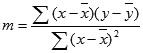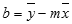Если в excel двум координатам

Как построить прямую в экселе по двум точкам?

Построить прямую линию по двум точкам в программе эксель задача дольно легко решаема. Рассмотрим подробную инструкцию, как это сделать.

Первый этап. Построим прямую линию функции y=x+6. Чтобы её построить, нужно получить две координаты, для этого в экселе рисуем небольшую таблицу с двумя столбцами и задаем вручную координаты «Х».

Второй этап. Посчитает координаты точек «Y», для этого пропишем в ячейке «В2» формулу: =A2+6, а в ячейке «В3»: =A3+6.

Третий этап. Выделим четыре данных точки, а на верхней панели настроек, провалимся в закладку «Вставка», чтобы в блоке «Диаграммы» отыскать иконку в виде осей и точек с подписью «Точечная».

Четвертый этап. Нажав на данную иконку, программа предложить выбрать тип диаграммы, выберем ту, что предлагает соединять прямыми линиями точки, она будет четвертой по счету.

В итоге мы построили в программе эксель прямую линию по двум точкам, что и требовалось сделать.

Видео

Функция ЛИНЕЙН

В этой статье описаны синтаксис формулы и использование функции LINEST в Microsoft Excel. Ссылки на дополнительные сведения о диаграммах и выполнении регрессионного анализа можно найти в разделе См. также.

Описание

Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Инструкции приведены в данной статье после примеров.

Уравнение для прямой линии имеет следующий вид:

y = m1x1 + m2x2 +. + b

если существует несколько диапазонов значений x, где зависимые значения y — функции независимых значений x. Значения m — коэффициенты, соответствующие каждому значению x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив . Функция ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.

Синтаксис

ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])

Аргументы функции ЛИНЕЙН описаны ниже.

Синтаксис

Известные_значения_y. Обязательный аргумент. Множество значений y, которые уже известны для соотношения y = mx + b.

Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.

Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.

Известные_значения_x. Необязательный аргумент. Множество значений x, которые уже известны для соотношения y = mx + b.

Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).

Если массив известные_значения_x опущен, то предполагается, что это массив <1;2;3;. >, имеющий такой же размер, что и массив известные_значения_y.

Конст. Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.

Если аргумент конст имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.

Если аргумент конст имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.

Статистика. Необязательный аргумент. Логическое значение, которое указывает, требуется ли вернуть дополнительную регрессионную статистику.

Если статистика имеет true, то LINEST возвращает дополнительную регрессию; в результате возвращается массив .

Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.

Дополнительная регрессионная статистика.

Стандартные значения ошибок для коэффициентов m1,m2. mn.

Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент конст имеет значение ЛОЖЬ).

Коэффициент определения. Сравнивает предполагаемые и фактические значения y и диапазоны значений от 0 до 1. Если значение 1, то в выборке будет отличная корреляция— разница между предполагаемым значением y и фактическим значением y не существует. С другой стороны, если коэффициент определения — 0, уравнение регрессии не помогает предсказать значение y. Сведения о том, как вычисляется 2, см. в разделе «Замечания» далее в этой теме.

Стандартная ошибка для оценки y.

F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными.

Степени свободы. Степени свободы используются для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Дополнительные сведения о вычислении величины df см. ниже в разделе «Замечания». Далее в примере 4 показано использование величин F и df.

Регрессионная сумма квадратов.

Остаточная сумма квадратов. Дополнительные сведения о расчете величин ssreg и ssresid см. в подразделе «Замечания» в конце данного раздела.

На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.

Замечания

Любую прямую можно описать ее наклоном и пересечением с осью y:

Наклон (m):
Чтобы найти наклон линии, обычно записанной как m, возьмите две точки на строке (x1;y1) и (x2;y2); наклон равен (y2 — y1)/(x2 — x1).

Y-перехват (b):
Y-пересечение строки, обычно записанное как b, — это значение y в точке, в которой линия пересекает ось y.

Уравнение прямой имеет вид y = mx + b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.

Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:

Наклон:
=ИНДЕКС( LINEST(known_y,known_x’s);1)

Y-перехват:
=ИНДЕКС( LINEST(known_y,known_x),2)

Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель ЛИНЕЙН. Функция ЛИНЕЙН использует для определения наилучшей аппроксимации данных метод наименьших квадратов. Когда имеется только одна независимая переменная x, значения m и b вычисляются по следующим формулам:

где x и y — выборочные средние значения, например x = СРЗНАЧ(известные_значения_x), а y = СРЗНАЧ( известные_значения_y ).

Функции ЛИННЕСТРОЙ и ЛОГЪЕСТ могут вычислять наилучшие прямые или экспоненциальное кривой, которые подходят для ваших данных. Однако необходимо решить, какой из двух результатов лучше всего подходит для ваших данных. Вы можетевычислить known_y( known_x) для прямой линии или РОСТ( known_y, known_x в ) для экспоненциальной кривой. Эти функции без аргумента new_x возвращают массив значений y, спрогнозируемых вдоль этой линии или кривой в фактических точках данных. Затем можно сравнить спрогнозируемые значения с фактическими значениями. Для наглядного сравнения можно отобразить оба этих диаграммы.

Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal — ssresid. Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента определения r 2 — индикатор того, насколько хорошо уравнение, выданное в результате регрессионного анализа, объясняет связь между переменными. Значение r 2 равно ssreg/sstotal.

В некоторых случаях один или несколько столбцов X (предполагается, что значения Y и X — в столбцах) могут не иметь дополнительного прогнозируемого значения при наличии других столбцов X. Другими словами, удаление одного или более столбцов X может привести к одинаковой точности предсказания значений Y. В этом случае эти избыточные столбцы X следует не использовать в модели регрессии. Этот вариант называется «коллинеарность», так как любой избыточный X-столбец может быть выражен как сумма многих не избыточных X-столбцов. Функция ЛИНЕЙН проверяет коллинеарность и удаляет все избыточные X-столбцы из модели регрессии при их идентификации. Удалены столбцы X распознаются в результатах LINEST как имеющие коэффициенты 0 в дополнение к значениям 0 se. Если один или несколько столбцов будут удалены как избыточные, это влияет на df, поскольку df зависит от числа X столбцов, фактически используемых для прогнозирования. Подробные сведения о вычислении df см. в примере 4. Если значение df изменилось из-за удаления избыточных X-столбцов, это также влияет на значения Sey и F. Коллинеарность должна быть относительно редкой на практике. Однако чаще всего возникают ситуации, когда некоторые столбцы X содержат только значения 0 и 1 в качестве индикаторов того, является ли тема в эксперименте участником определенной группы или не является ее участником. Если конст = ИСТИНА или опущен, функция LYST фактически вставляет дополнительный столбец X из всех 1 значений для моделирования перехвата. Если у вас есть столбец с значением 1 для каждой темы, если мальчик, или 0, а также столбец с 1 для каждой темы, если она является женщиной, или 0, последний столбец является избыточным, так как записи в нем могут быть получены из вычитания записи в столбце «самец» из записи в дополнительном столбце всех 1 значений, добавленных функцией LINEST.

Вычисление значения df для случаев, когда столбцы X удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n — k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.

При вводе константы массива (например, в качестве аргумента известные_значения_x) следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть другими в зависимости от региональных параметров.

Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.

Основной алгоритм, используемый в функции ЛИНЕЙН, отличается от основного алгоритма функций НАКЛОН и ОТРЕЗОК. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:

Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.

Наклон и ОТОКП возвращают #DIV/0! ошибка «#ЗНАЧ!». Алгоритм функций НАКЛОН и ОТОКП предназначен для поиска только одного ответа, и в этом случае может быть несколько ответов.

Помимо вычисления статистики для других типов регрессии с помощью функции ЛГРФПРИБЛ, для вычисления диапазонов некоторых других типов регрессий можно использовать функцию ЛИНЕЙН, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:

работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:

y = m1*x + m2*x^2 + m3*x^3 + b

Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.

Значение F-теста, возвращаемое функцией ЛИНЕЙН, отличается от значения, возвращаемого функцией ФТЕСТ. Функция ЛИНЕЙН возвращает F-статистику, в то время как ФТЕСТ возвращает вероятность.

Примеры

Пример 1. Наклон и Y-пересечение

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Вывести уравнение прямой по координатам двух точек

По введенным пользователем координатам двух точек вывести уравнение прямой, проходящей через эти точки.

Общее уравнение прямой имеет вид y = kx + b . Для какой-то конкретной прямой в уравнении коэффициенты k и b заменяются на числа, например, y = 4x — 2 . Задача сводится именно к нахождению этих коэффициентов.

Так как координаты точки это значения x и y , то мы имеем два уравнения. Пусть, например, координаты точки А(3;2), а координаты B(-1;-1). Получаем уравнения:
2 = k*3 + b,
-1 = k*(-1) + b.
Решая полученную систему уравнений находим значения k и b :
b = 2 — 3k
-1 = -k + 2 — 3k
4k = 3
k = 3/4 = 0.75
b = 2 — 3 * 0.75 = 2 — 2.25 = -0.25
Таким образом, получается уравнение конкретной прямой, проходящей через указанные точки: y = 0.75x — 0.25.

Алгоритм решения данной задаче на языке программирования будет таков:

1. Получить значения координат первой точки и присвоить их переменным, например x1 и y1 .
2. Получить значения координат ( x2, y2 ) второй точки.
3. Вычислить значение k по формуле k = (y1 — y2) / (x1 — x2) .
4. Вычислить значение b по формуле b = y2 — k * x2 .
5. Вывести на экран полученное уравнение.

Функция ЕСЛИ в Excel позволяет оценивать ситуацию с двух точек зрения, например, значение больше 0 или меньше, и в зависимости от ответа на этот вопрос, произведи дальнейшие расчеты по той или иной формуле. Однако, не редки ситуации, когда вам приходится работать более, чем с двумя условиями. В сегодняшней статье мы рассмотрим примеры создания формул в Excel с несколькими условиями ЕСЛИ.

Прежде, чем начать изучать данный урок, рекомендую прочитать статью про функцию ЕСЛИ, где описаны основные приемы работы.

Принцип создания формул с несколькими условиями ЕСЛИ заключается в том, что в одном из аргументов формулы (значение_если_ИСТИНА или значение_если_ЛОЖЬ) находится еще одна формула ЕСЛИ.

Например: =ЕСЛИ(A5=0;»НОЛЬ»;ЕСЛИ(A5<0;»МЕНЬШЕ НОЛЯ»;»БОЛЬШЕ НОЛЯ»)), где функция оценивает значение ячейки A5 два раза, первый, проверяет, равняется ли значение нулю, и возвращает текст – НОЛЬ, если ИСТИНА. Если результат оценки вернул значение ЛОЖЬ, происходит вторая оценка, функция проверяет, является ли значение ячейки A5 меньше ноля, и возвращает текст МЕНЬШЕ НОЛЯ, если результат ИСТИНА, в противном случае возвращает текст БОЛЬШЕ НОЛЯ.

Таким образом, в примере выше, формула вернет значение МЕНЬШЕ НОЛЯ, так как при первой оценке, результат оказался ЛОЖЬ, а при второй оценке ИСТИНА.

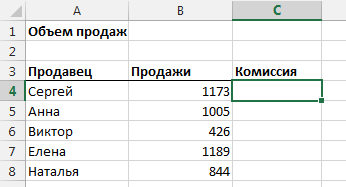
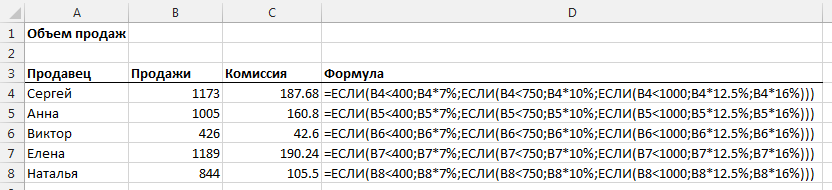
Давайте рассмотрим пример посложнее. Предположим, вам необходимо рассчитать размер комиссии каждого продавца в зависимости от объема его продаж.

Ваш план таков:

• Если продажи меньше или равны 500$, комиссия составляет 7%
• Если продажи больше 500$, но меньше или равны 750%, комиссия составляет 10%
• Если продажи больше 750$, но меньше или равны 1000%, комиссия составляет 12,5%
• Если продажи больше 1000$, комиссия составляет 16%

Вместо того, чтобы рассчитывать размер комиссии для каждого работника, можно создать формулу с несколькими условиями ЕСЛИ. Логика формулы будет следующая:

• Продажи меньше или равны 500$. Если ИСТИНА, рассчитываем комиссию.
• Если ЛОЖЬ, то продажи меньше или равны 750$. Если ИСТИНА, рассчитываем комиссию.
• Если ЛОЖЬ, то продажи меньше или равны 1000$. Если ИСТИНА, рассчитываем комиссию.
• Если ЛОЖЬ, рассчитываем комиссию, так как это будет означать, что продажи больше 1000$ и больше логических тестов проводить не нужно.

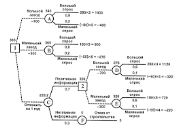
Давайте создадим формулу следуя данной логике для продавца Сергея. (Я выделил жирным проверку логики для лучшего понимания).

=ЕСЛИ(B4<400;B4*7%;ЕСЛИ(B4<750;B4*10%;ЕСЛИ(B4<1000;B4*12.5%;B4*16%)))

На первый взгляд может показаться, что это ужасная формула, но давайте попробуем разобраться:

Логическое выражение в первой формуле ЕСЛИ проверяет, является ли значение в ячейке B4 меньше 400, если ИСТИНА, формула умножает значение ячейки B4 на 7% и останавливает дальнейшие вычисления. Если значение ячейки B4 больше 400, мы переходим к следующей функции ЕСЛИ. Так будет продолжаться, пока мы не достигнем последнего значения, где значение ячейки умножается на 16%. Это значит, что ни одно из условий не удовлетворило требованиям, т.е. продажи составляют более 1000$.

Ниже вы видите, как будет выглядеть колонка Комиссия, когда все формулы будут введены. Также в колонке Формула отображены формулы для каждого продавца.

Можно проверить на примере Натальи правильность работы формулы. Продажи Натальи составили 844$, т.е. больше, чем 750$, но меньше чем 1000$. Соответственно, коэффициент комиссии будет равняться 12,5%, а сама комиссия составит 105,5$. Также важно отметить, о работе формулы с пограничными значениями. Предположим, что сумма продаж Натальи составила 750$, какой коэффициент должна применить формула? Коэффициент будет 12,5%, так как для коэффициента 10% сумма продаж должна равняться меньше 750. Это важное замечание, поэтому будьте аккуратны при составлении логики формулы.

Итак, как вы увидели, формула ЕСЛИ очень мощный инструмент при составлении логических выражений с несколькими условиями и позволяет экономить время на просчет каждой ячейки таблицы.