Equations for word problems

Worked-out word problems on linear equations with solutions explained step-by-step in different types of examples.

There are several problems which involve relations among known and unknown numbers and can be put in the form of equations. The equations are generally stated in words and it is for this reason we refer to these problems as word problems. With the help of equations in one variable, we have already practiced equations to solve some real life problems.

Step-by-step application of linear equations to solve practical word problems:

4. Aaron is 5 years younger than Ron. Four years later, Ron will be twice as old as Aaron. Find their present ages. 

More solved examples with detailed explanation on the word problems on linear equations.

Try to follow the methods of solving word problems on linear equations and then observe the detailed instruction on the application of equations to solve the problems.

● Equations

What is an Equation?

What is a Linear Equation?

How to Solve Linear Equations?

Solving Linear Equations

Problems on Linear Equations in One Variable

Word Problems on Linear Equations in One Variable

Practice Test on Linear Equations

Practice Test on Word Problems on Linear Equations

● Equations — Worksheets

Worksheet on Linear Equations

Worksheet on Word Problems on Linear Equation

Quadratic Equations — word problems with solutions

In this tutorial, you will learn:

In order to learn how to solve quadratic equations by four different methods, please follow this tutorial; it’s detailed and offers plenty of worked examples and practice questions.

In this tutorial, I assume you have already got a good skill in solving quadratic equations as explained in the above tutorial. This tutorial primarily focuses on solving real-world problems involving quadratic equations.

If you think you need a bit more practice before dealing with word problems, here is a question generator and a programme to check your answers:

The Equation Generator

The following programme is interactive: by clicking on the buttons, you can generate a random equation and its solutions: they are randomly generated — and unlimited in number.

The Quadratic Solver

A quadratic equation takes the form of ax² + bx + c where a and b are two integers, known as coefficients of x² and x respectively and c, a constant.

Enter a, b and c to find the solutions of the equations.

E.g.

x² — x — 6 = 0, where a = 1; b=-1; c=-6

Quadratic Word Problems

E.g.1

The sum of two numbers is 27 and their product is 50. Find the numbers.
Let one number be x. Then the other number is 50/x.
x + 50/x = 27
X => x x² + 50 = 27x
— 27x => x² — 27x + 50 = 0
(x -25)(x -2) = 0
(x -25) = 0 or (x -2) = 0
x = 25 or x = 2.

E.g.2

The length of a rectangle is 5 cm more than its width and the area is 50cm². Find the length, width and the perimeter.
Let the width be x. Then the length = x + 5.
x(x + 5) = 50
x² + 5x = 50
-50 => x² + 5x — 50 = 0
(x + 10)(x -5) =0
(x + 10) = 0 or (x -5) =0
x = -10 or x = 5 — x = -10 is impossible to be a width
Width = 5cm; so, the length = 10cm.
Perimeter = 30cm.

E.g.3

The three sides of a right-angled triangle are x, x+1 and 5. Find x and the area, if the longest side is 5.
The hypotenuse = 5
x² + (x+1)² = 5² (Pythagoras’ Theorem)
x² + x² + 2x + 1 = 25
-25 => x² + x² + 2x — 24 = 0
2x² + 2x — 24 = 0
x² + x — 12 = 0
(x — 3)(x + 4) = 0
(x + 4) = 0 or (x — 3) = 0
x = -4 or x = 3
x = 3;
Area = 1/2 x 3 x 4 = 6cm²

E.g.4

The product of two numbers is 24 and the mean is 5. Find the numbers.
Let one number = x; then the other = 24/x
(x + 24/x)/2 = 5
X 2 => x + 24/x = 10
X x => x² + 24 = 10x
— 10x => x² + -10x + 24 = 0
(x — 6)(x -4) = 0
(x — 6) = 0 or (x -4) = 0
x = 6 or x =4
The numbers are 6 or 4.

E.g.5

The sum of numbers is 9. The squares of the numbers is 41. Find the numbers.
These are quadratic simultaneous equations.
let the numbers be x and y.
x + y = 9
x² + y² = 41
From the first equation, y = (9-x)
Now substitute this in the second equation.
x² + (9-x)² = 41
x² + 81 — 18x + x² = 41
2x² — 16x + 81 = 41
2x² — 16x + 40 = 0
x² — 8x + 20 = 0
(x — 5)(x -4) =0
(x — 5) = 0 or (x -4) =0
x = 5 or x = 4
Substitute in the first equation, y = 5 or 4
The numbers are 5 and 4.

Mathematical Modelling with Quadratic Functions

There are quite a few real life situations that can be modelled by a quadratic function in an accurate way. For instance, the motion of a ball, thrown upwards to move under gravity, can be easily modelled by a quadratic equation. Using the model, we can calculate the height of the ball if the time is known or vice versa.

E.g.6

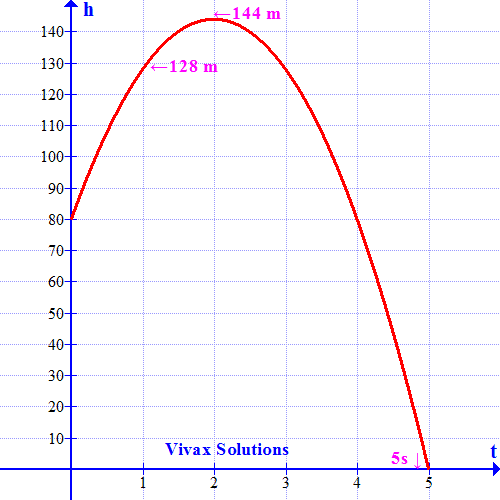
A ball is thrown upwards from a rooftop, 80m above the ground. It will reach a maximum vertical height and then fall back to the ground. The height of the ball from the ground at time t is h, which is given by,

h = -16t² + 64t + 80.

1. What is the height reached by the ball after 1 second?
2. What is the maximum height reached by the ball?
3. How long will it take before hitting the ground?

Follow the graph along with the calculation for a better understanding:

1) h = -16t² + 64t + 80
h = -16* 1*1 + 64*1 + 80 = 128m
2) Rearrange by the completing the square, we get:
h = -16[t² — 4t — 5]
h = -16[(t — 2)² — 9]
h = -16(t — 2)² + 144
When the height is maximum, t = 2; therefore, maximum height = 144m.
3) When the ball hits the ground, h = 0;
-16t² + 64t + 80 = 0
Divide the equation by -16
t² — 4t — 5 = 0
(t — 5)(t + 1) = 0
t = 5 or t = -1
The time cannot be negative; so, the time = 5 seconds.

E.g.7

A farmer wants to make a rectangular pen for his sheep. He has 60m fencing material to cover three sides with the other side being a brick wall. How should he use the fencing material to maximize the space for his sheep? How should he choose length and width of the pen to achieve his objective?

He just has to cover three sides; let the width be x.
Then the length = (60-2x)
Area of the pen = x(60-2x)
= 60x -2x²
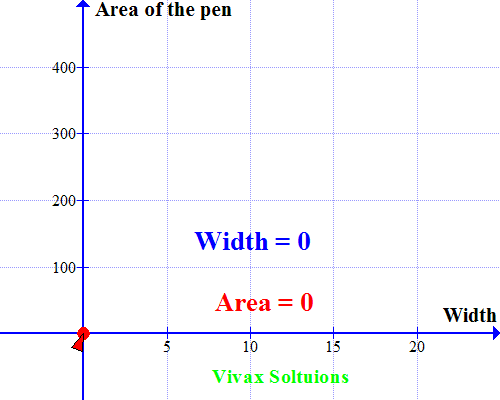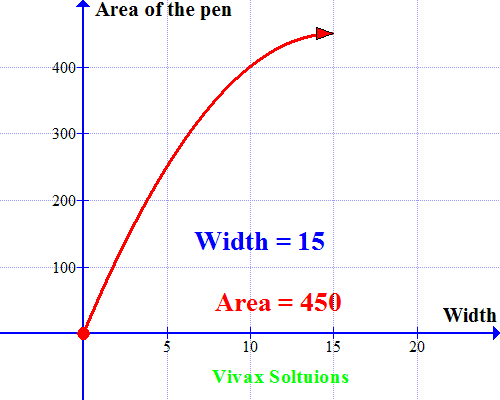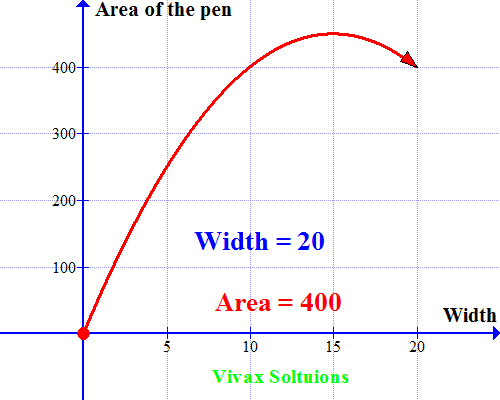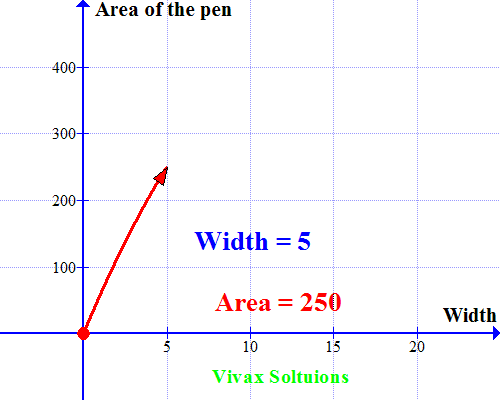
Now let’s sketch a graph for the quadratic equation. Which is as follows:

As you can see, the curve peaks at x = 15; when the width = 15m, the area is maximum. A very useful way to use quadratic equations in real life, indeed!

Amazon Ad: Phone Stand: it's Amazon's Choice

E.g.8

Two resistors, when connected in series, have a total resistance of 25 Ohms. If they are connected in parallel, the value goes down to 6 Ohms. Find the values.

When they are in series, if one resistor is x, then the other is 25-x
When they are in parallel, 1/6 = 1/x + 1/(25-x)
1/6 = 25/[x(25-x)] = 25/[25x — x²]
25x — x² = 150
If ax² + bx + c = 0, then
x = [-b ±√(b² — 4ac) ]/ 2a
x² — 25x + 150 = 0
a = 1; b = -25; c = 150
x = -(-25) ±√((-25)² — 4(1)(150)) / 2(1)
x = 25 ±√(625 — 600) / 2
x = 25 ±√(25) / 2

x = (25 ± 5 )/ 2
x = 15 or x = 10
So, the resistors are 15 Ohms or 10 Ohms.

E.g.9

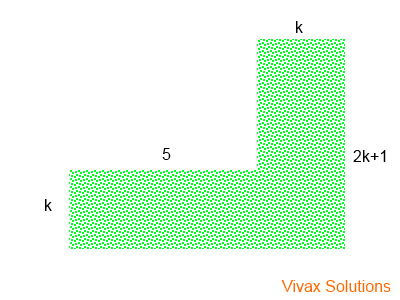
The following picture shows the shape of a certain grass patch. If the area of the patch is 80m², find k.

The total area = 5k + k(2k+1)
= 5k + 2k² + k
= 2k² + 6k
Since the area is 80m²
2k² + 6k = 80
2k² + 6k — 80 = 0
(2k — 10)(k + = 0
k = 5 or k = -8
Since the length cannot be negative, k = 5.

E.g.10

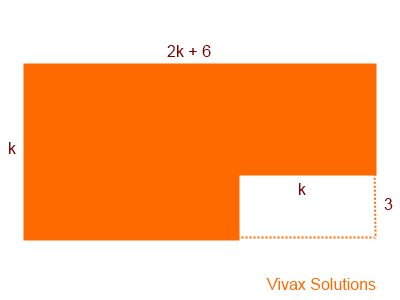
The following picture shows the shape of a rectangle from which a smaller rectangular part is removed. If the remaining area of the larger rectangle is 35cm², find k.

The remaining area = k(2k+6) — 3k
= 2k² + 6k -3k
= 2k² + 3k
Since the area is 35cm²
2k² + 3k = 35
2k² + 3k — 35 = 0
(2k -7)(k + 5) = 0
k = 3.5 or k = -5
Since the length cannot be negative, k = 3.5.

E.g.11

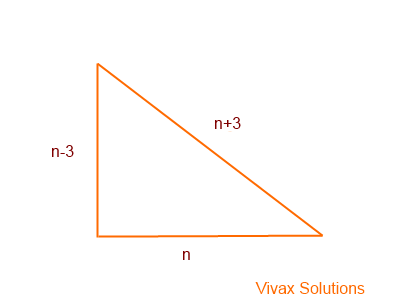
The shortest side of a right-angled triangle is 6cm shorter than its hypotenuse. The difference in length of other two sides is 3cm. If the shortest side is n-3, show that 2n² = 12n. Hence, find n.

If the length of the shortest side is n-3, the length of the hypotenuse and the other side are n+3 and n respectively.
So, using Pythagoras Theorem,
(n-3)² + n² = (n+3)²
n² — 6n + 9 + n² = n² + 6n + 9
n² = 12n
n² — 12n = 0
n(n — 12) = 0
n = 0 or n = 12.
Since the length cannot be zero, n = 12.

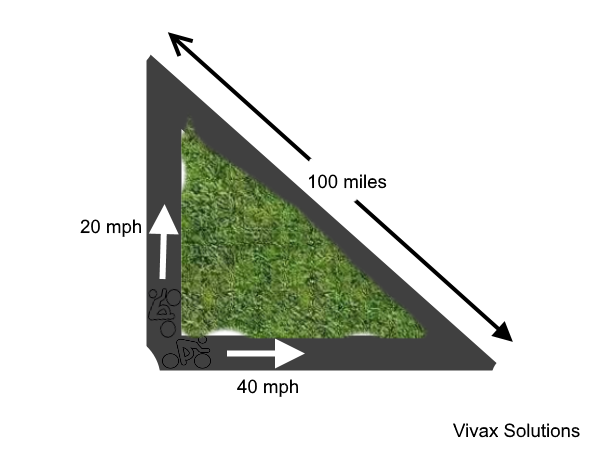
E.g.12

Two cyclists move away from a town along two perpendicular paths at 20 mph and 40 mph respectively. The second cyclist starts the journey an hour later than the first one. Find the time taken for them to be 100 miles apart.

Suppose the time taken by the first cyclist is t; then the time taken by the other cyclist = (t-1)
The distances travelled by them are 20t and 40(t-1) respectively.
Using Pythagoras Theorem,
(20t)² + [40(t-1)]² = 100²
400t² + 1600(t-1)² = 10000
t² + 4t² — 8t + 4 = 25
5t² — 8t -21 = 0
(5t + 7)(t -3) = 0
t = 3 or t = -1.4
Since time cannot be negative, t = 3hrs.

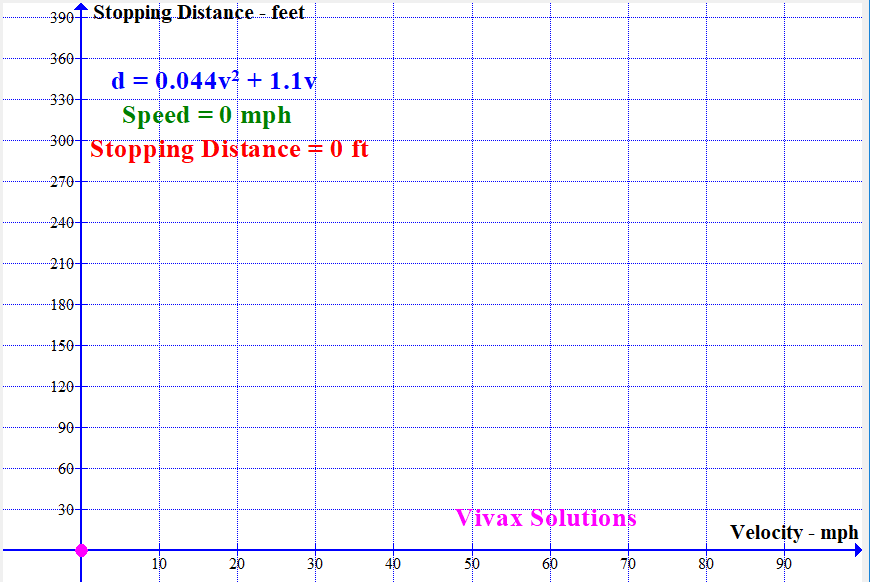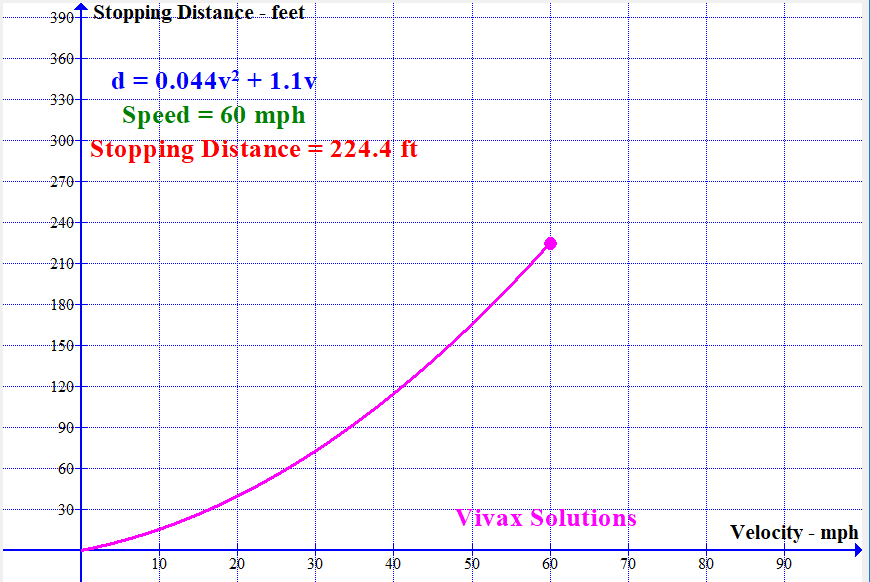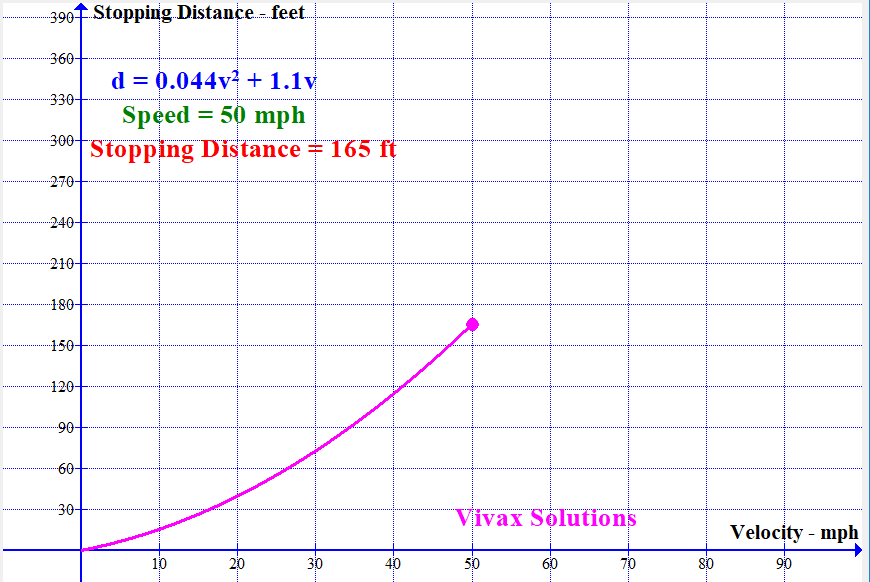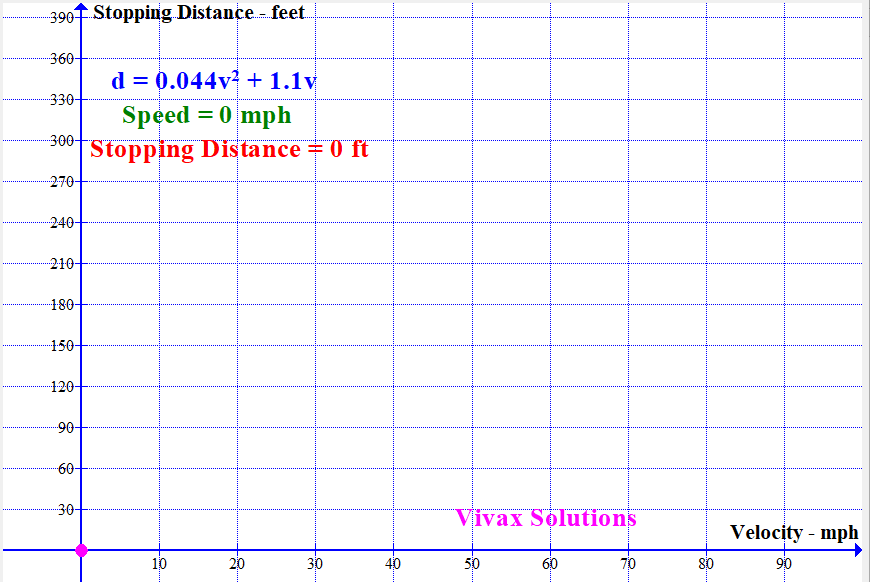
Modelling Stopping Distance of a Vehicle with Speed

With the available data, the stopping distance — sum of thinking distance and breaking distance — can be modelled by a quadratic function. It is as follows:

Stopping Distance
Thinking Distance	Breaking Distance

If the stopping distance = d and the speed = v,
d = 0.044v² + 1.1v

The following animation shows how the stopping distance, modelled by the above equation, changes with the speed:

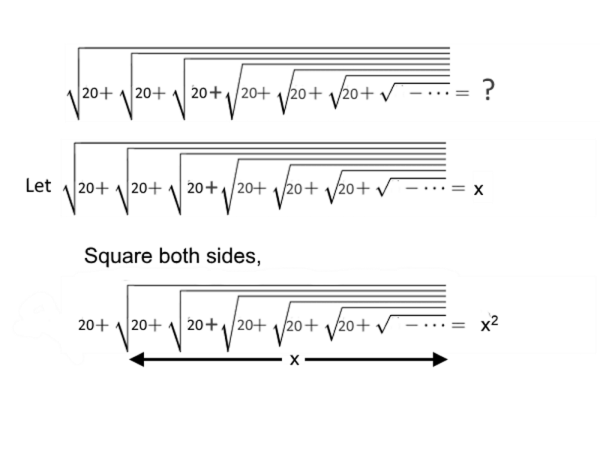
Infinite Square Root Problem

Solve the following infinite square root problem:

20 + x = x²
x² — x — 20 = 0
x = (1 ± √1 + 80)/2
x = (1 ± √81)/2
x = (1 ± 9)/2
x = 5 or x = -4
Since the square root of a negative number cannot be found, x = 5. So, the value of the above infinite square problem is 5.

🏆 Challenging Questions

Ad: The author of this site offers fully interactive tutorial on differentiation

Now, in order to complement what you have just learnt, work out the following questions:

Questions

1. The sum of squares of two consecutive even numbers is 244. Find the numbers.
2. The base length of a triangle is 2cm more than its height. The area is 24cm². Find the length of hypotenuse and the
   perimeter of the triangle.
3. The length of a square is increased by a 5^th so that its new area is 44cm² more than the original value. Find the difference in perimeter of two shapes.
4. The length and width of a rectangular garden are 150m and 120m. A foot path of regular width is added to the boundary of the garden and the total area of the garden
   becomes 2800m² more than its original area. Find the width of the footpath.
5. Adam is about to embark on a journey on a narrow country lane that covers 32km and decides to go at x km/h. On second thoughts, he calculates that if he increases the speed by 4km/h, his journey time can be cut down by 4 hrs. Find x.
6. The reciprocal of the sum of reciprocals of two numbers is 6. The sum of numbers is 25. Find the numbers.
7. The speed of an ant is (2t + 10) and after travelling for t minutes, it covers a distance of 12m. Find t.
8. Two chords and a diameter form a triangle inside a circle. The radius is 5cm and one chord is 2cm longer than the other one. Find the perimeter and the area of the
   triangle.
9. The sum of a number and it reciprocal is 26/5. Find the number.
10. The product of two numbers is 20. The sum of squares is 41. Find the numbers.
11. The dimensions of the glass plate of a wedding photo are 18cm and 12cm respectively. A new rectangular frame of equal width all, the way round the photo, is about to be fitted around the it so that the area of the frame is the same as that of the glass. Find the width of the frame.
12. A group of acquaints went to a restaurants for a meal. When the bill for £175 was brought by a waiter, two of the cheeky ones from the group just sneaked off before the bill was paid, which resulted in the payment of extra £10 by each remaining individual. How many were in the group at first?
13. Ashwin and Donald decided to set out from two towns on their bikes, which are 247 miles apart, connected by a straight
    t Roman road in England. When they finally met up somewhere between the two towns, Ashwin had been cycling for 9 miles a day. The number of days for the whole adventure is 3 more than the number of miles that Donald had been cycling in a day. How many miles did each cycle?
14. When a two-digit number is divided by the product of the two digits, the answer is 2 and if 27 is added to the number, the original number turns into a new number with the digits being swapped around. Find the number.
15. There are three numbers: the difference of the differences of them is 5. The sum and product are 44 and 1950 respectively. Find the numbers.
16. Find the two numbers, whose sum is 19 and the product of the difference and the greater, is 60.
17. A boy was asked his age: «If you add the square root of it to half of it, and then subtract 12, the answer will be nothing,» replied the boy. What was his age?
18. A group of army cadets, consisting of 1066 men, form two squares in front of a garrison. In the side of one square, there are 4 more men than the other. How many men are in each side of the squares?
19. The height of a triangle is 4cm less than three times its base length. If the area is 80 cm², find the lengths of the base and height.
20. An isosceles triangle is inscribed in a circle in such a way that its longest side, which goes through the centre is √50cm. Find the area of the triangle.
21. A butcher bought some pheasants for £100.00. Had each cost £1 less, he would have bought 5 more. How many pheasants did he buy?
22. The sum of reciprocals of two consecutive integers is 13/42. Find the integers.
23. The product of two numbers and the difference between them are 289 and 20 respectively. Find the numbers.
24. The sum of two numbers is 20. The sum of squares is 250. Find the numbers.
25. The area of a square exceeds twice that of another by 56cm². If the difference of the perimeter between the two is 24cm, find the area of the smaller square.

Answers

Move the mouse over, just below this, to see the answers:

1. 10, 12
2. 10cm, 24cm
3. 8cm
4. 5m
5. 4km/h
6. 10, 15
7. 1
8. 24cm, 24cm²
9. 5
10. 5 and 4
11. 3cm
12. 7
13. 117 and 130 miles
14. 36
15. 6, 13, 25
16. 12,7
17. 16
18. 21 and 25
19. 8cm, 20cm
20. 12.5cm²
21. 20
22. 6, 7
23. 27, 7
24. 15, 5
25. 100 or 4

Do you need detailed solutions to the above questions? Please click the following and I will send the answers:

Detailed Solutions
for the above
Quadratic Questions
As a PDF
for Just £3.99

Now that you have read this tutorial, you will find the following tutorials very helpful too:

REAL WORLD PROBLEMS:
How to Write Equations Based on Algebra Word Problems

I know that you often sit in class and wonder, «Why am I forced to learn about equations, Algebra and variables?»

But… trust me, there are real situations where you will use your
knowledge of Algebra and solving equations to solve a problem that is
not school related. And… if you can’t, you’re going to wish that you
remembered how.

It might be a time when you are trying to figure out how much you
should get paid for a job, or even more important, if you were paid
enough for a job that you’ve done. It could also be a time when you are
trying to figure out if you were over charged for a bill.

This is important stuff — when it comes time to spend YOUR money —
you are going to want to make sure that you are getting paid enough and
not spending more than you have to.

Ok… let’s put all this newly learned knowledge to work.

Click here if you need to review how to solve equations.

There are a few rules to remember when writing Algebra equations:

Let’s look at an example of an algebra word problem.

Example 1: Algebra Word Problems

---

Linda was selling tickets for the school play.  She sold 10 more adult tickets than children
tickets and she sold twice as many senior tickets as children tickets.

1. Let x represent the number of children’s tickets sold.
2. Write an expression to represent the number of adult tickets sold.
3. Write an expression to represent the number of senior tickets sold.
4. Adult tickets cost $5, children’s tickets cost $2, and senior tickets cost $3. Linda made $700. Write an equation to represent the total ticket sales.
5. How many children’s tickets were sold for the play? How many adult tickets were sold? How many senior tickets were sold?
   

---

As you can see, this problem is massive!  There are 5 questions to answer with many expressions to write. 

Solution

---

A few notes about this problem

---

1. In this problem, the variable was defined for
you.  Let x represent the number of
children’s tickets sold tells what x stands for in this problem.  If this had not been done for you, you might
have written it like this:

        Let x = the number of children’s tickets sold

2. For the first expression, I knew that 10 more adult
tickets were sold.  Since more means add,
my expression was x +10.  Since the
direction asked for an expression, I don’t need an equal sign.  An equation is written with an equal sign and
an expression is without an equal sign. 
At this point we don’t know the total number of tickets.

3. For the second expression, I knew that my key words,
twice as many meant two times as many. 
So my expression was 2x.

4. 
We know that to find the total
price we have to multiply the price of each ticket by the number of
tickets.  Take note that since x + 10 is the quantity of adult tickets, you must put
it in parentheses!  So, when you multiply
by the price of $5 you have to distribute the 5.

5.  Once I solve
for x, I know the number of children’s tickets and I can take my expressions
that I wrote for #1 and substitute 50 for x to figure out how many adult and
senior tickets were sold.

Example 2 — Identifying a Constant

---

A cell phone company charges a monthly rate of $12.95 and $0.25 a minute per call. The bill for m minutes is $21.20.

1. Write an equation that models this situation.

2. How many minutes were charged on this bill?

---

Solution

---

A cell phone company charges a monthly rate of $12.95 and $0.25 a minute per call. The bill for m minutes is $21.20.

1. Write an equation that models this situation.

Notes For Example 2

---

• $12.95 is a monthly rate. Since this is a set fee for each
  month, I know that this is a constant. The rate does not change;
  therefore, it is not associated with a variable.
• $0.25 per
  minute per call requires a variable because the total amount will change
  based on the number of minutes. Therefore, we use the expression 0.25m
• You must solve the equation to determine the value for m, which is the number of minutes charged.

The last example is a word problem that requires an equation with variables on both sides.

Example 3 — Equations with Variables on Both Sides

---

You have $60 and your sister has $120. You are saving $7 per week and your sister is saving $5 per week. How long will it be before you and your sister have the same amount of money? Write an equation and solve.

Solution

---

Notes for Example 3

---

• $60 and $120 are constants because this is the amount of money that they each have to begin with. This amount does not change.
• $7 per week and $5 per week are rates. They key word «per» in this situation means to multiply.
• The key word «same» in this problem means that I am going to set my two expressions equal to each other.
• When we set the two expressions equal, we now have an equation with variables on both sides.
• After solving the equation, you find that x = 30, which means that after 30 weeks, you and your sister will have the same amount of money.

I’m hoping that these three examples will help you as you solve real world problems in Algebra!

1. Home

>

2. Solving Equations

>

3. Algebra Word Problems

You are here: Home → Articles → How to set up an equation for a word problem

Students often have problems setting up an equation for a word problem in algebra. To do that, they need to see the RELATIONSHIP between the different quantities in the problem. This article explains some of those relationships.

I was asked, 

I need an easy and helpful way to teach writing equations.

Example: Helen has 2 inches of hair cut off each time she goes to the hair salon. If h equals the length of hair before she cuts it and c equals the length of hair after she cuts it, which equation would you use to find the
length of Helen’s hair after she visit the hair salon?

a) h = 2 − c       c) c = h − 2
b) c = 2 − h       d) h = c − 2

Is there a single method to teaching students how to write algebraic equations? I need help.

The first thing I do when trying to figure out how to teach something is to analyze my own thinking. How do I think when solving this
problem? What are the steps and fine details? It is these details and steps that I may do automatically that I need to explain to students
to help them.

Seeing the quantities and their relationship instead of numbers

In this problem there is seemingly lots of information, but really it’s about recognizing quantities and the simple relationship between
them. This is of course the exact same task as translating a situation explained in words into a mathematical expression using symbols.

Children manifest the difficulty in this task when they read a simple word problem and then ask, «Do I go this times this, or do I divide?», just guessing the operation to perform with the different numbers given in the problem.

Students need to see the quantities and the RELATIONSHIP between them. They need to step out of the 5, 2, 10, 789, or any others numbers in the problem, and see the general quantities involved and how those are related to each other. In very simple word problems that relationship usually involves just one of the four basic operations. Then in algebra, there may be more quantities and more operations between them.

Examples of addition word problems

Example. Jenny has 7 marbles and Kenny has 5. How many do they have together?

The keyword together tells us that ADDITION is probably the operation needed. The quantities here are Jenny’s marbles, Kenny’s marbles, and total marbles. The relationship between the three is

Jenny’s marbles  +  Kenny’s marbles  =  Total marbles

From this general relationship between the quantities it is easy to write an equation for the problem, which solves it:

Relationship:	Jenny’s marbles	+	Kenny’s marbles	=	Total marbles
Equation:	7	+	5	=	_____

I wrote ____ in the place of total marbles since that is what the problem is asking for (the unknown).

All of this may look oversimplified, but helping children to see the underlying relationship between the quantities is important. Consider now this problem:

Example: Jenny and Kenny together have 37 marbles, and Kenny has 15. How many does Jenny have?

Many teachers might try to explain this as a subtraction problem, but in the most fundamental level it is about addition! It still talks about two people having certain amount of marbles together. The relationship between the quantities is the SAME as above, so we still need to write an addition equation.

Relationship:	Jenny’s marbles	+	Kenny’s marbles	=	Total marbles
Equation:	_____	+	15	=	37

Then, we can solve the equation ____ + 15 = 37  by
subtracting. Using this kind of approach in the elementary grades will help children to set up equations
in algebra story problems later.

Example: Jenny, Kenny, and Penny together have 51 marbles.
Kenny has double as many marbles as Jenny has, and Penny has 12. How many does Jenny have?

The relationship between the quantities is the same, so it is solved the same way: by writing an addition equation. However, we need to denote the number of Jenny’s and Kenny’s marbles with something. Jenny’s marbles are unknown, so we can denote that with the variable n. Then Kenny has 2n marbles.

Relationship:	Jenny’s marbles	+	Kenny’s marbles	+	Penny’s marbles	=	Total marbles
Equation:	n	+	2n	+	12	=	51

Example: Jane is on page 79 of her book. The book has 254 pages. How many pages does she still have to read?

This time the word «still» clues us in to an additive relationship where one of the addends is missing. You can initially write an empty line for what is not known, and later replace that with a variable.

pages already read	+	pages still to read	=	pages total
	+		=

This equation is of course is then solved by subtraction, but it is better if you view it as an addition situation and write an addition equation for it.

Example:  The number of hours that were left in the day was one-third of the number of hours already passed. How many hours were left in the day?
(From Grade 5 word problems for kids)

Can you see the general principle governing this problem?  It talks about the hours of the day where some hours already passed and some hours left. This, of course, points to addition once again: we have one part of the day, another part, and a total.

The only quantity we know is the total hours for the day. We don’t know the hours already passed nor the hours left, so initially you can use two empty lines in the equation that shows the basic relationship between the quantities:

hours already passed	+	hours left	=	total hours
			=

Then, the information in the first sentence gives us another relationship:

«The number of hours that were left in the day was one-third of the number of hours already passed.»

We don’t know the amount of hours passed nor the hours left. So let’s use the variable p for the hours passed. Then we can write an expression involving p for the hours left, because «hours left is one-third of the hours passed,» or

hours left  =  1/3 p

Then writing 1/3p for the «hours left» in the first equation will give us:

hours already passed	+	hours left	=	total hours
p	+	1/3p	=	24

This can be solved using basic algebra or by guess & check.

Subtraction word problems

One situation that indicates subtraction is difference or  how many/much more. However, the presence of the word «more» can indicate either an addition or subtraction, so be careful.

Example:  Ted read 17 pages today, and Fred read 28. How many more pages did Fred read?

The solution is of course 28 − 17 = 11, but it’s not enough to simply announce that – children need also to understand that difference is the result of a subtraction and tells the answer to how many more.

Relationship:	Pages Fred read	−	pages Ted read	=	difference
Equation:	28	−	17	=	__

---

Example:  Greg has 17 more marbles than Jack. Jack has
15. How many does Greg have?

Here the word more has a different meaning. This
problem is not about the difference. The question asks how many does
Greg have – not what is the difference in the amounts of marbles. It simply states Greg has 17 more compared to Jack, so here the word more simply indicates addition: Greg has as many as Jack AND 17 more, so Greg has 15 + 17 marbles.

Example: The mass of the Great Pyramid is 557t greater than that of the Leaning Tower of Pisa. Stone Henge has a mass of 2695t which is 95t less than the Leaning Tower of Pisa. There once was a Greater Pyramid which had a mass twice that of the Great Pyramid. What was the mass of the Greater Pyramid?
(From Grade 5 word problems for kids)

Each of the first three sentences give information that can be translated into an equation. The question is not about how many more so it’s not about difference. One thing being greater than another implies you add. One thing being less than another implies you subtract. And one thing being twice something indicates multiplying by 2.

When I read this problem, I could immediately see that I could write equations from the different sentences in the problem, but I couldn’t
see the answer right away. I figured that after writing the equations I would see some way forwad; probably one equation is solved and gives an answer to another equation.

The first sentence says, «The mass of the Great Pyramid is 557t greater than that of the Leaning Tower of Pisa». What are the quantities and the relationship between them here?

mass of Great Pyramid

=

mass of the Leaning Tower of Pisa

+

557t

The second sentence says «Stonehenge has a mass of 2695t which is 95t less than the Leaning Tower of Pisa.» 
Here it gives you a relationship similar to the one above, and it
actually spells out the mass of Stonehenge. It’s like two separate pieces
of information: «Stonehenge weighs 95t less than the tower. 
Stonehenge weighs 2695t.»  Less means you subtract. If you have
trouble deciding which is subtracted from which, you can think in your mind
which is heavier: Stonehenge or the tower?  

either	mass of Stonehenge	=	mass of tower − 95t
or	mass of tower	=	mass of Stonehenge − 95t

Now since the mass of Stonehenge is given, you can solve this equation, and from that knowledge you
can solve the first equation, and from that go on to the mass of the «Greater Pyramid«.

If the teacher just jumps directly to the number sentences when solving word
problems, then the students won’t see the step that happens in the mind before
that. The quantities and the relationship between them have to be made
clear and written down before fiddling with the actual numbers. Finding
this relationship should be the most important part of the word problems. 
One could even omit the actual calculations and concentrate just finding the
quantities and relationships.

Problem of Helen’s hair length

Problem.  Helen has 2 inches of hair cut off each time she goes to the hair salon. If
h equals the length of hair before she cuts it and c equals the length of hair after she cuts it, which equation would you use to find the
length of Helen’s hair after she visit the hair salon?
a. h = 2 − c      c. c = h − 2
b. c = 2 − h      d. h = c − 2

Solution.  Ignoring the letters c and h for now,
what are the quantities?  What principle or relationship is there between
them? Which possibility of the ones listed below is right?  Which do you take away from which?

1.	cut hair	−	hair length before cutting	=	hair length after cutting
2.	cut hair	−	hair length after cutting	=	hair length before cutting
3.	hair length before cutting	−	cut hair	=	hair length after cutting
4.	hair length after cutting	−	cut hair	=	hair length before cutting

SIMPLE, isn’t it??  In the original problem, the equations are given
with the help of h and c instead of the long phrases «hair length before
cutting» and «hair length after cutting». You can
substitute the c, h, and 2 into the relationships above, and then match the equations (1) — (4) with the equations (a) through (d).

Helping students to write the algebraic equations

One idea that came to mind is to go through the examples above, and more, based on the typical word problems in the math books, and then turn the whole thing around and have students do exercises such as:

• Write 3 different story problems where the solution is based on the relationship

  money earned − money spent on this — money spent on that = money left

• Write 3 different story problems where the solution is based on the relationship

  original price − discount percent x original price = discounted price

• Write 3 different story problems where the solution is based on the relationships

  money earned each month − expenses/taxes each month = money to use each month AND

  money to use each month × number of months = money to use over a period of time

• Write 3 different story problems where the solution is based on the relationships

  speed × time = distance AND

  distance from A to B + distance from B to C = distance from A to C

I’m sure you can think of more similar exercises.

---

See also:

Why are math word problems SO difficult for elementary school children?
Hint: it has to do with a «recipe» that many math lessons follow.

The do’s and don’ts of teaching problem solving in math
General advice on how you can teach problem solving in elementary, middle, and high school math.

How I Teach Word Problems by Andre Toom (PDF)
This article is written by a Russian who immigrated to US and noticed how COLLEGE LEVEL students have difficulties even with the simplest word problems! He describes his ideas on how to fill in the gap formed when students haven’t learned how to solve word problems in earlier education.

A list of websites focusing on word problems and problem solving
Use these sites to find good word problems to solve. Most are free!

Comments

When solving word problems, students must first decide what quantity represents x and then must write all the other quuantities in terms of x. I teach the students to set up arrows according to the language in the problem. All arrows point to x.
Example. Harry had 10 less toys than Mark. Sue has twice as many toys as Harry. Set up arrows: Sue— Harry—Mark Therefore Mark is x, Harry is x-10 and Sue is 2(x-10). Students find this very helpful.

Sandy Denny

My idea is the math teacher might teach and understand the students at the same time and everyone would have a sense of humor. So I think she/he will know if the students are listening or not, when after the class, talk to the student and ask what is wrong. Don’t hurt the student’s feelings.

lorence

After you finish this lesson, view all of our Pre-Algebra lessons and practice problems. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.

Solving Word Problems

To solve a word problem using a system of equations, it is important to;
– Identify what we don’t know
– Declare variables
– Use sentences to create equations

An example on how to do this:

Mary and Jose each bought plants from the same store. Mary spent $188 on 7 cherry trees and 11 rose bushes. Jose spent $236 on 13 cherry trees and 11 rose bushes. Find the cost of one cherry tree and the cost of one rose bush.

Cost of a cherry tree:
Cost of a rose bush:
7 cherry trees and 11 rose bushes = $188

The y-values cancel each other out, so now you are left with only x-values and real numbers.

Then, you plug in your x-value into an original equation in order to find the y-value.

Cost of a cherry tree: $8
Cost of a rose bush: $12

Example 1

Three coffees and a cupcake cost a total of dollars. Two coffees and four cupcake cost a total of dollars. What is the individual price for a single coffee and a single cupcake?

Let’s solve this by following steps.

1. What we don’t know:

Cost of a single coffee

Cost of single cupcake

2. Declare variables:

Cost of a single coffee=

Cost of single cupcake=

3. Use sentences to create equations.

Three coffees and a cupcake cost a total of dollars.

Two coffees and four cupcake cost a total of dollars.

Now, we have a system of equations:

Let’s solve for one of the variables in one of the equations and then use that to substitute into the other.

Now, solve for the value of using the first equation.

Let’s solve the value of by substituting the value of to the bottom equation.

Distribute to each terms inside the parenthesis

Combine like terms

Now, let’s isolate the by subtracting on both sides.

Then divide both sides by ,

And we’ll have

Then, let’s plug the value of into one equation to get the value of .

Cost of a single coffee=

Cost of single cupcake=

Example 2

The senior class at High School A rented and filled vans and buses with students. High School B rented and filled vans and bus with students. Every van had the same number of students in it as did the buses. Find the number of students in each van and in each bus.

Let’s solve this by following steps.

1. What we don’t know:

Students in each van

Students in each bus

2. Declare variables:

Students in each van=

Students in each bus=

3. Use sentences to create equations.

High School A rented and filled 8 vans and 8 buses with 240 students.

High School B rented and filled 4 vans and 1 bus with 54 students.

Now, we have a system of equations:

Let’s solve for one of the variables in one of the equations and then use that to substitute into the other.

Now, solve for the value of using the second equation.

Let’s solve the value of by substituting the value of to the bottom equation.

Distribute to each terms inside the parenthesis

Combine like terms

Now, let’s isolate the by subtracting on both sides.

Then divide both sides by ,

And we’ll have

Then, let’s plug the value of into one equation to get the value of .

Students in each van=

Students in each bus=

Video-Lesson Transcript

To solve a word problem using system of equations, it is important to:
1. Identify what we don’t know
2. Declare variables.
3. Use sentences to create equations.

Let’s have an example:

Mary and Jose each bought plants from the same store. Mary spent on cherry trees and rose bushes. Jose spent on cherry trees and rose bushes. Find the cost of one cherry tree and the cost of one rose bush.

Let’s solve this by following steps above.

1. What we don’t know:
cost of a cherry tree
cost of a rose bush

2. Declare variables:
cost of a cherry tree :
cost of a rose bush :

3. Use sentences to create equations.

For Mary:
cherry trees and rose bushes

For Jose:
cherry trees and rose bushes

Now, we have a system of equations

We can solve this by process of substitution, elimination or fraction.

Since the value of is the same for both equations, let’s do the process of elimination.

First, let’s multiply the first equation by

Here we’ll have a negated equation

Let’s do the process of elimination now

We’ll have

Then, let’s isolate by dividing both sides by

Now, we have

Remember, our declared variable?

cost of a cherry tree :

Since

Now we can say that

cost of a cherry tree :

Now, let’s solve for the value of by getting one equation and plugging the value of .

Let’s use the first equation to plug in

Let’s isolate by subtracting on both sides of the equation

Then divide by

And we get

Now, we know that cost of a rose bush is .