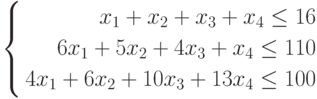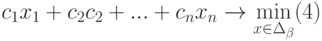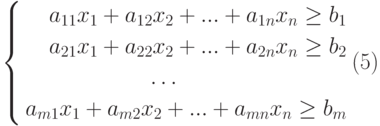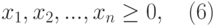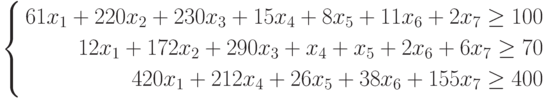Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
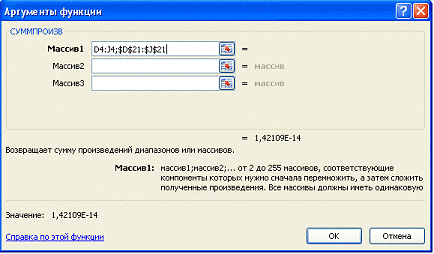
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
На сегодняшний день разработано большое количество специализированных программных продуктов для проведения экономических расчетов, однако сотрудники финансово-экономических служб чаще всего пользуются табличным редактором Excel. Причина популярности данного инструмента — обширный функционал Excel и постоянное его развитие практически в каждой новой версии табличного редактора.
В рамках одной статьи невозможно рассмотреть все достоинства Excel, которые экономисты могут применить в своей работе, поэтому остановимся на анализе лучших функций редактора, используемых для решения экономических задач.
Для удобства восприятия материала сгруппируем эти функции в три блока:
1. Функционал расчетных формул в Excel.
2. Функционал Excel для обработки табличных данных.
3. Инструменты Excel для моделирования и анализа экономических данных.
ФУНКЦИОНАЛ РАСЧЕТНЫХ ФОРМУЛ В EXCEL
Расчетные формулы являются изначальным и основополагающим функционалом табличного редактора Excel, поэтому рассмотрим их в первую очередь.
Пакет встроенных расчетных формул включает в себя десятки наименований, но самыми востребованными в работе экономистов являются следующие формулы: ЕСЛИ, СУММЕСЛИ и СУММЕСЛИМН, ВПР и ГПР, СУММПРОИЗВ, СЧЕТЕСЛИ.
Решение экономической задачи с помощью формулы ЕСЛИ
Формула ЕСЛИ — расчетная функция Excel, которую наиболее часто используют для решения несложных экономических расчетов. Она относится к группе логических формул и позволяет рассчитать необходимые данные по условиям, заданным пользователями.
С помощью формулы ЕСЛИ можно сравнить числовые или текстовые значения по прописанным в формуле условиям.
Запись расчетной формулы в заданной ячейке в общем виде выглядит так:
=ЕСЛИ(логическое_выражение;[значение_если_истина];[значение_если_ложь]),
где логическое выражение — данные, которые нужно проверить/сравнить (числовые или текстовые значения в ячейках);
значение_если_истина — результат, который появится в расчетной ячейке, если значение будет верным;
значение_если_ложь — результат, который появится в расчетной ячейке при неверном значении.
Задача № 1. Предприятие реализует три номенклатурные группы продукции: лимонад, минеральная вода и пиво. С 01.09.2020 запланировано установить скидку в размере 15 % на пиво.
Чтобы сформировать новый прайс на продукцию, сохраняем ее перечень в виде таблицы Excel. В первом столбце таблицы отражена номенклатура всей продукции в алфавитном порядке, во втором — признак группы продукции.
Для решения задачи создаем в таблице третий столбец и прописываем в первой ячейке номенклатуры формулу: =ЕСЛИ(C4=»пиво»;15%;0).
Эту формулу продлеваем до конца перечня номенклатуры продукции. В итоге получаем сведения о продукции, на которую с сентября снизится цена (табл. 1).
В данном примере показано использование формулы ЕСЛИ для обработки текстовых значений в исходных данных.
Решение экономической задачи с помощью формулы СУММЕСЛИ
Формулы СУММЕСЛИ и СУММЕСЛИМН также используют для экономических расчетов, но они обладают более широкими возможностями для выборки и обработки данных. Можно задать не одно, а несколько условий отборов и диапазонов.
Задача № 2. На основе ведомости начисления заработной платы сотрудникам магазина нужно определить общую сумму зарплаты продавцов.
Чтобы решить эту задачу, сохраняем ведомость из учетной базы данных в виде таблицы Excel. В данном случае нам нужно не просто произвести выборку значений, но и суммировать их результат. Поэтому будем использовать более сложную разновидность формулы ЕСЛИ — СУММЕСЛИ.
Для решения задачи добавим внизу таблицы еще одну строку «Всего продавцы». В ее ячейке под суммой зарплаты, начисленной сотрудникам магазина, пропишем следующую формулу:=СУММЕСЛИ(C4:C13;»продавец»;D4:D13).
Таким образом мы задали условие, при котором табличный редактор обращается к столбцу с наименованием должностей (столбец С), выбирает в нем значение «Продавец» и суммирует данные ячеек с начисленной заработной платой из столбца D в привязке к этой должности.
Результат решения задачи — в табл. 2.
Решение экономической задачи с помощью формул ВПР и ГПР
Формулы ВПР и ГПР используют для решения более сложных экономических задач. Они популярны среди экономистов, так как существенно облегчают поиск необходимых значений в больших массивах данных. Разница между формулами:
- ВПР предназначена для поиска значений в вертикальных списках (по строкам) исходных данных;
- ГПР используют для поиска значений в горизонтальных списках (по столбцам) исходных данных.
Формулы прописывают в общем виде следующим образом:
=ВПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер столбца, из которого будут подставлены данные; [интервал просмотра данных]);
=ГПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер строки, из которой будут подставлены данные; [интервал просмотра данных]).
Указанные формулы имеют ценность при решении задач, связанных с консолидацией данных, которые разбросаны на разных листах одной книги Excel, находятся в различных рабочих книгах Excel, и размещении их в одном месте для создания экономических отчетов и подсчета итогов.
Задача № 3. У экономиста есть данные в виде таблицы Excel о реализации продукции за сентябрь в натуральном измерении (декалитрах) и данные о реализации продукции в сумме (рублях) в другой таблице Excel. Экономисту нужно предоставить руководству отчет о реализации продукции с тремя параметрами:
- продажи в натуральном измерении;
- продажи в суммовом измерении;
- средняя цена реализации единицы продукции в рублях.
Для решения этой задачи с помощью формулы ВПР нужно последовательно выполнить следующие действия.
Шаг 1. Добавляем к таблице с данными о продажах в натуральном измерении два новых столбца. Первый — для показателя продаж в рублях, второй — для показателя цены реализации единицы продукции.
Шаг 2. В первой ячейке столбца с данными о продажах в рублях прописываем расчетную формулу: =ВПР(B4:B13;Табл.4!B4:D13;3;ЛОЖЬ).
Пояснения к формуле:
В4:В13 — диапазон поиска значений по номенклатуре продукции в создаваемом отчете;
Табл.4!B4:D13 — диапазон ячеек, где будет производиться поиск, с наименованием таблицы, в которой будет организован поиск;
3 — номер столбца, по которому нужно выбрать данные;
ЛОЖЬ — значение критерия поиска, которое означает необходимость строгого соответствия отбора наименований номенклатуры таблицы с суммовыми данными наименованиям номенклатуры в таблице с натуральными показателями.
Шаг 3. Продлеваем формулу первой ячейки до конца списка номенклатуры в создаваемом нами отчете.
Шаг 4. В первой ячейке столбца с данными о цене реализации единицы продукции прописываем простую формулу деления значения ячейки столбца с суммой продаж на значение ячейки столбца с объемом продаж (=E4/D4).
Шаг 5. Продлим формулу с расчетом цены реализации до конца списка номенклатуры в создаваемом нами отчете.
В результате выполненных действий появился искомый отчет о продажах (табл. 3).
На небольшом количестве условных данных эффективность формулы ВПР выглядит не столь внушительно. Однако представьте, что такой отчет нужно сделать не из заранее сгруппированных данных по номенклатуре продукции, а на основе реестра ежедневных продаж с общим количеством записей в несколько тысяч.
Тогда эта формула обеспечит такую скорость и точность выборки нужных данных, которой трудно добиться другими функциями Excel.
Решение экономической задачи с помощью формулы СУММПРОИЗВ
Формула СУММПРОИЗВ позволяет экономистам справиться практически с любой экономической задачей, для решения которой нужно работать с несколькими массивами данных. Она обладает всеми возможностями рассмотренных выше формул, умеет суммировать произведения данных из списка до 255 источников (массивов).
Задача № 4. Есть реестр продаж различной номенклатуры продукции за сентябрь 2020 г. Нужно рассчитать из общего реестра данные о суммах реализации по основным номенклатурным группам продукции.
Чтобы выполнить задачу, добавим внизу реестра три новые строки с указанием групп продукции и пропишем в ячейке с будущими данными о продажах первой группы (пиво) следующую формулу: =СУММПРОИЗВ(((C4:C13=C16)*D4:D13)). Здесь указано, что в ячейке должно быть выполнено суммирование произведений значений диапазона ячеек столбца с наименованием групп продукции (C4:C13) с условием отбора наименования группы «Пиво» (С16) на значения ячеек столбца с суммами продаж (D4:D13).
Далее копируем эту формулу на оставшиеся две ячейки, заменив в них условия отбора на группу «Лимонад» (С17) и группу «Минеральная вода» (С18).
Выполнив указанные действия, получим искомое решение задачи в табл. 4.
Решение экономической задачи с помощью формулы СЧЕТЕСЛИ
Формула СЧЕТЕСЛИ используется не так широко, как предыдущие, но она выручает экономистов, если нужно минимизировать ошибки при работе с таблицами Excel. Эта формула удобна для проверки корректности вводимых данных и установке различного рода запретов, что особенно важно, если с данными работает несколько пользователей.
Задача № 5. Экономисту поручили провести корректировку справочника номенклатуры ТМЦ в учетной базе данных компании. Справочник долгое время не проверяли, данные в него вносили порядка 10 человек, поэтому появилось много некорректных и дублирующих наименований.
Чтобы повысить качество работы, приняли решение создать обновленный справочник в книге Excel, а затем сопоставить его с данными в учетной базе и исправить их. Проблема заключалась в том, что перечень номенклатуры составляет порядка 3000 наименований. Вносить его в книгу будут шесть человек, а это создает риск дублирования позиций.
Экономист может решить эту проблему с помощью формулы СЧЕТЕСЛИ. Нужно выполнить следующие действия:
- выбираем диапазон ячеек, куда будут вноситься наименования номенклатуры (В5:В3005);
- в меню редактора выбираем путь: Данные → Проверка данных;
- в появившемся диалоговом окне выбираем вкладку Параметры и указываем в выпадающем списке Тип данных вариант Другой;
- в строке Формула указываем: =СЧЕТЕСЛИ($В$5:$В$3005;В5)<=1;
- в диалоговом окне на вкладке Сообщение об ошибке вводим текст сообщения и нажимаем кнопку «ОК».
Если кто-либо из сотрудников будет пытаться ввести в указанный диапазон ячеек наименование ТМЦ, которое уже есть в диапазоне, у него это не получится. Excel выдаст сообщение в таком виде (рис. 1).
ФУНКЦИОНАЛ EXCEL ДЛЯ ОБРАБОТКИ ТАБЛИЧНЫХ ДАННЫХ
Помимо расчетных формул в табличном редакторе Excel присутствует набор инструментов, значительно облегчающих жизнь экономистам, которые работают с большими объемами данных. К наиболее популярным из них можно отнести функцию сортировки данных, функцию фильтрации данных, функцию консолидации данных и функцию создания сводных таблиц.
Решение экономической задачи с применением функции сортировки данных
Функционал сортировки данных позволяет изменить расположение данных в таблице и выстроить их в новой последовательности. Это удобно, когда экономист консолидирует данные нескольких таблиц и ему нужно, чтобы во всех исходных таблицах данные располагались в одинаковой последовательности.
Другой пример целесообразности сортировки данных — подготовка отчетности руководству компании. С помощью функционала сортировки из одной таблицы с данными можно быстро сделать несколько аналитических отчетов.
Сортировку данных выполнить просто:
- выделяем курсором столбцы таблицы;
- заходим в меню редактора: Данные → Сортировка;
- выбираем нужные параметры сортировки и получаем новый вид табличных данных.
Задача № 6. Экономист должен подготовить отчет о заработной плате, начисленной сотрудникам магазина, с последовательностью от самой высокой до самой низкой зарплаты.
Для решения этой задачи берем табл. 2 в качестве исходных данных. Выделяем в ней диапазон ячеек с показателями начисления зарплат (B4:D13).
Далее в меню редактора вызываем сортировку данных и в появившемся окне указываем, что сортировка нужна по значениям столбца D (суммы начисленной зарплаты) в порядке убывания значений.
Нажимаем кнопку «ОК», и табл. 2 преобразуется в новую табл. 5, где в первой строке идут данные о зарплате директора в 50 000 руб., в последней — данные о зарплате грузчика в 18 000 руб.
Решение экономической задачи с использованием функционала Автофильтр
Функционал фильтрации данных выручает при решении задач по анализу данных, особенно если возникает необходимость проанализировать часть исходной таблицы, данные которой отвечают определенным условиям.
В табличном редакторе Excel есть два вида фильтров:
- автофильтр — используют для фильтрации данных по простым критериям;
- расширенный фильтр — применяют при фильтрации данных по нескольким заданным параметрам.
Автофильтр работает следующим образом:
- выделяем курсором диапазон таблицы, данные которого собираемся отфильтровать;
- заходим в меню редактора: Данные → Фильтр → Автофильтр;
- выбираем в таблице появившиеся значения автофильтра и получаем отфильтрованные данные.
Задача № 7. Из общих данных о реализации продукции за сентябрь 2020 г. (см. табл. 4) нужно выделить суммы продаж только по группе лимонадов.
Для решения этой задачи выделяем в таблице ячейки с данными по реализации продукции. Устанавливаем автофильтр из меню: Данные → Фильтр → Автофильтр. В появившемся меню столбца с группой продукции выбираем значение «Лимонад». В итоге в табл. 6 автоматически остаются значения продаж лимонадов, а данные по группам «Пиво» и «Минеральная вода» скрываются.
Для применения расширенного фильтра нужно предварительно подготовить «Диапазон условий» и «Диапазон, в который будут помещены результаты».
Чтобы организовать «Диапазон условий», следует выполнить следующие действия:
- в свободную строку вне таблицы копируем заголовки столбцов, на данные которых будут наложены ограничения (заголовки несмежных столбцов могут оказаться рядом);
- под каждым из заголовков задаем условие отбора данных.
Строка копий заголовков вместе с условиями отбора образуют «Диапазон условий».
Порядок работы с функционалом консолидации данных
Функционал консолидации данных помогает экономистам в решении задач по объединению данных из нескольких источников в одну общую таблицу. Например, экономисты холдинговых компаний часто создают однотипные таблицы с данными по разным компаниям холдинга и им требуется предоставить руководству сводные данные о работе всей группы компаний. Для упрощения формирования сводных показателей как раз и подходит функционал консолидации данных.
Консолидация работает только с идентичными таблицами Excel, поэтому для успеха все объединяемые таблицы должны отвечать следующим требованиям:
- макеты всех консолидируемых таблиц одинаковые;
- названия столбцов во всех консолидируемых таблицах идентичные;
- в консолидируемых таблицах нет пустых столбцов и строк.
Работа с функционалом консолидации включает ряд последовательных действий:
1) открываем файлы со всеми таблицами, из которых собираемся консолидировать данные;
2) в отдельном файле, где будет находиться консолидированный отчет, ставим курсор на первую ячейку диапазона консолидированной таблицы;
3) в меню Excel открываем вкладки: Данные → Работа с данными → Консолидация;
4) в открывшемся диалоговом окне выбираем функцию консолидации (как правило, это «сумма», потому что нам требуется суммировать значения нескольких таблиц);
5) в диалоговом окне консолидации указываем ссылки на диапазоны объединяемых таблиц (диапазоны должны быть одинаковые);
6) если требуется автоматическое обновление данных консолидированной таблицы при изменении данных исходных таблиц, ставим галочку напротив «Создавать связи с исходными данными»;
7) завершаем консолидацию нажатием кнопки «ОК». В итоге получаем сводную структурированную таблицу, объединяющую данные всех исходных таблиц.
Решение экономической задачи с использованием функционала сводной таблицы для создания нового отчета
Функционал сводных таблиц позволяет сформировать различного рода отчеты из одного или нескольких массивов данных с возможностью обновления отчетных данных в случае изменения информации в исходных массивах. Используя сводные таблицы, можно быстро перенастроить параметры отчета.
Для создания сводной таблицы нужно зайти в меню Excel и вызвать Мастера сводных таблиц. В моей версии редактора это выполняется через Вставка → Сводная таблица, в некоторых версиях нужно выбрать Данные → Сводная таблица.
В появившемся диалоговом окне формируем параметры будущей таблицы:
- указываем исходную таблицу или диапазон ячеек Excel, откуда будут взяты данные для сводной таблицы. В последних версиях Excel также можно выбрать вариант обработки данных из внешних источников;
- указываем место, куда размещать создаваемый отчет сводной таблицы (новый лист, ячейки открытого листа);
- в открывшемся конструкторе отчета указываем, какие исходные данные будут выведены в строки и столбцы отчета, при необходимости настраиваем фильтры для показателей сводной таблицы и создаем новый отчет.
Задача № 8. Экономисту нужно создать отчет на основе реестра данных о реализации продукции за сентябрь 2020 г. В отчете должно быть два уровня группировки данных. На первом уровне нужно вывести итоги по группам продукции, на втором уровне — по ее номенклатурным позициям. Чтобы решить эту задачу, вызываем Мастера сводных таблиц. Указываем, что данные берем из ячеек табл. 4, а отчет будем размещать на новом листе книги Excel. В конструкторе отчета указываем, что в первой колонке отчета будут показатели групп и номенклатурных единиц продукции, во второй — данные о суммах реализации. После этого даем команду создать сводную таблицу. Результат — в табл. 7.
ИНСТРУМЕНТЫ EXCEL ДЛЯ МОДЕЛИРОВАНИЯ И АНАЛИЗА ЭКОНОМИЧЕСКИХ ДАННЫХ
Постоянное развитие функционала табличного редактора Excel привело к тому, что появилось много новых инструментов, которые могут помочь экономистам в решении выполняемых ими задач. К числу наиболее значимых можно отнести функцию «Поиск решения», пакет расширенного анализа данных и специализированные надстройки.
Решение экономической задачи с помощью надстройки «Поиск решения»
Функция «Поиск решения» позволяет найти наиболее рациональный способ решения экономической задачи математическими методами. Она может автоматически выполнить расчеты для задач с несколькими вводными данными при условии накладывания определенных ограничений на искомое решение.
Такими экономическими задачами могут быть:
- расчет оптимального объема выпуска продукции при ограниченности сырья;
- минимизация транспортных расходов на доставку продукции покупателям;
- решение по оптимизации фонда оплаты труда.
Функция поиска решения является дополнительной надстройкой, поэтому в стандартном меню Excel мы ее не найдем. Чтобы использовать в своей работе функцию «Поиск решения», экономисту нужно сделать следующее:
- в меню Excel выбрать путь: Файл → Параметры → Надстройки;
- в появившемся списке надстроек выбрать «Поиск решения» и активировать эту надстройку;
- вернуться в меню Excel и выбрать: Данные → Поиск решения.
Задача № 9. Туристической компании необходимо организовать доставку 45 туристов в четыре гостиницы города с трех пунктов прибытия при минимально возможной сумме затрат. Для решения задачи составляем таблицу с исходными данными:
1. Количество прибывающих с каждого пункта — железнодорожный вокзал, аэропорт и автовокзал (ячейки Н6:Н8).
2. Количество забронированных для туристов мест в каждой из четырех гостиниц (ячейки D9:G9).
3. Стоимость доставки одного туриста с каждого пункта прибытия до каждой гостиницы размещения (диапазон ячеек D6:G8).
Исходные данные, размещенные таким образом, показаны в табл. 8.1.
Далее приступаем к подготовке поиска решения.
1. Создаем внизу исходной таблицы такую же таблицу для расчета оптимального количества доставки туристов при условии минимизации затрат на доставку с диапазоном ячеек D15:G17.
2. Выбираем на листе ячейку для расчета искомой функции минимизации затрат (J4) и прописываем в ячейке расчетную формулу: =СУММПРОИЗВ(D6:G8;D15:G17).
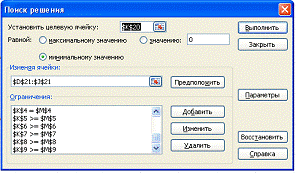
3. Заходим в меню Excel, вызываем диалоговое окно надстройки «Поиск решения» и указываем там требуемые параметры и ограничения (рис. 2):
- оптимизировать целевую функцию — ячейка J4;
- цель оптимизации — до минимума;
- изменения ячейки переменных — диапазон ячеек второй таблицы D15:G17;
- ограничения поиска решения:
– в диапазоне ячеек второй таблицы D15:G17 должны быть только целые значения (D15:G17=целое);
– значения диапазона ячеек второй таблицы D15:G17 должны быть только положительными (D15:G17>=0);
– количество мест для туристов в каждой гостинице таблицы для поиска решения должно быть равно количеству мест в исходной таблице (D18:G18 = D9:G9);
– количество туристов, прибывающих с каждого пункта, в таблице для поиска решения должно быть равно количеству туристов в исходной таблице (Н15:Н17 = Н6:Н8).
Далее даем команду найти решение, и надстройка рассчитывает нам результат оптимальной доставки туристов (табл. 8.2).
При такой схеме доставки целевое значение общей суммы расходов действительно минимальное и составляет 1750 руб.
Пакет расширенного анализа данных
Пакет расширенного анализа данных применяют, если нужно исследовать различного рода статистические анализы, ряды данных, спрогнозировать тренды и т. д.
Пакет является надстройкой к Excel, устанавливается в основное меню аналогично функции поиска решений (Файл → Параметры → Надстройки → Пакет анализа). Вызвать его можно командой Данные → Анализ данных через диалоговое окно, в котором отражены все заложенные в надстройке виды анализа (рис. 3).
Специализированные надстройки для финансово-экономической работы
В последние годы значительно расширился перечень специализированных надстроек к табличному редактору Excel, которые могут использовать в своей работе экономисты. Практически все они бесплатные, легко устанавливаются самим пользователем.
Не будем останавливаться на таких надстройках, как Power Query, Power Pivot, Power Quick, так как они в большей степени используются в целях бизнес-аналитики, чем для решения экономических задач.
Есть и другие надстройки к Excel, которые могут облегчить работу специалистов финансово-экономических служб. Интерес представляют две бесплатные надстройки — «Финансист» и PowerFin.
Надстройку «Финансист» можно установить на свою версию Excel как в автоматическом, так и ручном режиме. В надстройке собрано много полезных для экономистов функций. Достаточно перечислить основные блоки данной надстройки:
- финансовые функции (ликвидность, платежеспособность, финансовая устойчивость, рентабельность, оборачиваемость, безубыточность продаж, отсрочка платежа, налоги и т. д.);
- работа с формулами;
- работа с текстом;
- работа с книгами и листами Excel;
- работа с ячейками Excel;
- поиск дубликатов и сравнение диапазонов данных;
- вставка дат и примечаний к диапазонам данных;
- загрузка курсов валют;
- создание выпадающих списков.
Надстройка PowerFin будет полезна прежде всего экономистам, которые работают с кредитами и инвестициями. Она без проблем устанавливается в меню надстроек Excel и имеет следующие функции:
- кредитный калькулятор (с функцией выведения калькулятора на лист, в том числе с возможностью автоматического формирования графика платежей);
- депозитный калькулятор для вычисления основных параметров инвестиций (с функцией выведения калькулятора на лист);
- вычисление требуемой процентной ставки исходя из первоначальной и будущей стоимости инвестиций;
- набор основных формул для расчета эффективности проекта: дисконтированного денежного потока, чистого денежного дохода, внутренней нормы доходности, срока окупаемости.
Статья опубликована в журнале «Планово-экономический отдел» № 10, 2020.
На этой странице вы найдете примеры решений различных оптимизационных задач с использованием пакета электронных таблиц MS Excel (используется как надстройка Поиск решения, так и ручные вычисления).
Задачи оптимизации и Excel
Задачи оптимизации имеют огромное прикладное значение и возникают в самых разных разделах экономики, техники, военного дела и т.п. В таких задачах нас интересуют поиск некоторого оптимального решения (минимизующего или максимизирующего целевую функцию: прибыль, затраты, калорийность и т.п.) в условиях ограничений (наличия ресурсов, дорог, времени, продуктов и т.п.).
Вот некоторые примеры экономических задач: минимизация расходов при формировании состава сырья (например, на текстильных предприятиях), оптимизация раскроя (например, на швейных производствах), минимизация расходов при формировании штатного расписания, оптимизация калорийности и стоимости рациона (как для людей, так и для животных), минимизация расходов на перевозку грузов по маршрутам, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы и др.
Часто эти задачи (даже учебные, даже в случае линейности) содержат более десяти переменных(а в случае, например, транспортных задач, и вовсе десятки), что делает ручные расчеты нерациональными. В то же время привычная для всех программа Excel прекрасно подходит для поиска решения.
Алгоритм решения с помощью надстройки «Поиск решения» следующий:
- составить математическую модель задачи: выделить и обозначить переменные, ограничения на них в виде равенств и неравенств (естественные, например, неотрицательность количества, и дополнительные, например, «запасов железной руды не более 10 т»), целевую функцию (то, что нужно оптимизировать) выразить через переменные.
- выделить место под переменные задачи; внести ограничения (левые части — в виде формул от переменных, правые — в виде констант) в файл электронной таблицы Excel,
- внести в ячейку формулу для целевой функции,
- запустить надстройку Поиск решения,
- установить нужные параметры решения (ограничения в листе, ограничения неотрицательности, условие линейности при необходимости и т.п.) и запустить выполнение.
Excel вычислит оптимальные значения переменных и покажет их в ячейках, а также значение целевой функции. Дополнительно можно построить отчеты для анализа решения задачи.
Некоторые задачи оптимизации решаются не с помощью надстройки Поиск решения, а путем подбора параметра или ручных расчетов. Ниже вы найдете примеры разных задач, а также ссылки на другие разделы со сходными заданиями.
Лучшее спасибо — порекомендовать эту страницу
Задачи оптимизации: примеры в Excel
Задача 1. Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля $R_j$. Определена экономическая эффективность $К$ — каждого проекта в зависимости от рентабельности производства. По истечении трех сроков $S_i$ рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в следующей таблице (д. е.):
Выберите оптимальное решение в соответствии с критериями Лапласа, Вальда, Сэвиджа и Гурвица (при $а = 0,5$).
Задача 2. Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода каждого вида сырья на изготовление единицы продукции данного вида в таблице 6. В ней же указаны прибыль от реализации единицы изделия каждого вида и общее количество сырья данного, которое может быть использовано предприятием.
Требуется такой составить такой план производства изделий А и В, при котором прибыль от реализации будет максимальной?
Задача 3. Фирма N, имеющая филиалы (k), производит продукцию. Каждый филиал фирмы выпускает четыре вида продукции из пяти (i=1-5). Данные, характеризующие производство филиалов $b_{ki}$, приведены в табл.1.
Филиалы фирмы закупают сырье, из которого производят продукцию, у семи АО (j =1-7). Выход готового продукта из 1 тонны сырья $a_{ij}$ показан в табл.2.
Прибыль филиалов фирмы при закупке 1тн сырья у разных АО, $С_{kj}$ , показана в табл.3.
В разделе 1 работы требуется:
1.1.Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, ($x_j$), максимизируя прибыль филиала. Далее, студент формулирует экономико-математическую модель общей задачи линейного программирования (ОЗЛП).
1.2.С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы выпуска ассортимента продукции.
Задача 4. Для изготовления одного пирожка требуется 0,8 ед. начинки и 4 ед. теста, одного пирожного 4 ед. начинки и 0,5 ед. теста, одного рулета 2 ед. начинки и 2,5 ед. теста. Сколько пирожков, пирожных и рулетов нужно сделать кондитерской, если в наличии имеется 120 ед. теста и 300 ед. начинки?
Определите доход от реализации кондитерских изделий, если доход от продажи одного пирожка составляет 3 рубля, одного пирожного 2 рубля, одного рулета 1,5.
Для решения задачи используется ППП Excel.
Задача 5. Менеджер проекта по строительству нового торгового гипермаркета компании Наше дело надеется завершить проект за пару недель до Рождества.
После обзора оценок времени выполнения отдельных стадий выяснилось, что потребуются дополнительные инвестиции, чтобы сократить длительность проекта так, чтобы он действительно завершился вовремя. В таблице приведены оценки длительностей стадий и стоимость их сокращения на 1 и на 2 недели.
a. Нарисуйте сетевую диаграмму проекта и найдите критический путь.
b. Определите минимальную стоимость сокращения проекта на 5 недель.
Решаем задачи вручную и в Excel с отчетом
Полезные ссылки
|
|
Методички
- Решение оптимизационных задач в среде MS Excel 2013 Методические указания небольшого объема. Разобраны стандартные задачи: ЛП, транспортная, нелинейная, приведены скриншоты решения и пояснения.
- Решение задач оптимизации в Microsoft Excel 2010 Учебное пособие ТОГУ, 101 страница, более увесистый и подробный документ. Разбирается надстройка Поиск решения, решение задач линейного и нелинейного программирования и СЛАУ.
Решение задач экономико-математического моделирования с помощью программы Excel
Решение задач
экономико-математического моделирования с помощью программы Excel
Определить оптимальное сочетание
трех зерновых культур: пшеницы, ячменя и овса
Производство культур характеризуется
показатели таблицы.
|
Показатели |
Озимая пшеница |
Яровой ячмень |
Овес |
|
Урожайность с 1 га, ц. |
40 |
35 |
30 |
|
Затраты труда на 1 га, чел.-ч. |
20 |
15 |
13 |
|
Затраты удобрений на 1 га, руб. |
80 |
50 |
40 |
Производственные ресурсы: пашня-1600
га, труд — 27000 чел.-ч., удобрения — 99000 руб.
В структуре посевов площадь под оз.
пшеницы должна составлять не менее 50 %. Критерий оптимальности максимальное
производство зерна.
Решение.
Обозначим через:
х1-площадь оз. пшеницы, га.
х2-площадь яр. ячмень, га.
х3-площадь овса, га.
Запишем условие задач в виде системы
ограничений (уравнений и неравенств).
) По уборки площади посевов
трех зерновых, га
Х1+х2+х3=1600
) По использовании ресурсов
труда
*х1+15*х2+13*х3≤27000
) По затратам удобрений, руб.
*х1+50*х2+40*х3≤99000
) По структуре посевной
площади
х1≥0,5(х1+х2+х3)
х1≥0,5*х1+0,5*х2+0,5*х3
,5х1-0,5х2-0,5х3≥0
ЦФ= критерий max производства зерна.
ЦФ=40*х1+35*х2+30*х3→max
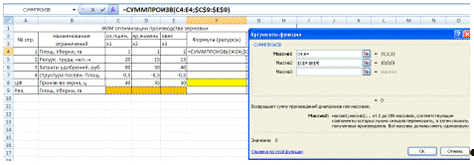
Решение задачи в Excel
В ячейку F4 вставим формулу «
=СУММПРОИЗВ(С4:Е4;$C$9:$E$9)», затем растянем форму до целевой ячейки
включительно.
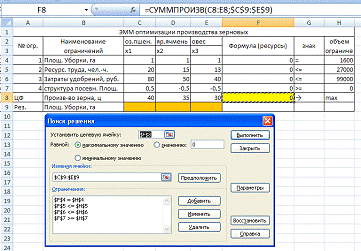
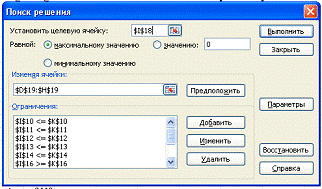
Затем находим решение задачи с
помощью «поиска решения». Находим: Данные→Анализ→Поиск решения. Как
видно на рисунке: устанавливаем целевую ячейку; равный- max значению; изменяя
ячейки и ограничение.
программирование excel оптимальный
модель
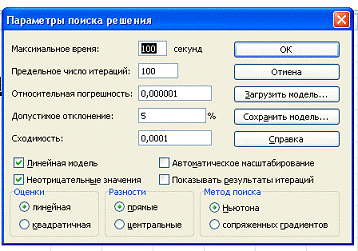
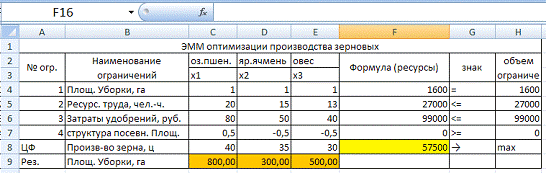
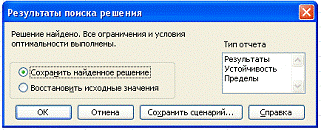
После выполненных операций нажимаем,
на «выполнить» и получаем возможное решение задачи:
Вывод: Оптимальное сочетание трех
зерновых культур, максимальное производства зерна будет при площади уборки: оз.
пшеницы — 800 га, яр. ячмень — 300 га, овес — 500 га.
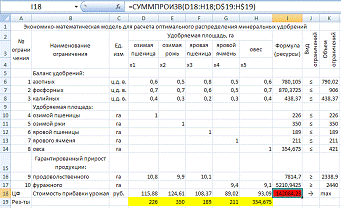
Экономико-математические модели для
расчета оптимального распределения минеральных удобрений
Рассчитать план распределения
минеральных удобрений, при котором достигается максимум стоимости прибавки
урожая. При этом по плану необходимо получить не менее 23 000 ц
продовольственного и 17 000 ц фуражного зерна. Площадь посева культур,
рекомендуемые дозы внесения удобрений и прибавка урожая показаны в табл.7.1.
Сведения о количестве, качестве и стоимости минеральных удобрений приведены в
табл.7.2.
Таблица 7.1
|
Показатели |
Озимая пшеница |
Озимая рожь |
Яровая пшеница |
Яровой ячмень |
Овес |
|||||
|
Площадь посева, га |
226 |
350 |
189 |
211 |
421 |
|||||
|
Урожайность без внесения удобрений с 1 га, ц |
29,7 |
26,3 |
25,1 |
28,9 |
20,1 |
|||||
|
Азотных |
0,6 |
0,5 |
0,8 |
0,5 |
0,6 |
|||||
|
Фосфорных |
0,7 |
0,7 |
0,6 |
0,5 |
0,7 |
|||||
|
Калийных |
0,4 |
0,3 |
0,2 |
0,3 |
0,4 |
|||||
|
Прибавка урожая за счет внесения удобрений с 1 га: |
||||||||||
|
ц |
10,8 |
9,9 |
10,1 |
9,4 |
9,1 |
|||||
|
руб |
115,88 |
124,61 |
108,37 |
89,02 |
93,09 |
Таблица 7.2
|
показатели |
Сульфат аммония N |
Суперфосфат Р2О5 |
Хлористый калий К2О |
|
Количество, ц |
3762 |
4530 |
743 |
|
Содержание действующего вещества, % |
21 |
20 |
59 |
|
Цена 1 ц, руб |
4,00 |
2,39 |
1,10 |
|
Стоимость внесения 1 ц, руб |
0,25 |
0,19 |
0,26 |
Решение:
ЭММ для расчета оптимальных рационов
кормления с/х животных
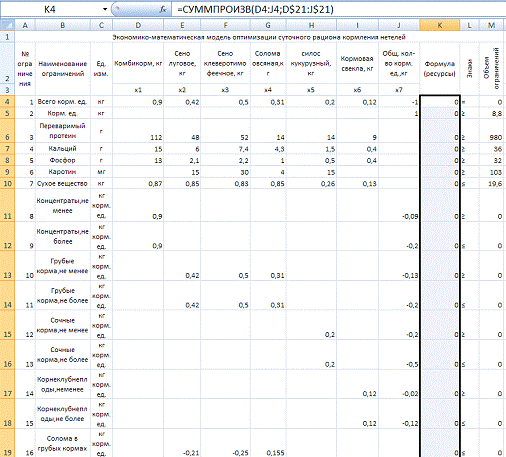
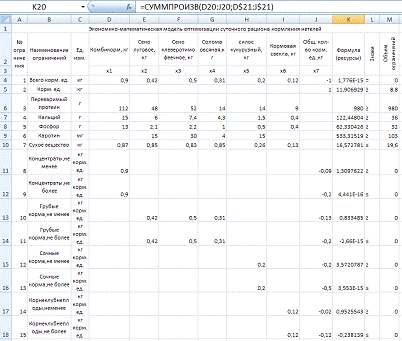
Рассчитать оптимальный суточный
рацион кормления нетелей средней живой массой 480 кг. В рационе должно
содержаться не менее 8,8 кг кормовых единиц, 980 г переваримого протеина, 36 г
кальция, 32 г фосфора, 103 мг каротина и не более 19,6 кг сухого вещества.
Рацион составляется из комбикорма,
сена лугового, сена клеверотимофеечного, соломы овсяной, силоса кукурузного и
кормовой свеклы. Содержание питательных веществ в кормах и их себестоимость
представлены в таблице 9.5.
В соответствии с зоотехническими
требованиями отдельные группы кормов в рационе могут изменяться в следующих
пределах, % к общему количеству кормовых единиц: концентрированные — от 9 до
20, грубые — от 13 до 20, сочные — от 20 до 50 и корнеклубнеплоды — от 2 до 12.
Удельный вес соломы в грубых кормах должен составлять не менее 50%.
Таблица 9.5
|
Корма |
Содержание в 1 кг корма |
Себестоимость 1 кг корма, коп |
|||||
|
Кормовых единиц, кг |
Переваримого протеина, г |
Кальция, г |
Фосфора, г |
Каротина, мг |
|||
|
Комбикорм |
0,9 |
112 |
15 |
13 |
— |
0,87 |
14,5 |
|
Сено луговое |
0,42 |
48 |
6 |
2,1 |
15 |
0,85 |
3,4 |
|
Сено клеверотимофеечное |
0,5 |
52 |
7,4 |
2,2 |
30 |
0,83 |
2,1 |
|
Солома овсяная |
0,31 |
14 |
4,3 |
1 |
4 |
0,85 |
0,2 |
|
Силос кукурузный |
0,2 |
14 |
1,5 |
0,5 |
15 |
0,23 |
0,6 |
|
Кормовая свекла |
0,12 |
9 |
0,4 |
0,4 |
— |
0,13 |
2,1 |
Решение:
Определим перечень переменных.
Количество кормов, которая может войти в рацион нетелей, обозначим через:
Х1-количество комбикорма в рационе,
кг
Х2-количество сена лугового в
рационе, кг
Х3-количество сена
клеверотимофеечного в рационе, кг
Х4-количество соломы овсяной в
рационе, кг
Х5-количество силоса кукурузного в
рационе, кг
Х6-количество кормовой свеклы в рационе,
кг
Х7-общее количество кормовых единиц
в рационе, кг
Запишем систему ограничений в
развернутом виде.
. Ограничения по балансу питательных
веществ в рационе:
) общее количество кормовых единиц
,9х1+0,42х2+0,5х3+0,31х4+0,2х5+0,12х6=х7
или после преобразования
,9х1+0,42х2+0,5х3+0,31х4+0,2х5+0,12х6-х7=0
) кормовые единицы не менее
Х7 ≥ 8,8
) переваримого протеина не менее
х1+48х2+52х3+14х4+14х5+9х6 ≥
980
) кальция не менее
х1+6х2+7,4х3+4,3х4+1,5х5+0,4х6 ≥
36
) фосфора не менее
) каротина не менее
х2+30х3+4х4+15х5 ≥ 103
. Ограничения по содержанию сухого
вещества в рационе:
)
0,87х1+0,85х2+0,83х3+0,85х4+0,26х5+0,13х6 ≤ 19,6
. Ограничения по содержанию
отдельных групп кормов в рационе:
) концентрированных не менее
,9х1 ≥ 0,09х7
или после преобразований
,9х1-0,2х7 ≥ 0
) концентрированных не более
,9х1 ≤ 0,2х7
или после преобразований
,9х1-0,2х7 ≤ 0
) грубых не менее
,42х2+0,5х3+0,31х4 ≥ 0,13х7
или после преобразований
,42х2+0,5х3+0,31х4-0,13х7 ≥ 0
) грубых не более
,42х2+0,5х3+0,31х4 ≤ 0,2х7
или после преобразований
,42х2+0,5х3+0,31х4-0,2х7 ≤ 0
) сочных не менее
,2х5≥0,2х7
или 0,2х5-0,2х7≥0
) сочных не более
,2х5≤0,5х7
или 0,2х5-0,5х7≤0
) корнеклубнеплодов не менее
,12х6≥0,02х7
или 0,2х6-0,02х7≥0
)корнеклубнеплодов не более
,12х6≤0,12х7
или 0,12х6-0,12х7≤0
. ограничения по содержанию
отдельных видов кормов
) удельный вес соломы в группе
грубых
,31х4≥0,5*(0,42х2+0,5х3+0,31х4)
или после преобразований
,21х2-0,25х3+0,155х4≥0
Целевая функция — минимальная
себестоимость рациона=14,5х1+3,4х2+2,1х3+0,2х4+0,6х5+2,1х6→min
Определить оптимальную структуру
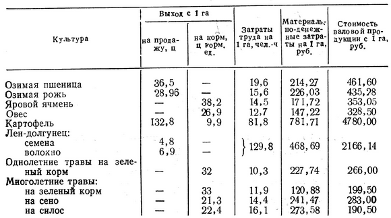
посевных площадей, обеспечивающую получение максимума валовой продукции. В
хозяйстве имеется 2377 га пашни. Ресурсы труда — 98700 чел.-ч.
Данные при возделывании культур
представлены в таблице:
Сельскохозяйственные культуры могут
размещаться по двум вариантам севооборотов:
Севооборот №1
. однолетние травы
. озимые зерновые
. картофель
. ячмень с подсевом многолетних трав
. многолетние травы
. озимые зерновые
. лен
. овес
Севооборот №2
. однолетние травы
. озимые зерновые с подсевом
многолетних трав
. многолетние травы
. лен
. картофель
. ячмень
. озимые зерновые
. картофель
. ячмень
Плановое задание по продажи
продукции государству, ц:
) картофель 56120
) льносемена 1050
) льноволокно 1830
Для обеспечения животноводства
кормами необходимо произвести следующее количество кормов, ц корм.ед.:
концентрированных 17930
грубых 2380
сочных 7280
зеленых 8760
Основные переменные:
В севообороте №1:
х11 — озимая пшеница
х21 — озимая рожь
х31 — яровой ячмень
х41 — овес
х51 — картофель
х61 — лен
х71 — однолетние травы
х81 — многолетние травы на зеленый
корм
х91 — многолетние травы на сено
х101 — многолетние травы на силос
х1 — площадь севооборота №1
В севообороте №2
х12 — озимая пшеница
х22 — озимая рожь
х32 — яровой ячмень
х52 — картофель
х62 — лен
х72- однолетние травы
х82 — многолетние травы на зеленый
корм
х92 — многолетние травы на сено
х102 — многолетние травы на силос
х2 — площадь севооборота №2
х3 — материально-денежные затраты,
руб.
х4 — Валовая продукция, руб.
Система ограничений:
. По площади пашни:
) х1+х2<=2377
. По площади севооборота №1:
)
х11+х21+х31+х41+х51+х61+х71+х81+х91+х101-х1<=0
. По площади отдельных
сельскохозяйственных культур внутри севооборота №1:
) озимые зерновые в севообороте
№1+x21=0,25×1
) ячмень-0,125×1=0
) овес-0,125×1=0
) картофель-0,125×1=0
) лен-0,125×1=0
) однолетние травы-0,125×1=0
) многолетние
травы+x91+x101-0,125×1=0
. По площади севооборота №2:
) x12+x22+x32+x52+x62+x72+x82+x92+x102-x2<=0
. По площади отдельных
сельскохозяйственных культур внутри севооборота №2:
) озимые зерновые+x22-0,22×2=0
) ячмень-0,22×2=0
) картофель-0,22×2=0
) лен-0,11×2=0
) однолетние травы-0,11×2=0
) многолетние
травы+x92+x102-0,11×2=0
. По использованию трудовых
ресурсов:
)
19,6×11+15,6×21+14,5×31+12,7×41+81,8×51+ 129,8×61+
10,37×71+11,9×81+14,4×91+16,1×10,1+19,6×12+15,6×22+14,5×32+81,8×52+129,8×62+10,37×72+11,9×82+14,4×92+16,1×10,2<=98700
. На продажу:
) зерно, ц+x21+x12+x22>=18030
) картофель, ц+x52>=56120
) льносемена
,8×6,1+4,8×6,2>=1050
) льноволокно
,9×61+6,9×62>=1830
. По производству кормов:
) концентрированные корма,
ц.корм.ед.
,2×3+26,9×41+38,2×32>=17930
) грубые корма
,3×91+21,3×92>=2380
,9×51+22,4×101+9,9×52+22,4×102>=7280
) зеленый корм
x71+33×81+32×72+33×82>=8760
. Материально-денежные затраты, руб.
)
214,27×11+226,03×21+171,72×31+147,22×41+781,71×51+468,69×61
+227,74×71+120,88×81+241,47×91+273,58×101+214,27×12+226,03×22+171,72×32+781,71×52+468,69×62+227,74×72+120,88×82+241,47×92+273,58×102-x3=0
. Валовая продукция, руб.
)
461,6×11+435,28×21+…+190,5×10,1+461,6×12+…+190,5×10,2-x4=0
ЦЕЛЕВАЯ ФУНКЦИЯ: х4 стремится к
максимуму
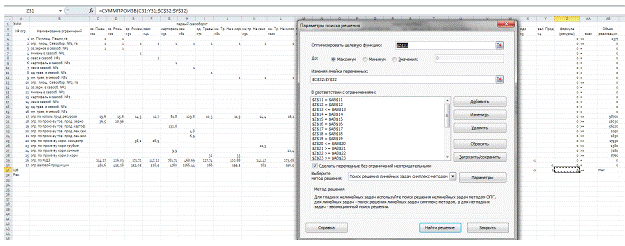
Решение задачи:
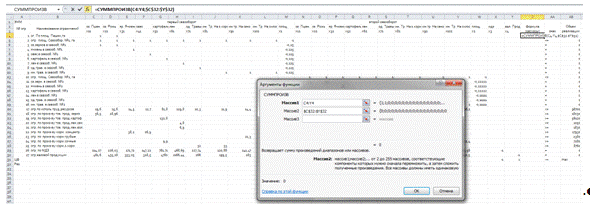
В ячейку Z4 вставим формулу «
=СУММПРОИЗВ(С4:Y4;$C$31:$Y$31)», затем растянем форму до целевой ячейки
включительно.
Затем находим решение задачи с помощью «поиска решения». Находим:
Данные→Анализ→Поиск решения. Как видно на рисунке: устанавливаем
целевую ячейку; равный- max значению; изменяя ячейки и ограничение.
Надстройка Поиск
решения
пакета MS Excel предназначена для выполнения
сложных вычислений, которые трудно
произвести вручную. Она позволяет
находить значения в целевой ячейке,
изменяя при этом до 200 переменных,
удовлетворяющих заданным критериям.
По желанию пользователя результаты
поиска могут быть представлены в виде
отчетов разных типов, которые можно
поместить в рабочую книгу.
Перед тем как
начать поиск решения, необходимо
произвести формализацию задачи, т. е.
составить ее экономико-математическую
модель.
Исходные данные
для запуска надстройки Поиск
решения
должны быть представлены в виде таблицы,
которая содержит формулы, отражающие
зависимости между данными таблицы.
Переход к надстройке
Поиск решения в MS
Office
2007 выполняется на вкладке Данные.
Рисунок 27. Справка
по элементам окна Поиск Решения
Рисунок 28.
Окно Поиск
решения
Рассмотрим работу
надстройки Поиск
решения на
примере.
Пример решения задачи
При продаже товаров
А
и В
торговое предприятие использует четыре
вида ресурсов. Нормы затрат ресурсов
на реализацию одной единицы товара и
объемы ресурсов указаны в табл. 7. Доход
от реализации единицы товара А
составляет 2 усл. ед., товара В
— 3 усл. ед. Определим оптимальный план
реализации товаров, обеспечивающий
торговому предприятию наибольшую
прибыль.
Таблица 7
Нормы затрат и
объем ресурсов, усл. ед.
|
Ресурсы |
Нормы затрат |
Количество |
|
|
А |
В |
||
|
1 |
2 |
2 |
12 |
|
2 |
1 |
2 |
8 |
|
3 |
4 |
0 |
16 |
|
4 |
0 |
4 |
12 |
Решение
1.
Составим
математическую модель задачи. Количество
товара А
обозначим х1,
В
— х2.
Доход от реализации товара А
составляет
2x1
усл. ед., товара В
— 3x2
усл. ед., общий доход — соответственно
F
2x1
+ 3x2.
Поскольку торговому
предприятию нужно получить наибольшую
прибыль, то ставится задача максимизации
целевой функции:
F
2x1
+ 3x2
max.
Ресурс 1-го вида
ограничен 12 единицами, при этом его
расходуется на реализацию товара А
2x1
единиц, а
на реализацию товара В
— 2x2
единиц.
Поскольку количество израсходованного
ресурса не должно превышать его запаса
на предприятии, можно записать следующее
ограничение:
2x1
+ 2x2
12.
Аналогично
записываются ограничения для других
ресурсов:
x1
+ 2x2
8;
4x1
16;
4x2
12.
Так как количество
реализованного товара не может быть
величиной отрицательной, то добавим
еще ограничения x1
0 и x2
0. Таким образом, математическая модель
задачи выглядит следующим образом:
2. Заполним ячейки
Excel соответствующими значениями (рис.
29).
Рисунок 29.
Экран Excel для
решения задачи линейного программирования
Ячейки А4:В4
отведены под значения переменных х1
и х2.
Этим ячейкам присваиваются начальные
значения (0; 0). После решения задачи Excel
запишет в эти ячейки найденные оптимальные
значения переменных х1
и х2.
Поэтому эти ячейки называются изменяемыми.
Далее нужно
подготовить данные для задания ограничений
задачи. В ячейки диапазона A7:B10
внесем коэффициенты при неизвестных в
ограничениях. Вычислим значение левой
части первого ограничения при начальных
значениях переменных. Для этого введем
в ячейку С7
формулу
=СУММПРОИЗВ($A$4:$B$4;A7:B7).
Ячейки С8:С10
заполняются формулами аналогично.
Формулу ячейки С7
можно скопировать с помощью автозаполнения.
Таким образом, ячейки C7:C10
содержат значения использованных
ресурсов (левые части ограничений). В
ячейки D7:D10
внесем количество ресурса, имеющегося
в наличии (правые части ограничений).
Вычислим значение
целевой функции при начальных значениях.
В ячейку А14
запишем формулу вычисления общего
дохода
=СУММПРОИЗВ(A4:B4;A12:B12).
Ячейка, содержащая
формулу вычисления значения целевой
функции модели, называется целевой.
Экран Excel в режиме
представления формул показан на рис.
30.
Рисунок 30.
Экран Excel в
режиме представления формул
3. Чтобы начать
процесс поиска решения, выполним команду
Сервис
/ Поиск
решения. На
экране появится окно Поиск
решения.
Замечание.
Если такого пункта в меню Сервис
не имеется, следует загрузить
соответствующую программу-надстройку.
Для этого выполним команду Сервис
/ Надстройки.
В открывшемся окне диалога установим
флажок в строке Поиск
решения
(рис. 31).
Рисунок 31.
Окно Надстройки
4. Установим курсор
в поле Установить
целевую
ячейку и
укажем ячейку модели, значение которой
должно быть изменено (максимизировано,
минимизировано или приравнено к
какому-либо определенному указанному
значению). В нашей модели целевой будет
ячейка, содержащая формулу расчета
прибыли А14
(рис. 32).
Рисунок 32.
Окно Поиск
решения
Целевая ячейка
должна содержать формулу, которая прямо
или косвенно ссылается на изменяемые
ячейки.
5. С помощью
переключателя Равной,
который может находиться в трех
положениях, зададим максимизацию,
минимизацию или установку определенного
значения целевой ячейки. В последнем
случае необходимо указать число в поле
Значение.
В данном примере установим переключатель
в положение Максимальному
значению.
6. В поле Изменяя
ячейки
установим ссылки на ячейки, которые
будут изменяться. Сделать это можно
двумя способами: введя адреса или имена
ячеек с клавиатуры либо указав ячейку
(диапазон ячеек) на рабочем листе с
помощью мыши.
При нажатии кнопки
Предположить
автоматически выделяются ячейки, на
которые есть прямая или косвенная ссылка
в формуле целевой ячейки.
Введем адрес
диапазона А4:В4.
7. Следующий этап
— определение ограничений. Для этого
нажмем кнопку Добавить.
На экране появится окно диалога Добавление
ограничения
(рис. 33).
В поле Ссылка
на ячейку
указывается адрес ячейки или диапазона
ячеек, для которых должно действовать
ограничение (левая часть ограничения).
В списке операторов нужно выбрать
оператор. В поле Ограничение
указывается число или делается ссылка
на какую-либо ячейку или диапазон (правая
часть ограничения).
Рисунок 33.
Окно Добавление
ограничения
Ограничения можно
задать как для изменяемых ячеек, так и
для целевой ячейки, а также для других
ячеек, прямо или косвенно присутствующих
в модели.
Если в поле
Ограничение
указана ссылка на диапазон ячеек, размер
этого диапазона должен совпадать с
размером диапазона, указанного в поле
Ссылка на
ячейку.
Введем первое
ограничение (требование неотрицательности
переменных):
$A$4:$B$4>=0.
Нажмем кнопку
Добавить,
чтобы продолжить ввод ограничений. Так
как все 4 ограничения имеют один и тот
же знак (),
то можно ввести их одной записью:
$С$7:$С$10<=$D$7:$D$10.
Далее нажмем кнопку
ОК,
чтобы завершить ввод ограничений и
вернуться в окно Поиск
решения.
Заданные условия появятся в списке
Ограничения.
С помощью кнопок
Добавить
и Изменить
можно при необходимости откорректировать
заданные ограничения.
Итак, целевая
ячейка, изменяемые ячейки и ограничения
для нашей модели заданы (см. рис. 32).
Далее мы можем
изменить параметры поиска решения,
заданные по умолчанию, а также сохранить
созданную модель поиска решения, чтобы
использовать ее в дальнейшем.
8. Нажмем кнопку
Параметры
в окне диалога Поиск
решения. На
экране появится окно Параметры
поиска решения
(рис. 34).
Рисунок 34.
Окно Параметры
поиска решения
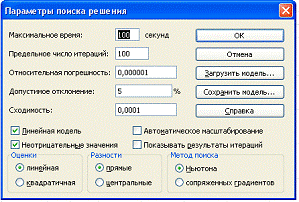
Н
следующие элементы этого окна:
-
Поле Максимальное
время,
служащее для ограничения времени,
отпускаемого на поиск решения задачи. -
Поле Предельное
число итераций,
ограничивающее число промежуточных
вычислений. -
Поля Относительная
погрешность
и Допустимое
отклонение,
служащие для задания точности, с которой
ищется решение. Рекомендуется найти
решение с величинами данных параметров,
заданными по умолчанию, а затем повторить
вычисления с меньшей погрешностью и
допустимым отклонением. -
Флажок Линейная
модель
должен быть установлен в случае линейной
задачи, а в случае нелинейной — сброшен. -
Флажок Показывать
результаты итераций
служит для приостановки поиска решения
и просмотра результатов промежуточных
вычислений. -
Флажок Автоматическое
масштабирование
служит для включения автоматической
нормализации входных и выходных
значений, качественно различающихся
по величине (например при максимизации
прибыли в процентах по отношению к
вложениям, исчисляемым в миллионах
рублей).
Установленные
параметры и ограничения поиска решения
можно сохранить в качестве модели. Для
этого служит кнопка Сохранить
модель
в окне Параметры
поиска решения.
В данном примере
следует установить флажок в строке
Линейная
модель
и вернуться в окно Поиск
решения,
нажав кнопку ОК.
После того, как
все параметры и ограничения будут
заданы, нужно только инициировать поиск.
9. Нажмем кнопку
Выполнить
в окне диалога Поиск
решения. По
мере того, как идет поиск, отдельные его
шаги будут отображаться в строке
состояния. Когда поиск закончится, в
таблицу будут внесены новые значения,
и на экране появится окно, сообщающее
о завершении операции (рис. 35).
Поскольку полученные
значения нас устраивают, установим
безымянный переключатель в положение
Сохранить
найденное решение,
тогда таблица будет обновлена. Отменить
результаты поиска можно, установив
переключатель в положение Восстановить
исходные
значения.
В случае, если
поиск закончился удачно, можно указать,
какие отчеты следует вставить в рабочую
книгу. Для этого в списке Тип
отчета
выделяется название нужного типа отчета
(или несколько названий с помощью клавиши
Ctrl). Оно будет вставлено на отдельном
листе в рабочую книгу перед листом с
исходными данными.
Когда
решение найти невозможно, Ехсе1 выводит
соответствующее сообщение в окне диалога
Результаты
поиска решения.
В этом случае возможность создать отчет
отсутствует, так как список Тип
отчета
становится недоступным.
Рисунок 35.
Результаты решения
Если планируется
использовать созданную модель в
дальнейшем, найденное решение можно
сохранить как сценарий, нажав кнопку
Сохранить
сценарий в
окне диалога Результаты
поиска решения.
Итак, нами получено
следующее решение задачи: х1
= 4; х2
= 2; Fmax
= 14. Таким образом, следует реализовывать
по 4 единицы товара А
и 2 — товара В.
При этом общая прибыль будет наибольшей
и составит 14 усл. ед. Левые части
ограничений представляют собой количество
ресурсов, которые будут израсходованы
при данном плане реализации товаров, а
правые части — количество имеющихся в
наличии ресурсов. Поэтому можно сделать
вывод о том, какие ресурсы будут
израсходованы полностью (левая часть
равна правой), а каких ресурсов имеется
остаток. Очевидно, что в данной задаче
имеется остаток только 4-го ресурса,
составляющий 12 – 8 = 4 усл. ед.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Найденные решения (значения изменяемых ячеек) можно сохранить в качестве сценария. Для этого нужно:
- В диалоговом окне Результаты поиска решения выбрать Сохранить сценарий.
- В поле Название сценария ввести имя сценария. Просмотреть сценарии можно с помощью команды Данные > Работа с данными > Анализ что-если > Диспетчер сценариев > Сценарии.
С помощью программы Поиск решения можно создать три типа отчетов по результатам, полученным при успешном завершении процедуры решения.
Каждый отчет создается на отдельном листе текущей рабочей книги.
Для создания отчета надо в диалоговом окне Результаты поиска решения выбрать нужный тип отчета в поле Тип отчета. Можно выбрать сразу несколько типов (при выделении нескольких строк используется клавиша ).
- Результаты – отчет содержит целевую ячейку, список изменяемых ячеек, их исходные и конечные значения, ограничения и сведения о них.
- Устойчивость – отчет содержит сведения о степени зависимости модели от изменений величин, входящих в формулы, применяемые в задаче (формулы модели и формулы ограничений).
- Пределы – выводится целевая ячейка и ее значение, а также список изменяемых ячеек, их значений, нижних и верхних пределов и целевых результатов.
Рассмотрим применение процессора Excel для решения ЗЛП на примерах.
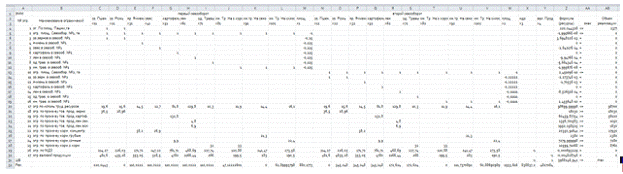
Задача 1. Планирование производства
Модель линейного программирования дает возможность определить наиболее выгодную производственную программу выпуска нескольких видов продукции при заданных ограничениях на ресурсы.
МП выпускает товары х1,х2,х3,х4, получая от реализации каждого прибыль в 60,70,120,130 руб. соответственно. Затраты на производство приведены в таблице.
| Затраты | х1 | х2 | x3 | х4 | Всего |
|---|---|---|---|---|---|
| Трудовые | 1 | 1 | 1 | 1 | 16 |
| Сырьевые | 6 | 5 | 4 | 1 | 110 |
| Финансы | 4 | 6 | 10 | 13 | 100 |
- Максимум прибыли в зависимости от оптимального распределения затрат.
- Минимум ресурсов, необходимых для получения максимальной прибыли.
Решение задачи средствами Excel состоит из 4 этапов:
- Создание математической модели задачи ЛП.
- Создание формы для ввода условий задачи, ввод в неё исходных данных и зависимостей из математической модели.
- Ввод данных из формы в окно Excel Поиск решения из меню Данные.
- Задание параметров поиска и решение задачи.
Создание математической модели задачи
Составим математическую модель процесса по описанию задачи:
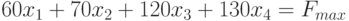
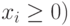
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее первого рабочего листа на Задача о производстве.
Создание формы
- Составление формы в виде:
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | Переменная | х7 | х2 | x3 | х4 | Формула | Знак | Св.член |
| 2 | Значение | |||||||
| 3 | Коэф. ЦФ | 60 | 70 | 120 | 130 | =СУММПРОИЗВ(В$2:Е$2;В3:Е3) | Max | |
| 4 | Трудовые | 1 | 1 | 1 | 1 | =СУММПРОИЗВ(В$2:Е$2;В4:Е4) |  |
16 |
| 5 | Сырьевые | 6 | 5 | 4 | 1 | =СУММПРОИЗВ(В$2:Е$2;В5:Е5) |  |
110 |
| 6 | Финансы | 4 | 6 | 10 | 13 | =СУММПРОИЗВ(В$2:Е$2;В6:Е6) |  |
100 |
- Запись в ячейки В3:Е3 коэффициентов целевой функции F (1), в В4:Е6 коэффициентов из системы ограничений (2) и в ячейки Н4:Н6 – свободных членов из системы (2).
- Ввод формул с помощью fx – Мастера функций.
Для ввода формулы в целевую ячейку (целевой функции): щелкнуть левой клавишей мыши по ячейке F3 , затем по значку Мастера функций fx на панели инструментов, в появившемся окне «Мастер функций, Шаг 1» выбрать категорию «Математические», далее выбрать функцию СУММПРОИЗВ, нажать клавишу ОК, в окне «Мастер функций Шаг 2» в поле Массив 1 ввести с клавиатуры В2:Е2 (ячейки, в которых будут варьироваться х1..х4), в поле Массив 2 ввести В3:Е3 (коэффициенты целевой функции ЦФ).
Примечание. Можно вводить В2:Е2 не с клавиатуры, а поставить курсор в окно Массив 1, а затем протащить курсор при нажатой левой клавише мыши по ячейкам В2:Е2, имена ячеек сами запишутся в окно. Аналогично поступить с полем Массив 2.
Нажать клавишу ОК, в ячейку F3 запишется формула 60х1+70х2+120х3+ 130х4 в виде СУММПРОИЗВ(В2:Е2;В3:Е3).
Чтобы не вводить формулы в другие ячейки, необходимо изменить тип адресации для ячеек В2:Е2 с относительной на абсолютную $B$2:$E$2 , установив курсор перед нужным адресом B2 и нажав функциональную клавишу F4 , затем повторить эти действия для адреса E2 . Формула примет следующий вид:
После внесенных изменений необходимо скопировать формулу в ячейки F4:F6 c помощью маркера заполнения. Для этого необходимо выделить ячейку F3 , содержащую нужную формулу, установить указатель мыши на черный квадратик в правом нижнем углу ячейки (он примет форму черного крестика) и протащить с помощью левой кнопки мыши на весь требуемый диапазон.
В результате копирования мы увидим следующие формулы:
- в ячейке F4 – СУММПРОИЗВ($В$2:$Е$2;В4:Е4),
- в ячейке F5 – СУММПРОИЗВ($В$2:$Е$2;В5:Е5),
- в ячейке F6 – СУММПРОИЗВ($В$2:$Е$2;В6:Е6).
Заполнение окна Поиск решения
Выбрать в пункте меню Данные команду Поиск решения, поставить курсор в поле целевой функции, выделить ячейку F3 в форме (или ввести F3 с клавиатуры), поставить переключатель в положение «Максимальному значению» (см. рис. 12.1 рис. 12.1). В поле «Изменяя ячейки» ввести $В$2:$Е$2(с клавиатуры или протащив мышью).
Нажать клавишу «Добавить», в окне «Добавление ограничения» в поле «Ссылка на ячейку» ввести F4 , выбрать через «стрелка вниз» знак «
Аналогично через «Добавить» ввести 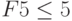
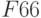
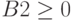
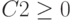
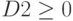
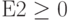
Также необходимо добавить ограничения для получения целочисленных величин по количеству товаров: B2=цел, C2=цел, D2=цел и Е2=цел.
После ввода последнего граничного условия вместо «Добавить» нажать клавишу ОК, появится окно «Поиск решения».
Для изменения или удаления ограничений и граничных условий используются клавиши Изменить, Удалить.
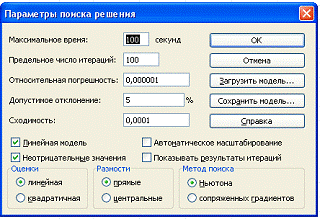
Параметры поиска
В окне «Поиск решения» нажать клавишу «Параметры», выбрать по умолчанию Максимальное время – 100 с, число итераций – 100 (для большинства задач это количество просчётов подходит с большим запасом), установить флажок в строке «Линейная модель», нажать ОК, в появившемся окне Поиск Решения нажать Выполнить (рис. 12. рис. 12.3).
Результаты поиска решения с таблицей результатов:
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | Переменная | X1 | X2 | X3 | X4 | Формула | Знак | Св.член |
| 2 | Значение | 10 | 0 | 6 | 0 | |||
| 3 | Коэф. ЦФ | 60 | 70 | 120 | 130 | 1320 | Max | |
| 4 | Трудовые | 1 | 1 | 1 | 1 | 16 |  |
16 |
| 5 | Сырьевые | 6 | 5 | 4 | 1 | 84 |  |
110 |
| 6 | Финансы | 4 | 6 | 10 | 13 | 100 |  |
100 |
Таким образом оптимальный план Х(Х1,Х2,Х3,Х4)=(10,0,6,0) при минимальном использовании ресурсов
- Трудовые – 16 (У1)
- Сырьевые – 84 (У2)
- Финансы – 100 (У3)
даёт максимум прибыли F в 1320 руб.
Вывод: Максимальная прибыль F в 1320 руб. получается при выпуске только товаров Х1 и Х3 в количестве 10 и 6 штук соответственно, товары Х3 и Х4 выпускать не нужно (это приведёт к снижению прибыли). Трудовые (У1) и финансовые (У3) ресурсы используются полностью, по сырьевым ресурсам (У2) есть запас в 110-84=26 ед.
Кроме того, это означает, что изменение трудовых ( y1 ) и финансовых ( y3 ) ресурсов приведёт к изменению прибыли F , а изменение сырьевых ресурсов ( y2 ) – нет.
Разности между плановыми ресурсами и использованными являются двойственными переменными y1, y2 и y3 сопряжённой задачи линейного программирования. В данном случае y1=y3=0 , а y2=26 ед. Таким образом, ресурс y2 можно уменьшить на 26 ед., тогда план по сырью тоже будет оптимальным.
Задача 2. Задача об оптимальной диете
Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа 

Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.
Ведем в рассмотрение следующие переменные: х – весовое количество продукта питания i-го типа в суточном рационе.
Тогда в общем случае математическая постановка задачи об оптимальной диете может быть сформулирована следующим образом:
где множество допустимых альтернатив 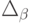
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи.
Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3).
Калорийность одной весовой единицы каждого из продуктов следующая:с1 = 2060,с2= 2430,с3= 3600,с4= 890,с5= 140,с6= 230, с7 = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы.
Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 100, в жирах b 2= 70, в углеводах b3 = 400.
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее второго рабочего листа на Задача о диете.
Таблица 1. Содержание питательных веществ в продуктах питания
| Продукты/питательные вещества | Хлеб ржаной | Мясо баранина | Сыр «Российский» | Банан | Огурцы | Помидоры | Виноград |
|---|---|---|---|---|---|---|---|
| Белки | 61 | 220 | 230 | 15 | 8 | 11 | 6 |
| Жиры | 12 | 172 | 290 | 1 | 1 | 2 | 2 |
| Углеводы | 420 | 0 | 0 | 212 | 26 | 38 | 155 |
Создание математической модели задачи
Составим математическую модель процесса по описанию задачи:

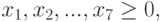
Создание формы
Для решения поставленной задачи выполним следующие подготовительные действия:
- Внесем необходимые надписи в ячейки A1:I1, A2:A7, B4, I4, J4 .
- В ячейки ВЗ:НЗ введем значения коэффициентов целевой функции: с1 = 2060, с2 = 2430, с3 = 3600, с4 = 890, с5 = 140, с6 = 230, с7 = 650.
- В ячейку I2 введем формулу: =СУММПРОИЗВ( b 2:Н2;B3:H3), которая представляет целевую функцию (4).
- В ячейки В5:Н7 введем значения коэффициентов ограничений, взятых из таблицы.
- В ячейки J5 :J7 введем значения правых частей ограничений, соответствующих минимальной суточной потребности в питательных веществах: в белках b 1=100 , жирах b 2= 70 и углеводах b3 = 400.
- В ячейку I5 введем формулу: =СУММПРОИЗВ($B$2:$H$2;В5:Н5), которая представляет левую часть первого ограничения (5).
- Скопируем формулу, введенную в ячейку I5 , в ячейки I6 и I7 .
- Внешний вид рабочего листа MS Office Excel с исходными данными для решения задачи об оптимальном рационе питания имеет следующий вид (pиc. 12.4).
Для отображения формул в ячейках рабочего листа необходимо выполнить команду меню: Формулы и на панели инструментов в группе Зависимости формул выбрать Показать формулы.
Заполнение окна Поиск решения
Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию: Данные > Поиск решения.
После появления диалогового окна Поиск решения следует выполнить следующие действия:
- В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $I$2 .
- Для группы Равной: выбрать вариант поиска решения – минимальному значению.
- В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $B$2:$H$2 .
- Добавить 3 ограничения, представляющие минимальные суточные потребности в питательных веществах. С этой целью выполнить следующие действия:
- для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить (рис. 12.5 рис. 12.5, а);
- в появившемся дополнительном окне выбрать ячейку $I$5 , которая должна отобразиться в поле с именем Ссылка на ячейку;
- в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство » «;
- в качестве значения правой части ограничения выбрать ячейку $J$5 ;
- для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;
- аналогичным образом задать оставшиеся два ограничения (рис. 12.5 рис. 12.5, б).
Параметры
В окне «Поиск решения» нажать клавишу «Параметры», выбрать «Поиск решения Линейных задач симплекс-методом», нажать ОК, затем нажать Найти Решение (рис. 12.6 рис. 12.6, б).
После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный на рис. 12. рис. 12.7.
Результатом решения задачи об оптимальной диете являются найденные оптимальные значения переменных: х1 = 0, х2 = 0,211, 3 = 0,109, х4= 1,887, х5 = 0, х6 = 0, х7 = 0, которым соответствует значение целевой функции: fопт= 2587,140. При выполнении расчетов для ячеек В2:I2 был выбран числовой формат с 3 знаками после запятой.
Анализ найденного решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы) следует использовать 211 г мяса баранины, 109 г сыра и 1887 г бананов, совсем отказавшись от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будет приближенно равна 2590 ккал, что вполне соответствует малоактивному образу жизни без серьезных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников интеллектуального труда (юристы, бухгалтера, врачи, педагоги) лежат в пределах 3000 ккал.
ЗАДАНИЕ
- Составить математическую модель задачи линейного программирования.
- Решить задачу линейного программирования в Excel с помощью Поиска решения.
- Сохранить в виде модели установочные параметры.
Предприятие легкой промышленности выпускает две модели машин, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 80 изделий, второй линии – 85 изделий. На машину первой модели расходуются 12 однотипных элементов электронных схем, на машину второй модели – 6 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одной машины первой и второй моделей равна $30 и $40 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.
Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех приборах. Время использования этих приборов для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.
Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Фирма производит два вида продукции – А и B . Объем сбыта продукции вида A составляет не менее 70% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 120 кг. Расход сырья на единицу продукции A составляет 3 кг, а на единицу продукции В – 5 кг. Цены продукции А и В равны $20 и $60 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.
Фирма выпускает женские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $6, а фасона 2 – $7. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.
Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:
Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства, максимизирующий чистую прибыль.
Завод выпускает изделия трех моделей ( I, II III ) Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 5000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:
Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.
Требуется распределить имеющиеся денежные средства по четырем альтернативным вариантам. Игра имеет три исхода. Ниже приведены размеры выигрыша (или проигрыша) на каждый доллар, вложенный в соответствующий альтернативный вариант, для любого из трех исходов. У игрока имеется $500, причем, использовать в игре их можно только один раз. Точный исход игры заранее неизвестен, и, учитывая эту неопределенность, игрок решил распределить деньги так, чтобы максимизировать максимальную отдачу от этой суммы.
Бройлерное хозяйство птицеводческой фермы насчитывает 80000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.
Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.
Смесь должна содержать:
- не менее 0.8%, но не более 1.2% кальция;
- не менее 22% белка;
- не более 5% клетчатки.
Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа 

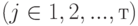
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность одной весовой единицы каждого из продуктов следующая:с1 = 2060,с2= 2430,с3= 3600,с4= 890,с5= 140,с6= 230, с7 = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме следующей таблицы (см. табл.).
Таблица 1. Содержание питательных веществ в продуктах питания
| Продукты/питательные вещества | Хлеб ржаной | Мясо баранина | Сыр «Российский» | Банан | Огурцы | Помидоры | Виноград |
|---|---|---|---|---|---|---|---|
| Белки | 66 | 225 | 235 | 20 | 13 | 16 | 11 |
| Жиры | 17 | 177 | 295 | 1 | 1 | 7 | 7 |
| Углеводы | 425 | 0 | 0 | 217 | 31 | 43 | 200 |
Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 105, в жирах b 2 = 75, в углеводах b 3 = 405.
Определить суточную потребности в питательных веществах (белки, жиры, углеводы) и общую калорийность оптимальной диеты.
Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуются 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.
Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.
Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Фирма производит два вида продукции – A и B . Объем сбыта продукции вида A составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции A составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны $20 и $40 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.
Фирма выпускает ковбойские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $8, а фасона 2 – $5. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.
Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:
Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства максимизирующий чистую прибыль.
Завод выпускает изделия трех моделей ( I, II III ). Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 4000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:
Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.
Некоторое производственное предприятие выпускает три вида клея. Для производства клея используется 4 типа химических веществ: крахмал, желатин, квасцы и мел. Расход этих веществ в кг для получения 1 кг каждого вида клея и их запас на складе предприятия представлены в таблице.
Таблица 1. Расход химических веществ на изготовления клея, их запас на складе
| Вид клея /Химические вещества | Клей № 1 | Клей № 2 | Клей № 3 | Запас на складе |
|---|---|---|---|---|
| Крахмал | 0,4 | 0,3 | 0,2 | 20 |
| Желатин | 0,2 | 0,3 | 0,4 | 35 |
| Квасцы | 0,05 | 0,07 | 0,1 | 7 |
| Мел | 0,01 | 0,05 | 0,15 | 10 |
Стоимость каждого вида клея для оптовых покупателей следующая:с1 = 380 руб/кг,с2 =430 руб/кг,с3 = 460 руб/кг. Требуется определить оптимальный объем выпуска клея каждого вида, обеспечивающий максимум общей стоимости готовой продукции.
Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.
Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.
Смесь должна содержать:
- не менее 0.8%, но не более 1.2% кальция;
- не менее 22% белка;
- не более 5% клетчатки.
Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Имеется конечное число видов продуктов питания: ананас, арбуз, грейпфрут, язык говяжий, сардельки говяжьи, хлеб «Бородинский», картофель ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность 1 кг каждого из продуктов следующая:с1 = 470,с2= 380,с3 = 350,с4 = 1460,с5 = 2150,с6 = 2070, с7 = 800. Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 100, в жирах b 2 = 70, в углеводах b3 = 400. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы (табл.).
Требуется определить такой рацион питания, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.
Поиск решения задач в Excel с примерами
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
источники:
http://intuit.ru/studies/courses/3659/901/lecture/32717
http://exceltable.com/vozmojnosti-excel/poisk-resheniya-v-excel