Экономическая моделирование в excel - Word и Excel - помощь в работе с программами

Любой бизнес-план нуждается в финансовых расчетах. А наиболее удобный инструмент для этого – табличный процессор Excel. Популярность программы объясняется простотой использования и многофункциональностью. Рассмотрим возможности редактора, которые будут полезны при составлении бизнес-модели.
Основы построение финансовой модели в Excel

Модель можно поместить на один лист или на разные листы. В любом случае, порядок расчетных таблиц должен соответствовать логике описания проекта:
таблицы для расчета инвестиций;
доходная и затратная часть;
финансирование;
итоговые отчетные формы, показатели.
Инвестиционный план

Основные элементы:
строительство и/или покупка зданий;
покупка оборудования;
расходы будущих периодов;
инвестиции в ЧОК (чистый оборотный капитал).
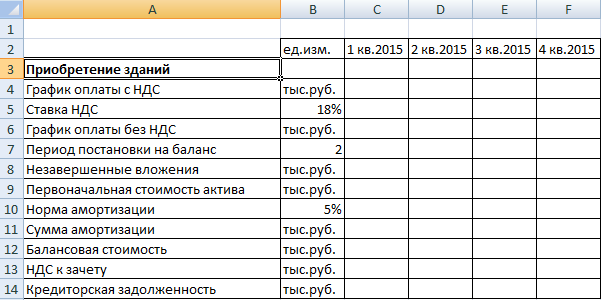
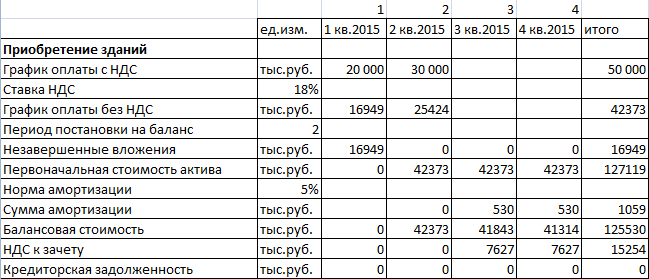
Исходные данные для расчета затрат на покупку или строительство зданий:
Расчеты:
График оплаты без НДС = Затраты с НДС / (1 + ставка НДС). Формула в Excel для ячейки С6: =C4/(1+$B$5).
Незавершенные вложения – сумма вложений в активы без учета НДС до периода их постановки на баланс. Формула в Excel для ячейки С8: =ЕСЛИ(C1<$B$7;СУММ($C6:C6);0).
Сумма амортизации начисляется со следующего периода. Формула в Excel для ячейки D11: =ЕСЛИ(D1>$B$7;ЕСЛИ(C12>0;ЕСЛИ(D9*$B$10/4>C12;C12;D9*$B$10/4);0);0).
Балансовая стоимость актива – разница между начальной стоимостью и амортизационными отчислениями за весь период существования актива. Формула в Excel для ячейки D12: =D9-СУММ($C11:D11).
Формула для расчета первоначальной стоимости актива — =ЕСЛИ(C1>=$B$7;$G$6;0).
НДС к зачету (в период постановки актива на баланс) – общая величина налога. Формула для ячейки С13: =ЕСЛИ(C1>$B$7;$G4-$G6;0).
Формула для расчета кредиторской задолженности: =ЕСЛИ(C1>=$B$7;$G6-СУММ($C6:C6);0).
Затраты на приобретение оборудования и элементы расходов будущих периодов в инвестиционном плане составляются аналогично. Особенности затрат будущих периодов:
оприходуются на баланс в составе текущих активов;
не облагаются налогом на имущество (в отличие от оборудования);
амортизируются быстрее, в течение 1-2 лет.
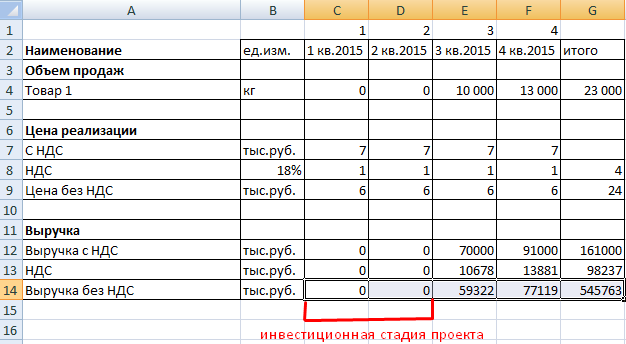
Прогнозирование доходов

Чтобы построить план продаж, нужно определить объем в натуральном выражении (для каждого вида продукции) и цену реализации (каждого вида продукции). Выручка определяется по каждому виду товара (работ и услуг) как произведение объема и цены.
В Excel составляются таблицы для каждого периода планирования и для каждого вида продукции с планируемым объемом выпуска (в натуральных единицах).
Из цены реализации нужно вычленять сумму налога на добавленную стоимость. Эти деньги не входят в состав выручки – они перечисляются в бюджет.
Формулы:
Цена без НДС = цена с НДС / (1 + налоговая ставка).
Величина НДС = (цена с НДС * налоговая ставка) / (1 + налоговая ставка).
Расчетная таблица может выглядеть следующим образом:
Формула для расчета цен без НДС: =C7/(1+$B$8).
Расчет налога на добавленную стоимость: =C7-C9.
Выручка с налогами: =C4*C7.
План текущих расходов

Элементы затрат:
сырье и материалы;
оплата труда;
начисления на зарплату;
амортизация;
прочие расходы.
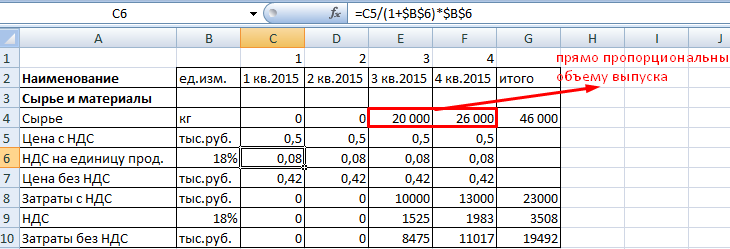
При учете затрат на материалы выделяем налог добавленной стоимости. Это необходимо для учета подлежащих возврату сумм (задолженность перед бюджетом уменьшится).
Затраты на сырье и материалы увеличиваются прямо пропорционально объему выпуска. Если, к примеру, на пошив одной сорочки требуется полтора метра ткани, то на две единицы продукции – 3 метра и т.д. Расход считается по формуле:
Количество материалов = удельный вес * объем производства.
Пример таблицы учета текущих затрат на сырье и материалы:
Формула для расчета налога на добавленную стоимость – в строке формул.
Формула вычисления цены без НДС: =C5/(1+$B$6).
Расчет затрат с НДС: =C4*C5.
Налог на ДС: =C4*C6.
Затраты без НДС: =C4*C7.
Прочие расходы:
аренда,
реклама,
оплата связи;
ремонт и т.д.
При составлении финансовой модели предприятия в Excel учитывается каждая статья расходов.
Финансовая модель предприятия в Excel

Когда спланированы продажи и затраты, можно приступать к формированию баланса, плана доходов и расходов, движения денежных средств. Чтобы модель пересчитывала значения в автоматическом режиме, данные в сводных отчетах рассчитываются с помощью формул или напрямую извлекаются из операционных планов (с помощью ссылок).
План доходов и расходов финансовой модели:
Доходы и расходы расписаны по статьям. Если планируется выпуск десятков наименований продукции, то лучше определить их в группы. Чтобы не перегружать отчет. В сводную таблицу добавлены аналитические показатели: рентабельность и прибыль с нарастающим итогом. Когда нужно больше аналитики, формируют отдельные таблицы.
План движения денежных средств:
Скачать пример финансовой модели предприятия в Excel
По теме: Финансовая модель в Excel при покупке бизнеса.
Предполагается, что предприятие не будет привлекать заемные средства. Поэтому раздел «Финансовая деятельность» отсутствует.
Источник
Хотите просчитать плановые значения выручки, прибыли и денежных потоков? На помощь придет финансовое моделирование в Excel. В статье рассказываем о базовых принципах построения модели и делимся готовым решением. На выходе вы получите прогнозную отчетность. Усильте с ее помощью контроль над процессами в организации.
Финансовая модель бизнеса: что это

Финансовая модель предприятия – это плановые показатели его деятельности по:
доходам;
расходам;
прибыли;
денежным потокам;
активам;
обязательствам.
Этим она похожа на систему бюджетов. Отличается от них бóльшими упрощениями и вариативными параметрами. Последнее объясняется целью создания: быстрая оценка изменений финансовых результатов и имущественного положения под влиянием разных факторов. Например, в результате смены условий расчетов с контрагентами, покупки нового оборудования, повышения зарплаты персоналу и т.п.
Обычно финансовая модель строится в Excel или Google-таблицах. Часть исходных данных вносится вручную (план по объему продаж, месячный фонд оплаты труда, нормы потребления материалов на единицу изделия и т.д.). Зависимые от них показатели задаются с помощью формул. Они обеспечивают моментальный пересчет итоговых значений выручки, операционной прибыли, дебиторки, денежных притоков и т.д.
Итоговый результат финансового моделирования – три формы отчетности:
баланс;
отчет о финансовых результатах (ОФР);
отчет о движении денежных средств (ОДДС).
Скачайте финансовую модель в Excel, о создании которой рассказываем в статье. Файл – Простая финансовая модель для торговли в Excel (Fail-Fin-model-v-Excel)
Финансовое моделирование проекта: что надо знать

Если вы решили самостоятельно построить финансовую модель в Excel, то идите от простого к сложному и от общих моментов к деталям. Так проще не запутаться в большом количестве формул и ссылок.
Вот пошаговый план реализации.
Рисунок 1. Построение финансовой модели: рекомендуемые этапы
Опробуем данный подход на практике. Рассмотрим пример для организации, которая занимается розничной торговлей. Такой выбор не случайный. Любое производство сложнее торговли, так как в нем предполагаются:
материальные затраты;
амортизация оборудования;
возможно, незавершенный производственный процесс на конец месяца, поэтому необходимость разделения затрат и расходов;
разнородные складские запасы в виде материалов и продукции.
Кроме того, продажи в розницу исключают вариант формирования дебиторской задолженности покупателей, если исходить из того, что отсрочки и рассрочки не предоставляются.
Финансовая модель (ФМ) в Excel: считаем доходы

Отправная точка на данном этапе – объем продаж. Можно пойти простым путем и внести только денежное значение выручки. Позже детализировать его как произведение цены и количества в разрезе номенклатурных позиций.
Мы сразу поступим вторым способом. Это даст количественный параметр, который необходим для корректного подсчета расходов на приобретение товаров.
Основная сложность этапа: откуда взять данные по плану продаж? Все зависит от вашей цели:
если она пока в том, чтобы построить и «обкатать» работоспособность ФМ, то берите любые данные. Например, за прошлый год или произвольные;
если вам одновременно нужны и модель, и качественные результаты расчета по ней, то займитесь планированием отдельно.
Мы ратуем за то, чтобы на данном этапе не уходить в детали. Но разумно уже сейчас подумать: чем будете усложнять и этим приближаться к реальности?
Вот два совета.
Первый. Покажите отдельно НДС, который «сидит» в цене реализации. Он приходит в поступлениях от покупателей, но это не доход вашей организации. Добавив его в таблицу, вы посчитаете выручку-нетто или чистый доход. Заодно определите будущие платежи в бюджет по данному налогу*.
____________________
Примечание: в бюджет платится разница между НДС, который начислен к уплате, и тем, который предъявляется к возмещению по собственным закупкам.
____________________
Второй. Введите аналитику по продажам. Самое простое – это номенклатурные позиции. Дополнительно к ним:
процент возврата товаров;
категория клиента (физическое лицо или организация);
номер магазина или наименование региона, если есть несколько точек продаж.
Помним: пока излишняя детализация лишь запутает. Поэтому получаем в Excel простой план по доходам.
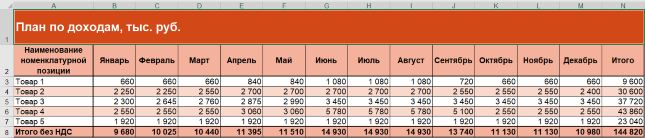
Рисунок 2. Упрощенный план по доходам в Excel
Построение финансовых моделей: пример планирования расходов

Определимся с расходами также пока в первом приближении. Обобщим полный перечень трат компании в разрезе элементов. Это будут:
материальные траты. В упрощенном варианте предположим, что к ним относятся только траты на покупку товара без НДС и что организация продает в течение месяца столько, сколько закупает. Значит, величину определим как произведение цены приобретения и объема продаж;
зарплата работников. Ограничимся единой суммой фонда оплаты труда за месяц без разбивки по составляющим;
социальные отчисления. Для них составим формульную зависимость. Обычно это 30% плюс процент взносов «на травматизм» в Фонд социального страхования от начисленной оплаты труда. Данный процент зависит от класса профессионального риска по организации. Мы взяли минимальное значение 0,2%;
амортизация. Вводим строку в ФМ, если в собственности предприятия есть основные средства и нематериальные активы. Указываем единую сумму для каждого месяца на основе средних фактических или предполагаемых значений;
прочие расходы. Это отчасти уход в детализацию. Однако если в компании есть постоянные легко планируемые траты, то зафиксируйте их. К ним относятся: арендные платежи, траты на рекламу, на командировки и т.п.
Для упрощенной ФМ такого списка достаточно. А это четыре совета на будущее о том, чем усложнить.
Первый. Введите дополнительные позиции в материальные расходы. Например, такие:
отопление, водоснабжение, электроэнергия;
упаковка;
ГСМ на автотранспорт, если он есть на балансе;
канцелярские принадлежности и т.п.
Второй. Отдельной строкой покажите входной НДС. Когда ставка – одна (20%), то его сумма – это произведение 20% на совокупные материальные траты без НДС. Когда примешивается еще 10%, тогда:
либо упрощайте и считайте налог по максимальной ставке;
либо усложняйте, применяя средневзвешенное значение ставки исходя из доли в закупках с НДС по 20% и 10% в прошлые периоды.
Третий. Разделите оплату труда на составляющие:
выделите в зарплате продавцов оклад (постоянную часть) и премию, зависящую от объема продаж (переменную компоненту);
покажите отдельной строкой зарплату других работников, которая не завязана на количественные показатели и является постоянной.
Четвертый. Учтите изменения амортизации, если в планах организации значатся покупка или продажа основных средств и нематериальных активов.
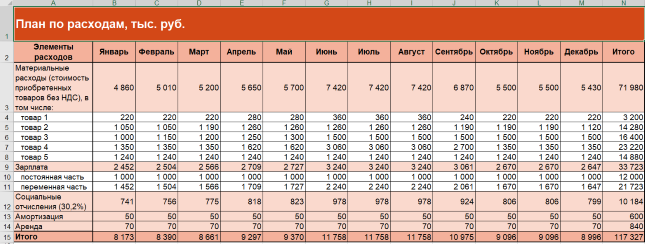
Рисунок 3. Финансовая модель бизнеса в Excel: план по расходам
То, что мы посчитали, является основой для:
вычисления прибыли/убытка в ОФР;
корректировки накопленного финансового результата в балансе;
построения притоков и оттоков в ОДДС.
Перейдем ко второму этапу – обобщению данных в системе финансовых отчетов. Рассмотрим, как это делается.
Составляем плановый отчет о финансовых результатах

Формирование фактической отчетности начинается с подсчета прибыли/убытка за период. Такое же правило действует для моделей и бюджетов. Ведь чтобы заполнить раздел баланса про собственный капитал, нужна величина финансового результата.
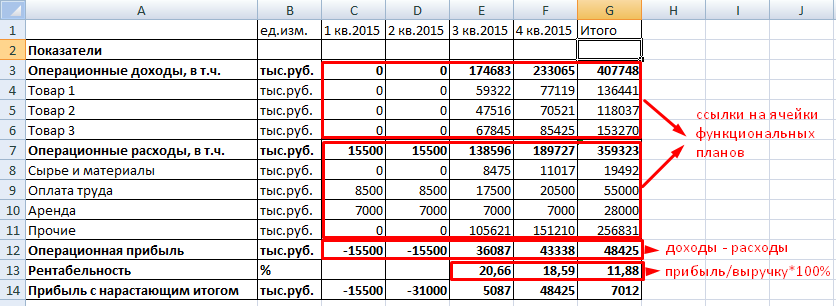
Мы подсчитали плановые доходы и расходы по операционной деятельности. Этого достаточно, чтобы составить упрощенный отчет. Вот его возможный вариант.
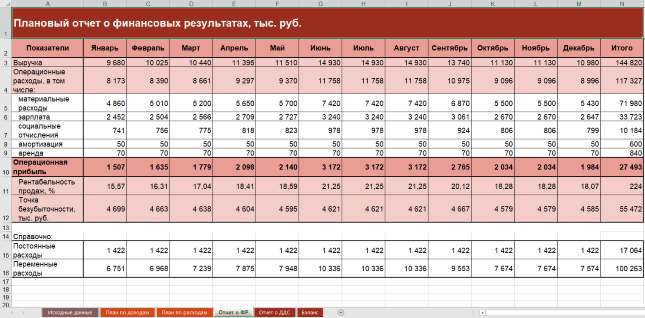
Рисунок 4. Упрощенный ОФР в Excel-модели
В нем разница между доходами и расходами показывает прибыль или убыток. Мы рассматриваем только основную деятельность без прочей. Поэтому выходим на операционный финансовый результат.
ОФР тесно связан с балансом и ОДДС. Смотрите в таблице, куда и какую информацию он передает.
Таблица 1. Взаимосвязь плановых ОФР, баланса и ОДДС
Строка ОФР	Связанная строка баланса	Связанная строка ОДДС
Операционная прибыль (убыток)	Нераспределенная прибыль (убыток) – добавляется к значениям предыдущего периода	–
Выручка (операционные доходы)	–	Поступления от покупателей и заказчиков – сумма выручки корректируется на авансы полученные и дебиторскую задолженность по формуле: Поступления = Выручка + Авансы полученные – Дебиторская задолженность*
Операционные расходы	–	Платежи по текущей деятельности – сумма денежных** расходов корректируется на авансы выданные и кредиторскую задолженность по формуле: Платежи = Денежные расходы + Авансы выданные – Кредиторская задолженность
Примечание: * в примере ФМ формируется по организации розничной торговли. Поэтому полагаем: авансов и дебиторки от покупателей нет. Значит, поступления равняются выручке; ** денежные расходы – те, которые приводят к оттоку денег (зарплата, налоги, материальные). Для сравнения: к неденежным относится амортизация
Чтобы плановый ОФР оказался более информативным, дополним строками:
рентабельность продаж. Это расчетный показатель, который равняется отношению прибыли (в данном случае – операционной) к выручке;
точка безубыточности в денежном выражении. Для ее расчета предварительно разделили расходы на постоянные и переменные. Об особенностях классификации затрат по такому принципу читайте в статье «Расчет себестоимости».
Формируем плановый отчет о движении денежных средств

Здесь задача:
обобщить денежные притоки и оттоки;
рассчитать чистый денежный поток как разницу между ними;
прибавить его значение к остатку денег на начало периода и вычислить остаток денег на конец. Через эту сумму ОДДС связан с балансом.
Для создаваемой ФМ исходим из допущений:
организация занимается только основной деятельностью. При этом не покупает оборудование и ценные бумаги, не берет и не дает взаймы, не принимает новых учредителей. Значит, формируется один вид денежных операций – текущий. О двух других – инвестиционных и финансовых – читайте в статье «Анализ движения денежных средств компании»;
товары оплачиваются поставщику двумя платежами: 60% – аванс в месяце, который предшествует поставке, 40% – окончательный расчет сразу после принятия на склад;
зарплата выплачивается двумя переводами: 50% – аванс в месяце начисления, 50% – перевод остатка в периоде, который следует за отработанным;
страховые взносы перечисляются в месяце, идущем за их начислением;
прочая составляющая расходов по обычным видам деятельности представлена арендой. Платежи по ней производятся в месяце начисления арендной платы.
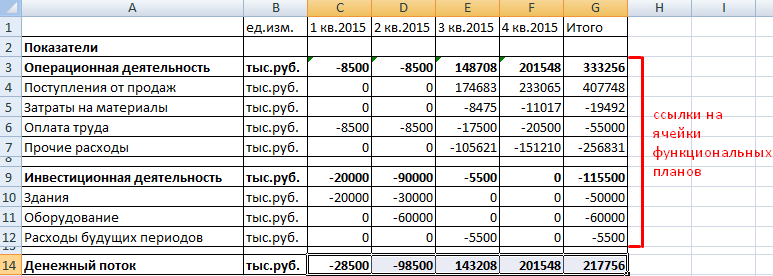
Получаем вариант ОДДС.
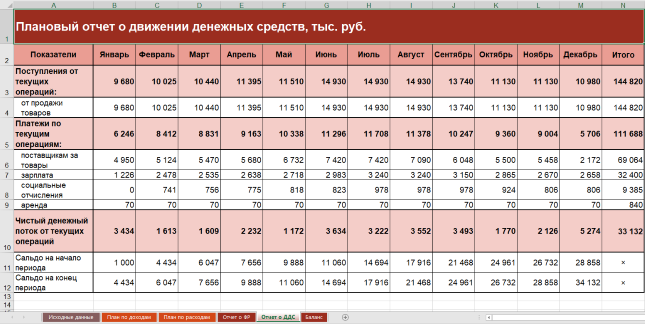
Рисунок 5. Упрощенный отчет о движении денежных средств в ФМ
Сводим плановый баланс

Предположим, что у организации:
нет входящих остатков по запасам, дебиторской и кредиторской задолженности;
имущество включает одно основное средство и деньги;
в пассиве – только уставный капитал и нераспределенная прибыль.
Схема заполнения балансовых строк окажется следующей.
Таблица 2. Техника сведения упрощенного баланса
Показатель на начало месяца	Расчетная формула	Пояснения
Основные средства	Основные средства на начало предыдущего месяца (баланс) – Амортизация за месяц (ОФР)	–
Запасы	–	Неизменны и равняются нулю из-за допущения: закупаемые товары полностью распродаются в течение месяца
Дебиторская задолженность	Дебиторская задолженность на начало предыдущего месяца (баланс) + Платежи поставщикам за товары (ОДДС) – Материальные расходы (ОФР)	В примере нет дебиторки покупателей, так как организация торгует в розницу
Денежные средства	Денежные средства на начало предыдущего месяца (баланс) + Чистый денежный поток за месяц (ОДДС)	–
Уставный капитал	–	Неизменен и равняется 1000 тыс. руб. из-за допущения: новых учредителей в течение года не было
Нераспределенная прибыль	Нераспределенная прибыль на начало предыдущего месяца (баланс) + Прибыль за месяц (ОФР)	–
Кредиторская задолженность	Кредиторская задолженность на начало предыдущего месяца + Начисления по зарплате, социальным отчислениям и аренде (ОФР) – Платежи по зарплате, социальным отчислениям и аренде (ОДДС)	–
Формат баланса будет таким.
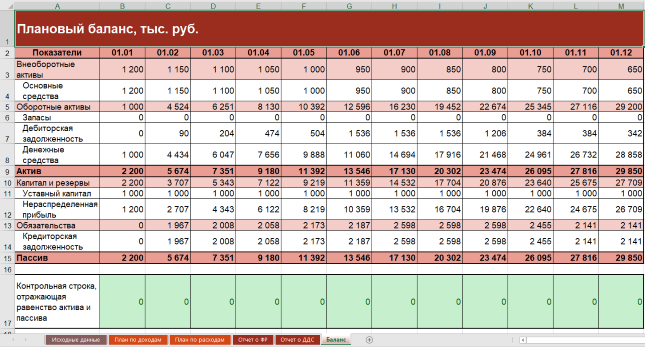
Рисунок 6. Упрощенный баланс в финансовой модели в Excel
Детализация финансовой модели в Excel
О возможных вариантах усложнения исходных данных рассказывали выше. Здесь остановимся на детализации строк плановой отчетности. Вот несколько советов:
используйте разные группировки расходов в ОФР. Мы обобщили их по элементам. Такой подход называется «по характеру расходов». Но он – не единственный. Можно одновременно с ним или вместо него использовать функциональную классификацию с выделением себестоимости продаж, а также расходов на сбыт и управление. Подробнее про такие варианты читайте в статье «БДР: бюджет доходов и расходов»;
добавьте другие виды прибыли в ОФР. Например, валовую. Она покажет разницу между продажной и закупочной ценами товаров. Если в организации есть прочие операции, то в отчете не обойтись без чистой прибыли. Читайте о видах финансового результата в материале «Анализ финансовых результатов деятельности компании»;
включите в ОФР строки для прочих доходов и расходов. Растущая организация не сможет обходиться без них. Например, взятие кредита приведет к появлению процентных платежей по нему. Они – это прочий расход;
расширьте ОДДС за счет инвестиционных и финансовых операций, если собираетесь приобретать оборудование и брать взаймы. Не смешивайте такие денежные потоки с текущими;
детализируйте сложносоставные строки в балансе. Например, из запасов выделите товары, материалы, готовую продукцию и незавершенное производство (последние два пункта – неактуальны для торговли). Из состава дебиторки: авансы выданные поставщикам и долги покупателей. По аналогии поступите с кредиторкой и покажите в отдельных статьях: авансы полученные, задолженность перед поставщиками, перед персоналом по оплате труда, по налогам и страховым взносам, перед учредителями по дивидендам.
Не забудьте скачать Excel-файл с полученной финансовой моделью из начала статьи.
Финансовое моделирование в Excel помогает понять:
как планируемые руководством мероприятия отразятся на величине имущества, капитала, обязательств, доходов, расходов и прибыли;
какие факторы больше других влияют на прибыль, ликвидность и финансовую устойчивость организации.
Важна роль ФМ и в план-фактном анализе. В течение отчетного периода сравнивайте ожидания из нее с тем, как получилось в реальности. Это хороший способ контролировать ситуацию: понимать суть нарождающихся тенденций и того, к чему они приведут бизнес.
Источник
                    ЭКОНОМИЧЕСКОЕ МОДЕЛИРОВАНИЕ
В MICROSOFT® EXCEL
ШЕСТОЕ ИЗДАНИЕ
ПРИЛАГАЕТСЯ
ДЖ. МУР • Л. УЗДЕРФОРД
г. эппен • Ф. ГУЛД • ч. ШМИДТ
КОМПАКТ-ДИСК
www.prenhall.com/more • www.williamspublishing.com
DECISION MODELING
WITH MICROSOFT® EXCEL
Jeffrey H. Moore
Stanford University
Larry R. Weatherford
University of Wyoming
Prentice
Hall
PRENTICE HALL
Upper Saddle River, New Jersey 07458
ЭКОНОМИЧЕСКОЕ МОДЕЛИРОВАНИЕ
В MICROSOFT® EXCEL
Джеффри X. Мур
Стэнфордский университет
Ларри Р. Уэдерфорд
Университет Вайоминга
Издательский дом “Вильямс"
Москва ♦ Санкт-Петербург • Киев
2004
ББК32 973 26-018 2 75
М91
УДК 681 3 07
Издательский дом “Вильямс”
Зав редакцией С.Н. Тригуб
Перевод с английского Р Г. Имамутдиновой, канд фнз -мат наук А А Минько,
Н.А. Ореховой
Под редакцией канд физ -мат наук А А Минько
По общим вопросам обращайтесь в Издательский дом “Вильямс” по адресу
infb@williamspublishing com, http //www williamspubhshing com
Мур, Джеффри, Уэдерфорд, Ларри P , и др.
М91 Экономическое моделирование в Microsoft Excel, 6-е изд. : Пер с англ — М
Издательский дом “Вильямс”, 2004. — 1024 с .ил. — Парад тит англ
ISBN 5-8459-0578-8 (рус )
Эта книга посвящена основным принципам моделирования, которые можно приме-
нить к широкому спектру различных управленческих задач, решаемых с помощью
Microsoft Excel В ней подробно рассматривается определенные классы моделей, ис-
пользуемые в самых разнообразных ситуациях. Цель книги — не составить сборник го-
товых “рецептов” моделей, а научить читателя самостоятельно готовить “здоровую пи-
щу” на основе нескольких типов моделей, приведенных в качестве примеров Она по-
может современным менеджерам в их карьерном росте, покажет реальные жизненные
ситуации, которые можно смоделировать с помощью электронных таблиц, и представит
методы построения и анализа моделей
Книга предназначена для широкого круга студентов, аспирантов и работающих спе-
циалистов
ББК 32.973.26-018.2.75
Все названия программных продуктов являются зарегистрированными торговыми марками соответст
вуюших фирм
Authorized translation from the English language edition published by Prentice Hall, Inc , Copyright © 2001
from the Publisher
Russian language edition published by Williams Publishing House according to the Agreement with R&l
Enterprises International, Copynght © 2004
ISBN 5-8459 0578 8 (pyc )
1SBN 0 13-017789 X (анп)
©Издательский дом Вильямс", 2004
©Prentice Hall, Inc , 2001
Оглавление
Предисловие	25
Часть I. Модели и моделирование	31
Глава 1. Введение в моделирование	33
Глава 2. Моделирование с помощью электронных таблиц 67
Часть II. Оптимизационные модели	119
Глава 3. Линейная оптимизация	121
Глава 4. Линейная оптимизация. Анализ чувствительности 201
Глава 5. Линейная оптимизация. Применение	297
Глава 6. Целочисленная оптимизация	381
Глава 7. Нелинейная оптимизация	435
Глава 8. Многоцелевые модели и эвристические методы 519
Часть III. Вероятностные модели	577
Глава 9. Анализ решений	579
Глава 10. Имитационное моделирование	659
Глава 11. Моделирование дискретных событий	741
Глава 12. Прогнозирование	793
Глава 13. Модели очередей	853
Часть IV. Реализация	893
Глава 14. Реализация моделей	895
Приложение А. Основные понятия теории вероятностей 923
Приложение Б. Средства моделирования Excel	933
Приложение В. Надстройка Поиск решения	973
Приложение Г. Ответы к задачам с нечетными номерами 987
Предметный указатель	1012
Содержание
Предисловие	25
Часть I. Модели и моделирование	31
Глава 1. Введение в моделирование	зз
I.]. Введение	35
1.2.	Процесс моделирования	36
Использование моделей на разных уровнях управления	38
Модели и менеджеры	39
1.3.	Немного философии	40
Реализм	40
Интуиция	40
1.4.	Типы моделей	43
Символические (количественные) модели	44
Модели принятия решений	45
Цели	45
1.5.	Построение моделей	46
Изучение среды	47
Формализация	47
Построение модели	50
1.6.	М оделирование на основе данных	50
1.7.	Детерминированные и вероятностные модели	52
Детерминированные модели	52
Вероятностные модели	53
1.8.	Последовательная разработка модели	54
1.9.	Моделирование и принятие решений в реальном мире	56
Проверка достоверности модели	57
1.10.	Подведение итогов	57
1.11.	Заключение	59
Основные термины	59
Контр	ольные вопросы	60
Вопро	сы для обсуждения	63
Л итература	66
Содержание
7
Глава 2. Моделирование с помощью
электронных таблиц	67
2.1.	Введение	69
2.2.	Пример 1 — Simon Pie	69
Этап 1. Изучение среды и структурирование ситуации	69
Этап 2 Формализация модели	70
Этап 3. Построение модели	72
Анализ “Что-если”	73
Уточнение модели	74
2.3.	Пример 2 — Simon Pie, продолжение	77
2.4.	Пример 3 — Simon Pie, окончание	84
2.5.	Пример 4 — XerTech Copy, Inc.	93
2.6.	Искусство моделирования	99
2.7.	Пример 5 — Oak Products	101
Оптимизационные модели	105
2.8.	Ограничения и условная оптимизация	106
2.9.	Заключение	107
Основные термины	108
Контрольные вопросы	108
Задачи	110
Kayo Computer	ИЗ
Компания Watson Truck Rental Company	114
Индивидуальный финансовый план	115
Компания Santa Rosa Raisins	117
Компания Ebel Mining (часть 1)	118
Литература	118
Часть II. Оптимизационные модели	119
Глава 3. Линейная оптимизация	121
3.1.	Введение в линейное программирование	123
3.2.	Формализация моделей линейного программирования	124
Ограничения	124
Целевая функция	124
Данные для модели	125
Определение ограничений	126
Оценивание решений	128
Исследование модели компании Oak Product	129
3.3.	Искусство создания моделей Л П	131
8
Содержание
3.4.	Невозвратные и переменные издержки	132
3.5.	Табличная модель компании Oak Product	133
3.6.	Модель Л П и ее представление в электронных таблицах	137
3.7.	Надстройка Поиск решения	139
Использование надстройки Поиск решения	139
Терминология средства Поиск решения	141
3.8.	Оптимизация модели Oak Product	142
3.9.	Рекомендации по поиску решения задач ЛП	151
3.10.	Пример транспортной модели	155
3.11.	Задача составления смесей	158
3.12.	Создание моделей Л П	161
3.13.	Пример 1. Задача об ассортименте продукции	161
3.14.	Пример 2. Задача составления смеси	162
3.15.	Пример 3. Составление расписания	162
3.16.	Пример 4. Анализ безубыточности при наличии ограничений 164
3.17.	Разработка моделей ЛП	165
3.18.	Заключение	167
3.19.	Решения примеров	168
Задача о составлении смесей	168
Пример 1. Задача об ассортименте продукции	169
Пример 2. Задача на составление смеси	170
Пример 3. Составление расписания	171
Пример 4. Анализ безубыточности	172
Основные термины	173
Контрольные вопросы	175
Учебные задачи	178
Прикладные задачи	179
Компания Ebel Mining (часть 1, продолжение)	191
Компания Red Brand Canners	191
Обмен валют в компании HiTech	195
Литература	200
Глава 4. Линейная оптимизация.
Анализ чувствительности	201
4.1.	Введение	203
4.2.	Графический метод решения задачи Oak Products	204
Графическое представление модели Oak Products	204
4.3.	Крайние точки и оптимальные решения	209
Содержание
9
4.4.	Графическое решение задачи минимизации	211
4.5.	Неограниченные и недопустимые модели	212
Неограниченные модели	212
Недопустимые модели	213
4.6.	Анализ чувствительности модели ЛП	215
4.7.	Изменения коэффициентов целевой функции	217
4.8.	Изменение правых частей ограничений	222
Устойчивость к изменениям правых частей
ограничений и теневые цены	223
4.9.	Анализ чувствительности с помощью
надстройки SolverTable	230
Изменение правых частей ограничений	231
Изменение коэффициентов целевой функции	234
Изменение технологических коэффициентов	235
4.10.	Анализ чувствительности в действии	237
Нормированная стоимость	238
4.11.	Характеристика отчета по устойчивости	244
4.12.	Использование отчета по устойчивости	245
Простые ограничения	250
Интерпретация теневой цены	252
4.13.	Вырождение моделей ЛП	252
Оптимальные значения переменных резерва и излишка	254
Положительные переменные и угловые решения	257
Вырожденные решения	257
4.14.	Заключение	258
Основные термины	260
Контрольные вопросы	261
Учебные задачи	266
Прикладные задачи	271
Симплекс-метод	279
Ebel Mining (часть 2)	280
Red Brand Canners, продолжение	282
Компания Saw Mill	284
Kiwi Computer	286
Компания Valley Chassis	292
Ферма Ельцина	293
Литература	296
10 Содержание
Глава 5. Линейная оптимизация. Применение	297
5.1.	Введение	299
5.2.	Транспортная модель	300
Формулировка и решение задачи ЛП	301
5.3.	Варианты транспортной модели	304
Максимизация транспортных моделей	304
Несбалансированные модели	304
Модель с недопустимыми путями	305
Целочисленные решения	305
Альтернативные оптимумы для нескольких целей	305
5.4.	Модель назначений	308
Задача организации проверок в Европейском отделении
компании AutoPower	308
Решение с помощью полного перебора	309
Формализация и решение задачи назначения	310
Связь между моделью назначений и транспортной моделью	312
Варианты модели назначений	312
Несбалансированная модель	312
Задачи максимизации	313
Недопустимые назначения	315
5.5.	Модель выбора средств массовой информации	315
Продвижение нового продукта	316
5.6.	Динамические модели	321
Динамические модели управления запасами	322
Словесная модель	323
Математическая модель	324
Динамическая модель управления запасами	324
Формализация модели управления запасами
в виде транспортной модели	332
5.7.	Динамическая модель планирования и управления запасами 335
5.8.	Динамическая модель управления финансами	337
5.9.	Модель управления финансами и планирования
производства	341
Финансовые требования	343
Влияние финансовых требований	345
5.10.	Сетевые модели	347
5.11.	Модель перевозок	348
Сетевая терминология	349
Формулировка задачи	349
Свойства модели	350
Содержание 11
Целочисленные оптимальные решения	352
Эффективные процедуры решения	352
5.12.	Поиск кратчайшего пути	352
5.13.	Модель замены оборудования	354
5.14.	Задача максимизации потока	357
Модель планирования городского строительства	358
5.15.	Заключение	360
Основные термины	361
Контрольные вопросы	362
Учебные задачи	365
Прикладные задачи	368
Планирование производства в компании Bumles	374
Ebel Mining (часть 3)	377
Ebel Mining (часть 4)	378
Литература	380
Глава 6. Целочисленная оптимизация	381
6.1.	Введение	383
Когда целочисленность решений играет основную роль	383
Сравнение моделей ЛП и ЦЛП	384
6.2.	Типы целочисленных оптимизационных моделей	385
6.3.	Графическое представление целочисленных моделей	386
Модель ЦЛП с двумя переменными	386
Упрощение модели ЦЛП	389
Округление решения	390
Решение методом перебора	391
6.4.	Применение двоичных переменных	392
Распределение бюджета	393
Логические условия	397
6.5.	Моделирование фиксированных затрат	399
Модель частично-целочисленного Л П	401
6.6.	Метод ветвей и границ	404
Пример модели ЦЛП	404
Модели частично-целочисленного линейного программирования 411
Применение метода ветвей и границ	411
Анализ чувствительности моделей ЦЛП	412
Эвристические методы	414
6.7.	Реализация моделей целочисленной оптимизации	414
Kelly-Springfield	414
Flying Tiger Line	414
12 Содержание
Hunt-Wesson Foods	415
6.8.	Заключение	416
Основные термины	416
Контрольные вопросы	417
Учебные задачи	422
Прикладные задачи	423
Назначение торговых представителей	428
Финансовое планирование	430
Ebel Mining (часть 5)	433
Литература	434
Глава 7. Нелинейная оптимизация	435
7.1.	Введение в нелинейные оптимизационные модели	436
7.2.	Безусловная оптимизация	437
7.3.	Нелинейная оптимизация: геометрическая интерпретация	439
Графический анализ задач НЛП	439
Сравнение моделей ЛП и НЛП	441
Задачи НЛП с ограничениями в форме равенств	443
7.4.	Использование средства Поиск решения
для решения задач НЛП	445
7.5.	Примеры нелинейных моделей	445
Экономическая интерпретация множителей Лагранжа
и нормированных градиентов	447
Оптимальность в моделях НЛП	450
Начальные предположения	455
7.6.	Параметры поиска решения	457
7.7.	Разрешимость задач НЛП	458
Разрешимые нелинейные модели: вогнутые
и выпуклые задачи НЛП	459
Нелинейные задачи, которые можно попытаться решить	462
7.8.	Генетический алгоритм	464
Понятие о методе эволюционного или генетического поиска	466
7.9.	Введение в квадратичное программирование	472
Решение задач КП с помощью средства Поиск решения	473
7.10.	Выбор портфеля инвестиций	475
Модель формирования инвестиционного портфеля	476
Формализация модели инвестиционного портфеля	476
7.11.	Пример модели портфельных инвестиций	479
Формулировка задачи	479
Содержание	13
Решение с помощью средства Поиск решения	480
7.12.	Модель управления запасами	483
Текущая политика компании STECO	485
Разработка модели ОРЗ	487
Оптимальный объем заказа в модели ОРЗ	490
Анализ чувствительности	491
7.13.	Модель управления запасами при наличии оптовых скидок	492
Оптовые скидки и оптимальное решение для компании STECO	492
7.14.	Производство и управление запасами	496
7.15.	Заключение	499
Основные термины	501
Контрольные вопросы по теме “Нелинейные модели”	502
Контрольные вопросы по теме
“Квадратичное программирование”	505
Контрольные вопросы по теме “ Модели управления запасами”	507
Учебные задачи	508
Прикладные задачи	509
Оперативные поставки	514
Abacus SFX	515
Литература	518
Глава 8. Многоцелевые модели и эвристические методы 519
8.1.	Введение	520
8.2.	Составление графика работы оборудования	522
Эвристические решения	523
8.3.	Составление графика работы оборудования
при ограниченности ресурсов	525
Простой пример	525
Эвристическая процедура выравнивания загрузки персонала	527
8.4.	Задачи со множеством целей	531
Целевое программирование	533
Абсолютные приоритеты	537
Комбинирование весовых коэффициентов
и абсолютных приоритетов	547
8.5.	Аналитический иерархический процесс	549
8.6.	Заключение	557
Основные термины	558
Контрольные вопросы	559
Учебные задачи	561
14 Содержание
Прикладные задачи	570
Объединение заводов	571
Литература	576
Часть III. Вероятностные модели	577
Глава 9. Анализ решений	579
9.1.	Введение	580
9.2.	Три класса моделей принятия решений	582
Принятие решений в условиях определенности	582
Принятие решений в условиях риска	583
Принятие решений в условиях неопределенности	590
9.3.	Принятие решений в условиях риска: ожидаемое
значение полной информации	594
9.4.	Полезность и принятие решения в условиях риска	595
Понятие полезности	595
Создание и применение функции полезности	598
9.5.	Промежуточные итоги	603
9.6.	Деревья решений	605
Альтернативные стратегии	605
Создание дерева решений	606
Ввод вероятностей и конечных значений	609
Обратный пересчет	610
9.7.	Анализ чувствительности	612
9.8.	Деревья решений: учет новой информации	614
Пересчет вероятностей с учетом новой информации	614
Включение апостериорных вероятностей в дерево решений	617
Ожидаемое значение дополнительной информации	621
9.9.	Последовательные решения	622
Анализ последовательных решений	622
Влияние функции полезности	624
Дополнительные возможности надстройки TreePlan	626
Чувствительность оптимального решения
к априорным вероятностям	627
9.10.	Менеджмент и теория принятия решений	629
Субъективные вероятности	630
9.11.	Анализ решений	631
9.12.	Заключение	631
9.13.	Условные вероятности и теорема Байеса	632
Основные термины	636
Содержание 15
Контрольные вопросы	637
Учебные задачи	640
Прикладные задачи	648
Компания Johnson’s Composite Materials	652
Бурить или не бурить?	653
Компания Shumway, Horch and Sager (часть 1)	654
Литература	658
Глава 10. Имитационное моделирование	659
10.1.	Введение	661
Применение имитационного моделирования	662
Имитация и случайные величины	663
10.2.	Генерирование случайных величин	665
Генераторы случайных чисел электронных таблиц	666
Генерирование значений дискретных случайных величин	666
Генерирование значений непрерывных случайных величин	669
Генерирование случайных величин с помощью надстроек	671
10.3.	Имитация в электронных таблицах	672
Модель финансового планирования	673
Модель со случайным спросом	674
Результаты имитации	675
10.4.	Имитация с помощью надстроек	679
Пример финансового планирования	680
Результаты имитации	682
Другие распределения спроса	686
10.5.	Модель управления запасами	688
Продвижение товара: определение объема заказа	688
Доход и объем заказа	690
Вычисление ожидаемого дохода	692
Краткие итоги	693
10.6.	Модель управления запасами с нормальным
распределением спроса	695
Нормальное распределение спроса	695
Результаты имитаций	697
10.7.	Модель авиаперевозок	699
10.8.	Баланс производственных мощностей	704
Моделирование производственного модуля	704
Имитация сбалансированных мощностей	705
Имитация несбалансированных мощностей	709
10.9.	Оптимизация в условиях неопределенности	710
16 Содержание
Распределение инвестиционных средств	710
Отбор проектов	716
10.10.	Некоторые выводы	721
10.11.	Заключение	722
Основные термины	723
Контрольные вопросы	724
Учебные задачи	727
Прикладные задачи	729
CyberLab	732
Mountain Realty	739
Литература	740
Глава 11. Моделирование дискретных событий	741
11.1.	Введение	742
11.2.	Имитационное моделирование в Excel	744
11.3.	Имитационное моделирование в Extend	749
Построение имитационной модели Хервиса	751
Имитация модели	758
11.4.	Расширенная модель Хервиса	761
11.5.	Изменение модели Хервиса	767
11.6.	Окончательная модель Хервиса	771
11.7.	Заключение	781
Основные термины	781
Контрольные вопросы	782
Учебные задачи	783
Прикладные задачи	783
Snowy Range Hardware	788
Баржи Миссисипи	790
Литература	792
Глава 12. Прогнозирование	793
12.1.	Введение	795
12.2.	Количественное прогнозирование	796
12.3.	Причинно-следственные модели прогнозирования	796
Подбор кривой по точкам	797
Какую кривую выбрать для приближения	808
Итоги	810
12.4.	Модели временных рядов	811
Экстраполяция статистических данных	811
Содержание
17
Подбор кривой	812
Метод скользящего среднего	813
Экспоненциальное сглаживание	819
Метод Хольта экспоненциального сглаживания	826
Сезонные изменения	829
12.5.	Статистические данные: разделяй и властвуй	835
12.6.	Качественное прогнозирование	837
Метод Дельфи	837
Прогнозирование и исследование рынка	838
12.7.	Заключение	839
Основные термины	840
Контрольные вопросы	841
Учебные задачи	842
Прикладные задачи	846
Ларамийский банк	846
Shumway, Horch и Sager (часть 2 )	849
Литература	852
Глава 13. Модели очередей	853
13.1.	Введение	855
13.2.	Базовая модель	857
Предположения о базовой модели	857
Характеристики базовой модели	859
13.3.	Классификация моделей очередей	862
13.4.	Формулы вычисления характеристик моделей очередей	863
13.5.	Очередь типа M/G/1	865
13.6.	Модель очереди M/M/s	867
13.7.	Экономический анализ моделей очередей	870
13.8.	Конечные очереди	874
13.9.	Очереди с конечным источником заданий	876
13.10.	Переходные процессы в моделях очередей	878
13.11.	Роль экспоненциального распределения	882
13.12.	Дисциплина очереди	884
13.13.	Заключение	884
Основные термины	885
Контрольные вопросы	885
Учебные задачи	887
Прикладные задачи	888
18 Содержание
Сколько необходимо телефонисток	891
Литература	892
Часть IV. Реализация	893
Глава 14. Реализация моделей	895
14.1.	Введение	896
14.2.	Что же такое модель	897
14.3.	Разделение функций игроков	899
14.4.	Размывание границ проекта	902
14.5.	Другие источники неудач	903
14.6.	Заключение	904
Основные термины	904
Задачи	905
Компания Australian Motors	905
Литература	921
Приложение А. Основные понятия теории вероятностей 923
А. 1. Введение	923
Случайные величины	923
Типы случайных величин	923
А.2. Дискретные случайные величины	923
Функция распределения	925
А.З. Непрерывные случайные величины	926
Функция распределения	926
Примеры непрерывных распределений	926
А.4. Математическое ожидание	928
Математическое ожидание случайной величины	928
Математическое ожидание функции от случайной величины	930
Дисперсия и стандартное отклонение случайной величины	930
А.5. Многомерные распределения	930
Совместное распределение	931
Независимые случайные величины	931
Математическое ожидание и дисперсия суммы случайных величин 932
Приложение Б. Средства моделирования Excel	933
Б. 1. Структура окна Excel	933
Б.2. Настройка Excel	934
Вкладка Вид	934
Вкладка Общие	934
Вкладка Переход	935
Содержание 19
Вкладка Правка	936
Вкладка Проверка ошибок	937
Б.З. Управление окнами и рабочими листами	938
Разделение окна рабочей книги	938
Закрепление областей	938
Масштабирование рабочих листов	939
Работа с несколькими окнами	940
Сокрытие окон рабочих книг	940
Сокрытие рабочих листов	941
Переименование рабочих листов	941
Б.4. Выделение ячеек	941
Выделение строки или столбца	941
Выделение нескольких смежных столбцов или строк	941
Выделение всех ячеек рабочего листа	942
Выделение диапазона ячеек	942
Выделение несмежных диапазонов ячеек	942
Выделение прямоугольного диапазона непустых ячеек	943
Выделение ячеек от табличного курсора до конца
непустого диапазона	943
Б.5. Работа с диапазонами ячеек	944
Редактирование содержимого ячеек	944
Абсолютные ссылки на ячейки	944
Относительные ссылки	945
Операция Вырезать	945
Операция Копировать	945
Операция Вставить	945
Перемещение и копирование диапазона ячеек	945
Копирование содержимого ячеек как рисунок	945
Команды Отменить и Повторить	946
Контекстные меню	946
Б.6. Заполнение ячеек	947
Команда Заполнить	947
Команда Прогрессия	947
Автозаполнение	948
Б.7. Форматирование	948
Изменение высоты строк	948
Изменение ширины столбцов	949
Форматирование числовых значении	949
Изменение шрифта	949
Выравнивание	950
Границы ячеек	950
20 Содержание
Форматы ячеек	950
Пользовательские форматы ячеек	952
Использование текста в форматах	953
Формат по образцу	953
Б.8. Массивы ячеек	954
Функция СУММПРОИЗВ	954
Функция ВПР	954
Формулы массивов’ результат в одной ячейке	955
Формулы массивов, результат в диапазоне ячеек	956
Пример формулы массива	956
Б.9. Поименованные ячейки	957
Создание имен для диапазонов ячеек	957
Автоматическое создание имен	958
Использование имен в формулах	959
Создание списка имен	959
Б. 10. Мастера Excel	960
Мастер функций	960
Мастер диаграмм	960
Мастер текстов	962
Б. 11. Другие часто используемые средства Excel	964
Сортировка	964
Отображение формул	964
Проверка формул	965
Вставка данных из Excel в Word	966
Специальная вставка	966
Вставка данных из Word в Excel	967
Панель инструментов Рисование	967
Справочная система Excel	968
Надстройки Excel	969
Таблица подстановки с одним входом	970
Приложение В. Надстройка Поиск решения	973
В. 1. Установка надстройки Поиск решения	973
В.2.	Введение	973
В.З.	Общие проблемы применения средства Поиск решения	975
В.4.	Замечания о работе средства Поиск решения	976
В.5.	Параметры средства Поиск решений	978
Параметр Максимальное время	978
Параметр Предельное число итераций	978
Параметр Относительная погрешность	978
Параметр Допустимое отклонение	979
Содержание 21
Параметр Сходимость	979
Параметр Неотрицательные значения	979
Параметр Автоматическое масштабирование	979
Параметр Показывать результаты итераций	979
Параметры Оценки, Разности и Метод поиска	980
Некоторые параметры диалоговых окон надстройки
Premium Edition Solver	980
Параметр Max Integer Solutions	980
Параметр Solve Without Integer Constraints	980
Параметр Convergence (оптимизатор Evolutionary Solver)	980
Параметр Population Size (оптимизатор	Evolutionary Solver)	980
Параметр Mutation Rate (оптимизатор Evolutionary Solver	980
Параметр Require Bounds On Variables (оптимизатор
Evolutionary Solver)	981
Диалоговое окно Limit Options (оптимизатор Evolutionary Solver) 981
B.6.	Сообщения средства Поиск решения	981
В.7.	Сообщения об успешном завершении работы	981
В.8.	Сообщения о неудачном завершении работы	982
В.9.	Загрузка и сохранение параметров поиска	984
В.	10. Отчеты надстроек Поиск решения и Premium Edition Solver 984
Диалоговое окно Результаты поиска решения	985
Отчет по результатам	985
Отчет по пределам	985
Отчет по устойчивости	985
Отчет Feasibility Report надстройки Premium Edition Solver	986
Отчет Linearity Report надстройки Premium Edition Solver	986
Отчет Population Report надстройки Premium Edition Solver	986
Приложение Г. Ответы к задачам с нечетными номерами 987
Предметный указатель	1012

Посвящение
Эшли и Аарону
Дженни, за ее потрясающую поддержку и неизменное дружеское отношение, а также
Марии, Кэролайн, Лауре, Бобу, Полу, Эми и Джошу за их любовь и воодушевление
Об авторах
Джеффри X. Мур (Jeffrey Н. Moore)
Джеффри X Мур после более 10 лет работы системным инжене-
ром, аналитиком компьютерных систем и аналитиком по проблемам
управления в 1972 году связал свою жизнь с Высшей школой бизнеса
(Giaduate School of Business) Стэнфордского университета (Stanioid
University), где он читает собственный специальный курс по инфор-
мационным технологиям для подготовки магистров и докторов Кро-
ме того, Джеффри читает основной курс моделирования и анализа и
является популярным лектором на старших курсах Стэнфордского
университета Его научные интересы сосредоточены в области ком
пьютерных технологий и систем поддержки принятия решении Он автор более 40 работ в
этих и других областях Мур является консультантом многих предприятий и фирм (как на-
ционального, так и международного масштаба) по применению информационных техно югии
и моделированию в процессе принятия решении Он участник нескольких проектов по разра-
ботке учебных курсов для аспирантов и магистров по использованию Excel для моделирова-
ния и поддержки процесса принятия решений Эти проекты выполнялись на основе грандов
от Microsoft, IBM и Hewlett Packard, а также на основе ботее ранних работ с Frontline Systems по
разработке и тестированию надстройки Solver (Поиск решения) для Excel, в частности для
решения задач линейной оптимизации. В конце 70-х годов Мур одним из первых разработал
курс для бизнес-колледжей по использованию электронных таблиц для моделирования, кото-
рый вскоре был переработан в основной курс по электронным таблицам для Стэнфордскою
университета Начиная с этого времени Джеффри Мур активно разрабатывает методы ис-
пользования электронных таблиц для моделирования и статистических расчетов Он создал
графический оптимизатор задач линейного программирования GLP и Regress, надстройку
Excel для регрессионного анализа, которая широко используется не только в Стэнфордском,
но и во многих других универсилетах Мур также является директором лаборатории техноло-
гий обучения SunTELL (Technology Educational Learning Laboratory) при Высшей школе бизнеса
Станфордского университета, которая основана компанией SUN Microsystems для изучения и
разработки методов использования информационных технологий в управлении, в том числе в
управлении образованием
В 1996 и 1998 годах он насаждался премией Sloan Teaching Excellence Award Станфорд
ского университета за курс лекции по моделированию в процессе принятия решении. Док-
тор Мур получил степень бака-лавра инженерных наук за разработку цифровых устройств в
Университете Цинциннати (University of Cincinnati), степень магистра экономики в Техас-
ском сельскохозяйственном университете (Texas А&М University), а степень доктора фило
Софии в области бизнеса — в университете Калифорнии в Беркли (University oi California,
Berkeley) Он также имеет сертификат профессионального инженера
Ларри Р. Уэдерфорд (Larry R. Weatherford)
Ларри Р Уэдерфорд — адъюнкт-профессор Колледжа бизнеса
(College of Business) Университета Вайоминга (University of Wyo-
ming) Он получил степень бакалавра в 1982 году в университете
Брайхем Янг (Bngham Young University), а степени магистра и док-
тора философии — в Высшей школе бизнеса Гардена (Garden
Graduate School of Business) Университета Виржинии (University of
Virginia) в 1991 году Уже в первый год работы профессором Кол-
леджа бизнеса Ларри был удостоен награды Outstanding Teaching
Award как лучший преподаватель В последующие годы он также награждался премиями
Outstanding Faculty Member от Alpha Карра Psi, Outstanding Junior Research Award Колледжа
бизнеса и межуниверситетской премией Ellbogen Meritorious Classroom Teaching Award Он
автор 17 научных статей, опубликованных в таких журналах, как Operation Reseach, Decision
Sciences, Transportation Science, Naval Reseach Logistics, Cornell Hotell and Restaurant
Administration Quarterly, International Journal of Technology Management, Journal of Combinatorial
Optimization и Omega
Ларри консультировал такие ведущие корпорации, как American Airlines, Northwest
Airlines, Lufthansa German Airlines, Swissair, Scandinavian Airlines, Air New Zealand, South
African Airways, Unisys Corporation, Walt Disney World и Hilton Hotels
Ларри счастлив в своем браке с любимой женой Дженни, с которой они воспитывают
семь детей' Редкое свободное время он посвящает семье и церкви, любит играть в теннис
и гольф, а также читать хорошие книги
Предисловие
Студентам, будущим менеджерам
Традиционно наукой управления называют построение подробно разработанных моде-
лей, после анализа которых принимаются управленческие решения
Новый словарь Вебстера определяет оксюморон как “оборот речи, содержащий сочетание
противоположных или взаимоисключающих идей и определений” Примерами таких сочета-
ний могут служить “сладкая горечь”, “громкое молчание”, “огромная малявка”, “спортивный
самосвал”, “бюрократичная оперативность”, “частный Госстандарт” — вы, вероятно, сможе-
те предложить другие примеры Ну, а наука управления9
В некоторых словарях управление определяется как “действие, искусство или способ
управлять чем-либо, те манипулировать, контролировать, направлять и тп” Если
управление является искусством, то не является ли оксюмороном сочетание “наука
управления”9
Нет, не является’
Наука как процесс (т е как научная деятельность) состоит из сбора и накопления эм-
пирических наблюдений и данных, выявления закономерностей на основе анализа нако-
пленных данных и построения научных теорий или моделей конкретной предметной об-
ласти, дающих ответы на поставленные исследователем вопросы Такой подход
(возможно, без этапа построения научных теорий) широко применяется и в других сфе-
рах практической деятельности человека, в частности в хозяйственной деятельности
и управлении Например, статистики в страховых обществах используют статистические
модели для определения страховых тарифов Во многих организациях для оценки капи-
тальных затрат используются различные модели финансовых потоков Продавцы явно
или неявно используют модели эластичного спроса при назначении цен на товар, а ме-
неджеры активно применяют инвестиционные модели для управления собственными
инвестиционными портфелями
Эта книга посвящена основным принципам моделирования, которые можно приме-
нить к широкому спектру различных управленческих ситуаций Кроме того, мы подроб-
но рассмотрим определенные классы моделей Например, модели финансовых потоков
можно использовать в ситуациях с различными временными периодами, скоростью об-
ращения и потоками Поэтому модели и концепции, изложенные в книге, можно приме-
нить к описанию самых разнообразных ситуаций.
По мере чтения книги вы обязательно заметите, что в ней много различных примеров
моделей — своеобразных рецептов по “приготовлению” моделей Но наша цель — не соста-
вить сборник готовых “рецептов” моделей, а научить вас самостоятельно готовить
“здоровую пищу” на основе, может быть, тех моделей, которые мы привели в качестве при-
меров Так, вы должны с осторожностью погружаться в технические детали моделей и их
представления с помощью Excel, чтобы не потерять из виду цели, для которых стр ится мо-
дель, — как с точки зрения менеджера, так и с точки зрения специалиста по моделирова-
нию Мы надеемся, что книга будет вам полезной по крайней мере в двух направлениях во-
первых, покажет реальные жизненные ситуации, которые можно смоделировать с помощью
электронных таблиц, и, во-вторых, представит методы построения и анализа моделей Про-
фессиональный менеджер в процессе принятия решений должен выделить те ситуации, ко-
26
Предисловие
торые можно с большей или меньшей точностью описать математически, т е для которых
можно построить соответствующие модели, и, конечно, должен уметь извлечь из этих мо-
делей необходимую для принятия решений информацию
Но эта книга не много даст вам в плане профессионального роста, если вы не будете
разрабатывать собственные модели Для этого необходимо пройти все этапы построения
моделей в Excel Ответственность за выполнение этого этапа обучения возлагается лично
на вас Однако для того, что стать хорошим разработчиком моделей и одновременно хоро-
шим менеджером, не достаточно освоить только механику моделирования с помощью
Excel Мы поможем вам в изучении методов моделирования и в освоении науки управле-
ния, но конечный результат будет зависеть только от ваших усилий
Преподавателям
Как сказано выше, науке управления, использующей модели, построенные с помо-
щью Excel, есть что предложить вашим студентам Мы надеемся, что материал нашей
книги, помноженный на ваше мастерство обучения и энтузиазм, поможет в формирова-
нии у завтрашних менеджеров навыков использования количественного моделирования
в повседневной деловой практике Тем более важно, что сегодня миллионы менеджеров
для анализа деловых задач применяют электронные таблицы Современные электронные
таблицы имеют много мощных средств, которые можно использовать для более точного
анализа моделей, вследствие чего могут приниматься более взвешенные и близкие к оп-
тимальным решения С учетом все более широкого применения электронных таблиц
в процессе управления ваша задача состоит в обучении студентов профессиональным на-
выкам разработки моделей — как “спланировать” чистый рабочий лист так, чтобы полу-
чить полезную и практичную модель деловой ситуации, не углубляясь в алгоритмические
и математические тонкости расчетов
Данная книга писалась как руководство для начальных курсов по моделированию
в процессе принятия решении с применением электронной таблицы Microsoft Excel, ко-
торое можно использовать при обучении студентов, аспирантов и магистров Что касает-
ся студентов, то необходимо подчеркнуть, насколько важно для их будущей профессио-
нальной деятельности освоить основные методы количественного моделирования в про-
цессе принятия решении Чтобы адресовать книгу более широкому кругу читателей,
в ней особое ударение делается на следующем
•	Строгий концептуальный фундаментдля всех рассматриваемых тем
•	Подчеркивание роли моделирования с помощью электронных таблиц для реше-
ния широкого круга задач принятия решении
Чтобы реализовать такой подход к изложению материала, шестое издание было зна-
чительно переработано с целью показать “искусство” использования средств Excel и дать
более широкий выбор материала для обучения студентов разных специальностей. По-
этому был сделан определенный “сдвиг” от простого рассмотрения процедур решения
и математических методов в сторону дополнительного материала, описывающего реаль-
ные управленческие ситуации Для этого в книгу добавлено более десятка новых врезок
“Практическое применение” Мы значительно увеличили количество задач, которые
приведены в конце большинства глав (причем, как задач начального учебного уровня,
так и более сложных и глубоких задач) Вместе с тем для более глубокого понимания ма-
тематической основы добавлены дополнительные темы, такие как вырожденность реше-
ний, методы ветвей и границ, условные вероятности, теорема Байеса и др
Предисловие
27
Мы адаптировали подход к моделированию, чтобы его можно было применить в раз-
личных областях финансовой деятельности, в управлении ресурсами, маркетинге, адми-
нистрировании и многих других сферах. Студенты предпочитают именно такой подход,
поскольку 1) они получают именно те знания, которые смогут использовать в своей бу-
дущей профессиональной деятельности, и, что более важно, 2) получают полезные навы-
ки моделирования и развивают интуицию в решении практических задач Многие сту-
денты сообщали нам, что это один из самых полезных курсов, которые они прослушали
в колледже, поскольку он сочетает четкую методологию моделирования и применение
моделей с изучением необходимых для этого средств.
Основное внимание в книге уделяется моделям — что это такое, как их создавать
и использовать, какую дополнительную информацию можно “выжать” из них — это кри-
тически важные вопросы для реализации любой управленческой деятельности В то же
время читатели, которые интересуются более глубокими аспектами этой темы, найдут
здесь описание методов оптимизации и теории принятия решений
Кроме пересмотра некоторых глав предыдущего издания, связанных с основами мо-
делирования в Excel, в это издание добавлены две новые главы В дополнение к главе,
описывающей имитационное моделирование, написана новая глава, посвященная моде-
лированию дискретных событий с помощью средств Excel и надстройки Extend Новая
глава о реализации моделей, в которой описываются организационные и управленческие
проблемы, возникающие в процессе придания моделям “законного” статуса, включает
описание многих реальных практических ситуаций, которые можно использовать при
проведении учебных дискуссий по этой действительно важной теме. Мы также значи-
тельно переработали главу, посвященную имитационному моделированию, добавили
примеры оптимизации имитационных моделей в Excel с помощью надстройки OptQuest
Продолжая прекрасную традицию предыдущих изданий, в конце каждой главы приво-
дятся “Ситуации для анализа”, для которых описывающие их сложные модели могут созда-
ваться постепенно, на основе материала нескольких глав (например, ситуация с компанией
Ebel Mining).
В данном издании продолжается объединение ранее разрозненного материала в отдельные
темы (что было начато еще в предыдущем издании). Так, ранее отдельные главы по графиче-
скому анализу и анализу чувствительности теперь объединены в одну главу, в которой также
описана надстройка SolverTable. Эта надстройка, разработанная в Стэнфордском университе-
те несколько лет назад, значительно расширяет возможности Excel по выполнению парамет-
рического анализа оптимизационных моделей, включая возможность создания отчета с табу-
лированными значениями, полученными при проведении анализа чувствительности
Наконец, в этом издании значительно увеличено количество примеров, в частности,
упрощенных примеров вводных моделей. Многочисленные “Советы”, разбросанные по
главам, помогут студентам избежать ловушек и ошибок в процессе построения моделей
в Excel Кроме того, детальное описание средств поиска решении и специальных средств
Excel, применяемых при моделировании и редко включаемых в стандартный курс изуче-
ния Excel, помогут студентам повысить свой уровень работы с этой замечательной элек-
тронной таблицей и оценить возможности Excel для построения моделей
Программные приложения для электронных таблиц и примеры из Microsoft Excel, вклю-
чая такие популярные надстройки для электронных таблиц, как Поиск решения, Crystal Ball.
@Risk и TreePlan, в книге рассматриваются через призму создания моделей. В этом издании
описан оптимизатор Evolutionary Solver, реализующий генетические алгоритмы, который
позволяет анализировать существенно нелинейные модели с использованием негладких
функций.
28
Предисловие
Особое внимание уделено пошаговому описанию процедур построения и анализа моде-
лей, для чего опять используется Excel и соответствующие надстройки. Примеры в этом из-
дании построены в Excel 2002, в книге приведено более 500 копий экранов. Особо подчерк-
нем, что в книге описано применение более десяти программных приложений, которые
студенты смогут использовать и после завершения курса.
•	Программа графической визуализации GLP для интерактивной оптимизации ли-
нейных моделей.
•	Программа Premium Edition Solver for Education, позволяющая отлаживать
вырожденные и нелинейные оптимизационные модели.
•	Надстройка SolverTable для параметрического анализа чувствительности оптими-
зационных моделей
•	Программа Evolutionary Solver (составная часть Premium Edition Solver for
Education), реализующая генетические алгоритмы для существенно нелинейных и
негладких моделей
•	Надстройка Crystal Ball версии Proffessional (со 140-дневным сроком использова-
ния), предназначенная для имитационного моделирования.
•	Надстройка TreePlan для анализа задач принятия решений.
•	Шаблоны Excel для выполнения вычислений в моделях очередей.
•	Программный пакет Extend LT для моделирования дискретных событий.
Книга разбита на четыре части' первая вводная часть посвящена общим вопросам мо-
делирования, вторая — детерминированным моделям, третья вероятностным
(стохастическим) моделям, а четвертая — вопросам реализации моделей. Структура
книги предполагает логическую связанность материала, которая позволяет с большей
выразительностью изложить такие актуальные и мощные методы, как оптимизация с по-
мощью генетических алгоритмов, аналитические иерархические процессы, имитацион-
ное моделирование, моделирование дискретных событий, многокритериальные задачи
принятия решений, а также общие методы моделирования посредством электронных
таблиц Этого материала значительно больше, чем можно прочитать в одном начальном
типовом курсе моделирования. Мы надеемся, что такая организация книги позволит ка-
ждому преподавателю выбрать тот материал, который в наибольшей степени соответст-
вует потребностям его аудитории.
Сопутствующие материалы
Каждый экземпляр книги шестого издания содержит компакт-диск со следующим
программным обеспечением.
•	Программа графической визуализации GLP для интерактивной оптимизации ли-
нейных моделей. Описывается и используется в главах 4 и 6.
•	Программа Premium Edition Solver for Education, позволяющая отлаживать
вырожденные и нелинейные оптимизационные модели. Описывается и использу-
ется в главах 3-7.
•	Надстройка SolverTable для параметрического анализа чувствительности оптими-
зационных моделей. Описывается и используется в главах 4—7.
Предисловие
29
•	Программа Evolutionary Solver (составная часть Premium Edition Solver for
Education), реализующая генетические алгоритмы для существенно нелинейных
и негладких моделей Описывается и используется в главе 7.
•	Надстройка Crystal Ball версии Proffessional (со 140-дневным сроком использова-
ния), предназначенная для имитационного моделирования Описывается и ис-
пользуется в главе 10. Она также включает оптимизатор OptQuest для имитацион-
ных моделей (см. главу 10)
•	Надстройка TreePlan для анализа задач принятия решений. Описывается и исполь-
зуется в главе 9
•	Программный пакет Extend LT для моделирования дискретных событий Описы-
вается и используется в главе 11
•	Программный пакет Microsoft Project 2000 (со 120-дневным сроком использования)
•	Шаблоны Excel для выполнения вычислений в моделях очередей
•	Файлы рабочих книг Excel для всех примеров, рассмотренных в книге
Благодарности от авторов шестого издания
Мы благодарны авторам первых четырех изданий Гари Эппену (Gary Ерреп) и Ф Дж
Гулду (F J Gould) и присоединившемуся к ним при написании пятого издания Чарльзу
Шмидту (Charles Schmidt) за их огромные усилия по созданию действительно прекрасной
книги, в которой было крайне сложно что-либо изменить
Огромное спасибо нашему редактору Тому Такеру (Tom Tucker) за наведение мостов
между нами и за его добрый и “направляющий” юмор во время подготовки данного из-
дания Мы уверены, что без его руководства книга никогда не вышла бы в свет
Большая благодарность всем рецензентам данного издания за их квалифицированные
комментарии и предложения Они значительно улучшили содержание книги
Благодарим более 300 преподавателей за их предложения и замечания, которые они
высказали после проверки в студенческой аудитории многих изменении, сделанных
в данном издании
Мы также говорим большое спасибо нашим секретарям Стефани О’Делл (Stephanie
O’Dell) и Хироми Ямпол (Hiromi Yampol) за долгие часы, проведенные за редактировани-
ем и приведением в порядок наших рукописей. Благодарим Кевина Льюиса (Kevin Lewis)
за помощь и создание многочисленных задач и примеров Спасибо преподавателям
Станфордского университета за проверку нового материала данного издания Особая
благодарность профессорам Джеймсу Петеллу (James Patel!) и Майклу Харрисону (Michael
Harrison) за проверку нового материала в своих учебных курсах
Хотим побла!одарить профессоров Чарльза Бонини (Charles Bonmi), Эвана Портеса
(Evan Porteus), Кришнана Ананда (Krishnan Anand), Джеймса Петелла (James Patell) и Хаи-
ма Мендельсона (Haim Mendelson) за предоставление материала практического примене-
ния и ситуаций для анализа и профессора Стефена Бредли (Stephen Bradley) за участие
в создании материала для главы, посвященной реализации моделей Спасибо профессо-
рам Дэвиду Эшли (David Ashley) и Майку Мидлтону (Mike Middlton) за предоставление
шаблонов Excel для моделей очередей и надстройки TreePlan соответственно
Мы хотим поблагодарить Дэниэла Филстру (Daniel Fylstra) и Джона Уотсона (John
Watson) из компаний Frontline Systems и Software Engines за подготовку рабочих книг
30 Предисловие
Excel Было очень приятно с ними работать Особая благодарность Дэну за создание Pre-
mium Edition Solver for Education для студентов, что мы рассматриваем как его щедрый
и благородный вклад в дело образования и, в частности, обучения менеджменту
Наконец, большое спасибо бывшим студентам Стэнфордского университета, ныне
работающим в Microsoft, Стиву Боллмеру (Steve Ballmer) и Питу Хиггенсу (Pete Higgins) за
их роль в создании средств Excel, что определило выбор этой электронной таблицы в ка-
честве инструмента для моделирования и анализа управленческих ситуаций. Сотрудни-
чество, при котором советы и предложения, исходящие из академических кругов, были
учтены при разработке программы Excel и ее инструментария, — это та модель сотрудни-
чества с компаниями, создающими программное обеспечение, которой мы хотели бы
следовать и в будущем
Мы надеемся, что эта книга и сопутствующие ей материалы помогут читателям в ос-
воении науки управления Мы всегда рады получить сообщение от читателя, особенно
если оно содержит идеи и предложения по улучшению содержания книги
Jeffrey Moore, Palo Alto. CA
Email moore_jeffiey@gsb Stanford edu
Phone (650) 723-4048
FAX (650) 725-7979
Larry R Weatherford, Laramie. WY
Email lrw@uwjoedu
Phone (307) 766-3639
FAX (307)766-3488
МОДЕЛИ
И МОДЕЛИРОВАНИЕ
Глава 1. Введение в моделирование
Глава 2. Моделирование с помощью электронных таблиц
В первой части книги мы предлагаем подход, позволяющий применять электронные таб-
лицы Excel для поддержки принятия управленческих решений. Сначала с помощью Excel
разрабатывается модель рассматриваемой ситуации, затем полученная модель анализи-
руется средствами Excel, после чего на основании проведенного анализа принимается
решение. Первые главы посвящены рассмотрению класса моделей, получивших назва-
ние детерминированных Что же собой представляют детерминированные модели?
Термин детерминированная модель означает, что все аспекты модели достоверно из-
вестны Например, в модели производства предполагается, что достоверно известно,
сколько времени требуется на изготовление определенной детали (скажем, 20 мин., или,
что то же самое, 3 детали в час) Таким образом, известно, что за 8 ч работы можно про-
извести 24 детали 8 часов х 3 детали в час = 24 детали
Мы все используем детерминированные модели. С тех пор как выяснилось, что четы-
ре 25-центовых пирожных стоят доллар, нам всегда при анализе были известны точные
значения всех факторов Естественно, возникает желание предположить, что окружаю-
щий мир является детерминированным Однако в действительности это не так В частно-
сти, в приведенном примере время изготовления некоторых деталей может оказаться
равным 19 мин , а других— 23 мин. Возможно, на изготовление 24 деталей потребуется
всего 7 ч 41 мин
Почему же детерминированные модели используются, несмотря на то, что они неточ-
но описывают действительность9 Ответ прост — эти модели полезны. Пусть детермини-
рованные модели несовершенны, но, как правило, они достаточно удовлетворительно
описывают реальность В любом случае это лучше, чем не иметь модели вовсе Получен-
ный с помощью таких моделей результат оправдывает усилия, затраченные на их созда-
ние и анализ Поэтому детерминированные модели нашли широкое применение в анали-
зе управленческих ситуаций с помощью электронных таблиц. Изучению детерминиро-
ванных моделей посвящены части 1 и 2 данной книги. В части 3 мы откажемся от
предположений о детерминированности, чтобы иметь возможность моделировать ситуа-
ции в условиях неопределенности
Введение в моделирование
В ЭТОЙ ГЛАВЕ...
1.1.	Введение
1.2.	Процесс моделирования
1.3.	Немного философии
1.4.	Типы моделей
1.5.	Построение моделей
1.6.	Моделирование на основе данных
1.7.	Детерминированные и вероятностные модели
1.8.	Последовательная разработка модели
1.9.	Моделирование и принятие решений в реальном мире
1.10.	Подведение итогов
1.11.	Заключение
I Основные термины
| Контрольные вопросы
i Вопросы для обсуждения
j Литература
34
ЧАСТЬ I Модели и моделирование
Практическое применение
Система принятия решений корпорации AT&T
Capital Corporation
Корпорация AT&T Capital Corporation (AT&T СС), активы которой составляют
более 12 миллиардов долларов, является крупнейшей открытой акционерной ком-
панией США в сфере лизинга и финансирования Мелкий коммерческий лизинг,
стоимость оборудования в котором составляет не более $50 000, является важней-
шим сегментом бизнеса AT&T СС, в котором вращаются многие миллиарды долла-
ров На этом рынке чрезвычайно высокий уровень конкуренции, поэтому корпора-
ция AT&T СС должна принимать соответствующие решения по кредитованию бы-
стро (иначе существует риск, что клиенты обратятся к другим арендодателям), точно
(в противном случае возможен риск непогашения долгов) и рентабельно (иначе за-
траты на принятие решения отрицательно скажутся на прибыли) Кроме того, необ-
ходимо эффективно управлять деятельностью, связанной с неоплаченными счетами,
чтобы контролировать потери от безнадежных долгов, уменьшить затраты на финан-
совое обслуживание и улучшить оборот наличных средств
AT&T СС разработала компьютерную систему принятия решений, которая по-
зволяет отслеживать риск, связанный с каждым кредитом клиента, на протяжении
всего периода его сотрудничества с компанией Были созданы модели и системы для
поддержки трех этапов отношений между клиентом и компанией 1) принятие пер-
воначального решения о предоставлении кредита, 2) управление кредитной линией
и последующие решения о кредитовании и 3) сбор отчетов Для каждого этапа моде-
ли оценки рисков и принятия решений определяют, какое решение будет принято.
Преимуществами такого подхода являются сокращение времени ответа клиентам,
увеличение объемов деловых операции AT&T СС и рост прибылей компании
При принятии первоначального решения о предоставлении кредита для оценки
будущей платежеспособности клиента используется информация о профиле кредита
и отчеты о кредитных операциях Выбор источников снабжения кредитной инфор-
мацией среди различных кредитных агентств осуществляется с помощью специаль-
ной оптимизационной модели Другая оптимизационная модель позволяет сформу-
лировать окончательное решение и определить лимит кредитования. При принятии
окончательного решения на основании информации о том, как клиент распоряжал-
ся средствами в прошлом, и оценок будущего использования кредита выбирается
одно из трех решении одобрить выделение кредита, отказать или направить для
дальнейшего рассмотрения В настоящее время данный процесс позволяет автомати-
зировать около 68% первоначальных решений о выделении кредита, благодаря чему
годовой объем операции увеличивается на $40 млн , а стоимость принятия решений
снижается на $500 тыс в год Другому подразделению AT&T СС использование дан-
ной модели позволяет снизить затраты более чем на $600 тыс ежегодно, при этом на
40% снижаются затраты на получение отчетов о кредитных операциях
Управление кредитной линией клиента состоит в постоянно проводимой оценке
его кредитоспособности с целью определения кредитного уровня Клиенты переводят-
ся на более высокий или низкий кредитный уровень, если моделью оценивания креди-
та предписывается новый порог Использование модели управления кредитной линиеи
позволяет ежегодно экономить $300 тыс и увеличить объем операций на $6 млн.
ГЛАВА 1. Введение в моделирование
35
Взыскание средств с клиентов-должников производится с помощью набора стати-
стических моделей, которые рекомендуют один из пяти видов взыскания платежей.
Модель управления портфелем кредитов автоматически выбирает клиентов-
должников и помещает их в порядке очередности в список для обслуживания Это по-
зволяет повысить производительность на 15%, сократить размеры неплатежей на
$16 млн и соответственно увеличить оборот наличных средств на $1 млн ежемесячно
В результате применения данной модели количество сомнительных клиентов в AT&T
СС сократилось на 15%, в то время как объем деловых операций возрос на 23%.
В целом применение указанных моделей (среди которых модели анализа рисков,
статистические и оптимизационные модели, а также модель управления портфелем
кредитов) позволило снизить затраты на принятие решений на $3,5 млн , увеличить
объем операций на $86 млн и сократить потери от невозвращения кредитов на
$1,1 млн ежегодно Согласно заключению AT&T СС инвестиции в “автоматизацию
и оптимизацию процесса принятия решений рассматриваются в качестве важного
источника повышения конкурентоспособности и прибыли” [ 1 ]
1.1. Введение
Изучив Excel, вы присоединились к тем 100 миллионам пользователей, которые сделали
электронные таблицы языком повседневного общения в менеджменте, что произвело под-
линную революцию в управлении два десятилетия назад. Данная книга не о том, как работать
в Excel, — она посвящена тому, как с помощью Excel создавать модели для анализа ситуаций
в сфере менеджмента Наша цель — изучить модели управления, основанные на электронных
таблицах что они собой представляют, как создаются, используются, и что можно узнать с их
помощью Например, в основе успеха компании AT&T СС (о которой говорится в начале гла-
вы) лежит набор управленческих моделей для поддержки процесса принятия решений в сфере
кредитования Как и в данной компании, наш подход будет состоять в разработке и после-
дующем анализе модели ситуации На основании проведенного анализа будут предлагаться
решения по улучшению рассматриваемой ситуации
Однако так получилось, что у менеджеров достаточно долго было двойственное от-
ношение к применению моделирования в процессе принятия решений Признавая опре-
деленные преимущества моделей, они зачастую воспринимали сам процесс моделирова-
ния как “черную магию”, которой владеют только математики, высокооплачиваемые
консультанты или специалисты-компьютерщики К сожалению, когда моделирование
поручалось специалистам, менеджер практически отстранялся отданного процесса, что,
как правило, приводило к неправильному применению или отказу от использования ре-
зультатов моделирования А это, в свою очередь, вело к усилению скептических настрое-
ний в среде менеджеров относительно реальной пользы моделирования (помимо созда-
ния стереотипных отчетов о результатах моделирования, которые часто так и оставались
непрочитанными) Таким образом, деньги и усилия тратились на ритуальные действия
по моделированию, которые в итоге практически никак не влияли ни на менеджера, ни
на организацию, для которой предназначалась модель, поскольку эта модель никого ни-
чему не учила, а процесс моделирования ничего не менял в работе организации
Применение электронных таблиц коренным образом изменило ситуацию, так как по-
зволило менеджерам самостоятельно создавать и анализировать модели Поэтому им для
создания собственных моделей уже не были нужны необходимые прежде аналитические
36
ЧАСТЬ I Модели и моделирование
способности профессиональных математиков, навыки программирования, алгоритмиче-
ское мышление и соответствующие технические знания Непосредственное использование
моделей для поддержки принятия решений не только повысило эффективность управленче-
ских решении, но и позволило самим менеджерам глубже вникнуть в суть решаемых про-
блем. Обучение в процессе моделирования позволяет менеджеру сосредоточиться на ос-
новной проблеме принятия решения — определить, на какие основные вопросы нужно от-
ветить, какие альтернативы исследовать и на что обратить особое внимание.
В данной книге описаны разнообразные модели, а также соответствующие концеп-
ции, которые обобщают приведенные примеры для всевозможных ситуаций, с которыми
сталкивается менеджер. Однако ключевой составляющей успешного моделирования
управленческих ситуаций с помощью Excel является сам менеджер Не следует забывать,
что ему придется конкурировать со 100 миллионами своих коллег, также применяющими
программы электронных таблиц. Но все ли из них умеют использовать Excel для успеш-
ного моделирования сложных управленческих ситуаций и опираются в своем анализе на
глубокие концептуальные принципы9
Может получиться, что читатель выполнит все предложенные в книге упражнения, но
это никак не поможет ему в работе. Чтобы такого не произошло, необходимо проник-
нуться идеями моделирования, т. е. эти идеи должны стать частью вашей интуиции.
Главное — приобретение собственного опыта моделирования с помощью Excel, а наша
книга поможет лучше понять связи между менеджментом и моделью В книге предлагается
множество конкретных моделей. Не следует слишком погружаться в технические под-
робности этих моделей и их представления с помощью Excel, чтобы не утратить понятие
об общих навыках, которые необходимы как хорошему менеджеру, так и специалисту
в сфере моделирования Работая с книгой, нужно уделять основное внимание реальным
ситуациям и роли табличных моделей (т.е. построенных с помощью электронных таб-
лиц) в разрешении этих ситуаций, а также заниматься самостоятельным построением
и анализом данных моделей. Это нелегко, но, чтобы чему-то научиться, всегда необхо-
димо приложить определенные усилия
Моделирование различных вариантов проекта будущей системы позволило компании
i Federal Express совершить ошибки только на бумаге. Компьютерное моделирование прино- °
i сит плоды; оно позволяет исследовать множество различных альтернатив и заставляет все- i
сторонне изучить проблему.
Фредерик У. Смит (Frederic W. Smith)'
Председатель правления и генеральный директор корпорации Federal Express
1.2. Процесс моделирования
На рис I I показаны этапы принятия управленческого решения. При наличии кон-
фликтующих или конкурирующих альтернатив менеджер анализирует сложившуюся си-
туацию, принимает решение, позволяющее разрешить конфликт; решение реализуется;
в результате организация получает определенную прибыль (не обязательно в виде денеж-
ных сумм) В книге рассматривается применение моделей, построенных с помощью
электронных таблиц, для поддержки принятия решений, т.е. для первых двух этапов —
анализа ситуации и принятия решения о выходе из нее Реализация принятых решений
также важна, этой теме будет посвящена глава 11.
ГЛАВА 1 Введение в моделирование
37
)—4 р^ци, )—►[
Прибыль
Рис. 1.1. Этапы принятия и реализации управленческих решений
На рис 1 2 представлен процесс моделирования применительно к первым двум этапам
принятия решения. Этот процесс будет постоянно использоваться в книге Диаграмма
процесса состоит из верхней и нижней частей, разделенных пунктирной линией Ниже
пунктирной линии находится реальный мир, с которым ежедневно сталкиваются менед-
жеры, призванные принимать решения в сложных ситуациях (например, распределять
ресурсы между конкурирующими задачами производства, составлять расписание дейст-
вий или разрабатывать маркетинговую стратегию) Процесс моделирования начинается
с исследования ситуации, требующей решения (в левом нижнем углу диаграммы)
В прошлом при принятии решений менеджеры привыкли полагаться главным образом на
свою интуицию Хотя интуиция, особенно опытных менеджеров, имеет большое значение,
она по определению лишена рационального аналитического начала Руководствуясь при при-
нятии решений исключительно интуицией, менеджер может делать выводы только из конеч-
ных результатов ранее принятых решений, а такое обучение слишком дорого обходится
Процесс моделирования, представленный на рис. 1 2 над пунктирной линией, реко-
мендует набор действий, которые должны дополнить (не заменить') интуицию при при-
нятии решений. При этом создается формализованная количественная модель проблем-
ных аспектов управленческой ситуации, представляющая существо проблемы
Построенная количественная модель анализируется с целью получения определенных
результатов или выводов, следующих исключительно из модели, независимо оттого, ка-
кие предположения и абстрактные построения лежали в ее основе После этого получен-
ные результаты интерпретируются для существующей реальной ситуации с учетом тех
факторов, которые не учитывались ранее в процессе формализации задачи. Процесс мо-
делирования, дополненный опытом и интуицией менеджера, позволяет принять более
удачное решение и многому научиться.
Как показано из рис 1 3, процесс моделирования сам по себе не является конкрет-
ным научным методом, реализацией которого должны заниматься исключительно спе-
циалисты Соображения оперативного управления оказывают влияние на все аспекты
процесса, поэтому непосредственное привлечение менеджера к процессу моделирования
является залогом успешного применения результатов моделирования в реальном мире
38
ЧАСТЬ I Модели и моделирование
Рис. 1.3. Роль мнения менеджера в процессе моделирования
Менеджеры играют очень важную роль как во время формирования абстракций, соз-
дания модели и ее интерпретации, так и при реализации решений Поэтому менеджер
должен понимать следующее
1.	Какие ситуации поддаются моделированию
2.	Как получить нужные для построения модели данные или как извлечь их из боль-
ших массивов данных, и какие существуют методы анализа моделей, помогающие
в принятии управленческих решений (причем в пределах разумных затрат времени
и средств)
3.	Что можно сделать, чтобы извлечь максимальную пользу из интерпретации модели
и реализации решения
Использование моделей на разных уровнях управления
Модели играют различную роль на разных уровнях управления компанией На верх-
нем уровне модели, как правило, предлагают информацию и помогают понять проблему,
причем не обязательно в форме рекомендуемых решений Они используются в качестве
средств стратегического планирования чтобы предвидеть будущее, исследовать альтер-
нативы, разработать несколько планов на случай непредвиденного развития событий,
повысить гибкость производства и сократить время реакции на требования времени На
более низком уровне модели чаще используются для того, чтобы предложить рекомен-
дуемые решения Например, на многих заводах операции на конвейере полностью авто-
матизированы Аналогично в некоторых случаях (как в примере с компанией AT&T СС)
решения принимаются исключительно на основании модели конкретной операции и по-
сле реализации требуют вмешательства менеджера тотько в исключительных ситуациях
Однако чаще вклад автоматизации в моделирование состоит в сборе и подготовке нуж-
ных данных Эти данные затем используются менеджерами для периодического обновле-
ния табличных моделей, построенных в электронных таблицах Пересмотренная модель
повторно анализируется, рекомендуются новые решения, которые вновь интерпретиру-
ются и реализуются
Модели по-разному используются на различных уровнях управления компанией по
ряду причин Чем ниже уровень организации, тем проще задачи и альтернативы Взаимо-
действия легче описать количественно, зачастую более доступны точные данные, более
определенной является и будущая среда реализации решения Кроме того, достаточно
часто повторяются ситуации принятия решений, что позволяет амортизировать затраты
ГЛАВА 1 Введение в моделирование
39
на сбор данных и разработку модели за счет ее многократного использования. Например,
на низшем уровне решение может заключаться в составлении расписания работы опре-
деленного станка Известно, какие изделия на нем можно изготавливать, а также стои-
мость переналадки станка при переходе с одного вида продукции на другой Задача моде-
ли — составить расписание, которое позволит изготовить необходимое количество изде-
лии в срок и минимизировать затраты на переналадку и хранение
Сравните эту простую и очевидную проблему с принятием на высшем уровне реше-
ния, следует ли “делать инвестиции в развитие” или “выжать максимум из производства”,
стоимость которого может составлять многие миллиарды долларов Конечно, модели
можно применять и для таких общих и неопределенных проблем, но тогда в самих моде-
лях оказывается слишком много неоднозначных предположений и неопределенностей
В таких случаях определить точность модели и достичь соглашения о ее целях бывает
столь же сложно, как и найти соответствующее решение
Модели и менеджеры
Способы использования моделей так же разнообразны, как и люди, которые их соз-
дают С помощью моделей можно продать идею или проект, заказать оптимальное коли-
чество синтетической пряжи или лучше организовать работу гигантской многонацио-
нальной корпорации В любом случае модели обеспечивают структуру для целостного
логического анализа Модели широко испотьзуются благодаря тому, что заставляют вы-
полнить следующие действия
1.	Явно определить цели.
2.	Определить и зафиксировать типы решений, которые влияют на достижение этих целей.
3.	Выявить и зафиксировать взаимосвязи и компромиссы между этими решениями.
4.	Тщательно изучить входящие в них переменные и определить возможность их из-
мерения.
5.	Разобраться, какие данные нужны для количественного определения значений
переменных и найти способ описать их взаимное влияние.
6.	Осознать, какие ограничения могут налагаться на значения этих переменных.
7.	Обсудить идеи, что помогает членам группы управления в совместной работе.
Как следует из перечисленного выше, модель можно использовать в качестве целост-
ного средства для оценки и обсуждения различных вариантов политики компании, если
каждый вариант или ряд решении оценивается с одних и тех же позиции, согласно тем же
формулам, описывающим взаимосвязи и ограничения Более того, модели можно прове-
рить непосредственно на практике и усовершенствовать, используя опыт, что является
разновидностью адаптивного обучения
Наконец, следует отметить, что основанные на электронных таблицах модели предос-
тавляют менеджерам возможность систематически использовать мощные аналитические
методы, прежде им недоступные Такие модели позволяют оперировать огромным чис-
лом переменных и описывать их взаимосвязи, что не под силу сделать в уме
; Модели позволяют одновременно использовать аналитические возможности электрон-
ных таблиц, возможности хранения данных и вычислительные ресурсы компьютеров.
40
ЧАСТЬ I Модели и моделирование
1.3. Немного философии
“Философия” моделирования призвана несколько сократить разрыв между способа-
ми использования моделей, показанными в нашей книге, и реальным опытом менедже-
ра В книге все задачи четко сформулированы (по крайней мере мы старались, чтобы это
было так), все данные точно известны, а решение можно охарактеризовать одним чис-
лом, приведенным в ответах в конце книги Очевидно, что в реальности все совсем иначе
Поэтому необходимо более подробно рассмотреть роль и место моделей в реальном мире.
Реализм
Начнем с темы, которая уже затрагивалась ранее Ни одна модель не в состоянии
полностью охватить реальность Каждая модель является некой абстракцией, т.е описы-
вает только некоторые возможные взаимосвязи реального мира и лишь приблизительно
представляет отношения между ними Из этого вытекает простое прагматическое прави-
ло, определяющее, когда следует использовать модели.
; Модель следует использовать в том случае, если с ее помощью принимаются более
удачные решения, чем без нее.
Данный подход во многом напоминает подходы, применяемые в науке и технике.
Модели могут не совсем точно описывать подъемные силы крыла самолета, но с их по-
мощью удается конструировать более совершенные самолеты, чем без них То же верно
и для принятия управленческих решений
Интуиция
Некоторые менеджеры продолжают думать, что модели и интуиция в управлении яв-
ляются вещами взаимоисключающими: “Или мы творчески подходим к разрешению си-
туации, или моделируем ее с помощью компьютера” Это в корне неверный подход Ус-
пешное (и творческое) использование моделей в значительной мере основано на сужде-
ниях и интуиции менеджера
Интуиция играет важную роль в осознании проблемы и создании модели. Сначала
нужно определить, где можно применить количественную модель, т е., прежде чем вкла-
дывать средства в процесс моделирования, необходимо интуитивно почувствовать, что
суть ситуации можно описать с помощью модели и получить полезный результат.
Интуиция не менее важна при интерпретации и реализации решения. Несмотря на то
что в ходе анализа многих предлагаемых в данной книге моделей получаются
“оптимальные” решения, важно понимать, что такие решения являются оптимальными
для формальных абстракций (находящихся над пунктирной линией на рис. 1.2), но они
могут и не быть таковыми в реальной ситуации.
Термин “оптимальность” относится к моделям, а не к реальности. То, что оптимально
в модели, отнюдь не всегда оптимально в реальной жизни.
Лишь иногда имеет смысл говорить об оптимальных решениях применительно к ре-
альным ситуациям в управлении бизнесом (гораздо реже, чем в государственном управ-
лении) Именно поэтому так важно, чтобы менеджер удостоверился, что предложенные
моделью решения имеют смысл и удовлетворяют его интуитивным требованиям. Если
рекомендации не соответствуют интуитивным соображениям менеджера, следует разо-
ГЛАВА 1. Введение в моделирование
41
браться, верна ли модель. Таким образом, для менеджера чрезвычайно важно оценить
модель и определить, насколько следует доверять ее рекомендациям. Может понадобить-
ся пересмотреть описание ситуации или даже формулировку модели. Важно понимать,
что моделирование ни в коем случае не заменяет интуицию менеджера. Для менеджера
было бы непростительной ошибкой слепо принять решение на основании модели лишь
потому, что “так следует из Excel”. Могла измениться деловая среда, и модель, дававшая
хорошие решения, может предложить плохой совет. Всегда нужно быть готовым к тому,
что возникнут какие-то изменения и старые решения перестанут срабатывать Тем
не менее существует немало доказательств, что процесс моделирования можно успешно
применять тогда, когда среда вокруг бизнес-ситуации меняется настолько, что стандарт-
ная политика или чисто практические методы становятся неадекватными
Безусловно, нельзя гарантировать, что использование “хорошей” модели всегда даст хоро-
ший результат; но, несмотря на его несовершенство, этот подход — наиболее рациональный
из всех возможных Более того, как и сам процесс моделирования, управленческие ситуации
в действительности развиваются скорее циклически, чем последовательно Это означает, что
они возникают повторно и нуждаются в повторном рассмотрении и обработке Этот факт
служит основной мотивацией для изучения количественных моделей, шансы правильно пред-
сказать, когда некая модель будет давать хорошие реальные результаты, а когда — нет, сущест-
венно возрастут, если понять концепции, используемые в данной модели.
Подведем итог. Чтобы лучше представить, что было сказано о процессе моделирова-
ния, поставьте себя на место менеджера в следующем диалоге.
МЕНЕДЖЕР. Позвольте удостовериться, что я правильно понял Поскольку раньше менеджеры
не привлекались к процессу моделирования, оказывалось, что усилия затрачиваются
впустую, во всяком случае в том, что касалось влияния моделей на процесс принятия
окончательных решений в реальном мире и на самих менеджеров
АВТОР. Да, это так
АВТОР.
МЕНЕДЖЕР.
АВТОР.
МЕНЕДЖЕР. Разработка мощных персональных компьютеров и электронных таблиц позволили ря-
довым менеджерам достаточно просто создавать собственные модели, не обращаясь за
помощью к специалистам
Да, во многих ситуациях
Подход, который состоит в построении модели, ее анализе и интерпретации, призван
дополнить, а не заменить собственную интуицию менеджера
Правильно, особенно в тех случаях, когда некоторые аспекты ситуации можно описать
в количественной модели, которая дополнит ваше интуитивное восприятие неизмеримых
аспектов данной ситуации
МЕНЕДЖЕР. Понятно Значит, с помощью моделирования я могу решить свои проблемы
АВТОР.
менеджер.
АВТОР.
Как ни странно, нет'
Вы издеваетесь9 Всем известно, что работа с электронными таблицами не такое про-
стое занятие А вы говорите, что моделирование с использованием электронных таб-
лиц не позволит решить мои управленческие проблемы9
Да, именно так
МЕНЕДЖЕР. Какой ж смысл использовать моделирование, если оно неспособно решить мои проблемы19
АВТОР. Подождите' Вы только что коснулись самого важного заблуждения относительно роли
моделирования в поддержке принятия решений Посмотрите еще раз на первые два рисун-
ка Не случайно ни на одном из них не встречается ни слово ‘ проблема , ни слово
‘ответ Наша конечная цель — содействовать общему совершенствованию принятия
решении в управленческих ситуациях, а не просто предлагать готовые 'ответы'
42
ЧАСТЬ I Модели и моделирование
МЕНЕДЖЕР.	Но у меня нет времени на бесплодные академические дискуссии о семантических раз- личиях'
АВТОР.	Это не входит и в мои планы Действите льно, в данной книге значительное внимание бу- дет уделено тому, чтобы получить для имеющейся задачи некие ответы (но не единст- венно верный ответ) Мне бы хотелось подчеркнуть, что, описывая реальную ситуацию в виде постановки проблемы, вы тем самым переходите на абстрактный уровень процесса моделирования Следовательно, проблемы как таковые действительно существуют в формальном мире, и, значит, существуют решения этих пробчем, но только в фор- мальном мире — а не в реальном Решения абстрактной проблемы редко могут служить готовыми решениями реальных управленческих ситуаций Эти решения нуждаются в тщательной интерпретации в реальном контексте, прежде чем будут сделаны оконча- тельные выводы В результате реализуемое решение может значительно отличаться от ответа, по ученного при анализе модели
МЕНЕДЖЕР.	Иными словами, я должен понять, ответы на какие абстрактные вопросы позволяет получить модель, и как эти ответы получаются, прежде чем смогу правильно интер- претировать их в виде решений, способных помочь мне в разрешении более хаотичной реальной ситуации
АВТОР.	Именно так Если воспринимать ответы не просто как результаты, а рассматривать их в совокупности с постановками проблем, можно обновить интуитивное первоначальное представление об управленческой ситуации. Такое ' обновление интуиции', позволяющее принимать более удачные решения в текущей ситуации, лежит в основе процесса обуче- ния Более того, получаемые от обучения преимущества накапливаются от ситуации к ситуации и в конце концов помогают достичь той мудрости, к которой мы все стре- мимся Таким образом, при моделировании нужно стараться глубже разобраться в си- туации, чтобы не только получить непосредственное преимущество в виде более удачного решения, но и отточить свою интуицию Совершенная интуиция (ичи мудрость) в управ- ленческих ситуациях является залогом успеха менеджера Никогда не следует забывать, что' “цельмоделирования — понимание, а не просто ответы'
МЕНЕДЖЕР.	Вы прямо построили вербальную “модель ’, чтобы помочь мне осознать, как я должен участвовать в процессе моделирования, чтобы “усовершенствовать” свою интуицию
АВТОР.	Точно'
МЕНЕДЖЕР.	Ранее вы отмечали, что процесс моделирования не является научным, а мне казалось, что в количественном моделировании максимально используются научные методы
АВТОР.	Напротив, в процессе моделирования не применяется научный метод Задача классиче- ского научного метода — устранить человеческие суждения, которые могут оказать не- объективное воздействие на знания Поэтому основой приобретения научных знаний явля- ется проверка теорий и результатов посредством повторения управляемых эксперимен- тов К сожалению, в разрешении управленческих ситуаций практически невозможно проводить повторяемые контролируемые эксперименты в силу стоимостных и временных ограничений Поэтому приходится использовать суждения менеджера в качестве (пусть и несовершенного) руководства на каждом шаге процесса моделирования В процессе моде- лирования этап анализа модели является намчным в том смысле, что дчя получения ра- циональных выводов применяются логика и вычисления, однако во всем остальном просле- живается субъективное влияние менеджера
МЕНЕДЖЕР.	Иными словами, моделирование и анализ, взятые в отдельности, не в состоянии осво- бодить меня от действий типа ‘ каков вопрос — таков ответ” при принятии решений
АВТОР.	Правильно И вы должны постоянно вмешиваться в процесс моделирования, поскольку только менеджер может выступать арбитром при выборе содержимого абстракций, ре- зультирующей модели, ее анализе, оценке результатов и их интерпретации В конце кон- цов, ведь именно менеджер несет ответственность за окончательное решение
ГЛАВА 1. Введение в моделирование
43
МЕНЕДЖЕР.
АВТОР.
МЕНЕДЖЕР.
АВТОР.
Все понятно Теперь мне ясно, какова моя роль в процессе моделирования и какие
преимущества я могу получить от моделирования
Мы еще не обсудили другое очень важное преимущество моделирования — полезность мо-
дели как средства общения участников процесса принятия решения Важные решения ред-
ко принимаются в одиночку, требуется сотрудничество многих людей, особенно при реа-
лизации окончательного решения При надлежащем осуществлении процесса моделирова-
ния результирующая модель и полученные с ее помощью рекомендации по принятию
решения могут стать мощными средствами командной стратегии, которые позволят
объяснять и обсуждать идеи, получать отклики и осуществлять кооперацию
Хорошо, я согласен в этом участвовать Теперь можно переходить к моделированию с
использованием электронных таблиц9
Не сразу Прежде необходимо рассмотреть еще несколько тем существующие типы ко-
личественных моделей, этапы построения моделей и роль данных в моделировании посред-
ством электронных таблиц
1.4. Типы моделей
Существует три типа моделей Конструкторы создают макеты самолетов, а архитекто-
ры — макеты городов Это физические модели Второй тип моделей — аналоговые модели —
используется настолько часто, что иногда это даже не осознается Эти модели представ-
ляют множество связей с помощью различных аналоговых посредников Карта основных
дорог является аналоговой моделью территории, автомобильный спидометр представля-
ет скорость с помощью аналогового отображения стрелки датчика, а круговая диаграмма
представляет результаты социологического опроса в виде секторов круга
Наиболее абстрактной является символическая модель, в которой все понятия выво-
дятся посредством количественно определенных переменных, а все связи представляют-
ся в математическом, а не физическом или аналоговом виде Например, физики создают
количественные модели вселенной, экономисты — количественные модели экономики
Поскольку в символических моделях используются количественно определенные пере-
менные, связанные уравнениями, их часто также называют математическими моделями,
количественными моделями или, как в нашем случае, табличными моделями (т е моделями
на основе электронных таблиц).
Менеджерам приходится работать со всеми тремя типами моделей, чаще всего —
с аналоговыми моделями в форме диаграмм и графиков, а также с символическими мо-
делями в виде электронной таблицы или отчетов информационно-управляющей систе-
мы Краткая характеристика трех типов моделей представлена в табл I I
Таблица 1.1. Типы моделей
Тип модели	Свойства	Примеры
Физическая	Осязаемость	Макет самолета,
модель	Понимание простое	макет дома,
Дублирование	и совместное использо- макет города
вание сложные
Модификация и манипулирование
сложные
Сфера использования наиболее узкая
44
ЧАСТЬ I. Модели и моделирование
Окончание табл. 1.1
Тип модели	Свойства	Примеры
Аналоговая модель	Неосязаемость Понимание более сложное Дублирование и совместное использо- вание более простые Модификация и манипулирование бо- лее простые Сфера использования более широкая	Карта дорог, спидометр, круговая диаграмма
Символическая модель	Неосязаемость Понимание самое сложное Дубтирование и совместное использо- вание самые простые Модификация и манипулирование са- мые простые Сфера использования самая широкая	Имитационная модель, алгебраическая модель, модель, построенная в электронной таблице
Несмотря на их различия, все модели имеют одно общее свойство.
I Любая модель является тщательно выбранной абстракцией реальности, которая отра-
: жает представления ее создателя о причинных связях в реальном мире.
В этой книге основное внимание будет уделено созданию символических моделей
(представленных в электронных таблицах) и их анализу с целью получения числовых
(в виде таблиц) и аналоговых (в виде диаграмм) результатов.
Символические (количественные) модели
Как следует из приведенного ранее определения, символические модели используют
математические закономерности для отображения связей между представляющими ин-
терес данными Необходимо, чтобы эти данные были количественными, т е их можно
было выразить в числовой форме
Рассмотрим часто встречающиеся примеры. В модели для оценки альтернативных
решений, состоящих в покупке дома или аренде жилья, учитываются требуемые авансо-
вые платежи, ипотечные ставки, график платежей, повышение стоимости и амортиза-
ция, говоря коротко, числовые данные В модели, которая помогает принять решение,
стоит ли получать степень магистра, должны рассматриваться время обучения, плата за
него и другие расходы, потенциальная заработная плата и тд , — опять числовые дан-
ные Таким образом, числовые данные — основное содержание символических моделей.
Рассмотрим более подробно простейший пример символической модели. Если чело-
век находится в Чикаго, штат Иллинойс, и планирует к обеду быть в Кливленде, штат
Огайо, ему требуется оценить время, которое нужно затратить, чтобы доехать на автомо-
биле из Чикаго в Кливленд. Для этого нужно с помощью атласа или Internet определить
расстояние между этими городами и разделить его на среднюю скорость движения. Та-
ким образом, модель имеет следующий вид:
T=D/S, где Т — время, D — расстояние, a S— скорость.
Такая модель, безусловно, полезна, однако она упрощает реальность, поскольку в ней
игнорируются многие факторы, которые могут заметно повлиять на время путешествия.
ГЛАВА 1 Введение в моделирование
45
В модели не учитываются разнообразные задержки, погодные условия, остановки для за-
правки и т.д Тем не менее, если планируется выехать в 9 утра, а Т= 6 часов, можно счи-
тать, что модель вполне удовлетворяет поставленным целям, т е показывает, что вполне
реально оказаться в Кливленде к обеду.
Теперь предположим, что выехать ранее полудня нельзя, а в 18 30 назначена важная
встреча в Кливленде В таком случае оказывается, что модель слишком проста, чтобы
чувствовать себя уверенно, и возникает желание приблизить ее к реальности, включив
дополнительные условия Можно, например, добавить выражение, отражающее оста-
новки в пути. Тогда модель примет следующий вид
Т = D/S + Rx N, где R — среднее время остановки,
a N— предполагаемое количество остановок
Можно продолжить совершенствование модели, учитывая все новые факторы Неко-
торые из них могут быть оценены только приблизительно. О моделях необходимо посто-
янно помнить следующее
1.	Модель всегда в той или иной степени упрощает реальность.
2.	Модель должна быть настолько подробной, чтобы
•	результат удовлетворял вашим потребностям;
•	степень подробности соответствовала доступным данным;
•	модель можно было проанализировать за то время, которое вы в состоянии уде-
лить этому занятию.
Модели принятия решений
В данной книге основное внимание уделяется моделям принятия решений, символи-
ческим моделям, в которых определенные переменные представляют решения, которые
нужно (или по крайней мере можно) принять Очевидно, что сократить расстояние меж-
ду Чикаго и Кливлендом невозможно. Однако можно выбрать скорость движения, коли-
чество остановок и время, затраченное на каждую из них Это и есть переменные реше-
ния. На эти переменные также могут налагаться определенные ограничения — нельзя
ехать со скоростью больше 300 миль/ч, бензобак имеет ограниченную емкость, заправка
требует определенного времени и т.д. Подобные ограничения будут обсуждаться в гла-
вах 2 и 3, поскольку они являются основой построения реалистических моделей
Цели
Обычно решения принимаются для достижения определенной цели. Таким образом,
помимо переменных модель принятия решения, как правило, содержит явный критерий
эффективности, который позволяет определить, насколько решение близко к цели. При
построении модели чрезвычайно важно указать, как переменные решения будут влиять
на указанный критерий. Рассмотрим следующие примеры
1.	Модель распределения торгового персонала Переменные решения — сколько
продавцов обслуживают торговую территорию Типичным критерием эффектив-
ности является доход, а цель состоит в максимизации дохода от продаж
2.	Составление расписания работы мастерской. Переменные решения — сколько ча-
сов конкретный станок обрабатывает определенные детали и в какой последова-
46
ЧАСТЬ I Модели и моделирование
тельности Возможные цели — минимизировать затраты, общее время выполне-
ния заказа или опоздания при поставках готовой продукции.
3.	Модель управления наличными средствами Переменными решения могут быть
суммы средств различных категорий (наличные, векселя, акции и облигации)
в каждом месяце Типичная цель может состоять в минимизации недополученного
процентного дохода в связи с поддержанием ликвидных активов — наличности
и ее эквивалентов
Подведем итог
1.	Модели принятия решений описывают управленческую ситуацию, но не всеох-
ватно, а выборочно.
2.	В моделях определяются переменные, влияющие на решения.
3.	В моделях принятия решений задаются критерии, отражающие цели моделирования.
1.5.	Построение моделей
Все модели (и простые, и сложные) создаются человеком К сожалению, не существу-
ет экспертных систем для построения моделей (за исключением очень узких специализи-
рованных приложений) Возможно, когда-нибудь революция в вычислительной технике
и программном обеспечении приведет к созданию автоматизированных пакетов для по-
строения моделей управления Однако в настоящее время построение моделей в значи-
тельной степени является искусством, которое требует определенного воображения,
а также владения техническими знаниями.
Для моделирования ситуации вначале нужно представить ее структурированным об-
разом, т е необходимо выработать некий способ, который позволит систематически об-
думать данную ситуацию Следует помнить, что чаще всего приходится иметь дело с фор-
мулировками управленческих ситуаций в виде неких признаков, а не в форме четкой по-
становки проблем Например, торговый представитель компании в Лос-Анджелесе со-
общает, что главный конкурент обошел вашу фирму, предложив обработку заказов по
электронной почте через Internet В повседневном смысле — это управленческая пробле-
ма, но в нашем понимании — это признак Постановка проблемы включает в себя воз-
можные решения и метод измерения их эффективности — две ключевые составные части
любой модели Структурирование — это искусство переходить от симптома к четкой по-
становке проблемы Это исключительно важное умение, которым должен обладать ме-
неджер, чтобы успешно разрабатывать модели
При количественном моделировании бизнес-среды необходимо описывать взаимо-
действия многих переменных. Для этого нужно сформулировать математическую модель.
В следующих главах приводится много примеров построения моделей. Чтобы конкрет-
ные примеры не ввели вас в заблуждение, необходимо помнить, что в реальном мире
обычно не существует единственно верного способа построения модели Различные мо-
дели могут дать различные представления об одной и той же ситуации, как на картинах
Пикассо и Ван-Гога один и тот же предмет будет выглядеть по-разному Хотя моделиро-
вание является искусством, в нем, как и в искусстве в целом, существуют общие принци-
пы Процесс моделирования можно условно разделить на три этапа
ГЛАВА 1 Введение в моделирование
47
1	. Изучение среды с целью структурирования управленческой ситуации
2	. Формализация представления о ситуации
3	. Построение символической (количественной) модели.
Изучение среды
Новички в моделировании обычно недооценивают значение первого этапа — изуче-
ния бизнес-среды с целью структурирования управленческой ситуации В результате по-
ставленная проблема зачастую является не адекватным обобщением реальной ситуации,
а всего лишь описывает некий ее признак Многие факторы, например, внутриорганиза-
ционные конфликты, различия в целях начальников и подчиненных, а также общая
сложность ситуации, могут мешать менеджеру правильно представить ситуацию Пред-
полагается, что определенные факты известны, в то время как на самом деле это не так
При структурировании управленческой ситуации создатель модели должен выбрать
и вычленить из всей среды аспекты, присущие рассматриваемой ситуации Важнейшей
составляющей успеха является опыт — как создания моделей, так и работы в соответст-
вующей среде
Формализация
Второй этап, формализация представления о ситуации, заключается в концептуаль-
ном анализе, во время которого необходимо принять определенные предположения
и упрощения Поскольку рассматриваемая управленческая ситуация включает в себя це-
ли и решения, их необходимо явно указать и определить Может существовать несколько
способов определить переменные решения, и не всегда сразу удается найти наиболее
подходящее определение Цели также могут быть не вполне ясны Даже самые способные
менеджеры могут не иметь точного представления о том, какие результаты они хотят по-
лучить Проблемы возникают и в том случае, когда целей слишком много и необходимо
выбрать одну из них (Как будет показано, обычно невозможно одновременно оптимизи-
ровать две различные цели Поэтому, как правило, бессмысленно пытаться получить
“наибольшую прибыль при минимальных вложениях” или “максимальные блага для
большинства людей”)
На рис 1.4 представлен первый (зачастую наиболее важный) этап формализации управ-
ленческого решения для формулировки задачи — выявление основных концептуальных со-
ставляющих модели На данном этапе детали работы модели не рассматриваются Основ-
ное внимание уделяется определению 1) входов, т е того, что модель должна обрабатывать,
и 2) выходов — того, что модель производит. Модель на данном этапе называется “черным
ящиком”, поскольку еще не известно, какая логика будет реализована в модели
ф Г Решения
s = (контролируемые)
11)
m ф Параметры
^(неконтролируемые)
Рис. 1.4. Модель в виде черного ящика "
После определения входов и выходов модели необходимо разбить их на две категории
Входы, именуемые внешними переменными, делятся на решения — переменные, контро-
48
ЧАСТЬ I Модели и моделирование
лируемые менеджером, и параметры — переменные, которыми менеджер управлять не мо-
жет 1 Примерами переменных решения могут служить сумма, в которую менеджер оценива-
ет свой продукт, размещение производственного оборудования или решение, продавать
филиал или нет Примеры параметров цены, назначаемые конкурентами на аналогичные
товары или услуги, физические ограничения объема складского помещения, стоимость
единицы сырья или прогнозируемое количество осадков. Многие неконтролируемые вход-
ные величины могут быть неизвестны заранее. Трактуя их как параметры, можно строить
модель так, как если бы они были известны. Позднее можно конкретизировать численные
значения данных величин, проанализировав данные и оценив эти значения, или просто за-
дать предполагаемые значения величин при анализе модели.
Выходы, называемые внутренними переменными, делятся на показатели эффективно-
сти (или критерии) — переменные, которые определяют степень приближения к цели,
и результирующие переменные, которые отражают другие следствия моделирования и по-
могают понимать и интерпретировать результаты работы модели. Критерии особенно
важны, так как именно они используются, чтобы определить, насколько удалось прибли-
зиться к конечной цели Поэтому критерии часто называют целевыми функциями. Приме-
рами целевых функций являются доход, доля рынка, совокупные издержки, дисциплина
работников, удовлетворение клиента, доходы от инвестиций. Примеры результирующих
переменных — разбивка дохода по статьям, количество проданных изделий, уплаченные
налоги и другие величины, которые полезно знать.
Несмотря на простоту концептуальной схемы “черного ящика”, она заставляет ме-
неджеров в самом начале процесса моделирования определить, что следует включить
в модель, а что исключить из нее, а также разобраться с классификацией соответствую-
щих факторов. Ниже приводятся некоторые вопросы, иллюстрирующие, на какие раз-
мышления могут натолкнуть менеджера простые идеи, представленные на рис. 1.4
•	Что такое прибыль для моей частной компании — решение или показатель эффек-
тивности9
•	Какими должны быть правильно сформированные множества переменных реше-
ний в отличие от второстепенных переменных9 Например, следует ли считать цену
на свой продукт единственным важным решением, предполагая, что бюджет на
рекламу зафиксирован (кем-то другим) на определенном уровне, или нужно рас-
сматривать и цену продукта, и бюджет на рекламу в качестве одновременно при-
нимаемых решений9
•	Действительно ли менеджер контролирует цену на свой продукт (в этом случае це-
на является переменной решения) или она определяется конкурирующими сила-
ми рынка (в таком случае цена является параметром)?
•	Является ли количество продукта, которое нужно продать, переменной решения,
т е контролируемым входом модели, или количество проданного продукта являет-
ся выходом модели (результирующей переменной), а входом является его цена9
•	Является ли дисциплина работников критерием, т е тем, на что менеджер может
повлиять административным способом, принимая решения о человеческих ресур-
Термин параметр в данном случае используется в самом широком смысле — это внешние факторы, такие
как рыночная цена или ставка налогообложения, которые помогают определить модель и задать ее поведе-
ние Некоторые специалисты по моделированию предпочитают использовать вместо термина параметр
термины неконтролируемая переменная или случайная переменная
ГЛАВА 1 Введение в моделирование
49
сах. Или это параметр, который нужно принимать как данность9 В любом случае,
как измерить дисциплинированность9 Если это понятие слишком расплывчато,
чтобы определять его в качестве переменной, может, следует не включать его в мо-
дель, а учесть позднее, на этапе интерпретации модели9 Или следует использовать
в качестве показателя дисциплины количество прогулов9 Какие факторы в таком
случае влияют на них, и какое подмножество этих факторов должно стать пере-
менными решения?
•	Если доля рынка должна быть критерием, каково точное определение рынка, на
долю которого повлияют решения менеджера? Имеется в виду доля регионально-
го, национального или международного рынка9 Или всех трех9 Идет ли речь о доле
рынка в текущем году, в следующем году или в последующие пять лет9 В чем изме-
ряется доля рынка — в количестве проданных единиц товара или в стоимостном
выражении?
•	Нужно ли включать в модель продажи конкурентов в качестве параметров9 Ведь
если считать продажи конкурентов внешними входами, это означает, что менед-
жер не может влиять на них и должен воспринимать их как заданные Однако ме-
неджер, безусловно, может повлиять на объемы продаж конкурентов посредством
активной системы скидок или усиленной рекламы, которые могут служить пере-
менными решения. В таком случае принадлежащая конкурентам доля рынка
должна быть внутренним выходом (результирующей переменной), а не внешним
входом модели. Но если это выход модели, может быть, следует считать долю рын-
ка, принадлежащую конкурентам, критерием, который нужно минимизировать9
•	Менеджер должен руководствоваться в своей модели своими собственными кри-
териями, временной шкалой и мировоззрением или обязан учитывать предпочте-
ния своего руководства9
•	Основное внимание в модели должно уделяться ежедневным оперативным решени-
ям, более долгосрочному стратегическому планированию или и тому, и другому9
•	Что нужно включить в модель в виде показателей эффективности или параметров,
исходящих от внешних заинтересованных лиц, таких как законодатели, группы
потребителей и акционеры?
Разрабатываемые в книге методы моделирования можно применять независимо от того,
как определены входы и выходы модели Однако приведенные выше вопросы иллюстрируют
важность суждений менеджера для четкого определения элементов “черного ящика”
Предлагается следующий подход к стадии формализации вначале определить цель и со-
ответствующий показатель качества (или несколько показателей), т е основные выходы
модели. Затем выяснить, какие входы модели (переменные решения и параметры) связаны
с достижением данной цели и оказывают влияние на показатели эффективности На осно-
вании этого делается следующий шаг определяются переменные решения и параметры,
которые непосредственно влияют на достижение цели В результате этих рассуждений,
производимых в обратном порядке, получается та же самая формализация модели в виде
“черного ящика” Однако такой подход зачастую проще, поскольку менеджерам легче ду-
мать о ситуациях в терминах целей и критериев (показателей эффективности)
50
ЧАСТЬ I Модели и моделирование
Построение модели
После завершения формализации (в устной или письменной форме) символическую
модель необходимо построить
Как следует из опыта, основной вклад менеджера в построение модели на данном
этапе состоит в том, чтобы разработать внутри “черного ящика” математические уравне-
ния, связывающие переменные Чтобы преодолеть при моделировании “синдром чис-
того листа”, можно вначале использовать упрощенные связи, которые затем уточняются.
К уточнению следует отнестись со всей ответственностью, поскольку эти связи в сово-
купности с данными становятся основой всего процесса моделирования. Этой теме уде-
лено достаточно внимания в последующих главах Главная же идея состоит в том, что
один менеджер с помощью современных методов использования электронных таблиц
в состоянии создать и проанализировать множество практических моделей Даже в более
сложных ситуациях, требующих создания межотраслевой группы, предварительное мо-
делирование может осуществить один эрудированный менеджер.
Основанием для такого утверждения может служить то, что большинство связей мо-
дели представляют собой простые бухгалтерские уравнения (Прибыль = Доход - Общие
расходы) или физические определения (Количество_месяцев = 12 х Количество_лет)
и, следовательно, знакомы и понятны каждому менеджеру Остальные связи модели раз-
работать сложнее, однако в большинстве управленческих моделей сложных уравнений
сравнительно немного Чтобы разработать корректное математическое представление
взаимосвязи двух или нескольких переменных как части общей логики модели, необхо-
дим определенный опыт Можно воспользоваться следующим методом начертить гра-
фик, отражающий требуемую зависимость, т е начать не с математического уравнения,
а с его графика, а затем подобрать соответствующее данному графику уравнение 2 Дан-
ный метод используется также для анализа необработанных данных, что может потребо-
ваться при оценке значений параметров Мы назвали этот метод “моделированием на ос-
нове данных”, ему посвящен следующий раздел.
1.6.	Моделирование на основе данных
Управленческие решения в значительной степени основаны на оценке и интерпретации
данных Однако интерпретация данных возможна только при наличии некой концептуальной
схемы Сложно сказать, что первично, схема или сбор данных Очевидно, что данные необхо-
димы для успешного моделирования Стремление создать более совершенную модель приво-
дит к сбору и хранению дополнительных данных или новых типов данных. Один из первых
приверженцев моделирования в сфере менеджмента, Черчмен (С West Churchman), заявлял,
что в действительности не существует “необработанных” данных, в том смысле, что сам факт
сбора и фиксации данных всегда отражает некие схемы мировоззрения, т.е определенную мо-
дель, построенную в уме (хотя эта модель может явно и не осознаваться) Тем не менее одной
из особенностей технологической цивилизации, по крайней мере в технической сфере, явля-
ется одновременные сбор и использование данных и моделей.
Количественные модели позволяют более целостно и подробно оценивать и интер-
претировать данные, чем “умственные” модели. Кроме того, количественные модели
можно использовать для генерирования данных, а для построения модели обычно необ-
Как будет показано в главе 2, в Excel имеются средства, позволяющие по графикам составлять уравнения
между зависимыми и независимыми переменными
ГЛАВА 1 Введение в моделирование
51
ходимы данные (например, чтобы оценить ее параметры) Часто успех иди неудача в мо-
делировании определяются доступностью данных, их точностью и правильностью выбо-
ра В практике построения и использования управленческих моделей многое зависит от
данных: модель, основанная на данных, может оказаться бесполезной, если необходимые
данные недоступны, или для их сбора требуется слишком много времени и средств
Рассмотрим вопросы, возникающие при использовании данных для построения мо-
делей, на примере гипотетической фирмы HiTech Решения в этой фирме в значительной
мере основаны на имеющейся информации, т е на оценке и интерпретации данных Как
уже отмечалось, с точки зрения моделирования рекомендованное моделью решение
должно представлять собой некое число, такое как цена или продаваемое количество то-
вара Кроме того, необходимо очень четко понимать, что подразумевается под данными
В нашем случае данные — это числа, которые количественным образом описывают фак-
ты, характеризующие управленческую ситуацию и ее среду
Чтобы увидеть, насколько тесно связаны числа и модели, рассмотрим, как в HiTech
принимается решение о том, сколько средств выделить на маркетинг в Европе Прежде
чем принять решение, руководство компании хочет получить представление о том, как
оно отразится на общем доходе от сбыта в Европе Для этого из корпоративной базы
данных запрашиваются данные о расходах на маркетинг в Европе и общем объеме дохо-
дов от сбыта за последние 12 лет, затем они помещаются в таблицы Excel, и создаются две
диаграммы, показанные на рис 1 5
Рис. 1.5. Расходы на маркетинг в Европе и общий доход от сбыта
После изучения представленных на рис 1 5 данных исполнительный директор может
предположить, что существует связь между расходами на маркетинг и доходами от сбыта
Например, он считает, что доход в определенном году напрямую зависит исключительно
от расходов на маркетинг в том же году и не зависит от дохода и маркетинговых расходов
предыдущих лет Он может выдвинуть и другие гипотезы, например, что доходы следуют
долгосрочной тенденции независимо от расходов на маркетинг, или на них влияет некая
комбинация маркетинговых расходов и долгосрочной тенденции Очевидно, что соответ-
ствующие связи будут зависеть от многих факторов, связанных с реальной средой, в ко-
торой оперирует компания HiTech А как же остальные факторы, такие как общие эко-
52
ЧАСТЬ I. Модели и моделирование
комические условия? Какие факторы реального мира могут стоять за различной степе-
нью эффективности маркетинга в разные годы9 Какие реальные отношения отражают
эти данные9 (Это могут быть различия в методах рекламы, в восприимчивости рынка
и спросе, которые в свою очередь являются следствиями различий в экономических ус-
ловиях, погоде или политике правительства.)
Приступая к интерпретации данных, менеджер обязан рассмотреть эти вопросы. Од-
нако главным следствием сказанного является следующее: как только возникают пред-
положения о любых связях между данными, начинается формулировка уравнений моде-
ли. Таким образом, данные интерпретируются как отражение важных внутренних зако-
номерностей Поэтому рис 1 5 играет особенно важную роль: он является выборочным
представлением реальности Раз так, то простая таблица данных удовлетворяет данному
ранее определению модели. Важно подчеркнуть, что сами по себе данные не представля-
ют никакую модель Абсолютные числа ничего не значат. Только когда данным припи-
сываются некие связи, получается модель (по меньшей мере в зачаточной ее форме).
1.7.	Детерминированные и вероятностные модели
Как уже отмечалось, данная книга посвящена моделям управленческих решений. Од-
нако это общее название объединяет много самых разнообразных моделей. Например,
модели для принятия решений часто классифицируются по выполняемым бизнес-
функциям, прикладным дисциплинам или отраслям В табл. I 2 перечислены некоторые
из этих классификаций.
Таблица 1.2 Классификация моделей	
Классификация	Примеры
По бизнес-функциям	Финансовые, маркетинговые, модели учета издержек, модели операций
По дисциплинам	Научные, технические, экономические
По отраслям	Военные, транспортные, телекоммуникационные, некоммерческие
По временному интервалу	На один временной период, на несколько времени ых периодов
По организационному уровню	Стратегические, тактические, операционные
По математическим свойствам	Линейные, нелинейные
По способу представления	Электронные таблицы, обычное программное обеспечение, ка- рандаш и бумага
По степени определенности	Детерминированные, вероятностные
Любая классификация помогает глубже понять, где применяются и как используются
те или иные модели Воспользуемся приведенной в табл 1.2 классификацией и будем от-
дельно рассматривать детерминированные и вероятностные модели.
Детерминированные модели
В детерминированных моделях все необходимые данные точно известны. Таким обра-
зом, в них предполагается, что при анализе модели будет доступна вся информация, не-
обходимая для принятия решения. Примером детерминированной модели может слу-
жить назначение экипажей на каждый из ежедневных авиарейсов в следующем месяце
при условии, что известны расписание рейсов, штат сотрудников, законодательные огра-
ГЛАВА 1. Введение в моделирование
53
ничения на количество рабочих часов, правила работы, установленные профсоюзами
и т.д. Как будет показано в главах, посвященных детерминированным моделям, такие
модели позволяют обрабатывать сложные ситуации, в которых существует много реше-
ний и ограничений. Детерминированные модели особенно полезны, когда в модели мало
неопределенных неконтролируемых входов. Поэтому они часто (но не всегда) использу-
ются для принятия внутренних по отношению к организации решений, как в примере
с назначением экипажей самолетов.
Детерминированным моделям посвящены части 1 и 2 данной книги. В части 1 рассмат-
риваются общие принципы моделирования с помощью электронных таблиц, а часть 2 в ос-
новном посвящена моделям условной оптимизации. В части 2 предлагается введение в ли-
нейное программирование, которое является основным инструментом исследования моделей
условной оптимизации? Вы научитесь создавать модели линейного программирования, оп-
тимизировать их и интерпретировать полученное решение. В части 2 также рассматривают-
ся другие модели, родственные моделям линейного программирования модели целочис-
ленного, нелинейного и многоцелевого программирования
Детерминированные модели важны по следующим причинам
1.	Множество разнообразных важных управленческих проблем можно формализо-
вать в виде детерминированных моделей.
2.	В детерминированных моделях легко налагать ограничения на переменные модели
3.	Существуют программы, позволяющие оптимизировать детерминированные мо-
дели с ограничениями, т.е. находить оптимальные решения; даже для моделей
большой размерности это делается быстро и надежно
4.	Условная оптимизация — очень хороший способ упорядоченного представления
ситуации даже в том случае, когда вы не собираетесь строить модель и оптимизи-
ровать ее.
5.	Практическая работа с детерминированными моделями позволяет усовершенст-
вовать общие навыки создания моделей
Поскольку центральная роль в разработке моделей принадлежит Excel, при чтении
книги потребуется знание этой программы. Краткое описание наиболее полезных при
моделировании свойств Excel содержится в приложении Б
Вероятностные модели
В вероятностных, или стохастических, моделях некоторые входы модели точно не из-
вестны Так, в них предполагается, что значения некоторых переменных не будут извест-
ны до принятия решения, и это необходимо отразить в модели. Примером вероятност-
ной модели может служить решение сделать Internet-компанию открытой (т е предло-
жить для продажи часть акций) до того, как станет известно, будет ли рыночная ситуация
благоприятной (растущий рынок), результатом чего явится высокая цена акций, или не-
благоприятной (рынок с тенденцией к снижению курсов), и, соответственно, цена акций
будет низкой. Как показано в части 3, неопределенность вводится в такие модели по-
В названии линейное программирование термин линейное отражает требование, чтобы все связи моде-
ли выражались линейными уравнениями, а программирование не имеет ничего общего с написанием про-
грамм для компьютера или разработкой программного обеспечения Оно означает нахождение расписания
или программы действий, позволяющей эффективно выполнить задачу ’
54
ЧАСТЬ I Модели и моделирование
средством случайных переменных (в данном случае такой переменной является будущее
состояние рынка ценных бумаг) Вероятностные модели наиболее успешно используют-
ся тогда, когда неопределенных входов модели немного, при условии, что ограничений
также немного или они отсутствуют вовсе. В результате вероятностные модели чаще
всего применяются для принятия стратегических решений, касающихся отношений ор-
ганизации и (неопределенной) среды, с которой она взаимодействует, как в примере
с продажей акций
В части 3 рассказывается о том, какие критерии можно использовать, когда сущест-
вует неопределенность, и как найти оптимальное решение в таких условиях. Это вновь
будут количественные модели принятия решений, в которых делается попытка оптими-
зировать некую функцию, зависящую от переменных решения В этой части книги опи-
сываются анализ решений, организация очередей, два типа имитационного моделирова-
ния, управление проектами и прогнозирование. Поскольку во всех этих моделях неопре-
деленность играет ключевую роль, при чтении данной части книги потребуются
определенные знания из области теории вероятности и статистики В приложении А
предлагается краткое введение в эти дисциплины Оно не в состоянии сделать читателя
экспертом, но может дать общее представление об основных понятиях, необходимых для
понимания соответствующих глав
1.8.	Последовательная разработка модели
Чтобы лучше понять взаимоотношения различных типов моделей в процессе модели-
рования, удобно представить классификацию символических моделей в виде ромба, как
показано на рис I 6 Правая и левая грани ромба отражают построение полярных моде-
лей детерминированных и вероятностных.
Конечно, ни одна модель не может быть полностью детерминированной (не содержа-
щей неопределенности в значениях ни одной переменной) или полностью вероятностной
(когда неопределенность присуща всем значениям переменных) Возвращаясь к ранее опи-
санным примерам, погода может внезапно привести к отмене рейса, а болезнь члена эки-
пажа — сделать невозможным его участие в полете, тем самым предложенное моделью рас-
писание экипажей будет нарушено Аналогично вдруг окажется, что условия на рынке цен-
ных бумаг можно предсказать с достаточной точностью, или модель может содержать
решение отложить в последнюю минуту продажу акций, если условия становятся неблаго-
приятными, тем самым воздействие неопределенности существенно снизится
Верхняя и нижняя части ромба описывают другие противоположности- нисходящее
и восходящее моделирование Нисходящее моделирование предполагает, что процесс может
происходить следующим образом сначала исходя из общих соображений определяются пе-
ременные, затем они связываются в модели на основании гипотез об алгебраических видах
их связей и предполагаемых значениях всех параметров В результате используется нисхо-
дящий способ моделирования, в котором основными являются общие знания и суждения
разработчика модели о значениях данных и математических связях между ними, а также
о будущем применении этих общих знаний. Полученные таким образом модели изначально
являются недостаточно обеспеченными данными и содержат лишь десятки или сотни эле-
ментов данных, часто выраженных как предполагаемые параметры модели
ГЛАВА 1. Введение в моделирование
55
Рис. 1.6. Типы моделей
При восходящем моделировании исходят из того, что модель можно разработать,
сфокусировав внимание на переменных, отражающих собранные данные, затем объеди-
нить их в модель, определив путем анализа данных связи между ними и оценив значения
всех параметров В результате модели строятся восходящим способом, а главным явля-
ются точные, легко доступные данные и суждения об их будущем применении Получен-
ные модели с самого начала хорошо обеспечены данными и содержат сотни или тысячи
элементов данных, которые впоследствии уточняются, чтобы оценить параметры модели
в процессе так называемого извлечения информации изданных
Изображенный на рисунке ромб также иллюстрирует, что все четыре его грани долж-
ны использоваться менеджерами в процессе построения модели, в частности на ранних
стадиях ее формирования Построение модели редко сводится к использованию одного
направления или к простому следованию некому рецепту комбинирования направлений
Элементы модели нужно опробовать, протестировать, оценить (часто вначале субъектив-
но), исправить, вновь оценить и так далее, последовательно переходя с одной “грани”
ромба на другую, используя при этом весь свой творческий потенциал Например, ме-
неджер компании HiTech может начать построение модели себестоимости продукта по-
средством “Моделирования решений”, предполагая или рассуждая (на основе дедук-
ции— нисходящее моделирование), что общая себестоимость проданных товаров со-
ставляет 60% от обшей выручки и это отношение известно (детерминировано) Таким
56
ЧАСТЬ I Модели и моделирование
образом, менеджер в своих построениях следует от вершины ромба вдоль правой сторо-
ны к некой детерминированной модели. Позднее в процессе моделирования менеджер
может рассмотреть данные о выручке и себестоимости прошлых временных периодов;
это означает движение по правой нижней грани ромба “Анализ данных”. В результате
анализа (интуитивного — восходящее моделирование) он может изменить значение про-
центного соотношения и сделать его равным 63%. После этого нужно исследовать, какое
влияние данное изменение окажет на себестоимость или прибыльность в модели HiTech
в целом, что заставляет менеджера вновь вернуться к правой грани “Моделирования ре-
шений”, чтобы субъективно оценить достоверность HiTech-модели.
Еще позже коллеги могут убедить менеджера, что процентное отношение не зафиксирова-
но на уровне 63%, а меняется случайным образом вследствие изменений оптовых цен на сы-
рье, закупаемое компанией HiTech. В результате процесс моделирования будет направлен
в левую часть диаграммы, чтобы найти зависимость между процентной долей себестоимости
в выручке и ценами на сырье (нисходящее моделирование) и проанализировать данные
(восходящее моделирование) для выяснения параметров вероятностного распределения, ко-
торому подчиняются значения процентной доли себестоимости в выручке.
Создание моделей последовательно (метод проб и ошибок) — творческий процесс.
Именно поэтому построение управленческих моделей является скорее искусством, неже-
ли наукой И, как в искусстве, чтобы чему-то научиться, необходим критический взгляд
на то, что сделано другими, а также практика, практика и практика.
1.9.	Моделирование и принятие решений в реальном
мире
Применение моделирования в процессе принятия реальных решений можно разде-
лить на четыре этапа, которые в значительной степени совпадают с представленными на
рис I I этапами самого процесса принятия решений.
1.	Три этапа моделирования (изучение среды, формализация задачи и построение
модели), которым соответствует процесс отбора реальных управленческих ситуа-
ций, их обобщение и формализация и последующая разработка математических
закономерностей символической модели.
2.	Анализ модели с целью получения результатов, т е “решение” модели — выпол-
нение вычислений и других необходимых действий.
3.	Интерпретация и проверка адекватности результатов моделирования, чтобы убе-
диться, что информация, полученная в результате анализа модели, приемлема
в контексте исходной реальной ситуации
4.	Реализация, т.е. применение новых знаний, полученных из интерпретации резуль-
татов моделирования, для принятия решений в реальных ситуациях.
Как и при построении моделей, перечисленные четыре этапа практически никогда
не выполняются строго последовательно Менеджеры реализуют их итеративно, по
крайней мере первые три этапа. Итеративно строится модель (как описано в предыдущем
разделе). Затем она анализируется с целью получения результатов; результаты критиче-
ски интерпретируются, чтобы получить рекомендации, которые зачастую не выдержива-
ют простейшей проверки- соответствуют ли полученные результаты и рекомендации
элементарному здравому смыслу?
ГЛАВА 1 Введение в моделирование
57
Соответствие здравому смыслу — наиболее очевидный тест для проверки достоверно-
сти модели. Если после устранения легко обнаружимых логических ошибок в модели ре-
зультаты или рекомендации противоречат требованиям здравого смысла, не остается ни-
чего иного как вернуться к предыдущему этапу, чтобы выяснить, что же произошло мо-
жет, неверно определена управленческая ситуация, или при формализации был утрачен
реализм, или сама модель оказалась несовершенной. Как правило, необходимо сделать
немало итераций по первым трем этапам моделирования, прежде чем будет получена
приемлемая модель или (иногда случается и такое) менеджер осознает, что его понима-
ние ситуации изначально неверно В любом случае не следует думать, что эта работа вы-
полнена напрасно: сам процесс является весьма поучительным и позволяет значительно
усовершенствовать как модель, так и понимание ситуации менеджером.
Проверка достоверности модели
Сам по себе здравый смысл вряд ли можно считать научным способом проверки дос-
товерности модели. К сожалению, другие методы проверки достоверности также имеют
свои недостатки. Например, часто в заключении о проверке модели говорится, что орга-
низация сэкономила X средств на издержках или получила Y дополнительной прибыли
в результате использования модели принятия решений. При этом возникает вопрос
вдруг такого же (или даже более значительного) повышения доходности можно добиться
безданной модели9
Поскольку в реальном мире бизнеса контролируемые эксперименты, как правило,
невозможны, одним из весьма несовершенных способов проверки правильности модели
является ее ретроспективное использование: данные о решениях, параметрах и результа-
тах для аналогичной ситуации, имевшей место в прошлом, помещаются в модель Затем
результаты, полученные с помощью модели, сравниваются с известными реальными ре-
зультатами Наконец, модель анализируется, и любое дополнительное улучшение реко-
мендаций по принятию решения становится доказательством того, что модель заслужи-
вает доверия
На этапе заключительного анализа следует помнить, что работа менеджера субъек-
тивно оценивается каждый день, причем условия принятия решений постоянно меняют-
ся Поскольку методы поддержки принятия решений предназначены для тех же самых
менеджеров, нет смысла подгонять модели под более высокие, практически недостижи-
мые научные стандарты. При заключительном анализе суждение о правильности модели,
равно как и о ее полезности, выносится на основании здравого смысла Как показывает
опыт, менеджеры, не вовлеченные непосредственно в процесс моделирования, не за-
трудняются при вынесении таких суждений.
1.10.	Подведение итогов
В разрешении разнообразных управленческих ситуаций часто применяются условная
оптимизация и принятие решений в условиях риска. Эти важные темы рассматриваются
в частях 2 и 3 К сожалению, для того, чтобы правильно использовать подобные модели,
не достаточно просто описать их Прежде чем использовать их на интуитивном уровне,
необходимо понять, как такие модели создаются, какие связи существуют между реше-
ниями и результатами. Нужно изучить модели и их применение в различных ситуациях,
только после этого могут появиться собственные идеи. Требуется уделить время критиче-
скому анализу чужих работ, а также попрактиковаться самому Поэтому в нашей книге
58
ЧАСТЬ I Модели и моделирование
много разнообразных примеров и их представлений в виде электронных таблиц, а также
задач, которые позволят читателю усовершенствовать свои навыки в моделировании.
В книге встретится множество бизнес-моделей, в результате анализа которых получают-
ся “оптимальные” решения Это звучит очень обнадеживающе — что может быть лучше
“оптимального” решения9 Однако не следует заблуждаться, в данном случае название
не совсем точно отражает лежащее в его основе понятие. Оптимальное решение дает наи-
лучшии ответ для абстрактной задачи, сформулированной в модели. Но будет ли это реше-
ние лучшим ответом в реальной ситуации, для которой создавалась модель9 На этот вопрос
необходимо ответить до того, как реализовать рекомендации модели Всегда приходится
принимать решение о том, следует ли реализовывать конкретную рекомендацию, но каче-
ство этого решения в значительной мере будет зависеть от того, насколько четко менеджер
видит взаимосвязь между моделью и реальной ситуацией, которую она отражает
Важно также оценить чувствительность результата, т е насколько рекомендуемые мо-
делью решения зависят от значений конкретных параметров, служащих входами модели.
Менеджеры предпочитают решения, которые остаются в силе для широкого диапазона
входных значений, следовательно, хорошее решение не должно превращаться в плохое
при незначительном изменении одного из входов модели. Поэтому в книге постоянно
уделяется внимание анализу чувствительности
Еще раз хотим напомнить, что в книге акцентируется внимание на управленческом
подходе к моделированию, представленном на рис I I. В этом подходе главным является
анализ и структурирование ситуаций, разработка моделей, их оценка, интерпретация ре-
зультатов и реализация решений, а не мастерство применения какого-либо конкретного
метода моделирования При описании способов построения моделей мы руководствова-
лись стремлением применить эти модели в реальном мире. Без этого пользователь элек-
тронных таблиц превратится в математика-программиста, а менеджер останется не у дел.
Надеемся, что данное введение подготовило читателя к восприятию главы 2, с кото-
рой начинается изучение построения управленческих моделей в Excel. Однако нам хоте-
лось бы в заключение сделать два замечания, об используемой терминологии и о здоро-
вом скептицизме
Большинство терминов, используемых при описании процесса моделирования, ин-
туитивно понятны, тем более, что по мере развития модели эта терминология приобрета-
ет все более точный смысл Но необходимость точного определения переменных и связей
модели (переменная решения, параметр, внешняя переменная и тп ) встречает опреде-
ленное сопротивление, возражения и непонимание со стороны других менеджеров, кото-
рые часто играют ключевую роль в реализации решений, полученных на основе анализа
модели В табл. 1 3 представлены термины, используемые в моделировании, их опреде-
ление и соответствующие примеры
Таблица 1 3. Терминология моделирования
Термин	Формальное определение	Пример
Переменная решения	Контролируемая внешняя входная величина	Объем инвестиций
Параметр	Неконтролируемая внешняя входная величина	Процентная ставка
Результирующая пере- менная	Внутренняя выходная переменная	Выплаченные ко- миссионные
Показатель эффективно- сти (критерий)	Внутренняя переменная, используемая для оценки решения (целевая функция)	Дивиденды
ГЛАВА 1 Введение в моделирование
59
Конечно же, менеджеру необходимо быть скептиком. Научитесь остерегаться экспер-
тов и решений, предлагаемых компьютерными моделями (и вашими, и, особенно, чужи-
ми) Доверяйте только своей интуиции Непосредственная работа с моделями учит ана-
лизировать и разбивать на части путь от начальных предположении к заключениям Для
иллюстрации этого в конце каждой главы предлагаются специально разработанные си-
туации для анализа Первый шаг на пути к хорошему решению — постановка правильных
вопросов Практикуясь в моделировании, вы получите возможность развить этот важный
навык.
1.11.	Заключение
В этой главе представлен краткий обзор использования количественных моделей приня-
тия решений, в котором особо подчеркнута роль моделей, построенных на основе данных,
в качестве инструментального средства менеджера Подробно описано взаимодействие ме-
неджера с моделью и его ведущая роль, поскольку именно он принимает окончательное реше-
ние, создает модели, использует и оценивает их Кроме того, мы показали связь между моде
лированием и интуицией менеджера в процессе принятия решений
Модели — это ограниченное представление реальности, поэтому результат анализа мо-
дели не обязательно является решением исходной управленческой задачи В частности, от-
мечалось, что понятие “оптимальное” является математической концепцией, а не концеп-
цией реального мира Однако, если модель правильно построена, а ее результаты тщательно
интерпретируются, она может предоставить менеджеру много ценной информации для
принятия решений
В данной главе были введены такие понятия, как переменные решения, параметры, ог-
раничения, цели и показатели эффективности, которые являются важными компонентами
моделей. Были описаны различные типы моделей и отмечена исключительно важная роль
данных в моделировании. Затем мы обсудили последовательный процесс построения моде-
лей, а также вопросы, связанные с проверкой их правильности Была отмечена роль, кото-
рую играют модели в совершенствовании понимания управления и в совместном обсужде-
нии управленческих ситуаций.
Основные термины
Анализ чувствительности Определение степени воздействия, оказываемого (незначительным) из-
менением внешней переменной на другую переменную
Аналоговая модель Модель, использующая различные средства для представления значении действи-
тельных величин (например, положение стрелок часов на циферблате для представления времени)
Вероятностная модель Модель, в которой некоторые данные не являются достоверно известными,
их неопределенность описывается посредством вероятностных распределений
Внешние переменные Количественные переменные, значения которых определяются вне симво-
лической модели, входы символической модели
Внутренние переменные Количественные переменные, значения которых определяются внутри
символической модели, выходы символической модели
Восходящее моделирование Построение количественной модели, при котором переменные, пара-
метры и математические связи между ними оцениваются на основании анализа имеющихся
данных
60
ЧАСТЬ I Модели и моделирование
Данные Числовые данные, которые количественно отражают взаимосвязи факторов управленче-
ской ситуации
Детерминированная модель Модель, в которой все данные достоверно известны
Линейное программирование Детерминированная модель, состоящая из линейных уравнений и не-
равенств и одного показателя эффективности (целевой функции), который нужно оптимизи-
ровать при наличии заданного набора ограничений
Методы управления Систематическое применение процесса моделирования в управленческих си-
туациях
Модель “черного ящика” Неполная символическая модель, в которой определены только пере-
менные входа и выхода, а математические связи не выявлены
Модель решения Символическая модель, в которой существуют переменные решения и хотя бы
один показатель эффективности
Нисходящее моделирование Построение символической модели, при котором переменные, параметры и
математические связи между ними определяются на основании ранее полученных знаний
Параметр Внешняя переменная, значение которой не зависит от решений, принимаемых менед-
жером, а определяется внешней средой
Поддержка принятия решений Процесс использования данных, моделей и результатов их анализа
для получения информации, помогающей при принятии решений
Показатель эффективности (критерий, целевая функция) Внутренняя переменная, позволяющая
определить, насколько модель близка к цели
Постановка проблемы Выявление возможных решений и метод измерения их эффективности
Процесс моделирования Итеративный процесс абстрагирования, построения модели, ее анализа и
интерпретации, дополненный интуицией и суждениями менеджера, призванный содейство-
вать принятию решений
Результирующая переменная Внутренняя переменная, поставляющая дополнительную информа-
цию, которая призвана помочь менеджеру в интерпретации результатов модели
Решение (переменная решения) Внешняя переменная, значение которой контролирует и определя-
ет принимающий решение менеджер
Символическая модель (количественная модель). Модель, использующая данные, переменные и ма-
тематические связи для представления абстрактных ситуаций (например, модель экономики
определенной страны)
Символическая модель линейного программирования Математическое представление модели ли-
нейного программирования
Структурирование Искусство перехода от признаков (ситуативных факторов) к четкой постановке
проблемы
Физическая модель. Модель, подобная модели самолета, компонентами которой являются физи-
ческие артефакты, обладающие действительными свойствами моделируемой сущности
Контрольные вопросы
Да/нет
1.	Чем сложнее модель, тем она полезней.
2.	В моделях значительная часть окружающего мира обычно игнорируется.
ГЛАВА 1 Введение в моделирование
61
3.	В моделях принятия решений переменные решения получают числовые значения
4.	Модель принятия решения, как правило, отражает взаимодействия и зависимости
между представляющими интерес переменными.
5.	Обычно невозможно указать единственно правильный способ построения модели
управленческой ситуации.
6.	Одним из преимуществ процесса моделирования является то, что он зачастую по-
зволяет избежать необходимости хорошо знать внешнюю среду.
7.	На практике модели иногда создаются группами специалистов, имеющих разные
специальности.
8.	Оптимизационные модели всегда обеспечивают наилучшее решение в реальной
ситуации
9.	Модель может с успехом заменить суждения и опыт менеджера.
10.	Важная роль управления заключается в оценке решения, предоставляемого моде-
лью (при этом решается, следует ли использовать модель и реализовывать ее ре-
зультаты).
11.	Хотя электронные таблицы позволяют легко выполнять вычисления, они не ока-
зывают заметного влияния на принятие решений.
12.	Модели, отвечающие на вопрос “Что будет, если...?”, полезны только для исследо-
вания изменений в значениях переменных решения
13.	Данные нужны только после того, как модель уже построена
14.	Начиная выдвигать гипотезы о существовании какой-либо связи между данными,
вы переходите к формулированию уравнений модели.
15.	Данные используются для построения моделей.
16.	Модель предлагает целостные средства интерпретации и оценки данных
17.	Агрегированные (сгруппированные) данные содержат больше информации, чем
неа третированные.
18.	Модели можно использовать для генерирования данных.
Выберите правильный ответ
19.	Модель — это:
а.	частичное представление реальности;
Ь.	абстракция;
с.	приближение;
d.	идеализация;
е все вышеперечисленное.
20.	Решения в реальных бизнес-ситуациях обычно основываются на:
а. оценке числовых данных;
b числовых значениях, полученных с помощью модели;
62
ЧАСТЬ I Модели и моделирование
с использовании интуитивных представлений;
d всем вышеперечисленном
21.	Модель
а не может быть полезной, если она не отражает реальную ситуацию во всех под-
робностях,
b является вспомогательным средством для человека, принимающего решения;
с после разработки редко пересматривается;
d обладает всеми вышеперечисленными свойствами
22.	Модель
а заставляет менеджера явно указать поставленные цели,
b заставляет менеджера явно указать типы решений, влияющих на цели;
с заставляет менеджера четко указать ограничения, налагаемые на значения, ко-
торые могут принимать переменные;
d обладает всеми вышеперечисленными качествами.
23.	Модели
а играют различные роли на разных уровнях управления компанией,
b редко используются в процессе стратегического планирования;
с дорогостоящий способ принятия рутинных ежедневных решений,
d все вышеперечисленное
24.	Условная оптимизация подразумевает
а лежащая в основе модель является очень точным представлением реальности,
b достижение наилучшего возможного (в математическом смысле) результата
с учетом ограничений;
с истинны оба приведенных выше высказывания
25.	Представим менеджера, интересы и возможности которого далеки от сферы коли-
чественных методов. При изучении курса количественного моделирования перед
ним встанут следующие задачи.
а осознанно принимать или отвергать использование количественных методов,
b получить в свое распоряжение новые способы исследования окружающей среды,
с ознакомиться с теми вспомогательными средствами, которые могут предоста-
вить электронные таблицы,
d все вышеперечисленные.
26.	В результате анализа “Что-если” можно гарантированно найти.
а оптимальное решение,
b хорошее решение;
с возможное решение (если такие решения существуют);
d ничего из вышеперечисленного.
ГЛАВА 1. Введение в моделирование
27.	В вероятностной модели некоторый элемент проблемы:
а. является случайной величиной с известным распределением,
Ь. является случайной величиной, о которой ничего не известно,
с принимает различные значения, которые необходимо точно оценить до начала
вычислений,
d не будет известен до тех пор, пока модель не будет четко формализована
28.	Менеджер, который желает максимизировать прибыль и минимизировать издержки
а должен задать две цели в своей модели;
Ь.	может получить желаемый результат при решении задачи максимизации (доход
минус издержки),
с.	поставил перед собой недостижимую задачу и должен выбрать одну цель,
d.	должен использовать вероятностную модель
29.	Каждая количественная модель-
а представляет данные в числовой форме,
Ь. требует использования компьютера для нахождения полного решения,
с должна быть детерминированной;
d обладает всеми вышеуказанными свойствами
30.	Использование моделей принятия решений.
а.	возможно только тогда, когда все переменные достоверно известны,
Ь.	снижает роль суждений и интуиции в принятии управленческих решении,
с требует от менеджеров высокой степени профессионализма в работе с компью-
тером,
d не обладает ни одним из вышеуказанных качеств
Ответы
1 Нет. 2. Да 3 Да 4 Да 5 Да 6. Нет 7. Да 8. Нет 9 Нет. 10 Да 11 Нет 12 Нет 13
Нет. 14. Да 15 Да 16. Да 17 Нет 18 Да 19 е. 20 d 21. b. 22 d 23 а. 24 b 25 d 26 d
27. а 28 с 29 а 30 d
Вопросы для обсуждения
1 1 “Для сложных управленческих ситуаций не существует моделей” Объясните это утвержде-
ние Приведите несколько примеров
1 2	В чем заключается связь между данными и моделями9
1 3 С какого момента таблица с определенными данными, представленная в электронной таб-
лице, начинает выполнять роль модели9
1 4 Что побуждает менеджера использовать модель для “предсказания” прошлых результатов ’
1 5 Предположим, вам предстоит принимать управленческие решения, но ваши профессио-
нальные навыки и интересы далеки от сферы вычислительной математики На что следует
обратить внимание при изучении моделирования с помощью электронных таблиц9
64
ЧАСТЬ I Модели и моделирование
1 6 Чем, на ваш взгляд, объясняется тот факт, что многие созданные модели никогда не реали-
зуются9
1 7 Как вы понимаете фразу “успешное применение модели”9
1 8 В качестве показателя эффективности предприятия (частного сектора) часто используется
максимизация прибыли Обязательно ли это9 Можете ли вы предложить другую подходя-
щую цель9 (Не беспокойтесь о том, чтобы цель можно было выразить количественно )
1 9 Часто говорят, что для сложных проблем в бизнесе не существует оптимальных решений
Однако оптимизационные модели дают “оптимальные решения” В каком смысле эти ре-
шения оптимальны9
1 10 Рассмотрите следующее утверждение “Наша производственная политика должна быть на-
правлена на достижение максимального выпуска при минимальных затратах” Проком-
ментируйте это утверждение
1 11 Что означает математическое уравнение, в котором данные (значения параметра) точно
не известны Какие предположения могут оправдать использование моделей в таких ус-
ловиях9
1 12 “Придать количественные значения элементам задачи — это не сложно, сложно выполнить
анализ модели ” Согласны ли вы с этим утверждением9 Объясните свой ответ
113 Вы проводите презентацию для генерального директора вашей компании с целью добиться
поддержки в реализации многомиллионного проекта продвижения на рынок нового про-
дукта Он прерывает вас на полуслове “Давайте сосредоточимся на главном Какие рычаги
вам нужны и какой меркой я буду измерять успех проекта в случае его одобрения9” Про-
интерпретируйте данный вопрос в контексте моделирования
1 14 Компания ABC Consulting специализируется на том, что за вознаграждение создает и ана-
лизирует модели решений для своих клиентов-менеджеров “Это очень прибыльный биз-
нес," — говорит Рик Джеймс, президент компании АВС “Мы приходим в организацию,
менеджер кратко описывает существующую проблему Затем мы ее оцениваем и запраши-
ваем необходимые данные После этого строим модель на наших компьютерах или при-
спосабливаем одну из уже существующих в нашей постоянно растущей библиотеке моде-
лей, анализируем ее и передаем клиенту, а также устраиваем для руководства презентацию
с нашими рекомендациями ” На вопрос, просматривают ли они вместе с менеджером
уравнения модели, передают ли ему копию модели, созданной с помощью электронных
таблиц, он ответил “Конечно, нет1 Вы сошли с ума1” Почему компания АВС не заинтере-
сована передавать менеджеру саму модель9 Почему ее клиенты не требуют этого9 В чем со-
стоят преимущества и недостатки такого подхода к моделированию9 Ответьте на послед-
ний вопрос сначала с точки зрения Рика Джеймса, а затем с позиции клиента-менеджера
115 В каких организационных условиях процесс моделирования будет более успешным, а в каких —
менее успешным в поддержке принятия решений в сфере бизнеса9 Чтобы ваш ответ был более
обоснованным, сравните следующие возможные принципы работы организаций
а Сравните организацию, в которой решение принимается коллегиально путем дости-
жения консенсуса, и организацию, в которой существуют внутренние противоречия, и
решения принимаются на основе конфликтующих аргументов
b Сравните крупную централизованную организацию, в которой все решения прини-
маются неким комитетом высокого уровня, и крупную децентрализованную организа-
цию, в которой большинство решений принимается менеджерами локального уровня
с Сравните небольшую организацию, которой управляет один предприниматель, и
крупную организацию, в которой менеджеры работают в различных подразделениях
финансовых, контролирующих, маркетинговых, производственных и т д
d Сравните работу менеджера по производству и менеджера по работе с персоналом
ГЛАВА 1. Введение в моделирование
65
1 19
1 20
е Сравните компанию, продвигающую новый продукт на новом рынке, с компанией,
занимающейся маркетингом известного продукта на традиционном рынке
f Сравните организацию, в которой все менеджеры владеют навыками работы с элек-
тронными таблицами, с компанией, в которой они этого не умеют
g Сравните организацию с централизованным отделом планирования, в котором сосре-
доточены эксперты, выполняющие разработку всех бизнес-моделей для компании, с
организацией, в которой такого отдела нет
h Сравните организации с высокой и невысокой текучестью управляющих кадров
1 Сравните организации с быстрым и медленным ростом доходов
j Сравните организации с высокими прибылями с организациями, терпящими убытки
к Сравните организации, которые занимаются производством, с организациями в сфере
обслуживания
1 Сравните организацию в стране с передовой экономикой, скажем, Франции, с органи-
зацией в развивающейся стране (например, во Вьетнаме)
m Сравните организацию, в которой менеджеры имеют фундаментальное или техниче-
ское образование, с организацией, где менеджеры имеют дипломы по искусствоведе-
“Чем сложнее становится управленческая ситуация, тем более важными становятся дета-
ли ” Почему верно это утверждение9 Какое отношение оно имеет к моделированию9
Что имел ввиду Черчмен, когда сказал, что необработанных данных не бывает9
Ваш новый начальник, исполнительный директор по международной торговле, вызвал вас
к себе в офис и проинформировал “Я решил открыть новый отдел сбыта в Сингапуре Но
мне нужно, чтобы во время встречи в следующую пятницу наш начальник, главный
исполнительный директор по маркетингу, согласился с этим решением Я хочу, чтобы вы
также участвовали в этой встрече и подготовили модель на основе электронных таблиц со
множеством уравнений, диаграмм и тому подобного, которые помогут мне убедить его
Смотрите, не ошибитесь я хочу, чтобы решение об открытии отдела в Сингапуре было ут-
верждено” Является ли такая тактика приемлемым использованием моделирования’ Что
вы будете делать в ответ на данное требование начальника и почему9
Существует мнение, что проверка достоверности, независимо от того, насколько неудовле-
творительны ее данные, никогда не приводит к отказу от модели К отказу от модели может
привести только появление другой модели Согласны ли вы с этим9 Объясните свои ответ
Если предположить, что утверждение справедливо, какова роль проверки достоверности
в построении моделей9
Председатель Совета директоров Федеральной резервной системы США Алан Гринспен
(Alan Greenspan) выступил 4 октября 1999 г с речью, посвященной измерению риска в 21-
м столетии В своем выступлении он, в частности, коснулся применения моделей для из-
мерения риска
“Более важно, что советы директоров, руководители и наблюдательные советы должны ис-
пользовать сбалансированный подход, опирающийся как на модели рисков, в которых отра-
жены лишь некоторые выборочные характеристики, так и на знания, опыт и суждения людей,
применяющих эти модели Способность определить, какая структурная модель наилучшим
образом описывает факторы, влияющие на стоимость активов в любой конкретный период
времени, сама по себе является бесценной Если перефразировать высказывание моего коллеги
Полный текст речи приведен на lVeb-странице Федеральной резервной системы США
(http//www federalreserve gov/)
66 Ч А С Т Ь I Модели и моделирование
Джерри Корригана (Jerry Comgan), появление сложных моделей оценки рисков не устранило
необходимость в умных и опытных людях '
Опишите, как соотносятся комментарии г-на Гринспена с представленным в данной главе
процессом разработки моделей
1 21 Какие преимущества и недостатки присущи физическим и символическим моделям9
1 22 Как можно использовать преимущества количественных моделей для построения более со-
вершенных моделей'’
Литература
1 George Curnow Gary Kochman, Steven Meerster, Debashish Sarkar, and Keith Wilton Automating
Credit and Collections at AT&T Capital Corporation, Interfaces 27, no 1, 1997 29-52
Моделирование с помощью
электронных таблиц
В этой главе...
2.1.	Введение
2.2.	Пример 1—Simon Pie
2	3. Пример 2 — Simon Pie, продолжение
2.4.	Пример 3 —Simon Pie, окончание
2.5.	Пример 4 —XerTech Copy, Inc
2.6.	Искусство моделирования
2	7.	Пример 5 — Oak Products
2	8. Ограничения и условная оптимизация
2.9.	Заключение
Основные термины
Контрольные вопросы
Задачи
Ситуация 1 Kayo Computer
Ситуация 2 Компания Watson Truck Rental Company
Ситуация 3 Индивидуальный финансовый план
Ситуация 4 Компания Santa Rosa Raisins
Ситуация 5 Компания Ebel Mining (часть 1)
Литература
68
Ч АСТЬ I. Модели и моделирование
Практическое применение
Моделирование тендера на закупку судов
береговой охраны США
Одной из функций береговой охраны США является поддержка 50 000 навигаци-
онных устройств, обеспечивающих безопасное плавание в прибрежных водах конти-
нентальных Соединенных Штатов, Аляски, Гавайских островов, а также территорий
США в Карибском море и западной части Тихого океана. К этим навигационным
средствам относятся маяки, буи с подсветкой и без подсветки, сигнальные огни
и дневные бакены Они могут быть плавучими (прикрепленными к якорю) и назем-
ными (установленными на земле или на сваях). С их помощью отмечаются подвод-
ные опасные места и пути для проводки судов. Большие океанские буи могут дости-
гать 3 м в диаметре, 11 м в высоту и весить более Ют Каждый навигационный буй
обслуживается раз в год. Для постоянного буя обслуживание заключается в проверке
его местоположения (уточняются значения его долготы и широты), ремонте обору-
дования и перекраске Среднее время обслуживания буя в зависимости от вида необ-
ходимых работ, а также погодных условий составляет от 25 до 260 мин.
Для размещения федеральных навигационных средств, их планового обслужива-
ния и реагирования на непредвиденные ситуации береговая охрана использует раз-
личные классы судов, из которых два наибольших класса судов составляют суда для
работы в открытом море и суда для работы в прибрежных водах Возникла необхо-
димость обновить флот судов. К этому моменту береговая охрана имела 26 судов для
работы в открытом море и 11 для работы в прибрежных водах, которые обслуживали
7500 навигационных устройств По оценкам специалистов, затраты на замену одного
судна для работы в открытом море составляют $50 млн , а судна для работы в при-
брежных водах — $20 млн Была построена компьютерная модель поддержки приня-
тия решений для замены флота береговой охраны Она должна была проанализиро-
вать расписание работы флота с целью наиболее эффективного обслуживания на-
вигационных устройств В модели учитывался объем необходимого обслуживания,
расстояния, которые должны преодолеть суда для обслуживания каждого буя, и свя-
занные с этим расходы
Задачу усложняло то, что суда должны были выполнять и другие задания, такие
как поиск и спасение на водах, борьба с нарушениями правопорядка и соглашений
мореходства, удаление нефтяных пятен и т п Кроме того, каждый тип судов имеет
различные возможности Например, судно для работы в открытом море может при-
нять груз до 20 т, способно плавать на глубинах свыше 6 футов и оставаться в море до
45 дней, а суда для плаванья в прибрежных водах работают на мелководье, куда не
могут подойти морские суда, они имеют меньшую грузоподъемность и прочность.
В модели также пытались оценить влияние погоды Суммарные потери времени
на обслуживание буев зависели от того, насколько они подвержены воздействию ок-
ружающей среды (незащищены, защищены частично, полностью защищены).
На основании модели принятия решений были получены следующие рекомендации:
оптимальным будет флот, состоящий из 16 морских и 14 прибрежных судов. При разумно
составленном расписании этого будет вполне достаточно Таким образом, флот можно
сократить на 7 судов и сэкономить $350 млн на капитальные затраты, а также сократить
на 500 человек обслуживающий штат (и связанные с этим расходы) [1]
ГЛАВА 2 Моделирование с помощью электронных таблиц
69
2.1.	Введение
В главе I изложены основные идеи и понятия численного моделирования, а также
кратко описан процесс построения моделей. Данная глава посвящена реализации детер-
минированных моделей с помощью электронных таблиц Мы рассмотрим следующие
вопросы.
•	Способы перехода от представлений в виде “черного ящика” к табличным моде-
лям на основе электронных таблиц.
•	Рекомендации по рациональному проектированию и макетированию электронных
таблиц, содержащих числовые модели.
•	Документирование моделей.
•	Средства Excel, используемые для моделирования и анализа
Отметим, что при этом будет представлено большое количество примеров моделей.
Моделирование — это искусство, чтобы научиться создавать модели, необходимо крити-
ческое изучение готовых примеров и, конечно же, практика.
Для удобства обучения будем рассматривать достаточно небольшие модели, построен-
ные с помощью электронных таблиц. Современные системы электронных таблицы, подоб-
ные Excel, позволяют поддерживать модели гораздо большей размерности Существует
множество примеров успешного использования таких больших моделей. Однако полез-
ность модели не определяется ее размерами или математической сложностью Простые не-
большие модели также могут принести большую пользу, если они содействуют принятию
решений Более того, сложные работоспособные модели практически всегда создаются на
основе успешного опыта работы с более примитивными предшественниками
Ни один менеджер не будет принимать всерьез модель, которую он не в состоянии
понять, или поддержка которой слишком обременительна. Грубейшей ошибкой менед-
жера на начальной стадии построения модели является попытка поместить в электрон-
ные таблицы как можно больше деталей, чтобы модель не утратила реализма. Всегда сле-
дует стремиться к простоте, особенно на ранних стадиях моделирования. Модель на ос-
нове электронных таблиц должна (по крайней мере вначале) успешно конкурировать со
своим предшественником — моделью, построенной на “обратной стороне конверта”.
2.2.	Пример 1 — Simon Pie
Вновь созданная компания Simon Pie специализируется на том, что делает из двух за-
купаемых компонентов (фруктов и замороженного теста) яблочные пироги, обрабатыва-
ет их (выпекает, упаковывает, доставляет) и продает местным бакалейным магазинам.
Основатель компании, Самуэль Саймон, хочет построить модель в электронной таблице
Excel, чтобы изучить возможности дальнейшего расширения своей компании Для этого
он выполняет первые три этапа построения модели.
Этап 1. Изучение среды и структурирование ситуации
Применяя идеи, изложенные в главе 1, Саймон обдумывает бизнес-план, анализирует
природу производства десертов и ситуацию на оптовом рынке этих продуктов Посколь-
ку Саймону необходимо немедленно получать прибыль, выбор показателя эффективно-
сти не вызывает сомнений, это — недельная прибыль. Обдумывая ситуацию, Саймон за-
70
ЧАСТЬ) Модели и моделирование
ключает, что наиболее важным его решением является определение оптовой цены на пи-
роги Маркетинговый план Саймона не предусматривает изменения размеров или каче-
ства его пирогов, а бакалейные магазины просто устанавливают свою надбавку к цене
пирога (оптовой цене, установленной Саймоном) Таким образом количество (и стои-
мость) проданных пирогов определяется оптовой ценой, заданной Саймоном. Поэтому
оптовая цена является переменной решения, и именно она наряду с параметрами издер-
жек будет определять прибыль
Этап 2. Формализация модели
В ходе разработки модели определяются переменные входа и выхода, образующие
представление модели в виде “черного ящика” Саймон начертил схему “черного ящика”
так, как показано на рис 2 1. Он исходил из того, что показателем эффективности явля-
ется недельная прибыль, и на основании этого определил концептуальные элементы сво-
ей модели Параметры затрат — это накладные расходы, которые слагаются из: ежеме-
сячной арендной платы, ежемесячных выплат процентов по кредиту и т д.; удельных за-
трат на закупку теста и яблок, удельной стоимости производства пирога (выпечки,
упаковки и доставки)
Цена пирога
Удельные затраты на покупку начинки
Удельные затраты на покупку теста
Удельные затраты на производство
Постоянные издержки
Прибыль
Рис. 2.1. Представление модели Simon Pie в виде “черного ящика”
Следующим этапом построения модели является разработка внутренней логики мо-
дели Многие менеджеры в этот момент испытывают затруднения, схожие с теми, что ис-
пытывают писатели, когда не знают, с чего начать Поскольку построение модели явля-
ется итеративным процессом, и первоначальный вариант будет многократно пересмат-
риваться, прежде чем получится удовлетворительная модель, главное — начать
Менеджеры, являющиеся новичками в моделировании, часто используют для струк-
туризации своих формулировок диаграммы влияния и незаметно преодолевают указан-
ное затруднение Диаграммы влияния позволяют организованно подойти к моделирова-
нию, кроме того, с них начинается создание документации модели, полезной для объяс-
нения содержащихся в ней идей Диаграмма влияния отражает связи между внешними
переменными модели и показателем эффективности, но не указывает явной математиче-
ской зависимости между ними Создание диаграммы начинается с переменной показате-
ля эффективности (Если показателей эффективности несколько, нужно выбрать один из
них ) Затем переменная показателя эффективности разбивается на несколько промежу-
точных переменных. которые в модели математически комбинируются, чтобы определить
значение данного показателя Эти промежуточные переменные — часть внутренней ло-
гики модели В свою очередь, промежуточные переменные разбиваются на более детали-
зированные промежуточные переменные Процесс разбиения продолжается до тех пор,
пока не будет определена внешняя переменная, те пока вы не выйдете за пределы
“черного ящика”, определив входную переменную решения, или параметр
ГЛАВА 2 Моделирование с помощью электронных таблиц
71
Не существует четких и простых правил, диктующих, какие переменные нужно вклю-
чить в диаграмму влияния, цель диаграммы — помочь начать (и упростить) построение
модели, а не выявить полностью все промежуточные переменные в виде окончательного
варианта модели В ходе разработки модели по мере дальнейшей формализации могут
возникать другие промежуточные переменные Проиллюстрируем данный процесс на
примере компании Simon Pie
Начнем с показателя эффективности — еженедельной прибыли Саймон определил
две ее составляющих — доход и общие затраты Каждая из этих промежуточных пере-
менных разбивается на составляющие, те, в свою очередь, подвергаются дальнейшему
разбиению и так далее, как показано на рис 2 2 Создание диаграммы заканчивается,
когда определены все входные переменные модели
Рис. 2.2. Диаграмма влияния для модели компании Simon Pie
Совет. Диаграммы подобного рода легко создавать в Excel Нужно перейти на новый рабочий
лист, отключить отображение сетки и вывести на экран панечь инструментов Рисова-
ние. Предлагаемые этой панечью средства позволяют построить множество разнообразных
схем Например, на рис 2 2 переменная решения — цена пирога — показана в виде прямо-
угольника, в то время как остальные переменные изображены прямоугольниками с закруглен-
ными углами Такого вида прямоугочьники (как и соединительные линии между ними) легко
создать с помощью инструментов панели Рисование
72
ЧАСТЬ I. Модели и моделирование
Исследование рис 2 1 и 2.2 может многое сказать об образе мыслей м-ра Саймона. Об
этом говорят не только те факторы, которые он считает важными для получения прибы-
ли от пирогов, но и те факторы, которые не включены в модель. Таким образом, диа-
грамма отражает бизнес-взгляды Саймона в виде выборочного представления действи-
тельности Например, из диаграммы следует, что ни реакция конкурентов, ни общая
экономическая ситуация не рассматриваются им как факторы, влияющие на прибыль,
по крайней мере в краткосрочном плане. Также не предусмотрены расходы на хранение,
возможно, потому, что пироги продаются сразу после выпечки. Нет переменных оборот-
ного капитала и движения платежей, поэтому они не могут заметным образом повлиять
на прибыль. Не учитываются факторы материально-технического обеспечения, график
выпечки и доставки, маркетинг и человеческие ресурсы. Возможно, он планирует доба-
вить эти и другие факторы на более поздних этапах процесса моделирования, а первона-
чальную модель строит максимально упрощенно (мудрая тактика).
Этап 3. Построение модели
На третьем этапе при непосредственном построении модели требуется ввести в элек-
тронную таблицу уравнения, связывающие переменные. В письменном виде большинст-
во предложенных Саймоном уравнений отражает простые бухгалтерские зависимости.
Прибыль = Доход — Общие затраты,
Доход = Цена пирога х Спрос,
Общие затраты = Затраты на обработку + Затраты на продукты + Постоянные издержки,
Затраты на продукты = К-во начинки х Удельные затраты на начинку + К-во теста х
хУдельные затраты на тесто.
На рис 2 3 показано представление в Excel полученной модели недельной прибыли.
Значения параметров, предложенных Саймоном, приведены в табл. 2.1.
Рис. 2.3. Исходный вариант модели еженедельной прибыли компании Simon Pie
Совет Сдвиг текста в ячейке достигается с помощью щелчка на кнопках Увеличить
отступ или Уменьшить отступ панели инструментов форматирования.
ГЛАВА 2. Моделирование с помощью электронных таблиц
73
Таблица 2.1. Значения входных параметров для модели Саймона
Цена пирога	$8,00
Спрос	16 тыс
Удельные (на один пирог) затраты на производство $2,05
Удельные затраты на закупку начинки	$3,48
Удельные затраты на закупку теста	$0,30
Постоянные недельные издержки	$12
Рассмотрим, как выглядит модель в Excel Ее представление структурировано, чтобы
облегчить интерпретацию модели В целом при построении моделей в электронных таб-
лицах необходимо следовать следующим рекомендациям.
1.	Переменные входа представляются вместе в виде отдельной поименованной таб-
лицы.
2.	Четко обозначаются выходные результаты модели.
3.	Там, где нужно, указываются единицы измерения
4.	Параметры хранятся в отдельных ячейках. Их подстановка в формулы произво-
дится посредством ссылок на соответствующие ячейки Хранение параметров от-
дельно от формул, в которых они используются, облегчает изменение, анализ и
документирование модели.
5.	Для удобства чтения таблиц следует использовать полужирный шрифт, сдвиг со-
держимого ячеек, подчеркивание и другие предлагаемые Excel возможности фор-
матирования.
После построения модели Саймон перешел ко второму этапу моделирования — ана-
лизу модели.
Анализ “Что-если”
Простейшим способом анализа моделей в электронных таблицах является составле-
ние последовательностей различных входов, получившее название анализ “Что-если”'.
Название очень точно отражает суть производимых действий. Например, Саймон хочет
узнать, что произойдет с интересующими его выходными переменными, если некая ха-
рактеристика среды (параметр) или переменная решения изменится определенным обра-
зом. Это основные вопросы любой управленческой задачи, поэтому анализ “Что-если”
является наиболее часто используемым способом анализа моделей, созданных в элек-
тронных таблицах. С помощью анализа “Что-если” Саймон может определить, как отра-
зятся на прибыли изменения в значениях параметров или переменных решения Напри-
мер, на рис. 2.4 показаны два различных значения прибыли при спросе 20 тыс пирогов
при цене $7,00 за штуку и 12 тыс. пирогов при цене $9,00
Иногда специалисты по моделированию называют этот вид анализа "прогнозированием но мы зарезерви-
руем этот термин для использования в вероятностных моделях
74
ЧАСТЬ! Модели и моделирование
	> ,	А	 2 >Переменные решения:	в jc	2 Переменные решения:		I В С
дЗудЦена пирога 4 'Спрос и объем продаж (тыс шт в неделю) 5 J 6 Параметры:	$7,1)0 20	хЗ.:хЦена пирога ___4 Спрос и объем продаж (тыс шт в неделю) J»/ 6 Параметры:		$9 00 12
с 7с J /дельные затрать! на обработку „8 > Удельные затраты на покупку начинки с 9_ j Удельные затраты на покупку теста 10' i Постоянные издержки		$2,05 $3,48 $0,30	7 Удельные затраты на обработку ofc	Удельные затраты на покупку начинки 9 Удельные затраты на покупку теста :: 10 ъ Постоянные издержки		$2,05 >- $3.49 $0.30	. $12 ;
12 Финансовые результаты		12 Финансовые ретультаты		
; 13 ! ДОХОД 14 1 Затраты на обработку 16 ; Затрать! на ингредиенты 16 • Накладные расходы _17_Юбщие издержки 18 (Прибыль (до уплаты налогов) 19 	$140 $41 $76 $12 $129 $11 '	13 Доход 14 ; Затраты на обработку 16 Затраты на ингредиенты 16 Накладные расходы ЛТ^Общие издержки 18и Прибыль (до уплаты налогов) 19 	$108 . $25 i $45 $12 $82 U $26
Рис. 2.4. Два результата анализа ' Что-если’ для модели Simon Pie
Уточнение модели
Анализируя модель и сравнивая ее с диаграммой влияния (см рис 2 2), Саймон замеча-
ет, что в его модели цена пирога и спрос считаются независимыми переменными Он по-
нимает, что данное предположение нереалистично при прочих равных условиях высокая
цена приведет к снижению спроса, а в его модели не отражена показанная на диаграмме
связь между этими переменными Уравнение, связывающее цену пирога и спрос, не оче-
видно — над его составлением необходимо подумать Простейшее уравнение, связывающее
две переменные, это линейное уравнение В данном случае зависимость должна быть об-
ратно пропорциональной, т е чем выше цена, тем меньше спрос (продажи) После некото-
рых размышлении Саймон пришел к заключению, что при цене, равной $12 за пирог, спрос
будет равен нулю, а при цене ниже S12 каждое снижение цены на $1,00 приведет к увеличе-
нию спроса на 4000 штук в неделю Поэтому он предположил, что зависимость спроса
(в тысячах штук в неделю) от цены выражается следующим линейным уравнением
Спрос = 48 - 4 х Цена пирога (для цен в диапазоне от Одо $12)
На рис 2 5 показана уточненная модель, в которой входная переменная Спрос явля-
ется линейной функцией переменной Цена пирога Чтобы Excel-модель была целостной
и понятной, мы следовали упомянутым выше правилам 1-5, Добавим еще одну рекомен-
дацию правило 6
6.	Физические результаты модели необходимо отделить от финансовых и экономи-
ческих
Как и ранее, Саймон может для своей новой модели провести анализ “Что-если”. Хо-
тя этот анализ в Excel выполняется достаточно просто, он имеет некоторые недостатки
•	Если не создавать отдельные распечатки, результаты нового анализа “Что-если”
при пересчете таблицы с новыми значениями замещают результаты предыдущего
анализа, что затрудняет их сравнение
•	Рассматривая результаты анализа “Что-если” по отдельности, сложно определить
чувствительность одной переменной к изменениям другой
•	Анализ “Что-если” недостаточно систематичен
ГЛАВА 2 Моделирование с помощью электронных таблиц
75
Simon Pie Со. - Модель недельной прибыли
2	Переменные решения'
3	Цена пирога
4	Параметры:
5	Удельные затраты на обработку
6	Удельные затраты на покупку начинки
1	Удельные затраты на покупку теста
в’"	Постоянные издержки
JL.	Коэффициенты уравнения спроса
10	Свободный член
п	Коэффициент пропорциональности
12	Физические результаты
1L	Спрос и объем продаж (тыс шт.)
14	Финансовые результаты
15	Доход
16	1 Затраты на обработку
17	1 Затраты на ингредиенты
18	( Накладные расходы
19 (Общие издержки
Рис. 2.5. Модель компании Simon Pie, в которой отражена связь между спросом и ценой пирога
К счастью, созданная Саймоном модель содержится в одном столбце рабочего лис-
та Excel В таких случаях наиболее простой способ зафиксировать множество результа-
тов анализа “Что-если” заключается в копировании всех данных модели в дополни-
тельные столбцы, по одному столбцу для каждого анализа “Что-если” 2 Фактически
каждый столбец становится копией исходной модели, что позволяет сравнивать между
собой последовательности множественных изменений данных, как показано на
рис 2 6 При систематическом изменении одной переменной такое расположение дан-
ных удобно для построения диаграмм и графиков, полезных для анализа чувствитель-
ности, а также для демонстрации и пояснения результатов моделирования В данном
примере показано, что прибыль будет наибольшей при значении цены около $9,ОО,3 а
точка безубыточности, в которой прибыль становится равной 0, соответствует цене,
приблизительно равной $6,25 Кроме того, из графика следует, что прибыль не слиш-
ком зависит от цены около $9,00
Совет. Для целей моделирования рекомендуется использовать точечный тип диаграмм, по-
скольку только он позволяет строить график зависимости Y от X согласно их значениям
Другие же типы диаграмм будут искажать действительный вид графика, если данные по
оси X распределены неравномерно Более подробно построение диаграмм Excel описано
в приложении Б.
Если модель занимает несколько столбцов, то альтернативным способом генерирования отчетов анализа
"Что-если" является использование сценариев (команда Сервис ^Сценарии)
Дальнейший анализ показывает, что прибыль будет примерно на $700 выше при цене $8,90, но такая точ-
ность обычно не требуется
ЧАСТЬ I Модели и моделирование
Рис. 2.6. Выходные результаты для различных значений цены в модели
компании Simon Pie
Для дальнейших исследований Саймон скопировал исходную модель на новый лист ра-
бочей книги и продолжил анализ модели Во-первых, для выполнения анализа чувстви-
тельности он выбрал в качестве базового значения цены $9,00. (Напомним, что в ходе ана-
лиза чувствительности исследуется воздействие (относительно незначительных) изменений
входных переменных на другие переменные, чаще всего — на показатель эффективности.)
В данном случае Саймона интересует воздействие малых изменений цены на прибыль, ко-
торая является критерием эффективности Чтобы не путаться в числах, он решает исследо-
вать, на сколько процентов изменится прибыль при заданном процентном изменении цены
(в экономике данный подход известен как анализ эластичности). Саймон включает в ис-
ходную модель дополнительные строки, чтобы вычислять процентные отношения
(рис 2 7) При этом он использовал команду Excel Окно^Разделить, чтобы скрыть лиш-
ние детали исходной модели. Обратите внимание на то, что Саймон использует абсолют-
ную адресацию в формулах вычисления процентов, таким образом, его формулы всегда
ссылаются на базовые ячейки при копировании формул в новые ячейки.
Совет. Команда Окно ^Разделить позволяет разделить окно рабочего листа горизонталь-
но и/или вертикально, что дает возможность сконцентрировать внимание только на опре-
деленных группах ячеек листа Более подробно использование этой команды рассматривает-
ся в приложении Б
ГЛАВА 2. Моделирование с помощью электронных таблиц
77
Рис. 2.7. Анализ чувствительности модели компании Simon Pie
Анализ чувствительности (рис 2.7) открыл Саймону важный факт- небольшое (5%)
уменьшение цены по сравнению с базовой приводит к заметному росту спроса и продаж
(15%) при совсем незначительном снижении недельной прибыли (менее 2%). Саймон
может предпочесть установить цену $8,10, что на 10% ниже базовой, и тем самым поте-
рять около 10% прибыли, чтобы добиться 30% увеличения недельного объема продаж
Это решение тем более привлекательно, что компания имеет статус вновь созданной,
и ей нужно быстро завоевывать рынок и привлечь клиентов Такие соображения часто
называют анализом компромиссов, поскольку они отражают, насколько нужно пожертво-
вать одним критерием эффективности (прибылью), чтобы добиться определенного
улучшения другого критерия (спрос и объем продаж).
Подведем итог Саймон начал разработку своей модели снизу вверх, с простых связей,
выявленных диаграммой влияния, после первичного анализа он дополнил модель, вклю-
чив в нее обратно пропорциональную зависимость между ценой и спросом Затем он
оценил модель с помощью анализа “Что-если”, нашел точку безубыточности, провел
анализ чувствительности и, наконец, анализ компромиссов Все это дало ему возмож-
ность получить ценную информацию.
2.3.	Пример 2 — Simon Pie, продолжение
Хотя Саймон поначалу был вполне доволен своей моделью, у него возникли опреде-
ленные проблемы. Как часто бывает с первым вариантом модели, оказалось, что дейст-
вительная недельная прибыль несколько меньше, чем предсказывалось моделью Изучая
поведение модели при более низких ценах, Саймон обнаруживает, что предлагаемая мо-
делью формула затрат на производство дает правильные значения затрат для базового
спроса в 12 тыс. штук, но не срабатывает для других значений спроса Саймон начинает
проверять достоверность данной части модели, уточняя данные о затратах на произвол-
78
ЧАСТЬ! Модели и моделирование
ство для различных объемов производства Эти данные и предсказанные исходной моде-
лью значения затрат на производство (= 2,05 х Спрос), а также построенный график
представлены на рис 2 8 На рисунке показано, что формула вычисления затрат на про-
изводство не обеспечивает должного соответствия действительным данным, что, в свою
очередь, может привести Саймона к принятию неверных решений.
I А _ _1 | Данные о К-во Зат пирогов O6f	..в	 затрата) раты на >а0отку	I с j < (тыс. $) Затраты на обработку	
2 । (тыс шт) (реальные)		(модель)	
3	6 $	10 10	$	12 30
4~1	8 $	11 20	$	16.40
~б1	10 $	16.50	$	20 50
6	12 $	24 60	$	24 60
	32 40	$	28.70
16 $	41 10	$	32.80
_9 I	18 $	45 30	$	36 90
10j	20 $	55 10	$	41 00
Il 1	22 $ 12  13 14 1 _15J		59.90	$	45.10
D	I Е |	F г,- I.. . 6 -	1 .. Н
	Затраты на обработку		
55 - 50 - . 45 - §40- 4 35 -	♦ Затраты ча обработку (реальные) •	З”;- '	 (модель)	♦ •	
^30- 25 - 20 - 15 -	• ♦		
f	5	0	10 12 14	16 10 20 К во пирогов (тыс шт)		22 24
Рис. 2.8. Сравнение действительных и вычисленных моделью значении затрат на производство
Хотя для уточнения уравнения затрат на производство можно использовать матема-
тические методы (или метод проб и ошибок), проще воспользоваться имеющимся в Excel
средством Линия тренда, чтобы получить уравнение непосредственно из реальных дан-
ных о затратах Для этого нужно щелкнуть на графике затрат на производство, т е выде-
лить данные, на основании которых построен график, затем щелкнуть правой кнопкой
мыши и выбрать в контекстном меню команду Добавить линию тренда, как показано на
рис 2 9 Откроется диалоговое окно Линия тренда
т 2	1 Даннь К-во ! пирогов ;(тыс шт )	В ie о затрата Затраты на обработ ку (реальные)	С < (тыс. $) Затраты на обработку (модель)
3	6	$	10 10	$	12 30
	8	$	11 20	$	16 40
б“	10	$	16 50	$	20.50
6	12	$	24 60	$	24 60
		$	32 40	$	28 70
8	16	$	4110	$	32 80
9	18	$	45 30	$	36 90
10	20	$	55 10	$	41 00
11	22	$	59 90	$	45.10
12			
13_			
			
_15_			
К во пирогов (тыс шт )
Рис. 2.9. Построение линии тренда на основании реальных значении затрат на производство
ГЛАВА 2 Моделирование с помощью электронных таблиц
79
Для простоты Саймон выбирает линейную зависимость и щелкает на вкладке Пара-
метры, где указывает, что нужно отобразить уравнение тренда на графике (рис 2.10).
Рис. 2.10. Подбор уравнения, соответствующего реальным значениям затрат на производство
Полученное уравнение показано на рис. 2 11. Конечно, для более точного соответст-
вия данным можно было выбрать и нелинейный тип для уравнения тренда, но Саймон
хочет сохранить пока более простой вид модели Проверка показала, что линейный тренд
гораздо лучше соответствует реальным данным о затратах на производство (по крайней
мере для спроса свыше 8 тыс штук, а это именно тот диапазон спроса, к которому при-
шел Саймон, исходя из результатов анализа чувствительности)4
На рис 2 12 представлена пересмотренная модель Саймона, в которую включено
уточненное уравнение затрат на производство.
Как и ранее, уточненная модель располагается в одном столбце рабочего листа, поэтому
можно зафиксировать множество решений анализа “Что-если”, скопировав данные модели
в соседние столбцы, по одному столбцу на каждый сценарий “Что-если” (рис 2 13) Срав-
нение представленных на рис 2 13 данных с результатами анализа чувствительности на
рис 2.7 показывает, что более реалистичное уравнение затрат на производство заметно по-
влияло на результаты вычислений в модели Как ни странно, но более высокие затраты
в этой более точной модели не слишком влияют на значение недельной прибыли, наблюда-
ется небольшое снижение (менее 1%) максимальной прибыли с $26,04 до $25,79 Однако
максимальное значение прибыли достигается при более высокой цене ($9,50 вместо $9,00)
и, как следствие, меньшем объеме спроса и продаж (примерно 10 тыс вместо 12 тыс , что
составляет около 17% всего объема продаж). Одна из задач моделирования состоит в том,
чтобы оценить неблагоприятные последствия снижения объема продаж Понятно, что
в данном случае Саймону нужно постараться снизить реальные затраты на производство,
4 Описанный способ определения уравнений тренда приемлем, если реальные данные расположены достаточно
близко к кривой тренда. Если среди реальных данных существуют точки, расположенные далеко от найден-
ной кривой, то используются вероятностные методы определения уравнения тренда Эти методы будут
рассмотрены в главе, посвященной прогнозированию
80
ЧАСТЬ I Модели и моделирование
чтобы приблизить их к изначально предполагавшейся зависимости. Аналогично можно
проанализировать точность других предполагаемых зависимостей модели, например, урав-
нений затрат на продукты или спроса и продаж.
Рис. 2.11. Новое уравнение затрат на производство
Рис. 2.12. Пересмотренная модель компании Simon Pie
ГЛАВА 2 Моделирование с помощью электронных таблиц
81
Рис. 2.13. Результаты расчетов в пересмотренной модели
Одним из результатов уточнения модели и включения в нее более точных уравнений
является появление в рабочей таблице Excel “технических” параметров, обычно не ото-
бражаемых в высокоуровневых управленческих моделях и соответствующих отчетах, по-
строенных по этим моделям Чтобы избежать появления таких параметров в отчетах,
многие разработчики моделей стремятся “спрятать” их в формулах ячеек рабочих таблиц
Однако это противоречит данным ранее рекомендациями по хорошему стилю моделиро-
вания. Более того, в таком случае затруднительно проводить анализ чувствительности
этих параметров. Вместо этого мы предлагаем использовать такую возможность Excel,
как создание структур на рабочих листах Она позволяет убрать технические подробно-
сти, временно скрыв соответствующие строки или столбцы при печати модели для отче-
та, и в то же время сохранить их в рабочих листах Excel для документирования и анализа
модели. Чтобы в пересмотренном варианте модели Simon Pie при печати отчетов убрать
технические параметры двух уравнений (спроса и затрат на производство), нужно выде-
лить соответствующие им строки и выбрать команду Данные^Группа и структура
Группировать, как показано на рис 2.14
Если щелкнуть на кнопке со знаком на панели структуры с правой стороны окна
рабочего листа (рис. 2 15), соответствующие строки будут скрыты
82
ЧАСТЬ I Модели и моделирование
Рис. 2.14. Группировка строк для создания структуры в модели компании Simon Pie
1 Simon Pie Со - Модель недельной прибыли _2 Переменные решения				{ р	Е	FIG	Н
; 3 Щена пирога	$8.50 : 4 Параметры:		$8.75	$9,00	$9,25 ;	$9,50 ; $9,75	$10.00,
- _5 ' Удельные затраты на покупку начин! $3.48	$3,48	$3.48	; $3,48 :	$з,48	$з,48	$3,48 8
r*6J Удельные затраты на покупку теста $0,30	$0,30	$0.30	; $0,30	$0,30	$0.30	$0,30 |
"~7 Постоянные издержки	 $12 ’	1 8., Коэффициенты уравнения спроса ,, .	$12	$12	$12 ;	$12 j , $12 .j	$12 г )
 19  j Свободный член	48 ' j Ю I Коэффициент пропорциональност -4 • (п Уравнение затрат на обработку	48	; 48	48	48	’48	" 48
		-4		4 . !	~4 ,
с у 12 '! Свободный член	-14 339	-14.339	-14,339	-14,339	-14 339 : -14 339 '	-14 339 -
‘ ! 19 ’ Коэффициент пропорциональност 3,375	3,375	3,375	! 3,375 !	3,375 J 3,375 	3,375 -
Гы"Фшическив ретультаты						
’ 15 1 Спрос и объем продаж (тыс шт )	14,0 !~16 Финансовые ретультаты		13,0	* l’2,o”'	11 .0	10.0 !	9,0	8.0	|
j 17(Доход 	$119		$114	$108	! $102' !	$95	$88^	$80
: 18 ' Затраты на обработку	$33	$29,54	’ $26,16	: $22.79 ;	$19,41 ! $16,04 !	$12,66 •'
•жгггттэ 1 Затраты на ингредиенты	$53	$49	$45	; $42 =	$38$34	$30
' .?8J Накладные расходы	$12	$12	$12	$12 •		$12	$12	$12 X
 ^ШОбщие издержки	$98	$91	$84	$76 .	$69	: $62	$55 г
•’*22”прибыль (до уплаты налогов)	$21.17 ' 23" 1	"	' •	$23,07	$24,5	$25,4	$25,8 : $25,7 !	$25,1
Рис. 2.15. Структура рабочего листа модели компании Simon Pie
Если потом щелкнуть на кнопке со знаком “+” (рис. 2 16), скрытые строки вновь ста-
нут доступными для дальнейшей работы и анализа
ГЛАВА 2 Моделирование с помощью электронных таблиц
83
	-в ч	С	I. О		F ' G L Н ...1		
I Simon Pie Co. - Модель недельной прибыли							
2 Переменные решения'							
1 3„ЛЦена пирога  <| 'Параметры:	$8.50	$8.75	 $9,00 :	$9.25"'"	Г $9,50	$9.75	" $1000
1 5 . удельные затраты на покупку начинг	$3 48	$3,48	$3.48 '	Г $3.48*	$3 48 '	$3.48 *	; $3.48 1.
'	:• j Удельные затраты на покупку теста	$0 30	$0 30	$0,30	: $0,30	 $0 30	$0 30	: $0 30 |
Постоянные издержки		$12	$12	• $12	; $12^	 $12 /	$12 ,	$12
+i 1 14 ; «Оптические ретультаты								
1в>я Спрос и объем продаж (тыс шт ) 1Е Финансовые ретультаты		14.0	13,0	12,Ь'	: 11,0	10.0	9.0	*80
' 'рЙЯДохОД	$119	$114	$108	: '$102 '	$9б' 	$88	$80 '
Ц1Й затраты на обработку	$33	$29.54	$26,16	: $22.79 	$19,41 5 $38	$16.04	$12,66 •;
Г1М Затраты на ингредиенты	$53		$49	 $45	$42		$34	$30
накладные расходы	$12	$12	$12	$12	$12	$12	$12 j
|,21 'p’W'e издержки	$98	$91	$84	$76	$69	$62	i $55	|
Прибыль (до уплаты налогов) 23	$21.17	$23,07	$24,5	$25,4 i	$25,8	$25.7	$25.1
Рис. 2.16. Модель со скрытыми строками
Совет Если группа ячеек содержит данные, на основе которых построен график, то сокры-
тие этой группы приведет к временному удалению этих данных из графика. Это позволяет
быстро изменять графики, отображая разные ряды данных
На рис. 2 13 столбцы используются для записи разных исходных данных модели, что
позволяет одновременно отобразить несколько сценариев анализа “Что-если” и увидеть
их взаимосвязи, а также провести анализ чувствительности (в данном случае для различ-
ных возможных значений цены пирога) В других вариантах модели столбцы могут соот-
ветствовать различным временным интервалам На рис 2 17, например, данные по четы-
рем практически одинаковым неделям (они отличаются только ценой пирога) обобщены
в модель, отображающую производство за месяц Столбец Итого этой модели представ-
ляет собой сумму “недельных” переменных В других случаях обобщение является более
сложным процессом, чем простое суммирование.
... А	.		1 в	С			Г S
i 1 Simon Pie Co. -- Модель прибыли >a месяц					
 2 j 3 Переменные решения:		Неделя 1	Неделя 2	Неделя 3	Неделя 4	• Итого
i 4 .Цена пирога	l. J9'00. .	’ $9,40 ,	$9,10	’ $9.20 '	
; Б Параметры:						
j 6 i Удельные затраты на покупку начинки	$3,48	$3.43	$3/52	$3,47	
; , 7 Удельные затраты на покупку теста	$0,30	$0,28	$0 31	$0,30	
} $ ' Постоянные издержки		$12	 $12	$12	$12	
4-1	16 Фитимеские ретупьтаты							
1 16 Спрос и объем продаж (тыс шт)	12 0	10,4	’ 11,6	11,2	15.2
; 17 Финансовые результаты						
S 18 ; Доход	$108,00	$97 76	$105,56	$103,04	$414,36 '
.19 , Затраты на обработку	: $26,16	: $20,76	$24 81	$23 46	 $95,19 k '
20 Затраты на ингредиенты	$45,36	; $38,58	$44 43	i $42,22	$170 60
(. 21 _ Накладные расходы	$12,00	$12,00	$12,00	 $12,00	$48,00
' 1 22 Общие издержки	$83,52	$71,35	$81,24	$77,69	$313 79
23 Прибыль (до уплаты налогов) 24	$24,48	$26,42	$24,32	$25,36	$10 ;
Рис. 2.17. Модель производства за месяц компании Simon Pie
84
ЧАСТЬ). Модели и моделирование
Подведем итог. Мы начали рассмотрение данного примера с простой модели компа-
нии Simon Pie (пример 1) и сравнили данные, полученные с помощью уравнения затрат
на производство, с реальными данными. На основании этих реальных данных с помо-
щью средств Excel построили новое более точное уравнение затрат на производство. При
получении дополнительных данных подобным образом можно уточнить каждое уравне-
ние модели Затем преобразованная модель вновь подверглась анализу (анализ “Что-
если” и анализ чувствительности) В примере Simon Pie аналогичные процедуры можно
провести для пересмотра других связей модели- для определения уравнений затрат на
продукты или для создания более реального (нелинейного) уравнения для спроса.
2.4.	Пример 3 — Simon Pie, окончание
Бизнес Саймона пошел в гору, и он собрался его расширить — взяться за выпечку и
продажу пирогов с другими начинками лимонной, клубничной и вишневой Расширить
модель с целью включить в нее дополнительные аналогичные продукты почти так же
просто, как и преобразовать модель недельного производства в модель месячного произ-
водства, показанную на рис 2 17, поскольку производство различных пирогов описыва-
ется той же самой моделью, отличаются лишь значения конкретных параметров Таким
образом, принципиально несложно моделировать множество аналогичных продуктов
или даже множество аналогичных продуктов на протяжении нескольких временных про-
межутков, при этом одна и та же форма модели просто многократно дублируется с под-
становкой конкретных значений соответствующих параметров Именно так зачастую ус-
пешно строятся большие модели путем дублирования одной и той же удачной неболь-
шой модели для нескольких продуктов и ряда временных периодов.
Однако не всегда можно расширить модель с помощью простого дублирования. На-
пример, ячейки, необходимые для размещения данных за несколько временных перио-
дов, могут быть заняты другими данными Кроме того, когда модель описывает произ-
водство нескольких продуктов, могут появиться дополнительные связи, налагаемые на
все производство. Например, продукты могут конкурировать за ограниченные ресурсы —
капитал или рабочую силу Как правило, модифицировать дублируемую модель с учетом
этих соображений относительно несложно Мы продемонстрируем, как это делается, на
примере модели Саймона расширим модель выпечки и продажи яблочных пирогов,
включив в нее пироги с другой начинкой.
На рис. 2 18 представлен результат изменения исходной модели, в которую теперь
включены три дополнительных вида начинки. В данном случае каждый столбец отвечает
определенному типу начинки, но они отличаются только значениями параметров. Чтобы
создать такую модель, исходную модель просто копируют в новые столбцы. Поскольку у
Саймона нет практического опыта изготовления новых пирогов, у него нет данных, по-
зволяющих оценить значения соответствующих параметров, поэтому при определении
этих значений он вынужден руководствоваться своей интуицией. Получив соответст-
вующие данные, он может пересмотреть значения указанных параметров, как это было
проделано в предыдущем примере
ГЛАВА 2. Моделирование с помощью электронных таблиц
85
	1	Переменные решения:
	4	Цена пирога		 		 Параметры:
	f 10. ТГ 16	Разность с ценой яблочного пирога Удельные затраты на покупку начинки • Удельные затраты на покупку теста	 Постоянные издержки	
		Коэффициенты уравнения спроса j СвоВодныйчлен 	 Коэффициент пропорциональности; Уравнение затрат на обработку	 Свободный член	; Коэффициент пропорциональности J Фиаические результаты
	т	Спрос и объем продаж (тыс шт.) Финансовые реаультаты
	& 20 1 .261	Доход	 Затраты на обработку	 Затраты на ингредиенты	; Накладные расходы Общие издержки	1 Прибыль (до уплаты налогов)	1
$9,32 ' 	$8,32	‘ ‘ $9.57
:	-$1,00	$0,25
$3,48		$2,20	$3,90
$0,30		$0,28	,	$0,35
.» . &......
-14,34	-11 66	-13,29
3,38	4,45	3.62
10,7 I ' 6,4	:	8,8
$99,91	<	$53,18	' $84,68
$21,84		$16,78	$18,74
$40,52		$15,85 :	$37,61
$62,36	:	$32,64	$56.35
$37.55		$20,54	$28.33
$
$0,00
$3.10
$ 
’-12,30	'
^'3,25''.
7,-	33.0
$65,80	$303,58
$10,65	$68,01
$24,22	$118,20
$34,86	$186.21
$30,94	$117,36
' 	$33,00
$84.36
Рис. 2.18. Модель производства нескольких типов продукции
Заметьте, что понадобилось произвести модификацию, чтобы учесть возросшие по-
стоянные накладные расходы' на аренду, процент по кредиту и т д , которые теперь оце-
ниваются в $33 000 в неделю. Поскольку эти накладные расходы являются общими для
всего производства и не связаны с каким-то конкретным типом пирогов, Саймон помес-
тил их в правый столбец, содержащий обобщенные итоговые показатели ' Поэтому он
также изменил некоторые заголовки в столбце А.
Другое отличие заключается в трактовке переменной решения (цены пирога) Саймон
знает, что пироги с вишневой начинкой продаются по той же цене, что и яблочные, с ли-
5 Предупреждение. Хотя так принято делать в финансовых отчетах, необходимо быть внимательным при
работе с такими таблицами (там, где накладные расходы распределены по отдельным продуктам), посколь-
ку эти постоянные расходы могут ошибочно трактоваться как переменные, что может привести к невер-
ным решениям Эта, безусловно, важная тема более подробно описывается в главе 3
86
ЧАСТЬ I Модели и моделирование
монной начинкой — на $1,00 дешевле, а с клубничной — на $0,25 дороже. Вместо того,
чтобы задавать эти цены по отдельности, Саймон записал зависимости между ними, в ре-
зультате цены остальных пирогов вычисляются как функции цены яблочного пирога.
Смысл такого решения в том, чтобы упростить анализ чувствительности для многопро-
дуктовой модели
Хотя Excel предлагает много различных типов диаграмм, с помощью которых можно
визуально представить числовые данные (некоторые из них, например объем-
ные, выглядят весьма привлекательно), зачастую для анализа данных удобнее использо-
вать простые диаграммы — гистограмму (столбчатую диаграмму) или линейчатую диа-
грамму 6 Пример нормированной гистограммы представлен на рис 2 19 В ней отражено
процентное распределение затрат для разных видов пирогов согласно представленной на
рис 2 18 модели
Рис. 2.19. Нормированная гистограмма для модели компании Simon Pie
Проанализировав результаты расчетов модели, Саймон понял, что не сможет произ-
водить планируемое количество пирогов (33 000 штук в неделю), если не введет на своем
заводе вторую смену Но это потребует дополнительных расходов на выплату сверхуроч-
ных, что отразится на производственных затратах Чтобы учесть эти изменения, нужно
модифицировать модель После консультации с управляющим завода Саймон пришел
к выводу, что с учетом добавления новых видов пирогов можно будет выпекать 25 000
пироюв в неделю при работе в одну смену Для каждого пирога свыше этого количества
к производственным затратам добавятся дополнительные затраты в размере $0,80, свя-
занные с введением второй смены Поскольку переход к двухсменной работе зависит от
общего объема производства, это изменение отражено в крайнем справа итоговом столб-
це на рис 2 20 Отметим, что были введены два новых параметра, предельный объем
производства (25 000 шт ) и дополнительные затраты на каждый пирог, произведенный
во вторую смену ($0,80) Обычные производственные затраты рассчитываются так же,
как и ранее, дополнительно вычисляются Затраты на сверхурочные Здесь формула со-
держит условную функцию ЕСЛИ, с помощью которой проверяется, превышает ли сум-
6 Здесь и даке названия типов диаграмм приводятся по русской версии Excel 2002 — Прим ред
ГЛАВА 2 Моделирование с помощью электронных таблиц
87
марный спрос предельное значение 25 000, если да, то добавляется $0,80 к удельным за-
тратам для всех пирогов, произведенных сверх этого количества Эти новые затраты
включаются в измененную формулу, по которой вычисляются Суммарные переменные
затраты Если сверхурочно производится 8 000 пирогов, Затраты на сверхурочные со-
ставят $6 400 Поскольку эти затраты являются переменными расходами, Саймон может
распределить их по столбцам, соответствующим определенным видам пирогов, основы-
ваясь на индивидуальных объемах производства, но в этом нет необходимости, если мо-
дель используется для обобщенного планирования
Пкмонныи
=$В$4+С6
=S0J4+DE
=СУММ'019Е13)
=(Р7+Р8)*Р19
=(С7*С8)*С1 9
Общие издержки
2
27
=СУММ(02ГЕ21) i
=СУММ(022 Е22) г
g = ECFIH(F1 9*F9,F1 0<
=СУММ(В24:Е24)
=Р16*Р17*Р19
Суммарные переменные затрат=СУММ(022 В24)=СУММ(С22:С24) =СУММ(Р22:Р24) =СУММ(Е22.Е24) =СУММ(Р22.Р24)
Всего	=021-025	=С21-С25	=D21-D25	=Е21-Е25	=F21-F25
ZU {Финансовые результат!
| Вв Доход
Рис. 2.20. Модель Simon Pie с учетом ограничений на объем производства
Клубничным


Совет. Условные выражения можно вычислять другими способами, не прибегая к использова-
нию функции ЕСЛИ. Например, формулу в ячейке F24 можно записать как
=MAX(F10*(F20-F9),0) или =(F20>F9)*F10*(F20-F9)
88
ЧАСТЬ I. Модели и моделирование
Хотя Саймона вполне устраивали цены на пироги и объемы продаж, а также распре-
деление прибыли по видам пирогов, он был неудовлетворен потерями прибыли, связан-
ными со сверхурочными работами, которые составили $6,4 тыс. в неделю, или более
$300 тыс в год Поэтому он решил получше разобраться в данном вопросе, проведя ана-
лиз чувствительности. При этом он преследовал две цели- 1) выяснить, можно ли в ка-
кой-то степени уменьшить потери от сверхурочных работ, если повысить цены и, таким
образом, уменьшить спрос; 2) определить, насколько вырастет прибыль, если удастся
увеличить производственную мощность (выше 25 000 шт.). Поскольку данная модель за-
нимает четыре столбца, соответствующих четырем типам производимых пирогов, теперь
невозможно проводить анализ чувствительности, создавая сценарии путем копирования
всей модели (состоящей из одного столбца), как это делалось в предыдущих примерах.
Вместо этого можно использовать таблицы подстановки Excel, которые позволяют полу-
чить аналогичный результат.
Средство Excel Таблица подстановки позволяет сразу получить полный набор сцена-
риев “Что-если”, при этом результаты заносятся в прямоугольный массив ячеек, это
удобно для построения графиков и анализа чувствительности.7 Таблицы подстановки
с двумя входами позволяют вычислять значения одной внутренней переменной (как пра-
вило, показателя эффективности) при изменении значений двух внешних переменных.
В модели Саймона показателем эффективности является общая прибыль, поэтому он
проводит анализ с помощью таблицы подстановки с двумя входами, меняя одну пере-
менную решения (цену яблочного пирога) и один параметр (производственную мощ-
ность) Поскольку цены на другие пироги привязаны к цене яблочного пирога, то ее из-
менение повлечет за собой соответствующие изменения этих цен
Создание таблицы подстановки с двумя входами начинается с создания диапазонов
значений двух внешних переменных в каком-либо свободном месте рабочего листа Excel,
как показано на рис. 2 21. Саймон меняет цену на яблочный пирог в диапазоне от $9,30
до $9,90 с шагом $0,05, а производственную мощность в диапазоне от 25 000 до 30 000
(штук) с шагом 1 000. Значения цены записываются в столбец, а производственной мощ-
ности — в строку
В левой верхней угловой ячейке таблицы подстановки указывается адрес ячейки, со-
держащей формулу, по которой вычисляется показатель эффективности, в данном случае
это ячейка F28 (см рис. 2.20). Затем выделяется весь диапазон ячеек таблицы подстанов-
ки (диапазон 13 016) и выбирается команда Данные^Таблица подстановки. На экране
появляется диалоговое окно (рис. 2 22), в котором необходимо указать ячейки со значе-
ниями внешних переменных, вместо которых в формулу показателя эффективности бу-
дут подставляться созданные последовательности значений. В поле ввода Подставлять
значения по столбцам диалогового окна Таблица подстановки указываем ячейку F9 —
это связывает последовательность значений в верхней строке таблицы со значением про-
изводственной мощности в модели (см рис. 2 20). Последовательность значений цены
яблочного пирога записана в столбце, поэтому она связывается с ячейкой В4 путем ука-
зания адреса этой ячейки в поле Подставлять значения по строкам диалогового окна
Таблица подстановки После щелчка на кнопке ОК в этом диалоговом окне Excel поме- В
В Excel имеются так называемые таблицы подстановки с одним входом, в которых значения одной изме-
няемой переменной подставляются в ряд формул (именно о такой таблице подстановки идет речь в данном
предложении), и таблицы подстановки с двумя входами, в которых значения двух изменяемых переменных
подставляются в одну формулу Далее в этом разделе описываются таблицы подстановки второго типа —
Прим ред
ГЛАВА 2. Моделирование с помощью электронных таблиц
89
щает каждую пару вводных значений в две указанные ячейки модели Simon Pies, пере-
считывает рабочую таблицу и помещает результирующее значение прибыли в соответст-
вующую ячейку таблицы подстановки, как показано на рис. 2.23
Рис. 2.21. Задание исходных данных для таблицы подстановки с двумя входами
Рис. 2.22. Привязка исходных значений таблицы подстановки к модели
Замечание. Ячейки, указываемые в диалоговом окне Таблица подстановки, должны со-
держать числа, а не формулы. Также отметим, что при задании ссылок на ячейки в диало-
говых окнах Excel посредством щелчка на соответствующей ячейке рабочего листа получа-
ются абсолютные адреса ячеек. Но независимо от того, абсолютные или относительные ад-
реса ячеек используются в диалоговом окне Таблица подстановки, результаты будут
одинаковыми.
90
ЧАСТЬ I Модели и моделирование
Рис. 2.23. Таблица значений прибыли для модели Simon Pies
Очевидным преимуществом таблиц подстановки является простота, с какой находит-
ся комбинация входных переменных, обеспечивающая максимальное значение прибыли.
Так, из таблицы, показанной на рис. 2.23, видно, что для любого значения производст-
венной мощности существует единственное значение цены яблочного пирога, дающее
максимальную прибыль
Менее очевидным, но также очень важным, является анализ поведения максималь-
ной прибыли Саймона интересует, зависит ли от производственной мощности цена яб-
лочного пирога, при которой достигается максимальная прибыль Ответить на подобные
вопросы поможет диаграмма Excel, которая дает возможность визуально представить со-
держимое таблицы подстановки Объемный график (в Excel этот тип диаграммы называ-
ется Поверхность), построенный на основании данных таблицы подстановки (и после
некоторого дополнительного форматирования), показан на рис 2 24.
Рис. 2.24. Объемный график прибыли для модели Simon Pies
Хотя рис 2.24 выглядит привлекательно, по объемному графику сложно проводить
анализ чувствительности, для определения зависимостей лучше использовать более про-
ГЛАВА 2 Моделирование с помощью электронных таблиц
91
стой двухмерный точечный график На рис. 2 25 представлены точечные графики для тех
же самых данных — по одному графику для каждого значения производственной мощно-
сти Очевидно, что Саймону следует повысить цену яблочного пирога с $9,38 до $9,50,
если производственная мощность зафиксирована на отметке 30 000 штук, а для любого
значения производственной мощности меньше 30 000 прибыль практически не зависит
от изменений цены в пределах от $9,50 до $9,70
Рис. 2.25. Точечные графики прибыли для модели Simon Pies
Чтобы исследовать другие возможные сценарии модели, можно воспользоваться таб-
лицей подстановки с одним входом, которая позволяет изменять только одну входную
переменную, но при этом рассчитывает значения нескольких выходных переменных
(а не одной, как в таблице подстановки с двумя входами) Для этого сначала необходимо
задать значения одной внешней переменной в свободном месте рабочего листа Значения
можно задать в виде столбца или строки В примере на рис 2 26 значения цены яблоч-
ного пирога заданы в строке. Все представляющие интерес внутренние выходные пере-
менные записываются в отдельных строках под первой строкой На количество расчет-
ных переменных ограничений нет Столбец, находящийся непосредственно слева от
строки со значениями внешней переменной (столбец I на рис 2 26), особый — он должен
содержать пустую ячейку (в данном случае это ячейка 122) в строке, где записываются
значения внешней переменной В ячейках столбца I (диапазон 123 126) необходимо ука-
зать ссылки на ячейки рабочего листа, содержащие формулы для вычисления значении
выходных переменных. В расположенном слева столбце, как правило, указываются на-
звания переменных (Эти названия служат для документирования модели и не являются
частью таблицы подстановки ) Общий вид таблицы подстановки с одним входом и соот-
ветствующими формулами показан на рис 2 26
92
ЧАСТЬ I Модели и моделирование
~ Н~ feL'd J I К I L I М-1 И I О I.P I, Q .1.
_21_	Цена яблочного пирога
1221!	$9,35: $9,40 $9,45 $3,50 $9,55 $9,60 $8,65 $9,70 $9,75^ $8,80
23 Спрос	: 33,о|	'	'	
24 Доход	$304
2Б ^Затраты на сверхурочны» $6.4
26 Прибыль	$78
27_____________________________________
...________н............m	М.
21 j	Цена яблочного пирога
B?2d	:9,35 I9.4	9,45 9,5	9,55 8,6	8,65 9,7	9,75 ^Э.б :
23 iCnpoc	=F19
24 Доход	=F21	;
25 ^Затраты на сверхурочны» =F23
26 (Прибыль	«F28
Рис. 2.26. Структура таблицы подстановки с одним входом для модели Simon Pies
После выделения диапазона ячеек 122-S26, содержащего все строки таблицы и левый
столбец со ссылками на ячейки модели (без столбца Н, содержащего названия), выбира-
ется команда Данные^Таблица подстановки. Поскольку в данном случае значения
внешней переменной задаются в первой строке, ссылка на ячейку рабочего листа, указы-
вающая, куда нужно подставлять эти значения, задается в поле Подставлять значения
по столбцам диалогового окна Таблица подстановки, как показано на рис. 2.27. (Если
бы значения внешней переменной были указаны в столбце, следовало бы выбрать поле
Подставлять значения по строкам ) В таблице подстановки с одним входом задается
только одна последовательность входных значений, поэтому второе поле ввода в диало-
говом окне Таблица подстановки остается пустым.
Рис. 2.27. Создание таблицы подстановки с одним входом
После щелчка на кнопке ОК в диалоговом окне Таблица подстановки рабочий лист
будет пересчитан для каждого значения внешней переменной, и все полученные значе-
ния заданных внутренних переменных модели будут записаны в таблицу подстановки,
как показано на рис. 2 28. Таким образом, в таблице содержатся значения спроса, общий
доход, затраты на сверхурочные работы и значения прибыли для различных значений це-
ны яблочного пирога На рис 2.28 не показано значение производственной мощности,
которое зафиксировано на исходном уровне 25 000 штук. Из таблицы подстановки вид-
но, что, если нельзя повысить производственную мощность, для снижения затрат на
сверхурочные работы необходимо повысить цену яблочного пирога (и, следовательно,
цены других пирогов) В частности, повысив цену яблочного пирога до значения, при ко-
тором достигается максимальная прибыль (примерно $9,65), можно уменьшить расходы
ГЛАВА 2. Моделирование с помощью электронных таблиц
93
на сверхурочные работы с $6 400 в неделю (при цене яблочного пирога $9,32) до менее
чем $2 000 в неделю. Однако при этом придется сократить объем продаж пирогов с 33 000
до 27 000.
Рис. 2.28. Окончательный вид таблицы подстановки с одним входом для модели Simon Pies
2.5.	Пример 4 — XerTech Copy, Inc.
Эмили и Билл Петерсоны решили основать компанию — XerTech Copy, Inc , которая
будет устанавливать копировальные самообслуживаемые машины в помещения заказчи-
ка — в библиотеки, университеты, институты, торговые центры и тд. Чтобы свести
к минимуму основные затраты, они собираются брать в аренду мощные копировальные
машины, к которым подключены автоматы для приема монет и платежных карт Помимо
платы за аренду и других расходов на копировальные машины, компания XerTech может
дополнительно платить организациям-клиентам, предоставляющим место для установки
этих машин Таким образом, оплата состоит из фиксированной ежемесячной платы за
аренду помещения плюс (необязательно) некоторые поощрительные выплаты В рамках
своего бизнес-плана Эмили и Билл сделали следующие предположения
Число арендуемых копировальных машин (переменная решения) 40
Количество копий, производимых в месяц одной машиной (переменная 30 000
решения)
Цена одной копии (переменная решения)	$0,05
Переменная затрат на одну копию (расходные материалы, ремонт и т д ) $0,03
Ежемесячная арендная плата за помещение для машины (переменная $150
решения)
Прочие ежемесячные расходы:
затраты на аренду одной копировальной машины	$250
затраты на инкасацию денег с одной машины	$35
прочие фиксированные затраты на одну машину	$50
Для анализа прибыльности нового предприятия была разработана модель на базе
электронной таблицы Excel, представленная на рис. 2.29. Как и в примере Simon Pies,
данная модель построена с учетом приведенных ранее рекомендаций, имеются заголовки
строк и столбцов, указаны единицы измерения для всех величин, в первых семи строках
содержатся основные входные параметры модели Также во всех формулах используются
ссылки на ячейки, содержащие параметры, а не числовые значения этих параметров.
В других строках модели содержатся основная входная переменная Число копий в месяц
на 1 машину и формулы для вычисления основного показателя эффективности — чис-
той ежемесячной пибыли.
94
ЧАСТЬ! Модели и моделирование
	 А	| В |	С	i D JE
2 "Г 4 5 6~ ~8" 9 10 11 12 13 14 15 16	XerTech Copy Inc. Средние хатраты на 1 машину в месяц	Количество машин 40 Аренда $250.00 Обслуживание $35.00	Цена	за	копию:	$0,05 р» Прочие постоянные затраты $50,00 Переменные затраты на копию $0 03 У-, Постоянные затраты на 1 машину: $335,00	Разность	на	копии:	$0,02 ss Ставка арендной платы на 1 машину::'	.. Число копий в месяц на 1 машину	-, -  - Средний доход в месяц Доход Стоимость проданного товара	ЛГо i и	 Валовая стоимость	-I . ii.i i. Общие и админ расходы	$10 400	•	у- Чистый ДОХОД	$4 600	'	: у-	.
А_________.....................L....1..:...с.....'.....L1.D;
XerTech Copy Inc
Рис. 2.29. Первоначальная модель компании XerTech
Петерсоны хотят изучить альтернативные варианты структуры арендной платы за вы-
деленную для копировальных машин площадь Помимо фиксированной ежемесячной
арендной платы $150 за одну машину можно попытаться предложить клиентам более
низкую арендную плату плюс определенные комиссионные с каждой сделанной копии
Например, организация-клиент может получать арендную плату за предоставленную для
одной машины площадь в размере $50 плюс комиссионные с каждой сделанной копии
в размере 0,5 цента Еще один возможный вариант —фиксированная арендная плата $75
плюс 1 цент комиссионных с каждой копии, сделанной сверх установленного ежемесяч-
ного лимита в 20 000 копий в месяц. Прежде чем обнародовать эти три альтернативные
схемы платы за аренду площадей, Петерсоны хотят сравнить объемы копирования, соот-
ветствующие точке безубыточности для данных вариантов
Вместо того, чтобы создавать и анализировать модель для каждого варианта арендной
платы в виде отдельной таблицы, предпочтительней представить все три альтернативы
в трех столбцах одной таблицы Это позволит сравнивать основные параметры альтерна-
тивных вариантов (рис. 2 30)
ГЛАВА 2 Моделирование с помощью электронных таблиц
95
;	А	В !	. .	. С , .	I-	D	|Е
t	XerTech Copy Inc. 2 Средние «атраты на 1 машину в месяц	Количество машин	до ЙЯ	Аренда $250.00	,	, Мч	Обслуживание	$35.00 :	Цена за копию	$0.05	~ г м&а	Прочие постоянные затраты	$50,00 Переменные затраты на копию	$0,03	 ЯП	Постоянные затраты на 1 машину $335,00 :	Разность на копии	$0,02	»?> R	Вариант!	Вариант 2	Варианта Арендная плата КJJ Постоянная^	Арендная плата	+комиссионныеза арендная )	+ комиссионные	сверхплановые		
9 110 JЧисло копий в месяц на 1 машину	плата 30 000	копии			. 	30	000	30 300 .
11 Ставка арендной платы на 1 машину	$150,00	$50,00	$75,00 I .
ЙЙ	Ставка комиссионных^ ЯЙ| Мин. к-во для начисления комиссионных? 14 i	Средний доход в месяц #5я Доход	’ $60 000 I	$0.005	$0,01 я.		 20 000 :	 $60 ООО '	$60 000 w
:Й6и СТОИМОСТЬ ПрОДЭННОГО ТОВЭра	$36 000 •		$36	000	$36 000
й17а Выплаченные комиссионные 1В; Валовая стоимость _Щ ООщие и админ расходы	$24 000 : $19400		$6 000	$4 000 Вд $18 000	$20 000 Жж 		$15 400	$16 400 W
20 Чистый доход "гГ	$4 600 :	$2 600	$3 600
1 В ' ] С I.	D
XerTech Copy Inc.
.Э«1	Аренда 250
кАж	Отслуживание 35	Цена за копию 0,05
))Д Прочие постоянные затраты 50___________________че затраты на копию 0,03____________________j
	Постоянные затраты на 1 машину =СУММ(ВЗ В5)		Разность на копии	=D4-D5	:
8		Вариант 1	Вариант 2	ВариантЗ
8 10	;Число копий в месяц на 1 машину	Постоянная арендная 30000	Арендная плата ) + комиссионные 30000		Арендная плата +комиссионнье за	; сверхплановые копии 30000	;
11	1авка арендной платы на 1 машину 150		50	75	;
Тз~	;	Ставка комиссионных)		?0,005	0 01
13- 14 15	k-во для начисления комиссионных) Средний доход в месяц Йоход	:	=$0$2*ВЮ*$0$4	=$D$2’C10*$D$4	20000 =$D$2*D10’$D$4
	i Стоимость проданного товара ,	=$О$2*ВЮ*$О$5	=$D$2*C10*$D$5	=$D$2*D1CT$D$5	!
17 :	Выплаченные комиссионные		=$D$2’C10’C12	=(D10>D13)*(D10-D13)*D2*D12 :
18	^Валовая стоимость	=В15-В16		:=С15-С16-С17	=D15-D16-D17
"1ST	i Общие и админ, расходы	=$D$2’($B$6+$B$11)	=$D$2*($B$6+C11)	=$D$2*($B$6+D11)
20	i Чистый доход	=В18-В19	=С18-С19	=D18-D19	;
211				
Рис. 2.30. Три варианта арендной платы компании XerTech
Совет. Условное выражение для вычисления комиссионных в ячейке D17 можно также запи-
сать с помощью функции ЕСЛИ
Совет. Формат ячейки, при котором разрешается переход текста на другую строку
(устанавливается во вкладке Выравнивание диалогового окна Формат ячеек), позволяет
более эффективно размещать длинные текстовые заголовки, не создавая слишком широких
столбцов. При вводе текста в такую ячейку переход на другую строку осуществ ыется на-
жатием комбинации клавиш <Alt+Enter>. Более подробно форматирование ячеек описыва-
ется в приложении Б
96
ЧАСТЬ! Модели и моделирование
Уточнить оценки выходных переменных модели можно с помощью средства Excel
Подбор параметра Это средство позволяет найти значение входной переменной моде-
ли, при котором получается заданное значение выходной переменной, как правило —
критерия эффективности. В данном случае можно использовать средство Подбор пара-
метра, чтобы найти значение числа копий в месяц, выполненных одной копировальной
машиной, соответствующее точке безубыточности. Выбираем команду Подбор пара-
метра в меню Сервис, как показано на рис. 2 31
Рис. 2.31. Команда Подбор параметра
В открывшемся диалоговом окне Подбор параметра нужно ввести в поле Устано-
вить в ячейке ссылку на ячейку, содержащую выходную переменную (в данном случае
это будет ячейка Чистый доход), ввести 0 в поле Значение (значение, соответствующее
точке безубыточности), ввести в поле Изменяя значение ячейки ссылку на ячейку, со-
держащую изменяемую переменную (здесь — ежемесячный объем производства копиро-
вальной машины), как показано на рис. 2 32, и затем щелкнуть на кнопке ОК.
Excel выполнит ряд последовательных вычислений, подставляя различные значения
в изменяемую ячейку, чтобы получить (если это возможно) желаемый результат в ячейке
В20, как показано на рис 2 33 * 8 В данном случае точка безубыточности в первом вариан-
те оплаты аренды достигается при объеме 24 250 копий в месяц для каждой машины.
* Последовательный поиск решения выполняется, начиная с исходного значения в изменяемой ячейке Если ис-
комый результат можно получить при нескольких значениях изменяемой ячейки, нахождение первого из них
приведет к остановке средства Подбор параметра Значение выходной переменной, указанной в поле Ус-
тановить в ячейке, может резко изменяться (например, вследствие использования в формулах функций
ЕСЛИ или других условных выражении), из-за чего Подбор параметра может не найти искомого значения
В таком случае выход заключается в повторном использовании средства Подбор параметра с другими на-
чальными значениями в изменяемой ячейке
ГЛАВА 2 Моделирование с помощью электронных таблиц
97
Рис. 2.32. Диалоговое окно Подбор параметра
Рис. 2.33. Ежемесячный объем, гарантирующий безубыточность при первом варианте оп-
латы аренды
Применив средство Подбор параметра к двум другим вариантам оплаты аренды
(в поле Установить в ячейке диалогового окна Подбор параметра указываются ячейки
С20 и D20 соответственно), можно сравнить значения, при которых достигаются точки
безубыточности, во всех трех вариантах (рис 2 34)
98
ЧАСТЬ I Модели и моделирование
	XerTech Copy Inc.			“  D	>
8		Вариант 1	Вариант 2	Вариант 3
		Постоянная	Арендная плата	Арендная плата fe
		арендная		+комиссионные за
, 9		плата		сверхплановые копии Ь
10	Число копий в месяц на 1 машину	24250’		 25	667’	21 ООО '
11	Ставка арендной плата на 1 машину	$150,00	$50,00 :	$75,00 ?'
	Ставка комиссионных»		$0,005	$0,01 я
~13"	Мин к-во для начисления комиссионных!			20 000//
14	Средний доход в месяц			
15'	Доход			$43 500 :	$51 334	$42 000^
Тб	Стоимость проданного товара	$29 100 '	$30 800		$25	200 '
J7	Выплаченные комиссионные		$5 133		$400 Я
18	Валовая стоимость	$19 400	$15400	$16 400
1U	ООщие и админ расходы	$19400 ’	$15400		  $16400	<
21	Чистый доход	$0	$0	$0
Рис. 2.34. Сравнение значений, при которых достигаются точки безубыточности
Петерсонов также интересуют так называемые точки безразличия, в которых чистая
прибыль не зависит от выбора альтернативных вариантов Пусть каждая копировальная
машина производит 30 000 копий в месяц, в 1-м варианте предусматривается фиксиро-
ванная арендная плата $150 в месяц за установку одной машины, альтернативные схемы
оплаты аренды представлены на рис 2 34 Какой должна быть фиксированная арендная
плата в других схемах оплаты, чтобы получить ту же чистую прибыль, что и в варианте I9
Чтобы ответить на этот вопрос, нужно добавить в таблицу, показанную на рис 2 30,
формулы, где из чистой прибыли варианта 1 вычитается чистая прибыль варианта 2 и ва-
рианта 3 соответственно (рис 2 35)
	' 	~	1 . ... _в	П	D	
ТТ	Xei 1 h Спру Inc Средний доход в mpi пц Доход	*$Р$2*В10‘$Э$4 Стоимость проданного т«$Р$2*В10*$Р$5		=$Р$2*С10*$Р$5	=$D$2*D10*$D$5	
*17"	Выплаченные комиссион!		•(dio>di3)-(Dio-di3)*d:	
¥	Валовая стоимость	-«615-616 Обшие и админ, расходы =$Р$2,|,($В$6<-$В$11) Чистый доход	«В18-В19 ход, вариант!-вариант	-Cl 5-С16-С17 МО$2‘($В$6»С11) :-С18-С19 2-В20-С20 оход. вариант! - вариант'	=015-016-017 -JD$2-(SB$6*D11) D18-D19 J =В20-Р20	
Рис. 2.35. Вычисление разностей значений чистой прибыли для различных вариантов
После этого с помощью средства Подбор параметра можно найти точку безразличия,
т е точку, в которой разность между чистой прибылью в вариантах 2 и 1 равна нулю, как
показано на рис 2 36 Аналогично находится точка безразличия для варианта 3 (по срав-
нению с вариантом 1), в данном случае устанавливается значение в ячейке D22, а изме-
няется значение в ячейке DI 1. Окончательный результат поиска точек безразличия пока-
зан на рис 2 37
Представленные на рис 2.37 результаты можно получить из исходной модели с по-
мощью простых алгебраических действий, но подходе использованием средства Подбор
параметра применяется и для более сложных моделей, в которых создание необходимых
формул не очевидно или затруднено.
ГЛАВА 2. Моделирование с помощью электронных таблиц
99
Рис. 2.36. Нало.ж<>сниеточки псчра i шчия для вариантов 1 и 2
Рис. 2.37. Точки безразличия для вариантов 2 и 3
2.6.	Искусство моделирования
Как следует из рассмотренных четырех примеров, моделирование с использованием
электронных таблиц не сводится к простому расчету уравнений, связывающих перемен-
ные При задании модели нужно предвидеть, как она будет анализироваться, и исходя из
этого так представить модель на рабочем листе Excel, чтобы она обладала следующими
свойствами.
1.	Была логически корректной
2.	Представляла основные альтернативы для сравнения.
3.	С ней удобно было проводить манипуляции, необходимые для анализа
100 ЧАСТЬ I Модели и моделирование
4.	Люди, не участвовавшие в создании модели, могли ее легко понять.
5.	Внешнее оформление модели было привлекательным.
Хотя многие “признаки” хорошей модели можно легко описать и зафиксировать, су-
ществуют определенные эстетические моменты, которыми можно овладеть только с по-
мощью практики. Ниже перечислены основные правила, которыми следует руководство-
ваться, чтобы создать качественную модель на основе электронных таблиц.
1.	Необходимо четко обозначить все переменные.
2.	Следует четко обозначить входы модели, переменные решения и параметры.
3.	Надо указать критерии эффективности и выходные переменные.
4.	Не следует жестко привязывать значения параметров к формулам — параметры
должны храниться в отдельных ячейках рабочего листа для удобства документиро-
вания и анализа.
5.	Если это возможно, надо отделять переменные, представляющие физические ве-
личины, от финансовых переменных
6.	Следует использовать предоставляемые Excel возможности форматирования для
выделения заголовков таблиц и ячеек.
Мы также рассмотрели проблему, с которой сталкиваются те, кто стремится полно-
стью документировать все параметры модели и в то же время пытается сделать рабочий
лист Excel, на котором представлена модель, компактным и свободным от излишних тех-
нических деталей В Excel существует две возможности, которые помогают разрешить это
противоречие структурирование, позволяющее скрыть строки и столбцы, содержащие
“технические” детали, и разделение окна рабочей книги на два или четыре подокна для
выполнения подобной задачи
Хотя анализ “Что-если” является основным видом анализа моделей, построенных
в электронных таблицах, мы видели, что он непригоден для серьезной оценки сложных
моделей При проведении этого анализа предшествующие результаты заменяются новы-
ми, поэтому невозможно одновременно представить результаты нескольких сценариев,
т е анализ является недостаточно систематичным В примере 1 был предложен подход,
при котором исходная модель записывается в одном столбце, тогда в другие столбцы
можно заносить копии модели, представляющие различные сценарии анализа “Что-
если”. Это упрощает анализ чувствительности и графическое представление его результа-
тов Кроме того, появляется возможность исследовать диапазон входных параметров для
поиска таких их значений, которые определяют если не оптимальные, то наиболее бла-
гоприятные значения критерия эффективности. Более подробно поиск оптимальных
решений рассматривается в последующих главах.
При расширении модели с целью включить в нее несколько временных периодов
(пример 2) или несколько продуктов (пример 3) следует учитывать два фактора Первый
заключается в том, что в хорошо структурированной модели базовая структура просто
дублируется для последующих временных периодов или других аналогичных продуктов,
что позволяет сохранить концептуальные основы модели. В этой структуре просто меня-
ются значения параметров, чтобы новые модели описывали новые продукты или вре-
менные периоды Именно так на основе небольшой удачной модели строятся крупные
модели Разобрав базовую структуру небольшой модели, несложно понять структуру го-
раздо более крупной, созданной на основе ее дублирования.
ГЛАВА 2. Моделирование с помощью электронных таблиц 101
Другой фактор (как следствие первого) заключается в том, что в созданных путем дуб-
лирования моделях данные и формулы располагаются в несколько строк и столбцов, по-
этому дальнейшее копирование модели, как это было с моделями, располагающимися
водном столбце, для проведения анализа чувствительности становится затруднитель-
ным, а то и вовсе невозможным. В этом случае, хотя мы и не обсуждали это в приведен-
ных примерах, можно скопировать модели на другие листы рабочей книги Excel, а затем
на одном листе свести в общую модель основные переменные со всех листов
Другим выходом из создавшегося положения является использование таблиц подста-
новки, описанных в примере 3 Существует два типа этих таблиц. Таблица подстановки
с двумя входами позволяет варьировать две входные переменные и вычислять одну вы-
ходную переменную (как правило, критерий эффективности). Таблица подстановки
с одним входом позволяет изменять одну входную переменную и вычислять при этом
любое число выходных переменных Оба варианта таблиц подстановки имеют опреде-
ленные ограничения, но творческий подход к их комбинированию обычно позволяет по-
лучить нужный результат Более того, созданный с помощью таблицы подстановки мас-
сив значений идеально подходит для проведения анализа чувствительности и визуаль-
ного представления зависимостей с помощью графиков
Наконец, в примере 4 мы рассмотрели средство Подбор параметра. Это средство ис-
пользуется, если известно желаемое значение выходной переменной (например, дохода
как критерия эффективности), и необходимо определить, при каком значении входной
переменной получится требуемый результат Кроме того, Подбор параметра можно ис-
пользовать для определения точки безубыточности, а также точки безразличия при суще-
ствовании альтернативных решении Несмотря на то что Подбор параметра — мощное
средство, у него есть определенные недостатки можно манипулировать только одной
входной переменной, нельзя одновременно применять его для нескольких выходных пе-
ременных, оно не позволяет проводить оптимизацию, осуществляя поиск наибольшего
или наименьшего значения выходной переменной, что часто требуется в управленческих
моделях.
Во всех рассмотренных до сих пор примерах слишком мало внимания уделено ограни-
чениям. В примере 3 содержалось одно ограничение на производственную мощность, од-
нако в реальных бизнес-ситуациях существует множество ограниченных ресурсов и, следо-
вательно, множество ограничений. Эта тема подробно рассматривается ниже в примере 5
В главе 3 мы покажем, как объединить ограничения, подбор параметров и оптимизацию
в единый аналитический механизм. Хотя приведенные примеры моделей не являются ис-
черпывающими, мы надеемся, что они позволят вам приступить к самостоятельному моде-
лированию.
2.7.	Пример 5 — Oak Products
Компания Oak Products, Inc (OP) производит несколько видов высококачественных
дубовых стульев. Ассортимент продукции насчитывает 6 типов изделий' Captain, Mate,
American High, American Low, Spanish King и Spanish Queen. Стулья сконструированы
так, что для их изготовления можно использовать ряд взаимозаменяемых деталей длин-
ные и короткие штифты, прочные и облегченные сиденья, а также тяжелые и легкие по-
перечины. Кроме того, каждый тип стульев имеет отличную от других направляющую, на
которую крепится спинка. Взаимозаменяемые детали помогают компании подстрахо-
ваться на случай внезапных изменений спроса. Директор завода Том Бар 15 ноября
встречается с Джимом Уайтом из отдела управления производством, чтобы составить
102 Ч А С Т Ь I Модели и моделирование
окончательный план производства на следующую неделю. В компании заключительные
действия по доводке деталей (шлифовка, окраска и сушка) занимают одну неделю. По-
этому на следующей неделе можно изготавливать стулья только из деталей, обработка ко-
торых уже завершена Джим Уайт разработал модель производства с помощью электрон-
ной таблицы Excel (рис 2.38)

2 Модель стульев
• 3 Удельная прибыль
4- Произведенное к-во
,6 Длинные штифты
~7' Короткие штифты
8 Ножки
9, Прочные сиденья
ДО Облегченные сиденья
11 Прочные поперечины
- $ 36 - $ 40 $ 45 Л 38 $ 35 $ 25 : ПриОыль
| 40	40	40 ; 40	40	40 I   $6 Тб5|
Суммарное Запас в начале Остаток в
потребление недели конце недели
ПотреСность в деталях
12 Облегченные поперечины
;:13 Спинки для Capt
14 Спинки для Mate
15 Спинки для Amer
16 Спинки для Span
lj Модель структуры недел!
~~tfiJCjDlE!PlGL
2 j Модель стульев
3J Удельная прибыль
4 ।Произведенное к-во
.6 ^Длинные штифты
7 короткие штифты
8 ; Ножки
10 ^Облегченные сиденья
Д1ДПрочные поперечины
12 ...Облегченные поперечинь
13'1 Спинки для Capt
-15 |Спинки для Amer
16 !спинки для Span
17 1
1280
1600
960
120
120:
600:
600
40
40
во:
80
1280
1900
1090
190
юоо:
юоо
110
93
85
300
130
70
50
400
400
70
32
О S < < W СО :
:эб 40 :45 38 :35 25 :__________Прибыль____________
|40 40 40 40 40 40 |-СУММПРОИЗВ($№>.-$6$4:ВЭ:ОЗ) |
Запас Остаток s
_________Суммарное потребление_____
4 =СУММПРОИЗВ($В$4:$С$4;В6:С6)
8 =СУММПРОИЗВ($В$4:$О$4,В7:С7)
4 =СУММПРОИЗВ($В$4:$С$4,88:С8)
1 =СУММПРОИЗВ($В$4:$С$4,В9:С9)
0 =СУММПРОИЗВ($В$4:$С$4;ВЮ:СЮ)
0 =СУММПРОИЗВ($В$4:$С$4;В11:G11)
6 =СУММПРОИЗВ($В$4:$О$4;В12:С12)
0 =СУММПРОИЗВ($В$4:$С$4;В13:С13)
0 =СУММПРОИ38($В$4:$С$4.В14:С14)
0 ;=СУММПРОИЗВ($В$4:$С$4;В15:С15)
1 =СУММПРОИЗВ($В$4:$0$4;В16:016)
1280
1900
1090
190
1000
1000
110
72
93
85
=18-Н8
:=19-Н9
-I10-H10
-I12-H12
=113-Н13
=|14-Н14
=И5-Н15
=116-Н16
Рис. 2.38. Первая модель для компании ОР
Совет. Во вкладке Выравнивание диалогового окна Формат ячейки можно изменить ори-
ентацию надписей Развернув названия типов стульев на 90° можно уменьшить ширину
столбцов в рабочем листе, как показано на рис. 2 38. Также отметим, что в столбце Н
в формулах вычисления общих затрат используется функция СУММПРОИЗВ. Эта функция
перемножает пары значений из диапазонов ячеек, заданных в качестве ее аргументов, а за-
тем складывает все полученные произведения. Данная функция часто используется в моде-
лях, построенных на базе электронных таблиц Более подробно форматирование ячеек
и функция СУММПРОИЗВ описаны в приложении Б
ГЛАВА 2. Моделирование с помощью электронных таблиц 103
Как и в других примерах, модель построена так, чтобы облегчить ее анализ и интерпре-
тацию. Чтобы был понятен смысл чисел, все строки и столбцы имеют заголовки Столбцы
таблицы представляют параметры решения — производство определенного типа стульев,
включая уровень производства и расход деталей. Так, число 4 в ячейке В7 показывает, что
для производства одного стула типа Captain требуется 4 коротких штифта Предлагаемый
план производства помешен в ячейках B4:G4. Таким образом, Джим предлагает произвести
по 40 стульев каждого типа, в результате недельная прибыль составит $8 760. Данные, со-
держащиеся, например, в ячейках Н7 J7, показывают следующее
1.	В соответствии с данным производственным планом будет использовано 1600 ко-
ротких штифтов.
2.	Запас коротких штифтов на складе (параметр) составляет 1900 штук.
3.	После выполнения плана в конце недели на складе останется 300 коротких штифтов
На рис. 2 39 показано использование имен диапазонов в формулах модели Это по-
зволит сделать формулы более удобочитаемыми по сравнению с формулами, которые
представлены на рис. 2.38. Имена можно использовать в любой табличной модели для ее
документирования.
	
	1	Прибыль
	|=СУММПРОИЗВ(П|>оиэееденное к вогУдельная прибыль)	|
5 ’	Суммарное потребление	св	Остаток в конце недели
j2 т~ 10 и *3 16 17	=СУММПРОИЗВ(Произведенное к	во.Длинные штифты)	1280	—Запас	в	начале	недели-Суммарное	потребле =СУММПРОИЗВ(Произведенное к	во;Короткие штифты)	1900	=3апас	в	начале	недели-Суммарное	потребле =СУММПРОИЗВ(Произведенное к	во;Ножки)	1090	-Запас	в	начале	недели-Суммарное	потребле =СУММПРОИЗВ(Произведенное к	во;Прочные сиденья)	190	—Запас	в	начале	недели-Суммарное	потребле =СУММПРОИЗВ(Произведенное к	во.Облегченные сиденья)	170	—Запас	в	начале	недели-Суммарное	потребле =СУММПРОИЗВ(Произведенное к	во;Прочные поперечины)	1000	-Запас	в	начале	недели-Суммарное	потребле =СУММПРОИЗВ(Произведенное к	во;Облегченные поперечины) 1000	=3апас	в	начале	недели-Суммарное	потребле =СУММПРОИЗВ(Произведенное	к	во;Спинки	для	Capt)	110	—Запас	в	начале	недели-Суммарное	потребле 1=СУММПРОИЗВ(Произведенное	к	во;Спинки	для	Mate)	72	—Запас	в	начале	недели-Суммарное	потребле |=СУММПРОИЗВ(Произведенное	к	во;Спинки	для	Amer.)	93	-Запас	в	начале	недели-Суммарное	потребле 1=СУММПРОИЗВ(Произведенное	к	во;Спинки	для	Span)	85	—Запас	в	начале	недели-Суммарное	потребле
Рис. 2.39. Использование имен диапазонов в формулах
Совет. Именованные переменные (точнее, имена диапазонов ячеек., в которых содержатся
значения этих переменных) являются глобальными для рабочей книги Excel, т е они доступ-
ны на всех листах данной книги Это позволяет формуле в ячейке на одном листе обращать-
ся по имени к переменной, находящейся на любом другом листе. Более подробно создание имен
диапазонов описано в приложении Б
Ниже приводится обсуждение планов выпуска, основанное на построенной модели
ДЖИМ. Я использовал стандартную процедуру определения структуры недельного
производства, количества различных продуктов считаются равными и макси-
мизируется общий выпуск В данном случае первыми закончатся длинные
штифты, но получатся неплохие результаты будет выпущено по 40 стульев
каждого вида и получено дохода $8 760.
ТОМ. Да, раньше мы всегда производили равные количества стульев каждого вида, од-
нако ситуация изменилась. Президент нашей компании сказал, что изделия из
цельного дерева сейчас в моде и мы сможем продать все свои стулья, независимо
от типа Он сказал, что нужно получить максимально возможную прибыль Как
это сделать9
104 Ч А С T b I Модели и моделирование
ДЖИМ. Я не могу дать готовый ответ, но у меня есть идея. Наиболее прибыльными
стульями являются American High, но на них идет больше всего длинных штиф-
тов, которых у нас мало. Если сократить выпуск American High на две единицы,
мы потеряем $90 прибыли, но у нас появится 24 длинных штифта, которые
можно использовать для изготовления трех стульев типа Captain, что принесет
$108 Что если сделать 100 Captain и отказаться от выпуска American High?
(Джим ввел новые предлагаемые значения в ячейки В4 G4, в результате получилась
таблица, представленная на рис. 2.40 )
U •	. А		0 •	! С D	I Е I. F,	L о	L н . 1	1	I'	J
1 ' (Модель структуры недельного проитводства компании Oak Products							
			5 ¥	о			
•'7-d Модель стульев	g.	1 I	| а				
^З’^Удельная прибыль	$ 36	$40 $45	$ 38 : $ 35	$25	Прибыль		
^Произведенное к-во	[	100	40	0	40	40	40	1	$91201		
					Суммарное	Запас в начале	Остаток в
..S';		Потребносп	гь в деталях		потребление	недели	конце недели
£	/Длинные штифты	8		0	8	4	1280	1280	0
7 Короткие штифты	4	12	0	12	4	8	1840	1900	60
8 /Ножки	4	4	4	4	4	4	1040	1090	50
"8 .Прочные сиденья	1	0	0	; 0	1	1	180	190	10
/18 а Облегченные сиденья	0	1	1			80	170	90
Дрочные поперечины	6	0	4	.05	0	800	1000	200
дёаЮблегченные поперечины	0	: 4	0	5 ; 0	6	600	1000;	400
13/Спинки для Capt	1	0	0	0	0	0	100	110:	10
М^Спинкидля Mate	0	1'0	0	0	0	40	72	32
ад/Спинки для Amer.	Q	. 0	1	1	0	0	40	93:	53
11Б/Спинки для Span	0	0	0	: 0 :	1	1	80	85	5
Т7~							
Рис. 2.40. Измененная таблица, предложенная Джимом
ТОМ. Отлично' Мы сможем повысить недельную прибыль на $360. Интересно, можно
ли добиться большего? Я уверен, что можно Попробуем вновь воспользоваться
твоей идеей На каждый Spanish King требуется 8 длинных штифтов, а на Span-
ish Queen — только 4. Отказавшись от выпуска одного Spanish King, мы потеря-
ем $35, но сможем сделать два Spanish Queen и получить $50 Что если отказать-
ся от производства King и выпустить 120 Queen? (Результат показан на
рис 2 41 )
ДЖИМ. Результат получился двойственным: недельная прибыль действительно воз-
росла бы на $600, но запас деталей на складе не позволит осуществить данный
план Я включил в формулы столбца К функцию ЕСЛИ, чтобы выводить со-
общение в соответствующих ячейках, если какие-то детали закончились. На-
пример, в данном случае для выполнения вашего плана потребуется больше
коротких штифтов, ножек и других деталей, чем у нас имеется. Так что осуще-
ствить его невозможно.
ТОМ. Понятно, это чересчур. Однако чтобы повысить прибыль, нам нужно каким-
то образом уменьшить выпуск Spanish King и увеличить выпуск Spanish
Queen Я думаю, нам удастся определить, как изменить выпуск при имеющих-
ся запасах деталей. Но как мы узнаем, что это действительно хорошее реше-
ние? Хочется, чтобы решение было оптимальным.
ГЛАВА 2. Моделирование с помощью электронных таблиц	105
Запас Остаток
в в конце
А	=СУММПРОИЗВ($В$4.$С$4;В6:С6)	1200
8	=СУММПРОИЗВ($В$4:$С$4,В7:С7)	1900
4	=СУММПРОИЗВ($В$4:$С$4;В8:С8)	1090
1	=СУММПРОИЗВ($В$4:$С$4;В9:О9)	190
0	=СУММПРОИЗВ($В$4:$С$4;ВЮ:С10)	170
0	=СУММПРОИЗВ($В$4:$С$4;В11:G11)	.1000
6	=СУММПРОИЗВ($В$4:$С$4;В12:С12)	1000
0	=СУММПРОИЗВ($В$4 $G$4;B13:G13)	110
О	•=СУММПР0ИЗВ($В$4.$С$4;В14:С14)	72
О	=СУММПРОИЗВ($В$4.$С$4,В15:G15)	93
1	=СУММПРОИЗВ'$В$4 $С$4.В16 С16)	85
недели
=16-Н6	=ЕСЛИ(36<0:А6&" закончились","")
=17-Н7	=ЕСЛИУ7<О:А7&” закончились":"”)
=18-Н8	=ЕСЛИ(38<0 A8S" закончились';'")
=19-Н9	=ЕСЛИ(39<0:А9&" закончились";"")
=110-Н10 =ЕСЛИ(Л0<0,А10&" закончились";"")
=111 -Н11 =ЕСЛИЦ 11 <0 А11 &" закончились","")
=112-Н12 «ЕСЛИ(Л 2<О;А12&" закончились",•)
=113-Н13 =ЕСЛИ(Л 3<0,А13&" закончились";"")
'=И4-Н14 =ЕСЛИ(Л4<0;А14&" закончились";"")
=115-Н15' =ЕСЛИ(315 < О А15&" закончились","")
«116-Н16 =ЕСЛИ(Л 6<0 А16&" закончились";”")
Рис. 2.41. Вторая измененная таблица, предложенная Томом
Совет. С помощью функции ЕСЛИ формулы столбца К проверяют ячейки столбца J, и при
появлении отрицательного значения в ячейках столбца К выводится соответствующее со-
общение; в противном случае эти ячейки остаются пустыми. Символ & обозначает опера-
цию конкатенации (объединения) символьных строк.
Оптимизационные модели
Как и модели в предыдущих примерах, модель Oak Products является количественной
моделью принятия решений. Она задает связи между переменными решения (сколько
стульев каждого типа выпускается) и параметрами (количество деталей, используемых для
изготовления одного стула определенного типа, и количество имеющихся деталей) и вы-
числяет показатель эффективности (прибыль), а также результирующие переменные
(значения ограниченных ресурсов). Однако данная модель не может дать ответ на вопрос
о том, сколько и каких стульев производить, поскольку точно не определена цель. Какую
цель мы преследуем? Может быть, мы хотим максимально использовать имеющиеся дета-
106
ЧАСТЬ! Модели и моделирование
ли? Или удовлетворить спрос потребителей на каждую из моделей? Более вероятно, что мы,
как и в предыдущем примере, захотим узнать, сколько стульев произвести, чтобы макси-
мально увеличить недельную прибыль компании К сожалению, ни один из рассмотренных
в данной главе аналитических методов не в состоянии учесть все имеющиеся ограничения
2.8.	Ограничения и условная оптимизация
Если Том и Джим хотят максимально увеличить недельную прибыль, модель Oak Prod-
ucts становится оптимизационной Данная модель является типичным примером задачи ус-
ловной оптимизации необходимо максимизировать (минимизировать) некий показатель
эффективности, зависящий от переменных решений, которые, в свою очередь, подчиняют-
ся ряду ограничений Ограничения сужают диапазон допустимых решений. В данном кон-
кретном случае ограничения — это количество различных деталей, из которых можно изго-
тавливать стулья, однако существует много других типов ограничений Как правило, ме-
неджеру приходится принимать большую часть решений в условиях, когда допустимые
решения тем или иным образом ограничены. В своей частной жизни мы также часто стал-
киваемся с ограничениями — с нехваткой времени, денег, пространства или сил. Менеджер
должен принимать во внимание требования к капиталовложениям, наличие персонала,
график поставок комплектующих, квоты на импорт, требования профсоюзов, производст-
венные возможности завода, требования по охране окружающей среды, затраты на хране-
ние, требования законодательства и множество других факторов Поэтому нет ничего уди-
вительного в том, что условная оптимизация — достижение наилучшего возможного ре-
зультата при наличии существующих ограничений — является одним из наиболее активно
развивающихся направлений исследований в науке управления.
	А 	'В !		С	I D .	Е	:F;!	 G	Н	1	J	
1	Модель структуры недельного производства компании Oak Products									
					5					
2	Модель стульев	8-	2	I	I					
3	Удельная прибыль	$36	$40	$45	$38	: $35	$25	Прибыль		
	Произведенное к во	|	100	72	40	53	: 0	: 0	1	$10 2941		
									Запас в	Остаток -
								: Суммарное	начале	в конце :
Б ;			Потребности		э в деталях			: потребление	недели ;	недели
6	Длинные штифты	6	0	12	0	8		1280	12В0:	0
	Короткие штифты	4	12	0	12	4	: 8	1900	1900!	0
_8_	Ножки	<4	4	4	4	4	4	1060	1090:	30
9 ,	Прочные сиденья	1	0	0	0	1	1	100	190:	90
_10_	Облегченные сиденья	Q			4	0	: 0	165	170:	5
11	Прочные поперечины	6	0	4	0	5	0	760	1000:	240
12	Облегченные поперечины	0	4	: 0	5	: 0	: 0	553	1000:	447
J3	Спинки для Capt	1	0	0	0	: 0	0	100	110	10
~14"	Спинки для Mate	0		о	0	0	Q	;	72	72:	0
15	Спинки для Amer.	0 ;	о	1	1	0	0	93	93	0
16	Спинки для Span	0	0	0	0	1	1	0	85:	85
J7_										
Рис. 2.42. Оптимальное решение для модели Oak Products
Модель Oak Products разработана в виде стандартной модели оптимального планирова-
ния, и найти наилучшую альтернативу, или оптимальное решение, достаточно просто. Су-
ществует несколько надстроек для программы Excel, предназначенных для оптимизации
ГЛАВА 2. Моделирование с помощью электронных таблиц	107
моделей при наличии ограничений. Примерами таких надстроек являются Solver (Поиск
решения) и What’s Best. Excel содержит сокращенную версию надстройки Поиск реше-
ния, с ее помощью получены результаты, представленные на рис 2 43 Интересно отметить,
что решение, полученное с помощью надстройки Поиск решения, должно принести при-
быль на $1 174 больше, чем план, предложенный Джимом, кроме того, в оптимальном ре-
шении нет стульев в испанском стиле (Spanish King и Spanish Queen), таким образом, опти-
мальное решение состоит в том, чтобы вовсе отказаться от производства стульев в испан-
ском стиле.
Более подробно использование надстройки Поиск решения для оптимизации моде-
лей будет рассматриваться в части 2.
2.9.	Заключение
В данной главе с помощью ряда коротких примеров представлены основы моделирова-
ния на базе электронных таблиц Были показаны пути преобразования модели “черного
ящика” в модель на основе электронных таблиц, даны рекомендации по стилю проектиро-
вания и макетирования моделей и советы по их документированию. Кроме того, были по-
казаны полезные средства Excel, используемые для моделирования и анализа
Диаграммы влияния облегчают построение моделей и служат для их документирова-
ния Уравнения модели строятся последовательным подбором математических отноше-
ний, соответствующих предполагаемым связям, содержащимся в данных Основным
средством анализа табличных моделей является анализ “Что-если”. При оценке чувстви-
тельности и компромиссов, а также сценариев анализа “Что-если” применяются такие
средства, как копирование модели, таблицы подстановки и построение графиков Для
нахождения точек безубыточности и точек безразличия при наличии нескольких альтер-
натив удобно использовать средство Excel Подбор параметра
При создании табличных моделей в Excel мы подчеркивали, что хорошая модель
должна обладать следующими свойствами
1.	Все переменные четко определены и обозначены
2.	Указаны входы модели, переменные решения и параметры
3.	Показатели эффективности и представляющие интерес результирующие перемен-
ные надлежащим образом обозначены, так что их легко наити
4.	Значения параметров хранятся в отдельных ячейках, а не включены непосредст-
венно в формулы, чтобы удобнее было документировать и анализировать модель
5.	Переменные, представляющие физические величины, нужно отделить от финан-
совых переменных
6.	Для выделения заголовков с целью улучшить внешний вид модели используются
предоставляемые Excel возможности форматирования
Для разработки хорошей модели (понятной, свободной от логических ошибок, легко
анализируемой и документируемой) исключительно важное значение имеет ее структура
и расположение на листе рабочей книги. Хорошему стилю моделирования присущи по-
нятная логика, отказ от помещения значений параметров в формулы, присвоение имен
всем переменным и их использование Наконец, в модели можно включать существую-
щие в Excel средства проверки выполнения условий, такие как функция ЕСЛИ, чтобы
предупреждать о возникновении исключительных ситуаций, когда, например, предла-
гаемый набор вводов приводит к нежелательным или невозможным последствиям
108 ЧАСТЬ I Модели и моделирование
Основные термины
Анализ “Что-если”. Подстановка значений входных переменных и/или параметров в модель, чтобы
определить их воздействие на показатель эффективности или результирующие переменные
Анализ компромиссов. Показывает, на сколько нужно снизить один показатель эффективности,
чтобы добиться улучшения другого показателя
Анализ чувствительности. Вычисление воздействия заданного изменения внешней переменной на
другую переменную
Диаграмма влияния. Иерархическая блок-схема, начинается с показателя эффективности, с помо-
щью стрелок показаны его связи с переменными и параметрами модели
Модель производства. Модель принятия решения, в которой переменные решения указывают, ка-
кое количество одного или нескольких товаров следует производить
Оптимальное решение. Допустимый набор значении переменных решения, оптимизирующий це-
левую функцию оптимизационной модели
Оптимизационная модель. Детерминированная модель принятия решения, содержащая единствен-
ный показатель эффективности (целевую функцию), который необходимо оптимизировать
при условии соблюдения набора заданных ограничений
Оптимизация. Максимизация или минимизация целевой функции
Подбор параметра. Нахождение значения внешней переменной, которое приводит к заданному
значению внутренней переменной
Промежуточные переменные. Внутренние переменные модели, созданные для удобства, которые
математически комбинируются с другими переменными, чтобы получить выходы модели —
показатель эффективности и результирующие переменные
Таблица подстановки. Представление значений показателя эффективности и/или результирующих
переменных в виде таблицы для заданного диапазона значений одной или двух внешних пере-
менных
Точка безубыточности. Набор значений входных переменных модели, который приводит к нулево-
му значению стоимостного показателя эффективности
Контрольные вопросы
Да/нет
1.	Не имеет большого значения, как модель представлена на листе рабочей книги,
если вычисления выполнены правильно.
2.	Помещение числовых значений в формулы позволяет улучшить документирова-
ние модели
3.	В табличную модель следует включать единицы измерения.
4.	На основе значений двух переменных средство Excel для построения линии тренда
позволяет исследовать зависимость между этими переменными и построить соот-
ветствующие формулы.
5.	Как правило, диаграмму влияния можно начертить несколькими способами.
6.	Временные значения всегда содержатся в столбцах модели Excel.
7.	В моделях показателем эффективности всегда является прибыль.
8.	Подбор параметра — это процедура для оптимизации табличных моделей.
ГЛАВА 2 Моделирование с помощью электронных таблиц 109
9.	Менеджерам не нужно разбираться в формулах модели, они имеют дело только с
результатами.
10.	С помощью группирования можно скрыть некоторые детали модели при печати
рабочего листа
11.	Удобно отделить вычисления промежуточных переменных, описывающих физиче-
ские величины, от вычисления переменных, описывающих финансовые показатели.
12.	Анализ “Что-если” пригоден исключительно для изучения изменений значений
переменных решения
13.	Для фиксирования результатов анализа “Что-если” полезно использовать таблицы
подстановки.
14.	Таблицы подстановки используются исключительно для создания данных, на
основе которых строятся диаграммы.
15.	С помощью средства Подбор параметра можно найти значение внешней пере-
менной, при котором значение показателя эффективности будет таким же, как
в альтернативном решении.
Выберите правильный ответ
16.	В хорошей модели на основе электронных таблиц:
а.	четко определены результаты;
Ь.	для переменных указаны единицы измерения,
с.	входные переменные отделены от внутренних переменных,
d.	четко видно, как внутренние переменные вычисляются на основании входных
переменных;
е.	все вышеперечисленное.
17.	Оптимизационная модель содержит:
а.	переменные решения,
Ь.	целевую функцию;
с.	и то и другое.
18.	Оптимизационная модель:
а.	предлагает наилучшее решение в математическом смысле;
Ь.	предлагает наилучшее решение с учетом ограничений модели;
с.	может служить средством оценки различных вариантов возможных управлен-
ческих решений,
d.	все вышеперечисленное.
19.	Анализ “Что-если” позволяет найти:
а.	оптимальное решение;
Ь.	хорошее решение;
с.	возможное решение (если оно существует);
d.	ничего из указанного выше.
20.	Оптимальное решение проблемы Oak Products позволяет:
а.	использовать все имеющиеся детали,
Ь.	использовать как можно больше наименее дорогих деталей;
с.	максимизировать разность между доходом и затратами,
110 ЧАСТЬ I Модели и моделирование
d максимизировать недельную прибыль,
е максимизировать общее количество произведенных стульев.
21.	При создании таблицы подстановки с одним входом'
а требуется задать диапазон значений для одной внешней переменной;
b можно указывать несколько внутренних переменных;
с и то и другое,
d ни то, ни другое
22.	При создании таблицы подстановки с двумя входами'
а требуется задавать диапазоны значений для двух внешних переменных,
Ь можно указывать несколько внутренних переменных,
с и то и другое,
d нито, ни другое
23.	Анализ чувствительности
а определяет степень изменения внутренних переменных в зависимости от изме-
нений внешних переменных;
Ь не может применяться к переменным решения,
с не может применяться для сравнения значений двух параметров,
d а и Ь,
е аис
24.	Именованные ячейки и именованные диапазоны
а упрощают интерпретацию формул;
b помогают документировать модели, построенные в электронных таблицах,
с служат для сокрытия структуры формул;
d а и Ь,
е а и с
25.	Чтобы облегчить интерпретацию и документирование моделей, можно использо-
вать следующие возможности Excel
а выделение шрифтом;
b сдвиг содержимого ячеек, содержащих заголовки и результаты;
с подчеркивание и заливка ячеек,
d рамки вокруг ячеек;
е все вышеперечисленные
Ответы
I Нет 2 Нет 3 Да 4 Да 5 Да 6 Нет 7 Нет 8 Нет. 9. Нет. 10 Да. И Да. 12 Нет.
13 Да 14 Нет 15. Да 16 е 17 с. 18 d 19 d 20 d 21. с 22 а. 23. а. 24. d. 25. е.
Задачи
2 1 Саймон не исследовал, верна ли его модель для цен, не попадающих в диапазон $6—11
Используя функцию ЕСЛИ и/или другие условные выражения Excel, измените модель
в примере 1 так, чтобы при попытке ввода значения цены, не входящего в указанный диа-
пазон, выдавалось предупреждение
ГЛАВА 2 Моделирование с помощью электронных таблиц
111
22	Петерсоны пришли к выводу, что переменные затраты в расчете на одну копию подчиняются более сложной закономерности, чем в существующей модели XerTech, где они вычисляются как сумма затрат на расходные материалы ($0,02 в расчете на копию) и амортизацию ($0,01 в расчете на одну копию) Они предполагают, что средние затраты на амортизацию в расчете на одну копию растут быстрее, чем простая пропорциональная зависимость от количества ко- пий, произведенных за месяц на одной копировальной машине Зависимость между этими величинами характеризуют данные, представленные ниже в таблице Измените модель XerTech, включив в нее новую информацию, и подготовьте отчете новыми результатами Данные за месяц Число копий на 1 копировальную	Затраты на амортизацию на 1 копировальную машину, тыс. шт.	машину, S 20	50 30	150 40	400 50	1000
23	С помощью таблицы подстановки исследуйте чувствительность прибыли в модели Simon Pie (раздел 2 3) к изменениям следующих параметров удельные затраты на начинку, удельные за- траты на тесто, постоянные затраты, коэффициент пропорциональности прямой спроса
24	Компания Bartel Job Shop получила предложение собрать примерно 15 тыс электронных калькуляторов по цене $26,50 Компания оценила, что при использовании существующих производственных мощностей переменные затраты на сборку одного калькулятора составят S21 В качестве альтернативного решения компания может заключить субконтракт и поручить некоторые операции по сборке компании Wizard Fabrication Со., сократив тем самым свои удельные затраты на сборку до $18 По контракту компания Bartel должна выплатить компа- нии Wizard фиксированную сумму $42 000 Еше один вариант может заключаться в том, чтобы взять в аренду робот-сборщик, что позволит компании Bartel снизить удельные переменные расходы на сборку до SI 1 Создайте модель прогнозирования валовой прибыли для каждого из описанных вариантов При каком уровне производства калькуляторов компанией Bartel дос- тигаются точки безразличия между использованием существующих мощностей и субконтрак- том, между субконтрактом и арендой робота9 Подготовьте отчет, содержащий рекомендации по возможным количествам выпускаемых калькуляторов
2 5.	Предположим, вы основали компанию по продаже компьютеров — “тонких клиентов”, кото- рые предназначены для обработки заключаемых через Internet сделок электронной коммер- ции в сфере пищевой промышленности Прежде чем вложить деньги в вашу компанию, инве- стор запросил предварительный отчет о доходах на 5 следующих лет, в котором должны быть показаны объем продаж (в количественном выражении), доход, суммарные переменные за- траты, расходы на маркетинг, постоянные затраты и прибыль до уплаты налогов Ожидается, что в первом году продажи составят 1600 единиц по цене $800 за штуку Благодаря росту по- пулярности Internet предполагается, что объем продаж будет ежегодно удваиваться на протя- жении последующих пяти лет С другой стороны, конкуренция будет приводить к ежегодному 15%-ному снижению цены. К счастью, технический прогресс позволит ежегодно снижать пе- ременные производственные затраты (первоначально составляющие $1000 на один компью- тер) на 6% Постоянные затраты оцениваются в $1 000 000 в год Расходы на маркетинг пред- полагаются в размере 14% годового дохода Если это окажется выгодным, можно взять в арен- ду устройство для автоматической сборки, что позволит снизить переменные производственные затраты на 20%, но вдвое увеличит ежегодные постоянные затраты, новые переменные производственные затраты также будут ежегодно снижаться на 6% Для агреги- рования потоков ежегодных доходов будет использоваться чистая текущая стоимость с дис- контной ставкой 15% в год Не учитывая соображения налогообложения, постройте для инве-
112 ЧАСТЬ I Модели и моделирование
стора модель в электронной таблице Сколько компьютеров необходимо продать в первый
год, чтобы 1) достичь точки безубыточности в первый год, 2) достичь точки безубыточности
во второй год9 К каким параметрам наиболее чувствительна чистая текущая стоимость9
Подготовьте отчет, отражающий итоги ваших исследований
2 6 Саймон решил изменить свою модель (пример 2) для зимнего сезона с низким уровнем продаж
На протяжении зимы заданного в модели недельного спроса на пироги можно добиться только
при очень активной рекламной компании При меньших затратах на рекламу объем заказов бу-
дет составлять лишь небольшой процент от указанного в модели количества Зависимость между
затратами на рекламу и объемом заказов показана в таблице Объем заказа 100% означает, что
количество проданных пирогов будет равно количеству, предсказанному исходной моделью,
а объем заказа 50% означает, что будет продана только половина этого количества Еженедель-
ные расходы на рекламу составляют от S5 ООО до S12 ООО Измените модель Simon Pie в приме-
ре 2, включив в нее эту новую информацию, дайте рекомендации по цене и расходам на рекламу
Исследуйте чувствительность недельной прибыли к затратам на рекламу
Расходы на рекламу, тыс. долл, в неделю	Объем заказа, %
5	40
7	65
10	78
12	88
2 7 Провайдер Internet-услуг, Surfing USA, собирается предложить в округе Ларами, штат Вис-
консин, услугу доступа к Internet через подключение к телевизионной сети Предполагае-
мая цена услуги для клиента составит S26 в месяц, удельные переменные затраты (в расчете
на одного потребителя) по предоставлению данной услуги — S17 в месяц Количество кли-
ентов в округе Ларами, которые, как предполагается, изъявят желание воспользоваться
этой услугой при заданной цене, — 20 000 в месяц
а Разработайте модель в Excel, чтобы найти максимальные ежемесячные постоянные за-
траты, которые компания Surfing USA в состоянии платить, чтобы не нести убытков
b Предположим, что ежемесячные постоянные затраты составляют S100 000, а ежеме-
сячные затраты на обслуживание клиента — S17 Цена, по которой предлагается об-
служивание, будет влиять на ежемесячный спрос Предположим, что для цены S26
в месяц услугой захотят воспользоваться 20 000 человек, а при каждом повышении це-
ны на S1 спрос сокращается на 2700 человек Разработайте модель, которая позволит
предложить рекомендации по цене и исследовать чувствительность ежемесячной при-
были к изменениям цены в диапазоне от S20 до S30
Президент компании Surfing USA Рон Сперри заявил “В нашем деле главный
показатель — удельная прибыль в расчете на одного клиента Чтобы получить как можно
больше денег, мы должны сделать ее как можно выше” Если компания установит цену,
позволяющую максимизировать среднюю удельную прибыль в расчете на одного клиента
(которая вычисляется делением ежемесячной прибыли на число клиентов), достигнет ли
она цели, провозглашенной Роном, — “получить как можно больше денег”9 Измените
свою модель и используйте ее, чтобы разъяснить Рону последствия его политики
с Компания Surfing USA может увеличить число своих клиентов в округе Ларами с по-
мощью рекламы Ежемесячные переменные затраты S17 на одного потребителя пред-
полагают 20 000 клиентов и отсутствие рекламы При использовании рекламы ежеме-
сячные переменные затраты по обслуживанию одного клиента будут возрастать на S1
при увеличении числа клиентов на 1000 человек сверх базовой цифры 20 000 Считая,
что цена обслуживания для каждого клиента составляет S26, а ежемесячные постоян-
ные затраты — S100 000, разработайте модель, чтобы предложить компании Surfing
ГЛАВА 2 Моделирование с помощью электронных таблиц
113
USA рекомендации по ежемесячным расходам на рекламу, и исследуйте чувствитель-
ность ежемесячной прибыли к затратам на рекламу
2 8 В салоне красоты Evermore работает семь мастеров, каждый получает повременную оплату
S18 в час Ежегодные постоянные издержки, которые включают арендную плату, проценты
по кредиту и тому подобное, составляют S48 ООО в год Все предлагаемые укладки волос
стоят одинаково S32 Считается, что каждый мастер работает 2000 часов в год Постойте
в Excel модель, которая позволит ответить на следующие вопросы
а Какое число укладок соответствует точке безубыточности9
b Какова прибыль салона Evermore, если в год делается 15 000 укладок9
с Сколько укладок будет соответствовать точке безубыточности при введении следующей
схемы оплаты труда мастеров повременная оплата S10 в час плюс S12 с каждой стрижки9
d Какое число укладок будет соответствовать точке безубыточности, если в схеме оплаты труда
повременная оплата будет равна 0, но за каждую стрижку мастер будет получать S259
е При выполнении 15 000 укладок в год какая из схем оплаты более привлекательна для
мастеров9 Какая схема предпочтительней для владельцев салона9
f При годовом объеме 15 000 укладок и использовании схемы, в которой не предусмот-
рена повременная оплата труда мастеров, сколько должен получать мастер за каждую
стрижку, чтобы владельцу было безразлично, использовать данную схему или платить
мастерам S18 в час9
Ситуация для анализа | Kayo Computer9
Компания Kayo Computer занимается сборкой и продажей персональных компью-
теров Для каждого компьютера нужна одна стандартная печатная плата Компания за-
ключила контракт на покупку печатных плат с фирмой Apex Manufactunng, производи-
телем печатных плат. Годичный контракт предусматривает, что Kayo платит Apex по
$200 за плату при объеме закупок до 2000 штук Если же годовой объем закупок пре-
вышает 2000 шт , компания Apex обязуется предоставить $40 скидки на каждую плату,
закупленную сверх этого количества, таким образом, плата продается по $160
Компания Kayo может покупать те же самые платы у другого производителя, TCI
Electronics, который предлагает более низкие цены — $120 за одну плату, но требует
внести единовременный взнос $100 000 на проектирование и разработку Инженеры
компании Kayo определили, что компания может использовать платы от этих произ-
водителей в любом сочетании, при этом не возникают дополнительные затраты или
проблемы совместимости.
Из плат и других компонентов компания Kayo собирает персональные компьюте-
ры. Переменные затраты на сборку каждого компьютера составляют $450, а годовые
постоянные издержки компании— $1500 000. Компания Kayo продает собранные
компьютеры по $1000. Никто не знает, сколько компьютеров компания сможет про-
дать в следующем году. Дженни Силк, заведующий финансовым отделом компании
Kayo Computer, сообщила, что через год компания прекратит выпуск данной модели
компьютера, поэтому все единовременные выплаты компании TCI нужно компенси-
ровать за счет продаж следующего года. Она попросила помочь оценить определенные
экономические и юридические аспекты ее финансового плана на будущий год
© 1999 Board of Trustees of the Leland Stanford Junior University All rights reserved
114 ЧАСТЬ I. Модели и моделирование
Вопросы
I. Постройте модель на основе электронных таблиц, позволяющую определить
прибыльность выпуска персонального компьютера Kayo в следующем году. Для
начала предположите, что в следующем году можно будет продать 5000 компью-
теров, при этом у компании Apex закупается только 1000 плат, остальные заку-
паются у компании TCI
2 Если общий объем продаж составляет 5000 штук, сколько плат следует купить у Apex,
а сколько — у TCI, чтобы максимизировать годовую прибыль? (Используйте таблицу
подстановки, чтобы найти наиболее удачные рекомендации)
3 В контракте с компанией Apex оговорено, что компания Kayo должна закупать как
минимум 20% плат (не менее 1000 штук) у Apex В контракте также содержится пункт
о том, что в случае невыполнения компанией Kayo обязательств она должна уплатить
неустойку $100 000 Какими будут экономические последствия, если непредвиден-
ные обстоятельства вынудят компанию Kayo отказаться от оговоренной контрактом
минимальной закупки (и купить больше плат у TCI) при условии, что в следующем
году будет продано 5000 компьютеров9 Предположим, что можно пересмотреть усло-
вия контракта с Apex Какие новые условия и/или максимальную сумму компенса-
ции вы рекомендуете для обсуждения? Подкрепите ваши рекомендации соответст-
вующими отчетами на базе электронных таблиц.
4 Анализ рынка показал, что объем продаж будет зависеть от цены компьютера.
При цене $1000 будет продано около 5000 компьютеров, а при каждом увеличе-
нии (уменьшении) цены на $100 объем продаж увеличится (уменьшится) на 1000
единиц Используйте таблицу подстановки с двумя входами, чтобы максимизи-
ровать прибыль компании Kayo в будущем году посредством нахождения (а) оп-
тимальной цены и (Ь) оптимального количества плат, закупаемых у Apex, при ус-
ловии, что исходный контракт останется в силе
| Ситуация для анализа | Компания Watson Truck Rental Company10
Компания Watson Truck Rental Company, владеющая 50 большегрузными автомо-
билями, сдаваемыми в аренду различным клиентам, выставляется на продажу за
$1000 000 Уотсон, продавец, хочет, чтобы вы провели трехгодичный экономиче-
ским анализ, который поможет покупателям оценить компанию
Компания платит налог на имущество $35 000 в год; административные расходы
и затраты на обслуживание парка автомобилей составляют $4 800 в расчете на один
грузовик. Ожидается, что налог будет ежегодно увеличиваться на 4%, а затраты на
обслуживание будут возрастать на 7% в год
В настоящее время плата за аренду грузовика составляет $1000 в месяц При такой
ставке арендной платы каждый месяц арендуется в среднем 60% грузовиков. Уотсон счи-
тает, что при снижении платы за аренду одного грузовика на $100 количество арендуемых
машин увеличится на 7%, и такое соотношение справедливо и для последующих сокра-
щений арендной ставки на $100 Так, при арендной ставке $600 ежемесячно будет арен-
доваться 88% грузовиков. Независимо от того, какой будет арендная ставка в первый год,
© 1999 Board of Trustees of the Leland Stanford Junior University AU rights reserved
ГЛАВА 2. Моделирование с помощью электронных таблиц 115
во 2- и 3-й год она будет увеличена на 9%. При этом средний процент арендуемых грузо-
виков останется таким же, как в I -й год, несмотря на увеличение арендной платы
Предположим, что по истечении трех лет покупатель продаст компанию с целью по-
лучения прибыли. Цена продажи будет равна утроенному годовому доходу в 3-м году
Выручка в каждом году предполагается равной чистой прибыли (валовый доход минус за-
траты) Влияние амортизации и других факторов, относящихся к подоходному налогу, не
учитывается Выручка в 3-м году включает также выручку от продажи дела Предполага-
ется, что в течение рассматриваемого периода грузовики не покупаются и не продаются
Вопросы
1	Определите переменные решения, внешние переменные, показатель эффективно-
сти, промежуточные переменные, а также все ограничения данной задачи и по-
стройте в Excel соответствующую модель
2	Используя таблицу подстановки, определите, какой должна быть исходная
арендная ставка, чтобы получить наибольшую общую прибыль от капиталовло-
жений после продажи компании через три года
3	Исследуйте чувствительность общей прибыли от капиталовложений к изменению сле-
дующих переменных цена покупки, удельные затраты на обслуживание (в расчете на
один грузовик), ежегодный налог на имущество, коэффициент умножения при прода-
же (Используйте для анализа значение арендной ставки, найденное при ответе на во-
прос 2) К какому фактору прибыль наиболее чувствительна7
4	. Подготовьте для Эрика Уотсона отчет, в котором отражены основные заключе-
ния и рекомендации.
Ситуация для анализа | Индивидуальный финансовый план11
Предположим, что вы получили наследство от вашего дядюшки Уилберфорса
и теперь решаете, что делать с деньгами
Зарплата
Суммарная зарплата вашей супружеской пары составляет $80 000 в год, и вы пред-
полагаете, что эта сумма будет расти со скоростью 15% в год. Вы решили жестко при-
держиваться бюджета и следить за тем, чтобы расходы семьи составляли определенный
постоянный процент от зарплаты (экспериментально установленный на уровне 75%)
По мере роста зарплаты соответственно увеличиваются расходы Заметим, что процент
берется от всей зарплаты, а не от чистого дохода после уплаты налогов
Налоги
Конгресс опубликовал новый закон о налогообложении — закон о фиксированном
подоходном налоге. Согласно данному закону для супружеской пары вводится необла-
гаемый минимум $15 000 и комбинированная ставка федерального и местного налога
35% со всех доходов, превышающих базовое значение $15 000. Кроме того, вводится на-
лог на прирост капитала 40% всего прироста капитала облагается как регулярный доход
© 1999 Board of Trustees of the Leland Stanford Junior University All rights reserved
116
ЧАСТЬ I Модели и моделирование
Инвестиции, снижающие налоги
У вас есть возможность вложить любое количество средств в недвижимость Од-
ним из преимуществ таких инвестиций является то, что на протяжении последую-
щих пяти лет их стоимость по счетам будет уменьшаться (соответственно, вследствие
амортизации уменьшится и налог), в то же время они будут приносить небольшую
(необлагаемую налогом) денежную прибыль. По прошествии 5 лет недвижимость
будет продана, вы получите свою долю прибыли и заплатите с этой прибыли налог
на прирост капитала На каждую $1000, вложенную в проект, влияют такие факторы.
Ежегодное снижение налога	$200
Ежегодные денежные выплаты	$40 (не облагаются налогом)
Сумма, возвращенная по окончании 5 лет $ 1 800
Обязательства по выплате налога на
прирост капитала на конец 5-го года	$2 200
Инвестиционная компания открытого типа
Другим видом инвестиций является некий инвестиционный фонд денежного
рынка Фонд платит 14% годовых, но этот доход подлежит налогообложению. Вы
можете внести в фонд любую сумму в любой момент.
Для удобства вычислений предположим, что ежегодный процент выплачивается
исходя из суммы, находившейся на счету на начало данного года (конец прошлого
года) Можно попробовать внести унаследованные $100 000 в фонд, а при необходи-
мости сразу же снять эту сумму
Вы хотите построить индивидуальную финансовую модель, чтобы увидеть, как
вырастет ваше благосостояние к концу пятилетнего периода, а также решить, сколь-
ко средств вложить в план снижения налогов, и исследовать чувствительность ва-
шего плана к различным предположениям.
Вопросы
Воспользуйтесь моделью, чтобы ответить на следующие вопросы.
1.	Сколько средств следует инвестировать в план снижения налогов?
2.	Предположим, ваша заработная плата увеличивается только на 10% ежегодно.
Как это повлияет на ваше благосостояние в конце пятилетнего периода? Объяс-
ните полученный результат
3.	Увеличьте по отдельности каждый из параметров налогосберегающей схемы на
10% Что окажет наибольшее влияние на конечный уровень вашего благосостоя-
ния по прошествии 5 лет?
4	Какую максимальную часть (в процентном выражении) зарплаты можно тра-
тить, чтобы не влезть в долги?
5	Какой должна быть отдача от денежного фонда, чтобы вам было безразлично,
инвестировать в недвижимость все средства или ничего?
ГЛАВА 2 Моделирование с помощью электронных таблиц 117
| Ситуация для анализа | Компания Santa Rosa Raisins
Компания по производству пищевых продуктов Santa Rosa Raisins (SRR) расположена
в Калифорнийской зоне виноделия. Осенью она закупает виноград у производителей,
сушит его, чтобы получить изюм, обливает глазурью и продает глазированный изюм про-
изводителям хлопьев для завтрака и кондитерским компаниям Весной, в начале сезона
выращивания винограда, компании SRR нужно принять несколько взаимосвязанных
решений. Во-первых, следует решить, сколько винограда купить по существующему кон-
тракту поставок, а во-вторых, определить цену на глазированный изюм
Компания SRR имеет контракт с производителем, который по заявке в начале сезона
должен поставить осенью указанное количество винограда по цене $0,25 за фунт Недос-
тающее количество винограда (разность между потребностями SRR и количеством, по-
ставленным производителем) компания SRR должна будет приобрести осенью по сво-
бодной рыночной цене, которая может колебаться в пределах от $0,15 до $0,35 за фунт
Следующие пункты, по мнению руководства, отражают положительный опыт в пе-
реговорах с клиентами о цене и количестве поставляемого изюма. На основании опыта
предыдущих лет руководство SRR считает, что 1) при цене засахаренного изюма $2,15
за фунт клиенты закажут 700 000 фунтов; 2) при каждом снижении цены от рыночного
значения $2,15 на $0,01 общий спрос будет возрастать на 15 000 фунтов
Глазированный изюм делается следующим образом виноград моется и высушива-
ется, а полученный изюм обрабатывается сахарной глазурью, которую компания SRR
покупает по цене $0,30 за фунт. Для изготовления 1 фунта глазированного изюма тре-
буется 2,5 фунта винограда и 0,5 фунта глазури (поскольку вода испаряется в процессе
сушки изюма). Помимо расходов на сырье (виноград и глазурь), компания также несет
затраты по превращению винограда в изюм (затраты на переработку), которые состав-
ляют $0,20 на переработку 1 фунта винограда при производственной мощности завода
компании 3 500 000 фунтов винограда. Переработка винограда сверх этого количества
потребует от SRR обращения к конкуренту, который берет $0,60 за превращение
1 фунта винограда в изюм Кроме того, у завода по переработке винограда есть посто-
янные накладные расходы, составляющие $200 000 в год.
Джейн Торстон, представляющая на переговорах компанию SRR, попросила вас
создать в Excel табличную модель, которая поможет ей проанализировать ситуацию
в свете предстоящих переговоров о цене и количестве глазированного изюма. Ее
цель — исследовать (с помощью анализа “Что-если”) воздействие различных факторов
на прибыль компании SRR. Прежде всего ее интересует оценка годовой прибыли до
уплаты налогов как функция цены на глазированный изюм и цены на виноград, при
условии, что по контракту закупается фиксированное количество винограда —
1 000 000 фунтов.
Также представляет интерес зависимость (если таковая существует) значения макси-
мальной прибыли до уплаты налогов от свободной цены на виноград, т е как цена изюма,
при которой достигается максимальная прибыль, зависит от свободной цены Для этого
Торнстон просит вас провести анализ чувствительности, чтобы увидеть (в процентном вы-
ражении), как различные значения свободной цены на виноград повлияют на прибыль при
определенной цене на глазированный изюм, в предположении, что SRR договорилась о за-
купке по контракту 1000 000 фунтов винограда по цене $0,25. В качестве базовой ситуации
она предлагает рассматривать свободную цену, равную прошлогоднему значению, — $0,25,
и закупку 1000 000 фунтов винограда. Ее также интересует, что будет, если по контракту бу-
дет закупаться количество винограда, отличное от базовых 1000 000 фунтов
118
ЧАСТЬ! Модели и моделирование
Разработайте документированную табличную модель, чтобы помочь Торстон
проанализировать данную управленческую ситуацию Модель должна рекомендо-
вать конкретные решения по цене глазированного изюма при различных значениях
свободной цены на виноград и объема его закупки. Кроме того, ваш отчет должен
сопровождаться анализом чувствительности в форме диаграмм или таблиц, чтобы
помочь Джейн понять и оценить основные закономерности
Ситуация для анализа | Компания Ebel Mining (часть 1)12
Компания Ebel Mining владеет различными шахтами, которые добывают определен-
ный тип руды Шахты расположены в разных концах страны, у них различные производ-
ственные мощности и качество руды. Добытая руда в зависимости от качества относится
к одному из трех классов: высококачественная, средняя и низкокачественная В конце
каждой рабочей пятидневки компания Ebel обязана по контракту поставлять плавильно-
му заводу не менее 12 т высококачественной руды, 8 т средней и 24 т низкокачественной.
Эксплуатация первой шахты обходится компании Ebel в $20 000, а второй— $16 000
вдень Однако в первой шахте добывается в день 6 т высококачественной руды, 2 т сред-
ней и 4т низкокачественной, в то время как во второй шахте ежедневно добывается 2 т
высококачественной руды, 2 т средней и 12 т низкокачественной.
Вопросы
Разработайте в Excel табличную модель, чтобы ответить наследующие вопросы
1	Сколько дней в неделю должна работать каждая шахта, чтобы выполнить обяза-
тельства Ebel наиболее экономичным способом9 (В расписании допускается,
чтобы шахта работала неполный день)
2	Насколько чувствительны общие еженедельные затраты компании Ebel к огово-
ренным контрактом объемам поставок высококачественной, средней и низкока-
чественной руды9
Литература
1 Mark Bucciarelli and Kip Brown A Desktop-OR Success Modeling Coast Guard Buoy Tender Op-
erations, Interfaces 25, no 4(1995), 1-11
12 © 1999 Board of Trustees of the Leland Stanford Junior University All rights reserved Это первая из предлагае-
мых вашему вниманию ситуаций для анализа на примере компании Ebel Mining. Все последующие примеры
базируются на этой постановке проблемы и используются для иллюстрации различных приемов и методов
моделирования
мизационные модели
Глава 3. Линейная оптимизация
Глава 4. Линейная оптимизация. Анализ чувствительности
Глава 5. Линейная оптимизация. Применение
Глава 6. Целочисленная оптимизация
Глава 7. Нелинейная оптимизация
Глава 8. Многоцелевая оптимизация
и эвристические методы
В конце главы 2 отмечалось, что основной интерес при создании моделей представ-
ляет поиск оптимального решения Эффективным средством поиска решений явля-
ется надстройка Excel Подбор параметра Однако у этого средства есть определен-
ные недостатки
1.	Средство Подбор параметра не позволяет налагать ограничения на пере-
менные
2.	С его помощью можно изменять только одну переменную.
3.	При использовании данного средства желаемое значение показателя эффек-
тивности необходимо указывать заранее, т е нужно знать оптимальное значе-
ние, чтобы с помощью средства Подбор параметра найти решение, опреде-
ляющее это значение.
В главах 3 и 4 будет описана надстройка Excel Поиск решения, которая лишена
указанных недостатков. Это мощное средство, но при его использовании нужно
быть внимательным, чтобы избежать возможных ошибок. Например, в некоторых
моделях использование средства Поиск решения приводит к решению, которое в
действительности не является оптимальным. Кроме того, существует риск невер-
ной интерпретации результатов поиска. Чтобы избежать подобных ловушек, необ-
ходимо разобраться в общих принципах построения оптимизационных моделей.
Сначала мы рассмотрим модели, в которых переменные связаны между собой ли-
нейными зависимостями. С линейными моделями гораздо проще работать, их
легче понимать и оптимизировать с помощью средства Поиск решения. В главе 5
будут представлены приложения, иллюстрирующие широкий спектр применения
линейной оптимизации к управленческим ситуациям Кроме того, теорию линей-
ной оптимизации можно применять к целочисленным и нелинейным моделям,
описанным в главах 6 и 7. Данная часть завершается главой 8, в которой рассмат-
ривается оптимизация при наличии нескольких критериев эффективности.
Глава
Линейная оптимизация
В этой главе...
3.1.	Введение в линейное программирование
3.2.	Формализация моделей линейного программирования
3.3.	Искусство создания моделей ЛП
3.4.	Невозвратные и переменные издержки
3.5.	Табличная модель компании Oak Product
3.6.	Модель ЛП и ее представление в электронных таблицах
3.7.	Надстройка Поиск решения
3.8.	Оптимизация модели Oak Product
3.9.	Рекомендации по поиску решения задач ЛП
3.10.	Пример транспортной модели
3.11.	Задача составления смесей
3.12.	Создание моделей ЛП
3.13.	Пример 1 Задача об ассортименте продукции
3.14.	Пример 2 Задача составления смеси
3.15.	Пример 3 Составление расписания
3.16.	Пример 4 Анализ безубыточности при наличии ограничений
3.17.	Разработка моделей ЛП
3.18.	Заключение
3.19.	Решения примеров
Основные термины
Контрольные вопросы
Задачи
Ситуация 1. Компания Ebel Mining (часть 1, продолжение)
Ситуация 2 Компания Red Brand Canners
Ситуация 3 Обмен валют в компании HiTech
Литература
122
ЧАСТЬ II Оптимизационные модели
Составление расписания полетов в компании
Delta Air Lines
Компания Delta Air Lines выполняет ежедневно более 2 500 внутренних рейсов,
используя около 450 самолетов 10 различных авиапарков. При составлении расписа-
ния полетов необходимо для каждого рейса выбрать самолет (Боинг 747, 757, DC-10
или MD-80) таким образом, чтобы как можно лучше заполнить пассажирский салон
Расписание — это основа функционирования авиакомпании. Компания Delta одной
из первых попыталась полностью решить проблему расписания, которая считается
наиботее сложной в отрасли авиаперевозок.
Место в самолете — самый “скоропортящийся товар” в мире. Каждый раз, когда
самолет поднимается в воздух с пустым креслом, возможность получения дохода теря-
ется безвозвратно Поэтому расписание должно разрабатываться так, чтобы извлечь
наибольшую выгоду максимизировать доходы при минимально возможных эксплуа-
тационных затратах Отрасль авиаперевозок соединяет в себе худшие черты двух секто-
ров экономики она обладает высокой капиталоемкостью промышленного сектора
и низкой долей прибыли, характерной для розничной торговли. Авиаперевозки требу-
ют больших затрат финансов, топлива и труда Выживание и успех на рынке зависят от
способности наиболее эффективно организовать расписание полетов.
Как размеры авиапарка, так и число самолетов различных моделей играют боль-
шую роль в составлении расписания Если авиакомпания выделит для определен-
ного рейса слишком маленький самолет, то часть потенциальных пассажиров оста-
нется “за бортом”, а выделение слишком большого самолета приведет к дополни-
тельным расходам на перевозку пустых мест. Другими словами, необходимо иметь
нужный самолет в нужное время в нужном месте, но множество эксплуатационных
ограничений делает эту цель труднодостижимой
Чтобы выбрать для выполнения рейсов наиболее подходящие самолеты, компа-
ния Delta разработала крупномасштабную модель линейного программирования,
которая позволяет минимизировать комбинацию эксплуатационных затрат и убыт-
ков от “потери” пассажиров с учетом разнообразных эксплуатационных ограниче-
ний Наиболее существенным ограничением является количество имеющихся в каж-
дом авиапарке самолетов Среди других факторов, которые необходимо учесть, мож-
но указать плановое обслуживание самолетов (т.е в каком городе его лучше
проводить), назначение на рейс пилотов, навыки которых позволяют им управлять
данным типом самолетов, обеспечение достаточного времени для отдыха пилотов;
дальность полета, скоростные характеристики самолета и ограничения, налагаемые
аэропортами (например, на уровень шума)
Типичная модель линейного программирования, которую ежедневно приходится
оптимизировать компании Delta, состоит из 40 000 ограничений и 60 000 переменных
решения Ожидается, что за последующие три года использование этой модели позво-
лит компании сэкономить $300 млн Компания American Airlines также сообщила, что
использование подобных моделей позволит ей сэкономить миллионы долларов [2]
ГЛАВА 3. Линейная оптимизация 123
3.1.	Введение в линейное программирование
Рассматривая в конце главы 2 пример компании Oak Production, мы убедились в важ-
ности моделей условной оптимизации, поскольку они отражают суть многих управленче-
ских ситуаций В модели условной оптимизации необходимо оптимизировать показатель
эффективности (целевую функцию) для допустимых значений переменных решения
Возможные значения переменных решения задаются множеством ограничении в виде
неравенств Таким образом, необходимо выбрать значения переменных решения в соот-
ветствии с ограничениями и при этом сделать показатель эффективности наибольшим
(модель максимизации) или наименьшим (модель минимизации) из всех возможных
Напомним, что в примере компании Oak Products задача состояла в нахождении значе-
ний шести переменных решения (определяющих, сколько стульев каждого типа будет про-
изведено) при соблюдении одиннадцати ограничений на имеющиеся ресурсы. Одним из
способов исследовать, к каким результатам приведут различные комбинации значений пе-
ременных решений, является применение анализа “Что-если”. Но в данной главе мы хотим
пойти дальше, и ответить на вопрос, какое решение будет “наилучшим”. При этом хотелось
бы избежать бессистемного перебора различных альтернативных решений, при котором
есть риск пропустить оптимальное решение Однако полный перебор сценариев “Что-если”
в диапазоне возможных решений для типичных моделей условной оптимизации быстро
становится утомительным даже для самых рьяных приверженцев электронных таблиц
Кроме того, вам не удастся воспользоваться таблицами подстановки Excel для автоматиза-
ции поиска, поскольку они позволяют изменять не более двух переменных одновременно
Но даже если использовать усовершенствованную версию таблиц подстановки
(позволяющую изменять более двух переменных), подумайте, сколько времени займет изуче-
ние модели компании Oak Products с помощью анализа “Что-если”, если предположить, что
каждая из шести переменных решения может принимать 100 различных значений Выполнить
полное исследование всех существующих комбинаций значений переменных практически не-
возможно, независимо от возможностей таблиц подстановки и быстродействия компьютера
Очевидно, что подавляющее большинство комбинаций переменных в примере Oak
Products нас не интересует, поскольку они нарушают одно или несколько ограничений мо-
дели или дают слишком низкую прибыль Но как выявить эти комбинации? Это трудно
сделать с помощью анализа “Что-если” В этом смысле оптимизационные модели сущест-
венно отличаются от простых моделей, рассмотренных ранее Необходимо найти быстрый
и эффективный способ просмотра комбинаций переменных для поиска допустимых реше-
ний Для этого можно “перевернуть таблицу”, сделав входы модели, используемые для по-
строения сценариев “Что-если” (обычно это переменные решения), выходами. Это позво-
лит прибегнуть к более эффективным процедурам поиска и избежать полного перебора
многих тысяч комбинаций переменных.
Пример Oak Products имеет шесть решений и одиннадцать ограничений Некоторые
современные оптимизационные модели содержат тысячи или даже десятки тысяч пере-
менных решения и ограничений, для работы с ними требуется специальное программное
обеспечение и мощные компьютеры Однако многие представляющие интерес модели
оптимального управления содержат десятки или сотни переменных и ограничений Для
моделей такого размера современные программы электронных таблиц часто являются
наиболее удачным средством оптимизации: электронные таблицы обеспечивают практи-
чески идеальное сочетание гибкости, удобства моделирования, простоты использования
и вычислительной мощности.
124	Ч А С Т Ь II Оптимизационные модели
Существуют эффективные методы поиска решений для моделей оптимизации с ли-
нейными ограничениями Модели с линейными ограничениями называются моделями
линейного программирования (ЛП) Однако, прежде чем перейти непосредственно к про-
цессу оптимизации моделей, следует уделить внимание представлению моделей ЛП
в электронных таблицах В этой главе мы рассмотрим: 1) методику формализации моде-
лей ЛП, 2) правила представления моделей ЛП в электронных таблицах, которые упро-
стят применение средства Excel Поиск решения, 3) использование средства Поиск реше-
ния для оптимизации моделей Л П.
3.2.	Формализация моделей линейного
программирования
Ограничения
Первым этапом формализации модели линейного программирования (ЛП) должно
стать выявление ограничений на переменные решения Ограничения сужают множество
допустимых решений Приведем конкретные примеры ограничений, возникающие в за-
дачах управления
1.	Менеджер по инвестициям имеет в своем распоряжении определенный капитал
Инвестиционные решения ограничены суммой данного капитала и распоряжения-
ми таких правительственных органов, как Комиссия по ценным бумагам и биржам.
2.	Решения директора завода ограничены производственной мощностью завода и имею-
щимися ресурсами.
3.	Планы полетов авиакомпании ограничены необходимостью обслуживания само-
летов и числом сотрудников
4.	Решение нефтяной компании использовать определенный тип нефти для производства
бензина диктуется характеристиками бензина, пользующегося спросом на рынке.
В моделировании ограничения на допустимые значения переменных решения явля-
ются очень важным понятием Ограничения в реальных управленческих моделях выра-
жаются в числовом виде, но в своей основе имеют физическую, экономическую или даже
политическую природу.
Целевая функция
Все модели линейного программирования имеют два общих основных свойства. Пер-
вое — это наличие ограничений Второе свойство заключается в том, что в каждой моде-
ли линейного программирования существует единственный показатель эффективности,
который необходимо максимизировать или минимизировать.1
В приведенных выше примерах менеджер по инвестициям, скорее всего, будет стре-
миться максимизировать прибыль от портфельных инвестиций; директор завода захочет
удовлетворить спрос при минимальных производственных затратах. Аналогично авиа-
компания будет стремиться реализовать заданное расписание с минимальными издерж-
Зачастую непросто найти единственный приемлемый критерий эффективности В случае наличия не-
скольких критериев эффективности оптимизация также возможна, эта тема рассмотрена в главе 12
ГЛАВА 3. Линейная оптимизация 125
ками, а нефтеперерабатывающая компания — использовать имеющуюся сырую нефть
с максимальной прибылью.
Таким образом, в каждом из этих примеров существует некий показатель эффектив-
ности, который при принятии решения желательно максимизировать (как правило, это
прибыль, эффективность или производительность) или минимизировать (обычно это за-
траты или время) В моделях оптимизации показатель эффективности, который следует
оптимизировать, называется целевой функцией.
Каждая модель линейного программирования имеет целевую функцию, которую необхо-
димо максимизировать или минимизировать, и ограничения.
Модели линейного программирования являются примером более широкого класса
моделей — моделей принятия решений при наличии ограничении, которые также назы-
ваются моделями условной оптимизации. Эти модели можно охарактеризовать следующим
образом
• Модель условной оптимизации призвана так распределить ограниченные ресурсы, что-
I бы оптимизировать целевую функцию.
В этом определении под “ограниченными ресурсами” подразумеваются ресурсы, на
которые распространяются ограничения
Хотя существуют модели принятия решений при наличии ограничении более общего
вида, во многих приложениях наиболее полезными являются модели линейного про-
граммирования Эти модели успешно применялись для решения тысяч различных задач
принятия решений, поэтому мы уделяем данной теме значительное внимание Начнем
с рассмотрения конкретного примера формулировки задачи линейного программирова-
ния для версии модели Oak Products, описанной в разделе 2 7 главы 2 Чтобы сконцен-
трировать внимание на механизме оптимизации, несколько упростим модель Oak Prod-
ucts и продемонстрируем использование надстройки Поиск решения для упрощенной
модели; позднее будет показано, как оптимизировать полную версию этой модели
Итак, в упрощенной версии компания Oak Products производит только два вида
стульев, Captain и Mate (вместо шести в полной версии), ее модель содержит шесть огра-
ничений (вместо одиннадцати). Значения параметров отличаются от исходной версии в
главе 2, однако форма модели остается прежней Составив экономический прогноз на
следующую неделю, Джим Уайт полагает, что можно будет продать все стулья марки
Captain и Mate, которые компания в состоянии произвести. Теперь Джим должен реко-
мендовать стратегию производства на следующую неделю, те. определить, сколько
стульев каждой марки нужно произвести, если руководство компании стремится макси-
мизировать недельную валовую прибыль (которая вычисляется как разность дохода и за-
трат).
Данные для модели
При принятии решения в данной модели необходимо учитывать следующие факторы
1.	Стулья, произведенные компанией, продаются на той же неделе, удельная валовая
прибыль (доход минус расход) составляет $56 для каждого проданного стула марки
Captain и $40 для каждого стула марки Mate
2.	Для сборки стула нужны длинные штифты, короткие штифты и одно из двух типов
сидений, которые имеются на складе в ограниченном количестве
126 ЧАСТЬ II Оптимизационные модели
3.	Запас длинных и коротких штифтов, которые можно будет использовать на сле-
дующей неделе, составляет 1280 и 1600 штук соответственно Для производства
одного стула марки Captain требуется 8 длинных и 4 коротких штифта, а для про-
изводства стула Mate — 4 длинных и 12 коротких штифтов (табл 3.1).
4.	Запас ножек на следующую неделю составляет 760 штук Для производства одного
стула любого типа требуется 4 ножки (табл. 3 2).
5.	Запас прочных и облегченных сидений составляет 140 и 120 штук соответственно
(табл 3 3) Для производства стульев Captain используются прочные сиденья, а для
Mate — облегченные
6.	Согласно договору между руководством компании и профсоюзом общее число
произведенных стульев не может быть менее 100
Таблица 3.1. Штифты			
Тип	Расход на 1 стул Captain	Расход на 1 стул Mate	Общий запас
Длинные штифты	8	4	1280
Короткие штифты	4	12	1600
Таблица 3.2 Ножки
Тип	Расход на 1 стул Captain	Расход на 1 стул Mate	Общий запас
Ножки	4	4	760
Таблица 3 3 Сиденья
Тип	Расход на 1 стул Captain	Расход на 1 стул Mate	Общий запас
Прочные	1	0	140
Облегченные	0	1	120
Задача Джима состоит в том, чтобы в данных условиях определить, сколько стульев
каждой марки необходимо произвести на следующей неделе. Используя терминологию
моделирования, он должен найти оптимальный ассортимент продуктов, или составить
оптимальный план производства Покажем, как данную ситуацию можно представить
в виде задачи линейного программирования, а затем — в виде оптимизационной модели
Excel Для этого необходимо определить ограничения и целевую функцию.
Определение ограничений
Как уже отмечалось, существует ограниченный запас деталей, из которых можно соби-
рать стулья Captain и Mate. Это ограничивает суммарное количество стульев, которые мож-
но собрать. Чтобы точно сформулировать ограничения, начнем с определения необходи-
мого количества длинных штифтов Длинные штифты требуются для производства обоих
видов стульев На изготовление одного стула Captain идет 8 длинных штифтов, a Mate — 4
Таким образом, для любого плана выпуска справедливо следующее равенство.
8 х (к-во произведенных Captain) + 4 х (к-во произведенных Mate)
= суммарная потребность в длинных штифтах.
ГЛАВА 3. Линейная оптимизация 127
Введем обозначения, пусть С — количество произведенных стульев Captain, М — ко-
личество произведенных стульев Mate. Тогда выражение для суммарной потребности
в длинных штифтах примет следующий вид'
8С + 4М = суммарная потребность в длинных штифтах
Однако запас длинных штифтов составляет 1280 штук. Поэтому переменные решения
С и Л/должны соответствовать ограничению
8С+4М<1280	(3 1)
Это ограничение на суммарную потребность в длинных штифтах. Условие (3 1) назы-
вается ограничением в виде неравенства Число 1280 называется правой частью неравенст-
ва Левая часть неравенства, которая зависит от неизвестных С И М, называется функцией
ограничения Неравенство (3 1)— символический способ представления ограничения,
требующего, чтобы суммарная потребность в длинных штифтах для производства С штук
стульев Capitan и М штук стульев Mate не превышала имеющийся запас — 1280 штук
длинных штифтов.
Для производства одного стула Captain требуется 4 коротких штифта, a Mate— 12
Поскольку запас коротких штифтов составляет 1600 штук, С и М должны также соответ-
ствовать ограничению
4С+12Л/< 1600.	(3 2)
Неравенства (3 1) и (3.2) — два ограничения данной модели Есть ли другие ограниче-
ния9 В перечне пунктов, которые необходимо учесть, говорится о существовании согла-
шения с профсоюзом Оно касается общего выпуска стульев
С + Л/>100.	(3 3)
Отметим, что условие (3 3) является неравенством типа “>” в отличие от условий (3 1)
и (3 2), которые являются неравенствами типа “<”
Еще одно ограничение отражает тот факт, что для сборки каждого стула требуется
4 ножки, а запас ножек составляет 760 штук
4С+4Л/< 760.	(3 4)
В пятом пункте списка говорится, что для изготовления стула Captain требуется проч-
ное сиденье, а для Mate — облегченное Указаны также запасы сидений обоих видов Эта
информация записывается в виде двух ограничений
С< 140 и Л/< 120	(3 5)
Мы сформулировали в сжатой форме шесть ограничений в виде неравенств для упро-
щенной модели Oak Products Поскольку количество изготовленных изделий не может при-
нимать отрицательное значение, необходимо включить два дополнительных ограничения
С>0иЛ/>0.	(3 6)
Условие вида (3.6), которое требует, чтобы переменные принимали неотрицательные
значения, называется условием неотрицательности. Следует помнить, что неотрицатель-
ность не то же самое, что положительность Неотрицательность допускает значение 0,
в то время как положительность не допускает нулевого значения.
128 ЧАСТЬ II Оптимизационные модели
Итак, сформулированы все ограничения и условие неотрицательности для упрощен-
ной модели Oak Product
Оценивание решений
Как и в предыдущих моделях, значение пары переменных С и М называется решени-
ем, сами переменные С и М называются переменными решения (поскольку именно эти ко-
личества контролирует Джим) В данной задаче решение — это структура производства
изделий (стульев) Например, С = 6, М = 5 — это решение сделать 6 стульев марки Captain
и 5 стульев Mate Некоторые неотрицательные решения будут соответствовать всем огра-
ничениям модели (3 1)—(3 5), другие — нет. Так, решение С = 6, М = 5 удовлетворяет ог-
раничениям (3 1), (3 2), (3 4), (3 5) и (3 6), но нарушает ограничение (3.3). Данное реше-
ние недопустимо, поскольку нарушает одно изограничений
Среди бесконечного множества неотрицательных пар чисел (С, Л/), включая дробные
значения, некоторые пары будут нарушать по крайней мере одно ограничение, а некото-
рые будут соответствовать всем ограничениям В нашей модели приемлемы только неот-
рицательные решения, соответствующие всем ограничениям Такие решения называют-
ся допустимыми
Целевая функция
Какое же из допустимых решений выбрать7 Как уже отмечалось, каждая модель ли-
нейного программирования наряду с ограничениями содержит конкретную цель Джим
хочет максимизировать прибыль, это и есть цель модели В данном случае у компании
Oak Products два источника прибыли
1. Прибыль от продажи стульев Captain
2. Прибыль от продажи стульев Mate
При перечислении основных производственных факторов отмечалось, что удельная
прибыль составляет $56 для стульев Captain и $40 для Mate. Тогда
56С — прибыль от продажи С стульев Captain,
40Л/— прибыль от продажи Л/стульев Mate
Таким образом, решение произвести С стульев марки Captain и Л/стульев марки Mate
приведет к получению суммарной прибыли, вычисляемой по формуле
суммарная прибыль — 56С+40Л/.	(3.7)
Заметим, что если известны только данные о доходах, единственное, что можно сделать —
это максимизировать доход при соблюдении ограничений Если же доступны только данные о
затратах (себестоимости), то нужно минимизировать затраты, связанные с производством оп-
ределенного ассортимента изделий Однако когда известны и данные о доходах, и данные о за-
тратах, предпочтительней максимизировать прибыль, а не просто доход.
Оптимальное решение
Среди бесконечного множества решений, удовлетворяющих всем ограничениям (т е.
среди допустимых решений), существует такое, которое обеспечивает наибольшую сум-
Очевидно, что дробные значения могут быть допустимы в модели, но не обязательно допустимы на прак-
тике, поскольку вряд ли можно продать часть стула Вопросы реализации дробных решений обсудим в конце
данного раздеча
ГЛАВА 3. Линейная оптимизация
129
марную валовую прибыль. Это решение будем называть решением задачи Oak Product,
или оптимальным решением. Таким образом, среди всех возможных допустимых решений
мы ищем решение, которое максимизирует недельную прибыль. Суммарная прибыль яв-
ляется функцией переменных С и М, поэтому выражение 56С+ 40Л/ называется целевой
функцией. Итак, надо найти допустимые значения С и М, которые оптимизируют (в на-
шем случае максимизируют) целевую функцию. В символической форме это можно за-
писать следующим образом:
максимизировать 56С + 40Л/,
или, еще короче,
Мах56С + 40Л/.	(3.8)
Целевую функцию необходимо максимизировать только на множестве допустимых ре-'
шений.
Исследование модели компании Oak Product
В следующем разделе показано, как найти оптимальное решение для данной и других
подобных моделей с помощью электронных таблиц, а также продемонстрированы воз-
можности надстройки Поиск решения Однако сначала запишем полную формулировку
задачи Oak Product и сделаем на ее основании некоторые заключения.
В предшествующих разделах мы преобразовали словесное описание ситуации реаль-
ного мира в символическую (математическую) модель, состоящую из целевой функции и
ограничений Эта модель называется моделью линейного программирования и имеет сле-
дующий вид
максимизировать 56С + 40Л/ (целевая функция)
при ограничениях
8С + 4Л/< 1280 (ограничение для длинных штифтов),
4С+ 12Л/< 1600 (ограничение для коротких штифтов),
С+ М> 100 (минимальный объем производства);
4С +4М< 760 (ограничение для ножек),
С< 140 (ограничение для прочных сидений),
М< 120 (ограничение для облегченных сидений);
С> 0 и М> 0 (условия неотрицательности)
Линейные функции
Заметьте, что в данной модели все функции ограничений, а также целевая функция
являются линейными функциями двух переменных решения. График линейной функции
двух переменных представляет собой прямую линию В общем случае линейная
функция — это такая функция, в которую каждая переменная вместе со своим коэффи-
циентом входит в виде отдельного члена (т.е переменные не умножаются, не делятся
друг на друга, не возводятся в степень (отличную от 1), нет логарифмических, экспонен-
циальных или тригонометрических выражений и тд.). Примером нелинейной функции
может служить функция 14С + 12СЛ/, поскольку слагаемое 12СЛ/ содержит произведение
переменных. Функция 9С2 +8Л/ также является нелинейной, так как переменная С воз-
водится во вторую степень. Другой пример нелинейной функции: 19LogC + ]2СгМ. При-
130 ЧАСТЬ II. Оптимизационные модели
мерами функций Excel, которые часто делают модели нелинейными, являются функции
ЕСЛИ, MAX, MIN, LN и ABS.
С математической точки зрения с нелинейными функциями работать значительно
сложнее, чем с линейными. Сила и привлекательность линейного программирования за-
ключается в простоте линейных связей (уравнений и неравенств) и в том, что менеджеры
и аналитики могут использовать линейные модели в практических приложениях, почти
не имея специальной математической подготовки. На данном этапе важно запомнить
следующее.
1. В задаче линейного программирования всегда присутствуют целевая функция ?
(которую необходимо максимизировать или минимизировать) и ограничения. !
2. Все функции (целевая функция и ограничения) в моделях Л П являются линейными. 
О целочисленности решений
Посмотрим еще раз на формулировку задачи Oak Product. Следует отметить, что если не
наложить дополнительные ограничения, требующие, чтобы значения переменных решения
были целыми, нам, скорее всего, придется рассматривать дробные решения. Для многих
моделей Л П, как и в данном случае, дробные значения переменных решения не имеют фи-
зического смысла Например, решение “произвести 3,12 стульев Captain и 6,88 стульев
Mate” реализовать невозможно С другой стороны, для многих задач дробные значения,
безусловно, имеют смысл (например, “произвести 98,65 галлонов бензина”). В тех случаях,
когда дробные ответы смысла не имеют, существует четыре возможных выхода.
1.	Добавить в модель ЛП так называемое условие целочисленности, которое требует,
чтобы одна или несколько переменных решения принимали только целые значе-
ния Это приведет к изменению модели, которая превратится в модель целочис-
ленной оптимизации или целочисленного программирования Модели целочислен-
ного программирования имеют дополнительные особенности, которые отличают
их от обычных моделей ЛП, поэтому на данном этапе мы их рассматривать не бу-
дем Целочисленному программированию посвящена глава 6.
2.	Решать задачу как обычную задачу линейного программирования, а затем округ-
лить (до ближайшего целого числа) все переменные решения, для которых дроб-
ные ответы невозможно реализовать. Однако во многих случаях эта простая и оче-
видная тактика может привести к недопустимым или неоптимальным решениям.
Недостатки данного подхода подробно обсуждаются в главе 6.
3.	Можно считать, что результаты работы модели задают средний недельный уровень
производства для периода из нескольких последующих недель. Например, решение
“произвести 70,5 стульев Captain и 80,25 стульев Mate” можно реализовать следую-
щим образом согласно производственному плану еженедельно производится 70,5
стульев Captain, но 1) каждую первую неделю продается 70 стульев Captain, а поло-
вина стула переходит на следующую неделю как полуфабрикат, который следует за-
кончить; 2) каждую вторую неделю продается 71 стул марки Captain. Аналогично
еженедельно производится 80,25 стульев марки Mate, но 1) каждые три недели про-
дается только 80 стульев этой марки, а все незаконченные части стула рассматрива-
ются как полуфабрикат, и 2) каждую четвертую неделю продается 81 стул Mate. Если
следовать этим правилам, то среднее недельное производство для четырехнедельного
периода действительно составит 70,5 Captain и 80,25 Mate, как предписывается ре-
ГЛАВА 3 Линейная оптимизация 131
шением задачи ЛП Преимущества и недостатки использования усредненной не-
дельной модели обсуждаются в главе 5 при описании динамических моделей.
4.	Можно рассматривать результаты использования модели Oak Product только как
ориентиры для планирования, а не как оперативные решения, которые следует
реализовывать В таком случае эти результаты будут служить основой для приня-
тия окончательного решения, которое неизбежно будет учитывать другие аспекты
реальной ситуации, не нашедшие отражения в абстрактной модели ЛП Весьма ве-
роятно, что эти аспекты все равно приведут к отклонению окончательных реше-
ний от нецелочисленных решений, полученных с помощью модели ЛП В таком
случае решение, предложенное моделью ЛП, служит точкой отсчета при рассмот-
рении дополнительных соображений и является основой для анализа ситуации,
для чего, собственно говоря, и разрабатываются модели
На практике применяются все вышеуказанные подходы На данном этапе будем счи-
тать, что дробные значения представляют некие средние уровни производства (вариант 3),
или модель разрабатывается в качестве основы для планирования и анализа (вариант 4)
3.3.	Искусство создания моделей АП
Чтобы описать управленческую ситуацию в виде символической (математической) мо-
дели, полезно сначала составить “словесную модель”. Это делается следующим образом.
1.	Описать словами цель и целевую функцию, т е показатель эффективности
2.	Дать словесное описание каждого ограничения, обращая особое внимание на то,
является данное ограничение требованием в форме неравенств или равенством
3.	Шаги 1 и 2 приведут к словесному описанию переменных решения
Очень важно правильно определить переменные решения Иногда существует не-
сколько возможных вариантов Например, должны ли переменные решения представ-
лять килограммы готовой продукции или килограммы сырья7 Советуем в этом случае за-
дать вопрос- “Какие решения нужно принять, чтобы оптимизировать целевую функцию?”.
Ответ на этот вопрос поможет правильно выявить переменные решения
После выполнения пп 1-3 следует присвоить обозначения (или имена) переменным
решения Затем необходимо выполнить такие действия.
4.	Выразить все ограничения через обозначенные переменные решения
5.	Выразить с помощью обозначенных переменных целевую функцию
На данном этапе следует проверить модель на соответствие единиц измерения Напри-
мер, если коэффициенты целевой функции даны в долларах за килограмм, то переменные
решения, входящие в целевую функцию, должны выражаться в килограммах, а не в тоннах
или унциях Аналогично нужно проверить соответствие единиц измерения в правой и левой
частях каждого ограничения Например, если налагается ограничение на число часов рабо-
чего времени, то в правой части ограничения должны быть указаны часы рабочего времени.
Тогда, если переменные решения измеряются в килограммах, то значения коэффициентов
для данной функции ограничения (т е числовые коэффициенты перед каждой переменной
решения в левой части ограничения) должны выражаться в часах рабочего времени, делен-
ных на килограмм Нельзя допускать, чтобы в одной части равенства или неравенства стоя-
ли часы, а в другой — минуты, секунды, килограммы или тонны.
132 ЧАСТЬ II Оптимизационные модели
Рассмотрим еще один аспект формирования модели ЛП. Как уже отмечалось, ограни-
чения могут иметь форму неравенств типа “<” или “>”. Студенты часто задают вопрос, бы-
вают ли в модели линейного программирования ограничения в виде строгих неравенств ти-
па “<” или “>”. Ответ — нет. Причина этого имеет математическую природу: так делается
для того, чтобы надлежащим образом сформулированная задача имела решение. Матема-
тическое доказательство данного утверждения не входит в нашу задачу. Однако не будет
преувеличением сказать, что практически в любой реальной жизненной ситуации,
в которой встречаются ограничения, неравенств типа “<” или “>” вполне достаточно, что-
бы передать реальный смысл. Например, если переменная ^должна быть < 15, то в модели
вполне можно использовать ограничение Х< 14,9999999999.
Обсудим теперь один из аспектов формирования моделей, который касается природы
используемых стоимостных данных.
3.4.	Невозвратные и переменные издержки
Во многих реальных задачах часто встречаются два типа издержек' невозвратные и пе-
ременные. Вопреки первому впечатлению невозвратные издержки не играют особой роли
в оптимизации
i В оптимизационных моделях учитываются только переменные издержки.
Невозвратные издержки уже были сделаны, это означает, что никакие будущие решения
не смогут повлиять на эти расходы Предположим, было закуплено с последующей доставкой
800 и 500 фунтов алюминия двух сортов (1 и 2) по фиксированным ценам $5 и $10 за фунт со-
ответственно, и контракт уже оплачен Задача состоит в том, чтобы определить, как опти-
мально использовать эти 1300 фунтов алюминия, чтобы максимизировать прибыль, получен-
ную от производства алюминиевых шарниров и трубок С каждым из двух изделий связан до-
ход и переменные затраты на его производство (затраты на механическую обработку,
штамповку и тд) При формировании модели невозвратные затраты $9000 на закупку алю-
миния роли не играют. Эта сумма уже потрачена, следовательно, количество закупленного
алюминия не является переменной решения Переменными будут количества изделий, кото-
рые следует произвести, и для их определения нужно учитывать только переменные издержки
Сформулируем модель, соответствующую данному описанию Пусть
К — количество производимых шарниров (переменная решения),
С — количество производимых трубок (переменная решения),
$ 10 — доход от продажи одного шарнира,
$30 — доход от продажи одной трубки,
$4 — затраты на производство шарнира (переменные издержки),
$12 — затраты на производство трубки (переменные издержки)
Для каждого продукта мы должны вычислить удельную валовую прибыль, т е разность
между удельным доходом и удельными переменными издержками Удельная валовая
прибыль составляет для шарниров $ 10 - $4 = $6, для трубок $30 - $ 12 = $ 18
Предположим, что для изготовления одного шарнира используется 1 фунт алюминия 1
сорта и 2 фунта алюминия 2 сорта. Для изготовления трубки требуется 3 фунта алюминия 1
сорта и 5 фунтов 2 сорта Получается следующая модель линейного программирования
Мах 6/Г + 18С
ГЛАВА 3. Линейная оптимизация 133
при ограничениях
К+ЗС < 800 (ограничение на количество алюминия I сорта);
IK + 5С < 500 (ограничение на количество алюминия 2 сорта),
^>0,С>0
Чтобы показать независимость решения от невозвратных издержек, заметим, что це-
левая функция в нашей формулировке является суммарной валовой прибылью Чистая
прибыль вычисляется следующим образом- чистая прибыль = валовая прибыль - невоз-
вратные издержки = 6^ + 180- 9000.
Найти допустимые значения К и С, максимизирующие выражение 6К+ 180 - 9000 все
равно, что найти допустимые значения Км С, максимизирующие выражение 6АЧ-180. Кон-
станту 9000 можно игнорировать. Таким образом, если к оптимизируемой функции прибавить
некую константу или умножить функцию на некоторое постоянное положительное число, ре-
зультат оптимизации не изменится, т е оптимальные значения переменных решения останут-
ся неизменными Однако если прибавить (или отнять) одно и то же постоянное число ко всем
коэффициентам переменных решения в целевой функции, результат может измениться.
Подведем итог. Невозвратные издержки в финансовых уравнениях влияют только на
чистую прибыль Они не отражаются на принятии решений, поскольку не связаны с бу-
дущими решениями, которые являются предметом моделирования. Поэтому можно уб-
рать невозвратные издержки из целевой функции модели, при этом оптимальное реше-
ние не изменится
Роль невозвратных и переменных издержек наглядно иллюстрируется в ситуации для
анализа “Red Brand Canners” в конце данной главы Там показано, как возникают невоз-
вратные и переменные издержки в реальных ситуациях
3.5.	Табличная модель компании Oak Product
Напомним, что модель ЛП недельного производства компании Oak Product выглядит
следующим образом (С — количество производимых стульев марки Captain, а М — коли-
чество производимых стульев Mate).
Максимизировать 560 + 40Л/(целевая функция)
при ограничениях
8С+ 4М< 1280 (ограничение для длинных штифтов);
4С+ 11М< 1600 (ограничение для коротких штифтов);
4С+ 4М< 760 (ограничение для ножек);
С< 140 (ограничение для прочных сидений);
М< 120 (ограничение для облегченных сидений);
С + М> 100 (минимальный объем производства),
С> 0 и М> 0 (условия неотрицательности).
Обратите внимание на то, что ограничения были перегруппированы так, чтобы одно-
типные неравенства находились рядом. Причина такой группировки станет понятна при
описании работы средства Поиск решения. Табличная версия упрошенной модели Oak
Product, созданная в рабочей книге Excel Стулья.xls, представлена на рис. 3.1. Здесь пока-
зан случай, когда производится 110 стульев Captain и 90 стульев Mate Заметим, что при та-
ком ассортименте нарушается ограничение для ножек — их требуется больше, чем имеется
134 ЧАСТЬ II Оптимизационные модели
т в	о~~тё f-:: -q
Упрощенная модель Oak Products
Captain Mate .
$ 56 : $ 40 । Прибыль । :
Стулья Мин производство
' 1 В | cj.-_..xxX^'A^dEj' . F л:.Х ‘х G_. S
j, '	ynpoi
Прибыль
Суммарное потребление
=СУММПРОИЗВ($В$4$С$4,В6:С6)
=СУММПРОИЗВ($В$4 $С$4.В7.С7)
=СУММПРОИЗВ($В$4 $С$4,В8 С8)
=СУММПРОИЗВ($В$4 $С$4,В9:С9) =
=СУММПРОИЗВ($В$4 $С$4.В10 СЮ)
Рис. 3.1. Упрощенная модель ЛП производства компании Oak Products
Совет. Наиболее простой способ ввода символов неравенства, таких как < в ячейке Е6, со-
стоит в том, чтобы ввести в ячейку символ <, а затем щелкнуть мышью на кнопке Под-
черкнутый на панели инструментов форматирования Excel.
Хотя содержимое показанного рабочего листа в особых пояснениях не нуждается,
следует сверить формулы на листе (см. рис. 3 1) с формулами математической модели
производства компании Oak Production. Обратим ваше внимание на некоторые
“неочевидные” аспекты данного рабочего листа.
Коэффициенты и переменные решения
Многие ячейки рабочего листа содержат числа Эти числа представляют
а числовые значения коэффициентов и правых частей неравенств, они называются
параметрами данной модели ЛП;
Ь. числовые значения двух переменных решения. Они называются значениями реше-
ний или просто решениями.
ГЛАВА 3 Линейная оптимизация 135
Формулы
Формулы в Excel используются для вычисления значений целевой функции, функций
ограничений и левых частей неравенств (записаны в столбце D). В некоторых случаях
используются вспомогательные формулы, с помощью которых вычисляются числовые
значения различных коэффициентов модели Таким образом, числовые значения одних
коэффициентов вводятся непосредственно, а других — вычисляются по формулам
Вычисление резерва
За исключением ячеек G11 и G12, все элементы таблицы имеют очевидный смысл Ос-
талось объяснить, что представляет собой элемент под названием Резерв в ячейке G12.
? В моделях ЯП термином резерв обозначается неотрицательная разность функции огра-
ничения и его правой части.3
Часто предпочтительней использовать более содержательные названия (чем
“резерв”), например, Конечный запас (т.е. запас на конец недели, как в ячейке G5) Бо-
лее того, вычисления в столбце G однотипны. Их назначение — показать, насколько
близко значение функции ограничения к значению правой части неравенства, при этом
нулевой резерв свидетельствует о том, что в ограничении достигнуто равенство Напри-
мер, формула =F6-D6 в ячейке G6 соответствует ограничению для длинных штифтов
8С+ 4Л/< 1280. Здесь из правой части данного ограничения вычитается левая часть. Та-
ким образом, значение запаса на конец периода (или “резерв” для данного
ограничения) — это количество неиспользованных длинных штифтов Однако в ячейке
G12, соответствующей ограничению С + М> 100, записана формула “левая часть ограни-
чения минус правая часть”, такой порядок вычитания обусловлен тем, что резерв должен
быть неотрицательной величиной для допустимых решений. Итак, сформулируем сле-
дующее правило.
 Для ограничений типа < при вычислении резерва из правой части неравенства вычита-
> ется левая часть.
Для ограничений типа > при вычислении резерва из левой части неравенства вычитает-
ся правая часть.
Хотя вычисление резерва и не является обязательным, оно очень полезно Например,
сразу становится очевидным, что производственный план на рис 3 1 недопустим, по-
скольку запас на конец периода в ячейке G8 получился отрицательным
Один из очевидных способов использования полученной модели компании Oak Product —
проведение анализа “Что-если” для различных решений (т е различных значений производ-
ства стульев Captain и Mate) Для этого следует ввести соответствующие значения в ячейки В4
и С4 и просмотреть значения в ячейке D4, представляющие недельную валовую прибыль При
этом нужно следить, чтобы значения резерва в ячейках G6G12 были неотрицательными
Именно так и поступали Джим и Том с исходной моделью Oak Product в главе 2 Если ввести
вячейку В4 значение 20, а в ячейку С4 значение 80 (что означает С= 20, М= 80), то результи-
рующая таблица будет выглядеть так, как показано на рис. 3.2.
Для этой разности также часто используется название остаток — Прим ред
136 ЧАСТЬ II Оптимизационные модели
Рис. 3.2. Модель производства компании Oak Products для С=20 и М=80
Совет Как вы увидите, знаки неравенств в столбце Е, разделяющие значения левых и правых
частей ограничений, не используются при работе со средством Поиск решения и поэтому не
являются обязательными Однако их использование помогает при формализации модели.
Используя рабочую книгу Стулья xls, попробуйте, подставляя различные значения
переменных С и М, получить максимальную прибыль, как это делали Том и Джим Вы
скоро поймете, что найти наибольшую прибыль, не нарушая ограничений, непростая за-
дача даже для такой упрощенной модели
Поиск оптимального решения
Средство Поиск решения позволяет найти оптимальное решение в любой модели ли-
нейного программирования с помощью нескольких щелчков кнопкой мыши На рис. 3 3
показано оптимальное решение для упрощенной модели Oak Product.
Облегченные сиденья
Произведено
Длинные штифты
Короткие штифты
Тип стульев
Удельная прибыль
Произведенное к-во
В . С . .. . D . Е;_______________F ________._.G
Упрощенная модель Oak Products
Captain Mate
$56	$40
| 130	60 Г
Потребность в
деталях
8	4
4	12
1	0
0	1
Прибыль
.. - ,$9 68р]
Суммарное
потребление
1280 <
1240 <
760 <
130 <
60 <
________Стулья:
190 >
Конечный
Начальный запас :	запас
1280	:	0
1600	360
760	।	0
140	10
120	60
Мин производство; Резерв
100	;	90
Рис. 3.3. Значения С и М, приносящие максимальную прибыль
ГЛАВА 3. Линейная оптимизация 137
3.6.	Модель ЛП и ее представление в электронных
таблицах
Итак, у нас есть два представления модели производства компании Oak Production,
символическая (математическая) модель ЛП и ее представление в электронной таблице,
которую будем называть табличной моделью.
В связи с этим может возникнуть несколько вопросов. Обязательно ли для каждой
моделируемой управленческой ситуации составлять обе модели (символическую и таб-
личную)9 Почему табличная модель Oak Production выглядит именно так, а не иначе?
Как использовалось средство Поиск решения для получения оптимального решения, по-
казанного на рис. З.З9
Ответим на первый вопрос- пока вы не обретете определенный опыт, следует записы-
вать обе версии модели, как символическую (математическую), так и табличную. Элек-
тронная таблица хорошо подходит для представления моделей ЛП, особенно при проведе-
нии анализа “Что-если”. Однако новичкам не следует формировать модель ЛП сразу
в электронной таблице. Пока нет достаточного опыта, для создания “правильной” модели
линейного программирования в Excel данный процесс лучше разбить на три этапа.
1.	Написание и проверка символической модели ЛП. Модель записывается на бумаге
в математическом виде; это не займет много времени и поможет при отладке
окончательного варианта табличной модели в Excel. Затем анализируются форму-
лировки математической задачи с целью выявления возможных логических оши-
бок.
2.	Создание и отладка табличной модели ЛП На основе символической модели ЛП
создается ее представление в Excel. Затем производится проверка полученной таб-
личной модели путем задания различных значений переменных решения с целью
выявить возможные очевидные ошибки (например, для заведомо допустимых ре-
шений нарушаются ограничения, значения в ячейках левых частей или критерий
эффективности оказываются лишенными смысла и т.д.).
3.	Попытка оптимизации модели с помощью надстройки Поиск решения. Если модель
некорректно сформирована, результатом чаще всего будет сообщение об ошибке.
Тогда нужно исправить модель, возможно, вернувшись к первому этапу.
Созданная на первом этапе математическая модель полезна для целей документации,
она позволяет увидеть всю модель целиком, что облегчает понимание табличной модели
в Excel Для достаточно сложных моделей проще сначала проанализировать структуру
символической модели ЛП, а не ее представление в Excel. Фактически после ответа на
оставшиеся два вопроса в последующих нескольких главах мы будем заниматься именно
объяснением структуры моделей Л П, представленных в Excel.
Ответим на второй вопрос (“Почему табличная модель Oak Product выглядит именно
так, а не иначе?”). Модель Oak Product в Excel построена в соответствии с рекомендациями
о представлении моделей в Excel, которые мы приводили как в главе 2, так в ранее в этой
главе Именно из-за неправильного построения моделей в Excel студентам часто не удается
получить нужные результаты на этапе оптимизации. Наши рекомендации позволяют вы-
явить скрытые ошибки в задании связей между ячейками в формулах и избежать опреде-
ленных проблем интерпретации результатов, получаемых с помощью средства Поиск ре-
шения. Накопив опыт формирования моделей линейного программирования в Excel, мож-
138 ЧАСТЬ II Оптимизационные модели
но пропускать этап написания символической модели Для тех, кто такого опыта пока не
имеет, предлагаем следующие рекомендации по созданию табличной модели Л П в Excel
•	Каждая переменная решения располагается в отдельной ячейке, ячейки груп-
пируются по строкам или столбцам; каждому ограничению отводится отдельная
строка или столбец таблицы. (Чаще всего переменные решения расположены
в столбцах, а ограничения — в строках.)
•	Переменные решения группируются в отдельный блок столбцов/строк; анало-
гично ограничения группируются в свой блок строк/столбцов.
•	Все ячейки, содержащие переменные решения и целевую функцию, имеют за- >
головки в верхней части своего столбца, а все ограничения имеют заголовки s
в крайней слева ячейке своей строки.
•	Коэффициенты целевой функции хранятся в отдельной строке, располагаясь
непосредственно под или над соответствующими переменными решения; фор-
мула для вычисления целевой функции находится в соседней ячейке.
•	Чтобы модель была понятней, ячейки с переменными решения и целевой
функцией выделяются рамкой по границе ячеек или заливкой ячеек.
•	Коэффициент перед определенной переменной решения в каком-либо ограниче-
нии записывается в ячейку на пересечении столбца (строки), содержащего дан-
ную переменную решения, и строки (столбца), содержащей это ограничение.
•	В каждой строке ограничений за ячейками, содержащими коэффициенты дан-
ного ограничения, следует ячейка, в которую записано вычисленное значение
функции ограничения (значение левой части неравенства), за ней следует ячей-
ка, в которой стоит соответствующий знак неравенства, а затем ячейка, содер-
жащая значение правой части неравенства. Дополнительно может включаться ;
ячейка с формулой вычисления резерва, т.е. разности между значениями левой ;
и правой частей неравенства, вычисляемой таким образом, чтобы она была не-
отрицательной при соответствии ограничению.
г • Ячейки, содержащие правые части ограничений, должны включать константы
или формулы, в которые не входят переменные решения, — все формулы в пра-
вой части, прямо или косвенно связанные с переменными решения, должны
быть перенесены в левую часть с помощью алгебраических преобразований
данного неравенства.
•	Не следует использовать в формулах модели ЯП функции Excel ЕСЛИ, ABS,
i MAX, MIN и другие нелинейные функции. Такие функции могут использоваться
в формулах рабочего листа, но только в том случае, если они не влияют (прямо :
или косвенно) на вычисление целевой функции.
•	Условия неотрицательности переменных решения не обязательно включать
в табличную модель. Как правило, они опускаются и указываются непосредст-
венно в диалоговом окне средства Поиск решения.
Одним из результатов выполнения этих рекомендаций является то, что все основные ко-
эффициенты модели содержатся в отдельных ячейках, поэтому их легко изменять, не меняя
формул модели Кроме того, группирование переменных решения и ограничений позволяет
копировать формулы для создания аналогичных формул Благодаря группированию также
ГЛАВА 3. Линейная оптимизация
139
упрощается работа со средством Поиск решения, поскольку для указания переменных реше-
ния или ограничений можно использовать диапазоны ячеек рабочего листа
3.7.	Надстройка Поиск решения
Поиск решения — это надстройка, входящая в поставку Excel, предназначенная для
оптимизации моделей при наличии ограничений, в том числе моделей линейного про-
граммирования. Для этого в надстройке используются методы и алгоритмы математиче-
ского программирования, которые позволяют находить оптимальные решения для таб-
личных моделей. Для задач линейного программирования Поиск решения использует
эффективный оптимизационный алгоритм (он подходит только для моделей ЛП) под на-
званием симплекс-метод
Средство Поиск решения позволяет оптимизировать линейные и нелинейные моде-
ли. (Пока мы рассматриваем более простые линейные модели ) Помните, что в оптими-
зируемой линейной модели все формулы, которые непосредственно содержат перемен-
ные решения и прямо или косвенно влияют на формулу, по которой вычисляется целе-
вая функция, должны быть линейными. Линейность модели позволяет использовать
в средстве Поиск решения алгоритм симплекс-метода, который правильно работает
только для формул, отображающих линейные взаимосвязи между переменными
г Все формулы Excel, используемые в табличной модели линейного программирования,
должны содержать только линейные отношения между переменными, если они прямо
или косвенно влияют на вычисление значения целевой функции или участвуют
в функциях ограничений.
Конечно, допускаются нелинейные формулы, даже содержащие переменные реше-
ния, если эти формулы не связаны с вычислением значения целевой функции — ни пря-
мо, ни косвенно, ни через ограничения.
Использование надстройки Поиск решения
Надстройка Поиск решения состоит из двух программных компонентов Первая —
это встроенная в Excel программа, написанная на языке Visual Basic, которая транслирует
представленную на рабочем листе информацию во внутреннее представление, исполь-
зуемое второй программой. Вторая программа находится в памяти компьютера в виде от-
дельного программного модуля; именно она выполняет оптимизацию и возвращает най-
денное решение первой программе, которая, в свою очередь, обновляет данные на рабо-
чем листе Эти две программы взаимодействуют при помощи внутреннего интерфейса
прикладных программ, подробности организации которого нас не интересуют Когда
выбирается команда Поиск решения в меню Excel Сервис, происходит обращение
к первой программе надстройки Поиск решения, которая подготавливает таблицу к оп-
тимизации и вызывает вторую программу-оптимизатор4
Таким образом, использование надстройки Поиск решения состоит из следующих
действий.
Надстройка Поиск решения, хотя и входит в поставку Excel, не подключается автоматически к этой
программе Поэтому, если в меню Сервис вы не находите команды Поиск решения, значит, надстройка не
подключена Для ее подключения выполните команду Сервис ^Надстройки и в открывшемся диалоговом
окне Надстройки установите флажок перед опцией Поиск решения — Прим ред
140
Ч А С Т Ь II Оптимизационные модели
1.	Откройте Excel и выполните обычные операции по созданию табличной модели.
Можно создать несколько сценариев анализа “Что-если” для проверки модели.
2.	После отладки модели переходите к этапу оптимизации, выбрав команду Поиск
решения в меню Сервис
Рис. 3.4. Этапы работы с надстройкой Поиск решения
ГЛАВА 3. Линейная оптимизация
141
3.	В открывшемся диалоговом окне Поиск решения укажите данные, необходимые
для процесса оптимизации.
4.	После задания необходимых данных (в какой ячейке содержится формула оптими-
зируемой целевой функции, какие ячейки включают переменные решения и т д.)
щелкните на кнопке Выполнить
5.	Поиск решения выполняет процесс оптимизации Для небольших моделей ЛП со-
временный персональных компьютер тратит на это всего несколько секунд, но для
очень больших моделей процесс может длиться несколько минут и дольше.
6.	Если в табличной модели нет ошибок, Поиск решения выведет на экран диалого-
вое окно Результаты поиска решения, где можно указать, обновить ли исходную
модель (т е занести ли в ячейки значения оптимального решения) и создавать ли
отчет (который впоследствии можно распечатать).
7.	После этого можно продолжить выполнение анализа “Что-если”, чтобы провести
анализ чувствительности оптимального решения.
Последовательность работы с надстройкой Поиск решения схематично показана на
рис. 3.4.
Терминология средство Поиск решения
После общего описания работы со средством Поиск решения вернемся к тому, какие
инструкции нужно дать программе, чтобы она оптимизировала модель линейного про-
граммирования Но сначала нужно разобраться в терминологии, которую использует это
средство при оптимизации моделей ЛП Применение специальной терминологии вызва-
но тем, что средство Поиск решения воспринимает только ячейки электронной таблицы,
а не символическое представление моделей ЛП С другой стороны, эти отличия чисто
номинальные Соответствие между терминами, используемыми в моделях ЛП и средстве
Поиск решения, показано в табл 3 4
Таблица 3.4. Терминология, используемая в надстройке Поиск решения
Термины моделей ЛП	Термины средства Поиск решения
Целевая функция	Целевая ячейка
Переменные решения	Изменяемые ячейки
Ограничения	Ограничения
Функция ограничения (левая часть нера- венств ограничений)	Адреса ячеек, содержащих функции ограничения
Правая часть неравенств ограничений	Ограничение или граница
Существует еще одно обстоятельство, о котором необходимо помнить при работе с мо-
делями ЛП. Часто отрицательные решения, например, отрицательное значение количества
производимых стульев в модели Oak Products и тому подобное, не имеют смысла, тогда на
переменные решения налагается ограничение неотрицательности Поскольку эти ограни-
чения очевидны, их, как правило, не перечисляют в табличной модели ЛП. Однако при ис-
пользовании средства Поиск решения условия неотрицательности переменных решения
необходимо указывать — их пропуск является распространенной ошибкой.
142 ЧАСТЬ II Оптимизационные модели
Если отрицательные решения не имеют смысла, необходимо наложить на решения мо-
дели ЛП ограничения неотрицательности, прежде чем оптимизировать модель с помо-
щью средства Поиск решения.
3.8.	Оптимизация модели Oak Product
Научиться работать с надстройкой Поиск решения лучше всего непосредственно за
компьютером Как показано на рис. 3.4, первым делом нужно загрузить Excel и открыть
рабочую книгу Стулья.xls, содержащую упрощенную табличную модель Oak Product.
После этого с помощью команды СервисЧ>Поиск решения вызывается средство Поиск
решения, как показано на рис 3.5
Потребное!
Средства в Интернете
16
Упрощенн
Captain^ 1
800
560
360
120
2 ,Тип стульев
3 Удельная прибыль
4 , Произведенное к-во
Л 2 Произведено
13_
5-,
6 ^Длинные штифты
7 - Короткие штифты
8. _ Ножки
9 •Прочные сиденья
10- Облегченные сиденья
Конечный
ьный запас : запас
1280
1600
760
140
120
зоизводство; Резерв
100 J 0

"IjJJ
Рис. 3.5. Выбор команды Поиск решения
После того как надстройка Поиск решения загрузится в память, на экране должно
появиться диалоговое окно, показанное на рис 3 6. Заметьте, что по умолчанию средство
Поиск решения настроено на модель максимизации, а курсор в этом диалоговом окне
находится в поле Установить целевую ячейку
Если вы установили версию надстройки Premium Solver for Education, содержащуюся
на прилагаемом к данной книге компакт-диске, у вас в диалоговом окне Поиск решения
ГЛАВА 3. Линейная оптимизация 143
появится дополнительная кнопка Premium.5 Настойчиво рекомендуем установить ее, по-
скольку в ней исправлены некоторые недочеты, содержащиеся в надстройке Поиск ре-
шения 6 Она также содержит два полезных отчета, несколько дополнительных парамет-
ров настройки и оптимизации, которые будут использованы в последующих главах кни-
ги. Надстройка Premium Solver for Education немного изменит внешний вид диалогового
окна Поиск решения, если щелкнуть на кнопке Premium (рис. 3 7).
Рис..?. 6. . [шьюгошк- окно Поиск решения
Рис. 3.7. Диалоговое окно надстройки Premium Solver
Мы пока будем работать со стандартной версией надстройки Поиск решения
(см рис. 3.6), но в следующих главах нам понадобятся некоторые возможности, предос-
тавляемые Premium Solver.
С помощью мыши можно передвигать по экрану диалоговое окно Поиск решения
так, чтобы были видны различные части таблицы модели Oak Product. Это удобно, по-
скольку лучший способ задать ссылку на ячейку в диалоговом окне Поиск решения —
щелкнуть непосредственно на данной ячейке рабочего листа. При таком способе указа-
ния ячеек не возникают опечатки.
Установка Premium Solver for Education в русской версии Excel меняет диалоговое окно Поиск решения на
англоязычное Поэтому при описании в данном разделе средства Поиск решения надстройка Premium Solver
не устанавливалась Работа с этой надстройкой рассмотрена в главе 7 — Прим ред
6 Инструкции по установке этой надстройки содержатся в приложении В
144	Ч А С Т Ь II Оптимизационные модели
В поле Установить целевую ячейку диалогового окна Поиск решения вводится адрес
ячейки, содержащей значение целевой функции. Для модели Oak Product в это поле сле-
дует ввести D4, но лучше щелкнуть указателем мыши на этой ячейке, чтобы ввести ее ад-
рес автоматически, как показано на рис. 3.8. Если адрес ячейки вводится с помощью
щелчка на ячейке, Excel добавляет символы $, которые указывают на абсолютную адре-
сацию Можно использовать как абсолютные адреса, так и относительные (если вводить
адрес ячейки вручную) В любом случае результаты будут одинаковыми
Рис. 3.8. Указание целевой ячейки
Совет. Если щелкнуть мышью на расположенной справа в поле ввода кнопке, диалоговое окно
свернется так, что будет отображаться только текущее поле (рис. 3.9). Это позволяет
видеть большую часть рабочего листа и удобно производить выбор ячеек. Чтобы вновь раз-
вернуть диалоговое окно, нужно нажать клавишу <Enter> или еще раз щелкнуть на кнопке,
расположенной справа в поле ввода.
Рис. 3.9. Сворачивание диалогового окна
Опции области Равной диалогового окна Поиск решения позволяют задать тип оп-
тимизации. В данном случае необходимо максимизировать значение показателя эффек-
тивности, т.е. прибыль компании Oak Product Для этого нужно щелкнуть на переключа-
теле максимальному значению. Щелчок на кнопке минимальному значению укажет,
что надо минимизировать целевую функцию (например, если показателем эффективно-
сти модели являются суммарные затраты). Можно также сделать значение целевой
функции равным заданному числу, установив переключатель значению и введя это чис-
ло. (Последний выбор позволяет с помощью средства Поиск решения проводить подбор
параметров в моделях, содержащих много переменных и ограничений, т.е. в тех случаях,
когда невозможно применить средство Подбор параметра, так как оно работает только
с одной переменной при отсутствии ограничений.)
ГЛАВА 3. Линейная оптимизация 145
Следующее поле Изменяя ячейки позволяет указать переменные решения модели,
в данном случае это диапазон В4:С4. Чтобы ввести их в данное поле, нужно щелкнуть на
этом поле, а затем выделить на рабочем листе ячейки В4.С4 (рис. 3 10) (Можно попро-
бовать воспользоваться кнопкой Предположить, но при этом обычно предлагаются не-
верные адреса ячеек переменных решения )
Рис. 3.10. Указание изменяемых ячеек
Совет. Если вы не создали в соответствии с нашими рекомендациями такую табличную мо-
дель, в которой все ячейки переменных решения расположены вместе (что позволяет выде-
лить сразу весь диапазон), можно указывать каждую переменную решения отдельно щелк-
нуть в ячейке, ввести в поле Изменяя ячейки точку с запятой, щелкнуть в ячейке следую-
щей переменной решения и т.д
Теперь необходимо задать для средства Поиск решения ограничения Щелчок на
кнопке Добавить открывает диалоговое окно Добавление ограничения, которое позво-
ляет вводить ограничения, как показано на рис. 3 И. По умолчанию предполагается, что
ограничение имеет вид неравенства со знаком <
Рис. 3.11. Задание левой части ограничения
146 ЧАСТЬ II Оптимизационные модели
Если модель организована так, что неравенства одного знака расположены рядом, то
их можно ввести все вместе, используя диапазоны ячеек В противном случае придется
вводить ограничения по отдельности, щелкая на кнопке Добавить диалогового окна До-
бавление ограничения.
Рассмотрим подробно, как задаются ограничения путем указания диапазона ячеек.
Сначала в диалоговом окне Добавление ограничения курсор находится слева в поле
Ссылка на ячейку Нужно выделить ячейки рабочего листа, содержащие суммы левых
частей пяти ограничений вида “<”, т.е. диапазон D6.D10, как показано на рис. 3.11. За-
метим, что в поле Ссылка на ячейку нельзя вводить формулы — это должны быть ссылки
на ячейки, которые, в свою очередь, могут содержать формулы.
Затем курсор переходит в правое поле ввода диалогового окна Добавление ограничения,
и в это поле помещаются адреса пяти ячеек, содержащих соответствующие правые части ог-
раничений, те диапазон F6.F10, как показано на рис. 3.12. Выполнив одно действие, мы в
действительности задали пять ограничений. Нужно следить, чтобы адресов ячеек левых частей
было ровно столько, сколько и адресов правых частей. После этого щелкните на кнопке До-
бавить диалогового окна Добавление ограничения, чтобы ввести эти ограничения в специ-
фикацию Ограничения диалогового окна Поиск решения и очистить поля диалогового окна
Добавление ограничения для ввода следующих ограничений.
Рис. 3.12. Задание правых частей ограничении
Теперь введем ограничения вида “>” Процедура их ввода такая же, как и для ограни-
чений вида “<” Курсор находится слева в поле Ссылка на ячейку, щелкаем на ячейке,
содержащей левую часть ограничения, т е на ячейке D12 В списке поля ввода диалого-
вого окна Добавление ограничения выбираем знак больше или равно >=, как показано
на рис 3 13 Обратите внимание на то, что в этом списке можно выбрать любой знак не-
равенства (<=, =, >=) (Пока мы не рассматриваем опции цел и двоич из этого списка;
они понадобятся при изучении моделей, в которых требуется, чтобы некоторые ячейки
переменных решения принимали целочисленные значения. Такие модели рассматрива-
ются в главе 6 )
ГЛАВА 3. Линейная оптимизация 147
После этого помещаем курсор в правое поле ввода диалогового окна Добавление ог-
раничения и щелкаем на ячейке F12 Введенное ограничение должно выглядеть так, как
показано на рис 3 14
Рис. 3.13. Задание левой части ограничения
9 / .Прочные сиденья 1	0	20:£	140	120
10 Облегченные сиденья 0:1	80 <	120	40
11*	Стулья: :Мин. производство Резерв
12с Произведено	1	1	100 >[_......100_______j 0
Рис. 3.14. Задание правой части ограничения
Далее надо не забывать об условиях неотрицательности для содержимого ячеек В4 и С4
Чтобы ввести эти ограничения, сначала следует вернуться в диалоговое окно Поиск реше-
ния из диалогового окна Добавление ограничения, щелкнув на кнопке ОК в этом окне
(Если вы случайно щелкнули на кнопке Добавить, щелкните на кнопке Отмена, и вы вер-
нетесь в диалоговое окно Поиск решения ) На данном этапе диалоговое окно Поиск реше-
ния для модели Oak Production должно выглядеть так, как показано на рис. 3 15.
Чтобы определить условия неотрицательности для переменных решения, необходимо
щелкнуть на кнопке Параметры диалогового окна Поиск решения Появится диалого-
вое окно Параметры поиска решения (рис 3 16)
Наконец, поскольку мы работаем с линейной моделью, в диалоговом окне Парамет-
ры поиска решения необходимо установить флажок опции Линейная модель, а также
Неотрицательные значения и Автоматическое масштабирование Первая из них со-
общает программе, что модель является линейной, вторая налагает ограничения неотри-
148
ЧАСТЬ II Оптимизационные модели
цательности на переменные решения Режим Автоматическое масштабирование будет
обсуждаться в следующем разделе Остальные опции этого окна мы пока рассматривать
не будем — они в основном относятся к оптимизации целочисленных и нелинейных мо-
делей Щелкните на кнопке ОК, чтобы вернуться в диалоговое окно Поиск решения.
Рис. 3.15. Параметры поиска решения для модели Oak Product
Рис. 3.16. Диалоговое окно Параметры поиска решения
Итак, полностью завершена спецификация оптимизационной модели. Мы ввели сле-
дующую информацию-
•	адрес ячейки, содержащей целевую функцию, которую необходимо оптимизиро-
вать (в данном случае максимизировать),
•	диапазон ячеек, которые программа должна изменять (переменные решения);
•	ограничения,
•	указание, что модель является моделью линейного программирования.
ГЛАВА 3. Линейная оптимизация
149
Теперь в диалоговом окне Поиск решения щелкните на кнопке Выполнить За тем,
как продвигается поиск решения, можно наблюдать в строке состояния в левом нижнем
углу окна Excel. Однако для такой маленькой модели, как наша, оптимизация завершит-
ся очень быстро, за это время можно и не увидеть сообщения, поступающие от програм-
мы. В общем случае в процессе вычислений в строке состояния показывается число ите-
раций и значения целевой функции при переборе множества допустимых решений зада-
чи. Эта информация позволяет следить, как продвигается процесс оптимизации больших
моделей, где он может длиться достаточно долго.
Диалоговое окно Результаты поиска решения сообщает о завершении поиска
(рис. 3.17). То, что программа Поиск решения завершила работу, не означает, что она
нашла оптимальное решение Поэтому всегда читайте сообщение, отображаемое в верх-
ней части данного окна! Если поспешить щелкнуть на кнопке ОК, чтобы убрать диалого-
вое окно Результаты поиска решения, не прочитав данное сообщение, можно пропус-
тить важную информацию о решении. Если оптимальное решение найдено, в диалоговом
окне Результаты поиска решения должно присутствовать два ключевых предложения
•	Решение найдено.
•	Все ограничения и условия оптимальности выполнены
Если хотя бы одного из этих предложений нет, программе не удалось оптимизировать
модель. В таком случае либо щелкните на кнопке Справка, чтобы получить дополнитель-
ную (зачастую несодержательную) информацию о результатах поиска, либо обратитесь
к приложению В данной книги, чтобы получить советы и указания, что делать дальше
Рис. 3.17. Диалоговое окно Результаты поиска решения
Если получено сообщение об успешном завершении поиска, как на рис. 3 17, можно
или сохранить найденное решение, выбрав соответствующую опцию, или отбросить его,
выбрав опцию Восстановить исходные значения, в результате ячейкам переменных ре-
шения будут возвращены значения, которые в них находились до запуска программы
Поиск решения. Существует возможность также получить отчеты о решении трех типов.
Каждый отчет выводится на новый лист рабочей книги.
Выберем отчет Результаты, что по умолчанию подразумевает сохранение найденного
решения, и щелкнем на кнопке ОК. Типы отчетов Устойчивость и Пределы рассмотрим
позднее. На рис. 3.18 показан отчет о результатах поиска оптимального решения для мо-
дели Oak Product. Он должен появиться на листе с названием Отчет по результатам 1
(если это имя не было использовано ранее для других листов рабочей книги) Содержи-
мое этого листа можно свободно форматировать, распечатывать или копировать на лю-
бой лист рабочей книги. Например, в отчете, показанном на рис. 3.18, некоторые строки
были удалены, а содержимое некоторых столбцов выровнено по центру
150	Ч А С Т Ь II. Оптимизационные модели
Рис. 3.18. Отчет о результатах для модели Oak Product
I Совет. Лист с отчетом о результатах — это просто рабочий лист Excel, у которого от-
। ключено отображение сетки Чтобы вернуть сетку, установите флажок опции Сетка
| в диалоговом окне Параметры (команда Сервис ^Параметры). Если вы забыли выбрать
I отчет и закрыли окно Результаты поиска решения, нет другого способа воссоздать от-
| чет, кроме как повторно оптимизировать модель, чтобы окно Результаты поиска реше-
| ния открылось вновь
Посте выполнения всех указанных выше действий исходная таблица модели Oak
Product будет выглядеть так, как показано на рис. 3 19 Средство Поиск решения записа-
ло в таблицу оптимальные значения переменных решения, определяющих, сколько
стульев Captain и Mate нужно произвести, — 130 и 60 штук соответственно После этого
таблица пересчитывается в последний раз, чтобы вычислить максимальное значение
прибыли — $9 680
Заметим, что значения ячеек в столбце G также были изменены Они показывают за-
пасы различных деталей после принятия оптимального решения. Если в ячейке резерва
для некоторого ограничения стоит 0, такое ограничение называется лимитирующим или
связывающим Лимитирующее ограничение не дает возможности добиться более высокой
прибыли Это значит, что увеличение прибыли путем дополнительного производства
стульев Captain и/или Mate приведет к тому, что значения одной или нескольких ячеек
резерва станут отрицательными, т е будет нарушено одно или несколько ограничений.
Ограничения, имеющие ненулевой резерв (исходя из определения, резерв тогда положи-
тельный), не являются лимитирующими Эти ограничения (по крайней мере на данном
ГЛАВА 3 Линейная оптимизация 151
этапе) не препятствуют возможности получения более высокой прибыли Таким обра-
зом, именно лимитирующие ограничения представляют интерес в любой модели ЛП
Нулевые значения резерва ограничений для длинных штифтов и ножек означают, что
в данном случае существует два лимитирующих ограничения, два “узких места”, которые
препятствуют компании Oak Product производить и продавать больше стульев и таким
образом получать большую прибыль.
Тип стульев
Удельная прибыль
I Произведенное к-во
Упрощенная модель Oak Products
Captain Mate
Прибыль
$9 680]
^Длинные штифты
. Короткие штифты
< Ножки
sПрочные сиденья
s Облегченные сиденья
Потребность в	Суммарное
деталях потребление
Конечный
Начальный запас запас
1280
1600
760
140
120
ь
9
12
J3_
I Произведено
1280 <
1240 <
760 <
130 <
60:<
Стулья Мин производство Резерв
190 >	100	90
Рис. 3.19. Решение, максимизирующее прибыль
Если сравнить рабочий лист на рис 3 19 с отчетом о результатах, показанным на
рис 3 18, можно заметить, что в таблице Oak Product представлена вся информация, со-
держащаяся в отчете о результатах Таким образом, за исключением различии в форма-
тировании, информация отчета о результатах полностью повторяется в исходной таблич-
ной модели Поэтому отчет о результатах в некоторой мере избыточен, и мы будем опус-
кать его в следующих примерах оптимизации с помощью средства Поиск решения
После нахождения оптимального решения можно исследовать различные альтерна-
тивные варианты, выполняя анализ “Что-если” в окрестности оптимальных значений
Кроме того, можно проследить, как отразится на прибыли увеличение запаса тех или
иных деталей, изменяя соответствующие ячейки правых частей ограничении и вновь за-
пуская Поиск решения для оптимизации измененной модели Это позволит узнать, на-
сколько такое изменение способствует повышению прибыли Также можно изменять ко-
эффициенты удельной прибыли и/или коэффициенты в ограничениях, чтобы увидеть,
как это отразится на прибыли После каждого изменения необходимо вновь использо-
вать Поиск решения для получения нового оптимального решения
Замечание. Все настройки диалогового окна Поиск решения для каждой модели сохраня-
ются при сохранении рабочей книги
3.9.	Рекомендации по поиску решения задач ЛП
Для удобства использования средства Поиск решения необходимо следовать трем
следующим принципам построения моделей линейного программирования
Во-первых, необходимо масштабировать числа в модели таким образом, чтобы раз-
ность между наибольшим и наименьшим числом в таблице не превышала шесть или семь
152 ЧАСТЬ II Оптимизационные модели
порядков Пусть, например, в модели одна из переменных решения — это процентная
ставка (имеющая значение порядка 5%, те 0,5), а показатель эффективности выражен
в долларах, тогда применение средства Поиск решения может привести к неверному ре-
зультату, если значение показателя эффективности будет выражаться 8-значным числом
($10 000 000, например) В этом случае разность между наименьшим (0,5) и наибольшим
(10 000 000) значениями ячеек модели составит 10 порядков Из-за этого ошибки округ-
ления, возникающие в процессе вычислений, приведут к такой потере точности, что По-
иск решения не сможет правильно завершить процесс. В результате будут получены не-
оптимальные решения или сообщение о том, что решение не найдено
В таких случаях нужно изменить масштаб измерения очень больших или очень ма-
леньких чисел модели В приведенном выше примере можно изменить денежные едини-
цы, и выражать прибыль в миллионах долларов, а не в долларах Это не приведет к потере
общности и позволит сделать числа модели достаточно небольшими' теперь самое ма-
ленькое значение (0,5) отличается от самого большого (10) всего на 3 порядка.
Плохое масштабирование моделей является второй по значимости причиной возник-
новения проблем при оптимизации моделей ЛП (первая — пропуск ограничений неот-
рицательности).
Совет. Начиная с версии Excel 97, помочь в разрешении проблем масштабирования может
опция Автоматическое масштабирование в диалоговом окне Параметры поиска ре-
шения (см. рис. 3 16). однако это не гарантирует успешного устранения всех проблем.
Другие причины отказов средства Поиск решения найти оптимальное решение обыч-
но легче обнаружить, особенно с помощью специальных отчетов об ошибках, содержа-
щихся в надстройке Premium Solver for Educational Edition Такой причиной может стать,
например, отсутствие допустимых решении в модели
Во-вторых, средство Поиск решения допускает, чтобы правые части неравенств были
числовыми константами, адресами ячеек или формулами, что никак не влияет на про-
цесс оптимизации Тем не менее не следует в правую часть ограничений помещать фор-
мулы или адреса ячеек, значения которых могут меняться при оптимизации, т.е которые
прямо или косвенно связаны со значениями переменных решения.
Кроме того, не рекомендуется задавать ограничения непосредственно в диалоговом
окне Поиск решения, не привязывая их к ячейкам рабочего листа и используя при этом
в качестве правых частей неравенств константы, а не ссылки на ячейки модели Рассмот-
рим еще один пример модели Oak Product Предположим, что исходя из определенных
соображений Джим решил, что на будущей неделе должно быть произведено не более
80 стульев Captain и не более 60 Mate Очевидно, что оптимальное решение, полученное
средством Поиск решения для исходной модели, не соответствует этим новым ограниче-
ниям, поэтому нужно исправить модель, включив в нее дополнительные ограничения,
а затем оптимизировать полученную модель Один из способов осуществления этого по-
казан на рис 3 20 Обратите внимание на два новых ограничения в верхней части списка
Ограничения диалогового oi«a Поиск решения Средство Поиск решения корректно
оптимизирует данную модель, новое решение показано на рис 3 21.
Обратите внимание на недостаток такой модификации модели Oak Production: в самой
таблице новых ограничений нет, при анализе таблицы на рис. 3.21 оказывается, что ни одно
ограничение не является лимитирующим В результате придется при каждой оптимизации
генерировать отчет о результатах и анализировать его, а также копировать информацию от-
чета обратно в таблицу. Кроме того, такой стиль работы со средством Поиск решения явля-
ется разновидностью жесткой привязки данных. Здесь данные вводятся непосредственно в
диалоговое окно Поиск решения, а не в ячейки рабочего листа И хотя на результат вычис-
ГЛАВА 3 Линейная оптимизация 153
лений это никак не влияет, структура модели становится трудно различимой, и при каждом
изменении модели приходится исправлять содержимое диалогового окна Поиск решения
Мы рекомендуем добавить два новых ограничения непосредственно в табличную модель
Oak Product на рабочем листе, а затем изменить диалоговое окно Поиск решения, чтобы
включить новые ограничения вместе с исходными.
Рис. 3.20. Новые параметры поиска решений для модели Oak Product
Рис. 3.21. Оптимальное решение
На основе вышесказанного можно сформулировать следующие правила хорошего
стиля моделирования	J
1.	При задании в диалоговом окне Поиск решения правых частей ограничений все-
гда следует указывать ссылки на ячейки в табличной модели.
2.	Ячейки правых частей неравенств в табличной модели должны содержать кон-
станты, а не формулы (точнее — не формулы, в которые явно или опосредованно
входят переменные решения).
154 Ч А С Т Ь II Оптимизационные модели
	ь...	I	BIC.	d t ;	г	G	н Ji J ।	К
	Модель структуры недельного проитводства компании Oak I	°	*	О a s “	| s ,.2 J Модель стульев	о S <	5	<Л	<л «ЗДУдельная прибыль	, $ 36 ‘ $ 40 ! $ 45 $ 38 ! $ 35 ‘ $ 25 , 4 д< Произведенное к во	| 100	72	40	53	0	0					Products Прибыль : ‘ 1	$10294| : Запас в Суммарное , начале	Остаток в конце
5	Потребность в деталях				потребление недели	недели
дбд Длинные штифты	8	0 :	12	0!	8 ‘		1280 <'	1280	0
 7?д Короткие штифты	4	12	0:12	4	8	1900 <	1900:	0
«8 .я Ножки	4	4	4	4	4	4	1060 <	1090!	30
9 Прочные сиденья	1 ! 0 ‘	0	0	1	1	100 <:	190	90
10 Облегченные сиденья	0	1	1	1	0	0	165 <	170	5
		‘Прочные поперечины	6	0	4 ‘ 0 ‘	5	0	760 <	1000!	240
‘ 12 «Облегченные поперечины	0 ‘ 4 !	0	5	0	6	553	1000	447
,_13_J Спинки для Capt	1	0	0	0	0	0	100 <	110	10
«14яСпинки для Mate	0	1	0 ‘ 0	о	0	72 <	72	Q
15^.Спинки для Amer	о ! о !	1	1	0 !	0	93 <	93	0
16 ‘Спинки для Span 17"	0	0	0 ‘ 0	1	1	0 <	85!	85
Рис. 3.22. Исходная модель Oak Products и ее оптимальное решение
ГЛАВА 3. Линейная оптимизация
155
В-третьих, документированию сложных моделей содействует присвоение имен ячейкам
показателя эффективности, переменных решения, функций ограничении (суммарным зна-
чениям левых частей) и ячейкам правых частей (такую возможность мы рассматривали
в главе 2). Если это сделать, Поиск решения будет автоматически подставлять имена диапа-
зонов для соответствующих ячеек в диалоговом окне Поиск решения.
На этом закончим изучение надстройки Поиск решения Теперь нужно записать ра-
бочую книгу Стулья на жесткий диск, сохраняя тем самым оптимальные решения моде-
ли ЛП и отчет о результатах.
В заключение оптимизируем более сложную исходную модель компании Oak Product,
построенную в главе 2. На рис 3 22 показана эта модель (слегка измененная) и опти-
мальное решение, найденное средством Поиск решения. В нижней части рисунка изо-
бражены диалоговые окна Поиск решения и Параметры поиска решения
Совет. Чтобы скопировать изображение с экрана монитора в буфер обмена, нужно нажать кла-
вишу <PnntScreen >. Чтобы копировать в буфер обмена изображение, находящееся на передне ч
плане (например, диалоговое окно), нужно нажать клавиши <Alt+PrintScreen> Из буфера обмена
рисунок можно вставить в рабочий лист Excel или в другой документ в качестве иллюстрации к
документации модели.
3.10.	Пример транспортной модели
У некой компании есть два завода и три оптовых магазина-склада Первый завод мо-
жет поставлять не более 100 единиц определенной продукции, а второй — не более 200
единиц. В первом магазине-складе может храниться не более 150 единиц продукции, во
втором — 200, а в третьем — 350 единиц Цена продажи единицы продукции в первом
магазине составляет $12, во втором — $14, в третьем — $15 Суммарные затраты на про-
изводство единицы продукции на заводе / и доставку ее в магазин-склад j приведены
в табл. 3.5. Компания хочет определить, сколько единиц продукции нужно отправить
с каждого завода каждому магазину, чтобы максимизировать прибыль
Таблица 3.5. Удельные суммарные затраты на производство и доставку
Магазин-склад, долл.
Завод	123
1	8	10	12
Заметим, что здесь выбор переменных решения продиктован самой постановкой за-
дачи. В формулировках моделей такого вида переменные решения, как правило, имеют
два индекса, поэтому в таблице модели переменные решения содержатся в нескольких
строках, а не в единственной строке, как это было в модели компании Oak Product Обо-
значим переменные решения через Хя — количество единиц продукции, произведенных
на заводе i и направленных в магазин-склад/.
156 ЧАСТЬ II Оптимизационные модели
а I в
2	Поставки
3	Завод 1
4	Завод 2
5	Всего
6
7	Емкость склада
8	Удельная прибыль
9	Доход
Стоимость
10 '	перевозки
_1Д_	Завод 1
12	Завод 2
13 Общие издержки
14 Прибыль
16 '
С О Е F' G Н
Всего Мощность завода
1	25~~< 100
] 20 < 200
Транспортная модель
Склад 1 - Склад 2 Склад 3
150	200	350
$12	$14	$15
$360	$140	$75
Склад 1 : Склад 2 Склад 3
$8		$10	$12
$7	$9	$11
$230	$90	$60
$130	:	$50	$15
Итого
,В ;	, С . _ i . D .„'Г- , Е щ, ‘МЛ:
Транспортная мо
Склад 1	Склад 2	Склад 3	Всего : Мощи,
20	0	"б	|=СУММ(БЗ:ОЗ)	<100
10	10 0 I =СУММ(В4: D4)	: < 200
=СУММ(ВЗВ4)	=СУММ(СЗ.С4)	=СУММ(ОЗ D4)
10
лкость склада 150
ельная прибы 12
Доход
| 200
=В5’В8
перевозки
Завод 1
Завод 2
350
15_____
=D5’D8
J2
' 13Т)бщие издержк=ВЗ’В11+В4*В12 =СЗ’С11+С4’С12 =D3’D11+D4’D12
15*
Прибыль ;=В9-В13
=D9-D13
Итого
|=СУММ(В14:О14) |
Рис. 3.23. Транспортная модель
Для каждой переменной решения Xt соответствующая удельная прибыль вычисляется как
цена единицы продукции в данном магазине-складе минус затраты на производство и достав-
ку этой единицы с завода i в магазин j. Например, для продукции, доставленной с завода 1
в магазин-склад 1, удельная прибыль составит $ 12 — $8 = $4. Выполнив аналогичные вычис-
ления для всех возможных комбинаций “завод-магазин”, получим коэффициенты при сла-
гаемых целевой функции Таким образом, символическая модель имеет следующий вид.
МаксимизироватьДХц + 5Х2| + 42(12 + 5%22+ ЗХ|3 + 4Х23
при ограничениях
Л| + Xt2 +Лз - 100 (производственная мощность 1 завода);
Т"21 + %2i +Лз - 200 (производственная мощность 2 завода);
Хи + Х21 < 150 (ограничение для 1 магазина-склада);
Т12 + Х22 < 200 (ограничение для 2 магазина-склада);
Х„ + Х2, < 350 (ограничение для 3 магазина-склада);
Х..> 0 для всех/,j
ГЛАВА 3 Линейная оптимизация 157
Очевидно, что транспортная модель имеет специфическую форму Например, все ко-
эффициенты при переменных XtJ в ограничениях равны 1 Фактически транспортные за-
дачи входят в особый класс задач линейного программирования, которые называются
сетевыми моделями Другие примеры сетевых моделей будут рассматриваться в главе 5.
При создании табличной модели в Excel можно разместить переменные решения XtJ
так, чтобы в результате получилась компактная таблица В данном случае переменные
решения будут занимать блок ячеек, а не отдельную строку, как в модели Oak Product
Табличная модель показана на рис 3 23 Переменные решения, записанные в диапазоне
B3:D4, задают объем продукции, произведенный определенным заводом и направлен-
ный для продажи в указанный магазин-склад В диапазоне G3.G4 задаются ограничения
производственных мощностей заводов, а в диапазоне В7 D7 — ограничения объемов
складов. Другие формулы имеют очевидный “бухгалтерский” смысл На рис 3 24 пока-
зано оптимальное решение данной модели, а также параметры средства Поиск решения
Рис. 3.24. Решение транспортной задачи
158
ЧАСТЬ II Оптимизационные модели
3.11.	Задача составления смесей
Несмотря на то что оба рассмотренных примера — Oak Product и транспортная мо-
дель— оказались моделями максимизации, многие реальные задачи сводятся к задачам
минимизации Когда целью является прибыль, ее необходимо максимизировать, но если
цель — уменьшить затраты, то приходим к задаче минимизации В качестве модели ми-
нимизации рассмотрим следующий пример
При создании сплава для новой продукции компании Eastern Steel используется же-
лезная руда, получаемая с четырех различных шахт Как показал анализ, чтобы получить
сплав с нужными свойствами, необходимо удовлетворить минимальные требования по
трем основным элементам, которые для простоты обозначили А, В и С. В частности, ка-
ждая тонна руды должна содержать не менее 5 фунтов элемента А, 100 фунтов элемента В
и 30 фунтов элемента С Эти данные приведены в табл. 3.6.
Таблица 3.6 Требования к содержанию основных элементов
Элемент	Минимальное содержание, фунт/т
В	5 100
С	30
Руда с каждой шахты содержит все три основных элемента, но в разных количествах.
Состав руды (содержание элементов) приведен в табл 3.7
Таблица 3 7. Состав руды с	: различных шахт
Элемент	Шахта (содержание элементов, фунт/т) 1	2	3	4
В	10	3	8	2 90	150	75	175 45	25	20	37
Заметим, что тонна руды с первой шахты содержит 10 фунтов элемента А и, следова-
тельно, удовлетворяет минимальному требованию к содержанию данного элемента
(5 фунтов в тонне) Кроме того, она содержит 90 фунтов элемента В и 45 фунтов элемен-
та С, таким образом требование к содержанию элемента С удовлетворяется, а к содержа-
нию элемента В — нет Аналогично тонна руды со второй шахты не удовлетворяет требо-
ваниям к содержанию элементов А и С, тонна руды с третьей шахты — требованиям
к содержанию В и С, а с четвертой — требованию к содержанию А. Однако можно соста-
вить разнообразные смеси (в которых в различных пропорциях будут смешиваться руды
с разных шахт), удовлетворяющие минимальным требованиям по всем основным эле-
ментам Пример такой смеси 1/2 тонны руды с шахты 1 и 1/2 тонны руды с шахты 4. Со-
держание элемента А в тонне такой смеси вычисляется по формуле:
содержание А = (1/2)х(содержание А в тонне руды с шахты 1) +
+ (1/2)х(содержание А в тонне руды с шахты 4).
ГЛАВА 3. Линейная оптимизация 159
Таким образом, содержание элемента А = (1/2)х10 + (1/2)х2 = 5+1=6
Поскольку 6 > 5, требование по минимальному содержанию элемента А удовлетворено
Аналогично можно рассчитать содержание элемента В в тонне смеси
содержание В = (1/2)х(содержание В в тонне руды с шахты 1) + (1/2)х
х(содержание В в тонне руды с шахты 4)
Следовательно, содержание элемента В = (1/2)х90 + (1/2)х175 = 132,5 Наконец, содер-
жание элемента С в тонне смеси равно (1/2)х45 + (1/2)х37 = 41
Сравнивая полученные значения с требуемым содержанием В (100 фунтов) и С
(30 фунтов), видим, что данная смесь (1/2 тонны с шахты 1 и 1/2 тонны с шахты 4) удов-
летворяет всем требованиям по минимальному содержанию элементов, следовательно,
она является допустимой смесью. Существует много других смесей, которые также удов-
летворяют всем требованиям и являются допустимыми Однако, поскольку руда с разных
шахт имеет различную стоимость, стоимость смесей также различается Стоимостные
данные содержатся в табл. 3.8.
Таблица 3.8. Стоимость руды с различных шахт
Шахта	Стоимость тонны руды, $
1	800
2	400
3	600
4	500
Например, стоимость допустимой смеси, тонна которой состоит из половины тонны
руды с шахты 1 и половины тонны руды с шахты 4, вычисляется по формуле
(1/2)х(стоимость тонны руды шахты 1) + (1/2)х(стоимость тонны руды шахты 4) =
= (1/2)х800 + (1/2)х500 = $650
Можно попробовать сравнить эту стоимость со стоимостью других допустимых сме-
сей. Цель компании Eastern Steel — найти самую дешевую допустимую смесь Сформули-
руем данную задачу в виде модели линейного программирования
Поскольку нужно найти оптимальный состав одной тонны смеси, зададим перемен-
ные решения следующим образом
Т} — часть тонны, состоящая из руды с шахты 1,
Т, — часть тонны, состоящая из руды с шахты 2,
7", — часть тонны, состоящая из руды с шахты 3,
Т4 — часть тонны, состоящая из руды с шахты 4
С помощью данных табл. 3.5 вычислим количества основных элементов в одной тон-
не смеси:
количество элемента А в 1	тсмеси = ЮГ, + ЗТ"2 + 87"3 + 2Т.,	(3 9)
количество элемента В в 1	тсмеси = 907", + 1507", + 7577, + 175Т„	(3	10)
количество элемента С в 1	т смеси = 457", + 2577, + 207"3 + 377/	(3	11)
160 ЧАСТЬ II Оптимизационные модели
Теперь скомбинируем выражения (3.9), (3.10) и (3 11) с требованиями по минималь-
ному содержанию элементов, приведенными в табл. 3.4, и получим три ограничения.
ЪТ3 + УГг + ЪТ + 2Т4>5,	(3.12)
907", + 1507", + 757", + 1757; > 100,	(3.13)
457", + 257;+ 207;+ 377; >30.	(3.14)
Существуют ли в данной модели другие ограничения7 Необходимо включить условия
неотрицательности переменных решения Тх, Tv Т3, Т4, однако есть еще одно важное ог-
раничение Поскольку тонна смеси состоит только из руды указанных четырех шахт,
сумма составляющих смеси должна быть равна 1:
7", + Т2+ Т3 + ТА = 1.	(3.15)
Последнее ограничение иногда называют условием материального баланса и ограниче-
нием в виде равенства Оно ограничивает значения переменных решения таким образом,
что левая часть в точности равна правой части
Ограничения модели линейного программирования могут быть как равенствами, так и
неравенствами.
Используя данные табл 3 7, легко получить формулу для вычисления стоимости тон-
ны любой смеси
стоимость 1 т смеси = 8007’, + 4007; + 6007; + 5007;
Теперь можем составить полную символическую модель
Минимизировать 8007’, + 4007; + 6007; + 5007;
при ограничениях
ЮТ,+ 37;+ 87;+ 27; >5,
907’, + 1507; + 757; + 1757; >100,
457’, + 257; + 207; + 377; >30,
1 + Тг + Т3 + ТА=,
тх, тг, т3, т; > о.
Все функции модели являются линейными, следовательно, это модель линейного
программирования
На этом закончим с формализацией моделей ЛП, предназначенных для последую-
щего применения средства Поиск решения. Вернемся к основной теме книги, т е созда-
нию моделей, которые могут помочь при принятии решений Однако прежде чем перехо-
дить к следующему разделу, рекомендуем читателям проверить свои возможности по соз-
данию моделей на базе электронных таблиц и применению средства Поиск решения на
основе модели составления рудной смеси для компании Eastern Steel. Реализуйте ее в ви-
де табличной модели в Excel, придерживаясь предложенных в данной главе рекоменда-
ций Затем оптимизируйте полученную модель с помощью средства Поиск решения.
Наша версия данной модели приводится в конце главы, но не спешите сразу посмотреть
на нее, не стоит отказываться от возможности проверить свои знания. Попробуйте сна-
чала самостоятельно создать табличную модель ЛП и найти решение задачи. Выполнив
это упражнение, а также справившись с несколькими более сложными примерами в сле-
дующем разделе, вы почувствуете себя более уверенно при разработке моделей в Excel и
применении средства Поиск решения
ГЛАВА 3. Линейная оптимизация
161
3.12.	Создание моделей ЛП
Оставшаяся часть данной главы содержит примеры, которые помогут вам усовершен-
ствовать свое умение переходить от реальных управленческих ситуаций к символическим
моделям ЛП, а затем к моделям в Excel, подготовленным к использованию средства По-
иск решения. Этот процесс создания табличных моделей — постановка задачи, форму-
лировка цели и ограничений — имеет исключительно важное значение
Чтобы попрактиковаться в формировании моделей, постарайтесь самостоятельно по-
строить модели для следующих задач. Ознакомившись с исходными данными, старайтесь
сразу же разработать символическую модель ЛП. На данном этапе не следует использо-
вать дополнительные ограничения, логические нюансы или полет фантазии, которые
могут, на ваш взгляд, сделать модель более реалистичной. Не нужно думать о том, что
случится на будущей неделе, если в задаче речь о следующей неделе не идет Предлагае-
мые задачи должны помочь вам научиться формулировать модели при условии, что этап
перехода от реальной ситуации к абстракции уже выполнен. Чтобы вы могли проверить
результаты своей работы, необходима однозначная формулировка задачи Иными слова-
ми, в отличие от реальных ситуаций, здесь для каждой задачи существует правильный от-
вет Позднее, когда у вас будет больше опыта, можно будет вносить в модели дополни-
тельные штрихи и нюансы реальной жизни. Поскольку тема формирования моделей
очень важна, а научиться этому можно лишь на практике, в конце данной главы приво-
дится длинный список задач
3.13.	Пример 1. Задача об ассортименте продукции
Компания производит две марки телевизоров — Astro и Cosmo Работают два конвей-
ера, каждый из которых выпускает телевизоры одной марки, и два цеха, занятых произ-
водством деталей для телевизоров обеих марок. Производственная мощность конвейера,
выпускающего Astro, составляет 70 телевизоров в день, а конвейера Cosmo — 50 телеви-
зоров в день. Цех А производит телевизионные трубки На производство трубки для теле-
визора Astro требуется 1 ч рабочего времени, а на производство трубки для Cosmo —2 ч.
На данном этапе в цеху А производству трубок для телевизоров обеих марок может быть
уделено не более 120 ч рабочего времени в день В цеху Б изготавливаются корпуса теле-
визоров, причем на производство одного корпуса как для Astro, так и для Cosmo требует-
ся 1 ч рабочего времени Цех Б может посвятить изготовлению корпусов не более 90 ч ра-
бочего времени вдень. Удельная валовая прибыль от реализации Astro и Cosmo составля-
ет 20 и 10 долларов соответственно. Эти данные представлены в табл 3 9
Таблица 3.9. Данные о производстве телевизоров
Удельные трудозатраты, ч
	Дневная производительность	Цех А	Цех Б	Удельная прибыль, долл.
Astro	70	1	1	20
Cosmo	50	2	1	10
Ресурс рабо- чего времени		120	90	
162	Ч А С Т Ь II. Оптимизационные модели
При условии, что компания может продать все произведенные телевизоры, каким
должен быть дневной план производства (т.е. сколько телевизоров каждой марки следует
производить ежедневно)? Вспомните модель Oak Product и попробуйте создать модель
для данной задачи. Постройте символическую модель ЛП, разработайте на ее основе таб-
личную модель и оптимизируйте полученную модель с помощью средства Поиск реше-
ния.
3.14.	Пример 2. Задача составления смеси
Жестяная банка корма для собак весом 16 унций должна содержать как минимум сле-
дующие количества питательных веществ: белков — 3 унции, углеводов — 5 унций и жи-
ров — 4 унции. Нужно смешать четыре вида каш в различных пропорциях, чтобы полу-
чить наиболее дешевую банку собачьего корма, удовлетворяющую требованиям по со-
держанию питательных веществ. Содержание питательных веществ и цена каждой каши
в расчете на 16 унций приводятся в табл 3.10.
Таблица 3.10. Данные о цене и содержании питательных веществ
Содержание питательных веществ и цена
Каша	Содержание белков, унции	Содержание углеводов, унции	Содержание жиров, унции	Цена, долл.
I 2	3 5	7 4	5	6
3	2	2	()	3
4	3	8	2	2
По аналогии с моделью составления рудной смеси создайте модель ЛП для данной за-
дачи. Постройте символическую модель, разработайте соответствующую табличную мо-
дель и оптимизируйте ее с помощью средства Поиск решения. Совет. Обозначьте через X,
количество 7-й каши в 16-унциевой банке собачьего корма, / = 1, 2, 3, 4
3.15.	Пример 3. Составление расписания
Управляющий персоналом университета должен составить расписание охраны терри-
тории университета, удовлетворяющее требованиям, представленным в табл. 3 11.
Таблица 3.11. Требования к организации охраны территории
Время	Минимальное число офицеров охраны
0 00-4 00	5
4 00-8 00	7
8 00-12 00	15
12 00-16 00	7
16 00-20 00	12
20 00-24 00	9
ГЛАВА 3. Линейная оптимизация 163
Офицеры дежурят посменно, продолжительность смены 8 ч. На каждый день уста-
новлено 6 смен. Время начала и конца каждой смены показано в табл. 3.12
Таблица 3.12. Расписание смен
Смена	Время начала	Время окончания
1	0 00	8 00
2	4 00	1200
3	8 00	16 00
4	12 00	20 00
5	16 00	24 00
6	20 00	4 00
Управляющий персоналом хочет определить, сколько офицеров назначить в каждую
смену, чтобы минимизировать их количество и при этом удовлетворить требования
к организации охраны. Переменные решения можно определить следующим образом.
— число офицеров, дежурящих в смену I;
Х2 — число офицеров, дежурящих в смену 2;
Х6 — число офицеров, дежурящих в смену 6.
Целевая функция имеет вид Xt + Х2 + X, + Xt + Xs + Хк. При формулировке ограниче-
ний нужно убедиться, что определенный набор значений переменных Xt, . , Хк удовле-
творяет требованиям по организации охраны территории. Нужно выбрать некий меха-
низм, который позволит определить, какие офицеры находятся на дежурстве в течение
каждого из указанных в требованиях интервалов времени. В этом может помочь
табл. 3.13. Так, офицеры, дежурящие в первую смену, находятся на посту в течение пер-
вых двух временных интервалов и т.д С помощью таблицы также можно определить
(суммируя значения в одном столбце), сколько офицеров находится на дежурстве в тече-
ние каждого временного интервала (например, в первый интервал дежурит Xt + Хк офи-
церов; поэтому первое ограничение выглядит следующим образом. Xt + Xf> 5).
Таблица 3.13. Количество офицеров, дежурящих в течение каждого
временного интервала
Временной интервал
Смена 0.00-4.00	4.00-8.00	8.00-12.00	12.00-16.00	16.00-20.00 20.00-24.00
А
Надо
164
ЧАСТЬ II Оптимизационные модели
Сформулируйте остальные ограничения для данной модели. Постройте символиче-
скую модель ЛП, на ее основе разработайте табличную модель и оптимизируйте ее с по-
мощью средства Поиск решения.
3.16.	Пример 4. Анализ безубыточности при наличии
ограничений
Компания Longer Boats производит три вида высококлассных гоночных яхт — Sting,
Ray и Breaker. Соответствующие данные о затратах и доходах на ближайший плановый
период представлены в табл. 3 14.
Таблица 3.14. Данные о затратах и доходах компании Longer Boats
Яхты	Цена, долл, за единицу	Переменные затраты, долл, за единицу	Фиксированные затраты, долл.
Sting	10 000	5 000	5 000 000
Ray	7 500	3 600	3 000 000
Breaker	15 000	8 000	10 000 000
Как свидетельствуют эти данные, фиксированные затраты в каждом случае весьма
значительные Фиксированные затраты — это всевозможные расходы, которые сущест-
вуют независимо от того, какое количество продукта производится Так, для яхт класса
Ray потребуется затратить те же самые $3 000 000 независимо от того, будет построена
I яхта этого класса, 40 яхт или 0 Высокие фиксированные затраты включают в себя за-
траты на модификацию проекта, создание макета и испытание яхты в бассейне
На рис 3 25 представлено определение точки безубыточности (критического объема
производства) для яхт класса Sting Как следует из графика, если компания Longer Boats
будет производить только яхты Sting, то для того, чтобы добиться безубыточности, ей по-
требуется выпустить не менее I 000 яхт
1 000 Количество произведенных яхт
Рис. 3.25. Анализ безубыточности для производства яхт Sting
Однако перед компанией Longer Boats стоит более сложная задача Во-первых, на
следующий плановый период руководство компании уже заключило контракт на произ-
водство 700 яхт Sting Во-вторых, еще один клиент заказал 400 яхт Breaker, и руководство
заинтересовано в выполнении данного заказа В-третьих, анализ рынка, проведенный
отделом маркетинга компании, свидетельствует, что следует произвести не более 300 яхт
Ray Руководство компании хочет выяснить, сколько каких яхт необходимо продать, что-
бы добиться безубыточности Таким образом, необходимо учесть наличие трех моделей,
а также заключенных соглашений
ГЛАВА 3 Линейная оптимизация 165
Начнем с общих положений’ точка безубыточности характеризуется тем, что суммар-
ный доход равняется суммарным затратам. Поскольку компания Longer Boats создана
относительно недавно и испытывает определенные сложности с платежами (что связано
с быстрым ростом компании), руководство заинтересовано в том, чтобы минимизиро-
вать расходы. Поскольку фиксированные затраты придется нести в любом случае, целью
можно считать минимизацию суммарных переменных затрат. Таким образом, поставлена
задача найти производственный план с наименьшими переменными затратами, соответ-
ствующий ограничениям и приносящий доход, равный суммарным затратам. Создайте
символическую модель ЛП, на ее основе разработайте табличную версию модели и опти-
мизируйте ее с помощью средства Поиск решения.
3.17.	Разработка моделей ЛП
Изучая рассмотренные примеры моделей линейного программирования, вы могли
убедиться, что их создание сводится к разумной и тщательной спецификации состав-
ляющих модели (переменных решения, ограничений, целевой функции и т д) в соответ-
ствии с символической линейной оптимизационной моделью Однако в формировании
моделей ЛП есть свои ловушки, которых следует избегать Рассмотрим некоторые ошиб-
ки, часто встречающиеся при создании моделей.
•	Как всегда при моделировании, не следует сразу излишне детализировать модель,
поскольку тогда трудно сформулировать целостную и согласованную модель При
создании табличной версии модели в Excel эти несогласованности превратятся
в трудно обнаружимые логические дефекты таблицы. Поэтому лучше начать с
формирования минимально достаточного множества переменных решения и ог-
раничений. Впоследствии можно усложнить изначально простую модель, добавив
дополнительные переменные и ограничения.
•	Не следует (по крайней мере на начальных этапах) включать в модель нелинейные
зависимости Старайтесь использовать линейные уравнения, для чего можно в уз-
ком диапазоне значений переменных (заданном с помощью дополнительных ог-
раничений) аппроксимировать более сложные нелинейные связи линейными за-
висимостями. Отметим, что оптимизировать нелинейную модель гораздо труднее
(как будет показано в главе 7). Кроме того, нелинейная оптимизация имеет свои
сложности и ловушки. Если же в модель необходимо включить некие нелинейные
связи, лучше сначала разработать упрощенную линейную модель, а нелинейные
связи добавить позже
Заметим, что некоторые нелинейные связи можно достаточно просто преобразо-
вать в линейные, не утратив общности модели. Предположим, Джим хочет ввести
в модель Oak Product ограничение на ассортимент выпуска, которое требует, что-
бы при выпуске 3 стульев Captain выпускался по меньшей мере один стул Mate
Можно записать данное ограничение в виде С/М< 3. Это выражение алгебраиче-
ски корректно, но функция ограничения является нелинейной по переменной Л/,
поскольку та выступает в качестве знаменателя отношения С помощью неслож-
ного преобразования можно получить эквивалентное неравенство С-ЗЛ/<0, ко-
торое уже является линейным по обеим переменным.
•	Не следует на ранних этапах заниматься выяснением, какими будут реальные по-
следствия нецелочисленных значений переменных оптимального решения. В главе 6
166 ЧАСТЬ II. Оптимизационные модели
мы рассмотрим модели, в которых переменные решения должны быть целочислен-
ными. Однако, как и нелинейные зависимости, требование целочисленности значе-
ний переменных вносит дополнительные сложности в процесс оптимизации, поэто-
му на первых этапах моделирования это требование лучше не вводить.
Во многих интересных моделях Л П принятия решений рассматривается несколько
временных периодов (например, задача определения производственного плана на
несколько недель при условии, что недели нельзя считать независимыми). В таких
случаях лучше сначала моделировать ситуацию для отдельного временного перио-
да (например, для одной недели), а затем модифицировать модель, добавляя более
сложные формулировки. Подобные модели рассмотрим в главе 5.
В противоположность сказанному выше отметим, что модели ЛП также не должны
быль слишком простыми и ограниченными. Например, если модель минимизации
затрат не содержит ни одного ограничения, вполне можно получить решение
(в реальной жизни не имеющее смысла), что все переменные решения равны нулю,
т.е предлагается минимизировать затраты за счет ликвидации бизнеса. Аналогично
в модели максимизации прибыли, не содержащей ни одного ограничения, можно
получить “приятное”, но нереальное решение с бесконечной прибылью за счет того,
что одна или несколько переменных решения в процессе оптимизации модели будут
стремиться к бесконечности. В линейном программировании последний результат
называется неограниченным решением.
Нужно очень внимательно относиться к ограничениям в виде равенств и сводить их
в моделях ЛП к минимуму, стараясь ограничиться только теми ситуациями, при ко-
торых с помощью равенств задаются связи, которые должны сохраниться в модели.
Например, в модель можно включить ограничение, отражающее уравнение
“Прибыль = доход - затраты”, или ограничение, отражающее уравнение материаль-
ного баланса “Запасы на конец периода = запасы на начало периода + производство
- отгрузка”. Однако даже такие ограничения снижают результативность модели.
Там, где возможно, такие ограничения лучше задавать в форме неравенств
“Прибыль < . ” или “Запасы на конец периода < ...”. В общем случае надо стараться
записывать ограничения в виде неравенств, даже если есть основания предполагать,
что в оптимальном случае они должны быть равенствами. Позднее, после того как
модель будет оптимизирована, можно проверить, действительно ли эти ограничения
являются лимитирующими, т е. выполняется ли равенство, как ожидалось. Если это
не так, следует внимательно разобраться, почему этого не происходит.
Включение в модель ограничения в виде равенства увеличивает риск получить че-
ресчур ограниченную модель, в результате оптимизации которой получатся реше-
ния с низким выигрышем, а в худшем случае допустимых решений может не ока-
заться вовсе Следует особенно внимательно подходить к включению в модель вы-
раженных в форме равенств ограничений, отражающих организационную
политику. Например, в некой компании XYZ существует неписаное правило:
“Назначать одного менеджера (5) на каждые 10 сотрудников (ИО”, которое пред-
полагает, что нужно наложить ограничение W= 105. Если не существует причины,
делающей включение данного ограничения неизбежным, можно улучшить значе-
ние целевой функции, не вводя его в модель. Если же такое ограничение включить
в модель необходимо, нужно попытаться ввести его в форме неравенства. Напри-
мер, приведенное выше ограничение можно сформулировать так: “Одному менед-
ГЛАВА 3. Линейная оптимизация 167
жеру может быть подчинено не более 10 сотрудников”, в результате получится ог-
раничение 105. При такой формулировке ограничения в ходе оптимизации
модели снижается вероятность получения ответа “допустимых решений не суще-
ствует”. Более того, может оказаться, что наилучшая стратегия состоит в том, что-
бы отказаться от исторически сложившейся традиции назначать менеджеров
в точной пропорции один к десяти.
• Не следует добавлять ограничения, которые не диктуются моделируемой ситуацией,
как это случается, когда в модель с самого начала вводят ограничения, основанные
на интуитивных предположениях (зачастую ошибочных) о природе оптимального
решения. В таком случае создается самореализующееся предсказание, поскольку
решение задачи определено до проведения оптимизации! В результате невозможно
узнать, правильны ли были интуитивные соображения Если же они были ошибоч-
ны, результатом оптимизации модели может быть ответ. “Допустимых решений не
существует”. Например, менеджер считает: “Очевидно, что в данной ситуации нельзя
говорить об эффективности, если запас на конец периода будет больше нуля. По-
этому для верности я добавлю в модель ограничение Запас на конец периода = О'. Та-
кие рассуждения не только повышают риск получить чересчур ограниченную мо-
дель. Если оптимальное решение задачи без данного ограничения приводит к поло-
жительному остатку, менеджер не сможет узнать об этом.
В последующих главах рассматриваются другие примеры моделей, которые вы можете
использовать для совершенствования своей способности осуществлять переход от реаль-
ной ситуации к ее модели линейного программирования. По мере совершенствования
навыков создания моделей вы сможете добавить свои советы и замечания к приведенно-
му выше списку.
3.18.	Заключение
В данной главе мы дали несколько определений Ограничения — это математические
условия, которые исключают определенные комбинации значений переменных реше-
ния. Допустимые решения — это значения переменных, удовлетворяющие всем ограни-
чениям. Линейное программирование занимается поиском допустимого решения, опти-
мизирующего линейную целевую функцию Задача линейного программирования — это
математическая модель, обладающая следующими свойствами
1.	Линейность целевой функции, которую необходимо максимизировать или мини-
мизировать.
2.	Линейность ограничений, каждое из которых представляет собой неравенство или
равенство.
Учитывая гибкость моделирования на базе электронных таблиц, необходимо следо-
вать определенным правилам, чтобы построить табличную модель, обладающую такими
свойствами: 1) точно соответствует модели ЛП, 2) легко документируется, 3) имеет фор-
му, пригодную для оптимизации с помощью средства Поиск решения, 4) не вызывает
проблем при интерпретации отчетов средства Поиск решения. Чтобы успешно использо-
вать средство Поиск решения, необходимо придерживаться следующих правил.
168 ЧАСТЬ II. Оптимизационные модели
1.	Все формулы, влияющие на целевую функцию или ограничения, должны быть ли-
нейными, если в них прямо или косвенно (через формулы других ячеек) входят
переменные решения
2.	Линейная модель является частным случаем нелинейной модели Однако для
средства Поиск решения такое суждение неправомерно эта надстройка использу-
ет разные алгоритмы для оптимизации разных классов моделей. Если в диалого-
вом окне Параметры поиска решения не установить опцию Линейная модель
и оптимизировать модель ЛП с помощью средства Поиск решения, можно не по-
лучить оптимального решения, даже если оптимальное решение будет получено,
отчеты для линейной и нелинейной моделей выглядят по-разному
3.	В диалоговом окне Поиск решения при задании правых частей ограничений необ-
ходимо ссылаться на ячейки рабочего листа, которые являются константами или
которые не будут меняться в процессе оптимизации Кроме того, не разрешается
вводить формулы при определении левых частей ограничений в диалоговом окне
Добавление ограничения. Чтобы избежать ошибок и ненужных сложностей, не
следует вводить формулы или константы непосредственно в поля левых или пра-
вых частей ограничений диалогового окна Добавление ограничения. Рекоменду-
ется помещать формулы и константы в ячейки таблицы, а в полях диалогового ок-
на Добавление ограничения указывать адреса соответствующих ячеек
4.	В моделях большого размера полезно присваивать имена диапазонам ячеек пере-
менных решения, ячейке показателя эффективности, группам ячеек, содержащих
левые части ограничений одного знака, и группам ячеек, содержащих правые час-
ти ограничений одного знака
Перед выполнением процесса оптимизации в диалоговом окне Поиск решения нужно
указать целевую ячейку, изменяемые ячейки, ограничения и установить флажок Линей-
ная модель Кроме того, если отрицательные значения переменных решения не имеют
смысла, нужно установить флажок опции Неотрицательные значения После заверше-
ния оптимизации на экране появится диалоговое окно Результаты поиска решения, со-
держащее сообщения о завершении вычислений и позволяющее создать один или не-
сколько отчетов о поиске решения.
Мы привели несколько примеров, демонстрирующих переход от реальной ситуации
к символической модели ЛП Если целью является увеличение прибыли, создается мо-
дель максимизации, а если цель — уменьшить затраты, получится модель минимизации
Ограничения записываются в виде неравенств со знаком < или >. В некоторых случаях
необходимо ввести ограничения в виде равенств.
3.19.	Решения примеров
Задача о составлении смесей
Табличное представление модели (см. раздел 3.11), ее оптимальное решение, диалого-
вое окно Поиск решения, а также формулы представлены на рис 3 26.
ГЛАВА 3. Линейная оптимизация 169
, ,А „,-л Ж-сХЕЕИ
Составление рудной смеси
Шахта	, Т1 - Т2 ТЗ - Т4	;
Доля в тонне смеси | 0,259 0 704 0,037	0 I Итого
Стоимость 1 тонны $800 $400 $600 $500 [	. '$511,1 V	I
Ограничения Содержание в тонне руды Содержание в смеси Требования Излишек
А	10	3	8	2	5,00 >5	0
В	90	150	75	175	131,67 >	100	31,67
С	45	25	20	37	30,00 >30	О
Баланс	^1-1	1 ; 1 ;	1,00 =	1	0
. a,.м-1 в.1йИ;дНе ..............й f.w
Шахта	Т1 ~2 ТЗ Т4	-	;
«ШЙ Доля в тонне jo 259.0 7010,03 0 I	Итого
4 / Стоимость 1 тс 800 400 600 500 =СУММПРОИЗВ($В$3:$Е$3;В4:Е4)|
;.-S»'sjОграничения держа-	-Содержание в смеси	'ребовани Излишек
А	10	3	8	2	=СУММПРОИЗВ($В$3 $Е$3;В6 Е6)	>	5	=F6-H6
' 1,	В	:90	150 75	175-=СУММПРОИЗВ($В$3:$Е$3;В7 Е7)	>	100	=F7-H7
ПТ"	С	45	25 20	37 =СУММПРОИЗВ($В$3 $Е$3,В8,Е8)	>	30	=F8-H8
*~дП Баланс	1	И	1	И	=СУММПРОИЗВ($В$3 $Е$3,В9 Е9)	=	1	-=F9-H9
чет	____________________________________
Рис. 3.26. Модель составления рудной смеси
Пример 1. Задача об ассортименте продукции
Символическая модель ЯП для данной задачи (см раздел 3 13) имеет следующий вид.
А — дневной выпуск телевизоров Astro (штук/день).
С — дневной выпуск телевизоров Cosmo (штук/день).
Максимизировать 20Я + ЮС
при ограничениях
А <70,
С<50,
А + 2С<П0,
А + С<90,
А,С>0.
170 ЧАСТЬ II. Оптимизационные модели
Заметим, что, как и в модели Oak Product, в некоторые ограничения входят не все пе-
ременные решения. Например, переменная С не входит в первое ограничение (А < 70).
В общем случае не обязательно, чтобы все переменные решения входили в каждое огра-
ничение. Табличная модель Excel для данной задачи с оптимальными решениями, а так-
же диалоговое окно Поиск решения представлены на рис. 3 27. Формулы для вычисле-
ния прибыли и суммарных значений в левых частях неравенств аналогичны соответст-
вующим формулам модели составления рудной смеси, поэтому здесь и в последующих
примерах мы их не приводим. Для ограничения по трудозатратам в цеху Б и для ограни-
чения производственной мощности по выпуску телевизоров Astro резерв оказался не в
точности равен нулю. Такая ситуация достаточно типична: во многих решениях, пред-
лагаемых средством Поиск решения, резерв может принимать очень маленькие положи-
тельные или отрицательные значения, поскольку программа имеет ограниченную точ-
ность вычислений Эти малые значения отражают предел вычислительной точности Ex-
cel и на практике могут считаться равными 0.
Рис. 3.27. Модель задачи об ассортименте продукции
Пример 2. Задача на составление смеси
Модель линейного программирования для задачи по составлению корма для собак
(см. раздел 3.14) имеет следующий вид.
Максимизировать 4х, + 6х2 + Зх3 + 2х4
при ограничениях
Зх, + 5х2 + 2х3 + Зх4 > 3,
7х, + 4х2 + 2х3 + 8х4 > 5,
5х, + 6х2 + 6х3 + 2х4 > 4,
х„х2,х3,х4>0.
Табличное представление модели, оптимальное решение, а также параметры для
средства Поиск решения показаны на рис. 3.28.
ГЛАВА 3. Линейная оптимизация 171
Рис. 3.28. Модель задачи по составлению оптимального корма для собак
Заметим, что в предыдущем примере дробные значения переменных решения могут
считаться недопустимыми (если не предполагать, что они представляют средний еже-
дневный выпуск) А в этом примере дробные значения естественны и допустимы.
Пример 3. Составление расписания
Символическая модель (см. раздел 3.15) имеет следующий вид.
Минимизировать х1 + х2 + х3 + х4 + х5 + х6
при ограничениях
х6+х,>5,
х,+х2>7,
х2 +х3> 15,
х3 + х4 > 7,
х4 + х5> 12,
X, + х6 > 9,
х,>0,7 = 1,2,..., 6.
Данная задача является еще одним примером, в котором переменные решения долж-
ны принимать целочисленные значения. Табличная модель с оптимальными решениями,
а также параметры для средства Поиск решения представлены на рис. 3 29.
Задачи такого типа использовались при составлении расписания дежурств операторов
телефонных станций. Как правило, каждый час разбивается на 15-минутные интервалы;
в сутках 24 часа, следовательно, имеется 94 ограничения. Количество переменных реше-
ния определяется тем, сколько существует возможных смен
172 ЧАСТЬ II. Оптимизационные модели
Рис. 3.29. Модель задачи по составлению расписания дежурств
Пример 4. Анализ безубыточности
Чтобы получить уравнение точки безубыточности в зависимости от количества про-
изведенных яхт (см. раздел 3.16), определим переменные решения следующим образом.
S — количество произведенных яхт класса Sting,
R — количество произведенных яхт Ray,
В — количество произведенных яхт Breaker.
Тогда уравнение точки безубыточности примет вид
100005 + 75005 + 150005 = 50005 + 36005 + 80005 + 18000000,
или
50005 + 39005 + 70005 = 18000000.
Заметим, что существует бесконечное число множеств значений 5, R и В, удовлетво-
ряющих данному ограничению, в многопродуктовой модели существует множество точек
безубыточности, в то время как для однопродуктовой модели точка безубыточности одна.
Поэтому при выпуске нескольких продуктов руководство должно указать дополнитель-
ные ограничения, которые позволят найти конкретную точку безубыточности, представ-
ляющую интерес. Постоянные затраты придется нести в полном объеме независимо от
количества произведенных яхт, поэтому, чтобы добиться минимизации инвестиций, не-
обходимо минимизировать суммарные переменные затраты. Таким образом, целевая
функция (суммарные переменные затраты) имеет вид
50005+36005+80005.
Полная модель с учетом ограничения безубыточности, предварительно установлен-
ных требований и ограничений спроса выглядит следующим образом:
минимизировать 50005 + 36005 + 80005
ГЛАВА 3. Линейная оптимизация 173
при ограничениях
50005 + 39005 + 70005 = 18 000 000,
5> 700,
В >400,
R <300,
5>0,5>0,5>0
Табличная модель, оптимальное решение и параметры для средства Поиск решения
представлены на рис. 3.30.
Л  -I.....С;. К.'.'О,-. .Ъ.^Е
31
Longer Boats
(Тыс долл. Г Stings Breakers Rays
Цена; $ 10,0
Переменные затраты $ 5 0
Фиксированные затраты $5 000
12
Модель безубыточности
Stings__________________________________
Произведено |	2806	400
Удельные затраты	$5 00	$8,00	
Ограничения	•_______Ресурсы
Точка безубыточности ।	$5 00	$7 00
Мин. проиэв. Stings 1
Мин. произв. Breakers :	1
Макс произв. Rays
Rays
Breakers
итого
$18 000 =
2806 >
400	:>
300	<
Итого
$18 000
Излишек
$18 000	0
700	2106
400 ;	0...
300	о
Рис. 3.30. Модель нахождения точки безубыточности

Основные термины
Допустимое решение. Решение, удовлетворяющее всем ограничениям модели, включая условия
неотрицательности
Значения решения. Набор числовых значений переменных решения
Излишек. Показывает, на сколько вычисленная при оптимальных значениях переменных левая
часть ограничения вида “>” превышает правую часть Излишек всегда неотрицателен
174	Ч А С Т Ь II. Оптимизационные модели
Лимитирующее ограничение. Ограничение, в котором при оптимальных значениях переменных ле-
вая часть равна правой
Линейная функция. Функция, в которую все переменные входят в виде отдельных членов В такой
функции нет степеней, отличных от 1, логарифмических, экспоненциальных, тригонометри-
ческих или подобных выражений
Модель условной оптимизации. Модель, цель которой состоит в том, чтобы найти значения пере-
менных решения, оптимизирующие целевую функцию при условии соблюдения ограничений
Невозвратные издержки. Затраты, значения которых уже определены, и поэтому на них не могут
повлиять будущие решения
Ограничение в форме неравенства. Ограничение, требующее, чтобы некая функция переменных
решения была больше или равна (>) или меньше или равна (<) определенной константы.
Ограничение в форме равенства. Ограничение, требующее, чтобы некая функция переменных ре-
шения была в точности равна некоторой константе
Ограничение. Математическое выражение в форме неравенства или равенства, которому должны
удовлетворять переменные модели
Оптимальное решение. Допустимое решение, оптимизирующее целевую функцию (т е обеспечи-
вающее максимум или минимум целевой функции).
Оптимальный ассортимент продукции. То же, что и оптимальный производственный план
Оптимальный производственный план. Оптимальное решение производственной модели, опреде-
ляющее оптимальные количества производимых продуктов
Оптимизировать. Максимизировать или минимизировать целевую функцию
Переменные затраты. Затраты, значения которых будут определяться выбранным решением.
Переменные решения. Переменные, значениями которых управляет человек, принимающий решение
Поиск решения. Надстройка (средство) Excel, которая может оптимизировать табличные модели Л П
Правая часть ограничения. Число, стоящее в правой части неравенства, задающего ограничение
Резерв. Показывает, на сколько левая часть ограничения вида “<”, вычисленная при оптимальных
значениях переменных, меньше, чем правая часть Резерв всегда принимает неотрицательные
значения
Символическая модель ЛП. Математическое представление задачи линейного программирования
Условие целочисленности. Требование, чтобы одна или несколько переменных модели принимали
только целочисленные значения
Условия неотрицательности. Условия модели, требующие, чтобы переменные решения принимали
только неотрицательные (положительные или нулевые) значения
Функция ограничения. Левая часть неравенства, задающего ограничение, зависит от переменных
решения
Целевая функция. В каждой задаче линейного программирования имеется линейная целевая
функция, представляющая показатель эффективности, которую необходимо максимизировать
или минимизировать
Целочисленное программирование. Модель, в которой одна или несколько переменных могут при-
нимать только целые значения
ГЛАВА 3. Линейная оптимизация 175
Контрольные вопросы
Да/нет
1.	В моделировании условия, сужающие область допустимых решений, называются
ограничениями.
2.	Модель Л П не обязательно содержит ограничения.
3.	Любая модель, содержащая целевую функцию, ограничения и переменные реше-
ния, является моделью линейного программирования.
4.	Ограничения задаются неравенствами типа “>”.
5.	Условия неотрицательности означают, что все переменные решения должны быть
положительными.
6.	Поскольку дробные значения переменных решения могут не иметь физического
смысла, на практике оптимальное решение задачи ЛП часто округляется до цело-
численных значений.
7.	Все ограничения в линейных моделях являются неравенствами.
8.	Правильное определение переменных решения является ключевым этапом фор-
мирования модели
9.	Целевая функция модели минимизации затрат должна учитывать только перемен-
ные затраты.
10.	Менеджер должен знать, каким образом реальная ситуация формализована в мо-
дели ЛП, поскольку рано или поздно ему придется оценить правильность данной
модели.
Выберите правильный ответ
11.	Ограничение сужает диапазон значений, которые.
а.	может принимать целевая функция;
Ь.	могут принимать переменные решения;
с.	ни одно из вышеуказанных;
d а и Ь.
12.	Ограничения могут отображать:
а.	требования;
Ь.	условия баланса;
с все вышеперечисленное
13.	Модель линейного программирования — это:
а.	модель условной оптимизации;
b	модель принятия решений при наличии ограничений;
с.	модель математического программирования,
d.	все перечисленное выше.
14.	В модели максимизации’
а.	находится максимум целевой функции;
176 ЧАСТЬ II Оптимизационные модели
b находится максимум целевой функции, а затем определятся, является ли дан-
ное решение допустимым;
с.	находится максимум целевой функции на множестве допустимых решений;
d.	все вышеперечисленное.
15.	Отличительной особенностью моделей линейного программирования
(выделяющей их из более общего класса моделей математического программиро-
вания) является то, что:
а.	модель Л П имеет целевую функцию и ограничения;
Ь.	все рассматриваемые функции линейны;
с.	находятся оптимальные значения переменных решения.
16.	При переходе от реальной проблемы к символической модели полезно:
а	словесно описать все ограничения;
Ь.	дать словесное описание цели;
с.	словесно определить переменные решения;
d сделать все вышеуказанное.
17.	Математическая формулировка модели важна потому, что:
а.	позволяет использовать математические методы,
Ь.	большинство менеджеров предпочитает работать с символическими моделями;
с	заставляет менеджера четко решить поставленную задачу;
d.	позволяет менеджеру отложить принятие решения, делая вид, что он занят.
18.	Требование неотрицательности включается в модель ЛП, поскольку:
а	такую модель легче решать;
b	такая модель больше соответствует реальной ситуации;
с.	ни первое, ни второе;
d.	и первое, и второе.
Вопросы с 19 по 26 относятся к следующей задаче
Три девушки, Лотта Андерсон, Клэр Мосли и Финни Джонс, направляются в Голли-
вуд на поиски счастья. Время полета 40 ч, стоимость самолетного топлива $100 за галлон.
В Голливуде они знакомятся со всем известным Питером Ренбергом. Чистый годовой до-
ход Питера составляет $40 000, а его выплаты по алиментам — $60 000. Питер знает прак-
тически всех в городе, поэтому он может занимательно рассказать трем искательницам
счастья, как становятся звездами. В настоящее время девушки работают контролерами
медицинских препаратов на фармацевтической фабрике. Капсула с препаратом помеща-
ется на специальный стол, где она просвечивается, и контролер визуально проверяет ее,
выявляя поврежденные, недостаточно наполненные или плохо закрытые капсулы. Лю-
бая из девушек может заниматься проверкой капсул Все девушки различаются по своим
внешним данным (росту), а также по скорости и точности выполнения работы, поэтому
их работодатель, Флора Сэйджер, установила им разные ставки почасовой оплаты. Дан-
ные о рабочих характеристиках и росте девушек приводятся в следующей таблице.
ГЛАВА 3 Линейная оптимизация 177
Контролер	Скорость, шт./ч	Точность, %	Почасовая ставка, $	Рост, см
Лотта	300	98	11,80	178
Клэр	200	99	10,40	132
Финни	350	96	11,00	164
Флоре нужно, чтобы за 8-часовой рабочий день было проверено не менее 2000 капсул,
причем ошибки проверки могут составлять не более 2% от общего количества. Кроме
того, из-за нарастающего утомления один контролер не может работать более 4-х часов
в день. Обозначим
%, — время, отработанное Лоттой,
Х2 — время, отработанное Клэр,
Ху — время, отработанное Финни.
Цель разрабатываемой модели — минимизировать затраты на 8-часовую проверку
препаратов. Предполагается, что процесс проверки длится все 8 ч; других контролеров,
кроме Лотты, Клэр и Финни, нет; одновременно может работать только один контролер;
контролер работает не более 4-х часов в день
19.	Какое из следующих неравенств не отражает ограничения для точности проверки9
а. 0,98х300хУ, + 0,99х200хУ2 + 0,96х350хУ3 > 2000,
Ь. 0,02х300хА'| + 0,01х200х%2 + 0,04х350х%3 < 0,02x2000,
с. -2Х2 + 7%3 < 0,
d. все
20.	Ограничение, выражающее требование к объему проверенных препаратов, запи-
сывается как 300Х, + 200%2 + 350Х, = 2000.
а.	Да.
Ь.	Нет.
21.	Исключая условия неотрицательности, правильная формулировка данной задачи
содержит 6 ограничений.
а Да
Ь. Нет.
22.	Может оказаться, что правильно сформулированная постановка данной задачи не
будет иметь допустимых решений. (Ответ нужно дать для приведенных данных )
а. Да.
Ь. Нет.
23.	Если бы не было ограничения, оговаривающего 4-часовый рабочий день контро-
лера, и требования к точности, оптимальное решение состояло бы в том, чтобы
работала только Финни.
а.	Да.
Ь.	Нет.
24.	В оптимальном решении требуется, чтобы работали как минимум два из трех кон-
тролеров.
178 ЧАСТЬ II Оптимизационные модели
а Да.
b Нет
25.	Следующие решения являются допустимыми.
а 4 часа работает Клэр, 4 часа — Финни;
b 4 часа работает Лотта, 4 часа — Клэр:
с и первое, и второе
26.	Пусть вариант А решения предполагает %, = 4, Х2 = 4, X, = 0, а вариант В — X, = 3,
Х2 = 4, Х} = 1 Оба варианта допустимы Поскольку в случае А проверяется 2000
капсул, а в случае В — 2050, вариант А предпочтительней
а Да
b Нет
27.	Рассмотрим ограничение 10С+ 15Л/<Я, где R — параметр Предположим, что
значение Л определяется формулой 200(1—где А — новая переменная реше-
ния Если подставить это выражение в исходное ограничение, оно примет вид
I0C + 15М < 200(1-е-0"5'*) Новое ограничение линейно по переменным С, Ми А
а Да
b Нет
28.	В табличной модели функция ограничения представляется формулой в ячейке ра-
бочего листа
а Да
b Нет
29.	Если в табличной модели существуют ячейки резерва, то для допустимых решений
эти ячейки будут содержать неотрицательные значения
а Да
b Нет
30.	Excel можно использовать для создания табличной модели ДП, но без средства
Поиск решения оптимизировать модель не удастся
а Да
b Нет
Ответы
1 Да 2 Нет 3 Нет 4 Нет 5 Нет. 6 Да 7 Нет. 8 Да. 9. Да 10. Да. 11. d 12 с 13. d.
14 с 15 b 16 d 17 с 18 b 19. с 20 b 21 а 22 b 23 Ь. 24 а 25 b 26. b 27. Ь. 28. а. 29.
Учебные задачи
3 1 Подберите каждому из следующих терминов наиболее подходящее определение
а задача линейного программирования,
b переменные затраты,
с невозвратные затраты,
ГЛАВА 3. Линейная оптимизация 179
d переменная решения,
е функция ограничения,
f ограничение
1	Неизвестные величины в модели ЯП, представляющие решения, которые предстоит
принять
2	Как правило, выражается в виде неравенства
3	Понятие, которое надлежит включать в модель
4	Обычно не включается в модель (исключение составляет анализ безубыточности)
5	Левая часть ограничения
6	Специальная разновидность модели условной оптимизации
3 2 Какие из следующих математических выражений могут встретиться в модели линейного
программирования Если какие-то из них не могут входить в модель ЛП, укажите причины
f х, + log(x,) = 5,
g log(10)x, + e‘x = 6,
h eA|+x2=23,
1 формула Excel для правой части ограничения, в которой F6 — переменная решения
=ЕСЛИ($1$6>=2,СУММ(С1 G1O),CYMM(G1 G5))
Прикладные задачи
3.3. Планирование производства Компания Swelte Glove производит и продает два изделия При
продаже каждой единицы изделия 1 компания получает прибыль S12, а при продаже еди-
ницы изделия 2 — $4 Требования к затратам рабочего времени на производство изделий в
трех цехах приводятся в таблице Начальники цехов оценили, что на следующей неделе ре-
сурс рабочего времени составит в первом цехе 800 ч, в цехе 2 — 600 ч, в цехе 3 — 2000 ч
Предполагая, что компания заинтересована в максимизации прибыли, разработайте мо-
дель линейного программирования для данной задачи
Затраты рабочего времени
Цех	Продукт 1	Продукт 2
1	1	2
Планирование производства Вуд Уолкер владеет небольшим мебельным магазином Он из-
готавливает три типа столов А, В и С При изготовлении каждого стола необходимо затра-
тить определенное время на производство составных частей, сборку и покраску Вуд может
продать все собранные столы Кроме того, модель С можно продавать без покраски Вуд
180 ЧАСТЬ II Оптимизационные модели
нанял несколько рабочих на условиях неполной занятости, поэтому время, затраченное на
изготовление столов, может от недели к неделе меняться Используя имеющиеся данные,
постройте модель ЛП, которая поможет Вуду определить ассортимент выпускаемой про-
дукции, максимизирующий его прибыль на следующей неделе
Модель	Изготовление частей, ч Сборка, ч	Окраска, ч Удельная прибыль, долл.
А	3	4	5	25
В	1	2	5	20
с	4	5	4	50
Неокрашенные столы С	4	5	0	30
Ресурс рабочего времени	150	200	300
Финансовое планирование Вилли Хене — президент инвестиционной фирмы, которая
управляет инвестиционными портфелями нескольких клиентов Новый клиент поручает
фирме управление своим портфелем в размере $100 000 Клиент хочет ограничиться по-
купкой акций трех компании, характеристики которых представлены в таблице Постройте
модель ЛП, которая позволит определить, сколько акций каждой компании должен купить
Вилли, чтобы оптимизировать ожидаемых годовой доход
Акции компании	Цена акции,	Ожидаемый годовой доход на акцию, долл.	Максимально возможные инвестиции, долл.
Gofer Crude	60	7	60 000
Can Oil	25	3	25 000
Sloth Petroleum	20	3	30 000
3 6 Задача составления смеси Дуглас Старр управляет питомником домашних животных Heav-
enly Hound Kennels, Inc Корм для собак в питомнике готовится из смеси трех зерновых
круп, чтобы обеспечить сбалансированное питание Соответствующие данные приведены
в таблице Дуглас хочет, чтобы каждая собака потребляла ежедневно не менее 8 унций бел-
ков, 1 унции углеводов и не более 0,5 унции жиров Сколько каждой крупы должна полу-
чать собака, чтобы минимизировать затраты9 (16 унций = 1 фунт )
Крупа	Стоимость 1 фунта, долл.	Белки, %	Углеводы, %	Жиры, %
А	0,45	62	5	3
В	0,38	55	10	2
С	0,27	36	20	1
Задача составления смеси Компания McNaughton, Inc производит два вида приправ для
мяса, Spicy Diablo и Red Baron Обе приправы готовятся из двух ингредиентов — А и В,
причем рецепты приправ допускают определенную вариативность Допустимое процент-
ное содержание ингредиентов, а также данные о доходах и затратах приводятся в таблице
Можно закупить до 40 кварт ингредиента А и до 30 кварт ингредиента В Компания в со-
стоянии продать все произведенные приправы Постройте модель ЛП, цель которой —
максимизировать чистый доход от продажи приправ
ГЛАВА 3. Линейная оптимизация 181
Приправа		Ингредиент			
	А	В		Цена за кварту, долл.
Spicy Diablo	не менее 25%	не менее 25%	3,35
Red Baron	не более 75%	произвольно	2,85
Цена за кварту, S	1,60	2,59	
3 8 Задача составления смеси У компании Corey Ander’s Spice имеются ограниченные запасы трех
ингредиентов, из которых изготавливаются приправы Ингредиенты НВ01, НВ02 и ВВОЗ идут
на производство двух приправ куркумы и паприки Отдел маркетинга сообщил, что компа-
ния сможет продать всю произведенную паприку, но не более 1700 бутылок куркумы Неис-
пользованные ингредиенты можно продать на свободном рынке Текущие цены ($ за унцию)
НВ01 — 0,60, НВ02 — 0,70, НВ03 — 0,55 Кроме того, компания заключила контракт на по-
ставку 600 бутылок паприки с Wal-Mart Другие данные представлены в таблице Сформули-
руйте задачу в виде модели ЯП максимизации дохода
	Ингредиенты			Спрос	Цена, долл.
	НВ01	НВ02	нвоз		
Куркума		2	1	1700	3,25
Паприка	3	2	3	Неограничен	2,75
Запас ингредиентов, унции	8 000	9 000	7 000		
3 9 Задача составления смеси Гай Чанг, администратор зданий и прилегающих территорий
университета Готхэма, планирует ранней весной внести удобрения для травы на лужайке
Для нормального роста траве нужны азот, фосфор и калий как минимум в следующих ко-
личествах
Вещество	Минимальное количество, фунты
Азот Фосфор Калий	10 7 5
На рынке предлагается три вида минеральных удобрений, содержание требуемых элементов
(в фунтах) и цена в расчете на 1000 фунтов представлены в следующей таблице Гай может ку-
пить любое количество каждого из удобрений и смешать их, прежде чем вносить в почву По-
стройте модель ЛП, которая позволит определить, сколько следует купить каждого удобре-
ния, чтобы минимизировать затраты
Удобрение	Содержание азота	Содержание фосфора	Содержание калия Цена, долл.
I	25	10	5	10
11	10	5	10	8
III		5	10	5	7
3 10 Планирование производства В выпуске двух продуктов задействованы три станка Чтобы
выпустить фунт продукта каждый станок должен отработать определенное количество ча-
сов Данные приводятся в таблице Ресурс рабочего времени для станка 1 составляет 10 ч,
для станка 2 — 16 ч и для станка 3 — 12 ч Удельная прибыль в расчете на 1 фунт составляет
$4 для продукта 1 и $3 для продукта 2 Определите переменные решения, сформулируйте
данную задачу в виде модели ЛП максимизации прибыли и решите ее
182	ЧАСТЬ II Оптимизационные модели
	Количество часов обработки Станок	Продукт 1	Продукт 2
3 11	1	3	2 2	1	4 3	5	3 Компания Solar Саг владеет заводом, который может выпускать семейные автомобили (седаны), пикапы и спортивные двухместные автомобили (купе) Удельная прибыль, время производства и фиксированные затраты представлены в таблице
3 12	Модель	Удельная прибыль, $ Время производства, ч Фиксированные затраты, S Седан	6 000	12	2	000	000 Пикап	8 000	15	3	000	000 Купе	11 000	24	7	000	000 Компания к настоящему моменту уже получила заказы на 100 седанов, 200 пикапов и 300 купе, которые она обязана выполнить Составьте производственный план, который позво- лит как можно быстрее достичь точки безубыточности, т е сделать валовый доход равным валовым фиксированным затратам, минимизировав суммарное время производства Сформулируйте данную задачу в виде модели ЛП и решите ее Анализ безубыточности Риз Эйлер производит воздухоочистители двух видов Umidaire и Depollinator Данные о цене и затратах приводятся в таблице Фирма Риза уже заключила контракт на поставку 500 Umidaire и хочет определить, какое количество воздухоочистите- лей обоих видов нужно произвести, чтобы достичь безубыточности Сформулируйте задачу ЛП минимизации затрат и найдите ее решение
3 13	Продукт	Цена 1 шт., Переменные затраты на 1 шт., S Фиксированные затраты, S	S Umidaire	450	240	150 000 Depollinator	700	360	240 000 Управление портфелем активов Инвестиционная компания должна определить, куда вло- жить средства в размере S10 млн Цель — максимизировать ожидаемый доход в следующем году Четыре возможных варианта вложения средств представлены в таблице Компания также приняла решение, что не менее 30% средств должно быть вложено в обыкновенные акции и долгосрочные казначейские облигации и не более 40% — в фонды денежного рын- ка и муниципальные облигации Необходимо инвестировать все имеющиеся $10 млн Сформулируйте задачу ЛП, позволяющую определить, куда и сколько вложить средств, и найдите ее решение Варианты инвестирования	Ожидаемый доход, Максимально возможная сумма ииве- %	стиций, млн. долл. Обыкновенные акции	8	5 Облигации казначейства	6	7 Фонд денежного рынка	12	2 Муниципальные облигации	9	4
Г Л А В А 3. Линейная оптимизация 183
3 14	Управление сельскохозяйственным производством Организация управляет четырьмя ферма- ми, производительность которых примерно одинакова Каждая ферма имеет определенную площадь сельхозугодий, ей требуется определенное количество часов рабочего времени, чтобы ухаживать за растениями и убирать урожай Данные для предстоящего сезона пред- ставлены в таблице
3 15	Ферма	Используемая площадь, акры Ресурс рабочего времени в месяц, ч 1	500	1700 2	900	3000 3	300	900 4	700	2200 Организация рассматривает варианты выращивания трех культур, которые отличаются ожидаемой удельной прибылью в расчете на один акр занимаемой ими площади и требуе- мыми трудозатратами, что отражено в следующей таблице Культура Максимальная площадь Трудозатраты, часы в месяц Ожидаемая прибыль на акр, S А	700	2	500 В	800	4	200 С	300	3	300 Общая площадь, выделенная под каждую определенную культуру, ограничена требованиями к уборочной технике Чтобы поддерживать примерно одинаковую рабочую нагрузку на фер- мах, руководство организации решило, что процентные отношения площадей, занятых опре- деленными культурами, должны быть одинаковы на всех фермах Однако ферма может вы- ращивать произвольную комбинацию культур, удовлетворяющую всем ограничениям (в том числе и требованию одинаковой нагрузки) Руководство организации хочет узнать, какие площади должны быть выделены под каждую из культур на каждой ферме, чтобы максимизи- ровать ожидаемую прибыль Сформулируйте задачу в виде модели ЛП и решите ее Задача составления смеси Винодел хочет из смеси четырех сортов винограда приготовить три сорта вина Имеющиеся количества винограда, требования к составу вина и цены, по которым данные вина продаются, приведены в таблице В частности, сорта винограда 2 и 3 в сумме должны составлять не менее 75% в смеси для приготовления вина А и не менее 35% в смеси для приготовления вина С Кроме того, смесь А должна содержать не менее 8% винограда сорта 4, а смесь В — не менее 10% сорта 2 и не более 35% сорта 4 Можно продать все произведенные вина Постройте модель ЛП, которая позволит наилучшим об- разом использовать выращенный виноград Виноград Вино	1	2	3	4	Цена за галлон А	произвольно	не	менее 75% 2 и 3 в лю-	не менее 8%	80 бой пропорции В	произвольно	не	менее произвольно	не более 35%	50 10% С	произвольно	не	менее 35% 2 и 3 в лю-	произвольно	35 бой пропорции Запас (галлон)	130	200	150	350
184	ЧАСТЬ II Оптимизационные модели
3 16	Задача составления расписания Ресторан работает 7 дней в неделю Официанты работают 6 часов в день Договор с профсоюзом предусматривает, что каждый должен работать 5 дней подряд, а затем 2 дня отдыхать У всех официантов одинаковый еженедельный оклад. Требо- вания штатного расписания представлены в таблице Предполагая, что эти требования цик- лически повторяются, а также игнорируя тот факт, что число нанятых официантов должно быть целым, постройте модель ЛП, которая позволит руководству составить расписание, удовлетворяющее заданным требованиям при минимальных затратах, и найдите решение по- лученной задачи
3 17	День недели	Минимальное необходимое количество часов работы официантов Понедельник	150 Вторник	200 Среда	400 Четверг	300 Пятница	700 Суббота	800 Воскресенье	300 Планирование производства Завод может производить четыре вида изделий А, В, С и D в произвольных комбинациях По технологии каждое изделие обрабатывается четырьмя машинами (время обработки в минутах в пересчете на фунт готовой продукции показано в таблице) Каждая машина может работать 60 ч в неделю Изделия могут продаваться по следующим ценам А — $9, В — S7, С —S6, D —S5 за фунт Переменные затраты на оплату труда составляют $2 в час для машин 1 и 2 и $3 в час для машин 3 и 4 Материальные затра- ты составляют S4 на каждый фунт продукции А и S1 на каждый фунт продукции В, С и D Сформулируйте задачу ЛП, максимизирующую прибыль при заданном максимальном спросе для каждого вида продукции и решите ее
3 18	Машина Продукция	1	2	3	4	Максимальный спрос А	5	10	6	3	400 В	3	6	4	8	100 С	4	5	3	3	150 D	4	2	1	2	500 Планирование производства В данном месяце необходимо выполнить четыре вида работ А, В, С и D Каждый вид работ может выполняться любым из трех цехов Время, требуемое на вы- полнение конкретного задания определенным цехом, стоимость часа работы каждого цеха и ресурс рабочего времени на данный месяц в каждом цехе представлены в таблице Каждое задание можно распределить по нескольким цехам в любой пропорции Например, четверть задания А может быть выполнена за 8 ч цехом 1, а треть задания С — за 9 ч цехом 3 Необхо- димо распределить выполнение заданий по цехам (сколько часов каждый цех должен выпол- нять каждое определенное задание), чтобы минимизировать затраты на выполнение всех за- даний Определите переменные решения, сформулируйте задачу Л П и решите ее
ГЛАВА 3. Линейная оптимизация 185
	Время, ч Цех	А	В	С	D	Стоимость часа Ресурс рабочего работы, S	времени, ч
3 19	1	32	151	72	118	89	160 2	39	147	61	126	81	160 3	46	155	57	121	84	160 Составление расписания Базирующийся в Стокгольме авианосец “Маити” с понедельника по пятницу находится на маневрах, а во время уик-энда — в порту На следующей неделе капитан хочет предоставить увольнение на берег во время уик-энда максимально возмож- ному числу моряков (Экипаж состоит из 2500 человек ) Однако при этом необходимо вы- полнить запланированные на неделю маневры и удовлетворить требования военно- морского регламента Требования таковы а Моряки работают в первую (от полуночи до полудня) или во вторую (от полудня до полуночи) смену, причем на протяжении недели каждый моряк все дни работает в од- ну и ту же смену b Каждый моряк должен дежурить ровно четыре дня, даже если в какой-то день реаль- ной работы недостаточно В таблице показано, сколько моряков должно дежурить каждый день в каждую смену Сформулируйте для данной задачи модель ЛП, чтобы узнать, сколько моряков должно ра- ботать каждый день
3 20	Пн.	Вт.	Ср.	Чт.	Пт. 1 смена	900	1000	450	800	700 2 смена	800	500	1000	300	750 Небольшая фирма использует два процесса для изготовления двух продуктов жидкости для стартера и жидкости для зажигалок Руководство фирмы пытается решить, сколько часов уде- лить каждому из процессов Данные о процессах (в пересчете на один час) приведены в таблице Пусть х, их, - число часов, выделенных компанией на проведение процессов 1 и 2 соответственно Федеральной программой компании выделено 300 единиц керосина и 450 единиц бензина Согласно торговым соглашениям компания должна произвести не менее 600 единиц жидкости для стартера и 225 единиц жидкости для зажигалок Почасовая прибыль, получаемая при проведении процесса 1 и 2, составляет $450 и $390 соответственно Сформу- лируйте задачу в виде модели Л П максимизации прибыли и решите ее
3 21	Исходные вещества	Конечные продукты Процесс Керосин Бензин Жидкость для стартеров	Жидкость для зажигалок 139	15	6 2	12	6	9	24 Составление расписания Ресторан работает 7 дней в неделю По условиям найма официан- ты работают 6 часов в день В ресторан приходят отдельные посетители и небольшие ком- пании, их посещения будем называть регулярным спросом Кроме того, более многочислен- ные группы (клубы по интересам и т п ) иногда собираются в ресторане на свои еженедель- ные встречи По соглашению с профсоюзом официант работает пять дней подряд, а затем
186	Ч А С Т Ь II Оптимизационные модели
два дня подряд отдыхает Все официанты получают одинаковую недельную заработную
плату Минимально необходимое ежедневное рабочее время зависит от регулярного еже-
дневного спроса, к которому добавлено количество рабочего времени, необходимого для
обслуживания запланированных на этот день крупных встреч Регулярный спрос
(выраженный в человеко-часах) и число встреч, запланированных на каждый день, пред-
ставлены в таблице
День недели	Регулярный спрос	Количество запланированных встреч
Понедельник	125	1
Вторник	200	0
Среда	350	1
Четверг	300	0
Пятница	650	3
Суббота	725	4
Воскресенье	250	2
Чтобы определить, сколько человеко-часов необходимо для обслуживания встреч, управляющий
использует следующую таблицу Необходимо составить расписание работы официантов, удовле-
творяющее потребности в обслуживании и минимизирующее затраты, предполагая, что данный
цикл неограниченно повторяется, и игнорируя тот факт, что число нанятых официантов должно
бьггь целым Поскольку спрос может со временем меняться, следует составить табличную модель
таким образом, чтобы данные вводились в ячейки (а не непосредственно в формулы) Оптими-
зируйте полученную модель при существующих значениях данных
Число запланированных встреч	Требуемое количество человеко-часов
О	О
1	24
2	36
3	52
4	64
5	80
3 22 Управление сельскохозяйственным производством Организация управляет четырьмя ферма-
ми, производительность которых примерно одинакова Каждая ферма имеет определенную
площадь сельхозугодий, ей требуется определенное количество часов рабочего времени,
чтобы ухаживать за растениями и убирать урожай Данные для предстоящего сезона пред-
ставлены в таблице задачи 3 14 Организация рассматривает варианты выращивания трех
культур, которые отличаются ожидаемой удельной прибылью в расчете на один акр зани-
маемой ими площади, что отражено во второй таблице задачи 3.14
Для каждой культуры требуется особая уборочная техника, затраты на которую различны
Общая площадь, отведенная под каждую конкретную культуру, ограничивается решением
о том, на сколько часов арендовать определенную уборочную технику Организация вло-
жила S19000 (фиксированные затраты) в кооператив уборочной техники Это позволяет ей
использовать комбайны любого из трех типов по ставкам аренды, указанным в таблице,
ГЛАВА 3. Линейная оптимизация
187
пока общая сумма не превысит $19000 Как правило, когда комбайн впервые попадает на
ферму, он работает достаточно медленно Однако с каждым сезоном рабочие все лучше ос-
ваивают машину и производительность повышается В данном случае скорость уборки по-
сле того, как отработано г часов, задается уравнением
скорость = n(l-e-v) акров в час,
где п — скорость уборки в долгосрочной перспективе, X — корректирующий множитель
для краткосрочного периода
Суммарную площадь, убираемую за определенный временной период, равный Т часов
можно вычислить, проинтегрировав скорость уборки по времени
площадь, убираемая за Тчасов, = £ n(-e~*)dt = п[Т - (1 -е ™ )]
Скорость уборки в долгосрочной перспективе и корректирующие множители для всех ви-
дов уборочных комбайнов приводятся таблице Руководство организации приняло реше-
ние использовать для уборки культуры А 400 машино-часов, культуры В — 315 машино-
часов и культуры С — 335 машино-часов Чтобы рабочая нагрузка на фермах была прибли-
зительно одинаковой, процентное отношение занимаемых различными культурами пло-
щадей на всех фермах должно быть одинаковым Однако каждая ферма может выращивать
произвольную комбинацию культур, удовлетворяющую всем ограничениям (в том числе
и требованию одинаковой нагрузки) Руководство организации хочет узнать, какие площа-
ди должны быть отведены под каждую из культур на каждой ферме, чтобы максимизиро-
вать ожидаемую прибыль
Культура	X	п	Стоимость мг	
			
А	0,02	2		15
В	0,02	3		20
С	0,03	1		20
а Создайте табличную модель ЛП, в которой часы аренды уборочных машин будут ис-
пользованы в качестве параметров
b Оптимизируйте полученную модель
с Предложите другие возможные значения часов аренды уборочных машин Получилась
ли у вас более высокая прибыль9 Существует ли набор значений часов аренды, кото-
рый позволит получить более высокую прибыль9
3 23 Производство бульдозеров и лесохозяйственной техники Пусть одна единица лесохозяйст-
венной техники приносит доход $802, для ее изготовления требуется 700 фунтов железа,
50 ч рабочего времени, 30 ч термической обработки и 1 коробка передач Один бульдозер
приносит чистый доход $660, для его изготовления требуется 4200 фунтов железа, 110 ч ра-
бочего времени, 12 ч тепловой обработки и 1 коробка передач Ресурсы компании на рас-
сматриваемый период составляют 680 000 фунтов железа, 21 000 ч рабочего времени,
6 000 ч тепловой обработки Коробки передач поставляются дочерней компанией, которая
производит их для всего семейства машин Таким образом, наличие коробок передач для
производимой техники определяется тем, сколько времени будет выделено на их произ-
водство на заводе дочерней компании Производство коробок передач состоит из трех эта-
пов наладка, запуск и регулярное производство Продолжительность каждого этапа и со-
ответствующая производительность указаны в таблице
188
Ч А С Т Ь II. Оптимизационные модели
Этап	Длительность, ч	Количество коробок передач, шт./ч
Наладка	8	0
Запуск	120	0,5
Регулярное производство	-	1
а Если лимит выделенного времени на дочернем заводе составляет 10 ч, то из этого вре-
мени 8 ч уйдет на наладку, во время которой ничего не производится, а 2 ч придется на
фазу запуска, за время которой будет произведено 2x0,5 = 1 коробка передач Если вы-
деленное время Н > 128 ч, то в первые 8 ч ничего не производится, в следующие 120 ч
производится 0,5 коробок в час, а в оставшиеся Н-128 ч будет производиться 1 короб-
ка в час Таким образом, общее количество произведенных коробок передач составит
60 + Н - 128 = Н - 68 шт Составьте уравнения, определяющие ограничение на произ-
водство коробок передач, если выделенное на дочернем заводе время составляет Т ч,
где Т = 6, Т = 108 и Т = 308
b Определите переменные решения и сформулируйте данную задачу в виде модели ЛП
максимизации дохода
с Найдите оптимальное решение, если на заводе дочерней компании на производство
коробок передач выделено 358 ч рабочего времени
3 24 Планирование производства Вернитесь к упрощенной модели Oak Product Предположим,
что прочные и облегченные сиденья производятся двумя цехами А и В соответственно Ко-
личество прочных сидений, производимых в неделю цехом А, и количество облегченных
сидений, производимых в неделю цехом В, зависят от того, сколько рабочих будет направ-
лено в каждый цех Руководство считает, что производственные мощности цехов описыва-
ются следующими функциями
производство прочных сидений в цехе А= 200(1 -е~°05т),
производство облегченных сидений в цехе В = 222(1-e“°“iwi),
где WA и WB — число рабочих, направленных в цех А и цех В соответственно В исходной
версии данной задачи предполагалось, что в цехеА работает 24 рабочих (те И01 = 24), а в
цехе В — 13 (IVВ = 13) Таким образом,
производство прочных сидений в цехе А = 200(1-е''2) = 139,8,
производство облегченных сидений в цехе В = 222 (1-е’° ”) = 120,23
(В упрощенной модели Oak Product эти числа были округлены до 140 и 120 соответственно )
а Измените рабочую книгу Стулья XLS так, чтобы число рабочих в цехах А и В можно
было вводить непосредственно в качестве параметров, и измените правые части огра-
ничений для прочных и легких сидений соответствующим образом
b Предположим, что в цех А направлено 20 рабочих, а в цех В — 6 С помощью средства
Поиск решения найдите оптимальное решение при WA = 20 и WB = 6 Может ли По-
иск решения оптимизировать данную модель как линейную? Ответ поясните
с Пусть WA = 20 Постройте график оптимальной прибыли как функции WB для значе-
ний WB, изменяющихся в пределах от 0 до 8 с шагом 1 Для этого необходимо 9 раз за-
пустить Поиск решения и копировать значения оптимальной прибыли и WB в ячейки
некой таблицы Затем с помощью мастера диаграмм постройте график Какое явление
иллюстрирует график данной функции9 (В главе 4 мы покажем, как выполнить подоб-
ные вычисления автоматически )
ГЛАВА 3. Линейная оптимизация
189
I 25	У компании Slick Oil есть три склада, с которых она может доставлять продукцию трем рознич- ным торговым точкам Спрос на продукт Gunkout составляет в первой точке 100 ящиков, во вто- рой — 250, в третьей — 150 Запас данного продукта на складе 1 составляет 50 ящиков, на складе 2 — 275 и на складе 3—175 Затраты на транспортировку одного ящика продукта Gunkout со складов в торговые точки представлены в таблице Постройте модель ЛП, позволяющую опре- делить, сколько ящиков следует доставить в каждую торговую точку с каждого склада, чтобы удовлетворить спрос с минимальными затратами
26	Торговые точки Склад	12	3 15	7	6 2	8	9	10 3	4	3	11 Компания HiTech управляет тремя Internet-серверами, каждый из которых может выполнять до трех типов запросов обращения к Web-страницам, запросы к базе данных и запросы к системе электронной коммерции Проще всего обрабатывать обращения к Web-страницам Компания оценивает пропускную способность своих серверов, исходя из того, сколько обращений к Web- страницам они могут обработать в течение дня Другие типы запросов обрабатывать сложнее, и HiTech учитывает обработку каждого такого запроса как выполнение нескольких обращений к Web-страницам Например, сервер 1 может обработать 230 тысяч обращений к Web-страницам в день, но обработка одного запроса к системе электронной коммерции для данного сервера эк- вивалентна обработке двух обращений к Web-страницам Поэтому для запросов к системе элек- тронной коммерции пропускная способность сервера 1 составит всего 115 тысяч запросов в день Общая пропускная способность серверов, выраженная в эквивалентах обращений к Web- страницам, представлена в таблице (НПО означает, что на данном сервере нет программного обеспечения, необходимого для обработки запросов соответствующего типа ) Сервер Обработка запроса в эквиваленте количества обращений	12	3 к Web-страиицам Обращение к Web-странице	1	1	1 Запрос к базе данных	2,5	НПО	4 Запрос к системе электронной коммерции	2	5	НПО Пропускная способность сервера, тыс	обращений	230	360	160 к Web-страницам/день Компания HiTech ожидает, что максимальный ежедневный спрос на запросы различных типов будет таким Тип запроса	Спрос, тыс. запросов/день Обращения к Web-страницам	310 Запросы к базе данных	40 Запросы к системе электронной коммерции	120
190 ЧАСТЬ II Оптимизационные модели
Компания заинтересована в том, чтобы обработать как можно больше запросов Разрабо-
тайте модель ЛП, которая позволит распределить запросы по серверам так, чтобы достичь
данной цели
3 27 Компания Candy’s Fragrances выпускает на своей фабрике, расположенной в Санта-Мария,
Калифорния, три вида продукции духи, шампунь и крем для лица Фабрика работает в две
смены В первую смену час рабочего времени стоит S15, а ресурс рабочего времени состав-
ляет не более 30 000 ч При работе во вторую смену платится надбавка $2 в час, поэтому
стоимость часа рабочего времени составляет $17 Ресурс рабочего времени второй смены не
превышает 20 000 ч Для производства каждого вида продукции используется три вида сы-
рья Компания платит $2 за фунт сырья А, $2,50 за фунт сырья В и $2 за фунт сырья С
Данные о трудозатратах, расходах сырья и спросе представлены в таблице
	Духи	Шампунь	Крем для лица
Трудозатраты, ч/упаковка	1,5	2	2
Расход сырья А, фунты/упаковка	5	7	4
Расход сырья В, фунты/упаковка	2	2	5
Расход сырья С, фунты/упаковка	3	5	3
Спрос, упаковка	10 000	7 000	15 000
Компания может также покупать шампунь и крем для лица у зарубежного поставщика
Расходы по доставке импортного шампуня составляют $50 за упаковку, а крема — $60 за
упаковку Сформулируйте табличную модель минимизации затрат при условии удовлетво-
рения (или превышения) спроса на продукцию компании
3 28 Компания Bear Lake Electronics выпускает три вида DVD-проигрывателей базовый, класса
люкс и портативный Компания хочет оптимизировать ассортимент продукции, выпускае-
мой на трех ее предприятиях Предположим, что компания может продать все произведен-
ные DVD-проигрыватели Производственные мощности предприятий по изготовлению
комплектующих и сборке представлены в следующей таблице
Предприятие	Сборка, ч	Изготовление комплектующих, ч
1	20 000	100 000
	30 000	100 000
3	10 000	70 000
Всего	60 000	270 000
Прибыль от продажи базовой модели составляет $75, модели класса люкс — $125, а порта-
тивной модели — $195 Время, необходимое для изготовления комплектующих и сборки
различных проигрывателей, приводится в таблице
Проигрыватель		
Базовая модель	3	8
Модель класса люкс	4	11
Портативная модель	8	16
Создайте табличную модель и найдите оптимальный ассортимент продукции для компа-
нии Bear Lake Electronics
3 29 Компания Environmental Energy Associates (EEA) владеет небольшим коммунальным предприятием
по производству электроэнергии в южной Калифорнии Предприятие генерирует электричество
следующим образом сжигая три вида топлива, нагревают паровой котел, а струя пара вращает тур-
бину генератора В качестве топлива для котла могут использоваться навоз, древесные отходы, а
также природный газ Компании необходимо минимизировать затраты на топливо, при этом про-
изводство электроэнергии в следующем месяце должно составить не менее 7200 МВтч Навоз по-
ГЛАВА 3. Линейная оптимизация 191
ставляется владельцами расположенных поблизости ранчо и откормочных хозяйств, которые пла-
тят компании ЕЕА $50 за утилизацию тонны навоза Древесные отходы закупаются на местной ле-
сопилке по цене $25 за тонну Природный газ поставляется по трубопроводу по цене $ 120 за милли-
он стандартных кубических футов В следующей таблице приводятся выход энергии, ресурс и
удельная стоимость каждого вида топлива
Топливо	Выход энергии	Ресурс	Стоимость
Навоз	10 МВт ч/т	100 т	-$50,00 за тонну
Древесные отходы	7 МВт ч/т	200 т	$25,00 за тонну
Природный газ	40 МВт ч/млн	Неограниченно	$120,00 за млн
	куб футов		куб футов
Разработайте в Excel табличную модель, которая позволит решить поставленную задачу
(минимизировать затраты при заданном уровне производства энергии) Сколько топлива
каждого вида следует использовать для выработки электроэнергии в следующем месяце9
| Ситуация для анализа) Компания Ebel Mining
(часть 1, продолжение)
Прочитайте еще раз описание ситуации для анализа компании Ebel Mining
(часть I) в конце главы 2 Сформируйте табличную модель линейного программиро-
вания и оптимизируйте ее с помощью средства Поиск решения
Ситуация для анализа | Компания Red Brand Canners7
Ниже предлагается простая, но интересная ситуация для анализа, которая содер-
жит несколько моментов, важных для формирования реальных моделей В любой
реальной ситуации менеджер должен отделить нужные данные и факты от ненуж-
ных Это бывает особенно трудно сделать из-за заблуждений и неверных концепций,
которых придерживается руководство В данном примере воспроизводится именно
такая ситуация Сейчас задача состоит в том, чтобы просто сформировать модель, но
мы еще вернемся к этому примеру в главе 4
В понедельник, 13 сентября 1996 года Митчел Гордон, вице-президент компании по
вопросам управления персоналом, пригласил на совещание экономиста, заведующего
отделом продаж и управляющего производством, чтобы обсудить с ними объемы про-
изводства продуктов из томатов в предстоящем сезоне. Урожай помидоров, закуплен-
ный у производителей, начнет поступать на консервный завод со следующего поне-
дельника. Red Brand Canners — компания средних размеров; она производит и продает
овощные и фруктовые консервы в западных штатах. Экономист Уильям Купер и заве-
дующий отделом продаж Чарльз Мерс первыми пришли в офис м-ра Гордона Управ-
ляющий производством Дэн Такер пришел несколькими минутами позже и сказал, что
располагает сведениями о последних оценках качества будущего урожая помидоров,
Стоимость отрицательна, поскольку компании ЕЕА платят за утилизацию данного вида топлива
© 1996 by the Board of Trustees of the Leland Stanford Junior University All rights reserved Составитель —

фессор Роберт Уилсон (Robert Wilson)
192	Ч А С Т Ь II. Оптимизационные модели
сделанных отделом контроля производства Согласно его отчету примерно 20% урожая
будет соответствовать сорту А, а оставшаяся часть (3 млн. фунтов) — сорту В.
На вопрос об объемах спроса Мерс ответил, что, судя по всему, компания сможет
продать все произведенные консервированные помидоры, а спрос на томатный сок и
пасту будет ограничен Затем он показал собеседникам последний прогноз спроса,
представленный в приложении 1, и сообщил, что цены установлены в соответствии
с долговременной стратегией компании, и потенциальные объемы продаж оценива-
лись для заданных значений цен.
Приложение 1. Прогноз спроса
Продукт(в 1 упаковке 24 банки по 2'/2 пинты)	Цена за упаковку, S	Прогнозируемый спрос, упаковки
Консервированные помидоры	12,00	800 000
Персики	16,20	10 000
Персиковый нектар	13,80	5 000
Томатный сок	13,50	50 000
Яблочный джем	14,70	15 000
Томатная паста	11,40	80 000
Посмотрев на оценки спроса, Билл Купер сказал, что в этом году компания смо-
жет неплохо заработать на помидорах С помощью новой системы учета ему удалось
вычислить удельную прибыль для каждого продукта, согласно проведенному анализу
удельная прибыль для консервированных помидоров оказалась выше, чем для лю-
бых других томатных продуктов. Купер вычислил значения удельной прибыли в мае,
после того, как компания заключила контракты на покупку будущего урожая поми-
доров по цене 18 центов за фунт (см приложение 2).
Приложение 2. Удельная прибыль для различных продуктов
Продукт (1 упаковка)	Помидоры	Персики	Персиковый Томатный		Яблочный джем	Томатная паста
			нектар	СОК		
Цена, S	12,00	16,20	13,80	13,50	14,70	11,40
Переменные затраты, S Прямые трудозатраты, $	3,54	4,20	3,81	3,96	2,10	1,62
Переменные накладные расходы, $	0,72	0,96	0,69	1,08	0,66	0,78
Переменные торговые затраты, S	1,20	0,90	1,20	2,55	0,84	1,14
Стоимость упаковки, S	2,10	1,68	1,80	1,95	2,10	2,31
Стоимость плодов, $	3,24	5,40	5,10	3,60	2,70	4,50
Суммарные перемен- ные затраты, $	10,80	13,14	12,60	13,14	8,40	10,35
Валовая прибыль, $	1,20	3,06	1,20	0,36	6,30	1,05
Накладные расходы, $	0,84	2,10	1,56	0,63	2,25	0,69
Чистая прибыль, S	0,36	0,96	-0,36	-0,27	4,05	0,36
ГЛАВА 3. Линейная оптимизация
193
Расход плодов при изготовлении продуктов приводится в следующей таблице.
Продукт	Расход плодов, фунты на упаковку
Помидоры Персики Персиковый нектар Томатный сок	18 18 17 20
Яблочный джем	27
Томатная паста	25
Дэн Такер, однако, заметил, что, несмотря на достаточные производственные
мощности, компания не сможет переработать весь урожай в консервированные по-
мидоры, поскольку только небольшую часть этого урожая можно отнести к сорту А
Компания использует числовую шкалу для обозначения качества поступающих пло-
дов и готовых продуктов Согласно данной шкале качество обозначается числом от О
до 10, причем, чем больше число, тем выше качество Так, фунт помидоров сорта А
имеет средний показатель качества 9 единиц, а сорта В — 5 единиц Минимальный
показатель качества плодов, используемых для изготовления консервированных по-
мидоров, составляет 8, а для приготовления томатного сока — 6 Томатную пасту
можно производить полностью из помидоров сорта В Это означает, что объем про-
изводства целых консервированных помидоров не может превысить 800 000 фунтов
Гордон настаивал, что это ограничение не является существенным, поскольку ему
только что предложили купить до 80 000 фунтов помидоров сорта А по цене 25,5 центов
за фунт. Он пока отклонил данное предложение, но еще не поздно его принять
Тем временем Мерс сделал кое-какие вычисления и сказал, что хотя он и согла-
сен с высказыванием, что “в этом году компания сможет неплохо заработать на по-
мидорах”, но это произойдет не за счет консервированных помидоров Мерс считает,
что при определении стоимости плодов нужно учитывать их качество и количество,
а не только количество, как это сделал Купер Исходя из этого, он пересчитал вало-
вую прибыль (приложение 3), получилось, что компании следует использовать
2 000 000 фунтов помидоров сорта В для производства томатной пасты, а оставшиеся
400 000 фунтов помидоров сорта В и все помидоры сорта А — для производства сока
Если ожидания относительно спроса оправдаются, то с урожая помидоров текущего
года компания получит прибыль $ 144 000.
Приложение 3. Анализ прибыли для продуктов из томатов
Z — стоимость фунта помидоров сорта А, выраженная в центах,
Y— стоимость фунта помидоров сорта В, выраженная в центах
600 000 х Z+ 2 400 000 х Y= 3 000 000 (фунты) х 18 (центы).
Z/9 = Y/5.
Z= 27,96 центов за фунт,
Y= 15,54 центов за фунт.
194
ЧАСТЬ II Оптимизационные модели
Продукт	Помидоры	Томатный сок	Томатная паста
Цена, $	12,00	13,50	11,40
Переменные затраты (без стоимости помидоров), $	7,56	9,54	5,85
	4,44	3,96	5,55
Стоимость помидоров, $	4,47	3,72	3,90
Валовая прибыль, $	-0,03	0,24	1,65
Вопросы
1	Почему Такер утверждал, что объем производства томатной продукции ограни-
чен 800 000 фунтами (откуда взялось значение 800 000)9
2	Почему неверно предложение Купера использовать весь урожай помидоров для
производства консервированных помидоров9
3	Каким образом Мерс вычисляет стоимость помидоров в приложении 3? Как он при-
шел к выводу, что компания должна использовать 2 000 000 фунтов помидоров сорта
В для производства пасты и оставшиеся 400 000 фунтов помидоров сорта В и все по-
мидоры сорта А для производства сока? Где ошибка в рассуждениях Мерса9
4	Не принимая во внимание предложенную Гордоном возможность дополнитель-
ной закупки помидоров, сформулируйте данную проблему в виде задачи линей-
ного программирования для определения оптимальной структуры производства.
Переменные решения должны измеряться в фунтах, а коэффициенты целевой
функции — в центах за фунт.
5	Как следует изменить модель, чтобы учесть возможность дополнительной закуп-
ки помидоров, предложенную Гордоном?
Дополнительные вопросы
Предположим, что отдел контроля качества при оценке качества урожая помидо-
ров относит помидоры к одному из трех сортов Фунт помидоров сорта А имеет
средний показатель качества 9 единиц, сорта В — 6 единиц, а сорта С — 3 единицы.
При такой системе оценки прогноз отдела выглядит следующим образом: 600 000
фунтов сорта А, 1 600 000 фунтов сорта В и 800 000 фунтов сорта С Для томатной
пасты не существует ограничений по минимальному показателю качества исполь-
зуемых помидоров
6	Каким будет максимальный объем производства консервированных помидоров?
Можно ли в данном случае реализовать предложение Купера9
Мерс проанализировал ситуацию с тремя сортами помидоров, его вычисления
представлены в приложении 4. На основании этих вычислений он рекомендует пе-
реработать все помидоры сорта С и 1 200 000 фунтов помидоров сорта В на томатную
пасту, а все помидоры сорта А и оставшиеся помидоры сорта В — на томатный сок.
ГЛАВА 3. Линейная оптимизация 195
Приложение 4. Анализ прибыли для продуктов из томатов
Z — стоимость фунта помидоров сорта А, выраженная в центах,
У — стоимость фунта помидоров сорта В, выраженная в центах,
X— стоимость фунта помидоров сорта С, выраженная в центах
800 OOOxZ + 1 600 ОООх Г + 800 000 xZ= 3 000 000 (фунты) х 18(центы).
Z/9 = У/6,
У/6=Л73.
Z = 27,93 центов за фунт,
Y= 18,61 центов за фунт,
X = 9,30 центов за фунт.
Продукт	Помидоры	Томатный сок	Томатная паста
Цена, $	12,00	13,50	11,40
Переменные затраты (без стоимости помидоров), $	7,56	9,54	5,85
	4,44	3,96	5,55
Стоимость помидоров, $	4,47	3,72	2,33	
Валовая прибыль, $	-0,03	0,24	3,22	
1.	Как Мерс вычислял стоимость помидоров в приложении 4? Как он пришел к
решению переработать все помидоры сорта С и 1 200 000 фунтов помидоров сор-
та В на томатную пасту, а все помидоры сорта А и оставшиеся помидоры сорта
В — на томатный сок? В чем его ошибка7
2.	Не принимая во внимание предложенную Гордоном возможность дополнитель-
ной закупки помидоров, сформулируйте данную проблему в виде задачи линей-
ного программирования для определения оптимальной структуры производства
Переменные решения должны измеряться в фунтах, а коэффициенты целевой
функции — в центах за фунт.
3.	Как следует изменить модель, чтобы учесть возможность дополнительной закуп-
ки помидоров, предложенную Гордоном?
Ситуация для анализа | Обмен валют в компании HiTech
Компания HiTech, Inc. осуществляет производственные и торговые операции в пя-
ти странах- США, Великобритании, Франции, Германии и Японии. В разное время в
разных странах возникают различные потребности в свободных средствах, поэтому
часто приходится перемещать имеющиеся средства из одной страны в другую и кон-
вертировать их В целом существует множество способов реорганизации денежных
фондов, позволяющих восполнить нехватку свободных средств в определенной стране.
В частности, в данное конкретное утро подразделения компании во Франции и Япо-
нии испытывают недостаток в средствах (7 млн. франков и 1040 млн. йен соответст-
венно) А подразделения в США, Великобритании и Германии имеют свободные сред-
ства (2 млн долларов, 5 млн. фунтов и 3 млн марок). Поскольку существует множество
196 ЧАСТЬ II Оптимизационные модели
вариантов перераспределения средств, позволяющих покрыть недостачи за счет из-
лишков, вопрос заключается в том, как сравнивать возможные стратегии конвертации.
Из-за высоких краткосрочных процентных ставок в США компания решила оценивать
свои конечные запасы свободных средств в долларовом эквиваленте.
Как и всегда, сегодня в 7 утра казначей корпорации Джек Уолкер и вице-
президент по зарубежным операциям Эзра Брукс встретились в штаб-квартире ком-
пании, чтобы определить, какие средства необходимо перевести сегодня Между ни-
ми состоялся следующий диалог (При чтении диалога полезны рис. 3.31 и 3.32 )
	A L В—1	1		... D | Е <		Г	.. G ’	I- Н ,1'	1 ..
	Медаль обмена валют						
2-		Доллар	Фунт	Фр франк	Нем. марка	Йена	.Сред стоимость, $
3	Доллар	1	0,591.	5,385	1,594	116,3	1,0000
	Фунт	1,665		9,12	2,607;	193,1	1,6785.
	Фр. франк	0,1823	0,1095;		0,2965	21,11	0.1840
$	Нем марка	0,6149	0,3694	3,351	1 .	72,14	0,6211
7	Иена	0,00847	0,005093;	0,0465:	0,01379	1	0,0085
дГ	Продажа/Покупка	Доллар	Фунт	Фр франк	Нем марка	Йена	Всего продано
10	Доллар	0	0	1 3		Q	10,300:
11	Фунт	4 3	о;	Q	0;	0	4,300:
12	Фр. франк	0	0:	0-	0	0	0,000;
13	Нем. марка	2		о;	0	0	2,000
14	Иена	0	0:	0	п	0	о.ооо;
	Всего куплено	8,389 Исходный	0 Куплено	7,001 Продано	Конечный	1047: Требования	Цена Остаток конечного
16		(млн )	(млн )	(млн )	(млн.)	(млн )	(Резерв) запаса,$
17	Доллар	2	В 389	10,300	0,089	>=0	:	0 089;$	0,089
18	Фунт	5		4,300	0.700	>=0	:	0,700 $	1,175
13	Фр франк	0	7,001		7.001	> = 7	о.ооо; $ 1,288
20	Нем марка	3		2,000	1,000	>=о	1,000 $ 0,621
21 22'	иена		1 047		1 047	>=1040	6,700- $	8,933 Totally 12.1061
Рис. 3.31. Модель обмена валют на базе электронных таблиц
ЭЗРА. Доброе утро, Джек Я хочу тебе кое-что показать Я попросила Фрэда построить на базе
электронных таблиц модель обмена валют Думаю, она заметно упростит нам жизнь
ДЖЕК. Идея мне нравится, но тебе придется объяснить мне данную модель
ЭЗРА. Конечно Модель содержит всю стандартную информацию Однако давай рассмотрим
ее шаг за шагом Цифры в ячейках с СЗ по G7 — это коэффициенты обмена Если ко-
эффициент на пересечении строки / и столбца j равен at, это значит, что одна единица
валюты i будет обмениваться на at единиц валюты j Фактически эти данные отражают
цены покупателя и продавца Например, за один фунт мы получаем 51,665 Таким об-
разом, 1,665 — это цена продажи фунта в долларах С другой стороны, за один доллар
мы получим 0,591 фунта Это означает, что мы можем купить фунт по цене 1/0,592 =
$ 1,692 (запрашиваемая цена в долларах за один фунт составляет 1,692) Следовательно,
разница между курсом продавцов и покупателей — 1,665 и 1,692 Если мы возьмем $1 и
купим на него фунты, а потом на полученную сумму вновь купим доллары, у нас ока-
жется 0,591x1,665 - 50,9810,те при обмене мы потеряли часть денег
ДЖЕК. Эго цена операции Очевидно, мы хотим минимизировать подобные издержки, не обмени-
вая денег больше, чем необходимо, чтобы избежать круговых обменов Однако где в модели
содержится информация о наших сегодняшних потребностях в свободных средствах9
ГЛАВА 3. Линейная оптимизация
197
ЭЗРА. Наши текущие запасы свободных средств показаны в столбце С (строки с 17 по 21)
Все Потребности в валюте показаны в тех же строках столбца G Как следует из этих
данных, нам требуется 7 млн французских франков и 1040 млн йен Наша задача —
удовлетворить потребности в валютах таким образом, чтобы максимизировать долла-
ровое значение конечного запаса средств
ДЖЕК. Отлично1 Что нужно делать дальше9
ЭЗРА. Мы помешаем наши выводы в соответствующие ячейки таблицы под названием
“Продажа/Покупка” Я уже ввела данные, которые соответствуют нашим типич-
ным решениям в таких ситуациях В ячейках с СЮ по С14 показано, что я решила
обменять 2 млн марок и 4,3 млн фунтов на доллары (получив 8,389 млн долл )
Затем на 1,3 млн долл покупается 7 млн франков, а на оставшиеся 9 млн долл
покупается 1047 млн йен Все соответствующие покупки содержатся в ячейках
СИ, С13, СЮ и G10 таблицы “Продажа/Покупка” Например, в ячейке СЮ пока-
зано, что мы использовали 1,3 млн долл на покупку франков, а значение в ячейке
С17 показывает, что в результате этой операции мы получили 7 млн франков
Сравнив значения ячеек с С17 по С21 со значениями ячеек с 117 по 121, можно
убедиться, что мы добились нашей цели Значения в ячейках с Н17 по Н21 пока-
зывают, сколько валюты (в долларовом эквиваленте) у нас получилось При вве-
денных мною данных конечные запасы валюты оцениваются в 12,106 млн долл
ДЖЕК. Я вижу, что мы удовлетворили наши потребности в свободных средствах Однако,
чтобы лучше понять происходящее, мне бы хотелось увидеть формулы, в соответст-
вии с которыми выполнены данные вычисления
ЭЗРА. Это несложно Я просто распечатаю формулы таблицы, и ты можешь смотреть на
них сколько угодно1
ДЖЕК. (Спустя какое-то время ) Я все понял, Эзра, но почему мы выбрали такую сложную
стратегию9
ЭЗРА. Как ты знаешь, мы всегда проводим наши обменные операции через Country Bank
в Нью-Йорке, эту стратегию нам рекомендовали они
ДЖЕК. Я считаю, что, представив задачу в виде табличной модели, проще обсуждать стра-
тегию Но мне бы хотелось узнать, действительно ли это хорошее решение
ЭЗРА. Я тоже об этом думаю, но валютный рынок для этих основных валют очень эффек-
тивен, поэтому, вероятно, разница между стратегиями будет не слишком велика
ДЖЕК. Не могу сказать, что банальные разговоры об эффективности меня убедили Я нажил
миллионы на использовании несовершенств рынка В любом случае, у меня сегодня
уже нет времени на поиски более удачного решения Будем работать с тем, что есть
Как нетрудно убедиться, модель обмена валют, представленная на рис 3 31 и 3 32,
является моделью линейного программирования, и оптимальное решение этой задачи
легко можно найти с помощью средства Поиск решения Рабочий лист с оптимальным
решением показан на рис 3 33. Оптимальное значение конечных валютных запасов
(в долларовом эквиваленте) составляет 12,184 млн по сравнению с 12,106 млн в реше-
нии, предложенном Эзрой Заметим, что в некотором смысле Эзра права разница со-
ставляет всего примерно 0,6%- (12,184- 12,106)/12,184 = 0,0064 С другой стороны, при
переводе крупных сумм даже маленький процент —это большие деньги В данном слу-
чае разница составляет $78 000, это та сумма, которую можно сэкономить практически
безо всяких усилий.
198 ЧАСТЬ It Оптимизационные модели
1	0,591	:5,385	1,594	116,3
1,665	1	:9,12	2,607	193,1
0,1823	0,1095	1	0,2965	21,11
0,6149	0,3694	3,351	1	72,14
0 00847 0,00509:0,0465	0,01379 1
Сред, стоимость/
=(СЗ+1/СЗ)/2
=(C4+1/D3)/2
=(С5+1/ЕЗ)/2
=(C6+1/F3)/2
=(C7+1/G3)/2
Всего продано ;
=СУММ(С10 G10);
=СУММ(С11:G11)
=СУММ(С12:С12);
=СУММ(С13:С13)
=СУММ(С14:С14):
Ж шено =СУММПРОИЗВ(СЗ:С7;С10:С14) =СУММГ=СУММ=СУММПРОИЗЕ=СУММГ
Исходный запас (млн )
Требов
Конечный ания	Щена конечного
: запас (млн.) (млн) Остаток (Резерв): запаса.$
-C17-E17+D17 0	i=F17-G17	;=H3*F17
:=C18-E18+D18 0	=F18-G16	t=H4’F18
=C19-E19+D19 7	=F19«G19	;=H5*F19
=C20-E20+D20 0	=F20-G20	=H6’F20
=C21-E21+D21 1040	=F21-G21	=H7*F21___________
Total|«C¥MM(tT7;l2l) I
Puc. 3.32. Формулы модели обмена валют
X	Доллар
Я.	фУнт
Фр франк
6_ Нем марка
1~	йена
ЭД
3 Продажа/Покупка
10	.	Доллар
11	Фунт
12	Фр франк
13:	Нем марка
14	Йена
Доллар
Йена
2 000
11,192
Всего продано
15 Всего куплено
45,600	11,445	1040-
5,000
38,600
11,192
0,000
;	ИСХОДНЫЙ
16 i	(млн)
17'	Доллар	2
18 .	Фунт	5
:19s	: Фр франк: 0
20 j Нем марка 3
21	Йена 0
22
2L___________________________
Конечный
Куплено	Продано	запас
(млн.) (млн.)	(млн.)
2 000
5,000
45,600	38 600	7,000
11,445	11,192	3,253
1 040	-	1 040
Требования	Остаток	конечного
(млн.)	(Резерв)	запаса. $
>=0	0,000	$	0,000
>=0	0,000	$
>=7	0,000	$	1,288
>=0	3,253	$ 2,020
>=1040	-0.009	$	8,876
Total|'$ :'Т2Л'Йл
0
Рис. 3.33. Оптимизированная модель обмена валют
Вопросы
1. Создайте собственную модель Л П для задачи обмена валют.
2. В диалоге Джек сказал: “Мы хотим минимизировать издержки операции, не об-
менивая денег больше, чем необходимо, чтобы избежать круговых обменов”.
Пусть И, — максимальная “средняя долларовая стоимость”, которую можно по-
лучить из начальной суммы
ГЛАВА 3. Линейная оптимизация	199
Заметим, что для нахождения значения И, мало просто выразить каждое началь-
ное значение в средней долларовой стоимости Например, средняя долларовая
стоимость 1 фунта равна $1,665, а если конвертировать 1 фунт в 9,12 франков
и оценить их среднюю долларовую стоимость, получится 9,12x0,180 = $1,67808.
Таким образом, предпочтительней конвертировать исходные средства в фунтах
во франки, а не оставлять их в неприкосновенности. Фактически для того, чтобы
найти значение необходимо решить задачу линейного программирования
Это решение показано на рис. 3 34. Здесь сначала требования к наличию валют
всех видов были установлены равными 0, после чего оптимизировалось значение
конечного суммарного запаса Получилось И, = 12,261. Пусть К,— максимальная
средняя долларовая стоимость конечного валютного запаса при соблюдении ог-
раничений для некоторых видов валюты, т.е. И, — оптимальное целевое значение
(И2= 12,184 на рис. 3.33).
LJ-A [ В ] стп o’
; 1	Модель обмена валют
Доллар
Фр. франк
Нем. марка
Продажа/Покупка
Доллар
Фр. франк
Нем. марка
15
чкЖем марка Йена
1	0.591	5,385.	1,594	1163
1,665	1	9,12-	2,607	193 1
0,1823	0,1095	1	0,2965	21,11
0,6149	0,3694	3,351	1	72,14
0.00847	0,005093;	0,0465.	0,01379	
Доллар	Фунт	Фр франк	Нем. марка	йена
Всего куплено
45,600
Продано
(млн.)
Куплено
(млн.)
Исходный
(млн.)
13,520	0
Конечный
запас Требования
(млн.) : (млн)
1,0000
1,6735
0,1840
0,6211
0,0085
Всего продано
0 000
5 000
45 600
0 000
0 000
J6

1S
го
Доллар
Фр франк
Нем марка
Остаток
(Резерв)
конечного
45 600
5,000
45,600
16,520
Total) $ 12,1
Рис. 3.34. Оптимизированная модель обмена валют, где конечные требования к наличию
валют равны нулю
В подобных случаях задача ЛП с более строгими ограничениями не может дать луч-
шее решение, чем модель с менее строгими ограничениями, поэтому всегда справед-
ливо неравенство V2 < И, Определим издержки операции как разность - И2
Если исходить из данного определения, верно ли утверждение Джека (т.е действи-
тельно ли оптимальное решение на рис. 3 33 минимизирует издержки операции)В 9
3 Используя таблицу, показанную на рис 3 31, ответьте на следующие вопросы.
а. Предположим, что коэффициенты обмена для двух валют (скажем, франка
и марки) таковы, что если взять 1 франк и выполнить следующие обмены
1 франк^марки^франки, то в результате получится более 1 франка Каким
будет оптимальное значение целевой функции при этих условиях9 Какой эко-
номический термин используется для обозначения такой ситуации9
200 ЧАСТЬ II Оптимизационные модели
b Прокомментируйте следующее утверждение Если у компании HiTech нет
требований к наличию определенных средств, оптимальным решением будет
отсутствие обменов (т.е. для оптимизации средней долларовой стоимости ко-
нечного запаса средств не следует выполнять обменные операции).
с Прокомментируйте следующее утверждение Поскольку валютный рынок ра-
ционален, наилучшее решение не намного лучше (в процентном отношении),
чем решение, предложенное Эзрой, по той же причине наихудшее решение
будет не намного хуже его (в процентном отношении). Совет Найдите реше-
ние, которое минимизирует среднюю долларовую стоимость конечного запаса
средств
d Прокомментируйте следующее утверждение Есть общая модель обмена ва-
лют, похожая на модель HiTech, которая может включать в себя сотни валют
Валюты, начальные запасы и конечная потребность в которых равны 0, мож-
но исключить из модели — это никак не отразится на оптимальном значении
целевой функции
Литература
1 Radhka Subramanian, Richard Scheff, John Quillman, Steve Wiper, and Roy Marsten Coldstart Fleet
Assignment at Delta Air Lines, Interfaces 24, no 1 (1994) 104-120
Линейная оптимизация. Анализ
чувствительности
В этой главе...
4.1.	Введение
4.2.	Графический метод решения задачи Oak Products
4.3.	Крайние точки и оптимальные решения
4.4.	Графическое решение задачи минимизации
4.5.	Неограниченные и недопустимые модели
4.6.	Анализ чувствительности модели ЛП
4.7.	Изменения коэффициентов целевой функции
4.8.	Изменение правых частей ограничений
4.9.	Анализ чувствительности с помощью надстройки SolverTable
4.10.	Анализ чувствительности в действии
4.11.	Характеристика отчета по устойчивости
4.12.	Использование отчета по устойчивости
4	13. Вырождение моделей ЛП
4.14.	Заключение
Основные термины
Контрольные вопросы
Задачи
Ситуация 1 Симплекс-метод
Ситуация 2 Ebel Mining (часть 2)
Ситуация 3 Red Brand Canners, продолжение
Ситуация 4 Компания Saw Mill
Ситуация 5 Kiwi Computer
Ситуация 6 Компания Valley Chassis
Ситуация 7 Ферма Ельцина
Литература
202	Ч А С Т Ь II Оптимизационные модели
Больше выстрелов за меньшую цену: ЛП помогает
армии США обновить свой арсенал
Военно-воздушные силы США выиграли много важных сражений. Американцы
с гордостью вспоминают успехи своих пилотов в небе Германии во время Второй
мировой войны и недавние победы в Персидском заливе. Успехи военных в немалой
степени являются результатом разработки новой тактики и техники. Неудивительно,
что в последние годы ВВС стали применять подход с использованием линейного
программирования при оценке и закупке новых систем вооружения, а также в своих
ежегодных баталиях за выделение средств
Ежегодно ВВС представляют Конгрессу план развития вооружений. Чтобы со-
ставить данный план, необходимо решить, какие новые проекты начать, какие те-
кущие проекты продолжить и какие проекты закрыть. Окончательные рекомендации
в значительной мере зависят от возможного уровня финансирования.
Основным принимаемым во внимание фактором является эффективность каж-
дой системы вооружений и ее возможный вклад (в составе других видов оружия)
в увеличение общей разрушительной способности Эффективность должна оцени-
ваться для всевозможных комбинаций самолетов-носителей, боеприпасов и мише-
ней (танки, командные пункты, коммуникации, мосты и т д ). Эти факторы взаимо-
действуют сложным образом Высота и время полета самолета, а также его способ-
ность противостоять средствам ПВО противника будут зависеть от того, какой тип
боеприпасов используется Даже небольшое изменение коэффициента потерь само-
летов может оказать заметное влияние на эффективность системы, не говоря уже
о потерях человеческих жизней
ВВС ежегодно приходится также учитывать последствия возможного увеличения
или уменьшения бюджета Изменения бюджета могут оказать заметное влияние на
ассортимент закупаемых систем вооружений, равно как и на количество каждого
приобретаемого вида оружия Количество закупаемого вооружения, в свою очередь,
может заметно отразиться на цене единицы оружия
Для анализа ситуаций подобного рода в ВВС применяется модель линейного
программирования, которая дает возможность оценить различные варианты выбора
как типов самолетов, так и типов вооружений. Она не только показывает оптималь-
ное сочетание вооружений, необходимое для уничтожения конкретного набора це-
лей, но и позволяет графически отобразить следующие параметры.
•	Отношение стоимости самолета к стоимости вооружения.
•	Суммарная разрушительная способность как функция расходов на вооружение.
•	Отношение суммарной разрушительной способности к расходам как функция
длительности конфликта
Эта информация отображается в виде надлежащим образом откалиброванных
двухмерных графиков, что позволяет руководству и аналитикам изучать возможные
варианты и выполнять анализ “Что-если”. [3]
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 203
4.1. Введение
В реальной жизни менеджеру ежедневно приходится сталкиваться с проблемой, как
применить на практике результаты табличной модели. В главе 3 мы оптимизировали мо-
дель линейного программирования (ЛП) компании Oak Products с помощью средства
Поиск решения. Однако не следует думать, что теперь у нас есть хорошее решение задачи
планирования компании Oak Products, и можно заняться другими проблемами Зачастую
такое суждение ошибочно. Как правило, решение является только отправной точкой
анализа ситуации. Необходимо помнить, что модель — это абстракция реальной ситуа-
ции. Например, Тому Барру, ответственному администратору компании Oak Products,
придется поставить множество дополнительных вопросов к модели, предложенной Джи-
мом Уайтом, прежде чем он будет настолько уверен в предложенных результатах, чтобы
реализовать рекомендуемые решения на практике. Например, могут существовать до-
вольно веские соображения, которые из-за их сложности не были включены в модель
Поскольку модель — упрощение действительности, всегда найдутся факторы (например,
политической или этической природы), которые в ней учесть не удалось Кроме того, не-
которые данные, вошедшие в модель в качестве параметров, могут содержать неточности
или неопределенности. Это достаточно сложно выразить количественно, но принять во
внимание необходимо. Таким образом, после оптимизации модели следует выяснить, на-
сколько оптимальное решение согласуется с другими соображениями, которые в модель
не вошли В реальных ситуациях это норма, а не исключение
Как уже отмечалось в главах 1 и 2, анализ чувствительности — вычисление результата воз-
действия (небольшого) изменения внешней переменной на переменные решения — дает важ-
ную информацию, которую можно использовать при принятии решения в реальной ситуации
Применительно к оптимизационным моделям анализом чувствительности называется про-
цесс анализа модели после нахождения оптимального решения В данной главе мы подробно
рассмотрим, как на практике воспользоваться той обширной информацией, которую предос-
тавляет средство Поиск решения при анализе чувствительности моделей Л П
Мы покажем, как модели ЛП оптимизируются с помощью средства Поиск решения
и как следует интерпретировать результаты анализа чувствительности На примере двух-
мерных графиков мы поясним общие понятия анализа чувствительности В частности, на
основе таких графиков можно предложить простой графический способ нахождения ре-
шения задачи ЛП, содержащей две переменные решения Большинство реальных задач
содержит гораздо больше переменных решения, и, следовательно, такой графический
метод решения не имеет широкого применения, однако он создаст основу для понима-
ния большей части того, что будет излагаться в дальнейшем Иными словами, в данной
главе мы хотим представить графические аспекты моделей ЛП в качестве средства, кото-
рое поможет понять, что нам дает анализ чувствительности моделей ЛП Мы рассмотрим
два средства, используемых для проведения анализа чувствительности моделей Л П отчет
по устойчивости, создаваемый средством Поиск решения, и надстройку SolverTable. Они
помогут интерпретировать результаты моделей ЛП во многих реальных приложениях
Наконец, в разделе 4 12 предлагается поучительная история о ловушках, которые могут
подстерегать менеджера при проведении анализа чувствительности
204
ЧАСТЬ II Оптимизационные модели
4.2. Графический метод решения задачи Oak Products
Графический метод — простой способ решения задач ЛП с двумя переменными. По-
скольку упрощенная модель Oak Products (см. главу 3) содержит только две переменные
решения, на ее примере можно проиллюстрировать применение графического метода
решения Напомним, как выглядела упрощенная линейная модель Oak Products.
С — количество произведенных и проданных стульев Captain,
М — количество произведенных и проданных стульев Mate
Максимизировать 56С +40Л/ (целевая функция)	(4.1)
при ограничениях
8С+4Л/< 1280 (ограничение для длинных штифтов),	(4.2)
4С + 12Л/< 1600 (ограничение для коротких штифтов),	(4.3)
С + М> 100 (минимальный объем производства),	(4.4)
4С + 4Л/< 760 (ограничение для ножек),	(4.5)
С< 140 (ограничение для прочных сидений),	(4 6)
М< 120 (ограничение для облегченных сидений),	(4 7)
С> 0 и М> 0 (условия неотрицательности)	(4.8)
Для построения графика и анализа модели ЛП мы будем использовать пакет Graphic
LP Optimizer GLP ехе, разработанный в Стэнфордском университете. Пакет GLP явля-
ется отдельной программой Windows1, не зависящей от Excel Чтобы понять, как произ-
водится графическая линейная оптимизация, лучше всего выполнять последующие дей-
ствия, запустив GLP на своем компьютере
Графическое представление модели Oak Products
Ha рис 4 1 показана верхняя часть окна программы GLP, в нижней части содержится
графическая панель, на которой будет показано графическое представление модели В
поля диалогового окна GLP можно вводить обозначения для осей X и Y, до 6 ограниче-
ний (предполагается, что всегда присутствуют условия неотрицательности, поэтому GLP
строит графики только в неотрицательном квадранте), а также целевую функцию
(помеченную как PAYOFF) После ввода ограничений и целевой функции GLP отобра-
жает их на графической панели окна
Рис. 4.1. Окно программы GLP
GLP будет работать лучше, если установить разрешение дисплея 800x600 (SuperVGA) или выше Поскольку
GLP — программа, работающая в среде Windows, она не будет выполняться на компьютерах Macintosh
Пользователи Macintosh могут запустить GLP с помощью такого эмулятора Windows, как Virtual PC ком-
пании Connectix
ГЛАВА 4. Линейная оптимизация Анализ чувствительности 205
Построение графического изображения множества ограничений является первым
шагом процедуры графического решения задачи ЛП. На рис. 4 2 показана линия ограни-
чения для длинных штифтов (не имеет значения, откладывать значения М по вертикали,
а значения Спо горизонтали или наоборот). Область, закрашенная серым цветом, пред-
ставляет множество всех неотрицательных точек плоскости, удовлетворяющих ограниче-
нию для длинных штифтов, заданному неравенством (4 2). Если перетащить с помощью
мыши линию ограничения, область допустимых значений можно изменить, но наклон
линии ограничения не изменяется, меняется только его правая часть — имеющийся за-
пас длинных штифтов Это происходит потому, что наклон линии ограничения опреде-
ляется отношением двух коэффициентов при переменных решения в формуле (4 2) Что-
бы убедиться в этом, решим уравнение линии ограничения 2С + 4Л/= 1280 относительно
М: М= 320 - 0,5С Таким образом, угол наклона для данного ограничения имеет фикси-
рованное значение -0,5, а изменение запаса имеющихся в наличии длинных штифтов
влияет только на положение точки пересечения линии ограничения с осью Y.
Замечание. При перетаскивании линии ограничения программа GLP пересчитывает значение
правой части ограничения
Рис. 4.2. Ограничение для длинных штифтов
Далее следует ввести остальные ограничения (4.3)—(4.7), программа GLP нанесет их
на график. Чтобы сэкономить время, рекомендуем открыть файл OakProd.glp, содержа-
щийся на компакт-диске книги, в котором представлено полное графическое изображе-
ние упрощенной модели ЛП компании Oak Products из главы 3 (рис. 4.3) Область, за-
крашенная серым цветом, представляет собой допустимое множество ограничений, или
допустимую область, т.е. множество всех возможных комбинаций переменных С и М,
удовлетворяющих всем ограничениям.
206
ЧАСТЬ II. Оптимизационные модели
: Множество всех значений переменных решения, удовлетворяющих одновременно всем ог-
раничениям, называется допустимым множеством ограничений или допустимой областью.
Можно поэкспериментировать, перетаскивая любую линию ограничения, чтобы уви-
деть, как изменения правой части данного ограничения отразятся на допустимой облас-
ти Если сравнить визуально рис 4 2 и рис. 4.3, становится очевидным следующий об-
щий принцип моделей оптимизации
; Добавление дополнительных ограничений никоим образом не может привести к увели- ;
чению допустимой области, а может лишь уменьшить ее или оставить неизменной.
i Удаление ограничений оставляет допустимую область неизменной или приводит к ее ;
расширению.
Теперь воспользуемся графиком, чтобы найти оптимальное решение упрощенной модели
Oak Products Поскольку данная задача линейного программирования является задачей мак-
симизации прибыли, необходимо найти такой допустимый план производства, который обес-
печивает наибольшее возможное значение целевой функции, заданной выражением (4.1).
Согласно определению допустимой области любой производственный план (пара
значений Си М), удовлетворяющий всем ограничениям, называется допустимым решени-
ем Эти допустимые решения и являются возможными производственными альтернати-
вами нашей модели Заметим, что некорректно говорить о допустимых значениях пере-
менной С или переменной М в отдельности — в данном двухмерном случае понятие до-
пустимости всегда применяется к паре значений, а не к отдельному значению.
На рис. 4.3 пунктирной линией в левом нижнем углу над стрелкой курсора показана
прямая, соответствующая целевой функции (4.1) (на графике она обозначена как Payoff,
т.е. выигрыш). Эта пунктирная линия соответствует множеству всех пар значений произ-
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 207
водственных решений С и М, которые дают прибыль, в точности равную $2000 Поэтому
данная линия называется изолинией прибыли $2000. Угол наклона этой прямой определя-
ется отношением коэффициентов при переменных в выражении (4 1), в чем можно убе-
диться, решив уравнение 56С + 40 Л/ = 2000 для М: М = 50 - 1,4С
Таким образом, наклон линии выигрыша фиксирован и равен -1,4, а изменения зна-
чения прибыли влияют только на координаты точки пересечения этой линии с осью Y.
Поскольку компания Oak Products хочет получить максимальную прибыль, это можно
сделать, перетаскивая с помощью мыши линию выигрыша После нескольких секунд
экспериментов легко убедиться, что оптимизирующим направлением является северо-
восток, поскольку в этом случае увеличивается прибыль, однако необходимо ограничить
свои аппетиты допустимыми значениями С и М, т.е. точками, находящимися внутри се-
рой области Поскольку угол наклона линии выигрыша фиксирован, множество допус-
тимых точек, максимизирующих прибыль, будет состоять из единственной точки, лежа-
щей в направлении увеличения значений целевой функции, определяемой в данном случае
пересечением ограничений для длинных штифтов и ножек (рис. 4.4)
Совет. При перемещении линии выигрыша программа GPL постоянно пересчитывает значе-
ния прибыли. Чтобы быстро найти максимальное значение, достаточно просто щелкнуть на
кнопке Auto Max (Автомаксимум) панели инструментов диалогового окна GLP (это кнопка,
на которой изображена стрелка, направленная вверх). Затем можно, как показано на
рис. 4 4, подвинуть само уравнение выигрыша поближе к окончательному положению пунк-
тирной линии и щелкнуть на кнопке Scissors (Ножницы) диалогового окна GLP, чтобы уб-
рать лишние отрезки линий ограничений.
208 ЧАСТЬ II Оптимизационные модели
В данной модели ЛП только одна точка допустимой области лежит на изолинии мак-
симальной прибыли, поэтому она называется единственным оптимальным решением зада-
чи. На рис 4 4 видно, что значение, соответствующее изолинии максимальной прибыли
(максимально возможная прибыль), равно $9680, что совпадает со значением, получен-
ным средством Поиск решения при оптимизации этой модели в главе 3.
С помощью нехитрых алгебраических приемов легко понять, откуда взялось это зна-
чение Сообщение в правом нижнем углу на рис. 4 4 свидетельствует, что оптимальное
значение С равно 130, а оптимальное значение М — 60. На рисунке также показано, что
оптимальное решение находится на пересечении двух линий ограничений, каждое из ко-
торых является в данном случае лимитирующим.
8С+4А/ = 1280 (ограничение для длинных штифтов),	(4.9)
4С+ 4М = 760 (ограничение для ножек).	(4 10)
Таким образом, имеется система двух линейных уравнений, которую можно решить
алгебраически (например, методом подстановки) и найти значения неизвестных С и М.
Выразим М из уравнения (4 10)- М = 190 - С. Подставим данное выражение в (4.9) и по-
сле преобразований получим С= 130. Теперь можно подставить это значение С в любое
из исходных уравнений и определить, что Л/=60. Это и есть решение уравнений (4 9)
и (4.10) относительно неизвестных С и М; именно так поступает программа GLP (и сред-
ство Поиск решения) для нахождения оптимальных значений переменных решения.
Обозначим оптимальные значения переменных решения как С' и Л/. Мы нашли опти-
мальный производственный план С = 130 и Ivf = 60. Это оптимальное решение, или просто
решение задачи Oak Products Используя оптимальные значения, легко вычислить макси-
мальное значение прибыли (также, как это делают программы GLPn Поиск решения):
56С + 40 Л/ = 56x130 + 40x60 = 7280 + 2400 = 9680.
Это значение называется оптимальным значением целевой функции, или просто опти-
мальным значением. Термин решение (оптимальное решение) всегда относится к оптималь-
ным значениям переменных решения. Термином оптимальное значение (в единственном
числе) обозначается значение целевой функции, вычисленное в точке решения. В модели
Oak Products решением является оптимальный производственный план (С'=130,
А/ = 60), а оптимальная прибыль $9680 является оптимальным значением. Теперь дадим
более четкие определения этих важнейших терминов и сделаем несколько заключений
о решениях моделей линейного программирования общего вида.
. Оптимальное решение любой модели ЛП не может находиться во внутренней точке до- >
' пустимой области.	!
• Геометрически лимитирующее ограничение — это ограничение, на линии которого рас- j
: положено оптимальное решение.
f Геометрически нелимитирующее ограничение — это ограничение, на линии которого нет i
оптимального решения.	I
i Добавление ограничений приведет к ухудшению оптимального значения или оставит
; его неизменным.
 Удаление ограничений приведет к улучшению оптимального значения или оставит его i
। неизменным.	i
: Введение дополнительных переменных решения улучшит оптимальное значение или
' оставит его неизменным.	;
Исключение переменных решения ухудшит оптимальное значение или оставит его не-,
. изменным.	
ГЛАВА 4 Линейная оптимизация. Анализ чувствительности 209
4.3.	Крайние точки и оптимальные решения
Таким образом, решение задачи ЛП Oak Products находится в угловой точке допусти-
мой области, а именно — в вершине угла, образованного при пересечении линий ограни-
чений для длинных штифтов и ножек. В линейном программировании углы допустимой
области называются крайними точками. В дальнейшем мы будем использовать оба тер-
мина, угловые точки и крайние точки, вкладывая в них один и тот же смысл
Чтобы понять, насколько важны крайние точки, рассмотрим различные линейные
целевые функции на одном и том же множестве ограничений и решим полученные зада-
чи ЛП. Предположим, что компания Oak Products изменит цену на стулья типа Mate,
и удельный доход в расчете на один стул будет составлять не $40, а $80 Посмотрим с по-
мощью программы GLP, как это изменение целевой функции повлияет на решение зада-
чи ЛП. Во-первых, поскольку изменению подверглась только целевая функция, допус-
тимая область останется неизменной. Изменится только целевая функция, т е линия,
соответствующая целевой функции, на графике будет иметь другой наклон В окне GLP
в поле ввода Payoff введем коэффициент 80 для переменной М и щелкнем на кнопке
Auto Мах, чтобы повторно оптимизировать модель. В результате получим оптимальное
решение, представленное на рис. 4.5.
Рис. 4.5. Решение задачи Oak Products для новой целевой функции
Как показано на рисунке, новую оптимальную точку определяют другие лимитирую-
щие ограничения. Теперь лимитирующими являются ограничения для коротких штиф-
тов и для ножек, в то время как в предыдущем случае лимитирующими были ограниче-
ния для длинных штифтов и ножек. Таким образом, изменение угла наклона целевой
210
Ч А С Т Ь II. Оптимизационные модели
функции привело к тому, что оптимальное решение сместилось из предыдущей угловой
точки в новую угловую точку Как можно было предвидеть, новая структура цен, в кото-
рой возросла относительная прибыльность стульев Mate, привела к новому оптимально-
му производственному плану, в котором количество стульев Captain сократилось со 130
до 85, а количество стульев Mate возросло с 60 до 105.
Можете самостоятельно провести эксперименты с программой GLP, чтобы убедить-
ся независимо от того, как будет изменяться целевая функция (оставаясь линейной), оп-
тимальным решением будет угловая точка. Можно изменить и множество ограничений,
оптимальное решение все равно будет угловым, пока уравнения модели остаются линей-
ными Это очень важное наблюдение, дополнительные подтверждения которого рас-
сматриваются ниже.
На рис 4 6 изображено произвольное шестистороннее множество ограничений
и прямые трех различных целевых функций, обозначенных f,gwh. Для каждой целевой
функции стрелка указывает направление, в котором оптимизируется соответствующая
целевая функция В каждом случае оптимальное решение окажется в некой в угловой
точке Целевая функция g на рис 4 6 иллюстрирует интересный случай, когда оптималь-
ная прямая целевой функции совпадает с одной из линий ограничений, составляющих границу
допустимой области Это может получиться только тогда, когда прямая целевой функции
имеет тот же угол наклона, что и линия ограничения. В таком случае будет бесконечно
много оптимальных решений, а именно — угловые точки В, С и все заключенные между ними
точки границы допустимой области Такие решения называются множественными опти-
мумами Однако даже в том случае, когда единственного оптимального значения нет, по-
прежнему верно утверждение, что существует оптимальное угловое решение (фактически
их два) Данная геометрическая иллюстрация подтверждает важный факт, справедливый
для моделей Л П с произвольным числом переменных решения.
Если модель ЛП имеет оптимальное решение, всегда существует по крайней мере одно I
угловое решение.
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 211
4.4.	Графическое решение задачи минимизации
Мы рассмотрели графическое представление модели максимизации Однако, как уже
отмечалось в главе 3, многие реальные модели призваны решать задачи минимизации
Примером такой модели может служить модель компании Eastern Steel, рассмотренная
в главе 3. Применение графического метода к моделям минимизации во многом анало-
гично поиску максимума; единственное отличие заключается в том, что оптимизирующим
направлением для прямой целевой функции является “спуск”, а не “подъем”. В модели мак-
симизации прямые целевой функции зачастую представляют собой изолинии прибыли
В моделях минимизации прямые целевой функции обычно являются изолиниями затрат
В модели минимизации необходимо найти угловую точку допустимой области, лежащую
на самой нижней прямой целевой функции, пересекающей допустимую область В каче-
стве примера используем программу GLP для поиска решения следующей простой зада-
чи минимизации с двумя переменными решения х, и х2.
Минимизироватьх, + 2х2
при ограничениях
—Зх, + 2х2 < 6,
—х, + Зх2 > 6,
х„х2>0.
На рис. 4 7 представлена GLP-версия данного примера Эту модель можно оптимизи-
ровать, сдвинув прямую целевой функции на юго-запад (или щелкнув на кнопке Auto
Min (Автоминимум), на которой изображена стрелка, направленная вниз)
212 ЧАСТЬ II Оптимизационные модели
Заметим, что оптимальное решение лежит на оси х2, на пересечении прямой третьего ог-
раничения и прямой ограничения неотрицательности. Ось х2 задается уравнением х1 = О
Таким образом, оптимальное решение определяется системой двух уравнений х*=0
и -х' + Зх,' = 6 , откуда следует х* = 0 и х2 = 2, как показано на рис 4 7. Этот пример демон-
стрирует, что если двигать прямую целевой функции в оптимизирующем направлении, гра-
фический анализ модели минимизации идентичен анализу модели максимизации.
Следует сделать одно предостережение. Студенты зачастую попадают в ловушку, счи-
тая, что решение задачи максимизации всегда находится в наиболее удаленном от начала
координат углу, а оптимальное решение задачи минимизации — в начале координат, ес-
ли данная точка входит в допустимую область, в противном случае (когда начало коорди-
нат не является допустимым решением) — в углу, ближайшем к началу координат. Такие
суждения могут оказаться неверными Они основаны на впечатлении, что подъем целевой
функции всегда направлен строго на северо-восток от начала координат, а спуска —
строго "на юго-запад к началу координат На самом деле не существует всеобщей связи
между подъемом или спуском целевой функции и началом координат.
4.5.	Неограниченные и недопустимые модели
Итак, мы рассмотрели геометрическое представление оптимизационных моделей ЛП
с двумя переменными решения Приведенные геометрические примеры позволили сде-
лать важное заключение если задача имеет оптимальное решение, всегда хотя бы одно
решение будет находиться в угловой точке области допустимых решений. Теперь рас-
смотрим, в каких случаях задача ЛП не имеет оптимального решения. Вновь воспользу-
емся геометрическим представлением.
Неограниченные модели
Вернемся к графическому изображению модели Oak Products на рис. 4.3, однако те-
перь изменим ее, предположив, что все ограничения, кроме (4 4) и (4.7), по невнима-
тельности были пропущены Графическое представление новой модели в программе GLP
показано на рис 4 8. Как видим, теперь допустимая область неограниченно простирается
в восточном направлении, поэтому можно сколь угодно далеко двигать линию целевой
функции в этом направлении Щелчок на кнопке Auto Мах приведет к появлению сооб-
щения о неограниченности допустимой области, показанного на рис 4.8.
Поскольку для данной конкретной модели оптимизирующим направлением является
восточное, можно найти допустимое решение со сколь угодно большими значениями целе-
вой функции. Иными словами, можно получить прибыль, стремящуюся к бесконечности.
У такой модели нет решения, поскольку целевая функция неограничена. Таким образом, для
любого набора допустимых значений переменных решения можно найти другие допусти-
мые значения, которые улучшат значение целевой функции. Модели такого типа называ-
ются неограниченными моделями Неограниченная модель — это аномалия. Такая модель
может получиться, если, как в представленном на рис. 4.8 случае, одно или несколько огра-
ничений были пропущены или были допущены ошибки при вводе неравенств, задающих
ограничения. В реальной жизни никому еще не удалось найти способ получения бесконеч-
ной прибыли, поэтому можно не сомневаться, что корректно сформулированная и пра-
вильно введенная модель не будет неограниченной. Заметим, что модель с неограниченной
допустимой областью не обязательно является неограниченной моделью. Например, если
на рис. 4.8 для другой целевой функции увеличение ее значений происходит при движении
в северо-западном направлении, такая задача будет иметь решение.
ГЛАВА 4. Линейная оптимизация Анализ чувствительности 213
Недопустимые модели
Как уже отмечалось в главе 3, существует другой тип аномалии, которой необходимо
избегать в линейном программировании. Это недопустимость (несогласованность) огра-
ничений Этим термином обозначаются модели, множество допустимых значений кото-
рых пусто, т е. ни одна комбинация значений переменных решения не удовлетворяет
всем ограничениям одновременно Приведем пример недопустимой модели линейного
программирования.
Максимизировать 50Е + 40Е
при ограничениях
Е+Е<5,	Ф
Е-ЗЕ<0,	®
10Е+ 15Е< 150, ®
20Е+ 10Е< 160, ®
30Е+ 10Е> 135, Ф
Е, Е> 0.
Графическое представление области решений для данной модели ЯП показано на
рис. 4.9. Нетрудно убедиться, что не существует пары значений EnF, соответствующей
всем ограничениям
214
ЧАСТЬ II Оптимизационные модели
Рис. 4.9. Недопустимая модель ЛП
Как следует из рис 4.9, отсутствие допустимых решений зависит только от ограничений
и не зависит от целевой функции Очевидно, что недопустимая задача Л П не имеет решений,
но аномалии такого рода не возникают в корректно разработанных моделях. Иными слова-
ми, недопустимость в правильно поставленной задаче всегда означает, что модель непра-
вильно описана возможно, ошибки могут заключаться в том, что ограничений слишком
много или неправильны некоторые неравенства ограничений Подведем итог.
Каждая задача линейного программирования относится к одной из трех взаимоисклю- ;
чающих категорий.
1.	Задача имеет оптимальное решение.
2.	Оптимального решения нет, поскольку модель является неограниченной.
3.	Оптимального решения нет, поскольку модель не имеет допустимых решений.
На практике корректно сформулированная задача ЛП всегда имеет решение Неогра-
ниченные и недопустимые модели являются результатом ошибок при формировании мо-
дели или вводе ограничений в Excel либо GLP
Модель рациона питания
Приготовить наилучшую возможную пищу с наименьшими затратами — цель ру-
ководителей большинства организаций общественного питания в больницах, шко-
лах, домах престарелых, тюрьмах и т д. Составление меню является ключевым ком-
понентом, так как именно меню определяет требования к продуктам, оборудованию
и персоналу Многие ошибочно склонны считать составление меню простой проце-
дурой На самом деле в модели рациона питания необходимо учитывать множество
ограничений Например, Комиссия по продуктам питания установила минимальные
уровни содержания для 29 питательных веществ Другие организации здравоохране-
ния ввели верхние пределы для уровней содержания жиров, холестерина и натрия.
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 215
Поэтому достаточно сложно составить меню, удовлетворяющее всем требованиям по
содержанию питательных веществ.
Однако обеспечить необходимое содержание питательных веществ — не единст-
венная цель модели рациона питания. Можно разработать простые модели на базе
электронных таблиц, позволяющие составить меню с необходимым содержанием
питательных веществ и минимальными затратами, но ни один нормальный человек
не сможет есть такую рекомендованную пищу. Подобная диета является эквивален-
том собачьих галет. Одну смешную историю поведал основатель теории линейного
программирования Георг Данциг (George Dantzig). Когда Данциг в начале 1950-х
впервые создал модель индивидуальной диеты, которая должна была помочь ему
сбросить лишний вес, модель рекомендовала ему кучу странных продуктов и 500 гал-
лонов уксуса После того как он исключил уксус в качестве возможной альтернати-
вы, новая оптимальная диета состояла из 200 бульонных кубиков в день На следую-
щий день Данциг попробовал выпить на завтрак горячую воду с растворенными
в ней 4 кубиками, но ему пришлось выплюнуть эту гадость После еще нескольких
нелепых попыток реализовать предложенные моделью пищевые наборы его жена,
наконец, сама занялась составлением диеты
Хотя данный случай и произошел на самом деле, в нем несколько преувеличена
неудовлетворительность рекомендуемой моделью диеты, основанной исключитель-
но на содержании питательных веществ Тем не менее учитывать предпочтения по-
требителя необходимо Хорошие модели должны содержать эти дополнительные ог-
раничения. Как правило, они включаются одним из двух способов путем задания
интервала времени между приемами отдельных видов продуктов или введения огра- ।
ничения на частоту потребления В первом случае указывается, сколько времени
должно пройти между двумя употреблениями определенного блюда (например, ни-
какого картофельного пюре ближайшие три дня) Во втором случае просто нужно
указать, сколько раз в неделю вы желаете потреблять определенное блюдо
Учреждения, которые воспользовались меню, рекомендованными моделями на
базе электронных таблиц, достигли следующих результатов 1) экономия средств со-
ставила от 10 до 30%, 2) полностью удовлетворены требования к содержанию пита-
тельных веществ, чего не всегда удавалось добиться ранее, 3) фактически пища на-
столько же приемлема для потребителей в плане вкусовых качеств, как и при состав-
лении меню традиционными методами
В конце данной главы обсуждается проблема составления диеты и описывается
вклад Данцига в разработку симплекс-метода, используемого для оптимизации мо-
делей линейного программирования [1,2]
4.6.	Анализ чувствительности модели ЛП
Мы рассмотрели графическое представление моделей ДП и их решении, при этом
наглядно показали, насколько важны крайние точки допустимой области при оптимиза-
ции линейных моделей Теперь нас интересует вопрос, насколько чувствительно опти-
мальное решение к небольшим изменениям исходных данных Допустим, мы оценили
среднее значение некоторого параметра модели и нашли решение, используя данную
оценку Что произойдет с оптимальным решением, если оценка изменится на 5%, 10%,
15% или больше? Решение и оптимальное значение целевой функции будут меняться
в широком диапазоне или останутся более-менее постоянными9 Как следует из приме-
216 ЧАСТЬ II Оптимизационные модели
ров анализа чувствительности в главе 2, ответ на эти вопросы определяет достоверность
рекомендаций, сформулированных на основе модели. Если оптимальное значение целе-
вой функции изменяется незначительно при достаточно больших изменениях значения
определенного параметра, можно не беспокоиться из-за неопределенности данного па-
раметра Если же оптимальное значение целевой функции меняется заметно даже при
незначительных изменениях параметра, нельзя допускать высокого уровня неопределен-
ности в его значении В таком случае, возможно, стоит затратить больше усилий на опре-
деление более точного значения этого параметра.
Хотя некоторые последующие рассуждения будут неформальными, в нашем распо-
ряжении есть также строгие и точные методы Эти методы относятся к области анализа
чувствительности оптимального решения Данная тема настолько важна, что оставшаяся
часть этой главы будет посвящена обсуждению информации, содержащейся в отчете по-
устойчивости, предлагаемом средством Поиск решения Графический подход позволит
показать, как изменения модели влияют на решение в двухмерном пространстве, а это,
в свою очередь, поможет понять изменения, которые возникнут в реальных моделях
большего размера
Важно отметить анализ чувствительности основан на предположении, что значения
всех параметров модели, за исключением одного, остаются неизменными Нас интересует
степень воздействия значений этого параметра, во-первых, на оптимальное значение
целевой функции и, во-вторых, на оптимальное решение, т е значения переменных
решения Математически анализ чувствительности сводится к нахождению частных
производных, когда все переменные, кроме одной, остаются постоянными. В эконо-
мике анализ чувствительности носит название анализа по предельным показателям или
маргинального анализа
Чтобы показать, как проводится анализ чувствительности, обратимся вновь к упро-
шенной модели ЛП Oak Products, представленной соотношениями (4.1)—(4 8). Цель дан-
ной модели — рекомендовать производственный план на предстоящий временной пери-
од Большинство прикладных моделей ЛП содержит подобные модели планирования,
в которых требуется определить будущие планы и политику Естественно, таким моделям
необходимы данные, которые точно будут известны только в будущем. В реальных ситуа-
циях эти данные на момент моделирования зачастую невозможно знать с абсолютной
точностью Например, значения удельного дохода в расчете на единицу продукции ($56
для стульев Captain и $40 для стульев Mate) являются только оценками, основанными на
ценах продажи и предполагаемых переменных затратах, которые могут измениться в бу-
дущем Поэтому мы вынуждены использовать текущие оценки параметров модели, отда-
вая себе отчет, что будущие реальные значения этих параметров наверняка будут отли-
чаться от используемых в модели. Но у нас могут быть достаточно веские соображения
относительно возможных диапазонов, в которых будут находиться истинные значения
этих параметров Например, $56 и $40 — наилучшие оценки середин этих диапазонов для
значений удельной прибыли
Еще один источник неопределенности содержится в ограничениях — чаще всего пло-
хо определены правые части ограничении Например, правая часть ограничения
(начальный запас) для длинных штифтов равна 1280. В реальных приложениях это число
может оказаться не соответствующим действительности, поскольку действительный на-
чальный запас длинных штифтов может быть иным по многим причинам. Таким обра-
зом, значение 1280 — всего лишь наилучшая оценка для правой части ограничения. По-
этому необходимо учитывать неопределенность в таких данных
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности
217
Последний источник неопределенности — коэффициенты функции ограничении,
т.е. коэффициенты при переменных решения в левых частях неравенств Поскольку эти
коэффициенты связывают переменные решения с ограничениями технологических ре-
сурсов (определяются правыми частями неравенств), их часто называют технологически-
ми коэффициентами В модели Oak Products нет неопределенности при задании техно-
логических коэффициентов, поскольку, например, для изготовления стула Captain не
может понадобиться больше четырех ножек Однако в других моделях ЛП возникновение
неопределенности в технических коэффициентах вполне вероятно Например, новое ог-
раничение для модели Oak Products может связывать время сборки и отделки одного сту-
ла с общим ресурсом рабочего времени В этом случае качество древесины или произво-
дительность труда могут внести неопределенность в коэффициент, отражающий время
сборки и отделки стульев
В приведенных ниже примерах первый иллюстрирует изменения коэффициентов целе-
вой функции, второй показывает изменения правых частей ограничении, а третий — измене-
ния технологических коэффициентов модели В главе 1 мы называли коэффициенты целе-
вой функции, правые части ограничений и технологические коэффициенты параметра-
ми модели, поэтому иногда исследование воздействия изменений этих величин называют
параметрическим анализом. Посмотрим, какую информацию о воздействии изменений
первого типа может предоставить нам графический анализ и отчет по устойчивости сред-
ства Поиск решения; изменения третьего типа будут исследоваться в разделе 4 9
4.7.	Изменения коэффициентов целевой функции
Предположим, что ограничения неизменны, а изменяются только коэффициенты це-
левой функции Тогда с геометрической точки зрения меняется только угол наклона
прямой целевой функции Что при этом происходит, мы уже наблюдали в разделе 4 3 На
рис. 4 5 все данные модели Oak Products остались прежними, лишь удельный доход для
стульев Mate возрос с $40 до $80 в расчете на один стул В результате данного изменения
изменился угол наклона прямой целевой функции, поэтому оптимальным стало новое
угловое решение.
Экспериментируя с коэффициентами целевой функции модели Oak Products в про-
грамме GLP, можно заметить, что некоторые изменения коэффициентов не приводят
к изменению оптимального решения, несмотря на то, что прямая целевой функции име-
ет другой угол наклона Например, заменим целевую функцию 560 + 40Л/новой функци-
ей 560 + 48Л/. Как показано на рис. 4.4, решением для исходной целевой функции явля-
лась пара значений С = 130, Л/’ = 60 В новой целевой функции переменной М соответст-
вует более высокая удельная прибыль Поэтому можно ожидать, что новое оптимальное
решение будет предусматривать производство большего количества М, поскольку их
прибыльность возросла Однако, как свидетельствуют представленные на рис 4 10 ре-
зультаты анализа новой модели программой GLP, этого не произошло Оптимальные
значения С и М не изменились, вновь было получено то же самое решение.
218 ЧАСТЬ II Оптимизационные модели
Совет Если щелкнуть правой кнопкой мыши на линии целевой функции поблизости точки ее
пересечения с одной из осей, а затем перетащить линию мышью, GLP будет поворачивать
линию целевой функции вокруг точки пересечения с другой осью. Это позволяет непосредст-
венно увидеть на графике связь между углом наклона линии целевой функции, угловыми точ-
ками и перемещениями оптимального решения из одной угловой точки в другую при измене-
нии угла наклона линии целевой функции.
Очевидно, что отрицательный наклон линий, связанных с каждой из трех рассмот-
ренных целевых функций (рис 4.4, 4 5 и 4. Ю), уменьшается по мере увеличения при-
быльности М по отношению к С (т.е при возрастании значения отношения коэффици-
ента при М к коэффициенту при С). Однако, хотя целевые функции 56С + 40Л/
и 56С + 48Л/ имеют разные углы наклона, эти углы недостаточно различны, чтобы полу-
чить новое решение Для обеих целевых функций оптимальное решение одно и то же:
С = 130, М‘ = 60. С другой стороны, поскольку коэффициент целевой функции изменил-
ся, оптимальное значение целевой функции изменится, что и показано на трех указан-
ных рисунках. Подведем итог.
Изменение коэффициентов целевой функции приводит к изменению угла наклона'
прямой целевой функции. Это может отразиться (а может и не отразиться) на опти- ;
мальном решении.
Сравнивая три вышеупомянутых рисунка, можно сделать вывод, что, если значение
отношения коэффициента при М к коэффициенту при С равно 1, прямая целевой функ-
ции будет иметь тот же наклон, что и линия ограничения для ножек. Более того, как
только значение данного отношения превысит 1, новое оптимальное решение (рис. 4 5)
станет предпочтительней, чем решение, показанное на рис 4 4. Если же значение этого
отношения равно 1, прямая целевой функции параллельна линии ограничения для но-
жек, и программам GLP или Поиск решения будет безразлично, какое из угловых реше-
ний (на рис 4.4 или на рис. 4.5) выбрать, поскольку оба решения дают одинаковое зна-
чение целевой функции
ГЛАВА 4 Линейная оптимизация. Анализ чувствительности 219
Напоминаем, что если в модели с двумя переменными прямая целевой функции парал-
лельна прямой какого-либо ограничения (в нашем случае это ограничение для ножек), то су-
ществует два оптимальных угловых решения текущее решение, находящееся на пересечении
ограничения для ножек и ограничения для длинных штифтов, и второе решение, задаваемое
пересечением ограничения для ножек и ограничения для коротких штифтов Более того, в та-
ком случае все точки прямой ограничения для ножек, находящиеся между этими угловыми
точками, также являются оптимальными В ситуации, когда имеется несколько наборов оп-
тимальных значений переменных решения, дающих одинаковое значение целевой функции,
используется термин множественные (альтернативные) оптимальные решения
Если задача ЛП имеет более одного оптимального решения, т.е. существуют множест-
венные оптимальные решения, то этих оптимальных решений бесконечно много.
Рассмотрим теперь результаты применения средства Поиск решения для этих трех
различных целевых функций, чтобы разобраться, как интерпретировать информацию,
содержащуюся в отчете по устойчивости, генерируемом этим средством. На рис 4 11
представлена таблица модели Oak Products, в которой показано оптимальное решение за-
дачи ЛП из главы 3, только вместо отчета о результатах был выбран отчет по устойчиво-
сти. Отчет по устойчивости располагается на отдельном рабочем листе, на котором убра-
ны линии сетки (см. рис. 4.11) Вторая строка верхней части отчета, озаглавленной Из-
меняемые ячейки, содержит значение 40 в столбце Целевой коэффициент (для стульев
Mate), а Допустимое увеличение для данного коэффициента равно 16 Это означает, что
если остальные данные модели останутся неизменными, то, увеличив коэффициент це-
левой функции для стульев Mate (т е удельный доход в расчете на единицу продукции) не
более чем на 16, мы получим то же самое оптимальное решение задачи ЛП, что и в ис-
ходном случае; если же прирост составит более 16, текущее решение, полученное с по-
мощью Поиск решения, уже не будет оптимальным Почему так происходит9
Замечание. При составлении отчета по устойчивости Поиск решения для каждой из ячеек
левых частей ограничений просматривает таблицу модели справа налево, пока не найдет заго-
ловок строки (если таковой существует) в строке данного ограничения Затем программа про-
сматривает таблицу вверх от рассматриваемой ячейки, пока не обнаружит заголовок столбца
(если он существует) в столбце данного ограничения Эти два заголовка соединяются и образу-
ют заголовок, соответствующий данному ограничению в отчете по устойчивости Аналогич-
ный процесс в отчете по устойчивости выполняется и с целью создания заголовков для ячеек
переменных решения Правильный выбор и размещение заголовков в табличном представлении
модели ЛП позволяют создать информативные заголовки в отчете по устойчивости
Если прирост коэффициента целевой функции при переменной М
...меньше 16, то значение отношения коэффициента при М к коэффициенту при Сбу-
дет меньше 1, как мы уже видели ранее в программе GLP, такого изменения целевой
функции недостаточно, чтобы решение сместилось из текущей угловой точки,
. .больше 16, значение отношения коэффициента при М к коэффициенту при С будет
больше 1, как следует из анализа, проведенного в GLP, такое изменение целевой функ-
ции приведет к смещению решения из текущей угловой точки в другую угловую точку,
...равно 16, значение отношения коэффициента при М к коэффициенту при С будет
равно 1; как следует из анализа, проведенного в GLP, это приведет к тому, что оба угло-
вых решения будут давать одно и то же значение целевой функции, т е существуют мно-
жественные оптимальные решения
220 ЧАСТЬ II Оптимизационные модели
А	'В 1 С Г	О	Е	F	]	G
1	. 2	Тип стульев 3	« Цельная прибыль 4	Произведенное к-во 5	Упрощенная модель Oak Products Captain Mate $ 56 s $ 4Q s	Прибыль 130	60 |	'	$9 680| Потребность в	Суммарное деталях	потребление		Начальный запас	Конечный запас
• блмДпинные штифты	8	4	1280 <	1280	0
7 'Короткие штифты	4	12	1240 <	1600	360
S 8 S 3 Ножки		760 <	760	0
9 Прочные сиденья	1	0	130 <	140	10
10 Облегченные сиденья	0	1	60 <	120	60
11			Стулья s	Мин производство	Резерв
12 Произведено	1	1	190 >	100	90
				
Microsoft Excel 10.0 Отчет по устойчивости						
		Результ	Нормир	Целевой	Допустимое	Допустимое
Ячейка	Имя		значение стоимост		ьКоэфсрициен	тУвеличение Уменьшение	
$В$4	Произведенное к-во Captain	130	0	56	24	16
$С$4	Произведенное к-во Mate	60	0	40	16		12
Ограничения	_______						
			Теневая	Ограничение Допустимое		Допустимое
Я ч р й к <	з	Имя	значение	Цена	Правая часть Увеличение		Уменьшение
2	Произведено Стулья	190	0.0	100	90	1Е*50	"
Ю$6	Длинные штисрты Суммарное пот	1290“ “	" 40	- -JJgg- -	" 19 "	““ “1W	
Ю$7	Короткие штисрты Суммарное пот	1240	0.0	1600_	'1Е*30		360
SDJS	Ножки Суммарное потребление '	““ 760	6.0	760	7?	39
$DS9	Прочные сиденья Суммарное потр	130	0.0 ‘	140	1Е*30	10“
$0*10	Облегченные сиденья Суммарное	60	0.0	“120	1Е*30	60 “
						
Рис. 4.11. Модель Oak Products и отчет по устойчивости
Аналогично, если остальные данные модели остаются неизменными, Допустимое
уменьшение целевого коэффициента для стульев Captain, равного 56, составляет 16. Та-
ким образом, чтобы значение отношения коэффициента при переменной М к коэффи-
циенту при переменной С стало равным 1, нужно уменьшить значение данного коэффи-
циента на 16, а это означает, что снижение коэффициента на меньшую величину не при-
ведет к изменению текущего решения, предложенного средством Поиск решения.
Итак, значения Допустимое увеличение и Допустимое уменьшение в таблице Изме-
няемые ячейки отчета по устойчивости показывают, на сколько можно изменить Целевой
коэффициент при заданной переменной решения в целевой функции, оставив неизмен-
ными остальные данные модели, чтобы при повторной оптимизации модели получить то
же самое решение. Иными словами, диапазоны целевого коэффициента задают пределы
изменений данного коэффициента (остальные данные остаются постоянными), которые не
вызовут изменений оптимального решения. Программа GLP позволяет увидеть, куда пере-
местится оптимальное решение задачи ЛП при изменении целевого коэффициента, выхо-
дящего за пределы указанного диапазона В отчете по устойчивости средства Поиск реше-
ния не содержится никакой информации о том, где будет находиться новое угловое реше-
ние Но отчет по устойчивости предоставляет информацию, пусть и ограниченную, для
моделей ЛП произвольной размерности, в то время как визуальные возможности програм-
мы GLP ограничены моделями с двумя переменными решения. Подведем итог.2
1 Решение задачи ЛП может оказаться вырожденным, в таком случае перечисленные далее пункты нужно
рассматривать как некое упрощение Более глубоко проблема вырождения в моделях ЛП рассматривается в
разделе 4 13
ГЛАВА 4 Линейная оптимизация Анализ чувствительности 221
1.	Значения в столбцах Допустимое увеличение и Допустимое уменьшение раздела
Изменяемые ячейки отчета по устойчивости показывают, на сколько можно уве-
личить или уменьшить коэффициент при переменной в целевой функции, чтобы
оптимальное решение (т е значения переменных решения) осталось неизменным,
при условии, что остальные данные считаются фиксированными При этом опти-
мальное значение целевой функции может измениться
2.	Если величина изменения целевого коэффициента меньше допустимой, текущее
оптимальное решение остается единственным.
3.	Если коэффициент при переменной в целевой функции увеличить или уменьшить
в точности на допустимую величину, появится альтернативное оптимальное решение
На основании отчета по устойчивости можно сделать еще один интересный вывод
о решении если для некоторой переменной из таблицы Изменяемые ячейки в столбце
Допустимое увеличение или Допустимое уменьшение содержится нулевое значение,
значит, для данной модели существует по крайней мере одна альтернативная угловая точка
оптимального решения Более того, если альтернативное оптимальное решение существу-
ет, обязательно появится такое нулевое значение Это правило проиллюстрировано на
рис. 4.12, где изображена гипотетическая линейная модель максимизации с двумя пере-
менными и тремя ограничениями-неравенствами Прямая целевой функции параллельна
прямой второго ограничения (помеченного цифрой 2) Видно, что угловые точки I и II
являются альтернативными оптимумами данной модели Поскольку Поиск решения ис-
пользует для оптимизации моделей ЛП метод, который просматривает угловые решения
по очереди, программа укажет в качестве оптимального решения только одно из них,
и отчет по устойчивости будет составлен только для этого углового решения * 4 Предполо-
жим, что с помощью средства Поиск решения найдено угловое решение I Из представ-
ленной на рис 4 12 геометрической интерпретации модели следует, что любое увеличе-
ние коэффициента при л; изменит угол наклона прямой целевой функции, например,
она приблизится к линии, нарисованной пунктиром, и единственным оптимальным ре-
шением станет угловая точка II. Отчет по устойчивости укажет на это, проставив нулевое
значение для х, в столбце Допустимое увеличение
Увеличивая в нашей модели коэффициент при переменной М (при фиксированном
значении коэффициента при переменной Q, в конце концов получим новое решение
(рис. 4 5), в котором оптимальное значение М больше исходного решения Этот результат
вполне соответствует интуитивным соображениям, поскольку увеличение прибыльности
М не должно приводить к снижению их выпуска' Данная ситуация иллюстрирует общее
положение.
; В модели максимизации увеличение коэффициента при какой-либо переменной реше-
ния (т.е. увеличение прибыльности деятельности, связанной с этой переменной) при
^условии постоянства остальных данных не может привести к снижению оптимального
значения этой переменной (т.е. не снижает уровня данной деятельности).
Более точно — о невырожденном решении
4 При наличии в модели ЛП альтернативных оптимумов незначительные отличия в точности выполнения
арифметических вычислении часто приводят к тому, что на одном компьютере Поиск решения находит
одно оптимальное решение, а на другом — альтернативное угловое решение
222
Ч А С Т Ь II Оптимизационные модели
Ситуация для модели минимизации прямо противоположна Поскольку в этом случае
минимизируются общие затраты, то увеличение затрат на некую деятельность при неиз-
менности остальных параметров не может привести к повышению оптимального уровня
данной деятельности Еще одно общее положение выглядит следующим образом.
В модели минимизации увеличение коэффициента при какой-либо переменной реше-„
ния (т.е увеличение затрат на деятельность, связанную с этой переменной) при посто-
янстве остальных данных не может привести к увеличению оптимального значения
этой переменной (т.е. не повышает уровень данной деятельности).
4.8.	Изменение правых частей ограничений
Теперь от изменения коэффициентов целевой функции перейдем к рассмотрению
изменений правых частей ограничений Начнем обсуждение с общих наблюдений, ка-
сающихся влияния изменений правых частей ограничений в виде неравенств. Чтобы
продемонстрировать воздействие изменений этих параметров, вновь обратимся к графи-
ческому анализу Предлагаем поэкспериментировать, перемещая линии ограничений
модели Oak Products на рис 4 3 путем присвоения различных значений правым частям
ограничений, чтобы увидеть разнообразие допустимых областей, получаемых в результа-
те этих простых манипуляций В программе GLP это можно делать, вводя различные
значения правых частей неравенств, перетаскивая линии ограничений или щелкая на
кнопках со значками + и -, находящихся справа от каждого поля ограничения в окне
GLP В результате экспериментов с перемещением ограничений модели Oak Products на
рис 4 3 можно сделать вывод, что увеличение правой части ограничения вида > усилива-
ет ограничение, т е такое ограничение становится сложнее удовлетворить. Аналогично,
если правая часть ограничения вида < уменьшается, такое ограничение также становится
сложнее удовлетворить, следовательно, оно усиливается.
ГЛАВА 4. Линейная оптимизация Анализ чувствительности
223
i Усиление ограничения-неравенства означает, что такое ограничение становится слож-
нее удовлетворить. Для ограничения вида > это происходит при увеличении правой час-
। ти. Для ограничения вида < это происходит при уменьшении правой части.
Процесс уменьшения правой части ограничения вида >, напротив, называется ослаб-
лением ограничения. Как показано на рис. 4.3, с уменьшением правой части ограничения
вида > появляется все больше комбинаций значений С и М, удовлетворяющих данному
ограничению. Таким образом, данное ограничение становится проще удовлетворить
Аналогично при увеличении правой части ограничения вида < его становится проще
удовлетворить, следовательно, происходит ослабление данного ограничения
( Ослабление ограничения-неравенства означает, что данное ограничение становится
i легче удовлетворить. Для ограничения вида > это происходит при уменьшении правой
части, а для ограничения вида < — при ее увеличении.
Подытожим наши наблюдения геометрических последствий усиления и ослабления
ограничений-неравенств.
i Усиление ограничения-неравенства приводит к уменьшению допустимой области или
оставляет ее неизменной. Ослабление ограничения-неравенства приводит к расшире-
нию допустимой области или оставляет ее неизменной.
Данные выводы справедливы для всех ограничений-неравенств и не зависят ни от
размерности модели (числа переменных решения), ни от вида ограничений (< или >)
Следует подчеркнуть, что при осуществлении анализа мы исходили из предположения,
что изменения затрагивают только одно ограничение, в то время как остальные ограни-
чения остаются фиксированными. Одновременное усиление (ослабление) нескольких
ограничений также приведет к уменьшению (расширению) допустимой области или ос-
тавит ее неизменной Однако если одни ограничения усиливаются, а другие в то же время
ослабляются, вряд ли можно сказать что-либо определенное о воздействии этих измене-
ний на допустимую область в общем случае. Наконец, как мы уже видели, чрезмерное ог-
раничение может привести к недопустимости модели. Эти выводы справедливы для мо-
делей с произвольным числом переменных решения
Посмотрим теперь, как эти выводы отражаются в отчете по устойчивости в таблице
Ограничения
Устойчивость к изменениям правых частей ограничений и теневые цены
Рассмотрим сначала ситуацию, при которой все числа в модели Oak Products остаются
фиксированными, за исключением запаса длинных штифтов Что если вместо 1280 штук
их запас составит 1281? Как это отразится на оптимальном значении целевой функции9
Поскольку данное ограничение имеет вид <, можно заключить, что увеличение правой
части приведет к ослаблению ограничения, т.е. его будет проще удовлетворить Следова-
тельно, данное изменение определенно не уменьшит значения целевой функции Однако
произойдет ли его увеличение, и если да, то насколько9
Чтобы ответить на эти вопросы, воспользуемся испытанным средством — графиче-
ским анализом, а затем свяжем результаты анализа с данными отчета по устойчивости,
генерируемого средством Поиск решения. Обозначим через L значение правой части ог-
раничения для длинных штифтов. Тогда первоначально L = 1280 В ходе экспериментов
224 ЧАСТЬ II Оптимизационные модели
с представленной на рис 4 4 моделью будем менять ограничение для длинных штифтов,
подставляя значения L = 1281, L = 1320 и L = 1350. Как мы показали в разделе 4.2, эти
новые значения L геометрически соответствуют параллельному переносу (в направлении
от начала координат) линии ограничения.
Поскольку увеличение L означает ослабление данного ограничения, в геометриче-
ском представлении допустимая область может измениться только в сторону расширения
(если она вообще будет меняться) Новые множества ограничений совместно с опреде-
ленными программой GLP оптимальными решениями, соответствующими значениям
запаса длинных штифтов 1281, 1320 и 1350, представлены на рис. 4.13, 4.14 и 4 16 соот-
ветственно Эти рисунки позволяют обнаружить некоторые интересные факты, которые
можно проверить, непосредственно изменяя модель Oak Products в программе GLP.
При £ = 1281 (рис 4 13) ограничения для ножек и длинных штифтов продолжают ос-
таваться лимитирующими, новое решение С= 130,25, М= 59,75, оптимальное значение
целевой функции равно $9684 Заметим, что последнее значение увеличилось на $4 по
сравнению с исходной моделью (было $9680)
Данный прирост $4 является, как показано на рис. 4 11, теневой ценой, соответствую-
щей ограничению для длинных штифтов Теневая цена ограничения для длинных штифтов
в отчете по устойчивости показывает, насколько изменится оптимальное значение целевой
функции, если правую часть данного ограничения увеличить на единицу при условии, что
остальные данные останутся фиксированными Термин цена означает, что данная величина
отражает максимальную цену, которую можно согласиться заплатить за приобретение до-
полнительного длинного штифта Термин теневая означает, что ее значение скрыто до тех
пор, пока не будет оптимизирована модель и проведен анализ чувствительности. В эконо-
мической теории теневую цену иногда называют ценой резервирования.
Теневую цену для заданного ограничения можно рассматривать как коэффициент из-
менения оптимального значения целевой функции при увеличении правой части этого i
ограничения при условии, что остальные данные остаются неизменными.
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 225
На рис. 4.14 показано, что при £= 1320 оптимальным решением является С= 140,
М = 50, лимитирующими становятся три ограничения — для длинных штифтов, для но-
жек и прочных сидений, а оптимальное значение целевой функции равно $9840.
Решение, предложенное средством Поиск решения, и отчет по устойчивости для дан-
ной модели показаны на рис 4.15. Мы видим нулевые значения конечного запаса для
трех лимитирующих ограничений В предыдущих случаях (при L = 1280 и 1281) в точке
оптимальности обе переменные решения были положительными и только два ограниче-
ния были лимитирующими. В данном случае в точке оптимальности обе переменные ре-
шения положительны, но связывающих лимитирующих ограничения — три Нестрого
говоря, решение задачи ЛП, для которого лимитирующих ограничений больше, чем по-
ложительных переменных, называется вырожденным, что может приводить к определен-
ным аномалиям при интерпретации отчета по устойчивости. Так, например, на рис. 4.15
показано, что допустимое увеличение и допустимое уменьшение для некоторых теневых
цен равны нулю.5
Совет. Отчет по устойчивости — это обычный рабочий лист с отключенной сеткой Мож-
но изменить форматирование его содержимого, чтобы придать ему более удобную форму.
Важно отметить, что теневая цена по умолчанию имеет тот же числовой формат, что и
ячейка левой части соответствующего ограничения в исходной таблице Excel. Если в фор-
мате этой ячейки десятичные знаки после запятой отсутствуют или их недостаточно,
это может привести к тому, что будет указано нулевое значение теневой цены, в то время
как фактически оно равно небольшому дробному числу, скажем, 0,023. Поэтому нужно
взять за правило просматривать нулевые элементы в отчете по устойчивости, чтобы про-
верить, действительно ли данный элемент равен 0, или же это небольшое число, требующее
числового формата с большим количеством знаков после запятой.
Вырожденность — просто обозначение особенности модели (указывает на то, что некоторые ограничения
избыточны — Прим ред ), однако она требует более тщательной интерпретации содержащейся в отчете
по устойчивости информации Подробнее тема избыточности рассмотрена в разделе 4 13
226	Ч А С Т Ь II. Оптимизационные модели
|Тип стульев
•'дельная прибыль
Произведенное к-во
6J Длинные штифты
^7.11 Короткие штифты
8 ННожки
8 Прочные сиденья
10_j' >блегченные сиденья;
12 /'роизведено
1 В С _D. -_jE
Упрощенная модель Oak Products
Captain Mate ;
$ 56 • $40	Прибыль	।
I 140	50	|	$9	840]
Потребность в	।	Суммарное
деталях	:	потребление
1320 <“
1160 <
760 <
140 <‘
50 <
• Конечный
Начальный запас ; запас
1320
1600
760
140
120
440
70
Стульям Мин производство Резерв
190 >	100	90
Microsoft Excel 10.0 Отчет по устойчивости
Ячейка_____________Имя________
1В14 Произведенное к-во Captain
Результ Нормир Целевой Допустимое Допустимое
значенивстоимостьКоэффициентУвеличениа Уменьшение
140	*	“
Ячейка_____________Имя
10112 Произведено Стуль
ИЖ Длинные штифты С
101? Короткие штиерты'
Резупьт Теневая Ограничение допустимое Допустимое
$019 Пре
tPil'S 0g?
ТЗЯГ
1160
140.
ТПГ
0,0
“ПИГ
TJgtT
1600
~75(Г
140
90
1Е-30
44IJ
"W
..55

Рис. 4.15. Оптимальное решение и отчет по устойчивости для L = 1320
При L = 1320 значение правой части ограничения для длинных штифтов увеличилось на
40 единиц по сравнению с исходным значением 1280. В соответствии с определенной ранее
теневой ценой (которая равна 4) значение целевой функции увеличилось на 9840 — 9680 =
= 160 = 4x40.
Если значение L превышает 1320, то, как показано на рис. 4 14 и рис. 4.16, ограничение
для длинных штифтов перестает быть лимитирующим, более того, оно становится избы-
точным, поскольку теперь его удаление никак не отражается на решении. Оптимальное ре-
шение остается точно таким же, как на рис. 4.14 и 4.15 Решение, предложенное средством
Поиск решения, и отчет по устойчивости для значения L = 1350 представлены на рис. 4.17.
Заметим, что теперь лимитирующими являются ограничения для ножек и коротких
штифтов (см. также рис. 4.16). Кроме того, теневая цена для ограничения длинных
штифтов снизилась с 4 до 0. Это изменение теневой цены показывает, что предыдущая ее
интерпретация верна только для определенного диапазона значений правой части огра-
ничения. Диапазон значений правой части ограничения, для которого теневая цена оста-
ется постоянной, называется допустимым. Соответствующий диапазон указан в таблице
Ограничения отчета по устойчивости в столбцах Допустимое увеличение и Допустимое
уменьшение.
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 227
	I		д_х	 в . с , Упрощенная мс	D >Et дель Oak Products	F	I	
[Тип стульев 3 ;Удельная прибыль 4 1 Произведенное к-во 2	Captain- Mate $ 56	$ 40 | 140 ' 50 [ Потребность в деталях	Прибыль * $9840| Суммарное потребление	Начальный запас		Конечный запас
6 '-^Длинные штифты	8	4	1320 <	1350	30
7J Короткие штифты	4	- 12	1160 <	1600	440
8 ,Ножки	4.4’	760 <	760	0
9 [Прочные сиденья	1	0	140 <	140	0
Ю_1Облегченные сиденья	0 i 1	50 <	120	70
JJLI <12 [Произведено			Стулья Мин.	производство	Резерв
	1	1	190 >	100	90
Microsoft Excel 10 0 Отчет по устойчивости
Изменяемые ячейки
Ячейка_________________________
$В$4 Произведенное к-во Captain
$С$4 Произведенное к-во Mate
Рмульт. Нормир.	Целевой Допустимое Допустимое
«качение стоимость КоеффициентУвеличениеУменьшеиие
140_______0 _______56_
5Р"0 40
40
Ограничения
Ре»ульт. Теневая Ограничение Допустимое Допустимое
Ячейка______________Имя_______________аначение Цена Правая часть УвеличениеУменьшение
$0$ 12 Произведено Стулья	_ 190 _ _ 0   100______________90_________1Е*30 
$О$6 Длинные штифты Суммарное потреОлег 1320 _____0________1350______1Е+30______30
$D$7 Короткие штифты Суммарное потребле! _1160____0_____1600_________1 Еч-30____440
$D$B’ Ножки Суммарной потребление ' ”760	10	760	_	30	_ 200
$D$9 _Прочные сидень_я Суммарное потреблег	140___16________140________7J5______55_____
$Р$10 Облегченные сиденья Суммарное потре	50 0 120
10
1б
1Е+30

Рис. 4.17. Оптимальное решение и отчет по устойчивости для L = 1350
228 ЧАСТЬ II Оптимизационные модели
Таким образом, из отчетов по устойчивости, приведенных на рис. 4.11, 4.15 и 4 17,
можно извлечь следующую информацию.
а При L = 1280 (см. рис. 4.11) теневая цена равна 4, допустимое увеличение вели-
чины L для ограничения длинных штифтов составляет 40 штук, а допустимое
уменьшение — 180. Как можно убедиться, для значений L, находящихся в диа-
пазоне 1100—1320, при каждом увеличении запаса (правой части ограничения) на
единицу при условии, что остальные данные остаются неизменными, прирост оп-
тимального значения целевой функции составит $4.
Ь. При £= 1320 (см. рис. 4.15) теневая цена остается равной 4, но допустимое
увеличение становится равным 0, а это означает, что для данных правой части
ограничения, превышающих 1320, значение 4 уже не будет верным. Геометри-
ческий анализ свидетельствует, что при L > 1320 данное ограничение становит-
ся нелимитирующим и, более того, избыточным. Незначительные изменения
правой части нелимитирующего ограничения не могут повлиять на оптимальное
значение целевой функции, следовательно, для нелимитирующего ограничения те-
невая цена всегда равна 0.
с. При L = 1350 (см рис. 4 17) данное ограничение является нелимитирующим, те-
невая цена равна нулю, а допустимое увеличение — бесконечности.6 Таким обра-
зом, при дальнейшем увеличении L данное ограничение останется нелимити-
рующим, а теневая цена — равной 0 Допустимое уменьшение имеет значение 30,
при этом правая часть ограничения вновь примет значение 1320. Для значений L,
меньше 1320, как показано на рис. 4 15, теневая цена составляет S4, а не 0.
Подведем итог.
1.	Теневая цена определенного ограничения может интерпретироваться как коэф-
фициент изменения оптимального значения целевой функции при увеличении
значения правой части данного ограничения на единицу при условии, что все ос-
тальные данные остаются неизменными. Данная интерпретация теневой цены
верна только в определенном диапазоне значений правой части. Этот диапазон за-
дается значениями, указанными в столбцах Допустимое уменьшение и Допусти-
мое увеличение в таблице Ограничения отчета по устойчивости. Именно в этом
диапазоне теневая цена постоянна и имеет указанное значение. Вне допустимого
диапазона теневая цена может принимать другие значения.
2.	Теневая цена нелимитирующего ограничения всегда равна 0. (“Нелимитирующее”
означает, что в точке оптимальности данное ограничение имеет ненулевой резерв
или излишек.)
3.	Таблица Ограничения отчета по устойчивости не содержит информации о том,
как меняются оптимальные значения переменных С и М В ней только показано,
как будет меняться оптимальное значение целевой функции при изменении пра-
вой части ограничения.
Наибольшее число, которое можно представить в Excel, равно 1Е+30, те 1 и 30 нулей Это число можно
считать бесконечно большим по сравнению с другими числами, фигурирующими в модели
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 229
Практическое применение
Линейное программирование помогает
компании экономить материалы
Компания Welborn Cabinet занимается производством шкафов в штате Алабама.
Производство состоит из лесопилки, четырех сушильных камер и сборочного завода
с фабрикой, производящей компоненты шкафов. Компания получает пиломатериа-
лы для производства шкафов: 1) приобретая бревна, которые обрабатываются на ле-
сопилке, чтобы получить доски, используемые затем на сборочном заводе; 2) приоб-
ретая доски у внешних поставщиков. В настоящее время около 73% досок поступает
с собственной лесопилки компании.
Бревна и доски относятся к первому или второму сорту, пиломатериалы первого
сорта более качественные и дорогие. В настоящее время около двух третей общего
объема закупленных компанией Wellborn бревен составляют бревна 1-го сорта. Заку-
пленные доски, составляющие около 27% общего объема используемых досок, были
двух видов: сырые (18%), которые необходимо сушить в сушильных камерах компа-
нии, и сухие (9%). Практически все сухие доски также были 1-го сорта.
Стоимость пиломатериалов составляет около 45% всех материальных затрат на
изготовление шкафов. Поэтому руководство компании хотело узнать, является ли
используемый компанией подход к покупке древесины наиболее экономичным.
Чтобы ответить на данный вопрос, Центр технической помощи при университете
Оборна в содружестве с Лесотехническим институтом проанализировали деятель-
ность компании. Была создана линейная оптимизационная модель производства
заготовок, ограничения которой учитывали производственные мощности лесопилки
и сушильных камер, требуемый объем производства заготовок и возможный объем
поставок сырья
В результате оптимизации обнаружилось, что компания может минимизировать
затраты на производство заготовок, покупая только два вида древесины бревна 2-го
сорта с диаметром тонкого конца 9—15 дюймов (88% объема закупок) и сырые доски
2-го сорта (12%). Такая политика закупок может почти на треть снизить затраты
компании Wellborn на сырье, что позволит сэкономить около $412 000 в год. Модель
также предоставила менеджерам множество дополнительной информации.
•	Теневые цены показывают возможность сделать более выгодную закупку бревен
различных размеров
•	Анализ чувствительности позволяет узнать диапазоны цен, для которых решение,
предлагаемое моделью, будет оставаться оптимальным. В частности, он свиде-
тельствует, что снижение цен на сухие доски или бревна 1 -го сорта вплоть до 20%
не повлияет на оптимальную политику закупок.
•	Нулевое значение резерва для процесса работы сушильных камер показывает, что
данный процесс является узким местом, т.е. производственная мощность сушиль-
ных камер — единственный фактор, сдерживающий увеличение производства. По-
вышение производственной мощности сушильных камер на 22% позволит увели-
чить выпуск заготовок на 29% безо всяких дополнительных изменений [5]
230	Ч А СI b II. Оптимизационные модели
4.9.	Анализ чувствительности с помощью надстройки
SolverTable
К недостаткам отчета по устойчивости, генерируемым средством Поиск решения, от-
носится то, что, во-первых, он предоставляет информацию по устойчивости решения
лишь в непосредственной близости от полученного оптимального решения, причем в от-
вет на изменения только одного параметра. Во-вторых, предоставляемая информация
касается только воздействия на оптимальное значение целевой функции, и, в-третьих,
в нем нет данных по устойчивости решения при изменении технологических коэффици-
ентов модели (т е коэффициентов в левых частях ограничений). Чтобы выяснить, каким
будет решение при значительных изменениях параметров, при одновременном измене-
нии нескольких параметров либо при изменении технологических коэффициентов, не-
обходимо вручную вносить новые данные, повторно находить решение задачи и вручную
фиксировать полученные результаты. В главе 2 при анализе чувствительности мы ис-
пользовали таблицы подстановки Excel, чтобы зафиксировать сразу несколько сценариев
“Что-если”. К сожалению, таблицы подстановки нельзя использовать для фиксирования
результатов оптимизации модели ЛП, поскольку в процессе создания таблиц подстанов-
ки Excel просто пересчитывает рабочий лист, но не может самостоятельно вызвать сред-
ство Поиск решения.
На прилагаемом к данной книге компакт-диске имеется надстройка SolverTable.xla.
Это средство содержит макрос, создающий таблицы, подобные таблицам подстановки, для
вновь оптимизированной модели ЛП после каждого изменения ее параметров. Кроме того,
SolverTable знает про отчет по устойчивости и может также фиксировать содержащуюся
в нем информацию Наконец, возможности SolverTable не ограничивается моделями с дву-
мя переменными (в отличие от GLP), она может работать с оптимизационными моделями
любой размерности, допустимой для встроенной в Excel надстройки Поиск решения или
программы Premium Edition Solver for Education. В данной главе мы проиллюстрируем ис-
пользование надстройки SolverTable на примере упрощенной модели Oak Products.
Для начала откройте с прилагаемого к книге компакт-диска рабочую книгу OakProd.xls.
Затем с помощью команды Файл^Открыть откройте файл надстройки SolverTable.xla.
Excel откроет диалоговое окно с предупреждением, показанное на рис. 4.18, в этом окне
щелкните на кнопке Не отключать макросы. После этого в меню Сервис появится новая
команда SolverTable Однако, как и при создании таблиц подстановки, сначала необходимо
сформировать таблицу результатов.
Рис. 4.18. У^тиноьКи Ни<ктроики .Sober fuble
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 231
Изменение правых частей ограничений
Чтобы проиллюстрировать работу с SolverTable, проведем анализ чувствительности
решения к изменениям правой части ограничения по длинным штифтам. Подобный
анализ мы проводили в главе 3 с помощью таблицы подстановки с одним входом. На-
помним, что таблица подстановки с одним входом позволяет менять только один пара-
метр, при этом можно фиксировать любое количество выходов модели. Сначала размес-
тим диапазон значений правой части ограничения в одном столбце (или строке) — на
рис. 4.19 значения правой части от 399 до 1350 внесены в ячейки 17.117. Затем, как и при
создании таблицы подстановки с одним входом, в верхнюю часть таблицы в ячейки J6P6
введем ссылки на ячейки, содержащие выходы модели (формулы в этих ячейках показа-
ны на рис. 419 в виде выносок). Формулы в ячейках J6:M6 ссылаются на значение левой
части ограничения по длинным штифтам, на два значения переменных решения и значе-
ния прибыли (целевой функции) соответственно. Формулы в ячейках N6 P6 указывают
на ячейки отчета по устойчивости средства Поиск решения, содержащие теневую цену,
допустимое увеличение и допустимое уменьшение для данного ограничения (ячейки, на
которые указывают ссылки, можно увидеть на рис. 4.11) Заголовки в ячейках 15.Р5 яв-
ляются необязательными и служат для удобства документирования.
Рис. 4.19. Создание таблицы для анализа решения в зависимости от значений правой части ог-
раничения по длинным штифтам
Замечание При использовании SolverTable требуется, чтобы модель ЛП была предвари-
тельно оптимизирована с помощью Поиск решения Если в создаваемой таблице предпо-
лагается фиксировать какие-либо элементы отчета по устойчивости, необходимо, чтобы
этот отчет был сгенерирован средством Поиск решения.
232	Ч А С Т Ь II. Оптимизационные модели
Длинные штифты правая часть	Длинные штифты, левая	i Теневая				Допустимое |	Допустимое
ограничения	ограничения	Captain	Mate	Прибыль i	цена	: увеличение ;	уменьшение
	1319	140	50	$9 836	4	39'	180
399	Infeasible	Infeasible .	Infeasible	Infeasible i	Infeasible	Infeasible	Infeasible
400	400	2211.121	100	$4 000 f	12.1O1.2'2	2221.60'221.2.	0
479	479				119.75		i	$4 790 2	100	1	79
4В0	400	0	120	$4 800 i	7.0 i	320	0
700		 700 2].	27.5		120	; $6 340 f	7.0			2 too 21111	220
800	800	"		40		120	 $7 040 I	6.4	300 J	0
	1000	1000	1	70	110	$8 320 ’			loo	!	' 200 ''
1100	Поп Г	85 I		105		$8 960 Г	2.4.° 2 2		"220 2)	0
1280	1280	;	130	60	Г $9 680 2	4.0	40	1	180
1320	1320	140 j	50	2 $9 640 	1	0.0	1E*30 i	0
1350		 1320		140	50	$9 840 i	0 0	IE-30	30
Рис. 4.20. Результаты вычислений с помощью SolverTable
Рис. 4.21. Графическое представление модели в программе GLP для различных значений
правой части ограничения по длинным штифтам
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 233
Затем созданную таблицу следует выделить и выбрать команду SolverTable из меню
Сервис. Как и при создании таблиц подстановки, SolverTable предлагает диалоговое ок-
но с двумя полями ввода, в которых указывается, где на рабочем листе расположены
ячейки, куда подставляются введенные значения. Поскольку в данном случае изменяется
только один параметр — правая часть ограничения длинных штифтов, и в созданной таб-
лице его значения помещены в столбец, адрес ячейки F6 вводится в поле Input Column
Cell7, а другое поле в диалоговом окне SolverTable остается пустым. После этого
SolverTable будет запускать Поиск решения для каждого из указанных значений правой
части ограничения. В данном случае будет выполнено 11 оптимизаций, и для каждой из
них зафиксируются перечисленные в таблице результаты модели (рис. 4.20).
На рис. 4 21 изображены различные представления модели Oak Products в программе
GLP для различных значений исходного запаса длинных штифтов L, содержащихся
в таблице на рис. 4 20. Здесь видно, что увеличение значений L с 400 до 1350 приводит
к расширению допустимой области до тех пор, пока ограничение по длинным штифтам
не становится избыточным. Более того, сравнение числовых результатов на рис. 4.20
и графических представлений модели на рис. 4.21 показывает, что теневая цена резко ме-
няется всякий раз, когда меняется комбинация ограничений, определяющих оптималь-
ное угловое решение. Также нетрудно заметить, что, поскольку значения теневой цены
уменьшаются (скачкообразно) по мере увеличения L, коэффициент возрастания опти-
мального значения целевой функции снижается, это явление достаточно типично для
моделей максимизации при ослаблении одного ограничения вида <.
В отчете по устойчивости одновременно изменяется только один параметр, остальные
данные при этом остаются фиксированными. SolverTable, как и таблица подстановки
с двумя входами, позволяет варьировать одновременно два параметра, однако при этом
можно фиксировать значения только одной итоговой ячейки. В качестве иллюстрации
рассмотрим различные диапазоны значений правых частей ограничений для длинных
и коротких штифтов Как и ранее, сначала создается таблица, в данном случае в ней ука-
заны значения обоих параметров После этого SolverTable запускает Поиск решения для
каждой пары значений правых частей ограничений по длинным и коротким штифтам;
в данном случае придется выполнить 108 оптимизаций, для каждой из которых в таблицу
заносится значение единственного результирующего показателя— значения целевой
функции (ссылка на соответствующую ячейку содержится в левом верхнем углу табли-
цы), как показано на рис 4.22. Неудивительно, что оптимальное значение целевой функ-
ции возрастает при увеличении одного или обоих значений правых частей. Далее с по-
мощью мастера диаграмм можно легко построить график зависимости оптимального
значения целевой функции от значений правых частей ограничения. Такой график на
рис. 4.22 показывает снижение прироста оптимального значения целевой функции по
мере ослабления ограничений.
При созданиии таблиц подстановки в диалоговом окне Таблица аналогичное поле называется Подстав-
лять значения по строкам — Прим ред.
234	Ч А С Т Ь II. Оптимизационные модели
Рис. 4.22. Результаты анализа с помощью SolverTable изменений правых частей ограни-
чений по длинным и коротким штифтам
Изменение коэффициентов целевой функции
Исследование влияния коэффициентов целевой функции с помощью SolverTable ана-
логично исследованию влияния правой части ограничений. Сначала создается таблица,
в столбец (или строку) которой заносятся значения исследуемого коэффициента целевой
функции На рис. 4.23 представлены результаты анализа влияния коэффициента целевой
функции, отражающего удельную прибыль для стульев Captain. При этих значениях ко-
эффициента решение задачи меняется, о чем говорят значения в столбце Допустимое
увеличение. На рис 4 24 показаны представления модели Oak Products в программе GLP
при различных значениях коэффициента Vцелевой функции для стульев Captain, задан-
ных в таблице на рис 4.23. При возрастании значений Кот 0 до 99999 прямая целевой
функции поворачивается, становясь из горизонтальной практически вертикальной. Бо-
лее того, сравнение данных на рис. 4 23 и 4.24 показывает, что оптимальное решение ме-
няется скачкообразно в точках критических значений V. Наконец, появление нулей
в столбце Допустимое увеличение или Допустимое уменьшение для критических зна-
чений Ипоказывает наличие множественных оптимальных решений.
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 235
Длинные							
Удельная прибыль Captain	штифты левая часть : ограничения	Captain :	Mate	Прибыль	Удельная : прибыль : Captain ;	Допустимое : увеличение	Допустимое  уменьшение
	1319	140	50	$9 836	56	24	16
Q	480	0	120	$4 800	0,0	0	1Е+30
0,001	800	40	120	$4 800	0,001	13,332	0,001
13,334	1100	85	105	$5 333	13,334	26,666	0,001
	40	1280	130	00	$7 600	40,0	40	0
80	1280	140	40	$12 800	’ 80 0 ‘	1Е+30	0
Рис. 4.23. Результаты анализа влияния показателя удельной прибыли для стульев Captain
Рис. 4.24. Графическое представление модели для различных значений показателя удель-
ной прибыли для стульев Captain
Изменение технологических коэффициентов
С помощью SolverTable можно достаточно просто исследовать альтернативные произ-
водственные технологии. Напомним, что функции ограничений и их коэффициенты оп-
ределяют вычисление левых частей, а следовательно — спрос на ресурсы, отражая тем
самым определенную технологию. Предположим, компания Oak Products рассматривает
возможность небольшого повышения или снижения прочности стульев Mate путем уве-
личения или уменьшения количества используемых для производства одного стула
длинных штифтов. Помимо инженерной оценки данных изменений, руководство ком-
пании хочет провести экономический анализ последствий уменьшения количества ис-
236	Ч А С Т Ь II. Оптимизационные модели
пользуемых для сборки одного стула Mate длинных штифтов с 4-х до 2-х и увеличения
свыше 4-х. Этот анализ не столь уж очевиден: данное изменение не только непосредст-
венно отразится на цене стула, но и повлияет на потребность в длинных штифтах, запас
которых ограничен. Это может сказаться на производственных возможностях, что в свою
очередь может привести к иным планам выпуска стульев обоих видов. Таким образом,
необходима повторная оптимизация модели с помощью SolverTable.
Процедура применения SolverTable в данном случае аналогична описанному выше
анализу влияния правой части ограничения: надо сформировать таблицу, задав различ-
ные значения технологического коэффициента в окрестности базового значения 4, а за-
тем запустить SolverTable, чтобы зафиксировать представляющие интерес итоговые пока-
затели модели. В результате получится таблица, содержащая показатели модели при из-
менении расхода длинных штифтов на изготовление одного стула Mate в диапазоне 2-10
(рис 4.25)8 Как и ожидалось, увеличение расхода длинных штифтов на изготовление од-
ного стула Mate с 4 до 6 приводит к уменьшению оптимального выпуска этих стульев, ко-
торое компенсируется увеличением выпуска стульев Captain, при этом происходит сни-
жение суммарной прибыли примерно на $570 Удивительно, но уменьшение расхода
длинных штифтов на изготовление одного стула Mate с 4 до 2 также приводит к сниже-
нию значения оптимального выпуска этих стульев и увеличению выпуска стульев
Captain, однако при этом общая прибыль возрастает Другие представленные на рис 4.25
результаты, в частности, теневая цена длинных штифтов, претерпевают аналогичные из-
менения Принимая во внимание, что все связи модели линейны, такие противоречащие
интуиции результаты решения задачи ЛП часто являются неожиданностью, поскольку
они отражают скрытые и порой непредсказуемые взаимодействия между ограничениями
даже простейшей модели линейного программирования.
Расход дл
штифтов на 1
Mate
Длинные
штифты левая
ограничения	Captain	Mate	Прибыль :	Теневая	: Допустимое  : увеличение	Допустимое уменьшение
1319	140	50	$9 836	4	39		180
1220	140	50	; $9 840 i	00	1Е+30	60
1280		i3o Г	60	$9 680 ’	4,0	40	180
1280	140 Г	26,67	$8 907	6.7		140	160
1280 ;	140	20		$8 640	5,0		240		160
1280	140 		16	$8 480	4,0	?		340		160
Рис. 4.25. Влияние значений коэффициента V для стульев Mate
На этом мы завершаем обсуждение данных, содержащихся в отчете по устойчивости.
Овладев изложенным материалом, вы сможете использовать модели линейного програм-
мирования на практике — формировать модели, оптимизировать их с помощью средства
Поиск решения, правильно интерпретировать отчет по устойчивости, а также использо-
вать надстройку SolverTable для более углубленного анализа параметров. Но мы еще не
рассмотрели пример анализа чувствительности для модели минимизации и не объяснили
значение данных Нормированная стоимость в отчете по устойчивости. Эти вопросы
рассматриваются в следующем разделе.
При выполнении расчетов предполагалось, что исследуемый коэффициент целевой функции (удельная при-
быль в расчете на один стул Mate) остался неизменным, т.е. влияние изменения расхода длинных штифтов
на переменные издержки не учитывалось.
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 237
4.10.	Анализ чувствительности в действии
Мы уже рассматривали модель компании Eastern Steel в разделе 3.10. Напомним по-
становку задачи. Для выплавки легированной стали смешивается руда, поступающая
с 4 месторождений. Каждая руда содержит три основных элемента, обозначенных для
простоты А, В и С, их минимальное содержание в рудной смеси должно быть не ниже оп-
ределенных пороговых значений. Компания платит разную цену за тонну руды с различ-
ных месторождений. Минимизирующая затраты рудная смесь получается с помощью
решения приведенной ниже задачи ЛП, где 7]— процентное содержание руды с место-
рождения I в тонне смеси. Решение данной задачи, найденное средством Поиск реше-
ния, а также отчет по устойчивости для оптимального решения показаны на рис. 4.26.
Минимизировать 8007', + 400Т2 + 600Т3 + 50074 (суммарные затраты)
при ограничениях
ЮТ| + ЗТ2 + 8Т3 + 2Т4>5
907’, + 150Г2+75Г3+ 17574> 100
457, + 25Т2 + 2073 + 37Т4 > 30
1 + Тг + Т, + Г4 = 1
Т(>0,/= 1,2, 3,4.
(требование к содержанию/!)
(требование к содержанию В)
(требование к содержанию С)
(условие составления смеси)
Л 	Составление рудной смеси
♦'	$7 Шахта	Т1 Т2 ТЗ	Т4
'•-'3  Доля в тонне смеси 10.259 0 704 0,037	0 I Итого
"л? Стоимость 1 тонны $800 $400 '$600 $500 | '«,
ание в тонне руды Содержание в смеси Требования Излишек
382	5 00	>	5	0
150	75	175	131,67	>	100	31	67
25	20	37	30,00 >30	0
1	1	1 100 =	1	'	0
Microsoft Excel 10.0 Отчет по устойчивости
Изменяемые ячейки_____________________________________________________________________
Реаульт, Нормир. Целевой Допустимое Допустимое
Ячейка___________Имя_____________аначение стоимость Коэффициент Увеличение Уменьшение
$В$3 Даля в тонне смеси Т1	0,259	0,000	800	223,64	120
$С$3....Доля в 'тонне смеси Т2... 0.704 ' 6,666...........400	’	66,85. ~	300
$D$3 Доля в тонне смеси ТЗ _ .0,037 ________0,000 __________ 600.____85,71____118,27
$Ё$3~~ Доля втонне~смесиТ4............0~	" вТ__________500 ~ ~	1Е+30 91,11111111
Ограничения___________________________________________________________________________
Реаульт. Теневая Ограничение Допустимое Допустимое
Ячейка Имя течение Цена Правая часть Увеличение Уменьшение
$Р$6 А Содержание в смеси	5,00	44,44	5	2,375	_ 0,25
$Р$7...В Содержание в смеси.......131,67......0,00  ....... '	ЮО ЗТбГ" ~ 1Еч-ЗО
Tf$8 С Содержание в смеси...........30,00.....4,44............30.........0,71..........7
$F$9 Баланс Содержание в смеси 1,66	155 56 1 6,25 6,043478261
Рис. 4.26. Решение и отчет по устойчивости для модели Eastern Steel
238	Ч А С Т Ь II. Оптимизационные модели
Нормированная стоимость
К настоящему моменту мы объяснили смысл всех элементов отчета по устойчивости
за исключением данных в столбце Нормированная стоимость. Эти данные можно ин-
терпретировать следующими способами.9
1.	Нормированная стоимость определенной переменной решения определяется как ве-
личина, на которую нужно изменить коэффициент при данной переменной в целе-
вой функции, чтобы оптимальное значение этой переменной стало положитель-
ным Таким образом, если переменная решения в точке оптимальности положи-
тельна, нормированная стоимость для нее равна нулю (см. переменные решения
задачи Oak Products на рис 4.5, 4 15 и 4.17). Если же оптимальное значение некой
переменной решения равно 0, то нормированная стоимость в строке, соответствую-
щей данной переменной, равна значению в столбцах Допустимое увеличение или
Допустимое уменьшение (одно из этих значений будет бесконечным, а второе равно
нормированной стоимости). Например, переменная решения Т4 в модели на
рис 4 26 в точке оптимальности имеет нулевое значение. Нормированной стоимо-
стью переменной Т4 является величина, на которую необходимо уменьшить соответ-
ствующие ей удельные затраты (коэффициент при ТА в целевой функции), чтобы по-
лучить оптимальное решение, содержащее положительное значение ТА Именно это
значение находится напротив переменной ТА в столбце Допустимое уменьшение.
В рассматриваемом случае при любом увеличении коэффициента при Т4 (что делает
ТА более дорогой) оптимальное значение ТА будет оставаться равным О
2.	Альтернативный способ интерпретации нормированной стоимости переменной
решения, текущее оптимальное значение которой равно 0, — использовать коэф-
фициент (удельной величины) уменьшения значения целевой функции при введе-
нии данной переменной в изначально оптимальное решение Следовательно,
нужно отказаться от предложенного средством Поиск решения нулевого значения
и заставить данную переменную принимать положительные значения. Если в оп-
тимальном решении ТА = 0, то оптимальная стоимость тонны смеси возрастет, ес-
ли искать оптимальное решение для модели с дополнительным ограничением,
скажем, ТА - 0,1 Этот коэффициент возрастания оптимальной стоимости при ус-
ловии, что ТА должна принимать положительные значения, и будет нормирован-
ной стоимостью ТА.
Напомним, что теневая цена ограничения — это коэффициент изменения оптималь-
ного значения целевой функции при увеличении значений правой части данного ограни-
чения. Поскольку в рассматриваемой модели ТА = 0, ограничение неотрицательности для
ТА является лимитирующим. Если мы заставляем ТА принимать положительные значения,
это то же самое, что увеличивать правую часть ограничения неотрицательности Отсюда
следует еще одна эквивалентная интерпретация- для модели, содержащей условия неот-
рицательности, нормированная стоимость является теневой ценой ограничения неотри-
цательности для рассматриваемой переменной решения.
9 Это еще один пример, когда для корректной интерпретации результатов отчета необходимо удостове-
риться, что данное оптимальное решение является невырожденным
Это стандартное определение нормированной стоимости для невырожденного решения. К сожалению, даже
при невырожденном решении в отчете по устойчивости в столбце Нормированная стоимость иногда появля-
ется другая информация, которая может ввести в заблуждение Пример рассматривается в разделе 412
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 239
Дополнительные примеры различных интерпретаций нормированной стоимости
можно найти в приведенном ниже диалоге, который должен показать, как информация
отчета по устойчивости применяется в реальных ситуациях. Представьте себя на месте
менеджера компании Eastern Steel, отвечающего за планирование производства. Вы за-
даете вопросы, а разработчик модели вам отвечает.
МЕНЕДЖЕР. Прежде всего, что собой представляет решение нашей задачи9
РАЗРАБОТЧИК. Под решением я подразумеваю оптимальные значения переменных решения Оп-
тимальные значения записаны в ячейках ВЗ ЕЗ рабочего листа модели и состав-
ляют (округленно) Т1-0,26, Т2 = 0,70, ТЗ~0,04, Т4~0,00 При этом мини-
мальная стоимость тонны смеси составляет $511,11 (ячейка F4)
МЕНЕДЖЕР. Мне бы хотелось, чтобы стоимость тонны смеси не превышала S500 Нет ли
способа добиться этого9 Я вижу в таблице столбец под названием Излишек
РАЗРАБОТЧИК. Если бы можно было найти более дешевую рудную смесь, удовлетворяющую огра-
ничениям, Поиск решения нашел бы это решение Столбец обозначен Излишек,
но, вообще говоря, подразумевается ‘‘резерв или превышение" — для каждой си-
туации выбирается более подходящее название В данном случае в этом столбце
показаны величины превышения ограничений
МЕНЕДЖЕР. Может быть, мне удастся изменить эти ограничения Превышение для ограничения
по элементу А равно 0 (ячейка 16), а требование к минимальному содержанию этого
элемента— 5 фунтов Это означает, что в тонне смеси содержится ровно 5 фунтов
элемента А Поскольку превышение в ячейке 18 также равно нулю, тонна оптималь-
ной смеси содержит ровно 30 фунтов элемента С Однако в ячейке 17, соответствую-
щей элементу В, я вижу превышение 31,67, таким образом, данное ограничение не яв-
ляется лимитирующим, и мы добавляем в смесь лишнее количество В
РАЗРАБОТЧИК. Да, это означает, что в оптимальной смеси требование к минимальному содер-
жанию элемента В (100 фунтов) превышено на 31,67, и действительное содержа-
ние его составляет 131,67 фунтов, что показано в ячейке F7
МЕНЕДЖЕР. Возможно, удастся составить более дешевую смесь, используя меньше Л9 За-
чем нам более 131 фунта элемента В, если необходимо только 100 фунтов9
РАЗРАБОТЧИК. Это интересный вопрос Оказалось, что тонна самой дешевой комбинации руд,
удовлетворяющей требованиям по элементам А и С, содержит более 100 фунтов
элемента В Любая комбинация руд, содержащая меньше В, либо не будет содер-
жать необходимого количества А и/или С, либо же будет стоить дороже, чем
$511,11 за тонну Иными словами, попытка сократить превышение по содержа-
нию элемента В при условии соблюдения требований по элементам А и С приведет
к повышению стоимости
МЕНЕДЖЕР. Понятно А как можно снизить общую стоимость тонны смеси до $500 или меньше9
РАЗРАБОТЧИК. Необходимо ослабить ограничения В данном случае нужно ослабить требования к
содержанию элементов А и С
МЕНЕДЖЕР. Почему не к элементу В9
РАЗРАБОТЧИК. Потому что, пытаясь удовлетворить требования по элементам А и С с минималь-
ными затратами, мы включили в смесь более 100 фунтов В, что превышает мини-
мальное пороговое значение Иными словами, требование к содержанию В не являет-
ся лимитирующим Если ослабить данное требование, задав меньшее пороговое зна-
чение, например 98, оптимальная смесь будет иметь все тот же состав и
стоимость Таким образом, ослабление требования к содержанию элемента В ни-
чего не даст Чтобы изменить стоимость смеси, необходимо ослабить одно из ли-
митирующих требований
240 Ч А С Т Ь 11, Оптимизационные модели
МЕНЕДЖЕР. Хорошо. Значит, я должен снизить требование к содержанию элемента А или
С Но какое именно и на сколько9
РАЗРАБОТЧИК. Для ответа на данный вопрос можно воспользоваться информацией, содержащей-
ся в столбце Теневая цена отчета по устойчивости. Значение теневой цены по-
казывает коэффициент изменения оптимального значения целевой функции при
увеличении правой части ограничения. Поскольку мы хотим ослабить ограничение
вида 2, нам нужно уменьшить значение правой части. Посмотрим на значение
теневой цены ограничения по элементу А Оно равно +44,44. Знак + означает, что
при увеличении правой части данного ограничения оптимальное значение стоимо-
сти повышается (т е ухудшается) Следовательно, при уменьшении значения
правой части оптимальное значение целевой функции уменьшается Это под-
тверждает основанное на здравом смысле предположение, что при ослаблении
требования к содержанию элемента А минимальная стоимость тонны смеси
снизится Теневая цена показывает, что она снижается на $44,44 при снижении
требования к содержанию А в тонне смеси на 1 фунт
МЕНЕДЖЕР. Итак, ослабить требование для элемента А значит снизить его с 5 фунтов до
некоего меньшего значения И теневая цена +44,44 показывает, что при каж-
дом уменьшении данного требования на 1 фунт общая стоимость тонны смеси
снижается на $44,44 Таким образом, если потребовать, чтобы смесь содержала
только 4 фунта А на тонну вместо 5, стоимость тонны смеси снизится пример-
но до $466 67, а это значительно меньше $500' Если же сократить требование
лишь до 4,5 фунтов, удастся сэкономить более $22 ((1/2)х44,44), и суммарная
стоимость все равно окажется меньше $500 Правильно9
РАЗРАБОТЧИК. В принципе, да Вы взяли правильный коэффициент изменения, однако данное зна-
чение коэффициента действует только в определенном интервале в окрестности
исходного значения 5 А соответствующий интервал может не позволить проана-
лизировать уменьшение правой части требования на целую единицу или даже на
половину единицы
МЕНЕДЖЕР. Понятно В столбце Допустимое уменьшение для ограничения элемента А
стоит значение 0,25 Это означает, что можно анализировать только уменьше-
ние правой части ограничения с 5 до 4,75 В этом случае экономия составит
0,25х$44,44 = $11,11, те тонна смеси будет стоить ровно $500 Но что будет,
если снизить требование несколько больше, скажем, до 4,59 Позволит ли это
дополнительно снизить стоимость9
РАЗРАБОТЧИК. Вероятно, однако я не могу точно определить, на сколько, так как коэффициент
изменения может стать другим при уменьшении требования более, чем на 0,25,
иными словами, теневая цена может измениться
МЕНЕДЖЕР. Теперь, чтобы убедиться, что я правильно все понял, попробую проанализировать
потенциальную экономию при снижении требования к содержанию элемента С
Исходное значение правой части равно 30 Как видно из отчета по устойчивости,
допустимое уменьшение составляет 7, следовательно, можно снизить данное требо-
вание до 23 Соответствующая теневая цена +4,44. Это коэффициент экономии при
снижении значения правой части. Таким образом, снизив данное требование до 23,
можно сэкономить 7x4,44 = $31,08, что позволит сделать стоимость тонны смеси
заметно ниже $500. Если снизить требование только на 2,5 фунта, можно приме-
нить тот же коэффициент, следовательно, экономия составит 2,5x4,44 “ $11,10, что
позволит получить стоимость практически равную $500 Правильно?
РАЗРАБОТЧИК. Абсолютно.
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 241
МЕНЕДЖЕР. Итак, мы выяснили, что можно снизить стоимость тонны смеси до $500 путем
снижения требования к содержанию элемента А до 4,75 фунтов в тонне или
требования к элементу С до 27,5 фунтов в тонне Теперь хотелось бы узнать,
что будет, если снизить оба требования (к содержанию элементов А и Q, воз-
можно, на меньшее значение, но одновременно9
РАЗРАБОТЧИК. К сожалению, отчет по устойчивости не содержит информации, которая позволи-
ла бы дать точный ответ на этот вопрос При интерпретации теневой цены одного
из ограничений необходимо сохранять неизменными остальные ограничения модели
Единственный способ ответить на вопрос, что будет при одновременном изменении
нескольких правых частей, — это многократно решить задачу для различных значе-
ний соответствующих правых частей с помощью средства типа SolverTable
МЕНЕДЖЕР. Хорошо, давайте посмотрим, что у нас получилось Известно, что можно сни-
зить стоимость 1 тонны смеси до $500, если снизить требование к содержанию
элемента А до 4,75 фунтов в тонне рудной смеси или требование к содержанию
элемента С до 27,5 фунтов в тонне Что делать дальше9
РАЗРАБОТЧИК. Отчет по устойчивости не может здесь помочь Теперь следует решить, какое
изменение более пагубно отразится на свойствах полученной смеси, а это уже
чисто технологический вопрос.
МЕНЕДЖЕР. Понятно Кстати, я думал, что столбец Допустимое увеличение позволяет
увеличивать значение правой части Не могли бы вы показать, что происходит
при увеличении правой части9
РАЗРАБОТЧИК. Рассмотрим требование к содержанию элемента А Предположим, что вы хоти-
те повысить данное требование
МЕНЕДЖЕР. Поскольку мы имеем дело с ограничением вида >, повышение подразумевает
увеличение правой части, т е требуемого содержания элемента А
РАЗРАБОТЧИК. Правильно Усиление ограничения никогда не приводит к улучшению оптимального зна-
чения целевой функции, а может только ухудшить его В данном случае теневая цена
+44,44 показывает, что увеличение правой части данного ограничения приведет к уве-
личению оптимальной стоимости тонны смеси Допустимое увеличение 2,375 означа-
ет, что при увеличении исходного показателя 5 на любое количество вплоть до 2,375
прирост стоимости составит 44,44, умноженное на данное количество
МЕНЕДЖЕР. Иными словами, одна и та же теневая цена действует как при увеличении, так
и при уменьшении правой части ограничения Таким образом, данная теневая
цена — это коэффициент изменения значения целевой функции при измене-
нии правой части в пределах всего допустимого диапазона
РАЗРАБОТЧИК. Да, и ослабление ограничения не только не приводит к ухудшению оптимального зна-
чения целевой функции, но и может его улучшить А усиление ограничения, не приво-
дя к улучшению оптимального значения целевой функции, может его ухудшить
МЕНЕДЖЕР- Мы уже говорили, что теневая цена элемента В равна нулю, это означает, что
любые отклонения В от значения 100 в пределах указанного диапазона никак
не повлияют на оптимальное значение целевой функции Раз ограничение по
В никак не влияет на решение, нельзя ли от него отказаться?
РАЗРАБОТЧИК. Я думаю, что нет Если когда-нибудь вы захотите изменить некоторые данные и
повторно найти решение задачи, ограничение по элементу В может стать лимити-
рующим. Например, значение допустимого прироста в данном случае составляет
31,67, а это значит, что если правая часть ограничения превысит 131,67, данное ог-
раничение станет лимитирующим Таким образом, удалять его из модели нельзя.
МЕНЕДЖЕР. Нельзя ли объяснить более понятно9
РАЗРАБОТЧИК. Хорошо. Предположим, что стоимость руды из месторождения 2 может возрасти
242 ЧАСТЬ II. Оптимизационные модели
МЕНЕДЖЕР. Должен признаться, я думал о подобной возможности Но как можно учесть
такую неопределенность9
РАЗРАБОТЧИК. Это связано с предыдущим вопросом. Стоимость руды из месторождения 2 — это
коэффициент при Т2 в целевой функции; в настоящий момент он имеет значение
400 Если эта стоимость возрастает, следует ожидать, что оптимальная ми-
нимальная стоимость также будет возрастать Если стоимость руды из место-
рождения 2 возрастет значительно, может получиться, что в оптимальной сме-
си этой руды станет меньше или даже не окажется вовсе Это означает, что бу-
дет использоваться больше других руд Следовательно, относительная важность
ограничений может измениться Ограничения, которые ранее были лимитирую-
щими, могут перестать быть таковыми, и наоборот Много всего может про-
изойти, когда вы начнете варьировать параметры модели
МЕНЕДЖЕР. Прекрасно Однако я так и не понял, какое отношение это имеет к стоимости
руды из месторождения 29
РАЗРАБОТЧИК. Рассмотрим стоимость руды из месторождения 2 На самом деле мы хотим оп-
ределить, в каком диапазоне она может изменяться, чтобы это не отразилось на
составе оптимальной смеси Обратимся к таблице Изменяемые ячейки отчета
по устойчивости, в которой есть столбцы Допустимое увеличение и Допус-
тимое уменьшение Значения в этих столбцах, соответствующих переменной
Т2, задают диапазон, в котором можно варьировать стоимость Т2 так, чтобы
это не привело к изменению состава оптимальной смеси
МЕНЕДЖЕР. Иными словами, в настоящий момент стоимость Т2 в нашей модели составляет
$400, и отчет по устойчивости свидетельствует, что для значений стоимости Т2
в пределах от $100 до $466,85 оптимальные решения останутся прежними Та-
ким образом, если цена возрастет с $400 до $450, нам не о чем беспокоиться
РАЗРАБОТЧИК. Не совсем так Мы знаем, что оптимальный состав смеси останется прежним
Это означает, что прежними останутся оптимальные значения всех переменных
Однако общая стоимость возрастет на величину, равную произведению 350 и зна-
чения Т2 в данном решении
МЕНЕДЖЕР. Значит, оптимальное значение целевой функции изменится с $511,11 до 511,11
+ 50x0,704 = $546,31, т е в данном диапазоне все останется неизменным, кро-
ме общей стоимости Интересно, а что произойдет, если стоимость Т2 увели-
чится назначение, которое превысит допустимое9
РАЗРАБОТЧИК. Как известно, в модели минимизации увеличение стоимости компонента не мо-
жет привести к увеличению его использования Поэтому при возрастании стои-
мости Т2 оптимальное значение Т2 увеличиться не может
МЕНЕДЖЕР. Таким образом, если удельная стоимость руды из шахты 2 вырастет более чем
на допустимое количество, мы получим оптимальное решение, в котором зна-
чение Т2 будет меньше или равно исходному
РАЗРАБОТЧИК. Да, и не только это Оптимальные значения некоторых других переменных также
могут измениться, но нельзя сказать, каких именно и на сколько Это означает,
что превышение, которое было положительным, может стать равным нулю, и,
следовательно, нелимитирующее ограничение может стать лимитирующим, и
наоборот
МЕНЕДЖЕР. Вы говорите об изменениях стоимости, превышающих допустимое значение
А что будет, если изменение в точности равно предельно допустимому9
РАЗРАБОТЧИК. Тогда появятся альтернативные оптимальные решения текущее решение и новые
решения с меньшим значением Тг
ГЛАВА 4. Линейная оптимизация Анализ чувствительности
243
РАЗРАБОТЧИК.
МЕНЕДЖЕР.
РАЗРАБОТЧИК.
МЕНЕДЖЕР.
РАЗРАБОТЧИК.
РАЗРАБОТЧИК.
МЕНЕДЖЕР. По-моему, это очень важная информация Я даже удивлен тем, как много
можно узнать о модели
РАЗРАБОТЧИК. Это происходит благодаря простоте вычисления данных по устойчивости реше-
ния для линейных моделей Разрешите в качестве проверки задать один вопрос
Как вы уже заметили, оптимальное значение Т4 равно нулю, предположим, что
стоимость Т, периодически может пересматриваться На сколько должна сни-
зиться цена Т4, чтобы вы захотели приобрести эту руду7
МЕНЕДЖЕР. Давайте посмотрим Текущее значение стоимости Т4 составляет $500 за тонну
Я думаю, что вопрос должен звучать так на сколько необходимо снизить данную
стоимость, чтобы получить оптимальное решение, в которое войдет переменная
Т49 Чтобы ответить на данный вопрос, обратимся к отчету по устойчивости, из
которого видно, что если стоимость Т4 снизится менее, чем на $91,11, оптималь-
ное значение данной переменной останется неизменным, т е нулевым Из этого
можно сделать вывод, что если снизить стоимость до значения меньше 408,89,
у модели будет новое оптимальное решение, в котором значение Т4 положитель-
но Однако что будет, если стоимость снизится ровно на $91,119 Вы сказали, что
в этом случае значение Т4 станет положительным Так ли это9
Не совсем В этом случае будет два оптимальных решения текущее и новое, со-
держащее положительное значение Т4 и новые значения других переменных реше-
ния Но какими станут значения других переменных, мне неизвестно
Не означает ли это, что при уменьшении стоимости Т4 на $91,11 общая стои-
мость внезапно снизится и станет меньше $511,119
Нет, поскольку оптимальное значение целевой функции будет равно $511,11 для
каждого решения
Можно ли узнать, каково значение Т4 для альтернативной смеси9
Можно, но не из отчета по устойчивости Все, что известно, — данная перемен-
ная будет иметь некое положительное значение Чтобы узнать ее точное значе-
ние нужно повторно решить задачу для значения стоимости Т4, уменьшенного на
величину, едва превышающую $91,11
И последний вопрос Что означает в отчете по устойчивости столбец с назва-
нием Нормированная стоимость9
Смысл имеют только ненулевые элементы нормированной стоимости Для пере-
менной решения, оптимальное значение которой равно нулю, существуют две эк-
вивалентные интерпретации ее нормированной стоимости В модели минимиза-
ции, такой как наша, нормированная стоимость, во-первых, показывает, на
скочько следует уменьшить удельную стоимость данной переменной решения,
чтобы оптимальное значение этой переменной стало ненулевым Во-вторых, это
теневая цена ограничения неотрицательности для данной переменной решения
Вспомним, что если переменная решения равна нулю, то ограничение неотрица-
тельности для данной переменной является лимитирующим, тогда, согласно оп-
ределению теневой цены, нормированная стоимость представляет собой коэффи-
циент ухудшения оптимального значения целевой функции в случае, если мы от-
вергнем решение, предложенное средством Поиск решения, и заставим данную
переменную принимать положительные значения, увеличив правую часть ограни-
чения неотрицательности
Первую интерпретацию нормированной стоимости иногда называют интерпре-
тацией вознаграждения — на сколько должна улучшиться данная удельная стои-
мость, чтобы Поиск решения увеличил соответствующую переменную решения
до положительного значения с целью понизить общую стоимость Вторую интер-
претацию нормированной стоимости иногда называют интерпретацией штра-
фа — на сколько испортится решение, если заставить Поиск решения увеличить
данную переменную решения до положительного значения
МЕНЕДЖЕР.
244 ЧАСТЬ II Оптимизационные модели
МЕНЕДЖЕР. Первая интерпретация относится к изменениям коэффициентов целевой функции,
а мы только что рассмотрели аналопшный вопрос для переменной Т4 В отчете по
устойчивости я вижу одно и то же значение 91,11 в столбце Допустимое уменьше-
ние и Нормированная стоимость Зачем нужен столбец Нормированная стои-
мость, если то же самое значение содержится в столбце Допустимое уменьшение9
РАЗРАБОТЧИК. Действительно, первая интерпретация нормированной стоимости связывает ее с из-
менениями коэффициентов целевой функции, поэтому одинаковые числа всегда содер-
жатся в столбце нормированной стоимости и в первом или втором столбце допусти-
мых изменений Однако размещение данных о нормированной стоимости в том же
столбце отчета по устойчивости, в котором находятся теневые цены, напоминает о
второй интерпретации, которая рассматривает нормированную стоимость в каче-
стве теневой цены Вы можете выбрать ту интерпретацию, которая вам удобней
МЕНЕДЖЕР. Спасибо, наша беседа была весьма плодотворной
4.11.	Характеристика отчета по устойчивости
После оптимизации модели линейного программирования таблица модели и отчет по
устойчивости средства Поиск решения содержат следующую информацию.
1.	Оптимальные значения переменных решения, значения резерва и излишка (раз-
ности между значениями левых и правых частей ограничений), а также значение
целевой функции. Ограничения с нулевым резервом или излишком называются
лимитирующими, они препятствуют дальнейшему улучшению целевой функции.
Ограничения с положительным значением резерва или излишка называются нели-
митирующими
2.	Теневая цена в отчете по устойчивости отражает коэффициент изменения опти-
мального значения целевой функции при увеличении правой части ограничения.
Допустимые увеличение и уменьшение задают допустимый диапазон изменений
правой части, в котором теневая цена сохраняет свое значение.
3.	Допустимые увеличение и уменьшение для коэффициентов целевой функции пока-
зывают, какие изменения можно вносить в коэффициенты целевой функции, чтобы
это не привело к изменению оптимального решения Если значение изменения ко-
эффициента целевой функции равно допустимому, это приведет к появлению аль-
тернативного оптимального решения с новыми значениями переменных (при усло-
вии невырожденности). Если изменение коэффициента превышает допустимое, оп-
тимальное решение изменится (также при условии невырожденности).
4.	Строго говоря, нормированная стоимость имеет смысл только для тех переменных
решения, оптимальное значение которых равно 0. В таком случае данный элемент
можно интерпретировать как теневую цену ограничения неотрицательности для
данной переменной (если такое ограничение существует); он содержит ту же ин-
формацию, что и допустимое увеличение или уменьшение для данной перемен-
ной Если значения как нормированной стоимости, так и переменной решения
ненулевые, это значит, что существует ограничение для данной переменной, кото-
рое является лимитирующим, и нормированная стоимость — теневая цена дан-
ного лимитирующего ограничения, а не ограничения неотрицательности."
Различные интерпретации нормированной стоимости также рассматриваются в разделе 4.12.
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 245
5.	В отчете по устойчивости не исследуются изменения технологических коэффици-
ентов или поведения модели, выходящие за пределы допустимого уменьшения или
увеличения. Подобную информацию можно получить с помощью средств, подоб-
ных надстройке SolverTable, которые позволяют зафиксировать данные, получен-
ные при повторных оптимизациях модели.
4.12.	Использование отчета по устойчивости
Рекомендованные нами в главе 3 принципы построения табличных моделей линейного
программирования несколько ограничены и порой приводят к созданию недостаточно
компактных таблиц, с которыми неудобно работать. Здесь мы покажем более компактное и
удобное табличное представление моделей ЛП (которое используется в транспортной зада-
че (см. главу 3) и в моделях ЛП в начале следующей главы). Но за достоинства данного
представления придется платить; необходимо потренироваться и быть более внимательным
при построении модели, а особенно — при интерпретации отчета по устойчивости средства
Поиск решения, чтобы избежать ряда ловушек. Однако вы уже достаточно освоились с эта-
пами формирования табличной модели ЛП и интерпретацией отчета по устойчивости, что-
бы воспринять эти дополнительные требования Лучше всего новую форму модели и ее ин-
терпретацию показать на простом примере.
Уэйн Фоли, недавно назначенный управляющим нового филиала кредитно-
финансовой компании Friendly Loan Company, полон страстного желания произвести
впечатление на своего босса, умело распорядившись 15-миллионным годовым бюдже-
том Каждый филиал компании Friendly извлекает прибыль, получая проценты по трем
типам ссуд: ипотечная ссуда на покупку недвижимости под 7% годовых, кредит на по-
купку мебели под залог приобретаемой мебели под 12% годовых и беззалоговая ссуда под
15% годовых Кредиты без обеспечения наиболее рискованные, поэтому для них уста-
новлена самая высокая процентная ставка.
Центральный офис компании установил для управляющих филиалами ограничения
на кредиты с высоким риском. Компания требует, чтобы не менее 60% ссуд составляли
ипотечные ссуды и не более 10% — ссуды без обеспечения (с высоким риском) Исполь-
зуя заданные процентные ставки, учитывая ограничения и то, что общий годовой бюджет
его филиала составляет $15 млн., Уэйн построил модель ЛП, представленную на рис 4 27
(на этом рисунке показаны сама модель, ее формулы, диалоговое окно Поиск решения
и оптимальное распределение имеющихся средств).
Отметим некоторые особенности модели Уэйна Во-первых, она компактна, в ней нет
вычислений значений левых частей ограничений, кроме того, для удобства ограничения
расположены в непосредственной близости от величин, на которые они влияют. Во-
вторых, фон всех пустых ячеек сделан темным, что помогает сконцентрировать внимание
на значимых частях модели. Наконец, в модели Уэйна некоторые ячейки выполняют
двойную функцию: содержат значение правой части ограничения и знак неравенства
Например, как следует из приведенной на рис. 4.27 формулы, ячейка G5 на самом деле
содержит данные о бюджете $15 млн. Знак “<=”, присутствующий в ячейке G5, не явля-
ется ее содержимым, это часть спецификации формата данной ячейки. Такой формат по-
зволяет отображать вместе с содержимым ячейки заданные пользователем строки симво-
лов, например, символы валюты. Аналогичное форматирование было применено и для
содержащих формулы ячеек С6 и F6. (Более подробно форматы описаны в приложе-
нии Б.) Кроме того, Уэйн ввел в ячейку G7 формулу вычисления среднего дохода кре-
246 ЧАСТЬ II. Оптимизационные модели
дитного портфеля (=F4/G5). Прежде чем продолжить работу, следует проверить, пра-
вильно ли модель отражает все три ограничения, касающиеся размера бюджета, ссуд без
обеспечения и ипотечных ссуд.
Рис. 4.27. Модель портфеля кредитов филиала компании Friendly
На основе решения данной задачи можно дать рекомендации выдать ссуды на сумму
$15 млн в следующих пропорциях. $9 млн. — ипотечные ссуды, $1,5 млн. — кредиты без
обеспечения и оставшиеся средства — ссуды под залог мебели. При этом суммарный го-
довой процентный доход должен составить $1 395 000. Вычисление в ячейке G7 показы-
вает, что средняя прибыль кредитного портфеля составляет 9,3%. Уэйн также заметил,
что все три ограничения модели являются лимитирующими (два ограничения по типам
ссуд и бюджетное ограничение).
Желая применить на практике свои недавно полученные знания по моделям линей-
ного программирования, Уэйн обратился к отчету по устойчивости, сгенерированному
средством Поиск решения (рис 4 28) и, посмотрев на теневую цену бюджетного ограни-
чения, сразу же бросился звонить своему начальнику, чтобы попросить его увеличить
бюджет Начальник был удивлен тем, что Уэйн обещает получить 12% прибыли с допол-
нительно выделенных средств, в то время как никто из остальных управляющих филиа-
ГЛАВА 4. Линейная оптимизация Анализ чувствительности 247
лами не может добиться более 9,33%. “Это потому, что они не разбираются в оптимиза-
ции, маргинальном анализе и роли теневых цен!” — ответил Уэйн. Начальник не стал ос-
тужать энтузиазм нового управляющего и спросил, сможет ли Уэйн получить 12% при-
были с дополнительных $5 000 000. Быстро проверив значение допустимого увеличения
для бюджетного ограничения, Уэйн попросил босса прислать его филиалу все $5 000 000
и даже больше.
Изменяемые ячейки
Ограничения
Ячейке	Имя	значение	Теневая Ограничение Допустимое Допустимое Цена Правая часть УвеличениеУменьшение
SFS5 О,	/мма займов Всего	$15 000	$0	15000	1Е+Э0	4500
Рис. 4.28. Отчет по устойчивости для модели филиала компании Friendly
Однако, повесив трубку, Уэйн ощутил некие сомнения- “В модели помимо ограниче-
ний неотрицательности было три ограничения Что же случилось в отчете по устойчиво-
сти с лимитирующими ограничениями для двух типов ссуд? Вместо одного там должно
быть три ограничения вместе с соответствующими теневыми ценами” Поскольку его
беспокойство росло, он решил проверить информацию отчета по устойчивости, введя
новое значение бюджета 20 000 в ячейку G5 Запустив Поиск решения для нового значе-
ния правой части ограничения, он получил результаты, показанные на рис 4 29 Уэйн
был шокирован, когда увидел, что средняя прибыль в ячейке G7 для новой модели оста-
лась неизменной и составила 9,3%. Поскольку удельная прибыль для дополнительных
$5 млн. составляет 12%, он ожидал, что средняя прибыль его портфеля также возрастет
Больше не доверяя ни средству Поиск решения, ни Excel, Уэйн схватил свой кальку-
лятор и, разделив разность двух значений суммарного процентного дохода, полученных
с помощью Поиск решения, на прирост бюджета ((1860—1395)/5000) увидел, что
удельная прибыль для дополнительных $5 млн. в действительности составляет 9,3%, а не
12%. Он скептически посмотрел на теневую цену бюджетного ограничения и допусти-
мый диапазон в новом отчете по устойчивости на рис. 4.29 и пришел к выводу, что про-
грамма дважды обманула его. В смущении Уэйн подошел к телефону, чтобы сообщить
начальнику о своей ошибке
Что же произошло7 Может быть, данные были неверно масштабированы, что привело
к неправильным отчетам средства Поиск решения? Или же Поиск решения действитель-
но дает неверные результаты для некоторых моделей7 Если это не так, как объяснить
значение 0,120 теневой цены бюджетного ограничения на рис. 4.28 и 4 297 И что случи-
лось с информацией о теневой цене для двух других ограничений, которая почему-то от-
сутствует в обоих отчетах по устойчивости?
248	Ч А С Т Ь II Оптимизационные модели

Бюджет
$20 000 <=$20 000
>=$12 000
Ср. ДОХОД
9.30%
У
FRIENDLY LOAN COMPANY (суммы В тыс. $)
Без обеспечения Под залог мебел| Ипотечный Всего
15%________________12%__________7%
|	$2 000	$6000	$12 000
s=$2 000
10%
3- Тип займов
•-Д/- Процентная ставка
1Е. СУмма займов	[
'6	Предельная сумма займов, $
7	Предельная сумма займов %
Microsoft Excel 10 0 Отчет по устойчивости Изменяемые ячейки				
Ячейка	Имя	значениеi	Нормир стоимость	Целевой Допустимое Допустимое Коэффициент Увеличение Уменьшение	
$С$5__ Сумма займов Без обеспечени	$2 000	0,03	0.15	1Е«30	0,03
$D$5 QjMMa займов Под залог мебе.	$6 000		0.00			0.12	ДОЗ	_ 0.05
$Et5 Сумме займов Ипотечный	—	-005	007	0.05	~lE*30
Ограничения				
Ячейка	Имя	Результ значение	Теневая	Ограничение Допустимое Допустимое Правая часть Увеличение Уменьшение	
SFJ5 Сумма займов Всего	$20 000	10	20000	1Е-30	1Е-30
Рис. 4.29. Модель филиала компании Friendly для бюджета 20 млн. долл.
Хотя подобное подозрение заслуживает внимания, в данном случае диапазон значе-
ний параметров модели недостаточно велик, чтобы привести к ошибкам в работе средст-
ва Поиск решения, что могут подтвердить результаты повторной оптимизации (нужно
установить опцию Автоматическое масштабирование в диалоговом окне Параметры
поиска решения и повторно выполнить оптимизацию). Чтобы разобраться, что про-
изошло на самом деле, переформируем модель, используя рекомендованные в главе 3
правила представления В результате получим оптимальное решение и отчет по устойчи-
вости (рис. 4 30)
Как показано на рис 4 27 и 4 30, обе формулировки задачи ЛП приводят к одним и
тем же оптимальным решениям по ссудам и одинаковому значению суммарного про-
центного дохода. Различия возникли в отчетах по устойчивости и их интерпретации Рас-
смотрим результаты работы модели ЛП, построенной согласно изложенным в главе 3
правилам. Во-первых, на рис. 4 30 в отчете по устойчивости присутствуют все три огра-
ничения, а также связанные с ними теневые цены и допустимые диапазоны изменений
правых частей Во-вторых, теневая цена бюджетного ограничения на рис. 4.30 имеет пра-
вильное значение 9,3%. В-третьих, те из вас, кто ознакомился уже с вопросами вырожде-
ния моделей ЛП, изложенными в разделе 4.13, могут заметить, что решения обеих задач
являются невырожденными (в чем легко убедиться, подсчитав на рис. 4.30 общее количе-
ство ненулевых переменных решения (равно 3) и сравнив его с числом ограничений
(также равно 3)). В-четвертых, в отличие от отчета по устойчивости первой модели Уэй-
на, в столбце Нормированная стоимость на рис. 4.30 правильно указаны нулевые значе-
ния для всех трех переменных решения, поскольку ни одна из них не равна нулю, т.е. ни
одно изограничений неотрицательности не является лимитирующим.
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 249
Рис. 4.30. Новая модель кредитного портфеля филиала компании Friendly
Из этого следует, что отчет по устойчивости для исходной модели Уэйна на
рис. 4 28 (с пропущенными теневыми ценами и диапазонами, неправильными данными
о нормированной стоимости и неверной теневой ценой бюджетного ограничения) со-
вершенно неудовлетворителен, а для стандартной формулировки задачи ЛП на рис 4 30
составлен вполне нормальный отчет С другой стороны, табличное представление Уэйна
на рис. 4 27 значительно легче понимать и интерпретировать, чем рекомендуемую фор-
мулировку задачи на рис. 4.30. Похоже, у нас нет выбора: удобное и компактное пред-
ставление приводит к неверным результатам в отчете по устойчивости, а корректную ин-
формацию о чувствительности решения можно получить только с помощью громоздкой
модели. Однако это не так обе модели совершенно корректны, и ошибок в отчетах по ус-
тойчивости нет. Таким образом, можно воспользоваться преимуществами более удоб-
ного представления и в то же время не получить ошибок в отчете по устойчивости Но
250 ЧАСТЬ II Оптимизационные модели
для этого требуется более глубокое понимание работы средства Поиск решения, чем есть
у Уэйна Итак, чтобы разрешить данный “парадокс”, рассмотрим более детально, как ра-
ботает средство Поиск решения
Простые ограничения
Сколько времени и машинной памяти потребуется средству Поиск решения для оп-
тимизации модели, определяется, главным образом, размерами матрицы коэффициен-
тов, составляющих левые части ограничений (например, содержащихся в ячейках C7:F9
на рис 4 30) Размерность матрицы коэффициентов ограничений вычисляется как про-
изведение числа переменных решения (столбцов) и числа ограничений (строк). Умень-
шив любое изданных чисел, можно уменьшить размер матрицы и, следовательно, сокра-
тить время оптимизации. Поиск решения включает в себя процедуру, которая позволяет
обрабатывать любые простые ограничения, где участвует только одна переменная реше-
ния (кроме ограничений неотрицательности), не рассматривая их как ограничения. Это
позволяет сделать матрицу коэффициентов меньше, сократить время оптимизации и по-
требность в оперативной памяти компьютера, или, что то же самое, позволяет на том же
компьютере оптимизировать модели ЛП большей размерности Платой за использование
этой возможности обработки простых ограничений является потеря некоторой инфор-
мации в отчете по устойчивости. Единственной информацией для всех простых ограни-
чений в этом отчете будут их теневые цены, которые не сопровождаются данными о диа-
пазонах их применимости
Поскольку, как правило, только одно простое ограничение может быть лимитирую-
щим для определенной переменной решения в точке оптимальности, а информация
о диапазоне отсутствует, для компактности отчета по устойчивости соответствующая не-
нулевая теневая цена простого ограничения (если таковая имеется) указывается после
своей переменной решения. Столбец Нормированная стоимость отчета по устойчивости
всегда содержит по одной ячейке для каждой переменной решения, поэтому Поиск ре-
шения помещает ненулевую теневую цену простого ограничения в столбец Нормирован-
ная стоимость после соответствующей переменной решения. Например, теневые цены
двух ограничений для типов ссуд указаны на рис. 4.30 в стандартном виде и составляют
3% для ограничения на ссуды без обеспечения и -5% для ограничения ипотечных ссуд
Те же самые значения представлены на рис. 4.28 в отчете для модели Уэйна в столбце
Нормированная стоимость сразу после соответствующих переменных решения. По-
скольку для каждой из двух переменных решения в модели ЛП задано по два ограниче-
ния, сразу непонятно, какие из них являются лимитирующими, и каким из них соответ-
ствуют ненулевые значения в столбце Нормированная стоимость отчета по устойчиво-
сти для модели Уэйна.
Для ссуд без обеспечения задано простое ограничение неотрицательности и простое
ограничение вида < $1500. Однако эти ограничения не могут быть лимитирующими од-
новременно В данном случае лимитирующим является второе ограничение; таким обра-
зом, число 0,03 в столбце Нормированная стоимость отчета для модели Уэйна должно
быть теневой ценой ограничения “Сумма ссуд без обеспечения <$1500”. Поскольку ог-
раничение “Сумма ссуд без обеспечения >0” не является лимитирующим, его теневая
цена должна быть нулевой.
Ддя переменной решения, определяющей сумму ипотечных ссуд, также задано два
ограничения “Сумма ипотечных ссуд > 0” и “Сумма ипотечных ссуд > 9000”, причем они
не могут быть лимитирующими одновременно. Поскольку значение данной переменной
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 251
решения составляет $9000, теневая цена в столбце Нормированная стоимость отчета для
модели Уэйна соответствует лимитирующему простому ограничению “Сумма ипотечных
ссуд > 9000” Поскольку второе ограничение (“Сумма ипотечных ссуд > 0”) лимитирую-
щим не является, его теневая цена равна нулю.
Таким образом, информация о теневой цене не теряется при использовании простых
ограничений в моделях ЛП, мы выяснили, где ее искать и как определить, какому огра-
ничению соответствует конкретное ненулевое значение теневой цены Поскольку зада-
ние простых ограничений на переменные решения приводит к более удобному представ-
лению таблицы и позволяет быстрее находить решение задачи (что немаловажно для мо-
делей больших размеров), их достаточно активно используют при формировании
табличных моделей ЛП. Однако следует помнить, что использование простых ограниче-
ний приводит к тому, что в отчете по устойчивости нарушается стандартная интерпрета-
ция нормированной стоимости, данная в разделе 4.10
Напомним, что в одной из интерпретаций нормированная стоимость переменной ре-
шения рассматривается как теневая цена ограничения неотрицательности для данной
переменной В моделях ЛП, содержащих простые ограничения, числа в столбце Норми-
рованная стоимость соответствуют теневым ценам тех ограничений, которые являются
лимитирующими для указанных переменных решения. В приведенной ниже таблице
представлена более сложная картина того, какими могут быть значения нормированной
стоимости в моделях ЛП, содержащих простые ограничения
Ограничение на переменную в точке оптимума	Нормированная стоимость, модель максимизации	Нормированная стоимость, модель минимизации
Лимитирующее простое ограни- чение вида >	Нулевая или отрицательная теневая цена	Нулевая или положительная те- невая цена
Лимитирующее простое ограни- чение вида <	Нулевая или положитель- ная теневая цена	Нулевая или отрицательная те- невая цена
Ни одно из ограничений не яв- ляется лимитирующим	Нулевая Теневая цена	Нулевая теневая цена
Есть ли возможность получить из отчета по устойчивости информацию о допустимых
диапазонах правых частей простых ограничений? К сожалению, нет. Если возможно,
Поиск решения всегда представляет отчет по устойчивости в такой форме, как на
рис. 4.30. Если информация о диапазонах правых частей простых ограничений важна,
необходимо перестроить табличное представление модели ЛП так, чтобы средство Поиск
решения не смогло обнаружить наличие в модели простых ограничений и повторно оп-
тимизировать полученную модель. Поиск решения не вызывает свою процедуру обра-
ботки простых ограничений, если они заданы в таблице неявно Для этого можно ис-
пользовать некоторую промежуточную формулу, как, например, на рис 4 30 формулы
в ячейках G7:G9, каждая из которых связывает переменную решения с ее правой частью
неравенства посредством значений трех ячеек, содержащих коэффициенты левых частей
ограничений. Если же Excel обнаружит в диалоговом окне Поиск решения адрес любой
из изменяемых ячеек в поле Ограничения (за исключением ограничений неотрицатель-
ности), будет вызвана специальная процедура обработки простых ограничений Напри-
мер, в модели Уэйна на рис. 4.27 адреса изменяемых ячеек С5 и Е5 для первых двух огра-
ничений перечислены в поле Ограничения диалогового окна Поиск решения, что при-
водит к вызову процедуры обработки простых ограничений
252	Ч А С Т Ь II. Оптимизационные модели
Интерпретация теневой цены
Как уже отмечалось, значение теневой цены бюджетного ограничения в модели Уэйна,
равное 0,120, оказалось неверным; более того, именно его интерпретация теневой цены
стала причиной всех неприятностей Уэйна. Заметим, что модель на рис. 4.27 содержит
формулы в правой части ограничений, задающих предельные значения для ссуд без обеспе-
чения и ипотечных ссуд, что является нарушением одной из рекомендаций по созданию
табличного представления (см главу 3). Напомним определение теневой цены: это измене-
ние оптимального значения целевой функции при изменении правой части заданного огра-
ничения на единицу, когда все другие параметры, включая правые части других ограниче-
ний, остаются постоянными Следовательно, теневую цену 0,120, содержащуюся в отчете
по устойчивости на рис 4.28, следует интерпретировать так: если зафиксировать правые
части ограничений, задающих предельные значения для ссуд без обеспечения и ипотечных
ссуд, на исходном уровне $1500 и $9000 соответственно, то улучшение значения целевой
функции составит 0,12 для каждого дополнительного бюджетного доллара.
Если оставить суммы ссуд без обеспечения и ипотечных ссуд на исходном уровне, до-
полнительный бюджетный доллар в модели Уэйна может пойти только на ссуду под залог
мебели, процентная ставка для которой составляет 12%. Таким образом, программа По-
иск решения совершенно правильно указала теневую цену для модели Уэйна. Очевидно,
что фиксация правых частей для ссуд без обеспечения и ипотечных ссуд на исходном
долларовом уровне не согласуется с результатами повторного решения, в котором изме-
няются все правые части, чтобы отразить новые предельные значения, обусловленные
появлением дополнительного бюджетного доллара. Уэйн ошибочно предположил, что
ограничения на объемы ссуд будут соблюдаться в отчете по устойчивости для его модели,
но этого не произошло из-за наличия формул в правых частях двух ограничений
В формулировке задачи ЛП на рис. 4 30 ошибочной интерпретации удалось избежать,
поместив все формулы в левые части ограничений и оставив в правых частях одни кон-
станты Когда все формулы связи с бюджетом находятся в левых частях ограничений,
Поиск решения вносит необходимые изменения во все левые части при оценке удель-
ного вклада дополнительного бюджетного доллара В результате этого согласования ле-
вых частей формируется отчет по устойчивости (см. рис 4 30), в котором указано верное
значение теневой цены 0,093 Модель на рис. 4 30 отражает все ограничения компании
Friendly, которые Уэйн пытался представить в своей модели
Из данного примера можно сделать следующий вывод использование простых огра-
ничений, а также формул в правых частях ограничений в формулировке задач ЛП позво-
ляет сделать их табличные представления более компактными и понятными. Поэтому мы
будем широко использовать такие представления моделей ЛП в последующих трех гла-
вах Однако следует помнить, что в таком случае потребуются дополнительные усилия
для извлечения необходимой для принятия решений информации из отчета по устойчи-
вости, сгенерированного средством Поиск решения.
4.13.	Вырождение моделей АП
Для оптимизации моделей линейного программирования средство Поиск решения
использует симплекс-метод, разработанный для решения моделей, содержащих только
ограничения в форме равенств Для приведения модели ЛП, содержащей ограничения-
неравенства, к нужному виду в модель вводятся новые внутренние переменные, назы-
ваемые переменными резерва и излишка. В качестве примера рассмотрим упрощенную мо-
дель Oak Products из главы 3.
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 253
Максимизировать 56С + 40 М
при ограничениях	8С + 4М< 1280,
4С+ 12Л/< 1600,
С + М> 100,
4С + 4Л/<760,
С< 140,
М< 120,
С>0иЛ/>0,	(411)
где С — количество произведенных и проданных стульев Captain, М— количество произ-
веденных и проданных стульев Mate
В этой модели ЛП две переменные решения и шесть ограничений (не считая ограни-
чения неотрицательности), одно из них вида > и пять — вида < Чтобы преобразовать
данную модель в модель, все ограничения которой имеют форму равенств, программа
Поиск решения прибавит переменные резерва к первому, второму, четвертому, пятому и
шестому ограничениям (ограничениям вида <) и вычтет переменную излишка из третьего
ограничения (ограничения вида >) Обозначим шесть новых переменных а,, у,,	s4, s5 и s6.
Тогда модель, оптимизируемая программой Поиск решения, будет выглядеть так
максимизировать 56С + 40 М
при ограничениях	8С+ 4Л/+ л, = 1280,
4С+ 12Л/ + s2 = 1600,
C+M-s,= 100,
4С + 4Л/+ = 760,
C + s5= 140,56
Л/ + а6= 120,
С, М, 5,, s2, s3, st, s„ s> 0	(4 12)
Отметим, что добавленные ограничения неотрицательности для новых переменных за-
ставляют их принимать только нулевые или положительные значения Таким образом, пе-
ременные резерва (излишка) представляют дополнительные количества, которые необхо-
димо прибавить (вычесть) клевым частям, чтобы превратить неравенства в равенства.
Итак, мы показали следующее.
( Любое ограничение вида < можно преобразовать в равенство, добавив к его к левой час-
ти новую неотрицательную переменную резерва.
i Любое ограничение вида > можно преобразовать в равенство, вычтя из его левой части
новую неотрицательную переменную излишка.
Внутреннее представление модели по-прежнему содержит шесть ограничений, одна-
ко введение переменных резерва и излишка привело к увеличению числа переменных
решения до восьми вместо двух Заметим, что переменные резерва и излишка не входят
явным образом в целевую функцию, рассматриваемую программой Поиск решения Но
можно считать, что новые переменные включены в целевую функцию с нулевыми коэф-
фициентами.
254 ЧАСТЬ II Оптимизационные модели
Оптимальные значения переменных резерва и излишка
В разделе 4 2 графическим методом было показано, что оптимальным решением зада-
чи (4 11) является С — 130 и Л/ = 60 Это означает, что оптимальные значения новых пе-
ременных в модели (4 12) с ограничениями-равенствами будут такими:
<	= 1280 - (8С + 4Л/) = 1280 - (1040 + 240) = 0,
s2'= 1600 - (4С‘ + 4Л/) = 1600 - (520 + 240) = 840,
<	= (С + М') - 100 = 130 + 60 - 100 = 90,
s4' = 760 - (4С + 4Л/‘) = 760 - (520 + 240) = 0,
<	= 135- С = 135 - 130 = 5,
<	= 120 - М' = 120-60 = 60.
Вспомним, что ограничение, для которого в точке оптимальности левая часть нера-
венства равна правой, называется лимитирующим. Для упрощенной модели ДП Oak
Products связывающими ограничениями являются первое и четвертое. Приведенные вы-
ше вычисления показывают, что соответствующие им переменные резерва 5,’ и s4’ равны
нулю Остальные ограничения нелимитирующие и их переменные резерва/излишка яв-
ляются положительными Можно обобщить данное наблюдение.
Лимитирующие ограничения — такие ограничения, для которых оптимальные значе-
ния переменных резерва или излишка равны нулю.
Нелимитирующие ограничения — такие ограничения, для которых оптимальные зна-
чения переменных резерва или излишка являются положительными.
В частности, если в точке оптимальности некое ограничение имеет нулевое значение
переменной резерва или излишка, это означает, что решение задачи лежит на прямой
данного ограничения С геометрической точки зрения можно также обнаружить свойст-
во, важное для правильной интерпретации отчета по устойчивости программы Поиск
решения Это свойство касается числа положительных переменных в любой угловой
точке (и, в частности, в оптимальной угловой точке) множества ограничений Все пере-
менные (переменные решение и переменные резерва и излишка) должны принимать не-
отрицательные значения. Покажем, что в любой угловой точке множества ограничений
(и, в частности, в оптимальной угловой точке) максимальное количество положительных
переменных среди всех переменных решения, резерва и излишка не превышает число ог-
раничений модели (не учитывая ограничения неотрицательности).
Проиллюстрируем это свойство на следующей модели.
Максимизировать х, + х2
при ограничениях
8х, + 7х2 < 56,	®
-6х,- 10х2>—60,	®
х, < 6,	®
-х,+х2<6,	®
х„х2>0.	(4 13)
Множество ограничений данной модели изображено на рис. 4 31, линии ограничений
снабжены метками от (1) до (4) в соответствии с номерами ограничений в модели (4.13).
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 255
Рассмотрим ту же самую модель, приведенную к виду, содержащему ограничения
только в форме равенств.
Макси мизироватьх, + х2
при ограничениях
8х, + 7х2 + s, = 56,	Ф
—6х, — 10х2 + т2 = —60,	@
X, + т, = 6,	®
-X, + х2 + 54 = 6,	Ф
х„ х2, 5„ s2, s5, s4 > 0.	(4 14)
Исходная модель содержала четыре ограничения и две переменные Форма модели
с ограничениями-равенствами содержит то же количество ограничений и шесть пере-
менных. Важно отметить, что, говоря о количестве переменных в модели с ограничения-
ми-равенствами, мы рассматриваем переменные резерва и излишка наравне с переменными
решения. Поскольку модель (4.14) содержит две переменные решения и четыре перемен-
ные резерва/излишка, в ней насчитывается шесть переменных. При подсчете количества
ограничений ограничения неотрицательности не учитываются.
Геометрическое представление модели (4.14) выглядит почти так же, как и (4 13),
единственное отличие заключается в том, что каждое ограничение будет снабжено мет-
кой соответствующей ему переменной резерва или излишка Это представление показано
на рис 4.32, где для удобства римскими цифрами обозначено пять угловых точек и отме-
чено несколько точек, которые будут представлять для нас интерес.
256 ЧАСТЬ II Оптимизационные модели
Рис. 4.32. Множество ограничений модели (4.14)
Исследование рис 4 32 позволяет сделать некоторые выводы
1. В любой внутренней точке допустимой области все переменные положительны.
Это показывает произвольно взятая точка Р(1 на рис 4.32. В данном случае это точ-
ка с координатами х, = 1 и х2 = 1. Используя эти значения и ограничения (4.14),
можно вычислить значения s2, s2 и s4 в точке Р„ и убедиться, что все они положи-
тельны Однако прибегать к алгебраическим вычислениям нет необходимости, по-
скольку непосредственно из рисунка видно, что в точке Р„ все значения резервов
и излишков положительны.
2. В любой точке границы допустимой области по крайней мере одна переменная бу-
дет равна нулю. Это показывают точки Р, и Р2. Как показано на рисунке, в точке Р,
переменная х2 = 0, все остальные переменные положительны. Аналогично в точке
Р2, лежащей на линии ограничения, только 5, равна 0. Особый интерес представ-
ляют угловые точки допустимой области Например, поскольку угол, обозначен-
ный цифрой III, лежит на пересечении линий первого и третьего ограничений,
в этом углу две переменные, 5, и s2, равны нулю, а остальные положительны. Эти
примеры показывают, что нулевые значения на границе допустимой области могут
принимать как переменные решения, так и переменные резерва или излишка. На-
пример, в углу V нулевые значения принимает переменная решения х2 и перемен-
ная резерва s3
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 257
Положительные переменные и угловые решения
На основании сделанных заключений можно проиллюстрировать основной результат
данного раздела, подсчитав количество положительных переменных в каждом из пяти уг-
лов множества ограничений (табл. 4.1). В таблице показано, какие переменные положи-
тельны в каждой угловой точке и сколько таких переменных.
Таблица 4.1. Количество положительных переменных в угловых точках множества огра-
ничений
Угловая точка Нулевые переменные Положительные переменные	Количество положительных переменных
I	*1»*2	4
II	X„S2,S4	X2,5„S3	3
HI	X,,X2, S3, 54	4
IV	5„53	X„X2,S2,34	4
Напомним, что в модели (4.14) четыре ограничения. Таким образом, приведенные в
таблице данные подтверждают следующее общее положение
В любой модели ЛП, содержащей только ограничения-равенства, в каждой угловой
точке допустимой области количество положительных переменных меньше или равно
числу ограничений.
Данный результат имеет очень большое значение для решения задачи ЛП программой
Поиск решения Как отмечалось выше, если модель ЛП имеет оптимальное решение, то
всегда существует оптимальное угловое решение (при этом могут быть и неугловые оп-
тимумы). Симплекс-метод, используемый средством Поиск решения для оптимизации
моделей ЛП, всегда находит угловое оптимальное решение (если модель не является не-
ограниченной или недопустимой). Более того, симплекс-метод решает задачу в форме,
содержащей только ограничения-равенства, а для такой модели, как только что отмеча-
лось, число положительных переменных в любой угловой точке допустимого множества
(следовательно, и в оптимальной угловой точке) меньше или равно числу ограничений.
Теперь становится понятно, почему это свойство представляет такой интерес
: Решение задачи ЛП, найденное средством Поиск решения, всегда содержит не более т '
положительных переменных, где/и — число ограничений модели.
Практическая значимость последнего утверждения заключается в следующем.
Если решение, найденное средством Поиск решения, содержит менее т положительных
I переменных, такое решение называется вырожденным. В этом случае особое внимание i
 необходимо уделить интерпретации отчета по устойчивости средства Поиск решения.	.
Вырожденные решения
Поскольку случаи вырожденности представляют особый интерес, определим фор-
мально данное понятие. Угловая точка, в которой число положительных переменных
меньше, чем число ограничений (как точка II на рис. 4.32), называется вырожденной угла-
258 ЧАСТЬ II Оптимизационные модели
вой точкой'2. Остальные угловые точки I, 111, IV и V, в которых число положительных пе-
ременных в точности равно числу ограничений, называются невырожденными. Если оп-
тимальное решение некой задачи ЛП содержит менее т положительных переменных, оно
называется вырожденным решением, поскольку оно расположено в вырожденной угловой
точке. Решение с числом положительных переменных, в точности равным т, называется
невырожденным
Итак, мы выяснили, что Поиск решения оптимизирует модель в форме, содержащей
только ограничения-равенства. Важное свойство такой модели заключается в том, что
любое оптимальное решение, полученное средством Поиск решения, содержит не более
т положительных переменных, где т — число ограничений данной модели. Наконец, для
корректной интерпретации отчета по устойчивости, генерируемого средством Поиск ре-
шения, необходимо знать, является оптимальное решение вырожденным или нет.
Как правило, о вырожденности оптимального решения задачи ЛП сигнализирует то,
что в отчете по устойчивости одно из значений Допустимое увеличение или Допустимое
уменьшение для некоторого ограничения равно нулю. Когда оптимальное решение ока-
зывается вырожденным, возможны следующие ситуации.
1.	С помощью Поиск решения можно получить два решения, в которых оптималь-
ные значения переменных решения и целевой функции одинаковы, а значения
некоторых или всех нормированных стоимостей и/или теневых цен (и их диапазо-
нов) в отчетах по устойчивости различаются. Возникающая в итоге неоднознач-
ность может вызвать затруднения при интерпретации отчета по устойчивости по-
добной модели для практических целей.
2.	Может оказаться, что коэффициенты целевой функции должны измениться зна-
чительно сильнее, чем указывают приведенные в отчете об устойчивости значения
в столбцах Допустимое уменьшение и Допустимое увеличение, чтобы опти-
мальное решение переместилось в другую угловую точку.
3.	Наличие в отчете об устойчивости нулевых значений в столбцах Допустимое уве-
личение или Допустимое уменьшение для коэффициентов целевой функции не
является достоверным признаком существования альтернативных оптимальных
решений.
4.14. Заключение
В данной главе мы воспользовались возможностями двухмерного геометрического
представления моделей ЛП, чтобы проиллюстрировать некоторые важные концепции
линейного программирования. В частности, такой подход к решению задач ЛП с двумя
переменными позволил продемонстрировать понятие лимитирующих и нелимитирую-
щих ограничений, показать связь между оптимальными решениями и угловыми точками
допустимой области, а также рассмотреть различные аномалии моделей линейного про-
граммирования.
Воспользовавшись графическим оптимизатором GLP, мы увидели, что графический
метод решения задачи ЛП состоит из двух этапов: определение множества допустимых
решений и выбор наилучшего из них. Использование графического метода позволило 12
12 Название "вырожденная угловая точка" не означает для модели ничего плохого С другой стороны, такое
эмоционально окрашенное название — хорошее напоминание о его смысле в угловой точке вырождение проис-
ходит тогда, когда слишком много ограничений накладываются друг на друга
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности	259
также продемонстрировать, что для решения задачи ЛП достаточно выявить лимити-
рующие ограничения. Тогда оптимальные значения переменных решения находятся
с помощью решения системы линейных алгебраических уравнений. С геометрической
точки зрения лимитирующие ограничения — это такие ограничения, для которых пря-
мые, их представляющие, проходят через оптимальную угловую точку допустимой облас-
ти. Алгебраически лимитирующее ограничение — это такое ограничение, для которого
вычисленная в точке оптимальности левая часть ограничения-неравенства равна правой
части. Для обозначения неотрицательной разности между двумя частями ограничения-
неравенства используются термины превышение и резерв. Термин превышение обычно ис-
пользуется для ограничений вида >, а резерв — для ограничений вида <. Раздел 4.2 посвя-
щен подведению итогов использования графического метода решения к моделям макси-
мизации, а в разделе 4 4 показано, что данный метод можно применять и для решения за-
дач минимизации.
В разделе 4.5 анализируются два аномальных случая, когда модель ЛП не имеет опти-
мального решения. В неограниченной модели максимизации целевая функция может
принимать произвольно большие значения (в неограниченной модели минимизации —
произвольно большие по модулю отрицательные значения). Как правило, это означает,
что при формулировке модели пропущено одно или несколько ограничений. Недопусти-
мая модель — это модель, для которой не существует допустимых решений, т.е. множест-
во значений переменных решения, удовлетворяющих всем ограничениям, пусто. Такой
результат может быть следствием некорректной формулировки, например, когда требу-
ется выполнение нескольких противоречащих друг другу ограничений.
Графический метод также использовался при анализе чувствительности. Общий под-
ход заключается в следующем: находится решение задачи ЛП, а затем исследуются воз-
действия различных изменений параметров модели на оптимальные значения перемен-
ных решения и на оптимальное значение целевой функции.
В разделе 4.7 показано, что изменение коэффициентов целевой функции изменяет
угол наклона прямой целевой функции, что может повлиять, а может и не повлиять на
оптимальное решение. В разделе 4.8 рассматривались изменения правых частей ограни-
чений. Было отмечено, что такие изменения приводят к параллельному сдвигу прямой
данного ограничения. Это может повлиять как на оптимальное решение, так и на опти-
мальное значение целевой функции.
Изменение правой части ограничения-неравенства можно рассматривать как усиле-
ние или ослабление данного ограничения. Усиление ограничения означает, что удовле-
творить его становится сложнее. С геометрической точки зрения усиление ограничения-
неравенства приводит к уменьшению допустимой области или оставляет ее неизменной.
Ослабление ограничения-неравенства приводит к расширению допустимой области или
оставляет ее неизменной.
Значительное внимание в данной главе уделено интерпретации отчета по устойчиво-
сти средства Поиск решения для моделей ЛП. Мы показали, какую информацию можно
извлечь из анализа чувствительности решения относительно правых частей ограничений
и коэффициентов целевой функции. В разделе 4.9 описано использование мощного
средства оценки моделей ЛП — надстройки SolverTable, позволяющей проводить более
углубленный анализ чувствительности, чем это может обеспечить стандартный отчет по
устойчивости.
В разделе 4 12 мы выяснили, что происходит с результатами отчета по устойчивости,
когда на переменные решения налагаются простые ограничения, а также рассмотрели
260 ЧАСТЬ II. Оптимизационные модели
проблемы интерпретации теневой цены, которые могут возникнуть при использовании
формул в правых частях ограничений.
В разделе 4.13 показано, что при оптимизации моделей ЛП средство Поиск решения
все ограничения-неравенства преобразует в равенства путем введения дополнительных
переменных. Сформулирован признак вырожденности решения: если в оптимальном
решении количество положительных переменных, считая и дополнительные перемен-
ные, меньше числа ограничений (без учета ограничений неотрицательности), то данное
решение вырожденное. Также кратко описано, как вырожденность решения может ото-
бржаться в отчете по устойчивости.
Основные термины
Альтернативные оптимумы. Оптимизируемая модель имеет несколько оптимальных решений
Анализ чувствительности. Исследование воздействия на оптимальное решение (значения перемен-
ных решения и значение целевой функции) изменений различных параметров модели
Вырожденное решение. Решение задачи ЛП, в котором число имеющих положительные значения
переменных меньше числа лимитирующих ограничений На вырожденное решение обычно
указывают теневые цены с нулевым значением допустимого увеличения или уменьшения
Графический метод решения. Двухмерный геометрический анализ моделей ЛП с двумя перемен-
ными решения
Диапазоны целевых коэффициентов. Задают диапазоны изменений коэффициентов целевой функ-
ции, при которых оптимальное решение не изменяется
Допустимая область. Множество значений переменных решения, удовлетворяющих всем ограни-
чениям и условиям неотрицательности одновременно, т е множество допустимых решений
Допустимое решение. Решение, которое удовлетворяет всем ограничениям Графически между до-
пустимыми решениями и точками допустимой области существует взаимно однозначное соот-
ветствие
Допустимый диапазон изменения правой части. Диапазон значений правой части, для которых тене-
вая цена остается постоянной
Избыточное ограничение. Ограничение, удаление которого не влияет на допустимую область
Крайняя точка. Угловая точка допустимого множества Если задача ЛП имеет решение, всегда су-
ществует как минимум одно решение в крайней точке.
Лимитирующее ограничение. Ограничение, для которого значение левой части, вычисленное в оп-
тимальной точке, равно значению правой части
Множественные оптимумы. То же, что и альтернативные оптимумы
Невырожденное решение. Решение задачи ЛП, в котором число имеющих положительные значе-
ния переменных равно числу лимитирующих ограничений Как правило, все теневые цены
невырожденного решения имеют ненулевые значения допустимого увеличения и допустимого
уменьшения
Недопустимая модель. Задача ЛП, область допустимых решений которой является пустым множе-
ством. Такая задача не имеет решений
Неограниченная допустимая область. Допустимая область, в которой по крайней мере одна пере-
менная решения может принимать произвольно большие значения.
Неограниченная модель. Модель ЛП, в которой значение целевой функции может неограниченно
увеличиваться (уменьшаться). Такая модель не имеет решения
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 261
Неограниченная целевая функция. Целевая функция, которая на допустимом множестве может
принимать в модели максимизации сколь угодно большие положительные, а в модели мини-
мизации — сколь угодно большие отрицательные значения
Оптимальное решение. Точка допустимой области, в которой целевая функция достигает оптимума
(максимума или минимума)
Оптимальное целевое значение (оптимальное значение). Оптимальное значение целевой функции,
т е значение целевой функции, вычисленное в точке оптимального решения
Ослабление ограничения. Изменение правой части ограничения-неравенства, в результате кото-
рого данное ограничение становится легче удовлетворить Это происходит при уменьшении
правой части ограничения вида > и при увеличении правой части ограничения вида <
Параметрический анализ. То же, что и анализ чувствительности
Превышение. Величина, на которую значение левой части ограничения вида >, вычисленное в оп-
тимальной точке, превышает значение правой части Превышение всегда неотрицательно
Прямая целевой функции. Множество всех значений переменных (х,, х.), при которых целевая
функция Дх,, х2) принимает указанное значение
Резерв. Величина, на которую значение левой части ограничения вида <, вычисленное в опти-
мальной точке, меньше значения правой части Резерв всегда неотрицателен
Теневая цена. Значение в столбце Теневая цена отчета по устойчивости средства Поиск
решения — это коэффициент изменения оптимального значения целевой функции при увели-
чении правой части ограничения на единицу
Технологические коэффициенты. Коэффициенты, на которые умножаются переменные решения,
образуя формулы левых частей ограничений
Усиление ограничения. Изменение правой части ограничения-неравенства, в результате которого
данное ограничение становится сложнее удовлетворить Это происходит при увеличении пра-
вой части ограничения вида > и при уменьшении правой части ограничения вида <
Контрольные вопросы
Да/нет
1.	Допустимая область — это множество всех точек, которые удовлетворяют хотя бы
одному ограничению.
2.	В двухмерных моделях пересечение двух любых ограничений определяет крайнюю
точку допустимой области.
3.	Оптимальное решение использует все имеющиеся ресурсы.
4.	Правильно сформулированная задача не окажется неограниченной или недопустимой
5.	Свойство недопустимости модели, в отличие от неограниченности, не связано с
целевой функцией.
6.	Если модель Л П не является недопустимой, она имеет оптимальное решение
7.	Произвольная точка границы допустимой области удовлетворяет всем ограничениям
8.	Лимитирующее ограничение-неравенство имеет нулевое превышение или ре-
зерв — это означает, что в точке оптимального решения данное ограничение вы-
полняется как равенство
9.	Анализ чувствительности значительно повышает вероятность того, что модель
окажется полезной при решении вопросов управления.
262	Ч А С Т Ь II. Оптимизационные модели
10.	Известно, что некоторые данные модели содержат ошибки или неточности
(например, являются оценками параметров, точное значение которых будет из-
вестно только в будущем). Предположим, анализ чувствительности показал, что
оптимальное решение очень чувствительно к изменениям этих параметров. Эта
информация придает дополнительную убедительность рекомендациям, построен-
ным на основе оптимального решения задачи.
11.	Анализ чувствительности — точный метод исследования решения линейной задачи.
12.	Изменение правой части ограничения приводит к изменению угла наклона пря-
мой, представляющей это ограничение.
13.	Изменение правой части ограничения не может повлиять на множество нелими-
тирующих ограничений.
14.	Ослабление ограничения-неравенства заключается в таком изменении его правой
части, при котором этому ограничению становится легче соответствовать.
15.	Увеличение правой части ограничения вида > приводит к его усилению.
16.	Усиление избыточного ограничения-неравенства не может повлиять на допусти-
мую область
17.	Для заданного множества данных нелимитирующие ограничения менее важны,
чем лимитирующие.
18.	Дополнительное ограничение модели может улучшить оптимальное значение це-
левой функции.
19.	Если ограничение вида < — нелимитирующее, соответствующий ему резерв отри-
цателен
20.	Наличие множественных оптимумов приводит к более простой интерпретации от-
чета по устойчивости средства Поиск решения
21.	Теневая цена ограничения — это коэффициент изменения оптимального значения
целевой функции при увеличении правой части данного ограничения.
22.	Теневая цена ограничения — это линейная функция от значения его правой части
в диапазоне, заданном допустимыми уменьшением и увеличением.
23.	Если ограничение в оптимальной точке имеет ненулевой резерв, это указывает на
его избыточность.
24.	Ограничение вида < с положительным значением резерва в точке оптимума всегда
имеет бесконечное значение допустимого увеличения для правой части.
Следующие два вопроса относятся к таблице, приведенной на рис. 4.26.
25.	Анализ чувствительности свидетельствует, что если требования к содержанию
элементов Л и С одновременно увеличить на 0,5 фунта, то оптимальная стоимость
возрастет на $24,44.
26.	Тот факт, что все теневые цены неотрицательны, объясняется исключительно тем,
что мы имеем дело с моделью минимизации.
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности	263
Ответы
1 Нет. 2 Нет. 3 Нет. 4 Да. 5. Да. 6. Нет. 7. Да. 8. Да. 9. Да. 10. Нет. 11. Да. 12. Нет.
13 Нет. 14 Да 15. Да 16. Нет. 17. Да. 18. Нет. 19. Нет. 20. Нет. 21. Да. 22. Нет. 23.
Да 24. Да. 25. Нет. 26. Нет.
Выберите правильный ответ
27.	Графический метод полезен тем, что:
а предлагает общий способ решения задач ЛП,
b предлагает геометрическую интерпретацию модели,
с а и b
28.	Термин неограниченная модель означает, что:
а все переменные решения могут принимать неограниченно большие значения, не вы-
ходя за пределы допустимой области,
b прямая целевой функции может перемещаться в оптимизирующем направлении сколь
угодно далеко, касаясь допустимой области по меньшей мере в одной точке;
с не все ограничения могут быть удовлетворены.
29.	Рассмотрим оптимальное решение некой задачи ЛП. Какие из следующих выска-
зываний верны?
а В точке оптимальности по крайней мере одно ограничение (не считая условий неот-
рицательности) является лимитирующим
b В точке оптимальности только одно ограничение (не считая условий неотрицательно-
сти) является лимитирующим
с Ни одно из этих утверждений
30.	Какие из следующих утверждений об оптимальном решении задачи ЛП являются
истинными?
а Все задачи ЛП имеют оптимальное решение
b Оптимальное решение всегда находится в крайней точке.
с Оптимальное решение использует все имеющиеся ресурсы.
d Если оптимальное решение существует, всегда найдется хотя бы одно угловое реше-
ние
е Верны все вышеперечисленные утверждения
31.	Каждая угловая точка допустимой области определяется:
а пересечением двух линий, соответствующих каким-либо ограничениям,
b некоторым подмножеством линий ограничений и условий неотрицательности;
с ни тем, ни другим
32.	Неограниченная допустимая область:
а получается в результате неверной формулировки задачи,
b означает, что целевая функция является неограниченной;
с ни одно из этих высказываний не верно,
d верны оба высказывания
33.	Анализ чувствительности"
а позволяет более содержательно интерпретировать оптимальное решение,
264 ЧАСТЬ II. Оптимизационные модели
Ь осуществляется после получения оптимального решения,
с иногда называется параметрическим анализом,
d все вышеперечисленное
34.	Анализ чувствительности:
а в двухмерном случае может проводиться графически,
b может укрепить наше доверие к модели,
с	может ослабить доверие к рекомендациям модели,
d все вышеперечисленное,
е ничего из вышеперечисленного
35.	В линейном программировании анализ чувствительности:
а позволяет исследовать изменения коэффициентов целевой функции,
b позволяет исследовать изменения правых частей ограничений;
с и то, и другое
36.	Изменение коэффициента в формуле целевой функции:
а приводит к новому оптимальному решению,
b изменяет угол наклона прямой целевой функции;
с дает новое оптимальное значение целевой функции,
d все вышеперечисленное
37.	Усиление ограничения-неравенства:
а улучшает оптимальное значение целевой функции,
b не может улучшить оптимальное значение целевой функции,
с ухудшает оптимальное значение целевой функции
38.	Избыточное ограничение.
а нелегко распознать до оптимизации модели,
b всегда следует удалять из модели,
с может перестать быть избыточным при изменении параметров модели,
d все вышеперечисленное,
е а и с,
f аи Ь,
g Ьис
39.	Вырожденное оптимальное решение:
а содержит менее т положительных переменных (т — число лимитирующих ограниче-
ний),
b не дает информации об альтернативных оптимумах,
с может не предоставить информацию о диапазоне допустимых коэффициентов увели-
чения и уменьшения целевой функции,
d все вышеперечисленное
40.	Термин улучшение в линейном программировании означает:
а увеличение оптимального значения целевой функции в модели максимизации,
b уменьшение оптимального значения целевой функции в модели минимизации,
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 265
41.	Если коэффициент с, целевой функции в модели максимизации увеличивается на
значение, в точности равное допустимому увеличению, то:
а оптимальное значение целевой функции может измениться;
Ь. предыдущее оптимальное решение останется оптимальным,
с появится новое оптимальное решение, с большим значением переменной х,;
d все вышеперечисленное
42.	Предположим, что в результате решения задачи минимизации, в которой присут-
ствуют условия неотрицательности, оптимальное значение переменной х, равно 0.
Необходимо выяснить, на сколько нужно уменьшить стоимость х, (коэффициент
перед этой переменной в формуле целевой функции), чтобы в оптимальном реше-
нии значение этой переменной стало положительным. Какие данные, приведен-
ные в отчете по устойчивости средства Поиск решения, могут помочь в этом?
а Значения переменных.
b Допустимые изменения правых частей для первого ограничения.
с Допустимое увеличение для коэффициента при х1
d Нормированная стоимость
43.	Предположим, что первое ограничение некой задачи ЛП в точке Р„ имеет нулевое
значение резерва. В этом случае:
а	точка Р„ лежит на границе допустимой области;
b точка Ро лежит на прямой первого ограничения,
с а и Ь
44.	Какие из следующих утверждений верны?
а Ограничение с нулевой теневой ценой является нелимитирующим
b Ограничение с положительной теневой ценой является лимитирующим.
с Оба утверждения
Следующие вопросы относятся к таблице, приведенной на рис. 4.26.
45.	Если требование к содержанию элементу Л изменится с 5 до 6,5, то:
а оптимальное значение целевой функции уменьшится на $66,66;
b оптимальное значение целевой функции улучшится на $66,66;
с оптимальное значение целевой функции возрастет на $66,66,
d оптимальное значение целевой функции не изменится
46.	Если требование к содержанию элементу С уменьшить с 30 до 20, то:
а.	оптимальное значение целевой функции уменьшится на $44,44,
Ь.	оптимальное значение целевой функции увеличится на $44,44,
с.	оптимальное значение целевой функции улучшится как минимум на $31,00.
47.	Если стоимость руды с месторождения 2 снизится до $300 за тонну, то:
а.	оптимальное значение целевой функции не изменится;
Ь.	оптимальное решение не изменится;
с ни первое, ни второе;
d.	и первое, и второе.
48.	Если стоимость руды из месторождения 1 снизится до $680 за тонну, то:
266 ЧАСТЬ II. Оптимизационные модели
а появится новое оптимальное решение с 1 > 0,259,
b появятся альтернативные оптимумы,
с. оптимальным останется прежнее решение,
d все вышеперечисленное
Ответы
27. Ь. 28. Ь. 29. а. 30. d. 31. b. 32. с. 33 d. 34. d. 35. с. 36. b 37. Ь. 38. е. 39. d. 40. с 41 d
42. d. 43. b. 44. b. 45. с. 46. с. 47. b. 48. d.
Учебные задачи
4.1 Небольшое предприятие Клэр Арчер продает стереоаппаратуру, при этом занимаясь сбор-
кой усилителей и предусилителей Для сборки усилителя требуется 12 ч и 4ч— для про-
верки его качества Сборка предусилителя длится 4 ч, а проверка качества 8 ч В следующем
месяце Клэр имеет возможность выделить 60 ч на сборку и 40 ч на проверку качества С
помощью программы GLP найдите комбинацию количества собранных усилителей и пре-
дусилителей, удовлетворяющую ограничениям
а.	по времени сборки,
Ь.	по времени проверки качества,
с обоим одновременно
4 2. Одна консервная банка корма для собак сорта А содержит 12 мг белка и 4 мг жира, а одна
банка корма сорта В — 3 мг белка и 8 мг жира Дэл Мэтью — директор небольшого собачь-
его питомника Чтобы прокормить своих собак, он хочет получить смесь, содержащую не
менее 30 мг белка и не менее 24 мг жира Используя программу GLP, покажите, сколько
банок сорта А и сорта В должен приобрести Дэл в соответствии с ограничениями
а по количеству белка,
b по количеству жира,
с.	а и b одновременно
4.3. Предположим, что в упражнении 4 1 Клэр получает S10 прибыли за каждый усилитель и S5
за каждый предусилитель С помощью программы GLP постройте прямые целевой функ-
ции для значений прибыли $10, $20 и $60
4 4 Предположим, что в упражнении 4 2 одна банка корма сорта А стоит $0,80, а сорта В —
$0,60 С помощью программы GLP покажите, какие комбинации банок двух сортов можно
приобрести за
а $4,80,
b $2,40
4.5. Вернемся к предприятию Клэр, описанному в упражнениях 4 1 и 4 3 В силу различных
причин она пришла к выводу, что в ее модель необходимо ввести два дополнительных ог-
раничения — в следующем месяце она сможет произвести не более 4 предусилителей и 6
усилителей Принимая во внимание все ограничения
а.	с помощью графического анализатора GLP найдите оптимальный (максимизирующий
прибыль) производственный план,
Ь.	вычислите оптимальное значение целевой функции
с.	Какие ограничения являются лимитирующими9
d.	Какие ограничения не являются лимитирующими, чему для них равно значение резерва9
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 267
4 6 При значениях цен, заданных в упражнении 4 4, найдите, сколько банок корма каждого
сорта Дэл должен приобрести, чтобы удовлетворить с минимальными затратами перечис-
ленные в упражнении 4 2 требования
4 7 Может ли пропуск двух любых ограничений сделать модель Клэр (упражнение 4 5) неогра-
ниченной9
4 8 Предположим, что Дэл оказался в магазине, где есть только корм сорта А, и у него нет воз-
можности приобрести корм где-нибудь в другом месте Изменит ли это обстоятельство ре-
шение, найденное в упражнении 4 6? Если да, то каким образом9
4 9 Предположим, что ограничение по объему производства усилителей в модели Клэр изменит-
ся с “не более 6 усилителей” на “не менее 6 усилителей” Как это отразится на ее модели9
4 10 Если Дэл должен купить не менее 3 банок корма сорта В, повлияет ли это на минимизи-
рующее общие затраты решение, найденное в упражнении 4 69 Если да, то каким образом9
(Замечание. В данном упражнении предполагается, что Дэн может покупать нецелое коли-
чество банок корма )
4 11 Рассмотрим следующую задачу линейного программирования
максимизировать х, + х2
при ограничениях	х, + 2х2 < 6,
Зх, + 2х2 < 12,
х„х2>0
а С помощью программы GLP найдите оптимальное решение
b Замените целевую функцию функцией 2x1 + 6x2 и найдите новое оптимальное решение
с Сколько крайних (угловых) точек имеет допустимая область9 Найдите значения пере-
менных решения в каждой угловой точке
4 12	Рассмотрим следующую задачу линейного программирования
максимизировать 2х, + Зх2
при ограничениях	Зх, + х2 > 6,
х, + 7х2 > 7,
хх2>0. ’
а С помощью GLP найдите оптимальное решение
b Замените целевую функцию функцией Зх, + 2х2 и найдите новое оптимальное решение
с Сколько угловых точек имеет допустимая область9 Найдите значения переменных ре-
шения в каждой угловой точке
4 13	Рассмотрим следующую задачу линейного программирования
максимизировать Зх, + 4х2
при ограничениях	-2х, + 4х2 < 16,
2х, + 4х2 < 24,
~6х, - Зх2 > -48,
х,,х2>0
а С помощью G LP найдите оптимальное решение
b Найдите значения резерва и превышения для каждого ограничения
4 14 Рассмотрим следующую задачу ЯП
максимизировать 6х, + 2х2
при ограничениях	2х, + 4х2 < 20,
Зх, + 5х2> 15,
х, > 3,
х2>0
268 ЧАСТЬ II Оптимизационные модели
а С помощью GLP найдите оптимальное решение.
b Найдите значения резерва и превышения для каждого ограничения.
4 15	Рассмотрим следующую задачу ЛП
минимизировать 5х, + 1хг
при ограничениях	3х1 + 6х2 £ 18,
5х, + 4х2 > 20,
8xj + 6х2 £ 16,
7х, + 6х2 < 42,
х„х2>0
а.	С помощью GLP найдите оптимальное решение
b Какие ограничения являются лимитирующими, а какие — нет9
с Какие значения резерва или превышения соответствуют каждому ограничению9
d Сколько угловых точек имеет допустимая область9
е Замените целевую функцию функцией 15х, + 12х2 Каким будет новое решение9
4 16 В упражнении 4 14 замените целевую функцию функцией х, + Зх2 Найдите новое опти-
мальное решение и определите лимитирующие ограничения
4 17 Рассмотрим следующую модель Л П
максимизировать 600£ + 1000F
при ограничениях	100 Е + 60Е< 21 000,
4000Е + 800Е<680 ООО,
Е+ Е<290,
12Е + 30F<6 000,
Е, F>0
а Откладывая переменную Е по горизонтальной оси, a F— по вертикальной, с помощью
программы GLP найдите оптимальное решение данной задачи.
b Одно из ограничений избыточно, т е оно не играет никакой роли в определении до-
пустимой области Какое именно9
с Каким должно быть минимальное изменение правой части избыточного ограничения,
чтобы оно стало лимитирующим9
d Коэффициент при Е в третьем ограничении равен 1 Какое минимальное увеличение
данного коэффициента может привести к тому, что данное ограничение станет лими-
тирующим9
е Предположим, что коэффициент при переменной Е в целевой функции, увеличивает-
ся, в то время как коэффициент при переменной Fостается фиксированным. При ка-
ком значении коэффициента при Евпервые появятся альтернативные оптимумы9
4 18. Рассмотрим следующую задачу ЛП:
максимизировать Зх, + х2
при ограничениях	6х, + Зх2 > 12,
4х, + 8х2 £ 16,
6х, + 5х2 £ 30,
6х, + 7х2 £ 36,
х„х2£0.
а С помощью программы GLP найдите оптимальное решение.
Ь.	Рассмотрим модель минимизации, допустимое множество которой совпадает с задан-
ным Пусть целевая функция имеет вид х, + Вх2. При каком наибольшем значении В
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 269
оптимальное решение будет находиться на пересечении прямых ограничений
6х, + Зх2 = 12 и 4х, + 8х2 = 16? Найдите оптимальное решение.
с Предположим, что целевая функция в модели максимизации имеет вид Ах, + Вх2. Оп-
ределите множество значений А и В, При которых оптимальное решение лежит на пе-
ресечении прямых ограничений 6х, + 5х2 = 30 и 6х, + 7х2 = 36. Изобразите графически
это множество значений А и В
4 19 Предположим, что в упрощенной модели Oak Products (см рис. 4.5) целевую функцию за-
менили функцией 58С + 20Л/
а. С помощью программы GLP определите, как это отразится на оптимальном решении,
b Как это повлияет на оптимальное значение целевой функции?
4 20. Предположим, что в упрощенной модели Oak Products целевую функцию заменили функ-
цией 25С + 50Л/
а С помощью программы GLP определите, как это отразится на оптимальном решении.
b Как это повлияет на оптимальное значение целевой функции9
4 21	Даны две целевые функции для упрощенной модели Oak Products 56С + 40 Л/и 56С + 80Л/
На рис 4 5 показано, что если удельная прибыль стульев Mate увеличивается с 40 до 80 при
фиксированном значении удельной прибыли для стульев Captain, оптимальное значение
переменной С убывает Почему оптимальное значение С зависит от коэффициента при пе-
ременной Л/9
4 22 Предположим, что в упрощенной модели Oak Products целевую функцию заменили функ-
цией 10С+ 100 М
а С помощью программы GLP определите, приведет ли это к новому оптимальному ре-
шению
b Как это повлияет на оптимальное значение целевой функции9
4 23 Рассмотрим следующую задачу Д П
максимизировать ЗОх, + 10х2
при ограничениях	2х, + х2 < 4,
2х, + 2х2<6,
х„х2>0
а	С помощью программы GLP найдите оптимальное решение данной задачи
b При условии, что все остальные параметры фиксированы, каким должен быть коэф-
фициент в формуле целевой функции при переменной, текущее оптимальное значе-
ние которой равно нулю, чтобы значение этой переменной в оптимальном решении
стало положительным9
с Сколько будет оптимальных решений после внесения изменения, описанного в пунк-
те Z>9 Какие это решения9
d На сколько можно увеличить (уменьшить) правую часть второго ограничения в исход-
ной модели, прежде чем оптимальное решение изменится9
е Ответьте на предыдущий вопрос для правой части Первого ограничения
f Как объяснить различие между ответами на два последних вопроса9
g. Как повлияет на исходную модель введение дополнительного ограничения
4х, + х2 = 4?
h Как повлияет на оптимальное решение исходной задачи введение дополнительного
ограничения Зх, + Зх2 £ 15?
4.24. Рассмотрим следующую задачу ЛП.
270 ЧАСТЬ!!. Оптимизационные модели
максимизировать 2х, + х2
Зх, + Зх2< 12,
х, + Зх2 < 6,
х„х2£0
при ограничениях
а.	Ответьте для данной модели на вопросы из упражнения 4 23
Ь.	Как повлияет на исходную модель добавление ограничения х, + х2 < I9
4 25. Даны два ограничения-неравенства -Зх, + 2х2 > -6 и -Зх, + 2х2 S -10
а.	Какое из них сильнее’
Ь.	Удовлетворяет ли какому-либо из этих ограничений точка (х, = 2, х2 = I)9 Если “да”,
укажите его.
с.	Ответьте на предыдущий вопрос для точки (х, = 3, х2 = 0).
4.26.	Даны два ограничения 4х, - Зх2 < 12 и 4х, - Зх2 < -12
а Какое из них сильнее?
Ь.	Удовлетворяет ли какому-либо из этих ограничений точка (х, = -2, х2 = З)9 Если “да”,
укажите его.
с.	Ответьте на предыдущий вопрос для точки (х, = 2, х2 = 3)
4.27.	Какое из двух ограничений в упражнении 4 25 слабее9
4.28.	Какое из двух ограничений в упражнении 4 26 слабее9
4.29.	Вставьте пропущенные слова “Увеличение правой части ограничения вида < означает, что
будет комбинаций значений переменных решения, удовлетворяющих данному
ограничению. Таким образом, это приводит к ограничения ”
4.30	Вставьте пропущенные слова. “Увеличение правой части ограничения вида > означает, что
будет комбинаций значений переменных решения, удовлетворяющих данному
ограничению Таким образом, это приводит к ограничения ”
4.31.	Используя слова из списка увеличить, уменьшить, сделать меньше, сделать больше, неизмен-
ной, вставьте пропущенные слова в предложение “Усиление ограничения не может
допустимую область, а может оставить ее или”
4.32.	Используя список слов из упражнения 4.31, вставьте пропущенные слова “Ослабление ог-
раничения не может допустимую область, а может оставить ее
или.”
4.33.	Предположим, что вы создали модель и выявили в ней избыточное ограничение Можно ли
утверждать, что такое ограничение всегда следует удалять из модели9 Объясните свой ответ
4.34.	Как изменится ответ на вопрос упражнения 4 33, если данная модель будет использоваться
только один-единственный раз?
4.35.	При определенных параметрах модели некое ограничение оказалось избыточным Следует
ли из этого, что данное ограничение будет также нелимитирующим9
4.36.	Для некоторого ограничения оптимальное значение резерва положительно Какой должна
быть теневая цена?
4.37.	Какое значение имеет теневая цена нелимитирующего ограничения9 Что можно сказать о
теневой цене лимитирующего ограничения9
4.38.	Объясните, как с помощью значений нормированной стоимости узнать, существуют ли
альтернативные оптимальные решения
Г ЛАВА 4. Линейная оптимизация. Анализ чувствительности 271
Прикладные задачи
4	39 На сколько можно увеличить правую часть ограничения для ножек в упрощенной модели
Oak Products, прежде чем оно станет избыточным9 До какого значения можно уменьшить
значение данной правой части, чтобы это не привело к недопустимости модели9
4	40 В упрощенной модели Oak Products измените значение правой части пятого ограничения
(запас прочных сидений) со 140 на 170 Как это отразится на допустимой области9
4	41 Какие ограничения являются избыточными в упрощенной модели Oak Products9 Останутся
ли эти ограничения избыточными, если их правые части увеличить на 10% при условии по-
стоянства остальных параметров модели9
4	42 Компания производит два вида шин Шины Last-Forever — это металлокордные, защи-
щенные от проколов, стойкие к износу шины Другой вид шин, Lane-Handler, — это про-
стые недорогие шины с гарантией на 40 000 миль Удельная прибыль компании составляет
$50 с каждой шины Last-Forever и $10 с каждой шины Lane-Handler Оба вида шин произ-
водятся на одном заводе, их производство осуществляется на одних и тех же станках
В двухэтапном процессе изготовления шин участвуют станок А и станок В. Время работы
станков, затраченное на изготовление одной шины, показано в таблице
	Lane-Handler Last-Forever	Суммарный ресурс рабочего времени, ч
Станок А	1	4	120
Станок В	2	2	100
Для важного дилера компании надо произвести 20 покрышек Lane-Handler, а 4 покрышки
Last-Forever были обещаны сыну владельца
а С помощью программы GLP составьте производственный план, максимизирующий
прибыль
b Чему равно оптимальное значение целевой функции9
с Как изменится оптимальное значение целевой функции, если ресурс рабочего време-
ни станка В увеличить до 120 ч9
d Что произойдет, если проблемы обслуживания станков приведут к сокращению ресур-
са рабочего времени станка А до 100 ч9
4 43 Полиграфическая компания выпускает рекламные издания LinksLetter и Ragged Edge, ко-
торые покупатели могут брать в местных магазинах и ресторанах Компания получает до-
ход, продавая место для размещения рекламы в своих изданиях Стоимость LinksLetter со-
ставляет $50 за тысячу экземпляров, а стоимость Ragged Edge — $100 за тысячу экземпля-
ров Чтобы напечатать тысячу экземпляров LinksLetter требуется один час, а печать тысячи
экземпляров Ragged Edge занимает всего полчаса На следующей неделе ресурс времени
печати составит 120 ч Обе рекламные газеты складываются фальцевальной машиной, ре-
сурс рабочего времени которой составляет 200 ч в неделю, причем она складывает обе газе-
ты с одинаковой скоростью 1000 экземпляров в час Компания хочет полностью использо-
вать время печатного станка, минимизировав при этом затраты на производство печатной
продукции С помощью программы GLP определите оптимальный производственный
план и его минимальную стоимость
4 44 Менеджер полиграфической компании из предыдущей задачи решил максимизировать по-
лучаемую от публикаций прибыль Он определил, что прибыль от тысячи экземпляров
LinksLetter составляет $25, а от тысячи экземпляров Ragged Edge — $45 Необходимо напе-
чатать не менее 60 000 экземпляров LinksLetter и не менее 30 000 экземпляров Ragged Edge
Ограничения на ресурс рабочего времени печатного станка и фальцевальной машины ос-
таются прежними
272	Ч А С Т Ь II. Оптимизационные модели
а С помощью программы GLP представьте графически данную модель.
b Каким будет производственный план?
с Какие ограничения являются лимитирующими9
4 45 Компания Кагта Computers производит две модели компьютеров. Standard и Deluxe Мо-
дель Standard имеет один дисковод и системный блок Standard. Модель Deluxe имеет два
дисковода и системный блок Deluxe Удельная чистая прибыль для модели Standard состав-
ляет $300, а для модели Deluxe — S400 В настоящее время компания имеет в своем распо-
ряжении 60 системных блоков Standard, 50 блоков Deluxe и 120 дисководов
а Разработайте модель ЛП для компании Каппа и создайте с помощью программы GLP
ее геометрическое представление
b Оптимизируйте модель с помощью программы GLP и используйте полученные ре-
зультаты, чтобы заполнить пустые ячейки в таблице на рис 4 33
—:	А | В : с I Р IE; F . i.G ,
KARMA COMPUTERS
Переменные решения  S________D ;
Количество	|	| Прибыль
Удельная прибыль	i $300	$4001	|
Ограничения.	: П часть Пр. часть  Резерв
Блоки Standard	i	1	<60
Блоки Deluxe ______________1	<	50
Дисководы	I	<| 
Рис. 4.33. Модель ЛП к задаче 4.45
с На основе данных из таблицы на рис 4 33 и с помощью GLP введите необходимые
значения в пустые ячейки отчета по устойчивости на рис 4 34
Microsoft Excel 10 0 Отчет по устойчивости Изменяемые ячейки				
PetynbT Нормир. Целевой Допустимое Допустимое Ячейка	Имя	значение стоимость Коеффициент Увеличение Уменьшение				
$В$3 Количество S			I	300]	I	I	
$С$3 Количество 0	I	L			I	400	200	400	
Ограничения				
Ре1ульт Теневая Ограничение Допустимое Допустимое Ячейка	Имя	сначение Цена Правая часть Увеличение Уменьшение				
$О$6 Блоки Standard Л. часть $D$7 Блоки Deluxe Л. часть $D$8 Дисководы Л. часть			60	60		|
			50|			20 	60
			. .... ... L. ... _.	
Рис. 4.34. Отчет по устойчивости к задаче 4.43
4 46 Вернитесь к результатам работы средства Поиск решения, показанным на рис. 4 11.
а Предположим, что запас коротких штифтов увеличился на 30 штук Как изменится оп-
тимальное значение целевой функции9
b Предположим, что запас коротких штифтов сократился на 300 штук Как изменится
оптимальное значение целевой функции9
с Для какого диапазона значений правой части действительна теневая цена ограничения
для коротких штифтов9
ГЛАВА 4 Линейная оптимизация. Анализ чувствительности
273
4 47
4 48
4 49
Вернитесь к результатам работы средства Поиск решения, показанным на рис 4 11
а Предположим, что правая часть ограничения для ножек равна 750 Как это отразится
на оптимальном значении целевой функции9
b Как можно усилить ограничение по суммарному производству стульев, прежде чем
изменится соответствующая ему теневая цена9
с Предположим, что запас ножек увеличился на 50 штук На сколько изменится опти-
мальное значение целевой функции9
Рассмотрим рис 4 11 Предположим, что удельная прибыль для стульев Mate снизилась до 830
а Каким будет новое оптимальное решение9
b На сколько изменится оптимальное значение целевой функции9
Предположим, что в модели, представленной на рис 4 11, удельная прибыль для стульев
Captain увеличилась до S80
а Каким будет новое оптимальное решение9
b На сколько изменится оптимальное значение целевой функции9
Рассмотрим рис 4 26
а На сколько необходимо уменьшить стоимость тонны руды из месторождения 4, чтобы
компания начала приобретать ее9
b Предположим, что стоимость тонны руды из месторождения 1 снизилась на S80 При-
ведет ли это к каким-либо изменениям в оптимальном решении9
с Предположим, что стоимость тонны руды из месторождения 1 увеличилась на S100
Приведет ли это к каким-либо изменениям в оптимальном решении9 Каким будет со-
ответствующее изменение стоимости тонны оптимальной смеси'
Рассмотрим рис 4 26
а Предположим, что стоимость тонны руды из месторождения 3 возросла на 850 Изме-
нится ли оптимальное решение9 На сколько изменится значение целевой функции'
b Исследуйте, как повлияет на оптимальное решение уменьшение стоимости тонны руды
из месторождения 3 ровно на 8118,269 (Останется ли оптимальным текущее решение9
Появится ли новое оптимальное решение, и если да, как его можно охарактеризовать9)
с Каким будет новое значение целевой функции для изменения, описанного в преды-
дущем пункте9
Бастер Сод — владелец орошаемой фермы площадью 800 акров в долине Красной реки
штата Аризона Основные направления хозяйственной деятельности фермы — выращива-
ние пшеницы и люцерны и производство говядины Департамент управления водными ре-
сурсами только что распределил лимиты воды на следующий год (ферме Сода выделено
1000 акро-футов) Сод приступил к разработке производственного плана на следующий
год Он считает, что цены на говядину составят примерно 8500 за тонну, а пшеница будет
продаваться по $2 за бушель Люцерну можно будет продавать по 822 за тонну, однако, ес-
ли для прокорма скота ему понадобится больше люцерны, чем он сможет вырастить, ее
придется приобретать по цене 828 за тонну
Урожайность пшеницы составляет 70 бушелей с акра, а урожайность люцерны — 4 т с акра
Остальные технологические детали представлены в следующей таблице
	Затраты,S	Потребность в воде, акро-футы	Потребность в земле, Потребность акры	в люцерне, т
1 акр пшеницы	20	2	1
1 акр люцерны	28	3	1
1 т говядины	50	0,05	0,1	5
274 ЧАСТЬ II. Оптимизационные модели
Определены следующие переменные
Пшеница — выращенная и проданная пшеница (измеряется в акрах, т е. это площадь, вы-
деленная под пшеницу)
Люцерна_В — выращенная люцерна (т)
Говядина — выращенная и проданная говядина (т)
ЛюцернаК — купленная люцерна (т)
Люцерна_П — проданная люцерна (т)
Microsoft Excel 10.0 Отчет по устойчивости Изменяемые ячейки					
Ячейка	Имя		Результ. значение	Нормир. стоимость	Целевой Допустимое Допустимое Коэффициент Увеличение Уменьшение	
$В$6 Пшеница		0	-2980	120	2980	1Е+30
$С$6 Люцерна_В		0	-754		754	1Е+30
$Р$6Говядина	8 000		450	1Е+30	298
$Е$6 Люцерна_К		40 000		-28	6	55,85
$F$6 Люцерна_П		0	-6	22	6	1Е+30
Ограничения				
Ячейка	Имя		Результ. значение	Теневая Цена	Ограничение Допустимое Допустимое Правая часть Увеличение Уменьшение	
$G$11 Баланс Всего		00	28	0	40000	1Е+30
$G$9 Лимит площади Всегс	800	3100	800	1200	800
$G$10 Лимит воды Всего	400	0	ЮОО	1Е+30	600
Рис. 4.35. Решение задачи ЛП и отчет по устойчивости к задаче 4 52
Модель данной задачи ЛП и ее решение показаны на рис. 4 35 Используя эту информа-
цию, ответьте на следующие вопросы
а Приведите вычисления, которые объясняют значения коэффициентов при перемен-
ных Пшеница и Люцерна_В в формуле целевой функции, а также коэффициентов при
переменной Люцерна_В в первом и втором ограничениях.
b Какое количество воды использовано9
с Какое количество говядины произведено9
ГЛАВА 4 Линейная оптимизация Анализ чувствительности 275
d Что предусматривает план покупку или продажу люцерны9
е Сколько должен заплатить Сод за приобретение дополнительного акро-фута воды9
f Как интерпретируется теневая цена 800 для ограничения Лимит площади9
g Что произойдет с оптимальным планом если цена пшеницы утроится9 Что произой-
дет со значением целевой функции9
h Какую прибыль получит Сод при оптимальном функционировании своей фермы9
1 Что произойдет с оптимальным значением целевой функции, если цена приобретае-
мой люцерны возрастет с S28 до S299
Замечание Текущее значение коэффициента при переменной Лкщерна_Ксоставляет -
S28, а станет —S29, т е коэффициент уменьшится на $1
j На сколько может уменьшиться цена покупки люцерны, прежде чем текущий опти-
мальный план изменится?
4 53 Завод, находящийся в некой развивающейся стране, может производить пять различных
продуктов в произвольном соотношении В выпуске каждого продукта принимают участие
три станка, как показано в таблице Все цифры даны в минутах на фунт продукта
Продукт	Время работы станка, мнн./фунт		
	1	2		3
А	12	8	5
В	7	9	10
С	8	4	7
D	10	0	3
Е	7	11	2
Ресурс рабочего времени каждого станка составляет 128 ч в неделю Все продукты конку-
рентоспособны и все их произведенное количество может быть продано по цене $5, S4, $5,
$4 и S4 за фунт продукта А, В, С, D и Е соответственно Переменные затраты на зарплату
составляют S4 в час шля станков 1 и 2 и S3 в час для станка 3 Стоимость материалов, затра-
ченных на выпуск каждого фунта продуктов А и С, составляет S2, а продуктов В, D и Е —
S1 Руководство хочет максимизировать прибыль компании Решение задачи ЛП и отчет по
устойчивости представлены на рис 4 36
а Как выглядит в Excel формула для ячейки В9, с помощью которой вычисляется значе-
ние коэффициента при первой переменной в целевой функции9
b Сколько часов отработает каждый станок, и в каких единицах измеряются теневые це-
ны для ограничений, задающих ресурс рабочего времени для станков9
с Какую цену фирма может позволить себе заплатить за получение дополнительного ча-
са рабочего времени станка 29
d На сколько может увеличиться цена продажи продукта А, прежде чем изменится оп-
тимальный производственный план9 Ответ должен быть выражен в надлежащих еди-
ницах
276 ЧАСТЬ II. Оптимизационные модели
Microsoft Excel 10.0 Отчет по устойчивости	[
Изменяемые ячейки _____________________________________________________________
Реэульт. Нормир. Целевой Допустимое Допустимое
Ячейке_______Имя________значение стоимость Коэффициент Увеличение Уменьшение
$В$8__Количестео/фунты А_______0______-1.3В ___	L417_ _____ 1 380	___1Е+30
$С$8	Количество/фунты В	0	” -0.245~	’1.433	"	0 245	'	1Е*30
$Р$8 Количество/фунты С 512____________-___________1 850______0 093_______0 041
$Е$8	Количество/фунты D_______0	-0 075________2.183______0,075______1Е+30
$F$8 Количество/фунты Е 512 0 1 7 0 113 0 08125
Ограничения____________________________________________________________________
Реэульт. Теневая Ограничение Допустимое Допустимое
Ячейка Имя значение Цена Правая часть Увеличение Уменьшение
$G$11	Станок	1.	мин Всего................... 7680..	0.226	7680	2671,304	2792,727
$G$12	Станок	2,	мин Всего	7680. 0,011.  7680. 4388,571	~	3840
$G$13	Станок	3,	мин Всего	4608 0 7680 1Е+30 3072
Рис. 4.36. Решение задачи ЛП и отчет по устойчивости к задаче 4.53
4 54 Компания Party Nut Company имеет в своем распоряжении 350 фунтов арахиса, 150 фунтов
орехов кешью, 90 фунтов бразильских орехов и 70 фунтов фундука Компания упаковывает
и продает четыре вида смесей орешков в стандартных 8-унциевых (полуфунтовых) банках
Требования к составу смесей и удельная прибыль в расчете на одну банку приведены в таб-
лице Компания может продать все, что она произведет Какие смеси следует производить
компании, чтобы максимизировать валовую прибыль?
Смесь	Состав	Прибыль на 1 банку, $
1	Только арахис	0,26
2	Не более 50% арахиса, не менее 15% кешью, не менее 10% бразильских орешков	0,40
3	Только орешки кешью	0,51
4	Не менее 30% кешью, не менее 20% бразильских ореш- ков, не менее 30% фундука	0,52
ГЛАВА 4. Линейная оптимизация Анализ чувствительности 277
Рис. 4.37. Решение задачи ЛПупражнения 4.54
278 Ч А С Т Ь II. Оптимизационные модели
Данную задачу можно представить в виде модели ЛП, показанной на рис 4 37 Обратите
внимание на то, что в целевой функции коэффициент при переменной, соответствующей
смеси 1, равен $52, а не $26, поскольку из одного фунта арахиса можно произвести две
8-унциевые банки этой смеси В отчете по устойчивости (рис. 4 38) мы специально удалили
некоторые теневые цены и нормированные стоимости Используя эти данные, ответьте на
предлагаемые вопросы Если ответить невозможно, укажите, почему.
а Приведите расчет, показывающий, как было получено значение коэффициента 1,02
при переменной, соответствующей смеси 3, в целевой функции
b Сколько банок смеси 2 производится при оптимальном решении9
с Какой знак у теневой цены ограничения G3 НЗ9 Объясните, почему
d Чему равно значение теневой цены для ограничения D18 > О9 Как вы это узнали9
е Почему содержимое ячейки D17 положительно9 Объясните, не используя термино-
логию линейного программирования
f Что произойдет с оптимальным решением, если цена продажи смеси 1 возрастет до
$0,27 за 8-унциевую банку9
g Чему равно числовое значение теневой цены ограничения G2 Н29 (Совет Проанали-
зируйте, что вы будете делать с дополнительным фунтом арахиса )
h Почему значение допустимого увеличения правой части ограничения G2 Н2 беско-
нечно9 (Совет Основой рассуждений должен служить ответ на предыдущий вопрос )
I. Объясните, почему решение может быть оптимальным, несмотря на положительное
превышение для ограничения D119
j Чему равны числовые значения нормированных стоимостей для арахиса в смеси 2
и кешью в смеси З9
Рис. 4.38. Отчет по устойчивости к упражнению 4 54
ГЛАВА 4 Линейная оптимизация Анализ чувствительности 279
4 55 Почему допустимое уменьшение коэффициента целевой функции при переменной М на
рис 4 11 равно 12, а на рис 4 15 — 409
4 56 Компания Encorporation производит устройства управления напряжением в сети Эти уст-
ройства используются для управления подачей энергии в крупных зданиях, таких как уни-
вермаг или офисный центр Приборы производятся с помощью трех процессов создание
электронных плат (сборка), изготовление корпуса (работа с листовым металлом) и поме-
щение плат в корпус (конечная сборка) Компания хочет минимизировать затраты на про-
изводство выпускаемых трех разновидностей приборов А, В и С Сборка прибора А длится
Зч, В—2чиС— 1ч Для изготовления корпусов приборов А, В и С требуется 6, 3 и 2 ч
соответственно Окончательная сборка любого прибора занимает 5 ч Затраты на А состав-
ляют $10, В — $20, а С — $30 Компания пообещала на следующей неделе поставить пять
приборов А, шесть В и пять С крупному розничному продавцу Ресурс рабочего времени
для каждого процесса составляет 80 ч Создайте табличную модель минимизации затрат
компании Encorporation, а также отчет по устойчивости
а Объясните смысл значении в столбце Допустимое уменьшение в таблице Изменяе-
мые ячейки отчета по устойчивости для оптимального решения данной задачи
b Почему Нормированная стоимость для каждого вида прибора равна нулю9
с Объясните, почему значения в столбце Допустимое уменьшение важны для ограниче-
ния времени производственных процессов
d Сколько в данной модели лимитирующих ограничений9
е (Дополнительный вопрос) Является ли данная модель вырожденной9
Ситуация для анализа | Симплекс-метод
Сегодня нет ничего необычного в умении решать задачи линейного программиро-
вания Даже новички быстро обучаются создавать табличные модели в форме, пригод-
ной для использования средства Поиск решения в Excel Но так было не всегда
В 1982 г Джордж Стиглер (George Stigler) получил Нобелевскую премию в области
экономики за “плодотворные исследования промышленных структур, функциониро-
вания рынков, а также причин и следствий общественного регулирования’’. Удиви-
тельно, но в начале своей карьеры Стиглер работал над тем, что мы теперь называем
задачей составления рациона Он пытался наити наиболее дешевый рацион, удовлетво-
ряющий 9 диетическим требованиям, сформулированным Национальным исследова-
тельским советом в 1943 г В наборе продуктов, из которых составлялся рацион, содер-
жалось 77 наименований, от пшеничной муки до клубничного джема Формулировка
была аналогична формулировке задачи на составление смеси (см раздел 3 14)
Подводя итоги своей работы в 1945 г в статье, озаглавленной “Затраты на пита-
ние’’, Стиглер писал “По всей видимости, не существует универсального метода на-
хождения минимума линеинои функции при условии соблюдения линейных ограни-
чений ” Разработав в конце 40-х годов симлекс-метод, Георг Данциг (George Dantzig)
совершил подлинный переворот 11 Не имея в своем арсенале симплекс-метода, Стиг-
лер решал свою задачу составления рациона с помощью комбинации эвристик и ре-
11 Первые постановки и методы решения задач линейного программирования принадлежат советскому ма-
тематику Л.В Канторовичу и выполнены им в конце 30-х годов К сожалению, в то время эти методы не
были востребованы и поэтому не получили широкой известности Г Данииг разработал симплекс-метод, не
зная о работах Л В Канторовича В русской научной литературе симплекс-метод часто называют методом
последовательного у/учшения шана — Прим ред
280 Ч А СТЬ II. Оптимизационные модели
шения “в лоб”. В то время он не мог доказать, что нашел хорошее решение (не гово-
ря уж об оптимальном). Позднее, когда данная задача была решена с помощью сим-
плекс-метода, оказалось, что методы Стиглера позволили найти решение, очень
близкое к оптимальному, хотя и не в точности равное ему.
Интересно, что еще 60 лет назад решение задачи составления рациона вызывало
затруднения у лучших экономистов того времени, а теперь это простое упражнение
для начинающих студентов.
Симплекс-метод, используемый средством Поиск решения, по сути, является ме-
тодом поиска экстремума. Программа находит некое угловое решение, затем про-
сматривает все соседние с ним углы допустимой области и выясняет, улучшится ли
значение целевой функции при перемещении в один из этих углов. При положи-
тельном ответе решение перемещается в такой угол, и программа снова проверяет
все соседние с ним углы — возможно ли дальнейшее улучшение. Если ответ отрица-
тельный, программа, отрапортовав об успехе, завершается.
Вопросы
1.	Рассмотрим рис. 4.3 и предположим, что средство Поиск решения начинает
свою работу с угловой точки, заданной пересечением ограничений С+ М> 100
иС>0. Покажите, что метод поиска экстремума позволит найти оптимальное
решение.
2.	Нарисуйте на бумаге график, аналогичный представленному на рис. 4.3, с другой
допустимой областью, для которой метод поиска экстремума не гарантирует по-
лучение оптимального или даже хорошего решения. Может ли допустимая об-
ласть, которую вы нарисовали, получиться в модели линейного программирова-
ния, можно ли создать такую область в программе GLP?
3.	Используя график, аналогичный рис. 4.3, проиллюстрируйте ситуацию, при ко-
торой метод поиска экстремума находит оптимальное решение за большое и ма-
лое количество шагов.
4.	Рассмотрим новый график для нелинейной модели, в которой всего одна пере-
менная решения. Откладывая по оси X значения переменной решения, а по оси
Y — значения целевой функции, докажите, что в общем случае метод поиска
экстремума не всегда приводит к оптимальному решению.
£§»гуация для анализа! Ebel Mining (часть 2)
Если компания Ebel предложит руду более высокого качества, чем предусматри-
валось исходными условиями договора, то клиенты с удовольствием будут ее исполь-
зовать. (См. ситуацию для анализа Ebel Mining (часть 1) в конце главы 2 и Ebel Min-
ing (часть 1, продолжение), в конце главы 3.)
“Зачем нужно рассматривать такой вариант? — спрашивает управляющий добы-
чей компании Ebel Трумэн Харди. — Я не хочу предпринимать никаких действий,
которые могут привести к увеличению количества рабочих дней на каждой из шахт,
необходимых, чтобы удовлетворить наши обязательства перед клиентами с мини-
мальными затратами. И мы, конечно, не хотим тратить лишние деньги, предлагая
клиентам, согласным на руду более низкого качества, более качественную руду.”
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 281
“Кстати, — продолжил он, — мне приходится заниматься продажей руды. Наше
производство руды превышает количество, обусловленное договорами. Похоже,
компании скоро придется нести огромные затраты, по меньшей мере $15 за тонну,
чтобы избавиться от лишней руды безопасным для окружающей среды образом.
Нельзя ли уменьшить общие расходы на добычу, избавившись от перепроизводства
на шахтах, а также от платы за утилизацию излишков?”
Вопросы
1.	Прав ли Трумэн, предполагая, что компания Ebel может снизить расходы, если
не будет производить руды больше, чем обусловлено договорами9 Объясните
свой ответ в доступной ему форме.
2.	Измените модель Ebel Mining, созданную в главе 3, включив в нее утилизацию
лишней руды, и оптимизируйте полученную модель. Как и прежде, предполага-
ется, что шахта может работать неполный день. Каким будет рекомендованное
расписание работы шахт при платной утилизации? Отличается ли оно от преды-
дущего расписания и почему?
3.	Может ли отгрузка некоторого количества руды более высокого качества потре-
бителям, заключившим договор на поставку руды более низкого качества, по-
мочь компании Ebel снизить затраты на добычу руды? Чтобы выяснить это, за-
пустите Поиск решения для исходной модели из главы 3 и изучите отчет по ус-
тойчивости Используя только информацию, представленную в отчете по
устойчивости, подготовьте краткое возражение на рассуждения Трумэна о недо-
пустимости поставлять руду более высокого качества, чем предусмотрено дого-
вором. Выполните те же самые действия для измененной модели из п. 2. Оста-
лись ли в силе сделанные ранее заключения для данной модели? Почему?
4.	Для более полного ответа на поставленный в п. 3 вопрос введем понятие диа-
граммы сетевых потоков. На диаграмме сетевых потоков физические перемен-
ные модели изображаются с помощью соединенных друг с другом дуг и узлов.
Дуги представляют физическое перемещение элементов (например, тонны руды,
доставленные потребителю), а узлы отражают накопление элементов (растущий
запас добытой руды). Диаграммы сетевых потоков помогают правильно постро-
ить модели ЛП, в которых присутствуют физические потоки. В таких случаях
часто необходимо составлять уравнения материального баланса. Чтобы их про-
верить, нужно убедиться, что сумма материальных потоков, входящих в узел,
равна сумме материальных потоков, выходящих из данного узла, плюс остав-
шийся запас Диаграмма сетевых потоков для Ebel показана на рис. 4.39.
5.	Используя измененную диаграмму, полученную в ответе на вопрос 4, определите
дополнительные переменные решения, отражающие объемы реклассификации
руд различных типов, для преобразованной модели ЛП в вопросе 3. Составьте
новую табличную модель, в которой отражено наличие новых дуг, представляю-
щих возможность замены низкокачественных руд высококачественными. Про-
верьте с помощью диаграммы, что в ограничениях новой модели правильно вы-
числяется материальный баланс руды, поступающей в любой узел и отправляе-
мой из него Найдите решение этой задачи с помощью средства Поиск решения.
282
ЧАСТЬ II Оптимизационные модели
Составьте полное заключение, содержащее всестороннее объяснение оптимального
решения, а подсчет экономии по сравнению с исходным решением задачи из главы 3
Какова экономическая интерпретация новых теневых цен9 Объясните, как следует
действовать компании Ebel в ответ на высокую стоимость утилизации не отправлен-
ной потребителям руды Если исходить только из результатов последней модели, сле-
дует ли компании Ebel добиваться снижения стоимости утилизации9
Потребителям руды низкого качества
Рис. 4.39. Диаграмма сетевых потоков для модели Ebel Mining
Потребителям руды высокого качества
Потребителям руды среднего качества
Измените диаграмму сетевых потоков, включив в нее новые дуги, представляю-
щие действия по реклассификации определенных количеств руды более высо-
кого качества в руду более низкого качества
| Ситуация для анализа | Red Brand Canners, продолжение
Работа компании Red Brand Canners (RBC) уже рассматривалась в главе 3. Про-
должим анализ данной модели
Вопросы
1	С помощью средства Поиск решения оптимизируйте модель производства ком-
пании Red Brand Canners, в которой не рассматривается вариант покупки допол-
нительных 80 000 фунтов помидоров сорта А
2	Чему равна чистая прибыль, полученная после вычитания стоимости помидоров?
3	Мерс утверждал, что чистая прибыль, полученная в результате реализации его
предложении, составит $144 000 Так ли это9 Если нет, то чему в действительности
будет равна чистая прибыль (как и в вопросе 2, нужно учесть стоимость плодов)9
4	Купер предлагает, сохраняя общую исходную схему расчетов, вычесть из каж-
дого коэффициента целевой функции стоимость плодов (18 центов за фунт) Из-
мените соответствующим образом формулировку и решите полученную задачу
Получится, что оптимальное значение целевой функции больше, чем в ответе на
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности	283
вопрос 2. Объясните это явное недоразумение (предполагается, что неиспользо-
ванные помидоры выбрасываются).
5.	Предположим, что неиспользованные помидоры можно перепродать по цене 18 цен-
тов за фунт. Какое решение предпочтительнее в этих условиях? На сколько можно
снизить цену перепродажи, чтобы это не повлияло на данное предпочтение9
6.	С помощью отчета по устойчивости, полученного в ответе на вопрос 1, определите,
стоит ли закупать дополнительное количество помидоров сорта А, не превышающее
80 000 фунтов. Можно ли сказать, сколько именно помидоров следует докупить9
7.	Постройте новую модель и получите оптимальный ассортимент продукции с учетом
возможности дополнительной закупки. В решении задачи необходимо явным обра-
зом показать, как следует использовать дополнительно закупленные помидоры
8.	Предположим, что в условиях, предложенных в вопросе 1, отдел маркетинговых
исследований пришел к выводу, что с помощью рекламной компании спрос на
сок можно увеличить на 25 000 ящиков. Какую сумму может выделить компания
Red Brand на эту рекламную компанию?
9.	Предположим, что в вопросе 1 цена сока возросла на 30 центов за ящик. Можно
ли узнать из отчета по устойчивости, изменится ли в таком случае оптимальный
производственный план?
10.	Предположим, что компания вынуждена перейти к производству только двух
продуктов на основе помидоров. Нужно ли повторно запускать Поиск решения,
чтобы ответить на вопрос, от производства какого продукта следует отказаться9
11.	Допустим, в вопросе 1 появилась возможность купить дополнительную партию
помидоров сорта В. Партия составляет 50 000 фунтов. Какую сумму компания
согласится заплатить за эту партию помидоров?
Дополнительные вопросы
1.	В следующих вопросах предполагается, что помидоры могут быть трех сортов,
как и в дополнительных вопросах к этой ситуации в главе 3.
2.	С помощью средства Поиск решения оптимизируйте модель ЛП в формулировке,
предложенной в вопросе 8 (см. дополнительные вопросы к ситуации в главе 3).
3.	Какова чистая прибыль, полученная после вычитания стоимости плодов?
4.	Мерс утверждает, что чистая прибыль при производстве 2 млн. фунтов томатной
пасты и 1 млн. фунтов сока составит $268 800. Так ли это? Если нет, чему в дейст-
вительности будет равна чистая прибыль (после вычитания стоимости плодов)?
5.	Купер предлагает, сохраняя общую исходную схему расчетов, вычесть из каждого ко-
эффициента целевой функции стоимость плодов. Измените соответствующим обра-
зом формулировку и решите полученную задачу, считая, что стоимость плодов со-
ставляет 21 цент за фунт. Полученное оптимальное значение целевой функции будет
отличаться от значения, полученного при ответе на вопрос 12. В каком решении чис-
тая прибыль будет больше (предполагается, что неиспользованные помидоры выбра-
сываются)? Правомерно ли включать стоимость помидоров в целевую функцию?
6.	Если в вопросе 15 неиспользованные помидоры можно продать по цене 21 цент
за фунт, какое решение предпочтительнее? На сколько можно снизить цену пе-
репродажи, чтобы это не отразилось на решении о перепродажи?
284 ЧАСТЬ II Оптимизационные модели
7	С помощью отчета по устойчивости, полученного в ответе на вопрос 12, опреде-
лите, стоит ли покупать дополнительное количество помидоров сорта А (не пре-
вышающее 80 000 фунтов) Можно ли сказать, сколько именно помидоров сле-
дует купить9
8	Создайте новую модель и получите оптимальный ассортимент продукции с учетом
возможности дополнительной закупки В решении задачи необходимо явным об-
разом показать, как следует использовать дополнительно закупленные помидоры
9	Предположим, что в условиях, предложенных в вопросе 12, отдел маркетинговых
исследовании пришел к выводу, что с помощью рекламной компании спрос на
томатную пасту можно увеличить на 3 000 ящиков Какую сумму согласится вы-
делить компания на эту рекламную компанию9
10	Предположим, что в вопросе 12 цена консервированных помидоров снизилась
на 48 центов за ящик Можно ли узнать из отчета по устойчивости, изменится ли
в таком случае оптимальный производственный план9
11	Допустим, в вопросе 12 появилась возможность купить дополнительную партию
помидоров сорта С Партия составляет 200 000 фунтов Какую сумму компания
согласится заплатить за эту партию помидоров сорта С9
| Ситуация для анализа | Компания Saw Mill14
Цель данного примера - потренироваться как в рассуждениях, так и в вычисле-
ниях Необходимо решить, какая информация необходима для решения поставлен-
ных задач После этого нужно формализовать модель ЛП (или несколько моделей),
оптимизировать ее и представить итоговый отчет со всеми результатами и выводами.
В понедельник 28 августа 2000 г управляющий мукомольной компании Saw Mill
Овертон созвал менеджеров по продажам и закупкам, чтобы обсудить политику ком-
пании на предстоящий месяц Компания Saw Mill уже приняла заказы от компаний
Turnbull Со и McClean Bros и рассматривает вариант принятия заказа от компании
Blue River, Inc Кроме того, компания имеет возможность купить дополнительное
количество кукурузы у Cochrane Farm До конца недели Овертон должен принять
решение, какие действия следует предпринять
Обычно все закупки кукурузы осуществляются до конца августа Однако компа-
ния Saw Mill все еще имеет возможность закупить дополнительное количество у
Cochrane Farm Это соглашение должно быть заключено до 1 сентября. Кукуруза
будет доставлена на элеватор Midwest Grain к 15 сентября. Этот элеватор выполняет
для Saw Mill роль хранилища
Неизменная политика компании состоит в том, что наценка на зерно кукурузы,
поставляемое заказчикам, составляет 15%. Отчисления элеватору рассматриваются
как накладные расходы и не влияют на данную политику Компании Turnbull,
McClean и Blue River согласились заплатить за сделанные заказы ту цену, которую
” Автор идеи Джонатан Корнблат (Jonathan Kornbluth), данные впервые опубликованы в книге Thomas Н
Naylor, Eugene Т Byrne, and John M Vernon, Introduction of Linear Programming Methods &Cases, 1971,
Wadsworth Publishing
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 285
запросит Saw Mill. Однако руководство компании понимает, что если цена окажется
слишком высокой, это поставит под угрозу будущие заказы.
Подробная информация о заказах, поступивших от компаний Turnbull, McClean
и Blue River, содержится в табл. 4.1.
Таблица 4.1. Данные заказов на покупку кукурузы
Компания -заказчик	Количество, бушель	Макс, про- цент влаги (на фунт)	Мин. вес на бушель, фунт	Макс, про- цент повреж- денного зерна (на фунт)	Макс, процент посторонних примесей(на фунт)	Дата по- ставки
Turnbull	40000-45000	13	56	2	2	20 09
McClean	32000-36000	15,5	54	5	3	22 09
River	50000-54000	15	56	2	4	26 09
Компания имеет возможность поставить любое количество кукурузы в указанных
пределах. Естественно, зерно должно удовлетворять оговоренным требованиям. К 4
сентября компания Saw Mill должна проинформировать компании Turnbull и McClean,
сколько зерна они получат. К этому же сроку необходимо сообщить компании Blue
River, принят ли ее заказ, и, если заказ принят, — сколько зерна будет поставлено.
Компания Saw Mill смешивает разные партии имеющейся в наличии кукурузы,
чтобы удовлетворить требования заказчиков. 28 августа на элеваторе хранится
326000 бушелей зерна Очевидно, что точно определить параметры каждого зерныш-
ка, хранящегося на элеваторе, невозможно. Поэтому в табл. 4.2 показаны обобщен-
ные характеристики различных партий кукурузы, доверенных компанией Saw Mill
элеватору Запас 326 000 бушелей состоит из 11 партий кукурузы, которые отличают-
ся качеством, ценой, процентным содержанием влаги, удельным весом в расчете на 1
бушель, процентом поврежденных зерен и процентом посторонних примесей.
Таблица 4.2. Характеристики партий кукурузы
Вид куку- рузы	Количество, бушель	Цена за бушель, $	Содержани е влаги, %	Вес буше- ля, фунт	Процент по- врежденных зерен (на фунт)	Процент посто- ронних примесей (на фунт)
1	30000	1,45	12	57	2	1,5
2	45000	1,44	15	57	2	1
3	25000	1,45	12	58	3	3
4	40000	1,42	13	56	4	2
5	20000	1,38	15	54	4	2
6	30000	1,37	15	55	5	3
7	75000	1,37	18	57	5	1
8	15000	1,39	14	58	2	4
9	16000	1,27	17	53	7	5
10	20000	1,28	15	55	8	3
11	10000	1,17	22	56	9	5
286 ЧАСТЬ II Оптимизационные модели
Кукуруза, предлагаемая Cochrane Farm, — это одна партия объемом до 50000 бу-
шелей, со средним содержанием влаги 15%, поврежденного зерна 3%, посторонних
примесей 2%, удельный вес составляет 57 фунтов на бушель Менеджер по закупкам
считает, что эту партию можно будет купить по цене $1,41 за бушель
Разработайте модель ЛП, чтобы помочь мистеру Овертону проанализировать си-
туацию (Предлагается использовать следующие обозначения Т:, М иИ - количест-
во бушелей кукурузы из партии /, которое должно быть продано компаниям Turnbull,
McClean и Blue River соответственно Кукурузу, закупленную у Cochrane Farm,
обозначим как партию 12 ) В небольшом отчете, объемом не более страницы,
изложите в сжатой форме информацию, которая может помочь мистеру Овертону
ответить на интересующие его вопросы Его главными целями являются
максимизация прибыли и удержание цен на достаточно низком уровне, чтобы
сохранить заказчиков Предполагается, что Овертон в состоянии самостоятельно
принять окончательное решение Ваша задача — предоставить ему информацию, ко-
торая позволит увидеть возможные компромиссы Можно также предложить свои
рекомендации
Ваше заключение должно осветить следующие вопросы
а покупать ли дополнительную партию кукурузы у Cochrane Farm,
b принимать ли заказ от компании Blue River,
с сколько кукурузы следует поставить компаниям Turnbull, McClean и Blue River
Ситуация для анализа | Kiwi Computer
Австралийская компания Kiwi Computer производит две модели персональных
компьютеров портативный “лэптоп" и дорогой настольный компьютер На единст-
венном заводе компании производятся корпуса, собираются печатные платы, а так-
же осуществляется окончательная сборка компьютеров Ежемесячная производи-
тельность завода ограничена производственными мощностями (табл 4.3).
Таблица 4.3 Производственные мощности (штук в месяц)
Компьютер
Операция	портативный	настольный
Производство корпусов	4000	2000
Сборка плат	2500	3000
Сборка компьютеров	200	1800
Таким образом, компания может произвести за месяц 4000 корпусов для порта-
тивных компьютеров и ни одного корпуса для настольных или 2000 корпусов для на-
стольных компьютеров и ни одного для портативных Если же уделить производству
тех и других корпусов одинаковое время, можно произвести 2000 корпусов для пор-
тативных компьютеров и 1000 для настольных Допустимый план производства ком-
пьютеров должен удовлетворять всем ограничениям одновременно. Множество до-
пустимых производственных планов показано на рис 4 40
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 287
Рис. 4.40
Оптовые цены, по которым компания поставляет компьютеры магазинам розничной
торговли, составляют $1500 за настольный и $1400 за портативный компьютер. В на-
стоящее время отрасль переживает подъем: компьютеры перестали быть средством,
предназначенным исключительно для профессионалов Рост армии пользователей при-
вел к тому, что спрос на компьютерном рынке превышает предложение, поэтому компа-
ния Kiwi может продать все произведенные компьютеры любой марки. В первом кварта-
ле текущего года компания выпускала ежемесячно 2000 портативных и 600 настольных
компьютеров. Производственные мощности по сборке печатных плат и портативных
компьютеров использовались полностью, однако оставался резерв по производству кор-
пусов и сборке настольных компьютеров. Бухгалтеры фирмы определили стандартные
издержки и накладные расходы (результаты представлены в табл. 4.4 и 4.5).
Таблица 4.4
	Компьютер	
	Настольные	Портативные
Прямые материальные затраты	800	690
Затраты на оплату труда		
Производство корпусов	20	15
Производство печатных плат	100	90
Сборка	5			10
Итого на оплату труда	125	115
Фиксированные накладные расходы		
Производство корпусов	95	95
Производство печатных плат	205	205
Сборка	415			115
Итого накладные расходы	715	415
Всего	$1640	$1220
288 ЧАСТЬ II Оптимизационные модели
Таблица 4 5
	Общие фиксированные на- Удельные фиксированные кладные расходы, тыс. долл, расходы, $
Производство корпусов Производство печатных плат Сборка настольных компьютеров Сборка портативных компьютеров Итого	247	95 533	205 249	415 	230	 115 1259
На собрании по итогам квартала руководство компании выразило недовольство
нынешним уровнем прибыли Kiwi Президент ожидал гораздо более высокой при-
были в сложившейся рыночной ситуации В ответ на это руководитель отдела про-
даж заметил, что компания не в состоянии с прибылью продавать настольные ком-
пьютеры Поэтому, чтобы повысить рентабельность, он предложил исключить дан-
ное изделие из ассортимента компании
Менеджер не со1ласился с данным предложением По его мнению, проблема с
настольными компьютерами состоит в том, что при небольшом объеме выпуска они
должны покрыть все постоянные накладные расходы цеха сборки настольных ком-
пьютеров Поэтому производство и продажа настольных компьютеров фактически
вносят положительный вклад в прибыль Этот вклад достаточно велик, чтобы по-
крыть фиксированные накладные расходы Он сказал “Если мы произведем больше
настольных компьютеров, мы сможем сделать фиксированные накладные расходы
окончательной сборки менее $415 Сейчас они высоки потому, что мы производим
слишком мало этих компьютеров ’
Заведующий отделом продаж возмутился, услышав это Именно менеджер отве-
чает за то, чтобы все руководители компании получали правдивую учетную инфор-
мацию, которая необходима им для принятия решений. А если его предположение
верно, то приведенные в табл 4 5 цифры затрат неверны
Следуя высказанному менеджером предположению, заведующий производством
предложил свои путь увеличения прибыли “Мы можем увеличить производство, если
заключим контракт с субподрядчиком на сборку некоторого количества печатных плат.
Мы можем поставлять ему компоненты и платить некие договорные цены (возможно,
различные) за сборку печатных плат для настольных и портативных компьютеров”.
В этот момент в дискуссию вмешался президент компании. Он попросил заве-
дующего отделом продаж, менеджера и заведующего производством собраться вме-
сте и подготовить рекомендации относительно ассортимента продукции и контрак-
тов с субподрядчиком Исходить следует из предположения, что спрос по-прежнему
будет высоким, а производственные мощности останутся неизменными В частно-
сти, он просил их совместно обсудить возникшие два вопроса
а Если производственные мощности и цены на компьютеры останутся неиз-
менными, и контрактов с субподрядчиками на сборку печатных плат не будет,
каким будет план наиболее рентабельного производства настольных и порта-
тивных компьютеров, будет ли он предполагать сокращение выпуска настоль-
ных компьютеров, как предлагал заведующий отделом продаж?
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 289
Ь. Чему будет равна максимальная цена, которую компания может заплатить
субподрядчику за сборку печатной платы, чтобы прибыль осталась на том же
уровне, что и при сборке всех печатных плат на собственном заводе?
Подготовьте небольшую служебную записку, основанную на анализе модели ЛП
данной ситуации. Дайте конкретные ответы на вопросы а и Ь.
Дополнительные вопросы
Часть А. Договоры с субподрядчиками не предусматриваются.
1	. В табл 4.4 накладные расходы, связанные с окончательной сборкой настольного
компьютера, составляют $415 Покажите, как была получена эта цифра
2	. а. Вносят ли настольные компьютеры вклад в общую прибыль? Иными словами,
если накладные расходы на некий небольшой срок можно считать фиксирован-
ными, повысится ли прибыль компании при прекращении выпуска настольных
компьютеров9
b Правильное вычисление удельной рентабельности показывает, что портатив-
ные компьютеры более прибыльны, чем настольные Означает ли это, что следу-
ет производить больше портативных компьютеров (или только их)9 Почему9
3	. Предположим, что сборку печатных плат нельзя поручить субподрядчику Соз-
дайте модель ЛП для определения оптимального производственного плана
4	Ответьте на первый из двух заданных президентом компании вопросов, оптими-
зировав модель с помощью средства Поиск решения, покажите оптимальный
план выпуска настольных и портативных компьютеров. В данной задаче допус-
тимы нецелые решения
5	Вычислите стандартные затраты компании, используя целочисленные решения
модели, и сравните их с приведенными в табл 4 4
6	. На сколько больше прибыль от нового производственного плана по сравнению с
предыдущим значением (при выпуске 600 настольных и 2000 портативных ком-
пьютеров)?
Часть Б. Возможен контракт с субподрядчиком.
Теперь сборка некоторого количества печатных плат может производиться суб-
подрядчиком Предполагается, что для производства корпуса и сборки компьютера в
этом случае требуется столько же времени, как и тогда, когда печатная плата собира-
ется на собственном заводе компании
7	Допустим, что субподрядчик намерен запросить $110 за сборку каждой печатной
платы настольного компьютера и $100 — портативного Компания Kiwi предос-
тавляет субподрядчику все необходимые материалы Следует ли компании в этих
условиях пользоваться услугами субподрядчика9 Объясните свои ответ, не при-
бегая к формулировке и решению новой задачи ЛП
8	. Создайте модель ЛП, учитывающую контракт с субподрядчиком В своей фор-
мулировке разделите компьютеры, производимые на основе печатных плат, соб-
ранных внутри и вне компании.
290 ЧАСТЬ II. Оптимизационные модели
9	Предположим, что в дополнение к оплате за сборку каждой печатной платы суб-
подрядчик хочет получать некую фиксированную сумму за сборку партии плат
(независимо от количества и типа плат). При каком значении этой фиксирован-
ной суммы компании Kiwi будет безразлично, заключать ли договор с субпод-
рядчиком или собирать все платы самостоятельно?
Часть В. Анализ чувствительности
10	Рассмотрите задачу линейного программирования в вопросе 8 Является ли оп-
тимальное решение вырожденным9 Объясните свой ответ.
11	Рассмотрите задачу линейного программирования в вопросе 8. Существуют ли
альтернативные оптимумы9 Обоснуйте ответ.
12	Рассмотрите задачу линейного программирования в вопросе 8 В настоящее
время субподрядчик получает $ 110 за каждую собранную печатную плату для на-
стольного компьютера На сколько нужно уменьшить данную сумму, чтобы оп-
тимальное решение для компании Kiwi предусматривало получение печатных
плат для настольных компьютеров от субподрядчика9 Объясните свой ответ
13	Рассмотрите задачу линейного программирования в вопросе 3 Предположим, что
компания Kiwi может увеличить мощности по сборке печатных плат, что позволит
собирать дополнительно 600 плат для настольных или 500 плат для портативных
компьютеров или любую эквивалентную их комбинацию. Следует ли компании на-
ращивать производственную мощность, если затраты при этом составят $175 000
в месяц9 Ответьте на данный вопрос, не прибегая к повторному решению задачи Л П
14	Рассмотрите задачу линейного программирования в вопросе 3. Предположим,
что конструкция печатной платы для настольного компьютера изменилась таким
образом, что прямые материальные затраты снизились на $200 Можно ли на ос-
новании отчета по устойчивости сказать, изменится ли оптимальный производ-
ственный план9
15	Ответьте на второй вопрос, заданный в конце дискуссии президентом компании
Альтернативные вопросы
Компания изучает возможность проведения окончательной сборки настольных и
портативных компьютеров в одном цеху. Этот новый цех сможет собрать за месяц
3000 портативных компьютеров и ни одного настольного или 2200 настольных и ни
одного портативного, если же время на сборку обоих видов компьютеров будет рас-
пределено поровну, цех сможет собрать 1500 портативных и 1100 настольных ком-
пьютеров Согласно оценкам, ежемесячные фиксированные накладные расходы для
данного цеха будут меньше, чем $479 000 — сумма текущих накладных расходов двух
цехов, осуществляющих сборку настольных и портативных компьютеров При ответе
на следующие вопросы предполагается, что цеха будут объединены.
Часть А. Договоры с субподрядчиками не предусматриваются.
1	Пусть D и Р— коэффициенты ежемесячного производства настольных и порта-
тивных компьютеров соответственно, a F— фиксированные накладные расходы
объединенного сборочного цеха Выразите общую прибыль как функцию D,Pw F
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности 291
2	Нужно ли знать значение F, чтобы определить оптимальный производственный
план9 Предполагается, что значения D и Рне влияют на фиксированные наклад-
ные расходы.
3.	Предположим, что печатные платы не могут поставляться субподрядчиком
Сформулируйте задачу линейного программирования для определения опти-
мального производственного плана.
4.	Оптимизируйте модель с помощью Поиск решения и укажите оптимальный ас-
сортимент выпуска настольных и портативных компьютеров. Допускаются не-
целочисленные ответы.
5.	Найдите наилучшее возможное целое решение, которое можно получить, округ-
лив до ближайших целых ответ на вопрос 4
6.	Предположим, что до объединения сборочных цехов оптимальное значение при-
были (доход минус все расходы) составляет $330 286. Каким может быть наи-
большее значение фиксированных накладных расходов объединенного сбороч-
ного цеха, чтобы компании все еще было выгодно провести это объединение9
Часть Б. Возможен контракт с субподрядчиком
7	Предположим, что субподрядчик намерен запросить $150 за сборку каждой пе-
чатной платы для настольного компьютера и $135 — для портативного компью-
тера Компания Kiwi предоставляет субподрядчику все необходимые материалы
Следует ли компании в этих условиях пользоваться услугами субподрядчика9
Объясните свой ответ, не прибегая к решению новой задачи ЛП.
8.	Сформулируйте задачу ЛП, в которой учитывается контракт с субподрядчиком
В своей формулировке разделите компьютеры, производимые на основе печат-
ных плат, собранных внутри и вне компании
9	Предположим, что в дополнение к оплате за сборку каждой печатной платы суб-
подрядчик хочет получать некую фиксированную сумму за сборку партии плат
(независимо от количества и типа плат) При каком значении этой фиксирован-
ной суммы компании Kiwi будет безразлично, заключать договор с субподрядчи-
ком или собирать все платы самостоятельно9
Часть В. Анализ чувствительности.
10	Рассмотрите задачу линейного программирования в вопросе 8. Является ли оп-
тимальное решение вырожденным? Объясните свой ответ.
11.	Рассмотрите задачу линейного программирования в вопросе 8. Существуют ли
альтернативные оптимумы? Как вы пришли к своему выводу?
12	Рассмотрите задачу линейного программирования в вопросе 8. В настоящее
время субподрядчик получает $150 за каждую собранную печатную плату для на-
стольного компьютера На сколько субподрядчик должен уменьшить данную
сумму, чтобы компании Kiwi было выгодно поручить ему изготовление печатных
плат для настольных компьютеров9 Объясните свой ответ.
13.	Рассмотрите задачу линейного программирования в вопросе 3 Предположим,
что компания Kiwi может увеличить мощности по сборке печатных плат, что по-
зволит собирать дополнительно 600 плат для настольных или 500 плат для порта-
тивных компьютеров или любую эквивалентную их комбинацию. Следует ли
компании наращивать производственную мощность, если издержки при этом
292 Ч А С Т Ь II. Оптимизационные модели
составят $175 000 в месяц? Ответьте на данный вопрос, не прибегая к повторно-
му решению задачи ЛП.
14.	Рассмотрите задачу линейного программирования в вопросе 3. Предположим,
что конструкция печатной платы для настольного компьютера изменилась таким
образом, что прямые материальные затраты снизились на $200. Можно ли на ос-
новании отчета по устойчивости сказать, изменится ли оптимальный производ-
ственный план?
| Ситуация для анализа | Компания Valley Chassis15
Компания Valley Chassis производит высококачественные полированные сталь-
ные и алюминиевые листы, а также два вида стоек высотой шесть футов, на которых
монтируются модемы, Internet-маршрутизаторы и другое телекоммуникационное
оборудование. При продаже металлических листов удельный валовой доход компа-
нии (прибыль плюс фиксированные затраты) составляет $0,40 за фунт стали и $0,60
за фунт алюминия. Например, цифра $0,40 за фунт стального листа вычисляется как
цена продажи (в расчете на один фунт) минус прямые затраты труда и материалов,
включая стоимость необработанной стали. При продаже стойки Standard удельная
прибыль составляет $12,00, а при продаже стойки Deluxe — $15,00.
В январе компания может приобрести и использовать для производства листов
или стоек до 25800 фунтов стали и 20400 фунтов алюминия (Напоминаем, что зна-
чения удельной прибыли для различных продуктов получены в результате вычитания
прямых затрат труда и материалов из удельной цены продажи.) Для изготовления
одной стойки Standard требуется 16 фунтов стали и 8 фунтов алюминия, а для изго-
товления стойки Deluxe — по 12 фунтов каждого металла.
Выпуск металлического листа ограничен исключительно производственной
мощностью полировальной машины В январе полировальная машина может обра-
ботать до 4000 фунтов металлического листа (независимо от вида металла).
При производстве стоек ограничивающими факторами могут быть как штампов-
ка, так и сборка, полировка в данном случае не применяется За месяц можно на-
штамповать не более 2500 стоек, ресурс времени сборки составляет 920 ч в месяц
Сборка стойки Standard занимает 24 мин , а стойки Deluxe — 36 мин.
Условия рынка таковы, что можно продать любое количество металлических лис-
тов, не более 1200 стоек Standard и не более 1000 стоек Deluxe.
Сформируйте табличную модель ЛП в Excel и оптимизируйте ее с помощью сред-
ства Поиск решения Используя результаты, представленные в отчете по устойчиво-
сти, ответьте на следующие вопросы
Вопросы
1	. Чему равен прирост прибыли, связанный с добавлением дополнительного часа к
ресурсу времени сборки9 Для какого диапазона увеличения действительно дан-
ное значение9
15 © 2000 Board of Trustees of the Leland Stanford Junior University All rights reserved Данный пример впервые
предложил Эван Портеус (Evan Porteus)
ГЛАВА 4. Линейная оптимизация. Анализ чувствительности
293
2	Чему равна стоимость дополнительной мощности полировальной машины9 На-
сколько можно увеличить и уменьшить данную производственную мощность,
прежде чем решение сместится в новую угловую точку9
3	. Предположим, что компания Standard Manufacturing хочет купить часть времени
сборки у компании Valley При какой наименьшей цене (в долларах за час) ком-
пании Valley следует принять предложение продать часть своего времени сборки9
Почему9 Для какого диапазона времени действительно данное значение9
4	. Согласно прогнозу, удельная прибыль от продажи стального листа в расчете на
один фунт возрастет с $0,40 до $0,43 Как это повлияет на текущее решение9
5	Насколько низкой можно сделать удельную прибыль стойки Deluxe, прежде чем это
приведет к снижению плана выпуска данных стоек9 Если удельная прибыль станет
чуть меньше этого критического значения, сколько стоек Deluxe следует произво-
дить9 Объясните, что еще происходит с оптимальным планом в данной точке
6	. Рекламное агентство Thornton разработало для компании Valley Chassis марке-
тинговый план, который позволит расширить рынок сбыта стоек Deluxe План
предусматривает увеличение спроса на 100 штук при затратах $200 в месяц Сле-
дует ли компании Valley принять данный план? Как следует поступить, если рас-
ходы составят всего $ 120 в месяц9 $ 160? Дайте в каждом случае наиболее полный
возможный ответ, не прибегая к повторному решению задачи Л П
7	Предположим, что можно добавить 4 ч к ресурсу времени сборки стоек Как это
отразится на производстве металлического листа и стоек9 Как изменится прибыль9
8	Предположим, что к ассортименту выпускаемой продукции предложено добавить
еще один вид стоек — самых лучших и легких Для изготовления такой стойки потре-
буется 8 фунтов стали и 16 фунтов алюминия, а также одна единица производствен-
ной мощности штамповочного пресса и 48 мин. на сборку При этом удельная при-
быль составит $ 16,00 Будет ли выпущена хотя бы одна такая стойка9 Объясните свой
ответ без повторного решения задачи. (Совет Вычислите коэффициент прибыльно-
сти для данного вида стоек исходя из предположения, что все ресурсы, необходимые
для производства этой одной стойки, берутся из ограниченных ресурсов существую-
щей модели, и используйте теневые цены.) Теперь сформируйте новую табличную
модель Л П, включив в нее новый вид продукции, решите эту задачу и сравните полу-
ченные результаты с результатами проведенного вами анализа
Ситуация для анализа | Ферма Ельцина
Игорь Ельцин руководит в России фермой еще со времен колхозной системы Ранее
ферма занималась выращиванием свиней для сдачи государству Руководитель фермы
ежегодно получал от государственных планирующих органов задание, сколько свиней
необходимо откормить, а также необходимые для выращивания животных корма При
переходе к рыночной экономике Игорь больше не получает инструкций и должен вести
хозяйство самостоятельно- закупать корма, откармливать свиней и находить покупателей
Свиней откармливают кукурузой и картофелем в пропорции, обеспечивающей мини-
мальное содержание протеина и калорий Поставки кукурузы и картофеля в последнее
время стали менее надежными, поэтому Игорь договорился о покупке пищевых отходов с
расположенным неподалеку пищевым комбинатом, чтобы дополнить рацион, состоящий
из картофеля и кукурузы. Представьте себя в роли консультанта из ООН, к которому
294 ЧАСТЬ II Оптимизационные модели
Игорь обратился с просьбой оказать помощь в управлении фермой в условиях нестабиль-
ной экономики Игорь уже заключил договор на поставку в следующем месяце 100 сви-
ней московскому мясокомбинату по цене 450 руб. за голову. Кроме того, он договорился
о покупке 800 кг пищевых отходов по цене 10 руб. за 1 кг. Он надеется, что сможет купить
практически любое количество кукурузы по 19 руб. за 1 кг и до 600 кг картофеля у бли-
жайшей фермы по 15 руб за 1 кг. В таблице представлена ежемесячная потребность од-
ного животного в протеинах и килокалориях, а также удельное содержание килокалорий
и протеина, приходящееся на килограмм каждого вида корма.
	Минимальная потребность	Кукуруза (на 1 кг)	Пищевые отходы (на 1 кг)	Картофель (на 1 кг)
Протеин	174	18	9	15
Килокалории	1400	30	120	80
Чтобы помочь Игорю разобраться в управлении фермой, консультант построил в Ex-
cel модель Л П (рабочая книга Ельцин xls), показанную на рис. 4 41. На основании полу-
ченных результатов необходимо ответить на вопросы Игоря относительно работы фермы.
Модель
Ельцина
Продано
______________свиней
Цена__________450
Решение |	100,00
Лимит поставки <=100
Содержание
питательных
веществ
Протеин
Килокалории
600 ОС
Удельная
потребность
-174
-1400
3|Щ
80
Закуплено
картофеля
120
Закуплено
пищевых закуплено
отходов кукурузы
/дельное содержание питательных
____________веществ____________
ДО
|=СУММПРОИЗВ($В$3 $Е$3 В2 Е2)|
Яч*йка_______________Имя_________________________
$В$3	Решение Продано свиней	100.00
$С$3	Решение Закуплено картофеля	_	__	600.00
$D$3	Решение Закуплено пищевых отходов	742.86
$Е$3	Решение Закуплено кукурузы 95.24
Р*аульт Нормир Целевой Допустимо* Допустимо»
аначени*стоимостьКоаффициентУвеличени*/меньшение
..........  "	""	1Е+30
1Е+30"
261.05
0.00
1 82
261.05
___<10
24.69
Ограничения
Ячейка______________Имя
$F$6 Протеин Превышение
$F$7 Килокалории Превышение
Реаульт Теневая Ограничение Допустимо* Допустимо*
значение Цена Правая часть Ув*пич*ниеУменьшение
0.00	-1.05	0	46800	1500
78000
46800
6000
450 _
Рис. 4.41. Модель фермы Ельцина
ГЛАВА 4. Линейная оптимизация Анализ чувствительности 295
На некоторые вопросы только на основе данных, показанных на рис. 4.41, отве-
тить нельзя. В таком случае необходимо дать наилучший возможный ответ и объяс-
нить, почему более точный ответ дать нельзя. После этого, если нужно, измените со-
держащуюся на прилагаемом к книге компакт-диске рабочую книгу Ельцин xls
и повторно оптимизируйте ее с помощью средства Поиск решения.
Вопросы
1	. “Если я последую вашим рекомендациям по максимизации производственной
прибыли в следующем месяце, сколько я смогу выручить за продажу 100 голов
свиней? Сколько голов свиней я должен буду в этом случае продать, какое ко-
личество кукурузы, пищевых отходов и картофеля купить9”
2	“Согласно рекомендациям мне следует купить нецелое количество килограм-
мов кукурузы и пищевых отходов, но мои закупки должны выражаться в целых
килограммах. Как быть?”
3	“Я думаю, что мне удастся договориться с мясокомбинатом, чтобы он купил
дополнительно 5 голов свиней по той же цене 450 рублей за голову Улучшится
ли ситуация, если я попытаюсь продать 105 голов вместо 1009 Насколько воз-
растет (и возрастет ли вообще) моя прибыль9”
4	“Вы должны понимать, что ситуация сейчас весьма нестабильна Например,
цена покупаемой мною кукурузы может внезапно измениться На сколько мо-
жет повыситься цена кукурузы, прежде чем мне придется менять производст-
венный план?”
5	. “К сожалению, договоры сейчас тоже не всегда выполняются Я боюсь, что по-
ставщик картофеля может не выполнить свое обещание поставить 600 кг Если
он поставит всего 500 кг, каковы будут мои потери и какие изменения нужно
будет внести в мои решения9”
6	. “Могу ли я получить ту же самую прибыль другим путем, скажем, при других
объемах закупки кукурузы, пищевых отходов или картофеля9 Если да, то как
именно9”
7	“Представитель международной компании Ralston-Punna предлагал мне ку-
пить упакованный сухой корм для свиней, импортированный из Польши Це-
на, включая доставку, составляет 16 руб за килограмм По его словам, каждый
килограмм корма содержит 16 единиц протеина и 150 килокалорий Следует ли
соглашаться на импорт корма из Польши? Если да, то сколько следует заку-
пить, и как это отразится на оптимальном значении прибыли9”
296 ЧАСТЬ II. Оптимизационные модели
Литература
1	George Dantzig The Diet Problem, Interfaces, 20, no 4(1990) 43-47.
2	Lily Lancaster The Evolution of the Diet Model in Managing Food Systems, Interfaces, 22, no 5 (1992)
p 59-68
3	. Robert J Might Decision Support for Aircraft and Munitions Procurement, Interfaces, 17, no 5 (1987)
p 55-63
4	Honono Carino and Clinton LeNoir Optimizing Wood Procurement in Cabinet Manufacturing, In-
terfaces, 18, no 2 (1988) p 101-19
Глава
Линейная оптимизация. Применение
В этой главе...
5.1.	Введение
5	2. Транспортная модель
5.3.	Варианты транспортной модели
5.4.	Модель назначений
5.5.	Модель выбора средств массовой информации
5.6.	Динамические модели
5.7.	Динамическая модель планирования и управления запасами
5.8.	Динамическая модель управления финансами
5.9.	Модель управления финансами и планирования производства
5.10.	Сетевые модели
5.11.	Модель перевозок
5.12.	Поиск кратчайшего пути
5.13.	Модель замены оборудования
5.14.	Задача максимизации потока
5.15.	Заключение
Основные термины
Контрольные вопросы
Задачи
Ситуация 1 Планирование производства в компании Bumles
Ситуация 2 Ebel Mining (часть 3)
Ситуация 3 Ebel Mining (часть 4)
Литература
298	Ч А С Т Ь II. Оптимизационные модели
Практическое применение^
Система HASTUS
Проблема снижения расходов на общественный транспорт носит всеобщий ха-
рактер Один из наиболее успешных подходов к решению данной проблемы был раз-
работан в Канаде управлением городскими перевозками Монреаля. Эта организа-
ция, в штате которой состоят 8000 сотрудников, а годовой бюджет составляет более
$575 млн , осуществляет более 400 млн. пассажирских перевозок в год. В ее распоря-
жении имеется 1700 автобусов и 750 вагонов метро, для обслуживания которых еже-
дневно требуется 3000 человек.
Эффективное расписание способствует улучшению качества обслуживания пас-
сажиров и может оказать заметное влияние на производственные затраты. Составле-
ние такого расписания — сложная задача, поскольку в течение дня наблюдаются
значительные колебания потока пассажиров. В часы пик требуется до 1500 единиц
транспорта, тогда как в периоды затишья достаточно одной пятой этого количества
Расписание должно учитывать интервалы движения транспорта на каждом маршруте
в течение дня, а также влияние на среднюю скорость условий движения в различные
периоды времени (например, дорожных пробок в часы пик)
Расписание составляется в два этапа. Начинают с расписания движения транс-
портных единиц Стоящая здесь задача — предоставить количество автобусов и ва-
гонов метро, необходимое для обеспечения нужной частоты движения на всех мар-
шрутах Затем составляется расписание для экипажей, при этом назначаются води-
тели для указанных транспортных средств Для содействия в решении данных задач
управление городскими перевозками Монреаля совместно с Центром транспортных
исследований университета Монреаля разработали систему HASTUS. Программа
состоит из трех основных программных модулей.
•	Первый модуль используется при составлении оптимального расписания движе-
ния транспортных средств и основан на сетевых методах
•	Второй модуль использует модели линейного программирования для получения
“хорошего” начального решения для расписания экипажей. Тщательно отобран-
ные упрощения позволили уменьшить огромное число переменных до 3000 и бы-
стро найти решение задачи
•	Последний модуль, использующий модели назначений и методы выбора крат-
чайшего пути, позволяет уточнить полученное ранее решение и составить под-
робное расписание для водителей
Отдел планирования сравнил затраты при решениях, найденных вручную и с по-
мощью компьютера Оказалось, что система HASTUS позволила снизить количество
ошибок в расписании и сэкономить не менее $100 000 в год за счет сокращения вы-
плат по зарплате за сверхурочные работы. Таким образом, система окупилась менее
чем за 3 месяца Кроме того, система HASTUS позволила сократить оплачиваемое
время простоев водителей и других работников на 20% по сравнению с решениями,
найденными вручную. Общая годовая экономия приблизилась к $4 млн • $3 млн. за
счет оптимального расписания для персонала и $ 1 млн. за счет оптимального распи-
сания для парка транспортных средств.
Система также позволяет менеджерам производить анализ чувствительности ре-
шений Имитационные эксперименты, на которые раньше потребовались бы неде-
ГЛАВА 5. Линейная оптимизация Применение
299
ли, теперь можно выполнять за считанные минуты. Это помогает руководству выби-
рать наиболее выгодные предложения на переговорах с профсоюзами
Система HASTUS оказалась достаточно простой в обращении и обучении. Она
быстро завоевала популярность среди плановиков, поскольку делает их работу более
интересной и содержательной. Успех программы настолько очевиден, что в настоя-
щее время версии HASTUS на нескольких языках помогают решать задачи планиро-
вания в 40 различных городах мира. [1]
5.1. Введение
Методы линейной оптимизации — основной рабочий инструмент в мире оптимиза-
ционных моделей. Широта диапазона моделей линейного программирования (ЯП) — от
простых моделей с несколькими дюжинами переменных до сложнейших моделей, кото-
рые содержат десятки тысяч переменных решения и ограничений и требуют огромного
количества итераций для нахождения решения, — делает их важнейшим средством ана-
лиза разнообразных бизнес-ситуаций.
В данной главе основное внимание уделяется применению линейной оптимизации
Мы рассмотрим различные постановки одиннадцати конкретных моделей, которые мо-
гут служить шаблонами при создании более крупных реальных моделей Раздел 5.2 по-
священ изучению одной из наиболее популярных моделей линейной оптимизации —
транспортной модели В данной модели ставится задача организации доставки хранящей-
ся в различных местах (на складах) продукции потребителям, чтобы удовлетворить суще-
ствующие требования с наименьшими затратами В разделе 5 3 рассматривается модель
назначений Эта модель позволяет исследовать распределение фиксированных ресурсов,
например, оптимальным образом распределять продавцов по отделам, задания по стан-
кам или задачи по компьютерам. Модель назначений является разновидностью транс-
портной модели
В разделе 5 4 исследуется разновидность модели сбыта — модель выбора средств мас-
совой информации, предназначенная для разработки успешной рекламной компании,
при которой решение ограничено общим объемом бюджетных средств, количеством мес-
та для размещения рекламы в различных источниках, а также субъективными соображе-
ниями собственного руководства Модель выбора СМИ — частный случай важного клас-
са управленческих моделей, в которых происходит снижение отдачи при увеличении
масштаба операций (в данном случае это уменьшение удельного дохода от рекламы),
а также комбинация решений (в данном случае требуется пропорциональное сочетание
различных рекламных источников)
В разделах 5 5-5 8 рассмотрены примеры динамических моделей, в которых необходимо
принять скоординированные решения на несколько временнь/х периодов Мы рассмотрим
три примера динамических моделей, в которых управление запасами влияет на будущее
производство, производственное планирование и управление финансовыми ресурсами
В разделе 5 9 представлена объединенная модель финансового и производственного пла-
нирования. Хотя данная модель относительно проста по сравнению с реальными приложе-
ниями, этот пример наглядно демонстрирует, как создаются объединенные модели, преду-
сматривающие оптимизацию как по производственным, так и финансовым показателям.
Транспортные модели и модели назначений являются частными случаями более об-
щего класса сетевых моделей, в которых рассматривается перемещение или распределе-
ние физических элементов (продукции, персонала, финансов, пакетов Internet и тд)
300 ЧАСТЬ II Оптимизационные модели
В оставшейся части главы описано несколько примеров сетевых моделей, используемых
для оптимизации перевозки грузов, нахождения кратчайшего пути и максимизации по-
тока в сети
5.2. Транспортная модель
Компания AutoPower выпускает аккумуляторы и источники бесперебойного питания,
которые используются в качестве резервных источников электроэнергии больницами,
Internet-проваидерами, в производстве полупроводников и химической продукции, т.е.
там, где недопустимы перебои в энергоснабжении. В Европе компания AutoPower имеет
четыре завода, на которых производится сборка больших дизельных генераторов для
бесперебойного питания Заводы расположены в городах Лейпциг, Германия (далее
обозначается цифрой 1), Нанси, Франция (обозначается 2); Льеж, Бельгия (3) и Тилбург,
Нидерланды (4) Дизельные моторы, используемые в этих генераторах, производятся в
США, доставляются в порты Амстердама (ниже обозначается буквой А), Антверпена
(будет обозначаться буквой В) и Гавра (С), откуда отправляются на сборочные заводы
Планы производства на третий квартал (с июля по сентябрь) уже сформированы
Требования к доставке моторов (спрос в местах назначения) сведены в табл 5 I.
Таблица 5.1. Спрос на моторы
Сборочный завод	Требуемое количество моторов
(I)	Лейпциг	400
(2)	Нанси	900
(З)Льеж	200
(4)	Тилбург	500
2000
В табл. 5.2 показаны количества моторов, которые будут доставлены в порты для ис-
пользования в третьем квартале (предложение в пунктах отправки).
Таблица 5.2. Предложение моторов
Порт	Количество	моторов
(А)	Амстердам	500
(В)	Антверпен	700
(С)	Гавр	800
2000
Обратите внимание на то, что данная модель является сбалансированной, т.е. сум-
марное предложение моторов равно их общему спросу. На рис. 5.1 представлена иллюст-
рация к данной модели. Число рядом с названием порта показывает существующее пред-
ложение, а число рядом с названием сборочного завода — требуемое количество моторов.
Линии показывают возможные пути доставки.
ГЛАВА 5 Линейная оптимизация. Применение 301
Рис. 5.1. Схема транспортной задачи для компании AutoPower
Компания AutoPower должна принять решение, сколько моторов будет отправлено из
каждого порта на каждый сборочный завод Моторы перевозятся обычными грузовика-
ми, и оплата производится исходя из количества перевезенных моторов. Соответствую-
щие расценки приведены в табл 5 3. Для упрощения будем обозначать порты буквами, а
заводы — цифрами, как указано выше.
Таблица 5.3. Затраты на транспортировку одного мотора, $
Пункт отправки	Место назначения			
	Лейпциг (1)	Нанси (2)	Льеж (3)	Тилбург (4)
(А) Амстердам	120	130	41	59,50
(В) Антверпен	61	40	100	ПО
(С) Гавр	102,50	90	122	42
Формулировка и решение задачи ЛП
Цель компании AutoPower — минимизировать суммарные затраты на транспортировку
моторов из портов на заводы Поскольку расходы на транспортировку для каждой комбина-
ции порт-завод (например, Антверпен-Нанси) прямо пропорциональны числу моторов, от-
правленных их данного порта на указанный завод (для комбинации Антверпен-Нанси коэф-
фициент пропорциональности равен $40), данную задачу можно сформулировать в виде мо-
дели линейного программирования Обозначим через* количество моторов, отправленных из
порта i на завод; (i = А, В, С; у = 1, 2, 3, 4) Тогда хС4 — количество моторов, отправленных из
порта С (Гавр) на завод 4 (Тилбург) Используя данные обозначения, целевую функцию —
общие транспортные расходы — можно записать как 120*Д1 + 130хЛ, + . +42хС4.
302
ЧАСТЬ II Оптимизационные модели
Модель содержит ограничения двух видов
1. Количество моторов, отправленных из любого порта, не может превышать коли-
чество моторов, имеющихся в данном порту. Например, общее количество мото-
ров, отправленных из порта А (Амстердам), составляет хА| +Хд, +хАЗ + хА4. По-
скольку предложение моторов в порту А равно 500, соответствующее ограничение
имеет вид хА1 + ха +	+ хА4 < 500
Аналогичные ограничения записываются для каждого пункта отправки. Заметим,
что в данном случае для задания ограничений вместо неравенств можно использо-
вать равенства Поскольку в этой модели спрос и предложение сбалансированы,
ограничения-неравенства в точке оптимальности будут лимитирующими, т е. пре-
вратятся в равенства
2. Необходимо удовлетворить спрос на всех заводах Например, пустьхА1 + хВ| + хС| —
общее количество моторов, отправленных на завод 1 (Лейпциг). Поскольку этому
заводу требуется 400 моторов, соответствующее ограничение будет иметь вид хА, +
+ хв, + хс| > 400
Аналогичные ограничения записываются для каждого завода. Как и ограничения
по объемам предложения, ограничения по спросу можно записать в виде равенств,
так как спрос и предложение сбалансированы.
Сформированная модель в Excel и ее оптимальное решение представлены на
рис 5.2 Заметим, что основные модули модели расположены в виде трех блоков
ячеек стоимостные параметры, переменные решения и общие затраты Как показа-
но на рис 5 2, используется 6 из 12 возможных маршрутов, и минимальная стои-
мость транспортировки составляет $121 450 Более того, из отчета по устойчивости
программы Поиск решения (рис 5 3) следует, что при снижении требований на по-
ставку моторов в Нанси общие затраты снизились бы на $107,5 за один мотор, уве-
личение запаса моторов в Антверпене также привело бы к снижению общих затрат
на $67,50 в расчете на один мотор.
Совет. В соответствии с данными в главе 3 рекомендациями табличные представления
моделей строятся с соблюдением следующих правил 1) параметры удельных за-
трат/прибыли, переменные решения и суммарные затраты/прибыль располагаются в от-
дельных диапазонах ячеек, 2) переменные решения выделяются рамкой, а ячейка со значе-
нием целевой функции — рамкой и затемненным фоном. Эти простые рекомендации об-
легчают восприятие модели Кроме того используются специальные форматы, задающие
отображение в одной ячейке числовых значений правых частей ограничений вместе с со-
ответствующим знаком неравенства Например, содержимое ячейки Н9 — число 500, но
формат данной ячейки позволяет отображать в ячейке и знак неравенства Более подроб-
но такие форматы описаны в приложении Б.
ГЛАВА 5. Линейная оптимизация. Применение 303
Рис. 5.2. Оптимальное решение транспортной задачи компании Auto Power
304 ЧАСТЬ II Оптимизационные модели
Microsoft Excel 10.0 Отчет по устойчивости Изменяемые ячейки						
Ячейка	Имя	значение	Нормир стоимость	Целевой Коаффициент	Допустимое Увеличение	Допустимое Уменьшение
$С$9	Амстердам Лейпциг	0	0	120	1Е+30	0
$D$9	Амстердам Нанси	0	22.5	130	i Ё+зб		22,5
$Е$9	Амстердам Льеж	200	0	41		98,5	41
$F$9	Амстердам ТилОург	300	б		59,5"'	Q		17,5
$С$10	Антверпен Лейпциг	0	8.5	61	1Е+30	8.5
$D$10	Антверпен Нанси.	700	б		40		ед’		1Е *30
$Ё$1 б	Антверпен Льеж	б	126.5	- Гбб"		126.0
$F$iб			б	i 18	iio 	......_	[е+зо	118
$С$11	Гавр Лейпциг			'	40б'~		  "о"		0 ...............		120
SD$ii		Гавр Нанси	200"	Q	90		8,5
$Ё$11	Г авр Льеж	......		7"	'99^"'	.'"i22		1Ё+30	98,5
$F$11	Гавр Тилбург	200	б	42	17.5	б
Ограничения	I	1						
		Результ	Теневая	Ограничение	Допустимое	Допустимое
Ячейка	Имя	значение	Цена	Правая часть	Увеличение	Уменьшение
$С$12		400	120	400		0			300
	Всего Нанси		—--gQQ		——	_•	”б"'	“200'
£Е£12	Всего Льеж	200	41	200		I	'""200
$F$12	Всего ТилОург	500	59.5	500	0	300
$G$9	Амстердам Всего		500			б""		500		iE+эб"	б
$G$10	Антверпен Всего	700	-68	700	200	о
$G$11	Та ер Всего		800	-18	800	300		0
Рис. 5.3. Отчет по устойчивости модели компании AutoPower
5.3.	Варианты транспортной модели
В общем случае транспортная модель — это модель ЛП, позволяющая найти самый
дешевый способ удовлетворить спрос в п пунктах назначения, осуществляя поставки из
т исходных (отправных) пунктов
Максимизация транспортных моделей
Предположим, что в рассмотренном примере целью является максимизация значения це-
левой функции, а не минимизация. Можно использовать ту же самую модель, внеся одно не-
большое, но важное, изменение, коэффициентами целевой функции должны стать значения
удельной прибыли, а не удельных затрат, и средство Поиск решения должно решать задачу
максимизации Аналогично изменяется интерпретация данных в отчете по устойчивости.
Несбалансированные модели
Предположим, что в нашем примере модели предложение моторов в порту А составляет
600 штук вместо 500 Тогда после удовлетворения спроса суммарное количество моторов,
оставшихся в трех отправных пунктах, будет равно 100 Поскольку в формулировке задачи
применялись неравенства, особых проблем при использовании средства Поиск решения не
возникнет Невостребованные моторы в каждом отправном пункте будут представлены
в виде резерва ограничения по объему предложения для данного пункта.
Если же спрос превышает предложение, модель Л П не имеет допустимых решений Одна-
ко компания AutoPower может в этой ситуации максимально удовлетворить спрос при мини-
мальных затратах Возможны два подхода к моделированию такой ситуации Можно перепи-
сать ограничения для запасов в виде равенств, тем самым заставив отгрузить на заводы все
имеющиеся в портах моторы, а все ограничения для спроса записать в виде неравенств вида <
Неудовлетворенный спрос в решении будет представлен резервом для каждого ограничения
ГЛАВА 5. Линейная оптимизация. Применение 305
спроса Второй подход заключается в том, чтобы переделать модель, введя в нее фиктивный
отправной пункт, запас в котором в точности соответствует разности между общим спросом
и предложением. Этот фиктивный пункт делает модель сбалансированной, когда предложе-
ние равно спросу. Стоимость доставки из этого пункта в любое место назначения равна нулю.
Каждая поставка из фиктивного пункта на любой завод интерпретируется как неудовлетво-
ренный спрос. Преимущество второго подхода состоит в том, что можно определить удельную
стоимость всех переменных решения, связывающих фиктивный пункт с определенным пунк-
том назначения. Если эти стоимости будут правильно отражать удельную стоимость неудовле-
творения спроса в соответствующих пунктах назначения, то Поиск решения сможет при оп-
тимизации учесть эти стоимости наряду с затратами на транспортировку и отразить соответст-
вующую информацию в отчете по устойчивости
Модель с недопустимыми путями
Предположим, что некоторые пути в транспортной модели являются недопустимыми.
Иногда в силу организационных условий, таких как региональные ограничения или время
доставки, некоторые отправные пункты не могут обслуживать определенные пункты на-
значения Предположим, что путь из Амстердама в Льеж нельзя использовать Для того что-
бы ввести это ограничение в формулировку транспортной задачи, следует присвоить произ-
вольно большое значение М удельным затратам для данного маршрута Значение Л/должно
быть значительно больше всех остальных удельных затрат модели Это заставит Поиск ре-
шения отказаться от данного пути, поскольку при его использовании затраты будут гораздо
больше, чем для всех других допустимых альтернатив В нашем случае, присвоив коэффи-
циенту удельных затрат на транспортировку в ячейке Е4 (см рис 5 2) значение $1 000 000,
можно не сомневаться, что Поиск решения не будет использовать данный путь
Целочисленные решения
Из предыдущих глав известно, что в общем случае модели J1П не дают целочисленных
решений Даже если все параметры модели линейного программирования общего вида
(коэффициенты в формуле целевой функции, коэффициенты технологических ограни-
чений и правые части) — целые числа, решение не всегда является целочисленным
Транспортная модель является исключением и имеет целочисленные решения при дос-
таточно общих условиях.
Если все значения спроса и предложения в транспортной модели являются целыми
числами, оптимальные значения переменных решения также будут целыми.
Альтернативные оптимумы для нескольких целей
Нулевые значения допустимых изменений целевых коэффициентов в отчете по ус-
тойчивости на рис 5 3 свидетельствуют о наличии альтернативных оптимумов.1 Можно
воспользоваться такой ситуацией, которая достаточно часто возникает в моделях ЛП,
особенно в транспортных. Предположим, что президент Европейского отделения компа-
нии AutoPower изучает риск повышения затрат в цепи поставок из-за возможной забас-
товки водителей грузовиков в Гавре. Он обратился с просьбой найти наиболее дешевые
пути транспортировки, при этом минимизировав затраты на вывоз моторов из Гавра
Понятно, что если бы более дешевые пути существовали, средство Поиск решения на-
Точнее, они указывают на наличие альтернативных оптимумов в невырожденном решении
306 ЧАСТЬ II Оптимизационные модели
шло бы их, но предложение уменьшить затраты на вывоз моторов из Гавра с целью
уменьшить риск Европейского отделения компании AutoPower нужно удовлетворить,
даже если при этом общие затраты несколько возрастут. В нашем случае наличие альтер-
нативных оптимумов может позволить президенту снизить риск, не увеличивая общие
расходы Итак, надо найти альтернативные оптимальные решения, которые к тому же
минимизируют расходы на транспортировку моторов из Гавра. В нашем распоряжении
есть средство минимизации Поиск решения; проблема в том, как уменьшить суммарные
затраты на транспортировку из Гавра, не повышая общих затрат Как следует из обсуж-
дения альтернативных оптимумов в разделе 4.7, для нашей модели существует бесконеч-
ное множество альтернативных оптимумов, которые приводят к одинаковому значению
затрат $121 450 Таким образом, исходную цель можно преобразовать в дополнительное
ограничение для общих затрат, это даст возможность средству Поиск решения миними-
зировать новую целевую функцию.
Рис. 5.4. Миннмишцин umipani на 1прчнсп<>ртир<м,ку ujJaupa
ГЛАВА 5 Линейная оптимизация Применение 307
На рис. 5.4 показано решение преобразованной задачи, при котором минимизируют-
ся затраты на транспортировку моторов из Гавра при наличии дополнительного ограни-
чения, требующего, чтобы общие затраты в ячейке G19 не превышали ранее найденное
минимальное значение $121 450 Это заставит Поиск решения рассматривать при мини-
мизации затрат на транспортировку из Гавра только те альтернативы, в которых общие
затраты не превышают ранее найденное (поэтому, очевидно, достижимое) значение.
В результате произойдет перераспределение затрат, и затраты на транспортировку на
других маршрутах возрастут более чем на $18 000
Преобразовывать исходное оптимальное значение в ограничение и задавать для Поиск
решения новую целевую функцию можно до тех пор, пока полученный отчет об устойчиво-
сти показывает наличие альтернативных оптимумов Данный подход можно применять
и при отсутствии альтернативных оптимумов, но в этом случае нужно ослабить дополни-
тельное ограничение по общим затратам, чтобы найти минимальное значение расходов на
транспортировку из Гавра при условии, что общие затраты не превысят заданную сумму,
которая будет больше исходного минимального значения, скажем, на 5% Очевидно, что
подход к многоцелевой оптимизации, использующий ограничения по исходному выигры-
шу, можно применять в любой модели ЛП, а не только в транспортной
В следующем разделе рассмотрим другой частный случай транспортной модели — мо-
дель назначений.
Практическое применение
Американская лига использует модель назначений
при составлении расписания работы судейских
бригад
Каждый год, справившись с трудной задачей составления расписания 162 матчей
для своих 14 команд, Американская бейсбольная лига должна назначить судейские
бригады, которые будут обслуживать каждый матч Как правило, команды проводят
друг с другом серии матчей, состоящие из 2, 3 или 4 игр, причем каждая команда за
26 недель игрового сезона проводит 52 серии. Каждую серию должна обслуживать
одна из семи судейских бригад лиги.
Неудивительно, что в условиях, когда команды находятся в городах, разбросан-
ных по всей Северной Америке, от Балтимора до Сиэтла и от Техаса до Торонто, од-
ной из главных целей при составлении расписания является минимизация расходов
на переезды Однако это не единственный фактор, который необходимо учитывать
Чтобы обеспечить непредвзятость судейства, вводится ограничение на то, сколько
раз определенная бригада судит матчи конкретной команды, как дома, так и на вы-
езде Более того, прилагается максимум усилий, чтобы одна и та же бригада не суди-
ла игры одной команды более двух серий подряд.
С переездами связаны дополнительные ограничения. Перечислим наиболее важ-
ные из них.
•	Бригада не может обслуживать вечерний матч в одном городе и дневной матч
в другом на следующий день
•	Из-за разницы во времени бригада не может попасть из города на Западном по-
бережье в Чикаго или любой другой город на востоке, не имея дневного перерыва
между сериями.
308 ЧАСТЬ II. Оптимизационные модели
•	Из-за ограничений, связанных с расписанием авиарейсов, переезд бригады в То-
ронто или из Торонто должен сопровождаться дневным перерывом для всех го-
родов, за исключением Нью-Йорка, Бостона, Детройта и Кливленда.
Несмотря на то что общее количество возможных назначений судейских бригад
слишком велико, чтобы их можно было проанализировать вручную, задачу назначе-
ния судей можно сформулировать в виде достаточно простой модели назначений.
Теперь лига использует систему поддержки принятия решений на базе персональных
компьютеров, разработанную доктором Джимом Эвансом (Jim Evans) из Универси-
тета Цинциннати. Данная система позволяет создать более удачное расписание за
вдвое меньшее время, чем прежде
При составлении расписания назначений программа отмечает определенным
цветом каждую судейскую бригаду Это позволяет легко отслеживать любую бригаду
и наблюдать за ее назначениями. Наряду с алгоритмом формирования назначений
система содержит программу статистических вычислений и базу данных, что позво-
ляет ей легко отслеживать комбинации бригада-команда. С вводом в действие этой
системы расписание работы судейских бригад заметно улучшилось. За первый год
использования система позволила Американской лиге сэкономить примерно $30 000
на транспортных расходах [2]
5.4.	Модель назначений
Модель назначений часто встречается в разнообразных управленческих ситуациях.
В моделях этого типа решается задача нахождения оптимального распределения п неде-
лимых агентов или объектов по п заданиям Это может быть распределение продавцов по
отделам, мастеров по вызовам, компьютеров по сетям, назначение консультантов для
клиентов, адвокатов для судебных слушаний или отбор актеров для рекламных роликов.
Распределяемые агенты или объекты являются неделимыми, т е. один агент не может за-
ниматься несколькими задачами Важное ограничение для агента заключается в том, что
он (она или оно) может быть назначен одной и только одной задаче.
Задача организации проверок в Европейском отделении компании
AutoPower
В качестве примера модели назначений рассмотрим следующую ситуацию Штаб-
квартира Европейского отделения компании AutoPower находится в Брюсселе. В этом году
президент Европейского отделения компании AutoPower решил, что в рамках ежегодной ре-
визии каждый из четырех вице-президентов должен посетить с проверкой один из сборочных
заводов компании в течение первых двух недель июня. Сборочные заводы расположены
в Лейпциге (Германия), Нанси (Франция), Льеже (Бельгия) и Тилбурге (Нидерланды).
Существует множество моментов, которые нужно учесть, выбирая, какой вице-президент
будет проверять конкретный завод Необходимо принять во внимание следующее.
1.	Следует обеспечить соответствие специализации вице-президента и наиболее
важных проблем конкретного завода.
2.	Нужно соотнести время, которое потребуется на проведение проверки, с другими
обязанностями каждого вице-президента в двухнедельном интервале проверок
ГЛАВА 5. Линейная оптимизация. Применение
309
3.	Вице-президент должен владеть языком, который является основным на прове-
ряемом заводе.
Удачно организовать проверку заводов с учетом всех этих факторов — достаточно
сложная задача Президент решил начать с оценки затрат на командировки Эти данные
представлены в табл. 5.4.
Таблица 5.4. Затраты на командировку, тыс долл
Специализация вице-президента	Завод			
	Лейпциг (1)	Нанси (2)	Льеж (3)	Тилбург (4)
Финансы (Ф)	24	10	21	11
Маркетинг (М)	14	22	10	15
Производство (П)	15	17	20	19
Персонал (Пл)	11	19	14	13
Исходя из этих данных, президент может оценить любой конкретный вариант коман-
дировки вице-президентов на заводы Например, если он выберет вариант, представлен-
ный в табл. 5.5, общие затраты составят $79 000.
Таблица 5.5. Вариант назначений
Вице-президент	Завод	Стоимость
Ф	1	24
М	2	22
п	3	20
Пл	4	13
Суммарные затраты		79
Решение с помощью полного перебора
Поскольку вице-президентов и заводов всего по 4 и возможных назначений конечное
число, можно попытаться осуществить полный перебор, т.е. вычислить затраты для каж-
дого возможного варианта и выбрать вариант с наименьшими затратами. Однако (как
и в примере Oak Products в главе 3) полный перебор всех возможных вариантов очень
скоро становится слишком обременительным. Посмотрим, сколько возможных вариан-
тов назначений в нашей модели. Предположим, что назначения осуществляются в таком
порядке: Ф, М, П, Пл. Тогда процесс перебора состоит из следующих этапов.
1.	Ф можно направить на любой из четырех заводов.
2.	После того как назначение Ф состоялось, М можно направить на один из трех ос-
тавшихся заводов.
3.	П можно направить на один из двух оставшихся заводов.
4.	Пл придется направить на последний завод.
310 ЧАСТЬ II Оптимизационные модели
Таким образом, число возможных решений 4хЗх2х1 = 24. В общем случае, когда имеет-
ся п вице-президентов и п заводов, возможных решений будет л(«-1)(я-2)(«-3) (2)(1) =
= п] (п факториал) По мере увеличения п п! возрастает чрезвычайно быстро. Ниже приво-
дятся значения и' для значений п в пределах от 1 до 20.
~ 1 2 3	4	5	6	7	8	9	10	20
л' 1 2 6 24 120 720 5 040	40 320	362 880	3 628 900	2.4х1018
Предположим, что президенту нужно решить вопрос о назначении 15 торговых предста-
вителей в региональных представительствах Европейского отделения компании AutoPower
Очевидно, что осуществить полный перебор в этом случае может оказаться не под силу да-
же с помощью Excel Данный пример показывает, насколько быстро увеличивается количе-
ство вариантов в комбинаторных задачах Поэтому, хотя небольшие модели иногда проще
решать с помощью перебора (или интуиции), даже при незначительном увеличении их раз-
мерности необходимы точные и эффективные методы оптимизации
Формализация и решение задачи назначения
Чтобы построить модель для задачи назначений, используем такое же обозначение пе-
ременных, как и в транспортной модели Пусть хя — число вице-президентов специализа-
ции I, направленных на заводу (z = Ф, М, П, Пл;у = 1, 2, 3,4)
Модель назначении для Европейского отделения компании AutoPower представлена на
рис 5 5, где также показаны минимальные затраты на командировки Поскольку имеется
только один вице-президент каждой специализации (предложение) и на каждом заводе тре-
буется только один вице-президент (спрос), модель сбалансирована, поскольку спрос равен
предложению Следовательно, вместо неравенств можно использовать ограничения в виде
равенств Числа в ячейках С18 F21 отражают затраты компании AutoPower при выборе ва-
рианта назначении
В представленной на рис 5 5 модели первое ограничение указывает, что число вице-
президентов по финансам не должно превышать 1. Аналогичные ограничения касаются и
других вице-президентов Поэтому все переменные решения в ячейках C10F13 могут
принимать только значения 0 или 1 (с учетом условия неотрицательности) Ограничение
для завода 1 показывает, что на этот завод необходимо прислать по меньшей мере одного
вице-президента Аналогичные ограничения существуют для других заводов.
На рис 5 5 показано также оптимальное решение, все переменные решения прини-
мают значения 0 или 1, а оптимальным является назначение, представленное в табл. 5.6.
Таблица 5 6. Оптимальное назначение
Вице-президент	Завод	Стоимость
Ф	2	10
М	3	10
п	1	15
Пл	4	13
Суммарные затраты, тыс долл	48
ГЛАВА 5 Линейная оптимизация. Применение 311
Рис. 5.5. Оптимальное решение задачи назначений компании AutoPower
312 Ч А С Т Ь II. Оптимизационные модели
Связь между моделью назначений и транспортной моделью
Модель назначений является разновидностью транспортной модели (см. раздел 5.2). Она
отличается только тем, что в ней единица предложения не может распределяться по несколь-
ким местам назначения (в данном примере каждый вице-президент должен отправиться толь-
ко на один завод) Напомним, что если в транспортной модели все значения спроса и предло-
жения являются целыми, то оптимальные значения переменных решения также будут целы-
ми В модели назначений все значения спроса и предложения равны единице, те. целые,
поэтому можно не сомневаться, что назначения, найденные средством Поиск решения, не
окажутся дробными В общем случае справедливо следующее утверждение
( Модель назначений можно построить в виде транспортной модели, в которой предло-
жение в каждой исходной точке и спрос в каждом конечном пункте равны 1.
Варианты модели назначений
Модель назначений Европейского отделения компании AutoPower — это модель (задача)
минимизации, в которой число вице-президентов равно числу заводов и все возможные на-
значения допустимы Рассмотрим модели, в которых эти условия не выполняются. В частно-
сти, рассмотрим модели, в которых: число назначаемых персон не равно количеству мест на-
значений (несбалансированная модель); надо максимизировать целевую функцию (а не ми-
нимизировать, как в предыдущем примере); существуют недопустимые назначения.
Несбалансированная модель
Рассмотрим два случая. Сначала предположим, что предложение превышает спрос.
Например, президент Европейского отделения компании сам решил провести инспек-
цию завода в Тилбурге. Теперь ему нужно решить, кого из четырех вице-президентов на-
править на три оставшихся завода. Затраты показаны в табл. 5.7.
Таблица 5.7. Затраты назначений, тыс долл				
Специализация вице-президента	1		Завод 2	3	Количество вице-президентов
Ф	24	10	21	1
М	14	22	10	1
П	15	17	20	1
Пл	И	19	14	1
Требуемое число вице-президентов	1	1	1	34
Чтобы построить новую модель, исключим ограничение, требующее направить вице-
президента на завод 4 (см. рис. 5.5). В результате в оптимальном решении резерв для од-
ного из четырех ограничений по вице-президентам будет равен 1, т.е. один вице-
президент не будет отправлен в командировку на завод.
Теперь рассмотрим ситуацию, когда спрос превышает предложение. Например, вице-
президент, отвечающий за работу с персоналом, должен в первые две недели июня нахо-
диться в штаб-квартире компании в США и поэтому не сможет принять участие в ин-
спекциях в Европе. В таком случае в задаче будут затраты, представленные в табл. 5.8.
ГЛАВА 5. Линейная оптимизация Применение 313
Таблица 5.8. Затраты назначений, тыс долл
Специализация вице-президента	Завод				Количество вице-президентов
	1	2		3	4	
ф	24	10	21	11	1
м	14	22	10	15	1
п	15	17	20	19	1
Требуемое число	1	1	1	1	43
вице-президентов					
Задача в такой постановке не имеет допустимых решений. Очевидно, что невозможно
удовлетворить потребность в четырех вице-президентах, имея только трех Если все же
надо выяснить, какие три завода следует проверить, чтобы минимизировать затраты,
нужно изменить неравенства в ограничениях таким же образом, как это делалось в при-
мере транспортной модели в разделе 5 3, когда спрос превышал предложение, или внести
данные о фиктивном вице-президенте в таблицу затрат, как показано в табл 5.9. В по-
следнем случае на какой-нибудь завод будет направлен фиктивный вице-президент
В действительности данный завод не будет инспектироваться. Как и в предыдущем при-
мере транспортной задачи, преимущество второго подхода заключается в том, что можно
определить ущерб, если данный завод не будет проинспектирован, а значения ущерба для
различных заводов могут отличаться. Новую строку в табличном представлении модели
можно обозначить как “Не проверяется” и ввести соответствующие значения в ее ячейки
Таблица 5.9. Введение фиктивного вице-президента
Специализация	Завод	Количество
вице-президента	1234	вице-президентов
Ф	24	10	21	И	1
М	14	22	10	15	1
п	15	17	20	19	1
Фиктивный	0	0	0	0	1
Требуемое число 1111	4
вице-президентов
Теперь благодаря введению фиктивного предложения предложение равняется спросу.
Также отметим, что фиктивному вице-президенту соответствуют нулевые затраты Здесь
оптимальное решение — это такое решение, которое минимизирует затраты на инспек-
ции, проводимые вице-президентами Ф, М и П. В любом случае, если спрос превышает
предложение, необходимо добавить к модели одну или несколько новых строк с подхо-
дящими значениями затрат, чтобы можно было найти допустимое решение
Задачи максимизации
Рассмотрим модель назначений, в которой каждому назначению поставлена в соот-
ветствие определенная прибыль, а не затраты. Например, предположим, что компании
AutoPower нужно направить коммивояжеров в новые районы сбыта. Имеется три вакан-
сии и четыре кандидата. Одному из кандидатов придется подождать, пока появится еще
одна вакансия.
314
Ч А С Т Ь II Оптимизационные модели
Назначения
В
Территория 1_______I ерритория 2____
0 999999999993339 0	О
О	.0.999999999993339 О
Территория 3
Всего =СУММ(С10 С13) =СУММ(Р10:Р13) =СУММ(Е10 Е1Э)
Необходимо 1	1	1
Суммарная
Территория 1
=С4*С10_______
=С6'С12
Территория 2
=04’010________
=Р5*Р11_______
=06*012
=07’013________
Территория 3
=Е4’Е10
=Е5*Е11
=Е6*Е12
=Е7*Е13
Всего =СУММ(С18 С211 =СУММ(О18 021) =СУММ(Е18 Е21)
Рис. 5.6. Модель назначений и соответствующее решение
ГЛАВА 5. Линейная оптимизация Применение 315
Результат назначения кандидата на определенное место измеряется ожидаемым уве-
личением удельной прибыли. Естественно, что компания заинтересована в максимиза-
ции общей прибыли Прибыль, которую могут дать конкретные коммивояжеры, показа-
на в табл 5.10
Таблица 5.10. Прибыль от назначений, тыс долл				
Коммивояжеры	Территория			Количество кандидатов
	1	2		3	
А	40	30	20	1
В	18	28	22	1
С	12	16	20	1
D	25	24	27	1
Число вакансий	1	1	1	34
Табличная модель в Excel и соответствующее оптимальное решение показаны на рис 5 6
Недопустимые назначения
Предположим, что в построенной модели назначений некоторые назначения являют-
ся недопустимыми. Например, вследствие личного конфликта президент Европейского
отделения компании AutoPower убежден, что вице-президент по вопросам производства
не должен инспектировать сборочный завод в Нанси (2). Чтобы учесть это обстоятельст-
во, нужно сделать значение соответствующих этому назначению удельных затрат (в ячей-
ке D6 на рис 5 5) значительно больше остальных значений Это автоматически исключит
командировку вице-президента П на завод 2 Здесь используется тот же общий подход,
который применялся в разделе 5 3, когда необходимо было гарантировать, что в опти-
мальное решение транспортной задачи не войдут недопустимые пути
5.5.	Модель выбора средств массовой информации
С задачей выбора средств массовой информации часто сталкиваются компании или рек-
ламные агентства при попытке разработать успешную рекламную компанию. Как правило,
вопрос заключается в том, сколько рекламных блоков фирме следует приобрести в каждом из
возможных средств массовой информации (радио, телевидение, газеты, журналы, Web-
страницы Internet). Цель — сделать рекламную компанию максимально эффективной Огра-
ничения, с которыми приходится считаться при принятии решения, обычно связаны с бюд-
жетом на рекламу и возможностями ее размещения в различных СМИ В свою очередь, руко-
водство компании может налагать дополнительные ограничения, настаивая, чтобы не менее
определенной суммы было потрачено на рекламу в конкретных СМИ (например, не менее
$10 000 необходимо потратить на газетную рекламу), или, напротив, требуя, чтобы па один
вид СМ И тратилось не более фиксированного процента бюджета
Наконец, на решение может оказать влияние “закон снижения отдачи” эффектив-
ность рекламного блока снижается с увеличением числа его показов в средствах массовой
информации на протяжении определенного временного периода Например, десятый
показ рекламного ролика на телевидении в течение недели, как правило, не оказывает
такого влияния на аудиторию, как первый или второй.
316 ЧАСТЬ II Оптимизационные модели
Рассмотрим выбор СМИ более подробно. Вначале важно подчеркнуть, что модель,
построенная для данной ситуации, имеет необычную целевую функцию. Естественно,
что руководство компании хочет выбрать такой вариант рекламной компании, который
максимизирует спрос на рекламируемый продукт. Следовательно, задача состоит в том,
чтобы найти вариант проведения рекламной компании, который максимизирует спрос и
удовлетворяет бюджетному и прочим ограничениям К сожалению, связь между спросом
на продукт и рекламной компанией недостаточно четкая, чтобы можно было на ее основе
построить полезную модель Поэтому обычно используется следующий подход- отдача от
определенной рекламы в определенных СМИ оценивается в специальных единицах, так
называемых единицах воздействия Это субъективная мера, основанная на оценке менед-
жером качества определенной рекламной продукции, на оценке восприимчивости по-
тенциального рынка и т д Иными словами, это некая мера ценных свойств конкретной
рекламы Единицу воздействия можно рассматривать как разновидность экономической
функции полезности В таком случае цель руководства — максимизировать сумму единиц
полезности, учитывая другие свойства модели (например, удельные затраты на привле-
чение потенциальных клиентов и т д.) Рассмотрим конкретный пример
Продвижение нового продукта
Компания RollOn хочет выйти на рынок транспортных средств для отдыха, предло-
жив машину типа мотоцикла с тремя большими колесами. Поскольку это новый вид
продукции, планируется в течение первого месяца развернуть рекламную компанию, на
которую выделены средства в размере $72 000 В своей рекламной компании RollOn на-
мерена задействовать дневное радио, вечернее ТВ и ежедневную газету Рекламный отдел
компании RollOn предоставил данные о затратах на рекламу в каждом из указанных
средств массовой информации и количестве купленных благодаря помещению рекламы
единиц товара (табл 5 11)
Таблица 5.11. Данные, характеризующие рекламу в различных СМИ
Размещение рекламы	Число единиц товара, купленных благодаря рекламе	Стоимость 1 рекламного объявления, $
Дневное радио	30 000	1700
Вечернее ТВ	60 000	2800
Ежедневная газета	45 000	1200
Как уже отмечалось, эффективность рекламы измеряется в ее воздействии на целевую
аудиторию Руководство компании RollOn произвольным образом выбрало шкалу от 0 до
100 для оценки каждого вида рекламы. В частности, первые 10 рекламных объявлений на
радио оцениваются в 60 единиц, а все последующие — в 40. На рис 5.7 представлен гра-
фик эффективности рекламы как функции количества рекламных объявлений на днев-
ном радио на протяжении месяца
По мнению руководства компании, аналогичная ситуация будет наблюдаться на теле-
видении и в газете, т е там также имеет место снижение отдачи Для простоты предпо-
лагается, что во всех трех случаях эффективность рекламного объявления изменяется на
десятом объявлении Однако эффективность объявлений в разных СМИ различна, соот-
ветствующие данные приведены в табл. 5.12 Графики эффективности как функции чис-
ла объявлений для каждого СМИ показаны на рис. 5.8
ГЛАВА 5. Линейная оптимизация. Применение	317
Рис. 5.7. Зависимость эффективности рекламных объявлений на радио от их
количества
Таблица 5.12. Эффективность рекламных объявлений в различных СМИ
Размещение рекламы	Первые 10 объявлений	Последующие объявления
Дневное радио	60	40
Вечернее ТВ	80	55
Ежедневная газета	70	35
Руководство компании RollOn хочет, чтобы рекламная компания проводилась в соот-
ветствии с определенными критериями. В частности. 1) в каждом СМИ должно быть
размещено не более 25 рекламных объявлений; 2) общими усилиями всех СМИ нужно
добиться покупки 1 800 000 единиц товара, 3) не менее одной четверти рекламных объяв-
лений должно выйти на вечернем ТВ Чтобы формализовать модель выбора СМИ в виде
задачи ЛП, введем следующие обозначения.
х, — число объявлений на дневном радио, если оно не превышает 10,
у, — число объявлений на дневном радио, превышающее 10,
х2 — число объявлений на вечернем ТВ, если оно не превышает 10;
у2 — число объявлений на вечернем ТВ, превышающее 10,
х3 — число объявлений в ежедневной газете, если оно не превышает 10;
у3 — число объявлений в ежедневной газете, превышающее 10.
318 ЧАСТЬ II. Оптимизационные модели
Рис. 5.8. Зависимость эффективности рекламных объявлений в различных
СМИ от их количества
В этих обозначениях эффективность объявлений по радио в пределах первого десятка
составит 60хи а последующих — 40у, Таким образом, целевая функция примет вид:
максимизировать 60х, + 40у, + 80х2 + 55у2 + 70х3 + З5у3.
Переходя к ограничениям, необходимо помнить, чтох, + у, равно общему количеству
объявлений по радио, х2 + у2— это общее количество объявлений на телевидении, х3 +
у, — общее количество объявлений в ежедневной газете
Из табл 5 11 следует, что затраты на каждое объявление по радио составляют $1700.
Общие расходы на радиорекламу составят 1700(х, + у,) Поскольку затраты на рекламное
объявление на ТВ составляют $2800, а в газете — $1200, общие расходы на рекламу соста-
вят 1700(х, + у,) + 2800 (х2 + у2) + 1200(х, + у,) Компания RollOn выделила на проведение
рекламной компании $72 000 Это ограничение выражается следующим неравенством.
1700х, + 1700у, + 28ООх2 + 2800у3 + 1200х3 + 1200у. < 72 000.
Ограничение на количество рекламных объявлений на радио (не более 25) записыва-
ется с помощью неравенства х, + у, <25 Аналогичные ограничения записываются для
других СМИ
ГЛАВА 5 Линейная оптимизация. Применение 319
Обратимся вновь к табл. 5 11, в которой показано, что каждое радиообъявление позво-
ляет продать 30 000 единиц товара. Таким образом, благодаря радиорекламе будет куплено
30 000(х, +у,) единиц товара Тогда требование к общей эффективности рекламной компа-
нии (продать не менее 1 800 000 единиц товара) будет выражено следующим неравенством
30 ОООх, + 30 ОООу, + 60 000х2 + 60 000у2 + 45 000х3 + 45 000у, > 1 800 000
Наконец, требование, чтобы не менее одной четверти рекламных объявлении вышло
на вечернем ТВ, выражается ограничением’
К сожалению, в этом неравенстве переменные решения присутствуют в знаменателе
дроби левой части Поэтому при попытке ввести данное ограничение в Excel и оптими-
зировать полученную модель появится сообщение, что предположение о линейности мо-
дели не выполняется Хотя оптимизация нелинейных моделей также возможна (см
гл. 7), проще сделать данное ограничение линейным, умножив обе его части на знамена-
тель дроби В результате получим
х2 + ^ > 0,25(х, + у, + х2 + у2 + х3 + у3)
Совет Этот способ представления в виде линейного неравенства требования, чтобы некий про-
дукт составлял определенную долю общего количества, часто используется в моделировании си-
туации, при которых производится смешивание чего-либо при смешивании нефтепродуктов, по-
лучении купированных вин, изготовлении кормов для животных, красителей или химических про-
дуктов Рекомендуется сначала записать условие смешивания в виде нелинейного неравенства, а
затем при переходе к представлению модели в Excel переписать данное ограничение в виде линей-
ного неравенства В противном случае легко ошибиться со знаком неравенства Если средство По-
иск решения генерирует сообщения, что не выполнено условие линейности модели или невозмож-
но найти допустимое решение, следует в первую очередь проверить, не забыли ли вы привести к
линейному виду какое-нибудь условие смешивания, и правилен ли знак неравенства
Законченная табличная модель в Excel и соответствующее оптимальное решение по-
казаны на рис 5 9. Три ограничения в ячейках 13.КЗ задают верхнюю границу 10 для пе-
ременных хр х2 и х3, а ограничения в ячейках 14.К4 задают в качестве верхней границы
для переменных ур у2 и у3 очень большое значение 1000. Однако следует отметить сле-
дующее согласно определению х, — это количество объявлений на дневном радио в пре-
делах первого десятка, ay, — количество объявлений на дневном радио после первых де-
сяти. Пусть х, и у, — оптимальные значения этих переменных Очевидно, что решение,
в котором х,' < 10, ay’ > 0, не имеет смысла В модели нет ограничений, которые препят-
ствовали бы появлению такого решения Тем не менее оно не появится Причина в том,
что удельная прибыль х, в целевой функции выше, чем удельная прибыль у, Если реше-
ние х, < 10, у, > 0 является допустимым, то, как следует из ограничений, решение х, + е,
у, — е, где е— очень маленькое положительное число, также допустимо Более того, это
решение улучшает значение целевой функции, поскольку коэффициент при х, в целевой
функции выше, чем коэффициент при уР Проще говоря, в процессе максимизации По-
иск решения всегда сначала доведет х, до ее предельного значения 10, прежде чем сделает
у, больше нуля, поскольку удельный выигрыш отх, больше, чем отур и они взаимозаме-
няемы Аналогичные заключения применимы к парам х2, у2 и х3, у3
320	Ч А С Т Ь II. Оптимизационные модели
Рис. 5.9. Табличное представление модели выбора СМИ
ГЛАВА 5. Линейная оптимизация. Применение 321
Совет Не забывайте о наших рекомендациях по созданию табличных моделей, поэтому ста-
райтесь при работе со средством Поиск решения избегать одновременного использования
в модели очень больших и очень маленьких чисел. В противном случае Поиск решения может
генерировать сообщения об "ошибках”, вызванные ошибками округления при выполнении ариф-
метических вычислений. Установите опцию Автоматическое масштабирование в диало-
говом окне Параметры поиска решения, проведите масштабирование параметров вручную
или выполните оба этих действия, поскольку Автоматическое масштабирование не все-
гда эффективно В данном примере параметры затрат выражены в тысячах долларов, а не
в долларах. Более подробно о сложностях, которые испытывает Поиск решения при решении
задач со слишком широким диапазоном чисел, рассказано в приложении В
Данная модель выбора СМИ иллюстрирует случай, когда снижение отдачи происхо-
дит в одной точке (для каждого СМИ после 10 рекламных объявлений). Чтобы более реа-
листично представить зависимость эффективности рекламы от количества рекламных
объявлений, можно рассмотреть несколько точек, где происходит снижение отдачи. На-
пример, предположим, что эффективность ТВ-объявления снижается с 55 до 45 единиц
для всех объявлений после двадцатого; аналогичное снижение отдачи наблюдается и для
двух других СМИ Чтобы учесть эти предположения в модели, необходимо заменить
в ячейках 14 К4 верхнюю границу 1000 на 20, вставить после строк 4, 10 и 14 новые стро-
ки с данными для второй точки снижения отдачи и изменить соответствующим образом
параметры поиска решения
5.6.	Динамические модели
Большинство рассмотренных до настоящего времени моделей были ограничены од-
ним временным периодом (неделей, месяцем, годом) Модели, разработанные для одного
временного периода, называются статическими моделями, поскольку время может вхо-
дить в такие модели только в качестве единиц измерения некоторых переменных В отли-
чие от них динамические модели охватывают несколько временных периодов, что, безус-
ловно, является более реалистичной абстракцией действительности Во многих моделях
принятия решений необходимо принимать решения в зависимости от времени, и реше-
ния, принятые раньше, влияют на последующие решения Зависимость принятия реше-
ний от времени делает динамическое моделирование исключительно полезным методом
анализа, так как человеческая интуиция часто заходит в тупик, когда взаимосвязанных
решений становится слишком много.
Конечно, за дополнительный реализм динамических моделей приходится платить
при создании динамических моделей необходимо уделять внимание большему количест-
ву деталей Во-первых, обычно каждый временной период имеет собственный критерий
эффективности, но для оптимизации требуется объединить эти индивидуальные крите-
рии эффективности в единый критерий, отражающий общую эффективность за все вре-
менные периоды. Как правило, в качестве единого критерия эффективности использует-
ся сумма всех критериев эффективности для отдельных периодов или (чаще) взвешенная
сумма, где весовые коэффициенты зависят от времени. Во-вторых, необходимо тщатель-
но определять синхронизацию событий, чтобы промежуточные результаты и решения
шли в правильном порядке Эти и другие аспекты разработки динамических моделей
лучше всего продемонстрировать на примере управления запасами.
322
ЧАСТЬ II. Оптимизационные модели
Динамические модели управления запасами
Динамические модели управления запасами (другое название многофазовые модели управле-
ния запасами) составляют важный класс моделей, которые применяются для управления за-
пасами материалов, финансов, трудовых ресурсов и тому подобного при переходе от одного
временного периода к следующему. Рассматриваемый пример — это классическая детер-
минированная “однопродуктовая” модель управления запасами. Она называется детерми-
нированной, поскольку мы предполагаем, что в начале временного периода 1 известен спрос
(количество заказов, которые необходимо удовлетворить) для всех последующих временнь/х
периодов Например, производитель полиуретана имеет заказы на последующие 6 недель
Обозначим через ф этот известный спрос (количество галлонов продукции, которое необ-
ходимо доставить потребителям на протяжении недели 0. Для простоты предположим, что
возврат заказов невозможен, те dt > 0 для всех/. ПустьС( — затраты на производство галло-
на полиуретана в течение недели z, а К,— максимальное количество продукции, которое
можно произвести за неделю z Обозначим через ф удельную стоимость хранения на складе
запасов на конец недели z (Таким образом, запас измеряется как количество галлонов, пе-
реходящих с недели z на неделю z+1 ) Предположим, что исходный запас (запас на начало
периода 1, для которого не взимается плата за хранение), составляет /„ галлонов. Необходи-
мо найти план производства, который позволит удовлетворить известный спрос в пред-
стоящие 6 недель с минимальными общими затратами.
Прежде чем формулировать задачу условной оптимизации, полезно записать выражение
для имеющегося запаса на конец каждого периода Поскольку существует плата за хранение,
это количество, очевидно, будет играть определенную роль в целевой функции. Обозначим
через I запас полиуретана в конце недели z. Определим переменную решения х как количество
галлонов полиуретана, произведенное за неделю z Тогда уравнение материального баланса
примет вид Ц = /„ +х, - ф Таким образом, наличный запас на конец недели 1 равен налично-
му запасу на конец недели 0 (начало недели 1) плюс произведенное за неделю 1 количество
продукции минус отгруженное ее количество за неделю 1. (Предполагается, что спрос должен
быть полностью удовлетворен Тогда, поскольку спрос на неделе z известен и равен d:, таким
же будет и объем отгрузки за неделю I) Аналогично для второй недели имеем /, = /, + х2 - d2
и для любой недели z. /, = Z(, + х, - dr
Итак, уравнение запасов — это уравнение материального баланса:
запас на конец периода t = запас на начало периода t + объем производства за период t —
- объем спроса за период t.
Здесь предполагается, что запас на конец недели г-1 равен запасу на начало недели t, т е. не
происходит сокращения запасов Подставив выражение для ф в уравнение для ф, получим
I2^Ia+xl-dl+x2-d2 = Io+Yx,-Xdl.
Словами это можно выразить так" новый запас = прежний запас + производство — спрос
Если подставить полученное выражение для ф в уравнение для ф, получим
АЧ-М*.
Повторяя данную процедуру, получаем уравнение запасов для любой недели Г.
I, = 4	•
ГЛАВА 5 Линейная оптимизация Применение 323
Последнее уравнение связывает запас на конец недели t с исходным запасом 1п, объемами
производства за все предшествующие недели (значения х) и величинами спроса (значения d)
Переменную /, иногда называют выводимой или определяемой переменной, поскольку она оп-
ределяется с помощью других переменных решения (значений х.) и известных параметров мо-
дели. Использование определяемых переменных иногда облегчает формулировку задач
Прежде чем переходить к созданию табличной модели, необходимо продумать, как
записать требование о том, чтобы объем производства в каждый временной период был
достаточен для удовлетворения спроса Для недели 1 это означает, что /„ + х, >d, или +
х, - > 0. Поскольку выражение в правой части последнего неравенства равно /,, то это
неравенство означает, что запас на конец недели 1 должен быть неотрицательным Удов-
летворение спроса за неделю 2 означает, что запас на начало недели 2 (или на конец не-
дели 1) плюс производство за неделю2 должны быть больше d2, те /, + х2 >d2 или /, + х2
— d2 > 0. Это эквивалентно утверждению, что запас на конец недели 2 должен быть неот-
рицательным. Итак, видна закономерность
1 Требование удовлетворения спроса за период t эквивалентно условию неотрицательно-
сти запаса/, на конец периода/.
Графическая иллюстрация данного утверждения приведена на рис 5 10
Рис. 5.10. Зависимость между запасами на начало и конец недели
Словесная модель
Минимизировать производственные затраты + стоимость хранения
при условии
запас на конец недели t > 0,	Г=1,2, .,6,
производство за неделю t <К:, /=1,2,. ,6,
производство за неделю t > 0, Г=1,2, ,6
324 Ч А С Т Ь II. Оптимизационные модели
Математическая модель
Пусть*, — объем производства за неделю t. Математическая формулировка задачи:
минимизировать +£h,I,
при ограничениях
-d,,}
х,<К„ Г = 1,2,...,6.
х,>К„1,>0. J
В общем случае поиск решений для подобных моделей — достаточно сложная задача.
Необходимо учитывать взаимодействия между многими переменными. Например, запас
на конец заданного временного периода г определяется всеми производственными реше-
ниями для временных периодов с 1 по Л Это видно из уравнения запасов, приведенного
выше. Затраты в период t также зависят от всех производственных решений в периоды с 1
по / Рассмотрим практический пример динамической модели управления запасами в си-
туации, с которой столкнулся Эндрю Тан
Динамическая модель управления запасами
Эндрю Тан отвечает за окончательную сборку и поставку дизельных электрогенерато-
ров фирмы AutoPower в Сингапуре. Генераторы собираются из импортируемых деталей
и испытываются в Сингапуре, а затем экспортируются потребителям в странах Азии.
В табл 5 13 показано количество проданных генераторов, которые необходимо поставить
в каждый из последующих четырех месяцев, а также оценка ежемесячной производст-
венной мощности и затрат на производство генераторов Различия в производственных
мощностях и затратах являются следствием неритмичной доставки деталей из-за грани-
цы и колебаний цен на рынке материалов, в частности, цен на медную проволоку
В табл 5 13 также указана стоимость хранения готового генератора на складе при перехо-
де запаса от одного месяца к следующему. Затраты на хранение больших дизельных гене-
раторов — важный фактор для Эндрю, поскольку в Сингапуре крайне ограничены зе-
мельные ресурсы Отметим, что именно возможность сохранять запас при переходе от
одного месяца к другому делает модель Эндрю динамической моделью, а не набором че-
тырех статических моделей, как при отсутствии накопления запасов.
Задача Эндрю — произвести и поставить потребителям требуемое количество генерато-
ров в каждый из 4 месяцев при минимальных суммарных затратах за эти 4 месяца, запас на
начало января составляет 15 генераторов. На рис 5.11 представлена табличная модель Энд-
рю. Она создана в соответствии с общим принципом построения динамических табличных
моделей каждому временному периоду соответствует отдельный столбец. В этой модели
значения конечного запаса в ячейках СЮ F10 являются выводимыми (определяемыми) пе-
ременными В данном случае они вычисляются для каждого месяца по формуле
конечный запас = производство + начальный запас - поставка.
Начальный запас для каждого периода (ячейки D8:F8) равен конечному запасу
для предшествующего периода (ячейки С 10:F10)2. Как и прежде, в диалоговом окне
Поиск решения необходимо добавить условие неотрицательности конечного запаса
2 В данном случае генераторы из запаса не теряются, не повреждаются и не воруются В других моделях управления
запасами можно учитывать сокращение запасов, для чего можно ввести коэффициент потерь (например, 1%)
ГЛАВА 5. Линейная оптимизация. Применение 325
для каждого месяца. Это не позволит средству Поиск решения искусственно снизить
затраты путем отгрузки в каком-либо месяце большего количества генераторов, чем
имеется в наличии.
Таблица 5.13. Ежемесячные данные о производстве генераторов
	Январь	Февраль	Март	Апрель
Объемы поставок	58	36	34	59
Производственная мощность	60	62	64	66
Удельные затраты на производство, тыс долл	28	27	27,8	29
Стоимость хранения 1 генератора, $	300	300	300	300
При построении модели (равно как и при построении любой динамической модели) Энд-
рю необходимо принять два решения: определить общий временной интервал, охватываемый
моделью (который также называется периодом планирования), и количество дискретных вре-
менных промежутков внутри данного интервала В модели Эндрю период планирования со-
ставляет четыре месяца, и этот период поделен на четыре временных промежутка продолжи-
тельностью I месяц. Оба эти решения могут оказать определяющее влияние на соответствие
модели рассматриваемой ситуации. Например, по определению четырехмесячный период
планирования означает, что модель не может учитывать требования к производству и доставке
после апреля, т.е. с точки зрения модели дело выглядит так, как будто производство и доставка
генераторов прекращаются после окончания апреля.
Кроме того, помесячное разбиение временного интервала требует, чтобы всякая дея-
тельность в пределах месяца представлялась одним числом. Например, конечный запас
в январе — это производство за январь плюс начальный запас минус январские поставки,
т.е единственное число, хотя в действительности объем запаса меняется каждый день
и каждую неделю по мере того, как генераторы производятся и отгружаются потребите-
лям. Чтобы пояснить, о чем идет речь, рассмотрим предельный случай, когда все генера-
торы производятся в первый, а отгрузка происходит в последний рабочий день января
Тогда стоимость хранения запаса в январе будет определяться суммой произведенного
количества и начального запаса, а не разностью этой суммы и доставленного количества.
В другом предельном случае, когда и производство и доставка происходят в последний
рабочий день января, стоимость хранения готовых генераторов будет зависеть только от
запаса на начало января. Предположив для простоты, что производство и доставка про-
исходят в течение месяца относительно равномерно, Эндрю решил вычислять затраты на
хранение, исходя из среднемесячного запаса для каждого месяца, который определяется
как (начальный запас + конечный запас)/2. Это эквивалентно предположению, что вы-
пуск и отгрузка происходят в середине месяца. Чтобы более точно отразить перемещение
генераторов в течение месяца, необходимо разбить модель на большее количество вре-
менных промежутков (например, длительностью одна неделя или один день или даже
один час). Разбиение временной шкалы на более мелкие части позволяет точнее учесть
действительные перемещения генераторов, их переход в запас и убытие из него, в резуль-
тате получится более точная оценка затрат на хранение.
326	Ч А С Т Ь II Оптимизационные модели
/’«<. 5. 11. r luiui мнил кап чаде и, j арак гении арап ;ыиЬ тки ч и jaaai ами
ГЛАВА 5. Линейная оптимизация. Применение 327
Помимо использования дробного разбиения временного интервала для определения
ежемесячных затрат, можно расширить период планирования модели, дополнив ее свя-
занными с различными видами деятельности стоимостными показателями для месяцев,
следующих за апрелем. К сожалению, попытка добиться большего реализма путем увели-
чения периода планирования и более мелкого разбиения временного интервала приводит
к экспоненциальному росту размерности динамической модели. Например, модель
с ежедневными показателями на период планирования один год будет содержать сотни
столбцов и быстро превысит существующий в Excel лимит в 256 столбцов и возможности
средства Поиск решения (200 переменных решения)3 Более того, если даже удастся пре-
одолеть эти технические барьеры, Эндрю придется оценивать значения многих сотен па-
раметров, таких как ежедневные требования по отгрузке, затраты на материалы и произ-
водственные мощности по выпуску генераторов Искушение придать модели дополни-
тельный реализм за счет более мелкого разбиения и увеличения периода планирования
в динамических моделях называется “проклятием размерности”. Добавление каждого но-
вого столбца увеличивает размер модели, что выражается в необходимости рассматривать
новые переменные решения, зависящие от времени связи между переменными решения
и зависимыми переменными, а также оценивать дополнительные параметры
Наконец, в каждой динамической модели необходимо уделять пристальное внимание
граничным условиям Речь идет о наборе параметров, для которых необходимо указать зна-
чения в начале и в конце временного интервала модели В модели Эндрю это значения на-
чального запаса для января и конечного запаса для апреля. В данном случае начальный за-
пас января составляет 15 генераторов, в общем случае начальное значение параметра, как
правило, известно или его легко оценить Однако конечное граничное условие гораздо ме-
нее надежно, поскольку оно должно выступать в роли разумного начального условия для
всего периода времени, выходящего за рамки периода планирования В данной модели Эн-
дрю решил, что запас на конец апреля в 7 генераторов — достаточно хорошее начальное ус-
ловие для работы в последующие месяцы.
На рис. 5 12 представлен результат четырехкратной оптимизации модели Эндрю
(отдельно для каждого из четырех месяцев) Сначала средство Поиск решения запуска-
лось только для января, в качестве переменной решения использовался объем производ-
ства в январе, а в качестве целевой функции — январские суммарные затраты Затем то
же самое делалось для февраля, марта и апреля. Отметим, что здесь нет переходов запаса
от одного месяца к следующему, поскольку каждый месяц трактуется как независимая
статическая модель4; производство сверх требуемого в данном месяце объема поставок
приводит к увеличению общих затрат, а компенсирующей экономии в статической моде-
ли нет. Именно поэтому статические модели часто называют близорукими, поскольку
в них полностью игнорируется влияние текущих решений на будущий выигрыш Чтобы
увидеть преимущество четырехмесячной динамической модели по сравнению с четырьмя
статическими моделями для каждого месяца в отдельности, сравним значения общих за-
трат за четыре месяца на рис. 5.11 и рис 5.12 применение динамической модели эконо-
мит более $64 000 Далее покажем, что для данной ситуации результат, полученный с по-
мощью динамической модели, никогда не окажется хуже, а зачастую будет значительно
лучше, чем результат запуска четырех статических моделей той же ситуации
Разработчик средства Solver (Поиск решения) компания Frontline Systems (MHw.frontsys.com) предлагает
платные надстройки, которые позволяют расширить возможности программы, однако динамические моде-
ли легко могут превысить даже возможности этих усовершенствованных версий средства Поиск решения
Числа в строке Затраты на хранение для января и апреля на рис 5 12 отражают стоимость хранения
в течение половины месяца январского начального запаса и требуемого апрельского конечного запаса
328 Ч А С Т Ь II Оптимизационные модели
Рис. 5.12. Модель, оптимизированная как четыре статические модели
На рис. 5.13 представлен отчет по устойчивости, созданный средством Поиск реше-
ния для динамической модели (см. рис 5.11). Поскольку четыре ограничения объема
производства были заданы в виде простых неравенств, ограничивающих сверху перемен-
ные решения, теневые цены для данных ограничений находятся в отчете по устойчивости
в столбце Нормированная стоимость, а информация о диапазоне для этих теневых цен
отсутствует.’
Microsoft Excel 10 0 Отчет по устойчивости
Ограничения
Ячейка	Имя	Результ значение	Теневая Цена	Ограничение Правая часть	Попустимое Допустимое Увеличение Уменьшение
$С$10	Конечный запас Январь	10		0	0	10	1Е+30
	Конечный запас Февраль	“”зГ			36	1Е*30
$Е$10	Конечный запас Март	66	0	0	66	1Е*30
SFS10	Конечный запас Апрель	7	29 05	7	7	10
Рис. 5.13. Отчет по устойчивости модели управления запасами за 4 месяца
’ Особенности работы средства Поиск решения, когда теневые цены для переменных решения, которые ог-
раничены простыми неравенствами, помещаются в столбец Нормированная стоимость отчета по ус-
тойчивости, обсуждались в разделе 4 12
ГЛАВА 5. Линейная оптимизация. Применение 329
Кроме того, на первый взгляд, коэффициенты целевой функции модели в отчете по
устойчивости также кажутся неправильными. Например, коэффициент целевой функ-
ции при переменной, обозначающей производство в январе, равен $29 050, в то время
как на рис. 5.11 четко указано, что переменные затраты на производство в январе состав-
ляют $28 000. Многие пользователи предполагают, что средство Поиск решения
“считывает” каждый коэффициент целевой функции из соответствующей ячейки рабо-
чего листа Excel. На самом деле Поиск решения так не поступает, поскольку вычисление
этого коэффициента может осуществляться по формулам, рассредоточенным по не-
скольким ячейкам исходной табличной модели. Вместо этого Поиск решения исследует
рабочий лист для каждой переменной решения отдельно, подставляя пробные значения
и фиксируя результат, который каждое такое изменение оказывает на значение целевой
функции после того, как Excel пересчитает таблицу. Исходя из этой информации Поиск
решения оценивает коэффициенты целевой функции.6 Конечно, это не дает ответа на
вопрос, почему возникло расхождение между переменными затратами на производство
в январе и целевым коэффициентом для январского производства, оцененным Поиск
решения и зафиксированным в отчете об устойчивости. Но нетрудно заметить, что число
29,05 тыс. долл, состоит из затрат на производство генератора в январе (28,00 тыс. долл.)
плюс 1,05тыс. долл. — стоимость хранения данного генератора до конца апреля (те
в течение 3,5 месяца). Напоминаем, что в своей модели Эндрю использовал средние зна-
чения для оценки уровней запасов, это эквивалентно предположению, что генераторы
выпускаются в середине месяца.
Чтобы убедиться, что 29,05 — правильное значение целевого коэффициента, можно
ввести в показанный на рис 5 11 рабочий лист (рабочая книга Сингапур.xls на прилагае-
мом к книге компакт-диске) любое решение для января, записать значение общих затрат
за четыре месяца, а затем добавить 1 к исходному производственному решению для янва-
ря. Вы увидите, что дополнительно произведенный в январе генератор будет добавлен ко
всем уровням запасов, это приведет к увеличению конечного запаса в апреле на единицу,
а общие затраты за четыре месяца возрастут на 29,05 тыс долл. Чтобы понять, почему
29,05 является правильным значением коэффициента для января, напомним, что все ос-
тальные элементы модели (количества генераторов, произведенных и отгруженных в те-
чение других месяцев) остались неизменными, поэтому дополнительный январский ге-
нератор может попасть только в конечный запас апреля Однако при оптимизации моде-
ли с помощью Поиск решения этот дополнительно произведенный в январе генератор
позволяет программе сократить на единицу производство в другом месяце. Например,
если дополнительно произведенный в январе генератор сократит объем производства
в феврале на единицу, то результатом будет разность между целевыми коэффициентами
для января и февраля, 29,05 -27,75 - 1,30 тыс. долл. Эта разность правильно отражает
стоимостной вклад двух одновременных изменений, т.е. перенос производства одного
генератора с февраля на январь повысит расходы на производство на 28 000 — 27 000
= $1 000 плюс $300 дополнительных затрат на хранение до середины февраля генератора,
произведенного в середине января. Таким образом, странные значения целевых коэф-
фициентов, содержащиеся в отчете по устойчивости, правильны и отражают более слож-
ные взаимосвязи переменных решения в динамической модели.
6 Именно оценкой коэффициентов Поиск решения занимается в то время, когда после щелчка на кнопке
Выполнить в строке состояния появляется сообщение “Постановка задачи ” (Для интересующихся ма-
тематическими аспектами работы программы на основании полученной информации строится ряд Тейлора
для целевой функции, затем этот ряд используется в процессе оптимизации )
330 Ч А СIЬ II. Оптимизационные модели
Рис. 5.14. M'i'le и,, в кчтчрчи ночи tt.ui.tu юное tint Kiiж/1ого ,wiяци является переменной
решения
ГЛАВА 5. Линейная оптимизация. Применение 331
На рис. 5.14 представлена вторая версия модели Эндрю. Она отличается от исходной
модели на рис 5 11 тем, что начальный запас для каждого месяца (ячейки D8F8) являет-
ся в данной модели не выводимой переменной, а переменной решения. Очевидно, чтобы
данный подход имел смысл, необходимо добавить определенные ограничения, которые
не позволят средству Поиск решения трактовать начальный запас как решение, незави-
симое от решений по объему производства В данном случае начальный запас каждого
месяца (ячейки D8.F8) не должен превышать конечный запас предыдущего месяца
(ячейки С10:ЕЮ). За исключением этого небольшого усложнения, модель на рис 5 14
эквивалентна исходной модели на рис 5 11 Однако преимущества новой формулировки
становятся очевидны, если обратиться к ее отчету по устойчивости (рис 5.15)
Microsoft Excel 10.0 Отчет по устойчивости Изменяемые ячейки
Результ Нормир	Целевой Допустимое Допустимое Ячейка	Имя	значение стоимость Коэффициент Увеличение Уменьшение
$С$6 Произведено Январь	53	0	28,15	0,1	0.8 $Р$6	Произведено Февраль	62	-1.3	27,15	1 3	1 Е*3£ $Е$6	Произведено Март	 64	 -0,8	_ __	27,95	_ _ _	JJ.8 	 1Е*30 _$F$6 _ Произведено Апрель 		_0	 __0,1	29.1J_ 	 __ 1Е+30	_	0.1 $Р$8	Начальный запас Февраль	10	  0	0,30	 0	1	0.8_
$Е$8 _	Начальный запас Март			 36		0	0,3		0.1 	 0.8 $F$8	Начальный запасАпрель	66	0	0 3	0 1	29.05
Ограничения
Результ Теневая Ограничение Допустимое Допустимое Ячейка	Имя	значение Щена	Правая часть Увеличение Уменьшение
$С$10 Конечный запас Январь	10	0	0	10	1Е*30 $P$io_ Конечный запас Февраль	___ 36 _ 	  0_	_	0		 35	_ 1Е+30 $Ё$10 КонечныйзапасМарт	_	66	0	б	66	1Ё+30 $Р$8	Начальный запас Февраль	10	-28	0	10	7 $Ё$8	Начальный запас Март	36	-28	б	J_0	 7
$F$8 Начальный запасАпрель		__66		-29			0	10	__	7 $F$10 Конечный запасАпрель	7	29 05	7	7	10
Рис. 5.15. Отчет по устойчивости для новой модели
Совет. Не являющиеся непрерывными диапазоны переменных решения можно вводить в поле
Изменяемые ячейки диалогового окна Поиск решения через точку с запятой Однако сле-
дует помнить, что в версиях Excel, предшествующих Excel 2000, количество вводимых сим-
волов во всех диалоговых окнах, включая Поиск решения, ограничено числом 256
В новом отчете по устойчивости появилась дополнительная информация, представ-
ляющая интерес для принятия решений. Например, теперь видна нечувствительность сум-
марных затрат к изменениям стоимости хранения запасов, поскольку в структуре модели на
рис 5.15 появились дополнительные переменные решения, отражающие уровень запасов,
а также соответствующие ограничения и, следовательно, — их теневые цены, которые от-
сутствовали, когда запас моделировался как выводимые переменные Отметим также еще
одно положительное свойство новой модели: моделирование запаса в виде переменной ре-
шения позволяет разделить удельные затраты на отдельные составляющие — производст-
венные коэффициенты (удельные затраты на производство плюс затраты на хранение в те-
чение половины месяца) и коэффициенты запасов; благодаря этому коэффициенты целе-
вой функции выглядят так, как в исходной табличной версии модели.
332 Ч А С T b II. Оптимизационные модели
Формализация модели управления запасами в виде транспортной
модели
Часто динамическую модель, подобную модели Эндрю, можно сформулировать в ви-
де транспортной модели, в которой источники (пункты отправления) представляют ре-
шения в определенный временной период, а пункты назначения представляют один или
несколько временных периодов, на которые эти решения оказывают влияние впоследст-
вии. На рис. 5 16 представлена преобразованная в транспортную модель исходная модель
Эндрю (рис. 5.11), а также соответствующее оптимальное решение, найденное с помо-
щью средства Поиск решения Как и в первом примере транспортной модели (рис. 5.2),
три блока ячеек на рис 5 16 представляют удельные затраты, решения и суммарные за-
траты соответственно.
Ячейки со светлым фоном в строках с 4 по 7 представляют удельную стоимость произ-
водства генератора в заданном месяце (пункт отправления) и доставки его определенному
потребителю в будущем месяце (пункт назначения), включая стоимость хранения $300 за
каждый дополнительный месяц Аналогичная интерпретация применяется в строке 8 для
вычисления удельных суммарных затрат на хранение начального январского запаса, пред-
назначенного для отгрузки в будущем месяце. Соответствующие решения в блоке ячеек От-
грузка представляют суммарное количество произведенных генераторов в данном месяце
(ячейка Всего), в других ячейках показано, сколько генераторов из числа произведенных
в этом месяце предназначено для отгрузки заказчикам в текущем или будущих месяцах
Аналогично строка 15 показывает, как распределяется по месяцам отгрузка начального за-
паса (15 генераторов) Содержимое ячеек СП G15 — значения переменных решения, най-
денные средством Поиск решения при минимизации суммарных затрат.
Новым элементом в модели на рис 5 16 являются ячейки с серым фоном в блоке
Удельные затраты в строках с 5 по 7. Согласно изложенному в разделе 5.3 методу ис-
ключения недопустимых путей с помощью задания очень больших значений стоимости
ввод в эти ячейки огромных значений удельных стоимостей ($1 млн.) ведет к тому, что
Поиск решения не поместит ни одного положительного значения в соответствующие
ячейки блока решений по отгрузке (эти ячейки в строках с 12 по 14 также выделены се-
рым цветом). В данном случае эти выделенные ячейки представляют решения с обрат-
ным временным порядком действий (например, произведенные в марте генераторы
предлагается отгрузить в прошедшем январе), что невозможно, поэтому Поиск решения
должен избегать таких решений.7 Однако в других обстоятельствах выделенные ячейки
можно использовать для представления более сложной ситуации, при которой допуска-
ется выполнение заказов с опозданием, например, отгрузка генераторов по январским
заказам двумя месяцами позже из числа произведенных в марте. В таком случае парамет-
ры удельных затрат для выделенных ячеек, представляющих невыполненные вовремя
отгрузки, отражают дополнительные затраты, связанные с неудовлетворенностью клиен-
та, и затраты на специальные переговоры и договоренности, вызванные этой задержкой.
Чтобы добиться того же эффекта другим способом, можно оставить выделенные серым цветом ячейки
блока удельных затрат незаполненными, поместить нулевые значения в ячейки С12, С13 D15 и С14 Е14 и
удалить эти ячейки из поля Изменяемые ячейки диалогового окна Поиск решения
ГЛАВА 5. Линейная оптимизация. Применение 333
Рис. 5.16. Динамическая модель производства и управления запасами в виде транспортной модели
334 ЧАСТЬ II Оптимизационные модели
Формулы в ячейках C8.F8 и G4.G8 отражают граничные условия динамической моде-
ли, в данном случае это дополнительные удельные затраты на хранение в течение поло-
вины месяца исходного запаса в первой половине января и конечного запаса во второй
половине апреля соответственно
Итак, мы разработали три эквивалентные модели, причем каждая последующая была
более подробной, содержала больше переменных решения и ограничений. Все модели
привели к одному и тому же оптимальному решению, поэтому может возникнуть вопрос-
зачем понадобилось создавать более подробные модели, чем необходимо для получения
решения9 Хотя создание моделей — процесс творческий и личные предпочтения несо-
мненно играют роль в выборе конкретной формализации, обычно модели с большим
числом переменных решения и ограничений предоставляют дополнительную полезную
для менеджеров информацию. В этом можно убедиться на предыдущем примере, когда
превращение месячных запасов в переменные решения привело к появлению дополни-
тельной информации в отчете по устойчивости.
Ячейка
$С$11 Г
53
Допустимое Допустимое
28
$Е$11_ Произведено в январе Март
SFS11 Произведено в январе Апрель
26
-
29.05"
10ОО
~Те*зо"
973.3
1Е+30
Имя
$D$12 Произведено в феврале Февр»
$Е$12 Произведено в феврале Март
$СЛ6	Всего Январь	58	28 __		58		7.0	
То$н[	Всего Февроль			36	"	28 3	36		50		 	10
$Е$16	Всего Март	34	28.6	34		5,0	10
$г$Т(Г	_ Всего Апрель	_ 				59			28.9			53			Ко				То"
SGH6	Всего Май		_29.0	7		5,0“	7
$HtiT'	Произведено в январе Всего	53~	0	бо-		1Е+30	
янгйГ	Произведено в феврале Всего		62		-1		62				1.3			5
$Н$13	Произведено в марте Всего	64	-1	64		10	5
$н$н	Произведено в апреле Всего __		0_		. _ 66 _		1Е-30		66_
'$ Н $ 15 ‘	Начальный запас Всего	15			Тб		“ " 53"	А 999999998
Рис. 5.17. Фрагмент отчета по устойчивости для транспортной модели Эндрю

Транспортная модель на рис. 5 16 также имеет преимущества по сравнению с моде-
лью на рис 5 11 Например, с помощью модели на рис 5.11 Эндрю может определить,
что в январе следует произвести 53 генератора и отгрузить 58, при этом конечный за-
пас, переходящий в запас следующего месяца, составит 10 генераторов. Но что именно
произойдет с этими генераторами, как долго их хранить и когда отгружать? Этой ин-
формации нет в модели на рис. 5.11, но ее легко получить из модели на рис. 5.16: три из
них хранятся в запасе и отгружаются в апреле, а оставшиеся семь составят конечный
запас модели, переходящий на май. Кроме того, структура модели на рис. 5.11 застав-
ляет вносить плату за хранение помесячно, а модель на рис. 5.16 отслеживает стои-
мость хранения для каждого генератора и позволяет вносить эту плату в том месяце,
ГЛАВА 5. Линейная оптимизация. Применение 335
когда происходит отгрузка данного генератора. В результате график помесячного рас-
пределения прямых затрат будет иметь другой вид, который больше соответствует
принципам накопительного учета Наконец, представленный на рис. 5 17 отчет по ус-
тойчивости для последней модели значительно подробнее отчета по устойчивости для
предыдущей модели. Помимо “сигналов” о наличии альтернативных оптимумов, дан-
ный отчет позволяет увидеть, как отразится на затратах небольшое изменение в требо-
ваниях к отгрузке в определенном месяце, увеличение или уменьшение начального за-
паса января и т д.
В целом, перед тем, как формулировать динамическую модель, следует обдумать,
что должно быть выводимой переменной, а что — переменной решения, и насколько
мелким должно быть временное разбиение переменных решения. Зачастую тщатель-
но продуманная формулировка задачи позволяет получить множество дополнитель-
ной полезной информации.
В следующем разделе мы рассмотрим еще два примера динамических моделей,
чтобы показать диапазон ситуаций для их применения. Первая модель является
примером более сложной динамической модели управления запасами, рассматри-
вающей одновременно производство и календарное планирование труда
5.7. Динамическая модель планирования и управления
запасами
Компания Bumles, Inc. использует часть производственных мощностей своего за-
вода в Мексике для изготовления традиционных расписанных вручную заварных
чайников, которые затем продаются на местном рынке На роспись одного чайника
художник тратит 0,5 ч рабочего времени В компании работает 30 художников Каж-
дую неделю завод занимается выпуском чайников в четверг, пятницу и субботу
В остальные дни недели производственные мощности заняты выпуском другого вида
продукции. Не обязательно должны быть заняты все 30 художников, но каждый за-
нятый художник может работать любой отрезок 8-часового дня 2 дня в неделю Для
художника может быть составлен любой двухдневный график работы, и оплата на-
числяется так, как будто он отработал 16 ч, независимо от того, когда он в действи-
тельности был занят производством чайников. Если продукции недостаточно, чтобы
полностью занять всех художников, работающих в этот день, оставшееся время ис-
пользуется для уборки территории завода и другой подобной работы
Если не учитывать затраты на оплату труда, прибыль от продажи одного чайника
составляет $15. Спрос необходимо удовлетворить в день его возникновения, иначе
заказ будет потерян. Произведенные в определенный день чайники могут использо-
ваться для удовлетворения спроса в этот день или последующие дни недели (т е
чайники, произведенные в четверг, могут поступать в запас и использоваться для
удовлетворения спроса в пятницу или субботу). Однако, поскольку с понедельника
по среду завод переходит на выпуск расписных статуэток, все произведенные за не-
делю чайники необходимо отгрузить на той же неделе (т е граничные условия пред-
писывают, что исходный запас чайников утром в четверг и конечный запас вечером
в субботу равны нулю) Хранение одного чайника до следующего дня обходится
в $0,50. Потеря единицы спроса выливается в комплексный убыток, составляющий
$1 в четверг, $3 в пятницу и $5 в субботу. Художники получают за час работы сумму
336 ЧАСТЬ II. Оптимизационные модели
в песо, эквивалентную $8. Каждую неделю спрос на чайники составляет 100 штук
в четверг, 300 в пятницу и 600 в субботу.
На рис. 5 18 представлена модель компании Bumles, оптимизированная с помощью
средства Поиск решения. Она показывает график работы художников и план производ-
ства, которые максимизируют разность дохода и затрат, где затраты слагаются из затрат
на оплату труда, стоимости хранения запаса и всех убытков, отражающих неудовлетво-
ренный спрос. Поскольку продажи могут оказаться меньше спроса, между продажами,
спросом и потерянными заказами в любой день существует следующая зависимость:
потерянные заказы вденьх = спрос в день х — продажи в деньх
Помимо данной зависимости, модель содержит уравнение материального баланса, свя-
зывающее производство, запас и продажи:
запас на конец дня х = запас на начало дня х + производство в день х - продажи в день х.
Наконец, как и ранее в модели Эндрю, в модель включены уравнения баланса при пере-
ходе от одного временного периода к следующему: требуется, чтобы начальный запас для
каждого дня был равен конечному запасу предшествующего дня. Эти связи отражены
в формулах для ячеек 13 К.7, где переменные решения для каждогодня (ячейки 14 К5) пока-
зывают, сколько чайников необходимо произвести и сколько — продать Таким образом,
потерянные заказы и конечный запас для каждого дня — это выводимые переменные.
Иными словами, запас и потерянные заказы являются зависимыми переменными.
Другими переменными решения в модели Bumles являются количество художников,
назначенных в каждую из трех двухдневных смен (ячейки С9 Cl 1) Ячейки D9 Fl 1 пока-
зывают распределение художников каждой смены по соответствующим дням В диалого-
вом окне Поиск решения содержатся ограничения 16:К7 >= 0 Поскольку невыполнен-
ных заказов для клиентов Bumles нет (невыполненные заказы просто теряются), эти ог-
раничения утверждают, что ни отрицательные запасы, ни отрицательные потерянные
заказы не могут возникнуть. Последнее требуется для гарантии того, что ни в какой день
продажи не смогут превысить спрос
Легко расширить данную модель, чтобы учесть больше дней производства и больше
вариантов распределения рабочей силы Для каждого дополнительного дня производства
вводится дополнительный столбец после столбцов F и К Дополнительные варианты на-
значений вводятся путем включения новых ячеек в левой половине модели выше строки
12, чтобы представить варианты назначений на новый рабочий день. Затем необходимо
изменить все суммирующие формулы и ввести значения параметров в новые ячейки На-
конец, необходимо изменить параметры в диалоговом окне Поиск решения, добавив до-
полнительные переменные решения и ограничения
В рассмотренных нами динамических моделях речь шла о запасах продукции, но те же
принципы применимы к ситуациям финансового планирования, когда в роли запаса вы-
ступают денежные средства, как будет показано в следующем примере.
ГЛАВА 5. Линейная оптимизация. Применение 337
Рис. 5.18. Mode и. прчи >«<яЛ шва компании Bumles
5.8. Динамическая модель управления финансами
Корпорация Winston-Salem Development Corporation (WSDC) хочет сформировать план
капиталовложений на следующие два года. В настоящий момент WSDC может инвестировать
$2 000 000. Через 6, 12 и 18 месяцев компания ожидает получить прибыль от предшествующих
инвестиций Соответствующие данные представлены в табл. 5.14. Существует два инвестици-
онных проекта, в которых компания WSDC может участвовать наряду с другими инвесторами
338
ЧАСТЬ II. Оптимизационные модели
1. При 100% уровне участия компании WSDC в проекте развития города Foster City
предполагаемое движение денежных средств показано в табл. 5.15 (отрицательные
числа — это инвестиции, а положительные — доходы). Таким образом, чтобы уча-
ствовать в данном проекте на уровне 100%, WSDC обязана немедленно внести
$I 000 000, через 6 месяцев — еще $700 000, затем она получит $1 800 000 и т.д.
2. Второй проект предусматривает приобретение предприятия Middle-Income
Housing (MIH) по сдаче жилья в аренду для людей со средними доходами при ус-
ловии, что будет сделан предварительный косметический ремонт Динамика фи-
нансов для данного проекта при 100% уровне участия показана в табл. 5.16.
Таблица 5.14. Денежный доход от предшествующих инвестиций
	6 месяцев	12 месяцев	18 месяцев
Доход, $	500 000	400 000	380 000
Таблица 5.15. Финансовая динамика проекта Forest City
	Начальный взнос	6 месяцев	12 месяцев	18 месяцев	24 месяца
Доход, $	-1 000 000	-700 000	1 800 000	400 000	600 000
Таблица 5.16. Финансовая динамика проекта MIH
	Начальный взнос	6 месяцев	12 месяцев	18 месяцев	24 месяца
Доход, $	-800 000	500 000	-200 000	-700 000	2 000 000
WSDC может участвовать в проектах менее, чем на 100% В этом случае недостающие
средства вносят другие инвесторы, а все затраты и поступления для WSDC уменьшаются
пропорционально доле участия. Например, если компания примет решение участвовать
в проекте Forest City на уровне 30%, все данные в табл. 5 15 надо умножить на 0,3. Прово-
димая компанией WSDC политика запрещает занимать деньги. Однако в начале каждого
6-месячного периода на все свободные средства (не вложенные в проекты Forest City
и Middle-Income Housing) можно купить депозитный сертификат, прибыль от которого
для 6-месячного периода составляет 7% Компании WSDC необходимо решить, какую
часть имеющихся $2 000 000 вложить в каждый из двух проектов, а какую часть просто
положить на депозит под 7% полугодовых Цель руководства компании — максимизиро-
вать средства компании по окончании 24 месяцев Чтобы построить математическую мо-
дель, необходимо определить переменные решения.
F— доля участия в проекте Forest City;
М — доля участия в проекте Middle-Income Housing;
5, — свободные средства (не вложенные в проекты F и М), которые инвестируются
в депозитный сертификат под 7%;
S2 — свободные средства, которые вкладываются в депозитный сертификат под 7%
через 6 месяцев,
5, — свободные средства, которые вкладываются в депозитный сертификат через
12 месяцев,
54 — свободные средства, которые вкладываются в депозитный сертификат через
18 месяцев.
ГЛАВА 5 Линейная оптимизация Применение 339
В ограничениях данной модели необходимо указать, что в начале каждого 6-
месячного периода вкладываемые средства не превышают имеющихся средств Первое
ограничение выглядит следующим образом.
1 000 000F + 800 000М + 5, < 2 000 000
Благодаря выплате процентов по депозитному вкладу по прошествии 6 месяцев 5,
превратится в 1,07^,, поэтому аналогичные ограничения для S2, S3 и 54 будут выглядеть
так:
700 000Л + S2 < 500 000Л/ +1,075,+ 500 000,
200 0004/ + 5, < 1800 000Л +1,0752+ 400 000,
700 0004/ + 5, < 400 000/ +1,075,+ 380 000.
Эти ограничения задают уравнения материального баланса для движения средств при
переходе от одного временного периода к другому. Заметим, что в ограничениях можно
использовать равенства вместо неравенств, поскольку неинвестированные средства не
приносят дохода, однако практика моделирования советует избегать равенств, если в них
нет необходимости. Формулировка подобных моделей с использованием неравенств по-
зволяет средству Поиск решения подтвердить эти предположения о незанятых средствах,
когда эти ограничения-неравенства станут лимитирующими в процессе оптимизации
Целевая функция, которую необходимо максимизировать, — это наличные средства
в конце 24-месячного периода (в данном случае без учета дисконтирования) 600 00QF +
+ 2 000 000Л/+ 1,0754.
Таким образом, мы получили следующую динамическую модель управления финан-
совыми потоками.
Максимизировать 600 000Л+ 2 000 000Л/+ 1,0754
при ограничениях
1 000 000/ + 800 0004/ + 5, < 2 000 000,
700 000/— 500 0004/- 1,075 + 52 < 500 000,
-1800 000/+200 0004/- 1,0752 + 5, < 400 000,
-400 000/+ 700 0004/- 1,0753 + 54 < 380 000,
/<1,Л/<1,
/>0, Л/>0, 5(>0, Z= 1,2, 3,4
Табличная модель и фрагмент отчета по устойчивости представлены на рис. 5.19 Пе-
ременные решения отражают количество свободных средств, вложенных в депозит
(ячейки D12-G12), и процент участия в двух инвестиционных проектах (ячейки С7 С8)
Инвестируемые суммы в ячейках D7.G8 вычисляются путем умножения процента уча-
стия на сумму необходимых инвестиций, указанную в ячейках D3.I4 Как видно из ре-
зультатов оптимизации модели, компании WSDC выгодно участвовать в обоих инвести-
ционных проектах на уровне 100%, а из отчета по устойчивости следует, что максималь-
ная прибыль для исходных средств компании составит 31 % за 24 месяца.
340 ЧАСТЬ II Оптимизационные модели
Инвестиции
<? - j —-Р_L__Е___L
Проект инвестиций компании Winston Salem
Начальный
Депозит 7% ванос 6 месяцев 12 месяцев 18 месяцев
Проект Foster City’ -$1 000	-$700	$1 800
-$800	$500	-$200
___________Распределение средств
Процент Начальные „	i
участия инвестиции месяцев 12 месяцев 18 месяцев
100% |	$1 000
$800
24 месяца
$400
-$700
$600
$2 000
Middle Income | 100% |
Вложения в депозит:
Доход от депозита
Необходимо средств
Вложения в депозит^
Инвестирование
Доступные средства
$700
-$500
-$400
______________-$2В
$1 800_______-$228
$400	$728
$2 200	$500
<=$2200	<=$500

-$1 800
$200
-$728
-$51
-$2 379
$2 779
$400
<=$400
$400
$700
Доход после 24
месяцев
$600
$2 000
$3 053
$214
-$195
-$2 673
$3 053
$380
<=$387
12 месяцев
18 месяцев
Доход после
24 месяцев
Распределение средств
т	Начальные
»! Процент участия
й	инвестиции
l=-$C7’D3
J= $C8’D4
- 9 Вложения в депозит
.10 । Доход от депозита_______________—
?11 Необходимо средств =СУММ(Р7Р10) =СУММ(Е7:Е10) =CyMM(F7 F10) =CyMM(G7G10)
>12‘|Вложения в депозитное
13 , Инвестирование =011+012
14 Доступные средства 2200
6 месяцев
=-$С7’ЕЗ
=-$С8’Е4
=-012
=-Р12*$С$2
=-$C7’F3
=-$C8*F4
-Е12
=-Е12’$С$2
=-$C7*G3
-$C8’G4
=-F12*$C$2
-се-м
728,000000000002778,96
=Е11+Е12
500
-Изменяя ячейки
Ограниченно
$Р*13
1ЕЯ3 Инвестирование 6 месяцев
¥g$'i3~
$500
_$400_
$380
3053,4872
=G11+G12

Теневая Ограничение Допустимое Допустимое
Цена Правая часть Увеличение Уменьшение
Я	2200	1Е+30	400
________Я___________500_______1Е-30__________728
_____Я______________400_______16*30________ 27710
~Я 380 "	16*30	~30~53 5~
1Е+30
Рис. 5.19. Модель инвестиций компании WSDC
ГЛАВА 5 Линейная оптимизация Применение 341
В данной модели учитывались только финансовые аспекты управления денежными
потоками, в то время как в предыдущих моделях рассматривалось только производство
без учета управления денежными средствами. Следующий пример иллюстрирует объеди-
нение в общую модель управления производством и денежными потоками
5.9.	Модель управления финансами и планирования
производства
Модель производства дизельных генераторов компании AutoPower Europe позволяет
решить, сколько генераторов моделей BigGen и SmallGen следует производить в каждом
месяце при наличии ряда ограничений Данные о производстве таковы.
1.	Финансовые данные, относящиеся к генераторам BigGen и SmallGen, приводятся
в табл. 5.17.
2.	Операции по производству и сборке генераторов осуществляются в двух производ-
ственных цехах А и В Ежемесячный ресурс рабочего времени составляет для них
150 и 160 ч соответственно.
3.	Для производства одного генератора BigGen требуется 10 ч обработки и сборки
в цеху А и 20 ч в цеху В, для производства генератора SmallGen требуется 15 ч в це-
ху А и 10 ч в цеху В.
4.	Проверка генераторов осуществляется в третьем цеху и не связана с деятельностью
цехов А и В Каждый генератор BigGen тестируется 30 ч, a SmallGen — 10 Преду-
смотрено, что общее количество рабочего времени проверки не должно быть
меньше 135 ч в месяц
Таблица 5.17. Финансовые данные
Продукция Цена продажи, тыс. долл. Удельные затраты (материальные Удельная прибыль,
и на оплату труда), тыс. долл.	тыс. долл.
BigGen	80	75	5
SmallGen	24	20	4
Обозначим через В количество генераторов BigGen, a .S’— количество генераторов
SmallGen, производимых ежемесячно Тогда математическая модель производства будет
выглядеть следующим образом:
максимизировать 55 + 45
при ограничениях
105 + 15У< 150,
205 + 105 < 160,
305+ 105> 135,
5, 5>0.
(ограничение на рабочее время цеха А)
(ограничение на рабочее время цеха В)
(ограничение на время проверки)
Табличная модель, оптимизированная в Excel с помощью Поиск решения, представ-
лена на рис. 5.20. (Напомним, что нецелое количество генераторов BigGen можно интер-
претировать как средний месячный объем производства и продаж, реальный объем про-
даж будет составлять 4 или 5 генераторов BigGen в месяц )
342 ЧАСТЬ II Оптимизационные модели
Рис. 5.20. Модель планирования производства
Управляющего производством такая модель вполне удовлетворяет, поскольку, с его
точки зрения, она правильно отражает суть ситуации. Он направляет в администрацию
компании AutoPower Europe предложение рассмотреть возможность реализации решений
задачи Однако, когда руководство компании приступает к рассмотрению предложенных на
предстоящий месяц действий, оказывается, что производственная модель охватывает толь-
ГЛАВА 5 Линейная оптимизация. Применение 343
ко часть реальной ситуации. В частности, в ней игнорируются некоторые важные финансо-
вые вопросы. Так, компания должна возместить материальные затраты и затраты на оплату
труда в следующем месяце, несмотря на то, что платежи от конечных потребителей в после-
дующие три месяца не будут поступать Кроме того, существующая модель не учитывает тот
факт, что компании придется занимать средства для покрытия части текущих расходов.
Финансовые требования
Компания AutoPower Europe выделила S100 000 на покрытие текущих материальных
расходов и затрат на оплату труда, остальные средства для покрытия этих расходов плани-
руется занять. Компания может взять кредит под 16% годовых, однако для снижения риска
банк требует, чтобы общая задолженность банку (сумма займа плюс проценты) не превы-
шала двух третей суммы наличных средств компании AutoPower Europe и дебиторской за-
долженности. Администрация считает, что при вычислении удельной прибыльности раз-
личных генераторов не была учтена зависимость стоимости денег от времени По ее мне-
нию, для оптимизации текущей стоимости следует производить меньше генераторов
BigGen и больше SmallGen. Однако администрации не удалось прийти к соглашению, ка-
кой должна быть соответствующая учетная ставка. Некоторые члены администрации счи-
тали, что она составит 12%, другие — 16%, а несколько человек утверждали, что 20%
Таким образом, перед компанией встала задача сформулировать новую целевую
функцию, определить, нужно ли занимать средства и сколько, и составить производст-
венный план с учетом этих данных Для моделирования данной ситуации удобно ввести
в модель новую переменную. Обозначим через D общую сумму кредита в тыс долл Тогда
сальдо финансов в следующем месяце составит D - 75В - 205, а три месяца спустя
(поскольку поступление платежей в ближайшие три месяца не ожидается) — 805 + 245 -
1,0407). Коэффициент 1,040 получен из условия, что компания AutuPower может взять
кредит под 16% годовых, что составляет 4% за три месяца Вычислим дисконт-фактор а
для данного периода, исходя из того, что годовая учетная ставка равна R- а = 1/(1+5/4)
Цель состоит в максимизации текущей стоимости денежных потоков, поэтому целевая
функция (в тыс. долл ) имеет следующий вид.
максимизировать D - 75В - 205 + а(805 + 245 - 1,040/)).
Например, если R = 20%, то а = 0,952381, и целевая функция примет вид
максимизировать 1,190485+ 2,857145+ 0,009523815
Отметим, что в этом случае коэффициент при D положителен, поскольку считается,
что компания может получить 20% от своих инвестиций, а по условиям кредитования она
должна платить за одолженную сумму только 16% Если R= 16% или R < 16%, то коэф-
фициент при D будет нулевым или отрицательным соответственно
Необходимо также ввести дополнительные ограничения.
1. Компания AutoPower Europe должна занять сумму, достаточную для покрытия ма-
териальных и трудовых затрат, связанных с производством Поскольку суммарное
использование средств не может превышать их суммарное наличие, справедливо
следующее неравенство:
затраты труда и материалов < сумма кредита + наличные средства.
Напомним, что компания имеет S100 000 наличных средств Кроме того, как вид-
но из табл. 5.17, общие затраты труда и материалов составляют $75 на каждую еди-
ницу 5 и $20 на каждую единицу 5 Таким образом, ограничение будет иметь вид
755 + 205< 5+100
344
Ч А С Т Ь II. Оптимизационные модели
Рис. 5.21. Модель финансов и производства компании AutoPower
ГЛАВА 5. Линейная оптимизация. Применение 345
2. Банк требует, чтобы общая сумма долга банку (кредит плюс проценты) не превы-
шала двух третей от суммы наличных средств компании и дебиторской задолжен-
ности. Иными словами:
сумма кредита + процент< 2/3 (наличные средства + дебиторская задолженность).
В табл. 5.17 показано, что каждый генератор В продается за $80, а каждый 5 — за $24.
Таким образом, общая дебиторская задолженность составляет 802? + 245, и ограничение
принимает следующий вид:
D 4- 0,042) < 2/3 (100 + 805 + 245) или
l,5xl,04D< 100 + 805 + 245.
Отметим, что нижняя граница суммы кредита D (неявно заданная ограничением в п. 1)
зависит от стоимости труда и материалов, а верхняя граница (неявно заданная ограничени-
ем в п. 2) определяется ценами продажи генераторов.
Новая версия производственной и финансовой модели компании AutoPower Europe,
некоторые ее формулы и оптимальное решение для случая R = 20% представлены на
рис. 5.21. Из решения видно, что компания должна взять кредит примерно на 279,49 тыс.
долл, и, как и ожидалось, уменьшить производство генераторов BigGen, увеличив произ-
водство генераторов SmallGen. Переменные резерва для ограничений по наличным сред-
ствам в строках 16 и 17 показывают, что (поскольку ограничение Дебиторский баланс
является лимитирующим) компания будет брать в кредит максимально возможную сум-
му, причем эта сумма больше, чем необходимо для покрытия затрат труда и материалов
(ограничение Баланс наличных средств имеет положительное значение резерва). Так
получается из-за того, что в модели предполагается возможность инвестировать остав-
шиеся средства, чтобы получить 20%, в то время как процентная ставка выплат по креди-
ту составляет только 16%.
Влияние финансовых требований
Включение в исходную модель производства финансовых аспектов привело к замет-
ному изменению плана. Новый план дает прибыль существенно меньше, чем прибыль,
определенная на основании исключительно производственных ограничений Оптималь-
ное значение целевой функции в финансово-производственной модели снизилось из-за
учета затрат на выплаты процентов по кредиту и дисконтирования будущих поступлений
наличных средств. На рис. 5.22 с помощью таблицы подстановки с одним входом рассчи-
таны финансовые показатели при изменении значений учетной ставки 5 от 12% до 20%
Оптимальный производственный план финансово-производственной модели не зависит
от величины учетной ставки внутри указанного диапазона (от 12% до 20%), те он не чув-
ствителен к R. Оптимальный размер кредита зависит от А, однако зависимость носит
простой характер: если А < 16%, следует занимать наименьшую возможную сумму,
а именно 192,5 тыс долл., если же А > 16%, занимаемая сумма должна быть как можно
больше, т е 279,49 тыс. долл. Если же А = 16, существуют альтернативные оптимальные
решения, в которых D принимает значения в пределах от 192,5 до 279,49 тыс. долл
346	Ч А С Т Ь II. Оптимизационные модели
Рис. 5.22. Финансовые показатели при изменении значений R
С помощью таблиц подстановки можно также исследовать поведение решения для
значений задержки платежей от 0 до 4 месяцев. Мы увидим, что компания AutoPower
Europe существенно выиграет, если сможет улучшить оборачиваемость своих средств,
поощряя потребителей быстрее оплачивать счета Это позволит компании не только пе-
рейти к более прибыльному ассортименту продукции, но и в зависимости от соотноше-
ния между годовой учетной ставкой и процентной ставкой за пользование кредитом
уменьшить издержки финансирования В таблице на рис. 5.23 в последнем столбце пока-
зано изменение прибыли (в процентах) в зависимости от срока задержки платежей по
сравнению с базовым вариантом, в котором этот срок составляет 3 месяца. Это измене-
ние вычисляется по формуле (прибыль — 30,162)/30,162, где 30,162 — значение прибыли
для базового варианта Например, если клиенты платят за генераторы через месяц вместо
трех, прибыль компании AutoPower Europe возрастет более чем на 40% в месяц, а немед-
ленная оплата позволит увеличить ежемесячную прибыль более чем на две трети.
Рис. 5.23. Зависимость прибыли от срока задержки платежей
Совет. Часто бывает, что при подстановке в модель определенного значения параметра Excel генери-
рует сообщение об ошибке, а это, в свою очередь, приводит к тому, что Поиск решения сообщает о
недопустимом решении. Если в ячейку G1 на рис 5.21 ввести значение 0, в формуле в ячейке СЗ воз-
никнет ошибка #ДЕЛ/0' (деление на 0) В таких случаях нужно использовать близкое к нулю значение
параметра, малое по сравнению с остальными числами модели. (В данном примере задание значения
срока задержки платежей 0,000001 позволит избежать указанной проблемы).
Практическое применение^
Сетевые модели помогают снижать
ранспортные расходы
Определение наиболее экономичного способа доставки товаров от поставщиков на
склады и со складов в магазины является большой проблемой для многих сетей роз-
ничной торговли Задача становится особенно сложной, когда компания растет со ско-
ростью 30% в год. Именно такая ситуация сложилась в компании Marshall’s, которая
Из-за быстрого появления все новых магазинов компании
ГЛАВА 5. Линейная оптимизация. Применение 347
необходимо быстро разрабатывать новые схемы доставки товаров, а также решать, где
размещать новые центры распределения товаров Чтобы помочь в решении данных во-
просов, компания внедрила компьютеризованную систему планирования перевозок
Одна из частей системы, модель сетевой оптимизации, состоит из трех программ-
ных модулей, предназначенных для минимизации расходов на транспортировку
•	Модуль “Прибытие” занимается потоком товаров от поставщиков на склады
и в центры обработки
•	Модуль “Убытие” занимается транспортировкой со складов и центров обработки
в магазины розничной торговли
•	Третий модуль анализирует размещение новых складов, что оказывает заметное
влияние на первые два модуля
Каждый модуль содержит четыре компонента
1	Генератор сетей, который строит узлы и дуги сети
2.	Редактор сетей, который позволяет модифицировать сеть, изменяя затраты,
спрос и ограничения
3.	Программа оптимизации
4.	Программный модуль, выполняющий преобразование результатов оптимиза-
ции в формат, удобный для использования
Каждый из трех модулей представляет собой отдельную модель, отражающую оп-
ределенную экономическую ситуацию и обеспечивающую выполнение необходимых
вычислений. Настоящей проблемой моделей прибытия и убытия являются их разме-
ры. Каждая из них первоначально требовала решения сетевой задачи, содержащей
350 000 связей Использование эвристических методов и других оригинальных под-
ходов позволило уменьшить это число приблизительно до 20 000 В результате упро-
щений задачи стало возможным решать на персональных компьютерах, а не на
больших ЭВМ. В настоящее время эти модели, являющиеся основой всей системы,
дают возможность менеджерам исследовать множество сценариев, изменяя такие
факторы, как количество используемых грузовиков, их грузоподъемность, затраты,
местонахождение складов, и быстро оптимизировать полученную модель
Использование вышеупомянутых моделей позволило компании Marshall’s оценить за-
траты и качество обслуживания для своей сети доставки продукции, получив при этом
около 250 000 долларов ежегодной экономии Кроме того, модель позволила определить
место для постройки нового распределительного центра, введение которого в строй, как
ожидается, обеспечит компании экономию в 1,4 млн долл, на расходах по доставке [3]
5.10. Сетевые модели
Рассматриваемые в разделах 5 2 и 5 3 транспортные модели и модели назначении яв-
ляются представителями более общего класса моделей, описывающих движение между
исходными пунктами и пунктами назначения, которые называются сетевыми моделями
Сетевые модели часто применяются при решении организационных вопросов и вопросов
распределения, а также в технике и информатике. Многие реальные модели сводятся
к сетевым моделям Как правило, с помощью сетевого подхода описываются очень мас-
штабные ситуации. Например, можно создать сетевую модель международной компании,
348
ЧАСТЬ II Оптимизационные модели
занимающейся производством бумаги. Сеть должна описывать всю систему прохождения
древесины на протяжении многих временнь/х периодов: из леса на склад древесины, за-
тем на различные бумажные фабрики, оттуда на широко разбросанные склады, учитывая
различные варианты транспортировки, и далее к оптовым продавцам в разных странах.
Динамическая модель системы поставок для такого множества операций позволяет
предприятию получить значительную выгоду в глобальных операциях.
В последние годы активно разрабатывается программное обеспечение для систем поста-
вок и планирования материальных ресурсов, основанное на сетевых моделях. Основное
внимание в этих программах обычно уделяется стратегическому планированию на стадиях
поставок и распределения. Термины поставки и распределение используются в достаточно
общем смысле, это могут быть потоки физической продукции, данных, транспортных
средств, валют разных стран и т д. В настоящее время уровень развития программных сете-
вых приложений позволяет оптимизировать модели, содержащие десятки тысяч перемен-
ных и ограничений (которые слишком велики для средства Поиск решения).
Применение сетевых моделей в реальных ситуациях требует высокой квалификации
и опыта в преобразовании моделей, которые первоначально могут казаться далекими от
сетевых, к сетевому представлению. Чтобы воспользоваться преимуществами большой
размерности сетевых структур, стоит потратить определенное время на осмысление мо-
дели и приведение ее исходной формулировки к сетевому представлению. Как правило,
это далеко не тривиальная задача, требующая глубоких знаний как в сфере формализа-
ции моделей, так и в моделируемой области.
Большое количество различных приложений сетевых моделей можно проиллюстри-
ровать с помощью нескольких простых примеров. Начнем с примера общей формы
транспортной модели, которая называется моделью перевозок с промежуточными пунк-
тами и широко используется в организации перевозок
5.11. Модель перевозок
Сеймур Майлз — начальник отдела сбыта компании Zigwell Inc., крупнейшего дист-
рибьютора продукции компании AutoPower в пяти штатах среднего запада США. В на-
стоящее время в распоряжении Сеймура имеется десять генераторов BigGen, которые на-
ходятся в пункте, обозначенном как пункт 1. Эти генераторы необходимо доставить
в пункты строительства, обозначенные как пункт 3 и пункт 4. В пункте 3 требуется три
генератора, а в пункте 4 — семь Из-за ограничений, касающихся наличия водителей, ге-
нераторы можно доставлять только по маршрутам, показанным на рис. 5.24.
Рис. 5.24. Сетевая диаграмма для модели Сеймура
ГЛАВА 5. Линейная оптимизация Применение 349
Сетевая терминология
На рис 5.24 показан пример сетевой диаграммы, или диаграммы потоков Каждая стрелка,
соединяющая пункты, называется дугой или ветвью сети Дуга, соединяющая пункты 2 и 4,
иногда символически обозначается парой чисел (2,4). Каждый пункт называется узлом сети
Возле пункта 1 на рис. 5.24 записано число +10. Это означает, что в данном пункте
находится десять генераторов BigGen (элементов поставки). Числа —3 и —7 рядом с пунк-
тами 3 и 4 обозначают потребности, или спрос, в этих пунктах. Из рисунка также следует,
что генераторы могут доставляться в пункт 3 по любым из возможных маршрутов
1—>2—>3, 1->2->4->3, 1->2->5->4->3 или 1 ->2->5->3.
Какой из возможных маршрутов будет выбран, определяется затратами, связанными
с каждым маршрутом, и его пропускной способностью. Эти данные показаны на рис 5 25,
где ctj — это удельные затраты (стоимость перевозки одного генератора), а — пропускная
способность. Например, затраты на перемещение одного генератора по дуге (5, 3) равны с5,
Затраты складываются главным образом из стоимости топлива, пошлин, а также зарплаты
водителя за среднее время пребывания в пути при движении поданному маршруту Соглас-
но заключенному ранее соглашению с профсоюзом компания Zigwel! должна менять води-
телей в каждом пункте маршрута Из-за ограничений по наличию водителей для каждой
дуги существует верхняя граница w.. для количества генераторов, которое можно по ней пе-
ревезти. Так, — верхняя граница, или пропускная способность, дуги (5, 3)
Рис. 5.25. Сетевая диаграмма с данными о затратах
и пропускной способности сети
Формулировка задачи
Задача Сеймура состоит в том, чтобы составить такой план перевозок, который удовлетво-
рит спрос с минимальными затратами при соблюдении ограничений по пропускной способ-
ности. Теперь оценим различные варианты перевозок. Например, если (с2, + сч) меньше, чем
с23, общие затраты для пути 1—>2—>5—>3 будут меньше, чем для пути 1—>2—>3, следовательно,
путь 1->2->5->3 предпочтительней, чем 1-э2-эЗ. Однако максимальное количество генерато-
ров, которое можно отправить по более выгодному пути, равно минимуму от чисел w12, w25 и и,3
Если этот минимум меньше 3 (количество генераторов, которое необходимо доставить в пункт
3), то не все перевозки удастся осуществить по маршруту 1 ->2->5->3 В нашей модели только
пять узлов и восемь дуг, но даже в таком простом примере оптимальное решение не всегда
очевидно. Представим, что подобная модель состоит из 300 или 400 узлов и многих тысяч дуг,
и станет понятно, насколько сложными являются задачи организации перевозок
350 ЧАСТЬ II. Оптимизационные модели
Предложенная модель практически эквивалентна рассматривавшейся ранее транс-
портной модели, но имеет две особенности
1. Любой завод или склад может осуществлять поставки любому другому заводу или
складу.
2. Для каждой перевозки (ветви) могут быть указаны верхние и/или нижние границы
пропускной способности
Данную модель легко сформулировать в виде модели линейного программирования.
Определим переменные решения
ху — общее количество генераторов BigGen, отправленных по дуге (z,y),
= поток из узла Z в узел j
Тогда модель примет следующий вид
минимизировать с|2х|2 + с23х23 + с14х24 + c2Sx25 + с34х34 + с43х43 + с53х53 + с,^
при ограничениях
хР=10,
"x'2+J’ + ?4tj' = -3
-х24+х43-х3>х”=-?;
—х2, + х53 + х54 = О,
0<х..<иудля всех дуг (z,у)
Свойства модели
Данная модель обладает следующими свойствами
1.	Это действительно модель линейного программирования. С каждой дугой сети,
изображенной на рис 5 25, связана одна переменная х/у Сеть содержит восемь дуг,
которым соответствует восемь переменных х|2, х23, х24, х25, х34, х43, х53 и хч. Цель —
минимизировать общие затраты (суммарную стоимость перевозок).
2.	С каждым узлом сети связано одно уравнение баланса потоков. Первое уравнение по-
казывает, что общий поток, выходящий из узла 1, составляет десять единиц (что рав-
но общему объему запаса в узле 1) Второе уравнение показывает, что общий поток,
выходящий из узла 2 (х23 + х24 + х25), минус общий поток х12, входящий в узел 2, равен
нулю Иными словами, поток, выходящий из узла 2, должен быть равен потоку, вхо-
дящему в узел 2 Третье уравнение показывает, что для узла 3 выходящий поток х„
должен быть на 3 единицы меньше, чем входящий (х23 + х43 +х53). Это математиче-
ский способ выразить требование, чтобы поставка в узел 3 составляла 3 единицы.
Аналогично интерпретируются уравнения для узлов 4 и 5. Таким образом, уравнение
для каждого узла отражает условия материального баланса, принимая во внимание
тот факт, что узел может быть точкой предложения, точкой спроса или ни тем, ни
другим Промежуточные узлы (такие как 2 и 5), которые не являются ни точками
предложения, ни точками спроса, часто называются узлами перевалки.
В общем виде баланс потоков для узлаj задается формулой:
суммарный поток, выходящий из узлаj, — суммарный поток, входящий в узел j =
= предложение в узле j,
ГЛАВА 5. Линейная оптимизация. Применение 351
Рис. 5.26. Модель перевозки грузов
где отрицательное предложение означает спрос Узлы с отрицательным предложени-
ем называются пунктами назначения, стоками или точками спроса Узлы с положи-
тельным значением предложения называются источниками или точками предложе-
ния. Узлы с нулевым значением предложения называются точками перевалки
352
ЧАСТЬ II Оптимизационные модели
3.	Положительные правые части соответствуют узлам, которые являются поставщи-
ками (источниками). Отрицательные правые части соответствуют узлам, являю-
щимся потребителями (стоками). Нулевые правые части соответствуют узлам пе-
ревалки, в которых не существует ни собственного спроса, ни предложения. Сум-
ма значений правых частей всех уравнений равна нулю, это означает, что
суммарное предложение в сети равно суммарному спросу.
На рис 5 26 показано табличное представление данной модели в Excel и соответст-
вующее оптимальное решение Матрица пропускных способностей дуг содержится
в ячейках СЗ G7, а матрица с. удельных стоимостей перевозок по дугам — в ячейках
J3 N7 Правые части ограничений, задающих значения спроса, введены в ячейки
С17 G17 Переменные решения содержатся в ячейках C10.G 14, а матрица суммарных за-
трат вычисляется по формулам в ячейках ПО.N14.
Целочисленные оптимальные решения
Если модель можно представить в виде сетевой модели, то получаем два преимущест-
ва Во-первых, теоретические результаты, установленные для сетевых моделей общего
вида, автоматически распространяются на ее частные случаи. (Второе преимущество
описано в следующем разделе ) Примером может служить свойство целочисленности се-
тевой модели Оно формулируется следующим образом.
Если в модели перевозки грузов все правые части ограничений и пропускные способ-
ности дуг и„ задаются целыми числами, то существует целочисленное оптимальное ре-
шение дан ной задачи.
Из предыдущих глав известно, что в общем случае задача ЛП не гарантирует сущест-
вование целочисленного оптимального решения Для сетевой модели с целыми значе-
ниями правых частей и пропускных способностей дуг целочисленное оптимальное реше-
ние существует
Эффективные процедуры решения
Второе преимущество сетевых моделей заключается в том, что структура такой модели
дает возможность применять специальные методы решения и программное обеспечение,
которые позволяют оптимизировать модель гораздо быстрее, чем более общий симплекс-
метод, используемый средством Поиск решения Благодаря этому можно оптимизировать
сетевые модели большой размерности быстрее и дешевле Результаты применения эффек-
тивных методов решения, основанных на специальной структуре сетевой модели, просто
поразительны Например, компания Internal Revenue Service создала сетевую модель, со-
держащую 50 000 ограничений и 600 миллионов переменных! Для оптимизации данной мо-
дели потребовался только час работы большой ЭВМ.
Далее рассмотрим две задачи, возникающие в сетевых моделях, — задачи нахождения
кратчайшего пути и максимального потока. Для каждой задачи представлены ее решения
в Excel и сетевая диаграмма модели
5.12.	Поиск кратчайшего пути
Задача нахождения кратчайшего пути возникает в сети, в которой с каждой дугой (JJ)
связано число с., интерпретируемое как расстояние (или, возможно, стоимость или вре-
мя движения) от узла i к узлу j. Маршрут, или путь, между двумя узлами — это произ-
ГЛАВА 5. Линейная оптимизация. Применение 353
вольная последовательность дуг, соединяющих данные узлы. Задача состоит в нахожде-
нии кратчайшего (требующего минимальных затрат или минимального времени) пути из
определенного узла в остальные узлы сети Эта задача естественна для моделей перевозки
продукции, пересылки пакетов данных по компьютерной сети и т.д
В качестве иллюстрации рассмотрим следующую модель Аарон Драннер занимается
регулярными поставками вина в семь различных пунктов На рис. 5 27 показаны эти пунк-
ты и соединяющие их маршруты. Заметим, что в данном случае, в отличие от модели пере-
возки грузов, дуги ненаправленные. Таким образом, по каждой дуге допускается движение
в обоих направлениях Можно, конечно, сделать дуги направленными, при этом стоимость
перевозки из узла 1 в узел 2 будет отличаться от стоимости перевозки из узла 2 в узел 1 Та-
кая модель соответствует ситуации, при которой интенсивность движения в одну сторону
заметно выше, или же из узла 1 в узел 2 движение возможно, а из 2 в 1 — нет (улица с одно-
сторонним движением) Каждой дуге на рис 5 27 соответствует число, обозначающее рас-
стояние между соединяемыми данной дугой узлами Исходный пункт обозначен Н Аарон
считает, что его суммарные затраты будут минимальны, если все поставки в любой задан-
ный пункт будут осуществляться по кратчайшему маршруту Поэтому его цель — отыскать
кратчайшие маршруты из узла Н во все остальные семь узлов.
Рис. 5.27. Сеть пунктов модели Аарона
На рис. 5 28 представлена модель Аарона в Excel, оптимальное решение — это крат-
чайшие пути между двумя любыми узлами. В данном случае показан оптимальный путь
из Н в пункт 5. Начальный узел Н и конечный узел 5 отмечены в строке 23 числами 1 и -1
соответственно В диапазоне М3 Т10 указаны расстояния вдоль различных дуг За ис-
ключением диапазона СЗ J10, где указано, как узлы соединены между собой посредством
дуг, модель имеет тот же вид, что и общая модель перевозки грузов, представленная на
рис. 5.26 Переменные решения должны принимать значения 0 или 1, как и в модели на-
значений, а целевая функция, которую необходимо минимизировать, представляет собой
суммарное расстояние.
354
ЧАСТЬ II Оптимизационные модели
Рис. 5.28. Модель для нахождения кратчайшего пути из узла Н в узел 5
5.13.	Модель замены оборудования
Задачу нахождения кратчайшего пути можно применить для оптимизации затрат на
оборудование в течение определенного времени. Майкл Кэрр отвечает в компании, за-
нимающейся печатью периодических изданий, за покупку оборудования, в частности,
печатных станков В этом году ему предстоит решить, приобрести ли новый дорогой пе-
чатный станок с низкими первоначальными расходами на обслуживание или продолжать
использовать приобретенный ранее печатный станок с высокими расходами на обслужи-
вание Для простоты предположим, что период планирования в модели Майкла состав-
ляет четыре года. Обозначим через с. расходы на приобретение нового оборудования
в начале года / (/ = 1, 2, 3,4) и обслуживание его до начала года j (j = 2, 3, 4, 5) Если обо-
рудование может работать только до начала года J, где j < 5, то в начале года j необходимо
снова приобретать новое оборудование Рассмотрим три возможных варианта поведения
ГЛАВА 5. Линейная оптимизация. Применение 355
1.	Приобретать новое оборудование в начале каждого года Такая политика приведет
к самым высоким расходам на приобретение и минимальным расходам на обслу-
живание. Общие расходы на приобретение и обслуживание в таком случае соста-
вят с12 + с23 + с34 + с45.
2.	Приобрести новое оборудование только в начале первого года, а затем заниматься
его ремонтом и обслуживанием в течение последующих лет. При такой политике
суммарные расходы на приобретение будут минимальны, а расходы на обслужива-
ние максимальны Общие расходы на приобретение и обслуживание составят с„.
3.	Новое оборудование приобретается в начале 1 и 4 годов. Суммарные расходы со-
ставят с14 + с4,.
Из всех возможных вариантов Майкл хочет выбрать вариант с минимальными сум-
марными затратами Чтобы решить эту задачу, необходимо найти кратчайший путь (в
данном случае — путь с минимальными затратами) из узла 1 в узел 5 для сети, показанной
на рис. 5.29 Каждый узел на кратчайшем пути означает замену оборудования в соответ-
ствующем году, т.е. в этом году необходимо приобрести новое оборудование.
Рис. 5.29. Модель для принятия решений по замене оборудования
В представленной на рис 5 30 табличной модели используется тот же общий макет
и формулы, что и на рис 5 26 Стоимостные параметры заданы в ячейках Н2 Н7. Пред-
полагается, что расходы составляют $1 600 000 на приобретение оборудования и $500 000
на его обслуживание в год приобретения; для каждого дополнительного года эксплуата-
ции ежегодные затраты на обслуживание составляют $1 000 000, $1 500 000 и $2 200 000
В ячейках J3‘N6 вычислены затраты на покупку и обслуживание печатного станка, если
он приобретен в одном году и эксплуатируется до начала другого указанного года Ячей-
ки переменных решения с серым фоном в диапазоне СЮ G14 соответствуют невозмож-
ным решениям с обратным ходом событий (например, приобретение станка в году 3 для
использования в году 1) Начальный и конечный годы использования оборудования от-
мечены в строке 17 с помощью чисел 1 и—1 В ячейках C3.G7 содержится матрица связей
между узлами, а в ячейках J10 N14 вычислены расходы для решений, записанных в ячей-
ках CIO G14 В данном случае оптимальной стратегией является приобретение нового
печатного станка в начале года 1, использование его в течение двух лет и замена в начале
года 3 новым печатным станком, который затем используется до начала года 5 При этом
общие расходы за четыре года составят 6,2 млн долл.
356 Ч А С Т Ь II. Оптимизационные модели
Рис. 5.30. Модель замены оборудования
Практическое применение^
Скоростная автострада Хансин в Японии
Первый участок скоростной автострады Хансин протяженностью всего 2,3 км
был построен в 1964 г Это была первая платная скоростная автомагистраль в Осаке.
Спустя два года была открыта скоростная дорога в городе Кобе, соединившая этот
город с Осакой В середине 60-х этой дорогой ежедневно пользовалось более 5000 ав-
томобилей Этот район Японии, расположенный на самом большом острове Хонсю,
является второй по населенности областью Японии (первое место принадлежит рай-
ону Токио) В 1992 году протяженность сети скоростных автомагистралей составила
200 км, ежедневно ее услугами пользовалось в среднем 828 000 автомобилей
Среднее количество автомобилей, приходящееся на единицу площади в Японии,
значительно больше, чем в США Практически все крупные города Японии страда-
ют от транспортных пробок. Считается, что из-за недостатка земли пропускная спо-
собность дорожной сети никогда не догонит спрос Поэтому так важно найти спосо-
бы максимизировать использование дорожных сетей, и эта задача останется акту-
альной в обозримом будущем
ГЛАВА 5. Линейная оптимизация. Применение 357
В 1970-х на скоростной автомагистрали стала работать автоматическая система
управления движением, призванная максимизировать общий транспортный поток,
проходящий по сети. Идея, лежащая в основе максимизации потока, довольно
сложна. Может показаться, что для максимизации потока следует позволить всем
желающим автомобилям входить в сеть и, возможно, даже снизить плату за проезд по
трассе, чтобы стимулировать спрос. Но если допустить в скоростную сеть слишком
много автомобилей, могут возникнуть большие пробки, что существенно уменьшит
поток в системе.
Одним из способов регулирования движения на магистрали Хансина является
ограничение количества автомобилей, попадающих на скоростную дорогу через ка-
ждый пропускной пункт. Максимально допустимые потоки транспорта вычисляют-
ся путем решения каждые пять минут задачи линейного программирования, исполь-
зующей данные приборов, установленных через каждые 500 м на трассе, а также на
всех пропускных пунктах. Целью задачи ЛП является максимизация потока транс-
порта на магистрали, что автоматически приводит к максимизации дохода. На осно-
вании решения задачи ЛП администрация скоростной автомагистрали определяет,
скольким новым автомобилям можно разрешить въезд на трассу на каждом из про-
пускных пунктов. Администрация может также использовать модель ЛП при воз-
никновении дорожно-транспортных происшествий (ДТП), чтобы определить,
сколько автомобилей должно покинуть трассу из-за аварии Чтобы избежать пробок,
администрация автомагистрали анализирует количество ДТП, число поврежденных
автомобилей, а также необходимый объем дорожных восстановительных работ Вто-
рой используемый метод управления движением состоит в снабжении водителей са-
мой свежей и полной информацией о ситуации на скоростной трассе и в ее окрест-
ностях, включая ожидаемое время поездки и информацию о ДТП
Администрации удается поддерживать расходы на систему управления движени-
ем в пределах 1% общего дохода от платы за пользование скоростной магистралью
Наибольшим преимуществом является сэкономленное водителями время По оцен-
кам, за десять лет в 1970-х годах удалось сэкономить 17 850 000 часов Исходя из
среднего часового дохода жителей Осаки, это время можно оценить в 27 300 000 000
йен (или 260 млн. долл. США по курсу 1994 года)! Модель ЛП для магистрали Хан-
сина явилась прототипом для других моделей, которые используются в Японии и на
Тайване для организации автоматического управления движением и позволяют по-
лучить аналогичную выгоду. [4]
5.14.	Задача максимизации потока
В задаче максимизации потока существует один узел-источник (вход в систему) и один
узел стока (выход из системы). Цель состоит в том, чтобы найти, какое максимальное коли-
чество (нефти, денег, пакетов Internet, транспортных средств) можно пропустить через дан-
ную физическую сеть (от источника до стока) за единицу времени. Поток в единицу време-
ни по каждой дуге сети ограничен ее пропускной способностью. Например, диаметр трубо-
провода ограничивает поток сырой нефти по звеньям трубопроводной системы. Для узлов
пропускные способности не задаются. Единственное требование состоит в том, что для ка-
ждого узла (кроме исходного и конечного) должен выполняться баланс потоков- поток, вы-
ходящий из узла, должен быть равен потоку, входящему в данный узел.
358 ЧАСТЬ II. Оптимизационные модели
Данная задача, как и задача нахождения кратчайшего пути, представляет самостоя-
тельный интерес Кроме того, она часто является частью других, более сложных, моде-
лей Поэтому, а также благодаря неким теоретическим положениям (которые мы здесь
рассматривать не будем) иногда утверждается, что эти две задачи (задача нахождения
кратчайшего пути и задача нахождения максимального потока) занимают центральное
место в теории сетей применительно к организации работы транспорта, компьютерных
сетей и т.д
Модель планирования городского строительства
Глория Стайм — член специальной исследовательской группы Комиссии по плани-
рованию городского строительства. В обязанности группы входит согласование строи-
тельства новой системы подземных переходов с государственным департаментом обслу-
живания автомагистралей Поскольку новая система подземных переходов строится ря-
дом с городской кольцевой дорогой, поток транспорта в восточном направлении
необходимо пустить в объезд. Объездной путь представляет собой сеть альтернативных
маршрутов, предложенных департаментом обслуживания автомагистралей. Из-за разли-
чий в ограничениях скорости и схемах движения пропускные способности разных дуг
предлагаемой сети отличаются друг от друга (рис 5 31)
Рис. 5.31. Предлагаемая сеть и пропускные способности
различных участков (тыс автомобилей в час)
Узел 1 обозначает начало объезда, т е. точку, в которой транспорт, идущий в восточ-
ном направлении, покидает окружную дорогу Узел 6 — это точка, в которой транспорт
возвращается на кольцевую дорогу Пропускные способности на рис 5.31 зависят от на-
правления движения Число 6 на дуге (1,3) означает, что пропускная способность при
движении в направлении из узла 1 в узел 3 составляет 6000 автомобилей в час Число 0 на
той же дуге означает, что при движении в направлении из 3 в 1 пропускная способность
равна нулю Это происходит потому, что дуга (1,3) обозначает улицу с односторонним
движением от I в 3 В данном примере все остальные дуги также обозначают улицы с од-
носторонним движением (Предлагаемая модель в Excel может также применяться в тех
случаях, когда допускается движение в обоих направлениях)
На рис 5 32 показана табличная модель данной сети, в которой оптимальное решение
позволяет наити максимальный поток За исключением отсутствия данных о затратах,
данная модель аналогична по форме предыдущим сетевым моделям Переменные реше-
ГЛАВА 5. Линейная оптимизация Применение 359
ния (неотрицательные) в ячейках С 10:Н 14 — это потоки из одного узла в другой, которые
не должны превышать соответствующие пропускные способности, заданные в ячейках
СЗ Н7 Если максимизировать поток, выходящий из пункта 1, то целевая функция для
этого случая записана в ячейке 110 Решение не изменится, если максимизировать поток,
входящий в узел 6, тогда целевая функция будет содержаться в ячейке Н15 Ограничения
в ячейках C17.G17 указывают, что результирующий поток в каждом промежуточном узле
должен быть равен нулю, т е. поток, входящий в узел, равен выходящему из него потоку
Рис. 5.32. Модель максимизации потока
Как следует из найденного оптимального решения, максимальный поток составляет
8000 автомобилей в час Отобразив найденное с помощью Excel решение в исходную се-
тевую диаграмму, получим схему движения, показанную на рис. 5.33
360 ЧАСТЬ II. Оптимизационные модели
Рис. 5.33. Схема движения с максимальным потоком
Как это часто случается в сетевых моделях, в данной модели есть альтернативные оп-
тимальные решения, показанные на рис. 5.34.
Рис. 5.34. Альтернативное оптимальное решение сетевой задачи
5.15.	Заключение
Данная глава посвящена приложениям линейного программирования. В разделе 5.2
рассматривалась транспортная модель. Такая модель позволяет определить, как с наи-
меньшими затратами удовлетворить спрос в ряде пунктов назначения, поставляя мате-
риалы, имеющиеся в наличии в нескольких исходных пунктах. Мы рассмотрели данную
модель на примере конкретной ситуации, с которой столкнулась компания AutoPower
Europe. Кроме того, обсудили изменения, необходимые для создания транспортной мо-
дели в тех случаях, когда модель отличается от исходной Затем, используя транспортную
ГЛАВА 5 Линейная оптимизация Применение 361
модель в качестве примера, показали, как можно решить задачу с несколькими целями
при наличии альтернативных оптимумов Наконец, было показано, что транспортная
модель обладает особым свойством: если все значения предложения и спроса являются
целыми величинами, то существует целочисленное оптимальное решение
В разделе 5 3 рассматривалась модель назначений как частный случай транспортной
модели. В общем случае в модели назначений требуется распределить п человек по п за-
дачам так, чтобы минимизировать общие расходы назначений Эту модель мы также рас-
смотрели на примере конкретной проблемы компании AutoPower Europe Отмечалось,
что модель назначений является частным случаем транспортной модели, в которой все
значения спроса и предложения равны 1.
В разделе 5 4 была построена модель ЛП для выбора средств массовой информации
при проведении рекламной компании Важным свойством этой модели было требование
к смешиванию решений, а также учет снижения отдачи от рекламных объявлений
Начиная с раздела 5 5 подробно рассматривались динамические модели Было пока-
зано различие между статическими (рассматривающими один временной период) и ди-
намическими моделями Было отмечено, что динамическая модель для заданного перио-
да планирования всегда дает решение не хуже, а во многих случаях — значительно лучше,
чем набор статических моделей для того же периода планирования Чтобы создавать точ-
ные динамические модели, необходимо уделять особое внимание определению перемен-
ных внутри временного периода, синхронизации видов деятельности и балансам потоков
при переходе от одного периода к другому Также необходимо определить граничные ус-
ловия для начального и конечного временных периодов Динамическая модель произ-
водственного планирования и управления запасами рассматривалась в разделе 5 6 Были
предложены три эквивалентные версии модели, из которых каждая последующая была
более подробной и, соответственно, содержала больше полезной информации В разде-
ле 5.7 представлена динамическая производственная модель, включающая в себя состав-
ление графика работы персонала. В разделе 5.8 рассматривалась динамическая модель
управления запасами и финансами. В разделе 5.9 показана интегрированная модель фи-
нансового и производственного планирования, иллюстрирующая взаимосвязи между
производством, финансированием и задержками платежей от клиентов.
В разделах 5 10-5.14 были рассмотрены четыре примера сетевых моделей Это широ-
кий класс моделей, которые применяются для моделирования управленческих ситуаций.
Как было показано, при наложении на данные достаточно мягких ограничений у таких
задач всегда существуют целочисленные оптимальные решения.
Основные термины
Ветвь. Другое название дуги
Динамическая модель управления запасами. Динамическая модель принятия решений об объеме за-
пасов в течение нескольких временных периодов
Динамическая модель. Модель, связывающая принятие решений в течение нескольких временнь/х
периодов, когда принятые в более ранние периоды времени решения оказывают влияние на
последующие допустимые решения
Дута. Соединение между двумя узлами сети.
Единица воздействия. Субъективная мера полезности рекламного объявления, используемая при
выборе средств массовой информации
362 ЧАСТЬ II Оптимизационные модели
Задача максимизации потока. Задача маршрутизации, позволяющая направить через сеть макси-
мальный поток
Задача нахождения кратчайшего пути. Задача нахождения кратчайших маршрутов от указанного уз-
ла (источника) до каждого из остальных узлов сети
Источник. Узел сети с положительным значением предложения
Место назначения. Узел сети с положительным значением спроса
Модель назначений. Модель определения оптимального распределения п неделимых агентов или
объектов по п заданиям
Модель перевозки грузов с учетом пропускных способностей. Сетевая модель, в которой одни пунк-
ты выступают источниками предложения, другие являются пунктами спроса, и существуют
альтернативные маршруты поставок, проходящие через промежуточные узлы от исходных
пунктов к пунктам назначения
Сетевая диаграмма. Схема, состоящая из узлов и дуг, по которым могут перемещаться потоки
Сетевая модель. Данный термин обычно применяется по отношению к модели перевозки грузов
с учетом пропускных способностей или одной из ее разновидностей
Статическая модель. Модель, в которой решения принимаются на один временной период незави-
симо от того, как это повлияет на будущие периоды
Транспортная модель. Модель линейного программирования для нахождения наиболее дешевого
способа удовлетворения спроса в п пунктах назначения посредством поставок из п исходных
пунктов
Узел. Элемент сети
Уравнение баланса потоков. В сетевой модели ограничение в виде уравнения баланса, которое пре-
дусматривает, что сумма предложения и входящего в узел суммарного потока должна быть
равна сумме спроса и потока, выходящего изданного узла
Фиктивный исходный пункт. Воображаемый источник поставок, который вводится в транспортную
модель, чтобы сделать суммарное предложение равным суммарному спросу
Контрольные вопросы
Да/нет
1.	Коэффициент при переменной xv в целевой функции транспортной модели — это
стоимость пересылки единицы товара из / ву.
2.	Если в транспортной модели суммарное предложение превышает суммарный
спрос, одним из способов нахождения решения является добавление фиктивного
пункта назначения, стоимость транспортировки в который из любого исходного
пункта равна нулю
3.	Транспортная модель не может иметь целочисленного оптимального решения, ес-
ли не будет выполнено условие о том, что все значения спроса, предложения и за-
трат на транспортировку — целые числа
4.	В модели перевозки грузов с учетом пропускных способностей с каждым узлом
связана одна переменная
5.	Транспортная модель — частный случай модели перевозки грузов с учетом пропу-
скных способностей.
6.	Если правая часть какого-либо неравенства, задающего пропускную способность
дуги в модели перевозки грузов, равна нулю, задача не имеет допустимых решений.
ГЛАВА 5. Линейная оптимизация. Применение 363
7.	Набор статических моделей для всех периодов планирования всегда дает результат
не хуже, чем единая динамическая модель, определенная для всего периода плани-
рования в целом
Выберите правильный ответ
8.	Транспортную модель можно использовать только в том случае, когда-
а спрос превышает предложение;
b предложение превышает спрос;
с. спрос и предложение равны,
d во всех вышеперечисленных случаях
9.	Модель назначений
а это частный случай транспортной модели,
Ь. может быть решена с помощью средства Поиск решения,
с всегда имеет целочисленное оптимальное решение,
d. обладает всеми вышеперечисленными свойствами.
10.	Положительная правая часть уравнения баланса потоков для любого узла модели
перевозки грузов означает, что.
а данный узел является источником,
Ь. данный узел является пунктом назначения,
с данный узел является промежуточным пунктом,
d. ничего из вышеперечисленного
11.	Выполнение каких из следующих условий гарантирует, что существует целочис-
ленное оптимальное решение задачи перевозки грузов9
а Правые части всех уравнений баланса потоков должны быть целыми числами
b Целыми должны быть значения пропускных способностей дуг
с Илия, или b
d. Ия, nb
12.	Кратчайший путь
а должен проходить через каждый узел,
b это множество всех дуг, составляющих кратчайший маршрут от начального уз-
ла до данного узла назначения,
с. и то, и другое
Вопросы с 13 по 17 относятся к следующей модели. Компания имеет два завода и
три товарных склада Первый завод может поставлять не более 500 фунтов некой
продукции, а второй завод — не более 200 фунтов Спрос на первом товарном
складе составляет 150, на втором — 200, а на третьем — 350 фунтов Затраты на
производство одного фунта продукции на заводе / и его доставку на складу приве-
дены в следующей таблице.
364 ЧАСТЬ II Оптимизационные модели
С завода	На склад	
	1	2	3
1	1	3	10,2	12,6
2	1	9	11,8
Модель должна определить схему перевозок, которая удовлетворит спрос с мини-
мальными затратами
13.	Данную модель можно отнести к классу:
а сетевых моделей,
b транспортных моделей,
с динамических моделей;
d ко всем вышеперечисленным классам;
е а и b
14.	Пусть х.. обозначает количество продукции, отправленное с завода / на товарный
склад j Правильно составленное ограничение для спроса на первом товарном
складе выглядит следующим образом.
а. х„+х2|= 150,
b х„+х21>150,
с обе записи правильны.
15.	Пусть xtj обозначает количество продукции, отправленное с завода /' на товарный
складj Тогда ограничения предложения можно записать следующим образом:
a ±xv<Sj, J = },2,
b.	±xij=Sj, J = ,2;
c.	£x,<57, /' = 1,2;
d.	все выражения неправильны;
e а и b.
16.	Средство Поиск решения всегда найдет целочисленное решение данной модели.
а Да.
Ь. Нет.
17.	Поскольку суммарное предложение равно суммарному спросу, все ограничения
для предложения и спроса можно записать в виде равенств.
а.	Да.
Ь.	Нет.
ГЛАВА 5. Линейная оптимизация. Применение	365
Ответы
1. Да. 2. Да. 3. Нет. 4. Нет. 5. Да. 6. Нет. 7. Нет 8. d. 9. d. 10 а. 11. d. 12 с 13. е. 14. с.
15 d. 16. а. 17. Ь.
Учебные задачи
5 1 Даны следующие линейные ограничения для модели перевозки грузов Начертите соответ-
ствующую сетевую диаграмму, поставив рядом с каждым узлом число, обозначающее пред-
ложение или спрос в данном узле
+ х12 + х,4 = 2,
-	х,2 + х24 = 1,
-	х„ + х25 = 0,
-	х24 - х]4 + х^ + x4S = 0,
-	x;; + xi6-x4, = 0,
х(/> 0 для всех i,j
5 2 Даны следующие ограничения
х12 + х|2 = 2,
-х,2 + х24 + х2! = О,
-х12 + х34 = О,
Постройте соответствующую сетевую диаграмму
5 3 Напишите линейные ограничения, соответствующие сетевой диаграмме на рис 5 35
5 4 Напишите линейные ограничения, соответствующие сетевой диаграмме на рис 5 36
Рис. 5.36
5 5 На рис 5 37 изображена сеть Найдите кратчайший путь из узла 1 в узел 7
5 6 На сколько необходимо уменьшить “цену” дуги от узла 1 до узла 3 на рис 5 37, чтобы эта
дуга стала частью кратчайшего пути из узла 1 в узел 79
5 7 Дана сеть, изображенная на рис 5 38 Найдите для этой сети кратчайший путь из узла 1 в узел 8
5 8 На сколько необходимо уменьшить “цену” дуги от узла 4 до узла 7 на рис 5 38, чтобы эта
дуга стала частью кратчайшего пути из узла 1 в узел 89
5 9 Дана сеть, показанная на рис 5 39 Узлы 1 и 5 — это заводы, которые производят 200 и 150
грузовиков товара соответственно Узлы 3, 6 и 9 — это торговые точки, спрос в которых со-
ГЛАВА 5 Линейная оптимизация Применение 367
ставляет 50, 250 и 50 грузовиков товара соответственно Число рядом с дугой (ij) показы-
вает затраты на транспортировку одного грузовика товара из узла / в j Предположим, что
затраты на транспортировку из / bj такие же, как и изу в /
а Определите наименьшую стоимость транспортировки одного грузовика продукции из
узла 1 в узлы 3, 6 и 9
b Определите наименьшую стоимость транспортировки одного грузовика продукции из
узла 5 в узлы 3, 6 и 9
с Сформулируйте и решите задачу перевозки грузов Чему равны минимальные суммар-
ные затраты9
Рис. 5.39
5 10 Определите максимальный поток из узла 1 в узел 6 для сети автомагистралей, показанной
на рис 5 40
Рис. 5.40
5 11 Дана сеть, показанная на рис 5 41 Найдите максимальный поток, предполагая, что 1 явля-
ется источником, а 7 — стоком
368 Ч А С Т Ь II. Оптимизационные модели
Рис. 5.41
5 12 Покажите, что транспортная модель с 5 источниками и D пунктами назначения является
частным случаем модели перевозки грузов с учетом пропускных способностей
5 13 Покажите, что модель назначений является частным случаем модели перевозки грузов
с учетом пропускных способностей
5 14 Покажите, что задачу нахождения маршрута с минимальными затратами можно предста-
вить как частный случай модели перевозки грузов с учетом пропускных способностей
Прикладные задачи
5 15 Распределение сырья Линдсей Дойл отвечает за транспортировку сырой нефти к несколь-
ким хранилищам Фрагмент трубопроводной сети показан на рис 5 42 Чему равен макси-
мальный поток из узла 1 в узел 79
Рис. 5.42
5 16	Мистер Кримедж руководит фитнес-центром в Чикаго, арендуя оборудование и помеще-
ние Недавно его арендодатель предложил долгосрочный договор лизинга Исходя из дол-
госрочного плана лизинга, Кримедж построил следующую таблицу, в которой отражены
ожидаемые суммарные затраты при аренде с начала года / до начала годаj (в тыс долл )
ГЛАВА 5 Линейная оптимизация. Применение 369
	/	2	3	4	5 1	13	25	37	45 2	12	21	30 3	10	20 4	9 Кримедж хочет выяснить, когда и на какой срок арендовать оборудование, чтобы миними- зировать расходы на протяжении последующих четырех лет Сформулируйте задачу и най- дите ее решение Существуют ли альтернативные оптимальные решения9
5 17	Компания Moebius Products столкнулась со следующей ситуацией В течение последующих четырех месяцев она должна ежемесячно поставлять 1000 бутылок вина Klein Удельные за- траты на производство одной бутылки составляют в первом месяце $5, во втором — $9, в третьем — S10 и в четвертом — $14. Стоимость хранения составляет S3 за одну бутылку в месяц Менеджер компании хочет определить наиболее эффективный план производства (т е когда и сколько бутылок следует производить), минимизирующий суммарные затраты Предположим, что производство осуществляется партиями по 1000 бутылок Представьте данную ситуацию в виде сетевой модели и решите эту задачу
5 18	У компании Slick Oil есть три склада, с которых она отгружает продукцию в три торговые точки Спрос на продукцию Gunkout составляет 100 банок в торговой точке 1, 250 банок — в точке 2 и 150 банок — в торговой точке 3 Запас данной продукции на складе 1 составляет 50 банок, на складе 2 — 275, а на складе 3—175 Стоимость транспортировки одной банки продукции со складов в торговые точки приводится в следующей таблице Торговые точки Склад	1	2	3 2	8	9	10 3	4	3	11 Постройте модель ЛП, позволяющую определить, сколько продукции необходимо отпра- вить с каждого склада в каждую торговую точку, чтобы удовлетворить существующий спрос с минимальными затратами
5 19	Боб Фрейп занимается упаковкой праздничных наборов экзотических фруктов Наборы упаковываются в двух пунктах, откуда затем рассылаются по пяти точкам оптовой торгов- ли Затраты на упаковку в пунктах 1 и 2 составляют $5,25 и $5,70 соответственно Прогно- зируемые значения спроса в точках оптовой торговли представлены в следующей таблице Точка оптовой торговли	1	2	3	4	5 Требуемый объем поставок	4000	6000	2000	10 000	8000 В пункте 1 производственная мощность по упаковке составляет 20000 наборов, а в пункте 2 — 12000 Стоимость доставки (в долл ) одного набора из пунктов упаковки в торговые точки приводится в следующей таблице Создайте модель ЛП, с помощью которой можно определить, сколько наборов следует отправить из каждого пункта упаковки в каждую торговую точку
370	Ч А С Т Ь II. Оптимизационные модели
	Точка оптовой торговли Пункт упаковки	1	2	3	4	5 1	0,60	0,40	1,20	0,90	0,50 2	1,50	0,90	0,50	0,80	0,80
5 20	Компании по изготовлению бижутерии Wonka Widget необходимо разработать модель управления запасами на три временных периода Удельные производственные затраты на изготовление бижутерии меняются от периода к периоду и составляют в расчете на едини- цу продукции $2, $4 и $5 для периодов 1, 2 и 3 соответственно Расходы на хранение каж- дой единицы продукции на складе при переходе от одного временного периода к следую- щему составляют $1 Спрос на бижутерию в периоды 1, 2 и 3 составляет соответственно 10 000, 20 000 и 30 000 штук Начальный и конечный запас равен нулю Постройте модель ЛП для определения количества продукции, производимой в течение каждого периода, так, чтобы удовлетворить спрос с наименьшими затратами
5 21	Джек Бьенсок отвечает за закупку консервированных продуктов для столовой крупного университета Ему известно, каким будет спрос в течение учебного года, он также прибли- зительно знает закупочные цены Эти данные для учебного года, начинающегося в сентяб- ре (9-й месяц), приводятся в следующей таблице Номер месяца 9	10	11	12	1	2	3	4	5 Спрос, ящики	1000	900	850	500	600	1000	1000	1000	500 Цена за ящик, $	20	20	20	21	21	21	22	22	22 Он может закупить требуемое количество впрок, чтобы избежать повышения цен, однако за хранение на складе запаса, оставшегося на конец месяца, необходимо платить 50,20 за ящик в месяц Начальный и конечный запасы равны нулю Сформулируйте и решите зада- чу ЛП минимизации затрат, которая поможет Джеку составить график закупок Совет Обозначьте через Р, количество ящиков, закупленных в месяце г, а через I, — число ящиков на складе в конце месяца t
5 22	Производитель столкнулся с проблемой управления запасами в течение трех временных периодов Цена продажи единицы товара постоянна и составляет 54 Удельные производ- ственные затраты в первый период составляют $4, а во второй и третий — $3 Спрос и стоимость хранения такие же, как и в задаче 5 20 Производитель не обязан полностью удовлетворять спрос Однако каждая единица неудовлетворенного спроса обходится ему в $1,50 Производственная мощность в первый период составляет не более 40 000 единиц, а в остальные два периода — не более 10 000 единиц продукции Начальный и конечный запасы равны нулю Постройте модель ЛП, которая позволит составить производственный план, дающий максимальную прибыль
5 23	Три завода компании Johnson Electric производят небольшие электрические моторы для четырех производителей бытовых приборов Удельные производственные затраты на заво- дах отличаются из-за различий в оборудовании и производительности труда Заказы клиен- тов на следующий месяц показаны в следующей таблице Клиент	Спрос 1	300 2	500 3	400 	4	600	
ГЛАВА 5. Линейная оптимизация Применение 371
Удельные производственные затраты и ежемесячные производственные мощности показа-
ны в следующей таблице
Завод	Удельные производственные	затраты, S	Ежемесячная производительность
А	17		800
В	20		600
с	24		700
Затраты на доставку продукции клиентам также различны Удельные затраты на транспор-
тировку в долларах приводятся в следующей таблице
Клиенту		
С завода	1	2	3	4
В	6	2	5 4	8 1	5	7 3 4
Руководство компании должно решить, сколько единиц продукции выпустить на каждом
заводе, и сколько отправить каждому клиенту с каждого завода При этом надо минимизи-
ровать суммарные производственные и транспортные расходы Сформулируйте данную за-
дачу в виде транспортной модели и найдите оптимальное решение
5 24 Модель планирования персонала Компания AutoPower приобрела новый завод по производ-
ству генераторов Вы должны ответить на следующий вопрос сколько новых сотрудников
нужно набрать и обучить в течение следующих шести месяцев9 Потребность в рабочем
времени обученных рабочих и ежемесячные тарифные ставки на следующие шесть месяцев
приводятся в таблице
	Месяц					
	Январь	Февраль	Март	Апрель	Май	Июнь
Необходимый ресурс рабочего времени, ч	7800	7500	7500	9200	10000	9000
Тарифная ставка, $	3600	3600	3900	3900	4200	4200
Стажеры набираются в начале каждого месяца Необходимо учитывать, что рабочие должны в
течение месяца проходить курс обучения, прежде чем они смогут работать на производстве
Следовательно, стажера нужно принять по крайней мере на месяц раньше, чем возникнет ре-
альная потребность в дополнительном рабочем На обучение каждого стажера тратится 80 ч
времени опытного производственного рабочего, следовательно, данный рабочий сможет уде-
лить собственно работе на производстве на 80 ч меньше Согласно контракту каждый обучен-
ный рабочий может работать до 195 часов в месяц (это суммарное время, в которое входит ра-
бота на производстве и обучение стажеров) Если ресурс рабочего времени обученных рабочих
превышает месячную потребность, руководство может в начале месяца временно уволить не
более 15% обученных рабочих Все рабочие получают полную месячную зарплату, даже если
они временно уволены Затраты на стажера составляют $1800 в месяц (зарплата и другие рас-
ходы) На начало января имеется 40 обученных рабочих Сформулируйте задачу найма и обу-
чения в виде модели линейного программирования
5 25 Руководство рекламного агентства должно решить, кто из четырех делопроизводителей бу-
дет работать со счетами каждого из четырех основных клиентов Затраты при каждом на-
значении для каждого делопроизводителя представлены в таблице Сформулируйте задачу
и найдите оптимальное решение
372	ЧАСТЬ II Оптимизационные модели
	Счет Делопроизводитель	1234
5 26	А	15	19	20	18 В	14	15	17	14 С	11	15	15	14 D	21	24	26	24 Финансовое планирование В начале каждого из четырех последовательных лет инвестор имеет возможность вложить средства в один из двух проектов, обозначенных Альфа и Бета Каждый доллар, вложенный в начале года в проект Альфа, дает доход через два года (как раз вовремя для немедленного реинвестирования) Доллар, вложенный в проект Бета, дает доход через три года В начале второго года появится третья инвестиционная возмож- ность— строительный проект Вложенный в строительство доллар дает доход уже через год (Эта возможность сохраняется также в начале третьего и четвертого года ) Стартовый капитал инвестора в начале первого года составляет $50000, и он хочет получить макси- мально возможную сумму денег в конце четвертого года. Значения удельной прибыли на инвестированный капитал приводятся в таблице
5 27	Альфа	1,50 Бета	1,80 Строительство	1,20 а Определите переменные решения и постройте математическую модель ЛП Совет Обозначьте через М, сумму наличных средств на начало года t и максимизируйте М5 при соблюдении соответствующих ограничений b Создайте табличную модель в Excel и найдите оптимальное решение с Можно ли найти решение математической задачи ЛП непосредственно, не используя средство Поиск решения9 Компании AutoPower нужно назначить четырех представителей в четыре региона Каждый представитель в разных регионах способен добиться разного объема продаж Объемы про- даж (в тыс долл ) при различных вариантах назначений показаны в следующей таблице
5 28	Регион Представитель	12	3	4 А	65	73	55	58 В	90	67	87	75 С	106	86	96	89 D	84	69	79	77 Компания хочет максимизировать суммарный объем продаж Однако назначить продавца В в регион 1 и продавца А в регион 2 нельзя, поскольку при этом будет нарушен принцип рота- ции персонала Постройте модель для данной ситуации и найдите оптимальное решение В распоряжении биржевого маклера находится элеватор емкостью 6000 бушелей для хра- нения кукурузы В начале первого месяца элеватор содержит 5000 бушелей кукурузы
ГЛАВА 5 Линейная оптимизация Применение 373
	Оценки закупочной цены и цены продажи кукурузы на следующие четыре месяца приво- дятся в таблице
5 29	Месяц	Закупочная цена за 1000 бушелей, S	Цена продажи за 1000 бушелей, S 1	45	40 2	50	45 3	60	56 4	70	65 Кукуруза, проданная в течение месяца, забирается из элеватора в начале следующего меся- ца Купленная в определенном месяце кукуруза помещается в элеватор, но она не может быть продана до начала следующего месяца Предполагается, что стоимость хранения ку- курузы исчисляется исходя из среднего объема запаса, хранение одного бушеля в течение одного месяца обходится в $0,01 За хранение нужно платить в конце месяца За все закуп- ки нужно платить наличными при доставке У маклера есть $100, которые можно инвести- ровать, и он не намерен брать кредит, чтобы закупать кукурузу или платить за ее хранение Следовательно, если у него не окажется наличных в начале месяца, он должен будет про- дать часть своего запаса, чтобы заплатить за хранение в конце месяца и купить при необхо- димости кукурузу Зная цены покупки и продажи, а также стоимость хранения, маклер хо- чет выяснить, сколько кукурузы следует покупать и продавать в каждом месяце, чтобы максимизировать суммарную прибыль в начале четвертого месяца Сформулируйте и най- дите решение задачи ЛП В распоряжении Сэма есть четыре ремонтных бокса в мастерской и три задания, которые нужно выполнить Поскольку в боксах находится различное оборудование, работают раз- ные люди, а выполняемые задания также имеют различные характеристики, время выпол- нения заданий различно Оценки времени, необходимого для выполнения каждого зада- ния в каждом боксе, приводятся в следующей таблице
5 30.	Задание Бокс	1	2	3 А	27	48	30 В	38	51	28 С	27	55	23 D	35	59	24 Сэм хочет минимизировать суммарное время, необходимое для выполнения заданий Сформулируйте задачу и найдите оптимальное решение. Существуют ли альтернативные оптимальные решения? Компания FemWood Lumber производит фанеру Затраты на производство 1000 кубических футов фанеры меняются от месяца к месяцу, поскольку меняется стоимость обработки, рас- ходы на оплату потребленной энергии и стоимость сырья. Удельные производственные затра- ты на 1000 кубических футов фанеры для последующих шести месяцев приводятся в таблице Мееяц	1	2	3	4	5	6 Производственные затраты, $	900	950	1250	1050	900	850 Спрос на ближайшие шесть месяцев показан в следующей таблице Месяц	1	2	3	4	5	6	Итого Спрос, тыс. куб футов	60	70	ПО	80	70	60	450
374
ЧАСТЬ II Оптимизационные модели
Компания может производить до 90 000 куб футов фанеры в месяц. Кроме того, у нее есть
возможность хранить запасы, при этом стоимость хранения при переходе запаса от одного
месяца к следующему составляет $25 за 1000 куб футов в месяц Кроме того, неудовлетво-
ренный в некотором месяце спрос можно удовлетворить позже, при этом пеня составляет
$40 за задержку 1000 куб футов на один месяц Начальный и конечный запасы равны ну-
лю Компания хочет определить объем производства в каждом месяце и величину запасов,
чтобы удовлетворить спрос с минимальными затратами Сформулируйте данную задачу
в виде транспортной модели и найдите оптимальное решение
[Ситуация для анализГ} Планирование производства
в компании Bumles
(Прежде чем приступить к решению данной задачи, полезно еще раз рассмотреть мо-
дель компании Bumles, описанную в разделе 5 7 ) Компания Bumles, 1пс использует часть
своих производственных мощностей для изготовления двух видов расписных статуэток.
Конечная продукция разделяется на две категории А и В Над росписью изделия А ху-
дожник работает 0,5 ч, а над В — 0,75 ч В компании работает 45 художников, но не обяза-
тельно все они задействованы. Завод занимается изготовлением расписных статуэток
в понедельник, вторник и среду каждую неделю В остальные дни недели производствен-
ные мощности заняты выпуском другой продукции Каждый художник, участвующий
в изготовлении статуэток, может работать любую часть восьмичасового дня два дня в не-
делю Художнику предлагается любой из двухдневных графиков работы, и он получает
оплату за 16 ч, независимо оттого, сколько времени в действительности был занят произ-
водством статуэток Если продукции недостаточно, чтобы все назначенные на данный
день рабочие были заняты полный рабочий день, оставшееся время они занимаются
уборкой территории и другой подобной работой Кроме того, компания может попросить
работающих в данный день художников отработать до 4 ч сверхурочно
Доход от продажи единицы продукции А составляет $21, а продукции В — $30
Спрос или удовлетворяется в день возникновения, или теряется. Произведенная
в определенный день продукция может использоваться для удовлетворения спроса
в этот день или последующие дни недели Однако все статуэтки, произведенные на
данной неделе, должны быть проданы на этой же неделе, т е утром в понедельник на
складе нет никаких запасов. При переходе запаса от одного дня к следующему стои-
мость хранения единицы продукции А составляет $0,25, а единицы продукции В —
$0,30 Потеря единицы спроса влечет за собой общие потери, которые для продук-
ции А составляют $2 в понедельник, $4 во вторник и $5 в среду, а для продукции В —
$5 в понедельник, $10 во вторник и $11 в среду. Художники получают $10 в час за ра-
боту в обычное время и $15 в час при сверхурочной работе
Спрос на продукцию компании может значительно изменяться. В качестве при-
зера в следующих таблицах представлены два характерных случая: наплыв покупа-
телей перед Рождеством и резкий спад спроса после Рождества
Увеличение спроса перед Рождеством
	Пн	Вт	Ср
Д	1500	1000	150
В	240	90	1100
ГЛАВА 5. Линейная оптимизация. Применение
375
Падение спроса после Рождества
Пн	Вт	Ср
А	240	48	64
В	160	32	64
Исполнительному директору компании Биллу Бамлесу известно, что удельная
прибыль при выпуске продукции А составляет 21/0,5 = $42 в расчете на час рабочего
времени, а продукции В — 30/0,75 = $40 Кроме того, потери от неудовлетворенного
спроса нарастают в течение недели Из этого он делает вывод, что компания сначала
должна полностью удовлетворить спрос на продукцию А в среду, во вторую оче-
редь — во вторник и в последнюю очередь — в понедельник, а после этого все остав-
шиеся возможности можно направить на производство продукции В
Вопросы
1 Прокомментируйте подход, предложенный Биллом Бамлесом
2 Игнорируя условия целочисленности (т е допуская возможность дробных зна-
чений всех переменных решения), создайте модель в Excel, позволяющую соста-
вить график работы художников и план производства таким образом, чтобы мак-
симизировать прибыль, где затраты вычисляются как стоимость оплаты труда
плюс неустойка за неудовлетворенный спрос плюс плата за хранение запасов
Модель должна быть верна для любых вариантов спроса В вашей формулировке
первые шесть ограничений должны отражать спрос на продукцию А в понедель-
ник, вторник и среду и спрос на продукцию В в эти же дни Тогда, чтобы решить
задачу для любых значений спроса, потребуется только подставить соответст-
вующие значения правых частей данных ограничений При формализации моде-
ли обратите особое внимание на связи между производством, продажами, поте-
рянными продажами, спросом и запасами в каждый день Например, спрос
в день t = продажи в день t + потерянные продажи в день Г
3. Как определить переменные решения?
4. Оптимизируйте модель для каждого из приведенных выше конкретных вариан-
тов спроса
После этого для обоих вариантов спроса составьте отчет для директора компа-
нии, в котором необходимо осветить следующие вопросы
5. Сколько единиц каждой продукции следует производитьв каждый изднеи
6 Как составить график работы занятых в производстве художников
7 Сколько часов сверхурочного труда следует использовать каждый день
8 Чему равны ежедневные запасы продукции каждого вида
9. Сколько единиц продажи теряется ежедневно
10. С помощью модели ответьте на следующий вопрос
11 Предположим, что 32 недели в году спрос ведет себя как во время предрождест-
венского бума, а 18 недель — как во время спада после Рождества. Компания хо-
чет, чтобы все 45 художников работали одинаковое число недель, сколько недель
в таком случае будет работать каждый художник* 1 2 * * * 6 7 8 9 * 11
376 ЧАСТЬ II Оптимизационные модели
Дополнительные условия
(При ответе на вопросы данного раздела следует использовать модель, созданную
в ответе на вопрос 2, вводя в нее новые параметры и выполняя дополнительный ана-
лиз там, где это необходимо )
Профсоюз художников предложил заключить договор об обеспечении гарантиро-
ванной годовой заработной платы. В частности, договор предусматривает, что ху-
дожник должен получать как минимум $11500 в год за работу по росписи статуэток.
Если в конце года выплаченная некоторому художнику сумма оказывается менее
$11500, фирма просто выдает ему чек на недостающую сумму Компания Bamles
планирует использовать всех 45 художников даже в том случае, если договор с проф-
союзом не будет принят, однако если он будет принят, всем 45 художникам будет
выплачиваться сумма не менее $11500 в год.
Чтобы оценить влияние данного предложения на работу компании Bamles,
Билл предполагает, что 30 недель в году из 50 спрос будет таким, как во время на-
плыва покупателей перед Рождеством, а остальные 20 недель — таким, как в сле-
дующей таблице
Пн Вт Ср
А	240	48	300
В 160 32 200
Кроме того, предполагается, что график работы можно составить так, что все ху-
дожники получат за год одинаковую заработную плату. Используя вашу модель ЛП и
предположения Билла, ответьте на следующие вопросы.
11 Какой будет суммарная годовая прибыль компании Bumles без принятия проф-
союзного договора?
12. Удовлетворяет ли полученное в ответе на вопрос 11 решение пункту договора об
обеспечении гарантированной годовой заработной платы? Какое влияние на
прибыльность компании Bumles окажет принятие договора (прибыльность уве-
личится, уменьшится или останется неизменной)? Приведите вычисления, под-
тверждающие ваш ответ,
13. Какой должна быть средняя недельная зарплата при низком спросе при годовой
заработной плате $11500? Постройте для недель с низким спросом модель ЛП,
которая поможет компании Bumles найти производственный план, позволяю-
щий обеспечить гарантированную заработную плату. Приведите обоснование
вашей модели и оптимизируйте ее.
14. Предположим, пункт о гарантированной годовой заработной плате принят.
Сколько средств сэкономит за год компания Bumles, используя план, найден-
ный в ответе на вопрос 13, вместо плана вопроса 11, при использовании кото-
рого художникам пришлось бы доплачивать в конце года?
ГЛАВА 5 Линейная оптимизация. Применение 377
Вопросы о чувствительности решений
(Ответы на эти вопросы строятся на основе отчетов по устойчивости для моделей,
созданных вами при ответе на вопросы 1-10.)
15	В полученном решении “предрождественской” версии модели при комбиниро-
вании основной и сверхурочной оплаты каждый художник получает $280 в не-
делю. Если появится дополнительный художник, какую максимальную недель-
ную зарплату сможет предложить ему компания?
16.	Предположим, что перед Рождеством спрос на продукцию А в понедельник
увеличится на 10 штук. Что произойдет со значением целевой функции9
17.	Ответьте на вопрос 16 для версии модели с низким спросом (как после Рождества)
18.	Чем обусловлено основное различие в ответах на вопросы 16 и 179
19.	Предположим, что, основываясь на предыдущем опыте, руководство считает
нужным изменить в предрождественской версии модели значение неустойки за
неудовлетворенный спрос на продукцию А в понедельник. Новое значение не-
устойки составит $3. Что произойдет с оптимальным решением и значением це-
левой функции9
20	Предположим, что новое значение неустойки в вопросе 19 составляет $4 Как
это отразится на оптимальном решении и значении целевой функции9
(Найдите наилучший возможный ответ, который можно получить на основании
информации, представленной в отчете по устойчивости.)
21	Предположим, что перед Рождеством цена единицы продукции А снизилась до
$15, а В — до $20 Можно ли указать новое значение целевой функции9
Ситуация для анализа | Ebel Mining (часть 3)’
Трумен Харди, главный управляющий добычей компании Ebel Mining, с восхище-
нием заметил. “Ваша идея о реклассификации руды более высокого качества и продаже
ее клиентам, согласным покупать руду более низкого качества, оказалась очень удач-
ной. Похоже, она позволит нам сэкономить определенные средства”. Далее он про-
должил “Мы уже рассматривали подобную идею, когда приобрели специальную ма-
шину для смешивания руд. Например, процентное содержание руды среднего качества
в поднимаемой породе оказывается ниже, чем содержание руды высокого качества
Фактически мы можем смешать низкокачественную и высококачественную руду в со-
отношении 0,6 к 0,4 (т.е. руды низкого качества в смеси должно быть в 1,5 раза больше,
чем руды высокого качества) и отгрузить эту смесь вместо руды среднего качества.
Смешивающее оборудование имеет производственную мощность 8 т руды в неделю,
что представляется достаточным. Однако мы решили не продавать смешанную руду,
поскольку смешивание приводит к дополнительным затратам $100 на тонну, чю, оче-
видно, повысит наши суммарные недельные расходы...”.
£>1998 By the Board of Trustees of the Leland Stanford Junior University All rights reserved
378 ЧАСТЬ II Оптимизационные модели
Вопросы
1	Измените диаграмму сетевых потоков (см. ситуацию для анализа компании Ebel
в конце главы 4), включив в нее возможность смешивать руду наряду с другими
действиями по реклассификации
2	Переформулируйте модель из главы 4, включив в нее новую переменную реше-
ния — количество руды среднего качества, полученной с помощью смешиваю-
щего оборудования, — и найдите оптимальное решение задачи, позволяющее
минимизировать суммарные недельные затраты. Убедитесь, что в ваших ограни-
чениях отражен материальный баланс по всем видам руды Увеличились ли сум-
марные недельные затраты, как утверждал Трумен Харди?
3	Объясните внесенные в модель изменения, полученные планы добычи, решения
по смешиванию и реклассификации, а также информацию, содержащуюся в те-
невых ценах в докладной записке на имя руководителей компании Ebel. Вклю-
чите в нее краткий комментарий рассуждений Харди о причинах отказа от воз-
можности продажи смешанных руд Опишите также, какое влияние этот новый
план окажет на реализацию любых излишков руды
| Ситуация для анализа | Ebel Mining (часть 4)’
Управляющий добычей компании Ebel Трумен Харди заявил- “При создании сво-
ей модели вы не учли реальное положение вещей. Во-первых, мы работаем согласно
месячному производственному плану, производя отгрузку в конце каждой недели
Во-вторых, нам обычно приходится создавать запас руды всех трех видов (высокого,
среднего и низкого качества), который переходит с одной недели на следующую
(общий объем запаса всей руды не превышает 75 т), поскольку каждый день работы
шахты — это 24 ч, а соглашение с профсоюзом предусматривает работу не более 5
дней в неделю. Если в какую-то неделю шахта будет работать менее пяти дней, нам
придется оповещать всех об этом заранее.
Учитывая данные факторы, необходимо составить план, в котором будут одновре-
менно отражены данные о производстве, запасах и отгрузке за весь месяц. Поэтому,
чтобы модель была реалистичной, необходимо преобразовать недельную модель,
включающую возможности реклассификации и смешивания руд, в 4-недельную мо-
дель для месяца Требования к отгрузке на следующий месяц (в тоннах) представлены
в таблице
Недельные объемы поставок руды, т
	Неделя 1	Неделя 2	Неделя 3	Неделя 4
Высокое качество	12	20	30	44
Среднее качество	8	22	38	35
Низкое качество	24	40	44	60
©1998 В'-; the Board of Trustees of the Leland Stanford Junior University AU rights reserved
ГЛАВА 5 Линейная оптимизация. Применение
379
Затраты на добычу также варьируются от недели к неделе из-за проведения работ
по обслуживанию и использования временных рабочих вместо рабочих, находящих-
ся в отпуске Эти затраты отражены в следующей таблице
Затраты на добычу, тыс. долл, в день
	Неделя 1	Неделя 2	Неделя 3	Неделя 4
Шахта 1	20	20,5	20,5	21
Шахта 2	16	16,4	16,4	16,4
Я считаю, что смешивающее оборудование по-прежнему сможет обрабатывать не
более восьми тонн руды в неделю, затраты при его использовании останутся на
прежнем уровне ($100 на тонну) и не будут меняться в течение месяца Реклассифи-
кация более качественной руды и отгрузка ее в счет поставок менее качественной не
будет связана для нас с дополнительными затратами, если мы захотим продолжать
эту абсурдную практику
Кстати, невозможно пройти ежемесячную проверку Агентства по охране окру-
жающей среды, если на территории хранится руда Следовательно, необходимо
спланировать все так, чтобы запас руды на конец месяца был равен нулю Вы творче-
ски подошли к решению моих проблем Однако теперь вы видите, что моя ситуация
слишком сложна, чтобы ее можно было описать с помощью вашей игрушечной таб-
личной модели Между прочим, мой аудитор хочет, чтобы при принятии решении
использовалась чистая приведенная стоимость, которая уменьшается на 1% в месяц
(= 0,25% в неделю), а это разрушает ваше упрощающее предположение о линейном
характере зависимостей модели Как видите, реальная ситуация в производстве руды
слишком сложна, мы должны с этим смириться и попытаться сделать лучшее из воз-
можного Рассмотрим требования по отгрузке Я считаю, что лучше создавать запасы
руды в первые недели ”
Вопросы
1	Прав ли Трумен, когда он утверждает, что переход к чистой приведенной стои-
мости нарушает предположение о линейности9 Аргументируйте свои ответ
2	Преобразуйте модель ЛП для ситуации Ebel Mining, часть 3, чтобы ее можно
было использовать в более реальной динамической ситуации, и составьте
производственный план Совет Перенесите четыре копии модели Ebel,
часть 3, на один рабочий лист, определите необходимые связи и добавьте но-
вые ограничения
3	В краткой докладной записке руководству компании Ebel объясните внесенные
в модель изменения, полученное расписание работы шахт, решения по реклас-
сификации, смешиванию и управлению запасами для каждой недели, а также
всю содержащуюся в теневых ценах информацию
380 ЧАСТЬ II Оптимизационные модели
Литература
1.	Jean-Yves Blais, Jacques Lamont and Jean-Marc Rousseau, The HASTUS Vehicle and Manpower
Scheduling System at the Societe de la Communaute urbaine de Montreal, Interfaces, 20, no. 1 (Jan.-
Feb , 1990)
2.	James Evans, A Microcomputer-Based Decision Support System Scheduling Umpires in the American
Baseball League, Interfaces, 18, no 6 (Nov-Dec., 1988)
3.	David Carlisle, Kenneth Nickerson, Stephen Porbst, Denise Rudolph, Yosef Sheffi, and Warren Pow-
ell, A Turnkey Microcomputer-Based Logistics Planning System, Interfaces, 17, no 4 (July-Aug , 1987)
4.	Tsuyoshi Yoshmo, Tsuna Sasaki, and Toshiharu Hasegawa, The Traffic-Control System on the Hanshin
Expressway, Interfaces, 25, no 1 (1995) p. 94-108
Глава
Целочисленная оптимизация
В этой главе...
6.1.	Введение
6.2.	Типы целочисленных оптимизационных моделей
6.3.	Графическое представление целочисленных моделей
6.4.	Применение двоичных переменных
6.5.	Моделирование фиксированных затрат
6.6.	Метод ветвей и границ
6.7.	Реализация моделей целочисленной оптимизации
6.8.	Заключение
Основные термины
Контрольные вопросы
Задачи
Ситуация 1 Назначение торговых представителей
Ситуация 2 Финансовое планирование
Ситуация 3 Ebel Mining (часть 5)
Литература
382 ЧАСТЬ II Оптимизационные модели
Практическое применение
Использование целочисленной оптимизации
в авиакомпании American Airlines
В компании American Airlines (АА), одной из крупнейших авиакомпаний США,
владеющей более чем 510 самолетами, работает свыше 8 300 пилотов и 16 200 стюар-
десс Суммарные затраты на содержание экипажей, включающие заработную плату,
премии и льготы, превышают 1,3 млрд долл в год и уступают только затратам на то-
пливо Однако, в отличие от затрат на топливо, значительной частью расходов на со-
держание экипажей можно управлять Поэтому приоритетной задачей департамента
летного состава компании АА является разработка планов, которые позволят дос-
тичь высоких уровней загрузки экипажей В значительной мере этому способствует
применение целочисленного программирования.
Компания АА составляет расписание полетов один раз в месяц. Каждому рейсу
должен быть назначен экипаж (пилоты и стюардессы) Экипажи приписаны к 12 раз-
личным пунктам, называемым базами приписки экипажей, таким образом, экипаж
должен обслуживать серию полетов, которая начинается и заканчивается в одном и том
же пункте приписки Эта последовательность полетов называется состыкованными рей-
сами, ее продолжительность, как правило, составляет 3 дня Ежемесячно экипаж вы-
полняет от четырех до пяти состыкованных рейсов
Составление графика состыкованных рейсов осложняется наличием правил регу-
лирования работы, составленных профсоюзами и Федеральной авиационной адми-
нистрацией Правила варьируются в зависимости от статуса члена экипажа (пилот
или стюардесса), размера экипажа, типа самолета и рейса (внутренний или междуна-
родный) Правила работы оговаривают длительность периодов дежурства и отдыха
Обязательное правило, установленное профсоюзом, предусматривает, что макси-
мальная длительность дежурства экипажа в течение дня составляет от 14 до 16 ч.
Требования Федеральной администрации направлены на уменьшение утомляемости
экипажей и повышение уровня безопасности пассажиров
Оценка затрат на состыкованные рейсы включает сложную формулу начисления
заработной платы, в которую входят гарантированные часы оплаты и реальное время
полета, а также более простые элементы, такие как оплата гостиницы и перемеще-
ний наземным транспортом Цель модели состоит в том, чтобы обеспечить экипа-
жами все рейсы предстоящего месяца, минимизировав суммарные затраты Данная
модель может также помочь принять решение о том, чтобы закрыть какой-либо су-
ществующий пункт приписки экипажей или открыть новый
Оптимизация стыковок рейсов чрезвычайно сложная комбинаторная задача Ее ис-
следования активно велись с начала 1950-х, поскольку даже незначительные улучше-
ния решения позволяли экономить крупные суммы. Фактически увеличение загрузки
экипажей АА на 1% дает возможность экономить $13 млн ежегодно По оценкам ком-
пании АА, ежегодная экономия средств при использовании данной модели превышает
$20 млн Успех модели был настолько очевидным, что она была продана 11 другим
крупным авиакомпаниям и одной железнодорожной компании. [1]
ГЛАВА 6. Целочисленная оптимизация 383
6.1.	Введение
В данной главе рассматриваются модели, которые строятся и оптимизируются как
обычные модели линейного программирования за исключением того усложняющего об-
стоятельства, что некоторые или все переменные модели должны принимать целые зна-
чения. Такие модели называются моделями целочисленного линейного программирования
(ЦЛП)'. Как и сетевые модели (см. главу 5), модели целочисленного линейного програм-
мирования стали важной отдельной областью оптимизационного моделирования В дан-
ном разделе мы затронем только лежащие на поверхности проблемы’ покажем важность
данной темы и приведем несколько поучительных примеров моделей ЦЛП
Как известно из предыдущих глав, в моделях линейного программирования перемен-
ные могут принимать дробные значения, и в соответствии с принципом “все, что может
произойти, произойдет” необходимо быть готовым к появлению нецелочисленных отве-
тов2. Тем не менее в реальной жизни переменные решения часто должны быть целыми
числами Например, если фирма производит корма в мешках для коров, то решение, при
котором требуется произвести и продать 3000,472 мешка, не имеет смысла В таких си-
туациях нецелочисленное решение делается целым зачастую путем простого округления
результатов до ближайших целых значений Этот метод приводит к получению так назы-
ваемого округленного решения Использование таких решений допустимо в тех ситуациях,
где округление, по сути, не имеет особого значения Так, для значений целевой функции
прибыли и ограничений практически все равно, производится 19 283,64 или 19 283 меш-
ка корма для коров На самом деле при сборе данных для модели, вероятно, использова-
лось достаточно приближений и допущений, чтобы руководство согласилось с любыми
цифрами производства на уровне порядка 19 200 мешков. В общем случае, чем больше
масштаб переменных решения, т е чем больше найденные при решении задачи ЛП зна-
чения переменных решения, тем выше вероятность, что округленный целочисленный
ответ окажется допустимым на практике
Когда целочисленность решений играет основную роль
Существует ряд моделей, где этот достаточно простой способ удовлетворения требований
целочисленности не срабатывает Это может быть обусловлено небольшим масштабом рас-
сматриваемых переменных решения. Например, если решение задачи ЛП предлагает ком-
пании Боинг произвести в будущем квартале 3,6 самолетов типа Boeing 747 и 4,8 типа Boe-
ing 777, руководство, вероятно, не согласится с тем, чтобы округлить эти значения и при-
нять решение построить четыре самолета Boeing 747 и пять Boeing 777 или просто
остановиться на любой другой округленной комбинации С одной стороны, в данном слу-
чае округление может привести к недопустимому решению, поскольку будут нарушены ог-
раничения по ресурсам Однако даже если округленное решение будет допустимым, целе-
сообразно определить наилучшее возможное целочисленное решение, поскольку с каждым
произведенным самолетом связаны большие объемы материальных и трудовых ресурсов
Модели целочисленного программирования не обязательно являются линейными, многие общие положения, ко-
торые мы будем обсуждать в данной главе, применимы как к линейным, так и к нелинейным целочисленным мо-
делям Однако поскольку в данном разделе речь идет только о линейных моделях, мы будем повсюду использовать
аббревиатуру ЦЛП, чтобы не вводить дополнительные термины и снизить риск возникновения недоразумений
Исключение из этого правила составляют описанные в главе 5 сетевые модели При оптимизации сетевых
моделей (в том числе транспортных моделей и моделей назначений) с целыми коэффициентами всегда полу-
чаются целочисленные решения
384 ЧАСТЬ II Оптимизационные модели
Примерами другого рода являются модели, в которых целочисленные переменные
используются в качестве индикаторов логических решений. Например, рассмотрим мо-
дель, в которой переменная Xравна 1, если следует построить склад в Канзас-Сити, и 0 —
в противном случае. Предположим, что в результате решения некой задачи ЛП для дан-
ной ситуации получается нецелое значение X (скажем, %=0,38). Очевидно, что такое
значение не дает никакой полезной информации о решении реальной задачи, поскольку
невозможно построить 0,38 склада. Можно построить склады различных размеров, но
все равно необходимо решить, будет склад в Канзас-Сити или нет Может показаться,
что в подобных случаях округление до ближайшего целого (в данном случае это 0) позво-
лит решить проблему К сожалению, такой подход не гарантирует получения хорошего
решения (не говоря об оптимальном). Как будет показано далее, округление в подобных
случаях не всегда ведет даже к получению допустимого решения.
Существует очень много управленческих моделей, которые можно считать линейны-
ми за исключением требования целочисленности переменных решения, и в которых не-
возможно найти хорошее решение, используя обычные методы линейной оптимизации,
заложенные в средстве Поиск решения, а затем округляя оптимальные значения пере-
менных решения Эти модели необходимо создавать с помощью методов, специально
разработанных для решения крупных задач целочисленного программирования.
Важность моделей целочисленного линейного программирования была осознана дав-
но, и много времени и усилий было потрачено на исследования и разработку методов их
оптимизации Эти усилия принесли свои плоды, и в данной области достигнут значи-
тельный прогресс Огромные успехи в развитии компьютерных технологий позволили
создавать большие модели целочисленного линейного программирования, что было не-
возможно еще десять лет назад.
Сравнение моделей АП и ЦАП
Несмотря на то что в настоящее время существует набор методов оптимизации моде-
лей целочисленного программирования, арсенал этих средств все еще заметно отличает-
ся от того, которым пользуются при решении задач, в которых переменные решения не
обязаны быть целыми. Многие модели, которые легко оптимизировать в виде задачи ли-
нейного программирования, практически невозможно решить, если потребовать, чтобы
переменные решения принимали целые значения (время и затраты, необходимые для на-
хождения оптимального решения, могут быть слишком велики). Это кажется неестест-
венным, поскольку добавление ограничений целочисленности уменьшает количество
допустимых вариантов, которые необходимо проанализировать, а уменьшение множест-
ва допустимых вариантов должно облегчить поиск оптимального решения. Однако на
практике для оптимизации моделей целочисленного программирования требуется, как
правило, в десятки, а зачастую в сотни и тысячи раз больше времени, чем для оптимиза-
ции аналогичных моделей без ограничений целочисленности.
В следующих разделах показаны два класса моделей целочисленного линейного про-
граммирования и графически проиллюстрирована связь между задачами линейного про-
граммирования и целочисленного линейного программирования и процессом округления
решений задачи ЛП для получения возможного решения задачи ЦЛП Графический подход
позволит понять природу целочисленной модели и покажет, почему неверны интуитивные
предположения о том, что модели ЦЛП проще оптимизировать. Затем рассматривается
специальное подмножество моделей ЦЛП, в которых целочисленные переменные могут
принимать только значения 0 или 1. Использование этих “индикаторов”, или “логических”
переменных, позволяет сформулировать разнообразные логические условия, которые
ГЛАВА 6. Целочисленная оптимизация
385
сложно описать иначе Многие практические модели содержат подобные условия, и мы об-
судим несколько таких формулировок. После этого обратимся к практическому использо-
ванию моделей целочисленного линейного программирования.
6.2.	Типы целочисленных оптимизационных моделей
Общий термин целочисленное программирование применяется к созданию оптимизацион-
ных моделей с условиями целочисленности (условия, требующие, чтобы некоторые или все пе-
ременные решения принимали целые значения) Как уже отмечалось, модели целочисленного
линейного программирования (ЦЛП) — это модели линейного программирования, содержа-
щие дополнительное требование, чтобы некоторые или все переменные решения принимали
только целые значения Существует несколько классов моделей данной категории.
Модель полностью целочисленного линейного программирования, как следует из назва-
ния, это модель, в которой все переменные решения должны принимать только целые
значения. Например, модель
минимизировать 6х, + 5х2 + 4х3
при ограничениях
108х, + 92х2 + 58х3 > 576,
7х, + 18х2+ 22х3>83,
х,,х2,х3>0 и целые
является полностью целочисленной Без дополнительных условий, оговаривающих, что
хр х2 и х3 должны быть целыми числами (т е без условий целочисленности), данная мо-
дель является обычной моделью линейного программирования
Модель, в которой некоторые переменные должны принимать только целые значе-
ния, а остальные переменные могут быть любыми, называется моделью частично-
целочисленного линейного программирования Предположим, что в приведенной модели
требуется, чтобы целыми были только переменные х, и х2, а для х3 допустимы дробные
значения. Тогда эта модель будет примером модели частично-целочисленного Л П.
В некоторых моделях целочисленные переменные могут принимать только значения О
или 1. Их называют моделями двоичного целочисленного линейного программирования Эти
модели особенно важны, поскольку двоичные переменные можно использовать для
представления дихотомических решений (решений типа “да-нет”). Разнообразные моде-
ли назначений, размещения заводов, производственного планирования и управления
инвестиционными портфелями являются примерами моделей двоичного ЦЛП. Эти мо-
дели подробно обсуждаются в разделе 6.4.
Совет. Умелое применение двоичных переменных позволяет включать в оптимизационную
модель проверку различных логических условий, тем самым заменяя функцию ЕСЛИ в форму-
лах Excel, использовать которую в моделях линейного программирования нельзя.
Напомним, что если для задания целевой функции либо ограничений прямо или косвенно ис-
пользуется функция ЕСЛИ или другие нелинейные функции, такие как ABS, МАКС и МИН,
то встроенные в средство Поиск решения методы линейной оптимизации, скорее всего, не
смогут найти оптимум.
Часто также рассматриваются модели линейного программирования, которые полу-
чаются из исходных моделей ЦЛП в результате отказа от ограничений целочисленности.
Такие модели Л П называются упрощением модели ЦЛП.
386 ЧАСТЬ II. Оптимизационные модели
6.3.	Графическое представление целочисленных моделей
Как показано в главе 3, графическое представление задачи ЛП с двумя переменными
значительно облегчает понимание природы и решения задач ЛП в целом. Аналогичный
подход применим и для моделей ЦЛП.
Модель ЦАП с двумя переменными
Рассмотрим приведенную ниже модель ЦЛП, предназначенную для определения ас-
сортимента выпускаемой продукции с двумя переменными Е и F, равными количеству
двух выпускаемых и продаваемых с целью получения прибыли продуктов. Будем считать,
что ограничения вида < отражают ограничения на ресурсы, а ограничения вида > опреде-
ляют соглашения о минимальных объемах производства.
Максимизировать 18£ + 6F
при ограничениях
E—3F<0,	(1)
42,8£ + 100£< 800,	(2)
20£ + 6£<142,	(3)
30£ + 10£> 135,	(4)
£, £> 0 и целые.
Единственное существенное отличие этой модели от аналогичных моделей ЛП, рас-
смотренных в предыдущих главах, заключается в слове целые. Как мы скоро увидим,
влияние этого единственного слова огромно
Чтобы оптимизировать данную модель графически, необходимо выполнить следую-
щие действия
1	Найти допустимое множество для упрощения модели ЦЛП.
2	Выявить целые точки внутри множества, определенного в п. 1.
3	Найти среди выявленных в п. 2 точек такую, которая оптимизирует целевую функцию.
На рис. 6 1 показано окно программы GLP (описанной в главе 4), где выполнены пер-
вые два из приведенных выше пунктов, а также табличное представление в Excel упро-
щения данной модели ЦЛП и решение, найденное с помощью Поиск решения. Заштри-
хованная область в верхней части рисунка — это допустимое множество решений упро-
щенной задачи ЛП, а темные точки — это точки с целочисленными координатами,
находящиеся внутри допустимой области задачи ЛП (Целочисленные точки можно ото-
бразить, щелкнув на кнопке Toggle Integer Dot (Переключатель целых точек) панели ин-
струментов GLP ) Данное множество целых точек является множеством допустимых ре-
шений задачи ЦЛП. Таким образом, у данной модели ЦЛП всего 13 допустимых реше-
ний (3, 6), (4, 6), (3, 5), (4, 5), (5, 5), (4, 4), (5, 4), (4, 3), (5, 3), (6, 3), (4, 2), (5, 2) и (6, 2).
Чтобы оптимизировать данную модель, необходимо определить, какая из допустимых
точек доставляет наибольшее значение целевой функции. Поступим так же, как и с моде-
лью ЛП’ будем двигать прямую целевой функции в направлении подъема (поскольку это мо-
дель максимизации) до тех пор, пока она не пересечет целую точку допустимой области.
Результат данного процесса показан в верхней части рис. 6.2 (для этого достаточно
щелкнуть на кнопке Auto Мах (Автомаксимум) панели инструментов GLP), в нижней
части рисунка приводится формулировка и решение данной задачи ЦЛП с помощью
средства Поиск решения. Оптимальным решением задачи ЦЛП является точка £=6,
£=3 Целевая функция задана формулой 18£+6£, поэтому ее оптимальное значение
равно 18x6 + 6x3 = 126, что и показано на рис. 6 2.
ГЛАВА 6. Целочисленная оптимизация 387
Рис. 6.1. Оптимальное решение упрощения и допустимое множество модели ЦЛП
388 ЧАСТЬ II. Оптимизационные модели
Рис. 6.2. Оптимальное целочисленное решение ш>ичи Ц.1П
ГЛАВА 6. Целочисленная оптимизация 389
Совет. Условие целочисленности задается в средстве Поиск решения в качестве ограниче-
ния, для чего необходимо выбрать опцию целое в раскрывающемся списке Ограничение
диалогового окна Добавление ограничения. Кроме того, следует установить равным 0 па-
раметр Допустимое отклонение в диалоговом окне Параметры поиска решения.
В противном случае решение задачи ЦЛП, найденное средством Поиск решения, может
оказаться неоптимальным. Более подробно данный вопрос обсуждается в разделе 6 4.
Упрощение модели ЦЛП
На рис. 6.3 схематически показан процесс нахождения решения программой GLP.
Воспользуемся данным рисунком, чтобы показать некоторые свойства модели ЛП, яв-
ляющейся упрощением модели ЦЛП. Во-первых, отметим, что оптимальное упрощение,
как следует из рис. 6 1, находится на пересечении линий ограничений (2) 42,8£ + 100£
= 800 и (3) 20£ + 6£= 142. Здесь оптимальные значения переменных решения задачи ЛП
равны £ = 5,39 и £ = 5,69, соответствующее оптимальное значение целевой функции со-
ставляет 131,21 Поскольку пересечение этихдвух ограничений происходит не в целочис-
ленной точке, оптимальное упрощение не является допустимым решением задачи ЦЛП.
Ближайшее округленное решение (5, 6)
Допустимое округленное
целое решение (5, 5)
Оптимальное решение
задачи ЦЛП (6, 3)
Рис. 6.3. Графическое решение задачи ЦЛП
Сравнивая оптимальные значения целевой функции (126 для модели ЦЛП и 131,21
для упрощения), видим, что значения целевой функции в упрощенной задаче ЛП боль-
ше, чем в исходной задаче ЦЛП Это проявление общей закономерности, которая обсуж-
далась в главе 4’ можно считать, что модель ЦЛП получается в результате добавления ог-
390 ЧАСТЬ II. Оптимизационные модели
раничений целочисленности к модели ЛП, являющейся ее упрощением. Как известно,
в любой оптимизационной модели при добавлении ограничений оптимальное значение целевой
функции не может улучшиться, а может только ухудшиться или остаться неизменным.
Поэтому при добавлении условий целочисленности оптимальное значение модели ухуд-
шается. На основании этого наблюдения сформулируем следующий общий вывод.
г 1. В модели максимизации оптимальное значение целевой функции упрощенной мо- j
дели является верхней границей оптимального значения целевой функции исходной 
i модели ЦЛП. Добавление ограничений целочисленности ухудшает или оставляет
неизменным оптимальное значение целевой функции упрощенной модели Л П.
2. В модели минимизации оптимальное значение целевой функции упрощенной мо- j
дели является нижней границей оптимального значения целевой функции исходной 
модели ЦЛП. Добавление ограничений целочисленности ухудшает или оставляет [
неизменным оптимальное значение целевой функции упрощенной модели ЛП.	<
Округление решения
Итак, оптимальное решение упрощенной задачи ЛП достигается в точке £’’ = 5,39,
X = 5,69 Значение каждой переменной можно округлить с недостатком или с избытком,
следовательно, возле оптимального решения упрощения имеется четыре округленных
решения (5, 5), (5, 6), (6, 5), (6, 6). В общем случае для двух переменных всегда существует
четыре соседних округленных решения. При п переменных количество таких точек равно
2", и последнее число растет очень быстро по мере увеличения п.
Рассмотрим более подробно проблемы, которые могут возникнуть при использова-
нии округленных решений. Обратимся к рис. 6.3. Если найти упрощение и округлить
значения переменных до ближайших целых чисел, то среди четырех ближайших целых
точек три являются недопустимыми. Единственной допустимой точкой, полученной
в результате округления, является точка (5, 5). Этот пример иллюстрирует два общих по-
ложения, касающихся округленных решений.
1. Округленное решение не обязательно оптимально. В данном случае значение целе-
вой функции для единственного допустимого округленного решения составляет
18x5 + 6x5= 120
Сравним это значение с оптимальным значением модели ЦЛП, которое равно 126.
Получается, что использование округленного решения вместо оптимального при-
водит к уменьшению значения целевой функции.
2. Округленное решение не обязательно находится рядом с оптимальным решением за-
дачи ЦЛП. Часто интуиция подсказывает, что даже если округленное решение не
является оптимальным, оно должно быть “рядом” с оптимальным решением зада-
чи ЦЛП На рис. 6.3 показано, что округленное решение не находится в непосред-
ственной близости от оптимального решения модели ЦЛП.
На рис. 6 4 представлен еще один пример задачи ЦЛП, который иллюстрирует про-
блему, связанную с округленными решениями. Заштрихованная область на рисунке —
это допустимое множество упрощения, точки — целочисленные решения, обведенная
кружком точка — единственное допустимое решение задачи ЦЛП. Оптимальное значе-
ние упрощения расположено на конце клиновидной допустимой области. Если взять за
основу оптимальное упрощение (приблизительно (3,3, 4,7)) и затем округлять его до лю-
бых соседних целочисленных точек, получатся недопустимые решения. Таким образом,
в данном примере ни одно округление не является допустимым решением.
ГЛАВА 6. Целочисленная оптимизация 391
Рис. 6.4. Все округленные решения являются недопустимыми
Подведем итог Интуитивно привлекательный способ решения задачи ЦЛП состоит
в том, чтобы найти решение упрощенной задачи ЛП исходной модели, а затем округлить
полученное значение до соседней целочисленной точки. Но при таком подходе могут
возникнуть следующие проблемы
1. Ни одна из соседних целочисленных точек не будет допустимой.
> 2. Даже если одна или несколько соседних целочисленных точек будут допустимы, >
то эта точка не обязательно станет оптимальной для модели ЦЛП. Более того, та-
1 кая точка может быть как угодно далека от оптимального решения задачи ЦЛП.	>
Решение методом перебора
Если посмотреть на решение задачи ЦЛП на рис. 6.2, становится понятно, почему до-
бавление условия целочисленности и, как следствие, значительное сокращение допусти-
мой области не упрощает поиск решения с помощью симплекс-метода Напомним, что
симплекс-метод основан на том факте, что решение задачи ЛП всегда лежит на границе
допустимой области. Таким образом, внутренние точки допустимой области не рассмат-
риваются Однако при оптимизации модели ЦЛП средству Поиск решения может пона-
добиться обойти многочисленные целые точки, находящиеся внутри допустимой облас-
ти, поэтому для решения задач ЦЛП симплекс-метод в чистом виде не применяется.3
Средство Поиск решения для решения линейных задач целочисленного программирования применяет метод
ветвей и границ, описанный далее в этой главе, а не симплекс-метод — Прим ред
392 ЧАСТЬ II. Оптимизационные модели
На рис. 6 1 видно, что в рассматриваемой модели ЦЛП только 13 допустимых цело-
численных точек. Можно прийти к ошибочному выводу, что нужно просто перебрать все
допустимые целочисленные точки, вычислить в каждой из них значение целевой функ-
ции и выбрать из них наилучшее, т.е. решить задачу путем полного перебора допустимых
целочисленных точек. В данном конкретном примере, конечно, можно так поступить.
Однако, к сожалению, полный перебор допустимых целочисленных точек для большин-
ства задач ЦЛП осуществить невозможно. Предположим, что модель ЦЛП содержит
всего 20 переменных решения, каждая из которых может принимать целые значения
в диапазоне от 1 до 50 В этом случае придется перебрать 502" (более чем 9,5х1033) точек
и проверить их допустимость! Даже с помощью самого мощного суперкомпьютера потре-
буются годы, чтобы осуществить этот перебор
Интересно сравнить метод полного перебора для задач ЦЛП с симплекс-методом оп-
тимизации, используемым средством Поиск решения для моделей ЛП. Уже отмечалось,
что симплекс-метод можно рассматривать как некий способ обхода угловых точек допус-
тимого множества и оценки целевой функции в этих точках. В крупной модели ЛП могут
быть миллиарды угловых точек, однако важным обстоятельством является то, что обхо-
дятся не все угловые точки. В действительности симплекс-метод очень эффективен. Он
работает так, что в каждой последующей посещаемой точке значение целевой функции
улучшается Если улучшение невозможно, Поиск решения прекращает работу и сообща-
ет, что оптимальное решение достигнуто Как правило, это происходит после посещения
очень небольшого подмножества всех угловых точек В настоящее время не существует
сравнимого по эффективности метода решения задач ЦЛП. Рассматриваемые в данной
главе методы решения задач ЦЛП значительно лучше, чем полный перебор, но они не
могут исключать большое количество возможных решений так же быстро и эффективно,
как это делает симплекс-метод в задачах ЛП
6.4. Применение двоичных переменных
Двоичные переменные (принимающие значения 0 или 1) играют исключительно важную
роль в прикладных моделях ЦЛП. Эти переменные позволяют включать в оптимизационные
модели решения, описываемые в Excel с помощью функции ЕСЛИ, которые иногда еще на-
зывают дихотомическими решениями Два небольших примера покажут, что имеется в виду.
1. В модели размещения производственных объектов х, = 1, если принимается реше-
ние разместить завод в пункте j, и xj = 0, если решено завод в данном пункте
не размещать
2. В модели маршрутизации xtjk = 1, если дорога к ведет из пункта i в пункт j, wxijk = G
в противном случае.
Как видно из этих примеров, использование двоичных переменных открывает новые
возможности в формировании разнообразных логических условий, не прибегая к операто-
рам, подобным функции ЕСЛИ в Excel Это очень важно, поскольку использование таких
операторов затрудняет оптимизацию модели с помощью средства Поиск решения. В дан-
ном разделе мы рассмотрим несколько примеров использования двоичных переменных
в различных приложениях, а также формулировки с их помощью логических условий.
ГЛАВА 6. Целочисленная оптимизация 393
Распределение бюджета
Многие компании ежегодно принимают решения о капиталовложениях. В крупных
компаниях такие решения, как правило, являются результатом длительного процесса,
который начинается со сбора предложений от отдельных подразделений, затем происхо-
дит обсуждение этих предложений на различных уровнях. Нередко окончательный выбор
остается за советом директоров. В небольших компаниях данный процесс не такой тру-
доемкий, тем не менее решение о выделении средств является основной частью ежегод-
ного финансового планирования компаний.
В простейшей форме решение о выделении средств заключается в выборе нескольких из
п вариантов капиталовложений, цель состоит в максимизации прибыли при наличии огра-
ничений на количество средств, которые можно вкладывать. В качестве конкретного при-
мера рассмотрим данные, которые поступили совету директоров компании AutoPower
(табл. 6.1). Совету директоров предстоит выбрать несколько вариантов из предложенных.
Если принимается решение о расширении завода в Бельгии, текущая стоимость чистой
прибыли составит $400 000. Этот проект требует выделения средств в размере $100 000
в первый год, $50 000 во второй год и т.д. Совет директоров ранее принял решение о выде-
лении до $500 000 на все капиталовложения в году 1, до $450 000 в году 2 и т.д.
Таблица 6.1. Варианты капиталовложений компании AutoPower
Чистая прибыль, тыс. долл. Вариант		Вложения по годам, тыс. долл.				
				3 1	4 1	5
Расширение завода в Бельгии	400	100	50	200	100	0
Расширение мощностей по произ- водству малых генераторов в США	700	300	200	100	100	100
Открытие нового завода в Чили	800	100	200	270	200	100
Расширение мощностей по произ- водству больших генераторов в США	1000	200	100	400	200	200
Имеющиеся средства		500	450	700	400	300
Модель ЦЛП для распределения бюджета компании AutoPower
Данную ситуацию можно представить с помощью модели ЦЛП, в которой все пере-
менные двоичные Такая модель называется двоичной моделью ЦЛП. Пусть переменная
х, = I, если проект i принимается, и х: = 0 в противном случае. Тогда модель примет сле-
дующий вид.
Максимизировать 400х, + 700х2 + 8ООх3 + Ю00х4
при ограничениях
ЮОх, + 300х2 + 100х3 + 200х4 < 500,
50х, + 200х2 + 200х3 + 100х4 < 450,
200х, + 100х2 + 270х3 + 400х4 < 700,
ЮОх, + 100х2 + 200х3 + 200х4 < 400,
100х2 + 100х3 + 200х4 < 300,
х, = 0 или 1,/= 1,..., 4.
394 ЧАСТЬ II. Оптимизационные модели
В данной модели целевая функция — это суммарная чистая прибыль, а ограничения
указывают на то, что в каждом году используется средств не больше, чем имеется в нали-
чии в этом году.
Упрощенная модель ЛП
Попробуем применить подход, в котором сначала решается задача ЛП, являющаяся уп-
рощением исходной задачи ЦЛП. Ее формулировка и решение представлены на рис. 6.5.
Отметим, что при переходе от модели ЦЛП к упрощенной модели ЛП требование двоично-
сти переменных х, игнорируется. Вместо этого к ограничениям неотрицательности добав-
ляются ограничениях,^ 1 (/= 1, 2, 3, 4), как показано на рис 6.5. Таким образом получает-
ся, что в упрощенной модели ЛП переменные х, принимают значения из интервала (0,1)
Если бы в оптимальном решении каждая переменная х, принимала одно из своих гранич-
ных значений 0 или 1, тогда исходная задача ЦЛП была бы решена. К сожалению, как пока-
зано на рис 6.5, так получилось только с переменной х4, значения же остальных перемен-
ных решения оказались дробными4 Поскольку переменная х3 равна 1, если компания
AutoPower принимает решение строить завод в Чили, и 0 в противном случае, результат
х3 = 0,33 не имеет смысла. Как известно, попытка найти решение задачи ЦЛП путем реше-
ния упрощенной задачи ЛП и последующего округления полученного результата не всегда
приводит к успеху. Стандартные правила округления до ближайших целых чисел (когда
числа меньше или равные 0,499 округляются до 0, а числа больше или равные 0,500 — до 1)
дают следующее решение- х, = 1, х2 = 1, х3 = 0, х4 = 1 Нетрудно убедиться, что данное реше-
ние недопустимо, поскольку нарушает первое ограничение.
Оптимальное решение задачи ЦАП
Чтобы получить оптимальное целочисленное решение в модели распределения
средств компании AutoPower, необходимо в средстве Поиск решения при задании огра-
ничений использовать опцию двоичное Формулировка и решение задачи ЦЛП показаны
на рис 6 6. Отметим, что четыре ограничения, требовавшие, чтобы х, не превышали 1,
удалены Ограничение C4-F4 = двоичное означает, что все четыре переменных решения
являются двоичными 5
Согласно представленному на рис 6.6 решению руководству компании AutoPower
следует принять первые три проекта; значение х4 теперь равно 0, хотя в упрощенной мо-
дели ЛП на рис. 6.5 оно было равно 1. Значение целевой функции в полученном решении
составляет 1900, что на 100 единиц (5%) меньше, чем оптимальное значение в упрощен-
ной модели. На практике иногда приходится решать задачи ЦЛП с сотнями двоичных
переменных. После показанного простого примера становится понятно, насколько важ-
ны встроенные в средство Поиск решения специальные методы решения задач ЦЛП,
причем для крупных и сложных моделей их значимость возрастает.
Ваше решение может отличаться от приведенного здесь, поскольку в данной модели имеются альтерна-
тивные оптимальные решения
Напоминаем, что Поиск решения при задании ограничений позволяет применять опции двоичное и целое
только к переменным решения, тек тем, которые указаны в поле Изменяемые ячейки

J
I
396 ЧАСТЬ II. Оптимизационные модели
Рис. 6.6. Модель ЦЛП для задачи распределения средств
Допустимое отклонение
Поскольку оптимизация моделей ЦЛП стандартных размеров зачастую является дли-
тельной процедурой даже на быстродействующем персональном компьютере, по умолча-
нию допускается, что для экономии времени средство Поиск решения может остано-
виться, немного не достигнув оптимальной точки. В диалоговом окне Параметры поиска
решения есть поле ввода Допустимое отклонение. По умолчанию значение допустимого
отклонения равно 5%. Это означает, что процедура оптимизации продолжается только до
тех пор, пока значение целевой функции будет отличаться от оптимального не более чем
на 5% Более высокие значения допустимого отклонения ускоряют работу средства По-
иск решения при оптимизации моделей ЦЛП, однако существует риск, что найденное
решение будет значительно отличаться от истинного оптимума соответствующей задачи
ЦЛП Устанавливая значение допустимого отклонения равным 0%, мы заставляем Поиск
решения находить истинный оптимум задачи ЦЛП за счет, возможно, более длительного
времени решения.
ГЛАВА 6. Целочисленная оптимизация 397
Как Поиск решения узнает о том, что находится внутри заданного процентного от-
клонения от оптимума? Первым делом Поиск решения отбрасывает ограничение цело-
численности и решает упрошенную задачу ЛП. Поскольку оптимальное значение целе-
вой функции задачи ЦЛП не может быть лучше, чем оптимальное значение целевой
функции упрощенной задачи ЛП, то последнее значение является верхней границей для
оптимального значения целевой функции задачи ЦЛП. Кроме того, в процессе оптими-
зации Поиск решения отслеживает наилучшее решение, найденное к данному моменту;
это решение задает нижнюю границу для оптимального значения целевой функции зада-
чи ЦЛП. Поскольку оптимальное значение целевой функции задачи ЦЛП заключено
в этих пределах, Поиск решения продолжает поиск до тех пор, пока не окажется, что
разность между границами не превышает допустимого отклонения.
Логические условия
Важной областью использования двоичных переменных является наложение ограни-
чений, которые вытекают из логических условий (принимающих значения “Истинно”
и “Ложно”). Ниже приводится несколько примеров таких условий.
Предположим, что задано целое число А:, ах((/= 1,...,/?) — двоичные переменные. Ог-
раничение х, + х2 + •• + хл < к означает, что можно выбрать не более к из возможных п ва-
риантов. Поскольку каждая переменная х, может принимать только значение 0 или 1, то
данное ограничение утверждает, что не более к из этих переменных могут быть равны 1.
Для примера предположим, что руководство компании AutoPower настроено принять не
более одного зарубежного проекта (данные приведены в табл. 6.1). Поэтому совет дирек-
торов хочет исключить варианты, которые включают одновременное расширение завода
в Бельгии и строительство нового завода в Чили. Добавление в модель ЦЛП ограничения
х, + х, 5 1 означает, что решение может содержать не более одного зарубежного проекта.
Зависимые решения
С помощью двоичных переменных можно описать зависимость между двумя или не-
сколькими переменными решения. Например, руководство компании AutoPower не хо-
чет принимать вариант к, если не будет принят вариант т. Это условие можно предста-
вить с помощью ограничения
х, 5 х„, или х, - хт < 0.
Отметим, что если вариант т не принят, то х„ = 0. В таком случае ограничение требу-
ет, чтобы значение х( также было равно 0 (т.е. вариант к принят не будет). Если же вари-
ант т принят, х„ = 1 и ограничение принимает вид хк 5 1. В этом случае Поиск решения
может выбрать хк = 1 или хк = 0.
В качестве примера предположим, что руководство компании AutoPower считает: если
планировать расширение производства в США, то для обеспечения конкурентоспособ-
ности необходимо в первую очередь расширить производственные мощности по выпуску
больших генераторов. Добавление к модели ЦЛП на рис. 6.6 ограничения хк <хт, (хк-х„
5 0) гарантирует, что в данной модели нельзя выбрать вариант расширения производст-
венных мощностей по выпуску малых генераторов, если не выбирается вариант расши-
рения производственных мощностей для больших генераторов.
Теперь предположим, что совет директоров решил: если принимается решение рас-
ширять производственные мощности внутри страны, следует увеличить производствен-
ные мощности по выпуску как больших, так и малых генераторов. В таком случае необ-
ходимо добавить к модели ЦЛП ограничение хк = хт, (или, что эквивалентно, хк - хт = 0),
тогда хк и х„ будут принимать одинаковые значения.
398 ЧАСТЬ II. Оптимизационные модели
Рассмотрим задачу управления портфелем инвестиций при наличии следующих усло-
вий. если ценные бумаги j покупаются, необходимо купить не менее 200 акций; и не раз-
решается покупать более 1000 акций вида j. Такое ограничение невозможно ввести в мо-
дель ЛП Обозначим через xt количество покупаемых акций вида j. Неравенство 200 <х
< 1000 не отражает данного ограничения, поскольку в нем требуется, чтобы х, всегда было
не меньше 200. Мы же хотим, чтобы выполнялось условие- или х? = 0, или 200 <xj < 1000.
Чтобы записать данное требование, введем для каждого вида ценных бумаг j двоичную
переменную уу, которая интерпретируется следующим образом:
•	если = 1, то акции видаj покупаются,
•	еслиу, = 0, то акции вида/ не покупаются
Рассмотрим теперь два ограничения.
х< 1000у,,	(6.1)
х^>200у/	(6 2)
Если уу = 1, то неравенства (6 1) и (6.2) эквивалентны неравенствам 200 <х7 < 1000
С другой стороны, еслиу, = 0, то (6.1) означает, чтох, <0, а из (6 2) следует, чтох, > 0, по-
этому х. = 0. Как удостовериться, что у, = 1, когда покупаются акции видар Это гаранти-
руется неравенством (6 1)- х, < 1000у,. Благодаря этому неравенству не может возникнуть
ситуация, когда одновременно х? > 0 и у? = 0. Следовательно, если х? > 0, то у, должно быть
равно 1. Таким образом, получается правильное описание налагаемых наху условий.
Рассмотрим еще один пример. Студент со Среднего Востока Миша Гаас, прибыл по об-
мену в университет для написания диссертации по всемирной истории Научный руководи-
тель сказал ему, что каждый, кто намерен получить степень доктора философии, чтобы
преподавать всемирную историю, должен удовлетворять хотя бы двум из трех следующих
критериев- быть одиноким, богатым или сумасшедшим К сожалению, Миша бьш беден
и женат. Кстати, прежде чем жениться, он несколько лет искал невесту, которая была бы
высокой, темноволосой, красивой и богатой Наконец, он сказал себе, что три из четырех
тоже неплохо, в результате девушка, которую он выбрал (и которая выбрала его), оказалась
высокой, темноволосой и красивой, но небогатой. Это примеры моделей, в которых необ-
ходимо удовлетворить к из т ограничений В общей постановке модель выглядит следую-
щим образом Задано множество из т ограничений для п (недвоичных) переменныхх;
g,(x„ ...,х„) <b„i = 1, ,.,т,
meg, — заданная функция ограничения от п переменных х. Введем в модель т дополни-
тельных двоичных переменных у, и зададим М — очень большое число, чтобы для всех /
неравенства g,(x.,..., х„) < М заведомо выполнялись Тогда следующие т + 1 ограничение
выражают нужное условие.
g,(x,,.. , х„) < by, + М( 1 - у,), / = 1,.. , т.
Ограничение j^y, = к требует, чтобы ровно к новых переменных решения у, прини-
мали значение 1. Это означает, что ровно к вышеприведенных ограничений-неравенств
будут эквивалентны неравенствам &(хр ...,х„) </>,. Оставшиеся т-к ограничений при-
нимают вид&(Х|, •• , х„) S А/, а поскольку М — очень большое число, все эти ограничения
оказываются избыточными и не влияют на оптимальное решение задачи
ГЛАВА 6. Целочисленная оптимизация 399
В качестве примера такой модели рассмотрим ситуацию, когда компания должна оп-
ределить планы выпуска трех видов продукции х„ х2 и ху Это часть большой модели ЛП,
где для этих трех видов продукции нужно выбрать одну из двух возможных технологий,
каждая из которых задана соответствующим ограничением. Таким образом, компания
должна выбрать ту или иную технологию (характеризующие эти технологии неравенства
приведены ниже), но не обе сразу.
ЗОх, + 20х2 + 10х3 < 100,	(технология I)
1 Ох, + 30х2 + 5х, < 110.	(технология 2)
Нельзя просто указать эти ограничения в модели ЛП, поскольку тогда это означало
бы, что в процессе производства должны выполняться оба ограничения одновременно,
а не одно из них. В данном случае в модель ЛП необходимо ввести две новые двоичные
переменные решения у, и у2, тем самым преобразовав ее в модель ЦЛП. Двоичные пере-
менные у, и у2 определяются следующим образом: если у, = 1, это означает выбор техно-
логии 1; если у, = 0, то технология 1 не выбирается, если у2 = 1, то выбирается технология
2; а если у2 = 0, технология 2 не выбирается.
После этого нужно изменить ограничения модели ЛП следующим образом
ЗОх, + 20х2 + 10х3 < ЮОу, + 999999(1 — у,),	(технология 1)
10х, + 30х2 + 5х3 < 110у2 + 999999(1 - у2)	(технология 1)
Теперь первое ограничение заставит Поиск решения выбрать только одну технологию,
а большое число (здесь выбрано 999999) необходимо подобрать так, чтобы или первое или
второе ограничение оказалось избыточным, если соответственно илиу„ илиу2 будут равны 1.
Теперь перейдем к одному из наиболее важных приложений ЦЛП — моделированию
ситуаций, когда еще до начала экономической деятельности необходимо сделать опреде-
ленные затраты Такая модель называется моделью фиксированных затрат
6.5.	Моделирование фиксированных затрат
Чтобы сэкономить средства, компания STECO, оптовый продавец электроники, арендует
для своих нужд региональные склады. В настоящий момент у компании есть список из трех
складов, которые можно взять в аренду Ежемесячная стоимость аренды склада / составляет Г,
при этом склад I может загрузить не более Т автофургонов с продукцией в месяц
Ежемесячная стоимость
аренды складов
Пропускная способность
(к-во грузовиков)
Склады
Районы
Ежемесячный спрос
Рис. 6.7. Расположение складов компании STECO
400 ЧАСТЬ II. Оптимизационные модели
Компания работает в четырех районах, среднемесячный спрос в районе j составляет rf,
автофургонов продукции; средние затраты отправки фургона со склада I в район j состав-
ляют се. Компания STECO решает, какие склады брать в аренду и сколько фургонов то-
вара отправлять с каждого склада в каждый район. Необходимо отметить, что компания
не вносит арендную плату за определенный склад, если она не планирует отправить
с него хотя бы один автофургон товара. Если же со склада отправляются фургоны с това-
ром, то необходимо вносить полную сумму ежемесячной арендной платы. Модели, в ко-
торых затраты ведут себя подобным образом, встречаются достаточно часто и носят на-
звание моделей фиксированных затрат. Представление модели компании STECO в виде
сетевой диаграммы показано на рис. 6.7.
Данные для этой модели представлены в табл. 6.2. Как видно из таблицы, аренда
склада А в течение месяца составляет $7750, и с этого склада можно загрузить и отпра-
вить потребителям до 200 автофургонов товара. Ежемесячный объем спроса в районе 1
равен 100 фургонам. Кроме того, в таблице представлены переменные затраты на от-
правку автофургона со склада z в район j.
Таблица 6.2. Данные для принятия решения о размещении складов
Склад	Затраты на отправку одного фургона, $			Ежемесячная пропускная способность, к-во фургонов	Ежемесячная стоимость аренды, S
	1 1 2 |	3 1	4		
А	170 40	70	160	200	7750
В	150 195	100	10	250	4000
С	100 240	140	60	300	5500
Ежемесячный спрос (фургоны)	100 90	ПО	60		
Если рассматривать данную задачу как модель частично-целочисленного программи-
рования, необходимо решить, какие переменные могут принимать только целые значе-
ния, а какие — действительные. Решение арендовать определенный склад или нет, по-
видимому, необходимо описывать с помощью двоичной переменной, поскольку стои-
мость аренды склада / не зависит от уровня активности использования склада (т.е. от ко-
личества отправленных с данного склада автофургонов). Определим двоичные перемен-
ные решениями положим д', = 1,если склад / арендуется, и у, = 0 в противном случае.
На первый взгляд кажется естественным считать количества автофургонов, отправ-
ленных с определенного склада в определенный район, как целочисленные переменные.
(Поскольку не имеет смысла говорить об отправке из одного места в другое половины
фургона.) Однако существуют следующие доводы считать количества автофургонов как
действительные переменные.
1.	Это модель планирования, а не подробная модель функционирования. При реаль-
ной работе спрос в торговых районах будет меняться, и руководству компании
STECO придется находить методы, позволяющие справиться с этой неопределен-
ностью. Автофургоны, приписанные к конкретному складу, могут при необходи-
мости распределяться по соседним районам, а для удовлетворения избыточного
спроса компания может воспользоваться услугами транспортного агентства. В лю-
бом случае количество фургонов, которое согласно решению нашей оптимизаци-
онной задачи должно быть направлено со склада / в район j, является только неким
приближением того, что в действительности будет происходить в любой конкрет-
ный день. Поэтому можно считать количества фургонов как действительные пере-
ГЛАВА 6. Целочисленная оптимизация 401
менные и округлять их до ближайших целых, чтобы определить, сколько авто-
фургонов следует приписать к каждому складу. Это позволит получить приблизи-
тельное представление о средних ежемесячных эксплуатационных расходах.
2.	Условие, что количества автофургонов описываются целочисленными переменны-
ми, может усложнить оптимизацию модели. Существует общая закономерность —
чем больше количество целочисленных переменных и чем больше значений может
принимать каждая из этих переменных, тем сложнее решить задачу ЦЛП.
3.	Очевидно, что расходы на аренду любого из складов значительно больше, чем на от-
правку автофургона со склада. Сравнив относительные величины этих затрат, можно
сделать вывод, что важнее трактовать как целочисленные переменные решения
“арендовать или не арендовать”, а не количество фургонов. Проиллюстрируем дан-
ное утверждение: аренда склада С обходится в $5500 в месяц, а отправка фургона со
склада С в район 4 — $60. Предположим, что данная задача рассматривается как
модель ЛП. Если в оптимальном решении ус =0,4, то в результате округления его
значения до 0 оптимальное значение целевой функции изменится на $2200, в то вре-
мя как округление хС4 = 57,8 в большую или меньшую строну приведет к изменению
оптимального значения целевой функции менее чем на $60.
Итак, из приведенных аргументов следует, что в данном примере незначительна целе-
сообразность считать количества автофургонов как целочисленные переменные. Поэто-
му создадим модель размещения складов компании STECO в виде модели частично-
целочисленного Л П.
Модель частично-целочисленного АП
Пусть у, = 1, если склад / арендуется, иу, = 0 в противном случае (/ = А, В, С); х^— ко-
личество автофургонов, отправленных со склада/в району (/ = А, В, С;у = 1, ...,4).
Теперь создадим модель, построив сначала целевую функцию. Выражение 170хА| +
+ 40хл2 + 70хЛ) + ••• + 60хС4 отражает полные затраты, связанные с отправкой фургонов,
а7750уА + 4000ув + 55ООус — это полная стоимость аренды. Таким образом, целевую
функцию минимизации затрат можно представить следующим образом:
минимизировать 7750ул + 4000ув + 5500ус + 170хА| + 40х^ + 70хм + + 60хС4.
Перейдем к рассмотрению ограничений. Необходимо учесть и спрос, и пропускную
способность складов. Следующее ограничение гарантирует удовлетворение спроса в рай-
оне 1: хА| + хВ1 + хС| > 100. Четыре аналогичных ограничения (по одному для каждого рай-
она) гарантируют удовлетворение спроса.
Следующее ограничение хА| +хА] +хА4 <200д (или хА| +хАЗ +хА4 -200^А <0)
служит двум целям. Во-первых, оно гарантирует, что пропускная способность склада А не
превышает 200 автофургонов, а во-вторых, оно заставляет арендовать склад А, если необхо-
димо что-то отправлять с данного склада. Чтобы убедиться в этом, вспомним, что у* должно
быть равно 0 или 1. Пусть ул= 1.Тогда неравенство примет вид хА| + хА2 +хА, +хА4 <200,
т.е. со склада А можно отправить не более 200 фургонов товара. Ограничения такого вида
уже встречались в транспортных моделях. Теперь рассмотрим случай, когдауА = 0. Тогда ог-
раничение будет выглядеть так: хА| +	+ хА, + хА4 < 0, т.е. со склада А невозможно отпра-
вить ни один автофургон. Таким образом, данное ограничение гарантирует, что со склада А
ничто не будет отправляться, пока д не станет равно 1. Отметим, что когда ул = 1, слагаемое
целевой функции 7750уА равно 7750. Таким образом, ничто не будет отправлено со склада
А, пока не будет внесена месячная арендная плата (фиксированные затраты) за данный
склад. В модели должно присутствовать три аналогичных ограничения (по одному для каж-
дого склада). Полная формулировка задачи и ее решение представлены на рис. 6.8.
402 ЧАСТЬ II. Оптимизационные модели
Рис. 6.8. Задача о размещении складов компании STECO
ГЛАВА 6. Целочисленная оптимизация 403
Анализ решения
Бросается в глаза, что оптимальные значения переменных, определяющие количества
автофургонов, целые числа, хотя в формулировке задачи допускается, чтобы эти пере-
менные принимали действительные значения. Что это, счастливая случайность9 Оказы-
вается, нет. Объясним, почему так получилось После того как принято решение, какие
склады арендовать, данная модель сводится к транспортной модели ЯП В главе 5 отме-
чалось, что если значения предложения на каждом складе и спроса в каждом районе яв-
ляются целыми числами, то оптимальное решение транспортной задачи также будет це-
лочисленным
Можно утверждать, что оптимальное решение данной задачи размещения складов
с целыми значениями предложения и спроса всегда будет содержать целочисленные зна-
чения переменных, определяющих количества фургонов Доказательство этого утвер-
ждения состоит из двух тезисов. 1) оптимальное решение заключается в аренде некого
множества складов, 2) для любого возможного числа арендованных складов получаются
целочисленные значения количеств фургонов, поскольку после выбора складов, по су-
ществу, решается транспортная задача Как видим, было бы неразумно включать в дан-
ную модель дополнительные ограничения, требующие, чтобы были целыми числами
Никогда не следует платить за товар, который предлагается бесплатно'
	Компания AT&T привлекает клиентов, экономя их средства с помощью модели частично-целочисленного программирования
Компания AT&T, крупнейший поставщик услуг в отрасли телемаркетинга, всегда
ищет способы помочь своим клиентам расширить объем их операций. Одна из про-
блем, с которой сталкиваются компании, активно занимающиеся телемаркетингом
(использующие для приема заказов клиентов бесплатные номера, начинающиеся на
800), заключается в принятии решений о количестве и местах расположения офисов
Компания AT&T заинтересована в разработке набора программ, которые способны
помочь ее клиентам в этом процессе.
Экономисты компании AT&T обнаружили, что вопреки первоначальным впечат-
лениям, местоположение офисов не всегда диктуется исключительно ценами на не-
движимость или затратами на коммуникации. Часто основную роль играют полити-
ческие или психологические соображения. Например, в компании считается, что
офис должен находиться в том же городе, что и региональная штаб-квартира, или
в городе, где хочет проводить время высшее руководство, даже если это не самые
удачные решения в плане затрат.
Компания AT&T разработала модель, которая анализирует затраты в зависимости
от места расположения офисов, и дает пользователям возможность оценить различные
варианты, учитывая как количественные, так и качественные факторы Эта модель
частично-целочисленного программирования решается с помощью программы, реали-
зующей метод ветвей и границ. Модель позволяет ответить на четыре вопроса.
1.	Сколько центров телемаркетинга следует открыть9
2.	Где должны располагаться эти центры9
3.	Какие географические регионы должен обслуживать каждый центр?
4.	Сколько человек обслуживающего персонала должно быть в каждом центре9
404 ЧАСТЬ II. Оптимизационные модели
Первоначально модель разрабатывалась на универсальной ЭВМ, но впоследствии
ее адаптировали для персональных компьютеров, при этом были добавлены дополни-
тельные графические возможности и средства общения с пользователем. Модель не
только предоставляет оптимальное решение, минимизирующее три составляющих
эксплуатационных расходов (коммуникации, оплата труда и недвижимость), но также
показывает альтернативные решения, благодаря чему пользователь может принять во
внимание иные факторы, отличные от затрат. Для этого к модели был добавлен анали-
тический блок, описанный в главе 12, который позволяет включать в процесс приня-
тия решений качественные или субъективные факторы.
Применение разработанной AT&T модели значительно ускорило процесс разме-
щения офисов, что позволило клиентам сэкономить время и средства, затраченные
на исследования и консультации. Некоторые компании оценивают, что экономия
составила до $240 000. Более того, ряд компаний-клиентов сообщили, что средняя
экономия составила 1 млн. долларов в год благодаря использованию предложенных
моделью мест размещения офисов вместо тех, что предусматривались ранее. В ре-
зультате операций, рекомендованных моделью, доля компании AT&T на данном
рынке возросла с 30% до 40%. [2]
6.6.	Метод ветвей и границ
Используемый средством Поиск решения алгоритм ветвей и границ является в на-
стоящее время наиболее эффективным универсальным методом оптимизации моделей
ЦЛП. Основная идея метода состоит в разбиении множества всех допустимых решений
данной задачи ЦЛП на непересекающиеся подмножества меньшего размера. После этого
вычисляются границы значения наилучшего решения для каждого подмножества реше-
ний. Алгоритм позволяет исключить из рассмотрения определенные подмножества ре-
шений, тем самым производится частичный перебор всех допустимых решений (в отличие
от полного перебора). Следующий пример показывает, как Поиск решения использует
метод ветвей и границ для оптимизации модели ЦЛП.
Пример модели ЦАП
Рассмотрим модель, которую будем называть Р1.
Максимизировать*, + 5х2
при ограничениях
11х, + 6х2 < 66,
5х, + 50х2 £ 225,
*,,*2й0 и целые.
Воспользуемся графическим способом решения, описанным в разделе 6.3.
Этап 1. Решение упрощенной задачи АП
Первый этап состоит в упрощении модели Р1. Если повезет, можно получить оптималь-
ное целочисленное решение уже на данном этапе, поскольку справедливо утверждение: ес-
ли упрощение является целочисленным, оно является оптимальным решением для исход-
ной модели ЦЛП. Воспользуемся графическим способом и посмотрим, насколько нам по-
везет. На рис. 6.9 штриховкой выделено допустимое множество упрощенной модели Л П.
ГЛАВА 6. Целочисленная оптимизация 405
Рис. 6.9. Упрощенная модель Р1
Точки в заштрихованной области — это допустимые целочисленные точки Таких то-
чек (включая лежащие на осях) насчитывается 27. На рис 6 9 также отмечена оптималь-
ная угловая точка модели ЛП, являющаяся точкой пересечения двух прямых, соответст-
вующих двум ограничениям. Чтобы найти числовые значения переменных решения, ре-
шим относительно х, и х2 систему уравнений, полученную из ограничений
11х, + 6х2 = 66 и 5х, + 50х2 = 225.
Получим х,’ = 3,75, х2’ = 4,125. Поскольку данные значения не являются целыми, модель
Р1 не оптимизирована. Однако мы получили определенную информацию о модели
1.	Найденное оптимальное значение целевой функции упрощенной модели ЛП зада-
ет верхнюю границу оптимального значения целевой функции модели Р1 Обозна-
чим эту верхнюю границу через U. Тогда, поскольку целевая функция имеет видх,
+ 5х2, можно записать
оптимальное значение целевой функции модели Р1 < 3,75 +5x4,125 = 24,375= U
2.	Как показано на рис. 6.9, если взять оптимальное решение упрощенной задачи
и округлить его в меньшую сторону до х, = 3, х2 = 4 (просто отбросить дробные
части), получим допустимое решение задачи Р1 Оценив целевую функцию в этой
точке (или в любой другой допустимой дочке), получим нижнюю границу опти-
мального значения целевой функции модели Р1 Назовем это значение F Тогда
оптимальное значение целевой функции модели Р1 > 3 + 5x4 = 23 = F
Значение F может оказаться равным или не равным оптимальному значению целевой
функции модели Р1, на данном этапе об этом судить невозможно. Все, что известно, это то,
что оптимальное значение целевой функции модели Р1 лежит в интервале от 23 до 24,375
Далее проводится ветвление. Последовательность решения методом ветвей и границ
обычно оформляется в виде древовидной диаграммы. Первый узел такой диаграммы по-
казан на рис. 6.10. Этот узел будет выглядеть несколько иначе, чем остальные узлы дере-
ва, так как мы поместили над ним значения текущей наилучшей верхней границы (будем
обозначать ее ВГ) и текущей наилучшей нижней границы (обозначается как НГ) опти-
мального значения целевой функции.
406
ЧАСТЬ II. Оптимизационные модели
Текущая наилучшая верхняя граница (ВГ) = 24,375
Текущая наилучшая нижняя граница (НГ) = 23,00
Рис. 6.10. Узел, соответствующий модели Р1
Этап 2. Ветвление
Разделим модель Р1 на две меньшие модели. Будем осуществлять ветвление по пере-
менной х,. Также можно было бы проводить ветвление по переменной х2. В процессе
ветвления используется тот факт, что в оптимальном решении задачи Р1 будет х, < 3 или
х,>4. Почему так происходит? Потому что в интервале, удаляемом наложением новых
ограничений х, < 3 и х, > 4, нет целых значений х,, поскольку удаляются значения х,, ле-
жащие в интервале 3 <х, < 4 Так как значение переменной х, должно быть целым, не
удалена ни одна допустимая точка из допустимого множества задачи Р1 Однако удалены
нецелочисленные точки из допустимого множества упрощения модели Р1. Оптимальное
значение х, упрощенной модели ЛП не удовлетворяет одновременно двум условиям х, < 3
их, > 4, поэтому в процессе ветвления текущая оптимальная точка (намеренно) исключа-
ется. В процессе ветвления создаются две новые модели путем добавления к исходной
модели Р1 ограниченийх, < 3 их, >4 (поодному к каждой модели) Таким образом, полу-
чаем две модели Р2 и РЗ. Модель Р2:
максимизироватьх, + 5х2
при ограничениях
11х, + 6х2 < 66,
5х, + 50х2 < 225,
х,<3,
х,,х2> 0 и целые.
Модель РЗ
максимизироватьх, + 5х2
при ограничениях
11х, + 6х2 < 66,
5х, + 50х2 < 225,
х, >4,
х,,х2 > 0 и целые.
Допустимые области этих моделей показаны на рис. 6.11. Можно сделать два вывода
из процесса ветвления
ГЛАВА 6 Целочисленная оптимизация 407
1. Допустимое множество модели Р1 разделилось на два подмножества, а исключен-
ная из рассмотрения область не содержит целочисленных точек.
2. Все допустимые целочисленные решения задачи Р1 теперь содержатся или в задаче
Р2 йли в задаче РЗ. Целевые функции моделей Pl, Р2 и РЗ одинаковы, отсюда сле-
дует, что или оптимальное решение задачи Р2, или оптимальное решение задачи РЗ
будет оптимальным решением задачи Р1, те. исходной задачи ЦЛП Таким обра-
зом, можно забыть о задаче Р1 и рассматривать только задачи Р2 и РЗ
Рис. 6.11. Модели Р2 и РЗ
Дерево решений
Процесс реализации метода ветвей и границ можно изобразить в виде дерева реше-
ний. Первый узел дерева — это задача Р1, узел 1 и узел 2— соответственно задачи Р2
и РЗ, как показано на рис. 6.12 Первый шаг процесса выполнения метода ветвей и гра-
ниц заключается в упрощении моделей Р2 и РЗ. Их оптимальные решения показаны на
рис. 6.11. В модели Р2 значение U (оптимальное значение целевой функции упрощения)
составляет 24,00, а в модели РЗ получаем U = 22,333 Как отмечалось, оптимальным ре-
шением задачи Р1 является или оптимальное решение задачи Р2, или оптимальное реше-
ние задачи РЗ. Поэтому оптимальное значение целевой функции задачи Р1 не превышает
максимума из значений U двух данных узлов Поскольку в узле 2 значение U равно 24,00,
а в узле 3 — 22,333, текущая наилучшая верхняя граница (ВГ) составляет 24,00 Поэтому
408 ЧАСТЬ II. Оптимизационные модели
изменяем значение ВГ над узлом 1. Чтобы заменить значение текущей наилучшей
нижней границы (НГ), необходимо найти допустимую точку задачи Р1, которая дает зна-
чение целевой функции больше, чем 23,00 (нынешнего значения НГ). Поскольку ни узел
2, ни узел 3 не дал полностью целочисленного решения, нового допустимого решения за-
дачи Р1 нет. Хотя в данном случае можно округлить в сторону уменьшения решения для
узлов 2 и 3, чтобы получить новые допустимые решения задачи Р1, в общем случае поиск
допустимых точек может оказаться затруднительным, поэтому продолжим процедуру без
поиска новых целочисленных решений в каждом узле. Тогда значение НГ останется
прежним Информация, полученная из задач Р2 и РЗ, также отмечается на дереве реше-
ний, как показано на рис. 6.12.
ВГ= 24,00
НГ= 23,00
Рис. 6.12. Дерево решений
Чтобы определить, что делать дальше, рассмотрим узлы в нижней части дерева, в дан-
ном случае это узлы 2 и 3. Верхняя граница для узла 3 составляет 22,333, а текущее значе-
ние нижней границы равно 23,00. Таким образом, найдено лучшее решение, чем можно об-
наружить в допустимом множестве модели РЗ. Следовательно, можно исключить из рас-
смотрения модель РЗ и сосредоточить усилия на задаче Р2. Чтобы показать, что модель
РЗ исключена из дальнейшего рассмотрения, поместим на рис. 6.12 букву П ниже узла 3,
что означает- дальнейшее исследование данной ветви дерева прекращено. В общем случае,
если после вычисления значения Uдля некого узла оказывается, что U< НГ, данный узел
можно исключить из дальнейшего рассмотрения.
Теперь продолжим исследование задачи Р2. Пока не получено оптимальное решение
этой задачи, поскольку значение х‘ все еще нецелое. Произведем еще одно ветвление.
В оптимальном решении для линейного упрощения модели Р2 переменная х, является
целой Поэтому ветвление нужно проводить по переменной х2 путем введения ограниче-
ний х2 < 4 и х2 > 5. В результате получим две новые модели Р4 и Р5. Модель Р4:
максимизировать*, + 5х2
ГЛАВА 6. Целочисленная оптимизация 409
при ограничениях
11х, + 6х2 < 66,
5х, + 50х2 < 225,
х,<3,
х2<4,
х,,х2>0ицелые.
Модель Р5:
максимизироватьх, + 5х2
при ограничениях
11х, + 6х2 < 66,
5х, + 50х2 < 225,
х2>б’
х,, х2 > 0 и целые.
Заметим, что ограничениями модели Р4 являются ограничения модели Р1 (Их, + 6х2
<66, 5х, + 50х2 <225), плюс ограничение, добавленное при определении модели Р2
(х, < 3), плюс новое ограничение, добавленное при определении Р4 (х2 < 4) Аналогично
формировались ограничения модели Р5. Результат этого ветвления показан на рис 6 13,
а новое дерево решений изображено на рис. 6 14
Рис. 6.13. Модели Р4 и Р5
410 ЧАСТЬ II Оптимизационные модели
ВГ = 23,00
НГ = 23,00
Сравнивая рис 6 13 и рис 6.11, необходимо отметить следующие моменты.
1.	Задача РЗ осталась неизменной
2.	Множество нецелочисленных решений, включая оптимальное решение упроще-
ния модели Р2, исключено из рассмотрения.
3.	Множество допустимых решений упрощения модели Р5 пусто, нет точек, которые
одновременно удовлетворяли бы ограничениям 5х, + 50х2 < 225, х, > 0 и х2 > 5 По-
этому модель Р5 можно исключить из рассмотрения.
Таким образом, осталось рассмотреть только модель Р4. Оптимальным решением уп-
рощения данной модели, как показано на рис 6 13, является полностью целочисленное
решение х,’ = 3, х2’ = 4 Тогда это решение является также оптимальным решением задачи
Р4 Поэтому задача Р4 является еще одним конечным узлом дерева решений. Таким об-
юм, окончание работы с узлом может происходить по трем причинам
1 его(/<НГ;
b узел представляет модель, имеющую пустую область допустимых решений,
с упрощенная задача ЛП дает решение целочисленной задачи, представляемой
данным узлом
Вернувшись вновь к рис. 6 14, можно заметить, что значение ВГ изменилось по срав-
нению с его значением на рис. 6 12. В результате ветвления в узле 2 получили узел 5 — не-
ГЛАВА 6. Целочисленная оптимизация 411
допустимую модель и узел 4 — модель с U= 23,00. Таким образом, текущая наилучшая
верхняя граница (ВГ) уменьшилась с 24,00 до 23,00. Кроме того в узле 4 было получено
полностью целочисленное решение, следовательно, оно является допустимым решением
задачи Р1. Оно доставляет целевой функции значение 23,00. Поскольку текущая наилуч-
шая нижняя граница равна 23,00, значение ВГ не меняется.
В общем случае, когда все узлы являются конечными, алгоритм ветвей и границ завер-
шается. Оптимальное решение исходной модели Р1 — это решение, определяющее наи-
лучшую нижнюю границу. В данном случае НГ равно 23,00 и х,’ = 3, х‘ = 4 является оп-
тимальным решением задачи Р1.
Модели частично-целочисленного линейного программирования
Описанный выше метод ветвей и границ можно легко модифицировать, чтобы решать
с его помощью задачи частично-целочисленного линейного программирования. Внесем
небольшое изменение в рассмотренную выше модель ЦЛП. Предположим, что модель
имеет следующий вид.
максимизировать*, + 5х2
при ограничениях
11х, + 6х2 < 66,
5х, + 50х2 < 225,
х, > 0 и целое, х2 > 0.
Единственное отличие от предыдущей модели заключается в том, что теперь не требу-
ется, чтобы значение переменной х2 было целым числом Чтобы решить данную задачу,
начнем, как и ранее, с упрощения, показанного на рис. 6.9. Поскольку х,’ не является це-
лым числом (равно 3,75), для получения начального значения Г можно округлить значе-
ние х,' в меньшую сторону до 3. Значение х2* можно оставить нецелым (равным 4,125).
Тогда F= 3 + 5x4,125 = 23,625. Как и ранее, ВГ = 24,375, но теперь НГ = 23,625. Прово-
дим ветвление по переменной х„ вводя новые ограничения х, < 3 и х, > 4. Результат полу-
чится такой же, как и на рис. 6.11. Из рисунка можно извлечь следующую информацию
1.	В узле 2 U = 24,00, а в узле 3 6/ = 22,333; поэтому ВГ становится равной 24,00.
2.	Оптимальное решение в узле 2 содержит целое значение х,; значит, это допустимое
решение задачи Р1. Из этого следует, что:
а.	имеем новую наилучшую нижнюю границу, равную 24,00,
Ь.	узел 2 является конечным.
3.	В узле 3 U< НГ; следовательно, узел 3 также конечный.
Поскольку оба узла являются конечными, оптимальным решением является решение,
определяющее НГ, т.е. х' = 3, х2‘ = 4,20.
Применение метода ветвей и границ
Завершим описание метода ветвей и границ для решения задач ЦЛП. Изменения, ко-
торые надо сделать в методе применительно к задаче частично-целочисленного ЛП, оче-
видны. Для решения упрощенных задач ЛП используется встроенный в средство Поиск
решения симплекс-метод. Повторим кратко последовательность действий, выполняе-
мых при решении задачи ЦЛП методом ветвей и границ.
412
ЧАСТЬ II. Оптимизационные модели
1.	Сначала находится решение упрощенной задачи ЛП, полученной из исходной мо-
дели ЦЛП. Оптимальное значение целевой функции упрощенной задачи является
значением U Если данное оптимальное решение полностью целочисленное, оно
является оптимальным для задачи ЦЛП В противном случае находится любая до-
пустимая точка задачи ЦЛП и значение целевой функции в ней обозначается
как F. Значение текущей наилучшей ВГ устанавливается равным U, а НГ — F.
2.	Берется любой узел, для которого решена упрощенная задача ЛП, не являющийся
конечным В этом узле производится ветвление путем создания двух новых узлов,
при этом оптимальное решение одной из новых задач ЦЛП будет оптимальным
решением исходной задачи ЦЛП Ветвление осуществляется путем выбора из оп-
тимального решения упрощенной задачи, имеющей в этом решении дробное зна-
чение Пусть [х’] — целая частьх' Одна из новых моделей представляет собой ис-
ходную модель, дополненную ограничением х, < [х,*] Вторая образуется путем до-
бавления к исходной модели ограничения х, > [х, ] + 1. После этого надо выбрать
следующий узел, для которого найдено решение, или перейти к п. 3.
3.	Выбирается любой узел, для которого пока не решена упрощенная задача ЛП,
и решается его упрощенная задача ЛП Оптимальное значение целевой функции
упрощения является значением U в данном узле Ветвь оканчивается, если область
допустимых упрощении пуста или для него U< НГ, либо его оптимальное решение
полностью целочисленное Если оптимальное решение полностью целочисленное,
полученное значение целевой функции обозначают как/7 Если F> НГ, полагают
НГ = F Если данная ветвь не окончена, повторяется п 3 или переходят к п 2 Ес-
ли узел конечен, переходят к п 4
4.	Если все узлы конечны, оптимальным решением для исходной модели ЦЛП явля-
ется полностью целочисленное решение, которое определило значение НГ.
Как следует из описания, алгоритм ветвей и границ предусматривает декомпозицию
исходной модели ЦЛП на последовательность моделей ЛП, содержащих дополнительные
ограничения на переменные решения, которые затем оптимизируются Таким образом,
метод ветвей и границ использует для решения задачи целочисленного программирова-
ния многократные оптимизации задач ЛП Поэтому в общем случае для решения задач
ЦЛП требуется значительно больше времени, чем для решения задач ЛП
Несколько слов о применении метода ветвей и границ для решения задач ЦЛП с дво-
ичными переменными Предположим, что ветвление производится по двоичной пере-
менной у. Тогда в одной подмодели у, = 0, а в другой у, = 1. Для очень больших моделей
ЦЛП с двоичными переменными достаточно успешно применяется другая разновид-
ность метода ветвей и границ (не используемая средством Поиск решения) — метод
частичного перебора.
Для оптимизации моделей ЦЛП и частично-целочисленных ЛП общего вида приме-
няются также другие методы, среди которых метод отсекающих плоскостей и метод Ла-
гранжа Но мы ограничились обсуждением только метода решения задачи ЦЛП, исполь-
зуемого средством Поиск решения.
Анализ чувствительности моделей ЦАП
Как было показано, используемый средством Поиск решения метод ветвей и границ
в общем случае требует гораздо больше времени для оптимизации модели ЦЛП, чем для оп-
тимизации модели ЛП К сожалению, решение задачи ЦЛП, полученное с помощью Поиск
ГЛАВА 6. Целочисленная оптимизация 413
решения также содержит меньше информации, чем решение задачи ЯП. Хотя диалоговое
окно Результаты поиска решения, которое появилось после успешной оптимизации мо-
дели ЦЛП компании STECO, содержит опцию, вроде бы позволяющую вывести отчет по
устойчивости, но после выбора этой опции появляется окно, сообщающее о том, что отчет
по устойчивости не применим для задач с целочисленными переменными (рис 6 8)' Это
происходит вследствие того, что в процессе решения средство Поиск решения не собирает
информацию о чувствительности оптимального значения целевой функции к изменениям
правых частей ограничений или к изменениям коэффициентов целевой функции Это не
означает, что изменения правых частей ограничений или коэффициентов целевой функции
не влияют на решение задачи ЦЛП Безусловно, влияют! В действительности решения за-
дач ЦЛП могут быть чрезвычайно чувствительны к изменениям значений параметров мо-
дели, что наглядно показывает следующий пример.
Рассмотрим задачу ЦЛП с двоичными переменными
Максимизировать 10х, + 100х2 + 1000х3
при ограничениях
29х, + 30х2 + З1х3 </>„
хр х2, х3 равны 0 или 1.
При заданном значении задача легко решается простым перебором решений В табл 6 3
показано оптимальное решение модели и оптимальное значение целевой функции для раз-
личных значений параметра правой части ограничения Из приведенных данных следует,
что изменение правой части ограничения на единицу (с 29 до 30) увеличивает оптимальное
значение целевой функции в 10 раз (с 10 до 100) Очевидно, что, зная о такой возможности,
следует с осторожностью производить подобные изменения.
Таблица 6.3. Чувствительность оптимального решения
Оптимальное решение
А,	х,	х2	х3	Значение целевой функции
29	1	0	0	10
30	0	1	0	100
31	0	0	1	1000
К сожалению, при решении этой или любой другой задачи ЦЛП с помощью средства
Поиск решения информация о чувствительности не предоставляется. Такую информа-
цию можно получить лишь путем повторной оптимизации модели ЦЛП р новыми значе-
ниями параметров Значительную помощь в проведении анализа чувствительности могла
бы оказать описанная в разделе 4.9 надстройка SolverTable, однако из-за отсутствия отче-
та по устойчивости невозможно определить наиболее влияющие на решение параметры
модели. Если модель содержит достаточно много ограничений и переменных решения,
то для получения данных о чувствительности модели ЦЛП может потребоваться много-
кратно запускать SolverTable. Причем при каждом запуске необходимо решить несколько
задач ЦЛП, а оптимизация может оказаться достаточно длительным процессом. Таким
образом, анализ устойчивости моделей ЦЛП может быть очень дорогим и длительным,
но это цена, которую приходится платить за удобства, которые дает включение в модели
условий целочисленности.
414 ЧАСТЬ II. Оптимизационные модели
Эвристические методы
Благодаря важности приложений целочисленной оптимизации в настоящее время
в данной области ведутся интенсивные исследования. Многие из них посвящены эври-
стическим методам Это методы, которые разрабатываются с целью эффективного поис-
ка хороших, хотя и не обязательно оптимальных, решений. В главе 7 мы рассмотрим
один пример эвристического подхода — используемый программой Solver Premium Edi-
tion for Education метод эволюции.
С точки зрения менеджера, эвристическая процедура может оказаться весьма приемле-
мой, а иногда даже более предпочтительной, чем более строгий метод решения задач
ЦЛП, дающий оптимальное решение. Основным критерием является полезная информа-
ция, которую может принести модель, а также затраты на получение данного результата.
6.7.	Реализация моделей целочисленной оптимизации
Целочисленность решений является существенным условием применения оптимиза-
ционных моделей во многих важных реальных ситуациях Успешные исследования и раз-
витие компьютерных технологий позволили достичь прогресса в оптимизации моделей,
содержащих целочисленные переменные. Рассмотрим несколько примеров.
Kelly-Springfield
Компания Kelly-Springfield (производящая автомобильные покрышки) использует
компьютерную систему для прогнозирования продаж, управления запасами, производст-
венного планирования Один из основных модулей системы — модель планирования
производства, определяющая время переналадки оборудования При производстве каж-
дого конкретного вида покрышек производится настройка оборудования путем установ-
ки типичного для производства именно этого вида покрышек штампа. Операция по за-
мене одного штампа другим занимает фиксированное время (и, следовательно, имеет
фиксированную стоимость) Иными словами, существуют фиксированные затраты на
переналадку при переходе от выпуска одного вида покрышек к другому, независимо от
того, сколько покрышек будет произведено после переналадки. Решение о переналадке
(т е. о производстве определенного типа покрышек в течение заданного производствен-
ного периода) или об отказе от нее задается в используемой для решения данной задачи
модели частично-целочисленного ЛП в виде двоичной переменной.
Система в целом (в которую входит модель планирования производства) согласно оцен-
кам уже принесла экономию $500 000 в год Усовершенствованная версия системы позво-
лила на 19% сократить средние товарные запасы, улучшить обслуживание клиентов, повы-
сить производительность; дополнительная экономия при этом составляет 7,9 млн. долл,
ежегодно
Flying Tiger Line
Другое интересное приложение — использование целочисленного программирования
авиакомпанией Flying Tiger Line (это принадлежащая компании Federal Express авиаком-
пания, которая занимается перевозкой грузов) для решения двух стратегических вопро-
сов- организации сети обслуживания, а также выбора и размещения парка самолетов.
Модель для 33 городов и 8 перевалочных пунктов содержала 843 ограничения, 3 807 дей-
ствительных переменных и 156 целочисленных переменных (описывающих выбор само-
ГЛАВА 6. Целочисленная оптимизация 415
летов). Презентация разработанной системы не содержит данных о достигнутой эконо-
мии средств, однако, судя по всему, руководство компании вполне удовлетворено моде-
лью, поскольку она эксплуатируется на постоянной основе.
Hunt-Wesson Foods
Третье приложение — это крупная модель системы распределения товаров компании
Hunt-Wesson Foods, Inc. Модель предназначена для выбора местоположения региональ-
ных распределительных центров, а также определения регионов, которые каждый из этих
центров должен обслуживать. Модель относится к типу частично-целочисленного ЛП,
количества отгружаемой продукции описываются действительными переменными, а два
типа целочисленных переменных означают следующее- ук = ], если пункт к используется
в качестве распределительного центра, и ук = 0 в противном случае; ук1= 1, если регион I
обслуживается складом к, и уи = 0 в противном случае.
Модель насчитывает 17 типов товаров, 14 заводов, 45 возможных пунктов размеще-
ния распределительных центров и 121 регион обслуживания. Размеры модели частично-
целочисленного ЛП, используемой для решения данной задачи, а также стоимость ее
решения просто ошеломляющие. В модели содержится 11 854 ограничения, 727 двоич-
ных переменных, а также 23 513 действительных переменных, для ее решения пришлось
разработать специальный метод оптимизации. Ежегодная экономия средств в результате
выполненного исследования оценивается семизначным числом
Все три кратко описанных приложения обладали рядом общих черт.
1.	В каждом случае решалась задача оптимизации большой модели, имеющей стра-
тегическое значение для соответствующей компании.
2.	Каждое приложение позволило успешно разрешить имеющиеся проблемы компании.
3.	В каждом случае строилась модель частично-целочисленного ЛП большой раз-
мерности.
4.	В каждом приложении требовалось применить для решения задачи специальные
методы.
5.	Для каждого проекта необходимо было найти источники финансирования и не-
стандартные управленческие решения
Приведенные примеры показывают, что хорошая модель позволяет руководству ком-
пании провести анализ на таком уровне, который иначе было бы невозможно обеспе-
чить, однако разработка таких моделей стоит дорого и зачастую требует длительного вре-
мени. Все приведенные примеры являются плодами тесного сотрудничества между раз-
работчиками и руководством компаний. Так, модель компании Kelly-Springfield
разрабатывалась более 15 лет, в результате было создано две версии модели. Таким обра-
зом, использование моделей для решения управленческих задач часто подразумевает во-
влечение высшего руководства в длительный процесс. Небольшие модели быстро и ус-
пешно оптимизируются с помощью электронных таблиц. С крупномасштабными стра-
тегическими моделями редко удается это сделать. Более подробно эти проблемы
рассматриваются в главе 15.
416 ЧАСТЬ II. Оптимизационные модели
6.8.	Заключение
Как отмечалось во введении, целочисленное линейное программирование (ЦЛП) явля-
ется важной для приложений областью условной оптимизации. В разделе 6.2 были перечис-
лены основные типы моделей ЦЛП — целочисленные и частично-целочисленные модели
ЛП В частично-целочисленных моделях линейного программирования только некоторые
переменные решения должны принимать целые значения. Далее обсуждались основные
свойства моделей, содержащих двоичные целочисленные переменные, принимающие зна-
чения только 0 или 1 И, наконец, было дано определение упрощения модели ЦЛП, яв-
ляющейся моделью ЛП и совпадающей с исходной моделью ЦЛП за исключением требо-
ваний целочисленности. В разделе 6 3 показано графическое решение задачи ЦЛП с двумя
переменными Это решение затем использовалось для исследования зависимостей между
моделью ЦЛП и ее упрощением В результате были сделаны следующие выводы.
1.	В модели максимизации оптимальное значение целевой функции упрощенной
модели ЛП всегда является верхней границей оптимального значения целевой
функции исходной модели ЦЛП
2.	В модели минимизации оптимальное значение целевой функции упрощенной мо-
дели ЛП всегда является нижней границей оптимального значения целевой функ-
ции исходной модели ЦЛП
В разделе 6 3 также обсуждалась проблема округления решения упрощенной модели
ЛП. В некоторых приложениях, как показано в разделе 6.1, округленное решение может
служить приемлемой заменой решения задачи ЦЛП. Однако в других случаях ни одно
округленное решение не может быть приемлемым
Раздел 6 4 посвящен использованию двоичных переменных в различных приложени-
ях В разделе 6 5 рассматривались условия, при которых задачи ЛП всегда имеют цело-
численные решения В разделе 6 6 описан метод ветвей и границ, используемый средст-
вом Поиск решения для оптимизации моделей ЦЛП. Запомните, что все методы оптими-
зации моделей ЦЛП (включая метод ветвей и границ) достаточно медленные. Также
отдельно указано, что в отличие от моделей ЛП средство Поиск решения не дает данных
о чувствительности решения задачи ЦЛП, тогда как решения задач ЦЛП могут быть
очень чувствительны к изменениям значений параметров модели Наконец, в разделе 6.7
перечислены некоторые реальные приложения целочисленного программирования.
Основные термины
Метод ветвей и границ. Метод оптимизации моделей ЦЛП, основанный на разбиении исходной
модели на последовательность подмоделей ЛП, решения которых не пересекаются
Модель двоичного целочисленного линейного программирования. Модель ЦЛП, в которой все пере-
менные решения могут принимать только два значения 0 или 1
Модель фиксированных затрат. Модель, в которой заданная переменная решения может быть от-
личной от нуля только после внесения фиксированной платы
Модель целочисленного линейного программирования (ЦЛП). Модель линейного программирова-
ния, в которой некоторые или все переменные должны принимать целочисленные значения
Модель частично-целочисленного линейного программирования. Модель целочисленного линейного
программирования, в которой только некоторые переменные должны быть целыми числами
ГЛАВА 6. Целочисленная оптимизация 417
Округленное решение. Допустимое решение задачи ЦЛП, найденное путем упрощения модели ЛП
и последующего округления всех переменных, которые должны принимать целые значения.
Полный перебор. Решение задачи ЦЛП, при котором совершается обход всех допустимых точек, в ка-
ждой из них вычисляется значение целевой функции и затем выбирается наилучшее решение.
Упрощение. Модель ЛП, которая получена из исходной модели ЦЛП путем удаления ограничений
целочисленности
Эвристический метод. Метод оптимизации, позволяющий находить хорошие, но не обязательно
оптимальные, решения задачи ЦЛП
Контрольные вопросы
Да/нет
1.	На практике часто производится округление решений задач ЛП, чтобы удовлетво-
рить требованию целочисленности переменных решения.
2.	В общем случае решить задачу ЦЛП не сложнее, чем решить задачу Л П.
3.	Двоичные переменные можно использовать в моделях ЦЛП вместо функции Excel
ЕСЛИ для представления дихотомических решений.
4.	В модели максимизации оптимальное значение целевой функции упрощенной
модели ЛП является нижней границей оптимального значения целевой функции
исходной модели ЦЛП или частично-целочисленного Л П.
5.	Первый шаг в получении округленного решения для модели частично-
целочисленного Л П заключается в решении ее упрощенной задачи ЛП
6.	Решение задачи ЦЛП методом полного перебора заключается в вычислении зна-
чений целевой функции во всех угловых точках допустимого множества ее упро-
щенной модели ЛП
7.	В упрощенной модели ЛП, построенной для модели ЦЛП распределения средств,
количество ограничений равно количеству временнь/х периодов.
8.	В модели ЦЛП с п двоичными переменными, каждая из которых показывает, вы-
бран или нет определенный вариант, ограничение, разрешающее выбирать не бо-
лее к вариантов, можно описать с помощью неравенствах, + х2 + + хп<к.
9.	В модели размещения складов компании STECO оптимальные количества авто-
фургонов, посылаемых с каждого склада на каждый завод, были целыми числами
потому, что после того, как склады выбраны, данная модель превращается в транс-
портную модель с целочисленными значениями предложения и спроса.
10.	Пустьх, ИХ; - двоичные переменные и х, = 1, если принято решение построить
завод в пункте I. Условие “завод в пункте 2 можно строить только в том случае, ес-
ли строится завод в пункте 1” записывается с помощью неравенствах, <х2.
11.	Рассмотрим транспортную модель с целыми значениями предложения и спроса,
в которой наложены дополнительные условия целочисленности на переменные
решения xtJ. Поскольку эта модель является моделью ЦЛП, при ее создании с по-
мощью средства Поиск решения нужно указать, что изменяемые ячейки должны
быть целыми.
418 ЧАСТЬ II. Оптимизационные модели
Выберите правильный ответ
12.	В модели ЦЛП
а. за исключением ограничений целочисленности, все функции ограничений ли-
нейны;
b все переменные решения должны быть целыми;
с. все переменные решения должны быть неотрицательными;
d а и b
13.	В модели частично-целочисленногоЛП’
а целевая функция линейна;
Ь. все переменные решения должны быть целыми;
с одни коэффициенты должны быть целыми, а другие нет;
d все вышеперечисленное.
14.	В упрощении модели ЦЛП’
а допускается нелинейность целевой функции;
b игнорируются ограничения целочисленности для переменных решения;
с. ослабляются ограничения неотрицательности для переменных решения;
d все вышеперечисленное
15.	Округленное решение задачи ЦЛП, в которой требуется максимизировать целевую
функцию, может оказаться недопустимым, поскольку.
а оно нарушает ограничения целочисленности;
b оно нарушает ограничения неотрицательности,
с его значение целевой функции меньше, чем значение целевой функции упро-
щения,
d. ничего из вышеперечисленного.
16.	Пусть хк их,- двоичные переменные для проектов к и т соответственно
(значение 1 означает выбор проекта), тогда ограничение х4 + хт < 0 означает, что:
а проект к не может быть выбран, пока не будет выбран проект /и;
b проект к должен быть выбран, если выбран проект /и;
с.	проект т не может быть выбран, пока не будет выбран проект к
d.	ничего из вышеперечисленного.
17.	Предположим, что продукция или не производится вовсе, или производится в ко-
личестве, не меньше L. Обозначим через х количество произведенной продукции.
Ситуации соответствуют два ограничения:
а.	х + Му <0,х - Ly > 0;
b.	х - Му >0,х - Ly > 0;
с х- My<0,x- Ly>Q-,
d х - Му < 0, х - Ly < 0;
где М — произвольное очень большое число, а у — двоичная переменная.
ГЛАВА 6. Целочисленная оптимизация 419
18.	При решении задачи ЦЛП, в которой необходимо максимизировать целевую
функцию, нижнюю границу оптимального значения целевой функции можно най-
ти следующим образом
а.	найти упрощение данной модели ЦЛП и использовать ее оптимальное значе-
ние целевой функции,
Ь.	найти допустимое решение для модели ЦЛП любым доступным способом
и использовать его значение целевой функции,
с.	решить упрощенную задачу ЛП, округлить решение и использовать значение
целевой функции округленного решения;
d ничего из вышесказанного
19.	Оптимизация модели ЦЛП с помощью метода ветвей и границ-
а начинается с решения упрощенной задачи ЛП данной модели;
b требует оптимизации многих моделей ЛП, если решение первоначальной уп-
рощенной задачи Л П содержит дробные значения целочисленных переменных,
с при наличии дробного значения целочисленной переменной требуется доба-
вить ограничение к исходной упрощенной модели Л П,
d все вышеперечисленное
20.	Решение задачи частично-целочисленного ЛП, полученное с помощью средства
Поиск решения
а не содержит информации о чувствительности решения,
b содержит информацию о чувствительности только для нецелочисленных пере-
менных,
с содержит информацию о чувствительности, относящуюся только к изменени-
ям правых частей ограничений,
d. содержит информацию о чувствительности только целевой функции
Более сложные вопросы
Следующие десять вопросов относятся к описанной ниже модели
Фирма имеет десять торговых точек, в каждую из которых необходимо поставлять оп-
ределенную продукцию Значения спроса (все положительные) в торговых точках равны
dt, d2, . , dm, и спрос должен быть в точности удовлетворен (т.е в торговую точку i должно
быть доставлено ровно d, единиц продукции) Фирма может удовлетворять спрос, достав-
ляя продукцию непосредственно от поставщика За каждую доставленную единицу про-
дукции поставщик получает $50, независимо от расположения торговой точки Если объ-
ем заказа превышает D единиц, то поставщику платится только $35 за доставку единицы
продукции независимо от местоположения торговой точки Но поскольку все </ < D, сис-
тема скидок не применяется. Фирма рассматривает вариант аренды склада за К долларов
и использования его в качестве промежуточного хранилища Склад может заказывать
любое количество продукции и распределять ее по любым торговым точкам Было при-
нято решение, что склад будет платить за доставку так же, как и торговые точки ($50 за
единицу продукции, если объем заказа меньше D, и $35 — если объем заказа больше D)
420 ЧАСТЬ II. Оптимизационные модели
Стоимость доставки единицы продукции со склада в торговую точку 7 равна С, (7=1,
2,	10). Предположим, что D<^dt . Руководство компании хочет выяснить следую-
щие вопросы.
1. Следует ли арендовать склад?
2. Если да, то какие торговые точки будет обслуживать склад, а какие будут обслужи-
ваться непосредственно поставщиком?
Для разработки модели, призванной ответить на эти вопросы, введем следующие обо-
значения: х,— количество продукции, направленное непосредственно от поставщика
в торговую точку 7, у, — количество продукции, отправленное со склада в торговую точку
7, z — количество продукции, отправленное поставщиком на склад.
Множество ограничений для данной модели запишем так:
x, + y=d„ i = 1,2,..., 10,
Z>tD,
z<tid”
^^,>0(1= 1,2,..., 10); z>0, / = 0 или 1.
21.	Данная модель должна иметь следующую целевую функцию.
а минимизировать ^50х, +^С,у, ,
Ь.	минимизировать ^50х, +^(С, + 35)у, + tK ,
с.	минимизировать ^50х, +35z + ^Clyl + tK ,
d.	минимизировать ^(50x, +C,y) + 35D,
e.	ничего из вышеперечисленного.
22.	При такой постановке задачи никогда не будет оптимальным решение, при кото-
ром склад заказывает количество продукции меньше D единиц:
а.	да;
Ь.	нет.
23.	Руководству компании следует принять решение об аренде склада, если:
а.	оптимальное значение D положительно;
Ь.	оптимальное значение tположительно;
с.	оптимальное значение z положительно;
d.	выполнены все перечисленные условия;
е. Ьис.
ГЛАВА 6. Целочисленная оптимизация 421
24.	Рассмотрим такую торговую точку к, при которой 35 + Ск > 50. Поскольку удель-
ные затраты на доставку непосредственно от поставщика в пункт к меньше, чем
удельные затраты на доставку через склад, в оптимальном решении данная торго-
вая точка не будет получать продукцию как со склада, так и непосредственно от
поставшика.
а.	Да.
Ь.	Нет
25.	В оптимальном решении ни одна торговая точка не снабжается из двух
источников — непосредственно поставщиком и через склад.
а. Да
b Нет.
26.	Пусть 35 + С: = 50 (/ = 1, ., 10). Тогда в оптимальном решении 1 = 0
а.	Да
Ь.	Нет.
27.	Данная модель может иметь оптимальное решение, при котором суммарное коли-
чество продукции, заказанное поставщику, превышает ^d,.
а.	Да.
Ь.	Нет.
28.	Если оптимальное значение z = ^d, , то оптимальное решение имеет вид х' = 0
(7=1,..., 10),у," = d: (i= 1, . , 10), t = 1.
а. Да
b Нет
29.	В данной модели допускается возможность того, что на складе останется запас
продукции после удовлетворения спроса во всех торговых точках.
а.	Да.
Ь.	Нет.
30.	Предположим, что все С: > 15.
а. Оптимальным решением задачи является х’ ^d^i^ 1, ..., 10), у' = 0 (/= 1, . ,
io),z‘ = r =0
Ь При некоторых значениях параметров dt решение может быть другим, поэтому
следует оптимизировать данную модель с помощью средства Поиск решения.
Ответы
1.	Да. 2. Нет. 3. Да. 4 Нет. 5. Да 6. Нет. 7. Нет. 8. Да. 9. Да. 10. Нет. 11. Нет. 12 d.
13. а. 14. Ь. 15. d. 16. d. 17. с. 18. b. 19. d. 20. а. 21. с. 22. а. 23. е. 24. Ь. 25. Ь. 26. а.
27. а. 28. а. 29. а. 30 а.
422 ЧАСТЬ II. Оптимизационные модели
Учебные задачи
6 1 Фирма производит два вида продукции, А и С Производственная мощность линии по вы-
пуску продукции А составляет 7 единиц в день Каждую единицу продукции С требуется
сушить 4 ч, ресурс времени сушки составляет 22 ч в день Кроме того, каждую единицу
продукции А необходимо шлифовать в течение 2 ч, а каждую единицу продукции С — 3 ч
Общий ресурс времени шлифовки составляет 19 ч в день Каждая единица продукции А
приносит прибыль $1, а каждая единица продукции С — $3 Фирма хочет составить еже-
дневный план выпуска, позволяющий получить максимальную прибыль Выпуск обоих
видов продукции может выражаться только целыми числами
а Формализуйте данную модель в виде задачи ЦЛП.
b С помощью программы GLP найдите оптимальное упрощение модели ЦЛП
с С помощью программы GLP найдите оптимальное решение задачи ЦЛП
d Найдите целочисленное решение путем округления решения упрощенной задачи ЛП
Является ли округленное решение допустимым9
е Какую сумму прибыли потеряет фирма, если примет данное округленное решение9
6 2 Дана модель ЦЛП
максимизироватьх, + 2х2
при ограничениях
Зх, +х2< 15,
Зх, + 7х2 < 42,
х,, х2 > 0 и целые
а С помощью программы GLP найдите оптимальное упрощение данной модели
b Сколько допустимых точек имеет задача9
с С помощью программы GLP найдите оптимальное решение задачи ЦЛП
d Найдите целочисленное допустимое решение путем округления ответа, полученного
для упрощенной модели ЛП Является ли округленное решение оптимальным9
6 3 Дана модель минимизации ЦЛП Какую границу — верхнюю или нижнюю — оптималь-
ного значения целевой функции задачи ЦЛП дает оптимальное значение целевой функции
ее упрощения9 Ответ поясните
6 4 Дана модель минимизации ЦЛП Значение целевой функции в некой допустимой точке,
полученной в результате округления, является верхней или нижней границей для опти-
мального значения модели ЦЛП9 Поясните свой ответ
6 5 Дана модель максимизации ЦЛП Какую границу — верхнюю или нижнюю — оптималь-
ного значения для задачи ЦЛП дает оптимальное значение целевой функции ее упроще-
ния9 Ответ поясните
6 6 Дана модель максимизации ЦЛП Значение целевой функции в некой допустимой точке,
полученной в результате округления, является верхней или нижней границей для опти-
мального значения модели ЦЛП9 Поясните свой ответ
6 7 Оптимизируйте модель из упражнения 4 54 главы 4 как модель ЦЛП Оцените, насколько
дольше происходит оптимизация модели ЦЛП по сравнению с соответствующей моделью
ЛП На сколько уменьшилось оптимальное значение целевой функции по сравнению
с решением исходной задачи ЛП9 На сколько отличается решение задачи ЦЛП от решения
задачи ЛП9
6 8 Дана модель из упражнения 6 1
максимизировать Л + ЗС
ГЛАВА 6. Целочисленная оптимизация 423
при ограничениях	А < 7,
4С<22,
24 + ЗС<19,
А, С> 0 и целые
Постройте график зависимости оптимального значения целевой функции от значений
правой части второго ограничения, изменяющихся в диапазоне от 0 до 24 Для получения
необходимых данных воспользуйтесь программами GLP или SolverTable
6 9 Дана модель ЦЛП из упражнения 6 2 Постройте график зависимости оптимального значе-
ния целевой функции от значений правой части ограничения Зх, + х2 < а, если а изменяет-
ся в диапазоне 0 < а < 24 Для получения необходимых данных воспользуйтесь программа-
ми GLP или SolverTable
6 10 Дана следующая модель ЦП П
Минимизировать 4х, + 5х2
при ограничениях
Зх, + 6х2> 18,
5х, + 4х2 > 20,
8х, + 2х2>16,
7х, + 6х2 < 42,
х,, х2 > 0 и целые
а С помощью программы GLP найдите оптимальное упрощение данной модели
b Перечислите все допустимые точки
с С помощью программы GLP найдите оптимальное решение задачи ЦЛП
d С помощью программы GLP найдите допустимое округленное решение
е Является ли найденное округленное решение оптимальным9
Прикладные задачи
6 11 Задача инвестирования Управляющему инвестиционным портфелем поручено распоря-
диться суммой $100 000 Выбор осуществляется из списка, в котором перечислено 20 видов
ценных бумаг Известно, что чистый доход от вложения $1 в акции t составляет г,, тогда при
вложении х долларов в акции i в конце периода будет получена сумма (1 +г)х Чтобы
обеспечить сбалансированность инвестиционного портфеля, менеджер использует сле-
дующие (основанные на здравом смысле) правила
а Не инвестировать более $20 000 в один вид ценных бумаг
b Если определенные акции покупаются, сумма покупки составляет не менее $5 000
Перед менеджером стоит задача максимизировать доход при условии соблюдения указан-
ных правил Сформулируйте данную задачу в виде модели частично-целочисленного Л П
6 12 Составление расписания полетов Авиакомпания Alpha Airline хочет составить расписание
полетов так, чтобы в нем было не более одного вылета из Чикаго в каждый из следующих
городов Колумбус, Денвер, Лос-Анджелес и Нью-Йорк Возможное время вылетов 8-00,
10-00 и 12-00 Компания арендует самолеты, стоимость аренды составляет $5000, если вы-
лет состоится до 10-00 включительно, и $3000 после 10-00 Допускается арендовать не бо-
лее двух самолетов на одно время вылета Кроме того, если в определенное время осущест-
вляется вылет в Нью-Йорк, в это же время должен производиться вылет в Лос-Анджелес
Ожидаемая удельная прибыль до внесения арендной платы в тысячах долларов в расчете на
один полет представлена в таблице Сформулируйте и решите задачу, которая позволит со-
ставить расписание, дающее максимальную прибыль
424 ЧАСТЬ II. Оптимизационные модели
	8-00	Время вылета 10-00	12-00
Колумбус	10	6	6
Денвер	9	10	9
Лос-Анджелес	14	11	10
Нью-Йорк	18	15	10
6 13 Коммунальное предприятие, занимающееся энергоснабжением, ежедневно вынуждено
решать, какие электрогенераторы запускать в работу Рассматриваемое предприятие имеет
в своем распоряжении три генератора, характеристики которых представлены в таблице
День можно условно разделить на два периода в первый период потребность в энергии со-
ставляет 2900 МВт, а во второй период — 3900 МВт Генератор, запущенный в первый пе-
риод, можно использовать во втором периоде без дополнительных затрат на запуск Все ге-
нераторы в конце каждого дня выключаются Сформулируйте задачу в виде модели час-
тично-целочисленного ЛП и решите ее
Генератор	Фиксированные затраты на запуск,S	Затраты на 1 МВт, S	Максимальная мощность за период, МВт
А	3000	5	2100
В	2000	4	1800
С	1000	7	3000
6 14 Производственное планирование Некая технологическая линия используется для выпуска двух
видов продукции Соответствующие данные приводятся в табл 6 4 Общий ресурс времени
(для производства и переналадки) составляет 80 ч в неделю В начале недели 1 и в конце неде-
ли 4 запасы продукции равны нулю Стоимость хранения единицы запаса при переходе от од-
ной недели к следующей составляет $4 для обоих видов продукции Единица неудовлетворен-
ного спроса оценивается в $10 для продукции А и в $15 для продукции В Данные о спросе
представлены в табл 6 5В конце каждой недели конвейер останавливается для профилакти-
ческого осмотра и наладки В течение недели может производиться только один вид продук-
ции Сформулируйте и решите задачу планирования на 4-недельный период как модель час-
тично-целочисленного ЛП Цель — максимизировать прибыль за период в 4 недели.
Таблица 6.4. Данные о продукции
Продукция
	А	В
Время запуска конвейера, ч	5	10
Время производства единицы продукции, ч	0,5	0,75
Затраты на настройку конвейера, $	200	400
Удельные затраты на производство единицы продукции, $	10	15
Цена продажи, $	20	30
ГЛАВА 6. Целочисленная оптимизация 425
	Таблица 6.5. Данные о спросе
6 15.	Неделя Продукция	12	3	4 А	80	100	75	80 В	15	20	50	30 Совет директоров крупного производственного предприятия рассматривает ряд инвести- ционных предложений, представленных в следующей таблице. Обозначим через А, сум- марный доход от инвестиционного проекта /, а через С, затраты на этот проект Совет ди- ректоров хочет максимизировать суммарный доход, при этом общий объем инвестиций не должен превышать М долларов Сформулируйте данную задачу как модель Щ1П. Дайте оп- ределение переменных решения и запишите уравнения модели.
6 16.	Инвестиционный проект Условия 1	Отсутствуют 2	Можно, если принят проект 1 3	Можно, если принят проект 2 4	Должен быть принят, если приняты проекты 1 и 2 5	Нет, если принят проект 1 или 2 6	Нет, если приняты проекты 2 и 3 7	Можно, если принят проект 2 и не принят проект 3 Компания-дистрибьютор хочет минимизировать затраты на транспортировку товаров с при- надлежащих ей складов А, В и С в торговые точки 1, 2 и 3. Затраты на транспортировку еди- ницы продукции со складов в торговые точки представлены в таблице.
6 17.	Торговые точки Склад	1	2	3 А	15	32	21 В	9	7	6 СИ	18	5 Спрос	200	150	175 Фиксированные затраты на открытие склада составляют $500 для склада А, $750 для склада В и $600 для склада С, причем компании необходимо открыть не менее двух складов Предполагается, что склады имеют неограниченный объем Сформулируйте и решите за- дачу ЦЛП, которая позволит определить, какие склады следует открыть, и сколько продук- ции будет доставлено с каждого склада в каждую торговую точку Некая работа состоит из пяти операций А, В, С, D и Е, каждая из которых может выполняться любым из двух станков (станок 1 или 2). Время, необходимое для выполнения каждой операции на каждом станке, приводится в таблице.
426	ЧАСТЬ II. Оптимизационные модели
	А	В	С	D	Е Станок 1	5	9	2	3	4 Станок 2	3	4	7	5	4 Сформулируйте и решите задачу ЦЛП, которая позволит распределить операции по стан- кам так, чтобы минимизировать величину Мах(Т1, Т2), где Т1 — суммарное время работы станка 1, а Т2 — суммарное время работы станка 2
6 18	Рассмотрим модель размещения складов компании STECO на рис 6.8 При заданном оп- тимальном решении об аренде складов А, В и С запишите в математической форме транс- портную модель, позволяющую оптимально распределить грузовики
6 19	Городской совет пришел к выводу, что для нужд города необходимо открыть пожарные стан- ции или в пунктах А, В и С или в А, С и D, либо в пунктах В, С и D Затраты на открытие по- жарной станции (в млн долл ) составляют в пункте А— 1,5, в В — 2,3, в С — 1,8 и в D — 2,1 Сформулируйте и решите задачу ЦЛП, которая позволит городскому совету определить, ка- кие пожарные станции открыть, чтобы обслуживать город с минимальными затратами
6 20	Коммунальное предприятие электроснабжения планирует расширение мощностей по про- изводству электроэнергии на протяжении следующих пяти лет В настоящее время генери- руюшая способность составляет 800 МВт, но, как следует из прогнозов спроса, предпри- ятию потребуются дополнительные мощности (см табл ) Год	Минимальная необходимая мощность, МВт 1	880 2	960 3	1050 4	1160 5	1280 Предприятие может повысить генерирующую способность путем установки дополнитель- ных генераторов на 10, 50 и 100 МВт Затраты на установку одного генератора зависят от его мощности и года подключения (см табл ) 	Год	 Мощность генератора, МВт	1	2	3	4	5 10	300	250	208	173	145 50	670	558	465	387	322 100	950	791	659	549	458 После того как генератор будет подключен, его мощность можно использовать для удовле- творения потребительского спроса в последующие годы. Сформулируйте и решите задачу ЦЛП, которая минимизирует затраты на подключение генераторов при условии удовлетво- рения требований к минимальной мощности
6 21	Компания Norco Home Cosmetics начинает продвижение своих товаров на рынок региона, находящегося на юге штата Юта и состоящего из шести округов Ниже схематически пока- зана карта, на которой представлено относительное расположение округов и численность их населения Р, Компания планирует назначить в данный регион двух торговых предста- вителей Каждый представитель будет отвечать за два округа (базовый и соседний) Округа считаются соседними, если они имеют общую сторону, наличия общего угла недостаточно
ГЛАВА 6. Целочисленная оптимизация 427
1‘	2	з’
pt 4	5	Рь
Так, на приведенной карте округа 1 и 2 являются соседними, а округа 1 и 5 — нет Компа-
ния стремится сделать так, чтобы суммарное население в округах с назначенными предста-
вителями было максимальным Пример допустимого решения выбрать базовым округ 4
с соседним округом 1, а также сделать базовым округ 3 с соседним 2 Значение целевой
функции для такого решения равно Р, + Р2 + Р5 + Р4
Введем следующие переменные Bt = 1, если округ j выбран в качестве базового, и В. = О
в противном случае (/' = 1,	6), At = 1, если округ i выбран в качестве соседнего для базо-
вого округа у, и Ав = 0 в противном случае (/ = 1, ,6, округи i и j — соседние) Таким
образом, заданы переменные решения А,, В2, В3, Ва, В.. Bt, A2I, Ап, Ап, AS2, Ai2,Л23, Л63 и т д
а В модели не должно быть двойного счета (т е в одном варианте назначения один и тот
же округ не должен одновременно выступать в качестве базового и соседнего) Запи-
шите ограничение, которое сделает невозможным двойной счет для округа 1
b Запишите ограничение “если торговый представитель назначается в базовый округ 2,
то этот же торговый представитель должен быть назначен в один из соседних округов”
с Запишите ограничение “если один из двух округов, соседних с округом 1, выбран в качестве
соседнего округа (к округу 1), то округ 1 должен использоваться в качестве базового”
d Верно ли утверждение, что данную модель можно описать с помощью ограничений
в виде 12 неравенств и 1 равенства'’
е Верно ли утверждение, что данную модель можно описать с помощью ограничений
в виде 7 неравенств и 6 равенств9
6 22 Прочитайте описание ситуации перед вопросом 21 в разделе “Контрольные вопросы”
Предположим, что в дополнение к указанным там условиям с каждой отправкой груза от
поставщика связаны фиксированные затраты А Тогда если поставщик производит 4 от-
грузки (непосредственно в торговые точки 3, 5 и 8 и на склад), то это влечет за собой до-
полнительные затраты в сумме 4А Сформулируйте задачу частично-целочисленного ЯП
6 23 Компания Bradford Electronics производит разнообразные DVD-дисководы, которые уста-
навливаются в домашние цифровые видеоплейеры У компании пять сборочных заводов,
где она может собирать DVD-дисководы Некоторые заводы более автоматизированы, по-
этому на них переменные затраты на сборку ниже, однако выше единовременные затраты
переналадки при переходе к выпуску определенной модели DVD-дисковода Компания
получила заказ на сборку 2500 DVD-дисководов определенной модели На основании при-
веденных в таблице данных о единовременных затратах на переналадку и переменных за-
тратах на сборку на каждом из пяти сборочных заводов определите, сколько DVD-
дисководов следует собрать на каждом заводе, чтобы минимизировать суммарные затраты
Сборочный завод	Удельные затраты иа сборку, S	Производственная мощность	Затраты на переналадку, S
1	62	500	12 000
2	68	600	6 000
3	72	700	3 000
4	78	450	1 500
5	85	1000	500
428 ЧАСТЬ II Оптимизационные модели
Ситуация для анализа | Назначение торговых представителей
Одна из основных идей, проводимых в данной книге, является идея о том, что ме-
неджер выполняет роль посредника между реальным миром и моделью. Именно ме-
неджер должен решить, приемлемы ли сделанные предположения и имеют ли предло-
женные моделью результаты смысл в контексте реальной решаемой проблемы.
Салли Эриксон заведует отделом сбыта отделения компании Lady Lynn Cosmetics
на Среднем Западе. Lady Lynn — быстро растущая компания, продающая косметику
через своих представителей. Представители, как правило, общаются с большинством
своих клиентов на специально организованных приемах и презентациях, демонстри-
руя продукцию компании и принимая заказы. Гости имеют возможность выиграть
образцы продукции и оформить заказы.
Перед Салли стоит задача назначить представителей в семь восточных округов
штата Айова (рис. 6.15). В настоящее время в ее распоряжении есть только два под-
готовленных представителя. Политика компании Lady Lynn состоит в том, что пред-
ставитель обслуживает базовый и один соседний округ. Действующий механизм на-
значений основан на эвристическом подходе, при котором представители назнача-
ются последовательно. Округ с наибольшей численностью населения выбирается
в качестве базового для первого представителя, к нему присоединяется соседний ок-
руг с наибольшим населением. В качестве следующего базового округа выбирается
свободный округ с наибольшим населением и т.д. Численность населения рассмат-
риваемых округов приводится ниже.
Рис. 6.15. Семь восточных округов штата Айова
ГЛАВА 6. Целочисленная оптимизация 429
1	Бучанан	16 000
2	Делавэр	15 000
3	Дубьюк	98 000
4	Линн	109 000
5	Джонс	4 000
6	Джэксон	6 000
7	Клинтон	100 000
Согласно схеме в качестве базового округа для первого представителя будет вы-
бран округ Линн Соседними округами являются Бучанан, Делавэр и Джонс. Из этих
трех округов наибольшее население имеет Бучанан, следовательно, он будет выбран
в качестве соседнего округа для первого представителя Второй представитель дол-
жен находиться в округе Клинтон, а соседним округом для него будет выбран
Джэксон Цель Салли —добиться, чтобы суммарное население округов с назначен-
ными представителями было максимальным. Поскольку население округа Дубьюк
почти такое же, как и округа Клинтон, Салли опасается, что предложенное решение
может не быть оптимальным, и краткий анализ показывает, что так оно и есть: пара
Дубьюк-Делавэр дает лучший результат, чем Клинтон-Джэксон. Поэтому Салли
принимает решение отказаться от традиционного способа назначений и создать мо-
дель ЦЛП. Хотя данная модель достаточно проста, предполагается, что ее можно бу-
дет модифицировать и использовать при назначении 60 представителей компании
в более чем 300 округах. В формулировке задачи используются следующие обозначе-
ния. Yt - 1, если округ j является базовым, и У^ = 0 в противном случае (/=1, ...,7);
Ху = 1, если соседний округ 7 присоединяется к базовому у, и Ху = 0 в противном слу-
чае (/ = 1,..., 7,j = 1,..., 7). Математическая модель приводится ниже.
Максимизировать 16 + 15 У2 + 98 У3 + 109 Г4 + 4У5 + 6У6 + 100 У, + 15А"21 + 109Х41 + 16Л12+ +
98%33 + 109Х42 + 4%„ + 15_¥33 + 4Л53 + 6Л63 + 16Л14 + 15%24 + 4Х„ + 15Л25 + 98Х5 + 109Л45 +
+6%65 + 100Л„ + 4Х„ + 98ХМ + 100%76 + 4Х„ + 6Х„
при ограничениях
Салли создала табличную версию модели и оптимизировала ее с помощью сред-
ства Поиск решения. В полученном решении У, = У, = 1 и %|4 =J41 = 1. Таким обра-
зом, округа Линн и Бучанан выбраны в качестве базовых, и те же самые округа вы-
браны в качестве прикрепленных соседних. Оптимальное значение целевой функции
оказалось равным 250, это означает, что два представителя будут обслуживать
250 000 человек. Решение, полученное с помощью эвристического подхода, действи-
тельно было неверным, и Салли была довольна, что обнаружила это до того, как по-
пыталась реализовать его. Ее несколько смущало, что в оптимальное решение не во-
шли ни Дубьюк, ни Клинтон, однако она была уверена, что средство Поиск решения
сделало оптимальный выбор, и собралась реализовать его.
430
ЧАСТЬ II. Оптимизационные модели
Вопросы
1	Очевидно, что полученное Салли решение неверно. Найдите путем просмотра
данных верное оптимальное решение Сколько альтернативных оптимумов су-
ществует в данном случае9
2	Какую ошибку допустила Салли9 Напишите дополнительные ограничения, ко-
торые позволят получить правильную формулировку.
3	Разработайте табличную версию исправленной модели, оптимизируйте ее с по-
мощью Поиск решения и найдите оптимальное решение.
Ситуация для анализа | Финансовое планирование
Часто необходимо организовать поток поступления денежных средств на протя-
жении определенного периода Например, в судебном деле о нанесении травмы ист-
цу необходимо компенсировать будущие медицинские расходы или потерю заработ-
ной платы или и то, и другое Обе стороны часто согласны на единовременную вы-
плату суммы, “эквивалентной по величине” поступлениям средств за определенное
время Но как определить, какой должна быть эта сумма? Истец, который хочет мак-
симизировать размер платежа, настаивает, что процентные ставки будут низкими,
поэтому единовременная выплата должна быть большой Ответчик утверждает, что
процентные ставки будут высокими, поэтому потребуется меньшая сумма
Одним из выходов может служить покупка портфеля облигаций с тем, чтобы до-
ход от облигаций обеспечивал необходимый приток средств Облигации предлагают
гарантированные ежегодные выплаты (определяемые процентной ставкой) и номи-
нальную стоимость при наступлении срока погашения Таким образом, можно опре-
делить, каким будет вклад каждой облигации в обеспечение притока средств Теку-
щая цена облигаций также известна, поэтому задача определения единовременной
суммы становится задачей нахождения портфеля облигаций наименьшей стоимости,
способного обеспечить заранее оговоренный приток денежных средств
Многие модели планирования пенсионных фондов можно рассматривать как мо-
дели обеспечения потоков финансов В этих моделях корпорация или профсоюз обя-
заны удовлетворять потребности пенсионного фонда в средствах на протяжении оп-
ределенного периода планирования. Цель состоит в покупке портфеля с низким
риском и минимальной стоимостью, который сможет обеспечить необходимый по-
ток доходов
Рассмотрим следующую простую, но концептуально достоверную модель прито-
ка средств. Потребности в средствах на следующие пять лет представлены в табл. 6.6.
Таблица 6.6. Потребности в денежных средствах, млн долл
Год_________________________2000______2001______2002______2003______2004
Потребности в средствах	10	И	12	14	15
Инвестиционный комитет рассматривает пять видов инвестиций с низким уров-
нем риска- депозиты фонда страхования денежного рынка, выплачивающие 5% го-
ГЛАВА 6. Целочисленная оптимизация
431
довых, и четыре вида облигаций Американской арбитражной ассоциации, характе-
ристики которых представлены в табл. 6.7.
Таблица 6.7. Стоимостные показатели облигаций, млн долл			
Облигация Текущая стоимость	Купон (ежегодный)	Количество лет до погашения	Номинальная стоимость
1	0,97	0,04	1	1,00
2	0,947	0,05	2	1,00
3	0,79	0,00	3	1,00
4	0,829	0,03	4	1,00
Предположим, что все переводы средств, связанные с инвестициями, происходят
1 января каждого года. В табл. 6 8 представлены поступления средств для облигаций
каждого вида.
Таблица 6.8. Стоимостные показатели облигаций, млн долл
Облигация	2000	2001	2002	2003	2004
1	-0,970	1,040			
2	-0,947	0,050	1,050		
3	-0,790	0,000	0,000	1,000	
4	-0,829	0,030	0,030	0,030	1,030
Отметим, что в год погашения облигации доход равен сумме купона и номи-
нальной стоимости облигации. Отметим также, что облигация 3 имеет нулевой об-
лигационный купон, т.е. до наступления срока погашения проценты по ней не
выплачиваются.
В большинстве моделей обеспечения притока средств существует также воз-
можность получения ссуды. В данной модели предполагается, что руководители
пенсионного фонда имеют возможность получить ссуду на любую желаемую сумму
под 1,3% годовых. Ссуды выдаются только на 1 год, т е. сумма, взятая в 2000 году,
должна быть возвращена в 2001. Однако сразу после этого можно взять новую ссу-
ду сроком на 1 год.
В реальности движение денежных средств (как приток, так и отток) происходит
в различные моменты на протяжении года. В нашей модели приняты следующие
предположения.
1. Весь капитал, поступающий в определенном году (доходы от облигаций; средст-
ва, инвестированные в фонд денежного рынка, а также полученные от этих фон-
дов проценты; ссуды, полученные в данный год, и исходная единовременная
сумма), доступен наутро 1 января.
2. Весь отток капитала в определенном году (средства, необходимые пенсионному
фонду, выплаты задолженности и процентов за предыдущие годы, депозиты)
происходит в полдень 1 января.
Эти предположения дают возможность описать взаимосвязи между различными
потоками средств.
432 ЧАСТЬ II. Оптимизационные модели
1	В 2000 году все средства (отток капитала), необходимые для удовлетворения
нужд пенсионного фонда, а также покупки акций или внесения денег на депо-
зит, должны поступить из исходной единовременной суммы или ссуд, взятых
в 2000 году.
2	. Долги и проценты по займам 2000 года могут быть оплачены из средств, взятых
взаймы в 2001 году
Вопросы
1.	Постройте кривую доходности для четырех видов облигаций, перечисленных
в табл. 6.7 Для этого необходимо сначала определить для каждой облигации про-
центную ставку, которая делает текущую стоимость денежных потоков для данной
облигации равной нулю. Затем строятся графики зависимости процентной ставки
от срока погашения облигации для указанных четырех видов облигаций.
2.	Прокомментируйте общую форму графиков функций, построенных в ответе на во-
прос 1 Какие выводы на основании формы этих графиков можно сделать о пред-
почтениях и ожиданиях кредиторов и заемщиков? Обязательно ли кривая доходно-
сти должна иметь такую форму? Какие предпочтения и ожидания заемщиков
и кредиторов могут вызвать изменение формы данной кривой?
3.	Пусть цель состоит в том, чтобы минимизировать первую выплачиваемую еди-
новременно сумму Сформулируйте модель частично-целочисленного ЛП для
решения данной задачи. Предполагается, что можно купить только целое число
облигаций и покупки осуществляются в январе 2000 года В пятом году (2004)
брать ссуду невозможно. В вашей модели для каждого года должно быть балан-
совое ограничение, требующее, чтобы поступления средств были равны исполь-
зованию средств
4	В реальной жизни данные табл. 6 6 являются оценками будущих потребностей,
поскольку точно знать их заранее невозможно. Какие другие предположения
были сделаны при создании этой модели?
5.	Всегда ли существует допустимое решение для модели общего вида, созданной
в ответе на вопрос З9 Поясните ответ
6.	Оптимизируйте сформулированную в ответе на вопрос 3 задачу с помощью сред-
ства Поиск решения
7.	Решите задачу, используя следующую эвристическую процедуру:
а.	решается задача из вопроса 3 как задача ЛП;
Ь.	округляется количество облигаций до ближайшего целого в большую сторону;
с.	фиксируются целые переменные на уровнях, определенных в предыдущем
пункте, и полученная модель оптимизируется как модель ЛП.
8.	Вычислите отношение оптимальных значений целевых функций задач вопроса 7,
с и 6. Как вы думаете, каким должно быть это значение — больше или меньше 1?
Почему? Какие выводы на основании величины этого отношения можно сделать
о решении реальных (более крупных) задач обеспечения притока средств?
9.	Как интерпретируются теневые цены, полученные при решении задачи ЛП в во-
просе 7, а!
ГЛАВА 6. Целочисленная оптимизация 433
10.	Прокомментируйте следующее утверждение: “одним из способов минимизиро-
вать исходную единовременную сумму является ограничение покупки облигаций
с наивысшей доходностью”.
11.	Прокомментируйте следующее утверждение- “если доходность депозита превы-
шает доходность всех видов облигаций, то существует оптимальное решение,
в котором присутствует только покупка депозита”.
Ситуация для анализа | Ebel Mining (часть 5)4
“Я думал, что ясно все объяснил во время нашей последней встречи,” — заявил
Трумен Харди, управляющий добычей компании Ebel “Как я уже отмечал, каждый
день работы шахты означает 24-часовой рабочий день и по договору с профсоюзом
мы можем работать не более пяти дней в неделю. Кроме того, мы должны предупре-
дить всех заранее, если в какую-то неделю шахта будет работать менее пяти дней Но
я никогда не думал, что вы порекомендуете нам, чтобы шахта работала нецелое ко-
личество дней в неделю. Это совершенно нереально' Ни один руководитель проф-
союза работников горнодобывающей отрасли не позволит нам составить такой гра-
фик работы и платить рабочим за часть дня А я не позволю оплачивать работу в те-
чение части дня как полный рабочий день, так как это позволит шахтерам получать
деньги даром. Пока я управляю этими шахтами, такого не будет'”
Набрав побольше воздуха, Трумен продолжил “Возьмите предыдущую таблич-
ную модель для четырехнедельного планового периода и переделайте ее так, чтобы
предложить мне более дешевый 4-недельный график работы, чем найденный ранее
(см ситуацию Ebel Mining, часть 4 в главе 5), и в то же время гарантировать, что
в этом графике не окажется нецелого количества дней работы шахт”
Вопросы
1	Что вы можете ответить на требование Трумена найти более дешевый график ра-
боты шахт, обеспечив при этом, чтобы шахты работали целое количество дней
в неделю? Объясните, на чем основан ваш ответ
2.	Преобразуйте 4-недельную модель ЛП из ситуации Ebel Mining, часть 4, чтобы с
ее помощью можно было удовлетворить требование целочисленности количест-
ва дней работы обеих шахт каждую неделю.
3.	Вернемся к вопросу утилизации неотгруженной руды Изменятся ли ваши реко-
мендации относительно использования неотгруженной руды в связи с новыми
требованиями Трумена?
4.	Объясните изменения модели и приведите всю имеющуюся информацию о тене-
вых ценах в краткой докладной записке, адресованной руководству компании Ebel
‘ © 2000 Board of Trustees of the Leland Stanford Junior University All rights reserved
434 ЧАСТЬ II. Оптимизационные модели
Литература
1	Anbil R , Gelman Е , Patty В , Tanga R Recent Advances in Crew-Pairing Optimization at American Air-
lines, Interfaces, 21, no 1 (1990) 62—74
2	Spenser T , Brigandi A , Dargon D , Sheehan M AT&T’s Telemarketing Site Selection System Offers
Customer Support, Interface, 20, no 1 (Jan —Feb , 1990)
Глава
Нелинейная оптимизация
В этой главе...
7.1.	Введение в нелинейные оптимизационные модели
7.2.	Безусловная оптимизация
7	3. Нелинейная оптимизация геометрическая интерпретация
7.4.	Использование средства Поиск решения для решения задач НЛП
7.5.	Примеры нелинейных моделей
7.6.	Параметры поиска решения
7.7.	Разрешимость задач НЛП
7.8.	Генетический алгоритм
7.9.	Введение в квадратичное программирование
7.10.	Выбор портфеля инвестиций
7.11.	Пример модели портфельных инвестиций
7.12.	Модель управления запасами
7.13.	Модель управления запасами при наличии оптовых скидок
7.14.	Производство и управление запасами
7.15.	Заключение
Основные термины
Контрольные вопросы
Задачи
Ситуация 1 Оперативные поставки
Ситуация 2 Abacus SFX
Литература
436 ЧАСТЬ II. Оптимизационные модели
Управление активами в компании Pacific Financial
Asset Management
При принятии решений об инвестициях необходимо учитывать конкретную си-
туацию, в которой находится инвестор. Человеку, которому скоро выходить на пен-
сию, следует выбирать менее рискованные операции, чем молодому человеку, кото-
рый вкладывает деньги в пенсионную программу с выплатой через 40 лет. Кроме
того, следует отличать инвесторов, которые должны платить со своих прибылей на-
логи, от институциональных инвесторов, таких как страховые компании или пенси-
онные фонды, которые, как правило, от налогов освобождены. Определение рисков
и вознаграждений, связанных с различными стратегиями инвестирования, также
должно учитывать конкретные обстоятельства.
Чтобы построить более точную модель инвестирования, компания Pacific
Financial Asset Management Company (PFAMC) на основе традиционной финансовой
модели учета активов Марковица и Шарпа разработала новую модель, в которой
учитываются как активы, так и пассивы Главная сложность состоит в том, чтобы
сбалансировать риски стратегических решений по инвестированию в соответствии
сдвижениями предполагаемых пассивов. Разработанная PFAMC модель является
моделью нелинейной оптимизации Модель реализована на персональном компью-
тере, что позволяет инвестору взаимодействовать с ней и таким образом учитывать
индивидуальные особенности и предпочтения в сфере рисков. Например, крупные
институциональные инвесторы должны решить, сколько средств вложить в каждую
из категории активов — государственные ценные бумаги, облигации, недвижимость
и т д Это решение является для них стратегическим
Хотя данный подход требует сбора большего количества информации, полученные
рекомендации более тесно связаны с нуждами и обстоятельствами инвесторов. Компа-
ния PFAMC и ее клиенты были весьма удовлетворены полученными результатами. [1]
7.1.	Введение в нелинейные оптимизационные модели
Во многих экономических и производственных задачах встречаются не только линей-
ные функции и отношения Среди реальных задач строго линейные задачи скорее явля-
ются исключением, чем правилом Например, в линейной модели обычно предполагает-
ся, что цена является постоянной, скажем р, а объем продаж, переменная х, не зависит от
цены Следовательно, доход вычисляется по формуле рх, т.е. можно сказать, что доход
пропорционален цене Это предположение о линейности было краеугольным камнем
нашего анализа в главах с 3 по 6, поскольку оно приводило к простой структуре моделей.
Однако в действительности цена может варьироваться, а объем продаж (и спрос) может
зависеть от цены Эта зависимость выражается формулой проданное количество =f(p), где
/— некая функция отр. Тогда доход вычисляется по формуле
доход = цена х объем продаж =р хДр),
которая является нелинейной по переменной р. В этом случае модель определения цены,
позволяющей максимизировать доход, окажется нелинейной.
В общем случае к нелинейности моделей могут привести любые физические, струк-
турные, биологические, экономические и логические взаимосвязи и их комбинации.
Следует еще раз подчеркнуть, что, хотя нелинейные явления широко распространены,
ГЛАВА 7. Нелинейная оптимизация
437
нелинейные модели существенно сложнее оптимизировать, чем линейные Например,
в отличие от задач линейного программирования (ЛП), нельзя рассчитывать, что опти-
мизационная процедура средства Поиск решения всегда сможет найти оптимальное ре-
шение любой нелинейной задачи. Этот факт, а также то обстоятельство, что линейные
модели зачастую являются достаточно хорошим приближением нелинейных моделей,
объясняет популярность линейных моделей.
Как известно, модель не является элементом реального мира. Она всего лишь абст-
рактное представление реальности. Создателю модели важно знать, при каких условиях
линейная версия модели обеспечивает адекватное представление нелинейного мира. От-
вет на этот фундаментальный вопрос дают опыт и эксперимент, но он не бывает одно-
значным и часто вызывает споры. В данной главе рассмотрим ситуации, в которых, как
принято считать, требуются нелинейные модели. Наша цель — описать понятия и сред-
ства, необходимые для работы с моделями нелинейного программирования, а также не-
которые вычислительные методы.
Глава организована следующим образом. Для тех, кто интересуется теоретическими
положениями, в разделе 7.2 предлагается краткий обзор фактов, касающихся безуслов-
ной оптимизации. Затем предлагается геометрическая интерпретация условной нели-
нейной оптимизации. Разделы с 7.3 по 7.6 посвящены формулированию и решению
с помощью средства Поиск решения задач нелинейного программирования (НЛП)
В разделе 7.7 мы определим понятия выпуклости и вогнутости применительно ко множе-
ствам и функциям, а также обсудим на качественном уровне, какие виды нелинейных за-
дач в общем случае разрешимы, а какие нет. В разделе 7 8 рассматривается специальная
процедура поиска решения задач НЛП, основанная на принципах генетики В разделе 7.9
перейдем к рассмотрению специального класса моделей НЛП, называемых квадратич-
ными, которые сравнительно легко оптимизировать. Эти модели нашли широкое приме-
нение в моделировании ситуаций принятия решений в финансовой сфере В разделе 7 12
рассмотрен пример из области управления запасами, где также широко применяются мо-
дели НЛП. Далее показана классическая модель определения экономически выгодного
размера заказа и представлены два примера ее расширения. Наконец, раздел 7 15 содер-
жит заключение и несколько замечаний о реализации моделей НЛП.
7.2.	Безусловная оптимизация
Пусть задана функцияот двух независимых переменных х, их, В этом случае
для нахождения локальных и глобальных оптимумов функции f используются частные
производные. Обозначим через fx первую частную производную функции f по перемен-
ной х/; через fxx — вторую частную производную и т д Точка (х,,х2), в которой все пер-
вые частные производные обращаются в нуль, называется стационарной точкой Сфор-
мулируем необходимое условие оптимальности.
В точке локального максимума или минимума все частные производные должны быть
равны нулю (т.е. Д = Д =0 ). Таким образом, локальный максимум (локальный мини-
рмум) всегда является стационарной точкой.
Однако не все стационарные точки являются точками максимума или минимума Нам
понадобится достаточное условие оптимальности (в котором используются вторые про-
изводные), более сложное, чем необходимое условие. Как и для функций одной пере-
438
ЧАСТЬ II. Оптимизационные модели
менной, для определения безусловного оптимума функции нескольких переменных при-
меняется критерий первого порядка (с использованием первых производных) и критерий
второго порядка (с использованием вторых производных). Эти критерии называются ус-
ловиями оптимальности первого порядка и условиями оптимальности второго порядка. От-
метим, что условия первого порядка являются необходимыми, а условия второго
порядка — достаточными Кроме того, условия второго порядка являются продолжением
условий первого порядка (т.е. в условиях второго порядка подразумевается, что (х,’, х2 ) —
стационарная точка).
При отсутствии дополнительной информации о свойствах функции (таких как вы-
пуклость или вогнутость) наибольшее, на что можно рассчитывать, это найти локальный
оптимум (а не глобальный). Критерий, основанный на первых производных
(необходимое условие), утверждает, что локальные оптимумы находятся среди стацио-
нарных точек функции. Критерий, основанный на вторых производных (достаточное ус-
ловие), позволяет отличать локальные максимумы и минимумы, а также точки, не яв-
ляющиеся ни тем, ни другим
Для дифференцируемой функции п переменных каждый локальный оптимум являет-
ся стационарной точкой Чтобы доказать, что некая стационарная точка является ло-
кальным максимумом, необходимо воспользоваться достаточным условием. Хотя эти два
типа условий оптимальности представляют теоретический интерес, для многих нелиней-
ных моделей, содержащих более двух переменных, их практическое значение ограниче-
но Причины этого следующие.
1.	Приравнивая к нулю первые частные производные, получаем систему п уравнений
с п неизвестными Если эта система не является линейной (т е. исходная функция
не была квадратичной), решить ее совсем непросто Вполне может оказаться, что
вручную сделать это невозможно.
2.	Достаточные условия второго порядка весьма сложны и требуют оценки определи-
телей подматриц матрицы вторых частных производных. Если функция f имеет
сложный вид, то даже при работе с одной или двумя переменными иногда невоз-
можно вручную проверить эти условия оптимальности.
Вышеперечисленные факты объясняют ведущую роль условий первого порядка в не-
линейной оптимизации. Эти условия используются неявно, т.е. они служат критерием
окончания для методов наискорейшего спуска, которые ищут локальные оптимумы. Дос-
таточные условия второго порядка для задачи общего вида с п переменными представля-
ют преимущественно теоретический интерес, поэтому мы не будем их обсуждать в дан-
ной главе, носящей вводный характер.
В заключение приведем еще один важный результат, относящийся к максимизации
вогнутой функции Для вогнутой функции стационарная точка является глобальным
максимумом (для выпуклой функции стационарная точка является глобальным миниму-
мом) Поскольку в общем случае оптимальное решение может быть локальным макси-
мумом или минимумом или ни тем, ни другим, при работе с выпуклой функцией гаран-
тируется, что любое решение является глобальным максимумом. Этот факт играет важ-
ную роль в оптимизации квадратичных нелинейных моделей (которым посвящен
раздел 7 9)
ГЛАВА 7. Нелинейная оптимизация 439
7.3.	Нелинейная оптимизация: геометрическая
интерпретация
Для нахождения локальных оптимумов нелинейных функций, зависящих от несколь-
ких переменных, было разработано такое специализированное программное обеспечение
оптимизации, как Поиск решения Зачастую подобное программное обеспечение осно-
вано на итерационных методах наискорейшего подъема или наискорейшего спуска'
В этих методах выбирается начальная точка (набор числовых значений переменных),
а затем определяется направление подъема путем вычисления первых частных производ-
ных целевой функции в этой начальной точке Интуиция подсказывает, что при безус-
ловной оптимизации метод движется из начальной точки вдоль линии возрастания зна-
чения целевой функции (те в направлении подъема) до наивысшей точки, которой
можно достигнуть на этой линии Затем выбирается новое направление подъема и про-
цедура продолжается Метод заканчивает свою работу, когда первые частные производ-
ные целевой функции становятся равными нулю (выполняется условие первого поряд-
ка) Такая точка всегда является локальным оптимумом, но в нелинейной задаче могут
быть другие оптимумы, которых можно достичь, выбрав иную начальную точку Для по-
иска других локальных максимумов процедура оптимизации выполняется из другой на-
чальной точки
Все, что мы говорили о нелинейной оптимизации до этого момента, касалось безус-
ловной оптимизации Однако в принятии управленческих решений гораздо чаще встре-
чаются задачи оптимизации при выполнении ограничении Ограничения могут иметь
форму равенств или неравенств, как и в задачах ЛП, однако в данном случае не подразу-
мевается линейность функций ограничений Математически общая задача НЛП записы-
вается так, как показано ниже, здесь/, g, и h, обозначают нелинейные функции от пере-
менных х, задающие целевую функцию, левые части ограничений-равенств и ограниче-
ний-неравенств соответственно
МаксимизироватьДх,, х2, ,хп)
при ограничениях
g,(x„x2, ,х„) = 6„
g2(x„x2,. ,Х„)=/>2,
g„,(X.’X2’ ’Х„)=Ь„.>
*,(*,> *2- .,х„)<г„
h2(x„x2, ...,х„)<г2,
^(х„х2, ^х„)^гк.
Графический анализ задач НЛП
Как и при работе с моделями ЛП, можно воспользоваться графическим представле-
нием, чтобы лучше понять природу задач НЛП. В качестве примера оптимизируем сле-
дующую модель НЛП
1 Используемый средством Поиск решения для оптимизации нелинейных моделей метод наискореишего
подъема/спуска, называемый методом обобщенного градиента, отличается от симплекс-метода, исполь-
зуемого для оптимизации моделей ЛП
440 ЧАСТЬ II. Оптимизационные модели
Максимизироватьх, — х2
при ограничениях
-х,2+х2>1,
х,+х2<3,
—х,+х2<2,
х,>0,х2>0.
Заметим, что в этой модели линейны все функции, за исключением первого ограни-
чения. Но если нелинейна хотя бы одна из функций ограничений или целевая функция,
то модель все равно будет моделью нелинейного программирования (НЛП).
Допустимая область
Чтобы оптимизировать данную модель графически, необходимо действовать так же, как
и при использовании моделей ЛП. Первым делом строится множество точек, которые од-
новременно удовлетворяют всем ограничениям. Это множество точек называется, как
и вЛП, множеством допустимых решений, допустимой областью или множеством ограниче-
ний. Чтобы найти допустимое решение, доставляющее максимум целевой функции, найдем
“самую высокую” (т.е. с наибольшим значением) изолинию, соответствующую целевой
функции, которая касается допустимого множества. Точка касания и будет неким опти-
мальным решением задачи? На рис. 7.1 показано графическое решение данной задачи.
Рис. 7.1. Пример графического решения нелинейной задачи
Как показано на рис. 7.1, наличие нелинейного ограничения привело к искривлению
границы допустимой области. В моделях ЛП графическое представление позволяло вы-
явить лимитирующие ограничения, а затем получить точное решение с помощью двух
уравнений с двумя неизвестными (при двух переменных решения). В общем случае этот ме-
тод для нелинейных моделей не срабатывает Существует только одно связывающее огра-
ничение, и решение не находится в угловой точке пересечения ограничений (см. рис. 7.1).
Обратите внимание на терминологию именно неким решением, а не единственным решением, поскольку в
моделях НЛП может существовать более одного локального оптимума
ГЛАВ A 7. Нелинейная оптимизация 441
Оптимум модели
Еще один пример модели НЛП показан на рис. 7.2, где изображена гипотетическая
нелинейная модель оптимизации при наличии ограничений в виде неравенств Здесь все
ограничения линейны, следовательно, множество допустимых решений является много-
угольником, но целевая функция нелинейна, и вновь оказывается, что решение не нахо-
дится в угловой точке допустимой области. Для некоторых нелинейных целевых функ-
ций оптимальное решение может находиться даже не на границе допустимой области,
а внутри нее. В некоторых моделях НЛП решение, конечно же, может находиться на
границе или в угловой точке допустимой области, однако важно подчеркнуть, что данное
свойство отнюдь не обязательно, как это было в линейных моделях Этот факт имеет
большое значение для методов оптимизации задач НЛП, поскольку чрезвычайно услож-
няет процедуру оптимизации
Рис. 7.2. Решение задачи НЛП
Сравнение моделей АП и НАП
Между моделями ЛП и НЛП существует ряд параллелей. Например, следующие че-
тыре утверждения справедливы для обоих типов моделей
1.	Увеличение (уменьшение) правой части ограничения вида < (вида >) ослабляет огра-
ничение Это не сузит множества допустимых решений, но может расширить его
2.	Увеличение (уменьшение) правой части ограничения вида > (вида <) усиливает огра-
ничение. Это не расширит множество допустимых решений, но может сузить его
3.	Ослабление ограничения не ухудшит, но может улучшить оптимальное значение
целевой функции.
4.	Усиление ограничения не улучшит, но может ухудшить оптимальное значение це-
левой функции.
442 ЧАСТЬ II. Оптимизационные модели
Еще одним общим понятием для моделей ЛП и НЛП является скорость изменений
значения целевой функции при изменении правой части одного ограничения, если ос-
тальные данные остаются фиксированными. Для моделей ЛП введено следующее опре-
деление (см главу 4) теневая цена определенного ограничения — это скорость изменения
значения целевой функции при изменении правой части данного ограничения и при неизмен-
ности остальных данных В силу исторических причин в моделях НЛП эта скорость из-
менения называется множителем Лагранжа, а не теневой ценой, однако смысл этого
термина практически тот же.
Множители Лагранжа
Теневая цена в модели ЛП обладает одним важным свойством, которого множитель Ла-
гранжа в общем случае лишен В модели Л П теневая цена постоянна для некоторого диапазо-
на значений правой части рассматриваемого ограничения. Легко показать, что в модели НЛП
это свойство в общем случае не выполняется В качестве иллюстрации рассмотрим следую-
щую простую модель НЛП максимизироватьх при ограничениях x<Z> их> 0.
Чтобы максимизировать х2, нужно сделать значение х как можно больше. Таким
образом, оптимальным решением будет х = Ь, а оптимальное значение целевой
функции равно (х’)2 = Ь2 Таким образом, оптимальное значение целевой функции
является функцией от Ь.
По определению теневая цена (множитель Лагранжа) — это скорость изменения оп-
тимального значения целевой функции по мере увеличения правой части ограничения
(т е Ь), а из теории дифференциального исчисления известно, что скорость изменения
функции — это производная от данной функции. В данном случае эта производная
в точке х = Ь равна 2Ь. Иными словами, здесь множитель Лагранжа не является постоян-
ным для некоторого диапазона значений правой части ограничения, как это было в ли-
нейных моделях, а непрерывно изменяется вместе с Ь.
Локальные и глобальные решения
Еще одно важное различие между моделями ЛП и НЛП заключается в отношени-
ях глобальных и локальных решений Для модели ЛП не может быть локального реше-
ния, которое не являлось бы глобальным Для моделей НЛП в общем случае это ут-
верждение не всегда справедливо Иными словами, такие модели могут иметь как
локальные, так и глобальные решения. Эта ситуация показана на рис 7 3 для неко-
торой модели максимизации
В общем случае модель НЛП должна удовлетворять дополнительным условиям
(например, условиям выпуклости или вогнутости), чтобы гарантировать, что локальный
условный оптимум является также глобальным Эти условия будут рассмотрены в разде-
ле 7 7 При отсутствии таких условий в общем случае нельзя утверждать, что найденное
решение задачи НЛП является глобальным оптимумом.
ГЛАВА 7. Нелинейная оптимизация
443
Рис. 7.3. Локальное и глобальное решения
Задачи НЛП с ограничениями в форме равенств
Многие нелинейные модели в экономике и бизнесе имеют следующий вид
Максимизировать (или минимизировать)/^, х2, , х„)
при ограничениях#,^,, х2, , х„) =/>,,/= 1, ,т(т<п).
Таким образом, цель задачи НЛП состоит в максимизации или минимизации целевой
функции п переменных при условии выполнения т ограничений-равенств Рассмотрим
три примера
Пример 1
Производитель может изготавливать продукцию на одном из двух станков Обозна-
чим черезх, количество продукции, изготовленное на станке I, а через х2 количество про-
дукции, изготовленное на станке 2. Пусть а/, + Ьрс2 — стоимость производства на стан-
ке 1, а^ + b^c2 — стоимость производства на станке 2 Необходимо найти значения х,
их;, которые бы минимизировали суммарные затраты при соблюдении требования, что
суммарное количество произведенной продукции должно быть равно заданному числу R
Эта модель имеет следующий вид.
Максимизировать ape, + Ь,х2 + арс. + Ьрс2
при ограничении х, + х2 = R
Пример 2 (классическая микроэкономическая модель)
Пусть pt,p2 и р2— заданные рыночные цены трех товаров, а В — заданная константа,
обозначающая личный бюджет некого субъекта Пусть s2 и s3 — определенные индиви-
дуальные параметры, характеризующие субъекта, а х1' +х5 +х'! обозначает “пользу”, ко-
торую субъект извлекает из потребления х, единиц товара 1, х2 единиц товара2 их, еди-
ниц товара 3 Необходимо определить потребительскую корзину, которая позволит субъ-
екту получить максимальную пользу при соблюдении бюджетного ограничения
Математически модель можно записать в виде
444 ЧАСТЬ II Оптимизационные модели
максимизировать х’1 +х'2 + *’’
при ограничениир,х, + ргх: + ррс = В
ПримерЗ
Рассмотрим модель максимизировать*,-х. при ограничении -*,2+*2 = 1.
Геометрическое представление этой модели (рис. 7.4) показывает, что в точке опти-
мального решения изолиния целевой функции является касательной к линии ограниче-
ния-равенства Оптимальное решение приблизительно равно*,’ = 0,5, х‘ = 1,25. Это под-
тверждает табличная модель в Excel, содержащая полученное с помощью средства Поиск
решения оптимальное решение (см рис 7 4).
Рис. 7.4. Решение задачи примера 3
ГЛАВА 7. Нелинейная оптимизация 445
7.4.	Использование средства Поиск решения
для решения задач НЛП
Как показано в предыдущих главах, создавать линейные модели с линейными огра-
ничениями и оптимизировать их с помощью средства Поиск решения несложно. Это
средство также позволяет достаточно легко оптимизировать модель, содержащую нели-
нейную целевую функцию и нелинейные функции ограничений. Однако следует пом-
нить, что Поиск решения использует различные методы оптимизации для моделей ЛП
и НЛП. При оптимизации модели ЛП используется симплекс-метод, а для моделей
НЛП — метод приведенного градиента Оптимизация нелинейных моделей состоит из
следующих этапов. Первым делом, используя начальные значения переменных решения,
указанные в поле Изменяемые ячейки диалогового окна Поиск решения, процедура на-
ходит допустимое решение, т.е. набор значений переменных, которые удовлетворяют
всем ограничениям. Затем для этой начальной точки находится направление, в котором
наиболее быстро улучшается значение целевой функции. В этом направлении изменяют-
ся значения переменных до тех пор, пока не будет достигнута линия ограничения или пе-
рестанет улучшаться значение целевой функции. Затем из новой точки вычисляется но-
вое направление и процесс повторяется Это продолжается до тех пор, пока дальнейшее
улучшение во всех направлениях станет невозможным, на чем процедура завершается
Указывать целевую функцию необязательно Если она не задана, Поиск решения бу-
дет пытаться найти некое допустимое решение Таким образом, это средство можно ис-
пользовать для проверки допустимости множества ограничений или для решения систем
линейных и нелинейных уравнений Также необязательно указывать ограничения, тогда
Поиск решения можно использовать для безусловной оптимизации моделей НЛП 3
7.5.	Примеры нелинейных моделей
Рассмотрим еще несколько примеров моделей НЛП Предлагаемые в данном разделе
модели будут содержать ограничения-неравенства в наиболее обшей форме
Расходы на рекламу
Средние ежедневные расходы ресторана на рекламу составляют $100, причем все
средства идут на рекламные объявления в газете и по радио. Обозначим через х, среднюю
сумму в день, потраченную на рекламные объявления в газете, а х2 — среднюю сумму
вдень, потраченную на рекламу по радио. Тогда суммарные годовые затраты ресторана
на содержание отдела рекламы, включая ежедневные расходы на рекламные объявления,
оцениваются следующей нелинейной функцией
затраты = С(х„ х2) = 20 000 - 440х, - ЗООх2 + 20х,2 + 12х22 + х,х2
Необходимо найти распределение бюджета ресторана, которое позволит минимизиро-
вать эти суммарные ежегодные расходы, сохранив ежедневные расходы на рекламу на
уровне $100. Математическая модель имеет вид
минимизировать 20 000 - 440х, - ЗООх2 + 20х,2 + 12х22 + х,х2
при ограничениях*, + х2 = 100 и х, > 0, х2 > 0.
Безусловная оптимизация имеет смысл только для нелинейных моделей
446
ЧАСТЬ II. Оптимизационные модели
Оптимизированная средством Поиск решения табличная версия данной модели вме-
сте с отчетом по устойчивости представлена на рис 7 5. Множитель Лагранжа показыва-
ет, что скорость увеличения годовых расходов отдела рекламы составляет около $1195
для каждого дополнительного доллара, ежедневно потраченного на рекламу
Изменяемые ячейки
Ячейка	Имя	Результ значение	Нормир градиент
$с$з	Решения. Газеты	$ 39.365	* „
$Р$3	Решения Радио	$ 60.645	$
Ограничения______________________________________
Результ Лагранжа
Ячейка Имя значение Множитель
$Е$6 Расходы Итого в день $100 00	$1194.84
Рис. 7.5. Модель расходов на рекламу
ГЛАВА 7. Нелинейная оптимизация
447
Совет. Средство Поиск решения чувствительно к ошибкам округления, вызванным ограни-
ченной точностью двоичной компьютерной арифметики. Эта проблема особенно актуальна
при оптимизации существенно нелинейных моделей, содержащих широкий диапазон числовых
значений. Если наименьшие числа модели отличаются от наибольших на шесть или семь по-
рядков, то это может привести к неверному решению, выдаваемому средством Поиск ре-
шения. Установка опции Автоматическое масштабирование в диалоговом окне Пара-
метры поиска решения во многих случаях поможет избежать таких ошибок Однако, как
и для моделей ЛП, выбор данной опции не гарантирует полного предотвращения проблемы
округления во всех случаях. Лучше сначала вручную изменить масштаб слишком больших или
слишком малых чисел во избежание подобных ошибок.
Экономическая интерпретация множителей Лагранжа и
нормированных градиентов
Множители Лагранжа имеют интересную и важную экономическую интерпретацию
Как уже отмечалось, множители Лагранжа в моделях НЛП интерпретируются практиче-
ски аналогично теневым ценам в моделях ЛП. Иными словами, в точке оптимальности
значение z-го множителя Лагранжа является мгновенной скоростью изменения опти-
мального значения целевой функции при увеличении правой части z-го ограничения />„
вто время как остальные данные модели остаются неизменными Используя экономиче-
скую терминологию, можно также сказать, что z-й множитель Лагранжа отражает
предельную стоимость z-го ресурса, поэтому он измеряется в единицах, которые
определяются как отношение единицы измерения целевой функции к единице измере-
ния правой части ограничения /.
Так, в примере 1, в котором производитель хотел минимизировать суммарные произ-
водственные затраты, целевая функция исчислялась в долларах, а ограничение выражало
суммарный объем производства двух продуктов в тоннах Множитель Лагранжа для дан-
ного ограничения выражается в долларах на тонну, а его значение представляет собой
мгновенную предельную стоимость производства единицы продукции.
Рассмотрим числа, приведенные в отчете по устойчивости для моделей НЛП Соответ-
ствующий некоторому ограничению множитель Лагранжа является мгновенной скоростью
изменения оптимального значения целевой функции при изменении правой части данного
ограничения. Как и теневые цены в моделях ЛП, положительное значение множителя Ла-
гранжа показывает, что увеличение правой части неравенства приведет к увеличению оп-
тимального значения целевой функции, а отрицательное значение множителя Лагранжа
показывает, что увеличение правой части неравенства приведет к уменьшению оптималь-
ного значения целевой функции. Однако, в отличие от задач линейного программирования,
в задачах НЛП ничего нельзя сказать о диапазоне увеличения или уменьшения правой час-
ти, для которого справедливо данное значение множителя Лагранжа. Обычной является си-
туация, когда множитель Лагранжа сам изменяется по мере изменения правой части Одна-
ко это не мешает использовать его, чтобы оценить, что будет происходить с оптимальным
значением целевой функции при изменении правой части ограничения
Значения нормированного градиента в отчете по устойчивости для моделей НЛП интер-
претируются аналогично значениям нормированной стоимости для моделей ЛП (см главу 4)
Как и нормированная стоимость, нормированный градиент переменной связан с заданием
верхних или нижних границ для переменных решения. Отрицательный нормированный гра-
диент для переменной решения показывает, что увеличение данной переменной приведет
448 ЧАСТЬ 11 Оптимизационные модели
к уменьшению оптимального значения целевой функции, а положительный — к увеличению.
Кроме того, как и в случае с нормированной стоимостью, если переменная решения достигает
своей верхней границы, нормированный градиент должен быть неотрицательным, чтобы ре-
шение задачи максимизации было оптимальным, в противном случае уменьшение значения
данной переменной сможет привести к улучшению значения целевой функции. Если пере-
менная решения достигает своей нижней границы, то, чтобы решение задачи максимизации
было оптимальным, нормированный градиент должен быть неположительным, в противном
случае увеличение значения данной переменной сможет привести к улучшению значения це-
левой функции. (Для задач минимизации верны противоположные заключения.) Если значе-
ние переменной решения заключено строго между ее верхней и нижней границами, нормиро-
ванный градиент, как и нормированная стоимость, в точке оптимальности должен быть равен
нулю (см рис 7 5)
Еще раз о модели производства телевизоров Astro и Cosmo
В главе 3 при формировании модели производства телевизоров Astro и Cosmo предпо-
лагалось, что удельная прибыль в расчете на один телевизор постоянна. Предположим
теперь, что больше телевизоров можно продать только в том случае, если снизить цену
продажи Допустим также, что спрос на телевизоры описывается формулами РА = 314 —
1,9А + 0,0А PC = 243 - 0,14С, где А — ежедневный выпуск телевизоров Astro, РА — це-
на продажи телевизоров Astro, С — ежедневный выпуск телевизоров Cosmo, PC— цена
продажи телевизоров Cosmo Здесь РА и PC — это цены, которые компания должна уста-
новить на телевизоры Astro и Cosmo, чтобы продать все произведенные ею телевизоры.
Получается, что теперь удельная прибыль зависит от общего объема производства Если
удельные переменные затраты на производство телевизора Astro составляют $210, а на
производство Cosmo — $230, то общая прибыль вычисляется по формуле
прибыль = (РА - 210)Л + (PC - 230)С.
Добавив остальные ограничения из исходной модели, получим приведенную ниже
модель НЛП Она содержит два ограничения-равенства, определяющих цену продажи
каждого продукта в зависимости от объема его производства. Одно из этих ограничений
нелинейно. Поскольку РА является функцией А, а PC функцией С, целевая функция так-
же нелинейна
Максимизировать (РА - 210)Л + (PC- 230)С
при ограничениях
РЛ = 0,01Л2- 1,9Л+314,
PC = —0,14С + 243,
А <70,
С<50,
А + 2С< 120,
А + С<90,
А, РА, С, PC >0.
(цена продажи Astro)
(цена продажи Cosmo)
(производственная мощность выпуска Astro)
(производственная мощность выпуска Cosmo)
(количество рабочего времени в цехе А)
(количество рабочего времени в цехе В)
ГЛАВА 7. Нелинейная оптимизация 449

в
Ограничения______________________
Ресурс рабочего времени в цехе А
Ресурс рабочего времени в цехе S
39.40
Устаноеигь целевую ячейку:
|! 9 Г S
K$6$W6 <= «7 «7
«13 «14 <= «13 «14
Коэффициенты спроса
Квадратичный член
Линейный член
Константа
Производство
Производственная мощность;
Цена
Себестоимость	j
Удельная прибыль
<=70
$254,67
$210,00
$44,67
$237,36
$230.00
$7 36
39,3952489151796	40.30237554241С2
=СУММПРОИЗВ( $С$6 $D$6: С13 013) 120
=СУММПРОИ38($С$6 $D$6.C14 D14) 90
Microsoft Excel 10 0 Отчет по устойчивости
Изменяемые ячейки______________________
Ячейка_________________Имя
$С$6	Производство Astro
$D$6	Производство Cosmo
Ограничения___________________
Результ Нормир
значение градиент
39.40	0.00
40 30	0 00
Ячейка_____________
Цена Astro
Цена Cosmo
Имя
$С$8	Цена Astro	$254.67
$D$8	Цена Cosmo	$237.36
$Е$13	Ресурс рабочего времени в цехе	А Всего____	120
$Е$14	Ресурс рабочего времени в цехе	В Всего 79,70
Результ Лагранжа
значение Множитель
$0.00
$0.00
0 8677
0.00
Рис. 7.6. Задача НЛП и ее решение
450
ЧАСТЬ II Оптимизационные модели
На рис 7 6 показана табличная версия данной модели в Excel, ее оптимальное решение
и отчет по устойчивости. Ограничение на количество рабочего времени в цехе А является ли-
митирующим. Множитель Лагранжа для данного ограничения показывает, что оптимальное
значение целевой функции увеличивается примерно на $0,86 на единицу дополнительного ра-
бочего времени в цехе А. Если ресурс рабочего времени в цехе А увеличится на 10 часов, то
значение целевой функции возрастет на 10x0,85766, или примерно на $8,58. Однако такая
оценка является неточной, поскольку в результате увеличения на 10 значения правой части
данного ограничения (ячейка F13) и повторной оптимизации модели новое значение целевой
функции оказывается равным $2061,51, при этом прирост составляет только $5,24. Данный
пример иллюстрирует рассмотренное выше утверждение, что в моделях НЛП множители Ла-
гранжа отражают только начальную скорость увеличения оптимального значения целевой
функции, и эта скорость может заметно меняться по мере изменения правой части ограниче-
ния Это справедливо даже для небольших изменений правой части В моделях НЛП единст-
венным надежным способом определения действительного влияния изменений правых час-
тей ограничений (и других изменений) является использование средства SolverTable для по-
строения таблицы изменений и последующее использование этих данных для определения
чувствительности модели, как это делалось в главе 5
Как отмечалось, для моделей ЛП справедливо утверждение: если оптимальное реше-
ние существует, то оно достигается в некоторой угловой точке допустимой области. На
рис 7 7 видно, что оптимальное решение данной модели не находится в угловой точке
допустимой области, хотя и лежит на ее границе
Рис. 7.7. Допустимая область модели Astro&Cosmo
Оптимальность в моделях НАП
Работая с моделями ЛП, мы привыкли, что оптимальное решение, найденное средст-
вом Поиск решения, действительно является оптимальным. С моделями НЛП все не так
просто Поиск решения может остановиться на решении, которое не является оптималь-
ным, или на таком, которое является лишь локальным, а не глобальным оптимумом. Не-
обходимо знать о существовании такой возможности и быть готовым предпринять соот-
ветствующие действия. В качестве иллюстрации рассмотрим следующий пример.
Модель компании Gulf Coast Oil
В главах 3 и 5 рассмотрены задачи смешивания, описываемые в виде линейных зависимо-
стей Однако некоторые смешивания требуют нелинейной формулировки. Рассмотрим дея-
тельность компании Gulf Coast Oil, которая изготавливает бензин из трех компонентов: смесь
отечественного производства, импортная смесь и специальная октановая добавка, которая
ГЛАВА 7. Нелинейная оптимизация 451
используется только в бензине Premium Импортная смесь, в свою очередь, получается из двух
компонентов. Ежемесячно импортная смесь доставляется компании Gulf Coast Oil в одном
отсеке большого танкера емкостью 8 млн. галлонов Поскольку компонент, поставляемый из
двух источников, заливается в отсек танкера и утрачивает свои индивидуальные свойства,
данная модель называется моделью объединения ресурсов. Этот процесс объединения приводит
к возникновению нелинейности в модели Октановые числа, удельная стоимость очистки
и информация о наличии каждого компонента представлены в табл 7.1
Таблица 7.1. Характеристики компонентов
Компонент	Октановое число	Затраты на один галлон, S	Возможность получения, тыс. галлонов в месяц
Смесь отечественного производства	85	0,65	10000
Импортная смесь			
Источник I	93	0,80	♦
Источник 2	97	0,90	♦
Специальная добавка	900	30	50
* Компания Gulf Coast Oil может получать в месяц в сумме не более 8 000 000 галлонов
из этих источников.
Компания Gulf Coast Oil должна решить, сколько галлонов бензина каждого сорта
(Regular, Midgrade, Premium) следует производить ежемесячно при условии, что согласно
заключенным контрактам она обязана поставлять не менее 100 000 галлонов бензина каж-
дого сорта. Для каждого сорта бензина установлено минимальное октановое число Окта-
новое число смеси вычисляется как взвешенное среднее октановых чисел его компонентов,
где в качестве веса выступает доля каждого компонента в смеси Данные о минимальных
октановых числах и отпускных ценах бензина оптовым дилерам представлены в табл 7 2.
Таблица 7.2. Характеристики сортов бензина
Сорт	Минимальное октановое число	Оптовая цена за галлон, S
Regular	87	1,18
Midgrade	89	1,25
Premium	94	1,40
В формулировке задачи используются следующие обозначения переменных решения
R — количество произведенного бензина Regular, М— количество произведенного бензина
Midgrade, Р — количество произведенного бензина Premium, D — объем закупки смеси оте-
чественного производства, А — объем закупки специальной добавки к бензину Premium,
RD — количество смеси отечественного производства в бензине Regular, RF — количество
смеси импортного производства в бензине Regular, MD — количество смеси отечественного
производства в бензине Midgrade, MF— количество смеси импортного производства
в бензине Midgrade, PD— количество смеси отечественного производства в бензине Pre-
mium, PF— количество смеси импортного производства в бензине Premium
Принимая во внимание, что в задаче речь идет об объединении ресурсов, необходимо
ввести три дополнительные переменные решения. 51 — объем закупки из источника I
(в тыс. галлонов), 52 — объем закупки из источника 2 (в тыс. галлонов), ОСТ — октановое
число полученной в результате объединения импортной смеси.
452 ЧАСТЬ II. Оптимизационные модели
Октановое число определяется как взвешенное среднее октановых чисел компонен-
тов согласно формуле
ОСТ= (9351 + 9752)/(51 + 52) или ОС7х(51 + 52) = 9351 + 9752.
Математическая запись модели приводится ниже (количество бензина и компонентов
измеряется в тыс галлонов). Отметим, что настоящими переменными решения являются
RD, RF, MD, MF, PD, PF, A, SI и 52. Все остальные переменные могут рассматриваться
как выводимые. Кроме того, ограничения, задающие минимальные октановые числа
сортов бензина, являются нелинейными.
Максимизировать 1,187? + 1,25 М + 1,40Р- 0,657) - 0,851 - 0,952 - ЗОЛ
при ограничениях
R = RD + RF, M=MD + MF, P = PD + PF + A, D = RD + MD + PD,	(состав бензина Regular) (состав бензина Midgrade) (состав бензина Premium) (количество использованной смеси отечественного производства)
RF+ MF+ PF=S + 52.	(использование импортной смеси должно быть равно объему ее поставки)
Следующие четыре ограничения представляют нелинейную часть модели.
857?7) + OCT*RF> 87R,	(минимальное октановое число бензина Regular)
85MD + OCT/MF> 89А/,	(минимальное октановое число бензина Midgrade)
85Р7) + ОСТ/PF + 900Л > 94 P,	(минимальное октановое число бензина Premium)
ОС7х(51 + 52) = 9351 + 9752,	(ограничение для внешних источников)
51 + 52 < 8000,	(ограничение емкости танкера)
D< 10000,	(предложение смеси отечественного производства)
А <50,	(предложение специальной добавки для Premium)
7?, М, Р> 100	(минимальный уровень производства)
Все переменные неотрицательные.
Табличная версия данной задачи в Excel и ее решение показаны на рис. 7.8.
Совет В процессе оптимизации модели НЛП средство Поиск решения определяет направле-
ние подъема, делает шаг в этом направлении, а затем оценивает ограничения (чтобы прове-
рить допустимость новой точки) и условия первого порядка (для определения нового направле-
ния или остановки). Может случиться, что шаг оказался слишком большим, поэтому нарушено
одно или несколько ограничений. В этом случае Поиск решения возвращается назад и делает
меньший шаг Но если новая точка вызывает в Excel появление сообщения об ошибке, средство
Поиск решения прерывает оптимизацию до того, как успеет вернуться к предыдущей точке.
Во избежание таких ситуаций применяются специальные приемы. В частности, формулы (без
ущерба для модели) изменяются таким образом, чтобы предотвратить появление сообщений
Excel об ошибках. Например, формула =СУММПРОИЗВ(Е6:Е8,$Н$6'$Н$8)/(Е9) в ячейке ЕН
(см. рис. 7.8) вычисляет октановое число бензина Premium. Входе оптимизации Поиск реше-
ния может установить производство бензина Premium равным нулю, тогда значение в ячейке
Е9 станет равно нулю. Это приведет к появлению сообщения Excel об ошибке #ДЕЛ/0! (деление
на 0), и Поиск решения остановится до того, как успеет обнаружить, что нарушено ограни-
чение в ячейке ЕЮ. Изменив делитель приведенной формулы на (Е9+1Е-30), т.е. добавив к не-
му очень маленькое положительное постоянное число, мы предотвращаем появление такой
ошибки, и Поиск решения сможет продолжить свою работу.
ГЛАВА 7. Нелинейная оптимизация 453
Рис. 7.8. Задача определения состава смесей компании Gulf Coast Oil и ее решение
Первые две группы ограничений в диалоговом окне Поиск решения (рис. 7.8) описы-
вают требования к минимальному октановому числу каждого вида бензина и произве-
денному количеству. Третье ограничение оговаривает, что суммарное количество во-
454
ЧАСТЬ II. Оптимизационные модели
шедшей во все виды бензина импортной смеси должно быть равно приобретенному ко-
личеству импортной смеси. Последняя группа ограничений утверждает, что объем ком-
понентов, использованных при изготовлении бензина, не должен превышать их наличие.
В диалоговом окне Параметры поиска решения установлена опция Неотрицательные
значения. Показанные на рис 7.8 значения девяти переменных решения не являются
допустимыми, тем не менее Поиск решения найдет начальную точку для своей процеду-
ры оптимизации
Первое решение, найденное средством Поиск решения, показано на рис. 7 9. При ос-
тановке Поиск решения сообщает, что “поиск свелся к текущему значению”.4 Это сооб-
щение наводит на мысль, что найден некий оптимум, на самом деле это не так. Чтобы это
было верно, в диалоговом окне Результаты поиска решения должно быть сообщение,
что “все ограничения и условия оптимальности выполнены”, т.е. удовлетворены условия
оптимальности первого порядка
MS
I
Продажа бензина
Октановое i Удельная
Модель проиаводства бензина	Внешние закупки_________число i стоимость
Внешний источник l|	и чяч чМИМИМ	93	'	$0,80
Внешний источник 2|	2 016 7иИИИН|	97	$0,90
=Куплено смеси из внешних
8 000,0	источников
Октановое; Удельная
Всего ; Наличие число стоимость
$0,83
$0,65
$30 00
18
19
18 000
94.01
85
900
8 000 <=8000
10 000 <=10 000
_____0 <=50
>=100
89,00
>=89
>=100
87,00
>=87	,-ui,
$255,82 $22 1 04.00'
$39,69 $6 479,54
Щена за галлон
Импортная смесь, галлон
Отечественная смесь,галлон
Спец, добавка галлон
Всего продано
Минимум продаж
Октановое число бензина
Минимальное октановое число
Доход
Стоимость импортной смеси ______ .
Стоимость отечественной смеси $109 66 $6 390 28
Стоимость добавки	_______________
Суммарные затраты	$149,35 $12 869,82	$82,50 $13 101,67
Прибыль	$106,48 $9 234,18	$57,50
= 100
94,00
>=94 Итого, тыс $
$140,00 ”---------
$82,44
$0,07
$0,00
$22 499,82
$6 601,67
$6 500,00
$0 00
I
Рис. 7.9. Первое решение задачи Gulf Coast Oil
Полученное сообщение о результатах поиска решения в действительности означает,
что программа остановила поиск, поскольку для последних пяти итераций скорость из-
менения значения целевой функции была ниже, чем значение, заданное в поле Сходи-
мость в диалоговом окне Параметры поиска решения (которое более подробно рас-
сматривается далее) Поскольку при оптимизации моделей НЛП Поиск решения всегда
начинает работу из заданной начальной точки, если она является допустимой, можно за-
пустить программу еше раз, чтобы посмотреть, не удастся ли ей улучшить решение. Для
этого достаточно вызвать Поиск решения еще раз и щелкнуть на кнопке Выполнить.
В результате получится решение, представленное на рис 7.10. Переменные решения из-
менились незначительно, однако сообщение о результатах теперь имеет желаемый вид:
“ .. Все ограничения и условия оптимальности выполнены” Это означает, что необходи-
мые условия оптимальности первого порядка выполнены. Предложенное программой
Полученный вами результат может оказаться иным Это зависит от начальных значений переменных ре-
шения, используемой версии Excel и типа процессора вашего компьютера
ГЛАВА 7. Нелинейная оптимизация 455
решение выглядит вполне приемлемо. Однако полезно попробовать другие начальные
значения переменных, поскольку данное решение может быть локальным, а не глобаль-
ным оптимумом
Е
la
Regular Midgrade ; Premium
$1 25
вооо
18 000
I 7 683,3
>=100
89,00
>=89.
>=100
87,00
>=87
$255,71 $22 1 04,13
$39,69 $6 479,53
Модель протводствэ бен:инэ
Внешний источник 1
: Внешний источник 2
Продажа бензина
Dl
Я
и I
I
в!
а I
Isa
цена за галлон
Импортная смесь, галлон
Отечественная смесь, галлон
Спец, добавка, галлон
Всего продано
Минимум продаж
Октановое число бензина
Минимальное октановое число
Доход
Стоимость импортной смеси _ . .
Стоимость отечественной смеси $109 59 $6 390 35
Стоимость добавкиКМЙМНММШН
Суммарные затраты	$149,28 $12 869,88 $82,50
Прибыль	$106,42 $ 9 234 2 5 $57,50
Октановое Удельная
чиг.по стоимость
mio
$0,90
=куплено смеси из внешних
источников
Октановое Удельная
Наличие число стоимость
$0.83
94,00
>=94 Итого, тыс. $
$140,00:
$82,44
$0,07
$0,00
$22 499,83
$6 601,66
$6 500,00
a

И

Рис. 7.10. Второе решение задачи Gulf Coast Oil
Начальные предположения
Когда Поиск решения начинает оптимизацию модели НЛП, оно использует набор
значений переменных, хранящийся в ячейках рабочего листа Как уже отмечалось, дан-
ный начальный набор значений (который не обязательно является допустимым — Поиск
решения это исправит) является стартовой точкой для метода приведенных градиентов
Из-за специфической формы нелинейных ограничении модели Gulf Coast Oil она назы-
вается невогнутой моделью. Как будет показано в следующем разделе, для невогнутых мо-
делей начальная точка может иметь достаточно большое значение, и для нахождения
“хорошего” решения может потребоваться несколько различных начальных точек Пред-
ложение в качестве начальной точки всех нулевых значений обычно является довольно
неудачным выбором для невогнутых моделей. Гораздо лучше предложить начальную
точку в окрестности глобального оптимума модели Получается замкнутый круг чтобы
определить хорошую начальную точку для нахождения глобального оптимального реше-
ния задачи, необходимо знать оптимальное решение задачи1 Ничего не поделать, это не-
приятное следствие нелинейности модели. В частности, для невогнутых моделей нельзя
гарантировать, что решение, найденное средством Поиск решения, является глобальным
оптимумом В нашем случае после двух попыток оптимизировать модель Gulf Coast Oil
программа нашла локальный оптимум (рис 7 10), а не глобальный Глобальным оптиму-
мом данной модели, по всей вероятности, является решение, показанное на рис 7 11
456 ЧАСТЬ II Оптимизационные модели

Модель прошеодстеа веи!ииа	Внешние закупки
Внешний источник 1 одМЦ
Внешний источник 2|	8 ООО.оИР
Продажа бензина
Regular Mldgrade Premium
$1 25	$1,40
цена за галлон
импортная смесь, галлон
Отечественная смесь,галлон
Спец, добавка, галлон
Всего продано
Минимум продаж
Октановое число бензина
Минимальное октановое числом
Доход	;--------------------------,
Стоимость импортной смеси $15,03 $3 917,97 $3 267,00*
Стоимость отечественной смеси $54,15 $5 659,36 $786,50
13 иьи,о
>=100
89,00
>=89
87,00'
>=87
Суммарные затраты
Прибыль
4 840,0
>=100
94,00
>=94 Итого, тыс. $
' $118,00 $16 325,00 $6 776,00: $23 219,00
------ -------------------- $7 200 00
$6 500,00
$0,00
! Октановое Удельная
число стоимость
I 93	; ЙЙ
J 97	$0,90
“Куплено смеси из внешних
8 000,0:	ИСТОЧНИКОВ
I Октановое Удельная
Всего । Наличие '• число стоимость
$0,90
$0,65
$30,00
$69,18 $9 577.33 $4 053,50 $13 700,00
$48,83 $6 747,68 $2 722,5оВ
97.00
1 210.0
900
8 000.<=8000 ।
ИЗ 000 х=10 000
____0 <=50
19 000
Реэулы
Нормир
Об
_JD$6
1Е»б'
$С$7
07
07
»Е$8
Импортная смесь галлон Regular
Отечественная смесь, галлон Regular
Спец. Добавка, I
»F$3
Внешний истонник 2 Внешние закупки
Ячейка___________________Имя____________
tCtll	Октановое число бензина Regular
t DS11	Октановое число бензина Midgrade
JE$11__Октаноеое число бензина Premium
$F$4____Premium Внешние закупки_________
JCJ9	Всего продано Regular
1D89____Всего продано Midgrade__________
8_Е$9_Всего продано Premium_____________
JFJ6	Импортная смесь, галлон Всего
8F87____Отечественная смесь галлон Всего
tF$B Спец добавка галлон Всего
16.7
4 353.3
3 630.0
1 210.0
_0.0
8 000.0
Результ Лагранжа
значение Множитель
87.00
89,00
____94.00_
_ sjqo.q_
’ юо.Ь
13 060.0
-3 00
-391.80
-145.20
8 000
10 000
Рис. 7.11. Оптимальное решение задачи Gulf Coast Oil
Представленное на рис. 7.11 решение, “по всей вероятности”, является глобальным
оптимумом модели Gulf Coast Oil, поскольку не существует достоверного теста, позво-
ляющего гарантировать это. Это решение было найдено в результате нескольких десят-
ков оптимизаций модели с использованием различных начальных точек (для чего каж-
дый раз в соответствующие ячейки вводился новый набор значений переменных реше-
ния) К сожалению, средство SolverTable не может существенно облегчить нудную
работу по повторной оптимизации. Чтобы задать новый набор начальных значений пе-
ременных модели Gulf Coast Oil, необходимо ввести девять значений, a SolverTable по-
ГЛАВА 7. Нелинейная оптимизация 457
зволяет вводить не более двух Однако не все так плохо, в разделе 7 8 мы опишем другой
подход к решению этой трудной задачи. Кроме того, существует класс “приятных” моде-
лей НЛП, так называемые вогнутые и выпуклые модели, в которых не нужно беспокоить-
ся о выборе начальной точки. Для этого класса моделей НЛП Поиск решения находит
глобальное оптимальное решение независимо от того, из какой точки начат поиск.
Полезно потренироваться в интерпретации информации о чувствительности реше-
ния, представленной на рис. 7.11. Например, покупка дополнительного галлона смеси из
источника 1 приведет к снижению прибыли на $0,02, а попытка добавить дополнитель-
ный галлон специальной добавки к бензину Premium будет уменьшать прибыль на $4,42
на галлон (значения нормированных градиентов). В то же время увеличение емкости
танкера на галлон увеличит прибыль на $0,59, а повышение требования к октановому
числу бензина Premium на единицу уменьшит прибыль на $145,20 (значения множителей
Лагранжа)
7.6.	Параметры поиска решения
Для улучшения работы средства Поиск решения при решении задач нелинейного
программирования (особенно для невогнутых или существенно нелинейных моделей,
как модель Gulf Coast Oil) можно попробовать настроить его параметры в диалоговом
окне Параметры поиска решения (рис. 7.12). Значение в поле Сходимость используется
для завершения процесса поиска решения, когда изменение целевой функции происхо-
дит очень медленно Если это изменение меньше или равно заданному по умолчанию
значению 0,0001 на протяжении пяти итераций, Поиск решения останавливается и выда-
ет сообщение об окончании поиска. Если установить меньшее значение сходимости, чем
предусмотрено по умолчанию, программа продолжит процесс оптимизации даже при ма-
лых изменениях целевой функции.
Рис. 7.12. Диалоговое окно Параметры поиска решения
Если установить в области Оценки переключатель квадратичная, Поиск решения бу-
дет применять для вычисления различных оценок более точную квадратичную аппрок-
симацию, а не линейную (переключатель линейная). Кроме того, установка в области
Разности переключателя центральные вместо переключателя прямые приведет к тому,
что Поиск решения для вычисления частных производных будет применять более точ-
458 ЧАСТЬ II Оптимизационные модели
ную аппроксимацию, используя большее количество точек Обе эти установки улучшают
вычисляемые числовые оценки функций нелинейной модели, однако могут увеличить
время решения, поскольку на каждой итерации требуется производить дополнительные
вычисления
В диалоговом окне Параметры поиска решения можно также задать метод поиска
решения Для этого в области Метод поиска нужно выбрать переключатель сопряжен-
ных градиентов или Ньютона Метод сопряженных градиентов в процессе оптимизации
использует меньше памяти, но требует большего количества вычислений при заданном
уровне точности, чем заданный по умолчанию метод Ньютона. В то же время, особенно
для больших нелинейных моделей, меньшее число обращений к памяти при использова-
нии метода сопряженных градиентов может в конечном итоге ускорить работу средства
Поиск решения
Значение в поле Относительная погрешность определяет, насколько точно должно
совпадать вычисленное значение левой части ограничения со значением правой части,
чтобы данное ограничение было выполнено. В любом случае совпадение не может быть
абсолютным из-за погрешностей вычислений компьютера. Если левая часть ограничения
отличается от его правой части на величину, меньше указанной в поле Относительная
погрешность, то считается, что ограничение выполняется как равенство, и, следователь-
но, это ограничение является лимитирующим
Для существенно нелинейных и невогнутых моделей НЛП одним из вариантов зада-
ния параметров поиска решения может быть следующий Оценки — квадратичная, Раз-
ности — центральные, Метод поиска—Ньютона, а Сходимость оставить на уровне, за-
данном по умолчанию, или установить не меньше 0,000001 Кроме того, следует вручную
произвести масштабирование числовых значений модели (как показано в главах 3 и 5),
а также установить флажок Автоматическое масштабирование. Наконец, если модель
НЛП содержит некоторые целые переменные, следует параметр Допустимое отклонение
сделать равным 0%, тогда Поиск решения будет продолжать поиск до нахождения цело-
численного оптимума, как описано в главе 6.
7.7.	Разрешимость задач НАП
Не существует универсального метода оптимизации задач НЛП. В научной литературе
можно без труда найти 10-15 методов оптимизации. Как уже отмечалось, Поиск реше-
ния использует при оптимизации моделей НЛП метод приведенных градиентов Но не-
линейное программирование — очень широкая тема, в литературе выделено множество
классов моделей НЛП, для которых разработаны специальные методы решения. Напри-
мер, ряд методов разработан специально для решения задач квадратичного программи-
рования, описанных в разделе 7.9, есть также специальные методы для “преиму-
щественно” линейных моделей, в которых нелинейные члены входят в целевую функцию
или ограничения неким особым способом.
Вместо того чтобы представить читателю конспективное изложение ряда методов ре-
шения задач НЛП, мы кратко опишем несколько основных классов нелинейных моде-
лей, которые могут встретиться в практических приложениях. Все множество моделей
НЛП разобьем на классы, основываясь на свойствах целевой функции и функций огра-
ничении, а затем обсудим наиболее простые способы оптимизации моделей этих клас-
сов С практической точки зрения важно знать, какие типы моделей НЛП могут встре-
титься и каковы перспективы их решения Как будет показано, перспективы решения
в значительной мере зависят от типа моделей.
ГЛАВА 7. Нелинейная оптимизация 459
Нелинейные модели делятся на два класса: класс моделей, которые поддаются опти-
мизации, и класс моделей, которые можно попытаться оптимизировать Оптимизируе-
мые модели, как правило, должны удовлетворять определенным требованиям Иерархия
моделей по нарастанию их вычислительной сложности представлена на рис. 7.13. Рас-
смотрим некоторые классы моделей НЛП более подробно.
ЗАДАЧИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задачи нелинейного
программирования общего вида
Вогнутые и выпуклые задачи
нелинейного программирования
Вогнутые или выпуклые задачи 1
квадратичного программирования |
ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ I
Рис. 7.13. Возрастание вычислительной
сложности моделей НЛП
Разрешимые нелинейные модели: вогнутые и выпуклые задачи НАП
Для определения данных задач необходимо ввести новое понятие — выпуклое множе-
ство точек Нестрого говоря, это множество точек без “дыр” и “углублений” Более фор-
мально, выпуклым называется множество точек, обладающее следующим свойством:
все возможные пары точек множества и отрезки, соединяющие эти пары точек, должны
находиться полностью внутри множества.
На рис 7 14 показаны двухмерные выпуклые множества точек, а также множества,
которые не удовлетворяют этому свойству и, следовательно, не являются выпуклыми.
Многоугольник на первом из двух рисунков напоминает допустимые множества задач
ЛП. Так и должно быть, поскольку допустимое множество любой задачи линейного
программирования является выпуклым. Задачи нелинейного программирования, о которых
можно с уверенностью утверждать, что они разрешимы, также должны иметь выпуклые
множества ограничений
460 ЧАСТЬ II. Оптимизационные модели
Рис. 7.14. Выпуклые и невыпуклые множества точек
Вогнутые и выпуклые функции
Следующий вопрос состоит в том, какие типы задач нелинейного программирования
имеют выпуклые допустимые множества ограничений? Для ответа на этот вопрос удобно
воспользоваться понятием выпуклых и вогнутых функций Функция двух независимых пе-
ременных является вогнутой, если она имеет форму перевернутой чаши. По определению
вогнутая функция обладает следующим свойством, отрезок, соединяющий любые две точки
графика функции, всегда ниже графика (если он всегда лежит строго ниже графика, функ-
ция называется строго вогнутой) Аналогично выпуклая функция двух переменных имеет
форму чаши По определению выпуклая функция обладает таким свойством, отрезок, со-
единяющий любые две точки графика функции, всегда выше графика (если он всегда лежит
строго выше графика, функция называется строго выпуклой). Аналогичные понятия суще-
ствуют для функций, имеющих одну переменную или несколько Отметим, что линейная
функция одновременно является и выпуклой, и вогнутой (отрезок, соединяющий две лю-
бые точки линейной функции, всегда лежит на ее графике).
Рассмотрим теперь задачу нелинейного программирования, все ограничения которой
имеют форму неравенств
i Если функции левых частей в ограничениях вида являются выпуклыми, а функции^
I левых частей в ограничениях вида £ являются вогнутыми, то множество ограничений !
I будет выпуклым множеством.	'
Иллюстрация данного факта представлена на рис. 7.15, где показана выпуклая
функция одной переменной g, заданная формулой g(x) =х2 + 1. Из рисунка видно, что
множество значений х, для которых g(x) < 2, является выпуклым (это множество
-1 <х<, 1), а множество значений х, для которых g(x) > 2, не является выпуклым (это
множество х<-1, х>1). Последнее множество не является выпуклым, поскольку
можно найти две точки данного множества (например, х = 2 и х = -2) такие, что отре-
зок, соединяющий эти точки, проходит через точки, не принадлежащие множеству
(например, через точку х= 0).
ГЛАВА 7. Нелинейная оптимизация 461
|	 Множество х, для которых д(х) < 2,
является выпуклым
Рис. 7.15. Множества ограничений
g(x) <2 и g(x)> 2
В данном примере функция g(x) является выпуклой, множество, заданное неравенст-
вом g(x) < 2, является выпуклым, а множество, заданное неравенством g(x) > 2, выпуклым
не является. Можно привести аналогичный пример, показывающий, что если функция
g(x) является вогнутой, то множество, заданное неравенством g(x)>2, является выпук-
лым, а множество, заданное неравенством g(x) < 2, выпуклым не является Таким обра-
зом, теоретически есть способ, позволяющий убедиться, что множество ограничений за-
дач НЛП является выпуклым. Но на практике очень сложно определить, является мно-
жество ограничений задачи НЛП выпуклым или нет Введем определения.
•	Вогнутая модель НЛП — это модель максимизации с вогнутой целевой функци- s
ей и выпуклым допустимым множеством ограничений.	!
•	Выпуклая модель НЛП — это модель минимизации с выпуклой целевой функ-
цией и выпуклым допустимым множеством ограничений.	j
Отметим, что модели ЛП удовлетворяют обоим определениям. Логическим обоснова-
нием выделения категории выпуклых и вогнутых моделей является то, что при нахожде-
нии максимума, как показывает пример с функцией одной переменной, очень удобно
работать с вогнутой целевой функцией благодаря математическим свойствам, связанным
с ее специфической формой перевернутой чаши Выпуклые целевые функции удобны
при минимизации. Наконец, выпуклость множества ограничений придает модели другие
привлекательные математические свойства, которые можно использовать как в теорети-
ческих построениях, так и при вычислениях. Наиболее важной характеристикой вогну-
тых (выпуклых) моделей НЛП является то, что для них локальное решение обязательно
является глобальным решением.
Процедуры решения
На рис. 7.13 показано, что простейшими задачами нелинейного программирования
являются вогнутые и выпуклые квадратичные модели. По определению эти модели име-
ют линейные ограничения (в форме равенств и неравенств). Целевая функция должна
быть квадратичной и вогнутой, если это модель нахождения максимума, и квадратичной
и выпуклой, если это модель минимизации Из этого следует, что для решения таких за-
дач можно использовать специальную модификацию симплекс-метода. Нередко ветре-
462
ЧАСТЬ II Оптимизационные модели
чаются квадратичные модели с сотнями ограничений и несколькими тысячами перемен-
ных Как будет показано в следующем разделе, финансовые модели, например, исполь-
зуемые при анализе портфельных инвестиций, часто являются квадратичными, поэтому
данный класс моделей представляет значительный практический интерес.
Следующими по уровню сложности (см рис 7.13) являются вогнутые и выпуклые
модели общего вида (неквадратичные) Существует множество математических методов
и соответствующих им оптимизационных процедур решения таких задач. Предположим,
например, что решаемая задача является моделью максимизации Аналогично
используемой средством Поиск решения процедуре метода приведенных градиентов
многие процедуры работают следующим образом.
1.	Находится начальная точка внутри допустимого множества ограничений (но не на
ею границе)
2.	Определяется направление подъема (или спуска для моделей минимизации) и про-
исходит движение вдоль этого направления или до достижения максимума (мини-
мума) в данном направлении, или до пересечения одной из границ допустимого
множества ограничении.
3.	Изменяется направление движения так, чтобы продолжить подъем (спуск), оста-
ваясь в пределах допустимой области
4.	Алгоритм завершается, когда найдена точка, удовлетворяющая необходимым ус-
ловиям оптимальности.
В процедурах такого типа, как и в большинстве других процедур, применяемых для
нелинейных неквадратичных задач, используются сложные вычисления, поэтому мы не
будем описывать их здесь подробно Достаточно сказать, что для вогнутых или выпуклых
моделей НЛП общего вида, в отличие от моделей ЛП, более важным показателем сложно-
сти модели представляется количество нелинейных переменных (т е переменных, входящих
в модель нелинейно), а не количество ограничений
Нелинейные задачи, которые можно попытаться решить
Рассмотрим теперь модели НЛП общего вида, составляющие уровень наивысшей
сложности на рис 7 13 Такие модели часто называют существенно нелинейными, это
обычно означает, что рассмотренные выше свойства выпуклости и вогнутости отсутст-
вуют. Для решения таких задач, как правило, используется та же процедура оптимиза-
ции, что и для вогнутых или выпуклых моделей общего вида. Однако результаты ее вы-
полнения различаются. Все алгоритмы оптимизации НЛП останавливаются, достигнув
точки, в которой выполнено необходимое условие оптимальности (т.е условие первого
порядка) Для вогнутой или выпуклой задачи гарантируется, что такая точка будет гло-
бальным оптимумом (если же целевая функция является строго вогнутой или строго вы-
пуклой, гарантируется, что такая точка будет единственным глобальным оптимумом) Но
для моделей НЛП общего вида это не обязательно выполняется, как можно было убе-
диться на примере модели Gulf Coast Oil или как это имеет место для модели с одной пе-
ременной на рис 7 16 Представленная на графике целевая функция не является ни вы-
пуклой, ни вогнутой Решением задачи является точка х, однако программа-
оптимизатор может остановиться в любой из точек х(, х2, х3 (поскольку они будут удовле-
творять условиям первого порядка) До настоящего времени не существует метода опти-
мизации, который полностью устранит такую возможность.
ГЛ ABA 7. Нелинейная оптимизация 463
Рис. 7.16. Невогнутая модель условной оптимизации
I — допустимая область
На практике эта трудность обычно преодолевается путем запуска оптимизирующей
программы из многих различных начальных точек, как это делалось для модели Gulf
Coast Oil Например, если начальная точка на рис. 7.16 будет близка к х, любой разум-
ный метод оптимизации сойдется кх’. Если ранее было найдено значение х,, оно теперь
будет отброшено, поскольку хотя и нельзя с уверенностью утверждать, чтох’ является оп-
тимальным, видно, что значение целевой функции в точке х, меньше, чем в точке х’
Зададимся таким вопросом как узнать, задача нелинейного программирования со
многими переменными является вогнутой, выпуклой или ни вогнутой, ни выпуклой9
Иными словами, как узнать, имеют ли целевая функция и ограничения нужную матема-
тическую форму? Есть несколько ответов на данный вопрос.
1.	Существуют математические критерии, с помощью которых иногда можно опре-
делить, являются функции вогнутыми, выпуклыми или ни теми, ни другими
2.	На основании экономической интуиции иногда можно утверждать, что такое-то яв-
ление отражает снижение предельной прибыли или увеличение предельных затрат,
и, следовательно, соответствующая функция является вогнутой или выпуклой
3.	Во многих реальных моделях на данный вопрос ответить невозможно Остается
просто попробовать оптимизировать модель, а затем исследовать практическую
полезность полученного решения Как уже отмечалось, если о модели известно
или предполагается, что она не является ни выпуклой, ни вогнутой, часто приме-
няется повторный запуск программы оптимизации из различных начальных точек,
чтобы исследовать возможность получения лучшего решения с более высоким
значением целевой функции.
Теперь мы можем обосновать совет избегать использования определенных негладких
функций Excel, которые обычно приводят к существенно нелинейному поведению моде-
лей. Примерами таких функций являются функции ЕСЛИ, ABS, ВЫБОР, ВПР, МИН,
МАКС и другие. В большинстве случаев эти функции делают модель нелинейной. Но они
также вызывают сложности и в моделях НЛП. Эти и другие негладкие функции могут
привести к возникновению резких изменений или разрывов в значениях целевой функ-
ции или функциях ограничений Резкие изменения в поведении функции возникают,
когда наклон ее графика (т.е. значения первых производных) резко меняется при некото-
рых пороговьгх значениях переменньгх, поскольку, например, функция ЕСЛИ обуслов-
ливает переход к связям (между переменными) другого вида. Аналогично непрерывность
функции нарушается, когда пороговые значения переменных вызывают переход к ново-
464 ЧАСТЬ II. Оптимизационные модели
му виду целевой функции или функций ограничений. Хотя при резких изменениях нет
разрыва функции, происходит нарушение непрерывности первых производных функ-
ции, которые используются для выбора направления поиска процедурой наискорейшего
подъема (спуска) средства Поиск решения В результате процедура не сходится к какому-
нибудь решению, так как программа “ходит” вокруг точки, в которой наблюдается раз-
рыв функции или ее производной, что в конечном итоге заставляет Поиск решения оста-
новиться. Эта проблема существует в дополнение ко всем сложностям, связанным с от-
сутствием вогнутости или выпуклости исходной задачи НЛП, которые могут привести
к сходимости к локальному оптимуму вместо глобального
7.8.	Генетический алгоритм
Как отмечалось, существенно нелинейные модели, подобные модели Gulf Coast Oil,
часто возникают в различных бизнес-ситуациях Кроме того, во многих существующих
табличных моделях широко используются негладкие функции Excel. Наличие сущест-
венно нелинейных и негладких функций, имеющих несколько локальных оптимумов,
обычно означает, что у данной модели отсутствуют свойства вогнутости или выпуклости,
необходимые средству Поиск решения, чтобы оптимизировать задачу НЛП и найти гло-
бальный оптимум На практике наличие в табличной модели негладких функций может
помешать средству Поиск решения найти даже локальный оптимум, поскольку его мето-
ды выбора направления поиска зависят от гладкости целевой функции
Чтобы проиллюстрировать сказанное, рассмотрим показанный на рис 7.17 график
целевой функций, которая является произведением двух негладких нелинейных функций
от двух переменных XI и Х2 При построении графика целевой функции Y для значений
XI и Х2 в диапазоне от 1 до 5 использовались значения этой функции, подсчитанньге
в таблице подстановки с двумя входами Приведенный график подтверждает невогну-
тость функции Y Данную модель можно рассматривать как модель бизнес-ситуации
с двумя переменными решения, в которой требуется максимизировать целевую функцию
прибыли Y Как показано на рисунке, существует множество локальных оптимумов, не-
которые из них с довольно плоскими вершинами, а другие с очень острыми вершинами.
С помощью средства Поиск решения мьг наверняка не получим глобальный оптимум,
находящийся приблизительно в точке XI = 1,42, Х2= 1,41 со значением целевой функ-
ции 22,28
На рис 7 18 показана крайне неприятная природа этой простой модели НЛП. При
первом запуске средства Поиск решения обеим переменным XI и Х2 было присвоено на-
чальное значение 3,3 Поиск решения нашел локальный оптимум, расположенный дале-
ко от глобального При повторном запуске средства Поиск решения переменным XI и Х2
было присвоено начальное значение 1, начальная точка находилась вблизи от глобаль-
ного оптимума, но Поиск решения вновь не нашел его. В этой простой модели можно от-
следить получаемые решения и сравнить их с известным глобальным максимумом, но
в более крупных моделях НЛП со многими переменньгми и ограничениями практически
невозможно представить форму графика целевой функции, поэтому весьма вероятно, что
будет принято “оптимальное” решение, которое может быть как угодно далеко от гло-
бального оптимального решения.
ГЛАВА 7. Нелинейная оптимизация 465
Рис. 7.17. Невогнутая модель НЛП со множеством оптимумов
466 ЧАСТЬ II Оптимизационные модели
Рис. 7.18. Два результата оптимизации модели НЛП
В настоящее время в теории оптимизации ведутся интенсивные исследования по соз-
данию устойчивых алгоритмов решения задач нелинейного программирования с неглад-
кими функциями, имеющими несколько оптимумов. При этом необходимо найти способ
выбора хороших начальных значений переменных, оценки промежуточных решений и их
использования для нахождения лучших значений переменных, не полагаясь на методы,
основанные на дифференцировании, которое часто невозможно выполнить вследствие
негладкости функций Именно это делает оптимизатор Evolutionary Solver, реализующий
генетический алгоритм
Понятие о методе эволюционного или генетического поиска5
Эволюционные алгоритмы, впервые разработанные Джоном Холландом (John Hol-
land) в 1970-х годах, сегодня чаще называют генетическими алгоритмами, поскольку они
имитируют процессы природного естественного отбора Первоначально эти алгоритмы
применялись в комбинаторной оптимизации и компьютерных исследованиях в области
искусственного интеллекта, однако в последнее время сфера их применения заметно
расширилась Благодаря быстрому совершенствованию компьютеров появилась возмож-
ность использовать генетические методы в оптимизационных моделях, которые не под-
даются решению с помощью традиционных методов, основанных на вычислении гради-
ентов Генетические алгоритмы гораздо реже, чем основанные на вычислении градиен-
тов методы поиска, останавливаются в точке локального оптимума или осциллируют
в окрестности точек разрыва С другой стороны, они требуют проведения очень боль-
шого количества вычислений и не гарантируют нахождения глобального оптимума
Основанный на биологических концепциях генетический алгоритм заметно отличает-
ся от большинства ранее описанных методов решения задач ЛП и НЛП. Сначала приве-
дем краткий перечень основных свойств, на которых строится работа алгоритма, а далее
опишем их более подробно
1.	Алгоритм использует случайно выбираемые начальные точки. Таким образом, это
недетерминированный метод
2.	В то время как в большинстве методов хранится только наилучшее решение, най-
денное в процессе поиска, в генетическом алгоритме хранится большое количест-
Дополнительные материалы по данной теме можно найти на Web-узле
http //www.geneticprogrammmg сот/Тutorial/mdex html
ГЛАВА 7. Нелинейная оптимизация 467
во промежуточных результатов, называемое популяцией возможных решений, не все
из которых являются хорошими решениями Данная популяция используется для
создания новых начальных точек, не обязательно в окрестности текущего наилуч-
шего решения, что помогает алгоритму избегать остановки в локальном оптимуме.
3.	Аналогично генным мутациям в биологии алгоритм время от времени производит
случайные изменения в одном или нескольких членах популяции для создания но-
вых потенциальных начальных точек-“потомков”, которые могут находиться дале-
ко от остальных членов данной популяции
4.	Как при половом способе размножения, элементы существующих в популяции
решений комбинируются друг с другом с помошью операции, напоминающей
скрещивание цепочек ДНК, чтобы создать новое потенциальное решение, обла-
дающее чертами каждого из родительских решений
5.	Любые нарушения ограничений новым решением приводят к вычитанию (в моде-
ли максимизации) из значения целевой функции для данного решения или при-
бавлению к нему (в модели минимизации) “штрафа”, сумма которого отражает
степень нарушения ограничений. Это измененное значение целевой функции ста-
новится мерой “пригодности” данного решения
6.	Аналогично естественному отбору начальные точки-потомки, которые не улуч-
шают значения целевой функции и не помогают получить новые начальные точки,
в конечном счете удаляются из популяции как “непригодные”.
В генетическом алгоритме решение задачи представляется в виде генома (или хромо-
сомы) Алгоритм работает с популяцией, содержащей десятки ичи даже сотни допусти-
мых решений Из этой популяции решений генетический алгоритм создает с помошью
операций мутации и скрещивания новые решения, чтобы получить набор претендентов
на “звание” наилучшего решения. Упрощенно говоря, в ходе скрещивания комбиниру-
ются две (родительские) хромосомы, чтобы получить новую хромосому (потомок) Как
и в половом размножении, идея скрещивания состоит в том, что новая хромосома может
оказаться лучше обеих родительских, если взять лучшие характеристики каждой из них
В отличие от скрещивания, операция мутации привносит некий элемент случайности
в новые хромосомы-потомки Ее задача заключается в том, чтобы помочь программе
найти такие решения-потомки, которые невозможно получить путем скрещивания Ре-
шения-потомки с низким значением выигрыша (“плохим” значением целевой функции)
сохраняются, поскольку они могут произвести в следующих поколениях потомков с вы-
соким выигрышем (лучшим значением целевой функции) Если этого не происходит, эти
потомки в конечном счете удаляются из популяции решении Согласно принципу выжи-
вания наиболее приспособленных, генетические алгоритмы— это алгоритмы поиска,
использующие структурированный обмен информацией (скрещивание) и рандомизацию
(мутации) для формирования процедуры поиска, обладающей свойствами природных
процессов, в каждом поколении создается новый набор решении, созданных из наиболее
подходящих экземпляров предыдущего поколения. Отметим, что генетический алгоритм
не является просто случайным движением по пространству возможных решений Это
было бы слишком неэффективно. Напротив, данный алгоритм эффективно использует
накопленную информацию для формирования новых решений, которые, как ожидается,
улучшат выигрыш Поэтому генетический алгоритм иногда называют методом направ-
ляемого случайного поиска.
468 ЧАСТЬ II Оптимизационные модели
Скрещивание
Обычно скрещиванием называют составление комбинации двух индивидуумов
(родителей) для получения двух новых индивидуумов (потомков). Однако в некоторых
генетических подходах используется неполовое скрещивание для получения одного по-
томка Главная задача операции скрещивания состоит в том, чтобы перенести генетиче-
ский материал, полученный от предыдущего поколения (значения переменных преды-
дущих возможных решений), в следующее поколение.
Первым шагом является селекция, в ходе которой определяется, сколько кандидатов
в популяции отбирается для скрещивания. Например, если всегда выбирается только од-
но лучшее решение из популяции, то будущие поколения популяции избранных реше-
нии быстро сойдутся к этому индивидууму. Поэтому селекция должна склоняться к вы-
бору лучших решений, но не только. Время от времени необходимо отбирать для скре-
щивания решения с низким выигрышем, чтобы поддерживать разнообразие в популяции
кандидатов
Некоторые наиболее часто применяемые методы отбора включают в себя механизм
рулетки (вероятность выбора решения-кандидата для скрещивания пропорциональна его
значению целевой функции), турнира (несколько кандидатов выбирается с помощью ме-
ханизма рулетки, а затем лучший из них отбирается для скрещивания) и упорядоченный
отбор (всякий раз выбираются самые лучшие кандидаты).
После того как решения-кандидаты будут выбраны, для составления комбинаций при-
меняется любой из множества существующих методов скрещивания. Приведем два из них.
Метод арифметического скрещивания создает выпуклую комбинацию пар значений
переменных родительских решений для образования двух новых решений-потомков
с помощью следующих операций.
Потомок! =/-Родитель! + (1 - г)Родитель2,
Потомок2 = (1 - г)Родитель! + гРодитель2,
где г — случайное значение из интервала от 0 до 1 (его выбор осуществляется перед каж-
дой операцией скрещивания)
При эвристическом методе скрещивания потомки создаются согласно формулам
Потомок! = Родитель1учший + г( Родитель^, - РодительВДШйй),
Потомок2 = Родительлучший,
где Родитель1учшйй и Родительхудш1[й выбраны, исходя из “качеств” родителей-кандидатов, а г
определяется так же, как и выше
Мутация
До недавнего времени мутация рассматривалась в качестве главной движущей опера-
ции в генетических стратегиях Мутацию можно реализовать, например, добавив “шум”
(случайную нормально распределенную величину с нулевым математическим ожидани-
ем) к каждой переменной решения При этом переменные решения, которые выходят за
пределы, заданные ограничениями модели, устанавливаются равными граничным значе-
ниям Часто (но не всегда) переменная в решении-кандидате имеет собственное значение
стандартного отклонения, также хранящееся в геноме, которое может изменяться вместе
с изменением значений переменных решения
ГЛАВА 7. Нелинейная оптимизация
469
Штрафные функции
Метод штрафных функций является наиболее общим подходом, позволяющим учесть
ограничения модели Штрафной функцией называется слагаемое, которое вычитается из
значения целевой функции (в моделях максимизации) или прибавляется к нему (в моделях
минимизации), если решение нарушает одно или несколько ограничений Значение штра-
фа пропорционально степени нарушения ограничения Часто размеры штрафов повыша-
ются в процессе работы алгоритма. Таким образом, нарушения ограничений допускаются
для ранних поколений, чтобы расширить возможности воспроизводства геномов, однако
для будущих поколений ситуация меняется. Использование штрафных функций имеет свои
слабые стороны Например, это очень грубый подход, поскольку он совершенно не исполь-
зует присущую конкретной модели информацию об ограничениях. Кроме того, выбор ве-
личин штрафов и их изменений с течением времени очень субъективен и может приносить
хорошие результаты в одних случаях, а в других быть неэффективным.
Более подробное описание генетического алгоритма не входит в задачу данной книги
Продемонстрируем его полезность при решении сложных задач НЛП, не поддающихся ре-
шению с помощью стандартного Поиск решения. Сокращенная версия генетического ал-
горитма в виде оптимизатора Evolutionary Solver встроена в надстройку Premium Edition
Solver for Education, которую можно найти на прилагаемом к книге компакт-диске Чтобы
активировать ее, необходимо щелкнуть на кнопке Premium в диалоговом окне Solver
Parameters (Поиск решения), после чего появится раскрывающийся список оптимизато-
ров (рис. 7.19).6 Установленные по умолчанию значения в диалоговом окне Solver Options
(Параметры поиска решения), также показанном на этом рисунке, должны подойти для
большинства моделей. Но отметим, что для быстрой работы оптимизатора Evolutionary
Solver для всех переменных необходимо задать верхние и нижние границы изменения, ко-
торые следует ввести в качестве новых ограничений. Хотя это условие не является необхо-
димым, его следует выполнить, поскольку, если переменные не имеют явно заданных гра-
ниц, оптимизатор должен рассматривать бесконечно большой диапазон возможных на-
чальных точек, что, в свою очередь, существенно снизит его эффективность.
Чтобы запустить оптимизатор Evolutionaty Solver, надо щелкнуть на кнопке Solve
(Выполнить). Для иллюстративной модели, представленной на рис. 7.17, этот оптимиза-
тор нашел самый высокий пик и сообщил решение, очень близкое к оптимальному, при-
мерно за Юс на медленном персональном компьютере, рассмотрев “всего лишь” около
2000 решений! Работа оптимизатора для средних моделей может продолжаться от не-
скольких минут до нескольких часов.
Следует отметить, что генетический алгоритм не является панацеей для решения лю-
бых задач НЛП. В действительности этот алгоритм даже не является оптимизатором
в точном смысле этого слова, поскольку он не обязательно находит оптимальное реше-
ние даже для хороших моделей. Например, при запуске оптимизатора Evolutionary Solver
для модели Gulf Coast Oil, когда в качестве начальной точки было выбрано представлен-
ное на рис. 7.8 решение, он не дал лучшего решения после многих минут работы и иссле-
дования более 30 000 решений. Однако запуск оптимизатора из точки конечного реше-
ния на рис. 7.10 привел к небольшому улучшению решения (рис. 7.20) после исследова-
6 Напомним, что установка надстройки Premium Edition Solver for Education меняет диалоговые окна сред-
ства Поиск решения на англоязычные окна Подробнее об установке этой надстройки см приложение В —
Прим ред
Поскольку в исходной формулировке задачи Gulf Coast Oil не указаны верхние и нижние границы для пере-
менных, их пришлось добавить, прежде чем использовать Evolutionary Solver
470 ЧАСТЬ II Оптимизационные модели
ния порядка 60 000 решений Заметим, что оптимизатор так и не определил наилучшее из
найденных решении, показанное на рис 7 11. Поскольку оптимизатор Evolutionary Solver
не является истинным оптимизатором в классическом смысле этого слова, его нужно
рассматривать как средство, которое производит интеллектуальный просмотр большого
множества потенциальных решений в поиске лучших
Рис. 7.19. Выбор оптимизатора Evolutionary Solver
, Совет. После того как оптимизатор Evolutionary Solver завершит работу и сообщит свое
I наилучшее решение, следует запустить средство Поиск решения снова, но теперь с обыч-
] ним нешнеиным оптимизатором. Если решение, найденное Evolutionary Solver, лежит в ок-
। рестности глобального оптимума, то использование этого решения в качестве начальной
! точки для Поиск решения может привести к быстрой сходимости к ближайшему опти-
[ му му который, можно надеяться, является глобальным
Насколько близко будет “лучшее” решение к глобальному оптимальному решению,
ни koi да не известно В общем случае остается только дать оптимизатору Evolutionary
Solver поработать достаточное количество времени и удовлетвориться наилучшим най-
денным решением
ГЛАВА 7. Нелинейная оптимизация 471
Модель прошводства бешина	Bi
Внешний источник 1
Внешний источник 2
Октановое удельная
число стоимость
$0,80
$0,90
=куплено смеси из внешних
источников
Октановое Удельная
Всего Наличие число стоимость
$0 90
$0 65
Regular Midgrade Premium
Продажа бензина
$1 25
10
Cell
$E$6
$F$3
a ooo <-8ooo
10 000 <=10 000
Цена за галлон
импортная смесь, галлон
Отечественная смесь, галлон
Спец, добавка, галлон
Всего продано
Минимум продаж
Октановое число бензина
Минимальное октановое число
1 249.1
Рис. 7.20. Решение задачи Gulf Coast Oil с помощью Evolutionary Solver
250.3
>=100
87.75
>=87
12 862.2
>=100
89,00
>=89
13 Доход	. .
* '-* 3 Стоимость импортной смеси $51,77 $3 868,50 $3 270,41
стоимость отечественной смеси $125,26 $5 562,90 $811,92
Стоимость добавкиМЙЯНМЙИМИЙИ $30,00
Суммарные затраты
Прибыль
"16
S1 IB 33 46 646 36 $2 731 71
Microsoft Excel ID 0 Population Report
Adjustable Cells
$Е$7 Отече
$Е$8
i

После завершения работы оптимизатора Evolutionary Solver на экран выводится диа-
логовое окно Solver Results (Результаты поиска решения) В этом окне предлагается но-
вый вид отчета, называемый Population Report (Отчет о популяции), который содержит
краткие характеристики созданной популяции решений В представленном на рис 7 20
фрагменте отчета показаны наилучшее и среднее значения всех переменных решения
и несколько показателей их изменчивости
Хотя процедура подстановки различных начальных решений, выполняемая вручную
с использованием обычного средства Поиск решения или автоматически с помощью
Evolutionary Solver, не гарантирует нахождения глобального оптимума, она вполне оп-
равдана с практической точки зрения. Если оптимизация с помощью Поиск решения
модели НЛП может дать лучшее решение, чем есть в настоящее время, то использование
модели НЛП вполне оправдано Это согласуется с общим положением, что на практике
нет ничего более “теоретического”, чем истинное оптимальное решение Как уже отме-
чалось, цель моделирования всегда состоит в том, чтобы помочь в поиске хороших решений
Общим критерием является сравнение стоимости улучшения решения (затраты на моде-
лирование и получение решения) и выгоды, принесенной новым решением
472 ЧАСТЬ II Оптимизационные модели
7.9.	Введение в квадратичное программирование
Как отмечалось в разделе 7 7, модели квадратичного программирования обладают
свойством вогнутости (выпуклости), что позволяет избежать сложностей оптимизации,
присущих моделям НЛП более общего вида Фактически модели квадратичного програм-
мирования (КП), как и модели целочисленного линейного программирования, являются
ближайшими родственниками моделей линейного программирования и обладают мно-
гими их свойствами. Проведем следующее сравнение.
•	Модель линейного программирования. Требуется максимизировать или минимизиро-
вать линейную целевую функцию при выполнении множества ограничений в виде
линейных равенств и неравенств, а также, возможно, условий неотрицательности
значений переменных.
•	Модель квадратичного программирования. Требуется максимизировать или мини-
мизировать квадратичную целевую функцию при выполнении множества ограни-
чений в виде линейных равенств и неравенств, а также, возможно, условий неот-
рицательности значений переменных.
Единственным различием двух моделей является вид целевой функции.
Квадратичные функции
Нам известно, что такое линейные функции. Приведем несколько примеров квадра-
тичных функций- 9х,2 + 4х, + 7, Зх,2 - 4х,х2 + 15х22 + 2 Ох, - 13х2 - 14.
Эти функции представляют собой суммы, содержащие квадраты переменных
(например, Зх,2), произведения двух переменных (4х,х2), а также линейные члены и кон-
станты В общем случае квадратичная функция N переменных представима в виде
лм
,-1	, = | / = (+1	/ = 1
Заметим, что если все коэффициенты Л, и Bt равны нулю, то такая функция будет линей-
ной. Следовательно, линейная функция является частным случаем квадратичной функции.
Следующий пример демонстрирует некоторые различия между моделями квадратич-
ного программирования (КП) и линейного программирования. Рассмотрим модель КП
минимизировать (х, - 6)2 + (х2 - 8)2
при ограничениях
х,<7.
х2<5,
х, + 2х2 < 12,
х,+х2<9,
х„х2>0.
Геометрическое представление модели
Геометрическое представление данной модели показано на рис. 7.21. Множество огра-
ничений, естественно, выглядит так же, как и в модели ЛП, поэтому в новых объяснениях
не нуждается. Чтобы показать, что данная целевая функция является частным случаем
квадратичной функции, ее можно переписать в видех, - 12х, + 36 +х22 - 16х2 + 64. Как вы,
возможно, помните, выражение (х, - 6)2 + (х2 - 8)2 = к2 является уравнением окружности
с радиусом к и центром в точке (6, 8). Таким образом, как показано на рис. 7.21, изолинии
целевой функции представляют собой концентрические окружности с центром в точке
(6, 8). Поскольку значение целевой функции на этих изолиниях увеличивается по мере уве-
ГЛАВА 7. Нелинейная оптимизация 473
личения радиуса к, а данная модель является моделью минимизации, оптимальное решение
находится в точке (4,4), как показано на рис 7.21. Ее можно охарактеризовать как точку,
в которой изолиния целевой функции впервые соприкасается с допустимым множеством.
В данном случае эта точка лежит на касательной, но в других случаях решение может ока-
заться в угловой точке, как и в задачах ЛП. Оптимальное значение целевой функции — это
ее значение в точке (4,4), т.е. (4 - 6)2 + (4 - 8)2 = 20.
Рис. 7.21. Графическое решение задачи КП
Сравнение с задачей АП
Данный пример ясно показывает, что отличает задачи КП от задач линейной оптими-
зации.
1. В данном случае, как и в моделях НЛП вообще, не обязательно существует угловое
решение. Поэтому для решения данной задачи нельзя использовать метод, анало-
гичный симплекс-методу, который ищет наилучшее угловое решение
2. Как прямое следствие пункта 1, в оптимальном решении может содержаться
больше ненулевых переменных, чем лимитирующих ограничений В данном при-
мере решение оказалось на границе допустимой области, но в других случаях оно
может находиться строго внутри нее.
Решение задач КП с помощью средства Поиск решения
Существует два подхода к оптимизации моделей КП. Один состоит в использовании
оптимизатора, общего для всех задач нелинейного программирования, например, как
Поиск решения, а второй — в использовании оптимизатора, созданного специально для
задач квадратичного программирования.8 Мы ограничимся рассмотрением надстройки
Excel Поиск решения.
Коммерческая версия надстройки Solver Premium Edition содержит специальный оптимизатор для задач
квадратичного программирования
474 ЧАСТЬ II. Оптимизационные модели
Microsoft Excel 10 0 О г moi по усюйчивости
Изменяемые ячейки________________________
Результ Нормир
Ячейка______Имя_______значение градиент
$В$3	XI___________________4.0_________0.0
$С$3	Х2 4,0 00
Ограничения__________________________________
Результ Лагранжа
Ячейка______Имя_______значение Множитель
Левая часть
$Р$5 ограничения 12 -3.999997854
Левая часть
$Р$6	ограничения	7.99999997 0
Рис. 7.22. Решение задачи КП
На рис 7 22 представлена модель, диалоговое окно Поиск решения, оптимальное ре-
шение и отчет по устойчивости для предыдущего примера Напомним, что приведено
в отчете по устойчивости
•	Числа в столбце Множитель Лагранжа соответствуют ограничениям. Как и в задачах
ЛП, он представляет скорость изменения оптимального значения целевой функции
при изменении правой части ограничения при неизменности других данных.
•	При отсутствии прямых ограничений на переменные числа в столбце Нормиро-
ванный градиент имеют значения для неотрицательных переменных, оптималь-
ные значения которых равны нулю Для таких переменных нормированный гради-
ент характеризует скорость ухудшения целевого значения, если они примут в оп-
тимальном решении положительные значения
ГЛАВА 7. Нелинейная оптимизация
475
На этом заканчиваем обсуждение квадратичного программирования и в следующем
разделе перейдем к рассмотрению приложений НЛП
Структуризация портфеля ценных бумаг
в компании Prudential Securities
Ha некоторых рынках ценных бумаг в последние годы наблюдались быстрый рост
и нововведения в сфере вторичной продажи жилья в кредит под его залог Рос был
стимулирован федеральными агентствами, которые должны были, увеличив приток
средств на ипотечное кредитование, способствовать росту количества владельцев
личных домов Эти агентства покупают ипотечные займы из первых рук и объеди-
няют их, чтобы создать ипотечные ценные бумаги.
Эти ценные бумаги вместе с ценными бумагами, выпускаемыми частными эми-
тентами, обращаются на рынках капитала вместе другими ценными бумагами с фик-
сированным доходом, такими, как казначейские билеты и облигации, а также их
корпоративными эквивалентами Выпуск ипотечных ценных бумаг достиг в послед-
нее время объема более 1 триллиона долларов, при этом оборот вторичного рынка
составляет более 5 миллиардов долларов в неделю Этот вторичный ипотечный ры-
нок сейчас сравним по размерам с рынком корпоративных облигации и сохраняй
потенциал для существенного роста, поскольку в ценные бумаги обращено только
40% ипотечного долга
В последние годы в компании Prudential был создан департамент первичных ипо-
течных ценных бумаг В силу сложности работы с данным типом ценных бумаг стан-
дартные средства оценки стоимости бумаг с фиксированным доходом оказались не-
пригодными Чтобы получить быструю и точную оценку, и, следовательно, эффек-
тивно торговать этими бумагами, компания использует целый ряд количественных
моделей, включающий модели линейного и нелинейного программирования
Кроме того, эти модели используются для страхования ценных бумаг, а также для
помощи клиентам в структурировании портфелей ценных бумаге целью добиться тре-
буемого результата (например, максимизировать ожидаемые доходы, минимизировать
инвестиционные риски и т п.) и при этом обеспечить выполнение некоторых ограни-
чений. К типичным ограничениям относятся минимальный и максимальный размер
портфеля, который позволено вложить в один конкретный тип обязательств, срок дей-
ствия ценных бумаг, а также общий объем инвестиций Модели используются сотни
раз за день маклерами, продавцами и клиентами. Благодаря внедрению данных моде-
лей компания Prudential превратилась из компании, даже не входящей в десятку круп-
нейших эмитентов, в компанию, постоянно входящую в первую тройку |2]
7.10.	Выбор портфеля инвестиций
Модель выбора инвестиционного портфеля является основной моделью современных
финансов. Об анализе инвестиционного портфеля написано немало книг Мы в своем
обсуждении только кратко коснемся этой интересной темы.
476
ЧАСТЬ II. Оптимизационные модели
Модель формирования инвестиционного портфеля
Постановка задачи анализа инвестиционного портфеля может выглядеть следующим об-
разом Инвестор имеет Р долларов, которые может вложить в п видов ценных бумаг; и он
хочет определить, сколько средств вкладывать в каждый вид бумаг. Выбранный набор цен-
ных бумаг называется инвестиционным портфелем. Инвестор хочет, чтобы портфель был
с высоким ожидаемым доходом и низким риском. Эти цели противоречивы, поскольку ча-
ще всего портфели с высоким ожидаемым доходом имеют также и высокий риск.
Приведем пример, чтобы объяснить, что в данном случае понимается под термином
доход Предположим, Dt долларов вложено в бумаги z и за определенный период времени
эти £), долларов выросли до 1,3.0,. В таком случае доход за данный период составляет
(1,3£)(- Д)/£), = 0,3. Понятие риска более тонкое и его сложнее объяснить. В нашем слу-
чае можно считать, что риск измеряется величиной возможного разброса (дисперсией или ва-
риацией) дохода инвестиционного портфеля. Это определение согласуется с тем, как боль-
шинство аналитиков в сфере портфельных инвестиций измеряют риск.
Поскольку задача состоит в обеспечении низкого риска и высокого дохода, можно
сформировать модель таким образом, чтобы минимизировать величину дисперсии дохо-
да (те минимизировать риск) при заданной нижней границе для ожидаемого дохода.
Кроме того, могут присутствовать некие ограничения, определяющие структуру портфе-
ля, т е какую часть средств позволено вкладывать в конкретные типы обязательств.
Формализация модели инвестиционного портфеля
Данная модель является моделью квадратичного программирования Обозначим че-
рез х, часть средств, вложенную в ценные бумаги i Например, если в модели необходимо
вложить Р долларов в два вида ценных бумаг и оптимальным решением оказалось
х, = 0,7, х2 = 0,3, то в ценные бумаги 1 будет вложена сумма ОДР долларов, а оставшаяся
сумма 0,ЗРдолларов будет вложена в ценные бумаги 2
Создадим модель для двух видов ценных бумаг В формулировке задачи используются
следующие обозначения о,1 2 3 4 5 — дисперсия годового дохода от ценных бумаг z (/= 1,2),
о12 — ковариация годового дохода от ценных бумаг 1 и 2, R, — ожидаемый годовой доход
от ценных бумаг i (z = 1,2), b — нижняя граница ожидаемого годового дохода от всех ин-
вестиций, S. — верхняя граница инвестиций в ценные бумаги i (z = 1,2).
Для построения модели примем без доказательства следующие факты.
1. Дисперсия годового дохода от ценных бумаг z — это число, описывающее изменчи-
вость дохода от года к году. Более строгое определение будет дано в следующем
разделе.
2. Ковариация годового дохода от ценных бумаг 1 и 2— это число, характеризующее,
в какой степени изменения доходов от двух видов ценных бумаг связаны друг
с другом Более строгое определение также будет дано в следующем разделе
3. Ожидаемый доход инвестиционного портфеля определяется как xtR, + x2R2.
4. Дисперсия дохода портфеля инвестиций — это оД,2 + 2о|2х,х2 + <32х2.
5. Стандартное отклонение дохода портфеля инвестиций вычисляется как квадрат-
ный корень дисперсии.
Исходя из данных определений модель инвестиционного портфеля можно записать
следующим образом.
ГЛАВА 7. Нелинейная оптимизация 477
Минимизировать о,*,2 +	+ о22х22
(дисперсия дохода)
при ограничениях
х>, + х2/?2’>Ь,
x2<s’
х„х2>0.
(необходимо вложить все средства)
(нижняя граница ожидаемого дохода инвестиционного портфеля)
(верхняя граница инвестиций в ценные бумаги 1)
(верхняя граница инвестиций в ценные бумаги 2)
(неотрицательность означает, что продажа ценных бумаг
без покрытия не допускается)
Предположим, что
о,2 = 0,09
о22 = 0,06
= 0,06
R2 = 0,02
5, = 0,75
S2 = 0,9
b = 0,03
о,2 = 0,02
Допустимое множество этой модели показано на рис 7 23, для удобства целевая
функция и ограничение ожидаемого дохода были умножены на 100 Из-за наличия огра-
ничения в форме равенства (х, + х2 = 1) допустимое множество представляет собой отре-
зок, соединяющий точки (0,25, 0,75) и (0,75, 0,25). Изолинии целевой функции пред-
ставляют собой эллипсы с центром в начале координат, малая полуось которых располо-
жена на прямой, составляющей угол 26,55° с осью х,. На рис 7.23 показаны изолинии
целевой функции для значений 2 и 4,54.
Рис. 7.23. Оптимальное решение задачи выбора инвестиционного портфеля
478
ЧАСТЬ II Оптимизационные модели
При увеличении значения целевой функции форма эллипса остается прежней, но его
размеры увеличиваются Задача состоит в том, чтобы выбрать наименьшее значение це-
левой функции, при котором эллипс коснется допустимого множества Как показано на
рис 7 23, при значении целевой функции 4,54 эллипс касается допустимого множества в
точке (%,’ = 0,36, х2’ = 0,64), которая является оптимальным решением
Как строится эллипс, знать необязательно В конечном счете реальные модели опти-
мизируются компьютером, а не графически Однако геометрическое представление по-
зволяет лучше разобраться в модели и помогает при интерпретации свойств решения.
В
С
о
Модель портфеля
инвестиций
Решение % вложении
Ограничения
Ожидаемый доход портфеля
Ценные Ценные
бумаги 1 бумаги 2 Всего
| 36 36%	63 64% |юо%
<=90% =100%
2%
Ценные
бумаги 2 Ковариация
<=75%
6%
Ценные
бумаги 1
3,455% >=3%
0 0243
0 0093
Показатели риска
Дислерсияковариация ценных бумаг
Дисперсияковариация портфеля 0 0119
Рис. ~.24. Решение шиичи выбора инвестиционного портфе.т

ГЛАВА 7. Нелинейная оптимизация 479
На рис. 7 24 показано решение задачи инвестиционного портфеля с помощью средст-
ва Поиск решения Лимитирующим является только ограничение, требующее вложения
всех средств Это видно и в геометрической интерпретации на рис. 7 23 Судя по значе-
нию левой части ограничения минимального дохода, ожидаемый доход данного портфе-
ля составляет 3,454% Сравнивая оптимальные значения х,' и х2’, можно заметить, что оп-
тимальный портфель содержит больше ценных бумаг с более низким ожидаемым годо-
вым доходом (те ценных бумаг2) Причина заключается в том, что дисперсия для
ценных бумаг 2 ниже, чем для ценных бумаг 1
Следует заметить, что с помощью Поиск решения можно оптимизировать данную
модель, в которой будет максимизироваться доход портфеля при условии, что его дис-
персия не превысит заданной верхней границы Поскольку в такой формулировке квад-
ратичная функция является частью одного из ограничений, а не целевой функцией, та-
кая модель, строго говоря, не является квадратичной. Однако такая формулировка не вы-
зывает сложностей при применении средства Поиск решения, и многие разработчики
моделей предпочитают использовать именно такую формулировку при оптимизации ин-
вестиционного портфеля.
7.11.	Пример модели портфельных инвестиций
В данном разделе мы рассмотрим пример с тремя видами ценных бумаг В отличие от
предыдущего примера, в котором все параметры были заданы, здесь нужно будет испоть-
зовать данные для оценки параметров модели После этого модель будет оптимизирована
средством Поиск решения, и мы обсудим полученное решение
Формулировка задачи
Обозначим три вида ценных бумаг какх, у и z Пусть X — доля ценных бумаг х в инве-
стиционном портфеле, У — доля ценных бумагу, Z— доля ценных бумаг z в инвестици-
онном портфеле.
Для обозначения любого из видов ценных бумаг (х, у или г) будет также использоваться
выражение “ценные бумаги Г. В предыдущих разделах модель портфельных инвестиций
была представлена так, как будто параметры, описывающие распределение будущих дохо-
дов, известны, те предполагается, что известны ожидаемые доходы, вариации и ковариа-
ции ценных бумаг На практике эти параметры необходимо оценивать на основании дан-
ных за прошлые годы В общем случае, если имеются данные за п периодов (лет), то для
каждого вида ценных бумаг z известны значения А,', связанные с каждым периодом /, где t
изменяется от I до п Иными словами, для каждого вида ценных бумаг имеется п значении
дохода за прошлые годы Ожидаемый доход за предстоящий период от ценных бумаг z оце-
нивается формулой R: =	, те является средним арифметическим доходов за про-
«7^
шлые периоды Значения А,' дохода за прошлые периоды также используются для оценки
дисперсии и ковариации. Соответствующие формулы имеют следующий вид’
Читатели, изучавшие статистику, могут заметить, что эти оценочные формулы не учитывают степени
свободы Мы используем эти формулы, несмотря на небольшое отклонение оценок, чтобы обеспечить согла
сование с функцией Excel КОВАР
480 ЧАСТЬ II. Оптимизационные модели
оценка дисперсии дохода от ценных бумаг/: о2 =—	-R,)2,
оценка ковариации дохода от ценных бумаг / иу: о2 = —^(Я' -/?,)(/?' -Л,).
Введем дополнительные обозначения- b — нижняя граница ожидаемого дохода инве-
стиционного портфеля, SI — верхняя граница доли, которую ценные бумаги / могут со-
ставлять в структуре портфеля.
Формулировка задачи для трех типов ценных бумаг выглядит следующим образом.
Минимизировать о2Х2 + о2К2 + o2Z2 + 2ojvAT + 2ox.XZ + 2ov.KZ
при ограничениях
ЯТ + R Y + RZ>b,
Х + Y+Z= 1,'
^<5,
Г<5,
Z<S,
X, r,Z>0.
Целевой функцией является дисперсия дохода портфеля, которая, как отмечалось
в предыдущем разделе, обычно считается мерой риска портфеля инвестиций Первое ог-
раничение устанавливает нижнюю границу для ожидаемого дохода инвестиционного
портфеля Второе ограничение утверждает, что сумма долей инвестиций должна соста-
вить единицу, а оставшиеся ограничения задают верхние границы долей различных цен-
ных бумаг в структуре портфеля
Если в портфель может входить более трех видов ценных бумаг, ожидаемый доход вы-
числяется по формуле . Как и ранее, R: — это ожидаемый доход от ценных бумаг i,
а X, — доля ценных бумаг / в инвестиционном портфеле В общем случае, когда портфель
может состоять из А видов ценных бумаг, дисперсия дохода портфеля вычисляется по
формуле
Решение с помощью средства Поиск решения
После подстановки численных оценок параметров данную модель квадратичного
программирования можно оптимизировать с помощью средства Поиск решения В каче-
стве конкретного примера рассмотрим три вида ценных бумаг, для которых есть данные
о доходах за прошедшие 12 лет: это акции компаний AT&T, General Motors и USS — хол-
динга компании US Steel Показатели дохода от акций приводятся в табл. 7.3. Доход в го-
ду п вычисляется по формуле
10 В матричном представлении дисперсия дохода портфеля записывается как XTYX, где X — это вектор-
столбец (X,, , XJ, a Y— симметричная матрица ковариаций, (1, ))-й элемент которой равен ац(<хЙ = of)
Если X является вектор-строкой, то дисперсия дохода портфеля вычисляется как XYXT
ГЛАВ A 7. Нелинейная оптимизация 481
(заключительная цена, я) — (заключительная цена, я — 1) + (дивиденды, я)
(заключительная цена, я - 1)
Здесь заключительные цены и дивиденды выражены в долларах на акцию.
Таблица 7.3. Доход от акций за последние 12 лет, %
Год	AT&T	GM	USS
1	30,0	22,5	14,9
2	10,3	29,0	26,0
3	21,6	21,6	41,9
4	-4,6	-27,2	-7,8
5	-7,1	14,4	16,9
6	5,6	10,7	-3,5
7	3,8	32,1	13,3
8	8,9	30,5	73,2
9	9,0	19,5	2,1
10	8,3	39,0	13,1
И	3.5	-7,2	0,6
12	17,6	71,5	90,8
Предположим, что мы хотим минимизировать дисперсию дохода инвестиционного
портфеля при условии, что ожидаемый доход составит не менее 15% и не более 75% об-
щей суммы средств, которые можно вложить в акции любого одного вида Табличная мо-
дель, решение, найденное с помощью средства Поиск решения, и отчет по устойчивости
представлены на рис 7 25.
Решение предусматривает, что примерно 53% портфеля будут составлять акции АТТ,
35,6% акции GM и 11,35% US Steel. Ожидаемый годовой доход в точности равен 15%
Оптимальное значение целевой функции показывает, что вариация годового дохода
портфеля составляет примерно 0,0205, таким образом, стандартное отклонение равно
примерно 14,33% Если считать, что данная модель правильна, и предположить, что до-
ход инвестиционного портфеля является нормально распределенной величиной со сред-
ним значением 15% и стандартным отклонением 14,33%, то согласно теории вероятно-
стей с достаточной уверенностью (доверительный уровень 95%) можно ожидать, что дан-
ный портфель в следующие годы будет давать доход от -13,7% до +43,7% (те
15% ± 2x14,33%) Фактические доходы трех рассматриваемых видов акций в последую-
щие три года были такими, как показано в табл. 7 4 Здесь же показаны действительные
доходы инвестиционного портфеля, рассчитанные на предложенных моделью оптималь-
ных долях.
482 ЧАСТЬ II. Оптимизационные модели
Рис. 7.25. Решение задачи выбора инвестиционного портфеля
ГЛАВА 7. Нелинейная оптимизация 483
Таблица 7.4. Действительные доходы от ценных бумаг, %
Акции	Год 1	Год 2	ГодЗ
AT&T	10,3	3,9	3,0
GM	51,2	-5,0	-20,0
USS	64,7	32,2	-26,6
Доход портфеля	31,1	3,9	-8,6
Значение множителя Лагранжа в отчете по устойчивости показывает, что увеличение
ожидаемого дохода на 1%(те увеличение на 0,01 значения в ячейке G21) приведет к уве-
личению дисперсии примерно на 0,00324 Следовательно, новая дисперсия портфеля со-
ставит около 0,0238, а стандартное отклонение будет равно 15,4% Эти числа являются
приблизительными, поскольку множители Лагранжа определяют мгновенные скорости
изменения оптимального значения целевой функции при изменении значений правых
частей ограничений (в задачах ЛП теневые цены (аналог множителей Лагранжа) посто-
янны в определенных интервалах изменения правых частей ограничений). Для модели
инвестиционного портфеля это видно из общей формы зависимости дисперсии портфе-
ля от значения Ь, показанной на рис 7 26 При создании данного графика использова-
лась таблица подстановки с одним входом, чтобы подсчитать оптимальное значение дис-
персии портфеля для значении ожидаемого дохода в пределах от 10 до 20%.
График показывает, что усиление ограничения для ожидаемого дохода (т е увеличе-
ние значения ожидаемого дохода Ь) ухудшает оптимальное значение целевой функции
На языке финансистов данный график называется границей эффективности портфеля Ее
свойства изучаются в курсах по финансированию Мы же просто отметим, что это кусоч-
но-квадратичная выпуклая функция.
Рис. 7.26. Граница эффективности портфеля
7.12.	Модель управления запасами
По определению запасы — это отложенный товар в хранилище, ожидающий своего
использования. Существует множество типов запасов, например, запасы сырья, запасы
полуфабрикатов, запасы конечных продуктов, запасы валюты и даже запасы людских ре-
сурсов. Запасы создаются по ряду причин.
484 ЧАСТЬ II Оптимизационные модели
1.	Запасы сглаживают разрыв между предложением и спросом. Например, урожай
кукурузы собирается в сентябре и октябре, а спрос на кукурузу практически по-
стоянен на протяжении года Поэтому урожай необходимо хранить в виде запаса
для последующего использования
2.	Возможность хранения запасов часто позволяет снизить производственные из-
держки, поскольку некоторые изделия более экономично производить большими
партиями даже при отсутствии заказов в данный момент.
3.	Создание запасов — способ хранения труда. Например, наличие трудовых ресур-
сов для производства может оказаться лимитирующим ограничением в более
поздний период, но нелимитирующим в более ранние периоды. Возможность
произвести дополнительную продукцию в эти более ранние периоды и затем хра-
нить ее в запасах высвобождает трудовые ресурсы в последующие периоды, позво-
ляет найти им другое применение
4.	Наконец, запас обеспечивает возможность быстрого обслуживания клиентов сразу
же при возникновении потребности, и потребители готовы платить за это удобство.
Существует три типа затрат, связанных с деятельностью по организации запасов- из-
держки хранения, издержки размещения заказа и издержки возможного дефицита. Лучше
всего объяснить смысл этих расходов на примере. Помимо другой продукции на складе
компании STECO хранится короткомерный волоконно-оптический сетевой кабель (СК),
используемый для подключения Internet-маршрутизаторов к локальному сетевому обо-
рудованию
Издержки хранения
В настоящий момент запасы СК компании STECO составляют 3000 штук. Каждый
СК обходится компании в $8. Получается, что в виде запасов кабеля находятся средства
на сумму 8x3000 = $24000 Предположим, что компании пришлось сократить эти запасы
до 1000 штук, в результате стоимость запасов сократилась до $8000. В таком случае мож-
но инвестировать часть высвободившихся средств ($16000) Иными словами, владея за-
пасами, компания STECO отказывается от возможности вложить деньги во что-нибудь
другое Эта так называемая цена шанса (издержки в результате принятия альтернативного
решения) является, возможно, наиболее важной составляющей издержек хранения запа-
сов Ее величина тесно связана с рыночной процентной ставкой Есть также другие со-
ставляющие связанных с хранением запасов расходов возмещение за поломку, хищения,
страхование, складирование и специальные требования по обработке Чем больше запасы,
тем больше затраты на их хранение
Издержки размещения заказа
Каждый раз когда компания STECO размещает заказ на пополнение своих запасов,
это связано с определенными затратами на выполнение заказа Эти затраты не зависят
от заказанного количества, они связаны с количеством времени, необходимым сотрудни-
кам для осуществления учета, выписки счета-фактуры, проверки заказа и т д
Издержки возможного дефицита
Дефицит означает, что у фирмы закончились запасы Как правило, данный термин обо-
значает явление, когда заказы клиентов продолжают поступать после исчерпания запасов.
Существует, по крайней мере в контексте данной модели, два способа трактовки таких за-
казов. Первый состоит в том, что заказы сохраняются и выполняются после пополнения
ГЛ ABA 7. Нелинейная оптимизация 485
запасов. Такая схема действий называется задержкой заказов В управлении запасами
встречаются модели с возможностью дефицита, в одних допускается задержка заказов, в
других — нет. В любом случае существуют издержки дефицита Эти издержки включают в
себя потерю прибыли при невыполнении заказа (в случае недопустимости задержки зака-
зов) или при его задержке (если разрешено выполнение заказов с опозданием), а также по-
тери, связанные с такими менее материальными факторами, как возможность потерять
клиента, потеря расположения или получение плохого отзыва об обслуживании В случае
дефицита без возможности задержки заказов обычно используется термин убыток, кото-
рый отражает удельную стоимость неудовлетворенного спроса В случае дефицита с воз-
можностью выполнения заказов с опозданием говорят об издержках, связанных с задержкой
заказов, что означает стоимость единицы отложенного спроса
Для такой компании, как STECO, в которой сотни тысяч долларов вложены в запасы,
существуют различные способы управления запасами, которые порождают похожие про-
блемы. Основные проблемы понятны, с одной стороны, хорошо иметь запас, поскольку
это позволит гарантировать выполнение заказов клиентов (т.е избежать издержек дефи-
цита), с другой стороны, содержание запаса связано с издержками хранения Эти издерж-
ки можно уменьшить, чаще заказывая малые количества товара, но такой подход приво-
дит к росту издержек размещения заказов Таким образом, необходимо сбалансировать
три указанные составляющие затрат
Если известно, что именно следует запасать, остальные вопросы одинаковы для всех
систем управления запасами Для каждого типа запасов необходимо ответить на два ключе-
вых вопроса 1) когда следует размещать заказ на пополнение запасов, и 2) каким должен
быть размер заказа или заказываемое количество9 Необходимость учета многих факторов
делает эту задачу достаточно сложной Ниже перечислены наиболее важные факторы
1.	Насколько хорошо известна величина будущего спроса
2.	Издержки дефицита и административная политика (допускается выполнение за-
казов клиентов с опозданием или нет)
3.	Издержки хранения и размещения заказов на пополнение запасов
4.	Возможность длительных промежутков времени между размещением заказа на по-
полнение запасов и получением продукции.
5.	Наличие планов закупки с оптовыми скидками
Текущая политика компании STECO
Ежемесячный спрос на СК за предыдущий год представлен в табл 7 5 Термин спрос
обозначает имеющиеся заказы потребителей и не обязательно совпадает с объемом про-
даж Например, в январе прошлого года было заказано 5300 штук Если в запасе имелось
хотя бы 5300 штук, то объем продаж равен спросу (т е 5300 штук) Если же запас состав-
лял менее 5300 штук, например, только 5000, то объем продаж составил 5000 штук, что
меньше спроса, следовательно, возник дефицит.
Таблица 7.5. Ежемесячный спрос на СК
Месяц	Спрос,	шт.
Январь	5 300
Февраль	5 100
Март	4 800
486 ЧАСТЬ II. Оптимизационные модели
Окончание табл. 7.5
Месяц	Спрос, шт.
Апрель	4 700
Май	5 000
Июнь	5 200
Июль	5 300
Август	4 900
Сентябрь	4 800
Октябрь	5 000
Ноябрь	4 800
Декабрь	5 100
Совокупный годовой спрос	60 000
Средний ежемесячный спрос	5 000
В течение нескольких лет спрос на кабель оставался постоянным и составлял при-
мерно 5000 штук в месяц Исходя из этого, компания STECO избрала политику, которая
заключается в ежемесячном добавлении в запас 5000 штук СК Поскольку ожидается, что
спрос останется примерно на этом же уровне в будущем, предполагается сохранить суще-
ствующую политику управления запасами. Однако насколько хороша эта политика, если
учесть имеющиеся данныеВ 9
Чтобы ответить на этот вопрос, можно оценить, какими будут издержки политики
ежемесячного заказа 5000 СК в упрощенной модели при следующих предположениях.
1.	Доставка всегда производится в первый день месяца
2.	Спрос известен, возникает равномерно и его уровень составляет 5000 штук в месяц.
3.	Весь спрос удовлетворяется без задержки заказов, иными словами, возникновение
дефицита запрещено
В таком случае график наличного запаса в любой момент времени можно изобразить
так, как показано на рис. 7 27 В начале каждого месяца в результате доставки заказан-
ного количества запас возрастает до 5000 штук, а затем постепенно снижается до 0 с по-
стоянной скоростью 5000 штук в месяц (постоянный ежемесячный уровень спроса) От-
метим также, что пополняющая запас поставка от производителя происходит в момент,
когда наличный запас равен нулю Поэтому дефицит не возникает. При выполнении пе-
речисленных предположений затраты функционирования системы, показанной на
рис 7 27, зависят только от того, сколько новых единиц хранения заказано, а также от из-
держек хранения и размещения заказа Посмотрим, как вычисляются затраты функциони-
рования Во-первых, отметим, что если ежемесячно заказывается 5000 штук СК и спрос
составляет 5000 штук в месяц, то среднемесячный объем запаса составляет 2500 штук
(рис 7 27)
ГЛАВА 7. Нелинейная оптимизация 487
5	6 Время —-
Рис. 7.27. Наличный запас, объем заказов 5000 штук
На рис. 7 28 показано, как будет вести себя запас, если заказывать по 10 000 штук СК
каждый второй месяц Если спрос остается на уровне 5000 штук в месяц, средний объем
запаса удвоится, но ежегодное количество заказов на пополнение запаса сократится
вдвое Таким образом, политика увеличения объема заказов приводит к увеличению из-
держек хранения, поскольку увеличивается средний запас, и уменьшению годовых из-
держек размещения заказов, поскольку пополнения производятся реже
6 Время
Рис. 7.28. Наличный запас, объем заказов 10 000 штук
Для ответа на два поставленных выше вопроса воспользуемся простои моделью, на-
зываемой моделью определения оптимального размера заказа (ОРЗ), которая призвана сба-
лансировать издержки размещения заказов и хранения запасов
Разработка модели ОРЗ
Простейшая форма модели ОРЗ основывается на следующих предположениях
1.	Дефицит не допускается Таким образом, как только уровень запасов достигает
нуля, делается новый заказ на их пополнение
2.	Уровень спроса является постоянным
3.	Учитываются только издержки размещения заказов и издержки хранения запасов
Модель ОРЗ находит оптимальный объем заказа (оптимальное заказываемое количе-
ство), определяемый как количество, которое при выполнении трех вышеуказанных
предположений минимизирует суммарные годовые издержки размещения заказов на СК и
хранения его запаса В модели используются следующие обозначения
1. Издержки размещения заказа С Каждый раз при размещении заказа отдел закупок
должен связаться с поставщиком и определить текущую цену и время доставки,
заполнить бланк заказа на Web-сайте или отправить его по электронной почте, пе-
реслать заказ в систему управления запасами компании STECO и инициировать
488 ЧАСТЬ II. Оптимизационные модели
создание записей о получении и хранении товара При поступлении заказа получа-
тель должен заполнить поля записей о получении и хранении товара и обновить
базу данных компании STECO, отражающую состояние заказов. Все эти операции
стоят денег Компания оценивает стоимость размещения одного заказа на СК (вне
зависимости от количества заказанных единиц) в $25. В эту стоимость входит $20,
направленных на оплату труда канцелярских работников и агентов по закупке,
и $5 на материальные расходы и оплату услуг связи.
2. Издержки хранения запаса Сх. Каждый вложенный в запасы доллар компания
STECO могла бы использовать другим образом. Например, можно положить
деньги в банк или приобрести казначейские векселя и получать процентный до-
ход Вкладывая доллар в запасы, STECO теряет возможность вложить его в другие
проекты, следовательно, возникают издержки в результате потерянных возможно-
стей Как правило, эти издержки составляют большую часть издержек хранения
запасов Кроме того, существуют такие накладные расходы, как арендная плата,
оплата коммунальных услуг, страховка, которые относятся к единице хранимой
продукции
Стоимость хранения запасов обычно определяется как стоимость хранения одной
единицы продукции в течение года и исчисляется как процентная доля от стоимости
данной единицы По оценке компании STECO, стоимость хранения одного СК в течение
года составляет 24% его отпускной цены Поскольку каждый СК стоит $8, издержки хра-
нения в запасе одной штуки в течение года составляют Сх — 0,24х$8,00 = $1,92.
Годовые издержки хранения и размещения заказов
Для вычисления минимизирующего затраты объема заказов сначала необходимо вы-
разить годовые издержки хранения и размещения заказов (ГХР) как функцию заказывае-
мого количества Эти издержки состоят из двух частей' годовых издержек размещения
заказов и годовых издержек хранения
Годовые издержки размещения заказов = С?х(число заказов за год).	(7.1)
Если заказываемое количество составляет 5000 штук, компании требуется размещать
12 заказов в год, поскольку суммарный спрос составляет 60 000 штук, а 60 000/5000 = 12.
Общая формула имеет вид
N = D/Q,	(7.2)
где А — число заказов в год, D — годовой объем спроса, a Q — объем заказа. Таким образом,
годовые издержки размещения заказов = CN= C^D/Q).	(7 3)
При вычислении годовых издержек хранения учитывается следующее годовые издерж-
ки хранения равны произведению Сх на средний объем запаса, при равномерном спросе
средний объем запаса равен половине максимального запаса. Поскольку заказываемое ко-
личество одновременно является максимальным наличным запасом (см. рис. 7.27 и 7.28),
получаем
годовые издержки хранения = Cx(Q/2).
(7.4)
ГЛАВА 7. Нелинейная оптимизация 489
Сложив выражения (7.3) и (7.4), получим следующую формулу для годовых издержек
хранения и размещения заказов как функции заказываемого количества Q
ГХР(0) = Cpx(D/Q) + Cx(Q/2).	(7.5)
Поскольку уровень спроса составляет D штук в год, Q штук заказа будут израсходованы
за Q/D лет, именно в этот момент уровень запасов дойдет до нуля Например, если Q = 5000,
a Z) = 60 000, заказанное количество 5000 штук будет израсходовано через
5000/60 000 = 1/12 года = 1 месяц. Подставив в формулу (7.5) значения Ср, D и Сх, получим
ГХР(0) = $25х(6ОООО/0) + $ 1,92х(0/2) = 1 500 000/0 + 0,96Q.	(7 6)
При Q = 5000 имеем ГХР(5000) = $300 + $4800 = $5100. Используя выражение (7.6),
можно построить график зависимости годовых издержек хранения и размещения заказов
от объема заказа Q (рис. 7.29). Из графика видно, что оптимальный объем заказов
(доставляющий минимум функции ГХР(0)) несколько больше 1000 штук.
Рис. 7.29. Годовые издержки хранения и размещения заказов STECO
На рис. 7.30 представлена табличная версия модели управления запасами компании
STECO Данная модель является нелинейной, поскольку Q входит в качестве знаменате-
ля в формулу целевой функции. Формулы в ячейках С16:С17 описывают издержки раз-
мещения заказов и издержки хранения запасов. Поскольку стоимость закупки постоянна
и не зависит от Q (стоимость закупки = закупочная цена х годовой спрос), она не исполь-
зуется для вычисления оптимального значения Q. Она включена в модель для полноты
определения суммарных годовых затрат. Ограничение, требующее, чтобы в течение года
был размещен хотя бы один заказ, включено в модель для того, чтобы средство Поиск
решения не проверяло (бессмысленный) вариант 0 = 0, что приведет к ошибке деления
на 0 в формуле издержек размещения заказов и может прервать процесс оптимизации.
Полученное оптимальное решение согласуется с графическим представлением, показан-
ным на рис. 7.29.
490 ЧАСТЬ II Оптимизационные модели
Рис. 7.30. Модель ОРЗ компании STECO
Оптимальный объем заказа в модели ОРЗ
Найдем формулу для вычисления Q‘, оптимального объема заказов (звездочка пока-
зывает, что это оптимальное решение задачи) Благодаря простой форме модели можно
вывести формулу для Q‘ как значения, доставляющего минимум функции ГХР(С) Про-
ГЛАВА 7. Нелинейная оптимизация 491
дифференцировав выражение (7.5) по Q и приравняв производную 0, видим, что в точке
оптимума годовые издержки хранения равны годовым издержкам размещения заказов:"
Cx(Q/2) = Cx(D/Q),	(7 7)
(Q)2 = 2CpD/C,	(7 8)
Иногда удобно оценивать Сх, исходя из предположения, что это определенная про-
центная доля i закупочной цены Р, т.е. Сх = iP Тогда формулу (7 9) можно записать в виде
В нашем примере закупочная цена кабеля Р составляет $8, а доля i, используемая для
вычисления С, равна 24%
Количество Q* часто называют экономически выгодным размером заказа, и оно опреде-
ляется входными параметрами С, D и С Подставив в формулу (7 9) числовые значения
этих параметров для СК, определим, что оптимальный объем заказа для сетевых кабелей
(2x60000x25
составляет О =--------------= 1250 .
V 1,92
Подставив это значение в выражение (7 6) для годовых издержек хранения и разме-
щения заказов, получим
ГХР((2‘) = ГХР( 1250) = 150000/1250 + 0,96x1250 = $1200 + $1200 = $2400
Эти значения совпадают со значением на рис. 7 30, найденным средством Поиск ре-
шения.
Анализ чувствительности
Будет ли использоваться решение задачи ОРЗ, зависит от того, насколько реально это
решение В конце концов, модель ОРЗ, как и все другие модели, идеализирована Она
является абстрактным и приближенным представлением реальности В данном случае,
как и всегда в моделировании, основным является вопрос насколько чувствительны ре-
зультаты моделирования к сделанным предположениям и данным9
Поскольку модель достаточно реалистична, создается впечатление, что затраты на со-
держание запасов, подсчитанные с помощью модели, являются достаточно хорошими
оценками реальных затрат компании STECO. Следовательно, использование предло-
женной моделью оптимальной политики (объем заказа 1250 штук) представляется более
предпочтительным, чем традиционная политика заказа 5000 штук Однако компании не-
обходимо выяснить, насколько чувствительны оптимальный объем заказа и, что более
важно, оптимальные годовые издержки к изменению данных В конечном счете парамет-
ры С и Сх сами являются оценочными. Если компания STECO ошибется в оценке дан-
Утверждение, что в точке оптимума выполняется равенство годовых издержек хранения и годовых из-
держек размещения заказов, верно только для рассматриваемой конкретной функции Это не является об-
щим положением
492 ЧАСТЬ II Оптимизационные модели
ных параметров, как это повлияет на разность между вычисленными 0 и ГХР' и истин-
ными Q' и ГХР’9 Если результаты тесно связаны со значениями данных оценок, неясно,
следует ли компании реализовать рекомендованную моделью оптимальную политику.
Рассмотрим, как результаты модели ОРЗ могут меняться при изменении оценок издер-
жек хранения и размещения заказов В компании STECO предполагают, что С =$1,92,
а С = $25 Рассмотрим четыре ситуации, когда значения параметров отличаются от значе-
ний, выбранных STECO Эти значения показаны в первых двух столбцах табл. 7.6.
Таблица 7.6. Анализ чувствительности
Сл Ср Оптимальное Q Минимальные затраты Решение" STECO Затраты STECO Потери, %
1,72	23	1267	2179	Q = 1250	2179	0
1,72	27	1372	2361	(2= 1250	2371	0 42
2,12	23	1141	2419	Q = 1250	2429	0 41
2,12	27	1236	2621	Q = 1250	2621	0
’ Подсчитано при Сх = $1,92 и Ср = $25
В первом случае компания STECO ошиблась в большую сторону в оценке каждого из
двух параметров примерно на 10% Если бы компания правильно оценила эти парамет-
ры, ей следовало бы заказывать по 1267 штук кабеля, что привело бы к годовым издерж-
кам хранения и размещения заказов, равным $2179. Но вычисленное значение ГХР при
этих параметрах и оптимальном значении Q = 1267 дает то же значение затрат компании
STECO Поэтому ошибка в оценке никак не отразится на годовых издержках хранения
и размещения заказов
Другие три примера показывают, что воздействие на годовые издержки хранения
и размещения заказов приведенных комбинаций оценок Сх и Ср является совершенно не-
значительным. Таким образом, анализ свидетельствует, что в данном случае модель ОРЗ
устойчива даже к 10% отклонений или ошибок в оценке затрат. Оказывается, что данное
приятное свойство присуще моделям ОРЗ в целом.
7.13.	Модель управления запасами при наличии оптовых
скидок
Модель управления запасами компании STECO — это классическая модель ОРЗ, ми-
нимизирующая годовые издержки хранения запасов и размещения заказов на их попол-
нение На практике существует множество вариаций этой классической модели ОРЗ, ка-
ждая из которых требует новой формулировки зависимостей между элементами модели
и повторного вычисления экономически выгодного объема заказов. В этом и следующем
разделе мы приведем два примера подобных моделей
Оптовые скидки и оптимальное решение для компании STECO
Хотя затраты на закупку продукции были включены в табличную модель на рис. 7.30,
их не нужно было учитывать, поскольку предполагалось, что стоимость единицы заку-
паемой продукции постоянна и не зависит от объема заказа Q. Предположим теперь, что
поставщик сетевого кабеля предлагает компании STECO оптовые скидки в качестве сти-
мула развития деловой активности. Он согласен предоставить скидку $0,10 на каждый
ГЛАВА 7 Нелинейная оптимизация 493
купленный кабель, если размер заказов компании будет не менее 5000 штук. Больший
размер заказов приведет к уменьшению количества заказов и, соответственно, снижению
годовых издержек размещения заказов. Как уже отмечалось (при сравнении рис. 7.27
и 7 28), больший размер заказа приводит к увеличению среднего уровня запасов и повы-
шению издержек хранения. В такой ситуации не ясно, будет ли выгодна компании
STECO оптовая скидка
Будем действовать, как и прежде- построим кривую годовых затрат и найдем размер
заказа, который минимизирует эти затраты Годовые совокупные затраты ГСЗ(0 — это
сумма годовых издержек хранения и размещения заказов ГХР(0 и годовой стоимости
закупок ГЗ ГСЗ(0 = ГХР(0 + ГЗ
Из уравнения (7 5) и равенства СЛ = iP получаем ГХР(0 = Crx{D/Q) + iPx(Q/2) Отметим,
что, поскольку Сх зависит от закупочной цены единицы продукции, выражение для ГХР также
содержит Р. Годовые затраты на закупку продукции вычисляются как произведение цены
единицы продукции на годовой спрос ГЗ = PD, тогда ГСЗ(0 = Cpx(D/Q) + iPAQ/T) + PD
Чтобы увидеть влияние оптовых скидок, оценим данную функцию для двух различ-
ных цен- нормальной цены $8,00 за штуку и возможной цены со скидкой $7,90 Уравне-
ние для нормальной цены
ГСЗ(0) = (25х6ОООО)/0 + О,24х8,ООх(0/2) + 8,00x60000
Уравнение для цены со скидкой
ГСЗ(0) = (25х6ОООО)/0 + О,24х7,9Ох(0/2) + 7,90x60000
Общая форма этих кривых показана на рис 7 31 Необходимо отметить следующее
1.	Кривая для цены со скидкой лежит ниже кривой с нормальным значением цены
Это происходит потому, что каждое слагаемое в выражении для ГСЗ(2) при нор-
мальной цене больше или равно соответствующему слагаемому выражения для
ГСЗ(2) при цене со скидкой
2.	Значение Q, минимизирующее ГСЗ при цене со скидкой (обозначим это значение
как Qd), больше, чем значение Q, минимизирующее ГСЗ при обычной цене
(обозначим Qr ), поскольку согласно (7 10)
. _ [2x25x60000	[2x25x60000	.
0,24x7,90	 0,24x8,00 ~^к
Очевидно, что компания STECO хотела бы минимизировать годовые совокупные за-
траты ГСЗ(0. Если бы компания могла получить цену со скидкой независимо от заказы-
ваемого количества продукции, она, естественно, выбрала бы размер заказа Qd. Предпо-
ложим, однако, что ценовая скидка действует только в том случае, если компания
STECO заказывает за один раз не менее В штук Могут возникнуть две ситуации, которые
показаны на рис. 7.32.
Участки кривых, проведенные жирной линией на рис 7 32, показывают действитель-
ный вид функции затрат компании STECO. Для объемов заказов, не превышающих В,
следует использовать кривую с нормальным значением цены, а для превышающих В —
кривую для цены со скидкой.
494 ЧАСТЬ II Оптимизационные модели
Рис. 7.31. Годовые совокупные затраты дм нормальной цены и цены со скидкой
Рис. 7.32. Влияние минимального размера заказа
Таким образом, если B<Qn, STECO добьется минимальных затрат, делая заказ объе-
ма Если же В > Qd , оптимальное решение в общем случае трудно указать сразу. Луч-
шее, что может сделать компания STECO при обычном значении цены, — заказывать Q^.
Лучшее, что можно сделать при цене со скидкой, — заказывать В Чтобы определить, ка-
кое решение является оптимальным, необходимо вычислить ГСЗ(0 в этих двух точках
и сравнить их Общее правило выглядит следующим образом
< Если В< Q„, заказывать Q,'.
Если B>Qd, заказывать Qx если ГСЗ((?/) < ГСЗ(Д): в противном случае заказывать В.
Компания STECO должна заказать не менее 5000 штук СК, чтобы получить скидку, сле-
довательно, В= 5000 На рис 7 33 представлена табличная версия модели управления запа-
сами с оптовыми скидками В отличие от предложенного выше подхода, модель в Excel
сформирована так, что годовые затраты записываются как годовые затраты при отсутствии
скидки в ячейках CI6 С19 минус поправка на сумму скидки, если такая имеет место. Таким
образом, если скидка получена, то в слагаемые годовых затрат Издержки хранения и Стои-
мость закупки вносятся соответствующие поправки, отражающие сумму скидки. Эти затра-
ты объединяются в Совокупные чистые затраты в ячейках Е16 Е19 Такой подход позволя-
ет трактовать получение скидки как двоичную переменную решения (ячейка D13). Форму-
ГЛАВА 7. Нелинейная оптимизация 495
ла в ячейке Е13 имеет вид =D7*D13 Таким образом, если Поиск решения устанавливает
в ячейке D13 значение 0 (нет скидки), то ограничение принимает вид Размер заказа>0
Если же в D13 установлено значение 1 (скидка получена), то поправки к затратам становят-
ся отличными от нуля, а ограничение принимает вид Размер заказа>5000.
Со скидкой
Минимальный объем заказа
Закупочная цена
Издержки хранения
Издержки хранения
Стоимость размещения заказа
Годовой объем спроса
40.10
40 024
Модель управления запасами
Без скидки
24%
$25,00
60000
$25.01
60001
$0,10
5000
$480 000
$495 100
Г одовые затраты
$300
Удельные затраты
$9.00
__________ $1,92
]=07*Р1з
Рис. 7.33. Модель ОРЗ с оптовыми скидками компании STECO
Стоимость размещения заказа
Издержки хранения
Стоимость закупки
Совокупные затраты
Закусочная цена
Издержки >ранения
Размер заказа Получение скидки
5000
46 000
$6 060
Удельные затраты Учет скидки
"	= D6	=СУММ(С9 09)
=РЗ*О9	=СУММ(С10Р10
=СЗ*С9
Размер заказа Получение скидки Минимальный объ{
5000
Годовые затраты	Учет скидки Чистые затраты
-	=СУММ(С16О16)
=D13*D10’C13/2 =СУММ(С17 D17)
=Р13*О9*О5	=СУММ(С18:Р18)
Стоимость размещения заказа =С4’С5/С 13
Издержки хранения	=010*013/2
Стоимость закупки	=С9*С5__________
Совокупные затраты	=СУММ(С16 С18) =СУММ(О16 D18) |=С

496
ЧАСТЬ II. Оптимизационные модели
Средство Поиск решения оптимизирует частично-целочисленную модель нелиней-
ного программирования, чтобы оценить две функции ГСЗ (со скидкой и без скидки).
Чтобы отразить в модели существование системы скидок (т.е. когда существует несколь-
ко пороговых значений размера заказа, с каждым из которых связаны “поправки” к об-
щим затратам), необходимо ввести дополнительные двоичные переменные, ограничения
для отражения минимальных количеств и внести соответствующие изменения в форму-
лы В рассматриваемом случае решение задачи для компании STECO на рис 7.33 означа-
ет, что компании следует заказывать по 5000 штук кабеля, чтобы воспользоваться пре-
имуществами скидки. Это позволит экономить $482 400 - $479 040 = $3360 в год по
сравнению с решением заказывать Очевидно, что система скидок может играть важ-
ную роль в определении оптимальной политики управления запасами.
7.14.	Производство и управление запасами
Хотя компания STECO преимущественно специализируется в оптовой торговле, у нее
есть и собственные производственные мощности. В частности, компания имеет совре-
менное высокопроизводительное оборудование для термической герметизации волокон-
нооптического кабеля, которое она использует для производства ряда типов кабеля, хра-
нящихся затем в запасах Следует отметить две важные характеристики данного оборудо-
вания. с его настройкой для выпуска определенного типа продукции связаны
значительные затраты на переналадку, после завершения процесса наладки производи-
тельность постоянна и известна
Затраты на переналадку, аналогичные издержкам размещения заказа в модели ОРЗ,
возникают из-за того, что необходимо производить замену литейных форм для пластико-
вых деталей и вносить изменения в температурный режим тепловой обработки, чтобы
удовлетворить требования, предъявляемые к кабелям соответствующими стандартами
Кроме того, каждый кабель должен иметь разъем. Таким образом, заказанное количество
сетевых кабелей не попадает с производства в запас все сразу, а поступает постепенно на
протяжении нескольких дней Такое изменение модели требует изменения формул, даже
если остаются в силе предположения о постоянном уровне спроса и о том, что затраты на
содержание запаса равны произведению С и среднего объема запасов.
Обычно, работая с такой моделью, удобней рассматривать дневные показатели про-
изводительности и спроса Введем следующие обозначения: d — ежедневный объем
спроса, выраженный в единицах продукции; р — количество ежедневно выпускаемых
единиц продукции, Ср — затраты на переналадку (не зависящие от производимого коли-
чества продукции), сх — ежедневные издержки хранения запасов (обозначение несколько
изменено, чтобы подчеркнуть, что это издержки хранения задень).
Очевидно, для того, чтобы задача представляла интерес, р должно быть больше d. (Если
р < d, то спрос превышает производственные возможности компании STECO, и управление
запасами продукции становится неактуальным.) На рис. 7 34 показан график наличного за-
паса продукции, если компания STECO примет решение выпускать продукцию партиями
по Q штук Необходимо отметить несколько моментов, которые следует учитывать при вы-
числении средних дневных затрат хранения и стоимости переналадки
1.	В процессе производства продукция добавляется к запасу равномерно со скоро-
стью р единиц в день и изымается из него со скоростью d штук в день. В результате
запас увеличивается в день на/? — d штук.
ГЛАВА 7. Нелинейная оптимизация 497
2.	Если производство “стоит”, то продукция изымается из запаса со скоростью d
штук в день.
3.	Поскольку за период производства изготавливается Q единиц продукции, а в день
производитсяр единиц, то каждый период производства длится Q/p дней
4.	Поскольку за период производства выпускается Q единиц продукции, а ежеднев-
ный уровень спроса составляет d единиц, продолжительность цикла (т е. интервал
от начала процесса пополнения запасов до ближайшего следующего начала ана-
логичного процесса) составляет (9/г/дней.
На основе вышесказанного можно вычислить максимальный объем наличного запаса
(рис. 7 34) по формуле (р - d)x(Q/p). Средний объем запаса равен половине максималь-
ного запаса (р - d)x(Q/p)/2 После перегруппировки членов получим, что средний объем
запаса равен (£>/2)х(1 - d/p) Тогда ежедневные издержки хранения можно вычислить по
формуле cx(Q/2)x(l - d/p).
Поскольку каждый цикл включает в себя одну переналадку, и продолжительность
цикла составляет Q/d дней, затраты на переналадку в день составляют Срx(d/Q)
Обозначим ежедневные затраты на переналадку и хранение как ЕПХ(0, тогда
ЕПХ(0 = Cx(d/Q) + c;x(Q/2)x(l — d/p}. Если считать множитель с;х (1 — d/p} констан-
той, то данное выражение принимает ту же форму, что и выражение (7.5) для годовых из-
держек хранения и размещения заказов в модели ОРЗ Из этого следует, что значение Q,
доставляющее минимум ЕПХ(0), задается уравнением (7.9). Таким образом, в модели оп-
ределения оптимального размера партии
Подставив Q вместо Q в выражение ЕПХ((?) и произведя необходимые упрощения, полу-
чаем следующее выражение для вычисления минимальных затрат на переналадку и хранение:
ЕПХ(е’) = ^2С/сх|--£|.
Отметим, что данное выражение не зависит от Q, и оно верно только для значения
размера партии, заданного выражением (7.11).
498
ЧАСТЬ II Оптимизационные модели
Чтобы воспользоваться данной моделью для анализа производства определенной
продукции, необходимо оценить различные параметры производства данной продукции
и подставить в формулу (7 11), чтобы вычислить £)’.

Модель производства и управления запасами
Количество рабочих дней в году
Годовые издержки хранения
4 Затраты на переналадку
Годовой спрос
Ежедневный спрос
Ежедневная производительность
_2_
Переменные производственные затраты
Ежедневные издержки хранения
240
24%
$100
48000
200
400
Удельные затраты
$1.00
________	$0001
Размер партии
8944
Стоимость размещения заказа
Издержки хранения
Производственные затраты
Итого
Ежедневные затраты
$2,24
$2,2361
$400.00
I	$40447,
Рис. 7.35. Модель определения оптимального размера партии продукции
ГЛАВА 7 Нелинейная оптимизация 499
Рассмотрим числовой пример. Предположим, что спрос на сетевой кабель (СК) состав-
ляет в среднем 200 штук в день. Затраты, связанные с переходом на выпуск данного кабеля,
составляют $100, а производственная мощность равна 400 штук в день Согласно оценке
компании STECO ежедневные издержки хранения составляют $1x0,24/240 =$0,001, где
$1 — это стоимость производства одного СК, 0,24— годовая процентная ставка, а 240 —
количество рабочих дней в году В таком случае оптимальный размер партии продукции со-
ставит
а минимальные ежедневные затраты на хранение и переналадку —
j2x200xI00x0,00l| 1-—|=$4,47
V	I 400)
Такой партии продукции достаточно, чтобы удовлетворять спрос в течение 8944/200 =
44,72 дней.
Для оптимизации данной модели можно использовать Поиск решения, что позволит не
выводить формулы, аналогичные приведенным выше, которые при изменении некоторых
предположений могут оказаться неприменимыми Табличная модель НЛП в Excel для оп-
ределения оптимального размера партии продукции представлена на рис 7 35 На практике
компания STECO может уточнить размер партии, принимая во внимание тот факт, что при
выпуске других видов продукции также используется оборудование для термической герме-
тизации. Кроме того, компания, вероятно, проведет анализ чувствительности данного ре-
шения аналогично тому, как это делалось для модели ОРЗ в разделе 7 12
Другие разновидности данной модели или модели ОРЗ учитывают наличие резервного за-
паса в начале производственного цикла, что допускает возможность возникновения спроса,
опережающего предложение Еще одно изменение модели может заключаться в том, чтобы
учесть возможность отставания запасов, при этом убытки, связанные с отсутствием запасов,
компенсируются экономией от снижения среднего уровня запасов
7.15.	Заключение
Практическое применение моделей НЛП является искусством даже в большей мере,
чем использование моделей ЛП. Практически все программы оптимизации моделей ЛП
в главных чертах одинаковы, поскольку все они используют симплекс-метод 12 В то же
время, можно выделить 10-15 различных методов решения задач НЛП, из которых толь-
ко один используется средством Поиск решения. Чтобы найти наилучший метод реше-
ния конкретной задачи или даже просто осознать существующие между разными подхо-
дами различия, необходимо обладать серьезной математической подготовкой Еще одна
сложность заключается в существовании большого количества различных с математиче-
ской точки зрения типов нелинейных моделей с различными теоретическими свойствами
(в то время как все модели ЛП относятся к одному типу) В ряде случаев приходится
12 В последние годы были разработаны новые методы оптимизации ЛП, основанные на подходах, отличных
от симплекс-метода Однако имеющиеся данные о их применении свидетельствуют, что эти новые методы
наиболее эффективны для очень больших моделей ЛП, содержащих тысячи переменных
500
ЧАСТЬ II. Оптимизационные модели
сталкиваться с существованием локальных, а не только глобальных решений. Поэтому
необходимо иметь достаточно полные знания о математической структуре рассматривае-
мой модели, чтобы можно было хотя бы оценить, какое решение (локальное или гло-
бальное) получено средством Поиск решения. Чтобы найти улучшенные решения, часто
требуется экспериментировать вручную или с помощью средства Evolutionary Solver.
Хотя большинство программ-оптимизаторов НЛП, таких как Поиск решения, наряду
с решением приводят значения множителей Лагранжа (т.е. теневых цен) и нормирован-
ных градиентов, провести дальнейший анализ чувствительности в общем случае невоз-
можно без повторных оптимизаций, проводимых вручную или с помощью средства
SolverTable. Таким образом, при решении управленческих задач модель НЛП предостав-
ляет существенно меньше полезной информации, чем модельЛП.
Модели НЛП можно применять для решения широкого спектра задач, однако чаще
всего они применяются в ситуациях, когда модель имеет особую структуру, например,
как модели квадратичного программирования. Например, ограничения линейны, а целе-
вая функция нелинейна и т.д. В таких случаях есть надежда получить решение достаточно
крупномасштабных моделей Понятие крупномасштабных моделей в НЛП значительно
менее ясно определено, чем в моделях ЛП Для вогнутых или выпуклых квадратичных за-
дач допускается несколько тысяч ограничений и переменных, поскольку для решения
таких задач часто применяются специальные методы Однако для нелинейных моделей
общего вида, в которых невозможно воспользоваться преимуществами специальной
структуры, содержащая более 2000 переменных задача оказывается слишком крупной
даже для больших вычислительных машин
Замечание. Надстройки Excel Поиск решения и Premium Edition for Education Solver опти-
мизируют модели НЛП, которые могут содержать не более 200 переменных решения и не бо-
лее 100 ограничений, не считая простых ограничений верхних и нижних границ для перемен-
ных Коммерческая программа Long Scale GRG Solver, которая в состоянии оптимизировать
крупные модели НЛП (до 4000 переменных решения), содержит специальный оптимизатор
для моделей квадратичного программирования
Последние три раздела данной главы были посвящены применению нелинейной мо-
дели портфельных инвестиций в финансовой сфере, а также базовой модели определе-
ния экономически выгодного размера заказа и ее различным модификациям. В послед-
нем примере показано, как необходимо изменить базовую модель при наличии оптовых
скидок, а также в том случае, когда запасаемая продукция не заказывается внешнему по-
ставщику, а производится самой компанией
Рассматриваемые в разделах с 7.10 по 7.14 два класса моделей НЛП удовлетворяют
требованиям вогнутости и выпуклости, что существенно повышает привлекательность
работы с моделями НЛП. В результате модели НЛП нашли широкое применение в сфере
финансов и управления запасами. Среди других областей применения моделей НЛП
можно назвать инженерное проектирование, нелинейное статистическое оценивание,
распределение продукции, а также физические приложения, такие как бурение нефтя-
ных скважин, и, наконец, составление оптимального расписания работы и загрузки обо-
рудования при условии нелинейности затрат.
ГЛАВА 7. Нелинейная оптимизация 501
Основные термины
Анализ инвестиционного портфеля. Модель минимизации дисперсии дохода при условии обеспече-
ния требуемого уровня ожидаемого дохода
Вогнутая задача НЛП. Модель нахождения максимума с вогнутой целевой функцией и выпуклым
множеством ограничений
Выпуклая задача НЛП. Модель нахождения минимума с выпуклой целевой функцией и выпуклым
множеством ограничений
Выпуклое множество точек. Множество точек, обладающее следующим свойством для любой пары
точек, принадлежащих данному множеству, соединяющий данные точки отрезок также при-
надлежит этому множеству
Граница эффективности. В анализе портфельных инвестиций оптимальное значение целевой функ-
ции как функции параметра ожидаемого дохода в моделях квадратичного программирования
Дефицит. Недостаточное количество наличных запасов для удовлетворения спроса
Дисперсия (вариация). Статистическая мера риска
Задержка заказов. Практика доставки товаров потребителям не сразу после получения заказа,
а спустя некоторое время
Запасы. Товары, деньги или рабочая сила, хранящиеся в ожидании будущих потребностей
Издержки дефицита. Выражаются в убытках или в издержках, связанных с задержкой заказов
Издержки размещения заказа. Один из стоимостных параметров модели ОРЗ Предельная стои-
мость размещения одного заказа
Издержки хранения запасов. Один из стоимостных параметров модели ОРЗ Стоимость содержания
некой продукции в запасах в течение указанного времени
Издержки хранения. Издержки хранения запасов, включают в себя цену шанса (издержки в резуль-
тате неиспользования альтернативных возможностей) плюс прямые затраты, такие как убытки
от краж, страховые выплаты и моральный износ
Издержки, связанные с задержкой заказов. Один из стоимостных параметров модели ОРЗ, в кото-
рой допускается выполнение заказов с опозданием Стоимость задержки единицы продукции
на указанное время
Ковариация. Статистическая мера степени зависимости двух случайных величин
Множитель Лагранжа. Связан с ограничением и характеризует скорость изменения оптимального
значения целевой функции при изменении правой части данного ограничения Аналогичен
теневой цене в моделях Л П (см главу 4)
Модели квадратичного программирования (КП). Нелинейные модели, в которых минимизируется
или максимизируется значение квадратичной целевой функции при условии соблюдения ли-
нейных ограничений и условий неотрицательности
Модель нелинейного программирования (НЛП). Модель математического программирования, в кото-
рой нелинейной является по меньшей мере одна функция ограничения или целевая функция
Модель определения оптимального размера заказа (ОРЗ). Модель управления запасами с постоян-
ным уровнем спроса, в которой учитываются издержки хранения и размещения заказов, а так-
же, возможно, задержки заказов
Модель определения размера партии продукции. Модификация модели ОРЗ, в которой учитывается
конечность скорости поступления продукции
Нормированный градиент. Связан с переменной решения, отражает начальную скорость изменения
оптимального значения целевой функции при изменении значений данной переменной Если
неотрицательная переменная в точке оптимальности равна нулю, нормированный градиент
502 ЧАСТЬ II Оптимизационные модели
показывает скорость ухудшения значения целевой функции, если данной переменной присво-
ить ненулевые значения Аналогичен нормированной стоимости в моделях ЛП (см главу 4)
Ожидаемый доход. Взвешенное среднее доходов от входящих в инвестиционный портфель ценных
бумаг
Оптимальный размер заказа. Количество определенной продукции, минимизирующее совокупные
годовые издержки хранения и размещения заказов этой продукции
Оптовая скидка. План закупок, согласно которому продавец предлагает покупателю специальную
цену при покупке указанного или большего количества продукции
Продолжительность цикла. Интервал времени между появлением двух последовательных заказов
на пополнение запасов
Размер заказа. Часть системы управления запасами Количество единиц продукции, заказываемое
всякий раз при размещении заказа для пополнения запасов
Спрос. Заказанное потребителями количество единиц продукции В условиях дефицита может не
совпадать с количеством проданных единиц продукции
Стандартное отклонение. Квадратный корень из дисперсии
Стационарная точка. Точка, в которой все частные производные целевой функции обращаются в нуль
Убытки. Потери в не допускающих задержки заказов моделях, связанные с невозможностью удов-
петворить спрос, обычно определяются как стоимость единицы неудовлетворенного спроса
Условия оптимальности второго порядка. Достаточные условия существования оптимума
Условия оптимальности первого порядка. Необходимые условия существования оптимума — все ча-
стные производные целевой функции должны быть равны нулю
Цена шанса. Если выбор определенного действия (скажем, А) означает отказ от другого действия
(В), чистый доход, связанный с действием В, является ценой шанса при принятии решения
о действии А
Экономически выгодный размер заказа. Оптимальный размер заказа, определенный с помощью мо-
дели ОРЗ
Контрольные вопросы по теме “Нелинейные модели”
Да/нет
1.	Экономия, обусловленная ростом масштаба производства, описывается нелиней-
ным уравнением
2.	Прикладную задачу, содержащую нелинейную связь, нельзя описать с помощью
модели Л П
3.	Если в некой точке выполнены необходимые условия локального максимума, то
эта точка является локальным максимумом
4.	В точке локального минимума выполнены необходимые условия локального ми-
нимума
5.	Единственной точкой, в которой выполнены достаточные условия локального
минимума, является точка, в которой локальный минимум является глобальным.
6.	Прямая линия не является ни выпуклой, ни вогнутой функцией.
7.	В модели НЛП, как и в модели ЛП, усиление ограничения не улучшит решение,
но может ухудшить его.
8.	В модели максимизации множитель Лагранжа в отчете по устойчивости средства
Поиск решения имеет ту же интерпретацию, что и теневая цена из подобного от-
ГЛАВА 7. Нелинейная оптимизация 503
чета для моделей ЛП, но в общем случае он не является постоянным для опреде-
ленного интервала изменений правой части ограничения
9.	Модель квадратичного программирования является частным случаем вогнутой
модели.
10.	Модель НЛП всегда является выпуклой или вогнутой моделью
11.	Множество ограничений, заданное следующими неравенствами, является выпуклым
9х + 4у < 36,
4х + 12у<20.
12.	На практике, чтобы найти локальный максимум функции нескольких перемен-
ных, необходимо сначала найти все стационарные точки, а затем проверить для
них условия второго порядка
13.	Хотя нелинейные модели сложнее, чем модели ЛП, для нахождения их оп шмаль
ного решения можно применять метод поиска по угловым точкам допустимого
множества решений
14.	Одной из проблем в нелинейном программировании является необходимость от-
личать локальные решения от глобальных
Выберите правильный ответ
В предлагаемых ниже вопросах/(х) и/'(х) обозначают первую и вторую производные
функции одной переменнойДх), ах — стационарную точку
15.	Пустьf — функция одной переменной Неравенство/'(х) > О
а. является необходимым условием локального минимума,
b является достаточным условием локального минимума,
с является достаточным условием локального максимума,
d ни одно из вышеперечисленных утверждений не верно
16.	Пусть/—функция одной переменной Равенство/(х ) = О
а.	является необходимым условием, чтобы точка х была точкой локального мак-
симума;
Ь.	является необходимым условием, чтобы точка х была точкой локального ми-
нимума;
с.	является необходимым условием, чтобы точка х была точкой глобального ми-
нимума,
d.	верны все вышеприведенные утверждения
17.	В нелинейных моделях прибегают к дифференцированию, чтобы
а.	исключить локальные решения;
Ь.	выразить условия оптимальности,
с верны оба утверждения;
d оба утверждения неверны
18.	Точках*, для которой/(х) = 0 и/'(х) > 0, удовлетворяет достаточному условию
а. локального максимума,
504 ЧАСТЬ II. Оптимизационные модели
Ь.	локального минимума;
с.	оба утверждения неверны.
19.	Какие из следующих утверждений справедливы для вогнутой функции?
а.	Можно найти глобальный максимум с помощью программы, реализующей ме-
тод наискорейшего подъема.
Ь.	Любой локальный максимум является глобальным.
с.	Верны оба вышеприведенных утверждения.
20.	Какое из следующих утверждений справедливо?
а Условия оптимальности непосредственно используются для решения задач НЛП
общего вида, т.е. оптимизационные программы, подобные средству Поиск ре-
шения, получают решение задачи НЛП непосредственно из этих условий.
b Условия оптимальности используются неявно для решения задач НЛП общего
вида, т.е. оптимизационные программы, подобные средству Поиск решения,
решают задачу НЛП, например, с помощью метода наискорейшего подъема,
а условия оптимальности служат критерием окончания работы алгоритма.
с. Условия оптимальности представляют исключительно теоретический интерес.
21.	Для вогнутых моделей
а более полезны условия второго порядка;
b любой локальный оптимум является глобальным;
с. множество ограничений и целевая функция должны быть вогнутыми.
22.	Выпуклость
а это понятие, применяемое как ко множествам точек, так и к функциям;
Ь.	важное математическое свойство, гарантирующее, что локальные решения яв-
ляются также глобальными;
с.	полезна как в безусловной, так и в условной оптимизации;
d.	все вышеперечисленное.
23.	Какое из следующих утверждений в обшем случае не справедливо для множителя
Лагранжа?
а Экономический смысл множителя Лагранжа аналогичен смыслу теневой цены.
b Множитель Лагранжа — это скорость изменения оптимального значения целе-
вой функции при увеличении правой части ограничения.
с. Множитель Лагранжа постоянен внутри некоторого диапазона значений пра-
вой части ограничения
24.	Какое из следующих утверждений неверно?
а.	Несмотря на то что гарантировать получение глобальных решений невозмож-
но, оптимизация нелинейных моделей является полезным средством при при-
нятии решений.
Ь.	В моделях ЛП не приходится беспокоиться о локальных решениях (т.е. любое
локальное решение является глобальным).
с.	Поскольку исключительно для моделей, обладающих свойствами выпуклости
или вогнутости, можно гарантировать, что локальное решение является глобаль-
ным, это единственные типы моделей НЛП, дающие полезную информацию.
25.	Какое из высказываний справедливо по отношению к угловым решениям задач НЛП?
а.	Вне зависимости от формы целевой функции оптимальное решение всегда бу-
дет находиться в угловой точке
ГЛАВА 7. Нелинейная оптимизация 505
Ь.	Угловые точки могут быть решениями только при линейной целевой функции.
с В общем случае оптимум может находиться не в угловой точке.
Ответы
1 Да. 2 Нет 3 Нет 4. Да 5 Нет. 6 Нет. 7 Да 8 Да. 9. Нет. 10 Нет 11. Да 12 Нет
13 Нет. 14. Да. 15. d. 16. d 17. b. 18. b. 19. с. 20 b. 21. b. 22 d 23. c 24. c 25 c
Контрольные вопросы по теме “Квадратичное
программирование”
Да/нет
1.	Модели квадратичного программирования могут содержать квадратичные функ-
ции ограничений
2.	Модель квадратичного программирования заключается в максимизации или ми-
нимизации произвольной нелинейной целевой функции на множестве ограниче-
ний, состоящем из линейных ограничений в форме равенств и неравенств, а также
условий неотрицательности переменных решения
3.	Любую задачу ЛП можно решить с помощью процедуры оптимизации моделей КП
4.	Невозможно выделить угловые точки допустимой области задачи КП
5.	Оптимальное решение задачи КП не обязательно является угловым
6.	Оптимальное решение задачи КП должно содержать по крайней мере столько же
положительных переменных, сколько ограничений в модели
7.	Ослабление ограничения в задаче КЛ улучшит оптимальное значение целевой
функции или оставит его неизменным
8.	В модели максимизации скорость улучшения оптимального значения целевой
функции всегда противоположна значению множителя Лагранжа.
9.	Изменение коэффициента перед неким слагаемым в целевой функции всегда при-
водит к изменению оптимального решения
10.	Дисперсия (вариация) дохода инвестиционного портфеля является линейной
функцией средств, инвестированных в каждый вид акций портфеля
11.	Если портфель состоит из трех видов ценных бумаг, то допустимая область будет
представлять собой линию на плоскости
12.	Модель инвестиционного портфеля содержит нижнюю границу ожидаемого дохо-
да. В общем случае это ограничение не обязательно является лимитирующим
Выберите правильный ответ
13.	Согласно определению модель КП не содержит.
а.	квадратичных функций ограничений;
Ь.	линейных ограничений-равенств;
с.	нелинейных членов в целевой функции.
14.	В модели КП с л переменными х|;. ., хп целевая функция не может содержать чле-
ны вида:
506 ЧАСТЬ II Оптимизационные модели
с! 9л,
15.	МодельЛП является частным случаем модели КП, поскольку:
а допустимая область модели ЛП является частным случаем допустимой области
модели КП,
b функции ограничений модели ЛП являются частным случаем функций огра-
ничении модели КП,
с моделям ЛП присущи условия неотрицательности,
с! целевая функция модели ЛП является частным случаем целевой функции мо-
дели КП
16.	Оптимальное решение задачи КП с п ограничениями неотрицательности не долж-
на содержать
а отрицательных значений переменных решения;
b более п положительных переменных решения;
с менее п положительных переменных решения;
d пулевых значений некоторых переменных решения.
17.	Оптимальное решение задачи КП.
а должно находиться в угловой точке допустимой области,
b не может находиться в угловой точке допустимой области;
с всегда является невырожденным;
d ничего из перечисленного
18.	В оптимальном решении задачи КП вычисление резервов-
а не имеет смысла,
b имеет тот же смысл, что и в модели ЛП;
с имеет другой смысл, чем в модели Л П;
d дает неограниченные значения.
19.	Средство Поиск решения можно использовать для решения:
а задач нелинейного программирования общего вида;
b задач КП,
с задач ЛП,
d всех вышеперечисленных задач.
20.	Ослабление какого-либо ограничения в модели минимизации дисперсии дохода
инвестиционного портфеля
а должно увеличить множитель Лагранжа для данного ограничения,
b должно уменьшить множитель Лагранжа для данного ограничения,
с может изменить знак множителя Лагранжа для данного ограничения,
d не может увеличить значение целевой функции.
Отвг ы
Нет 2 Нет 3 Да 4 Нет 5 Да 6 Нет 7 Да 8 Нет 9 Нет 10 Нет 11 Да 12 Да 13 а 14 с
15. d 16 а 17 d 18 b 19 d 20 d
ГЛАВА 7 Нелинейная оптимизация 507
Контрольные вопросы по теме “Модели управления
запасами”
Да/нет
1.	Составляющая издержек хранения запасов, называемая ценой шанса, определяется
такими факторами, как порча, хищения и страховые выплаты
2.	В моделях управления запасами спрос всегда больше или равен объему продаж
3.	В модели ОРЗ годовые издержки размещения заказов прямо пропорциональны
объему заказа.
4.	В модели ОРЗ годовые издержки хранения запасов и размещения заказов доста-
точно устойчивы к ошибкам в оценке стоимостных параметров
5.	Поскольку в модели определения размера партии продукции уровень производст-
ва постоянен, затраты на переналадку в модель не включаются
Выберите правильный ответ
6.	Ниже перечислены мотивы создания запасов-
а защита от неопределенности спроса,
b снижение производственных затрат,
с способ сохранения труда,
d. все вышеперечисленное.
7.	В число факторов, которые необходимо учитывать при принятии решения о том,
когда размещать заказ на пополнение запасов и каким должен быть объем заказа,
не входят следующие факторы
а время выполнения заказа,
b доля, которую цена шанса составляет в издержках хранения запасов,
с возможность оптовых скидок,
d. степень определенности будущего спроса
8.	В модели ОРЗ.
а.	каждая поставка производится в виде единого пакета,
Ь.	спрос известен и его уровень постоянен;
с спрос должен быть полностью удовлетворен,
d. все вышеперечисленное.
9.	Если в модели ОРЗ цена продукции увеличивается, а все остальные параметры ос-
таются прежними, оптимальный объем заказа, как правило, будет
а увеличиваться;
Ь. уменьшаться;
с останется прежним.
10.	В модели ОРЗ оптимальное число заказов за год-
а увеличивается пропорционально годовому уровню спроса,
b увеличивается пропорционально квадратному корню из годового уровня спроса,
с. пропорционально уменьшается с ростом годового уровня спроса,
d. не изменяется с ростом годового уровня спроса.
508 ЧАСТЬ II Оптимизационные модели
11.	В модели определения размера партии продукции при увеличении уровня произ-
водства оптимальное число размещаемых за год заказов-
а увеличивается,
b не изменяется,
с уменьшается.
Ответы
1 Нет 2 Да 3 Нет 4 Да 5 Нет 6 d 7 b 8 d 9 b 10 b 11 а
Учебные задачи
7 1 a С помощью средства Поиск решения найдите максимум функции/(х) = -8х2 — 14х — 32
b С помощью средства Поиск решения найдите максимум данной функции на интервале
1 <х< 10
с Можно ли определить, является данная функция вогнутой или выпуклой9
7 2 а С помощью средства Поиск решения найдите максимум функции/(х) = —х2 + 4х + 6
b С помощью средства Поиск решения найдите максимум данной функции на интервале
3<х< 12
с Можно ли определить, является данная функция вогнутой или выпуклой9
7 3 Является ли образуемое данным набором ограничений множество выпуклым9 Почему9
х + у<20,
—2х + у> 10,
х+2х+ 1 < 100,
-х -2х + 60 > 36
7 4 С помощью средства Поиск решения найдите минимум функцииДх, у) = х + 1ху + 2у -8х
-12у + 6 Используя таблицу подстановки и мастер диаграмм, постройте график функции
Лх, У)
7 5 Требуется построить цилиндр объемом 2л Какими должны быть радиус его основания г
и высота Л, чтобы площадь поверхности цилиндра (включая оба основания) была мини-
мальной9 Подсказка объем цилиндра вычисляется по формуле лг2й, а площадь поверхно-
сти — 2лгЛ + 2лг
7 6 Линейная регрессия В модели линейной регрессии имеются данные за прошлые периоды
(х„ у), i = 1, , п На основе этих данных строится линия регрессии у = ах + Ь, где а и Ь выбра-
ны так, чтобы минимизировать сумму квадратов отклонений S(a,b) = У,(у, - (ах, + b))2
а Постройте линию регрессии для следующих данных
8	6
6	14
b Постройте линию регрессии для таких данных
х I 10	17,4	20,1	12,6	14,9
25
20
ГЛАВА 7. Нелинейная оптимизация 509
7 7 а Решите следующую задачу минимизировать 2х,2 + Зх22 + х, - 9х2 + 16 при ограничении х, +
b На основе отчета по устойчивости оцените, как изменится оптимальное значение целе-
вой функции, если правую часть ограничения увеличить с 5 до 8, и сравните полученную
оценку с действительным изменением
7 8 а Решите задачу максимизировать —Зх,2 + 42х, -Зх/ + 48xj — 339 при ограничении 4х, + 6х2 = 24
b На основе отчета по устойчивости оцените, как изменится оптимальное значение целе-
вой функции, если правую часть ограничения увеличить с 24 до 28, и сравните полученную
оценку с действительным изменением
Прикладные задачи
7 9 Хут Спа импортирует кокосовое масло из своего родного города на Ямайке Это масло он
использует для производства крема для загара двух видов, Sear и Chat Цена, по которой он
может продавать свою продукцию, зависит от того, сколько крема каждого вида произво-
дится В частности, если производится х, кг крема Sear и х2 кг крема Chat, то вся произве-
денная продукция может продаваться по следующим ценам
цена за 1 кг Sear = 120 - х,, цена за 1 кг Chat = 150 — х2
Стоимость производствах, кг крема Sear и х2 кг крема Chat вычисляется по формуле 1,2х, +
+ 16,8х2 + 1,3х,х2
Предполагая, что он может продать всю произведенную продукцию, Хут хочет определить,
сколько килограммов каждого крема следует производить, чтобы максимизировать прибыль
7 10 При использовании х единиц труда и у единиц капитала производительность компании
Ore industries вычисляется по формуле Дх,у) = 2ху + Злу2 + 2у’ Если стоимость труда со-
ставляет S50 за единицу, а стоимость капитала $100 за единицу, сколько единиц труда и ка-
питала должна использовать компания при условии, что ее бюджет составляет $150 0009
Предполагается, что компания может выступать в роли как потребителя, так и поставщика
труда и капитала, т е переменные решения могут принимать отрицательные значения
а Сформулируйте задачу и оптимизируйте ее с помощью средства Поиск решения, вы-
брав в качестве начальной точки х = 0, у = 1
b Оптимизируйте модель, выбрав в качестве начальной точки х = 1 000 000, у = 1 000 000
с Объясните полученные результаты
7 11 Покажите, что найденное в модели оптимизации расходов на рекламу решение (см раз-
дел 7 5) является глобальным, а не локальным оптимумом
7 12 Покажите, что оптимальное решение задачи 7 10 удовлетворяет условию
предельная производительность труда/предельная производительность капитала =
=удельная цена труда/удельная цена капитала
Совет. Удалите бюджетное ограничение и введите ограничения для х и у, чтобы каждое из
них не превышало оптимальных значений, найденных в процессе решения задачи 7 10
7 13 Решите пример 2 из раздела 7 3 при следующих значениях параметров модели 5, = 1/2
(/ = 1, 2, 3), р, = 2, р2 = 2,8, р3 = 4 и В = 250 Чему равен множитель Лагранжа для бюджет-
ного ограничения9
7 14 Ленард Крамб, управляющий компанией Crumb Baking Services, рассматривает предложе-
ние дистрибутьюра, который предлагает растворимый полуфабрикат теста для рогаликов
Общая стоимостьх фунтов полуфабриката определяется формулой х3 - 50х2 + 750х
Какое количество полуфабриката минимизирует стоимость в расчете на один фунт9
510 ЧАСТЬ II Оптимизационные модели
7 15	Модель смешивания Два химических продукта X и У изготавливаются путем смешивания трех химических компонентов Л, йиС Исходные компоненты загрязнены серой, а конеч- ные продукты должны удовлетворять природоохранным ограничениям по содержанию се- ры. Три исходных компонента доставляются в двух цистернах компонент Л перевозится в цистерне I, компонент С — в цистерне 2, а компонент В в цистерне 1 и/или цистерне 2 Продать можно нс более 100 единиц продукта Хи не более 200 единиц У Используя содер- жащиеся в таблице данные, сформулируйте задачу НЛП максимизации прибыли и опти- мизируйте ее с помощью Поиск решения Компонент	Стоимость единицы, долл.	Содержание серы, % Л	6	3 В	16	1 С	10	2 Удельная цена продажи X	9	не более 2,5 У	15	не более 1,5
7 I6	Рассмотрим модель инвестиционного портфеля из раздела 7 11 Предположим, что изуча- ется возможность включения в инвестиционную модель акций корпорации IMCRZY Эти акции имеют отрицательный ожидаемый доход При каких условиях модель может вклю- чить акции этой корпорации в портфель инвестиций9
7 17	Рассмотрим модель инвестиционного портфеля из раздела 7 11 Чему равно допустимое уменьшение правой части ограничения, устанавливающего, что акции GM должны состав- лять не более 75% портфеля?
7 IS	Как и в моделях ЛП, с решением задачи НЛП связан отчет по устойчивости средства Поиск решения Содержит ли отчет по устойчивости для модели НЛП допустимые увеличения и уменьшения для правых частей ограничений9 Почему?
7 19	Рассмогрим модель инвестиционного портфеля из раздела 7 11 Предположим, что цель состоит в максимизации дохода при условии, что дисперсия портфеля не превысит задан- ное значение V Перепишите математическую модель с учетом этого изменения
7 20	Пусть в условии задачи 7 19 V= 0,0205 Если в исходной модели нет других оптимумов, че- му равен максимальный ожидаемый доход в измененной модели9 Объясните, почему
7 21	Акции х у и z имеют соответственно ожидаемый доход 7, 6 и 10% и следующую матрицу ковариаций х	0,01 У	0,001	0,04 z	0,001	-0,04	0,08 а Определите, какую долю портфеля должны составлять акции каждого вида, чтобы ми- нимизировать дисперсию портфеля при условии, что минимальный ожидаемый доход портфеля составляет 8% b Может ли дисперсия портфеля быть меньше, чем дисперсия любых отдельно взятых акций ’ Объясните свой ответ
ГЛАВА 7. Нелинейная оптимизация 511
с На основании предоставляемой множителями Лагранжа информации оцените, что
произойдет с дисперсией оптимального инвестиционного портфеля, если минималь-
ный ожидаемый доход повысится до 9% Сравните полученную оценку с действитель-
ным значением, полученным при повторном решении задачи
7 22 Спрос на общие тетради в книжном магазине университета постоянен и составляет 18000
штук в год Менеджер удовлетворяет этот спрос без отсрочки выполнения заказов При вы-
числении оптимального размера заказа он исходит из того, что стоимость размещения за-
каза составляет $30, а годовые издержки хранения — $3 за тетрадь Предполагается, что
в году 250 рабочих дней Чему равны значения Q , N и ГХР(2')9
7 23 Местный магазин скобяных изделий продает 364000 фунтов гвоздей в год В настоящее
время магазин заказывает 14000 фунтов гвоздей каждые две недели по цене $0,50 за фунт
Предполагается, что 1) уровень спроса постоянен, 2) стоимость размещения заказа состав-
ляет $50 независимо от размера заказа, 3) годовые издержки хранения запасов составляют
12% от среднего уровня запасов, 4) эти факторы не меняются с течением времени
а Чему равен средний уровень запасов9
b Чему равны годовые издержки хранения9
с Чему равны годовые расходы на размещение заказов9
d Чему равны годовые издержки хранения и размещения заказов9
е Чему равны годовые совокупные затраты9
f Владельцу выгоднее заказывать более крупные партии (но реже) или более мелкие
партии (но чаще)9
7 24 Расположенный на территории студенческого городка магазин мороженого продает 180
кварт ванильного мороженого каждый месяц В настоящее время магазин пополняет свои
запасы в начале каждого месяца Оптовая цена мороженого составляет $3 за кварту Пред-
полагается, что 1) уровень спроса постоянен, 2) годовые издержки хранения запасов со-
ставляют 25% от среднего уровня запасов, 3) за последний год совокупные затраты соста-
вили $7 627,50, 4) эти факторы не меняются с течением времени
а	Вычислите средний уровень запасов
b	Вычислите годовые издержки хранения
с Вычислите годовые расходы на размещение заказов
d С помощью таблицы подстановки постройте графики зависимости годовых издержек хра-
нения, годовых издержек размещения заказов и ГХР в зависимости от размера заказов
е В какой точке достигается минимум ГХР9 Сколько сможет сэкономить магазин, ис-
пользуя оптимальный размер заказа9
7 25 Начинающий предприниматель продает карандаши по 25 штук в день Каждый карандаш
стоит $0,05 Если стоимость размещения заказа составляет $5, а издержки хранения состав-
ляют 20% стоимости среднего уровня запасов, чему равны оптимальный размер заказа
и оптимальное количество заказов, сделанных за год9
7 26 Годовой доход компании по обслуживанию кредитных карт составляет $ 100 тыс Как часто
компания должна рассылать счета за обслуживание, если стоимость рассылки счетов со-
ставляет $30 000, а существующая процентная ставка — 6%9
7 27 Компания Specific Electric — крупный производитель электроприборов в США Она ис-
пользует электромоторы, которые приобретает у других фирм Совокупные затраты на за-
купки за год составляют $2 400 000 Стоимость размещения заказа составляет $100, а годо-
вые издержки хранения — 20% от среднего уровня запасов
а Чему равен оптимальный объем заказа в долларовом выражении9
Ь Сколько заказов в год должна размещать компания9
512 ЧАСТЬ II. Оптимизационные модели
с Чему равна оптимальная продолжительность цикла в годах и днях, если считать, что
в году 250 рабочих дней9
7 28 Предположим, что в задаче 7 24 стоимость размещения заказа удвоилась Как изменится
оптимальный объем заказа9
7 29 Strumm and Howell — магазин по продаже звукозаписей, который специализируется на му-
зыке в стиле кантри В последние годы дела шли достаточно успешно, и объем розничных
продаж составлял S400 ООО в год Уровень продаж в течение года постоянен Магазин заку-
пает записи у крупной звукозаписывающей компании Розничная цена продажи составляет
5/3 от затрат магазина Стоимость размещения заказа на каждую поставку независимо от ее
объема равна $75 Годовые издержки хранения составляют 10% от стоимости среднего
уровня запасов
а Чему равен оптимальный объем заказа в долларовом выражении9
b Сколько заказов в год должен размещать магазин9
с Чему равна оптимальная продолжительность цикла в годах9
7	30 Если в задаче 7 24 оптовик предлагает мороженое по цене $2,43 за кварту и если объем за-
купаемой партии составляет не менее 1000 кварт, то какой будет оптимальная стратегия за-
купок9
7	31 Магазин компании Cheep Chicks в г Уокон, штат Айова, заказывает цыплят с централь-
ного инкубатора компании в г Де-Мойн Каждый день в течение 360-дневного финансо-
вого года спрос составляет 22,5 дюжины цыплят Размещение заказа обходится в $40 неза-
висимо от того, сколько цыплят заказано, а стоимость хранения дюжины цыплят в запасах
в течение года составляет $80 Предположим, что компания вычисляет издержки хранения
запасов, исходя из среднего уровня запасов
а Чему равен оптимальный объем заказа9
b Сколько заказов в год должен делать магазин9
с Чему равна оптимальная продолжительность цикла в годах и днях9
7 32 Компания Napa Wine — крупнейший дистрибьютор вина в Калифорнии Спрос на ее наи-
более популярную продукцию Wino Delux постоянен и составляет 192 ящика в месяц
Стоимость размещения заказа $100, годовые издержки хранения составляют 25% среднего
уровня запасов, а стоимость продукции $200 за ящик В настоящее время у компании нет
отложенного спроса и она использует оптимальный размер заказа В году 200 рабочих дней
Найдите Q, /if, ГХР(б')
7 33 Компания Bed Bug, производящая ортопедические матрасы, в настоящее время для удов-
летворения производственных потребностей в спиральных пружинах (500 штук в день) ис-
пользует модель ОРЗ, в которой стоимость размещения заказа составляет $90, стоимость
одной пружины $1, а издержки хранения равны 15% стоимости среднего уровня запасов
Поставщик пружин, компания Springy Steel, предложила скидку 0,5%, если Bed Bug будет
заказывать не менее 20000 штук пружин за один раз, и 0,7%, если заказы будут размещаться
один раз в квартал Предполагается, что в году 240 рабочих дней
а Найдите Q и годовые совокупные затраты при существующих стоимостных показателях
b Вычислите годовые совокупные затраты для каждого варианта скидок
с Какой должна быть политика компании Bed Bug в отношении скидок9 •
7 34 Если в задаче 7 24 издержки хранения в процентном выражении удвоятся, как изменится
оптимальный объем заказа9
7 35 Крупная фармацевтическая фабрика XXX Distillery производит свою продукцию партиями
В начале каждого производственного периода этап подготовки в производству стоит $900
В процессе производства выпускается 60 галлонов продукции в день, хранение одного гал-
ГЛАВА 7. Нелинейная оптимизация 513
лона в течение дня стоит $0,025 Спрос постоянен и составляет 1125 галлонов в месяц
Предполагается, что в году 12 месяцев, 300 дней, а в месяце 25 дней
а Найдите Q, У и продолжительность цикла при оптимальном размере партии
Ь Определите максимальный уровень запасов и продолжительность (в днях) производст-
венного периода при оптимальном размере партии
с Вычислите ЕПХ(б')
7 36 В силу важных конфиденциальных деловых соображений компания XXX Distillery из зада-
чи 7 35 принимает решение запускать производственный процесс три раза в год
а Найдите размер партии продукции Q, продолжительность цикла (в днях), продолжи-
тельность периода производства и максимальный уровень запасов
b Вычислите ЕПХ
7 37 Вернитесь к задаче 7 35
а Предположим, что компания XXX Distillery не производит, а закупает продукцию,
и стоимость размещения заказа составляет $900 Найдите Q и ГХР((?)
Ь Как ГХР(б’) соотносится с ЕПХ(б’) при уровне производства 60 галлонов в день9 Объ-
ясните это соотношение
с С помощью таблицы подстановки постройте график зависимости ЕПХ((? (/>)) в зави-
симости от ежедневной производительности р
d Благодаря экономии при увеличении объема производства удельные производствен-
ные затраты снижаются по мере увеличения р Зависимость выражается формулой
С(р) = 30/р, где С(р) — удельные производственные затраты при производительности р
Найдите минимальное значение ЕПХ и дневных производственных затрат для р = 45
и р = 60
7 39.
Из-за технической отсталости оборудования компания XXX Distillery (см задачу 7 35) пре-
кратила производство и функционирует исключительно как торговая организация, прода-
вая продукцию другого производителя Чтобы получить оптовую скидку, размер заказа на
покупку должен составлять не менее 1000 галлонов Какой должна быть минимальная
скидка в расчете на галлон, чтобы компании было выгодно заказывать 1000 галлонов9
Предполагается, что Р = $5, С„ = $2,50, Ср = $200
Рассмотрим пример модели, приведенной на рис 7 17, применительно к организации, со-
стоящей из нескольких подразделений Каждому подразделению штаб-квартира выделяет*
средств, и оно возвращает штаб-квартире доход у, состоящий из двух частей Первая
часть — это доход, полученный в результате собственного размещения капитала, вторая
часть — доход, являющийся следствием сотрудничества с другим подразделением, который
принимается равным половине дохода последнего Штаб-квартира может выделить макси-
мум $10 млн , ее доход состоит из суммы доходов ее подразделений плюс нераспределен-
ный капитал Минимально выделяемая каждому подразделению сумма составляет $1,1
млн Эта модель показана на рис 7 36 Представьте модель в виде задачи НЛ П и найдите
для нее оптимальное решение с помощью средства Поиск решения, используя минималь-
но возможные выделяемые суммы в качестве начального решения
Рассмотрим модель из задачи 7 39 Воспользуйтесь SolverTable и Evolutionary Solver, чтобы
определить, какие суммы следует выделять каждому из подразделений, если суммарный
выделяемый капитал последовательно уменьшается с 10 до $5 млн Прокомментируйте по-
лученные решения
514 ЧАСТЬ II. Оптимизационные модели
Рис. 7.36
Ситуация для анализа | Оперативные поставки
Хотя концепция оперативных поставок (just-in-time) появилась совсем недавно,
от силы I5 лет назад, она настолько укоренилась в американской системе производ-
ства и предоставления услуг, что стала практически стереотипом Вероятно, это про-
изошло потому, что сама идея является очень простой и привлекательной Если го-
ворить коротко, стратегия оперативных поставок означает “иметь нужный продукт
в нужное время в нужном месте” Это означает, что в процессе производства или
предоставления услуг создается ровно то количество продукции, которое требуется
для выполнения следующего этапа. Это правило применяется ко всем этапам произ-
водственного процесса Предположим, что на заводе все изделия проходят через
операцию сверления, а затем шлифовки. При использовании стратегии оперативных
поставок просверливаются только те детали, которые затем шлифуются Тот же
принцип применяется на последнем этапе, т е. система производит только то, что
нужно потребителю
Для внедрения системы оперативных поставок обычно необходимо уделить вни-
мание следующим аспектам производственного процесса
1 Снижение времени и стоимости запуска процесса. В данном случае надо сделать
выгодным производство сверхмалых партий. В идеале такая партия состоит из
одного изделия
2 Профилактическое обслуживание. Этот аспект важен потому, что процесс про-
изводства должен всегда быть готов к запуску тогда, когда это окажется нужно,
чтобы осуществлять оперативные поставки.
ГЛАВ A 7. Нелинейная оптимизация 515
3. Постоянное совершенствование процесса с целью гарантировать высокое качество
продукции Чтобы производить точно заданное количество изделий, необходимо
быть уверенным, что все они — хорошего качества, поскольку данный подход не
позволяет выбирать изделия хорошего качества из большего количества. Постоян-
ное совершенствование процесса обычно основывается на высокой степени заин-
тересованности работников и предоставлении им значительных прав
4. Сокращение времени подготовки операции посредством активного использования
информационных технологий и тесных отношений с продавцами продукции
Во многих публикациях оперативные поставки рассматриваются в качестве кон-
цепции, противоположной модели определения оптимального размера заказа (ОРЗ).
Модель ОРЗ представляется в них устаревшей, не соответствующей времени и при-
водящей к многочисленным проблемам в работе компаний производственной сфе-
ры Хотелось бы предложить несколько иную трактовку положения дел возможно,
понятия, на которых основывается модель ОРЗ, вполне совместимы с философией
оперативных поставок, а проблема заключается в интерпретации и реализации9 По-
пробуем разобраться в данном вопросе
Вопросы
1	. Какое влияние оказывает снижение стоимости пуско-наладочных работ на раз-
мер партии в модели ОРЗ9 Аналогична ли ситуация в системе оперативных по-
ставок9
2	Какова роль качества и профилактического обслуживания в модели ОРЗ9 Почему9
3	Ощущаете ли вы разницу между подходом, заключенным в модели ОРЗ, и в опе-
ративных поставках9 В частности, на какие аспекты проблемы производства
продукции можно влиять в каждом случае?
4	. Существуют ли некие общие уроки, касающиеся моделирования, которые мож-
но извлечь, анализируя проблему перехода от модели ОРЗ к подходу оператив-
ных поставок?
Ситуация для анализа | Abacus SFX
Расположенная в Голливуде компания Abacus SFX представляет собой небольшое
недавно созданное предприятие в сфере высоких технологий, специализирующееся на
создании цифровых спецэффектов для научно-фантастических фильмов Расходы
компании для каждого отдельного проекта, связанного с созданием нового фильма, со-
ставляют $20 000 за настройку отдельного компьютера с установленным на нем графи-
ческим сервером плюс $25 000 за каждого мультипликатора, включаемого в группу по
исполнению данного проекта Компенсировать эти расходы призваны два типа дохо-
дов. платеж “за готовность к сотрудничеству”, если компания соглашается взяться за
проект (аванс), а также оплата счетов, связанных с проектом
Как принято в данной отрасли, когда Abacus берется за выполнение проекта, она по-
лучает аванс от компании — производителя фильмов Сумма такого аванса может ме-
няться от проекта к проекту. На следующий месяц Abacus рассматривает возможность
принять участие в пяти проектах В табл 7 7 показано, какие платежи за готовность к со-
516 ЧАСТЬ II. Оптимизационные модели
трудничеству ожидают компанию в случае участия в каждом из этих проектов. Также учи-
тывается, что при увеличении количества занятых в каждом отдельном проекте мультип-
ликаторов время его выполнения сокращается, что позволяет требовать более высоких
гонораров, если в группе работает больше сотрудников. В настоящее время Abacus берет
с производителей картин по $90 000 за каждого мультипликатора, занятого в проекте. Эта
сумма добавляется к платежу за готовность к сотрудничеству.
Если компания Abacus соглашается на участие в проекте, она должна назначить
для участия в нем как минимум одного мультипликатора. В компании не принято
назначать одного мультипликатора одновременно на несколько проектов, т.е. в каж-
дом проекте может участвовать только целое число мультипликаторов. У Abacus есть
восемь мультипликаторов, которых она может направить для участия в различных
проектах в следующем месяце, чтобы максимально увеличить прибыль.
Таблица 7.7
Проект	Аванс, тыс. долл.
1	18
2	20
3	8
4	26
5	22
Вопросы
1	Постройте модель, чтобы определить, какие проекты выбрать и сколько мульти-
пликаторов прикрепить к каждому из них Предполагается, что нет проектов, ко-
торые начаты раньше и продолжаются в данный момент времени Найдите оп-
тимальное решение для модели с помощью средства Поиск решения.
2	Компании Abacus нужно исследовать возможность распределения мультиплика-
торов по нескольким проектам одновременно, при Котором они должны иметь
возможность одновременно участвовать в нескольких проектах и соответственно
строить свою работу При таком способе организации труда заказчики должны
оплачивать соответствующую часть суммы ($90 000) стоимости работы одного
мультипликатора, а мультипликаторы будут получать соответствующую часть
своей зарплаты в $25 000 На основе табличной модели, построенной для ответа
на вопрос 1, создайте новую табличную модель с тем, чтобы появилась возмож-
ность прикреплять к каждому из проектов дробное число мультипликаторов при
условии, что в каждый момент времени каждым отдельным проектом занимается
не менее одного мультипликатора. Найдите оптимальное решение задачи с по-
мощью средства Поиск решения
3	Вернемся к модели и постановке задачи из вопроса 1 Компания Abacus может
привлечь от 5 до 10 мультипликаторов к работе над пятью проектами в следую-
щем месяце Используйте SolverTable для построения таблицы, показывающей
распределение мультипликаторов по принятым проектам и итоговую прибыль
при изменении числа мультипликаторов от 10 до 5 включительно. Насколько
чувствительна прибыль к количеству мультипликаторов, которых можно при-
влекать к участию в проектах9
ГЛАВА 7. Нелинейная оптимизация 517
4	. Компания Abacus пришла к выводу, что модель, построенная для ответа на во-
прос 1, не соответствует действительности в том, что касается определения за-
трат на участие в проекте. В частности, увеличение числа участников проекта
приводит к уменьшению их производительности. Предполагается, что все затра-
ты, платеж за готовность к сотрудничеству, требование прикреплять к проекту
как минимум одного мультипликатора остались прежними Однако оплата стои-
мости работы группы сотрудников (вычисляется как $90 ОООхколичество сотруд-
ников) понижается путем умножения на некий коэффициент, установленный
руководством компании Abacus (см. табл. 7 8) Например, за работу группы из
трех человек будет выплачено 3x90000x0,63 долларов Измените модель, постро-
енную для ответа на вопрос 1, так, чтобы учесть соответствующие изменения
(рекомендуем использовать функцию Excel ВПР) Предполагая, что ранее не бы-
ло принято ни одного проекта, а в распоряжении компании имеется восемь
мультипликаторов, найдите оптимальное решение задачи с помощью средства
Поиск решения.
Таблица 7.8	
Численность участников проекта	Доля выплачиваемого вознаграждения
1	1,00
2	0,77
3	0,63
4	0,54
5	0,46
6	0,40
7	0,35
8	0,31
9	0,27
10	0,23
11	0,20
12	0,17
13	0,15
14	0,12
5 Еще раз рассмотрим модель и условия, заданные в вопросе 4 Компания Abacus
имеет возможность привлечь к выполнению любого из пяти проектов, запускае-
мых в следующем месяце, от 5 до 10 мультипликаторов С помощью SolverTable
постройте таблицу, определяющую распределение мультипликаторов по проек-
там и результирующую прибыль при изменении числа мультипликаторов от 10
до 5 включительно. Насколько чувствительна результирующая прибыль к изме-
нению количества мультипликаторов, которых можно привлечь к работе5 * * * 9
518 ЧАСТЬ II Оптимизационные модели
6. Обобщите результаты, полученные по итогам рассмотрения вопросов 4 и 5, в ви-
де отчета, предоставляемого руководству компании Abacus. Выскажите свои со-
ображения относительно того, что следует делать компании Abacus в случае, если
у нее в распоряжении окажется больше или меньше восьми мультипликаторов
для пяти проектов в следующем месяце.
Литература
1 Mulvey J An Asset-Liability Investment System Interfaces, 24, по 3 (1994) p 24-23
2 Ben-Dov Y , Hayre L , Pica V Mortgage Valuation Models at Prudential Securities Interfaces, 22, no
1 (1992) p 55-71
Глава
Многоцелевые модели
и эвристические методы
В этой главе...
8.1.	Введение
8.2.	Составление графика работы оборудования
8.3.	Составление графика работы оборудования при ограниченности ресурсов
8 4 Задачи со множеством целей
8.5.	Аналитический иерархический процесс
8.6.	Заключение
Основные термины
Контрольные вопросы
Задачи
Ситуация 1 Объединение заводов
Литература
520 ЧАСТЬ II Оптимизационные модели
► Рациональное использование лесных угодий
За последние два десятилетия в мировой практике использования лесных угодий про-
изошел ряд изменении. Рост населения и эксплуатация природных ресурсов привели
к тому, что производство многих продуктов лесоводства достигло максимально допусти-
мого уровня или превысило его Все более актуальной становится задача охраны лесных
экосистем, сохранения широкого спектра лесных ресурсов, защиты исчезающих видов
растений и животных, их естественной среды обитания, неповторимой красоты и разно-
образия природы Как следствие, основной акцент в управлении лесными угодьями сме-
стился от производства товаров и услуг (сельскохозяйственная модель) к сохранению
здоровья леса, его биологического разнообразия и продуктивности (модель экосистемы).
Учитывая возросший интерес общественности к вопросам управления лесным хозяйст-
вом, неудивительно, что процесс принятия решений в данной области стал более откры-
тым, политизированным и сложным.
Находящимися в общественной собственности лесами пользуется множество
людей, причем пользуется по-разному Некоторые лесные ресурсы — древесина, ле-
карственные растения, места отдыха и вода — имеют непосредственную экономиче-
скую ценность Стоимость других ресурсов измерить сложнее живописная красота,
нетронутые ландшафты, разнообразие живой природы, исчезающие виды растений
и животных Важными являются также социальные и экономические вопросы, ка-
сающиеся жителей лесных районов За последнее десятилетие заметно повысилось
внимание поддерживаемых общественностью экологических групп к решению во-
просов охраны окружающей среды
Две наиболее интенсивно используемые в управлении лесным хозяйством много-
критериальные модели базируются на многоцелевой линейной оптимизации В об-
щем случае эти модели определяют набор решений по управлению лесным хозяйст-
вом с учетом нескольких целей
Мноые комплексные задачи управления лесным хозяйством приходится решать
в обстановке состязания за ресурсы, когда существуют законодательные ограниче-
ния, цель которых — обеспечить удовлетворительный уровень таких бесценных об-
щественных ресурсов, как вода, рыба, дикая природа Компромиссные решения на-
ходятся за столом переговоров, при этом многокритериальные компьютерные моде-
ли помогают проводить обсуждение более обоснованно и доказательно. [6]
8.1. Введение
Иногда задача менеджера настолько сложна, что построенная для ее решения математи-
ческая модель неразрешима с помощью имеющихся в распоряжении аналитика традици-
онных методов Можно указать следующие причины возникновения подобной ситуации
I “Корректно формализованная” модель оказывается слишком большой, существенно
нелинейной или чрезмерно сложной (например, при ее формулировке приходится
использовать большое количество двоичных переменных)
2 Введение упрощающих предположений и приближений, которые могли бы помочь
в решении задачи, нарушают структуру модели, делая ее слишком далекой от реаль-
ности, чтобы быть полезной
ГЛАВА 8 Многоцелевые модели и эвристические методы 521
Налицо дилемма- существующая модель слишком сложна, чтобы ее можно было ре-
шить, в то же время упрощать ее нежелательно Что делать в таком случае?
Стремление найти выход из данной ситуации стало одной из причин развития эври-
стических методов Говоря, что задача слишком сложна, чтобы ее можно было решить,
мы употребляем слово решить в строгом математическом смысле. Подразумевалось, что
данная математическая задача настолько сложна, что, хотя существует ее строгое реше-
ние (оптимальное решение в модели оптимизации), наити его с помощью современных
знаний и методов слишком трудно или даже невозможно В таком случае применяется
эвристический алгоритм.
Эвристический алгоритм позволяет эффективно находить хорошие приблизительные
решения данной задачи Часто (однако отнюдь не всегда) при применении такого алго-
ритма можно точно измерить, насколько “хорошим” является это приближение Напри-
мер, применительно к задачам оптимизации для некоторых эвристических алгоритмов
и при определенных предположениях можно получить оценку близости полученного ре-
шения к оптимальному Важным свойством эвристического алгоритма является то, что
он никогда не дает “плохих” решений.
Часто встречается термин эвристика. Эвристики — это практические приемы и спо-
собы решения определенных частных задач. В некоторых компьютерных программах,
предназначенных для решения задач линейного программирования (таких как Поиск
решения в Excel), эвристики используются на начальном этапе применения симплекс-
метода, чтобы быстро найти начальное угловое решение С этой же целью эвристики
применяются при решении транспортных задач В математическом программировании
эвристики часто являются частью или частным случаем более обшей или более строгой
стратегии решения задач.
Важно помнить, что, несмотря на интуитивную привлекательность эвристической про-
< цедуры или алгоритма, о их результатах можно говорить только в статистическом смыс-
: ле или с определенной мерой достоверности. Они применяются главным образом для
 повышения эффективности — чтобы быстро получить хорошие, если не оптимальные,
* результаты. С точки зрения менеджера, эвристическая процедура столь же приемлема,
i а иногда даже предпочтительнее (в смысле затрат), чем более точный алгоритм, даю-
ший оптимальное решение.
В первой части главы мы рассмотрим несколько примеров эвристических алгорит-
мов, применяемых для решения крупных задач комбинаторной оптимизации Термин
комбинаторная оптимизация означает, что существует конечное число допустимых вари-
антов, и, перебрав все эти варианты, можно найти оптимальное решение Проблема
в том, что на практике это конечное число составляет миллионы или миллиарды вариан-
тов, поэтому полный перебор даже с помощью быстродействующего компьютера невоз-
можен. Хотя подобные модели можно сформулировать в виде задач целочисленного
программирования (ЦП) с двоичными переменными, зачастую они настолько велики,
что полученную формулировку в виде задачи ЦП слишком дорого оптимизировать по-
средством обычного метода ветвей и границ или частичного перебора
Далее рассмотрим модели, построенные для поиска приемлемых значений несколь-
ких критериев эффективности, и приведем примеры моделей с несколькими конфлик-
тующими целями. Наличие нескольких конфликтующих целей типично для бизнес-
приложений. Такими моделями занимается целевое программирование Данная область
тесно связана с эвристическими методами, поскольку в определенном смысле само целе-
522 ЧАСТЬ II Оптимизационные модели
вое программирование может рассматриваться как некий эвристический подход для по-
иска решения при наличии нескольких целей
Следующая часть главы посвящена рассмотрению аналитических иерархических про-
цессов (АИП) АИП — это метод, посредством которого менеджер осуществляет выбор
среди множества различных альтернативных решений, когда для сравнения этих реше-
ний используется несколько критериев Можно привести множество примеров, где пра-
вомерно использование этого метода, поскольку он позволяет найти решение при нали-
чии многих конкурирующих целей
8.2. Составление графика работы оборудования
Рассмотрим производственное оборудование (например, компьютер, сверлильный
станок или оборудование для производства мороженого), на котором последовательно
может выполняться несколько заданий Обычно после завершения одного задания обо-
рудование останавливается и настраивается для выполнения следующего Это время
простоя оборудования называется временем подготовки к работе или временем переналад-
ки Продолжительность этого времени зависит от того, какое задание предстоит выпол-
нить и какое было только что завершено Если следующие друг за другом задания ана-
логичны (например, после английского ванильного выпускается французское ванильное
мороженое), время подготовки (требуемое для мойки машины) будет меньше, чем при
переходе к совершенно иному заданию (выпуск французского ванильного после гол-
ландского шоколадного) Типичная управленческая задача упорядочить задания таким
образом, чтобы минимизировать суммарное время переналадки оборудования перед выполне-
нием нового задания
Заметим, что если данную модель рассматривать как комбинаторную, она может ока-
заться очень большой Если возможных заданий всего три, например, А, В и С, тогда любое
из них можно выбрать в качестве первого, затем любое из двух оставшихся в качестве вто-
рого, после чего третье будет определяться однозначно Возможные последовательности
выполнения заданий можно изобразить в виде дерева, каждая ветвь которого представляет
определенную последовательность заданий Шесть возможных случаев представлены на
рис 8 1 В общем случае, когда имеется п заданий, существует = п(п— 1)(н-2) . 1 возмож-
ных комбинаций или последовательностей (я1 называется в математике “и факториал”)
При наличии 10 заданий получится 10' = 3 628 800 различных последовательностей,
т е число возможных последовательностей выполнения работ п' возрастает чрезвычайно
быстро с увеличением п
Рис. 8.1. Дерево шести возмож-
ных последовательностей вы-
полнения трех заданий
Очевидным способом решения приведенной выше задачи минимизации является пол-
ный перебор Для этого строятся все и' возможных последовательностей выполнения зада-
ний и для каждой последовательности вычисляется суммарное время переналадки Хотя
ГЛАВА 8. Многоцелевые модели и эвристические методы 523
данный алгоритм позволяет найти оптимальное решение, он непрактичен даже для относи-
тельно небольших значений п, поскольку приходится рассматривать слишком большое ко-
личество возможных последовательностей Для 20 заданий компьютеру, способному вы-
полнять 6 500 000 000 команд в секунду (“6500 MIPS” на “компьютерном” языке), потребу-
ется 11 лет, чтобы найти оптимальное решение методом полного перебора
Эвристические решения
В таких моделях часто применяются эвристические правила, которые хотя и не гаран-
тируют получение оптимального решения, но обычно достаточно быстро позволяют по-
лучить удовлетворительное решение.
В качестве примера рассмотрим следующую ситуацию оператору некой машины
в понедельник после обеда нужно выполнить три достаточно длительных задания Машина
к этому моменту свободна Для каждого задания существует время подготовки (очистка
машины после выполнения последней работы, установка оснастки, необходимой для вы-
полнения новой работы и т д ), как показано в табл 8 1 Поскольку возможных последова-
тельностей всего 3' = 3x2 = 6, можно осуществить их полный перебор Результаты представ-
лены в табл 8 2 Из таблицы видно, что оптимальной последовательностью работ (с мини-
мальным временем подготовки и переналадки) является 0-+A-+C-+B
Таблица 8.1. Время переналадки в минутах
	Задание А	Задание В	Задание С
Подготовка (0)	27	21	32
Задание А		35	22
Задание В	49		46
Задание С	46	12	
Таблица 8 2 Полный перебор последовательностей работ
Последовательность работ	Время переналадки	Итого, мин.
0—>А—>В—>С	27+35+46	108
0—>А—>С—>В	27+22+12	61
0—>В—>С—>А	21+46+46	113
ОчВчАчС	21+49+22	92
О^С^А^В	32+46+35	113
0—>С—>В—>А	32+12+49	93
Поглощающий алгоритм
Попробуем теперь применить к данной модели некое эвристическое правило Прави-
ло, применение которого мы хотим продемонстрировать, называется правилом выбора
следующего наилучшего или поглощающим алгоритмом 1 Оно заключается в следующем
Этот алгоритм иногда называется жадным алгоритмом, поскольку на каждом шаге он выбирает
(поглощает) наилучшее возможное (на данном шаге) решение — Прим рсд
524 ЧАСТЬ II Оптимизационные модели
1. На первом шаге (при выборе первого задания) выбирается задание с наименьшим
начальным временем.
2. На каждом последующем шаге выбирается задание, требующее наименьшего вре-
мени переналадки
Применим это правило к приведенным в табл 8.1 данным Задание с наименьшим
начальным временем подготовки — это задание В. Следовательно, первым шагом явля-
ется ОчВ В соответствии с поглощающим алгоритмом после окончания задания В сле-
дует выбрать задание С, поскольку время переналадки для В->С меньше, чем для В->А.
Таким образом, задания выполняются в таком порядке. О—>В—>С, последним заданием
может быть только А Получается последовательность работ 0—> В—>С—>А с суммарным
временем подготовки и переналадки 21+46+46 = 113.
Как видно, данный результат далек от оптимального. Фактически в данном примере
интуитивно привлекательный поглощающий алгоритм приводит к выбору наихудшей
возможной последовательности работ. Хотя в общем случае поглощающий алгоритм не
приводит к оптимальному решению, тем не менее существует несколько моделей специ-
ального вида, для которых найденное с помощью данного алгоритма решение будет оп-
тимальным, например, в задачах нахождения минимального пути (см. главу 5) Кроме
того, данный алгоритм чрезвычайно просто реализуется, а исследования его применения
показали, что статистически он работает неплохо. Например, статья [3] доказывает, что
эта эвристика очень часто дает лучшие результаты, чем те, которые можно получить
с помощью простого случайного выбора заданий.
В этой статье также показано, что следующая эвристическая процедура дает еще луч-
шие результаты
1. Преобразовывается таблица исходных данных путем вычитания в каждом столбце
минимального времени, содержащегося в этом столбце, из всех элементов данного
столбца. В нашем примере из табл. 8.1 получится новая табл. 8 3.
2. Применяется поглощающий алгоритм к преобразованным данным. В нашем примере
в результате получится новая последовательность выполнения заданий 0-эА->С->В,
которая, как мы уже видели, является оптимальной для данной модели.
Таблица 8.3. Преобразованные данные
	Задание А	Задание В	Задание С
Подготовка (0)	0	9	10
Задание А		23	0
Задание В	22		24
Задание С	19	0	
Хотя эта модифицированная эвристическая процедура не всегда дает оптимальное
решение, ее легко реализовать, и, как показывает практика, для больших моделей она
часто дает достаточно хорошие результаты.
ГЛАВА 8. Многоцелевые модели и эвристические методы 525
8.3. Составление графика работы оборудования при
ограниченности ресурсов
Предположим, что для выполнения проекта необходимо составить календарный план
работ. Базовые модели позволяют составить график работ, минимизирующий суммарное
время выполнения проекта с учетом того, что некоторые виды деятельности не могут на-
чаться раньше, чем будут завершены другие При этом, как правило, считается, что необ-
ходимые для выполнения отдельных заданий ресурсы (финансы, рабочая сила, оборудо-
вание и т д ) доступны в необходимых объемах Однако в действительности эти ресурсы
могут быть ограничены, и в этом случае появляются дополнительные ограничения
Простой пример
В качестве простого примера рассмотрим модель составления графика работ, пред-
ставленную на рис. 8.2 и в табл. 8 4. На рис. 8.2 представлены отношения предшествова-
ния между различными видами работ, т.е. показано, какие задания необходимо выпол-
нить до того, как приступить к другим Например, выполнение задания VIII нельзя начи-
нать, пока не будет выполнено задание VII, а к заданию VII нельзя приступать до
завершения задания I В табл 8 4 показана длительность выполнения каждого задания
(в неделях) и необходимые ресурсы (количество человек).
Таблица 8.4. Время и трудовые ресурсы, необходимые для выполнения заданий
Задание Время выполнения, недели Необходимое количество людей в неделю
VI	4
VII	1
VIII	2
IX 2
526 ЧАСТЬ II Оптимизационные модели
Если не учитывать ограничения на количество людей, задача является простой,
и найти кратчайшее возможное время окончания проекта просто оно составляет 9 не-
дель На рис 8 3 показан предлагаемый график выполнения заданий, при котором дос-
тигается это время Выполнение заданий I, II и III начинается немедленно (в начале не-
дели 1) Работы IV, V, VII и IX стартуют в начале недели 4. Выполнение задания VI начи-
нается в начале недели 6, а задания VIII — в начале недели 5.
Теперь рассмотрим количество человек в неделю, необходимое для реализации предло-
женного графика Сопоставив данные о потребностях в персонале из табл 8 4с представ-
ленным на рис 8 3 графиком работ, можно получить схему загрузки персонала, показанную
на рис 8 4 Как видно, предлагаемый график приводит к неравномерному использованию
персонала, потребности в рабочей силе изменяются от 15 человек в неделю (неделя 4) до 5
(недели 7, 8 и 9) Обычно удобней иметь график с более равномерным использованием ре-
сурсов Для достижения этой цели часто применяются эвристические методы.
ГЛАВА 8 Многоцелевые модели и эвристические методы 527
Эвристическая процедура выравнивания загрузки персонала
Прежде чем приступить к обсуждению одной из таких эвристических процедур, опре-
делим для каждого задания проектарезерв
Резерв — это максимальное время задержки начала задания, которое не приведет к за-
держке выполнения проекта в целом.
Если задержать выполнение задания V (см рис 8 3), то задание VI не сможет начаться
в начале недели 6, и проект не будет завершен к концу девятой недели Таким образом,
задание V не имеет резерва Напротив, выполнение задания VIII можно задержать на 3
недели, при этом выполнение проекта в целом не задержится Следовательно, задание
VIII имеет резерв 3 недели
Используя данное понятие, опишем эвристическую процедуру, призванную выров-
нять рабочую нагрузку на протяжении всего времени выполнения проекта
1. Определяется максимум требуемых ресурсов в имеющемся графике работ, скажем,
т рабочих в неделю
2. Для каждой недели устанавливается новый верхний предел использования ресур-
сов в размере т- 1, и, если возможно, существующий график работ преобразуется
так, чтобы он удовлетворял этому ограничению Преобразование осуществляется
следующим образом
а Начиная с первой недели, для которой нарушено данное ограничение, рас-
сматриваются выполняемые в это время задания, задание с наибольшим резер-
вом сдвигается на минимально возможное время, обеспечивающее выполне-
ние ограничения по нагрузке, но не приводящее к задержке окончания проекта
в целом (это означает, что задания с нулевым временным резервом сдвигать
нельзя) При наличии равнозначных вариантов следует сдвигать вперед зада-
ние, вносящее наименьший вклад в перегрузку (т е. требующее минимального
количества человек)
b Эвристическая процедура завершается, когда текущий уровень нагрузки нельзя
понизить
Чтобы продемонстрировать применение описанной процедуры, изобразим график
выполнения проекта так, как показано на рис 8 5 На этом рисунке под каждой стрелкой
указан номер задания (I, II и т д.), а над стрелкой — количество человек, требуемое каж-
дую неделю Например, цифра 6 над стрелкой, соответствующей заданию I, означает, что
каждую из трех недель над выполнением задания I должны работать 6 человек Таким об-
разом, легко подсчитать, сколько человек требуется каждую неделю Например, посколь-
ку в течение недели 2 выполняются задания I и II, соответствующее число в строке По-
требность в персонале равно 9 Расстояние от стрелки в конце задания до конца неде-
ли 9 показывает, чему равен резерв для этого задания Так, задание IV имеет резерв 5
недель, а задание VIII — 3 недели и тд Для задания VII, не являющегося последним,
можно вычислить резерв, исходя из того, что после него выполняется только задание
VIII Поскольку резерв для задания VIII составляет 3 недели, резерв для задания VII так-
же составит 3 недели Кроме того, отметим, что задания I, V и VI имеют нулевой резерв,
и поэтому их нельзя сдвигать вперед, не увеличив общее время выполнения проекта При
использовании данной эвристической процедуры сдвигаются вперед только задания
с положительным резервом
528 ЧАСТЬ II Оптимизационные модели
Применение эвристической процедуры
Применим эвристическую процедуру в нашем примере. Для первого графика работ
(рис 8 5) максимальное количество требуемых ресурсов составляет 15 человек (для неде-
ли 4) Согласно шагу 2 процедуры для каждой недели задаем новое ограничение сверху,
составляющее 14 человек. Это ограничение нарушается только для четвертой недели.
В это время выполняются допускающие смещение задания IV, VII и IX. Из них наиболь-
шим резервом обладает задание IV. Смещая начало выполнения задания IV вперед на
1 неделю, мы уменьшаем необходимое в течение недели 4 количество работников на 3,
что составит 12 человек, при этом дополнительные 3 человека потребуются в течение не-
дели 5, тогда суммарное количество работников на этой неделе составит 16 человек, что
приведет к превышению ограничения в 14 человек. Следовательно, задание необходимо
передвигать вперед Если передвинуть задание IV вперед на две недели (на неделю 6, как
показано стрелкой без номера на рис. 8.5), ограничение нигде не будет нарушено. В ре-
зультате получаем второй график работ, представленный на рис. 8.6.
На рис 8.6 максимальное необходимое количество работников составляет 13 человек.
Далее необходимо уменьшить это значение до 12. Единственное нарушение нового огра-
ничения возникает на протяжении недели 5, когда выполняются задания VIII и IX. Зада-
ние IX имеет больший резерв, и начало его выполнения следует передвинуть на 3 недели
вперед — на начало недели 7, как показано на рис. 8.6. В результате получится третий
график работ, представленный на рис. 8.7. Здесь верхний предел равен 12 человек, и его
следует уменьшить до 11. Нарушения последнего ограничения происходят в течение не-
дель 1 и 6. В соответствии с алгоритмом сначала сдвигаем вперед на 2 недели начало вы-
полнения задания III, а затем перемещаем задание IV на 1 неделю. Продолжая эту проце-
дуру, получаем четвертый и пятый графики работ, показанные на рис. 8.8 и 8.9.
ГЛАВА 8 Многоцелевые модели и эвристические методы 529
Рис. 8.7. Третий график работ
530
ЧАСТЬ II Оптимизационные модели
Завершение эвристической процедуры
Улучшить пятый график работ алгоритм уже не в состоянии, поскольку уменьшить
нагрузку в течение недели 5 можно только путем сдвига вперед задания VIII, однако
сдвиг этого задания на 1, 2 или 3 недели увеличит потребность в персонале в течение не-
дель 7 и 8 или 8 и 9 до 12 человек Таким образом, последнее условие эвристического ал-
горитма выполнено, следовательно, пятый график работ является решением В этом гра-
фике использование персонала значительно более равномерное, чем в исходном, пред-
ставленном на рис 8 4, максимальная потребность в персонале составляет 10 человек
(неделя 5), а минимальная — 8
ГЛАВА 8 Многоцелевые модели и эвристические методы
531
Можно иначе посмотреть на данную модель и считать оптимальным график работ,
минимизирующий максимальное использование персонала Оптимальный план, соответст-
вующий этому минимаксному критерию, представлен на рис 8 10 В этом графике макси-
мальная потребность в персонале составляет 9 человек Хотя эвристический алгоритм не
привел к этому оптимальному решению (необходимо отметить, что использование пер-
сонала в оптимальном решении более равномерное, чем в графике на рис 8 9), все же ре-
Вышеописанное можно рассматривать только как краткое введение в важную тему
эвристических алгоритмов Еще один пример модели размещения оборудования рас-
сматривается в задачах 8 2, 83и84в конце данной главы
8.4. Задачи со множеством целей
Во многих приложениях в модели закладывается поиск нескольких целей, среди ко-
торых трудно выделить одну Рассмотрим задачу планирования, долгосрочными целями
которого являются 1) максимизация прибыли, 2) максимизация доли рынка на конец
планового периода и 3) максимизация основного капитала на конец планового периода
Эти цели несопоставимы в том смысле, что они не поддаются непосредственному срав-
нению или комбинированию Также ясно, что это конфликтующие цели, т е ослабление
требований к одной цели приведет к возможности получить более высокие результаты по
другим Например, если потратить меньше денег на маркетинг (уменьшение расходов),
это может привести к сокращению доли рынка, тем самым помешает компании в дости-
жении ее второй цели Однако эти средства можно направить на закупку нового оборудо-
вания, чтобы увеличить основной капитал и тем самым достичь третьей цели
Моделирование при наличии многих целей является относительно молодой, но важ-
ной областью исследований В настоящее время многоцелевые модели не так часто при-
меняются на практике, как, например, модели линейного программирования, прогнози-
532 ЧАСТЬ II Оптимизационные модели
рования, управления ресурсами и имитационные модели. Однако концепции, на кото-
рых строятся многоцелевые модели, достаточно важны, и некоторые ведущие специали-
сты в теории управления считают, что в ближайшем будущем их важность еще больше
возрастет Эти модели оказались особенно полезны при решении задач государственного
управления
Разработано несколько подходов к многоцелевым моделям (называемым также мно-
гокритериальным принятием решений), среди них использование теории полезности, по-
иск Парето-оптимальных решений с помощью многокритериального линейного про-
граммирования, аналитический иерархический процесс (АИП) и целевое программиро-
вание Мы ограничимся обсуждением двух последних подходов. АИП и целевого
программирования Метод АИП был разработан Томасом Саати (Thomas Saaty, [5]) и яв-
ляется относительно новым подходом, призванным помочь менеджерам осуществить
выбор среди многих альтернативных решений при наличии нескольких критериев По-
нятие целевого программирования (ЦП) было введено Чансом (Abraham Charnes) и Ку-
пером (William Cooper) [2]. Его можно рассматривать как эвристический подход для
многоцелевых моделей, основанный на концепциях линейного программирования. Оба
указанных подхода представляют в настоящее время значительный интерес и являются
предметом интенсивных исследований, поэтому они важны для будущих менеджеров.
Практическое применение
Размещение оборудования в университете
штата Миссури
В академической среде обеспечение высокого качества преподавания, научных ис-
следований и обмена опытом предъявляет особые требования к специалисту, ответст-
венному за размещение оборудования. Отдел технического администрирования уни-
верситета Миссури-Ролла умело воспользовался значительным расширением произ-
водственных площадей в 1987 году. Тогда была организована лаборатория систем
автоматизации производства (САП) для обучения, проведения исследований и обмена
опытом Она была призвана повысить интерес к изучению и исследованию производ-
ственных систем и должна была со временем развиться в центр обмена передовым
опытом для промышленных предприятий штата.
В университете считали, что новая лаборатория САП будет обслуживать потреб-
ности всего учебного заведения, включая различные университетские исследова-
тельские центры. Из-за этого возникла дискуссия о наиболее рациональном разме-
щении оборудования в новой лаборатории, занимающей площадь 5072 квадратных
фута. Для решения задачи была создана специальная рабочая группа. После выявле-
ния альтернативных предложений по размещению оборудования в лаборатории бы-
ло выделено 15 секций (секции физического моделирования, автоматического про-
ектирования, робототехнических систем и другие). Для каждой секции оценивалась
идеальная площадь. Сумма идеальных площадей составила 6035 квадратных футов,
примерно на 1 000 больше, чем имелось в распоряжении
Группа должна была предложить некий систематический способ распределения
помещений между секциями, который соответствовал бы общим задачам универси-
тета. Было сформулировано пять целей (разработка новых учебных курсов, повыше-
ние уровня осведомленности в промышленности о концепциях САП и т.д.). Для оп-
ределения приоритетов этих целей использовался аналитический иерархический
процесс, а для определения относительных приоритетов была предложена анкета.
ГЛАВА 8 Многоцелевые модели и эвристические методы 533
Предварительным анализ ответов выявил некоторые несоответствия в попарном
сравнении приоритетов. Респонденты имели возможность проверить и уточнить
свои ответы, повысив согласованность сравнений
После задания приоритетов для выделения площадей каждой из 15 секций была ис-
пользована модель целевого программирования Для девяти из 15 секций коэффициент
назначения оказался меньше 1, т.е они получили площади меньше, чем им требовалось
в идеале. Площади четырех секций претерпели существенное сокращение Комиссия ис-
пользовала рекомендованный план распределения площадей в качестве руководства при
разработке первоначального плана размещения оборудования в лаборатории Был также
проведен анализ устойчивости для определения влияния изменения приоритетов, кото-
рый показал, что модель достаточно устойчива к изменениям приоритетов
Аналитический иерархический процесс позволил достичь консенсуса при реше-
нии достаточно сложной задачи перспективного планирования в значительно поли-
тизированной группе. Благодаря применению данного метода университет быстро
принял предложенный план размещения лаборатории, а лаборатория САП достигла
поставленных целей в сфере обучения, исследований и обмена опытом [ 1 ]
Целевое программирование
Целевое программирование в общем случае применяется к линейным моделям, это рас-
ширение задач ЛП, которое позволяет вплотную подойти к достижению различных целей
иограничений. Лицо, принимающее решение, по крайней мере на эвристическом уровне,
может использовать свою систему предпочтений при работе со многими противоречивыми
целями Иногда целевое программирование рассматривают как попытку математической
интерпретации понятия удовлетворительности (satisficing). Этот термин ввел лауреат Нобе-
левской премии в области экономики Херберт Саймон (Herbert Simon), чтобы охарактери-
зовать достаточно часто возникающую ситуацию, когда люди ищут не оптимальные, а “дос-
таточно хорошие” решения. Иными словами, требуется довести несколько целей одновре-
менно хотя бы до минимально удовлетворительных уровней. Чтобы показать работу метода
целевого программирования, рассмотрим несколько примеров.
Предположим, что в модели разработки образовательной программы введены две пере-
менные решения х, и х2, где х, — часы работы студентов в аудитории, а х2 — часы работы
в лаборатории Существует следующее ограничение на общее время работы х,+х2 < 100
(общее количество часов, выделенных на программу).
Два вида ограничений
В целевом программировании выделяется два вида ограничений: системные ограниче-
ния (так называемые жесткие ограничения), которые нарушать нельзя, и целевые ограни-
чения (так называемые мягкие ограничения) которые при необходимости могут нару-
шаться. Приведенное выше ограничение суммарного количества часов, выделенных на
программу, является примером системного ограничения
Теперь предположим, что из каждого часа работы в аудитории 12 мин уделяется работе
небольшими группами и 19 мин. — индивидуальному решению задач, а из каждого часа лабо-
раторных занятий 29 мин. уделяется работе по группам и 11 мин. — индивидуальному реше-
нию задач. Общее время, отведенное на программу, составляет не более 6 000 мин (100 чхбО
мин./ч). Разработчики программы преследуют две цели: желательно, чтобы студент посвятил
примерно четверть максимально отведенного на программу времени работе в группах и треть
этого времени — решению задач. Эти условия записываются следующим образом:
534 ЧАСТЬ II Оптимизационные модели
12х, + 29х2 = 1 500 (работа по группам),
19х, + 11х2 = 2 000 (индивидуальное решение задач)
Символ = означает желательно, чтобы левая часть была как можно ближе к правой
части Если бы удалось найти план, который в точности соответствовал обеим целям
(т е в обоих выражениях будет достигнуто точное равенство), не нарушив системное ог-
раничение суммарного количества отведенных на программу часов, то он и был бы ре-
шением задачи Однако простой геометрический анализ показывает, что такого плана не
существует Следовательно, чтобы удовлетворить системное ограничение, придется на-
рушить строгое равенство по крайней мере для одной цели.
Прежде чем применить метод целевого программирования, перепишем условие для
работы по группам в виде целевого ограничения.
12х, + 29х2 + м, - v, = 1 500 (и, > 0, у, > 0),
где //, показывает, на сколько минут время работы по группам меньше величины 1 500,
а г, — на сколько минут время работы по группам превышает 1 500.
Переменные отклонения
Переменные и, и у, называются переменными отклонения, поскольку они показывают,
на сколько значение, полученное в решении, отклоняется от цели По определению хотя
бы одна из переменных л, или v, (или обе) должна быть равна нулю, поскольку получен-
ное значение не может одновременно быть больше и меньше 1 500 Чтобы значение сум-
мы 12х1 + 29х2 было как можно ближе к 1 500, достаточно сделать малой сумму и, + v,
Аналогично запишем в виде целевого ограничения условие для времени индивиду-
ального решения задач
19х, + 11х2 + и2 - v2 = 2 000 (и2 > 0, v2 > 0)
В данном случае также необходимо, чтобы сумма двух переменных отклонения и2 + v2
была как можно меньше. Таким образом, наша иллюстративная модель примет следую-
щий вид
Минимизировать и, + v,+ и2 + v2
при ограничениях
х, +х2 < 100 (общее количество часов, выделенных на программу),
12х1 + 29х2 + и, - у, = 1 500 (время работы по группам),
19х1 + 11х2 + и2 — v2 = 2 000 (время индивидуального решения задач),
х,, х2, ир Vp и2, v2 > 0
Это стандартная модель Л П, которую можно легко решить в Excel Оптимальные пе-
ременные решения будут удовлетворять системному ограничению (общее количество ча-
сов, выделенных на программу) Кроме того, оказывается, что программа Поиск реше-
ния (в силу технических причин, которые мы обсуждать не будем) гарантирует, что одно
из значений или у, (или оба) будет равно нулю, тем самым эти переменные автоматиче-
ски удовлетворяют требуемому условию То же самое справедливо для переменных и2
и v„ а в общем случае — для любой пары переменных отклонения.
Целевая функция представляет собой сумму переменных отклонения. Такой выбор
целевой функции показывает, что у нас нет предпочтений при рассмотрении отклонений
от намеченных целей Например, все три перечисленных ниже решения являются допус-
тимыми 1) решение, в котором целевой показатель времени работы по группам превы-
ГЛАВА 8 Многоцелевые модели и эвристические методы 535
шен на 5 мин , а время решения задач в точности совпадает с целевым, 2) время работы
по группам совпадает с целевым, а решению задач отводится на 5 мин меньше желае-
мого; и 3) каждому виду работ отводится на 2,5 мин. меньше желаемого Иными словами,
нам все равно, какое из трех решений выбрать
1)	//, = 0,	2) м,=0,	3) и, = 2,5,
	Л = 5,	v, = 0,	г, =0,
	«2 = 0,	«2 = 5,	«2 = 2,5,
	v2 = 0	v2 = 0	v2 = 0
Мы не должны иметь предпочтений, поскольку каждое из этих трех решении достав-
ляет одно и то же значение 5 целевой функции
Весовые коэффициенты для переменных отклонения
В моделях целевого программирования отнюдь не всегда наблюдается отсутствие
предпочтений относительно различных решений Даже простые различия в единицах из-
мерения показателей могут привести к возникновению определенных предпочтений по
отношению к переменным отклонения Предположим, что ограничение по индивиду-
альному решению задач выражено в часах и выглядит следующим образом
19/60 х, + 11/60 x2 + u2-v2 = 2 000/60
Кроме того, очевидно, что составителю программы предпочтительней превысить на
одну минуту показатель времени работы в группах (v1 = 1), чем снизить на 1 час время
решения задач (w2 = 1)
Одним из способов описания предпочтений среди различных целей является при-
своение различных коэффициентов переменным отклонения в целевой функции В на-
шем примере целевая функция может выглядеть следующим образом минимизировать
Юи, + 2v, + 20w2 + v.
Минимальный коэффициент при v2 (превышение времени индивидуального решения
задач) указывает на то, что разработчики программы скорее предпочтут иметь положи-
тельное значение этой переменной, чем других переменных отклонения (положительное
значение данной переменной приводит к наименьшим потерям)
Интервальные целевые ограничения
Существует еще один тип целевых ограничений — интервальные целевые ограничения
Такое ограничение задает интервал изменения целевого показателя, а не конкретное чи-
словое значение Пусть, например, в рассматриваемом примере разработчики считают
одинаково приемлемыми программы, в которых время индивидуального решения задач
заключено в следующих пределах 1 800 < время решения задач (в минутах) <2 100,
те 1 800 < 19х, + 11х2<2 100.
В этом случае целевой интервал можно описать с помощью двух целевых ограничении
19х, + 11х2 - г, < 2 100 (v, > 0),
19х, + 11х2 + М1< 1 800 (и, > 0)
Включив слагаемые г/, и г, в целевую функцию, модель можно попытаться опти-
мизировать Если в точке оптимальности и}' = 0 и у/ = 0 (их минимальные возмож-
ные значения), то общее время решения задач 19х, + 11х2 попадет в желаемый диапа-
536 ЧАСТЬ II Оптимизационные модели
зон (те 1 800 < 19х, + 11х2 < 2 100) Если же окажется, что в точке оптимальности
одна из этих двух переменных положительна, а вторая равна нулю, значит, можно
удовлетворить только одну часть двойного неравенства.
Использование целевых ограничений
Подведем итог и кратко охарактеризуем различные способы формирования и приме-
нения целевых ограничений Каждое целевое ограничение состоит из левой части, обо-
значим ее g(xp ..., хл), и правой части b Целевое ограничение записывается с использо-
ванием неотрицательных переменных отклонения и, и v, В точке оптимальности по
крайней мере одна из переменных, и, или у, всегда должна быть равна нулю. Переменная
и, обозначает недостачу, а у — избыток по сравнению с заданным значением правой час-
ти при этом и, прибавляется к £,(х,, , хД, а у вычитается из g(xp .... хД. В целевую
функцию входят только переменные отклонения (или некое их подмножество), и задача
заключается в минимизации этой целевой функции. Переменные решения х (/ = 1, . ., п)
не входят в целевую функцию Мы рассмотрели четыре типа целей.
1.	Достижение намеченного показателя. Сделать g(xp .., хД как можно более близкой
к b Для этого целевое ограничение записывается следующим образом:
g,(x„ ...,хп) + u-v=bt (и,>0, у SO),
и цель состоит в минимизации (и, + у) В точке оптимальности по крайней мере
одна из пары переменных и„ у будет равна нулю.
2.	Минимизация недостачи. Для этого можно записать целевое ограничение в виде
g,(x{,. ,хп) + п- у= Ь: (п,>0, у>0),
а целью будет минимизация недостачи и,. Поскольку у входит только в целевое ог-
раничение и не входит в целевую функцию, данное ограничение можно перепи-
сать в виде
+	6,	(и,>0)
Если оптимальное и' положительно, это ограничение будет жестким, поскольку
в противном случае и' можно было бы уменьшить. Этот же вывод можно сделать,
анализируя ограничение в форме равенства. Если и, > 0, то у' должно быть равно
нулю и g(xp .. , хД + н/ = Ьг
3.	Минимизация превышения. Для этого целевое ограничение записывается в виде
g,(Xp ...,хД +u-v=b,	(н,>0, у>0),
а целью является минимизация превышения у. Поскольку в данном случае и, не
входит в целевую функцию, ограничение можно переписать в виде
g,(xp ...,хД - у <6,	(v,S0).
Если оптимальное значение у положительно, ограничение будет жестким.
4.	Интервальное целевое ограничение. В этом случае цель состоит в том, чтобы как
можно ближе подойти к удовлетворению двойного неравенства
a;<g(Xp .. ,хД +u,-v<bl.
Чтобы записать это условие в виде целевого ограничения, сначала увеличим ин-
тервал-
а, - и, <g,(x„ .., хД < />, + у (и, > 0, у > 0),
ГЛАВА 8. Многоцелевые модели и эвристические методы 537
что эквивалентно двум ограничениям
+ и,>а„	g,(x„ .,х„) + и,- 1< = я,	(Му>0, И,>0),
g,(Xi,...,x„)-v,<^,	gl(xl,...,xli) + Ul-v, = al	(Ut>0, v > 0)
В данном случае минимизируется целевая функция и, + v, Переменные V и U
представляют собой просто излишек и недостаток соответственно (а не перемен-
ные отклонения). Как и всегда, в точке оптимальности по крайней мере одна из
пары переменных отклонения и,, v будет равна нулю. Когда целевой интервал
представлен двумя ограничениями, жестким будет ограничение с ненулевой пере-
менной отклонения (если таковая имеется).
В общем случае целевые ограничения чаще всего записываются в форме соответст-
вующих равенств с использованием переменных отклонения, излишка и недостатка,
а приведенные эквивалентные неравенства позволяют в моделях с двумя переменными
решения получить геометрическое представление о процедуре решения.
Абсолютные приоритеты
Иногда менеджеры не хотят выражать свои предпочтения по отношению к различным
целям с помощью взвешенных переменных отклонения, поскольку процесс присвоения
весовых коэффициентов кажется им произвольным и субъективным В таких случаях бо-
лее приемлемо сформулировать предпочтения в виде абсолютных приоритетоз различ-
ных целей (а не весовых коэффициентов) Рассмотрим на конкретном примере подход,
в котором цели удовлетворяются в определенном порядке. При использовании весовых
коэффициентов задача целевого программирования решается только один раз При ис-
пользовании абсолютных приоритетов задача целевого программирования решается по-
этапно как последовательность задач
Модель выбора СМИ
Том Свенсон, главный компаньон рекламного агентства, заключил соглашение с
фармацевтической фирмой о проведении на радио и телевидении рекламной компании
для продвижения на рынок нового продукта — майлонала Общие расходы на рекламную
компанию не должны превышать $120 000 Заказчик хочет с помощью этой компании
информировать различные группы потребителей Чтобы определить, насколько эффек-
тивно каждая отдельная рекламная акция удовлетворяет потребности заказчика, агентст-
во использует оценку ее воздействия на различные группы потребителей Это воздейст-
вие определяется коэффициентом информирования, показывающим, сколько человек
увидело или услышало рекламу в течение месяца Два типа СМИ, радио и телевидение,
услугами которых намерено воспользоваться агентство, обеспечивают различный уро-
вень информирования разных групп потребителей Соответствующие данные о реклам-
ной компании майлонала приводятся в табл 8.5
Таблица 8.5. Количество проинформированных граждан на каждую S1000 затрат
ТВ	Радио
Всего	14	000	6 000
Граждане с высокими дохо-	1 200	1 200
дами
538 ЧАСТЬ II Оптимизационные модели
После длительных дискуссий с заказчиком Том сформулировал следующие цели рек-
ламной компании, порядок, в котором они перечислены, отражает их абсолютные при-
оритеты
1.	Желательно, чтобы общее количество проинформированных составило не менее
840 000
2.	Для поддержания дружеских отношений с ведущей радиостанцией желательно по-
тратить на ТВ-рекламу не более $90 000
3.	В ходе рекламной компании желательно проинформировать не менее 168 000 гра-
ждан с высоким уровнем доходов
4.	Наконец, если все остальные цели будут достигнуты, хотелось бы как можно бли-
же подойти к максимально возможному числу проинформированных Известно,
что если потратить все $120 000 на ТВ-рекламу, то будет проинформировано
1 680 000 человек (120x14 000), это и есть максимально возможное число
В данной модели имеется ряд ограничений, однако она не является типичной моде-
лью математического программирования, поскольку в ней присутствуют несколько це-
лей Тем не менее основанный на математическом программировании подход может по-
мочь понять и решить данную задачу. Поэтому Том действовал стандартным образом.
Для формализации своей задачи он ввел следующие обозначения х, — сумма, потрачен-
ная на ТВ-рекламу (тыс долл.), х2 — сумма, потраченная на радиорекламу (тыс долл )
Поскольку целью с наивысшим приоритетом является суммарное количество проин-
формированных, разумно при моделировании задачи использовать в качестве целевой
функции это суммарное число проинформированных, а остальные цели трактовать как
ограничения
Недопустимая модель
Табличная модель и решение задачи (рабочая книга Свенсон XLS) представлены на
рис 8 11 Информация в диалоговом окне Результаты поиска решения свидетельст-
вует, что у данной модели нет допустимых решений Следовательно, не существует
способа удовлетворить одновременно три цели (по суммарным расходам, расходам на
ТВ-рекламу и информированию людей с высокими доходами), которые были сформу-
лированы в качестве ограничений Поскольку модель содержит только две переменные
решения, можно исследовать модель графически Показанное на рис 8.12 графическое
представление модели ясно показывает, что не существует точек, удовлетворяющих
одновременно первому (суммарные расходы) и третьему (информирование людей
с высокими доходами) ограничениям. На этом этапе Том решил попробовать исполь-
зовать другой подход изменить одну или несколько целей или, возможно, целевую
функцию и начать все сначала. Однако в общем случае такой способ действий непри-
емлем В моделях с большим количеством переменных решения и несколькими проти-
воречивыми целями реструктуризация модели с целью создать модель, имеющую до-
пустимые решения, может оказаться слишком сложной задачей. Более того, в ходе
этой реструктуризации можно утратить основу реальной ситуации
ГЛАВА 8 Многоцелевые модели и эвристические методы 539
ill
Рис. 8.11. Максимизация суммарного числа проинформированных
540 ЧАСТЬ II Оптимизационные модели
Рис. 8.12. Графическое представление модели
Напомним, что различные цели для Тома неравнозначны — для каждой из них уста-
новлены свои абсолютные приоритеты Для такой ситуации, возникающей в процессе
принятия решений, предназначен метод целевого программирования с абсолютными
приоритетами Он представляет собой последовательный процесс, в котором цели добав-
ляются к модели ЛП по одной (в порядке убывания приоритетов).
Модель целевого программирования
Прежде чем формализовать модель в виде задачи целевого программирования, Том
заметил, что если достичь первой цели невозможно, то она окажется недовыполненной,
если нельзя достичь второй цели — она будет перевыполненной, и т д. С учетом этих на-
блюдений он вновь сформулировал цели в порядке убывания приоритетов.
1.	Минимизировать недостачу в достижении показателя 840 000 по числу информиро-
ванных ( те надо минимизировать и, при условии 14000х1 + 6000х2 + и1 > 840 000
и w, > 0)
2.	Минимизировать расходы на ТВ-рекламу, превышающие $90 000 (т.е. надо мини-
мизировать у2 при условии, что х, — v2 < 90 и v2 > 0).
3.	Минимизировать недостачу в количестве проинформированных людей с высоки-
ми доходами по сравнению с показателем 168 000 (минимизировать и3 при условии
1 200х, + 1 2ООх2 + w, > 168 000 и и, > 0)
4.	Минимизировать недостачу суммарного количества проинформированных людей
по сравнению с максимально возможным показателем 1 680 000 (т.е. минимизиро-
вать и4 при условии 14000х, + 6000х2 + и4> 1 680 000 и и4> 0).
Теперь приоритеты Тома явно сформулированы в виде задач минимизации недостачи
(минимизации и) или минимизации превышения (минимизации у,), а его цели выражены
в форме неравенств Такой подход упрощает проведение графического анализа модели.
При условии, что приоритеты сформулированы правильно, Тому необходимо выде-
лить системные ограничения (ограничения, которые нельзя нарушать) и целевые ограниче-
ния В данной модели единственным системным ограничением является условие, что
суммарные расходы не должны превышать $120 000. Поскольку х1 и х2 измеряются в ты-
сячах долларов, это ограничение имеет видх, +х2< 120.
ГЛАВА 8. Многоцелевые модели и эвристические методы 541
Таким образом, модель Тома можно записать в виде следующей задачи целевого
программирования.
Минимизировать P.w, + P2v2 + Р3и3 + Р4и4
при ограничениях
х,+х2< 120,	(S)
14000х, + 6000х2 + «, > 840 000,	(1)
х,-у2<90,	(2)
1200х, + 1 200х2 + и3 > 168 000,	(3)
14000Xj + 6000х2 + и4 > 1 680 000,	(4)
х„х2, и„у2, w„w4>0
Отметим, что целевая функция состоит исключительно из переменных отклонения
и требует минимизации. Как уже отмечалось, все задачи целевого программирования яв-
ляются задачами минимизации, поскольку необходимо подойти как можно ближе к на-
меченным целевым показателям. Коэффициенты Р: в целевой функции служат для отра-
жения приоритетов, Р, обозначает наивысший приоритет и т.д. Приведенная постановка
задачи означает следующее.
1.	Необходимо найти множество переменных решения, удовлетворяющих систем-
ному ограничению S и доставляющих минимально возможное значение и, при со-
блюдении ограничений 1 и хр х2, и, > 0 Назовем это множество решений допусти-
мой областью 1 Если рассматривать только цель с наивысшим приоритетом, все
точки этой области являются “оптимальными” (т е наилучшими из возможных),
и поэтому Тому безразлично, какую из этих точек выбрать
2.	Далее ищем подмножество точек допустимой области 1, доставляющих минимальное
возможное значение переменной у2 при условии выполнения ограничений 2 и v2>0
Назовем это подмножество допустимой областью 2 С точки зрения достижения двух
целей с наивысшими приоритетами все точки этой области являются“оптимальными”,
и поэтому опять Тому безразлично, какую из этих точек выбрать
3.	Назовем допустимой областью 3 подмножество точек допустимой области 2, ми-
нимизирующих и3 при соблюдении ограничений 3 и и, >0
4.	Назовем допустимой областью 4 подмножество точек допустимой области 3, ми-
нимизирующих и4 при соблюдении ограничений 4 и w4>0 Любая точка этой об-
ласти является оптимальным решением полной исходной задачи
Графический анализ и реализация процедуры решения
Поскольку модель содержит всего две переменные решения, описанный выше метод
решения можно дополнить графическим анализом Отметим, что во всех реальных моде-
лях для поиска решения используются электронные таблицы и средство Поиск решения
1. Из таблицы (лист Первая цель в рабочей книге Свенсон XLS) и геометрического
представления, показанных на рис 8 13, следует, что минимум ut при ограничени
ях S, 1 и х,, х2, w, > 0 достигается при и,’ = 0 Хотя Поиск решения предоставляет
также оптимальные значения х, и х2’, эти значения интереса пока не представля-
ют Результат ut = 0 свидетельствует о том, что первая цель достижима Альтерна-
тивными оптимумами для данной модели являются все пары значении (хих2),
удовлетворяющие условиям, определяющим допустимую область 1
542
ЧАСТЫI Оптимизационные модели
х,+х2<120,
14000х, + 6000х2 > 840 000,
х„х2>0.
В любой из этих точек достигается и, = 0, поэтому с точки зрения удовлетворения
первой цели эти решения одинаково предпочтительны. На рис. 8.13 допустимая
область I показана в виде заштрихованной области АВС.
Линия, обозначенная (1), представляет первую цель Во всех точках справа от этой
линии первая цель достижима
2. В таблице на рис 8 14 (рабочий лист Цель 2) имеются ограничения, задающие до-
пустимую область! (ячейки B10D11), а также новое ограничение 2 (ячейки
D12 D12) Мы видим, что решением задачи минимизации v2 является v‘ = 0. До-
пустимая область 2 определяется неравенствами
х,+х2<120,
14000х, + 6000х2 > 840 000,
х, < 90,
х„х2>0
Допустимая область 2 (заштрихованная область ABDE на рис. 8.14) является под-
множеством допустимой области 1.
Продолжая процедуру последовательного построения допустимых областей для разных
целей, получаем допустимую область 3, которая состоит только из линейного отрезка BD
(рис 8 15) В этом случае w3 = 24000 Хотя первые две цели достигнуты (ut = v2’ = 0), до-
биться полного соответствия третьей цели не удалось, поскольку иу > 0. Допустимая об-
ласть 3 определяется системой неравенств
х,+х2<120,
14000х, + 6000х2 > 840 000,
х,<90,
1200х, + 1 200х2 >168000 - 24000 = 144 000,
х„х2>0.
Наконец, на рис 8 16 (лист Оптимум рабочей книги Свенсон) показано оптимальное
решение, которым является точка D Напомним, что четвертая цель состоит в макси-
мальном приближении к наибольшему возможному числу проинформированных, рав-
ному 1 680 000 Таким образом, необходимо минимизировать недостачу иа при условии
14000х, + 6000х2 + w4 > 1 680 000.
В последней задаче найден единственный оптимум х,' = 90, х2' = 30, таким образом,
Тому Свенсону следует потратить $90 000 на ТВ-рекламу и $30 000 на радиорекламу Это
же решение вытекает из геометрического представления модели — точка D (х,=90, х2=30)
ближе к задающей цель 4 линии (14000х, + 6000х2 = 1 680 000), чем любая другая точка
допустимой области 3 (т е. чем любая другая точка отрезка BD). Заметим также, что
w4’ = 240 000, поэтому количество проинформированных составит только 1 680 000 -
240 000 = 1 440 000 человек
Как видно изданного примера, целевое программирование с абсолютными приорите-
тами позволяет менеджеру находить удовлетворительное решение даже тогда, когда не
существует решения, удовлетворяющего всем целям. В этом случае менеджер может ука-
зать абсолютные приоритеты целей и последовательно ограничивать свое внимание теми
точками, которые как можно ближе подходят к достижению каждой цели.
ГЛАВА 8 Многоцелевые модели и эвристические методы 543
Рис. 8.13. Первая цель
544
ЧАСТЬ II Оптимизационные модели
Рис. 8.14. Вторая цель
ГЛАВА 8. Многоцелевые модели и эвристические методы 545
60	90	120 140
Рис. 8.15. Третья цель
546 ЧАСТЬ II Оптимизационные модели
Рис. 8.16. Оптимальное решение
ГЛАВА 8. Многоцелевые модели и эвристические методы 547
Комбинирование весовых коэффициентов и абсолютных
приоритетов
Можно совместно использовать весовые коэффициенты целей и их абсолютные при-
оритеты В качестве иллюстрации рассмотрим вновь модель проведения рекламной ком-
пании Тома Свенсона.
Пересматривая результаты задания абсолютных приоритетов, Том и его клиент отме-
тили важную роль пожилых людей на рынке майлонала В частности, они решили обра-
тить особое внимание на количество проинформированных людей в возрасте старше
50 лет Оказалось, что эффективность радио и телевидения в информировании этой ка-
тегории населения неодинакова. Количество проинформированных на $1 000 рекламных
расходов приводится в табл. 8.6.
Таблица 8.6
Группа информируемых потребителей	ТВ	Радио
50 лет и старше 3000 8000
При отсутствии других соображений Том хотел бы проинформировать как можно
больше людей старше 50 лет Поскольку радио обеспечивает более высокий показатель ин-
формирования, чем ТВ (8000 > 3000), максимально возможное количество людей старше
50 лет будет проинформировано, если направить всю имеющуюся сумму $120 000 на радио-
рекламу Таким образом максимально можно проинформировать 960 000 (= 120x8000) че-
ловек старше 50 Том и его клиент хотят как можно ближе подойти к этой цели после того,
как будут удовлетворены первые три Однако они также хотят после удовлетворения первых
трех целей подойти как можно ближе к цели достижения суммарного показателя проин-
формированных 1680 000 (те минимизировать недостачу). Чтобы разрешить конфликт
двух последних целей, было решено на последнем этапе вместо применения метода абсо-
лютных приоритетов использовать в качестве целевой функции взвешенную сумму соот-
ветствующих переменных отклонения По мнению Тома и его клиента, недостача в дости-
жении пятой цели (информирование 960 000 людей старше 50 лет) в три раза серьезней, чем
недостача в достижении четвертой цели (суммарное число проинформированных
1 680 000). Табличная модель, решение задачи (лист Веса в рабочей книге Свенсон) и гра-
фический анализ модели представлены на рис. 8 17.
Из таблицы следует, что оптимальным решением данной задачи является точка В
(3:,"= 15, х2’ = 105) Напомним, что когда задача заключалась в минимизации иа, опти-
мальным решением была точка D (х,‘ = 90, х2‘ = 30) На графике видно, что новая целевая
функция привела к смещению оптимального решения в другую точку допустимой облас-
ти 3. Можно провести анализ чувствительности для весовых коэффициентов целевой
функции, чтобы увидеть, когда решение смещается из точки D в точку В.
На этом мы завершаем анализ модели рекламной компании Тома Свенсона. В общем
случае описанная процедура последовательного решения задач ЛП для моделей целевого
программирования с абсолютными приоритетами может применяться к любым моделям,
у которых системные и целевые ограничения сформулированы в виде линейных функ-
ций Для перехода к новой задаче ЛП в предыдущую задачу вводится одно дополнитель-
ное ограничение и изменяется целевая функция. Модель может иметь достаточно боль-
шое количество переменных решения. Пример с двумя переменными полезен потому,
что позволяет наряду с табличными результатами представить геометрические интерпре-
тации, которые помогают лучше понять метод решения.
548 ЧАСТЬ II. Оптимизационные модели
Рис. 8.17. Использование весовых коэффициентов
ГЛАВА 8 Многоцелевые модели и эвристические методы 549
На примере следующей модели мы покажем, как с помощью целевого программирова-
ния можно одновременно учитывать конфликтующие и несоразмерные цели (например,
производственные и политические) Это позволит понять, почему целевое программирова-
ние считается многообещающим и полезным средством при анализе вопросов обществен-
ной политики
8.5.	Аналитический иерархический процесс
Данный раздел посвящен часто встречающейся в реальной жизни ситуации, когда необ-
ходимо принимать решение с учетом множества целей и критериев Ежедневно мы сталки-
ваемся с многочисленными примерами таких решений. Перечислим некоторые из них
•	Выбор работы из нескольких предложенных вакансий
•	Выбор компьютера (автомобиля, холодильника и т п )
•	Принятие решения о том, какой новый продукт выпускать первым.
•	Выбор места для нового ресторана, отеля, производственного объекта и т д
•	Выбор учебного заведения.
•	Составление рейтинга городов по условиям проживания
•	Выбор для компании новой информационной системы, которая осуществляет об-
работку платежных ведомостей, счетов и т п (или выбор нового пакета приклад-
ных программ конкурирующих производителей).
•	Выбор системы налогообложения для граждан
При покупке автомобиля, например, необходимо учитывать множество факторов,
среди которых цена, безопасность, объем двигателя, экономия топлива и т д В каждом
из перечисленных выше примеров при принятии сложных решений требуется учитывать
множество факторов
Простейшим способом принятия решений в подобных ситуациях является присвое-
ние критериям, определяющим качество решения, весовых коэффициентов и вычисле-
ние для альтернативных решений оценок по шкале от 1 (наихудшее) до 10 (наилучшее)
путем суммирования произведений значении каждого критерия на его весовой коэффи-
циент Решение с наивысшей суммой будет наиболее предпочтительным
Рассмотрим пример, в котором необходимо выбрать новый компьютер для офиса
Выбор осуществляется среди трех моделей модель А с процессором AMD K6-II с часто-
той 400 МГц, модель В с процессором Celeron с частотой 333 МГц и модель С с процес-
сором Pentium II с частотой 450 МГц При выборе учитываются следующие критерии
цена, эффективность (частота процессора), емкость жесткого диска и наличие гарантии
и обслуживания Далее решаем, что при принятии решения цене присваивается весовой
коэффициент, например, 0,50 (50% общего веса), эффективности — 0,15 (15%), емкости
жесткого диска — 0,20 (20%) и наличию гарантии — 0,15 (15% общего веса). Затем произ-
водится оценка каждой модели компьютера по указанным четырем критериям Их оцен-
ки по шкале от 1 до 10 (как описывалось выше) показаны в табличной модели на
рис 8 18 (рабочая книга Компьютер XLS)
550 ЧАСТЬ II Оптимизационные модели
Рис. 8.18. Модель принятия решения при покупке компьютера
Как видим, наибольшую сумму баллов 7,05 набрала модель В, поэтому ее следует ку-
пить Данный пример достаточно упрощенный, в практических моделях существуют
сложности при задании оценочных шкал для разнородных критериев
Аналитический иерархический процесс (АИП) также основан на идее использования
взвешенных средних, однако в нем применяется более надежный и согласованный метод
присвоения оценок и весовых коэффициентов, чем простой метод, описанный выше
АИП основывается на попарном сравнении альтернативных решений по каждому крите-
рию Затем проводится аналогичный ряд сравнений, чтобы оценить относительную важ-
ность каждого критерия и таким образом определить весовые коэффициенты. Основная
процедура выглядит так
1.	Определяются рейтинги всех возможных вариантов решений по каждому крите-
рию следующим образом
•	создается матрица попарных сравнений по всем критериям,
•	полученная матрица нормализуется,
•	для получения соответствующих рейтингов усредняются значения в каждой
строке,
•	вычисляются и проверяются коэффициенты согласованности.
2.	Определяются весовые коэффициенты критериев.
•	создается матрица попарных сравнений по всем критериям,
•	полученная матрица нормализуется,
•	для получения весовых коэффициентов усредняются значения в каждой строке,
•	вычисляются и проверяются коэффициенты согласованности.
3.	Вычисляется взвешенный средний рейтинг для каждого варианта решения и вы-
бирается решение, набравшее наибольшее количество баллов
ГЛАВА 8 Многоцелевые модели и эвристические методы	551
Продемонстрируем применение данной процедуры на новом примере. Компании
Sleepwell Hotels нужно выбрать наилучший пакет бухгалтерского программного обеспе-
чения из предлагаемых несколькими поставщиками. Эта задача была поручена заведую-
щему отделом Марку Джеймсу. Он выделил трех поставщиков, предлагаемое программ-
ное обеспечение которых сможет удовлетворить основные потребности компании Reve-
nue Technology Corporation (RTC), PRAISE Strategic Solutions (PSS) и El Cheapo (EC)
Критерии, которые он считает важными в выборе программного обеспечения. 1) общая
стоимость программной системы, 2) обеспечение обслуживания на протяжении следую-
щего года, 3) сложность и надежность лежащих в основе математических процедур и 4)
возможность адаптации системы под условия Sleepwell. Первый шаг процедуры АИП со-
стоит в попарном сравнении продавцов по каждому критерию. Для этого используем
стандартную шкалу сравнения, приведенную в следующей таблице
Рейтинг	Описание
3 5 7	Одинаковое предпочтение Умеренное предпочтение Явное предпочтение Очевидное предпочтение Исключительное предпочтение
Также можно присваивать значения рейтинга 2, 4, 6 и 8, которые определяются как
средние от ближайших рейтингов
Марк начал с первого критерия (общая стоимость) и внес в лист Стоимость рабочей
книги ПО XLS данные, показанные на рис 8.19 Таблицу следует читать таким образом
указанный в строке поставщик сравнивается с поставщиком, указанным в столбце. Если
указанный в строке поставщик предпочтительней, то соответствующее число от 1 до 9
записывается в ячейку на пересечении строки и столбца Если же предпочтительней по-
ставщик, указанный в столбце, то 1 делится на соответствующее число от 1 до 9, и резуль-
тат записывается в ячейку на пересечении строки и столбца. Очевидно, что поскольку
любой поставщик одинаково предпочтителен по сравнению с самим собой, то во все
диагональные ячейки заносится значение 1 По показателю общей стоимости поставщи-
ку 1 отдается среднее между умеренным и явным предпочтение в сравнении с поставщи-
ком 2, поэтому в ячейку второго столбца первой строки заносится число 4 (ячейка С4)
Поставщику 3 (ЕС) отдается предпочтение от одинакового до умеренного перед постав-
щиком 1 (RTC), поэтому в ячейке третьего столбца первой строки записано число 1/2
(ячейка D4). Марк так запрограммировал свою таблицу, что после ввода элементов спра-
ва от диагонали (ячейки С4, D4 и D5) обратные предпочтения вычисляются автоматиче-
ски Например, поскольку при сравнении поставщика 1 с поставщиком 2 было записано
4, то при сравнении поставщика 2 с поставщиком 1 автоматически получается 1/4
(ячейка В5).
552 ЧАСТЬ II Оптимизационные модели
Рис. 8.19. Попарное сравнение по показа-
телю стоимости
После выполнения всех попарных сравнений матрицу необходимо нормализовать.
Это выполняется путем суммирования чисел в каждом столбце и последующего деления
каждого элемента столбца на полученную для данного столбца сумму Результаты данной
операции представлены в ячейках B12.D14 на рис. 8.20. Следующий шаг состоит в вы-
числении балла для каждого продавца по критерию общей стоимости. Эти значения по-
казаны на рис 8.20 в столбце Е Видно, что наивысший средний балл по данному крите-
рию имеет поставщик ЕС
Рис. 8.20. Нормализованная матрица для критерия общей стоимости
ГЛАВА 8. Многоцелевые модели и эвристические методы 553
Завершив нормализацию матрицы, необходимо вычислить коэффициент согласован-
ности и проверить его значение. Цель этой операции состоит в том, чтобы убедиться
в согласованности задания предпочтений в исходной таблице. Например, если по крите-
рию общей стоимости задана явная предпочтительность поставщика 1 перед поставщи-
ком 2 и умеренная предпочтительность поставщика 2 по сравнению с поставщиком 3, то
при сравнении поставщиков 1 и 3 задание одинаковой предпочтительности приведет к
несогласованности, еще большая несогласованность возникнет при указании, что 3
предпочтительней 1. Вычисление коэффициента согласованности состоит из трех этапов.
1.	Вычисляется мера согласованности для каждого поставщика.
2.	Определяется индекс согласованности ИС.
3.	Вычисляется коэффициент согласованности как отношение ИС/ИР, где ИР —
индекс рандомизации
Для вычисления меры согласованности можно воспользоваться функцией умножения
матриц Excel МУМНОЖ. Как показано на рис. 8.21, для поставщика 1 (RTC) средний
рейтинг каждого поставщика (ячейки Е12:Е14) умножается на соответствующее количе-
ство баллов в первой строке (ячейки B4.D4), эти произведения суммируются, и сумма де-
лится на средний рейтинг первого поставщика (ячейка Е12) Аналогичные вычисления
осуществляются для 2 и 3 поставщика В идеальном случае меры согласованности долж-
ны быть равны числу возможных альтернативных решений (в нашем случае имеется
3 решения, т.е. 3 поставщика) Для вычисления индекса согласованности определяется
средняя мера согласованности всех трех поставщиков, из нее вычитается количество
возможных вариантов решения п и результат делится на и-1. Индекс согласованности
ИС показан на рис 8 21 в ячейке F16, его значение равно 0,001. Последний этап опреде-
ления коэффициента согласованности заключается в делении ИС на индекс рандомиза-
ции ИР, значения которого для различных значений п вычисляются в методе АИП спе-
циальным образом и приведены в таблице ниже.
л Индекс рандомизации
2	0,00
3	0,58
4	0,90
5	1,12
6	1,24
7	1,32
8	1,41
9	1,45
10	1,51
Коэффициент согласованности записан в ячейке F20 и равен 0,002.
554 ЧАСТЬ II Оптимизационные модели
Рис. 8.21. Коэффициент согласованности для критерия общей стоимости
Рис. 8.22. Коэффициент согласованности для критерия обслуживания
ГЛАВА 8. Многоцелевые модели и эвристические методы 555
Рис. 8.23. Коэффициент согласованности для критерия <. тжности
Рис. 8.24. Коэффициент согласованности для критерия адаптации
556 ЧАСТЬ II. Оптимизационные модели

Рис. 8.25. Коэффициент согласованности для весов критериев
В случае абсолютной согласованности предпочтений мера согласованности будет
равна п, следовательно, ИС будут равны нулю, и коэффициент согласованности также
будет равен нулю. Если этот коэффициент слишком велик (больше 0,10 по оценке
Саати), значит, менеджер был недостаточно последователен в своих оценках, поэтому
следует вернуться назад и пересмотреть результаты попарных сравнений (в большинстве
случаев обнаруживается элементарная ошибка, и коэффициент согласованности
сигнализирует о ее наличии).
Теперь необходимо проделать то же самое для остальных трех критериев. Для этого
следует трижды скопировать рабочий лист Стоимость, создав тем самым три новых ра-
бочих листа (назовем их Обслуживание, Сложность и Адаптация), а затем надо просто
изменить параметры попарных сравнений. Результаты этих действий показаны на
ГЛАВА 8. Многоцелевые модели и эвристические методы 557
рис. 8.22-8.24 Во всех случаях значения коэффициента согласованности заключены
в пределах от 0 до 0,047, это означает, что Марк был достаточно последователен в своих
оценках Кроме того, можно заметить, что компания PSS оказалась лучшей по критерию
обслуживания, RTC и PSS — лучшие по критерию сложности, a PSS — лучшая по крите-
рию адаптации.
На этом первый этап процедуры заканчивается На втором этапе процедуры осущест-
вляются аналогичные попарные сравнения для определения весов критериев Процесс
аналогичен предыдущему в том, что опять производятся сравнения, однако теперь срав-
ниваются не поставщики, как это было на этапе 1, а критерии Эти действия выполняют-
ся на рабочем листе Веса, показанном на рис. 8 25
Оказалось, что показатель сложности и надежности математических алгоритмов име-
ет наибольший вес (52,5% в ячейке F14), за ним идет стоимость (30,4% в ячейке F12).
Приятно, что меры согласованности оказались близки к 4, поэтому индекс согласован-
ности и коэффициент согласованности близки к нулю.
Последний шаг состоит в вычислении взвешенных средних оценок для каждого вари-
анта решения и применении полученных результатов для принятия решения о том, у ка-
кого поставщика будет куплено новое программное обеспечение. Заключительные вы-
числения сделаны на листе Сравнение в той же самой рабочей книге nO.XLS (рис. 8.26).
На основании полученных результатов можно сделать вывод, что компания RTC
(показатель 0 378 в ячейке С8) несколько превосходит компанию PSS (0 376 в ячейке
D8), а компания ЕС от них заметно отстала
Рис. S.26. Взвешенное среднее рейтингов с использованием весов
8.6. Заключение
Эвристические подходы, как и большинство других методов оптимизации количествен-
ных моделей, чаще всего реализуются с помощью электронных таблиц или других компью-
терных программ. На практике различие между использованием эвристических процедур
и более формальных методов линейного и нелинейного программирования состоит в том,
558 ЧАСТЬ II Оптимизационные модели
что для последних уже разработано готовое программное обеспечение При использовании
эвристических процедур часто приходится разрабатывать программное обеспечение само-
стоятельно Как уже отмечалось, типичной сферой применения эвристических методов яв-
ляется область больших комбинаторных моделей, для которых получить решение с помо-
щью перебора, формальных математических моделей или моделей целочисленного про-
граммирования слишком дорого При применении эвристических процедур всегда неявно
присутствует убеждение, что целесообразно стремиться к “приемлемости” решения, а не
к его “оптимальности”. Такой подход целесообразен для моделей с неопределенной постановкой,
таких как многоуровневые модели с несколькими противоречивыми критериями, для которых
сложно сформулировать единую целевую функцию
До настоящего времени наиболее часто эвристические методы в сфере управления
применялись в производственных моделях, моделях календарного планирования работы
предприятий и распределения ресурсов Однако в последнее время произошло расшире-
ние сферы их применения в таких областях, как маркетинговая задача выбора СМИ, ад-
министративное районирование, календарное планирование занятий в университетах
и размещение градообразующих систем.
В реализации эвристических методов взаимодействие между разработчиком модели
и менеджером должно играть, возможно, даже более заметную роль, чем при более фор-
мальном моделировании, поскольку при использовании эвристического подхода менед-
жер должен иметь доступ не только к самой модели, но и к эвристическому алгоритму.
Суждения менеджера необходимы потому, что для одной и той же модели различные эври-
стические методы приведут к различным решениям.
Эта тесная взаимосвязь между моделью и лицом, принимающим решения, также ярко
проявляется в целевом программировании, когда принимающий решения человек дол-
жен присвоить приоритеты различным целям, например в форме обычного упорядоче-
ния (задание абсолютных приоритетов) Целевое программирование представляет собой
интуитивно понятный “почти эвристический” подход к моделям с несколькими целями.
В целевом программировании с абсолютными приоритетами менеджер должен тщатель-
но изучить относительную важность или полезность своих целей. Исходя из результатов
моделирования лицо, принимающее решения, может изменить приоритеты или даже ко-
личество целей и оптимизировать модель повторно. Иными словами, как и в линейном
программировании, анализ чувствительности является важным аспектом реализации та-
ких многоцелевых моделей Поскольку целевое программирование — сравнительно мо-
лодое направление, его теоретические аспекты быстро развиваются и, судя по всему, это
приведет ко все более широкому использованию данного метода
В настоящее время существуют компьютерные программы для решения крупномас-
штабных задач целевого программирования, но они, как правило, не являются частью
библиотек стандартных программ. Для моделей средних размеров идеально подходит
диалоговый режим реализации методов последовательного выполнения определенных
действий, приводящих к приемлемым решениям.
Основные термины
Абсолютные приоритеты. Разновидность целевого программирования, когда цели должны удовле-
творяться в указанном порядке
Аналитический иерархический процесс (АИП). Процедура, в которой для осуществления выбора из
конкурирующих решений при наличии нескольких важных критериев используются попар-
ные сравнения критериев и решений
ГЛАВА 8. Многоцелевые модели и эвристические методы 559
Интервальное целевое ограничение. Ограничение, в котором цели задаются интервалом значений,
а не одним числовым значением
Комбинаторная оптимизация. Оптимизационная модель с конечным числом возможных вариантов
решений.
Отношения предшествования. Отношения между определенными видами деятельности или опера-
циями, когда некоторые операции должны быть завершены до того, как смогут начаться другие
Переменные отклонения. Переменные, используемые в целевом программировании для измерения
степени невыполнения определенной цели
Поглощающий алгоритм. Алгоритм, в котором на каждом шаге последовательного процесса долж-
но достигаться максимальное улучшение решения
Резерв. В календарном планировании работы над проектом данный термин обозначает макси-
мальное время задержки начала выполнения определенной деятельности, которое не приведет
к задержке окончания проекта в целом
Схема загрузки персонала. Гистограмма, показывающая, какое количество человек требуется в не-
делю для выполнения заданного графика работ
Целевое программирование. Поиск допустимых решений, которые как можно ближе подходят
к достижению указанных целей
Эвристика. Практический прием или способ решения определенных частных задач
Эвристический алгоритм. Алгоритм, обеспечивающий эффективный поиск хороших приближен-
ных решений для заданной модели Часто позволяет получить оценки близости найденного
решения к оптимальному
Контрольные вопросы
Да/нет
1.	Эвристические алгоритмы с гарантией дают результат, отличающийся от опти-
мального не более, чем на указанный процент
2.	Оптимальное решение комбинаторной оптимизационной модели, в принципе,
можно найти методом полного перебора.
3.	Альтернативный подход к модели календарного планирования с ограниченными
ресурсами состоит в переносе вперед начала деятельности, использующей наи-
большее количество людей.
4.	Целевое программирование — единственный количественный метод, разработан-
ный для моделей с несколькими целями.
5.	В целевом программировании с абсолютными приоритетами на каждом этапе вво-
дится новая цель и исключаются из дальнейшего рассмотрения все текущие воз-
можные решения, которые не удовлетворяют эту новую цель настолько, насколько
это возможно.
6.	Одним из способов задания приоритетов целей является присвоение весовых ко-
эффициентов переменным отклонения.
7.	Имеется интервальное целевое ограничение 180 <4х, + 12х2 <250 Правильная
формулировка цели выглядит следующим образом
4х, + 12х2 — v,<250,
4х, + 12х2 — и,> 180.
560 ЧАСТЬ II Оптимизационные модели
8.	Если интервальное целевое ограничение невозможно удовлетворить, то одна пе-
ременная отклонения будет положительной, а ограничение, в которое входит эта
переменная, будет жестким.
9.	В целевом программировании не разрешается нарушать системное ограничение.
10.	Модель целевого программирования не может быть недопустимой
Выберите правильный ответ
11.	Если время переналадки при выполнении п заданий на одной машине зависит от
последовательности выполнения заданий, задача минимизации суммарного вре-
мени переналадки требует рассмотрения:
а п последовательностей заданий,
b одной последовательности заданий,
с. л! последовательностей заданий.
12.	Интуитивно привлекательная идея, лежащая в основе поглощающего алгоритма,
состоит в том, чтобы-
а подойти как можно ближе к оптимальному решению,
b сделать все возможное для улучшения на данном этапе,
с минимизировать количество необходимых шагов,
d ничего из вышеперечисленного.
13.	В модели составления графика работы оборудования вычитание минимального
времени переналадки в столбце из остальных элементов данного столбца:
а делается для того, чтобы получить относительные показатели,
b гарантирует, что в результате применения каскадного алгоритма получится оп-
тимальное решение,
с делает поглощающий алгоритм бесполезным,
d все вышеперечисленное
14.	Если модель целевого программирования содержит ограничениеg,(x,,..., х„) + w, - у, = Ь
и в целевую функцию входит член 6ut + 2vp то лицо, принимающее решение:
а. предпочитает, чтобыхп) было больше, а не меньше
b предпочитает, чтобы g((xp , хп) было меньше, а не больше Ь„
с. безразлично к тому, будетg,(x,,..., х„) меньше или больше Ь,.
15.	Задачи с несколькими целями:
а.	сложны, поскольку обычно улучшение одного целевого показателя приводит
к ухудшению другого,
Ь.	сложны, поскольку целевые показатели могут выражаться в несоразмерных
единицах,
с.	могут иногда решаться методами целевого программирования,
d. все вышеперечисленное.
Ответы
1. Нет. 2. Да. 3. Да. 4. Нет. 5. Да. 6. Да. 7. Нет. 8. Да. 9. Да. 10 Нет. И. с. 12. Ь. 13. а. 14.
ГЛАВА 8. Многоцелевые модели и эвристические методы 561
Учебные задачи
8 1 Для минимаксной модели календарного планирования найдите оптимальное решение,
альтернативное для приведенного на рис. 8 10 решения
Упражнения 8 2, 8 3 и 8 4 относятся к следующему примеру модем размещения оборудования
Соломона Фарсона, консультанта по вопросам управления, пригласили для реконструкции
небольшого банка В банке четыре основных отдела отдел кредитов, недвижимости, бухгалтерия
и отдел сбережений Необходимо разместить эти четыре отдела по четырем помещениям, расстоя-
ния между помещениями даны в табл 8 7 Например, расстояние от помещения 2 до помешения
4составляет 1 условную единицу и тд Результаты измерения (в некоторых условных единицах)
ежедневных удельных потоков между этими отделами представлены в табл 8 8
Таблица 8.7. Расстояния между помещениями
______________________________Помещение___________________________
Помещение	12	3	4
i	о	2	з	i
2	2	0	3	1
3	3	3	0	2
4 1 1 2 0
Таблица 8.8. Удельные потоки между отделами
______________________________Отдел_______________________________
______Отдел_____________1	2_______________3	4________
1	0_15	20_16
2	15	0	13	9
3	29	13	0	19
4 16 9 19 0
Задача распределить отделы по помещениям (по одному отделу в каждом помещении) таким
образом, чтобы минимизировать сумму произведений ежедневных потоков на соответствующие
расстояния Например, если разместить отделы следующим образом 1—>1, 2—>2, 3—>3, 4->4, то зна-
чение целевой функции (суммарного потока) составит
суммарный поток между отделами 1	и 2	= расстояние	х	поток = 2 х 15 = 30,
суммарный поток между отделами 1	и 3	= расстояние х поток = 3 х 20 = 60,
суммарный поток между отделами 1	и 4	= расстояние х поток =1x16=16,
суммарный поток между отделами 2	и 3	= расстояние х	поток = 3 х 13 = 39,
суммарный поток между отделами 2 и 4 = расстояние х поток =1x9 = 9,
суммарный поток между отделами 3 и 4 = расстояние х поток = 2x19 = 38,__________
суммарный поток = 192.
8 2 Предположим, что Соломон предложил разместить отдел 1 в помещении 4, отдел 2 — в по-
мещении 3, отдел 3 — в помещении 1 и отдел 4 — в помещении I
а Чему равны расстояния между отделами4 * * * 8 9
b	Чему равен суммарный поток9
с Сколько возможных вариантов размещения отделов необходимо рассмотреть, если
пытаться решить данную задачу методом полного перебора9
d Чему равно число возможных вариантов размещения п объектов по п пунктам9
8.3 Предположим, что отдел 1 разместили в помещении 1 Начертите дерево, аналогичное
приведенному на рис 8 1, показывающее оставшиеся возможные размещения отделов 2, 3
и 4 по помещениям 2, 3 и 4
562 ЧАСТЬ II Оптимизационные модели
8 4 Ответьте на следующие вопросы
а Сколько различных пар можно образовать из четырех отделов'’
b В качестве отправной точки используем ответ на первый пункт упражнения 8 2 и по-
пытаемся улучшить размещение с помощью описанного ниже эвристического метода
попарных перестановок (В литературе предлагается множество эвристических мето-
дов для решения модели размещений Сообщается (см [4]), что для одной модели, со-
держащей 12 объектов, с помощью алгоритма ветвей и границ был найден истинный
оптимум, что потребовало 2 ч работы высокоскоростного компьютера За 7 с процеду-
ра попарных перестановок для этой же модели позволила найти решение, в котором
значение целевой функции отличалось от оптимального не более, чем на 3% ) На
сколько удалось улучшить целевую функцию в данном примере'’
Этап 1 Путем перестановок пар отделов ищется множество размещений, потенциаль-
но улучшающих целевую функцию Например, если отделы 1 и 2 поменять местами,
новое размещение примет вид 1->3, 2->4, 3->2, 4—>1, т е отделы 1 и 2 поменялись мес-
тами, а 3 и 4 остались в прежних помещениях
Этап 2 Производится перестановка двух отделов, при которой максимально улучша-
ется значение целевой функции Эта процедура повторяется до тех пор, пока не оста-
нется попарных перестановок, улучшающих целевую функцию
8 5 Сэм Халл — заведующий отделом маркетинга фармацевтической компании Ему нужно на-
значить пять ответственных представителей в пять больниц Ожидаемые объемы продаж
представлены в табл 8 9
Таблица 0.9
Больница
Представитель______А____________В___________С____________D_____________Е______
1	25	18	23	22	16
2	20	21	18	15	12
3	23	19	20	21	20
4	30	26	25	22	20
5 28 22 23 20 18
а Используя поглощающий алгоритм, предложите назначение представителей в боль-
ницы, максимизирующее суммарные ожидаемые продажи
b Используйте предложенный в разделе 8 2 модифицированный эвристический алго-
ритм для получения нового решения (преобразуйте данные путем вычитания макси-
мального числа продаж в каждом столбце из всех остальных элементов этого столбца,
затем воспользуйтесь процедурой поглощающего алгоритма) Насколько лучше ре-
зультат, полученный с помощью модифицированного алгоритма, по сравнению с по-
лученным в предыдущем пункте9
8 6 На токарном станке необходимо выполнить три задания Л, J2 и J3 Стоимость переналадки
станка зависит от того, на какое предыдущее задание был настроен станок (см табл 8 10)
В начальный момент станок не настроен ни на одно задание
Таблица 8.10
	Л	J2	J3
Нет заданий	$50	$35	$39
Л	—	$30	$34
J2	$41	—	$30
J3	$35	$25	—
ГЛАВА 8 Многоцелевые модели и эвристические методы 563
а Составьте график работ, используя поглощающий алгоритм Цель состоит в миними-
зации суммарных затрат на переналадку
b Составьте график работ, используя модифицированную эвристическую процедуру,
описанную в разделе 8 2
с Всегда ли модифицированная процедура дает лучшие результаты, чем простой погло-
щающий алгоритм9
8 7 Эрма Мак-Зил отвечает за контроль качества водопроводной воды в Чикаго. В настоящее
время существует три станции контроля качества воды на озере Мичиган Станции имеют
следующие координаты (координаты измеряются в милях)
станция 1 х, = 2, х2 = 10,
станция 2 х, = 6, х, = 6,
станция 3 х, = 1, х2 = 3
Требуется так расположить новую станцию, чтобы минимизировать суммарное расстояние
от нее до трех существующих станций Предположим, что расстояние между станциями
измеряется вдоль сторон прямоугольника Например, если новая станция располагается
в точке (х, = 3, х2 = 4), то она находится на расстоянии |3—2| + [4—10[ = 1 + 6 = 7 от станции
1 и т д Обозначим координаты новой станции (х,, х2) Сформулируйте данную задачу в ви-
де модели целевого программирования
8 8 На рис 8 27 представлена диаграмма предшествования для заданий некого проекта Время
и количество сотрудников, необходимые для выполнения каждого задания, показаны
в табл 8 11 Используя эвристический метод выравнивания нагрузки, составьте календар-
ный план работ для данного проекта
D
Е
Таблица 0.11	Рис. 8.27	
Задание	Длительность	Персонал
В	I 2	4 5
D	2	2
Е	2	7
G	I	5
Н	I	4
564 ЧАСТЬ II Оптимизационные модели
8 9	Компания производит два вида продукции Каждый из них проходит обработку на двух стан-
ках, каждый станок работает 240 мин в день Каждая единица продукции 1 требует 20 мин
обработки на станке 1 и 12 мин обработки на станке 2 Каждая единица продукции 2 требует
12 мин обработки на станке 1 и 20 мин обработки на станке 2 При определении ежедневного
ассортимента продукции руководство компании ставит перед собой следующие цели
1 Добиться общего уровня производства не менее 12 единиц продукции
2 Произвести 9 единиц продукции 2
3 Произвести 10 единиц продукции 1
Предположим, что целям присвоены предварительно определенные веса и'|, w2 и и", соот-
ветственно Сформулируйте данную задачу в виде модели целевого программирования
8 10 Компания Т&С Furniture Company (TCFC) производит столы и стулья Запишите целевые
ограничения для следующих целей
а Для изготовления стола требуется 10 часов, а стула — 5 часов Ресурс рабочего времени
за рассматриваемый период составляет 3200 часов Хотя возможны простой и сверх-
урочная работа, компания хочет, чтобы суммарное количество рабочих часов было как
можно ближе к числу 3200
b Для изготовления стола требуется 1 лист фанеры, а для изготовления стула — половина
листа, в течение рассматриваемого периода можно использовать не более 300 листов
Компания TCFC хочет использовать за один период как можно больше имеющейся
у нее фанеры
с Компания TCFC изготавливает столы по заказу и у нее заключен договор о поставке 200 сто-
лов Дополнительно произведенные столы, если таковые будут, придется хранить на складе,
компания хочет минимизировать количество хранимых на складе столов
d Спрос на стулья точно неизвестен, однако, по оценкам, он составит от 200 до 250 штук
Компания хочет, чтобы количество произведенных стульев оказалось как можно ближе
к этому интервалу
8 11 Дана модель целевого программирования
минимизировать Ру, + Ру2 + Ру} + Р4(«4 + v4)
при ограничениях
х2 + и, - г, = 100,
х, + х2 + и2 - v2 = 80,
х2 + и, = 40,
х, + 2х2 + ut — v4 = 160,
х,, х2, и,, и2, и„ и„, Vp v2, v,, v4 > 0
а Решите данную задачу графическим методом
b Объясните третью цель х2 + и2 = 40
с Замените х2 + и, = 40 неравенством х2 + щ > 40 Какова новая интерпретация этого ус-
ловия9
d Найдите решение графическим методом данной задачи с неравенством из предыду-
щего пункта
8 12 Дана модель целевого программирования
минимизировать Ру, + Ру2 + Ру} + Р,(и2 + v4)
при ограничениях
х2 + и,-у, = 100,
х, + х2 + и2 — v2 = 80,
ГЛАВА 8. Многоцелевые модели и эвристические методы
565
Xj ~ Vj = 40,
х, + 2х2 + ut - v4 = 160,
х1; ut, и2, и2, ut, V,, Vj, v„ v4 £ О
а Решите данную задачу графическим методом.
b Объясните третью цель х2 - v2 = 40
с Замените х2 - v2 = 40 неравенством х2 - v2 £ 40 Какова новая интерпретация этого ус-
ловия'’
d Найдите решение данной задачи с неравенством из предыдущего пункта графическим
методом
8 13 Дана модель целевого программирования
минимизировать Р.и2 + P2v, + Р,и,
при ограничениях
х, +х2 + «, - v1 = 80,
х, + и2 - v2 = 80,
х2 + и} > 45,
X,, Х2, Ut, U2, U,, Vj, v2 > 0
а Решите данную задачу графическим методом
b Достигается ли первая по приоритету цель'’
с Достигаются ли вторая и третья (по приоритетам) цели9
Укажите конкретное числовое значение недостижения цели
8 14 Транспортная компания обслуживает склады и доставляет товары по точкам розничной
торговли Склады компании расположены в пяти различных местах и обслуживают четы-
рех розничных торговцев Показатели удельной стоимости транспортировки, спроса
и стоимости обслуживания складов показаны в табл 8 12 Все склады имеют неограничен-
ную емкость Компания хочет решить, какие склады должны работать, а какие следует за-
крыть Эвристический подход к решению данной задачи состоит в том, чтобы открыть
склад, который экономит более всего средств, и продолжать открывать склады до тех пор,
пока это позволяет экономить деньги
Таблица 8.12
Продавцы
Склад	А	В	С	D	Стоимость обслуживания складов
1	5		1	6	31
2	9	7	3	5	35
3	8	1	7	4	20
		3	6	2	29
5	6	3	5	2	38
Спрос	10	15	6	5	
а Решите данную задачу, используя поглощающий алгоритм Какие склады оказались
открытыми9
b Сколько при этом удалось сэкономить9
566 ЧАСТЬ II Оптимизационные модели
8 15 На двух станках 1 и 2 необходимо выполнить шесть заданий В каждом задании изделия
сначала обрабатываются на станке А, а затем на станке Б Последовательность выполнения
заданий на обоих станках одинакова
В табл 8 13 показано время (в часах), необходимое для выполнения заданий на каждом из
станков Цель — составить такой график, чтобы минимизировать время, необходимое для
выполнения всех заданий
Таблица в 13
Время, необходимое для выполнения задания, ч
	А	В	с	D	Е	F
Станок 1	3	4	2	1	5	3
Станок 2	2	5	2	1	3	4
Итого	5	9	4	2	8	7
а Сколько вариантов решения необходимо рассмотреть в случае полного перебора9
b Какое время потребуется для окончания всех работ, если задания выполняются в по-
рядке возрастания суммарного времени обработки9
Замечание Полезно нарисовать график, аналогичный рис 8 7В данном случае следует по-
местить все задания для станка 1 в первую строку, а все задания для станка 2 — во вторую
8 16 Используя метод АИП, помогите Мику Мотту выбрать университет для получения выс-
шего образования Ему предлагают стипендии два университета (Гарвард и Стэнфорд),
и он определил для себя четыре критерия выбора университета размер стипендии, престиж
университета, стоимость жизни и достоинства города, где находится университет Соответ-
ствующие данные представлены на рис 8 28 (и в рабочей книге Колледж на компакт-
диске, прилагаемом к книге)
Рис. 8.28
а Чему равны средние рейтинги университетов по критерию престижа9
b Чему равны средние веса критериев9
с В какой университет вы посоветуете поступить Мику9
8 17 Компания Wyoming Bentonite Inc владеет тремя месторождениями бентонита, который до-
бывается для производства кошачьих туалетов Бентонит — это глиноподобное вещество
с хорошими впитывающими свойствами, добываемое в центре штата Вайоминг Добывае-
мый компанией из трех ее месторождений бентонит имеет немного разные характеристи-
ки, что определяется содержанием в нем кальция и натрия Повышенное содержания
кальция дает более светлый цвет, а повышенное содержание натрия улучшает впитываю-
щие свойства Заказчику важны цена, впитывающие свойства и белизна Согласно специ-
фикации заказчика показатель белизны должен быть в пределах от 67,2 до 67,8, показатель
впитываемости от 200 до 275 Характеристики бентонита, добываемого на каждом из ме-
сторождений, представлены в табл 8 14
ГЛАВА 8 Многоцелевые модели и эвристические методы 567
Таблица 0.14			
Месторождение	Белизна	Впнтываемость	Цена за тонну
д	67,1	175	50
В	68,3	410	НО
С	67,7	180	95
Руководство компании требует, чтобы в смесь входило как минимум 15% бентонита с каж-
дого месторождения
а Найти минимальную цену смеси
b Если цена не так важна, как белизна и впитывающие свойства, найдите состав смеси, при
котором ее характеристики будут как можно ближе к середине заданных в спецификации
интервалов для показателей белизны и впитываемости Какой будет цена такой смеси9
8 18 Кэрол должна выполнить некий проект для нового Internet-продавца Она определила,
сколько программистов необходимо для выполнения каждого задания, а также порядок
следования заданий (табл 8 15)
Таблица 0.15
Задание Начинается после завершения заданий Время (недели) Количество работников
I	—	6	6
II	—	4	3
III	—	2	3
IV	III	2	3
V	III	2	3
VI	V	8	5
VII	VI	1	3
VIII	I, II, IV, VII	4	4
С помощью эвристической процедуры выравнивания нагрузки определите использование
персонала в проекте
8 19 Рассмотрим время подготовки к работе станков компании Stamped Metal Необходимо вы-
полнить четыре вида работ, для подготовки к каждому из них требуется определенное вре-
мя, зависящее оттого, какое задание выполнялось перед этим (табл 8 16) Различия времен
подготовки связаны с тем, что для каждого вида работ станок снабжается особой оснаст-
кой Задание ноль — это исходное состояние станка, отправная точка для начала работы
Таблица 0 16			
Задания	1	2	3	
0	50	29	35	42
1 -	15	54	36
2	36	—	24	42
3	34	27	—	37
4	48	55	58	—
С помощью поглощающего алгоритма минимизируйте суммарное время подготовки к ра-
боте для данных четырех заданий
8 20 Производящая электронные приборы фирма собирает сигнализационные системы для до-
машнего использования Компания производит три вида таких систем Guard Dog, Home
Guard и самую совершенную из них Terminator III Сборка одной системы Guard Dog за-
568 ЧАСТЬ II. Оптимизационные модели
нимает 1,5 ч, системы Home Guard — 2 ч и Terminator III — 2,5 ч Ресурс рабочего времени
равен 240 ч Удельная прибыль от Guard Dog составляет $320, Home Guard — $320, и Ter-
minator III — S35O По прогнозам отдела продаж, на следующей неделе можно будет про-
дать по 60 единиц каждой продукции Руководство сформулировало несколько целей, оди-
наково важных для компании.
а произвести 60 единиц каждой продукции,
b использовать весь ресурс рабочего времени,
с получить прибыль не менее S3600
Сформулируйте и решите соответствующую задачу целевого программирования
8 21 Коммерческий директор нового ресторана, специализирующегося на мясных блюдах, в го-
роде Одесса, штат Техас, пришел к выводу, что для повышения объема продаж необходима
рекламная компания Совместно с владельцем ресторана они решили, что максимальный
объем средств, потраченных на рост доходов ресторана, не должен превысить $75 000 Иде-
альным изданием для размещения рекламы ресторана является местный журнал о рестора-
нах Permian Eats Полная страница рекламы в журнале Permian Eats стоит $1 000, а число
проинформированных оценивается в 60 000 человек 30-секундный рекламный блок в ме-
стной телекомпании KOIL стоит $6 000, и каждую рекламу увидит порядка 600 000 человек
Коммерческий директор хочет разместить по меньшей мере пять рекламных блоков на ТВ
и десять рекламных объявлений в журнале Кроме того, он намерен потратить как можно
меньше денег из своего бюджета, чтобы остались средства для альтернативных действий,
если рекламная компания не принесет желаемых результатов Он преследует следующие
цели проинформировать по крайней мере 35 млн чел и потратить не более 60 тыс долл
а Создать табличную модель для достижения данных целей
b Прокомментировать полученные результаты
8 22 Gert’s Sports — быстро развивающаяся сеть спортивных магазинов на Восточном побере-
жье Владелец сети Боб Гертц скопил солидный капитал, чтобы открыть новые магазины
в районе Чикаго Он может построить магазины трех типов супермаркеты, торговые цен-
тры и Интернет-магазин Постройка одного супермаркета стоит $3,5 млн , в нем работает
150 человек, постройка торгового центра стоит $ 1,7 млн , в нем работает 65 человек, откры-
тие Интернет-магазина стоит $1млн и в нем занято 50 человек Гертц может вложить в от-
крытие магазинов до $10 млн , при этом он хочет достичь ряда целей, в частности, макси-
мизировать дивиденды наряду с максимизацией количества занятых Ожидаемый доход
для супермаркета, торгового магазина и Интернет-магазина составляет 1, 0,5 и 1 млн долл
соответственно Количество магазинов каждого типа ограничено демографическими фак-
торами региона Интернет-магазинов может быть не более одного, супермаркетов — не бо-
лее трех, а торговых центров — не более семи Оцените ситуацию с помощью метода АИП
Предполагается, что учитываются два критерия — доход и количество занятых Боб оценил
рейтинги по обоим критериям, используя описанную в тексте главы шкалу Результаты
представлены в табл 8 17 и 8 18
Таблица 0.17. Рейтинг доходности
	Супермаркет	Торговый центр	Интернет-магазин
Супермаркет	I	4	7
Торговый центр	0,25	1	5
Интернет-магазин	0,142857	0,2	1
ГЛАВА 8. Многоцелевые модели и эвристические методы 569
	Таблица 0.10. Рейтинг по количеству занятых
8 23	Супермаркет	Торговый центр	Интернет-магазин Супермаркет	I	0,25	0,333333 Торговый центр	4	I	0,5 Интернет-магазин	3	2	I а На основании данных рейтингов с помощью алгоритма АИП найдите наилучшие ре- шения по строительству магазинов b Оцените согласованность рейтингов Для снабжения новых магазинов компании Гертца (см задачу 8 22) потребуется расширить склады За поддержкой он может обратиться к услугам одной из трех финансовых компа- ний У каждой из них есть свои преимущества в условиях кредита и обслуживании клиен- тов Боб оценил рейтинги этих компаний (табл 8 19 и 8 20) Таблица 0.19. Рейтинги по условиям кредита
8 24	Big Bank	Little Bank	Bucks R Us Big Bank	I	2	0,143 Little Bank	0,5	1	6,000 Bucks R Us	7	0,167	1 Таблица 0.20. Рейтинги по обслуживанию клиентов Big Bank	Little Bank	Bucks R Us Big Bank	1	0,25	1 Little Bank	4	1	0,5 Bucks R Us	1	2	1 С помощью АИП определите единственный источник финансирования для компании Гертца Гертц (см задачу 8 22) ищет поставщиков хоккейного снаряжения Он ожидает резкого по- вышения уровня продаж в связи с необычно холодной зимой Он пришел к выводу, что при выборе поставщика нужно исходить из его способности обеспечить своевременную доставку заказа Рейтинги четырех возможных поставщиков Боб оценил так, как показано в табл 8 21 Таблица 0.21. Рейтинги поставщиков Sticks Supply	Puck’s House	Rinks Inc.	Goal Tenders Sticks Supply	I	3	I	0,5 Puck’s House	0,333333	I	0,5	0,25 Rinks Inc	I	2	I	I Goal Tenders	2	4	I	I
а Методом АИП выберите двух лучших поставщиков
b Был ли Боб последователен в оценке рейтингов'’
570 ЧАСТЬ II Оптимизационные модели
Прикладные задачи
8 25 Вернитесь к упражнению 8 15 Можно ли получить более удачный график выполнения ра-
бот с помощью следующего эвристического алгоритма?
Этап 1 Составляется список заданий с указанием времен обработки на станках 1 и 2
Этап 2 Находится задание с наименьшим временем обработки Если наименьшее время
соответствует времени обработки на станке 1, поставить данное задание на возможно более
ранее время, если же это время соответствует времени обработки на станке 2, поставить
данное задание на наиболее позднее возможное время При наличии нескольких заданий
с наименьшим временем обработки выбирается любое из них произвольным образом
Этап 3 Удаляется выбранное задание из списка
Этап 4 Повторяются этапы 2 и 3 до тех пор, пока все задания не будут выбраны
8 26 Городские власти рассматривают два проекта Осуществление одного цикла действий
в рамках проекта А обходится в $400, приводит к созданию 20 рабочих мест и приносит
к концу года доход $200 Осуществление одного цикла действий в рамках проекта В обхо-
дится в $600, приводит к созданию 40 рабочих мест и приносит к концу года доход $200
При составлении плана ставятся следующие цели
1	Сохранить суммарные расходы на уровне не более $2400
2	Создать не менее 120 рабочих мест
3	Максимизировать доход на конец года
Цели перечислены в порядке убывания их абсолютных приоритетов
а Найдите графически оптимальное количество циклов действий в рамках каждого проекта
b Достигаются ли при этом цели и в какой степени9
с Чему равны суммарные расходы и число созданных рабочих мест9
8 27 Опишем еще один эвристический подход для решения задачи 8 14 В этом подходе считает-
ся, что в начальный момент все склады открыты, и закрывается склад, ликвидация кото-
рого принесет максимальную экономию. Процесс продолжается до тех пор, пока окажется
невозможно закрыть склад, не понеся убытки
а Решите задачу 8 14 с помощью описанного алгоритма
b Улучшит ли этот алгоритм полученное решение9
8 28 Используя метод АИП, помогите Марлен Уитт выбрать работу после окончания колледжа
Она получила три предложения от работодателей в Бакерсфилде, Фресно и Ойлдейле (все
города штата Калифорния) и определила три важных для нее критерия выбора заработная
плата, стабильность работы и привлекательность города Соответствующие данные пред-
ставлены на рис 8 29 (рабочая книга Работа на компакт-диске, прилагаемом к книге)
SJ Ойлдейл	2 0,14285714	1
Рис. 8.29
а Чему равны средние рейтинги по критерию зарплаты9
b Согласованы ли заданные Марлен оценки9 Как можно изменить попарные оценки,
чтобы согласовать их9
с Чему равны средние веса критериев9
d Какую работу вы посоветуете выбрать9
ГЛАВА 8. Многоцелевые модели и эвристические методы 571
8 29. Используя метод АИП, помогите Чарльзу Шумвею выбрать новый автомобиль Он остановил
свой выбор на трех моделях, Buick Regal, Toyota Camry и Honda Accord, и указал три основных
для него критерия цена, надежность (по отзывам покупателей), скорость Соответствующие
данные представлены на рис 8 30 (рабочая книга Авто на компакт-диске, прилагаемом к книге)
Рис. 8.30
а Чему равны средние рейтинги по критерию скорости9
b Чему равны средние веса критериев9
с Был ли Чарльз последователен при задании весов9
d Какой автомобиль вы рекомендуете купить9
8 30 Вернитесь к задаче 8 19 Существует ли лучшее решение задачи минимизации времени
подготовки к работе в компании Stamped Metal Parts9
8 31 Вернитесь к задаче 8 22
а Методами линейного программирования определите, сколько магазинов каждого вида
следует открыть, чтобы максимизировать доход
b Определите, сколько магазинов каждого вида следует открыть, чтобы максимизиро-
вать количество созданных рабочих мест
с Измените модель ЛП таким образом, чтобы можно было реализовать обе цели
8 32 Нефтеперерабатывающий завод производит дизельное топливо, бензин и битум Удельная
прибыль одного барреля дизельного топлива составляет $3, бензина — $2,5 и битума —
$3,50 Завод хочет максимизировать прибыль, но должен также заботиться о безопасности
производства Последние данные показали, что при производстве битума несчастные слу-
чаи с потерей работоспособности происходят вдвое чаще, чем при производстве дизель-
ного топлива или бензина Количество несчастных случаев при производстве битума со-
ставляет 0,2 случая на миллион баррелей произведенного продукта В следующем месяце
завод может произвести всего до 10 млн баррелей продукции, а также необходимо произ-
вести 5 млн баррелей бензина для важного клиента
Сформулируйте задачу целевого программирования, которая позволит в равной мере ми-
нимизировать недостижение целей по получению прибыли и обеспечению безопасности
Ситуация для анализа | Объединение заводов2
Специальному помощнику президента компании Sleepmore Mattress Manufacturing
Карлу Легосу поручили изучить предложение по объединению предприятий, располо-
женных в трех различных пунктах. В результате приобретения фирмы-конкурента у ком-
пании появилось несколько новых заводов, некоторые из них находятся там же, где и уже
существующие предприятия компании Президент компании считает, что экономию
средств от объединения подсчитать легко, но качественные факторы и неизбежные ком-
Данный пример следует использовать в качестве основы для обсуждения, а не в качестве иллюстрации эф-
фективности или неэффективности при разрешении административной ситуации © 1990, Darden Graduate
Business School Foundation
572 ЧАСТЬ II Оптимизационные модели
промиссы описать сложнее Именно этому вопросу должен уделить основное внимание
в своей работе Карл
Главные цели при оценке плана объединения расположенных в разных пунктах
предприятий состоят в максимизации производственных возможностей, получении
преимуществ в сфере продаж и прямых финансовых выгод. Эти цели характеризуют-
ся 13 показателями (влияющими факторами) (см. приложение 1). Проанализировав
каждый показатель в отдельности, Карл и его сотрудники упорядочили их по убыва-
нию важности Кроме того, были добавлены наилучший и наихудший возможный
результат по каждому из показателей (приложение 2).
Приложение 1. Иерархия целей и показатели
I Увеличение производственных возможностей.
А Трудовой коллектив.
В Эффективность управления.
1	Управленческие кадры.
2	Размер предприятия (объем продаж).
С. Производительность.
1	Сложность производственной специализации.
2	Обучение персонала.
3	. Стабильность производства.
D Помещения.
1	Планировка.
2	. Местонахождение.
3	Наличие свободных помещений.
II	Максимизация преимуществ в сфере продаж.
А Увеличение сферы обслуживания.
В.	Увеличение качества обслуживания.
III	Максимизация прямых финансовых выгод.
А.	Минимизация исходных затрат.
В.	Максимизация будущей прибыли.
Приложение 2. Показатели целей
Ранг Показатель	Худший результат	Лучший результат
1 Трудовой коллектив	Наличие враждебного профсоюза	Отсутствие враждебного профсоюза
2 Качество	Заметное ухудшение качества	Заметное улучшение ка- чества
3 Обслуживание	Утрата бизнеса	Расширение бизнеса
4 Годовая экономия	Потеря 1 млн долл	Экономия 1 млн долл
5	Первоначальные за- траты	Затраты 5 млн долл	Экономия 5 млн долл
6 Управление	Заметное ухудшение управления	Заметное улучшение управления
7 Размер предприятия	Создание предприятия стоимостью	Создание предприятия
(объем продаж)	35 млн долл	стоимостью 15 млн долл
ГЛАВА 8 Многоцелевые модели и эвристические методы 573
Ранг Показатель	Худший результат		Лучший результат
8	Местоположение	Перенос из сельской местности в предприятия	город 9	Сложность производи- Увеличение ассортимента продукции венной специализации 10	Наличие свободных	Требуется новое помещение помещений	(100000 кв футов) 11	Стабильность произ-	Увеличение колебаний спроса водства 12	Обучение персонала	Необходимо обучать весь персонал 13	Планировка предпри-	Неудачная планировка предприятия ятия			Перенос из города в сель- скую местность Сокращение ассортимен- та продукции Освобождается помеще- ние 100000 кв футов Снижение колебании спроса Обучать новый персонал не нужно Избавление от неудачной планировки
Измерения показателей Каждому показателю присваивалось значение от 0 до 10, где 10 обозначало наи- лучший возможный результат, указанный в приложении 2 Три рассматриваемых пункта возможного объединения предприятий находятся в различных регионах, и для каждого из них нужно принять решение, объединять ли расположенные в дан- ном пункте предприятия или сохранить их самостоятельность В приложениях 3, 4 и 5 дано краткое описание и оценка трех возможных вариантов объединения Оце- нивается только вариант объединения без сравнения с вариантом “не объединять” Приведенные оценки являются относительными оценками показателей по отноше- нию к имеющейся ситуации, когда предприятия существуют отдельно Присвоенные оценки базируются на субъективном мнении Карла после бесед с менеджерами и по- сещения данных пунктов. Приложение 3. Оценка объединения в пункте 1: поглощение предприятия 1А предприятием 1В			
Показатель	Предприятие 1А	Предприятие 1В	Оценка объединения
Трудовой коллектив Качество Обслуживание Ежегодная экономия Первоначальные за- траты Управленческие кадры Объемы продаж Расположение пред- приятия Сложность производ- ственной специали- зации Наличие свободных помещений	Плохой Плохое Плохое Высокие накладные расходы При слиянии эконо- мится 1 млн долл Плохие 3 млн долл Большой город 2 основных вида продукции Нет данных	Отличный	9, значительное улучшение Хорошее	9 Хорошее	8 Эффективное, слияние — экономит 1 млн долл Нет данных	— Отличные	9 27 млн долл	— Сельская местность	10 2 отдельных конвейера 0, очень сложно Имеются, новые пло- — щади не нужны	
574 ЧАСТЬ II Оптимизационные модели
Показатель	Предприятие 1А	Предприятие 1В	Оценка объединения		
Стабильность произ-	Низкий спрос/вы- Высокий спрос/незна- 7, уменьшение из-		
водства	сокая неопределен- чительная неопреде- менчивости		
	ность	ленность		
Обучение персонала	Нет данных	Есть резерв кадров	7,5		
Планировка пред-	Перегруженное	Хорошо спроектиро- 7,5		
приятия	предприятие	ванное предприятие		
Приложение 4. Оценка объединения в пункте 2: предприятие 2В вливается в 2А			
Показатель	Предприятие 2А	Предприятие 2В	Оценка объе- динения
Трудовой коллектив	Средний	Плохой	6
Качество	Среднее	Среднее	5
Обслуживание	Среднее	Хорошее	7
Ежегодная экономия	Недогрузка мощно- стей, слияние сэко- номит 500 тыс долл	Недогрузка мощностей	—
Первоначальные затраты	। Нет данных	При слиянии экономится 1 млн долл	—
Управленческие кадры	Средние	Хорошие	6
Объем продаж	5 млн долл	10 млн долл	—
Расположение предпри	Промышленная зона	Большой город	6
ятия			
Сложность производст-	2 основных вида	2 отдельных конвейера	0, очень сложно
венной специализации	продукции		
Наличие свободных по-	При слиянии необ-	Нет	—
мещений	ходимо добавить 50 000 кв футов		
Стабильность произвол	Низкий спрос/ вы-	Высокий спрос	9, уменьше-
ства	сокая неопределен-		ние изменчи-
	ность		вости
Обучение персонала	Недогрузка персонала	Недогрузка персонала	9, временное увольнение
Планировка предприятия Отличная		Плохая	9
Приложение 5. Оценка объединения в пункте 3: предприятие ЗВ вливается в ЗА			
Показатель	Предприятие ЗА	Предприятие ЗВ	Оценка объ-
			единения
Трудовой коллектив	Ниже среднего	Хороший	3
Качество	Среднее	Среднее	5
Обслуживание	Среднее	Хорошее	6
Ежегодная экономия	Недогрузка мощностей, слия- Эффективное пред-		—
	ние сэкономит 200 тыс	долл приятие	
Первоначальные затраты	1 Нет данных	При слиянии эко- номится 2 млн долл	—
Управленческие кадры	Средние	Ниже средних	6
Объем продаж	9 млн долл	18 млн долл	—
ГЛАВА 8. Многоцелевые модели и эвристические методы 575
Показатель	Предприятие ЗА	Предприятие ЗВ	Оценка объ- единения
Расположение пред- приятия	Большой город	Пригород	4
Сложность производст- венной специализации	2 основных вида продукции	2 отдельных кон- вейера	0, очень сложно
Наличие свободных помещений	При слиянии необходимо до- бавить 30 000 кв футов	Нет	—
Стабильность произ- водства	Низкий спрос/ высокая неоп- ределенность	Неустойчивый спрос	6
Обучение персонала	Недогрузка персонала	Нет данных	3, часть пер- сонала увольняется
Планировка предпри- ятия	Хорошая	Стесненная в про- странстве	7
Определение весов показателей
После оценки показателей Карл столкнулся с более сложной задачей, оценить, на-
сколько важен один показатель по сравнению с другим Сравнить количественные по-
казатели относительно несложно, однако Карл точно не знал, как именно это сделать
Он слышал, что президент компании сказал- “Чем меньше предприятие, тем лете им
управлять При сокращении размера предприятия (объема продаж) с 35 до 15 млн долл
полученная выгода будет эквивалентна экономии 1 млн долл в год производственных
расходов при сохранении существующего положения” На основании данного высказы-
вания Карл быстро подсчитал в уме, что весовой коэффициент размеров предприятия
должен составлять одну вторую от весового коэффициента годовой экономии, однако
этот результат нуждался в последующем уточнении
Если для объединения необходимо строительство нового помещения или значи-
тельное расширение существующего, трудность перемещения, а также скрытые рас-
ходы будут дополнительными отрицательными факторами Дополнительные расхо-
ды на каждый дополнительный квадратный фут площади составят $25
Чтобы оценить весовые коэффициенты других (качественных) показателей, Карл
использовал свои заметки, сделанные на встрече с участием президента компании,
вице-президента по вопросам производства и вице-президента по работе с кадрами
На этой встрече, проводившейся во время приобретения компании-конкурента, был
составлен список целей и обсуждалась относительная важность каждого показателя
(см приложение 2).
Вице-президент по работе с кадрами сказал: “Кадры важнее всего, поскольку ка-
чество кадров определяет основные аспекты функционирования предприятия
(качество, прибыльность и т.д ) Опыт свидетельствует, что с хорошими кадрами
можно преодолеть множество препятствий, а с плохим коллективом неизбежны на-
рушения производственного процесса. Я считаю, что кадры вдвое важнее, чем сред-
няя важность всех 13 показателей”.
Вице-президент по вопросам производства согласился с высказыванием относи-
тельно важности кадров и сказал: “Я считаю, что хотя качество и обслуживание не-
много менее важны, чем кадры, эти два показателя имеют вес выше среднего”.
576 ЧАСТЬ II Оптимизационные модели
Казалось, что следующим по важности показателем будут признаны управленче-
ские кадры, поскольку они, наряду с трудовым коллективом, определяют судьбу
предприятия Однако в отличие от трудового коллектива руководство достаточно
легко поменять Поэтому данный показатель был признан средним по важности
Президент компании высказался в пользу показателя местонахождения предпри-
ятия “Местонахождение завода столь же важно, как и размеры предприятия. Наши
данные свидетельствуют, что предприятия в перенаселенных местах (города) менее
прибыльны, чем в сельской местности”.
Вице-президент по вопросам производства сказал’ “Поскольку наша компания
производит разнообразную продукцию на различных предприятиях, объединение зна-
чительно увеличит сложность и уменьшит эффективность в долгосрочной перспективе.
Я считаю, что сложность производственного ассортимента должна быть следующим по
важности качественным показателем после управленческих кадров, по-моему, ее важ-
ность составляет примерно две трети важности управленческих кадров”.
Было признано, что оставшиеся три показателя (стабильность, обучение персо-
нала и планировка предприятия) по отдельности имеют незначительное влияние, но
их совокупный вклад примерно вдвое больше, чем влияние сложности производст-
венного ассортимента
Самой сложной задачей оказалось описать, какие компромиссы между количест-
венными и качественными показателями устроили бы руководство В частности, пре-
зидент компании сказал, что ему сложно выбрать между ситуацией, когда экономится
7 млн долл , и ситуацией, когда устраняются враждебно настроенные профсоюзы.
Решение
Карлу необходимо найти эффективный способ учета всей имеющейся информа-
ции как о количественных, так и о качественных показателях, чтобы принять реше-
ние, стоит ли производить слияние предприятий в каждом из трех пунктов. Кроме
того, ему надо знать, насколько его решения будут устойчивы к значениям весовых
коэффициентов показателей.
Литература
1	Benjamin С , Ehie I , Omurtag Y Planning Facilities at the University of Missoun-Rolla, Interfaces,
22, no 4(1992) p 95-105
2	Charnes A, Cooper W Management Models and Industnal Applications of Linear Programming
(New York John Wiley, 1961)
3	Gavett W Three Heunstic Rules for Sequencing Jobs to a Single Production Facility, Management
Science, 11 (1965) B166-176
4	Mojena R , Vollmann T , Okamoto Y On Predicting Computational Time of a Branch-and-Bound Al-
gonthm for the Assignment of Facilities, Decision Sciences, 7, no 4(1976) p 856-867
5	. SaatyT The Analytic Hierarchy Process New York McGraw-Hill, 1988
6	Weintraub A , Bare В New Issues in Forest Land Management from an Operations Research Perspec-
tive, Interfaces, 26, no 5 (1996) p 9-25
Дероятностные модели
Глава 9. Анализ решений
Глава 10. Имитационное моделирование
Глава 11. Моделирование дискретных событий
Глава 12. Прогнозирование
Глава 13. Модели очередей
Мы все знаем выражение, что в этом мире только две вещи неизбежны —
смерть и налоги Хотя эту фразу можно рассматривать как комплемент правитель-
ству, но это скорее мировоззренческий взгляд на природу и человеческую деятель-
ность Суть этого высказывания в том, что большинство явлений нашего мира ха-
рактеризует некоторый элемент неопределенности и непредсказуемости. Библей-
ский Экклезиаст сделал подобное же заключение о людях и их делах. “Но время
и случай для всех их”
Мы реагируем на этот свойство жизни по-разному. В некоторых ситуациях мы
полностью игнорируем неопределенность, в других — стараемся ее учесть В пре-
дыдущих восьми главах мы не обращали внимания на неопределенность, прису-
щую любой ситуации. В следующих пяти главах будет описано много ситуаций,
в которых уровень неопределенности настолько высок, что его нельзя игнориро-
вать, и мы как менеджеры должны его учитывать.
Эта часть книги расшифровывает понятие неопределенности и предлагает ме-
тоды для анализа вероятностных моделей принятия решений Наша цель — очер-
тить круг проблем, в которых неопределенность играет решающую роль, и пред-
ложить несколько полезных методов решения таких проблем Мы рассмотрим си-
туации, в которых управление стоит перед выбором одной из нескольких
альтернатив При этом ситуации осложняются тем, что мы можем не знать точной
цены выбора той или иной альтернативы
Теория вероятностей — это область математики, которая составит фундамент
для анализа проблем, рассматриваемых в данной части книги Заметим, что язык
теории вероятностей мы широко используем в своей повседневной практике:
прогноз погоды предсказывает на завтра дождь с вероятностью 30%, в газетах при-
водятся шансы на победу спортивных команд, правительство озабочено вероятным
эффектом от принятия нового закона о налогах и т д. Однако попытка точно опре-
делить эти выражения часто приводит к недоразумениям Чтобы лучше понять ма-
териал данной части, изучите некоторые основные концепции теории вероятно-
стей, которые кратко описаны в приложении А. Здесь приведены определения
и понятия, необходимые для освоения материала данной части книги
Теория вероятностей часто становится камнем преткновения для многих студен-
тов Но вы можете не испытывать особых затруднений при чтении глав этой части
или при выполнении упражнений, поскольку основная сложность заключается
в привнесении вероятностных понятий в ваш подход к решению проблем Вероят-
ности могут “прятаться” в таких естественных понятиях, как распределение дохода,
время ожидания, время выполнения запроса и тому подобное, и они “покажут себя”
при выборе средств, подходящих для решения ваших конкретных проблем Еще раз
напомним, что вычислительный аспект решения практических задач играет важную
роль, особенно в имитационном моделировании Для анализа имитационных моде-
лей мы будем использовать электронные таблицы и специальные надстройки Crystal
Ball и ©RISK Эти средства будут рассмотрены в главе 10 В других главах будут опи-
саны другие программные продукты, необходимые для успешного решения задач,
рассматриваемых в этой части
Анализ решений
В этой главе...
91 Введение
9.2 Три класса моделей принятия решении
9 3 Принятие решений в условиях риска ожидаемое значение полной информации
9 4 Полезность и принятие решения в условиях риска
9 5 Промежуточные итоги
9 6 Деревья решений
9 7 Анализ чувствительности
9 8. Деревья решений учет новой информации
9 9 Последовательные решения
9 10 Менеджмент и теория принятия решений
9 11 Анализ решений
912 Заключение
9 13 Условные вероятности и теорема Байеса
Основные термины
Контрольные вопросы
Задачи
Ситуация 1 I
Ситуация 2 i
Ситуация 3 I
Литература
Компания Johnson s Composite Materials
Бурить или не бурить"’
Компания Shumway Horch and Sager (часть 1)
580 ЧАСТЬ III Вероятностные модели
Практическое применение^
Альтернативы коррекции зрения для близоруких
Приблизительно 70 млн американцев страдает миопией, которую обычно назы-
вают близорукостью До 80-х годов близорукость лечилась почти исключительно
с помощью внешней корректирующей оптики в виде очков либо контактных линз
Эти корректирующие вогнутые линзы возвращают точку фокусировки глазного яб-
лока на сетчатку
В последние 20 лет популярной альтернативой корректирующим линзам стано-
вится хирургическая операция, называемая радиальной кератотомией (РК), которая
заключается в нанесении многочисленных очень тонких разрезов на роговицу Со-
гласно Consumers Reports этой операции в 1992 году подверглось более 200 тыс аме-
риканцев. что на 667% больше, чем в 1987 году В 1995 году была разработана хи-
рургическая операция фоторефракционнои кератектомии (ФК), при которой с по-
мощью лазера изменялась форма рогови цы
Таким образом, в настоящее время у взрослого близорукого человека в процессе
последовательной коррекции своего зрения есть три альтернативы В каждом узле
принятия решения, ести он ранее не подвергался хирургическим операциям, он мо-
жет продолжать лечение без хирургического вмешательства, либо может рискнуть на
операцию Если он выбирает хирургическую операцию, то после нее зрение может
восстановиться потностью, либо частично Кроме того, зрение может ухудшиться
в течение последующих после операции лет В любом случае у пациента, согласив-
шегося на хирургическую коррекцию зрения, в дальнейшем может возникнуть необ-
ходимость следующего акта принятия решения о том, каким образом дальше бороть-
ся со своей близорукостью
Близорукий человек имеет три основные целевые функции, которые влияют на
его решения при выборе альтернативы коррекции зрения Это максимальная острота
зрения на всю оставшуюся жизнь (те максимальная полезность), минимальная
стоимость коррекции зрения в течение оставшейся жизни и минимальная временная
стоимость коррекции (имеется в виду время, потраченное на саму процедуру кор-
рекции, и время, необходимое для дальнейшей поддержки качества зрения)
Хотя принимаемые решения обязательно будут зависеть от индивидуальных пред-
почтений человека (возможно, ему нравится носить очки), интересны некоторые вы-
воды анализа возможных альтернатив Во-первых, альтернатива операции ФК пред-
почтительнее альтернативы операции РК, поскольку имеет большую ожидаемую по-
лезность в первый год после операции, а риски последующего ухудшения зрения
не выше, чем после операции РК Во-вторых, стоимость поддержки зрения после опе-
рации в течение 40 лет примерно равна стоимости постоянного ношения контактных
линз за такой же период В-третьих, известная заранее стоимость операций примерно
совпадает с денежным эквивалентом экономии средств на поддержку зрения в течение
40 лет, полученной в результате лечения хирургическими методами [2]
9.1.	Введение
Анализ решений предлагает общую основу для проведения анализа широкого круга
управленческих моделей Это подразумевает наличие I) системы классификации моде-
лей принятия решении в зависимости от информации, заложенной в моделях, и 2) кри-
ГЛАВА 9 Анализ решений 581
териев решений, т е наличие возможности измерить “доброкачественность” решений
в рамках каждой модели
В первой части этой главы мы представим основы теории принятия решений и пока-
жем ее связь с ранее рассмотренными моделями Вторая часть главы посвящена деревьям
решений С их помощью общие концепции теории принятия решений применяются
к последовательным решениям в условиях неопределенности и риска
В общем случае теория принятия решении трактует решения как решения, прини-
маемые против природы Это означает, что результат отдельного решения зависит от
действий другого игрока (природы), которого вы не можете контролировать Например,
результат решения брать или не брать зонтик, выходя излома, зависит только от состоя-
ния погоды Здесь важно отметить, что в этой модели результат проявляется только после
вашего акта принятия решения — природа сама не делает первого шага и ей безразлично
принятое вами решение В этом заключается кардинальное отличие теории принятия
решений от теории игр В теории игр оба игрока имеют экономическим интерес
В моделях теории принятия решений основной формой данных служит таблица пла-
тежей, подобная табл 9 1 В этой таблице альтернативы решений располагаются в левом
столбце таблицы, а возможные состояния природы являются заголовками столбцов, рас-
положенных справа от столбца альтернатив.
Таблица 9.1. Таблица платежей
Решения	Состояния природы	
	1	2	т
	/-Ц	Г|,	г1т
d2	'22	Л,„
d„	'Э	г„г		А™	
В таблице представлены значения платежей для всех возможных комбинаций решений
и состояний природы Процесс принятия решения можно описать следующим образом
1.	Вы, как лицо, принимающее решение, выбираете одно из возможных альтерна-
тивных решений Предположим, вы выбрали решение d,
2.	После выбора решения проверяется текущее состояние природы Пусть природа
находится в состоянии 2
3.	Теперь ваш платеж (выигрыш или проигрыш, если значение платежа отрицатель-
ное), полученный в результате принятия вами определенного решения, находится
в таблице платежей Поскольку вы приняли решение d;, а природа находится в со-
стоянии 2, то ваш платеж равен rs2
Еще раз повторим, что сначала принимается решение, затем определяется состояние
природы После принятия решения вы не можете изменять состояние природы Как же
решить, какую альтернативу выбрать9 Выбираемая альтернатива определяется макси-
мально возможным платежом ги, где i — номер соответствующей альтернативы, а; — но-
мер состояния природы (если платеж — это выигрыш) Обычно решение принимается
в зависимости от того, какое состояние природы мы ожидаем. Если мы предполагаем,
что ожидается состояние 1, то выбираем решение, которое соответствует максимальному
платежу при этом состоянии природы
582 ЧАСТЬ III Вероятностные модели
В следующем разделе мы рассмотрим различные предположения о поведении приро-
ды Каждое предположение порождает свои критерий выбора “наилучшего” решения и,
следовательно, свою процедуру выбора такого решения
9.2.	Три класса моделей принятия решений
В этом разделе представлены три класса моделей принятия решений, причем каждый
класс определяется своими предположениями о поведении природы Это классы моделей
принятия решении в условиях определенности, риска и неопределенности Конечно,
наиболее интересным является класс моделей принятия решений в условиях риска, но
без описания других двух классов не будет полной картины моделей принятия решений
Принятие решений в условиях определенности
Этот класс моделей соответствует ситуации, когда мы знаем, в каком состоянии будет
находиться природа после принятия нами решения Это условие можно интерпретировать
и так, что природа может находиться только в одном-единственном состоянии Допустим,
утром вы решаете, взять ли вам зонтик на работу, если вы уверены, что во второй половине
дня (во время возвращения с работы) обязательно будет дождь В таблице платежей для
этой модели (табл 9 2) решению не брать зонтик соответствует платеж -$7 (стоимость чи-
стки костюма, если вы попадете под дождь) Знак минус здесь указывает на то, что
“выигрыш” в игре против природы будет отрицательным, те такую сумму вы потеряете
при выборе этого решения Конечно же, оптимальным решением будет взять зонтик
Таблица 9 2 Таблица платежей для примера с зонтиком
Решение	Состояние природы: дождь
Взять зонтик	О
Не брать зонтик	—7,00
Все модели линейного программирования, целочисленного программирования, нели-
нейного программирования и другие детерминированные модели можно рассматривать как
модели принятия решении против природы, которая имеет только одно состояние Это
следует из того, что мы всегда получаем какои-либо платеж (в зависимости от конкретной
модели) посте принятия любого решения, и этот платеж повторится, если мы опять повто-
рим данное решение Чтобы проиллюстрировать это положение, рассмотрим простую мо-
дель линейного программирования, которая уже описывалась в главе 3
Мах 5000£ + 4000£
при ограничениях
10£ + 15£< 150,
20£+ 10£< 160,
30£ + 10£> 135,
£-3£<0,
£+£>5,
£, £>0
В табл 9 3 представлена эта модель в виде таблицы платежей В этой таблице платеж
-оо означает недопустимое решение Например, поскольку решения £= 0, £= 0 наруша-
ют третье и пятое ограничения, то соответствующий платеж определен как — оо Для лю-
ГЛАВА 9 Анализ решений 583
бой допустимой пары значении (Е, F) платеж определяется как соответствующее значе-
ние целевой функции, те подсчитывается по формуле 5000Е + 4000F Изучая эту мо-
дель, мы точно знаем, какой платеж получим в результате принятия того или иного ре-
шения (решение — выбор пары значений Е и F) Мы можем выписать все возможные
значения платежей в одном столбце, который соответствует одному состоянию природы
Таблица 9 3. Таблица платежей для модели линейного программирования
Решение	Состояние природы
£=0, F=0	-оо
Е=5 F=b	41 000
£=6, £=3,5	44 000
В принципе, не трудно наити решение для модели с одним состоянием природы На-
до просто выбрать то решение, которому соответствует наибольший выигрыш Но на
практике эта простота “в принципе” может повернуться другой стороной Поскольку Е
и Лмогут принимать бесконечное количество значении, то и количество строк в табл 9 3
также должно быть бесконечным Даже в такой простои модели бесконечное количество
альтернатив не позволяет выбрать наилучшее решение В этом случае необходим допол-
нительный математический анализ модели (для рассмотренной модели приюдится сред-
ство Excel Поиск решения)
Принятие решений в условиях риска
Отсутствие определенности относительно будущих событии — характерная черта
многих (но не всех) управленческих моделей принятия решений Представьте финансо-
вого вице-президента страховой компании, который при принятии решений точно знает
только то, что изменения на финансовом рынке обязательно будут Очевидно, что мно-
гие модели реальных ситуации характеризуются отсутствием определенности
В количественных моделях с неопределенностью можно ‘ бороться” разными спосо-
бами Например, в моделях линейного программирования каким-либо способом можно
построить оценку для данных, относящихся к будущим событиям Во многих моделях
линейного программирования, описывающих производственные ситуации, обычно пер-
вое ограничение описывает производственные возможности (это может быть рабочее
время персонала, мощности оборудования и т п ) которые будут доступны в течение рас-
четного периода времени Эти возможности, конечно, зависят от факторов, которые мо-
гут проявиться в будущем, и которые заранее трудно учесть Но производственный план
составляется сегодня, а не задним числом, поэтому менеджер просто обязан оценить бу-
дущие производственные возможности и только затем на их основе выполнять анализ
чувствительности (как показано в главе 4)
Определение риска
Теория принятия решении предлагает свои подход к моделям с неполной определен-
ностью Этот подход называется принятие решений в условиях риска Здесь термин риск
имеет вполне определенный и четко очерченный смысл В классе моделей принятия ре-
шении в условиях риска рассматривается несколько состояний природы и мы можем
сделать предположения о вероятностях наступления каждого возможного состояния приро-
584 ЧАСТЬ III Вероятностные модели
ды Пусть, например, имеется т (т> 1) состояний природы, и р,— оценка вероятности
наступления события j В общем случае значение вероятности оценивается на основа-
нии каких-либо статистических данных за прошлые периоды времени, где зафиксирова-
ны проявления события j в течение времени наблюдений Например, если в течение по-
следних 1000 дней мы зафиксировали 200 дождливых дней, то оценкой вероятности дож-
дя в данный день будет число 0,20 (=200/1000) Если статистические данные отсутствуют
или недоступны, либо если менеджер в силу каких-нибудь причин не может спроециро-
вать их на будущее, то он все равно должен оценить эти вероятности, пусть даже субъек-
тивно Подход с субъективным оцениванием вероятностей мы рассмотрим в разделе 9 10
Напомним, что ожидаемое значение любой случайной величины вычисляется как
взвешенное среднее всех возможных значений этой случайной величины, где веса явля-
ются вероятностями принятия случайной величиной данных значений Поскольку ре-
зультат принятия того или иного решения зависит от состояний природы, ожидаемый ре-
зультат, связанный с решением л вычисляется как сумма по всем возможным состояни-
ям j произведений платежа (результат от решения i при j-ом состоянии природы)
и вероятности pj (вероятность состояния у) Таким образом, ER:, ожидаемый результат' от
принятия решения i, вычисляется по формуле
ER' = £л Р> =r'iPi + г^ + "+гтРт	(9 1)
Для любых типов моделей менеджмент должен выбирать такое решение, которое мак-
симизировало бы ожидаемый результат 2 Другими словами, i* будет оптимальным реше-
нием, если
ER. = максимум ER по всем i
Модель газетного киоска
Для иллюстрации положении предыдущего раздела рассмотрим модель газетного ки-
оска (Подобные модели подробно исследованы в главе 10 ) Продавец газетного киоска
может купить газету Wall Street Journal по 40 центов за каждый экземпляр и продать их по
75 центов Но, конечно, он должен закупить газеты до того, как будет знать, сколько ре-
ально он их продаст Если он закупит газет больше, чем сможет продать, то он понесет
убытки, равные стоимости непроданных газет Если он закупит слишком мало газет, то
он потеряет потенциальных покупателей сегодня и, возможно, в будущем (неудовлетво-
ренный покупатель может перестать покупать в этом газетном киоске свою любимую га-
зету) Предположим, что будущие потери (т.е. упущенную выгоду) можно обобщенно
оценить в 50 центов на одного неудовлетворенного покупателя. Чтобы не “затенять
идею” модели и для простоты вычислении предположим, что продавец оценил вероятно-
сти спроса на газету следующим образом.
Рп == Р{ спрос = 0) =0,1;
Pt = Л спрос - 1) = 0,3,
Р2 - Pfcnpcc = 2) - 0,4,
Р, = Рспрос = 3) = 0,2
ER — сокращение от Игре tied Reluin, что означает ожидаемый возврат, или ожидаемый результат. —
Прим перев
Далее мы покажем, что это требование эквивалентно другому критерию — м инимизации ожидаемых потерь
ГЛАВА 9 Анализ решений 585
Итак, в этой модели четыре значения спроса соответствуют четырем состояниям при-
роды, а количество закупаемых продавцом газет является решением В табл 9 4 пред-
ставлена таблица платежей для данной модели
Таблица 9.4 Таблица платежей для модели газетного киоска
Решение	Состояния природы (спрос)			
	0	1		2	3
0	0	-50	-100	-150
1	-40	35	-15	-65
2	-80	-5	70	20
3	-120	-45	30	105
Платежи в этой таблице, вычисляемые для каждой комбинации решения и спроса,
определяют прибыль или упущенную выгоду, если количество закупленных газет не со-
ответствует спросу на них Эти платежи вычисляются по следующей формуле
Платеж = 75 х (Количество проданных газет) - 40 х (Количество закупленных газет) -
— 50 х (Неудовлетворенный спрос)
Здесь 75 центов — стоимость проданной газеты, 40 центов — покупная стоимость газеты
и 50 центов — стоимость потери покупателя (упущенная выгода)
Рассматривая эту модель, важно понять, что количество проданных газет и спрос не
являются тождественными величинами Количество проданных газет — это минимум
двух величин количества закупленных газет и реального спроса Например, если не за-
куплено ни одного экземпляра газеты, то, очевидно, количество проданных газет равно
нулю, независимо от спроса, и неудовлетворенный спрос равен самому спросу Таким
образом, платежи в первой строке таблице платежей вычисляются как 75x0 — 40x0 -
50 х Спрос = -50 х Спрос Если закуплен один экземпляр газеты, а спроса нет, то эта га-
зета не продана, неудовлетворенный спрос равен 0, а платеж вычисляется как 75 х 0 -
40 х 1 — 50 х 0 = —40, что соответствует значению первого платежа во второй строке таб-
лицы платежей Но если закуплен один экземпляр газеты и спрос на газету не нулевой, то
этот экземпляр газеты обязательно будет продан, а неудовлетворенный спрос будет на 1
меньше самого спроса В этом случае платеж вычисляется как 75 x1 - 40 х 1 -
50 х (Спрос - 1)= 85 - 50 х Спрос Подобным образом вычисляются другие значения
платежей в табл 9 4
Когда определены все значения платежей, далее нахождение оптимального решения
является делом математической техники Мы используем формулу (9 1) для вычисления
ожидаемого результата (платежа) для каждого решения и выберем то решение, для кото-
рого ожидаемый платеж будет наибольшим Сначала выполним вычисления вручную,
а затем покажем, как это сделать в электронной таблице.
Если закуплено, например, два экземпляра газеты, то
ER2 = -80 х 0,1 - 5 х 0.3 + 70 х 0,4 + 20 х 0,2 = 22,5
Здесь первое слагаемое является произведением значения платежа при нулевом спросе
(и если закуплено 2 экземпляра газеты) и вероятности нулевого спроса Второе слагаемое
также вычисляется как значение платежа при спросе, равном 1 (и если закуплено 2 эк-
586 ЧАСТЬ III Вероятностные модели
земпляра газеты, см табл 9 4), умноженном на вероятность такою значения спроса Два
следующих слагаемых определяются аналогично
Вычистим ожидаемые платежи для остальных возможных решений
£«„ = 0x0,1 - 50 x0,3 - 100x 0,4 - 150x 0,2 = -85,
ERt = -40 х 0,1 + 35 х 0,3 - 15 х 0,4 - 65 х 0,2 = -12,5,
£«, = —120x0,1 - 45 x 0,3 + 30x 0,4 + 105 x 0,2 = 7,5
Поскольку максимальное значение имеет £«2, оптимальным решением будет заку-
пить два экземпляра газеты
Другой путь нахождения оптимальною решения заключается в сравнении графиков
профилен рисков Профичь риска показывает для конкретного решения все возможные
выходы (значения платежей) с соответствующими вероятностями, что позволяет менед-
жеру сортировать возможные выходы в соответствии со своими критериями или пред-
почтениями Некоторые менеджеры находят профили рисков более полезными, чем про-
стое использование одного числа (г е значения ожидаемого результата), которое обоб-
щает всю возможную информацию о решении (вероятности и потенциальные выходы,
которые в явном виде представлены на графике профиля риска) На рис 9 1 показаны
профи пи рисков для четырех решений рассматриваемой задачи
На рис 9 1 видно, чго все четыре возможных выхода для “Решение 0” меньше или рав-
ны нулю (т е при этом решении возможны лишь одни убытки) В “Решение 1” три из четы-
рех выходов отрицательны, а в “Решение 2” и “Решение 3“ отрицательна половина выхо-
дов Из профилен рисков также видно, что в “Решение 2” наибольшую возможную вероят-
ность (0,4) имеет второй по величине положительный платеж (70 центов) Конечно, вся эта
информация представлена в исходной таблице платежей, но часто бывает полезным пред-
ставить эт информацию не безликими числами, а в виде наглядных графиков
Упущенная выгода: анализ чувствительности
Решения в модели газетного киоска базируются на значениях прибыли и упущенной
выюды, которые определяются менее точно, чем два других параметра модели — цена при-
обретения газеты и отпускная (розничная) цена Возникает вопрос каким может быть оп-
ГЛАВА 9 Анализ решений 587
тимальное решение, если изменится значение упущенной выгоды9 Чтобы ответить на этот
вопрос, надо выполнить анализ чувствительности относительно этого параметра модели
Один из способов анализа чувствительности заключается в задании разных значений
упущенной выгоды, пересчете таблицы платежей, повторном вычислении ожидаемых
платежей и выборе на их основе нового оптимального решения Это можно выполнить
вручную, но, естественно, более рационально использовать для этого Excel На рис 9 2
показан рабочий лист Базовый (из рабочей книги Газеты xls), на котором рассчитыва-
ются таблица платежей и ожидаемые платежи
Рис. 9.2. Рабочий лист для вычисления таблицы платежей и значении ожидаемых платежей
На этом листе в ячейки Bl ВЗ введены значения цены покупки газеты и ее розничной
цены, а также значение упущенной выгоды На рис 9 2 также показаны формулы, по ко-
торым вычисляются значения в таблице платежей и ожидаемые платежи Отметим, что
формула в ячейке В7 построена с использованием относительных, смешанных и абсо-
лютных ссылок на ячейки, что позволяет ее скопировать на все остальные ячейки табли-
цы платежей Формулы в диапазоне F7 F10 используют функцию СУММПРОИЗВ, кото-
рая позволяет легко найти сумму произведении платежей из соответствующей строки
таблицы платежей на их вероятности, записанные в диапазоне В12 Е12
С помощью таблиц подстановки Excel можно легко создать таблицу расчета ожидае-
мых платежей для каждого решения в зависимости от величины упущенной выгоды Мы
покажем, как это сделать, в той же рабочей книге Газеты, но на новом рабочем листе, ко-
торый назовем Анализ чувствительности Значения упущенной выгоды будем изменять
от 0 до 150 центов с шагом в 5 центов Для создания таблицы подстановки выполните
следующие действия
1.	Скопируйте данные с рабочего листа Базовый на лист Анализ чувствительности
2.	Введите значение 0 (начальное значение упущенной выгоды) в ячейку А16
588 ЧАСТЬ III Вероятностные модели
3.	Снова щелкните кнопкой мыши на ячейке А16 и выполните команду Прав-
ка^Заполнить^Прогрессия
4.	В открывшемся диалоговом окне Прогрессия щелкните на переключателе Распо-
ложение по столбцам, введите значение 5 в поле Шаг и значение 150 в поле Пре-
дельное значение Затем щелкните на кнопке ОК
5.	В ячейку В15 введите формулу =F7, которая даст значение ожидаемого платежа
для решения, при котором газета не закупается совсем (решение 0) В ячейки
С15 Е15 введите формулы =F8, =F9 и =F7, которые дадут значения ожидаемых
платежей для решений 1, 2 и 3 соответственно.
6.	Выделите диапазон А15 Е46 и выполните команду Данные^Таблица подстанов-
ки В диалоговом окне Таблица подстановки в поле Подставлять значения по
строкам в введите $В$3, как показано на рис 9.3 Этим вы говорите Excel, что
значения, введенные в столбце А, следует подставить в ячейку ВЗ (по одному зна-
чению за один раз), пересчитать формулы в диапазоне F7 F10 и вычисленные зна-
чения поставить в столбцы В, С и D соответственно
Рис. 9.3. Создание таблицы подстановки
Результаты, представленные в таблице подстановки, можно представить в графиче-
ском виде, для чего используем мастер построения диаграмм Excel
1.	Выделите диапазон с данными, которые вы хотите отобразить на диаграмме. В данном
случае это диапазон В16.Е46
2.	Щелкните на кнопке Мастер диаграмм, которая находится на стандартной пане-
ли инструментов Последовательно откроется ряд диалоговых окон мастера диа-
грамм, которые помогут построить нужную вам диаграмму.
3.	В первом диалоговом окне Мастер диаграмм следует указать желаемый тип диа-
граммы. Щелкните в списке Тип на типе График и далее выберите подтип диа-
граммы, например График с маркерами Затем щелкните на кнопке Далее.
ГЛАВА 9 Анализ решений 589
4.	В следующем окне Мастер диаграмм будет показан образец вашего графика.
В этом окне перейдите на вкладку Ряд и в поле Подписи оси X введите ‘Анализ
чувствительности’!$А$16.$А$46 (либо укажите этот диапазон на рабочем листе)
как показано на рис 9.4. Далее в списке Ряд поочередно выделяйте Ряд1, Ряд2,
РядЗ и Ряд4, при этом в поле Имя вводите соответственно Решение 0, Реше-
ние 1, Решение 2 и Решение 3. Затем щелкните на кнопке Далее
5.	В следующем диалоговом окне введите заголовки для диаграммы и для осей X и Y
Щелкните на кнопке Далее.
6.	В последнем диалоговом окне Мастер диаграмм укажите, что вы хотите помес-
тить диаграмму на текущем активном листе (выбор по умолчанию) и щелкните на
кнопке Готово
7.	На рабочем листе Анализ чувствительности появится график, показанный на рис 9 5
Рис. 9.4. Второе диалоговое окно мастера диаграмм
На построенном графике видно, что при возрастании значения упущенной выгоды
ожидаемые платежи убывают (для решении 0, 1 и 2) или остаются постоянными (для ре-
шения 3). Если значение упущенной выгоды меньше 125 центов, то оптимальным будет
решение 2 Для значения упущенной выгоды 125 центов оптимальными будут решение 2
и 3 Если значение упущенной выгоды больше 125 центов, то оптимальным будет реше-
ние 3. Таким образом, нет необходимости знать точное значение упущенной выгоды —
чтобы определить оптимальное решение достаточно знать, будет ли оно больше или
меньше 125 центов. Этот результат напоминает результаты анализа чувствительности мо-
делей линейного программирования, когда оптимальное решение не меняется при изме-
нении в определенных пределах коэффициентов модели
590 ЧАСТЬ III Вероятностные модели
На рассмотренном примере модели газетного киоска мы показали важный класс мо-
делей принятия решении — принятие решении в условиях риска, и соответствующий
критерии определения оптимального решения — критерий максимизации ожидаемого
результата
Принятие решений в условиях неопределенности
В моделях принятия решений в условиях неопределенности мы снова имеем несколь-
ко (ботее одного) состояний природы, но в данном случае нам неизвестны вероятности
проявления этих состоянии природы Можно долго рассуждать о том, как поступить
в такой ситуации неопределенности Во всяком случае при принятии любого решения
будет присутствовать большой элемент субъективности, если каким-либо способом вы
сами будете указывать вероятности возможных событий природы. Но, поскольку в ре-
альной жизни трудно представить подобную ситуацию, особенно в деловой сфере, оста-
вим философам возможность порассуждать о природе неопределенности и путях ее пре-
одоления Мы же рассмотрим несколько различных подходов к анализу класса моделей,
работающих в условиях неопределенности Отметим, что данный раздел является необя-
зательным в том смысле, что его содержание не будет использоваться в дальнейшем По-
этому те читатели, которых больше интересует тема принятия решений в условиях риска,
могут спокойно пропустить этот раздел и перейти к разделу 9 3
Критерий Лапласа
При использовании критерия Лапласа условие неопределенности интерпретируется как
предположение о равных вероятностях появления всех возможных состояний природы
Например, в модели газетного киоска из предположения о равновероятности всех состоя-
нии природы следует, что вероятности всех четырех событии (соответствующих разным ве-
личинам спроса) будут одинаковыми и равными 0,25 Далее можно пересчитать модель
принятия решения в условиях риска с этими вероятностями и получить ожидаемые значе-
ния платежей Нетрудно проверить, что в модели газетного киоска после такого пересчета
оптимальным снова будет решение 2, в соответствии с которым следует закупить два экзем-
ГЛАВА 9 Анализ решений 591
пляра газеты Поскольку при использовании критерия Лапласа все вероятности равны, для
определения наилучшего решения можно просто просуммировать значения платежей, со-
ответствующих каждому решению, и выбрать то решение, которое будет иметь максималь-
ную сумму (что также соответствует максимальному ожидаемому платежу)
Хотя во многих ситуациях “равновероятностный” подход дает вполне приемлемое
решение, в других ситуациях он дает заведомо неверные решения Причина этого заклю-
чается именно в условии равновероятности состояний природы Наше незнание вероят-
ностей состояний вовсе не гарантирует равенства их реальных значении Если в какой-
нибудь ситуации вероятность проявления одного или нескольких состояний явно и зна-
чительно превосходит вероятности проявления других состояний природы, то решение,
полученное на основании критерия Лапласа, очевидно, будет далеким от наилучшего
По этой причине разработано три других критерия принятия решении в условиях не-
определенности, которые не опираются на вероятности состояний природы Это макси-
минный и максимаксный критерии и критерий минимаксных потерь Ниже эти критерии
будут проиллюстрированы с помощью модели газетного киоска
Максиминный критерий
Этот критерий очень консервативен, он реализует пессимистический подход к приня-
тию решений При использовании этого критерия для каждого решения определяются
наибольшие потери, возможные в случае принятия данного решения Другими словами,
каждое решение оценивается минимумом платежей, возможных при данном решении
В модели газетного киоска, например, решению 3 (решению купить три экземпляра газе-
ты) соответствует минимальный платеж, равный —120 Таким образом, каждому реше-
нию ставится в соответствие минимальное значение в его строке в таблице платежей Для
модели газетного киоска в результате таких действий получим табл 9 5В качестве иско-
мого решения выбираем то решение, которому будет соответствовать максимум мини-
мального значения платежа (отсюда название “максиминныи критерии") В нашем слу-
чае продавец газетного киоска должен купить только один экземпляр газеты (решение 1)
Таблица 9.5 Минимальные платежи для модели газетного киоска
Решение	Минимальный платеж
0	-150
1	-65
2	-80
3	-120
Максиминный критерий часто используется в ситуациях, когда принимающий реше-
ние менеджер не может допустить самого худшего исхода (Примерами таких ситуаций
могут служить планирование оборонных мероприятий или ситуации в медицине, когда
речь идет о сохранении человеческой жизни ) В этом случае менеджер выбирает реше-
ние, которое заведомо избегает наихудшего (наиболее пессимистического) исхода
Конечно, нетрудно привести примеры, когда для большинства людей будет неприем-
лемым решение, полученное на основе максиминного критерия Рассмотрим, например,
таблицу платежей 9 6 Здесь очевидно предпочтительное решение I Оно дает значитель-
но большие платежи для всех состояний природы, кроме третьего, платеж при котором
незначительно хуже платежей решения 2 Однако максиминный критерии выберет
592 ЧАСТЬ III Вероятностные модели
именно решение 2 3 В связи с этим возникает естественный вопрос: если даже на таком
простом примере максиминный критерий дает неудовлетворительное решение, то можно
ли доверять ему в более сложных и ответственных моделях9 Однозначного ответа на та-
кой вопрос не существует Ответ зависит от понимания своих целей и предпочтений ли-
ца, принимающего решения И в связи с этим замечанием будет полезным рассмотреть
еще один критерий, в некотором смысле антипод максиминного критерия, который так-
же применяется при принятии решений в условиях неопределенности.
Таблица 9.6. Пример таблицы платежей
Решение	Состояния природы					
	1	2	3	4	5	6	7	8	9
1 2	100	100	2 3	100	100	100	100	100 3	100 3
Максимаксный критерий
Этот критерии так же оптимистичен, как максиминный пессимистичен Здесь для
каждого решения определяется наибольший соответствующий ему платеж и затем в ка-
честве оптимального решения выбирается решение, которому соответствует максималь-
ный возможный платеж Например, для модели газетного киоска сначала строится таб-
лица (табл. 9 7), содержащая для каждого решения соответствующий ему максимальный
возможный платеж, т е максимальное значение в строке таблицы платежей для данного
решения Тогда искомым решением будет решение 3, т е продавец должен закупить три
экземпляра газеты
Таблица 9.7. Максимальные платежи для модели газетного киоска
Решение	Максимальные платежи
0	0
1	35
2	70
3	105
Максимаксныи критерий можно критиковать с тех же позиций, что и максиминный
Например, на основе таблицы платежей 9 8 максимаксный критерий выберет решение 2,
хотя решение 1 очевидно лучше
Таблица 9.8 Пример таблицы платежей
				Состояния природы			
Решение	1	2	3	4	5	6	7	8	9
1	100	100	100	100	100	100	100	100	100
2	3	3	101	3	3	3	3	3	3
Отметим, что в данном случае критерий Лапласа даст "правильное”решение ] — Прим ред
ГЛАВА 9. Анализ решений 593
Критерий минимаксных потерь
Потери вводят новую меру для определения качества решений, для чего создается но-
вая таблица платежей. Обычно в таблице платежей приводятся значения чистого дохода
или выплат для каждой комбинации возможного решения и возможного состояния при-
роды При использовании критерия минимаксных потерь в таблице платежей приводят-
ся значения потерь, также рассчитанных для каждой возможной комбинации решения
и состояния природы. Покажем расчет потерь для модели газетного киоска (исходная
таблица платежей для этой модели приведена в табл. 9.4).
1. Находим в табл. 9.4 максимальное значение для каждого столбца, соответствую-
щего состоянию природы (например, в столбце, соответствующем состоянию 2,
максимальное значение равно 70).
2. Вычисляем значения таблицы потерь путем вычитания из максимального значе-
ния столбца текущего значения платежа. Например, значение потерь во второй
строке и третьем столбце (состояние природы 2) вычисляется так: 70 — (—15) = 85.
В результате таких вычислений получаем таблицу потерь (табл. 9 9).
Таблица 9.9. Таблица потерь для модели газетного киоска
Состояния природы
Решение	0	1		2	3
0	0	85	170	255
1	40	0	85	170
2	80	40	0	85
3	120	80	40	0
Каждое значение потерь показывает, сколько мы потеряем при различных состояниях
природы, если наше решение будет отличаться от наилучшего (для данного состояния приро-
ды) решения Отсюда следует, что менеджер должен принять такое решение, которое бы ми-
нимизировало потери, но он не знает, каким будет состояние природы Если было бы извест-
но распределение вероятностей состояний природы, то можно было бы выбрать решение, ко-
торому соответствует минимальное ожидаемое значение потерь. (В следующем разделе мы
покажем, что такое решение эквивалентно решению, максимизирующему ожидаемые плате-
жи ) Если вероятности неизвестны, то возникает естественная мысль использовать консерва-
тивный минимаксный критерий выбрать то решение, которому бы соответствовали наимень-
шие из максимальных потерь (т.е следует выбрать наилучшее из наихудшего)
Для модели газетного киоска на основе таблицы потерь (см. табл 9 9) построим таб-
лицу максимальных потерь, выбрав для каждого решения максимальное значение в его
строке в таблице потерь Результат показан в табл. 9.10.
Таблица 9.10. Максимальные потери для модели газетного киоска
Решение	Максимум	потерь
0	255
1	170
2	85
3	120
594 ЧАСТЬ III Вероятностные модели
Теперь выбираем решение, которое минимизирует максимум потерь. В данном случае
критерий минимаксных потерь укажет на решение 2.
В этом разделе мы показали, что в условиях неопределенности без использования ка-
ких-либо предположений о распределении вероятностей состояний природы три критерия
(максиминный, максимаксный и минимаксный) могут дать различные “оптимальные” ре-
шения
9.3.	Принятие решений в условиях риска: ожидаемое
значение полной информации
Вернемся к модели газетного киоска принятия решения в условиях риска
(вероятности спроса указаны в строке 12 рабочего листа Excel на рис 9 2) Напомним,
что в этом примере оптимальным решением для продавца будет закупить два экземпляра
газеты, и ожидаемый результат равен 22 5 Рассмотрим эту модель в немного фантастиче-
ской манере, чтобы было легче ввести понятие ожидаемого значения полной информа-
ции Предположим, что в обычный рабочий день продавца газетного киоска происходят
следующие события (это будет “текущая последовательность событий”)
1.	Волшебник на основе известного распределения спроса на газеты определяет, ка-
ким будет спрос в этот день
2.	Продавец газет, не зная, что спрос на газеты уже определен, но зная распределение
вероятностей спроса, закупил газеты для своего киоска.
3.	В течение рабочего дня проявляется реальный спрос на газеты, и продавец получа-
ет фактический (в отличие от ожидаемого) результат, определяемый тем решени-
ем, которое он принял при закупке газет
Теперь рассмотрим новый сценарий событий Продавец каким-то образом договари-
вается с волшебником В этом случае реализуется другая последовательность событий.
1.	Продавец дает волшебнику взятку
2.	Волшебник определяет спрос на текущий день Здесь важно отметить, что вол-
шебник не может самостоятельно установить спрос Он только обладает знанием о
том, каким сегодня будет спрос на газеты, и это знание (т е информацию) он про-
дает продавцу газетного киоска
3.	Волшебник сообщает продавцу, каким будет спрос на газеты
4.	В соответствии с этой информацией продавец закупает нужное количество экзем-
пляров газет
5.	Продавец в конце рабочего дня получает результат, который, естественно, зависит
от спроса и количества закупленных газет
Возникает вопрос какую максимальную цену за информацию может заплатить про-
давец волшебнику9 Эта наибольшая цена называется ожидаемым значением полной ин-
формации и определяется формулой
цена = ожидаемый результат при знании состояния природы - ожидаемый результат
в текущей последовательности событий (без знания состояния природы)
Зная значение спроса на текущий день, продавец, конечно, закупит столько экземп-
ляров газет, чтобы получить максимальную прибыль Но здесь есть одна сложность- про-
ГЛАВА 9 Анализ решений 595
давец платит волшебнику до того, как он узнает будущий спрос Возвращаясь к таблице
платежей 9 4, мы видим, что если спрос равен нулю, то продавец не должен вообще по-
купать этих газет, и тогда его максимальная ожидаемая прибыль будет равна нулю Нуле-
вой спрос будет реализоваться достаточно редко (его вероятность 0,1), но если волшеб-
ник скажет продавцу, что сегодня фактический спрос равен нулю, то все равно в этот
день у продавца будет нулевая прибыль Аналогично, если с вероятностью 0,3 реализует-
ся спрос, равный 1, то в этом случае максимальная прибыль продавца составит 35 центов
Рассуждая подобным образом, нетрудно прийти к выводу, что в данном случае
ожидаемый результат при знании состояния природы = 0x0,1 + 35 x0,3 + 70x0,4 +
+ 105 x0,2 = 59,5
Ранее мы уже показали, что ожидаемый результат в этой модели (при отсутствии знания
состояния природы) равен 22,5 центов Поэтому
ожидаемое значение полной информации = 59,5 — 22,5 = 37,0 центов
Это максимальная сумма, которую наш продавец газет может заплатить “доброму”
волшебнику за его информацию Хотя рассказанная нами история фантастична, ожи-
даемое значение полной информации имеет большое практическое значение Это верх-
няя граница той суммы платежей, которую вы можете получить при наличии информа-
ции о том, каким будет состояние природы Маркетинговые и другие подобные органи-
зации тратят миллионы долларов для того, чтобы определить состояние природы в том
бизнес-проекте, для которого они проводят исследования Здесь ожидаемое значение
полной информации указывает на ожидаемую величину прибыли от таких исследований,
а также показывает верхнюю границу цены, которую можно заплатить за дополнитель-
ную информацию о возможном состоянии природы
9.4.	Полезность и принятие решения в условиях риска
Полезность — это еще один способ измерить привлекательность или приемлемость
принимаемых решений Другими словами, это еще один способ заполнить таблицу пла-
тежей Мы уже рассмотрели два способа заполнения таблицы платежей значениями при-
были (или убытков), выраженными в денежном эквиваленте, и значениями потерь как
двух мер “доброкачественности” разных комбинаций принимаемых решений и состоя-
ний природы Полезность предлагает другой тип измерения “доброкачественности”
Понятие полезности
В предыдущем разделе мы видели, что максиминный и максимаксныи критерии дают
неприемлемые решения даже на простых иллюстративных моделях Покажем, что крите-
рий максимума ожидаемого значения результата, имеющего денежное выражение, в мо-
делях принятия решений в условиях риска также может привести к неприемлемым ре-
шениям Для примера рассмотрим модель урны В урне содержится 99 белых шаров
и один черный Вам предложили сыграть в следующую игру вы не глядя выбираете один
шар из урны (т е все шары имеют одинаковую вероятность быть выбранным) Если вы
вытянули белый шар, то платите 10 тыс долл , а если черный — получаете I млн долл
Вы должны решить, играть в такую игру или нет Таблица платежей для этой игры пока-
зана в табл. 9 11
596 ЧАСТЬ III Вероятностные модели
Таблица 9.11. Таблица платежей
Решение	Состояния природы	
	Белый шар	Черный шар
Играть	-10 000	1 000 000
Не играть	0	0
Используя значения платежей и значения вероятностей 0,99 (вероятность вытянуть
белый шар) и 0,01 (вероятность вытянуть черный шар), подсчитаем ожидаемый результат
для каждого возможного решения
ЕЯ(играть) = -10 000 х 0,99 + I 000 000 х 0,01 = -9900 + 10000 = 100,
ЕЯ(не играть) = 0 х 0,99 + 0 х 0,01 = 0
Поскольку ЕЯ(играть) > ЕЯ(не играть), то в соответствии с критерием максимизации
ожидаемого результата выбираем решение “играть”.
Теперь вернитесь на шаг назад и спросите себя, хотите ли вы сыграть в такую игру
Помните, что вероятность потерять 10 тыс долл составляет 0,99 Многие люди найдут
такой большой риск потери неприемлемым, т е они скорее всего отбросят решение, по-
лученное в соответствии с критерием максимизации ожидаемого результата. Таким обра-
зом, мы снова приходим к проблеме выбора подходящего критерия Эта проблема вста-
нет еще более остро, если рассматривать не простые иллюстративные примеры,
а сложные модели, отображающие реальные жизненные ситуации Наглядный пример из
реальной жизни, когда люди отказываются следовать за решением, полученным в соот-
ветствии с критерием максимизации ожидаемого результата, — это страхование приобре-
тенного автомобиля Предположим, вы купили новый спортивный автомобиль и теперь
решаете, страховать ли его от возможных аварий или нет Фактически вы выбираете ме-
жду покупкой страховки и азартной игрой (что вы не попадете в аварию) Многие люди
выбирают покупку страховки, даже если они уверены в том, что страховые взносы пре-
вышают стоимость возмещения ущерба от аварии
К счастью, нет необходимости полностью отказываться от критерия максимального
ожидаемого результата — нужно только осознать, что платежи, выраженные в денежном
эквиваленте, не всегда отображают предпочтительность результата, получаемого от при-
нимаемого решения Чтобы прояснить эту мысль, спросите себя, хотите ли вы рискнуть
10 центами, сыграв с судьбой в орлянку, т е выиграть или потерять 10 центов в зависи-
мости от того, как упадет монета после подбрасывания (Уверен, что большинство людей
согласятся ) Ну, а если в зависимости от подбрасывания этой же монеты вы можете вы-
играть или потерять 10 тыс долл 9 (Уверен, что большинство людей не согласятся ) В чем
же разница9 В первом случае прибыль в 10 центов уравновешивается потерей 10 центов
Почему же прибыль в 10 тыс долл не уравновешивается потерей тех же 10 тыс долл 9
Ответ заключается в том, что большинство людей избегают риска Это значит, что для них
сама возможность потери 10 тыс долл настолько болезненна, что она не компенсируется
возможной прибылью в 10 тыс долл
Анализ решений, учитывающий подобные психологические аспекты поведения лю-
дей, требует введения специальной функции, которая бы измеряла “привлекательность”
денег Такая функция называется функцией полезности, здесь слово полезность трактуется
как мера “удовлетворительности” Типичная функция полезности для лица, избегаю-
щего риск, показана на рис 9 6 Эта функция имеет следующие свойства
ГЛАВА 9 Анализ решений 597
1. Она не убывает, поскольку больше денег всегда предпочтительнее меньшего их
количества
2. Ее график вогнутый Это означает, что относительная полезность денег не возрас-
тает Рассмотрим подробнее этот феномен, опираясь на график функции полезно-
сти (рис 9 6)
Рис. 9.6. Типичная функция полезности для лица, избе-
гающего риска
Сначала предположим, что у вас есть $100 и некто дал вам еще $100 В этом случае по-
лезность денег возрастет на величину
£7(200) - £7(100) = 0,680 - 0,524 = 0,156.
Если же у вас есть $400 и некто снова дает вам $100, то в этом случае полезность воз-
растет на величину
£7(500) - £7(400) = 0,910 - 0,850 = 0,060.
Другими словами, 100 дополнительных долларов для вас менее привлекательны, если у вас
на руках уже есть $400, чем если бы у вас было только $100, Можно посмотреть на этот фено-
мен с другой точки зрения: при выигрыше определенной суммы полезность возрастает на
меньшую величину, чем величина убывания полезности при потере такой же суммы Напри-
мер, мы уже видели, при выигрыше $100 при имеющейся сумме $400 полезность возрастает на
величину 0,060 Если же при начальной сумме $400 потерять $100, то полезность уменьшится
на величину £7(400) - £7(300) = 0,850 - 0,775 = 0,075, что больше величины 0,060,
На рис. 9 7 показаны функции полезности двух других основных типов. Первая функ-
ция — это функция полезности для лица, настроенного на риск Здесь при выигрыше оп-
ределенной суммы денег полезность возрастает на большую величину, чем величина убы-
вания полезности при потере той же суммы денег. Например, если при начальной сумме
$200 вы выиграете $100, то полезность возрастет на величину
£7(300) - £7(200) = 0,590 - 0,260 = 0,330.
Если же при начальной сумме $200 вы проиграете $100, то полезность уменьшится на ве-
личину
£7(200) - 6/(100) = 0,260 - 0,075 = 0,185.
598 ЧАСТЬ III Вероятностные модели
Таким образом, для лица, настроенного на риск, более привлекателен выигрыш, на про-
игрыш он обращает значительно меньше внимания Эта позиция противоположна пози-
ции лица, избегающего риска, чья функция полезности показана на рис. 9 6
Функция полезности для лица, нейтрального к риску, показана с правой стороны на
рис 9 7 Здесь выигрыш или потеря одинаковой суммы денег изменяет значение полез-
ности на одинаковую величину
Настроенность на риск	Нейтральность к риску
Рис. 9.7. Другие типы функции полезности
Создание и применение функции полезности
Рассмотрим два метода построения функции полезности Первый метод точнее, но бо-
лее сложный и длительный Второй метод более быстрый, поскольку предусматривает, что
известна форма функции полезности В первом методе менеджеру (в нашем случае это бу-
дет продавец газет) предлагается сделать серию выборов между гарантированной суммой
денег и случайным выигрышем Этот метод называется методом эквивалентной лотереи
Рассмотрим подробнее построение функции полезности с помощью этого метода.
Сначала надо определить диапазон изменения аргумента функции полезности, а так-
же диапазон изменения самой функции. Обычно за минимальное значение аргумента
принимается наименьшее значение денежного платежа, при этом значение функции по-
лезности считается равным нулю, за максимальное значение аргумента принимается
наибольшее значение денежного платежа, значение функции при этом считается рав-
ным 1 В примере газетного киоска наименьшее значение денежного платежа равно —150
(см табл 9 4), а наибольшее — +105, поэтому (/(-150) = 0 и (7(105) = 1.
Наступает самый сложный этап определения значений функции полезности. Напри-
мер, мы хотим определить значение функции полезности от аргумента 10 (т е. надо найти
значение 17(10)) Продавец газет должен выбрать такую вероятность р, при которой сле-
дующие альтернативы будут для него равнозначными.
1. Получить гарантированный платеж 10
2. Участвовать в лотерее, в которой с вероятностью р можно выиграть 105 или с веро-
ятностью 1 — р потерять 150 (т е получить платеж —150)
Очевидно, что если р = 1, то лицо, принимающее решение, предпочитает второй ва-
риант, поскольку в этом случае он также гарантированно получает платеж 105 вместо 10
ГЛАВА 9 Анализ решений 599
Аналогично, если р = 0, то лицо, принимающее решение, предпочитает первый вариант,
так как в этом случае он получает гарантированный платеж 10 вместо —150. Таким обра-
зом, приходим в выводу, что если эти две альтернативы действительно равнозначны для
лица, принимающего решения, то значение р должно находиться между 0 и 1 и не должно
равняться этим крайним значениям После того как лицо, принимающее решение, в со-
ответствии со своими предпочтениями определит значение р, оно принимается за значе-
ние функции £/(10) Допустим, менеджер определил, чтор = 0,6 Тогда ожидаемое значе-
ние платежа в лотерее равно 0,6 х 105 + 0,4 х (-150) = 3. Таким образом, менеджеру оди-
наково “интересно” получить гарантированно 10 или сыграть в игру с меньшим
ожидаемым выигрышем (равным 3) Это означает, что наш менеджер настроен на риск,
поскольку он готов заплатить (потерять гарантированный платеж 10) за возможность
сыграть с судьбой в лотерею больше, чем ожидаемый выигрыш в этой лотерее
Теперь предположим, что менеджер выбрал вероятность р - 0,8 Тогда ожидаемый
платеж игры в лотерею равен 0,8 х 105+ 0,2 х (-150) = 54,0 Это означает, что данный
менеджер избегает риска, поскольку ему требуется значительный ожидаемый платеж
в лотерее (по сравнению с гарантированным платежом), чтобы согласиться на игру Оче-
видно, что, чем больше выбираемое значение вероятности р, тем больше лицо, прини-
мающее решение, избегает риска
Решив уравнение
р х 105 + (1 - р) х (-150) = 10,
255/? — 150= 10,
р= 160/255 = 0,6275,
найдем значение р, для которого ожидаемое значение результата лотереи равно гаранти-
рованному платежу 10 Если человек, принимающий решение, выбирает значение р
больше 0,6275. это значит, что он избегает риска Если р равно 0,6275, он нейтрален
к риску, и, еслир меньше этой величины, он настроен на риск
Повторяя описанную процедуру для других значении аргумента функции полезности,
мы определяем ее значения Это достаточно сложная и кропотливая работа, требующая
как знания теории вероятностей, так и большого терпения Иногда определяю, функцию
полезности не как индивидуальные предпочтения лица, принимающего решения, а как
отношение фирмы к денежному риску, те определяют корпоративную (обобщенную)
точку зрения Очевидны различия между индивидуальной функцией полезности (когда
индивидуум боится потерять несколько тысяч долларов) и корпоративной (когда фирма
оперирует миллионами долларов) Поэтому мы не утверждаем, что определение вероят-
ностей р с помощью лотереи является объективным способом построения функции по-
лезности Мы также не будем открывать дискуссию по поводу, почему все-таки этот под-
ход работает и используется на практике, поскольку эта тема выходит за рамки нашей
книги — мы ее оставим для более развернутого курса
Из-за сложностей, которые упоминались выше, разработан другой метод оценивания
функции полезности, когда заранее определена ее форма Обычно за основу берется >кс-
поненциальная функция (в таком случае это функция полезности для лица, избегающего
риска), где требуется определить только один параметр Такая функция используется при
анализе решений, связанных с инвестициями, и во многих других бизнес-приложеииях
Функция имеет вид
U(x) = 1 - е
600 ЧАСТЬ III Вероятностные модели
где х— денежная сумма, которой мы должны приписать определенное значение
полезности Функция зависит от одного неизвестного параметра г, который определяет
меру предрасположенности к риску Чем больше значение г, тем меньше компания или
индивидуум избегает риска (т е они могут пойти на больший риск) И, наоборот, чем
меньше значение г, тем больше компания или индивидуум избегает риска.
Существует много способов определения значения параметра г Два простейших спо-
соба будут показаны ниже В первом менеджер должен определить такую денежную сум-
му г, чтобы для него были бы равнозначны следующие два варианта
1. Игра, где с вероятностью 50 на 50 можно было бы выиграть г долларов или поте-
рять г/2 долларов
2. Не играть и “остаться при своих’’ (нулевой платеж)
Например, продавцу газет одинаково “привлекательно” ничего не потерять и не при-
обрести или с вероятностью 0,5 выиграть $100 с возможностью с такой же вероятностью
потерять $50 В этом случае г равно $100
Второй способ определения величины г основан на эмпирических данных, собранных
известным специалистом в области теории принятия решений Роном Ховардом (Ron How-
ard) Д-р Ховард консультирует многие компании, он нашел очень полезную эмпирическую
зависимость между величинами чистой прибыли, капитала, объемом чистых продаж ком-
пании и ее предрасположенностью к риску Он считает, что значение г приблизительно
равно 124% от чистой прибыли, 15,7% от капитала и 6,4% от объема чистых продаж (в де-
нежном эквиваленте) Например, большая компания с чистым доходом в 1 млрд долл име-
ет г порядка 1,24 млрд , тогда как небольшая компания, у которой объем продаж составляет
5 млн долл , имеет значение г, приблизительно равное 320 000 Конечно, эти значения
только оценочные, но они очень полезны и показывают, что большие компании имеют
большее значение г и, следовательно, в меньшей степени избегают риска
Вернемся к нашему продавцу газет и определим для него функцию полезности. По-
скольку его бизнес очень маленький (т е он не может позволить себе расходы на построе-
ние функции полезности с помощью первого метода), предпочтительнее использовать экс-
поненциальную функцию полезности, опредетив один параметр г. Далее с помощью опи-
санного выше подхода (равнозначность нулевого платежа и игры с вероятностью 50 на 50
выиграть г долларов или потерять г/2 долларов) он определил, что значение г равно $100.
Теперь он хочет ввести функцию полезности в рабочую книгу Газеты на новый рабочий
лист Полезность и рассчитать полезность для всех возможных денежных платежей. На ос-
нове рассчитанных значений полезности можно найти новое оптимальное решение, ис-
пользуя процесс вычисления ожидаемого результата при условии, что известны вероятно-
сти всех состояний природы. Здесь важно понять, что на основе построенной функции по-
лезности продавец газет создает новую таблицу платежей, где вместо денежных платежей
приведены их значения полезности Например, в таблице платежей 9 4 решению 2 и треть-
ему состоянию природы (когда спрос на газеты равен 2) соответствует денежный платеж 70
центов Функция полезности (рис. 9.8) переводит это денежное значение в значение полез-
ности, равное 0,50. Именно это значение теперь будет платежом для данной комбинации
решения и состояния природы. Далее процесс нахождения оптимального решения хорошо
известен вычисляются ожидаемые значения результата (полезности) для каждого решения
и выбирается то решение, для которого ожидаемое значение будет наибольшим На рис. 9 8
вычисленные ожидаемые значения полезности приведены в столбце F. На этом же рисунке
показана построенная функция полезности.
ГЛАВА 9 Анализ решений 601
Рис. 9.8. Рабочий лист Полезность
Для создания рабочего листа Полезность необходимо выполнить следующие действия
1.	В рабочей книге Газеты вставьте новый лист и назовите его Полезность.
2.	Скопируйте ячейки А5 F12 с рабочего листа Базовый на новый рабочий лист По-
лезность. Введите значение 100 (значение параметра г) в ячейку В14. Затем изме-
ните формулу в ячейке В7 на =1-ЕХР(-Базовый!В7/$В$14) и скопируйте ее в диа-
пазон В7:Е 10
3.	Теперь введите начальное значение-150 в ячейку Al 7.
4.	Далее вернитесь в ячейку А17 и выполните команды Правка^Заполнить^
Прогрессия.
5.	Убедитесь, что в открывшемся диалоговом окне Прогрессия установлен переклю-
чатель Расположение по столбцам, введите шаг 5 и предельное значение 105
Щелкните на кнопке ОК
602 ЧАСТЬ III Вероятностные модели
6.	Введите показанную на рис 9 8 формулу в ячейку В17 и скопируйте ее вниз до
ячейки В68
7.	На основе данных диапазона А17 В68 с помощью мастера диаграмм постройте
график функции полезности
В столбце F на рис. 9 8 показаны ожидаемые значения полезности для каждого воз-
можного решения Максимальное значение имеет решение 2 (ожидаемое значение по-
гезности равно 0,10), поэтому в данном случае для продавца газет оптимальным будет это
решение, что совпадает с решением, полученным в разделе 9 2 при рассмотрении модели
принятия решения в условиях риска Однако так бывает далеко не всегда. Это скорее ис-
ключение из правила — обычно решения, принимаемые на основе критерия максимума
ожидаемых значений денежных платежей, не совпадают с решениями, полученными на
основе функции полезности Чтобы проиллюстрировать это утверждение, рассмотрим
более реальный пример страхования автомобилей
Кэрол Лейн уже 10 лет как закончила Стэнфордскую высшую школу бизнеса и сейчас
имеет возможность купить новый великолепный автомобиль Lexus Она позвонила
в страховую компанию и узнала, что ежегодная страховая премия за безаварийную езду
составляет $1000 с обязательным платежом $250 (т е страховой полис стоит $1250, из ко-
торых ей возвращается $1000, если она не попадет в аварию в текущем году) Поскольку
Кэрол очень осторожно водит автомобиль, вероятность аварии в следующем году состав-
ляет 0,50%, стоимость потерь в случае аварии составляет $50 000 При покупке автомоби-
ля она сразу внесла все деньги (купила не в рассрочку), поэтому она является полной
владелицей этого чуда на колесах и ей не требуется обязательная страховка Возникает
вопрос страховать Lexus или не страховать9
Платежи
. I. в
1 .Ежегодная премия 1000
2 Обязательный плат 250
Состоя
Авария Нет до; Ожидаемый платеж
Страховать =В2+В1 =В1
Не cmpaxoeat =В6	0
Вероятности
=СУММПРОИЗВ(ЕЭ.РЗ;$Е$6:$Р$6)
=СУММПРОИ
5 Вероятность аварие0.005
6 Потери при аварии 50000
Рис. 9.9. Рабочая книга Автострах
Кэрол смоделировала свою ситуацию в рабочей книге Excel, показанной на рис 9 9
(книга названа Автострах) Исходя из критерия максимизации ожидаемого результата
для нее лучшим решением будет не страховать автомобиль (потеря, в среднем, $250 про-
тив потери $1001,25) Однако она понимает, что решение не может быть таким простым,
и чувствует некоторый душевный дискомфорт Она вспомнила о концепции полезности,
которую изучала в школе бизнеса, и решила применить ее к своей ситуации Себя она
ГЛАВА 9 Анализ решений 603
считает не склонной к риску Поэтому для построения функции полезности использова-
ла экспоненциальную функцию, где параметр г определила равным $10 000 (Первый ме-
тод (на основе игры 50 на 50) определения параметра предопределенной функции полез-
ности ) Она создала новый рабочий лист Полезность в той же самой рабочей книге, пе-
ренеся на этот лист данные с первого листа Этот лист показан на рис 9 10
Результаты расчетов на листе Полезность показывают, что решение “Страховать”
максимизирует ожидаемое значение полезности (-0,11 против -0,74) (Отрицательные
значения полезности указывают на возможные денежные потери ) Кэрол приняза это
решение, купила страховой полис и успокоила себя тем, что в случае аварии ей не при-
дется одной выкладывать все $50 000 на возмещение ущерба
Рис. 9.10. Рабочий лист Полезность
9.5.	Промежуточные итоги
Предыдущие разделы являются теоретическим фундаментом для материала остав-
шейся части этой главы Далее мы опишем методы и процедуры, которые играют важную
роль в исследовании моделей принятия решений для реальных управленческих ситуаций
Перед тем как двигаться дальше, будет полезным подвести промежуточные итоги того,
что мы уже знаем
В разделе 9 2 предложена классификация моделей, определенных как модели приня-
тия решений против природы Эти модели описываются таблицами платежей, в которых
604 ЧАСТЬ III Вероятностные модели
приведены значения платежей (возвращаемого результата), зависящих от выбираемого
решения и возможного состояния природы. Мы описали три класса таких моделей.
1.	Модели принятия решений в условиях определенности. Здесь лицо, принимающее
решение, точно знает, в каком состоянии будет природа. Остается “только” вы-
брать наилучшее решение Моделями этого класса являются детерминированные
модели, такие как модели линейного, целочисленного и нелинейного программи-
рования и другие оптимизационные модели.
2.	Модели принятия решений в условиях риска. В этих моделях известно распределе-
ние вероятностей всех состояний природы, для выбора “наилучшего решения”
применяются следующие критерии
а.	Максимизация ожидаемого результата, выраженного в виде денежных платежей
Ь.	Минимизация ожидаемых потерь
с.	Максимизация ожидаемого результата, выраженного в виде значения полез-
ности.
Мы показали, что критерии а и b всегда приводят к одинаковым решениям. Боль-
шинство управленческих моделей принадлежат классу моделей принятия решения
в условиях риска.
3.	Модели принятия решений в условиях неопределенности. Здесь лицо, принимающее
решения, не знает вероятностей наступления того или иного состояния природы
В этой ситуации можно применить критерий Лапласа: присвоить всем возможным
состояниям природы одинаковые вероятности их осуществления и затем выбрать
решение, максимизирующее ожидаемый результат. Альтернативой критерию Лап-
ласа могут служить критерии, не использующие вероятности состояний природы.
Существует три таких критерия.
а.	Максиминный критерий, максимизирующий минимум денежных платежей.
Ь.	Максимаксный критерий, максимизирующий максимум денежных платежей
с.	Критерий минимаксных потерь, минимизирующий максимум потерь.
Эти критерии в общем случае порождают различные решения.
В разделе 9.3 описано понятие ожидаемого значения полной информации. Это поня-
тие играет важную роль, поскольку устанавливает верхнюю границу для цены за инфор-
мацию о том, в каком состоянии будет природа.
Наконец, в разделе 9.4 мы рассмотрели полезность как меру приемлемости для каж-
дой комбинации возможного решения и возможного состояния природы. Функция по-
лезности используется в тех случаях, когда решения, максимизирующие ожидаемые де-
нежные платежи, в силу тех или иных причин (часто субъективных) не приемлемы. Мы
также рассмотрели методы построения функции полезности.
В оставшейся части этой главы мы углубленно исследуем наиболее общие модели
принятия решений — модели принятия решения в условиях риска. Мы опишем деревья
решений, полезный метод практического исследования моделей принятия решений, для
их построения используем надстройку TreePlan. Также рассмотрим два важных подхода:
использование новой информации в процессе принятия решений и анализ моделей по-
следовательных решений.
ГЛАВА 9 Анализ решений 605
9.6.	Деревья решений
Деревья решений — это графическое средство анализа решений в условиях риска Де-
ревья решений создаются для использования в моделях, в которых принимается последо-
вательность решений, каждая из которых ведет к некоторому результату (выходу моде-
ли). Например, концессионеры решают, сколько заявок послать на региональные торги
Но результат этого решения не определен, пока они не решат, в каких торгах участвовать
Только после этого можно решить, на какие суммы посылать заявки. Но и после этого
результат, если его рассматривать как доход от торгов, не определен, поскольку не извес-
тен спрос на их товар.
Наше обсуждение деревьев решений будет построено следующим образом в этом
разделе будут введены основные понятия, относящиеся к деревьям решений, и будет
описана надстройка TreePlan, создающая эти деревья в электронных таблицах Эта над-
стройка разработана Майклом Мидлтоном (Michael Middleton) и является условно-
бесплатной программой (Если вам понравится эта программа и вы захотите использо-
вать ее в дальнейшем, вам необходимо будет сделать небольшой регистрационный взнос
Подробности можно найти в справочной системе программы TreePlan или на Web-узле
http //www treeplan com )4 В разделе 9 7 будет проведен анализ чувствительности опти-
мального решения при изменении значении вероятностей состояний природы В разде-
ле 9 8 будет показано, как с помощью теоремы Байеса можно включить новую информа-
цию в процесс принятия решений Модель последовательных решений рассмотрена
в разделе 9 9 Дальнейший материал будет проиллюстрирован на модели принятия реше-
ний для фирмы Sonorola, которая занимается производством мобильных телефонов
Альтернативные стратегии
В фирме Sonorola заканчивается этап разработки и тестирования нового ряда моделей
мобильных телефонов Высшее руководство фирмы разрабатывает стратегию производ-
ства и продвижения на рынок этих моделей телефонов. Рассматриваются три основные
стратегии (решения)
1.	Агрессивная стратегия Эта стратегия в наибольшей степени соответствует ожида-
ниям фирмы от разработанного ряда моделей Основные капитальные вложения
будут сделаны в разработку нового и эффективного производственного оборудо-
вания. Большие инвестиции должны гарантировать продвижение на рынок всех
разработанных моделей телефонов Маркетинговая компания предусматривает
покупку рекламного времени на телевидении всех основных мировых рынков
и скидки для дилеров
2.	Базовая стратегия Производство текущих моделей телефонов переносится из То-
кио в Осаку, что, очевидно, вызовет “головную боль” у руководства фирмы В то
же время существующая производственная линия в Токио модернизируется и пе-
реналаживается для производства новых моделей телефонов Значительные инве-
стиции будут сделаны для продвижения на рынок только наиболее популярных
моделей Фирма рассчитывает на проведение локальных и региональных реклам-
ных компаний, не выходя на глобальный уровень рекламной компании
Версия Education данной надстройки, помещенная на компакт-диск книги, является бесплатной для чита-
телей, купивших эту книгу — Прим ред
606
ЧАСТЬ III Вероятностные модели
3.	Осторожная стратегия При этой стратегии для производства новых моделей теле-
фонов будут использоваться только “излишки” производственных мощностей, за-
действованные в настоящее время для производства текущих моделей телефонов
Модернизация производственных средств сведена до минимума. Объем производ-
ства новых телефонов ограничен спросом Рекламные материалы рассылаются
выборочно региональным дилерам.
Руководство фирмы решило оценивать ситуацию на рынке мобильных телефонов
(т е спрос на их продукцию) по двум градациям, как благоприятную и как неблагоприят-
ную (Конечно, в реальности спрос является непрерывной величиной, но для простоты мы
ограничимся двумя состояниями рынка благоприятным и неблагоприятным ) На рис 9 11
представлена рабочая книга (называется Sonorola), в которую введены таблица платежей и
оценки вероятностей состояния рынка Значения платежей измеряются в миллионах
долларов и вычисляются с учетом объемов продаж, цен и прибыли, рассчитанных для всех
комбинации решений (стратегий) и состояний природы (состояний рынка) Интересно
отметить, что осторожная стратегия дает наибольший доход в условиях неблагоприятного
рынка, а агрессивная — в условиях благоприятного Однако оптимальным решением,
найденным в соответствии с критерием максимизации ожидаемого результата, является ба-
зовая стратегия, для которой ожидаемое значение платежей составляет $12,85 млн
(см данные в столбце D на рис 9 11)
Рис. 9.11. Рабочий лист с моделью принятия решений для фирмы Sonorola
Создание дерева решений
Рассмотренную модель можно также представить в виде дерева решений, как будет пока-
зано ниже Введем некоторые определения для деревьев решений Узел решений (обозначается
квадратиком, вТгееР1ап называется decision node) соответствует точке, в которой принимаются
решения, каждая линия, выходящая из квадратика, соответствует какому-нибудь решению
Узел событии (обозначается кружочком, в TreePlan называется event node) соответствует ситуа-
ции, в которой выход модели не определен Линии, выходящие из кружочка, представляют
соответствующие выходы модели Термин ветви (branches в TreePlan) обозначает линии, со-
ГЛАВА 9 Анализ решений 607
единяющие узды любых типов Опишем последовательность действий, необходимых для соз-
дания дерева решений для модели фирмы Sonorola
1.	Установите табличный курсор в ячейке А10 и выполните команду Сервис^
Decision Tree (Если в меню Сервис нет команды Decision Tree, значит, над-
стройка TreePlan еще не установлена Чтобы ее установить, выполните команду
Сервис=Жадстройки, в диалоговом окне Надстройки щелкните на кнопке Обзор
и найдите файл TREEPLAN XLA на своем жестком диске (или в сети) Дважды
щелкните на найденном файле TREEPLAN XLA, затем на кнопке ОК в окне Над-
стройки. Команда Decision Tree появится в меню Сервис )
2.	В открывшемся диалоговом окне TreePlan New щелкните на кнопке New Tree
(Новое дерево). Программа по умолчанию нарисует простое дерево с одним узлом
решений и двумя исходящими из него ветвями
3.	Поскольку Sonorola имеет три стратегии-решения, необходимо добавить еше одну
ветвь Для этого нажмите комбинацию клавиш <Ctrl+t>, которая вызывает контек-
стное меню TreePlan
4.	В открывшемся диалоговом окне TreePlan Decision щелкните на переключателе
Add branch (Добавить ветвь), а затем — на кнопке ОК
5.	В ячейках рабочего листа, в которых сейчас для ветвей записаны метки Decision 1,
Decision 2 и Decisions (Решение 1, Решение 2 и тд), задаваемые TreePlan по
умолчанию, введите названия Агрессивное, Базовое и Осторожное
6.	Далее надо заменить конечные узлы, которыми заканчиваются ветви, узлами со-
бытий Для этого щелкните на конечном узле (точнее, на ячейке рабочего листа,
где заканчивается ветвь) и нажмите комбинацию клавиш <Ctrl+t> Откроется диа-
логовое окно TreePlan Terminal, показанное на рис 9 12
7.	Щелкните сначала на переключателе Change to event node (Изменить на узел со-
бытий), затем в области Branches (Ветви) установите переключатель Two (Два),
указывая тем самым, что надо вставить узел событий с двумя ветвями Затем
щелкните на кнопке ОК
8.	TreePlan добавит к дереву новый узел, как показано на рис 9 13 Отметим, что ка-
ждому событию по умолчанию присваивается вероятность 0,5 и даются имена
(в данном случае Event 4 и Event 5 (События 4 и 5))
9.	Измените названия событий Event 4 и Event 5 на Благоприятное и Неблагоприятное
Замечание. Теперь надо повторить п 6—9 для того, чтобы заменить два других конеч-
ных узла узлами событий Однако TreePlan имеет средство копирования узлов (и частей
деревьев), которым мы сейчас воспользуемся
10.	Чтобы скопировать узел (или часть дерева), щелкните на ячейке, содержащей этот
узел, и нажмите <Ctrl+t>.
11.	В окне TreePlan Event щелкните на переключателе Copy subtree (Копировать
поддерево) и затем на кнопке ОК
12.	Щелкните на ячейке, в которую хотите скопировать узел (в данном случае конеч-
ный узел, которым заканчивается ветвь от решения Базовая), нажмите <Ctrl+t>
В открывшемся окне TreePlan Terminal щелкните на переключателе Paste subtree
(Вставить поддерево) и затем на кнопке ОК
608 ЧАСТЬ III Вероятностные модели
13.	Повторите последние действия (п. 10-12) для последнего конечного узла.
14.	В результате описанных действий вы получите дерево, подобное показанному на
рис. 9 14.
Рис. 9.12. Добавление узла событий к дереву решений
Рис. 9.13. Часть дерева решений для модели Sonorola
ГЛАВА 9. Анализ решений 609
Рис. 9.14. Дерево решений для модели Sonorola
Для завершения дерева решений надо еще задать конечные значения для ветвей ре-
шений и вероятности для событий, что мы сделаем в следующем разделе Рассмотрим
сначала полученное дерево решений Как показано на рис. 9.14, начальный узел дерева
расположен в ячейке В24. Поскольку этот узел изображен в виде квадратика, значит, это
узел решений. Менеджер может выбрать одно из трех возможных решений, которые со-
ответствуют агрессивной, базовой или осторожной стратегиям. В зависимости от вы-
бранного решения мы приходим к новой позиции на дереве решений. Например, выбор
агрессивной стратегии приведет от ячейки В24 к ячейке F14, в которой расположен узел
событий (обозначен кружком). Из этого узла можно достичь конечных узлов (terminal
nodes), расположенных в ячейках J12 и J17 Но какой из этих узлов будет достигнут, зара-
нее не известно. Известны только вероятности осуществления событий, соответствую-
щих ветвям, исходящим из узла событий. В данной модели такими случайными собы-
тиями являются состояния рынка (благоприятное или нет).
Ввод вероятностей и конечных значений
Дерево решений — прекрасный способ визуализации взаимосвязей между принимае-
мыми решениями и случайными событиями, от которых зависят результаты решений
Но, чтобы с помощью дерева решений найти оптимальное решение, необходимо на
диаграмму дерева добавить числовые значения для каждого конечного узла. Эти значе-
ния в TreePlan называются конечными значениями (terminal value). Необходимо также за-
дать вероятности для каждой ветви, исходящей из узлов событий. Для этого выполните
следующие действия.
610 ЧАСТЫП Вероятностные модели
1. В ячейках НЮ и Н15 замените значения вероятностей 0,5, заданных TreePlan по
умолчанию, формулами =В1 (даст значение 0,45) и =С1 (даст значение 0,55) соот-
ветственно. Аналогичные изменения сделайте в ячейках Н20, Н25, Н30 и Н35.
(Отметим, что если сумма вероятностей, приписанных ветвям, исходящим из од-
ного узла события, не равняется единице, то вместо значения ожидаемого резуль-
тата для узла события в ячейке, расположенной слева от этого узла, появится со-
общение об ошибке #Н/Д, что указывает на необходимость изменения значения
вероятностей.)
2. Измените значения для ветвей, которые в TreePlan по умолчанию установлены ну-
левыми Например, в ячейке Н13 (соответствует комбинации агрессивной стра-
тегии и благоприятному состоянию рынка) введите формулу =В5 (соответствует
платежу $30 млн в таблице платежей на рис. 9.11). Далее в ячейку Н18
(соответствует комбинации агрессивной стратегии и неблагоприятному состоя-
нию рынка) введите формулу =С5 (соответствует платежу -30 в таблице плате-
жей). Подобным образом в ячейки Н23, Н28, НЗЗ и Н38 введите формулы =В6,
=С6, =В7 и =С7 соответственно.
Дерево решений после ввода значений и вероятностей показано на рис 9.15.
Рис. 9.15. Законченное дерево решений для модели Sonorola
Обратный пересчет
Теперь на основе построенного дерева решений необходимо найти оптимальное решение.
Надстройка TreePlan выполняет необходимые для этого вычисления автоматически. Эти вы-
числения выполняются в обратном порядке, начиная не с корневого узла, ас конечных узлов
событий, для которых вычисляются ожидаемые значения (такой процесс вычислений называ-
ГЛАВА 9. Анализ решений 611
ется обратным пересчетом). Для примера рассмотрим узел событий, расположенный в ячейке
F14(cm рис 9.15) Ожидаемое значение для этого узла вычисляется так:
ожидаемое значение = 30 х 0,45 + (-8) х 0,55 = 9,10.
Это значение записывается рядом с данным узлом в ячейке Е14. Аналогично выполняют-
ся вычисления для узлов событий F24 и F34. Отметим, что вычисленные ожидаемые зна-
чения для узлов событий (см рис 9.15) совпадают с ожидаемыми результатами для соот-
ветствующих решений, которые показаны на рис. 9 11. Теперь менеджер должен просто
выбрать решение, которому соответствует наибольшее ожидаемое решение. В данном
случае это будет решение 2 (базовая стратегия), на что указывает и TreePlan, поместив
цифру 2 (вторая ветвь) в ячейку В24 узла решений.
Вычисления на более сложных деревьях TreePlan производит таким же способом. Для
каждого узла событий вычисляется сумма ожидаемых значений всех ветвей, исходящих
из этого узла, а для каждого узла решений определяется “наилучшая” ветвь (имеющая
наибольшее ожидаемое значение) среди всех ветвей, исходящих из этого узла.
В данном разделе приведен простой пример анализа модели принятия решений с по-
мощью дерева решений. В разделах 9.8 и 9.9 будут показаны более сложные деревья ре-
шений и способы их использования Здесь мы еще раз подчеркнем, что деревья решений
предлагают только другое представление (графическое) исходной модели принятия решений.
Вычисления, необходимые для определения оптимального решения, используются как
в табличных моделях, так и в случае представления моделей в виде деревьев решений
	Oglethorpe Power Corporation: делать ли
	инвестиции в систему передачи электроэнергии?
В последние годы оптовый рынок электроэнергии на юго-востоке США стано-
вится все более активным Население Флориды и его потребность в электроэнергии
растут быстрее, чем возможности производства электроэнергии этого штата В то же
время в соседних штатах, таких как Джорджия, имеются излишки электроэнергии.
В результате часть энергии из соседних штатов (Джорджия, Алабама и Южная Каро-
лина) передается во Флориду
Компания Oglethorpe Power Corporation (ОРС) — это генерирующее и постав-
ляющее электроэнергию на оптовый рынок предприятие. Оно производит и продает
примерно 20% электроэнергии штата Джорджия. В 1990 году руководство ОРС узна-
ет, что компания из Флориды Florida Power Corporation (FPC) хочет увеличить по-
ставку электроэнергии из Джорджии с помощью новой 500-киловольтной линии
электропередач (ЛЭП) с пропускной способностью более 1000 МВ. Перед компани-
ей ОРС встает вопрос- участвовать ли в строительстве новой линии электропередач
и, если участвовать, то в какой форме. Возможны три решения: 1) строить ЛЭП
в одиночку, 2) строить совместно с компанией Georgia Power, 3) не участвовать
в строительстве В зависимости от структуры инвестиций и формы дальнейшего
управления новой ЛЭП компании ОРС надо вложить не менее $100 млн. с после-
дующей ежегодной прибылью более $20 млн. Такие инвестиции в компании счита-
ются очень большими, в то время как прибыль составляет всего несколько процен-
тов от ее годового бюджета.
Поскольку принимается серьезное решение, компания ОРС проводит формальный
анализ всех вариантов. Отметим, что благодаря усилиям исследовательского института
электроэнергии (Electric Power Research Institute) в CHIA в последнее время анализ на
612	ЧАСТЬ III. Вероятностные модели
основе теории принятия решений завоевывает все большую популярность в энергетике.
После анализа возможных решений в ОРС пришли к выводу, что ни одно из них не имеет
явных преимуществ. При этом были выявлены пять основных неопределенностей,
которые значительно влияют на решения стоимость строительства новой ЛЭП, объем
спроса на электроэнергию во Флориде, конкурентная ситуация, доля рынка
электроэнергии, контролируемая ОРС, и реальная отпускная цена на электроэнергию.
Вероятные значения этих неопределенностей в комбинации с возможными решениями
приводят к созданию 8 000 ветвей в дереве решений. Оптимальное решение искалось на
основе критерия максимизации ожидаемой прибыли После проведения анализа
чувствительности компания решила, что перед принятием окончательного решения
необходимо дополнительное исследование одного неопределенного фактора —
конкурентной ситуации на рынке электроэнергии штата Флорида. После этого наиболее
интересным и коммерчески выгодным признано решение строить линию электропередач
совместно с компанией Georgia Power [ 1 ]
9.7.	Анализ чувствительности
Прежде чем начать следующую большую тему (связанную с учетом новой информа-
ции о вероятностях случайных событии), проведем анализ чувствительности решения
в зависимости от вероятностей благоприятной или неблагоприятной ситуации на рынке
мобильных телефонов Как показано выше, ожидаемый результат для агрессивной стра-
тегии (обозначим ее как решение А) вычисляется по формуле
££(А) = 30 х Р(Б) + (-8) х Р(Н),
где Р(Б) — вероятность благоприятной, а Р(Н) — неблагоприятной ситуации на рынке.
Очевидно, что
Р(Б) + Р(Н) = 1 или Р(Н) = 1 - Р(Б).
Тогда
£Л(А) = 30 х £(Б) + (-8) х (1 - Р(Б)) = -8 + 38Р(Б).
Таким образом, ожидаемый результат ER(A) является линейной функцией от вероятно-
сти Р(Б) благоприятной ситуации на рынке. Аналогично можно выразить ожидаемые ре-
зультаты от принятия базовой и осторожной стратегий (будем обозначать их как решения
В и С соответственно) через вероятность £(Б):
££(В) = 20 х Р(Б) + 7 х (1 - Р(Б)) = 7 + 1 ЗР(Б),
££(С) = 5 х Р(Б) + 15 х (1 -Р(Б))= 15- 10Р(Б).
С помощью таблицы подстановки Excel следует подсчитать значения этих функций
в зависимости от значений вероятности Р(Б) и затем построить их графики. Для этого
выполните следующие действия.
1.	В рабочей книге Sonorola скопируйте диапазон Al D7 с рабочего листа Базовый
на новый рабочий лист (назовем его Анализ). Измените в ячейке С1 значение 0,55 на
формулу =1-В1 Это позволит использовать таблицу подстановки с одним входом.
2.	В ячейке А10 введите начальное значение 0.
ГЛАВА 9. Анализ решений 613
3.	Снова щелкните на ячейке А10 и выполните команду Правка^Заполнить1^
Прогрессия
4.	В открывшемся диалоговом окне Прогрессия щелкните на переключателе Распо-
ложение по столбцам, введите в поле Шаг значение 0,05 и 1 в поле Предельное
значение. Щелкните на кнопке ОК
5.	В ячейки В9, С9 и D9 введите формулы =D5, =D6 и =D7 соответственно. Таким об-
разом мы свяжем формулы для вычисления ожидаемых значений ER(Ay ER(B)
и £ДС) с создаваемой таблицей подстановки.
6.	Выделите диапазон A9.D30 и выполните команду Данные^Таблица подстановки.
7.	В диалоговом окне Таблица подстановки в поле Подставлять значения по стро-
кам введите $В$ 1 и щелкните на кнопке ОК
8.	Excel автоматически вычислит значения ожидаемых результатов для всех трех
стратегий при изменении вероятности Р(Б) от 0 до 1 с шагом 0,05.
9.	С помощью мастера диаграмм постройте графики функций ER(A), ER(B) и ER(C).
У вас должны получиться графики, подобные показанным на рис 9.16.
Рис. 9.16. Ожидаемые результаты реше-
ний как функции от вероятности Р(Б)
На рис. 9.16 видно, что при ДБ) = 0 ожидаемые значения равны платежам в случае не-
благоприятной ситуации на рынке, а при ДБ) = 1 — платежам при благоприятной ситуа-
ции (сравните с таблицей платежей на рис. 9.11). На рис. 9.16 также легко определить опти-
мальное решение для любого значения вероятности ДБ). Например, если Р(Б) ~ 0,45, то на
рис 9.16 видно, что при этом значении вероятности выполняются неравенства £ДВ)>
ER(C) > ER(A) Следовательно, при данном значении вероятности ДБ) оптимальным будет
решение В (базовая стратегия). Но если ДБ) = 0,8, то выполняются неравенства £ДА)>
£ДВ) > £ДС), и оптимальным будет решение А (агрессивная стратегия).
На рис 9 16 видно, что если вероятность ДБ) больше значения ДБ), при котором пересе-
каются графики функций £ДА) и £ДВ), то следует выбрать в качестве оптимального реше-
ние А. Это значение ДБ), при котором становится оптимальным решение А, можно найти,
приравняв функции ER(A) и £ДВ) и определив с помощью этого уравнения значение ДБ).
614 ЧАСТЬ III. Вероятностные модели
£Л(А) = ££(В),
-8 + 38Р(Б) = 7 + 13Р(Б),
25£(Б)= 15,
ДБ) = 0,6.
Аналогично можно определить, что графики функций £Л(В) и £Л(С) пересекаются
при Р(Б) = 0,348. Таким образом, оптимальным будет решение В, если вероятность Р(Б)
лежит в пределах от 0,348 до 0,6 В этот же интервал входит значение вероятности 0,45,
для которого мы ранее определили то же оптимальное решение В. Но графики на
рис. 9.16 дают дополнительную информацию. Например, в случае оптимального реше-
ния при Р(Б) = 0,45 видно, что это решение не очень чувствительно к точности опреде-
ления значения данной вероятности — это решение остается оптимальным, даже если
истинное значение вероятности Р(Б) отличается от значения 0,45 на 0,1 в большую или
меньшую сторону.
Хотя графики, подобные показанным на рис. 9.16, можно использовать только при
двух состояниях природы, проведенный анализ показывает методику оценки чувстви-
тельности решений в зависимости от значений вероятности этих состояний. Для моде-
лей, учитывающих большее количество состояний природы, также существуют соответ-
ствующие методы проведения анализа чувствительности, но их описание выходит за
рамки данной главы, которую можно рассматривать лишь как вводную для темы вероят-
ностных моделей принятия решений.
9.8.	Деревья решений: учет новой информации
Руководство компании Sonorola уже было готово рекомендовать базовую маркетинго-
вую и производственную стратегию (см. раздел 9.6), когда совет директоров настоял, что-
бы перед принятием окончательного решения были проведены дополнительные марке-
тинговые исследования. Вследствие этого решения совета директоров группе маркетин-
говых исследований в штаб-квартире в Токио было поручено провести соответствующий
анализ с предоставлением через месяц отчета о результатах. Таким образом, через месяц
будет получена новая информация, которую необходимо учесть перед окончательным
выбором стратегии производства новых моделей телефонов.
Новая информация может повлиять на оценку значения Р(Б), вероятности благопри-
ятной ситуации на рынке мобильных телефонов. Если отчет группы маркетинговых ис-
следований будет оптимистическим, то эту вероятность следует увеличить, а если песси-
мистическим, то уменьшить. Возникает вопрос: как учесть новую информацию и изме-
нить значение Р(Б)? Существует формальный способ пересчета вероятности Р(Б),
основанный на концепции условных вероятностей. Этот способ требует определенного
уровня математической подготовки менеджеров, поэтому он описан в дополнительном
разделе 9.13. Здесь же мы рассмотрим подход к учету новой информации, основанный на
использовании электронных таблиц.
Пересчет вероятностей с учетом новой информации
Пусть отчет с результатами маркетинговых исследований оценивается либо как опти-
мистический (О), либо как пессимистический (П). Если считать результаты исследова-
ний абсолютно точными, то оптимистический отчет означает гарантированную благо-
приятную ситуацию на рынке; и, наоборот, пессимистический отчет гарантирует небла-
гоприятную обстановку на рынке. Другими словами, если результаты исследований
ГЛАВА 9. Анализ решений 615
абсолютно точны, то отчет однозначно определяет истинное состояние природы
(ситуацию на рынке). Но даже если нельзя гарантировать абсолютную точность результа-
тов отчета, такие исследования очень полезны, поскольку позволяют уточнить степень
надежности наших представлений о ситуации на рынке. Чтобы количественно выразить
влияние надежности новой информации на вероятности состояний природы, использу-
ют условные вероятности
Условные вероятности
Обозначим через А и В два случайных события. Нестрогое определение условной веро-
ятности ДА1В): это вероятность осуществления события А при условии, что осуществи-
лось событие В Например, ДО1Б) — условная вероятность, что отчет группы маркетин-
говых исследований будет оптимистичным, при условии, что ситуация на рынке дейст-
вительно благоприятная. Если исследования выполнены абсолютно точно, то эта
вероятность равна 1, т.е. в этом случае отчет точно отображает ситуацию на рынке. До-
пустим, в прошлом, когда ситуация на рынке была благоприятной, оптимистический от-
чет представлялся в 60% случаев. Тогда можно считать, что ДО1Б) = 0,6. Поскольку у нас
только два типа отчета: оптимистический и пессимистический, то значение вероятности
ДП1Б) =1 — 0,6 = 0,4, т.е. примерно в 40% случаев отчет будет пессимистическим, хотя
ситуация на рынке будет благоприятной.
Если ситуация на рынке неблагоприятная, маркетинговые исследования должны это
почувствовать и отразить, но, скорее всего, не с абсолютной точностью: пусть
Р(П1Н) = 0,7 В этом случае Р(О1Н) = 0,3. Эти условные вероятности характеризуют на-
дежность маркетинговых исследований
Вычисление апостериорных вероятностей
Предположим, что группа маркетинговых исследований предоставила оптимистиче-
ский отчет. Какова в этом случае вероятность благоприятной ситуации на рынке? После
получения новой информации (маркетингового отчета) эта вероятность будет условной
вероятностью ДБ1О). (Эта вероятность не совпадает с условной вероятностью ДО1Б),
которую мы считаем известной и равной 0,6.) Первоначальная оценка вероятности ДБ)
называется априорной вероятностью, а условная вероятность ДБЮ) называется апосте-
риорной вероятностью. Мы уже имеем оценку априорных вероятностей: ДБ) = 0,45
и ДН) = 0,55 (см. таблицу на рис. 9.11).
Основой для вычисления апостериорных вероятностей служит теорема Байеса. Здесь
мы используем формулы пересчета вероятностей, которые являются следствием этой
теоремы и приведены в разделе 9.13. Процесс вычисления вероятностей мы организуем
на новом листе (назовем его Вероятности) в рабочей книге Sonarola. Законченный рабо-
чий лист и используемые формулы показаны на рис. 9.17. Для создания такого листа вы-
полните следующие действия.
1.	В ячейки Al ,С4 введите значения условных вероятностей, характеризующие надеж-
ность маркетинговых исследований (т.е. вероятностей ДО1Б), ДО1Н), ДП1Б)
и ДП1Н)). Эти значения образуют таблицу, озаглавленную “Надежность отчета”
(см. рис 9.17) Сумма значений в каждом столбце должна быть равной 1, сумма зна-
чений по строкам может быть любой. Замечание. Будем придерживаться соглашения,
что условная вероятность ДА1В) находится на пересечении строки, соответствующей
событию А, и столбца, соответствующего событию В.
616 ЧАСТЬ III. Вероятностные модели
2.	Создайте новую таблицу путем умножения каждого столбца таблицы надежности
на соответствующую априорную вероятность Например, каждый элемент столбца
Благоприятный умножьте на вероятность Р(Б) благоприятной ситуации на рынке
и получите значения совместного распределения вероятностей (см. раздел 9.13).
3.	Для каждой строки новой таблицы вычисляется сумма ее элементов. Получаем
значения безусловных (частных) вероятностей событий Р(О) и Р(П) в ячейках D12
и D13
4.	Вычисляем значения таблицы “Апостериорные вероятности” путем деления каж-
дого значения совместной вероятности на соответствующее значение безусловной
вероятности (например, значение в ячейке В12 делится назначение из ячейки D12).
Рис. 9.17. Вычисление апостериорных вероятностей
Здесь таблицы “Надежность отчета” и “Априорные вероятности” содержат исходные
данные, а две другие — вычисляемые данные. Этот же рабочий лист можно использовать
для анализа чувствительности апостериорных вероятностей к изменениям вероятностей
надежности и априорных вероятностей. Для этого можно создать таблицу подстановки,
в которой были бы представлены значения условных вероятностей Р(БЮ) и Р(Б1П) в за-
висимости от изменения значения априорной вероятности Р(Б) в интервале от 0 до 1
ГЛАВА 9. Анализ решений 617
с шагом 0,1. Такая таблица показана на рис. 9.18. Чтобы создать ее в Excel, выполните
следующие действия.
1.	В ячейку 13 введите начальное значение 0.
2.	Снова щелкните на ячейке 13 и выполните команду Правка^Заполнить1^
Прогрессия.
3.	В открывшемся диалоговом окне Прогрессия щелкните на переключателе Распо-
ложение по столбцам, введите в поле Шаг значение 0,1 и 1 в поле Предельное
значение. Щелкните на кнопке ОК.
4.	В ячейки J2 и К2 введите формулы =В19 и =В20 соответственно. Таким образом
мы свяжем формулы для вычисления условных вероятностей ДБЮ) и Р(Б1П)
с создаваемой таблицей подстановки
5.	Выделите диапазон 12.К13 и выполните команду Данные^Таблица подстановки.
6.	В диалоговом окне Таблица подстановки в поле Подставлять значения по стро-
кам введите $В$8 и щелкните на кнопке ОК.
7.	Excel автоматически вычислит значения условных вероятностей при изменении
вероятности Р(Б) от 0 до 1 с шагом 0,1.
J . 1 Р(Б)	J ...1 р(Е|о; 0.621	К'.Н 0,31 э
	0.162	0,060:
0,2	0,333	0,125
0.3	0 462	0,197
0 4	0,571	0,276
0,5	0,667	0,364
0.6	0,750	0,462
0,7	0,824	0,571
о.а	0.869	0,696:
0,9	0,947	0,837
Рис. 9.18. Зависимость апо-
стериорных вероятностей
от априорных
Отметим, что при возрастании априорной вероятности Р(Б) возрастает и апостериор-
ная вероятность Р(БЮ) благополучной ситуации на рынке при условии, что результаты
маркетинговых исследований оптимистичны. Также интересно отметить, что апостери-
орная вероятность благоприятной ситуации выше, чем априорная, если отчет оптими-
стичен, и ниже априорной, если отчет пессимистичен (за исключением ситуации при
Р(Б) — 0 и Р(Б) = 1, когда все вероятности совпадают).
Включение апостериорных вероятностей в дерево решений
Теперь рассмотрим данную модель, представленную в виде дерева решений, показан-
ного на рис. 9.19. Первый узел этого дерева (обозначен как I) соответствует выполнению
маркетинговых исследований Он является узлом событий, поскольку результат этих ис-
следований заранее не определен. Из этого узла выходят две ветви, которые соответству-
618 ЧАСТЬ III Вероятностные модели
ют оптимистическому (О) и пессимистическому (П) результату маркетинговых исследо-
ваний. Вероятности ДО) и ДП) этих результатов подсчитаны в ячейках D12 и D13 рабо-
чего листа Вероятности (см. рис. 9.17).
Рис. 9.19. Дерево решений с узлом маркетинговых исследований
Если результат маркетинговых исследований оптимистичен, мы по дереву решений
переходим к узлу П, который является узлом решений. В этом узле необходимо выбрать
одно из трех возможных решений — А, В или С, которые соответствуют агрессивной, ба-
зовой и осторожной стратегиям. Предположим, выбрано решение А. Это решение ведет
к узлу событий IV, из которого исходят две ветви, соответствующие случайным событи-
ям: ситуация на рынке будет благоприятной (Б) и ситуация будет неблагоприятной (Н).
ГЛАВА 9. Анализ решений	619
Если ситуация на рынке мобильных телефонов для компании Sonorola будет благоприят-
ной, то она получит чистый доход 30 (млн. долл.) — конечное значение данной ветви.
Важно отметить, что дерево создается в “хронологическом” порядке, т е. в том поряд-
ке, в каком становится доступной информация и в каком принимаются решения. Следо-
вательно, сначала проводятся маркетинговые исследования (результат оптимистичен или
пессимистичен), затем принимается решение (выбирается агрессивная, базовая или ос-
торожная стратегия), после этого проявляются условия на рынке (благоприятная ситуа-
ция или неблагоприятная).
Чтобы найти оптимальное решение с помощью этого дерева, надо указать для него
значения вероятностей Р(БЮ), Р(НЮ), Р(Б1П), Р(Н1П), Р(О) и Р(П) Первые четыре зна-
чения можно найти в таблице “Апостериорные вероятности” рабочего листа Вероятно-
сти (см. рис. 9.17). Например, значение вероятности Р(НЮ) находится на пересечении
столбца “Неблагоприятный” и строки “Оптимистический” и равно 0,379. (Напомним
о соглашении, что значение условной вероятности Р(А1В) находится на пересечении
строки, соответствующей событию А, и столбца, соответствующего событию В.)
Для ветви, соответствующей оптимистическому результату маркетинговых исследо-
ваний, на основе теоремы Байеса априорные вероятности Р(Б) и Р(Н) заменяются услов-
ными (апостериорными) вероятностями Р(Б1О) и Р(Н1О). Аналогично для ветви, соответ-
ствующей пессимистическому результату маркетинговых исследований, вероятности
Р(Б) и Р(Н) заменяются условными вероятностями Р(Б1П) и Р(Н1П) Затем TreePlan ав-
томатически производит пересчет ожидаемых значений на дереве решений (в обратном
порядке, начиная с конечных узлов) Результаты расчетов показаны на рис 9.20 и 9 21
620 ЧАСТЬ III. Вероятностные модели
Рис. 9.21. Нижняя часть нового дерева решений
Чтобы создать такое дерево, выполните следующие действия. (Отметим, что TreePlan
не может создать более одного дерева решений в одной рабочей книге, поэтому данное
дерево мы создаем в новой книге Excel.)
1.	Откройте новую рабочую книгу и выполните команду Cepenc^Decision Tree.
В открывшемся диалоговом окне TreePlan New щелкните на кнопке New Tree
(Новое дерево)
2.	TreePlan создаст дерево решений с одним узлом. Щелкните на этом узле и нажмите
комбинацию клавиш <Ctrl+t>. В открывшемся диалоговом окне установите пере-
ключатель Change to event (Преобразовать в событие) и щелкните на кнопке ОК.
3.	Щелкните на конечном узле, нажмите <Ctrl+t> и в открывшемся диалоговом окне
установите переключатель Change to decision node (Преобразовать в узел реше-
ний) и переключатель Three (Три) в секции Branches (Ветви) диалогового окна.
Щелкните на кнопке ОК.
4.	Повторите действия, описанные в предыдущем пункте, для другого конечного узла.
5.	Щелкните на новом конечном узле в верхней части дерева решений, нажмите
<Ctrl+t> и в открывшемся диалоговом окне установите переключатель Change to
event node (Преобразовать в узел событий) и переключатель Two (Два) в секции
Branches (Ветви) диалогового окна. Щелкните на кнопке ОК.
6.	Скопируйте узел, созданный в предыдущем пункте, в другие два конечных узла.
(Для копирования используйте команды TreePlan Copy subtree (Копировать под-
дерево) и Paste subtree (Вставить поддерево), а не средства копирования Excel.)
ГЛАВА 9. Анализ решений 621
7.	Далее аналогичные действия выполните для нижней части дерева решений.
(Можно также скопировать узел, который на схеме рис. 9.19 обозначен как узел II,
в узел Ш)
Построение дерева решений закончено. Далее следует ввести значения вероятностей
и платежей.
Построенное дерево решений можно использовать для выбора оптимального решения.
Очевидно, что если результат маркетинговых исследований будет оптимистичен (ветвь “О”
на рис 9.19), то мы придем к узлу П (ячейка F22 на рис. 9.20). Тогда максимальное ожидае-
мое значение мы получим при выборе решения А (агрессивная стратегия). (TreePlan указы-
вает на это решение, помещая “1” в ячейку F22, что обозначает первую ветвь, исходящую из
этого узла.) Аналогично, если результат маркетинговых исследований будет пессимистич-
ным (ветвь “П” на рис. 9.19), то мы придем к узлу Ш (ячейка F52 на рис. 9.21). Тогда макси-
мальное ожидаемое значение мы получим при выборе решения С (осторожная стратегия).
Ожидаемое значение дополнительной информации
Ожидаемый результат оптимального решения, записанный в ячейке F37 на схеме де-
рева решений (рис. 9.20 и 9 21), составляет
ER= 15,586x 0,435 + 11,814 х 0,565 = 13,455.
Это значение ожидаемого результата, если будет выполнено маркетинговое исследование
и затем, в зависимости от результата исследований, выбрано соответствующее оптималь-
ное решение.
В разделе 9.6 мы видели, что если маркетинговые исследования не выполнялись, то
оптимальным решением будет базовая стратегия, при этом ожидаемый результат равен
12,85. Очевидно, что проведение маркетинговых исследований увеличило ожидаемый ре-
зультат на 80,61 млн. (13,46 - 12,85 = 0,61). Даже если результаты маркетинговых иссле-
дований не абсолютно надежны, они чего-то стоят (если быть точным, то стоят они
80,61 млн.). Эта разность между ожидаемым результатом при дополнительной информа-
ции и ожидаемым результатом без нее называется ожидаемым значением дополнительной
информации. Это верхняя граница цены, которую можно заплатить за какую-либо част-
ную дополнительную информацию.
Подсчитаем в данной ситуации ожидаемое значение полной информации. Напомним
(см. раздел 9.3), что это цена точной информации о том, какое состояние природы осу-
ществится. Исходная таблица платежей представлена на рис. 9.11. Если мы уверены, что
рынок будет благоприятным, то наилучшей будет агрессивная стратегия, которая вернет
платеж в размере 30. Если мы уверены, что рынок будет неблагоприятным, то наилучшей
будет осторожная стратегия, которая вернет платеж в размере 15. За сколько можно ку-
пить полную информацию о состоянии рынка9 Поскольку вероятность благоприятной
ситуации на рынке равна 0,45, а неблагоприятной — 0,55, то
ожидаемое значение полной информации = 30 х 0,45 + 15 х 0,55 - 12,85 = 21,75 -
- 12,85 = 8,90.
Последние вычисления говорят о том, что полная информация о состоянии рынка может
принести $8,90 млн. сверх того ожидаемого результата, который мы можем получить без нее.
В данном случае ожидаемое значение полной информации значительно больше того, что мы
622 ЧАСТЬ 111. Вероятностные модели
можем получить, проведя маркетинговые исследования (ожидаемое значение информации,
полученной от этих исследований, равно $0,61 млн ). Но чем точнее будут проведены марке-
тинговые исследования (т.е. чем больше будут вероятности Р(ОБ) и Р(П1Н)), тем меньше бу-
дет разность между ожидаемыми значениями полной и дополнительной информации. В част-
ности, если Р(О1Б) = 1 и ЛП1Н) = 1, то эти ожидаемые значения совпадут.
9.9.	Последовательные решения
В предыдущем разделе мы предположили, что совет директоров компании Sonorola
перед выбором окончательной стратегии решил провести маркетинговые исследования
рынка мобильных телефонов. Затем мы рассмотрели, как можно использовать информа-
цию, полученную в результате маркетинговых исследований, и как при этом изменится
модель принятия решений для этой компании. Теперь сделаем шаг назад — очевидно,
что решение провести маркетинговое решение ничем не отличается от других принимае-
мых решений, например, от решений, какую выбрать стратегию производства. Руково-
дство компании может подсчитать, что стоимость маркетинговых исследований больше
возможной прибыли от них. Допустим, что для проведения этих исследований необхо-
димо $500 000. Также очевидно, что решение проводить или нет маркетинговые исследо-
вания не изолировано от других принимаемых решений — если маркетинговые исследо-
вания проведены, то на основе их результатов будут приняты одни стратегии производст-
ва, а если нет, то другие. Другими словами, от начального решения зависят последующие
решения и случайные события, вытекающие из этого решения. Такая ситуация называ-
ется моделью последовательных решений.
Анализ последовательных решений
Это очень распространенный тип управленческих моделей, и обычно для их анализа
используются деревья решений В ситуациях, когда существует несколько взаимосвязан-
ных решений и событий, графическое представление моделей особенно полезно
На рис. 9.22 и 9.23 показано дерево решений из предыдущего раздела, к которому добав-
лен новый узел решений, соответствующий принятию решения о том, проводить или нет
маркетинговые исследования. Из этого узла выходят две ветви Верхняя ветвь (рис 9 22)
соответствует решению провести маркетинговые исследования и совпадает с деревом ре-
шений, показанным на рис. 9.20 и 9.21. Нижняя ветвь соответствует решению не проводить
исследование и совпадает с деревом решений, показанным на рис 9.15 Это дерево реше-
ний построено в новой рабочей книге Excel с помощью надстройки TreePlan (методика по-
строения деревьев подробно описана в предыдущих разделах).
Числовые значения на этом дереве решений требуют некоторых пояснений Задание
и вычисление этих значений осуществляется в два этапа.
1.	Сначала назначаются платежи для всех решений и случайных событий. В этой мо-
дели мы предположили, что маркетинговые исследования стоят $500 000. По-
скольку для всех денежных сумм в этой модели выбран масштаб в 1 млн , то пла-
теж за маркетинговые исследования составит -0,5, и это число следует поместить
на ветвь, соответствующую принятию решения о проведении исследований
(точнее, в ячейку D46, см. рис. 9.22). Аналогично на ветвь, соответствующую при-
нятию решения об отказе проведения исследований, следует поместить 0 (ячейка
ГЛАВА 9. Анализ решений	623
D91 на рис. 9.23). Подобным образом вводятся значения других платежей, напри-
мер, значение 30 — в ячейку Р19 (см. рис. 9.22), что соответствует платежу при вы-
боре агрессивной стратегии производства и благоприятной ситуации на рынке.
2.	Далее TreePlan вычисляет конечные значения путем суммирования всех платежей,
начиная от первого узла и до данного конечного. Например, верхнее конечное
значение (ячейка S18 на рис. 9 22) будет равно 29,5, что соответствует сумме пла-
тежей на ветвях Исследование — Оптимистический результат — Агрессивная стра-
тегия — Благоприятный рынок (т.е. —0,5 + 0 + 0 + 30 = 29,5).
Надстройка TreePlan снова произведет вычисления от конечных узлов и далее до пер-
вого При этом для узлов событий вычисляются ожидаемые значения, а для узлов реше-
ний значения принимаются равными наибольшему из ожидаемых значений узлов собы-
тий, подчиненных данному узлу решений.
Рис. 9.22. Верхняя часть нового дерева решений
624 ЧАСТЬ III. Вероятностные модели
Оптимальная стратегия — это план действий, основанный на анализе всего дерева
решений, где перечисляются необходимые решения, которые могут меняться в зависи-
мости от того, какое случайное событие может осуществиться. Для примера рассмотрим
дерево решений, показанное на рис. 9.22 и 9.23. В первом узле решения этого дерева мы
видим, что компании Sonorola следует принять решение о проведении маркетинговых ис-
следований, поскольку этому решению соответствует наибольший ожидаемый результат
(12,96 > 12,85). Если результат маркетинговых решений будет оптимистическим, то наи-
лучшим выбором будет агрессивная производственная стратегия (этой стратегии соот-
ветствует наибольший ожидаемый результат, равный 15,098). Если же результат исследо-
ваний будет пессимистичным, то наилучшим решением будет осторожная стратегия
с ожидаемым результатом 11,31.
Влияние функции полезности
Найти оптимальное решение по дереву решений с учетом функции полезности не-
трудно. Для этого строится обычное дерево решений, но вместо платежей на нем указы-
ваются значения функции полезности, соответствующие этим платежам. Пусть функция
полезности задана своими значениями, представленными в табл. 9.12 (как вычисляются
такие значения, показано в разделе 9.4). График этой функции показывает, что компания
Sonorola не склонна к риску. В самом деле при возрастании платежей от значения 20 до 30
полезность возрастает только на 0,020 (= 0,963 - 0,943), тогда как при возрастании пла-
тежей от 5 до 15 полезность возрастает на 0,205 (= 0,914 - 0,709).
ГЛАВА 9. Анализ решений 625
Таблица 9.12. Функция полезности
Платеж	Полезность
-8,5	0,300
-8	0,320
4,5	0,695
5	0,709
6,5	0,748
7	0,760
14,5	0,910
15	0,914
19,5	0,941
20	0,943
29,5	0,962
30	0,963
Итак, чтобы включить функцию полезности в дерево решений, следует просто заме-
нить значения платежей значениями функции полезности, соответствующими этим пла-
тежам, и затем заново пересчитать ожидаемые значения. На рис. 9.24 и 9.25 показано то
же дерево решений, что и на рис. 9.22 и 9.23, но вместо платежей используются значения
функции полезности. Обратите внимание на то, что теперь при оптимистическом резуль-
тате маркетинговых исследований оптимальным решением будет не агрессивная произ-
водственная стратегия, а базовая стратегия, поскольку в данном случае именно этой
стратегии соответствует наибольший ожидаемый результат 0,868.
Рис. 9.24. Верхняя часть дерева решений с применением функции полезности
626 ЧАСТЬ III Вероятностные модели
Рис. 9.25. Нижняя часть дерева решений с применением функции полезности
Дополнительные возможности надстройки TreePlan
Если в диалоговых окнах надстройки TreePlan щелкнуть на кнопке Options
(Параметры), откроется диалоговое окно TreePlan Options (рис. 9.26), которое представ-
ляет дополнительные средства TreePlan. Среди этих средств прежде всего отметим встро-
енную экспоненциальную функцию полезности. Если установить переключатель Use
Exponential Utility Function (Использовать экспоненциальную функцию полезности), то
TreePlan автоматически пересчитает платежи на дереве решений в значения функции по-
лезности Во второй секции окна TreePlan Options по умолчанию установлен переключа-
тель Maximize Profits (Максимизировать прибыль), который указывает на то, что значе-
ние узла решений определяется как максимум платежей на ветвях, исходящих из этого
узла Если вы исследуете модель, в которой необходимо минимизировать стоимость или
потери, следует установить переключатель Minimize Cost (Минимизировать стоимость).
Тогда значение узла решений будет определяться как минимум платежей на ветвях, исхо-
дящих из этого узла Также отметим, что при возникновении каких-либо затруднений
в вашем распоряжении всегда имеется справочная система надстройки (кнопка Help
(Справка)).
ГЛАВА 9 Анализ решений 627
Рис. 9.26. Диалоговое окно TreePlan
Options
Чувствительность оптимального решения к априорным
вероятностям
Найдя с помощью дерева решений оптимальное решение, важно провести анализ
чувствительности этого решения по отношению к различным параметрам модели На-
пример, насколько оптимальное решение зависит от первоначальной оценки вероятно-
сти /’(Б) того, что ситуация на рынке мобильных телефонов будет благоприятной Рабо-
чий лист Excel, показанный на рис 9.27, подготовлен для графического анализа чувстви-
тельности оптимального решения, найденного с помощью дерева решений,
приведенного на рис 9 24 и 9 25. Этот лист создан в новой рабочей книге Excel путем ко-
пирования в него содержимого рабочего листа Вероятности (рис 9 17) из рабочей книги
Sonorola (эта часть листа на рис. 9 27 не показана) и посредством ввода значений и фор-
мул, которые показаны на рис 9 27
На рис 9 28 показан график зависимости ожидаемого результата для решений прово-
дить маркетинговые исследования или не проводить от значений вероятности Р(Б), ко-
торые изменяются от 0 до 1 с шагом 0,01 Чтобы построить такой график, надо сначала
создать таблицу значений вероятности Р(Б) и соответствующих значений ожидаемых ре-
зультатов Проще всего такую таблицу создать как таблицу подстановки с одним входом
Для этого необходимо выполнить следующие действия.
1.	В ячейку А24 введите начальное значение 0
2.	Снова щелкните на ячейке А24 и выполните команду Правка^Заполнить^
Прогрессия.
3.	В открывшемся диалоговом окне Прогрессия щелкните на переключателе Распо-
ложение по столбцам, введите в поле Шаг значение 0,01 и 1 в поле Предельное
значение Щелкните на кнопке ОК
4.	В ячейки В23 и С23 введите формулы =G1 и =112 соответственно Таким образом
мы свяжем формулы для вычисления ожидаемых результатов с создаваемой таб-
лицей подстановки
5.	Выделите диапазон А23’С 124 и выполните команду Данные^Таблица подстановки
6.	В диалоговом окне Таблица подстановки в поле Подставлять значения по стро-
кам введите $В$8 и щелкните на кнопке ОК
7.	Excel автоматически заполнит таблицу значений ожидаемых результатов при из-
менении вероятности Р(Б) от 0 до 1 с шагом 0,01
628 ЧАСТЬ III Вероятностные модели
Рис. 9.27. Рабочий лист для проведения анализа чувствительности
На рис. 9.28 сплошная линия представляет ожидаемый результат решения проводить,
а точечная линия — не проводить маркетинговые исследования. Там, где эти линии пере-
секаются, оптимальное решение изменяется (т.е если оптимальным было решение про-
водить маркетинговые исследования, то теперь оптимальным будет решение не прово-
дить их, и наоборот) Эти линии пересекаются четыре раза (хотя четвертое пересечение
трудно увидеть, поскольку линии при значениях Р(Б), близких к 1, почти сливаются).
Решение проводить маркетинговые исследования будет оптимальным при значениях ве-
роятности Р(Б) в интервалах (приблизительно) от 0,29 до 0,50 и от 0,94 до 0,96 Решение
не проводить эти исследования будет оптимальным при значениях вероятности Р(Б)
в интервалах от 0 до 0,29, от 0,50 до 0,94 и от 0,96 до 1
ГЛАВА 9. Анализ решений 629
Рис. 9.28. Зависимость ожидаемых результатов от априорной вероятности Р(Б)
9.10.	Менеджмент и теория принятия решений
Типичное управленческое решение имеет следующие характеристики.
1.	Решение принимается один-единственный раз (например, покупать сегодня 100
акций компании Intel или нет).
2.	Результат принятого решения зависит от неопределенных (случайных) событий,
которые могут осуществиться в будущем (например, поднимется или упадет цена
на акции компании Intel), причем практически никакой надежной информации об
этих событиях нет.
Конечно, имеется определенная информация о подобных событиях в прошлом, которая
может что-то сказать нам о правдоподобии различных результатов решения (например, мы
знаем о поведении цены акций за последнюю неделю или даже за последние 52 недели). Но
мы не можем провести эксперимент, чтобы получить надежную оценку вероятностей инте-
ресующих нас событий (т.е. мы не можем экспериментально оценить вероятности повыше-
ния или понижения цены акций на следующей неделе).
Как материал этой главы может содействовать выходу из подобных ситуаций9 Если вы-
ражаться кратко, то рекомендации данной главы можно свести к следующим положениям.
1.	Для каждого решения следует определить полезность (платеж) всех возможных
выходных результатов.
2.	Необходимо определить вероятность каждого выходного результата.
3.	Надо вычислить ожидаемую полезность (ожидаемый результат) для каждого решения
4.	В качестве наилучшего решения следует выбрать то решение, которое имеет наи-
большую ожидаемую полезность.
Последние две рекомендации выполнить относительно просто (по крайней мере, тео-
ретически), но первым двум следовать сложно. В самом деле, как нам узнать значения
вероятностей и полезности?
630 ЧАСТЬ III Вероятностные модели
Ответ заключается в том, что мы в принципе не можем знать эти значения — не суще-
ствует “истинных” значений, которые мы можем выявить экспериментально или анали-
тически. Напротив, эти параметры, вероятности и полезности, субъективны по своей
природе и отражают мнения и предпочтения менеджера. Конечно, на оценку менеджером
этих параметров могут влиять какие-либо внешние факторы (например, мнения экспер-
тов), но здесь говорится о том, что оценки этих параметров мы не можем получить объек-
тивным способом, как это делается в физических или биологических науках.
Однако существуют подходы, которые не дают нам утонуть в море субъективности
Эти подходы используют логическое “устройство”, которое называется эквивалентной
лотерей. Они дают достаточно твердую основу для оценки как вероятностей, так и полез-
ностей С эквивалентной лотереей мы уже встречались в разделе 9.4 при построении
функций полезности
Субъективные вероятности
Менеджер может использовать эквивалентную лотерею для получения значений
субъективных вероятностей Предположим, вы хотите определить вероятность того, что
Хиллари Клинтон будет кандидатом в Президенты от демократической партии на выбо-
рах 2004 года Сначала придумаем две игры. В первой игре вы получаете $100, если Хил-
лари будет кандидатом, и 0 — в противном случае. Во второй игре вы получаете $100 с ве-
роятностью р и 0 с вероятностью 1 - р. Теперь вы подбираете такое значение р, при кото-
ром для вас будет равнозначно сыграть или в первую, или во вторую игру. Это значение р
и будет вашей субъективной вероятностью того, что Хиллари Клинтон будет кандидатом
в Президенты от демократической партии на выборах 2004 года Очевидно, что ваша
оценка шансов Хиллари может отличаться от аналогичной оценки самой Хиллари Клин-
тон или кого-нибудь другого.
Эквивалентная лотерея позволяет оценивать как вероятности, так и полезности. Но еще
раз подчеркнем, что этот процесс очень субъективный, и, конечно, разные люди получают
различные оценки. Почему бы и нет? Описанный подход позволяет менеджеру использо-
вать знания (и опыт) других людей, поскольку, очевидно, мы не можем надеяться, что есть
человек, который знает “абсолютно все” об интересующих нас в данный момент решениях.
Однако скептик может спросить, а зачем вообще “городить этот огород”, если в этих
оценках такую важную роль играют индивидуальные предпочтения и мнения? Не будет ли
честнее просто выбрать то решение, которое интуитивно кажется нам наилучшим? Что мы
выигрываем, определяя значения субъективных вероятностей и полезностей по отдельно-
сти? Ответ очевиден — это позволяет менеджеру сосредоточить свое внимание на одном из
этих параметров Проблема простого интуитивного выбора решений заключается в том, что
человеку обычно трудно сосредоточиться сразу на двух вещах. Если он размышляет о воз-
можных платежах, получаемых в результате принятия какого-нибудь решения, ему трудно
одновременно с этим оценивать правдоподобие возможных случайных событий, связанных
с данным решением, и практически невозможно скомбинировать их в одно решение. Ин-
туитивный подход обычно позволяет найти какое-нибудь отдельное “выдающееся” реше-
ние, но, как правило, при этом не учитывается тот факт, что вероятность осуществления
этого решения крайне мала. Например, многие люди боятся летать на самолетах, но без
особой боязни пользуются автомобилями, даже зная, что вероятность погибнуть в автока-
тастрофе значительно выше, чем в авиакатастрофе. (Вероятно, они рассчитывают выжить
в автокатастрофе, тогда как в авиакатастрофе это практически невозможно.) Раздельное
оценивание вероятностей и полезностей принуждает менеджера сконцентрировать свое вни-
мание на каждом из них перед тем, как скомбинировать на их основе конечное решение.
ГЛАВА 9. Анализ решений 631
Появление персональных компьютеров и бурный рост индустрии программного
обеспечения дали новый толчок для теории принятия решений Еще десятилетие назад
практически не было свободно продаваемых программ, предназначенных для анализа
решений Некоторые компании разработали свои программы для этих целей, но они, как
правило, не появлялись на рынке программных продуктов В этой главе мы продемонст-
рировали использование очень популярной надстройки для электронных таблиц
TreePlan Также отметим, что существуют другие подобные надстройки для электронных
таблиц (например, PrecisionTree от Polisade) и отдельные программные пакеты (DPL от
Applied Decision Analysis, DATA, Arborist, Riskcalc и Supertree) Многие из этих пакетов
имеют средства для создания диаграмм влияния, которые помогают менеджеру понять
структуру переменных модели и взаимосвязи между ними.
9.11.	Анализ решений
Ральф Киней (Ralph Keeney), ведущий специалист в области теории принятия реше-
ний ([5], [6]), определил анализ решений как “формализацию здравого смысла в виде мо-
делей принятия решений, которые слишком сложны для неформального применения
здравого смысла” Теория принятия решений и анализ решений основываются на осно-
вополагающих работах Джона фон Неймана и Оскара Моргенштерна Модели принятия
решений, которые отображают реальные управленческие и производственные ситуации,
как правило, очень сложны Процесс их создания и анализа можно условно разбить на
четыре этапа I) создание структуры модели, 2) определение значений вероятностей воз-
можных выходных результатов, 3) определение значений полезности возможных выход-
ных результатов, 4) оценка альтернатив и выбор стратегии
Материал этой главы, в основном, описывает последний этап анализа решении,
те оценку альтернатив и выбор оптимальной стратегии. Это сердцевина анализа реше-
ний Но на практике обычно это самый легкий этап анализа. Значительно больших уси-
лий требуют первые три этапа Создание структуры модели, что включает в себя форму-
лирование альтернатив и задание целевой функции, часто является наиболее сложным
и “волюнтаристским” этапом анализа, особенно, если модель отражает реальные ситуа-
ции, например, в охране окружающей среды, здравоохранении или безопасности
Важно понять, что анализ решений не предполагает полностью объективного анализа
моделей принятия решений Многие аспекты анализа решений требуют личных сужде-
ний — это относится к структуре модели, определению значений вероятностей и полез-
ностей. Во многих сложных моделях, отражающих реальные ситуации, просто не хватает
эмпирических данных для полного анализа. Однако практика показывает, что даже в та-
ких случаях анализ решений приносит несомненную пользу Кроме того, в процесс при-
нятия решения неизбежно включаются многочисленные качественные и трудно форма-
лизуемые факторы Поэтому задача анализа решений состоит не в том, чтобы сделать его
полностью “объективным” или исключить любые субъективные суждения, а чтобы по-
нять, согласовать и исключить противоречия между всеми видами факторов, влияющих
на модель.
9.12.	Заключение
Первая часть данной главы посвящена фундаментальным основам теории принятия
решений Заключение по этой части главы приведено в разделе 9 5.
632 ЧАСТЬ III Вероятностные модели
Следующие четыре раздела главы показывали роль деревьев решений в процессе при-
нятия решений Деревья решений — это графическое представление моделей, требующее
принять последовательность решений. Эти решения перемежаются случайными собы-
тиями, порождающими разные выходные результаты. Типичное дерево решений состоит
из узлов решений и узлов случайных событий. Ветви, исходящие из узла решения, пред-
ставляют возможные решения, а ветви, исходящие из узла событий, соответствуют раз-
личным выходам (выходным результатам). В законченном дереве решений путь от на-
чального узла дерева до какого-нибудь конечного узла представляет последовательность
решений и возможных случайных событий.
Вычисления в дереве решений выполняются по схеме обратного пересчета, начиная
от конечных узлов и заканчивая начальным узлом дерева При этом для узлов событий
вычисляются ожидаемые значения от случайных событий, а для узлов решений в качест-
ве значения выбирается максимальное ожидаемое значение, вычисленное для ветвей, ис-
ходящих из узла решений Процесс обратного пересчета в надстройке TreePlan полностью
автоматизирован По дереву решений определяется оптимальная стратегия — последова-
тельность решений, которые должны выполняться при возникновении тех или иных слу-
чайных событий.
При работе с деревьями решений большую роль играет теорема Байеса, поскольку она
дает формальный метод, позволяющий в процессе принятия решений учесть новую ин-
формацию Применение теоремы Байеса требует введения понятия условных вероятно-
стей, этой теме была посвящена часть материала данной главы.
Ожидаемое значение дополнительной информации — это цена новой информации в про-
цессе принятия решений в условиях неопределенности. Ожидаемое значение полной инфор-
мации является верхней границей ожидаемого значения дополнительной информации.
9.13.	Условные вероятности и теорема Байеса5
Хотя игральные кости и урны, заполненные шарами, на первый взгляд, не имеют ни-
какого отношения к теории принятия решений, с их помощью легко ввести понятие ве-
роятностей и затем через условные вероятности прийти к теореме Байеса. Предположим,
мы вытаскиваем шар из урны согласно следующему двухэтапному процессу (рис. 9.29).
1.	Выбрасывается кость.
2.	Значение на кости определяет, из какой урны будет вытаскиваться шар.
Каждая урна содержит 100 шаров, но разное количество белых (Б) и черных (Ч) ша-
ров Если кость упала так, что на верхней грани значение 1, то выбирается первая урна,
в которой 28 белых и 72 черных шара. Урна 2, содержащая 40 белых и 60 черных шаров,
выбирается в случае, если значение кости 2 или 3 Если значение кости 4, 5 или 6, выби-
рается урна 3, содержащая 92 белых и 8 черных шаров
Если кость правильная и мы ее бросаем “честно”, то вероятность выбора урны 1 равна
1/6 (обозначим Р(1) = 1/6) Поскольку урна 2 выбирается, если выпадут два значения
кости (2 или 3), то вероятность выбрать эту урну равна 2/6 (т е Р(2) = 2/6) Аналогично:
урна 3 выбирается, если выпадет хотя бы одно из трех значений кости (значения 4, 5 или
6) Поэтому Р(3) = 3/6. (Эти вероятности показаны рис. 9 29 ) Если вам эти кости и урны
Это дополнительный раздел для данной главы, который в американском издании книги находился на прила-
гаемом к книге компакт-диске — Прим ред
ГЛАВА 9. Анализ решений 633
с шарами кажутся слишком абстрактными и не связанными с реальной жизнью, можете
интерпретировать урны как три состояния природы, соответствующих трем уровням ры-
ночного спроса некоего продукта, где урна 1 представляет наименьший уровень спроса,
а урна 3 — наибольший Два типа шаров могут соответствовать двум возможным резуль-
татам маркетинговых исследований белый шар представляет благоприятный результат
исследований (для данного продукта), а черный — неблагоприятный
Условные вероятности
Запись Р(Б11) обозначает условную вероятность и читается как “вероятность события
Б при условии, что произошло событие 1” В данном случае это вероятность вытащить
белый шар при условии, что выбрана урна 1 (или вероятность благоприятного результата
маркетинговых исследований при условии, что уровень реального спроса на продукт
очень низок) Напомним, что если урна выбрана, то шар из нее выбирается случайным
образом, те считается, что все шары в урне имеют одинаковые вероятности быть вы-
бранными На рис 9 29 показано, что
Р(Б11) = 0,28 и Р(Ч11) = 0,72,
Р(Б12) = 0,40 и Р(Ч12) = 0,60,
Р(Б13) = 0,92 и Р(Ч13) = 0,08.
В примере с маркетинговыми исследованиями эти вероятности точно определить
нельзя Обычно они оцениваются на основе данных о предыдущих маркетинговых ис-
следованиях других продуктов и предположении, что эти данные можно распространить
на исследования данного продукта Например, приведенные выше значения вероятно-
стей Р(Б11) и Р(Ч11) могут быть получены в том случае, если в предыдущих 100 исследова-
ниях при низком уровне спроса в 28 исследованиях был получен благоприятный резуль-
тат, а в 72 исследованиях — неблагоприятный
В примере с маркетинговыми исследованиями нас также может интересовать вероят-
ность Р( 114) — вероятность того, что на рынке на самом деле низкий уровень спроса, ес-
ли результат исследований неблагоприятный В примере с костью и урнами это вероят-
ность того, что вытащенный в результате двухэтапного процесса черный шар был выта-
щен именно из первой урны.
Прежде чем определить значение этой вероятности, найдем вероятность вытащить
любой шар из урны 1, независимо от цвета шара. В нашем случае эта безусловная вероят-
ность Р(1) вытащить шар из первой урны известна и равна 1/6 В примере с маркетинго-
выми исследованиями данная вероятность — это вероятность пониженного спроса, оп-
ределенная перед проведением маркетинговых исследований
634
ЧАСТЬ III Вероятностные модели
Если мы знаем, что вытащен черный шар, а в первой урне преобладают черные шары, то
интуитивно мы чувствуем, что вероятность Р(11Ч) должна быть очень высокой. Но, чтобы
найти точное значение этой вероятности, надо ввести еще один “тип” вероятностей.
Совместные вероятности
Пусть X и Y —два произвольных случайных события Тогда
Р(Х и Y) = AXIY) Р(У),	(9.2)
Р(Х и Y) = P(Y и X),	(9.3)
P(Y и X) = AYIX) Р(Х),	(9 4)
WX) = WW)	(9.5)
Р(Х)
Первое из этих равенств дает формулу для определения совместной вероятности по-
явления обоих событий X и Y Второе равенство показывает равнозначность обозначений
Р(Х и Y) и P(Y и X) Третье равенство — это просто другой способ записи первого равен-
ства, поскольку для нас события X и Y равнозначны Последнее равенство является след-
ствием предыдущих трех равенств, оно дает возможность вычислить условную вероят-
ность через известную “обратную” условную вероятность
Чтобы применить эти общие равенства в нашем случае, допустим, что Y = 1 и X = Ч.
Тогда на основе формулы (9 5) получаем
P(1IQ) = P(QI^P-(1).	(9 6)
P(Q)
Мы знаем вероятности Р(ЧИ) и Р(1), но чему равна вероятность Р(Ч)? Чтобы найти
значение этой вероятности, используем прием, который часто применяется в теории ве-
роятностей Событие Ч (т е событие, которое заключается в том, что будет вынут черный
шар) возможно только тогда, когда шар, вынутый из урны 1, будет черным, или шар, вы-
нутый из урны 2, будет черным, либо шар, вынутый из урны 3, также будет черным Та-
ким образом,
Р(Ч) = Р(1 и Ч) + Р(2 и Ч) + Р(3 и Ч) =
= Р(Ч и 1) + Р(Ч и 2) + Р(Ч и 3) =
= Р(Ч11) Р(1) + Р(Ч12) Р(2) + Р(Ч13) Р(3)	(9.7)
Теорема Байеса и вычисление апостериорных вероятностей
Подставив последнее выражение для Р(Ч) в формулу (9.6), получим пример примене-
ния теоремы Байеса
Р(1 | Q) = —------Р^Н)Р(1)------------- (9.8)
P(Qll)P(l) + P(Ql2)P(2) + P(Ql3)P(3)
Поскольку все выражения в правой части формулы (9 8) нам известны, можем вычис-
лить вероятность Р( 114).
flllS)=72/ x/Jy°Xxyt8/ x3/4	(9'9)
/100 /6+ /100 /6+/100 /6
ГЛАВА 9. Анализ решений	635
Напомним, что безусловная вероятность вынуть шар из первой урны равна 1/6. Но если
мы знаем, что вынут именно черный шар, то вероятность того, что этот шар достали из пер-
вой урны, возросла в два раза (равна 1/3). В интерпретации примера с маркетинговыми ис-
следованиями это означает, что до проведения исследований вероятность того, что рынок
имеет низкий уровень спроса (1), принималась равной 1/6, а после проведения исследова-
ний и получения неблагоприятного результата (Ч) эта вероятность возросла до 1/3
Подобным образом мы можем вычислить ДПБ) и другие условные вероятности, для
чего следует использовать формулу (9.8). Но вместо этого мы покажем табличный подход
к вычислению вероятностей, который легко реализуется в программах электронных таблиц
Приведенные ниже табл. 9.13 и 9.14 содержат первоначальные значения известных
вероятностей. Если придерживаться примера маркетинговых исследований, то вероятно-
сти в табл. 9.13 следует называть “надежностями”, поскольку они характеризуют надеж-
ность результатов маркетинговых исследований; вероятности в табл. 9 14 — это априор-
ные вероятности состояний природы Совместные вероятности в табл 9 15 вычисляются
путем деления каждого элемента столбца i табл. 9.13 на такой же элемент столбца i
табл 9.14. Суммы элементов строк и столбцов этой таблицы дают значения безусловных
вероятностей Апостериорные вероятности в табл. 9 16 определяются путем деления зна-
чений совместных вероятностей в каждой строке табл. 9 15 на соответствующие значения
безусловных вероятностей, которые вычисляются как суммы этих же строк
Таблица 9.13. "Надежности"
Результат исследований		Состояния природы		
	1	2		3
Ч	ДЧП) =0,72	ДЧ12) = 0,60	/’(413) = 0,08
Б Суммы по столбцам	ДБП) =0,28	ДБ12) = 0,40 1	ДБ13) = 0,92
Таблица 9.14. Априорные вероятности
Состояния природы
	2	3	Сумма
Д1) = 1/6	Д2) = 2/6	Р(3) = 3/6	1
Таблица 9.15. Совместные и безусловные вероятности
Состояния природы
Результаты исследований	1	2	3	Суммы по строкам
Ч	ДЧи1)=0,12 ДЧ и 2) = 0,20	ДЧ и 3) = 0,04	ДЧ)=О,36
Б	ДБ и 1) = 0,0467 ДБ и 2) = 0,1333	ДБ и 3) = 0,46	ДБ) = 0,64
Суммы по столбцам	Д1) = 0,1667	Д2) = 0,3333	ДЗ) = 0,50	1
Таблица 9.16. Апостериорные вероятности
Состояния природы
Результаты исследований	1	2		3	Суммы по строкам
Ч	Д11Ч) = 0,333	Д21Ч) = 0,556	Д31Ч) =0,111	1
Б	Д11Б) = 0,073	Д21Б) = 0,208	Д31Б) =0,719	1
636
ЧАСТЬ III Вероятностные модели
Мы закончим этот раздел рассмотрением одного интересного вопроса, который часто
возникает на практике. Если в примере с маркетинговыми исследованиями надежность
этих исследований оценивается по имеющимся статистическим данным, то почему мы
не можем использовать эти данные для оценки апостериорных вероятностей? Допустим,
имеются данные о 300 проведенных ранее маркетинговых исследованиях (табл. 9.17).
Исходя из этих данных мы оцениваем вероятность /’(ЧП) как 72/100 = 0,72. Почему тогда
нельзя считать, что вероятность Р(ПЧ) равна 72/140?
Таблица 9.17. Данные по 300 маркетинговым исследованиям
Состояния природы
Результаты исследований	12	3	Суммы по строкам
Ч	72	60	8	140
Б	28	40	92	160
Суммы по столбцам	100	100	100	300
Прежде всего заметим, что значение 72/140 (=0,514) для вероятности /’(ПЧ) отлича-
ется от значения 0,333, полученного нами по формуле (9 9). Причина этого заключается
в различных значениях априорных вероятностей Предположив, что Z’(l) = Р(2) = Р(3) =
= 1/3, как это следует из данных табл. 9.17, и применив теорему Байеса, мы действитель-
но получим /’(ПЧ) = 0,514 Но если в нашем распоряжении будут другие первоначальные
оценки вероятностей состояний природы, то мы получим другие значения апостериор-
ных вероятностей Предположим, что мы уверены на 100%, что уровень спроса на нашу
продукцию очень высоким, т е считаем, что Р(3) = 1,0. Тогда применение теоремы Байе-
са дает /’(114) = 0, /Д2|Ч) = 0 и /"(314) = 1,0. Другими словами, в этом случае даже неблаго-
приятный результат маркетинговых исследований не может изменить априорных веро-
ятностей Вывод апостериорные вероятности зависят от значений априорных вероятно-
стей, сегодняшние оценки априорных вероятностей состояний природы могут не совпадать
с оценками, полученными на основе статистических данных.
Основные термины
Апостериорные вероятности Новые значения вероятностей, пересчитанные на основе теоремы
Байеса из априорных вероятностей с учетом новой информации
Априорные вероятности Исходные значения вероятностей
Ветви Линии, исходящие из узлов дерева решений
Дерево решений Графическое представление модели принятия решений в условиях риска.
Конечная позиция Окончание ветви, исходящей из конечного узла
Конечное значение Платеж, соответствующий конечной позиции
Конечный узел Узел дерева решений, не имеющий следующих за ним узлов
Критерий минимаксных потерь. Критерий принятия решений, минимизирующий максимум потерь
Потери — мера измерения качества решений (отличная от платежей), характеризующая
“стоимость” решения
Лицо, избегающее риска Лицо, для которого в условиях риска более значим проигрыш, а не выиг-
рыш Такая позиция отображается в виде вогнутой функции полезности
ГЛАВА 9. Анализ решений
637
Лицо, настроенное на риск Лицо, для которого в условиях риска более привлекателен выигрыш
и менее значим проигрыш Настроенность на риск отображается в виде выпуклой функции
полезности
Лицо, нейтральное к риску Функция полезности для такого лица является прямой линиеи
Максимаксный критерий Оптимистический критерий принятия решений, максимизирующий
максимум возвращаемого результата (платежа)
Максиминный критерий Консервативный (пессимистический) критерий принятия решении, мак-
симизирующий минимум возвращаемого результата (платежа)
Модель последовательных решений Модель, в которой оптимальное решение (оптимальная стра-
тегия) состоит из последовательности других решении, зависящих от случайных событии
Обратный пересчет Процесс вычисления значений дерева решении, начинающийся в конечных
узлах и заканчивающийся в начальном узле дерева
Ожидаемое значение дополнительной информации Разность между максимально возможными ожи-
даемыми результатами с учетом и без учета дополнительной информации
Ожидаемое значение полной информации Верхняя граница “цены” новой информации
Полезность В этой главе — мера “привлекательности” выходного результата для индивидуума
Принятие решений в условиях неопределенности. Принятие решений против природы, когда неиз-
вестны вероятности проявления состояний природы
Принятие решений в условиях определенности Принятие решений против природы, когда известно,
в каком состоянии будет находиться природа после принятия решения
Принятие решений в условиях риска. Принятие решений против природы, когда известны вероят-
ности наступления каждого возможного состояния природы
Профиль риска. Для конкретного решения профиль риска показывает все возможные выходы
(значения платежей) с соответствующими вероятностями Обычно профиль риска представля-
ется в виде графика
Таблица платежей При принятии решений против природы эта таблица показывает возвращае-
мый результат для каждой комбинации состояния природы и принимаемого решения
Узел решений Узел дерева решении, в котором должно быть принято какое-либо решение
Узел событий Узел дерева решений, представляющий случайные события
Условная вероятность Вероятность события (скажем, события В), зависящая от наступления дру-
гого события (события А) Обозначается как ABIA) и определяется ABIA) = АВ и А)/АА)
Эквивалентная лотерея Метод создания функции полезности
Контрольные вопросы
Да/нет
1.	Дерево решений содержит последовательность решений и случайных выходных
результатов
2.	В теории принятия решений считается, что результаты принятых решении зависят
от безличностного и беспристрастного противника, которого называют “природа”
3.	Один из основополагающих фактов теории принятия решений состоит в том, что
независимо от наших предположений о состояниях природы (точнее, о вероятно-
стях этих состояний) для выбора “наилучшего решения” всегда используется еди-
ный критерий
638 ЧАСТЬ 111 Вероятностные модели
4.	Многие детерминированные оптимизационные модели можно рассматривать как
модели принятия решений в условиях определенности, когда существует только
одно состояние природы.
5.	Один из способов создания моделей принятия решений в условиях полной неоп-
ределенности состоит в том, чтобы считать, что все состояния природы равнове-
роятны
6.	Вычисление ожидаемого значения полной информации основывается на предпо-
ложении, что исключены все возможные случайности
7.	Критерий максимизации ожидаемого денежного платежа всегда приводит к тако-
му же решению, что и критерий минимизации ожидаемых потерь.
8.	Функция полезности для лица, избегающего риска, выпукла
9.	Поиск решения по дереву решении происходит с помощью обратного пересчета
10.	Теорема Байеса предлагает метод изменения априорных вероятностей с учетом
поступившей новой информации
Выберите правильный ответ
11.	Теория принятия решений уделяет большое внимание:
а всей доступной информации, необходимой для построения модели принятия
решений;
b критерию для измерения “качества” решения;
с выбору оптимального решения,
d всему вышеперечисленному.
12.	Какое из следующих утверждений неверно для моделей принятия решений в усло-
виях риска9
а Для принятия решения необходимо знать вероятность каждого возможного со-
стояния природы
b Для принятия решения используется критерий максимизации результата
с Для принятия решения используется критерий максимизации ожидаемого ре-
зультата
d Для принятия решения используется критерий минимизации ожидаемых потерь
13.	Какой из следующих критериев не используется при принятии решений в условиях
неопределенности9
а Максимизации минимума результата.
b Максимизации максимума результата.
с Минимизации максимума потерь
d. Максимизации минимума ожидаемых потерь
14.	Максиминный критерий, максимаксный критерий и критерий минимаксных потерь:
а приводят к одному и тому же оптимальному решению;
b можно использовать без знания вероятностей состояний природы;
с а и b
15.	Ожидаемое значение полной информации-
ГЛАВА 9. Анализ решений 639
а.	определяет двухстороннюю границу объема собранной информации,
Ь.	можно определить без использования значений вероятностей,
с.	показывает полезность собранной информации;
d.	численно равно ожидаемым потерям оптимального решения в условиях риска.
16. Полезность — это
а.	мера привлекательности денег;
b	мера неприятия риска;
с.	мера предрасположенности к риску;
d.	я ий;
е а, b и с
17.	Какое из следующих утверждений не применимо к деревьям решений9
а.	Узлы решений — это точки, в которых необходимо выбрать одно из возможных
решений
Ь.	Узлы событий означают “встречу с неопределенностью”.
с.	Выбирается последовательность решений, имеющих наибольшие вероятности
успеха.
d Основное внимание обращается на максимизацию ожидаемого результата
18.	Ожидаемое значение полной информации
а показывает стоимость получения полной информации о событиях, которые
произойдут в будущем,
Ь. показывает максимальное возрастание ожидаемого результата при полной ин-
формации,
с показывает ожидаемый объем информации, необходимой для выбора опти-
мального решения,
d все вышеперечисленное.
19.	Вычисляя ожидаемое значение полной информации, необходимо учитывать пла-
тежи, сделанные:
а.	до получения информации,
Ь.	после получения информации,
с.	безвозвратно;
d.	лис.
20.	Если решения принимаются заблаговременно и последовательно, то-
а деревья решений не используются;
b должна использоваться теорема Байеса;
с. конечное значение конечной позиции каждой последовательности ветвей яв-
ляется платежом этой последовательности;
d конечное значение конечной позиции каждой последовательности ветвей яв-
ляется ожидаемым платежом этой последовательности
640 ЧАСТЬ III Вероятностные модели
Ответы
1 Да 2 Да 3 Нет 4 Да. 5. Да 6. Нет 7. Да. 8. Нет. 9. Нет. 10. Да. 11. d. 12. b. 13 d. 14.
b 15. d 16 е 17 с 18. b 19 d 20. с
Учебные задачи
9 I В табл 9 18 представлена таблица платежей в денежном выражении Предположим, что при-
нимается решение в условиях отсутствия информации о вероятностях состояний природы
а Каким будет оптимальное решение, если используется критерий Лапласа9
b Каким будет оптимальное решение, если используется максиминный критерий9
с Каким будет оптимальное решение, если используется максимаксный критерий?
d Создайте таблицу платежей со значениями потерь
е Каким будет оптимальное решение, если используется критерий минимизации мак-
симума потерь9
Таблица 9.18
_______________________Состояния природы______________________
Решение I 2 3 4
35	22	25	12
9 2 В табл 9 19 представлена таблица платежей в денежном выражении Предположим, что при-
нимается решение в условиях отсутствия информации о вероятностях состояний природы
а Каким будет оптимальное решение, если используется критерий Лапласа9
b Каким будет оптимальное решение, если используется максиминный критерий9
с Каким будет оптимальное решение, если используется максимаксный критерий9
d Создайте таблицу платежей со значениями потерь
е Каким будет оптимальное решение, если используется критерий минимизации мак-
симума потерь9
Таблица 9.19
Состояния природы
Решение	12	3
9 3 В табл 9 18 представлена таблица платежей в денежном выражении Предположим, что со-
стояния природы имеют следующие вероятности Р(1) = 0,1, Р(2) = 0,4, Р(3) = 0,3, Р(4) = 0,2
а Найдите решение, которое максимизирует ожидаемый платеж
b Найдите решение, которое минимизирует ожидаемые потери
с Объясните полученные решения
ГЛАВА 9. Анализ решений 641
В табл. 9.19 представлена таблица платежей в денежном выражении Предположим, что со-
стояния природы имеют следующие вероятности. Р(1) = 0,3, Р(2) =0,6, Р(3) = 0,1
а. Найдите решение, которое максимизирует ожидаемый платеж.
b Найдите решение, которое минимизирует ожидаемые потери Предположите, что зна-
чения вероятностей Р(1) и Р(2) неизвестны, а Р(3) =0,1.
с Создайте графики ожидаемых платежей для трех решений в зависимости от значений
вероятности Р(2) и найдите значения этой вероятности, при которых будет оптималь-
ным каждое из решений
d Создайте графики ожидаемых потерь для трех решений в зависимости от значений ве-
роятности Р(2) и найдите значения этой вероятности, при которых будет оптимальным
каждое из решений
е Объясните полученные решения
Перед директором компании Johnson’s Printing из Чикаго Филом Джонсоном стоит дилем-
ма заняться заключением контракта с правительством на печатные работы, либо вылететь
в Лос-Анджелес для заключения другого договора на печать рекламных брошюр Ситуация
складывается таким образом, что он не может одновременно начать процесс заключения
обоих контрактов, и в любом случае решение о подписании договора с правительством он
должен принять до заключения контракта на печать брошюр Оценки Джонсоном плате-
жей для этой ситуации приведены в табл 9 20
а Каким будет оптимальное решение, основанное на максиминном критерии9
b Если вероятность получить контракт на печать брошюр равна 1/3, то какое решение
обеспечивает максимум ожидаемого платежа9
с Обозначим через Р(К) вероятность заключить контракт на печать брошюр Создайте гра-
фики зависимости ожидаемых результатов для каждого решения от вероятности Р(К)
d Каково наименьшее значение вероятности Р(К), при котором Фил Джонсон должен
лететь в Лос-Анджелес9
е Каким будет оптимальное решение в соответствии с критерием минимаксных потерь9
f Каким будет оптимальное решение, если применяется критерий минимизации ожи-
даемых потерь и Р(К) = 1/39
g Предположим, что агент, который занимается заключением контракта на печать бро-
шюр, уже выбрал типографию, но Фил еще не знает его решения Какую максималь-
ную цену может заплатить Фил за эту информацию, если еще надеется, что с вероят-
ностью 1/3 он может выиграть данный тендер9
h Как называется цена информации, полученная в предыдущем пункте9
Таблица 9.20
__________________Состояния природы_________________
Не получить контракт на печать Получить контракт на печать
Решение_______________________________брошюр___________________брошюр__________
Заключать правительствен-	1000	1000
ный контракт
Заключать контракт на пе-	-1000	4000
чать брошюр
Продавец сувениров обнаружил, что объемы продаж в июле очень сильно зависят от пого-
ды Однако сувениры он должен заказывать еще в январе Оптовый продавец сувениров
поставляет продукцию малыми, средними и большими партиями, причем оптовая цена су-
642
ЧАСТЬ III Вероятностные модели
вениров в этих партиях различна Таблица денежных платежей для этой ситуации показана
в табл 9 21, а функция полезности для продавца сувениров — на рис 9 30 Продавец пред-
полагает, что все состояния природы равновероятны
а Какое решение максимизирует ожидаемый денежный результат9
b Какое решение максимизирует ожидаемую полезность9
с Объясните полученные решения
Таблица 9.21
Состояния природы
Решение	Холодно	Прохладно	Тепло	Жарко
Малая партия	0	ЮОО	2000	3000
Средняя партия	-ЮОО	0	3000	6000
Большая партия-3000-ЮОО 4000 8000
Полезность
-4000j -2000	0	| 2000 | 4000	6000	8 000	Доллары
-3 000	1 000	3 000
Рис. 9.30. Функция полезности
Фил Джонсон (см задачу 9 5) решил использовать функцию полезности, показанную на
рис 9 30, чтобы определить, стоит ли ему заключать контракт на печать брошюр
а Каким будет оптимальное решение, если применить критерий максимизации ожидае-
мого денежного результата, и вероятность получить контракт на печать брошюр равна
1 /З9 Какова величина ожидаемого денежного результата в этом случае9
b Изменится ли оптимальное решение, если применить критерий максимизации ожи-
даемой полезности9 Объясните ответ
с Каково значение ожидаемой полезности оптимального решения9
d Каково значение функции полезности от ожидаемого результата решения заключать
контракт на печать брошюр9
е	Каково значение ожидаемой полезности решения заключать контракт на печать брошюр9
f Должны ли совпадать ответы на вопросы пунктов d и е9
ГЛАВА 9. Анализ решений 643
9 8 Пусть значение функции полезности равно 0 для платежа — S20 ООО и 1 для платежа S50 ООО
Постройте собственную функцию полезности, выполнив следующие действия
а С помощью метода эквивалентных лотерей найдите значения функции полезности для
платежей SO и $20 000
b Отложите на графике четыре точки вашей функции полезности и соедините их пря-
мыми линиями
с На основе построенной функции полезности определите категорию лиц (склонных
к риску, уклоняющихся от риска, безразличных к риску, либо ничего из перечислен-
ного), к которой вы себя отнесете
9 9 Менеджер, отвечающий за работу с клиентами в компании Sonorola, должен быстро обра-
батывать заказы, поступившие с опозданием Чтобы делать эту работу эффективно, он
должен определить причину опоздания заказа Причин может быть только две неправиль-
ное оформление заказа и задержка в доставке заявки Система обработки заказов такова,
что причиной задержки может быть только одна из этих причин Из своего опыта менед-
жер знает, что ошибки оформления встречаются в 8 из 20 случаев, тогда как в 8 из 10 случа-
ев виновата доставка заявок Вместе с тем статистика говорит, что на 1 000 заказов 30 зака-
зов будут оформлены с ошибками, а 10 будут доставлены с опозданием Менеджер держит
в руках заявку, поступившую с опозданием Какова вероятность, что этот заказ оформлен
с ошибками, и какова вероятность, что в опоздании виновата служба доставки9
9 10 Шоу дрессированных собак Вальтера в соответствии с расписанием турне должно высту-
пать в городе N 10 июля Доход от выступления напрямую зависит от погоды Если будет
идти дождь, то шоу может потерять $15 000, а если будет солнечная погода, то прибыль мо-
жет составить $10 000 (Будем предполагать, что в этом городе N погода может быть только
двух видов или идет дождь или светит солнце ) Вальтер может отменить свое шоу, но
в этом случае он потеряет залог на выступление в размере S1 000 Из исторических хроник
за последние 100 лет известно, что 10 июля в городе N дождь идет с вероятностью 1/4
а Какое решение должен принять Вальтер для максимизации ожидаемого дохода9
b Каково ожидаемое значение полной информации для этой ситуации9
9 11 Ситуация предыдущей задачи Вальтер хочет купить прогноз погоды на 10 июля у предска-
зателя погоды Виктора Конечно, Виктор дает прогнозы не со 100% точности Известно,
что если он предсказывает дождь, то дождь действительно идет в 90% случаев Прогноз
солнечной погоды не такой точный — он сбывается только в 80% случаев
а Какой стратегии должен придерживаться Вальтер для максимизации ожидаемого до-
хода при наличии прогноза от Виктора9
b Какую сумму может заплатить Вальтер за прогноз погоды9
9 12 Игроку предложено сыграть в следующую двухэтапную игру На первом этапе он платит $5 и
случайным образом вытаскивает шар из урны, содержащей пять белых и пять красных шаров
После этого игрок может или выйти из игры или, доплатив еще $10, перейти ко второму этапу
игры Если вначале игрок вытащил белый шар, то на втором этапе он случайным образом вы-
таскивает шар из белой урны, содержащей два синих и восемь зеленых шаров Если на первом
этапе игрок вытащил красный шар, то на втором этапе он вытаскивает шар из красной урны,
содержащей шесть синих и четыре зеленых шаров Если на втором этапе игрок вытащит си-
ний шар, он получит выигрыш $35 Если же вытащит зеленый шар, то не получит ничего С
помощью дерева решений найдите для игрока оптимальную стратегию
9 13 Некая инвестиционная компания делит всех своих клиентов, обращающихся за кредитом,
на две категории лица с повышенным риском невозврата кредита и лица с обычным рис-
ком невозврата кредита Статистика показывает, что среди всего населения примерно
10% — это лица с повышенным риском (по критериям компании) Для решения о выдаче
кредита компания использует систему оценки кредитоспособности клиентов Опыт пока-
644	ЧАСТЬ III Вероятностные модели
	зывает, что если система считает клиента кредитоспособным, то он получит кредит с веро- ятностью 90% Если же система считает клиента лицом с повышенным риском, то имеется только 20% шансов, что он получит кредит. Руководство компании считает, что клиенты, обращающиеся к ним за кредитом, составляют случайную выборку из всего населения. Ка- кова вероятность того, что клиент, получивший кредит, является лицом с повышенным риском невозврата кредита9 (Используйте теорему Байеса )
9 14	Трое рабочих производят некоторые детали с одинаковой производительностью Ларри в среднем допускает три бракованных детали на сотню, тогда как Мои и Карл делают по шесть и девять бракованных деталей на сотню соответственно а. Сколько бракованных деталей следует ожидать в 1000 деталях, произведенных этими рабочими9 b Какова вероятность того, что наугад выбранная бракованная деталь произведена Карлом9
9 15	Компания Johnson’s Composite Materials (JCM), производящая корпуса из композитных мате- риалов для мобильных телефонов, принимает решение о том, участвовать ли в тендере на производство корпусов для мобильных телефонов компании Sonorola Чтобы заключить кон- тракт с Sonorola, компании JCM надо предварительно разработать (или модернизировать су- ществующий) технологический процесс производства корпусов и создать 10 моделей корпу- сов, которые необходимо передать Sonorola для оценки Стоимость этого предварительного этапа составляет $50 000, и эти деньги будут потеряны, если не будет заключен контракт с So- norola Если же JCM заключит контракт с Sonorola (специалисты оценивают вероятность выиг- рать тендер как 0,4), то появится возможность продать Sonorola 10 000 корпусов по цене $50 за штуку JCM может использовать для нового заказа существующие производственные мощно- сти, при этом их переналадка обойдется в $40 000, а себестоимость корпусов составит $20 Од- нако существует риск, что в зависимости от ситуации с другими выполняемыми JCM заказа- ми, может понадобиться вводить сверхурочные работы Стоимость сверхурочных работ в за- висимости от ситуации с выполнением других заказов показана в табл 9 22 JCM может закупить новую технологическую линию стоимостью $260 000, в этом случае отпадет необхо- димость в сверхурочных работах, а себестоимость корпусов для мобильных телефонов соста- вит $10 С помощью дерева решений найдите оптимальную стратегию для компании JCM Таблица 9.22. Стоимость и вероятность сверхурочных работ для компании JCM Ситуация с другими заказами	Вероятность	Стоимость сверхурочных работ Тяжелая	0,2	$200	000 Обычная	0,7	$100	000 Легкая	0,1	0
9 16	Дженни Линд — автор любовных романов Кинокомпания и телекомпания хотят получить эксклюзивные права на ее наиболее популярный роман для экранизации Если Дженни продаст права телекомпании, то она получит одноразовую фиксированную сумму $900 000 Если же она продаст права кинокомпании, то ее гонорар будет зависеть от прокатного ус- пеха кинокартины Таблица платежей для данной ситуации приведена в табл 9 23 Опреде- лите, кому Дженни должна продать права на свой роман, если вероятность малого успеха будущей картины оценивается как 0,3, среднего — 0,6, а большого — 0,1 Таблица 9.23 	Состояния природы	 Решение	Малый успех Средний успех	Большой успех Продать права кинокомпании	$200 000	$ 1 000 000	$3 000 000 Продать права телекомпании	$900 000	$900 000	$900 000
ГЛАВА 9. Анализ решений	645
9 17 Компания Kelly Construction хочет принять участие в строительстве студенческих общежитий
Для этого компания должна сначала выкупить участок земли, на котором можно построить
комплекс на 100, 200 или 300 жилых модулей В строительстве участвуют многие компании,
причем строительство их комплексов находится на разных стадиях готовности Поэтому в на-
стоящий момент очень сложно прогнозировать спрос на студенческое жилье В табл 9 24
приведены возможные платежи компании Kelly Construction для разных уровней спроса
а Каково оптимальное решение в соответствии с максиминным критерием9
b Каково оптимальное решение в соответствии с максимаксным критерием9
с Каково оптимальное решение в соответствии с критерием минимаксных потерь9
d Пусть вероятность низкого спроса равна 0,3, среднего спроса — 0,5 и высокого — 0,2
Какое решение обеспечит максимизацию минимума ожидаемых платежей9
е Найдите ожидаемое значение полной информации
Таблица 9.24
Решение		Спрос, долл.	 Низкий	Средний	Высокий
Строить 100 модулей Строить 200 модулей Строить 300 модулей	400 000	400 000	400 000 100 000	800 000	800 000 -200 000	500 000	1 200 000
9 18 Компания Marple Manufactonng планирует производство нового изделия Одна из деталей
этого изделия имеет высокую стоимость, поэтому компания рассматривает варианты как
закупки этого компонента на стороне, так и производства его собственными силами Но
получаемый доход в том и другом случае значительно зависит от спроса на выпускаемое
изделие, как показано в табл 9 25 Вероятность низкого спроса равна 0,4, а вероятности
среднего и высокого спроса — 0,3 Создайте дерево решений и определите, следует компа-
нии покупать или производить эту деталь
Таблица 9.25
Решение	Спрос		
	Низкий	Средний	Высокий
Производить деталь	11	32	53
Покупать деталь	15	30	45
9 19 Чак каждую среду ездит в Паоло-Альто в командировку (он работает консультантом в кон-
салтинговой фирме), возвращаясь домой в Сан-Хосе в тот же день вечером Проделав
многократно маршрут Паоло-Альто — Сан-Хосе, он заметил, что если он едет по шоссе
280, то время поездки может значительно отличаться, а если он едет через Эль-Камино, то
время поездки всегда примерно одинаково На основе этого опыта Чак составил таблицу
платежей (табл 9 26), где в качестве платежей указана длительность поездки в минутах Он
считает, что примерно в 90% случаях движение не интенсивно Какой ему следует выбрать
маршрут, чтобы минимизировать ожидаемое время поездки9
Таблица 9.26
Решение	Состояния природы Неинтенсивное движение	Интенсивное движение
Шоссе 280 Через Эль-Камино	25	55 35	40
646 ЧАСТЬ III. Вероятностные модели
9 20	Небольшая больница в деревне Альбемарль покупает кровь в городском банке крови Закуп- ленная кровь не может храниться более месяца, поэтому ее запасы ежемесячно обновляются Если кровь заказывается заблаговременно, ее стоимость для больницы составляет $10 за еди- ницу Если кровь нужна срочно и в больнице ее нет, то стоимость единицы крови возрастает до $100 Данные о потребности крови за последние три года показаны в табл 9 27 а Составьте для больницы таблицу платежей b Сколько единиц крови должна заказывать больница в месяц9 Таблица 9.27 Использовано единиц крови	Количество	месяцев 0	24	месяца 1	8	месяцев 2	4 месяца Всего	36 месяцев
921	Боб Дэвидсон из компании Marple Manufactortng, отвечающий за закупку комплектующих, должен решить, у каких производителей покупать определенный компонент, необходимый для производства изделия, которое выпускает их компания Производитель А поставляет эту деталь партиями в 1 000 штук по цене $10 за штуку, тогда как у производителя В цена составляет $9,50 за штуку Однако в 20% поставляемых производителем В партиях содер- жится 10% дефектных деталей, а в 80% — 1% брака В 99% партий, поставляемых произво- дителем А, содержится только 1 % брака, и в 1% партий — 3% дефектных деталей Для ком- пании Marple Manufactonng каждый дефектный компонент приносит убыток в $100 вслед- ствие затрат на тестирование и переделку готовых изделий, содержащих дефектную деталь а Создайте дерево решений для этой ситуации b На основе критерия ожидаемой стоимости определите, у какого производителя следу- ет покупать компоненты
9 22	Рик О’Шин — независимый автоперевозчик из Таксона Он хочет определиться, занимать- ся ему доставкой груза в Денвер или в Солт-Лейк При доставке грузов в Денвер, он в 90% случаев будет также иметь обратный груз (т е не будет возвращаться в Таксон пустым), то- гда как в Солт-Лейке он только в половине случаев сможет найти обратный груз Платежи для этой ситуации показаны в табл 9 28 а Создайте дерево решений для этой ситуации b На основе критерия ожидаемого результата определите, в какой город лучше всего доставлять грузы Таблица 9.28 Есть обратный груз	Нет обратного груза Солт-Лейк	$4000	$3500 Денвер	$3850	$3350
9 23	Дана таблица платежей (см табл 9 29) а Какие акции выберет беспристрастный инвестор9 b Какие акции выберет оптимистичный инвестор9 с Какие акции выберет пессимистичный инвестор9 d Какие акции принесут наибольший ожидаемый доход, если предположить, что веро- ятность неблагоприятного состояния экономики равна 0,1, благоприятного — 0,5, а отличного — 0,4
ГЛАВА 9 Анализ решений 647
	Таблица 9.29 Состояния экономики Акции	Неблагоприятное	Благоприятное	Отличное IBM	10	15	18 Т	5	15	20 Q	-15	25	45 WFT	-15	0	15
9 24	Производитель одноразовых фотокамер готовится к сезону праздников Вероятности и объемы спроса на одноразовые фотокамеры, рассчитанные на основании данных за предыдущие годы, показаны в табл 9 30 Доход с каждой фотокамеры, проданной в течение сезона праздников, со- ставляет S5, тогда как фотокамеры, не проданные за это время, приносят только S1 дохода а Создайте дерево решений для данной ситуации b Какое решение должен принять производитель, чтобы максимизировать свою прибыль9 Таблица 9.30 Спрос	Вероятность 5 000	0,4 9 000	0,6
9 25	Фотограф готовится к съемкам на южных пляжах Гавайских островов Расписание съемок составлено заранее, и на съемки приглашена только на один день супермодель Нацио- нальное бюро погоды прогнозирует на день съемок с вероятностью 40% дождь Если дейст- вительно в день съемок будет дождь, то фотограф потеряет S250 000, а если будет солнечная погода, то он заработает S1 000 000 а Покупать ли фотографу страховку от потерь в случае дождя9 b Какую максимальную цену можно заплатить за такую страховку9
926	Фред — владелец театра на Бродвее Сейчас он решает вопрос о том, какую пьесу принять к постановке Постановка первой пьесы (которая называется Собаки) требует S2 млн , тогда как постановка второй пьесы (называется Ушедшие со снегом) требует S4 млн Однако вто- рую пьесу можно будет играть значительно дольше, чем первую Вероятности успеха каж- дой пьесы и возможные доходы от них представлены в табл 9 31 а С помощью дерева решений определите, какую пьесу следует принять к постановке b Каков ожидаемый результат от постановки каждой пьесы9 Таблица 9.31 Вероятности	Доход, млн. долл. Уровень успеха	Собаки	Ушедшие со снегом Собаки Ушедшие со снегом Хит сезона	0,3	0,4	5	25 Умеренный	0,3	0,3	4	15 Низкий	0,3	0,2	2	2 Провал	0,1	0,1	0,5	0,75
648 ЧАСТЬ III Вероятностные модели
9 27 Скульптор может продать свой последний шедевр за $10 ООО посреднику для последующей
продажи на еженедельной выставке искусств, но эта цена действует только одну неделю
Он также может выставить свое произведение на аукционе в Internet, для чего должен сна-
чала внести сумму $500 Если торги будут удачными, то он может выручить за свою скульп-
туру не менее $15 000, а если нет — не более $3 000 Вероятности активных и пассивных
торгов (на основе данных предыдущих аукционов) приведены в табл 9 32
а Создайте дерево решений для этой ситуации
b Какое решение должен принять скульптор9
Таблица 9.32
Торги	Вероятности
Активные	0,75
Пассивные	0,25
9 28 “Биогенетика” — небольшая фирма, занимающаяся разработкой медикаментов Фирма
имеет ограниченные ресурсы, поэтому она может разработать не более двух лекарственных
препаратов в следующем году Поэтому ей необходимо выбрать из четырех возможных раз-
работок только две, которые могут принести фирме наибольшую прибыль Отметим, что
в данной отрасли очень большая вероятность неудачи при разработке нового продукта
Данные о возможных прибылях и потерях приведены в табл 9 33
а На основе критерия Лапласа выберите препараты, которые стоит разрабатывать
b На основе максиминного критерия выберите препараты, которые стоит разрабатывать
с На основе максимаксного критерия выберите препараты, которые стоит разрабатывать
Таблица 9.33
Платежи, долл.
Препарат	Неудача	Успех
А	-500 000	7 000 000
В	-1 000 000	27 000 000
С	-400 000	10 000 000
D	-700 000	17 000 000
9 29 В фирме “Биогенетика” (см задачу 9 28) считают, что вероятность потерпеть неудачу при
разработке любого препарата равна 80%, вероятность добиться успеха — 20%
а Какие два препарата следует выбрать для разработки, чтобы максимизировать ожидае-
мый результат9
b Какие два препарата следует выбрать для разработки, чтобы минимизировать ожидае-
мые потери9
Прикладные задачи
9 30 Предположим, что вы опасаетесь риска Для вашей функции полезности известны две
крайние точки (/(-30) = 0, (/(70) = 1
а Какая нижняя граница для значений (/(30)9
ГЛАВА 9. Анализ решений	649
Ь Предположим, что для вас равнозначно получить гарантированный платеж 30 или сыграть
в лотерею, где с вероятностью 0,7 вы можете выиграть 70 и с вероятностью 0,3 потерять 30
с Какова нижняя граница для значений £7(50)’
d Каково минимальное значение верхней границы для U( 10)’
9 31 Предположим, что на вашей функции полезности известны две крайние точки. £/(—30) = 0,
£/(70) = 1
Допустим, что для вас равнозначно получить гарантированный платеж 30 или сыграть в лоте-
рею, где с вероятностью 0,3 вы можете выиграть 70 и с вероятностью 0,7 потерять 30 Кроме
того, вам все равно, получить гарантированный платеж 10 или сыграть в игру, где с вероятно-
стью 0,9 вы можете потерять 30 и с вероятностью 0,1 выиграть 30
а	Как можно описать вашу функцию полезности9 Являетесь ли вы лицом, склонным к риску9
b	Каковы верхняя и нижняя границы для значений £/(50)9
с	Каковы верхняя и нижняя границы для значений £/(25)9
9 32 Фирма Scrub Professional Cleaning Service занимается обслуживанием зеленых насаждений
возле жилых домов (подрезка деревьев и кустарников, уборка, очистка участков и т п )
Предварительные заявки на обслуживание она получает или от собственного агента или от
управляющих домами, причем примерно четверть заказов она получает от собственного
агента, а три четверти — от управляющих домами К сожалению, не все предварительные
заявки реализуются Например, только 3/8 предварительных заявок, полученных от управ-
ляющих домами, доходят до стадии реализации, тогда как 7/8 предварительных заявок, по-
лученных от собственного агента, реализуются Чистый доход от одной реализованной за-
явки составляет S1 000, на каждой нереализованной заявке фирма теряет S150
а Какова вероятность того, что предварительная заявка будет выполнена9 Какой ожи-
даемый доход от каждой предварительной заявки9
b Кто, агент или управляющие домами, приносит больший ожидаемый доход9
Фирма хранит всю информацию о всех ранее выполненных работах, причем данные
о заказах собственного агента и управляющих домами хранятся отдельно Фирма хочет
найти информацию о работах, которую они ранее выполняли для Джона Джонса
с В данных о каких заказах (выполненных по предварительным заявкам собственного
агента или по заявкам управляющих домами) наиболее вероятно найти информацию
о работах для Джона Джонса9
9 33 Небольшая угледобывающая компания продает уголь близлежащим городкам партиями
в 2, 1 и 0,5 т Вероятность, что компания получит заказ на уголь от города А, равна 0,20, ве-
роятность, что компания получит заказ от города В, равна 0,30, и аналогичная вероятность
для города С составляет 0,50 Относительная повторяемость (частота) объемов заказов для
каждого города приведена в табл 9.34 Величины доходов от поставок различного количе-
ства угля во все города даны в табл 9 35.
а Какова вероятность того, что будет получен заказ на 0,5 т9
b Если есть заказ объемом 0,5 т, то какова вероятность, что это заказ от города А9
с. Найдите ожидаемый доход для компании.
Таблица 9.34. Относительная повторяемость объемов заказов
	Объем заказа, т				
Город	0,5	1	2		
А	0,50	0,00	0,50
В	0,00	0,50	0,50
С	0,25	0,75	0,00
650 ЧАСТЬ III Вероятностные модели
Таблица 9.35. Размеры доходов
Город	Объем заказа, т 0,5	1	2
В	100	190	370 90	200	360 70	130	270
9 34 Руководитель компании Kelly Construction (см задачу 9 17) хочет уменьшить неопределен-
ность относительно спроса на студенческое жилье Он обратился в строительное управле-
ние муниципалитета, где ему могут сделать прогноз спроса, однако результат прогноза
можно охарактеризовать только как “малый спрос” (обозначим такой прогноз как Л/,),
“средний спрос” (обозначим как М2) и “большой спрос” (Л/,) Надежность такого прогноза
показана в табл 9 36, а таблица платежей (несколько отличная от аналогичной таблицы
в задаче 9 17) — в табл 9 37
а Создайте дерево решений для данной ситуации
b Найдите оптимальную стратегию
с Вычислите ожидаемые значения дополнительной и полной информации
Таблица 9.36
Прогноз			
	£>1	d2	D3
Mt	0.7	0.3	0,1
мг	0,2	0.4	0,3
М3	0,1	0,3	0,6
Таблица 9 37			
Спрос, долл.			
Решение	Низкий (Z>i)	Средний (Z>2)	Высокий (£>з)
Строить 100 модулей	500 000	500 000	500 000
Строить 200 модулей	0	1 000 000	1 000 000
Строить 300 модулей	-700 000	400 000	1 500 000
Вероятность	0,3	0,5	0,2
9 35 Таблица платежей для Дженни Линд (см задачу 9 16) повторена в табл 9 38 Она хочет на-
нять фирму, занимающуюся маркетинговыми исследованиями, чтобы эта фирма провела
исследование по прогнозированию успеха (У) или неуспеха (Н) будущей кинокартины,
снятой по ее роману За это Дженни согласна заплатить S100 ООО Точность прогноза опре-
деляется следующими условными вероятностями Р(У1М) = 0,3, Р(У1С) = 0,6, Р(У1Б) = 0,8,
Р(Н1М) = 0,7, Р(Н1С) = 0,4, Р(Н1Б) = 0,2
а Создайте дерево решений для данной модели
b Должна ли Дженни обращаться за проведением маркетинговых исследований7 Как
следует использовать результат исследований9
с Вычислите ожидаемое значение дополнительной информации Какую наибольшую
цену она может заплатить за исследования9
ГЛАВА 9 Анализ решений 651
	Таблица 9.38 Состояние природы Решение	Малый успех (М) Средний успех (С) Большой успех (Б) Продать права кинокомпании	$200 000	$1000 000	$ 3 000 000 Продать права телекомпании	$900 000	$900 000	$900 000 Вероятность	0,3	0,6	0,1
9 36	Джим, отставной геолог, разработал программу, определяющую возможное месторождение нефти по геологическим данным и данным сейсморазведки Это программное обеспечение использует сложный алгоритм, который значительно превосходит существующие Джим мо- жет продать права на эту программу компании Dundee Software Services за $100 000 либо выйти с ней на рынок программного обеспечения самостоятельно Проведя небольшое исследова- ние рынка программных продуктов, Джим оценил вероятность большого успеха своей про- граммы как 0,15 (при этом он может заработать $350 000), вероятность умеренного успеха — 0,70 с прибылью $80 000 и вероятность провала — 0,15, при этом он потеряет $110 000 а Постройте дерево решений для этой ситуации b Что должен предпринять Джим и почему9
9 37	Таблица платежей для больницы деревни Альбемарль (см задачу 9 20) приведена в табл 9 39 Администрация больницы хочет на основе количества планируемых операций на следующий месяц спрогнозировать количество необходимого запаса крови Условные вероятности, свя- зывающие количество операций и потребности в крови, приведены в табл 9 40 а Создайте дерево решений для этой модели b Вычислите ожидаемое значение дополнительной информации с Сколько денежных средств может сохранить больница, если будет использовать про- гноз в потребности крови на основе количества планируемых операций9 Таблица 9.39 Потребность Заказано	0 (ОД	1 (Di)	2 (О3) 0(Ql)	0	100	200 1 (Q2)	10	10	НО 2 (Q3)	20	20	20 Вероятность	2/3	2/9	1/9 Таблица 9.40 	P(S}D}	 Количество операций	£>i	Di	D3 0(Sl)	0 95	0,05	0 02 1 (S2)	0,04	0,80	0,08 2 (S3)	0,01	0,15	0,90
9 38	Фабрика Fly Rods выпускает высококачественные спиннинги для серьезных рыбаков В на- стоящее время для изготовления продукции используются старые машины, которые в еле-
652
ЧАСТЬ III. Вероятностные модели
дующие два года, скорее всего, потребуют ремонта Стоимость каждого ремонта составляет
$25 000 Вероятность необходимости ремонта в последующие два года оценивается как
очень высокая Выходом из такой ситуации может служить покупка бывших в употребле-
нии машин, которые также, возможно, придется в будущем ремонтировать (стоимость их
ремонта тоже равна $25 000), но вероятность их поломки значительно ниже Альтернати-
вой этому решению является покупка новой машины стоимостью $100 000, которая гаран-
тированно будет работать без ремонта по крайней мере два года
а Создайте дерево решений для этой ситуации
Ь Каково наилучшее решение для фабрики Fly Rods* 1 2 3 * * * * * 9
с	Какой должна быть стоимость новой машины, чтобы для фабрики было выгодно ее купить9
d Какой должна быть стоимость ремонта, чтобы изменилось решение, полученное в п Ь9
Ситуация для анализа | Компания Johnson’s Composite Materials
Ширли Джонсон, президенту компании Johnson’s Composite Materials (JCM), необхо-
димо принять решение в ситуации, описанной в задаче 9 15. Но в данный момент в этой
ситуации появился новый элемент. Ширли хочет привлечь консалтинговую компанию
Compal, чтобы она провела “анализ конкуренции” Compal должна изучить другие фир-
мы, также добивающиеся контракта с Sonorola на производство корпусов для ее мобиль-
ных телефонов, и сделать прогноз о том, каковы шансы у JCM получить этот контракт.
Если прогноз Compal будет благоприятным, следовательно, JCM может получить
контракт с вероятностью 0,5, а если неблагоприятным — с вероятностью не более
0,35 Вместе с тем шансы получить как благоприятный, так неблагоприятный про-
гнозы от Compal одинаковы. Эта компания берет за свои услуги $1000.
Ширли поручила своему помощнику Линусу Дроу найти оптимальные стратегии
и определиться, следует ли вообще привлекать компанию Compal. Линус создал де-
рево решений и по нему нашел следующую оптимальную стратегию.
1. Привлечь Compal для получения прогноза.
2. Если прогноз будет благоприятным, то:
а) выполнить предварительный этап;
Ь) если JCM получит контракт, использовать имеющееся оборудование.
3. Если прогноз будет неблагоприятным, то:
а) выполнить предварительный этап;
Ь) если JCM получит контракт, использовать имеющееся оборудование.
Линус пришел к Ширли показать полученные результаты. Между ними состоялся
следующий разговор.
ШИРЛИ. Линус, я вижу впечатляющее дерево решений, но полученный результат не имеет
никакого смысла Зачем я должна платить Compal $1000, если мы должны делать
одно и то же что с прогнозом, что без него9
ЛИНУС. Извините, Ширли, но вы не понимаете, что анализ решений нельзя сделать по-
другому Дерево решений дает информацию о всех возможных решениях — как же
без него можно найти оптимальную стратегию9
ГЛАВА 9. Анализ решений	653
ШИРЛИ. Линус, я вас спрашиваю не о том' По вашему, наилучшей стратегией будет выпол-
нение предварительного этапа, а затем в случае заключения контракта следует ис-
пользовать существующее оборудование Но эта стратегия не зависит от того, ка-
кой прогноз сделает Compal' Вы это можете объяснить9
ЛИНУС. Я этого не могу объяснить, но я знаю, что дерево решений всегда дает верный ре-
зультат
ШИРЛИ. У меня нет времени и желания разбираться в деталях вашего анализа Я хочу, что-
бы завтра утром у меня было решение о компании Compal Это решение должно
быть обоснованным, и обоснование должно иметь смысл'
Вопросы
I.	Ширли права. Как обосновать Линусу оптимальность полученного решения?
2	Линус прав Как обосновать корректность результата, полученного с помощью
дерева решений9
3.	Поставьте себя на место Линуса и подготовьте обоснование решения о том, при-
влекать компанию Compal или нет.
Ситуация для анализа | Бурить или не бурить?
Терри Андехилл недавно принят в отдел экономического анализа нефтедобы-
вающей компании Global Oil От компании Prescot Oil поступило предложение выку-
пить у Global Oil аренду участка “Горящая долина” за $15 000 Этот участок размером
320 акров находится на западе Оклахомы, его аренда дает компании Global право на
бурильные работы и эксплуатацию найденных месторождений. Терри поручено
подготовить ответ на это предложение Фактически он должен определить, какая из
двух альтернатив, продать аренду участка или проводить бурильные работы, более
выгодна для его компании
Результат бурения, конечно, нельзя определить заранее. На основе записей о бу-
рении в западной Оклахоме и существующих ценах на бурильные работы и нефте-
и газопродукцию Терри подготовил таблицу, в которой показаны возможные резуль-
таты бурения, вероятности этих результатов и чистая прибыль, получаемая компани-
ей в случае осуществления этих результатов (табл. 9.41).
Но Терри понимает, что данные о предыдущих бурениях — это не слишком на-
дежная основа для принятия решений Компания Drilling Resource, Inc. (DRI) за
$6 000 может выполнить работы по определению геологических формаций, распо-
ложенных в районе “Горящей долины”. Возможные геологические структуры в дан-
ном районе могут быть отнесены к трем категориям: базальтовая плита, смешанные
структуры и гребень месторождения. В табл 9 42 показаны результаты 50 изысканий
DRI и соответствующие результаты бурения, проведенные после изысканий.
С другой стороны, желание Global Oil продать аренду на “Горящую долину” после
проведения изысканий DRI будет указывать на то, что найти нефть на этом участке
маловероятно. Поэтому цена на этот участок может значительно снизиться.
654 ЧАСТЬ III Вероятностные модели
Вопросы
1	На основе приведенных данных определите, что более выгодно для Global Oil:
бурить или продать участок
2	За какую максимальную цену Global Oil может купить информацию о том, каким
будет результат бурения6 7
3	С помощью дерева решений найдите оптимальную стратегию для компании
Global Oil (привлекать DRI или нет, бурить или продать участок и т д )
4	Какова величина ожидаемого результата при оптимальной стратегии7
5	Какую дополнительную сумму может заплатить Global Oil компании DRI за про-
веденные изыскания7
Таблица 9.41
Результат бурения	Вероятность	Чистый доход (потери)
Пустое бурение	0,2	-100 000
Месторождение газа	0,4	40 000
Месторождение газа и нефти	0,3	90 000
Месторождение нефти	0,1	200 000
Таблица 9.42		
Результат изысканий		
Результат бурения	Плита Смешанные структуры Гребень	Всего	
Пустое бурение	8	2	0	10
Месторождение газа	2	16	2	20
Месторождение газа и нефти	0	14	1	15
Месторождение нефти	0	0	5	5
	10	32	8	50
		
I Ситуация для анализа! Компания Shumway, Horch and Sager
--------------------- (часть 1)‘
Клейр Кристенсен (Claire Christensen), второй год работающая в консалтинговой
фирме Shumway, Horch and Sager (SHS), приступила к выполнению нового проекта
Этот проект ей кажется несложным и она рассчитывает быстро и качественно закон-
чить его
6 Эту ситуацию рекомендуем использовать для обсуждения, не следует ее рассматривать как описание эф-
фективных (или не очень) действии при решении административных проблем © 1990 Darden Graduate Busi-
ness School Foundation Описание данной ситуации можно найти на Web-странице
иии darden Virginia edu/puhlishing
ГЛАВА 9. Анализ решений 655
Ее клиент владеет издательством, специализирующимся в основном на журналь-
ной продукции. “Внезапно” он обнаруживает, что теряет большие суммы на печати
изданий, которые не продаются Конечно, принятая издательская практика преду-
сматривает печать и распространение по газетным киоскам большего количества
журналов, чем может быть продано. Это делается для того, чтобы читатель при необ-
ходимости мог найти в газетном киоске любой номер интересующего его журнала
Однако такая практика приводит к огромному количеству непроданных журналов
Консалтинговая фирма SHS получила задание пересмотреть такую практику и выра-
ботать рекомендации, улучшающие существующую ситуацию
Еще одно задание для SHS связано с определением базового уровня тиража для
установки цен на рекламу, которая печатается в журналах. В частности, надо опреде-
лить гарантированно продаваемый тираж журнала Good Housekeeping (Домоводство)
и на основе величины этого тиража — стоимость рекламы в журнале (Если тираж
будет меньше продаваемого, то потери будут пропорциональны дефициту журналу,
а если тираж будет больше продаваемого, то возникнут потери от непроданных эк-
земпляров журнала, однако возрастет доход от рекламы, поскольку доход от рекламы
прямо пропорционален тиражу.)
Кристенсен решила сначала найти способ прогнозировать объем продаж журнала
Good Housekeeping В финансовых отчетах издательства она нашла объемы проданных
тиражей журнала за последние 9 лет (с июля 1979 по июнь 1988 года) Данные о по-
следних 6 месяцах она хочет использовать для проверки своего метода прогнозиро-
вания Данные за восемь с половиной лет приведены в табл 9 43 (см также рабочую
книгу Excel SHSA.XLS).
Таблица 9.43
№ п/п	Дата	Тираж	№ п/п	Дата	Тираж	№ п/п	Дата	Тираж
1	7/79	5264165	35		5367404	69		5253739
2		5313127	36		5316957	70		5138210
3		5117969	37	7/82	5412745	71		5251664
4		5098771	38		5387779	72		5450869
5		5187708	39		5439224	73	7/85	5022522
6		5645295	40		5341392	74		5206132
1	1/80	5023173	41		5396853	75		5042725
8		5333352	42		5961612	76		5096277
9		5224234	43	1/83	5335737	77		5067717
10		5079207	44		5618540	78		5508198
11		5167277	45		5604606	79	1/86	5133963
12		5006445	46		5343116	80		5180897
13	7/80	5150974	47		5294990	81		5161222
14		5180346	48		5327995	82		5174238
15		5223467	49	7/83	5177176	83		5047775
16		5153303	50		5290109	84		5152063
656 ЧАСТЬ III. Вероятностные модели
Окончание табл. 9.43
№ п/п	Дата	Тираж	№ п/п	Дата	Тираж	№ п/п	Дата	Тираж
17		5247109	51		5449099	85	7/86	5001222
18		5789798	52		5344570	86		5232314
19	1/81	5350502	53		5334053	87		5235207
20		5371371	54		5763516	88		5009584
21		5327700	55	1/84	5198585	89		5352370
22		5269993	56		5501741	90		5498755
23		5240438	57		5329592	91	1/87	5159840
24		5273266	58		5322838	92		5274075
25	7/81	5439920	59		5178815	93		5179002
26		5378584	60		5247590	94		5269295
27		5329516	61	7/84	5194827	95		5005048
28		5292129	62		5118408	96		5166569
29		5378127	63		5291564	97	7/87	5068848
30		5736465	64		5047946	98		5007388
31	1/82	5073651	65		5105056	99		5265191
32		5553245	66		5448542	100		5046595
33		5439363	67	1/85	5023818	101		5300978
34		5363948	68		5099829	102		5526153
Кристенсен, глядя на график изменения проданного тиража журнала Good
Housekeeping (рис 9 31), размышляет о том, как ей предугадать будущий тираж, чтобы
он был полностью продан Сама она не является читателем этого журнала, но видела
его в приемной у дантиста и даже дома у своей тетушки. Она также знает, что в декабре
продажи журнала возрастают, поскольку в нем приводятся кулинарные рецепты и со-
веты по выбору подарков к рождественским и новогодним праздникам В январе после
праздников продажи всегда снижаются. Также объемы продаж журнала зависят от его
содержания.
5800000
J 5000000
° 4800000
4600000
4400000
Год
Рис. 9.31. Объемы продаж журнала Good Housekeeping
ГЛАВА 9 Анализ решений 657
Кристенсен подобрала подходящий метод прогнозирования спроса на журнал, кото-
рый проверила на данных из табл 9.43, результаты сравнила с данными 6 других месяцев
(из исходных данных спроса за 9 лет). Эти тестовые данные приведены в табл. 9.44.
Таблица 9.44
№ п/п	Тираж
103	5012276
104	5056537
105	5061844
106	5005226
107	5000500
108	5030805
После того как был проверен метод прогнозирования, перед Кристенсен встал сле-
дующий вопрос, каким должен быть тираж журнала — больше или меньше прогнози-
рованного спроса9 От этого зависит стоимость рекламы в журнале (чем больше тираж
журнала, тем выше стоимость рекламных объявлений) Она знает, что экземпляр жур-
нала продается в газетном киоске за $1,95, тогда как его себестоимость составляет
$0,70, оптовая цена равна $1,20, а к продавцу киоска он поступает по цене $1,50 При
этом только оптовый продавец не несет потерь от непроданных экземпляров журнала
Доход от рекламы вычисляется по простой формуле $1 умножается на базовый
уровень тиража Но если спрос на журнал будет меньше напечатанного тиража, то
будет потеряно $ 1,5 на каждом непроданном экземпляре журнала
На данном этапе тираж журнала составляет 4,78 млн. экземпляров. Редакция
журнала хочет повысить его в июле 1988 года до 5,1 млн Кристенсен должна опреде-
лить, нужен ли такой тираж.
Вопросы
1	Предположим, спрос на журнал в июле будет распределяться так
Спрос	Вероятность
4 875 000	0,2
4 932 000	0,2
4 983 000	0,2
5 034 000	0,2
5 109 000	0,2
Должна ли Кристенсен рекомендовать повышение базового уровня тиража на
этот месяц?
2	. Предположим, что предсказанное значение спроса в январе 1988 года имеет
нормальное распределение со средним 5 082 329 и стандартным отклонением
98 324. Какой тираж журнала должен быть в этом месяце9
658 ЧАСТЬ III. Вероятностные модели
Литература
1	. Bonson Adam Oglethorpe Power Corporation Decides about Investing in a Major Transmission Sys-
tem, Interfaces, 25, no 2 (1995), p 25-36
2	Brown Mark Evaluation of Vision Correction Alternatives for Myopic Adults, Interfaces, 27, no 2(1997),
p 66-84
3	Howard Ron Heathens, Heretics, and Cults The Religious Spectrum of Decision Aiding, Interfaces,
22, no 6(1992), p 15-27
4	Keeney Ralph Decision Analysis. An Overview, Operations Research, 30, no 5 (1982), p 803-838
5	Keeney Ralph Value-Focused Thinking, Cambridge, MA Harvard University Press, 1992
6	Keeney Ralph and Raiffa Howard Decisions with Multiple Objectives Preferences and Value Trade-
offs, New York Wiley, 1976
Глава
10
Имитационное моделирование
В этой главе...
10.1.	Введение
10.2	Генерирование случайных величин
10.3.	Имитация в электронных таблицах
10.4.	Имитация с помощью надстроек
10.5.	Модель управления запасами
10.6.	Модель управления запасами с нормальным распределением спроса
10.7.	Модель авиаперевозок
10.8.	Баланс производственных мощностей
10.9.	Оптимизация в условиях неопределенности
10.10.	Некоторые выводы
10.11.	Заключение
Основные термины
Контрольные вопросы
Задачи
Ситуация 1 CyberLab
Ситуация 2 Mountain Realty
Литература
660 ЧАСТЬ III. Вероятностные модели
Практическое применение
Имитация обработки вызовов в AT&T
Во второй половине 1970-х годов в Штатах широкую популярность получила те-
лефонная служба 1-800, через которую можно было получить самую разнообразную
информацию (от наличия товаров в магазинах до расписания авиарейсов) и сделать
заказы в магазинах. Это вызвало рост индустрии центров обработки телефонных вы-
зовов. Такие центры в свой состав включают линии телекоммуникаций, состоящие
из телефонных линий данного района, коммутаторов, сортирующих и распределяю-
щих входящие звонки, и операторов, отвечающих на звонки. Первоначально центры
обработки вызовов отвечали на вопросы о наличии товаров в магазинах (в соответст-
вии с предоставляемыми магазинами каталогами товаров), о расписании полетов
самолетов, бронировали места в отелях и т п.
Центры обработки вызовов эволюционировали в отдельную сервисную службу,
связывающую клиентов и покупателей с индустрией обслуживания и транспортными
агентствами В 1993 году в приблизительно 350 тыс. центрах обработки вызовов рабо-
тало 6,5 млн человек. По сравнению с 1990 годом количество таких центров увеличи-
лось на 20%, и прогнозируется, что вскоре их число возрастет вдвое. Этому способст-
вуют такие факторы, как уменьшение времени, которое покупатели тратят на покупку
(при росте числа одиноких людей и семей, состоящих из двух человек), увеличение за-
трат на организацию процесса продаж типа “продавец-покупатель”, расширение воз-
можностей, предоставляемых индустрией телекоммуникаций. Кроме того, недавние
изменения законодательства увеличивают рентабельность инвестиций и конкуренцию
в этой сфере. Компания AT&T также занимается этим видом бизнеса.
Поскольку затраты, связанные с содержанием персонала и обслуживанием теле-
коммуникационных центров, возрастают, компании, занимающиеся этим бизнесом,
стараются удешевить обработку звонков клиентов. В компании AT&T разработана
имитационная модель, позволяющая проанализировать различные сценарии обра-
ботки вызовов клиентов Эта модель помогает рассмотреть влияние на количество
обрабатываемых вызовов таких факторов, как квалификация персонала, длитель-
ность телефонных звонков, количество телефонных линий на номер 800, число заня-
тых линий и т п Можно также смоделировать поведение абонентов. Если абонент
дозвонился до центра, но оператор занят, то одни клиенты сразу бросают трубку,
вторые ожидают короткое время, а третьи могут ждать достаточно долго, пока опера-
тор их обслужит. Те клиенты, которые не дождались обслуживания, либо позвонят
еще раз, либо наберут номер конкурирующей службы. Первоначальная имитацион-
ная модель AT&T была разработана для центра, занимающегося заказами билетов на
самолеты Поскольку эта модель показала высокую эффективность, было принято
решение разработать подобные модели для других центров.
Внедрение рекомендаций, полученных в результате исследований имитационных
моделей, позволило компании AT&T только в центре, занимающемся заказами
авиабилетов, на 20% увеличить количество обрабатываемых звонков, на 20% умень-
шить затраты на персонал, на 27% сократить количество сверхурочных часов. Число
заказанных авиабилетов возросло на 5%. Общая годовая прибыль компании увели-
чилась на 750 млн. долл. [1]
ГЛАВА 10. Имитационное моделирование 661
10.1.	Введение
Многие люди утверждают, что опыт — это наилучший учитель К сожалению, часто
весьма затратно (по деньгам или по времени) получить реальный опыт Это замечание
наталкивает на мысль использовать имитацию — быстрый и экономный путь приобрете-
ния знаний, которые обычно можно получить только из опыта или эксперимента
? Основная идея имитации — создать экспериментальное устройство, т.е. имитатор, ко-
торое в основных чертах повторяет (имитирует) поведение интересующей нас реальной
системы, причем быстро и экономно.
Цель имитационного моделирования — создать среду или устройство, позволяющие
путем эксперимента получить нужную информацию об объектах окружающего мира, не
общаясь непосредственно с этими объектами. Имитация является основой многих при-
кладных экспериментов Она используется, например, при проверке медицинских пре-
паратов на животных, которые имитируют реакцию человеческого организма, при тес-
тировании автомобилей на испытательных стендах, когда имитируется дорожная среда,
при испытании моделей самолетов в аэродинамической трубе, где имитируются условия
полета реального самолета, при тренинге пилотов на самолетных тренажерах, где на эк-
ранах мониторов имитируются условия реального полета.
При проведении количественного анализа имитация является основой эксперимен-
тов, проводимых на математических моделях Хотя и при имитации и при оптимизации
используются количественные модели, эти модели строятся, исходя из разных концеп-
ций Основное различие этих моделей заключается в той роли, которую играют в них пе-
ременные решения
i • В моделях оптимизации значения переменных решения являются выходом моде- =
ли. Выходным результатом процесса оптимизации модели будут значения пере-
i менных решений, которые максимизируют (или минимизируют) целевую .
функцию.
i • В имитационных моделях значения переменных решений являются входом моде-
i ли — выходным результатом процесса имитации модели будет значение целевой
к функции, соответствующее данным входным значениям переменных решения. ?
Чтобы сделать это различие между моделями оптимизации и имитации более нагляд-
ным, рассмотрим следующий пример. Предположим, что руководство супермаркета хо-
чет определить, сколько кассиров и упаковщиков должно находиться на выходе торговых
секций для того, чтобы минимизировать затраты на персонал, не нарушить профсоюз-
ные соглашения и сократить время обслуживания покупателей.
Если для решения этой проблемы используется оптимизационная модель, то необхо-
димо задать параметры этой модели. Такими параметрами, скорее всего, будут интенсив-
ность прихода покупателей, распределение времени обслуживания покупателя в случае,
если продавец упаковывает или не упаковывает товар, и другие подобные количествен-
ные параметры. В результате оптимизации такой модели мы будем знать оптимальное
количество работников, соответствующее значение целевой функции (стоимость персо-
нала), а также лимитирующие ограничения. Такие модели рассмотрены в предыдущих
главах книги.
662 ЧАСТЬ III Вероятностные модели
В имитационной модели входными параметрами модели будут (как и в модели опти-
мизации) интенсивность прихода покупателей, распределение времени обслуживания
покупателя и другие, математическое выражение для вычисления целевой функции,
а также количество работников Выходом модели будет множество различных измерений,
таких как стоимость (персонала), время ожидания покупателя, загруженность работни-
ков и тд. В общем случае модель позволяет измерить количественные характеристики
ожидаемого решения, которое может принимать различные значения в процессе имита-
ции вследствие вероятностной природы некоторых входных параметров модели. Имита-
ционное моделирование предполагает проведение многочисленных испытаний модели
и тесное общение с ее разработчиком, но здесь не ставится цель найти оптимальное ре-
шение Такое моделирование позволяет дешево и быстро определить значения представ-
ляющих практический интерес числовых факторов реальных ситуаций
Применение имитационного моделирования
После такого введения возникает вопрос, нужно ли вообще имитационное моделирова-
ние, если оно не может найти оптимального решения? Еще в недалеком прошлом имитация
считалась методом “второго сорта”, который применялся только тогда, когда “пробуксо-
вывали” аналитические методы И действительно, если уже построена аналитическая модель,
то обычно с помощью того или иного метода оптимизации можно найти оптимальное детер-
минированное решение. Однако сегодня имитация считается одним из самых популярных
и полезных методов количественного анализа В чем же причина такой популярности?
1.	Во-первых, аналитические модели часто трудны для формализации и построения,
а иногда их вообще невозможно построить. Любая аналитическая модель имеет
свои “затрудняющие” факторы, которые зависят от специфики данной модели.
Например, в финансовых моделях таким фактором может быть случайный
(непрогнозируемый) спрос, в моделях очередей — вероятностное распределение
переменных, отличное от экспоненциального, в производственных моделях —
большое число поставщиков материалов и комплектующих и т п.
2.	Аналитические модели обычно дают среднестатистическое или стационарное
(долговременное) решение На практике часто важно именно нестационарное по-
ведение системы или ее характеристики на коротком временном интервале, что не
дает возможности получить “средние” значения.
3.	Для имитационного моделирования можно использовать очень широкий круг
программного обеспечения — от “обычных” электронных таблиц (Excel, Lotus)
и разнообразных надстроек для них (Crystal Ball, ©Risk) до программ, написанных
как на общих языках программирования (Pascal, C++), так и с применением язы-
ков, специально разработанных для создания имитационных моделей (SIMAN).
Имитационные модели могут создаваться и использоваться на персональных ком-
пьютерах, уровень компьютерной и математической подготовки, необходимый
для создания и выполнения полезных имитаторов, сегодня значительно снижен.
В настоящее время во многих случаях имитационные модели строятся не вместо ана-
литических, а параллельно с ними, поскольку они относительно просты для создания
и позволяют исследовать такие параметры реальных систем, которые невозможно ото-
бразить в аналитических моделях.
ГЛАВА 10 Имитационное моделирование
663
Имитация и случайные величины
Имитационные модели часто используются для анализа решений, принимаемых в ус-
ловиях риска, т е для анализа моделей, в которых поведение (или значение) нескольких
факторов заранее не известно Такие факторы называются случайными переменными или
случайными величинами Поведение случайных величин описывается распределением веро-
ятностей (Мы предполагаем, что читатель владеет основными понятиями теории веро-
ятностей Основные определения и понятия теории вероятностей приведены в приложе-
нии А ) Этот тип имитации иногда называют методом Монте-Карло “в честь” рулеток
Монте-Карло, генерирующих случайные переменные и случайные события Рассмотрим
несколько примеров, “провоцирующих” такой тип имитационного моделирования
Проектирование погрузочно-разгрузочной площадки
Типичная схема погрузочно-разгрузочной площадки, обслуживающая грузовые авто-
мобили, показана на рис 10 1 Грузовики (возможно, различных типов) по очереди подъ-
езжают к погрузочным платформам, где осуществляются погрузочно-разгрузочные рабо-
ты Неопределенными, т е случайными, факторами здесь будут время прибытия грузо-
виков, тип и объем груза, время обработки груза (погрузки или разгрузки) При создании
модели эти неопределенные факторы описываются случайными величинами, каждая из
которых имеет свое распределение вероятностей Целью моделирования данной ситуа-
ции могут быть ответы на следующие вопросы
1.	Сколько необходимо иметь погрузочно-разгрузочных платформ7
2.	Какого типа и сколько нужно иметь оборудования, обслуживающего погрузочно-
разгрузочные работы7
3.	Сколько рабочих следует использовать на этих работах7
Выезд
Въезд
Рис. 10.1. Схема погрузочно-разгрузочной площадки
При проектировании погрузочно-разгрузочных площадок необходимо учитывать
стоимость всего сооружения и требования, предъявляемые к погрузочно-разгрузочным
работам Стоимость можно уменьшить, построив минимальное количество платформ,
664
ЧАСТЬ III Вероятностные модели
закупив по минимуму оборудование и наняв только нескольких рабочих. Однако при
этом может возрасти время как непосредственно погрузочно-разгрузочных работ, так
и ожидания грузовиками начала этих работ. Менеджер должен найти разумный компро-
мисс между стоимостью сооружения, его обслуживанием и стоимостью времени обслу-
живания и ожидания грузовых автомобилей.
Подобные модели часто применяются при проектировании нефтеналивных прича-
лов, обслуживающих нефтяные танкеры. Стоимость простоя танкеров очень высока. Эти
модели формально определяются как “модели очередей” (см. главу 13). Если они удовле-
творяют достаточно строгим предположениям, например, предположению об экспонен-
циальном распределении времени обслуживания и ожидания, то для их анализа можно
применить аналитические методы, описанные в главе 13. Однако если модель очень
сложная и не выполняются предположения об экспоненциальном распределении или
какие-либо другие стандартные условия моделей очередей, то получение аналитических
результатов становится проблематичным делом, если вообще возможным. В этом случае
используются имитационные модели.
Управление запасами
Имитация часто применяется для изучения широкого класса моделей управления за-
пасами Одна из ситуаций управления запасами показана на рис. 10.2. Здесь завод произ-
водит некую продукцию, рассылаемую по региональным складам, которые, в свою оче-
редь, должны удовлетворять местный спрос на эту продукцию. Предполагается, что
спрос на продукцию в каждом регионе и время перевозки продукции от завода до скла-
да — случайные величины Модель, построенная для этой ситуации, должна помочь от-
ветить на следующие вопросы
1. Сколько и с какой периодичностью следует доставлять продукции на склады?
2. Какой запас продукции должен быть на заводе, чтобы удовлетворить заявки складов?
Л Завод к
I Склад 1 "I I Склад 2 I •.. I Склад N I
Спрос	Спрос	Спрос
Рис. 10.2. Схема распределения продукции
Основными стоимостными параметрами в такой модели будут стоимости хранения
запаса продукции, перевозки продукции с завода на склады и стоимость неудовлетворен-
ного спроса, если продукции нет на складе. Поскольку спрос точно предсказать нельзя,
может наступить момент, когда невозможно будет удовлетворить возникший спрос на
каком-нибудь складе (если, конечно, не держать на складе очень большой запас продук-
ции, но это решение очевидно увеличивает затраты на хранение). Альтернативным ре-
шением является увеличение частоты доставки продукции с завода на склады. Такое ре-
шение уменьшает стоимость хранения продукции, однако возрастают затраты на пере-
возки. Моделирование таких ситуаций позволит определить размер минимальных
запасов на заводе и складах, уменьшить транспортные расходы и удовлетворить опреде-
ленную часть спроса потребителей продукции.
ГЛАВА 10. Имитационное моделирование 665
В общей теории управления запасами получено много аналитических результатов для
относительно простых моделей, описывающих только один вид продукции Модели, ис-
пользующиеся для управления запасами нескольких типов продукции, расположенных
в разных местах, значительно сложнее, поэтому для их исследования часто используется
имитация. В этой главе описываются методы имитационного моделирования на основе
электронных таблиц, а также с использованием популярных надстроек Crystal Ball и @Risk
Чтобы прояснить природу имитационных моделей, следующий раздел мы посвятим
рассмотрению методов генерирования случайных величин, а затем построим несколько
имитационных моделей финансового планирования и проведем их анализ В конце гла-
вы мы затронем интересную тему оптимизации в условиях неопределенности, обобщая
и комбинируя материал предыдущих и данной глав
10.2. Генерирование случайных величин
В этом разделе мы покажем, как осуществлять случайную выборку из генеральной со-
вокупности, имеющей заданное вероятностное распределение, что является синонимом
генерирования случайных величин Существует два типа случайных величин дискретные
и непрерывные Дискретная случайная величина может принимать только определенные
значения (например, только целые), тогда как непрерывная случайная — любое значение
(включая дробные) из заданного непрерывного интервала
Рассмотрим сначала способы генерирования произвольных дискретных случайных
величин с помощью электронных таблиц Это даст нам основу для работы со случайны-
ми элементами. Затем опишем методы генерирования непрерывных случайных величин,
в частности, случайных величин, распределенных по экспоненциальному и нормальному
законам В конце раздела покажем способы генерирования случайных величин с помо-
щью надстроек электронных таблиц
Не трудно придумать физическое устройство, которое генерировало бы значения дис-
кретных случайных величин, например, значения спроса для последней модели управле-
ния запасами Такое устройство в виде диска со стрелкой показано на рис Ю 3 После
вращения остановившаяся стрелка с равной вероятностью может указать на любую точку
окружности Поэтому вероятность, что стрелка укажет на какую-либо точку на дуге, за-
нимающей 30% длины окружности (или, что то же самое, на точку сектора, занимающего
30% площади круга), равна 0,3. Если отношения площадей секторов к общей площади
круга соответствуют числовым значениям вероятности, что случайная величина примет
некое конкретное значение, то такое устройство можно использовать для получения раз-
личных значений случайной величины. Пусть, например, спрос (случайная величина)
в 10% случаев принимает значение 8 (каких-либо единиц), в 20% случаев спрос равен 9,
в 30% — 10, в 20% — 11, в 10% случаев спрос равен 12, также с вероятностью 10% спрос
составляет 13 Если круг разделить на секторы так, как показано на рис 10 3, то остано-
вившаяся стрелка, указывающая на сектор, занимающий 20% площади круга, генерирует
значение спроса, равное 9 единиц. Чтобы генерировать другие значения случайного
спроса, надо просто еще раз раскрутить стрелку.
666 ЧАСТЬ III Вероятностные модели
Рис. 10.3. Устройство для генерирования зна-
чений дискретной случайной величины
Генераторы случайных чисел электронных таблиц
Несмотря на то что устройство, описанное выше, просто в использовании, оно не
удобно, если необходимо, например, получить несколько тысяч значений случайной ве-
личины либо выполнить процесс генерирования случайных чисел на компьютере. Для
последнего случая разработаны генераторы случайных чисел электронных таблиц, кото-
рые генерируют случайные числа, равномерно распределенные на интервале от 0 до 1.
Чтобы генерировать значения случайного спроса, вероятности которого приведены
выше, необходимо разбить интервал 0-1 на ряд подынтервалов, длина которых совпада-
ла бы со значениями этих вероятностей Одно из возможных разбиений интервала 0-1 на
соответствующие подынтервалы показано на рис 10 4 Очевидно, что такое разбиение не
единственное, обычно оно производится последовательно в соответствии с возрастаю-
щим порядком значений спроса Если случайное число, полученное от генератора слу-
чайных чисел, попадает в какой-либо из определенных интервалов, принимается значе-
ние спроса, соответствующее этому интервалу
Случайное число Спрос
0,0-0,09999	8
0,1-0,29999	9
0,3-0,59999	10
0 6-0 79999	11
0 8-0,89999	12
0 9-0 99999	13
Рис. 10.4. Интервалы случай-
ных чисел и значения спроса
Генерирование значений дискретных случайных величин
Описанный выше метод применяется только для генерирования значений дискрет-
ных случайных величин Но во многих моделях необходимо генерировать значения как
дискретных, так и непрерывных величин Здесь мы опишем общий метод, который по-
зволяет генерировать значения дискретных и непрерывных случайных величин
ГЛАВА 10 Имитационное моделирование 667
Чтобы получить значение произвольной дискретной случайной величины, необходи-
мо иметь 1) значение непрерывной равномерно распределенной случайной величины
и 2) распределение вероятностей дискретной случайной величины, значения которой ге-
нерируются. Аналогично, чтобы получить значение непрерывной случайной величины,
необходимо иметь 1) значение непрерывной равномерно распределенной случайной ве-
личины и 2) распределение вероятностей (в виде функции распределения) непрерывной
случайной величины, значения которой генерируются.
Равномерно распределенные случайные величины
Для понимания дальнейшего материала очень важно различать случайную величину,
в частности, имеющую равномерное распределение на интервале от 0 до 1 (обозначим ее
U), и значения, которые может принимать эта случайная величина (значения случайной
величины U будем обозначать как и). Можно предложить один способ генерирования
значений равномерно распределенной непрерывной случайной величины U— использо-
вать описанный выше круг с вращающейся стрелкой (но без разделения на секторы, как
показано на рис 10 5). С каждой точкой на окружности можно сопоставить число, лежа-
щее в интервале от 0 до 1 Например, точке на окружности, соответствующей трем часам
на циферблате часов, можно сопоставить число 0,25.
Такое устройство помогает понять природу равномерно распределенных случайных
величин, однако оно имеет невысокую точность (например, на этом устройстве практи-
чески невозможно увидеть разность между значениями 0,500000 и 0,499999) Конечно, на
практике применяются не такие “аналоговые” генераторы случайных чисел, а функция
СЛЧИС, которая генерирует равномерно распределенные случайные числа в электрон-
ной таблице Excel и позволяет задать любое число десятичных знаков в записи значения
случайного числа
Рис. 10.5. Устройство для генерирования
равномерно распределенных случайных чисел
Функция распределения
Рассмотрим понятие функции распределения случайной величины, для чего вспомним
о распределении случайного спроса (обозначим его D) в модели управления запасами.
Функция распределения F(x) случайной величины D определяется как вероятность собы-
тия, что D меньше или равна х, т.е F(x) = P{D<x}. Если известны вероятности конкрет-
668 ЧАСТЬ III Вероятностные модели
ных значений дискретной случайной величины, то построить функцию распределения не
составляет особого труда Например, для спроса D функция распределения будет иметь
следующие значения 1
I	х	I	8	9	10	11	12	13	I
I	F(x)	|	0,1	0,3	0,6	0,8	0,9	1,0	|
Общая схема генерирования значений дискретной случайной величины с использова-
нием функции распределения показана на рис. 10.6 Сначала генерируется значение и рав-
номерной случайной величины и определяется положение этого значения на вертикальной
оси графика функции распределения. От этого значения на вертикальной оси проводится
горизонтальная линия до пересечения с графиком функции распределения, и от точки пе-
ресечения опускается перпендикуляр на горизонтальную ось Основание этого перпенди-
куляра определяет значение случайной величины Например, если и = 0,5, то d, значение
случайного спроса D, будет равным 10, как показано на рис 10 6.
Рис. 10.6. Функция распределения случайного спроса
Почему работает описанная процедура? Потому что здесь вероятность получить ка-
кое-либо конкретное значение случайной величины равна вероятности того, что данная
случайная величина примет это значение.2 Например, мы хотим, чтобы спрос принимал
значение 10 с вероятностью 0,3. Значение 10 можно получить, если значение и лежит ме-
жду 0,3 и 0,6 на вертикальной оси рис. 10 6. Поскольку случайная величина U равномер-
но распределена на интервале от 0 до 1, то вероятность того, что значение и попадет в ин-
тервал от 0,3 до 0,6, равна длине этого интервала, т.е. 0,6 - 0,3 = 0,3, что совпадает с ве-
Если известны вероятности PfD =j), то значения функции F(x) вычисляются по формуле
F(.x) = ^ ^P[D = j} Более подробно о функциях распределения сказано в приложении А — Прим ред
Здесь "работает" доказанный в теории вероятностей факт, что если случайная величина D имеет функ-
цию распределения F(x), то случайная величина £= F(D) будет равномерно распределена на интервале 0—1
величина D = F-l(£), где F—1— функция, обратная к функции F(x), будет иметь функцию распределения
F(x) — Прим ред
ГЛАВА 10. Имитационное моделирование 669
роятностью того, что спрос примет значение 10. Аналогично пусть спрос принимает зна-
чение 11 с вероятностью 0,2. Значение 11 можно получить, если и будет принадлежать
интервалу от 0,6 до 0,8, что может случиться с вероятностью 0,8 - 0,6 = 0,2, и т.д. (Но что
мы должны предпринять, если и будет точно равняться 0,6 — какое значение, 10 или 11,
мы должны приписать спросу? Ответ на этот вопрос не имеет большого значения, по-
скольку вероятность того, что и будет точно равняться 0,6, равна нулю.3 Однако считает-
ся, что если и = 1, то спрос полагается равным 13.)
Описанный способ генерирования значений случайных величин можно применить
для моделирования любых дискретных величин. Рассмотрим моделирование дискретного
равномерного распределения, где целые значения от 8 до 12 должны иметь равные вероят-
ности. Напомним, что функция Excel СЛЧИС возвращает случайное число из интервала
от 0 до 1, т.е. она моделирует непрерывное равномерное распределение Возникает вопрос
можно ли использовать непрерывное равномерное распределение для моделирования
дискретного равномерного распределения? Заметим, что формула =5*СЛЧИС() будет
возвращать равномерно распределенные случайные числа из интервала 0-5, поэтому
формула =8+5*СЛЧИС() будет генерировать равномерно распределенные случайные чис-
ла из интервала 8-13. Теперь, если мы используем функцию Excel ЦЕЛОЕ, которая воз-
вращает целую часть числа, то формула =ЦЕЛОЕ(8+5*СЛЧИС()) будет генерировать дис-
кретное равномерное распределение целых чисел от 8 до 12.
На рис. 10 7 показано, каким интервалам должны принадлежать значения функции
СЛЧИС, чтобы соответствовать определенным случайным целым числам Поскольку все
эти интервалы имеют одинаковую длину (равную 1/5), то все целые числа имеют одина-
ковую вероятность (также равную 1/5). В общем случае для того, чтобы моделировать
равномерное дискретное распределение целых чисел, принимающих значения от х до у,
можно использовать формулу =ЦЕЛОЕ(х+(х-у+1)*СЛЧИС()) В разделе 10 7 будет приве-
ден пример генерирования случайных чисел, подчиняющихся биноминальному распре-
делению, которое также дискретно.
Значение функции СЛЧИС	=ЦЕЛОЕ(8+5'СЛЧИСО)
0<=СЛЧИС()<0.2	8
0 2<=СЛЧИС()<0,4	9
0,4<=СЛЧИС()<0,6	10
0.6<=СЛЧИС()<0,8	
0 8<=СЛЧИС( )<1 0	12
Рис. 10.7. Использование функции СЛЧИС для ге-
нерирования дискретных случайных чисел
Генерирование значений непрерывных случайных величин
Описанный выше общий метод генерирования значений дискретных случайных ве-
личин легко использовать для непрерывных случайных величин. Как показано на
рис. 10.8, главным элементом для генерирования значений w случайной величины Появ-
ляется ее функция распределения Е(х) = P{lV<x}. Показанная на этом рисунке функция
распределения является типичной — она изменяется от 0 до 1, не убывает и непрерывна
(т.е. не имеет скачков, которые присутствуют у функций распределения дискретных слу-
чайных величин). Для того чтобы получить значение w случайной величины W вначале
1 Из определения функции распределения F(x) = Р/D <х/ следует, что если и будет равняться 0,6, то следует
принять значение спроса, равное 10 — Прим ред
670 ЧАСТЬ III Вероятностные модели
следует получить значение и равномерно распределенной случайной величины Uи опре-
делить положение этого значения на вертикальной оси графика функции распределения.
Затем проводится горизонтальная линия от этого значения до пересечения с графиком
функции распределения, откуда опускается перпендикуляр на горизонтальную ось. Ос-
нование этого перпендикуляра дает искомое значение w. На рис. 10.8 значению и = 0,8
соответствует значение w = 5,2 (приблизительно)
Рис. 10.8. Схема получения значений непрерывной случайной величины
Мы описали только общую схему генерирования значений случайных величин. На
практике такая работа обычно поручается компьютеру Но при этом используются два
разных алгоритма в зависимости от того, задана функция распределения аналитически
или в табличном форме в виде ряда своих значений Чтобы по значению и найти значе-
ние w, надо решить уравнение
и = F(w) = P{lF<w}
относительно w Если функция F{w) задана простым математическим выражением, то
часто удается аналитически решить такое уравнение, т е в явном виде выразить w как
функцию от и.
Моделирование экспоненциального распределения
Экспоненциальное распределение часто используется в моделях очередей для задания
времени между поступлениями клиентов в систему обслуживания (см. главу 13). Функ-
ция этого распределения задается формулой
F(w) = Р{ IV< и] = 1 - е
где 1А равняется среднему (математическому ожиданию) случайной величины W Отсю-
да нетрудно наити решение (относительно w) уравнения
и = 1 - е	(10 1)
Этим решением будет
и' = -1/Х1п(1 -и)	(10 2)
ГЛАВА 10. Имитационное моделирование 671
Предположим, что необходимо в электронной таблице получить одно значение экс-
поненциально распределенной случайной величины, у которой математическое ожида-
ние равно 20 (т.е. 1 /X = 20). Для этого выполним такие действия.
1. С помощью функции СПЧИС получаем значение и равномерно распределенной
случайной величины Пусть для определенности и = 0,75.
2. Подставляем значение 0,75 в формулу (10.2) вместо и и выполняем вычисления:
w = -1/X ln( 1 - и) = -20х1п(1 - 0,75) = -20х1п(0,25) = - 20х(-1,386) = 27,72.
В общем случае, если надо получить несколько значений экспоненциально распреде-
ленной случайной величины с математическим ожиданием 20, можно записать в ячейку
электронной таблицы формулу =20*1_М(1-СЛЧИС()), которая будет генерировать нужные
значения.
Моделирование нормального распределения
Нормальное распределение играет большую роль в имитационных и аналитических
моделях. В имитационных моделях часто предполагается, что какие-либо количествен-
ные параметры распределены по нормальному закону. Например, в модели из раздела
10.6 принято предположение о том, что спрос имеет нормальное распределение со сред-
ним (математическим ожиданием) р. = 1000 и стандартным отклонением о = 100. Чтобы
смоделировать такое распределение, заметим следующее: если Z— случайная величина,
имеющая стандартное нормальное распределение (т.е. нормальное распределение
с нулевым математическим ожиданием и единичным стандартным отклонением), то
случайная величина ц + oZ имеет нормальное распределение со средним ц и стандарт-
ным отклонением о. Таким образом, задача моделирования любых нормально распреде-
ленных случайных величин сводится к задаче моделирования случайной величины, под-
чиняющейся стандартному нормальному закону.
К сожалению, функция распределения этого закона не позволяет получить в явном виде
аналитическое выражение для w как функции от и. Но в Excel есть встроенная функция
НОРМОБР, которая возвращает значение w при известном значении и. Например, чтобы по-
лучить значение нормально распределенной случайной величины со средним 1000 и стан-
дартным отклонением 100, надо применить формулу Excel =НОРМОБР(СЛЧИС(), 1000; 100)
Генерирование случайных величин с помощью надстроек
Значения случайных величин можно также генерировать с помощью надстроек Crystal Ball
и @Risk для электронных таблиц Эти надстройки используют разные подходы В надстройке
Crystal Ball каждая ячейка выделенного диапазона на рабочем листе представляет случайную
величину, для задания распределений и их параметров необходимо пройти через меню Define
Assumption (Предположения) В надстройке @Risk в каждой ячейке рабочего листа, соответ-
ствующей случайной величине, надо ввести формулу, которая обозначает тип распределения
Обе эти надстройки значительно расширяют возможности Excel. Во-первых, они позволяют
задавать больше типов распределения, чем непосредственно Excel. Во-вторых, с их помощью
можно установить количество генерируемых случайных чисел (без ограничений в Crystal Ball и
до 32 767 в @Risk). Наконец, они автоматически генерируют статистические отчеты (с по-
строением различных диаграмм и графиков) по результатам имитации.
В Crystal Ball параметры моделируемого распределения задаются с помощью меню, как
показано в примерах разделов 10 4, 10.5 и 10.6. В надстройке @Risk, как уже говорилось,
моделируемые распределения задаются с помощью формул. Некоторые такие формулы, за-
дающие часто используемые распределения, приведены в табл. 10.1 (их применение пока-
зано в разделе 10 7).
672 ЧАСТЬ III Вероятностные модели
Таблица 10.1
Распределение	Формула в @Risk	Описание
Биномиальное	=RiskBmomial(n,p)	Возвращает количество “успехов” в п испы- таниях, р — вероятность успеха в одном ис- пытании
Хи-квадрат	=RiskChisq(X)	Возвращает значение случайной величины, имеющей распределение хи-квадрат со сред- ним X
Общее	=RiskCumul(a,b,{xi,x2, . ,xn}, {Pl,P2, ,Pn})	Возвращает значение случайной величины, функция распределения которой задана пара- ми значений х„ а и b — соответственно ми- нимальное и максимальное значение, которые может принимать данная случайная величина
Дискретное	=RiskDiscrete(a,b,{x1,x2, ,Xn},	Возвращает одно из п значений хр ,х, ,р: —
(общее)	{P1,P2, ,Pn})	вероятность значения х
Дискретное (равномерное)	=RiskDuniform({x1,x2, ,Xn})	Возвращает с равными вероятностями одно из л значений х,,	,х„
Экспоненциальное	=RiskExp(P)	Возвращает значение случайной величины, имеющей экспоненциальное распределение со средним р
Логнормальное	=RiskLognorm(p,o)	Возвращает значение случайной величины, имеющей логнормальное распределение со средним ц и стандартным отклонением о
Нормальное	=RiskNormal(p,o)	Возвращает значение случайной величины, имеющей нормальное распределение со средним ц и стандартным отклонением о
Пуассона	=RiskPoisson(X)	Возвращает значение случайной величины, имеющей распределение Пуассона со средним X
Треугольное	=RiskTnang(a,b,c)	Возвращает значение случайной величины, имеющей треугольное распределение с пара- метрами а, b и с (а — минимальное, b — мак- симальное, а с — наиболее вероятное значе- ние случайной величины)
Равномерное (непрерывное)	=RiskUniform(a,b)	Возвращает значение случайной величины, имеющей равномерное распределение с па- раметрами а и b (а — минимальное, Ь — мак- симальное значение случайной величины)
В следующем разделе рассмотрим примеры моделирования случайных величин в Excel
без применения описанных надстроек, а в последующих разделах — с их использованием
10.3. Имитация в электронных таблицах
Большинство имитационных моделей строятся и выполняются в электронных табли-
цах, поскольку процесс имитации требует выполнения многочисленных и разнообраз-
ных вычислений В этом разделе на примере финансового планирования мы покажем
процесс построения имитационной модели и ее выполнение в Excel без привлечения до-
полнительных надстроек
ГЛАВА 10 Имитационное моделирование 673
Модель финансового планирования
Джон Вильсон работает в компании Airbus Industry, занимающейся проектированием
и выпуском самолетов В настоящий момент он рассматривает финансовые последствия
запуска в производство новой модели самолета АЗXX Начальные затраты, которые
включают стоимость разработки и проектирования, создания и испытания опытного об-
разца составляют $150 млн (эта и другие приведенные суммы в рабочей книге Вильсон
(см рис 10 9) выражаются в тысячах долларов) Новый самолет будет продаваться по це-
не $35 млн за единицу Постоянные затраты оцениваются в $15 млн в год, тогда как пе-
ременные затраты в год составляют 75% от дохода.
Рис. 10.9. Первоначальная модель Вильсона
Амортизационные отчисления на новое оборудование составляют $ 10 млн в год в те-
чение 4 лет прогнозируемого периода производства самолета АЗХХ Остаточную стои-
мость оборудования после 4 лет эксплуатации предсказать достаточно сложно, поэтому
674 ЧАСТЬ III Вероятностные модели
Джон определяет ее по консервативному принципу, т е. полагает равной нулю. Для ком-
пании Airbus Industry стоимость капитала составляет 10%, а налоговая ставка — 34%.
Неопределенным фактором рассматриваемой модели является спрос на новую про-
дукцию Зная величину спроса, с помощью функции Excel ЧПС нетрудно вычислить
чистую приведенную стоимость (ЧПС) Например, если предположить, что спрос на
АЗХХ ежегодно будет составлять 10 единиц, то, как показано на рис. 10.9 (рабочая книга
Вильсон), ЧПС составит $12 455,60
Модель со случайным спросом
Невозможно точно предсказать спрос на 4 года вперед Более реалистична модель, где
спрос не фиксирован по годам, а является последовательностью случайных величин. Мож-
но установить базовый уровень спроса, например, 10, в таком случае точные значения
спроса по годам будут случайными флуктуациями относительно этого базового уровня
Генерирование случайного спроса
Джон Вильсон решил генерировать случайный спрос на 4 года, чтобы увидеть, как мо-
жет меняться значение ЧПС Он предположил, что спрос может принимать значения 8, 9,
10, 11 и 12 с равными вероятностями Это пример равномерного дискретного распределе-
ния Почерпнув нужные сведения из раздела 10 2 данной книги, он в своей рабочей книге
в ячейки, содержащие значения спроса, ввел формулу =ЦЕЛОЕ(8+5*СЛЧИС()), которая бу-
дет возвращать целые значения 8, 9, 10, И или 12 с равными вероятностями Поскольку
функция СЛЧИС изменяет возвращаемое ею значение каждый раз при пересчете рабочего
листа, то Джон может легко выполнить множественные испытания своей модели (т е задать
новые значения для спроса и выполнить соответствующие вычисления) — для этого доста-
точно нажать клавишу, которая инициировала бы пересчет рабочего листа (в Excel такой
клавишей является <F9>)
Рис. 10.10. Модель Вильсона со случайным спросом
ГЛАВА 10. Имитационное моделирование
675
На рис 10 10 показано значение ЧПС при некоторых значениях спроса Если сейчас
Джон нажмет клавишу <F9>, будет получено другое значение ЧПС Поскольку в этой
модели спрос является случайной величиной, то ЧПС также является случайной величи-
ной. Проведя несколько испытаний, Джон обнаружил, что ЧПС может принимать отри-
цательные значения
Результаты имитации
Джон построил имитационную модель, чтобы она помогла ему ответить на два вопроса
относительно распределения ЧПС’ 1) чему равно математическое ожидание {ожидаемое
значение) ЧПС и 2) какова вероятность того, что ЧПС примет отрицательное значение9
Чтобы ответить на эти вопросы, надо несколько раз выполнить имитацию и полученные
значения ЧПС сохранить в отдельной таблице, лучше на отдельном рабочем листе, для чего
можно использовать таблицы подстановки Excel Сначала выполните следующие действия
(Предполагаем, что открыта рабочая книга Вильсон, лист с моделью случайного спроса на-
зван Случайный спрос)
1.	Выполните команду Вставка^Лист. Excel вставит в рабочую книгу новый лист
2.	Дважды щелкните на корешке нового листа и дайте ему новое имя, например, 100
итераций
3.	Введите начальное значение 1 в ячейку А2 и нажмите <Enter>
4.	Вернитесь в ячейку А2 и выполните команду Правка^ЗаполнитьФПрогрессия
5.	В открывшемся диалоговом окне Прогрессия установите переключатель По
столбцам и введите значение 100 в поле Предельное значение
6.	Щелкните на кнопке ОК
Рис. 10.11. Результаты ими-
тации модели Вильсона
676 ЧАСТЬ III Вероятностные модели
Excel автоматически заполнит 100 ячеек столбца А начиная с ячейки А2 последова-
тельными значениями от 1 до 100 Далее введите в ячейку В2 нового рабочего листа фор-
мулу ='Случайный спрос'! В19. Можно ввести заголовки столбцов в ячейки А1 и В1. Те-
перь создадим таблицу подстановки
1.	Выделите диапазон А2 В101
2.	Выполните команду ДанныеФТаблица подстановки.
3.	В диалоговом окне Таблица подстановки введите С1 в поле Подставлять значе-
ния по строкам.
4.	Щелкните на кнопке ОК
Excel подставит по очереди все значения из диапазона А2 А101 в ячейку С1 (что не
произведет никакого эффекта), пересчитает рабочую книгу и сохранит полученные зна-
чения ЧПС в соседних ячейках столбца В, как показано на рис. 10.11.
Поскольку значения функции СЛЧИС изменяются при каждом пересчете рабочего
листа, то и полученные значения ЧПС также будут в дальнейшем изменяться при любых
вычислениях Чтобы зафиксировать полученные значения ЧПС (так, чтобы они не изме-
нялись при пересчете рабочего листа), надо преобразовать формулы в столбце В листа
100 итераций в значения Для этого выполните простые действия.
1.	Выделите диапазон В2 В101
2.	Скопируйте содержимое этого диапазона в буфер обмена с помощью, например,
команды ПравкаФКопировать
3.	Выполните команду ПравкаФСпециальная вставка.
4.	В открывшемся диалоговом окне Специальная вставка установите переключа-
тель Значения и щелкните на кнопке ОК
Статистический анализ полученных значений ЧПС можно провести с помощью встро-
енных средств Excel (Если в меню Сервис нет команды Анализ данных, выполните ко-
манду СервисФНадстройки и в диалоговом окне Надстройки выберите Пакет анализа)
Средство Excel Анализ данных позволяет получить многочисленные статистические харак-
теристики (среднее, стандартное отклонение, минимальное и максимальное значения
и т д). Чтобы воспользоваться этим средством, необходимо предпринять следующее.
1.	Выполните команду СервисФАнализ данных.
2.	В диалоговом окне Анализ данных в списке Инструменты анализа выберите
Описательная статистика и щелкните на кнопке ОК
3.	Заполните открывшееся диалоговое окно Описательная статистика так, как по-
казано на рис 10 12 Щелкните на кнопке ОК.
Результаты работы средства Анализ данных показаны на рис 10 13, среднее ЧПС
равно $12 115,19, а стандартное отклонение — $1247,62
Полученные результаты также показывают, что значения ЧПС могут изменяться от
$39 955,37 до -$11 100,37 — это интервал возможных значений ЧПС
ГЛАВА 10. Имитационное моделирование 677
Рис. 10.12. Диалоговое окно Описательная статистика
Рис. 10.13. Результаты анализа данных
Распределение ЧПС
Несмотря на то что данные на рис 10 13 достаточно полно характеризуют ЧПС, они не
позволяют ответить на некоторые существенные вопросы Например, какова вероятность
крайних значений ЧПС (т.е наилучшего и наихудшего вариантов)9 Чтобы ответить на по-
добные вопросы, необходимо знать распределение ЧПС Для этого Excel имеет встроенные
678 ЧАСТЬ III Вероятностные модели
средства Чтобы получить гистограмму (графическое представление распределения вероят-
ностей), функцию распределения и таблицу частот, надо выполнить такие действия
1.	Выполните команду Сервис^Анализ данных.
2.	В диалоговом окне Анализ данных в списке Инструменты анализа выберите Гис-
тограмма и щелкните на кнопке ОК
3.	Заполните открывшееся диалоговое окно Гистограмма так, как показано на рис. 10 14,
и щелкните на кнопке ОК.
Рис. 10.14. ,[ui:.Kic<>b'ie окно Гистограмма
В данном случае результаты представлены на отдельном рабочем листе (рис. 10 15)
Данные в столбце В показывают, сколько значений ЧПС (из ста) попали в интервалы,
определенные Excel в столбце А (эти интервалы называются карманами) Например,
только одно значение ЧПС меньше или равно —$ 11 100,37 Пять значений лежат в преде-
лах от —$5427,44 до $245,49 Наибольшее количество значений (19) лежит в интервале
$11 591,34-17 269,27 Данные в столбце С показывают, что примерно 15% значений ЧПС
отрицательны
Карман
Рис. 10.15. Гистограмма и таблица частот
ГЛАВА 10. Имитационное моделирование 679
Надежность результатов имитационного моделирования
Джону необходимо было ответить на два вопроса относительно распределения ЧПС
Во-первых, каково среднее значение ЧПС (ответ — $12 115) Во-вторых, какова вероят-
ность отрицательных значений ЧПС (ответ — не менее 15%) Теперь пришло время за-
дать другие вопросы какова надежность полученных ответов и можно ли ее повысить,
увеличив количество испытаний (имитаций) модели9
Интуиция подсказывает, что, увеличивая количество проведенных испытаний имита-
ционной модели, мы повышаем надежность полученных результатов Но как численно
оценить эту надежность, если мы провели ровно 100 испытаний9 Из курса математиче-
ской статистики вы должны знать, что на основе полученных в результате испытаний
данных можно построить доверительный интервал для интересующих нас статистиче-
ских характеристик Например, можно построить доверительный интервал, который
с вероятностью 95% содержал бы истинное значение среднего ЧПС Этот интервал стро-
ится так- нижняя граница этого интервала равна полученному значению среднего минус
1,96 стандартного отклонения, деленного на корень из числа испытаний, верхняя грани-
ца этого интервала равна полученному значению среднего плюс 1,96 стандартного от-
клонения, деленного на корень из числа испытаний Такой доверительный интервал для
среднего ($9679,44, $14521,30) построен на рабочем листе, показанном на рис 10 13 Та-
ким образом, кроме текущего предположения, что среднее равно $12 100, можно утвер-
ждать, что с надежностью (вероятностью) 95% истинное (неизвестное) значение среднего
лежит в пределах от $9669,86 до $ 14560,52
При проведении таких вычислений следует избегать ловушки “среднего значения”
многие студенты уверены, что истинное среднее какои-либо вычисляемой случайной пе-
ременной всегда можно рассчитать, подставив вместо случайных величин, от которых за-
висит данная переменная, их истинные средние. Например, истинное значение среднего
ЧПС вычисляют, подставив вместо значений случайного спроса его среднее, те. значе-
ние 10 (как это сделано в исходном рабочем листе на рис 10 9) Это глубоко ошибочный
подход — зависимости между средними (математическими ожиданиями) случайных ве-
личин обычно настолько сложны и нелинейны и настолько зависят от их вероятностных
распределений, что только в отдельных исключительных случаях можно описанным спо-
собом найти среднее вычисляемой случайной переменной
Итак, если Джон Вильсон хочет повысить надежность полученных результатов, ему
необходимо увеличить количество проведенных испытаний.
10.4. Имитация с помощью надстроек
Такие надстройки электронных таблиц, как Crystal Ball и ©Risk, значительно облег-
чают построение и испытание имитационных моделей. Они упрощают генерирование
случайных величин и сбор статистических результатов. В этом разделе на примере фи-
нансового планирования Джона Вильсона мы покажем использование надстройки Crys-
tal Ball (версии 4 0g). В следующем разделе на другом примере мы продолжим демонстра-
цию использования Crystal Ball, но той ее версии, которая распространяется вместе
с данной книгой Работа с надстройкой @Risk будет кратко описана в разделе 10 7.
Процесс имитации в электронных таблицах без соответствующих надстроек может
быть длительным и утомительным даже для простых моделей. Тем более это утверждение
справедливо для сложных моделей, использующих “нестандартные” вероятностные рас-
пределения и требующих проведения большого количества испытаний. Как мы увидим,
680 ЧАСТЬ III Вероятностные модели
перечисленные надстройки имеют многочисленные средства, позволяющие автоматизи-
ровать процесс генерирования случайных величин. В настоящее время, как правило,
“профессиональное” имитационное моделирование выполняется с помощью специаль-
ных надстроек электронных таблиц.
Пример финансового планирования
Данный пример описан в начале раздела 10 3. В этом примере рассматривается мо-
дель, на основании которой менеджер Джон Вильсон должен дать рекомендацию, начи-
нать ли производство нового типа самолета Начальная модель с постоянным спросом
показана на рис. 10 16 (рабочая книга Вильсон_Кристалл).
Далее Джон преобразует модель в модель со случайным спросом, предполагая, что
ежегодно спрос может принимать значения 8, 9, 10, 11 и 12 с равными вероятностями
(эти вероятности равны 0,2) Для генерирования случайного спроса с этими вероятно-
стями он применяет надстройку Crystal Ball, предварительно введя значения спроса и их
вероятности в столбцы I и J рабочей таблицы, как показано на рис. 10.16. Далее надо ука-
зать на эти вероятности надстройке Crystal Ball, выполнив следующие действия.4
1.	Щелкните на ячейке С9, где Crystal Ball будет генерировать случайные значения
спроса для первого года производства.
2.	Щелкните на кнопке Define Assumption (Предположения) панели инструментов
Crystal Ball
Предполагается, что надстройка Crystal Ball уже установлена и подключена к Excel Чтобы установить
эту надстройку, сначала запустите на исполнение файл Setup, который находится в папке Crystal Ball на
компакт-диске данной книги Если при установке надстройки вы указали, чтобы Crystal Ball не запускалась
автоматически при открытии Excel (установка по умолчанию), то далее необходимо подключить ее к Excel
Для этого выполните команду Сервис ^Надстройки, затем в списке Доступные надстройки выберите
Crystal Ball (эта опция появится в данном списке, если надстройка правильно установлена на компьютере)
В окне Excel появится дополнительная панель инструментов Crystal Ball, о которой идет речь ниже —
Прим рсд
ГЛАВА 10. Имитационное моделирование	681
3.	В открывшемся диалоговом окне Distribution Gallery (Набор распределений)
щелкните на типе распределения Custom (Пользовательский) и затем на кнопке
ОК (см. рис. 10 17).
4.	В новом окне Custom Distribution (Пользовательское распределение) щелкните на
кнопке Data (Данные) и введите в то поле, где будет находиться курсор, I3:J7 —
диапазон ячеек, где находятся данные о моделируемом распределении. Затем
щелкните на кнопке ОК.
5.	Crystal Ball воспроизведет заданное вами распределение, как показано на
рис. 10.18. Щелкните на кнопке ОК.
6.	Повторите описанные действия для ячеек D9:F9, задающих значения спроса для 2,
3 и 4 годов производства. Можно также воспользоваться кнопками Copy Data
(Копировать данные) и Paste Data (Вставить данные) панели Crystal Ball.
Рис. 10.17. Предлагаемые Crystal Ball типы распределений
Рис. 10.18. Распределение, которое будет генерировать
Crystal Ball
Чтобы средство Crystal Ball сгенерировало одно значение для случайного спроса, надо
щелкнуть на кнопке Single Step (Один шаг) панели инструментов Crystal Ball (эта кноп-
682
ЧАСТЬ III. Вероятностные модели
ка показана на рис. 10 19) После этого Excel пересчитает все формулы, и Джон получит
значение ЧПС для этих значений спроса, как показано на рис. 10 19. Щелкнув на кнопке
Single Step снова, Джон получит новое значение ЧПС. Таким образом, последовательно
генерируя значения случайного спроса, можно просмотреть случайные значения вычис-
ляемой ЧПС.
Рис. 10.19. Рабочий мет модели Вильсона, готовый для проведения испытаний
Результаты имитации
Имитационная модель должна помочь Джону ответить на два вопроса относительно
распределения ЧПС 1) чему равно математическое ожидание (или ожидаемое значение)
ЧПС и 2) какова вероятность того, что ЧПС примет отрицательное значение9 Чтобы от-
ветить на эти вопросы, надо несколько раз выполнить имитацию и сохранить получен-
ные значения ЧПС Для того чтобы поручить Crystal Ball эту работу, выполните следую-
щие действия (Предполагаем, что открыта рабочая книга Вильсон_Кристалл )
1.	Щелкните на ячейке В19, в которой находится формула для вычисления ЧПС
2.	Щелкните на кнопке Define Forecast (Параметры прогноза) панели инструментов
Crystal Ball.
3.	Откроется одноименное диалоговое окно, в котором надо установить переключа-
тели Large (Большое) и When Stopped (После остановки), как показано на
рис 10 20 Можно также щелкнуть на кнопке Set Default (Установить по умолча-
нию), если вы хотите, чтобы сделанные вами изменения стали установками по
умолчанию.
4.	Щелкните на кнопке ОК.
5.	Щелкните на кнопке Run Preferences (Параметры выполнения) панели Crystal
Ball Откроется одноименное диалоговое окно, введите в поле Maximum Number of
Trials (Максимальное число испытаний) число 500, как показано на рис. 10.21.
6.	Щелкните на кнопке ОК.
ГЛАВА 10 Имитационное моделирование 683
7.	Щелкните на кнопке Start Simulation (Начало имитации), и после того, как Crystal
Ball выполнит 500 имитаций, будет выведено сообщение “Maximum number of
trials reached” (Максимальное число испытаний достигнуто) Щелкните на кнопке
ОК в окне сообщения, автоматически будет построена гистограмма, показанная на
рис 10 22
8.	Чтобы просмотреть полученные статистические характеристики, в окне Forecast
(Прогноз) выполните команду View=>Statistics (Вид^Статистики) Crystal Ball
отобразит таблицу, показанную на рис. 10.23
Рис. 10.20. Диалоговое окно Define Forecast
Рис. 10.21. Диалоговое окно Run Preferences
Отметим, что 500 испытаний в Crystal Ball выполняются намного быстрее, чем 20 или
100 испытаний непосредственно в рабочем листе Excel Результаты работы этой над-
стройки показаны на рис 10 23. Из них видно, что среднее ЧПС равно $12 130,86, а стан-
дартное отклонение — $12 747,88 Конечно, у вас могут быть несколько иные результаты
684 ЧАСТЬ III Вероятностные модели
испытаний, поскольку, не забывайте, процедура имитации “выбирает” только несколько
(500) значении из бесконечного множества возможных значений случайных величин
Отметим также, что в данном примере значение среднего ЧПС ближе к его истинному
значению, чем значение, полученное в разделе 10.3.
Рис. 30.23. Статистические результаты имитации
Полученные результаты также показывают, что значения ЧПС могут изменяться от
$49 067,55 до — $20 211,94 — это интервал возможных значений ЧПС.
Распределение ЧПС
Данные на рис. 10.23 достаточно полно характеризуют ЧПС, однако они не позволя-
ют ответить на некоторые существенные вопросы. Например, какова вероятность край-
них значений ЧПС (т е наилучшего и наихудшего вариантов)? Чтобы ответить на подоб-
ные вопросы, необходимо знать распределение ЧПС. Для этого Crystal Ball имеет встро-
енные средства. На рис. 10 22 показана гистограмма распределения частот значений
ГЛАВА 10 Имитационное моделирование 685
ЧПС, построенная Crystal Ball. Одно из замечательных свойств надстройки Crystal Ball
заключается в том, что в ней после проведения имитаций уже табулированы многие ста-
тистические характеристики и показатели. Например, чтобы определить значение веро-
ятности отрицательных значений ЧПС, достаточно в нижней части окна с гистограммой
ввести в правое поле (помеченное символом <) число 0, как показано на рис. 10.24.
Crystal Ball автоматически покажет значение этой вероятности в поле Certainty
(Достоверность). В нашем случае значение этой вероятности равно 17,6%, т е. в 18 случа-
ях из 100 (в среднем) ЧПС будет принимать отрицательные значения. Значения ЧПС, со-
ответствующие заданным вероятностям (10%, 20%, ..., 90%), можно получить, выполнив
в окне Forecast команду Vie w<=> Percentiles (Вид^Процентили). Отметим, что Crystal Ball
предоставляет значительно больше разнообразной статистической информации, чем
встроенные средства Excel Гистограмма и Описательная статистика.
Рис. 10.24. Определение вероятности отрицательных значении ЧПС
Рис. 10.25. Доверительный интервал для среднего значения ЧПС
686
ЧАСТЬ III Вероятностные модели
Как описано в разделе 10 3, в данной ситуации также можно построить доверитель-
ные интервалы для интересующих нас статистических характеристик ЧПС. Поскольку
в данном случае проведено больше испытаний, длина этих интервалов будет меньше, чем
при проведении 100 испытаний (как было сделано в разделе 10.3), т.е. будут получены
более точные оценки неизвестных параметров распределения ЧПС. Например, довери-
тельный интервал для неизвестного математического ожидания ЧПС, показанный на
рис 10 25, почти в два раза меньше аналогичного интервала, приведенного на рис. 10 13.
Другие распределения спроса
Джон задумался о том, правильно ли он оценивает спрос на 4 года вперед В преды-
дущих моделях он предполагал, что средний ежегодный спрос будет равен 10 Однако,
если конъюнктура рынка ухудшится, то средний спрос, очевидно, уменьшится
(например, до 8), а если ситуация на рынке будет благоприятной, то средний спрос дол-
жен увеличиться (по некоторым оценкам, до 13). После некоторых размышлений Джон
решил, что средний спрос должен быть случайной величиной, принимающей с равными
вероятностями любые значения из интервала от 6 до 14 Другими словами, средний спрос
должен иметь непрерывное равномерное распределение на интервале от 6 до 14.
Далее Джон решил, что спрос должен иметь сравнительно небольшой разброс воз-
можного среднего значения В литературе по теории вероятности и математической ста-
тистике он вычитал, что для такой ситуации подойдет распределение Пуассона Это рас-
пределение зависит от одного параметра — математического ожидания, которое полно-
стью определяет это распределение. Распределение Пуассона является дискретным
распределением — случайная величина, подчиняющаяся этому закону, принимает толь-
ко неотрицательные целые значения
Джон заложил эту информацию в новую рабочую книгу Excel (книга называется Виль-
сон_Кристалл_2) Распределения случайных величин он задал с помощью надстройки
Crystal Ball Чтобы задать распределение среднего спроса, он щелкнул на ячейке D6
(содержащей это значение), затем — на кнопке Define Assumption панели инструментов
Crystal Ball В открывшемся диалоговом окне он выбрал равномерное (uniform) распреде-
ление, дважды щелкнув на нем В следующем окне Uniform Distribution (Равномерное рас-
пределение) в поле Min (Минимум) он ввел число 6, а в поле Мах (Максимум) — 14. Для за-
дания распределения спроса он щелкнул на ячейке С9 (значение спроса для первого года
производства) и на кнопке Define Assumption, в открывшемся диалоговом окне выбрал
распределение Пуассона (Poisson), дважды щелкнув на нем В следующем окне Poisson
Distribution (Распределение Пуассона) в поле Rate (Коэффициент) Джон ввел формулу
=$D$6, указав тем самым ячейку, где находится значение математического ожидания дан-
ного распределения (рис 10.26). Затем с помощью кнопок Copy Data и Paste Data панели
инструментов Crystal Ball он скопировал эту информацию из ячейки С9 в ячейки D9 F9.
Джон выполнил 1000 испытаний новой модели, задав в окне Run Preferences в поле
Maximum Number of Trials значение 1000. Чтобы надстройка Crystal Ball отслеживала ха-
рактеристики именно значений ЧПС, в окне Define Forecast в поле Forecast Name он
указал ячейку С19, содержащую формулу вычисления ЧПС. Выполнив процесс имита-
ции, Crystal Ball вывела окно с гистограммой частот значений ЧПС (рис. 10 27) По этой
гистограмме нетрудно определить, что ЧПС может принимать отрицательные значения
с вероятностью 49,7% (что значительно больше, чем в предыдущей модели). Также легко
просмотреть все статистические характеристики ЧПС.
ГЛАВА 10 Имитационное моделирование 687
Рис. 10.26. Задание распределения Пуассона
Рис. 10.27. Гистограмма распределения ЧПС
Итак, Джон имеет три модели, с детерминированным спросом (рис 10 16), случай-
ным равномерно распределенным спросом (рис 10.19, проведено 500 испытаний) и слу-
чайным спросом, распределенным по закону Пуассона (рис. 10 27, проведено 1000 испы-
таний). Какие из этого можно сделать выводы9
1.	Чем больше проведено испытаний (имитаций), тем более точные оценки парамет-
ров модели мы получаем Но необходимо помнить, что даже при очень большом
количестве испытаний полученные оценки будут отличаться от истинных значе-
ний этих параметров
2.	Имитация дает полезную информацию Во второй модели даже относительно неболь-
шое количество испытаний (500) показало, что с вероятностью не менее 0,18 возможны
отрицательные значения ЧПС (т е потери вместо прибыли) Такую информацию не-
возможно (или очень сложно) получить только на основе анализа модели
3.	Результаты имитационного моделирования очень чувствительны к исходным
предположениям относительно параметров модели Вы видели, что, изменив
предположение о типе распределения спроса (вместо равномерного дискретного
распределения применив распределение Пуассона с тем же средним 10), мы резко
увеличили вероятность отрицательных значений ЧПС
688 ЧАСТЬ III. Вероятностные модели
Вероятно, наиболее важно применение имитационного моделирования в процессе
принятия решений Если бы Джон не испытал имитационные модели, он, наверное, дал
бы рекомендацию на начало производства нового типа самолета. Однако после проведе-
ния имитации он понял, что это очень рискованно, причем, что очень важно, он может
показать степень риска, основываясь на результатах, полученных в процессе имитации.
Подчеркнем еще раз, что модели не ограничивают менеджера в принятии решений и не
снимают с него ответственности — они только предоставляют дополнительную инфор-
мацию, которую можно и нужно учитывать при принятии решений.
10.5. Модель управления запасами
В рассмотренных моделях финансового планирования Джона Вильсона имитация ис-
пользовалась в ситуации, где надо было ответить на вопрос “да или нет” — должен ли
Джон дать рекомендацию на производство нового самолета или нет. Однако на практике
часто возникает необходимость ответить на вопросы типа “сколько, когда или по какой
цене?” Имитационные модели могут помочь и в этом случае.
Продвижение товара: определение объема заказа
Мэри Форд руководит отделом, занимающимся оптовыми закупками посуды для
компании Foslins, одного из ведущих предприятий розничной торговли в Денвере Она
отвечает за разработку долгосрочной стратегии розничной торговли компании. Ей также
подчиняется группа менеджеров, занимающаяся удовлетворением покупательского
спроса по различным группам товаров.
Некоторые подразделения отдела, которым руководит Форд, уже второй год подряд
испытывают определенные трудности Конкурирующие предприятия стали серьезно по-
сягать на те сегменты рынка, которые традиционно считались вотчиной Foslins. Таким
образом, подразделения, занимающиеся продажей стеклянной и нержавеющей посуды,
перестали приносить прибыль, достаточную хотя бы для покрытия расходов по содержа-
нию складских помещений
Мэри хочет разобраться в сложившейся ситуации и переломить негативный ход раз-
вития бизнеса Она реорганизовала убыточные подразделения, открыла при своем отделе
магазин посуды (как у конкурентов), оснащенный специальной техникой и освещением
Она также решила в октябре провести месячник “Международные столовые принадлеж-
ности”. В течение этого месяца будут продаваться пять специальных наборов посуды, все
из разных стран. Например, будут продаваться особые (для приготовления омлетов) ско-
вородки из Франции, созданные специально для компании Foslins, набор из 12 предме-
тов огнеупорной стеклянной посуды из Испании и т.д Наборы необходимо заказать не
позднее, чем за 6 месяцев до начала этой акции. Мэри отвечает за ценовую политику ме-
сячника Если какой-либо набор не будет продан до конца октября, он будет реализован
со скидкой Кроме тою, если закончится специально заказанный для месячника товар,
то вместо него по той же цене будет продаваться подобная “обычная” посуда (т е. та, ко-
торая не заказана специально для месячника, но, конечно, соответствующего качества).
Особые сковородки Foslins будет закупать по цене $22 и продавать по $35. Если они
не будут проданы в течение месяца, то как уцененные товары будут реализованы по $15
за штуку Если заказанные особые сковородки будут проданы, то вместо них будут вы-
ставляться обычные сковородки, которые также будут продаваться по цене $35. Эти ско-
вородки обычно продаются по $65 при закупочной цене $32
ГЛАВА 10. Имитационное моделирование 689
Мэри должна определить, сколько надо заказать особых сковородок, не зная будущий
спрос на них. Например, предположим, что заказано 1000 сковородок, а спрос составит
1100 сковородок. Тогда надо будет продать дополнительно 100 сковородок, у которых
покупная цена $32 (у 1000 сковородок покупная цена $22). Но все сковородки будут про-
даны по цене $35. В этом случае доход составит
$35x1100 - $32x100 - $22x1000 = $12 300.
Если обозначить через у количество заказанных сковородок, а через D — спрос на них, то
при D >у
доход = 35Д - 32(Р - у) - 22у = 3D + 10у.
Если же Мэри закажет 1000 сковородок, а спрос составит всего 200 сковородок, то
только 200 сковородок будет продано по цене $35, а остальные 800 уйдут по цене $15
в сеть уцененных товаров. Тогда доход составит
$35x200 + $15x800 - $22x1000 = -$3000.
В общем случае, если D < у
доход = 35D + 15(у - D) - 22у = 20D - 7у.
(Если D = y, то приведенные формулы вычисления дохода, как нетрудно заметить, сов-
падают.)
Для вычисления дохода по этим формулам Мэри создала рабочую книгу Форд_1, по-
казанную на рис. 10.28. Здесь для пробы Мэри ввела у = 11 (т е заказано 11 сковородок),
а спрос положила равным 8 (т.е D = 8). Электронная таблица подсчитала, что доход бу-
дет равен $83.
J ~ А~ ~ i	I с I D j Е, I F
1	Определение объема заказа сковородок
2	Специальные сковородки
3	Объем заказа	Цена продажи	:	 и
4	Цена после уценки J	1' ;н
5	Случайный спрос	Стоимость	$	22,00 >>	I
7	Не продано	:	Обычные сковородки
S		Стоимость	S	<п0
9	Неудовлетворенный спрос	О
11 Доход	$	83.П0
I  а 	/  в ,	' 
6 |"...'	~ ~~	:	TLx
7 He продано	_
v].. .	'с.-z	'
9 Неудовлетворенный спрос =MAKC(0,B5-B3)	''	’ •'
11 Доход	=ЕСЛИ(ВЗ>=®5.ЕЗ*В5+Е4"В7-Е5'ВЗ;ЕЗ-В5-Е8’ВЭ-Е5’ВЗ)
Рис. 10.28. Ничи.шныи рибочии шип
690 ЧАСТЬ III Вероятностные модели
Доход и объем заказа
Мэри, естественно, интересует, какой объем заказа увеличит ожидаемый доход. Для
того чтобы получить ответ с помощью имитационной модели, надо сначала сформировать
предположение о распределении случайного спроса. В разделе 10.6 предполагается, что
спрос распределен по нормальному закону, а здесь вероятности спроса имеют следующие
значения Р{спрос = 8} =0,1, Р{спрос = 9} =0,2, Р{спрос=10} =0,3, Р{спрос=11} =0,2,
Р{спрос = 12} = 0,1, Р{спрос = 13} = 0,1.
Для генерирования значений случайного спроса в соответствии с этим вероятност-
ным распределением с помощью надстройки Crystal Ball Мэри сначала ввела значения
спроса и их вероятности в столбцы G и Н своего рабочего листа (рис. 10 29). Далее она
выполнила следующие действия
1.	Щелкнула на ячейке В5, где будут находиться значения случайного спроса.
2.	Щелкнула на кнопке Define Assumption панели инструментов Crystal Ball
3.	В открывшемся диалоговом окне Distribution Gallery щелкнула на типе распреде-
ления Custom и затем на кнопке ОК (см рис 10 17)
4.	В новом окне Custom Distribution щелкнула на кнопке Data и ввела в поле, в кото-
ром находится курсор, G3 Н8 — диапазон ячеек, где размещены данные о модели-
руемом распределении (рис 10 29) Затем щелкнула на кнопке ОК.
5.	Надстройка Crystal Ball воспроизвела заданное распределение (рис. 10 29)
В*-.| С I	D	I Е I F
Распределение спроса
Значение Вероятность
Enter Cell Range Containing Custom Data Points (e.g. A1:B9):
I" Cumulative Data (two columns only)
Puc. 10.29. Задание распределения случайного спроса
Теперь надо указать Crystal Ball, характеристики какой величины отслеживать при
проведении имитаций, а также количество испытаний. Для этого Мэри выполнила такие
действия
1.	Щелкнула на ячейке Bl 1, в которой находится формула для вычисления дохода
2.	Щелкнула на кнопке Define Forecast панели инструментов Crystal Ball.
3.	Открылось одноименное диалоговое окно, в котором Мэри установила переклю-
чатели Large и When Stopped (как показано на рис 10 20). Можно также щелк-
ГЛАВА 1 0. Имитационное моделирование 691
нуть на кнопке Set Default, если вы хотите, чтобы сделанные вами изменения ста-
ли установками по умолчанию.
4.	Щелкнула на кнопке ОК
5.	После щелчка на кнопке Run Preferences панели Crystal Ball открылось одно-
именное диалоговое окно, где в поле Maximum Number of Trials Мэри ввела число
500 (как показано на рис 10 21)
6.	Щелкнула на кнопке ОК
7.	Щелкнула на кнопке Start Simulation (Начало имитации), и после того, как Crystal
Ball выполнила 500 имитации, Мэри получила сообщение “Maximum number of
trials reached” (Максимальное число испытаний достигнуто) После щелчка на
кнопке ОК в окне сообщения была автоматически построена гистограмма, пока-
занная на рис. 10 30
8.	Чтобы просмотреть полученные статистические характеристики, в окне Forecast
Мэри выполнила команду View^Statistics Crystal Ball отобразила таблицу, пока-
занную на рис. 10 31.
Если вы повторите описанные действия, то числа, которые получатся в результате
имитаций, могут немного отличаться от приведенных на рис 10 31 Не забывайте, что
Crystal Ball генерирует только 500 значений из потенциально бесконечного множества,
поэтому набор значений, которые Crystal Ball сгенерирует в вашем случае, наверняка бу-
дет отличаться от набора, сгенерированного в процессе нашей имитации По этой же
причине, повторив имитацию с теми же данными, Мэри получит характеристики дохода,
несколько отличающиеся от показанных
В соответствии с данными на рис 10 31 оценка среднего дохода составляет $123,74
Мэри может использовать созданную рабочую книгу для вычисления среднего при дру-
гих значениях объема заказа Для этого надо ввести новое число в ячейку ВЗ и повторить
процесс имитации
ЧАСТЬ III Вероятностные модели
Рис. 10. ?/. Cmamucmuuet кие характеристики дохода
Вычисление ожидаемого дохода
В этом простом примере можно легко вычислить истинное ожидаемое (среднее) зна-
чение дохода Для этого можно использовать рабочий лист, показанный на рис 10.28.
Сначала в этом листе надо вычислить значения дохода, который будет получен при всех
шести возможных значениях спроса (8, 9, , 13). Соответствующие значения спроса и
дохода можно поместить в столбцы В и С на новом листе (см. табл 10 2). Поскольку для
каждого значения спроса доход вычисляется однозначно, то вероятности спроса будут
также вероятностями этих значений. Другими словами, мы имеем распределение случай-
ного дохода Чтобы найти математическое ожидание (ожидаемое значение) дохода, надо
каждое из шести значений вычисленного дохода умножить на соответствующее значение
вероятности и затем все эти произведения сложить В рабочем листе для удобства вычис-
лений значения вероятностей можно поместить в столбец D, произведение значений до-
хода и вероятности — в столбец Е Теперь останется только просуммировать данные
в столбце Е Эти вычисления показаны в табл. 10.2
Таблица 10.2. Вычисление ожидаемого дохода
А	В	С	D		Е
Объем заказа	Спрос	Доход	Вероятность	Произведение (доходхвероятность)	
11	8	83	0,10		8,3
11	9	103	0,20		20,6
11	10	123	0,30		36,8
11	11	143	0,20		28,6
11	12	146	0,10		14,6
11	13	149	0,10		14,9
			Ожидаемый доход -	$123,9	
ГЛАВА 10. Имитационное моделирование 693
Вычисления или имитация?
Мэри поставила цель: определить объем заказа, который принесет максимальную
прибыль Для этого можно, например, вычислить ожидаемый доход для всех возможных
объемов заказа, как это сделано выше, и затем выбрать объем заказа, обеспечивающий
максимальную прибыль. Но если использовать имитацию, то для вас уже не должно быть
сюрпризом, что полученное в ее процессе среднее какой-либо случайной величины не
будет в точности совпадать с истинным значением математического ожидания той же ве-
личины. Причины этого уже обсуждались выше В табл 10 3 приведены значения вычис-
ленных средних дохода и значений этих же величин, полученные после 500 испытаний
имитационной модели для разных значений объема заказа.
Таблица 10.3
Объем заказа	Истинный ожидаемый доход, $	Средний доход после 500 испытаний, $
9	119,2	118,88
10	124,1	124,18
И	123,9	124,30
12	120,3	118,81
Таким образом, если Мэри основывает свое решение только на результатах имита-
ции, то она должна сделать заказ в 11 сковородок, а если она учитывает истинные сред-
ние дохода, то заказ должен составлять Ю сковородок. Конечно, это очень упрощенный
пример, но он прекрасно иллюстрирует положение, что в общем случае результаты ими-
тационного моделирования не гарантируют достижения оптимальности.
В описанной ситуации решение заказывать 10 или 11 сковородок не критично, посколь-
ку истинные значения среднего дохода при этих значениях заказа отличаются менее, чем на
0,2%. Но в других случаях имитация может привести к решению, которое будет очень дале-
ко от оптимального. Можно ли повысить точность имитационного моделирования, чтобы
получить именно оптимальное решение? Хотя природа имитационного моделирования та-
кова, что нельзя гарантировать достижение оптимального решения, существует очень про-
стой способ увеличить точность результатов имитации — увеличить число испытаний моде-
ли. Чем больше число испытаний, тем надежнее результаты имитации.
1 Чтобы решение, принятое на основе результатов испытаний имитационной модели, было;
। обоснованным, следует провести достаточное количество испытаний этой модели. .	'
Еще раз подчеркнем, что в моделях, описывающих реальные ситуации, как правило,
невозможно или крайне сложно получить истинные ожидаемые значения случайных ве-
личин. Поэтому и используется имитация, чтобы хотя бы таким способом получить оцен-
ки этих значений. Приведенный выше пример просто иллюстрирует взаимоотношения
между имитационной и аналитической моделями.
Краткие итоги
Подведем краткие итоги, проанализировав имитационную модель Мэри Форд.
1.	Имитационная модель, построенная в электронных таблицах, требует использо-
вать в качестве входных данных значения определенных параметров (задание рас-
пределений случайных величин) и значения решений, в качестве выходных дан-
694
ЧАСТЬ III Вероятностные модели
ных модели выступают измерения статистических характеристик наблюдаемых
случайных величин
2.	Каждая имитация модели (для одних и тех же значений входных параметров и ре-
шений) генерирует разные значения измеряемых характеристик.
3.	В модели Мэри Форд наблюдаемой случайной величиной был доход. После 500
испытаний модели было получено значение основной характеристики случайного
дохода — средний (ожидаемый) доход
Отметим, что в процессе имитации получен значительный объем информации, а не
только значение среднего дохода (см рис 10.31) Также можно получить дополнитель-
ную информацию, если в качестве наблюдаемой случайной величины взять не доход, а,
например, количество случаев, когда спрос был неудовлетворен (значение ячейки В9 на
рис 10 28 равно величине неудовлетворенного спроса) Для этого надо в окне Define
Forecast надстройки Crystal Ball указать ячейку В9 и повторить процесс имитации Ре-
зультат этой имитации показан на рис 10 32 Здесь видно, что спрос не был удовлетворен
в 104 случаях при 500 испытаниях (20,8%)
Рис. 10.32. Распределение неудовлетворенного спроса
Еще одну важную информацию можно извлечь из результатов имитации, показанных на
рис 10 31 Это данные о распределении дохода, доход может изменяться от $83 до $149 со
средним $123,74. Гистограмма этого распределения (см рис 10 30) показывает, насколько
может изменяться величина дохода в зависимости от спроса, или, в конечном счете, от эко-
номической политики менеджмента компании. Менеджмент обычно выбирает такую поли-
тику, которая обеспечивает максимальный гарантированный выход (например, доход), но при
минимальной его возможной изменчивости
4.	Увеличение числа испытаний имитационной модели обычно ведет к увеличению
точности получаемых оценок статистических характеристик наблюдаемых случай-
ных величин
5.	Имитационная модель никогда не позволяет наити точное оптимальное решение.
Однако для неизвестных параметров решения можно построить доверительные
интервалы, содержащие эти значения с заданным доверительным уровнем 95%
или даже 99% (Однако невозможно построить в принципе доверительные интер-
валы с доверительным уровнем 100% )
ГЛАВА 10 Имитационное моделирование 695
6.	Для того чтобы корректно использовать результаты имитации, надо ответить на
следующие вопросы
а. Насколько точно модель отображает существенные черты реальной ситуации?
(Этот вопрос будет обсуждаться в разделе 10 10 )
b Как начальные условия влияют на результаты имитации7 (Этот вопрос на кон-
кретном примере рассмотрен в разделе 10 8)
с.	Сколько необходимо выполнить испытаний модели, чтобы оценка среднего
наблюдаемой случайной величины незначительно отличалась от истинного
значения ее математического ожидания7
d Как оценить близость решения, полученного в процессе имитации, к опти-
мальному решению7
10.6.	Модель управления запасами с нормальным
распределением спроса
В предыдущем разделе в модели Мэри Форд учитывалось упрощенное распределение
спроса, тогда как более реалистичным будет предположение, что спрос распределен по
нормальному закону со средним 1000 и стандартным отклонением, равным 100 В этом
разделе в модели Мэри Форд будет реализовано предположение о нормальном распреде-
лении спроса, выполнено 1000 испытаний этой модели и найден оптимальный объем за-
каза Кроме того, мы покажем, как оценивать различие между решениями и разность ме-
жду значением среднего, полученного в процессе имитации, и истинным математиче-
ским ожиданием
Нормальное распределение спроса
Первоначальная модель Мэри Форд показана на рис I0 28 (рабочая книга Форд_1) Но-
вую модель (с другим распределением спроса) создадим в новой рабочей книге (назовем ее
Форд_2) и скопируем в нее содержимое первого листа книги Форд_1 Далее укажем объем за-
каза (1020) ис помощью надстройки Crystal Ball зададим распределение значений спроса —
нормальное распределение с математическим ожиданием 1000 и стандартным отклонением
100, как показано на рис 10 33 (Замечание Чтобы генерировать значения нормально распре-
деленной случайной величины без применения надстройки Crystal Ball, введите в ячейку В5,
содержащую значение случайного спроса, формулу =НОРМОБР(СПЧИС(),1000,100) Конеч-
но, числовые значения в этой формуле можно заменить ссылками на ячейки, содержащими
эти значения)
Как показано в разделе 10.5, задавать количество испытаний модели (в данном случае
1000 испытаний) надо в диалоговом окне Crystal Ball Run Preference В данной модели
есть необходимость провести имитации для разных значений объема заказа, при этом
желательно, чтобы в каждой серии испытаний использовались одни и те же значения
случайного спроса Чтобы в каждой серии испытаний генерировались одни и те же слу-
чайные значения, надо задать начальное число, которое будет определять генерируемую
последовательность случайных значений Чтобы задать это начальное число в настройке
Crystal Ball, выполните следующие действия (предполагается, что открыто диалоговое
окно Run Preference)
696 ЧАСТЬ III Вероятностные модели
1.	В диалоговом окне Run Preference щелкните на кнопке Sampling (Выборка).
2.	В новом открывшемся диалоговом окне установите флажок опции Use Same
Sequence of Random Numbers (Использовать одинаковую последовательность
случайных чисел).
3.	Введите в поле Initial Seed Value (Начальное число) какое-либо целое число (мы
ввели число 422, как показано на рис 10.34).
4.	Щелкните на кнопке ОК.
Рис. 10.33. ЗиОания норма /ьногорашрсде и'ния input а
Рис. 10.34. Задание начального числа, определяющего
последовательность случайных чисел
Использование одной и той же последовательности случайных значений при разных
имитациях очень важно, поскольку мы хотим сравнить средний доход для различных зна-
чений объема заказа, но при одинаковых значениях спроса. В этом случае различие в зна-
чениях дохода будет определяться только различием заказов, а не различием в значениях
случайного спроса
ГЛАВА 10. Имитационное моделирование 697
Использование одной и той же последовательности значений случайных величин зна-
чительно снижает изменчивость результатов имитации и позволяет уменьшить количест-
во вычислений, необходимых для получения надежных результатов имитации. Исполь-
зование одинаковых последовательностей значений случайных чисел — это уникальное
и очень полезное свойство имитационного моделирования, особенно при сравнении раз-
личных возможных решений.
Результаты имитаций
На рис. 10.35 показана гистограмма распределения дохода после 1000 испытаний мо-
дели (предполагается, что объем заказа равен 1020). Средний доход равен $12 237,84
(рис 10.36). Чтобы повторить процесс имитации с другим значением объема заказа и тем
же самым набором значений случайного спроса, выполните такие действия.
1.	Введите новое значение объема заказа в ячейку ВЗ.
2.	Щелкните на кнопке Reset Simulation (Восстановление имитации) панели инст-
рументов Crystal Ball и на кнопке ОК в открывшемся диалоговом окне с вопросом.
3.	Щелкните на кнопке Start Simulation (Начать имитацию) панели инструментов
Crystal Ball.
Рис. 10.35. Гистограмма распределения дохода для объема заказа 1020
Чтобы найти оптимальное значение объема заказа, надо несколько раз повторить
процесс имитации с разными значениями объема заказа Итак, при объеме заказа 1020
ожидаемый доход составляет $12 237,84 Далее Мэри выполнила имитацию (1000 испы-
таний с той же последовательностью значений случайного спроса) для объемов заказа
1010 и 1030 и получила значения ожидаемого дохода соответственно $12 228,95 и
$12 224,60 Объему заказа 1020 по-прежнему соответствует наибольший ожидаемый до-
ход. Поэтому Мэри решила найти значения дохода в более узкой области вокруг значе-
ния заказа 1020. Она выполнила имитацию для заказа 1015 и 1025 и получила значения
ожидаемого дохода соответственно $12 237,70 и $12 228,34. Теперь наибольшее значение
дохода ожидается при объеме заказа 1015. Далее Мэри проверила значения дохода для
объемов заказов 1013 и 1017 и получила значения $12 237,29 и $12 237,87 соответственно
698 ЧАСТЬ III Вероятностные модели
Таким образом, объем заказа 1017 дает наибольший ожидаемый доход Чтобы удостове-
риться в этом, Мэри вычислила ожидаемый доход для объемов заказа 1016 и 1018. Были
получены значения дохода $12 237,76 и $12 237,81 соответственно. Действительно объем
заказа 1017 дает наибольший ожидаемый доход, хотя здесь разница с ближайшим дохо-
дом составляет всего несколько центов
Edit Preferences View Рцп Це1р			
Cell В11	Statistics		
	Statistic	Value	
	Standard Deviation Kurtosis Coeti of Variability Range Maximum Range Width Mean Std Error	1 г 8 г is s is в is й i ; i 8	
			
Рис. 10.36. Статистические характеристики дохода
В результате описанного процесса вычислений Мэри определила, что средний доход
для данного набора значений спроса будет иметь максимальное значение при объеме заказа
1017 сковородок Как мы уже говорили выше, нельзя гарантировать, что “оптимальное”
решение, найденное в процессе имитации, действительно является оптимальным реше-
нием Но, с другой стороны, не следует забывать, что оптимальное решение — это неко-
торая теоретическая абстракция, которая только в определенной степени соответствует
ситуации реального мира В лучшем случае оптимальное решение соответствует просто
“хорошему решению” реальной проблемы. В рассматриваемом примере значения сред-
него дохода для объемов заказа от 1015 до 1018 отличаются всего на несколько центов.
Поэтому, даже если мы не нашли точное оптимальное решение, то, по крайней мере, на-
ходимся достаточно близко от него
Вероятностное распределение дохода
Обычно нас интересует не только среднее значение случайной величины, полученное
в результате имитации для оптимального решения, но и другие параметры ее вероятност-
ного распределения Например, в данном примере нас может интересовать разброс зна-
чений дохода вокруг среднего, возможные максимальные и минимальные значения до-
хода, вероятности малых и больших значений и т.п На эти и подобные вопросы можно
найти ответ, исходя из вида графика плотности вероятности (гистограммы) дохода, пока-
занной на рис 10 37
ГЛАВА 10. Имитационное моделирование
699
Рис. 10.37. Гистограмма распределения дохода для объема заказа 1017
Напомним, что данная гистограмма получена после проведения 1000 испытании моде-
ли, этого вполне достаточно для получения четкой картины вероятностного распределения
дохода График плотности вероятности имеет явно выраженный пик в районе среднего
с быстрым убыванием вправо и длинным “хвостом” влево “Хвост” влево говорит о том, что
доход может принимать значения значительно меньше среднего, но вероятность таких со-
бытий относительно невелика Минимальное значение дохода, полученное в 1000 испыта-
ний, составляет $4 370, что намного меньше среднего значения $12 237,84
10.7.	Модель авиаперевозок
Большинство моделей, которые мы рассмотрели в этой главе, были построены на
примерах из производственного сектора экономики (примеры компаний Airbus Industry
и Foslins) Но известно, что более половины внутреннего валового продукта Соединен-
ных Штатов создается в сфере обслуживания. Во многих отраслях этого сектора эконо-
мики давно используются на практике различные численные методы, получившие общее
название управление доходами. Лидером по использованию таких методов считается авиа-
компания American Airlines. Эта компания от применения подобных методов только при
продаже билетов получает ежегодно дополнительную прибыль более 200 млн. долл [4]
Рассмотрим пример весьма успешной региональной авиакомпании Midwest Express
Airlines. Штаб-квартира этой компании находится в г. Милуоки, штат Висконсин В этой
компании управлением доходами занимается менеджер Лаура Соренсен В настоящий
момент она просматривает статистические данные по своей компании, относящиеся
к отказу пассажиров от забронированных билетов или их неявке В частности, ее интере-
сует рейс 227 из Милуоки в Сан-Франциско Она подсчитала, что таких недисциплини-
рованных пассажиров приходится в среднем 15% на рейс. Самолет MD88, совершающий
этот рейс, имеет 112 мест на борту в одном салоне (По меркам Midwest Express это салон
не первого и не бизнес-класса, хотя предусмотрено обслуживание по первому классу )
Лаура хочет определить, сколько “лишних” билетов продавать на рейс, чтобы с уче-
том отказов максимально заполнить самолет Средняя стоимость перелета одного пас-
сажира этим рейсом составляет $400. Если Лаура выделит только 112 билетов на этот
рейс, то почти наверняка часть мест полетит пустыми, что увеличит стоимость рейса
700 ЧАСТЬ III. Вероятностные модели
из-за упущенной выгоды, которую мог дать пассажир, и плюс $400 — стоимость пере-
возки пустого кресла. С другой стороны, если продать билетов больше, чем мест в са-
молете, то возникает риск, что даже с учетом отказов могут оказаться пассажиры, ко-
торым не хватило мест в самолете. Обычная процедура в таком случае заключается
в том, что таким пассажирам, естественно, отказывают в посадке на самолет, но пред-
лагают лететь следующим ближайшим рейсом, компенсируя это неудобство скидками
на билеты в будущем и возможностью бесплатного питания и проживания в отеле до
следующего рейса. Это должно смягчить естественное раздражение и неудовольствие
“лишних” пассажиров. Лаура подсчитала, что “лишние” пассажиры обходятся компа-
нии в среднем в $600.
Чтобы решить поставленную задачу, Лаура разработала в Excel табличную модель, ко-
торая показана на рис. 10.38 (рабочая книга Мидвест). На примере этой модели мы про-
демонстрируем использование надстройки @Risk.
Рис. 10.38. Модель компании Midwest Express
В ячейке В12 с помощью ©Risk будут генерироваться значения биномиально рас-
пределенной случайной величины. Для каждого количества билетов, которое Midwest
Express выделяет для продажи, модель случайным образом определяет количество пас-
ГЛАВА 10. Имитационное моделирование	701
сажиров, которые действительно собираются лететь этим рейсом Простые вычисле-
ния дают количество пустых мест в самолете (ячейка В16) и количество “лишних” пас-
сажиров (ячейка В14) — очень важно отслеживать эти параметры модели. Лаура хочет
определить оптимальное количество выделяемых для продажи билетов, чтобы макси-
мизировать доход компании. Формула, по которой вычисляется доход (ячейка В18),
показана в строке формул на рис. 10 38 Доход вычисляется как произведение количе-
ства летящих пассажиров и стоимости перелета, минус количество “лишних” пассажи-
ров, умноженное на “стоимость” такого пассажира В этой модели для простоты пред-
полагается, что стоимость билета полностью окупает стоимость перелета, а если пас-
сажир отказался от полета, то он ничего не платит.
Поскольку значение, генерируемое @Risk, изменяется при каждом пересчете ра-
бочего листа, Лауре легко выполнить любое количество испытаний модели — для
этого достаточно нажать клавишу пересчета листа (обычно это клавиша <F9>) По-
сле проведения ряда испытаний Лаура может с удивлением обнаружить, что в неко-
торых случаях прибыль на несколько тысяч долларов меньше $38 тысяч, принятых
Лаурой как базовое значение прибыли. Но, чтобы увидеть отдельные результаты ис-
пытаний, а не среднее значение по ряду испытаний, надо соответствующим образом
настроить @Risk.
1.	В окне надстройки @Risk щелкните на кнопке Simulation Settings (Установки
имитации, третья кнопка слева), затем в открывшемся одноименном диалоговом
окне щелкните на корешке вкладки Sampling (Выборка)
2.	Во вкладке Sampling в разделе Standard Recalc (Стандартный пересчет) установи-
те переключатель Monte Carlo (Монте-Карло) (по умолчанию установлен пере-
ключатель Espected Value (Ожидаемое значение)), как показано на рис 10 39.
। Iterations Sampling | Convergence | Macro | External |
Sampling Type
(• Latin Hypercube
C Monte Carlo
Standard Recalc
Г Expected Value
(• Monte Carlo
C True EV
Bandom Number
Generator Seed -
fx Colled Distribution Samples
.OK | Cancel
Puc. 10.39. Вкладка Sampling диалогового окна Simulation
Settings
Итак, модель настроена и можно проводить испытания. Напомним, что Лауре надо опре-
делить количество билетов, выделяемых для продажи, максимизирующее прибыль Очевидно,
что если выделяться будет ровно 112 билетов, то “лишних” пассажиров не будет, но весьма ве-
702 ЧАСТЬ III Вероятностные модели
роятно, что в самолете будут пустые места Поэтому Лаура хочет проверить значения от 112 до
146 (с шагом 2) количества выделяемых билетов и выбрать из них то, которое обеспечивает
максимум прибыли Сильной стороной надстройки ©Risk является возможность проводить
“большую” имитацию для заданного набора параметров, когда для каждого заданного значе-
ния параметра проводятся отдельные испытания модели. Чтобы реализовать такую возмож-
ность ©Risk в рассматриваемой модели, надо выполнить следующие действия.
1.	В ячейку В10 введите формулу =RiskSimtable({112;114;..;146;148}) (см рис. 10 38)
2.	В окне ©Risk щелкните на кнопке Simulation Settings, затем в открывшемся диа-
логовом окне щелкните на вкладке Iterations (Итерации) и укажите, что для каж-
дой из 18 имитаций надо провести по 1000 итераций (испытаний).
3.	Щелкните на ячейке В18 и на кнопке Add Output Cell (Добавить выходную ячей-
ку) в окне ©Risk
Надстройка @Risk автоматически отобразит результаты 18 имитаций (рис. 10.40) Мож-
но объединить эти результаты в один отчет, щелкнув на кнопке Merge Sim#’s (Объединить
имитации) в окне ©Risk Объединенный результат представлен на рис 10 41
Рис. 10.40. Результаты имитации
Просматривая результаты имитации, Лаура видит, что если выделять для продажи 112 би-
летов, то средняя прибыль составит $38 080 (имитация Sim#l). При увеличении количества
выделяемых билетов прибыль также возрастает. Например, имитация Sim#4 (118 выделяемых
билетов) показывает среднюю прибыль $40 118,8 Максимальная средняя прибыль $43 901 бу-
дет при 134 выделенных билетах (имитация Sim#12). Это на 15,3% больше базового значения
прибыли' При этом следует продавать на 22 билета больше, чем емкость самолета. Таким об-
разом , Лаура нашла ответ для своей задачи
ГЛАВА 10. Имитационное моделирование 703
Рис. 10.41. Объединенный результат имитации
В задаче 10 22 мы рассмотрим версию данной модели с другим вероятностным рас-
пределением числа пассажиров, действительно желающих лететь этим рейсом
*7^	Проведение буровых работ на дамбе w	в Новой Зеландии
Дамба Клайд на Южном острове Новой Зеландии построена в зоне большей неус-
тойчивости, чем предполагалось при ее проектировании Она была построена более
10 лет назад и является наибольшей среди дамб Новой Зеландии Новозеландская ком-
пания Electricity Corporation подписала контракт на укрепление дамбы, в котором пре-
дусмотрено сооружение подземного барьера длиной 1 362 метра вдоль реки Клата Та-
кой барьер строится путем сверления скважин, в которые под давлением закачивается
бетон Для проведения буровых работ компании нужно арендовать специальное обору-
дование, при этом для снижения затрат необходимо минимизировать время бурения и,
соответственно, время аренды оборудования и выполнения всего проекта
Когда было пробурено несколько скважин, компания обнаружила, что некоторые
скважины не сразу заполняются бетоном из-за того, что в соседних скважинах вы-
полняются другие работы, что задерживает и бурильные работы Поскольку аренда
бурового оборудования стоит $227 в час (здесь и далее в этом разделе цены указыва-
ются в новозеландских долларах), на время простоя обратили особое внимание
Процесс создания защитного барьера состоит из пяти этапов 1) бурение скважины,
2) очистка скважины, 3) проверка ее на герметичность, 4) заполнение скважины
жидким бетоном и 5) усадка бетона. После пятого этапа, когда бетон затвердеет, за-
ливку скважины бетоном повторяют Длительность каждого этапа зависит от многих
факторов Например, скорость бурения зависит от геологических условии в месте
бурения, время заполнения скважины бетоном зависит от угла наклона скважины
Кроме того, разброс времени затвердевания бетона может составлять до 18%
В компании для выработки оптимальной стратегии бурения была создана имита-
ционная модель, в которой учитывались не только те факторы, которые упомина-
лись выше, но и количество бурильного оборудования и бурильных станков, рас-
704 ЧАСТЬ III. Вероятностные модели
стояние между скважинами, находящимися на разных этапах готовности, глубина
каждой скважины и другие факторы Выходными параметрами модели были время
завершения работ и время простоя/использования бурильного оборудования.
На основе результатов испытаний имитационной модели были выработаны ре-
комендации, которые позволили завершить проект за 27 недель (сокращение време-
ни на 26% по сравнению с запланированным), общее время бурения сократили на
34 041 ч (сокращение 7%), время простоя бурильного оборудования сократили на
692 ч, а стоимость всех работ уменьшили на $580 000. [3]
10.8.	Баланс производственных мощностей
Имитация является мощным средством привнесения экономических показателей
в процесс планирования и управления производственными мощностями В этом разделе
мы рассмотрим, как можно сбалансировать производственные мощности в виде произ-
водственного плана Мы увидим, что “игра” на времени продолжительности производст-
венных процессов может привести к неожиданным результатам. Рассмотренный ниже
пример покажет, как можно использовать электронные таблицы для моделирования
многоэтапных процессов, когда результаты выполнения одного этапа влияют на реали-
зацию последующих, как составить заключение о величине рисков на основе относи-
тельно небольших испытаний имитационной модели; как управлять последовательно-
стью производственных операций
Моделирование производственного модуля
Инженер Пол Михаэльсон пытается определить необходимую мощность небольшого
производственного модуля (рис Ю 42) Этот модуль сначала обрабатывает исходные ма-
териалы (сырье) на первой рабочей станции (PCI), сохраняет полуфабрикаты на пло-
щадке временного хранения, если вторая рабочая станция (РС2) занята, и затем обраба-
тывает их на станции РС2 Готовая продукция должна поступать на одну из сборочных
линий предприятия со скоростью 3 изделия в час. Определим, сколько будет стоить для
предприятия реализация и тестирование производственного модуля, и сравним эту стои-
мость со стоимостью, определенной в процессе имитации табличной модели
Рис. 10.42. Производственный модуль
При проектировании производственного модуля Пол ставит перед собой несколько
целей Он должен рассчитать производительность рабочих станций, чтобы количество
выпускаемой продукции удовлетворяло потребность сборочной линии, определить коли-
чество временно хранимых полуфабрикатов и, в конечном счете, минимизировать необ-
ходимую производительность рабочих станций (конечно, при соблюдении условия, что
потребность сборочной линии в его продукции будет удовлетворена). Для решения по-
ставленных задач Пол решил использовать имитационную модель.
ГЛАВА 1 0. Имитационное моделирование 705
Имитация сбалансированных мощностей
Поскольку на сборочную линию продукция производственного модуля должна по-
ступать с частотой 3 изделия в час, Пол первоначально установил для рабочих станций
производительность 3 изделия (полуфабриката) в час. Таким образом, производственные
мощности обеих рабочих станций сбалансированы. Но поскольку время обработки одного
изделия может изменяться (в зависимости от разнообразных факторов), то рабочая стан-
ция может выпускать от 1 до 5 изделий в час Предположим, что в течение часа рабочая
станция с равной вероятностью может обработать 1, 2, 3, 4 или 5 изделий (имеем равно-
мерное дискретное распределение) Тогда средняя производительность рабочей станции
составит 3 изделия в час, если не будет задержек сырья (для РС1) и полуфабрикатов (для
РС2). Пол предполагает, что сырье для станции РС1 всегда есть в избытке Однако из-за
различного времени обработки сырья на РС1 может возникнуть ситуация, когда рабочая
станция РС2 будет простаивать из-за отсутствия полуфабрикатов.
Начальные условия
На рис 10 43 показан рабочий лист из книги Михаэль xls, представлюший первые 16 ими-
тационных часов работы производственного модуля Начальные условия — это условия на
начало первого имитируемого часа, когда рабочие станции еще не приступили к работе и нет
полуфабрикатов (на рабочем листе количество полуфабрикатов обозначено как ПФ) Далее
Полу необходимо ввести в ячейку СЮ значения дискретной равномерно распределенной слу-
чайной величины, имитирующеи выход РС1, и аналогичные значения, имитирующие выход
станции РС2, — в ячейку D10 Проще всего это сделать с помощью надстройки Crystall Ball
Сначала Пол ввел значения случайной величины и их вероятности в диапазон ячеек Cl D6,
как показано в следующей таблице
Производительность	Вероятность
1	0,2
2	0,2
3	0,2
4	0,2
5	0,2
В ячейке ЕЮ (фактический выход станции РС2) записана формула =MHH(D10,B10)
Таким образом, реальный выход (количество произведенных изделий) рабочей станции
РС2 не может превышать количество имеющихся полуфабрикатов (ячейка В10) и, ко-
нечно, не превысит производительности станции, заданной для текущего часа работы
(ячейка D10) Количество полуфабрикатов на конец текущего часа (столбец Конечное
ПФ) вычисляется как сумма количества полуфабрикатов на начало часа (столбец На-
чальное ПФ) и полуфабрикатов, произведенных станцией РС1 (столбец Выход РС1),
минус количество полуфабрикатов, фактически использованных станцией РС2 за этот
час (столбец Фактический выход РС2) Начальное количество полуфабрикатов для те-
кущего часа — это просто конечное число полуфабрикатов предыдущего часа Среднее
количество полуфабрикатов (столбец Среднее ПФ) вычисляется как среднее значений
в столбце Конечное ПФ, начиная от значения первого и до текущего часа
706 ЧАСТЬ III Вероятностные модели
 1 'А	В	<	с	i	D ,	; е ! f		G	
1 :Рабочая станция 1 2,М|П и>д /час ЗМах ихд /час	Производительность Вероятность Рабочая станция 2 1	1	0,2 Min ихдЗчас 5	2	0.2 Мах иадЗчас 3	0.2 4	0.2 5	0,2			5		
9 Часы работы Начально» ПФ Выход РС1 10	1	° ЙП	2	3 32g	3	3 13;	4	3 в	5	3 gS4	6	3 1Ё1	7	3 8 3 18,i	9	3 Й9Я	10	3 ай	и	з 21л	12	3 221	13	3 23J	14	3 24;	15	3 2S1	16	3		Прогнох Выход РС2 3	3 3	3 3	3 3	3 3	3 3	3 3	3 3	3 3	3 3	3 3	3 3	3 3	3 3	3 3	3 3	3	Фактический Выход РС2 Конечное ПФ Средне» ПФ 0	3	3 3	3	3,00 3	3	3,00 3	3	3,00 3	3	3,00 3	3-	3,00 3	3	3,00 3	3	3,00 3	3	3,00 3	3	3,00 3	3	3,00 3	3	3,00 3	3	3,00 3	3	3.00 3	з;	3,00 3	3	3,00			
А J ',в . L JL	С J ' D Прогно»	L . . Е :.L Фактический	. F .	...	G	Й11ИИ.	
9 Часы Начальное ПФ Выход РС1 Выход РС2 Выход РС2
10 1	"	~	-	.........
1€7
=F13
=F14
1В 9
=Р16
21 -12
J2!13
=F19
=F20
=F21
=МИН(010,В10)
=МИН(О11;В11)
=MHH(D12;B12)
=MI4H(D13;B13)
=МИН(О14,В14)
=MHH(D15;B15)
=МИН(О16,В16)
=MHH(D17,B17)
=MHH(D18;B18)
-MHH(D19;B19)
=MHH(D20.B20)
=МИН(О21;В21)
=МИН(О22;В22)
=МИН(О23;В2Э)
=МИН(Р25В25)
Конечное ПФ Среднее ПФ
=B10+C1Q-E10 =CP3HA4(F10)
=В11+С11-Е11 =CP3HA4($F$10 ;F11)
=В12+С12-Е12 ,=CP3HA4($F$IDF12)
=В13+С13-Е13 =CP3HA4($F$10:F13)
=В14+С14-Е14 =CP3HA4($F$10;F14)
=В15+С15-Е15 ,=CP3HA4($F$10:F1S)
=В16+С16-Е16 =CP3HA4($F$10:F16)
=В 17*С 17-Е 17 =CP3HA4($F$ 10F 17)
=В18+С18-Е18 =CP3HA4($F$10:F18)
=В19+С19-Е19 =CP3HA4($F$10:F19)
=В20+С20-Е20 :=CP3HA4($F$10:F20)
=В21+С21-Е21 =CP3HA4($F$10 F21)
=В22+С22-Е22 =CP3HA4($F$10:F22)
=В23+С23-Е2Э =CP3HA4($F$10:F23)
=В24+С24-Е24 =CP3HA4($F$10:F24)
=В25+С25-Е25 =СРЗНА 4($F$ 10 F25)
Рис. 10.43. Рабочий лист Михаэльсона
Чтобы с помощью надстройки Crystal Ball ввести в модель значения случайных вели-
чин, задающих производительность рабочих станций для каждого часа, выполните сле-
дующие действия
1. Щелкните на ячейке СЮ — первой ячейке, где Crystal Ball будет генерировать зна-
чения случайной величины, задающие производительность станции РС1 в первый
час работы Замечание Студенческая версия надстройки Crystal Ball имеет ограни-
чение задать генерирование значений случайных величин можно только для
ГЛАВА 10. Имитационное моделирование 707
6 ячеек, отслеживать результаты испытаний также можно только в 6 ячейках.
В данной же модели надо сгенерировать значения случайных величин в 32 ячей-
ках, а результаты отслеживать в 16 ячейках Чтобы обойти это ограничение, при-
меним следующий прием.
2.	Введите в ячейку СЮ формулу =CB.Custom($C$2:$D$6). Эта формула задает такое
же распределение случайной величины, как и при аналогичном распределении
с помощью диалоговых окон Crystal Ball
3.	Crystal Ball покажет гистограмму распределения, которое вы задали Щелкните на
кнопке ОК
4.	Снова поместите табличный курсор на ячейку СЮ и щелкните на кнопке Копиро-
вать стандартной панели инструментов Excel
5.	Выделите диапазон ячеек СЮ D25 и затем щелкните на кнопке Вставить стан-
дартной панели инструментов Excel Копия первоначальной формулы будет встав-
лена во все 32 ячейки.
6.	В идеале, мы должны были бы выделить все 16 ячеек в столбце Среднее ПФ для
отслеживания их значений с помощью Crystal Ball Но поскольку в студенческой
версии Crystal Ball мы ограничены шестью наблюдаемыми ячейками, исследуем
ячейки GIO, G13, G16, С22и G25
7.	После щелчка на каждой из перечисленных выше ячеек щелкните на кнопке Define
Forecast в окне Crystal Ball Откроется одноименное диалоговое окно (см рис 10 20)
8.	Установите в окне Define Forecast переключатели Large и When Stopped (faster),
если они не установлены по умолчанию Вы также можете дать имя наблюдаемой
ячейке. Щелкните на кнопке ОК
9.	Повторите предыдущий пункт для всех шести наблюдаемых ячеек
10.	Щелкните на кнопке Run Preferences в окне Crystal Ball и в открывшемся окне
в поле Maximum Number of Trials введите число 1000— количество испытаний
(см рис 10 21)
11.	Щелкните на кнопке ОК.
12.	Щелкните на кнопке Start Simulation в окне Crystal Ball, и после того, как Crystal
Ball выполнит 1000 испытаний модели, автоматически отобразятся окна с гисто-
граммами распределений значений каждой наблюдаемой ячейки
13.	Если вам трудно охватить сразу все 6 гистограмм, щелкните в окне Crystal Ball на
кнопке Run, затем в открывшемся диалоговом окне установите переключатель
Open Trend Chart, и вы получите более простую обобщенную гистограмму, по-
добную той, что показана на рис. 10.44.
Надстройка Crystal Ball создает график распределения среднего количества полуфаб-
рикатов (среднее ПФ) за первых 16 часов работы производственного модуля на основе
наблюдений за этой величиной в шести указанных ячейках На графике более светлым
цветом выделена область математического ожидания среднего ПФ плюс-минус 25% (т е
показан доверительный интервал 50%). Более темным цветом показан доверительный
интервал 95% для среднего ПФ На графике видно, что среднее ПФ медленно возрастает
с течением времени, а его распределение постепенно “расплывается” Рабочая книга Ми-
xasnb_1.XLS с законченной данной моделью содержится на компакт-диске, прилагае-
мом к данной книге.
708
ЧАСТЬ III Вероятностные модели
Рис. 10.44. Изменения среднего количества полуфабрикатов,
баланс мощностей
Влияние начальных условий
Пол решил, что результаты, имитирующие только 16 ч работы производственного мо-
дуля, не надежны Поэтому он скопировал все формулы модели на 184 строки вниз рабо-
чего листа, теперь модель будет имитировать работу производственного модуля 200 ч (это
он сделал в новой рабочей книге) Повторно запустив Crystal Ball, он получил график,
отображающий распределение среднего ПФ за 200 ч работы (рис 10 45). Он думал, что
вначале среднее ПФ будет возрастать (как в предыдущей модели, имитирующей 16 ч ра-
боты), но затем стабилизируется на каком-нибудь уровне Пол не ожидал увидеть, что
среднее ПФ будет непрерывно возрастать Это указывает на то, что чем дольше работает
производственный модуль, тем больше накапливаются полуфабрикаты на площадке
временного хранения Это неожиданный результат, поскольку средняя производитель-
ность обеих рабочих станций составляет 3 изделия в час и нет видимых причин для уве-
личения количества промежуточных полуфабрикатов
Рис. 10.45. Среднее количество полуфабрикатов, баланс
мощностей
ГЛАВА 10. Имитационное моделирование 709
Однако даже простая модель очереди может предсказать это неожиданное, на первый
взгляд, увеличение количества промежуточных полуфабрикатов. Как мы покажем в гла-
ве 13, если средняя скорость поступления клиентов в очередь равна средней скорости об-
служивания, то количество клиентов в очереди будет неограниченно возрастать. В моде-
ли Пола “клиенты” — это полуфабрикаты, производимые рабочей станцией РС1, а оче-
редь— площадка временного хранения перед станцией РС2 Поскольку количество
сырья не ограничено, производительность РС1 и, следовательно, скорость поступления
в очередь, составляет 3 единицы (полуфабриката) в час. Средняя скорость обслуживания
(т е. производительность РС2) также составляет 3 единицы в час. Таким образом, ско-
рость поступления “клиентов” в очередь и скорость их обслуживания совпадают. Други-
ми словами, производительность рабочих станций сбалансирована. Это и является при-
чиной непрерывного роста среднего количества полуфабрикатов.
Имитация несбалансированных мощностей
Пол решает увеличить среднюю производительность станции РС2 до 3,5 изделий в час
(используя для этого дискретное целочисленное равномерное распределение от 2 до 5).
Новую модель он создал на рабочем листе в книге Михаэль_2.Х1_8. Сначала Пол скопи-
ровал рабочий лист из книги Михаэль.XLS в новую книгу, а затем ввел в ячейки G1.H5
следующую таблицу, задающую распределение производительности РС2.
Производительность___Вероятность
2	0,25
3	0,25
4	0,25
5 0,25
Затем Пол изменил формулы в ячейках D10.D209 на формулу =СВ Custom($G$2.$H$5).
Он выбрал шесть наблюдаемых ячеек и выполнил 1000 испытаний модели. Полученный
новый график, отображающий распределение среднего ПФ в зависимости от времени, по-
казан на рис. 10.46. В этой модели среднее ПФ не возрастает неограниченно, а с течением
времени стабилизируется на величине, равной примерно 5-7 единицам.
Рис. 10.46. Изменение среднего количества полуфабрикатов,
мощности не сбалансированы
710 ЧАСТЬ III. Вероятностные модели
Пол сделал вывод, что мощности двух рабочих станций не должны быть равными. Ес-
ли требуется, чтобы хранимый запас полуфабрикатов был на приемлемом уровне, необ-
ходимо, чтобы производительность второй станции была немного выше производитель-
ности первой станции. Если бы Пол имитировал значительно меньше часов работы мо-
дуля, чем 200, то он скорее всего получил бы неверное представление о долговременном
поведении среднего ПФ При имитации длительного временного периода уменьшается
влияние начальных условий, задаваемых в модели, и проясняется поведение исследуе-
мого параметра модели в долговременной перспективе.
10.9. Оптимизация в условиях неопределенности
Часто спрашивают, можно ли совместно использовать методы оптимизации и имитаци-
онное моделирование Ответ положительный. Но, как показано в предыдущих главах, сред-
ство Excel Поиск решения прекрасно находит оптимальное решение только в условиях оп-
ределенности, т е когда точно заданы все параметры модели. На практике, конечно, мно-
гие параметры известны неточно или являются случайными величинами В этом разделе
мы покажем, как решаются задачи оптимизации в условиях неопределенности с помощью
наиболее мощной на сегодняшний день программы оптимизации OptQuest. Она содержит-
ся в надстройке Crystal Ball Professional. Мы покажем использование OptQuest на двух дос-
таточно общих примерах — распределение инвестиционных средств и выбор проекта. Мы
также сравним полученные результаты с результатами “стандартной” оптимизации с по-
мощью Поиск решения
Распределение инвестиционных средств
Рассмотрим пример, подобный описанному в главе 7, посвященной нелинейной оп-
тимизации Итак, предположим, что мы стоим перед выбором, можно вложить средства
в акции компании Intel, Microsoft и Proctor & Gamble или положить их на депозитный
счет. Введем переменные решения IV, X, YmZ, где
W — процент средств, положенных на депозитный счет,
X — процент средств, вложенных в акции компании Intel;
У— процент средств, вложенных в акции компании Microsoft,
Z— процент средств, вложенных в акции компании Proctor & Gamble
Основываясь на данных последних девяти лет, мы знаем, что средняя годовая доходность
акций компании Intel составляет 46,6% (см. www mtc com/intel/fmance/investorfactors), Micro-
soft — 62,1 % (см www microsoft com/msfi/stock htm), Proctor & Gamble — 20,8% (cm. www.
pg com/investor), а средняя годовая доходность типового депозитного счета составляет 5,2%.
На объемы инвестиций каждого вида налагаются обычные ограничения: доля инвестиции
любого вида не должна превышать 50% общей суммы инвестиций, и сумма всех переменных
решения (общая сумма инвестиций в процентах) не должна превышать 100%. Чтобы приме-
нить стандартную методику оптимизации портфеля инвестиций (см. главу 7), надо сначала
сделать выбор либо максимизировать доход с “удержанием” риска на приемлемом уровне,
либо минимизировать риск при получении дохода на некотором приемлемом уровне. Выбе-
рем последнее (минимизация риска) и создадим простую табличную модель, показанную на
рис 10 47 (рабочая книга Портфель XLS). Подобная модель подробно рассмотрена в главе 7.
ГЛАВА 10. Имитационное моделирование 711
Рис. 10.47. Модель распределения инвестиции
Здесь в качестве начального решения мы установили все переменные решения равными
25%. Эти переменные содержатся в ячейках C17-F17, формула вычисления целевой функ-
ции находится в ячейке Н17 Ограничения заданы следующим образом 1) содержимое
ячейки G19 (доход) должно быть не меньше содержимого ячейки Н19, в которой находится
значение 25%, 2) сумма переменных решения должна равняться 100% (т е должны совпа-
дать значения в ячейках G17 и G18); 3) значение каждой переменной решения не должно
превышать 50% (ограничение вида С17.F17<=С 18 F18). Результат оптимизации этой моде-
ли с помощью средства Поиск решения показан на рис 10 48. В этом решении инвестиции
вакцин Intel составляют всего 0,51 %, Microsoft — 20,7%, Proctol & Gamble 50% и 28,8% сле-
дует положить на депозитный счет с ожидаемой доходностью 25,0% и минимизированной
дисперсией 0,0127 Поскольку мы минимизировали риск, вложения в высокодоходные, но
рисковые, акции компаний Intel и Microsoft минимальны.
712 ЧАСТЬ III. Вероятностные модели
Рис. 10.48. Результат оптимизации модели
Чтобы оптимизировать модель с помощью OptQuest, надо выполнить следующие
действия.
1.	Поскольку ячейки, значения которых будут использованы для задания параметров
распределений, должны содержать числа, а не формулы, сначала преобразуем со-
держимое ячеек С1 Г. Fl 1 в значения Для этого выделим диапазон Cl 1:F11 и затем
выполним команду Excel ПравкаФКопировать После этого (не снимая выделения
с диапазона) выполним команду ПравкаФСпециальная вставка и в открывшемся
диалоговом окне Специальная вставка установим переключатель Значения, по-
сле чего щелкнем на кнопке ОК
2.	Теперь зададим в ячейках СИ F11 случайные величины, каждая из которых имеет
нормальное распределение с математическим ожиданием, совпадающим
с исходными значениями в этих ячейках (т.е. 46,6, 62,1, 20,8 и 5,2%) и стандартным
отклонением соответственно -^/0,3188 =0,5646 , ^0,599 =0,3999 , л/о,О178 =0,1334
и ^/0,0002 =0,0141 Стандартную процедуру задания случайных величин покажем
на примере ячейки СП. Сначала в окне Crystal Ball щелкнем на кнопке Define
Assumption (Предположения), в открывшемся окне Distribution Gallery (Набор рас-
пределений) выберем тип распределения Normal (Нормальный), который указан по
умолчанию, и затем щелкнем на кнопке ОК. В следующем окне (см. рис. 10.49) в по-
ле Std Dev (Стандартное отклонение) введем 0,5646, щелкнем на кнопке Enter
(Ввод) и ОК. Повторим эту процедуру для ячеек D11:F11.
ГЛАВА 10 Имитационное моделирование 713
Рис. 10.49. Задание нормально распределенной случайной
величины
3.	Теперь надо задать наблюдаемую ячейку (это будет ячейка Н17 со значением целе-
вой функции). Для этого щелкнем на ячейке Н17, затем — на кнопке Define
Forecast (Параметры прогноза) панели инструментов надстройки Crystal Ball
В открывшемся окне введем имя (например, Portfolio Variance) для наблюдаемой
величины и щелкнем на кнопке ОК
4.	Щелкнем на кнопке Run Preferences (Параметры выполнения) панели Crystal
Ball. Откроется одноименное диалоговое окно, где в поле Maximum Number of
Trials (Максимальное число испытаний) введем число 1000, щелкнем на кнопке
Sampling (Выборка), затем в следующем диалоговом окне в области Sampling
Method (Выборочный метод) установим переключатель Latin Hypercube
(Латинский гиперкуб), отметим опцию Use Same Sequence of Random Numbers
(Использовать одну последовательность случайных чисел) и введем в поле Initial
Seed Value (Начальное число) число 999 (число, задающее последовательность
случайных чисел), как показано на рис 10.50 Щелкнем на кнопке ОК.
I - Random Numbar Generation---------------- 	> I ——I
I P Use Same Sequence of Random Numbers | 1 I q ,,np|inl) I
I	Initial Seed Value: Iw	'
------------------------------------------------- Speed |
Puc. 10.50. Диалоговое окно Run Preferences
714 ЧАСТЬ III Вероятностные модели
5.	Теперь определим ячейки С17 F17 как ячейки, содержащие переменные решения
(каждая переменная непрерывна и принимает значения от 0% до 50%). Стандарт-
ную процедуру задания переменных решения покажем на примере ячейки С17.
Сначала щелкнем в окне Crystal Ball на кнопке Define Decision (Определение ре-
шения), в отрывшемся диалоговом окне Define Decision Variable (Определение
переменной решения) введем имя переменной lntel% (поле Name), в полях Lower
(Нижняя) и Upper (Верхняя) введем значения нижней и верхней границ перемен-
ной, те 0% и 50% соответственно, укажем, что переменная непрерывная
(переключатель Continuous), как показано на рис. 10.51, и щелкнем на кнопке ОК
Повторим эту процедуру для ячеек D17-F17.
6.	Чтобы запустить OptQuest, щелкнем в окне Crystal Ball на крайней справа кнопке
панели инструментов или выполним команду CepBUC^OptQuest.
7.	В окне OptQuest выполним команду File^New (Файл^Создать). В отрывшемся
окне Decision Variable Selection (Выбор переменных решения) установим “Yes”
(Да) перед всеми переменными решения Проверим, правильно ли для этих пере-
менных указаны нижняя и верхняя границы и их тип (рис. 10 52). Щелкнем на
кнопке ОК
Рис. 10.51. Диалоговое окно определения перемен-
ной решения в Crystal Ball
Рис. 10.52. Задание переменных решения в OptQuest
ГЛАВА 10. Имитационное моделирование 715
8.	Определим ограничения следующим образом
lntel% + Microsoft% + P&G% + ММ% = 1;
Intel% <= 0,5;
Microsoft% <= 0,5,
P&G% <= 0,5,
MM% <= 0,5,
O,466xlntel% + 0,621xMicrosoft% + 0,208xP&G% + 0,052xMM% >= 0,25
Диалоговое окно OptQuest, задающее ограничения, показано на рис. 10 53.
9.	В раскрывающемся меню Select (Выбор) выберем Minimize Objective (Минимизи-
ровать целевую функцию), как показано на рис 10 54 Щелкнем на кнопке ОК
Рис. 10.53. Диалоговое окно OptQuest, задающее ограничения
Рис. 10.54. Диалоговое окно OptQuest, задающее целевую функцию
10.	В диалоговом окне Options (Параметры) щелкнем на кнопке ОК, принимая предло-
женные по умолчанию параметры процесса имитации (Отметим, что по умолчанию
задано 10 мин на выполнение процесса имитации ) Для начала процесса оптимиза-
ции щелкнем на кнопке Yes (Да) По прошествии 10 мин вы увидите результат, по-
добный показанному на рис. 10.55. Конечно, количество испытаний модели, прове-
денных за 10 мин , будет зависеть от частоты процессора вашего компьютера
716 ЧАСТЬ III Вероятностные модели
II.	Чтобы перенести полученные результаты на исходный рабочий лист, выполним
команду Excel Правка^Копировать. Также автоматически будет показана итого-
вая диаграмма частот выбранной (наблюдаемой) статистики (в нашем случае это
дисперсия, значения которой находятся в ячейке Н17). Если необходимо получить
итоговые статистические данные, выполните в окне Forecast (Прогноз) команду
View^Statistics (Вид^с» Статистики).
р Optimization File-
Optimization is Complete
UnNsmedopt;
Ctystal BaJ Simulation i
Simulation	Minimize Objective Portfolio Variance Mean	InteIX	MicrosoftX	P&GX	MMX	
63	1 2714E-02	0.00000	0 212592	0 493814	0 293594	
67	1 2700E-02	0 00000	0 210976	0 499710	0 289314	
76	1.2696E-02	1 3642E-03	0.209986	0 499701	0 288949	
77	1 2693E-02	3.4104E-03	0.208501	0 499687	0 288402	
78	1 2692E-02	5.4566Е-0Э	0 207016	0 499673	0 287855	
109	1 2692E-02	4.9925E-03	0.207353	0 499676	0 287979	
110 118 123 Best: 129 ’ «и		1 2692E-02 1 2692E-02 1 2692E-02	5.2246E-03 4 7206E-03 4.9726E-03	0 207184 0 207537 0 207361	0 499674 0 499725 0 499700	0 287917 0 288017 0 287967	
Puc. 10.55. Результаты оптимизации модели с помощью OptQuest
Как показано в этом примере, OptQuest выдает практически то же самое решение, что
и Поиск решения (но затратив значительно больше времени). Возникает естественный во-
прос, стоило ли привлекать новую программу, если решение, полученное с ее помощью, такое
же, как и решение, полученное с помощью стандартного средства Поиск решения. Но, во-
первых, решение, полученное с помощью OptQuest, подтверждается и поддерживается реше-
нием средства Поиск решения Во-вторых, использование в средстве Поиск решения вместо
случайных величин их математических ожиданий может привести к неверному или необосно-
ванному решению, что уже обсуждалось в разделе 10 4. Следующий пример покажет возмож-
ности программы OptQuest, которые нельзя реализовать при проведении “чистой” оптимиза-
ции или простого имитационного моделирования
Отбор проектов
Компании необходимо отобрать для реализации в текущем году несколько исследователь-
ских проектов из восьми предложенных. Для каждого проекта подсчитана сумма начальных
вложений и предполагаемая чистая приведенная стоимость (ЧПС). Финансовый отдел ком-
пании может выделить в текущем году на эти проекты не более 2 млн. долл. Для реализации
всех восьми проектов необходимо 2,8 млн долл. Поэтому нужно отобрать проекты с наи-
большей предполагаемой ЧПС, не выходя за рамки бюджета Используя методы целочислен-
ной оптимизации из главы 6, мы построили оптимизационную модель, где все переменные
ГЛАВА 10 Имитационное моделирование
717
решения могут принимать только два значения 0 и 1 (0, если соответствующий проект откло-
няется, и 1 — если принимается) Рабочий лист Начальный, содержащий эту модель (рабочая
книга Проекты), показан на рис 10 56 Применение средства Поиск решения показывает, что
следует выбрать проекты 1, 2, 3, 4 и 7, что обеспечит максимальную ЧПС в размере
3,55 млн долл, и потребует все 2 млн долл бюджетных денег. Это непосредственное приме-
нение методов целочисленного программирования требует полной определенности относи-
тельно значений ЧПС всех проектов Если мы внесем некоторую неопределенность в успех
реализации каждого проекта, как это сделано на рабочем листе Измененный в той же рабочей
книге (рис. 10 57), то какие проекты в этом случае предпочтительнее9 Повторно запустим По-
иск решения с учетом ожидаемых значений ЧПС (изменяя значения в ячейках Е5 Е12, мак-
симизируем значение в ячейке G15 с учетом простого ограничения С15 <= С14) и получим но-
вое решение (рекомендуется выбрать проекты 1,2,4, 6, 7 и 8) с ожидаемым суммарным значе-
нием ЧПС 2,184 млн долл и использованием только 1,85 млн долл из 2 бюджетных млн
долл Но как убедиться, что это действительно наилучшее решение с учетом неопределенно-
сти в реализации проектов9 Если компания старается избегать риска, то следует как-то мини-
мизировать риск от неправильного выбора проектов.
Рис. 10.56. Модель отбора проектов
718 ЧАСТЫП Вероятностные модели
Рис. 10.57. Измененная модель отбора проектов
С помощью программы OptQuest можно просмотреть все возможные решения (таких
комбинаций всего 2Л8 = 256) и выбрать среди них наилучшее Для этого надо выполнить
такие действия
1.	Щелкнув в окне Crystal Ball на кнопке Define Assumption, задать в ячейках F5 F12
случайные величины, каждая из которых имеет биномиальное распределение с веро-
ятностями успеха, совпадающими с исходными значениями в этих ячейках, и одним
испытанием.
2.	Щелкнув в окне Crystal Ball на кнопке Define Decision, определить ячейки C17.F17 как
ячейки, содержащие переменные решения (каждая переменная дискретна с нижней
границей 0 и верхней границей 1).
3.	Задавая наблюдаемую ячейку (ячейка G15 с итоговым значением ЧПС), щелкнуть
на кнопке Define Forecast панели инструментов надстройки Crystal Ball.
4.	Щелкнуть на кнопке Run Preferences панели окна Crystal Ball и установить макси-
мальное число испытаний, равное 1000, задать выборочный метод Latin Hypercube
(Латинский гиперкуб), установить флажок опции Use Same Sequence of Random
Numbers (Использовать одну последовательность случайных чисел) и ввести началь-
ное число 999, задающее последовательность случайных чисел
5.	Чтобы запустить OptQuest, щелкнуть в окне Crystal Ball на крайней справа кнопке
панели инструментов или выполнить команду Ceparic^OptQuest.
6.	В окне OptQuest выполнить команду File^New (Файл^Создать). В отрывшемся
окне Decision Variable Selection установить “Yes” (Да) перед всеми переменными
решения Проверить, правильно ли для этих переменных указаны нижняя и верх-
няя границы и их тип
7.	Определить 01 раничение-
ГЛАВА 10. Имитационное моделирование 719
250хПроект1 + 650хПроект2 + 250хПроектЗ + 500хПроект4 + 700хПроект5 +
+30хПроект6 + 350хПроект7 + 70хПроект8 <= 2000
8.	В раскрывающемся меню Select выбрать Minimize Objective В поле Forecast Statistic
(Статистика прогноза) вместо значения Mean (Среднее) установить Percentile
(Персентиль) и в следующем диалоговом окне ввести 25, как показано на рис 10 58.
9.	В диалоговом окне Options (Параметры) щелкнуть на кнопке ОК, принимая пред-
ложенные по умолчанию параметры процесса имитации (по умолчанию задано
10 мин ) Для начала процесса оптимизации щелкните на кнопке Yes (Да) Через
10 мин будет получен результат имитации
Рис. 10.58. Диалоговое окно OptQuest, задающее целевую функцию
Рис. 10.59. График функции распределения
10.	Чтобы перенести эти результаты на исходный рабочий лист, выполните команду Excel
Правка^Копировать Также автоматически будет показана итоговая диаграмма частот
выбранной (наблюдаемой) статистики (в нашем случае это ЧПС) В окне Forecast
(Прогноз) выполните команду View^Cumulative Chart (Вид^График функции рас-
пределения) и введите в правое поле значение $1,6 млн (наилучшее значение, найден-
ное OptQuest) Полученный график функции распределения показан на рис 10 59.
Т20 ЧАСТЬ III Вероятностные модели
Выполнив в окне Forecast команду View^Statistics, вы увидите итоговые статистиче-
ские данные (рис 10 60) Они показывают, что наилучшим выбором будут проекты 1, 2, 5, 6
и 7, что потребует $1,98 млн бюджетных денег (рис. 10.61), а максимальное значение 25%
персентиля составляет $ 1,6 млн OptQuest также позволяет определить различные множества
решений, которые наилучшим образом соответствуют вашему отношению к риску и мини-
мизируют предельную нижнюю границу потенциальных потерь (рисков) Таким образом,
мы видим, что OptQuest является мощным средством, которое позволяет проводить опти-
мизацию в условиях неопределенности, минимизируя при этом потенциальные риски —
ничего этого нельзя сделать, используя только средство Excel Поиск решения
Рис. 10.60. Итоговые статистические данные
Рис. 10.61. Результаты применения OptQuest
ГЛАВА 1 0. Имитационное моделирование 721
10.10. Некоторые выводы
Имитация является мощным и гибким инструментом изучения широкого круга
управленческих моделей В основном, имитация используется, если не существует хоро-
шей аналитической модели или она слишком сложна В процессе имитации можно
учесть изменчивость параметров модели и определить время выхода модели на стацио-
нарный (устойчивый) режим С помощью имитационных моделей можно представить
большинство реальных задач, стоящих перед менеджером, поэтому техника работы с та-
кими моделями в настоящее время широко используется при разрешении управленче-
ских ситуаций Однако перед тем, как использовать имитационное моделирование, ме-
неджеру необходимо рассмотреть и учесть несколько важных факторов
Имитация или аналитическая модель?
Как указывалось выше, имитация часто применяется из-за отсутствия подходящей
аналитической модели. В аналитических моделях можно использовать широкий арсенал
математических методов, что часто позволяет найти оптимальное решение и иногда про-
вести анализ чувствительности (конечно, если сложность модели не препятствует этому)
А при имитационном моделировании случайных событий оптимальность решения не га-
рантирована и даже более того — часто трудно получить решение, хотя бы в какой-то
степени близкое к оптимальному Иногда требуется провести много испытаний имита-
ционной модели, чтобы получить приемлемую достоверность “добротности” какого-
либо решения Однако с помощью имитационного моделирования можно получить та-
кие данные, которые с помощью аналитических моделей получить очень сложно или со-
всем невозможно, например, определить влияние изменчивости параметров модели, по-
ведение модели до достижения ею установившегося состояния и т п
Разработка имитационных моделей в электронных таблицах
Общей и часто фатальной ошибкой при разработке имитационных моделей является
попытка “вместить” в модель все, что только можно, делая ее излишне сложной Это
можно рассматривать как гиперреакцию на свободу, полученную после перехода от ана-
литических моделей к имитационным. Предположения, на которых базируются анали-
тические модели, часто бывают очень ограничительными Как только мы уходим от
предположения о линейности функций или других подобных упрощающих предположе-
ний, как сразу в астрономических размерах возрастают математические сложности, свя-
занные с аналитической моделью В этом кроется причина того, что многие аналитиче-
ские модели имеют ограниченное применение на практике Имитационные модели
в этом плане более “либеральны” Поскольку в процессе имитационного моделирования
наблюдаются значения функций (а не решаются системы уравнений), то здесь свойство
линейности функций не играет такой заметной роли, как в аналитических моделях.
Какой бы ни была мотивация, но зачастую действительно слишком много факторов
и параметров включается в имитационную модель. С другой стороны, нет каких-либо тео-
ретических препятствий, чтобы не делать этого Например, чтобы учесть какой-нибудь но-
вый фактор в модели, достаточно ввести его в рабочий лист и инкорпорировать в модель.
Большие сложные имитационные модели менеджерам кажутся очень “жизнеподобными”.
Однако такой подход может породить серьезные проблемы. Во-первых, такие модели ока-
зываются “дорогим удовольствием”. Во-вторых, сложные имитационные модели порож-
дают большой объем новых данных, эти данные трудно интерпретировать и для их анализа
требуются дополнительные усилия.
722 ЧАСТЬ III Вероятностные модели
Залогом успешного применения имитационных моделей является включение в мо-
дель только самых существенных черт реальной проблемы, не загроможденных излиш-
ними деталями и подробностями. (Впрочем, это же можно сказать о моделях любого ти-
па ) Наши наблюдения показывают, что многие проекты имитационного моделирования
“умирают” от излишней “тучности” первоначальных предположений (включенных в мо-
дель) чаше, чем от каких-либо других “болезней”.
Также отметим важную роль, которую играют в имитационном моделировании, реа-
лизованном в электронных таблицах, различные надстройки и дополнительное про-
граммное обеспечение, значительно расширяющие встроенные средства электронных
таблиц (например, Excel). Они часто предоставляют такие возможности, которые недос-
тупны в самих электронных таблицах. Некоторые подобные программы мы рассмотрели
в этой главе Без их использования решение имитационных задач только встроенными
средствами Excel часто или не продуктивно, или не эффективно.
Документирование
Имитационные модели необходимо хорошо документировать. Любой менеджер, ко-
торый знакомится с имитационной моделью, должен легко понять требования, предъяв-
ляемые к модели, предположения, на которых построена модель, входные данные и вы-
ходные результаты, полученные с ее помощью. Все это требует ясной и четкой докумен-
тации, описывающей модель.
Документация также необходима при общении разработчика модели с заказчиком
или конечным пользователем Конечный пользователь должен понимать, как вводить
значения переменных, изменять параметры модели и анализировать результаты имита-
ции Пользователь также должен уяснить, какие основные стороны реальной проблемы
отражены в имитационной модели, поскольку именно он знает существо проблемы и ему
делать вывод о том, какие решения “хороши”, а какие — нет.
10.11. Заключение
В разделе 10 I отмечается, что эксперимент, в результате которого оцениваются воз-
можные альтернативы, является важной частью прикладных наук, а имитация на основе
электронных таблиц — наиболее общим подходом при моделировании управленческих
ситуаций принятия решений В этом разделе также обсуждается использование имита-
ции при принятии решений в условиях риска, другими словами, рассматриваются моде-
ли, в которых поведение некоторых факторов можно описать с помощью вероятностных
распределений
В основе методов имитации случайных событий лежат случайные величины. В разде-
ле 10 2 представлены надстройки Crystall Ball и @Risk, позволяющие генерировать слу-
чайные величины с различными вероятностными распределениями (как дискретными,
так и непрерывными)
В разделе 10 3 приведен пример модели финансового планирования, которая включа-
ет труднопрогнозируемый элемент (спрос). Здесь показаны возможности электронных
таблиц по имитационному моделированию. Раздел Ю.4 повторяет пример из предыду-
щего раздела, но с использованием в процессе моделирования надстройки Crystall Ball.
В разделе I0.5 рассмотрены модели управления запасами, которые также содержат
элементы со стохастическим поведением, и показано, как можно учесть в имитационной
модели случайные события. Эти примеры доказывают, что результаты, полученные на
основе испытаний имитационных моделей, совсем не обязательно ведут к такому же ре-
ГЛАВА 1 0. Имитационное моделирование 723
шению, какое можно получить в аналитических моделях оптимизации Но в общем слу-
чае при использовании очень большого числа испытаний имитационной модели можно
надеяться, что средние значения отслеживаемых параметров будут достаточно близки
к теоретическим На примерах данного раздела также показаны различные способы из-
мерения критериев качества моделей В разделе 10 6 рассмотрена та же модель управле-
ния запасами, но с использованием более реалистических предположений о распределе-
нии случайных параметров
В разделе Ю 7 рассматривается модель определения оптимального количества авиа-
билетов, выделяемых для продажи через кассы Здесь же описывается новое вероятност-
ное распределение (биномиальное)
В разделе 10 8 исследуется вопрос о том, всегда ли сбалансированные производитель-
ности рабочих станций ведут к оптимальному результату Этот пример иллюстрирует
важное положение имитационного моделирования, которое заключается в том, чтобы по
возможности исключить влияние начальных условий на конечный результат имитации
Другая область применения имитационного моделирования рассмотрена в разделе 10 9
Здесь описан способ оптимизации вероятностной модели в условиях неопределенности
Два примера этого раздела показывают возможности нового программного обеспечения
для поиска оптимального решения в очень сложных ситуациях.
В последнем разделе обсуждаются такие обшие вопросы имитационного моделиро-
вания, как преимущества и недостатки имитационных моделей (по сравнению с анали-
тическими), проблемы разработки таких моделей, роль документирования
Основные термины
Вероятностное распределение Способ определить вероятность того, что случайная величина при-
мет конкретное числовое значение
Дискретное равномерное распределение Вероятностное распределение, задающее равные вероятно-
сти всем членам конечного множества чисел
Имитатор Устройство для экспериментирования, которое имитирует некоторые основные черты
поведения реальных систем
Имитационная модель Последовательность логических и математических операторов, ведущая
к получению оценок определенного множества значений параметров или переменных решения
Испытание Однократное вычисление имитационной модели
Метод Монте-Карло Тип имитации, при котором используются вероятностные распределения
наступления случайных событий
Непрерывное равномерное распределение Вероятностное распределение, задающее равные вероят-
ности всем действительным числам из конечного интервала (В приложении А приведена ма-
тематическая формулировка этого распределения )
Нормальное распределение Вероятностное распределение, которое хорошо описывает многие яв-
ления, происходящие как в природе, так и в бизнесе, например, изменения спроса и предто-
жения или распределение вычисленного выборочного среднего значения какои-либо случай-
ной величины (Более подробно это распределение описано в приложении А )
Ожидаемое значение Среднее значение или математическое ожидание некоторой случайной вели-
чины, имеющей заданное вероятностное распределение
Распределение Пуассона Вероятностное распределение, которое часто используется для описания
количества поступлений в систему очереди в течение указанного интервала времени
724
ЧАСТЬ III Вероятностные модели
Случайная величина Величина, которая с определенной вероятностью может принимать различ-
ные числовые значения из определенного множества Распределение вероятностей принимае-
мых случайной величиной числовых значений описывается функцией распределения
Функция распределения Вероятность того, что случайная величина примет значение, не превы-
шающее значения аргумента функции распределения
Экспоненциальное распределение Вероятностное распределение, обычно используемое для описа-
ния времени между поступлениями заказов в систему очереди (В приложении А приведена
математическая формулировка этого распределения )
Контрольные вопросы
Да/нет
1.	Основой имитации является построение устройства для экспериментов, которое
в основных чертах повторяет поведение интересующей нас системы.
2.	В качестве имитационной модели можно использовать детерминированную мо-
дель (т е модель, не содержащую вероятностных элементов).
3.	Если имитационная модель содержит вероятностные элементы, то два испытания
этой модели дадут одинаковые значения наблюдаемых выходов модели.
4.	В имитационной модели со случайными элементами невозможно гарантировать
получение решения, обеспечивающего максимум целевой функции.
5.	В процессе решения реальных проблем общей практикой является сопоставление
ожидаемых значений параметров решения со средними значениями этих парамет-
ров, полученными в результате имитационного моделирования.
6.	Если в процессе имитации получено несколько различных случайных выходных
результатов, то корректная связь между случайными числами и событиями пред-
полагает, что каждому случайному числу должен соответствовать один случайный
результат
7.	При проведении малого числа испытаний имитационной модели результаты ими-
тации очень чувствительны к начальным условиям модели
8.	Имитационное моделирование часто считается последним средством решения ре-
альных проблем, поскольку его не применяют до тех пор, пока аналитические мо-
дели хорошо работают и адекватно отражают реальную ситуацию.
9.	Общей ошибкой при разработке имитационных моделей является использование
ограничительных предположений, при которых модель перестает адекватно отра-
жать сущность реальной проблемы.
10.	Добавление дополнительных параметров в имитационную модель не только уве-
личивает стоимость имитационного процесса, но и повышает качество получае-
мого решения.
Выберите правильный ответ
11.	В типичной имитационной модели входными данными являются:
а.	значения параметров;
Ь.	значения переменных решения;
с	значения наблюдаемых переменных;
ГЛАВА 10. Имитационное моделирование 725
d.	все выше перечисленное;
е.	а и Ь.
12.	К достоинствам имитационного моделирования (в сравнении с аналитическими
моделями оптимизации) можно отнести’
а возможность многократного измерения интересующих нас параметров модели,
Ь. возможность получения оценки изменчивости выходных результатов модели,
с. возможность исследования сложных сценариев поведения системы,
d. все выше перечисленное
13.	Рассмотрим имитатор со случайными элементами, где в качестве показателя эф-
фективности системы используется доход Справедливы следующие утверждения
а. В качестве оценки значения ожидаемого дохода можно использовать значение
дохода, усредненное по большому количеству испытаний имитатора
b При возрастании количества испытаний имитатора среднее значение дохода,
полученное в результате имитации, стремится к ожидаемому значению дохода
с. Значение среднего дохода всегда одинаково в течение десяти испытаний ими-
татора
d Ничего из вышеперечисленного
14.	Случайное число, полученное с помощью генератора случайных чисел электрон-
ной таблицы, это.
а действительное число из интервала от 0 до 1, причем все числа из этого интер-
вала имеют одинаковую вероятность,
Ь. число, выбранное наугад из множества чисел, на котором задано равномерное
распределение,
с число, выбранное случайно из множества чисел, на котором вероятностное
распределение задано менеджером,
d ничего из вышеперечисленного
15.	Пусть с помощью генератора случайных чисел получено случайное число 0,63 Со-
ответствующее значение у случайной величины, имеющей нормальное распределе-
ние, определяется следующим образом'-
а у — это “вероятность того, что нормально распределенная случайная величина
<0,63”;
b у — это такое число, что “вероятность того, что нормально распределенная
случайная величина < у”, равна 0,63,
с. у— это такое число, что “вероятность того, что нормально распределенная
случайная величина равна у”, равна 0,63,
d ничего из вышеперечисленного
16.	Полученные ранее аналитические результаты используются перед процессом ими-
тации для того, чтобы определить’
а.	“хорошие значения” системных параметров,
Имеется в виду способ генерирования значений случайных величин, описанный в разделе “Генерирование зна-
чений непрерывных случайных величин" — Прим ред
726 ЧАСТЬ III. Вероятностные модели
b.	оптимальное решение;
с “хорошие значения” переменных решения для заданного набора значений сис-
темных параметров,
d все вышеперечисленное.
17.	Чтобы уменьшить влияние начальных условий на результаты имитации, можно:
а варьировать значения системных параметров;
b увеличить количество рассматриваемых альтернативных решений;
с увеличить количество испытаний и не рассматривать данные, полученные во
время первых испытаний модели для всех наборов параметров и решений;
d все вышеперечисленное.
18.	Как аналитические, так и имитационные модели можно использовать для реше-
ния задач, включающих случайные события. При этом часто аналитические моде-
ли предпочтительнее имитационных по следующим причинам:
а имитационное моделирование требует проведения большого числа испытаний,
чтобы получить хорошую оценку значения целевой функции для каждого от-
дельного решения,
b с помощью аналитической модели можно получить оптимальное решение;
с решение задачи с помощью имитационного моделирования требует оценить
большое количество возможных альтернативных решений;
d все вышеперечисленное.
19.	Большие сложные имитационные модели порождают такие проблемы.
а трудно оценить средние значения параметров модели;
b сложно имитировать случайные события;
с модель становиться дорогостоящей;
d все вышеперечисленное.
20.	Использование имитационного моделирования целесообразно в следующих си-
туациях
а полученные ранее решения можно использовать для предсказания (с после-
дующей проверкой) других решений,
b можно провести большое количество испытаний для каждого решения;
с для имитации всех возможных решений;
d ничего из вышеперечисленного
Ответы
1 Да 2 Да 3 Нет 4 Да 5 Нет. 6. Нет. 7 Да 8 Да. 9. Нет. 10. Да. 11. е. 12. d. 13. а. 14.
а 15 b 16 с 17 с 18 d. 19 с 20. а
ГЛАВА 1 0. Имитационное моделирование 727
Учебные задачи
В следующих задачах необходимо провести несколько испытаний имитационных мо-
делей Помните, что, поскольку применяются различные генераторы случайных чисел,
ваши ответы могут отличаться от ответов, приведенных в конце книги
10 1 Приведите примеры использования имитационного моделирования (в широком понима-
нии) в военном деле
10 2 Приведите примеры использования имитационного моделирования (в широком понима-
нии) в профессиональном спорте
10 3 Рассмотрим следующую модель линейного программирования
максимизировать 20/1 + 30С
при ограничениях
А <70,
С <50,
Л + 2С<120,
А, С>0
а Постройте блок-схему, представляющую эту задачу в виде имитационной модели
b Используя построенную блок-схему, оцените значение целевой функции для двух
возможных решений (А = 40, С = 30) и (А = 50, С = 30)
10 4 В следующей таблице отражены объемы продаж автомобилей компанией Solar Саг за 50 недель
Количество продаж в неделю	Количество недель
0	2
3	16
4	8
а Подберите вероятностное распределение для спроса на автомобили, которое бы в точ-
ности соответствовало приведенному распределению продаж
b Имитируйте спрос на автомобили в течение 120 недель с помощью надстроек для элек-
тронных таблиц (или в течение 12 недель, если использовать только встроенные воз-
можности Excel)
10 5 Прокомментируйте следующее утверждение Алгоритм симплекс-метода является разно-
видностью имитации, поскольку в процессе поиска оптимального решения он оценивает
различные альтернативные варианты
10 6 Джерри Тейт имеет парк специализированных автомобилей, которые он предоставляет
электрической компании, занимающейся прокладкой и обслуживанием линий электропе-
редачи Джерри хочет купить новые автомобили с выдвижной стрелой для высотных работ.
Чтобы определиться с объемом покупки, он хочет смоделировать котичсство аварий
в электросетях, требующих использования таких автомобилей, которые произойдут в сле-
дующие 20 лет У Тейта есть данные о подобных авариях за предыдущие 10 лет, которые
приведены в следующей таблице
728
ЧАСТЬ III. Вероятностные модели
Количество аварий в год	Количество лет
0	4
10'
101
10'
10
10
10
Создайте для Джерри имитатор, генерирующий число аварий по годам на период в 20 лет
7	Компания Sonorola испытывает трудности в управлении денежными потоками Финансо-
вый баланс подводится каждое утро нового рабочего дня Изменения в балансе текущего
дня, по сравнению с предыдущим, являются случайными величинами В частности, воз-
растание дохода на $10 000 происходит с вероятностью 0,3, уменьшение дохода на такую же
величину происходит с вероятностью 0,2, а неизменным доход остается с вероятностью 0,5
Если вы будете моделировать изменение дохода с помощью генератора случайных чисел
Excel, то в соответствии с какими значениями случайных чисел будет назначаться то или
иное изменение в финансовом балансе9
В примере из раздела 10 5 мы вычислили истинное значение ожидаемого (среднего) дохода
и нашли оценку этого значения, выполнив 500 испытаний имитационной модели, при ус-
ловии, что объем заказа составляет 11 сковородок Найдите эти же величины (истинное
значение ожидаемого дохода и оценку этого значения, выполнив 500 испытаний имитаци-
онной модели), предполагая, что объем заказа равен 9
8	Решите задачу 10 8, предполагая, что объем заказа равен 10
9	Решите задачу 10 8, предполагая, что объем заказа равен 11
10	Функция плотности вероятности распределения Пуассона имеет вид
р(хД) = —х = 0,1,
Пусть /. = 2 Вычислите вероятность значений х = 0, 1, , 5 и значения функции распреде-
ления F(x) при этих значениях х
11	Имитируйте 50 раз продажи сковородок для примера, описанного в разделе 10 5 (10 раз,
если вы используете только встроенные средства Excel) Предполагается, что каждый раз на
начало продаж имеется 10 сковородок Подберите подходящее вероятностное распределе-
ние для моделирования спроса поданным, приведенным в разделе 10 5
а По результатам имитации вычислите средний доход.
b Определите, сколько раз спрос будет превышать предложение (те. подсчитайте,
сколько раз спрос будет больше 10)
12	Недельный спрос на молоко в местном магазине за последние 50 недель показан в сле-
дующей таблице
____________Спрос, упаковки	Количество недель___________________
40_________________________________________________________________________________4
41	10
42	12
43	9
44	8
__________________45________________________________________7_____________________
Всего 50
ГЛАВА 1 0. Имитационное моделирование 729
10 13	a С помощью генератора равномерно распределенных случайных чисел смоделируйте распределение спроса так, чтобы вероятность каждого значения спроса совпадала с относительной частотой его реализации в течение 50 приведенных недель b Магазин еженедельно заказывает 42 упаковки молока. Каково среднее значение дефи- цита и избытка молока, если имитировать 100 недель продажи9 (Если вы используете только встроенные средства Excel, то имитируйте 10 недель ) с Подсчитайте среднее значение дефицита и среднее значение избытка молока Время между прибытиями клиентов в банк показано в следующей таблице Все клиенты поступают в одну очередь и обслуживаются в том порядке, каком они пришли Предполо- жим, что все клиенты обслуживаются точно 8 мин Также предположим, что, когда пришел первый клиент, не было других ни обслуживаемых, ни ожидающих клиентов Имитируйте приход 800 клиентов в банк (80 клиентов, если вы используете только встроенные средства Excel) и подсчитайте количество клиентов, которым пришлось ждать обслуживания
10 14	Время между прибытиями клиентов, мин.	Вероятность 5	0,25 10	0,50 15	0,25 Инвестиционная компания рассматривает возможность реализации 6 проектов, данные о которых приведены в следующей таблице В текущем году компания на эти проекты мо- жет выделить не более $10 млн Измените рабочую книгу Проекты и с помощью OptQuest определите набор проектов, который максимизировал бы ожидаемое значение ЧПС Также определите набор проектов, который максимизировал бы 35% персентиль ЧПС Должны ли совпадать эти два набора проектов9 Если нет, то почему9 Проект	Стоимость, тыс. долл.	Вероятность успеха, % ЧПС, тыс. долл. 1	2 000	80	3	500 2	3 000	55	2	700 3	1 500	72	1	100 4	2 500	90	2	000 5	4 000	65	5	500 6	750	40	3 000
Прикладные задачи
10 15.	Рассмотрим вероятностную модель, которая изучает поведение покупателей — любителей пива Данные о поведении покупателей, которые могут выбрать один из трех сортов пива (А, В и С), приведены в следующей таблице Из этой таблицы видно, что если покупатель в первую неделю покупает пиво А, то на следующей неделе с вероятностью 0,90 он купит это же пиво, либо с вероятностью 0,06 — пиво В или с вероятностью 0,04 — пиво С Это данные первой строки таблицы Данные в других строках таблицы интерпретируются по- добным образом Вы хотите имитировать поведение покупателя в течение 10 недель Пусть покупатель в первую неделю купил пиво А, тогда на второй неделе он может купить пи- во А, В или С с вероятностями соответственно 0,90, 0,06 и 0,04 Если на второй неделе он купил пиво В, тогда на третей неделе он купит пиво А, В или С с вероятностями 0,12, 0,78 и 0,10 соответственно Задайте в модели последовательность случайных событии (покупку того или иного сорта пива) и соответствующие вероятности этих событий
730	ЧАСТЬ III Вероятностные модели
	Вероятности покупки в неделю / + 1 Пиво, купленное в неделю i	А	В	С
10 16	А	0,90	0,06	0,04 В	0,12	0,78	0,10 С	0,09	0,07	0,84 Количество тормозных дисков, отремонтированных на станции технического обслужива- ния автомобилей в течение последних 30 недель, приведено в следующей таблице
10 17	Количество отремонтированных дисков	Количество недель 6	8 7	9 8	6 9	4 Всего	30 а С помошью генератора равномерно распределенных случайных чисел смоделируйте рас- пределение ремонтных работ так, чтобы вероятность каждого значения отремонтирован- ных дисков совпадала с относительной частотой его реализации в течение 30 приведен- ных недель b Имитируйте выполнение ремонтных работ в течение 100 недель (10 недель, если вы используете только встроенные средства Excel) Каково среднее количество дисков, отремонтированных за одну неделю9 Компания STECO поставляет листы нержавеющей стали в два близлежащих города Лос-Гатос (Л) и Аламеда (А) Недельный спрос на сталь (в грузовых платформах) и вероятности спроса показаны в приведенной ниже таблице Предполагается, что спрос в городах не зависит друг от друга Каждую неделю в Л ос-Г атос поставляется 4 платформы стали, а в Аламеду — 6 Вероятности Спрос	Л	А 1	0,2 2	0,3 3	0,3	0,1 4	0,1	0,1 5	0,1	0,3 6	0,3 7	0,2 а Имитируйте спрос в течение 500 недель в Лос-Гатосе (20 недель, если вы пользуетесь только встроенными средствами Excel) и подсчитайте количество случаев, когда пред- ложение превышает спрос
ГЛАВА 10. Имитационное моделирование 731
b Имитируйте спрос в течение 500 недель в Аламеде (20 недель, если вы пользуетесь
только встроенными средствами Excel) и подсчитайте количество случаев, когда пред-
ложение превышает спрос
Предположим, что компания STECO централизировала поставки стали и теперь удовле-
творяет спрос на сталь в Лос-Гатосе и Аламеде с одного товарного склада (назовем его ЛА)
с Если в начале каждой недели в склад ЛА поступает 10 платформ стали, то как изменится
положение с удовлетворением спроса на сталь в городах Лос-Гатос и Аламеда и почему9
d На основе той же случайной последовательности спроса, которая использовалась в п а
и Ь, имитируйте работу склада ЛА в течение 500 недель (20 недель, если вы пользуетесь
только встроенными средствами Excel) и подсчитайте количество случаев, когда предло-
жение превышает спрос Должен ли полученный результат отличаться от ответа на п с ’
10 18 В разделе 10 7 рассматривалась модель компании Midwest Express продажи авиабилетов
Предположим, что количество пассажиров, желающих лететь данным рейсом, подчиняется
следующему дискретному вероятностному распределению
К-во пассажиров	100	105	ПО	115	120	125	130	135	140	145
Вероятность	0,03	0,05	0,08	0,12	0,18	0,20	0,12	0,10	0,08	0,04
Измените рабочую книгу Мидвест в соответствии с новым распределением количества
пассажиров
а Как, по вашему мнению, изменится значение оптимального количества билетов, вы-
деляемых для продажи, в связи с новым распределением9
b Каково новое значение оптимального количества билетов, выделяемых для продажи,
и каким при этом будет ожидаемый доход9
10 19 Организация волонтеров проводит ежегодный сбор пожертвований, совершая обход 3 000
домов Волонтеры предлагают сделать или обычное пожертвование в размере $10 или
именное в размере $25 Анализ данных о проведении сбора пожертвований за предыдущие
годы показывает, что в 15% случаев при посещении дома хозяева отсутствуют (в таком слу-
чае в этот дом не возвращаются и, следовательно, пожертвовании нет) В 80% случаях дверь
открывает женщина, а в 20% — мужчина 40% женщин делают пожертвования, из которых
70% простые пожертвования и 30% именные Мужчины делают пожертвования в 70% слу-
чаев, из них 25% простые и 75% именные
а Какова ожидаемая общая сумма пожертвований9
b Создайте блок-схему вычисления общей суммы пожертвований
с Используя созданную блок-схему, имитируйте 200 посещений домов (20 посещении,
если вы пользуетесь только встроенными средствами Excel) и подсчитайте общую сум-
му пожертвований Какова ваша оценка общей суммы пожертвований, основанная на
результатах имитации9
d Имитируйте 1000 посещений домов (100 посещений, если вы пользуетесь только встро-
енными средствами Excel) и ответьте на те же вопросы, что и предыдущем пункте
10 20 Измените рабочую книгу Портфель, которая использовалась в разделе 10 9, включив в нес
акции еще четырех компаний (например, Yahoo, Dell Computer или America Online) Дан-
ные о доходности акций за предыдущие годы найдите на Web-узлах этих компаний и под-
считайте дисперсию доходности новых акций Определите долю акции каждой компании
в инвестиционном портфеле так, чтобы минимизировать общую дисперсию, а средняя до-
ходность всего портфеля была не ниже 30% Результат будет зависеть от того, воспользуе-
тесь вы средством Поиск решения или OptQuest
10 21 Лора Лин владеет цветочным киоском возле нового международного аэропорта Ден-
вера Она покупает цветы в оптовом магазине по $0,25 за штуку, а продает по $0,50
Лаура хочет определить оптимальное количество цветов, покупаемых на базе каждый
732 ЧАСТЬ III Вероятностные модели
день Основываясь на своих наблюдениях за три последние годы она считает, что
спрос на цветы можно примерно описать нормальным распределением со средним
100 и стандартным отклонением 20 Если в конце рабочего дня остаются не продан-
ные цветы, она реализует их оптом по S0,05 за штуку Если цветы заканчиваются
раньше конца рабочего дня и есть еще покупатели, то в этом случае она считает поте-
ри как двойную упущенную выгоду (т е 2xSO,25), поскольку по ее наблюдениям не-
удовлетворенный покупатель в будущем по меньшей мере два раза проигнорирует ее
киоск и только на третий раз рискнет купить у нее цветы
а Создайте в электронных таблицах имитационную модель и выполните 1000 ее испыта-
ний (100 испытаний, если вы пользуетесь только встроенными средствами Excel) Оп-
ределите оптимальное количество закупаемых на один день цветов Используйте
функцию Excel ЦЕЛОЕ для преобразования генерируемых нормально распределенных
случайных чисел в целочисленные значения
b Постройте 95% доверительный интервал для ожидаемого дохода в случае оптималь-
ного решения
Ситуация для анализа | CyberLab6
CyberLab — новая компания, разрабатывающая и производящая автоматизирован-
ное лабораторное оборудование Компания имеет находящийся на рассмотрении па-
тент на систему CyberLab и заканчивает строительство небольшого предприятия
в городе Нью-Милфорд, шт Коннектикут. Она также обладает действующими прото-
типами всех своих разработок, но в настоящее время требует денежного “вливания”
для разработки основного производственного оборудования и пополнения оборотных
средств, необходимых для расширения производства. CyberLab предлагает для продажи
30% своих акций компании Precision Instrument Corporation (PRICO) за $1 млн. и за
соглашение о том, что CyberLab будет распространять свою продукцию через
международную дистрибьютерскую сеть PRICO. Компания PRICO является одним из
основных производителей лабораторного оборудования Некоторые аспекты
предложения CyberLab Джеймсу Кемпбеллу, президенту компании PR1CO, кажутся
привлекательными, но другие вызывают определенное внутреннее сопротивление. Он
хочет понять, каково действительное положение компании CyberLab и какую финан-
совую выгоду может получитьего компания от сделки с ней.
Как родилась компания CyberLab
Компания CyberLab появилась как результат разочарований биохимика доктора
Мельтцера, работающего в Нью-Йоркском психиатрическом институте. Д-р Мельтцер
готовил и тестировал биопробы человеческих энзимов.7 Подготовка таких проб требует
особых усилий и затрат времени, поскольку человеческие энзимы чрезвычайно дороги,
а ручная подготовка проб приводит к некоторой их потере. Д-р Мельтцер хотел бы ав-
' Эту ситуацию для анализа можно использовать как основу для обсуждения в аудитории © 1988 Darden
Graduate Business School Foundation Краткое описание этой ситуации можно найти по Internet-adpecy
www darden Virginia edu/publishing
Энзимы — сложные белковые субстанции, необходимые для жизни Они действуют как катализаторы
клеточных реакций без деструктивного вмешательства в ход самих реакций Биопробы определяют отно-
сительную эффективность новых биологических субстанций путем сравнения их эффективности на тесто-
вых организмах с эталонными субстанциями
ГЛАВА 1 0. Имитационное моделирование 733
томатизировать подготовку своих проб, но в то время не существовало такого лабора-
торного оборудования, которое подходило бы для его целей. Тогда он поделился свои-
ми проблемами с сыном Уолтером, который взялся за разработку автоматизированной
системы. Так возникла компания CyberLab.
Через два года был готов опытный образец системы CyberLab, при этом Уолтер
исходил из выдвинутого им предположения, что основные элементы системы будут
изготовляться субподрядчиками, а остальные — закупаться.
Лабораторные роботы
Фрэнсис Зини, президент компании Zymark Corporation, наибольшего
разработчика и производителя лабораторных роботов, так обосновывает необходи-
мость автоматизации лабораторных работ. “За последние 10 или 20 лет мы получили
отличные измерительные инструменты, и при этом поток данных значительно умень-
шился, но подготовка препаратов к измерениям осталась такой же, как и в средние ве-
ка ” Компания Zymark потратила шесть месяцев, задавая лабораторным химикам и ра-
ботникам химической индустрии только один вопрос. “В чем ваша наибольшая про-
блема?”. И чаще всего ответ звучал так- “Подготовка образцов для анализа” Zymark
определила самое “больное” место химической индустрии и в 1982 году выпустила
первый лабораторный робот
Сотрудники лабораторий работают в двух измерениях рутина и ответственность8
Подготовка лабораторных образцов очень утомительна и требует высокой концен-
трации внимания Человек может работать так же быстро, как и робот, но робот мо-
жет поддерживать быстрый темп практически бесконечно (за исключением времени
профилактических и ремонтных работ) и при этом не сделает такой распространен-
ной (для человека) ошибки, как смешение образцов К достоинствам лабораторных
роботов также относится высокая производительность, постоянно высокое качество
подготовленных образцов и низкая стоимость эксплуатации Большинство совре-
менных лабораторных роботов действует по принципу рабочей станции, где цикли-
чески используются закрепленные на консолях инструментальные средства
Система CyberLab 800
Система CyberLab 800 работает несколько иначе, чем описано выше Здесь под
управлением компьютера инструменты могут перемещаться не только в одной плоско-
сти, как у других роботов, но и в трех измерениях. Критическим фактором в этом слу-
чае является точное начало и остановка движения инструмента Также отметим, что
для подготовки различных образцов здесь применяются разные программы Эта систе-
ма состоит из трех отдельных частей и управляющего компьютера (см рис 10 62) Уп-
рощенно, CyberLab 800 — это устройства для перемещения жидкости или пробирок
с жидкостью. Эта система способна выполнять любые повторяющиеся лабораторные
процедуры с жидкими препаратами
S В оригинале игра слов “2-D environment dull and demanding”, m e “двухмерное окружение нудное и требо-
вательное" — Прим перев
734
ЧАСТЬ III Вероятностные модели
Рис. 10.62. Система Cyber Lab 800
В конце лета 1987 года одна полная система CyberLab 800 работала в Нью-
Йоркском психиатрическом институте Д-р Мельтцер на ее покупку использовал по-
лученный федеральный гранд Эта система заменила двух лаборантов и сэкономила
в первый год работы более $70 000 Д-р Мельтцер отмечает, что новая система гото-
вит биопробы с меньшей потерей энзимов и значительно более аккуратно и качест-
венно Уже к концу июля 1988 года компания CyberLab продала 4 таких системы
и получила заказы еще на 25 систем
Конкуренция на рынке лабораторных роботов
В Соединенных Штатах насчитывается 18 тысяч лабораторий, которые могли бы
иметь лабораторных роботов Кроме того, Zymark указывает, что во всем мире таких ла-
боратории от 30 до 50 тысяч Однако на конец второго квартала 1988 года только 3 050 ла-
бораторий имели такое оборудование В настоящее время 42% установленного автомати-
зированного оборудования принадлежит компании Zymark, первой открывшей рынок
лабораторных роботов в 1982 году Два других конкурента, компании Cetus и Micromedic,
вышли на рынок в 1983 году и им принадлежит соответственно 15% и 17% установлен-
ного оборудования Компания Cetus в 1986 году была куплена Perkin-Elmer, большой
корпорацией, занимающейся производством аналитического инструментария, объем ее
продаж в 1987 финансовом году составил 1,6 млрд додп Три других производителя лабо-
раторного автоматизированного оборудования появились в 1985 году, один из которых,
Beckman Instruments, является дочерней компанией большой медицинской корпорации
SmithKline Beckman В 1987 году на рынке лабораторных роботов появились компании
Hewlett-Packard и Dynatech Другая информация об участниках этого рынка на 1987 год
приведена в табл 10 4
ГЛАВА 10. Имитационное моделирование 735
Таблица 10.4
Компания	K-bo лет на рынке	К-во продан- Доля ного оборудо- рынка, вания	Общие объемы % продаж, млн. долл.	Объемы продаж лаборатор- ного оборудования, млн. долл.
Zymark	6	1000	42	15	15
Micromedic	5	400	17	43	17
Perkin-Elmer/ Cetus	5	350	15	1334	416
Tecan	3	300	13		99
Beckman	2,5	175	7	4329	693
Hamilton	3	100	4	25	25
HP/ Genenchem	1	50	2	8090	405
Dynatech	1	4	0,2	305	13
Компания CyberLab собирается потеснить основных игроков на рынке лабора-
торных роботов, поскольку ни одна из восьми основных компании не может пред-
ложить систему, подобную CyberLab 800, за аналогичную цену Эта система стоит
$32 470 и может заменить одного химика (средняя зарплата химика в 1987 году со-
ставляла $41 800) Таким образом, она окупает себя за 0,78 года
Текущее финансовое состояние
С целью получения инвестиций Том Фредландер, генеральный директор Cyber-
Lab, обратился в компанию Dean Witter and Salomon Brothers, но получил отказ То-
гда он нанял на полную ставку консультанта из большой компании для помощи
в поиске денег Этот консультант заинтересовал в предложениях CyberLab партнера
своей компании фирму PRICO. CyberLab предлагает 30% своих акций и право про-
давать свою продукцию через международную дистрибьюторскую сеть PRICO в об-
мен на 1 млн долл В соответствии с этим соглашением PRICO становится едино-
личным покупателем и продавцом систем CyberLab Компания CyberLab производит
свои системы и продает их PRICO по заранее согласованной цене На рис 10 63 по-
казан рабочий лист из книги Cyber9, разработанной CyberLab для оценки объемов
производства при условии выполнения этого соглашения (финансовые условия со-
глашения представлены в табл на рис 10 65).
' Эта рабочая книга не русифицирована — Прим ред
736 ЧАСТЬ III Вероятностные модели
в	।	с	I	D	-	|,-  г. •			
26 j	CYBERLAB'. J29JSelling Price/Unit 30?Matrl Labor/Unit ЭХ-Units Sold	PRO FORMA INCOME 625 000	STATEMENT: MANUFACTURING ONLY 625 000	625 000 <8 651	<8 651	
33 Sales Revenue	6725 000	61 175 000	61 275 000
34 Material,Dir Labor	250 879	406 597	441 201
35  Overhead	138 000	196 430	207 641
36 Cost Of Goods Sold	t388 879	6603 027	6648 842
37 Gross Margin	f 336 121	6571 973	6626 158
38iSelling, Gen c Admin	<258 044	<343 047	6344 908
39 Depreciation	16 000	9 600	5 760
40 Profit before tax	?62 077	< 219 326	6275 490
41 -Taxes	624 631	<87 730	6110 196
Profit after tax	<37 246	Я31 596	<165 294
44_RETURN ON SALES	5,14%	11,20%	12,96%
EQUITY AT 48 BEGINNING OF YEAR	<1 000 000	fl 037 246	61 168 842
47_ RETURN ON EQUITY	3,72%	12,69%	14,14%
_49_ YEAR	7	2	3 TERM VALUE
50 ; PAT	37 246	131 596	165 294
51, DE? N ADD BACK	16 000	9 600	5 760
S2 CHANGE IN U0RK CAP	-47 176	-58 841	-72 912
_53_CASH FLOW FR OPNS	<1 141 090		98 142	1 635 700
Рис. 10.63
Фирме PRICO необходимо оценить предложения в двух направлениях рыночные
возможности реализации продукции CyberLab и возможности покупки ее акций
Чтобы предложение было приемлемым и привлекательным, надо определить стои-
мость покупаемой продукции CyberLab и минимальную возможную прибыль
(маржу) и определить, стоят ли 30% акций CyberLab 1 млн долл (или, возможно, за
эту сумму можно приобрести больше акций)
На рынке лабораторного оборудования компания PRICO имеет имя, торговую сеть
и рекламу, в которую вкладывает 23% прибыли Компания занимается продажей лабо-
раторного оборудования более 50 лет, имеет в Соединенных Штатах 100 центров по
продаже и обслуживанию своего оборудования и 220 таких центров в 60 странах мира
Исходя из этих позиции и цены патента на CyberLab 800 $700 000, м-р Кемпбелл счита-
ет эффективным дать CyberLab ссуду В этом случае компания получит чистого дохода
не менее $262 258, как показывают расчеты в таблице на рис 10 64
Чтобы компания PRICO смогла организовать продажу продуктов CyberLab, ей
необходимо одноразово потратить $150 000 на проведение семинара для продавцов
и выпуск брошюры о новых продуктах Затем в первый год надо вложить $51 000 и по
$60 000 в последующие два года Кроме того, следует учесть $600 комиссионных за
каждую проданную систему CyberLab
ГЛАВА 10 Имитационное моделирование 737
Рис. 10.64
Рис. 10.65
Средняя прибыль от продаж (до уплаты налогов) в индустрии производства лабо-
раторного оборудования составляет 5,1% Доходность акции основных производите-
лей составляет от 12 до 13%.
Итак, потратив миллион, PR1CO может получить или 30% акций CyberLab, или сумму
$342 327 (0,3x$ 1 141 090) плюс $262 258 за торговое соглашение И все-таки м-р Кемпбелл
сомневается, заключать ли эту сделку
738 ЧАСТЬ III Вероятностные модели
Вопросы
1	С учетом приведенной ниже дополнительной информации постройте имитаци-
онную модель и оцените привлекательность с точки зрения компании PRICO
предложений, сделанных CyberLab.
2	Проведите пять испытаний этой модели
3	Предположим, что вам доступны результаты многих испытаний модели. Как вы
используете эти результаты для решения вопроса о том, следует ли PRICO при-
нимать предложение CyberLab9
Рост рынка лабораторных роботов
По оценкам экспертов, емкость этого рынка в 1988 году равняется 1,2 млрд долл
с ожидаемым увеличением к 2000 году до 25 млрд долл , т е со среднегодовым рос-
том 28,8% В ближайшие годы прогнозируется рост 7-9% Продажи лабораторного
оборудования за пределы США должны вырасти от 1,65 млрд долл, в 1985 году до
2,35 млрд долл в 1990 году, т е ежегодный прирост составит 7,3%, при этом за бли-
жайшие два года продажи возрастут соответственно на 5 и 9% Эксперты прогнози-
руют рост с равной вероятностью в пределах 6—8% (со средним значением 7%), но
возможны годы, когда рост будет превышать 10% или опускаться до 0
Доля рынка CyberLab
Уолтер Мельтцер считает, что его компания в первый год продажи системы Cy-
berLab 800 может занять с равной вероятностью от 4 до 6% рынка со средним значе-
нием 5% Во второй и последующие годы объемы продаж должны возрасти на 2,5%
относительно уровня, достигнутого в первый год
Себестоимость системы CyberLab
По расчетам Уолтера Мельтцера, себестоимость системы не должна превышать
$8 651 Однако в последующие годы из-за изменения цены комплектующих и стоимо-
сти рабочей силы себестоимость может возрасти, но не более, чем на 5%, или умень-
шиться максимум на 9% Вероятности изменения себестоимости показаны в следую-
щей таблице
Изменение себестоимости, Вероятность, что изменение будет меньше указанного значения или
%	равно ему
-10	0
-5	0,25
—2	0,50
0	0,75
+5 1,0
ГЛАВА 10. Имитационное моделирование 739
Ситуация для анализа | Mountain Realty10
Компания Mountain Realty обслуживает портфель разнообразных коммерческих
предложений, полученных из района Ларами, для сотрудничества с большими инве-
сторами из Денвера. Сотрудница этой компании Бренда Шуте по поручению прези-
дента компании Билла Вита должна провести анализ инвестиций в строительство
жилого комплекса, расположенного недалеко от университета Вайоминга Билл Вит
хочет оценить привлекательность этих инвестиций, предполагая, что они должны
приносить ежегодную прибыль от 12 до 16%.
Бренда сформулировала известные ей данные следующим образом
•	Строятся пять жилых блоков площадью 750 кв. футов каждый В настоящее вре-
мя аренда таких помещений стоит $500 в месяц Таким образом, ожидаемый об-
щий доход (ООД) в первый год составит $30 000 В последующие годы ожидается
рост ООД от 3 до 8% в год, но наиболее вероятно — на 5%
•	Норма допустимых потерь для Ларами равняется 1 —2%, но может возрасти до 4%
на пятый год.
•	Каждую статью расходов следует учитывать в расчетах за каждый год, представ-
ляя их в итоговых суммах как процент от ООД Расчеты Бренды показывают, что
расходы составляют 40% от ООД со стандартным отклонением 2,5%
•	Жилой комплекс стоит $160 000, из которых $24 000 — это стоимость земельного
участка, а $136 000 — стоимость зданий Таким образом, стоимость одного квад-
ратного фута жилья стоит $42,66 (общая площадь комплекса 3 750 кв футов)
•	Западный банк предлагает стандартный заем в $120 000 под 12% годовых на 25
лет. Бренда подсчитала, что ежегодные платежи за такой заем составят $15 300.
•	Амортизационные отчисления будут равномерными в течение всех 27,5 заплани-
рованных лет эксплуатации комплекса.
•	Основываясь на прогнозах рынка жилья в районе Ларами, можно ожидать еже-
годный 3% рост стоимости жилья со стандартным отклонением 1,5%
•	Инвестиционная деятельность облагается налогом в 28%.
•	За участие в продаже устанавливаются твердые комиссионные в размере $6 000
•	Инвестиционный проект рассчитывается по годам на период 5 лет.
Для стандартного анализа данного инвестиционного предложения Бренда созда-
ла рабочую книгу Mountain11, показанную на рис 10 66 Она подставляла различные
начальные значения, чтобы определить степень чувствительности решений для ин-
весторов из Денвера Однако инвесторов не удовлетворил такой поверхностный ана-
лиз чувствительности и они хотят, чтобы Бренда учла в своем анализе вероятности
всех возможных случайных величин и событий Инвесторы не принадлежат к людям,
склонным рисковать, поэтому хотят вложить свои деньги в проект с умеренной сте-
пенью риска
10 Эта ситуация подготовлена Фредом Хиршом, Реем Роджерсом и Ларри Уэдерфордом (Fred Hirsh, Ray
Rogers, Larry Weatherford) Copyright © 1993, Larame, WY
11 Эта рабочая книга не русифицирована — Прим ред
740 ЧАСТЬ III Вероятностные модели
Рис. 10.66
Сын Билла Джек прослушал новый курс по теории принятия решений в универси-
тете Вайоминга На практических занятиях он убедился в исключительной полезности
новых программных продуктов Crystall Ball и ©Risk, которые применяются при имита-
ционном моделировании в электронных таблицах. По совету Билла Бренда решила ис-
пользовать эти надстройки в процессе анализа инвестиционного проекта.
Вопросы
1	Каково значение чистой приведенной стоимости (ЧПС) при налоге 12% на не-
движимость9 А при 16%9
2	Какова вероятность того, что ЧПС будет отрицательной при налоге на недвижи-
мость 12%9
3	. Что Бренда может порекомендовать инвесторам из Денвера для осуществления
данного проекта9
Литература
1	Anthony Bngandt, Dennis Dargon, Michhael Sheehan, and Thomas Spencer AT&T’s Call Processing
Simulator (CAPS) Operation Design for Inbound Call Centers, Interfaces, 24, no 1 (1994), p 6-28
2	James Bookbinder and Terrence Kotwa Modeling an AGV Automobile Body-Flaming System, Inter-
faces, 17, no 6 (1987), p 41-50
3	1 M.Premachandra and Liliana Gonzalez A Simulation Model Solved the Problem of Scheduling
Drilling Rigs at Clyde Dam, Interfaces, 26, no 2 (1996); p 80—91
4	Barry Smith, John Leimkuhler, and Ross Darrow Yield Management at American Airlines, Interfaces,
22, no 1 (1992), p 8-31
Моделирование дискретных
событий
В этой главе...
11.1.	Введение
11.2.	Имитационное моделирование в Excel
11.3.	Имитационное моделирование в Extend
11.4.	Расширенная модель Хервиса
11.5.	Изменение модели Хервиса
11.6.	Окончательная модель Хервиса
11.7.	Заключение
Основные термины
Контрольные вопросы
Задачи
Ситуация 1. Snowy Range Hardware
Ситуация 2 Баржи Миссисипи
Литература
742 ЧАСТЬ III. Вероятностные модели
Процесс обработки запроса на установку линии
DS1 в компании US WEST
Исторически так сложилось, что моделирование дискретных событий использо-
валось в основном при имитации промышленных и производственных процессов
На сегодняшний день, как показывает следующий пример, значительно расшири-
лась сфера применения этого вида моделирования. В настоящее время растет спрос
на сети с линиями связи типа DS1 Это очень мощные и высокоскоростные сети.
Компания US WEST хочет, чтобы мощность и скорость обработки запросов на уста-
новку линий связи DS1 были сравнимы с мощностью и скоростью самих линий.
Компания для определения лучшей модели обработки запросов решила воспользо-
ваться моделированием дискретных событий.
Процесс установки линии DS1 начинается с запроса от владельцев телекоммуни-
кационных линий связи (частных или государственных организаций). Этот запрос
принимается центром обслуживания коммуникационных линий или отделом марке-
тинга центра обслуживания, который оформляет заказ на работу. Заказ направляется
в центр обеспечения работ Здесь выявляются ошибки в оформлении запроса, и за-
прос с ошибками отсылают на доработку в центр обслуживания коммуникационных
линий или отдел маркетинга центра обслуживания. Если в запросе нет ошибок, центр
обеспечения работ изготавливает подробный план проведения работ. Этот план может
быть послан в одно из трех мест. Если все необходимые (в соответствии с планом)
материалы и кабели имеются на месте, план посылают непосредственно в центр об-
служивания для немедленного исполнения. В случае отсутствия необходимых мате-
риалов или кабелей план посылается в центр текущего планирования или в центр
управления строительством Как только эти центры обеспечат необходимыми мате-
риалами и кабелями, запрос передается центру обслуживания для завершения работ.
Для отображения этого процесса была разработана модель, в которой для представ-
ления различных этапов обработки запроса использовались очереди. Имитация модели
проводилась на компьютере с помощью приложения Extend Рекомендации, основан-
ные на имитационных экспериментах, должны были быть применены в Де-Мойне,
штат Айова Вначале менеджеры в Де-Мойне не решались действовать в соответствии
с этими рекомендациями Однако, столкнувшись с проблемами в процессе обслужива-
ния, точно предсказанными имитационной моделью, менеджеры приняли предложе-
ния, полученные на основе результатов дискретной модели Они наняли для каждого
участка последовательного обслуживания запроса соответствующее количество персо-
нала, что помогло устранить “узкие” места и улучшило обслуживание клиентов [ I ]
11.1.	Введение
В некотором смысле все модели являются имитацией реальных явлений. Однако, как
правило, термин имитационное моделирование относится к определенному классу дина-
мических моделей, включающих детальное наблюдение за сложной вероятностной сис-
темой на протяжении какого-то промежутка времени. Чтобы получить представление об
имитационном моделировании, обратитесь к разделу 10 1 предыдущей главы.
Имитационные модели, описанные в главе 10, содержат агрегированные переменные,
которые со временем изменяются более или менее непрерывно. Поэтому такие модели
ГЛАВА 11. Моделирование дискретных событий 743
называются непрерывными (аналоговыми) имитационными моделями. В этой главе мы рас-
смотрим моделирование дискретных событий, которое обычно применяется в тех случаях,
когда отслеживаются отдельные случайные элементы, вероятностное распределение ко-
торых имеет разрывы (негладкое распределение). Например модель, отслеживающая ба-
зовый процент на ссуды в течение какого-то времени как функцию других макроэконо-
мических переменных (таких как курс иностранных валют, безработица, государствен-
ные расходы и капиталовложения коммерческих предприятий), может быть построена
или как простая детерминированная модель или, если присутствует неопределенность,
как непрерывная имитационная модель. В таких макроэкономических моделях обычно
используются переменные, представляющие обобщенные единицы измерения, которые
одновременно учитывают множество событий на рынке, а эти события слишком много-
численны и громоздки для моделирования по отдельности. В противоположность этому
моделирование дискретных событий обычно используется тогда, когда желательно учесть
в модели подобные события.
В качестве другого примера можно привести модели линейного программирования
или модели анализа решений, которые полезны при планировании производства про-
дукции в заданном периоде времени и для определения необходимых ресурсов Однако
в таких моделях довольно сложно включить подробные тактические решения, влияющие
на производство Такие тактические решения могут включать планирование занятых ра-
ботников, установку (или удаление) производственного оборудования, обеспечение
сырьем, учет полуфабрикатов и готовых изделий, а также решения, касающиеся внепла-
нового ремонта оборудования и отсутствия работников Имитационные модели дискрет-
ных событий могут использоваться для глубокого изучения мельчайших подробностей
сложных систем со многими взаимодействиями. Разумеется, необходимо платить за та-
кой реализм имитационные модели дискретных событий могут стать чрезвычайно слож-
ными для построения и соответствующего анализа, особенно если их разрабатывать
в электронных таблицах
Наиболее часто имитационное моделирование дискретных событий используется для
создания действующих систем с конфликтующими процессами, которые выполняются
параллельно и которым одновременно могут потребоваться дефицитные (в системе) ре-
сурсы Примером такого моделирования может служить моделирование очередей, состоя-
щих из заданий, ожидающих обслуживания (например, люди в очереди к банковскому
служащему, пакеты Internet, передаваемые через маршрутизаторы, или поток комплек-
тующих на сборочном конвейере завода). Созданная однажды подобная имитационная
модель намного удобнее и надежнее для исследования, чем сама реальная система. Кро-
ме того, в модели дискретных событий можно относительно просто изменить сценарии
управления ключевыми переменными для наблюдения за их воздействием на показатели
качества работы системы.
Построим в Excel имитационную модель для простой ситуации — организации очереди
для получения обслуживания. Как будет показано, имитационные модели дискретных со-
бытий трудно представить в табличном виде (приемлемом для электронных таблиц), по-
этому для построения и изучения сложных систем используются специализированные
программы В этой главе будет показана одна такая программа, Extend, урезанная версия
которой (Extend LT) находится на компакт-диске, прилагаемом к этой книге. Программа
Extend может использоваться как для создания аналоговых моделей, так и для моделирова-
ния дискретных событий. Аналоговые модели уже рассматривались в главе 10, поэтому
здесь будут показаны возможности Extend для моделирования только дискретных событий
744
ЧАСТЬ III Вероятностные модели
11.2.	Имитационное моделирование в Excel
Рассмотрим следующий пример. Генри Хервис основал фирму по прокату автомоби-
лей в аэропорту Он надеется, что более низкие накладные расходы и эффективное об-
служивание привлекут клиентов и позволят конкурировать с более крупными фирмами.
Чтобы исследовать эффективность своего бизнеса, Хервис собирает статистику о пере-
мещении клиентов через свой офис, где они арендуют автомобили. Клиенты прибывают
в автофургонах аэропорта и становятся в очередь. Прибывший первым обслуживается
у стойки по оформлению проката. В общей ситуации каждый клиент становится в начало
очереди и, если служащий, оформляющий прокат, не занят, то клиенту предоставляется
обслуживание, которое состоит из заполнения бланков по аренде автомобиля, выбора
вариантов арендной платы, получения некоторых инструкций по вождению автомобиля
и т п Затем клиенты покидают офис, чтобы забрать взятые напрокат автомобили и уе-
хать. Хервис собрал данные по прибытию в свой офис клиентов, которые обычно приез-
жают маленькими группами после приземления в аэропорту самолетов. В табл. I l.l при-
ведены собранные им данные по распределению прибытия клиентов в течение суток с 5-
минутным интервалом времени. В таблице также вычислены интегральные вероятности
(функция распределения) прибытия одного, не менее двух и не менее трех клиентов.
Таблица 11.1
Количество прибывающих клиентов Вероятность, %	Интегральная вероятность, %
О	70	70
I	12	82
2	16	98
3	2	100
Хервис решил смоделировать круглосуточные операции по оформлению проката ав-
томобилей в течение недели, а время разбить на 5-минутные интервалы. Для упрощения
он предположил, что обслуживание одного клиента всегда занимает ровно 5 мин. В его
модели это привело к 7x24x60/5 = 2016 временным интервалам. Поскольку в Excel суще-
ствует ограничение на максимальное количество столбцов, равное 256, то временные ин-
тервалы необходимо представить в строках. В подробной имитационной модели отсле-
живаются все перемещения клиента в пределах каждого 5-минутного временного интер-
вала, а затем эти перемещения обобщаются в статистические данные интенсивности
работы офиса Чтобы построить в Excel такую модель, необходимо обозначить времен-
ные интервалы, для чего используется диалоговое окно Прогрессия (рис. 11.1), которое
открывается после выполнения команды Правка^Заполнить^Прогрессия
Затем в диапазоне J4 K7 необходимо создать таблицу распределения вероятностей,
как показано на рис. 11.2. Обратите внимание на единственную формулу, содержащуюся
в ячейке К8, которая вычисляет ожидаемое количество клиентов, прибывающих в каж-
дый 5-минутный интервал (равное в среднем половине клиента) с помощью функции
СУММПРОИЗВ.
ГЛАВА 11. Моделирование дискретных событий 745
Рис. 11.1. Создание последовательности целых чисел для обозначения
временных интервалов
Рис. 11.2. Распределение вероятностей для имитационной модели очереди
Совет Перечитайте раздел 10.2 в главе 10, чтобы вспомнить способы моделирования в ими-
тационных моделях случайных величин с заданными вероятностями.
Имитационная модель будет управляться случайными числами, генерируемыми Excel,
которые задают вероятности количества клиентов, прибывающих в любой 5-минутный ин-
тервал времени. Для каждого из 2016 временных интервалов функция СЛЧИС выдает слу-
чайное число из интервала от 0 до 1 каждый раз, когда в рабочем листе происходят какие-
либо изменения, что ведет к постоянно изменяющимся значениям рабочего листа, нежела-
тельным при разработке модели. Чтобы избежать постоянного пересчета рабочего листа,
установите ручной режим пересчета. Для этого надо установить переключатель Вручную во
вкладке Вычисления в диалоговом окне Параметры (рис. 11.3), которое открывается по
команде СервисФПараметры.
746 ЧАСТЬ III Вероятностные модели
Рис. 11.3. Задание ручного режима пересчета рабочего листа
Совет В режиме ручного пересчета рабочий лист пересчитывается при нажатии на клави-
шу <F9>. Если в рабочем листе сделаны какие-либо изменения, требующие вычислений, Excel
поместит в строке состояния слово “Вычислить ”.
После ввода формулы =СЛЧИС() в ячейку В5 необходимо скопировать ее в нижние
ячейки до В2020, чтобы создать 2016 случайных величин. Теперь создадим в диапазоне
M4-N7 таблицу функции распределения количества поступивших клиентов (рис. 11 4)
По этой таблице функция ВПР (показанная в ячейке С5 на рис. 11 4) в соответствии со
значением случайного числа в столбце В определяет количество прибывших клиентов 1
(Обратите внимание на то, что в отличие от первоначальной табл. 11.1 данная таблица
должна соответствовать синтаксису функции ВПР ) Таким образом, 2016 случайных ве-
личин, результаты работы функции СЛЧИС, содержащиеся в диапазоне В6 В2020, с по-
мощью функции ВПР преобразуются в количество прибывших клиентов, записанных
в диапазоне С6 С2020
	С5	’	А	=ВПР(В5,$М$4 $N$7,2)			
	.. В ..	к..Л.:„.С J С . Е F GHI.	J		К	|L.	М	_ N		...
~2~	К Прока	тавтоиооилеи	Данные наблюдений Табл, для определения числа клиентов			
3	Случайное	К во : прибывающих	К-во прибывающих клиентов	Вероятность	К во Интегральная прибывающих вероятность клиентов	
Ж! в	0,195 0,195	0	2	70% 12% 16%	0%	0 70%	1 82%	2	
	0,195	2	:	3	2%	-	98%	3	
Г 9 10 11	0,195 0,195 0,195 0.195	3 0 2	Ожидаемое к-во прибывающих	0.5		
Рис. 11.4. Таблица функции распределения и функция ВПР
Для завершения построения модели необходимо ввести формулы в ячейки D5:F2020,
как показано на рис. 11 5 Формулы в столбце D для каждого временного интервала вы-
числяют количество клиентов в очереди, включая обслуживаемого у стойки, суммируя
Функция ВПР ищет заданное значение в левом столбце указанной таблицы (если такого значения нет,
ищет ближайшее, превышающее заданное) и возвращает значение, содержащееся в той же строке, где най-
дено совпадение, из указанного столбца таблицы Эта функция описана в приложении Б — Прим ред
ГЛАВА 11. Моделирование дискретных событий 747
число вновь прибывших в текущем 5-минутном интервале и еще не обслуженных клиен-
тов из предыдущего интервала (если таковые имеются). Формулы в столбце Е вычисляют
количество клиентов, обслуживающихся у стоек, как минимум от длины очереди
(которая может быть равна нулю) и количества стоек (задается в ячейке С2) Число кли-
ентов, остающихся необслуженными в конце 5-минутного временного интервала, вы-
числяется в столбце F как разность между содержимым столбцов D и Е
Прокат автовобилей
4 i	К-во	Као	К ео	К-во
^-аинутные Случайное прибывающих клиентов в обслуживаевых ожидающих
.3.1 интервалы число клиентов очереди клиентов клиентов
0,195
0,195
0,195
0,195
То7
2011
2012
2013
2014
2015
2016
0,195
0,195
0,195
0,195
1937
0,961
1005
0 499
вину Случайн К во прибывающих
К во клиентов в К-во обслуживаевых К-во ожидающих
очереди клиентов клиентов
=CB4HCQ =ВПР(В5.1М$4$М$7;2)
=СЛЧИС0 =BnP(B6;$M$4:$N$7,2)
=СЛЧИС0 =ВПР(В7;$М$4 $N$7;2)
=СЛЧИС0 =ВПР(В8;$М$4:1М7;2)
=СЛЧИС0 =ВПР(В9.$М$4:$М7;2)
=СЛЧИС0 =BnP(B10;$M$4:$N$7;2)
=СЛЧИС0 =BnP(B11,$M$4;$N$7,2)
=СЛЧИС0 =ВПР(В12;$М14.$1М$7;2)
=C5+F4
=C6+F5
=МИН(05,$С$2)
>МИН(06;$С$2)
=МИН(О7,$С12)
=МИН(08;$С$2)
=MHH(D9,JCJ2)
=МИН(010;$С$2)
=МИН(011;$С$2)
=МИН(012;$С$2)
=МИН(Э2015,$С$2)
=МИН(02016,$С$2)
=МИН(02017.$С$2)
=МИН(О2О10,$С12)
=МИН(02019;$С$2)
_____________________1=МИН(Р2020;$С$2)_______________________
=MAKC(D$5:D$2O2O)	=MAKC(EJ5:EJ2020)	=MAKC(FJ5 FI2020)
=СУММ(015:0$2020)	=СУММ(Е$5:Е$2020) =СУММ(Е$5.Е$2020)
=CP3HA4(Dt5 D62020) =СРЗНАЧ(Е65:Е62020) =CP3HA4(FK:Ft2020)
=C9tF8
=C10+F9
=D6-E6
=О7-Е7
=08-ЕВ
=09 Е9
=010-Е10
=C12+F11
1512011 =СЛЧИС0 =ВПР(В2015;$М$4 JNJ7.2) =С2015+Е2014
1612012 =СЛЧИС0 =ВПР(В2016.$ММ:б1М»7.2) =С2016+Г2015
2017_2013 =СЛЧИС0 =ВПР(В2017;$М$4:$К1$7;2) =С2017+Е2016
2ЙВ; 2014 =СЛЧИС() =ВПР(В2018,бМ$4.$М»7;2) =C2018+F2017
201912015 =СЛЧИС0 =BFIP(B2019;$M$4:$N$7;2) =C2019+F2018
202012016 =СЛЧИС0 =ВПР(В2020;бМб4:бИб7 2) =02020+62019
23213 Максиаув=МАКС(Сб5:С$2020) =мдкглт<д пт
2022- Всего =СУММ(С$5:С$2020)
2023*	Среднее =СРЗНАЧ(С65:С62О2О)
=012-Е12
=02015-Е2015
=02016-Е2016
=02017-Е2017
=02018- Е2018
=02019-52019
Рис. 11.5. Законченная модель очереди
Совет. Возможность разделить в Excel окно рабочей книги на две части, как показано на
рис. 11.5, полезна для копирования формул в больших листах и просмотра их различных участков
Формулы в диапазоне C2021.F2023 вычисляют статистические данные, необходимые
Хервису для оценки эффективности работы его офиса. Эти формулы вычисляют максимум,
общее количество и среднее значение для каждого столбца Обратите внимание на то, что
748 ЧАСТЬ III. Вероятностные модели
эти показатели являются случайными величинами из-за вероятностной природы имитаци-
онного моделирования. Числа, полученные в вашей рабочей книге, конечно, будут не-
сколько отличаться от приведенных здесь, поскольку нажатие на клавишу <F9> заполнит
таблицу другими 2016 случайными числами для моделирования другой недели. Повторные
нажатия на <F9> дадут возможность прочувствовать непостоянство этих величин.
Результаты моделирования очередей почти всегда неожиданны, поскольку человеческая
интуиция ненадежна при анализе нелинейных ситуаций, приводящих к очередям. Напри-
мер, в ячейке К8 вычислено, что в каждый 5-минутный интервал времени в среднем при-
бывает только “половина” клиента, или в среднем каждые 10 мин. прибывает один клиент.
А чтобы обслужить этого клиента, всегда требуется только один 5-минутный интервал. Та-
ким образом, в среднем стойка по оформлению проката занята только половину времени,
что приводит в модели Хервиса к значительным простоям соответствующих служащих. Тем
не менее в течение недели возникают случаи предельной загрузки, когда сразу 9 клиентов
ожидают обслуживания. Поскольку обслуживание клиента занимает 5 мин., последний
клиент, чтобы получить автомобиль, должен ждать 45 мин. Способ удовлетворения клиен-
тов, основанный на повышении эффективности работы служащего у стойки во время пре-
дельной загрузки, вряд ли приемлем для Хервиса, поскольку предполагается, что служащий
всегда работает с постоянной высокой скоростью.
Для Хервиса очевидным выходом является добавление еще одной стойки по оформ-
лению проката, что позволит обслуживать одновременно двух ожидающих клиентов. Это
должно привести приблизительно к двойному сокращению предполагаемых задержек,
разумеется, за счет удвоения текущих расходов офиса Хервиса Но в действительности
интуиция снова подводит, что подтверждается результатом испытаний модели для двух
стоек На рис 11 6 полученные статистические данные для модели с двумя стойками по-
казывают, что максимальное количество клиентов, получающих обслуживание с задерж-
кой, падает почти на порядок, а среднее количество клиентов, получающих обслужива-
ние с задержкой, уменьшается почти в двадцать раз. Впечатляющий результат!
Рис. 11.6. Результаты имитации модели с двумя стойками
ГЛАВА 11. Моделирование дискретных событий 749
11.3.	Имитационное моделирование в Extend
Как показано в предыдущем разделе, использование Excel для моделирования дискретных
событий страдает от двух главных недостатков. Во-первых, для больших моделей рабочий лист
Excel быстро заполняется ячейками, занятыми формулами. Например, если в модели Хервиса
предусмотреть, что клиенты приходят не в начале каждого 5-минутного интервала времени,
а в любую минуту, то это немедленно увеличит размер модели в 5 раз, поскольку в этом случае
минимальный временной интервал будет равен I, а не 5 мин , как ранее Кроме того, модели-
рования одной недели недостаточно для оценки работы офиса в течение месяца Моделиро-
вание работы в течение месяца увеличило бы модель еще в 4 раза (от одной недели до четы-
рех) Это увеличение модели при расширении моделируемого периода уже упоминалось в гла-
ве 5 как “проклятие размерности” для динамических моделей, и имитационные модели почти
всегда являются экстремальным случаем этого “проклятия”.
Во-вторых, имитационные модели дискретных событий в Excel плохо масштабируют-
ся. Например, в модели Хервиса было относительно просто расширить количество стоек
по оформлению проката от I до 2, но для увеличения моделируемого периода (от недели
до месяца) или для использования более мелкого временного интервала необходимо
полностью переделать всю модель (копируя формулы, вставляя ячейки и т.д ) Другими
словами, нельзя определить в качестве параметров модели коэффициенты, в соответст-
вии с которыми изменяется размер модели. Чтобы проиллюстрировать эту проблему, до-
пустим, что в модели Хервиса время обслуживания клиента не равно точно 5 мин , а про-
извольно изменяется, скажем, от 4,5 до 5,3 мин В этом случае единицей измерения вре-
мени должна быть 0,1 мин , что ведет к десятикратному увеличению размера модели,
требующего многочисленных вставок ячеек, копирования формул и тд Все это может
быстро сокрушить даже большие размеры рабочего листа Excel Отметим, что в этой
расширенной модели многие ячейки содержали бы нулевые значения, отражая как от-
сутствие клиентов, так и отсутствие событий по их обслуживанию Эти пустые ячейки
занимают значительное пространство на рабочем листе, а структура рабочего листа Excel
не позволяет их исключить
Итак, чтобы быстро и качественно построить имитационную модель и провести ими-
тацию, необходимо иметь возможность вводить более мелкие временные интервалы и
изменять период имитации без коренной переделки модели, без потери пространства ра-
бочего листа и значительного увеличения объема работы. Во-вторых, представление мо-
дели должно быть компактным для того, чтобы избежать формирования гигантских таб-
лиц, неудобных для манипулирования и отладки. В-третьих, модели должны быть про-
сты для проведения имитации и получения ее результатов без обременительного
программирования. В-четвертых, чтобы облегчить построение моделей и документиро-
вание, среда разработки моделей должна иметь графический интерфейс пользователя.
Это именно то, чем обладают такие современные программные приложения для дис-
кретного моделирования событий, как Extend.2 Платой за использование этих программ
является отказ от Excel.
Совет. На компакт-диске, прилагаемом к книге, содержится урезанная версия этой про-
граммы. На Web-узле разработчика Extend wv,w.imaginethatine сот доступна расширенная
версия программы, а также версия для Macintosh.
750 ЧАСТЬ III Вероятностные модели
Применение Extend для дискретного моделирования очередей будет показано на
примере переработанной модели Хервиса Вы увидите, что с помощью Extend намного
проще моделировать сложные системы с временной зависимостью, чем в Excel. Кроме
того, Extend обладает расширенными возможностями документирования и предоставля-
ет привлекательный графический интерфейс для визуального построения, наблюдения,
отладки и анализа имитационных моделей дискретных событий. У Extend есть даже про-
стая анимация, которая позволяет отображать перемещение клиентов или заданий в мо-
делируемой системе. Наконец, Extend может экспортировать свои результаты в виде таб-
лиц для последующего их анализа в Excel.
Дискретные модели Extend являются объектно-ориентированными и строятся с по-
мощью предопределенных стандартных блоков. Блок — это объект Extend, предназна-
ченный для определения действия, процесса, накопления данных, статистического обоб-
щения Другими словами, это объект, предназначенный для моделирования. Связанные
между собой блоки Extend формируют сеть взаимовлияющих активностей Элементы
модели (например, клиенты или автомобили на прокат), поведение которых представля-
ет интерес, перемещаются через связанную сеть блоков, a Extend собирает статистиче-
ские данные об этом. Extend отслеживает любое ожидание или время задержки при пере-
мещении элементов В Extend также имеются блоки специального назначения, исполь-
зуемые для сведения в таблицы статистических данных (таких как длина очереди и время
ожидания) и построения на их основе диаграмм Предопределенные блоки приложения
Extend хранятся в файлах-библиотеках. Поэтому при построении новой модели следует
открыть необходимые библиотеки, чтобы можно было скопировать эти блоки
в создаваемую модель.
Существуют четыре типа связей между блоками: два типа для входа и выхода элементов, и
два — для входа и выхода значений Связи для входа и выхода элементов образуют пути,
по которым элементы перемещаются через блоки модели Эти связи изображаются в ви-
де линий, соединяющих маленькие коннекторы (разъемы), расположенные на одной из
сторон каждого блока Связи для входа и выхода значения передают данные и параметры
элементов между блоками и также изображаются в виде линий, соединяющих коннекто-
ры блоков. В Extend доступ к блоку осуществляется двойным щелчком на нем, каждый
блок имеет диалоговое окно для задания параметров и просмотра результатов после ис-
пытаний модели. В качестве примера на рис. 11.7 показан блок Activity, Delay
(Активность, Задержка) используемый обычно для задержки элемента в течение некото-
рого времени, после чего элемент переходит к следующему блоку.3 Для модели Хервиса
это время задержки равно 5 мин , которые клиент проводит у стойки по оформлению
проката Элементы (клиенты) входят в блок через левый коннектор и после задержки вы-
ходят через правый Как только элемент (отдельный клиент) входит в блок, он удержива-
ется в нем ровно 5 мин., как указано в поле Delay (Задержка) в диалоговом окне блока.
Это диалоговое окно вызывается двойным щелчком на блоке. Как показано на рис. 11.7,
блоку можно задать имя в поле, расположенном в нижней части окна (в этом примере —
Задержка-сервис4) Для получения более подробной информации о блоке Activity, Delay
можно щелкнуть на кнопке Help (Справка), находящейся в этом диалоговом окне. В диа-
логовом окне Help можно увидеть, для каких целей предназначены три других коннекто-
Extend также можно использовать для построения непрерывных имитационных моделей В главе 10 для
этих целей использовалась надстройка Crystal Ball
Для удобства названия предопределенных блоков Extend будут выделяться курсивом
В Extend максимальная длина задаваемых имен блоков составляет 15 символов — Прим ред
ГЛАВА 1 1. Моделирование дискретных событий 751
ра этого блока Коннектор D применяется для входа значения, которое отменяет время
задержки, установленное в диалоговом окне блока. Этот коннектор можно использовать
для задания произвольного времени задержки во время испытания модели вместо фик-
сированной 5-минутной задержки Коннекторы Т и U предназначены для выхода значе-
ний и могут использоваться для предоставления информации о занятости и проценте ис-
пользования этого блока, передаваемой другим блокам во время испытания модели
Г Utilize blocking
Г "Г connector Is true/false
11 model default
Ие»о1|Эадержка-с( < |
Рис. 11.7 Блок Activity, Delay, его диалоговое окно и окно справки
После окончания процесса имитации, дважды щелкнув на блоке, снова вызовите диа-
логовое окно Во вкладке Results (Результаты) показана информация, записанная в бло-
ке во время имитации, например, среднее значение использования блока (процент заня-
тости сервиса) и количество элементов, вышедших из блока (т е. количество обслужен-
ных клиентов). Все блоки Extend обладают одинаковой базовой структурой, состоящей
из входных и выходных коннекторов, используемых для задания маршрутов элементов
в системе, диалогового окна блока для установки параметров и записи собранных в про-
цессе имитации статистических данных, а также коннекторов для входа или выхода зна-
чений во время испытаний модели
Построение имитационной модели Хервиса
После запуска программы Extend автоматически открывается окно новой модели.
В меню Run (Выполнить) выберите команду Simulation Setup (Установки моделирова-
ния), открывающую одноименное диалоговое окно (рис. 11.8). Это диалоговое окно по-
зволяет определить, каким образом и как долго будет осуществляться имитация модели.
752
ЧАСТЬ III Вероятностные модели
Обычно единственными параметрами, которые устанавливаются в этом окне, являются
единицы измерения времени и время окончания имитации модели Для большинства
моделей имитация начинается с заданного по умолчанию нулерого момента времени.
Опцию Number of runs (Количество испытаний) можно оставить равной 1, если нет не-
обходимости отслеживать вариации результатов во время многократных испытаний мо-
дели Поскольку Хервис моделирует операции по прокату автомобилей поминутно в те-
чение недели, необходимо открыть список Global time units (Глобальные единицы вре-
мени) и выбрать опцию Minutes (Минуты) Как и для предыдущей модели, построенной
в Excel, Хервис выполнит имитацию в течение недели моделируемого времени, которое
равно 10 080 мин (24x7x60) Поэтому необходимо ввести число 10080 в поле End
simulation at time (Время окончания имитации), как показано на рис 11 8, и щелкнуть на
кнопке ОК Для каждого испытания модели Extend повторно использует значения пара-
метров, которые были определены в диалоговом окне Simulation Setup.
Рис. 11.8. Диалоговое окно Simulation Setup
Если в Extend была открыта какая-либо модель, для начала создания новой модели сле-
дует выбрать File^New Model (Файл^Новая модель); Extend откроет окно для новой моде-
ли Для добавления блока в окно модели необходимо выполнить следующие действия.
1.	Открыть при необходимости библиотеку, содержащую предопределенные блоки
Extend
2.	Выбрать требуемый блок из библиотеки и добавить его к модели.
3.	Поместить этот блок в нужную позицию в окне модели
4.	Соединить его с другими блоками
Совет. Выполнив команду Edit^Preferences (Правка ^Предпочтения) и щелкнув в от-
крывшемся диалоговом окне на вкладке Libraries (Библиотеки), можно ввести имена биб-
лиотек в список Preload libraries (Предварительно загруженные библиотеки). Тогда каж-
дый раз при запуске Extend будет автоматически открывать эти библиотеки.
ГЛАВА 11. Моделирование дискретных событий 753
Для того чтобы скопировать предопределенный блок Extend в модель, библиотека,
в которой хранится этот блок, должна быть открытой. Для создания модели Хервиса не-
обходимо открыть библиотеки Generic (Общая), Discrete Event (Дискретные события),
Plotter (Графопостроитель) и Stats (Статистика). Чтобы открыть библиотеку Discrete
Event, следует выполнить команду Library=>Open Library (Библиотека^Открыть библио-
теку), найти папку Libs, выбрать библиотеку Discrete Event (файл DE lix) и щелкнуть на
кнопке Открыть. Для открытия библиотек Generic (файл GENERIC Их), Plotter (файл
PLOTTER.lix) и Stats (файл STATS Irx) выполняется такая же последовательность дейст-
вий. Обратите внимание на другое расширение 1гх в имени библиотеки STATS
После того как вы откроете нужные библиотеки, в меню Library появится список этих
библиотек, а когда вы установите курсор на имени библиотеки — откроется список типов
объектов, содержащихся в данной библиотеке. Типы объектов, в свою очередь, открыва-
ют список названий блоков этого типа Теперь, чтобы добавить блок к модели, нужно
в меню Library выбрать имя библиотеки, тип блока и его название, после чего копия бло-
ка помещается в окно Extend.
При моделировании дискретных событий всегда необходим блок Executive (Диспетчер)
из библиотеки Discrete Event (файл DE.ltx), который помещается слева у самого края окна
модели Этот блок (с пиктограммой часов) определяет продолжительность имитации, усло-
вия остановки и оперирует деталями планирования событий Обычно соединение с блоком
Executive отсутствует
Модель Хервиса начинается с прибытия автофургона с клиентами, которым нужны
прокатные автомобили Прибытие автофургона представлено в модели блоком Generator
(Генератор) и добавляется в модель с помощью описанных выше действий из подменю
Generators библиотеки Discrete Event Двойной щелчок на блоке вызывает его диалого-
вое окно, показанное на рис. 11 9. Поскольку автофургоны аэропорта прибывают через
5-минутные интервалы, в этом диалоговом окне в списке Distribution (Распределение)
выбирается опция Constant (Постоянное) и в поле Constant вводится значение 5 Если
ранее не была установлена общая единица измерения времени, то в списке Time Units
(Единицы измерения времени) выбирается опция Minutes (Минуты) В нижнее поле ок-
на введем имя блока Клиенты (потребуется для документирования)
Рис. 11.9. Параметры блока Generator
754 ЧАСТЫН. Вероятностные модели
Совет, Extend всегда помещает новые блоки на место последнего щелчка кнопкой мыши в ок-
не модели После вставки блок можно легко переместить с помощью мыши. Более точное
позиционирование блока в окне модели выполняется с помощью клавиш управления курсором.
Каждый прибывающий от самолета автофургон содержит разное количество клиен-
тов, вероятностное распределение этого количества дано в табл 111. По умолчанию
блок Generator создает один клиент, но любое количество генерируемых клиентов можно
задать посредством ввода значений через коннектор V В данном случае случайное число
клиентов создается с помощью блока Input Random Number (Ввод случайного числа), ко-
торый находится в библиотеке GENERIC.lix в подменю Inputs/Outputs (Ввод/Вывод).
Добавив блок Input Random Number, дважды щелкните на нем, откроется его диалоговое
окно (рис 11 10) После выбора в списке Distribution (Распределение) опции Empirical
Table (Эмпирическая таблица) в диалоговом окне появляется таблица, куда можно вве-
сти данные из табл 111, как это показано на рис 11.10 Для обозначения этого блока
в модели можно задать имя блока К-во клиентов. Кроме того, в окно модели можно до-
бавить прямоугольник с текстом “Прибывающие клиенты” для документирования этого
раздела модели Прямоугольник с текстом создается просто двойным щелчком мыши
в свободной области окна модели и последующим вводом текста. Параметры текста
можно изменить с помощью меню Тext (Текст)
Рис. 11.10. Параметры блока Input Random Number
Совет. Прямоугольники с текстом позволяют документировать модель Их можно переме-
щать с помощью мыши, а для редактирования текста следует дважды щелкнуть на них.
Пронумерованные коннекторы блока Input Random Number (в данной модели они не
нужны) используются для задания значений параметров для таких типов распределения,
как нормальное, экспоненциальное, равномерное и др. Другой коннектор на правой сто-
роне блока предназначен для вывода значения, в данном случае он подключается к вход-
ГЛАВА 11. Моделирование дискретных событий	755
ному коннектору V блока Generator. Связь между блоками показывается с помощью ли-
ний, соединяющих коннекторы блоков. Чтобы соединить блоки, необходимо поместить
указатель мыши на коннектор, указатель примет вид чертежного пера. Затем перо при
нажатой кнопке мыши надо переместить к другому коннектору Соединение состоялось,
когда тонкую линию заменит толстая (рис 1111) Отпустив кнопку мыши, увидите два
коннектора, соединенных тонкой сплошной линией Теперь наша пара связанных бло-
ков будет генерировать каждые 5 мин прибытие клиентов, количество которых будет из-
меняется от 0 до 3 в соответствии с вероятностями из табл 111.
Рис. 11.11. Соединение
коннекторов двух блоков
Совет. Обычно соединение блоков обозначается с помощью прямой линии между двумя кон-
некторами Extend также позволяет производить соединение посредством многосегментных
и именованных соединений. Эти два способа соединения блоков расширяют возможности мо-
дели Многосегментные соединения создаются с использованием одной или нескольких точек
привязки в каждом изломе соединяющей линии. Точка привязки создается при отпускании
нажатой кнопки мыши и последующего щелчка левой кнопкой мыши во время перемещения
чертежного пера.
Далее группу поступивших клиентов нужно поставить в очередь перед пунктом по
оформлению проката, которую они проходят в порядке поступления (такая дисциплина
очереди называется FIFO, от First In, First Out, т e. первый пришел — первый вышел) Для
этого добавляются блоки Queue, FIFO (Очередь, FIFO) из подменю Queues (Очереди) биб-
лиотеки DE.lix. Затем входной коннектор этого блока соединяется с выходным коннекто-
ром блока Generator, помещая клиентов в очередь (рис 11 12). Обратите внимание на диа-
логовое окно блока Queue, FIFO, где задан параметр Maximum queue length (Максимальная
длина очереди) со значением 1000, что фактически создает неограниченную очередь Кон-
некторы для выхода значений L и W этого блока во время имитации дают информацию
о количестве элементов в очереди и о времени ожидания клиентов
Обратите внимание на то, что соединительные линии, по которым элементы
(клиенты) перемещаются между блоками, двойные (как бы полые), а линии для передачи
информации (значений) обозначаются тонкими сплошными линиями
Важно отметить, что элементы (в данном случае клиенты), создаваемые блоком Genera-
tor, сразу из него выходят, поэтому в модели должно быть какое-нибудь место, куда они
могут войти. Это обычно требует прямого подсоединения блока Generator к одному из бло-
ков Queue или Resource (Ресурс) В противном случае можно потерять элементы, генерируе-
мые блоком Generator, что приведет к неверным статистическим результатам имитации
756 ЧАСТЫН Вероятностные модели
Рис. 11.12. Присоединение клиентов к очереди
Заполнение контракта на прокат автомобиля требует времени В первоначальной мо-
дели Хервиса служащий, отвечающий за оформление контрактов, задерживает каждого
клиента в течение 5 мин для завершения сделки по аренде автомобиля Чтобы ввести эту
задержку, можно использовать блок Activity, Delay (Активность, Задержка), который рас-
сматривался выше Однако этот блок вмещает только один элемент, а Хервис хотел бы
изучить ситуацию, при которой оформление документов на прокат выполняют несколь-
ко служащих В таком случае следует использовать блок Activity, Multiple (Активность,
Множественная), который можно найти в подменю Activities (Активности) библиотеки
DE lix Этот блок позволяет задерживать несколько элементов, т е. предоставлять одно-
временное обслуживание нескольким клиентам. Заключив договор на прокат, клиент
выходит из офиса для получения автомобиля Элементы покидают имитационную мо-
дель через блок Exit (Выход), который находится в подменю Routing (Маршрутизация)
библиотеки DE lix
На рис II 13 показаны блок Activity, Multiple со своим диалоговым окном и окном
Help справочной системы, блок Exit, а также прямоугольники с поясняющим текстом
Диалоговое окно блока Activity, Multiple отражает первоначальную модель с одним слу-
жащим, у которого время обслуживания клиента занимает ровно 5 мин. Назначение
других коннекторов блока Activity, Multiple описано в справочном окне.
На этом построение базовой модели Хервиса завершается. Но Extend имеет дополни-
тельные блоки для сбора данных в процессе имитации и для ее графического отображе-
ния Наиболее полезным из них является блок Plotter, Discrete Event (Плоттер, Дискретное
событие), находящийся в библиотеке PLOTTER.lix. Этот блок фиксирует данные и во
время имитации модели вычерчивает диаграммы для нескольких (до четырех) перемен-
ных Он также может хранить эти и другие данные, полученные в результате многократ-
ных имитации модели, в виде многостраничных выходных данных для их дальнейшего
анализа Переменные, которые должны быть собраны и представлены в виде диаграмм,
определяются коннекторами блоков, подключенными к блоку Plotter, Discrete Event. Как
ГЛАВА 11. Моделирование дискретных событий 757
показано на рис. 11.14, блок Plotter, Discrete Event будет фиксировать степень занятости
служащих, оформляющих прокат (данные, получаемые от блока Activity, Multiple), и полу-
чаемые от блока Queue, FIFO данные о времени, в течение которого клиент ожидает об-
служивания. На рис. 11.14 также показан простой блок Help (Справка), который можно
найти в библиотеке GENERIC.lix в подменю Inputs/Outputs. Этот блок при двойном
щелчке мышью на нем позволяет ввести некоторый текст для описания модели
Оформление
авт™™11"
Прибывающие
клиенты
автомобилей
I inis асиипц can work on menu Hems at once.
Activity. Multiple (DE LIX)
Virtual Memoiy(MB) 399 c
The item output connector is the delayed item
К-во клиентов
C Maximum number in block This overrides the maximum number in in lhe dialog il
connected. If this connector has a value of less than the number of items currently m lhe
capacity will be reduced as each item leaves until the actual capacity matches the
F Outputs 1 when the block is full otherwise outputs 0
L Number ol items in the block
W Wait time for items leaving the block
Topic* I Next I Preulou»| Print | Search | Cancel |
Рис. 11.13. Добавление к модели блоков Activity, Multiple и Exit
758 ЧАСТЬ III Вероятностные модели
Имитация модели
Чтобы начать имитацию, необходимо выполнить команду Run^Run Simulation
(Выполнить^Выполнить имитацию) или на панели инструментов Extend щелкнуть на кнопке
с нарисованной стрелкой, направленной вправо В начале имитации Extend отображает
в нижней части экрана строку состояния, где показаны значения параметров настройки, оп-
ределенные в диалоговом окне Simulation Setup, и открывает окно плоттера (рис. И 15), в ко-
торое динамически выводятся данные, передаваемые на блок Plotter, Discrete Event (в данном
случае это информация о занятости служащего, обслуживающего клиентов, и о времени ожи-
дания в очереди) В процессе имитации модели можно заметить, что время ожидания для кли-
ентов увеличивается и уменьшается на время, кратное 5 мин., а максимальное время ожида-
ния равняется 35 мин Также нетрудно заметить, что средний процент занятости служащего
близок к 50%, те служащий будет занят только половину времени (в среднем) Результаты,
полученные в следующей имитации, будут отличаться от этих результатов из-за случайного
характера количества поступающих клиентов
После окончания имитации можно просмотреть таблицу данных в нижней части окна
плоттера, чтобы увидеть значения, по которым строились диаграммы. Можно также по-
местить курсор на линии диаграммы, при этом Extend отобразит координаты точки, на
которую указывает курсор.
Обращаем ваше внимание на панель инструментов в окне плоттера, которая предна-
значена для изменения параметров настройки плоттера, заданных по умолчанию, на-
пример, автоматического изменения осей координат и т д Щелчок на крайней слева
кнопке этой панели инструментов открывает окно свойств диаграммы, показанное на
рис И 16 Каждой переменной, отображаемой плоттером, отводится в этом окне две
строки, одна для свойств аргумента (времени) переменной, другая — для свойств самой
переменной Параметры, заданные в столбцах окна, указывают обозначение для пере-
менной, цвет, толщину и тип линии, числовой формат данных и другое.
Совет. Если величины, отображаемые в окне плоттера, имеют разный масштаб, то удобно
использовать две оси значений, как показано на рис. 11.15.
Статистические данные, собранные в блоках Queue, FIFO и Activity, Multiple в резуль-
тате имитации, можно просмотреть во вкладках Results (Результаты) диалоговых окон
этих блоков, как показано на рис. 1117 (окна открываются двойным щелчком мыши на
ГЛАВА 11. Моделирование дискретных событий
759
этих блоках). Эти данные показывают, что в данной имитации среднее время ожидания
для клиента было меньше 5 мин. (4,162 мин ), а максимальное время ожидания, по край-
ней мере для одного клиента, равнялось 25 мин Длина очереди была в среднем менее по-
ловины клиента (0,42 элемента), но возрастала, по крайней мере в одном случае, до
8 клиентов.5 Служащий, оформляющий прокат, был занят приблизительно 50% времени
Рис. 11.15. Результаты имитации модели Хервиса
Рис. 11.16. Окно свойств диаграммы
Совет. Результаты имитации сохраняются при сохранении модели Позже их можно еще
раз просмотреть, дважды щелкнув на соответствующем блоке
В самом худшем случае восьмой клиент прибывает в то время, когда начато обслуживание первого клиен-
та, а остальные 7 клиентов ожидают обслуживания Обслуживание занимает 5 мин , т е седьмому к тен-
ту приходится ожидать начала обслуживания 35мин
760 ЧАСТЬ 111. Вероятностные модели
Рис. 11.17. Результаты имитации в блоках
Queue, FIFO и Activity, Multiple
Как и при построении модели в Excel, Хервис хочет видеть эффект от добавления еще
одной стоики (и, соответственно, еще одного служащего) для обслуживания клиентов.
Он должен удостовериться в том, что добавление еще одного служащего произведет такое
же сокращение максимальной длины очереди клиентов, как и полученное ранее в Excel.
Чтобы сделать это, ему необходимо дважды щелкнуть на блоке Activity, Multiple и изме-
нить параметр Maximum Number in Activity (Максимальное количество элементов в дей-
ствии) с 1 на 2 в диалоговом окне, показанном на рис. 11.13 Повторная имитация модели
дает результаты, показанные на рис 1118, схожие с результатами, полученными в Excel.
Как и ожидалось, средний процент использования этих двух сервисов меняется до 25%.
Максимальная длина очереди снижается до четырех, и клиенты ожидают обслуживания
не более 5 мин. Это в семь раз меньше предыдущего результата.6
6 В самом худшем случае четвертый клиент прибывает в то время, когда только начато обслуживание пер-
вых двух клиентов, а оставшиеся два клиента ожидают окончания обслуживания этих двух первых клиен-
тов Обслуживание занимает 5 мин , следовательно, каждый из двух ожидающих обслуживания в очереди
ожидает начала своего обслуживания максимум 5 мин
ГЛАВА 11. Моделирование дискретных событий 761
Рис. 11.18. Модель Хервиса с двумя служащими
11.4.	Расширенная модель Хервиса
Легкость изменения и анализа моделей дискретных событий, разработанных в Extend,
по сравнению с моделями в Excel становится очевидной по мере того, как Хервис иссле-
дует другие аспекты этой ситуации. Например, Хервис знает по опыту, что автобусы мо-
762
ЧАСТЬ III Вероятностные модели
гут задерживаться и не всегда прибывают ровно через каждые 5 мин. Для того чтобы из-
менить модель с учетом этого обстоятельства, ему достаточно только определить характер
этой дополнительной изменчивости На рис 11.19 показано, как изменить в Extend пер-
воначальную модель, чтобы задать интервал времени между последовательными прибы-
тиями автофургонов от 3 до 7 мин с наиболее вероятным значением, равным, как и пре-
жде, 5 мин До некоторой степени произвольно для описания времени между прибытия-
ми автофургонов Хервис выбирает простое треугольное распределение.7 Чтобы задать это
распределение, Хервису надо только указать тип распределения (приблизительно из 20
стандартных типов, предоставляемых приложением Extend) и определить его параметры
в диалоговом окне блока Generator
Рис. 11.19. Задание распределения времени прибытия автофургонов
Далее Хервис задумался о правильности предположения о том, что служащему для
оформления контракта на прокат автомобиля всегда необходимо ровно 5 мин. Он решает
также учесть некоторую изменчивость этого фактора своей модели Однако блок Activity,
Multiple не имеет, в отличие от блока Generator, встроенного источника случайных вели-
чин Но из описания коннектора D на рис 11 13, видно, что можно добавить другой блок
Input Random Number (Ввод случайных чисел) (из подменю Inputs/Outputs библиотеки
GENERIC lix), генерирующий случайные числа с заданным распределением, который
можно подсоединить к коннектору D блока Activity, Multiple, таким образом отменяя
фиксированное времени задержки в этом блоке. Это соединение блоков показано на
рис 11 20 Для описания времени обслуживания выбрано экспоненциальное распреде-
ление со средним временем задержки, как и прежде, 5 мин.8
Для большей точности Хервис должен собрать фактические значения интервалов времени между прибытиями
автофургонов и определить, насколько собранные данные соответствуют треугольному распределению.
S Вновь Хервис должен собрать эмпирические данные относительно длительности подготовки контракта по
прокату автомобиля для того, чтобы проверить предположение об экспоненциальном типе распределения
ГЛАВА 1 1. Моделирование дискретных событий 763
Рис. 11.20. Задание распределения времени обслуживания
Хервис полагает, что введение в модель дополнительных факторов изменчивости (для
большей реалистичности) приведет к большей вариативности итоговых значений време-
ни ожидания и длины очереди Он также предполагает, что эти нововведения не скажут-
ся на средних значениях длины очереди и времени ожидания, поскольку средние значе-
ния обоих распределений такие же, как в его первоначальной модели
Чтобы проверить свои предположения, Хервис провел имитацию последней модели
(рис. 1120) Результаты имитации показаны на рис 1121 Новый фактор изменчивости су-
щественно увеличил максимальное время ожидания (44,8 мин) и немного — максималь-
ную длину очереди (8 клиентов). Однако, несмотря на то, что средние значения новых слу-
чайных величин (т е. времени между прибытием автофургонов и времени обслуживания)
совпадают со значениями этих параметров первоначальной модели, полученные результаты
(рис. 11 21) показывают, что увеличилось среднее значение времени ожидания (5,92 мин )
и среднее значение длины очереди (0,592 клиентов) После некоторых размышлений мож-
но убедиться в обоснованности полученных результатов и ошибочности первоначальных
предположений Хервиса. Такое проникновение в суть исследуемых простых имитационных
моделей важно для обобщений, особенно при анализе сложных систем.
Испытывая отчаяние от того, что модели предсказывают низкую производительность его
офиса, Хервис выполнил еще одну имитацию, чтобы увидеть, произведет ли добавление еще
одного служащего столь же впечатляющий эффект, как и ранее. Для этого двойным щелчком
на блоке Activity, Multiple он открывает диалоговое окно этого блока и изменяет в нем значение
параметра Maximum Number in Activity с 1 на 2, а затем выполняет имитацию Результаты этой
имитации показаны на рис. 11 22 К счастью, новые значения среднего и максимального вре-
мени ожидания выглядят приемлемыми среднее время ожидания равно примерно 0,41 мин ,
а максимальное время ожидания менее 13 мин. Конечно, Хервису необходимо выполнить
большее количество имитаций для подтверждения достоверности полученных результатов
ЧАСТЬ III Вероятностные модели

Рис. 11.21. Результаты имитации модем со случайными интерва-
лами времени между прибытием автофургонов и случайным време-
нем обслуживания
ГЛАВА 11. Моделирование дискретных событий 765
Рис. 11.22. Результаты имитации модели со слу-
чайными факторами и двумя служащими
Имитационное моделирование в химическом
производстве
В химической промышленности предприятия могут выбирать один из двух спо-
собов производства продукции. Первый способ — это непрерывный технологиче-
ский процесс, в котором производится один вид химического продукта различной
концентрации Переход на изготовление нового продукта является дорогостоящим,
поскольку перед производством нового продукта вся технологическая система долж-
766 ЧАСТЬ 111 Вероятностные модели
на быть промыта и осмотрена. Поэтому большинство химических предприятий с не-
прерывным технологическим процессом выпускают только один вид продукции.
Другой способ предусматривает загрузку сырья в технологическую систему по типу
рецептов, тогда можно произвести широкий ассортимент продуктов, которые затем
превращаются в несколько различных химических соединений с помощью следую-
щего метода
Сырье подается в резервуары для предварительного смешивания. Затем смесь
транспортируется к основным резервуарам для дальнейшего смешивания До того
как сырье будет запущено в процесс предварительного смешивания, основные ре-
зервуары, так же как и трубопроводы, ведущие к ним, подготавливаются и очищают-
ся После основного смешивания химические продукты отправляют в одно из трех
мест резервуары для дальнейшей переработки, распределительные резервуары или
резервуары для выдержки В резервуарах для переработки хранят химикаты, которые
не отвечают стандартам В этих резервуарах химикаты перерабатываются в целях по-
вышения их качества до такой степени, чтобы их можно было продать. Если это не
удается, то химикаты выбрасывают Если переработка проведена успешно, то хими-
каты отправляют в резервуары для хранения готовой продукции. Химикаты, отправ-
ленные непосредственно в распределительный резервуар, перемещают в резервуар
для хранения продукции, где они содержатся до момента продажи. Если химикаты
были отправлены в резервуар для выдержки, то они позже направляются через рас-
пределительный резервуар в резервуар для хранения готовой продукции, где они на-
ходятся до момента их продажи Трубопроводы между различными типами резервуа-
ров должны тщательно очищаться для гарантии того, что в пути продукция не будет
загрязняться
Большие химические предприятия могут значительно улучшить свою работу,
правильно спроектировав производство. Это особенно верно в тех случаях, когда
проектировщики определяют, какая продукция будет производиться на том или
ином типе оборудования и какие резервуары для выдержки будут использоваться.
При таком проектировании выискиваются ошибки в критических параметрах, обес-
печивается гарантия качества продукции и производится анализ стадий производст-
ва на предприятии
Эдвард Ф Уотсон (Edward F Watson) из университета штата Луизиана использо-
вал имитационную модель дискретных событий, чтобы помочь большому произво-
дителю химической продукции в проектировании нового предприятия. Уотсон для
моделирования процессов на химическом предприятии разработал систему модель-
ных блоков резервуаров и трубопроводов (типа зон обслуживания и очередей). Ис-
пользуя данные по существующему предприятию, он проанализировал такие факто-
ры, как методика выбора основного резервуара, гарантии качества, транспортировки
смеси и т д На основе результатов моделирования он разработал рекомендации для
рационального и эффективного проектирования нового предприятия. Используя
имитационную модель, компания смогла выявить свои производственные пробле-
мы, связанные с проектированием новых предприятий и оценить предложенные
усовершенствования до их реализации, экономя таким образом значительные сред-
ства и время [2]
ГЛАВА 1 1. Моделирование дискретных событий 767
11.5.	Изменение модели Хервиса
Стоя в очереди в супермаркете, Хервис обдумывал новые результаты своей имитаци-
онной модели. Разумеется, с помощью Extend он может быстро строить имитационные
модели своего предприятия по прокату автомобилей. Больше всего его удивляет, как
“разрушительно” воздействует на время ожидания в очереди добавление изменчивости
к распределению времени между прибытиями автофургонов и к распределению времени
обслуживания, хотя их средние значения оставались такими же, как в предыдущей моде-
ли Это навело его на мысль, что уменьшение изменчивости, как в расписании прибытия
автофургонов, так и во времени обслуживания клиентов, увеличит среднюю производи-
тельность его офиса.
Размышляя над этими проблемами, он обратил внимание на то, что менеджер супер-
маркета по мере удлинения очередей начал открывать дополнительные кассы по обслу-
живанию покупателей Это подало Хервису идею Он может использовать часть персона-
ла по обслуживанию автомобилей, чтобы при необходимости увеличить количество сто-
ек по оформлению проката. Это позволит ему сократить персонал до количества, которое
необходимо для двух стоек в периоды низкого спроса, а в часы пик довести число служа-
щих, занимающихся оформлением контрактов, до трех или даже четырех
Хервис, заинтригованный этой идеей, задался вопросом, как преобразовать свою мо-
дель в Extend, чтобы она динамически изменяла свое поведение во время моделирования
в соответствии с собственной статистикой производительности Необходимо найти спо-
соб заставить Extend изменять значение в поле Maximum Number in Activity диалогового
окна блока Activity, Multiple во время имитации на большее или меньшее число при увели-
чении и уменьшении длины очереди Хервис, рассматривая свою модель на рис Н 13,
замечает, что в имитационной модели уже есть средства, необходимые для реализации
этой идеи
Сначала, дважды щелкнув на блоке Queue, FIFO, он вызвал его диалоговое окно
и щелкнул на кнопке Help (Справка), чтобы удостовериться в том, что коннектор L во
время имитации передает значение длины очереди. Затем он нашел в справочной систе-
ме, что коннектор С блока Activity, Multiple можно использовать для ввода значения, ко-
торое заменяет число в поле Maximum Number in Activity. Теперь Хервису необходим
способ для передачи значения от коннектора L блока Queue, FIFO к коннектору С блока
Activity, Multiple во время имитации модели.
В Extend есть блок для преобразования значений коннектора L в значения, приемле-
мые для коннектора С Этот блок называется Conversion Table (Таблица преобразования),
его можно найти в подменю Math (Математика) библиотеки GENERIC lix На рис. 11 23
показана модель Хервиса с добавленным блоком Conversion Table. На вход этого блока
подаются значения от коннектора L блока Queue, FIFO, а его результаты передаются на
коннектор С блока Activity Multiple В прямоугольнике с текстом также показано правило,
в соответствии с которым увеличивается количество служащих в пункте проката Это
правило реализуется в диалоговом окне блока Conversion Table. В этом окне входные зна-
чения записываются в столбце х in, а выходные (преобразованные) — в столбце у out
Отметим, что Хервис не предполагает, что очередь будет более 7 человек
768 ЧАСТЬ III Вероятностные модели
Рис. 11.23. Модель Хервиса с изменяемым количеством служащих
Стремясь поскорее увидеть улучшение в обслуживании клиентов, Хервис щелкает на
кнопке Run Simulation (кнопка со стрелкой, направленной вправо) панели инструментов
Extend, чтобы выполнить имитацию новой версии своей модели Результаты этой имита-
ции показаны на рис 11 24
Рассматривая результаты, Хервис удивляется тому, насколько плохо работает его схема
динамического использования персонала Выходит, что увеличение в два раза персонала во
время прибытия максимального количества клиентов ухудшает статистику, отражающую
время ожидания обслуживания Сравнивая результаты, показанные на рис. 11.24, с резуль-
татами на рис 11.22 (использование двух служащих, занятых полный рабочий день), Хервис
видит, что среднее время ожидания для клиента увеличивается более чем в пять раз прибли-
зительно с 0,41 до 4,41 мин., а максимальное время ожидания в очереди возросло почти до
34 мин ' Это ухудшение связано с ростом среднего количества ожидающих клиентов с 0,04
до более чем 0,42. Но как это может быть9
После проверки логики модели Хервис приходит к заключению, что этот случайный
результат был вызван неблагоприятной последовательностью случайных чисел при ими-
тации модели Но верно ли это заключение9 Проверить этот вывод можно, только мно-
гократно выполнив имитацию модели и сравнив полученные результаты, чтобы удосто-
вериться в нетипичности результатов на рис. 11 24 Но такой подход является бессистем-
ным, поскольку он зависит от человеческой памяти, субъективно оценивающей
результаты многократных имитаций модели К счастью, в Extend в библиотеке STATS 1гх
имеется блок Queue Stats (Статистики очереди), предназначенный для сведения в таблицу
статистических данных об очереди, полученных в результате многократных имитаций
модели, что помогает систематично оценивать влияние случайностей, присущих модели,
на показатели очереди На рис 11 25 показан блок Queue Stats, который можно поместить
в любой точке окна модели, вместе с его диалоговым окном. Для того чтобы свести в таб-
ГЛАВА 11. Моделирование дискретных событий 769
лицу результаты многократных имитаций, необходимо установить опцию Append new
updates (Новые данные добавить в конец) и опцию (для ускорения процесса имитации)
Update at end of simulation (Обновлять в конце имитации). Затем следует с помощью ко-
манды Run^Simulation Setup вызвать диалоговое окно Simulation Setup (Установки
имитации) (см. рис. 11.8) и изменить значение в поле Number of runs (Количество испы-
таний) с 1 на, скажем, 20. Это будет командой для Extend выполнить 20 независимых
имитаций модели Хервиса и свести в единую таблицу блока Queue Stats статистические
данные об очереди, полученные в каждой имитации.
Рис. 11.24. Результаты имитации модели с из-
меняемым количеством служащих
770 ЧАСТЬ III Вероятностные модели
Щелчок кнопкой мыши на кнопке Run Simulation приведет к 20 имитациям модели. На
это требуется определенное время, процесс имитаций отображается в строке состояния
в нижней части окна Extend Если по окончании имитаций дважды щелкнуть на блоке Queue
Stats, откроется окно с таблицей результатов, показанное на рис. 11.26. Щелчок на кнопке
Confidence Interval (Доверительный интервал) в диалоговом окне блока Queue Stats приводит
к построению 95-процентных доверительных интервалов для наблюдаемых величин.
Рис. 11.25. Диалоговое окно блока Queue Stats
И1ШЖ1ТОИЯВ^МИШИИ
necords statistics on all queue-tqpe
Пурирль JS'irup F1FO.CI ^^43^7Я1Л 0ЛЛЛЛППЛГ1^4 П£П5ЯЕ371^3ЯЯякя40Л4< ]
ГЮрпрлк Лпаия FlFO.n ЗЯЯ227ЯЯЯЛ ППЛПЛППЛО.З Я_ЗЯ1734Я8.37 4Я71 7ЯЕ?Н
..П.ияпр.л.к..4аиаир..Е1ЕСХ0..424Я1.49.38;5..0ЛЛП0ПЛЛ0‘4.Ш.43.7ЛЯЯ;ЗЕ..ЗЗП9.1.22Й|
Лирпрпн Лиаир FIFO.!! 4ЛЯЯПЯЯД9Л ППППЛПЛППЛ ПЯ7ЕЯЯ5Я4.4П.34ЯЯ24.3Я<
Пирпрпн Лиаир F1FO.O 3244123ПЛЛЛПЛПЛПППЛ.З 81 ЯШЕЯЯ4.32 Л713Я4ЯЛ
Лирпрпн ЛиаиР FiFO.fl 4ЯП1Я774Я.ЕППЛЛЛПЛП0.4 Ч4ЯЯ87Я.30.4Е2ЯЕЯ.34П4-
Оирпр л к ЛлаиР НРаЛ..ЗЯ2ЯЯЯ7£45..0ПППЛПППП=4..0.337.3222Я13Я.22П74Я.ЗЯ=
ЛиРПР.л.н..’С)цр.ир...Е1ЕСНП..3.7.ЯЕЛЛ9Я2ЛЛПЛПЛДПДЛ;З..ЯЕ2.7ЛЕПП1;3.1..Е7.7.941Н21
ПиРПРпн iQiiPUP FlFClin 41Я18.3Я935 ЛПППЛПЛПП14..2.17ПЗЯЗЕ7142.ЕЯЗЕБПБП= ДИ
Пирпрлн AiauP F1FD.0 ЗЯЛ44ДЯ12.Я ЛЯПЛЛЛППЛЛ ЯЯ4Я2ЯЯЯ4.3Я45.39Я8.33; ,
...Пирлр.лъ...Лиаий...Е1ЕСШЯ4ЕПЗБЕ2;5..ППППЛПШ1П14..ЛД1ЕЕ35.4П13.1..19Я4.1.7ЯЛ=^1
Sort by block I Sort bg time |
ч Continence Interval
open selected block» |
17 Append new updates
Г Clear statistics after update
|7 Update at end of simulation
ГUpdate continuously
Рис. 11.26. Статистические данные для отдельных имитации
г*
ГЛАВА 11. Моделирование дискретных событий 771
Результаты на рис. 11 26 показывают, что данные, которые так удивили Хервиса, не
были нетипичными, и что предложенная им гибкая политика использования персонала
оказалась плохой идеей. Эта политика последовательно ведет к увеличению среднего
и максимального времени ожидания клиентами обслуживания по сравнению с использо-
ванием двух постоянных служащих.
Этот пример ясно показывает, что моделирование является мощным инструментом,
дополняющим и проверяющим интуицию, которая часто ошибается в предсказании по-
ведения сложных систем в условиях перегрузки В качестве упражнения на основе ре-
зультатов моделирования объясните, почему предложенная Хервисом политика исполь-
зования персонала ошибочна.
11.6.	Окончательная модель Хервиса
Отказавшись на основе результатов моделирования от своей идеи гибко использовать
персонал, Хервис возвращается к своей первоначальной политике двух постоянных слу-
жащих, занятых оформлением проката Его окончательная модель, отображающая эту
ситуацию, показана на рис. 11 27
Но теперь Хервис считает, что быстрого обслуживания клиентов при оформлении про-
ката для его предприятия мало Он должен также обеспечить достаточное количество авто-
мобилей Хервис предполагает, что есть только два типа клиентов те, которые хотят не-
большие автомобили экономичного класса, и те, кто желает арендовать большие и мощные
автомобили класса люкс. Полагая, что большинство клиентов будет привлечено в его фир-
му благодаря умеренной цене, Хервис считает, что 70% его клиентов предпочтут экономич-
ные автомобили, а остальные выберут большие автомобили Очень важно правильно опре-
делить количество автомобилей каждого типа. Прошлый опыт убедил его в том, что клиен-
ты, арендующие экономичные автомобили, берут их на один или два дня, а срок аренды
больших автомобилей немного больше, обычно два дня плюс-минус половина дня Для мо-
делирования времени проката экономичных автомобилей Хервис выбирает равномерное
распределение, а больших автомобилей — нормальное распределение со стандартным от-
клонением, равным половине дня
772 ЧАСТЬ III. Вероятностные модели
Совет. Возможно, лучшим выбором для распределения времени аренды больших автомобилей
вместо нормального будет логнормальное распределение. Это распределение гарантирует
отсутствие отрицательного времени аренды, а нормальное распределение — нет.
Чтобы упростить визуальное представление своей новой модели, Хервис решает вос-
пользоваться иерархическими блоками Extend. Это позволяет создавать модели, состав-
ленные из подмоделей, каждая из которых является логически связанной группой блоков.
Таким образом можно создавать “суперблоки”, каждый из которых является подмоде-
лью, составленной из множества блоков Extend. Чтобы это сделать, откройте модель, вы-
берите группу связанных блоков и выполните команду Model^Make Selection Hierarchi-
cal (МодельюСоздать иерархию). Extend “спрячет” выбранные блоки в суперблок, кото-
рый можно обозначить и подсоединить, в свою очередь, к другим блокам или
суперблокам, что в результате приводит к очень компактной модели. Например, теперь,
когда Хервис обращает свое внимание на моделирование управления парком автомоби-
лей, ему хочется скрыть блоки, относящиеся к модели офиса (рис 11 27), в виде отдель-
ного суперблока
Чтобы это сделать, необходимо выделить все блоки, щелкая на них левой кнопкой
мыши при нажатой клавише <Shift>, кроме блоков Executive и Exit, и выполнить команду
Model^Make Selection Hierarchical. Будет открыто диалоговое окно, где надо задать имя
новому суперблоку, как показано на рис. 11 28 Назовем его Office9, затем щелкнем на
кнопке Make Н-В1оск (Создать иерархический блок) в этом окне. Все выбранные блоки
станут частью подмодели, подсоединенной к блоку Exit Это можно проверить с помо-
щью двойного щелчка на новом блоке — откроется окно со всеми выбранными блоками.
После закрытия окна подмодели окно основной модели будет иметь вид, как окно
в нижней части рис 11 28 Теперь Хервис может добавить к этой упрощенной модели на
место блока Exit новые блоки так, чтобы клиенты, выходящие из подмодели Офис, попа-
дали в блок управления парком автомобилей.
Чтобы смоделировать передачу клиентам автомобилей, Хервис должен отличать кли-
ентов, желающих арендовать экономичные автомобили от тех, которые хотят большие
машины Для этого он сначала удаляет блок Exit, выделив его и нажив клавишу <Delete>,
и начинает моделировать парк автомобилей, добавив два новых блока, показанных на
рис 11 29 Часть диалогового окна нового блока Input Random Number (из подменю In-
put/Output библиотеки GENERIC.Их) отображена в нижней части этого рисунка. Обра-
тите внимание на использование опции Empirical Table (Эмпирическая таблица) для за-
дания распределения случайной величины, принимающей значение 0 (обозначает, что
требуется экономичный автомобиль) с вероятностью 0,7 и значение 1 (требуется боль-
шой автомобиль) с вероятностью 0,3. Выход этого блока соединен с входным коннекто-
ром нового блока Select DE Output (Выход выбранного дискретного события) из подменю
Routing библиотеки DE Их Этот блок разделяет поток элементов (клиентов) и направля-
ет на один из двух выходных коннекторов на основе значения, поступившего на его кон-
нектор Select (Выбор). В диалоговом окне этого блока (рис. 11.29) видно, что входяший
клиент направляется к верхнему выходу (коннектор “а”), если случайное число на кон-
некторе Select равно 0 и направляется к нижнему выходу (коннектор “Ь”), если случай-
9 Здесь задается имя блока, под которым он будет известен программе Extend Это имя лучше задавать ла-
тинскими буквами, поскольку Extend не всегда корректно работает с кириллическими шрифтами Чтобы
задать имя блока, которое будет отображаться на экране в окне модели, надо дважды щелкнуть на этом
блоке и ввести это имя в нижней части открывшегося окна с содержимым блока — Прим ред
ГЛАВА 11. Моделирование дискретных событий 773
ное число на коннекторе Select равно 1. Итак, два новых блока направляют клиента, вы-
ходящего из блока Офис, к верхнему выходу блока Select DE Output (экономичный авто-
мобиль) с вероятностью 0,7 и к нижнему (большой автомобиль) с вероятностью 0,3.
Рис. 11.28. Преобразование модели офиса в иерархический блок
Разделив клиентов в соответствии с типом арендуемых автомобилей, Хервис может
далее смоделировать передачу автомобилей клиентам. Он начинает с клиентов, арен-
дующих большие автомобили, и вводит еще два блока. Эти блоки, Resource Pool
(Накопитель ресурсов) (из подменю Resources (Ресурсы) библиотеки DE lix) и Queue,
Resource Pool (Очередь, Накопитель ресурсов) (из подменю Queues (Очереди) библиоте-
ки DE.lix), и их диалоговые окна показаны на рис. 11.30. Resource Pool — это перемен-
ная, которая показывает количество доступных элементов ограниченного ресурса, в дан-
ном случае — больших автомобилей. Основываясь на своем прогнозе еженедельного
максимального спроса на большие автомобили, Хервис в диалоговом окне Resource Pool
вводит в поле Initial number (Начальное значение) число 100 (количество имеющихся
в наличии больших автомобилей) Блок Queue, Resource Pool задерживает элементы
(клиентов, арендующих большие автомобили) до тех пор, пока не будет доступно опреде-
ленное количество элементов (в данном случае один) в блоке Resource Pool Deluxe Car,
774 ЧАСТЬ III Вероятностные модели
а затем выводит элемент и уменьшает на I число элементов в блоке, таким образом моде-
лируя передачу клиенту автомобиля Обращаем внимание на то, что блок Resource Pool
является глобально доступной переменной и не имеет соединений с другими блоками.
Рис. 11.29. Разделение клиентов по типу арендуемого автомобиля
Теперь, когда богатый клиент получил большой автомобиль, Хервис должен смодели-
ровать интервал времени проката этого автомобиля Как показано на рис 11 31, для
этого используется блок Activity, Multiple (из подменю Activities библиотеки DE.lix), осу-
ществляющий задержку, время которой определяет новый блок Input Random Number (из
подменю Inputs/Outputs библиотеки GENERIC lix), где задано нормальное распределе-
ние случайной задержки, среднее значение которой равно 2 дням (2880 мин.), а стан-
дартное отклонение составляет 0,5 дня (720 мин ). Пропускная способность блока Activ-
ity, Multiple задана значением 1000 Такое большое число гарантирует, что ни один эле-
мент не будет задержан при входе в этот блок По истечению времени проката (случайной
задержки) автомобиль возвращается в ресурс больших автомобилей (становится доступ-
ным для последующей аренды) с помощью блока Release Resource Pool (Освобождение
элементов ресурса) из подменю Resources библиотеки DE lix Этот блок и его диалого-
вое окно показаны на рис. 11 31.
ГЛАВА 11 Моделирование дискретных событий 775
Рис. 11.31. Моделирование времени проката и возвращение больших автомобилей
776 ЧАСТЬ III. Вероятностные модели
Как показано на рис. 11.32, моделирование клиентов, арендующих экономичные ав-
томобили, ничем не отличается от моделирования клиентов больших автомобилей. Для
экономичных автомобилей добавляется другой блок Resource Pool, где снова, руково-
дствуясь своим мнением о спросе на такие автомобили, Хервис устанавливает их началь-
ное количество — 140. Также добавлен блок Queue, Resource Pool, где клиент получает ав-
томобиль (если экономичные автомобили имеются в наличии) Далее следуют блоки
Queue, Multiple и Input Random Number, моделирующие время проката. Затем идет блок
Release Resource Pool, возвращающий автомобили для повторного проката. Наконец, для
выхода клиентов обоих типов из модели используется блок Exit (4) (из подменю Routing
библиотеки DE Их)
Чтобы сохранить расположение клиентов, Хервис хочет усовершенствовать обслужи-
вание клиентов экономичных автомобилей, предоставляя им, если возможно, большие
автомобили в случае отсутствия экономичных автомобилей. Это реализовано в диалого-
вом окне блока Queue, Resource Pool Econ. Car, показанном на рис. 11.32. Обращаем вни-
мание на то, что оба накопителя ресурсов поименованы, и Extend начинает поиск ресур-
сов в том накопителе ресурсов, имя которого стоит первым в списке Pool name (Имя на-
копителя) диалогового окна блока Econ. Саг В данном случае Extend будет пытаться
сначала взять автомобиль из ресурсов Econ. Саг. Если этот накопитель ресурсов пуст,
рассматривается накопитель ресурсов Deluxe Саг, и будет взят большой автомобиль
в случае, если он доступен. В противном случае клиент будет удерживаться до тех пор,
пока один автомобиль любого типа не станет доступным Это то, чего хочет Хервис. Од-
нако в результате такого подхода возникает “бухгалтерская” проблема. В модели должно
ГЛАВА 11 Моделирование дискретных событий 777
быть известно, какого типа автомобиль арендован для того, чтобы позже, при возвраще-
нии автомобиля из проката, вернуть его в соответствующий накопитель ресурсов.
Диалоговое окно на рис. 11 32 позволяет создавать атрибуты элементов. Атрибут при-
лагается к элементу (клиенту) и следует за ним через все блоки модели. В данном случае
атрибут Саг Туре (Тип авто) был создан с помощью щелчка на кнопке pool name (имя
накопителя) и ввода имени атрибута в открывшемся диалоговом окне (на рис. 11 32 это
окно не показано). Во время имитации модели клиентам, желающим арендовать эконо-
мичные автомобили, передаются для проката автомобили из одного из двух возможных
накопителей ресурсов, при этом атрибуту Саг Туре будет присвоено имя того накопителя
ресурсов, из которого был взят автомобиль.
Как показано в диалоговом окне блока Release Resource Pool на рис 11 33, возвращен-
ный из проката автомобиль передается в один из двух накопителей ресурсов в зависимо-
сти от значения атрибута Саг Туре. На этом рисунке также показано диалоговое окно
блока Input Random Number, задающего случайное время задержки для блока очереди
Queue, Multiple (время проката автомобиля). Эта задержка моделируется равномерным
распределением из диапазона от 1440 до 2880 мин., т.е равным одному-двум дням, как
и было определено Хервисом.
Рис. 11.33. Задание распределения времени задержки и возвращение в накопители ресурсов
автомобилей, взятых напрокат
На рис. 11.34 показана законченная модель с новыми блоками Queue Stats (из библио-
теки STATS.lrx), Help (из подменю Inputs/Outputs библиотеки GENERIC.Их) и Plotter,
Discrete Event (из библиотеки PLOTTER.lix), а также новый блок Activity Stats (из библио-
теки STATS,Их). Последний блок собирает статистические данные для блоков Activity так
же, как блок Queue Stats делает это для блоков Queue. Блоки Activity Stats и Queue Stats
можно размещать в любом месте окна модели. Интерпретация результатов, содержащих-
ся в этих блоках, облегчается, если всем блокам Activity, Multiple присвоить имена (после
двойного щелчка на блоке открывается его диалоговое окно, имя вводится в поле рядом
с кнопкой Help). Как показано на рис. 11.34, блоки Activity, Multiple названы соответст-
778 ЧАСТЬ III Вероятностные модели
венно Эконом, прокат и Люкс прокат. Для накопления результатов на протяжении мно-
гократных имитаций модели в диалоговом окне блока Activity Stats (здесь не показанного)
необходимо задать опции Append new updates и Update at end of simulation (как было
сделано ранее в окне блока Queue Stats на рис. 11.25).
Рис. 11.34. Окончательная модель проката автомобилей
На рис 11.35 представлены графики изменения наблюдаемых переменных, получен-
ные в результате одной имитации модели, где заданы начальные значения количества ре-
сурсов, равные 140 экономичным автомобилям и 100 большим автомобилям Этого ко-
личества автомобилей, как предполагает Хервис, должно быть достаточно Два графика,
выполненных тонкими линиями, используют левую шкалу и показывают количество ав-
томобилей каждого типа, арендуемых в течение недели (верхняя линия — количество
экономичных автомобилей, в число которых иногда включаются большие автомобили
согласно политике Хервиса) Для оценки модели Хервису более важны два графика, вы-
полненные толстыми линиями, которые используют правую шкалу Эти графики пока-
зывают количество клиентов, которые не могут сразу получить в аренду автомобиль из-за
их отсутствия
Как свидетельствуют графики, начального количества автомобилей не достаточно для
удовлетворения всех требований клиентов Это не случайный результат, что подтверждают
показанные на рис 11 36 окна блоков Queue Stats и Activity Stats с 95-процентными довери-
тельными интервалами, построенные после 20 имитаций модели. Например, среднее время
ожидания автомобиля для клиентов больших автомобилей равно 140 ±49 мин., для клиен-
тов экономичных автомобилей время ожидания любого типа автомобиля в среднем было
вдва раза меньше. Но еще хуже максимальное время ожидания: 513 ±96 мин. для клиента
больших автомобилей и 316 ±90 мин. для клиента экономичных автомобилей Поскольку
ГЛАВА 11 Моделирование дискретных событий
779
ни один клиент не будет ожидать автомобиль от одного до двух часов (в среднем) или более
того (максимальное время ожидания — до десяти часов), Хервис должен увеличить число
своих автомобилей Но на сколько9 Надо ли их количество удвоить или утроить, что, ко-
нечно, удвоит или утроит его затраты на автомобили, или же можно увеличить на меньшее
число9
Рис. 11.35. Результаты первой имитации модели проката автомобилей
Рис. 11.36. Доверительные интервалы для статистических данных
Почувствовав, насколько зависит время ожидания клиентов от количества автомоби-
лей, Хервис решил поэкспериментировать, увеличивая начальные количества автомоби-
лей каждого типа примерно на 15%, начав с 115 больших автомобилей и 160 экономич-
ных К его утешению, следующая имитация показывает значительное уменьшение вре-
мени ожидания клиентов, как показано на рис. 11.37 На этом рисунке также показаны
95-процентные доверительные интервалы для наблюдаемых величин после 20 имитации
модели Среднее время ожидания, равное 2,8± 3,3 мин для клиентов больших автомоби-
лей и 0,93 ± 1,3 мин. для клиентов экономичных автомобилей, говорит о том, что Хервис
ненамного ошибся в отношении количества автомобилей
780 ЧАСТЬ III Вероятностные модели
Рис. 11.37. Новые результаты имитации
Совет. Extend поддерживает анимацию моделей. Хотя анимация замедляет выполнение
имитаций, она полезна при отладке и демонстрации модели. Отдельные блоки Extend также
позволяют определять стоимостные показатели, предоставляя возможность собирать ин-
формацию о совокупных издержках производства. Наконец, полная версия Extend обеспечи-
вает оптимизацию модели. Например, оптимизация позволила бы Хервису определить коли-
чество автомобилей, минимизирующих общие издержки.
Хотя средние значения времени ожидания, показанные на рис. 11.37, для Хервиса
приемлемы, но максимальные значения времени ожидания все еще слишком велики.
Хервис решает провести другую серию имитаций модели, используя еще большие на-
чальные количества автомобилей, равные 170 и 125 соответственно для экономичных
и больших автомобилей. На рис. 11.38 показаны 95-процентные доверительные интерва-
лы для наблюдаемых величин после 20 имитаций модели.
Рис. 11.38. Результаты имитаций для 170 и 125 автомобилей
Хервис удовлетворен показанными на рис. 11.38 результатами, но хочет продолжить
дальнейший анализ влияния на основные показатели модели начальных количеств авто-
мобилей и надеется улучшить результаты, изменив распределение времени проката авто-
ГЛАВА 11 Моделирование дискретных событий	781
мобилей и прибытия клиентов Он полагает, что время ожидания клиентов тоже может
зависеть от этих параметров, поэтому необходим дальнейший анализ модели перед при-
нятием окончательных решений, касающихся его предприятия
11.7.	Заключение
Эта глава посвящена имитационному моделированию дискретных событии Модели
дискретных событий детально отслеживают перемещение неких элементов по сложной ве-
роятностной системе на протяжении заданного времени, в результате чего оцениваются
различные параметры, связанные с этими перемещениями На примере модели обслужива-
ния клиентов сначала было показано, как моделирование дискретных событий можно реа-
лизовать с помощью средств Excel Поскольку требуется детальное отслеживание переме-
щения отдельных элементов (клиентов) по системе, большая часть рабочего листа Excel за-
нята формулами Такие большие табличные модели слишком сложны и громоздки для
построения, документирования и расчетов Кроме того модели, построенные в Excel, плохо
масштабируются, т е изменения длительности моделируемых периодов, длины минималь-
ных временных интервалов или других параметров системы требуют кардинального изме-
нения всей табличной модели, часто вынуждая строить модель заново
Недостатки имитационного моделирования дискретных событий в Excel преодолеваются
с помощью приложения Extend, специально предназначенного для моделирования Построе-
ние моделей в Extend требует перехода от табличного представления модели, состоящей из
столбцов и строк электронной таблицы, к структуре имитационной модели, основанной на
стандартных блоках Extend Модель, составленная из таких блоков, позволяет визуализиро-
вать потоки элементов и информации в системе. Хотя в этой главе была представлена только
часть из более чем 100 доступных блоков Extend, очевидно, что блочная конструкция позволя-
ет легко строить имитационные модели любой степени сложности, которые можно проанали-
зировать с помощью средств, также предоставляемых программой Extend
Метод имитационного моделирования дискретных событий, проиллюстрированный
в данной главе, подчеркивает основы методики моделирования, рассматриваемые в этой
книге Они заключаются в том, что следует начинать с простой модели реальной ситуа-
ции и постепенно ее усложнять до получения усовершенствованных моделей, более пол-
но отражающих моделируемую ситуацию. При учете в имитационной модели дополни-
тельных факторов реальной жизни полезно использовать иерархические блоки Extend
Создание подмоделей с помощью этих блоков является полезным способом поддержки
модульности системы и возможности документирования модели.
Читатели, которые хотят получить более полную информацию по вопросу моделиро-
вания дискретных событий с помощью Extend, могут посмотреть руководство, которое
находится на компакт-диске, прилагаемом к этой книге. В это руководство включены
дополнительные примеры моделей, которые иллюстрируют множество других блоков,
полезных при построении моделей дискретных событий, а также примеры аналогового
моделирования и возможности Extend, которые не рассматривались в этой главе.
Основные термины
Extend Доступное программное приложение, предназначенное для построения дискретных и не-
прерывных имитационных моделей.
Аналоговое (непрерывное) моделирование Моделирование, включающее агрегированные перемен-
ные, которые со временем изменяются более или менее непрерывно
782 ЧАСТЬ III Вероятностные модели
Блок Модуль, описывающий часть имитационной модели в Extend
Иерархический блок То же самое, что и подмодель
Моделирование дискретных событий Моделирование, при котором отслеживаются отдельные случай-
ные элементы, вероятностное распределение которых имеет разрывы (негладкое распределение)
Моделирование очереди Моделирование дискретных событий, включающее ожидание элементов
в очередях
Моделирование Детальное наблюдение за моделью сложной вероятностной системы на протяже-
нии заданного интервала времени
Подмодель Группа связанных блоков Extend, которой можно дать имя и использовать в качестве
нового блока
Связи Соединения между блоками имитационной модели в Extend, по которым происходит пере-
мещение элементов или передача данных
Контрольные вопросы
Да/нет
1.	Моделирование заменяет анализ ситуаций
2.	Результат моделирования дискретных событий — это совокупность данных на-
блюдения за их (событий) поведением на протяжении какого-то времени
3.	Повторные имитации модели, содержащей случайные элементы, будут всегда
приводить к одинаковым результатам
4.	В результате моделирования системы очереди получаем данные, которые значи-
тельно зависят от параметров вероятностных распределении
5.	Сложные имитационные модели дискретных событий очень легко создавать в Excel
6.	Сложные имитационные модели дискретных событий, построенные в Extend, об-
ладают полезной возможностью документирования
7.	При построении в Excel сложных имитационных моделей дискретных событий их
легко изменить при введении более мелких временных интервалов и моделирова-
нии более длительных временных периодов
8.	Имитационные модели дискретных событий легче создавать и анализировать
в Extend, чем в Excel
9.	Имитационная модель дискретных событий является хорошей заменой опыта
и интуиции исполнителя
10.	Extend облегчает выбор типа распределения вероятностей, который следует ис-
пользовать в имитационной модели
11.	Использование обобщенных данных наблюдений, полученных в результате мно-
гократных имитаций одной и той же модели дискретных событий, всегда предпоч-
тительнее использования данных наблюдений, полученных в результате одной
имитации этой модели
12.	В Extend нетрудно ввести в модель дополнительные факторы с помошью вставки
новых блоков
Ответы
1 Нет 2. Да 3 Нет 4 Да 5 Нет 6 Да 7 Нет 8 Да 9 Нет 10 Нет. 11 Да 12 Да.
ГЛАВА 11 Моделирование дискретных событий	783
Учебные задачи
Имитационная модель дискретных событий в Extend является примером
а физической модели,
b аналоговой модели,
с символической (математической) модели
Предположим, что в модели Хервиса изменилось расписание прибытия автофургонов с пас-
сажирами Теперь автофургоны прибывают в два раза реже, те каждые 10 мин вместо 5 Но
число клиентов, доставляемых каждым автофургоном, возрастает в два раза со следующим
распределением количества клиентов 0 клиентов с вероятностью 0,7, 2 — с вероятностью
0,12, 4 — с вероятностью 0,16 и 6 — с вероятностью 0,02 В этом случае среднее количество
клиентов, прибывающих каждые 10 мин , равно 1 Таким образом, новая средняя интенсив-
ность входного потока клиентов эквивалентна предыдущей аналогичной интенсивности,
равной 0,5 клиента каждые 5 мин Изменится ли время ожидания клиентами автомобилей по
сравнению со значением, приведенным на рис 1117, для ситуации, когда прокат оформляет
один служащий'' Реализуйте в модели Хервис1.тох (см рис 11 14) указанные изменения,
выполните ее имитацию и найдите новое среднее время ожидания клиентов
Консультант порекомендовал Хервису для определения интервалов времени между прибылыми
автофургонов применить экспоненциальное распределение с той же средней интенсивностью
входного потока, равной 1 фургону каждые 5 мин Изменится ли после этого время ожидания кли-
ентами автомобилей по сравнению со значением, приведенным на рис 1121, когда прокат оформ-
ляет только один служащий9 Реализуйте в модели Hervisl глох (показана на рис 11 14) указанные
изменения, выполните ее имитацию и найдите новое среднее время ожидания клиентов
Объясните с точки зрения науки управления, почему предпринятая Хервисом гибкая по-
литика обеспечения персоналом, описанная в разделе 11 5, ухудшила показатели времени
ожидания клиентами по сравнению с аналогичными показателями постоянного использо-
вания двух служащих
Статистические данные, полученные после имитации законченной модели Хервиса, могут вве-
сти в заблуждение, поскольку он предположил, что оба ресурса автомобилей (экономичных
и больших) в начале каждой недели содержат столько автомобилей, сколько им предписывается
начальными значениями Как показано на рис 11 37, это привело к недолгому ожиданию клиен-
тов в начале недели, поскольку здесь неявно предполагается, что все автомобили в конце преды-
дущей недели немедленно возвращаются в парк Каким образом Хервис может преодолеть или
уменьшить влияние этого неявного предположения на статистику значений времени ожидания9
Прикладные задачи
116 В модели офиса по прокату автомобилей, представленной на рис И 20, предполагается, что
клиенты сразу после заключения контракта по аренде берут автомобиль и уезжают Пусть это
правило распространяется на 95% клиентов, а остальные 5% клиентов возвращаются в офис,
поскольку их контракт содержит ошибки Предположим, что после возвращения в офис они
становятся в конец очереди и, по сути, повторяют процесс заключения контракта в качестве
нового клиента Измените модель Hervis2 mox (рис 11 20) с учетом повторного обслуживания
5% клиентов Выполните имитацию измененной модели и сравните полученные результаты
с результатами, показанными на рис И 21 (Совет Рассмотрите возможность использования
блока Combine из подменю Routing библиотеки DE lix )
11 7 Смоделируйте ситуацию, приведенную в предыдущем пункте, но теперь для повторного
обслуживания эти 5% клиентов становятся не в конец, а в начало очереди Выполните
имитацию модели и сравните полученные результаты с результатами, показанными на
рис 1121 (Совет Рассмотрите возможность использования блоков Set Priority из подменю
Attributes и Queue Priority из подменю Queues библиотеки DE lix )
784 ЧАСТЬ III Вероятностные модели
И 8 Гибкая политика обеспечения персоналом, описанная в разделе II 5, привела к увеличе-
нию времени ожидания клиентами обслуживания Для исследования причин этого факта
измените в таблице преобразования, приведенной на рис 11 23, значения числа служащих
на новые значения, которые, по вашему мнению, лучше, чем у Хервиса, и выполните ими-
тацию модели Будут ли новые результаты лучше тех результатов, которые дает модель
с двумя постоянными служащими'' Если это так, то каково среднее число занятых служа-
щих* * * 9 (Совет Рассмотрите возможность использования блока Mean and Variance из подме-
ню Statistics библиотеки GENERIC lix для отслеживания числа занятых служащих )
11 9 Хервис решил пересмотреть свою модель, которая показана на рис 11 20 Пусть на проти-
воположной стороне улицы, где расположен офис Хервиса, находится конкурирующая
фирма по прокату автомобилей Клиенты, ожидающие обслуживания в очереди в офисе
Хервиса более 15 мин , теряют терпение и покидают офис Хервиса, чтобы воспользоваться
услугами конкурирующей фирмы Измените модель Hervis2 глох (рис 11 20), чтобы учесть
“сбежавших” клиентов Выполните имитацию измененной модели и сравните полученные
результаты с результатами, показанными на рис 1121 Как зависит число ушедших клиен-
тов (в среднем) от числа служащих, оформляющих прокат9 (Совет Рассмотрите возмож-
ность использования блока Queue, Reneging из подменю Queues библиотеки MFG 1гх )
1110 Пусть действуют условия предыдущей задачи, но теперь 10% клиентов, пришедших в офис
Хервиса, сразу покидают его, если в нем находится более шести клиентов, ожидающих об-
служивания, и переходят к конкуренту Остальные 90% клиентов становятся в очередь не-
зависимо от ее длины Измените модель Hervis2 глох (рис 1120), чтобы учесть
“сбежавших” клиентов Выполните имитацию измененной модели и сравните полученные
результаты с результатами, показанными на рис 1121 Как зависит число ушедших клиен-
тов (в среднем) от числа служащих, оформляющих прокат9
1111 Хервис выпустил “золотые” карточки для 10% своих клиентов С обладателями таких карто-
чек заключены постоянные контракты и они без оформления проката после выхода из авто-
фургонов по предъявлению своих “золотых” карточек, с которых считывается номер клиента,
сразу получают автомобиль для проката Среди таких клиентов 50% предпочитают большие
автомобили, а 50% —экономичные Таким клиентам при отсутствии экономичных авто пре-
доставляются большие машины “Золотые” клиенты обычно арендуют автомобили на более
длительное время большие автомобили сроком на три дня, плюс-минус половина дня, а эко-
номичные автомобили сроком на два или три дня. (Хервис предполагает, что для описания
времени аренды автомобилей в этом случае подходят те же самые типы распределения, что
и для времени проката обычных клиентов, т е нормальное для больших автомобилей и рав-
номерное для экономичных.) Измените модель Hervis4 mox (рис 11 34), чтобы учесть
“золотых” клиентов Выполните имитацию измененной модели и сравните полученные ре-
зультаты с результатами, показанными на рис 11 38 Каким образом эти изменения повлияют
на начальные количества экономичных и больших автомобилей9
11 12 Хервис понимает, что предположения, на которых построены его модели, далеки от реаль-
ности Поэтому он решил внести в модели следующие изменения Во-первых, Хервис ре-
шил использовать экспоненциальное распределение для задания временных интервалов
между последовательными прибытиями фургонов как наиболее реалистичное Во-вторых,
поскольку активность аэропорта различна в разное время суток, поток прибывших клиен-
тов не может быть постоянным Так, объем пассажирских перевозок в аэропорту уменьша-
ется в вечерние часы, существенно снижается после полуночи, а утром снова возрастает.
Поэтому Хервис хочет изменить свою модель, применив экспоненциальное распределение
для задания временных интервалов между последовательными прибытиями автофургонов
Эти интервалы изменяются в течение суток в соответствии с приведенной ниже таблицей.
Время суток_____________Среднее время между прибытием автофургонов, мин.________
00 00-5 59	30
6 00-8 59	15
9 00-1159	10
ГЛАВА 11. Моделирование дискретных событий 785
Время суток	Среднее время между прибытием автофургонов, мин.
12 00-18 59	5
19 00-20 59	10
21 00-23 59	15
Измените модель Hervis4 mox (рис 11 34), чтобы учесть изменение времени между прибы-
тиями автофургонов в зависимости от времени суток, при этом пусть начальный момент
имитационного времени соответствует полуночи первого дня Выполните имитацию изме-
ненной модели и сравните полученные результаты с результатами, показанными на
рис 11 38 Каким образом эти изменения повлияют на начальные количества экономич-
ных и больших автомобилей7 (Совет Рассмотрите возможность использования блока Input
data из подменю I пр ut/Output библиотеки GENERIC lix )
11 13 Недавно ресторан быстрого обслуживания Бегущий гамбургер провел большую рекламную
кампанию с целью привлечения клиентов-автомобилистов в полуденное время, используя
так называемое “обслуживание на колесах” Ресторан гарантирует, что в 12-13 часов их
клиентам потребуется в среднем не более четырех минут с момента их въезда на террито-
рию ресторана и до момента получения пищи Чтобы гарантировать успех своей новой
кампании, владелец Бегущего гамбургера должен определить, какое количество служащих
потребуется в полуденное время и где каждый из них должен работать, чтобы клиенты по-
лучали свои заказы в среднем в течение четырех или менее минут Для этого необходимо
учесть следующие факторы Во-первых, клиенты “на колесах” обслуживаются в очереди по
принципу “первым прибыл, первым обслуживаешься” Чтобы получить пищу, они должны
пройти через три пункта обслуживания окно заказа, окно оплаты и окно выдачи заказа
Во-вторых, обычный персонал в Бегущем гамбургере во время ленча состоит из 3-5 человек
На каждое окно должно быть назначено не менее одного работника В-третьих, предпола-
гается, что интервалы времени между последовательными прибытиями клиентов в полу-
денные часы распределены экспоненциально со средним значением 3 мин , и в полдень
перед началом обслуживания нет клиентов Наконец, последнее Предполагается, что вре-
мя обслуживания в каждом окне имеет следующие распределения вероятностей
Время обслуживания в окне заказа, мин.	Вероятность
0,60	0,07
0,65	0,10
0,70	0,14
0,75	0,26
0,80	0,22
0,85	0,16
0,90	0,05
	
Время обслуживания в окне оплаты, мин.	Вероятность
0,1	0,05
0,2	0,11
0,3	0,13
0,4	0,23
0,5	0,18
0,6	0,21
0,7	0,09
786 ЧАСТЬ III Вероятностные модели
Время обслуживания в окне выдачи, мин.	Вероятность
0,4 0,5 0,6 0,7 0,8 0,9 1,0	0,05 0,11 0,13 0,23 0,18 0,21 0,09
а Каково среднее время полного обслуживания клиента во время ленча при наличии трех ра-
ботников, по одному в каждом окне9 Время полного обслуживания — это время с момента
въезда клиента в ресторан до момента получения заказанной еды (Совет Рассмотрите воз-
можность использования при создании модели в Extend блоков System Variable (библиотека
Genenc lix), Set Attribute (библиотека DE lix), Get Attribute (библиотека DE hx), Subtract
(библиотека Genenc lix) и Mean and Variance (библиотека Genenc hx))
b	Какой процент клиентов получит свой заказ в течение четырех минут9 (Совет Рассмотрите
возможность использования блока Histogram Plotter (библиотека Plotter hx) для создания гис-
тограммы распределения времени полного обслуживания клиента)
с Если Бегущий гамбургер может выделить пять дополнительных работников, то какие
окна они должны обслуживать и как это повлияет на среднее время обслуживания
клиентов9 Какой процент клиентов получит обслуживание в течение четырех минут9
d В Бегущем гамбургере территория, прилегающая к ресторану, ограничена Перед окном
кассы есть место только для двух автомобилей, столько же места и перед окном выдачи
заказа Насколько изменятся (и изменятся ли) ваши рекомендации по привлечению до-
полнительных работников при этом новом условии9 Каким будет среднее время полного
обслуживания клиента9 Какой процент клиентов получит заказ в течение четырех минут9
е Предположим, что ресторан может перепланировать свою территорию таким образом,
чтобы три автомобиля могли находиться в очереди к окну оплаты, но при этом остает-
ся место только для одного автомобиля в очереди к окну выдачи заказа В качестве аль-
тернативы можно перепланировать территорию так, чтобы три автомобиля могли на-
ходиться в очереди к окну выдачи заказа, но при этом остается место только для од-
ного автомобиля в очереди в кассу Какую из трех конфигураций очереди (одна
описана в пункте d и две здесь) можно порекомендовать ресторану9 Насколько изме-
нятся (и изменятся ли) ваши рекомендации по привлечению дополнительных работ-
ников в этих условиях9 Каким будет среднее время полного обслуживания клиентов9
Какой процент клиентов будет обслужен в течение четырех минут9
f Вместо перепланировки территории, описанной в предыдущем пункте, предположим,
что ресторан может объединить операции оплаты и выдачи заказа Тогда окно оплаты
будет закрыто, а оплата и выдача заказа будут производиться в окне выдачи заказа
Предполагается, что время для выполнения объединенной операции по оплате и вы-
даче заказа равно сумме времени, если бы эти операции выполнялись по отдельности,
при этом надо учитывать вероятностные распределения времени каждой операции,
приведенные выше Пространство перед объединенным окном позволяет находиться
в очереди четырем автомобилям Как изменятся (и изменятся ли) ваши рекомендации
по привлечению дополнительных работников в этих условиях9 Каким будет среднее
время полного обслуживания клиентов9 Какой процент клиентов будет обслужен в те-
чение четырех минут9
Подготовьте рекомендации для руководства ресторана Бегущий гамбургер относительно не-
обходимого количества персонала и организации обслуживания клиентов-автомобилистов
в полуденное время
ГЛАВА 11. Моделирование дискретных событий 787
Сью Круз, директор магазина по продаже смазочных материалов, решила повысить эффек-
тивность своей работы, поскольку недавно на этой же улице конкуренты открыли подоб-
ный магазин Магазин Сью располагает четырьмя площадками для замены масла, т е од-
новременно могут обслуживаться не более четырех автомобилей Когда все четыре пло-
щадки заняты, клиенты стоят в очереди, организованной по принципу “первым пришел,
первым обслужен”, дожидаясь свободной площадки Распределения вероятностей времени
между прибытием клиентов и заменой масла даны в следующих таблицах
Время между прибытиями, мин.	Вероятность
3	0,45
4	0,23
5	0,15
6	о,н
7	0,06
Время замены масла, мин.	Вероятность
8	0,22
10	0,19
12	0,32
14	0,27
В процессе замены масла автомеханики пытаются убедить клиентов в необходимости по-
купки новых воздушных фильтров Клиенты, которые не видят необходимости в замене
воздушного фильтра, выезжают со своей площадки сразу после замены масла Клиенты,
которые хотят купить воздушный фильтр, продолжают занимать площадку в течение вре-
мени, которое требуется на его замену Наблюдения Сью показывают, что примерно 10%
клиентов согласны заменить воздушный фильтр, распределение вероятностей времени ус-
тановки нового фильтра дано в следующей таблице
Время замены фильтра, мин.	Вероятность
5	0,07
6	0,25
7	0,43
8	0,25
Замена воздушного фильтра в автомобиле не начинается до тех пор, пока не закончится
замена масла Работники магазина Сью могут производить одновременно не более трех за-
мен масла и двух замен воздушных фильтров Но, конечно, общее количество замен масла
и фильтров, сделанных в одно и то же время, не превышает количества доступных площа-
док (равного четырем) Сью решила, что для ее бизнеса плохо, когда среднее время ожида-
ния в очереди превышает четыре минуты Создайте средствами Extend модель бизнеса
Сью Предполагается, что магазин Сью открыт 16 ч в сутки и пуст при открытии
а Сколько в среднем клиенту приходится ждать, чтобы попасть на одну из четырех пло-
щадок этого магазина9
b Как можно увеличить продажу воздушных фильтров, не превышая среднее время ожи-
дания 4 мин 9
с Если Сью увеличит количество своих служащих, чтобы производить одновременно бо-
лее трех замен масла, то повлияет ли это на среднее значение ожидания клиентов9
788 ЧАСТЫН Вероятностные модели
1115 Пат Уэст управляет маленьким копировальным бюро в Иствилле Поскольку Иствилл — ма-
ленький провинциальный городок, для получения новых картриджей с тонером (красящим
порошком) для своих копировальных устройств требуется две недели Одного картриджа хва-
тает на 10 000 копий Копировальное бюро располагает такой информацией по еженедельным
средним количествам сделанных копий
Количество копий за неделю	Вероятность
10 000	0,12
20 000	0,25
30 000	0,41
40 000	0,17
50 000	0,05
Пат теряет $7 000 в неделю, если его бюро простаивает Каждое размещение заказа на
картридж стоит S10, а один картридж — $100 Разработайте в Excel имитационную мо-
дель, чтобы ответить на следующие вопросы
а Смоделируйте работу бюро в течение 52 недель, предположив, что Пат делает заказ на
10 картриджей в конце каждой недели всякий раз, когда его запасы снижаются до 6
или менее картриджей Какой процент времени бюро простаивает из-за отсутствия
картриджей9 Насколько это приемлемо9
b Предположим, что время получения новых картриджей случайно и распределено сле-
дующим образом получение картриджей в течение 1 недели с вероятностью 25%, 2 не-
дель — 50%, 3 недель — 25% Каков оптимальный объем заказа картриджей и когда
следует делать заказ в этой ситуации9
с Допустим, что продолжительность использования картриджа также является случай-
ной величиной и распределена следующим образом 8 тыс копий с вероятностью 10%,
9тыс копий с вероятностью 15%, Ютыс копий с вероятностью 50%, 11 тыс копий
с вероятностью 15% и 12 тыс копий с вероятностью 10% Каков оптимальный объем
заказа картриджей и когда следует делать заказ в этой ситуации9
Ситуация для анализа | Snowy Range Hardware10
Компания Snowy Range Hardware (SRH) продает электробуры Асе. Ежедневный
спрос на электробуры сравнительно низок и подвержен изменчивости. Количество
продаж за последние 300 дней показано в столбце 2 табл. 11.2. Эти данные преобра-
зованы в распределение вероятностей случайного ежедневного спроса (столбец 3).
Значения его функции распределения показаны в столбце 4. В последнем столбце
табл. 11.2 рассчитаны интервалы значений равномерно распределенных случайных
чисел, соответствующие распределению возможных значений ежедневного спроса.
Когда фирма SRH подает заказ на пополнение запаса электробуров, поставки
выполняются в срок от 1 до 3 дней. Это означает, что время реализации заказа также
можно рассматривать как случайную величину. Сроки поставки последних 50 зака-
зов и построенное на этих данных распределение сроков показаны в табл. 11.3
(структура этой таблицы аналогична структуре табл. 11.1).
° Этот адаптированный пример взят из книги Heizer and Render. Operations Management, 1999 (5-ih
•ditiim), Prentice Hall
ГЛАВА 1 1. Моделирование дискретных событий 789
Таблица 11.2. Распределение ежедневного спроса на буры Асе
Спрос на буры	Количество дней	Вероятности	Функция распределения	Интервалы слу- чайных чисел
1	2	3	4		5	
0	15	0,05	0,05	0,00-0,0499
1	30	0,10	0,15	0,05-0,1499
2	60	0,20	0,35	0,15-0,3499
3	120	0,40	0,75	0,35-0,7499
4	45	0,15	0,90	0,75-0,8999
5	30	0,10	1,00	0,90-0,9999
300 дней	1,00
Истинное среднее = 0x0,05 + 1x0,10 + 2x0,20 + 3x0,40 + 4x0,15 + 5x0,10 = 2,80
Таблица 11.3. Распределение срока поставки заказа
Сроки постав- ки (дни)	Количество за- казов	Вероятности	Функция распределения	Интервал случай- ных чисел
1	2	3	4		5	
1	10	0,20	0,20	0,00-0,1999
2	25	0,50	0,70	0,20-0,6999
3	15	0,30	1,00	0,70-0,9999
	50 заказов	1,00		
	Истинное среднее = 1x0,20		+ 2x0,50+ 3x0,30 = 2,10	
Компания SRH хочет смоделировать и оценить свою политику управления запа-
сами. в конце рабочего дня, когда имеющийся запас буров равен 5 или меньше, вече-
ром того же дня заказывается еще Ю буров.
Результат имитации Ю-дневного периода показан в табл. 11 4. Предполагалось, что
запас на 1-й день равен 10 бурам. Случайные числа (столбец 4) сгенерированы в Excel.
Таблица 11.4. Имитация запасов буров в течение 10 дней
День Получен Начальные Случайное			Спрос Остаток запаса	Потерянные Заказ Случайное		Срок по- ставки
заказ	запасы	число		продажи	число	
1	2	3	4	5	6	7	8	9	10
1	10	0,06	1	9	0	Нет	
2	0	9	0,63	3	6	0	Нет	
3	0	6	0,57	3	3"	0	Да	0,02	1
4	0	3	0,94	5	0	2	Нет”	
5	10”	10	0,52	3	7	0	Нет	
" Первый раз, когда запасы опустились до уровня, требующего нового заказа 5 буров
11 Заказ не был сделан, поскольку есть невыполненный заказ предыдущего дня
Срок выполнения первого заказа равен 1-му дню, но заказ прибывает не следующим утром после заказа, а
через день. Таким образом, первый заказ прибывает в начале 5-го дня
790 ЧАСТЫН. Вероятностные модели
Окончание табл. 11.4
День Получен	Начальные	Случайное Спрос	Остаток	Потерянные Заказ	Случайное	Срок по-
заказ	запасы	ЧИСЛО	запаса	продажи	число	ставки
1	2	3	4	5	6	7	8	9	10
0,69	3	4
0,32	2	2
0,30	2	0
0,48	3	7
0,88	4	3
0	Да
0	Нет
0	Нет
0	Нет
_0_____ Да
Всего 41	2
Результаты даже одной имитации позволяют вычислить некоторые важные пара-
метры модели
Среднее число ежедневных остатков = 41 (общая сумма остатков)/Ю дней = 4,1 бу-
ров в день
Среднее количество потерянных продаж = 2/10 дней = 0,2 потери вдень.
Среднее количество заказов =3/10 дней = 0,3 заказа в день.
Вопросы
1	Представьте описанную ситуацию в виде имитационной модели в Excel и вы-
полните 20 имитаций 10-дневных периодов
2	Какое значение объема заказа и уровня остатков, при котором делается заказ,
уменьшат количество потерянных продаж? Каково среднее количество остатков
в этом случае9
| Ситуация для анализа | Баржи Миссисипи1
Груженые баржи, возвращаясь из долгого путешествия из промышленных горо-
дов Среднего Запада вниз по Миссисипи, прибывают ночью в Новый Орлеан Коли-
чество таких барж находится в диапазоне от 0 до 5 Распределение вероятностей ко-
личества прибывающих барж показано в табл. 11.5 В той же самой таблице приведе-
ны интервалы равномерно распределенных случайных чисел, соответствующих
каждому возможному значению количества барж
Таблица 11.5. Распределение количества прибывающих барж
Количество барж	Вероятность	Функция распределения	Интервал случайных чисел
0	0,13	0,13	0,00-0,1299
1	0,17	0,30	0,13-0,2999
2	0,15	0,45	0,30-0,4499
3	0,25	0,70	0,45-0,6999
Прибытие заказа, поданного в конце 6-го дня К счастью для SRH, в течение 2-х дней до прибытия заказа
не произошло ни одного случая потери продажи
Этот адаптированный пример взят из книги Helper and Render. Operations Management, 7999 (5-th edition),
Prentice Hall
ГЛАВА 1 1. Моделирование дискретных событий 791
Окончание табл. 11.5
Количество барж	Вероятность	Функция распределения	Интервал случайных чисел
	0,20	0,90	0,70-0,8999
5	0,10	1,00	0,90-0,9999
	1,00		
Истинное среднее = 0x0,13 + 1x0,17 + 2x0,15 + 3x0,25 + 4x0,20 + 5x0 10 = 2,52			
Наблюдения управляющего разгрузочным причалом показывают, что количество
разгруженных барж изо дня в день также колеблется Распределение вероятностей
разгруженных барж показано в табл. Н 6
Таблица 11.6. Распределение количества разгруженных барж
Количество разгруженных Вероятность Функция распределения Интервал случайных чисел
барж
1	0,05	0,05	0,00-0,0499
2	0,15	0,20	0,05-0,1999
3	0,50	0,70	0,20-0,6999
4	0,20	0,90	0,70-0,8999
5	0,10	_	1,00	0,90-0,9999
1,00		
Истинное среднее = 1x0,05	+ 2x0,15 + 3x0,50 + 4x0,20	+ 5x0,10 = 3,15
Баржи разгружаются по принципу “первым пришел, первым разгрузился” Все
баржи, не разгруженные в день прибытия, должны ждать до следующего дня Но
держать баржи у причала невыгодно, и управляющий не может игнорировать серди-
тые звонки от владельцев барж, напоминающих ему, что “время — деньги1” Перед
тем как обратиться к руководству порта с просьбой о предоставлении дополнитель-
ной команды грузчиков, управляющий хочет самостоятельно разобраться с ситуаци-
ей, для чего решает создать в Excel модель прибытия барж, их разгрузки и задержки
Было бы идеально имитировать 100-дневный интервал времени, но для ускорения
работы управляющий начинает с имитации более короткого 15-дневного интервала
Результаты имитации показаны в табл 11 7
Таблица 11.7. Имитация прибытия и разгрузки барж
День Количество нераз- груженных барж, пришедших накануне	Случайные	Количество прибывших	Общее количе- ство барж под разгрузкой	Случайные числа	Количество разгруженных барж
1	0	0,52	3	3	0,37	3
2	0	0,06	0	0	0,63	0"
3	0	0,50	3	3	0,28	3
4	0	0,88	4	4	0,02	1
5	3	0,53	3	6	0,74	4
16 В этом случае баржи можно было разгрузить во 2-и день Или же не было ни одной прибывшей баржи и ни
одной задержанной разгрузки
792 ЧАСТЬ III. Вероятностные модели
Окончание табл. 11.7
День	Количество нераз- груженных барж, пришедших накануне	Случайные числа	Количество прибывших	Общее количе- ство барж под разгрузкой	Случайные числа	Количество разгруженных барж
6	2	0,29	1	3	0,35	3
7	0	0,10	0	0	0,24	О'7
8	0	0,47	3	3	0,03	1
9	2	0,99	5	7	0,29	3
10	4	0,37	2	6	0,60	3
11	3	0,66	3	6	0,74	4
12	2	0,91	5	7	0,85	4
13	3	0,35	2	5	0,89	4
14	1	0,32	2	3	0,73	3"
15	0	0,94	5	5	0,59	3
	20		41			39
Даже одна имитация модели может дать управляющему важную для него инфор-
мацию
Среднее количество барж, разгрузка которых задержана до следующего дня, равно
20/15 = 1,33 барж вдень.
Среднее количество прибывающих барж равно 41/15 = 2,73 баржи.
Среднее количество барж, разгружаемых каждые сутки, равно 39/15 = 2,60 барж.
Вопросы
1.	Представьте описанную ситуацию в виде имитационной модели в Excel и вы-
полните имитацию работы причала в течение 100 дней.
2.	Создайте модель в Extend и выполните имитацию работы причала в течение 100 дней.
3.	Что может сделать управляющий для того, чтобы уменьшить количество барж,
разгрузка которых задерживается на день?
Литература
1. Youngho Lee and Arnie Elcan, Simulation Modeling for Process Reengineering in the Telecommuni-
cations Industry, Interfaces, 26, no. 3 (1996), 1-9,
2. Edward Watson, An Application of Discrete-Event Simulation for Batch-Process Chemical-Plant Design,
Interfaces, 27, no 6 (1997); 35-50
17 В данном случае имеет место такая же ситуация, какая описана в предыдущей сноске
м В этот раз можно было разгрузить 4 баржи, но поскольку в очереди было только 3 баржи, то количество
разгруженных записано равным 3
Глава
12
Прогнозирование
В этой главе...
12.1.	Введение
12.2.	Количественное прогнозирование
12.3.	Причинно-следственные модели прогнозирования
12.4.	Модели временных рядов
12.5.	Статистические данные разделяй и властвуй
12.6.	Качественное прогнозирование
12.7	Заключение
Основные термины
Контрольные вопросы
Задачи
Ситуация 1 Ларамийский банк
Ситуация 2 Shumway, Horch и Sager (часть 2)
Литература
794 ЧАСТЬ III. Вероятностные модели
Практическое применение
Прогнозирование Бина
Л Л Бин (L L Bean) — известный розничный торговец высококачественной
одеждой и товарами для спорта и отдыха. Товары в основном реализуются по теле-
фонным заказам Звонки поступают на номера с кодом 800 Эта служба была образо-
вана в 1986 году В 1993 году доход компании составил 870 млн. долл., 10% из кото-
рых были получены от продаж в розничных магазинах, 18% — от заказов по почте,
оставшаяся часть (72%) были получены через телефонный центр компании.
Клиентов, звонящих в телефонный центр, можно разделить на две категории, по-
купатели и желающие получить справку. Каждая группа клиентов звонит по разным
номерам Клиенты, звонящие в справочную службу, как правило, спрашивают о со-
стоянии их заказов, сообщают о проблемах, которые у них возникли в связи с зака-
зами и т д Количество звонков и средняя продолжительность разговора значительно
различаются для этих двух групп. Количество звонков за год в службу телемарке-
тинга (ТМ) в несколько раз больше, чем в справочную службу, но их средняя про-
должительность разговора значительно меньше Телефонисты справочной службы
должны уметь ответить на различные вопросы клиентов, поэтому они проходят спе-
циальную подготовку Таким образом, важно точно спрогнозировать входящий объ-
ем звонков в службу ТМ и справочную службу, чтобы правильно составить расписа-
ние работы телефонистов этих служб
В данном случае прогноз нужно сделать на три недели вперед Затем следует соста-
вить понедельное расписание и сообщить телефонистам об их графике работ на две не-
дели вперед Ошибочный прогноз может дорого стоить для Бина Недостаточное число
телефонистов в службе ТМ увеличит затраты из-за потери части заказов (клиенты, ко-
торые сразу не дозвонились, как правило, больше звонить не будут). Недостаточное
число телефонистов в справочной службе приведет к снижению доверия клиентов
к компании, вследствие чего компания также может потерять клиентов В обоих случа-
ях нехватка телефонистов увеличит время ожидания клиентов в очереди, и плата за те-
лефонные разговоры значительно возрастет С другой стороны, избыточное число те-
лефонистов в любой из служб приведет к их низкой загруженности и увеличению за-
трат на оплату труда
Составить график работ достаточно просто, если не учитывать изменчивый ха-
рактер и сезонные скачки спроса в бизнесе Бина. Например, последние три недели
перед Рождеством могут принести как огромные прибыли, так и убытки, поскольку
почти 20% звонков, совершаемых за год, приходятся на этот короткий период. Как
правило, Бин удваивает число телефонистов на это время и увеличивает в 4 раза чис-
ло телефонных линий После Рождества возникает относительное затишье Более
того, существует строгая закономерность, наблюдаемая на протяжении всего года
для обеих служб в понедельник возникает наибольшая интенсивность звонков, ко-
торая постепенно убывает до своего минимального значения в воскресенье
Существует еще один фактор, который нужно учитывать при создании модели
прогнозирования, — выпуск нового каталога товаров Как правило, каталоги товаров
обновляются во вторник, что значительно влияет на интенсивность поступления
звонков Множество жаждущих клиентов начинают заказывать новые товары, что
приводит к росту интенсивности звонков в компанию во время появления нового
каталога и держится еще какое-то время после его выхода В компании была разра-
ботана модель прогнозирования, которая давала более точный прогноз, чем это де-
ГЛАВА ^.Прогнозирование
795
лая ранее лично Бин. В частности, абсолютная погрешность (в процентах) между
предыдущими прогнозами Бина и новой моделью, основанная на данных за послед-
ние пять лет, составляла 7,4% для службы ТМ и 11,4% для справочной службы. По
крайней мере прогнозы на будущие три недели, выполненные с помощью модели
прогнозирования, имели приблизительно такую же точность, какая была продемон-
стрирована на данных за прошлые годы. Более высокая точность прогнозов позво-
лила составлять более эффективное расписание, что привело к сокращению расхо-
дов на 300 тыс. долл, в год. [ 1 ]
12.1.	Введение
15 июня 1941 года Иохим фон Риббентроп, специальный посол Гитлера, встречался
в Вене с итальянским министром иностранных дел графом Циано Во время этой встречи
Риббентроп сказал: “Дорогой Циано, я пока что не могу ничего сказать вам конкретного,
поскольку любое решение фюрера находится в строжайшем секрете Однако одно могу ска-
зать наверняка если мы нападем, то сталинская Россия будут стерта с карты мира не позд-
нее, чем через восемь недель ”. (См. [3].) Через семь дней нацистская Германия привела
в действие план Барбаросса и объявила войну России После этого решения произошла
цепь событий, в результате которых пал третий рейх и был изменен весь ход истории
Несмотря на то что последствия некоторых решений значительны, очевидно, что сами
последствия от решений, принятых отдельными людьми или организациями, определяются
только по истечении некоторого периода времени. Ниже представлено несколько “мудрых”
высказываний, которые иллюстрируют обещания и разочарования прогнозирования
•	“Трудно сделать правдивый прогноз, особенно если он касается будущего ”
•	“Предсказать не сложно, сложно предсказать правильно ”
•	“Числа, если их правильно преподнести, могут сказать о чем угодно.”
Экономическое прогнозирование является важной частью экономической науки
и практики Политика государства в области экономики основана на прогнозировании
внутреннего валового продукта. Требует прогнозирования уровень безработицы, спрос на
холодильники и многое другое. Среди больших страховых компаний трудно найти такую,
у которой не был бы заключен постоянный контракт с экспертом или компанией для полу-
чения экономических прогнозов. На их основе миллиарды долларов вкладываются в займы
и облигации Более 2 000 людей собираются на ежегодный обед, спонсируемый Чикагским
университетом, чтобы послушать мнения трех специалистов относительно экономических
перспектив Подобные примеры можно приводить до бесконечности.
Именно поэтому количественные модели играют все более заметную роль в построении
прогнозов Яркий пример тому — программы управления запасами, которые включают под-
программы прогнозирования. Другой пример — это доверие к точным прогнозам спроса
в сфере обслуживания (пассажирские авиаперевозки, отели, прокат автомобилей, туристиче-
ские компании), где применяются сложные математические модели оптимизации доходов
При расчетах таких показателей, как внутренний валовой продукт или курсы валют, многие
компании надеются на эконометрические модели с их возможностями прогнозирования
Существует множество классификаций моделей прогнозирования, и в зависимости от
классификации формируется терминология. Например, в экономической литературе
можно встретить “долгосрочные”, “среднесрочные” и “краткосрочные” модели. В дру-
796 ЧАСТЬ III. Вероятностные модели
гих изданиях эти модели называются “регрессионными”, “экстраполяционными”,
“условными”, “основанными на прецедентах” или же “ближайшими”. Мы в дальнейшем
будем различать количественные и качественные модели прогнозирования.
12.2.	Количественное прогнозирование
Количественные модели прогнозирования обладают двумя важными и привлекатель-
ными свойствами
1.	Они записываются в математической форме. Поэтому ясно виден и понятен метод
прогнозирования, что позволяет обмениваться данными между людьми, которые
занимаются прогнозированием Более того, модели этого типа предоставляют
возможность для систематического изменения и улучшения методов прогнозиро-
вания В количественной модели можно изменять коэффициенты или добавлять
условия, пока модель не будет давать надежные результаты.
2.	При использовании электронных таблиц количественные модели могут содержать
огромное количество параметров, что позволяет стоить модели, адекватно отра-
жающие экономическую ситуацию как отдельного предприятия, так и целых от-
раслей Например, без количественных моделей и компьютеров было бы невоз-
можно сконструировать системы управления запасами, которые требуют ежеме-
сячных прогнозов для тысяч наименований товаров.
Существует огромное количество специальной литературы о количественном прогнози-
ровании, где, чтобы разобраться во всех тонкостях моделей, требуется высокий уровень
знаний математической статистики. В следующих двух разделах мы опишем некоторые
важные характеристики и области применения моделей прогнозирования без глубокого
проникновения в технические и математические вопросы Будем различать две категории
моделей — причинно-следственные (каузальные) модели и модели временных рядов.
12.3.	Причинно-следственные модели прогнозирования
В причинно-следственных моделях прогнозирование изменения значения какой-то вели-
чины осуществляется на основе известных значений другой величины или набора величин.
Другими словами, зная значение одной переменной (или, возможно, нескольких перемен-
ных), можно предсказать значение другой Математически это выражается следующим об-
разом Пусть у — действительное значение некоторой интересующей нас переменной,
а у — предсказанное или спрогнозированное ее значение. Тогда у = /(х,,х2,...,х„), где/—
функция прогнозирования, х,, х2,..., х„ — набор переменных.
В этом представлении переменные х называются независимыми переменными, а у —
зависимой (или переменной отклика). Таким образом, зная значения независимых пере-
менных, можно предсказать значение зависимой.
Приведем примеры таких зависимостей.
1.	Если через у выражается спрос на еду для младенцев, то х— количество детей
в возрасте от 7 до 24 месяцев.
2.	Если у — это медицинское оборудование, то х, и х2 должны выражать соответст-
венно число строящихся и уже работающих больниц.
ГЛАВА ^.Прогнозирование 797
3.	Если через у выразить поток автомобилей по автомагистрали, то х, и х2 — потоки
автомобилей по двум ближайшим магистралям.
Причинно-следственные модели используются в том случае, если независимые пере-
менные известны заранее, или же их спрогнозировать проще, чем зависимую перемен-
ную у. Например, функциональное отношение объемов продаж капусты и угля за год
может быть интересно для социологов, но как бы ни было просто предсказать спрос на
капусту, это вряд ли будет иметь какое-то значение для угольной промышленности Во-
обще говоря, в компаниях, как правило, ищут связь между объемами продаж и объемами
внутреннего валового продукта за тот же период. Таким образом можно достаточно точно
спрогнозировать объем продаж компании на следующий месяц, используя данные об
ожидаемом объеме внутреннего валового продукта. Единственная трудность заключается
в том, чтобы определить, действительно ли величина, которую нужно спрогнозировать,
зависит от независимой переменной?
Поэтому для выбора причинно-следственный модели прогнозирования должны вы-
полняться два условия.
1. Должна существовать связь, которую можно установить на основе данных за про-
шлый период, между зависимой переменной и независимыми.
2. Значения независимой переменной за период, на который необходимо сделать
прогноз, должны быть известны.
Прежде чем продолжить, следует еще раз подчеркнуть значение пункта 1 Только то,
что зависимость между двумя переменными можно выразить математическими форму-
лами, не гарантирует, что одна из них является причиной, а другая — следствием На-
пример, с того времени, как в 1967 году впервые был разыгран Суперкубок по футболу,
практически всегда, когда выигрывали команды Национальной футбольной конферен-
ции, показатель фондовой биржи Standard & Poor 500 возрастал Если же выигрывала
команда Американской футбольной конференции, показатель понижался За 32 года су-
ществования Суперкубка это правило срабатывало в 88% случаев (при 28 из 32 побед ко-
манд Национальной футбольной конференции)1 Но можно ли считать, что есть взаимо-
связь между тем, какая команда выиграла Суперкубок, и показателем фондовой биржи,
и на этой основе прогнозировать положение на бирже9
В причинно-следственных моделях прогнозирования часто используется подход, на-
зываемый подбором кривой по точкам
Подбор кривой по точкам
Основную идею метода подбора кривой можно проще показать на примере, где для
прогнозирования значения зависимой переменной используется одна независимая пере-
менная Рассмотрим модель нефтяной компании, руководство которой решило расши-
рять сеть современных автозаправочных станций самообслуживания В этой модели ис-
пользуются две величины: поток автомобилей (измеряется как среднее число машин
в час) и прогноз продаж (измеряется как средний объем продаж в час).
В компании более года работало пять автозаправочных станций Данные за год по
этим станциям использовались для вычисления средних значений потока автомобилей
и объема продаж, результаты представлены на рис 12 1 (рабочая книга Abto.XLS) На
рис. 12.2 показано графическое представление этих данных Такой график называется
точечным Чтобы создать такой график в Excel, нужно выполнить следующие действия.
798 ЧАСТЬ III. Вероятностные модели
Рис. 12.1. Данные по объему продаж и потоку
автомобилей
Автомобили в час
Рис. 12.2. Точечный график зависимости объема продаж от потока
автомобилей
1.	Выделите диапазон данных В2 С6, затем щелкните на кнопке Мастер диаграмм
стандартной панели инструментов
2.	В первом диалоговом окне Мастер диаграмм выберите тип диаграммы Точечная
без соединяющих линий.
3.	Второе диалоговое окно мастера диаграмм можно пропустить, щелкнув на кнопке
Далее, поскольку в данном случае подходят все параметры, установленные по
умолчанию
4.	В третьем диалоговом окне мастера диаграмм введите названия осей и затем
щел кн ите на кноп ке Далее
5.	В последнем диалоговом окне Мастер диаграмм установите переключатель от-
дельном, чтобы разместить диаграмму на отдельном листе, который будет назы-
ваться Диаграмма!, после этого щелкните на кнопке Готово.
Далее нужно использовать эти данные для построения функции, которая отражала бы
зависимость объема продаж бензина от потока автомобилей.
ГЛАВА 12. Прогнозирование
799
Подбор кривой методом наименьших квадратов
Метод наименьших квадратов — это формальная процедура для подбора кривой по
точкам, которая выполняется едва этапа.
1. Задается вид функции (линейная функция, квадратичная или какая-либо другая).
2. Среди функций выбранного вида нужно выбрать функцию, для которой сумма
квадратов разностей между точками данных и значениями функции была бы ми-
нимальна
Чтобы проиллюстрировать этот процесс, вернемся к нашему примеру Сначала выби-
раем линейный тип функции, т е. функцию вида у = а + Ьх Следующий шаг показан на
рис 12.3, где определены значения коэффициентов а и b (далее опишем, как можно бы-
стро найти эти значения в Excel) На этом рисунке также нарисована прямая линия у =
а + bx и показаны разности между точками данных и функцией Например, = у, -
(a + bxj =220 - (а + 1506), где у, — фактический (измеренный) объем продаж на стан-
ции 1, х, — фактический (измеренный) поток автомобилей на станции 1, а — длина от-
резка вертикальной оси, отсекаемый прямой линией, b — угловой коэффициент прямой
Значение d2 показывает, насколько близки значение функции а + 1506 и измеренное
значение у,, другими словами, оно показывает, насколько выбранная функция подходит
в данной точке
300
50
50	100	150	200 л
Поток машин (в час)
Рис. 12.3. Иллюстрация к методу наи-
меньших квадратов
Затем нужно определить, насколько подходит выбранная функция для всех точек
данных. Чтобы это сделать, следует найти сумму квадратов отклонений в каждой точке
800 ЧАСТЫП Вероятностные модели
£<У,2 . Теперь рассмотрим общий случай, когда количество измеренных значений п не
обязательно равно пяти. Тогда сумма квадратов отклонений может быть записана так:
£42=£(y,-(a + fct,))2.	(12.1)
В методе наименьших квадратов коэффициенты а и b выбираются так, чтобы мини-
мизировать сумму (12.1). Существуют формулы для вычисления значений а и Ь, миними-
зирующих эту сумму. Чтобы получить эти формулы, найдем частную производную по а
суммы (12.1) и полученное выражение приравняем к нулю. Это будет первое уравнение.
Второе уравнение получается аналогично, но частная производная берется по Ь. В ре-
зультате получим систему уравнений относительно а и Ь:
£-2(у,-(а + Ц)) = 0 и ^-2х,(у,-(а + Ьх,)) = 0.
Решение этой системы запишется следующим образом:
„ =	(12.2)
...
Теперь можно найти значения а и Ь, вычислив значения сумм, входящих в эти выра-
жения, и выполнив обычные арифметические операции
-Входные данные-------—
акодной интервал Y1.
Входной интервал X:
Г уровень надежности:
Рис. 12.4. Диалоговое окно Регрессия
Вычисление коэффициентов а и b можно поручить Excel, поскольку в этой программе
есть необходимые средства. Для этого нужно выполнить такие действия.
ГЛАВА ^.Прогнозирование 801
1.	Выберите Сервис^Анализ данных (Если у вас нет этого пункта меню, то вам не-
обходимо выполнить команду Сервис^ Надстройки и в открывшемся диалоговом
окне установить надстройку Пакет анализа.)
2.	В диалоговом окне Анализ данных в списке Инструменты анализа выберите Рег-
рессия, в результате появится одноименное диалоговое окно, показанное на
рис 12 4 В поле Входной интервал Y введите $С$2 $С$6, а в поле Входной ин-
тервал X — $В$2 $В$6.
3.	Укажите, что результаты надо вывести на отдельном рабочем листе, и задайте имя
листа, например, Результаты Щелкните на кнопке ОК.
Результаты вычислений показаны на рис 12 5.
Г	"I - В • . с . i о . J . Е . L F.. ! . G . J Н ! . I ... ВЫВОД ИТОГОВ	:
3	Регрессионная статистика
_4 6 J	Множественный R	0,833037289. R-квадрат	:	0,693951125: Нормированный R-квадрат	0,591934833 Стандартная ошибка	:	44.17659631: Наблюдения	5
9~ ТО'	Дисперсионный анализ
12 ЧТ	itY	QQ	fl/Q	Р	ймдилмоглтц. F
	Регрессия	j	1:	13275,28502^	13275,28502	6,8023559:	0.07981342 Остаток	"	3:	5854,714984;	1 951,571661: Итого	 4	19130
ЧТ	
1$	: Стандартная	: Коэффициенты ошибка Статистика Р-Знаиение Н1лкние 95% Верхние 95%Нижние 95,0%Верхние 95,0?
~ТГ	Y-пересечение	57,10423453	50,38799691:	1,133290427	0,3394713 -103,25301	217,46148	-103,253011	217,461479( ПеременнаяХ1	0.929967427	0,356564467:	2.608132647	0.0798134 -0 2047809 2 06471576	-0 20478091	2 06471576'
	
Рис. 12.5. Результаты вычислений
В полученном отчете приведено много информации, но данные, которые нас интере-
суют, находятся в ячейках В17 В18 Они называются Y-пересечение (коэффициент а)
и Переменная X 1 (коэффициент Ь) Имеем а - 57,104 и b = 0,92997
Чтобы построить по исходным данным прямую, соответствующую линейной функ-
ции, найденной методом наименьших квадратов, выполните такие действия.
1.	Щелкните на ярлыке Диаграмма! листа с точечной диаграммой.
2.	Щелкните на любой точке данных на диаграмме, все точки данных будут выделены
3.	Выполните команду Диаграмма^Добавить линию тренда
4.	В открывшемся диалоговом окне Линия тренда по умолчанию будет выбран ли-
нейный тип функции
5.	Щелкните на кнопке ОК.
После этого на графике появится прямая линия тренда (рис 12 6) 1
Чтобы добавить к линии тренда ее уравнение, установите опцию Показывать уравнение на диаграмме
на вкладке Параметры диалогового окна Линия тренда — Прим ред
802 ЧАСТЬ III. Вероятностные модели
Рис. 12.6. Прямая линия тренда, построенная методом
наименьших квадратов
Итак, построена линейная функция, которая минимизирует сумму (12.1), и которую
можно использовать для прогнозирования Такая функция (не обязательно линейная,
как в нашем случае) называется функцией регрессии. Теперь разберемся с тем, какую еще
мы получили информацию, использовав средство Регрессия (см рис. 12 5). Значение Fl-
квадрат в ячейке В5 равно 0,694 (69,4%). Это мера адекватности между исходными дан-
ными и построенной функцией, как и сумма квадратов отклонений. Это статистика Л2,
которая известна всем, кто изучал хотя бы начальный курс математической статистики.2
Она принимает значения от 0 до 1 и показывает, насколько велико общее отклонение по
оси Y построенной линии от фактических значений величины у. С другой стороны, ста-
тистики любят говорить о трех различных суммах погрешностей, общая сумма квадратов
(ОСК), сумма квадратов отклонений (СКО) и сумма квадратов регрессии (СКР). Зави-
симость между ними следующая: ОСК = СКО + СКР. Эти величины вычисляются по та-
ким формулам ’•
ОСК = £(у,-у)2 , СКО = Х(у,-у,)2, СКР = Х(у,-у)2	(12.3)
С помощью средства Регрессия минимизировано значение суммы квадратов откло-
нений СКО. Величину Л2 можно найти, используя формулу R2 =	. Если найдена
идеальная линия регрессии (тогда СКО = 0), то СКР = ОСК и Л2 = 1 (максимальное зна-
чение) В нашем случае Л2 = 0,694. Это значит, что только приблизительно 70% всех зна-
чений у можно выразить через переменнуюх.
Вернемся к первоначальным данным и рассмотрим вопрос, следует ли строить стан-
цию около г. Буффало, где поток автомобилей составляет 183 машины в час? Лучшее, что
Статистика R2 называется коэффициентом детерминации В случае парной линейной регрессии R~ равно
квадрату коэффициенту корреляции между хиу — Прим ред.
В этих формулах у — среднее значений у,, т е у = -^у, . — Прим ред
ГЛАВА 12. Прогнозирование
803
можно сейчас сделать, — это найти прогнозируемый объем продаж, подставив значение
183 вместо переменной* в полученное уравнение регрессии:
объем продаж (в час) = 57,104 + 0,92997 х 183 машины (в час).
Находим, что объем продаж (в час) будет равен $227,29. Но насколько можно быть уве-
ренным в правильности этого прогноза? Для этого надо построить доверительный интер-
вал, который бы с вероятностью 95% содержал фактическое значение объема продаж.
Необходимые для этого данные имеются на рабочем листе Результаты (рис. 12.5).
В ячейке В7 записано значение стандартной ошибки Sc, равное 44,18. Эта величина пока-
зывает величину разброса исходных данных относительно линии регрессии, что похоже
на сумму квадратов отклонений Стандартная ошибка вычисляется по формуле
X(y.-yf
(12.4)
где п — число точек данных (5 в нашем примере), к — количество независимых переменных
(1 в данном примере) Очевидно, что формулу (12.4) можно записать как Se =	.
Если известно значение стандартной ошибки можно воспользоваться эмпириче-
ским правилом (основанным на свойствах нормального распределения), которое гласит,
что с вероятностью 68% (или 95%) можно утверждать, что фактическое значение прогно-
зируемой величины будет находиться в окрестности найденного значения прогноза
(значение $227,29) с разбросом ±5 (или ±25с).4 В нашем случае получим 95% доверитель-
ный интервал [227,29 - 2x44,18, 227,29 + 2x44,18] или [$138,93; $315,65].
Чтобы убедиться в том, насколько правильно и точно был определен доверительный ин-
тервал, требуется вычислить значение 5, стандартной ошибки прогнозирования, значение
которой всегда больше значения 5. Но вывод формулы для определения 5р достаточно сло-
жен и выходит за рамки данной книги. Отметим только, что, чем меньше разброс значений
независимой переменной х относительно своего среднего, тем 5 будет ближе к 5.
Теперь рассмотрим другие данные, приведенные в отчете средства Регрессия и отно-
сящиеся к коэффициенту b (ячейки DI 1:G18), и прежде всего /-статистику (ячейки D18)
и P-значение (ячейка Е18), поскольку посредством этих величин строится доверитель-
ный интервал для коэффициента Ь. В данном случае P-значение равно 0,0798. Но жела-
тельно, чтобы P-значение в данном случае было меньше 0,05. Тогда с вероятностью по
крайней мере 95% можно было бы утверждать, что коэффициент b статистически значи-
мо отличается от нуля. Если коэффициент b равен нулю, это указывает на отсутствие ста-
тистической зависимости между у и х. Средство Регрессия уже построило 95%-ный до-
верительный интервал для коэффициента Ь. Границы этого интервала -0,205 и 2,064 за-
писаны в ячейках F18 и G18 соответственно. Этот интервал показывает, что в данном
случае нельзя исключать того, что истинное значение b может быть равным нулю.
Более надежно другое эмпирическое правило, так называемое правило 3S, не использующее гипотезу о нор-
мальности распределения, которое справедливо для широкого класса одномодальных (имеющих одну моду)
распределении Согласно этому правилу случайная величина £ с вероятностью 95% будет принимать значе-
ния из интервала (х-35,х + 35), где х и S — соответственно выборочные среднее и среднеквадратическое
отклонение случайной величины £ — Прим ред
804 ЧАСТЬ III. Вероятностные модели
Обратите внимание на то, что можно получить те же самые значения коэффициентов
а и b с помощью средства Поиск решения (для этого нужно задать целевую функцию как
сумму квадратов отклонений, а коэффициенты а и b — искомыми переменными).
В заключение отметим, что функция регрессии “предсказывает” получение прибыли
$57,10 (значение переменной а) при х = 0, т е когда через автозаправочную станцию не
проезжают автомобили. Поэтому следует установить границы (например, от 30 до 250 ав-
томобилей в час), в пределах которых прогноз обоснован, или же найти логическое объ-
яснение этому факту Например, на территории многих станций находятся магазины,
покупателями в которых могут быть просто прохожие Поэтому значение а может пока-
зывать объем продаж для пешеходов, который, конечно, не зависит от интенсивности
потока автомобилей
Подбор квадратичной функции
Выше была описана процедура подбора линейной функции от одной независимой
переменной Но метод наименьших квадратов можно применять при любом количестве
независимых переменных и для функции регрессии произвольного вида Например,
предположим, что необходимо подобрать квадратичную функцию у = а„ + а:х + а ус на
основе прежних данных с помощью метода наименьших квадратов Решение сводится
к тому, чтобы найти такие коэффициенты а, и а2, которые бы минимизировали сумму
квадратов отклонении
_(йо +ал +й2г.2»2	(12 5)
Начнем с того, что приравняем к нулю частные производные от выражения (12 5) по
а„, а, и а2 Это даст уравнения
Ч + (£>. )«> + (£ х,2	= £ У, ,
(£ли++(Ex’i°2
(Ex-2iao+(Zv’)oi+(S^4)o2=Ev2x	(126)
Мы получили систему трех линейных уравнений с тремя неизвестными а„, а, и а2.
В электронных таблицах не составляет труда найти числовые значения этих коэффици-
ентов Но сейчас для их вычисления вместо средства Excel Регрессия применим средство
Поиск решения. Для этого создадим новый рабочий лист Квадратичная в той же книге
Авто XLS Этот лист показан на рис 12.7.
Ниже приведена последовательность действий, которую необходимо выполнить для
определения оптимальных значений параметров «0, а, и а2
1.	Выберите команду Сервис=>Поиск решения
2.	В диалоговом окне Поиск решения сделайте такие установки, как показано на
рис. 12 8. Это установки для модели безусловной нелинейной оптимизации, в ко-
торой изменяемые ячейки В2 В4 содержат значения искомых переменных, а в ро-
ли целевой функции выступает сумма квадратов ошибок (ячейка F13) Щелкните
на кнопке Выполнить
3.	После завершения вычислений будет выведено диалоговое окно с сообщением
о том, что решение найдено Щелкните на кнопке ОК. Результаты вычислений по-
казаны на рис. 12.9
ГЛАВА 12. Прогнозирование 805
Рис. 12.7. Новый рабочий лист
Рис. 12.8. Диалоговое окно Поиск решения
806 ЧАСТЬ III. Вероятностные модели
Рис. 12.9. Результаты поиска оптимальных параметров
Получены оптимальные значения параметров аи = -13,586, а, = 2,147 и а2 = -0,0044,
для которых сумма квадратов отклонений равна 4954. Замечание. В Excel имеется встро-
енная функция, которая непосредственно вычисляет сумму квадратов ошибок (тогда не
надо вычислять значения в столбцах Е и F). Эта функция СУММКВРАЗН(диапазон1,
диапазон2), записанная в ячейке F15 на рис. 12.9. Функция берет значения из диапазон2
и вычитает их из значений диапазон! (одно за раз), возводит в квадрат полученную раз-
ность, а затем суммирует квадраты разностей.
Чтобы построить графики исходных данных и полученную квадратичную функцию с
помощью мастера диаграмм, выполните следующие действия.
1.	На рабочем листе Квадратичная выделите диапазон В7:С11 с исходными данны-
ми, затем щелкните на кнопке Мастер диаграмм.
2.	В первом диалоговом окне мастера диаграмм выберите точечный тип диаграммы
без соединяющих линий.
3.	Во втором диалоговом окне мастера диаграмм щелкните на кнопке Далее, по-
скольку все установки по умолчанию в этом окне в данном случае нам подходят.
4.	В третьем диалоговом окне введите заголовки для осей X и Y, затем щелкните на
кнопке Далее.
5.	В последнем диалоговом окне мастера диаграмм установите переключатель от-
дельном, чтобы разместить диаграмму на отдельном листе; щелкните на кнопке
Готово.
6.	На полученной диаграмме щелкните на любой точке ряда данных (выделится весь
ряд данных).
7.	Выберите команду Диаграмма^Добавить линию тренда.
8.	В диалоговом окне Линия тренда выберите полиномиальный тип линии степени 2.
9.	Щелкните на кнопке ОК и вы получите график, показанный на рис. 12.10.
ГЛАВА 12. Прогнозирование 807
Рис. 12.10. Квадратичная функция, соответствующая исходным данным
Сравнение линейного и квадратичного приближений
В методе наименьших квадратов мы использовали сумму квадратов отклонений как
“критерий адекватности” приближения По этому же критерию можно сравнить линей-
ное и квадратичное приближения. Для этого с помощью рабочего листа Данные, содер-
жащего исходные данные, необходимо вычислить сумму квадратов отклонений для ли-
нейной регрессии (используя значения коэффициентов а и Ь, записанные на листе Ре-
зультаты), как показано на рис. 12 11.
D2 -г '  ..* =Реэультаты1$В$17+Результаты1$В$18’В2
А I . В- к .^..Сул-
1	Станция	Автомобили	Продажи в час	Прогноз продаж в час	Ошибка	Квадрат ошибки
2^	1	150	$	220,00	I	196,60|	23,40	547,59
з_	9	55	$	75,00	108,25	-33,25	1 105,72
	3	220'	$	250,00	261,70'	-11,70	136,82
5~	4	130	$	145,00	178,00	-33,00	1 089,00
6	5	95	$	200,00		145,45	54,55'	2 975 58
Продажи в час Прогноз продаж в час
220
75
250
145
200
=Результаты!$В$17+Результаты!$В$18*В2
=Результаты1$8$17+Результаты1$В$18’ВЗ
=Результаты!$В$17+Результаты!$В$18*В4
=Результаты!$В$17+Результаты!$В$18’В5
=Резулыаты1$В$17+Результаты1$В$18*В6
Ошибка
=C2-D2
=C3-D3
=C4-D4
=C5-D5
=C6-D6
Квадрат ошибки
=ЕЗЛ2
=Е4Л2
=E5n2
=Е6Л2
Рис. 12.11. Результаты вычисления суммы квадратов отклонений для линейной регрессии
808 ЧАСТЬ III Вероятностные модели
Сумма квадратов отклонений для квадратичной функции меньше, чем для линейной
функции (4954 < 5854,7), т е. квадратичная функция приблизительно на 15% уменьшает
сумму квадратов отклонений. Отсюда можно сделать вывод: как правило, с помощью
квадратичной функции можно выполнить более точное приближение, чем с помощью
линейной. Следует помнить, что линейная функция является частным случаем квадра-
тичной (когда коэффициент при х1 равен 0), поэтому приближение квадратичной функ-
цией должно быть по крайней мере не хуже приближения линейной функцией.
Какую кривую выбрать для приближения
Если квадратичное приближение дает как минимум такую же точность, как и линей-
ное, то почему бы для приближения не выбрать более общую форму кривой, например,
многочлен третьей или четвертой степени, и таким образом получить более точное при-
ближение9 На практике действительно часто используются функции вида у = а„ +
+ аре2 +	+ а ус (для простоты рассмотрим случай одной независимой переменной). Та-
кая функция называется многочленом степени п и представляет широкий класс функций
(при п = 2 получим квадратную функцию, при п = 3 кубическую и т.д.) С помощью
многочленов можно построить огромное количество разнообразных кривых, поэтому
они широко используются на практике Но применять полиномиальные функции для
приближения данных нужно осторожно В общем случае можно найти многочлен степе-
ни (к — 1), который будет идеально описывать к точек исходных данных. Например,
предположим, что имеется семь измеренных точек данных (х.,у.) (i = 1, 2,..., 7). Тогда
можно найти многочлен шестой степени у = а„ + atx + аус1 + ... + аусь, график которого
точно проходит через каждую из этих точек (рис 12.12).
Рис. 12.12. Многочлен шестой степени обеспечивает иде-
альное приближение
Это идеальное приближение (сумма квадратов отклонений равна нулю), тем не менее,
обманчиво, поскольку оно не информативно для получения прогнозируемых значениях.
Например (см. рис. 12.12), если независимая переменная в какой-нибудь момент време-
ни в будущем примет значениех8, а истинное значение)' равноу8, то спрогнозированное
ГЛАВА 12. Прогнозирование 809
значение будет равно у8, что значительно отличается от истинного значения у. Таким
образом, несмотря на идеальное приближение функции, прогноз будет неточен. В этом
случае линейное приближение (те. многочлен первой степени), как показано на
рис. 12.12, может обеспечить более правдоподобный прогноз, даже несмотря на то, что
этот многочлен не дал такого точного приближения, как многочлен шестой степени. Бо-
лее того, чем больше степень многочлена, тем выше изменчивость значений многочлена
на относительно коротких интервалах Поэтому, например, значения х, незначительно
отличающиеся отх6, дадут значения переменной у, значительно отличающиеся оту6.
Для того чтобы определить, какое приближение “лучше”, можно использовать срав-
нение по величине среднего квадратов ошибок, которое вычисляется как сумма квадратов
отклонений, поделенная на число точек данных минус число параметров кривой при-
ближения. Для линейного приближения число параметров равно 2 (коэффициенты а
иЬ), тогда среднее квадратов ошибок равно 5854/(5 - 2) = 1951,3; а для квадратичного
приближения среднее квадратов ошибок равно 4954/(5 — 3) = 2477,0. Итак, в данном
случае больше подходит линейное приближение, несмотря на то, что сумма квадратов
отклонений квадратичного приближения меньше Но, даже используя новый критерий
сравнения, нужно быть внимательным, потому что, если получится идеальное прибли-
жение, то как общая сумма квадратов отклонений, так и среднее квадратов ошибок будут
равны нулю Отметим, что большинство программ прогнозирования выполняют при-
ближение на основе многочлена третьей степени или ниже, поскольку многочлены более
высокого порядка не отражают общую тенденцию статистических данных ’
Какое приближение считать подходящим
Одной из задач вышеизложенного было показать, что модель прогнозирования, для
которой на основе статистических данных построена достаточно точная приближающая
кривая, может давать неправдоподобные результаты при прогнозировании Приближе-
ние, точно описывающее статистические данные, может иметь низкий уровень точности
прогноза. Так какое же приближение лучше9
Ответ на этот вопрос может быть как философским, так и техническим Прежде всего,
у создателя модели должно быть достаточно полное представление о реальном процессе,
который он выражает через функциональное отношение переменных хм у. Чтобы модель
прогнозирования была эффективной, функция прогнозирования должна отражать ос-
новные характеристики этого процесса С другой стороны, важно понимать, что данные
об этом процессе обычно формулируются на языке математической статистики. Напри-
мер, линейное приближение в статистике называется линейной регрессией. Если в точно-
сти выполнены статистические предположения о модели линейной регрессии (т е. ошиб-
ки распределены по нормальному закону относительно линии регрессии), то можно точ-
но и обоснованно утверждать, что линейное приближение является наилучшим
На практике, к сожалению, все оказывается не так просто. Как правило, мы не имеем
полного представления о моделируемом процессе В нашем распоряжении может быть
только небольшая (и недостаточная) последовательность данных за прошлый период.
Выбор оптимальной степени аппроксимирующего многочлена зависит от многих факторов Прежде всего,
от свойств аппроксимируемой функции у =f(x) (от ее гладкости), во-вторых, от статистических харак-
теристик наблюдаемых значений у (особенно от дисперсии) Если априорная информация о функции f(x)
и статистических характеристиках наблюдаемых значений минимальна или отсутствует, то на практике
не более 6-8 — Прим ред
810 ЧАСТЬ III. Вероятностные модели
Тогда возникает вопрос: насколько можно быть уверенным в том, что моделируемый
процесс удовлетворяет определенному набору статистических предположений? К сча-
стью, с помощью статистического анализа, по крайней мере для класса таких простых
моделей, как линейная регрессия, можно определить, действительно ли имеющиеся дан-
ные удовлетворяют этим предположениям.
А что же делать, если статистические предположения не выполняются? Можно попы-
таться построить другую модель. Но давайте на время отвлечемся от прогнозирования
и обратимся к “философии” использования оптимизационных моделей. (Что собой
представляет метод наименьших квадратов? Это безусловная нелинейная оптимизация )
В основе создаваемой модели лежит реальный процесс, а модель отражает некоторое
представление этого процесса. Как определить, подходит ли модель (или представление)
для данного процесса? Как правило, точно это определить нельзя Наилучший способ
проверить точность прогноза построенной модели — это достаточно большой опыт ее
использования на практике. Если при многократном использовании будет видно, что
с помощью данной модели можно получить достаточно точные результаты, то с опреде-
ленной уверенностью можно сказать, что модель правильно отражает реальный процесс.
Но какая уверенность может быть в самом начале создания модели?
Проверка моделей
Человек, проводящий испытания модели, однажды задал вопрос, который очень точно
подходит к данной теме. Предположим, что модель использовалась для принятия предыду-
щих решений; насколько успешным оказался прогноз? Такое приближение “создает” опыт
использования модели путем имитации прошлого. Этот процесс часто называют обоснова-
нием адекватности модели Принцип использования этого приближения в контексте про-
гнозирования называется “разделяй и властвуй”, он будет обсуждаться в разделе 12.5. Как
правило, для создания модели (например, при подборе полиномиальной кривой заданной
степени) используется только часть имеющихся данных за прошедший период Оставшаяся
часть данных используется для того, чтобы оценить точность прогноза Эта процедура более
детально описана в разделе 12.5. На данном этапе следует помнить, что при подборе кривой
вопрос “наилучшего приближения” является как философским, так и техническим, и нель-
зя терять из виду ни один из этих аспектов.
Итоги
В количественных моделях прогнозирования используется одна или несколько неза-
висимых переменных для прогноза значения зависимой переменной (переменной откли-
ка). Модель создается путем подбора кривой (функции прогноза) на существующем на-
боре данных, а затем эта кривая используется для определения отклика на новые значе-
ния независимых переменных. Метод наименьших квадратов— один из наиболее
используемых методов подбора функции прогноза. Мы показали основную идею этого
метода и рассмотрели характерные проблемы, которые возникают при подборе линей-
ной, квадратичной функций и полиномиальных функций высших порядков. Для просто-
ты во всех рассматриваемых моделях присутствовала только одна независимая перемен-
ная, но в моделях с несколькими независимыми переменными применяется тот же спо-
соб подбора функции прогноза.
Несколько приведенных выше примеров количественных моделей прогнозирования
показывают, что для построения даже простых моделей необходимо выполнить доста-
точно большой объем вычислений. Электронные таблицы в значительной мере снимают
проблему больших вычислений. Но остается другой важный вопрос: может ли построен-
ГЛАВА 12. Прогнозирование 811
ная модель предложить достоверный прогноз, и имеются ли в наличии данные, необхо-
димые для построения такой модели? Комментарии по поводу роли количественных мо-
делей при принятии решений будут приведены в разделе 12.7. Далее рассмотрим модели
временных рядов.
12.4.	Модели временных рядов
Другой класс методов количественного прогнозирования составляют методы прогно-
зирования временного ряда. Эти методы осуществляют прогноз путем экстраполяции зна-
чений отдельной переменной на основе статистических данных за прошлый временной пери-
од. Модель временного ряда, т.е. экстраполяционная функция, экстраполирует
(продолжает) “прошлые” значения переменной в “будущее”. Данные временного ряда —
это статистические данные за прошлый временной период, упорядоченные в хронологи-
ческом порядке, причем каждому отслеживаемому моменту времени соответствует толь-
ко одно значение наблюдаемой переменной. Поэтому данные по автозаправочным стан-
циям, которые использовались в предыдущем разделе, не являются данными временного
ряда, и их нельзя анализировать методами, рассматриваемыми в этом разделе.
Экстраполяция статистических данных
Рассмотрим несколько примеров использования метода экстраполяции. Предполо-
жим, что в журнале Wall Street Journal приведена сводка за последние 12 дней (включая
сегодняшний) цен на какао, сложившихся на момент закрытия биржи. Используя эти
данные, нужно предсказать завтрашнюю цену на какао (также на момент закрытия бир-
жи). Рассмотрим несколько способов сделать это.
1.	Если все имеющиеся значения цен существенны и имеют равную ценность для
прогноза, можно найти среднее всех 12 значений, и это будет наилучший прогноз
на завтра.
2.	Если последнее (сегодняшнее) значение наиболее значимо по сравнению с ос-
тальными, то оно является наилучшим прогнозом на завтра.
3.	Возможно, из-за быстрого изменения цен на бирже первые шесть значений уже
устарели и не актуальны, в то время как последние шесть значимы и имеют рав-
ную ценность для прогноза Тогда в качестве прогноза на завтра можно взять сред-
нее последних шести значений.
4.	Если все значения существенны, но сегодняшнее 12-е значение наиболее значимо,
а предыдущие 11-е, 10-е, 9-е и т.д. имеют все меньшую и меньшую значимость,
следует найти взвешенное среднее всех 12 значений. Причем весовые коэффициен-
ты для последних значений должны быть больше, чем для предыдущих, и сумма
всех весовых коэффициентов должна равняться 1.
5.	Можно на основе имеющихся 12 значений построить точечный график, а затем
максимально близко к этим значениям провести линию регрессии. Значение на
этой линии можно использовать для прогноза на завтра.
Теперь предположим, что мы знаем завтрашнюю цену на какао и надо построить
прогноз на послезавтра, используя уже 13 значений В этой ситуации можно применить
первый и второй описанные способы построения прогноза. Рассмотрим третий способ.
Нужно взять завтрашнее известное значение, сегодняшнее и значения за последние че-
812 ЧАСТЬ III Вероятностные модели
тире дня, чтобы получить среднее значение за последние 6 дней. Этот способ называется
построением скользящего среднего, о нем будет рассказано в следующих разделах.
Рассмотрим четвертый способ. В этом случае, поскольку используются 13 значений,
а не 12, весовые коэффициенты будут другими. Многие модели прогнозирования ис-
пользуют такой подход, называемый экспоненциальным сглаживанием. Более подробно
этот подход будет описан ниже.
И, наконец, рассмотрим пятый способ. Это пример прогнозирования, использующий
метод подбора кривой Как уже говорилось ранее, когда существуют значения перемен-
ной, зависящей от времени, эти значения, как правило, называются временным рядом,
методы анализа и экстраполяции таких данных называются анализом временных рядов.
В настоящее время эта область математической статистики активно развивается. Не имея
возможности подробно рассмотреть эти методы, приведем некоторые формальные по-
ложения этого анализа, которые будут интересны для менеджеров, применяющих модели
прогнозирования В частности, в этом разделе при построении функций прогнозирова-
ния в качестве критерия подбора кривых будут использоваться средние абсолютных от-
клонений и средние абсолютных ошибок в процентах вместо среднего квадратов откло-
нений, которое использовалось в разделе 12 3.
Подбор кривой
Выше уже рассматривался метод подбора кривой для моделей прогнозирования. Ос-
новное отличие в применении этого метода в моделях временных рядов состоит в том,
что здесь независимой переменной является время Статистические данные, т.е. значе-
ния зависимой переменной, наносятся на график в соответствии со временем, а затем по
этим данным подбирается кривая Для получения прогноза кривая продолжается дальше
“в будущее” В данном случае продление кривой означает вычисление значений полу-
ченной функции (кривой) для значений времени t, выходящих за интервал значений, по
которым строилась кривая Эта процедура для линейной функции показана на рис. 12.13.
Использование времени в качестве независимой переменной влечет за собой более
серьезные последствия, чем просто изменение вида нескольких формул, поэтому менеджер
должен понимать существенную разницу между методами подбора кривой в количествен-
ных моделях и моделях временных рядов. Одним из предположений при подборе кривой
является то, что все данные одинаково значимы (имеют равный вес). Этот метод позволяет
получать стабильный прогноз, который мало чувствителен к изменению данных.
ГЛАВА ^.Прогнозирование 813
Математические методы, используемые при подборе кривых в этих двух видах моде-
лей идентичны, но обоснование их применения различно. Чтобы понять это различие,
рассмотрим изменения переменной у, значения которой порождает какой-то процесс
или система. В количественных моделях предполагается, что лежащая в основе система
меняется и тем самым порождает другие значения у, система также порождает соответст-
вующие изменения независимых переменных. Поэтому, зная значения независимых пе-
ременных, с достаточной точностью можно спрогнозировать значение переменной у.
В моделях временных рядов предполагается, что система, порождающая значения у, ста-
ционарна (т е стабильна) и в будущем будет вести себя так же, как и в прошлом Характер
поведения переменной у в будущем практически совпадает с характером ее поведения
в прошлом Если система порождает существенно разные значения переменной у
(например, из-за изменений окружающей среды, технологии или государственной поли-
тики), то в этом случае предположение о стационарном процессе не выполняется и, сле-
довательно, прогноз скорее всего будет ошибочным.
В моделях временных рядов, как и в количественных моделях, для экстраполяции
данных можно использовать не только линейные функции. Например, можно предполо-
жить, что у — это многочлен от t порядка к вида у, = Z>„ + bj + Z>/ + ... + Z>/. Как и ранее,
значения коэффициентов Z>„, Z, Z>2, , bk можно вычислить на основе имеющихся данных.
Однако использование многочленов высокого порядка чревато проблемами, которые
описывались ранее, — можно получить идеальное приближение, которое будет давать не-
точные прогнозы.
Метод скользящего среднего
Одним из предположений, лежащих в основе данного метода, является то, что более
точный прогноз на будущее можно получить, если использовались недавние наблюде-
ния, причем, чем “новее” данные, тем их вес для прогноза должен быть больше. Удиви-
тельно, но такой “наивный” подход оказывается чрезвычайно полезным для практики.
Например, многие авиакомпании используют частный тип скользящего среднего для
создания прогнозов спроса на авиаперелеты, которые, в свою очередь, используются
в сложных механизмах управления и оптимизации доходов. Более того, практически все
программные пакеты управления запасами содержат модули, выполняющие прогнозы на
основе того или иного типа скользящего среднего. Исходя из критерия “частота исполь-
зования” метод скользящего среднего, несомненно, является одной из самых важных
и полезных процедур прогнозирования
Рассмотрим практический пример. Виктор Ковальский, новый вице-президент по
производству компании STECO, проявляет интерес к использованию простых моделей
прогнозирования. Этот интерес вызван создаваемыми им моделями управления запаса-
ми, которые были описаны в главе?. Поскольку его модели должны учитывать тысячи
наименований товаров, в данном случае важны простые (и недорогие) модели прогнози-
рования. Ознакомившись с различными методами прогнозирования, он решил
“опробовать” их на некотором наборе статистических данных — конкретно, на данных за
прошлый год об объемах продаж стоек из нержавеющей стали.
Модели прогнозирования представлены в математическом виде, и Виктор использо-
вал одинаковые обозначения для всех моделей:
у,., — фактический объем продаж стоек за месяц t — 1,
у, — прогнозируемый объем продаж стоек за месяц t.
814 ЧАСТЬ III. Вероятностные модели
На основе известных значений ур у,_, Виктор вычислял прогнозируемый объем
продаж у, на один месяц вперед. Другими словами, он использовал значения объемов
продаж до мая, чтобы получить прогнозируемый объем продаж в июне; затем, используя
значения объемов продаж до июня, получал прогноз на июль и т.д. Таким образом, он
получил последовательность значений у,, которую можно сравнить с фактическими зна-
чениями у,. В результате можно оценить точность прогноза с помощью того или иного
метода.
Простое скользящее среднее
Из группы методов скользящего среднего самым простым является метод скользящего
среднего по п узлам. В этом методе среднее фиксированного числа п последних наблюде-
ний используется для оценки следующего значения у. Например, если п равняется 4
и существует 15 фактических значений^, то значение для у|6 определяется по формуле
с _ Ун + У|4 + У,3 +У|2
Jis -	4
В общем случае формула скользящего среднего для п узлов выглядит следующим об-
разом:
У,+1 =-(Л +X-I +-+У,-„+|) 
п
Применение скользящего среднего для 3 и 4 узлов к данным объема продаж компании
STECO показано в табл. 12.1.
Таблица 12.1. Скользящее среднее для трех и четырех узлов
Месяц	Объем продаж, тыс. долл.	Прогноз на основе скользящего среднего за 3 месяца	Прогноз на основе скользя- щего среднего за 4 месяца
Январь	20		
Февраль	24		
Март	27		
Апрель	31	(20 + 24 + 27J/3 = 23,67	
Май	37	(24 + 27 + 31)/3 = 27,33	(20 + 24 + 27 + 311/4= 25,50
Июнь	47	(27 + 31 + 37)/3 = 31,67	(24 + 27 + 31 + 37)/4 = 29,75
Июль	53	(31 + 37 + 47)/3 = 38,33	(27 + 31 + 37 +471/4 = 35,50
Август	62	(37 + 47 + 531/3 = 45,67	(31 +37 + 47 + 531/4 = 42,00
Сентябрь	54	(47 + 53 + 62)/3 = 54,00	(37 + 47 + 53 + 62)/4 = 49,75
Октябрь	36	(53 + 62 + 54J/3 = 56,33	(47 + 53 + 62 + 54)/4 = 54,00
Ноябрь	32	(62 + 54 + 36)/3 = 50,67	(53 + 62 + 54 + 36)/4 = 51,25
Декабрь	29	(54 + 36 + 32)/3 = 40,67	(62 + 54 + 36 + 32)/4 = 46,00
ГЛАВА 12. Прогнозирование 815
Как видно, прогноз объема продаж в апреле на основе скользящего среднего за три
месяца — это среднее объемов продаж за январь, февраль и март, т.е. (20 + 24 + 27)/3 =
= 23,67. Фактический объем продаж в апреле составил 31. Поэтому в данном случае
спрогнозированный объем продаж отличается от фактического на 7,33 (= 31 - 23,67).
Если сравнить фактические объемы продаж с прогнозами, видно, что ни один из ме-
тодов прогнозирования не является достаточно точным. Тем не менее пора перейти от
качественного сравнения к некоторой количественной величине, по которой можно судить
о точности прогнозов разных методов. Мерой сравнения, которая будет использоваться
в этом разделе, является среднее абсолютных отклонений (САО) и среднее относитель-
ных ошибок в процентах (СООП), где:
У, |факт.продажи - прогноз|
САО = с.е.^озь.--------------------- ,
количество прогнозов
у |Факт- продажи - пРогноз1х100%
сооп = ссп'Хозы Факт, продажи	< j 2
количество прогнозов
Значения среднего абсолютных отклонений для прогноза на основе скользящего
среднего за 3 и 4 месяцев можно найти в рабочей книге СТОЙКИ.XLS, которая показана
на рис. 12.14. Для скользящего среднего за три месяца значение САО равно 12,67
(ячейка D16), тогда как для скользящего среднего за 4 месяца значение САО равно 15,59
(ячейка F16), это значит, что использование большего количества статистических дан-
ных скорее ухудшает, чем улучшает точность прогноза методом скользящего среднего.
Значение прогноза, полученное методом простого скользящего среднего, всегда
меньше фактического значения, если исходные данные монотонно возрастают, и больше
фактического значения, если исходные данные монотонно убывают. Поэтому, если дан-
ные монотонно возрастают или убывают, то с помощью простого скользящего среднего
нельзя получить точных прогнозов. Этот метод лучше всего подходит для данных с не-
большими случайными отклонениями от некоторого постоянного или медленно меняю-
щегося значения.
Метод простого скользящего среднего имеет два недостатка. Первый возникает в ре-
зультате того, что при вычислении прогнозируемого значения самое последнее наблюде-
ние имеет такой же вес (т.е. значимость), как и предыдущие. Это происходит потому, что
вес всех п последних наблюдений, участвующих в вычислении скользящего среднего, ра-
вен 1/л. Присвоение равного веса противоречит интуитивному представлению о том, что
во многих случаях последние данные могут больше сказать о том, что произойдет в бли-
жайшем будущем, чем предыдущие (это же показывает анализ данных на рис 12.14).
Второй недостаток состоит в том, что если скользящее среднее вычисляется по п уз-
лам, то эти данные должны где-то храниться. Когда требуется выполнить небольшое
число прогнозов по небольшому количеству узлов, то это не такая уж и серьезная про-
блема. Но ситуация кардинально меняется, когда, например, необходимо прогнозиро-
вать спрос на тысячи различных продуктов, выполняя эти прогнозы отдельно для каж-
дого наименования товара. Если, предположим, компании STECO необходимо спрогно-
зировать спрос на основе скользящего среднего по 8 узлам на 5 000 изделий, то
необходимо будет хранить 40 000 значений данных. На практике требования к памяти
компьютера, как и время, затраченное на вычисления, могут стать лимитирующими фак-
торами при проектировании прогнозирующей системы.
816 ЧАСТЬ III. Вероятностные модели
Абсолютная
Т
Абсолютная
ошибка
Прогноз на основе
ск. среднего за 4
месяца
.5.
=СРЗНАЧ(В2 В5)
=СРЗНАЧ(ВЗ.В6)
=СРЗНАЧ(В4 В7)
=СРЗНАЧ(В5.В8)
=СРЗНАЧ(В6 В9)
=СРЗНАЧ(В7 В10)
=СРЗНАЧ(В8 В11)
=СРЗНАЧ(В9 В12)
=ABS(B6-E6)
=ABS(B7-E7)
=ABS(B8-E8)
=ABS(B9-E9)
=ABS(B10-E10)
=ABS(B11-E11)
=ABS(B12-E12)
=ABS(B13-E13)
=ABS(B5-C5)
=ABS(B6-C6)
=ABS(B7-C7)
=ABS(B8-C8)
=ABS(B9-C9)
=ABS(B10-C10)
=ABS(B11-C11)
=ABS(B12-C12)
=СРЗНАЧ(В2,В4)
=СРЗНАЧ(ВЗ:В5)
=СРЗНАЧ(В4 В6)
=СРЗНАЧ(В5 В7)
Д i=CP3HA4(B6 В8)
ЯШ=СРЗНАЧ(В7В9)
|ГЙг1=СРЗНАЧ(В8 В10)
=СРЗНАЧ(В9 В11)
=СРЗНАЧ(В10 В12) =ABS(B13-C13)
ошибка
I Прогноз на основе
ск. среднего за 3
месяца
Сумма =
CAO =
=СУММ(Р5Р13) ' Сумма =
|*СРЗНАЧ(Р5:Р13) |САО =
=CyMM(F5F13)
|=CP3HA4(F5 F13)
Рис. 12.14. Сравнение значений САО для прогнозов методом скользящего среднего заЗи4 месяца
Взвешенное скользящее среднее
Идея, что более поздние данные важнее более старых, лежит в основе метода взвешенного
скользящего среднего по п узлам. Данный метод — обобщение метода простого скользящего
среднего по п узлам, где каждый узел имел вес /п. Например, при п = 3 взвешенное среднее
вычисляется по формуле у7 = су6 + оу, + оу4, где коэффициенты оу а, и оу называемые ве-
сами, представляют собой неотрицательные числа, которые выбираются исходя из условий,
что более ранние данные обладают меньшим весом и общий вес всех узлов равен 1. Конечно
же, существует бесконечное множество наборов значений а, которые удовлетворяют этим
критериям. Например, можно определить взвешенное среднее по трем последним наблюде-
ГЛАВА 12. Прогнозирование 817
ниям с помощью формулы
.	3	2	1
Л=-Л+^№+-)’4-
Но возможен и такой вариант:
5	3	2
у7 =—у6 +—у5 +—у4. В обеих случаях значения а убывают, а их сумма равняется 1. На
практике для нахождения подходящих значений а в Excel проще всего воспользоваться сред-
ством Поиск решения.
Рис. 12.15. Использование взвешенного среднего за 3 месяца

818 ЧАСТЬ III Вероятностные модели
Виктор, чтобы проверить точность метода взвешенного скользящего среднего за 3 меся-
ца, применил этот метод к статистическим данным объема продаж, при этом он назначил
веса 3/6, 2/6 и 1/6. Полученный прогноз и значение среднего абсолютных отклонений по-
казаны на новом рабочем листе Веса, который находится в той же рабочей книге
СТОЙКИ XLS (см рис 12.15). Сравнение нового значения среднего абсолютных отклоне-
ний, равного 11,04 (ячейка G16), со значениями средних абсолютных отклонений, полу-
ченных при использовании простого скользящего среднего за 3 (САО = 12,67) и за 4 месяца
(САО = 15,59), подтверждает предположение о том, что более поздние данные являются
лучшим показателем прогнозируемого объема продаж, чем более ранние данные.
Используя средство Поиск решения, можно определить более оптимальный вес уз-
лов, чем тот, который использовался вначале. Чтобы определить вес узлов с помощью
средства Поиск решения, при котором значение среднего абсолютных отклонений было
бы минимально, выполните такие действия
1.	Выберите команду Сервис^ Поиск решения.
2.	В открывшемся диалоговом окне Поиск решения установите ячейку G16 целевой
и укажите, что ее значение должно быть минимальным.
3.	В поле Изменяя ячейки введите диапазон В 1:ВЗ.
4.	Введите ограничения В4 = 1,0, В1.ВЗ > 0, В1 :ВЗ < 1, Bl < В2 и В2 < ВЗ.
5.	Щелкнув на кнопке Выполнить, получите результат, показанный на рис. 12.16.
Рис. 12.16. Применение взвешенного среднего за 3 месяца при оптимальном весе узлов
Полученные результаты показывают, что оптимальное распределение весов таково,
что весь вес сосредоточен на самом последнем наблюдении, при этом значение среднего
абсолютных отклонений равно 7,56. Этот результат подтверждает предположение о том,
что более поздние наблюдения должны иметь больший вес.
Несмотря на то что в методе взвешенного скользящего среднего более поздним на-
блюдениям назначается больший вес, этот метод не решает практическую проблему, свя-
ГЛАВА 12. Прогнозирование 819
занную с хранением данных, поскольку для вычисления одного значения прогноза все
равно необходимо хранить п значений статистических данных. Рассмотрим метод взве-
шенного среднего, который решает эту проблему.
Экспоненциальное сглаживание
Очевидно, что в методе взвешенного скользящего среднего существует множество
способов задавать значения весов так, чтобы их сумма была равной 1. Один из таких спо-
собов называется экспоненциальным сглаживанием В этой схеме метода взвешенного
среднего для любого t > 1 прогнозируемое значение у,+, в момент времени г + 1 представ-
ляет собой взвешенную сумму фактического объема продаж yt за период времени t и про-
гнозируемого объема продаж у, за период времени t Другими словами,
у,+|=ау, + (1-а)у,,	(12.8)
где а — определенная константа такая, что 0<а< 1. Значение константы а определяет
значение веса, которое имеет самое последнее наблюдение при вычислении прогнози-
руемого значения на следующий период. Если в уравнении (12 8) значение а будет близ-
ко к 1, то практически весь вес будет приходиться на наблюдение за период t
Экспоненциальное сглаживание имеет вычислительные преимущества. Здесь, чтобы
вычислить у,+| , необходимо знать только значения у, и у, (вместе со значением а). На-
пример, если компании STECO нужно спрогнозировать спрос для 5 000 наименований
изделий в каждый период времени, то в этом случае необходимо хранить 10 001 значений
данных (5 000 значений у,, 5 000 значений у, и значение а), в то время как для выполне-
ния прогноза на основе скользящего среднего по 8 узлам требовалось 40 000 значений
данных. В зависимости от поведения данных, возможно, потребуется хранить различные
значения а для каждого изделия, но даже в этом случае количество хранимой информа-
ции значительно меньше, чем при использовании скользящего среднего Положительная
особенность экспоненциального сглаживания состоит в том, что, сохраняя а и послед-
ний прогноз, все предыдущие прогнозы также неявно сохраняются.
Чтобы лучше раскрыть метод экспоненциального сглаживания, заметим, что при t = 1
у2 вычисляется как у2 = ay, +(1 -a)yt. В этом выражении у, представляет собой “началь-
ное предположение” значения у в момент времени 1, а у, равно фактическому значению
в момент времени 1. Итак, чтобы осуществить прогноз с помощью экспоненциального
сглаживания, необходимо знать “начальное предположение”. Существует несколько спо-
собов его вычисления. Наиболее часто предполагается, что у, = у, (т.е. предыдущий про-
гноз был “идеальным”). Следующий способ предполагает использование всех доступных
статистических данных, при этом у, = у (т е У, равно среднему всех доступных данных).
Иногда предполагается, что у, равно среднему только нескольких последних наблюдений.
Рассмотрим первый способ определения у, 
Виктор использовал рабочий лист Экспо, который содержится в той же книге
СТОЙКИ XLS, для применения метода экспоненциального сглаживания к данным об
объеме продаж На рис. 12.17 показаны фактические и спрогнозированные объемы про-
даж за 12 месяцев при значении а = 0,5.
820 ЧАСТЬ III. Вероятностные модели
Объемы
продаж,
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Прогноз
=Е2
=$B$1’E2+(1-$B$1)’F2
=$B$1’E3+(1-$B$1)*F3
=$B$1*E4+(1-$B$1)’F4
=$B$1*E5+(1-$B$1)'F5
=$B$TE6+(1-$B$1)*F6
=$B$1*E7+(1-$B$1 )’F7
=$B$1’E8+(1-$B$1)’F8
=$B$1’E9+(1-$B$1)’F9
=$B$1’E1O(1-$B$1)*F10
=$B$1’E11+(1-$B$1)*F11
=$B$1’E12t(1-$B$1),F12
____G______
Абсолютная
ошибка
=ABS(E3-F3)
=ABS(E4-F4)
=ABS(E5-F5)
=ABS(E6-F6)
=ABS(E7-F7)
=ABS(E8-F8)
=ABS(E9-F9)
=ABS(E10-F10)
=ABS(E11-F11)
=ABS(E12-F12)
=ABS(E13-F13)
Сумма=
CAO =
=CyMM(G3:G13)
Puc. 12.17. Прогнозирование методом экспоненциального сглаживания при значении а =0,5
Ковальский также вычислил среднее абсолютных отклонений прогноза с февраля по
декабрь. В модели экспоненциального сглаживания при а = 0,5 получено меньшее зна-
чение среднего абсолютных отклонений (9,92, ячейка G16), чем в моделях скользящего
среднего (см. рис. 12.14) и в начальной модели взвешенного среднего (см. рис. 12 15).
Полученное значение среднего абсолютных отклонений меньше, чем в прошлых моде-
лях, при этом вычисления достаточно просты С этой точки зрения разумно рассматри-
вать экспоненциальное сглаживание как достаточно недорогой и простой способ прогно-
зирован ия объемов продаж для многих продуктов компании STECO.
Виктор знает, что с помощью средства Поиск решения можно найти оптимальное
значение а, при котором среднее абсолютных отклонений будет минимально Чтобы
найти такое значение а, выполните следующие действия.
ГЛАВА 12. Прогнозирование 821
1.	Выберите команду Сервис^Поиск решения
2.	В открывшемся диалоговом окне Поиск решения установите целевую ячейку G16
и укажите, что ее значение должно быть минимальным.
3.	Укажите, что изменяемой ячейкой является ячейка В1.
4.	Введите ограничения В1 > 0 и Bl < 1
5.	Щелкнув на кнопке Выполнить, получите результат, показанный на рис. 12 18
Рис. 12.18. Прогноз с помощью метода экспоненциального сглаживания при
оптимальном значении а
Опять, как и в методе взвешенного скользящего среднего, наилучший прогноз будет
получен, если назначить весь вес последнему наблюдению. Следовательно, оптимальное
значение а равно 1, при этом среднее абсолютных отклонений равно 6,82 (ячейка G16)
Виктор получил прогноз, который уже видел ранее.
Поскольку модель экспоненциального сглаживания является достаточно важной,
изучим более детально, как она работает и когда ее можно применять. Рассмотрим неко-
торые ее свойства Для начала заметим, что если Г > 2, то в формуле (12.8) t можно заме-
нить на Г - 1, т е. у, = «у,., + (1 - а)у,., • Подставив это выражение в первоначальную фор-
мулу (12.8) для у,+1, при t> 2 получим у,+| = ау, +сг(1-«)у,_1 +(1-«)2у,.| •
Выполняя последовательно аналогичные подстановки, получим следующее выраже-
ние для у,+]:
у,+, = ау, + а(1 - а)у,_, + а(1 - ау у,_2 +... + а(1 - а)"' у, + (1 - а)1 у,.	(12 9)
Поскольку из неравенства 0 < а < 1 следует, что 0 < 1 - а < 1, то а > а( 1 - а) > а( 1 - а)2.
Другими словами, наблюдение у, имеет больший вес, чем наблюдение у,_р которое, в свою
очередь, имеет больший вес, чем у,_2. Это иллюстрирует основное свойство модели экспо-
ненциального сглаживания — коэффициенты при ук убывают при уменьшении номера к. Так-
822 ЧАСТЬ III. Вероятностные модели
же можно показать, что сумма всех коэффициентов (включая коэффициент при у,) равна 1.
Поэтому, например, если t = 4, то
а + а(1 - а) +а(1 -а)2 + (1 -а)3 = 1.
Из формулы (12 9) видно, что значением у,+| является взвешенная сумма всех предыду-
щих наблюдений (включая последнее наблюдение у). Последнее слагаемое суммы (12.9) яв-
ляется не статистическим наблюдением, а “предположением” у,. Очевидно, что с ростом t
влияние у, на у,+| уменьшается, и в определенный момент им можно будет пренебречь.
Чтобы это увидеть, заметим, что коэффициент при у, в формуле (12.9) равен (1 - а)'. Этот
коэффициент экспоненциально убывает с увеличением t Даже если значение а достаточно
малое (такое, что 1 - а приблизительно равно 1), значение (1 - а)' будет быстро убывать.
Например,еслиа = 0,1 и/=20,то(1 -а)' = 0,12. Еслижеа = 0,1 иг = 40,то(1 -а)' = 0,015.
Поэтому при достаточно большом числе t значение y,tl перестанет зависеть от выбора зна-
чения у,.
Очевидно, что значение параметра а сильно влияет на функционирование модели прогно-
зирования, поскольку а представляет собой вес самого последнего наблюдения уг Это значит,
что следует назначать большее значение а в том случае, когда в модели наиболее прогностиче-
ским является именно последнее наблюдение Если же а близко к 0, это означает практически
полное доверие к прошлому прогнозу и игнорирование последнего наблюдения. В табл. 12.2
представлены значения весов из формулы (12.9) при а = 0,1; 0,3 и 0,5.
Таблица 12.2. Веса данных при различных значениях а
Переменная	Коэффициент	а = 0,1	а =0,3	а= 0,5
У,	а	0,1	0,3	0,5
У, i	а(1—а)	0,09	0,21	0,25
У, 2	а(1—а)2	0,081	0,147	0,125
У, 3	а(1 -а)’	0,07290	0,10290	0,0625
У, 4	а(1 — а)4	0,06561	0,07203	0,03125
у, ,	а(1—а)5	0,05905	0,05042	0,01563
у, 6	а(1 - а)”	0,05314	0,03530	0,00781
У, 7	а(1—а)7	0,04783	0,02471	0,00391
У, 8	а(1 - а)8	0,04305	0,01729	0,00195
У, 9	а(1—а)’	0,03874	0,01211	0,00098
У, К)	о(1 - а)1”	0,03487	0,00847	0,00049
Сум ма весов		0,68619	0,98023	0,99610
Рассмотрим три ситуации, иллюстрирующих различный выбор значения параметра а.
ГЛАВА 12. Прогнозирование 823
Ситуация 1 (реакция на скачок)
Предположим, что в определенный момент времени лежащая в основе процесса сис-
тема испытывает быстрый и резкий скачок При каком значении параметра а прогноз
наиболее быстро предскажет этот скачок9 Поскольку этот пример иллюстративный, рас-
смотрим крайний случай, когда у, = 0 для t = 1, 2, ..., 99 и у, = 1 для t = 100, 101, ... Этаси-
туация графически показана на рис. 12 19 Заметьте, что если у(=0,тои у1Оо = ° при лю-
бом значении а, поскольку взвешенная сумма (12 9) состоит из нулей.
У<
0	•
95	96	97	98	99 100 101 102	(
Рис. 12.19. При t = 100 система меняется
Итак, наилучшим прогнозируемым значением у||Ю будет 0, тогда как действительное
значение равно 1 Возникает вопрос- как быстро прогнозирующая система отреагирует на
изменения в системе9
Чтобы ответить на этот вопрос, построим графики зависимости прогноза у,+| от t при а = 0,5
и а = 0,1, которые представлены на рис 12 20 Заметьте, что при а = 0,5 у](|6=0,984 (т.е прогно-
зируемое значение у|06 будет равно 0,984, в то время как действительное значение равно 1) Если
же а = 0,1, прогнозируемое значение переменной у№ будет только 0,468
0,3
0,2
Рис. 12.20. Прогноз у, при разных значениях а
824 ЧАСТЬ III Вероятностные модели
Как видно, прогнозирующая система при а = 0,5 значительно быстрее отреагирует на
изменения данных, чем при а = 0,1. Поэтому следует использовать относительно боль-
шие значения параметра а в том случае, когда система характеризуется низким уровнем
случайных воздействий, но подвержена редким и значительным по величине скачкам.
Ситуация 2 (реакция на постоянные изменения)
В противоположность системе с редкими и большими скачками, рассмотренной вы-
ше, предположим теперь, что система испытывает постоянные и относительно неболь-
шие изменения значений переменной у Пример такого типа изменений (пример линей-
ного роста) показан на рис 12.21 Опять возникает вопрос- как на такие изменения будет
реагировать модель экспоненциального сглаживания, и как эта реакция будет зависеть от
значения параметра а?
И
Рис. 12.21. Линейный рост переменной у,
Вспомним, что у,+| = ау, +а(-а)у1_1 + Поскольку значения у...... y,_t меньше у„
и сумма весов равна 1, очевидно, что при любых значениях а между 0 и 1 у,+| < у, Далее,
поскольку > у„ то, очевидно, у,+1 < У, < 3',+| Поэтому прогноз всегда будет занижен-
ным И наконец, так как малые значения а увеличивают вес “старых” данных, малые
значения параметра а ухудшают качество прогноза Но даже при значениях а, очень
близких к 1, прогноз также будет неточным при достаточно быстром росте значений у.
Отсюда можно сделать вывод, что экспоненциальное сглаживание (равно как и любое
взвешенное скользящее среднее) не является подходящим средством прогнозирования
для монотонно возрастающих или убывающих статистических данных Метод можно
скорректировать, включив в него направление изменения значений у, такой метод носит
название метода Хольта или экспоненциального сглаживания с учетом тренда. Об этом
методе будет рассказано в следующем разделе
Ситуация 3 (реакция на сезонные изменения)
Предположим, что система испытывает постоянные сезонные изменения переменной у
(такие, например, как если бы переменная у представляла спрос на купальные костюмы
в Денвере). Пример структуры сезонных колебаний показан на рис. 12 22 Предположим,
что необходимо экстраполировать эти данные на несколько периодов вперед. Предполо-
жим, что нужно спрогнозировать спрос на 8-11 периоды, имея данные только до 7-го пе-
риода включительно. Тогда уЙ = ау1+(1-а)у1. Поскольку в наличии имеются данные
только семи периодов, чтобы вычислить значение уд, допустим, что уя = у8. Тогда
ГЛАВА 12. Прогнозирование 825
у, =	+ (1	= «Л + (1 -	= Л •
Аналогично можно показать, что ун = у|0 = у9 = у8 • Другими словами, у8 является наи-
лучшим приближением для всех будущих прогнозов.
Посмотрим, насколько точными являются эти прогнозы. Известно, что
у,+| =ау, + a(l-a)y,_t + (1-сг)2у,_, + . . Предположим, что выбрано небольшое значение
параметра а. В табл. 12 2 показано, что, когда значение а мало (например, равно 0,1),
коэффициенты при недавних значениях у изменяются относительно медленно
(т е они приблизительно равны). В таком случае вычисление значения у,+1 имеет
сходство с вычислением простого скользящего среднего Тогда будущие прогнозы бу-
дут приблизительно равны среднему прошлых наблюдений. Такой прогноз, по сущест-
ву, игнорирует структуру сезонных колебаний. Если выбрано большое значение а, то
значение будет равно у8, которое в свою очередь приблизительно равно у7 Такой
прогноз, очевидно, является плохим. Другими словами, вне зависимости от значения
параметра а методом экспоненциального сглаживания в модели с сезонными измене-
ниями получить удовлетворительные прогнозы не удастся.
Метод экспоненциального сглаживания хорошо работает в ситуациях, когда интере-
сующая нас переменная ведет себя стационарно, а ее отклонения от постоянного значе-
ния вызваны случайными факторами и не носят регулярного характера. Это называется
гипотезой стационарности. Поэтому не удивительно, что метод экспоненциального
сглаживания не дает удовлетворительных результатов, когда его применяют в ситуациях,
где не подтверждается гипотеза о стационарности (например, при линейном росте пере-
менной у или при наличии сезонных колебаний) С другой стороны, надо отметить, что
определение гипотезы стационарности не очень конструктивно и в чистом виде редко
встречается на практике
Но что делать в ситуациях, когда метод экспоненциального сглаживания не подходит
для имеющихся данных9 При периодических колебаниях можно воспользоваться про-
стым приближением по методу экспоненциального сглаживания на отдельных
“подходящих” статистических данных. Например, авиакомпании или отели, испыты-
вающие сильные колебания спроса в зависимости от дня недели, для получения прогноза
на спрос в будущий понедельник могут воспользоваться сглаженным средним спросом
в предыдущие понедельники. Аналогично можно поступить, если данные испытывают
сезонные колебания. Тогда можно применить сглаженное среднее к объему продаж за
июнь за прошлые несколько лет для того, чтобы спрогнозировать объем продаж в буду-
щем июне. Но описанный метод прогнозирования порождает по крайней мере две про-
блемы Во-первых, не используется большая часть имеющейся информации.
(Информация об уровне спроса со вторника по воскресенье, конечно же, содержит ин-
формацию о наиболее вероятном уровне спроса в этот понедельник) Во-вторых, если
период колебаний достаточно велик, скажем, год, то, чтобы получить приемлемый объем
выборки, для прогнозирования используются старые данные В этом случае труднее про-
верить и принять гипотезу о стационарности интересующей переменной на такой дли-
тельный срок.
Если статистические данные монотонно изменяются или подвержены сезонным из-
менениям, необходимы специальные методы прогнозирования, которые будут рассмот-
рены ниже
826	ЧАСТЫ 11 Вероятностные модели
Метод Хольта экспоненциального сглаживания
Как уже обсуждалось ранее, простые методы экспоненциального сглаживания не да-
ют удовлетворительных результатов, если статистические данные монотонно возрастают
или убывают Для таких случаев Хольтом (Holt) разработан метод, основанный на сле-
дующих вычислениях:
= Ц + кТ,, где
Д = ау,+ (1 -«)(£,_, + Т,.,),
7]	= р(£,-£,_,) + (!-₽)7](12.10)
Метод Хольта6 позволяет прогнозировать на к периодов времени вперед. Значения
параметров аир находятся в пределах от 0 до 1. Переменная L, указывает на долгосроч-
ный уровень значений или базовое значение данных временного ряда. Переменная Т,
указывает на возможное возрастание или убывание значений за один период.
Рассмотрим работу этого метода на новом примере. Эми Луфорд работает аналитиком
в большой брокерской фирме. На основе имеющихся у нее квартальных отчетов компа-
нии Startup Airlines она хочет спрогнозировать доход этой компании в следующем квар-
тале Имеющиеся данные и диаграмма, построенная на их основе, находятся в рабочей
книге STARTUP.XLS (рис 12 23). Видно, что данные имеют явный тренд (почти моно-
тонно возрастают). Эми Луфорд хочет применить метод Хольта, чтобы спрогнозировать
значение прибыли на одну акцию (П/А) на тринадцатый квартал. Полученный прогноз
показан на рис 12 24 Чтобы его вычислить, необходимо задать начальные значения для
L и Т Есть несколько вариантов выбора 1) £, равно значению П/А за первый квартал
и Т = 0; 2) £, равно среднему значению П/А за 12 кварталов и Г, равно среднему изме-
нению за все 12 кварталов. Существуют другие варианты начальных значений для £ и Т,
но Эми выбрала первый вариант.
Рис. J2.23. Доходы компании Startup Airlines
Метод Хольта также называют методом экспоненциального сглаживания с учетом тренда и двухпара-
метрическим методом экспоненциального сглаживания — Прим ред
ГЛАВА 12. Прогнозирование 827

Ti
0
. =$B$2*(C6-C5)+( 14B$2)*D5
=$B$2*(C7-C8)+(14B$2)’D6
=$B$2*(C8-C7)+(14B$2)*D7
=4B$2’(C9-C8)+(14B$2)*D8
=$B$2*(C1O-C9)+(14B$2)*D9
Абс. ошибка. %
Не определено
=ABS(B6-E6)/B6
=ABS(B7-E7)/B7
=ABS(B8-EB)/B8
=ABS(B9-E9)7B9
=ABS(B10-E10)/B10
Прогно> П/А
He определено
=СУММ(С5:О5)
=СУММ(С6.О6)
=СУММ(С7О7)
=СУММ(С8 D8)
=СУММ(С9:О9)
S=B5
Xj=$B$1*B6+(1-$B$WS+D5)
"fl =$B$ 1’B7+( 1 -$B$ 1 )*(C6+D6)
_0 '=TBf1’B8+(1-$B$1)*(C7+D7)
9 !=$B$1*B9+(1-$B$1)’(C8+D8)
jO 5 =$B$ ГВ10+( 1-$B$ 1 )*(C9+D9)
11 -5l41’B11+(14B$1)*(C10+D10) =$B$2*(C11-C10)+(14B$2)’D10 =СУММ(С10 D10) =ABS(B11-E11)7811
T5l=$B$1*B12+(14B$1)*(C11+D11) =$B$2*(C12-C11)+(1-$B$2)*D11 =СУММ(С11:D11) =ABS(B12-E12)/B 12
J3j=$B$1*B13+(1-$B$1)*(C12+D12) =$B$2*(C13-C12)+(14B$2)*D12 =СУММ(С12.О12) =ABS(B13 E13J7B13
ЙГ-Р41’В14+(1-$В$1Г(С13+О13) =$B$2*(C14-C13)+(14B$2)*D13 =СУММ(С13 D13) =ABS(B14 E14)/B14
_15j=$B$1*B1S+(14B$1)’(C14+D14) =4B$2*(C1S-C14)+(14B$2)*D14 =СУММ(С14 014) =ABS(B15-E15)/B15
16 '-ГВИ,В16-»-(1-$В$1),(С15+Р15) ;=$В$2*(С16-С15)+(1-$В$2),Р15 -СУММ(С15 DIS) =ABS(B16-E16)7B16
Puc. 12.24. Метод Холыпа для компании Startup Airlines
Положив первоначально а = 0,5 и р = 0,5, она увидела, что среднее абсолютных оши-
бок в процентах равняется 43,3% (ячейка F18). Поскольку это значение достаточно вели-
ко, Эми ввела в ячейку В2 новое значение для р, равное нулю (в этом случае метод Хольта
равнозначен простому экспоненциальному сглаживанию). В результате (см. рис 12 25)
значение среднего абсолютных ошибок в процентах возросло до 78,1% Таким образом,
метод Хольта дает лучший прогноз, чем простое экспоненциальное сглаживание
Наконец Эми решила воспользоваться средством Поиск решения, чтобы наити опти-
мальное значение параметров аир, при которых значение среднего абсолютных ошибок
в процентах было бы минимально. Для этого она выполнила такие действия.
1.	Выбрала команду Сервис^Поиск решения.
2.	В открывшемся диалоговом окне Поиск решения задала ячейку F18 в качестве це-
левой и указала, что ее значение следует минимизировать
828 ЧАСТЬ III. Вероятностные модели
3.	В поле Изменяя ячейки ввела диапазон ячеек В1 :В2.
4.	Добавила ограничения В1:В2> О и В 1:В2 < 1.
5.	Щелкнула на кнопке Выполнить и получила результат, представленный на
рис. 12 26.
Рис. 12.25. Простое экспоненциальное сглаживание для компании Startup
Airlines
Рис. 12.26. Оптимальное экспоненциальное сглаживание с учетом тренда
ГЛАВА 12 Прогнозирование 829
Как видно, оптимальными оказались значения а = 0,59 и 0’ = 0,42, при этом среднее
абсолютных ошибок в процентах равно 38%, что примерно на 12,5% меньше, чем при
значениях а = 0,5 и 0 = 0,5
Сезонные изменения
При прогнозировании на основе данных временного ряда следует учитывать сезонные
изменения Сезонные изменения — это колебания вверх и вниз с постоянным периодом
в значениях переменной
Например, если посмотреть на объемы продаж мороженого по месяцам, то можно
увидеть в теплые месяцы (с июня по август в северном полушарии) более высокий уро-
вень продаж, чем зимой, и так каждый год Здесь сезонные колебания имеют период
в 12 месяцев Если используются данные, собранные по неделям, то структура сезонных
колебаний будет повторяться через каждые 52 недели Другой пример анализируются
еженедельные отчеты о количестве постояльцев, которые оставались на ночь в отеле,
расположенном в бизнес-центре города Предположительно можно сказать, что большое
число клиентов ожидается в ночи на вторник, среду и четверг, меньше всего клиентов бу-
дет в ночи на субботу и воскресенье, и среднее число постояльцев ожидается в ночи на
пятницу и понедельник Такая структура данных, отображающая количество клиентов
в разные дни недели, будет повторяться через каждые семь дней
Процедура, которая позволяет сделать прогноз с учетом сезонных изменении, состоит
из таких четырех этапов
I На основе исходных данных определяется структура сезонных колебаний и период
этих колебаний
2	Используя численный метод, описанный в следующем разделе, из исходных данных
исключают сезонную составляющую
3	На основе данных, из которых исключена сезонная составляющая, делается наилуч-
ший возможный прогноз
4	К полученному прогнозу добавляется сезонная составляющая
Время (год и квартал)
Рис. 12.27. Объем сбыта угля за девять лет
830 ЧАСТЬ III Вероятностные модели
Проиллюстрируем этот подход на данных об объемах сбыта угля (измеряемого в ты-
сячах тонн) в США на протяжении девяти лет Фрэнк Китч работает менеджером в ком-
пании Gillette Coal Mine, ему необходимо спрогнозировать спрос на уголь на ближайшие
два квартала. Он ввел данные по всей угольной отрасли 7 в рабочую книгу Уголь XLS
и построил по этим данным график, который показан на рис 12 27. На графике видно,
что объемы продаж выше среднего уровня в первом и четвертом кварталах (зимнее время
года) и ниже среднего во втором и третьем кварталах (весенне-летние месяцы)
Исключение сезонной составляющей
Процедура исключения сезонной составляющей из данных достаточно проста Сна-
чала необходимо вычислить среднее значение всех отклонений за один период сезонных
изменений Чтобы исключить сезонную составляющую в пределах одного года, исполь-
зуются данные за четыре периода (квартала) А чтобы исключить сезонную составляю-
щую из всего временного ряда, вычисляется последовательность скользящих средних по
т узлам, где т — продолжительность сезонных колебаний Для выполнения необходи-
мых вычислений Фрэнк Китч использовал столбцы С и D, как показано на рис 12 28
Столбец С содержит значения скользящего среднего по 4 узлам на основе данных, кото-
рые находятся в столбце В
Теперь Фрэнку надо назначить полученные значения скользящего среднего средним
точкам последовательности данных, на основе которых эти значения были вычислены
Эта операция называется центрированием значений Если т нечетное, то первое значение
скользящего среднего (среднее значений от первой до /и-й точки) надо присвоить
(т + 1 )/2 точке (например, если т = 7, то первое скользящее среднее будет назначено
четвертой точке) Аналогично среднее значений от второй до (т + 1)-й точки центриру-
ется в (т + 3)/2 точке и т д
Если т четное, как в случае, рассматриваемом Фрэнком, то задача несколько усложняется,
поскольку здесь центральные (средние) точки расположены между точками, по которым вы-
числялось значение скользящего среднего Например, центральная точка среднего значения
от первых четырех точек находится между второй и третьей точками, а центральная точка
среднего значения от второй до пятой точки находится посередине между третьей и четвертой
точками Поэтому центрированное значение для третьей точки вычисляется как среднее пер-
вого и второго значений скользящего среднего Например, первое число в столбце D отцен-
трированных средних на рис. 12.28 равняется (16)3 + 1594)/2 = 1603. На рис 12 29 показаны
графики исходных данных и отцентрированных средних
Далее находим отношения значений точек данных к соответствующим значениям от-
центрированных средних. Поскольку точкам в начале и конце последовательности дан-
ных нет соответствующих отцентрированных средних, такое действие на эти точки не
распространяется Эти отношения показывают степень отклонения значений данных от-
носительно типового уровня, определяемого отцентрированными средними Заметим,
что значения отношений для третьих кварталов меньше 1, а для четвертых — больше 1
' См [5]
ГЛАВА ^.Прогнозирование 831
J в; .1	С	.	D	Г	г
6 ^сходные	Скользящее	Центрированные тошекяя дамньа	Сезонные
	средние	средние	^мроваммым ср<	индексы
У1203		 		-$Е$2
:1$!11094	-СРЗНЛЧ(88:Bl1) -СРЗНЛЧ(С 10:Cl1) -B10/D10	-$Е$3
IX]1996	-СРЗНЛЧ(89:В12) -СРЗНАЧ (СИ : С12 ) «811/811	-SES4
	•СРЗНЛЧ(В 10:В13) -СРЗНЛЧ(С12:С13 ) -B12/D12	-SES1
13, ‘1332	-СРЗНХЧ(811:В141 -СРЗНЛЧ(С13:С14) -B13/D13	“SES2
14^1476	-СРЗНЛЧ(В12:B1S) -СРЗНЛЧ(С14:C1S) -B14/D14	-$Е$3
15 ,2533	“СРЗНЛЧ(813:В16) -СРЗНЛЧ(С15:С16) -В15/В15	-US4
16 <2249	-СРЗНЛЧ£814:B17J -СРЗНЛЧ(С1б:С17) -B16/D16	-UU
1533	«СРЗНЛЧ(В15:В18) -СРЗНЛЧ(С17:С18) -B17/D17	-$Е$2
-«18'^1935	-СРЗНЛЧ(816:B19J -СРЗНЛЧ(С18:С19) -B18/D18	“$Е$3
1>]2523	-СРЗНЛЧ(817;В20) -СРЗНЛЧ(С19:С20) -B19/D19	-$Е$4
Жр206	-СРЗНЛЧ(В18:В21) -СРЗНЛЧ(С2О:С21) -B20/D20	-SES1
1597	-СРЗНЛЧ(819:822) -СРЗНЛЧ(С21:С22) “B21/D21	-$Е$2
ljjl917	•СРЗНЛЧ(В20:В23) “СРЗНЛЧ(С22:С23) -B22/D22	“SES3
S3 2726	-СРЗНЛЧ(821:В24) -СРЗНЛЧ(С23:С24) -B23/D23	-SES4
zjF* 2612	“СРЗНЛЧ(В22:В25) -СРЗНЛЧ(С24:С25) -B24/D24	-$Е$1
25 1931	“СРЗНЛЧ(823:В26) -CP3HX4(C2SiC26) -B25/D2S	-$Е$2
24J2223	-СРЗНЛЧ(В24:В27) -СРЗНЛЧ(С26:С27) -B26/D26	-$Е$3
Z7J2363 Ж!2074	“СРЗНЛЧ(825:В28) -СРЗНЛЧ(С27:С28) “B27/D27	-SES4
	-СРЗНЛЧ(В2б:В29);-СРЗНЛЧ(С28;С29) -B26/D28	-$Е$1
29 .1589	-СРЗНЛЧ(827:ВЗО) -CP3HA4(C29iC30) -B29/D29	-$Е$2
Рис. 12.28. Данные, из которых будет исключаться сезонная составляющая
832 ЧАСТЫН Вероятностные модели
Время (год и квартал)
Рис. 12.29. Графики исходных данных и отцентрированных средних
Эти отношения являются основой для создания сезонных индексов Для их вычисления
группируются вычисленные отношения по кварталам, как показано на рис. 12.30
в столбцах G-0 Затем находятся средние значения отношений по каждому кварталу
(столбец Е) Например, среднее всех отношений для первого квартала равно 1,108 Это
значение является сезонным индексом первого квартала, на основе которого Фрэнк де-
лает вывод, что объем сбыта угля за первый квартал составляет в среднем около 110,8%
относительного среднего годового объема сбыта
:РЗНЛЧ(Н1:О1)
-CP3HA4tG3:N3)
-СРЗНЛЧ(С4 N4)
l-й к».	'	-----'1,24350164326262	1,12162583380089
2-й и».	-----0,744610232753196	0,743723468766951
3-я кь.	0,68236394623015’0,786570743405276	0,941663118194537
1-я га>	1,24004038207657 1,31746960535726	1,22609646458511
Рис. 12.30. Вычисление сезонных индексов
Сезонный индекс — это среднее отношение данных, относящихся к одному сезону
(в данном случае сезоном является квартал), ко всем данным Если сезонный индекс
больше 1, значит, показатели этого сезона выше средних показателей за год, аналогично,
если сезонный индекс ниже 1, то показатели сезона ниже средних показателей за год.
Наконец, чтобы исключить из исходных данных сезонную составляющую, следует
поделить значения исходных данных на соответствующий сезонный индекс. Результаты
этой операции приведены в столбцах F и G на рис 12 31 График данных, которые уже не
содержат сезонной составляющей, представлен на рис. 12 32
ГЛАВА 12. Прогнозирование
833
	Л • • (	С. '1	-Z 0	t ' /  . :	1	Г	L	с .	1. и
S			к Сезонные	составляйте* Прогноз
в	2 159		 		—		1 948,1	1 948,1
.:	]_ 203			—-					0,784	1 535,4	1 948,1
из	1 094	1 613	1 603	0	< 682	0,860	1 272,3	1 678,5
И	1 996	1 594	1 610	1	,240	1,234	1 617,8	1 413,1
Ш	2 001	1 626	1 674	1	,244	1, 108	1 877,8	1 546,8
ка	1 332	1 721	1 708	0	, 745	0,784	1 700,0	1 763,0
шз	1 476	1 05b	1 077	0	787	□ , 860	1 716,6	1 721,9
из	2 533	1 898	1 923	1	,317	1,234	2 053,1	1 718,4
	2 249	1 948	2 005	1	122	1, 108	2 029,3	1 937,1
17	1 533	2 063	2 061	0	744	Q 784	1 956,5	1 997,4
18	1 935	2 060	2 055	0	942	0,060	2 250,4	1 970,7
9	2 523	2 050	2 058	1	,22 6	1,234	2 045,0	2 153,4
20	2 20S	2 066	2 064	1.	070	1, 108	1 992,3	2 082,6
Й 1	1 597	2 061	2 087	0	,765	0, 784	2 038,2	2 023,6
JJZ	1 917	2 112	2 163	0,	, 886	0,860	2 229,5	2 033,2
23	2 726	2 213	2 255	1.	,209	1,234	2 209, 5	2 161,4
24	2 612	2 297	2 335	1.	119	1, 108	2 356,9	2 192,8
25	1 931	2 373	2 328	0,	830	0 784	2 464,5	2 300,0
26	2 223	2 202	2 215	1.	004	0, 860	2 585,3	2 407,5
*7	2 363	2 148	2 105	1.	123	1,234	1 915,3	2 523,7
28	2 074	2 0ь2	1 994	1	040	1, 108	1871,4	2 126,2
29	1 589	1 925	1 935	0		0, 784	2 028,0	1 959,7
	' с • . 1	0	- ( - к.. ' 1	г	}	0	и
	Скользящие	Центрированные ошекмя дакны	Сезонные	манные oes с	-е
•7	средние	средние	ированнын ср	нмдекснт	с о с т ав л ямце в	[	Прогноз
3		 		-$Е$1	-B8/F8	-G8
9		-$Е$2	-B9/F9	-$J$7*G8+(1-$J$7)*Н0
10	-СРЗНАЧ (В8: ВИ) :-СРЗНАЧ(СЮ:СИ) -B10/D10	-$Е$3	-B10/F10	«$J$7*G9+(1-SJ§7)*Н9
11	-СРЗНАЧ (В9: В12 ) “СРЗНАЧ (СИ : С12 ) -B11/D11	-$Е$4	-Bl1/F11	-SJS7*G1O+(1-$JS7)»Н10
12	“СРЗНАЧ(В10:В13) «СРЗНАЧ(С12:С13) «B12/D12	«SES1	-B12/F12	-$J$7«G11+(1-$J$7) «НИ
* 3	-СРЗНАЧ(Bl1:В14) -СРЗНАЧ(С 13:С14) -B13/D13	-SES2	-В13/F13	-$JS7*G12+(1-SJS7) >Н12
fgl	-СРЗНАЧ(В12:В15) »СРЗНАЧ(С14:С15) -B14/D14	“SE53	-B14/F14	- $JS7*G13 + (1-SJ57) *Н13
	-СРЗНАЧ(В13:В1 б) -СРЗНАЧ(С15:С16) -B15/D15	-$Е$4	“B15/F15	“$J$7*G14+(1~$J$7)"Н14
Tel	«СРЗНАЧ(В14:В17) «СРЗНАЧ(С16:С17) -B16/D16	-SES1	—B16/F16	«§JS7*G15+(l-SJ$7)«Н15
17 .	«СРЗНАЧ(В15:В18) -СРЗНАЧ(С17:С18) -B17/D17	-SES2	-B17/F17	-$JS7*G16+(l-$J$7)»H16
ia’	-СРЗНАЧ(В16:В19) -СРЗНАЧ(С18:С19) -B18/D18	-$Е$3	-B18/F18	«$J$7*G17+(1-$ J$7) *H17
19	»СРЗНАЧ(В17:В20) -СРЗНАЧ(С19:С20) -B19/D19	“$Е$4	-B19/F19	•=$JS7’G18+(1-$J$7) »H18
го	-СРЗНАЧ(В18:В21) -СРЗНАЧ(С20:С21) -B20/D20	-SES1	-B2O/F2O	•$JS7*G19+(1-$J$7)’H19
'1	вСРЗНАЧ(В19:В22) «СРЗНАЧ(С21:С22) «В21/В21	«$Е$2	-В21/F21	«$JS7*G20+(1-SJS7)*H20
22	«СРЗНАЧ(В20:В23) :-СРЗНАЧ(С22:С23) -B22/D22	-SES3	«В22/F22	-$J$7’G21+(1-SJS7)«Н21
	«СРЗНАЧ(В21:В24) «СРЗНАЧ(С23:С24) «B23/D23	-$Е54	-B23/F23	«$J$7*G22+(1-SJS7)*H22
24	-СРЗНАЧ(В22:В25) -СРЗНАЧ(С24:С25) -B24/D24	-SE51	-В24/F2 4	- $J$7"G23+(1-5J37)’H23
2Ь	“СРЗНАЧ(В23:В26) -СРЗНАЧ(С25:С2б) -B25/D25	-SES2	-B25/F25	- §JS7*G24+(1-5JS7)*H24
26	-СРЗНАЧ(В24:В27) :-СРЗНАЧ(С2б:С27) -B26/D26	“$Е$3	“B2 6/F26	-$JS7*G25+(1-?J$7)*H25
27	-СРЗНАЧ(B2S:В28) -СРЗНАЧ(С27;С28) -B27/D27	-$Е$4	-В27/F27	-$J$7*G26+(1-SJS7)*H26
28	-СРЗНАЧ(В26:В29) -СРЗНАЧ(С28:С29) -B28/D28	«SE51	-B28/F28	-sJ$7*G27+(l-sJS7)*H27
29~	-СРЗНАЧ(В27:ВЗО) -СРЗНАЧ(С29.СЗО) -B29/D29	-SES2	-B29/F29	- S J $7*G28+(1-$ J $ 7) ’H28
Рис. 12.31. Исключение сезонной составляющей
834 ЧАСТЬ III Вероятностные модели
Рис. 12.32. График данных, не содержащих сезонную составляющую
Прогнозирование
На основе данных, из которых исключена сезонная составляющая, строится прогноз.
Для этого используется соответствующий метод, который учитывает характер поведения
данных (например, данные имеют тренд или относительно постоянны). В этом примере
Фрэнк решил построить прогноз спроса на уголь на первый квартал десятого года с по-
мощью простого экспоненциального сглаживания. Оптимальное значение параметра а
равно 0,653 (что он нашел с помощью средства Поиск решения), при этом среднее абсо-
лютных отклонений равно 47,920 (рис 12 33) Прогнозируемый спрос на уголь в первом
квартале следующего года составляет 1726 тыс тонн (ячейка Н44). На основе этих дан-
ных таким же оказался прогноз спроса во втором квартале.
Рис. 12.33. Прогноз, выполненный методом экспоненциального сглаживания
ГЛАВА ^.Прогнозирование 835
Учет сезонной структуры
Теперь Фрэнку нужно учесть в полученном прогнозе (который равен 1726) сезонную
составляющую Для этого следует умножить 1726 на сезонный индекс первого квартала
1,108, в результате чего получим значение 1912 Аналогичная операция (умножение 1726
на сезонный индекс 0,784) даст прогноз на второй квартал, равный 1353
Рассмотренные выше методы скользящего среднею и экспоненциального сглажива-
ния — это относительно простые методы анализа временных рядов В последнее время на
практике стали применяться более сложные методы, которые в значительной степени
основаны на исследованиях Бокса и Дженкинса (G. Е Р Box and G М Jenkins, [2])
(метод Бокса-Дженкинса встроен во многие компьютерные пакеты прогнозирования)
12.5.	Статистические данные: разделяй и властвуй
При создании и тестировании моделей прогнозирования очень важную роль играют
статистические данные Как правило, созданию количественной модели прогнозирова-
ния предшествует ее логическое обоснование выявление причинно-следственных связей
и формализация зависимостей между независимыми переменными и зависимой пере-
менной, что невозможно сделать без статистических данных С другой стороны, хорошим
показателем качества модели является имитация “поведения в прошлом” этих данных
В любом случае, если строится количественная модель, то необходимо определить пара-
метры модели Приведем несколько примеров
1.	Для применения в модели линейной прогнозирующей функции у = а + Ьх необхо-
димо определить значения параметров а и Ь
2.	Чтобы применить взвешенное скользящее среднее по п узлам
5,+| = аоу, +а1х,_1 + +а„.|3,_„+, , надо определить количество узлов л и значения
весов а,„ а,,	, а„ ,
3.	Для использования метода экспоненциального сглаживания у,+1 = ay, +(1 -а)у
должно быть определено значение параметра а
Во всех моделях для определения значений параметров, как правило, используются
статистические данные Эти данные обычно применяются в соответствии с принципом
“разделяй и властвуй” часть данных используется для определения параметров, а остав-
шаяся часть — для тестирования модели На практике также важно “почистить” дан-
ные — проверить их на наличие явных отклонении от “нормы”, отметить пропуски или
какие-либо особые отличия и привести их в соответствие с остальными данными
Пусть, например, имеются еженедельные данные об объеме продаж одного товара за
последние два года (104 наблюдения), и планируется для прогнозирования будущих объ-
емов продаж использовать модель экспоненциального сглаживания Для этого необхо-
димо выполнить следующие действия
1.	Выбрать какое-то значение а и сравнить значения прогнозов у1+| и реальных дан-
ных у;>| для Г от 25 до 75 Первые 24 значения не используются для исключения на-
чального или “стартового” эффекта, т е чтобы свести к минимуму влияние на-
чального предположения о величине у. Подбор значений а следует продолжать
до тех пор, пока модель не будет выдавать значения прогноза, близкие к истин-
ным, на всем промежутке от t = 25 до t = 75.
836 ЧАСТЬ III Вероятностные модели
2.	Протестировать полученную модель на оставшихся 29 значениях данных. Иными
словами, используя наилучшее значение параметра а (определено в п.1), сравнить
значения у,+| и у, +| для/от 76 до 104.
Если на последних статистических данных модель работает достаточно точно, то, ве-
роятнее всего, при прогнозировании будущих значений результат также окажется доста-
точно точным. С другой стороны, если модель не будет давать близкие к истинным про-
гнозы на 76-104 недели, целесообразность ее использования вызывает сомнения. В этом
случае нужно применять другой метод прогнозирования.
Стратегию “разделяй и властвуй” можно использовать в любом методе прогнозирова-
ния Это эквивалентно имитации работы модели на статистических данных. Таким обра-
зом строится один из популярных методов тестирования моделей. Но здесь необходимо
учитывать следующее. Если модель не дает удовлетворительных результатов на статисти-
ческих данных, то вероятнее всего, что она в данном случае просто не подходит Если же
модель дает значения прогноза, близкие к имеющимся данным, то все равно нельзя быть
уверенным, что она будет хорошо работать в будущем, — возможно, реальная система, ле-
жащая в основе модели прогнозирования, изменилась.
С помощью модели прогнозирования
корпорации Taco Bell сократила расходы
на оплату труда на несколько миллионов
Корпорация Taco Bell имеет около 6,5 тысяч филиалов и офисов в 50 странах ми-
ра Суммарный годовой объем продаж составляет примерно 4,6 млрд, долл В конце
80-х годов для повышения эффективности управления и рентабельности компания
реструктуризировала свой бизнес Корпорация разработала комплексный набор мо-
делей принятия решений, среди которых были также модели прогнозирования За
1997 год с помощью этих моделей удалось сэкономить более $53 миллионов на рас-
ходах по заработной плате
В компании Taco Bell на эту статью расходов отчисляется приблизительно 30%
с каждого заработанного доллара, и эти расходы принадлежат к числу наибольших
контролируемых расходов Кроме того, ими наиболее тяжело управлять, поскольку
существует прямая связь между объемом продаж и количеством занятых работников
Из-за того, что продаваемые продукты должны быть свежими, их нельзя произво-
дить в большом количестве и складировать во время низкого спроса, а затем, когда
спрос повысится, продавать С другой стороны, заказываемый продукт должен быть
готов немедленно Кроме того, поскольку спрос в значительной мере колеблется
и сосредоточен в районе обеденного перерыва (52% всех продаж за день совершают-
ся во время трехчасового периода с 11 до 14 часов), то определение расписания коли-
чества работников и распределение обязанностей между ними в данный промежуток
времени — весьма сложная и утомительная задача.
Операции с клиентами во время любого 15-минутного интервала зависят от мно-
жества факторов изменчивости, включая день недели, неделю месяца и месяц года.
Чтобы исключить максимально возможное число факторов изменчивости, все дан-
ные об операциях с клиентами были разделены на некоторое число независимых
временных рядов, каждый из которых представлял собой архив соответствующего
15-минутного интервала в течение определенного дня недели. Например, данные об
операциях с клиентами в отдельно взятом магазине за все прошлые пятницы с 9:00
ГЛАВА ^.Прогнозирование 837
до 9 15 составляют временной ряд, используемый для прогноза сделок в этом мага-
зине в будущие пятницы с 9:00 до 9:15.
Было опробовано множество методов прогнозирования на основе временных ря-
дов, после чего был сделан вывод, что наилучшим методом в данном случае является
простое скользящее среднее по данным шести недель (в этом случае среднее квадра-
тов ошибок было минимальным). С помощью новой системы прогнозирования ме-
неджер получает прогнозы на следующую неделю, результаты которых он использует
при составлении расписания работ. [4]
12.6.	Качественное прогнозирование
Множество реальных прогнозов не были основаны на формальных моделях. В первую
очередь это касается сферы международных отношений, так сказать, вопросов войны
и мира. Более неожиданным может показаться то, что это относится и к вопросам эко-
номики Например, во время высоких процентных ставок в 1980 и 1981 годах большинст-
во влиятельных прогнозов были сделаны не с помощью популярных тогда эконометри-
ческих моделей, а двумя специалистами, Генри Кауфманом (Henry Kaufman) из компа-
нии Salomon Brothers и Альбертом Войнилауером (Albert Wojnilower) из Первого банка
Бостона. Эти джентльмены объединили неформальным способом важные экономиче-
ские факторы (денежные запасы и уровень безработицы) с результатами использования
количественных моделей и получили прогнозы, которые имели большой уровень дове-
рия и произвели значительное воздействие на финансовые круги.
Для менеджеров мораль этой истории такова: прогнозирование на качественном
уровне (без построения формальных моделей) также может быть важным источником
информации. Менеджеры должны просмотреть большое число источников информации,
прежде чем принимать решение. Нельзя игнорировать и мнение экспертов. Ниже рас-
сматривается метод качественного прогнозирования, который объединяет прогнозы,
сделанные различными группами экспертов.
Метод Дельфи
Этот метод решает проблему получения объединенного прогноза, составленного на
основе заключения группы экспертов. Один из возможных подходов к получению такого
прогноза состоит в том, чтобы собрать экспертов вместе в одной комнате для обсуждения
какого-либо вопроса до тех пор, пока не возникнет между ними согласие по этому вопро-
су. Но этот подход имеет недостаток, так как существует объективная динамика поведе-
ния такого коллектива — одна сильная личность может подавить остальных В таком слу-
чае тщательный анализ рассматриваемого вопроса может быть отодвинут на второй план.
Метод Дельфи был разработан Rand Corporation для сохранения мощи коллективного
прогнозирования, при этом исключается влияние поведения коллектива. В этом методе
участвует координатор и группа экспертов. Ни один из экспертов не знает, кто еще нахо-
дится в этой группе, поскольку все контакты проходят через координатора. Подобный
процесс иллюстрируется на рис. 12.34.
838 ЧАСТЬ III Вероятностные модели
Рис. 12.34. Метод Дельфи
После трех-четырех проходов этого процесса, как правило, достигается соглашение
по данному прогнозу Принятый прогноз может быть чем-то средним между первона-
чальными предложениями, но если прогноз, который был отброшен при первоначаль-
ном рассмотрении, подтвердится после строгого анализа, то скорее всего окажется, что
этот прогноз будет очень похож на тот, который был принят группой экспертов после
третьего или четвертого обсуждения.
Прогнозирование и исследование рынка
Другие качественные методы прогнозирования в основном сосредоточены на пред-
сказании спроса на продукт или группу продуктов. Они основаны на концепции опроса
тех, кто непосредственно общается с конечными потребителями (например, продавцов),
изучении мнения потребителей о самом продукте или о их планах на его покупку.
Опрос продавцов
Обычно продавцов опрашивают для прогнозирования спроса на определенный про-
дукт в районе, где расположен их магазин В наиболее упрощенном подходе эти опросы
суммируются для того, чтобы получить итоговый прогноз спроса. При более сложном
подходе отдельные прогнозы или же общий прогноз модифицируется на основе стати-
стической корреляции между прогнозом продавца и фактическим объемом продаж. Эта
процедура позволяет избавиться от стереотипного оптимизма продавцов.
Массовые опросы имеют преимущество, которое заключается в том, что собирается
большое количество детализированных сведений. Продавцы обычно очень хорошо знают
ГЛАВА 12 Прогнозирование 839
ситуацию в своем районе и могут сделать лучшие прогнозы, чем формальные модели
Тем не менее при таком способе прогнозирования возникает несколько проблем
1.	Высокая стоимость. Во время опроса продавцы временно ничего не продают,
вследствие чего несут убытки Некоторые эксперты считают, что высокая стои-
мость такого прогнозирования является его основным недостатком
2.	Потенциальный конфликт интересов Прогнозы объема продаж можно легко пре-
вратить в требуемый показатель сбыта, который будет выгоден продавцу Это мо-
жет привести к умышленному занижению прогноза некоторыми продавцами
3.	Товарная шизофрения (стереотипный оптимизм продавца) Для продавцов важно
быть оптимистами по отношению к продаваемым товарам и к их потенциальной
пользе Но ясно, что этот энтузиазм не всегда согласуется с беспристрастной
оценкой рыночного потенциала
Обобщив сказанное, можно сделать вывод, что массовый опрос не всегда согласуется
с целями прогнозирования, и поэтому он может быть не эффективным.
Опрос потребителей
Исследование рынка — это большая и важная тема, в рамках которой разработаны
собственные правила и методы прогнозирования, от опроса потребителей и потребитель-
ских инспекций до пробного маркетинга Конечной целью исследования рынка являют-
ся предсказание объема и структуры рынка каких-либо товаров или услуг Эти предска-
зания (прогнозы) обычно основаны на небольших выборках и выражены в качественной
форме, поскольку исходными данными, как правило, являются субъективные оценки
потребителей Существует большое число методов анализа таких данных
12.7.	Заключение
В любых сферах общественной и производственной деятельности в явном или неяв-
ном виде присутствует необходимость оценивать будущие события Вследствие этого
управление процессом прогнозирования является важной обязанностью любого менед-
жера Менеджер должен решить, какие ресурсы необходимы для осуществления прогно-
за и какой подход использовать для его выполнения При решении вопроса о ресурсах он
должен учитыват г следующие факторы
1.	Важность прогноза или, точнее, допустимое время ожидания прогноза, требуемого
для принятия решения, и влияние этого прогноза на решение
2.	Качество прогноза как функция от затраченных ресурсов
Другими словами, насколько важен прогноз и сколько он стоит Это те вопросы, ко-
торые менеджер должен задать себе и ответить на них, чтобы принять решение о начале
процесса прогнозирования
На практике выбор подходящего метода прогнозирования для конкретной ситуации
зависит от множества факторов Существуют некоторые характеристики, которые отли-
чают одну ситуацию от другой
1.	Важность решения.
2.	Наличие значимых данных
3.	Временной диапазон прогнозирования
840 ЧАСТЬ III Вероятностные модели
4.	Стоимость прогноза.
5.	Промежуток времени, по истечению которого прогноз не будет нужен.
6.	Количество раз использования модели прогнозирования
7.	Стабильность окружающей среды.
Важность принятия решения, наверное, играет главную роль при выборе метода
прогнозирования. Отметим, что качественные методы (в отличие от количественных)
преобладают во всех прогнозах.
На нижнем конце шкалы важности стоят прогнозы, которые являются простыми
бизнес-решениями, принимаемыми менеджерами супермаркетов- какие проводить ак-
ции, какие товары выставлять в конце полок, сколько требуется нанять упаковщиков
и т п Цена неверного прогноза здесь не достаточно велика, чтобы использовать фор-
мальные модели прогнозирования и их всесторонний анализ.
Наверху шкалы важности находятся очень важные (и, как правило, очень сложные)
прогнозы, которые полностью можно описать только количественными моделями. На-
пример, будущее компании, не говоря уже о будущем исполнительного директора, зави-
сит от хорошего прогноза и соответствующего решения, принимаемого на его основе.
Количественные модели прогнозирования здесь обязательны, но их использование ограничено
При принятии очень важных решений итоговый прогноз составляется не только на осно-
ве количественной хорошо обоснованной модели, но и на заключениях исполнительного
директора и его коллег и обязательно с учетом мнений экспертов.
Количественные модели прогнозирования на практике играют решающую роль, как пра-
вило, в ситуациях, которые можно считать “средними по уровню важности”. Это справедливо
при принятии краткосрочных (до одного месяца) и среднесрочных (от одного месяца до двух
лет) решении Модели на основе временных рядов чаще всего применяются в периодически
повторяющихся прогнозах среднего уровня важности и в относительно стабильном окруже-
нии. Причинно-следственные модели активно “конкурируют” с мнениями экспертов в про-
гнозировании разнообразных среднесрочных экономических явлений среднего уровня важ-
ности Количественные модели разрабатываются для ситуаций, которые часто повторяются
и в которых доступны статистические данные. Для таких ситуаций разработано много удач-
ных моделей
Основные термины
Взвешенное скользящее среднее по п узлам. Для прогноза используется взвешенная сумма последних п
наблюдений Сумма весов равна 1 Для вычислений необходимо п последних наблюдений.
Линейная регрессия. Статистический метод, используемый для определения коэффициентов та-
кого многочлена, который “наилучшим образом” описывает набор данных
Метод Дельфи. Метод достижения согласия в группе экспертов, при котором исключается их лич-
ное общение
Метод наименьших квадратов. Процедура, выполняемая на наборе данных для подбора кривой,
минимизирующей сумму квадратов отклонений исходных данных от кривой.
Многочлен степени п. Функция вида у = аа +	+ ар? + .. + арх'. Часто используется в качестве
подбираемой кривой, коэффициенты которой находятся по методу наименьших квадратов
Модель Хольта. Разновидность экспоненциального сглаживания, учитывающая тренд данных
Подбор кривой. Выбор функции, график которой на диаграмме проходит достаточно близко к точ-
кам данных
ГЛАВА 12 Прогнозирование 841
Причинно-следственное прогнозирование. Прогноз интересующей величины, определенной в виде
функции от других переменных
Проверка достоверности. Процесс проверки модели прогнозирования на данных за прошлый пе-
риод для оценки правильности модели
Прогнозирование временного ряда. Прогнозируемая переменная является функцией от времени
и экстраполируется в будущее с помошью специальных методов
Простое скользящее среднее по п узлам. Для прогноза используется среднее арифметическое значе-
ний последних п точек данных Для вычислений необходимо п последних наблюдений
Сезонные колебания. Структура изменений данных временного ряда, при которой колебания зна-
чений данных имеют постоянную периодичность
Экспоненциальное сглаживание. Взвешенная сумма всех наблюдений Сумма весов равна 1 Для вычисле-
ний необходимо одно последние наблюдение и предыдущий прогноз
Контрольные вопросы
Да/нет
1.	Минимум суммы отклонений является разумным критерием определения
“подходящего приближения”
2.	Подбор кривых методом наименьших квадратов можно использовать для многих
видов функций, в том числе для линейных.
3.	Регрессионный анализ можно использовать для доказательства того, что метод
наименьших квадратов обеспечивает наилучшее возможное приближение для лю-
бой реальной модели
4.	Метод наименьших квадратов применяется в причинно-следственных моделях так
же, как и в моделях временных рядов.
5.	При прогнозировании методом взвешенного скользящего среднего по трем узлам
существуют разные способы назначения веса.
6.	При экспоненциальном сглаживании веса назначаются автоматически, причем
они убывают на более “старых” данных.
7.	Среднее квадратов ошибок является одним из способов сравнения различных ме-
тодов прогнозирования.
8.	Проверка достоверности модели — это процесс определения правильности резуль-
татов работы модели путем имитации ее работы на данных за прошлые периоды.
Выберите правильный ответ
9.	Линейная регрессия (с одной независимой переменной)'
а	требует определения трех параметров;
Ь.	является особым случаем многочлена, определяемого методом наименьших
квадратов;
с.	использует сумму отклонений в качестве меры точного подбора кривой.
10.	Проблема при использовании метода скользящего среднего по к узлам состоит
в том, что:
842 ЧАСТЬ III Вероятностные модели
а всем наблюдениям назначается равный вес,
b последним к наблюдениям назначается одинаковый вес,
с в памяти нужно хранить к точек данных,
d ничего из перечисленного выше
11.	В методе экспоненциального сглаживания при больших значениях а больший вес
назначается
а последним данным,
b ранее полученным данным
12.	Если наблюдаемые данные можно описать как случайные отклонения от стацио-
нарного значения, то в модели экспоненциального сглаживания предпочтительнее
использовать значение параметра а
а большое,
b малое
13.	Стратегия “разделяй и властвуй” означает
а разделение процедуры создания модели прогнозирования на две части' во-
первых, все данные используются для оценки значений параметров, и, во-
вторых, проверяется адекватность модели,
b разделение данных на две части первая часть используется для определения
параметров модели, а вторая — для проверки адекватности модели,
с сравнение двух моделей на одном и том же наборе данных,
d ничего из перечисленного выше
14.	Метод Дельфи
а полагается на силу сформулированных письменно аргументов;
b настаивает на разрешении противоречий посредством дискуссий экспертов,
с используется как альтернатива методу экспоненциального сглаживания,
d ничего из перечисленного выше
Ответы
1. Нет 2. Да 3. Нет 4. Да 5. Да 6. Да 7. Да 8. Да 9. b 10. с 11. а. 12. b 13. b 14. а
Учебные задачи
12 1 Ниже представлены данные
х	|	100	70	30	40	80	60	50	20	10	90
уI	57	40	35	33	56	46	45	26	26	53
а На основе этих данных постройте точечную диаграмму
b Методом наименьших квадратов подберите линейную функцию приближения
с Используя построенную функцию, спрогнозируйте значение переменной у при х= 120
12 2 Дан следующий набор данных, где х — независимая переменная, а у — зависимая
х |	30 25 20 L5 10 5
у	15	20	30	35	45	60
ГЛАВА 12. Прогнозирование 843
а. Постройте точечную диаграмму на основе этих данных
b Подберите методом наименьших квадратов линейную функцию
12 3 Приводится следующее множество данных
х |	1______2__________3_______4__________5_________6__________7
у | 2ДЮ П50	ф504~005^50	ф506Д)
а Постройте точечную диаграмму этих данных
b Методом наименьших квадратов подберите линейную функцию и постройте ее график
с На основе данных подберите методом наименьших квадратов квадратичную функцию
и постройте ее график
12 4 На основе данных задачи 12 2 методом наименьших квадратов подберите квадратичную
функцию
12 5 Для данных задачи 12 3 подсчитайте сумму квадратов отклонений для полученных методом
наименьших квадратов линейной и квадратичной функций Сравните полученные значения
12 6 Вычислив суммы квадратов отклонений, сравните адекватность данным задачи 12 2 ли-
нейной функции, построенной методом наименьших квадратов, и квадратичной функции,
полученной тем же методом в задаче 12 4
12 7 Пусть переменная х в задаче 12 1 представляет собой момент времени, когда было получе-
но данное наблюдение, умноженный 10, а у является переменной спроса Например, в 10-й
момент времени спрос был равен 57, а в моменты времени 1 и 2 значения спроса равны 26
а Постройте график зависимости спроса от времени
b Используя простое скользящее среднее по 4 узлам, спрогнозируйте спрос в 11-и мо-
мент времени
с Подходит такой метод прогнозирования для этих данных или нет9 Почему9
12 8 Рассмотрите следующую последовательность данных
Время |	1	2	3	4	5	6	7	89	10	11	12
Спрос | 10	14	1926	31	3539	44	51	55	61	54
а Постройте график этого временного ряда Соедините точки отрезками прямых
b Используя простое скользящее среднее по 4 узлам, спрогнозируйте спрос для узлов 5— 13
с Найдите среднее абсолютных отклонений
d Целесообразно ли использовать данный метод прогнозирования для представленных
данных9
129 Рассмотрите данные задачи 12 7
а Используя взвешенное скользящее среднее по 4 узлам и назначив веса 4/10, 3/10, 2/10,
1/10, спрогнозируйте спрос в момент времени И Больший вес следует назначить бо-
лее поздним наблюдениям
b Является ли данное приближение более предпочтительным по отношению к простому
скользящему среднему по 4 узлам, которое использовалось в задаче 12 79 Почему9
с С помощью средства Поиск решения найдите оптимальные веса узлов Насколько
уменьшилась ошибка приближения9
12 10 Вернитесь к данным, представленным в задаче 12 8
844 ЧАСТЬ III. Вероятностные модели
а Воспользуйтесь методом взвешенного скользящего среднего по 4 узлам, назначив веса
0,1,0,2, 0,3 и 0,4, чтобы получить прогноз спроса в моменты времени 5—13 Больший
вес следует назначить более поздним наблюдениям
b Найдите среднее абсолютных отклонений
с Считаете ли вы, что данное приближение более предпочтительно по сравнению с мо-
делью простого скользящего среднего по 4 узлам, которая применялась в задаче 12 89
Почему9
d С помощью средства Поиск решения найдите оптимальные веса узлов На сколько
удалось уменьшить значение ошибки9
12 11 Рассмотрите данные временного ряда из задачи 12 7
а Пусть у, = 22 и а = 0,4 Спрогнозируйте спрос в 11-й момент времени методом экспо-
ненциального сглаживания
b Если бы вы использовали метод экспоненциального сглаживания для прогнозов этого
временного ряда, вы бы предпочли большее (>0,4) или меньшее значение параметра
а9 Почему9
с Путем минимизации среднего абсолютных ошибок в процентах определите с помо-
щью средства Поиск решения оптимальное значение а
12 12 Вернитесь к данным временного ряда, представленного в задаче 12 8
а Пусть у, = 8 и а = 0,3 Используйте метод экспоненциального сглаживания для про-
гноза спроса в периоды 2-13
b Найдите значение среднего абсолютных ошибок в процентах
с Повторите пункты а и />, используя значение а = 0,5
d Если бы вы использовали метод экспоненциального сглаживания для осуществления
прогнозов этого временного ряда, какое значение параметра а вы бы выбрали9 Почему9
е Чему равно оптимальное значение а9 На сколько при этом меньше значение среднего
абсолютных ошибок в процентах по сравнению с пунктом а9
12 13 Президент компании Quacker Mills хочет оценить потенциал рынка новых продуктов Для
этого создана группа, в которую входят вице-президент, менеджер по маркетингу и десять
региональных представителей в западном регионе Обсудите преимущества и недостатки
этой группы по принятию решений и возможности применения метода Дельфи для полу-
чения этой оценки
12 14 Пусть yt задается формулой yt = yt — 1 + е, где е — случайная величина со средним 0, и у1 = 1,
у1 = 2, уЗ = 1,5, у4 = 0,8, у5 = 1 Какой наилучший прогноз для величины уб9
12 15 Оцените достоинства критерия “среднее квадратов ошибок ” Всегда ли лучше тот метод,
при использовании которого значение среднего квадратов ошибок меньше?
12 16 Оцените преимущества и недостатки среднего квадратов ошибок, среднего абсолютных от-
клонений и среднего абсолютных ошибок в процентах, рассматривая их как критерии аде-
кватности моделей прогнозирования Почему в разных ситуациях один критерий предпоч-
тительнее другого9
12 17 Менеджер по маркетингу небольшой развивающейся компании, содержащей сеть продо-
вольственных магазинов, хочет получить прогноз объема продаж в магазине, открываю-
щемся в небольшом городке на среднем западе Он собрал статистические данные о насе-
лении и об объемах продаж в десяти других работающих магазинах корпорации. Эти дан-
ные представлены в табл 12 3.
а Постройте точечную диаграмму на основе этих данных.
b Методом наименьших квадратов подберите к этим данным линейную функцию.
ГЛАВА ^.Прогнозирование 845
с Спрогнозируйте объем продаж в новом магазине, если численность населения в городе
составляет 50 000
Таблица 12.3
Номер магазина	Объем продаж, S	Население, чел.
I	400 000	10 000
2	1 250 000	65 000
3	1 300 000	72 000
4	1 100 000	54 000
5	450 000	42 500
6	540 000	36 800
7	500 000	27 500
8	1 425 000	85 000
9	1 700 000	98 000
Ю	475 000	37 500
12 18 Менеджер по маркетингу небольшой развивающейся компании, содержащей сеть продо-
вольственных магазинов, обладает информацией об объемах продаж за все время сущест-
вования самого прибыльного магазина (табл 12 4)
а Используя простое скользящее среднее по 3 узлам, спрогнозируйте значения в узлах
с 4 до 11
b Используя взвешенное скользящее среднее по 3 узлам, спрогнозируйте значения в уз-
лах с 4 до ] ] Для определения оптимальных весов воспользуйтесь средством Поиск
решения
с Методом экспоненциального сглаживания спрогнозируйте значения в узлах 2—11 Оп-
ределите оптимальное значение параметра а с помощью средства Поиск решения
Таблица 12.4
Период	Объем продаж, S
1	750 000
2	790 000
3	810 000
4	875 000
5	990 000
6	1 090 000
7	950 000
8	1 050 000
9	1 150 000
10	1 200 000
11	1 250 000
846 ЧАСТЬ III Вероятностные модели
12 19 Оцените, насколько стратегия “разделяй и властвуй” подходит для применения в прогно-
зировании временных рядов Какие альтернативные варианты можно рассмотреть, если ре-
зультаты, полученные после использования этой стратегии, нс будут вас удовлетворять'’
12 20 Обсудите роль теории вероятностей в создании моделей прогнозирования В каких случаях
в моделях прогнозирования удобно использовать случайные переменные и какой тип ста-
тистических зависимостей можно применять в этих моделях9
Прикладные задачи
12 22
12 23
В некоторых случаях можно получить более точные прогнозы с помощью прогноза, учиты-
вающего тренд
а Используя метод Хольта со значением у, = 22, спрогнозируйте последовательность
значении спроса для задачи 12 7
b Используя среднее квадратов ошибок, сравните результаты, полученные с помощью
методов экспоненциального сглаживания (задача 12 11) и Хольта
В некоторых случаях можно получить более точные прогнозы с помощью прогноза, учиты-
вающего тренд
а Используя метод Хольта со значением , = 8 , спрогнозируйте последовательность
значений спроса для задачи 12 8
b Используя среднее квадратов ошибок, сравните результаты, полученные с помошью
методов экспоненциального сглаживания (задача 12 12) и Хольта
В разделе 12 4 была представлена модель прогнозов доходов компании Startup Airlines На
основе данных этой модели
а разработайте модель линейной регрессии, учитывающей тренд, в которой независи-
мой переменной будет время,
b оцените эффективность построенной модели, сравнив се с моделью Хольта
12 24 В рабочей книге Busmess_Week XLS приведены данные из журнала Business Week по еже-
месячным об-ьемам продаж автомобилей за 43 месяца
а Исключите из этих данных сезонную составляющую
b Определите наилучший метод прогнозирования для имеющихся данных
с	Чему равен прогноз для 44-го периода ’
d Насколько вы уверены в этом прогнозе9
12 25 К данным, представленным в рабочей книге Заправка XLS, примените средство Excel Рег-
рессия для подбора по этим данным квадратичной функции Сравните эти результаты
с теми, которые были получены в разделе 12 3 с использованием средства Поиск решения
Ситуация для анализа | Ларамийский банк
Джим Коуэн (Jim Cowan), директор Ларамийского банка, пересматривает штат-
ное расписание операционнт о отдела
Ларамийский банк проводит индивидуальные и корпоративные банковские опе-
рации и обеспечивает полный спектр кредитных услуг для своих клиентов Общий
актив банка составляет 19 млн долл с чистым доходом в 300 тыс долл
ГЛАВА 12. Прогнозирование
847
Операционный отдел
Операционный отдел занимается чековыми операциями Отдел получает и обра-
батывает чеки и другие документы и проводит по ним расчеты Ежедневно в отдел
поступает чеков в среднем на сумму 450 тыс долл На отделе лежит ответственность
за сортировку чеков, проверку правильности депозитов и запись ежедневных тран-
закций банка Отдел работает с 8 00 до 17 30 с понедельника по пятницу. Несмотря
на распространенную практику других банков обрабатывать чеки практически круг-
лосуточно, в Ларамийском банке служащие работают нормальный рабочий день
Количество обрабатываемых операционным отделом чеков значительно увели-
чилось за последние два года с 780 тыс до 1,6 млн. за год Также усложнилась задача
составления расписания работ этого отдела из-за неравномерного поступления че-
ков В табл. 12 5 содержатся данные, из которых была исключена сезонная состав-
ляющая, об объеме обрабатываемых отделом чеков по неделям от начала прошлого
года. Зная временную структуру поступлений чеков, руководство может использо-
вать частично занятых рабочих для того, чтобы покрыть максимальные нагрузки
В данный момент одна треть операторов работает полный рабочий день, а две тре-
ти — неполный. Каждый оператор в среднем обрабатывает 700 чеков за один час
Таблица 12.5. Недельный объем поступающих в отдел чеков
Неделя	Объем, тыс.	Неделя	Объем, тыс.
I	23,4	34	31,1
2	26,4	35	31,0
3	28,7	36	29,6
4	26,4	37	31,5
5	28,6	38	31,3
	29,4	39	31,1
7	29,9	40	34,9
8	29,3	41	32,3
9	32,2	42	35,6
Ю	28,7	43	33,8
И	27,8	44	31,3
12	31,1	45	31,2
13	32,7	46	30,4
14	32,5	47	31,1
15	28,9	48	32,7
16	31,8	49	34,8
17	32,8	50	34,5
18	32,7	51	36,0
19	31,7	52	28,3
20	32,5	53	27,8
21	32,7	54	30,4
22	30,9	55	28,4
23	30,5	56	29,3
24	31,3	57	28,9
848 ЧАСТЬ III Вероятностные модели
Окончание табл. 12.S
Неделя	Объем, тыс.	Неделя	Объем, тыс.
25	30,1	58	33,5
26	32,4	59	32,6
27	28,5	60	32,0
28	29,9	51	30,6
29	31,7	62	31,9
30	30,7	63	31,3
31	31,6	64	31,6
32	32,1	65	31,1
33	30,1	66	32,0
Прогнозирование
В первую очередь м-ру Коуэну необходимо спрогнозировать спрос (количество че-
ков) на следующую, 67-ю, неделю, а затем в соответствии с прогнозом — составить
расписание работы служащих, занятых полный и неполный рабочий день. Для него
привлекательны два простых метода прогнозирования — использовать известное зна-
чение спроса на прошлой неделе для прогноза на следующую или же использовать
среднее значение за все 66 недель При этом его, конечно, интересует, насколько точ-
ными являются эти простые методы, и какой из них лучше Джим хотел использовать
свой прогноз для того, чтобы определить, сколько часов работы служащих с неполным
рабочим днем следует включить в расписание на следующую неделю Основное распи-
сание составлено так, чтобы вовремя обработать 15 000 чеков, но Коуэн может вклю-
чить в него любое число дополнительных часов (Основное расписание основано на
количестве чеков, которые будут обработаны одним служащим, работающим полный
рабочий день, и двумя, работающими неполный день Также предусмотрено, что слу-
жащие должны выполнять и другие свои обязанности ) Если он запланирует дополни-
тельные часы работы, то за них необходимо будет заплатить даже в том случае, если
служащие закончат обработку чеков досрочно С другой стороны, если объем чеков бу-
дет настолько велик, что они не будут обработаны в запланированное время, то при-
дется работать сверхурочно (стоимость такой работы на 50% выше обычной). Не суще-
ствует требования, чтобы обработка чеков, поступивших в какой-то определенный
день, была закончена в этот же день, но все накопившиеся за неделю чеки должны
быть обработаны до обеда в пятницу.
Коуэн должен построить модель прогнозирования, а затем на основе получен-
ного прогноза определить число дополнительных часов работы служащих с непол-
ной занятостью
Вопросы
I Рассмотрите пять следующих методов прогнозирования недельного объема ра-
бот для операционного отдела.
•	Метод 1 Простая схема прогнозирования, когда значение за прошлую неделю
принимается за прогноз на следующую неделю.
•	Метод 2 В качестве прогноза используется средний объем за все предыдущие не-
дели.
ГЛАВА ^.Прогнозирование 849
•	Метод 3. Метод экспоненциального сглаживания с параметром 0,5 Этот метод реа-
лизован в рабочей книге Банк XLS, в которую уже введены данные из табл 12 5.
•	Метод 4 Это метод скользящего среднего. Число узлов выбираете вы Попробуй-
те воспользоваться несколькими различными значениями числа узлов
•	Метод 5. Это метод линейной регрессии Как правило, здесь требуется подобрать
по имеющимся данным линейную функцию, рассматриваемую как тренд данных
2 Какой из представленных выше методов прогнозирования вы порекомендовали
бы для прогноза недельного объема работ? Если нужно, подберите константу
сглаживания в методе 3 для того, чтобы добиться более точных результатов
3. Сколько дополнительных часов работы м-ру Коуэну следует включить в распи-
сание на следующую неделю?
Ситуация для анализа | Shumway, Horch и Sager (часть 2 )8
Кристенсен занимается изучением данных о распространении ежемесячных жур-
налов Первый набор данных — о журнале Working Woman (представлены на листе
Женщина рабочей книги Журналы XLS и на рис 12 35), который рассчитан на дело-
вых женщин. Журнал включает разделы, посвященные предпринимательству, ново-
стям бизнеса, тенденциям развития экономики, технологиям, политике, карьерному
росту, социологии и психологии, моде и здоровью Тираж этого журнала практиче-
ски полностью распространяется по подписке, как свидетельствуют последние дан-
ные о тираже (823,6 тыс. из 887,8 тыс было распространено по подписке)
Working Woman
Время (месяцы)
Рис. 12.35. Тиражи журнала Working Woman
Этот материал может служить основой для обсуждения в аудитории Он не является иллюстрацией эффектив-
ного или неэффективного подхода к решению административных ситуации © 1990 by the Darden Graduate Business
School Foundation Резюме этого материала приведено на lVeb-узле wwk datden Virginia edu/pubhshtng
850 ЧАСТЫП Вероятностные модели
Следующий график содержит данные о тиражах журнала Country Living
(находится на листе Село рабочей книги Журналы.XLS и показан на рис. 12 36).
Этот журнал уделяет основное внимание практическим вопросам сельского хозяйст-
ва и духовным интересам жизни на земле. Он продается людям, живущим в сельской
местности либо там, где есть работающие фермы, загородные дома или же клубы от-
дыха, работающие по выходным
Третий набор данных относится к журналу Health (представлены на листе Здоро-
вье рабочей книги Журналы.XLS и на рис 12 37) Журнал в основном рассчитан на
женщин, и в нем представлена информация о питании, медицине, психологии и мо-
де для женщин, ведущих активный образ жизни
Рис. 12.37. Тиражи журнала Health
ГЛАВА 12. Прогнозирование
851
На рис 12 38 показаны данные по журналу Better Homes and Gardens (находятся на
листе Дом рабочей книги Журналы XLS) Он рассчитан для семейного чтения. В нем
глубоко рассматриваются темы дома и семьи, пища и кухонные приборы, строительство
и рукоделие, украшения, управление семейным бюджетом, садоводство, путешествия,
здоровье, бытовая техника и семейные вечеринки, информация о новых продуктах и ма-
газинах Объем тиражей этого журнала кажется изменчивым, но постоянно растущим
Время (месяцы)
Рис. 12.38. Тиражи журнала Better Homes and Gardens
Последним представленным здесь журналом является True Story (лист Истории
рабочей книги Журналы XLS, рис 12 39) Это журнал для чтения, рассчитанный на
молодых женщин Кроме занимательных историй в нем много тематических статей
рецепты и свойства пищи, статьи о красоте и здоровье, домашние хитрости и личные
советы Тираж этого журнала имеет четко выраженную тенденцию спада на протя-
жении последних девяти лет
1	7 13 19 25 31 37 43 49 55 51 67 73 79 85 91 97
Время (месяцы)
Рис. 12.39. Тиражи журнала True Story
852 ЧАСТЫП Вероятностные модели
Вопрос
Какой метод прогнозирования является оптимальным для каждого представлен-
ного журнала? При тестировании различных методов прогнозирования воспользуй-
тесь концепцией “разделяй и властвуй”
Литература
1	Bruce Andrews and Shawn Cunningham L L Bean Improves Call-Center Forecasting, Interfaces, 25,
no 6 (1995), p 1-13
2	George E P Box and Gwilym M Jenkins, Time Senes Analysis, Forecasting and Control San Fran-
cisco Holden-Day, Inc., 1970
3	Alan L C Bullock, Hitler A Study in Tyranny New York Harper & Row, 1962
4	Jackie Hueter and William Swart, An Integrated Labor-Management System for Taco Bell, Interfaces,
28, no 1 (1998), p 75-91
Модели очередей
В этой главе...
13.1	Введение
13.2.	Базовая модель
13.3.	Классификация моделей очередей
13.4.	Формулы вычисления характеристик моделей очередей
13.5.	Очередь типа M/G/1
13.6.	Модель очереди M/M/s
13.7.	Экономический анализ моделей очередей
13.8.	Конечные очереди
13.9.	Очереди с конечным источником заданий
13.10.	Переходные процессы в моделях очередей
13.11.	Роль экспоненциального распределения
13.12.	Дисциплина очереди
13.13.	Заключение
Основные термины
 Контрольные вопросы
| Задачи
| Ситуация 1 Сколько необходимо телефонисток
। Литература
854 ЧАСТЬ III Вероятностные модели
Сокращение времени между арестом
и предъявлением обвинения в полицейских
участках Нью-Йорка
В 1988 году в Нью-Йорке арестованные находились под охраной в ожидании предъ-
явленного им обвинения в среднем 44 часа, а порой и больше 72 часов Более того, они
находились в переполненной шумной камере, что приводило к эмоциональным стрес-
сам, заболеваниям и часто к физическим травмам В марте 1990 года вышел номер газе-
ты New York Times со статьей на первой странице о женщине, которую держали 45 часов
в камере предварительного заключения в Бронксе Арестованным не была предостав-
лена возможность воспользоваться услугами адвоката сразу после задержания, и эта
длительная задержка значительно уменьшила эффективность правовой системы В том
же году Верховный Суд Нью-Йорка постановил, что город должен либо предъявить об-
винение не позже чем через 24 часа, либо освободить задержанного.
Принимая во внимание эти обстоятельства, Нью-Йорк самостоятельно принял ре-
шение уменьшить время между задержанием подозреваемого и предъявлением ему об-
винения Город состоит из четырех основных районов (Манхэттен, Бронкс, Бруклин
и Квинс), каждый из которых имеет свой характерный способ ведения дел. Процесс за-
держания включает длинную последовательность действий, выполняемых поочередно,
арест офицером полиции, доставка задержанного в ближайший полицейский участок,
снятие отпечатков пальцев задержанного, содержание его под стражей, пока не будет
написан отчет, передача в центральное бюро запросов отпечатков пальцев, где они бу-
дут отправлены факсом в столицу штата для идентификации и получения досье задер-
жанного, далее офицер, арестовавший задержанного, вместе с помощником прокурора
штата составляют более полный отчет, включающий исковое заявление, после чего
арестованный остается в полицейском участке, ожидая предъявления обвинения.
В 1988 году в этих четырех районах было проведено более 325 тысяч арестов. При
этом задержанные содержались под стражей, ожидая предъявленного им обвинения
К сожалению, в Соединенных Штатах есть другие правоохранительные органы,
многие из которых также занимаются преступлениями насильственного характера
и борьбой с наркотиками (в Нью-Йорке преобладают преступления такого характе-
ра) Поэтому арестованный по обвинению в насильственном преступлении может
быть повторно задержан или обвинен, например, за хранение наркотиков, которые
были обнаружены у него при первом задержании
Команда разработчиков нового законопроекта опиралась на результаты, получен-
ные за два года интенсивных исследований Основным объектом этих исследований
был промежуток времени между арестом и предъявлением обвинения Как выяснилось
в ходе исследований, больше всего времени проходит после того, как офицер, аресто-
вавший подозреваемого, передаст отпечатки пальцев в центральное бюро, и до того,
как будет оформлено исковое заявление В среднем на это тратилось более восьми ча-
сов Большую часть времени офицер ожидал ответа на свой запрос, тогда как собствен-
но сама процедура занимала не более 30 минут Он ждал ответа 7 с половиной часов!
Весь процесс был смоделирован как последовательность этапов Некоторые из
этапов были смоделированы как очереди, обслуживаемые одним исполнителем,
другие — как очереди, обслуживаемые несколькими исполнителями, а некоторые
этапы были еще более сложными. Каждый этап был разделен на более простые дей-
ствия, также были определены параметры, от которых зависит срок выполнения
этих действий После этого вся модель была представлена как множество различных
сценариев “Что-если”, содержащих возможные комбинации необходимого объема
ГЛАВА 1 3. Модели очередей 855
работ, выполняемых полицейскими при задержании С помощью этой модели было
получено нескотько результатов, которые включали среднее количество времени, за-
траченное на весь процесс, и среднее время, необходимое для выполнения каждого
этапа данного процесса Стоимость каждого из этих сценариев оценивалась с помо-
щью модели, построенной в электронной таблице Власти Нью-Йорка должны были
из вариантов, имеющих разную стоимость и эффективность, выбрать один
В мае 1990 года мэр Нью-Йорка Дэвид Динкинс (David Dinkins) собрал пресс-
конференцию, на которой одобрил один из представленных ему вариантов и подписал
распоряжение об изменениях в полицейской системе Новая модель экономит городу
более 10 млн долл в год только на затратах за сверхурочные часы работы полицейских
Среднее время содержания под стражей подозреваемого до предъявления обвинения
сократилось с 44 до 24 часов в среднем по городу Арестованные получили право на
скорейшее судебное разбирательство и возможность находиться в камерах с ужасными
условиями не дольше, чем это действительно необходимо Город также экономит на
стоимости перевозки и содержания подозреваемого под стражей около 11 млн долл
В год В заключение своей пресс-конференции мэр порекомендовал сократить отдель-
ные подразделения суда, находящиеся при полицейских участках, что привело к до-
полнительной экономии в 9,5 млн долп для города и штата [2]
13.1.	Введение
Очереди вездесущи Самолеты, подлетающие к аэропорту, совершают несколько
кругов перед посадкой, ожидая разрешения на посадку, т е они ожидают своей очереди,
позже на земле они опять ожидают разрешения на взлет Люди стоят в очереди за биле-
тами и в кассы магазинов — практически всегда мы находимся в какой-нибудь очереди
В компьютерах задания находятся в очереди на выполнение, вновь поступившие заказы
выполняются после выполнения предыдущих, т е становятся в очередь и т д Как вы, на-
верное, уже догадались, очередь — это любая последовательность, члены которой ожида-
ют обслуживания Датскому инженеру А К Эрлангу приписывают создание основ тео-
рии массового обслуживания, одним из разделов которой является теория очередей Он
разрабатывал телефонные коммутаторы в Копенгагене для Датской телефонной компа-
нии Многие полученные им теоретические результаты и сегодня широко используются
Пример использования теории массового обслуживания в Соединенных Штатах — это
анализ автомобильных транспортных потоков, т е изучение количества и качества дорог
и их пропускных способностей, количества светофоров, регулируюшихдвижение, и т д
Монти Джексон может не соглашаться с мнением, что вся наша жизнь — это очередь,
но как административный директор госпиталя Св Луки в Филадельфии он постоянно
сталкивается со множеством ситуаций, которые могут быть описаны как модели очере-
дей Если говорить кратко, модель очереди - это последовательность элементов
(например, людей), ожидающих обслуживания, как показано на рис 13 I В данный мо-
мент Монти занят тремя различными “моделями очередей”, связанными с реорганиза-
цией работы вверенного ему госпиталя
Поступления
00000 -------Средство обслуживания |--------►
Рис. 13.1. Общий вид модели очереди
856 ЧАСТЬ III Вероятностные модели
Модель 1. Лаборатория гематологии
В госпиталь Св Луки обращается большое количество амбулаторных пациентов —
эти пациенты приходят на прием к врачам для диагностики и лечения, но они не ложатся
на стационарное лечение в госпиталь. Амбулаторные пациенты плюс те, которые нахо-
дятся на стационарном лечении в госпитале, рассчитанном на 600 человек, ежедневно
создают большой поток пациентов. Каждый пациент должен быть обследован лаборан-
том Система работает следующим образом После приема у врача пациент отправляется
в лабораторию на обследование, где его регистрирует медсестра. Пациенты обследуются
в кабинетах по принципу “первым пришел — первым обслужен” Когда обследование за-
кончено, пациент идет дальше по своему маршруту (например, на рентген), а к лаборанту
заходит новый пациент
Монти должен определить рациональное количество лаборантов’ большое их количе-
ство увеличивает расходы для госпиталя, но при этом ускоряет обслуживание пациентов.
Модель 2. Добавление новых телефонных линий
Реконструкция госпиталя Св Луки включает внедрение новой коммуникационной
системы Монти должен решить, сколько новых линий глобальной службы телефонной
сети WATS (Wide Area Telephone Service) необходимо приобрести госпиталю Глобальная
служба телефонной сети — это служба, предоставляющая специальный единый тариф
для междугородних и международных телефонных разговоров, поддерживаемая некото-
рыми телефонными компаниями Монти хочет, чтобы любой человек мог дозвониться в
его госпиталь с первого раза Но не совсем ясно, сколько телефонных линий необходимо
приобрести, чтобы достичь требуемого результата за разумную цену.
Модель 3. Наем ремонтников
Госпиталю Св Луки необходимо нанять работников, которые обслуживали бы 20
различных устройств электронного оборудования Это оборудование включает такие из-
мерительные устройства, как кардиографы, небольшие специализированные компьюте-
ры, используемые, например, для обследования легких, и другие устройства, в том числе
сканер для компьютерной томографии Если какое-то устройство сломано, а все механи-
ки заняты, то необходимо время, пока кто-нибудь не освободится и не устранит поломку.
Монти нужно решить, сколько ремонтников следует нанять Он должен найти опти-
мальное соотношение между расходами на обслуживающий персонал и стоимостью про-
стоя поломанного оборудования.
Как показано в табл 13.1, все три модели подходят под базовое описание модели оче-
реди Монти может найти решение этих проблем, используя аналитические и имитаци-
онные методы. Однако прежде, чем анализировать модели Монти, необходимо потратить
некоторое время на изучение базовых моделей очередей и способов их создания.
Таблица 13.1. Модели очередей
Проблема	Объект обслуживания	Средство обслуживания
I	Пациенты	Лаборанты
2	Телефонные звонки	Коммутатор
3	Сломанное оборудование	Персонал
ГЛАВА 13. Модели очередей 857
13.2.	Базовая модель
Рассмотрим копировальный аппарат Xerox, который расположен на четвертом этаже
в секретариате фирмы. Допустим, пользователи подходят к аппарату для ксерокопирова-
ния, образуя одну очередь Каждый прибывший использует копировальный аппарат для
выполнения своего индивидуального задания Эти задания различны от получения ко-
пии одностраничного письма до изготовления ста копий 25-страничного отчета Эта сис-
тема называется очередью с одним сервисом (одноканальной очередью). Любой метод иссле-
дования системы очереди (и построения соответствующей модели) прежде всего требует
определения следующих величин.
1.	Количество клиентов в системе: число клиентов, обслуживаемых в данный мо-
мент, и клиентов, находящихся в очереди на обслуживание
2.	Количество клиентов в очереди: число клиентов, ожидающих обслуживания
3.	Продолжительность пребывания клиента в системе интервал времени от момента,
когда клиент вошел в систему, и до момента, когда он ее покинул Заметим, что
этот интервал времени включает и время обслуживания
4.	Продолжительность пребывания клиента в очереди: интервал между моментом вре-
мени, когда клиент вошел в систему, и до момента, когда его начали обслуживать
Предположения о базовой модели
1.	Поступление в систему. Каждый поступивший клиент называется “заданием” По-
скольку время между поступлениями заданий точно не известно, нужно определить
его вероятностное распределение. В базовой модели часто используется распреде-
ление, называемое экспоненциальным. Это распределение играет основную роль во
многих моделях очередей. Оно обеспечивает приемлемое представление процесса
поступления заданий в большинстве ситуаций. Экспоненциальное распределение
обладает также свойством, которое называется отсутствием последствия, что об-
легчает получение аналитических результатов. Экспоненциальное распределение
не симметрично, в то время как многие люди думают, что “среднее значение”
должно делить все множество возможных значений пополам, т е количество зна-
чений, больше и меньше среднего, должно быть одинаковым. Например, если по-
купатели приходят в среднем каждые пять минут, то согласно экспоненциальному
распределению приблизительно 2/3 из них придут с интервалом менее, чем пять
минут, и только около трети с интервалом больше, чем пять минут. С помошью
экспоненциального распределения можно описать множество сервисов (работа
кассиров в банке, клерков почтового отделения и т.п.).
Если время между поступлениями заданий определяется экспоненциальным рас-
пределением, то для описания процесса поступления также используют термин
поток Пуассона: существует взаимосвязь между распределением Пуассона и экс-
поненциальным распределением. В частности, если время между поступлениями
заданий определяется экспоненциальным распределением, то количество поступ-
лений за определенный промежуток времени (скажем, за три часа) будет опреде-
ляться распределением Пуассона.
Связь между экспоненциальным распределением и распределением Пуассона бу-
дет рассмотрена более подробно в разделе 13.11. На данном этапе важно знать, что
858 ЧАСТЬ III. Вероятностные модели
экспоненциальное распределение полностью определяется только одним пара-
метром Этот параметр, обозначаемый X, называется интенсивностью поступления
и показывает, сколько поступает новых заданий (в среднем) за определенный пе-
риод времени Рассмотрим пример, в котором Х = 0,05 задании в минуту Это оз-
начает, что в среднем 5/100 заданий поступает каждую минуту Возможно, привыч-
нее было бы оперировать более длинными интервалами времени Тогда можно
сказать, что в среднем каждые 20 мин поступает одно задание Также можно ска-
зать, что время между поступлениями равно 20 мин , понимая под временем между
поступлениями среднее время между двумя заданиями Отсюда
среднее время между заданиями =
= среднее время между поступлениями = 1/Х	(13 1)
Поэтому, если X = 0,05, то
среднее время между поступлениями = 1/Х = 1/0,05 = 20.
2.	Обслуживание. В базовой модели время, необходимое на выполнение задания
(время обслуживания), также определяется экспоненциальным распределением
Параметр ц определяет данное экспоненциальное распределение Он показывает
среднюю интенсивность обслуживания — количество выполненных заданий в ми-
нуту Другими словами, ц7 — это количество заданий, которые будут выполнены
(в среднем) за время Т Рассмотрим пример Пусть ц = 0,10 Это означает, что
в среднем каждую минуту будет выполняться 0,10 задании Можно также сказать,
что в среднем каждые десять минут будет выполняться одно задание Среднее время
обслуживания (среднее время, затраченное на выполнение одного задания) равно
1/ц Если ц, средняя интенсивность обслуживания, равна 0,10, то среднее время
обслуживания равно 10, поскольку 1/ц = 1/0,10 = 10
3.	Длина (емкость) очереди. Если количество задании в очереди не ограничено, то такая
очередь называется бесконечной В противном случае считается, что очередь конечна
4.	Дисциплина очереди. Задания обрабатываются по принципу “первым пришел —
первым обслуживаешься”. Это значит, что задания обслуживаются в том же по-
рядке, в котором они поступили в очередь 1
5.	Временной горизонт. Промежуток времени, в течение которого работает система
6.	Источник заданий. Генерирует задания, подлежащие обслуживанию Характеризу-
ется емкостью (конечной или бесконечной)
Рассмотрим эти предположения в контексте предоставленной выше модели копиро-
вального аппарата Xerox Предположим, что среднее время между поступлениями зада-
ний составляет 20 мин Пусть время между поступлениями определяется экспоненциаль-
ным распределением, тогда 1/Х = 20, а Х = 0,05, т е задания поступают с интенсивностью
0,05 задании в минуту Аналогично, если среднее время, затраченное на выполнение за-
дания, равно 10 мин , то 1/ц = 10 и ц = 0,10, другими словами, задания обслуживаются с
интенсивностью 0,10 заданий в минуту.
Дисциплина очереди — это правило, по которому отбираются на обслуживание задания, стоящие в очере-
ди Правило “первым пришел — первым обслуживаешься” является только одним из возможных подобных
правил. В теории массового обслуживания также рассматриваются другие типы дисциплины очереди, не-
которые из которых описаны ниже в разделе 15 12 — Прим ред
ГЛАВА 1 3. Модели очередей 859
Характеристики базовой модели
Для вычисления основныхрабочих характеристик базовой модели достаточно (вместе
с предположениями о модели) знать значения двух основных параметров модели. X —
интенсивность поступления заданий в систему, и ц — интенсивность обслуживания за-
даний сервисом Формулы для вычисления других характеристик модели приведены в
табл 13 2 ВНИМАНИЕ' Формулы в этой таблице выполняются только при условии, что
Х<ц. Если это условие не выполняется (те при Х>ц), количество заданий в очереди
может неограниченно возрастать.
Таблица 13.2. Рабочие характеристики базовой модели
Характеристика	Обозначение	Формула
Коэффициент загрузки системы	-	Х/ц
Среднее количество заданий в системе	L	Х/(ц-Х)
Среднее количество заданий в очереди (средняя длина очереди)	L4	Х2/ц(ц - X)
Среднее время пребывания в системе	W	W-X)
Среднее время ожидания в очереди		1/ц(ц-Х)
Вероятность того, что система пуста	Р„	1-Х/р
Рассмотрим пример, когда Х = 0,25 и ц= 0,10 Напомним, что величина 1/Х равна
среднему интервалу времени между поступлениями. Поскольку 1/Х = 1/0,25 = 4, в сред-
нем задания поступают в систему каждые 4 мин Аналогично 1/ц — среднее время обслу-
живания (выполнения) одного задания. Поскольку 1/ц = 1/0,10 = 10, в среднем десять
минут тратится на выполнение одного задания Очевидно, что в этом случае количество
заданий в системе будет расти (очередь будет увеличиваться) с течением времени
Вернемся к модели копировального аппарата, в которой X. < ц, и к формулам
табл. 13.2. Электронные таблицы — наилучшее средство для выполнения вычислений по
формулам. Мы будем использовать рабочую книгу Excel Q.XLS, которая была разработа-
на профессором Дэвидом Эшли (David Ashley), и в которую уже введены все формулы,
приведенные в табл. 13 2. Впервые открыв таблицу, вы увидите начальную страницу, по-
казанную на рис. 13 2 (заметьте, что данная книга содержит еще четыре рабочих листа,
названных MMs, MG1, Конечная очередь, Конечный источник, доступ к которым вы
можете получить, щелкнув на ярлыке соответствующего рабочего листа).2
Введя числовые значения рассматриваемой модели Х = 0,05 иц = 0,10 в ячейки Е2
и ЕЗ рабочего листа MMs, получим результат, показанный на рис 13 3 Также нужно ука-
зать, что в модели имеется только один сервис (т.е. один копировальный аппарат) и что
время измеряется в минутах.
Эта рабочая книга, находящаяся на прилагаемом компакт-диске, полностью русифицирована —
Прим ред
860 ЧАСТЬ III Вероятностные модели
$1' Й 90%	Times New Roman
| ШАБЛОНЫ ОЧЕРЕДЕЙ |
© 1995 by David W Asliley
Revised September 14, 1998
Эта рабочая книга выполняет вычисление характеристик
моделей очередей следующих типов:
М / М / s
М / М / s с конечной длиной очереди
М / М / s с конечным источником заданий
M'G/1
Для выполнения расчетов перейдите на соответствующий
рабочий лист и введите необходимые параметры модели
Параметры всех моделей ссылаются на параметры модели MTVI/s.
Вьггисления ограничены 100 сервисами в моделях M/M/s
емкость источника заданий ограничена числом 500	yj
ведениеZ НМ» Z КднгИКЫЙжд». /,КЯ»Ч№1ЙИСТ<ЙНИК~/МЙТ7I <11,	'*• V ? JElfT
NUM	. 
Рис. 13.2. Начальная страница книги шаблонов очередей
Стационарное состояние
Полученные результаты требуют некоторого пояснения. Например, полученное зна-
чение L — это ожидаемое (среднее) количество клиентов в системе (т.е. тех, кто обслужи-
вается, и тех, кто ожидает в очереди) после того, как очередь достигнет стационарного со-
стояния В данном случае стационарное состояние означает, что вероятность того, что
в системе будет определенное количество клиентов (скажем, 2) не зависит от момента
времени, для которого вычисляется это значение. Если стационарное состояние достиг-
нуто, то вероятность наличия в системе двух клиентов (обслуживаемых и/или ожидаю-
щих обслуживания) будет одинаковой и в 14:30 и в 16:00.
Значения других характеристик (рис. 13.3) интерпретируются подобным образом.
Так, в стационарном состоянии система пуста с вероятностью 50% (ячейка F7 показыва-
ет, что Рп = 0,5); в среднем 0,5 клиента находится в очереди (ячейка F8:	= 0,5); клиент
в среднем ожидает 10 мин., чтобы воспользоваться копировальным аппаратом (ячейка
F10. 1У = 10); и клиент находится в системе в среднем 20 мин. (ячейка Fl 1: W= 10). На-
поминаем, что это средние значения случайных величин, которые имеют определенное
вероятностное распределение. Если они имеют экспоненциальное распределение, то 2/3
их значений меньше среднего, а 1/3 — больше. Поэтому 2/3 клиентов будут ожидать
в очереди менее 10 мин., тогда как 1/3 будет ожидать более 10 мин.
ГЛАВА 13 Модели очередей
861
~6 | .Коэффициент загрузки системы
7_J ’ вероятность того, что система пуста
' Lq,-средняя длина очереди
L, среднее количество заданий в системе
Wq. среднее время ожидания в очереди
 ;W. средняя время пребывания в системе
Вероятность ожидания в очереди
50,00%
0,5000
0,5000
1,0000
10.0000
20,0000
0 5000
Рис. 13.3. Вычисление рабочих характеристик базовой модели
Использование результатов
Полученные результаты, а также значения параметров X и ц — это основные характе-
ристики базовой модели Данная информация используется для анализа системы обслу-
живания Рассмотрим пример с копировальным аппаратом, эта система обслуживания
характеризуется следующими показателями Поскольку Х = 0,05, то в среднем 5/100 за-
даний (клиентов) поступает в систему каждую минуту Восьмичасовой рабочий день со-
ставляет 480 мин. (8 х 60 = 480) Поэтому среднее количество прошедших через систему
клиентов равно 0,05 х 480 = 24
На основе результатов вычислении, показанных на рис 13 3, определяем, что средняя
продолжительность пребывания каждого клиента в системе равна 20 мин (20) Поэто-
му общее время пребывания всех клиентов в данной системе равно 24 (поступивших клиен-
та за день) х 20 (минут пребывания одного клиента в системе) = 480 мин , или 8 ч Менед-
жер должен понимать, что это слишком длительное время обслуживания, а значит, и слиш-
ком дорогое “удовольствие” Существуют различные способы выхода из такой ситуации
1.	Приобрести новый более производительный копировальный аппарат
2.	Приобрести еще один копировальный аппарат и использовать оба аппарата Это
создаст новую систему очереди с двумя сервисами
3.	Направить часть клиентов к другому копировальному аппарату (если таковой име-
ется), тем самым уменьшив нагрузку на данную машину Это решение изменит
процесс поступления в систему.
Менеджер должен выбрать один из этих вариантов или принять другое решение Но
в любом случае нужно найти оптимальное соотношение между стоимостью улучшения
обслуживания и стоимостью времени, потраченного сотрудниками на ожидание в очере-
ди. Данные, приведенные на рис. 13 3, и подобные характеристики, полученные для
других систем, послужат основой для анализа сложившейся ситуации. Способы анализа
очередей будут рассмотрены ниже более подробно на примере моделей Монти Джексона
862 ЧАСТЬ III Вероятностные модели
13.3.	Классификация моделей очередей
Существует множество различных моделей очередей Например, определив время
между поступлениями в систему по другому закону распределения (не экспоненциаль-
ному), мы получим другой тип модели, в которой нельзя использовать предыдущие фор-
мулы для вычисления характеристик (подобных L, L, и т д ) Чтобы упорядочить различ-
ные модели очередей, Д Г Кендалл (D. G Kendall) предложил классификацию моделей,
основанную на обозначениях А/B/s, где А — тип вероятностного распределения момен-
тов времени поступлений клиентов в систему, В— тип вероятностного распределения
продолжительности обслуживания, х — количество сервисов ’
Для обозначения каждого типа распределения используются различные буквы Как
правило, применяются следующие условные обозначения М— экспоненциальное рас-
пределение, D — детерминированный (фиксированный) интервал времени между посту-
плениями клиентов в систему (детерминированная продолжительность обслуживания
клиентов), G— произвольный (общий) тип распределения продолжительности обслужи-
вания, GI— произвольный (общий) тип распределения поступления клиентов
Согласно этой классификации описанная выше модель копировальных аппаратов яв-
ляется моделью вида М/М/ Следовательно, это очередь с одним сервисом с экспонен-
циальными распределениями времени между поступлениями клиентов и времени обслу-
живания
Как имитационная модель очереди помогла
устранить автомобильные пробки
Завод компании The Westinghouse Hanford в г Ричланд, штат Вашингтон, является
секретным объектом Все транспортные средства и пассажиры останавливаются возле
контрольного пункта, где после проверки их пропускают на территорию завода При
въезде на территорию компании создаются огромные пробки в часы пик Поскольку пер-
сонал постоянно задерживается в очередях на пропускном пункте, компания ощущает
значительное снижение производительности труда Поэтому руководство дало задание
группе инженеров компании изучить проблему и предложить пути ее устранения.
В процессе исследования выяснилось, что каждый рабочий день утром на завод
приезжает в среднем 7 автобусов и 283 легковые и грузовые машины Весь транспорт
выстраивается в одну очередь для проезда через пропускной пункт, в котором в час пик
работает два охранника Очередь увеличивается, занимая весь подъездной путь к заводу
(который вмещает только 40 автомобилей) и выходит на примыкающую к нему трассу,
что создает аварийно-опасные ситуации Когда очередь становится очень длинной, во-
дители вновь прибывших автомобилей часто едут дальше по шоссе к другому въезду на
завод Этот выбор означает дополнительное время и расстояние, преодолеваемое ра-
ботниками компании, однако не гарантирует, что они попадут на завод быстрее, по-
скольку неизвестно, насколько велика очередь на втором пропускном пункте.
Прим ред
ГЛАВА 13. Модели очередей 863
Стандартная аналитическая модель очереди показала, что скорость обслужива-
ния на пропускном пункте значительно ниже скорости поступлений в очередь, по-
этому очередь будет продолжать неограниченно возрастать, пока будут подъезжать
автомобили. Но это лишь подтверждает то, что уже и так было известно Поэтому
была построена имитационная модель очереди с целью воспроизвести сложившуюся
ситуацию и попытаться найти способы выхода из нее.
•	Первый способ предполагает увеличение числа охранников на контрольном
пункте до трех при одном потоке автомобилей Это позволяет уменьшить макси-
мальную длину очереди с 45,5 до 28 автомобилей, но увеличивает стоимость об-
служивания
•	Второй способ предполагает две очереди, причем каждую обслуживает только
один охранник Автобус занимает по своим габаритам сразу две полосы движе-
ния. Поэтому, как только он поступает в очередь, он сразу обслуживается одним
из охранников, в то время как второй временно обслуживает сразу две очереди
Это решение позволит уменьшить максимальную длину очереди до 14 автомоби-
лей, а время ожидания в очереди — до 15 мин (против существующих 30 мин )
Второй способ является лучшим решением, так как он не требует дополнитель-
ных затрат. Когда автомобили начали обслуживать по этому сценарию, длина очере-
ди значительно сократилась Но большое удивление вызвало то, что количество
транспортных средств, проезжающих каждый день через контрольный пункт, увели-
чилось в среднем с 285 до 345 Очевидно, автомобили, которые обычно проезжали
мимо основных ворот и ехали ко вторым, снова начали использовать этот пропуск-
ной пункт Благодаря тому, что очереди стали значительно короче, новая система
пропуска легко справилась с возросшим потоком автомобилей [1]
13.4.	Формулы вычисления характеристик моделей
очередей
Можно доказать, что для стационарной модели очереди справедливо равенство
Л = Ж	(132)
где L — среднее количество клиентов в системе; X — интенсивность поступления клиен-
тов в систему, W— время ожидания клиента в системе Нетрудно убедиться, что показа-
тель/, для модели копировальных аппаратов (рис. 13 3) удовлетворяет равенству (13 2)
L= 1,0 = 0,05x 20 = Х(К	(133)
Чтобы наглядно пояснить полученный результат, рассмотрим две схемы на рис 13 4
На первой схеме клиент только поступил в систему и присоединился к очереди На вто-
рой схеме он только что обслужен Поскольку система находится в стационарном режи-
ме, среднее число клиентов в системе не зависит от времени, что позволяет вычислить
эту величину в тот момент, когда клиент уже обслужен. В этом случае количество клиен-
тов, находящихся в системе, соответствует общему числу поступивших клиентов во вре-
мя пребывания в системе клиента. Поэтому, если W— длительность его пребывания
в системе, и новые клиенты поступают с интенсивностью X, то мы можем ожидать, что L,
среднее количество клиентов в системе, равно W.
864
ЧАСТЫН Вероятностные модели
Клиент поступил
в систему
С»а, Q ООООО [
ООО 000 I IQSZ..
Клиенты, поступившие в систему во время
пребывания нашего клиента в очереди
Рис. 13.4. Пояснения к формуле Литтла
Формулу (13 2) часто называют формулой Литтла. Заметим, что эту формулу можно
применить для любого процесса в модели, находящейся в стационарном режиме. Напри-
мер, можно утверждать, что среднее количество клиентов, находящихся в очереди, равно:
(13.4)
Вычислим значение этого показателя для модели копировального аппарата:
Ьч = 0,5 = 0,05 х 10 = Щ.
Полученный результат совпадает со значением этого показателя (см рис. 13 3).
Необходимо быть внимательным, применяя эту формулу Очень важно, чтобы значе-
нием X была интенсивность поступления клиентов в очередь Это значение может отли-
чаться от фактической интенсивности поступления клиентов в систему Рассмотрим
пример с ограниченным количеством клиентов в очереди (т.е. модель конечной очереди)
Современное телефонное оборудование, которое может поддерживать определенное ко-
личество вызовов в очереди (скажем, 10), пока коммутатор не выполнит соединение, —
хороший пример конечной очереди Если система полна, клиент просто услышит сигнал
“занято” —те получит отказ при попытке входа в систему Это значит, что клиент не
поступит в очередь Данная ситуация называется отказом. Поэтому, если Х = 0,25
(интенсивность входящих звонков), то среднее время между звонками составляет 4 мин ,
но это не интенсивность поступления клиентов в очередь Следовательно, в этой системе
равенство L = 0 25 Wвыполняться не будет Аналогично покупателю может надоесть сто-
ять в очереди, и он покинет ее без обслуживания Это называется изменением решения.
Опять же в этом случае равенство (13 4) не будет выполняться для такой системы
Сделаем еще один важный вывод
среднее время ожидания = среднее временя ожидания в очереди +
+ среднее время обслуживания.
В базовой модели
среднее время обслуживания = 1/ц.
Тогда
И^=И;+1/ц.	(13 5)
Для модели копировальных аппаратов получим И/=	+ 1/р. = 10 + 1/0,10 = 20. Формула
(13 5) верна не только для базовой модели, но и для всех моделей очередей в стационар-
ном режиме
Уравнения (13 2), (13 4) и (13.5) позволяют вычислять четыре основные характери-
стики модели L, L4, Wи ГС, если известна хотя бы одна из них. Чтобы убедиться в этом,
ГЛАВА 13. Модели очередей 865
снова вычислим все рабочие характеристики модели копировального аппарата. Сначала
найдем L — среднее количество клиентов в системе. Для этого воспользуемся второй
формулой из табл. 13 2:
L = _L_ = _-9:o5._. = 1.
р-Х 0,10-0,05
Для вычисления остальных характеристик можно воспользоваться формулами из
табл. 13.2, но мы применим формулы, которые привели выше. Прежде всего воспользу-
емся формулой Литтла (13.2) L = W. Зная, что L = 1 иХ = 0,05, получим W= L/k = 20.
Далее из формулы (13.5) найдем И':
И/= W- 1/ц = 20- 1/0,10= 10.
И, наконец, применим формулу (13.4):
£, = Х»; = 0,05х 10 = 0,5.
Этот способ вычисления рабочих характеристик часто используется при анализе и бо-
лее сложных систем, чем базовая.
13.5.	Очередь типа M/G/1
Экспоненциальное распределение может хорошо описывать процесс поступления
клиентов в систему, но оно может не соответствовать процессу обслуживания Существу-
ет обобщение базовой модели, которое позволяет не задавать в явном виде распределение
времени обслуживания одного клиента Здесь необязательно знать закон распределения
времени обслуживания, достаточно знать его среднее (математическое ожидание) 1/ц
и дисперсию о2 Формулы для вычисления рабочих характеристик обобщенной модели
приведены в табл 13.3
Таблица 13.3. Рабочие характеристики обобщенной модели
Характеристика	Обозначение	Формула
Коэффициент загрузки системы	-	ь/н
Среднее количество заданий в системе	L	А, + Vn
Среднее количество заданий в очереди		Х2<г + (А/ц)2
		2(1-Х/ц)
Среднее время пребывания в системе	W	и; + 1/ц
Среднее время ожидания в очереди	И/,	
Вероятность того, что система пуста	Л	1 -Х/ц
Заметьте, что в обобщенной модели можно использовать формулы, приведенные
в разделе 13 4, для вычисления всех рабочих характеристик, за исключением L Прове-
рим справедливость этих формул, учитывая, что распределение времени обслуживания
подчиняется экспоненциальному закону. Для экспоненциального распределения дис-
персия равна (1/ц)2, если среднее равно 1/ц Поэтому
866 ЧАСТЬ III Вероятностные модели
L Х2(1/ц)г+ (Х/р)2 X2
2(1-Х/ц)	ц(ц-Х)’
Полученная формула не отличается от аналогичной формулы для базовой модели
При увеличении значения дисперсии о2 значения характеристик L, L:i. W и РИ также
увеличиваются Это значит, что постоянство параметров работы средств обслуживания
так же важно, как и скорость обслуживания Предположим, нужно нанять на работу сек-
ретаря, и вы должны выбрать одного из двух кандидатов на эту должность Первый пре-
тендент работает с постоянной скоростью любой документ печатает ровно за 15 мин
Второй кандидат работает немного быстрее Его средняя производительность — один до-
кумент за 14 мин , но время, затраченное на печать документа, может изменяться в соот-
ветствии с экспоненциальным распределением Средний объем работ в офисе — три до-
кумента в час, время между поступлениями которых определяется экспоненциальным
распределением У какого секретаря среднее время возврата напечатанных документов
будет короче9 Эту задачу легко решить в рабочих листах MG1 или MMs рабочей книги
Excel Секретари XLS (рис 13 5 и 13 6)
Рис. 13.5. Временной цикл работы первого секретаря
Поскольку первый секретарь печатает каждый документ ровно 15 мин,, то дисперсия
о2 равна 0 Значения остальных параметров следующие интенсивность поступления за-
дании (документов) X = 3 в час (или 0,05 в минуту), интенсивность обслуживания
(скорость печати) ц = 1/15 Эти значения вводятся в ячейки ЕЗ Е6 на рабочем листе
MMs Введенные значения автоматически скопируются в соответствующие ячейки листа
MG1 Результаты вычислений показаны на рис 13 5 Можно проверить справедливость
полученных результатов, выполнив вычисления вручную на основе формул, приведен-
ных в табл 13 3
Чтобы получить значения характеристик модели для второго секретаря, надо ввести
значения параметров X = 0,05, р = 1/14 в минуту и о = 14 мин. Полученные результаты
представлены на рис 13 6 Чтобы проверить полученные результаты, можно использо-
вать формулы как базовой (табл 13 2), так и обобщенной модели (табл 13 3).
ГЛАВА 13. Модели очередей	867
Несмотря на то что второй секретарь работает “быстрее”, его временной цикл печати
документов больше (№= 46,67 мин.), чем аналогичный показатель у первого секретаря
(Ж= 37,5 мин).
А. в .!. с D
1  Характеристики очереди M/G/1
2
3	Интенсивность поступления заданий
4	Среднее времени обслуживания
5	Ст. отклонение времени обслуживания
6	Единицы времени
7	'
 Е xF-..'-| G ! Н
Средняя интенсивност
О 05 работы/минуты обслуживания
14 минуты 0,0714 работы/минуть
14 минуты
8
9  Коэффициент загрузки системы	70,00%
10  Р(0) вероятность того что система пуста	0,3000
11 Lq средняя длина очереди	1,6333
12	L среднее количество заданий в системе	2,3333
13	Wq среднее время ожидания в очереди	______32,6667
14 । W средняя время пребывания в системе |	46,6667 I
“15
Рис. 13.6. Временной цикл работы второго секретаря
13.6.	Модель очереди M/M/s
Напомним, что в начале этой главе мы поставили задачу найти решение проблем гос-
питаля Св Луки с помощью моделей очередей В предыдущих разделах были описаны
основы построения таких моделей Мы рассмотрели характеристики моделей очередей
(ожидаемое число клиентов в очереди, среднее время ожидания и т д.), а также рабочую
книгу Excel, которая автоматически вычисляет рабочие характеристики моделей Кроме
того, были приведены некоторые общие формулы (в частности, формула Литтла), кото-
рые понадобятся нам в будущем. Сейчас вернемся к моделям Монти Джексона
Система очереди, описанная в модели I раздела 13 I (модель лаборатории гематоло-
гии), показана на рис. 13.7 Заметьте, что все пациенты стоят в общей очереди, и, попав
в начало очереди, заходят в первый освободившийся кабинет для обследований Не пу-
тайте этот тип системы с системой, в которой формируется отдельная очередь возле каж-
дого сервиса, как, например, очереди в кассы в обычном магазине.
Рис. 13.7. Очередь с несколькими сервисами
868 ЧАСТЬ III. Вероятностные модели
Предположим, что время между поступлениями клиентов определяется экспоненци-
альным распределением с интенсивностью поступлений X = 0,20 в мин. Это значит, что в
среднем каждые пять минут в очередь поступает новый пациент, поскольку среднее вре-
мя между поступлениями равно 1/А. = 1/0,20 = 5.
Также предположим, что все средства обслуживания одинаковы, и время обслужива-
ния имеет экспоненциальное распределение с параметром ц= 0,125 (в минуту). Отсюда
следует, что среднее время обслуживания равно 8 мин., поскольку среднее время обслу-
живания для каждого сервиса равно 1/(1= 1/0,125 = 8.
Если бы в системе был только один сервис, то в этом случае очередь могла неограни-
ченно увеличиваться, поскольку А. > ц (0,20 > 0,125). Однако очередь с несколькими сер-
висами будет иметь стационарное состояние, если выполняется неравенство А. < sfi, где
s — количество сервисов. Например, если есть два сервиса, то система будет находиться в
стационарном состоянии, поскольку выполняется неравенство 0,20 < 0,25 (= 2 х 0,125).
Основные формулы
Необходимо вычислить значения характеристик £, W и И/. Но, поскольку в дан-
ном случае мы имеем дело с очередью с несколькими сервисами (в отличие от модели ко-
пировального аппарата с одним сервисом), для вычислений нужно использовать другие
формулы. Начнем вычисления с формулы для вероятности Р„ того, что система пуста.
Для нашей модели формула принимает следующий вид’
R =------------—;---------(13.6)
| (АУц/Г 1
Чтобы вычислить ожидаемое число клиентов в очереди £?, применим формулу.
Формулы (13 6) и (13 7), а также формулы (13 2), (13.4) и (13 5) позволяют вычислить
значения характеристик И7 и L при любых значениях параметров А. и ц, а также для
любого числа сервисов (значение s) Эти новые формулы уже введены в лист MMs рабо-
чей книги шаблона очередей Гематология.XLS.
Пример вычислений
Предположим, что Монти решил принять на работу двух лаборантов. Тогда х = 2,
А. = 0,20 и ц = 0,125 Эти значения вводятся в соответствующие ячейки листа MMs рабочей
книги Гематология XLS Получим результаты, показанные на рис. 13 8. Мы видим, что ко-
эффициент загрузки системы составляет 0,8 (ячейка F6), а вероятность того, что система
пуста, равна 0,11 (ячейка F7) Эти два значения используются в формуле (13 7) для нахож-
дения L, (= 2,84, ячейка F8) Поэтому ожидаемое число клиентов в очереди чуть меньше 3.
Результат вычисления по формуле (13.4) показывает, что в среднем пациент находится
в очереди 14,22 мин (ячейка F10), прежде чем попасть в кабинет для обследований.
ГЛАВА 13. Модели очередей
869
80 00%
чеповек/минуты Првдполагавтся«чтягврвмя’ЬрСтуп
человек/^инуты в систе&ур ервмя.обслуживйния/
(не более 40),_ падчиняютсяэкспбменииалв^му!:
Цсраднее количество заданий в системе
Wq. среднее время ожидания в очереди
W. средняя время пребывания в системе
вероятность ожидания в очереди " '
, в ; с и.„у о.
Характеристики очереди M/M/s
Рис. 13.8. Результаты вычислений для модели с двумя сервисами
Интенсивность обслуживания
Количество сервисов
Единицы времени
Коэффициент загрузки системы
Р(С). вероятность того, что система пуста
Для вычисления среднего времени ожидания в системе суммируются среднее время
ожидания в очереди и среднее (ожидаемое) время обслуживания В результате W= 22,22
мин (ячейка Fl 1) Итак, в среднем пациент находится в лаборатории 22,10 мин , ожидая
приема, проходя обследование или сдавая анализы.
Теперь Монти хочет узнать, что произойдет, если он примет на работу еще одного или
двух лаборантов (добавит еще один или два сервиса). Полученные результаты представ-
лены на рис 13 9 и 13 10 соответственно
Рис. 13.9. Результаты вычислений для модели с тремя сервисами
870 ЧАСТЬ III Вероятностные модели
40.00%
0.1991
0.0605
1.ВБ05
0.090/
Количество задании в систеие
Рис. 13.10. Результаты вычислений для модели с четырьмя сервисами
очереди M/M/s
Интенсивность поступления заданий
Интенсивность обслуживания
Количество сервисов
Единицы времени
Коэффициент загрузки системы
Р(0}, вероятность того, что система пуста
Lq. средняя длина очереди.  
L среднее количество заданий в системе
Wq, среднее время ожидания в очереди
W. средняя время пребывания в системе
Вероятность ожидания в очереди
Добавление еще одного лаборанта значительно сокращает время ожидания в очереди
(И'' = 1,57 мин ), но требует дополнительных затрат. Добавление же четвертого лаборанта
уже не дает столь значительного результата — время ожидания сокращается до 0,30 мин
Посмотрим на изменения другого показателя насколько заняты лаборанты в каждой мо-
дели На рис 13 8-13 10 показано, что коэффициент загрузки сервисов (лаборантов) па-
дает с 80% до 53,3% во втором случае и до 40% в третьем Добавление большего количест-
ва лаборантов увеличивает процент их свободного времени Сотрудники начнут скучать
на работе и, вполне вероятно, небрежно относиться к клиентам
Эти вычисления предоставляют достаточно информации, чтобы Монти мог принять
решение При одном лаборанте, поскольку к > ц, система будет нестационарной, и оче-
редь может неограниченно возрастать. Такое решение безответственно. Если нанять на
работу двух лаборантов, то среднее время ожидания в очереди будет меньше 15 мин По
текущим стандартам госпиталя — это небольшое и приемлемое значение. Очевидно, что,
приняв на работу большее число лаборантов, Монти может сократить время ожидания,
но это решение приведет к существенным затратам для госпиталя. Поэтому Монти
больше нравится идея приема на работу двух лаборантов с полным рабочим днем
Заметим, что рассмотренная в этом примере модель аналогична модели ресторанов быст-
рого питания, когда менеджер решает, сколько нужно нанять на работу продавцов, чтобы
среднее время ожидания клиентов было ниже определенного значения. Судя по отчетам сети
ресторанов McDonalds, они теряют клиента, если общее время ожидания больше пяти минут.
13.7.	Экономический анализ моделей очередей
Монти определил число лаборантов, требуемых для его лаборатории, принимая во
внимание рабочие характеристики моделей и используя свой опыт Это обычный подход
при решении подобных задач в некоммерческой сфере Но Монти хочет найти опти-
мальное соотношение между затратами на содержание лаборантов и стоимостью времени
ожидания пациентов Стоимость содержания лаборантов подсчитать нетрудно, в отличие
от определения стоимости времени ожидания.
ГЛАВА 13. Модели очередей	871
Монти заметил, что во время анализа моделей очередей его не заботили пациенты,
которые стоят в очереди (надо только, чтобы время их ожидания было приемлемым).
Действительно, не имеет значения, кто ждет в очереди- больной, который платит за кон-
сультацию врача $250 в час, или безработный, который не может заплатить за свое лече-
ние Но так будет только до тех пор, пока время ожидания не вынудит первого пациента
воспользоваться услугами другого медицинского учреждения. Это объясняет, почему не-
которые некоммерческие организации могут не обращать внимания на время ожидания
клиентов. Но в данном случае это недопустимо'
Более того, это может привести к тому, что лаборатория гематологии станет убыточ-
ной для госпиталя, если из-за нее уменьшится количество платных пациентов Это про-
изойдет, если, например, в клинику, обслуживающую амбулаторных пациентов, каждый
день будет обращаться 50 новых пациентов, а лаборатория гематологии сможет обслу-
жить только 10. Но несмотря на все сказанное выше, все еще не ясно, как определить
стоимость времени ожидания пациентов.
Стоимостные параметры моделей
В принципе, построить стоимостную модель очереди нетрудно. Рассмотрим опять
модель лаборатории гематологии (или, другими словами, очередь с несколькими серви-
сами и с экспоненциальными распределениями времени поступления клиентов и време-
ни обслуживания) и предположим, что менеджер каким-либо способом определил две
стоимостные характеристики.
С — стоимость (в час) содержания средства обслуживания,
Q — стоимость (в час) ожидания клиента в системе
Найдем общую стоимость обслуживания нескольких сервисов Начнем с вычисления
общей стоимости обслуживания двух сервисов за восьмичасовой рабочий день
стоимость обслуживания = С, х 2 х 8,
где С — стоимость обслуживания (в час) одного сервиса, 2 — количество сервисов и 8 —
количество часов работы каждого сервиса. Аналогично
стоимость ожидания = Си х L2 х 8,
где L2 — количество клиентов в очереди, когда работает два сервиса Поясним эту фор-
мулу Если своей очереди ожидают в среднем L2 клиентов, и в системе имеется два серви-
са, то L2, умноженное на восемь, — это среднее количество “часов” ожидания в день
Следовательно, С х L2 х 8 — средняя стоимость ожидания за восьмичасовой рабочий
день. Если надо вычислить общую стоимость использования 4 сервисов за 6-часовой ра-
бочий день, следует применить формулу
С х 4 х 6 + С, х Л4 х 6 = (С х 4 + Q х Л4) х 6
Здесь выражение в скобках представляет общую стоимость (в час) использования 4
средств обслуживания.
Общая стоимость (в час)
Обозначим через OC(s) общую стоимость (в час) использования s средств обслужива-
ния. Очевидно, что
OC(.S') =C,xj + C,xI,
8Т2. ЧАСТЬ III Вероятностные модели
Нужно найти такое 5, количество сервисов, чтобы эта функция принимала наимень-
шее значение. Очевидно, что если 5 возрастает, то стоимость времени ожидания умень-
шается, а стоимость обслуживания увеличивается. Наша цель — найти такое значение 5,
чтобы сумма этих двух стоимостей была минимальна.
На рис 13 И показан рабочий лист Анализ из рабочей книги Гематология.ХЬЗ, создан-
ный для вычисления оптимального значения s К сожалению, невозможно вывести формулу,
дающую оптимальное значение s (в отличие от моделей, рассмотренных в главе 7).
В данном примере примем относительно высокую стоимость ожидания и посмотрим,
будет ли полученное решение отличаться от решения Монти использовать два средства
обслуживания Допустим, что С = $50 (сервис/час) иС = $100 (клиент/час) (значения в
ячейках В1 и В2), далее вычислим стоимость обслуживания и стоимость ожидания для 2,
3 и 4 средств обслуживания (сервисов).
Стоимость обслуживания в час
Стоимость ожидания в час
с : D Е
Длительность
смены, часы
в
Количество сервисов
Ср длина Стоимость Стоимость
очереди сервиса ожидания
Общая
Длительность
смены, часы
Ср длина очереди Стоимость сервиса Стоимость ожидания Общая стоимость
=СУММ(С6 D6)
=СУММ(С7О7)
=СУММ(С8Р8)
Рис. 13.11. Экономический анализ модели с 2, Зи4сервисами
Сравним общую стоимость для 8-часового рабочего дня (количество часов задается
в ячейке Е1) при разном количестве сервисов, для этого необходимо ввести в ячейки
В6:В8 значения L (среднее число клиентов в системе) для каждого рассматриваемого зна-
чения s (эти значения можно получить из таблиц на рис. 13.8-13.10). Как видно, при
3 сервисах общая стоимость минимальна и равна $2 730 (ячейка Е7).
ГЛАВА 13. Модели очередей 873
Далее Монти создал таблицу подстановки для определения чувствительности этого
решения по отношению к стоимости Сн. Он решил исследовать значения Ск от 0 до $180.
Для этого Монти выполнил такие действия.
1.	Ввел начальное значение 0 в ячейку Al 1.
2.	Опять выделил ячейку АН, затем выполнил команду Правкам Заполнить^
Прогрессия
3.	Щелкнул на переключателе Расположение по столбцам, ввел шаг 20 и предель-
ное значение 180. Затем щелкнул на кнопке ОК.
4.	Ввел в ячейки BIO D10 формулы =Е6, =Е7 и =Е8, которые установили связь с ве-
личинами общей стоимости при 2 сервисах, 3 сервисах и 4 сервисах.
5.	Выделил диапазон ячеек А10 D20 и выбрал команду Данные^Таблица подстановки.
6.	В поле Подставлять значения по строкам ввел В2 Щелкнул на кнопке ОК
7.	Excel автоматически заполнитдиапазон ячеек A 10.D20, как показано на рис. 13.11
Монти также решил построить график, чтобы проследить характер поведения полу-
ченных значений общей стоимости. Для этого он выделил диапазон ячеек A11.D20,
щелкнул на кнопке Мастер диаграмм стандартной панели инструментов и выполнил все
действия для создания диаграммы, которая показана на рис 13 12.
Рис. 13.12. Зависимость общей стоимости от стоимости ожидания
Как видно, два сервиса — это оптимальное решение при С„ < $20, тогда как три серви-
са является лучшим решением при значениях Cw от $20 до $180. Четыре сервиса имеет
смысл использовать только при Си > $200.
Подведем итоги в исследовании модели лаборатории гематологии. Мы узнали, как
находить значения характеристик L, L4, И' и И'. Эти значения используются при выборе
оптимального числа лаборантов (средств обслуживания). Также был проведен анализ за-
висимости решения от параметра Q. Перейдем ко второй модели Монти.
874 ЧАСТЬ III Вероятностные модели
13.8.	Конечные очереди
Напомним, что вторая модель должна помочь Монти выбрать подходящее для госпита-
ля Св Луки количество линий телефонной связи К счастью, в этом случае он может рас-
считывать на помощь телефонной компании. Большое значение имеет опыт людей, рабо-
тающих в ней, поскольку модели очередей широко применяются при исследовании нагру-
зок в телефонных линиях Задача о том, сколько линий необходимо закупить, обычно
решается с использованием моделей типа M/G/s. Это тип модели с s сервисами (s телефон-
ных линий), экспоненциальным распределением времени между звонками и произволь-
ным типом распределения времени обслуживания (в этом примере время обслуживания —
это длительность телефонного разговора) Обычные телефонные коммутаторы обладают
свойством, которое на профессиональном жаргоне называется “освобождение от заблоки-
рованных клиентов”. Это значит, что если вновь поступивший клиент видит, что все средст-
ва обслуживания заняты (все линии связи заняты), то он не встанет в очередь, а просто поки-
нет систему Существуют более совершенные системы, которые удерживают конечное ко-
личество клиентов в очереди в ожидании освобождения линии, а некоторые даже
позволяют послушать при этом, например, Элтона Джона или песню “Macarena”.
Вероятность того, что сервисы заняты
Проблема выбора подходящего числа телефонных линий (сервисов) сводится к вы-
числению вероятности того, что в стационарном состоянии системы равноj линий будет
занято Очевидно, что если имеется в наличии з телефонных линий и все они заняты, то
следующий клиент не сможет позвонить
Вероятность того, что в стационарном состоянии системы точно j сервисов будет за-
нято при наличии s линий (сервисов), можно вычислить по формуле
Р1= (ХУц2--/7’ ,	(13 8)
где X — интенсивность поступлений заданий (частота, с которой поступают звонки); 1/ц —
среднее время обслуживания (средняя продолжительность телефонного разговора); s — ко-
личество сервисов (телефонных линий). Эта формула называется формулой Эрланга
Рассмотрим систему, в которой X = 1 (интенсивность поступлений — один звонок в мину-
ту) и 1/р. = 10 (средняя продолжительность разговора— 10 мин ) Следовательно, л/М- = Ю
Допустим, что в системе пять телефонных линий (з = 5), и нужно найти вероятность того, что
в стационарном режиме системы две из них будут заняты (/ = 2) По формуле (13 8) находим
р QJytflV
gaw/*'
=_______________________10;/(2 1)_____________________=
“ 1 +1 О'/1 +101 2 */(2 1) + 10’/(3 2 1) + 104/(4 3 2 1) + 105/(5 4 3 2 1)
1 + 10 + 50+166,67 + 416,67 + 833,33 1477,67	’
Другими словами, в среднем две линии будут заняты 3,4% времени. Другие значения можно
достаточно просто подсчитать в электронных таблицах, применяя следующую формулу, опи-
сывающую зависимость между последовательными значениями этих вероятностей’
ГЛАВА 13 Модели очередей 875
Л=Л-.(Ш/'
Например, если известно значение Р2, то значение Р, вычисляется таким образом-
Р3 = Р2х 10/3 = 0,034 х 10/3 = 0,1133
Аналогично находится значение Р4-
Р4 = Р3х 10/4 = 0,1133 х 10/4 = 0,2833
Итак, чтобы получить следующее значение Р, нужно предыдущее значение А , умножить
на Х/Н и затем разделить на i
Найдем вероятность того, что все линии будут заняты. Если j = s = 5, то
А, = Р4 х 10/5 = 0,2833 х 10/5 = 0,564
Это значит, что в среднем все сервисы в системе будут заняты 56,4% времени
Еще раз повторим, что достаточно просто реализовать и использовать эти формулы в
электронных таблицах Вероятность того, что система будет занята (все сервисы будут
обслуживать клиентов) можно вычислить с помощью рабочего листа Конечная очередь
рабочей книги Ожидание XLS На рис 13 13 видно, что эта вероятность равна 0,564
(значение в ячейке F13) Естественно, это значение совпадает с вычисленным ранее ре-
зультатом Также нетрудно построить таблицу подстановки, в которой будут вычислены
значения искомой вероятности при различных значениях5 Такая таблица показана на
рис 13 14, где з варьируется от 0 до 10 К этой таблице добавлен столбец D, в котором вы-
числяются изменения вероятности при каждом добавлении нового сервиса Эти измене-
ния вероятности тем меньше, чем больше в системе сервисов Например, если в системе
имеется один сервис, то добавление второго уменьшит вероятность занятости системы на
0,089, тогда как добавление десятого сервиса уменьшит эту вероятность только на 0,059
Характеристики конечной очереди M/M/s
Интенсивность поступления заданий _
Интенсивность обслуживания >	_
Количество сервисов	_
Максимальная длина очереди	L
Коэффициентзагрузки системы	< j;,/: к)
Р'0) probability that the system is empty ‘	j;
Lq. expected queue length	’ /////’
L. expected number in system 7   //§  Г/F;
v/q expected ВДИЙтдирМ
W. expected total time in system	   .
Probability that a customer watts 7
Вероятность полной занятости системы / /
1А|, В j, С  j , D I Е	G | Н?
5
(не более 40)
(не более 40)
87.21%
0.0007
0.0000
4.3605
0.0000
10.0000
0.0000
| 0.5640 |
Рис. 13.13. Рабочий лист с вычисленными характеристиками очереди с 5 сервисами
876 ЧАСТЬ III Вероятностные модели
Рис. 13.14. Таблица значений вероятности полной занято-
сти системы при различных значениях числа сервисов
Среднее число занятых сервисов
Еще одна широко используемая при установке телефонных линий характеристика —
это среднее число занятых линий. Пусть Д'— среднее число занятых сервисов, тогда
W = (Х/ц) х (1 - вероятность полной занятости системы).	(13 9)
Телефонная модель для госпиталя Св. Луки имеет параметры X = 1 и 1/ц = 10 Поэтому,
если Монти закупит 10 линий, то (см рис. 13 14) вероятность того, что все 10 линий будут
заняты, равна 0,215 (ячейка СЗЗ) Из формулы (13.9) следует, что N= 10х(1 - 0,215) = 7,85.
Другими словами, все средства обслуживания будут заняты с вероятностью 0,215 (т.е.
около пятой части времени работы), и в среднем почти восемь телефонных линий будут
постоянно заняты. Вычислив значение N, коэффициент загрузки системы можно опре-
делить путем деления N Has (число сервисов). Для нашей модели коэффициент загрузки
системы равен 7,85/10 = 78,5% Это значит, что каждый сервис будет обслуживать клиен-
тов 78,5% всего времени работы (в среднем) и будет свободным 21,5% времени.
Монти решил, что установка 10 телефонных линий является подходящим решением.
Может показаться, что такое количество линий избыточно, но, с другой стороны, только
в 70-80 случаях из ста можно будет свободно дозвониться, что, впрочем, допустимо для
госпиталя. Если Монти не устраивает решение, основанное на выборе приемлемого зна-
чения вероятности полной занятости системы, он может определить стоимость каждого
утраченного звонка и решить, сколько необходимо телефонных линий, чтобы ожидаемая
стоимость была минимальной. Способы определения этой стоимости описаны в разде-
лах 13.6 и 13.7.
13.9.	Очереди с конечным источником заданий
С помощью третьей модели Монти должен решить, сколько ему необходимо принять
на работу ремонтников, чтобы поддерживать в рабочем состоянии 20 электронных уст-
ройств. Рабочие ремонтируют их по схеме “первым пришел (точнее, первым сломался) —
первым обслужен”. Каждый ремонтник может починить любое устройство. Поэтому по-
ломанное устройство становится в конец очереди, которая обслуживается несколькими
параллельными сервисами (ремонтниками).
ГЛАВА 13. Модели очередей 877
Это другой тип модели M/M/s, отличающийся от модели, рассмотренной в разделе 13 6.
В данной модели количество клиентов, которые могут войти в систему, ограничено числом
20 (в отличие от модели лаборатории, в которой число возможных клиентов не ограничива-
лось). Если в модели очереди может быть только ограниченное число клиентов, то говорят,
что это модель с конечным источником заданий. И, наоборот, модель с неограниченным чис-
лом возможных клиентов называется моделью с бесконечным источником заданий.
Рассмотрим модель из 20 устройств и 2 ремонтников. Допустим, что время между полом-
ками оборудования имеет экспоненциальное распределение с параметром X = 0,25 (в час), т.е.
среднее время между поломками 1/Х = 4 ч. Аналогично предположим, что время, требуемое на
починку одного устройства, является случайной величиной, распределенной по экспоненци-
альному закону со средним 0,50 ч (т.е. 1/ц = 0,50). Поэтому данная модель является моделью
вида MIMI2 с максимальной длиной очереди 18 (всего 20 заданий, включая двух, находящихся
на обслуживании) и конечным источником. Поэтому одна из основных характеристик моде-
ли, вероятность того, что в стационарном режиме в системе будет находиться п заданий, будет
функцией четырех переменных: X, ц, 5 (число сервисов) и N (максимальное число заданий).
Эта формула имеет следующий вид.
Р" = и 5’ м(ХУц)"Р"’ если 0 ~ " - s’
n’(N-n)’
Р„ =-----—------QJP)"Pa, ecms<n<N.	(13 10)
" (N - ny.sls"-1 °
Присоединив равенство
(13 11)
/1=0
получим систему, состоящую из N+ 1 линейных уравнений (У уравнений, задаваемых
формулами (13 10), и уравнение (13.11)) с N+ 1 неизвестными (Р„, Р„ , Рп) Из этой
системы можно найти (часто для этого требуются большие усилия) значения вероятно-
стей Ря для любой модели Как можно заметить, по мере усложнения моделей все более
сложными становятся формулы для вычисления Р„.
К сожалению, не существует для этого типа очередей простых формул вычисления
среднего числа заданий в системе или среднего времени ожидания Но если значения Ря
вычислены, то найти значение среднего числа клиентов в системе несложно Для этого
можно применить формулу
среднее число клиентов в системе = L = ^пРп
/1=0
Если бы господь предположил, что люди станут вручную вычислять подобные выра-
жения, то он не способствовал бы изобретению электронных таблиц На рис. 13 15 пока-
зан рабочий лист Конечный источник из рабочей книги PewioHT.XLS. Эту книгу можно
использовать для вычисления значений вероятностей Ро, среднего (ожидаемого) числа
клиентов в системе и ожидаемой продолжительности пребывания клиента в системе для
различных моделей данного типа Для этого следует ввести значения стандартных пара-
метров X, р. и i в соответствующие ячейки рабочего листа MMs, затем нужно ввести зна-
чение максимального количества клиентов в ячейку Е5 рабочего листа Конечный источ-
ник, все остальное сделает электронная таблица. В данном случае “остальное” — это вы-
числение значений Р„ и использование их для поиска среднего количества клиентов
в системе Отметим, что при использовании этой рабочей книги в лист MMs вводится
значение не X, а Л'хХ, т.е. общая интенсивность поступления клиентов.
878 ЧАСТЬ III Вероятностные модели
Характеристики очереди M/M/s 
Интенсивность поступления заданий
Интенсивность обслуживания
Количество сервисов
Ратмер источника
Коэффициент загрузки системы
Р(0) вероятность того, что система пуста
Lq средняя длина очереди
L, среднее количество заданий в системе
Wq. среднее время ожидания в очереди
W средняя время пребывания в системе
Вероятность ожидания в очереди
с конечным источником
0.25
поступления заданий
20
(одного сервиса)
(не более 40)
(не более 100)
92.51%
0.033277
3.347725
5.197978
0.904667 часов
1,404667 часов
0,88353 I
12 14 16 18 20 22 24 26 28 30 32 34 36 38 40
Количество заданий в системе
П1Ш111
Рис. 13.15. Модель очереди с конечным источником
Как показано на рис 13 15, для нашей модели Lq среднее число устройств, ожидаю-
щих ремонта, равно 3,348 (ячейка F8), a W, ожидаемая продолжительность ремонта од-
ного устройства, равна 1,405 часа (ячейка Fl 1) Коэффициент загрузки ремонтников дос-
таточно высок — 92,5%, а вероятность того, что они простаивают, равна всего 3,3%.
В среднем одновременно ремонта требуют 5,19 устройств
13.10.	Переходные процессы в моделях очередей
В этом разделе мы рассмотрим переходные режимы системы, а для получения ответов на
интересующие вопросы используем имитационную модель очереди В частности, производст-
венный процесс можно рассматривать как сложную систему очередей. При этом наиболее
часто используемым средством анализа таких систем являются имитационные модели.
Рассмотрим пример Ларри Луджак — плановик производственного отдела компании
Sonorola, недавно окончивший школу бизнеса Чикагского университета. Для того чтобы
определить сроки выполнения нового заказа клиента, Ларри хочет воспользоваться зна-
ниями о моделях очередей, которые он приобрел в университете. Компания получила за-
каз на производство 20 единиц изделия, изготовление которого требует последователь-
ной обработки на двух автоматизированных станках. Среднее время обработки изделия
на каждом станке составляет 4 ч Каждый станок работает 8 ч в рабочий день.
Ларри вычислил, что на выполнение заказа потребуется 10,5 дней. Действительно,
последнее изделие будет находиться в очереди на обработку первым станком, пока не бу-
дут обработаны первые 19 изделий, после чего это (последнее) изделие будет обработано
первым станком и затем вторым. Предположив, что изделия, прошедшие обработку на
первом станке, сразу поступают на второй станок, Ларри вывел следующую формулу:
(19 изделий х 4 ч на изделие + 4ч + 4 ч) / 8 ч в день = 10,5 дней
Однако это упрощенная формула. Она не учитывает, что время обработки может быть
различным, вследствие чего может образоваться очередь на втором станке. Ларри счита-
ГЛАВА 13 Модели очередей 879
ет, что экспоненциальное распределение вполне подходит для задания времени обработ-
ки на станках, поскольку, если в среднем обработка длится 4 ч, то на практике обработка
одного изделия чаще будет занимать немного меньше 4 ч и лишь изредка больше 4 ч (см
раздел 13 11) Такие задержки могут возникать, например, при поломке станков во время
обработки изделий
Далее Ларри проверил, выполняются ли предположения базовой модели очередей
Изделия, обработанные первым станком, поступают на второй, причем интервал време-
ни между поступлениями является экспоненциально распределенной случайной величи-
ной, поскольку время обработки на первом станке подчиняется экспоненциальному за-
кону. Время обработки изделий на втором станке также определяется экспоненциальным
распределением Изделия обрабатываются на втором станке по принципу “первым при-
был — первым обслужен” Площадка для временного хранения изделии между станками
достаточно вместительна, поэтому длина очереди может быть в принципе не ограничена
Но предположение о неограниченном временном горизонте в этой модели не выполняет-
ся, поскольку Ларри интересует поведение системы только до того момента, пока не за-
вершится обработка двадцатого изделия
Ларри решил воспользоваться базовой моделью как простейшей. Ему надо определить
время изготовления 20 изделий Очевидно, что последнее из 20 изделий будет обработано
на первом станке через 20 х 4 = 80 ч после начала всей работы Далее последнее изделие бу-
дет ожидать в очереди обработки на втором станке. После обработки на этом станке все 20
изделий будут готовы Промежуток времени между выходом последнего изделия с первого
станка и выходом его же после обработки со второго станка (т.е время, проведенное этим
изделием в системе) обозначим через Ж. Итак, искомое время изготовления заказа вычис-
ляется по формуле 20 х 4 + Ж, причем в базовой модели Ж = 1/(ц - Л) Нов данном случае
перед Ларри возникла проблема в его модели ц и X равны (одно изделие за 4 ч), а последняя
формула справедлива только тогда, когда ц больше X
Ларри создал рабочую книгу Заказ XLS, чтобы с ее помощью имитировать обработку
20 изделий на двух станках Первый лист этой книги показан на рис 13 16 Ларри пред-
положил, что на первом станке (С1) всегда имеется достаточный запас заготовок, поэто-
му обработка очередного изделия на первом станке начнется сразу же, как будет законче-
на обработка предыдущего изделия Это значит, что время начала обработки очередного
изделия совпадает со временем окончания обработки предыдущего изделия Поэтому в
рабочей книге Заказ XLS ячейки в столбце В (время начала обработки изделия на первом
станке) ссылаются на значения ячеек столбца С (время окончания обработки изделия на
первом станке), расположенных на одну строку выше относительно данной (например, в
ячейке В8 записана формула =С7) Время поступления изделия на второй станок совпа-
дает либо со временем окончания обработки этого изделия на первом станке либо со
временем окончания обработки предыдущего изделия на втором станке в зависимости от
того, которое из этих времен больше Поэтому, например, в ячейке D8 содержится фор-
мула =МАКС(С8;Е7) Время выполнения заказа в днях показано в ячейке F2, оно вычис-
лено путем деления времени окончания обработки последнего изделия на втором станке
на число часов в рабочий день (значение 8 в ячейке F1). Полученное значение времени
выполнения заказа 10,5 дней, показанное на рис. 13.16, справедливо, если каждое изде-
лие обрабатывалось ровно 4 ч на каждом станке.
880 ЧАСТЬ III Вероятностные модели
1	А	I	В , С		□		F 1 G
Среднее время |					К-во часов в	
1 .обработки на С1 I			часы		рабочий день	8
, J Среднее время |					Выполнение	
2	обработки на С2 |		часы		заказа	10,5 дней
3						
4-.1						
5]		Станок 1		Станок 2		
6	Номер изделия	Начало	Конец	Начало	Конец,	
		0			8	
8	2	4	8	8	12	
	з	8	12	12	16	
10'	А	12	16	16	20	
Й	5	16	20	20	24	
12ч	6	20	24	24	28	
	7	24	28	28	32	
14	8	28	32	32	36	
15	9	32	36	36 ’	40	
-16J 17	10	36	40	40	44	
	11	40	44	44	48	
w"	12	44	48	48	52	
	13	48	52	52	56	
ж		14—		52.		56—		55		ео_	
	,	В ' '	' I '	с	I	D	Е
6 	|	Начало	Конец	Начало	Коней
7		=$В$1+В7	=С7	=D7+$B$2
8	=С7	=$В$1+В8	=МАКС(С8,Е7)	=О8+$В$2
9	=08	'=$В$1 + В9	=МАКС(С9,Е8)	=D9+$B$2
10	=С9	МВ$1 + В10	=МАКС(С10.Е9)	=D10+$B$2
11	=С10	МВ61+В11	=МАКС(С11,Е10)	=D11+$B$2
12	=С11	=$В$1+В12	=МАКС(С12,Е11)	=D12+$B$2
13	=С12	=$В$1 + В13	=МАКС(С13;Е12)	=D13+$B$2
14	=С13	=$В$1+В14	=МАКС(С14;Е13)	=D14+$B$2
15	=С14	=$В$1 + В15	=МАКС(С15,Е14)	=D15+$B$2
16	=015	=$В$1 + В16	=МАКС(С16,Е15)	=D16+$B$2
17	=016	=$В$1+В17	!=МАКС(С17;Е16)	=D17+$B$2
*ij8-:	—С 17	=$В$1+В18	=МАКС(С18;Е17)	=D18+$B$2
19	=С18	=$В$1 + В19	=МАКС(С19,Е18)	=D19+$B$2
20	=019	=$В$1+В20	=МАКС(С20;Е19)	=D20+$B$2
21	=020	=$В$1+В21	=МАКС(С21,Е20)	=D21 + $B$2
22	=С21	=$В$1+В22	=МАКС(С22,Е21)	=D22+$B$2
23	=С22	=$В$1+В23	=МАКС(С23:Е22)	=D23+$B$2
24	=023	•=$В$1+В24	=МАКС(С24;Е23)	=D24+$B$2
25	I =С24	=$В$1+В25	=МАКС(С25,Е24)	=D25+$B$2
26	1=025	=$В$1+В26	=МАКС(С26 Е25)	=D26+$B$2
Рис. 13.16. Таблица времени выполнения заказа
Чтобы проанализировать влияние времени обработки на длительность выполнения за-
каза, Ларри заменил в рабочей таблице константу 4, равную времени обработки для стан-
ков, значениями случайных величин, имеющих такое же среднее (в надстройке Crystal Ball
надо просто выбрать экспоненциальное распределение; при использовании надстройки
ГЛАВА 13. Модели очередей 881
@RISK следует заменить ссылки на ячейки В1 и В2 формулами =RiskExpon($B$1)
и =RiskExpon($B$1)). В этом случае время выполнения заказа будет случайной величиной.
Ларри хочет получить значение времени выполнения заказа, которое будет соответствовать
действительности с вероятностью 99% (т.е. в 99 случаях из 100 время выполнения заказа не
превысит это значение).
В электронных таблицах с помощью надстроек Crystal Ball и @RISK достаточно про-
сто найти это значение На рис 13.17 показано окно надстройки @RISK, где представле-
ны вероятностные характеристики для значения ячейки F2 (время выполнения заказа
в днях), основанные на 1000 имитациях обработки 20 изделий на двух станках. Сразу за-
метим, что среднее время выполнения заказа (значение в поле Mean для ячейки F2,
см рис. 13.17) составляет 12,52 дня, что на 2 дня больше, чем значение, вычисленное
Ларри Дополнительные 2 дня — это среднее время пребывания изделий в очереди, вы-
званное непостоянством значений времени обработки изделий Если Ларри хочет быть
уверенным на 99%, что заказ будет выполнен в назначенный им срок, он должен устано-
вить его равным 18,28 дня (значение Target#1 (Value) на рис. 13 17).
Рис. 13.17. Статистические характеристики модели выполнения заказа
Очередь, которая образовывается на втором станке, увеличивает время реализации за-
каза (время, проведшее с момента поступления заказало момента его выполнения) почти
на 8 дней (18,28 дня вместо 10,5) На рис 13 18 показана гистограмма (эмпирическая
плотность вероятности) времени выполнения заказа Как видно из этого рисунка, про-
должительность выполнения заказа варьируется от 6,5 дней до 21 дня
882 ЧАСТЬ 111. Вероятностные модели
Рис. 13.18. Гистограмма времени выполнения заказа
Даже несмотря на то, что базовая модель очереди не полностью подходит для описа-
ния данной ситуации, она помогла Ларри разработать собственную модель и найти ре-
шение, применив имитационное моделирование на основе электронной таблицы
13.11.	Роль экспоненциального распределения
Существует огромная научная литература, посвященная теории массового обслужи-
вания и моделям очередей, в которой обычному менеджеру очень сложно разобраться
Приведем несколько рекомендаций, которые могут помочь ему в этом. Прежде всего
подчеркнем роль экспоненциального распределения в аналитических моделях очередей.
Трудно получить какие-либо аналитические результаты на основе модели очереди,
если не использовать экспоненциальное распределение для вычисления времени поступ-
ления заданий (клиентов) в систему и/или для определения времени обслуживания Учи-
тывая это обстоятельство, менеджерам важно понять, в каких случаях можно предполо-
жить, что события будут происходить в соответствии с экспоненциальным распределени-
ем Опишем некоторые свойства экспоненциального распределения, которые помогут
распознать такие случаи.
1.	Отсутствие последствия. Это свойство означает, что вероятность того, что новый
клиент поступит в систему в некоторый момент времени, не зависит от момента вре-
мени, когда поступил предыдущий клиент. Другими словами, система “не помнит”,
что произошло мгновение назад Такие ситуации возникают, когда 1) существует
большое количество клиентов, которые потенциально могут вступить в систему;
2) каждый клиент сам решает, когда ему вступить в систему, и его решение не зави-
сит от других клиентов, 3) каждый клиент выбирает время вхождения в систему слу-
ГЛАВА 13. Модели очередей
883
чайно. Очевидно, что распределение поступлений звонков по экспоненциальному
закону очень хорошо подходит для моделей телефонных станций
2.	Короткое время обслуживания. При экспоненциальном распределении в большинстве
случаев время обслуживания меньше его среднего На рис 13 19 изображен график ве-
роятности того, что время обслуживания 5 меньше или равно /, если среднее время об-
служивания равно 10, т е ц = 0,1 и 1/ц = 10 Заметьте, что при малых значениях t гра-
фик быстро возрастает, а затем медленно приближается к значению 1 Это указывает на
достаточно большую вероятность того, что время обслуживания будет коротким На-
пример, при t= 10 вероятность того, что 5 <t, равна 0,632 Другими словами, более 63%
значений времени обслуживания будут меньше среднего значения этой величины По-
этому экспоненциальное распределение применяется для определения времени обслу-
живания в системах, в которых большинство клиентов обслуживается быстро, и только
некоторые из них требуют более длительного обслуживания.
Говорят, инженеры думают, что весь мир экспоненциально распределен, а ученые
считают, что вселенная распределена по нормальному закону Чтобы определить,
какой тип распределения лучше описывает ваши данные, следует посмотреть, на-
сколько близко расположены значения среднего (математического ожидания)
и стандартного отклонения Если эти значения близки, то, скорее всего, эти дан-
ные подчиняются экспоненциальному закону Если значение стандартного откло-
нения составляет примерно 1/3 или меньше от среднего, то, скорее всего, данные
распределены по нормальному закону4
3.	Связь с распределением Пуассона. При описании базовой модели (см раздел 13 2)
мы упоминали о связи между экспоненциальным распределением и распределени-
ем Пуассона В частности, если время между поступлениями в систему имеет экс-
поненциальное распределение с параметром X, то число поступлении в систему Д'
заданий за период времени Т будет иметь распределение Пуассона с параметром
XT Вероятность Р{Х=п] того, что X равно некоторому положительному целому
числу/?, вычисляется по формуле
Рис. 13.19. Высокая вероятность короткого времени обслуживания
Последнюю рекомендацию можно принять только тогда, когда все эмпирические данные положительны —
Прим ред
884
ЧАСТЬ Ш Вероятностные модели
Взаимосвязь между экспоненциальным распределением и распределением Пуассона
играет важную роль в аналитических построениях теории массового обслуживания. Кро-
ме того, эта связь также имеет практическое применение. Сравнивая количество зада-
ний, поступающих на средство обслуживания на протяжении определенного отрезка
времени, с числом, определенным распределением Пуассона, менеджер может выяснить,
насколько точно он выбрал значения параметров модели.
13.12.	Дисциплина очереди
В предыдущих разделах мы характеризовали системы очередей типом распределения
поступлений клиентов, значением среднего времени обслуживания и числом средств об-
служивания (сервисов) Дисциплина очереди — еще один компонент полной характеристи-
ки системы очереди Во всех рассмотренных ранее моделях мы предполагали, что посту-
пившие в систему клиенты будут обслуживаться по принципу “первым прибыл — первым
обслужен” (стандартная аббревиатура для этого вида дисциплины очереди — FIFO, от англ,
“first-in, first-out”). Очевидно, что такая дисциплина подходит для многих моделей, в кото-
рых клиентами являются поступившие в очередь люди. Тем не менее существуют модели,
где ее использовать не стоит. Например, последний человек, вошедший в лифт, выходит
первым (такая дисциплина очереди называется “последним прибыл — первым обслужен”
или LIFO, от англ “last-in, first-out”) Еще один тип дисциплины очереди подсказывает рас-
смотренная выше модель ремонта оборудования. На практике не всегда разумно ремонти-
ровать оборудование в той последовательности, в которой оно поступило на ремонт Если
какое-либо устройство можно отремонтировать за 5 мин., то лучше сначала починить
именно его Дисциплина очереди, в которой есть возможность произвольного выбора кли-
ентов, как правило, приводит к усложнению модели
13.13.	Заключение
В этой главе мы познакомились с моделированием очередей В разделе 13 2 рассмотрена
базовая модель очереди с одним сервисом, в которой время между поступлениями заданий
в систему и время обслуживания имеют экспоненциальные распределения. Были представле-
ны формулы для вычисления четырех основных характеристик системы, ожидаемое (среднее)
число клиентов в системе L, ожидаемое (среднее) число клиентов в очереди L4, среднее время
ожидания в системе Wи среднее время ожидания в очереди IT. Эти характеристики являются
функциями от параметров процессов поступления и обслуживания заданий в системе.
В разделе 13.3 введена система обозначений, применяемая для описания моделей очере-
дей В разделе 13.4 представлена формула Литтла L = которая вместе с равенством
И/= IV + среднее время обслуживания
предоставляет альтернативный способ вычисления характеристик очереди.
В разделе 13 5 показано использование базовой модели при произвольном распреде-
лении времени обслуживания Очереди с несколькими сервисами рассмотрены в разде-
ле 13 6 Раздел 13 7 посвяшен экономическому анализу моделей В разделах 13.8 и 13 9
продолжено изучение очередей с несколькими сервисами В разделе 13 8 рассмотрена
модель очереди типа M/G/s, в которой, если все сервисы заняты, вновь поступившие
клиенты не ожидают в очереди, а покидают систему. Этот тип модели особенно часто
применяется при анализе телефонных систем.
ГЛАВА 13. Модели очередей 885
В разделе 13.9 рассмотрена модель типа M/M/s с конечным источником заданий.
В разделе 13.10 показан пример использования имитационного моделирования с помо-
щью электронных таблиц для исследования системы в переходном режиме
Важность экспоненциального распределения при анализе моделей очередей показана
вразделе 13.11. И, наконец, вразделе 13.12 кратко рассмотрены виды дисциплины очереди
Основные термины
Время между поступлениями заданий в систему. Интервал времени между двумя последовательными
поступлениями заданий в систему Как правило, эта характеристика модели является случай-
ной величиной
Время обслуживания. Интервал времени обслуживания одним сервисом одного задания Эта ха-
рактеристика модели, как правило, является случайной величиной
Дисциплина очереди. Правило, по которому выбирается из очереди задание для обслуживания
Наиболее часто используется правило “первым пришел — первым обслужен”
Длина очереди. Максимальное число заданий, которые могут ожидать обслуживания в очереди
Источник заданий. Общее число заданий, которые могут поступить в систему для обслуживания, —
один из параметров, определяющих процесс поступления заданий в систему
Канал. Синоним сервиса (средства обслуживания) в модели очереди Например, одноканальная
очередь — это очередь с одним сервисом
Конечная очередь. Очередь, в которой может находиться ограниченное число задании
Модель очереди. Модель, в которой отражается состояние ожидания в очереди
Отсутствие последствия. Свойство экспоненциального распределения, позволяющее получать ана-
литические результаты для многих моделей очередей
Процесс обслуживания. Часть модели очереди, которая определяет время обслуживания для каж-
дого задания в системе
Процесс поступлений заданий в систему. Часть модели очереди, которая определяет характер посту-
плений заданий в систему
Рабочие характеристики. Величины, например, среднее число заданий в очереди, которые характе-
ризуют модель (систему) очереди
Стационарный режим. Состояние системы, при котором значения рабочих характеристик
(например, вероятность того, что очередь пуста) не зависят от момента времени, для которого
вычисляются эти величины
Контрольные вопросы
Да/нет
1.	Число клиентов в системе — это число клиентов, ожидающих обслуживания в очереди
2.	Время обслуживания в системе включает время ожидания в очереди.
3.	Экспоненциальное распределение определяется двумя параметрами — средним
и стандартным отклонением.
4.	Среднее время между поступлениями — это обратная величина к средней интен-
сивности поступлений, а среднее время обслуживания — это обратная величина
к средней интенсивности обслуживания.
5.	Базовая модель — это модель типа М/М/.
886 ЧАСТЬ III Вероятностные модели
6.	При увеличении числа сервисов стоимость ожидания возрастает.
7.	Если средняя интенсивность обслуживания меньше средней интенсивности по-
ступления, то этого достаточно, чтобы исключить возможность образования бес-
конечнодлинной очереди.
8.	Формула Литтла устанавливает прямо пропорциональную зависимость между
средним временем ожидания в системе и средним числом клиентов в системе
9.	Обозначение G/M/1 означает, что в модели очереди распределение времени об-
служивания произвольное, распределение между поступлениями экспоненциаль-
ное, и в системе находится два параллельных сервиса.
Выберите правильный ответ
10.	Какое предположение не выполняется для базовой модели?
а Экспоненциальное распределение времени поступления заданий в систему.
b Экспоненциальное распределение времени обслуживания
с Конечный временной горизонт
d Неограниченный объем очереди
е Дисциплина очереди “первым пришел — первым обслужен”.
11.	Основная цель моделирования очередей
а минимизировать стоимость обслуживания,
b помочь менеджеру уменьшить стоимость обслуживания,
с максимизировать ожидаемый результат,
d оптимизировать характеристики системы
12.	Характеристики системы, такие как “ожидаемое число клиентов в очереди”
а имеют отношение только к системам, находящимся в стационарном режиме;
b являются вероятностными,
с зависят от конкретной модели;
d все вышеперечисленное
13.	Какие утверждения не верны для формулы Литтла9
а X— это постоянный коэффициент пропорциональности между ожидаемым
числом клиентов в очереди и средним временем ожидания в очереди
b X— это постоянный коэффициент пропорциональности между ожидаемым
числом клиентов в системе и средним временем ожидания в системе
с л — это интенсивность поступлений клиентов в систему, включая тех клиен-
тов, которые решили не поступать в систему.
14.	Сложнее всего при выполнении экономического анализа модели очереди оценить:
а стоимость обслуживания;
b стоимость ожидания,
с коэффициент использования.
15.	Какие из приведенных ниже характеристик не относятся к экспоненциальному
распределению9
ГЛАВА 13 Модели очередей 887
а. Отсутствие последствия.
b Как правило, выборочное значение больше среднего
с Распределение зависит от одного параметра
Ответы
1 Нет 2 Да 3 Нет 4 Да 5 Да 6 Нет 7 Нет. 8 Да 9. Нет. 10 с. 11b 12 d 13 с
14. b 15 Ь.
Учебные задачи
13 1 Баржи поступают в шлюз в Ла Кроссе на реке Миссисипи в среднем с интенсивностью одна
баржа за 2 ч Если время между поступлениями распределено экспоненциально, то определите
а значение X,
b среднее время между поступлениями барж,
с среднюю интенсивность поступления барж
13 2 Машины поступают на станцию технического обслуживания для смены машинного масла
каждые 15 мин , причем время между поступлениями определяется по экспоненциальному
закону Станция может обслужить 18 автомобилей за 8-часовой рабочий день, работая без
перерыва Предположим, что время обслуживания является случайной величиной с экспо-
ненциальным распределением Определите
а значение X,
b среднюю интенсивность поступлений автомашин,
с значение р,
d среднее время обслуживания,
е среднюю интенсивность обслуживания
13 3 Сотрудник иммиграционной службы аэропорта Хитроу в Лондоне может обслужить
в среднем 120 человек, прилетающих в страну, за его 8-часовое дежурство Если время об-
служивания каждого прилетающего является случайной величиной с экспоненциальным
распределением, то вычислите
а значение р,
b среднее время обслуживания,
с среднюю интенсивность обслуживания
13 4 Используя данные задачи 13 2, определите
а среднее число автомобилей в системе,
b среднее число автомобилей в очереди,
с среднее время пребывания в системе,
d среднее время ожидания в очереди;
е вероятность того, что система пуста
13 5 Предположим, что в задаче 13 3 модель построена на основе базовой Напомним, что при
постоянной загрузке сотрудник может обслужить 120 клиентов за 8-часовую рабочую сме-
ну, т е в среднем каждые 6 мин поступает один клиент Определите
а ожидаемое число клиентов в системе,
b ожидаемое число клиентов в очереди,
с среднее время ожидания в системе,
d среднее время ожидания в очереди,
е вероятность того, что система пуста
888 ЧАСТЬ III Вероятностные модели
13 6 Рассмотрим очередь с одним сервисом Для описания работы этой очереди используется
базовая модель Прокомментируйте следующую схему вычисления Л пусть N — число кли-
ентов, поступивших в систему с 8 00 до 16 00, тогда X = 8/7V
13 7 Рассмотрим базовую модель Пусть X = 5 Постройте график значений ожидаемого числа
клиентов в системе для р = 6, 7, ,15
13 8 Рассмотрим базовую модель Пусть ц = 10 Постройте график значений вероятности того,
что система пуста, для X = 0, 1, ,10
13 9 Выведите формулу вычисления И7для базовой модели, используя формулы Литтла и соот-
ношение L = Х/(ц - X)
13 10 Используя формулу Литтла, выражение для среднего времени обслуживания и формулу L
= Х/(р - X), найдите для базовой модели формулу вычисления Wq
13 11 Врач тратит на осмотр пациента в среднем 20 мин Если среднее время ожидания в систе-
ме — полчаса, то каково среднее время ожидания в очереди9
13 12 Пусть в условиях предыдущей задачи пациенты поступают с интенсивностью семь человек
в час Прокомментируйте эту ситуацию
13 13 Опишите словами модель очереди типа M/D/3
Прикладные задачи
13 14 Пусть работу шлюза из задачи 13 1 можно приемлемо описать с помощью базовой модели Для
нового навигационного сезона сделана новая оценка среднего времени между поступлениями
барж — 60 мин , при этом через шлюз баржа будет проходить в среднем 30 мин Найдите
а среднее число барж в системе,
b среднее число барж в очереди,
с среднее время ожидания в системе,
d среднее время ожидания в очереди,
е вероятность того, что система пуста,
f наибольшее среднее время обслуживания, при котором среднее время ожидания в очереди
будет меньше 45 мин
13 15 Покажите, что в условиях предыдущей задачи выполняются равенства Литтла
13 16 Решите задачу 13 14, предположив, что используется обобщенная модель, и отклонение
распределения времени обслуживания равно его среднему
13 17 В Гамбургском сберегательном банке клиенты, покупающие депозитные сертификаты, об-
служиваются одним банковским служащим, т е находятся в одной очереди и обслужива-
ются по правилу “первым прибыл — первым обслужен” Время обслуживания подчиняется
нормальному закону со средним 5 мин и стандартным отклонением 1 мин Интенсивность
поступления клиентов — один новый клиент каждые 8 мин. Анализ временных затрат по-
казал, что клиенты находятся в банке в среднем 11,833 мин (время ожидания + время об-
служивания). Найдите среднее число клиентов в банке
13 18 В Гамбургском сберегательном банке в субботу работают три кассира Время поступления
и время обслуживания клиентов подчиняются экспоненциальному распределению. Ин-
тенсивность поступления клиентов составляет 20 клиентов в час, среднее время обслужи-
вания равно 6 мин Клиенты образуют одну очередь и обслуживаются первым освободив-
шимся кассиром. Считая, что система работает в стационарном режиме, определите
а вероятность того, что система пуста,
b среднее число клиентов в очереди,
с среднее время ожидания в очереди;
d среднее время ожидания в системе,
е среднее число клиентов в системе
ГЛАВА 13. Модели очередей 889
13 19 В Дарденской школе бизнеса имеется десять высокоскоростных модемов на каждом фа-
культете, которые используются для обеспечения связи между школьной сетью и домаш-
ними компьютерами Если студент попытается войти в сеть в момент, когда все модемы
заняты, он получит сообщение об этом, и ему придется позже попытаться подключиться
еще раз Руководитель отдела информационных технологий хочет определить характери-
стики системы, предположив, что количество клиентов ограничено и равно 100, а очередь
может быть бесконечной Каждому студенту нужно входить в сеть в среднем каждые 8 ч,
причем время между поступлениями распределено экспоненциально Время соединения
также распределено экспоненциально и в среднем равно 30 мин Вычислите
а вероятность того, что все модемы свободны,
b среднее число клиентов в очереди,
с среднее время ожидания в системе,
d среднее время ожидания в очереди,
е среднее число клиентов в системе
13 20 В условиях задачи 13 19 с помощью рабочей книги Excel Q.XLS найдите вероятность того,
что все модемы заняты (Рассмотрите модель M/G/s, в которой число клиентов не ограни-
чено, а интенсивность поступлений равна 100 )
13 21 Компания STECO имеет 100 торговых представителей в Соединенных Штатах Они по теле-
фону отправляют заказы в центральный офис, где служащий, используя централизованную
систему управления запасами, подтверждает наличие товара на складе, его цену и срок по-
ставки Представители, как правило, звонят из офиса клиента перед подписанием контракта
Звонки находятся в очереди и обслуживаются первым освободившимся служащим по прин-
ципу “первым пришел — первым обслужен” Интенсивность звонков составляет 40 (в час), а
среднее время обслуживания — 6 мин Компания выплачивает за час работы торговому пред-
ставителю $20, а служащему офиса $12 Постройте модель этой компании, используя очередь
типа M/M/s с бесконечным количеством клиентов, и вычислите ожидаемую общую стоимость
в час (см раздел 13 7), если в центральном офисе работает пять служащих
13 22 Вычислите ожидаемую общую стоимость (в час) в условиях задачи 13 21, если в централь-
ном офисе работает шесть служащих
13 23 Используя результаты, полученные в задачах 13 21 и 13 22, определите отношение стоимо-
сти работы сервиса к стоимости ожидания в очереди С,/С, (см раздел 13 7), при котором
система будет индифферентна к тому, сколько служащих работает в центральном офисе —
пять или шесть
13 24 В производственном цехе один механик обслуживает четыре станка Время между полом-
ками станков распределено экспоненциально, среднее значение этого времени равно че-
тырем часам В среднем на ремонт станка тратится 30 мин Определите
а вероятность того, что 0, 1, 2, 3 или 4 станка требуют ремонта,
b среднее число станков, требующих ремонта
13 25 Телефонная станция имеет семь линий Звонки поступают с интенсивностью в два звонка в ми-
нуту, а время между поступлениями подчиняется экспоненциальному распределению Длитель-
ность разговора подчиняется нормальному распределению со средним 5 мин и стандартным от-
клонением 1 мин Если заняты все семьлиний, звонящий услышит сигнал “занято”
а Какова вероятность того, что заняты три линии9
b Какова вероятность того, что вся система занята9
с Сколько линий занято в среднем9
13 26 В группу маркетинговых исследований входят три сотрудника, которые берут интервью
у посетителей трех магазинов, расположенных рядом в одном торговом центре Интер-
вьюеры подходят к посетителям и спрашивают, не против ли они, чтобы им задали не-
сколько вопросов Подсчитано, что посетители, согласившиеся на опрос, поступают с ин-
тенсивностью в 15 человек в час, причем время между поступлениями распределено экс-
890 ЧАСТЬ III Вероятностные модели
поненциально Интервью длится в среднем 15 мин Если все интервьюеры заняты, то посе-
тители идут дальше по своим делам
а Прокомментируйте следующее утверждение поскольку в данном случае X > цх, то чис-
ло клиентов в системе будет расти бесконечно
b Вычислите вероятность того, что один интервьюер будет занят
с	Найдите вероятность того, что все три интервьюера будут заняты
d Определите среднее число занятых интервьюеров
13 Т1 Вернитесь к модели шлюза, рассмотренной в задачах 13 1 и 13 14 Предположим, что сред-
нее время между поступлениями барж составляет 60 мин , одна баржа проходит через шлюз
в среднем за 30 мин , стандартное отклонение времени обслуживания равно 3 мин Учиты-
вая новые данные, найдите ответы на вопросы а-/задачи 13 14 Насколько изменятся отве-
ты и почему9
13 28 В многоквартирном доме мелкий текущий ремонт производит один рабочий по мере по-
ступления заявок на ремонт В среднем поступает одна заявка в час Время, затраченное на
ремонт, подчиняется нормальному закону со средним 30 мин и стандартным отклонением
15 мин Сколько в среднем проходит времени с момента поступления заявки и до момента
окончания ремонта9
13 29 Ларри Луджака не устраивает время выполнения заказа (см раздел 13 10), поскольку при
такой длительности Sonorola будет терять клиентов, которые могут обратиться к конкурен-
там, предлагающим более быстрое выполнение заказа Изначально Ларри предположил,
что время обработки подчиняется экспоненциальному распределению Подробнее изучив
имеющиеся данные, он определил, что в 90% случаев время обработки на станках состав-
ляет 3 ч, и в 10% случаев она длится 13 ч Поэтому среднее время обработки на одном стан-
ке равно 0,9x3 + 0,1x13 = 4 ч От начальника цеха он узнал, что 13 ч требуется для обработ-
ки, если оборудование все время ломается Как правило, на ремонт одного станка уходит
10 ч Ларри знает, что профилактическое обслуживание может уменьшить вероятность ре-
монта станка с 10 до 1 %
а Используйте надстройку Crystal Ball или ©RISK для определения времени выполнения
заказа, которое не будет превышено с вероятностью 99%, при условии, что вероят-
ность поломки станка во время обработки изделия равна 10% На сколько это значе-
ние отличается от полученного в разделе 13 10, где время обслуживания имело экспо-
ненциальное распределение9
b Предположим, что вероятность поломки станка составляет 1% Сколько времени мо-
жет длиться профилактическое обслуживание, если оно уменьшает вероятность по-
ломки до такого уровня9
13 30 Допустим, что Ларри Луджаку (см раздел 13 10) нужно определить время выполнения
другого заказа Для этого заказа также нужно изготовить 20 изделий, но среднее время об-
работки на первом станке составляет 6 ч, а на втором — 4ч
а Используя базовую модель, определите время выполнения заказа
b Пусть время обслуживания распределено экспоненциально Используя модель, по-
строенную с помощью электронных таблиц, вычислите срок выполнения заказа На
сколько полученное значение отличается от подобного значения, найденного в преды-
дущем пункте9
с Если время между поступлениями изделий и время обработки распределены экспо-
ненциально, то сумма этих времен также подчиняется экспоненциальному закону
Учитывая этот факт, оцените аналитически (без имитации) значение времени выпол-
нения заказа, которое не будет превышено с вероятностью 99%
d Используя надстройку Crystal Ball или ©RISK, найдите значение времени выполнения
заказа, которое не будет превышено с вероятностью 99% Сравните с ответом, полу-
ченным в предыдущем пункте
ГЛАВА 13. Модели очереде “1	891
Ситуация для анализа | Сколько необходимо телефонисток
М-р J1 Л Бин занимается организацией почтовых переводов Заказы принима-
ются по телефону 24 часа в сутки и 365 дней в году. Средняя интенсивность звон-
ков — 78 000 в день. Звонки поступают с различной интенсивностью в разное время
суток. Заказы принимают операторы-телефонистки. Одни телефонистки трудятся
полный рабочий день, другие — неполный, третьи работают временно Такая стра-
тегия набора работников обеспечивает необходимую гибкость, учитывающую не-
равномерность поступления заказов
Однако остается открытым вопрос сколько операторов нужно м-ру Бину и когда9
Очевидно, что компании нужно найти разумное соотношение между качеством обслужи-
вания клиентов и затратами на обслуживающий персонал Допустим, что период, на ко-
торый нужно набрать персонал, составляет 168 ч в неделю Для каждого отдельного часа
этого периода смоделируем систему очереди типа M/M/s, т е очередь с несколькими па-
раллельными сервисами с экспоненциальным законом распределения времени между
поступлениями звонков и временем обслуживания и cs сервисами (операторами) Ин-
тенсивность поступления и обслуживания определена на основе данных за прошлые пе-
риоды Соотношение затрат должен обеспечить определенный стандарт обслуживания
компании не более 15% клиентов ожидают соединения с оператором более 20 с
Рассмотрим упрощенную модель Предположим, что работает только одна теле-
фонная линия, принимающая звонки в период от 1 часа ночи до 5 часов утра (самое
“неактивное” время) Существуют статистические данные о сотне звонков, сделан-
ных за этот период Эти данные содержатся в рабочей книге Бин XLS (рис 13 20)
	L	А	I	В [	С	D 1	....Ес	:	••Г ....		F
		: Звонки		(Длительность разговора			
Tl	Номер звонка	Время звонка	Занято?	(минуты) Конец разговора		Стоимость	
3_"		0,452	0		3,660 (	4 112	$	51 40
	9	0.945	1	Нет	4 112'	Нет	
б	з	7,553	0		2,086 Г	9,639	$	58,12
6	4	10,803	0	(	1.217;	12.020J	$	55,86
7 |	5	12 217	0	1914	14 131	$	37 81
8	6	16,426	0	0,319	16 745	$	61 82
9		:	18 136	0	•	1,012	19,148	$	43 44
10	8	25 242	0	6 883	32 125	$	49 15
11	9	27 753	1	[Нет J	32,125	Нет	
12 :	ю	30,159	1	Нет	32,125	Нет	
13		31,395	1	Нет	32,125	Нет	
14 j	12	32 042	т	Нет	32 125	Нет	
"(б	13	32,380	0	Г 0,049	32 429	$	37.75
16		14	36,803	' 0	2 165	38,968	$	56,18
17	15	36 911	1	Нет	38 968	Нет	
18	16	40,864	0	2,434	43 299	$	63 83
19	17	45,586	0	5,860	51,445	J .	59,18
20 '	18	46,211	1	Нет	51 445	Нет	
21	19	46,446	1	Нет	51 445	Нет	
22	20	53 127	0	4 807	57 933	$	66 81
Рис. 13.20. Статистика звонков
892 ЧАСТЬ III Вероятностные модели
Вопросы
1	Проанализируйте данные и определите среднюю продолжительность звонка Ка-
кое среднее время между поступлениями звонков9 Какова средняя сумма заказа?
2	Представьте графически статистические данные и определите, подчиняются ли
моменты времени поступления звонков и длительность обслуживания экспо-
ненциальному распределению {Совет. Надстройка Crystal Ball обладает встро-
енной возможностью определить тип распределения, наилучшим образом опи-
сывающий представленные данные)
3	. Какой процент времени оператор занят9
4	Каков процент звонков утрачивается из-за занятости линии9
В этой модели клиенты слышат сигнал “занято”, если оператор разговаривает
с другим клиентом Бин добавил дополнительные линии, которые будут удерживать кли-
ентов, пока телефонистка не освободится Если все дополнительные линии будут заняты,
новые клиенты также будут слышать сигнал “занято” Допустим, что каждая новая линия
обходится компании в 35 долл в месяц и в среднем каждый звонок стоит 2 долл. Бин хо-
чет знать, как изменятся показатели системы, если добавить новые телефонные линии.
Предположим также, что прибыль компании составляет 45 долл с каждого заказа.
Вопросы
5	Используя рабочий лист Конечные очереди из книги Бин XLS, определите, на
сколько увеличится количество звонков, если установят 1, 2, 3, 4 или 5 дополни-
тельных линий Определите, на сколько увеличится прибыль и затраты компа-
нии для каждого из этих случаев
6	Приведут ли дополнительные затраты на телефонные линии к увеличению стои-
мости заказов9 Какое число линий требуется добавить, чтобы добиться опти-
мального соотношения прибыли и затрат9
Литература
1 Edwin Laudauer and Linda Becker, “Reducing Waiting Time at Security Checkpoints”, Interfaces, 19,
no 5 (1989) 57-70
2 Richard Larson, Michael Cahn, and Martin Shell, “Improving the New York City Arrest-to-
Arraignment System”, Interfaces, 23, no 1 (1993) 76-96
лизсщия
Глава 14. Реализация моделей
Можно с уверенностью утверждать, что читатель уже привык к мысли о возмож-
ности использовать моделирование в электронных таблицах в процессе принятия
решений Цель этой части состоит в том, чтобы показать, что для построения по-
настоящему эффективной модели поддержки принятия решений необходимо не
только знать Excel и уметь создавать табличные модели, но и разбираться в основных
концепциях процесса моделирования Многолетний опыт большинства профессио-
налов подтверждает следующее наблюдение создания самой модели недостаточно
для принятия оптимального решения в реальной ситуации В этой части представле-
ны три основные группы причин появления неудачных проектов моделирования
и перечень “обычных” причин, почему моделирование не улучшает процесс приня-
тия решения В завершение описана реальная компания, в которой многообещаю-
щие усилия по моделированию столкнулись с большими проблемами.
Реализация моделей
В этой главе...
14.1.	Введение
14.2.	Что же такое модель
14.3.	Разделение функций игроков
14.4.	Размывание границ проекта
14.5.	Другие источники неудач
14.6.	Заключение
Основные термины
Задачи
Ситуация 1 Компания Australian Motors
Литература
896 ЧАСТЬ IV. Реализация
14.1	Введение
Читателю, дошедшему до этой главы, идея использования табличных моделей в про-
цессе принятия решений должна казаться вполне обоснованной. Несомненно, элек-
тронные таблицы и модели, построенные на их основе, — это мощная комбинация, спо-
собствующая лучшему пониманию ситуаций, в которых необходимо принимать ком-
плексные решения Перед нами стояла задача показать возможности Excel для создания
и анализа табличных моделей Мы также хотели показать, при каких обстоятельствах Ex-
cel не является лучшим выбором среды моделирования, например, при моделировании
дискретных событий Мы надеемся, что справились со своей задачей. Однако цель этой
главы состоит в том, чтобы показать, что для построения по-настоящему действенной
модели поддержки принятия решений необходимо понимать весь процесс реализации
проекта по созданию модели
Последнее утверждение иногда с удивлением воспринимается студентами, которые
плохо знакомы с использованием электронных таблиц для моделирования задач приня-
тия решений Освоение концепций моделирования на основе электронных таблиц явля-
ется трудным делом, особенно вначале Несмотря на это, опыт большинства профессио-
налов подтверждает следующий факт: создания самой модели еще недостаточно для
принятия лучших решений Существует много причин, почему лица, от которых зависят
решения, в реальных ситуациях не принимают хороших решений, и одна из них — это
неадекватное моделирование Но из этого не следует, что повышение только качества
моделирования обязательно приводит к лучшим реальным принимаемым решениям Для
этого имеется много причин, и цель этой главы состоит в том, чтобы их определить
и описать
Целью данной книги не является полный обзор и анализ того, что необходимо для ка-
чественного принятия решении в организациях Мы ограничимся рассмотрением основ-
ных ошибок, которые совершают менеджеры, плохо знающие основы моделирования,
при попытке применить модели в реальных ситуациях В этой главе рассмотрены в ос-
новном те ошибки и оплошности, о которых сообщалось как об основных причинах не-
удач в известных случаях применения моделирования в бизнесе и в нескольких научных
исследованиях
Нам бы не хотелось, чтобы у читателей создалось впечатление, что любые попытки
моделирования связаны с проблемами или, более того, приводят к неудаче Просто
“хорошие новости не интересны”, поэтому мало сообщений о растущем числе успешных
применении моделирования с использованием электронных таблиц в процессе принятия
решений Однако краткие врезки “Практическое применение”, которыми сопровожда-
ются главы этой книги, показывают многочисленные примеры успешного и эффектив-
ного применения моделирования в реальных ситуациях С другой стороны, утверждение,
что лучше всего учиться на чужих ошибках (на неудачных проектах моделирования), яв-
ляется справедливым В этой главе мы хотим сбалансировать приведенное в предыдущих
главах описание потенциальных преимуществ моделирования обсуждением его недос-
татков для того, чтобы читатель мог взвесить все “за” и “против”, принимая решение об
использовании моделей
Данная глава заканчивается большой врезкой “Ситуация для анализа”, описывающей
реальную компанию (ее название изменено) Усилия, предпринятые читателем для того,
чтобы понять, почему у этой компании возникли проблемы при моделировании, помогут
ему при построении и реализации собственных моделей
ГЛАВА 14. Реализация моделей	897
14.2.	Что же такое модель
Вы, вероятно, думаете, что каждый, кто занимается бизнесом, хочет знать, что такое мо-
дель Разумеется, к этому времени читатель сам может ответить на этот вопрос (не прибегая
к определениям из главы I). Например, можно предложить следующую формулировку:
“модель — это абстрактное описание деловой ситуации, удобное для анализа в электронной
таблице; этот анализ служит основой при принятии решения и способствует углубленному
пониманию рассматриваемой ситуации”. Такое определение является вполне приемлемым,
поскольку оно отражает цели данной книги. Но попробуйте задать коллегам вопрос о том,
что такое “модель поддержки принятия решений” или “экономическая модель”, и вы уди-
витесь разнообразию полученных ответов В частности, само понятие “модель” достаточно
расплывчато Большинство людей приписывают ему разнообразные значения
Так, все по-разному оценивают уровень готовности модели В этой книге многократ-
но подчеркивалось, что модели часто приблизительны или делаются “быстро и дешево”,
т е. они невелики, нацелены на конкретное решение и разрабатываются быстро для при-
менения только в определенной ситуации Но большинство менеджеров считают, что
модель готова, только если она совершенна и безукоризненна с профессиональной точки
зрения, наглядна, снабжена документацией, проста в использовании, проверена на адек-
ватность и может применяться в различных условиях множеством разных пользователей
В основном, именно такое мнение вызывает большинство проблем, связанных с приме-
нением моделей На рис 14 I представлена схема, которая показывает эволюцию поня-
тия модели В основе этой схемы лежат аналогичные схемы, которые были разработаны
для других дисциплин- Бруксом (Brooks) для систем программного обеспечения, Горри
и Скотт-Мортоном (Gorry and Scott-Morton) для информационных систем
Модель-прототип
Закончена
Отлажена
Эксплуатируется ее автором
Проверена на тестовых данных
Полезность модели принимается на веру
Институциональная модель
Полезность модели не вызывает сомнения
Интегрирована в процессы принятия решения
в организации
Функционально согласована с другими
моделями и системами
► Используется другими менеджерами
Поддерживается и расширяется пользователями
Обеспечена необходимыми данными
Усилия и затраты: 1Х
——4-----------------------------------
Модель-приложение
Эксплуатируется менеджером,
работающим с клиентами
Хорошо документирована
Имеет средства проверки вводимых-данных
Расширяется автором или менеджером
Проверена на реальных данных
Полезность модели признана
Усилия и затраты: 10Х-100Х
—i—
Институциональная
модель-приложение
Усилия и затраты: 10Х
Усилия и затраты: 100Х-1000Х
Рис. 14.1. Эволюция моделей
898
ЧАСТЬ IV Реализация
В верхнем левом углу схемы приведены характеристики “простой” модели, которая
называется модель-прототип Это законченная модель (отображает основные черты мо-
делируемой деловой ситуации), она не содержит очевидных логических ошибок, с ней
работает, в основном, только ее автор. Проверка адекватности проведена на тестовых
данных Считается, что модель отвечает бизнес-целям, но это еще необходимо доказать
Для окончательного завершения модели-прототипа ее тестируют на правдоподобных
входных данных, и, если она продуцирует также правдоподобные выходные результаты,
то считается, что работа по созданию модели завершена. Такая модель часто создается
очень быстро и без больших затрат Но она в действительности является только прототи-
пом и нуждается в большой доработке, чтобы превратиться в полезный продукт для дру-
гих (не только для автора модели), который можно было бы даже продать
Сделать экспериментальную модель-прототип полезной для других означает, что, во-
первых, ее необходимо преобразовать в модель-приложение Другими словами, преобра-
зовать ее во что-то понятное не только автору этой модели, но и конечному менеджеру,
работающему с клиентами Для этого необходимо, чтобы модель была хорошо докумен-
тирована В ней обязательно должна быть проверка входных данных И, что наиболее
важно, она должна быть проверена на адекватность на реальных, а не только тестовых
данных Модель также должна быть легко расширяемой, т.е она должна позволять без
особых усилии и переделок увеличивать число переменных решения и период модели-
руемого времени, учитывать большее количество вариантов возможного решения и тд.
Один из безошибочных показателей успешного преобразования модели-прототипа в мо-
дель-приложение заключается в том, что деловая ценность данного приложения не под-
вергается сомнению, и оно может быть использовано другими пользователями без кон-
сультации с его автором Как показано на рис 14.1, преобразование модели-прототипа
в модель-приложение является трудоемким процессом Оно требует почти десятикрат-
ных затрат по сравнению с затратами на создание первоначальной модели Затраты могут
определяться в стоимостных показателях, трудозатратах или количестве времени, по-
скольку эти величины в высокой степени коррелированны.
Несмотря на то что модель-приложение является законченной моделью, большинст-
во менеджеров все же определяют модель в более широком смысле, как институциональ-
ную (наделенную законным статусом) модель. Следовательно, модель-приложение рас-
сматривается в качестве автономного продукта, который является законченным, но
только в отношении самого себя Институциональная модель интегрируется в действую-
щие процессы организации Под интеграцией подразумевается, что эта модель скоорди-
нирована с функционированием других моделей, процессами принятия решений, систе-
мами и процедурами, которые уже используются организацией. Это также означает, что
модель может работать с различными начальными параметрами, задаваемыми другими
менеджерами, функциональные обязанности которых не совпадают с обязанностями ме-
неджера, для которого первоначально была предназначена модель Модель будет жизне-
способной, если ее смогут использовать не только автор или менеджер, работающий
с клиентами, но и сотрудники, исполняющие другие обязанности. Кроме того, необхо-
димо, чтобы модель была пригодна для эксплуатации другими сотрудниками в организа-
ции, которые, возможно, не были связаны с первоначальной разработкой модели, а так-
же она должна обладать возможностью расширения. Наконец, это означает, что ответст-
венность за текущее обеспечение необходимыми данными и поддержку самой модели
берут на себя другие сотрудники организации Преобразование модели-прототипа в ин-
ституциональную модель, в сущности, означает преобразование автономного продукта
в продукт “всеобщего пользования”, что, естественно, требует соответствующих затрат,
поскольку в процесс преобразования вовлекается множество специалистов (а не только
ГЛАВА 14 Реализация моделей 899
автор модели и ее конечный пользователь) Обычно на реализацию институциональной
модели требуется на один или даже два порядка больше трудозатрат, чем на создание
первоначальной модели-прототипа
Большинство менеджеров, особенно старших менеджеров, не соглашаются на созда-
ние институциональной модели-приложения, пока не будут завершены разработки как
“простой” институциональной модели, так и модели-приложения Институциональная
модель-приложение обладает всеми характеристиками других трех типов моделей, пока-
занных на рис. 14 1 К сожалению, затраты на создание институциональной модели-
приложения не прибавляются, а умножаются Таким образом, общие затраты на ее соз-
дание могут быть в сто (до тысячи) раз больше затрат, необходимых на создание первона-
чальной модели-прототипа Перспектива в достаточной степени устрашающая
Нет ничего необычного в том, что на начальной стадии планирования проекта моде-
лирования автор модели имеет в виду разработку модели-прототипа, в то время как ме-
неджер, финансирующий разработку модели, думает о модели-приложении или даже об
институциональной модели-приложении Таким образом, осложнения, недоразумения
и проблемы могут возникнуть уже тогда, когда модель-прототип представляется прини-
мающим лицам, которые ожидают гораздо большего Такую ситуацию обычно называют
неоправдавшимся ожиданием Это особенно характерно для проектов с большим количе-
ством участников Затем следует этап выяснения причин “неудачного моделирования’’.
14.3.	Разделение функций игроков
На рис 14 2 представлена новая схема, которая является разновидностью одной из
схем, предложенных Черчманом (С. West Churchman) и его коллегами Черчман — один
из первых поборников моделирования в процессе принятия управленческих решений
В этой схеме на первый план выдвигается источник осложнении, возникающих в том
случае, когда один человек выполняет множество функций функции лица, принимаю-
щего решение, клиента, разработчика модели и руководителя проекта Затем эти функ-
ции передаются другим людям, которые могут быть отделены друг от друга и физически
и организационно Этих людей называют игроками, чтобы подчеркнуть их роль в качестве
активных участников, выполняющих определенные функции. Можно себе представить,
насколько упрощается жизнь, когда все функции выполняет один человек Именно по
этой причине мы неоднократно подчеркивали важность того факта, что менеджер сам
проводит моделирование в Excel К сожалению, это не всегда возможно.
По предложенной схеме разработчик модели — это человек, отвечающий за виды дея-
тельности, которые были рассмотрены в этой книге, а именно за разработку, испытание,
отладку и начальную оценку модели Руководитель проекта отвечает за обеспечение ресур-
сами, необходимыми для получения результата проекта по созданию модели Результат
проекта может быть представлен в виде модели-приложения, институциональной модели,
а также в виде институциональной модели-приложения. Кроме того, руководитель проекта
отвечает за координацию работ, управление ресурсами и составление бюджета Лицо, при-
нимающее решение, — это человек, который фактически будет использовать модель под-
держки принятия решений И он, разумеется, является основным игроком Клиент — тот
человек, для которого, в конечном счете, предназначается этот проект, и, следовательно, он
определяет критерии оценки модели. Различие между лицом, принимающим решение,
и клиентом заключается в том, что первый обладает правом дать “добро” на использование
модели, тогда как клиент только извлекает выгоду в результате использования модели, он
может физически находиться вдали от места создания и использования модели
900 ЧАСТЬ IV Реализация
Разработчик модели
Руководитель проекта
Лицо, принимающее решенияГ
Клиент
Рис. 14.2. Разделение функций в проекте создания модели
Даже в ситуациях, в которых все четыре функции выполняются одним человеком, на
заключительном этапе реализации модели эти функции могут быть разделены между не-
сколькими людьми Это разделение игроков может стать источником осложнений в реали-
зации модели. Проблемы возникают в результате того, что конкретные функции берут на
себя люди, имеющие различные убеждения, предпочтения, распорядок дня, навыки
и мотивации, которые могут мешать успешному завершению проекта Даже в тех случаях,
когда игроки составляют единую команду, необходимы нетривиальные действия, направ-
ленные на координацию их работы и на обеспечение связи между ними, блаюдаря чему
достигается эффективность команды В реальной ситуации зачастую лицо, принимающее
решение, и клиент являются разными людьми В этом случае лицо, принимающее реше-
ние, действует в качестве агента для клиента Но поскольку лицо, принимающее решение,
может иметь представления и предпочтения, отличные от представлений клиента, он мо-
жет использовать проект для достижения собственных целей, а не целей клиента Этот фак-
тор называется несовместимостью стимулов
Разделение функций игроков становится причиной многих потенциальных проблем
при разработке моделей Например, разработчик модели в таких условиях может сосредото-
читься на непосредственно самой разработке модели, не обращая достаточного внимания
на сложности реализации всего проекта Даже в команде узкая специализация ее членов мо-
жет привести к сложностям в общении и несогласованности действий
Выше при описании ролей (руководителя проекта, лица, принимающего решение,
клиента и разработчика модели) подразумевалось, что каждую из этих ролей выполняет от-
дельный человек Но любую из них одновременно могут выполнять несколько человек, ко-
торые, в свою очередь, могут внести свои разнообразные проблемы в общение и согласо-
ванность действий
Мы рассматриваем разделение функций и специализацию игроков в проектах создания
моделей как “проклятие разделения игроков”, поскольку в результате этого разделения
возникает множество потенциальных проблем, связанных с поведенческими, политиче-
скими, коммуникационными свойствами индивидуальных игроков. Хотя мы не рассмат-
риваем все аспекты этого “проклятия”, но один вывод очевиден: необходимо уделять
достаточно внимания поведенческим проблемам управления в пределах маленьких групп.
Решение этих проблем может быть важнее, чем решение любых технических проблем са-
мой модели. Недостаточное внимание к ним зачастую приводит к окончательному прова-
лу проекта создания модели. Важно отметить, что риск потерпеть неудачу растет в геомет-
ГЛАВА 14. Реализация моделей 901
рической прогрессии по мере увеличения группы игроков, исполняющих эти четыре роли.
Кроме того, чем уже специализация игроков, тем больше проблем она вызывает. К сожа-
лению, зачастую разработчик модели не обладает ни властью, ни темпераментом для то-
го, чтобы взять ответственность за управление проектом и нивелировать последствия,
возникающие в результате разделения игроков. Во многих случаях лучше ограничить раз-
меры группы, даже если для этого придется пожертвовать некоторыми аспектами
“совершенной” модели и другими не основными задачами моделирования.
Одним из самых важных факторов успешного завершения любого проекта моделирова-
ния является наличие влиятельного борца за этот проект, отстаивающего его среди клиен-
тов и лиц, принимающих решения. Борец за проект “одержим” этим проектом и наблюдает
за тем, насколько проект пользуется успехом и воспринимается клиентами и каждым из лиц,
принимающих решения. Очень важно, чтобы борец за проект имел определенное положе-
ние внутри организации. Иметь определенное положение означает, что борец за проект
воспринимается в качестве легитимного лица, что он компетентен и настолько уверен
в успехе проекта, что готов пожертвовать своей профессиональной репутацией Таким
образом, борец за проект — это больше чем проповедник или оратор, представляющий
проект, и, конечно же, больше, чем разработчик модели или руководитель команды, ра-
ботающей над этим проектом.
Другим фактором успешного завершения проекта моделирования является наличие
знающего и заслуживающего доверия интерпретатора модели, который в доступной
форме может рассказать о преимуществах модели тем, чьи знания и опыт в области элек-
тронных таблиц или математики недостаточны для профессиональной оценки модели
Если работа над проектом делится между многими исполнителями, то разработчику мо-
дели зачастую приходится выполнять двойные обязанности, быть технически опытным
разработчиком табличной модели, а также ее толкователем для специалистов, обладаю-
щих низкой квалификацией в вопросах моделирования. Иногда человек, прекрасно раз-
бирающийся в проблемах моделирования, не может объяснить преимущества модели для
организации Тогда обязанность по интерпретации модели должна быть передана борцу
за проект
При участии в процессе моделирования множества людей проект зачастую терпит не-
удачу, поскольку о реализации модели задумываются только по окончании процесса мо-
делирования. Часто на реализацию модели, как и на разработку документации, должное
внимание обращают слишком поздно. Команды, на счету которых успешные проекты,
и которые сталкивались с трудностями, возникающими в результате разделения функций
между исполнителями, всегда беспокоятся о проблемах реализации с начала проведения
работ по разработке модели и зачастую в соответствии с ними строят последовательность
действий самого процесса моделирования.
Для того чтобы избежать трудностей, возникающих в результате разделения функ-
ций между исполнителями, следует включить клиентов и лиц, принимающих решения,
во все этапы работ по моделированию для того, чтобы они определяли показатели за-
вершения этапов проекта. Каждый из этапов должен завершаться понятными для них
результатами. Необходимо создать ощущение, что право собственности на саму мо-
дель, которой обладает организация, превышает право разработчика модели Недоста-
точное внимание к этим обычным аспектам управления зачастую приводит к провалу
проекта моделирования
902 ЧАСТЬ IV. Реализация
14.4.	Размывание границ проекта
На схеме рис 14.3 показано размывание границ проектов моделирования, особенно
проектов разработки институциональных моделей Вначале работы по моделированию
сфокусированы на ограниченной области, и в них участвует всего несколько исполните-
лей Проект таких размеров поддается управлению Но такой узкоспециализированный
проект порождает проблемы масштабирования как самой модели, так и поддерживаю-
щих модель информационной системы и базы данных. Такой проект мало заметен внут-
ри организации и обладает небольшим влиянием. По разнообразным причинам в орга-
низации возникает интерес к расширению проекта Причины заключаются не только
в том, что модель может быть полезной в будущем для организации, но и в том, что мно-
гим хочется принять участие в успешных работах по моделированию. В свою очередь, это
может привести к значительному росту популярности модели внутри организации и, в ко-
нечном счете, к увеличению ее стоимости. А это также приводит к размыванию границ про-
екта, поскольку остальные сотрудники предлагают свои расширения, возможности, новые
программные модули и т д Незапланированные расширения модели (размывание границ)
могут навредить проекту и, в конечном счете, привести к его провалу. К сожалению, допол-
нительные этапы работ и привлечение к проекту новых участников может привести к раз-
мыванию границ проекта со всеми сопутствующими затратами и осложнениями, связанными
с проблемой разделения функций между игроками
Узкий проект моделирования
Отдельная модель
Реализация одной цели
Узкая специализация
Небольшое количество исполнителей
Небольшое количество заинтересованных сторон
Небольшие трудозатраты
Невысокий риск разработки
Неофициальное согласование “
и управление проектом
Доступность проекта для узкого круга лиц
Проблемы масштабирования модели
Проблемы масштабирования базы
данных поддержки модели
Проблемы в применении модели
при уходе ее сторонников
Небольшое влияние модели в организации
Размывание
границ проекта
Расширенный проект моделирования
Множество (похожих) моделей
Реализация нескольких целей
Широкая специализация
Большое количество исполнителей
Большое количество заинтересованных сторон
Большие трудозатраты
,	Высокая стоимость
•—►	Высокий риск разработки
,та Официальное согласование
и управление проектом
Доступность проекта для широкого круга лиц
Проблемы масштабирования моделей
Проблемы масштабирования базы
данных поддержки моделей
Поддержка моделей независимо от разработчиков
Влияние моделей на всю организацию
Рис. 14.3. Размывание границ проекта
Большинство успешных крупных проектов развивалось из небольших проектов, по-
этому расширение проектов неизбежно, но этот процесс необходимо контролировать
Естественный способ предотвратить размывание границ состоит в тщательном разграни-
чении проектных работ по этапам При этом во избежание размывания границ проекта
снизу необходимо, чтобы ранние этапы проекта были небольших размеров (по длительно-
сти и трудозатратам) Нет необходимости в изначальном отказе от расширения проекта моде-
лирования — просто это расширение необходимо отложить до того времени, пока не будет
протестирован первичный проект Это требует достаточно убедительных доводов в пользу
умеренных шагов при создании институциональной модели, чтобы противопоставить их
аргументам в пользу быстрого завершения проекта (и, как следствие, быстрого получе-
ния вознаграждения, что является очень убедительным аргументом). Это вновь полнима-
ГЛАВА 14 Реализация моделей	903
ет проблемы организационного характера, которые выходят далеко за рамки технических
проблем разработки модели. И в данном случае важную роль играет борец за проект Он
должен отстоять четкий и выполнимый план и предотвратить искушение в преждевре-
менном расширении проекта, поскольку на успешном выполнении именно “узкого”
проекта строится возможность его будущего расширения.
14.5.	Другие источники неудач
При разработке модели необходимо позаботиться о политической поддержке проекта
внутри организации Информация, предоставляемая моделью, никогда не является полити-
чески нейтральной Почти всегда, особенно при использовании институциональных мо-
делей, применение модели вызывает перемещение прав на принятие решения от одной
группы лиц к другой Это влияет на политику распределения поощрений и вознаграждений
внутри организации и, в свою очередь, приводит к победителям и к проигравшим, которые
в результате этого теряют свою политическую власть В составе участников проекта также
происходят изменения Именно эти политические проблемы из-за недостаточного к ним
внимания наиболее часто становятся причиной неудач в моделировании, а не техниче-
ские проблемы, касающиеся логики модели и ее несогласованности, которым уделяется
большее внимание.
К сожалению, зачастую “козлом отпущения” становится сама модель, и именно ее рас-
сматривают как главную причину неудачи Поскольку модель — неодушевленный объект, и,
следовательно, является беззащитной, ее легче обвинить в неудаче, что приводит к непра-
вильной оценке причин неудачного проекта Обычно проект терпит неудачу в результате ряда
причин, возникающих из-за несогласованности всего процесса разработки и реализации мо-
дели Кроме того, мифы вокруг неудачного проекта могут послужить препятствием для бу-
дущих работ по моделированию на многие годы Очень важно перед тем, как начать новый
проект по моделированию, ознакомиться со всеми прошлыми неудачами и определить их
истинные причины
Другая проблема, которая может возникнуть даже при создании “узкого” проекта модели-
рования, заключается в возможной потере преемственности во время разработки модели или
позже во время ее реализации Это может быть вызвано уходом основных разработчиков, утра-
той документации о модели либо другими подобными причинами Через какое-то время, осо-
бенно при создании неинституциональной модели, это может привести к осложнениям в ее
использовании.
Одной из возможных причин возникновения проблем в реализации проекта по созданию
модели является попытка разработать модель-приложение до оценки пригодности имеющихся
данных, необходимых для поддержки этого приложения Несмотря на достижения в создании
корпоративных баз данных, большая часть хранящейся в них информации состоит только из
таких сведений, которые легко собираются и записываются в базы данных и являются
“промежуточным продуктом” деятельности фирмы Эти данные зачастую не пригодны для
использования в процессе создания, тестирования и эксплуатации модели Например, рас-
смотрим финансовые данные Большинство денежно-кредитных сведении, зафиксирован-
ных организациями, касается сделок и финансового учета С другой стороны, построение
модели требует доступа к данным о затратах организации, включая данные о ежедневных затра-
тах и издержках, а не финансовые данные, касающиеся прошлых сделок Эти данные могут
быть недоступными, а их сбор и обработка — очень трудоемкими Во избежание этой проблемы
на начальной стадии проекта можно создать приближенную модель (точнее, модель, построен-
904 ЧАСТЬ IV Реализация
ную на имеющихся неточных данных) и одновременно сформировать инфраструктуру сбора,
обработки и поддержки данных, состоящую из соответствующих информационных систем
и баз данных Это в первую очередь относится к проектам построения институциональных мо-
делей, где средства поддержки данных являются необходимым атрибутом. С другой стороны,
разработчики модели не редко недооценивают затраты, необходимые для создания информа-
ционных систем и баз данных, а эти затраты нужно оценить до того, как будет принято ре-
шение о моделировании.
14.6.	Заключение
В этой главе описаны причины проблем, которые могут возникнуть в процессе реализа-
ции проекта по созданию моделей Безусловно, основная “философская” проблема, стоя-
щая перед разработчиками табличных моделей и пользователями этих моделей, возникает
при распространении идеи использования моделирования в процессе принятия решений
в рамках организации. Мы также предполагаем, что одна из основных проблем, которая
встанет перед менеджерами в двадцать первом столетии, коснется неизбежных изменений
в организации, необходимых для более эффективного использования все увеличивающего-
ся объема данных и применения для этих данных существующих моделей. Это в большей
степени является проблемой реализации моделей, а не их разработки. Менеджеры, которые
осознают и ценят возможности, предоставляемые моделированием, а также способны
пройти через “минные поля” организационных изменений, необходимых для эффективного
применения моделей в процессе принятия решений, в конце концов, окажутся в выигрыше.
Основные термины
Агент Лицо, принимающее решение, которое представляет клиента в процессе разработки модели
Борец Влиятельный защитник проекта моделирования
Игрок Активный участник процесса реализации проекта моделирования
Институциональная модель Модель-прототип, интегрированная в процессы организации, согласо-
ванная с другими моделями, процедурами, и системами организации, поддерживаемая и обес-
печиваемая данными другими сотрудниками, жизнеспособная в отсутствие своих создателей
Институциональная модель-приложение Модель, обладающая всеми характеристиками модели-
приложения и институциональной модели
Интерпретатор Человек, который в доступной форме преподносит сведения о модели, ее исполь-
зовании и потенциальных выгодах
Клиент Человек, который извлекает выгоду из решения, принятого на основании результатов ис-
пользования модели
Лицо, принимающее решение Человек, который использует модель в процессе принятия решений
Модель-приложение Хорошо документированная модель-прототип, которая всесторонне протестирована
и проверена на достоверность на реальных данных, имеет средства проверки входных данных, а также
признана полезной в процессе принятия решения Эта модель используется не только ее автором, но
и другими пользователями
Модель-прототип Законченная модель, проверенная на достоверность на тестовых данных и признан-
ная полезной для поддержки принятия решений Используется, в основном, только ее автором
Несовместимость стимулов Различия во мнениях, предпочтениях, видах на вознаграждение и последова-
тельность действий у агента и его клиента
Разделение функций между игроками Возникновение при моделировании ситуации, в которой разра-
ботчик модели, лицо, принимающее решение, руководитель проекта и клиент — разные люди
ГЛАВА 14. Реализация моделей 905
Размывание границ проекта Расширение проекта моделирования посредством добавления новых
моделей, вариантов возможного решения, характеристик, элементов, целей, видов вознаграж-
дения и игроков
Разработчик модели. Человек, который создает модель, тестирует ее и подтверждает ее правильность
Руководитель проекта Человек, отвечающий за преобразование модели-прототипа в другой тип модели
Задачи
14 1 Кого из четырех игроков, которые определены как основные участники проекта моделиро-
вания, лучше всего выбрать в качестве борца за проект и почему9
14 2 Почему происходит размывание границ проекта9
14 3 Происходит ли размывание границ проекта преимущественно в больших организациях9
Обоснуйте ответ
14 4 Какова ваша интерпретация фразы “успешное применение модели”9
14 5 Структура разделения функций между игроками определяет четырех игроков, каждый из
которых может находиться в относительной изоляции от других Выберите из них трех иг-
роков, которые тесно взаимодействуют между собой и могут составить команду, оставив
четвертого в относительной изоляции Конкретизируйте возможные проблемы реализации
модели, которые могут возникнуть в результате меньшего участия в проекте одного из иг-
роков Каким образом можно преодолеть эти проблемы9
14 6 Структура разделения функций между игроками определяет четырех игроков, некоторые
из них могут находиться в относительной изоляции Четырех игроков можно разделить на
пары шестью разными способами Двое игроков в паре, тесно общаясь, могут стать коман-
дой, а двое будут представлены как отдельные игроки Необходимо выбрать одно из воз-
можных сочетаний, в котором два игрока составляют пару, а двое других находятся в отно-
сительной изоляции от этой пары и друг от друга Конкретизируйте возможные проблемы,
которые могут возникнуть в результате такого разделения на этапе реализации модели Ка-
ким образом можно преодолеть эти проблемы9
Ситуация для анализа | Компания Australian Motors1
Введение
В январе 1996 года Майкл Йетс, вице-президент по планированию в компании
Australian Motors (AM), столкнулся с трудностями, касающимися развертывания но-
вой модели оптимизации для управления парком грузовых автомобилей своей ком-
пании. Его команда работала 18 месяцев над разработкой комплексной модели ли-
нейного программирования для управления сложным процессом приобретения
и обслуживания большого парка грузовиков. Йетс убежден в том, что автоматизация
принятия решений по аренде, покупке и продаже грузовых транспортных средств
предоставит новые возможности компании для увеличения как производительности,
так и эффективности поставки транспортных средств в Австралию, Тайвань, Синга-
пур, Корею и Японию. Йетс организовал команду из четырех человек, которая соз-
дала модель оптимизации. Теперь он представил эту модель компании AM.
Впервые данная ситуация описана профессором Стивеном П Брэдли (Stephen Р Bradley) Все имена людей,
названия компаний и данные изменены Деньги приводятся в австралийских долларах.
Copyright © 2000 by the Trustees of Leland Stanford University
906 ЧАСТЬ IV Реализация
Йетса беспокоит то, как руководство воспримет этот проект, и пожелает ли гене-
ральный управляющий компании AM Питер Расселл согласиться с его предложением
применить модель для управления транспортным парком всей компании Более того,
решение должно быть принято как можно скорее, иначе система не сможет своевре-
менно определить модели грузовых автомобилей, которые необходимо приобрести для
следующего 1997 года Расселл высказал свое мнение относительно этого предложения
Итак, мы будем работать с системой, которая должна помогать нам в приобрете-
нии грузовых транспортных средств для нашего парка и в управлении этим парком По-
хоже на то, что эта новая модель устранит несогласованность наших действий и по-
может сэкономить в среднем больше 200 тыс долл ежегодно для каждого из 10 боль-
ших отделений компании AM. Но в AM никогда не занимались крупномасштабными
работами по моделированию, и в компании нет специалистов, глубоко разбирающихся в
технических аспектах математического программирования Об этом свидетельству-
ют прошлогодние сомнительные результаты нашей первой попытки применить подоб-
ную систему Если сбор данных дчя этой новой системы оптимизации и их анализ не бу-
дут проделаны должным образом, мы не сможем своевременно заключить контракты
на закупку и договоры на аренду на 1997 год. Более того, я не думаю, что менеджеры
отделении захотят предоставить нам другой шанс, если мы пропустим этот период
времени Похоже, этот проект является очень рискованным для компании AM
Предыстория проекта
Компания Australian Motors, основанная в Сиднее в 1960 году, планировала заняться
краткосрочной арендой грузовиков для доставки товаров Клиентами компании были
торговцы, подрядчики, строительные фирмы и другие компании, от небольших до
средних, которые хотели избежать затрат на содержание собственного транспортного
парка и проблем, связанных с его управлением По мере роста бизнеса компания AM
расширялась и открывала свои филиалы в других австралийских городах, а позже —
в Азии В Азии компания AM охватила своей деятельностью Сингапур, Тайвань, Ко-
рею и Японию В Японии компания AM и японская фирма по сдаче в аренду грузовых
транспортных средств организовали совместную компанию Во время затянувшегося
экономического спада в конце 1980-х потребность компании AM в капитале привела ее
к продаже своих акции британской финансовой холдинговой компании British Finan-
cial До недавнего времени эта холдинговая компания обеспечивала финансовую под-
держку AM, но своим приобретением акций она содействовала децентрализации ее
управления Рост конкуренции в индустрии проката грузовиков и продолжающееся
ослабление австралийского доллара стало причиной того, что AM стала одним из наи-
менее выгодных предприятий британской финансовой холдинговой компании В ре-
зультате для увеличения прибыли на свой инвестированный капитал, большая часть
которого использовалась в качестве оборотного капитала компании AM, британская
финансовая компания начала принимать более активное участие в деятельности AM
Парк грузовых транспортных средств компании AM состоит из автобусов, грузо-
виков с погрузчиками, больших и малых грузовиков для доставки товаров, микроав-
тобусов и универсальных грузовиков
В администрацию компании AM входят четыре менеджера — представители
стран, в которых находятся отделения компании Каждый из них отвечает за свой
регион Исключением являлось японское совместное предприятие Каждое отделе-
ние — это отдельное структурное подразделение, результаты деятельности которого
измеряются полученной прибылью Отделение управляется менеджером Каждый из
ГЛАВА 14 Реализация моделей	907
этих менеджеров отвечает за политику управления транспортным парком своего ре-
гиона, заключение договоров аренды и соглашений о покупке-продаже транспорт-
ных средств с их изготовителями Менеджеры — представители стран отвечают за
проверку работы менеджеров своих отделений по приобретению автомобилей и их
эксплуатацию (Исключением является Сингапур, где менеджер-представитель яв-
ляется и менеджером отделения ) В штаб-квартире компании AM, которая находит-
ся в Сиднее, контроль за деятельностью менеджеров — представителей стран заклю-
чается в проверке транспортного парка каждого отделения Эта проверка основана
на трех критериях качества работы совокупном доходе, доходе от одного транспорт-
ного средства и общей прибыли отделения Пока эти числа приемлемы и менед-
жер — представитель страны остается в рамках политики компании AM, опреде-
ляющей общий состав транспортного парка, ему предоставляется свобода в заказе
транспортных средств для парка отделения.
Компания AM требует ежегодных прогнозов на доход и приобретение грузови-
ков Поскольку договоры на аренду или приобретение транспортных средств могут
заключаться в конце года (те оказаться вне бюджетного года), бюджетный анализ
производится для двухлетнего периода планирования В среднем компания AM по-
полняет свой парк каждые 18 месяцев
Ежегодное планирование менеджеры отделений выполняют вручную Менеджер
каждого отделения на основе данных прошлых отчетов прогнозирует ежемесячный
доход на следующий 24-месячный период Аргументация и опыт играют существен-
ную роль в получении этих прогнозов Также оценивается доход от одного транс-
портного средства в месяц, и исходя из этого рассчитывается ежемесячный средний
размер транспортного парка для следующего планируемого двухлетнего периода.
План заказов, предлагаемый менеджером отделения, представляет ежемесячный
список приобретений автомобилей и их передачи в аренду или в собственность
Из-за большого количества вариантов приобретения транспортных средств
и множества способов ими распорядиться определение планируемого заказа было
трудоемким процессом, выполняемым каждым менеджером отделения методом проб
и ошибок Есть две основные альтернативы использования грузовых транспортных
средств, которые предлагаются их изготовителями, — аренда и покупка. Кроме того,
можно выбирать самих изготовителей. Многие из этих вариантов содержат детали-
зированные ограничения и условия, например, количество грузовиков, которые бу-
дут доступны через год, зависит от количества сданных в аренду автомобилей в тече-
ние первой половины года Что касается купленных транспортных средств, то ме-
неджер отделения должен также предвидеть цены, которые ожидаются на
подержанные транспортные средства вплоть до истечения 24 месяцев после их по-
ставки, чтобы решить, когда организовать их перепродажу Планирование срока
продажи зависит как от рынка подержанных автомобилей, так и от количества по-
добных транспортных средств, сданных в аренду в транспортном парке отделения
Например, дата возврата сданных в аренду автомобилей и план замены возвращен-
ных транспортных средств влияют на график перепродажи купленных ранее автомо-
билей Поэтому для ежегодного составления бюджета управления транспортным
парком требуются сложные согласования времени приобретения автомобилей и их
передачи в аренду или продажи
Как правило, менеджеры отделений определяют ожидаемые затраты на единицу
транспортного средства в месяц для каждого варианта и рекомендуют тот вариант, ко-
торый обладает наиболее низкими удельными затратами Кроме того, большинство
менеджеров отделений предпочитают продажу с выгодой подержанных автомобилей
908 ЧАСТЬ IV. Реализация
вместо долгосрочных арендных договоров, по крайней мере, для популярных на рынке
видов транспортных средств Наконец, менеджеры — представители стран часто изме-
няют количество закупаемых машин, предлагаемых менеджерами отделений
В начале 1994 г некоторые изготовители грузовых транспортных средств отмени-
ли большинство скидок, предлагаемых оптовым покупателям. Это вызвало рост
средних издержек на содержание транспортного парка компании AM более чем на
15% Это катастрофический результате точки зрения компании British Financial
В середине 1994 г начата разработка модели линейного программирования для
управления транспортным парком В течение зимы 1995 г. модель использовалась
для уменьшения затрат на содержание этого парка. К сожалению, модель пользова-
лась ограниченным успехом, и ее вклад в работу компании AM в течение этого года
был весьма спорным Снижение доходов компании AM в 1995 г. было меньше ожи-
даемого По предположению некоторых старших менеджеров, это частично объяс-
няется некоторым улучшением в использовании транспортного парка, произошед-
шим благодаря применению модели Однако, по мнению других членов правления
компании AM, улучшение в использовании транспортного парка — это результат
внимания, проявленного к персоналу транспортного парка и его дисциплине, а не
результат использования модели Правление компании AM все же решило продол-
жить применение модели, поскольку это могло в будущем снизить затраты.
В январе 1996 г Йетс обдумывал, как лучше всего использовать модель при со-
ставлении плана закупок для транспортного парка на следующий год. Этот план вес-
ной должен быть окончательно оформлен. Но большинство региональных менедже-
ров сопротивлялось использованию модели Таким образом, Йетс столкнулся с не-
обходимостью решить, что же делать с моделью при планировании транспортного
парка для следующего года.
История модели
Идея создания модели для планирования парка транспортных средств родилась
в 1994 г. Тогда, в начале года, генеральный директор компании AM Джон Харринг-
тон посещал курсы по подготовке администраторов, где познакомился с методами
моделирования с помощью электронных таблиц, в частности, с моделями линейного
программирования Впоследствии идея использования модели планирования транс-
портного парка овладела Майклом Йетсом, когда его, штатного аналитика компании
British Financial, имеющего большой опыт в применении компьютерного моделиро-
вания в нефтяной промышленности, в апреле 1994 г. назначили вице-президентом
компании AM, отвечающим за планирование. Обсудив варианты с Питером Рассел-
лом, генеральным управляющим компании AM, Йетс попросил предоставить ему
двух человек: одного — специалиста-транспортника и второго — бухгалтера. В июле
1994 года Курт Килан и Гита Рао, оба из Сиднейской штаб-квартиры компании AM,
начали работу над проектом Килан, служащий компании AM с 1975 года, вначале
работал в качестве агента в одном из районных отделений AM и, в конце концов,
стал одним из региональных менеджеров компании. Последующее продвижение по
службе привело его в Сиднейскую штаб-квартиру компании в качестве члена прав-
ления компании AM, отвечающего за администрирование парка грузовых транс-
портных средств Рао пришла в бухгалтерию компании AM в 1990 г. и четыре года
обучалась на главного бухгалтера на вечерних курсах в университете Южного Уэльса.
К моменту начала работы над проектом она уже получила степень магистра и была
в компании менеджером по финансовому учету.
ГЛАВА 14. Реализация моделей 909
Сбор данных и построение модели
В сентябре 1994 года группа под руководством Йетса начала изучение работы
транспортного парка Сиднейского отделения компании. Этот парк имел от 800 до
1 000 транспортных средств Для разработки модели оптимизации был заключен
контракт с местной консалтинговой компанией Decision Technology, имеющей опыт
в построении таких моделей На работу над проектом модели был назначен сотруд-
ник данной компании Джон Эллис
С весны 1994 и до января 1995 года исследования, проводимые Киланом и Рао,
и работа Эллиса над моделью линейного программирования велись параллельно
Эллис, Килан и Рао часто совместно обсуждали ход выполнения проекта и помогали
друг другу в разработке модели Например, Эллис использовал результаты работы
Килана и Рао в качестве предварительных данных и при определении переменных,
описывающих работу транспортного парка
С самого начала было ясно, что сбор и предварительная обработка данных станут
проблемой Что вскоре подтвердилось и, главным образом, это коснулось группы
Килан—Рао Данные, находящиеся в компьютерных файлах компании AM, состояли
прежде всего из статей финансовых отчетов, а не числовых значений себестоимости,
необходимых для модели Кроме того, система учета основных фондов в компании
AM была разработана для налоговых целей, и в ней не содержалось подробной ин-
формации о типах грузовых транспортных средств. Для получения нужной инфор-
мации пришлось проводить трудоемкий поиск в бумажном архиве заказов на закуп-
ку и контрактов на аренду грузовиков
Йетс по мере развития работ над проектом начал большую часть своего времени
уделять работе с Эллисом над построением модели (модель описана ниже в прило-
жении 4) К концу 1994 года было выполнены следующее работы
1	Определены переменные решения и ограничения для модели
2	Описаны данные
3	Написана программа на языке Java, предназначенная для проверки входных
данных и подготовки их к импорту в Microsoft Excel.
4	Для структурирования данных в виде, пригодном для надстройки Solver (Поиск
решения), на языке Visual Basic for Excel написана отдельная программа
Поскольку работа над компьютеризацией модели начала требовать больших усилий,
в январе 1995 года к Эллису присоединился Си Хун Чанг, системный аналитик вычисли-
тельного центра компании British Financial. Роль Чанга заключалась в обработке первич-
ных данных (для получения значений параметров модели), в помощи при отладке про-
грамм, в документировании модели и соответствующего программного обеспечения
В начале февраля 1995 года были получены первые пригодные для использования
результаты модели Сразу стали очевидными существенные различия между планами
для транспортного парка, рекомендованными моделью, и планами, которые на самом
деле реализовывались сиднейским отделением компании Для обоснования этих полу-
ченных данных и, поскольку модель опоздала к составлению весеннего плана закупки
грузовиков, Йетс развернул проект во всех пяти отделениях Австралии
Под руководством Килана и Рао персонал этих пяти отделений начал собирать
и обобщать сведения об использовании своих транспортных парков. Некоторые из не-
обходимых данных стали доступными в течение месяца благодаря накопленному опы-
ту сбора информации в сиднейском отделении компании. Для того чтобы сэкономить
910 ЧАСТЬ IV Реализация
время на определение значений параметров модели, группа разработчиков попросила
районных менеджеров определить эти значения. Но вскоре от этого отказались, по-
скольку, за исключением сиднейского отделения, менеджеры не могли ответить на
срочные запросы разработчиков Впоследствии менеджеры отделений утверждали, что
они не понимали, чего от них требовали Даже сиднейское отделение, более склонное
к сотрудничеству, часто предоставляло противоречивые данные. Подобные недоразу-
мения, ошибки и проблемы в процессе сбора и передачи информации сделали необхо-
димым почти ежедневный контакт группы разработчиков с отделениями К этому вре-
мени Килан и Рао стали специалистами по сбору и обработке данных
Объем обрабатываемых данных был огромен Для модели планирования транс-
портного парка были необходимы прогнозируемые данные на 24 месяца вперед (для
расчета ожидаемой прибыли), данные о средней прибыли от одного грузового транс-
портного средства, ежемесячном составе транспортного парка, ценах на грузовики,
бывшие в употреблении, и количестве грузовиков, пригодных для продажи по этим
ценам, переменных издержках и переменных накладных расходах; а также ежеме-
сячных ограничениях в каждом отделении на количество грузовиков, которые могут
поступать в парк или убывать из него
Летом 1995 года из-за недостатка нужных данных и нехватки времени Эллис не-
сколько изменил модель. Во-первых, цикл планирования был изменен с еженедель-
ного на ежемесячный с целью уменьшения размера модели Даже после этого модель
имела более 200 ограничений и 1500 переменных решения, что потребовало приобре-
тения расширенной версии надстройки Premium Edition of Solver и использования са-
мого быстрого (на то время) компьютера класса Pentium Затем Эллис на основе опыта
и интуиции определил отсутствующие значения параметров и коэффициентов модели.
К марту 1995 года были готовы модели для пяти австралийских отделений, и в сидней-
скую штаб-квартиру компании AM были приглашены менеджеры этих отделений. На
встрече также присутствовали вице-президент по вопросам торговых и финансовых сделок
Ян Шафер и другие представители персонала штаб-квартиры компании AM, которых инте-
ресовали финансовые операции, проводимые с транспортными средствами Встреча прово-
дилась под руководством Йетса и членов проектной группы Килана, Рао и Чанга. Целью
встречи было представление менеджерам отделений моделей плана закупки транспортных
средств, показ результатов моделирования по отделениям и обмен мнениями До этого ме-
неджеры отделений ничего о модели не знали. Единственное их участие в проекте заключа-
лось в ответе группе Килан—Рао на запрашиваемую ими информацию
После презентации модели и результатов моделирования состоялась дискуссия
между менеджерами отделений и проектной группой Шафер подвел итоги встречи,
высказав свое мнение о применении моделирования в развитии и совершенствова-
нии бизнеса, которым занимается их компания После длительной и энергичной
дискуссии менеджеры отделений сформулировали следующие замечания
1	Модель предлагает ежемесячное планирование вместо более точного еженедельного.
2	В модели ежемесячного планирования предполагается, что транспортные сред-
ства всегда прибывают в первый день месяца и всегда распределяются в послед-
ний день месяца На самом деле машины поступают в парк и покидают его
(продаются или возвращаются после окончания срока аренды) постоянно
3	Модель ограничивается одним типом транспортного средства от каждого произ-
водителя В реальности используется смешанный состав транспортных средств,
состоящий из грузовиков стандартного размера и фургонов разной вместимости.
Также в модели полностью игнорируется грузовой транспорт дальнего следова-
ния, который приносит большую прибыль
ГЛАВА 14. Реализация моделей	911
Во время последующей встречи с Шафером Йетс пообещал рассмотреть возмож-
ность построения модели еженедельного планирования с включением не менее дю-
жины типов транспортных средств Эффект от этого предлагаемого изменения мо-
дели может быть существенным, но требует значительных ресурсов, необходимых
для реализации изменений в модели (см приложение 1)
Март 1995 года для проектной группы прошел в спорах по расширению модели
для включения большего количества типов транспортных средств и по использова-
нию более мелкой временной сетки Впервые внутри группы возник конфликт Ки-
лан и Рао были против этих изменений, утверждая, что доступных данных недоста-
точно для большей модели Эллис и Чанг были убеждены в том, что имеющаяся мо-
дель слишком упрощена и что проектная группа обязана учесть предложения
менеджеров отделений Йетс приказал группе рассчитать затраты на разработку
расширенной модели и исследовать перспективы этой модели (см. приложение 2)
Приложение 1. Расширенная модель
Дата	Среда, 8 марта 1995 г 12 30 49-0800
От кого:	Джон Эллис <jellis@dectech com au>
Кому	Майкл Йетс <yates@britfin com uk>
Тема:	Пересмотр модели
Мистер Йетс'
Это дополнение к нашему разювору на прошлой неделе, в котором Вы попроси-
ли меня рассмотреть последствия расширения модели приблизительно для дюжины
типов транспортных средств и ее перевода на еженедельный временной цикл вместо
ежемесячного Как я уже говорил, это существенно увеличит количество перемен-
ных и количество ограничений
В настоящее время в модели определены следующие переменные.
Тип переменной	Количество переменных
Сегменты спроса	з
Переменные прибыли Варианты покупки-продажи транспортных средств Варианты аренды транспортных средств Количество изготовителей транспортных средств	3 5
Переменные, связанные с приобретением транспортных средств Затраты на содержание парка	60
Переменные затраты Страна Тип грузового транспортного средства	61
Количество временных периодов в месяц Количество месяцев	24
Общее количество переменных	1 536
Модель также содержит следующие ограничения
912 ЧАСТЬ IV. Реализация
Тип ограничения	Количество ограничений
Уровень запасов	24
Размер парка	24
Связывание сегментов спроса	24
Границы сегментов спроса	72
Типы транспортных средств одного производителя	24
Контракты аренды	24
Право распоряжаться транспортными средствами	24
Ограничения на вторую покупку транспортных средств		10	
Всего		 			226	
Расширение до 12 типов транспортных средств в течение каждой из четырех не-	
дель в месяц увеличит приведенные итоговые числа примерно в 50 раз. По моим рас-	
четам, расширенная модель будет иметь следующее количество переменных	
Тип переменной	Количество переменных
Сегмент спроса		3	
Переменные прибыли	3
Варианты покупки-продажи транспортных средств	6
Варианты аренды транспортных средств	6
Количество изготовителей транспортных средств		5	
Переменные, связанные с приобретением транспортных средств		60	
Затраты на содержание парка		1	
Переменные затраты		61	
Страна	1
Тип грузового транспортного средства	14
Количество временных периодов в месяц	4
Количество месяцев		24	
Общее количество переменных				73 728	
В расширенной модели будут следующие ограничения.	
Тип ограничения	Количество ограничений
Уровень запасов	24
Размер парка	24
Связывание сегментов спроса	24
Границы сегментов спроса	72
Типы транспортных средств одного производителя	24
Контракты аренды	24
Право распоряжаться транспортными средствами	24
Ограничения на вторую покупку транспортных средств	10
Всего	226
Страны	1
Типы транспортных средств	12
Количество временных периодов в месяц	
Общее количество ограничений	10 848
ГЛАВА 14. Реализация моделей 913
Как можно увидеть, модель значительно разрастается. Из этой ситуации единст-
венным выходом является перенос модели на мэйнфрейм Hitachi, находящийся в
вычислительном центре сиднейского отделения компании British Financial. При
этом возникает необходимость в преобразовании модели из формата программы
Solver в формат оптимизатора IBM MPSX. Предполагаю, что преобразование модели
займет приблизительно две недели.
Построение расширенной модели потребует дополнительной работы От Курта
потребуется отдельная программа по структурированию данных. Кроме того, необ-
ходимо разработать инструментальные средства для упрощения загрузки матрицы
коэффициентов (которая теперь увеличилась примерно в 2500 раз) и ее проверки.
Проверка и отладка расширенной модели также потребуют длительного времени
По нашей оценке, выполнение оптимизации потребует от 30 до 40 минут машинного
времени на Hitachi, приблизительно в 15 раз больше, чем требуется для меньшей мо-
дели, реализованной на Pentium.
Я надеюсь, что предоставил необходимую Вам информацию
Джон
Приложение 2. Оценка затрат на разработку расширенной модели
Дата:	11 марта 1995 г. 12-3022-0100
От кого:	Курт Килан <kkeelan@am.com.au>
Кому:	Майкл Йетс <yates@britfm com uk>
Тема:	Пересмотр модели
Майкл!
Я уверен, что компания British Financial предоставит нам машинное время для
работы на Hitachi Оплата составляет $400 за час машинного времени Нам потребу-
ется свыше 100 прогонов модели в месяц во время ее отладки и тестирования Общие
затраты на машинное время рассчитать трудно, но, по моей оценке, на одного разра-
ботчика в месяц потребуется приблизительно $500. Затраты на хранение данных на
диске и печать добавят еще приблизительно $900 в месяц.
По оценке Си Хуна, нам дополнительно потребуется не менее двух программи-
стов из вычислительного центра для помощи в преобразовании и тестировании мо-
дели. Компании AM придется платить каждому из них по $10 000 в месяц. Это не
включает оплату дополнительных консультантов по моделированию, которые, по
мнению Джона, также необходимы
Мы уже получаем много жалоб от персонала отделений на то, что им приходится
предоставлять информацию для модели. Нам нужно будет им в этом помочь Для
достижения запланированных к весне целей, по моей оценке, нам потребуется не
менее двух штатных бухгалтеров для каждого из этих пяти отделений в течение сле-
дующих пяти месяцев. Гита говорит, что бухгалтерии не располагают свободным
персоналом, который можно было бы использовать для этих целей. Поэтому нужно
нанять временных служащих за $35 в час, но для этого нам необходимо решить, кто
их будет обучать и контролировать Я не советую рассчитывать на то, что менеджеры
отделений возьмут на себя эту обязанность.
Курт
914 ЧАСТЬ IV Реализация
9 марта 1995 г.
Мистеру Майклу Йетсу
Компания Australian Motors, Ltd
Сидней
Австралия
Мистер Йетс!
Компания Decision Technology рада предоставить компании Australian Motors
свою помощь по разработке расширенной модели оптимизации и ее преобразовании
для реализации на ЭВМ Hitachi, принадлежащей компании British Financial.
По нашей оценке, процесс расширения и преобразования модели потребует услуг
двух дополнительных сотрудников компании Decision Technology, занятых непол-
ную рабочую неделю на протяжении приблизительно четырех месяцев Джон Эллис
продолжит свою работу на основе неполной рабочей недели в течение последующих
шести месяцев и будет непосредственно контролировать этих сотрудников
Ориентировочные затраты-
2 сотрудника х S160 в час в течение 20 часов в неделю х 16 недель	= $102 400
Джон Эллис х S25O в час в течение 20 часов в неделю х 24 недели	=$ 120 000
Итого$222 400
Компании Decision Technology интересны ваши работы по повышению эффек-
тивности управления транспортным парком в Australian Motors, и я с нетерпением
ожидаю работы с Вами над расширенным проектом
Искренне Ваша
Сандра Бентлей
Главный менеджер
Дата	Четверг, 9 марта 1995 г 02.30-22-0700
От кого	Си Хун Чанг <chang@bntfin.com аи>
Кому	Майкл Йейтс <yates@britfin com uk>
Тема	Компьютерные проблемы
Майкл’
Обеспечение связи между проектной группой компании AM и компанией BF
(точнее, машиной Hitachi) может стать проблемой. Сетевые службы компании BF ре-
комендуют компании AM для этого проекта купить выделенный канал связи ($3 500
единоразово + $1 600 в месяц) и заменить свой маршрутизатор на модель Cisco 7510
($25 000 единоразово) На эту модернизацию потребуется около четырех недель
Поскольку база данных проекта стала очень большой, то они также рекомендуют рас-
смотреть возможность ее конвертирования в базу данных на платформе Oracle SQL, кото-
рая полностью поддерживается Hitachi В этом случае единственными дополнительными
издержками будут работы по конвертированию, которые смогут выполнить новые про-
граммисты На эти работы нам будет необходимо приблизительно две недели, в этой си-
туации я советую нанять администратора базы данных на полную рабочую неделю.
ГЛАВА 14. Реализация моделей 915
Наконец, Курт Килан и Гита Рао могут изучить язык SQL, а Джон может адапти-
ровать модель для выполнения удаленных запросов к Oracle SQL Это может потре-
бовать дополнительного программного обеспечения от IBM
Альтернативой использованию Hitachi может быть система SUN Ultra 4000
SPARC UNIX и ее подключение к отдельному серверу NT-SQL. Имеющийся ком-
пьютер Pentium можно преобразовать в сервер SQL с программным обеспечением от
Microsoft Система SPARC расширяема до многопроцессорной конфигурации, если
это потребуется для расширенной модели SPARC может постоянно находиться
в офисе проектной группы, тогда мы сэкономили бы на затратах по модернизации
линии связи и на оплате машинного времени Hitachi Но в этом случае надо приоб-
рести программный пакет оптимизатора AM PL Plus, работающий в системе SPARC
Вот приблизительная оценка стоимости этой альтернативы
SUN Ultra 4000 SPARC, двухпроцессорный, RAM 256 Мбайт, диск S66 000
на 18,4 Гбайт
Программное обеспечение SQL Server, обновленная версия NT, же- S18 000
сткии диск на 9 Гбайт
Оптимизатор AMPL плюс утилиты	S10 000
Итого	$94 000
СиХун
Вопросы, связанные с системой учета в компании AM, всплыли после записки от
Гиты Рао к ее прежнему начальнику Ютаке Хирота в компании AM. Текущая систе-
ма учета компании AM, разработанная более двух десятилетий назад, была ориенти-
рована в большей степени на финансовую отчетность Рао утверждала, что значи-
тельное количество данных по стоимости, собираемых для модели, может быть ис-
точником ценной информации и за рамками планирования транспортного парка
Но пока компания AM не заменит свою устаревшую систему учета на более совре-
менную систему, ей придется поддерживать две отдельные системы учета, реализо-
ванные на двух несовместимых компьютерах
К концу марта Йетс решил отказаться от обоих предложений как от конвертиро-
вания модели для Hitachi, так и от приобретения рабочей станции SPARC и сервера
базы данных SQL Он обосновал это следующим образом, даже если не обращать
внимания на значительные дополнительные затраты, следствием каждого из этих
предложений будут задержки и технические риски при разработке окончательного
проекта Эллису дали указание, чтобы при продолжении работ по расширению мо-
дели в максимально возможной степени использовались существующие аппаратные
и программные средства Основываясь на дальнейшем анализе Эллиса, Йетс сооб-
щил Шаферу о возможных изменениях (см приложение 3)
В июне 1995 года измененная модель была представлена высшему руководству
компании AM, включая Харингтона (исполнительного директора компании),
Шафера и его шефа Питера Расселла (генерального директора отдела грузовых
транспортных средств) Также на встрече присутствовали Хью Эдельман
(исполнительный вице-президент компании British Financial) и Сандра Бентлей из
компании Decision Technology и Майкл Йетс. Доклад, сделанный Йетсом, кроме
описания недавних изменений в модели, напоминал сообщение, которое было сде-
лано проектной группой в марте на встрече с менеджерами отделений
916 ЧАСТЬ IV. Реализация
Приложение 3. Переписка с Яном Шафером
Кому
От кого-
Тема
Ян Шафер
Майкл Йетс
Пересмотр модели
30 марта 1995 г.
Это письмо продолжает нашу дискуссию прошлого месяца о расширении модели
линейного программирования для включения более реальной информации от отде-
лений. Оказывается, что добавление в модель данных о дюжине типов грузовых
транспортных средств и ее переход на еженедельное планирование увеличит размер
модели примерно в 50 раз Это потребует от нас перестройки модели и использова-
ния более мощного компьютера Поэтому финансовые и временнь/е затраты на пе-
рестройку модели являются препятствием для получения каких-либо результатов
моделирования в период весенних закупок автомобилей
Однако можно кое-что сделать. Можно увеличить модель только в два раза за счет
использования двухнедельного планирования. Если допустить, что транспортные
средства поставляются и удаляются равномерно в течение месяца, то из модели
можно удалить условие, что поставка грузовых транспортных средств осуществляет-
ся только в начале месяца, их передача арендодателю или продажа выполняется
только в конце месяца
К сожалению, без существенных изменений модель нельзя приспособить для бо-
лее чем одного типа транспортного средства каждого изготовителя Нам необходимо
определить универсальное “комбинированное” транспортное средство каждого из-
готовителя, для которого прогнозируемые затраты и прибыли составляют среднее от
затрат и прибылей для желаемой комбинации транспортных средств, производимых
данным изготовителем. Это позволит значительно сократить размер модели. Но
в этом случае мы вынуждены в модели опустить учет автотрейлеров Возможно, ко-
гда-нибудь мы построим для них отдельную модель.
Мы сможем предоставить измененную модель в следующем году после ее перено-
са на более мощную компьютерную систему. Тем временем, пожалуйста, сообщите
об этих изменениях менеджерам австралийских отделений и скажите им, что Курт
будет контактировать с ними в течение следующих нескольких месяцев, пока будут
проводиться работы по изменению модели.
Дата	18 апреля 1995 г.
Кому	Ян Шафер
От кого	Джоэл Бети
Копия.	Питер Расселл
Тема	Проект модели
Ян'
Я только что поговорил по телефону с другими менеджерами отделений. Они
подтверждают, что группа Йетса разослала им письма, подобные тому, которое я по-
лучил вчера Вы можете поверить в то, что мы, как предполагается в модели, сможем
объединить многотонный грузовик с пикапом для доставки небольших грузов? Ко-
му, черт возьми, мы собираемся арендовать такое транспортное “чудо”?
ГЛАВА 14. Реализация моделей 917
Мы и так уже затратили слишком много времени, отвечая этим людям из группы
Йетса, а теперь они запрашивают вдвое больше данных. Я сказал Курту Килану, что
мы едва ли сможем уделить больше времени этому их проекту.
Я знаю, вы, сиднейские парни, располагаете большим количеством свободного
времени. Но у нас здесь в Мельбурне достаточно своей работы, и она на первом мес-
те, не так ли?
Эдельман выразил глубокую обеспокоенность по поводу высокой стоимости про-
екта и отсутствия до сих пор весомой отдачи от него. Он также был сильно удивлен
тем, что модель ограничивается пределами Австралии, игнорируя другие страны, в
которых компания AM имеет свои филиалы. Расселл, хотя и не был в восторге от
модели, против нее не выступил. После длительных дебатов Харрингтон решил вве-
сти проект в завершающую стадию. Он спросил Йетса, сколько отделений компании
можно внести в модель. Йетс пообещал ввести в модель 10 самых больших транс-
портных парков компании AM, что составило приблизительно 75% всех грузовых
транспортных средств, управляемых компанией AM в Австралии и Азии
Обещание, данное Йетсом, поставило перед его группой огромную проблему, по-
скольку изменить модель надо было в течение месяца, чтобы повлиять на сентябрь-
ские заказы поставок транспортных средств для 1996 года Опыт первой половины
1995 года показал, что группе Килан-Рао будет необходимо активно контролировать
сбор данных Кроме того, до сих пор не было разработано программное обеспечение,
учитывающее курсы обмена валют для азиатских отделений компании при импорте-
экспорте новых и подержанных грузовых транспортных средств
20 июня Гита Рао ушла из компании AM в группу учета British Financial в Лондоне
Первого июля истек срок контракта компании Decision Technology, и Джон Эл-
лис покинул проектную группу. Бентлей объяснила, что теперь у Эллиса другая ра-
бота, и его деятельность как консультанта и участника группы по созданию модели,
по существу, закончена, поскольку включение в модель других стран будет скорее
касаться вопросов сбора данных, а не моделирования.
Кроме Йетса осталось только два человека, знающих модель, Чанг и Килан
Группа теперь состояла из Сандры Бентлей, представителя компании Decision Tech-
nology, Курта Килана и Си Хун Чанга. Поскольку Чанг работал над компьютериза-
цией модели, Йетс поручил ему взять на себя работы, ранее выполняемые Эллисом
Бентлей будет исполнять роль координатора проекта. Курту Килану было поручено
руководство той частью работ, которая проводилась в отделениях К счастью, Йетс
еще в апреле поручил Килану сформировать группу из пяти человек, представляю-
щих более молодую и перспективную часть персонала отделений. Они стали основ-
ными специалистами по сбору данных в других странах. Кроме того, группа решила
упростить модель, выполняя ее прогоны в отдельности для каждой страны и игнори-
руя зависимости между отделениями компании в разных странах. Деятельность
Чанга по документированию модели также была временно приостановлена
В начале августа стали возможными первые оптимизационные прогоны модели.
После подтверждения результатов прогона модели фактическими планами 1995 года
была обнаружена новая проблема: менеджеры отделений наложили новые ограниче-
ния, касающиеся “урезания пика” спроса в случае нехватки транспортных средств.
При этом большая часть доступных данных, описывающая эти ограничения, была
противоречивой или ненадежной, а часть вообще отсутствовала. Курт Килан попро-
918 ЧАСТЬ IV Реализация
сил Чанга пересмотреть модель для внесения новых ограничений и проверить досто-
верность измененной модели
К сожалению, не предусмотренные заранее изменения модели послужили при-
чиной задержки проекта К сентябрю 1995 г. стало очевидно, что результаты модели
будут получены слишком поздно, чтобы непосредственно повлиять на процесс зака-
за транспортных средств для 1996 г , как было обещано Йетсом Но, так или иначе,
полученные результаты могли быть использованы для последующих заказов транс-
портных средств Уровень доверия менеджеров отделений к результатам моделиро-
вания оставался низким, только менеджеры австралийских отделений компании
всегда просматривали эти результаты Но даже они полагались на свои собственные
планы, составленные вручную, проверяя по ним результаты модели.
В октябре 1995 г возникла ситуация, когда сиднейское отделение предложило за-
купку большого количества грузовых автомобилей вопреки результатам, предостав-
ленным моделью Йетс возражал против закупки, и Расселл остановил заказ до того
момента, пока не будет принято окончательное решение Чанг и Килан работали с
сиднеиским отделением для повторного прогона модели, налагая на нее в качестве
ограничения предложенный сиднейским отделением заказ План закупок, выданный
моделью с учетом введенных ограничений, оказался на $110 000 дешевле плана, со-
ставленного вручную Этот эксперимент убедил менеджера сиднейского отделения в
полезности модели
Остаток 1995 года группа провела в разработке документации к модели, легко
воспринимаемой менеджерами отделений и правлением компании С января 1996 г
работы ни по документированию модели, ни над моделью вообще не возобновля-
лись Также у Йетса не было никаких дальнейших контактов с Хирота относительно
возможной замены системы учета компании AM В конце концов Си Хун подтолк-
нул его к решению перенести модель на систему SUN UNIX
Приложение 4. Общая структура модели компании AM2
Общую структуру модели можно показать посредством очень упрощенного при-
мера, который предусматривает только 6-месячный период планирования В полной
модели компании AM переменными решения являются транспортные средства кон-
кретного производителя, которые куплены или арендованы в данном месяце. Разли-
чают несколько вариантов аренды, зависящих от видов оплаты и от сроков аренды
(например, 6 месяцев или 8 месяцев) В упрощенном примере рассматривается толь-
ко один изготовитель грузовых автомобилей и один вид аренды Единственный из-
меняемый показатель — это срок аренды Для простоты рассматриваются кратко-
срочные арендные договоры на 2, 3, 4 или 5 месяцев. Для описания арендных дого-
воров вводятся следующие обозначения.
А:	— количество грузовиков, арендованных в месяце / сроком на 2 месяца (т е.
грузовики будут возвращены в конце периода t + 2);
В,	— количество грузовиков, арендованных в месяце t сроком на 3 месяца;
С,	— количество грузовиков, арендованных в месяце t сроком на 4 месяца,
£>, — количество грузовиков, арендованных в месяце t сроком на 5 месяцев
Модель разработана профессором Чарльзом Бонини (Charles Ботт)
ГЛАВА 14. Реализация моделей 919
В модели также определены переменные FSr — размер парка (среднее количество
транспортных средств) в течение месяца t и /, — количество транспортных средств в
конце месяца t
Цель модели заключается в выработке такой стратегии аренды, которая обеспе-
чит потребности компании AM в транспортных средствах с минимальными затрата-
ми Но определение этой “потребности” является сложным делом. Точное количест-
во транспортных средств, необходимых в каком-либо будущем месяце, не определе-
но Чтобы выити из этого положения, весь возможный спрос был разбит на три
части (сегмента), грузовики, соответствующие тому или иному сегменту спроса,
приносили разную прибыль Например, если в автопарке имеется только 100 грузо-
виков, то все они могут быть сданы в аренду, и каждый из них может приносить при-
быль $1 000 в месяц Если существует 100 дополнительных грузовиков (общее коли-
чество 200), и из этих дополнительных 100 грузовиков может быть сдана в аренду
только половина, то средняя прибыль, приносимая одним грузовиком в месяц, со-
ставит $500 Если имеется еще 100 дополнительных грузовиков (общее количество
300), и из этих дополнительных 100 грузовиков может быть сдана в аренду только де-
сятая часть, то средняя прибыль, приносимая одним грузовиком в месяц, составит
только $100 Дополнительное количество грузовиков (свыше 300) не может быть
сдано в аренду В таком случае в течение этого месяца имеется три сегмента спроса
Сегмент спроса	Максимальный размер сегмента	Размер парка	Прибыль от 1 грузовика, $
Первый	100	100	1000
Второй	100	200	500
Третий	100	300	100
Модель пытается удовлетворять спрос только до того момента, пока ожидаемая
прибыль равна или превышает расходы на грузовик В этой упрощенной модели
в течение каждого месяца / рассматриваются только два сегмента спроса, DSlr и £>52,
Предположим, что спрос в течение следующих 6 месяцев распределяется следующим
образом
	Январь	Февраль	Март	Апрель	Май	Июнь
Сегмент DS,	240	НО	110	100	150	100
Сегмент DS2,	60	80	70	80	100	50
Допустим, размер прибыли от одного грузовика в сегменте спроса 1 равен $1000 в
месяц и $800 в месяц в сегменте спроса 2
Ограничения
Количество грузовиков в конце месяца. Первый набор ограничений касается коли-
чества грузовиков, имеющихся в распоряжении в конце каждого месяца В общем
случае количество грузовиков в конце месяца равно количеству грузовиков в начале
месяца, плюс количество грузовиков, полученных в аренду в течение месяца, минус
количество грузовиков, у которых закончился в текущем месяце срок аренды или ко-
торые были проданы в этом месяце
920 ЧАСТЬ IV. Реализация
Для примера предположим, что в парке в начале января было 300 грузовиков.
В результате арендных договоров в январе получено 100 грузовиков, которые необ-
ходимо возвратить в этом же месяце, также получено 120 грузовиков, которые надо
возвратить в феврале, и 80 грузовиков, которые надо возвратить в марте. Тогда для
января имеем уравнение баланса
/, = 300 + (А, +В,+С,+ D,) - 100,
где 2, — количество грузовиков в конце января; Л,, Bt, и D, — количество грузови-
ков, полученных в январе по аренде на различный срок. Аналогичные уравнения со-
ставим для остальных месяцев.
Февраль
/2 = 2, + (А2 + В2 + С2 + D2) - 120;
март
Ц = 12 + (А, + В3 + С3 + £>3) - 80-Л,
(А, — это количество грузовиков, взятых в аренду в январе на два полных месяца
и поэтому возвращаемых в марте);
апрель
/4 = Ц + (А4 + В4 + С4 + Р4)-(А2 + 5,),
май.
Ц = 24 + (Л5 + В, + С5 + £>,) - (А, + В2 + С,);
июнь
/6 = /5 + (А6 + В6 + С6 + Db) - (А4 + вз + С2 + 2),).
Размер парка. Если грузовики поступают и покидают транспортный парк в тече-
ние месяца равномерно, средний размер транспортного парка в течение месяца ра-
вен среднему значению количества грузовиков в начале и конце месяца. Для любого
месяца t FS, =(1,, + 2,)/2.
Сегменты спроса. Этот набор ограничений связывает размер транспортного парка
с сегментами спроса, которые обсуждались выше. Для любого месяца t имеем FS, =
DS, + DS2t + избыток
Эти уравнения позволяют модели удовлетворять такому количеству сегментов
спроса, которое экономически выгодно. Кроме того, существуют верхние границы
на размер любого сегмента спроса.
Январь	Февраль	Июнь
2)51, <240	2)512< ПО	2)516< 100
2)52, <60	2)522 < 80	2)526 < 50
Другие ограничения. Для реальной модели компании AM имеется несколько дру-
гих наборов ограничений, которые сложно показать в этом упрощенном случае.
Среди них следующие.
1.	Ограничения на марки автомобилей (например, не менее 51% транспортных
средств должны быть марки Toyota).
2	Ограничения на соотношение арендованных и купленных транспортных
средств
ГЛАВА 14. Реализация моделей 921
3.	Ограничения на количество транспортных средств, которыми можно распоря-
диться в течение какого-либо месяца (например, не более 100 грузовиков могут
быть возвращены или проданы в июне).
4.	Ограничения на вторую покупку Производители автомобилей часто налагают
ограничения на количество арендуемых или покупаемых транспортных средств
во второй половине года в зависимости от количества заключенных договоров
аренды или продажи в первой половине года.
Целевая функция
Модель максимизирует целевую функцию, которая подсчитывается как доход от
эксплуатации транспортного парка
Литература
1.	Horst, W J Rittel, and Melvin M Webber, “Dilemmas in a General Theory of Planning”, Policy Sci-
ences, 4 (1973) 155-169
2.	Levasseur, R E , “People Skills How to Improve the Odds of a Successful Project Implementation”,
Interfaces, 23 (4 July-August 1993) 85-87.
3	Churchman, C W, “Managerial Acceptance of Scientific Recommendations”, California Manage-
ment Review, 7 (Fall 1964) 31-38
4.	Walsham, Geoff, “Implementation of Operational Research Some Lessons from Organizational The-
ory”, Operational Research, 42, no 5 (1990)- 37-47
5	Swanson, E В , “Churchman's Theory of Design Integrity”, Interfaces, 24 (4 July-August 1994). 54-59
6.	Schultz, R L , D P Slevin, and J К Pinto, “Strategy and Tactics in a Process Model of Project Im-
plementation”, Interfaces, 17 (3 May-June 1987) 34-46

Основные понятия теории
вероятностей
А.1. Введение
Теория вероятностей — это область математики, которая занимается изучением не-
определенностей, случайных изменении и случайных событий, возникающих в природе,
науке, экономике и любых видах человеческой деятельности Биологи используют ее дтя
создания моделей развития на генетическом уровне, физики — изучения поведения элек-
тронов в атоме, а экономисты — для определения изменения стоимости товаров Очень
часто в учебниках по теории вероятностей используют примеры азартных игр, чтобы по-
казать природу случайных событий Например, в теории вероятностей нетрудно смоде-
лировать результат бросания игральных костей Эта наука позволяет использовать знания
о простых случайных событиях для вычисления вероятностей более сложных их проявле-
нии Таким образом можно использовать простую модель игры в кости для того, чтобы
определить возможность и вероятность выигрыша в более сложных ситуациях
Случайные величины
Невозможно говорить о вероятностях, не затрагивая понятия случайных величинах
К сожалению, трудно ввести это понятие без использования более абстрактных понятий,
на которые не хватит места в этом маленьком приложении, но которые достаточно важны
для рассматриваемой темы Для простоты будем считать, что случайные величины — это
случайные события, в результате которых получаем числовые значения Например, слу-
чайными величинами будут число, выпавшее в результате подбрасывания игральных кос-
тей, количество купальников, проданных в супермаркете за июль, стоимость товаров Ya-
hoo' в конце недели, количество снежных дней в 2005 году и т д
Типы случайных величин
Существует два типа случайных величин дискретные и непрерывные С точки
зрения управленческих наук различия между ними не имеют особого значения Тем не
менее каждый тип случайных величин “эксплуатирует” свою отдельную область мате-
матики Для работы с дискретными случайными величинами необходима только
арифметика, но для описания и работы с непрерывными случайными величинами по-
надобятся интегральное и дифференциальное исчисления
А.2. Дискретные случайные величины
Дискретные случайные величины описываются с помощью вероятностной меры
f(x) Функция f(x) — это вероятность того, что рассматриваемая случайная величина
примет значение х Рассмотрим несколько примеров
924 ПРИЛОЖЕНИЕ А. Основные понятия теории вероятностей
Пример 1. Дискретное равномерное распределение
Предположим, что в игре в кости каждая грань игрального кубика выпадает с одинако-
вой вероятностью. Тогда f(x) = 1/6 для* = 1,2, 3,4,5,6 и f(*) = 0 для всех других значений*.
График вероятностной меры этого распределения показан на рис. А. 1.
f(x)
1	2	3	4	5	6 х
Рис. А. 1. График вероятностной меры
Пример 2. Произвольное дискретное распределение
Предположим, что урна содержит пять шаров, которые отличаются написанными
на них номерами На двух шарах стоит число 23, а на остальных трех — 37. С равной
вероятностью выбираем один шар. Получим f(23) = 2/5, f(37) = 3/5 и f(*) = 0 для всех
других значений*
Отметим, что f(*) > 0 и £f(*) = 1 Эти два условия должны выполняться для любой
вероятностной меры
Пример 3. Биномиальное распределение
Это распределение используется для моделирования серии независимых испыта-
ний, где в каждом испытании может произойти или не произойти определенное собы-
тие (Определение независимых событий см. в разделе А.5 ) В главе 10 упоминалось об
этом распределении, где оно использовалось в системе управления доходами аэропорта
для задания вероятности, с какой пассажир может заказать билет на самолет. Биноми-
нальное распределение имеет два параметра- п — количество испытаний и р — вероят-
ность того, что в испытании событие произойдет. Отсюда следует, что (1 - р) — это ве-
роятность того, что событие не произойдет. (Часто используемый пример, для описа-
ния которого используется биномиальное распределение, — это подбрасывание
монеты, событием здесь является выпадение “орла”, при этом предполагается, что для
“правильной” монеты р = 0,5.) Биноминальное распределение также позволяет под-
считать вероятность того, что при п испытаниях событие произойдет ровно * раз. На-
пример, из 10 подбрасываний монеты 9 раз она выпадет “орлом” вверх. Вероятностная
мера этого распределения задается формулой
f(x) =	//(1-р)"'х при* = 0,1,..., п и f(*) = 0 в противном случае.
ПРИЛОЖЕНИЕ А. Основные понятия теории вероятностей	925
Значение J — это количество способов, которыми можно выбрать х элементов
из множества п элементов Оно вычисляется по формуле
n'j _ л1 ______________л(л-1) 1_________
х) х'(п-х)' [x(x-l) l][(zi —x)(w - х —1) 1]
Например, если вероятность выпадения “орла” при одном подбрасывании монеты
равна 0,5, то вероятность того, что из 10 подбрасываний 7 раз выпадет “орел”, равна
f (7) = уу7<0’5)7(°-5)’ = 0,117 .
Пример 4. Распределение Пуассона
Очень часто распределение Пуассона используется в системах массового обслужи-
вания (см. главы И и 13) Вероятностная мера этого распределения задается следую-
щей формулой, где М— положительный параметр.
е-м м‘
f (х) =-— прих = 0,1,.. и f(x) = 0 в противном случае
Функция распределения
Функция распределения F(x) — это вероятность того, что случайная величина примет
значение меньше или равное х Исходя из того, что функция f(x) — это вероятность того,
что случайная величина будет равна х, получим F(x) =	f (у)
Пример 1 (продолжение). Дискретное равномерное
распределение
Если случайная величина — значения на игральной кости, то
х	I	х< I_____1________2__________3______4________5_______6<
F(x)	I 0	1/6	2/6	3/6	4/6	5/6 Г
График функции распределения приведен на рис. А 2.
Рис. А.2. График функции распределения
926 ПРИЛОЖЕНИЕ А Основные понятия теории вероятностей
Пример 2 (продолжение). Произвольное дискретное
распределение
х<23
23<х<37
37<х
F(x)
2/5
А.З. Непрерывные случайные величины
Непрерывные случайные величины описываются функцией плотности распределе-
ния вероятностей Если f(x) — это функция плотности распределения случайной величи-
ны, то для всехх f(x) > 0 и j* f ( t)<7. = 1 Эта функция — аналог вероятностной меры дис-
кретных случайных величин
Функция распределения
Функции распределения одинаково определяется как для дискретных, так и для не-
прерывных случайных величин F(x) — это вероятность того, что случайная величина
примет значение, которое меньше или равно х Связь между функцией плотности рас-
пределения и функцией распределения для непрерывных случайных величин выражается
формулой F(r) = £ f (r)di Результатом интегрирования плотности распределения в пре-
делах от -оо до х будет вероятность того, что случайная величина примет значение, кото-
рое меньше или равно х
Примеры непрерывных распределений
Рассмотрим три распределения, играющих важную роль в прикладных задачах
Пример 5. Непрерывное равномерное распределение
Равномерно распределенная непрерывная случайная величина с равной вероятно-
стью принимает любое числовое значение из интервала от 0 до 1.
{1, если 0 < х < 1,
О в противном случае
По определению функции распределения
10, если х<0,
х, если 0 < х;
1, если 1 < х.
Графики функции плотности распределения и функции распределения показаны на
рис А 3 и А4 Равномерное распределение играет большую роль в моделировании при
генерировании случайных величин (см главу 10).
ПРИЛОЖЕНИЕ А. Основные понятия теории вероятностей 927
А.4. Функция распределения
А.З. Функция плотности равно-
мерного распределения
Пример 6. Экспоненциальное распределение
Экспоненциальное распределение используется в системах массового обслуживания
для задания временного интервала между событиями (см главы 11 и 13) Это распределе-
ние имеет один параметр, обычно обозначаемый как X Функция плотности и функция
распределения имеют вид
Хе'и, еслих>0,
О в противном случае.
f 1-е-'-', еслих>0,
FW= „
[О в противном случае.
На рис А 5 изображены графики функции плотности и функции распределения для
параметра X = 1
Рис. А. 5. Функция плотности и функция распределения экспоненциального закона
Пример 7. Нормальное распределение
Нормальное распределение играет большую роль в теории вероятностей и математи-
ческой статистике В этой книге оно уже использовалось несколько раз (см главу 10)
928 ПРИЛОЖЕНИЕ А. Основные понятия теории вероятностей
Нормальное распределение имеет два параметра, математическое ожидание (среднее зна-
чение) ц и стандартное отклонение о, которое всегда больше 0. Поскольку нам в дальнейшем
не понадобится функция плотности нормального распределения, здесь мы не будем приво-
дить ее формулу. Функция нормального распределения как интеграл от функции плотности в
элементарных функциях не выражается. Однако значения функции распределения табулиро-
ваны, и соответствующие таблицы приводятся в любой книге по теории вероятностей или ма-
тематической статистике. В электронной таблице Excel есть встроенная функция
НОРМСТРАСП, которая вычисляет значение функции распределения стандартного нор-
мального распределения (при нулевом математическом ожидании и единичном стандартном
отклонении), а также функция НОРМРАСП, которая вычисляет значения плотности и функ-
ции распределения при любых значениях математического ожидания и стандартного откло-
нения На рис А 6 приведен график плотности нормального распределения и показано значе-
ние функции распределения как величина площади под кривой плотности.
Рис. А. 6. Функция плотности и значе-
ние функции распределения нормально
распределенной случайной величины.
А.4. Математическое ожидание
Ожидаемые прибыль или расход часто являются критериями решений, принимаемых
в условиях неопределенности, т е. в решениях проблем, результат которых является слу-
чайной величиной Сначала познакомимся с ожидаемым значением (в теории вероятно-
стей чаще употребляется термин математическое ожидание) случайной величины, а за-
тем рассмотрим математическое ожидание функции от случайной величины
Математическое ожидание случайной величины
Математическое ожидание случайной величины X записывается как М(Л). Это
среднее значение случайной величины X, обычно обозначаемое греческой буквой ц.
Ниже приведены определения математического ожидания для дискретных и непре-
рывных случайных величин.
Дискретные случайные величины
Математическое ожидание дискретной случайной величины с заданной вероятно-
стной мерой f(x) вычисляется по формуле
М(Х) = ц= £xf(x).
Приведем несколько примеров.
ПРИЛОЖЕНИЕ А. Основные понятия теории вероятностей 929
Пример 1 (продолжение). Равномерное дискретное
распределение
Стоит заметить, что математическое ожидание случайной величины не обязательно
должно быть одним из ее возможных значений. Например, в результате бросания костей
не может выпасть число 3,5. Физическая интерпретация математического ожидания
представляет его как “центр тяжести” значений вероятностной меры Математическое
ожидание имеет еще одну наглядную интерпретацию. Рассмотрим ряд независимых на-
блюдений за случайной величиной. Подсчитав среднее арифметическое наблюдений,
получим числовое значение, которое будет близко к математическому ожиданию.
Пример 2 (продолжение). Произвольное дискретное
распределение
М(Х) = 23 | + 37 |=-31,4
ПримерЗ (продолжение). Биномиальное распределение
Для случайной величины, имеющей биномиальное распределение с параметрами п и
р, математическое ожидание вычисляется по формуле (приводим без доказательства)
М(Х) = пр Эта формула интуитивно понятна Например, если подбрасывать симметрич-
ную монету 10 раз, то в среднем 5 раз должен выпасть “орел”
Пример 4 (продолжение). Распределение Пуассона
В распределении Пуассона математическое ожидание равно его дисперсии, которая
совпадаете параметром М
Непрерывные случайные величины
Формулы вычисления математического ожидания непрерывных случайных величин
подобны аналогичным формулам для дискретных случайных величин. Отличаются они
тем, что здесь нужно использовать функцию плотности распределения и интегрирование,
т.е. М(Х) = £ xf(x)dx.
Пример 5 (продолжение). Непрерывное равномерное
распределение
М(Х)=£л 1	=
930	ПРИЛОЖЕНИЕ А. Основные понятия теории вероятностей
Пример 6 (продолжение). Экспоненциальное распределение
м(Х)=
Здесь для вычисления интеграла нужно воспользоваться техникой интегрирования по
частям
Математическое ожидание функции от случайной величины
Пусть G(x) — некоторая функция переменной х и X— дискретная случайная величина
с вероятностной мерой f(x). Тогда математическое ожидание случайной величины G(X)
вычисляется по формуле
M(G(X)) = £c(x)f(x)
Для непрерывных случайных величин используется аналогичная формула, но вместо
суммы берется интеграл
Дисперсия и стандартное отклонение случайной величины
Дисперсия — это мера рассеивания значений случайной величины Обычно она обо-
значается как о2 и определяется формулой
D(X) = о2 = М((Х -М(Х)2) = £ (х-M(X))2f(х).
Дисперсия играет важную роль в математической статистике, поскольку она определяет
степень рассеивания распределения случайной величины Чтобы показать роль дисперсии
как численной меры рассеивания, рассмотрим две случайные величины X и К. Пусть f/x) —
вероятностная мера первой случайной величины, a f,(y) — второй Положим
{—, если х = 4,6,
2
0 в противном случае,
и
= ес""Л=|'9-
[о в противном случае.
Заметим, что математическое ожидание обеих случайных величин равно 5. Нетрудно
проверить, что D(X) = 1 и D(X) = 16. Интуиция подсказывает, что дисперсия будет боль-
ше у той случайной величины, у которой выше вероятность находиться дальше от сред-
него значения Это можно проверить на приведенном примере.
Стандартное отклонение обозначается буквой о и вычисляется как квадратный ко-
рень из дисперсии, т е о = (о2)'/2.
А.5. Многомерные распределения
Этот раздел представляет ситуации, в которых одновременно участвует несколько
случайных переменных. Многомерные случайные величины неявно были представлены
в разделе 9 13, где обсуждалась теорема Байеса. Рассмотрим более подробно многомер-
ные случайные величины.
ПРИЛОЖЕНИЕ А. Основные понятия теории вероятностей 931
Совместное распределение
Дискретные случайные величины
Рассматривая многомерные случайные величины, полезно ввести несколько новых
обозначений Пусть ft /х, у) — вероятность того, что случайная величина Xпримет значе-
ние х, а Y — значение у Тогда ,.(х, у) будет совместной вероятностной мерой случайных
величин Хи Y
Рассмотрим игру, которая описана в разделе 9 13.
1. Бросается игральная кость
2 Выпавшее значение определяет урну, из которой будет взят шар Примем, что ве-
роятность быть вынутым для всех шаров одинакова.
В следующей таблице приведены условия этой игры
Выпавшее значение	Урна	Содержимое урны
2 или 3 4, 5 или 6	2 3	28 белых и 72 черных шара 40 белых и 60 черных шаров 92 белых и 8 черных шаров
Построим для этой игры совместное распределение следующих случайных величин
X— номер выбранной урны, случайная величина У равна 1, если из урны выбран белый
шар и Y= 2, если выбран черный Значения совместной вероятностной меры Гхг(х,у) по-
казаны ниже
X	У= 1	У=2
2 3	(1/6)х(28/100) = 0,0467 (2/6)х(40/100) = 0,1333 (3/6)х(92/100) = 0,4600	(1/6)х(72/100) = 0,12 (2/6)х(60/100) = 0,20 (3/6)х(8/100) = 0,04
Эти значения получены на основе формул условной вероятности (см раздел 9.13)
fx^x,y) = f/x) f^Xylx)
Непрерывные случайные величины
Многомерные распределения также можно построить на основе непрерывных слу-
чайных величин Последнее равенство, задающее зависимость между совместной и ус-
ловной вероятностями, используется для определения функции совместной плотности и
функций плотностей условных вероятностей.
Независимые случайные величины
Случайные величины Хи Yназываются независимыми, если ГЛ)(х,у) = f^xjxf/y). По-
скольку в общем случае fA.r(x,}') = f^/x^xf/y), поэтому Хи Yнезависимы только тогда,
когда f^/xly) = f/x).
932 ПРИЛОЖЕНИЕ А. Основные понятия теории вероятностей
Математическое ожидание и дисперсия суммы случайных величин
Математическое ожидание суммы
Всегда верно (пне зависимости от того, будут л и Д'и У независимыми иди нет), что
М(%+ У) = М(Л) + М(У).
Дисперсия суммы
Дисперсия суммы случайных величин X + Yвычисляется по формуле
D(%+ У) = D(A) + D(y> + 2Cov(%, У)
или
о2^г = <зх + о2г + 2оЛГ
Ковариация X и Y
В предыдущем выражении было использовано Cov(%, У) — ковариация случайных ве-
личин Ей У Она обозначается как аху и определяется формулой
Cov(X У) = о„,= М([Л'-М(Л)][У-М(У)])
Ковариация определяет степень зависимости между величинами X и У, но на практи-
ке для этой цели чаще используется коэффициент корреляции. Заметим, если X и У неза-
висимы, то о„= О
Коэффициент корреляции
Коэффициент корреляции величиной У обозначается как рЛ), и определяется формулой
_ Соу(Х,У) _ оХ1
PAr ~ 7D(X)D(y) ~
Коэффициент корреляции может принимать значения от —1 до 1 Если коэффициент
корреляции положителен, то значения случайных величин X и У имеют тенденцию изме-
няться в одном направлении — если Xпринимает большие значения, то с большой вероят-
ностью У также примет большие значения, и наоборот. Отрицательное значение коэффи-
циента корреляции говорит о том, что значения случайных величин X и У имеют тенденцию
изменяться в противоположных направлениях — если X принимает большие значения, то
с большой вероятностью У примет малые значения, и наоборот Если рХ|, = 0, говорят, что
случайные величины Хи У некоррелированные (но это не означает, что они независимы).
Математическое ожидание и дисперсия суммы нескольких случайных
величин
Пусть Z = £x, , те Z является суммой N случайных величин Xt, Х2, .. , XN. Тогда
M(Z) = ^M(X ) Таким образом, математическое ожидание суммы случайных величин
равняется сумме их математических ожиданий
Дисперсия суммы случайных величин вычисляется по формуле
D(Z) = gD(X,) + 2XXCov(X,, XJ).
Таким образом, дисперсия суммы случайных величин равняется сумме их дисперсий
и суммы ковариаций всех возможных пар случайных величин
Приложение
Средства моделирования Excel
В данном приложении представлены средства, часто применяемые при создании таб-
личных моделей в Excel В первых разделах кратко описаны общие вопросы работы
с программой Excel и ее настройки В последующих разделах материал изложен в виде
отдельных процедур, выполняемых в Excel. Но подчеркнем, что изложение полного кур-
са работы в Excel не является целью данного приложения Это приложение организовано
таким образом, что им можно пользоваться как справочником Если вы хотите
“освежить” свои знания о каких-либо действиях или процедурах, выполняемых в Excel,
найдите нужный раздел в этом приложении Дополнительную информацию о рассматри-
ваемых вопросах можно найти в справочной системе Excel.
Б.1. Структура окна Excel
Ha рис Б 1 показаны основные элементы окон программы Excel и рабочей книги
Рис. Б.1. Элементы окна Excel и окна рабочей книги
934
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
Б.2. Настройка Excel
Большинство опций управления как самой программой Excel, так и внешним видом
окон и рабочих книг, сосредоточено в диалоговом окне Параметры, которое открывает-
ся по команде Сервис^ Параметры Это диалоговое окно содержит 13 вкладок (в Excel
2002, в предыдущих версиях количество вкладок другое) Кратко опишем некоторые
вкладки этого окна и их основные опции.
Вкладка Вид
Большинством элементов окон, показанных на рис Б 1, можно управлять с помощью
опций, расположенных во вкладке Вид диалогового окна Параметры Если установлен
флажок или переключатель, помеченный названием элемента окна, то данный элемент
будет отображен на экране Опции, установленные по умолчанию в этой вкладке, пока-
заны на рис Б 2 Установка флажка Формулы приведет к тому, что в ячейках, содержа-
щих формулы, вместо чисел будут отображаться формулы, по которым они вычислены
Международные | Сохранен» | Проверка оимйж | Орфография | Безопасность Вид | Вычислено) | Правка | Общие | Переход | Списки | Диаграмма | Цвет .Отображать-';; , ~	z	'	- - F область задач при запуске F строку формул F строку состояния Р окна на данеги задач ' Дэшечания	‘—----- - -	—-——						— не отображать	г только индикатор	' X* примечание и инаиквтор , т7 отображать	только онертания	4g отображать Параметры окна	  - 	— 	-	—	 , Г арторазбиение на страницы . Ргагалсвки стртжи столбцов Р бсриэонтальная полоса прокрутки :' Г фордолы	. - ' Р символы структуры	I7 вертикальная полоса прокрутки ’ Р’^еуа'1	.	.	17 долевые значения	17 ярлычки лист»	- Цвет птл сетки: | Авто	] 1
’	| ОК | Отмена	
Рис. Б.2. Вкиадкч Вид днаюгомк-о окна Параметры
Вкладка Общие
Эта вкладка (рис Б 3) содержит основные опции управления рабочими книгами
Excel Обратите внимание на опции Помнить список файлов (устанавливает количество
файлов, которые будут отображаться внизу списка команд меню Файл), Листов в новой
книге (устанавливает количество рабочих листов по умолчанию в новой рабочей книге),
Стандартный шрифт (шрифт и его размер, который по умолчанию применяется в рабо-
чих книгах) и Имя пользователя (это имя будет автоматически “подписывать” ваши ра-
бочие книги)
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 935
Рис. Б.З. Вкладка Общие диалогового окна Параметры
Вкладка Переход
Параметры этой вкладки обеспечивают обратную совместимость с предыдущими вер-
сиями Excel и файлами электронной таблицы Lotus 1-2-3 (рис Б 4)
Рис. Б.4. Вкладка Переход диалогового окна Параметры
936 ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
Вкладка Правка
При выборе вкладки Правка станут доступными опции, показанные на рис Б 5 Что-
бы редактировать значения прямо в ячейках, дважды щелкнув на них мышкой (без ис-
пользования строки формул), установите флажок опции Правка прямо в ячейке Если
установлен флажок опции Переход к другой ячейке после ввода, то после нажатия кла-
виши <Enter> курсор переместится в том направлении, которое указано в поле Направ-
ление Если же эта опция отключена, то после нажатия <Enter> ячейка, в которую вво-
дилось значение, останется выделенной
Международные | Сохранение | Гроеерка ошибок	|	Орфография | безопасность
Вид | Вычисления j Правка "|| Общие | Переход | Списки | Диаграмма | Цвет '
...... Параметры" «	.................................
.Правка прямо в ячейке	Р Расширять форматы и формулы в сгмоех
F Перехаживание ячеек	'Г Автоматический ввод процентов '
Р Предупреждать перед перезаписью ячеек F Отображать меню параметров ^ставки
" Г Ореход к другой ячейке после ввода,	Р Отображать дано параметров добавления
виапрое.лемии.	f Т]
Г Фиксированный двсатичиьй формат при вводе,
десятичных разрядов:	§
17 Перемещать рбъекгы вместе с ячейками	,	'
Р Запрашивать об о&ювлении автоматических .	.
Г" Пдавная вставка и удалетдае ячеек; • 
Г Автодаеершение значений ячеек
j ОК ] Отмена [
Рис. Б.5. Вкладка Правка диалогового окна Параметры
Вкладка Вычисления
Опции, показанные на рис Б 6, станут доступными после перехода во вкладку Вы-
числения Если вы создаете большие табличные модели, установите переключатель ре-
жима вычислений Автоматически кроме таблиц или Вручную, что ускорит работу при
редактировании больших таблиц В любом случае Excel сообщит, когда потребуется пе-
ресчет таблиц и формул, отобразив в строке сообщений слово Вычислить Когда это не-
обходимо, формулы рабочего листа можно пересчитать, нажав клавишу <F9> или же
комбинацию клавиш <Ctrl+=>
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 937
Рис. Б. 6. Вкладка Вычисления диалогового окна Параметры
Вкладка Проверка ошибок
Эта вкладка (рис Б 7) появилась в окне Параметры только в Excel 2002, ранее ее не
было Опции этой вкладки позволяют включить режим фоновой проверки ошибок
(опция Включить фоновую проверку ошибок) и определить ошибки, на которые Excel
будет обращать внимание (опции в области Проверять наличие следующих ошибок)
Рис. Б. 7. Вкладка Проверка ошибок диалогового окна Параметры
938 ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
Б.З. Управление окнами и рабочими листами
Разделение окна рабочей книги
Поместив указатель мыши на один из разделителей окна (рис Б 8), а затем перетащив
его, вы разделите рабочий лист на две области. Повторив эту процедуру для другого раз-
делителя, можно получить еще две области, как показано на рис. Б.9 В окне рабочей
книги появились дополнительные полосы прокрутки, с помощью которых можно неза-
висимо прокручивать данные в разных областях. Чтобы удалить разделение окна, нужно
перетащить линию раздела к границе окна или дважды щелкнуть на ней. Разделить окно
также можно с помощью команды Окно1*Разделить.
Рис. Б.Х. I’tijile mine i и окна
Рис. Б.9. Разделенное окно
Закрепление областей
После выполнения команды ОкноФЗакрепить области окно также разбивается на
две или четыре области. Однако в этом случае нельзя прокручивать области, находящие-
ся выше и левее линий разделения. Закрепление областей часто используется тогда, когда
надо зафиксировать заголовки столбцов и строк для удобства прокрутки больших таблиц.
Чтобы закрепить области, поставьте курсор в верхнюю левую ячейку области, которая
должна оставаться незакрепленной (прокручиваемой), затем выберите команду Ок-
ноФЗакрепить области На рис. Б. 10 строки 1,2 и 3 и столбцы А и В закреплены. Чтобы
удалить закрепление областей, выполните команду Окно^Снять закрепление областей.
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 939

С19
____В.
• f, 30456
_CZZJ с
Джексон С imp.
Доходы и >асходы
21
22
23
24"
26
Сентябрь
30
Октябрь
Доход Расход Прибыль
ЗО456|
85201
15926'
75369
8520
74561•
14578'
56248'
14563
63580
472922
9632
14785
85201
15926
/ £тобразить.,
'7 Разделить
:(3 201.05xls
25874
75369
8520
35742
5736
30201
2478
35741
10230
8520
74561
5470
..3145
75369
8520
4582
39627
44360
12100
20507-
4333
55060^
398361'
4162!
11640
9832
7406


Рис. Б. 10. Закрепление областей
Масштабирование рабочих листов
Инструмент Масштаб, расположенный на стандартной панели инструментов, позволя-
ет увеличить или уменьшить масштаб отображения активного окна рабочей книги, как по-
казано на рис Б 11
Рис. Б. 11. Возможности масштабирования
940
ПРИЛОЖЕНИЕ Б Средства моделирования Excel
Чем меньше масштаб, тем больше ячеек отображается на экране. Чтобы выделенный
диапазон занимал весь экран, в списке инструмента Масштаб выберите пункт По выде-
лению Чтобы вернуться к стандартному масштабу, выберите пункт 100%.
Работа с несколькими окнами
После выполнения команды ОкноФНовое откроется еще одно окно активной рабо-
чей книги, с которым можно работать независимо от первого окна. Тем не менее оба ок-
на отображают данные одной и той же рабочей книги Если в диалоговом окне Располо-
жение окон (это окно открывается по команде ОкноФРасположить) установить пере-
ключатель Рядом (рис Б 12), то это действие приведет к тому, что в окне программы
Excel будут видны все окна открытых на данный момент рабочих книг, как показано на
рис Б 13 Используя несколько окон одной рабочей книги, можно одновременно видеть
на экране несколько листов этой книги Более того, каждое окно можно разделить на не-
сколько областей Это предоставляет широкие возможности для отображения на экране
моделей с большим объемом данных. Например, на рис. Б. 13 в правом окне отображены
формулы, а в левом представлены результаты вычислений по этим формулам.
Рис. Б. 12. Диалоговое окно
Расположение окон
।Wjjb 4» 90% ; jf; J Anal Cyr "	V 10 УуУк	Ф}	Д B3 ’	~	' fi' 1234 		
	Ф	AZ! .	.1	- >в ./И
i 1	Темп роста ;> । Квартал 1 К К । И Доход	|	$1 234 001 % 4a Стоимость	$740,40 ft ДиРазмер налога	$493,60 |si jj	у	sfes	|Темп роста аЙ1	Квартал	1 ВЛ Доход	1234 Дм Стоимость	1=$Е$1*ВЗ	 ЛЯРазмер налога	jsB3-B4
Рис. Б. 13. Два окна одной рабочей книги, расположенные рядом
Сокрытие окон рабочих книг
Если открыто много окон рабочих книг и какое-то из них временно не нужно, его
можно скрыть, выбрав команду ОкноФСкрыть. Чтобы снова открыть скрытое окно, вы-
полните команду ОкноФОтобразить.
ПРИЛОЖЕНИЕ Б Средства моделирования Excel 941
Сокрытие рабочих листов
Так же, как и окна, можно скрывать отдельные рабочие листы Выберите команду
Формат'^Лист^Скрыть. после чего активный рабочий лист будет скрыт Команда Ото-
бразить из того же меню выполняет обратное действие
Переименование рабочих листов
Чтобы изменить имя рабочего листа, выберите команду Формат^Лист^Переименовать
(или дважды щелкните на ярлыке листа), после чего введите новое имя, как показано на
рис Б 14
Рис. Б. 14. Переименование ра-
бочего листа
Б.4. Выделение ячеек
Выделение нескольких смежных столбцов или строк
Чтобы выделить несколько смежных столбцов или строк, перетащите указатель мыши
по заголовкам этих строк или столбцов (рис Б. 16).
Рис. Б. 16. Выделение нескольких смежных столбцов и строк
942 ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
Выделение всех ячеек рабочего листа
Чтобы выделить все ячейки активного рабочего листа, щелкните на пустой кнопке,
которая находится в верхнем левом углу листа (на пересечении заголовков строк и столб-
цов), как показано на рис Б. 17.
Выделение диапазона ячеек
Для выделения диапазона ячеек нажмите кнопку мыши и перетащите указатель мыши
по этому диапазону ячеек так, как показано на рис. Б 18
Рис. Б. 18. Выделение диапазона ячеек
Диапазон ячеек также можно выделить, выполнив следующую последовательность
действий
1.	Выделите первую ячейку диапазона.
2.	Нажмите и удерживайте клавишу <Shift> или нажмите клавишу <F8>, чтобы
включить режим выделения.
3.	Нажимая клавиши управления курсором, выделите нужный диапазон ячеек.
4.	Отпустите клавишу <Shift> или нажмите клавишу <F8>, чтобы отключить режим
выделения
Выделение несмежных диапазонов ячеек
Чтобы выделить несмежные ячейки, строки или столбцы, выделите первый диапазон
ячеек Затем, нажав и удерживая клавишу <Ctrl>, выделите следующий диапазон, и т.д.
(рис. Б 19).
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 943
Рис. Б. 19. Несмежные выделения
Тот же результат можно получить, выполнив следующую последовательность действий.
1.	Выделите первую ячейку или диапазон ячеек
2.	Нажмите комбинацию клавиш <Shift+F8>, чтобы включить режим добавления
ячеек.
3.	Выделите первую ячейку следующего диапазона.
4.	Нажмите клавишу <F8>, чтобы включить режим выделения
5.	Повторите п. 2—4 для каждого нового диапазона ячеек
6.	Нажмите клавишу <F8>, чтобы отключить режим выделения
Выделение прямоугольного диапазона непустых ячеек
Чтобы выделить прямоугольный диапазон непустых ячеек, выделите любую ячейку из
этого диапазона и затем нажмите комбинацию клавиш <Ctrl+Shift+8> (Используйте
клавишу <8> на основной клавиатуре, а не на дополнительной )
Выделение ячеек от табличного курсора до конца непустого
диапазона
Щелкните на первой ячейке диапазона, затем нажмите комбинацию клавиш
<Ctrl+Shift+KnaBHina управления курсором>. Будет выделен диапазон ячеек от первой
ячейки до края непустого диапазона в том направлении, какое указывает нажатая клави-
ша управления курсором. В примере на рис. Б.20 табличный курсор был установлен в
ячейке В2, потом была нажата комбинация клавиш <Ctrl+Shift+-L> Если затем нажать
<Shift+«—>, то будет выделен диапазон А2 В4
Рис. Б. 20. Выбор диапазона ячеек
944 ПРИЛОЖЕНИЕ Б Средства моделирования Excel
Б.5. Работа с диапазонами ячеек
Редактирование содержимого ячеек
Чтобы отредактировать содержимое ячейки (формулу, числовое или текстовое значение),
поместите на ячейку табличный курсор, содержимое ячейки отобразится в строке формул
(рис Б 21) Щелкните в строке формул и приступайте к редактированию (удаляйте символы
с помощью клавиш <Delete> и <Backspace> или вводите новые). Затем нажмите клавишу
<Enter> для завершения редактирования ячейки или клавишу <Esc> для отмены редактиро-
вания и возврата к предыдущему содержимому ячейки. Если дважды щелкнуть на ячейке (или
нажать клавишу <F2>), можно редактировать непосредственно в ячейке, как показано на
рис Б 22 (Чтобы последняя возможность была доступной, необходимо установить флажок
Правка прямо в ячейке во вкладке Правка диалогового окна Параметры, см рис Б 5 )
Рис. Б.21. Редактирование в строке формул
Рис. Б. 22. Редактирование в ячейке
Чтобы вставить в ячейку одну из предопределенных функций Excel, щелкните в стро-
ке формул на кнопке Вставка функции (рис Б 23) Откроется панель средства Мастер
функций, которое будет описано ниже В поле Имя отображается список последних ис-
пользовавшихся функций, которые можно вставить в создаваемую формулу.
А.У В =ВЗЧ1<1)~
• Встаека функции
Рис. Б.23. Кнопка Вставка функции
Абсолютные ссылки на ячейки
Абсолютные ссылки на ячейки, применяемые в формулах, не меняются при копиро-
вании или перемещении этих формул В абсолютных ссылках необходимо перед буквой
столбца и номером строки поставить знаки доллара ($). Например, ссылка $Е$5 является
абсолютной Если формулу с этой ссылкой переместить или скопировать из исходной
ячейки в любую другую, формула в новой ячейке всегда будет указывать на ту же ячейку
Е5 Возможно использование смешанных ссылок, в которых абсолютной является только
ссылка на строку или только на столбец Например, ссылка Е$5 всегда будет указывать
на строку с номером 5, вне зависимости от того, куда она будет скопирована. Аналогично
ссылка $Е5 всегда будет указывать на столбец Е При вводе или выделении адреса ячейки
в формуле путем нажатия клавиши <F4> знак доллара будет добавлен в ссылку автомати-
чески Повторное нажатие этой клавиши приведет к циклическому перебору всех воз-
можных комбинаций расположения знака $ в ссылке.
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 945
Относительные ссылки
Если в формуле ссылка не содержит знака доллара, то она является относительной
В этом случае Excel запоминает ссылку на ячейку относительно той ячейки, в которой
находится формула со ссылкой. Например, если в ячейке G10 содержится формула
=F10+G9, и эта формула копируется в ячейку Gl 1, то в этой ячейке формула примет вид
=F11+G10, поскольку относительная ссылка содержит не адрес ячейки, а ее положение
относительно содержащей ссылку ячейки.
Операция Вырезать
Выбрав команду Правка^Вырезать, нажав комбинацию клавиш <Ctrl+X> либо
щелкнув на соответствующей кнопке стандартной панели инструментов, можно пере-
местить содержимое и формат ячейки или диапазона ячеек в буфер обмена, как правило,
для вставки в другое место рабочего листа.
Операция Копировать
С помощью команды Правка^ Копировать, комбинации клавиш <Ctrl+C> либо
щелчка на соответствующей кнопке стандартной панели инструментов можно перемес-
тить содержимое и формат ячейки или диапазона ячеек в буфер обмена, как правило, для
вставки в какое-либо другое место рабочего листа
Операция Вставить
Чтобы вставить диапазон ячеек, предварительно скопированный или вырезанный в бу-
фер обмена (при этом все имеющиеся данные в ячейках, куда будет осуществлена вставка,
будут удалены), выберите команду Правка^Вставить, нажмите комбинацию клавиш
<Ctrl+V> либо щелкните на соответствующей кнопке стандартной панели инструментов
Перемещение и копирование диапазона ячеек
Если навести указатель мыши на рамку выделения диапазона ячеек, а затем перета-
щить ее в другое место, то содержимое выделенных ячеек будет перемещено на новое ме-
сто, как показано на рис. Б 24 Если при этом нажать и удерживать клавишу <Shift>, то
данные будут вставлены между ячейками. Если же нажать и удерживать кнопку <Ctrl>,
то выделенные данные будут скопированы
Рис. Б.24. Перемещение выделенных ячеек
Копирование содержимого ячеек как рисунок
Чтобы скопировать и вставить любой объект Excel как рисунок, используйте команду
Копировать рисунок Выделите графический объект или диапазон ячеек, который нужно
скопировать. Нажав и удерживая клавишу <Sliift>, выберите команду Прав-
ка^ Копировать рисунок. После этого на экране появится диалоговое окно Копировать
рисунок (рис. Б.25). Если установлен переключатель Вид как на экране, то после вставки
946 ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
рисунка через буфер обмена будет получено такое же изображение объекта или диапазо-
на ячеек, как и то, что вы видите в данный момент на экране Например, если на экране
видны линии сетки, то они будут присутствовать и в скопированном изображении Если
в диалоговом окне Копировать рисунок установить переключатель Вид как на печати, то
в буфер обмена объект будет скопирован в том виде, в котором он будет выведен на пе-
чать Например, если в диалоговом окне Параметры страницы установлены опции так,
что при выводе на печать будут печататься линии сетки и заголовки строк и столбцов, то
они будут содержаться и в скопированном рисунке
Рис. Б.25. Диалоговое окно
Копировать рисунок
Команды Отменить и Повторить
Большинство команд Excel можно отменить или же повторить для другой выделенной
области, для чего надо щелкнуть на соответствующей кнопке стандартной панели инстру-
ментов Также можно воспользоваться клавишами <Ctrl+Z> (отменить) и <Ctrl+Y>
(повторить) Excel “помнит” 16 последних команд и операций, которые выполнял пользо-
ватель и которые можно отменить или повторить Если щелкнуть на стрелке, направленной
вниз, возле кнопки Отменить, откроется список команд, которые можно отменить.
Контекстные меню
Если щелкнуть правой кнопкой мыши на любом объекте окна Excel, то откроется ме-
ню, содержащее команды, относящиеся к этому объекту В зависимости от того, на чем
установлен указатель мыши (ячейка, объект, диаграмма, панель инструментов, заголовок
столбца или строки и т д ), будут отображаться разные контекстные меню. На рис Б.26
показаны два примера контекстных меню, одно из которых содержит команды, выпол-
няемые над отдельной ячейкой, а второе — над столбцом ячеек.
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 947
Рис. Б.26. Контекстные меню
Б.6. Заполнение ячеек
Команда Заполнить
Команда Правка^Заполнить часто используется при копировании формул и другого
содержимого ячейки в соседние ячейки. Введите данные в первую ячейку, выделите диа-
пазон ячеек, которые необходимо заполнить (включая и первую ячейку), затем выберите
Правка^Заполнить1^Вниз (либо Вправо, Вверх, Влево) В результате все пустые ячей-
ки из выделенного диапазона будут заполнены
Команда Прогрессия
Эта команда используется для создания числовых последовательностей и последова-
тельностей, состоящих из дат Выделите ячейку, с которой будет начинаться прогрессия,
и введите в нее первое значение создаваемой последовательности. Затем выберите команду
Правка^Заполнить^Прогрессия В открывшемся диалоговом окне Прогрессия укажите
расположение последовательности, по строкам или по столбцам, тип прогрессии арифме-
тическая, геометрическая или состоящая из дат (рис Б 27) Кроме того, требуется опреде-
лить значение шага прогрессии, ее предельное значение, а затем щелкнуть на кнопке ОК
Также можно выделить несколько ячеек, а затем выполнить команду Прогрессия, при этом
не надо вводить предельное значение. В примере на рис Б 27 будет создана расположенная
в столбце последовательность значений арифметической прогрессии с начальным значени-
ем 10 с шагом 15, причем последнее значение последовательности не превысит 75
Рис. Б. 27. Диалоговое окно Прогрессия
948
ПРИЛОЖЕНИЕ Б Средства моделирования Excel
Автозаполнение
Выделите одну или несколько ячеек, которые содержат какой-то ряд данных Помес-
тите указатель на маркер заполнения в правом нижнем углу выделенной области, чтобы
указатель принял форму маленького черного крестика После этого нажмите кнопку'
мыши и перетащите указатель вправо (в данном примере), чтобы заполнить ячейки, рас-
положенные справа (если в заполняемых ячейках содержались какие-либо данные, то
они будут утеряны), как показано на рис Б 28 Если в выделенных первоначально ячей-
ках содержатся числовые значения или стандартная последовательность текстовых запи-
сей, то Excel продотжит эти значения на все выделенные ячейки
(ноябрь"
Февраль |
Рис. Б.28. Автозаполнение
Чтобы отключить автозаполнение и просто скопировать содержимое выделенных ячеек,
нажмите клавишу <Ctrl> и, удерживая ее, перетащите маркер заполнения Если же при пе-
ретаскивании маркера заполнения будет нажата клавиша <Shift>. то вместо копирования
выделенные ячейки будут очищены от содержимого (кроме первоначально выделенных)
Автозаполнение также можно применить ко всей строке или столбцу рабочего листа,
при этом маркер заполнения будет находиться возле первой ячейки строки или столбца
Б.7. Форматирование
Изменение высоты строк
Установите указатель мыши на нижней границе заголовка строки, чтобы он изменил свою
форму, как показано на рис Б 29 После этого двойной щелчок приведет к автоматическому
подбору высоты строки в соответствии с содержимым ячеек данной строки Этот же результат
можно получить, выбрав команду Формат^ Строка^Автоподбор высоты Также можно пе-
ретащить нижнюю границу, чтобы вручную установить требуемую высоту строки
Рис. Б.29. Установка высоты строки
Чтобы изменить высоту нескольких строк, выделите их, а затем перетащите одну из
нижних границ выделенных строк. В результате все выделенные строки будут иметь оди-
наковую высоту Другим способом установки высоты строк является команда Фор-
мат^Строка^Высота (см. рис Б.29) На экране появится диалоговое окно, в котором
надо ввести требуемую высоту строки (в пунктах). Ввод нуля приведет к сокрытию строк
(тот же результат, что и после выбора команды Формат^Строка^Скрыть). Команда
Формат^Строка^Отобразить выводит на экран ранее скрытые строки
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 949
Изменение ширины столбцов
Установите указатель мыши на границе заголовка строки так, чтобы он изменил свою
форму, как показано на рис. Б 30. После этого двойной щелчок приведет к автоматическому
подбору ширины в соответствии с содержимым ячеек данного столбца Этот же результат
можно получить, выбрав команду Формат^ Столбец^ Автоподбор ширины Также можно
перетащить разделитель столбцов, чтобы вручную установить требуемую ширину столбца
	А .4 в
1 ~2	
Рис. Б.ЗО. Установка ширины столбца
Для изменения ширины нескольких столбцов выделите их заголовки, затем перета-
щите один из разделителей выделенных столбцов. В результате все выделенные столбцы
будут иметь одинаковую ширину. Задать ширину столбцов также можно с помощью ко-
манды Формат^Столбец^Ширина (см рис. Б.ЗО). На экране появится диалоговое окно,
в котором в поле Ширина столбца следует ввести нужное значение ширины столбцов
(в символах). Ввод нуля приведет к сокрытию выделенных столбцов (то же самое про-
изойдет после выполнения команды Формат^СтолбецоСкрыть) Команда Формат^
СтолбецФОтобразить выводит на экран ранее скрытые столбцы.
Форматирование числовых значений
Выделите ячейку или диапазон ячеек и, чтобы применить один из часто используемых
числовых форматов, щелкните на одной из кнопок панели инструментов форматирования,
показанных на рис. Б.31. Две кнопки, расположенные справа, увеличивают и уменьшают
количество отображаемых дробных знаков. (Числовой формат никогда не изменяет
содержимое ячейки, а лишь изменяет внешний вид значения )
Рис. Б.31. Инструменты форма-
тирования числовых значений
Изменение шрифта
Выделите ячейку или диапазон ячеек и щелкните на одной из кнопок, представленной
на рис. Б.32. Чтобы установить полужирное начертание, курсив или подчеркивание, щелк-
ните на нужной кнопке. Шрифт и его размер выбирается из соответствующих списков.
I Arial Cyr	V 10	-K.’.-g |
Рис. Б.32. Изменение шрифта в ячейках
950 ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
Выравнивание
Чтобы задать тип выравнивания в ячейках, выделите ячейку или диапазон ячеек, а за-
тем щелкните на одной из кнопок панели инструментов форматирования, показанных на
рис Б 33
Рис. Б.ЗЗ. Инструменты выравнивания
Кнопка Объединить и поместить в центре (рис Б 34) объединяет выделенные ячейки
и помещает в центре объединенной ячейки содержимое левой ячейки Эта возможность часто
используется при оформлении заголовков Ее также можно применить для диапазонов,
содержащих несколько строк. Отменить объединение ячеек можно в диалоговом окне Формат
ячеек, которое описано ниже.
Е~	~	» 10 71 Ж Л Я »|g Ф X ОТ	.
В1	»	* д Модель прсгнсЭД’г.^°="-"'’° r>nvr.no
------------------------------- 1 •’.—I—-Т--------------------——Объединить и поместить е центре
Z - - а...........................................«3=2..4
| и д. , IH , дозирования дохода ,	П
Рис. Б.34. Применение инструмента Объединить и поместить
в центре
Границы ячеек
Выделите ячейку или диапазон ячеек, щелкните на стрелке, направленной вниз, рядом
с кнопкой Границы и в открывшейся палитре типов границ выберите необходимый тип
рамки (рис Б 35) Тип рамки, который использовался в последний раз, становится типом
по умолчанию и им можно воспользоваться, просто щелкнув на кнопке Границы.
IОбщая стоимость I
I
Рис. Б.35. Типы границ ячеек
Форматы ячеек
Диалоговое окно Формат ячеек (рис. Б 36) предоставляет больше возможностей по
форматированию, чем отдельные кнопки панели инструментов форматирования
Выделите ячейку или диапазон ячеек и выберите команду Формат^Ячейки или нажмите
<Ctrl+1 > Откроется диалоговое окно Формат ячеек, в котором выберите нужные опции,
затем щелкните на кнопке ОК
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 951
Рис. Б.36. Диалоговое окно Формат ячеек
При вводе длинных заголовков строк и столбцов лучше не разбивать их на фрагмен-
ты, а установить флажок опции Переносить по словам во вкладке Выравнивание диа-
логового окна Формат ячеек Там же можно задать тип выравнивания заголовков по вер-
тикали и горизонтали, как показано на рис Б 37 Можно не использовать опцию Пере-
носить по словам, а установить курсор в место, где должен быть перенос, а затем нажать
клавиши <Alt+Enter>
Прибыль
Доход Стоимость до уплаты
налогов
Прибыль
Доход Стоимость
уплаты
налогов
Рис. Б.37. Перенос по словам длинных заголовков
Также можно располагать текст в ячейках вертикально и объединять ячейки в верти-
кальном направлении (рис Б 38).
952
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
Доход
Рис. Б.38. Перенос текста и объединение ячеек в вертикальном направлении
Пользовательские форматы ячеек
В Excel можно определять собственные форматы, например, дробный денежный
формат, представленный на рис. Б 39. Значение в поле Образец вкладки Число диалого-
вого окна Формат ячеек позволяет увидеть, как выбранная ячейка будет выглядеть после
применения формата Можно в одном формате задавать разные форматы для положи-
тельных, отрицательных, нулевых и текстовых значений, при этом форматы для отдель-
ных типов значений разделяются точкой с запятой.
Рис. Б.39. Создание новых форматов
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 953
В частности, если применить к ячейке формат то содержимое ячейки будет
скрыто Можно также создавать условные форматы, когда в зависимости от значений,
содержащихся в ячейке, применяются разные форматы Альтернативой условных форма-
тов является команда Формат^Условное форматирование, которая предоставляет те
же возможности, но без непосредственного написания кодов форматов Более подробно
о создании собственных форматов можно узнать из справочной системы Excel.
Использование текста в форматах
Строку символов, заключенную в кавычки, можно вставить в пользовательский формат
Эти символы будут отображаться на экране вместе с другими элементами форматирования
В примере на рис Б 40 содержимое ячейки (число 50) будет отформатировано и выведено на
экран в виде <=$50,00 Такое форматирование часто используется для представления ограни-
чений в моделях Excel, которые оптимизируются с помощью средства Поиск решения
Рис. Б. 40. Пример текстового поля в формате ячейки
Формат по образцу
Выделите ячейку, которая отформатирована нужным образом, и щелкните на кнопке
Формат по образцу, расположенной на стандартной панели инструментов Затем выде-
лите диапазон ячеек, к нему сразу будет применен выбранный формат. Для многократ-
ного переноса формата дважды щелкните на кнопке Формат по образцу После того как
выбранный формат будет применен ко всем нужным ячейкам, опять щелкните на этой
кнопке или нажмите клавишу <Esc>.
954
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
Б.8. Массивы ячеек
В Excel массивом называется прямоугольный диапазон смежных ячеек на рабочем
листе Массивы записываются следующим образом- адрес верхней левой ячейки, двоето-
чие, после чего идет адрес нижней правой ячейки Например, Al ВЗ обозначает массив,
состоящий из ячеек Al, А2, АЗ, Bl, В2 и ВЗ. Многие функции Excel поддерживают мас-
сивы, у таких функции в качестве входных аргументов могут быть массивы, а результат
вычислении — число, записанное в одной ячейке Например, функция =СУММ(А1:ВЗ)
суммирует значения всех ячеек в диапазоне А1 ВЗ.
Функция СУММПРОИЗВ
Эта функция перемножает соответствующие значения ячеек заданных массивов, а за-
тем подсчитывает сумму произведений (рис Б 41). Синтаксис функции следующий:
=СУММПР0ИЗВ(массив1 ;массив2; . )
Здесь массив1 и массив2 — массивы, соответствующие ячейки которых перемножаются.
Массивы должны иметь одинаковую размерность, т.е число столбцов и строк в этих мас-
сивах должно совпадать, в противном случае функция возвращает значение ошибки
#ЗНАЧ' Например, на рис Б 41 Cl, С2, СЗ — стоимость единиц товара трех наименова-
нии, KI, К2, КЗ — количество проданных единиц соответствующего товара Общая
стоимость вычисляется как сумма произведений стоимости на количество для каждого
наименования товара Для обработки больших массивов более эффективно использовать
функцию СУММПРОИЗВ, чем писать вручную одну большую формулу, выполняющую
те же вычисления Отметим, что функция СУММПРОИЗВ рассматривает нечисловые
элементы массивов как нулевые
Рис. Б.41. Применение функции СУММПРОИЗВ
Функция ВПР
Функция ВПР (функция ГПР выполняет аналогичные действия) ищет в крайнем слева
столбце массива значение, совпадающее с заданным, и возвращает значение из указанного
столбца массива и той строки, где найдено совпадение Функция имеет следующий синтаксис
ВПР(искомое_значение,таблица;номер_столбца;просмотр),
где искомое_значение — вводимое значение, таблица — массив данных; номер_столбца —
номер столбца, из которого будет возвращено значение, просмотр — необязательный логиче-
ский аргумент если введено значение ЛОЖЬ, то аргумент искомое_значение должен точно
соответствовать значению из первого столбца массива Если значение аргумента просмотр не
определено, то по умолчанию оно считается равным ИСТИНА — это значит, что точного соот-
ветствия не требуется В этом случае значения в первом столбце массива должны быть упоря-
дочены по возрастанию
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 955
Ha рис. Б.42 представлены данные о средней сумме страховки на автомобиль в боль-
ших и малых городах в зависимости от возраста водителей Диапазону B3D7 присвоено
имя Таблица
2	Возраст
3	16
4	18
5'	21
е	25
7	60
Город (более 1 млн )
$714
$630
$441
$420
$462
Город (менее 1 млн )
$630
$588
$420
$420
$462
Рис. Б. 42. Пример применения функции ВПР
По данным, приведенным на рис Б.42, получим следующие значения функции
ВПР(16,Таблица;3) равно 630, поскольку 16-летние водители в малых городах платят
страховку в размере $630
ВПР(23;Таблица,2) равно 441. В данном случае функция возвратит значение $441 для
любых значений параметра искомое_значение в диапазоне от 31 до 24 99999)
ВПР(65,Таблица;3) равняется 462 При любом значении аргумента искомое_значение,
равного или превышающего 60, в данном примере будет возвращено значение 462
ВПР(15,Таблица,2) вернет значение ошибки #Н/Д, так как число I5 меньше любого
значения из столбца В.
ВПР(23,Таблица,2,ЛОЖЬ) также вернет значение ошибки #Н/Д вследствие того, что
значение аргумента просмотр равно ЛОЖЬ — это значит, что значение аргумента искомое_
значение должно точно соответствовать значению из столбца В
Формулы массивов: результат в одной ячейке
Как говорилось ранее, функции могут использовать в качестве аргументов массивы
Но на практике этого бывает недостаточно Предположим, что вместо формулы
=СУММ(А1 ВЗ), которая суммирует значения в шести ячейках, нужно написать формулу,
вычисляющую сумму квадратов значений в этих ячейках По “логике” подходит формула
=СУММ(А1 ВЗЛ2), но она не будет работать, и Excel вернет значение ошибки #ЗНАЧ',
поскольку промежуточная операция возведения в степень не разрешена для аргументов-
массивов Но если объявить эту формулу как формулу массива, то такая конструкция бу-
дет правильной С помощью формул массивов можно работать с массивами, как с про-
стым одиночным значением
Чтобы указать, что данная формула является формулой массива, надо ввести формулу
обычным образом и по окончанию ввода нажать комбинацию клавиш <Ctrl+Shift+Enter>
Excel автоматически добавит фигурные скобки вокруг формулы — это наглядное отли-
чие формулы массива от обычной формулы В приведенном выше примере сумму
квадратов элементов массива можно правильно вычислить, используя формулу масси-
ва {=СУММ(А1 ВЗЛ2)}.
Еще раз подчеркнем, что, завершив создание или редактирование формулы массива,
вы должны нажать комбинацию клавиш <Ctrl+Shift+Enter>. Не вводите фигурные скоб-
ки вручную.
956 ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
Формулы массивов: результат в диапазоне ячеек
Формулы массивов можно использовать для вычисления не одного, а целого массива
значений Обычно результат вычисления формулы массива можно получить, копируя
одну формулу во все ячейки массива, но формулы массивов требуют меньше памяти, вы-
числяются быстрее, а также их проще использовать, особенно в больших моделях.
Для ввода формулы массива в диапазон ячеек 1) выделите диапазон ячеек, каждая из ко-
торых получит одно значение из вычисленного массива результатов, 2) введите формулу, 3)
нажмите комбинацию клавиш <Ctrl+Shift+Enter>, чтобы указать, что введенная формула
является формулой массива Excel применит эту формулу ко всем выделенным целевым
ячейкам, используя соответствующие значения из входного диапазона ячеек, если он был
введен Например, на рис Б 43 был выделен диапазон В5Е5, после этого была введена
формула, в которой в качестве аргументов использовались два диапазона ячеек. Эта форму-
ла вычисляет разности между соответствующими значениями ячеек этих диапазонов.
Рис. Б.43. Пример ввода формулы массива
Для завершения ввода формулы нажмите комбинацию клавиш <Ctrl+Shift+Enter>, по-
сле этого Excel вычислит значение для каждой ячейки диапазона В5 Е5, как показано на
рис Б 44 Если в данном случае (при выделенном диапазоне ячеек) для завершения ввода
формулы будет нажата клавиша <Enter>, то будет выведено сообщение об ошибке. Кроме
того, нельзя по отдельности редактировать содержимое ячеек диапазона, в который введена
формула массива, можно редактировать только общую формулу массива всего диапазона.
Рис. Б.44. Результат вычисления формулы массива
Пример формулы массива
Предположим, что для некой модели необходимо вычесть из каждой ячейки в нижней
строке значение соответствующей ячейки из правого столбца (рис. Б.45).
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 957
Рис. Б. 45. Пример массивов
ю‘
Ч "Г И5
35
40
22 24. 39’ 42
Один из вариантов решения этой задачи — сделать горизонтальную копию правого
столбца (либо вертикальную копию строки, для этого надо скопировать столбец и далее
перед вставкой копии в рабочий лист с помощью команды Правка^Специальная
вставка открыть одноименное диалоговое окно, установив в нем опцию Транспониро-
вать) Затем можно выполнить попарные вычитания из ячеек, которые находятся в двух
строках, либо с помощью обычных формул, либо с помощью одной формулы массива
Можно обойтись без копирования, выполнив все вычисления за одну операцию с по-
мощью формулы массива Для этого сначала выделите ячейки, в которых будет храниться
результат, например, В19.Е19 Затем в первую ячейку В19 введите формулу, показанную на
рис Б 46 После ввода формулы нажмите комбинацию клавиш <Ctrl+Shift+Enter>, и, как
показано на рис Б 47, во всех выделенных ячейках будет вычислен результат
	ЧоТ 15 35 40j
I	22	24	39	42	
|=В18 Е18-ТРАНСП(Г1' - ’Л	-	.	
Рис. Б. 46. Формула массива
Рис. Б.47. Результат, вычисленным по формуле массива
Б.9. Поименованные ячейки
Создание имен для диапазонов ячеек
Сначала выделите ячейку или диапазон ячеек, которые надо назвать, затем выберите
команду Вставка^Имя^Присвоить, после чего откроется диалоговое окно Присвоение
имени (рис. Б.48).
958 ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
Рис. Б. 48. Диалоговое окно Присвоение имени
Введите имя ячейки или выделенного диапазона в текстовое поле Имя В именах не
разрешается использовать пробелы (а также символы пунктуации), поэтому такие сим-
волы часто заменяются подчеркиванием (см рис Б 48) Кроме того, присвоить имя так-
же можно через поле Имя, расположенное в строке формул Выделите ячейку или диапа-
зон ячеек и введите имя прямо в поле Имя, как показано на рис. Б 49.
Рис. Б.49. Использование
поля Имя
Отметим, что имена в рабочей книге глобальны, поскольку каждое имя содержит
также имя рабочего листа, которое предшествует ссылке на ячейку (или диапазон) По-
этому в формулах можно использовать имена для ссылок на ячейки, которые содержатся
в других рабочих листах
Автоматическое создание имен
Если столбец (или строка) содержат текст, который можно использовать в качестве
имен для смежных ячеек, то можно создать имена для этих ячеек автоматически, выпол-
нив команду Вставка^Имя^Создать Откроется диалоговое окно Создать имена
(рис. Б 50) Убедитесь, что Excel правильно определила столбец, на основе которого сле-
дует создавать имена В созданных именах Excel автоматически заменит все пробелы
и другие недопустимые символы символами подчеркивания.
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 959
Рис. Б. 50. Диалоговое окно Создать имена
Использование имен в формулах
Использование имен сделает формулы более понятными, а также поможет при доку-
ментировании моделей Чтобы использовать ранее определенное имя в формуле, можно
ввести его вручную или выбрать из раскрывающегося списка поля Имя (рис Б 51)
Рис. Б.51. Использование имен в формулах
Создание списка имен
Для документирования модели можно вставить в рабочий лист список всех определенных
имен, а также ссылки на ячейки, которым эти имена присвоены. Для этого выделите ячейку
в пустой области рабочего листа, затем выберите команду Вставка^ИмяФВставить В поя-
вившемся диалоговом окне Вставка имени щелкните на кнопке Все имена (рис Б 52)
Рис. Б. 52. Диалоговое окно Вставка имени
960 ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
В результате список со всеми определенными именами ячеек и диапазонов будет
вставлен в активный рабочий лист, как показано на рис. Б.53. Отметим, что здесь перед
каждой ссылкой на ячейку или диапазон пишется имя рабочего листа.
I Доход	,=Лист111$В$3:$Е$3
Размер_налога =Лист111$В$5:$Е$5
Стоимость	=Лист111$В$4:$Е$4
Рис. Б. 53. Список всех имен рабочей книги
Б.10. Мастера Excel
Мастер функций
Щелкнув на кнопке Вставить функцию, расположенной в строке формул, можно вы-
брать нужную функцию и получить о ней детальную информацию (рис. Б.54).
Рис. Б. 54. Вставка функции Excel
После щелчка на кнопке ОК выбранная функция будет выведена в строку формул,
а также появится палитра формул Excel (рис. Б 55). На этой палитре представлены все
аргументы (обязательные аргументы выделены жирным шрифтом), которые необходимо
задать для работы функции.
Мастер диаграмм
Наилучший способ создания диаграмм в Excel — использовать мастер диаграмм, первое
окно которого показано на рис. Б.56. Сначала выделите диапазон ячеек, в котором хранятся
данные для построения диаграммы, затем щелкните на кнопке Мастер диаграмм стан-
дартной панели инструментов. Далее следуйте указаниям мастера диаграмм, который со-
стоит из четырех диалоговых окон. Если возникают затруднения, щелкните на кнопке
Справка, чтобы получить дополнительную информацию о каждом из диалоговых окон.
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 961
Рис. Б.56. Стандартные типы диаграмм
Создание диаграмм с помощью мастера значительно упрощается, если в первом столбце
(когда ряды данных расположены по столбцам) или в первой строке (когда ряды данных
расположены по строкам) содержатся данные, которые будут откладываться по оси X
962 ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
Отметим, что точечный тип диаграммы, показанный на рис. Б.56, является одним из
немногих, в котором по оси X также откладываются значения. В большинстве других ти-
пов диаграмм значения откладываются по оси Y, а по оси X откладываются равные про-
межутки независимо от значений Например, на рис. Б.57 слева построена диаграмма ти-
па “график”, а справа — точечная диаграмма для того же набора данных.
Мастер текстов
Вставка или импорт данных в Excel из других приложений (например, Word) часто
приводит к тому, что все данные помещаются в один столбец, что не соответствует струк-
туре импортируемых данных Чтобы разделить данные на несколько отдельных столбцов,
выделите столбец ячеек, в который вставлены импортируемые данные (рис. Б 58) Затем
выберите команду Данные^Текст по столбцам.
Рис. Б.58. Выделение данных для
мастера текстов
В первом диалоговом окне Мастер текстов укажите формат исходных данных (если
мастер предложил неправильный вариант), как показано на рис. Б.59 (Если столбцы ис-
ходных данных разделяются, например, запятыми или символами табуляции, то реко-
мендуется воспользоваться форматом С разделителями. В противном случае установите
переключатель в положение Фиксированной ширины — в большинстве случаев при дан-
ном формате исходных данных также можно добиться требуемых результатов )
ПРИЛОЖЕНИЕ Б Средства моделирования Excel 963
• ртов° * -I ’
Рис. Б.59. Первый шаг разбора текста с помощью мастера текстов
Во втором диалоговом окне (рис Б 60) выберите символ-разделитель Затем в третьем
диалоговом окне установите формат данных для каждого столбца
Рис. Б. 60. Второе диалоговое окно мастера текстов
Результат разбора текста по столбцам представлен на рис Б 61 Возможно, придется
подправить полученные данные вручную
964 ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
: Изделие 1	6	7	9
:Изделие 2	10:	11	5
Всего	16:	18	14
Рис. Б. 61. Результат рабо-
ты мастера текстов
Б.11. Другие часто используемые средства Excel
Сортировка
Для сортировки данных на рабочем листе можно использовать инструменты Сорти-
ровка по возрастанию и Сортировка по убыванию, находящиеся на стандартной панели
инструментов, и команду Данные^Сортировка Если выделен диапазон ячеек, то сорти-
ровка осуществляется по левому столбцу выделенного диапазона Если же была выделена
только одна ячейка, то вокруг активной ячейки автоматически выделяется прямоуголь-
ный диапазон непустых ячеек, а сортировка выполняется по столбцу, в котором находит-
ся активная ячейка. Диалоговое окно Сортировка диапазона (рис Б.62), открывающее-
ся по команде Данные^Сортировка, предоставляет значительно больше возможностей
для систематизации данных (в частности, возможность сортировать по нескольким
столбцам или строкам), чем простые инструменты Сортировка по возрастанию и Сор-
тировка по убыванию
Рис. Б. 62. Диалоговое окно Сорти-
ровка диапазона
Отображение формул
Чтобы отобразить и вывести на печать формулы, содержащиеся на рабочем листе, реко-
мендуется сначала сделать копию данного рабочего листа Для этого следует выбрать ко-
манду Правка^Переместить/скопировать лист. В результате появится диалоговое окно
Переместить или скопировать, показанное на рис. Б 63, где надо указать, что лист будет
копироваться (а не перемещаться), и определить местоположение копии в рабочей книге.
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 965
Рис. Б. 63. Копирование рабочего
листа
Перейдите на скопированный лист и выберите команду Сервис^Пареметры В от-
крывшемся диалоговом окне Параметры перейдите во вкладку Вид и, установив флажок
опции Формулы, щелкните на кнопке ОК. На рабочем листе в ячейках вместо значений
будут отображаться формулы, по которым эти значения подсчитаны (рис. Б.64) Далее,
если нужно, измените ширину столбцов или форматирование, чтобы было легче читать
формулы.
Рис. Б. 64. Формулы на рабочем листе
Проверка формул
Выделите ячейку или диапазон, содержащий формулы, затем выберите одну из команд
подменю Сервис=>3ависимости формул В результате на экране стрелками будут показа-
ны связи между ячейками (рис. Б.65), что очень удобно при документировании и отладке 1
Для отладки и проверки формул также полезна панель инструментов Зависимости, которая содержит
дополнительные инструменты — Прим ред
966 ПРИЛОЖЕНИЕ Б. Средства моделирования Excel
Рис. Б. 65. Проверка формул
Вставка данных из Excel в Word
Если в Excel скопировать в буфер диапазон ячеек, после чего в программе Microsoft
Word воспользоваться командой Вставить, то содержимое ячеек будет вставлено в виде
таблицы После этого можно редактировать содержимое любой ячейки. Если же диапа-
зон был скопирован с помощью команды Копировать рисунок, то он будет вставлен как
графический объект Содержание ячеек нельзя будет редактировать, но при этом его
можно будет масштабировать или “обрезать” изображение.
Специальная вставка
Команда Правка^Специальная вставка позволяет выбрать способ вставки скопиро-
ванных данных, отличный от стандартного, выполняемого с помощью команды Вста-
вить Например, можно вставить только формулы, только значения или форматирование
и тд Также можно указать арифметическую операцию, которую при вставке следует
произвести между содержимым буфера обмена и содержимым ячеек, куда вставляется
скопированный диапазон. Для этого в диалоговом окне Специальная вставка (рис. Б.66)
следует установить нужный переключатель в секции Операция.
Если в диалоговом окне Специальная вставка установить флажок Транспонировать,
то в результате строки копируемого диапазона будут вставлены как столбцы, а столбцы —
как строки Если вы щелкните на кнопке Вставить связь (см рис Б.66), то вставленный
диапазон будет связан с первоначально копируемыми ячейками Изменения, внесенные
в эти ячейки, также отразятся во вставленных ячейках.
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 967
Рис. Б. 66. Диалоговое окно Специальная вставка
Вставка данных из Word в Excel
Если в буфере обмена содержатся данные, которые были вырезаны или скопированы
в Microsoft Word или аналогичном приложении, то в Excel диалоговое окно Специальная
вставка изменится в соответствии с данными, которые содержатся в буфере обмена,
и будет выглядеть так, как показано на рис Б 67 Установите переключатель Связать,
чтобы поддерживать “активную” связь с документом-источником. Выберите тип данных
Объект Документ Microsoft Word, чтобы в будущем можно было редактировать встав-
ленные данные с помощью средств программы Word Выберите тип Метафайл Windows,
чтобы вставить данные как 1рафический объект Но, как правило, выбирается тип Текст,
при этом скопированные данные будут вставлены в одну ичи несколько ячеек
Панель инструментов Рисование
Средства рисования часто используются при документировании моделей Эти средст-
ва расположены на отдельной панели инструментов Рисование Чтобы открыть ее,
щелкните на кнопке Рисование стандартной панели инструментов или выберите коман-
ду Вид^Панели инструментовФРисование
968
ПРИЛОЖЕНИЕ Б Средства моделирования Excel
Инструменты рисования Надпись и Стрелка часто используются для создания при-
мечаний в модели или же для представления основных формул (для этого из строки фор-
мул скопируйте формулу, а затем вставьте ее в текстовое поле объекта Надпись), как по-
казано на рис Б 68 Другие инструменты рисования можно использовать для создания
специальных визуальных эффектов или выносок.
Доход
Стоимость
Год 1	Год 2 Изменение
$1 234	$1 518'	23%
$567	$879	55%
| Быстрый рост Y f
стоимости | |=(E9-D9)/D9~~|
Рис. Б. 68. Применение инструментов рисования
Справочная система Excel
В Excel существует несколько способов получения справочной информации Во-
первых, это экранные подсказки — если навести указатель мыши на какой-либо элемент
окна Excel (прежде всего это относится к кнопкам панелей инструментов) и немного по-
дождать, то, как показано на рис Б 69, на экране появится название этого элемента
100%
!* .. ,
с - Справю Microsoft Excel (Fl)
Рис. Б.69. Экранная подсказка
После щелчка на кнопке Справка. Microsoft Excel (находится справа на стандартной па-
нели инструментов) на экране появится либо диалоговое окно справочной системы Excel
(рис Б 70). если у вас отключен помощник, либо сам помощник (рис Б 71), которому вы мо-
жете задать вопрос по интересующей вас теме Вопрос к справочной системе можно также за-
дать через поле ввода Задать вопрос, которое обычно находится справа в строке меню
После выполнения команды Справка^Что это такое? изменится указатель мыши
справа от стрелки появится знак вопроса Щелкните на каком-либо элементе окна и вы
получите краткое описание этого элемента.
Если отключен помощник, то доступ к справочной системе Excel можно получить не-
сколькими способами- щелкнув на кнопке Справка Microsoft Excel, выбрав команду
Справка^Справка: Microsoft Excel или нажав клавишу <F1>. После этих действий от-
крывается диалоговое окно Справка Microsoft Excel, которое имеет три вкладки. Содер-
жание, Мастер ответов и Указатель Перейдя во вкладку Указатель, можно найти нуж-
ный раздел справки по ключевым словам. В примере на рис Б 70 показан результат по-
иска по ключевому слову ЧПС Каждая тема справочной системы помимо документации
и примеров содержит много полезных пошаговых инструкций
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 969
□"и'ф	’' . ъ., ъ ,	*	'	">• > •
Мастер ответов «1 » 1. Введите ключе» Jl_±£q 2. Или выберите кл Microsoft Exes xlS	# баланс	. возврат  возвращать И J 3. Выберите раздет * Различия между» ЧИСТНЗ	Kj я	е Л Л -	-	чпе Ч.Ч **3 дисконтирования, а также стоимости будущих выплат (отрицательньи значения) и поступлений Синтаксис	, ЧПС^ставкаэмачение1,значение2, Значение 1, эначение2, ,.. — от 1 до 29 аргументов, представляющих расходы и доходы должны осуществляться в конце каждого периода. •	ЧПС использует порядок аргументов значение!, эмачение2, .. для определения порядка правильном порядке. ♦	Аргументы, которые являются числами пустыми ячейками, логическими значениями или ошибки или текстами, которые не могут быть преобразованы в числа, игнорируются •	Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, период до даты денежного взноса змачение/и заканчивается с последним денежным взносом в  списке. Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый к результату функции ЧПС, но не включать в список аргументов Для получения более
Рис. Б. 70. Окно справочной системы Excel
Рис. Б. 71. Помощник
Надстройки Excel
Возможности самой программы Excel можно расширить с помощью надстроек. Вы-
берите команду Сервис^Надстройки, откроется диалоговое окно Надстройки, через ко-
торое можно подключить новые надстройки к Excel (рис. Б.72) Вместе с Excel поставля-
ется ряд надстроек, среди которых Пакет анализа, которая содержит множество функ-
ций для статистических и инженерных расчетов; Мастер подстановок, помогающая при
создании формул для нахождения данных в списках; а также Поиск решения, которая
необходима для оптимизации моделей.
Наличие надстроек зависит от типа инсталляции программы Excel. Например, если
при инсталляции был выбран тип Стандартная, то надстройка Поиск решения устанав-
ливаться не будет. Если средство Поиск решения отсутствует в списке надстроек и в ме-
ню Сервис, то запустите программу инсталляции с установочного диска, затем установи-
те флажок напротив соответствующего компонента для его установки
Если при инсталляции Excel установлены файлы надстроек, то после установки
в диалоговом окне Надстройки флажков возле названий надстроек в меню Сервис поя-
вятся команды, вызывающие эти надстройки.
970 ПРИЛОЖЕНИЕ Б Средства моделирования Excel
Обзор... |
Автоматизация... |

-Пекк решения---------------------------------------
Инструмент для поиска решения уравнений и задач
оптимизации
Рис. Б. 72. Диалоговое окно Надстройки
Таблица подстановки с одним входом
Таблица подстановки с одним входом представляет собой диапазон ячеек, которые со-
держат результат вычислений по одной или нескоиьким формулам при подстановке раз-
личных значений одного параметра (Таблица подстановки с двумя входами описана в главе
2, раздел 2 4 ) В примере на рис Б 73 необходимо создать таблицу, в которой содержались
бы значения функций Доход и Размер налога за четвертый квартал в зависимости от зна-
чений параметра Темп роста На рис Б 74 показана структура таблицы подстановки Здесь
в ячейках В10 и С10 содержатся формулы =ЕЗ и =Е5 соответственно, которые ссылаются на
ячейки, содержащие формулы для вычисления функций Доход и Размер налога В табли-
це подстановки каждое значение темпа роста из столбца А будет подставлено во входную
ячейку С1 Результирующие значения будут заноситься в таблицу диапазона В11 С20
Квартал 1 Квартал 2 Квартал 3 Квартал 4
З'ЗДоход	$1234,00	$1 320 38	$1412,81	$1511,70
4 .Ctommoi	$740,40	$792 23	$847,68	$907,02
'5-. Размер	$493 60	$528 15	$565 12	$604 68
8
Рис. Б. 73. Модель, дчя которой создается таблица подстановки
ПРИЛОЖЕНИЕ Б. Средства моделирования Excel 971
Рис. Б. 74. Макет таблицы подстановки
с одним входом
Чтобы создать таблицу подстановки с одним входом в данном примере, выделите
диапазон ячеек А10 С20, который содержит строку с формулами (В10С10) и столбец со
значениями параметра для подстановки (А10 А20), затем выберите команду Данные^
Таблица подстановки, как показано на рис Б.75.
Рис. Б. 75. Выбор команды Данные ^Таблица подстановки
На экране появится диалоговое окно Таблица подстановки (рис. Б 76) Поскольку
значения для подстановки находятся в столбце, введите ссылку С1 в поле Подставлять
значения по строкам в, а второе поле оставьте пустым (при использовании таблицы под-
становки с двумя входами используются оба поля) Затем щелкните на кнопке ОК.
972 ПРИЛОЖЕНИЕ Б Средства моделирования Excel
<}
60%
Квартал 4
$1 511,70
$907,02
$604,68
-т~-в-> Г'-с > -ч ~Т—
J	Темп роста .....___7%]Стоимость
।	Квартал 1 Квартал 2 Квартал 3
$1 234,00	$1 320,38 $1 412,81
$740 40______$792 23
$493 60
4. | Доход
4 [Стоимость
5 । Размер налога
____________$847 68
$528,15	$565,12
Рис. Б. 76. Задание входной ячейки для таблицы подстановки с одним входом
На рис Б.77 показана созданная таблица. Данные из таблицы подстановки удобно
использовать для графического представления полученных результатов.
	Доход	Размер налога
Темп роста	$1 511 70	$604,68
5.0%	$1 428,51	$571,40
5 5%		$1'449'01	$579,61
6 0%	$1 469,71	$587,89
6,5%	$1 490,61	$596,24
7 0%'	$1 511,70		$604	68
7,5%	$1 532,99	$613,20
8,0%,	$1 554,48'	$621,79'
8 5%:	$1 576,17		$63047
9,0%	$1 598,07	$639,23
9,5%	$1 620,16'	$648,06
Рис. Б. 77. Результаты таблица под-
становки
Если бы значения параметра Темп роста первоначально были занесены в строку, а не
в столбец, то в диалоговом окне Таблица подстановки (рис Б.76) ссылку на ячейку С1
нужно было бы поместить в поле Подставлять значения по столбцам в.
Надстройка Поиск решения
В.1.	Установка надстройки Поиск решения
Компания Frontline Systems (http //www frontsys com) разработала несколько версий
программы поиска решении Solver1 для фирмы Microsoft, одна из которых поставляется
вместе с программой Excel Frontline Systems также разработала несколько расширенных
коммерческих про!рамм-оптимизаторов, в том числе надстройку Premium Edition Solver
for Education, которая содержится на компакт-диске, прилагаемом к этой книге Premium
Edition Solver — более расширенная версия программы поиска решении по сравнению
с Поиск решения — содержит несколько способов коррекции ошибок, что делает ее бо-
лее предпочтительной, чем Поиск решения
Для установки Premium Edition Solver for Education необходимо, чтобы надстройка
Поиск решения уже была инсталлирована Но надстройка Поиск решения не устанавли-
вается автоматически при инсталляции Microsoft Office или Excel Если после инсталля-
ции Excel в меню Сервис нет команды Поиск решения, необходимо выполнить команду
Сервис^ Надстройки и в открывшемся диалоговом окне Надстройки установить опцию
Поиск решения
Как только команда Поиск решения появится в меню Сервис, можно перейти к уста-
новке Premium Edition Solver for Education Файл SOLVPREM EXE содержит все файлы
этой надстройки в виде архива, и его запуск проведет вас через процесс установки
(Файлы Premium Edition Solver for Education, скопированные из другого компьютера, не
будут работать, необходим запуск именно программы SOLVPREM EXE ) Для удаления
Premium Edition Solver for Education запустите снова программу SOLVPREM EXE и вы-
берите опцию ее удаления После этого восстановится предыдущая версия надстройки
Поиск решения Работа с надстройкой Premium Edition Solver for Education кратко опи-
сана в главе 3, а также в 1лаве 7 при изложении эволюционных методов 2
В.2.	Введение
В диалоговых окнах надстройки Поиск решения используется несколько иная терми-
нология, отличающаяся от испочьзуемой в моделях оптимизации Различия в термино-
логии приведены в табл В 1
Надстройка Solver в русской версии Excel называется Поиск решения Далее мы предполагаем, что у чи-
тателя установлена русскоязычная версия Excel 2002 Поэтому все команды меню, названия диалоговых
окон и тому подобное будем приводить в соответствии с этой версией Excel — Прим ред
Установка надстройки Premium Edition Solver for Education в русской версии Excel заменяет русскоязычные
диалоговые окна надстройки Поиск решения англоязычными Но после ее уда 1ения русскоязычная надстрой-
ка Поиск решения восстанавливается корректно — Прим ред
974 ПРИЛОЖЕНИЕ В. Надстройка Поиск решения
Таблица В.1. Терминология, используемая в надстройке Поиск решения
Терминология моделей оптимизации	Терминология надстройки Поиск решения
Целевая функция Переменные решения Ограничения Левая часть ограничения Правая часть ограничения	Целевая ячейка Изменяемые ячейки Ограничения Ссылка на ячейку (в окне Добавление ограничения) Ограничение (в окне Добавление ограничения)
Ниже приведены четыре основных типа задач оптимизации, которые можно решить с по-
мощью средства Поиск решения Оптимизация при наличии ограничений — самый общий
тип задачи оптимизации, другие типы задач появляются при ограничениях специального вида
или их отсутствия Эти задачи могут решаться как задачи линейного программирования (тогда
Поиск решения использует симплекс-метод), так и как задачи нелинейного программирова-
ния (в этом случае Поиск решения использует метод приведенного градиента)
1.	Поиск допустимого решения. Если не задавать целевую ячейку (в поле ввода Уста-
новить целевую ячейку в диалоговом окне Поиск решения), то средство Поиск
решения остановится, найдя допустимое решение задачи, т е набор значений для
изменяемых ячеек, которые удовлетворяют всем ограничениям Если все функции
ограничении линейные, то установка флажка Линейная модель в диалоговом ок-
не Параметры поиска решения ускорит поиск допустимого решения
2.	Подбор параметров. Целевая ячейка не задается, указываются только ограничения
в виде равенств, либо задается конкретное значение для целевой ячейки без опреде-
ления каких-либо ограничений В первом случае выполняется поиск тех значений
изменяемых ячеек, которые удовлетворяют заданной системе ограничений, т е , по
сути, решается система уравнении, в которой неизвестными являются значения из-
меняемых ячеек (Если некоторые ограничения заданы в виде неравенств, Поиск
решения находит допустимое решение, определяемое заданной системой ограниче-
ний (см выше задачу 1)) Во втором случае (задано конкретное значение целевой
функции без указания ограничении) Поиск решения работает подобно средству Ex-
cel Подбор параметра, используя другой алгоритм поиска Кроме того, в отличие от
средства Подбор параметра, Поиск решения может проводить подбор нескольких
параметров, доставляющих заданное значение целевой функции
3.	Поиск безусловного оптимума — задача нахождения максимума или минимума целе-
вой функции при отсутствии ограничении Эта задача имеет смысл только в том слу-
чае, если целевая функция является нелинейной (по отношению к значениям из-
меняемых ячеек) В случае попытки поиска оптимума линейной целевой функции
(без задания ограничений) будет выводиться сообщение о неограниченном реше-
нии Если целевая функция имеет несколько максимумов или минимумов, то По-
иск решения находит один из них (локальный оптимум), который может не совпа-
дать с глобальным оптимумом Какой конкретно будет найден локальный опти-
мум, зависит от начальных значений изменяемых ячеек
4.	Поиск оптимума при наличии ограничений. Наиболее общей задачей является задача
условной оптимизации, когда заданы ограничения и адрес ячейки целевой функции,
которую необходимо максимизировать или минимизировать Если целевая функция
и все ограничения линейны, то это задача линейной оптимизации или линейного
программирования. Решение этой задачи будет найдено быстрее, надежнее и с более
ПРИЛОЖЕНИЕ В Надстройка Поиск решения 975
подробной дополнительной информацией, если в диалоговом окне Параметры по-
иска решения установлен флажок Линейная модель или при использовании над-
стройки Premium Edition Solver выбрана опция Standard Simplex LP В противном
случае Поиск решения использует метод приведенного градиента. В надстройке
Premium Edition Solver для решения задачи нелинейной оптимизации можно также
использовать оптимизатор Evolutionary Solver.
Если целевая функция имеет несколько оптимумов, которые удовлетворяют огра-
ничениям, то Поиск решения найдет один из них (т е. локальный оптимум), кото-
рый может не быть глобальным. Какой конкретно будет найден локальный опти-
мум, зависит от начальных значений изменяемых ячеек.
В задачах 3 и 4, приведенных выше, при наличии нескольких оптимумов, чтобы найти
глобальный оптимум, необходимо повторно решить задачу с различными начальными
значениями изменяемых ячеек либо применить оптимизатор Evolutionary Solver над-
стройки Premium Edition Solver Для больших моделей перебор начальных значений из-
меняемых ячеек или использование оптимизатора Evolutionary Solver не всегда приводят
к глобальному оптимуму Поэтому для нелинейных моделей всегда есть риск, что гло-
бальные оптимумы не будут найдены.
В.З.	Общие проблемы применения средства Поиск
решения
Надстройка Поиск решения — нетривиальная программа, выполняющая сложные вы-
числения по табличной модели, расположенной на рабочем листе Excel В процессе фор-
мирования модели, при задании параметров в диалоговых окнах средства Поиск решения,
в процедурах оптимизации и при интерпретации результатов поиска существует множество
возможностей для возникновения ошибок и других проблем Кроме того, как оптимизатор
надстройки Поиск решения, так и оптимизатор Evolutionary Solver надстройки Premium
Edition Solver могут не найти глобальный оптимум даже для корректно сформированной
модели, если целевая функция имеет несколько оптимумов. Причем зачастую Поиск реше-
ния не выдает сообщений об ошибках и проблемах, возникающих в процессе оптимизации.
Но даже когда выводятся сообщения об ошибках, они мало информативны. Поэтому при-
веденные ниже меры предосторожности помогут избежать многих часов, проводимых
в тщетной попытке решить возникшие в процессе оптимизации проблемы
1.	Большинство проблем, возникающих в процессе оптимизации табличных моделей,
связано не с самим средством Поиск решения, а с неправильной постановкой зада-
чи. Запись на бумаге символической (математической) модели помогает разрешить
многие противоречия в постановке задачи Точное отображение символической мо-
дели в табличную модель на рабочем листе Excel облегчает понимание табличной
модели и упрощает ее документирование В конечном счете это приводит к умень-
шению времени, затрачиваемого на разработку и отладку табличной модели
2.	Вторым источником проблем является противоречивость ограничений модели,
что приводит к отсутствию допустимых решений. Необходима тщательная про-
верка знаков неравенств во всех ограничениях (не использован ли знак ко-
гда требовалось использовать “>=”). Следует избегать ограничений в виде равен-
ства, если это не продиктовано моделируемой ситуацией Во многих случаях огра-
ничение в виде равенства можно представить в виде ограничения-неравенства, что
позволит средству Поиск решения найти оптимальное решение
976 ПРИЛОЖЕНИЕ В. Надстройка Поиск решения
3.	Одна из обычных ошибок разработчика модели состоит в том, что он забывает об
ограничениях неотрицательности для значений изменяемых ячеек. Ограничения
неотрицательности задаются путем установки опции Неотрицательные значения
в диалоговом окне Параметры поиска решений или с помощью явного задания
ограничений неотрицательности в диалоговом окне Добавление ограничения. Но
не нужно использовать оба варианта задания таких ограничений. Несмотря на то
что они эквивалентны, применение обоих вариантов создает избыточные ограни-
чения, которые могут стать причиной того, что Поиск решения не будет сходиться
к оптимуму для некоторых типов задач
4.	Плохо масштабированные модели часто вызывают преждевременную остановку
средства Поиск решения или приводят к выводу малопонятных сообщений об
ошибках. Особенно чувствительны к масштабированию нелинейные модели. Сле-
дует избегать ситуаций, когда некоторые переменные принимают значения, отли-
чающиеся по величине на пять или более порядков от значений других перемен-
ных Такие ситуации приводят к накоплению ошибок округления в процессе вы-
числений, что, в свою очередь, может привести к неверному решению или к
ложным сообщениям об ошибках Не трудно изменить масштаб представления
некоторых данных для уменьшения разброса в значениях переменных, при этом
не потеряется ни универсальность модели, ни точность вычислений Например,
объемы продукции можно измерять не в килограммах, а в тоннах (уменьшая мас-
штаб числовых значений этих показателей в тысячу раз, т.е. на три порядка), фи-
нансовые суммы можно записывать не в долларах, а в миллионах долларов
(уменьшая масштаб финансовых показателей в миллион раз, т.е. на шесть поряд-
ков), и т п Автоматическое изменение масштаба в средстве Поиск решения
(опция Автоматическое масштабирование диалогового окна Параметры поиска
решения) может оказаться недостаточным для избежания этой проблемы, осо-
бенно в нелинейных моделях. (Попутно отметим, что в версиях Excel, предшест-
вующих Excel 97, опция Автоматическое масштабирование была недоступна, ес-
ли был установлен флажок опции Линейная модель, т.е. в этих версиях Excel ав-
томасштабирование применялось только для нелинейных моделей.)
5.	Наконец, использование негладких функций, таких как функция Excel ЕСЛИ,
в формулах вычисления целевой функции или функций ограничений, вероятно,
спровоцирует проблемы в работе средства Поиск решения. Функции, подобные
функции ЕСЛИ, не только делают модель нелинейной, но и нарушают целостность
области допустимых решений или вносят разрывы во множество возможных значе-
ний целевой функции Это, в свою очередь, влияет на оценку частных производных,
вычисляемых средством Поиск решения в процессе поиска оптимума. Ни один из-
вестный алгоритм оптимизации не гарантирует в таких условиях нахождения опти-
мума Если модель требует использования негладких функций, необходимо приме-
нить оптимизатор Evolutionary Solver надстройки Premium Edition Solver. Однако,
как отмечалось в разделе 7.8, Evolutionary Solver на самом деле не является оптимиза-
тором Это мощный механизм поиска решений, близких к оптимальному, но кото-
рый не гарантирует нахождения оптимального или даже “хорошего” решения.
В.4.	Замечания о работе средства Поиск решения
• Известно, что некоторые ошибки в самой программе Excel 2000 (не в надстройке
Поиск решения) при использовании средства Поиск решения порождают ложные
сообщения об ошибках. Одна из документально подтвержденных причин этих
ПРИЛОЖЕНИЕ В Надстройка Поиск решения 977
ложных ошибок состоит в использовании объединенных ячеек в рабочих листах
Excel. Советуем не объединять ячейки в тех табличных моделях, которые будут оп-
тимизироваться с помощью средства Поиск решения.
Для нелинейных моделей, включая те, которые должны оптимизироваться с по-
мощью Evolutionary Solver, начальные значения переменных решения берутся из
ячеек, определяемых как изменяемые ячейки. Для линейных моделей значения
в изменяемых ячейках игнорируются — средство Поиск решения использует от-
дельную процедуру для нахождения начального набора допустимых значений
Помещать формулы в правую часть ограничений в диалоговых окнах Добавление
ограничения и Изменение ограничения не желательно, хотя Поиск решения это
допускает Рекомендуется вместо формул использовать ссылки на ячейки рабочего
листа, содержащие формулы Но если ячейки, задающие значения правых частей ог-
раничений, содержат формулы, это может вызвать проблемы интерпретации данных
в отчете по устойчивости, когда эти формулы будут пересчитываться во время опти-
мизации модели. В практике моделирования все формулы, вычисляющие ограниче-
ния, принято помещать в левую часть неравенств, оставляя в правой части только
константу В разделе 4 12 рассмотрен пример, поясняющий эту проблему
Ограничения целочисленности и двоичности могут налагаться только на перемен-
ные решения (содержащиеся в изменяемых ячейках). Для ввода таких ограничений
достаточно в диалоговых окнах Добавление ограничения или Изменения ограни-
чения указать адреса изменяемых ячеек и выбрать опцию цел или двоич в раскры-
вающихся списках этих окон
Параметр Относительная погрешность в диалоговом окне Параметры поиска реше-
ния задает точность выполнения ограничения. Ограничение считается выполненным
в виде равенства, если модуль разности между значениями правой и левой частей огра-
ничения не выходит за интервал, определяемый параметром Относительная погреш-
ность. Для хорошо масштабированных моделей (если сомневаетесь, установите фла-
жок Автоматическое масштабирование) можно оставить без изменения значение
этого параметра, заданного по умолчанию Считается, что значение параметра Относи-
тельная погрешность должно быть в пределах от 0,0001 до 0,000001
Не следует задавать для каких-либо значений несколько различных простых усло-
вий, ограничивающих эти значения сверху или снизу, поскольку в этом случае
Поиск решения будет использовать только одно из этих ограничений, причем не-
возможно сказать заранее, какое из них Например, если введены ограничения
В2:В10<=8 и А5.С5<=3, значит, тем самым для ячейки В5 заданы два простых не-
равенства В5<=8 и В5<=3 Поиск решения использует одно из этих ограничений,
и определить, какое из них будет использовано, невозможно.
При оптимизации моделей целочисленного программирования средство Поиск
решения проводит большой объем вычислений. Чтобы быстрее найти решение,
в диалоговом окне Параметры поиска решения по умолчанию следует задать зна-
чение допустимого отклонения, равное 5%. В этом случае процесс оптимизации
завершится, если относительная разность между последовательными значениями
целевой функции будет меньше 5%. Если необходимо получить точное решение,
то следует ввести в поле Допустимое отклонение значение 0, но нужно помнить,
что при этом может значительно увеличиться время оптимизации модели.
Из опыта работы в Excel 2002 могу сделать заключение, что эта ошибка в данной версии Excel исправлена
Средство Поиск решения корректно работает с объединенными ячейками — Прим ред
978
ПРИЛОЖЕНИЕ В Надстройка Поиск решения
В отчетах, генерируемых средством Поиск решения, при отображении данных на-
следуется форматирование соответствующих ячеек табличной модели Excel. Часто
унаследованный формат не дает достаточной точности для отображения данных
Например, в отчете могут выводиться нулевые значения, хотя на самом деле это
дробные числа, меньше 0,5 Следует проверять форматы всех “подозрительных”
значении в отчетах, генерируемых средством Поиск решения
В нелинейных моделях изменение в диалоговом окне Параметры поиска решения оп-
ции Прямые разности (задаваемой по умолчанию) на Центральные разности в неко-
торых случаях может привести к некорректным результатам в отчете по устойчивости
Не пытайтесь оптимизировать модель, если рабочий лист или рабочая книга, со-
держащие модель, защищены паролем.
В некоторых ранних версиях Excel нельзя использовать более 16 несмежных диа-
пазонов изменяемых ячеек.
В.5.	Параметры средства Поиск решений
Для большинства небольших моделей очень редко возникает необходимость в изме-
нении установленных по умолчанию параметров диалоговых окон (исключение состав-
ляют параметры Неотрицательные значения и Автоматическое масштабирование)
Тем не менее значения параметров средства Поиск решения требуют изменения при не-
которых обстоятельствах, описанных ниже (Общая информация, касающаяся установки
параметров диалоговых окон Поиск решения и Параметры поиска решения, для линей-
ных моделей дается в разделе 3 4, а для нелинейных моделей — в разделе 7 6 )
Параметр Максимальное время
Этот параметр диалогового окна Параметры поиска решения задает максимальное
количество времени (в секундах), которое отводится средству Поиск решения для нахож-
дения решения (значение по умолчанию равно 100 с) По достижению этого времени по-
является диалоговое окно Текущее состояние поиска решения, предлагающее два вари-
анта дальнейших действий остановка или продолжение работы средства Поиск реше-
ния Замечание Поиск решения можно остановить, нажав клавишу <Esc>.
Параметр Предельное число итераций
Этот параметр определяет максимальное количество итераций, которые Поиск реше-
ния может выполнить в процессе одной оптимизации (по умолчанию равно 100). Для це-
лочисленных моделей данный параметр задает максимальное количество итераций для
каждой подзадачи Когда Поиск решения выполнит заданное количество итераций, поя-
вится диалоговое окно Текущее состояние поиска решения, предлагающее два варианта
дальнейших действии остановка или продолжение работы средства Поиск решения.
Параметр Относительная погрешность
Параметр Относительная погрешность в диалоговом окне Параметры поиска ре-
шения задает точность выполнения ограничения Ограничение считается выполненным
в виде равенства, если модуль разности между значениями правой и левой частями огра-
ничения не выходит за интервал, определяемым параметром Относительная погреш-
ность Для хорошо масштабированных моделей можно оставить без изменения значение
этого параметра, заданного по умолчанию Считается, что значение параметра Относи-
тельная погрешность должно быть в пределах от 0,0001 до 0,000001.
ПРИЛОЖЕНИЕ В Надстройка Поиск решения 979
Параметр Допустимое отклонение
Этот параметр используется только при решении задач целочисленного программиро-
вания для ускорения вычислений Для ускоренного нахождения решения в диалоговом ок-
не Параметры поиска решения по умолчанию задается значение допустимою отклонения,
равное 5% В этом случае процесс оптимизации завершится, если относительная разность
между последовательными значениями целевой функции будет меньше 5% Если необхо-
димо получить точное решение, то следует ввести в поле Допустимое отклонение значение
О, но нужно помнить, что при этом может значительно увеличиться время оптимизации мо-
дели В надстройке Premium Edition Solver for Education параметр Tolerance (Допустимое
отклонение) находится в диалоговом окне Integer Options (Целочисленные параметры)
Параметр Сходимость
Этот параметр применяется при оптимизации нелинейных моделей и описывается
ниже и в разделе 7 6
Параметр Неотрицательные значения
Установка этого параметра эквивалентна добавлению ограничения неотрицательности,
означающего, что значения всех изменяемых ячеек должны быть больше или равны 0 Но не
нужно одновременно устанавливать этот параметр и задавать в явном виде ограничения неот-
рицательности Несмотря на то что оба варианта задания таких ограничений эквивалентны,
их совместное использование создает избыточные ограничения, которые могут стать причи-
ной того, что Поиск решения не будет сходиться к оптимуму для некоторых типов задач
Параметр Автоматическое масштабирование
При установке флажка этой опции Поиск решения производит масштабирование значе-
ний целевой функции и функции ограничения с целью уменьшить разность между возмож-
ными минимальными и максимальными значениями. Плохо масштабированные модели час-
то вызывают преждевременную остановку средства Поиск решения или приводят к выводу
сообщений об ошибках Особенно чувствительны к масштабированию нелинейные модели
Следует избегать ситуации, когда некоторые переменные принимают значения, отличающие-
ся по величине на пять или более порядков от значений других переменных Такие ситуации
приводят к накоплению ошибок округления в процессе оптимизации модели, что, в свою оче-
редь, может привести к неверному решению или к ложным сообщениям об ошибках Следует
изменить масштаб представления некоторых данных для уменьшения разброса в значениях
переменных, при этом не потеряется ни универсальность модели, ни точность вычислении
Автоматического изменения масштаба в средстве Поиск решения (опция Автоматическое
масштабирование в диалоговом окне Параметры поиска решения) может оказаться недос-
таточно, особенно в нелинейных моделях
Параметр Показывать результаты итераций
Если установить этот флажок, то средство Поиск решения будет останавливаться по-
сле выполнения каждой итерации и будет выводиться диалоговое окно Текущее состоя-
ние поиска решения с полученным на данный момент решением Щелчок на кнопках
Продолжить или Стоп соответственно продолжает или останавливает работу средства
Поиск решения Щелчок на кнопке Сохранить сценарий позволяет сохранить текущее
решение в поименованном сценарии.
980 ПРИЛОЖЕНИЕ В Надстройка Поиск решения
Параметры Оценки, Разности и Метод поиска
Эти параметры (описанные в разделе 7 6) управляют процессом оптимизации нели-
нейных моделей
Некоторые параметры диалоговых окон надстройки Premium
Edition Solver
Параметр Max Subproblems
Параметр Max Subproblems (Максимальное количество подзадач) в диалоговом окне
Integer Options (Целочисленные параметры) задает максимальное количество подзадач,
решаемых в методе ветвей и границ Если это число превышается, программа Premium Edi-
tion Solver останавливает работу и открывает диалоговое окно Show Trial Solution (Текущее
состояние поиска решения), предлагая остановить вычисления или продолжить их
Параметр Max Integer Solutions
Параметр Max Integer Solutions (Максимальное количество целочисленных решений)
в диалоговом окне Integer Options определяет максимальное количество вариантов цело-
численных решении, рассматриваемых в методе ветвей и границ Если это число превы-
шается, программа Premium Edition Solver останавливает работу и открывает диалоговое
окно Show Тrial Solution, предлагая остановить вычисления или продолжить их.
Параметр Solve Without Integer Constraints
Установка в диалоговом окне Integer Options опции Solve Without Integer Constraints
(Решать без ограничений целочисленности) означает, что нужно игнорировать ограни-
чения целочисленности для оптимизации модели. При отладке целочисленных моделей
проще установить эту опцию, чем удалять ограничения целочисленности и затем после
отладки добавлять их вновь
Параметр Convergence (оптимизатор Evolutionary Solver)
Если почти все решения в популяции имеют похожие значения (степень “похожести”
задается параметром Convergence (Сходимость)), оптимизатор Evolutionary Solver оста-
навливается и отображает сообщение Solver has converged to the current solution (Поиск
свелся к текущему решению) Если есть подозрение, что Evolutionary Solver останавлива-
ется преждевременно, необходимо уменьшить значение этого параметра Кроме того,
можно увеличить скорость мутации (параметр Mutation Rate) или размер популяции
(параметр Population Size).
Параметр Population Size (оптимизатор Evolutionary Solver)
Параметр Population Size (Размер популяции) устанавливает количество решений
в популяции, с которыми работает оптимизатор Evolutionary Solver Минимальный раз-
мер популяции равен 10, а максимальный — 200 Хорошим начальным значением этого
параметра является значение 100 (значение по умолчанию) или в 10 раз увеличенное ко-
личество переменных решения.
Параметр Mutation Rate (оптимизатор Evolutionary Solver)
Скорость мутации (параметр Mutation Rate) — это вероятность мутации решения,
создающего пробное решение, которое может стать новым решением. Увеличение этой
вероятности добавляет разнообразие в популяцию решений.
ПРИЛОЖЕНИЕ В Надстройка Поиск решения
981
Параметр Require Bounds On Variables (оптимизатор Evolutionary Solver)
При выбранной опции Require Bounds On Variables (Необходимы границы на пере-
менные) оптимизатор Evolutionary Solver выдаст сообщение об ошибке в том случае, если
какая-нибудь из переменных решения (содержащихся в изменяемых ячейках) не имеет
нижней или верхней границы, заданных в виде ограничения. Если удалить флажок этой
опции (по умолчанию он установлен), отсутствие границ для значений переменных реше-
ния может замедлить работу оптимизатора Evolutionary Solver.
Диалоговое окно Limit Options (оптимизатор Evolutionary Solver)
При щелчке на кнопке Limit Options (Параметры ограничений) открывается одноимен-
ное диалоговое окно. Оптимизатор Evolutionary Solver при решении задач целочисленного
программирования не использует метод ветвей и границ программы, однако, как и этот ме-
тод, оптимизатор Evolutionary Solver решает последовательность подзадач линейного про-
граммирования. В диалоговом окне Limit Options задаются параметры, управляющие про-
цессом решения задач целочисленного программирования.
В.6.	Сообщения средства Поиск решения
При остановке средства Поиск решения в изменяемые ячейки рабочего листа записы-
ваются результаты полученного решения, и затем Excel пересчитывает формулы рабочего
листа, на которые влияют изменяемые ячейки. Одновременно появляется диалоговое окно
Результаты поиска решения с сообщением о причине остановки процесса оптимизации
Появление диалогового окна Результаты поиска решения не обязательно означает, что
средство Поиск решения нашло оптимальное решение — это только означает, что законче-
на процедура оптимизации. Должно появиться окно Результаты поиска решения с сооб-
щением о том, что решение найдено, только тогда можно говорить о том, что оптимум, воз-
можно, найден. Повторим, что завершение процесса оптимизации не означает, что опти-
мальное решение найдено, и даже если появится одно из сообщений о том, что решение
найдено, это не обязательно означает, что найдено оптимальное решение. Например, ли-
нейная модель может иметь альтернативные оптимумы, но средством Поиск решения будет
найден только один из возможных оптимумов, либо для нелинейной модели процесс опти-
мизации может закончиться на локальном оптимуме вместо глобального.
После завершения работы средства Поиск решения в диалоговом окне Результаты
поиска решения можно щелкнуть на кнопке ОК, тем самым сохранив полученные зна-
чения изменяемых ячеек, или щелкнуть на кнопке Отмена, восстановив содержимое
ячеек, которое было в них перед запуском средства Поиск решения. В следующих двух
разделах приведены некоторые сообщения, генерируемые средством Поиск решения.
В.7.	Сообщения об успешном завершении работы
Решение найдено. Все ограничения и условия оптимальности выполнены
Это самое желанное сообщение о завершении работы средства Поиск решения Оно
означает, что все ограничения удовлетворены с точностью, установленной в диалоговом
окне Параметры поиска решения, и найдено оптимальное (максимальное или мини-
мальное) значение целевой функции. Для модели целочисленного программирования
оно означает, что найденное оптимальное значение находится в пределах допустимого
отклонения от истинного оптимума.
982 ПРИЛОЖЕНИЕ В Надстройка Поиск решения
Для линеинои модели (когда в диалоговом окне Параметры поиска решения уста-
новлен флажок Линейная модель), это сообщение означает, что средство Поиск реше-
ния нашло оптимальное решение Но возможно, что есть другие решения с тем же самым
значением целевой функции, т е другие альтернативные оптимальные решения. В таком
случае существует бесконечное количество альтернативных оптимальных решений
(каждое с различными значениями переменных решения), но все они порождают то же
самое оптимальное значение целевой функции и удовлетворяют ограничениям.
Если решение не вырождено и модель линейна, то о существовании альтернативных
оптимальных решении сигнализируют нулевые значения в столбцах Допустимое увели-
чение или Допустимое уменьшение для некоторых переменных решения в отчете по ус-
тойчивости, генерируемом средством Поиск решения. Кроме этого, в отчете по устойчи-
вости нет другой информации об альтернативных оптимальных решениях. Необходим
повторный запуск средства Поиск решения с немного отличающимися значениями пе-
ременных решения для нахождения другого оптимума
Для нелинейной модели (в диалоговом окне Параметры поиска решения не установ-
лен флажок Линейная модель) это сообщение означает, что средство Поиск решения
нашло локальное оптимальное решение Возможны другие наборы значений переменных
решения, которые приводят к тем же самым (альтернативные оптимумы) или лучшим
(другие локальные оптимумы) значениям целевой функции. Из отчетов средства Поиск
решения невозможно узнать, является решение локальным или глобальным оптимумом
и есть ли альтернативные оптимумы Процесс многократной оптимизации модели с по-
мощью некоторой систематической стратегии перебора начальных значений переменных
решения — это единственный способ обнаружить другие оптимумы и, в конечном счете,
глобальный оптимум Однако для больших моделей такой подход непрактичен. Таким
образом, всегда есть риск, что глобальный оптимум не будет обнаружен
Даже если известно, что задача имеет единственный оптимум, на близость получен-
ного решения к истинному влияют установленные в диалоговом окне Параметры поиска
решения параметры (например, значение параметра Относительная погрешность), вид
нелинейной целевой функции и нелинейных ограничений и начальные значения пере-
менных решения, скорость сходимости решения к оптимуму, а также параметры процес-
сора, на котором выполняются вычисления.
Поиск свелся к текущему решению. Все ограничения выполнены
Это сообщение может появиться только для нелинейных моделей. Поиск решения пре-
кращается, поскольку значения целевой функции за N последних итераций изменяются очень
медленно, со скоростью ниже заданной скорости сходимости В версиях, предшествующих
Excel 97, значения N и скорости сходимости задавались внутри надстройки Поиск решения, и
пользователь не мог на них повлиять Начиная с версии Excel 97, в диалоговом окне Парамет-
ры поиска решения появилось поле Сходимость для задания скорости сходимости, но значе-
ние N по-прежнему недоступно (косвенные данные показывают, что 7V равно 5) Уменьшение
значения параметра Сходимость, равного по умолчанию 0,0001, до 0,00001 предоставляет
возможность продолжить поиск оптимального решения, если получено данное сообщение.
В.8.	Сообщения о неудачном завершении работы
Поиск не может улучшить текущее решение. Все ограничения выполнены
Для линейных моделей это сообщение не должно выводиться. Оно редко появляется
для нелинейных моделей и означает, что, хотя оптимальное решение не было найдено,
Поиск решения не может найти набор значений изменяемых ячеек лучше, чем отобра-
ПРИЛОЖЕНИЕ В Надстройка Поиск решения 983
жаемые на рабочем листе. Одной из причин этого может быть то, что модель вырождена,
и решения циклически повторяются. Если появилось это сообщение, необходимо прове-
рить, не являются ли некоторые ограничения в модели избыточными Например, избы-
точные ограничения появляются при явном задании ограничений неотрицательности
и установке флажка Неотрицательные значения в диалоговом окне Параметры поиска
решения Если присутствует такая избыточность, то, удалив избыточные ограничения,
можно исключить вырождение и устранить зацикливание поиска
При использовании оптимизатора Evolutionary Solver надстройки Premium Edition
Solver подобное сообщение появляется часто и означает, что оптимизатор не может най-
ти нового улучшенного решения Поскольку оптимизатор Evolutionary Solver не обладает
критерием оптимальности, он обычно останавливается с сообщением Solver converged
to the current solution (Поиск свелся к текущему решению) или с сообщением Solver
cannot improve the current solution (Поиск не может улучшить текущее решение)
Средство не может найти подходящего решения
Средство Поиск решения не смогло найти набор значении изменяемых ячеек, которые
удовлетворяли бы всем ограничениям в пределах точности, задаваемой параметром Отно-
сительное отклонение диалогового окна Параметры поиска решения Это сообщение
обычно появляется тогда, когда ограничения модели противоречивы Причиной появления
этого сообщения для нелинейных моделей может быть то, что процедура поиска не может
найти допустимое решение вблизи начальных значений изменяемых ячеек В этом случае
нужно ввести другие значения в изменяемые ячейки и повторно запустить Поиск решения
При поиске решения обнаружено ошибочное значение в целевой ячейке
или в ячейке ограничения
При последнем пересчете формул модели в ячейках рабочего листа обнаружены
ошибки, такие как #ДЕП/0( или ЙЧИСЛО1 В этих условиях Поиск решения останавлива-
ет свою работу Найдите ячейку, содержащую ошибку, и исправьте формулу Можно
также добавить ограничения, исключающие значения, при которых возникают ошибки
Поиск остановлен по требованию пользователя
Процесс решения прерван нажатием клавиши <Esc> и щелчком на кнопке Стоп в диало-
говом окне Текущее состояние поиска решения после остановки средства Поиск решения
Условия для линейной модели не выполняются
В диалоговом окне Параметры поиска решения установлен флажок Линейная модель,
но расчеты, выполняемые средством Поиск решения, не согласуются с линейной моделью
В этой ситуации следует либо пересмотреть логику модели, чтобы определить и устранить
источник нелинейности, либо принять нелинейную формулировку модели и отказаться от
линейной оптимизации Это сообщение может также появиться при оптимизации плохо
масштабированных моделей Установите флажок опции Автоматическое масштабирова-
ние в диалоговом окне Параметры поиска решения и повторите запуск Поиск решения
Поиск остановлен (истекло заданное на поиск время) и Поиск остановлен
(достигнуто максимальное число итераций)
Истекло время, отведенное на процесс оптимизации, или выполнено максимальное
количество итераций (параметры Максимальное время и Предельное число итераций
в диалоговом окне Параметры поиска решения), но достичь оптимального решения
не удалось При появлении этих сообщений можно увеличить значение указанных пара-
984
ПРИЛОЖЕНИЕ В, Надстройка Поиск решения
метров, но сначала необходимо исследовать текущие решения и найти причину длитель-
ного процесса вычислений, быть может, это большой разброс возможных значений пе-
ременных решения (плохо масштабированная модель).
Значения целевой ячейки не сходятся
Значения целевой функции неограниченно возрастают (или убывают), даже если все ог-
раничения выполняются. Наиболее вероятной причиной появления такого сообщения яв-
ляются пропущенные ограничения. Проверьте, так это и нет ли других логических ошибок,
которые делают “неработающими” некоторые ограничения. Для нелинейной модели, воз-
можно, была неправильно определена формула для вычисления целевой функции.
Не поставлена задача для поиска решения
В диалоговом окне Поиск решения пропущена необходимая информация. Например,
не были заданы изменяемые ячейки или не определена целевая ячейка.
Мало памяти для решения задачи
Это сообщение появляется, когда Поиск решения определяет, что для оптимизации
модели недостаточно памяти. Часто это сообщение появляется в тех случаях, когда в Ex-
cel открыто слишком много рабочих книг или в дополнение к Excel открыто много дру-
гих приложений Попробуйте закрыть рабочие книги и приложения, не имеющие отно-
шения к решаемой задаче.
Другой экземпляр Microsoft Excel использует SOLVER.DLL
Надстройку Поиск решения не могут одновременно использовать несколько экземпля-
ров программы Excel. Это сообщение появляется, если в данной рабочей книге вы пытае-
тесь запустить средство Поиск решения, используемое в другой рабочей книге. Надо подо-
ждать, пока Поиск решения закончит свою работу. Но если это сообщение появляется то-
гда, когда открыта одна рабочая книга, значит, необходимо перезагрузить компьютер,
поскольку в этом случае, скорее всего, проблемы возникли в операционной системе
В.9.	Загрузка и сохранение параметров поиска
Обычно табличная модель содержит только одну спецификацию параметров поиска,
используемых в процессе оптимизации надстройкой Поиск решения, которая хранится
в виде скрытых переменных вместе с рабочим листом. Тем не менее спецификации па-
раметров поиска можно также сохранить в явном виде на рабочем листе и впоследствии
повторно использовать с помощью кнопок Сохранить модель и Загрузить модель, на-
ходящихся в диалоговом окне Параметры поиска решения Сохраняется и восстанавли-
вается информация, необходимая для осуществления поиска: адреса изменяемых ячеек,
ограничения, адрес ячейки с целевой функцией и параметры, установленные в диалого-
вом окне Параметры поиска решения.
В.10.	Отчеты надстроек Поиск решения и Premium Edition
Solver
Средство Поиск решения создает несколько типов отчетов, которые сохраняются на
новых рабочих листах в активной рабочей книге. Поскольку отчеты находятся на рабочих
листах, их можно редактировать и копировать так же, как и любую другую информацию,
содержащуюся на рабочем листе. Кроме того, на ячейки отчета можно ссылаться в фор-
мулах или использовать их для создания диаграмм.
ПРИЛОЖЕНИЕ В. Надстройка Поиск решения	985
В отчетах форматирование ячеек, содержащих данные, наследуется от соответствую-
щих ячеек табличной модели. Часто унаследованный формат дает недостаточную точ-
ность отображения данных Например, данные могут быть представлены в виде чисел О
или 1, хотя в действительности они имеют дробные значения, такие как 0,3 или 1,48 со-
ответственно Во избежание неверного истолкования данных отчетов, вызванного недос-
таточной точностью форматов чисел, переформатируйте отчет или, по крайней мере, по-
местите табличный курсор на ячейку с данными, чтобы увидеть в строке формул точное
значение, содержащееся в этой ячейке
В большинстве отчетов имена переменных в столбце Имя создаются путем соедине-
ния первой текстовой ячейки слева (если таковая имеется) и первой текстовой ячейки
выше изменяемой ячейки, содержащей эту переменную Структура табличной модели,
содержащая текстовые заголовки столбцов и строк (как рекомендовано в главе 3), делает
имена переменных в отчетах средства Поиск решения информативными и понятными
Диалоговое окно Результаты поиска решения
При любом завершении работы средства Поиск решения (в результате нахождения
оптимального решения или вследствие какой-либо ошибки) на экране появляется диа-
логовое окно Результаты поиска решений Чтобы выбрать один или несколько отчетов,
перечисленных в окне списка Тип отчета, щелкните на названии отчета Если работа
средства Поиск решения закончилась из-за ошибки или была прервана, то названия от-
четов в списке Тип отчета будут не доступны.
Затем можно выбрать опцию Сохранить найденное решение или Восстановить исход-
ные значения, а также сохранить значения переменных решения в поименованном сценарии,
щелкнув на кнопке Сохранить сценарий Щелчок на кнопке Отмена отменяет создание от-
четов Отчеты (на отдельных рабочих листах) создаются после щелчка на кнопке ОК
Отчет по результатам
В этом отчете приводятся исходные и оптимальные значения переменных решения
и целевой функции, а также показывается, какие ограничения являются связывающими
(лимитирующими)
Отчет по пределам
Этот отчет представляет ограниченный вариант отчета по устойчивости Здесь показаны
наименьшее и наибольшее значения, которые может принимать каждая переменная решения
при удовлетворении ограничений и при постоянстве значений всех остальных переменных
Отчет по устойчивости
Этот отчет дает основную информацию для анализа чувствительности линейных и не-
линейных моделей. Этот анализ показывает, насколько чувствительно оптимальное ре-
шение к небольшим изменениям параметров модели, при этом предполагается, что зна-
чения всех параметров, за исключением одного, остаются неизменными
Отчет содержит две таблицы Изменяемые ячейки и Ограничения В линейных моделях
в таблице Изменяемые ячейки для каждой переменной решения приводятся ее значение,
нормированная стоимость, целевой коэффициент, допустимое увеличение и допустимое
уменьшение Нормированная стоимость показывает, на сколько изменится значение целе-
вой функции при изменении на единицу значения переменной Этот показатель будет от-
личным о г нуля только тогда, когда значение переменной равно ее верхнему или нижнему
предельному допустимому значению (и модель является невырожденной без альтернатив-
986 ПРИЛОЖЕНИЕ В. Надстройка Поиск решения
ных оптимальных решений). Числа в столбцах Допустимое увеличение и Допустимое
уменьшение показывают, на сколько можно изменить целевой коэффициент (т е коэф-
фициент при данной переменной в формуле целевой функции), не меняя текущего опти-
мальною решения Для нелинейных моделей в таблице Изменяемые ячейки приводятся
только результирующее значение переменной решения и нормированный градиент, кото-
рый обозначает то же, что и нормированная стоимость в отчете для линейных моделей
Для линейных моделей в таблице Ограничения для каждого ограничения приводятся
результирующее значение левой части (функции ограничения), теневая цена, значение
правой части, допустимое увеличение и допустимое уменьшение В нелинейных моделях
в этой таблице отображаются только результирующее значение левой части ограничения
и множитель Лагранжа (аналог теневой цены) Простые верхние и нижние ограничения,
налагаемые на переменные решения, в таблице Ограничения не отображаются, поскольку
обрабатываются средством Поиск решения иначе, чем остальные неравенства (более под-
робно это описывается в разделе 4 12) Теневая цена и множитель Лагранжа отличны от ну-
ля только тогда, когда данное ограничение в оптимальном решении является лимитирую-
щим (и решение не вырождено) Они показывают, на сколько изменится значение целевой
функции при изменении на единицу значения правой части этого ограничения Для линей-
ных моделей теневая цена остается постоянной в диапазоне, заданном значениями допус-
тимого увеличения и допустимого уменьшения Множители Лагранжа являются частными
производными, т.е мгновенными скоростями изменения целевой функции, поэтому для
них невозможно рассчитать интервал, в котором они бы принимали постоянные значения
В случае вырожденности моделей анализ отчета по устойчивости имеет свои особен-
ности и требует особой осторожности.
Отчет Feasibility Report надстройки Premium Edition Solver
Этот отчет создается в тех случаях, когда оптимизационные методы линейного или
нелинейного программирования не могут найти допустимого решения В отчете Feasibil-
ity (Допустимость) указаны ограничения, из-за которых, возможно, не были найдены до-
пустимые решения Анализируются ограничения и простые границы переменных по-
средством их исключения из модели до тех пор, пока не будет найдено наименьшее под-
множество ограничений, которое порождает пустую область допустимых решений Для
больших моделей выполнение такого анализа может занять значительное время Тем не
менее этот отчет предоставляет полезную диагностическую информацию
Отчет Linearity Report надстройки Premium Edition Solver
Создается только в тех случаях, когда при оптимизации линейной модели выдается со-
общение The linearity conditions required by this Solver engine are not satisfied (Условия
линейности не выполняются) Отчет Linearity (Линейность) помогает найти и удалить не-
линейные зависимости в табличной модели В этом отчете приводится список, состоящий
из целевой функции, всех переменных решения и всех ограничений с указанием того, яв-
ляются ли они линейными (целевая функция и ограничения), и входят ли переменные ре-
шения в модель линейно или нелинейно
Отчет Population Report надстройки Premium Edition Solver
В отчете Population (Популяция), доступном только при использовании оптимизатора
Evolutionary Solver, приводится совокупность решений, порождаемых во время поиска
оптимального решения. В этом отчете для каждой переменной и каждого ограничения
показано лучшее найденное значение, среднее значение и среднеквадратичное отклоне-
ние значений, а также максимальное и минимальное значения
Приложение
Ответы к задачам с нечетными
номерами
Глава 2
• j ' /	.’А'.’	; В J С 1 О ; Е i.' F f G ; н
1	~fsimon Pi* Co. - Модель недельной прибыли
•^йЗпеременные решения: Цена пирога должна быть в пределах от $ 5,00 идо $ 11.00
ШШена пирога ~	| $4,00 | $8,75 J $9,00 ; $9,25	$9.50	$9 75 | $12,00 |
ЯлЯ Не верно*..Не верно!
 ।	, F /	I	 Н .. ~ ~Т
2	, ;5	и__________________________________________
3	J 9.5	112	~~	]
4 =ЕСЛИ(ИЛИ(РЗ<$Р$2.РЗ»$Н$2)."Не верно!":"")=ЕС'лИ(ИЛИ(НЗ<$Т$2:НЗ>$Н$21'"Не верно!":"’!
-Е_1______________________________._____:_______________L_________________________:___,
1) 1825 штук, 2) около 1330 штук
а $180 000
б Рекомендуемая цена составляет $25,25 Прибыль практически не зависит от цены при се
малых колебаниях (±5% от $25,25) и весьма чувствительна при се больших изменениях От
ношение прибыль/количество клиентов максимально при цене примерно $27 50, но при
этом прибыль снижается почти на 17% относительно наибольшего возможного значения
в Оптимальное количество клиентов составляет примерно 33 000 Прибыль нс чувствительна к
изменению количества клиентов, если это изменение не превышает ±15% от 33 000
988 ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами
Глава 3
31	Зс4</1 е5/2
3 3 Максимальная прибыль составит $7200
3 5 Максимальный годовой доход составит $12 750
3 7 Максимальная прибыль составит $82,50
3 9 Следует закупить 80 фунтов удобрений при минимальной стоимости $6,55
3 11 Минимальное время производства равно 23 587,5
3 13 Максимальная прибыль составит $880 000
3 15 Максимальная прибыль — $46 000,30
3 17 Максимальная прибыль составит $3 501,25
3 19 Минимальное число матросов — 2 000
3 21 Стоимость минимальна, если занято 131,5 официантов
3 23 Максимальная прибыль составит $201 556
3 25 Минимальные транспортные расходы равны $3 300
3 27 Минимальные затраты равны $1 746 250
3 29 Минимальная стоимость производства равна $13 600
Глава 4
4 1 Обозначим через А — количество усилителей, Р — количество предусилителей Ограниче-
ние на время сборки 12А + 4Р < 60 Ограничение на время проверки качества 4Л + 8Р < 40
ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами 989
а А = 4, Р - 3 b Оптимальное значение целевой функции = 10/f + 5Р'= S55
с Лимитирующими являются ограничения на время сборки и время проверки качества
d Нелимитирующие ограничения А < 6 (резерв = 2), Р < 4 (резерв = 1)
Нет
Сделает модель недопустимой
а х, = 3, х2 = 1,5, значение целевой функции = 4,5 b х/ = 0, х2 =3 с Существуют четыре
угловые точки (0, 0), (4, 0), (3, 1,5) и (0, 3)
990 ПРИЛОЖЕНИЕ Г Ответы к задачам с нечетными номерами
4 13 ах, = 6,67, х,’= 2,67, значение целевой функции = 30,67 b Первое ограничение имеет резерв
18,67, для второго ограничения резерв равен 0, третье ограничение имеет превышение 0
4 15 а л,’= 1,091, х2’ = 3,64, значение целевой функции = 12,73 b Лимитирующими являются
второе и третье ограничения, нелимитирующие — первое и четвертое с Первое ограниче-
ние имеет превышение 7,091, четвертое ограничение имеет резерв 12,55, остальные огра-
ничения имеют нулевые резервы d 4 е (х,‘ = 1,091, х2’ = 3,64), (х,‘ = 2,67, х2' = 1,67)
ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами 991
4 17
4 19
4 21
4 23
4 25
4 27
4 29
431
4 33
4 35
4 37
4 39
4 41
4 43
а Е = 118,4, F = 152,6, значение целевой функции = 223,684 b Третье ограничение с -
18 496 d 0 1599 е 1667
а Новое решение С' = 140, Л/ = 40 b Новое оптимальное значение целевой функции ран
но 8920
Поскольку прибыльность стульев М возрастает, это провоцирует увеличение их произвол
ства Но, так как ресурсы для производства ограничены, увеличение производства ctjjIlcb
Л/возможно только при уменьшении количества произведенных стульев С
а х,’ = 2, х2' = 0, значение целевой функции = 60 b Надо увеличить коэффициент при пс
ременной х2 в формуле целевой функции до значения 15 с 2 решения- (х, = 2, х = 0)
и (х,‘ = 1, х2’ = 2) d Увеличить можно на любую величину, уменьшить — на 2 е Любое из
менение приведет к изменению оптимального решения / Первое ограничение лимити-
рующее, второе — нелимитируюшее g Приведет к новому решению (х/ = 0,333, х2 = 2 67)
й Оптимальное решение не изменится
а Первое неравенство более сильное b Точка (2, I) удовлетворяет обоим неравенствам
с Точка (3, 0) удовлетворяет второму неравенству и не удовлетворяет первому
Второе ограничение
Больше, ослабление
Увеличить, неизменной, сделать меньше
Нет, при изменении каких-либо параметров модели это ограничение может стать
“неизлишним”
Нет
Теневая цена нелимитирующего ограничения всегда равна нулю В общем случае юневая
цена лимитирующего ограничения отлична от нуля, но если решение вырождено теневая
цена лимитирующего ограничения может быть равной нулю
Можно увеличить на 72 Минимальное значение — 400
Первое ограничение Нет
Следует напечатать 120 000 экземпляров LinksLetter, Ragged Edge не печатать Обшая стой
мость печати составит $6000
992 ПРИЛОЖЕНИЕ Г Ответы к задачам с нечетными номерами
4 47	а Уменьшится на величину 6x10 = 60 b 90 с Увеличится на величину 50x6 = 300
4 49	а Множественные оптимумы Одно из решений С'=130, Л/= 60 Ь Значение целевой
функции = 130x80 + 60x40
4 51 а Оптимальное решение не изменится Значение целевой функции возрастет на величину
50x0,037 =1,85 b Поскольку решение не вырождено, появится альтернативный оптимум,
где используется больше руды с месторождения 3 с Новое оптимальное значение целевой
функции = 511,11 - 118,269x0,037 = 506,735
4 53 а =В2-СУММПРОИЗВ(ВЗ В5 В11 B13J/60-B6 b 7680/60 = 128 ч для станков 1 и 2,
4608/60 = 76,8 ч для станка 3, теневые цены измеряются в долларах в минуту с 60x0,011 =
66 центов d 51,38 на фунт
4 55 Эти значения допустимого уменьшения связаны с разными ограничениями с ограничени-
ем на длинные штифты в первом случае (см рис 4 10) и с ограничением на прочные сиде-
нья во втором случае (см рис 4 14)
Глава 5
+2( 1
ПРИЛОЖЕНИЕ Г Ответы к задачам с нечетными номерами 993
-Х2,+Х,4=О,
Х21 + Х24 + Х25 ~
х36 = 8,
-Х,4-Х24 + Х47 = -1,
-Х25 - Х„5 + Х;7 = О,
-хз6-х65 = О,
-Х,7 - Х,9 = —9
5 5	Кратчайший путь из узла 1 в узел 7 “стоит” 20 единиц
5 7	Кратчайший путь из узла 1 в узел 8 “стоит” 9 единиц
5 9 а 5, 4 и 10 соответственно
b 8, 6 и 11 соответственно
с Минимальная стоимость перевозок равна 2000
5 11 Максимальный поток из узла 1 в узел 7 — 12 единиц
5 13 Модель назначений является частным случаем транспортной модели (см раздел 5 4), кото-
рая, в свою очередь, является частным случаем модели перевозок (см раздел 5 10)
5 15 Максимальный поток из узла 1 в узел 7 равен 22 единицы
5 17 Минимальные затраты на производство в течение 4-х месяцев составят S36 000
5 19	Минимальные транспортные расходы составят S17 800
5 21	Минимальные затраты — $ 150 340
5 23 Минимальные расходы составят S40 500
5 25 Минимальная стоимость назначения равна S68
5 27 Максимальный объем продаж составит $320 000
5 29 Минимальное время выполнения заданий составляет 99 мин Альтернативных решений нет
Глава 6
6 1 а Максимизировать А + ЗС
при ограничениях А < 7,
4С <22,
2Л + ЗС< 19,
А, С> 0 и целые
b А =,25, С = 5,5 с А = 2, С = 5 d А= 1, С =5 Да, является допустимым е $1
6 3	Нижняя граница
6 5	Верхняя граница
6 7 Решение задачи Щ1П занимает примерно в пять раз больше времени, чем решение задачи
ЛП Оптимальное значение целевой функции задачи ЦЛП на $0,24 меньше оптимального
значения целевой функции задачи ЛП
994 ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами
6 11 Введем переменные х,— сумма вложений в акции i, у, = 1, если покупаются акции i,
и у, = 0 в противном случае Формулировка модели
20
максимизировать £>;х,
при ограничениях
fx, <100000 ,
х, < 20000у„ t = 1, ,20,
х, >5000у„/ = 1, ,20,
у, = 0, 1, х > 0 для всех i
6 13 Минимальные затраты равны $35 400
6 15 Введем переменные у = 1, если сделаны инвестиции в проект I, и у, = 0 в противном случае
Формулировка задачи
максимизировать ^Ry,
при ограничениях
У5< 1 -уь
У5< 1 -У2,
Уб<2-у2-уз,
2у7 < Уз + 1 - Уз,
ХСу,<М ,
у, = 0 или 1,1=1, ,7
6 17 Минимальное значение величины Мах(Т1, Т2) равно 9
6 19 Минимальные затраты равны $5,4
6 21 а В, + Л2, + Л4| < 1 b В2 <Л|2 +ЛЯ + Л32. с А21 + Atl < В d Верно е Верно.
6 23 Минимальные суммарные затраты равны $201 050
Глава 7
7 1 а х = —7/8 b х =  с Данная функция вогнутая, поскольку ее вторая производная отри-
цательна для всехх
ПРИЛОЖЕНИЕ Г Ответы к задачам с нечетными номерами 995
Следует воспользоваться известным математическим фактом если функции в левой части
неравенств вида < вогнуты, а функции в левой части неравенств вида > выпуклы, то множе-
ство ограничений будет выпуклым В данном случае множество ограничений выпукло
Площадь поверхности минимальна при r= 1 и h = 2
а Минимальное значение целевой функции равно 26 b Значение целевой функции увеличится
примерно до 27 На самом деле минимальное значение целевой функции станет равным 37,8
7 11
7 13
7 15
7 17
7 19
7 21
7 23
7 25
7 27
7 29
7 31
7 33
7 35
7 37
7 39
Максимальная прибыль составит $4 024,99
Стационарная точка единственная, поэтому найденное решение будет глобальным
Множитель Лагранжа равен 0,03327
Оптимальный доход составляет $466,67
Возможное уменьшение составляет 75% - 35,64% = 39,36%
Максимизировать 0,0891Z + 0,213 Y+ 0,2346ZnpH ограничениях
0,00992^ + 0,0535 Y2 + 0,0864Z2 + 2x0,0114АТ+ 2xO,O12OAZ + 2x0,0508YZ< V,
X + Y+Z = 1,
Z, r,Z>0,Z r,Z< 75%
а Оптимальные доли трех видов акций равны соответственно 19,51%, 35,37% и 45,12%
Минимальная дисперсия равна 0,00922
b Да, как показывает этот пример Отрицательная ковариация между акциями X и Z
уменьшает дисперсию портфеля инвестиций
с Множитель Лагранжа для ограничения на ожидаемый минимальный доход равен 1,293
Поэтому возможно увеличение дисперсии портфеля на величину 0,01x1,293 = 0,1293 Фак-
тический рост дисперсии будет 0,0325 - 0,00922 = 0,02328
а 7000 Ь $420 с $1300 d $1720 е 183 720 f Более выгодны большие партии
Q' = 3020,76,	= 3,02
а $48 989,79 b 48,99 с 0,020 года = 5,10 дня
а $18 974 Ь 12,65 с 0,079 года
а 90 дюжин b 90 заказов в год с 0,011 года = 4 дня
a Q' = 12 000, ГСЗ = $121 800 b При скидке 0,5% ГСЗ = $121 432,50, при скидке 0,7% ГСЗ
= $121 754,25 с Заказ объема 20 000 при скидке 0,5%.
а 2'= 3600,// = 3,75 Продолжительность цикла составляет 80 дней b Максимальный за-
пас равен 900 галлонов с ЕПХ(£?*) = $22,50
a Q' = 1800 галлонов, ЕПХ(£?*) = $13 500, с См рисунок ниже d При р = 45 ЕПХ = $30,
при р = 60 ЕПХ = $45
Р
Максимум целевой функции равен 33,42
996 ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами
Глава 8
8 1 Надо начать выполнение задания 1П в первую неделю, а задания II во вторую, и/или начать вы-
полнение задания IX в пятую неделю, а задания VII в седьмую, и/или начать выполнение задания
IV в третью неделю и задания Ш в четвертую Всего существует 7 альтернативных оптимумов
8 3 На приведенном ниже рисунке (/,/) обозначает размещение отдела / в помещении j
8 5 а Назначения 4->А, 1->С, 5->В, 3->D, 2->Е Суммарные продажи составят 108
b Преобразованные данные представлены ниже
В	С	D	Е
Назначения 4-»А, 1 ->D, 3^>Е, 5->С, 2—>В Суммарные продажи составят 116
8 7 Задача целевого программирования записывается следующим образом
минимизировать
при ограничениях
8 9 Задача целевого программирования записывается следующим образом
минимизировать Wiut + w2u2 + w2u2
при ограничениях
20х, + 12х2<240,
12х, + 20х, <240,
х,+х2 + и, — v, = 120,
х„х2>0, и„ v,>0, * = 1, 2, 3.
ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами 997
8 11 а х,' = 40, х2’ - 40 b Следует найти решение х2, которое будет как можно ближе к значению
40, но превышать это значение х2 не может с Следует найти решение х2, которое будет как
можно ближе к значению 40, при этом х2 может превышать значение 40 d х, =0, х, =80
8 13 а х,‘ = 100, х2 = 0 b Первая цель достигается, при этом v,‘ = 20 с Вторая цель достигается
всегда Для третьей цели и3‘ = 20
998 ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами
8 15 а Всего вариантов 6' = 6х5х4хЗх2х1 - 720 b Последовательность работ D->C->A->F->E->B.
Полное время обработки составит 23 ч
Станок
С.но.2 . И ITI ГГ1 I , 1 , I I A I I . А . I , ,
О 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
8 17 а Смесь с минимальной ценой $65,75 состоит из 70% бентонита из месторождения А и по
15% из месторождений В и С b Минимальная цена составит $72,52
8 19 Последовательность работ 0—>2—>3—>1 —>4 Время переналадки составит 123 мин
8 23 Наиболее подходящей финансовой компанией является Little Bank.
8 25
Задание Станок 1 Станок 2
В	4	5
С	2	2
D	1	1
Е	5	3
F 3 4
Последовательность выполнения заданий	D—>F—>В—>Е—>А—>С Суммарное время обработ-
ки составит 20 ч
Станок 1
8 29 В соответствии с описанным алгоритмом следует поочередно закрыть 2, 4 и 5 склады или
открыть 1 и 3 склады Стоимость составит 142 Это решение лучше полученного ранее
8 31 a Regal = 0,777, Camry = 0,155, Accord = 0,069 b Вес цены = 0,179, вес надежности - 0,129,
вес скорости = 0,692 с Чарльз не был последователен при задании весов d Regal
8 33 а Следует открыть 5 торговых центров и 1 Интернет-магазин Доход составит 3,5 млн долл
b Следует открыть 2 супермаркета, 1 торговый центр и 1 Интернет-магазин Количество заня-
тых работников составит 415 человек с Следует открыть 2 супермаркета, 1 торговый центр и
1 Интернет-магазин Обе цели будут достигнуты
Глава 9
9 1 а 4 b 3 с 1
ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами 999
Состояния природы
а 4 b 4 с Критерий максимизации ожидаемого результата и критерий минимизации
ожидаемых потерь всегда приводят к одному и тому же решению
а Заключать правительственный контракт b Заключать правительственный контракт
d 0,4 е Заключать контракт на печать брошюр f Заключать правительственный контракт
g 1000 h Ожидаемое значение полной информации
а Заключать правительственный контракт 1000 b Нет с 0,73
d U(666,67) = 0,66 + 666,67 (0,73-0,66) = 0,71 е 0,66 f В общем случае - нет
Дошибка в оформленииЬпоздание) = 0,6, /’(виновата доставка!опоздание) = 0,4
9 11. а Оптимальная стратегия если прогноз “солнечно”, то провести выступление, если про-
гноз “дождь”, то отменить выступление b Ожидаемое значение дополнительной инфор-
мации - $6250 - $4750 = $1500
9 13 Р (повышенный риск1получил кредит) = 0,024
9 15 Оптимальная стратегия 1 Участвовать в тендере 2 Если контракт заключен, использовать
существующие мощности
9 17 а Строить 100 модулей b Строить 300 модулей с. Строить 200 модулей d Строить 200 мо-
дулей е $240 000
9 19 Шоссе 280
10ОО	ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами
921 а
b Следует выбрать производителя А.
9 23. а Покупать акции Q b Покупать акции Q с. Покупать акции IBM d Покупать акции Q
9 25 а Да, покупать Ь $100 000
9 27 а
Ь Скульптор должен выставить свое произведение на аукционе в Internet
9 29	а Следует выбрать препараты В и D Ь Следует выбрать препараты В и D
9 31	а £7(30) = 0,3(7(70) + 0,7(7(—30) = 0,3; £7(10) = 0,1(7(30) + 0,9(/(-30) = 0,1. Функция полез-
ности выпуклая, поэтому вы лицо, склонное к риску Ь Верхняя граница £7(50) =
0,5х[£7(30) + £7(70)] = 0,65 Нижняя граница £7(50) = £7(30) + 0,05х[(7(30) - (7( 10)]х20 = 0,5
с Верхняя граница (/(25)= £7(10) + О,О5х[£7(1О) - (/(7О)]х(25 - 10) = 0,25 Нижняя граница
(7(25) = МАХ(0,1 + 0,025х[£7( 10) - (7(-30)]х(25 - 10), 0,03 + 0,025х[(7(70) - (7(30)]х(25 - 30) =
МАХ(0,1375, 0,2125) = 0,2125
9 33 а = 0,225. b P(h\/2) = 0,44 с $188,50
9.35. а
Ь Нет Но если результат прогноза известен, то следует продать права кинокомпании, если
прогнозируется успех, и надо продавать права телекомпании, если прогнозируется неудача
с Ожидаемое значение дополнительной информации = (940 000 + 100 000) - 960 000 =
$80 000 Дженни может заплатить за прогноз не более $80 000
ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами 1001
1002 ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами
Ь Ожидаемое значение дополнительной информации = 20 — 7,38 = $12,62 с. $12,62
Глава 10
10 1 Компьютеризированные военные игры, военные учения, занятия боевой подготовкой
ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами 1003
Ь 4 = 40, С =30, BEST =1700
л = 50, С =30, BEST = 1900
10 5 Не верно Симплекс-метод гарантированно находит оптимальное решение
Событие			Случайное число	
Возрастание дохода			0,00 - 0,299	
Неизменный доход			0,30 - 0,799	
Уменьшение дохода			0,80 - 0,999	
Истинное значение ожидаемого дохода при объеме заказа 10 сковородок				
а	ь	С	d	е
Объем заказа	Спрос	Доход, долл.	Вероятность спроса	cxd
10	8	90	0,10	9,0
10	9	110	0,20	22,0
10	10	130	0,30	39,0
10	11	133	0,20	26,6
10	12	136	0,10	13,6
10	13	139	0,10	13,9
	Истинное значение ожидаемого дохода = $J24,1			
Среднее значение дохода, полученное в результате 500 испытаний имитационной модели,
может (и должно) быть различным на разных компьютерах, но не должно значительно от-
личаться от истинного значения ожидаемого дохода
1004	ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами
10 11	X	0	1	2	3	4	5 р(х,2)	0,135	0,271	0,270	0,180	0,09	0,036 Дх)	0,135	0,406	0,677	0,857	0,947	0,983
10 13	а Спрос	Относительная частота	Случайное число 40	4/50 =	0,08	0,00 - 0,0799 41	10/50	=	0,20	0,08 -0,2799 42	12/50	=	0,24	0,28 - 0,5199 43	9/50 =	0,18	0,52 -0,6999 44	8/50 =	0,16	0,70-0,8599 45	7/50 =	0,14	0,86 -0,9999 Ь Результаты имитации, если использовать только встроенные средства Excel Неделя	123456789	10 Случ число	0,97	0,02	0,80	0,66	0,96	0,55	0,50	0,29	0,58	0,51 Спрос	45	40	44	43	45	43	42	42	43	42 Дефицит	3	2	13	1	1 Излишек	2 Среднее значение дефицита = (3 + 2+1 + 3+1 + 1 )/10 = 1,1 Среднее значение излишка = 2/10 = 0,2 В результате имитации 100 недель с помощью Crystall Ball получим среднее значение де- фицита = 0,85 и среднее значение излишка = 0,34 Результаты вашей имитации могут от- личаться от приведенных с Ожидаемое значение дефицита = 0,18х(43 - 42) + 0,16х(44 - 42) + 0,14х(45 - 42) = 0,92 Ожидаемое значение излишка = 0,08х(40 - 42) + 0,20х(41 - 42) = 0,36
10 15	Максимизируют среднее значение ЧПС проекты 1, 4, 5 и 6, при этом среднее значение ЧПС равно $9343 Максимизируют 35% персентиль ЧПС проекты 1, 4, 5 и 6, при этом значение персентиля равно $8500 В данном случае оба набора проектов совпали, но это не обязательно в общем случае, по- скольку решения значительно зависят от начальных условий (в данном случае это стои- мость проектов, ЧПС, вероятности успеха и т д )
10 17	а Количество ремонтов	Относительная частота	Случайное число 5	3/30 = 0,10	0,00-0,099 6	8/30 = 0,267	0,10-0,367 7	9/30 = 0,30	0,368 -0,667 8	6/30 = 0,20	0,668 -0,867 9	4/30 = 0,133	0,868 -0,999 Ь Результаты имитации, если использовать только встроенные средства Excel Случайные числа 0,20 0,82	0,74 0,08	0,01	0,69 0,36	0,35	0,52	0,99 Число ремонтов 6885586679
ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами 1005
Среднее число ремонтов в неделю = (6 + 8+ +7 + 9)/10 = 6,8
После имитации 100 недель с помощью Crystall Ball получим среднее число ремонтов в не-
делю, равное 6,96
(Ваши случайные числа и результаты имитации могут отличаться от приведенных здесь )
10 19 а Вероятность, что женщина пожертвует $10, равна 0,85x0,8x0,4x0,7 =0,1904 Вероят-
ность, что женщина пожертвует $25, равна 0,85x0,8x0,4x0,3 =0,0816 Вероятность, что
мужчина пожертвует $10, равна 0,85x0,2x0,7x0,25 =0,02975 Вероятность, что мужчина
пожертвует $25, равна 0,85x0,2x0,7x0,75 = 0,08925 Ожидаемая сумма пожертвований от
посещения одного дома равна 10х(0,1904 + 0,02975) + 25х(О,О816 + 0,0925) = 6,47275 Ожи-
даемая сумма пожертвований от посещения 3 000 домов равна 6,47275x3000 = 19 418 25
b Пусть N — число испытаний, i — номер испытаний, a D — сумма пожертвований На
схеме RN обозначает случайное число
с Результаты имитации, если использовать только встроенные средства Excel, представле-
ны ниже
1006 ПРИЛОЖЕНИЕ Г Ответы к задачам с нечетными номерами
'i^'-'Сл. число	Событие  'Пожертвование-		
V	0 11 Никого нет дома	0
2	0,91 Дверь открывают 0,99 Мужчина 0,57 Пожертвование 0 28	25	25
3	0,61 Дверь открывают: 0,7 Женщина 0,33 Пожертвование 0 91	25	
4	0,67 Дверь открывают 0,97 Мужчина 0 61 Пожертвование 011	10	10
5	0.5 Дверь открывают 0,86 Мужчина 0,25.Пожертвование 06^	10	10
После 200 испытаний, выполненных с помощью Crystall Ball, получим среднее значение
пожертвований от посещения одного дома, равное $6,28 Средняя общая сумма пожертво-
ваний от посещения 3 000 домов равна 3000x6,28 = $18 840
d Результаты имитации, если использовать только встроенные средства Excel, показаны ниже
ПРИЛОЖЕНИЕ Г Ответы к задачам с нечетными номерами	1007
Общая сумма пожертвований (от посещения 5 домов) равна $70 Средняя общая сумма по-
жертвований от посещения 3 000 домов равна 70x3000/5 = $42 000
Общая сумма пожертвований (от посещения 10 домов) равна $85 Средняя общая сумма
пожертвований от посещения 3 000 домов равна 85x3000/10 = $25 000
После 1000 испытаний, выполненных с помощью Crystall Ball, получим среднее значение по-
жертвований от посещения одного дома, равное $7,11 Средняя общая сумма пожертвований от
посещения 3 000 домов равна 3000x7,11 = $21 330 Отметим, что здесь оценка общей суммы по-
жертвовании, полученная после 200 испытаний, ближе к истинному значению этой величины,
чем такая же оценка, полученная после 1000 испытаний В этом нет ошибки, поскольку резуль-
таты зависят от случайных чисел Ваши результаты могут отличаться от приведенных здесь
10 21 Результаты имитации, если использовать только встроенные средства Excel
а)	на основе 100 испытаний определяем, что оптимальной будет закупка 112 цветов в день,
при этом средний доход составит $19,44,
Ь)	95%-ный доверительный интервал составляет ($18,23, $20,65)
Результаты имитации, если использовать надстройку ©Risk
а)	на основе 1000 испытаний определяем, что оптимальной будет закупка 116 цветов в день,
при этом средний доход составит $19,39,
Ь)	95% доверительного интервала составляет ($18,06, $20,72)
Глава ИИ
11 1 Аналоговая модель Но в модели, построенные в Extend, можно включать элементы как
аналоговой, так и символической моделей
11 3 Время ожидания клиентов возрастет
11 5 Следует увеличить имитационное время модели до нескольких недель
11 7 Добавление блока Queue Stats в модель на рис 11 20 и выполнение 98 имитаций этой
модели даст значение среднего времени ожидания 6,92 ±0,199 мин , максимальное время
ожидания составит 62,1 ±2,56 мин Выполнение 98 имитаций измененной модели, когда
5% клиентов возвращаются в офис для переоформления контракта, даст значение среднего
времени ожидания 7,85 ± 0,283 мин , максимальное время ожидания составит 69,5 ± 3,43
мин Значения, полученные вами, могут немного отличаться от вышеприведенных
11 9 После 15 мин ожидания уйдет приблизительно 10% клиентов Выполнение 20 имитаций
модели покажет среднее время ожидания оставшихся клиентов, равное 4,34 ±0,01 мин ,
максимальное время ожидания будет равно в точности 15 мин
1111 В следующей таблице показаны результаты 20 имитаций измененной модели
11 13 а 10 имитаций модели, построенной в Extend, показывают 95%-ный доверительный интер-
вал для времени обслуживания клиентов Этот интервал равен 8,09 ± 3,07 мин , что более
чем в два раза больше запланированных 4 мин обслуживания
Ь В среднем 16% клиентов (при разбросе от 7% до 30%) получат полное обслуживания
в течение 4 мин
с Среднее время обслуживания составит примерно 3,59 мин , если дополнительные работ-
ники будут принимать заказы и выдавать пищу, а в окне оплаты останется один работник
Около 66% клиентов получат полное обслуживание в течение 4 мин
1008 ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами
d Среднее время обслуживания составит примерно 3,75 мин , если дополнительные работ-
ники будут принимать заказы и выдавать пищу, а в окне оплаты останется один работник
Около 71% клиентов получат полное обслуживание в течение 4 мин
е Если максимальная длина очереди перед окном оплаты составляет три автомобиля, а перед
окном выдачи пищи один, то минимальное среднее время обслуживания равно приблизи-
тельно 3,84 мин при двух работниках в окнах заказа и выдачи и одном в окне оплаты Если же
максимальная длина очереди (три автомобиля) будет перед окном выдачи заказа, а перед ок-
ном оплаты один автомобиль, то минимальное среднее время обслуживания составит при-
близительно 3,29 мин при двух работниках в окнах заказа и выдачи и одном в окне оплаты
Последняя организация обслуживания обеспечивает минимальное время обслуживания, при
этом в среднем 64% клиентов получат обслуживание менее чем за 4 мин
f Минимальное среднее время обслуживания составит примерно 3,1 мин , если в объеди-
ненном окне будут работать три человека, а в окне приема заказов — двое Около 90% кли-
ентов получат полное обслуживание в течение 4 мин Значения, полученные в результате
имитаций вашей модели, могут отличаться от приведенных выше
1115 а Следует провести имитацию работы бюро в течение года с интервалом в 1 неделю (всего
52 недели), предполагая, что новый год бюро начинает с 10 новыми картриджами Прове-
дение 100 имитаций модели дает следующие результаты среднее время простоя бюро со-
ставит 14,6% при разбросе от 3,8% до 25%, средняя величина затрат (потери от простоя
плюс стоимость заказов и картриджей) равняется $66 000 при разбросе от $26 000 до
$104 000 Полученные результаты неприемлемы для работы бюро Если заказывать 10 кар-
триджей тогда, когда остается 10 или менее картриджей, то уже только это сократит время
простоя бюро (в среднем) до 0,8%, а затраты (тоже в среднем) — до $18 000
b Сделанное предположение ведет к увеличению времени простоя бюро и затрат В част-
ности, затраты возрастут (в среднем) до $69 700 Если оставить прежним объем заказа (10
картриджей), но последовательно провести новые имитации модели с условием, что заказ
на картриджи делается тогда, когда картриджей остается меньше 7, 8, 9, 10, 15 и 20 штук, то
обнаружим, что минимальные средние затраты составят $16 800, если заказ делать при ми-
нимальном запасе в 15 картриджей
с Создать имитационную модель в Excel при данных предположениях наиболее сложно Сде-
ланное предположение увеличивает время простоя бюро и затрат В частности, затраты возрастут
(в среднем) до $68 000 Если поэкспериментировать с объемом заказа и с условием, при котором
делается заказ на новые картриджи, то обнаружим, что минимальные средние затраты составят
$15 800, если делать заказ на 8 картриджей при минимальном запасе в 16 картриджей Значения,
полученные в результате имитаций вашей модели, могут отличаться от приведенных выше
Глава 12
12 1 а
50
50
Ь Функция приближения у = 21,87 +0,361х
W0 х
ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами 1009
Ь Линейная функция приближения у = 1,29 + О,68х
с Квадратичная функция приближения у = 0,428 + 1,250х + 0,071x2
12 5 Сумма квадратов отклонений для линейной функции равна 4,11 и для квадратичной — 3,68
12 7 а
У	,
50 -	*
5	10
b Спрос в 11-й момент времени будет равен 51,50 с Нет, поскольку в данном случае прогно-
зирование методом простого скользящего среднего будет недооценивать будущий спрос
12 9 а уи=53,9 b Да с Оптимальные веса wi = 0,613, w2 = 0,387, w3 = w4 =0 Ошибка прибли-
жения уменьшится на 23,6%
12 11 а Ju =52,24 b Предпочтительнее большее значение параметра а, поскольку график трен-
да показывает, что больший вес должны иметь последние наблюдения с а = 0,799
12 17
1010 ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами
с Прогнозируемое значение объема продаж составляет $865 767
1221 См рабочую книгу 12-21.xls
12 23 См рабочую книгу 12-23 xls
Глава 13
13 1 а Л = 0,5 баржи в час Ь 2 ч с 0,5 баржи в час
13 3	а ц = 15 человек в час. Ь 0,067 ч на человека с 15 человек в час
13 5	a L=2b L, = 0,75 с W= 0,2 ч на человека d W4 = 2/15 ч на человека е Ро = 1/3
13 7	£ = 5/(ц - 5)
ПРИЛОЖЕНИЕ Г. Ответы к задачам с нечетными номерами 1011
139
13 11
13 13
13 15
13 17
13 19
13 21
13 23
13 25
13 27
13 29
W=Lfr.= [А/(ц - Л)]/Л = 1/(ц - Л)
W= W4 + 1/ц, 1/ц = 20 мин , W4 = W- 1/ц = 30 - 20 = 10 мин
Очередь с тремя сервисами, поступление заданий в систему имеет Пуассоновское распре-
деление (экспоненциальное распределение времени между поступлениями), длительность
обслуживания на любом сервисе постоянна
Надо проверить соотношения L = ХИ'и L, = ЛИ/,.
L= 1,4791
Для решения этой задачи можно использовать рабочую книгу Excel Q XLS а 0,0023
Ь 0,0983 с 0,0084 ч = 0,5 мин d 0,5083 ч е 5,9745
ОС(5) = $184,80 в час
С/С. = 1,67
а Р3 = 0,034 b 0,409 с 5,91
a L = 0,7525 b L4 = 0,2525 с W= 0,7525 ч d W„ = 0,2525 ч е Ро = 1/2
а После 5000 имитационных итераций в Crystal Ball получим среднее время выполнения за-
каза равно 11,69 дней, с вероятностью 99% время выполнения заказа не превысит 15,4 дней
Ваши результаты могут незначительно отличаться от этих данных
b В этих условиях в 99% случаев обработка изделий на одном станке будет составлять 3 ч,
а в 1% случаев —13 ч После 5000 имитационных итераций в Crystal Ball получим среднее
время выполнения заказа равно 8,49 дней, с вероятностью 99% время выполнения заказа
не превысит 10,8 дней Ваши результаты могут незначительно отличаться от этих данных
Время профилактического обслуживания не должно превышать 15,4 - 10,8 = 4,6 дней
Предметный указатель
@
@Risk, 671,679, 700, 881
С
Crystal Ball, 671; 679; 686, 690, 695, 881
Crystall Ball, 705
E
Extend, 749, 751, 761,767
библиотеки, 753
G
GLP, 204,220
T
TreePlan, 606, 620
A
Абсолютные ссылки, 944
Алгоритм
генетический, 464
поглощающий, 523
эвристический,521
Анализ
безубыточности, 172
безубыточности при наличии ограни-
чений, 164
временных рядов, 812
инвестиционного портфеля, 476
компромисов, 77
параметрический, 217
решении, 580
эластичности, 76
Анализ “Что-если”, 73
сценарии, 79
Анализ данных, 676
Анализ решении, 580, 622; 629, 631
Анализ чувствительности, 58; 76, 203;
237; 491,612
изменение коэффициентов целевой
функции, 217; 234
изменение правых частей ограниче-
ний, 222, 231
изменение технологических коэффи-
циентов, 235
модели линейного
программирования, 215
нормированная стоимость, 238
отчет по устойчивости, 219
теневые цены, 224
Аналитические иерархические процес-
сы, 522, 549
Апостериорные вероятности, 615
Априорные вероятности, 615
Б
Безусловная оптимизация, 437
В
Вероятности
апостериорные, 615
априорные, 615
совместные, 634
субъективные, 630
условные, 615, 632
Вогнутые и выпуклые задачи НЛП, 459
Г
Генераторы случайных чисел, 666
Генерирование
случайного спроса, 674
случайных величин, 665, 666; 669
Генетический алгоритм, 464; 466
Предметный указатель 1013
д
Дерево решений, 407
обратный пересчет, 610
Деревья решений, 605
создание, 606
учет новой информации, 614
Диаграмма
влияния, 71
линейчатая, 86
потоков, 349
сетевая, 349
Диалоговое окно
Анализ данных, 678, 801
Добавление ограничения, 145
Линия тренда, 78
Параметры, 934
Параметры поиска решения, 147
Подбор параметра, 96
Поиск решения, 142
Прогрессия, 947
Регрессия, 801
Результаты поиска решения, 149, 985
Таблица подстановки, 88
Формат ячейки, 102
Динамические модели, 321
планирования и управления запаса-
ми, 335
управления
запасами, 324
производством и запасами, 325
финансами, 337
Дискретные модели Extend, 750
Дисперсия, 930
Дисциплина очереди, 858; 884
Допустимая область, 205
Допустимое множество ограниче-
ний, 205
3
Задача
максимизации потока, 357
об ассортименте продукции, 161; 169
составления расписания, 162; 171
составления смесей, 158,162,
168, 170
И
Игроки, 899
Издержки
невозвратные, 132
переменные, 132
Излишек, 174
Имитатор, 661
Имитационное моделирование, 661;
662,672,682, 721, 742; 744
в Extend, 749
влияние начальных условий, 708
надежность результатов, 679
Имитационные модели
аналоговые, 742
дискретные, 742
непрерывные, 742
Имитация
несбалансированных мощностей, 709
сбалансированных мощностей, 705
Индекс
рандомизации, 553
сезонный, 832
согласованности, 553
Исключение сезонной составляю-
щей, 830
К
Ковариация, 932
Комбинаторная оптимизация, 521
Коэффициент
согласованности, 553
Коэффициент корреляции, 932
Критерий
Лапласа, 590
максимаксный, 592
максиминный, 591
минимаксных потерь, 593
Л
Линия тренда, 78
м
Массивы, 954
Мастер
диаграмм, 960
1014 Предметный указатель
текстов, 962
функций, 960
Математическое ожидание, 928
функции от случайной величины, 930
Метод
ветвей и границ, 404
взвешенного скользящего средне-
го, 816
Дельфи, 837
Монте-Карло, 663
наименьших квадратов, 799
скользящего среднего, 813, 814
Хольта, 826
эквивалентной лотереи, 598
экспоненциального сглаживания, 819
Методы эвристические, 521
Множители Лагранжа, 442, 447
Модели, 35, 897
аналоговые, 43
вероятностные, 52; 53
временных рядов, 811
детерминированные, 52
динамические, 321
имитационные, 661
использование, 38
квадратичного программирования, 472
классификация, 52
количественные, 43; 44
линейного программирования,
124, 299
математические, 43
недопустимые, 213
нелинейного программирования, 437
неограниченные, 212
оптимизационные, 105
очередей, 743
поддержки принятия решений, 36
портфельных инвестиций, 479
построение, 46
принятия решений, 45; 582
прогнозирования,796
сетевые, 347
символические, 43; 44
стохастические, 53
табличные, 43
типы,43
транспортные, 155
управления запасами, 322
условной оптимизации, 123; 125; 174
физические, 43
фиксированных затрат, 399
целевого программирования, 522
целочисленного линейного програм-
мирования, 383
целочисленной оптимизации, 130
эволюция, 898
Модели квадратичного программирова-
ния, 472
поиск решения, 473
Модели линейного программирова-
ния, 124
анализ чувствительности, 203
вырожденные, 252
графическое решение, 211
задание целевой функции, 128
искусство создания, 131
лимитирующие ограничения, 150
ограничения, 124
определение ограничений, 126
оптимальное решение, 129
параметры, 134
решения, 134
создание, 161; 165
формализация, 124
целевая функция, 124
Модели нелинейного программирова-
ния, 437
анализ чувствительности, 447
вогнутые и выпуклые задачи, 459
графическое представление, 439
допустимая область, 440
множители Лагранжа, 442
начальные предположения, 455
оптимальное решение, 441
оптимальность, 450
поиск решения, 445; 457
примеры,445
разрешимость, 458
решения глобальные, 442
решения локальные, 442
Модели очередей, 855
базовые, 857
классификация, 862
переходные процессы, 878
стационарное состояние, 860
характеристики, 863
экономический анализ, 870
Модели прогнозирования, 796
причинно-следственные, 796
Предметный указатель 1015
Модели целочисленного линейного
программирования, 383
анализ чувствительности, 412
графическое представление, 386
метод ветвей и границ, 404
округленные решения, 390
применение двоичных перемен-
ных, 392
типы моделей, 385
упрощение модели, 389
эвристические методы, 414
Моделирование, 35; 69
восходящее, 54
дискретных событий, 743
как искусство, 99
нисходящее, 54
процесс, 37
терминология, 58
Модель
авиаперевозок, 699
внешние переменные, 48
внутренние переменные, 48
входы, 123
выбора средств массовой информа-
ции, 315
выходы, 123
замены оборудования, 354
институциональная, 898
критерии, 48
критерий эффективности, 45
назначений, 308
недопустимая, 538
определения оптимального размера
заказа, 487
параметры, 48
перевозок, 348
планирования городского строитель-
ства, 358
показатели эффективности, 48
построение, 50, 72
проверка достоверности, 57
производства, 102
производства и управления запаса-
ми, 496
производственного модуля, 704
промежуточные переменные, 70
разработка, 54
результирующие переменные, 48
решения, 48
со случайным спросом, 674
табличная, 133
транспортная, 300
транспортная, несбалансирован-
ная, 304
управления запасами, 483, 659; 664;
688, 695
управления
запасами при наличии оптовых ски-
док, 492
финансами и планирования произ-
водства, 341
финансового планирования, 673
формализация, 47
формирования инвестиционного
портфеля, 476
целевая функция, 48
целевого программирования, 540
Модель назначений, 308
несбалансированная, 312
формализация, 3 10
Модель управления запасами
как транспортная модель, 332
Модель-приложение, 898
институциональная, 899
Модель-прототип, 898
н
Надстройка
©Risk, 671
Crystal Ball, 671
Premium Edition Solver, 973
Premium Edition Solver for Education,
469
Premium Solver for Education, 142
SolverTable, 230
TreePlan, 626
Поиск решения, 139, 973
Надстройки Excel, 969
Нормированная стоимость, 238
О
Ограничение
лимитирующее, 150, 208
связывающее, 150
Ограничения, 127, 173
допустимое множество, 205
жесткие, 533
1016 Предметный указатель
интервальные целевые, 535
лимитирующие, 173
мягкие, 533
простые, 250
системные, 533
функция, 127
целевые, 533
Ожидаемое значение
дополнительной информации, 621
полной информации,594
Описательная статистика, 676
Оптимизатор
Evolutionary Solver, 469
OptQuest, 714
Оптимизация
безусловная, 437
в условиях неопределенности, 710
условная, 57; 106
Относительные ссылки, 945
Отношения предшествования, 525
Отчет
Feasibility Report, 986
Linearity Report, 986
Population Report, 986
по пределам, 985
по результатам, 149; 985
по устойчивости, 219, 220, 244, 985
Отчеты надстройки Premium Edition
Solver, 984
Отчеты надстройки Поиск решения, 984
Очередь, 855
бесконечная, 858
дисциплина, 858; 884
конечная, 858, 874
одноканальная, 857
с конечным источником заданий, 876
с одним сервисом, 857
типа M/G/1, 865
типа M/M/s, 867
п
Параметры надстройки Premium Edition
Solver, 980
Параметры средства Поиск решений,
978
Переменные
внутренние, 48
отклика, 796
отклонения, 534
промежуточные, 70
результирующие, 48
решения, 128, 174
случайные, 663
Подбор кривой, 804, 808; 812
методом наименьших квадратов, 799
по точкам,797
Подбор параметра, 96
Поиск кратчайшего пути, 352
Поиск решения, 129; 136; 139
автоматическое масштабирование, 147
добавление ограничений, 145
изменяемые ячейки, 145
надстройка, 139
отчет по устойчивости, 219
отчеты, 149
рекомендации, 151
терминология, 141
целевая ячейка, 142
Полезность, 595
Поток Пуассона, 857
Пример
Eastern Steel, 237
Friendly Loan Company, 245
Gulf Coast 011,450
Kelly-Spnngfield, 414
Midwest Express Airlines, 699
Oak Product,
Oak Products, 101; 125; 129, 142;
204; 217
Simon Pie, 67; 69; 77, 84
Sonorola, 605, 612
STECO, 484; 496; 813
Winston-Salem Development, 337
XerTech Copy, 67; 93
Вильсона, 675, 680
выбор СМИ, 316; 537
газетного киоска, 584
Джексона, 855
компании Airbus Industry, 673
компании AutoPower, 300; 308; 324;
341; 393
компании Bumles, 335
компании Zigwell, 348
Михаэльсона, 704
Монти, 870
отбор проектов, 716
производство телевизоров, 448
Хервиса, 744; 749; 761; 767
Предметный указатель 1017
Принятие решений
в условиях
неопределенности, 590; 604
определенности, 582; 604
риска, 57; 579; 583; 594; 604
Проверка моделей, 810
Прогнозирование, 795; 812; 834
качественное, 837
количественное, 796
Проект создания модели, 899
источники неудач, 903
размывание границ, 902
Профиль риска, 586
Р
Разделение
игроков, 900
функций игроков, 899, 900
Распределение вероятностей, 663
биномиальное, 924
дискретное равномерное, 669, 924
многомерное, 930
неперерывное равномерное, 669
непрерывное равномерное, 926
нормальное, 671; 695; 927
Пуассона, 857, 883; 925
равномерное, 667
совместное, 931
экспоненциальное, 670, 857; 882, 927
Регрессия, 801
Резерв, 135; 174
Решение
допустимое, 128, 174,206
оптимальное, 106, 129, 174
целочисленное, 130
Решения
альтернативные, 219
вырожденные, 257
Риск, 583
профиль, 586
С
Сглаживание экспоненциальное, 819
Сезонные изменения, 829
Сетевые модели,347
задача максимизации потока, 357
модель замены оборудования, 354
нахождение кратчайшего пути, 352
процедуры решения, 352
Симплекс-метод, 139
Случайные величины, 663, 923
генерирование, 666, 669
дискретные, 665, 923
независимые, 931
непрерывные, 665; 926
равномерно распределенные, 667
Совместные вероятности, 634
Сообщения средства Поиск реше-
ния, 981
Состояние природы, 584
Среднее квадратов ошибок, 809
Статистические данные, 793, 835
Субъективные вероятности, 630
т
Таблица подстановки, 88; 970
с двумя входами, 88
создание, 88
Теневые цены, 224
интерпретация, 252
Теорема Байеса, 632, 634
Точка
безразличия, 98
безубыточности, 94
стационарная, 437
Точки
крайние, 209
угловые, 209
Транспортная модель, 300
несбалансированная, 304
фиктивные пункты, 305
формулировка, 301
целочисленные решения, 305
У
Уравнение баланса потоков, 350
Условие
неотрицательности, 127, 174
целочисленности, 130, 174
Условия оптимальности, 437
Условные вероятности, 615
Условные выражения, 87
1018 Предметный указатель
Ф
Формула Литтла, 864
Формулы массивов, 955
Функции
вогнутые, 460
выпуклые, 460
квадратичные, 472
линейные, 129
нелинейные, 129
штрафные, 469
Функция
ограничения, 174
полезности, 596, 624
распределения, 667, 925; 926
регрессии, 802
экстраполяционная, 811
ц
Целевая функция, 48; 124; 174
Целевое программирование, 533
Целочисленное программирование,
130;174
Цена резервирования, 224
ч
Чистая приведенная стоимость, 674
э
Эволюционные алгоритмы, 466
Эвристики,521
Эвристические методы, 521
Эвристический алгоритм, 521
Экспоненциальное сглаживание, 819
Научно-популярное издание
Джеффри Мур, Ларри Р. Уэдерфорд и др.
Экономическое моделирование
в Microsoft Excel
6-е издание
Литературный редактор О Ю. Белазовская
Верстка О В. Мишутпина
Художественный редактор Е П. Дынник
Корректоры ЗВ Александрова, Л А. Гордиенко,
Т.А Корзун, О В. Мишутина,
Л.В. Чернокозинская
Издательский дом “Вильямс”
101509, Москва, ул Лесная, д 43, стр 1
Изд лиц ЛР№ 090230 от 23.06 99
Госкомитета РФ по печати
Подписано в печать 30 01 2004 Формат 70X100/16
Гарнитура Times Печать офсетная
Усл печ л 82,56 Уч -изд л 70,00
Тираж 3500 зкз Заказ № 1729
Отпечатано с диапозитивов в ФГУП “Печатный двор”
Министерства РФ по делам печати,
телерадиовещания и средств массовых коммуникаций
197110, Санкт-Петербург, Чкаловский пр , 15
Источник
Финансовая модель — это функциональный инструмент, который поможет оперативно просчитать влияние различных факторов и изменений на результаты работы и финансовое состояние организации. За счёт формул и уравнений расчётов после изменения исходных данных все зависимые характеристики, будут пересчитаны программой автоматически.
Для финансового моделирования наиболее удобен и доступен формат Excel. Использовать его могут как бухгалтеры, так и руководители различных уровней.
Набор показателей для финансовой модели зависит от специфики деятельности организации. Основных групп, как правило, четыре:
активы — имущество, принадлежащее организации;
пассивы — обязательства;
финансовые потоки — различные денежные поступления и платежи;
доходы и расходы.
Результаты расчётов можно представить в виде баланса, отчётов о доходах и расходах и о движении денежных средств (по состоянию на определённую дату).
Алгоритм построения финансовой модели

Начните финансовое моделирование в Excel с создания простой модели. Из внешних параметров можно, например, взять стоимость продукции и спрос на неё. Например, в качестве внутренних показателей можно взять размер выручки и затрат. На первом этапе количество элементов может быть минимальным, а особой точностью можно пренебречь. Основная цель — установить рабочие взаимосвязи для автоматического пересчёта. Далее модель можно развивать, детализировать и усложнять.
Рассмотрим пример простого моделирования в Excel с небольшим количеством ключевых переменных. Для каждой таблицы необходимо отвести отдельную страницу.
1. Задаём исходные параметры
Попробуем спрогнозировать выручку. За основу можно взять план реализации товаров или услуг за год. Размер выручки на первом этапе можно округлить или указать приблизительные данные (рисунок 1).
Рисунок 1 — План реализации услуг (тыс.руб.)
Выручка рассчитывается как сумма услуг.
2. Определяем переменные затраты
В качестве переменных введём затраты на заработную плату сотрудникам. Допустим, она зависит от объёма реализованных услуг и составляет 25% от выручки. Зарплата рассчитывается помесячно как произведение коэффициента 0,25 (25/100) и плана продаж на конкретный месяц.
Расходы на аренду и управление внесём как фиксированные значения.
Например, чтобы посчитать зарплату за январь, берём план реализации на январь и умножаем на коэффициент
151 * 0,25 = 38 тыс. руб.
В Excel прописываем формулу: fx = 0,25*название страницы с таблицей по плану реализации!B8
Общий размер планируемых затрат будет равен сумме зарплаты, аренды и управленческих расходов (рисунок 2).
Рисунок 2 — План затрат
3. Составляем план доходов и расходов
Обратите внимание на строки «операционные доходы» и «операционные расходы» (рисунок 3). Чтобы их заполнить, потребуется прописать ссылки на соответствующие ячейки функциональных планов.
Рисунок 3 — План доходов и расходов, тыс. руб.
Так, операционные доходы будут равны суммам от услуг 1-4. Например, чтобы рассчитать операционный доход за январь, складываем 15+30+46+60. Получаем 151 тыс. руб.
В формулу прописываем: fх =СУММ(B5:B8)
Числовые значения по услугам прописываем ссылками на ячейки таблицы «План реализации услуг».
Графа «Итого» считается как сумма ячеек с B4 по M4
fх =СУММ(B4:M4)
Аналогично рассчитываются операционные расходы. Данные синхронизируем с таблицей «План затрат».
Операционная прибыль рассчитывается как разность операционные доходы — операционные расходы.
Например, операционная прибыль за январь равна: 151 — 96 = 55 тыс. руб.
Рентабельность рассчитывается как отношение операционной прибыли к операционному доходу помноженное на 100.
За январь получаем: 55/151*100 = 36,69%
fх = B13/B4*100
Обратите внимание, что итоговая рентабельность рассчитывается не как сумма за предыдущие месяцы, а как отношение итоговой операционной прибыли к итоговому операционному доходу.
Прибыль нарастающим итогом — это прибыли (убытки) за прошлый и текущий отчётные периоды. В январе мы берём данные операционной прибыли, равные 55 тысячам рублей. В феврале прибавляем 58 тысяч. Получаем 113 тысяч рублей. В марте прибавляем ещё 64 тысячи. Получаем 176 тысяч. И так суммируем по каждому месяцу.
В нашем финансовом плане прибыль нарастающим итогом за февраль будет прописываться формулой: fх=B15+C13
4. Составляем план движения денежных средств
Допустим, что в организации осуществляется только операционная деятельность, без капитальных вложений и заёмных средств. Также для упрощения исключим дебиторскую задолженность, допустив что время оплаты и время оказания услуг совпадают.
Платежи по заработной плате и аренде происходят в месяце, следующем за месяцем их начисления, а управленческие расходы — в месяц их осуществления (рисунок 4).
Рисунок 4 — План движения денежных средств, тыс. руб.
Платежи по операционной деятельности рассчитываются, как сумма зарплата + аренда + управленческие расходы.
Сальдо по операционной деятельности — это разность поступлений по операционной деятельности и платежей по операционной деятельности.
Сальдо операционной деятельности за январь будет равно: 151 — 38 = 113 тысяч рублей.
Сальдо на конец периода рассчитывается как сумма сальдо на начало периода и сальдо по операционной деятельности. Если принять сальдо на начало января равное 10 тысячам рублей, сальдо на конец периода будет равно 123 тысячам рублей.
5. Делаем прогнозный баланс
На основании плана доходов и расходов и плана движения денежных средств можно построить прогнозный баланс. Начальные остатки нужно взять из баланса предыдущего периода. Допустим, что все они равны 10 тысячам рублей (рисунок 5).
Рисунок 5 — Прогнозный баланс, тыс. руб.
В графу «денежные средства» подставляем значение сальдо на конец периода предыдущего месяца. Так, денежные средства за февраль = 123 тысячам рублей.
Активы будут равны сумме: денежные средства + основные средства + дебиторская задолженность.
Кредиторская задолженность рассчитывается: кредиторская задолженность предыдущего периода + планируемые затраты на заработную плату и аренду предыдущего месяца — планируемы движения денежных средств по зарплате и аренде предыдущего месяца.
Так, кредиторская задолженность на 1 февраля составит 58 тысяч рублей
0+38+20-0-0.
Капитал = капитал за предыдущий период + операционная прибыль предыдущего периода.
Капитал на 1 февраля составляет 65 тысяч рублей. 10+55.
Пассив — это сумма капитала и кредиторской задолженности
Обратите внимание, что дебиторская задолженность будет рассчитываться как дебиторская задолженность за предыдущую дату + отгрузка периода — поступление денежных средств.
Далее финансовую модель можно детализировать. Например, разбить по видам управленческие расходы, расписать зарплаты по сотрудникам, детализировать план продаж.
Финансовую модель можно корректировать, заменять плановые данные фактическими, отслеживать риски и контролировать финансовые результаты.
Узнайте больше о финансовом моделировании в Excel и прогнозировании финансового состояния бизнеса на семинаре в Учебном центре «Финконт».
Источник
Финансовое моделирование в Excel относится к инструментам, используемым для подготовки ожидаемых финансовых отчетов, прогнозирующих финансовые результаты компании в будущем периоде с использованием допущений и исторической информации о результатах. Такие финансовые модели можно использовать при оценке DCF, слияниях и поглощениях, прямых инвестициях, проектном финансировании и т. д.
Финансовое моделирование в Excel находится во всем Интернете. Об обучении финансовому моделированию написано много. Тем не менее, большинство учебных материалов по финансовому моделированию одинаковы. Он выходит за рамки обычной тарабарщины и исследует практическое финансовое моделирование, используемое инвестиционными банкирамиИнвестиционные банкирыИнвестиционно-банковские услуги — это специализированный банковский поток, который помогает бизнес-структурам, правительству и другим организациям генерировать капитал за счет долгов и акционерного капитала, реорганизации, слияний и поглощений и т. д. подробнее и аналитики-исследователи.
В этом бесплатном руководстве по финансовому моделированию в Excel мы возьмем пример Colgate Palmolive (2016–2020) и подготовим полностью интегрированную финансовую модель с нуля.
Это руководство состоит из более чем 5000 слов и заняло у меня три недели. Поэтому сохраните эту страницу для дальнейшего использования и не забудьте поделиться ею.
Обучение финансовому моделированию в Excel — прочтите сначала

Шаг 1 — Загрузите шаблон финансовой модели Colgate.
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать эти шаблоны финансового моделирования Colgate (решенные/нерешенные) здесь – Шаблоны финансового моделирования Colgate (решено/нерешено)
Шаг 2 — Обратите внимание, что вы получите два шаблона: 1) нерешенная финансовая модель Colgate Palmolive и 2) решенная финансовая модель Colgate Palmolive.
Шаг 3- Вы будете работать на Нераскрытый шаблон финансовой модели Colgate Palmolive. Следуйте пошаговым инструкциям, чтобы подготовить полностью интегрированную финансовую модель.
Шаг 4 — Приятного обучения!
Если вы новичок в финансовом моделировании, ознакомьтесь с этим руководством Что такое финансовое моделирование? Что такое финансовое моделирование? Финансовое моделирование относится к использованию моделей на основе Excel для отражения прогнозируемых финансовых показателей компании. Такие модели представляют финансовую ситуацию с учетом рисков и будущих предположений, которые имеют решающее значение для принятия важных решений в будущем, таких как привлечение капитала или оценка бизнеса, и интерпретации их влияния.Подробнее
Как построить финансовую модель в Excel?

Давайте посмотрим, как можно построить финансовую модель с нуля. Это подробное руководство по финансовому моделированию содержит пошаговые инструкции по созданию финансовой модели. Основной подход, используемый в этом руководстве по финансовому моделированию, заключается в следующем. Модульный. Модульная система, по сути, означает создание основных отчетов, таких как отчеты о прибылях и убытках, балансовые отчеты и отчеты о движении денежных средств, с использованием различных модулей/листов. Основное внимание уделяется подготовке каждого оператора шаг за шагом и подключению всех вспомогательных программ к основным операторам по завершении. Мы понимаем, что сейчас это может быть неясно. Однако вы поймете, что это очень просто, когда мы будем двигаться вперед.
Шаг 1 – Финансовая модель Colgate – историческая
Шаг 2 – Анализ соотношения Colgate Palmolive
Шаг 3 – Прогнозирование отчета о прибылях и убытках
Шаг 4- Прогноз оборотного капитала
Шаг 5 – Прогноз амортизации
Шаг 6 – Прогноз амортизации
Шаг 7 – Другой долгосрочный прогноз
Шаг 8 – Заполнение отчета о прибылях и убытках
Шаг 9 – Прогноз акционерного капитала
Шаг 10 – Делится невыполненным прогнозом
Шаг 11 – Заполнение отчетов о движении денежных средств
Шаг 12 — Прогноз долга и процентов
Обратите внимание на следующее –
Основными отчетами являются отчет о прибылях и убытках. Отчет о прибылях и убытках. Отчет о прибылях и убытках — это один из финансовых отчетов компании, в котором обобщаются все доходы и расходы компании с течением времени, чтобы определить прибыль или убыток компании и измерить ее деловую активность с течением времени на основе требований пользователей. читать подробнее, Балансовый отчетБалансовый отчетБалансовый отчет является одним из финансовых отчетов компании, который представляет акционерный капитал, обязательства и активы компании в определенный момент времени. Он основан на уравнении бухгалтерского учета, в котором говорится, что сумма общих обязательств и капитала владельца равна общей сумме активов компании. Читать далее, и Денежные потоки.
Различные листы представляют собой амортизациюАмортизацияАмортизация — это систематический метод распределения, используемый для учета затрат на любые физические или материальные активы на протяжении всего срока их полезного использования. Его значение показывает, какая часть стоимости актива была использована. Амортизация позволяет компаниям получать доход от своих активов, взимая только часть стоимости актива, используемого каждый год. подробнее прогноз, прогноз оборотного капитала, прогноз нематериальных активов, акционерный капитал Акционерный капитал Акционерный капитал представляет собой остаточную долю акционеров в компании и рассчитывается как разница между Активами и Обязательствами. Отчет об акционерном капитале в балансовом отчете подробно описывает изменение стоимости акционерного капитала с начала до конца отчетного периода. Подробнее прогноз, прогноз других долгосрочных статей, график прогноза долга График прогноза долга График долга представляет собой список долги, которые должен бизнес, включая срочные кредиты, долговые обязательства, кредит наличными и т. д. Бизнес-организации составляют этот график, чтобы знать точную сумму обязательств компании перед другими и управлять своими денежными потоками, чтобы предотвратить финансовый кризис и обеспечить более эффективное управление долгом. читать больше и т. д.
Различные расписания связаны с основными утверждениями после их завершения.
В этом руководстве по финансовому моделированию будет построена пошаговая интегрированная экономическая модель Colgate Palmolive с нуля.
Шаг 1 — Финансовое моделирование в Excel — проецирование исторических данных

Первым шагом в руководстве по финансовому моделированию является подготовка исторических данных.
Загрузить отчеты Colgate 10K Reports
Один готовит финансовые модели в Excel. Первые шаги начинаются с понимания того, как обстоят дела в отрасли в последнее время. Понимание прошлого может дать ценную информацию о будущем компании. Поэтому первым шагом является загрузка всех финансовых отчетов компании и их заполнение на листе Excel. Для Colgate Palmolive вы можете загрузить годовые отчеты Colgate Palmolive с их Секция по связям с инвесторами.
Вертикальный анализ Colgate
В отчете о прибылях и убытках вертикальный анализ является универсальным инструментом для измерения относительной эффективности фирмы из года в год с точки зрения затрат и прибыльности. Поэтому его всегда следует включать в любой финансовый анализ. Здесь проценты рассчитываются относительно чистых продаж, которые считаются 100%. Этот вертикальный анализ в отчете о прибылях и убытках часто называют анализом маржи, поскольку он дает разные маржи в отношении продаж.
Найти чистое увеличение (уменьшение) денежных средств и их эквивалентов
Заполните отчеты о движении денежных средств
Найдите денежные средства и их эквиваленты на конец года.
Свяжите денежные средства и их эквиваленты с балансовым отчетом.
Теперь мы готовы позаботиться о нашем последнем и окончательном графике, т.е. графике долгов и процентов.
Шаг 12 – Финансовое моделирование в Excel – График долгов и процентов

Следующим шагом в этом онлайн-финансовом моделировании является заполнение графика задолженности и процентов. Резюме Долг и проценты – График.
Настройте график погашения задолженности
Ссылка на денежный поток, доступный для финансирования
Ссылка на все источники собственного капитала и использование денежных средств
Рассчитать денежный поток от погашения долга
Ссылка на начальный остаток денежных средств из бухгалтерского баланса.
Вычесть минимальный остаток денежных средств. Мы предположили, что Colgate хотела бы иметь как минимум 500 миллионов долларов в год.
Пропустите выпуск/погашение долгосрочных долговых обязательств, денежные средства, доступные для возобновляемой кредитной линии, и раздел револьвера.
В отчете Colgate 10K отмечена доступная информация о возобновляемой кредитной линии.
Colgate 2020 – 10K, стр. 49
Также в дополнительной информации о долге приводится совершенная долгосрочная задолженность по погашению.
Colgate 2020 – 10K, стр. 50
Рассчитайте окончательную долгосрочную задолженность.
Мы используем приведенный выше график погашения долгосрочного долга и рассчитываем конечное сальдо погашения долгосрочного долга.
Связать долгосрочные выплаты долга
Рассчитайте дискреционные заимствования/выплаты.
Используя формулу расчета денежных средств, как показано ниже, рассчитайте дискреционные займы/выплату.
Рассчитать процентные расходы по возобновляемой кредитной линии
Сделайте разумное предположение относительно процентной ставки на основе информации, представленной в отчете 10K.
Найдите средний остаток возобновляемой кредитной линии и умножьте его на предполагаемую процентную ставку.
Рассчитать процентные расходы по долгосрочному долгу
Свяжите исторические средние остатки и процентные расходы. Найдите подразумеваемую процентную ставку за исторические годы.
Предположим, что процентная ставка по долгосрочному долгу основана на подразумеваемой процентной ставке. Затем умножьте средний долгосрочный долг на предполагаемую процентную ставку.
Рассчитать Общие процентные расходы = средний остаток долга x процентная ставка
Найдите общие процентные расходы = проценты (возобновляемая кредитная линия) + проценты (долгосрочная задолженность)
Свяжите долговые и револьверные просадки с денежными потоками
Ссылка на текущий и долгосрочный периоды в балансовый отчет
Разграничение текущей части долгосрочного долгаТекущая часть долгосрочного долгаТекущая часть долгосрочного долга (CPLTD) подлежит оплате в течение следующего года с даты составления баланса и отделяется от долгосрочного долга, поскольку они должны быть выплачивается в течение следующего года с использованием денежных потоков компании или с использованием ее оборотных активов и долгосрочной задолженности, как показано ниже.
Свяжите возобновляемую кредитную линию, долгосрочный долг и текущую часть долгосрочного долга с балансом.
Ссылка Неконтролирующая доля участия в отчете о прибылях и убытках
Рассчитайте процентный доход, используя средний остаток денежных средств
Связывание процентных расходов и процентных доходов с отчетом о прибылях и убытках
Выполните проверку баланса: общие активы = обязательства + акционерный капитал.
Аудит баланса
Нам нужно проверить модель и проверить наличие ошибок связи, если есть какие-либо расхождения.
Что дальше?

Если вы узнали что-то новое или вам понравилось это финансовое моделирование в Excel, оставьте комментарий ниже. Дайте мне знать, что вы думаете. Большое спасибо, и берегите себя. Счастливого обучения!
Источник
Грамотный расчет плановых показателей по движению денежных потоков, выручки и прибыли — один из ключевых факторов в управлении организацией. На сегодняшний день разработано немало инструментов, призванных облегчить решение поставленной задачи. Однако многие из них требуют длительного освоения и высокого уровня базовых навыков, да и стоимость подобных решений не всегда соизмерима с функционалом, которые они обеспечивают. Впрочем, есть и альтернативный вариант, позволяющий провести анализ данных в нужном формате, и получить на выходе желаемый результат. Финансовая модель бизнеса в Excel, построенная с соблюдением принципов, гарантирует получение качественной прогнозной отчетности, необходимой для эффективного контроля за организационными процессами.
Общее представление

При разработке шаблонов для экономического планирования учитываются основные показатели деятельности предприятия, к числу которых относятся:
доходы и расходы;
прибыль;
денежные потоки;
активы и обязательства.
Несмотря на внешнюю схожесть с бюджетной системой, специфика использования такого инструмента, как финансовое моделирование в эксель, предусматривает большее количество упрощений и вариативных параметров. Подобный подход обуславливается целевыми задачами, решение которых является целью прогнозирования. Отчетная таблица призвана обеспечить возможность быстрой оценки потенциальных результатов операционной деятельности и стабильности состояния организации при изменении внешних и внутренних факторов.
Построение финмодели в Excel от Microsoft или в Google docs предусматривает внесение части информации вручную, тогда как зависимые данные определяются с помощью базовых формул. Благодаря этому любая корректировка позволяет моментально пересчитать итоговые значения, оценить риски и проанализировать перспективы получения прибыли.
За счет проделанной работы формируются три типа отчетности:
балансовые показатели предприятия;
аналитика результатов (ОФР);
отчет по движению денежных средств (ОДДС).
Грамотное применение полученных результатов упрощает управленческий процесс — так же, как и использование программных решений от компании «Клеверенс», исключающих вероятность технических ошибок при учете активов организации.
Финансовое моделирование проекта в Excel: что нужно знать

Для тех, кто планирует самостоятельно разобраться в особенностях и нюансах создания рабочей модели, лучшим вариантом станет последовательный переход от простых вещей к более сложным. Планомерный подход позволит избежать неточностей, связанных с использованием формул и подстановкой значений. Пошаговый план выглядит следующим образом:
Создайте предварительный вариант с минимальным количеством данных, и задайте локальные критерии расчета для зависимых переменных. В качестве примера можно привести выручку относительно цены продукции и объемов реализации, фонд оплаты труда при сдельной работе, социальные отчисления ФОТ и т.д.
Обобщите параметры в рамках общей системы, и проведите предварительную проверку функциональности готовой структуры. Ключевой критерий — схождение баланса, отклонения в котором свидетельствуют о допущенных ошибках. Небольшое количество формул позволяет без особых усилий выявить проблемные зоны, требующие корректировки.
Детализируйте финансовый расчет бизнес-плана в Excel, дополнив его новыми базовыми показателями. Раскройте специфику формирования себестоимости продукции, уточните периоды взаиморасчетов с поставщиками исходя из имеющихся коммерческих условий, привяжите к производственным объемам корреляцию, учитывающую величину переходящего товарного остатка. При добавлении параметров также следует проверять работоспособность системы, чтобы исключить «перекос» формульных значений.
Поэтапная реализация проекта управления отчетностью позволяет не только отследить взаимозависимость ключевых факторов, но и лучше понять структуру доходов и расходов, исходя из которой можно выбрать грамотный курс развития организации.
Готовые решения для всех направлений

Сократите издержки в работе склада до 70% : ускорьте складские операции, устраните ошибки человеческого фактора и забудьте про потерю и пересортицу товаров.
Узнать больше
У вас всегда будут актуальные ценники на товарах и витринах, товар перестанет теряться при перемещении между магазинами, а в вашей системе учета — только точные остатки по товарам.
Узнать больше
С маркировкой вы на 100% исключите приемку контрафактного товара на свой склад, а также сможете отслеживать полную цепочку поставок товара от производителя.
Узнать больше
Скорость, точность приёмки и отгрузки товаров на складе — краеугольный камень в E-commerce бизнесе. Начни использовать современные, более эффективные мобильные инструменты.
Узнать больше
Повысьте точность учета имущества организации, уровень контроля сохранности и перемещения каждой единицы. Мобильный учет снизит вероятность краж и естественных потерь.
Узнать больше
Повысьте эффективность деятельности производственного предприятия за счет внедрения мобильной автоматизации для учёта товарно-материальных ценностей.
Узнать больше
RFID
Первое в России готовое решение для учёта товара по RFID-меткам на каждом из этапов цепочки поставок.
Узнать больше
Исключи ошибки сопоставления и считывания акцизных марок алкогольной продукции при помощи мобильных инструментов учёта.
Узнать больше
Получение сертифицированного статуса партнёра «Клеверенс» позволит вашей компании выйти на новый уровень решения задач на предприятиях ваших клиентов..
Узнать больше
Используй современные мобильные инструменты для проведения инвентаризации товара. Повысь скорость и точность бизнес-процесса.
Узнать больше
Показать все решения по автоматизации
Как построить финансовую модель компании в Excel: инструкция пошагово

В качестве наглядного примера рассмотрим вариант для предприятия, специализирующегося на розничной торговле. Подобный выбор не случаен, поскольку производственные процессы априори отличаются более сложной структурой, предполагающей материальные затраты, амортизацию, незавершенные к окончанию периода циклы, а также разнородные формы складских запасов. Кроме того, коммерческая деятельность, связанная с продажами, допускает исключение дебиторской задолженности — в тех ситуациях, когда клиентам не предоставляются опции с рассрочкой или отсрочкой платежей.
Подсчет доходов

Ключевым фактором на первом этапе выступает объем реализации. Самый простой вариант — внесение в фин модель, формируемую в Эксель, показателя выручки в денежном выражении, который позже может быть детализирован как производная от перемножения цены и количества для каждой позиции в номенклатуре. Подобный параметр также позволяет грамотно рассчитать расходы на закупку продукции.
Одной из главных сложностей на этой стадии выступает построение плана продаж. В ситуациях, когда отчетная таблица составляется для обычного тестирования, можно взять любые значения «с потолка», однако, если вы сразу рассчитываете на результат, способный принести практическую пользу — стоит заняться планированием более детально.
К числу важных факторов, требующих учета при прогнозировании, следует отнести величину налога на добавленную стоимость, по умолчанию включенного в цену реализации. Несмотря на то что налоговые отчисления формально поступают в структуре выручки, их нельзя отнести к доходной статье, поэтому выделение НДС позволит рассчитать чистую прибыль с каждой позиции.
Кроме того, нелишним станет добавление аналитики по номенклатуре, отражающей такие характеристики операционной деятельности, как:
доля возврата продукции;
типы клиентов (физические или юридические лица);
реквизиты торговой точки или региона продаж.
Важно понимать, что на предварительном этапе чрезмерно подробная детализация может привести к лишней путанице, тогда как основной задачей проекта выступает составление базового плана по доходности.
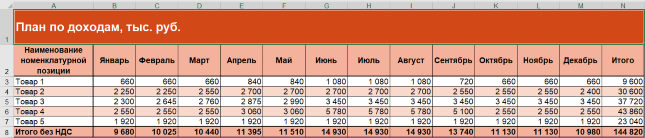
Пример планирования расходов

Расходные статьи изначально также рассматриваются в общей перспективе. Для обобщенной структуры достаточно выделить несколько элементов, таких как:
Материальные затраты. В рамках упрощенной версии будем считать, что в эту категорию входит только приобретение товаров без НДС, количество которых полностью совпадает с объемом реализации. Исходя из этого, критериями получаемой величины станут стоимость закупки и количество продаж.
Зарплатный фонд. Опять же, для базового варианта достаточно указать общую сумму, без дробления на отдельные элементы.
Социальные отчисления. В этом случае используются зависимые переменные, рассчитываемые с помощью формулы. Как правило, стандартным показателем считается 30% от величины ФОТ, плюс дополнительные страховые взносы, размер которых определяется классом риска профессиональной деятельности, определенным для предприятия. В качестве примера возьмем минимально возможный размер, составляющий 0,2%.
Амортизация. Даже с учетом того, что наше условное предприятие занимается исключительно розничной торговлей, на его балансе все равно могут быть основные средства и нематериальные активы, относящиеся к собственности. Стандартная практика — расчет среднемесячной суммы, базирующийся на теоретических или практических критериях.
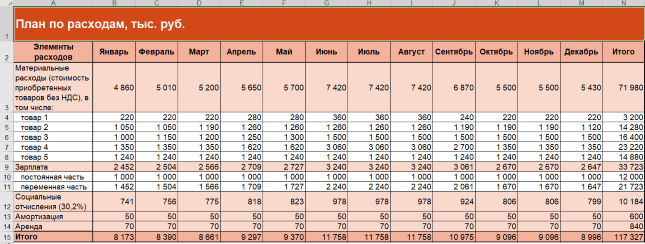
Иные расходы. Фактически начальная стадия детализации, предполагающая отражение постоянных трат компании, легко поддающихся планированию. В рассматриваемую категорию можно включить затраты на аренду торговых площадей, размещение рекламы, представительские и командировочные компенсации, и т.п.
Указанного списка вполне достаточно для реализации проектной модели, после проверки которой можно перейти сначала к дроблению базовых значений, а затем и к обобщению полученных данных.
Составление планового отчета о финансовых результатах

Отправной точкой формирования отчетности выступает подсчет прибылей и убытков за отдельно взятый период. Аналогичное правило применяется и к построению бюджетной аналитики, поскольку для заполнения балансового раздела необходимы результирующие показатели. В случае с тестовой версией достаточно взять плановые значения основной операционной деятельности, где разность между доходами и расходами определяет итог на конкретном временном этапе.
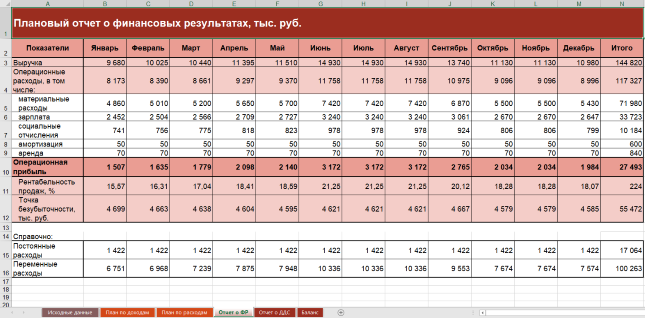
Это позволяет перейти к построению ОФР, для которого характерна взаимосвязь с балансом и ОДДС:
Финансовые результаты	Балансовая строка	ДДС
Прибыль или убыток от операционной деятельности	Нераспределенная величина добавляется к данным за предшествующий период	—
Выручка	—	Входящие поступления от взаиморасчетов с клиентами. Суммовой параметр корректируется с учетом переведенных авансов и текущей задолженности по следующей формуле: Поступления = Выручка + Авансовые платежи — Задолженность по отгрузкам
Расходы	—	Выплаты, учитывающие предоплату и долговые обязательства перед кредиторами. Для расчета применяется формульное значение: Платежи = Денежные затраты + Авансы выданные — Кредиторская задолженность
Для большей информативности следует дополнить отчет еще двумя строками:
Рентабельность реализации — расчетный критерий, равный соотношению между операционной прибылью и выручкой.
Порог безубыточности, выраженный в деньгах — предусматривает предварительное разделение постоянных и переменных расходных статей.
Формирование отчетности ОДДС

На этой стадии основной задачей выступает обобщение денежных поступлений и оттоков, расчет чистой разницы между ними, и суммирование полученного значения с оставшимися средствами на начало периода, позволяющее вычислить планируемый остаток. Результирующая сумма связывает аналитический базис с балансом. В рамках рассматриваемого примера возьмем за основу несколько допущений:
Предприятие специализируется только на профильной деятельности, не осуществляя сторонних закупок и финансовых операций, и не меняя состав учредителей. Единственным видом операций остается текущая категория.
Оплата поставляемой продукции делится на две стадии: 60% авансовым платежом, перечисляемым в месяце, предшествующем отгрузке товара, и 40% — расчет по факту приемки на склад.
Для выплат в рамках ФОТ также предусмотрены два перевода: половину составляет аванс, выдаваемый в период начисления, вторые 50% оплачиваются в следующем календарном отрезке так же, как и страховые взносы.
В качестве прочих расходов можно взять арендную плату — взаиморасчеты с собственником торгового помещения проводятся ежемесячно, сразу после выставления счета.
Результатом подстановки указанных значений становится модель ОДДС, отражающая специфику движения денежных потоков в рамках деятельности организации.
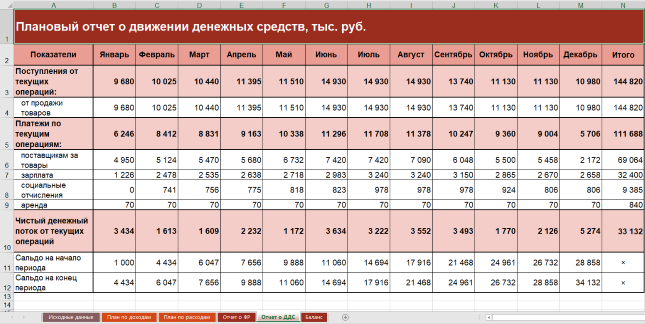
Сведение планового баланса

Обобщим технику составления в сводной таблице:
Показатель на начало периода	Формула	Пояснения
Основные средства	Баланс на начало предыдущего месяца — Амортизация за месяц (ОФР)	—
Запасы	—	Неизменны и равняются нулю из-за допущения, согласно которому весь объем реализуется за период
Дебиторская задолженность	Баланс на первое число предыдущего месяца + Платежи контрагентам за поставку (ОДДС) — Материальные расходы (ОФР)	В рассматриваемом примере отсутствует дебиторская задолженность
Денежные средства	Остаток на момент начала периода (баланс) + Чистый поток (ОДДС)	—
Уставный капитал	—	1000 рублей (ввиду условия об отсутствии новых учредителей)
Нераспределенная прибыль	Начальный показатель (баланс) + Поступление за месяц (ОФР)	—
Кредиторская задолженность	Значение отправной точки + Начисления ФОТ, социальным выплатам и аренде (ОФР) — Соответствующие платежи (ОДДС)
Общие требования

Примеры построения проекта финансовой модели предприятия в программе Excel, в том числе рассмотренный в данной статье, позволяют вывести ряд основных критериев, которые нужно учитывать при планировании. Итоговый результат моделирования должен соответствовать следующим стандартам.
Простота

Очевидно, что чем сложнее структура деятельности организации — тем более детализированными должны быть аналитические инструменты, используемые для анализа эффективности. Однако практика показывает, что грамотный подход к упрощению позволяет избежать ошибок в процессе построения, и способствует более быстрому освоению функциональных механизмов на начальных этапах.
Удобство использования

Последовательная организация блоков гарантирует формирование комплексного представления об экономической составляющей, а также о нюансах составления и ведения отчетности на различных временных интервалах.
Наглядность

Распространенный недостаток — разнесение предпосылок и выводов, затрудняющее определение взаимосвязи между корректируемыми данными и показателями, на которые они влияют. Грамотная визуализация — важный аспект, исключающий сложности адаптации.
Как подготовить финансовую модель

В процессе моделирования можно учитывать различные факторы, включая не только персональные управленческие потребности, но и банковские требования, актуальные в ситуациях, когда необходимо представить подробный инвестиционный проект. Отсутствие практических навыков и наличие достаточного свободного времени — повод для самостоятельного освоения такого эффективного аналитического инструмента, как Эксель. Однако в ситуациях, когда отчет требуется быстро, и должен соответствовать строгим критериям — лучше обратиться за помощью к специалистам.
Заключение

Приведенный пример рассматривает алгоритм создания базовой отчетности, оставляющей широкий диапазон возможностей для дальнейшей оптимизации. Структурирование категорий, группировка данных, учет большего количества внешних факторов — все это позволяет получить более точные результаты, которые станут основой для принятия верных решений, направленных на развитие бизнеса. Финансовое моделирование в Excel помогает понять, как планируемые мероприятия отразятся на прибыли и убытках предприятия, и какие аспекты имеют наибольшее влияние с точки зрения увеличения показателей экономической стабильности и ликвидности — как в текущем периоде, так и в долгосрочной перспективе.
Количество показов: 25550
Источник
Основы построение финансовой модели в Excel

Инвестиционный план

Прогнозирование доходов

План текущих расходов

Финансовая модель предприятия в Excel

Финансовая модель бизнеса: что это

Финансовое моделирование проекта: что надо знать

Финансовая модель (ФМ) в Excel: считаем доходы

Построение финансовых моделей: пример планирования расходов

Составляем плановый отчет о финансовых результатах

Формируем плановый отчет о движении денежных средств

Сводим плановый баланс

Алгоритм построения финансовой модели

Обучение финансовому моделированию в Excel — прочтите сначала

Как построить финансовую модель в Excel?

Шаг 1 — Финансовое моделирование в Excel — проецирование исторических данных

Шаг 12 – Финансовое моделирование в Excel – График долгов и процентов

Рекомендуемые статьи

Что дальше?

Общее представление

Финансовое моделирование проекта в Excel: что нужно знать

Готовые решения для всех направлений

Как построить финансовую модель компании в Excel: инструкция пошагово

Подсчет доходов

Пример планирования расходов

Составление планового отчета о финансовых результатах

Формирование отчетности ОДДС

Сведение планового баланса

Общие требования

Простота

Удобство использования

Наглядность

Как подготовить финансовую модель

Заключение
