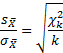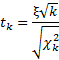Рассмотрим использование MS EXCEL при проверке статистических гипотез о разнице средних значений 2-х распределений в случае неизвестных дисперсий (парный тест). Вычислим значение тестовой статистики
t
0
, рассмотрим соответствующую процедуру «двухвыборочный
t
-тест», вычислим Р-значение (Р-
value
). С помощью надстройки Пакет анализа сделаем «Парный двухвыборочный t-тест для средних».
Здесь рассмотрен специальный случай
двухвыборочного t-теста
, когда наблюдения случайных величин из двух распределений производятся не независимо, а парами.
Примечание
: Процедура
двухвыборочного t-теста
также изложена в статьях
Двухвыборочный t-тест с одинаковыми дисперсиями
и
Двухвыборочный t-тест с различными дисперсиями
, где
выборки
из распределений считались независимыми.
СОВЕТ
: При первом знакомстве с процедурой
двухвыборочного
t
-теста
может быть полезным освежить в памяти
процедуру одновыброчного t-теста для среднего при неизвестной дисперсии
.
СОВЕТ
: Для
проверки гипотез
нам потребуется знание следующих понятий:
-
дисперсия и стандартное отклонение
,
-
выборочное распределение статистики
,
-
уровень доверия/ уровень значимости
,
-
нормальное распределение
,
-
t-распределение Стьюдента
и
его квантили
.
Приведем пример
. Имеется 2 прибора измеряющих твердость металлических образцов. Необходимо проверить, что эти приборы показывают одинаковые результаты на одном и том же образце (
нулевая гипотеза
).
Если для испытания на приборах образцы отбирать случайным образом: половину для проверки на приборе №1, другую на приборе №2, и использовать для проверки
нулевой
гипотезы
t-тест с одинаковыми (или различающимися) дисперсиями,
то можно сделать ошибочное заключение. Дело в том, что металлические образцы могут быть изготовлены из различных заготовок, прошедших различную термообработку и, следовательно, они могут иметь различную твердость. Таким образом, наблюденная разность между средними значениями твердости, полученными на каждом из приборов (Х
ср1
и Х
ср2
), будет также включать различие в твердости, обусловленную самими образцами. Другими словами, при таком методе исследования у нас имеется 2 источника неопределенности (случайности): несовершенство приборов и случайные колебания твердости самих образцов.
Чтобы исключить случайность, обусловленную различием образцов, и тем самым увеличить мощность
t
-теста
, используют парные
выборки
. В нашем случае, измерения одного и того же образца будем проводить сначала на одном, затем на другом приборе (предполагается, что после измерения твердости на первом приборе, образец не портится).
Таким образом, процедура
проверки гипотезы
сводится к определению разности твердостей полученных приборами на одном и том же образце. Если приборы настроены одинаково, то среднее разностей должно быть около 0 (отклонение не должно быть статистически значимым).
Пусть имеется набор из n пар наблюдений (n образцов). Т.к. результат каждого наблюдения является случайной величиной (приборы не идеальны, присутствует случайная ошибка измерений), то эти случайные величины имеют распределения с неизвестными средними значениями μ
1
и μ
2
(измерения полученные на приборе №1 и №2, соответственно). Дисперсии этих распределений неизвестны (обозначим их σ
1
2
и σ
2
2
).
Будем рассматривать не сами наблюдения, а их разницу. Обозначим D
i
– разницу измерений, полученную приборами №1 и №2 на i-м образце. Разницу между μ
1
и μ
2
, которую нам необходимо оценить, обозначим μ
D
.
Проведем
проверку гипотезы
о равенстве μ
D
заданному значению Δ
0
, т.е.
парный
t
-тест
(англ. The Paired t-Test). Если Δ
0
равно 0, то речь идет о проверке равенства средних двух распределений.
На самом деле, этот
t
-тест
сводится к
одновыборочному t-тесту
:
Нулевая гипотеза
H
0
: μ
D
=Δ
0
Альтернативная гипотеза
H
1
:
μ
D
<>Δ
0
Т.е. нам требуется проверить
двухстороннюю гипотезу
.
Тестовой статистикой
является случайная величина t:
где D
ср
– среднее значение разностей, S
d
– стандартное отклонение этих разностей.
Как известно из статьи про
одновыборочный t-тест
, данная
тестовая статистика
, имеет
t-распределение
c n-1 степенью свободы. Значение, которое приняла эта
t
-статистика,
обозначим t
0
.
Установим требуемый
уровень значимости
α (альфа) = 0,05 (допустимую для данной задачи
ошибку первого рода
, т.е. вероятность отклонить
нулевую гипотезу
, когда она верна).
Если вычисленное на основе
выборок
значение t
0
, в случае
двухсторонней гипотезы
, не попадет в область значений ограниченной
нижним
и
верхним α/2-квантилями
t
—
распределения
с n–1
степенями свободы,
то у нас будет основание отвергнуть
нулевую гипотезу.
Это утверждение эквивалентно случаю, когда D
ср
окажется вне пределов соответствующего
доверительного интервала.
В
файле примера на листе Парный тест
показана эквивалентность
доверительного интервала
и соответствующего
t
-теста.
Примечание
:
Верхний α/2-квантиль
— этотакое значение случайной величины
t
n–1
,
что
P
(
t
n-1
>=t
α/2
,
n-1
)
=α/2. Верхний α/2-квантиль
t
—
распределения с
n
-1 степенью свободы
обычно обозначают
t
α
/2,
n-1
. Подробнее о
квантилях
распределений см. статью
Квантили распределений MS EXCEL
.
В нашем случае, необходимо будет вычислить только верхний α/2-квантиль, т.к. он равен соответствующему нижнему
квантилю
со знаком минус. Следовательно, условие отклонения
нулевой гипотезы
можно записать как |t
0
|>t
α/2
,
n-1
.
Чтобы в MS EXCEL вычислить значение t
α/2
,
n-1
для различных
уровней значимости
(10%; 5%; 1%) и
степеней свобод
можно использовать несколько формул:
=СТЬЮДЕНТ.ОБР.2Х(α; n-1) =СТЬЮДЕНТ.ОБР(1- α/2; n-1) =-СТЬЮДЕНТ.ОБР(α/2; n-1) =СТЬЮДРАСПОБР(α; n-1)
Примечание
: Подробнее про функции MS EXCEL, связанные с
t
—
распределением
см.
статью t-распределение
.
Итак, если при проверке
двухсторонней гипотезы
формула
=ABS(t
0
)
вернет значение больше, чем результат формулы
=СТЬЮДЕНТ.ОБР.2Х(α; n-1)
, то это означает, что необходимо отвергнуть
нулевую гипотезу
(вычисления приведены в
файле примера на листе Парный тест
)
.
Для
односторонней
альтернативной гипотезы
μ
D
>Δ
0
,
нулевая гипотеза
будет отвергнута в случае t
0
> t
α
,
n-1
.
Для
односторонней
альтернативной гипотезы
μ
D
<Δ
0
,
нулевая гипотеза
будет отвергнута в случае t
0
<-t
α
,
n-1
.
Примечание
: Вышеуказанные распределения не обязательно должны быть
нормальными
. Однако, требуется чтобы выполнялись условия применимости
Центральной предельной теоремы
. Если размеры
выборок
меньше 30, то для справедливости сделанных здесь выводов, необходимо, чтобы
выборки
были сделаны из
нормального распределения
.
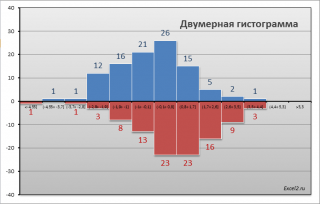
СОВЕТ
: Перед
проверкой гипотез
о равенстве средних значений
полезно построить
двумерную гистограмму
, чтобы визуально определить
центральную тенденцию
и
разброс данных
в обеих
выборок
.
Р-значение
При
проверке гипотез,
помимо
t
-теста,
большое распространение получил еще один эквивалентный подход, основанный на вычислении
p
-значения
(p-value).
Если
p-значение
меньше чем заданный
уровень значимости α
, то
нулевая гипотеза
отвергается и принимается
альтернативная гипотеза
. И наоборот, если
p-значение
больше α, то
нулевая гипотеза
не отвергается.
В случае
двусторонней гипотезы
p-значение
равно суммарной вероятности, что
t
-статистика
примет значение больше |t
0
| и меньше -|t
0
|.
Подробнее про
p
-значение
см., например,
статью про двухвыборочный z-тест
.
В MS EXCEL
p
-значение
для
двухсторонней гипотезы
в случае
парного
t
-теста
вычисляется по формуле:
=2*(1-СТЬЮДЕНТ.РАСП(ABS(t
0
); n-1;ИСТИНА))
Примечание
: Вычисления приведены в
файле примера на листе Парный тест
.
Для
односторонней гипотезы
μ
1
-μ
2
>Δ
0
p
-значение
вычисляется по формуле:
=1-СТЬЮДЕНТ.РАСП(t
0
; n-1;ИСТИНА)
В этом случае
p-значение
равно вероятности, что
t
-статистика
примет значение больше t
0
.
Для
односторонней гипотезы
μ
1
-μ
2
<Δ
0
p
-значение
вычисляется по формуле:
= СТЬЮДЕНТ.РАСП(t
0
; n-1;ИСТИНА)
В этом случае
p-значение
равно вероятности, что
t
-статистика
примет значение меньше t
0
.
В
файле примера на листе Парный
тест показана эквивалентность
проверки гипотезы
через
доверительный интервал
,
статистику t
0
(
t
-тест)
и
p
-значение
.
В MS EXCEL есть функция
СТЬЮДЕНТ.TEСT()
, которая вычисляет
p-значение
для 3-х различных
двухвыборочных
t
-тестов
(см. следующий раздел статьи)
.
К сожалению, эта функция может быть использована только для
проверки гипотез
с Δ
0
=0, то есть для
проверки гипотез
о равенстве средних μ
1
=μ
2
. Об этом легко догадаться, т.к. среди ее параметров отсутствует параметр
Гипотетическая разность средних
, т.е. Δ
0
.
Функция
СТЬЮДЕНТ.ТЕСТ()
Функция
СТЬЮДЕНТ.ТЕСТ()
используется для оценки различия двух
выборочных средних
. До
MS EXCEL 2010
имелась аналогичная функция
ТТЕСТ()
.
Примечание
: В английской версии функция носит название T.TEST(), старая версия — TTEST().
Функция
СТЬЮДЕНТ.ТЕСТ()
имеет 4 параметра. Первые два – это ссылки на диапазоны ячеек, содержащие
выборки
из 2-х сравниваемых распределений.
Третий параметр имеет название «хвосты». Этот параметр задает тип проверяемой гипотезы: односторонняя (=1) или двухсторонняя (=2). Если мы проверяем
двухстороннюю гипотезу
, то смотрим, не попало ли значение
тестовой статистики
в один из 2-х хвостов соответствующего
t-распределения
. Если мы проверяем
одностороннюю гипотезу
(имеется ввиду гипотеза μ
1
<μ
2
), то «хвост» всего один.
Как было сказано выше, эта функция вычисляет
p
-значение
для 3-х различных
двухвыборочных
t
-тестов
. За это отвечает четвертый параметр функции, который принимает значения от 1 до 3:
Парный двухвыборочный t-тест для средних;
-
Двухвыборочный t-тест с одинаковыми дисперсиями
;
-
Двухвыборочный t-тест с разными дисперсиями
.
Таким образом,
p
-значение
для
двухсторонней гипотезы
(равные
дисперсии
) вычисляется по формуле (см.
файл примера
):
=СТЬЮДЕНТ.ТЕСТ(
выборка1
;
выборка2
; 2; 1)
или
=2*(1-СТЬЮДЕНТ.РАСП(ABS(t
0
); n-1;ИСТИНА))
Для
односторонней гипотезы
μ
1
<μ
2
p
-значение
вычисляется по формуле:
=СТЬЮДЕНТ.ТЕСТ(
выборка1
;
выборка2
; 1; 1)
или
=СТЬЮДЕНТ.РАСП(t
0
; n-1;ИСТИНА)
Для
односторонней гипотезы
μ
1
>μ
2
p
-значение
вычисляется по формуле:
=1-СТЬЮДЕНТ.ТЕСТ(
выборка1
;
выборка2
; 1; 1)
или
=1-СТЬЮДЕНТ.РАСП(t
0
; n-1;ИСТИНА)
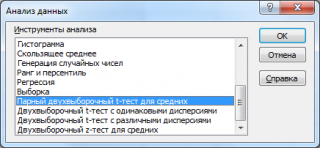
Пакет анализа
В
надстройке Пакет анализа
для проведения
Парного
двухвыборочного
t
-теста
имеется одноименный инструмент:
Парный
двухвыборочный
t
-тест для средних
(t-Test: Paired Two-Sample for Means).
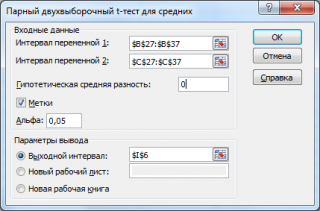
После выбора инструмента откроется окно, в котором требуется заполнить следующие поля (см.
файл примера лист Пакет анализа
):
интервал переменной 1
: ссылка на значения первой
выборки
. Ссылку указывать лучше с заголовком. В этом случае, при выводе результата надстройка выводит заголовки, которые делают результат нагляднее (в окне требуется установить галочку
Метки
);
интервал переменной 2
: ссылка на значения второй
выборки
;
гипотетическая средняя разность
: укажите значение Δ
0
, т.е. μ
1
-μ
2
. В нашем случае, введем 0;
Метки:
если в полях
интервал переменной 1
и
интервал переменной 2
указаны ссылки вместе с заголовками столбцов, то эту галочку нужно установить. В противном случае надстройка не позволит провести вычисления и пожалуется, что «
входной интервал содержит нечисловые данные
»;
Альфа:
уровень значимости;
Выходной интервал:
диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона.
В результате вычислений будет заполнен указанный
Выходной интервал.
Тот же результат можно получить с помощью формул (см.
файл примера лист Пакет анализа
):
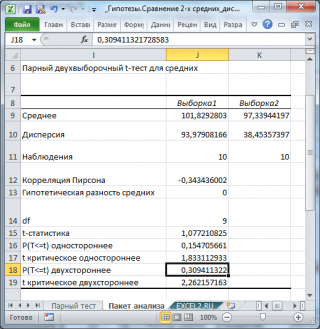
Разберем результаты вычислений, выполненных надстройкой:
Среднее
:
средние значения
обеих
выборок
Хср
1
и Хср
2
. Вычисления можно сделать с помощью функции
СРЗНАЧ()
;
Дисперсия
:
дисперсии
обеих
выборок.
Вычисления можно сделать с помощью функции
ДИСП.В()
Наблюдения
: размер
выборок.
Вычисления можно сделать с помощью функции
СЧЁТ()
Корреляция Пирсона
: коэффициент корреляции двух
выборок
. Вычисления можно сделать с помощью функции
КОРРЕЛ()
или
PEARSON()
Df
: число
степеней свободы
: n-1, где n размер
выборок
;
t
-статистика
: значение
тестовой статистики
t
(в наших обозначениях – это t
0
). Вычисление t
0
приведено в ячейке
Е1
5
;
P(T<=t) одностороннее
:
р-значение
в случае
односторонней альтернативной гипотезы
μ
1
-μ
2
>Δ
0
. Эквивалентная формула
=1-СТЬЮДЕНТ.РАСП(t
0
; n-1;ИСТИНА)
;
t критическое одностороннее
: Верхний α-квантиль t-распределения. Эквивалентная формула
=СТЬЮДЕНТ.ОБР(1- α; n-1)
;
P(T<=t) двухстороннее: р-значение
в случае
двухсторонней альтернативной гипотезы
μ
1
-μ
2
<>Δ
0
. Эквивалентная формула
=2*(1-СТЬЮДЕНТ.РАСП(ABS(t
0
); n-1;ИСТИНА))
;
t критическое двухстороннее: Верхний α/2-Квантиль t-распределения
. Эквивалентная формула
=СТЬЮДЕНТ.ОБР(1- α/2; n-1)
.
СОВЕТ
: О проверке других видов гипотез см. статью
Проверка статистических гипотез в MS EXCEL
.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает вероятность, соответствующую t-тесту Стьюдента. Функция СТЬЮДЕНТ.ТЕСТ позволяет определить вероятность того, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.
Синтаксис
СТЬЮДЕНТ.ТЕСТ(массив1;массив2;хвосты;тип)
Аргументы функции СТЬЮДЕНТ.ТЕСТ описаны ниже.
-
Массив1 Обязательный. Первый набор данных.
-
Массив2 Обязательный. Второй набор данных.
-
Хвосты Обязательный. Число хвостов распределения. Если значение «хвосты» = 1, функция СТЬЮДЕНТ.ТЕСТ возвращает одностороннее распределение. Если значение «хвосты» = 2, функция СТЬЮДЕНТ.ТЕСТ возвращает двустороннее распределение.
-
Тип Обязательный. Вид выполняемого t-теста.
Параметры
|
Тип |
Выполняемый тест |
|
1 |
Парный |
|
2 |
Двухвыборочный с равными дисперсиями (гомоскедастический) |
|
3 |
Двухвыборочный с неравными дисперсиями (гетероскедастический) |
Замечания
-
Если аргументы «массив1» и «массив2» имеют различное число точек данных, а «тип» = 1 (парный), то функция СТЬЮДЕНТ.ТЕСТ возвращает значение ошибки #Н/Д.
-
Аргументы «хвосты» и «тип» усекаются до целых значений.
-
Если «хвосты» или «тип» не является числом, возвращается #VALUE! значение ошибки #ЗНАЧ!.
-
Если «хвосты» — любое значение, кроме 1 или 2, возвращается значение #NUM! значение ошибки #ЗНАЧ!.
-
Функция СТЬЮДЕНТ.ТЕСТ использует данные аргументов «массив1» и «массив2» для вычисления неотрицательной t-статистики. Если «хвосты» = 1, СТЬЮДЕНТ.ТЕСТ возвращает вероятность более высокого значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими к генеральной совокупности с одним и тем же средним. Значение, возвращаемое функцией СТЬЮДЕНТ.ТЕСТ в случае, когда «хвосты» = 2, вдвое больше значения, возвращаемого, когда «хвосты» = 1, и соответствует вероятности более высокого абсолютного значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими к генеральной совокупности с одним и тем же средним.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные 1 |
Данные 2 |
|
|
3 |
6 |
|
|
4 |
19 |
|
|
5 |
3 |
|
|
8 |
2 |
|
|
9 |
14 |
|
|
1 |
4 |
|
|
2 |
5 |
|
|
4 |
17 |
|
|
5 |
1 |
|
|
Формула |
Описание |
Результат |
|
=СТЬЮДЕНТ.ТЕСТ(A2:A10;B2:B10;2;1) |
Вероятность, соответствующая парному критерию Стьюдента, с двусторонним распределением |
0,196016 |
Нужна дополнительная помощь?
Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух совокупностей.
В этом руководстве объясняется, как провести t-критерий с двумя образцами в Excel.
Как провести двухвыборочный t-тест в Excel
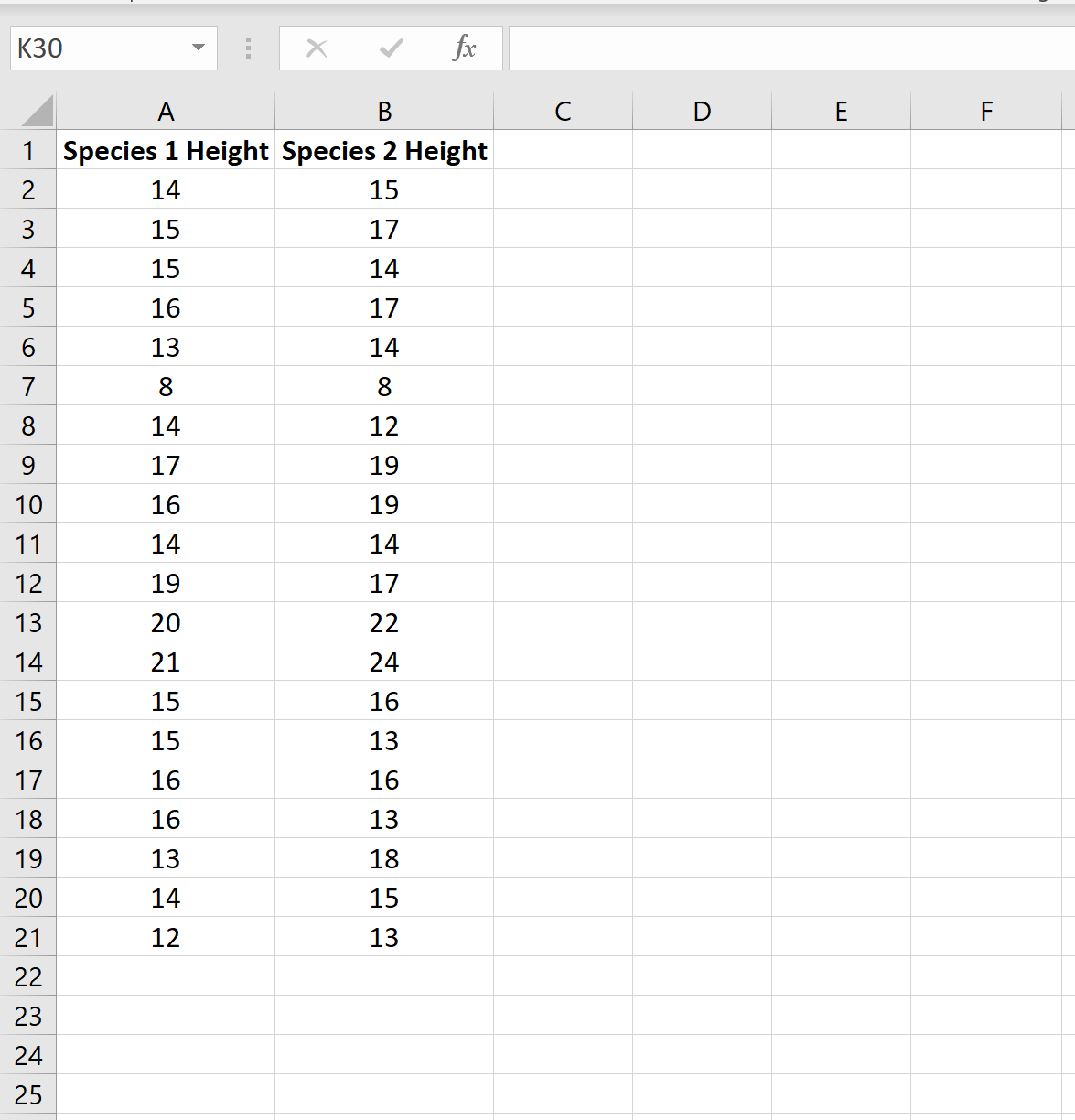
Предположим, исследователи хотят знать, имеют ли два разных вида растений в определенной стране одинаковую среднюю высоту. Поскольку обход и измерение каждого растения заняло бы слишком много времени, они решили собрать образец из 20 растений каждого вида.
На следующем изображении показана высота (в дюймах) каждого растения в каждом образце:
Мы можем провести двухвыборочный t-тест, чтобы определить, имеют ли два вида одинаковую среднюю высоту, используя следующие шаги:
Шаг 1: Определите, равны ли дисперсии генеральной совокупности .
Когда мы проводим двухвыборочный t-критерий, мы должны сначала решить, будем ли мы предполагать, что две совокупности имеют равные или неравные дисперсии. Как правило, мы можем предположить, что совокупности имеют равные дисперсии, если отношение большей выборочной дисперсии к меньшей выборочной дисперсии составляет менее 4:1.
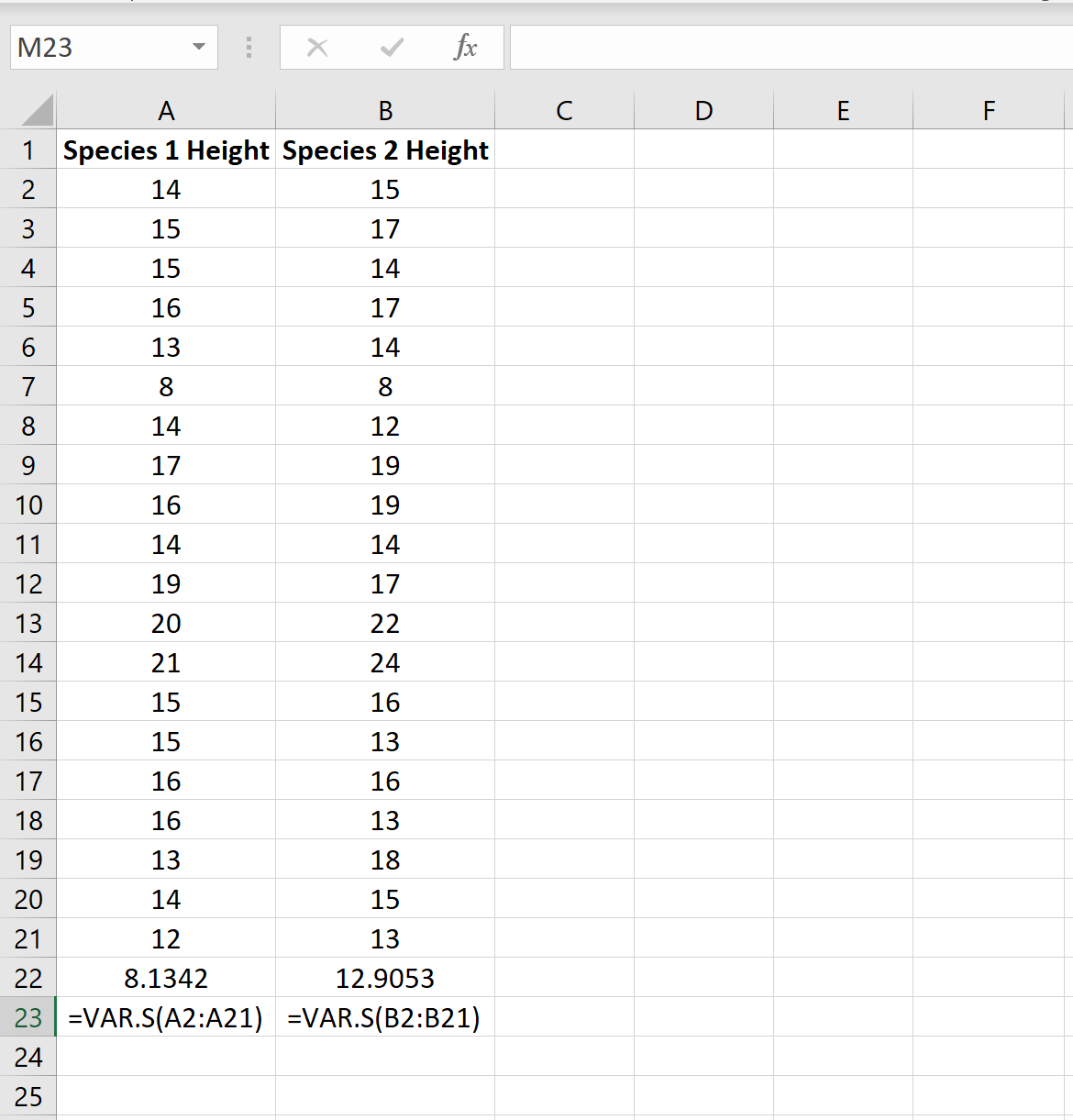
Мы можем найти дисперсию для каждого образца, используя функцию Excel =VAR.S(диапазон ячеек) , как показано на следующем рисунке:
Отношение большей дисперсии выборки к меньшей дисперсии выборки составляет 12,9053 / 8,1342 = 1,586 , что меньше 4. Это означает, что мы можем предположить, что дисперсии генеральной совокупности равны.
Шаг 2: Откройте пакет инструментов анализа .
На вкладке «Данные» на верхней ленте нажмите «Анализ данных».
Если вы не видите этот вариант для выбора, вам необходимо сначала загрузить пакет инструментов анализа , который является совершенно бесплатным.
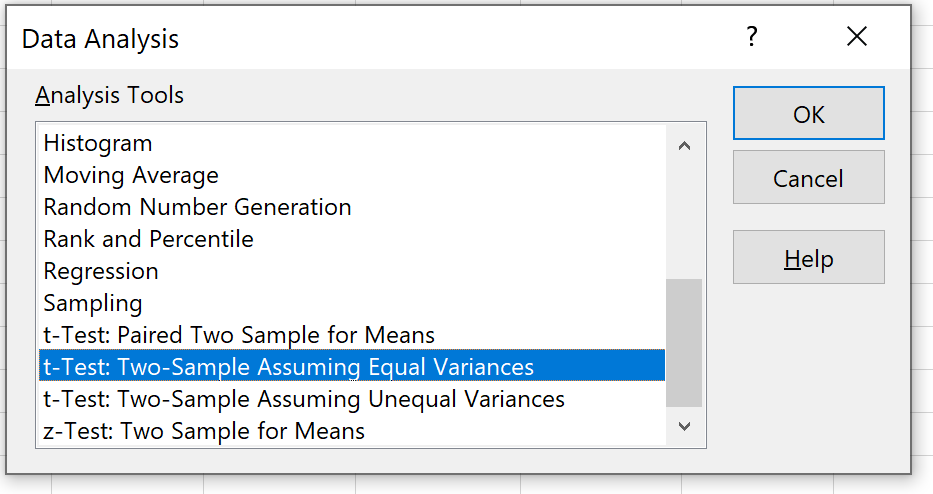
Шаг 3: Выберите подходящий тест для использования.
Выберите вариант с надписью t-Test: Two-Sample Assassining Equal Variances и нажмите OK.
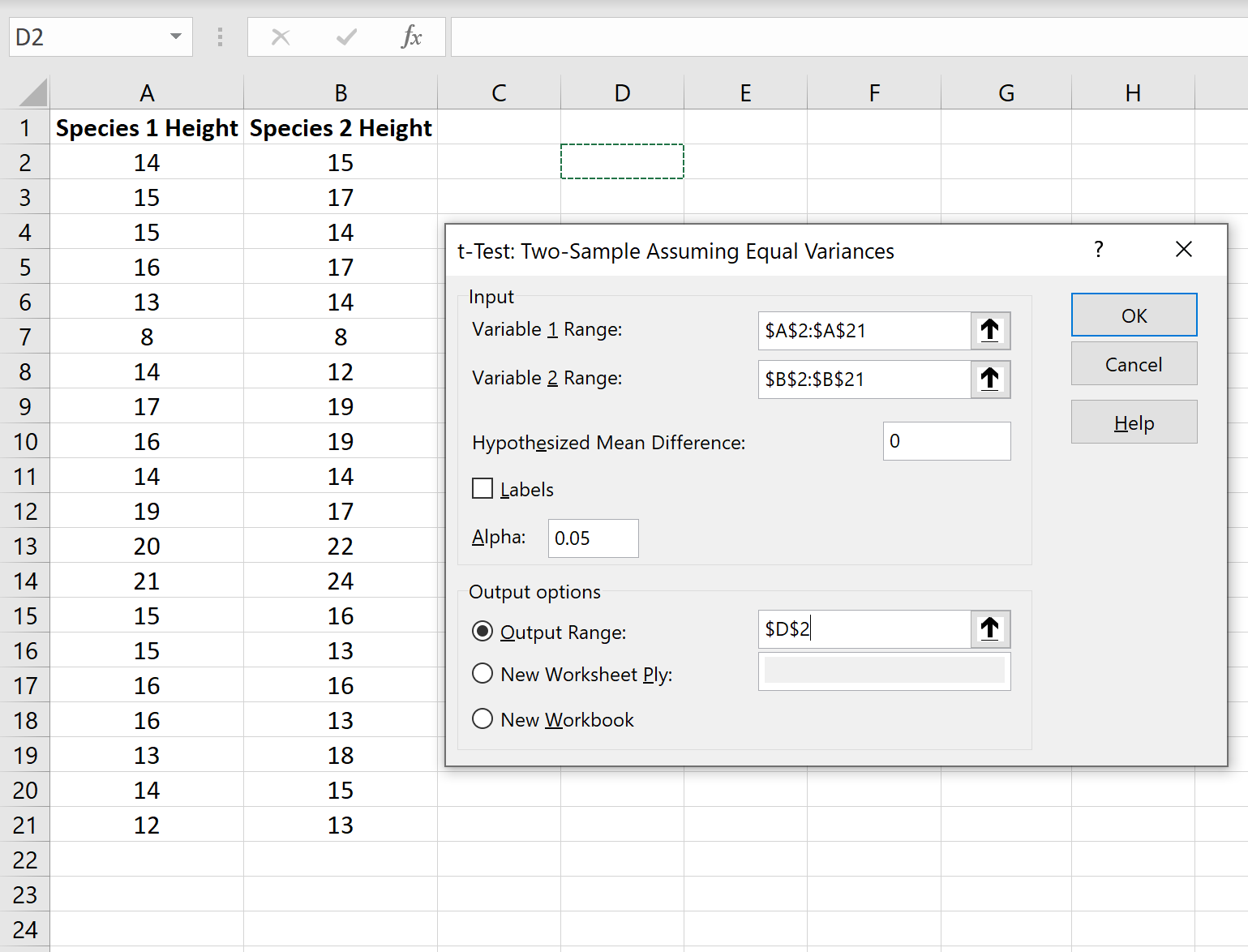
Шаг 4: Введите необходимую информацию .
Введите диапазон значений для переменной 1 (наша первая выборка), переменной 2 (наша вторая выборка), гипотетической средней разницы (в этом случае мы поместили «0», потому что мы хотим знать, равна ли истинная средняя разница генеральной совокупности 0), и выходной диапазон, в котором мы хотели бы видеть результаты t-теста. Затем нажмите ОК.
Шаг 5: интерпретируйте результаты .
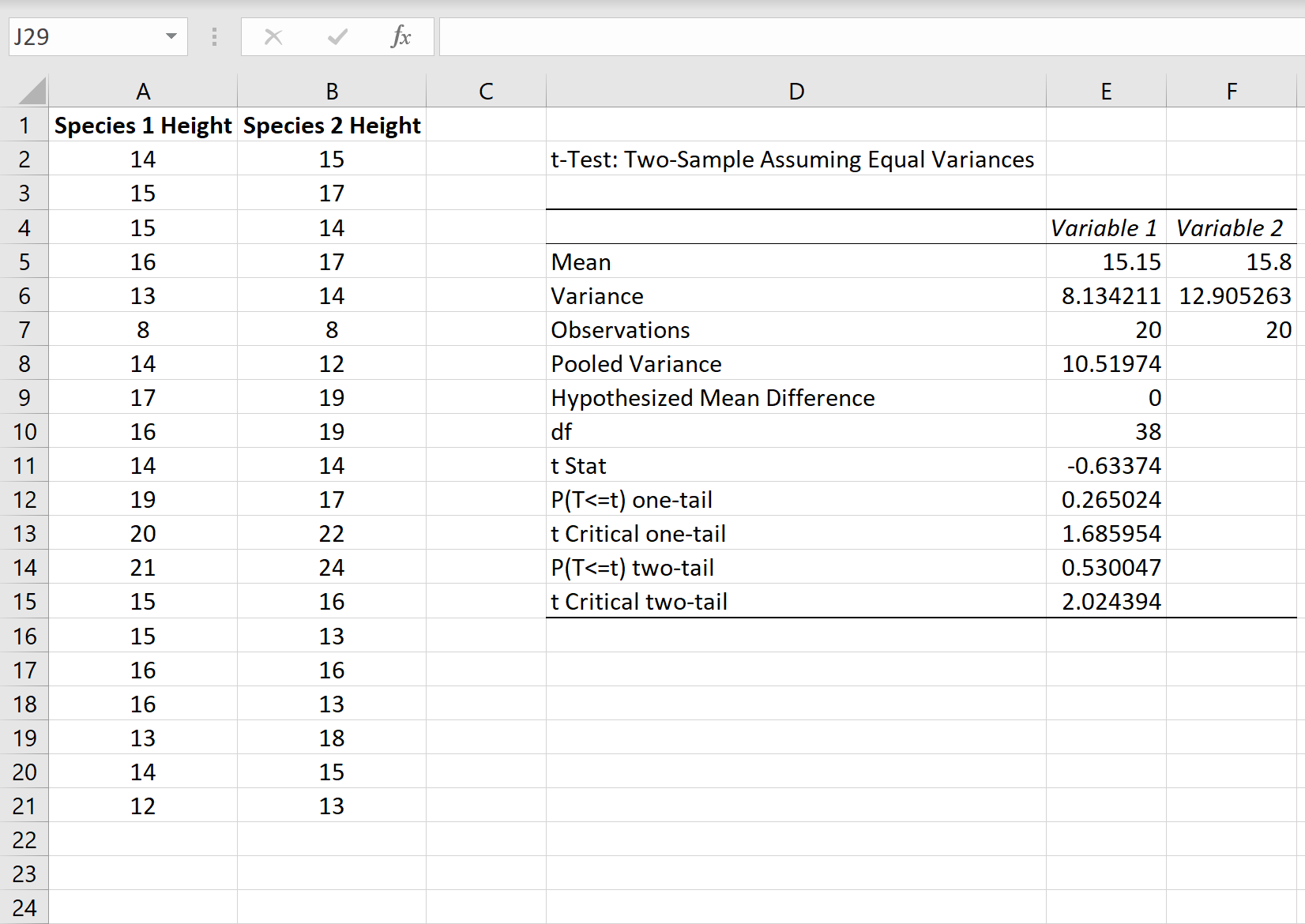
После того, как вы нажмете OK на предыдущем шаге, отобразятся результаты t-теста.
Вот как интерпретировать результаты:
Среднее значение: это среднее значение для каждого образца. Образец 1 имеет среднюю высоту 15,15 , а образец 2 имеет среднюю высоту 15,8 .
Дисперсия: это дисперсия для каждого образца. Выборка 1 имеет дисперсию 8,13 , а выборка 2 — 12,90 .
Наблюдения: это количество наблюдений в каждой выборке. Обе выборки содержат по 20 наблюдений (например, по 20 отдельных растений в каждой выборке).
Объединенная дисперсия: Число , которое рассчитывается путем «объединения» дисперсий каждой выборки вместе по формуле +n 2 -2), что оказывается равным 10,51974.Это число позже используется при вычислении тестовой статистики t .
Гипотетическая средняя разница: число, которое мы «предполагаем», представляет собой разницу между двумя средними значениями совокупности. В данном случае мы выбрали 0 , потому что хотим проверить, равна ли разница между двумя популяциями в среднем 0, например, разницы нет.
df: Степени свободы для t-критерия, рассчитанные как n 1 + n 2 -2 = 20 + 20 – 2 = 38 .
t Stat: тестовая статистика t , рассчитанная как t = [ x 1 – x 2 ] / √ [ s 2 p (1/n 1 + 1/n 2 )]
В этом случае t = [15,15-15,8] / √ [10,51974(1/20+1/20)] = -0,63374 .
P(T<=t) двухсторонний: значение p для двустороннего t-критерия. В этом случае р = 0,530047.Это намного больше, чем альфа = 0,05, поэтому мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что два средних значения населения различны.
t Критический двухсторонний: это критическое значение теста, найденное путем определения значения в таблице распределения t , которое соответствует двустороннему тесту с альфа = 0,05 и df = 38. Получается 2,024394.Поскольку наша тестовая статистика t меньше этого значения, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что два средних значения населения различны.
Обратите внимание, что подход с использованием p-значения и критического значения приведет к одному и тому же выводу.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие типы t-тестов в Excel:
Как провести одновыборочный t-тест в Excel
Как провести t-тест для парных выборок в Excel
Содержание
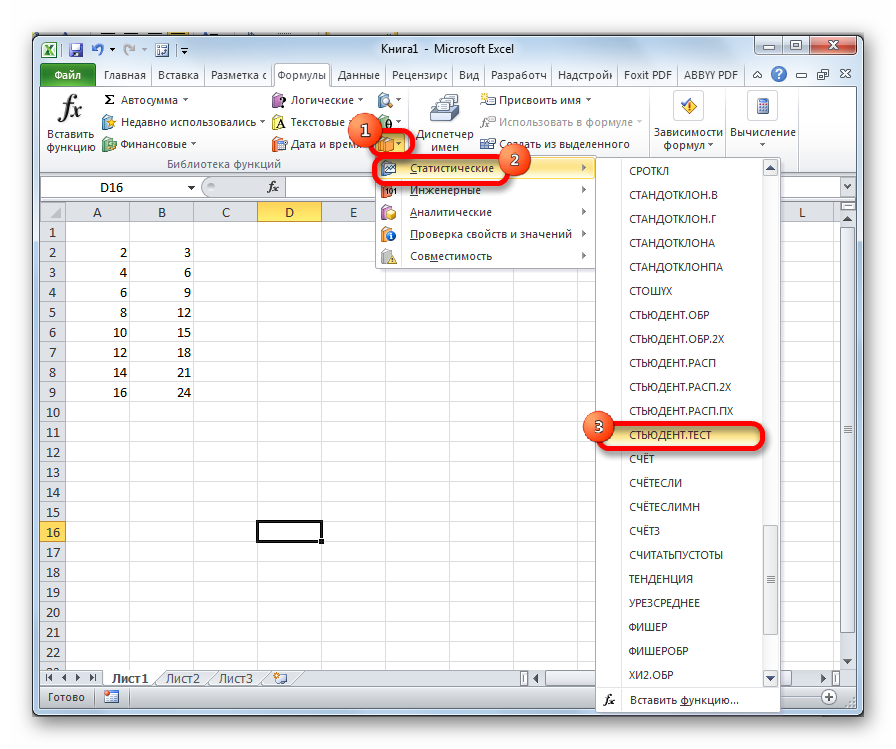
- Определение термина
- Расчет показателя в Excel
- Способ 1: Мастер функций
- Способ 2: работа со вкладкой «Формулы»
- Способ 3: ручной ввод
- Вопросы и ответы
Одним из наиболее известных статистических инструментов является критерий Стьюдента. Он используется для измерения статистической значимости различных парных величин. Microsoft Excel обладает специальной функцией для расчета данного показателя. Давайте узнаем, как рассчитать критерий Стьюдента в Экселе.
Определение термина
Но, для начала давайте все-таки выясним, что представляет собой критерий Стьюдента в общем. Данный показатель применяется для проверки равенства средних значений двух выборок. То есть, он определяет достоверность различий между двумя группами данных. При этом, для определения этого критерия используется целый набор методов. Показатель можно рассчитывать с учетом одностороннего или двухстороннего распределения.
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Способ 1: Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.
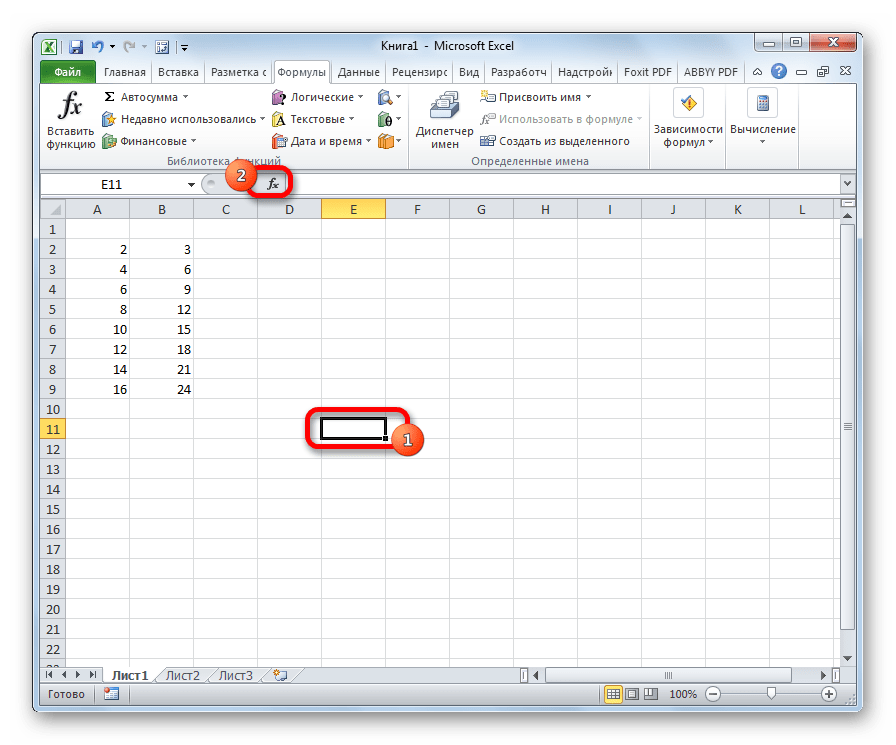
- Строим таблицу с двумя рядами переменных.
- Кликаем по любой пустой ячейке. Жмем на кнопку «Вставить функцию» для вызова Мастера функций.
- После того, как Мастер функций открылся. Ищем в списке значение ТТЕСТ или СТЬЮДЕНТ.ТЕСТ. Выделяем его и жмем на кнопку «OK».
- Открывается окно аргументов. В полях «Массив1» и «Массив2» вводим координаты соответствующих двух рядов переменных. Это можно сделать, просто выделив курсором нужные ячейки.
В поле «Хвосты» вписываем значение «1», если будет производиться расчет методом одностороннего распределения, и «2» в случае двухстороннего распределения.
В поле «Тип» вводятся следующие значения:
- 1 – выборка состоит из зависимых величин;
- 2 – выборка состоит из независимых величин;
- 3 – выборка состоит из независимых величин с неравным отклонением.
Когда все данные заполнены, жмем на кнопку «OK».
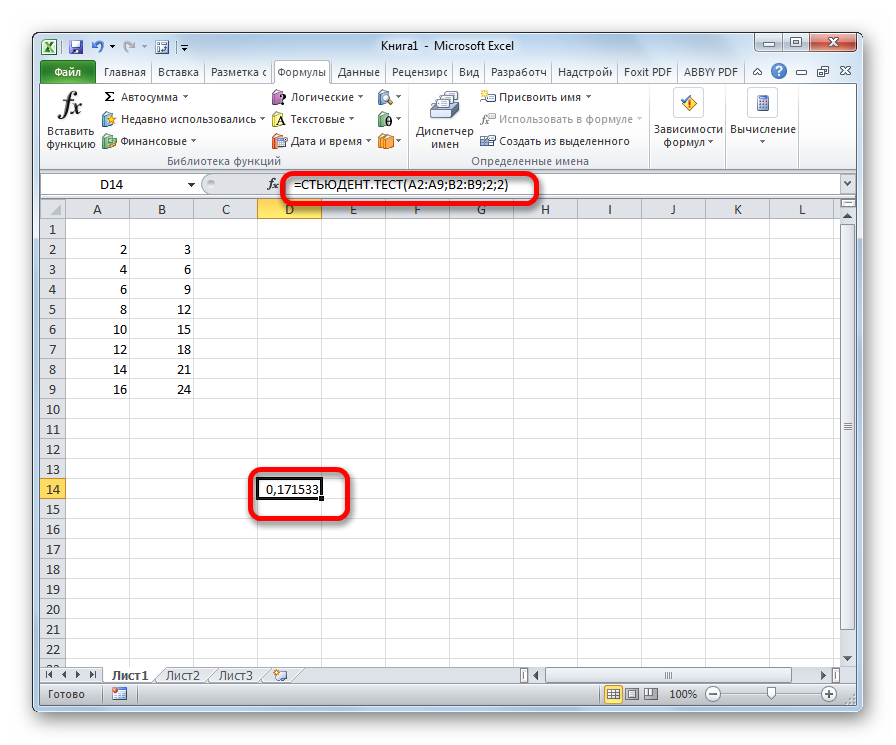
Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.
Способ 2: работа со вкладкой «Формулы»
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.
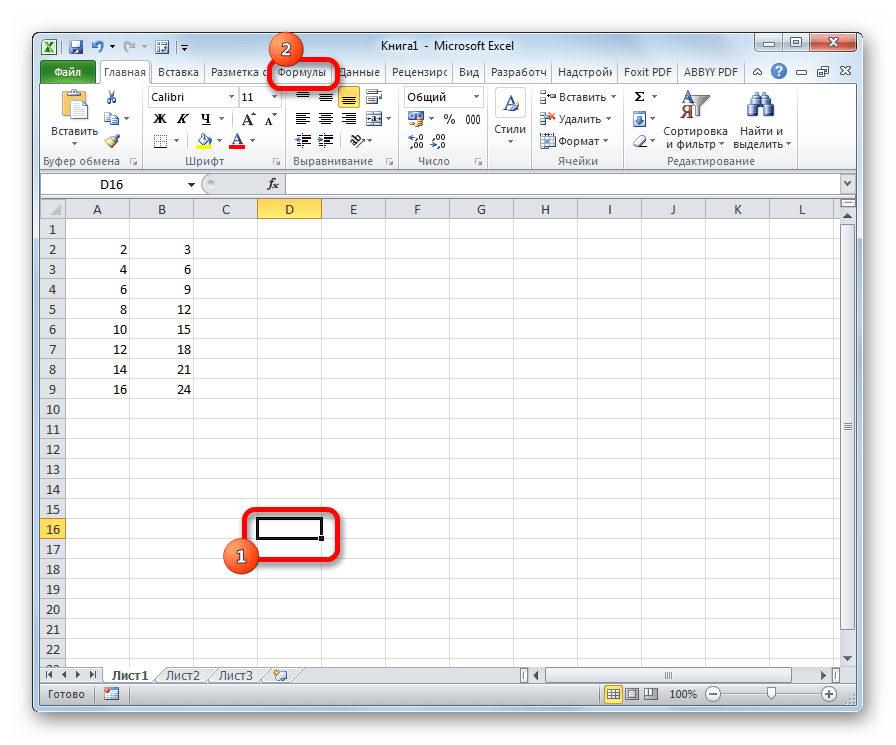
- Выделяем ячейку для вывода результата на лист. Выполняем переход во вкладку «Формулы».
- Делаем клик по кнопке «Другие функции», расположенной на ленте в блоке инструментов «Библиотека функций». В раскрывшемся списке переходим в раздел «Статистические». Из представленных вариантов выбираем «СТЬЮДЕНТ.ТЕСТ».
- Открывается окно аргументов, которые мы подробно изучили при описании предыдущего способа. Все дальнейшие действия точно такие же, как и в нём.
Способ 3: ручной ввод
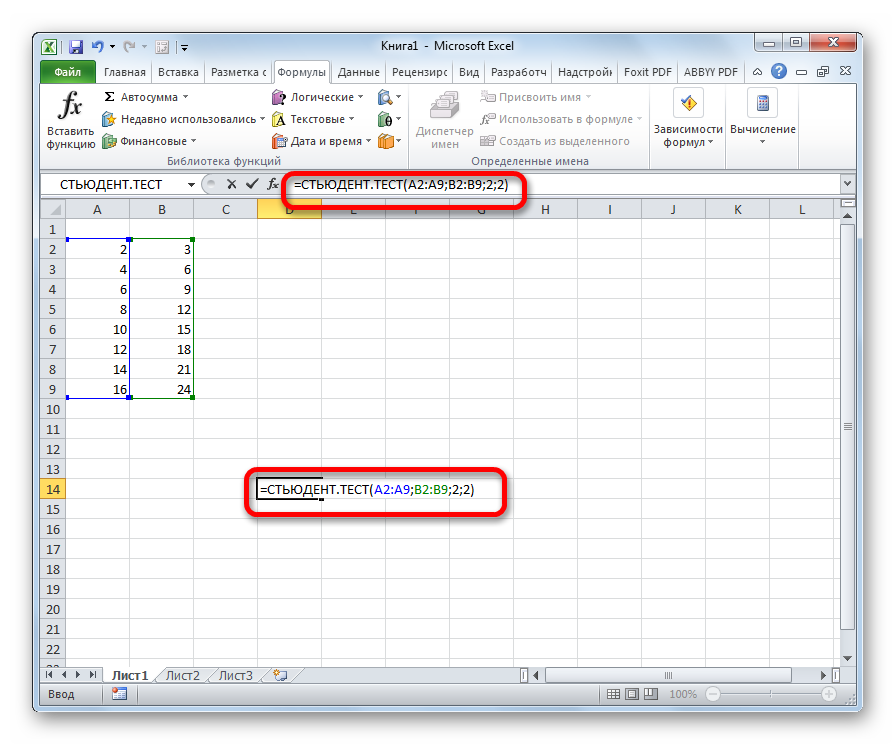
Формулу СТЬЮДЕНТ.ТЕСТ также можно ввести вручную в любую ячейку на листе или в строку функций. Её синтаксический вид выглядит следующим образом:
= СТЬЮДЕНТ.ТЕСТ(Массив1;Массив2;Хвосты;Тип)
Что означает каждый из аргументов, было рассмотрено при разборе первого способа. Эти значения и следует подставлять в данную функцию.
После того, как данные введены, жмем кнопку Enter для вывода результата на экран.
Как видим, вычисляется критерий Стьюдента в Excel очень просто и быстро. Главное, пользователь, который проводит вычисления, должен понимать, что он собой представляет и какие вводимые данные за что отвечают. Непосредственный расчет программа выполняет сама.
Еще статьи по данной теме:
Помогла ли Вам статья?
Microsoft Excel имеет мощные инструменты для анализа и визуализации статистики. В этой статье мы продемонстрируем их на примере классической статистической процедуры: теста Стьюдента или t-теста.
t-тест: что это такое, и зачем это нужно?
t-тест или тест Стьюдента был разработан английским математиком Уильямом Госсетом. В начале XX века он трудился на пивоваренном заводе «Гиннесс» в Ирландии, разрабатывая математические методы оценки качества сырья, из которого варят пиво.
По условиям контракта, Госсет не имел права публиковать свои разработки под собственным именем. Поэтому первая публикация методики теста появилась в журнале «Биометрика» под псевдонимом Student, что значит «студент». Так тест и остался в истории под названием теста Стьюдента.
Тест Стьюдента позволяет сравнивать случайные выборки данных — либо с некой нормой, либо между собой. Например, завод выпускает шурупы, и нужно оценить, соответствуют ли они в норме по длине. Или в больнице ведется клиническое исследование лекарства, и нужно оценить его эффект на пациентах до и после приема.
В обоих случаях должно выполняться требование нормальности распределения исследуемого признака в каждой из сравниваемых групп. Результатом выполнения теста является число, отражающее данный показатель — t-критерий, или критерий Стьюдента.
t-тест: как выполнить в MS Excel?
Вне зависимости от того, для чего вам может понадобиться вычислить критерий Стьюдента, в Microsoft Excel есть функция TTEST, которая позволяет это сделать. Она доступна в надстройке Пакет анализа. Рассмотрим, как использовать функцию на примере Microsoft Excel 2013 в Windows 7.
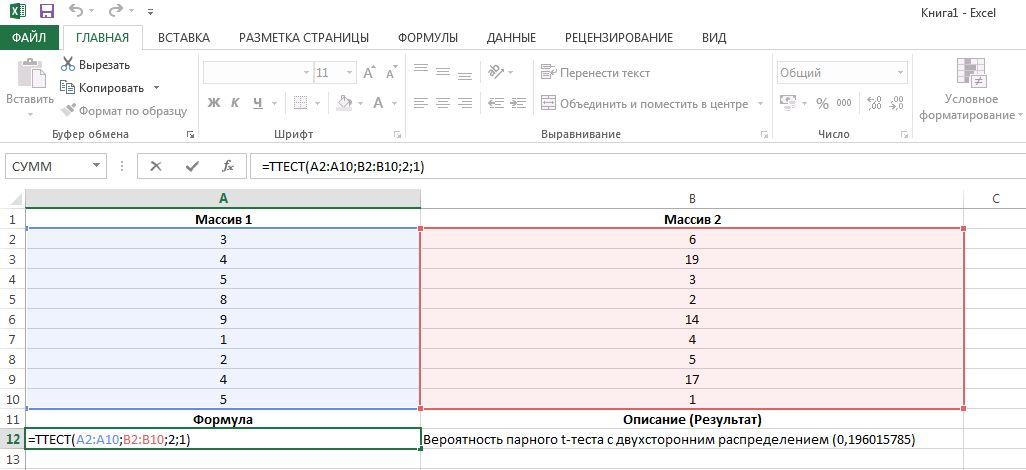
Синтаксис функции следующий: ТТЕСТ(массив1;массив2;хвосты;тип). Скопируйте эту формулу в любое поле вашего документа Excel.
- Первый набор данных называется «массив1», а «массив2», соответственно, обозначает второй набор данных. В примере (см. изображение) «массив1» имеет значение «A2:A10».
- Переменная «хвосты» определяет тип распределения. Если в ячейке имеется значение «1», используется одностороннее распределение; если имеется значение «2», то используется двустороннее распределение.
- Переменная «тип» указывает, какой тип теста применять. Если значение равно «1», используется тест «Парный». Если выбрать «2», то будет использоваться тип «Двухпарный», если 3 — «Двухпарный с неравным отклонением».
Читайте также:
- Как выполнять расчеты времени в Excel
- Как сделать сводную таблицу в Excel
- Excel: 10 формул для работы в офисе
Фото: авторские, pxhere.com
Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).
Распределение Стьюдента
Общий подход в проверке гипотез описан здесь, поэтому сразу к делу. Предположим для начала, что выборка извлечена из нормальной совокупности случайных величин X с генеральной средней μ и дисперсией σ2. Средняя арифметическая из этой выборки, очевидно, сама является случайной величиной. Если извлечь много таких выборок и посчитать по ним средние, то они также будут иметь нормальное распределение с математическим ожиданием μ и дисперсией
Тогда случайная величина
имеет стандартное нормальное распределение со всеми вытекающими отсюда последствиями. Например, с вероятностью 95% ее значение не выйдет за пределы ±1,96.
Однако такой подход будет корректным, если известна генеральная дисперсия. В реальности, как правило, она не известна. Вместо нее берут оценку – несмещенную выборочную дисперсию:
где
Возникает вопрос: будет ли генеральная средняя c вероятностью 95% находиться в пределах ±1,96sx̅. Другими словами, являются ли распределения случайных величин
и
эквивалентными.
Впервые этот вопрос был поставлен (и решен) одним химиком, который трудился на пивной фабрике Гиннесса в г. Дублин (Ирландия). Химика звали Уильям Сили Госсет и он брал пробы пива для проведения химического анализа. В какой-то момент, видимо, Уильяма стали терзать смутные сомнения на счет распределения средних. Оно получалось немного более размазанным, чем должно быть у нормального распределения.
Собрав математическое обоснование и рассчитав значения функции обнаруженного им распределения, химик из Дублина Уильям Госсет написал заметку, которая была опубликована в мартовском выпуске 1908 года журнала «Биометрика» (главред – Карл Пирсон). Гиннесс строго-настрого запретил выдавать секреты пивоварения, и Госсет подписался псевдонимом Стьюдент.
Несмотря на то что, К. Пирсон уже изобрел распределение Хи-квадрат, все-таки всеобщее представление о нормальности еще доминировало. Никто не собирался думать, что распределение выборочных оценок может быть не нормальным. Поэтому статья У. Госсета осталась практически не замеченной и забытой. И только Рональд Фишер по достоинству оценил открытие Госсета. Фишер использовал новое распределение в своих работах и дал ему название t-распределение Стьюдента. Критерий для проверки гипотез, соответственно, стал t-критерием Стьюдента. Так произошла «революция» в статистике, которая шагнула в эру анализа выборочных данных. Это был краткий экскурс в историю.
Посмотрим, что же мог увидеть У. Госсет. Сгенерируем 20 тысяч нормальных выборок из 6-ти наблюдений со средней (X̅) 50 и среднеквадратичным отклонением (σ) 10. Затем нормируем выборочные средние, используя генеральную дисперсию:
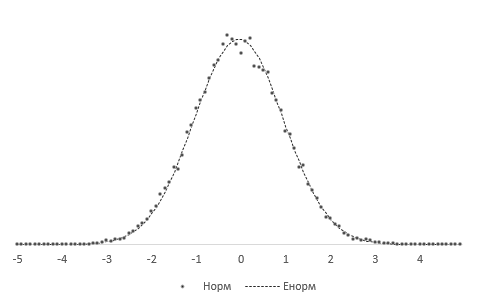
Получившиеся 20 тысяч средних сгруппируем в интервалы длинной 0,1 и подсчитаем частоты. Изобразим на диаграмме фактическое (Norm) и теоретическое (ENorm) распределение частот выборочных средних.
Точки (наблюдаемые частоты) практически совпадают с линией (теоретическими частотами). Оно и понятно, ведь данные взяты из одной и то же генеральной совокупности, а отличия – это лишь ошибки выборки.
Проведем новый эксперимент. Нормируем средние, используя выборочную дисперсию.
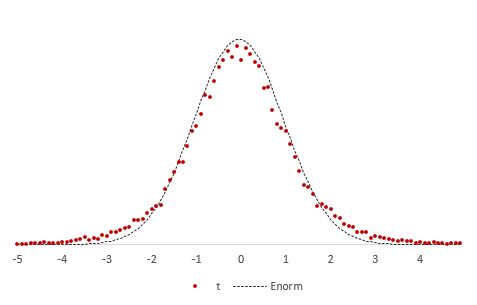
Снова подсчитаем частоты и нанесем их на диаграмму в виде точек, оставив для сравнения линию стандартного нормального распределения. Обозначим эмпирическое частоты средних, скажем, через букву t.
Видно, что распределения на этот раз не очень-то и совпадают. Близки, да, но не одинаковы. Хвосты стали более «тяжелыми».
У Госсета-Стьюдента не было последней версии MS Excel, но именно этот эффект он и заметил. Почему так получается? Объяснение заключается в том, что случайная величина
зависит не только от ошибки выборки (числителя), но и от стандартной ошибки средней (знаменателя), которая также является случайной величиной.
Давайте немного разберемся, какое распределение должно быть у такой случайной величины. Вначале придется кое-что вспомнить (или узнать) из математической статистики. Есть такая теорема Фишера, которая гласит, что в выборке из нормального распределения:
1. средняя X̅ и выборочная дисперсия s2 являются независимыми величинами;
2. соотношение выборочной и генеральной дисперсии, умноженное на количество степеней свободы, имеет распределение χ2(хи-квадрат) с таким же количеством степеней свободы, т.е.
где k – количество степеней свободы (на английском degrees of freedom (d.f.))
Вернемся к распределению средней. Разделим числитель и знаменатель выражения
на σX̅. Получим
Числитель – это стандартная нормальная случайная величина (обозначим ξ (кси)). Знаменатель выразим из теоремы Фишера.
Тогда исходное выражение примет вид
Это и есть t-критерий Стьюдента в общем виде (стьюдентово отношение). Вывести функцию его распределения можно уже непосредственно, т.к. распределения обеих случайных величин в данном выражении известны. Оставим это удовольствие математикам.
Функция t-распределения Стьюдента имеет довольно сложную для понимания формулу, поэтому не имеет смысла ее разбирать. Вероятности и квантили t-критерия приведены в специальных таблицах распределения Стьюдента и забиты в функции разных ПО вроде Excel.
Итак, вооружившись новыми знаниями, вы сможете понять официальное определение распределения Стьюдента.
Случайной величиной, подчиняющейся распределению Стьюдента с k степенями свободы, называется отношение независимых случайных величин
где ξ распределена по стандартному нормальному закону, а χ2k подчиняется распределению χ2 c k степенями свободы.
Таким образом, формула критерия Стьюдента для средней арифметической
есть частный случай стьюдентова отношения
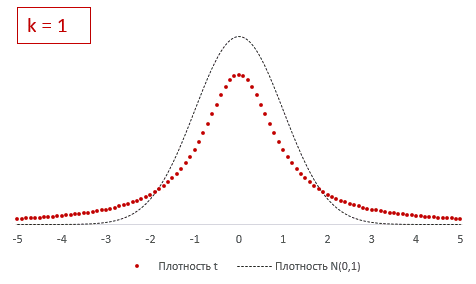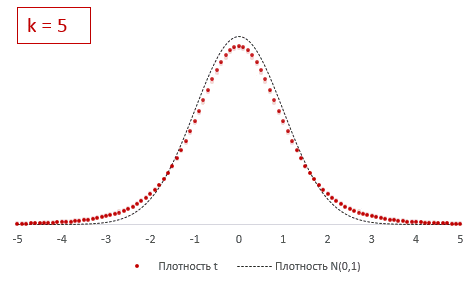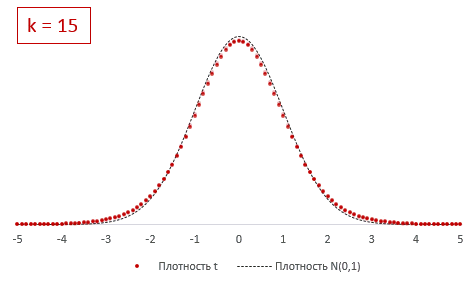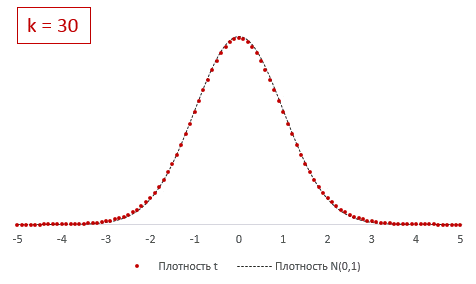
Из формулы и определения следует, что распределение т-критерия Стьюдента зависит лишь от количества степеней свободы.
При k > 30 t-критерий практически не отличается от стандартного нормального распределения.
В отличие от хи-квадрат, t-критерий может быть одно- и двусторонним. Обычно пользуются двусторонним, предполагая, что отклонение может происходить в обе стороны от средней. Но если условие задачи допускает отклонение только в одну сторону, то разумно применять односторонний критерий. От этого немного увеличивается мощность критерия.
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
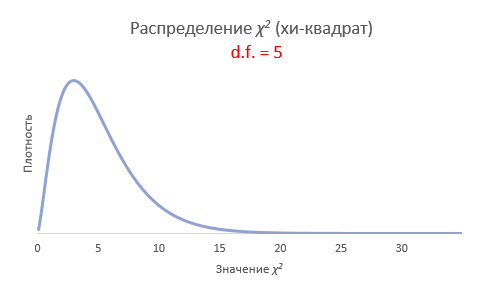
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.
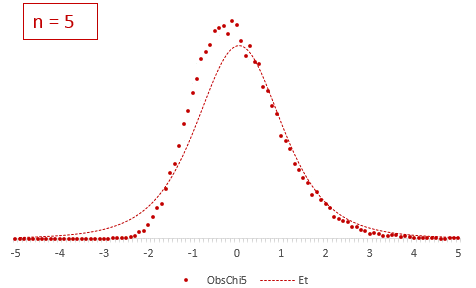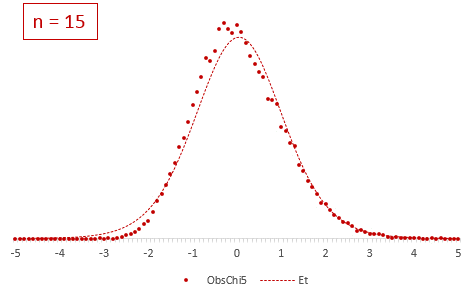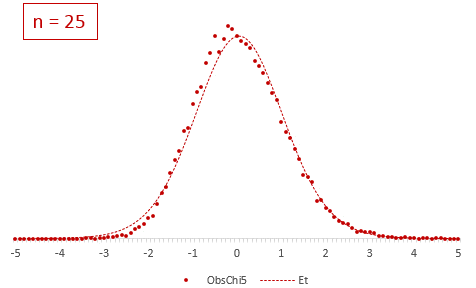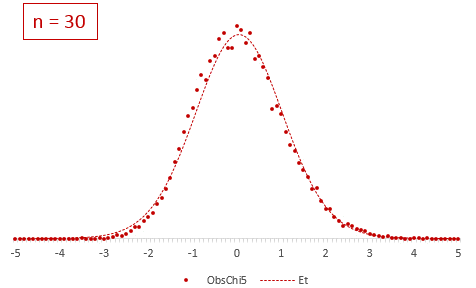
Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.
Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.
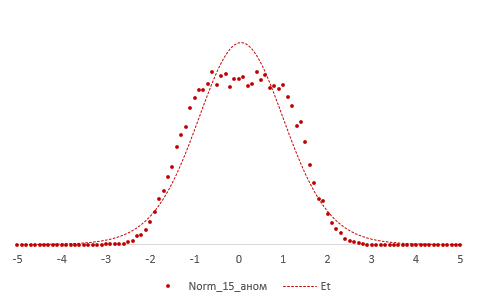
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.
Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.
СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.
СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).
СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.
СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.
СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058
СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.
ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.
Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.
Краткое условие в обще принятых обозначениях выглядит так.
H0: μ = 50 кг
Ha: μ ≠ 50 кг
Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.
Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:
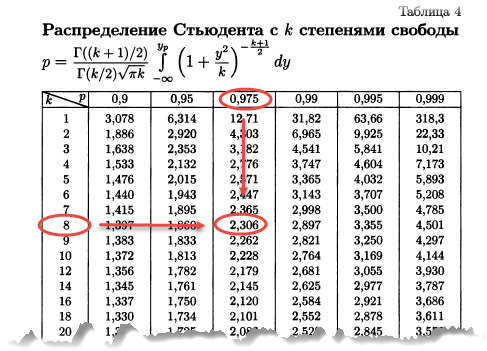
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).
По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H0 о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.
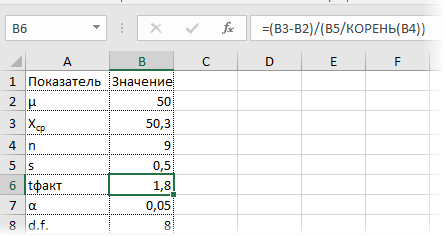
Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.
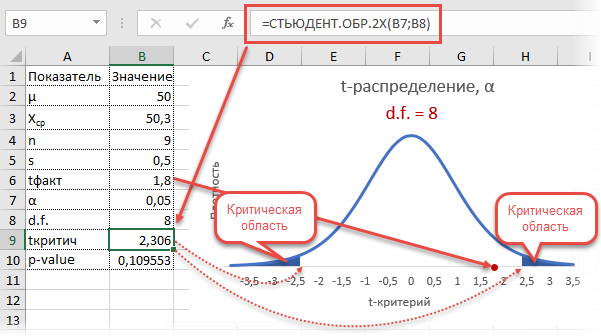
Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.
Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.
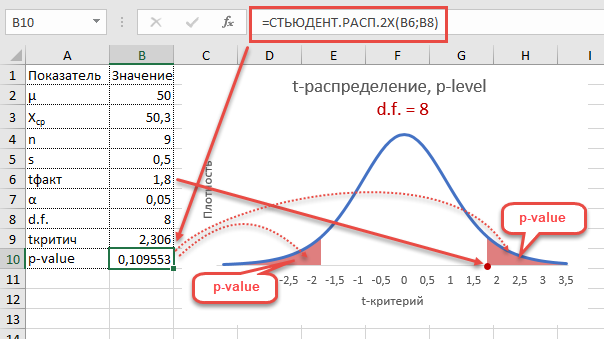
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.
P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
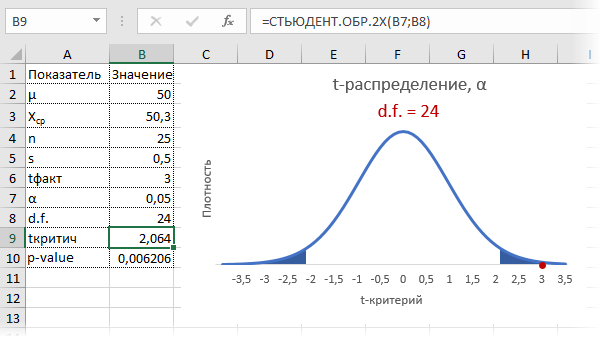
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.
Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.
Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.
Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel
С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.
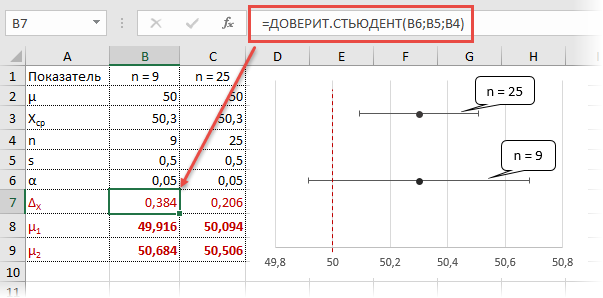
Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.
Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.
Таким образом, мы решили одну и ту же задачу тремя способами:
1. Древним подходом, сравнивая расчетное и табличное значение t-критерия
2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.
3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.
Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.
Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.
Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.
Скачать файл с примером.
Всего доброго, будьте здоровы.
Поделиться в социальных сетях:
Критерий Стьюдента – обобщенное название группы статистических тестов (обычно перед словом “критерий” добавляется латинская буква “t”). Чаще всего он применяется для проверки равенства средних значений в двух выборках. Давайте посмотрим, как рассчитать данный критерий в программе Excel с помощью специальной функции.
-
Расчет t-критерия Стьюдента
- Метод 1: пользуемся Мастером функций
- Метод 2: вставляем функцию через “Формулы”
- Метод 3: ручной ввод формулы
- Заключение
Для того, чтобы выполнить соответствующие расчеты, понадобится функция “СТЬЮДЕНТ.ТЕСТ”, в ранних версиях Excel (2007 и старше) – “ТТЕСТ”, которая есть и в современных редакциях для сохранения совместимости со старыми документам.
Использовать функцию можно по-разному. Давайте разберем каждый вариант отдельно на примере таблицы с двумя рядами-столбцами числовых значений.
Метод 1: пользуемся Мастером функций
Этот способ хорош тем, что не нужно запоминать формулу функции (список ее аргументов). Итак, алгоритм действий следующий:
- Встаем в любую свободную ячейку, затем щелкаем по значку “Вставить функцию” слева от строки формул.
- В открывшемся окне Мастера функций выбираем категорию “Полный алфавитный перечень”, в списке ниже находим оператор “СТЬЮДЕНТ.ТЕСТ”, отмечаем его и щелкаем OK.
- На экране отобразится окно, в котором заполняем аргументы функции, после чего нажимаем OK:
- “Массив1” и “Массив2” – указываем диапазоны ячеек, содержащие ряды чисел (в нашем случае это “A2:A7” и “B2:B7”). Мы можем сделать это вручную, введя координаты с клавиатуры, или просто выделяем нужные элементы в самой таблице.
- “Хвосты” – пишем цифру “1”, если требуется выполнить расчет методом одностороннего распределения, или “2” – для двухстороннего.
- “Тип” – в этом поле указываем: “1” – если выборка состоит из зависимых величин; “2” – из независимых; “3” – из независимых величин с неравным отклонением.
- В результате в нашей ячейке с функцией появится рассчитанное значение критерия.
Метод 2: вставляем функцию через “Формулы”
- Переключаемся во вкладку “Формулы”, где также представлена кнопка “Вставить функцию”, которая нам и нужна.
- В результате откроется Мастер функций, дальнейшие действия в котором аналогичны описанным выше.
Через вкладку “Формулы” функцию “СТЬЮДЕНТ.ТЕСТ” можно запустить по-другому:
- В группе инструментов “Библиотека функций” жмем по значку “Другие функции”, после чего раскроется список, в котором выбираем раздел “Статистические”. Пролистав предложенный перечень мы сможем найти нужный нам оператор.
- На экране отобразится окно для заполнения аргументов, с которым мы уже познакомились ранее.
Метод 3: ручной ввод формулы
Опытные пользователи могут обходиться без Мастера функций и в требуемой ячейке сразу вводить формулу со ссылками на нужные диапазоны данных и прочими параметрами. Синтаксис функции в общем виде выглядит так:
= СТЬЮДЕНТ.ТЕСТ(Массив1;Массив2;Хвосты;Тип)
Каждый из аргументов мы разобрали в первом разделе публикации. Все, что остается сделать после набора формулы – нажать Enter для выполнения расчета.
Заключение
Таким образом, рассчитать t-критерий Стьюдента в программе Excel можно с помощью специальной функции, которую можно запустить разными способами. Также у пользователя есть возможность сразу ввести формулу функции в нужной ячейке, однако в этом случае придется запоминать ее синтаксис, что может быть хлопотно из-за того, что применяется она не так часто.
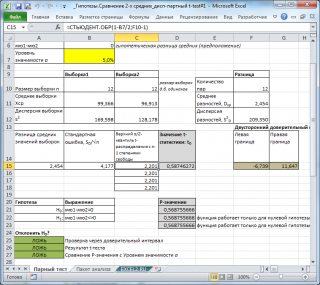
Это средство анализа служит для проверки
гипотезы о равенстве средних парных
наблюдений, когда наблюдения собраны
в пары, и нужно исследовать разницу
между ними.
Для проверки необходимо заполнить
диалоговое окно, приведенное на рис.4.14.,
назначение всех полей очевидно. Результат
работы представлен на рис.4.15. Сравните
полученные результаты с результатами,
полученными вручную.
Рис.4.14 Диалоговое
окно средства анализа «Парный
двухвыборочный t-тест для средних»
надстройки «Пакет анализа»MSExcel
Рис.4.15. Результат
работы средства анализа «Парный
двухвыборочный t-тест для средних»
надстройки «Пакет анализа»MSExcel
ЗАДАНИЕ
Задача 1
Проверка гипотезы о согласии выборочных
данных с нормальным законом распределения.
Имеется выборка объема n
из непрерывно распределенной
генеральной совокупности.
Требуется проверить гипотезу, состоящую
в том, что выборочные данные получены
из нормально распределенной генеральной
совокупности.
Варианты
заданий взять из лабораторной работы
№ 3.
Решение
задачи 1 приведено выше (см. пример
4.2) .
Задача 2
Текст задачи в зависимости от варианта
приведен ниже.
Пример задачи 2
В рабочей книге MSExcelЛечебницы.xlsсодержатся статистические данные,
связанные с работой городских и загородных
лечебниц, собранные Отделом здравоохранения
штата Нью-Мексико. Фрагмент этой книги
приведен на рис. 4.16.
Рис.4.16 Фрагмент
рабочего листа Excelс
исходными данными для задачи 2
Выяснить, есть ли разница между доходами
городских и загородных лечебниц.
Решение
Выдвигаем гипотезу H0:
средние значения доходов городских
и загородных лечебниц выборок равны,
альтернативная гипотезаH1: доходы не равны. Чтобы проверить эту
гипотезу с помощьюt-критерия,
необходимо выполнить ряд операций:
-
Разделить всю выборку на две части: для
городских и для загородных лечебниц.
Считать эти выборки самостоятельными; -
Выяснить, имеют ли эти выборки одинаковую
дисперсию, если «да», то перейти к пункту
3, в противном случае перейти к пункту
4; -
Применить двухвыборочный t-тест с
одинаковыми дисперсиями; -
Применить двухвыборочный t-тест с
различными дисперсиями.
Пункт 1.Для разделения
выборки воспользоваться командойДанныеСортировка. Результат приведен на
рис.4.17. В интервале строк 59:76 содержатся
данные, относящиеся к городским
лечебницам. В интервале строк 77:110 —
данные, относящиеся к загородным
лечебницам.
Рис.4.17 Фрагмент
рабочего листа Excelс
данными для задачи 2 после сортировки
Пункт 2.Для проверки
предположения, что эти выборки имеют
одинаковую дисперсию, воспользуемся
критерием Фишера.
Выдвигаем гипотезу H0:
дисперсии выборок равны, альтернативная
гипотезаH1:
дисперсии не равны.
Воспользуемся надстройкой MSExcel«Пакет анализа»
«Двухвыборочный F-тест для дисперсии».
Результат расчета приведен на рис. 4.18.
Рис.4.18.
Фрагмент рабочего листа MSExcelс данными для проверки
равенства
дисперсий
Поскольку
(вычисленное значение критерия
не больше критического),
то принимается гипотезаH0(дисперсии выборок равны). Отсюда следует,
что можно применить двухвыборочныйt-тест с одинаковыми дисперсиями.
Выдвигаем гипотезу H0:
средние арифметические значения
выборок равны, альтернативная гипотезаH1: эти
значения не равны. Воспользуемся
надстройкойMSExcel«Пакет анализа» «Двухвыборочныйt-тест
с одинаковыми дисперсиями»; результат
работы приведен на рис. 4.19.
Рис. 4.19. Фрагмент
рабочего листа MSExcelс данными для проверки равенства
средних
В качестве
следует рассматривать двустороннее
значение. Так как,
,
то,
следовательно, гипотезаH0
отклоняется, гипотезаH1—
принимается. Из этого делаем вывод о
том, что средние значения доходов
городских и загородных лечебниц различны.
Соседние файлы в папке Эконометрика 1 лекция
- #
- #
- #
- #
- #
- #
Для того, чтобы рассчитать t-критерий Стьюдента (для зависимых и для независимых выборок) в Excell необходимо сделать следующие шаги:
1.Вносим значения для двух переменных в таблицу (Например Переменная 1 и Переменная 2)
2. Ставим курсор в пустую ячейку
3. На панеле инструментов нажимаем кнопку fx (вставить формулу)
4. В открывшемся окне «Мастер функций» в поле «Категории» выбираем Полный алфавитный перечень
5. Затем в поле «Выберите функцию» находим функцию TTECT, которая возвращает вероятность, соответствующую критерию Стьюдента.
5.1. Нажимаем Ок
6. В открывшемся окне «Аргументы функции» в поле Массив1 вносим номера ячеек, содержащие значения Переменной 1, в поле Массив2 вносим номера ячеек, содержащие значения Переменной2.
7. В поле «Хвосты» пишем 2 (критерий будет рассчитываться используя двустороннее распределение, как и в SPSS); либо 1 (критерий будет рассчитываться используя одностороннее распределение).
Важно!
8. В поле «Тип» пишем 1 (рассчитывается, если выборки зависимые); либо 2 или 3 (если выборки независимые).
9. Нажимаем Ок
10. Смотрим получившийся результат