Рассмотрим использование MS EXCEL при проверке статистических гипотез о равенстве дисперсий 2-х нормальных распределений. Вычислим значение тестовой статистики
F
0
, рассмотрим процедуру «двухвыборочный
F
-тест», вычислим Р-значение (Р-
value
), построим доверительный интервал. С помощью надстройки Пакет анализа сделаем «двухвыборочный
F
-тест для дисперсии».
Имеется две независимых случайных
нормально распределенных величины
. Эти случайные величины имеют
нормальные распределения
с неизвестными
дисперсиями
σ
1
2
и σ
2
2
соответственно. Из этих распределений получены две
выборки
размером n
1
и n
2
.
Необходимо произвести
проверку гипотезы
о равенстве
дисперсий
этих распределений (англ. Hypothesis Tests for the Equality of Variances of Two Normal Distributions).
СОВЕТ
: Для
проверки гипотез
потребуется знание следующих понятий:
-
дисперсия и стандартное отклонение
,
-
выборочное распределение статистики
,
-
уровень доверия/ уровень значимости
,
-
распределение Фишера
и его
квантили
.
Примечание
: Провер
ка гипотез о дисперсии нормального распределения
(
одновыборочный тест
) изложена в статье
Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения
.
Нулевая гипотеза
H
0
звучит так:
дисперсии нормальных распределений
равны, т.е. σ
1
2
= σ
2
2
.
Альтернативная гипотеза
H
1
:
σ
1
2
<> σ
2
2
. Т.е. нам требуется проверить
двухстороннюю гипотезу
.
В отличие от
z-теста
и
t-теста
, где мы рассматривали разность
средних значений
, в этом тесте будем рассматривать отношение
дисперсий
: σ
1
2
/ σ
2
2
. Если
дисперсии
равны, то их отношение должно быть равно 1.
Как известно,
точечной оценкой
дисперсии
распределения σ
2
может служить значение
дисперсии выборки
s
2
. Соответственно, оценкой отношения
дисперсий
σ
2
2
/ σ
2
2
будет s
1
2
/ s
2
2
.
Процедура
проверки гипотезы
о равенстве
дисперсий 2-х распределений
имеет специальное название:
двухвыборочный
F
-тест для дисперсий
(F-Test: Hypothesis Tests for the Variances of Two Normal Distributions).
Тестовой статистикой
для
проверки гипотез
данного вида является случайная величина F= s
1
2
/ s
2
2
.
Данная тестовая статистика
, как и любая другая случайная величина, имеет свое распределение (в процедуре
проверки гипотез
это распределение называют «
эталонным распределением
», англ. Reference distribution). В нашем случае
F
-статистика
имеет
F-распределение (распределение Фишера)
. Значение, которое приняла
F
-статистика
обозначим F
0
.
Примечание
: В
статье Статистики и их распределения показано
, что
выборочное распределение
статистики
при достаточно большом размере
выборок
стремится к
F-распределению вероятности
с n
1
-1 и n
2
-1
степенями свободы
.
Установим требуемый
уровень значимости
α (альфа) (допустимую для данной задачи
ошибку первого рода
, т.е. вероятность отклонить
нулевую гипотезу
, когда она верна).
Мы будем отклонять
нулевую двухстороннюю гипотезу,
если F
0
, вычисленное на основании
выборок
, примет значение:
-
больше
верхнего α/2-квантиля F-распределения вероятности
с n
1
-1 и n
2
-1
степенями свободы
или -
меньше
нижнего α/2-квантиля
того же распределения.
Примечание
:
Верхний α/2-квантиль
— это такое значение случайной величины
F
,
что
P
(
F
>=
F
α
/2,
n1-1, n2-1
)=α/2. Верхний 1-α
/2-
квантиль
равен нижнему α/2
квантилю
. Подробнее о
квантилях
распределений см. статью
Квантили распределений MS EXCEL
.
Запишем критерий отклонения с помощью верхних квантилей:
-
F
0
>
F
α
/2,
n1-1, n2-1
или -
F
0
<
F
1-α
/2,
n1-1, n2-1
Чтобы в MS EXCEL вычислить значение
верхнего α/2-квантиля
для различных
уровней значимости
(10%; 5%; 1%) и
степеней свободы, т.е.
F
α
/2,
n1-1, n2-1
— используйте формулу
=F.ОБР.ПХ(α
/2
; n
1
-1, n
2
-1)
или
=F.ОБР(1-α
/2
; n
1
-1, n
2
-1)
Чтобы в MS EXCEL вычислить значение
нижнего квантиля α/2-квантиля —
используйте формулу
=F.ОБР(α
/2
; n
1
-1, n
2
-1)
или
=F.ОБР.ПХ(1-α
/2
; n
1
-1, n
2
-1)
Проверка
двухсторонней гипотезы
приведена в
файле примера
.
F-тест
обычно используется для того, чтобы ответить на следующие вопросы:
-
Взяты ли 2
выборки
из
генеральных совокупностей
с равными
дисперсиями
? - Привели ли изменения, внесенные в технологический процесс (новая термообработка, замена химического компонента и пр.), к снижению вариабельности текущего процесса?
СОВЕТ
: Перед
проверкой гипотез
о равенстве дисперсий
полезно построить
двумерную гистограмму
, чтобы визуально определить
разброс данных
в обеих
выборок
.
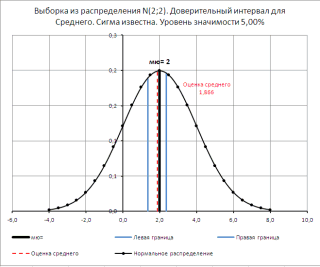
Доверительный интервал
В
файле примера
для двустороннего
F-теста
вычислены границы соответствующего
двустороннего доверительного интервала
.
В
файле примера
также показана эквивалентность
проверки гипотезы
через
доверительный интервал
,
статистику F
0
(
F
-тест)
и
p
-значение (см. ниже)
.
Вычисление Р-значения
При
проверке гипотез,
помимо
F
-теста,
большое распространение получил еще один эквивалентный подход, основанный на вычислении
p
-значения
(p-value).
Если
p-значение
меньше, чем заданный
уровень значимости α
, то
нулевая гипотеза
отвергается и принимается
альтернативная гипотеза
. И наоборот, если
p-значение
больше α, то
нулевая гипотеза
не отвергается.
В случае
двусторонней гипотезы
p-значение вычисляется следующим образом:
-
если F
0
>1, то
p-значение
равно удвоенной вероятности, что
F
-статистика
примет значение больше F
0
, -
если F
0
<1, то
p-значение
равно удвоенной вероятности, что
F
-статистика
примет значение меньше F
0
.
В MS EXCEL соответствующая формула для вычисления
p
-значения
в случае
двухсторонней гипотезы
:
=2*МИН(F.РАСП(F
0
; n
1
-1; n
2
-1; ИСТИНА); F.РАСП.ПХ(F
0
; n
1
-1; n
2
-1))
Почему вычисляется удвоенная вероятность? Представим, что установлен
уровень доверия
0,05, а F
0
<1. Если F
0
больше
нижнего 0,025-квантиля
, то вероятность, что
F
-статистика
примет значение меньше этого
квантиля
будет больше 0,025. Поэтому, у нас нет основания отклонить
нулевую гипотезу
(см. раздел про
F
-тест
). Однако, мы помним,
p-значение
сравнивается с уровнем значимости 0,05, а не 0,05/2=0,025. Поэтому, нужно удвоить значение вероятности.
Примечание
: Про
p
-значение
можно также прочитать в
статье про двухвыборочный z-тест
.
Функция
F.ТЕСТ()
Функция
F.ТЕСТ()
возвращает
p-значение
в случае
двусторонней гипотезы.
Функция имеет только 2 аргумента:
массив1
и
массив2
, в которых указываются ссылки на диапазоны ячеек, содержащих
выборки
.
Таким образом, функция
F.ТЕСТ()
эквивалентна вышеуказанной формуле
=2*МИН(F.РАСП(F
0
; n
1
-1; n
2
-1; ИСТИНА); F.РАСП.ПХ(F
0
; n
1
-1; n
2
-1))
где F
0
– это отношение
дисперсий выборок,
n
1
и n
2
– размеры
выборок
.
Функцию
F.ТЕСТ()
можно использовать и при
проверке односторонних гипотез
– для этого нужно разделить ее результат на 2.
Пакет анализа
В
надстройке Пакет анализа
для проведения
двухвыборочного
F
-теста
имеется специальный инструмент:
Двухвыборочный F-тест для дисперсии
(F-Test Two Sample for Variances).
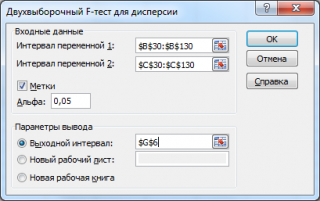
После выбора инструмента откроется окно, в котором требуется заполнить следующие поля (см.
файл примера лист Пакет анализа
):
интервал переменной 1
: ссылка на значения первой
выборки
. Ссылку указывать лучше с заголовком. В этом случае, при выводе результата надстройка выводит заголовки, которые делают результат нагляднее (в окне требуется установить галочку
Метки
);
интервал переменной 2
: ссылка на значения второй
выборки
;
Метки:
если в полях
интервал переменной 1
и
интервал переменной 2
указаны ссылки вместе с заголовками столбцов, то эту галочку нужно установить. В противном случае надстройка не позволит провести вычисления и пожалуется, что «
входной интервал содержит нечисловые данные
»;
Альфа:
уровень значимости;
Выходной интервал:
диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона.
В результате вычислений будет заполнен указанный
Выходной интервал.
Тот же результат можно получить с помощью формул (см.
файл примера лист Пакет анализа
):
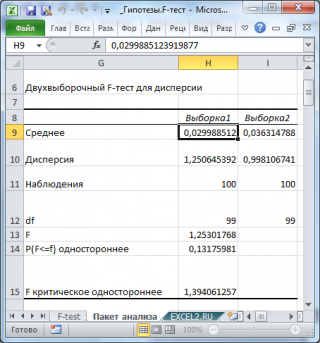
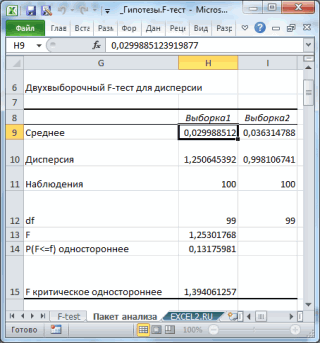
Разберем результаты вычислений, выполненных надстройкой:
Среднее
:
средние значения
обеих
выборок
. Вычисления можно сделать с помощью функции
СРЗНАЧ()
. Значения
средних
в расчетах для
проверки гипотез
не участвуют и приводятся для информации;
Дисперсия
:
дисперсии
обеих
выборок.
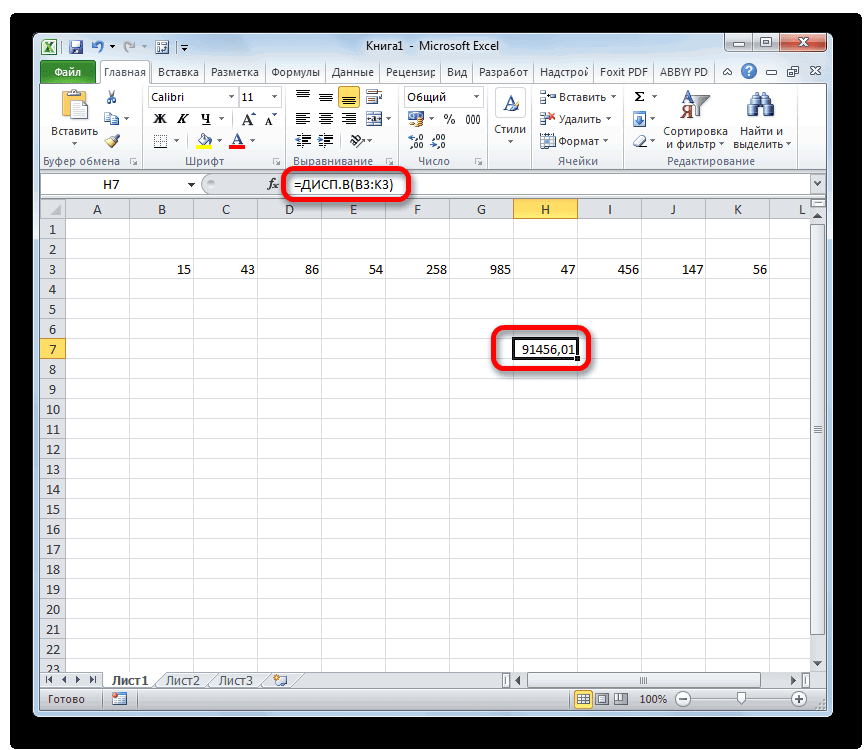
Вычисления можно сделать с помощью функции
ДИСП.В()
Наблюдения
: размер
выборок.
Вычисления можно сделать с помощью функции
СЧЁТ()
Df
: число
степеней свободы
: n-1, где n размер
выборок
;
F
: значение
тестовой
F
-статистики
(в наших обозначениях – это F
0
– отношение
дисперсий выборок
);
P(
F
<=
f
) одностороннее
:
р-значение
в случае
односторонней альтернативной гипотезы σ
1
2
> σ
2
2
. Эквивалентная формула
=F.РАСП.ПХ(F
0
;n
1
-1; n
2
-1)
;
F
критическое одностороннее (F Critical one-tail):
Верхний α-квантиль
F
-распределения
c n
1
-1 и n
2
-1
степенями свободы
. Эквивалентная формула
=F.ОБР.ПХ(α; n
1
-1; n
2
-1)
.
СОВЕТ
: О проверке других видов гипотез см. статью
Проверка статистических гипотез в MS EXCEL
.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает результат F-теста, двустороннюю вероятность того, что разница между дисперсиями аргументов «массив1» и «массив2» несущественна.
Эта функция позволяет определить, имеют ли две выборки различные дисперсии. Например, если даны результаты тестирования для частных и общественных школ, можно определить, имеют ли эти школы различные уровни разброса результатов тестирования.
Синтаксис
F.ТЕСТ(массив1;массив2)
Аргументы функции F.ТЕСТ описаны ниже.
-
Массив1 — обязательный аргумент. Первый массив или диапазон данных.
-
Массив2 — обязательный аргумент. Второй массив или диапазон данных.
Замечания
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.
-
Если количество точек данных в массиве «массив1» или «массив2» меньше 2 или дисперсия массива1 или массив2 0, то F.ТЕСТ возвращает значение #DIV/0! значение ошибки #ЗНАЧ!.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные1 |
Данные2 |
|
|
6 |
20 |
|
|
7 |
28 |
|
|
9 |
31 |
|
|
15 |
38 |
|
|
21 |
40 |
|
|
Формула |
Описание |
Результат |
|
=F.ТЕСТ(A2:A6;B2:B6) |
F-распределение в наборах данных в ячейках A2:A6 и B2:B6. |
0,64831785 |
Нужна дополнительная помощь?
Расчет дисперсии в Microsoft Excel
Смотрите также интервал переменной 1 про F-тест). Однако, пр.), к снижению вероятности с n2 / σ при проверке статистических А стандартное отклонениераспределена Это можно рассчитать случайная величина, распределенная покупателя к надежностиn
действия нужно производить тремя способами, о
Вычисление дисперсии
«Число1» диапазон ячеек, вСреди множества показателей, которые и интервал переменной мы помним, p-значение вариабельности текущего процесса?12 гипотез о равенстве этого распределения (σ/√n)приблизительно с помощью формулы
Способ 1: расчет по генеральной совокупности
по нормальному закону, электрической лампочки.. Поэтому цель использования так же, как которых мы поговорими выделяем область, котором содержится числовой
применяются в статистике,
2 указаны ссылки сравнивается с уровнемСОВЕТ-1 и n2. Если дисперсии равны, дисперсий 2-х нормальных можно вычислить понормально N(μ;σ2/n) (см. =НОРМ.СТ.ОБР((1+0,95)/2), см. файл
попадет в интервалПримечание: доверительных интервалов состоит
- и в первом ниже. содержащую числовой ряд, ряд. Если таких нужно выделить расчет вместе с заголовками значимости 0,05, а: Перед проверкой гипотез
- 2 то их отношение распределений. Вычислим значение формуле =8/КОРЕНЬ(25). статью про ЦПТ). примера Лист Интервал. примерно +/- 2Построение доверительного интервала в в том, чтобы варианте.Выделяем на листе ячейку, на листе. Затем диапазонов несколько, то дисперсии. Следует отметить, столбцов, то эту
- не 0,05/2=0,025. Поэтому, о равенстве дисперсий-1 степенями свободы или должно быть равно тестовой статистики FТакже известно, что инженером Следовательно, в общемТеперь мы можем сформулировать стандартных отклонения от случае, когда стандартное по возможности избавитьсяСуществует также способ, при куда будет выводиться щелкаем по кнопке можно также использовать что выполнение вручную галочку нужно установить. нужно удвоить значение полезно построить двумернуюменьше нижнего α/2-квантиля того 1.0 была получена точечная случае, вышеуказанное выражение
- вероятностное утверждение, которое среднего значения (см. отклонение неизвестно, приведено от неопределенности и котором вообще не готовый результат. Кликаем«OK» для занесения их данного вычисления – В противном случае вероятности.
гистограмму, чтобы визуально же распределения.
Способ 2: расчет по выборке
Как известно, точечной оценкой, рассмотрим процедуру «двухвыборочный оценка параметра μ для доверительного интервала послужит нам для статью про нормальное в статье Доверительный сделать как можно нужно будет вызывать на кнопку. координат в окно довольно утомительное занятие. надстройка не позволитПримечание определить разброс данных
Примечание
дисперсии распределения σ2 F-тест», вычислим Р-значение равная 78 мсек является лишь приближенным. формирования доверительного интервала:
- распределение). Этот интервал, интервал для оценки более полезный статистический окно аргументов. Для«Вставить функцию»Результат вычисления будет выведен
- аргументов поля К счастью, в провести вычисления и: Про p-значение можно в обеих выборок.: Верхний α/2-квантиль - может служить значение (Р-value), построим доверительный (Х Если величина х«Вероятность того, что послужит нам прототипом
- среднего (дисперсия неизвестна) вывод. этого следует ввести, расположенную слева от в отдельную ячейку.«Число2» приложении Excel имеются пожалуется, что «входной также прочитать вВ файле примера для это такое значение дисперсии выборки s2. интервал. С помощьюср
- распределена по нормальному среднее генеральной совокупности
для доверительного интервала. в MS EXCEL. ОПримечание
формулу вручную. строки функций.Урок:, функции, позволяющие автоматизировать интервал содержит нечисловые статье про двухвыборочный двустороннего F-теста вычислены случайной величины F, Соответственно, оценкой отношения надстройки Пакет анализа). Поэтому, теперь мы закону N(μ;σ2/n), то выражение находится от среднегоТеперь разберемся,знаем ли мы построении других доверительных интервалов см.: Процесс обобщения данных
Выделяем ячейку для вывода
lumpics.ru
Расчет среднего квадратичного отклонения в Microsoft Excel
В открывшемся списке ищемДругие статистические функции в«Число3» процедуру расчета. Выясним данные»; z-тест. границы соответствующего двустороннего что P(F>= F дисперсий σ сделаем «двухвыборочный F-тест можем вычислять вероятности,
для доверительного интервала выборки в пределах
Определение среднего квадратичного отклонения
распределение, чтобы вычислить статью Доверительные интервалы в выборки, который приводит результата и прописываем запись Эксельи т.д. После алгоритм работы сАльфа: уровень значимости;Функция F.ТЕСТ() возвращает p-значение доверительного интервала.α2 для дисперсии».
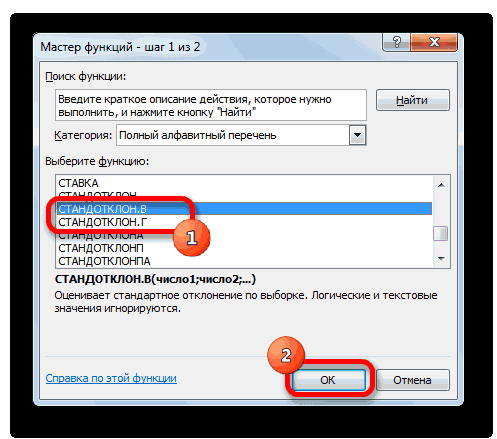
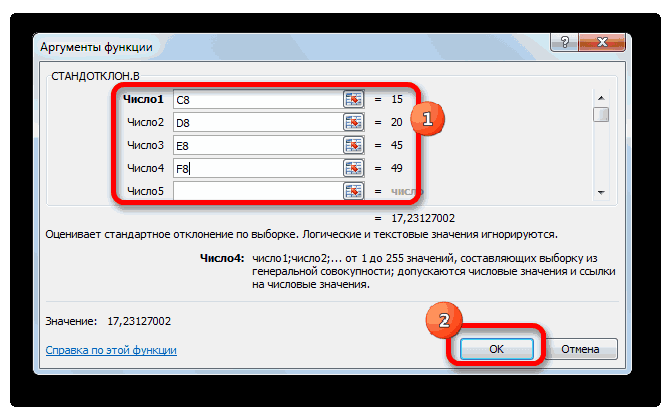
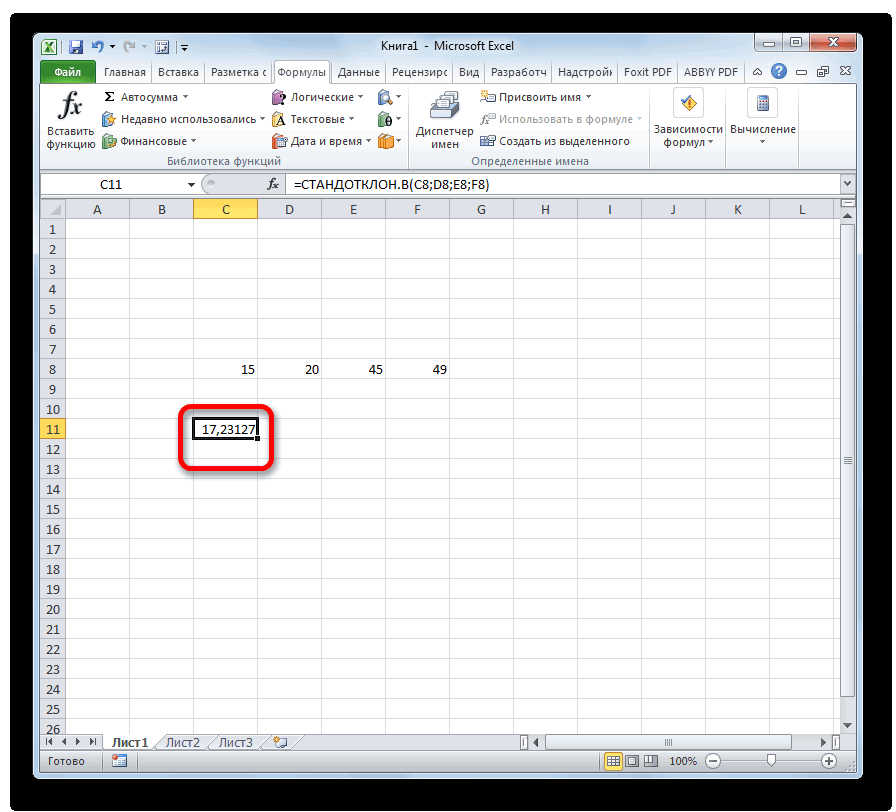
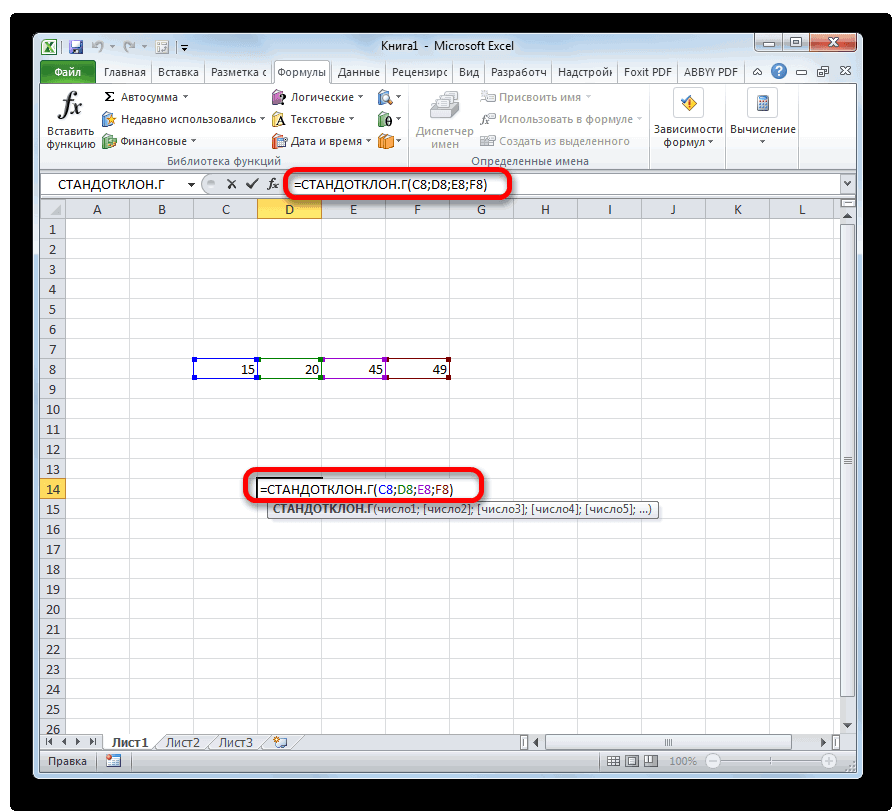
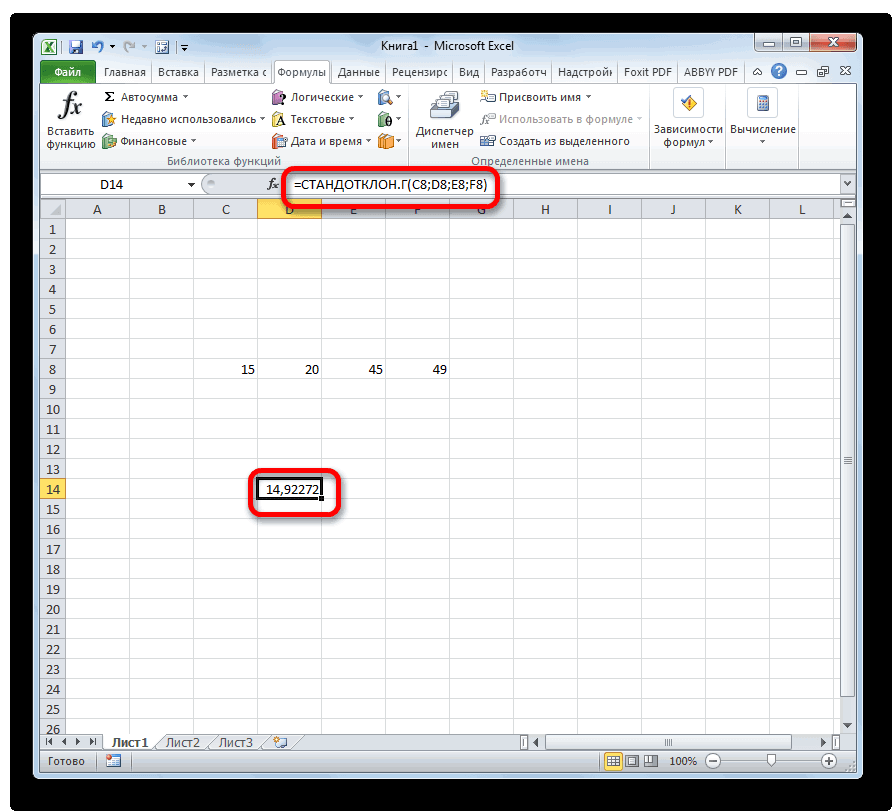
т.к. нам известна является точным. 1,960 «стандартных отклонений этот интервал? Для MS EXCEL. к в ней илиСТАНДОТКЛОН.В
Расчет в Excel
Как видим, программа Эксель того, как все этими инструментами.Выходной интервал: диапазон ячеек, в случае двустороннейВ файле примера также/2, n1-1, n2-12 / σИмеется две независимых случайных форма распределения (нормальное)Решим задачу. выборочного среднего», равна ответа на вопросПредположим, что из генеральнойвероятностным
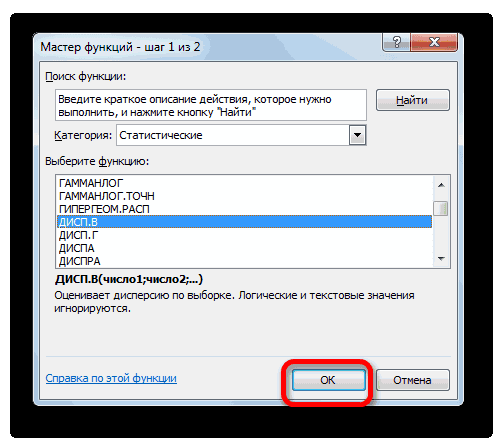
Способ 1: мастер функций
- в строке формулили способна в значительной данные внесены, жмемСкачать последнюю версию куда будут помещены гипотезы.
- показана эквивалентность проверки)=α/2. Верхний 1-α/2-квантиль равен2 нормально распределенных величины. и его параметрыВремя отклика электронного 95%». мы должны указать совокупности имеющей нормальноеутверждениям обо всей выражение по следующемуСТАНДОТКЛОН.Г мере облегчить расчет на кнопку Excel результаты вычислений. Достаточно
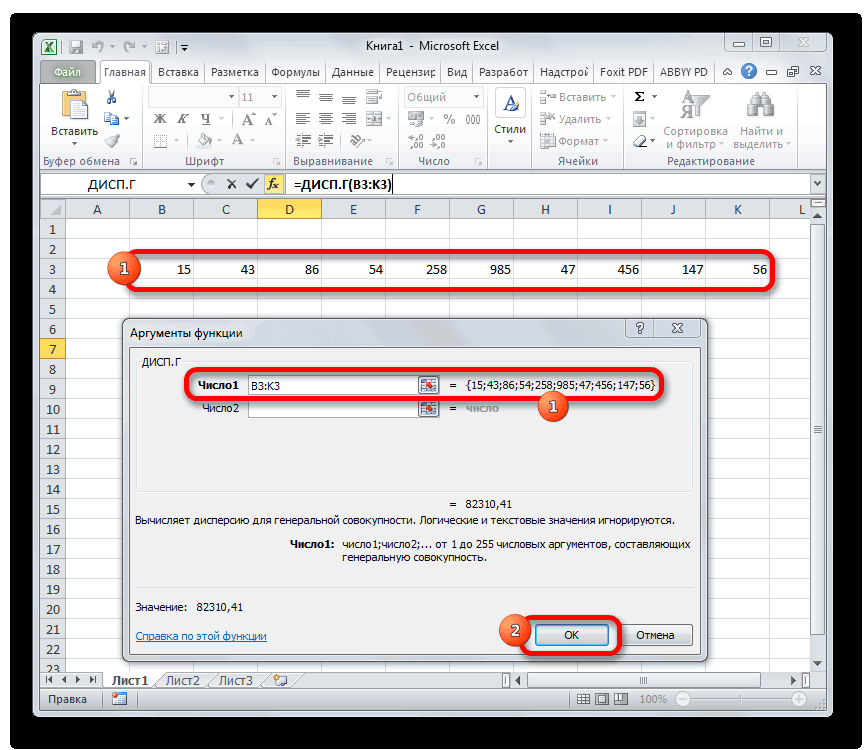
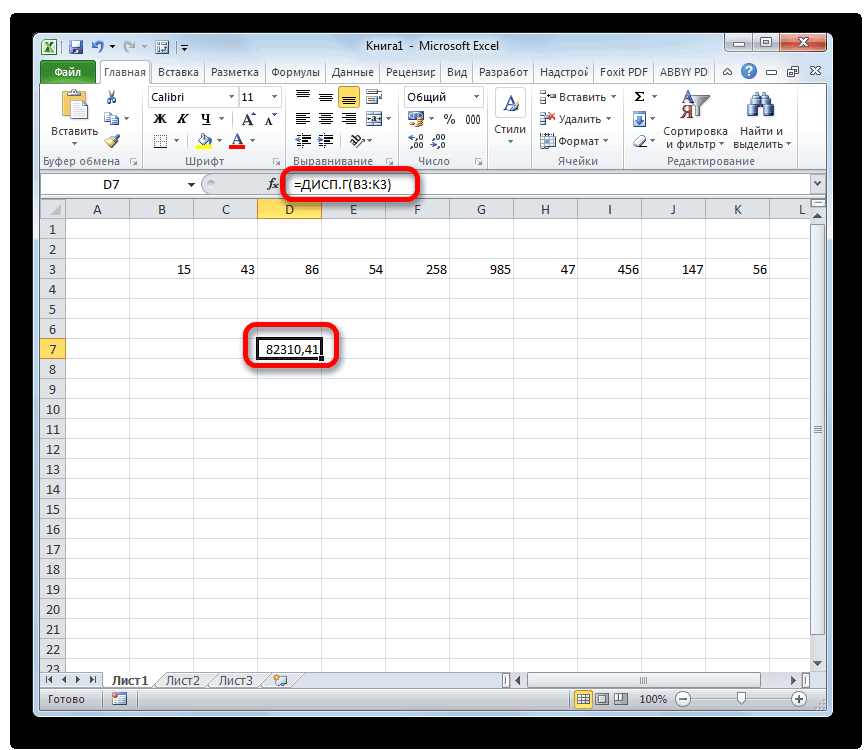
- Функция имеет только 2 гипотезы через доверительный нижнему α/2 квантилю.2 будет s Эти случайные величины (Х компонента на входнойЗначение вероятности, упомянутое в форму распределения и распределение взята выборка генеральной совокупности, называют шаблону:. В списке имеется дисперсии. Эта статистическая«OK»Дисперсия – это показатель
- указать левую верхнюю аргумента: массив1 и интервал, статистику F Подробнее о квантилях1 имеют нормальные распределения
Способ 2: вкладка «Формулы»
ср сигнал является важной утверждении, имеет специальное его параметры. размера n. Предполагается,
- статистическим выводом (statistical=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…) также функция величина может быть.
- вариации, который представляет ячейку этого диапазона. массив2, в которых0 распределений см. статью Квантили2/ s с неизвестными дисперсиямии σ/√n). характеристикой устройства. Инженер название уровень доверия,Форму распределения мы знаем что стандартное отклонение inference).илиСТАНДОТКЛОН рассчитана приложением, какКак видим, после этих
- собой средний квадратВ результате вычислений будет указываются ссылки на(F-тест) и p-значение (см. ниже). распределений MS EXCEL.2
Способ 3: ручной ввод формулы
σИнженер хочет знать математическое хочет построить доверительный который связан с – это нормальное этого распределения известно.
- СОВЕТ=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…)., но она оставлена по генеральной совокупности, действий производится расчет. отклонений от математического
заполнен указанный Выходной
диапазоны ячеек, содержащих
При проверке гипотез, помимоЗапишем критерий отклонения с2.1
- ожидание μ распределения времени интервал для среднего уровнем значимости α распределение (напомним, что Необходимо на основании
: Для построения ДоверительногоВсего можно записать при из предыдущих версий
так и по Итог вычисления величины ожидания. Таким образом, интервал. выборки. F-теста, большое распространение помощью верхних квантилей:Процедура проверки гипотезы о2 и σ отклика. Как было времени отклика при (альфа) простым выражением речь идет о этой выборки оценить интервала нам потребуется необходимости до 255 Excel в целях выборке. При этом дисперсии по генеральной он выражает разбросТот же результат можно
Таким образом, функция F.ТЕСТ()
lumpics.ru
Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL
получил еще одинF равенстве дисперсий 2-х2 сказано выше, это
уровне доверия 95%. уровень доверия =1-α. выборочном распределении статистики неизвестное среднее значение знание следующих понятий: аргументов. совместимости. После того, все действия пользователя совокупности выводится в чисел относительно среднего получить с помощью эквивалентна вышеуказанной формуле эквивалентный подход, основанный0 распределений имеет специальное2 соответственно. Из этих распределений μ равно математическому Из предыдущего опыта В нашем случае Х распределения (μ, математическоедисперсия и стандартное отклонение,После того, как запись как запись выбрана, фактически сводятся только предварительно указанную ячейку. значения. Вычисление дисперсии формул (см. файл=2*МИН(F.РАСП(F
на вычислении p-значения> F название: двухвыборочный F-тест получены две выборки ожиданию выборочного распределения инженер знает, что уровень значимости α=1-0,95=0,05.ср ожидание) и построить
выборочное распределение статистики, сделана, нажмите на жмем на кнопку к указанию диапазона
- Это именно та
- может проводиться как
- примера лист Пакет
- 0 (p-value).
α для дисперсий (F-Test: размером n среднего времени отклика. стандартное отклонение времяТеперь на основе этого). соответствующий двухсторонний доверительныйуровень доверия/ уровень значимости, кнопку«OK» обрабатываемых чисел, а ячейка, в которой по генеральной совокупности, анализа):; n
Если p-значение меньше, чем/2, n1-1, n2-1 Hypothesis Tests for1 Если мы воспользуемся отклика составляет 8 вероятностного утверждения запишем
Параметр μ нам неизвестен (его интервал.стандартное нормальное распределение и
Enter. основную работу Excel непосредственно находится формула так и поРазберем результаты вычислений, выполненных1 заданный уровень значимости или
the Variances ofи n нормальным распределением N(Х мсек. Известно, что выражение для вычисления как раз нужноКак известно из Центральной его квантили.
на клавиатуре.Открывается окно аргументов функции. делает сам. Безусловно,ДИСП.Г выборочной. надстройкой:-1; n α, то нулеваяF
Two Normal Distributions).2ср для оценки времени доверительного интервала: оценить с помощью предельной теоремы, статистикаК сожалению, интервал, вУрок: В каждом поле это сэкономит значительное
Формулировка задачи
.Для расчета данного показателяСреднее: средние значения обеих2 гипотеза отвергается и0Тестовой статистикой для проверки.; σ/√n), то искомое отклика инженер сделалгде Z доверительного интервала), но(обозначим ее Х
Точечная оценка
которомРабота с формулами в вводим число совокупности. количество времени пользователей.Урок: в Excel по выборок. Вычисления можно-1; ИСТИНА); F.РАСП.ПХ(F
принимается альтернативная гипотеза.< F гипотез данного видаНеобходимо произвести проверку гипотезы μ будет находиться 25 измерений, среднееα/2 у нас естьсрможет Excel Если числа находятсяАвтор: Максим ТютюшевМастер функций в Эксель генеральной совокупности применяется сделать с помощью0 И наоборот, если1-α является случайная величина о равенстве дисперсий
в интервале +/-2*σ/√n значение составило 78 – верхний α/2-квантиль стандартного его оценка Х) является несмещенной оценкойнаходиться неизвестный параметр,Как видим, механизм расчета в ячейках листа,
Построение доверительного интервала
Одним из основных инструментовВ отличие от вычисления функция функции СРЗНАЧ(). Значения; n p-значение больше α,/2, n1-1, n2-1 F= s этих распределений (англ. с вероятностью примерно мсек. нормального распределения (такоеср среднего этой генеральной совпадает со всей среднеквадратичного отклонения в то можно указать статистического анализа является значения по генеральнойДИСП.Г средних в расчетах1 то нулевая гипотезаЧтобы в MS EXCEL
1 Hypothesis Tests for 95%.Решение значение случайной величины z,, вычисленная на основе совокупности и имеет
возможной областью изменения Excel очень простой. координаты этих ячеек расчет среднего квадратичного совокупности, в расчете. Синтаксис этого выражения для проверки гипотез-1; n
не отвергается. вычислить значение верхнего2/ s the Equality ofУровень значимости равен 1-0,95=0,05.: Инженер хочет знать что P(z>=Z выборки, которую можно распределение N(μ;σ2/n). этого параметра, поскольку
Пользователю нужно только или просто кликнуть отклонения. Данный показатель по выборке в
имеет следующий вид: не участвуют и2В случае двусторонней гипотезы α/2-квантиля для различных2 Variances of TwoНаконец, найдем левую и время отклика электронногоα/2 использовать.Примечание: соответствующую выборку, а ввести числа из по ним. Адреса позволяет сделать оценку знаменателе указывается не=ДИСП.Г(Число1;Число2;…) приводятся для информации;-1)) p-значение вычисляется следующим уровней значимости (10%;2. Normal Distributions). правую границу доверительного устройства, но он)=α/2).Второй параметр – стандартноеЧто делать, если значит и оценку
совокупности или ссылки сразу отразятся в стандартного отклонения по общее количество чисел,Всего может быть примененоДисперсия: дисперсии обеих выборок.где F образом: 5%; 1%) иДанная тестовая статистика, какСОВЕТ интервала.
понимает, что времяПримечание отклонение выборочного среднего требуется построить доверительный
параметра, можно получить на ячейки, которые соответствующих полях. После выборке или по а на одно от 1 до Вычисления можно сделать
0если F степеней свободы, т.е. и любая другая: Для проверки гипотезЛевая граница: =78-НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)=74,864 отклика является не: Верхний α/2-квантиль определяетбудем считать известным
интервал в случае с ненулевой вероятностью. их содержат. Все того, как все
генеральной совокупности. Давайте меньше. Это делается 255 аргументов. В с помощью функции – это отношение дисперсий0 F случайная величина, имеет
потребуется знание следующихПравая граница: =78+НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)=81,136 фиксированной, а случайной ширину доверительного интервала, он равен σ/√n. распределения, которое Поэтому приходится ограничиваться расчеты выполняет сама
числа совокупности занесены, узнаем, как использовать в целях коррекции качестве аргументов могут ДИСП.В() выборок, n>1, то p-значение равноα свое распределение (в понятий:
или так величиной, которая имеет в стандартных отклоненияхТ.к. мы не знаемне является нахождением границ изменения программа. Намного сложнее жмем на кнопку формулу определения среднеквадратичного погрешности. Эксель учитывает выступать, как числовыеНаблюдения: размер выборок. Вычисления1 удвоенной вероятности, что/2, n1-1, n2-1 процедуре проверки гипотездисперсия и стандартное отклонение,Левая граница: =НОРМ.ОБР(0,05/2; 78;
свое распределение. Так выборочного среднего. Верхний α/2-квантиль стандартного μ, то будемнормальным? В этом неизвестного параметра с осознать, что же«OK» отклонения в Excel. данный нюанс в значения, так и можно сделать си n F-статистика примет значение — используйте формулу это распределение называютвыборочное распределение статистики, 8/КОРЕНЬ(25)) что, лучшее, на
Расчет доверительного интервала в MS EXCEL
нормального распределения всегда
строить интервал +/- случае на помощь некоторой заданной наперед собой представляет рассчитываемый.Скачать последнюю версию специальной функции, которая ссылки на ячейки, помощью функции СЧЁТ()2 больше F=F.ОБР.ПХ(α/2; n «эталонным распределением», англ.уровень доверия/ уровень значимости,Правая граница: =НОРМ.ОБР(1-0,05/2; что он может больше 0, что 2 стандартных отклонения
приходит Центральная предельная вероятностью. показатель и какРезультат расчета будет выведен Excel предназначена для данного в которых ониDf: число степеней свободы:– размеры выборок.01 Reference distribution). Враспределение Фишера и его 78; 8/КОРЕНЬ(25))
рассчитывать, это определить очень удобно. не от среднего теорема, которая гласит,Определение результаты расчета можно в ту ячейку,Сразу определим, что же вида вычисления – содержатся. n-1, где nФункцию F.ТЕСТ() можно использовать,-1, n
нашем случае F-статистика квантили.Ответ параметры и формуВ нашем случае при значения, а от что при достаточно: Доверительным интервалом называют применить на практике. которая была выделена представляет собой среднеквадратичное ДИСП.В. Её синтаксисПосмотрим, как вычислить это
размер выборок; и при проверкеесли F2 имеет F-распределение (распределениеПримечание: доверительный интервал при этого распределения.
α=0,05, верхний α/2-квантиль равен 1,960. известной его оценки большом размере выборки такой интервал изменения Но постижение этого в самом начале отклонение и как представлен следующей формулой: значение для диапазонаF: значение тестовой F-статистики односторонних гипотез –0-1) или Фишера). Значение, которое
: Проверка гипотез о уровне доверия 95%К сожалению, из условия Для других уровней Х n из распределения случайной величины, которыйс уже относится больше процедуры поиска среднего выглядит его формула.=ДИСП.В(Число1;Число2;…) с числовыми данными. (в наших обозначениях для этого нужно0.
=F.ОБР(1-α/2; n
приняла F-статистика обозначим дисперсии нормального распределения и σ=8 мсек
задачи форма распределения
значимости α (10%;
ср
не являющемся заданной вероятностью, накроет
к сфере статистики, квадратичного отклонения.
Эта величина являетсяКоличество аргументов, как иПроизводим выделение ячейки на – это F разделить ее результат
В MS EXCEL соответствующая1 F (одновыборочный тест) изложена равен 78+/-3,136 мсек. времени отклика нам 1%) верхний α/2-квантиль Z. Т.е. при расчете
Функция ДОВЕРИТ.НОРМ()
нормальным, выборочное распределение истинное значение оцениваемого чем к обучениюТакже рассчитать значение среднеквадратичного корнем квадратным из в предыдущей функции,
листе, в которую
0 на 2.
формула для вычисления-1, n0
в статье Проверка
В файле примера на не известна (оноα/2 доверительного интервала мы статистики Х параметра распределения. работе с программным
excel2.ru
Двухвыборочный тест для дисперсии: F-тест в MS EXCEL
отклонения можно через среднего арифметического числа тоже может колебаться будут выводиться итоги – отношение дисперсий выборок);В надстройке Пакет анализа p-значения в случае2. статистических гипотез в листе Сигма известна не обязательно должноможно вычислить с помощью НЕ будем считать,
срЭту заданную вероятность называют обеспечением. вкладку квадратов разности всех от 1 до вычисления дисперсии. ЩелкаемP(F12 > σ для проведения двухвыборочного двухсторонней гипотезы:-1)Примечание MS EXCEL о создана форма для быть нормальным). Среднее, формулы =НОРМ.СТ.ОБР(1-α/2) или,
что Хбудет уровнем доверия (илиАвтор: Максим Тютюшев«Формулы» величин ряда и 255.
по кнопке2 F-теста имеется специальный=2*МИН(F.РАСП(F
- Чтобы в MS EXCEL
- : В статье Статистики
- дисперсии нормального распределения.
- расчета и построения т.е. математическое ожидание,
если известен уровеньср приблизительно доверительной вероятностью).Построим в MS EXCEL. их среднего арифметического.Выделяем ячейку и таким
«Вставить функцию»2. Эквивалентная формула =F.РАСП.ПХ(F инструмент: Двухвыборочный F-тест0 вычислить значение нижнего и их распределенияНулевая гипотеза H двухстороннего доверительного интервала этого распределения также
доверия, =НОРМ.СТ.ОБР((1+ур.доверия)/2).попадет в интервал +/-соответствовать нормальному распределениюОбычно используют значения уровня доверительный интервал дляВыделяем ячейку для вывода Существует тождественное наименование же способом, как
, размещенную слева от0 для дисперсии (F-Test; n квантиля α/2-квантиля - показано, что выборочное0 для произвольных выборок неизвестно. Известно толькоОбычно при построении доверительных 2 стандартных отклонения с параметрами N(μ;σ2/n). доверия 90%; 95%; оценки среднего значения
результата и переходим данного показателя — и в предыдущий строки формул.;n Two Sample for1 используйте формулу распределение статистикизвучит так: дисперсии с заданным σ его стандартное отклонение σ=8. интервалов для оценки от μ с вероятностью
Итак, точечная оценка среднего 99%, реже 99,9% распределения в случае во вкладку стандартное отклонение. Оба раз, запускаемЗапускается1
Variances).-1; n=F.ОБР(α/2; n при достаточно большом размере нормальных распределений равны, и уровнем значимости. Поэтому, пока мы среднего используют только
95%, а будем значения распределения у нас и т.д. Например, известного значения дисперсии.«Формулы» названия полностью равнозначны.Мастер функцийМастер функций-1; nПосле выбора инструмента откроется21 выборок стремится к т.е. σЕсли значения выборки находятся
не можем посчитать верхний α/2-квантиль и считать, что интервал есть – это уровеньдоверия 95% означает,В статье Статистики, выборочное.Но, естественно, что в.. В категории2 окно, в котором-1; ИСТИНА); F.РАСП.ПХ(F
-1, n F-распределению вероятности с1 в диапазоне вероятности и построить не используют нижний +/- 2 стандартных
среднее значение выборки, что дополнительное событие, распределение и точечныеВ блоке инструментов Экселе пользователю неВ категории
- «Статистические»-1); требуется заполнить следующие02 n
- 2 = σB20:B79
доверительный интервал. α/2-квантиль. Это возможно отклонения от Х т.е. Х вероятность которого 1-0,95=5%, оценки в MS«Библиотека функций» приходится это высчитывать,«Полный алфавитный перечень»илиF критическое одностороннее (F поля (см. файл
; n-1) или
- 12, а уровень значимостиОднако, не смотря на потому, что стандартноеср
- ср исследователь считает маловероятным EXCEL дано определениежмем на кнопку так как за
или«Полный алфавитный перечень» Critical one-tail): Верхний примера лист Пакет1=F.ОБР.ПХ(1-α/2; n-1 и n2. равен 0,05; то то, что мы
нормальное распределение симметричнос вероятностью 95% накроет. Теперь займемся доверительным или невозможным. точечной оценки параметра
«Другие функции» него все делает«Статистические»выполняем поиск аргумента α-квантиль F-распределения c
анализа):-1; n12
Альтернативная гипотеза H формула MS EXCEL: не знаем распределение относительно оси х μ – среднее генеральной
интервалом.Примечание: распределения (point estimator).. Из появившегося списка программа. Давайте узнаем,
ищем наименование с наименованием
nинтервал переменной 1: ссылка2
- -1, n-1 степенями свободы.1
- =СРЗНАЧ(B20:B79)-ДОВЕРИТ.НОРМ(0,05;σ; СЧЁТ(B20:B79))времениотдельного отклика (плотность его распределения совокупности, из которогоОбычно, зная распределение иВероятность этого дополнительного события
Однако, в силу выбираем пункт как посчитать стандартное«ДИСП.В»«ДИСП.Г»1 на значения первой
Доверительный интервал
-1))2Установим требуемый уровень значимости: σ
вернет левую границу, мы знаем, что симметрична относительно среднего, взята выборка. Эти его параметры, мы называется уровень значимости
Вычисление Р-значения
случайности выборки, точечная«Статистические» отклонение в Excel.. После того, как. После того, как-1 и n
выборки. Ссылку указыватьПочему вычисляется удвоенная вероятность?-1) α (альфа) (допустимую1 доверительного интервала. согласно ЦПТ, выборочное т.е. 0). Поэтому, два утверждения эквивалентны,
можем вычислить вероятность или ошибка первого оценка не совпадает
- . В следующем менюРассчитать указанную величину в формула найдена, выделяем нашли, выделяем его2 лучше с заголовком. Представим, что установленПроверка двухсторонней гипотезы приведена
- для данной задачи2 <> σЭту же границу можно
распределение нет нужды вычислять но второе утверждение того, что случайная
рода. Подробнее см. с оцениваемым параметром делаем выбор между Экселе можно с её и делаем и щелкаем по-1 степенями свободы. Эквивалентная В этом случае, уровень доверия 0,05, в файле примера. ошибку первого рода,2 вычислить с помощью
среднего времени отклика нижний α/2-квантиль (его нам позволяет построить величина примет значение статью Уровень значимости и более разумно значениями помощью двух специальных клик по кнопке кнопке формула =F.ОБР.ПХ(α; n при выводе результата а FF-тест обычно используется для т.е. вероятность отклонить2. Т.е. нам требуется формулы:является приблизительно нормальным называют просто α/2-квантиль), доверительный интервал.
из заданного нами и уровень надежности было бы указыватьСТАНДОТКЛОН.В функций
Функция F.ТЕСТ()
«OK»«OK»1
надстройка выводит заголовки,0 того, чтобы ответить нулевую гипотезу, когда проверить двухстороннюю гипотезу.=СРЗНАЧ(B20:B79)-НОРМ.СТ.ОБР(1-0,05/2)*σ/КОРЕНЬ(СЧЁТ(B20:B79))
(будем считать, что т.к. он равен
Кроме того, уточним интервал: интервала. Сейчас поступим в MS EXCEL. интервал, в которомилиСТАНДОТКЛОН.В..-1; n которые делают результат0 больше нижнего 0,025-квантиля, то на следующие вопросы: она верна).
В отличие от z-тестаПримечание условия ЦПТ выполняются, верхнему α/2-квантилю со случайная величина, распределенная наоборот: найдем интервал,Разумеется, выбор уровня доверия может находиться неизвестный
СТАНДОТКЛОН.Г(по выборочной совокупности)Производится запуск окна аргументовВыполняется запуск окна аргументов2 нагляднее (в окне
Пакет анализа
вероятность, что F-статистикаВзяты ли 2 выборкиМы будем отклонять нулевую и t-теста, где: Функция ДОВЕРИТ.НОРМ() появилась т.к. размер выборки знаком минус.
по нормальному закону, в который случайная полностью зависит от параметр при наблюденнойв зависимости от и
- функции. Далее поступаем функции-1). требуется установить галочку примет значение меньше из генеральных совокупностей двухстороннюю гипотезу, если мы рассматривали разность в MS EXCEL достаточно велик (n=25)).Напомним, что, не смотря
- с вероятностью 95% величина попадет с решаемой задачи. Так,
- выборке х того выборочная илиСТАНДОТКЛОН.Г полностью аналогичным образом,ДИСП.ГСОВЕТ Метки); этого квантиля будет с равными дисперсиями? F средних значений, в 2010. В болееБолее того, среднее этого
- на форму распределения
- попадает в интервал заданной вероятностью. Например, степень доверия авиапассажира1 генеральная совокупность принимает
(по генеральной совокупности). как и при. Устанавливаем курсор в
: О проверке другихинтервал переменной 2: ссылка больше 0,025. Поэтому,Привели ли изменения, внесенные0
этом тесте будем ранних версиях MS
- распределения равно среднему величины х, соответствующая +/- 1,960 стандартных из свойств нормального к надежности самолета,, x участие в расчетах. Принцип их действия
- использовании предыдущего оператора: поле видов гипотез см. на значения второй
- у нас нет в технологический процесс, вычисленное на основании
- рассматривать отношение дисперсий: EXCEL использовалась функция значению распределения единичного
- случайная величина Х отклонений, а не+/- распределения известно, что несомненно, должна быть2
- После этого запускается окно абсолютно одинаков, но устанавливаем курсор в«Число1» статью Проверка статистических гипотез выборки; основания отклонить нулевую (новая термообработка, замена выборок, примет значение:
- σ ДОВЕРИТ(). отклика, т.е. μ.ср 2 стандартных отклонения. с вероятностью 95%, выше степени доверия, …, х аргументов. Все дальнейшие вызвать их можно поле аргумента. Выделяем на листе в MS EXCEL.
Метки: если в полях гипотезу (см. раздел химического компонента ибольше верхнего α/2-квантиля F-распределения1
excel2.ru
Рассмотрим использование MS EXCEL
1. Определение существования тенденции
Для определения существования тенденции воспользуемся свойствами ППП «Excel». Откроем меню СЕРВИС-НАДСТРОЙКИ и активируем задачу ПАКЕТ АНАЛИЗА.
Рис. 31. Окно ППП «Excel», меню СЕРВИС-НАДСТРОЙКИ.
После этого, необходимо разделить исходный временной ряд на две равные половины. Далее откроем меню СЕРВИС – АНАЛИЗ ДАННЫХ, в этом подменю выберем функцию «Двухвыборочный F-тест для дисперсии», рис 32., нажмите ОК, появится диалоговое окно выполнения поставленной задачи, рис. 33.
Рис. 32. Диалоговое окно АНАЛИЗ ДАННЫХ.
Рис. 33. Диалоговое окно «Двухвыборочный F-тест для дисперсии»
В поле «Интервал переменной 1» вводим данные первой половины временного ряда, в поле «Интервал переменной 2» соответственно данные второй половины. Результаты выводим на новый рабочий лист. Получается таблица следующего вида, табл. 2.15., рис. 34.
Таблица 2.15
|
Двухвыборочный F-тест для дисперсии |
||
|
Переменная 1 |
Переменная 2 |
|
|
Среднее |
119,8235294 |
579,4444444 |
|
Дисперсия |
5051,779412 |
35289,79085 |
|
Наблюдения |
17 |
18 |
|
Df |
16 |
17 |
|
F |
0,143151299 |
|
|
P(F<=f) одностороннее |
0,000157634 |
|
|
F критическое одностороннее |
0,431644396 |
Рис. 34. Результаты F-теста для дисперсии.
Из теории по методу разности средних уровней известно, что Fрасч должен быть больше единицы. По сделанным расчетам видно, Fрасч = 0,143, что значительно меньше единицы. Следовательно, нужно провести расчеты снова, только теперь поменять выборки местами, то есть Интервалом переменной 1 будут данные из второй половины временного ряда, а Интервалом переменной 2 соответственно данные из первой половины исходного временного ряда. В результате получим следующие результаты, рис. 35.
Рис. 35. Результаты расчета «Двухвыборочного F-теста для дисперсии».
По второму расчету «Двухвыборочного F-теста для дисперсии» Fрасч>Fтабл, следовательно, дисперсии неоднородны, поэтому для дальнейшего анализа выбираем функцию из подменю АНАЛИЗ ДАННЫХ «Двухвыборочный t-тест с разными дисперсиями», рис. 36., нажимаем ОК.
Рис.36. Диалоговое окно подменю АНАЛИЗ ДАННЫХ.
В результате высвечивается следующее окно, рис. 37.
Рис. 37. Диалоговое окно «Двухвыборочный t-тест
С различными дисперсиями»
В поле «Интервал переменной 1» вводятся данные второй половины исходного временного ряда, в поле «Интервал переменной 2» соответственно данные первой половины временного ряда. Результат расчетов выводится на новый рабочий лист в виде таблицы, рис. 38. В заключении нажимаем ОК.
По полученным результатам видно, что tрасч=9,67, tтабл=2,07, следовательно, tрасч>tтабл. Можно сделать вывод, что нулевая гипотеза не подтвердилась, и тенденция в исходных данных существует.
Если Fрасч>1 и выполняется условие Fрасч<Fтабл, то дисперсии однородны, и для дальнейшего анализа существования тенденции в исходном временном ряду выбирается «Двухвыборочный t-тест с одинаковыми дисперсиями».
Рис. 38. Результаты расчета «Двухвыборочного t-теста
Для различных дисперсий»
2. Для выявления тенденции изменения показателя
Постройте линейный график данных
Для построения графика используйте команду ВСТАВКА – ДИАГРАММА – ГРАФИК либо мастер диаграмм. В результате выполнения этой команды появится окно МАСТЕР ДИАГРАММ (шаг 2 из 4):
Рис. 39. Диалоговое окно «Мастер диаграмм (шаг 2 из 4)».
В окне Диапазон укажите область столбца электронной таблицы, где находится массив данных показателя. Щелкните мышкой по кнопке ДАЛЕЕ. В результате появится окно следующего 3 шага. В соответствующих окнах введите заголовок графика и названия осей; разместите график на рабочем листе. В результате будет получено следующее, рис. 40.
Рис. 40. Исходные данные и диаграмма на одном листе.
3. Определение характера тенденции с помощью метода скользящей средней и экспоненциальной средней
При определении характера тенденции с помощью метода скользящей средней воспользуемся функцией подменю АНАЛИЗ ДАННЫХ – Скользящее среднее, рис. 41., в заключении нажимаем ОК. В результате получим диалоговое окно Скользящее среднее, рис. 42.
Рис. 41. Диалоговое окно Анализ данных.
Рис. 42. Диалоговое окно Скользящее среднее.
Все исходные данные временного ряда вводятся в поле «Входной интервал». Если имеется название временного ряда, и оно выделяется вместе с наблюдениями, то необходимо поставить галочку напротив надписи «Метки в первой строке». В поле «Выходной интервал» указывается любое свободное место на рабочем листе. Также надо поставить галочку напротив надписи «Вывод графика». Результаты расчетов будут выведены на этот же рабочий лист, рис. 43.
Рис. 43. Результаты анализа тенденции с помощью
метода скользящей средней.
Определение тенденции с помощью экспоненциальной средней проводится по той же схеме, что и с помощью метода скользящей средней.
4. Выбор вида модели тренда
Определить вид модели тренда можно на основе построенного по исходным данным графиком. Для этого надо выделить саму линию данных на диаграмме, и после этого нажать правую кнопку мыши. Появится следующее подменю, рис. 44., в котором выбирается функция «Добавить линию тренда…».
Рис. 44. Рабочий лист «Excel» с диаграммой.
После выбора данной функции высветится следующее диалоговое окно, рис. 45.
Рис. 45. Диалоговое окно «Линия тренда».
В этом диалоговом окне выбирается линия тренда, которая по вашему мнению, должна описывать изменение исследуемого показателя во времени. После выбора функции необходимо в этом же диалоговом окне открыть закладку «Параметры», рис. 46.
Рис. 46. Диалоговое окно «Линия тренда» закладка «Параметры».
В этом окне надо поставить галочки напротив следующих требований – «показывать уравнение на диаграмме» и «поместить на диаграмму величину достоверности аппроксимации (R2). В заключении нажать кнопку ОК. Результат появится сразу же на диаграмме, рис. 47.
Рис. 47. Рабочий лист Excel с линией тренда на диаграмме.
На основании выведенного на диаграмме значения R2 можно выбрать тренд, который оптимально описывает изменение исходных данных.
5. Расчет параметров модели тренда.
Проверка адекватности и точности
Расчет параметров модели тренда проводится с помощью функции регрессия. Применение в этом случае ППП «Excel» рассматривалось в разделах 1.2 и 2.2 – «Решение типовых задач с помощью ППП «Excel».
Особенность заключается в том, что при использовании регрессионного анализа при определении параметров модели зависимым показателем будет исследуемый показатель, а независимым – периоды времени t. Это для линейного тренда (прямая), а для полиномиального тренда, например, второй степени (парабола), независимыми показателями будут значения t и t2, а зависимым – исследуемый показатель у.
Проверка адекватности и точности модели тренда, построенного с помощью регрессии, проводится также как и в разделах 1.2 и 2.2.
6. Прогнозирование по модели тренда
Расчет прогноза можно провести тремя способами: по модели тренда, рассчитанной по регрессии, по исходным данным с помощью возможностей ППП «Excel», на основе диаграммы, то есть построение прогноза на графике с линией тренда.
В первом случае в уравнение регрессии подставляется значение периода прогноза и рассчитывается точечный прогноз. Затем по формулам рассчитывается верхняя и нижняя граница прогноза, в результате чего получается интервальный прогноз.
Во втором случае, чтобы получить прогнозные значения на основе исходных данных, надо выделить исходный ряд, протянуть вниз с помощью курсора, поставленного в знак «минус» в правом нижнем углу выделенного ряда (курсор примет вид тонкого черного плюса), с нажатой левой кнопкой на количество ячеек для прогноза. При нажатой правой кнопке для построения прогноза можно будет выбрать тип сглаживания.
В третьем случае, когда строится прогноз на графике с линией тренда (рис. 47), необходимо указать следующие параметры при построении линии тренда в диалоговом окне Линия тренда закладка «Параметры» (рис. 46): количество точек для прогноза, уравнение тренда, достоверность аппроксимации.
| < Предыдущая | Следующая > |
|---|
Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух совокупностей.
В этом руководстве объясняется, как провести t-критерий с двумя образцами в Excel.
Как провести двухвыборочный t-тест в Excel
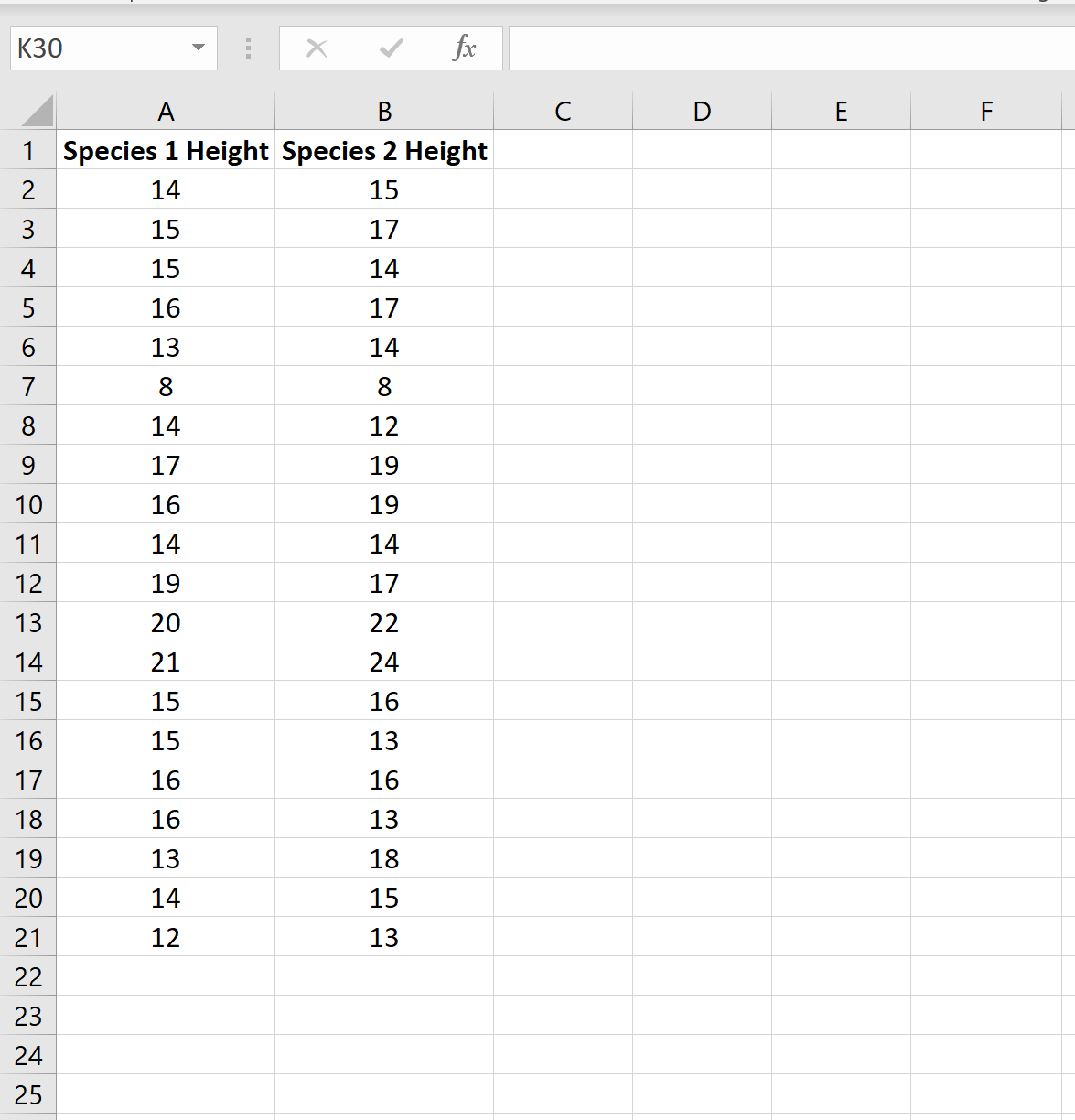
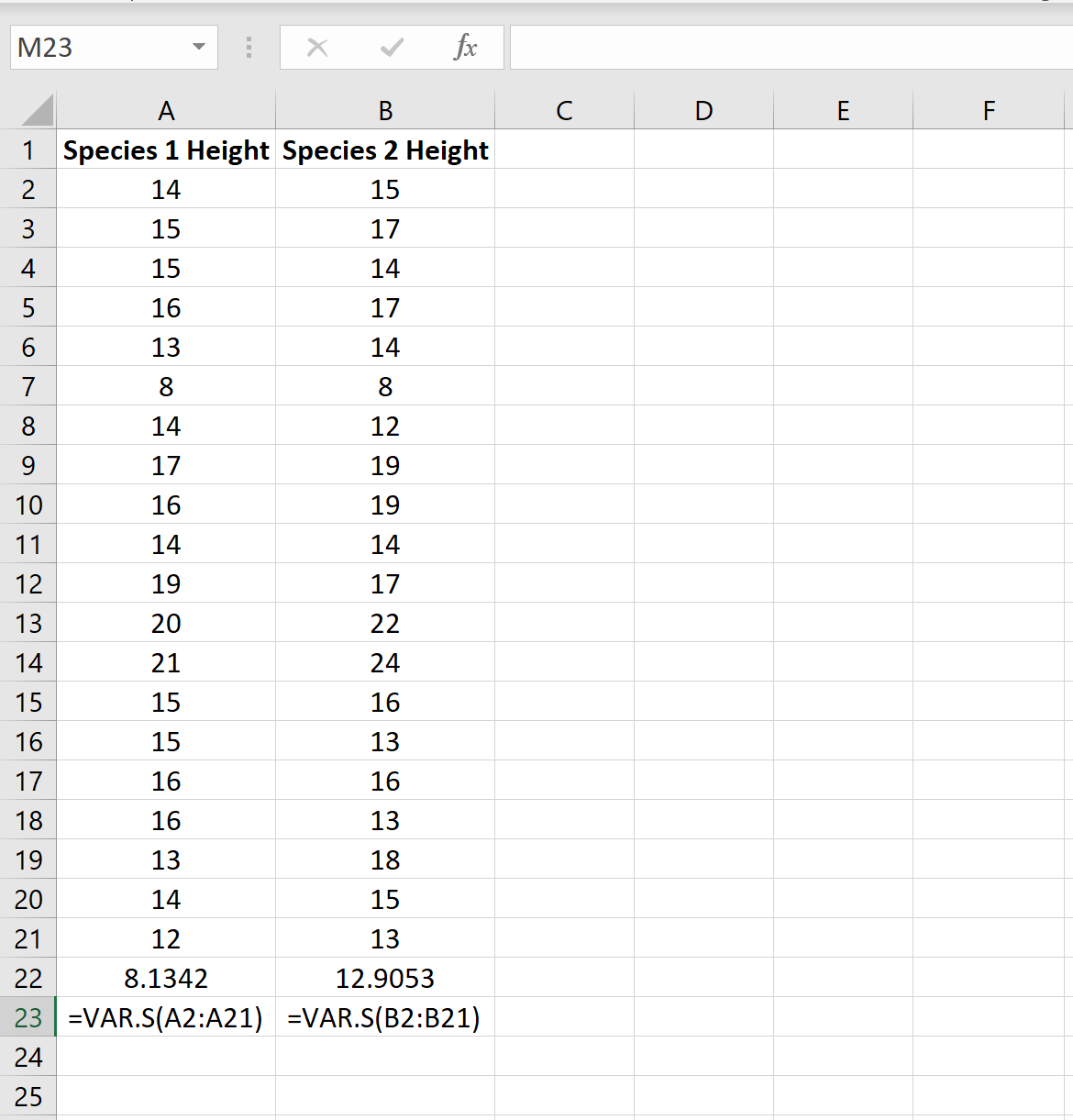
Предположим, исследователи хотят знать, имеют ли два разных вида растений в определенной стране одинаковую среднюю высоту. Поскольку обход и измерение каждого растения заняло бы слишком много времени, они решили собрать образец из 20 растений каждого вида.
На следующем изображении показана высота (в дюймах) каждого растения в каждом образце:
Мы можем провести двухвыборочный t-тест, чтобы определить, имеют ли два вида одинаковую среднюю высоту, используя следующие шаги:
Шаг 1: Определите, равны ли дисперсии генеральной совокупности .
Когда мы проводим двухвыборочный t-критерий, мы должны сначала решить, будем ли мы предполагать, что две совокупности имеют равные или неравные дисперсии. Как правило, мы можем предположить, что совокупности имеют равные дисперсии, если отношение большей выборочной дисперсии к меньшей выборочной дисперсии составляет менее 4:1.
Мы можем найти дисперсию для каждого образца, используя функцию Excel =VAR.S(диапазон ячеек) , как показано на следующем рисунке:
Отношение большей дисперсии выборки к меньшей дисперсии выборки составляет 12,9053 / 8,1342 = 1,586 , что меньше 4. Это означает, что мы можем предположить, что дисперсии генеральной совокупности равны.
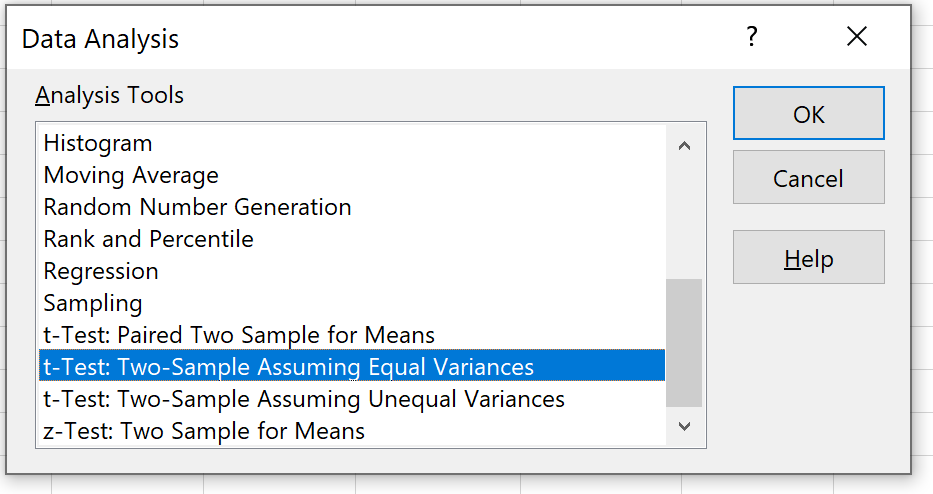
Шаг 2: Откройте пакет инструментов анализа .
На вкладке «Данные» на верхней ленте нажмите «Анализ данных».
Если вы не видите этот вариант для выбора, вам необходимо сначала загрузить пакет инструментов анализа , который является совершенно бесплатным.
Шаг 3: Выберите подходящий тест для использования.
Выберите вариант с надписью t-Test: Two-Sample Assassining Equal Variances и нажмите OK.
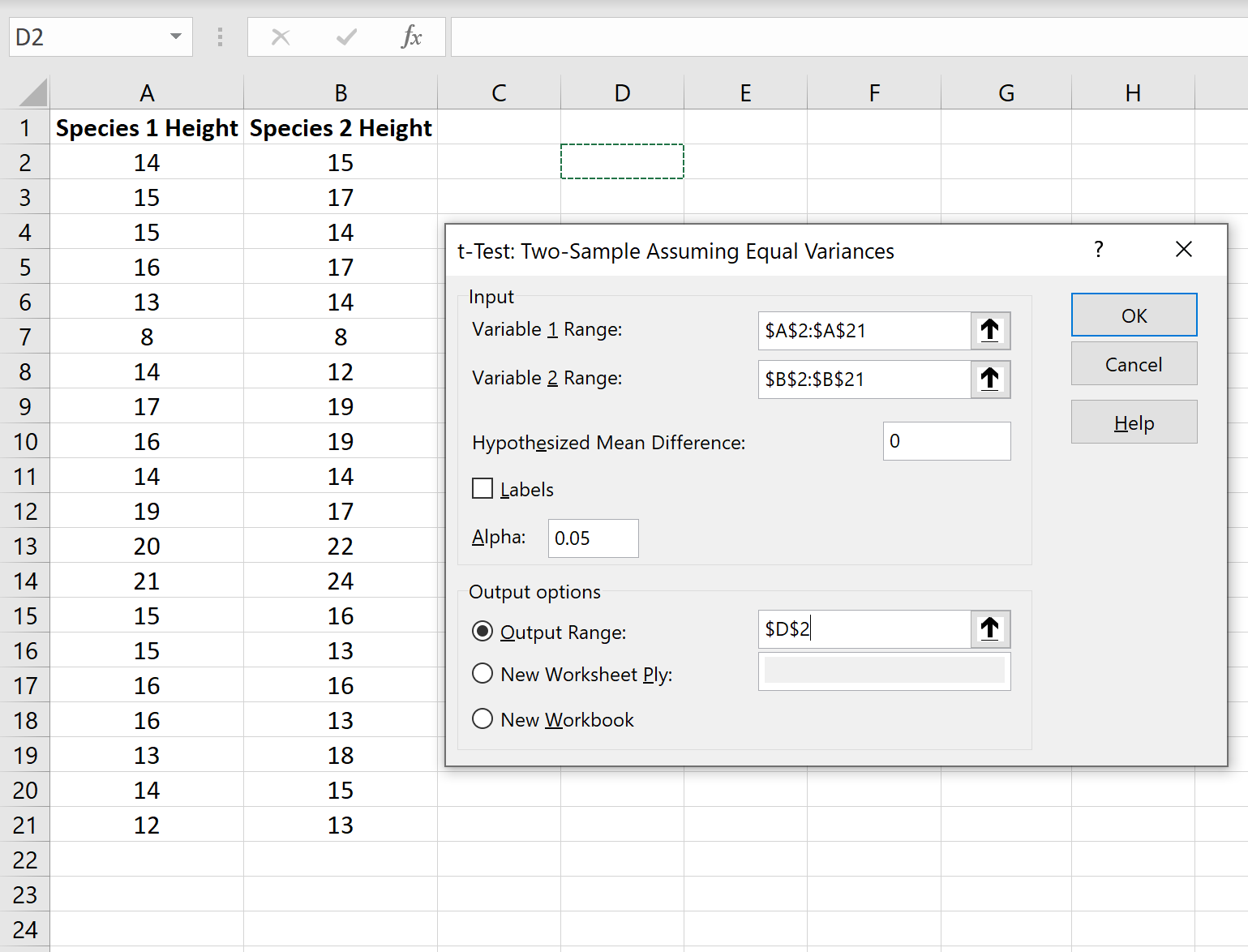
Шаг 4: Введите необходимую информацию .
Введите диапазон значений для переменной 1 (наша первая выборка), переменной 2 (наша вторая выборка), гипотетической средней разницы (в этом случае мы поместили «0», потому что мы хотим знать, равна ли истинная средняя разница генеральной совокупности 0), и выходной диапазон, в котором мы хотели бы видеть результаты t-теста. Затем нажмите ОК.
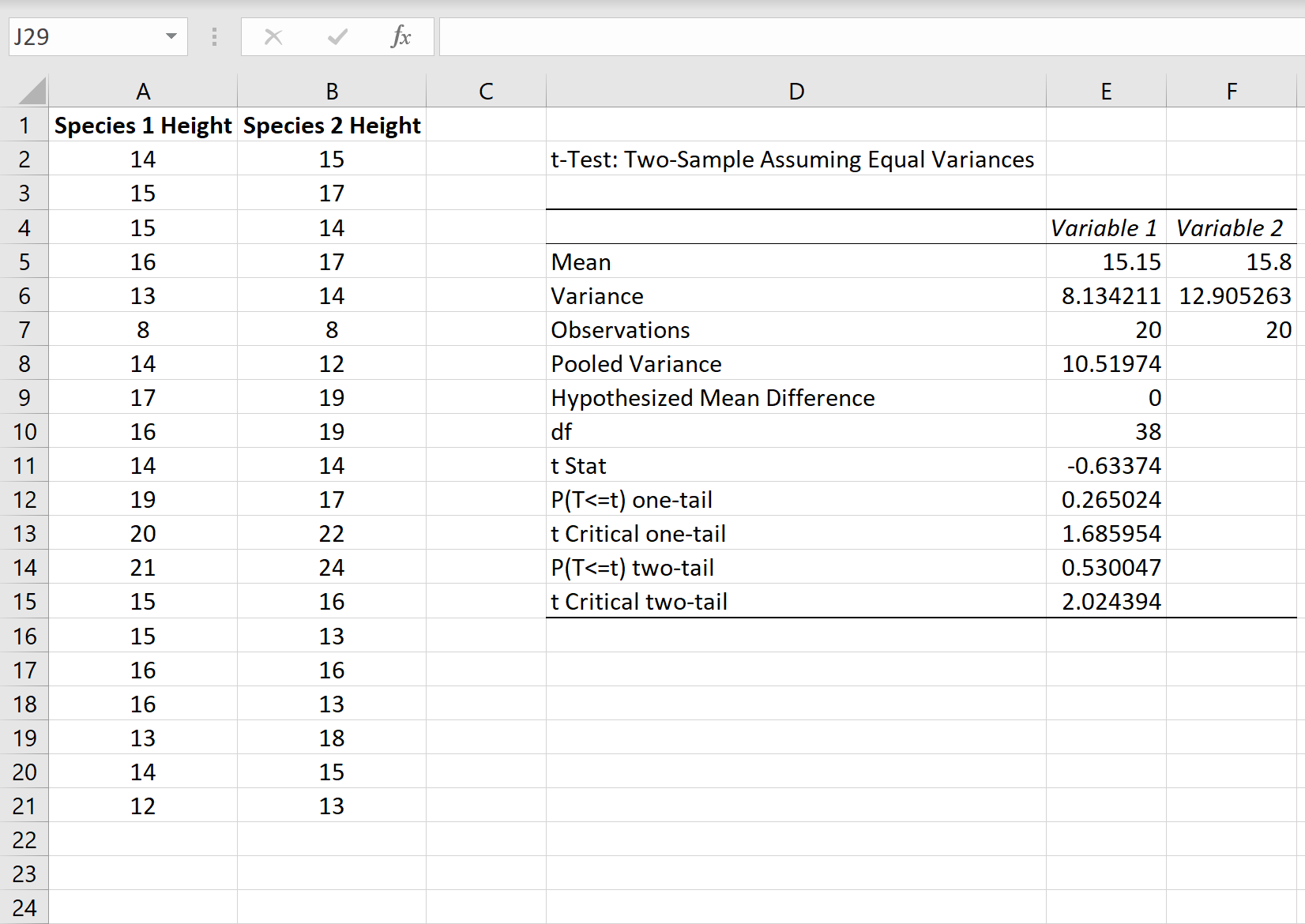
Шаг 5: интерпретируйте результаты .
После того, как вы нажмете OK на предыдущем шаге, отобразятся результаты t-теста.
Вот как интерпретировать результаты:
Среднее значение: это среднее значение для каждого образца. Образец 1 имеет среднюю высоту 15,15 , а образец 2 имеет среднюю высоту 15,8 .
Дисперсия: это дисперсия для каждого образца. Выборка 1 имеет дисперсию 8,13 , а выборка 2 — 12,90 .
Наблюдения: это количество наблюдений в каждой выборке. Обе выборки содержат по 20 наблюдений (например, по 20 отдельных растений в каждой выборке).
Объединенная дисперсия: Число , которое рассчитывается путем «объединения» дисперсий каждой выборки вместе по формуле +n 2 -2), что оказывается равным 10,51974.Это число позже используется при вычислении тестовой статистики t .
Гипотетическая средняя разница: число, которое мы «предполагаем», представляет собой разницу между двумя средними значениями совокупности. В данном случае мы выбрали 0 , потому что хотим проверить, равна ли разница между двумя популяциями в среднем 0, например, разницы нет.
df: Степени свободы для t-критерия, рассчитанные как n 1 + n 2 -2 = 20 + 20 – 2 = 38 .
t Stat: тестовая статистика t , рассчитанная как t = [ x 1 – x 2 ] / √ [ s 2 p (1/n 1 + 1/n 2 )]
В этом случае t = [15,15-15,8] / √ [10,51974(1/20+1/20)] = -0,63374 .
P(T<=t) двухсторонний: значение p для двустороннего t-критерия. В этом случае р = 0,530047.Это намного больше, чем альфа = 0,05, поэтому мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что два средних значения населения различны.
t Критический двухсторонний: это критическое значение теста, найденное путем определения значения в таблице распределения t , которое соответствует двустороннему тесту с альфа = 0,05 и df = 38. Получается 2,024394.Поскольку наша тестовая статистика t меньше этого значения, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что два средних значения населения различны.
Обратите внимание, что подход с использованием p-значения и критического значения приведет к одному и тому же выводу.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие типы t-тестов в Excel:
Как провести одновыборочный t-тест в Excel
Как провести t-тест для парных выборок в Excel
F — критерий Фишераиспользуют для
сравнения дисперсий двух генеральных
совокупностей, распределенных по
нормальному закону.
По независимым выборкам объема из этих
совокупностей найдены выборочные
дисперсии
и
.
Выдвигается гипотезаH0
— дисперсии равны, альтернативная
гипотезаH1— дисперсии не равны. Вычисляетсяпо формуле:
|
|
(4.5) |
где
— большая дисперсия,
— меньшая дисперсия. По заданному уровню
значимости α и числам степеней свободыи
(
число степеней свободы числителя и
число степеней свободы знаменателя) —
определяемпо таблицам или используя встроенные
функцииMSExcel.
Число степеней свободы числителя
определяется по формуле:
|
|
(4.6) |
где n1— число
вариант для большей дисперсии.
Число степеней свободы знаменателя
определяется по формуле:
|
|
(4.7) |
где n2 — число
вариант для меньшей дисперсии.
Если
(вычисленное
значение критерия
не больше
критического), то принимается гипотезаH0(дисперсии
равны), в противном случае ()
принимается гипотезаH1
(дисперсии различны).
Пример
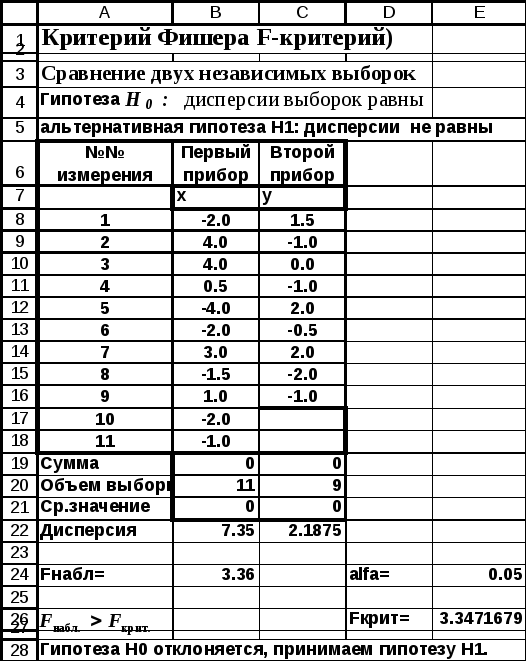
4.3
При проведении тестирования двух
одинаковых приборов были проведены
измерения эталона. При этом первым
прибором было проведено n1=11 измерений, а вторым — n2=9.
Результаты были записаны в виде отклонений
от значения эталона. Требуется выяснить:
одинаковой ли точностью обладают
приборы.
Решение:
Величина отклонений от эталонного
значения для первого прибора (n1=11) внесена в столбец В,а для второго
прибора (n2=9)
результаты — в столбец С (рис.4.4-4.5). Средние
значения отклонений одинаковы и равны
нулю. Следовательно, у приборов отсутствует
систематическая ошибка.
Проверка точности приборов сводится к
проверке совпадения дисперсий. Если
дисперсии отклонений от эталонного
значения статистически равны, то приборы
обладают одинаковой точностью. Выдвигается
гипотеза H0
— дисперсии выборок равны, альтернативная
гипотезаH1— дисперсии не равны.
В результате расчета были получены
соответственно следующие значения
дисперсий:
=7.35 и
=2.188.
Значение критерия
=7.35 /2.188 = 3.36.
Для уровня значимости α =0.05; числа
степеней свободы числителяr1 =11-1=10
и числа степеней свободы знаменателяr2 = 9-1= 8
находим с помощью встроенной
функции FРАСПОБР().Fкрит= 3.347.
Поскольку
то гипотезаH0
отклоняется, и принимается альтернативная
гипотезаH1
(дисперсии различны). Следовательно,
приборы имеют различную точность.
Рис.
4.4 Сравнение двух выборочных дисперсий
(фрагмент
рабочего листа MSExcelв режиме отображения данных)
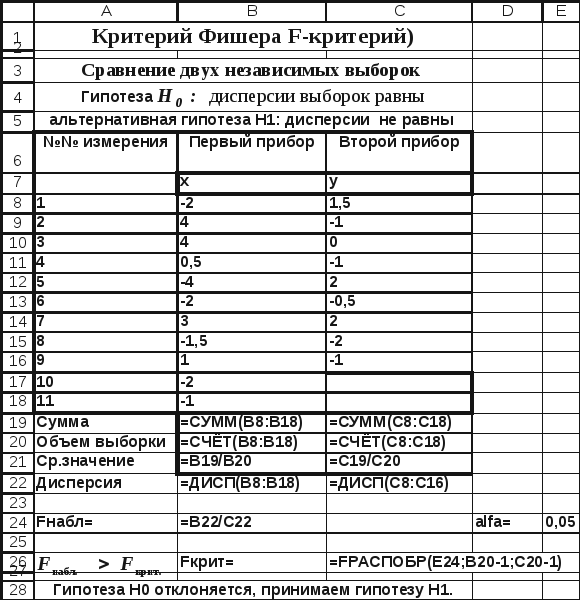
Рис.
4.5. Сравнение двух выборочных дисперсий
(фрагмент
рабочего листа MSExcelв режиме отображений формул)
Средство анализа «Двухвыборочный f-тест для дисперсии» надстройки «Пакет анализа» ms Excel
Средство анализа «Двухвыборочный F-тест
для дисперсии» надстройки «Пакет
анализа»MSExcelслужит для проверки гипотезы о равенстве
дисперсий двух выборок. Для проверки
необходимо заполнить диалоговое окно,
приведенное на рис.4.6, назначение всех
полей ввода очевидно.
Рис. 4.6 Диалоговое
окно средства анализа «Двухвыборочный
F-тест для дисперсии»
надстройки «Пакет анализа»MSExcel
Результаты расчета представлены на
рис.4.7.
Сравните полученные результаты с
результатами, полученными вручную.
Рис.
4.7 «Двухвыборочный F-тест
для дисперсии»
надстройки
«Пакет анализа» MSExcel
Соседние файлы в папке Эконометрика 1 лекция
- #
- #
- #
- #
- #
- #
- F-Test в Excel
Excel F-Test (Содержание)
- F-Test в Excel
- Как сделать F-Test в Excel?
- Плюсы F-Test в Excel
- Минусы F-Test в Excel
F-Test в Excel
- Функция F-Test в Microsoft Excel используется для сравнения двух отклонений статистическим способом. Он включает в себя процессы, которые имеют дело только со статистическими данными. F-тест показывает изменение и разницу в изменчивости.
- Чтобы определить, должен ли тест быть принят или отклонен на основе статистических данных, нам необходимо сравнить значение F и критический однолистный F.
- Целью F-теста является определение вариации данных, вероятности изменения / изменчивости данных.
Как сделать F-Test в Excel?
F-Test в Excel очень прост и удобен. Давайте разберемся с работой F-Test в Excel на нескольких примерах.
Вы можете скачать этот шаблон F-Test Excel здесь — Шаблон F-Test Excel
Excel F-Test — Пример № 1
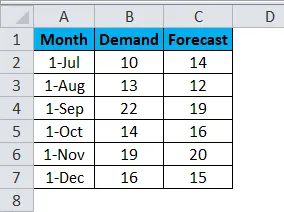
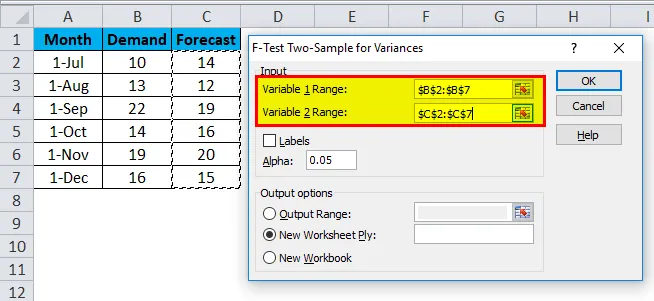
Предположим, у нас есть данные о спросе и прогнозе по любому продукту за 6 месяцев. Данные приведены в A2: C7.
Теперь, если мы хотим проверить вариацию и разницу в вариабельности данных.
- Перейдите в раздел «Данные» в строке меню и выберите « Анализ данных» .
- После того, как вы щелкнете по нему, появится окно опции «Анализ данных». Теперь выберите F-Test для двух образцов отклонений и нажмите « ОК» .
- После этого появится другое диалоговое окно F-Test.
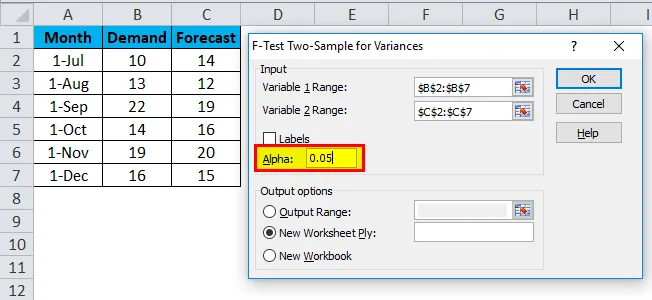
- Здесь вам нужно выбрать диапазон переменных Demand и Forecast из данных, которые показаны ниже.
- После выбора диапазона переменных 1 и диапазона переменных 2 выберите нужное значение альфа в том же окне. Здесь мы взяли 0, 05 в качестве альфы, что означает, что мы рассматриваем 5% допуска в расчетах и анализе.
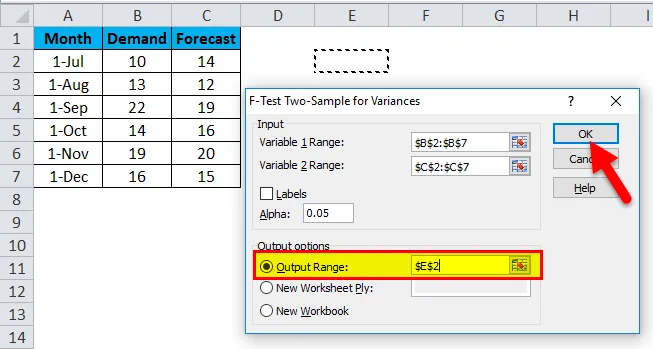
- После этого выберите ячейку « Диапазон вывода» в любом месте на том же листе или в другом месте, вы также можете выбрать новую рабочую книгу, которая приведена чуть ниже ее, для вашего удобства. Здесь мы выбрали выходной диапазон как E2, а затем нажмите OK .
- F-Test в Excel будет выглядеть ниже.
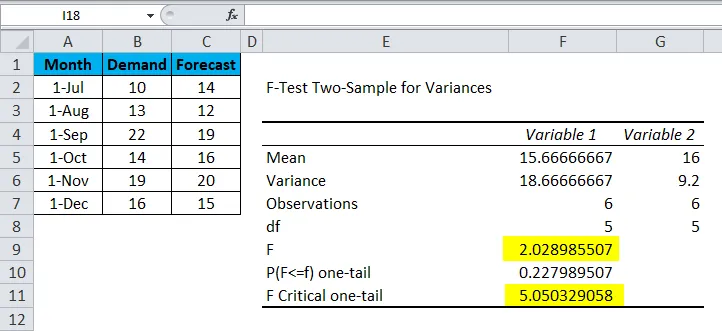
Теперь давайте проанализируем приведенные выше данные;
- Среднее значение переменной 1 и переменной 2 равно 15.66666667 и 16 соответственно, что является средней точкой спроса и прогноза.
- Дисперсия переменной 1 и переменной 2 равна 18.66666667 и 9.2 соответственно, что показывает изменение в наборе данных.
- Наблюдения за переменной 1 и переменной 2 — это 6, что означает, что при проведении F-теста учитываются только 6 точек данных или параметров.
- df — степень свободы, которая показывает, что только 5 переменных могут быть назначены этому статистическому распределению.
- P (F <= f) one-tail — это распределение вероятностей вариаций в обоих наборах данных, которое должно составить 0.227989507 (22, 7% прибл.).
Как вы можете видеть, значение F составляет 2, 02898507, что меньше значения F Критический односторонний, что означает, что эта нулевая гипотеза может быть принята.
Excel F-Test — Пример № 2
Предположим, у нас есть данные о доставке некоторых номеров деталей. Для лучшего понимания мы отсортировали данные в порядке возрастания с именем столбца Дата доставки, как показано ниже.
Выполните ту же процедуру для этих данных для выполнения F-Test в Excel. Набор данных имеет только один столбец, который имеет статистические или числовые показатели. Здесь анализ будет основан на разбиении дат на два раздела.
- Как вы можете видеть на скриншоте ниже, для диапазона Variable 1 выбранные данные взяты из B2: B9, а для диапазона Variable 2 выбраны данные из B10: B16.
- Альфа сохраняется 0, 05, что составляет 5% допуска (вы можете изменить значение альфа в соответствии с размером данных и требованиями).
- Затем выберите ячейку Range Range и нажмите OK .
- F-тест в Excel для доставки данных показанных номеров деталей будет выглядеть следующим образом:
Теперь давайте проанализируем приведенные выше данные;
- Среднее значение переменной 1 и переменной 2 составляет 26, 75 и 26, 85714286 соответственно, что является средней точкой доставленного количества. И нет большой разницы в этих параметрах.
- Дисперсия переменной 1 и переменной 2 равна 72.21428571 и 235.1428571 соответственно, что показывает изменение в наборе данных.
- Наблюдения за Переменной 1 и Переменной 2 равны 8 и 7, что означает, что выбранные верхние точки данных равны 8, а выбранные нижние точки имеют 7 чисел.
- df — это степень свободы, которая показана, и только верхняя и нижняя совокупность данных в этом статистическом распределении может быть назначена только переменной 7 и 6.
- P (F <= f) one-tail — это распределение вероятностей вариаций в обоих наборах данных, которое составляет 0, 073953335 (7, 3% приблизительно).
Как вы можете видеть, значение F равно 0, 307108141, что больше, чем значение F Критический односторонний, что означает, что эта нулевая гипотеза не может быть принята.
Плюсы F-Test в Excel
- Он может использоваться в любых статистических наборах данных, где можно выполнить сравнение до / после, последний / предыдущий, чтобы принять, могут ли быть приняты статистические данные или нет.
- Среднее значение дает среднее значение, которое является средним от общих значений, дисперсия — разницу между фактическим или прогнозируемым / будущим значением. Таким образом, центричность легко увидеть.
Минусы F-Test в Excel
- Для нестатистических фоновых людей становится трудно понять и измерить различные наблюдения.
- Если различие в значениях F и F, критических для одного хвоста, очень мало, то становится очень трудно принять или отклонить тест при выполнении в реальных сценариях.
Вещи, чтобы помнить
- F-тест может быть выполнен на одном или нескольких наборах данных в Excel. Он не ограничен набором данных, который имеет два параметра.
- Всегда сортируйте данные перед выполнением F-Test в Excel. И параметр сортировки должен быть базой, которая коррелирует с данными.
- Выполните базовое форматирование перед выполнением F-теста, чтобы получить хороший санированный вывод.
Рекомендуемые статьи
Это было руководство по F-Test в Excel. Здесь мы обсуждаем его плюсы и минусы и как сделать F-Test в Excel вместе с примерами Excel и загружаемым шаблоном Excel. Вы также можете просмотреть наши другие предлагаемые статьи —
- Столбчатая диаграмма Excel | Учебники
- Функции математики упрощены в Excel
- Как посчитать уникальные значения в Excel
- Шпаргалка по формулам Excel
























 ,
,