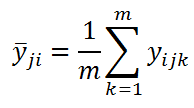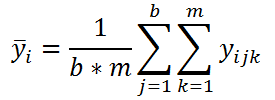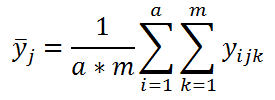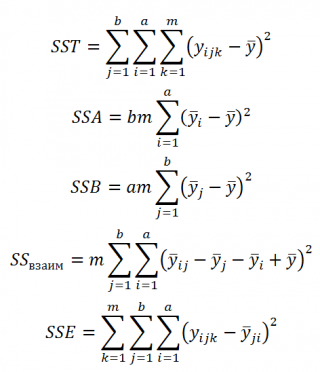17 авг. 2022 г.
читать 3 мин
Двухфакторный дисперсионный анализ («дисперсионный анализ») используется для определения того, существует ли статистически значимое различие между средними значениями трех или более независимых групп, разделенных на два фактора.
В этом руководстве объясняется, как выполнить двусторонний дисперсионный анализ в Excel.
Пример. Двухфакторный дисперсионный анализ в Excel
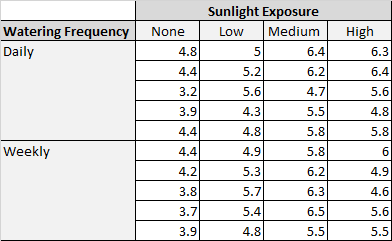
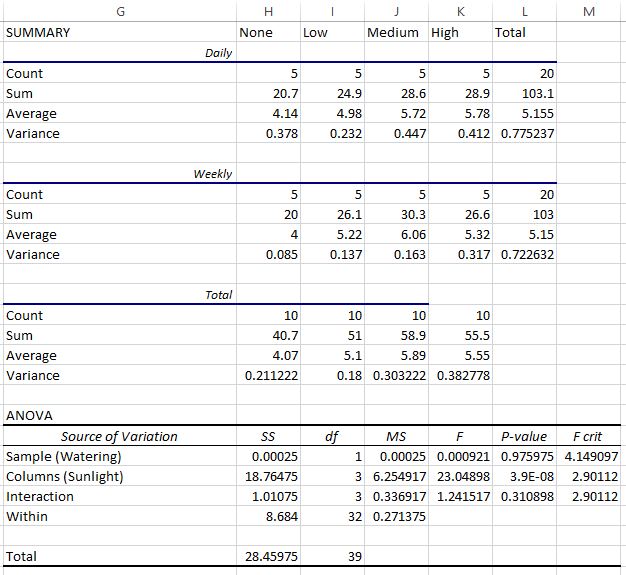
Ботаник хочет знать, влияет ли на рост растений воздействие солнечного света и частота полива. Она сажает 40 семян и дает им расти в течение двух месяцев при различных условиях солнечного света и частоты полива. Через два месяца она записывает высоту каждого растения. Результаты показаны ниже:
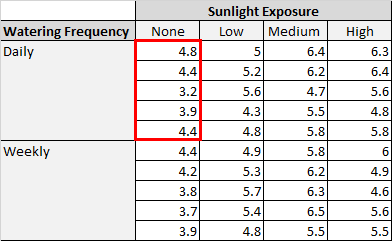
В таблице выше мы видим, что в каждой комбинации условий выращивалось по пять растений. Например, было пять растений, выращенных с ежедневным поливом и без солнечного света, и их высота через два месяца составила 4,8 дюйма, 4,4 дюйма, 3,2 дюйма, 3,9 дюйма и 4,4 дюйма:
Мы можем использовать следующие шаги для выполнения двустороннего анализа этих данных:
Шаг 1: Выберите пакет инструментов анализа данных.
На вкладке « Данные » нажмите « Анализ данных» :
Если вы не видите этот вариант, вам нужно сначала загрузить бесплатный пакет инструментов для анализа данных .
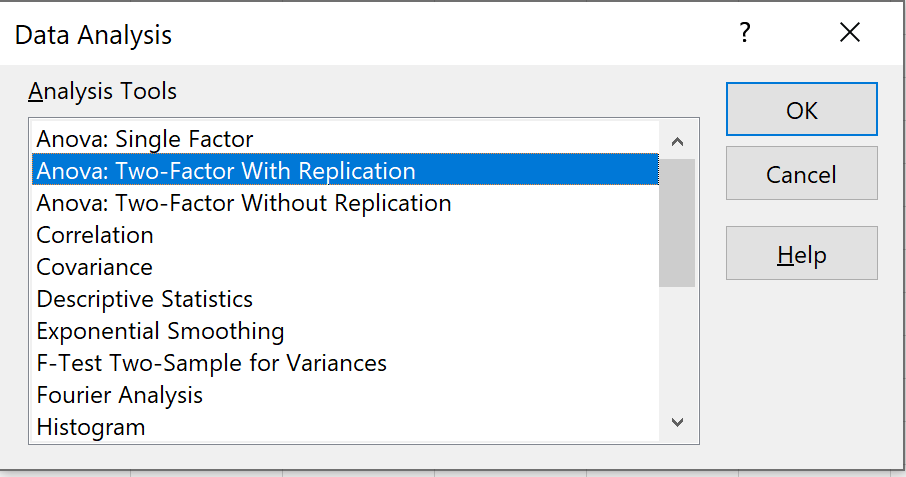
2. Выберите Anova: двухфакторный с репликацией
Выберите вариант с надписью Anova: Two-Factor With Replication , затем нажмите OK .
В этом контексте «повторение» означает наличие нескольких наблюдений в каждой группе. Например, было несколько растений, которые выращивались без воздействия солнечного света и ежедневного полива. Если бы вместо этого мы выращивали только одно растение в каждой комбинации условий, мы бы использовали «без повторения», но размер нашей выборки был бы намного меньше.
3. Введите необходимые значения.
Далее заполните следующие значения:
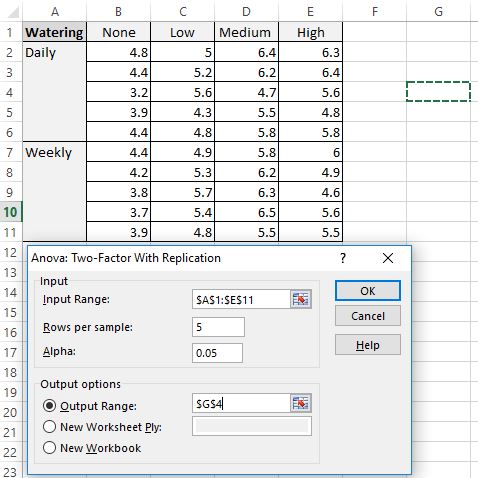
- Диапазон ввода: выберите диапазон ячеек, в котором находятся наши данные, включая заголовки.
- Рядов на образец: введите «5», поскольку в каждом образце 5 растений.
- Альфа: выберите уровень значимости для использования. Мы выберем 0,05.
- Выходной диапазон: выберите ячейку, в которой должны появиться выходные данные двухфакторного дисперсионного анализа. Мы выберем ячейку $G$4.
Шаг 4: Интерпретируйте вывод.
Как только мы нажмем OK , появятся результаты двухфакторного дисперсионного анализа:
Первые три таблицы показывают сводную статистику для каждой группы. Например:
- Средняя высота растений, которые ежедневно поливали, но не освещали солнечным светом, составляла 4,14 дюйма.
- Средняя высота растений, которые поливали еженедельно и получали мало солнечного света, составляла 5,22 дюйма.
- Средняя высота всех ежедневно поливаемых растений составляла 5,115 дюйма.
- Средняя высота всех растений, которые поливали еженедельно, составляла 5,15 дюйма.
- Средняя высота всех растений, получавших много солнечного света, составляла 5,55 дюйма.
И так далее.
В последней таблице показан результат двухфакторного дисперсионного анализа. Мы можем наблюдать следующее:
- Значение p для взаимодействия между частотой полива и воздействием солнечного света составило 0,310898.Это не является статистически значимым при уровне альфа 0,05.
- Значение p для частоты полива составило 0,975975.Это не является статистически значимым при уровне альфа 0,05.
- Значение p для воздействия солнечного света составило 3,9E-8 (0,000000039).Это статистически значимо при уровне альфа 0,05.
Эти результаты показывают, что воздействие солнечного света является единственным фактором, статистически значимо влияющим на высоту растений. А поскольку эффекта взаимодействия нет, эффект воздействия солнечного света одинаков для каждого уровня частоты полива. То есть, поливают ли растение ежедневно или еженедельно, это не влияет на то, как воздействие солнечного света влияет на растение.
Пусть имеется случайная переменная
Y
, значения которой мы можем измерять. Исследователь предполагает, что эта переменная зависит от 2-х факторов, значения которых мы можем контролировать, т.е. задавать с требуемой точностью. Покажем как методом дисперсионного анализа проверить гипотезу о наличии или отсутствии влияния указанных факторов на зависимую переменную
Y
.
Disclaimer
: Эта статья – о применении MS EXCEL для целей
Дисперсионного анализа, поэтому
данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения теории
Дисперсионного анализа
– плохая идея. Хорошая идея — найти в этой статье формулы MS EXCEL для проведения
Дисперсионного анализа.
Напомним, что
дисперсионный анализ
(ANOVA, ANalysis Of VAriance) позволяет
проверить гипотезу
о равенстве
средних значений
выборок (взяты ли выборки из одного распределения или из разных распределений). Данная задача возникает, например, когда необходимо исследовать зависимость некой
количественной
величины Y от одной или нескольких переменных (факторов), которые мы можем контролировать (устанавливать их значения). Действительно, если фактор оказывает влияние на зависимую переменную Y, то при разных уровнях фактора мы должны
в среднем
получать различные значения Y, т.е. мы должны получить «заметно отличающиеся»
средние значения выборок
. В статье будет показано, что значит
средние выборок
«заметно отличаются».
В этой статье рассмотрим метод дисперсионного анализа в случае двух факторов (Фактор А и Фактор В) (Two Factor ANOVA with Replication).
СОВЕТ
: Перед прочтением этой статьи рекомендуется освежить в памяти
Однофакторный дисперсионный анализ
.
Обозначения
Отдельные, заданные значения каждого фактора называются уровнями (
levels
) или испытаниями (
treatments
).
Уровни фактора А будем обозначать буквой j (j изменяется от 1 до
a
). Уровни фактора В будем обозначать буквой i (i изменяется от 1 до
b
). Каждой паре уровней факторов соответствует одна выборка, которая состоит из
m
измерений, каждое измерение будем обозначать буквой k (k от 1 до m). Таким образом, измеренные значения Y при уровне j фактора А и при уровне i фактора В будем обозначать y ijk . Всего выборок
a*b
.
Предполагается, что
дисперсии
всех выборок σ 2 неизвестны, но равны между собой.
Рассмотрим
двухфакторный дисперсионный анализ
при решении задачи.
Задача
В компании, изготавливающей изделия путем механообработки, необходимо исследовать влияние на качество изделия двух факторов: Метода обработки поверхности детали, и Исходного материала детали (используется сталь с различным легированием).
Метод обработки представляет собой
фактор А
, который может принимать 3 значения (Метод 1, Метод 2, Метод 3), а Исходный материал
представляет собой
фактор В
, который может принимать 2 значения (№ 1, № 2). Качество изделий будем определять по количеству дефектных изделий в партии (это будет зависимой переменной Y).
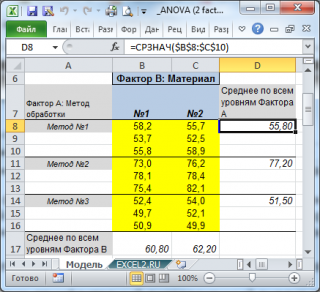
Всего различных комбинаций 2-х факторов 6=3*2=a*b. Для каждой комбинации факторов было проведено по 3 измерения (т.е. m=3). Исходные данные приведены в файле примера .
Другими словами мы имеем 6 выборок по 3 значения в каждой. Средние этих выборок для каждой комбинации факторов ij можно вычислить по формуле:
Также для дальнейших вычислений нам потребуется вычислить еще несколько средних значений. Во-первых, вычислим среднее всех измерений, относящихся к каждому уровню i Фактора А:
Во-вторых, вычислим среднее всех измерений, относящихся к каждому уровню j Фактора В:
Взаимодействие факторов
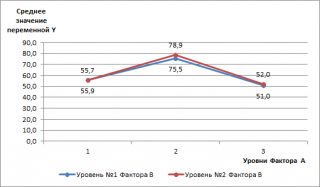
Теперь, используя эти 6 средних значений, построим диаграмму, которая
состоит из 2-х рядов
.
По оси Х (абсцисс) отложены уровни
Фактора А
, по оси ординат отложены средние значения переменной Y (среднее количество дефектов для заданных уровней факторов). Средние значения сгруппированы по 2-м уровням Фактора В (Синяя и красная линии. Каждая линия представляет собой отдельный ряд диаграммы).
Как видно из диаграммы – синяя и красная линии практически параллельны друг другу. Это означает, что взаимодействие между факторами практически отсутствует (они не влияют друг на друга). Действительно, выбор метода обработки никак не может влиять на выбор конкретного исходного материала.
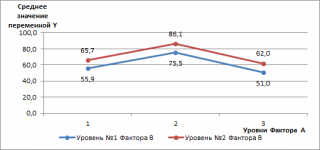
Вот еще одна диаграмма, демонстрирующая независимость 2-х факторов.
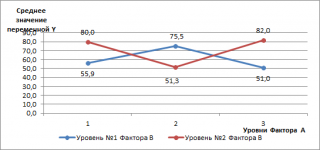
Обратная ситуация показана на диаграмме ниже, когда оба фактора взаимодействуют.
Из этой диаграммы видно, что при
уровне №1 фактора В
(синяя линия) количество дефектов сначала возрастает, затем снижается (когда мы переходим от метода №1 к №2, затем к №3). Мы наблюдаем диаметрально противоположную ситуацию при
уровне №2 фактора В
(красная линия): количество дефектов сначала снижается, а затем возрастает. В этом случае говорят о наличии взаимодействия факторов.
В случае взаимодействия факторов А и В, эффект от их взаимодействия может быть рассмотрен как некий
третий фактор АВ
. Чтобы пояснить это рассмотрим задачу анализа влияния на урожайность свеклы 2-х факторов:
Вид семян
и
Тип почвы
. Очевидно, что факторы
Вид семян
и
Тип почвы
не являются независимыми: можно утверждать, что для всех с/х культур на разных почвах разные типы семян дадут разную всхожесть. Различные комбинации
Вид семян
—
Тип почвы
могут сильно влиять на урожайность и поэтому взаимодействие факторов может вносить определенный вклад в разброс исходных данных.
Взаимодействие факторов было рассмотрено столь подробно, так как отсутствие или наличие взаимодействия принципиально влияет на ход
дисперсионного анализа
. При отсутствии взаимодействия влияние каждого фактора на переменную Y может быть рассмотрено по отдельности. При наличии взаимодействия анализировать влияние каждого фактора по отдельности нельзя. Альтернативным вариантом анализа в этом случае является
однофакторный дисперсионный анализ,
целью которого может быть поиск оптимального сочетания 2-х факторов.
Возвращаемся к диаграммам взаимодействия. Очевидно, что делать заключение о наличии или отсутствии взаимодействия факторов невозможно лишь по взаимному расположению линий на диаграмме. Для формулирования утверждения о взаимодействии требуется составить математическое выражение. Это выражение должно вычисляться на основании исходных данных, а результат должен сравниваться с неким критическим значением. Займемся этим в следующем разделе.
Определяем причины изменчивости исходных данных
По аналогии с однофакторным
дисперсионным анализом
общую изменчивость (разброс) значений Y относительно
общего среднего
(SST = Sum of Squares Total, общая сумма квадратов) определим как сумму нескольких компонентов, в данном случае 4-х:
SST=SSA+SSB+ SS взаим +SSE
- SSA – изменчивость, которую можно объяснить выбором метода обработки (фактор А)
- SSВ — изменчивость обусловленная выбором материала детали (фактор В)
- SS взаим — изменчивость обусловленная взаимодействием 2-х факторов
- SSE — ошибка модели (Error Sum of Squares).
SST и все 4 компонента вычисляются на основании имеющихся исходных данных:
Примечание
: Вычисления SST и всех 4-х компонентов выполнены в файле примера .
Также в
дисперсионном анализе
используется понятие
среднего квадрата отклонений
(Mean Square) или сокращенно MS. Соответственно для SST имеем MST=SST/(N-1), где N= a*b*m является общим количеством измерений (18). Для других SS степени свободы приведены в таблице ниже.
Таким образом, MS имеет смысл средней изменчивости на 1 наблюдение (с некоторой поправкой). Эта поправка отражает тот факт, что MS должна вычисляться не делением SS на соответствующее количество наблюдений, а делением на число
степеней свободы
(degrees of freedom, DF). Например, чтобы вычислить MST, мы из N (общего количества наблюдений) должны вычесть 1, т.к. в выражении SST присутствует одно (1) среднее значение (аналогично тому, как мы делали при
вычислении дисперсии
).
В случае
двухфакторного дисперсионного анализа
формируется 3
нулевых гипотезы
.
- Гипотеза Н 0 взаим об отсутствии взаимодействия Фактора А и Фактора В. Альтернативная гипотеза Н 1взаим формулируется о наличии взаимодействия.
- гипотеза Н 01 заключается в том, что уровень фактора А (метод обработки поверхности) не влияет на измеренные значения Y (количество дефектов), т.е. средние значения выборок, относящиеся к различным уровням Фактора А не отличаются статистически значимо (их различие может быть объяснено лишь случайностью выборок).
- гипотеза Н 0 2 заключается в том, что уровень фактора В (Исходный материал) не влияет на измеренные значения Y (количество дефектов), т.е. средние значения выборок, относящиеся к различным уровням Фактора В не отличаются статистически значимо.
Сначала тестируют гипотезу об отсутствии взаимодействия между факторами. Мы можем отклонить Н 0 взаим в пользу Н 1взаим при заданном
уровне значимости
α (альфа), если вычисленное значение тестовой статистики F= MS взаим /MSE больше F критич альфа – значения случайной величины F имеющей
распределение Фишера
с (b-1)*(a-1) и a*b*(m-1) степенями свободы.
Если взаимодействие между факторами отсутствует, то можно начинать тестировать гипотезы Н 01 и Н 0 2 . При наличии взаимодействия анализировать влияние каждого фактора по отдельности нельзя. Альтернативным вариантом анализа в этом случае является
однофакторный дисперсионный анализ
, целью которого может быть поиск оптимального сочетания 2-х факторов.
Чтобы проверить гипотезы необходимо вычислить значения тестовых статистик и сравнить их с соответствующими критическими значениями F крит ич , вычисленными для заданного уровня значимости
альфа
. Если вычисленное значение F 01 = MSА/MSE больше F 1крит ич , то нулевую гипотезу Н 0 1 об отсутствии влияния уровней Фактора А отклоняют. Аналогичные умозаключения справедливы и для Фактора В.
Проверить гипотезу Н 01 можно и через вычисление
p
-значения,
которое представляет собой вероятность того, что случайная величина F 1 = MSА/MSE примет значение более F 01 . Далее
p
-значение
сравнивают с уровнем значимости. Если
p
-значение
менее уровня значимости, то нулевую гипотезу отклоняют. Действительно, если вычисленное значение F 01 получить маловероятно, то это ставит под сомнение справедливость того, что случайная величина F 1 = MSА/MSE имеет
распределение Фишера
с
a
-1
и
a
*
b
*(
m
-1)
степенями свободы, а следовательно и саму нулевую гипотезу. В этом случае мы можем считать, что справедлива альтернативная гипотеза: уровни фактора А влияют на зависимую переменную Y.
Вычисления в MS EXCEL
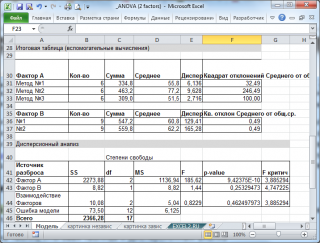
В файле примера приведено решение вышеуказанной задачи: вычислены средние значения выборок, суммы квадратов (SS), степеней свобод, средние квадратов отклонений (MS).
Для вычислений критических значений в MS EXCEL имеется специальная функция = F.ОБР.ПХ()
Формула для вычисления F 1критич = F.ОБР.ПХ(a-1; a*b*(m-1);альфа)
В MS EXCEL первое
p
-значение
(вероятность того, что случайная величина F 1 = MSА/MSE примет значение более F 01 ) можно вычислить по формуле:
= F.РАСП.ПХ((MSА/MSE; a-1; a*b*(m-1))
Второе
p
-значение
(вероятность того, что случайная величина F 2 = MSВ/MSE примет значение более F 0 2 ) вычисляется по аналогичным формулам.
В нашей задаче
p
-значения
получились 0,000 и 0,253, что значительно меньше обычно принимаемого в качестве
уровня значимости
0,05. Таким образом, обе нулевых гипотезы отклоняются.
В программе MS Excel
для статистического анализа данных
имеется надстройка «Пакет анализа»,
которая позволяет проводить дисперсионный
анализ следующих видов:
-
однофакторный
дисперсионный анализ, -
двухфакторный
дисперсионный анализ без повторений, -
двухфакторный
дисперсионный анализ с повторениями.
Последний вид
двухфакторного анализа используется
в том случае, когда в каждой группе
данных имеется более одной выборки.
3. Расчет однофакторного комплекса.
Рассмотрим задачу
проверки влияния дозы мерказолила на
время Y (в сутках) устранения тиреотоксикоза
у больных диффузным токсическим зобом.
При этом исследуемый фактор A имеет три
уровня:
A1
— 30 мг/сутки
A2
— 25 мг/сутки
A3
— 20 мг/сутки.
Статистический
комплекс представлен на рисунке 2. Он
включает 3 группы и в каждой группе
имеется по 2 наблюдения, т.е. n = 2, к =3.
|
ВАРИАНТЫ |
||
|
Уровень |
Уровень |
Уровень |
|
фактора |
фактора |
фактора |
|
54 |
67 |
73 |
|
57 |
63 |
70 |
Рисунок
2
Для выполнения
расчетов в MS Excel:
1. Сформируйте
таблицу с исходными данными (Рисунок
3):
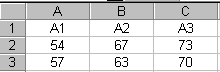
Рисунок 3
2.Выполните
команду Анализ
данных
из меню Сервис.
3.Выберите в
появившемся диалоговом окне метод
«Однофакторный дисперсионный анализ»
и нажмите кнопку [OK].
4.В окне «Однофакторный
дисперсионный анализ» (Рисунок 4)
установите для входных данных следующие
параметры:
-
входной
интервал равен $A$1:$C$3, -
входной
диапазон содержит метки в первой строке, -
альфа
(уровень значимости) равен
0,05.
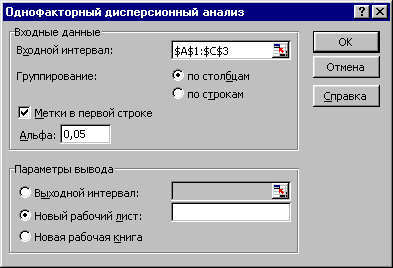
Рисунок 4
5.Для параметров
вывода установите переключатель в
положение «Новый рабочий лист».
6.После завершения
настройки параметров нажмите кнопку
[OK].
Результаты
дисперсионного анализа будут представлены
на новом листе и состоять из двух таблиц
(Рисунок 5). В первой таблице для каждой
строки и каждого столбца исходной
таблицы приведены числовые параметры:
количество чисел, сумма, среднее и
дисперсия.
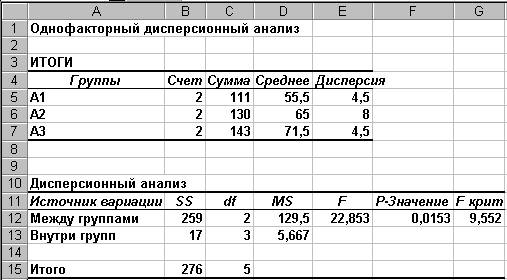
Рисунок 5
Вторая часть –
это результаты дисперсионного анализа.
В таблице результатов Excel использует
следующие обозначения:
В таблице результатов
MS Excel использует следующие обозначения:
-
SS
— сумма квадратов, -
df
— степени свободы, -
MS
— средний квадрат (дисперсия), -
F
– наблюдаемое значение F-статистики
Фишера, -
p-значение
— значимость критерия Фишера, -
F-критическое
— критическое значение F-статистики при
p=0,05.
Проанализируем
полученные результаты. В соответствии
с рисунком 5 имеем F = 22,85 и Fкр.
= 9,55, т.е. F > Fкр.
Следовательно влияние фактора на
результативный признак можно считать
достоверным, что и подтверждается
величиной значимости (p=0.0153), которая
меньше 0.05.
Итак,
конкурирующая гипотеза о достоверности
влияния фактора А может быть принята с
вероятностью 0.95. При этом сила влияния
мерказолила на устранение тиреотоксикоза
оценивается в
соответствии с формулой (10) величиной:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Чтобы проанализировать изменчивость признака под воздействием контролируемых переменных, применяется дисперсионный метод.
Для изучения связи между значениями – факторный метод. Рассмотрим подробнее аналитические инструменты: факторный, дисперсионный и двухфакторный дисперсионный метод оценки изменчивости.
Дисперсионный анализ в Excel
Условно цель дисперсионного метода можно сформулировать так: вычленить из общей вариативности параметра 3 частные вариативности:
- 1 – определенную действием каждого из изучаемых значений;
- 2 – продиктованную взаимосвязью между исследуемыми значениями;
- 3 – случайную, продиктованную всеми неучтенными обстоятельствами.
В программе Microsoft Excel дисперсионный анализ можно выполнить с помощью инструмента «Анализ данных» (вкладка «Данные» — «Анализ»). Это надстройка табличного процессора. Если надстройка недоступна, нужно открыть «Параметры Excel» и включить настройку для анализа.
Работа начинается с оформления таблицы. Правила:
- В каждом столбце должны быть значения одного исследуемого фактора.
- Столбцы расположить по возрастанию/убыванию величины исследуемого параметра.
Рассмотрим дисперсионный анализ в Excel на примере.
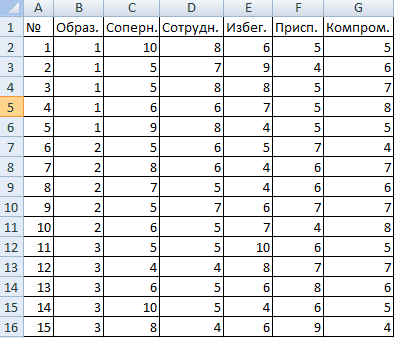
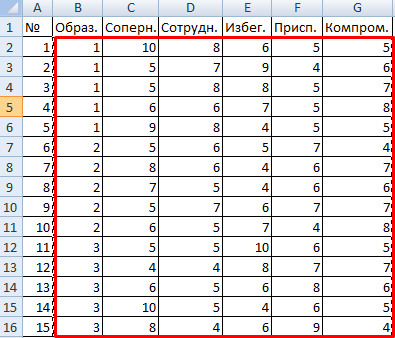
Психолог фирмы проанализировал с помощью специальной методики стратегии поведения сотрудников в конфликтной ситуации. Предполагается, что на поведение влияет уровень образования (1 – среднее, 2 – среднее специальное, 3 – высшее).
Внесем данные в таблицу Excel:
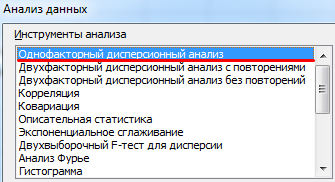
- Открываем диалоговое окно нашего аналитического инструмента. В раскрывшемся списке выбираем «Однофакторный дисперсионный анализ» и нажимаем ОК.
- В поле «Входной интервал» ввести ссылку на диапазон ячеек, содержащихся во всех столбцах таблицы.
- «Группирование» назначить по столбцам.
- «Параметры вывода» — новый рабочий лист. Если нужно указать выходной диапазон на имеющемся листе, то переключатель ставим в положение «Выходной интервал» и ссылаемся на левую верхнюю ячейку диапазона для выводимых данных. Размеры определятся автоматически.
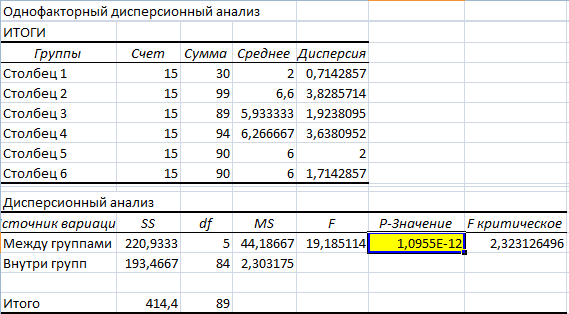
- Результаты анализа выводятся на отдельный лист (в нашем примере).
Значимый параметр залит желтым цветом. Так как Р-Значение между группами больше 1, критерий Фишера нельзя считать значимым. Следовательно, поведение в конфликтной ситуации не зависит от уровня образования.
Факторный анализ в Excel: пример
Факторным называют многомерный анализ взаимосвязей между значениями переменных. С помощью данного метода можно решить важнейшие задачи:
- всесторонне описать измеряемый объект (причем емко, компактно);
- выявить скрытые переменные значения, определяющие наличие линейных статистических корреляций;
- классифицировать переменные (определить взаимосвязи между ними);
- сократить число необходимых переменных.
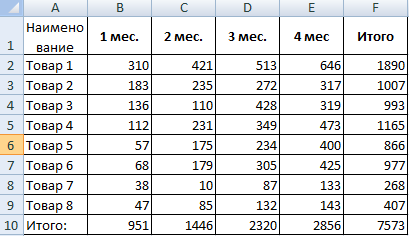
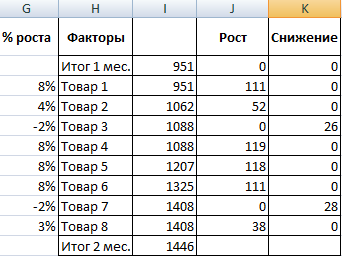
Рассмотрим на примере проведение факторного анализа. Допустим, нам известны продажи каких-либо товаров за последние 4 месяца. Необходимо проанализировать, какие наименования пользуются спросом, а какие нет.
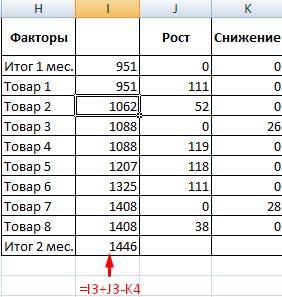
- Посмотрим, за счет, каких наименований произошел основной рост по итогам второго месяца. Если продажи какого-то товара выросли, положительная дельта – в столбец «Рост». Отрицательная – «Снижение». Формула в Excel для «роста»: =ЕСЛИ((C2-B2)>0;C2-B2;0), где С2-В2 – разница между 2 и 1 месяцем. Формула для «снижения»: =ЕСЛИ(J3=0;B2-C2;0), где J3 – ссылка на ячейку слева («Рост»). Во втором столбце – сумма предыдущего значения и предыдущего роста за вычетом текущего снижения.
- Рассчитаем процент роста по каждому наименованию товара. Формула: =ЕСЛИ(J3/$I$11=0;-K3/$I$11;J3/$I$11). Где J3/$I$11 – отношение «роста» к итогу за 2 месяц, ;-K3/$I$11 – отношение «снижения» к итогу за 2 месяц.
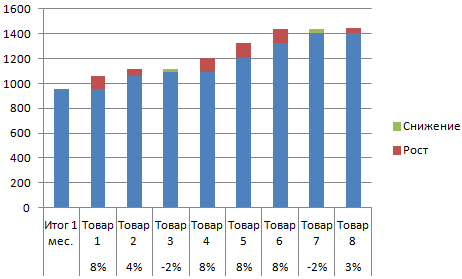
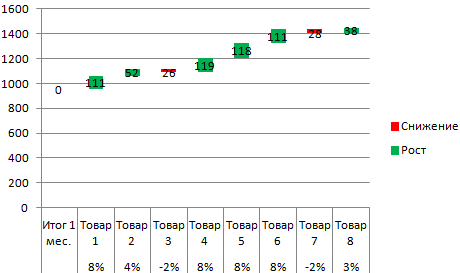
- Выделяем область данных для построения диаграммы. Переходим на вкладку «Вставка» — «Гистограмма».
- Поработаем с подписями и цветами. Уберем накопительный итог через «Формат ряда данных» — «Заливка» («Нет заливки»). С помощью данного инструментария меняем цвет для «снижения» и «роста».
Теперь наглядно видно, продажи какого товара дают основной рост.
Двухфакторный дисперсионный анализ в Excel
Показывает, как влияет два фактора на изменение значения случайной величины. Рассмотрим двухфакторный дисперсионный анализ в Excel на примере.
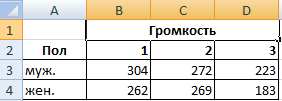
Задача. Группе мужчин и женщин предъявляли звук разной громкости: 1 – 10 дБ, 2 – 30 дБ, 3 – 50 дБ. Время ответа фиксировали в миллисекундах. Необходимо определить, влияет ли пол на реакцию; влияет ли громкость на реакцию.
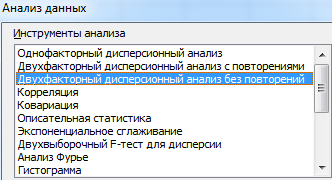
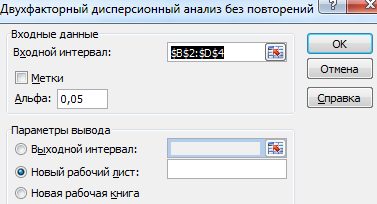
- Переходим на вкладку «Данные» — «Анализ данных» Выбираем из списка «Двухфакторный дисперсионный анализ без повторений».
- Заполняем поля. В диапазон должны войти только числовые значения.
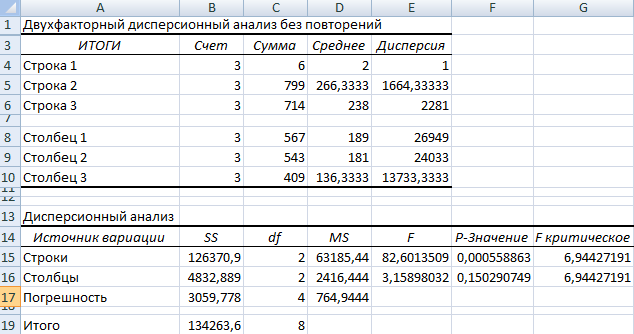
- Результат анализа выводится на новый лист (как было задано).
Та как F-статистики (столбец «F») для фактора «Пол» больше критического уровня F-распределения (столбец «F-критическое»), данный фактор имеет влияние на анализируемый параметр (время реакции на звук).
Скачать пример факторного и дисперсионного анализа
скачать факторный анализ отклонений
скачать пример 2
Для фактора «Громкость»: 3,16 < 6,94. Следовательно, данный фактор не влияет на время ответа.
Для примера также прилагаем факторный анализ отклонений в маржинальном доходе.
Двухфакторный дисперсионный анализ с повторными измерениями в Excel рассмотрим на примере.
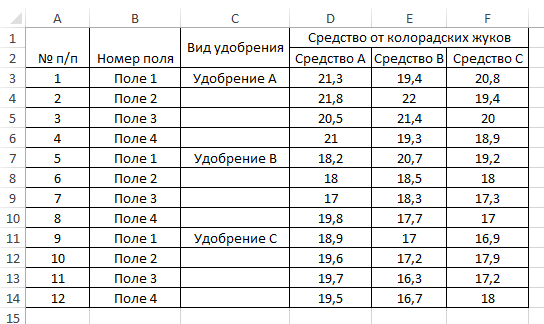
Ниже приведена статистика в виде таблицы об урожайности картофеля с 1 га. при применении разных видов удобрения и химических средств для борьбы с колорадскими жуками. На уровне значимости α=0.05 определить какие факторы влияют на урожайность картофеля.
| № п/п | Номер поля | Вид удобрения | Средство от колорадских жуков | ||
| Средство A | Средство B | Средство C | |||
| 1 | Поле 1 | Удобрение A | 21,3 | 19,4 | 20,8 |
| 2 | Поле 2 | 21,8 | 22 | 19,4 | |
| 3 | Поле 3 | 20,5 | 21,4 | 20 | |
| 4 | Поле 4 | 21 | 19,3 | 18,9 | |
| 5 | Поле 1 | Удобрение B | 18,2 | 20,7 | 19,2 |
| 6 | Поле 2 | 18 | 18,5 | 18 | |
| 7 | Поле 3 | 17 | 18,3 | 17,3 | |
| 8 | Поле 4 | 19,8 | 17,7 | 17 | |
| 9 | Поле 1 | Удобрение C | 18,9 | 17 | 16,9 |
| 10 | Поле 2 | 19,6 | 17,2 | 17,9 | |
| 11 | Поле 3 | 19,7 | 16,3 | 17,2 | |
| 12 | Поле 4 | 19,5 | 16,7 | 18 |
Итак, решаем данную задачу в Excel. Переходим на вкладку Данные -> Анализ данных. Выбираем однофакторный дисперсионный анализ c повторениями и жмём Ок.
Во входном интервале ставим выбираем диапазон ячеек $C$2:$F$14, число строк для выборки указываем 4, альфа ставим 0,05 и в выходном интервале ячейку $A$17 и далее Ок.
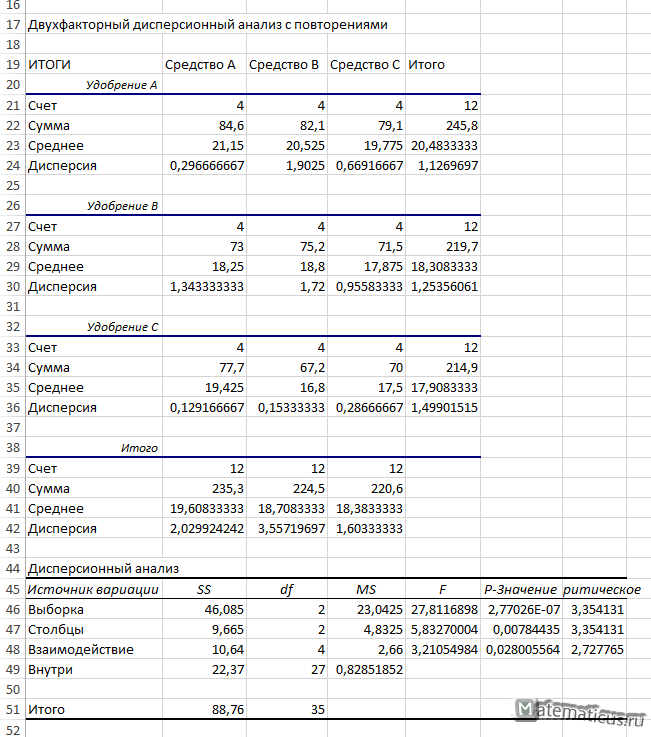
Получаем таблицу двухфакторного дисперсионного анализа с повторениями в Excel
| Двухфакторный дисперсионный анализ с повторениями | ||||
| ИТОГИ | Средство A | Средство B | Средство C | Итого |
| Удобрение A | ||||
| Счет | 4 | 4 | 4 | 12 |
| Сумма | 84,6 | 82,1 | 79,1 | 245,8 |
| Среднее | 21,15 | 20,525 | 19,775 | 20,4833333 |
| Дисперсия | 0,296666667 | 1,9025 | 0,66916667 | 1,1269697 |
| Удобрение B | ||||
| Счет | 4 | 4 | 4 | 12 |
| Сумма | 73 | 75,2 | 71,5 | 219,7 |
| Среднее | 18,25 | 18,8 | 17,875 | 18,3083333 |
| Дисперсия | 1,343333333 | 1,72 | 0,95583333 | 1,25356061 |
| Удобрение C | ||||
| Счет | 4 | 4 | 4 | 12 |
| Сумма | 77,7 | 67,2 | 70 | 214,9 |
| Среднее | 19,425 | 16,8 | 17,5 | 17,9083333 |
| Дисперсия | 0,129166667 | 0,15333333 | 0,28666667 | 1,49901515 |
| Итого | ||||
| Счет | 12 | 12 | 12 | |
| Сумма | 235,3 | 224,5 | 220,6 | |
| Среднее | 19,60833333 | 18,7083333 | 18,3833333 | |
| Дисперсия | 2,029924242 | 3,55719697 | 1,60333333 |
| Дисперсионный анализ | ||||||
| Источник вариации | SS | df | MS | F | P-Значение | F критическое |
| Выборка | 46,085 | 2 | 23,0425 | 27,8116898 | 2,77026E-07 | 3,354131 |
| Столбцы | 9,665 | 2 | 4,8325 | 5,83270004 | 0,00784435 | 3,354131 |
| Взаимодействие | 10,64 | 4 | 2,66 | 3,21054984 | 0,028005564 | 2,727765 |
| Внутри | 22,37 | 27 | 0,82851852 | |||
| Итого | 88,76 | 35 |
Значение F-критерия фактора А — влияния удобрения на урожайность картофеля, Fнабл= 27.81, а Fкрит лежит в интервале (3.35; +∞). Fнабл не лежит в критической области, следовательно, принимаем, что удобрения влияют на урожайность картофеля.
Выборочный коэффициент детерминации для фактора — удобрения:
${R^2} = frac{{frac{{46,085}}{{36}}}}{{frac{{88,76}}{{36}}}} approx 0,52$
это означает, что 52% общей выборочной вариации урожайности картофеля зависит от удобрения.
Значение F-критерия фактора В — средство для борьбы с колорадскими жуками Fнабл= 5.83, а Fкрит=3,35. Fнабл находится в критической области, следовательно средство для борьбы с колорадскими жуками влияет на урожайность картофеля.
Выборочный коэффициент детерминации для фактора — средства для борьбы с колорадскими жуками равен:
${R^2} = frac{{frac{{9,665}}{{36}}}}{{frac{{88,76}}{{36}}}} approx 0,11$
11% общей выборочной вариации урожайности картофеля зависит от средства для борьбы с колорадскими жуками.
И в дополнении, найдём взаимодействие факторов Fкрит=2,73, a Fнабл=3,21. Так как Fнабл входит в интервал (2.73; +∞), значит полезность видов удобрения изменяется в зависимости от использования различных средств борьбы с колорадскими жуками.
4873