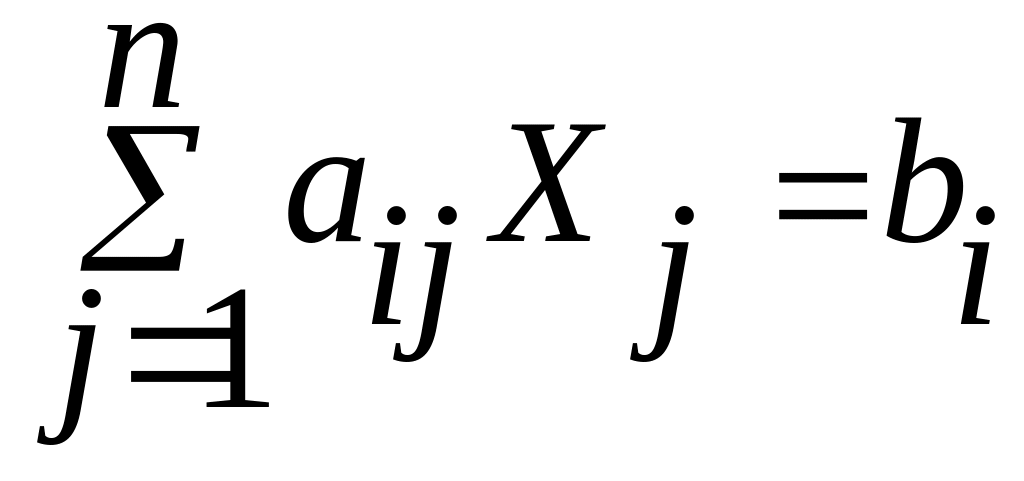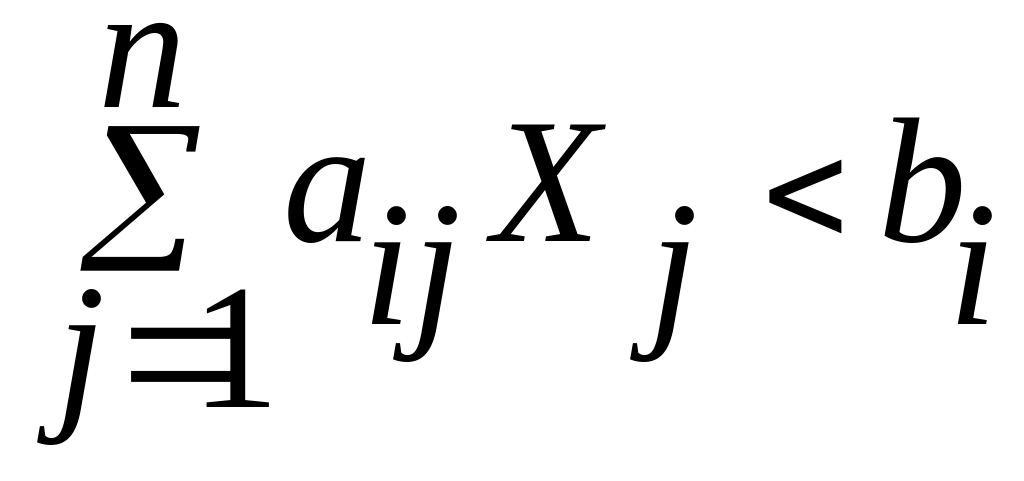Решение
двойственной задачи можно найти в Отчете
по устойчивости решения исходной задачи
(рис. 2.1).
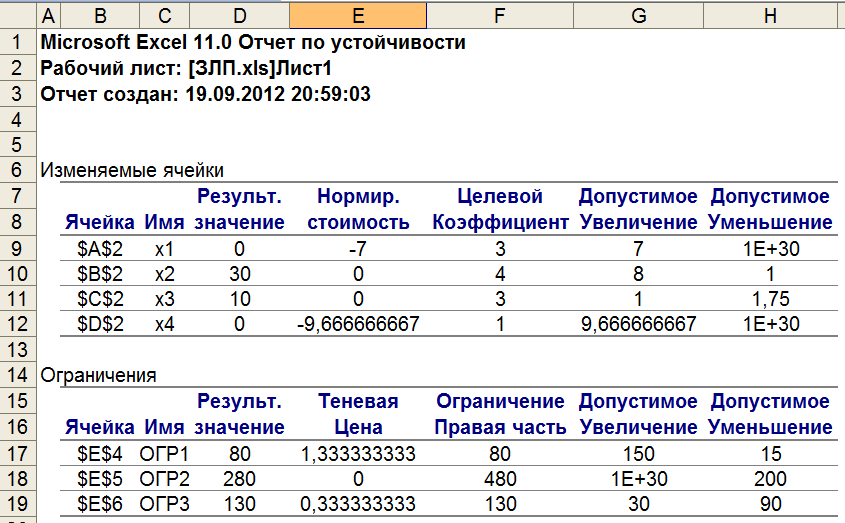
Рис. 2.1. Содержание
отчета по устойчивости
Отчет
по устойчивости содержит
информацию, относящуюся к переменным:
-
Результат решения
задачи. -
«Нормированная
стоимость» показывает, на сколько
изменится значение целевой функции в
случае принудительного включения
единицы этой продукции в оптимальное
решение. Например, в отчете по устойчивости
для рассматриваемой задачи (см. рис.
2.1) нормированная стоимость для ковров
первого типа равна -7 тыс. руб./шт. Это
означает, что если мы,
несмотря на оптимальное решение (0; 30;
10; 0), попробуем включить
в план выпуска один ковер первого типа,
то новый план
выпуска принесет нам доход 143 тыс. руб.,
что на 7 тыс. руб. меньше,
чем прежнее оптимальное решение. -
Коэффициенты
целевой функции. -
Предельные
значения приращения целевых коэффициентов
Δсj,
при которых
сохраняется первоначальное оптимальное
решение.
Например, допустимое
увеличение цены на ковер первого типа
равно
7 тыс. руб./шт., а допустимое уменьшение
— практически не
ограничено.
Это означает, что если цена ковра
первого типа возрастет более чем на 7
тыс.
руб./шт.,
то
оптимальное
решение изменится: станет целесообразным
выпускать
ковры первого типа.
А
если их цена будет снижаться вплоть до
нуля, то оптимальное
решение (0; 30; 10; 0) останется прежним.
Во второй части
Отчета по устойчивости содержится
информация, относящаяся к ограничениям:
-
Величина
использованных ресурсов в колонке
Результирующее значение. -
Предельные значения
приращения ресурсов Δbi.
В графе Допустимое
уменьшение (увеличение) показано, на
сколько можно уменьшить (увеличить)
ресурс, сохранив при этом оптимальное
решение.
Рассмотрим анализ
дефицитных
ресурсов.
Анализируя
отчет по результатам, мы установили,
что существуют причины
(ограничения), не позволяющие фабрике
выпускать больше ковров, чем в оптимальном
решении, и получать более высокий доход.
В рассматриваемой задаче такими
ограничениями
являются дефицитные ресурсы «труд» и
«оборудование». Поскольку
знак ограничений этих запасов имеет
вид ≤, то возникает вопрос, на сколько
максимально должен возрасти запас этих
ресурсов, чтобы обеспечить увеличение
выпуска продукции. Ответ дает графа
«Допустимое увеличение». Ресурс «труд»
имеет смысл увеличить максимум на 150
чел.- дней, а ресурс «оборудование» — на
30 станко –часов.
• Ценность
дополнительной единицы ресурса (теневые
цены) рассчитываются только для дефицитных
ресурсов.
2. Анализ оптимального решения исходной задачи с помощью двойственных оценок
Анализ
использования ресурсов в оптимальном
плане
выполняется
с помощью следствия второй теоремы
двойственности:
если Yi
> 0, то
,
i=1,…,m;
если
,
то
Yi
= 0,
i=1,…,m.
Ресурсы
«труд» и «оборудование» имеют отличные
от нуля оценки 4/3 и 1/3 — эти ресурсы
полностью используются в оптимальном
плане и являются дефицитными, т.е.
сдерживающими рост целевой функции.
Правые части этих ограничений равны
левым
частям:
7Х1
+ 2Х2
+ 2Х3
+ 6Х4
≤ 80,
2Х1
+ 4Х2
+ Х3
+ 8Х4
≤ 130,
7
∙ 0 + 2 ∙ 30 + 2 ∙ 10 + 6 ∙ 0 = 80
= 80,
2
∙ 0 + 4 ∙ 30 + 1 ∙ 10 + 8 ∙ 0 = 130
= 130.
Ресурс
«сырье» используется не полностью (280
< 480), поэтому имеет нулевую двойственную
оценку (Y2
= 0).
5Х1
+ 8Х2
+ 4Х3
+ 3Х4
≤ 480,
5
∙ 0 + 8 ∙ 30 + 4 ∙ 10 + 3 ∙ 0 = 280
< 480.
Этот
ресурс не влияет на план выпуска
продукции. Общая стоимость используемых
ресурсов при выпуске 30 ковров второго
вида и 10 ковров третьего вида составит
150 тыс. руб.:
F
= 80 ∙ Y1
+ 480 ∙ Y2
+ 130 ∙ Y3
=
80 ∙ 4/3 + 480 ∙ 0 + 130 ∙ 1/3 = 150 тыс. руб.
Нулевая
оценка ресурса «сырье» свидетельствует
о его недефицитности. Недефицитность
ресурса возникает не из-за его
неограниченных запасов (в задаче они
составляют 480 кг), а из-за невозможности
его полного использования в оптимальном
плане. Так как суммарный расход
недефицитного ресурса меньше его общего
количества, то план производства им не
лимитируется. Данный ресурс не препятствует
и дальше максимизировать целевую
функцию F(X).
Замечание.
Ценность различных видов ресурсов
нельзя отождествлять с действительными
ценами, по которым осуществляется его
закупка. В данном случае речь идет о
некоторой мере, имеющей экономическую
природу, которая характеризует ценность
ресурса только относительно полученного
оптимального решения.
Анализ
эффективности отдельных изделий
выполняется на основе соотношений
следствия
второй теоремы двойственности:
если Хj
> 0, то
,
j=1,…,n;
если
,
то
Хj
= 0,
j=1,…,n.
Поясним
равенство нулю Х1
и Х4.
Если изделие вошло в оптимальный
план (Xj
> 0), то в двойственных оценках оно не
убыточно, т.е. стоимость ресурсов,
затраченных на производство единицы
изделия, равна его цене. Такие изделия
эффективны,
выгодны с точки зрения принятого критерия
оптимальности. В рассматриваемой задаче
— это ковры второго и третьего видов.
Если
стоимость ресурсов, затраченных на
производство одного изделия, больше
его цены, то это изделие не войдет в
оптимальный план из-за его убыточности.
В рассматриваемой задаче в план выпуска
не вошли ковры первого и четвертого
видов, потому что затраты по ним превышают
цену на 7 (10 — 3 = 7) тыс. руб. и 9,666 (10,666 — 1
=9,666) тыс. руб. соответственно. Этот факт
можно подтвердить, подставив в ограничения
двойственной задачи оптимальные значения
вектора Y:
7∙4/3
+ 5∙0 + 2∙1/3 = 30/3 = 10
> 3,
2∙4/3
+ 8∙0 + 4∙1/3 = 12/3 = 4
= 4,
2∙4/3
+ 4∙0+1∙1/3 = 9/3 = 3
= 3,
6∙4/3
+ 3∙0 + 8∙1/3 = 32/3 = 10,666
> 1.
Разницу
между правыми и левыми частями ограничений
двойственной задачи можно найти в
Отчете по устойчивости в столбце
Нормируемая
стоимость.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Лабораторная работа №2 Решение двойственных задач линейного программирования с использованием microsoft excel
- 1. Порядок выполнения лабораторной работы
- Инструкция по использованию microsoft excel при решении двойственных задач линейного программирования
- Решение двойственной задачи с помощью надстройки Excel Поиск решения
- Решение оптимизационной задачи линейного программирования в Excel
- Решение оптимизационных задач средствами EXCEL (стр. 3 )
Лабораторная работа №2 Решение двойственных задач линейного программирования с использованием microsoft excel
Целью работы является приобретение навыков построения математических моделей двойственных задач линейного программирования и их решения в среде Microsoft Excel.
1. Порядок выполнения лабораторной работы
Для выполнения лабораторной работы необходимо:
повторить теоретический материал, относящийся к данному занятию;
по номеру своего варианта выбрать условие задачи (см. лаб. раб. №1) и построить математическую модель двойственной задачи;
решить двойственную задачу линейного программирования с помощью надстройки Поиск решений в среде Excel (см. п.2);
после выполнения всех пунктов задания необходимо защитить отчет по работе.
Отчет по лабораторной работе должен занимать 5-7 страниц и содержать:
постановку экономической задачи (исходные данные варианта);
экономико-математическую модель с необходимыми комментариями по ее элементам с указанием всех единиц измерения;
протокол решения задачи, куда должны входить:
а) фрагмент исходного рабочего листа Excel;
б) диалоговое окно Поиск решения;
в) отчет по устойчивости и результаты его анализа;
г) предложения (рекомендации) лицу, ответственному за принятие решений, по оптимальному управленческому поведению.
Отчет оформляется в установленные преподавателем сроки.
Инструкция по использованию microsoft excel при решении двойственных задач линейного программирования
Рассмотрим в качестве примера решение средствами Microsoft Excel двойственной задачи к задаче о коврах:
В распоряжении фабрики имеется определенное количество ресурсов: рабочая сила (труд), сырье и оборудование. Фабрика может выпускать ковры четырех видов. Данные о запасах ресурсов, количестве единиц каждого ресурса, необходимых для производства одного ковра каждого вида, и доходах, получаемых предприятием от единицы каждого вида ковров, приведены в таблице:
Источник
Решение двойственной задачи с помощью надстройки Excel Поиск решения
Лабораторная работа №2
Решение двойственных задач линейного программирования с использованием MICROSOFT EXCEL
Целью работы является приобретение навыков построения математических моделей двойственных задач линейного программирования и их решения в среде Microsoft Excel.
Порядок выполнения лабораторной работы
Для выполнения лабораторной работы необходимо:
1) повторить теоретический материал, относящийся к данному занятию;
2) по номеру своего варианта выбрать условие задачи (см. лаб. раб. №1) и построить математическую модель двойственной задачи;
3) решить двойственную задачу линейного программирования с помощью надстройки Поиск решений в среде Excel (см. п.2);
4) после выполнения всех пунктов задания необходимо защитить отчет по работе.
Отчет по лабораторной работе должен занимать 5-7 страниц и содержать:
• постановку экономической задачи (исходные данные варианта);
• экономико-математическую модель с необходимыми комментариями по ее элементам с указанием всех единиц измерения;
• протокол решения задачи, куда должны входить:
а) фрагмент исходного рабочего листа Excel;
б) диалоговое окно Поиск решения;
в) отчет по устойчивости и результаты его анализа c ответами на вопросы:
· Какие ресурсы в решенной задаче являются дефицитными?
· На сколько максимально можно увеличить запасы дефицитных ресурсов, сохранив при этом оптимальное решение?
· Как изменится целевая функция задачи, если один из дефицитных ресурсов максимально увеличить?
· Какие изделия являются эффективными в решаемой задаче? Показать с помощью теневых цен.
г) предложения (рекомендации) лицу, ответственному за принятие решений, по оптимальному управленческому поведению.
Отчет оформляется в установленные преподавателем сроки.
2. Инструкция по использованию
MICROSOFT EXCEL при решении двойственных задач линейного программирования
Рассмотрим в качестве примера решение средствами Microsoft Excel двойственной задачи к задаче о коврах:
В распоряжении фабрики имеется определенное количество ресурсов: рабочая сила (труд), сырье и оборудование. Фабрика может выпускать ковры четырех видов. Данные о запасах ресурсов, количестве единиц каждого ресурса, необходимых для производства одного ковра каждого вида, и доходах, получаемых предприятием от единицы каждого вида ковров, приведены в таблице:
| Ресурсы | Запасы ресурсов | Нормы расходов ресурсов на единицу изделия | |
| Ковер Тип 1 | Ковер Тип 2 | Ковер Тип 3 | Ковер Тип 4 |
| Труд, чел.- дн. | |||
| Сырье, кг | |||
| Оборудование, станко — час | |||
| Цена ед. изделия, тыс. руб. |
Требуется найти такой план выпуска продукции, при котором стоимость выпущенной продукции будет максимальной.
Экономико-математическая модель двойственной задачи имеет вид:
где y1 – теневая цена ресурса «труд»;
y2 — теневая цена ресурса «сырье»;
y3 — теневая цена ресурса «оборудование».
Решение двойственной задачи с помощью надстройки Excel Поиск решения
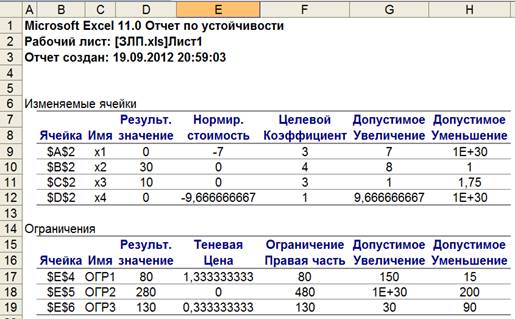
Решение двойственной задачи можно найти в Отчете по устойчивости решения исходной задачи (рис. 2.1).
Рис. 2.1. Содержание отчета по устойчивости
Отчет по устойчивости содержит информацию, относящуюся к переменным:
• Результат решения задачи.
• «Нормированная стоимость» показывает, на сколько изменится значение целевой функции в случае принудительного включения единицы этой продукции в оптимальное решение. Например, в отчете по устойчивости для рассматриваемой задачи (см. рис. 2.1) нормированная стоимость для ковров первого типа равна -7 тыс. руб./шт. Это означает, что если мы, несмотря на оптимальное решение (0; 30; 10; 0), попробуем включить в план выпуска один ковер первого типа, то новый план выпуска принесет нам доход 143 тыс. руб., что на 7 тыс. руб. меньше, чем прежнее оптимальное решение.
• Коэффициенты целевой функции.
• Предельные значения приращения целевых коэффициентов Δсj, при которых сохраняется первоначальное оптимальное решение. Например, допустимое увеличение цены на ковер первого типа равно 7 тыс. руб./шт., а допустимое уменьшение — практически не ограничено. Это означает, что если цена ковра первого типа возрастет более чем на 7 тыс. руб./шт ., то оптимальное решение изменится: станет целесообразным выпускать ковры первого типа.А если их цена будет снижаться вплоть до нуля, то оптимальное решение (0; 30; 10; 0) останется прежним.
Во второй части Отчета по устойчивости содержится информация, относящаяся к ограничениям:
• Величина использованных ресурсов в колонке Результирующее значение.
• Предельные значения приращения ресурсов Δbi. В графе Допустимое уменьшение (увеличение) показано, на сколько можно уменьшить (увеличить) ресурс, сохранив при этом оптимальное решение.
Рассмотрим анализ дефицитных ресурсов. Анализируя отчет по результатам, мы установили, что существуют причины (ограничения), не позволяющие фабрике выпускать больше ковров, чем в оптимальном решении, и получать более высокий доход. В рассматриваемой задаче такими ограничениями являются дефицитные ресурсы «труд» и «оборудование». Поскольку знак ограничений этих запасов имеет вид ≤, то возникает вопрос, на сколько максимально должен возрасти запас этих ресурсов, чтобы обеспечить увеличение выпуска продукции. Ответ дает графа «Допустимое увеличение». Ресурс «труд» имеет смысл увеличить максимум на 150 чел.- дней, а ресурс «оборудование» — на 30 станко –часов.
• Ценность дополнительной единицы ресурса (теневые цены) рассчитываются только для дефицитных ресурсов.
Источник
Решение оптимизационной задачи линейного программирования в Excel
Пусть предприятие (например, мебельная фабрика) производит столы и стулья. Расход ресурсов на их производство и прибыль от их реализации представлены ниже:
Расход древесины на изделие, м 3
Прибыль от реализации
единицы изделия, руб.
Кроме того, на производство 80 столов заключен контракт с муниципалитетом, который, безусловно, должен быть выполнен. Необходимо найти такую оптимальную производственную программу, чтобы прибыль от реализации продукции была максимальной.
Тогда система ограничений и целевая функция запишутся следующим образом:
1 
x1 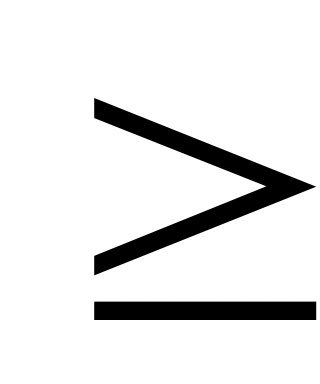
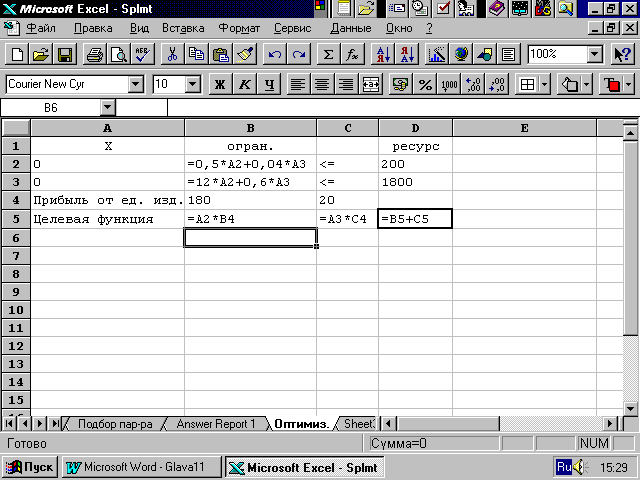
Для решения задачи в Excel запишем ее виде, представленном на рис. 3.4.
Рис. 3.4. Запись исходных данных для решения задачи линейной оптимизации
Для решения задачи вызовем меню Сервис-Поиск решения (Tools-Solver).
В открывшемся диалоговом окне Поиск решения (рис. 3.5.) укажем:
адрес целевой ячейки (в нашем примере D5);
Источник
Решение оптимизационных задач средствами EXCEL (стр. 3 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
1. Сформулируем экономико — математическую модель задачи.
Обозначим через Х1, Х2, Х3, Х4 количество ковров каждого типа.
Целевая функция — это выражение, которое необходимо максимизировать f(x) = 3Х1 +4Х2 +3Х3 +Х4
Ограничения по ресурсам
7Х1 +2Х2 +2Х3 +6Х4 
5Х1 +8Х2 +4Х3 +3Х4
2Х1 +4Х2 +Х3 +8Х4
Х1, Х2, Х3, Х4
1. Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки).
Обозначьте через Х1, Х2, Хз, Х4 количество ковров каждого типа. В нашей задаче оптимальные значения вектора Х =(Х1, Х2, Хз, Х4) будут помещены в ячейках ВЗ:ЕЗ, оптимальное значение целевой функции в ячейке F4.
2. Ввести исходные данные.
)Введем исходные данные в созданную форму. В результате получим (Рисунок 14):

3 Введем зависимость для целевой функции
• Курсор на кнопку Мастер функций.
На экране диалоговое окно Мастер функций шаг 1 из 2.
• Курсор в окно Категория на категорию Математические.
Рисунок 15. Вводится функция для вычисления целевой функции.
• Курсор в окно Функции на СУММПРОИЗВ.
• В массив 1 ввести[3] В$3:E$3.
• В массив 2 ввести В4:E4.
• Готово. На экране: в F4 введена функция, как показано на Рисунке 15.
4. Введем зависимость для левых частей ограничений:
• Вставить из буфера.
• Вставить из буфера.
• Вставить из буфера.
На этом ввод зависимостей закончен.
Запуск Поиска решения.
6) Назначение целевой функции (установить целевую ячейку).
¨ Курсор в поле Установить целевую ячейку.
¨ Ввести адрес $F$4.
¨ Ввести направление целевой функции: Максимальному значению.
Ввести адреса искомых переменных:
¨ Курсор в поле Изменяя ячейки.
¨ Ввести адреса В$3:E$3.
5. Ввод ограничений.
Курсор в поле Добавить. Появится диалоговое окно Добавление ограничения (Рисунок 16.).
Рисунок 16. Ввод правых и левых частей ограничений.
· В окне Ссылка на ячейку ввести $F$7.
· Ввести знак ограничение £..
· Курсор в правое окно.
· Добавить. На экране опять диалоговое окно Добавление ограничения. Ввести остальные ограничения.
· После ввода последнего ограничения ввести ОК.
На экране появится диалоговое окно Поиск решения с введенными условиями (Рисунок 17).
Рисунок 17. Введены все условия для решения задачи.

§ Открыть окно Параметры поиска решения.
§ Установить флажок Линейная модель, что обеспечивает применение симплекс-метода.
§ Установить флажок Неотрицательные значения.
§ ОК (На экране диалоговое окно поиска решения).
§ Выполнить (На экране диалоговое окно результаты поиска решения – Рисунок 19.).
Рисунок 18. Ввод параметров.
Рисунок 19. Решение найдено.
Полученное решение означает, что максимальный доход 150 тыс. руб. фабрика может получить при выпуске 30 ковров второго вида и 10 ковров третьего вида. При этом ресурсы труд и оборудование будут использованы полностью, а из 480 кг пряжи (ресурс сырье) будет использовано 280 кг.
Создание отчета по результатам поиска решения
Excel позволяет представить результаты поиска решения в форме отчёта. Существует три типа таких отчетов:
§ Результаты (Answer). В отчет включаются исходные и конечные значения целевой и влияющих ячеек, дополнительные сведения об ограничениях
§ Устойчивость (Sensitivity). Отчет, содержащий сведения о чувствительности решения к малым изменениям в изменяемых ячейках иди в формулах ограничений.
§ Пределы (Limits). Помимо исходных и конечных значений изменяемых и целевой ячеек в отчет включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.
1. Отчет по результатам.
Отчет по результатам
Целевая ячейка (Максимум)
труд левая часть
$F$7 0), то в двойственных оценках оно не убыточно, то есть, стоимость ресурсов, затраченных на производство единицы изделия равна его цене. Такие изделия эффективны, выгодны с точки зрения принятого критерия оптимальности. В нашей задаче это ковры второго и третьего видов.
Если стоимость ресурсов, затраченных на производство одного изделия больше его цены, то это изделие не войдет в оптимальный план из-за его убыточности. В нашей задаче в план выпуска не вошли ковры первого и четвертого видов, потому что затраты по ним превышают цену на 7 (10-3) тыс. руб. и 9.тыс. руб. соответственно. Это можно подтвердить, подставив в ограничения двойственной задачи оптимальные значения вектора Y.
2 ´4/3 + 4´0+ 1´1/3= 9/3= 3= 3
Разницу между правыми и левыми частями ограничений двойственной задачи можно найти в Отчете по устойчивости в столбце Нормируемая стоимость.
2) Анализ влияния изменения правых частей ограничений на значения целевой функции (Чувствительность решения к изменению запасов сырья).
Предположим, что запас сырья ресурса «труд» изменился на 12 единиц, т. е. теперь он составляет 80 + 12 = 92 единиц. Из теоремы об оценках, известно, что колебание величины bi приводит к увеличению или уменьшению f(X). Оно определяется величиной yi в случае, когда при изменении величин bi значения переменных yi в оптимальном плане соответствующей двойственной задачи остаются неизменными. В нашей задаче увеличение запасов ресурса «труд» приведет к увеличению значения целевой функции на 16 тыс. руб.(Df(x)= D b1´ y1 =12´4/3 = 16). Для двойственных оценок оптимального плана весьма существенное значение имеет их предельный характер. Точной мерой влияния ограничений на функционал оценки являются лишь при малом приращении ограничения. Известно, что оценки не меняют своей величины, если не меняется набор векторов, входящих в базис оптимального плана, тогда как интенсивность этих векторов (значения неизвестных) в плане могут меняться.
Источник
Решим данную задачу графическим методом в табличном редакторе Microsoft Excel (рис. 1). Для построения ОДР, и линий уровня воспользуемся Мастером диаграмм
. ОДР представляет собой многоугольник с вершинами в точках: (0;0), (0;6), (2;5), (4;3), (5;0).
При перемещении линии уровня в направлении вектора получаем оптимальное решение в точке с координатами (2;5).
Аналогичным образом можно решить данную задачу графическим методом в табличном редакторе OpenOffice.org Calc воспользовавшись пунктом меню Диаграмма
.
Решение ЗЛП в Microsoft Excel и OpenOffice.org Calc с помощью встроенной функции Поиск решения
В табличном процессоре Microsoft Excel существует встроенная функция Поиск решения
, с помощью которой можно решить задачу линейного программирования. Если данный модуль установлен, его можно запустить выбрав команду Сервис/Поиск решения
(рис. 2). На экране появится диалоговое окно Поиск решения
(рис. 3).

Р и с. 2. Р и с. 3.
Если такого пункта в меню Сервис
не оказалось, следует загрузить соответствующую программу-надстройку. Для этого выберите команду Сервис/Надстройки
(рис. 4) и в диалоговом окне Надстройки
установите флажок в строке Поиск решения
(рис. 5).
Разберем решение ЗЛП с помощью функции Поиск решения
на примере задачи 1.
1. Создадим таблицу для ввода исходных данных: переменных, целевой функции, ограничений.
2. Введем начальные нулевые значения для и .
3. Зададим целевую функцию в ячейке D41 и ограничения в ячейках Е39, Е40 и E41 (рис. 6).
Р и с. 4. Р и с. 5.
4. Выберем команду Сервис/Поиск решения
, в открывшемся окне Поиск решения
установим целевую ячейку D41, зададим условие отыскания максимального значения (рис. 7).
5. В поле Изменяя ячейки
установим ссылку на ячейки С40 и С41, которые будут изменены (можно ввести адреса или имена ячеек с клавиатуры или указать диапазон ячеек на рабочем листе с помощью мыши). При щелчке на кнопке Предположить
автоматически выделяются ячейки, на которые есть прямая или косвенная ссылка в формуле целевой ячейки (рис. 7).
6. Определим ограничения, для этого щелчком по кнопке Добавить
откроем диалоговое окно Добавление ограничения
. Введем ограничения для ячеек E39, E40, E41. Ограничения можно задать как для изменяемых ячеек, так и для целевой ячейки, а также для других ячеек, прямо или косвенно присутствующих в модели (рис. 8, 9).
Р и с. 8. Р и с. 9.
7. Щелчком на кнопке Параметры
откроем диалоговое окно Параметры поиска решения
. В данном окне выберем линейную модель и неотрицательные значения (неотрицательные значения для ячеек С40 и С41 можно было также установить при определении ограничений). Подробнее узнать о задаваемых параметрах можно щелкнув на кнопке Справка
(рис. 10).
8. После того как все параметры и ограничения заданы, запускаем поиск решения, щелкнув на кнопке Выполнить
(рис. 9). По мере того как идет поиск, отдельные его шаги отражаются в строке состояния. Когда поиск будет закончен, в таблицу будут внесены новые значения и на экране появится диалоговое окно Результаты поиска решения
, сообщающие о завершении операции (рис. 11).
Решение найдено. Все ограничения и условия оптимальности выполнены. Сохраним найденное решение. В этом случае таблица будет обновлена. В случае необходимости всегда можно будет восстановить исходные данные с помощью отчета. Для выбора типа отчета достаточно выделить название нужного отчета в списке Тип отчета
(или несколько названий, удерживая нажатой клавишу Сtrl
). Они будут вставлены на отдельных листах в рабочую книгу перед листом с исходными данными.
Предлагаемые отчеты содержат следующую информацию:
отчет Результаты
содержит сведения о начальных и текущих значениях целевой ячейки и изменяемых ячеек, а также о соответствии значений заданным ограничениям;
отчет Устойчивость
отражает найденный результат, а также нижние и верхние предельные значения для изменяемых ячеек;
отчет Пределы
показывает зависимость решений от изменения формулы или ограничений.
Если планируется использовать созданную модель в дальнейшем, найденное решение можно сохранить как сценарий. Для этого в диалоговом окне Результаты поиска решения
необходимо щелкнуть на кнопке Сохранить сценарий
.
Аналогично Поиск решения
осуществляется в OpenOffice.org Calc.
Задание
1. Решить задачи 2 и 3 графическим методом.
2. Решить задачи 2 и 3 в редакторе Microsoft Excel или OpenOffice.org Calc используя встроенную функцию Поиск решения
.
3. Сравнить и проанализировать полученные результаты.
4. Ответить на контрольные вопросы.
5. Оформить отчет.
Задача 2. Фармацевтическая фирма Ozark ежедневно производит не менее 800 фунтов некой пищевой добавки – смеси кукурузной и соевой муки, состав которой представлен в таблице 2.
Таблица 2
Диетологи требуют, чтобы в пищевой добавке было не менее 30% белка и не более 5% клетчатки. Фирма Ozark хочет определить рецептуру смеси минимальной стоимости с учетом требований диетологов.
Задача 3.
Предприятие, специализирующееся на производстве трикотажного полотна двух видов, использует для своего производства четыре вида сырья (шерстяную, хлопковую, вискозную, и акриловую нити), запасы которого на планируемый период составляют соответственно 80, 80, 260 и 410 бобин. В приведенной ниже таблице даны технологические коэффициенты, т.е. расход каждого вида сырья на производство одного метра каждого вида трикотажа.
Таблица 3
Прибыль от реализации 1м трикотажного полотна первого вида составляет 2 у.е., а трикотажного полотна второго вида 3 у.е. Необходимо определить оптимальный план выпуска трикотажного полотна первого и второго вида, чтобы обеспечить максимальную прибыль от их реализации.
Контрольные вопросы
1. Что означает составить математическую модель ЗЛП?
2. Из каких этапов состоит графический метод решения ЗЛП?
3. Какова геометрическая интерпретация решения системы линейных неравенств с двумя переменными?
4. Как определяется направление наискорейшего возрастания целевой функции?
5. Какое решение называется оптимальным решением ЗЛП?
6. В каком случае ЗЛП имеет множество решений?
7. При каких условиях ЗЛП может быть неразрешима?
8. Как установить модуль Поиск решения
?
9. Для чего предназначена кнопка Предположить
в окне Поиск решения
?
10. Какие типы отчетов можно получить при решении ЗЛП с помощью встроенной функции Поиск решения
?
Лабораторная работа №2
Симплексный метод. Задача определения оптимального плана выпуска продукции. Использование встроенных функций редакторов Microsoft Excel и OpenOffice.org Calc для построения математической модели и решения ЗЛП.
Цель лабораторного занятия:
Приобретение навыков решения ЗЛП симплекс-методом. Освоение приемов записи математической модели ЗЛП с большим количеством неизвестных в табличных редакторах Microsoft Excel и OpenOffice.org Calc с помощью встроенной функций СУММПРОИЗВ. Приобретение навыков решения ЗЛП с большим количеством неизвестных с помощью функции Поиск решения
.
Задачи лабораторного занятия:
1. Освоение симплекс-метода решения ЗЛП.
2. Построение математической модели задачи в табличных редакторах Microsoft Excel и OpenOffice.org Calc с помощью встроенной функций СУММПРОИЗВ.
3. Нахождение максимума (минимума) целевой функции с помощью команды Поиск решения
.
4. Анализ полученных результатов.
5. Оформление отчета.
1. Краткие теоретические сведения.
2. Решение ЗЛП симплекс методом без использования табличных редакторов.
3. Решение ЗЛП на определение оптимального плана выпуска продукции в Microsoft Excel и OpenOffice.org Calc с помощью встроенной функции Поиск решения
.
4. Задание.
5. Контрольные вопросы.
Краткие теоретические сведения
В основу симплекс-метода (симплексного метода) легла идея последовательного улучшения решения.
Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений (называемой первоначальной) к соседней, в которой линейная целевая функция принимает лучшее или, по крайней мере, не худшее значение. Этот процесс осуществляется до тех пор, пока не будет найдено оптимальное решение – вершина, где достигается оптимальное значение целевой функции (если задача имеет конечный оптимум).
Реализация симплекс-метода предусматривает содержание трех основных элементов:
1. Определение какого-либо первоначального допустимого базисного решения задачи (базисное решение называется допустимым, если значения, входящих в него переменных неотрицательны);
2. Правила перехода к лучшему (точнее, не худшему) решению;
3. Критерий проверки оптимальности найденного решения.
Для использования симплексного метода задача линейного программирования должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена в виде уравнений.
Практические расчеты при решении прикладных задач симплексным методом выполняются в настоящее время с помощью компьютерных программ, таких как табличный процессор Microsoft Excel, пакеты прикладных программ MathCAD, Math Lab и др. Однако, если расчеты осуществляются вручную, удобно использовать так называемые симплексные таблицы.
Рассмотрим пример задачи линейного программирования.
Требуется определить, в каком количестве надо выпустить продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье и финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены на рис. 1.
|
Ресурс |
Прод1 |
Прод2 |
Прод3 |
Прод4 |
Знак |
Наличие |
|
Прибыль |
||||||
|
Трудовые |
||||||
|
Сырье |
||||||
|
Финансы |
Рисунок 1.
Математическая модель задачи имеет вид:
где x j – количество выпускаемой продукции j-го типа; F – функция цели; в левых частях выражений ограничений указаны величины потребного ресурса
, а правые части показывают количество имеющегося ресурса
.
Ввод условий задачи
Для решения задачи с помощью Excel следует создать форму для ввода исходных данных и ввести их. Форма ввода показана на рис. 2.
В ячейку F6 введено выражение целевой функции как суммы произведений значений прибыли от выпуска единицы продукции каждого типа на количество выпускаемой продукции соответствующего типа. Для наглядности на рис. 3 представлена форма ввода исходных данных в режиме вывода формул.
В ячейки F8:F10 введены левые части ограничений для ресурсов каждого вида.
Рисунок 2.
Рисунок 3.
Решение задачи линейного программирования
Для решения задач линейного программирования в Excel используется мощный инструмент, называемый Поиск решения
.
Обращение к Поиску решения осуществляется из меню Сервис
, на экран выводится диалоговое окно Поиска решения (рис. 4).
Рисунок 4.
Ввод условий задачи для поиска ее решения состоит из следующих шагов:
1 Назначить целевую функцию, для чего установить курсор в поле Установить целевую ячейку
окна Поиск решения и щелкнуть в ячейке F6 в форме ввода;
2 Включить переключатель значения целевой функции, т.е. указать ее Равной Максимальному значению
;
3 Ввести адреса изменяемых переменных (x j): для этого установить курсор в поле Изменяя ячейки
окна Поиск решения, а затем выделить диапазон ячеек B3:E3 в форме ввода;
4 Нажать кнопку Добавить
окна Поиск решения для ввода ограничений задачи линейного программирования; на экран выводится окно Добавление ограничения
(рис. 5)
:
Ввести граничные условия для переменных x j (x j ³0), для этого в поле Ссылка на ячейку
указать ячейку В3, соответствующую х 1 , выбрать из списка нужный знак (³), в поле Ограничение
указать ячейку формы ввода, в которой хранится соответствующее значение граничного условия, (ячейка В4), нажать кнопку Добавить
; повторить описанные действия для переменных х 2 , х 3 и х 4 ;
Ввести ограничения для каждого вида ресурса, для этого в поле Ссылка на ячейку
окна Добавление ограничения
указать ячейку F9 формы ввода, в которой содержится выражение левой части ограничения, наложенного на трудовые ресурсы, в полях Ограничение
указать знак £ и адрес Н9 правой части ограничения, нажать кнопку Добавить
; аналогично ввести ограничения на остальные виды ресурсов;
После ввода последнего ограничения вместо Добавить
нажать ОК
и возвратиться в окно Поиск решения.
Рисунок 5.
Решение задачи линейного программирования начинается с установки параметров поиска:
В окне Поиск решения
нажать кнопку Параметры
, на экран выводится окно Параметры поиска решения
(рис. 6);
Установить флажок Линейная модель,
что обеспечивает применение симплекс-метода;
Указать предельное число итераций (по умолчанию – 100, что подходит для решения большинства задач);
Установить флажок
, если необходимо просмотреть все этапы поиска оптимального решения;
Нажать ОК
, возврат в окно Поиск решения
.
Рисунок 6.
Для решения задачи нажать кнопку Выполнить
в окне Поиск решения
, на экране – окно Результаты поиска решения
(рис. 7), в котором содержится сообщение Решение найдено. Все ограничения и условия оптимальности выполнены.
Если условия задачи несовместны, то выводится сообщение Поиск не может найти подходящего решения
. Если целевая функция не ограничена, то появляется сообщение Значения целевой ячейки не сходятся
.
Рисунок 7.
Для рассматриваемого примера решение найдено и результат оптимального решения задачи выводится в форме ввода: значение целевой функции, соответствующее максимальной прибыли и равное 1320, указывается в ячейке F6 формы ввода,
оптимальный план выпуска продукции х 1 =10, х 2 =0, х 3 =6, х 4 =0 указывается в ячейках В3:С3 формы ввода (рис. 8).
Количество использованных для выпуска продукции ресурсов выводится в ячейки F9:F11: трудовых – 16, сырья – 84, финансов – 100.
Рисунок 8.
Если при установке параметров в окне Параметры поиска решения
(рис. 6) был установлен флажок Показывать результаты итераций
, то будут показаны последовательно все шаги поиска. На экран будет выводиться окно
(рис. 9). При этом текущие значения переменных и функции цели будут показаны в форме ввода. Так, результаты первой итерации поиска решения исходной задачи представлены в форме ввода на рисунке 10 .
Рисунок 9.
Рисунок 10.
Чтобы продолжить поиск решения, следует нажимать кнопку Продолжить
в окне Текущее состояние поиска решения
.
Анализ оптимального решения
Прежде чем, перейти к анализу результатов решения, представим исходную задачу в форме
введя дополнительные переменные у i , представляющие собой величины неиспользованных ресурсов.
Составим для исходной задачи двойственную задачу и введем дополнительные двойственные переменные v i .
Анализ результатов поиска решения позволит увязать их с переменными исходной и двойственной задач.
С помощью окна Результаты поиска решения
можно вызвать отчеты трех типов, позволяющие анализировать найденное оптимальное решение:
Результаты,
Устойчивость,
Пределы.
Для вызова отчета в поле Тип отчета
выделить название нужного типа и нажать ОК
.
1 Отчет по результатам
(рис. 11) состоит из трех таблиц:
Таблица 1 содержит сведения о целевой функции; в столбце Исходно
указывается значение целевой функции до начала вычислений;
Таблица 2 содержит значения искомых переменных x j , полученных в результате решения задачи (оптимальный план выпуска продукции);
Таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
Для Ограничений
в графе Формула
приведены зависимости, которые были введены при задании ограничений в окне Поиск решения
; в графе Значение
указаны величины использованного ресурса; в графе Разница
показано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе Состояние
выводится сообщение связанное
; при неполном использовании ресурса в этой графе указывается не связан.
Для Граничных условий
приводятся аналогичные величины с той лишь разницей, что вместо неиспользованного ресурса показана разность между значением переменной x j в найденном оптимальном решении и заданным для нее граничным условием (x j ³0).
Именно в графе Разница
можно увидеть значения дополнительных переменных y i исходной задачи в формулировке (2). Здесь у 1 =у 3 =0, т.е. величины неиспользованных трудовых и финансовых ресурсов равны нулю. Эти ресурсы используются полностью. Вместе с тем, величина неиспользованных ресурсов для сырья у 2 =26, значит, имеются излишки сырья.
Рисунок 11.
2 Отчет по устойчивости
(рис. 12)состоит из двух таблиц.
В таблице 1 приводятся следующие значения:
Результат решения задачи (оптимальный план выпуска);
— Нормир. стоимость
, т.е. величины, показывающие, насколько изменится целевая функция при принудительном включении единицы продукции соответствующего типа в оптимальный план;
Коэффициенты целевой функции;
Предельные значения приращения коэффициентов целевой функции, при которых сохраняется оптимальный план выпуска.
В таблице 2 содержатся аналогичные данные для ограничений:
Величины использованных ресурсов;
— Теневая цена
, показывающая, как изменится целевая функция при изменении величины соответствующего ресурса на единицу;
Допустимые значения приращений ресурсов, при которых сохраняется оптимальный план выпуска продукции.
Рисунок 12.
Отчет по устойчивости позволяет позволяет получить двойственные оценки.
Как известно, двойственные переменные z i показывают, как изменится целевая функция при изменении ресурса i-го типа на единицу. В отчете Excel двойственная оценка называется Теневой ценой
.
В нашем примере сырье не используется полностью и его ресурс у 2 =26. Очевидно, что увеличение количества сырья, например, до 111 не повлечет за собой увеличения целевой функции. Следовательно, для второго ограничения двойственная переменная z 2 =0. Таким образом, если по данному ресурсу есть резерв, то дополнительная переменная
будет больше нуля, а двойственная оценка
этого ограничения равна нулю.
В рассматриваемом примере трудовые ресурсы и финансы использовались полностью, поэтому их дополнительные переменные равны нулю (у 1 =у 3 =0). Если ресурс используется полностью, то его увеличение или уменьшение повлияет на объем выпускаемой продукции, и следовательно, на величину целевой функции. Двойственные оценки ограничений на трудовые и финансовые ресурсы отличны от нуля, т.е. z 1 =20, z 3 =10.
Значения двойственных оценок находим в Отчете по устойчивости
, в таблице 2, в графе Теневая цена
.
При увеличении (уменьшении) трудовых ресурсов на единицу целевая функция увеличится (уменьшится) на 20 единиц и будет равна
F=1320+20×1=1340 (при увеличении).
Аналогично, при увеличении объема финансов на единицу целевая функция будет
F=1320+10×1=1330.
Здесь же, в графах Допустимое увеличение
и Допустимое уменьшение
таблицы 2, показаны допустимые пределы изменения количества ресурсов j-го вида. Например, для при изменении приращения величины трудовых ресурсов в пределах от –6 до 3,55, как показано в таблице, структура оптимального решения сохраняется, т.е наибольшую прибыль обеспечивает выпуск Прод1 и Прод3, но в других количествах.
Дополнительные двойственные переменные также отражены в Отчете по устойчивости
в графе Нормир. стоимость
таблицы 1.
Если основные переменные не вошли в оптимальное решение, т.е. равны нулю (в примере х 2 =х 4 =0), то соответствующие им дополнительные переменные имеют положительные значения (v 2 =10, v 4 =20). Если же основные переменные вошли в оптимальное решение (х 1 =10, х 3 =6), то их дополнительные двойственные переменные равны нулю (v 1 =0, v 3 =0).
Эти величины показывают, насколько уменьшится (поэтому знак минус в значениях переменных v 2 и v 4) целевая функция при принудительном выпуске единицы данной продукции. Следовательно, если мы захотим принудительно выпустить единицу продукции вида Прод3, то целевая функция уменьшится на 10 единиц и будет равна 1320 -10×1 =1310.
Обозначим через Dс j изменение коэффициентов целевой функции в исходной модели (1). Эти коэффициенты определяют прибыль, получаемую при реализации единицы продукции j-го вида.
В графах Допустимое увеличение
и Допустимое Уменьшение
таблицы 1 Отчета по устойчивости
показаны пределы изменения Dс j , при которых сохраняется структура оптимального плана, т.е. будет выгодно по-прежнему выпускать продукцию вида Продj. Например, при изменении Dс 1 в пределах -12£ Dс 1 £ 40, как показано в отчете, по-прежнему будет выгодно выпускать продукцию вида Прод1. При этом значение целевой функции будет F=1320+x 1 ×Dс j =1320+10×Dс j .
3 Отчет по пределам
приведен на рис. 13. В нем показывается, в каких пределах могут изменяться значения x j , вошедшие в оптимальное решение, при сохранении структуры оптимального решения. Кроме этого, для каждого типа продукции приводятся значения целевой функции, получаемые при подстановке в оптимальное решение значения нижнего предела выпуска изделий соответствующего типа при неизменных значениях выпуска остальных типов. Например, если при оптимальном решении х 1 =10, х 2 =0, х 3 =6, х 4 =0 положить х 1 =0 (нижний предел) при неизменных х 2 , х 3 и х 4 , то значение целевой функции будет равно 60×0+70×0+120×6+130×0=720.
Цель работы:
изучение современных программных
средств решения задачи линейного
программирования; практическое решение
задач линейного программирования
графическим методом, симплекс-методом
и средствами программыMicrosoftExcel; программная реализация
симплекс-метода на языке программирования
высокого уровня.
1. Теоретическая часть
Для решения задач
линейного программирования в программе
Microsoft
Excel
имеется надстройка Поиск
решения
,
обращение
к которой производится из меню Сервис
.
Если команда
Поиск решения
отсутствует в меню Сервис
,
то требуется установить надстройку
«Поиск решения». Для этого в меню Сервис
выбирается команда Надстройки
,
которая открывает диалоговое окно,
показанное на рис. 1.
Покажем использование
надстройки
«Поиск решения» на примере решения
следующей задачи.
Постановка задачи
Предприятие
изготавливает и реализует три вида
продукции – P
1 ,
Р
2
и Р
3 .
Для производства продукции используются
три вида ресурсов – комплектующие
изделия, сырье и материалы. Запасы
ресурсов и их расход на изготовление
единицы продукции каждого вида приведены
в табл. 1.
Таблица 1
Прибыль от реализации
единицы продукции каждого вида составляет
240, 210 и 180 денежных единиц для P
1 ,
Р
2
и Р
3
соответственно.
Требуется определить
производственную программу предприятия
таким образом, чтобы прибыль от реализации
продукции была максимальной.
Математическая модель задачи
Обозначим переменными
x
1 ,
x
2
и x
3
искомые объемы производства продукции
видов P
1 ,
Р
2
и Р
2 ,
а через F
– прибыль предприятия. Тогда математическая
постановка представленной задачи
принимает следующий вид.
Определить значения
переменных x
1 ,
x
2
и x
3 ,
для которых достигается максимум целевой
функции
F
=
240 x
1
+ 210 х
2
+ 180 x
3
при ограничениях:
Целевая функция
описывает суммарную прибыль от реализации
произведенной продукции всех трех
видов. Ограничения (1), (2) и (3) учитывают
расход и запасы комплектующих изделий,
сырья и материалов соответственно.
Поскольку объемы производства продукции
не могут быть отрицательными, добавляются
условия
x
1
≥ 0; x
2
≥ 0; x
3
≥ 0.
Порядок оптимального решения задачи
Примерные действия,
необходимые для решения задачи линейного
программирования средствами программы
Excel,
представим в виде последовательности
шагов.
Шаг 1.
Исходные данные задачи записываются
на рабочем листе электронной таблицы.
Один из вариантов показан на рис. 2.
Замечание.
Если известно исходное допустимое
базисное решение, то можно несколько
ускорить процесс поиска оптимального
решения. Для этого начальные значения
некоторых или всех переменных могут
быть заданы вручную. В данном примере
для их хранения используются ячейки
$B$2,
$C$2
и $D$2.
Если допустимое базисное решение не
задано, то программа Excel
автоматически определяет начальные
значения переменных задачи.
Шаг 2.
В ячейку E3
вводится формула
СУММПРОИЗВ(В3:D3;
$B$2:$D$2)
для вычисления
текущего значения целевой функции,
которая находит сумму попарных
произведений ячеек (В3:D3)
с коэффициентами при переменных в
выражении целевой функции на ячейки
($B$2:$D$2)
с текущими значениями переменных.
Шаг 3.
Чтобы задать ограничения решаемой
задачи, в ячейки E5,
E6
и E7
копируется формула из ячейки E3.
После этого в указанных ячейках должны
быть получены формулы, представленные
в табл. 2.
Таблица
2
|
СУММПРОИЗВ(В5:D5; |
|
|
СУММПРОИЗВ(В6:D6; |
|
|
СУММПРОИЗВ(В7:D7; |
Шаг 4.
После создания таблицы с исходными
данными курсор устанавливается в ячейку
E3,
содержащую формулу для вычисления
целевой функции. Далее в меню Сервис
выбирается
команда Поиск
решения
,
которая открывает диалоговое окно,
приведенное на рис. 3.
В поле Установить
целевую ячейку
окна «Поиск решения», показанного на
рис. 3, должен
появиться адрес ячейки с формулой
целевой функции (в данном примере это
ячейка $E$3).
Затем в этом окне
(рис. 3) заполняются следующие поля этого
окна:
В поле Равной
переключатель вида экстремума целевой
функции устанавливается в положение
максимальное
значение
(или минимальное
значение
при
соответствующей постановке задачи);
В поле Изменяя
ячейки
указывается
диапазон ячеек со значениями переменных
задачи, выделяемый на рабочем листе
электронной таблицы (в примере это
ячейки $B$2:$D$2);
В поле Ограничения
задаются
ограничения исходной задачи. Для этого
курсор устанавливается в поле ввода
ограничений и нажимается кнопка Добавить
.
В результате
выводится диалоговое окно «Добавление
ограничения», показанное на рис. 4.
В этом окне в поле
Ссылка на
ячейку
вводится
адрес ячейки
с формулой соответствующего ограничения
(например, для ограничения (1) это будет
ячейка E5),
а в поле Ограничение
указывается
предельное значение, которое может
принимать выбранное ограничение (в
данном примере правая часть ограничения
(1) находится в ячейке G5).
Следует заметить,
что заполнение полей Ссылка
на ячейку
и Ограничение
в окне «Добавление
ограничения» можно выполнить выделением
соответствующих ячеек рабочего листа
электронной таблицы.
Затем выбирается
вид отношения, связывающего левую и
правую части ограничения, что показано
на рис. 5.
После нажатия
кнопки Добавить
в окне
«Добавление ограничения»
(или кнопки
ОК
для
ввода
последнего ограничения) данное ограничение
попадает в список ограничений решаемой
задачи. С помощью кнопок Удалить
и Изменить
можно удалять
выделенные в списке ограничения или
вносить в них исправления.
Замечание
.
В окне «Добавление
ограничения» можно указать, что все или
некоторые переменные должны принимать
только целые значения (рис. 5). Это
позволяет получать решения задач
целочисленного линейного программирования
(полностью или частично целочисленных).
Шаг 5.
После заполнения всех полей окна «Поиск
решения» нажимается кнопка Параметры
(рис. 3),
которая открывает диалоговое окно
«Параметры поиска решения», показанное
на рис. 6.
В этом окне требуется
установить флажки Линейная
модель
для решения
задачи линейного программирования и
Неотрицательные
значения
,
если такое
условие накладываются на все переменные
задачи.
Здесь (рис. 6) также
можно определить параметры процесса
решения: предельное время поиска решения,
максимальное количество итераций,
точность и т.п. Флажок Показывать
результаты
итераций
позволяет по шагам следить за поиском
решения. Флажок Автоматическое
масштабирование
включается
в том случае, когда разброс значений
переменных очень велик.
Шаг 6.
Задав необходимые параметры в окне
«Параметры
поиска решения»,
следует нажать на кнопку Выполнить
для поиска
решения задачи (рис. 3) в
окне «Поиск решения».
Если решение найдено, то на экран
выводится окно с соответствующим
сообщением (рис. 7).
Полученные
результаты отображаются на рабочем
листе электронной таблицы, как это
показано на рис. 8. В частности, значения
переменных — в ячейках $B$2:$D$2,
значение целевой функции – в ячейке
E3.
Таким образом,
получено оптимальное решение исходной
задачи в виде вектора

где


для которого значение целевой функцииF
максимально и составляет F
*
= 129825.
Результаты решения
задачи линейного программирования
также можно сохранить в виде отдельных
рабочих листов с именами Отчет
по результатам
,
Отчет
по устойчивости
и Отчет
по пределам
.
Для сохранения
результатов в виде отчетов необходимо
предварительно в поле Тип
отчета
выделить
требуемые типы отчетов (рис. 7). В этом
же окне можно отказаться от полученных
решений и восстановить исходные значения
переменных.
Отчет по результатам
для рассмотренной задачи показан
на рис. 9.
В данном отчете
представлены оптимальное решение задачи
линейного программирования и его
расположение в области допустимых
решений. В графах Результат
выводятся
оптимальные значения целевой функции
F
*
и переменных задачи

а также их значения для исходного
базисного решения, с которого начинался
поиск оптимального решения (графаИсходное
значение
).
Состояние
ограничений (графа Статус
)
характеризует расположение точки

показывает разности между значениями
левых и правых частей ограничений
(невязки). Для связанного ограничения
невязка равна нулю, что свидетельствует
о расположение точки

которая задается этим ограничением.
Если ограничение являются не связанным,
то оно не влияет на оптимальное решение.
Замечание
.
В экономической интерпретации связанные
ограничения соответствуют дефицитным
ресурсам. Для не связанных ограничений
графа Разница
показывает оставшиеся объемы
неиспользованных не дефицитных ресурсов.
В рассмотренной задаче ограничения (1)
и (3) соответствуют комплектующим изделиям
и материалам, которые являются дефицитными
ресурсами. Ограничение (2) является не
связанным, т.е. не влияет на оптимальный
план производства продукции по критерию
максимальной прибыли. Это означает, что
второй ресурс (сырье) не использован в
объеме 292,5 ед.
В
отчете по устойчивости (рис.
10)
приведены
границы устойчивости переменных задачи
(графы Допустимое
увеличение
и Допустимое
уменьшение
коэффициентов целевой функции), а также
границы устойчивости теневых цен (т.е.
переменных двойственной задачи), в
пределах которых оптимальное решение
не изменяется. Большие
значения пределов (1Е+30)
означают фактическое
отсутствие соответствующих границ,
т.е. переменная может изменяться до
бесконечности.
В графе Нормированная
стоимость
элемент во второй строке
(-150) показывает,
на сколько уменьшится значение функции,
если в решении переменную x
2
увеличить на единицу. С другой стороны,
при допустимом увеличении коэффициента
функции при неизвестной x
2
на 150 единиц значение этой переменной
не изменится, т.е. неизвестная x
2
будет равна нулю, а если выйти за пределы
допустимого увеличения (коэффициент
при x
2
увеличить более чем на 150), то неизвестная
x
2
в решении будет больше нуля.
В
отчете
по пределам
(рис. 11) показаны нижние и верхние пределы
возможного изменения переменных (в
пределах области допустимых решений)
и соответствующие значения целевой
функции (графа Целевой
результат
)
при этих изменениях. В частности, если
x
1
= 0, а x
2
и x
3
остаются без изменений, то F
= 2400
+ 2100
+ 180191,25
= 34425; при x
3
= 0 и неизменных x
1
и x
2
получим F
= 240397,5
+ 2100
+ 1800
= 95400.
Требуется определить, в каком количестве надо выпустить продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье и финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены на рис. 1.
|
Ресурс |
Прод1 |
Прод2 |
Прод3 |
Прод4 |
Знак |
Наличие |
|
Прибыль |
||||||
|
Трудовые |
||||||
|
Сырье |
||||||
|
Финансы |
Рисунок 1.
Математическая модель задачи имеет вид:
где x j – количество выпускаемой продукции j-го типа; F – функция цели; в левых частях выражений ограничений указаны величины потребного ресурса
, а правые части показывают количество имеющегося ресурса
.
Ввод условий задачи
Для решения задачи с помощью Excel следует создать форму для ввода исходных данных и ввести их. Форма ввода показана на рис. 2.
В ячейку F6 введено выражение целевой функции как суммы произведений значений прибыли от выпуска единицы продукции каждого типа на количество выпускаемой продукции соответствующего типа. Для наглядности на рис. 3 представлена форма ввода исходных данных в режиме вывода формул.
В ячейки F8:F10 введены левые части ограничений для ресурсов каждого вида.
Рисунок 2.
Рисунок 3.
Решение задачи линейного программирования
Для решения задач линейного программирования в Excel используется мощный инструмент, называемый Поиск решения
.
Обращение к Поиску решения осуществляется из меню Сервис
, на экран выводится диалоговое окно Поиска решения (рис. 4).
Рисунок 4.
Ввод условий задачи для поиска ее решения состоит из следующих шагов:
1 Назначить целевую функцию, для чего установить курсор в поле Установить целевую ячейку
окна Поиск решения и щелкнуть в ячейке F6 в форме ввода;
2 Включить переключатель значения целевой функции, т.е. указать ее Равной Максимальному значению
;
3 Ввести адреса изменяемых переменных (x j): для этого установить курсор в поле Изменяя ячейки
окна Поиск решения, а затем выделить диапазон ячеек B3:E3 в форме ввода;
4 Нажать кнопку Добавить
окна Поиск решения для ввода ограничений задачи линейного программирования; на экран выводится окно Добавление ограничения
(рис. 5)
:
Ввести граничные условия для переменных x j (x j ³0), для этого в поле Ссылка на ячейку
указать ячейку В3, соответствующую х 1 , выбрать из списка нужный знак (³), в поле Ограничение
указать ячейку формы ввода, в которой хранится соответствующее значение граничного условия, (ячейка В4), нажать кнопку Добавить
; повторить описанные действия для переменных х 2 , х 3 и х 4 ;
Ввести ограничения для каждого вида ресурса, для этого в поле Ссылка на ячейку
окна Добавление ограничения
указать ячейку F9 формы ввода, в которой содержится выражение левой части ограничения, наложенного на трудовые ресурсы, в полях Ограничение
указать знак £ и адрес Н9 правой части ограничения, нажать кнопку Добавить
; аналогично ввести ограничения на остальные виды ресурсов;
После ввода последнего ограничения вместо Добавить
нажать ОК
и возвратиться в окно Поиск решения.
Рисунок 5.
Решение задачи линейного программирования начинается с установки параметров поиска:
В окне Поиск решения
нажать кнопку Параметры
, на экран выводится окно Параметры поиска решения
(рис. 6);
Установить флажок Линейная модель,
что обеспечивает применение симплекс-метода;
Указать предельное число итераций (по умолчанию – 100, что подходит для решения большинства задач);
Установить флажок
, если необходимо просмотреть все этапы поиска оптимального решения;
Нажать ОК
, возврат в окно Поиск решения
.
Рисунок 6.
Для решения задачи нажать кнопку Выполнить
в окне Поиск решения
, на экране – окно Результаты поиска решения
(рис. 7), в котором содержится сообщение Решение найдено. Все ограничения и условия оптимальности выполнены.
Если условия задачи несовместны, то выводится сообщение Поиск не может найти подходящего решения
. Если целевая функция не ограничена, то появляется сообщение Значения целевой ячейки не сходятся
.
Рисунок 7.
Для рассматриваемого примера решение найдено и результат оптимального решения задачи выводится в форме ввода: значение целевой функции, соответствующее максимальной прибыли и равное 1320, указывается в ячейке F6 формы ввода,
оптимальный план выпуска продукции х 1 =10, х 2 =0, х 3 =6, х 4 =0 указывается в ячейках В3:С3 формы ввода (рис. 8).
Количество использованных для выпуска продукции ресурсов выводится в ячейки F9:F11: трудовых – 16, сырья – 84, финансов – 100.
Рисунок 8.
Если при установке параметров в окне Параметры поиска решения
(рис. 6) был установлен флажок Показывать результаты итераций
, то будут показаны последовательно все шаги поиска. На экран будет выводиться окно
(рис. 9). При этом текущие значения переменных и функции цели будут показаны в форме ввода. Так, результаты первой итерации поиска решения исходной задачи представлены в форме ввода на рисунке 10 .
Рисунок 9.
Рисунок 10.
Чтобы продолжить поиск решения, следует нажимать кнопку Продолжить
в окне Текущее состояние поиска решения
.
Анализ оптимального решения
Прежде чем, перейти к анализу результатов решения, представим исходную задачу в форме
введя дополнительные переменные у i , представляющие собой величины неиспользованных ресурсов.
Составим для исходной задачи двойственную задачу и введем дополнительные двойственные переменные v i .
Анализ результатов поиска решения позволит увязать их с переменными исходной и двойственной задач.
С помощью окна Результаты поиска решения
можно вызвать отчеты трех типов, позволяющие анализировать найденное оптимальное решение:
Результаты,
Устойчивость,
Пределы.
Для вызова отчета в поле Тип отчета
выделить название нужного типа и нажать ОК
.
1 Отчет по результатам
(рис. 11) состоит из трех таблиц:
Таблица 1 содержит сведения о целевой функции; в столбце Исходно
указывается значение целевой функции до начала вычислений;
Таблица 2 содержит значения искомых переменных x j , полученных в результате решения задачи (оптимальный план выпуска продукции);
Таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
Для Ограничений
в графе Формула
приведены зависимости, которые были введены при задании ограничений в окне Поиск решения
; в графе Значение
указаны величины использованного ресурса; в графе Разница
показано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе Состояние
выводится сообщение связанное
; при неполном использовании ресурса в этой графе указывается не связан.
Для Граничных условий
приводятся аналогичные величины с той лишь разницей, что вместо неиспользованного ресурса показана разность между значением переменной x j в найденном оптимальном решении и заданным для нее граничным условием (x j ³0).
Именно в графе Разница
можно увидеть значения дополнительных переменных y i исходной задачи в формулировке (2). Здесь у 1 =у 3 =0, т.е. величины неиспользованных трудовых и финансовых ресурсов равны нулю. Эти ресурсы используются полностью. Вместе с тем, величина неиспользованных ресурсов для сырья у 2 =26, значит, имеются излишки сырья.
Рисунок 11.
2 Отчет по устойчивости
(рис. 12)состоит из двух таблиц.
В таблице 1 приводятся следующие значения:
Результат решения задачи (оптимальный план выпуска);
— Нормир. стоимость
, т.е. величины, показывающие, насколько изменится целевая функция при принудительном включении единицы продукции соответствующего типа в оптимальный план;
Коэффициенты целевой функции;
Предельные значения приращения коэффициентов целевой функции, при которых сохраняется оптимальный план выпуска.
В таблице 2 содержатся аналогичные данные для ограничений:
Величины использованных ресурсов;
— Теневая цена
, показывающая, как изменится целевая функция при изменении величины соответствующего ресурса на единицу;
Допустимые значения приращений ресурсов, при которых сохраняется оптимальный план выпуска продукции.
Рисунок 12.
Отчет по устойчивости позволяет позволяет получить двойственные оценки.
Как известно, двойственные переменные z i показывают, как изменится целевая функция при изменении ресурса i-го типа на единицу. В отчете Excel двойственная оценка называется Теневой ценой
.
В нашем примере сырье не используется полностью и его ресурс у 2 =26. Очевидно, что увеличение количества сырья, например, до 111 не повлечет за собой увеличения целевой функции. Следовательно, для второго ограничения двойственная переменная z 2 =0. Таким образом, если по данному ресурсу есть резерв, то дополнительная переменная
будет больше нуля, а двойственная оценка
этого ограничения равна нулю.
В рассматриваемом примере трудовые ресурсы и финансы использовались полностью, поэтому их дополнительные переменные равны нулю (у 1 =у 3 =0). Если ресурс используется полностью, то его увеличение или уменьшение повлияет на объем выпускаемой продукции, и следовательно, на величину целевой функции. Двойственные оценки ограничений на трудовые и финансовые ресурсы отличны от нуля, т.е. z 1 =20, z 3 =10.
Значения двойственных оценок находим в Отчете по устойчивости
, в таблице 2, в графе Теневая цена
.
При увеличении (уменьшении) трудовых ресурсов на единицу целевая функция увеличится (уменьшится) на 20 единиц и будет равна
F=1320+20×1=1340 (при увеличении).
Аналогично, при увеличении объема финансов на единицу целевая функция будет
F=1320+10×1=1330.
Здесь же, в графах Допустимое увеличение
и Допустимое уменьшение
таблицы 2, показаны допустимые пределы изменения количества ресурсов j-го вида. Например, для при изменении приращения величины трудовых ресурсов в пределах от –6 до 3,55, как показано в таблице, структура оптимального решения сохраняется, т.е наибольшую прибыль обеспечивает выпуск Прод1 и Прод3, но в других количествах.
Дополнительные двойственные переменные также отражены в Отчете по устойчивости
в графе Нормир. стоимость
таблицы 1.
Если основные переменные не вошли в оптимальное решение, т.е. равны нулю (в примере х 2 =х 4 =0), то соответствующие им дополнительные переменные имеют положительные значения (v 2 =10, v 4 =20). Если же основные переменные вошли в оптимальное решение (х 1 =10, х 3 =6), то их дополнительные двойственные переменные равны нулю (v 1 =0, v 3 =0).
Эти величины показывают, насколько уменьшится (поэтому знак минус в значениях переменных v 2 и v 4) целевая функция при принудительном выпуске единицы данной продукции. Следовательно, если мы захотим принудительно выпустить единицу продукции вида Прод3, то целевая функция уменьшится на 10 единиц и будет равна 1320 -10×1 =1310.
Обозначим через Dс j изменение коэффициентов целевой функции в исходной модели (1). Эти коэффициенты определяют прибыль, получаемую при реализации единицы продукции j-го вида.
В графах Допустимое увеличение
и Допустимое Уменьшение
таблицы 1 Отчета по устойчивости
показаны пределы изменения Dс j , при которых сохраняется структура оптимального плана, т.е. будет выгодно по-прежнему выпускать продукцию вида Продj. Например, при изменении Dс 1 в пределах -12£ Dс 1 £ 40, как показано в отчете, по-прежнему будет выгодно выпускать продукцию вида Прод1. При этом значение целевой функции будет F=1320+x 1 ×Dс j =1320+10×Dс j .
3 Отчет по пределам
приведен на рис. 13. В нем показывается, в каких пределах могут изменяться значения x j , вошедшие в оптимальное решение, при сохранении структуры оптимального решения. Кроме этого, для каждого типа продукции приводятся значения целевой функции, получаемые при подстановке в оптимальное решение значения нижнего предела выпуска изделий соответствующего типа при неизменных значениях выпуска остальных типов. Например, если при оптимальном решении х 1 =10, х 2 =0, х 3 =6, х 4 =0 положить х 1 =0 (нижний предел) при неизменных х 2 , х 3 и х 4 , то значение целевой функции будет равно 60×0+70×0+120×6+130×0=720.
Линейное программирование является разделом, с которого начала развиваться дисциплина «математическое программирование». Термин «программирование» в названии дисциплины ничего общего с термином «программирование (т.е. составление программ) для ЭВМ» не имеет, так как дисциплина «линейное программирование» возникла еще до того времени, когда ЭВМ стали широко применяться при решении математических, инженерных, экономических и других задач. Термин «линейное программирование» возник в результате неточного перевода английского «linear programming». Одно из значений слова «programming» — составление планов, планирование. Следовательно, правильным переводом «linear programming» было бы не «линейное программирование», а «линейное планирование», что более точно отражает содержание дисциплины. Однако, термин линейное программирование, нелинейное программирование и т.д. в нашей литературе стали общепринятыми. Задачи линейного программирования является удобной математической моделью для большого числа экономических задач (планирование производства, расходование материалов, транспортные перевозки и т.д.). Использование метода линейного программирования представляет собой важность и ценность — оптимальный вариант выбирается из достаточно значительного количества альтернативных вариантов. Также все экономические задачи, решаемые с применением линейного программирования, отличаются альтернативностью решения и определенными ограничивающими условиями.В электронных таблицах Excel с помощью функции поиска решения можно вести поиск значения в целевой ячейке, изменения значения переменных. При этом для каждой переменной можно задать ограничения, например верхнюю границу. Перед тем как запустить поиск решения, необходимо четко сформулировать в модели решаемую проблему, т.е. определить условия, выполняемые при оптимизации. Отправленной точкой при поиске оптимального решения является модель вычисления, созданная в рабочем листе. Программе поиска решения при этом необходимы следующие данные. 1. Целевая ячейка — это ячейка в модели вычисления, значения в которой должно быть максимизировано, минимизировано или же равняться определенному указанному значению. Она должна содержать формулу, которая прямо или косвенно ссылается на изменяемые ячейки, или же самой быть изменяемой. 2. Значения в изменяемых ячейках будут последовательно (методом итераций) изменяться до тех пор, пока не будет получено нужное значение в целевой ячейке. Эти ячейки, следовательно, прямо или косвенно должны влиять на значение целевой ячейки. 3. Вы можете задать как для целевой, так и для изменяемых ячеек, ограничения и граничные условия. Можно задать также ограничения для других ячеек. Прямо или косвенно присутствующих в модели. Программа предоставляет возможность задать специальные параметры, определяющие процесс поиска решения. После задания всех необходимых параметров можно запустить поиск решения. Функция поиска решения создаст по итогам своей работы три отчета, которые можно пометить в рабочую книгу.Ограничения — это условия, которые должны быть выполнены аппаратом поиска решения при оптимизации модели.
Изучение литературы показало, что:
1. Линейное программирование — это один из первых и наиболее подробно изученных разделов математического программирования. Именно линейное программирование явилось тем разделом, с которого начала развиваться сама дисциплина «математическое программирование».
Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи:
- · рационального использования сырья и материалов; задачи оптимизации раскроя;
- · оптимизации производственной программы предприятий;
- · оптимального размещения и концентрации производства;
- · составления оптимального плана перевозок, работы транспорта;
- · управления производственными запасами;
- · и многие другие, принадлежащие сфере оптимального планирования.
- 2. Графический метод довольно прост и нагляден для решения задач линейного программирования с двумя переменными. Он основан на геометрическом представлении допустимых решений и ЦФ задачи.
Суть графического метода заключается в следующем. По направлению (против направления) вектора в ОДР производится поиск оптимальной точки. Оптимальной считается точка, через которую проходит линия уровня, соответствующая наибольшему (наименьшему) значению функции. Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.