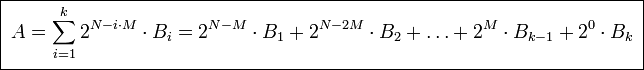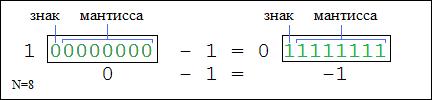First thing, always understand your data, the x86 memory is addressable by bytes. It doesn’t matter what kind of logical structure you use to write the data into the memory, if anybody else is watching the memory content, and they don’t know about your logical structure, they see only bytes.
a dd 12345678h,1A2B3Ch,78h
So this compiles as 12 (3 * 4) bytes:
78 67 34 12 3C 2B 1A 00 78 00 00 00
To condense such array by removing zeroes you don’t even need to work with double words, just copy it byte by byte (voluntarily dropping away your knowledge that it was meant as double word array originally), skipping zero values.
code segment
start:
mov ax,data
mov ds,ax
lea si,[a] ; original array offset
lea di,[n] ; destination array offset
mov cx,l ; byte (!) length of original array
repeta:
; load single byte from original array
mov al,[si]
inc si
; skip zeroes
test al,al
jz skipping_zero
; store non-zero to destination
mov [di],al
inc di
skipping_zero:
loop repeta
; fill remaining bytes of destination with zeroes - init
xor al,al
lea si,[n+l] ; end() offset of "n"
; jump first to test, so filling is skipped when no zero
jmp fill_remaining_test
fill_remaining_loop:
; clear one more byte in destination
mov [di],al
inc di
fill_remaining_test:
; test if some more bytes are to be cleared
cmp di,si ; current offset < end() offset
jb fill_remaining_loop
; exit back to DOS
mov ax,4C00h
int 21h
code ends
end start
But this is complete rewrite of your code, unfortunately, so I will try to add some explanations what’s wrong in yours.
About MUL, and especially about multiplying by power of two value:
mov bx,si ; bx = si (index into array?)
mul pat ; dx:ax = ax * word(4)
As you can see, the mul doesn’t use either bx, or si, and it results into 32 bit value, split into dx (upper word) and ax (lower word).
To multiply si by 4 you would have either to do:
mov ax,si ; ax = si
mul [pat] ; dx:ax = ax * word(4)
Or simply exploiting that computers are working with bits, and binary encoding of integer values, so to multiply by 4 you need only to shift bit values in the value by two positions «up» (left).
shl si,2 ; si *= 4 (truncated to 16 bit value)
But that destroys original si («index»), so instead of doing this people usually adjust the loop increment. You will start with si = 0, but instead of inc si you would do add si,4. No multiply needed any more.
add bx,1 hurts my eyes, I prefer inc bx in human Assembly (although on some generations of x86 CPUs the add bx,1 was faster, but on modern x86 the inc is again fine).
mov al,byte ptr a[si]+1 is very weird syntax, I prefer to keep things «Intel-like» simple, ie. mov al,byte ptr [si + a + 1]. It’s not C array, it’s really loading value from memory from address inside the brackets. Mimicking C-array syntax will probably just confuse you over time. Also the byte ptr can be removed from that, as al defines the data width already (unless you are using some MASM which enforces this upon dd array, but I don’t want to touch that microsoft stuff with ten foot pole).
Same goes for mov n[bx],al = mov [n + bx],al or mov [bx + n],al, whichever makes more sense in the code.
But overall it’s a bit unusual to use index inside loop, usually you want to convert all indexes into addresses ahead of loop in the init part, and use final pointers without any calculation inside loop (incrementing them by element size, ie. add si,4 for double words). Then you don’t need to do any index multiplication.
Especially in 16 bit mode, where the addressing modes are very limited, in 32/64b mode you can at least multiply one register with common sizes (1, 2, 4, 8), ie. mov [n + ebx * 4],eax = no need to multiply it separately.
EDIT: there’s no scale (multiply by 1/2/4/8 of «index» part) in 16b mode available, the possible example [si*4] would not work.
New variant storing bytes from most-significant dword byte (ie. reversing the little-endian scheme of x86 dword):
code segment
start:
mov ax,data
mov ds,ax
lea si,[a] ; original array offset
lea di,[n] ; destination array offset
mov cx,l1 ; element-length of original array
repeta:
; load four bytes in MSB-first order from original array
; and store only non-zero bytes to destination
mov al,[si+3]
call storeNonZeroAL
mov al,[si+2]
call storeNonZeroAL
mov al,[si+1]
call storeNonZeroAL
mov al,[si]
call storeNonZeroAL
; advance source pointer to next dword in array
add si,4
loop repeta
; Different ending variant, does NOT zero remaining bytes
; but calculates how many bytes in "n" are set => into CX:
lea cx,[n] ; destination begin() offset
sub cx,di
neg cx ; cx = number of written bytes into "n"
; exit back to DOS
mov ax,4C00h
int 21h
; helper function to store non-zero AL into [di] array
storeNonZeroAL:
test al,al
jz ignoreZeroAL
mov [di],al
inc di
ignoreZeroAL:
ret
code ends
end start
Written in a way to keep it short and simple, not for performance (and I strongly suggest you to aim for the same, until you feel really comfortable with the language, it’s difficult enough for beginner even if written in simple way without any expert-trickery).
BTW, you should find some debugger which works for you, so it would be possible for you to step instruction by instruction and watch how that resulting values in «n» are being added, and why. Or you would probably notice sooner that the bx+si vs mul don’t do what you expect and the remaining code is operating on wrong indices. Programming in Assembly without debugger is like trying to assemble a robot blindfolded.
Очень часто в программах приходится выполнять действия с числами разного размера, например складывать или умножать байт и слово. Напрямую процессор не умеет выполнять такие операции, поэтому в этом случае необходимо выполнять преобразование типов. Сложность представляет преобразование меньших типов в большие (байта в слово, слова в двойное слово и т.д.)
Преобразовать больший тип в меньший гораздо проще — достаточно отбросить старшую часть. Но такое преобразование небезопасно и может привести к ошибке. Например, если значение слова без знака больше 255, то сделав из него байт, вы получите некорректное значение. Будьте внимательны, если вы используете такие трюки в своей программе.
Преобразование типов без знака
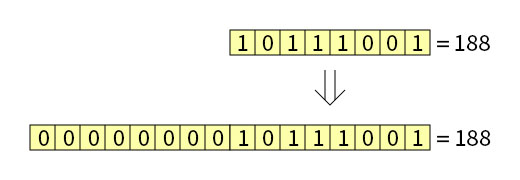
Преобразование типов выполняется по-разному для чисел со знаком и без. Для преобразования чисел без знака необходимо просто заполнить все старшие биты нулями. Например, так будет выглядеть преобразование байта в слово:
Такое преобразование можно выполнить с помощью обычной команды MOV (x объявлен как байт):
mov bl,[x] mov bh,0 ;BX = x ;Или вот так: mov bl,[x] sub bh,bh ;BX = x
Но кроме того в системе команд процессора существует специальная команда — MOVZX (копирование с нулевым расширением). Первый операнд команды имеет размер 16 бит (слово), а второй — 8 бит (байт). Тот же результат можно получить так:
Преобразование типов со знаком
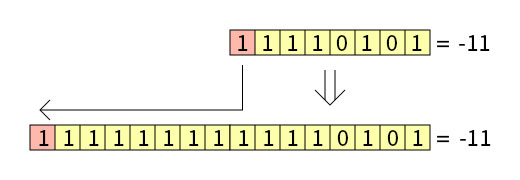
Для чисел со знаком всё немного сложнее. Если мы просто заполним старшую часть нулями, то результат будет положительным, а это не всегда верно. Поэтому преобразование выполняется путём копирования знакового бита на всю старшую часть. То есть для положительного числа со знаком старшая часть будет заполняться нулями, а для отрицательного — единицами:
Для такого преобразования предназначена команда MOVSX (копирование со знаковым расширением). Первый операнд — слово, второй операнд — байт. Например (y объявлен как байт):
Существуют ещё две команды для преобразования типов со знаком: CBW (Convert Byte to Word — преобразовать байт в слово) и CWD (Convert Word to Double word — преобразовать слово в двойное слово). У этих команд нет явных операндов. Команда CBW преобразует байт, находящийся в регистре AL, в слово в регистре AX. Команда CWD преобразует слово, находящееся в регистре AX, в двойное слово в регистрах DX:AX. Эти команды удобно использовать вместе с командами умножения и деления. Например:
mov al,[y] cbw ;AX = y cwd ;DX:AX = y
Пример программы
Допустим, требуется вычислить значение формулы x = (a + b) / c. Все числа со знаком. Размер x — двойное слово, размер a — байт, размер b и c — слово.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
use16 ;Генерировать 16-битный код org 100h ;Программа начинается с адреса 100h movsx ax,[a] ;AX = a add ax,[b] ;AX = a+b cwd ;DX:AX = a+b idiv [c] ;AX = (a+b)/c, в DX остаток cwd ;DX:AX = (a+b)/c mov word[x],ax ; mov word[x+2],dx ;/ x = DX:AX mov ax,4C00h ; int 21h ;/ Завершение программы ;------------------------------------------------------- a db -55 b dw -3145 c dw 100 x dd ? |
Упражнение
Напишите программу для вычисления формулы z = (x·y) / (x + y). Все числа со знаком. Размер x — байт, размер y — слово, размер z — двойное слово. Проверьте работу программы в отладчике. Результаты можете выкладывать в комментариях.
Следующая часть »
|
VlaDO5 0 / 0 / 0 Регистрация: 04.10.2018 Сообщений: 5 |
||||
|
1 |
||||
|
MASM 13.10.2018, 17:48. Показов 5894. Ответов 7 Метки нет (Все метки)
Здравствуйте. Помогите пожалуйста, как dword/byte.
0 |
|
Модератор 8297 / 4200 / 1598 Регистрация: 01.02.2015 Сообщений: 13,065 Записей в блоге: 4 |
|
|
13.10.2018, 21:05 |
2 |
|
Загрузите байт в AL и последовательными инструкциями расширьте его до двойного слова, результат перенесите в какой нибудь регистр. О расширении регистров (имеется в виду знаки чисел) прочтите в главе 10 среди «деления» и «изменения размеров числа».
1 |
|
0 / 0 / 0 Регистрация: 04.10.2018 Сообщений: 5 |
|
|
13.10.2018, 22:43 [ТС] |
3 |
|
За объяснение спасибо. Пожалуйста не могли бы вы мне, отправить сам код который нужно написать в Ассемблере? Так как я пока не понимаю как это сделать.
0 |
|
Модератор 8297 / 4200 / 1598 Регистрация: 01.02.2015 Сообщений: 13,065 Записей в блоге: 4 |
|
|
13.10.2018, 22:59 |
4 |
|
Попробуйте прочесть два раздела главы 10. Станет легче.
0 |
|
VlaDO5 0 / 0 / 0 Регистрация: 04.10.2018 Сообщений: 5 |
||||
|
14.10.2018, 17:56 [ТС] |
5 |
|||
0 |
|
ФедосеевПавел Модератор 8297 / 4200 / 1598 Регистрация: 01.02.2015 Сообщений: 13,065 Записей в блоге: 4 |
||||
|
14.10.2018, 18:23 |
6 |
|||
|
Можно так. А я бы попробовал
1 |
|
Mikl___ Ушел с форума 15852 / 7433 / 996 Регистрация: 11.11.2010 Сообщений: 13,402 |
||||
|
14.10.2018, 18:24 |
7 |
|||
|
РешениеVlaDO5,
4 |
|
Модератор 8297 / 4200 / 1598 Регистрация: 01.02.2015 Сообщений: 13,065 Записей в блоге: 4 |
|
|
14.10.2018, 18:25 |
8 |
|
Точно, есть же копирование с расширением знака
0 |
This function block allows you to convert a variable WORD in two variables BYTE. The 8 high bits of In will be transferred to the operand MSB, low 8 bits will be transferred to the operand LSB.
Function lock
CODESYS: Not available
LogicLab: eLLabUtyLib
In (WORD) Variable to convert.
MSB (BYTE) MSB of the input value.
LSB (BYTE) LSB of the input value.
Examples
How to use the examples.
In the example a variable WORD with value 16 # 1234 is transferred in two variables BYTE which will have value 16 # 12 and 16 # 34. In the example in language ST it is highlighted how the same operation is much simpler by writing it directly with the operands of the language.
LogicLab (Ptp114)
PROGRAM ST_WordToByte
VAR
WData : WORD := 16#1234; (* Word data *)
High : ARRAY[ 0..1 ] OF BYTE; (* MSB byte *)
Low : ARRAY[ 0..1 ] OF BYTE; (* LSB byte *)
WDec : WordToByte; (* Word decompress *)
END_VAR
// *****************************************************************************
// PROGRAM "ST_WordToByte"
// *****************************************************************************
// This program shows the use of WordToByte function block.
// -----------------------------------------------------------------------------
// -------------------------------------------------------------------------
// DECOMPRESS WORD
// -------------------------------------------------------------------------
// Decompress word using the FB.
WDec(In:=WData);
High[0]:=WDec.MSB; //MSB byte
Low[0]:=WDec.LSB; //LSB byte
// -------------------------------------------------------------------------
// DECOMPRESS WORD
// -------------------------------------------------------------------------
// The same operation as above executed directly using ST statements.
High[1]:=TO_BYTE(WData/256); //MSB byte
Low[1]:=TO_BYTE(WData); //LSB byte
// [End of file]
Was this article helpful?
Статья основана на материале xrnd с сайта asmworld (из учебного курса по программированию на ассемблер 16-битного процессора 8086 под DOS).
Очень часто в программах приходится выполнять действия с числами разного размера, например складывать или умножать байт и слово. Напрямую процессор не умеет выполнять такие операции, поэтому в этом случае необходимо выполнять преобразование типов. Сложность представляет преобразование меньших типов в большие (байта в слово, слова в двойное слово и т.д.)
Преобразовать больший тип в меньший гораздо проще — достаточно отбросить старшую часть. Но такое преобразование небезопасно и может привести к ошибке. Например, если значение слова без знака больше 255, то сделав из него байт, вы получите некорректное значение. Будьте внимательны, если вы используете такие трюки в своей программе.
Преобразование типов без знака
Преобразование типов выполняется по-разному для чисел со знаком и без. Для преобразования чисел без знака необходимо просто заполнить все старшие биты нулями. Например, так будет выглядеть преобразование байта в слово:
Такое преобразование можно выполнить с помощью обычной команды MOV (x объявлен как байт):
mov bl,[x]
mov bh,0 ;BX = x
;Или вот так:
mov bl,[x]
sub bh,bh ;BX = x
Но кроме того в системе команд процессора существует специальная команда — MOVZX (копирование с нулевым расширением). Первый операнд команды имеет размер 16 бит (слово), а второй — 8 бит (байт). Тот же результат можно получить так:
movzx bx,[x] ;BX = x
Преобразование типов со знаком
Для чисел со знаком всё немного сложнее. Если мы просто заполним старшую часть нулями, то результат будет положительным, а это не всегда верно. Поэтому преобразование выполняется путём копирования знакового бита на всю старшую часть. То есть для положительного числа со знаком старшая часть будет заполняться нулями, а для отрицательного — единицами:
Для такого преобразования предназначена команда MOVSX (копирование со знаковым расширением). Первый операнд — слово, второй операнд — байт. Например (y объявлен как байт):
movsx cx,[y] ;CX = y
Существуют ещё две команды для преобразования типов со знаком: CBW (Convert Byte to Word — преобразовать байт в слово) и CWD (Convert Word to Double word — преобразовать слово в двойное слово). У этих команд нет явных операндов. Команда CBW преобразует байт, находящийся в регистре AL, в слово в регистре AX. Команда CWD преобразует слово, находящееся в регистре AX, в двойное слово в регистрах DX:AX. Эти команды удобно использовать вместе с командами умножения и деления. Например:
mov al,[y]
cbw ;AX = y
cwd ;DX:AX = y
Пример программы
Допустим, требуется вычислить значение формулы
$$x = frac{a + b}{c}$$
Все числа со знаком. Размер x — двойное слово, размер a — байт, размер b и c — слово.
use16 ;Генерировать 16-битный код
org 100h ;Программа начинается с адреса 100h
movsx ax,[a] ;AX = a
add ax,[b] ;AX = a+b
cwd ;DX:AX = a+b
idiv [c] ;AX = (a+b)/c, в DX остаток
cwd ;DX:AX = (a+b)/c
mov word[x],ax ;
mov word[x+2],dx ;/ x = DX:AX
mov ax,4C00h ;
int 21h ;/ Завершение программы
;-------------------------------------------------------
a db -55
b dw -3145
c dw 100
x dd ?
Упражнение
Напишите программу для вычисления формулы
$$z = frac{x cdot y}{x + y}$$
Все числа со знаком. Размер x — байт, размер y — слово, размер z — двойное слово. Проверьте работу программы в отладчике. Результаты можете выкладывать в комментариях.
Часть команд процессор может обработать только со значениями одной разрядности. Процессор без колебаний перемножит байт на байт и слово на слово. Но никак не байт на слово, или двойное слово на слово. Чтобы складывать, перемножать и выполнять другие операции со значениями разных размеров, программист должен озаботиться преобразованием типов в своей программе.
Под преобразованием типов я подразумеваю изменение разрядности операнда от большего к меньшему (например, двойное слово в слово), или от меньшего к большему (например, байт в слово). Для преобразования больших типов в меньшие отбрасывается старшая часть значения. Операция может быть не безопасной, если утрачивается часть значения, хранимого в старшей части (например, беззнаковое слово хранит число 500, а его преобразование в байт отсекает всё выше 255). В таком случае преобразование приводит к ошибочному результату.
Преобразование типов без знака
Беззнаковое преобразовании с увеличением разряда происходит через добавление к исходному значению старшей части, биты которой заполняется нулями. На картинке показан пример расширения из байта в слово:
Преобразование беззнакового значения происходит просто. В программе на ассемблере для преобразования такого типа используется команда MOV:
|
mov dl,[a] mov dh,0 ;Другой вариант: mov dl,[a] xor dh,dh ;Вот еще один: mov dl,[a] sub dh,dh ;… a db 118 |
Также для беззнаковых преобразований в ассемблере есть специальная команда MOVZX (move with Zero-Extend, т.е. переместить с нулевым расширением). Она копирует содержимое операнда источника (регистр или значение в памяти) в операнд назначения (регистр). Старшая часть расширения заполняется нулями. Операнд назначения определяет размер расширения.
Преобразование командой MOVZX происходит так:
|
movzx cx,[b] ;CX = b ;… b db 193 |
Преобразование типов со знаком
Существует нюанс, касающийся старшего бита, который, как мы помним из Урока 8. Числа со знаком и без, является знаковым битом, то есть битом, определяющим, стоит перед числом знак «минус» или нет. Поэтому преобразования знакового числа происходит через прибавление старшей части и её заполнением знаковым битом. Говоря проще, если число было отрицательным, то старшая часть заполняется единицами, а если положительным – то нулями:
В ассемблере за преобразование типов знаковых значений отвечает команда MOVSX (Move with Sign-Extension, т.е. переместить со знаковым расширением). Она копирует содержание операнда источника (регистр или значение в памяти) в операнд назначения (регистр), расширяя значение знаковым битом:
Дополнительно в ассемблере есть еще команды для преобразования знаковых операндов: CBW – преобразует байт в слово (Convert Byte to Word) и CWD – преобразует слово в двойное слово (Convert Word to Double word). Они не получают явных операндов. Вместо этого CBW расширяет значение-байт в регистре AL в слово в регистре AX. В свою очередь CWD преобразует значение-слово в AX в двойное слово DX:AX. На практике обе команды часто сопутствуют операциями на умножении и деление.
Пример программы
Найдем решение формулы m = (a + 1) / (b – c). Все операнды со знаком. Размер m – слово, размер a – двойное слово, размер b – слово, размер c – байт.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
use16 ;Генерировать 16—битный код org 100h ;Программа начинается с адреса 100h mov ax,[b] ;AX = b movsx cx,[c] ;CX = c sub ax,cx ;AX = (b — c) mov cx,ax ;Запоминаем результат в CX mov ax,word[a] ;AX = младшая часть a mov dx,word[a+2] ;DX = старшая часть a add ax,1 ; adc dx,0 ;/DX:AX = (a + 1) idiv cx ;AX = (a + 1) / (b — c), в DX остаток mov [m],ax ;m = AX, в DX остаток int 20h ;Завершение программы a dd 12299 b dw 128 c db —16 m dw ? |
Упражнение
Теперь упражнение для самостоятельной работы. Закрепите пройденный урок написанием программы для решения формулы m = a^2 / (a + b). Все операнды со знаком. Размер a – слово, размеры b – байт, размер m – двойное слово. После компиляции откройте программу в Turbo Debugger, выполните все строки и проверьте, какое значение записалось по адресу переменной m. Результат отправьте в комментарии к уроку.
Целые числа
Данные каким-либо образом необходимо представлять в памяти компьютера. Существует множество различных типов данных, простых и довольно сложных, имеющих большое число компонентов и свойств. Однако, для компьютера необходимо использовать некий унифицированный способ представления данных, некоторые элементарные составляющие, с помощью которых можно представить данные абсолютно любых типов. Этими составляющими являются числа, а вернее, цифры, из которых они состоят. С помощью цифр можно закодировать практически любую дискретную информацию. Поэтому такая информация часто называется цифровой (в отличие от аналоговой, непрерывной).
Первым делом необходимо выбрать систему счисления, наиболее подходящую для применения в конкретных устройствах. Для электронных устройств самой простой реализацией является двоичная система: есть ток — нет тока, или малый уровень тока — большой уровень тока. Хотя наиболее эффективной являлась бы троичная система. Наверное, выбор двоичной системы связан еще и с использование перфокарт, в которых она проявляется в виде наличия или отсутствия отверстия. Отсюда в качестве цифр для представления информации используются 0 и 1.
Таким образом данные в компьютере представляются в виде потока нулей и единиц. Один разряд этого потока называется битом. Однако в таком виде неудобно оперировать с данными вручную. Стандартом стало разделение всего потока на равные последовательные группы из 8 битов — байты или октеты. Далее несколько байтов могут составлять слово. Здесь следует разделять машинное слово и слово как тип данных. В первом случае его разрядность обычно равна разрядности процессора, т.к. машинное слово является наиболее эффективным элементом для его работы. В случае, когда слово трактуется как тип данных (word), его разрядность всегда равна 16 битам (два последовательных байта). Также как типы данных существую двойные слова (double word, dword, 32 бита), четверные слова (quad word, qword, 64 бита) и т.п.
Теперь мы вплотную подошли к представлению целых чисел в памяти. Т.к. у нас есть байты и различные слова, то можно создать целочисленные типы данных, которые будут соответствовать этим элементарным элементам: byte (8 бит), word (16 бит), dword (32 бита), qword (64 бита) и т.д. При этом любое число этих типов имеет обычное двоичное представление, дополненное нулями до соответствующей размерности. Можно заметить, что число меньшей размерности можно легко представить в виде числа большей размерности, дополнив его нулями, однако в обратном случае это не верно. Поэтому для представления числа большей размерности необходимо использовать несколько чисел меньшей размерности. Например:
- qword (64 бита) можно представить в виде 2 dword (32 бита) или 4 word (16 бит) или 8 byte (8 бит);
- dword (32 бита) можно представить в виде 2 word (16 бит) или 4 byte (8 бит);
- word (16 бит) можно представить в виде 2 byte (8 бит);
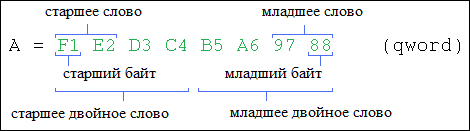
Если A — число, B1..Bk — части числа, N — разрядность числа, M — разрядность части, N = k*M, то:
Например:
- A = F1E2D3C4B5A69788 (qword)
- A = 232 * F1E2D3C4 (dword) + 20 * B5A69788 (dword)
- A = 248 * F1E2 (word) + 232 * D3C4 (word) + 216 * B5A6 (word) + 20 * 9788 (word)
- A = 256 * F1 (byte) + 248 * E2 (byte) + … + 28 * 97 (byte) + 20 * 88 (byte)
Существуют понятия младшая часть (low) и старшая часть (hi) числа. Старшая часть входит в число с коэффициентом 2N-M, а младшая с коэффициентом 20. Например:
Байты числа можно хранить в памяти в различном порядке. В настоящее время используются два способа расположения: в прямом порядке байт и в обратном порядке байт. В первом случае старший байт записывается в начале, затем последовательно записываются остальные байты, вплоть до младшего. Такой способ используется в процессорах Motorola и SPARC. Во втором случае, наоборот, сначала записывает младший байт, а затем последовательно остальные байты, вплоть до старшего. Такой способ используется в процессорах архитектуры x86 и x64. Далее приведен пример:
Используя подобные целочисленные типы можно представить большое количество неотрицательных чисел: от 0 до 2N-1, где N — разрядность типа. Однако, целочисленный тип подразумевает представление также и отрицательных чисел. Можно ввести отдельные типы для отрицательных чисел от -2N до -1, но тогда такие типы потеряют универсальность хранить и неотрицательные, и отрицательные числа. Поэтому для определения знака числа можно выделить один бит из двоичного представления. По соглашению, это старший бит. Остальная часть числа называется мантиссой.
Если старший бит равен нулю, то мантисса есть обычное представление числа от 0 до 2N-1-1. Если же старший бит равен 1, то число является отрицательным и мантисса представляет собой так называемый дополнительный код числа. Поясним на примере:
Как видно из рисунка, дополнительный код равен разнице между числом 2N-1 и модулем исходного отрицательного числа (127 (1111111) = 128 (10000000) — |-1| (0000001)). Из этого вытекает, что сумма основного и дополнительного кода одного и того же числа равна 2N-1.
Из вышеописанного получается, что можно использовать только целочисленные типы со знаком для описания чисел. Однако существует множество сущностей, которые не требуют отрицательных значений, а значит, место под знак можно включить в представление неотрицательного числа, удвоив количество различных неотрицательных значений. Как результат, в современных компьютерах используются как типы со знаком или знаковые типы, так и типы без знака или беззнаковые типы.
В итоге можно составить таблицу наиболее используемых целочисленных типов данных:
| Общее название | Название в Pascal | Название в C++ | Описание | Диапазон значений |
| unsigned byte | byte | unsigned char | беззнаковый 8 бит | 0..255 |
| signed byte | shortint | char | знаковый 8 бит | -128..127 |
| unsigned word | word | unsigned short | беззнаковый 16 бит | 0..65535 |
| signed word | smallint | short | знаковый 16 бит | -32768..32767 |
| unsigned double word | cardinal | unsigned int | беззнаковый 32 бита | 0..232-1 |
| signed double word | integer | int | знаковый 32 бита | -231..231-1 |
| unsigned quad word | uint64 | unsigned long long unsigned __int64_t (VC++) |
беззнаковый 64 бита | 0..264-1 |
| signed quad word | int64 | long long __int64_t (VC++) |
знаковый 64 бита | -263..263-1 |




 Сообщение было отмечено ФедосеевПавел как решение
Сообщение было отмечено ФедосеевПавел как решение