Доходность к погашению облигации формула excel

Финансовые показатели облигаций могут быстро рассчитываться в Excel. Для этого используется функция ДОХОД. С ее помощью вычисляется доходность ценных бумаг, по которым периодически выплачиваются проценты (дивиденды).

Как работает функция ДОХОД в Excel?

Облигации – это финансовый инструмент. Предприятие, выпустившее облигации, выступает в роли заемщика. Нуждаясь в привлечении средств, оно выпускает и выбрасывает на рынок такие ценные бумаги. Покупатель облигаций, фактически, является заимодавцем. Ставка купона – это процент, который получает покупатель облигации за то, что предоставил свои средства в пользование.

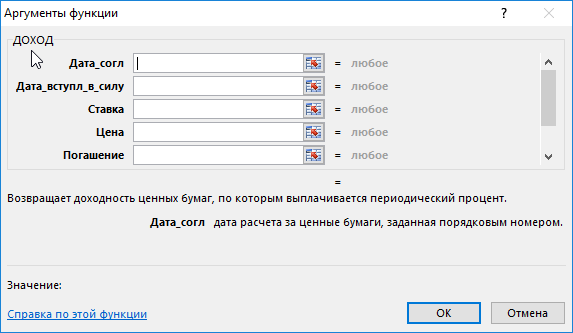
Как рассчитать доходность облигаций в Excel? Для решения данной задачи используется функция ДОХОД. Как и любая другая функция, ее синтаксис состоит из имени и аргументов. В строке формул сначала ставится знак равенства, после прописывается имя функции, а затем заполняем ее аргументы входящими значениями всех необходимых показателей.

Всего аргументов у сложной функции 7. Из них 6 обязательных для заполнения:

1. Дата_согл. Расчетный день, когда облигация продана. Дата, когда долговые обязательства переданы покупателю. Не стоит путать ее с датой выпуска облигации.
2. Дата_вступл_в_силу. День, когда заем возвращается покупателю. Это срок погашения облигации, когда истекает срок ее действия.
3. Ставка. Годовая ставка процентов по облигации. Процент, который получает покупатель ценных бумаг.
4. Цена. Показатель определяет цену облигации на 100 рублей номинала.
5. Погашение. Стоимость, по которой выкупаются ценные бумаги.
6. Частота. Число выплат по облигации в год. Может быть равна 1, 2 или 4.
7. Базис. Этот аргумент не является обязательным. Поэтому он заключается в квадратные скобки. Он определяет способ вычисления дней.

Существует 5 видов базиса:

• — 0 – Американский 30/360;
• — 1 – факт/факт;
• — 2 – факт/360;
• — 3 – факт/365;
• — 4 – Европейский 30/360.

Аргументы всегда берутся в круглые скобки. Все они перечисляются по порядку. Между ними ставится знак «;».

Синтаксис функции прописывается следующим образом:

=ДОХОД(дата_согл; дата_вступл_в_силу; ставка; цена; погашение; частота; [базис])

Обязательно учитывать то, что все даты в Excel записываются в виде последовательных чисел. Недопустимо использование текстового формата. За 1 принято 1 января 1900 года. Все последующие даты просто прибавляют число прошедших дней. Поэтому все значения рассчитываются с помощью функции «ДАТА».

Результатом применения функции является определение прибыльности облигаций. Программа может выдать не результат, а знак ошибки #ЧИСЛО! Это происходит в нескольких случаях:

• введены даты без использования функции «ДАТА»;
• значение ставки меньше нуля;
• указана цена меньше или равная нулю;
• погашение указано меньше или равно нулю;
• базис меньше нуля или больше четырех.



Примеры использования функции ДОХОД для анализа облигаций

Для вычисления доходности ценных бумаг нужно ввести в первый столбик таблицы все аргументы функции.

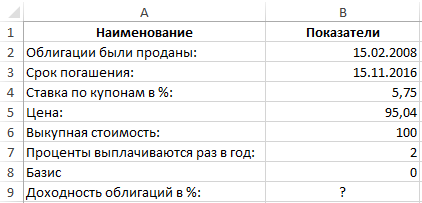
Пример 1. Необходимо вычислить доходность облигаций при следующих условиях:

1. Облигации были проданы 15 февраля 2008 года.
2. Срок погашения – 15 ноября 2016.
3. Ставка по купонам определена 5,75%.
4. Цена составляет 95.04 номиналов.
5. Выкупная стоимость — 100 номиналов.
6. Проценты выплачиваются раз в полгода.
7. Значение базиса – 0 (30/360).

Последовательно вводите все значения заполняя таблицу с данными:

В ячейку B9 вводите данные для аргументов функции ДОХОД. Формула будет выглядеть так:

Доходность облигаций составляет 4,26%.

Можно вводить формулу с клавиатуры или указывать соответствующие ячейки мышью. При этом прописать имя функции нужно вручную. Затем откройте скобку и последовательно через «пробел» укажите все ячейки, которые должны быть учтены.

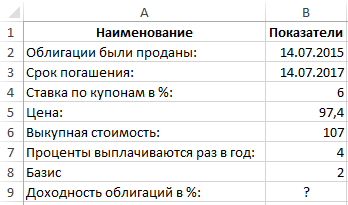
Пример 2. Предприятие продало облигации 14 июля 2015. Установлен небольшой срок их погашения 14 июля 2017. Предлагается ставка 6%. Цена бумаг 97,4 номинальных значений. Стоимость для выкупа – 107 номиналов. Выплата процентов проводится 4 раза в год. Базис 2 – (48/360).

Для вычисления прибыльности облигации введите данные в таблицу по принципу, который стал понятен из примера 1:

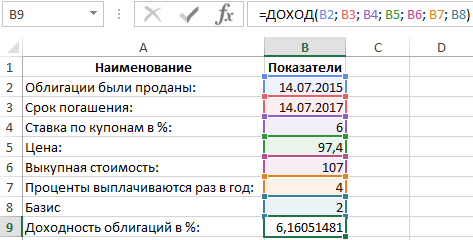
В итоговой ячейке B9 приписываем функцию:

Это обозначает, что расчет доходности к погашению облигаций составляет (6,16% х 2года)=12,32%.

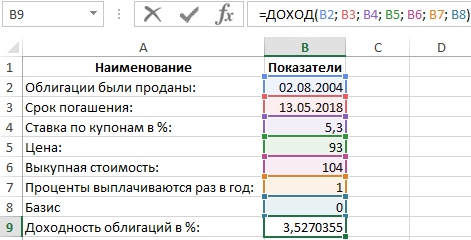
Пример 3. Ценные бумаги проданы 2 августа 2004. Погашение произошло 13 мая 2018. Купонная ставка по ним – 5,3%. Цена бумаг – 93 номинала. Стоимость для выкупа – 104 номинала. Проценты начисляются раз в год. Базис – 0 (30/360).

По аналогии составляем таблицу, используя функцию =ДОХОД():

Прибыльность акций оценена в 3,52%.

С помощью программы Excel удалось всего за несколько минут установить, что самыми прибыльными инвестициями являются облигации из второго примера.

Этот текст написан в Сообществе, в нем сохранены авторский стиль и орфография

Возник у меня как-то вопрос: насколько корректно отображается доходность к погашению у облигаций в приложениях брокера и на различных сервисах наподобие РУСБОНДС. И, как оказалось, действительно реальная доходность может отличаться от указанной, а иногда даже быть отрицательной. Да, да, вы не ослышались. Об этом подробнее расскажу ниже. А сначала продемонстрирую таблицу, благодаря которой я пришел к такому выводу.

Преимущество данной таблицы заключается в том, что вам необходимо заполнить только желтые ячейки:

1. Налог,
2. Комиссия брокера,
3. Код облигации
4. Их количество.

И всё! Остальное все таблица сделает за вас: покажет название облигации, номинал, цену, дату погашения, НКД, купон, периодичность выплаты и даже дату оферты (если она есть). Данные подтягиваются с сайта Московской биржы. Ну, и самое главное — таблица рассчитает реальную доходность с учетом НДФЛ и без него, с учетом комиссии и без нее. Но я рекомендую смотреть на доходность с учетом комиссии и НДФЛ. В этом-то и смысл этой таблицы. Если вы снимите галочку «с учетом комиссии», то она не будет учитываться. Помимо этого, для облигации сформируется график денежного потока. И качестве бонуса — есть визуализация денежного потока.

В процессе работы с этой таблицей у меня для некоторых облигаций получалась отрицательная реальная доходность. Я начал разбираться и оказалось, что так и есть, таблицу не обманешь:). Дело в том, что с 01.01.2021 купоны по облигациям стали облагаться налогом. И из налогооблагаемой базы почему-то не вычитают потраченные средства на НКД — накопленный купонный доход. То есть если я покупаю облигацию за пару дней до выплаты купона — допустим 30 Р, то я дополнительно к цене облигации еще плачу НКД — допустим 29 Р. Справочно по колхозному: НКД равен 0 в день выплаты купона, затем каждый день он увеличивается на определенное значение, пока в день выплаты купона он не станет равным величине купона. В этот день он опять обнуляется и так далее до следующей выплаты.

Так вот получается я отдал 29 Р, а получил 30 Р — 13% налога, то есть всего 26,1 Р. Если последующих выплат еще много, то данная «несправедливость» не значительно уменьшит вашу доходность, а если эта выплата была последней (то есть в день погашения облигации), то получается вы вложите больше, чем вам вернется. То есть получите отрицательную реальную доходность!

Именно поэтому данная таблица имеет преимущество перед сторонними сервисами, которые не учитывают нюансы налогооблажения и комиссию брокера.

Сделаем вывод: облигацию выгодно покупать сразу после выплаты купона, когда НКД минимален. А таблица вам в этом поможет.

Ссылка на таблицу

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Understanding a bond’s yield to maturity (YTM) is an essential task for fixed-income investors. But to fully grasp YTM, we must first discuss how to price bonds in general. The price of a traditional bond is determined by combining the present value of all future interest payments (cash flows), with the repayment of principal (the face value or par value) of the bond at maturity.

The rate used to discount these cash flows and principal is called the «required rate of return,» which is the rate of return required by investors who are weighing the risks associated with the investment. 

How to Price a Bond

The formula to price a traditional bond is: 

PV

=

P

(

1

+

r

)

1

+

P

(

1

+

r

)

2

+

⋯

+

P

+

Principal

(

1

+

r

)

n

where:

PV

=

present value of the bond

P

=

payment, or coupon rate

×

par value

÷

number of

payments per year

r

=

required rate of return

÷

number of payments

per year

Principal

=

par (face) value of the bond

n

=

number of years until maturity

begin{aligned} &text{PV} = frac { text{P} }{ ( 1 + r ) ^ 1 } + frac { text{P} }{ ( 1 + r ) ^ 2 } + cdots + text{P} + frac { text{Principal} }{ ( 1 + r ) ^ n } \ &textbf{where:} \ &text{PV} = text{present value of the bond} \ &text{P} = text{payment, or coupon rate} times text{par value} div text{number of} \ &text{payments per year} \ &r = text{required rate of return} div text{number of payments} \ &text{per year} \ &text{Principal} = text{par (face) value of the bond} \ &n = text{number of years until maturity} \ end{aligned}

​PV=(1+r)1P​+(1+r)2P​+⋯+P+(1+r)nPrincipal​where:PV=present value of the bondP=payment, or coupon rate×par value÷number ofpayments per yearr=required rate of return÷number of paymentsper yearPrincipal=par (face) value of the bondn=number of years until maturity​

The pricing of a bond is therefore critically dependent on the difference between the coupon rate, which is a known figure, and the required rate, which is inferred.

Suppose the coupon rate on a $100 bond is 5%, meaning the bond pays $5 per year, and the required rate—given the risk of the bond—is 5%. Because these two figures are identical, the bond will be priced at par, or $100.

This is shown below (note: if tables are hard to read, hover over the graphic and select the magnification icon):

Pricing a Bond After It’s Issued

Bonds trade at par when they are first issued. Frequently, the coupon rate and required return don’t match in the subsequent months and years because events impact the interest rate environment. A failure of these two rates to match causes the price of the bond to appreciate above par (trade at a premium to its face value) or decline below par (trade at a discount to its face value) in order to compensate for the rate difference.

Take the same bond as above (5% coupon, pays out $5 a year on a $100 principal) with five years left until maturity. If the current Federal Reserve rate is 1%, and other similar-risk bonds are at 2.5% (they pay out $2.50 a year on a $100 principal), this bond looks very attractive: offering 5% in interest—double that of comparable debt instruments.

Given this scenario, the market will adjust the price of the bond proportionally, in order to reflect this difference in rates. In this case, the bond would trade at a premium amount of $111.61. The current price of $111.61 is higher than the $100 you will receive at maturity, and that $11.61 represents the difference in the present value of the extra cash flow you receive over the life of the bond (the 5% versus the required return of 2.5%). 

In other words, in order to get that 5% interest when all other rates are much lower, you must buy something today for $111.61 that you know in the future will only be worth $100. The rate that normalizes this difference is the yield to maturity. 

Calculating the Yield to Maturity in Excel

The above examples break out each cash flow stream by year. This is a sound method for most financial modeling because best practices dictate that the sources and assumptions of all calculations should be easily auditable. However, when it comes to pricing a bond, we can make an exception to this rule because of the following truths:

• Some bonds have many years (decades) to maturity, and a yearly analysis, like that shown above, may not be practical
• Most of the information is known and fixed: We know the par value, we know the coupon, and we know the years to maturity.

For these reasons, we’ll set up the calculator as follows:

In the above example, the scenario is made slightly more realistic by using two coupon payments per year, which is why the YTM is 2.51—slightly above the 2.5% required rate of return in the first examples.

Открыть эту статью в PDF

Определение доходности к погашению

Доходность к погашению (Yield To Maturity, YTM) — доходность, которую получит покупатель облигации, если он приобретет ее сегодня по рыночной цене и будет держать до полного погашения, то есть получит все денежные выплаты по купонам и итоговую выплату номинальной стоимости облигации.

Именно доходность к погашению обычно является главным показателем доходности облигаций.

Доходность к погашению рассчитывают, как внутреннюю норму рентабельности всех денежных потоков, связанных с приобретением облигации.

Доходность к погашению и другие виды доходности

Необходимость использовать в анализе облигаций именно доходность к погашению определяется двумя факторами:

• Доход от вложения в облигацию обычно получают не только за счет выплаты купонов, но также и за счет разницы между текущей ценой облигации и ее номинальной стоимостью (face value), которая будет выплачена в конце срока. Более того, существуют бескупонные облигации, которые приносят доход только за счет разницы этих цен.
• Облигация может быть куплена не только в начале, в день выпуска, но и в любой другой момент. Это значит, что время до ближайших купонных выплат может быть разным и не составлять целый период начисления купона.

Из-за этих особенностей только YTM может продемонстрировать инвестору ожидаемую доходность облигации. Тем не менее, в данных об облигациях встречается еще два показателя доходности.

Купонная доходность показывает отношение суммы выплачиваемых купонов (т. е. процентов по облигации) к номинальной стоимости облигации. Как правило, облигации имеют полугодовой или годовой график выплаты купонов. Купонный доход в любом случае использует сумму за полный год.

Например, если на облигацию номиналом 1000 руб. дважды в год выплачивается купон 25 руб., то купонная доходность облигации равна (25+25)/1000 = 5%.

Текущая доходность — отношение годовых выплат купона к текущей рыночной стоимости облигации.

Например, если в предыдущем примере облигация сейчас имеет рыночную цену 900 рублей, то ее текущая доходность равна (25+25)/900 = 5,56%.

Расчет доходности к погашению

Для расчета доходности к погашению в Excel существует функция ДОХОД (в английской версии — YIELD), однако эта функция не может учесть ситуацию, когда облигация покупается в середине купонного периода, кроме того, у некоторых облигаций ставка купона может меняться.

Поэтому наиболее корректным будет считать доходность к погашению как IRR всех денежных потоков, то есть как решение уравнения:

В этой формуле CF — платежи по облигации, включая и купоны, и погашение номинала. Время здесь условно обозначено как t, но применение этой формулы отличается от базового уравнения IRR, так как шаг платежей часто равен 6 месяцам, а первый период может иметь свою собственную длительность, если облигация была куплена в середине периода.

На практике это означает, что для расчета YTM не используют функцию ВСД(). Вместо этого для каждого платежа указывается его дата, а затем расчет IRR выполняется с помощью функции ЧИСТВНДОХ(), которая в качестве второго параметра принимает точные даты платежей.

Ниже показан пример такого расчета:

Excel предлагает ряд функций, используемых для вычисления различных финансовых показателей облигаций. Облигацией называется финансовый инструмент, в котором покупатель выступает в роли заимодателя, а учреждение или государство, выпустившее облигации, — в роли заемщика. Однако многие функции, связанные с облигациями, выходят за рамки материала настоящей книги. В этой статье представлены примеры некоторых наиболее распространенных функций.

Некоторые свойства облигаций являются также и аргументами функций, связанных с облигациями.

• Расчетный день. Дата, в которую долговые обязательства переходят к покупателю.
• Срок погашения. Дата, в которую заем (представленный облигацией) возвращается покупателю.
• Ставка (также называемая купоном). Процентная ставка, которую выпустивший облигацию выплачивает покупателю.
• Доходность. Норма прибыли, получаемая покупателем. Включает в себя выплаты по процентам и дисконт.
• Погашение. Выкупная стоимость ценных бумаг за 100 долларов номинальной стоимости.
• Частота. Количество выплат дивидендов за год.

Оценка облигаций

Предприятия, выпускающие ценные бумаги, устанавливают перечисленные выше показатели, основываясь на текущей рыночной конъюнктуре. Когда конъюнктура меняется, стоимость облигаций тоже изменяется.

Для примера предположим, что некоторая компания выпустила облигации с номинальной стоимостью 100 долларов, сроком погашения 10 лет и 6%-ной ставкой, выплачиваемой дважды в год.

• Если процентная ставка по кредитам растет, ставка в 6% становится не такой уж и привлекательной. Покупатели уже не захотят платить 100 долларов за облигацию — они будут их покупать за меньшую сумму.
• Если процентная ставка по кредитам падает, ставка в 6% становится привлекательной. В данном случае покупатели готовы платить больше номинальной стоимости.

Функция ЦЕНА вычисляет сумму, которую покупатели потенциально готовы заплатить за облигацию в ожидании определенного дохода. Синтаксис этой функции таков: ЦЕНА(расчетный_день;срок_погашения;ставка;доходность;погашение;частота;базис). Учитывая приведенные выше факты, инвестор, желающий получить 7,5% годовых, должен использовать следующую формулу для вычисления приемлемой цены облигации, срок погашения которой наступает через 8 лет: =ЦЕНА(СЕГОДНЯ();СЕГОДНЯ()+ДАТА(8;1;0);,06;,075;100;2).

Результатом этой формулы будет 91,10 долларов — именно такую сумму стоит заплатить за облигацию номиналом в 100 долларов с шестью процентами годовых, чтобы прибыльность составила 7,5%. Каждый год инвестор будет получать 6%*100 долларов, плюс при погашении облигации он получит дополнительную прибыль в 8,90 долларов. Эти два компонента — проценты и дисконт — формируют доходность облигаций. Фактическая дата выпуска облигации может отличаться от даты ее покупки инвестором. Облигации выпускают многие организации, так производитель кондиционеров кватро клима имеет достаточно высокую ликвидность своих ценных бумаг, которая основывается на качестве продукции.

В рассмотренном примере облигации были выпущены за два года до их покупки, следовательно, инвестор будет получать за них проценты только в течение 8 лет. Если же процентная ставка упала с момента выпуска и инвестору достаточно 5,2%, формула слегка изменится: =ЦЕНА(СЕГОДНЯ();СЕГОДНЯ()+ДАТА(8;1;0);,06;,052;100;2). При этих обстоятельствах инвестор может заплатить за стодолларовую облигацию 105,18 долларов. На рис. 11.17 эти вычисления показаны на рабочем листе.

Вычисление доходности

В предыдущем примере инвестор знал необходимую ему доходность и вычислял такую цену облигации, чтобы получить ее. Если же, наоборот, он знает цену облигации, то функция ДОХОД поможет вычислить прибыльность инвестиций. Синтаксис этой функции следующий: ДОХОД (расчетный_день;срок_погашения;ставка;цена_покупки;номинал;частота;базис).

Инвестор все еще заинтересован в покупке десятилетней облигации с 6 процентами, выплачиваемыми дважды в год, однако на этот раз он хочет заплатить всего 93,95 долларов за стодолларовую облигацию. Следующая формула вычисляет процентную ставку за восемь лет, оставшихся до даты погашения: =ДОХОД(СЕГОДНЯ();СЕГОДНЯ()+ДАТА(8;1;0);,06;93,95;100;2). Если инвестор заплатит за облигацию 93,95 долларов, то получит от своих инвестиций 7%. Если бы он заплатил за облигацию больше ста долларов, то получил бы от инвестиций меньше 6% (рис. 2).

Перейти к контенту