Для вычисления значения функции y sin 2 x 3 в ms excel - Word и Excel

Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.

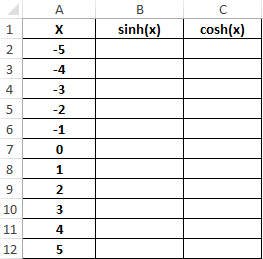
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.

Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.

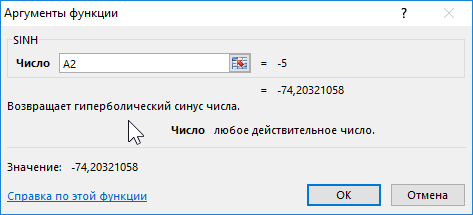
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.

Примеры использования функций SIN, SINH, COS и COSH в Excel

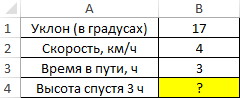
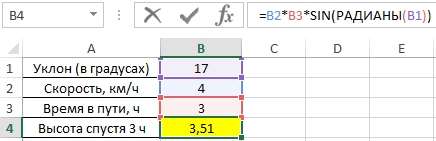
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.

Таблица данных:

Для решения используем формулу:

=B2*B3*SIN(РАДИАНЫ(B1))

Описание аргументов:

B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.

В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.

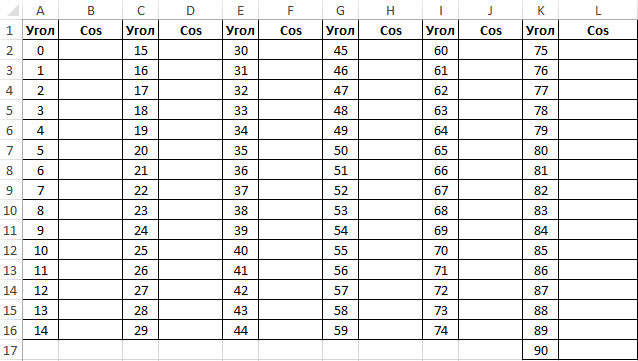
Таблица синусов и косинусов в Excel

Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?

Заполним столбцы значениями углов в градусах:

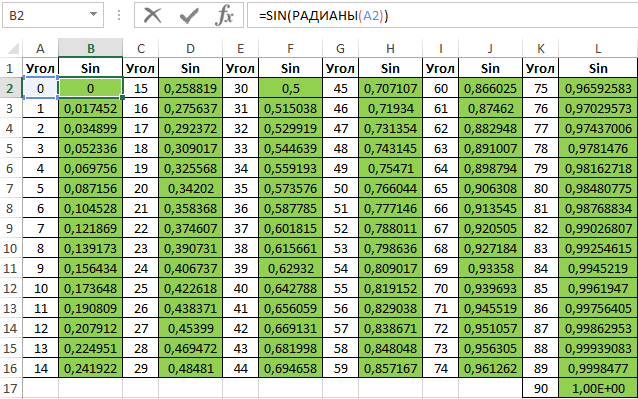
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:

=COS(РАДИАНЫ(A2:A16))

Вычислим значения для всех значений углов. Полученный результат:

Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.

Аналогичным способом создадим таблицу синусов в Excel:

Построение графика функций SINH и COSH в Excel

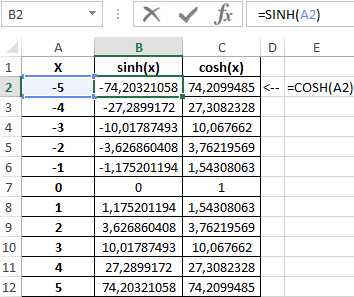
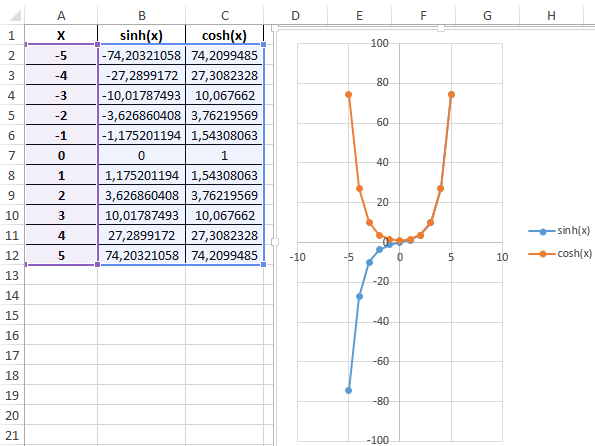
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.

Исходные данные:

Формула для нахождения синусов гиперболических:

=SINH(A2:A12)

Формула для нахождения косинусов гиперболических:

=COSH(A2:A12)

Таблица полученных значений:

COSH.

Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:

Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.

Особенности использования тригонометрических функций в Excel

Синтаксис функции SIN:

=SIN(число)

Синтаксис функции SINH:

=SINH(число)

Синтаксис функции COS:

=COS(число)

Синтаксис функции COSH:

>=COSH(число)

Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).

Примечания 1:

Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
Все рассматриваемые функции могут быть использованы в качестве формул массива.

Примечения 2:

Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:

Скачать примеры тригонометрических функций SIN и COS

Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
Выражение ПИ()*угол_в_градусах/180.

Источник

Пример 1

Дана функция:

Нужно построить ее график на промежутке [-5;5] с шагом равным 1.

Создание таблицы

Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.

Вычисление значений функции

Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).

Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).

Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.

Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.

Построение графика

Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).

Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.

Пример 2

Даны функции:

и y=50x+2. Нужно построить графики этих функций в одной системе координат.

Создание таблицы и вычисление значений функций

Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.

Мы получили таблицу значений переменной х и обеих функций в этих точках.

Построение графиков

Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.

Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.

Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Источник

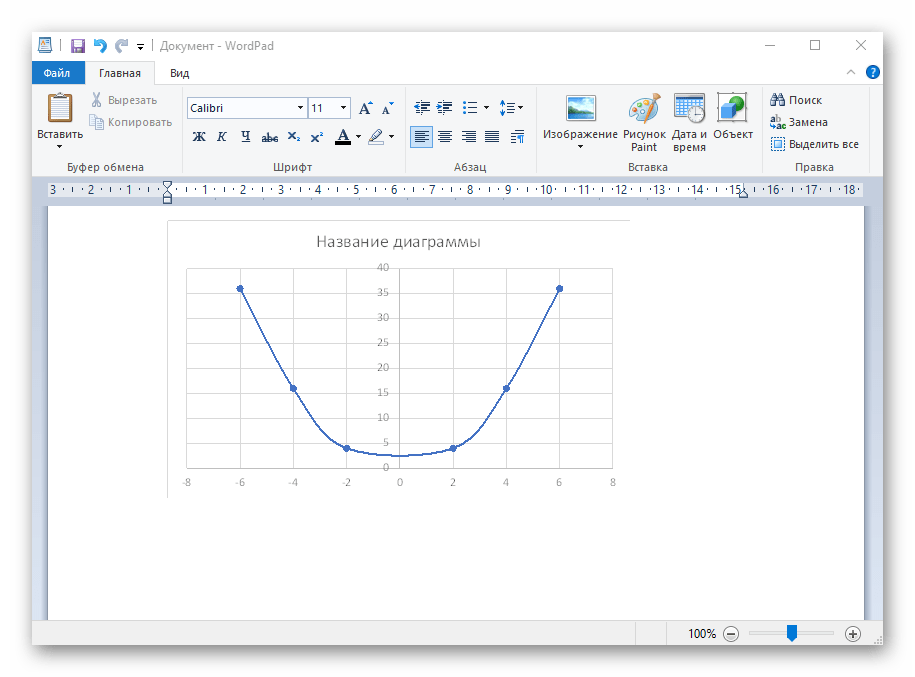
Вариант 1: График функции X^2

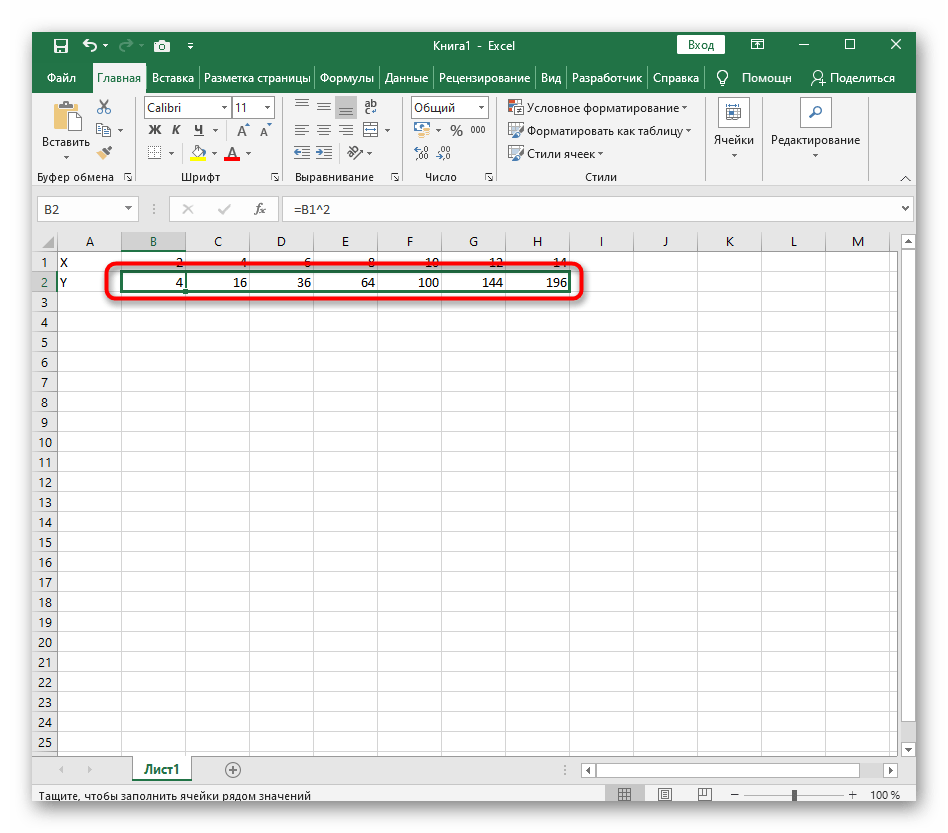
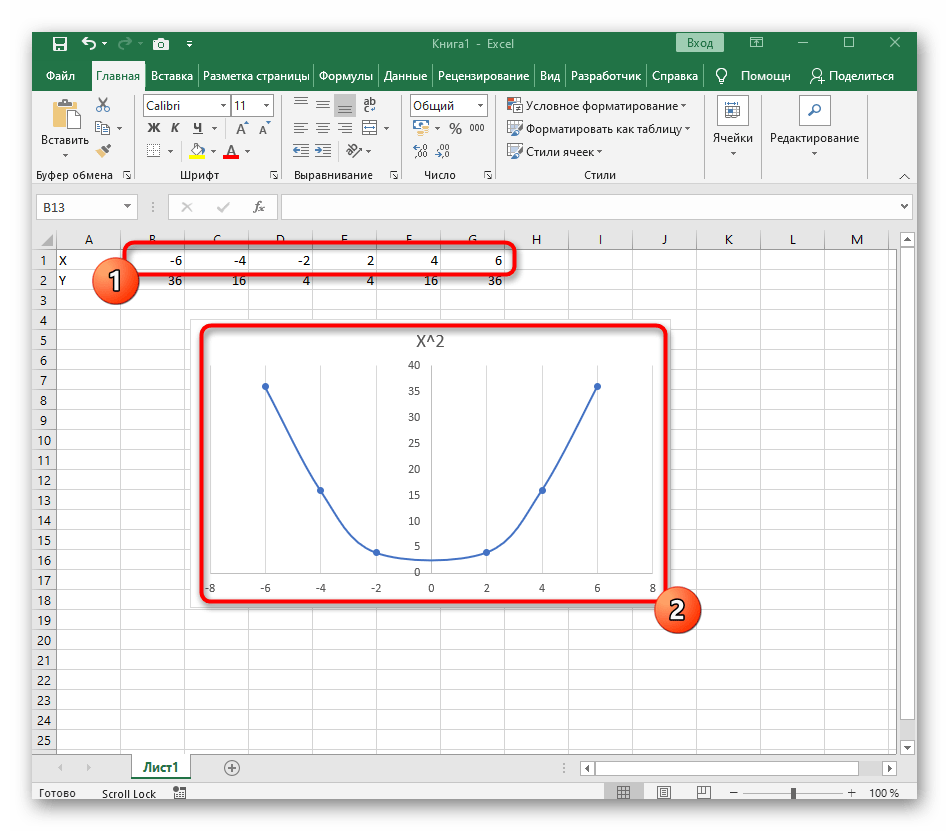
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.

Создайте строку X, где укажите необходимый диапазон чисел для графика функции.

Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.

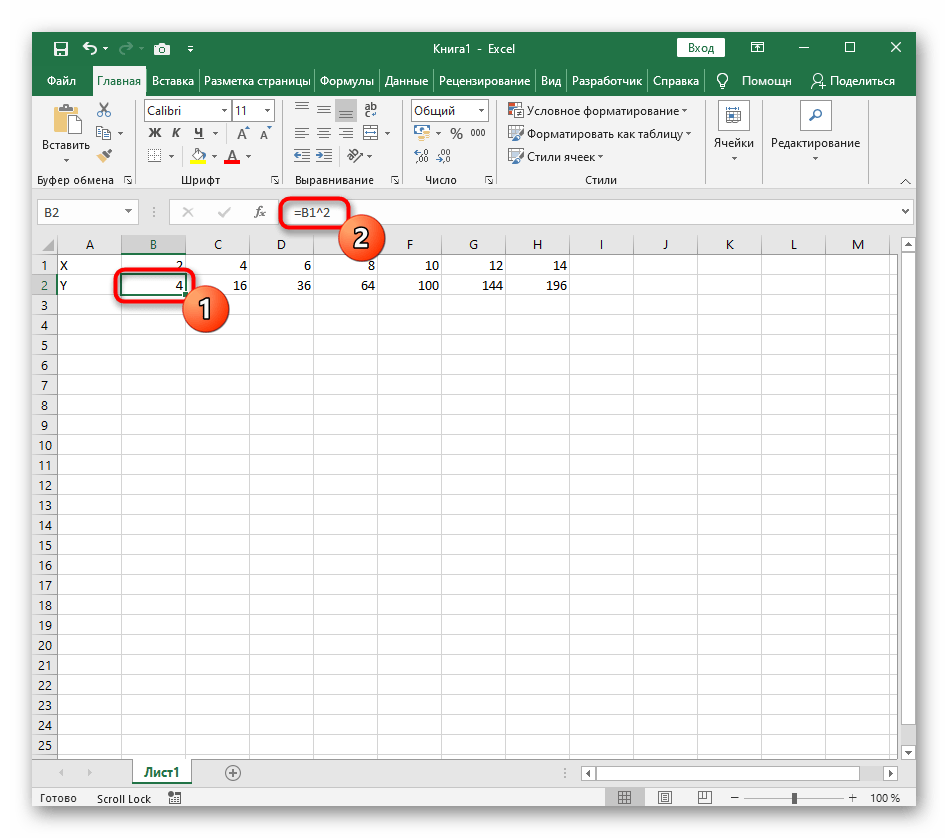
Нажмите по первой ячейке и впишите =B1^2, что значит автоматическое возведение указанной ячейки в квадрат.

Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.

Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».

На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».

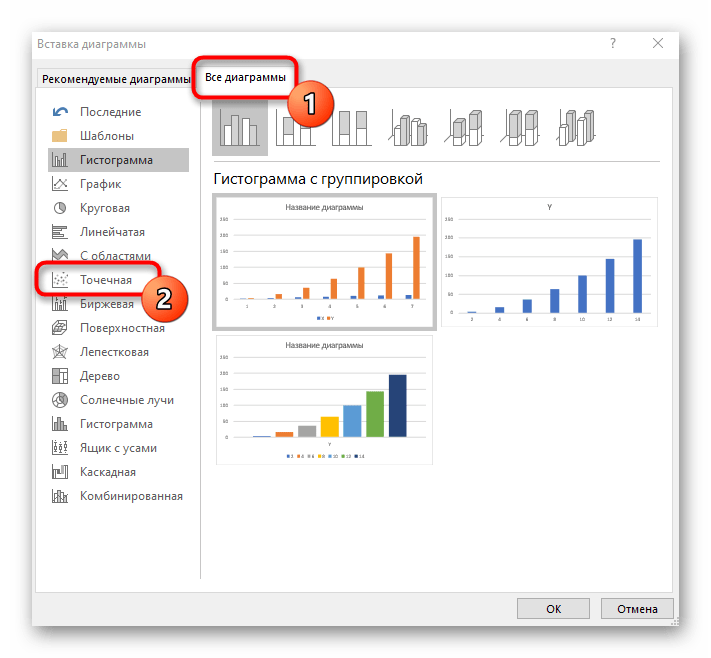
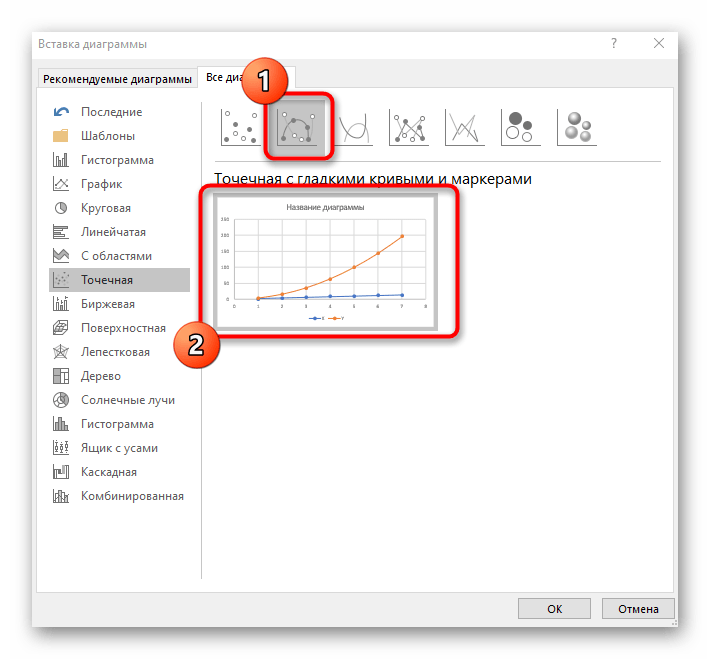
В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».

Подойдет вариант «Точечная с гладкими кривыми и маркерами».

После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.

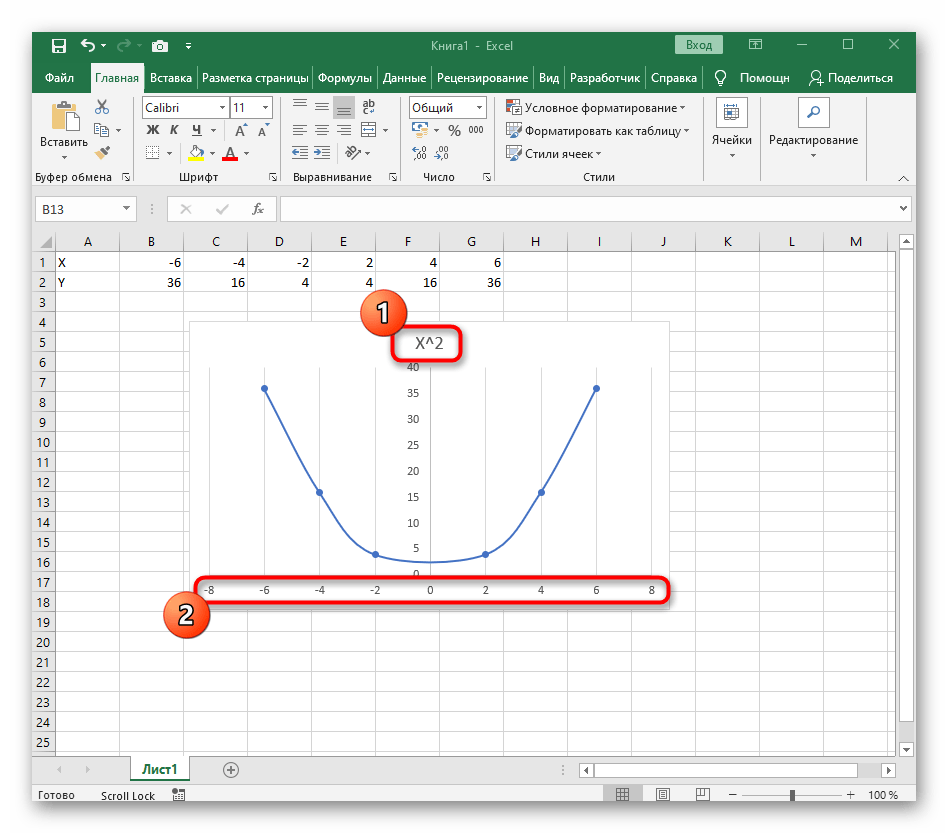
Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.

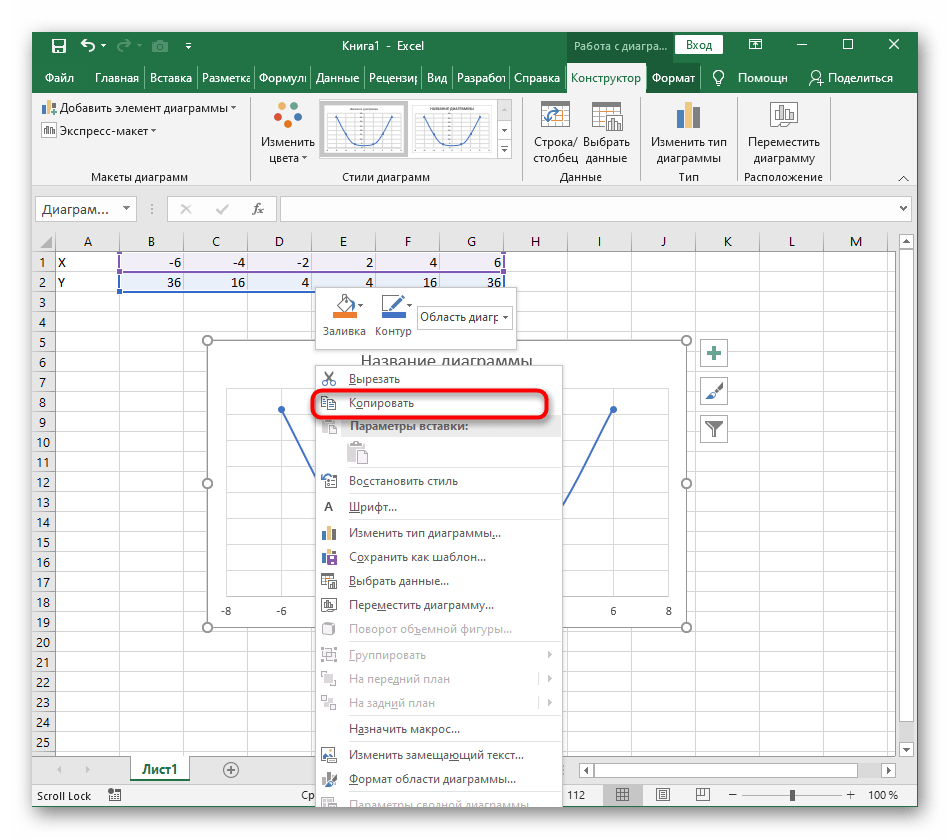
Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».

Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.

Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.

Вариант 2: График функции y=sin(x)

Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.

Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.

Создайте сразу два столбца — X и Y, куда будете записывать данные.

Запишите самостоятельно первые два или три значения с указанным шагом.

Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.

Перейдите к столбцу Y и объявите функцию =SIN(, а в качестве числа укажите первое значение X.

Сама функция автоматически высчитает синус заданного числа.

Растяните столбец точно так же, как это было показано ранее.

Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.

Выделите столбец с Y и перейдите на вкладку «Вставка».

Создайте стандартный график, развернув выпадающее меню.

График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Задание. Создать таблицу с
использованием математических функций,
которая рассчитывает значения функции
y=sin(2x/ 3)*cos(x/2)
на интервале значений х от -
до +2 с шагом 0,1, вычисляет максимальное
и минимальное значения функции на данном
интервале области определения, а также
строит график данной функции.

Запустите программу Excel и для получения
подсказки о синтаксисе тригонометрических
функций в окне справки Excel на вкладке
Содержание выберите раздел Справка
по функциям, тема Математические
функции. Для просмотра информации
щелкните по ссылкам SIN, COS и ПИ. Для
возврата к предыдущему окну справки
щелкайте кнопку «Назад».

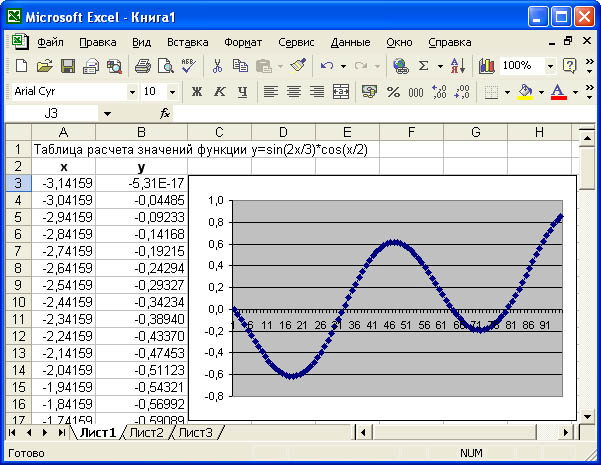
Рис. 1. Таблица расчета значений функции
y=sin(2x/3)*cos(x/2)

После просмотра справки закройте окно
справки любым из стандартных способов.

В ячейку А1 введите заголовок таблицы
«Таблица значений функции
y=sin(2x/3)*cos(x/2). Задайте в ячейке А2 формулу
= -ПИ() для ввода начального значения х.

В ячейке A3 задайте формулу = А2+0,1 для
вычисления следующего значения х,
изменяющегося с шагом 0,1. Скопируйте
формулу из A3 в диапазон (А4:А97).

В ячейку В2 введите формулу расчета
значения функции =SIN(2*A3/3)*COS(A3/2). Затем
скопируйте формулу из ячейкиВ2 в диапазон
(ВЗ:В97).
В ячейку С2 введите формулу определения
минимума функции =МИН(В2:В97), а в ячейку
СЗ — формулу определения максимума
функции =МАКС(В2:В97).

В результате получится таблица, фрагмент
которой показан на рис. 1.

Для построения графика функции выделите
диапазон ячеек (В2:В97) и, щелкнув кнопку

на
панели инструментов Стандартная,
вызовите Мастер диаграмм. На первом
шаге диалога с Мастером диаграмм
выберите тип диаграмм График и
щелкните кнопку «Далее». На втором шаге
определите, что данные для построения
диаграммы берутся из ряда в столбце и
уточните значение диапазона В2:В97.
Щелкнув кнопку «Далее», определите
параметры диаграммы: заголовки, подписи
данных, положение легенды, линии сетки
и т.д. На последнем шаге определите
положение диаграммы на имеющемся листе
и щелкните кнопку «Готово».
Сохраните полученную таблицу, выбрав
в меню Файл команду Сохранить
как, а затем в диалоговом окне
Сохранение документа, открыв нужную
папку, задайте в поле имя файла SIN_COS
и щелкните кнопку «Сохранить».
Для просмотра вида таблицы на бумаге
выберите в меню Файл команду
Предварительный просмотр. Для
перехода к другим страницам щелкните
клавиши Далее или Назад. Для
печати таблицы на бумаге выберите
команду Печать в меню Файл. В
окне Печать укажите номера печатаемых
страниц и количество копий, после чего
щелкните кнопку «ОК» для начала печати.
Закройте окно Excel.

Лабораторная работа 2. Использование логических функций

Задание. Создать таблицу,
которая формирует ведомость на выплату
зарплаты с прогрессивной шкалой
подоходного налога.

Пусть налог исчисляется по прогрессивной
шкале следующим образом: с зарплаты, не
превышающей 1000 руб., налог составляет
12%, а с части зарплаты, превышающей 1000
руб., взыскивается налог 20% от этой части.

1. Вначале определим исходные
данные задачи: фамилии работников
(текст) и размер зарплаты (число с двумя
цифрами в дробной части).

Установим, что мы должны рассчитать в
задаче величины подоходного налога и
получаемой каждым работником суммы.

2. Для выполнения расчетов
запустите Excel, опишите структуру таблицы
и введите исходные данные следующим
образом.

	А	В	С	D
1	Расчет зарплаты с прогрессивной шкалой подоходного налога
2	Фамилия	Зарплата	Налог	Получить
3	Иванов	1234,56
4	Петров	1000
5	Сидоров	1563,35
6	Фролов	986,54
7	Итого	4784,45
8

3. В ячейку СЗ поместите формулу
расчета величины подоходного налога,
вычисляемого по прогрессивной шкале.
Для этого выделите ячейку СЗ и введите
формулу =ЕСЛИ(ВЗ<=1000;
ВЗ*0,12;1000*0,12+(ВЗ-1000)*0,2). В этой формуле
проверяется условие В3<=1000. Если условие
соблюдается, то налог вычисляется по
формуле В3*0,12. Если условие ложно, то
налог вычисляется по формуле
1000*0,12+(ВЗ-1000)*0,2 (12% от суммы зарплаты в
1000 руб. + 20% от суммы, превышающей 1000
руб.).

4. В ячейку D3 введите формулу
=ВЗ-СЗ для определения суммы разности
зарплаты и налога.

5. Скопируйте формулы из
диапазона C3:D3 в диапазон C4:D6. В ячейку
В7 введите формулы суммирования результата
по столбцу В, для чего, выделив ячейки
ВЗ:В6, щелкните кнопку «Автосумма» в
панели инструментов Стандартная.
Скопируйте формулу вычисления суммы
столбца из В7 в C7:D7.

6. Оформите таблицу, выделив
диапазон A2:D7 и выбрав команду Автоформат
в меню Формат. В диалоговом окне
Автоформат из списка форматов
выберите вариант Финансовый 3 и щелкните
кнопку «ОК». Измените формат отображения
значений в ячейках B3:D7, для чего, выделив
этот диапазон, выберите в меню Формат
команду ячейки, затем в диалоговом окне
Формат ячеек выберите Финансовый
формат, в поле Число десятичных
знаков задайте отображение двух цифр
в дробной части, в поле Обозначение
выберите р и щелкните кнопку «ОК»
для применения заданного формата ячеек.
После этого таблица будет иметь следующий
вид .

	А	В	С	D
1	Расчет зарплаты с прогрессивной шкалой подоходного налога
2	Фамилия	Зарплата	Налог	Получить
3	Иванов	1234,56р.	166,91р.	1067,65р.
4	Петров	1000,00р.	120,00р.	880,00р.
5	Сидоров	1563,35р.	232,67р.	1330,68р.
6	Фролов	986,54р.	118,38р.	868,16р.
7	Итого	4784,45р.	637,97р.	4146,48р.

7. Сохраните таблицу под именем
Расчет зарплаты. Для этого в меню
Файл выберите команду Сохранить
как, затем в диалоговом окне Сохранение
файла выберите папку, задайте имя
файла и щелкните кнопку «Сохранить».

8. Завершите работу приложения
Microsoft Excel одним из стандартных способов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Задание . Табулирование функции с параметром. Рассчитайте
таблицу значений функции f(x) = ax² + 7, где x меняется от -2 до 2 с шагом 0, 5. рассчитаем значения
аргумента и значения функции в таблице.

Заполнение диапазона x рис. 8. В ячейку B3
вводим – 2 в ячейку B4 – формулу B3+0,5. Этой формулой
заполняем значения аргументов. Используем автозаполнение.

Рис. 8. Заполнение диапазона x

Заполнение диапазона y рис. 9. В ячейку C3
вводим формулу =$D$3*B3*B3+7. Заполняем этой формулой значения функции.
Используем автозаполнение.

Рис. 9. Заполнение диапазона y

Построение графика, тип диаграммы точечная, рис. 10.

Рис. 10 График функции

Построение
графиков функций

1.
Запустите табличный
процессор OpenOffice.org Calc.

2.
Выделите ячейки А1:F1 и объедините их, используя кнопку –
объединить ячейки на панели инструментов Форматирование.

3.
Введите в объединенные
ячейки заголовок Построение графиков функций.

4.
В ячейку А3 введите
x, а в ячейку В3 – y=sin(x).

5.
В ячейку А4 введите
значение — 6, в А5 – значение —5,5. Выделите
эти две ячейки и наведите указатель мыши на правый нижний угол выделения –
черный квадратик (маркер заполнения). После того, как указатель примет
форму черного крестика, растяните область выделения до значения 6.

6.
В ячейку В4 введите
формулу =sin(A4) и
нажмите клавишу Enter.

7.
Используя маркер
заполнения, скопируйте формулу в остальные ячейки.

8.
Выделите значения двух
столбиков и запустите Мастер диаграмм (Вставка ► Диаграмма).

9.
Выберите тип диаграммы – Диаграмма
XY (только линии).

10.
Приведите диаграмму к
виду, представленному на рис. 2.

Рисунок 2. График функции у=sin(x)

11. Переименуйте Лист1 в Графики функций.

12. Постройте на этом же листе график функции:

на отрезке [-3;3] с шагом 0,2 (рис. 3).

Для того чтобы записать функцию y
воспользуемся логической функцией IF(Логическое выражение; значение_если
истина; значение_если ложь).

Функция IF проверяет
выполняется ли условие, и возвращает одно значение, если оно истинно и другое
значение, если нет.

В нашем случае если xÎ[-1;1], то y = 1–x², в противном случае y = |x|–1.

Чтобы записать условие xÎ[-1;1] воспользуемся логической функцией

AND(логическое
выражение1; логическое выражение2; …).

В нашем случае получим AND(x >=
– 1;x <= 1).

Таким образом формула для нахождения значения функции
будет выглядеть следующим образом:

=IF(AND(А15 >= – 1;А15 <= 1); 1 – А15*А15; ABS(A15) –
1).

Для вычисления модуля используется функция ABS(число).

Рисунок 3. График функции

13.
На втором листе рабочей
книги самостоятельно постройте еще 2 графика:
y = |x²+5x-10|,
[-10;5], шаг 0,5

, [-3;3], шаг 0,5.

Задания на внеаудиторную
самостоятельную работу:

Постройте графики функций.

1	y = x⁵+x²–10, [-10;10], шаг 1
2	y = (tg(x))×x, [-1;1], шаг 0,5
3	y = cos(x+x⁵)–2, [-2;2], шаг 0,5
4	y = \|x³+x –10\|, [-2;2], шаг 0,5
10	y = x+5, [-10;10], шаг 1

Источник