Для решения уравнения с одним неизвестным в excel можно использовать опцию - Word и Excel

Решение уравнений в excel — примеры решений

Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.

Первый метод

Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».

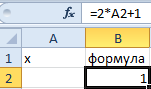
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.

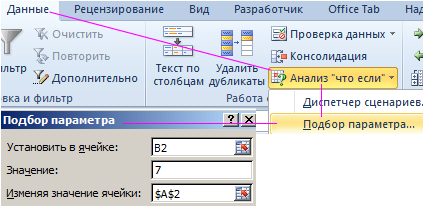
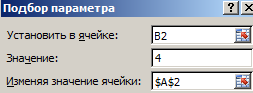
2. Переходите к инструменту и заполняете все необходимые поля

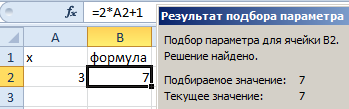
3. После проведения вычислений программа выдаст результат в ячейке с иксом.

4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.

Второй метод

Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.

1. Создаете два диапазона.

На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.

2. Переходите во вкладку Вставка и выбираете обычный график.

3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.

Важно! В настройках оси поставьте положение по делениям.

4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.

Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.

Третий метод

Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.

1. Записываете произвольную систему уравнений.

2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.

3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.

4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.

Жми «Нравится» и получай только лучшие посты в Facebook ↓

Задачи на подбор параметра в excel

Главная > Решение

Информация о документе

Дата добавления:

Размер:

Доступные форматы для скачивания:

Решение задач – Подбор параметра

Задачи оптимизации с одним неизвестным

Задача оптимизации затрат

Подбор параметра и таблицы подстановки

РЕШЕНИЕ ЗАДАЧ – Подбор параметра

Решение задач – одно из важных применений Excel. Самый простой инструмент предназначен для подбора значений и называется «что-если» анализ: задается некоторая целевая функция и ее числовое значение, Excel автоматически подбирает параметры целевой функции до получения целевого значения. Формула в целевой функции должна логически зависеть от подбираемого параметра.

В Excel встроены инструменты для решения задач статистического и инженерного анализа, сложных задач со многими неизвестными и ограничениями, в частности, решения уравнений и задач оптимизации. Эти инструменты поставляются в виде надстроек Поиск решения и Пакет анализа ; устанавливаются через пункт меню Сервис  Надстройки…, далее пометить пункты Поиск решения и Пакет анализа . Смотрите справку – клавиша F1.

Эти инструменты Excel (будут рассмотрены в следующих разделах) полезны экономистам, администраторам, менеджерам, которым для решения деловых проблем и принятия решений в сферах финансов, бухгалтерского учета, маркетинга, управления операциями, экономики, менеджмента необходимо применять количественные методы анализа и прогнозирования.

В качестве примера разберем расчет прибыли от продаж, показанный на рис. 1.20. В ячейках А3, А4 и А7 записаны формулы – формулы для наглядности продублированы в скобках. Поскольку Другие затраты и Количество здесь постоянны, то нужную прибыль можно получить подбором Цены единицы или Себестоимости единицы товара. Попробуем получить прибыль 20000, изменяя Цену единицы . Проделайте следующие действия:

Встаньте на целевую ячейку А7. Выберите пункт меню С е рвис  П одбор параметра… . Введите значение ожидаемой прибыли. Для ввода адреса изменяемой ячейки, перейдите в нижнее поле и встаньте на ячейку А9 в таблице – адрес будет записан автоматически в поле. Нажмите ОК.

В следующем окне можно либо принять, либо отменить результат подбора параметра. Результат:

Самостоятельно попробуйте подобрать Себестоимость единицы , чтобы получить прибыль 20000 при Цене единицы =200.

Далее приводятся другие применения инструмента Подбор параметра .

Задачи оптимизации с одним неизвестным

Часто уравнения не имеют точного аналитического решения. Тогда их решают методом последовательных приближений (итераций) неизвестных параметров так, чтобы они давали минимум ошибки целевой функции.

Для численного решения уравнений с одним неизвестным в Excel имеется эффективный инструмент Подбор параметра . Целевая функция может быть линейной, квадратичной, третьей и выше степени.

Инструмент Подбор параметра был рассмотрен в предыдущем разделе для расчета прибыли от продаж. Здесь рассмотрим его применение для решения некоторого уравнения, например 2х 3 -3х 2 +х-5=0.

Решение задачи состоит из двух этапов. На первом этапе следует ввести уравнение в ячейку (В2), а в другую ячейку (А2) ввести некоторое ориентировочное значение, здесь 1:

На втором этапе следует воспользоваться инструментом Подбор параметра :

Встаньте на ячейку В2 и вызовите его – С е рвис  П одбор параметра… .

В открывшемся окне введите искомое значение функции и адрес изменяемой ячейки:

После нажатия кнопки ОК Вы получите следующее решение:

Найденное решение приближенное, поэтому можно считать, что при х=1,918578609 значение уравнения 2х 3 -3х 2 +х-5 стремится к нулю, т.е. к 0,000107348. Смело установите для ячеек А2 и В2 числовой формат отображения данных и получите следующее:

Следует отметить, что уравнение может иметь более одного решения. Поэтому рекомендуется выполнить подбор параметра для разных начальных значений Х, указывая положительные, отрицательные, большие и малые значения. В нашем примере установите начальное значение А2=–1 и повторите подбор. Решение будет таким же.

Задача оптимизации затрат

С помощью подбора параметров можно решать задачи оптимального распределения ресурсов следующего плана. Требуется закупить составляющие (конфета карамельная, конфета шоколадная, упаковка печенья и мармелада) для комплектования подарочных наборов так, чтобы цена набора не превышала 100 руб. При этом известны соотношения цен относительно одной из компонент (здесь карамели): цена шоколадной конфеты в 2.5 раза выше цены карамели, цена печенья на 10 руб. больше карамели и цена мармелада в 8.5 раза выше цены карамели. В наборе должно быть 5-10 конфет карамель, 4-6 шоколадных конфет, 1-2 упаковки печенья и 1 упаковка мармелада. Рассчитать закупочные цены для разных комплектов.

Ниже показаны расчеты закупочных цен для максимального и минимального комплектов:

В ячейки В4:В6 запишите формулы: =B3*2.5, =B3+10 и =B3*8.5. В колонки D3:D6 поставьте формулы вычисления сумм по строкам, а в D7 вычислите общую сумму: =СУММ(D3:D6). В итоге целевая функция – стоимость набора D7 есть C3* x +C4*2.5* x +C5*( x +10)+C6*8.5* x , где x =B3 цена одной компоненты – конфеты карамель. Параметры инструмента Подбор параметра заполните так:

Подбор параметра и таблицы подстановки

В паре с инструментом Подбор параметра обычно применяют инструмент Таблица подстановки , который позволяет расширить количество одновременно рассчитываемых вариантов решений. Таблицы подстановки создаются на основе одной или двух изменяемых параметров.

Рассмотрим пример. Фирма производит изделия и продает их по цене 90руб. Ежемесячные постоянные затраты составляют 5000руб., переменные затраты на единицу изделия – 30руб. Необходимо определить точку безубыточности, т.е. вычислить количество изделий, при котором прибыль равна 0. Кроме того, требуется определить изменение прибыли для 10 следующих значений количества с шагом 5, а также прибыль при этих значениях количества для цен 80, 85, 95 и 100руб.

Решение. Введите в Excel исходные данные, приведенные ниже:

В точке безубыточности валовая прибыль равна валовым затратам, т.е. (В3*В4)-(В1+В2*В4)=0. Вызовите Подбор параметра , заполните параметры и нажмите ОК – в ячейке В4 будет вычислено значение 83.33 (рис. 17).

На следующем шаге рассчитаем 10 значений прибыли для следующих значений количества с шагом 5. Используем для этого таблицу подстановки с одним изменяемым параметром. Подготовьте исходные данные (рис. 2.35) : в ячейки C4:C13 запишите значения количества с шагом 5, а в колонке справа в строке выше (ячейка D3) — формулу из ячейки В7.

Примените инструмент Таблица подстановки к подготовленным данным: выделите диапазон C3:D13 (рис. 2.36), вызовите пункт Д анные  Т аблица подстановки… , укажите изменяемую ячейку ($B$4) и порядок расположения исходных данных (в строках) в окне запроса – рис. 2.36. После нажатия ОК в ячейках D4:D13 будут рассчитаны значения прибыли.

На последнем шаге рассчитаем значения прибыли для тех же значений количества при ценах 80, 85, 95 и 100руб. Используем для этого таблицу подстановки с двумя изменяемыми параметрами. Результат показан на рис. 2.37.

Для его получения подготовьте исходные данные : в ячейки F4:F13 запишите значения количества, в строке G3:J3 запишите значения цен, на пересечении строки и столбца с данными в ячейке F3 запишите формулу из ячейки В7. Примените инструмент Таблица подстановки к подготовленным данным: выделите диапазон F3:F13 (рис. 2.37), вызовите пункт Д анные  Т аблица подстановки… , укажите изменяемую ячейку по строкам ($B$4) и по столбцам ($B$3) в окне запроса – рис. 2.38. После нажатия ОК в ячейках G4:J13 будут рассчитаны значения прибыли.

Задания для самостоятельного выполнения:

Найдите решение уравнения х 3 +5х 2 -х+1=0

Найдите два решения уравнения х 2 -3х+2=0.

Найдите решение уравнения е х =20000.

Примените инструмент Таблица подстановки при решении предыдущей задачи комплектования подарочных наборов.

Часто нам нужно предварительно спрогнозировать, какие будут результаты вычислений при определенных входящих параметрах. Например, если получить кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?

При разных поставленных подобных задачах, результаты вычислений могут завесить от одного или нескольких изменяемых условий. В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.

Подбор параметра и решение уравнений в Excel

Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:

y =7 является функцией x ;
нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.

Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:

Заполните ячейки листа, так как показано на рисунке:
Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:

В результате мы получили правильное значение 3.

Получили максимально точный результат: 2*3+1=7

Второй пример использования подбора параметра для уравнений

Немного усложним задачу. На этот раз формула выглядит следующим образом:

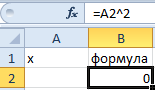
Заполните ячейку B2 формулой как показано на рисунке:
Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
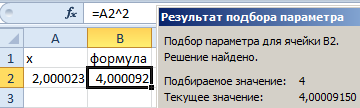
Сравните 2 результата вычисления:

Обратите внимание! В первом примере мы получили максимально точный результат, а во втором – максимально приближенный.

Это простые примеры быстрого поиска решений формул с помощью Excel. Сегодня каждый школьник знает, как найти значение x. Например:

Excel в своих алгоритмах инструментов анализа данных использует более простой метод – подстановки. Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.

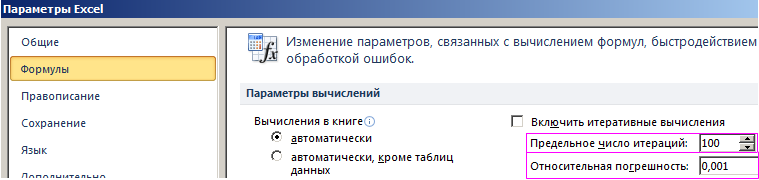
По умолчанию инструмент выполняет 100 повторений (итераций) с точностью 0.001. Если нужно увеличить количество повторений или повысить точность вычисления измените настройки: «Файл»-«Параметры»-«Формулы»-«Параметры вычислений»:

Таким образом, если нас не устраивает результат вычислений, можно:

Увеличить в настройках параметр предельного числа итераций.
Изменить относительную погрешность.
В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).

Используя эти способы настроек можно существенно облегчить и ускорить процесс поиска максимально точного решения.

О подборе нескольких параметров в Excel узнаем из примеров следующего урока.

Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную — скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра.

В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным.

Простейший пример

Найдем значение параметра b в уравнении 2*а+3*b=x, при котором x=21, параметр а=3.

Подготовим исходные данные.

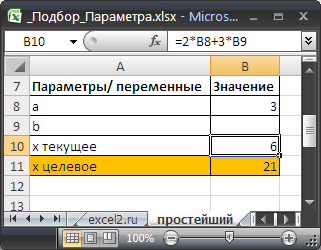
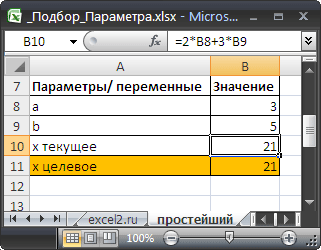
Значения параметров а и b введены в ячейках B8 и B9. В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x). Целевое значение x в ячейке B11 введено для информации.

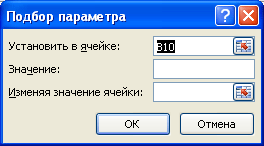
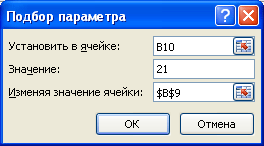
Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…).

В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b).

Инструмент Подбор параметра подобрал значение параметра b равное 5.

Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно.

Примечание: Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b, которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший.

Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X — аналитический. Решение b=(X-2*a)/3) очевидно. Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).

Калькуляция, подбираем значение прибыли

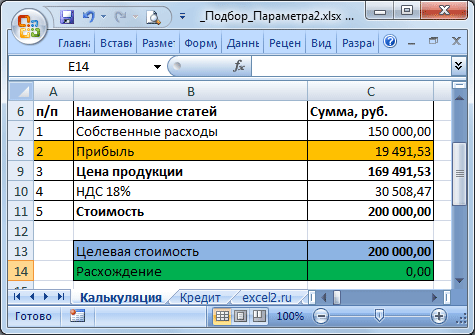
Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.

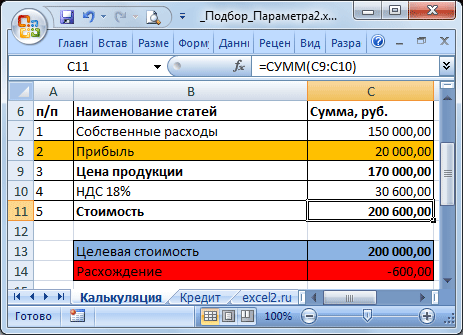
Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли (С8), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение (С14) равно 0.

В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль ( =С7+С8 ). Стоимость договора (ячейка С11) вычисляется как Цена продукции + НДС (= СУММ(С9:C10) ).

Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент Подбор параметра.

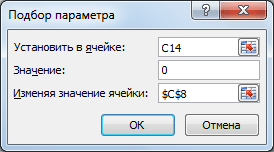
Выделите ячейку С14, вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…). В качестве целевого значения для ячейки С14 укажите 0, изменять будем ячейку С8 (Прибыль).

Теперь, о том когда этот инструмент работает.
1. Изменяемая ячейка не должна содержать формулу, только значение.
2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.
3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0

Примечание : В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.

Подбор суммы кредита

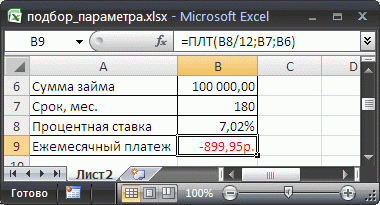
Предположим, что нам необходимо определить максимальную сумму кредита, которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).

В EXCEL существует функция ПЛТ() для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см. статьи про аннуитет). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции ПЛТ() ) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента Подбор параметра сумму займа пришлось бы подбирать в ручную с помощью функции ПЛТ() или использовать соответствующую формулу.

Введем в ячейку B6 ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку B7, % ставку по кредиту введем в ячейку B8, а формулу =ПЛТ(B8/12;B7;B6) для расчета суммы ежемесячного платежа в ячейку B9 (см. файл примера ).

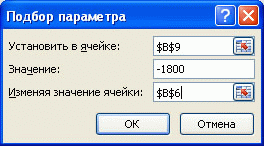
Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:

на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…;
в поле Установить введите ссылку на ячейку, содержащую формулу. В данном примере — это ячейка B9;
введите искомый результат в поле Значение. В данном примере он равен -1800;
В поле Изменяя значение ячейки введите ссылку на ячейку, значение которой нужно подобрать. В данном примере — это ячейка B6;
Нажмите ОК

Что же сделал Подбор параметра? Инструмент Подбор параметра изменял по своему внутреннему алгоритму сумму в ячейке B6 до тех пор, пока размер платежа в ячейке B9 не стал равен 1800,00 руб. Был получен результат — 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.

Подбор параметра подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте инструмент Поиск решения. Точность подбора параметра можно задать через меню Кнопка офис/ Параметры Excel/ Формулы/ Параметры вычислений . Вопросом об единственности найденного решения Подбор параметра не занимается, вероятно выводится первое подходящее решение.

Иными словами, инструмент Подбор параметра позволяет сэкономить несколько минут по сравнению с ручным перебором.

Урок по теме «Решение уравнений в среде MS Excel»

Одна из наиболее актуальных проблем компьютерного обучения – проблема отбора и использования педагогически целесообразных обучающих программ.

При изучении отдельных тем и решении некоторых задач на уроках математики в старших классах громоздкие вычисления как, например, при решении уравнений методом деления отрезка пополам или методом последовательных приближений, затмевают существо математической задачи, не дают увидеть красоту, рациональность применяемого метода решения.

В данной статье я представила те задачи, решение которых с помощью MS EXCEL позволяет получить наглядное, доступное для понимания учащимися решение, показать его логику, рациональность. Попутно учащиеся получают устойчивые навыки работы с программой.

Нахождение корней уравнения с помощью подбора параметра

Пример 1.

Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующая хозяйством и заведующий больницей. Общий месячный фонд зарплаты составляет 1000 000 условных единиц. Необходимо определить, какими должны быть оклады сотрудников больницы.

Решение такой задачи можно искать методом перебора. Однако в лучшем случае на это уходит много времени. Можно предложить другой способ решения. В EXCEL он реализован как поиск значения параметра формулы, удовлетворяющего ее конкретному значению.

Построим модель решения этой задачи. За основу возьмем оклад санитарки, а остальные оклады будем вычислять, исходя из него: во столько-то раз или на столько-то больше. Говоря математическим языком, каждый оклад является линейной функцией от оклада санитарки: A_i*С+В_i, где С – оклад санитарки; А_i и В_i – коэффициенты, которые для каждой должности определяют следующим образом:

медсестра получает в 1,5 раза больше санитарки (А₂=1,5; В₂=0);
врач – в 3 раза больше санитарки (А₃=3; В₃=0);
заведующий отделением – на 30 y.e. больше, чем врач (А₄=3; B₄=30);
заведующий аптекой – в 2 раза больше санитарки (А₅=2; В₅=0);
заведующий хозяйством – на 40 y.e. больше медсестры (А₆=1,5; В₆=40);
заведующий больницей – на 20 y.e. больше главного врача (А₈=4; В₈=20);
главный врач – в 4 раза больше санитарки (А₇=4; В₇=0);

Зная количество человек на каждой должности, нашу модель можно записать как уравнение: N₁*(A₁*C+B₁)+N₂*(A₂*C+B₂)+. +N₈*(A₈*C+B₈) = 1000000, где N₁ – число санитарок, N₂ – число медсестер и т.д.

В этом уравнении нам известны A₁. A₈, B₁. B₈ и N₁. N₈, а С неизвестно. Анализ уравнения показывает, что задача вычисления заработной платы свелась к решению линейного уравнения относительно С. Предположим, что зарплата у санитарки 150,00 y.e.

Введите исходные данные в рабочий лист электронной таблицы, как показано ниже.

Оклад мед. Работников

Общий фонд равен

В столбце D вычислите заработную плату для каждой должности. Например, для ячейки D4 формула расчета имеет вид =B4*$D$3+C4.

В столбце F вычислите заработную плату всех работников данной должности. Например, для ячейки F3 формула расчета имеет вид =D3*E3.

В ячейке F11вычислите суммарный фонд заработной платы больницы. Рабочий лист электронной таблицы будет выглядеть, как показано ниже.

Оклад мед. Работников

Общий фонд равен

Чтобы определите оклад санитарки так, чтобы расчетный фонд был равен заданному надо:

Активизировать команду Подбор параметра во вкладке Данные / Работа с данными /Анализ «Что, если»;
В поле «Установить в ячейке» появившегося окна ввести ссылку на ячейку F11, содержащую формулу;
В поле «Значение» набрать искомый результат 1000000;
В поле «Изменяя значение ячейки» ввести ссылку на изменяемую ячейку D3 и щелкните на кнопке ОК.

Анализ задачи показывает, что с помощью Excel можно решать линейные уравнения. Конечно, такое уравнение может решить любой школьник. Однако, благодаря этому простому примеру стало, очевидным, что поиск значения параметра формулы, удовлетворяющего ее конкретному значению, – это не что иное, как численное решение уравнений. Другими словами, используя Excel, можно решать любые уравнения с одной переменной.

Задание для учащихся:

Составить несколько вариантов штатного расписания с использованием функции Подбор параметра и оформить их в виде таблицы:

Изменить количество сотрудников на различных должностях;
Подобрать зарплату санитарки в новых условиях;
Составить таблицу нескольких вариантов штатного расписания.

Рассмотрим еще один пример нахождения корней уравнения с помощью подбора параметра. При решении этого уравнения используется также метод последовательных приближений. Учащиеся в классах с углубленным изучением математики знакомы с этим методом. Поэтому, чтобы этот пример был доступен для других учащихся, предлагаю краткую теорию этого метода.

Пусть дано уравнение, записанное в виде x=F(x). Выбирают некоторое начальное приближение x₁ и подставляют его вместо x в F(x). Полученное значение x₂=F(x₁) этой функции считают вторым приближением. Далее находят третье приближение по формуле x₃=F(x₂) и так далее. Таким образом, получаем последовательность x₁, x₂, x₃,…, x_n,… чисел, имеющая предел α. Тогда если функция F(x) непрерывна, из равенства x_n+1=F(x_n) получаем α=F(α). Это означает, что α является решением уравнения x=F(x).

Пример 2.

Пусть нам дан многочлен третьей степени:

x 3 -0,01x 2 -0,7044x+0,139104=0.

Так как мы ищем корни полинома третьей степени, то имеются не более трех вещественных корней. Для нахождения корней их первоначально надо локализовать, то есть найти интервалы, на которых они существуют. Такими интервалами локализации корней могут служить промежутки, на концах которых функция имеет противоположный знак. С целью нахождения интервалов, на концах которых функция изменяет знак, необходимо построить ее график или протабулировать ее. Составим таблицу значений функции на интервале [-1;1] с шагом 0,2. Для этого необходимо:

источники:

http://planshet-info.ru/kompjutery/zadachi-na-podbor-parametra-v-excel

http://urok.1sept.ru/articles/606276

Источник

Очень полезной функцией в программе Microsoft Excel является Подбор параметра. Но, далеко не каждый пользователь знает о возможностях данного инструмента. С его помощью, можно подобрать исходное значение, отталкиваясь от конечного результата, которого нужно достичь. Давайте выясним, как можно использовать функцию подбора параметра в Microsoft Excel.

Суть функции

Если упрощенно говорить о сути функции Подбор параметра, то она заключается в том, что пользователь, может вычислить необходимые исходные данные для достижения конкретного результата. Эта функция похожа на инструмент Поиск решения, но является более упрощенным вариантом. Её можно использовать только в одиночных формулах, то есть для вычисления в каждой отдельной ячейке нужно запускать всякий раз данный инструмент заново. Кроме того, функция подбора параметра может оперировать только одним вводным, и одним искомым значением, что говорит о ней, как об инструменте с ограниченным функционалом.

Применение функции на практике

Для того, чтобы понять, как работает данная функция, лучше всего объяснить её суть на практическом примере. Мы будем объяснять работу инструмента на примере программы Microsoft Excel 2010, но алгоритм действий практически идентичен и в более поздних версиях этой программы, и в версии 2007 года.

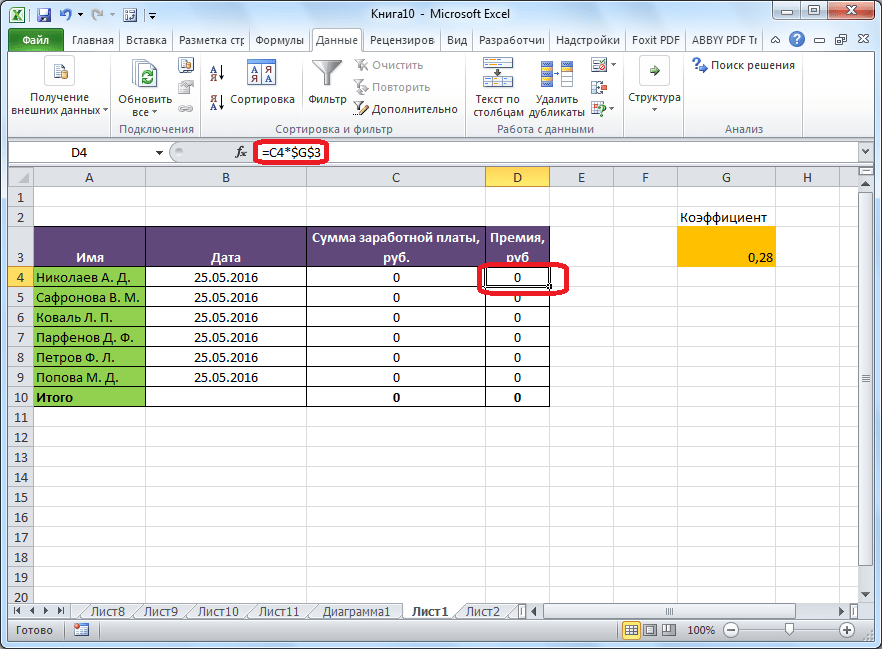
Имеем таблицу выплат заработной платы и премии работникам предприятия. Известны только премии работников. Например, премия одного из них — Николаева А. Д, составляет 6035,68 рублей. Также, известно, что премия рассчитывается путем умножения заработной платы на коэффициент 0,28. Нам предстоит найти заработную плату работников.

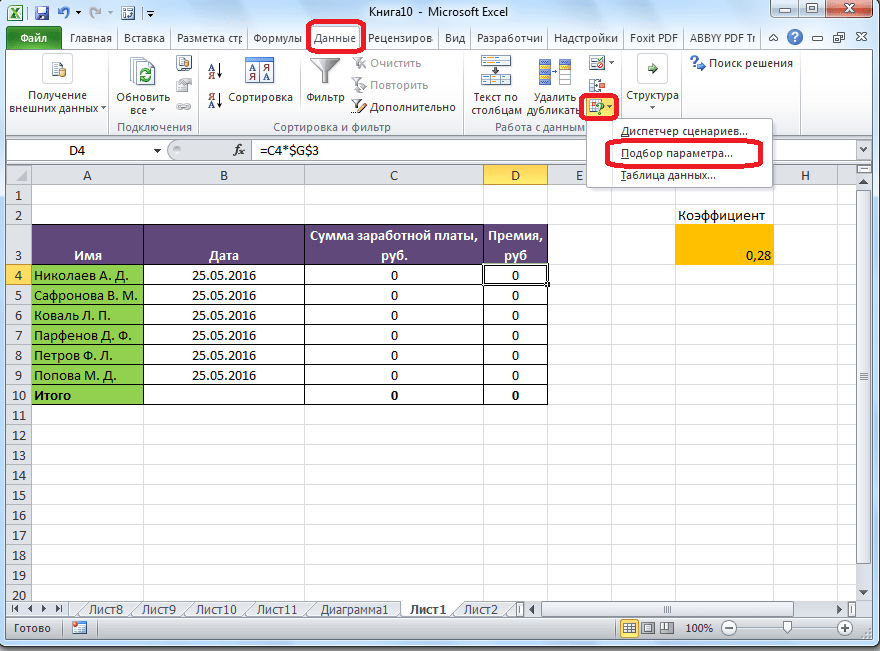
Для того, чтобы запустить функцию, находясь во вкладке «Данные», жмем на кнопку «Анализ «что если»», которая расположена в блоке инструментов «Работа с данными» на ленте. Появляется меню, в котором нужно выбрать пункт «Подбор параметра…».

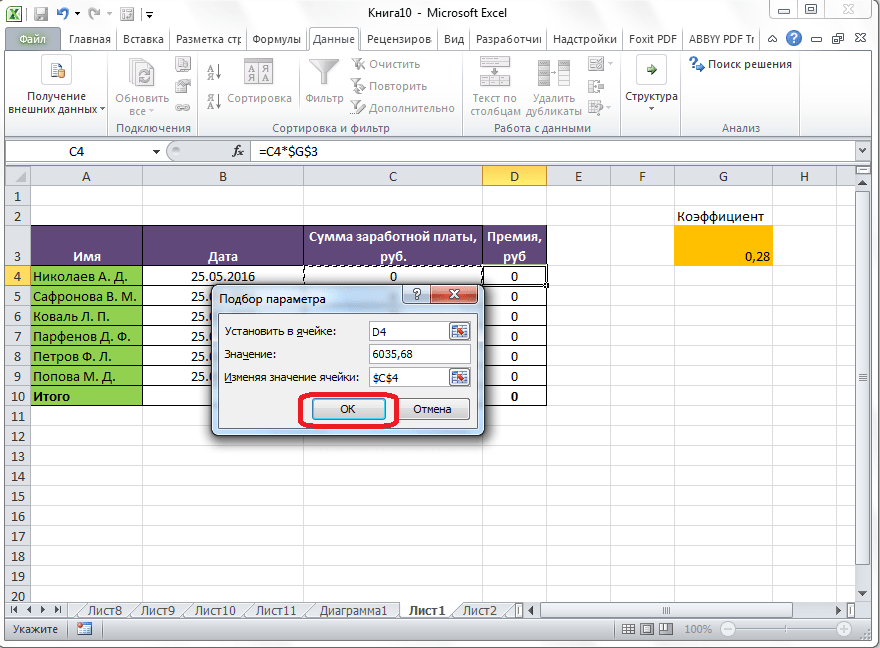
После этого, открывается окно подбора параметра. В поле «Установить в ячейке» нужно указать ее адрес, содержащей известные нам конечные данные, под которые мы будем подгонять расчет. В данном случае, это ячейка, где установлена премия работника Николаева. Адрес можно указать вручную, вбив его координаты в соответствующее поле. Если вы затрудняетесь, это сделать, или считаете неудобным, то просто кликните по нужной ячейке, и адрес будет вписан в поле.

В поле «Значение» требуется указать конкретное значение премии. В нашем случае, это будет 6035,68. В поле «Изменяя значения ячейки» вписываем ее адрес, содержащей исходные данные, которые нам нужно рассчитать, то есть сумму зарплаты работника. Это можно сделать теми же способами, о которых мы говорили выше: вбить координаты вручную, или кликнуть по соответствующей ячейке.

Когда все данные окна параметров заполнены, жмем на кнопку «OK».

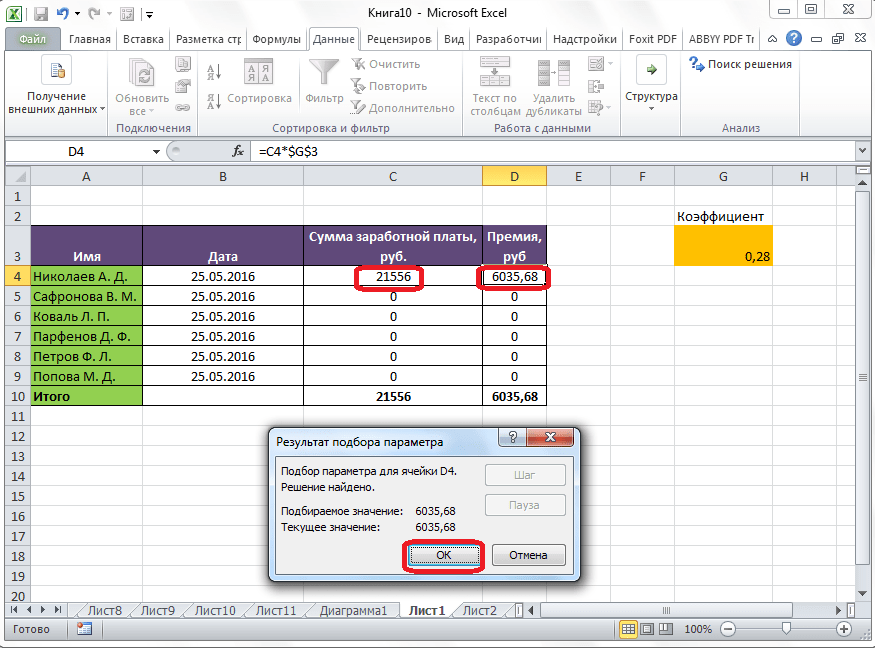
После этого, совершается расчет, и в ячейки вписываются подобранные значения, о чем сообщает специальное информационное окно.

Подобную операцию можно проделать и для других строк таблицы, если известна величина премии остальных сотрудников предприятия.

Решение уравнений

Кроме того, хотя это и не является профильной возможностью данной функции, её можно использовать для решения уравнений. Правда, инструмент подбора параметра можно с успехом использовать только относительно уравнений с одним неизвестным.

Допустим, имеем уравнение: 15x+18x=46. Записываем его левую часть, как формулу, в одну из ячеек. Как и для любой формулы в Экселе, перед уравнением ставим знак «=». Но, при этом, вместо знака x устанавливаем адрес ячейки, куда будет выводиться результат искомого значения.

В нашем случае, формулу мы запишем в C2, а искомое значение будет выводиться в B2. Таким образом, запись в ячейке C2 будет иметь следующий вид: «=15*B2+18*B2».

Запускаем функцию тем же способом, как было описано выше, то есть, нажав на кнопку «Анализ «что если»» на ленте», и перейдя по пункту «Подбор параметра…».

В открывшемся окне подбора параметра, в поле «Установить в ячейке» указываем адрес, по которому мы записали уравнение (C2). В поле «Значение» вписываем число 45, так как мы помним, что уравнение выглядит следующим образом: 15x+18x=46. В поле «Изменяя значения ячейки» мы указываем адрес, куда будет выводиться значение x, то есть, собственно, решение уравнения (B2). После того, как мы ввели эти данные, жмем на кнопку «OK».

Как видим, программа Microsoft Excel успешно решила уравнение. Значение x будет равно 1,39 в периоде.

Изучив инструмент Подбор параметра, мы выяснили, что это довольно простая, но вместе с тем полезная и удобная функция для поиска неизвестного числа. Её можно использовать как для табличных вычислений, так и для решения уравнений с одним неизвестным. Вместе с тем, по функционалу она уступает более мощному инструменту Поиск решения.

Источник

В
экономической работе и других областях
деятельности часто приходится сталкиваться
с задачами по вычислению какого-либо
параметра математического выражения.
Рассмотрим несколько примеров.

Уровень
инфляции 30% в год. Чему равен ежемесячный
рост цен? Для определения увеличения
цен за месяц необходимо решить уравнение
(1+Х)¹²=1,30

В
ячейку А1
рабочего листа Excel 2000 вносим какое-либо
число, которое, по нашему мнению, может
быть решением, например, 1.
В др. ячейку, например, В1
записываем формулу зависимости годовой
величины инфляции от ежемесячного роста
цен. Последняя ячейка должна остаться
выделенной. Затем даём команду
Сервис—›Подбор
параметра.
На экране появится диалоговое окно, в
котором потребуется заполнить 3 строки:

1
— указать адрес ячейки, в которую записана
формула,

2
— указать требуемое значение этой
формулы,

3
— указать адрес ячейки, где находится
изменяемый параметр. В нашем случае в
первой строке появится адрес выделенной
ячейки, т.е. нужное значение в ней появится
автоматически. Во 2-ю строку надо записать
число 1,30
(целая часть от дробной отделяется
запятой, а не точкой), а в 3-ю —
А1. Далее
следует щёлкнуть мышью по кнопке «ОК»,
и через мгновение будет получен ответ
0,022115,
т.е. ежемесячный рост цен ~2,2%.
Очевидно, между величинами, помещёнными
в 1-ю и 3-ю строки окна диалога должна
существовать функциональная зависимость.
Если в качестве изменяемой указать
ячейку, содержание которой не влияет
на результат, то программа даст ответ
«Решение не найдено».

Допустимо
совместное использование функций
рабочего листа и процедуры подбора
параметра.

§ 11 Графическое представление данных с помощью диаграмм

	Таблица 22
ТИП ТРАК	ВЫРАБОТКА
МТЗ-52	3600
Т-75	1742
ДТ-54А	6054

Диаграммы, как
правило, используются для наглядного
представления соотношений между
какими-либо величинами или динамики их
изменения. Excel 2000 предоставляет в
распоряжение пользователя целый ряд
средств для работы с диаграммами
(Мастер диаграмм). Во многих случаях
целесообразно перед созданием диаграммы
выделить ячейки, содержащие необходимые
данные.

Для
вызова мастера диаграмм достаточно
либо дать команду Вставка
—› Диаграмма,
либо нажать соответствующую кнопку на
стандартной панели инструментов. После
этого откроется диалог, состоящий из
4-х шагов. На каждом шаге требуется
выбрать один из предлагаемых вариантов,
после чего щёлкнуть по кнопке «Далее»
— переход к следующему шагу, «Готово»
— автоматическое завершение процесса
создания диаграммы в соответствии с
установками программы по умолчанию,
«Назад»
— возврат к предыдущему шагу, «Отмена»
— отказ от построения диаграммы. На
первом
этапе в
диалоговом окне необходимо указать вид
тип диаграммы, например, гистограмма
или круговая на вкладке «Стандартные».
Второй
шаг
– указать
диапазон ячеек, в котором содержится
исходная информация, а также определить
«направление» последовательности
данных, в строках или в столбцах. Если
диапазон был выделен до начала построения,
соответствующая информация будет
введена в программу автоматически.
Названия строк и столбцов таблицы должны
быть включены в выделенную область.
Третий шаг
– ввод дополнительной информации
(названия диаграммы и осей, включение
или невключение в диаграмму легенды и
таблицы данных и т.д.). Четвёртый
шаг
–разместить диаграмму на текущем листе
или на отдельном. Далее пользователь
нажимает на кнопку «Готово»,
и диаграмма появляется на экране
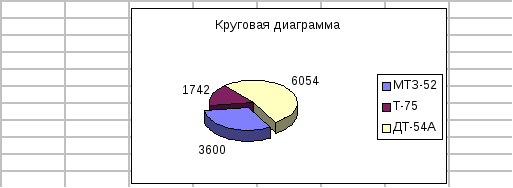
монитора. В качестве примера на рис 2а,б
показаны гистограмма и круговая
диаграмма, построенные на основе данных
таблицы 22.

Рис.
2б

ледует также отметить, что вертикальная
ось — ось значений, а горизонтальная —
ось категорий, т.е. на ней все названия,
даже, если они имеют форму цифровых
значений, воспринимаются как текст и
располагаются на равных расстояниях.
Это следует иметь в виду при построении
графиков, что тоже возможно. Если дважды
щёлкнуть мышью по созданной диаграмме,
вокруг неё появится контур, что
свидетельствует о возможности
редактирования диаграммы.

В
частности, потянув левой клавишей мыши
какой-либо из квадратов на этом контуре,
можно изменять размер области диаграммы.
Изменяется также содержание ряда
пунктов меню, расположенного в верхней
части окна. Это относится, главным
образом, к пунктам «Вставка»
и «Формат».
Через команды меню «Вставка»
пользователь имеет возможность дополнить
диаграмму новыми данными, например,
ввести новый тип трактора, а также ввести
числовые метки, легенду, если она
отсутствует, и т.д. В пункте «Формат»
появляются команды, позволяющие изменить
формат диаграммы, например, круговую
диаграмму превратить в гистограмму или
изменить объёмное положение диаграммы
путём поворота вокруг одной из осей, и
т.д. Щёлкнув мышью по средней части
диаграммы, области построения, пользователь
получает возможность редактировать
отдельные её элементы, например, линии
сетки, шкалу вертикальной оси и т.д.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Уравнение с одной неизвестной в эксель

Если в ячейку Excel введена формула, содержащая ссылку на эту же самую ячейку (может быть и не напрямую, а опосредованно — через цепочку других ссылок), то говорят, что имеет место циклическая ссылка (цикл). На практике к циклическим ссылкам прибегают, когда речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. В обычном режиме Excel обнаруживает цикл и выдает сообщение о возникшей ситуации, требуя ее устранения. Excel не может провести вычисления, так как циклические ссылки порождают бесконечное количество вычислений. Есть два выхода из этой ситуации: устранить циклические ссылки или допустить вычисления по формулам с циклическими ссылками (в последнем случае число повторений цикла должно быть конечным).

Рассмотрим задачу нахождения корня уравнения методом Ньютона с использованием циклических ссылок. Возьмем для примера квадратное уравнение: х 2 — 5х + 6=0, графическое представление которого приведено на рис. 8. Найти корень этого (и любого другого) уравнения можно, используя всего одну ячейку Excel.

Для включения режима циклических вычислений в меню Сервис/Параметры/вкладка Вычисления включаем флажок Итерации, при необходимости изменяем число повторений цикла в поле Предельное число итераций и точность вычислений в поле Относительная погрешность (по умолчанию их значения равны 100 и 0,0001 соответственно). Кроме этих установок выбираем вариант ведения вычислений: автоматически или вручную. При автоматическом вычислении Excel выдает сразу конечный результат, при вычислениях, производимых вручную, можно наблюдать результат каждой итерации.

Рис. 8. График функции

Выберем произвольную ячейку, присвоим ей новое имя, скажем — Х, и введем в нее рекуррентную формулу, задающую вычисления по методу Ньютона:

где F и F1 задают соответственно выражения для вычисления значений функции и ее производной. Для нашего квадратного уравнения после ввода формулы в ячейке появится значение 2, соответствующее одному из корней уравнения (рис. 8). В нашем случае начальное приближение не задавалось, итерационный вычислительный процесс начинался со значения, по умолчанию хранимого в ячейке Х и равного нулю. А как получить второй корень? Обычно это можно сделать изменением начального приближения. Решать проблему задания начальных установок в каждом случае можно по-разному. Мы продемонстрируем один прием, основанный на использовании функции ЕСЛИ. С целью повышения наглядности вычислений ячейкам были присвоены содержательные имена (рис. 9).

В ячейку Хнач (В4) заносим начальное приближение — 5.
В ячейку Хтекущ (С4) записываем формулу:
=ЕСЛИ(Хтекущ=0;Хнач; Хтекущ-(Хтекущ^2-5*Хтекущ+6)/(2*Хтекущ-5)).
В ячейку D4 помещаем формулу, задающую вычисление значения функции в точке Хтекущ, что позволит следить за процессом решения.
Заметьте, что на первом шаге вычислений в ячейку Хтекущ будет помещено начальное значение, а затем уже начнется счет по формуле на последующих шагах.

Чтобы сменить начальное приближение, недостаточно изменить содержимое ячейки Хнач и запустить процесс вычислений. В этом случае вычисления будут продолжены, начиная с последнего вычисленного

Рис. 9. Определение начальных установок

значения. Чтобы обнулить значение, хранящееся в ячейке Хтекущ, нужно заново записать туда формулу. Для этого достаточно для редактирования выбрать ячейку, содержащую формулу, дважды щелкнув мышью на ней (при этом содержимое ячейки отобразится в строке формул). Щелчок по кнопке (нажатие клавиши) Enter запустит вычисления с новым начальным приближением.

2.2. Подбор параметра

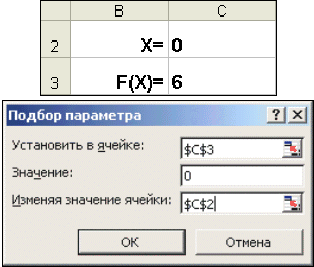
Когда желаемый результат вычислений по формуле известен, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.

Возьмем в качестве примера все то же квадратное уравнение х 2 -5х+6=0. Для нахождения корней уравнения выполним следующие действия:

В ячейку С3 (рис. 10) введем формулу для вычисления значения функции,

Рис. 10. Окно диалога Подбор параметра

стоящей в уравнении слева от знака равенства. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6.

В окне диалога Подбор параметра (рис. 10) в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение — ожидаемый результат, в поле Изменяя значения ячейки — ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).
После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки. Для восстановления значения, которое было в ячейке С2 до использования команды Подбор параметра, нажмите кнопку Отмена.

При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка Продолжить — для возврата в обычный режим подбора параметра.

Вернемся к примеру. Опять возникает вопрос: как получить второй корень? Как и в предыдущем случае необходимо задать начальное приближение. Это можно сделать следующим образом (рис. 11,а):

В ячейку Х (С2) вводим начальное приближение.
В ячейку Х_i (С3) вводим формулу для вычисления очередного приближения к корню, т.е.
=X-(X^2-5*X+6)/(2*X-5).
В ячейку С4 поместим формулу, задающую вычисление значения функции, стоящей в левой части исходного уравнения, в точке Х_i.
После этого выбираем команду Подбор параметра, где в качестве изменяемой ячейки принимаем ячейку С2. Результат вычислений изображен на рис. 11,б (в ячейке С2 — конечное значение, а в ячейке С3 — предыдущее).

Однако все это можно сделать и несколько проще. Для того чтобы найти второй корень, достаточно в качестве начального приближения (рис. 10) в ячейку C2 поместить константу 5 и после этого запустить процесс Подбор параметра.

2.3. Поиск решения

Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения, зависящего от одного неизвестного параметра. Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню Сервис/Поиск решения.

Задачи, которые можно решать с помощью Поиска решения, в общей постановке формулируются так:

Искомые переменные — ячейки рабочего листа Excel — называются регулируемыми ячейками. Целевая функция F(х₁, х₂, … , х_n), называемая иногда просто целью, должна задаваться в виде формулы в ячейке рабочего листа. Эта формула может содержать функции, определенные пользователем, и должна зависеть (ссылаться) от регулируемых ячеек. В момент постановки задачи определяется, что делать с целевой функцией. Возможен выбор одного из вариантов:

найти максимум целевой функции F(х₁, х₂, … , х_n);
найти минимум целевой функции F(х₁, х₂, … , х_n);
добиться того, чтобы целевая функция F(х₁, х₂, … , х_n) имела фиксированное значение: F(х₁, х₂, … , х_n) = a.

Функции G(х₁, х₂, … , х_n) называются ограничениями. Их можно задать как в виде равенств, так и неравенств. На регулируемые ячейки можно наложить дополнительные ограничения: неотрицательности и/или целочисленности, тогда искомое решение ищется в области положительных и/или целых чисел.

Под эту постановку попадает самый широкий круг задач оптимизации, в том числе решение различных уравнений и систем уравнений, задачи линейного и нелинейного программирования. Такие задачи обычно проще сформулировать, чем решать. И тогда для решения конкретной оптимизационной задачи требуется специально для нее сконструированный метод. Решатель имеет в своем арсенале мощные средства решения подобных задач: метод обобщенного градиента, симплекс-метод, метод ветвей и границ.

Выше для нахождения корней квадратного уравнения был применен метод Ньютона (п. 1.4) с использованием циклических ссылок (п. 2.1) и средство Подбор параметра (п. 2.2). Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.

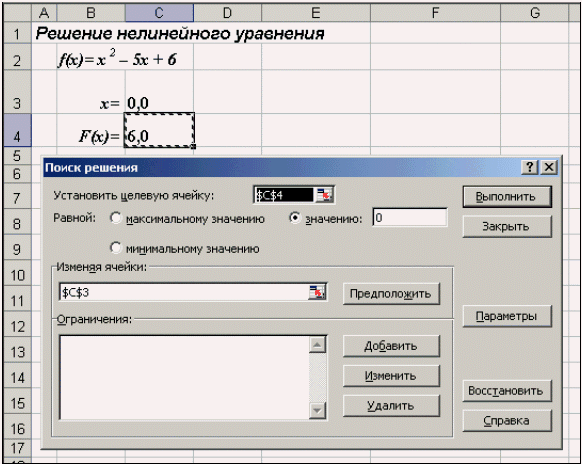Рис. 12. Окно диалога Поиск решения

После открытия диалога Поиск решения (рис. 12) необходимо выполнить следующие действия:

в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем примере целевая ячейка — это С4, а формула в ней имеет вид: = C3^2 — 5*C3 + 6;
для максимизации значения целевой ячейки, установить переключатель максимальному значению в положение 8 , для минимизации используется переключатель минимальному значению, в нашем случае устанавливаем переключатель в положение значению и вводим значение 0;
в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции (С3), разделяя их знаком «;» (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического поиска всех влияющих на решение ячеек используется кнопка Предположить;
в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;
для запуска процесса поиска решения нажать кнопку Выполнить.

Рис. 13. Результаты поиска

Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис. 13. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.

Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения), следующие (рис. 14):

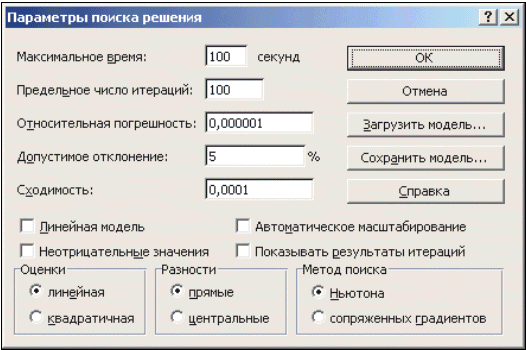Рис. 14. Настройка параметров Решателя

Максимальное время — ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).
Предельное число итераций — еще один способ ограничения времени поиска путем задания максимального числа итераций. По умолчанию задано 100, и, чаще всего, если решение не получено за 100 итераций, то при увеличении их количества (в поле можно ввести время, не превышающее 32767 секунд) вероятность получить результат мала. Лучше попытаться изменить начальное приближение и запустить процесс поиска заново.
Относительная погрешность — задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).
Допустимое отклонение — задается в % только для задач с целочисленными ограничениями. Поиск решения в таких задачах сначала находит оптимальное нецелочисленное решение, а потом пытается найти ближайшую целочисленную точку, решение в которой отличалось бы от оптимального не более, чем на указанное данным параметром количество процентов.
Сходимость — когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа (дробь из интервала от 0 до 1), указанного в данном параметре, поиск прекращается.
Линейная модель — этот флажок следует включать, когда целевая функция и ограничения — линейные функции. Это ускоряет процесс поиска решения.
Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.
Автоматическое масштабирование — этот флажок следует включать, когда масштаб значений входных переменных и целевой функции и ограничений отличается, возможно, на порядки. Например, переменные задаются в штуках, а целевая функция, определяющая максимальную прибыль, измеряется в миллиардах рублей.
Показывать результаты итераций — этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.
Оценки — эта группа служит для указания метода экстраполяции — линейная или квадратичная, — используемого для получения исходных оценок значений переменных в каждом одномерном поиске. Линейная служит для использования линейной экстраполяции вдоль касательного вектора. Квадратичная служит для использования квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач.
Разности (производные) — эта группа служит для указания метода численного дифференцирования, который используется для вычисления частных производных целевых и ограничивающих функций. Параметр Прямые используется в большинстве задач, где скорость изменения ограничений относительно невысока. Параметр Центральные используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдается сообщение о том, что получить более точное решение не удается.
Метод поиска — служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях.

Сохранить модель поиска решения можно следующими способами:

при сохранении книги Excel после поиска решения все значения, введенные в окнах диалога Поиск решения, сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров Поиска решения;
если в пределах одного рабочего листа Excel необходимо рассмотреть несколько моделей оптимизации (например найти максимум и минимум одной функции, или максимальные значения нескольких функций), то удобнее сохранить эти модели, используя кнопку Параметры/Сохранить модель окна Поиск решения. Диапазон для сохраняемой модели содержит информацию о целевой ячейке, об изменяемых ячейках, о каждом из ограничений и все значения диалога Параметры. Выбор модели для решения конкретной оптимизационной задачи осуществляется с помощью кнопки Параметры/Загрузить модель диалога Поиск решения;
еще один способ сохранения параметров поиска — сохранение их в виде именованных сценариев. Для этого необходимо нажать на кнопку Сохранить сценарий диалогового окна Результаты поиска решений.

Кроме вставки оптимальных значений в изменяемые ячейки Поиск решения позволяет представлять результаты в виде трех отчетов: Результаты, Устойчивость и Пределы. Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога Результаты поиска решения. Рассмотрим более подробно каждый из них.

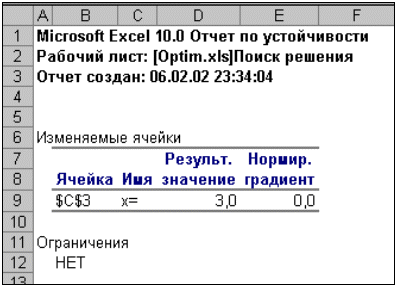Рис. 15. Отчет по устойчивости

Отчет по устойчивости (рис.15) содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных. Этот отчет имеет два раздела: один для изменяемых ячеек, а второй для ограничений. Правый столбец в каждом разделе содержит информацию о чувствительности. Каждая изменяемая ячейка и ограничения приводятся в отдельной строке. Раздел для изменяемых ячеек содержит значение нормированного градиента, которое показывает, как целая ячейка реагирует на увеличение значения в соответствующей изменяемой ячейке на одну единицу. Подобным образом, множитель Лагранжа в разделе для ограничений показывает, как целевая ячейка реагирует на увеличение соответствующего значения ограничения на одну единицу. При использовании целочисленных ограничений Excel выводит сообщение Отчеты устойчивость и Пределы не применимы для задач с целочисленными ограничениями. Если в окне диалога Параметры поиска решения установлен флажок Линейная модель, то отчет по устойчивости содержит несколько дополнительных столбцов информации.

Рис. 16. Отчет по результатам

Отчет по результатам (рис.16) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй — значения искомых переменных, полученные в результате решения задачи, в третьей — результаты оптимального решения для ограничений. Этот отчет также содержит информацию о таких параметрах каждого ограничения, как статус и разница. Статус может принимать три состояния: связанное, несвязанное или невыполненное. Значение разницы — это разность между значением, выводимым в ячейке ограничения при получении решения, и числом, заданным в правой части формулы ограничения. Связанное ограничение — это ограничение, для которого значение разницы равно нулю. Несвязанное ограничение — это ограничение, которое было выполнено с ненулевым значением разницы.

Отчет по пределам содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Уравнения и задачи на подбор параметра в Excel

Подбор параметра и решение уравнений в Excel

y =7 является функцией x ;
нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.

Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:

Заполните ячейки листа, так как показано на рисунке:
Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:

В результате мы получили правильное значение 3.

Получили максимально точный результат: 2*3+1=7

Второй пример использования подбора параметра для уравнений

Немного усложним задачу. На этот раз формула выглядит следующим образом:

Заполните ячейку B2 формулой как показано на рисунке:
Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
Сравните 2 результата вычисления:

Таким образом, если нас не устраивает результат вычислений, можно:

Увеличить в настройках параметр предельного числа итераций.
Изменить относительную погрешность.
В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).