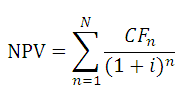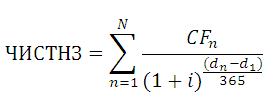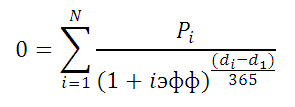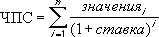Дисконтированная сумма в excel

К наиболее типичным методам финансового анализа можно отнести анализ затрат, период окупаемости инвестиций, денежный поток и внутрифирменный коэффициент окупаемости инвестиций. Каждый из этих методов мы рассмотрим далее.

Анализ затрат

Анализ затрат является довольно простым методом. В этом случае вы определяете стоимость производства продукта (которым в нашем случае является проект) и сопоставляете ее с ожидаемыми выгодами. Если выгоды перекрывают затраты, то, скорее всего, данный проект будет принят к исполнению.

При выполнении этого анализа не забывайте включить все затраты. Обычно сюда входит совокупная стоимость таких процессов, как практическая реализация проекта, текущая поддержка, сопровождение (техобслуживание), содержание соответствующего персонала, устранение проблем, которые не удалось решить в ходе выполнения проекта, и т.д. В этой методике полная стоимость проекта рассчитывается не по факту выполненных работ, а на основании результатов, полученных в итоге выполнения этого проекта, и только после того, как они будут внедрены в данной организации.

Период окупаемости инвестиций

Период окупаемости инвестиций — это количество времени, которое требуется для того, чтобы окупились первоначальные инвестиции в данный проект. Совокупная стоимость проекта сравнивается с получаемыми доходами и вычисляется время, которое требуется для того, чтобы полученные доходы превысили затраты на реализацию данного проекта. Когда выполняется сравнение двух или большего числа проектов сходного масштаба и сложности, как правило, выбирается проект с наименьшим периодом окупаемости инвестиций. У этого метода нет «универсальной» формулы, которая позволяла бы быстро найти требуемое решение. Если, например, себестоимость проекта равняется 100 000 долл., а ожидаемые доходы составляют 25 000 долл. в квартал, то период окупаемости инвестиций составит один год.

Дисконтированные (приведенные) денежные потоки

Если вам предложат 1 000 долл. сегодня или те же 1 000 долл. через два года, какой вариант вы предпочтете? Ответ предсказуем, поскольку вложив сейчас эту сумму в банк или какое-либо предприятие, через два года вы будете иметь с нее прибыль. Например, под 6% годовых такая инвестиция на двухлетний период составит 1 123,60 долл. (в нынешних долларах, разумеется).

Метод дисконтированного (приведенного) денежного потока сравнивает стоимость будущих денежных потоков с нынешними долларами. Иными словами, он выполняет операцию, противоположную той, которую мы только что объяснили. Зная, что ваш проект принесет через два года сумму, равную 1 123,60 долл. (это так называемая будущая стоимость — Future Value, или FV), вы бы смогли с помощью метода дисконтированного (приведенного) денежного потока определить нынешнюю стоимость этой суммы. Ответ, конечно же, таков: 1 000 долл.

Чтобы иметь представление о дисконтированных денежных потоках, вы должны знать стоимость соответствующих инвестиций в нынешних долларах, иначе говоря, приведенную стоимостью (Present Value, или PV), которая вычисляется следующим образом: PV=FV/(1+i)n. Эта формула говорит о том, что приведенная стоимость равняется будущей стоимости инвестиций, деленной на один, плюс процентная ставка, возведенная в степень, равную количеству периодов, на которые мы инвестируем нашу сумму.

Вам не нравится математика? Но это же так просто! В Excel предусмотрена встроенная функция для вычисления приведенной стоимости (наряду со множеством других функций, позволяющих выполнять финансовые расчеты). На рисунке ниже показана группа Function Library (Библиотека функций), предусмотренная на вкладке Formulas (Формулы), и часть списка финансовых функций, встроенных в Excel.

Вернемся, однако, к нашей формуле для вычисления приведенной стоимости инвестиций. Выберите в списке функций элемент PV (в русифицированной версии Excel — ПС (Приведенная стоимость)). На экране появится диалоговое окно Function Arguments (Аргументы функции), показанное на рис. 2.

Диалоговое окно Function Arguments предназначено для ввода значений отдельных элементов выбранной вами функции, которые необходимы для вычисления приведенной стоимости. В текстовом поле Rate (Ставка) этого диалогового окна следует ввести величину процентной ставки за определенный временной период. Вы можете ввести 6% или 0,06 (предполагается, что процент начисляется ежегодно по методу сложных процентов). Если бы процент начислялся ежеквартально (по тому же методу), тогда вам нужно было бы разделить указанную величину процентной ставки на 4, а затем ввести полученный результат в поле Rate (Ставка).

Ниже находится поле Nper (Кпер), в котором вводят количество временных периодов. Мы инвестируем нашу сумму на два года. Величина выплаты (поле Pmt (Плт)) равняется 0, поскольку мы не производим выплат по этой инвестиции, а просто хотим знать величину всей этой суммы в нынешних долларах. Далее находится поле FV (Бс), в котором вводят значение будущей стоимости. В нашем примере будущая стоимость инвестиции равняется -1 123,60 долл. Если в поле FV (Бс) ввести положительное число, то результат вычисления этой функции будет отрицательным. На рис. 3. показано диалоговое окно Function Arguments со значениями аргументов функции PV (Приведенная стоимость), введенных в соответствующие поля.

Вместо числовых значений в полях диалогового окна Function Arguments (Аргументы функции) можно дать адрес ячейки, в которой введено нужное вам значение. Предположим, например, что в ячейке С1 введено число 0,06. В этом случае в текстовом поле Rate (Процентная ставка) диалогового окна Function Arguments достаточно указать только адрес упомянутой выше ячейки, т.е. С1. Непосредственно под текстовыми полями диалогового окна Function Arguments представлен результат наших вычислений функции PV (Приведенная стоимость). В нашем случае PV=1000. Помимо диалогового окна Function Arguments аргументы данной функции отображены в строке формул программы Excel, а также в активизированной ячейке (А1 в данном случае) (см. рис. 3.).

Как видите, сначала следует значение процентной ставки, затем количество периодов и будущая стоимость. Обратите внимание, что в данной функции отсутствует значение между двумя запятыми. Это означает, что один из аргументов функции равен нулю (в нашем случае величина выплаты (поле Pmt (Плт)). (В русифицированной версии программы Excel аргументы функций следует отделять друг от друга точкой с запятой (;)) Как только вы
щелкнете на кнопке ОК, в ячейке А1 появится результат вычисления функции, в нашем случае — 1 000 долл.

Для того чтобы воспользоваться функцией PV (ПС), не обязательно перебирать ряд интерфейсных элементов программы. Для этого достаточно просто ввести =pv() в ячейке А1. В результате ваших действий на экране появится экранная подсказка, в которой приведен синтаксис данной функции, т.е. сокращенные названия и очередность ее аргументов (рис. 4).

Если вы не знаете точно, какие значения следует вводить в качестве аргументов функции, откройте окно справочной системы Excel. В единственном текстовом поле этого окна введите PV (ПС для русифицированной Excel) и нажмите клавишу Enter. Справочная система немедленно отобразит всю необходимую информацию по интересующей вас функции.

Если вы, как и большинство других пользователей, раздражаетесь из-за того, что окно справочной системы Excel время от времени скрывается за вашей электронной таблицей (когда вы пытаетесь выполнять пошаговые инструкции, приведенные в этом окне), выполните следующее: скопируйте, а затем вставьте информацию, представленную в окне справки, в электронную таблицу, а затем, когда вы введете нужные значения в формулу, удалите эту информацию.

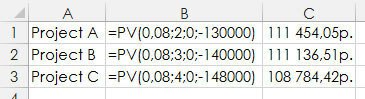
Допустим, что ваш комитет по отбору проектов рассматривает три проекта, из которых необходимо выбрать самый подходящий. Ожидается, что проект А принесет через два года 130 000 долл. прибыли; проект В — 140 000 долл. через три года; а проект С — 148 000 долл. через четыре года. Какому из этих проектов должен отдать предпочтение комитет, если свое решение он основывает лишь на использовании метода дисконтированного (приведенного) денежного потока, полагая, что процентная ставка равняется 8%? Самую высокую прибыль обеспечивает проект А. На рис. 5 показаны расчетные формулы по каждому проекту и полученные с их помощью результаты.

Расчет приведенной или дисконтированной стоимости может потребоваться в различных случаях. В том числе с 2022 года выполнять его придется всем бухгалтерам, у кого есть договоры аренды, признаваемой неоперационной, и лизинга. Постараемся рассказать простыми словами, что такое приведенная стоимость и как и зачем ее вычислять.

Дисконтирование простыми словами

Рассмотрим пример

Банк сделал Васе персональное предложение по кредиту на сумму 200 тыс. руб. по ставке 10% годовых, сроком на год. Причем вернуть сумму с процентами можно всю сразу по завершении этого года.

Вася рассказал об этом своему другу Пете. И заметил, что все 200 тыс. руб. ему не нужны, но некоторой суммой он бы воспользовался. Петя предложил Васе взять весь кредит и ссудить часть суммы ему, а он, по прошествии года, вернет ее с такими же процентами.

Вася прикинул свои возможности и понял, что на возврат кредита он сможет набрать через год порядка 120 тыс. руб. Значит, вторую часть – еще 100 тысяч – должен к тому моменту вернуть Петя.

Сколько же нужно сегодня ссудить Пете под 10% годовых, чтобы через год он вернул 100 тысяч?

Считать нужно, исходя из формулы банковского (сложного) процента.

Например, общая сумма к возврату по Васиному кредиту:

S=200*(1+0,10)¹ = 220

Степень 1 в формуле означает, что у кредита только один период выплаты – через год. Если бы срок был 2 года – в степень в формулу следовало бы поставить 2. И так далее.

Чтобы узнать, какая сумма, выданная под 10% годовых, через год превратиться в 220, нужно принять 200 тыс. руб. за Х и решить получившееся уравнение.

Х = 220/(1+0,10)¹ = 200

А теперь Вася по той же методике посчитает, какая сумма превратится в 100 тыс. руб.

100/(1+0,10)¹ = 90,91 тыс. руб.

Вася произвел дисконтирование и получил приведенную стоимость Петиной ссуды к возврату.

А мы запомним формулу дисконтирования:

   К

ПС = ————-

        (1+ r) ^t

ПС – приведенная (дисконтированная) стоимость

К – дисконтируемая сумма

r – процентная ставка

t – период кредитования

Зачем вообще это нужно

Продолжим пример

О том, что у Васи есть свободные средства, узнал Федя. Пришел к Васе и сказал:

— Инвестируй в мой бизнес свободные 100 тысяч и через 2 года я выплачу тебе 120 тысяч. Ты компенсируешь проценты, которые заплатишь банку по всему кредиту.

— Я подумаю, — сказал Вася и снова занялся подсчетами.

Потенциальный доход от вложения в бизнес Феди получится:

S=100*(1+ r)² = 120

Решив уравнение, Вася выяснил, что на таких условиях он выдаст Феде деньги под 9,5% годовых. В то время как сам получит их под 10%. Да и воспользоваться ими сможет только через 2 года.

А вот, если Петя согласится взять еще 100 тысяч и вернуть через 2 года по ставке 10% годовых, то Вася получит:

S=100*(1+ 0,1)² = 121 (побольше, чем от Феди).

В бытовых ситуациях, как у Васи из примера, можно обойтись базовыми формулами и не долгими подсчетами. Но что делать, если обсчитать надо большой и долгосрочный проект? Где много денежных потоков и двигаться они будут на отрезке времени длиннее, чем 1-2 года?

Есть два способа привести все потоки инвестпроекта к общему знаменателю, чтобы можно было сравнить разные проекты:

1. Рассчитать будущую доходность от инвестируемой суммы и сравнить результат по разным проектам. Это будет процесс обратный дисконтированию и называется он компаундинг. (Примерно то, что сделал Вася, оценивая предложение Феди).
2. Взять за основу прогнозные данные по получаемым в результате инвестирования денежным поступлениям и дисконтировать на текущий момент. Если, например, два проекта обещают поступления 1 миллион рублей через 3 года, но в результате приведения вложений оказалось, что в первый надо вложить 900 тысяч, а во второй 850, то второй проект можно рассматривать как более предпочтительный.

Зачем берется банковская ставка

Снова приведем пример

Костя выиграл в лотерею. После уплаты налогов у него остался 1 миллион рублей. Костя решил открыть свой бизнес – небольшое кафе. Арендовал помещение, купил оборудование, нанял персонал, сам за всем следил, практически в своем кафе поселился… Через год получил первую чистую прибыль – 50 тысяч рублей.

В то время как на момент открытия кафе можно было положить деньги в банк на депозит по 6% годовых. И получить по окончании года доход в 60 тысяч рублей, миллион обратно в свое распоряжение и все это не особо напрягаясь и с минимальными рисками.

С этим примером мы вплотную подошли к тому, для кого в идеале делается бухгалтерская отчетность по МСФО. А делается она для потенциальных инвесторов, которые, посмотрев на нее, должны принять решение: вложить свои деньги в эту компанию или проще отнести их в банк на депозит?

То есть инвестор, анализируя состояние дел компании по отчетности, подготовленной по принципам МСФО, оценивает выбор между двумя инвестиционными проектами – с компанией и с банком.

А, поскольку, в бухотчетности мы отражаем то, что есть именно на текущий момент, то для информативного отражения, например, расчетов по аренде и лизингу, мы пользуемся вторым способом, позволяющим сравнить разные проекты – дисконтированием. И из этих же соображений часто подставляем в формулу ставку дисконтирования – величину банковского процента.

Как определить ставку дисконтирования

Отметим, что в случае с долгосрочной арендой или лизингом у сторон сделки будет немного разный подход к оценке.

Арендатор (или лизингополучатель) должен показать, что для него взять объект в аренду или лизинг выгоднее, чем взять кредит и купить такой же объект. (Ну, или не выгоднее, и тогда отражение по приведенной стоимости даст убыток). Поэтому арендатор в качестве ставки для подстановки в формулу дисконтирования берет ставку, по которой он мог бы взять кредит на приобретение аналогичного объекта.

Если у арендатора уже есть подобные кредиты – можно опираться на ставку по ним. Если нет – нужно определять по какой ставке арендатор, на дату получения объекта,  мог бы взять кредит с аналогичным сроком и обеспечением для приобретения примерно такого же.

Важно! В МСФО процесс выбора ставки дисконтирования гораздо более обусловлен и имеет несколько вариантов расчета. Причем выбранный вариант еще надо обосновать аудиторам. Российские ФСБУ, дублируя необходимость применения дисконтирования, пока не настолько усложнены и можно следовать общим предписаниям стандарта и логике.

У арендо- и лизингодателя ситуация больше похожа на ситуацию Кости, получившего миллион. У Кости заключен договор аренды, куплено оборудование и мебель. Как отбить обратно свой миллион, чтобы подумать, куда его дальше лучше вложить?

Продолжим пример

Костя нашел арендатора, который готов арендовать его кафе. Помещение, соответственно, пойдет в субаренду, а оборудование и мебель – в аренду от самого Кости. Договор заключен на 4 года, для упрощения расчетов примем, что арендатор рассчитывается сразу за год по 250 000 рублей. То есть, через 4 года Костя вернет свой миллион.

При этом у Кости уже есть вложения по объекту аренды:

480 000 – аренда (опять же, чтобы не перегружать пример, будем считать, что Костя оплатил всю сумму на 5 лет авансом);

280 000 – затраты на покупку оборудования и мебели;

40 000 – расходы на монтаж и обслуживание оборудования.

Итого можно определить стоимость инвестиционного вложения Кости – 800 тыс. руб.

То есть, следуя все тем же формулам, выполняется равенство:

800*(1+ r)⁴ = 1 000 000

Вот эта ставка r, при которой валовая стоимость инвестиции в аренду (будущий 1 миллион) равна справедливой стоимости вложений арендодателя (800 тысяч) и будет ставкой дисконтирования, которая нужна арендодателю. Зависящей от условий конкретного договора и позволяющей сравнивать его с другими подобными договорами.

Для полноты картины следует учесть, что оборудование и мебель, которые вернутся к Косте по окончании срока аренды, возможно, еще будут иметь какую-то ценность. Например, их можно будет продать как б/у, но еще годные к использованию. Поэтому, на практике, нужно эту ценность, называемую негарантированной ликвидационной стоимостью, оценить и добавить в равенство, приплюсовав к поступлениям от аренды.

Допустим, Костя договорился по окончании срока аренды помещения продать оптом находящееся в нем к тому моменту имущество (мебель и оборудование) за 50 000 рублей.

Тогда равенство для вычисления ставки дисконтирования примет вид

800*(1+ r)⁴ = 1 050 000 (1 000 000 + 50 000)

Отметим также, что на практике решить как уравнение подобное равенство для большого временного отрезка, а потом вычислить дисконтированные величины арендных платежей не так просто. Не всякий и не со всяким калькулятором справится. Поэтому далее мы поговорим о том, какие есть способы упростить расчеты.

Как считать показатели для приведенной стоимости в Excel

Традиционной палочкой-выручалочкой для бухгалтеров в случаях, когда надо дисконтировать, является Excel. В нем имеются функции как для расчета, например, ставки дисконтирования для арендодателя, так и для вычисления самих приведенных сумм.

Функция ЧИСТВНДОХ

С помощью этого средства как раз можно вычислить ставку внутренней доходности для арендодателя (лизингодателя).

Чтобы воспользоваться данным инструментом, нужно внести в лист Excel данные по датам и платежам договора. А в первой строке отразить величину инвестиционных вложений со знаком «-».

Возьмем данные из примера про сдачу в аренду Костиного кафе. Пусть кафе он передал арендатору 01.01.2022, а платит арендатор по истечении года. Для упрощения не станем учитывать негарантированную ликвидационную стоимость.

Далее ставим курсор в свободную ячейку и нажимаем на значок формул. Формула ЧИСТВНДОХ находится в разделе Финансовые. В англоязычном Excel она же называется XIRR.

Вносим данные для расчета, выделяя нужные области. На первое место ставим суммовые значения, на второе – даты

Далее жмем ОК и получаем ставку дисконтирования, с помощью которой арендодателю надо производить вычисления для отражения в отчетности договоров по ФСБУ 25/2018.

Важно!

Переписывать по датам обязательно нужно все платежи по условиям договора. Если у вас, к примеру, договор заключен на 5 лет с платежами ежемесячно, то придется заполнить 60 строк под каждый платеж.

А вот такие параметры как периодичность, аннуитетность – на точность вычислений не влияют. С помощью формулы можно рассчитывать ставку внутренней доходности и в случае, если платежи идут произвольно, и в случае, если их суммы не равные.

Функция ЧИСТНЗ

С помощью этой формулы, зная ставку дисконтирования, можно быстро вычислить чистую стоимость инвестиций в аренду на дату отражения в отчетности. Английская аббревиатура функции XNPV. Эта формула тоже больше подойдет для арендодателя (лизингодателя).

Для вычислений можно завести еще один столбец в табличке, которая получилась из платежей и их дат.

На момент передачи стоимость инвестиций принимаем равной справедливой стоимости вложений в объект аренды или лизинг. Скажем по секрету, что если объект ОС, передаваемый в аренду, учитывался с соблюдением правил приема на баланс, оценки и тестирования на обесценение, то его стоимость при  передаче вполне можно считать справедливой.

А далее начинаем вычислять чистую стоимость инвестиций для каждого последнего дня года.

Важно! Если на дату, на которую определяется приведенная чистая стоимость инвестиций, приходится и дата платежа по договору, то сумму платежа нужно вычесть из значения, получившегося по формуле ЧИСТНЗ.

Выбираем значения, начиная от того, на дату которого считаем и далее до конца договора. Даты выбираем соответственно.

Вычитаем из получившегося по формуле значения сумму платежа по договору, чтобы получить справедливое значение на конец дня 31 декабря.

При наступлении следующей даты поступаем так же. Расчеты рекомендуется сохранить для каждого договора.

Дальнейшие вычисления для арендодателя

Используя полученные значения, арендодатель  может определить величину дохода по процентам для отражения в учете по правилам ФСБУ 25/2018.

И получившаяся расчетная табличка целиком, на всякий случай.

Приведенная стоимость у арендатора

Описанный далее функционал больше подойдет арендаторам. Например, для вычисления приведенной стоимости платежей по договору.

В принципе, определив ставку дисконтирования, с помощью Excel можно производить расчеты и просто через формулы. Напомним, что значок степени в формуле Excel выставляется как комбинация «^число», например, чтобы возвести в 3-ю степень нужно ввести в формулу «^3».

Например, покажем, какая приведенная стоимость получится у платежей по договору у арендатора Костиного кафе. Допустим, что для покупки всего того, что он арендует у Кости, ему бы понадобилось взять кредит в банке по ставке 11,5% годовых.

Помним, что в данном случае дисконтируется каждый платеж. А t принимает значение количества периодов, оставшихся до платежа.

Если t выражено не в годах, а в более мелких периодах: кварталах или месяцах, то для подстановки в формулу дисконтирования нужно вычислить соответствующую периоду ставку исходя из годовой.

r = ((1 + годовая ставка/100)^{1/число периодов в году} Х 100%

Например, при ежеквартальных платежах в степени будет 1/4

r = ((1 + годовая ставка/100)^1/4 Х 100%

Также можно воспользоваться функцией ПС (приведенная стоимость, в английском PV). Помните, что она корректно работает только для единой процентной ставки и фиксированного размера периодического платежа.

Попробуем вычислить приведенную стоимость платежей по договору с помощью функции ПС

Ставка – указываем значение ставки за период платежа. Например, за квартал квартальную, рассчитав ее по предложенной выше формуле.

Кпер – количество периодов, за которые будут производятся платежи до конца договора. Мы вычисляем для всех платежей, поэтому ставим 4.

Плт – фиксированная сумма платежа за период. Если считаем поступления (например, от инвестиций), ставим значение с плюсом. Если считаем выплаты – ставим с минусом.

Бс – будущая стоимость. Желаемый остаток средств  после завершения платежей. В данном случае он не нужен. Если ячейка не заполнена, программа автоматом считает 0.

Тип – характеристика выплаты: в начале периода – 1, в конце периода – 0. Если не заполнено, автоматически считается 0 (конец периода). У нас как раз конец периода, поэтому не заполняем.

Когда все внесено, нажимаем Ок.

Как видим, общая сумма дисконтированных платежей, рассчитанная по периодам, и сумма, полученная с помощью функции ПС одинаковы.

ЧПС – еще одна похожая функция. Удобна тем, что можно выбирать любые значения размера платежа из уже внесенных в таблицу.

Полученный результат совпадет с полученным по ПС и из сложения дисконтированных сумм каждого платежа.

Таблицы дисконтирования

Как вы, должно быть, уже успели заметить, дисконтированная сумма всегда меньше приводимой. И чем больше периодов дисконтирования, тем меньше итоговый результат.

То есть, можно сказать, что величина, которую мы дисконтируем, уменьшается в пропорции к количеству периодов и зависит от значения ставки.

Это давно подметили финансисты и высчитали закономерности для разных значений периодов и ставок. В результате мы можем пользоваться таблицами дисконтирования, которые есть в свободном доступе.

По вертикали в таких таблицах обычно идут периоды, а по горизонтали ставки. Единственный минус – ставки, как правило, выражены только в целых числах.

В остальном же работа с таблицами очень проста. Достаточно выбрать строку с нужным количеством периодов и столбец с нужным процентом, а на их пересечении будет ячейка с коэффициентом, на который надо умножить сумму, чтобы получить ее приведенное значение.

Вспомним Васю, который прикидывал, сколько денег дать Пете на 1 год под 10%, чтобы Петя вернул 100 тыс. руб.

Вася мог бы не проводить расчеты, а взять коэффициент из таблицы и умножить на него 100 000.

Бухгалтерские программы

На текущий момент (осень 2021 года) можно найти отдельно написанные программки, предназначенные для проведения вычислений, которые мы описали выше. Сделали их после появления ФСБУ 25/2018 для тех, кто хотел перейти на стандарт раньше установленного срока. Как вы понимаете, особенной популярностью это ПО не пользовалось. Даже то, которое коннектилось с 1С.

Что же касается 1С, то корректно работающий функционал для расчетов с приведенной стоимостью есть в 1С МСФО (там все настроено на МСФО и даже после внедрения ФСБУ логика расчетов все равно может отличаться) и в 1С Управление предприятием 2 (Бюджетирование лизинговых платежей).

Следует ожидать, что разработчики 1С отреагируют на необходимость ведения учета по ФСБУ 25/2018 и к 01.01.2022 появится необходимый функционал и в Бухгалтерии. Как только он появится – мы сразу же подготовим подробную инструкцию со скриншотами по работе с ним.

---

Автор материала:
Оксана Лим

Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул

MS

EXCEL.

Начнем с определения, точнее с определений.

Чистой приведённой стоимостью (Net present value, NPV) называют

сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню

(взято из Википедии). Или так:

Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт

cfin.

ru)

Или так:

Текущая

стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика

.

Толковыйсловарь

. —

М

.

:

»

ИНФРА

—

М

«,

Издательство

»

ВесьМир

«.

Дж

.

Блэк

.)

Примечание1

. Чистую приведённую стоимость также часто называют Чистой текущей стоимостью, Чистым дисконтированным доходом (ЧДД). Но, т.к. соответствующая функция MS EXCEL называется

ЧПС()

, то и мы будем придерживаться этой терминологии. Кроме того, термин Чистая Приведённая Стоимость (ЧПС) явно указывает на связь с

Приведенной стоимостью

.

Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма

Приведенных стоимостей

денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.

Совет

: при первом знакомстве с понятием Чистой приведённой стоимости имеет смысл познакомиться с материалами статьи

Приведенная стоимость

.

Это более формализованное определение без ссылок на проекты, инвестиции и ценные бумаги, т.к. этот метод может применяться для оценки денежных потоков любой природы (хотя, действительно, метод NPV часто применяется для оценки эффективности проектов, в том числе для сравнения проектов с различными денежными потоками). Также в определении отсутствует понятие дисконтирование, т.к. процедура дисконтирования – это, по сути, вычисление приведенной стоимости по методу

сложных процентов

.

Как было сказано, в MS EXCEL для вычисления Чистой приведённой стоимости используется функция

ЧПС()

(английский вариант — NPV()). В ее основе используется формула:

CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).

Примечание2

. Т.к. денежный поток может присутствовать не в каждый период, то определение NPV можно уточнить:

Чистая приведённая стоимость — это Приведенная стоимость денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через промежутки времени, кратные определенному периоду (месяц, квартал или год)

. Например, начальные инвестиции были сделаны в 1-м и 2-м квартале (указываются со знаком минус), в 3-м, 4-м и 7-м квартале денежных потоков не было, а в 5-6 и 9-м квартале поступила выручка по проекту (указываются со знаком плюс). Для этого случая NPV считается точно также, как и для регулярных платежей (суммы в 3-м, 4-м и 7-м квартале нужно указать =0).

Если сумма приведенных денежных потоков представляющих собой доходы (те, что со знаком +) больше, чем сумма приведенных денежных потоков представляющих собой инвестиции (расходы, со знаком минус), то NPV >0 (проект/ инвестиция окупается). В противном случае NPV <0 и проект убыточен.

Выбор периода дисконтирования для функции ЧПС()

При выборе периода дисконтирования нужно задать себе вопрос: «Если мы прогнозируем на 5 лет вперед, то можем ли мы предсказать денежные потоки с точностью до месяца/ до квартала/ до года?». На практике, как правило, первые 1-2 года поступления и выплаты можно спрогнозировать более точно, скажем ежемесячно, а в последующие года сроки денежных потоков могут быть определены, скажем, один раз в квартал.

Примечание3

. Естественно, все проекты индивидуальны и никакого единого правила для определения периода существовать не может. Управляющий проекта должен определить наиболее вероятные даты поступления сумм исходя из действующих реалий.

Определившись со сроками денежных потоков, для функции

ЧПС()

нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы  ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см.

файл примера, лист NPV

).

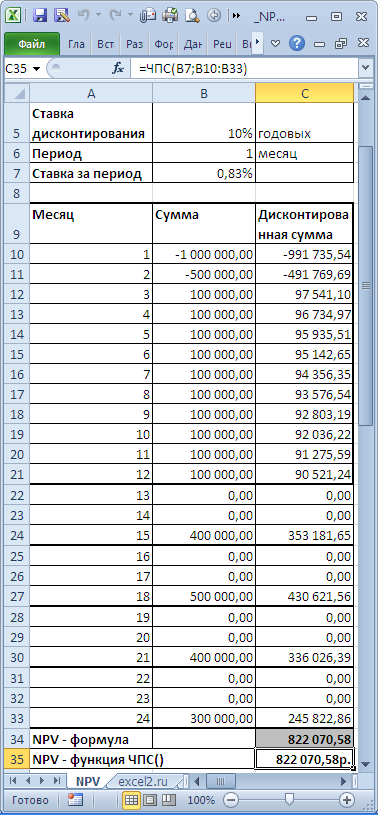
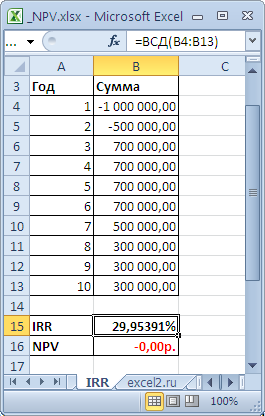
В таблице NPV подсчитан двумя способами: через функцию

ЧПС()

и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.) Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода. Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции

ЧПС()

, а нужно просто прибавить к получившемуся результату (см.

файл примера

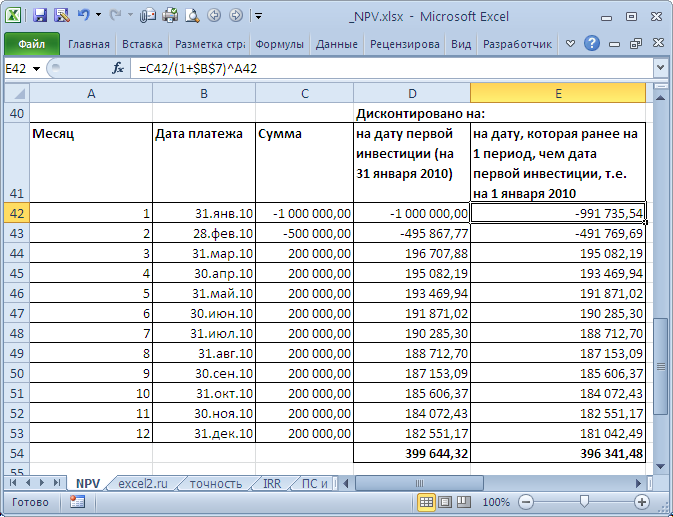
). Сравнение 2-х вариантов дисконтирования приведено в

файле примера

, лист NPV:

О точности расчета ставки дисконтирования

Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см.

файл примера, лист Точность

).

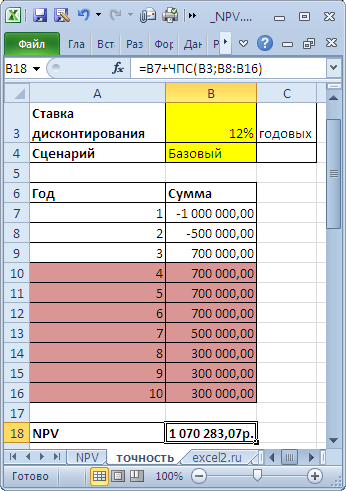
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.

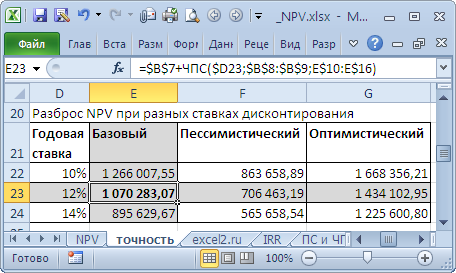
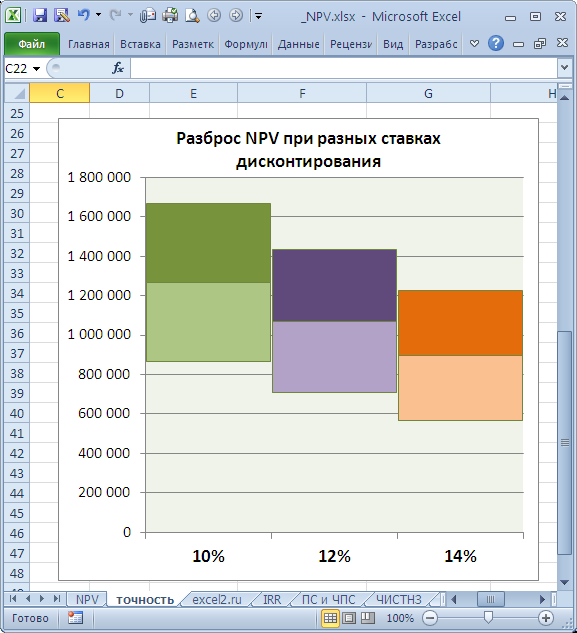
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):

Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.

Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.

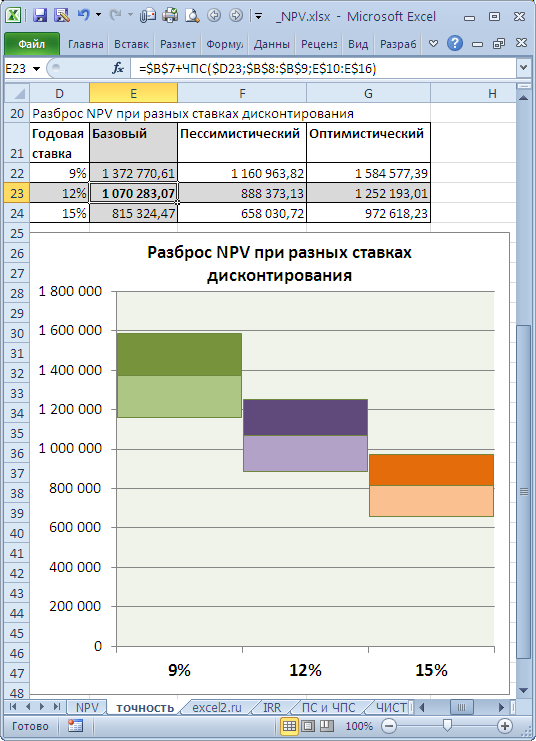
Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0

Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.

Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.

После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.

Внутренняя ставка доходности

IRR

(ВСД)

Внутренняя ставка доходности (англ.

internal rate of return

, IRR (ВСД)) — это ставка дисконтирования, при которой Чистая приведённая стоимость (NPV) равна 0. Также используется термин Внутренняя норма доходности (ВНД) (см.

файл примера, лист IRR

).

Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.

Для расчета IRR используется функция

ВСД()

(английский вариант – IRR()). Эта функция тесно связана с функцией

ЧПС()

. Для одних и тех же денежных потоков (B5:B14) Ставка доходности, вычисляемая функцией

ВСД()

, всегда приводит к нулевой Чистой приведённой стоимости. Взаимосвязь функций отражена в следующей формуле:

=ЧПС(ВСД(B5:B14);B5:B14)

Примечание4

. IRR можно рассчитать и без функции

ВСД()

: достаточно иметь функцию

ЧПС()

. Для этого нужно использовать инструмент

Подбор параметра

(поле «Установить в ячейке» должно ссылаться на формулу с

ЧПС()

, в поле «Значение» установите 0, поле «Изменяя значение ячейки» должно содержать ссылку на ячейку со ставкой).

Расчет NPV при постоянных денежных потоках с помощью функции ПС()

Напомним, что

аннуитет

представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию

ПС()

(см.

файл примера, лист ПС и ЧПС

).

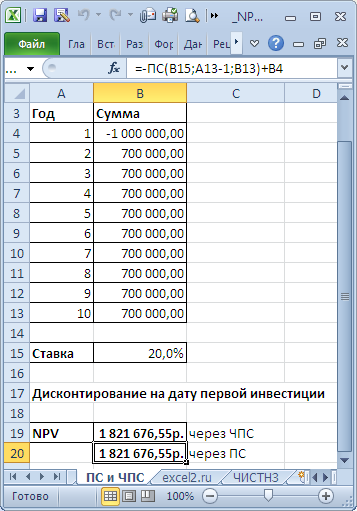
В этом случае все денежные потоки (диапазон

В5:В13

, 9 одинаковых платежей) дисконтируются на дату первой (и единственной) суммы инвестиции, расположенной в ячейке

В4

. Ставка дисконтирования расположена в ячейке

В15

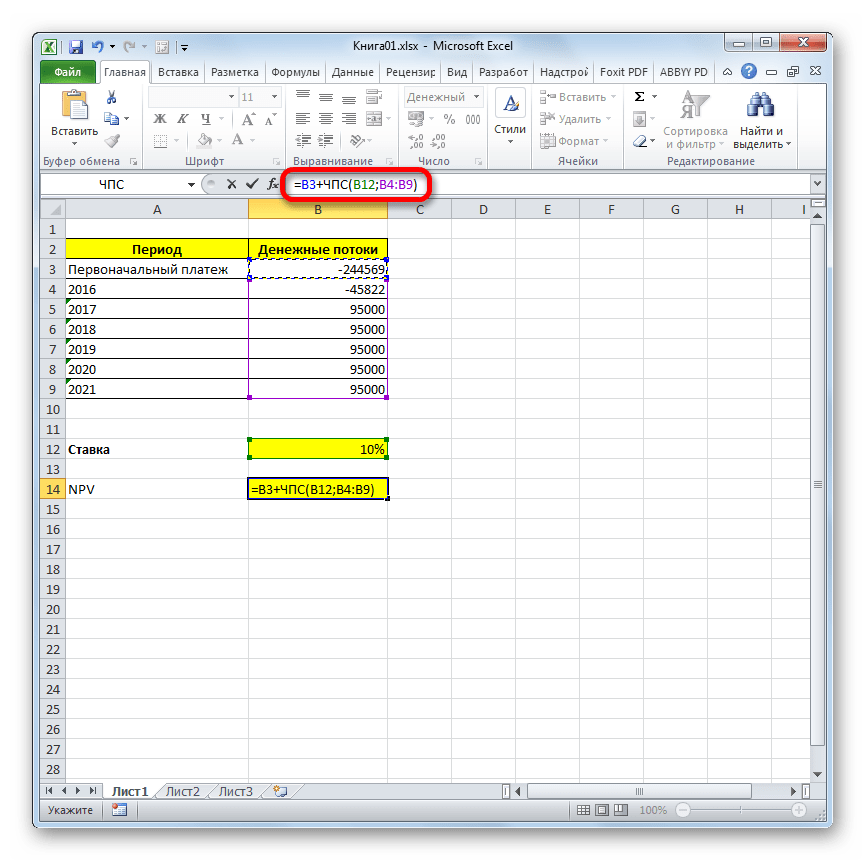
со знаком минус. В этом случае формула

=B4+ЧПС(B15;B5:B13)

дает тот же результат, что и

= B4-ПС(B15;9;B13)

Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени

Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за

любые

промежутки времени, то используется функция

ЧИСТНЗ()

(английский вариант – XNPV()).

Функция

ЧИСТНЗ()

возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:

Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.

Принципиальным отличием от

ЧПС()

является то, что денежный поток привязан не к конкретным периодам, а к датам. Другое отличие: ставка у

ЧИСТНЗ()

всегда годовая, т.к. указана база 365 дней, а не за период, как у

ЧПС()

. Еще отличие от

ЧПС()

: все денежные потоки всегда дисконтируются на дату первого платежа.

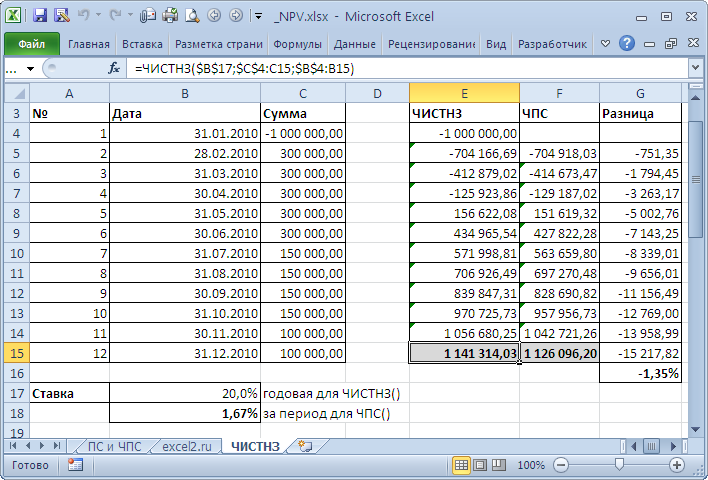
В случае, когда платежи осуществляются регулярно можно сравнить вычисления функций

ЧИСТНЗ()

и

ЧПС()

. Эти функции возвращают несколько отличающиеся результаты. Для задачи из

файла примера, Лист ЧИСТНЗ

разница составила порядка 1% (период = 1 месяцу).

Это связано с тем, что у

ЧИСТНЗ()

длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у

ЧПС()

указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет

високосного

года).

Внутренняя ставка доходности ЧИСТВНДОХ()

По аналогии с

ЧПС()

, у которой имеется родственная ей функция

ВСД()

, у

ЧИСТНЗ()

есть функция

ЧИСТВНДОХ()

, которая вычисляет годовую ставку дисконтирования, при которой

ЧИСТНЗ()

возвращает 0.

Расчеты в функции

ЧИСТВНДОХ()

производятся по формуле:

Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).

Примечание5

. Функция

ЧИСТВНДОХ()

используется для

расчета эффективной ставки по потребительским кредитам

.

В статье подробно расскажем про дисконтирование денежных потоков, формулу расчета и анализа в Excel.

Дисконтирование денежных потоков. Определение

Дисконтирование денежных потоков (англ. Discounted cash flow, DCF, дисконтированная стоимость) – это приведение стоимости будущих (ожидаемых) денежных платежей к текущему моменту времени. Дисконтирование денежных потоков основывается на важном экономическом законе убывающей стоимости денег. Другими словами, со временем деньги теряют свою стоимость по сравнению с текущей, поэтому необходимо за точку отсчета взять текущий момент оценки и все будущие денежные поступления (прибыли/убытки) привести к настоящему времени. Для этих целей используют коэффициент дисконтирования.

Как рассчитать коэффициент дисконтирования?

★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут Коэффициент дисконтирования используется для приведения будущих доходов к текущей стоимости за счет перемножения коэффициента дисконтирования и потоков платежей. Ниже показана формула расчета коэффициента дисконтирования: 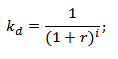где: r – ставка дисконтирования, i  – номер временного периода.

Дисконтирование денежных потоков. Формула расчета

где: DCF (Discounted cash flow) – дисконтированный денежный поток; CF (Cash Flow) – денежный поток в период времени I; r – ставка дисконтирования (норма дохода); n – количество временных периодов, по которым появляются денежные потоки. Ключевым элементов в формуле дисконтирования денежных потоков является ставка дисконтирования. Ставка дисконтирования показывает, какую норму прибыли следует ожидать инвестору при вложении в тот или иной инвестиционный проект. Ставка дисконтирования использует множество факторов, которые зависят от объекта оценки, и может в себя включать: инфляционную составляющую, доходность по безрисковым активам, дополнительную норму прибыли за риск, ставку рефинансирования, средневзвешенную стоимость капитала, процент по банковским вкладам и т.д.

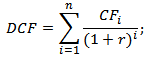
Расчет нормы дохода (r) для дисконтирования денежных потоков

Существует достаточно много различных способов и методов оценки ставки дисконтирования (нормы дохода) в инвестиционном анализе. Рассмотрим более подробно достоинства и недостатки некоторых методов расчета нормы доходности. Данный анализ представлен в таблице ниже.

Методы оценки ставки дисконтирования	Достоинства	Недостатки
Модели CAPM	Возможность учета рыночного риска	Однофакторность, необходимость наличия обыкновенных акций на фондовом рынке
Модель Гордона	Простота расчета	Необходимость наличия обыкновенных акций и постоянных дивидендных выплат
Модель средневзвешенной стоимости капитала (WACC)	Учет нормы дохода как собственного, так и заемного капитала	Сложность оценки доходности собственного капитала
Модель ROA, ROE, ROCE, ROACE	Возможность учета рентабельности капиталов проекта	Не учет дополнительных макро, микро факторов риска
Метод E/P	Учет рыночного риска проекта	Наличие котировок на фондовом рынке
Метод оценки премий на риск	Использование дополнительных критериев риска в оценке ставки дисконтирования	Субъективность оценки премии за риск
Метод оценки на основе экспертных заключений	Возможность учесть слабоформализуемые факторы риска проекта	Субъективность экспертной оценки

Вы можете более подробно узнать про подходы в расчете ставки дисконтирования в статье «Ставка дисконтирования.10 современных методов оценки».

Пример расчета дисконтированного денежного потока в Excel

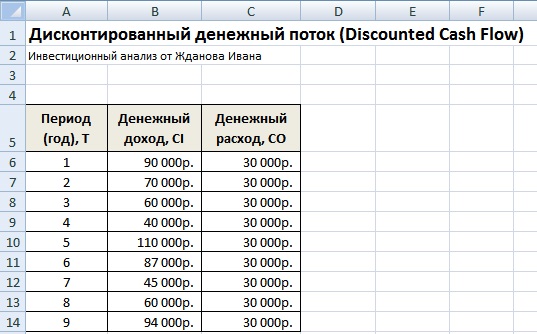
Для того чтобы рассчитать дисконтированные денежные потоки необходимо по выбранному временному периоду (в нашем случае годовые интервалы) расписать подробно все ожидаемые положительные и отрицательные денежные платежи (CI – Cash Inflow, CO – Cash Outflow). За денежные потоки в оценочной практике берут следующие платежи:

• Чистый операционный доход;
• Чистый поток наличности за исключением затрат на эксплуатацию, земельного налога и реконструирования объекта;
• Облагаемая налогом прибыль.

В отечественной практике, как правило, используют период 3-5 лет, в иностранной практике период оценки составляет 5-10 лет. Введенные данные являются базой для дальнейшего расчета. На рисунке ниже показан пример ввода первоначальных данных в Excel.

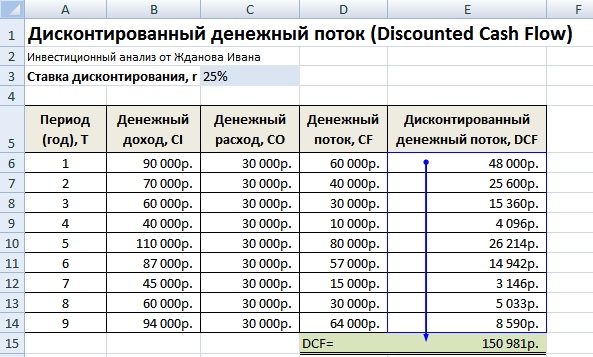
На следующем этапе рассчитывается денежный поток по каждому из временных периодов (колонка D). Одной из ключевых задач оценки денежных потоков является расчет ставки дисконтирования, в нашем случае она составляет 25%. И была получена по следующей формуле: Ставка дисконтирования = Безрисковая ставка + Премия за риск За безрисковую ставку была взята ключевая ставка ЦБ РФ. Ключевая ставка ЦБ РФ на настоящий момент составляет 15% и премия за риски (производственные, технологические, инновационные и др.) была рассчитана экспертно на уровне 10%. Ключевая ставка отражает доходность по безрисковому активу, а премия за риск показывает дополнительную норму прибыли на существующие риски проекта. Более подробно узнать про расчет безрисковой ставки можно в следующей статье: «Безрисковая ставка доходности. 5 современных методов расчета» После необходимо привести полученные денежные потоки к первоначальному периоду, то есть умножить их на коэффициент дисконтирования. В результате сумма всех дисконтированных денежных потоков даст дисконтированную стоимость инвестиционного объекта. Формулы расчета будут следующие: Денежный поток (CF) = B6-C6 Дисконтированный денежный поток (DCF) = D6/(1+$C$3)^A6 Суммарный дисконтированный денежный поток (DCF) = СУММ(E6:E14)

В результате расчета мы получили дисконтированную стоимость всех денежных потоков (DCF) равную 150 981 руб. Данный денежный поток имеет положительное значение, это свидетельствует о возможности дальнейшего анализа. При проведении инвестиционного анализа необходимо сопоставить итоговые значения дисконтированного денежного потока по различным альтернативным проектам, это позволит проранжировать их по степени привлекательности и эффективности в создании стоимости.

Методы инвестиционного анализа, использующие дисконтированные денежные потоки

Следует заметить, что дисконтированный денежный поток (DCF) в своей формуле расчета сильно походит на чистый дисконтированный доход (NPV). Главное отличие заключается во включении первоначальных инвестиционных затрат в формулу NPV. Дисконтированный денежный поток (DCF) используется во многих методах оценки эффективности инвестиционных проектов. Из-за того, что данные методы используют дисконтирование денежных потоков, их называют динамическими.

• Динамические методы оценки инвестиционных проектов
  • Чистый дисконтированный доход (NPV, Net Present Value)
  • Внутренняя норма прибыли (IRR, Internal Rate of Return)
  • Индекс прибыльности (PI, Profitability index)
  • Эквивалент ежегодной ренты (NUS, Net Uniform Series)
  • Чистая норма доходности (NRR, Net Rate of Return)
  • Чистая будущая стоимость (NFV, Net Future Value)
  • Дисконтированный срок окупаемости (DPP, Discounted Payback Period)

Более подробно узнать про методы расчета эффективности инвестиционных проектов вы можете в статье «6 методов оценки эффективности инвестиций в Excel. Пример расчета NPV, PP, DPP, IRR, ARR, PI». Помимо только дисконтирования денежных потоков существую более сложные методы, которые в дополнение учитывают реинвестирование денежных платежей.

• Модифицированная чистая норма рентабельности (MNPV, Modified Net Rate of Return)
• Модифицированная норма прибыли (MIRR, Modified Internal Rate of Return)
• Модифицированный чистый дисконтированный доход (MNPV, Modified Present Value)

Достоинства и недостатки показателя DCF дисконтирования денежных потоков

+) Использование ставки дисконтирования является несомненным достоинством данного метода, так как позволяет привести будущие платежи к текущей стоимости и учесть возможные факторы риска при оценке инвестиционной привлекательности проекта. -) К недостаткам можно отнести сложность прогнозирования будущих денежных потоков по инвестиционному проекту. К тому же трудно отразить в ставке дисконтирования изменения внешней среды. Резюме Дисконтирование денежных потоков является основой для расчета многих коэффициентов оценки инвестиционной привлекательности проекта. Мы разобрали на примере алгоритм расчета дисконтированных денежных потоков в Excel, их существующие достоинства и недостатки. С вами был Иван Жданов, спасибо за внимание.

Автор: к.э.н. Жданов Иван Юрьевич

Каждый человек, который серьезно занимался финансовой деятельностью или профессиональным инвестированием, сталкивался с таким показателем, как чистый дисконтированный доход или NPV. Этот показатель отражает инвестиционную эффективность изучаемого проекта. В программе Excel имеются инструменты, которые помогают рассчитать это значение. Давайте выясним, как их можно использовать на практике.

Расчет чистого дисконтированного дохода

Показатель чистого дисконтированного дохода (ЧДД) по-английски называется Net present value, поэтому общепринято сокращенно его называть NPV. Существует ещё альтернативное его наименование – Чистая приведенная стоимость.

NPV определяет сумму приведенных к нынешнему дню дисконтированных значений платежей, которые являются разностью между притоками и оттоками. Если говорить простым языком, то данный показатель определяет, какую сумму прибыли планирует получить инвестор за вычетом всех оттоков после того, как окупится первоначальный вклад.

В программе Excel имеется функция, которая специально предназначена для вычисления NPV. Она относится к финансовой категории операторов и называется ЧПС. Синтаксис у этой функции следующий:

=ЧПС(ставка;значение1;значение2;…)

Аргумент «Ставка» представляет собой установленную величину ставки дисконтирования на один период.

Аргумент «Значение» указывает величину выплат или поступлений. В первом случае он имеет отрицательный знак, а во втором – положительный. Данного вида аргументов в функции может быть от 1 до 254. Они могут выступать, как в виде чисел, так и представлять собой ссылки на ячейки, в которых эти числа содержатся, впрочем, как и аргумент «Ставка».

Проблема состоит в том, что функция хотя и называется ЧПС, но расчет NPV она проводит не совсем корректно. Связано это с тем, что она не учитывает первоначальную инвестицию, которая по правилам относится не к текущему, а к нулевому периоду. Поэтому в Экселе формулу вычисления NPV правильнее было бы записать так:

=Первоначальная_инвестиция+ ЧПС(ставка;значение1;значение2;…)

Естественно, первоначальная инвестиция, как и любой вид вложения, будет со знаком «-».

Пример вычисления NPV

Давайте рассмотрим применение данной функции для определения величины NPV на конкретном примере.

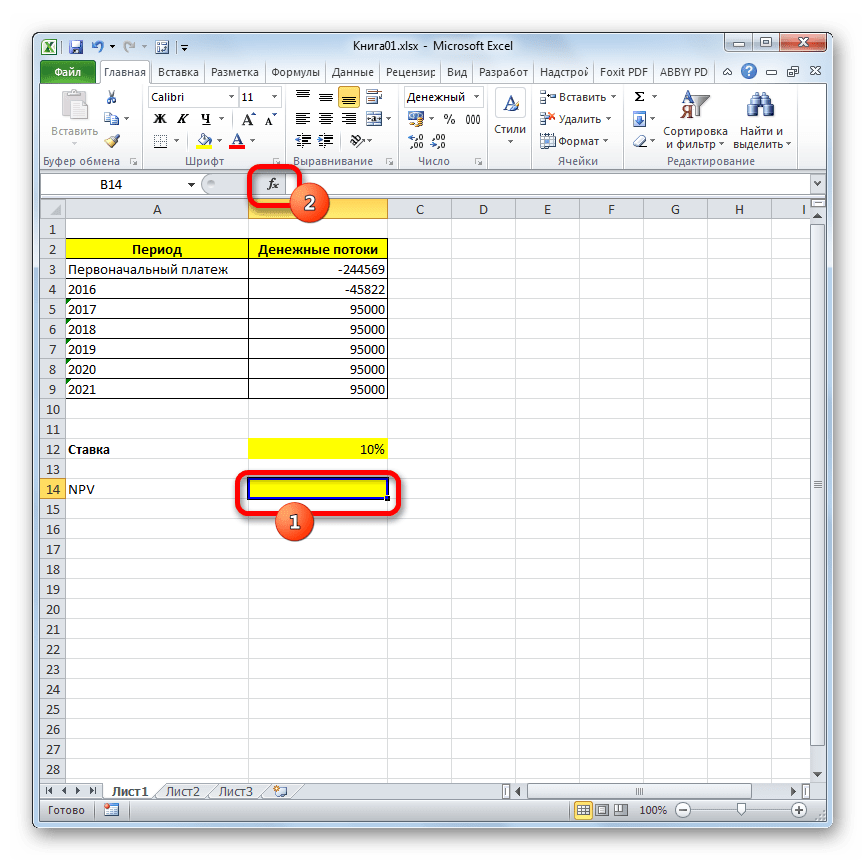
1. Выделяем ячейку, в которой будет выведен результат расчета NPV. Кликаем по значку «Вставить функцию», размещенному около строки формул.



2. Запускается окошко Мастера функций. Переходим в категорию «Финансовые» или «Полный алфавитный перечень». Выбираем в нем запись «ЧПС» и жмем на кнопку «OK».



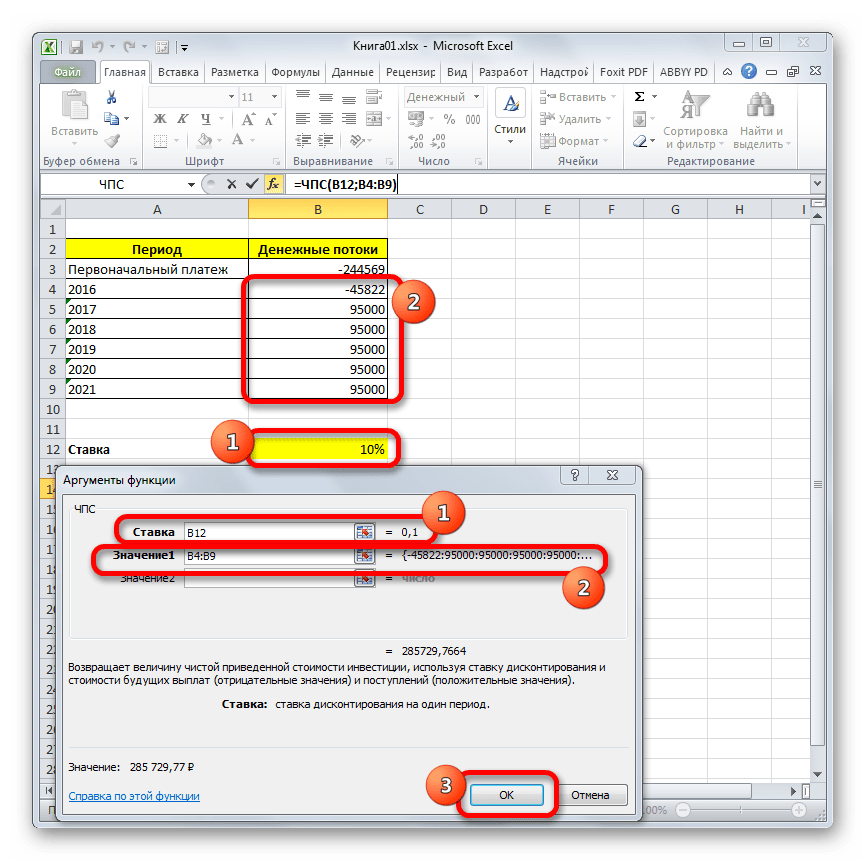
3. После этого будет открыто окно аргументов данного оператора. Оно имеет число полей равное количеству аргументов функции. Обязательными для заполнения является поле «Ставка» и хотя бы одно из полей «Значение».

   В поле «Ставка» нужно указать текущую ставку дисконтирования. Её величину можно вбить вручную, но в нашем случае её значение размещается в ячейке на листе, поэтому указываем адрес этой ячейки.

   

   В поле «Значение1» нужно указать координаты диапазона, содержащего фактические и предполагаемые в будущем денежные потоки, исключая первоначальный платеж. Это тоже можно сделать вручную, но гораздо проще установить курсор в соответствующее поле и с зажатой левой кнопкой мыши выделить соответствующий диапазон на листе.

   Так как в нашем случае денежные потоки размещены на листе цельным массивом, то вносить данные в остальные поля не нужно. Просто жмем на кнопку «OK».



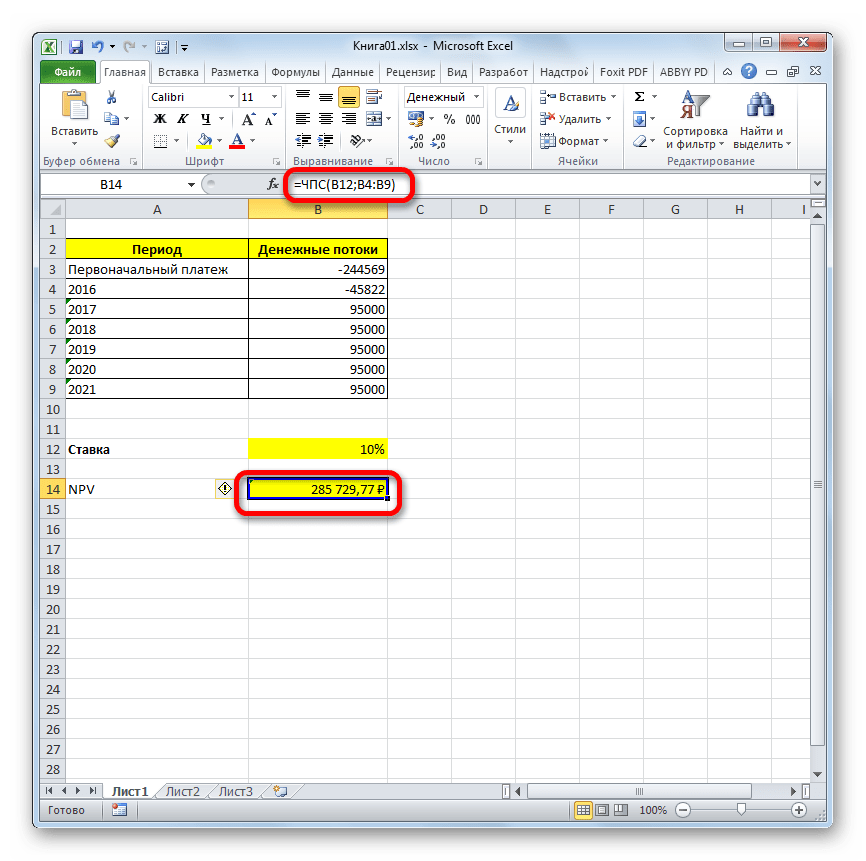
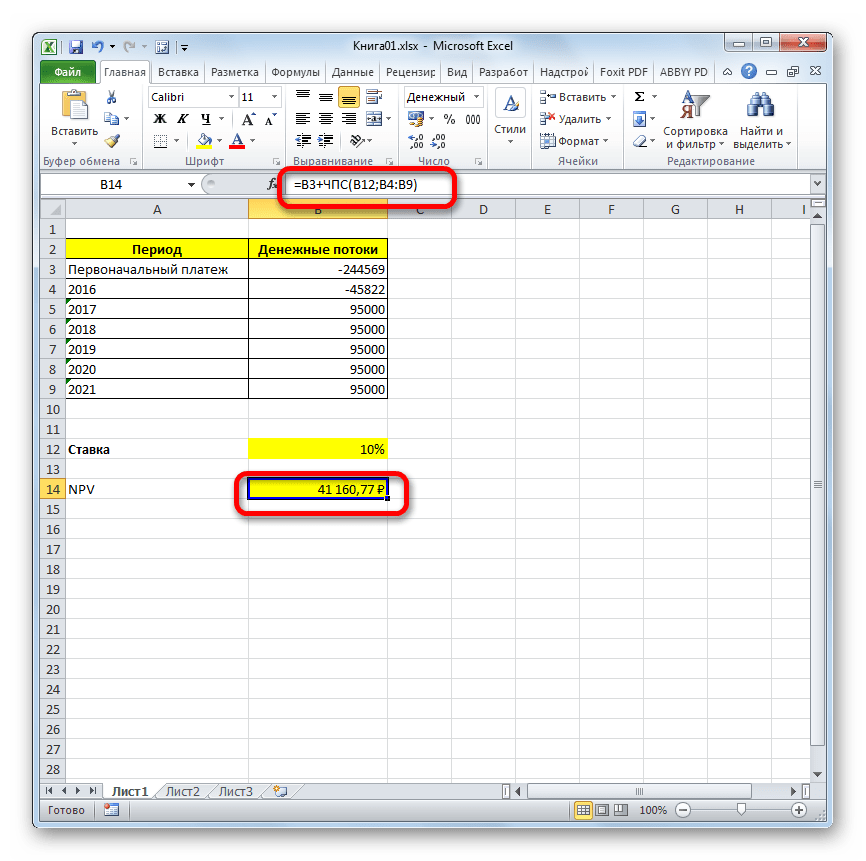
4. Расчет функции отобразился в ячейке, которую мы выделили в первом пункте инструкции. Но, как мы помним, у нас неучтенной осталась первоначальная инвестиция. Для того, чтобы завершить расчет NPV, выделяем ячейку, содержащую функцию ЧПС. В строке формул появляется её значение.



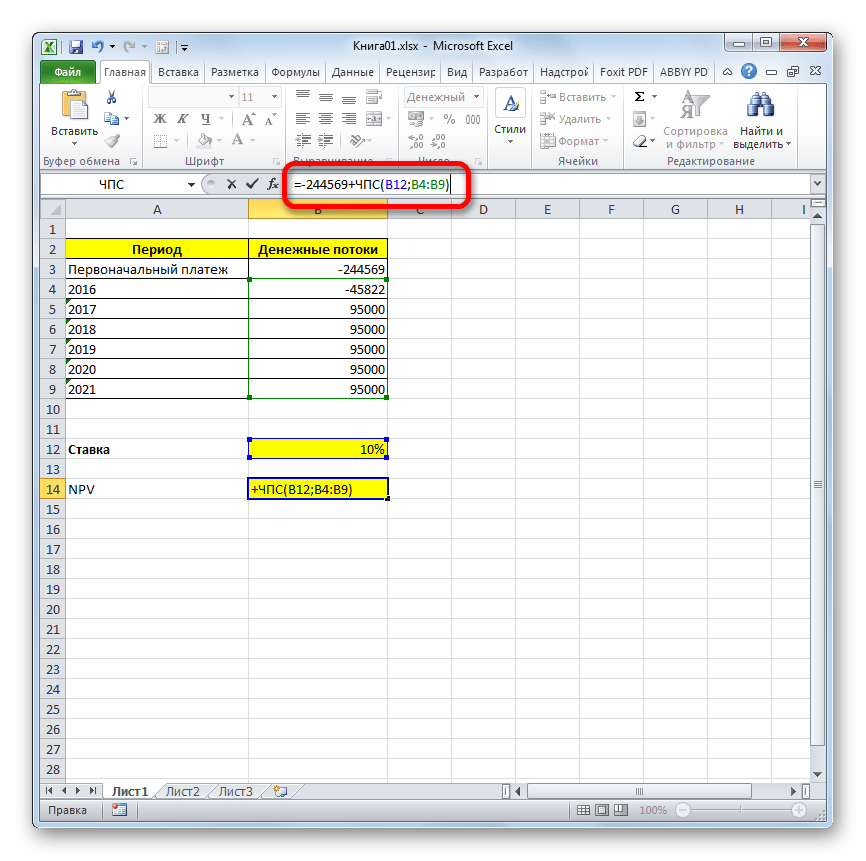
5. После символа «=» дописываем сумму первоначального платежа со знаком «-», а после неё ставим знак «+», который должен находиться перед оператором ЧПС.
   

   Можно также вместо числа указать адрес ячейки на листе, в которой содержится первоначальный взнос.



6. Для того чтобы совершить расчет и вывести результат в ячейку, жмем на кнопку Enter.

Результат выведен и в нашем случае чистый дисконтированный доход равен 41160,77 рублей. Именно эту сумму инвестор после вычета всех вложений, а также с учетом дисконтной ставки, может рассчитывать получить в виде прибыли. Теперь, зная данный показатель, он может решать, стоит ему вкладывать деньги в проект или нет.

Урок: Финансовые функции в Excel

Как видим, при наличии всех входящих данных, выполнить расчет NPV при помощи инструментов Эксель довольно просто. Единственное неудобство составляет то, что функция, предназначенная для решения данной задачи, не учитывает первоначальный платеж. Но и эту проблему решить несложно, просто подставив соответствующее значение в итоговый расчет.

For discounted cash flow analysis, the discount rate refers to the interest rate used when calculating the net present value (NPV) of an investment. It represents the time value of money.

NPV is a core component of corporate budgeting and is a comprehensive way to calculate whether a proposed project will add value or not.

For this article, when we look at the discount rate, we will be solving for the rate that results in the NPV equaling zero. Doing so allows us to determine the internal rate of return (IRR) of a project or asset.

Discount Rate

First, let’s examine each step of NPV in order. The formula is:

NPV = ∑ {After-Tax Cash Flow / (1+r)^t} — Initial Investment

Broken down, each period’s after-tax cash flow at time t is discounted by some rate, shown as r. The sum of all these discounted cash flows is then offset by the initial investment, which equals the current NPV. Any NPV greater than $0 is a value-added project.

In the decision-making process relating to competing yet comparable projects, a project with the highest NPV should tip the scale toward its selection.

The NPV, IRR, and discount rate are all connected concepts. With an NPV, you know the amount and timing of cash flows. You also know the weighted average cost of capital (WACC), which is designated as r when solving for the NPV. With an IRR, you know the same details, and you can solve for the NPV expressed as a percentage return. 

The question is, what is the discount rate that sets the IRR to zero? This is the same rate that will give the NPV a value of zero. As you will see below, if the discount rate equals the IRR, then the NPV is zero. Or to put it another way, if the cost of capital equals the return of capital, then the project will break even and have an NPV of 0. 

Calculating the Discount Rate in Excel

In Excel, you can solve for the discount rate in two ways:

• You can find the IRR and use that as the discount rate, which causes NPV to equal zero. 
• You can use What-If analysis, a built-in calculator in Excel, to solve for the discount rate that equals zero.

Method One

To illustrate the first method, we will take our NPV/IRR example. Using a hypothetical outlay, our WACC risk-free rate, and expected after-tax cash flows, we’ve calculated an NPV of $472,169 with an IRR of 57%.

We’ve already defined the discount rate as a WACC that causes the IRR to equal 0. So, we can just take our calculated IRR and put it in place of WACC to get the NPV of 0. That calculation is shown below:

Method Two

Let’s now look at the second method, using Excel’s What-If calculator. This assumes that we did not calculate the IRR of 57%, as we did above, and have no idea what the correct discount rate is.

To get to the What-If solver, go to the Data Tab —> What-If Analysis Menu —> Goal Seek. Then simply plug in the numbers and Excel will solve for the correct value. When you select «OK,» Excel will recalculate WACC to equal the discount rate that makes the NPV zero (57%).

Discount Factor

When working with the discount rate, you may come across the discount factor, as well. They aren’t the same thing although they may be used together in calculations. The discount factor, when multiplied by a cash flow value, discounts that value and provides a present value.

It’s used by Excel to shed added light on the NPV formula and the impact that discounting can have.

Here’s a comparison of the discount rate and the discount factor.

Discount Rate

• Along with time period, it’s used in the formula that calculates the discount factor.
• It represents the time value of money.
• It’s a rate of return determined by a company.
• It’s used in the calculation of present value.

Discount Factor

• As the discount rate increases due to compounding over time, the discount factor increases.
• It facilitates audits of a discounted cash flow model.
• It illustrates the effect of compounding.
• It’s an alternative to using the XNPV and XIRR functions in Excel.

Временная стоимость денег (Time Value of Money, TVM) – это важный показатель в бухгалтерской и финансовой отрасли. Идея заключается в том, что рубль сегодня стоит меньше чем тот же самый рубль завтра. Разница между этими двумя финансовыми значениями является прибыль, которую можно извлечь с одного рубля или убыток. Например, данная прибыль может быть получена с процентов, начисленных на банковском счете или в качестве дивидендов от инвестиций. Но также может быть убыток при оплате процентов за погашение кредитного долга.

Пример с расчетом текущей дисконтированной стоимости инвестиций в Excel

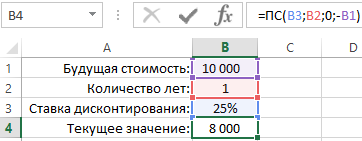
Программа Excel предлагает несколько финансовых функций для вычисления стоимости денег во времени. Например, функция ПС (приведенная стоимость) возвращает текущую стоимость инвестиций. Простыми словами, данная функция снижает сумму на размер процента дисконтирования и возвращает текущую стоимость для этой суммы. Если инвестиционный проект предполагает принести прибыль в размере 10 000 через год. Вопрос: какой максимальной суммой рационально рискнуть чтобы инвестировать в данных проект?

Например, в России розничный бизнес иногда делает прибыль до 35% годовых, а оптовый не более 15%. Учитывая небольшую сумму инвестиций предполагается, что инвестиционный объект не является оптовым бизнесом, а значит следует ожидать прибыль больше чем 15% годовых. Ниже на рисунке провиден пример формулы калькулятора доходности инвестиций в процентах:

Как мы видим на рисунке калькулятор нам отображает, чтобы получить сумму 10 000 за 1 год при доходности 25% нам необходимо вложить 8 000 финансовых средств. То есть если бы у нас была сумма 8 000 и мы вложили ее под 25% годовых через год мы заработали бы 10 000.

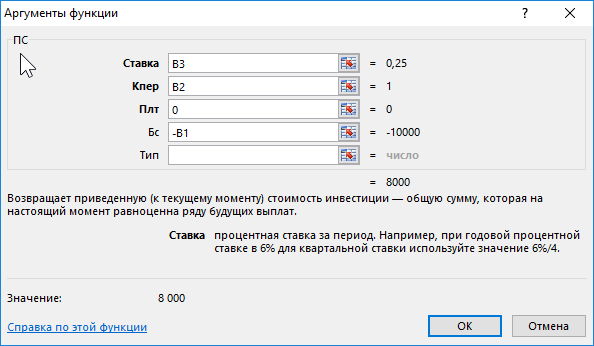
Функция ПС имеет 5 аргументов:

1. Ставка – процентная ставка дисконтирования. Это прибыль в процентах, на которую можно рассчитывать за период дисконтирования. Это значение имеет наибольшее влияние на вычисление текущей стоимости инвестиций, но его наиболее сложно точно определить. Осторожные инвесторы чаще всего занижают процентную ставку до максимально реально достижимого уровня при тех или иных условиях. Если же финансовые средства предназначены для погашения кредита, в таком случае данный аргумент определяется легко.
2. Количество периодов (Кпер) – период времени на протяжении которого дисконтируется будущая сумма. В данном примере указан 1 год (записанный в ячейке B2). Процентная ставка и количество лет должны быть выражены в соответственных единицах измерения. Это значит, что вы используете годовую ставку, тогда числовое значение в данном аргументе значит количество лет. Если указана процентная ставка в первом аргументе для месяцев (например, 2,5% ежемесячных), тогда число во втором аргументе значит количество месяцев.
3. Платеж (Плт) – сумма, которая периодически платится на протяжении периода дисконтирования. Если предусмотрен в условиях инвестирования только один платеж, как в выше приведенном примере, тогда данная сумма является будущей стоимостью денег, а сам платеж равен =0. Данный аргумент должен быть согласован со вторым аргументом количества периодов. Если количество периодов дисконтирования равно 10, а третий аргумент не равен <>0, тогда функция ПС посчитает как 10 платежей на сумму, указанную в третьем аргументе (Плт). Ниже на следующем примере изображено как вычисляется текущая стоимость денег при нескольких взносах отдельными платежами.
4. Будущая стоимость (БС) – это сумма, которую следует получить в конце периода дисконтирования. Финансовые функции Excel основаны на вычислениях наличного потока. Это значит, что будущая стоимость и текущая стоимость инвестиций имеют противоположные знаки чисел. В данном примере будущая стоимость является отрицательным числом, поэтому формула в результате вычислений возвращает положительное число.
5. Тип – данный аргумент должен иметь значение 0, если выплата итоговой суммы припадает на конец периода дисконтирования, или число 1 – если на его начало. В данном примере значение данного аргумента не имеет значения и никак не повлияет на итоговый результат вычисления. Так как платежный взнос равен нулю и аргумент определяющий тип может быть опущен. В таком случае функция по умолчанию присваивает данному аргументу значение 0.



Формула расчета текущей стоимости денег с учетом инфляции в Excel

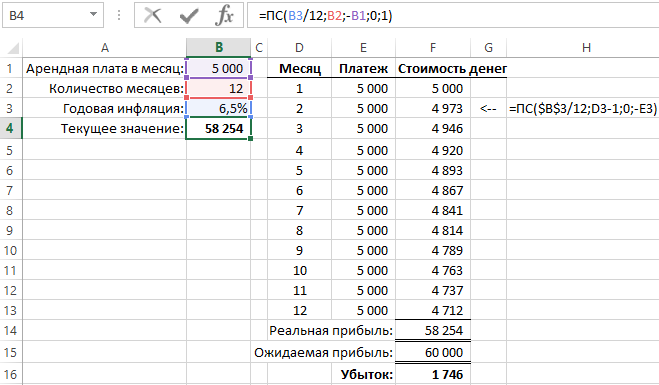
В другом примере применения функции ПС выполняется вычисление будущей стоимости денег сразу для целой серии будущих равных платежных взносов. Если, например, по договору аренды офиса арендатор должен платить по 5000 каждый месяц на протяжении одного года, тогда арендодатель с помощью функции ПС сможет посчитать сколько он потеряет дохода при учете 6,5% годовой инфляции:

В данном примере пятый аргумент «Тип» имеет числовое значение 1, так как оплата за аренду платится в начале каждого месяца.

В случае наличия суммы регулярных платежей функция ПС в реальности вычисляет текущую стоимость денег отдельно для каждого платежа и суммирует полученные результаты. На рисунке видны результаты вычисления стоимости для каждого платежа. Текущая стоимость первого платежа такая же, как и сумма платежа, так как платится сейчас по факту. Платеж в следующем месяце будет проплачен через месяц и уже уменьшается его текущая денежная стоимость (обесценивается). Он дисконтирован до суммы 4 973. Изменения не значительные, но последний платеж, который буде проплачен через 11 месяцев имеет стоимость уже существенно ниже – 4 712. Все результаты вычисления значений текущей стоимости инвестиций необходимо суммировать. Функция ПС выполняет всю эту работу автоматически без необходимости составления хронологического графика платежей за весь период.

В этой статье описаны синтаксис формулы и использование функции ЧПС в Microsoft Excel.

Описание

Возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также последовательность будущих выплат (отрицательные значения) и поступлений (положительные значения).

Синтаксис

ЧПС(ставка; значение1; [значение2],…)

Аргументы функции ЧПС описаны ниже.

• Ставка    Обязательный аргумент. Ставка дисконтирования за один период.

• Значение1, значение2,…    Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 254 аргументов, представляющих выплаты и поступления.

  • Аргументы «значение1, значение2, …» должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.

  • Функция ЧПС использует порядок аргументов «значение1, значение2, …» для определения порядка поступлений и платежей. Убедитесь в том, что ваши платежи и поступления введены в правильном порядке.

  • Аргументы, которые являются пустыми ячейками, логическими значениями или текстовыми представлениями чисел, значениями ошибок или текстом, который невозможно преобразовать в числа, игнорируются.

  • Если аргумент является массивом или ссылкой, то учитываются только числа в массиве или ссылке. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.

Замечания

• Считается, что инвестиция, значение которой вычисляет функция ЧПС, начинается за один период до даты денежного взноса «значение1» и заканчивается с последним денежным взносом в списке. Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС, но не включать в список аргументов. Дополнительные сведения см. в приведенных ниже примерах.

• Если n — количество денежных потоков в списке значений, формула для функции ЧПС имеет следующий вид:

  

• ЧПС аналогична функции ПС (текущее значение). Основное различие между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В функции ЧПС денежные взносы могут быть переменной величиной, тогда как в функции ПС они должны быть постоянными на протяжении всего периода инвестиции. Сведения о функциях платежей по ссуде и финансовых функциях см. в описании функции ПС.

• ЧПС связана также с функцией ВСД (внутренняя ставка доходности). ВСД — это ставка, для которой ЧПС равняется нулю: ЧПС(ВСД(…); …) = 0.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
0,1	Годовая ставка дисконтирования
-10 000	Начальная стоимость инвестиции через один год
3000	Доход за первый год
4200	Доход за второй год
6800	Доход за третий год
Формула	Описание	Результат
=ЧПС(A2; A3; A4; A5; A6)	Чистая приведенная стоимость данной инвестиции	1 188,44 ₽

Пример 2

Данные	Описание
0,08	Годовая ставка дисконтирования. Она может представлять показатель инфляции или процентную ставку по конкурирующим инвестициям.
-40 000	Начальная стоимость инвестиции
8000	Доход за первый год
9200	Доход за второй год
10000	Доход за третий год
12000	Доход за четвертый год
14500	Доход за пятый год
Формула	Описание	Результат
=ЧПС(A2; A4:A8)+A3	Чистая приведенная стоимость данной инвестиции	1 922,06 ₽
=ЧПС(A2; A4:A8; -9000)+A3	Чистая приведенная стоимость данной инвестиции с учетом убытка (9000) на шестом году	(3 749,47 ₽)

К началу страницы