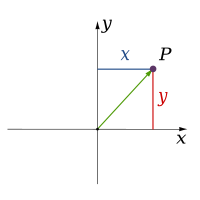На основании Вашего запроса эти примеры могут содержать грубую лексику.
На основании Вашего запроса эти примеры могут содержать разговорную лексику.
I hate him in all possible dimensions of the word.
You put your foot right into it and speak of four dimensions and of the word «mystic,» and you tell me that all of us would have a long reaction time to such stimulus words.
Этого-то как раз вы и коснулись, заговорив о четырех измерениях, о слове «мистика» и сказав мне, что на эти слова-раздражители у нас у всех будет замедленная реакция.
CSM: I’d felt that the use of quotes indicate a dimension of irony about the word «Heroes» or about the whole concept of heroism.
ЧШМ: Мне показалось, что использование кавычек указывает на иронический подтекст слова «Герои», а то и самого понятия «героизм».
In our civilization, which is totally identified with the outer and ignorant of the inner dimension of spirit, the word old has mainly negative connotations.
В нашей цивилизации, полностью отождествленной с внешним измерением и невежественной в отношении внутреннего измерения духа, слово «старый» имеет в основном негативный оттенок.
Результатов: 141193. Точных совпадений: 1. Затраченное время: 366 мс
Documents
Корпоративные решения
Спряжение
Синонимы
Корректор
Справка и о нас
Индекс слова: 1-300, 301-600, 601-900
Индекс выражения: 1-400, 401-800, 801-1200
Индекс фразы: 1-400, 401-800, 801-1200
Noun
She carefully measured each dimension of the room.
The social dimensions of the problem must also be taken into account.
Recent Examples on the Web
The typical dimensions of a mini backpack will be near 12 x 10 x 5 inches, give or take a few inches.
—
The interactive dimension of this revival sets up logistical complications that can leave a gimmicky impression (despite the attractive immersive design of Sara Beil).
—
The Madison Square Garden arena itself would be surrounded by a roughly 90-foot-tall glass podium designed to mirror the dimensions of the Beaux-Arts-style James A. Farley Building across the street.
—
Rice was wearing a T-shirt showing the dimensions of the short-faced bear: eleven feet six inches tall, weighing a ton.
—
Taylor: Sometimes, the song gains a whole new dimension of excitement from that.
—
Much of this dimension of self-awareness comes down to paying attention.
—
Material: Plastic | Handle length: 42 inches | Blade dimensions: 18 x 18 inches | Weight: 4.8 lbs.
—
In recent years, the acceleration in raw computer speeds has become less reliable, and our traditional definition of Moore’s Law is approaching its end game as the dimensions of the circuits imprinted on chips shrink to nearly atomic size.
—
Aaron Judge, New York Yankees: Another huge man with huge power playing in the same Little League-dimensioned ballpark as Stanton.
—
Each barn is covered top to bottom in oversized shingles dimensioned to make the volume look smaller.
—
See More
These examples are programmatically compiled from various online sources to illustrate current usage of the word ‘dimension.’ Any opinions expressed in the examples do not represent those of Merriam-Webster or its editors. Send us feedback about these examples.
размер, измерение, размерность, величина, проставлять размеры
существительное
- размеры
- размер
Мои примеры
Словосочетания
the spatial dimensions of a room — пространственные габариты помещения 
a rather biggish table for a dining room of modest dimensions — стол, который великоват для столовой скромных размеров. 
human dimensions of global environmental change — человеческое измерение глобальных экологических изменений 
campaign of nation-wide dimensions — общенациональная кампания 
orthogonal dimensions — ортогональные размеры 
outline dimensions — габаритные размеры 
outside dimensions — наружные линейные размеры; внешние размеры 
ample dimensions — размеры с достаточным запасом; размеры, взятые с запасом 
precise dimensions — габаритные размеры; точные размеры 
preferred dimensions — предпочтительные размерный; предпочтительные размеры 
minimum qualifying dimensions — минимальные квалификационные размеры 
regain one’s original dimensions — снова приобрести свои первоначальные размеры 
Примеры с переводом
The issue assumed serious dimensions. 
Дело приняло серьёзный оборот.
A diagram represents things in only two dimensions. 
Схема представляет всё только в двух измерениях.
We’ll need to know the exact dimensions of the room. 
Нам нужно будет знать точные размеры помещения.
The social dimensions of the problem must also be taken into account. 
Также необходимо принять во внимание социальные аспекты данной проблемы.
Tokens of this vowel varied on dimensions of height, rounding and length. 
Реализации этой гласной фонемы различались по параметрам высоты, лабиализации и долготы.
Возможные однокоренные слова
dimension — размер, измерение, размерность, величина, проставлять размеры
dimensioned — измеренный, масштабный, размерный, с размерами
dimensionless — безразмерный, без указания размеров, не поддающийся измерению, огромный
Other forms: dimensions; dimensioned; dimensioning
A dimension is the measurement of something in physical space. You might give the painters every dimension of the rooms you want painted, including depth, height, and width.
In addition to physical objects, dimension can describe something less tangible, such as the magnitude or extent of something. You might be shocked by the dimension of damage from the explosion down the street. Dimension can also be a feature of something, such as an experience, situation, flavor, or thing. Painting your bedroom purple will add a mystical dimension to your dwelling, especially if you add unicorn accents.
Definitions of dimension
-
noun
a construct whereby objects or individuals can be distinguished
-
synonyms:
attribute, property
see moresee less-
types:
- show 15 types…
- hide 15 types…
-
character, lineament, quality
a characteristic property that defines the apparent individual nature of something
-
characteristic, feature
a prominent attribute or aspect of something
-
feature, feature of speech
(linguistics) a distinctive characteristic of a linguistic unit that serves to distinguish it from other units of the same kind
-
sex character, sex characteristic, sexual characteristic
those characteristics (both anatomical and psychological) that are strongly associated with one sex relative to the other
-
texture
the essential quality of something
-
invariant
a feature (quantity or property or function) that remains unchanged when a particular transformation is applied to it
-
aspect, facet
a distinct feature or element in a problem
-
attracter, attraction, attractive feature, attractor, magnet
a characteristic that provides pleasure and attracts
-
badge
any feature that is regarded as a sign of status (a particular power or quality or rank)
-
centerpiece, centrepiece
the central or most important feature
-
contour
a feature (or the order or arrangement of features) of anything having a complex structure
-
excellence, excellency
an outstanding feature; something in which something or someone excels
-
external
outward features
-
distinctive feature, distinguishing characteristic, peculiarity
an odd or unusual characteristic
-
safety feature
feature of an artifact that is added to insure a user’s safety
-
type of:
-
concept, conception, construct
an abstract or general idea inferred or derived from specific instances
-
noun
the magnitude of something in a particular direction (especially length or width or height)
see moresee less-
types:
- show 18 types…
- hide 18 types…
-
thickness
the dimension through an object as opposed to its length or width
-
slenderness, tenuity, thinness
relatively small dimension through an object as opposed to its length or width
-
length
the linear extent in space from one end to the other; the longest dimension of something that is fixed in place
-
breadth, width
the extent of something from side to side
-
height, tallness
the vertical dimension of extension; distance from the base of something to the top
-
third dimension
the dimension whereby a solid object differs from a two-dimensional drawing of it
-
fourth dimension, time
the fourth coordinate that is required (along with three spatial dimensions) to specify a physical event
-
circumference
the length of the closed curve of a circle
-
diam, diameter
the length of a straight line passing through the center of a circle and connecting two points on the circumference
-
r, radius
the length of a line segment between the center and circumference of a circle or sphere
-
gauge
the thickness of wire
-
longness
the property of being of long spatial extent
-
shortness
the property of being of short spatial extent
-
broadness, wideness
the property of being wide; having great width
-
beam
(nautical) breadth amidships
-
narrowness
the property of being narrow; having little width
-
highness, loftiness
the quality of being high or lofty
-
lowness
the quality of being low; lacking height
-
type of:
-
magnitude
the property of relative size or extent (whether large or small)
-
noun
one of three Cartesian coordinates that determine a position in space
see moresee less-
type of:
-
Cartesian coordinate
one of the coordinates in a system of coordinates that locates a point on a plane or in space by its distance from two lines or three planes respectively; the two lines or the intersections of the three planes are the coordinate axes
-
Cartesian coordinate
-
verb
indicate the dimensions on
“These techniques permit us to
dimension the human heart” -
verb
shape or form to required dimensions
DISCLAIMER: These example sentences appear in various news sources and books to reflect the usage of the word ‘dimension’.
Views expressed in the examples do not represent the opinion of Vocabulary.com or its editors.
Send us feedback
EDITOR’S CHOICE
Look up dimension for the last time
Close your vocabulary gaps with personalized learning that focuses on teaching the
words you need to know.
Sign up now (it’s free!)
Whether you’re a teacher or a learner, Vocabulary.com can put you or your class on the path to systematic vocabulary improvement.
Get started
Answer
A Word Embedding is just a mapping from words to vectors. Dimensionality in word
embeddings refers to the length of these vectors.
Additional Info
These mappings come in different formats. Most pre-trained embeddings are
available as a space-separated text file, where each line contains a word in the
first position, and its vector representation next to it. If you were to split
these lines, you would find out that they are of length 1 + dim, where dim
is the dimensionality of the word vectors, and 1 corresponds to the word being represented. See the GloVe pre-trained
vectors for a real example.
For example, if you download glove.twitter.27B.zip, unzip it, and run the following python code:
#!/usr/bin/python3
with open('glove.twitter.27B.50d.txt') as f:
lines = f.readlines()
lines = [line.rstrip().split() for line in lines]
print(len(lines)) # number of words (aka vocabulary size)
print(len(lines[0])) # length of a line
print(lines[130][0]) # word 130
print(lines[130][1:]) # vector representation of word 130
print(len(lines[130][1:])) # dimensionality of word 130
you would get the output
1193514
51
people
['1.4653', '0.4827', ..., '-0.10117', '0.077996'] # shortened for illustration purposes
50
Somewhat unrelated, but equally important, is that lines in these files are sorted according to the word frequency found in the corpus in which the embeddings were trained (most frequent words first).
You could also represent these embeddings as a dictionary where
the keys are the words and the values are lists representing word vectors. The length
of these lists would be the dimensionality of your word vectors.
A more common practice is to represent them as matrices (also called lookup
tables), of dimension (V x D), where V is the vocabulary size (i.e., how
many words you have), and D is the dimensionality of each word vector. In
this case you need to keep a separate dictionary mapping each word to its
corresponding row in the matrix.
Background
Regarding your question about the role dimensionality plays, you’ll need some theoretical background. But in a few words, the space in which words are embedded presents nice properties that allow NLP systems to perform better. One of these properties is that words that have similar meaning are spatially close to each other, that is, have similar vector representations, as measured by a distance metric such as the Euclidean distance or the cosine similarity.
You can visualize a 3D projection of several word embeddings here, and see, for example, that the closest words to «roads» are «highways», «road», and «routes» in the Word2Vec 10K embedding.
For a more detailed explanation I recommend reading the section «Word Embeddings» of this post by Christopher Olah.
For more theory on why using word embeddings, which are an instance of distributed representations, is better than using, for example, one-hot encodings (local representations), I recommend reading the first sections of Distributed Representations by Geoffrey Hinton et al.
- Top Definitions
- Synonyms
- Quiz
- Related Content
- Examples
- British
- Scientific
This shows grade level based on the word’s complexity.
[ dih-men-shuhn, dahy- ]
/ dɪˈmɛn ʃən, daɪ- /
This shows grade level based on the word’s complexity.
noun
Mathematics.
- a property of space; extension in a given direction: A straight line has one dimension, a parallelogram has two dimensions, and a parallelepiped has three dimensions.
- the generalization of this property to spaces with curvilinear extension, as the surface of a sphere.
- the generalization of this property to vector spaces and to Hilbert space.
- the generalization of this property to fractals, which can have dimensions that are noninteger real numbers.
- extension in time: Space-time has three dimensions of space and one of time.
Usually dimensions.
- measurement in length, width, and thickness.
- scope; importance: the dimensions of a problem.
an aspect, feature, or angle: A study abroad experience can add a cultural dimension to your language learning.We haven’t addressed that dimension of the issue.
Topology.
- a magnitude that, independently or in conjunction with other such magnitudes, serves to define the location of an element within a given set, as of a point on a line, an object in a space, or an event in space-time.
- the number of elements in a finite basis of a given vector space.
Physics. any of a set of basic kinds of quantity, as mass, length, and time, in terms of which all other kinds of quantity can be expressed: usually denoted by capital letters, with appropriate exponents, placed in brackets: The dimensions of velocity are [LT−1].Compare dimensional analysis.
Also called al·ter·nate di·men·sion [awl-ter-nit di-men-shuhn, dahy-] /ˈɔl tər nɪt dɪˈmɛn ʃən, daɪ-/ . (in science fiction, fantasy, etc.) a hypothetical universe or world that is different from our known universe and reachable by traveling in directions that are not the perceptible axes of space and time, as with the use of futuristic technology or magic: Your enemies are villains, cultists, terrible monsters, and unfathomable entities from alternate dimensions or the cosmos beyond.Compare parallel universe (def. 3).
dimensions, Informal. the measurements of a woman’s bust, waist, and hips, in that order: The dressmaker noted that the customer’s dimensions were 38-24-36.
verb (used with object)
to shape or fashion to the desired dimensions:Dimension the shelves so that they fit securely into the cabinet.
to indicate the dimensions of an item, area, etc., on (a sketch or drawing).
QUIZ
CAN YOU ANSWER THESE COMMON GRAMMAR DEBATES?
There are grammar debates that never die; and the ones highlighted in the questions in this quiz are sure to rile everyone up once again. Do you know how to answer the questions that cause some of the greatest grammar debates?
Which sentence is correct?
Origin of dimension
First recorded in 1375–1425; late Middle English dimensioun, from Anglo-French or directly from Latin dīmēnsiōn- (stem of dīmēnsiō ) “a measuring,” equivalent to dīmēns(us) “measured out” (past participle of dīmētīrī, equivalent to dī- di-2 + mētīrī “to measure”) + -iōn- -ion
OTHER WORDS FROM dimension
di·men·sion·al, adjectivedi·men·sion·al·i·ty [dih-men-shuh—nal-i-tee, dahy-], /dɪˌmɛn ʃəˈnæl ɪ ti, daɪ-/, noundi·men·sion·al·ly, adverbdi·men·sion·less, adjective
mul·ti·di·men·sion·al, adjectivenon·di·men·sioned, adjectiveun·di·men·sioned, adjective
Words nearby dimension
dime, dime a dozen, dime bag, dimenhydrinate, dime novel, dimension, dimensional analysis, dimensionless number, dimension lumber, dimension stone, dimer
Dictionary.com Unabridged
Based on the Random House Unabridged Dictionary, © Random House, Inc. 2023
Words related to dimension
aspect, element, extent, height, importance, length, magnitude, proportion, quality, range, scope, size, thickness, bulk, capacity, mass, time, volume
How to use dimension in a sentence
-
Almost every dimension of inequity has been accentuated here.
-
At times he’s proposed worlds where the rules of the universe that we take for granted — about space, dimensions, the human body, the nature of dreams — are bent into strange new shapes.
-
All the while, lidar measured the exact dimensions of their bodies.
-
Psychologists call this misleading feeling of helplessness the “pseudoinefficacy effect,” and it has a political dimension that may keep individuals from working to help others.
-
A simple argument shows that once the conjecture is false in one dimension, it’s necessarily false in all higher dimensions.
-
A Europe which is no longer open to the transcendent dimension of life is a Europe which risks slowly losing its own soul.
-
Underneath, a miniature version of the bug-crazy man is revealed, himself thwacking away in an alternate dimension.
-
There needs to be a fully thought out strategy with a political dimension that involves the opposition.
-
Trippy, echoing sound effects give “A Brain In A Bottle” a sense of fullness and dimension—as they do for “Guess Again!”
-
In the case of Hollywood actresses, too, this expectation takes on an even more pernicious dimension.
-
For copying by engraving, &c. the exact dimension required of any picture may at once be given to be copied from.
-
By varying the distances between a and c, and c and b, any dimension required may be given to the positive impression.
-
It was a genuine western, with high horn and high cantle and two cinches, but much reduced in every dimension.
-
Dimension lines and centre lines are best put in of different colour.
-
The arrow-heads at the ends of the dimension lines are now put in with black ink, and so are the figures for the dimensions.
British Dictionary definitions for dimension
noun
(often plural) a measurement of the size of something in a particular direction, such as the length, width, height, or diameter
(often plural) scope; size; extenta problem of enormous dimensions
aspecta new dimension to politics
maths the number of coordinates required to locate a point in space
physics
- the product or the quotient of the fundamental physical quantities (such as mass, length, or time) raised to the appropriate power in a derived physical quantitythe dimensions of velocity are length divided by time
- the power to which such a fundamental quantity has to be raised in a derived quantity
verb
(tr) mainly US
- to shape or cut to specified dimensions
- to mark with specified dimensions
Derived forms of dimension
dimensional, adjectivedimensionality, noundimensionally, adverbdimensionless, adjective
Word Origin for dimension
C14: from Old French, from Latin dīmensiō an extent, from dīmētīrī to measure out, from mētīrī
Collins English Dictionary — Complete & Unabridged 2012 Digital Edition
© William Collins Sons & Co. Ltd. 1979, 1986 © HarperCollins
Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Scientific definitions for dimension
- Any one of the three physical or spatial properties of length, area, and volume. In geometry, a point is said to have zero dimension; a figure having only length, such as a line, has one dimension; a plane or surface, two dimensions; and a figure having volume, three dimensions. The fourth dimension is often said to be time, as in the theory of General Relativity. Higher dimensions can be dealt with mathematically but cannot be represented visually.
- The measurement of a length, width, or thickness.
A unit, such as mass, time, or charge, associated with a physical quantity and used as the basis for other measurements, such as acceleration.
The American Heritage® Science Dictionary
Copyright © 2011. Published by Houghton Mifflin Harcourt Publishing Company. All rights reserved.
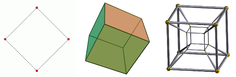
The first four spatial dimensions, represented in a two-dimensional picture.
- Two points can be connected to create a line segment.
- Two parallel line segments can be connected to form a square.
- Two parallel squares can be connected to form a cube.
- Two parallel cubes can be connected to form a tesseract.
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it.[1][2] Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on it – for example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on it – for example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces.
In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that was found necessary to describe electromagnetism. The four dimensions (4D) of spacetime consist of events that are not absolutely defined spatially and temporally, but rather are known relative to the motion of an observer. Minkowski space first approximates the universe without gravity; the pseudo-Riemannian manifolds of general relativity describe spacetime with matter and gravity. 10 dimensions are used to describe superstring theory (6D hyperspace + 4D), 11 dimensions can describe supergravity and M-theory (7D hyperspace + 4D), and the state-space of quantum mechanics is an infinite-dimensional function space.
The concept of dimension is not restricted to physical objects. High-dimensional spaces frequently occur in mathematics and the sciences. They may be Euclidean spaces or more general parameter spaces or configuration spaces such as in Lagrangian or Hamiltonian mechanics; these are abstract spaces, independent of the physical space in which we live.
In mathematics[edit]
In mathematics, the dimension of an object is, roughly speaking, the number of degrees of freedom of a point that moves on this object. In other words, the dimension is the number of independent parameters or coordinates that are needed for defining the position of a point that is constrained to be on the object. For example, the dimension of a point is zero; the dimension of a line is one, as a point can move on a line in only one direction (or its opposite); the dimension of a plane is two, etc.
The dimension is an intrinsic property of an object, in the sense that it is independent of the dimension of the space in which the object is or can be embedded. For example, a curve, such as a circle, is of dimension one, because the position of a point on a curve is determined by its signed distance along the curve to a fixed point on the curve. This is independent from the fact that a curve cannot be embedded in a Euclidean space of dimension lower than two, unless it is a line.
The dimension of Euclidean n-space En is n. When trying to generalize to other types of spaces, one is faced with the question «what makes En n-dimensional?» One answer is that to cover a fixed ball in En by small balls of radius ε, one needs on the order of ε−n such small balls. This observation leads to the definition of the Minkowski dimension and its more sophisticated variant, the Hausdorff dimension, but there are also other answers to that question. For example, the boundary of a ball in En looks locally like En-1 and this leads to the notion of the inductive dimension. While these notions agree on En, they turn out to be different when one looks at more general spaces.
A tesseract is an example of a four-dimensional object. Whereas outside mathematics the use of the term «dimension» is as in: «A tesseract has four dimensions«, mathematicians usually express this as: «The tesseract has dimension 4«, or: «The dimension of the tesseract is 4″ or: 4D.
Although the notion of higher dimensions goes back to René Descartes, substantial development of a higher-dimensional geometry only began in the 19th century, via the work of Arthur Cayley, William Rowan Hamilton, Ludwig Schläfli and Bernhard Riemann. Riemann’s 1854 Habilitationsschrift, Schläfli’s 1852 Theorie der vielfachen Kontinuität, and Hamilton’s discovery of the quaternions and John T. Graves’ discovery of the octonions in 1843 marked the beginning of higher-dimensional geometry.
The rest of this section examines some of the more important mathematical definitions of dimension.
Vector spaces[edit]
The dimension of a vector space is the number of vectors in any basis for the space, i.e. the number of coordinates necessary to specify any vector. This notion of dimension (the cardinality of a basis) is often referred to as the Hamel dimension or algebraic dimension to distinguish it from other notions of dimension.
For the non-free case, this generalizes to the notion of the length of a module.
Manifolds[edit]
The uniquely defined dimension of every connected topological manifold can be calculated. A connected topological manifold is locally homeomorphic to Euclidean n-space, in which the number n is the manifold’s dimension.
For connected differentiable manifolds, the dimension is also the dimension of the tangent vector space at any point.
In geometric topology, the theory of manifolds is characterized by the way dimensions 1 and 2 are relatively elementary, the high-dimensional cases n > 4 are simplified by having extra space in which to «work»; and the cases n = 3 and 4 are in some senses the most difficult. This state of affairs was highly marked in the various cases of the Poincaré conjecture, in which four different proof methods are applied.
Complex dimension[edit]
The dimension of a manifold depends on the base field with respect to which Euclidean space is defined. While analysis usually assumes a manifold to be over the real numbers, it is sometimes useful in the study of complex manifolds and algebraic varieties to work over the complex numbers instead. A complex number (x + iy) has a real part x and an imaginary part y, in which x and y are both real numbers; hence, the complex dimension is half the real dimension.
Conversely, in algebraically unconstrained contexts, a single complex coordinate system may be applied to an object having two real dimensions. For example, an ordinary two-dimensional spherical surface, when given a complex metric, becomes a Riemann sphere of one complex dimension.[3]
Varieties[edit]
The dimension of an algebraic variety may be defined in various equivalent ways. The most intuitive way is probably the dimension of the tangent space at any Regular point of an algebraic variety. Another intuitive way is to define the dimension as the number of hyperplanes that are needed in order to have an intersection with the variety that is reduced to a finite number of points (dimension zero). This definition is based on the fact that the intersection of a variety with a hyperplane reduces the dimension by one unless if the hyperplane contains the variety.
An algebraic set being a finite union of algebraic varieties, its dimension is the maximum of the dimensions of its components. It is equal to the maximal length of the chains 

Each variety can be considered as an algebraic stack, and its dimension as variety agrees with its dimension as stack. There are however many stacks which do not correspond to varieties, and some of these have negative dimension. Specifically, if V is a variety of dimension m and G is an algebraic group of dimension n acting on V, then the quotient stack [V/G] has dimension m − n.[4]
Krull dimension[edit]
The Krull dimension of a commutative ring is the maximal length of chains of prime ideals in it, a chain of length n being a sequence 
For an algebra over a field, the dimension as vector space is finite if and only if its Krull dimension is 0.
Topological spaces[edit]
For any normal topological space X, the Lebesgue covering dimension of X is defined to be the smallest integer n for which the following holds: any open cover has an open refinement (a second open cover in which each element is a subset of an element in the first cover) such that no point is included in more than n + 1 elements. In this case dim X = n. For X a manifold, this coincides with the dimension mentioned above. If no such integer n exists, then the dimension of X is said to be infinite, and one writes dim X = ∞. Moreover, X has dimension −1, i.e. dim X = −1 if and only if X is empty. This definition of covering dimension can be extended from the class of normal spaces to all Tychonoff spaces merely by replacing the term «open» in the definition by the term «functionally open«.
An inductive dimension may be defined inductively as follows. Consider a discrete set of points (such as a finite collection of points) to be 0-dimensional. By dragging a 0-dimensional object in some direction, one obtains a 1-dimensional object. By dragging a 1-dimensional object in a new direction, one obtains a 2-dimensional object. In general one obtains an (n + 1)-dimensional object by dragging an n-dimensional object in a new direction. The inductive dimension of a topological space may refer to the small inductive dimension or the large inductive dimension, and is based on the analogy that, in the case of metric spaces, (n + 1)-dimensional balls have n-dimensional boundaries, permitting an inductive definition based on the dimension of the boundaries of open sets. Moreover, the boundary of a discrete set of points is the empty set, and therefore the empty set can be taken to have dimension -1.[5]
Similarly, for the class of CW complexes, the dimension of an object is the largest n for which the n-skeleton is nontrivial. Intuitively, this can be described as follows: if the original space can be continuously deformed into a collection of higher-dimensional triangles joined at their faces with a complicated surface, then the dimension of the object is the dimension of those triangles.[citation needed]
Hausdorff dimension[edit]
The Hausdorff dimension is useful for studying structurally complicated sets, especially fractals. The Hausdorff dimension is defined for all metric spaces and, unlike the dimensions considered above, can also have non-integer real values.[6] The box dimension or Minkowski dimension is a variant of the same idea. In general, there exist more definitions of fractal dimensions that work for highly irregular sets and attain non-integer positive real values.
Hilbert spaces[edit]
Every Hilbert space admits an orthonormal basis, and any two such bases for a particular space have the same cardinality. This cardinality is called the dimension of the Hilbert space. This dimension is finite if and only if the space’s Hamel dimension is finite, and in this case the two dimensions coincide.
In physics[edit]
Spatial dimensions[edit]
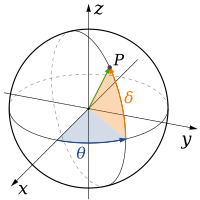
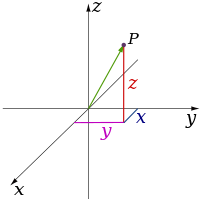
Classical physics theories describe three physical dimensions: from a particular point in space, the basic directions in which we can move are up/down, left/right, and forward/backward. Movement in any other direction can be expressed in terms of just these three. Moving down is the same as moving up a negative distance. Moving diagonally upward and forward is just as the name of the direction implies; i.e., moving in a linear combination of up and forward. In its simplest form: a line describes one dimension, a plane describes two dimensions, and a cube describes three dimensions. (See Space and Cartesian coordinate system.)
|
Number of |
Example co-ordinate systems | |||
|---|---|---|---|---|
| 1 |
|
|||
| 2 |
|
|||
| 3 |
|
Time[edit]
A temporal dimension, or time dimension, is a dimension of time. Time is often referred to as the «fourth dimension» for this reason, but that is not to imply that it is a spatial dimension. A temporal dimension is one way to measure physical change. It is perceived differently from the three spatial dimensions in that there is only one of it, and that we cannot move freely in time but subjectively move in one direction.
The equations used in physics to model reality do not treat time in the same way that humans commonly perceive it. The equations of classical mechanics are symmetric with respect to time, and equations of quantum mechanics are typically symmetric if both time and other quantities (such as charge and parity) are reversed. In these models, the perception of time flowing in one direction is an artifact of the laws of thermodynamics (we perceive time as flowing in the direction of increasing entropy).
The best-known treatment of time as a dimension is Poincaré and Einstein’s special relativity (and extended to general relativity), which treats perceived space and time as components of a four-dimensional manifold, known as spacetime, and in the special, flat case as Minkowski space. Time is different from other spatial dimensions as time operates in all spatial dimensions. Time operates in the first, second and third as well as theoretical spatial dimensions such as a fourth spatial dimension. Time is not however present in a single point of absolute infinite singularity as defined as a geometric point, as an infinitely small point can have no change and therefore no time. Just as when an object moves through positions in space, it also moves through positions in time. In this sense the force moving any object to change is time.[7][8][9]
Additional dimensions[edit]
In physics, three dimensions of space and one of time is the accepted norm. However, there are theories that attempt to unify the four fundamental forces by introducing extra dimensions/hyperspace. Most notably, superstring theory requires 10 spacetime dimensions, and originates from a more fundamental 11-dimensional theory tentatively called M-theory which subsumes five previously distinct superstring theories. Supergravity theory also promotes 11D spacetime = 7D hyperspace + 4 common dimensions. To date, no direct experimental or observational evidence is available to support the existence of these extra dimensions. If hyperspace exists, it must be hidden from us by some physical mechanism. One well-studied possibility is that the extra dimensions may be «curled up» at such tiny scales as to be effectively invisible to current experiments.
In 1921, Kaluza–Klein theory presented 5D including an extra dimension of space. At the level of quantum field theory, Kaluza–Klein theory unifies gravity with gauge interactions, based on the realization that gravity propagating in small, compact extra dimensions is equivalent to gauge interactions at long distances. In particular when the geometry of the extra dimensions is trivial, it reproduces electromagnetism. However at sufficiently high energies or short distances, this setup still suffers from the same pathologies that famously obstruct direct attempts to describe quantum gravity. Therefore, these models still require a UV completion, of the kind that string theory is intended to provide. In particular, superstring theory requires six compact dimensions (6D hyperspace) forming a Calabi–Yau manifold. Thus Kaluza-Klein theory may be considered either as an incomplete description on its own, or as a subset of string theory model building.
In addition to small and curled up extra dimensions, there may be extra dimensions that instead aren’t apparent because the matter associated with our visible universe is localized on a (3 + 1)-dimensional subspace. Thus the extra dimensions need not be small and compact but may be large extra dimensions. D-branes are dynamical extended objects of various dimensionalities predicted by string theory that could play this role. They have the property that open string excitations, which are associated with gauge interactions, are confined to the brane by their endpoints, whereas the closed strings that mediate the gravitational interaction are free to propagate into the whole spacetime, or «the bulk». This could be related to why gravity is exponentially weaker than the other forces, as it effectively dilutes itself as it propagates into a higher-dimensional volume.
Some aspects of brane physics have been applied to cosmology. For example, brane gas cosmology[10][11] attempts to explain why there are three dimensions of space using topological and thermodynamic considerations. According to this idea it would be since three is the largest number of spatial dimensions in which strings can generically intersect. If initially there are many windings of strings around compact dimensions, space could only expand to macroscopic sizes once these windings are eliminated, which requires oppositely wound strings to find each other and annihilate. But strings can only find each other to annihilate at a meaningful rate in three dimensions, so it follows that only three dimensions of space are allowed to grow large given this kind of initial configuration.
Extra dimensions are said to be universal if all fields are equally free to propagate within them.
In computer graphics and spatial data[edit]
Several types of digital systems are based on the storage, analysis, and visualization of geometric shapes, including illustration software, Computer-aided design, and Geographic information systems. Different vector systems use a wide variety of data structures to represent shapes, but almost all are fundamentally based on a set of geometric primitives corresponding to the spatial dimensions:[12]
- Point (0-dimensional), a single coordinate in a Cartesian coordinate system.
- Line or Polyline (1-dimensional), usually represented as an ordered list of points sampled from a continuous line, whereupon the software is expected to interpolate the intervening shape of the line as straight or curved line segments.
- Polygon (2-dimensional), usually represented as a line that closes at its endpoints, representing the boundary of a two-dimensional region. The software is expected to use this boundary to partition 2-dimensional space into an interior and exterior.
- Surface (3-dimensional), represented using a variety of strategies, such as a polyhedron consisting of connected polygon faces. The software is expected to use this surface to partition 3-dimensional space into an interior and exterior.
Frequently in these systems, especially GIS and Cartography, a representation of a real-world phenomena may have a different (usually lower) dimension than the phenomenon being represented. For example, a city (a two-dimensional region) may be represented as a point, or a road (a three-dimensional volume of material) may be represented as a line. This dimensional generalization correlates with tendencies in spatial cognition. For example, asking the distance between two cities presumes a conceptual model of the cities as points, while giving directions involving travel «up,» «down,» or «along» a road imply a one-dimensional conceptual model. This is frequently done for purposes of data efficiency, visual simplicity, or cognitive efficiency, and is acceptable if the distinction between the representation and the represented is understood, but can cause confusion if information users assume that the digital shape is a perfect representation of reality (i.e., believing that roads really are lines).
More dimensions[edit]
- Degrees of freedom
- in mechanics
- in physics and chemistry
- in statistics
- Exterior dimension
- Hurst exponent
- Isoperimetric dimension
- Metric dimension
- Order dimension
- q-dimension
- Fractal (q = 1)
- Correlation (q = 2)
List of topics by dimension[edit]
- Zero
- Point
- Zero-dimensional space
- Integer
- One
- Line
- Curve
- Graph (combinatorics)
- Real number
- Length
- Two
- Plane
- Surface
- Polygon
- Net
- Complex number
- Cartesian coordinate system
- List of uniform tilings
- Area
- Three
- Platonic solid
- Polyhedron
- Stereoscopy (3-D imaging)
- 3-manifold
- Axis of rotation
- Knots
- Skew lines
- Skew polygon
- Volume
- Four
- Spacetime
- Fourth spatial dimension
- Convex regular 4-polytope
- Quaternion
- 4-manifold
- Polychoron
- Rotations in 4-dimensional Euclidean space
- Fourth dimension in art
- Fourth dimension in literature
- Higher dimensions
- in mathematics
- Octonion
- Vector space
- Plane of rotation
- Curse of dimensionality
- in physics
- Kaluza–Klein theory
- String theory
- M-theory
- in mathematics
- Infinite
- Hilbert space
- Function space
See also[edit]
- Dimension (data warehouse)
- Dimension tables
- Dimensional analysis
- Hyperspace (disambiguation)
- Intrinsic dimension
- Multidimensional analysis
- Space-filling curve
- Mean dimension
References[edit]
- ^ «Curious About Astronomy». Curious.astro.cornell.edu. Archived from the original on 2014-01-11. Retrieved 2014-03-03.
- ^ «MathWorld: Dimension». Mathworld.wolfram.com. 2014-02-27. Archived from the original on 2014-03-25. Retrieved 2014-03-03.
- ^ Yau, Shing-Tung; Nadis, Steve (2010). «4. Too Good to be True». The Shape of Inner Space: String Theory and the Geometry of the Universe’s Hidden Dimensions. Basic Books. pp. 60–. ISBN 978-0-465-02266-3.
- ^ Fantechi, Barbara (2001), «Stacks for everybody» (PDF), European Congress of Mathematics Volume I, Progr. Math., vol. 201, Birkhäuser, pp. 349–359, archived (PDF) from the original on 2006-01-17
- ^ Hurewicz, Witold; Wallman, Henry (2015). Dimension Theory (PMS-4), Volume 4. Princeton University Press. p. 24. ISBN 978-1-4008-7566-5. Extract of page 24
- ^ Fractal Dimension Archived 2006-10-27 at the Wayback Machine, Boston University Department of Mathematics and Statistics
- ^ Rylov, Yuri A. (2007). «Non-Euclidean method of the generalized geometry construction and its application to space-time geometry». arXiv:math/0702552.
- ^ Lane, Paul M.; Lindquist, Jay D. (May 22, 2015). «Definitions for The Fourth Dimension: A Proposed Time Classification System1». In Bahn, Kenneth D. (ed.). Proceedings of the 1988 Academy of Marketing Science (AMS) Annual Conference. Developments in Marketing Science: Proceedings of the Academy of Marketing Science. Springer International Publishing. pp. 38–46. doi:10.1007/978-3-319-17046-6_8. ISBN 978-3-319-17045-9 – via Springer Link.
- ^ Wilson, Edwin B.; Lewis, Gilbert N. (1912). «The Space-Time Manifold of Relativity. The Non-Euclidean Geometry of Mechanics and Electromagnetics». Proceedings of the American Academy of Arts and Sciences. 48 (11): 389–507. doi:10.2307/20022840. JSTOR 20022840 – via JSTOR.
- ^ Brandenberger, R.; Vafa, C. (1989). «Superstrings in the early universe». Nuclear Physics B. 316 (2): 391–410. Bibcode:1989NuPhB.316..391B. doi:10.1016/0550-3213(89)90037-0.
- ^ Scott Watson, Brane Gas Cosmology Archived 2014-10-27 at the Wayback Machine (pdf).
- ^ Vector Data Models, Essentials of Geographic Information Systems, Saylor Academy, 2012
Further reading[edit]
- Murty, Katta G. (2014). «1. Systems of Simultaneous Linear Equations» (PDF). Computational and Algorithmic Linear Algebra and n-Dimensional Geometry. World Scientific Publishing. doi:10.1142/8261. ISBN 978-981-4366-62-5.
- Abbott, Edwin A. (1884). Flatland: A Romance of Many Dimensions. London: Seely & Co.
- —. Flatland: … Project Gutenberg.
- —; Stewart, Ian (2008). The Annotated Flatland: A Romance of Many Dimensions. Basic Books. ISBN 978-0-7867-2183-2.
- Banchoff, Thomas F. (1996). Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions. Scientific American Library. ISBN 978-0-7167-6015-3.
- Pickover, Clifford A. (2001). Surfing through Hyperspace: Understanding Higher Universes in Six Easy Lessons. Oxford University Press. ISBN 978-0-19-992381-6.
- Rucker, Rudy (2014) [1984]. The Fourth Dimension: Toward a Geometry of Higher Reality. Courier Corporation. ISBN 978-0-486-77978-2. Google preview
- Kaku, Michio (1994). Hyperspace, a Scientific Odyssey Through the 10th Dimension. Oxford University Press. ISBN 978-0-19-286189-4.
- Krauss, Lawrence M. (2005). Hiding in the Mirror. Viking Press. ISBN 978-0-670-03395-9.
External links[edit]
Wikiquote has quotations related to Dimension.
Wikimedia Commons has media related to Dimensions.
- Copeland, Ed (2009). «Extra Dimensions». Sixty Symbols. Brady Haran for the University of Nottingham.
- aspect
- element
- extent
- height
- importance
- length
- magnitude
- proportion
- quality
- range
- scope
- size
- thickness
- bulk
- capacity
- mass
- time
- volume
On this page you’ll find 39 synonyms, antonyms, and words related to dimension, such as: aspect, element, extent, height, importance, and length.
Roget’s 21st Century Thesaurus, Third Edition Copyright © 2013 by the Philip Lief Group.
TRY USING dimension
See how your sentence looks with different synonyms.
How to use dimension in a sentence
SYNONYM OF THE DAY
OCTOBER 26, 1985
WORDS RELATED TO DIMENSION
- amplitude
- area
- compass
- comprehensiveness
- dimension
- expanse
- extensiveness
- fullness
- gamut
- greatness
- inclusiveness
- largeness
- magnitude
- measure
- orbit
- range
- reach
- scale
- scope
- size
- space
- spread
- stretch
- sweep
- vastness
- borders
- bounds
- circumference
- compass
- country
- dimension
- edge
- end
- environs
- extent
- limits
- orbit
- periphery
- precinct
- proportions
- purlieus
- purview
- radius
- range
- reach
- region
- scope
- sweep
- term
- terrain
- territory
- amount
- amplitude
- caliber
- dimension
- division
- expanse
- extent
- gauge
- gradation
- grade
- height
- intensity
- interval
- length
- limit
- line
- link
- mark
- notch
- period
- plane
- point
- proportion
- quality
- quantity
- range
- rate
- ratio
- reach
- rung
- scale
- scope
- severity
- shade
- size
- space
- stage
- stair
- standard
- step
- stint
- strength
- tenor
- term
- tier
- breadth
- compass
- continuance
- diameter
- dimension
- duration
- elongation
- endlessness
- expanse
- expansion
- extensiveness
- height
- interval
- lastingness
- lengthiness
- limit
- linearity
- loftiness
- longitude
- longness
- magnitude
- measure
- mileage
- orbit
- panorama
- period
- piece
- portion
- protractedness
- purview
- quantity
- radius
- range
- ranginess
- reach
- realm
- remoteness
- season
- section
- segment
- space
- spaciousness
- span
- stretch
- stride
- tallness
- term
- unit
- width
- year
- admeasurement
- amount
- amplitude
- bigness
- breadth
- bulk
- capacity
- compass
- dimension
- dimensions
- enormity
- enormousness
- expanse
- extent
- greatness
- hugeness
- immensity
- intensity
- largeness
- mass
- measure
- measurement
- proportion
- proportions
- quantity
- range
- reach
- sizableness
- space
- strength
- tremendousness
- vastness
- volume
- dimension
- extent
- greatness
- magnitude
- size
- span
- volume
Roget’s 21st Century Thesaurus, Third Edition Copyright © 2013 by the Philip Lief Group.