Дифференцированный калькулятор в excel

Составим в MS EXCEL график погашения кредита дифференцированными платежами.

При расчете графика погашения кредита дифференцированными платежами сумма основного долга делится на равные части пропорционально сроку кредитования. Регулярно, в течение всего срока погашения кредита, заемщик выплачивает банку эти части основного долга плюс начисленные на его остаток проценты. Если кредитным договором период погашения установлен равным месяцу, то из месяца в месяц сумма основного долга пропорционально уменьшается. Поэтому при дифференцированных платежах основные расходы заемщик несет в начале кредитования, размеры ежемесячных платежей в этот период самые большие. Но постепенно, с уменьшением остатка ссудной задолженности, уменьшается и сумма начисленных процентов по кредиту. Выплаты по кредиту значительно сокращаются и становятся не такими обременительными для заемщика.

Примечание

. При расчете кредита дифференцированными платежами сумма переплаты по процентам будет ниже, чем при

аннуитетных платежах

. Не удивительно, что сегодня практически все российские банки применяют в расчетах аннуитетную схему погашения кредита. Сравнение двух графиков погашения кредита приведено в статье

Сравнение графиков погашения кредита дифференцированными аннуитетными платежами в MS EXCEL

.

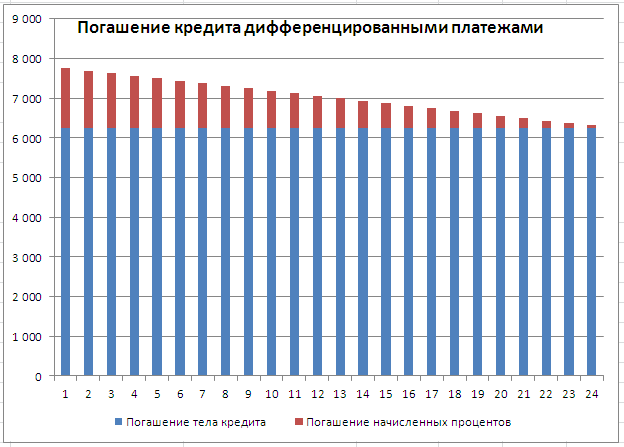
График погашения кредита дифференцированными платежами

Задача

. Сумма кредита =150т.р. Срок кредита =2 года, Ставка по кредиту = 12%. Погашение кредита ежемесячное, в конце каждого периода (месяца).

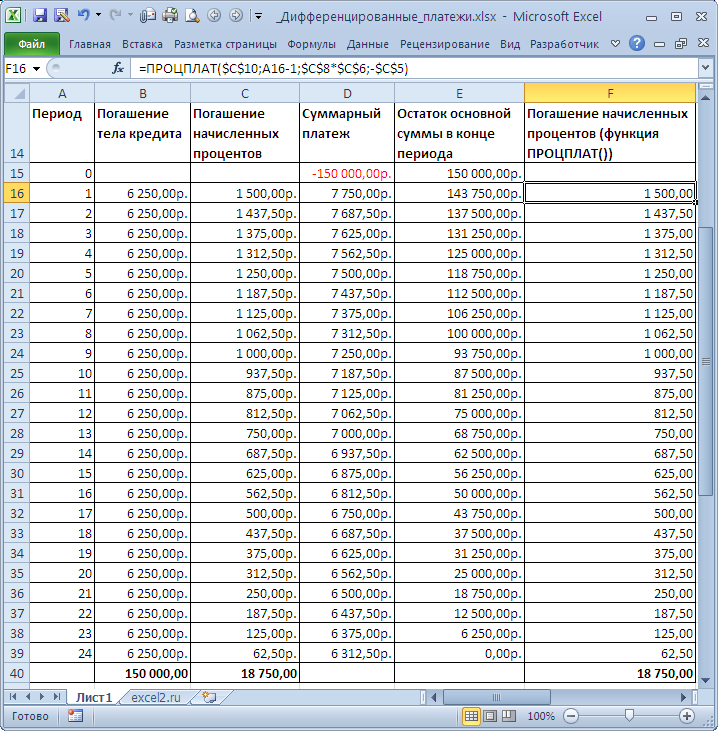
Решение. Сначала вычислим часть (долю) основной суммы кредита, которую заемщик выплачивает за период: =150т.р./2/12, т.е. 6250р. (сумму кредита мы разделили на общее количество периодов выплат =2года*12 (мес. в году)). Каждый период заемщик выплачивает банку эту часть основного долга плюс начисленные на его остаток проценты. Расчет начисленных процентов на остаток долга приведен в таблице ниже – это и есть график платежей.

Для расчета начисленных процентов может быть использована функция ПРОЦПЛАТ(ставка;период;кпер;пс), где Ставка — процентная ставка

за период

;

Период

– номер периода, для которого требуется найти величину начисленных процентов;

Кпер

— общее число периодов начислений;

ПС

–

приведенная стоимость

на текущий момент (для кредита ПС — это сумма кредита, для вклада ПС – начальная сумма вклада).

Примечание

. Не смотря на то, что названия аргументов совпадают с названиями аргументов

функций аннуитета

–

ПРОЦПЛАТ()

не входит в группу этих функций (не может быть использована для расчета параметров аннуитета).

Примечание

. Английский вариант функции — ISPMT(rate, per, nper, pv)

Функция

ПРОЦПЛАТ()

предполагает начисление процентов

в начале каждого периода

(хотя в справке MS EXCEL это не сказано). Но, функцию можно использовать для расчета процентов, начисляемых и в конце периода для это нужно записать ее в виде ПРОЦПЛАТ(ставка;период-1;кпер;пс), т.е. «сдвинуть» вычисления на 1 период раньше (см.

файл примера

). Функция

ПРОЦПЛАТ()

начисленные проценты за пользование кредитом указывает с противоположным знаком, чтобы отличить денежные потоки (если выдача кредита – положительный денежный поток («в карман» заемщика), то регулярные выплаты – отрицательный поток «из кармана»).

Расчет суммарных процентов, уплаченных с даты выдачи кредита

Выведем формулу для нахождения суммы процентов, начисленных за определенное количество периодов с даты начала действия кредитного договора. Запишем суммы процентов начисленных в первых периодов (начисление и выплата в конце периода): ПС*ставка (ПС-ПС/кпер)*ставка (ПС-2*ПС/кпер)*ставка (ПС-3*ПС/кпер)*ставка … Просуммируем полученные выражения и, используя формулу суммы арифметической прогрессии, получим результат. =ПС*Ставка* период*(1 — (период-1)/2/кпер) Где, Ставка – это процентная ставка за период (=годовая ставка / число выплат в году), период – период, до которого требуется найти сумму процентов. Например, сумма процентов, выплаченных за первые полгода пользования кредитом (см. условия задачи выше) = 150000*(12%/12)*6*(1-(6-1)/2/(2*12))=8062,50р. За весь срок будет выплачено =ПС*Ставка*(кпер+1)/2=18750р. Через функцию

ПРОЦПЛАТ()

формула будет сложнее: =СУММПРОИЗВ(ПРОЦПЛАТ(ставка;СТРОКА(ДВССЫЛ(«1:»&кпер))-1;кпер;-ПС))

Excel – это универсальный аналитическо-вычислительный инструмент, который часто используют кредиторы (банки, инвесторы и т.п.) и заемщики (предприниматели, компании, частные лица и т.д.).

Быстро сориентироваться в мудреных формулах, рассчитать проценты, суммы выплат, переплату позволяют функции программы Microsoft Excel.

Как рассчитать платежи по кредиту в Excel

Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:

1. Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.

Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.

Расчет аннуитетных платежей по кредиту в Excel

Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:

А = К * S

где:

• А – сумма платежа по кредиту;
• К – коэффициент аннуитетного платежа;
• S – величина займа.

Формула коэффициента аннуитета:

К = (i * (1 + i)^n) / ((1+i)^n-1)

• где i – процентная ставка за месяц, результат деления годовой ставки на 12;
• n – срок кредита в месяцах.

В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:

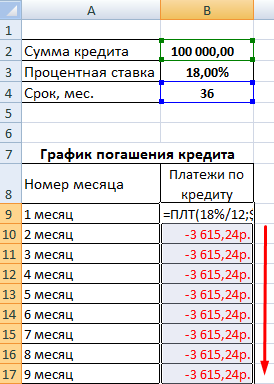
1. Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.



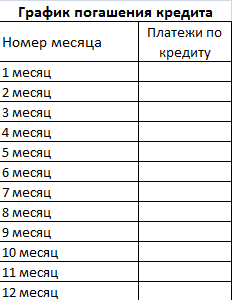
2. Составим график погашения кредита. Пока пустой.



3. В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).

Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.



Расчет платежей в Excel по дифференцированной схеме погашения

Дифференцированный способ оплаты предполагает, что:

• сумма основного долга распределена по периодам выплат равными долями;
• проценты по кредиту начисляются на остаток.

Формула расчета дифференцированного платежа:

ДП = ОСЗ / (ПП + ОСЗ * ПС)

где:

• ДП – ежемесячный платеж по кредиту;
• ОСЗ – остаток займа;
• ПП – число оставшихся до конца срока погашения периодов;
• ПС – процентная ставка за месяц (годовую ставку делим на 12).

Составим график погашения предыдущего кредита по дифференцированной схеме.

Входные данные те же:

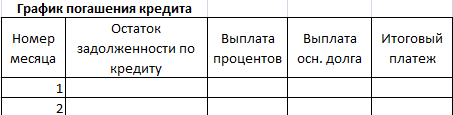
Составим график погашения займа:

Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.

Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).

Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9<=$B$4;$B$2/$B$4;0).

Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.

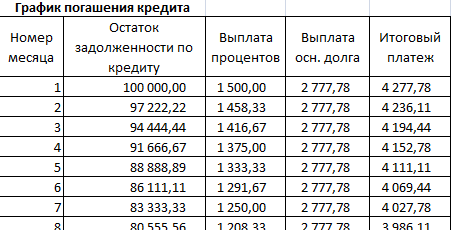
Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.

Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:

Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.

Формула расчета процентов по кредиту в Excel

Проведем расчет процентов по кредиту в Excel и вычислим эффективную процентную ставку, имея следующую информацию по предлагаемому банком кредиту:

Рассчитаем ежемесячную процентную ставку и платежи по кредиту:

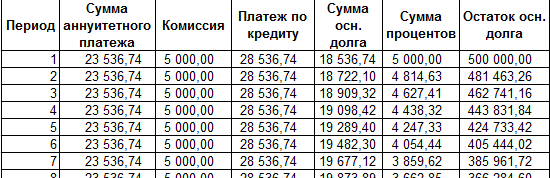
Заполним таблицу вида:

Комиссия берется ежемесячно со всей суммы. Общий платеж по кредиту – это аннуитетный платеж плюс комиссия. Сумма основного долга и сумма процентов – составляющие части аннуитетного платежа.

Сумма основного долга = аннуитетный платеж – проценты.

Сумма процентов = остаток долга * месячную процентную ставку.

Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.

Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:

• взяли кредит 500 000 руб.;
• вернули в банк – 684 881,67 руб. (сумма всех платежей по кредиту);
• переплата составила 184 881, 67 руб.;
• процентная ставка – 184 881, 67 / 500 000 * 100, или 37%.
• Безобидная комиссия в 1 % обошлась кредитополучателю очень дорого.

Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.

Расчет полной стоимости кредита в Excel

Согласно Закону о потребительском кредите для расчета полной стоимости кредита (ПСК) теперь применяется новая формула. ПСК определяется в процентах с точностью до третьего знака после запятой по следующей формуле:

• ПСК = i * ЧБП * 100;
• где i – процентная ставка базового периода;
• ЧБП – число базовых периодов в календарном году.

Возьмем для примера следующие данные по кредиту:

Для расчета полной стоимости кредита нужно составить график платежей (порядок см. выше).

Нужно определить базовый период (БП). В законе сказано, что это стандартный временной интервал, который встречается в графике погашения чаще всего. В примере БП = 28 дней.

Далее находим ЧБП: 365 / 28 = 13.

Теперь можно найти процентную ставку базового периода:

У нас имеются все необходимые данные – подставляем их в формулу ПСК: =B9*B8

Примечание. Чтобы получить проценты в Excel, не нужно умножать на 100. Достаточно выставить для ячейки с результатом процентный формат.

ПСК по новой формуле совпала с годовой процентной ставкой по кредиту.

Скачать кредитный калькулятор в Excel

Таким образом, для расчета аннуитетных платежей по кредиту используется простейшая функция ПЛТ. Как видите, дифференцированный способ погашения несколько сложнее.

Автоматизировать процесс дифференцированного расчёта кредита можно при помощи кредитного калькулятора, разработанного в программе Microsoft Excel. В этой публикации мы вам расскажем и покажем, как это делается. Давайте приступим!

Где можно бесплатно скачать такой калькулятор

Не удивляйтесь, друзья, но вначале вам действительно надо скачать готовый калькулятор дифференцированных платежей, который мы разработали в Excel. Именно его мы и будем «разбирать на запчасти». Также, при желании, вы сможете его доработать под свои требования.

На примере этого калькулятора вы немного познакомитесь с программой Microsoft Excel, а также автоматизируете расчёт дифференцированных платежей по кредиту. Бесплатно скачать калькулятор можно перейдя по ссылке ниже:

Получилось? Вот и отлично! Приступаем к «разбору полётов»!

Разрабатываем калькулятор дифференцированных платежей в Excel

Прежде всего давайте разберемся, по какому принципу работает наш калькулятор. Откройте скачанный «экселевкий» файл. В верхнем левом углу страницы вы увидите две таблицы. Они называются: «Укажите данные для расчёта» и «Результаты расчёта». Также сверху над всеми столбцами нашей страницы Excel есть буквы A, B, C, D, E, F и т.д., а слева напротив строк – цифры 1, 2, 3, 4, 5, 6 и т. д. Именно эти буквы и цифры определяют координаты каждой ячейки таблицы.

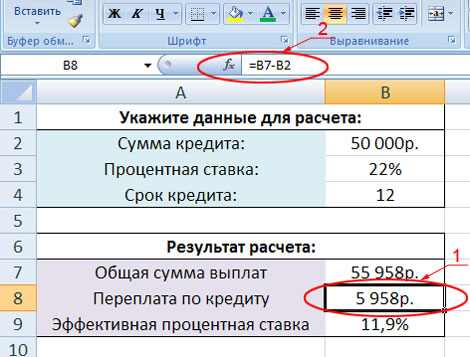
Кликните левой кнопкой мыши по ячейке со значением «5958р.», которое находится в результатах расчёта в строке «Переплата по кредиту». В нашем калькуляторе эта ячейка имеет координаты B8. Вот вам картинка для наглядности:

На изображении данную ячейку мы обвели красной линией и обозначили цифрой один. Обратите внимание ещё вот на что. Когда вы кликаете по какой-либо ячейке в таблице Excel, то эта ячейка выделяется чёрной жирной рамкой, а её буквенно-цифровые координаты сверху и слева окрашиваются другим фоном. Например, на нашем изображении буква B сверху и цифра 8 слева изменили цвет фона с серо-голубого на желтоватый. Также в верхней строке формул, слева от которой есть кнопка «fx» (на рисунке она обведена красным и обозначена цифрой два) указано значение или формула, по которой выполняется расчёт данных для выделенной ячейки. В нашем примере для ячейки с координатой B8 выполняется расчёт по следующей формуле: =B7-B2. В окне с координатой B7 указана общая сумма выплат по кредиту, которая в нашем примере равна 55 958 рублей, а B2 – это сам кредит, который равен 50 000 рублей. Выполнив простое математическое вычисление, наша программа занесла в ячейку B8 значение 5958 (55 958 – 50 000=5958).

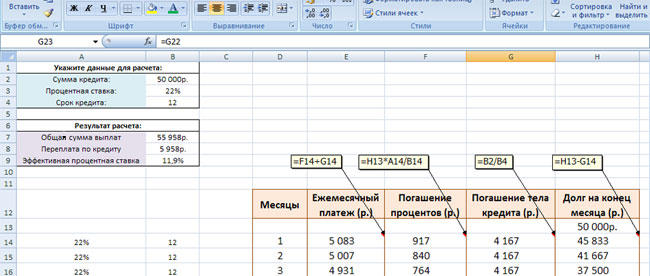
Как видите, Microsoft Excel работает достаточно просто. По аналогичному принципу заданы формулы и значения для остальных ячеек нашего кредитного калькулятора дифференцированных платежей. Давайте рассмотрим, как они рассчитаны. Щёлкаем мышкой по изображению:

Итак, правее в оранжевой рамке вы видите график дифференцированных платежей по кредиту. Все значения в этой таблице рассчитываются автоматически по формулам, которые мы рассматривали в предыдущей публикации. Именно эти формулы и прописаны в ячейках нашего калькулятора. Давайте их детально рассмотрим на примере первой строки графика погашения кредита.

• «Ежемесячный платёж» – это ежемесячный дифференцированный платёж по займу. Он состоит из двух частей: суммы, идущей на погашение процентов (ячейка F14), и суммы, идущей на погашение тела кредита (ячейка G14). Именно потому ежемесячный платёж в первой строке рассчитан по формуле: =F14+ G14.
• «Погашение процентов» – здесь работает формула расчёта процентов по кредиту за данный период: остаток задолженности (в первом платеже он равен сумме кредита 50 000 руб., вынесенную в ячейку H13) умножить на годовую процентную ставку (она равна 22% и вынесена в ячейку A14) и разделить на 12 (мы вынесли это значение в ячейку B14). Собственно, эти условия и прописаны в формуле для ячейки F14: =H13*A14/B14. Кстати, вместо B14 можно просто указать фиксированную цифру – 12.
• «Погашение тела кредита» – это фиксированное значение, которое не меняется на протяжении всего срока кредитования. Рассчитывается этот показатель очень просто: сумма кредита (ячейка B2) делится на общий срок кредитования (ячейка B4). В итоге для ячейки G14 получаем такую формулу: = B2/B4.
• «Долг на конец месяца» – из суммы долга на конец предыдущего месяца (в первом платеже он у нас равен сумме кредита – 50 000 рублей и вынесен в ячейку H13) вычитаем выплату по телу кредита в текущем периоде (4167 рублей – ячейка G14). В результате, долг на конец месяца по первому платежу у нас равен 45 833 рубля (50 000 – 4167 = 45 833), что и записано в формуле для ячейки H14: = H13- G14.

Вот таким нехитрым способом разработан кредитный калькулятор дифференцированных платежей в Excel. Он рассчитан на кредиты сроком до 12 месяцев. При желании, вы можете его усовершенствовать и расширить данный диапазон до 24, 36 и более месяцев. В общем, теперь всё в ваших руках, друзья. Как говорится, мы вам дали удочку, а вы сами решайте, что с ней дальше делать.

Портал temabiz.com – ваш надёжный информационный помощник в вопросах кредитования. Оставайтесь с нами!

⇧

Расчет кредита в Excel

Кто как, а я считаю кредиты злом. Особенно потребительские. Кредиты для бизнеса — другое дело, а для обычных людей мышеловка»деньги за 15 минут, нужен только паспорт» срабатывает безотказно, предлагая удовольствие здесь и сейчас, а расплату за него когда-нибудь потом. И главная проблема, по-моему, даже не в грабительских процентах или в том, что это «потом» все равно когда-нибудь наступит. Кредит убивает мотивацию к росту. Зачем напрягаться, учиться, развиваться, искать дополнительные источники дохода, если можно тупо зайти в ближайший банк и там тебе за полчаса оформят кредит на кабальных условиях, попутно грамотно разведя на страхование и прочие допы?

Так что очень надеюсь, что изложенный ниже материал вам не пригодится.

Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. «Помассажировать числа» заранее, как я это называю 🙂 Microsoft Excel может сильно помочь в этом вопросе.

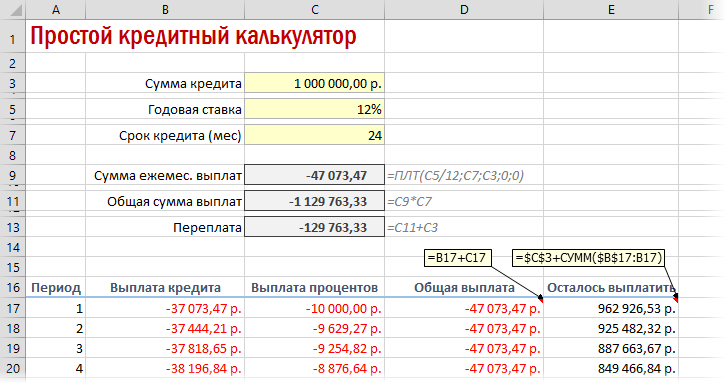
Вариант 1. Простой кредитный калькулятор в Excel

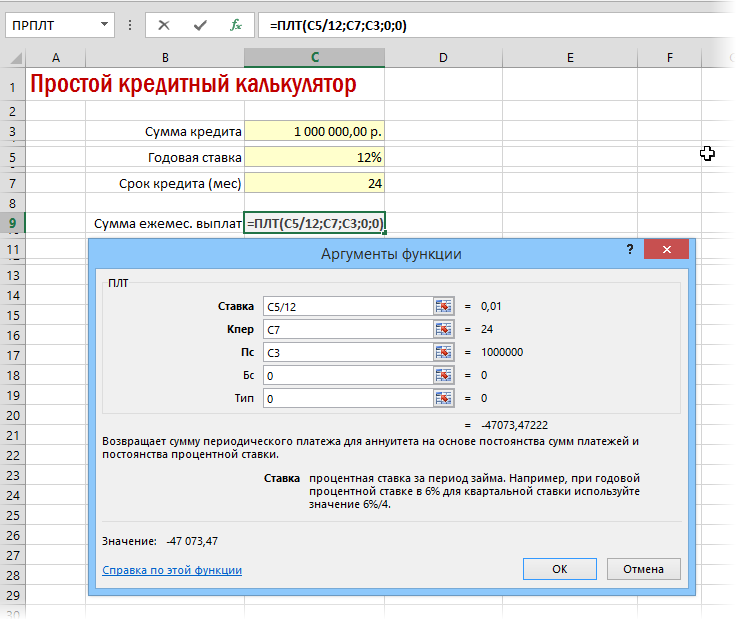
Для быстрой прикидки кредитный калькулятор в Excel можно сделать за пару минут с помощью всего одной функции и пары простых формул. Для расчета ежемесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты производятся равными суммами — таких сейчас большинство) в Excel есть специальная функция ПЛТ (PMT) из категории Финансовые (Financial) . Выделяем ячейку, где хотим получить результат, жмем на кнопку fx в строке формул, находим функцию ПЛТ в списке и жмем ОК. В следующем окне нужно будет ввести аргументы для расчета:

• Ставка — процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годовая ставка 12%, то на один месяц должно приходиться по 1% соответственно.
• Кпер — количество периодов, т.е. срок кредита в месяцах.
• Пс — начальный баланс, т.е. сумма кредита.
• Бс — конечный баланс, т.е. баланс с которым мы должны по идее прийти к концу срока. Очевидно =0, т.е. никто никому ничего не должен.
• Тип — способ учета ежемесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в России абсолютное большинство банков работает по второму варианту, поэтому вводим 0.

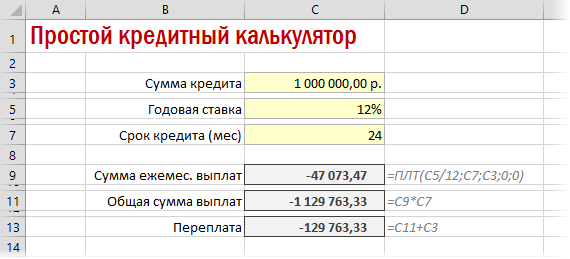
Также полезно будет прикинуть общий объем выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно использование его денег. Это можно сделать с помощью простых формул:

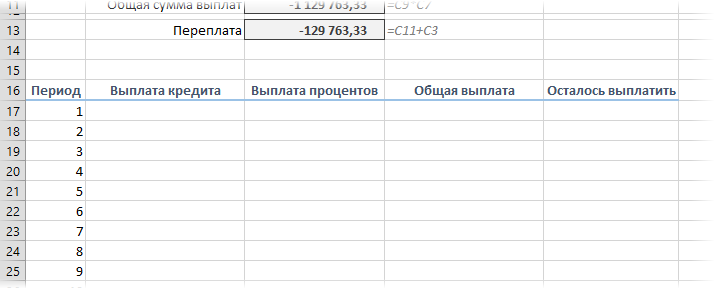
Вариант 2. Добавляем детализацию

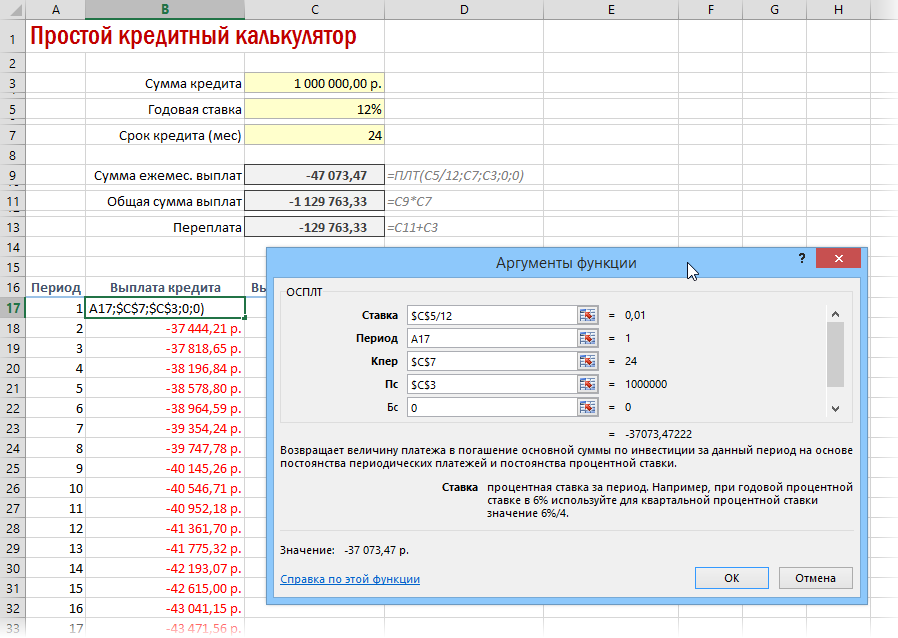
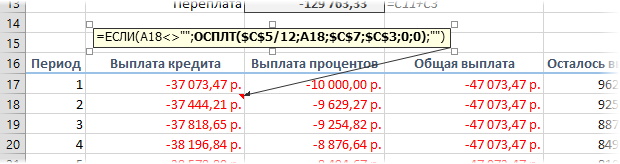
Если хочется более детализированного расчета, то можно воспользоваться еще двумя полезными финансовыми функциями Excel — ОСПЛТ (PPMT) и ПРПЛТ (IPMT) . Первая из них вычисляет ту часть очередного платежа, которая приходится на выплату самого кредита (тела кредита), а вторая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предыдущему примеру небольшую шапку таблицы с подробным расчетом и номера периодов (месяцев):

Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:

Добавился только параметр Период с номером текущего месяца (выплаты) и закрепление знаком $ некоторых ссылок, т.к. впоследствии мы эту формулу будем копировать вниз. Функция ПРПЛТ (IPMT) для вычисления процентной части вводится аналогично. Осталось скопировать введенные формулы вниз до последнего периода кредита и добавить столбцы с простыми формулами для вычисления общей суммы ежемесячных выплат (она постоянна и равна вычисленной выше в ячейке C7) и, ради интереса, оставшейся сумме долга:

Чтобы сделать наш калькулятор более универсальным и способным автоматически подстраиваться под любой срок кредита, имеет смысл немного подправить формулы. В ячейке А18 лучше использовать формулу вида:

Эта формула проверяет с помощью функции ЕСЛИ (IF) достигли мы последнего периода или нет, и выводит пустую текстовую строку («») в том случае, если достигли, либо номер следующего периода. При копировании такой формулы вниз на большое количество строк мы получим номера периодов как раз до нужного предела (срока кредита). В остальных ячейках этой строки можно использовать похожую конструкцию с проверкой на присутствие номера периода:

=ЕСЛИ(A18<>«»; текущая формула; «»)

Т.е. если номер периода не пустой, то мы вычисляем сумму выплат с помощью наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строку:

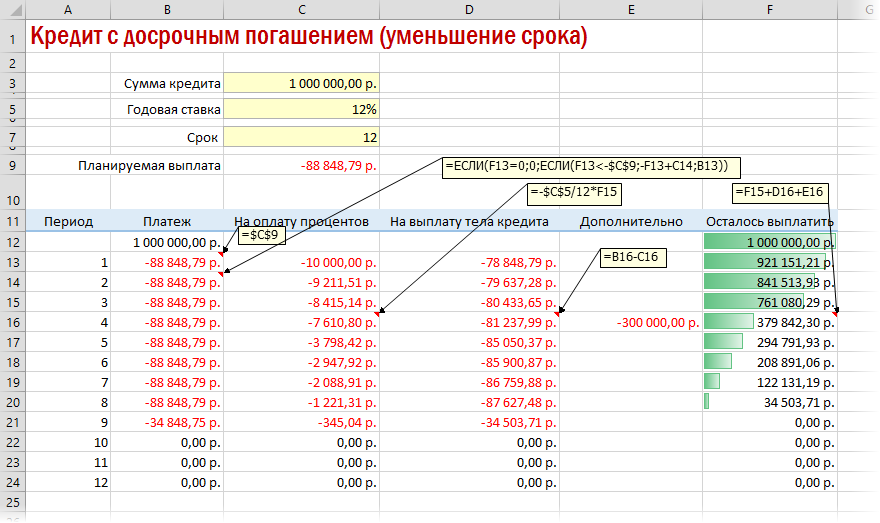
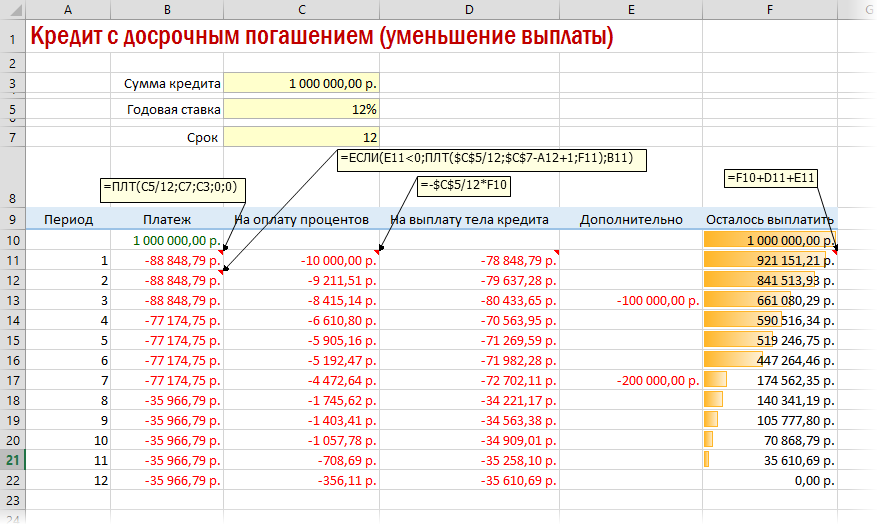
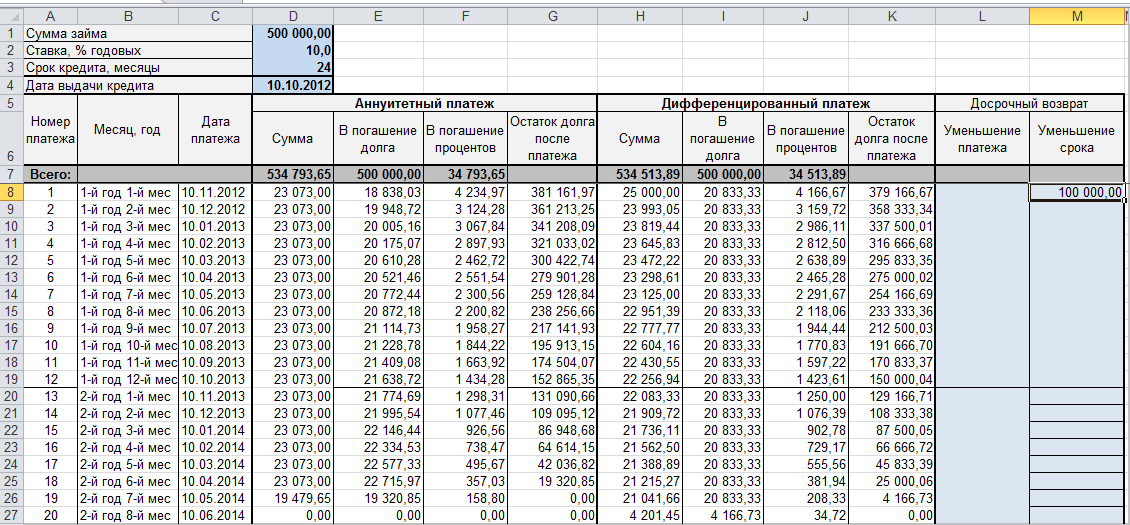
Вариант 3. Досрочное погашение с уменьшением срока или выплаты

Реализованный в предыдущем варианте калькулятор неплох, но не учитывает один важный момент: в реальной жизни вы, скорее всего, будете вносить дополнительные платежи для досрочного погашения при удобной возможности. Для реализации этого можно добавить в нашу модель столбец с дополнительными выплатами, которые будут уменьшать остаток. Однако, большинство банков в подобных случаях предлагают на выбор: сокращать либо сумму ежемесячной выплаты, либо срок. Каждый такой сценарий для наглядности лучше посчитать отдельно.

В случае уменьшения срока придется дополнительно с помощью функции ЕСЛИ (IF) проверять — не достигли мы нулевого баланса раньше срока:

А в случае уменьшения выплаты — заново пересчитывать ежемесячный взнос начиная со следующего после досрочной выплаты периода:

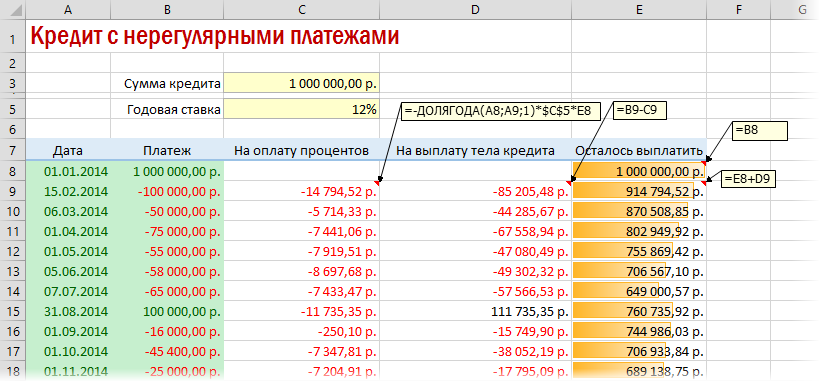
Вариант 4. Кредитный калькулятор с нерегулярными выплатами

Существуют варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таким кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще денег в дополнение к имеющемуся кредиту. Для расчета по такой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до дня:

• в зеленые ячейки пользователь вводит произвольные даты платежей и их суммы
• отрицательные суммы — наши выплаты банку, положительные — берем дополнительный кредит к уже имеющемуся
• подсчитать точное количество дней между двумя датами (и процентов, которые на них приходятся) лучше с помощью функции ДОЛЯГОДА (YEARFRAC)

Ипотечный кредитный калькулятор в Excel. Как правильно рассчитать кредит в Excel?

Когда вы взяли кредит, вы так или иначе думаете о досрочном погашении.
Есть люди которые платят кредит и все. А есть те, которые каждый раз смотрят, сколько осталось платить, какая сумма основного долга. Я отношу себя ко второму типу людей, я смотрю сколько сейчас сумма основного долга, пытаюсь рассчитать, сколько будет платеж, если я сделаю досрочное погашение.
На данный момент у меня есть два калькулятора кредита для своих расчетов. Оба калькулятора сделаны в Excel. Калькуляторы позволяют достаточно быстро и просто рассчитать ипотеку.
Читайте также: Как рассчитать кредит в Excel самому?

Скачать кредитный калькулятор в Excel

Первый кредитный калькулятор в Excel можно скачать по ссылке.
Но Excel есть не на всех компьютерах. Пользователи MAC и Linux не пользуются Excel обычно, т.к. это продукт Microsoft.
Для расчета досрочного погашения можно также воспользоваться онлайн версией калькулятора с досрочным погашением. В нем предусмотрена возможность экспорта результатов расчета в Excel.

На основе этого калькулятора был разработан ипотечный калькулятор для Android и iPhone. Найти и скачать мобильные версии калькуляторов можно с главной страницы сайта.

Достоинства данного калькулятора:

1. Кредитный калькулятор в Excel практически точно считает аннуитетный график платежей и дифференцированный график платежей
2. Изменения в графике платежей — учет досрочных погашений в уменьшение суммы основного долга
3. Построение и расчет графика платежей в виде таблицы в Excel. Таблица графика платежей может также редактироваться
4. При расчете учитывается високосный и невисокосный год. За счет этого сумма начисленных процентов практически совпадает с значениями, рассчитываемыми ВТБ24 и Сбербанком
5. Точность расчетов — рассчеты совпадают с расчетами кредитного калькулятора ВТБ24 и Сбербанка
6. Калькулятор можно редактировать под себя, задавая разные варианты расчета.

Недостатки калькулятора

1. Нет учета возможное изменение процентной ставки во время выплат кредита
2. Если сделать расчет, делая досрочные платежи в изменение срока и суммы, то расчет будет неверным
3. Если сумма процентов, начисленных за период больше суммы аннуитетного платежа, то расчет будет не верным
4. Не рассчитывается вариант — первый платеж только проценты. В случае когда дата выдачи не совпадает с датой первого платежа, вам нужно будет заплатить проценты банку за период между датой выдачи и датой первого платежа.
5. Расчет производится для процентой ставки с 2мя знаками после запятой.

Всех выше названных недостатков лишен кредитный калькулятор для iPad/iPhone. В целом недостатки не сильно критичны и они присущи любому кредитному калькулятору онлайн.
Другой кредитный калькулятор в Excel можно скачать по данной ссылке. Данный кредитный калькулятор не позволяет рассчитать досрочное погашение. Однако его плюс в том, что он рассчитывает кредит с несколькими процентными периодами. Если сумма процентов по кредиту за данный месяц больше суммы аннуитетного платежа, то график для первого кредитного калькулятора в excel строится некорректно. В графике получаются отрицательные суммы.

Попробуйте посчитать к примеру кредит 1 млн. руб под 90 процентов на срок 30 лет.
У второго калькулятора нет данного недостатка. Однако он делит кредит на 2 периода, т.е. возможно что после деления в графике снова будут отрицательные значения. Тогда график платежей нужно делить на 3 и более периода.
Естественно сам файл также можно отредактировать под свои нужды.

Калькулятор расчета кредита в Excel и формулы ежемесячных платежей

Excel – это универсальный аналитическо-вычислительный инструмент, который часто используют кредиторы (банки, инвесторы и т.п.) и заемщики (предприниматели, компании, частные лица и т.д.).

Быстро сориентироваться в мудреных формулах, рассчитать проценты, суммы выплат, переплату позволяют функции программы Microsoft Excel.

Как рассчитать платежи по кредиту в Excel

Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:

1. Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.

Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.

Расчет аннуитетных платежей по кредиту в Excel

Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:

• А – сумма платежа по кредиту;
• К – коэффициент аннуитетного платежа;
• S – величина займа.

Формула коэффициента аннуитета:

К = (i * (1 + i)^n) / ((1+i)^n-1)

• где i – процентная ставка за месяц, результат деления годовой ставки на 12;
• n – срок кредита в месяцах.

В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:

1. Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.
2. Составим график погашения кредита. Пока пустой.
3. В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).

Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.

Расчет платежей в Excel по дифференцированной схеме погашения

Дифференцированный способ оплаты предполагает, что:

• сумма основного долга распределена по периодам выплат равными долями;
• проценты по кредиту начисляются на остаток.

Формула расчета дифференцированного платежа:

ДП = ОСЗ / (ПП + ОСЗ * ПС)

• ДП – ежемесячный платеж по кредиту;
• ОСЗ – остаток займа;
• ПП – число оставшихся до конца срока погашения периодов;
• ПС – процентная ставка за месяц (годовую ставку делим на 12).

Составим график погашения предыдущего кредита по дифференцированной схеме.

Входные данные те же:

Составим график погашения займа:

Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.

Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).

Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9<=$B$4;$B$2/$B$4;0).

Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.

Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.

Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:

Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.

Формула расчета процентов по кредиту в Excel

Проведем расчет процентов по кредиту в Excel и вычислим эффективную процентную ставку, имея следующую информацию по предлагаемому банком кредиту:

Рассчитаем ежемесячную процентную ставку и платежи по кредиту:

Заполним таблицу вида:

Комиссия берется ежемесячно со всей суммы. Общий платеж по кредиту – это аннуитетный платеж плюс комиссия. Сумма основного долга и сумма процентов – составляющие части аннуитетного платежа.

Сумма основного долга = аннуитетный платеж – проценты.

Сумма процентов = остаток долга * месячную процентную ставку.

Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.

Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:

• взяли кредит 500 000 руб.;
• вернули в банк – 684 881,67 руб. (сумма всех платежей по кредиту);
• переплата составила 184 881, 67 руб.;
• процентная ставка – 184 881, 67 / 500 000 * 100, или 37%.
• Безобидная комиссия в 1 % обошлась кредитополучателю очень дорого.

Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.

Расчет полной стоимости кредита в Excel

Согласно Закону о потребительском кредите для расчета полной стоимости кредита (ПСК) теперь применяется новая формула. ПСК определяется в процентах с точностью до третьего знака после запятой по следующей формуле:

• ПСК = i * ЧБП * 100;
• где i – процентная ставка базового периода;
• ЧБП – число базовых периодов в календарном году.

Возьмем для примера следующие данные по кредиту:

Для расчета полной стоимости кредита нужно составить график платежей (порядок см. выше).

Нужно определить базовый период (БП). В законе сказано, что это стандартный временной интервал, который встречается в графике погашения чаще всего. В примере БП = 28 дней.

Далее находим ЧБП: 365 / 28 = 13.

Теперь можно найти процентную ставку базового периода:

У нас имеются все необходимые данные – подставляем их в формулу ПСК: =B9*B8

Примечание. Чтобы получить проценты в Excel, не нужно умножать на 100. Достаточно выставить для ячейки с результатом процентный формат.

ПСК по новой формуле совпала с годовой процентной ставкой по кредиту.

Таким образом, для расчета аннуитетных платежей по кредиту используется простейшая функция ПЛТ. Как видите, дифференцированный способ погашения несколько сложнее.

Расчет кредита в excel: скачайте готовые формулы и калькуляторы

Если вы хотите расчитать платежи по кредиту (аннуитетные или дифференцированные), переплату и график платежей по месяцам в excel, то скачайте следующие xls-файлы:

Альтернатива использованию MS Excel — кредитный калькулятор on-line (функционал практически такой же, ничего качать на компьютер не нужно: все операции выполняются на нашем сайте).

Расскажем о файлах подробнее: дадим мини-инструкции.

Кредитный калькулятор в Excel

• Считать оба вида платежей.
• Показывать полный график платежей.
• Разбивать сумму выплаты на «погашение долга» и «погашение процентов».
• Учитывать досрочные возвраты (отдельно для уменьшения срока и уменьшения размера выплат).

Пользоваться файлом довольно удобно: вбиваете значения в верхние четыре поля (сумма, процентная ставка, срок в месяцах, дата получения — последнее нужно для определения точного графика) и умное детище Билла Гейтса тут же заполняет все графы таблицы актуальной информацией.

Простая функция для платежей

Вы и сами может сконстурировать подобный расчет — подробно это описано в статье про расчет по формуле аннуитета. Ничего сложного нет, но для удобства мы подготовили специальный файл.

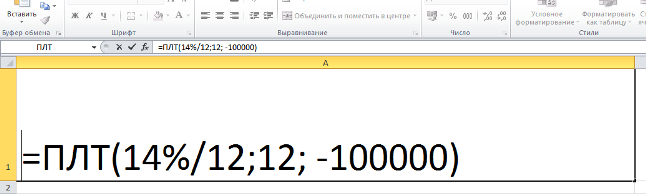
Содержит всего одну функциональную ячейку:

Поменяйте значения на свои (вместо 14 — свою ставку, вместо 12 во втором случае — свой срок кредита в месяцах, вместо 100000 — свою сумму займа).

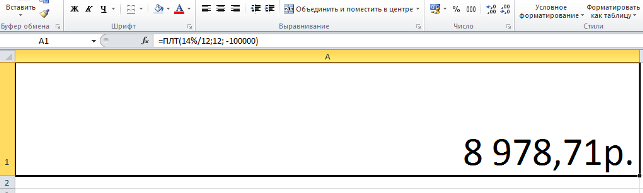
После смены данных достаточно нажать на «Энтер», чтобы получить результат:

Напоминаем, ссылки на оба xls-файла представлены в начале страницы.

Что такое кредитный калькулятор в Excel

Кредитный калькулятор в Excel – это программа, которая позволяет осуществлять расчеты выплат по кредиту без выхода в интернет. Для этого достаточно просто скачать файл программы и использовать его в любое удобное время. Программа в Excel позволяет осуществлять любые математические расчеты. Неспроста она широко используется в бухгалтерии.

Конечно, можно использовать обычный кредитный калькулятор, который расположен на сайтах различных банков, но лучше иметь дома свой собственный кредитный калькулятор в Excel.

Для всех подсчетов потребуются следующие данные:

• — размер кредита;
• — цель кредита;
• — размер процентов по кредиту.

Пользование программой Excel может доставить некоторые сложности тем, кто видит ее впервые, но небольшая таблица все упростит. Все строки таблицы заполняются конкретными данными, при этом используются специальные функции:

• — функция КПЕР – сумма кредита;
• — функция СТАВКА – ставка процентов по кредиту;
• — функция ПС – цель кредита;
• — функция ПЛТ – ежемесячный платеж по кредиту.

Если программа знает первые три показателя, то последний она рассчитает самостоятельно.

В программе можно составить собственный график гашения кредита, но потребуется дата его начала, которая обычно указывается в кредитном договоре.

При желании, можно погасить кредит досрочно, при этом никаких комиссий или штрафов банк не должен требовать.

Достоверная информация о кредите, ежемесячных платежах, фактической переплате доступна у кредитора. Стоит помнить и о том, что некоторые кредитные программы включают в себя скрытые комиссии, а значит, ежемесячный платеж и прочие показатели по кредиту могут отличаться от заранее рассчитанных. Так же может изменяться и размер процентной ставки.

Перед оформлением любого кредитного продукта рекомендуется воспользоваться специальными калькуляторами или программами, с помощью которых определяется полная стоимость кредита, ежемесячный платеж, переплата и другие параметры. Для этих целей актуально пользоваться специальным вычислительным и аналитическим инструментом, представленным программой Excel.

Если хорошо разобраться в функционале программы, то без проблем можно произвести расчеты по любому кредитному продукту, предлагаемому банковскими учреждениями. Для этого не нужно разбираться в сложных формулах или на калькуляторе рассчитывать проценты и переплату.

В статье расскажем как правильно сделать расчеты с помощью кредитного калькулятора Exel.

Правила расчета в Ексель

Перед началом расчета важно определиться, какую схему погашения долга предлагает кредитор. Для этого выбирается один из следующих вариантов:

• Аннуитетные выплаты. Такая схема считается наиболее распространенной, поэтому предлагается по потребительским займам, автокредитам или ипотечным займам. Предполагается, что заемщик ежемесячно вносит одинаковую сумму, которая не меняется с течением времени. По такому способу переплата считается довольно высокой, но при этом легко планировать свои расходы и доходы.
• Дифференцированная схема. При таком способе размер процентов полностью зависит от остатка долга, поэтому ежемесячно производится перерасчет. В первые месяцы сотрудничества заемщику приходится вносить наиболее крупные выплаты за счет наличия значительного долга. С течением времени плата существенно снижается. При таких условиях обеспечивается уменьшение переплаты.

Аннуитетная схема считается не только наиболее удобной для заемщика, но и выгодна каждому банковскому учреждению, представленному кредитором.

Полезно также почитать: Можно ли погасить потребительский кредит материнским капиталом

Формулы расчета аннуитетных платежей

Для расчета кредитов приходится пользоваться специальными формулами, с помощью которых определяется ежемесячный платеж и другие показатели.

Например, чтобы понять, какую сумму придется вносить ежемесячно по кредиту, применяется формула:

Сумма = коэффициент выплаты * размер кредита.

Для определения коэффициента платежа (аннуитета), применяется формула:

Коэффициент = (i * (1 + i)^n) / ((1+i)^n-1), где

1. i – это месячная ставка, определяемая путем деления основной ставки на 12,
2. n – период кредитования.

Чтобы не пользоваться этими громоздкими формулами, можно применять специальные функции программы Excel. Здесь существует особая функция, называемая ПЛТ. Она предназначена для расчета аннуитетных выплат.

Чтобы ею воспользоваться, выполняются следующие действия:

• Вводится основная информация по кредиту, представленная полученной заемной суммой, ставкой и сроком кредитования.
• Ниже формируется график погашения долга. В первом столбце указывается номер месяца, а второй предназначается для ежемесячных выплат.
• В первую ячейка столбца, предназначенного для расчета платежей, вводится формула, позволяющая определить плату на основании аннуитетной схемы. Для этого используется следующая формула: ПЛТ($B$3/12; $B$4; $B$2). Для закрепления ячейки рекомендуется пользоваться абсолютными ссылками. Допускается вводить вместо ссылок на ячейки с информацией непосредственные показатели, поэтому формула будет иметь следующий вид: =ПЛТ(15%/12; 48; 50000), где 15% — это годовая ставка процента, 48 — период кредитования в месяцах, а 50000 – размер займа.

После выполнения всех действий производится автоматический расчет. В ячейках, предназначенных для отображения ежемесячных аннуитетных платежей, появляются суммы, которые придется каждый месяц перечислять банку. Данные значения окрашиваются в красный цвет, а также отражаются со знаком минус, поскольку представлены расходом человека, так как эти суммы придется ежемесячно отдавать банковскому учреждению.

Расчет дифференцированных платежей

Если для погашения кредита выбирается дифференцированная схема, то размер основной задолженности распределяется по всему периоду кредитованию равными частями, а вот проценты начисляются исключительно на остаток, поэтому уменьшаются по мере погашения долга.

Чтобы определить размер выплаты по такой схеме, применяется стандартная формула:

Ежемесячный платеж = остаток долга / (число месяцев, оставшихся до погашения задолженности + остаток долга * месячная ставка)

Но можно не пользоваться этой громоздкой формулой, если применить уникальный функционал программы Excel.

Для этого выполняются следующие действия:

• Открывается программа Excel.
• Формируется график погашения задолженности на основании дифференцированных платежей, для чего указывается общий размер займа, ставка процента и период кредитования в месяцах. Для этих целей можно воспользоваться исходными данными, например, мужчина оформил потребительский кредит в размере 50 тыс. руб. на 4 года по ставке 15%.
• Составляется график погашения долга. Для этого используется 5 столбцов: номер месяца, остаток долга по займу, проценты, плата по основной задолженности и общая выплата за 1 месяц.
• За первый период погашения кредита остаток долга составляет 50 тыс. руб. В последующие месяцы для расчета данного показателя применяется следующая формула: ЕСЛИ(D10>$B$4;0;E9-G9). В этой формуле D10 – это месяц, за который производится расчет, а В4 – это срок кредитования. Е9 – остаток долга по займу в предыдущем месяце, а G9 – основной долг за прошлый период.
• Размер процентов рассчитывается путем умножения остатка долга за текущий период на ставку за 1 период. Для определения данной ставки нужно годовой процент разделить на 12. Поэтому для определения показателя применяется следующая формула: =E9*($B$3/12).
• Размер основного долга по займу определяется с помощью деления общей суммы займа на период кредитования: =ЕСЛИ(D9<=$B$4;$B$2/$B$4;0).
• Общий ежемесячный платеж. Он определяется путем складывания суммы процентов с основным долгом: =F8+G8.

Как только формулы будут внесены в необходимые столбцы, нужно скопировать их на всю таблицу, для чего учитывается 48 месяцев кредитования. На основании выполненных действий осуществляется автоматический расчет, позволяющий определить, какую сумму придется платить в тот или иной месяц.

Справка! Если сравнить показатели с аннуитетными выплатами, то переплата по дифференцированным платежам будет немного меньше, хотя в первые месяцы придется вносить крупные суммы.

Этапы расчета процентов

С помощью программы Excel можно определить не только размер ежемесячного платежа, но и общую сумму процентов. Это позволит выявить эффективную ставку. Для этих целей первоначально вводятся следующие данные:

К ежемесячным платежам относится:

Далее заполняется стандартная таблица:

Комиссия составляет 1%, причем она ежемесячно рассчитывается от общей кредитной суммы. Поэтому выплата по займу формируется путем сложения комиссии с аннуитетным платежом, состоящим из основного долга и процентов. Для расчета основной задолженности нужно из аннуитетного платежа вычесть проценты. Для определения процентов остаток долга умножается на месячную ставку.

На основании полученных сведений легко рассчитывается эффективная процентная ставка:

• гражданин оформил займ на сумму 50 тыс. руб.;
• в банк заемщик вернул 80397,72 руб., причем сюда входят проценты, основной долг и комиссия;
• переплата составляет 30397,72 руб.;
• процентная ставка равна: 30397,72/50000*100=60,8%, причем такой высокий показатель обусловлен комиссией в размере 1%, которая взималась на протяжении всех 36 месяцев;
• если не используется комиссия, то гражданин выплатит 62397,72 руб., поэтому переплата составит 12397,72 руб., а эффективная ставка снижается до 24,8%.

Поэтому перед оформлением кредита желательно рассчитать данный показатель, чтобы рассчитать целесообразность получения заемных средств по невыгодным условиям.

Как определить полную стоимость займа

По новым требованиям законодательства для определения полной стоимости кредита используется новая формула:

ПСК = ставка процента за базовый период (i) * число периодов за 1 календарный год (ЧБП) * 100

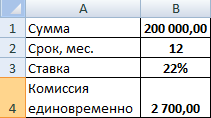
Например, мужчина оформил кредит на сумму 200 тыс. долларов на 1 год по ставке 22%. При этом ему пришлось внести единовременную комиссию 2,7 тыс. долларов.

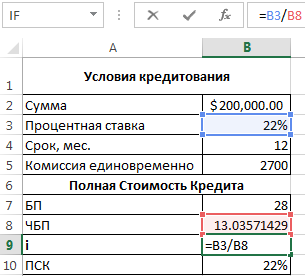
Для определения полной стоимости займа формируется график:

Базовый период (БП) представлен интервалом времени, встречающимся в графике наиболее часто. На примере он представлен 28 днями. В этом случае число периодов составляет: 365/28=13. Только после этого рассчитывается ставка базового периода:

В результате легко рассчитывается полная стоимость кредита (ПСК), которая составляет 22%. Благодаря использованию новой формулы данный показатель равен годовой ставке по займу.

Полезно также почитать: Как встать на биржу труда через Госуслуги

Полезное видео

Наглядно посмотреть порядок расчета можно в видео:


Заключение

Перед оформлением любого займа рекомендуется рассчитать основные показатели по кредиту. К ним относятся не только ежемесячные платежи, но и полная стоимость, а также эффективная процентная ставка. Это позволит определить  точную переплату, а также выявить наличие скрытых платежей.