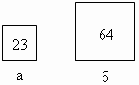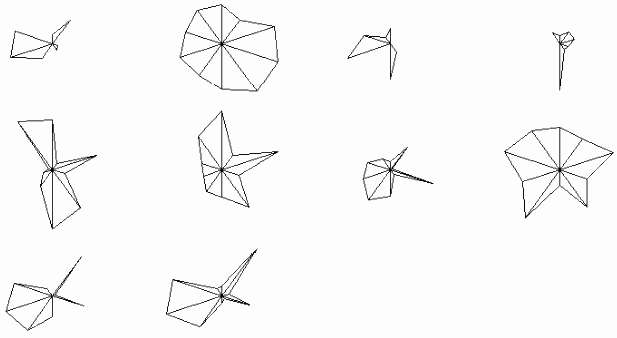Анализ
данных c
помощью графического метода является
одним из наиболее эффективных и доступных
видов анализа. Основным его преимуществом
выступает простота применения и
наглядность полученных результатов,
которые впоследствии используются для
принятия решений. Широкое применение
этого метода стало возможным благодаря
развитию компьютерной техники и
информатики.
Построение
основных типов графиков и диаграмм,
обычно, осуществляется с помощью наиболее
распространенной и популярной программы
Microsoft
Excel.
Графический
метод включает разнообразные типы
графиков, применение которых зависит
от цели, вида, особенностей
социально-экономических процессов и
условий их протекания. Наибольшее
распространение имеют два основных
вида графиков: диаграммы
и ста-тистические карты.
Диаграмма
– это
плоскостное или фигурное графическое
изображение статистических данных,
наглядно показывающее соотношение
между сравниваемыми величинами. Диаграммы
могут быть линейные,
столбиковые, полосовые, радиальные,
круговые, треугольные, квадратные и
графики фигур-знаков.
Статистические
карты
разделяются на картограммы
и картодиаграммы. В
статистических картах цифровые данные
изображаются путем нанесения на контурные
географические карты условных знаков
в виде точек, различной штриховки или
раскраски, диаграммных знаков. На
статистических картах пространственная
ориентировка задается контурной сеткой,
определяющей те территории, к которым
относятся статистические характеристики.
Любой
график имеет общие
элементы:
1)
графический образ; 2)
по-ле графика; 3) масштабные ориентиры;
4) экспликация графика и 5) система
координат.
Графический
образ –
геометрические знаки, совокупности
точек, линии, фигуры, с помощью которых
изображаются статистические величины.
Поле графика
– это пространство, в котором размещаются
геометрические знаки. Масштабные
ориентиры
определяются масштабом
и масштабной шкалой.
Масштаб
статистического графика – это мера
перевода числовой величины в графическую,
а масштабная
шкала – это
линия
(носитель шкалы) и отдельные расположенные
на ней в определенном порядке точки,
которые могут быть прочитаны как
конкретные числа. Носитель шкалы может
быть представлен прямой или кривой
линией, поэтому шкалы называются
прямолинейными и криволинейными
(круговые и дуговые).
Шкалы
могут быть равномерными
и неравномерными.
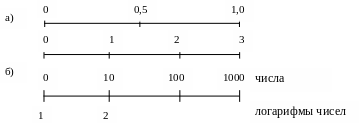
Одним из видов неравномерной шкалы
является логарифмическая. На этой шкале
отрезки пропорциональны не изображаемым
величинам, а их логарифмам (рис.3.1).
Экспликация графика – это словесное
описание его содержания. Оно включает
название графика, которое в краткой
форме передает его содержание; подписи
(надписи) вдоль масштабных шкал и
пояснения к отдельным частям графика.
Для
размещения геометрических знаков в
поле графика используется система
координат.
Наиболее распространенной при построении
статистических графиков является
система прямоугольных координат.
Наилучшим соотношением масштаба по
осям абсцисс и ординат является 1,62:1,
известное под названием “золотого
сечения”.
4
3
Рис.3.1. Масштабные
шкалы: а) равномерные; б) неравномерная.
По
форме
графического образа
наиболее распространенные в статистике
диаграммы подразделяют на:
-
линейные (рис.
3.9); -
плоскостные (рис.
3.8); -
изобразительные
(рис. 3.10).
По задачам
изображения различают диаграммы:
-
структурные
(рис. 3.3, в типовой задаче № 1, рис.3.15); -
динамики структуры
(рис. 3.4, 3.6); -
балансовые (рис.
3.7);
-
сравнения
(рис. 3.5, 3.8); -
выполнения плана.
Линейные диаграммы
широко применяются для характеристики
изменений явлений во времени, хода
выполнения плановых заданий, для изучения
рядов распределения, а также для выявления
связи между явлениями. Линейные диаграммы
строятся на координатной сетке.
Геометрическими знаками в линейных
диаграммах служат точки и последовательно
соединяющие их отрезки прямой, которые
складываются в ломаные “кривые”.
Методика построения таких кривых не
отличается от построения графика рис.
3.9.
На одной линейной
диаграмме можно привести несколько
кривых, которые дают сравнительную
характеристику динамики различных
показателей или одного и того же
показателя для разных территорий (на
рис. 3.9 – одна линия).
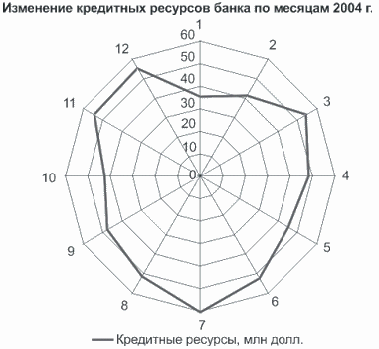
Р
азновидностью
линейного графика являются радиальные
диаграммы,
которые строятся в полярной системе
координат. Их используют для наглядного
изображения циклического изменения
явления во времени. В радиальных
диаграммах радиусы обозначают периоды
времени, а полученная фигура, окружность
— величину изучаемого явления (рис.3.2).
Рис.
3.2. Сезонные колебания продажи творога
на колхозных рынках области по месяцам
2002 г.
Плоскостная
диаграмма отображает
размеры явлений площадями геометрических
фигур (квадратов, кругов, прямоугольников,
треугольников).
Изобразительные
диаграммы (фигур-знаков)
представляют собой графические
изображения в виде рисунков, силуэтов,
фигур, соответствующих содержанию
статистических данных. Отдельные
величины на них изображаются определенным
количеством (упрощенных) одинаковых
(увеличивающихся или уменьшающихся) по
размеру и типу фигур (рис. 3.10) или
геометрическими фигурами (столбцами,
кругами, квадратами).
Существует
три типа диаграмм, в которых применяются
изобразительные символы:
-
размеры
изобразительных символов пропорциональны
изображаемым величинам; -
каждый из символов
представляет определенную и неизменную
величину; -
диаграмма,
основные графические элементы которой
сопровождаются иллюстрациями,
художественным фоном.
Структурные
диаграммы
показывают состав (структуру) целого,
разделенного на части. Они подразделяются
на:
-
секторные (рис.
3.3); -
столбиковые (рис.
3.4, 3.6); -
треугольные
(рис.3.1 – тип. задача № 1) и др.
Секторная
диаграмма позволяет сопоставить
различные части целого при помощи
площадей, образуемых секторами круга
пропорционально удельному весу частей
в целом (рис.3.3).
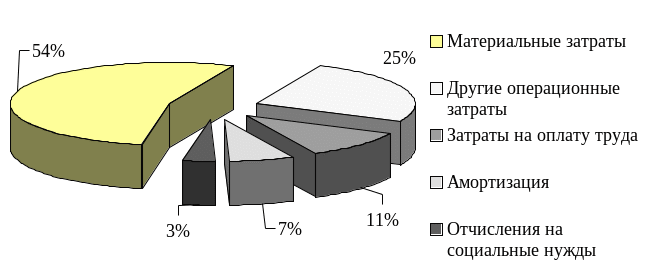
Рис.
3.3. Структура операционных затрат на
производство продукции
При
их построении вся величина явления
принимается за 100%, рассчитываются доли
отдельных его частей в процентах. Круг
разбивается на секторы пропорционально
долям изображаемого целого.
Треугольная
диаграмма
(рис.3.15 – тип. задача № 1) применяется
при изучении структуры для одновременного
изображения трех переменных, представляющих
элементы или составные части целого.
Столбиковая
диаграмма (рис.3.5) изображает
статистические величины в форме
прямоугольников – столбиков, равных
по величине основания и размещенных
вертикально рядом или на одинаковом
расстоянии друг от друга. Высота этих
столбиков в соответствии с принятым
масштабом пропорциональна изображаемым
величинам.
Рис.3.4. Динамика
структуры потребления
При помощи
столбиковой диаграммы можно сравнивать
явления (рис.3.5), а при помощи столбиков,
разделенных на части, — изучать структурные
сдвиги (рис.3.4, 3.6).
При
построении столбиковой диаграммы
необходимо выполнение следующих
требований:
1) наличие вертикальной масштабной
шкалы; 2) шкала, по которой устанавливается
высота столбика, должна начинаться с
нуля; 3) шкала должна быть, как правило,
непре-рывной; 4) основания столбиков —
равны между собой; 5) столбики могут
размещаться на одинаковом расстоянии
друг от друга, вплотную один к другому
или наплывом (один столбик частично
накладывается на другой); 6) наряду с
разметкой шкалы соответствующими
ц
ифровыми
надписями следует снабжать и столбцы.
Р
Годы
ис. 3.5 Сравнительная динамика
производства ВВП по странам.
Диаграмма
динамики структуры
является разновидностью структурных
диаграмм (рис.3.4, 3.6). Она отображает
изменения удельных весов и соотношений
составных частей явлений для нескольких
периодов (моментов) времени.
Изобразительными средствами могут
служить столбиковые (общая высота
столбика принимается равной 100%, а
отдельные его части выражают удельные
веса), секторные или треугольные
диаграммы. Изображаемые части явлений
как в столбиках, так и в секторах должны
иметь различную раскраску или штриховку
и располагаться в определенной
последовательности: в секторных
диаграммах – по движению часовой
стрелки, в столбиковых – от верха к
низу.
Ленточные
(полосовые) диаграммы строятся
аналогично столбиковым, но располагаются
горизонтально (полосами, лентами). В
этом случае масштабной шкалой будет
горизонтальная ось.
В
квадратных
и круговых диаграммах
величина изображаемого явления выражается
размером площади. Для ее построения
необходимо вначале определить сторону
квадрата-графика. Для этого из сравниваемых
статистических величин следует извлечь
квадратные корни, а затем начертить
квадраты с соответствующими сторонами.
Построение показано в типовой задаче
№ 3 (рис.3.17).
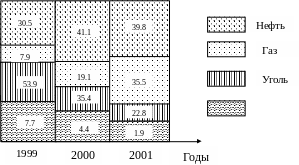
Прочие виды топлива
Рис. 3.6. Добыча
топлива по видам.
Круговые
диаграммы
строятся аналогично. Разница состоит
лишь в том, что на графике вычерчиваются
круги, площади которых пропорциональны
радиусам изображаемых величин (рис.3.8).
Запас на начало периода
Поступление
Расход
Запас
на конец периода
Рис.3.7. Баланс
товарных
запасов
Для одновременного
сопоставления трех величин, связанных
между собой так, что одна величина
является произведением двух других,
применяют диаграммы, называемые “Знаком
Варзара”. Знак Варзара представляет
собой прямоугольник, у которого один
сомножитель принят за основание, другой
– за высоту, а вся площадь, равная
произведению этих двух величин, изображает
объем изучаемого явления. Так можно
изобразить, например, размер посевной
площади под пшеницей, величину урожайности
и объем валового сбора в определенном
году; численность работающих, уровень
их производительности труда и объем
произведенной продукции для предприятия,
отрасли или страны за период.
Балансовую
диаграмму применяют
для характеристики балансовых соотношений
в какой-либо области. Данный вид диаграммы
строится в виде четырех расположенных
особым образом прямоугольников, из
которых два крайних изображают запасы
на начало и конец периода, два средних
– их поступление и использование
(рис.3.7).
17075,4
603,7
Россия
207,6
Украина
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
4.2. Графическое представление статистических данных
Важное место в современном статистическом анализе социально-экономических явлений и процессов занимает графический метод. Без графиков не обходится ни одно статистическое исследование — они позволяют с наименьшими временными затратами выявить закономерности в развитии явления и его структуру, а также наглядно представить взаимосвязи показателей. Графический образ часто более нагляден и понятен, чем многие страницы текста. Арсенал используемых в статистике графиков обширен. Более того, с появлением новых программных средств он непрерывно увеличивается: на замену плоскостным графикам приходят объемные, матричные, категоризованные графики и пиктографики.
График — это схематичное изображение статистической информации с помощью различных геометрических образов, которыми могут быть линии, точки, плоскостные либо объемные фигуры (круги, прямоугольники и т.д.), символы со многими элементами (звезды, лучи, многоугольники, «лица Чернова», «японские свечи», «ящики с усами» и т.д.).
Любой статистический график содержит графический образ и вспомогательные элементы. Под графическим образом понимают совокупность выбранных для изображения конкретной статистической информации линий, фигур, точек или символов, имеющих определенный формат изображения. Вспомогательные элементы графика — это, во-первых, поле графика (пространство, на котором располагается геометрический образ, при этом длина и ширина поля графика, как правило, имеют между собой определенное соотношение), во-вторых, система координат и масштабные ориентиры (декартовы, полярные координаты, контурные линии или сетки с нанесенной на них масштабной шкалой), и, в-третьих, экспликация графика, которая представляет собой необходимый разъяснительный текст, прилагаемый к графику: его название, подписи масштабных шкал, смысловое содержание применяемых символов и знаков (легенда графика).
Статистические графики можно классифицировать по следующим признакам:
- аналитическое предназначение;
- способ построения;
- символы геометрического образа.
По аналитическому предназначению различают графики сравнения, структуры, динамики, изображения вариационных рядов, графики взаимосвязи показателей.
По способу построения графики делятся на диаграммы и статистические карты.
Согласно используемым символам геометрического образа графики бывают точечные, линейные, фигурные (плоскостные или объемные) и пиктографики.
Для сравнения одноименных показателей, относящихся к различным временным периодам, объектам или территориям, применяют линейные графики и различные виды диаграмм: столбиковую, ленточную, фигурную; а также пиктографики.
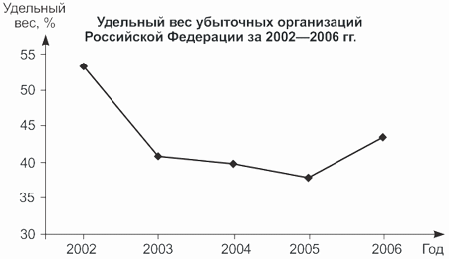
У линейного графика по оси абсцисс отмечаются временные периоды, объекты или территории, а по оси ординат — соответствующие им значения рассматриваемого показателя. Например, по данным табл. 4.10 построим линейный график изменения удельного веса убыточных организаций за период 2002-2006 гг. для экономики в целом (рис. 4.1).
| Отрасль экономики | Год | ||||
|---|---|---|---|---|---|
| 2002 | 2003 | 2004 | 2005 | 2006 | |
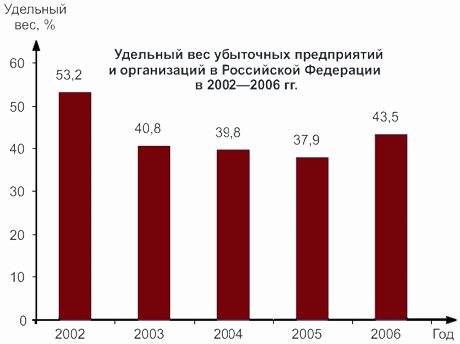
| Всего в экономике, в том числе: | 53,2 | 40,8 | 39,8 | 37,9 | 43,5 |
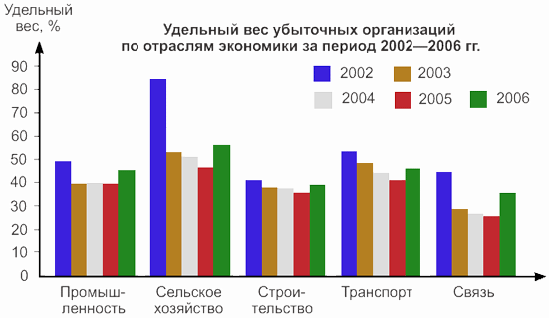
| промышленность | 48,8 | 39,1 | 39,7 | 39,3 | 45,1 |
| сельское хозяйство | 84,4 | 52,7 | 50,7 | 46,3 | 55,6 |
| строительство | 40,6 | 37,7 | 37,2 | 35,4 | 38,6 |
| транспорт | 53,4 | 47,9 | 44,1 | 40,9 | 45,6 |
| связь | 44,3 | 28,4 | 26,1 | 25,4 | 35,1 |
| торговля и общественное питание | 45,3 | 32,7 | 31,4 | 27,7 | 31,2 |
Рис.
4.1.
Линейный график
Столбиковая диаграмма несет тот же аналитический смысл, что и линейный график. При ее построении на оси X располагаются элементы, подлежащие сравнению, которыми могут быть временные периоды, территории, либо объекты. Они находятся на одинаковом расстоянии друг от друга. Затем рисуются прямоугольники (столбики): сторона, являющаяся шириной, одинакова для всех сравниваемых элементов и располагается на оси X, высота прямоугольников откладывается по оси Y пропорционально значению сравниваемого показателя. Таким образом, ось Y должна иметь определенную масштабную шкалу, обязательно начинающуюся с нуля. Так, используя данные табл. 4.10, построим столбиковую диаграмму изменения удельного веса убыточных предприятий и организаций по всей экономике в целом (рис. 4.2).
Прямоугольники столбиковой диаграммы могут располагаться и вплотную друг к другу — расстояние между ними определяется произвольно, масштаб имеет лишь высота прямоугольников.
Рис.
4.2.
Столбиковая диаграмма
Столбиковые диаграммы могут одновременно демонстрировать изменение нескольких показателей. Для примера изобразим динамику удельного веса убыточных предприятий и организаций по отраслям экономики за несколько временных периодов (рис. 4.3).
Рис.
4.3.
Столбиковые диаграммы для нескольких объектов
Для четырех отраслей построим линейный график (рис. 4.4).
Рис.
4.4.
Линейные графики для нескольких объектов
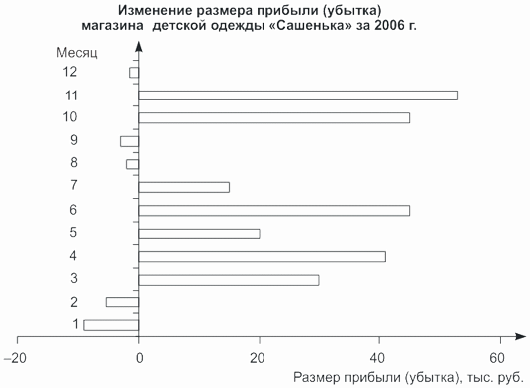
Ленточная (полосовая) диаграмма строится по тем же правилам, что и столбиковая, но прямоугольники, изображающие размеры показателя, располагаются не вертикально, а горизонтально. Данный вид диаграммы удобно применять в тех случаях, когда сравниваемые показатели могут принимать отрицательные значения. Например, магазин детской одежды «Сашенька» в течение года имел не только прибыль (+), но и нес убытки (рис. 4.5).
Рис.
4.5.
Ленточная диаграмма
Для получения диаграмм сравнения могут использоваться и различные геометрические фигуры. Предположим, что количество заключенных договоров личного страхования, заключенных страховой компанией, составляло в 2003 г. 23 тыс., в 2004 г. — 64 тыс. Изобразим эти данные графически, для чего выберем в качестве фигурного знака квадрат. Чтобы найти стороны квадратов нужно извлечь квадратные корни из значений показателей: 
Рис.
4.6.
Количество договоров личного страхования, заключенных страховой компанией в 2003-2004 гг., тыс.: а — 2003 г.; б — 2004 г.
Вместо квадратов часто используются круги. Тогда изображаемые величины должны быть пропорциональны площади круга. Наглядность данного вида диаграмм тем больше, чем сильнее различаются между собой сравниваемые показатели. Действительно, если различия небольшие, то подобный график теряет свой смысл.
В динамических сравнениях, особенно если приводятся данные по месяцам года и в них присутствуют так называемые сезонные колебания, используются радиальные диаграммы. Для этого вычерчивается круг такого радиуса, чтобы при нанесении на него масштабной шкалы верхнее значение шкалы соответствовало наибольшему значению показателя. Затем весь круг делится на 12 частей (если мы рассматриваем помесячные данные) и проставляются номера либо названия месяцев около каждого радиуса. После этого на них откладываются в принятом масштабе значения показателей соответствующих месяцев, и полученные точки соединяются отрезками — образуется замкнутая ломаная линия. Пример построения радиальной диаграммы приведен на рис. 4.7.
Рис.
4.7.
Радиальная диаграмма
Для изображения структуры явления используются прямоугольные или секторные диаграммы.
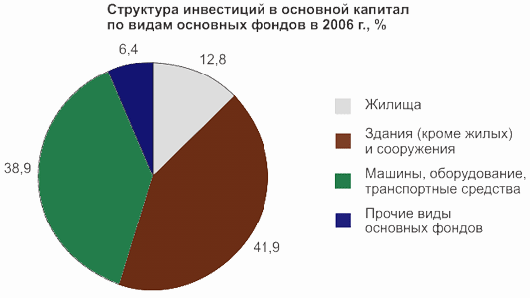
Продемонстрируем построение круговой секторной диаграммы на данных табл. 4.11.
| Вид основных фондов | Удельный вес инвестиций в их общем объеме, % |
|---|---|
| Жилища | 12,8 |
| Здания (кроме жилых) и сооружения | 41,9 |
| Машины, оборудование, транспортные средства | 38,9 |
| Прочие виды основных фондов | 6,4 |
Для того чтобы построить секторную диаграмму, необходимо определить величину углов секторов: 100% соответствует 360°, тогда 1% равен 3,6°. Пересчитаем наши данные:
- жилища: 12,8 * 3,6 = 46°;
- здания (кроме жилых) и сооружения: 41,9 * 3,6 = 151°;
- машины, оборудование, транспортные средства: 38,9 * 3,6 = 140°;
- прочие виды основных фондов: 6,4 * 3,6 = 23°.
Начертим круг произвольного радиуса и разделим его на четыре соответствующих сектора (рис. 4.8).
Рис.
4.8.
Круговая секторная диаграмма
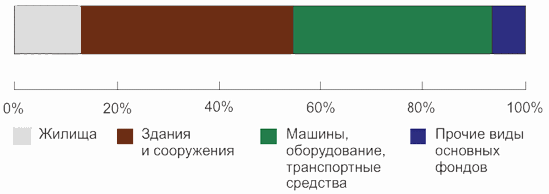
Изобразить графически структуру явления можно также с помощью ленточных (полосовых) диаграмм. В этом случае вычерчивается прямоугольник произвольной длины и ширины. Значение его длины принимается за 100%. Затем прямоугольник делится на части, соответствующие значениям долей тех компонент, из которых состоит явление. Так, по данным табл. 4.10 получим полосовую диаграмму, представленную на рис. 4.9.
Рис.
4.9.
Ленточная (полосовая) диаграмма
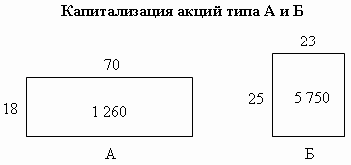
Для одновременного изображения трех величин, одна из которых является произведением двух других, применяется особый график, называемый знаком Варзара. Поясним процедуру его построения на условном примере.
Знак Варзара имеет вид прямоугольника, длина и ширина которого соответствуют двум множителям произведения, а площадь — значению произведения, т.д. третьей величине. Так, в табл. 4.12 показатель «Капитализация» рассчитан как произведение рыночной стоимости акции на количество акций данного вида:
| Тип акции | Количество акций, находящихся в обращении, тыс. шт. | Рыночная стоимость акции, ден. ед. | Капитализация, тыс. ден. ед. |
|---|---|---|---|
| А | 70 | 18 | 12 492 |
| Б | 23 | 25 | 575 |
Основание прямоугольников примем за показатель количества, а высоту — за цену. Тогда площадь полученных прямоугольников будет изображать капитализацию. При построении знаков Варзара следует помнить, что основание и высота прямоугольников откладываются в своем масштабе независимо друг от друга (рис. 4.10).
Рис.
4.10.
Знаки Варзара
Особое место в графическом анализе финансовой информации занимают биржевые статистические графики.
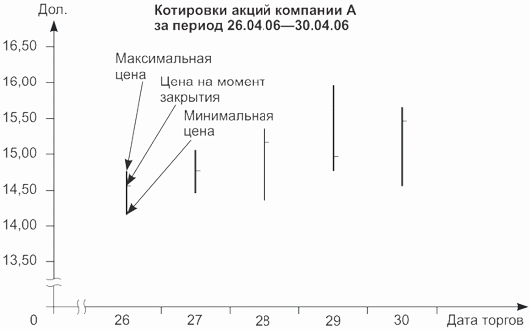
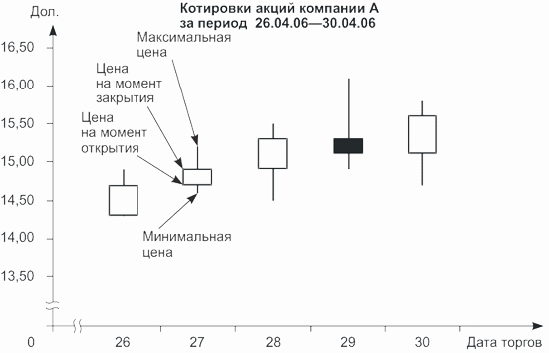
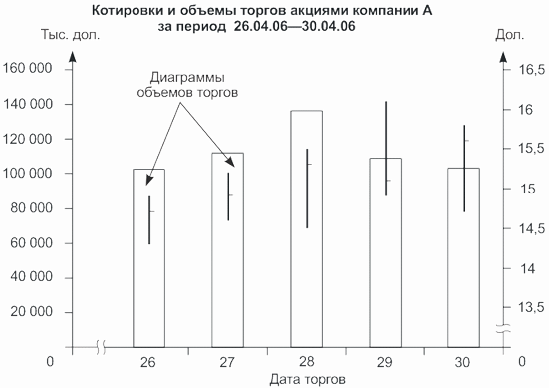
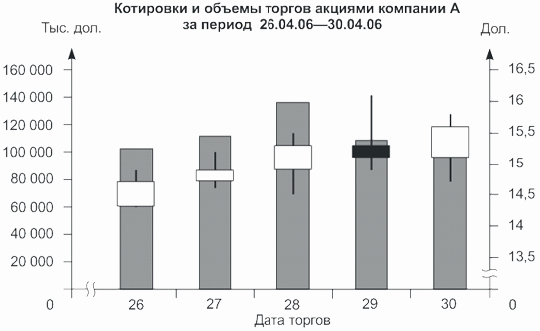
Для анализа данных фондовых, товарных и фьючерсных рынков чаще всего используют столбиковые биржевые графики (табл. 4.13).
| Дата торгов | Цена открытия | Максимальная цена дня | Минимальная цена дня | Цена закрытия | Объем торгов |
|---|---|---|---|---|---|
| 26 | 14,3 | 14,9 | 14,3 | 14,7 | 102 548 |
| 27 | 14,7 | 15,2 | 14,6 | 14,9 | 112 054 |
| 28 | 14,9 | 15,5 | 14,5 | 15,3 | 136 250 |
| 29 | 15,3 | 16,1 | 14,9 | 15,1 | 108 914 |
| 30 | 15,1 | 15,8 | 14,7 | 15,6 | 103 145 |
По данным табл. 4.13 построим столбиковый биржевой график (рис. 4.11).
На столбиковом биржевом графике для каждого дня строится вертикальная черта (столбик): начало столбика соответствует значению минимальной в течение дня цены на акцию, вершина — максимальной цене, горизонтальная черта на столбике — цена в момент закрытия торгов.
Рис.
4.11.
Столбиковый биржевой график
Для одновременного изображения цен открытия и закрытия торгов, а также минимального и максимального значений цены служит график, часто называемый в литературе «ящики с усами». Для данных табл. 4.13 он выглядит так, как показано на рис. 4.12.
Рис.
4.12.
«Ящики с усами»
Здесь, в отличие от графика, приведенного на рис. 4.11, у каждого столбика имеется еще и «ящик» (отсюда и название — «ящики с усами»). Основание белого «ящика» соответствует цене открытия торгов, высота — цене закрытия; черный цвет «ящика» означает, что цена закрытия была ниже цены открытия торгов — в этом случае на графике они меняются местами.
Столбиковый график можно дополнить диаграммами показателя объема торгов. Для данных табл. 4.13 получим графический образ, представленный на рис. 4.13.
Рис.
4.13.
Столбиковый биржевой график с диаграммой объемов торгов
Поскольку график дополняется диаграммами, показывающими объемы торгов, то он имеет две вертикальные масштабные шкалы: слева находится шкала для показателя объема торгов, справа — для котировок акций.
График «ящики с усами» также можно дополнить диаграммами показателя объема торгов (рис. 4.14).
Рис.
4.14.
Биржевой график «ящики с усами» с диаграммой объемов торгов
В современных статистических пакетах прикладных программ для графического представления статистической информации предлагается особый вид графиков — пиктографики.
Пиктографики составляются для каждого наблюдения, они имеют вид графических объектов (определенных символов) со многими элементами. Значения показателей соответствуют свойствам или размерам элементов пиктографика. С изменением значений показателей при переходе от одной единицы наблюдения к другой внешний вид пиктограммы меняется. Таким образом возникает возможность визуально классифицировать наблюдения по однородным группам.
Предположим, что имеется совокупность 10 промышленных предприятий, характеризующихся следующими показателями (табл. 4.14).
| Номер предприятия | Рентабельность, % | Удельный вес рабочих в составе промышленного производственного персонала, % | Коэффициент сменности оборудования | Удельный вес потерь от брака, % | Фондоотдача на 1 руб. фондов | Среднегодовая численность промышленного производственного персонала, чел. | Среднегодовая стоимость основных производственных фондов, млн. руб. | Оборачиваемость нормируемых оборотных средств, дн. | Оборачиваемость ненормируемых оборотных средств, дн. | Непроизводственные расходы, млн. руб. |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 13,28 | 0,80 | 1,14 | 0,27 | 1,07 | 1 257 | 50,79 | 80,12 | 22,46 | 18,20 |
| 2 | 22,31 | 0,80 | 1,85 | 0,38 | 2,45 | 1 687 | 58,12 | 80,12 | 22,37 | 38,45 |
| 3 | 15,27 | 0,78 | 1,14 | 0,26 | 1,14 | 1 588 | 44,20 | 80,45 | 21,74 | 22,13 |
| 4 | 12,99 | 0,79 | 1,33 | 0,28 | 1,05 | 1 696 | 44,57 | 68,17 | 20,11 | 24,56 |
| 5 | 25,78 | 0,78 | 1,74 | 0,29 | 2,12 | 1 804 | 51,43 | 70,82 | 20,37 | 46,75 |
| 6 | 28,47 | 0,79 | 1,90 | 0,30 | 2,09 | 1 512 | 53,96 | 73,47 | 21,38 | 38,16 |
| 7 | 12,97 | 0,80 | 1,16 | 0,35 | 1,03 | 1 499 | 57,58 | 76,12 | 21,52 | 24,58 |
| 8 | 23,47 | 0,81 | 1,86 | 0,32 | 2,11 | 1 403 | 65,34 | 78,77 | 23,58 | 41,78 |
| 9 | 10,47 | 0,81 | 1,17 | 0,33 | 0,87 | 1 451 | 59,34 | 81,42 | 22,47 | 22,79 |
| 10 | 13,58 | 0,82 | 1,23 | 0,32 | 0,97 | 1 327 | 57,83 | 84,07 | 23,17 | 22,47 |
Проанализируем имеющуюся информацию графически с помощью пиктографиков.
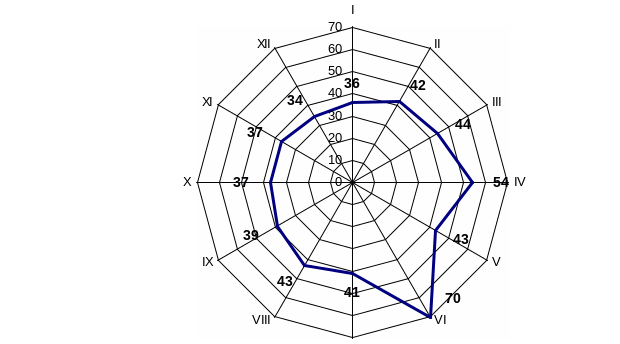
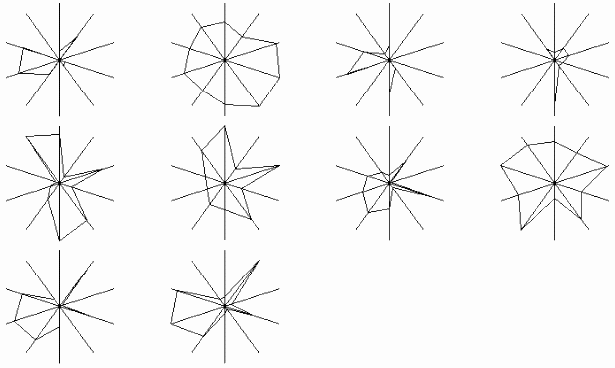
Пиктографики «лучи» имеют вид «велосипедного колеса», в котором количество «спиц» соответствует количеству переменных. Каждая спица — числовая ось, на которой откладывается значение показателя в своем масштабе независимо от масштаба других показателей, причем шкалы начинаются не с нулевого значения, а с наименьшего в данном числовом массиве. Цель пиктографика — продемонстрировать различия в значениях аналогичных показателей у разных единиц наблюдения.
По данным табл. 4.14 построим пиктографики «лучи» (рис. 4.14а).
Рис.
4.14а.
Пиктографики «лучи»
Как видим, на рис. 4.14а пиктографиков столько, сколько имеется наблюдений. Число лучей каждого пиктографика равно количеству показателей, которые располагаются друг за другом по часовой стрелке, начиная с первого, который находится на верхнем луче, соответствующем 12 часам, если проводить аналогию с часовым механизмом.
Итак, визуальный анализ данных показывает, что сходными по своим экономическим показателям являются предприятия 2 и 8; 5 и 6; 7 и 9.
Преимущество данного способа анализа возрастает с увеличением числа наблюдений, так как при большом их количестве все труднее становится систематизировать полученную информацию, изучая цифры табличным методом.
Другой вид часто применяющихся пиктографиков — «звезды» (рис. 4.14б). Их построение и анализ абсолютно аналогичен пиктографикам «лучи» (у «звезд» лучи не продолжаются за отметками показателей на осях).
Рис.
4.14б.
Пиктографики «звезды»
Отметим, что в каждом конкретном случае выбор «звезд» или «лучей» — сугубо индивидуальный процесс: кому-то удобнее работать со «звездами», чем с «лучами», а кому-то наоборот.
Следующий, наиболее экзотичный, вид пиктографиков — «лица Чернова» (рис. 4.14в). Здесь для каждого наблюдения рисуется отдельное лицо. Черты лица соответствуют значениям показателей: овал лица — показатель первый, размер ушей — показатель второй, длина носа — показатель третий, форма ушей — показатель четвертый, тип улыбки — показатель пятый, угол наклона бровей — показатель шестой и т.д. Конечно, по данному графику нельзя определить конкретные значения показателей — преследуется вовсе не эта цель, но для классификации наблюдений по однородным группам, выявления взаимосвязей между показателями (если скажем, длина носа меняется с изменением овала лица) «лица Чернова» могут быть полезны.
Рис.
4.14в.
Пиктографики «лица Чернова»
Роль и место данной темы в курсе:
в курсе математики тема «Диаграммы» стала одной из актуальной тем современности. Именно здесь начинается формирование умения работать с информацией, представленной в форме диаграммы, которая широко используется в СМИ, Интернет-ресурсах и т.п. У учащихся формируются представления о приемах сбора необходимых данных и наглядном изображении, что также способствует умению анализировать, сравнивать и делать соответствующие выводы.
Основные вопросы темы:
- Столбчатые диаграммы.
- Чтение диаграмм.
- Построение диаграмм.
Краткий обзор материала, изученного на предыдущих уроках:
из курса математики в 5-м классе учащимся известно: понятие о диаграммах; чтение и построение круговых диаграмм.
Перечень вопросов, изучаемых в данной теме:
- Столбчатые диаграммы (назначение, преимущества, недостатки);
- Чтение диаграммы и решение задач по ней;
- Анализ и сравнение данных;
- Построение столбчатой диаграммы ручным способом и с помощью компьютера.
Основные особенности использования цифровых образовательных ресурсов (компакт-диски, интернет-ресурсы) и компьютерных программных средств.
Для проведения уроков по данной теме, благодаря интернет-ресурсам, можно подобрать большой объем интереснейшей информации. У детей формируется умение работать с информацией, повышается интерес к современным компьютерным технологиям, совершенствуются навыки работы с компьютерной техникой.
Средства обучения(в том числе технические средства обучения)
Компьютеры, мультимедийный проектор, экран, принтер, таблицы с диаграммами, печатные средства (раздаточный материал).
Программные средства.
- Microsoft Word
- Microsoft Power Point
- Microsoft Excel
- Internet Explorer.
Ресурсы Интернет.
http://www.sekret1.info/
http://anti-smoking.ru/statistic
http://www.alkandtab.info/index7.html
Использование компьютера при подготовке учителя к уроку: Стандартные программы операционной системы Windows позволяют создать такие материалы к уроку как:
- Презентации.
- Таблицы.
- Практические задания.
- Раздаточный материал.
Ожидаемые результаты обучения.
Изучив тему «Столбчатые диаграммы» ученики должны:
- Знать назначение, преимущества, недостатки столбчатых диаграмм.
- Уметь читать и решать задачи по ней.
- Выделять и группировать данные, которые должны быть отражены на диаграмме.
- Интерпретировать количественную информацию, представленную в диаграмме.
- Освоить построение диаграмм ручным способом и с помощью компьютера.
- Применять построение диаграмм в практической деятельности.
Урок
Цель:
познакомить учащихся со столбчатыми диаграммами, их назначением и построением.
Задачи:
Образовательные:
- Формировать у учащихся понятие по теме: «Столбчатые диаграммы»;
- Выделять и группировать данные, которые отражены на диаграмме;
- Учить сравнивать данные, анализировать их, обобщать и делать выводы.
Воспитательные:
- Воспитывать у учащихся навыки учебного труда;
- Формировать ответственность;
- Воспитывать познавательную активность.
Развивающие:
- Развивать мыслительные операции, посредством наблюдений, сравнений, сопоставлений, обобщений, конкретизацией, сознательного восприятия материала;
- Способствовать творческой деятельности учащихся;
- Продолжать развитие навыков работы с информационными технологиями.
Оборудование:
Компьютеры, мультимедийный проектор, экран, принтер, таблицы с диаграммами, печатные средства (раздаточный материал).
Программные средства.
- Microsoft Word
- Microsoft Power Point
- Microsoft Excel
- Internet Explorer.
- Электронный учебник «Математика 5-11»
План-конспект.
I
.
Организационный момент.
II
. Повторение ранее изученного материала.
а) Диаграммы – всякий чертёж, для геометрического или иного объяснения. (объяснительный чертёж или рисунок в красках для наглядного изображения какого либо явления в описательных науках, особенно в статистике).
б) виды диаграмм: линейные, круговые, столбчатые
в) Фронтальный опрос.
- Какой вид диаграмм вы изучили ранее(в 5 классе)?
- Что называется круговой диаграммой?
- Для чего и где используется круговая диаграмма?
- В чём заключается принцип построения диаграмм? Слайд 1.
III
. Изучение нового материала.
Учитель
:
на сегодняшнем уроке мы с вами познакомимся с одним из видов диаграмм – столбчатые диаграммы.
Назначение столбчатых диаграмм: сравнение нескольких величин в нескольких точках. Чтобы наглядно сравнить какие-то цифровые данные, часто используют диаграммы. При их построении не обойтись без чисел, пропорциональных данным. /Учитель демонстрирует через проектор электронное учебное пособие «Математика 5-11, раздел «Чтение и построение диаграмм»./
Учитель
:
по данным диаграммы можно анализировать, сравнивать данные и решать задачи. Презентация к уроку. Слайд 2.
Данная диаграмма показывает количество банок мёда, съеденного Вини-Пухом за неделю в гостях у друзей. Используя диаграмму, ответьте на вопросы. Слайд 3.
Вопросы классу:
- В какой день Винни-Пух побывал в гостях у самых гостеприимных хозяев?
- В какой несчастливый день ему не удалось попасть в гости?
- Сколько всего банок мёда съел медвежонок за неделю?
- На сколько больше банок мёда съел медвежонок в четверг, чем в субботу?
- В какой день было съедено одинаковое количество мёда?
- Сколько в среднем съел бочонков мёда Винни-Пух? Почему в ответе применили округление?
Построение столбчатых диаграмм.
Учитель:
рассмотрим два способа построения диаграмм.
Первый способ
/ручной
/: заключается в том, что для изображения чисел (величин) используется, как вы заметили столбики, высота которых пропорциональна этим числам.
/Учитель на доске показывает построение столбчатой диаграммы «Массы вымерших динозавров»/.
Второй способ
/с помощью компьютера
/: заключается в построении столбчатых диаграмм с помощью электронных таблиц в Microsoft Excel. /Учитель демонстрирует через проектор построение столбчатой диаграммы «Массы вымерших динозавров» с помощью электронных таблиц в Microsoft Excel/. Слайд 4.
IV
.
Практическая работа /в группах/.
1-я группа выполняет построение столбчатой диаграммы по карточке- заготовке, ручным способом, используя линейку, цветные карандаши.
2-я группа выполняет построение на компьютере с помощью электронного учебного пособия «Математика 5-11», раздел «Анализ данных» (можно с помощью Excel).
Карточка №1
Инструкция.
1. По данным таблицы постройте столбчатую диаграмму, для этого:
1.1. Изобразите данные числа столбиками, высоты которых пропорциональны этим числам: отрезок длиной 1 см будет изображать число 10, 10 см – число 100 и т.д.
2. Оформите диаграмму, с учётом, что диаграмма должна быть видна и понятна для всех участников.
Карточка №2
Построить столбчатую диаграмму выпадения осадков /мм/ за год в Чистополе.
Инструкция.
1. Воспользуйтесь данными и постройте таблицу в Excel.
2. По введённым данным постройте диаграмму, для этого:
2.1. Выделите ячейки с данными и вызовите «Мастер диаграмм».
2.2. На 1-м шаге выберите тип диаграммы – гистограмма.
2.3. На 2-м шаге введите заголовок диаграммы.
2.4. На 3-м шаге выберите размещение диаграммы на отдельном листе.
3. Оформите диаграмму, с учётом, что диаграмма должна быть видна и понятна для всех участников.
Диаграмма выводится на экран с помощью проектора для обмена информацией и обсуждения результатов. Слайд 4.
V
. Итоги урока.
Для чего используются столбчатые диаграммы?
Какой способ построения диаграмм более рациональный? Почему?
Выполнить упражнения №5, 6,7 из ЭУ «Математика 5-11».
VI
. Домашняя работа.
- Найти информацию в СМИ, Интернет-ресурсах
Статистические графики отличаются большим разнообразием. В зависимости от способа построения их можно разделить на две большие группы: 1) диаграммы и 2) статистические карты.
Диаграммы — это условное изображение числовых величин и их соотношений с помощью геометрических знаков. Термин «графика» тождественный термину «статистический график». Диаграммы являются наиболее распространенным видом графиков. Выделяют такие основные виды диаграмм: линейные, столбиковые, ленточные, квадратные, круговые, радиальные, треугольные, фигурные, знак Варзара и др.
в Зависимости от круга решаемых задач все диаграммы можно разделить на диаграммы сравнения, структуры и динамики.
Рассмотрим методику и технику построения статистических графиков, которые чаще всего применяются на практике.
самым Распространенным видом показательных диаграмм являются линейные диаграммы, которые используются в основном для характеристики динамических рядов и рядов распределения. Наряду с этим линейные диаграммы широко используются для изучения взаимосвязей между явлениями, сравнение нескольких показателей, хода исполнения планов и т.д.
Линейные диаграммы дают возможность изображать явления в виде линий, которые соединяют точки, расположенные в координатном поле. Ломаные линии, образующиеся показывают характер развития явления во времени или особенности его распределения по величине какого-либо признака, или связи явлений.
По способу построения — это графики с равномерной (арифметическим) шкале. При их построении используют прямоугольную систему координат. Расположение любой точки в этой системе определяется двумя параметрами — абсциссой и ординатой. Иногда поле в пределах осей координат для удобства нанесения геометрических знаков и чтения графика покрывается горизонтальными и вертикальными линиями, проведенными по принятому масштабу. Эти линии образуют координатную числовую сетку.
На горизонтальной оси (ось абсцисс) откладывают одинаковые по длине отрезки, отражающие периоды (годы, месяцы, декады, дни и т.д.). На вертикальной оси (ось ординат) в определенном масштабе наносят значения исследуемой величины. На пересечении перпендикуляров соответствующих значений исследуемого признака и временных дат до осей координат получают точки. Ломаная линия, соединяющая эти точки, характеризует изменение исследуемого явления во времени.
Построение простой линейной диаграммы рассмотрим на следующем примере (табл. 12.1).
Таблица 12.1. Динамика производства молока в агрофирме за 2001 — 2010 гг.
|
производство |
||||||||||
В прямоугольной системе координат на вот абсцисс нанесем показатели времени (годы с 2001 по 2010), принимая масштаб летнего периода равен 1 см. Тогда длина горизонтальной шкалы будет равна 10 см (1 см х 10 лет). На оси ординат исходя из оптимального соотношения осей ординат и абсцисс как 1: 1,5, то есть длиной 6,7 см (10: 1,5), нанесем в определенном масштабе значения валового производство молока от 26 до 38 тыс. ц. Возьмем 1 см за 2 тыс. ц. При этом для большей наглядности на оси ординат сделаем разрыв, поскольку минимальное значение производства молока значительно отличается от нуля. На поле графика точками отложим соответствующие значения валового производства молока по годам. Полученные точки соединим отрезками прямой линии (рис. 12. 1).
Построенный график показывает постоянный рост производства молока. Ломаная кривая, которая имеет небольшие взлома, непрерывно направляется вверх.
Линейные диаграммы могут быть построены с целью изучения взаимосвязей между двумя признаками: результативным и факторным (например, между урожайностью и качеством почв). При этом на оси абсцисс откладывают
Рис. 12.1. Динамика валового производства молока в агрофирме за 2001 — 2010 гг.
значение факторного признака (качества почв), а на оси ординат — значения результативного признака (урожайности).
Линейные диаграммы удобны для изображения нескольких параллельных рядов с целью их сравнения (например, динамики продуктивности коров и уровня кормления или других качественно отличительных признаков). В этом случае строят две (при двух признаках) или несколько шкал. Вторую шкалу строят справа.
Особое место имеют линейные диаграммы со специальными базовыми линиями. Наиболее типичными являются два случая. В первом случае значение вертикальной шкалы в начале координат принимают за 100%, то есть линия, выходящая из этой точки, отображает уровень базисной величины, которая равна 100%. Все значения величин, которые превышают базисную, располагают выше этой линии, а значения, которые менее уровня базисной величины, располагают ниже.
Во втором случае при изображении отклонений от среднего значения уровня (чаще в процентах) базовая линия, которая характеризует средний уровень, является нулевой. Положительные отклонения (превышения) от среднего уровня откладывают выше этой линии, отрицательные — ниже.
Диаграммы в виде вертикальных столбиков и лент являются наиболее простыми и достаточно эффективными для анализа социально — экономических явлений видом графического изображения.
Столбиковые и ленточные диаграммы преимущественно применяются для сравнения различных показателей в пространстве и во времени, а также анализа структуры явлений.
Столбиковые диаграммы
— это графики, в которых различные величины представлены в виде столбиков одинаковой ширины, которые расположены друг от друга на одинаковом расстоянии или плотно. Если колонки расположены не по вертикали, а по горизонтали, то такие диаграммы называются ленточными.
Основа сравнения в столбиковых и ленточных диаграммах — линейная (одномерная). Высота столбиков и длина лент в соответствии с принятым масштабом пропорциональна величине изображаемых явлений.
При построении столбиковых (ленточных) диаграмм нужно придерживаться таких основных правил. Основания столбиков (лент) должны быть равными. Столбики (ленты) могут быть размещены на одинаковом расстоянии друг от друга или плотно. Конечно соблюдают правила, чтобы ширина зазоров была вдвое меньшей ширины самих столбиков (лент). Высота столбиков и длина лент должны строго соответствовать изображаемым цифрам.
Рекомендуется включение в диаграмму масштабной шкалы, которая дает возможность определить высоту столбика и длину ленты. Шкала может совпадать с гранью первого столбца или ленты или располагаться на отдельной линии слева (в столбиковой диаграмме) или в верхней части (в ленточной диаграмме). Шкала, по которой устанавливается высота столбиков или длина лент должна быть непрерывным и начинаться с нуля. Надписи и указания цифр в конце столбиков (лент) делать не рекомендуется, ибо это может создать зореве удлинение столбиков (лент). Цифры показателей лучше всего писать внутри столбиков (лент), или расположить в один ряд над ними на уровне окончания шкалы по оси ординат.
Столбики (ленты) для лучшей наглядности могут быть закрашены краской сплошной, если столбик (лента) отражает целое явление, или несколькими красками, если изображаются сравнения различных структур явлений, каждому из которых отведена часть столбика (ленты).
Ленточной диаграммой можно изображать то же самое что и стовпчиковою. Однако вертикальные столбики лучше лент, если числа выражают идею высоты (уровень роста) и если небольшие пояснительные надписи к каждому столбику. Горизонтальные ленты нагляднее, если изображаемые величины выражают идею подовженості (автомобильных дорог, рек и т.п.) и если пояснительный текст к ним небольшой.
Столбиковые и ленточные диаграммы лучше линейные прежде всего в тех случаях, когда сравниваемых величин не так много, нарушается непрерывность во времени (сравнивают не смежные периоды) и нужно обратить внимание не на относительное изменение, а на абсолютную величину сравниваемых уровней.
Порядок построения столбиковой диаграммы покажем на следующем примере (табл. 12.2).
Таблица 12.2. Посевные площади сельскохозяйственных культур в TOB района за 2009 и 2010 гг., тыс. га
Сравним с помощью столбиковой диаграммы общую посевную площадь в TOB района за 2009 и 2010 гг., которая соответственно составила 55,0 и 60,0 тыс. га.
Для этого на оси абсцисс построим два столбика с основами по 3 см на расстоянии 1 см друг от друга. Масштаб на оси ординат примем равным такому соотношению: 10 тыс. га на 1 см. Цифры, характеризующие общий размер посевной площади, напишем в середине столбиков. Для наглядности столбики рекомендуется закрасить или заштриховать.
Построим столбиковая диаграмма (рис. 12.2).
Рис. 12.2. Посевные площади в TOB района за 2009 и 2010 гг.
Столбчатая диаграмма может быть использована не только для характеристики общего размера и структуры того или иного явления. При
построении столбиковой структурной диаграммы высоту столбика принимают за 100% и делят на части пропорционально структуре явлений (табл. 12.3).
Таблица 12.3. Структура посевных площадей в ООО района за 2009 и 2010 гг.
Чтобы облегчить чтение и анализ таких диаграмм, отдельные составные части раскрашивают разным цветом или штриховкой.
Используя данные табл. 12.3, построим столбиковая структурную диаграмму (рис. 12.3).
Под круговыми (квадратными)
диаграммами понимают графики, которые выражают однородные величины через площади кругов (квадратов).
Чтобы построить круговую и квадратную диаграмму из сравниваемых статистических величин нужно извлечь квадратные корни, а потом изобразить круги и квадраты со сторонами, пропорциональными полученным результатам.
Сравним между собой за 2010 г размер посевных площадей технических (4,0 тыс. га), картофеля и овоще-бахчевых (3,3 тыс. га) культур. Корни квадратные из посевных площадей соответственно составляют =2,0 и ^/3,3 =1,8.
Рис. 12.4. Посевные площади технических, картофеля и овоще-бахчевых культур в TOB района в 2010 г.
тот, кто читает диаграмму по-разному ее воспринимает, принимая за сравнение или высоту фигуры, или ее площадь.
В связи с этим предпочтение следует отдавать основном одномерным (линейным) сравнением, используя для этих целей столбиковые или ленточные диаграммы.
диаграмма
представляет собой круг, разделенный радиусами на отдельные секторы, каждый из которых характеризует удельный вес соответствующей части в общем объеме изображаемой величины. Круговые диаграммы используются преимущественно для характеристики структуры явлений. При сравнении различных структур общие площади кругов принимают одинаковыми. Каждый сектор выделяют цветом или штриховкой; кроме того в каждом секторе нередко дают и цифровое обозначение его удельного веса. При малом угле сектора экспликация к нему указывается стрелкой.
При построении круговой диаграммы круг разделяют на секторы, площади которых пропорциональны долям частей исследуемого явления. Площадь круга изображает общий размер явления и принимают ее равной 100% или 3600. Перед построением диаграммы абсолютные величины переводят в проценты, а проценты в градусы. Каждый процент равен 3,6° (360:100).
Последовательность размещения секторов определяется их величиной: самый большой размещается сверху, а остальные — по ходу часовой стрелки в порядке уменьшения.
В круговой диаграмме можно в основной круг вписать малый круг, указав в нем базу, равную 100%.
Иногда вместо круга используют напівкруги, разделены на секторы, где 1% равен 1,80.
Круговые диаграммы наглядные только тогда, когда исследуемая совокупность разделяется не более как на 4 — 5 секторов и наблюдается значительная структурная дифференциация. Если совокупность делится на большее количество секторов и структурная дифференциация незначительна, то для изображения структуры явлений целесообразно применять столбиковая или ленточную диаграмму.
Построение круговой диаграммы покажем на примере данных табл. 12.3. Для построения круговой диаграммы используем данные этой таблицы и условные обозначения рис. 12.3. С помощью транспортира найдем нужные углы и поделим одинаковые круги на сектора. Для лучшей наглядности графика секторы круга изобразим разной штриховкой (рис. 12.5).
Рис. 12.5. Структура посевных площадей в ООО района в 2009 и 2010 гг.
Радиальные диаграммы используются для изображения явлений, которые периодически изменяются во времени (преимущественно сезонных колебаний). Для их построения используют полярную систему координат. Круг делится на 12 равных частей, каждая из которых означает определенный месяц. Величину радиуса берут за среднемесячный уровень (100%) и соответственно к этому масштаба на лучах, начиная от центра круга, откладывают отрезки, изображающие месячные уровне. Концы этих отрезков соединяют между собой, в результате чего образуется замкнутая фигура дванадцятикутник, характеризующий сезонные колебания изучаемого явления.
В радиальной диаграмме за вот абсцисс берут круг, а за вот ординат — его радиусы, которые являются носителями масштабной шкалы с точкой отсчета от центра круга.
в Зависимости от того, какой изображается цикл исследуемого явления — замкнутый или продолжаемое (из периода в период) — различают замкнутые и спиральные радиальные диаграммы. Например, если изображаются данные по месяцам за несколько лет, то при соединении уровня декабря данного года с уровнем января этого же года диаграмма будет замкнутой; при соединении уровня декабря данного года с уровнем января следующего года образуется спиральная диаграмма. Спиральная диаграмма применяется в том случае, если наряду с сезонными колебаниями происходит систематический рост исследуемого явления.
Проиллюстрируем построение замкнутой радиальной диаграммы на следующем примере (табл. 12.4).
Определим средний уровень ряда динамики — среднемесячное производство молока:
Таблица 12.4. Производство молока в агрофирме по месяцам 2010 г.
|
Месяц |
Производство молока, тыс. т |
Показатели сезонности, % |
Длина радиуса, см |
|
Вместе |
Рассчитаем показатели сезонности как отношение уровня каждого месяца в процентах к среднемесячному. Например, для января(1526: 2000) -100 = 76,3%, для февраля (1616: 2000) o 100 = 80,8% и т.д.
Вычислим длину радиуса для каждого месяца, приняв среднемесячный уровень равным 3 см. Тогда величина радиуса для января составит (3 -76,3) : 100 = 2,3 см, для февраля — (3 -80,8) : 100 = 2,4 см и т.д.
График показывает, что наибольшее производство молока наблюдается в мае — августе, а меньше всего — в декабре — марте.
Построим радиальную диаграмму (рис. 12.6).
Рис. 12.6. Сезонность производства молока в агрофирме
Особой разновидностью плоскостных диаграмм являются графические статистические знаки, предложенные российским статистиком В.Е. Варзаром (1851 — 1940 гг.). в Знак Варзара
представляет собой плоскостную диаграмму в виде прямоугольника. Этот вид диаграмм используют для изображения показателей, которые являются результатом перемножения двух других связанных между собой показателей — факторов.
Применение знаков Варзара эффективно для анализа показателей валового производства за складаючими (в растениеводстве — за урожайность и площадь, в животноводстве — продуктивность одной головы и поголовья) и других сложных показателей с выявлением роли отдельных факторов. Так, например, при помощи знаков Варзара можно графически изобразить динамические и территориальные изменения таких показателей как валовой сбор сельскохозяйственных культур (произведение урожайности на посевную площадь), валовая продукция (произведение производительности труда — производство продукции на одного работника — на численность работников), объем грузоперевозок (произведение выработки на одну автомашину на среднесписочную численность автомашин) и т.д.
Знак Варзара строят в виде прямоугольника, основание и высота которого определяются по масштабу двумя факторами — співмножниками, а площадь — величине результативного показателя — добутка. Построение знака Варзара (рис. 12.7) рассмотрим на следующем примере (табл. 12.5).
Таблица 12.5. Поголовье, продуктивность коров и валовой надой молока в ООО
Для построения диаграммы примем такой масштаб: по оси ординат (надой на корову) 10 ц на 1 см, по оси абсцисс (среднегодовое поголовье) — 100 голов на 1 см.
Рис. 12.7. Поголовье, продуктивность коров и валовой надой молока в ООО
Как видно из рис. 12.7., валовой надой молока в двух TOB одинаковый, но в TOB №1 его получили от меньшего поголовья за счет более высокой продуктивности коров.
Линейные напівлогарифмічні диаграммы
(графики отношений) строят таким образом, чтобы одна из шкал отражалась как логарифмическая, а вторая — как арифметическая. В данном случае логарифмический масштаб наносится на оси
ординат, а на оси абсцисс располагают равномерную (арифметическую) шкалу для отсчета времени по принятым интервалам (годы, месяцы, дни и т.д.).
Логарифмический масштаб характерен тем, что в нем отрезки шкалы пропорциональны не изображаемым числовым величинам, а их логарифмам.
Напівлогарифмічні диаграммы целесообразно и эффективно применять для сравнения относительных изменений в динамических рядах с существенно различными абсолютными уровнями. Этот вид диаграмм имеет особую ценность для изображения пропорциональных и процентных отношений, поскольку на этом графике угол наклона кривой выражает относительные изменения, например темпов роста.
Разности ординат точек кривой (их прирост) пропорциональны темпам роста, так же как и на обычной шкале эти ординаты пропорциональны уровням ряда. Итак, по логарифмической шкале можно определить процентное отношение между любыми ее точками.
Преимущество напівлогарифмічних диаграмм в анализе рядов динамики заключается в том, что они дают более правильное представление о темпах динамики. Поэтому линейные напівлогарифмічні диаграммы называют диаграммами темпов. Диаграмма с равномерной арифметической шкале правильно передает абсолютные приросты объемов того или иного явления, а относительные приросты (темпы) искажает. Так, если производство продукции растет равномерно, увеличиваясь из года в год, например, на 3%, то это означает, что абсолютные годовые приросты будут все время увеличиваться. На равномерной координатной сетке линия динамики будет иметь вид возрастающей кривой, а на напівлогарифмічній — вид прямой. Напівлогарифмічний график правильнее покажет темпы изменения исследуемого явления, что имеет большое значение для анализа динамики, особенно за длительный период.
Проиллюстрируем это на следующем примере. На рис. 12.8 изображен рост урожайности кукурузы на зерно в 2010 г. по сравнению с 2002 г. двух предприятий: предприятия №1 с 20 до 30 ц/га и предприятия №2-с 40 до 60 ц/га.
Рис. 12.8. Напівлогарифмічна (А) и арифметическая (Б) линейные диаграммы динамики урожайности кукурузы на зерно
В обоих предприятиях одинаковый темп роста урожайности, то есть увеличение в 1,5 раза, что улавливается напівлогарифмічною диаграммой (рис. 12.8, А) без расчета относительных величин, а на арифметической диаграмме (рис. 12.8, Б) на направление линий влияет величина абсолютного прироста (у предприятия №1 рост урожайности составляет 10 ц/га, а у предприятия №2 — 20 ц/га).
Техника построения логарифмической шкалы такова (рис. 12.9).
Рис. 12.9. Логарифмическая шкала
Сначала нужно найти логарифмы исходных чисел, начертить ординату и разделить ее на несколько равных частей. Затем нанести на ординату (или равную ей параллельную линию) отрезки, пропорциональные абсолютным приростам этих логарифмов.
Далее записать соответствующие логарифмы чисел и их антилогарифми, например 0,0000; 0,3010; 0,4771; 0,6021; …; 1,0000, что дает 1, 2, 3, 4, 10. Полученные антилогарифми дают конечный вид искомой шкалы на ординаті. На логарифмической шкале нет нулевой базовой линии, так как ^ 0 — <ю.
Приведем пример построения напівлогарифмічної диаграммы. Предположим, что нужно изобразить на графике уровень энергообеспеченности предприятия за 1980 — 2010 гг. За эти годы она выросла в 3,3 раза. Найдем логарифмы для каждого уровня динамического ряда (табл. 12.6).
Определив минимальное и максимальное значение логарифмов энергообеспеченности, построим масштаб с таким расчетом, чтобы все данные разместились на графике
Учитывая масштаб, найдем соответствующие точки, соединим прямыми линиями, в результате получим график (рис. 12.9) с использованием логарифмического масштаба на оси ординат. Он называется диаграммой на напівлогарифмічній сетке.
Таблица 12.6. Динамика энергообеспеченности предприятия за 1980 — 2010 гг.
в Полной логарифмической диаграмме он станет в том случае, если на оси абсцисс будет построен логарифмический масштаб. В рядах динамики это никогда не применяется, так как логарифмирование времени теряет всякий смысл.
Применение логарифмического масштаба дает возможность без каких-либо вычислений характеризовать динамику явления. Если кривая на логарифмическом масштабе несколько отклонена от прямой и становится угнутою к оси абсцисс, значит, имеет место снижение темпов; когда кривая приближается к прямой — стабильность темпов; если она отклоняется от прямой в сторону, выпуклую к оси абсцисс (как в нашем примере), исследуемое явление (енергозабезпеченість) имеет тенденцию к росту с растущими темпами.
Напівлогарифмічні диаграммы широко используются при изображены относительных изменений величин, выраженных в разных единицах измерения. Это позволяет на одной диаграмме сравнивать темпы роста средней заработной платы, производительности труда, выпуска продукции и другие показатели.
В этом случае логарифмическая шкала делится на несколько циклов. Цифры каждого цикла в 10 раз больше цифр низшего цикла. Например, в пределах низшего цикла значения показателя изменяются от 1 до 10, второй от 10 до
100 и т.д. Каждый цикл соответствует изменению характеристики логарифма на единицу. Для построения логарифмической шкалы нужно масштаб цикла (например, один цикл равен 5 см) умножить на логарифмы чисел от 1 до 10 и полученные произведения нанести на вертикальную шкалу в пределах каждого цикла. Число самих циклов определяется амплитудой колебания уровней (разницей между максимальным и минимальным значением).
наиболее отчетливо и такими, которые легко воспринимаются, является изобразительные (картинные, фигурные диаграммы),
на которых дают художественное изображение какого-либо явления. Геометрические знаки (точки, линии и т.п.) в изобразительных диаграммах заменяются фигурами, что в какой-то степени символизируют внешний образ изображаемого на графике явления. Например, поголовье коров, свиней, овец в хозяйстве или хозяйствах района (области, страны) может быть изображен рядом фигур этих животных.
Достоинство таких графиков заключается в высокой степени наглядности, в получении наилучшего отображения сравниваемых явлений. Фигурные диаграммы могут быть построены по двум основным принципам: количественном и пропорциональном. Для количественного діаграмування характерно использование равных по размеру фигур — знаков, число которых показывает величину изображаемых явлений.
Фигуры, изображающие ту или иную величину, располагают слева направо на одинаковом расстоянии. В этом отношении фигурные диаграммы является разновидностью линейных диаграмм, в которых сочетаются положительные стороны столбиковых и ленточных диаграмм и преимущества символического изображения по сравнению с геометрическим.
При построении фигурных диаграмм каждой фигуре предоставляется конкретное числовое значение и определенные стандартные размеры. Сама же исследуемая статистическая величина изображается определенным количеством одинаковых по размеру фигур. Однако в большинстве случаев не удается изобразить статистический показатель целым числом фигур. Последнюю из них приходится делить на части, так как по масштабу один знак является слишком крупной единицей измерения. Сложность ее определения является недостатком фигурных диаграмм. Однако большая точность изображения статистических данных в фигурных диаграммах не требуется, и результаты здержуються вполне удовлетворительными.
Принцип пропорционального построения фигурных диаграмм основывается на отраженные величины сравниваемых показателей размеру фигур в соответствующей пропорции с изображаемыми явлениями. Недостатки этого способа, по сути, повторяют недостатки рассмотренных выше круговых и квадратных диаграмм. Вследствие возможного довольно значительного искажения при восприятии в исключительных случаях.
Покажем пример построения фигурной диаграммы по данным о численности фермерских хозяйств в двух областях (условно А и Б) в 2010 г.
Рис. 12.10. Численность фермерских хозяйств в двух областях в 2010 г.
Примем условно за один фігуро-знак 500 хозяйств. Тогда число фермерских хозяйств в области, А в количестве 2550 будет изображен 5,1 фигурами, а в области Б в количестве 3250 — 6,5 фигурами.
Особое место в системе графических изображений отчетных и плановых данных занимают контрольно-плановые графики. Основная задача этих графиков оперативная характеристика выполнения тех или иных производственных процессов и их соответствие плановым заданием. Большим преимуществом контрольно-плановых графиков является то, что они дают возможность наглядного сравнения выполнения плана по большому кругу взаимосвязанных объектов (бригад, звеньев, видов работ и т.д.).
Контрольно-плановые графики бывают разных видов и степени сложности в зависимости от числа объектов и количества признаков, подлежащих графическому изображению.
Среди большого разнообразия контрольно-плановых графиков для изучения хода выполнения плана чаще всего используют график Ганта. Этот вид графика изображает уровень выполнения плана по нескольким объектам как за отдельные периоды, так и за отчетный период в целом.
Порядок построения контрольно-планового графика (графика Ганта) рассмотрим на следующем примере (табл. 12.7).
Таблица 12.7. Данные о ходе сева озимой пшеницы по двух отделениях агрофирмы
Этот график построим на специально розграфленій сетке, в которой по горизонтали в определенном масштабе отложим периоды времени (дни), а по вертикали укажем объекты наблюдения.
Каждый отрезок по горизонтали, который означает отрезок времени (день), примем равным 100% и делим его на 5 равных частей, каждая из которых равна 20% планового задания. На графике эту шкалу дадим нарастающим итогом. При этом отметки 0 и 100%, чтобы не усложнять график не давать.
Степень выполнения плана на графике изобразим двумя линиями: тонкой и жирной. Тонкая линия покажет степень выполнения плана за весь прошедший период. Жирная линия является своеобразной суммарной линией, характеризует степень выполнения плана по состоянию на каждый день.
Построим контрольно-плановый график (рис. 12.11).
Рис. 12.11. График выполнения плана сева озимой пшеницы по отделениях агрофирмы
Построение графика начнем с данных по первому отделению. Плановое задание первого дня (25.08) выполнено на 90%. Согласно этого показателя на диаграмме проведем тонкую линию, которая занимает 90% всего дневного промежутка, или 4,5 деления. За второй день (26.08) план выполнен на 100%. Соответственно проведем тонкую линию, которая занимает весь дневной отрезок (100%). Плановое задание третьего дня (27.08) выполнено на 110%. Поэтому тонкая линия займет все пять частей дневного отрезка (100%), под линией в первой части проведем дополнительный отрезок, который равен половине первой части (10%). Эта дополнительная линия показывает перевыполнение плана за третий день на 10%. За четвертый день (28.08) план сева выполнен на 90%. На диаграмме проведем тонкую линию, которая занимает четыре части дня отрезке (80%) и половину последней пятой части, что составляет 10% планового задания.
Нанесем на график жирную линию. На ней одновременно с ее построением сделаем отметки о ежесуточное выполнение плана. За первый день ее длина будет равна длине тонкой линии (90%). За второй день план выполнен на 100%, а за первый и второй день суммарный процент составит 190% (90 + 100), то есть жирную линию за первый день доведем до 100%, а за второй день — до деления, что соответствует 90%. Жирная линия показывает, что за первые два дня план не выполнен на 10%, или на 20 га (400-380). За третий день план выполнен на 110%, а за три дня вместе суммарный процент составит 300% (90+100+110). Жирная линия займет три полных дневных отрезки. За четвертый день план сева выполнен на 90%. Соответственно суммарный процент за 4 дня составит 390% (90+100+110+90). Жирную линию по четвертый день продлим до отметки 90%.
Аналогично нанесем тонкую и жирную линии согласно данных отделения №2.
Анализ контрольно-планового графика показывает, что за первые четыре дня посевных работ отделения №1 не выполнило план на 10%, или на 20 га (800-780), а отделение №2 выполнило плановое задание на 100%.
В статистических карт относят картограммы и картодиаграммы. Для характеристики территориального размещения каких-либо социально-экономических явлений (плотность населения по регионам страны, распределение районов по уровню урожайности, продуктивности животных и т.д.) применяют картограммы.
Картограмма
представляет собой схематическую географическую карту, на которой разной краской или штриховкой показано распределение какого-либо явления в пределах изображаемой на карте территории.
Картограммы могут быть выполнены по материалам отдельного хозяйства (внутрихозяйственный разрез по бригадах, участках, полях севооборота), района (в разрезе хозяйств), области (в разрезе районов) и т.д.
Картограммы делятся на фоновые и точечные. в Фоновая картограмма
— вид картограммы, на которой штриховкой различной густоты или краской разной степени насыщенности показывают интенсивность какого-либо показателя в пределах территориальной единицы. Этот вид картограмм, как правило, используются для изображения средних и относительных показателей.
При построении фоновых картограмм предварительно осуществляется группировка данных по исследуемой признаку. При этом обычно выделяют небольшое количество групп (не более 5-6), а для наглядности интервалы закругляют. Для каждой группы устанавливаются своя штриховка (интенсивность ее должна возрастать по мере роста показателя). Группа хозяйств (район), попадающих в тот или иной интервал, обозначается на карте соответствующей штриховкой.
Точечная диаграмма
— вид картограммы, на которой уровень изучаемого показателя изображается с помощью точек. Точки изображают одну единицу совокупности или некоторое их количество, показывая на географической карте плотность или частоту появления определенного признака. Этот вид картограмм используется в основном для отображения размещения и концентрации абсолютных показателей — площади угодий, посевов, численности скота и т.д. При этом размер того или иного показателя по территориальных единицах характеризуется определенным количеством точек.
При построении точечной диаграммы все точки, нанесенные на карту, должны иметь одинаковый размер, так как каждая из них характеризует определенную величину. Точки легко подсчитать на карте. Необходимо продумать, какую величину будет означать каждая точка; если это очень малое значение, то нужно будет очень большое количество точек, и, наоборот, малое количество точек не даст впечатление густоты.
Построим точечную картограмму размещения посевов сахарной свеклы в южной подзоне области (рис. 12.12).
Рис. 12.12. Точечная картограмма размещения посевов сахарной свеклы по районам южной подзоны области
Точечная диаграмма построена по следующим данным о площади посева сахарной свеклы: в районе А — 3500 га, Б — 5000, В — 6000, Г — 8000 га. Масштаб выражено следующим соотношением: 1 точка равна 500 га. Соответственно количество точек по районам составит: А — 7 точек, Б — 10, В — 12, Г — 16 точек.
Общим недостатком картограмм является то, что в пределах выделенной территориальной участки колебания статистических показателей четко не улавливается. Кроме того, нецелесообразно изображать абсолютные величины, так как они относятся к разным по величине территорий.
Картодіаграма — это сочетание схематической географической карты с одной из рассмотренных выше диаграмм (круговой, квадратной, стовпчиковою и др.). Примером картодиаграмм есть географическая карта, на которой численность крупных городов изображена в виде кругов различной величины.
4. Классификация и правила построения
статистических графиков.
Статистические графики
различают по содержанию и способу
построения.
По способу построения различают:
столбиковые
ленточные
линейные
квадратные
круговые
секторные
диаграммы
При построении столбиковых
диаграмм используется прямоугольная
система координат. При этом каждое
значение изучаемого показателя
изображается в виде вертикального
столбика. По оси абсцисс размещается
основание столбиков. Их ширина может
быть произвольной, но обязательно
одинаковой для каждого столбика. Высота
столбиков (в соответствии с принятым
по оси ординат масштабом) должна строго
соответствовать изображаемым данным.
Количество столбиков определяется
числом изучаемых показаний (данных).
Расстояние между столбиками должно
быть одинаковым. У основания столбиков
дается название изучаемого показателя.
Разновидности столбиковых
диаграмм составляют так называ-емыеленточные
диаграммы
.В этих диаграммах основания
столбиков располагаются вертикально,
а масштабная шкала наносится на
горизонтальную ось. По своей форме
ленточная диаграмма представляет ряд
простирающихся по оси абсцисс полос
одинаковой ширины. Длина полос (лент)
соответствует значениям изображаемых
показателей. При построении ленточных
диаграмм соблюдаются те же требования,
что и при построении столбиковых графиков
(одинаковая ширина полос, начало
масштабной шкалы от нулевой отметки и
др.).
Для построения линейных
графиков применяют систему пря-моугольных
координат. Обычно по оси абсцисс
откладывается время (годы, месяцы),
а по оси ординат —
размеры изоб-ражаемых явлений или
процессов. На оси ординат наносят
мас-штабы. Особое внимание следует
обратить на их выбор, так как от этого
зависит общий вид графика. Обеспечение
равновесия, пропорциональности между
осями координат необходимо в гра-фике
в связи с тем, что нарушение равновесия
между осями ко-ординат дает неправильное
изображение развития явления.
Нередко на одном линейном графике
приводится несколько кри-вых, которые
дают сравнительную характеристику
динамики раз-личных показателей или
одного и того же показателя.
Однако на
одном графике не следует помещать более
трех-че-тырех кривых, так как большое
их количество неизбежно ослож-няет
чертеж и линейная диаграмма теряет
наглядность.
Для простого сравнения независимых
друг от друга показателей могут
использоваться диаграммы, принцип
построения кото-рых состоит в том,
что сравниваемые величины изображаются
в виде правильных геометрических фигур,
которые строятся так, чтобы площади их
относились между собой как количества,
этими фигурами изображаемые. Иными
словами,эти
диаграммы выражают вели-чину
изображаемого явления размером своей
площади.
Для получения диаграмм
рассматриваемого типа используют
разнообразные геометрические фигуры
— квадрат,
круг
. Известно, что площадь
квадрата равна квадрату его стороны, а
площадь круга определяется пропорционально
квадрату его
радиуса. Поэтому для построения диаграмм
необходимо сначала из сравниваемых
величин извлечь квадратный корень.
Затем на базе полученных результатов
определить сторону квадрата или радиус
круга соответственно принятому масштабу.
Широкое
применение в статистике находят
секторные
диаграммы
.
В этих диаграммах площадь окружности
принимается за величину всей изучаемой
статистической совокупности, а площади
отдельных секторов отображают удельный
вес (долю) ее составных частей. То есть
площадь круга в ней принимается за 100%,
а величины секторов пропорциональны
соотношению составных частей целого в
их общем итоге. Структуру
изображают в процентах, при этом один
процент равен 3,6 градуса.
графики
сравнения
графики
динамики
графики
структуры
графики
выполнения плана
графики
вариационных рядов
графики
взаимосвязанных показателей
При построении
графиков необходимо придерживаться
следующих правил:
Каждый график
должен иметь название, которое
располагается под ним. В названии в
краткой форме следует отразить
содержание, место и время явления.
Все графики
в тексте последовательно нумеруются
и именуются «рисунком».
Оси координат
должны быть названы и иметь единицы
измерения.
На оси ординат
и на числовой оси должны быть отложены
цифры в равном масштабе. Заканчиваться
числовая ось должна той величиной,
которая немного больше максимальной
величины в исходной совокупности.
Под рисунком
(где это необходимо) следует давать
пояснения условных изображений,
используемых на графике.
В текстовой
части работы график следует помещать
после ссылки на него в тексте на той же
странице или на следующей.
Каждый график
в текстовой части работы должен быть
прокомментирован.
Рассмотрим на конкретных примерах
каждый вид графиков и соответствующие
способы графического изображения
статистических данных.
5. Примеры практического использования
графиков.
5.1.Графики сравнения.
Диаграмма сравнения — показывает
соотношение признака статистической
совокупности. При построении графиков
сравнения могут использоваться
столбиковые (рис.1), ленточные (рис.2),
квадратные (рис.3) и круговые (рис.4)
диаграммы.
В качестве примера столбиковой
диаграммы возьмем данные по товарной
продукции различных предприятий за
отчетный период: предприятие №1 – 103099
млн.руб., предприятие №2 – 122282млн.руб.,
предприятие №3 – 89329 млн.руб., предприятие
№4 – 88716 млн.руб.
Как видно из графика, наибольшее
количество товарной продукции приходится
на долю предприятия №2, немного меньше
на предприятие №1, а наименьшее число
— на предприятия №3 и №4, у которых
число товарной продукции примерно
равно.
Для построения ленточной диаграммы
возьмем следующие данные: изменение
затрат на 1 руб. товарной продукции на
предприятии за отчетный год (в % к
предыдущему году) характеризуются
следующими значениями: предприятие №1
– (+0,26%), предприятие №2 – (-0,74%), предприятие
№3 – (-0,79%), предприятие №4 – (-0,24%),
предприятие №5 – (-0,5%).
Проанализировав график, можно
сказать, что лишь на предприятии №1
затраты на 1 руб. товарной продукции
увеличились (на 0.26%), на остальных же –
снизились, причем наибольшее снижение
произошло на предприятии №3 (-0.79%).
Квадратную и круговую диаграммы
целесообразно строить в том случае,
когда между сравниваемыми показателями
разница настолько велика, что установление
подходящего масштаба становится
затруднительным. Для нахождения стороны
квадрата, как уже говорилось ранее,
находят квадратный корень из соответствующей
величины. Тогда площадь квадратов
визуально будет характеризовать
соответствующую исходную величину.
Рассмотрим следующие данные:
выпуск отдельных видов продукции
предприятия характеризуется следующими
данными: продукция №1 – 4225 млн.руб.,
продукция №2 – 2500 млн.руб., продукция
№3 – 625 млн.руб. Тогда стороны квадратов
составят: №1 — √4225 = 65, №2 — √2500 = 50, №3 —
√625 = 25. Установим масштаб: 1см = 25 млн.руб.
Тогда получим следующую диаграмму.
Как видно из диаграммы, продукции
№1 произведено наибольшее количество,
продукции №2 – меньше, а продукции №3
произведено наименьшее количество.
Для построения круговой диаграммы
возьмем данные из предыдущего примера.
Для нахождения радиуса, возьмем корень
квадратный из соответствующих величин,
тогда имеем следующую диаграмму:
И, судя по диаграмме, наибольшее
количество произведено продукции №1,
затем- продукции №2 и меньше всего
произведено продукции №3.
5.2. Графики динамики.
Диаграмма динамики — показывает
изменение явления во времени. Построение
графиков динамики осуществляется, как
правило с помощью линейной (рис.5,
рис.5.1.) или столбиковой (рис.6) диаграмм.
Для построения линейной диаграммы
динамики возьмем следующие данные:
темпы роста производства продукции на
предприятии №1 (в % к декабрю предыдущего
года) составили: январь – 104%, февраль –
101%, март – 107,3%, апрель – 111,3%, май – 115%.
В данных условиях рекомендуется
строить шкалу без вертикального нуля,
т. е. шкала значений раз-рывается
недалеко от нулевой линии и на диаграмму
попадает лишь часть всего возможного
поля графика. Это не приводит к искажениям
в изображении динамики явления, и процесс
его из-менения рисуется диаграммой
более четко.
Можно сделать вывод, что за
рассматриваемый период наблюдается
ежемесячное увеличение выпуска продукции,
причем наиболее значительно выпуск
продукции увеличился в мае (на 15%), в то
время, как в феврале увеличение было
незначительно (1%).
Для примера изображения нескольких
показателей на линейной диаграмме, к
предыдущим данным добавим показатели
предприятия №2 темпы роста производства
продукции на котором (в % к декабрю
предыдущего года) составили: январь –
109%, февраль – 111%, март – 114,3%, апрель –
119,3%, май – 125%.
Как видно из данного графика за
рассматриваемый период наблюдается
ежемесячное увеличение выпуска продукции
на обоих предприятиях, причем максимального
увеличения выпуска продукции оба
предприятия достигли в мае, а меньше
всего рост выпуска продукции составил
на предприятии №1 в феврале, а на
предприятии №2 – в январе. Однако, в
общем, наиболее значительно выпуск
продукции увеличился на предприятии
№2.
В качестве примера столбиковой
диаграммы возьмем данные по сбору
сахарной свеклы: в 2002 году он составил
15.7 млн.тонн, в 2003 – 19.4 млн.тонн, в 2004 –
21.8 млн.тонн, 2005 – 21.4 млн.тонн и в 2006 –
30.9 млн.тонн.
Как видно из графика, меньше
всего сахарной свеклы за данный период
было собрано в 2002 году (15.7 млн.тонн),
тогда как наибольший сбор приходится
на 2006 год (30.9 млн.тонн). А в целом, сборы
сахарной свеклы с каждым годом
увеличивались, за исключение небольшого
спада в 2005 году.
5.3. Графики структуры.
Структурная диаграмма — позволяет
сопоставить статистические совокупности
по составу. При построении графиков
структуры могут использоваться секторные
(рис.7) и столбиковые (рис.8) диаграммы.
Площадь круга в секторной
диаграмме принимается за 100%, а величины
секторов пропорциональны процентному
соотношению составных частей целого в
их общем итоге.
Возьмем следующие данные: в цехе
работают рабочие 6 тарифных разрядов,
численность рабочих 1 разряда в общей
численности рабочих составляет 1,5%, 2
разряда – 6,1%, 3 разряда – 32%, 4 разряда –
34,5%, 5 разряда – 17,3% и 6 разряда – 8,6%.
Как видно из секторной диаграммы
наименьшую долю в общей численности
рабочих цеха составляют рабочие 1 разряда
– 1.5%, затем, в порядке возрастания идут
рабочие 2 и 6 разрядов, которые составляют
примерно равные доли, 6.1% и 8.6 % соответственно,
за ними- 5 разряд – 17.3% и самыми
многочисленными являются рабочие 3 и 4
разрядов, которые составляют соответственно
32% и 34.5%.
Для изображения графика структуры
с помощью столбиковой диаграммы
рассмотрим структуру занятых в экономике
по видам экономической деятельности.
В сельском хозяйстве (1)
занято — 10.8%, в добыче полезных ископаемых,
обрабатывающем производстве, производстве
и распределении электроэнергии, газа
и воды (2) – 21.3%, в строительстве (3) –
7.6%, в оптовой и розничной торговле (4) –
18.6%, транспорт и связь (5) – 8.1%,
государственное управление, обязательное
социальное обеспечение (6) – 6.6%, образование
и здравоохранение (7) – 15.8%, другие виды
деятельности (8) — 11.2%. Построим диаграмму.
Как видно, больше всего
людей занято во 2 категории — добыча
полезных ископаемых, производство и
распределение электроэнергии, газа и
воды (21.3%), а также в категории № 4 — оптовая
и розничная торговля (18.6%). Далее идет 7
категория — образование и здравоохранение
(15.8%). Затем следуют 8 и 1 категории – это
соответственно другие виды деятельности
(11.2%) и сельское хозяйство (10.8%). И наименьшая
доля занятых приходится на категории
5, 3 и 6 – это транспорт и связь, строительство
и государственное управление, обязательное
социальное обеспечение, соответственно,
доля каждой из этих категорий не превышает
9% к общей численности занятых.
5.4. Графики выполнения плана.
Показатели выполнения плана
можно изобразить графически в виде
линейной (рис.9) и столбиковой (рис.10)
диаграмм.
Для построения линейной диаграммы
возьмем следующие данные: выполнение
плана выпуска товарной продукции цехом
характеризуется следующими данными:
январь – 108%, февраль – 110%, март – 104%,
апрель – 108%, май – 112%.
По графику можно сделать следующий
вывод: более высокий процент перевыполнения
плана приходится на февраль отчетного
периода – 110%, тогда как в марте он
составил минимальное значение – 104%.
Выполнение плана выпуска товарной
продукции цехом характеризуется
следующими данными: I квартал – 110%, II
квартал – 107%, III квартал – 109%, IV
квартал – 108%, на основе этих данных
построим столбиковую диаграмму выполнения
плана.
Из графика видно, что наиболее
высокий процент перевыполнения плана
приходится на I квартал – 110%, тогда как
минимальным этот показатель был во II
квартале, когда он составил 107%.
5.5. Графики вариационных рядов.
Среди вариационных рядов
распределения выделяют дискретные
(когда отдельные варианты имеют
определенные конкретные значения) и
интервальные (когда варианты колеблются
в определенных пределах) ряды. Дискретные
вариационные ряды изображают в виде
так называемого полигона распределения
(Рис.11). Варианты откладываются на оси
абсцисс, частоты – на оси ординат. Точки
пересечения соединяются отрезками
прямой.
Возьмем данные по распределению
рабочих на предприятии согласно их
тарифным разрядам: 1 разряд – 10 человека,
2 разряд – 15, 3- 22, 4 – 109, 5- 96 и 6 разряд –
32 человека.
Как видно из графика, наибольшее
число составляют рабочие 4 и 5 разрядов
– 109 и 96 человек соответственно, тогда
как численность рабочих 6, 3 и 2 разрядов
не на много отличается друг от друга и
колеблется в районе 15 – 30 человек, и
самую маленькую группу составляют
рабочее 1 разряда – 10 человек.
Интервальные вариационные ряды
изображают в виде гистограммы (Рис.12).
При построении гистограммы интервальных
вариационных рядов с равными интервалами
на оси абсцисс откладывают границы
интервалов, на оси ординат – число
единиц совокупности, приходящееся на
данный интервал. Строят прямоугольники
с равными основаниями. При построении
гистограммы с неравными интервалами
на оси абсцисс так же откладывают границы
интервалов, на оси ординат – число
единиц совокупности, приходящееся на
единицу ширины интервала. Строят
прямоугольники
Пример. Распределение рабочих
по стажу лет на предприятии: 0-5 лет –
210 человек, 5-10 – 250 человек, 10-15 – 300
человек, 15-20 – 270 человек, 20 – 25 лет –
200 человек.
Как видно, наибольшее число
рабочих на предприятии – со стажем от
10 до 15 лет, тогда как наименьшая численность
приходится на людей со стажем 20 – 25 лет.
5.6. Графики взаимосвязанных показателей.
Графики взаимосвязанных
показателей, один из которых равен
произведению двух других можно построить
с помощью так называемых «знаков
Варзара». «Знак Варзара» строится вне
системы прямоугольных координат в виде
прямоугольника, основание которого
пропорционально одному показателю-сомножителю,
а высота — другому. Площадь
прямоугольника равна величине третьего
показателя, являющегося произведением
двух первых. Располагая рядом несколько
прямоугольников, относящихся к разным
показателям, можно сравнивать не только
размеры показателя — произведения, но
и значения показателей — сомножителей.
Пример. Имеются следующие данные
за 2001 год по всему миру: ВНП – 46403
млрд.долл., ВНП на душу населения – 7570
долл., средняя численность населения –
6.1298 млрд.чел. Взаимосвязь этих показателей
можно представить в виде:
Как видно из графика общее
производство ВНП в мире зависит от
средней численности населения и от
производства ВНП, приходящегося на душу
населения.
6. Заключение.
Проделав данную работу, мы
действительно убедились, что графики
делают статистический материал более
понятным и доступным даже неспециалистам,
упрощают восприятие данных. Однако
графические изображения не только
иллюстративны, они носят и аналитический
характер. С помощью графического
изображения возможны изучение
закономерностей развития явления,
установление существующих взаимосвязей.
В настоящее время графики широко
применяются в учетной и статистической
практике предприятий и учреждений, в
научно-исследовательской работе, в
производственно-хозяйственной
деятельности, в учебном процессе,
пропаганде и других областях. Трудно
переоценить их роль в жизни общества.Применение
графического
метода
в социально
—экономических
явлениях
Реферат >> Маркетинг
Дисциплине «Статистика» на тему: Применение
графического
метода
в социально
—экономических
явлениях
Преподаватель: Горемыкина Т.К. Студент: … ЗАКЛЮЧЕНИЕ Значение графического
метода
в анализе
и обобщении различных данных неоценимо. Графическое
изображение, …
Социально
—экономические
явления
и методы
исследования связей между ними
Реферат >> Экономика
… социально
— экономических
явлений
Основные статистические методы
выявления корреляционной связи Корреляционно-регрессионный анализ
. Уравнение парной регрессия: экономическая
…
Методы
экспертных оценок (1)
Реферат >> Маркетинг
Теоретические основы использования экспертных методов
в анализе
социально
—экономических
явлений
5 2. Метод
Дельфы 20 3. Практические… в словесной, математической, графической
или другой форме суждения… эксперимента. Известны случаи применения
метода
Дельфы, в…
Социально
-культурная деятельность (2)
Учебное пособие >> Социология
Средств и методов
научного анализа
социально
—экономических
, духовных… вероятных последствий их применения
, и положительных… анализом
социально
-культурной ситуации, когда с помощью объективно фиксируемых фактов и явлений
… языка экономного графического
знака, …
Численность населения
1.
Столбчатые диаграммы на рисунке 9 показывают численность населения крупнейших стран мира. Надпишите названия этих стран и определите место России по этому показателю.
(По данным на 2013г. Россия занимает 9 место; 5 – Бразилия (201 млн), 6 – Пакистан, 7 – Нигерия, 8 – Бангладеш)
1 – Китай; 2 – Индия; 3 – США; 4 – Индонезия; 5 – Пакистан; 6 – Нигерия; 7 – Бангладеш; 8 – Россия; 9 – Япония.
2.
Изменение численности населения страны зависит от двух основных процессов. Надпишите на схеме: а) их название; б) их слагающие.
3.
Постройте и проанализируйте график изменения естественного прироста населения России (на 1000 жителей) (рис. 10).
С 1960 года естественный прирост населения России был положительным, но снижался, а начиная с 2000-ых годов, ЕП стал отрицательным.
4.
Естественный прирост в разных районах страны неодинаков. Перечислите причины, влияющие на его величину.
5.
Назовите виды миграций населения, их причины и характер. Отразите это на схеме.
6.
Перечислите и проанализируйте основные направления миграций в России:
Городское и сельское население
1.
Постройте и проанализируйте диаграмму изменения соотношения городского и сельского населения России.
Доля городского населения России с 1913 по 2002 г. Постепенно увеличивалась и с каждым годом продолжала свой рост, а доля сельского населения напротив – уменьшалась.
Доля городского населения России, %
1913г. – 17
1940г. – 34
1950г. – 43
1960г. – 54
1970г. – 62
1980г. – 70
2010г. — 73
2.
Назовите причины изменения доли городского населения. В какие периоды развития страны городское население росло особенно быстро и почему?
Особенно быстро число городов (а, следовательно, и доля городского населения) возрастало в советский период. Это связано с активным развитием промышленности, возможностью найти работу, условиями труда и жизни.
3.
Дополните схему. Приведите примеры городов России с различными функциями.
4.
Сельские населенные пункты еще более разнообразны, нежели города. Они различаются:
а) по происхождению.
Назовите районы, в которых встречаются эти типы сельских пунктов:
хутор — Европейская часть России, кроме южных районов
село – центральные районы России
деревня – центральные районы России
станица — южные районы России
аул – районы Северного Кавказа
б) по функциям.
Дополните схему.
Национальный состав
1.
На рисунке 11 надпишите названия и численность трех крупнейших народов, проживающих в России.
2.
Приведите примеры народов России, принадлежащих к разным языковым семьям.
3.
Напишите названия крупнейших народов, проживающих в различных частях России.
Сравнение определенных показателей в разных сферах жизнедеятельности человека очень удобно проводить посредством диаграмм. Программа Excel предлагает достаточно разнообразные виды для сопоставления любых типов данных. Построим сравнительные диаграммы.
Для сравнения разных типов данных могут использоваться следующие виды диаграмм:
- Круговые.
Позволяют сопоставить доли отдельных элементов в общем значении. Такие диаграммы не совсем удобны для сравнения. - Линейчатые.
Позволяют сравнивать несколько значений в определенном диапазоне данных. - Гистограммы.
Вертикальные столбики для сопоставления значений в одном или нескольких диапазонах. - Графики.
Используются для иллюстрации тенденции изменения показателя. Если нужно сравнить несколько рядов данных, то в одной области строится несколько графиков. - Точечные.
Показывают взаимосвязь между двумя наборами данных. Представляют собой точки в области построения. - Лепестковые.
Отображают функциональную зависимость нескольких переменных. Данный тип диаграммы имеет вид криволинейного многоугольника с несколькими векторами, выходящими из центра. Векторные линии – оси координат по каждой категории.
Все эти примеры можно скачать в одном файле в конце статьи. Построение любого типа сравнительной диаграммы начинается с составления таблицы с исходными данными. Общие требования:
- Все ячейки исходного диапазона заполнены.
- Строки и столбцы имеют подписи, которые Excel автоматически генерирует в подписи осей координат.
Как программа воспринимает данные для столбчатых и линейчатых диаграмм и графиков:
- Каждая строка воспринимается Excel как отдельный ряд данных. На диаграмме это обособленная линия или столбик одного цвета.
- Каждое значение в строке – это точка на линейном графике или высота (длина) столбика.
- Заголовки строк – названия рядов данных (легенда).
- Заголовки столбцов – подписи одной из осей.
Как Excel интерпретирует данные для круговых диаграмм:
- Программе нужен только один ряд данных (один столбец со значениями).
- Каждое значение в столбце – это сектор круга.
- Заголовки строк – подписи секторов (легенда).
- Название столбца – наименование ряда данных.
В точечной диаграмме координаты каждой точки – значения из двух наборов данных. Из первого столбца – координата по оси Х. Из второго столбца – по оси Y.
Рассмотрим на примере, как строится лепестковая сравнительная диаграмма:
Изменения ВВП и инфляции показаны относительно одного центра.
Показатели уровня экономического развития страны
Используем диаграммы Excel для отображения некоторых сравнительных показателей экономического развития России. Уровень экономического развития определяют, в основном,
- уровень ВВП / НД на душу населения;
- отраслевая структура экспорта и импорта;
- уровень и качество жизни.
Ведущий показатель – ВВП.
Сравним с помощью гистограммы значения ВВП на душу населения в США, Великобритании, Японии, Канаде и России за последние три года:
Проанализируем диаграмму, сравнительные показатели экономического развития и сделаем все возможные выводы. Данные для построения взяты из Википедии (по списку МВФ). Сравнительные показатели экономического развития стран мало поменялись со времен Советского Союза. Вот диаграмма на основе значений 1991 года (ВВП на душу населения – цифра 1):
Сравним ВНД на душу населения в этих же странах в 2015 году. Используем линейчатую диаграмму:
Для иллюстрации уровня жизни населения возьмем индекс развития человеческого потенциала как наиболее широкий показатель, который можно представить в количественном виде. Помимо экономических данных, ИРЧП учитывает ожидаемую продолжительность жизни, уровень грамотности и образования. Сравним индексы по странам с помощью лепестковой диаграммы (данные взяты за 2014 год из Википедии):
Для сопоставления доли каждой отрасли в структуре экономики страны лучше использовать круговые диаграммы. Показатели по России за 2014 год:
Так как доля сельского хозяйства и других областей первичного сектора достаточно низкая, вторичные и третичные сектора (производство, услуги, образование) преобладают, Россию можно охарактеризовать как развитую страну. Но индекс человеческого развития немногим выше среднемирового значения (ИРЧП в 2014 году в РФ – 0,798, в том же 1985 – 0,811).
Обновлено: 14.04.2023
Более редкими, но не менее важными являются прямоугольные диаграммы, так называемые знаки Варзара [21, с. 447-449].
Знаки Варзара применяются для графического сравнения трех разноименных мультипликативно связанных показателей, т.е. таких, один из которых представляет собой произведение двух других, являющихся сомножителями.
Используя свойство прямоугольника, производный показатель, который является произведением двух других показателей-сомножителей, изображают его площадью; при этом основание прямоугольника пропорционально величине одного из показателей-сомножителей, а высота — второму показателю-сомножителю. Основание прямоугольника служит, как правило, для изображения объемных показателей (численности населения, выработанной энергии, объема вредных выбросов тепловых электростанций и т.д.), а его высота — для изображения качественных показателей (плотности населения, доли выработки электроэнергии определенным видом электростанций, процентного содержания вредных веществ и т.п.). При сравнении показателей, которые принадлежат к разным статистическим единицам — объектам или территориям, прямоугольники располагаются на горизонтальной базовой линии, или рядом друг с другом, или один на одном так, чтобы совмещались их нижние левые углы.
Пример знаков Варзара приведен на рис. 1.14 по данным табл. 1.7, в которой учтены данные табл. 1.5.
Таблица 1.7. Производство электроэнергии Украины, Германии, Франции в 1999 г.
Общая выработка электроэнергии,
Доля выработки АЭС от общего производства
электроэнергии в стране, %
Выработка электроэнергии АЭС, млрд кВт-ч
На графике показан общий объем производства электроэнергии, доля в ней атомной энергетики и объем производства электроэнергии атомными энергоблоками Украины, Германии, Франции в 1999 г.
Связь названных показателей имеет следующий вид: если за основание прямоугольника принять общую выработку электроэнергии млрд. кВт-ч, а за его высоту -% выработки АЭС от общего производства электроэнергии в стране, то площадь прямоугольника будет отображать общую выработку электроэнергии на АЭС, млрд. кВт-ч. Для построения прямоугольников по соответствующим показателям каждой страны установим масштаб для их основания 1 см — 200 млрд. кВт-ч, а для их высоты — 1 см = 20%. В соответствии с выбранным масштабом прямоугольник, который отображает общий объем производства электроэнергии АЭС Украины, млрд. кВт-ч, имеет основание и высоту, равные соответственно 0,77 и 2,17 см.
Рис. 1.14. Доля выработки электроэнергии на АЭС от общего производства электроэнергии в Украине, Германии, Франции в 1999 г.
Прямоугольники, изображенные на рис. 1.14, имеют разные площади. Они наглядно показывают, что в Германии и Франции в 1999 г. почти при равном объеме выработки электроэнергии доля АЭС в Германии в 2,5 раза меньше, чем во Франции. При сравнении Украины и Германии видно, что доля АЭС в Украине превышает аналогичный показатель Германии в 1,5 раза, в то время как общее производство электроэнергии в Украине в 3,5 раза меньше, чем в Германии.
Отметим, что недостатком знаков Варзара является то, что при незначительных отличиях показателей очень трудно оценить на глаз соотношения площадей прямоугольников, поэтому в таких случаях их использование становится нецелесообразным и малоэффективным.
Для графического изображения трех взаимосвязанных показателей, один из которых равен произведению двух других, российский статистик проф. В.Е. Варзар предложил использовать прямоугольную диаграмму, названную им «статистическим знаком». В настоящее время такие диаграммы часто называют знаком Варзара.
Знак Варзара строится в виде прямоугольника, основание которого пропорционально одному показателю-сомножителю, а высота — второму показателю сомножителю. Тогда произведение этих показателей, т.е. третий показатель, будет изображаться площадью прямоугольника.
Пример. Имеются следующие данные в 2001 г. по всему миру:
ВНП — 46403 млрд. долл.
ВНП на душу населения — 7570 долл.
Средняя численность населения — 6,1298 млрд. чел.
Нужно изобразить эти данные с помощью знака Варзара (рис. 3.1). Взаимосвязь этих показателей можно представить в виде:
Рис. 3.1 — Зависимость общего производства ВНП от производства ВНП на душу населения и средней численности населения мира в 2001 г.
Лица Чернова (Chernoff Faces) — это схема визуального представления мультивариативных данных в виде человеческого лица. Каждая часть лица: нос, глаза, рот — представляет собой значение определенной переменной, назначенной для этой части.
Каждое лицо — это массив из 18 элементов, каждый из которых принимает значение от 0 до 1. Значению соответствует внешний вид соответствующей части лица. Параметры исследуемых объектов приводятся к этим значениям. Экстремумы реальных данных будут приняты как 0 и 1. Все остальное — лежащим в этом промежутке. По полученному массиву конструируется лицо.
Вот какие параметры задаются у лица:
- 1. Размер глаза
- 2. Размер зрачка
- 3. Позиция зрачка
- 4. Наклон глаза
- 5. Горизонтальная позиция глаза
- 6. Вертикальная позиция глаза
- 7. Изгиб брови
- 8. Плотность брови
- 9. Горизонтальная позиция брови
- 10. Вертикальная позиция брови
- 11. Верхняя граница волос
- 12. Нижняя граница волос
- 13. Обвод лица
- 14. Темнота волос
- 15. Наклон штриховки волос
- 16. Нос
- 17. Размер рта
- 18. Изгиб рта
Сложность заключается в правильном сопоставлении исследуемых переменных с частями лица. При ошибке важные закономерности могут остаться незамеченными.
В 1981 году Бернард Флури и Ганс Ридвил улучшили концепцию и добавили лицам Чернова асимметрию. Таким образом, количество переменных увеличилось вдвое — до 36.
Флури приводит пример удачного анализа с помощью лиц. Он проанализировал 100 реальных и 100 поддельных банкнот по параметрам размера границ, отступов и диагоналей. Вот что получилось (рис. 4.1):
Рис. 4.1 — Пример графика «Лица Чернова»
Читайте также:
- Идет ли far cry 3 на xbox 360
- Utorrent отключить вкладку воспроизведение
- Где находятся звуковые файлы майнкрафт
- Digma 1025n не включается
- Видео проблема с компьютером бесплатно
Статистические графики по направлению использования характеризуются значительным разнообразием. их научная классификация предусматривает такие признаки, как общее назначение, виды, формы и типы основных элементов. Традиционно теория статистики рассматривает классификацию графиков по видам их поля. По этому принципу графические изображения разделяют на диаграммы, картограммы и картодиаграммы.
Диаграммы —
это условные изображения числовых величин и их соотношений с помощью геометрических знаков.
Картограммы
— изображение числовых величин и их соотношений с помощью нанесения условной штриховки или расцветки на карту — схему.
Картодиаграммы —
это сочетание диаграммы с картой — схемой. При построении диаграммы устанавливается определенный масштаб, то есть соотношение между размерами величин на графике и действительной величиной изображаемого явления в натуре.
Наиболее распространенным видом статистических графиков являются диаграммы. В зависимости от способа изображения статистических данных они могут быть в одном измерения, когда эти данные изображают в виде прямых линий или полос одинаковой ширины, и в двух измерениях (плоскости), на каких данных изображают с помощью площадей геометрических фигур (прямоугольников, квадратов, кругов.).
К первому виду диаграмм относятся линейные, столбиковые, ленточные и др.; ко второму — прямоугольные (квадратные, «Знак Варвара»), круговые, секторные, радиальные, фигурные.
Линейная диаграмма
отображает размер показателя в форме линий разной длины, которые образуются в результате соединения точек в координатном поле. Одним из видов линейных диаграмм является линейный график выполнения плана и учетно-плановый график (рис. 27, 28).
Рис. 27. Линейный график динамики поголовья лошадей в хозяйстве
Рис. 28. Учетно-плановый график выполнения предприятием плана производством продукции в течение месяца: а
— за декаду; б — нарастающим итогом
Применяют линейные диаграммы в основном для изучения развития явлений во времени.
Строению линейных диаграмм ставят следующие требования:
2) на оси ординат обязательно сказывается нулевая величина. В случаях, когда соблюдение этого правила связано со значительным уменьшением масштаба и ухудшением наглядности, следует сделать разрыв по всем ординатах (при этом нулевая линия сохраняется.)
3) отрезки на оси абсцисс должны соответствовать интервалам (для рядов динамики — периода времени);
4) нулевая линия должна резко отличаться от других параллельных линий;
5) при построении диаграммы с применением процентной шкалы нужно четко выделить линию, которая означает 100%;
6) кривая линия диаграммы должна резко отличаться от линий сетки
7) цифровые показатели размещают на графике таким образом, чтобы их можно было легко прочитать;

данные изображают в виде прямоугольников (столбиков) одинаковой ширины. Располагают их вертикально или горизонтально. Величину явлений характеризует высота столбика (рис. 29).
Рис. 29. Столбиковая диаграмма динамики валового производства продукции предприятием
Колонке диаграммы применяются: 1) при сравнении между собой различных явлений; 2) для изображения явлений во времени; 3) для отображения структуры явлений.
Рассмотрим основные правила построения столбиковых диаграмм:
1) ширина столбиков и расстояние между ними должны быть одинаковыми;
2) столбики располагают от меньшего к большему или наоборот (пространственная модель);
3) в основе столбиков проводится и выделяется базовая линия;
4) указывается название и цифровые данные столбиков;
5) на шкале должны быть деления, основные из которых обозначаются цифрами;
6) указывают единицу измерения.
Разновидностью столбиковой диаграммы является гистограмма, с помощью которой изображаются вариационные ряды распределения.
Ленточные диаграммы.
В отличие от столбиковых, при построении ленточных диаграмм прямоугольники, которыми изображают размер явлений, располагают не по вертикали, а по горизонтали (рис. 33). Требования, предъявляемые к построению этого вида диаграмм, аналогичные требованиям к столбиковых диаграмм.
Рис. 30. Ленточная диаграмма дневной заработной платы на предприятиях
Секторные диаграммы
представляют собой круг, разделенный на секторы, величины которых соответствуют (в пропорциях) изображаемым размерам явлений. Секторные диаграммы строят для отображения структуры явлений (рис. 31).
Рис. 31. Секторная диаграмма структуры посевных площадей сельскохозяйственного предприятия
Прямоугольные диаграммы.
Этот вид диаграмм величину исследуемых явлений изображает в виде площадей. Прямоугольные диаграммы применяют для изображения явлений, которые изменяются во времени, а также для сравнения различных величин в пространстве.
К прямоугольных диаграмм относятся квадратные диаграммы и «Знак Варвара».
Квадратные диаграммы
используют при сравнении абсолютных величин. Для определения стороны квадрата следует добыть квадратный корень из испытуемых (диаграмованих) величин. По данным таблицы 95 проводим соответствующие расчеты, приняв масштаб 30 = 1 см. Переводим в масштабные единицы показатели, полученные после извлечения квадратного корня из величин площадей сельскохозяйственных угодий: 81,2: 30 = 2,7 см; 76,8: 30 = 2,6 см; 72,8: 30 = 2,4 см полученные числовые значения принимаются величины стороны квадрата (рис.32).
Таблица 95
Выходные и расчетные данные для построения квадратных и круговых диаграмм
«Знак Варзара».
Используется для сравнения трех связанных между собой величин. Он представляет собой прямоугольник, в
котором длина отображает величину одного явления, ширина — другого, а площадь его характеризует произведение этих в двомасштабному сравнении: один масштаб — для основы прямоугольника, второй — для его высоты.
«Знаком Варзара» одновременно сравнивается, как уже упоминалось, три связанные между собой величины, то есть диаграмовий показатель является произведением двух других. Например, если площадь прямоугольника диаграммы иллюстрирует сбор, то одна его длина — посевную площадь, вторая — высота — урожайность. Этот вид диаграммы изображен на рисунке 33.
Рис. 32. Квадратная диаграмма размеров площадей сельскохозяйственных угодий предприятия
Рис.33. Прямоугольная диаграмма «Знак Варзара».
Круговые диаграммы своей площади отражают величину исследуемых явлений. Они основываются на использовании площади круга для иллюстрации сравниваемых однородных величин. При их построении учитывается, что площади кругов относятся между собой как квадраты их радиусов. Для определения радиуса круга необходимо добыть квадратный корень из диаграмовои величины; на этой основе наметить его в определенном масштабе и по его величине описать круг. На рисунке 34 показано круговую диаграмму по данным таблицы 95.
Радиальные диаграммы. Этот вид диаграмм применяется для графического изображения явлений, которые изменяются в замкнутые календарные сроки. В основу их построения положен полярную систему координат, где по оси абсцисс принимается круг, за все ординат — его радиусы.
В зависимости от того, какой изображается цикл диаграмованого явления -замкнутая или продолжаемое (с периода в период) — различают радиальные диаграммы замкнутые и спиральные.
Например, если весь цикл изменения изображаемого явления охватывает летний период, радиальную диаграмму строят по форме замкнутой.
Рис. 34. Круговая диаграмма размеров площадей сельскохозяйственных угодий
предприятия
Рис. 35. Радиальная диаграмма отработанных человеко-часов на предприятии в течение года
Если же изменение явления изучается в течение цикла диаграмованого периода (например, декабрь одного года соединяется с январем второго года и т.д.), ряд динамики изображается в виде сплошной кривой, которая визуально имеет вид спирали.
При построении радиальных диаграмм началом отсчета (полюсом) может быть центр окружность. Если за полюс принято центр круга, то радиальную диаграмму строят в такой последовательности: круг делят на столько частей, сколько периодов имеет диаграмований цикл (например, год — 12 мес.), И строят соответственно им радиусы (в данном случае — 12). Периоды размещают по часовой стрелке и на каждом радиусе в масштабном измерении откладывают отрезки (от центра круга), пропорциональны размерам явлений. Концы отрезков на радиусах соединяют, в результате чего образуется концентрическая ломаная линия. Пример замкнутой радиальной диаграммы с началом отсчета от центра окружности приведены на рис. 35.
Метод фигур — знаков.
Этот метод изображения диаграмованих явлений предусматривает замену геометрических фигур рисунками, которые соответствуют содержанию статистических данных (рис. 36). То есть величина показателя изображается с помощью фигур (символов, рисунков): например, поголовье лошадей — в виде силуэта лошади, производство автомобилей — в виде рисунка автомобиля и т.п. Преимущества такого вида диаграмм перед геометрическим — их наглядность и доходчивость. Символическое изображение делает диаграмму выразительной и привлекательной.
Рис. 36. Динамика книжных изданий по вопросам рыночной экономики в районной библиотеке
Метод фигур — знаков (так называемый венский) имеет свои особенности и характеризуется более насыщенным содержанием, имеет принципиальное значение и требует соблюдения определенных правил построения таких диаграмм, а именно:
1) символы должны быть понятными сами по себе и не требовать детальных объяснений. Как правило, они изображают контур или силуэт диаграмованих объектов;
2) обеспечивать однозначность трактовки;
3) однозначность темы;
4) групувальни признаки располагают вертикально, а показатели, которые характеризуют, — горизонтально;
5) изображения знаков — символов должно соответствовать принципам хорошего рисунке;
6) исключительными считаются излишняя детализация и украшения;
7) стандартизация знаков — символов. Компоновка диаграммы должно осуществляться стандартизированными знаками — символами, изготовленными в типографии и монтируемые методом аппликации. Существуют специальные образцы таких знаков;

Полулогарифмическая графики.
Этот вид статистического графика строится в системе координат. Числа, характеризующие диаграмоване явление, находятся в масштабе логарифмов. Логарифмы точек располагают на оси ординат, а дату явления (года) — на оси абсцисс (рис. 37).
Рис. 37. полулогарифмическая график динамики показателей дневной заработной платы на предприятии
Картограммы и картодиаграммы.
Картограммы представляют собой контурную географическую карту или схему, на которой штриховкой различной густоты, точками или красками различной степени насыщенности изображена сравнительная интенсивность какого-либо показателя в пределах каждой единицы нанесенного на карту территориального деления. На картограммами, как правило, изображают явления, характеризующиеся относительными или средними величинами (например, количество работающих пенсионеров в общей численности работающих по регионам, мелиорованисть земель в процентах к общей площади, средняя заработная плата на предприятиях по районам области и т.д.) .
По способу изображения диаграмованих явлений различают картограммы точечные и фоновые.
В первых уровень явления показывают с помощью точек, расположенных на контурной карте территориальной единицы. Для наглядности изображения плотности или частоты появления определенного признака точкой обозначают одну или несколько единиц совокупности.
На фоновых картограммами штриховкой различной густоты или краской различной степени насыщенности изображают интенсивность какого-либо показателя в пределах территориальной единицы. Один из случаев картограмм показано на рисунке 38.
Рис. 38. Картограмма плотности поголовья коров на 100 га сельскохозяйственных угодий в хозяйствах района
Если на контурную карту наносятся статистические данные в виде диаграмм, получают картодиаграму. Ярким ее примером является географическая карта, на которой численность населения крупных городов изображена в виде кругов различной величины.
Кроме рассмотренных способов графического изображения исследуемых явлений, существуют и другие. Практическое их использование при отражении динамики явлений, их структуры и взаимосвязей рассмотрено в предыдущих главах.
Большую группу графиков составляют структурные диаграммы.
Это такие диаграммы, в которых отдельные статистические совокупности сопоставляются по их структуре, характеризующейся соотношением разных параметров совокупности или ее отдельных частей.
Широко распространенный метод графического изображения структуры статистических данных заключается в составлении структурных круговых или секторных диаграмм. Секторные диаграммы
удобно строить следующим образом: всю величину явления принимают за 100%, рассчитывают доли отдельных частей в процентах. Круг разбивают на секторы пропорционально частям изображаемого целого. Таким образом, на 1% приходится 3,6°. Для получения центральных углов секторов, изображающих доли частей целого, необходимо их процентное выражение умножить на 3,6°. Секторные диаграммы позволяют не только разделить целое па части, но и сгруппировать отдельные части, давая как бы комбинированную группировку долей по двум признакам.
Пример. Рассмотрим построение секторной диаграммы по данным, приведенным в табл. 4.3.
Таблица 4.3/
Данные об охвате населения телевизионным вещанием на конец 2010 г. в N-м регионе
Построение секторной диаграммы начинается с определения центральных углов секторов.
Для этого процентное выражение отдельных частей совокупности но каждой категории умножим на 3,6°. Три и более телевизионные программы — 131,7°; две — 207°; одна — 14,8°; ни одной — 7,6°. По найденным значениям углов круг делится на соответствующие сектора (рис. 4.11).
Рис. 4.11.
Другим видом структурных статистических диаграмм являются полосовые диаграммы удельных весов,
отражающие структуры сравниваемых совокупностей по процентному соотношению в них отдельных частей, выделяемых потому или иному количественному или атрибутивному признаку. Эти диаграммы получены путем преобразования простой полосовой диаграммы с подразделенными полосами. Полосовые диаграммы удельных весов могут вскрыть существенные особенности многих изучаемых экономических явлений.
Пример.
Необходимо изобразить графически данные, приведенные в табл. 4.4.
Таблица 4.4/
Данные, характеризующие структуру потребительских расходов населения в N-м регионе за период 2009-2010 гг., %
Рис. 4.12.
Значительными преимуществами полосовых структурных диаграмм по сравнению с другими видами являются их большая емкость, возможность отразить на небольшом пространстве большой объем полезной информации. Секторные же диаграммы выглядят убедительно при существенных различиях сравниваемых структур, а при небольших различиях они могут быть недостаточно выразительны.
Диаграммы динамики
Для изображения и внесения суждений о развитии явления во времени строят диаграммы динамики.
Для наглядного изображения динамики явлений используют многие диаграммы: столбиковые, ленточные, квадратные, круговые, линейные, радиальные и др. Выбор вида диаграмм зависит в основном от особенностей исходных данных, от цели исследования. Например, если имеется ряд динамики с неравно отстоящими уровнями во времени (1913, 1940, 1950, 1980, 2000, 2010 гг.), то часто для наглядности используют столбиковые, квадратные или круговые диаграммы. Они зрительно впечатляют, хорошо запоминаются, но не годны для изображения большого числа уровней, так как громоздки. Если число уровней в ряду динамики велико, то целесообразно применять линейные диаграммы, которые воспроизводят непрерывность процесса развития в виде непрерывной ломаной линии.
Для построения линейных диаграмм
используют систему прямоугольных координат. Обычно но оси абсцисс откладывают время (годы, месяцы и т.д.), а по оси ординат наносят масштабы для отображения явлений или процессов. Особое внимание следует обратить на масштаб осей координат, поскольку от этого зависит общий вид графика. Обеспечение равновесия, пропорциональности между осями координат необходимо в диаграмме, так как нарушение равновесия дает неправильное изображение развития явления. Если масштаб для шкалы на оси абсцисс очень растянут по сравнению с масштабом на оси ординат, то колебания в динамике явлений мало выделяются, и наоборот, преувеличение масштаба по оси ординат по сравнению с масштабом на оси абсцисс дает резкие колебания. Если в ряду динамики данные за некоторые годы отсутствуют, это должно быть учтено при построении графика. Равным периодам времени и размерам уровня должны соответствовать равные отрезки масштабной шкалы.
Пример.
Рассмотрим построение линейной диаграммы на основании следующих данных по динамике производства газетной бумаги в регионе за период 2001-2010 гг.:
Год………….2001 2002 2003 2004 2005 2006 2007 2008 2009 2010
Производство,
Млн.т………..237 179 189 158 186 192 172 191 210 211
Изображение динамики производства газетной бумаги на координатной сетке с неразрывной шкалой значений, начинающихся от нуля, вряд ли целесообразно, так как 2/3 ноля диаграммы остается неиспользованным, и это ничего не даст для выразительности изображения. Поэтому в данных условиях рекомендуется строить шкалу без вертикального нуля, т.е. шкала значений разрывается недалеко от нулевой линии, и на диаграмму попадает лишь часть возможного поля графика. Это не приводит к искажениям в изображении динамики изучаемого процесса, и его изменения показываются диаграммой более четко (рис. 4.13).
Рис. 4.13.
Нередко на одном линейном графике приводится несколько кривых, которые дают сравнительную характеристику динамики различных показателей или одного и того же показателя в разных странах. Примером графического изображения сразу нескольких показателей служит рис. 4.14.
Рис. 4.14.
Линейные диаграммы с равномерной шкалой имеют недостаток, снижающий их познавательную ценность. Этот недостаток заключается в том, что равномерная шкала позволяет измерять и сравнивать только отраженные на диаграмме абсолютные приросты или уменьшения показателен на протяжении исследуемого периода. Однако при изучении динамики важно знать и относительные изменения исследуемых показателей по сравнению с достигнутым уровнем или темпы их изменения.
Именно относительные изменения экономических показателей в динамике искажаются при изображении их на координатной диаграмме с равномерной вертикальной шкалой. Кроме того, в обычных координатах теряет всякую наглядность и даже становится невозможным изображение рядов динамики с резко изменяющимися уровнями, которые обычно имеют место в динамических рядах за длительный период времени.
В этих случаях следует отказаться от равномерной шкалы и положить в основу графика полулогарифмическую систему. Полулогарифмической системой называется система, в которой на одной оси нанесен линейный масштаб, а на другой — логарифмический. В данном случае логарифмический масштаб наносят на ось ординат, а на оси абсцисс располагают равномерную шкалу для отсчета времени по принятым интервалам (годам, кварталам, месяцам, дням и т.д.). Техника построения логарифмической шкалы следующая: найти логарифмы исходных чисел; построить ординату и разделить на несколько равных частей. Затем нанести на ординату (или равную ей параллельную линию) отрезки, пропорциональные абсолютным приростам этих логарифмов. Далее записать соответствующие логарифмы чисел и их антилогарифмы, например 0″.000; 0,3010; 0,4771; 0,6021; …; 1,000, что дает 1, 2,3,4,10. Полученные антилогарифмы окончательно дают вид искомой шкалы на ординате.
Пример
. Допустим, нужно изобразить на графике динамику производства угля в регионе за 1980-2010 гг., за эти годы его рост составил 9,1 раза. С этой целью найдем логарифмы для каждого уровня ряда (табл. 4.5).
Найдя минимальное и максимальное значения логарифмов производства угля, построим масштаб с таким расчетом, чтобы все данные разместились на графике. В соответствии с масштабом найдем соответствующие точки, которые соединим прямыми линиями. В результате получим график (рис. 4.15) с использованием логарифмического масштаба на оси ординат.
Таблица 4.5
Динамика производства угля в регионе за период 1980-2010 гг., млн т
|
Производство К, |
||
Рис. 4.15.
К диаграммам динамики относятся и радиальные диаграммы, построенные в полярных координатах и предназначенные для отражения процессов, ритмически повторяющихся во времени. Чаще всего эти диаграммы применяют для иллюстрации сезонных колебаний, и в этом отношении они имеют преимущество перед статистическими кривыми. Радиальные диаграммы подразделяют на два вида: замкнутые и спиральные. Эти два вида диаграмм отличаются друг от друга по технике построения; все зависит от того, что взято в качестве базы отсчета — центр круга или окружность.
Замкнутые диаграммы
отражают весь внутригодовой цикл динамики одного года. Их построение сводится к следующему: строят круг, среднемесячный показатель приравнивают к радиусу этого круга, затем весь круг делят на 12 равных секторов посредством проведения радиусов, которые изображают в виде топких линий. Каждый радиус изображает месяц, причем расположение месяцев аналогично циферблату часов. На каждом радиусе делают отметку в определенном месте согласно масштабу, исходя из данных на соответствующий месяц. Если данные превышают среднегодовой уровень, то отметку ставят вне окружности па продолжении радиуса. Затем отметки различных месяцев соединяют отрезками.
Пример. Необходимо изобразить с помощью замкнутой диаграммы динамику индексов потребительских цен на все товары и услуги в одном из регионов по месяцам 2010 г. по следующим данным, % к декабрю прошлого года:
Январь……………………………………………………..101,68
Февраль…………………………………………………..102,81
Март………………………………………………………..103,42
Апрель…………………………………………………….104,01
Май………………………………………………………….104,67
Июнь……………………………………………………….105,66
Июль……………………………………………………….106,58
Август……………………………………………………..106,68
Сентябрь…………………………………………………107,52
Октябрь…………………………………………………..109,28
Ноябрь…………………………………………………….110,62
Декабрь……………………………………………………111,87
Среднемесячный индекс равен 106,2
Построим круг радиусом, равным среднемесячному показателю. 11а горизонтальном диаметре построим шкалу, взяв длину радиуса, равную 4 см. Следовательно, 1 см = 106,2/4 = 26,6% (рис. 4.16).
Рис. 4.16.
Если в качестве базы отсчета берется окружность, такого рода диаграммы называют спиральными. Спиральные диаграммы
отличаются от замкнутых тем, что в них декабрь одного года соединяется не с январем данного же года, а с январем следующего года. Это дает возможность изобразить весь динамический ряд за несколько лет в виде одной кривой. Особенно наглядна такая диаграмма тогда, когда наряду с сезонным ритмом ряд обнаруживает неуклонный рост из года в год.
Для отображения зависимости одного показателя от другого используют диаграмму взаимосвязи.
Один показатель принимают за X,
а другой за У
(т.е. функцию от X),
затем строят прямоугольную систему координат с масштабами для показателей, в которой формируется рисунок.
С повышением стоимости основных производственных фондов происходит увеличение затрат на реализацию продукции. Данная зависимость этих показателей может быть выражена линейной связью (рис. 4.17).
Рис. 4.17.
Диаграммы взаимосвязи имеют большое значение на практике, так как множество различных показателей связаны между собой либо прямой, либо обратной формой связи. Они могут использоваться также для отображения различных циклических процессов (например, инфляционной спирали), взаимно накладывающихся явлений и т.п.
Дата:
9 января 2017
Категория:
Задумываясь над тем, в, я предлагаю разобраться, какие бывают графики в Эксель и как правильно их применять. От правильного выбора типа диаграммы зависит корректность подачи графической информации, её наглядность и доступность. А чтобы сделать выбор – нужно продумать, какую цель преследует диаграмма и какой тип данных будет на ней изображен.
Например, вы можете строить графики изменения величин во времени, гистограммы для сравнения каких-то показателей, круговые диаграммы долевого участия в общем показателе и многое другое. Для такой визуализации нужно подобрать оптимальный вид диаграммы и получить максимальный эффект от возможностей Microsoft Excel. Давайте разбираться какие графики позволяет строить нам программа.
Гистограмма
Гистограмма – это вид диаграммы, который позволяет отобразить и, главное, сравнить некоторые дискретные данные. Выглядит она, как набор столбиков, характеризующих значение показателя для определенной категории. В примерах я буду приводить диаграммы продаж четырех работников за 6 лет (по годам). Гистограммы бывают таких типов:
- Гистограмма с группировкой
– отображает значения из рядов данных, располагая их рядом для удобного сравнения.
- – располагает данные не рядом а в одном столбце. Это позволяет не только сравнить отдельные ряды данных, но и суммарный показатель в целом. В нашем примере мы сможем сравнить продажи по продавцам и суммарные продажи по годам.
- – подобна предыдущей, но здесь значения нормированы, т.е. приведены к процентам. Суммарный показатель всегда – 100%. Так проще оценить долевое участие каждого из рядов (в нашем случае – продавцов) в совокупном результате.
- Трехмерная гистограмма с группировкой
– то же, что и в п.1, только добавлен эффект объема. Впрочем, график все равно остается двумерным, просто добавляется визуальный эффект. Такие же варианты есть для гистограммы с накоплением и для нормированной.
- – это диаграмма, построенная уже в трех измерениях. Хотя выглядит это эффектно, на практике не всегда наглядно и удобно, поэтому применяйте её осторожно, когда это действительно оправдано.
Графики в Excel
Графики лучше всего подходят для отображения непрерывных процессов или дискретных с высокой частотой дискретизации, например, ежедневных продаж, изменения температуры и др. Графики делятся на такие виды:
- График
– показывает изменение ряда с течением времени. Самый простой и наглядный вариант
- График с накоплением
– здесь каждый следующий ряд «ложится» на предыдущий. На диаграмме с рисунка продажи Иванова (первый ряд) первого числа составили 22,2 у.е., а Зимы (второй ряд) – 32,69. На графике точка продажи Иванова – 22,2 у.е., а Зимы – 22,20 + 32,69 = 54,9 у.е. То есть, началом отсчета для графика второго ряда будет не ось X, а график предыдущего ряда. Такая визуализация позволяет оценить долевой вклад каждого ряда в суммарном прогрессе с течением времени.
- Нормированный график с накоплением.
Здесь последний накопительный ряд принят за базис, 100%. Остальные графики показаны в процентном отношении к нему. Соотношение значений в суммарном прогрессе отслеживается очень хорошо, но нельзя оценить, как изменяется сумма величин.
- Графики с маркерами
это группа графиков, дублирующая предыдущие три, но каждая точка такого графика будет обозначена маркером, внешний вид которого можно настраивать.
- очень похож на обычный (из п.1), но изображается не линиями, а лентами, имитируя объем. Такое представление выглядит эффектно, но редко оправдано на практике.
Линейчатая диаграмма практически не отличается от гистограммы, только столбцы в ней располагаются не вдоль горизонтальной оси, а вдоль вертикальной. Типы диаграммы те же, что и у гистограммы, за исключением объемного варианта, он недоступен. Я применяю линейчатую диаграмму, когда названия категорий представляют собой достаточно длинный текст, и отобразить его под горизонтальной осью — проблематично.
Круговые диаграммы в Эксель
Круговые диаграммы изображаются в виде круга с сегментами, по размерам которых легко определить соотношение величин. В нашем примере рассмотрим состав одной буханки пшеничного хлеба. У круговой диаграммы есть такие разновидности:
- – самый простой вариант – круг, разделенный на секторы.
- – похожа на предыдущую, но кажется объемной. Эффектно смотрится и может придать диаграмме современного, продуманного вида.
- – отображает на дополнительной диаграмме те величины, которые слишком мало, чтобы их разглядеть.
- – то же, что и в предыдущем примере, только вспомогательная диаграмма не круговая, а линейчатая.
- – схожа с обычной круговой, но выполнена в форме кольца, а не круга. Выглядит менее громоздкой и достаточно практичной.
Точечные диаграммы
Такие диаграммы подходят, например, для визуализации результатов научного эксперимента или статистической выборки. Здесь по обоим осям откладываются значения, а на диаграмме точками отображается соотношение между ними. У этого вида диаграмм есть такие разновидности:
- Точечная
– набор точек на пересечении двух величин. На рисунке я представил пример такого набора с линией тренда, характеризующей усредненное соотношение для всей совокупности данных.
- Точечная с гладкими кривыми (с маркерами и без)
– здесь точки данных соединены сглаженными линиям для отображения тенденции. Сглаживание применяется, когда речь идет о непрерывных данных
- Точечная с прямыми отрезками (с маркерами и без)
– то же, что и в прошлом пункте, но линии не сглажены.
- Пузырьковая диаграмма (плоская или объемная)
– отображает ту же зависимость, что и точечная, но может нести в себе дополнительный ряд данных, который будет влиять на размер каждого пузырька. То есть, такая диаграмма отображает не два параметра, а три.
Диаграммы с областями в Эксель
Диаграммы с областями – это обычные графики, только области от оси до графика залиты цветом. Это может добавлять визуальной привлекательности диаграмме, а может, наоборот, мешать. По аналогии с графиками и гистограммами, есть такие типы диаграмм с областями:
- : график с залитыми участками от оси до линии графика.
- Диаграмма с областями с накоплением
– график последующего ряда «ложится» на график предыдущего. Удобно для оценки общего прогресса и сравнения рядов данных между собой.
- Нормированная диаграмма с накоплением
– данные приведены к процентному соотношению, где базис – накопленный уровень последнего ряда. Очень удобно для визуального сопоставления вклада каждого ряда в общий прогресс.
Все перечисленные виды диаграмм доступны как двумерными, так и объемными.
Лепестковые диаграммы
Лепестковая диаграмма имеет столько осей (выстроенных по кругу), сколько задано категорий. А значение ряда для данной категории откладывается на этой оси. Таким образом, у нас получается замкнутая линия, похожая на петлю и демонстрирующая тенденции по категориям.
Есть три вида этих диаграмм:
- – только линии на осях, как на рисунке выше.
- Лепестковая с маркерами
– в каждой точке на оси изображается маркер. - Заполненная лепестковая
– фигуры, очерченные диаграммами, заполняются цветом.
Практическая ценность этого вида диаграмм ограничена, но в некоторых случаях она может выглядеть интереснее гистограммы, например. Проверяйте опытным путем.
Поверхностные диаграммы
Это еще один способ, кроме пузырьковых, отобразить три параметра на одном рисунке. Такие диаграммы дают возможность реализовать трехмерные графики, где это уместно и полезно. Поверхностные диаграммы бывают:
- Поверхность
– трехмерная диаграмма, напоминающая рельеф. Может быть обычной, закрашенной, либо «проволочной», где отображается, как будто, каркас рельефа. Целесообразность построения проверяем только экспериментально, ведь некоторые участки могут перекрывать другие данные. Если этого не происходит, поверхность может быть очень полезной.
- Контурная
– отображает вид сверху и напоминает топографическую карту с отображением уровней. Как и у поверхности, можно сделать залитую диаграмму или проволочную. Мне ни разу не приходилось применять в практике этот вид диаграмм, но очевидно, кому-то он может быть полезен.
Биржевые диаграммы
Название диаграммы говорит само за себя, она призвана визуализировать изменение биржевых котировок, облегчая работу аналитикам. Хотя, многие умельцы научились применять их и для других статистических данных. Всего разработчики предлагают четыре вида диаграмм, отображающие перечисленные биржевые показатели:
- Максимальная цена, минимальная цена, средняя цена
. Минимальная и максимальная цены будут отображены прямой линией, средняя – меткой.
- Курс открытия, максимальная цена, минимальная цена, курс закрытия.
Максимальная и минимальная цены, так же, отображаются линией, а курсы открытия и закрытия – цилиндром. Если цилиндр залит – курс закрытия ниже открытия.
- Объем продаж, максимальная цена, минимальная цена, курс закрытия.
Здесь добавляется еще объем продаж в виде залитого столбика.
- Объем продаж, курс открытия, максимальная цена, минимальная цена, курс закрытия.
Самый детальный график, в нем отображаются сразу все перечисленные выше показатели.
Особый вид диаграмм составляют комбинированные. Они включают в себя визуализации нескольких видов, благодаря чему достигается наилучший эффект от применения диаграмм и графиков в Microsoft Excel.
Пожалуй, это и все диаграммы, которые мы рассмотрели на примере Microsoft Excel 2013. В других редакциях программы этот список может отличаться, но отличия небольшие.
На этом я статью завершаю, а следующий пост будет посвящен . Жду Вас на страницах своего блога!
— В некотором смысле, показывая человеку круговую диаграмму, вы можете оскорбить его интеллектуальные способности
К. Г. Карстен, «Диаграммы и графики» (1923)
Первые негативные выпады в сторону круговых (секторных) диаграмм начались более 100 лет назад. В 1914 году инженер и сторонник визуализации, Виллард Бринтон (Willard Brinton), опубликовал работу под названием «Графические методы», которую принято считать первой книгой о правильной визуализации данных для широкой аудитории. Он был Эдвардом Тафтом своего времени: пропагандистом наглядного обмена информацией и памфлетистом плохих форм.
Значительная часть книги Бринтона предостерегает читателей от использования круговых диаграмм (pie chart). В самой первой главе, описывая «составные элементы», автор объясняет:
«Круговая диаграмма, вероятно, используется гораздо чаще, чем любая другая форма, для демонстрации пропорций элементов. Однако, круг с секторами — это далеко не оптимальная форма, поскольку он и близко не обладает такой же выразительностью, как столбиковые диаграммы. Недостатком секторного представления является невозможность размещения частей таким образом, чтобы их можно было легко сравнить или просуммировать».
С тех пор, как Бринтон написал эти слова, многие статистики и эксперты в области визуализации выступили против секторных диаграмм и настаивали на использовании различных альтернатив. Хотя изначально в своих суждениях критики апеллировали к логике, за последние 40 лет они отыскали экспериментальные доказательства, которые указывают на неполноценность таких диаграмм в плане точности передачи информации.
Тем не менее, круговые диаграммы остаются весьма востребованными. Крупные издательства и медиа-корпорации, например, The Walt Street Journal и Target Corporation, до сих пор используют их, чтобы отображать свои данные. Кроме того, некоторые веб-ресурсы также задействуют этот довольно спорный графический метод.
Чтобы понять суть проблемы, вернемся к ее истокам и рассмотрим аргументы сторонников и критиков секторных диаграмм.
История возникновения
Отцом современной визуализации данных можно по праву назвать Уильяма Плейфэра (William Playfair). Он родился в Шотландии в 1759 году и вел очень увлекательный образ жизни. Плейфэр принимал участие во взятии Бастилии, внес свой вклад в развитие телеграфа и, конечно же, опубликовал первую круговую диаграмму. Он также является создателем столбиковой и линейной диаграмм.
Круговая диаграмма является одной из многих инноваций шотландского «мошенника» Уильяма Плейфэра
На рубеже XVIII века, использование иллюстраций в серьезной интеллектуальной литературе считалось слишком детским подходом. Но, как свободно мыслящего человека, Плейфэра это не остановило.
В 1801 году он опубликовал «Статистический Бревиарий» (Statistical Breviary) — книгу, посвященную демографическим и экономическим данным европейских государств. В этой работе, которая содержала первую круговую диаграмму, Плейфэр аргументирует ценность использования графических элементов: «Создание визуального образа для наших глаз при сохранении всех пропорций и размеров — это наиболее оптимальный и читабельный способ выражения определенной идеи».
Секторная диаграмма, опубликованная на страницах «Статистического Бревиария», показана ниже. На ней изображены доли земельных участков Турецкой Империи, расположенных в Азии, Африке и Европе тех времен. Этот рисунок принято считать первой круговой диаграммой, где идея о целом была представлена в виде круга, а для различия секторов использовался цвет.
Распределение площади Турецкой Империи является первой известной секторной диаграммой
Но как Плейфэр пришел к такой идее?
Некоторые эксперты считают, что секторная диаграмма обязана своим появлением кругам, которые использовались для представления понятий в философии и математике. Брат Плейфэра, Джон, был уважаемым математиком и ученым. Вполне вероятно, что Уильям увидел разделенный круг, изображающий составные части категории, в одной из его работ. Математики и философы применяют этот тип иллюстрации еще с XIV века.
Пример использования круга для представления составных частей в XIV веке
Секторная диаграмма, впрочем как и другие инновации Плейфэра, обрела широкое распространение не сразу. В то время Уильяма считали «мошенником» и нечистым на руку бизнесменом, поэтому, как правило, его идеи игнорировались.
Так продолжалось до 1850-х годов, пока круговая диаграмма не обрела еще одного важного сторонника — французского инженера Чарльза Джозефа-Минарда (Charles Joseph-Minard), который подтвердил эффективность данного метода. Минард был «пионером» статистических графиков и, по мнению многих, создателем самых гениальных методик визуализации данных.
Будучи в первую очередь картографом, Минард дополнил круговыми диаграммами свои карты. На размещенном ниже примере он изобразил в виде таких диаграмм количество мяса, поставляемого в парижские магазины из различных регионов Франции. Размер круга представляет общее количество мяса, и каждый круг разделен пропорционально на доли баранины, телятины и говядины:
Карта, созданная пионером визуализации данных Чарльзом Джозефом-Минардом в 1858 году, с использованием круговых диаграмм
Изобретение секторной диаграммы иногда ошибочно приписывают легендарной британской медсестре и общественному деятелю Флоренс Найтингейл (Florence Nightingale). В 1858 году она распределила причины смертности британских солдат в Крымской войне по месяцам. Флоренс использовала эту диаграмму, чтобы убедить правительство Великобритании улучшить санитарные условия и питание в военных лагерях.
Несмотря на то, что ее чертеж смотрится очень мощно и убедительно, на самом деле он не является круговой диаграммой. Это так называемая областная диаграмма (polar-area chart), в которой круг делится на ровные части, но их длина зависит от величины переменной:
Областная диаграмма Флоренс Найтингейл, которую часто путают с круговой диаграммой
Критика в адрес круговой диаграммы
Первые сто лет истории круговой диаграммы были мирным временем, но буря уже надвигалась. Слова Бринтона, которые мы цитировали в начале поста, являются самым ранним примером критики в сторону данной инновации, но к 1920 году в мире появилось еще больше литературы, резко осуждающий этот метод.
В 1923 году американский экономист Карл Густав Карстен (Karl G. Karsten) согласился с предупреждением Бринтона касательно секторных диаграмм. Заявления Карстена в его книге «Диаграммы и графики» (Charts and Graphs) удивительно похожи на те, что мы слышим сегодня:
«У секторной диаграммы очень много недостатков. Во-первых, человеческий глаз не может нормально сравнить длину дуги окружности, поскольку секторы направлены в различные стороны. Во-вторых, человеческое зрение не приспособлено к сравнению углов в принципе…
Наконец, невозможно эффективно оценить величину областей, особенно если они представлены в виде неравномерных секторов в круге. Не существует способа, который бы позволял сравнивать компоненты круглой фигуры так же быстро и точно, как части прямой линии или столбца»
Однако, хотя подобные выпады звучали все чаще, статистик Вальтер Кросби Иллс (Walter Crosby Eells) отметил, что многие критические замечания основываются «исключительно на личных предпочтениях». Иллс и другие решили проверить это предположение.
Ранние исследования в этой области были направлены на то, чтобы выяснить, пропорции какой разделенной фигуры — круга или столбца — люди определяют более точно. В ходе эксперимента 1927 года, проведенного Фредериком Крокстоном (Frederick Croxton) и Роем Страйкером (Roy Stryker), ученые попросили более 800 испытуемых угадать пропорции каждого компонента различных сегментированных фигур:
В данном случае пропорции практически идентичны.
Исследователи рассчитали среднюю погрешность предположений респондентов, но в этом эксперименте и многих других экспериментах ученым так и не удалось отыскать серьезных доводов, дискредитирующих круговые диаграммы. Сторонники данного типа визуализации до сих пор используют результаты проведенных в 1927 году исследований, чтобы аргументировать свою точку зрения.
Тем не менее, как отметил ученый Майкл Макдональд-Росс (Michael Macdonald-Ross) в обширном обзоре «Конфронтации круга и столбца», эти первоначальные эксперименты на самом деле не отображают реальное положение вещей. Несмотря на то, что сегментированный столбец в то время считался основной альтернативой кругу, сегодня специалисты практически всегда предлагают использовать гистограммы или точечные диаграммы.
Основной и, возможно, наиболее мощный удар по секторным диаграммам пришелся на 1980-е года, благодаря усилиям статистика Уильяма Кливленда (William Cleveland). Кливленд является автором новаторской книги «Элементы графических данных», в результате которой, как многие считают, визуализация данных обрела научную основу. Его работа не только описывает базовые «задачи восприятия», решаемые при просмотре диаграммы (например, суждения касаемо длины или площади), но и утверждает, с какими из них люди справляются лучше всего.
В эксперименте, проведенном в 1984 году, Кливленд и его друг, исследователь Роберт МакГилл (Robet McGill) тестировали круговую диаграмму. Вместо того, чтобы сравнивать ее с сегментированным столбцом, они сопоставили разделенный на части круг с его истинным конкурентом — гистограммой:.
В эксперименте Кливленда задачей восприятия гистограммы было определение позиции на шкале, а при просмотре круговых диаграмм — угол сегмента. Ученые обнаружили, что гипотез на счет высоты столбцов гистограммы были в 1,96 раз точнее, чем суждения, касающиеся угла. Кливленд отметил: «Круговые диаграммы не обеспечивают эффективную передачу информацию о разнице значений».
После этого, статистик Наоми Роббинс (Naomi Robbins) проводила исследования, чтобы понять, почему мы так плохо определяем углы. В книге «Создание более эффективных графиков» (Creating More Effective Graphs) она пишет, что, как правило, люди склонны недооценивать острые углы и переоценивать тупые. Роббинс также утверждает, что сегменты круга, направленные в стороны, кажутся большими, чем те, что размещены вверху или внизу.
Это исследование подбодрило ярых противников секторных диаграмм, к которым относятся и сегодняшние ведущие специалисты в области визуализации данных — Эдвард Тафт (Edward Tuft) и Стивен Фью (Spethen Few). Тафт пишет: «Таблица практически всегда лучше, чем дурацкая круговая диаграмма, а Фью добавляет: «Пироги можете оставить на десерт» (pie — пирог по-английски).
Кроме того, круговые диаграммы постоянно высмеиваются популярными СМИ, например, в Washington Post, и в New York Times:
Круговая диаграмма, демонстрирующая эффективность круговой диаграммы
Тем не менее, у этого инструмента есть и свои защитники.
Доводы в защиту круговой диаграммы
По мнению многих пользователей, основным преимуществом круговой диаграммы является то, что все сегменты выглядят частью чего-то целого. К примеру, рассматривая график населения страны, распределенного по возрастным группам, зритель понимает, что представленные данные касаются всех людей, проживающих в этой стране. Это допущение не будет столь очевидным в случае с гистограммами.
Некоторые ученые также оспаривают эмпирическую литературу, которая резко критикует секторные диаграммы. Пожалуй, ни один человек не потратил больше времени на поиск аргументов в пользу этих диаграмм, чем психолог Ян Спенс (Ian Spence). В своей книге «Возникновение и использование статистических диаграмм (No Humble Pie: The Origins and Usage of a Statistical Chart) он активно защищает этот осуждаемый многими визуальный элемент.
Спенс утверждает, что исследования восприятия «пирожковых» диаграмм плохо проработаны. Он считает работу Кливленда ошибочной, поскольку в ней испытуемых просят сравнить размеры отдельных сегментов круга, а не оценить величину сегмента по отношению к целой фигуре. По его мнению, круговые диаграммы чаще используются для второй цели. Ссылаясь на другое исследование 1987 года, Спенс заявляет, что в этом плане секторные диаграммы и сегментированные столбцы абсолютно идентичны. Он пишет:
«На мой взгляд, чаще всего круговые диаграммы критиковали люди, которые хотели сделать больше, чем могли на самом деле. Секторная диаграмма — это простой информационный график, и его основное назначение заключается в демонстрации связи между сегментом и целой фигурой»
Исследование 2013 года о толковании человеком круговых диаграмм и столбцов дало сторонникам «пирогов» еще больше аргументов. В ходе эксперимента, проведенного Университетом Тафтса для измерения психической энергии, требуемой при просмотре различных графиков, использовалась около инфра-красная спектроскопия. Авторы обнаружили, что круговые диаграммы оцениваются не менее точно и что среднестатистический человек не считает их изучение более утомительным, чем просмотр гистограмм.
Однако, критикуя данное исследование, Стивен Фью утверждает, что заявления, сделанные психологами, ошибочны и безответственны. Эксперимент проверял способность людей делать гипотезы касаемо отдельных диаграмм (круговой и столбиковой), а не одной и той же. По словам Фью, на самом деле, глядя на эти графики, респонденты должны были действовать не совсем так, поэтому данная работа не имеет большого значения.
Другие считают, что секторная диаграмма может быть полезной, когда она используется редко и в эстетических целях. Нейтан Яу (Nathan Yau) из Flowing Datapoints говорит, что даже если предположения об углах в круговой диаграмме не так точны, как в других случаях, это не особо важно, ведь на практике выдвигать такие допущения не нужно практически никогда (в частности, когда на чертеже изображено только два или три значения). При определенных обстоятельствах, круговую диаграмму выбрать даже лучше, чисто из дизайнерских соображений:
Эта диаграмма не очень информативна с точки зрения представления данных, но она красива и оригинальна (Sky — небо, Sunny side of pyramid — солнечная сторона пирамиды, Shady side of pyramid — теневая сторона пирамиды)
Вместо заключения
Даже после столетних споров об их полезности, круговые диаграммы никуда не делись. На защиту (как и на критику) этого визуального инструмента представления данных было затрачено много энергии, при этом ученым так и не удалось объяснить привлекательность данной фигуры. Возможно, она связана с тем, что это первый тип диаграмм, с которыми люди сталкиваются еще в школе, или же нам попросту нравятся круги. А может, стоит винить Microsoft за то, что они добавили секторные диаграммы в Excel.
Так или иначе, по мере увеличения роли информации и цифровых данных в современной жизни, их грамотная визуализация требует все больше внимания. Многие уже выступают за то, чтобы статистика стала обязательной дисциплиной для изучения в старших классах. Как знать, возможно, благодаря более широкому использованию гистограмм и других графических методик, круговые диаграммы наконец утратят свою актуальность. Или нет.
Данные в столбцах или строках листа можно представить в виде гистограммы. В гистограмме категории обычно отображаются по горизонтальной оси, а значения — по вертикальной оси, как показано на этой диаграмме:
Типы гистограмм
-
диапазоны значений (например, количество элементов);
специфические шкалы (например, шкала Ликерта с масками, такими как «Полностью согласен», «Согласен», «Не знаю», «Не согласен», «Полностью не согласен»);
неупорядоченные имена (например, названия элементов, географические названия или имена людей).
На гистограмме с группировкой значения выводятся в виде плоских столбцов. Используйте этот тип диаграммы при наличии категорий, представляющих:
Гистограмма с накоплением
Гистограмма с накоплением представляет значения в виде плоских столбцов с накоплением. Используйте этот тип диаграммы, когда есть несколько ряд данных и нужно подчеркнуть итоговое значение.
Нормированная гистограмма
Нормированная гистограмма представляет значения в виде плоских нормированных столбцов с накоплением для представления 100 %. Используйте этот тип диаграммы, когда есть несколько рядов данных и нужно подчеркнуть их вклад в итоговое значение, особенно если итоговое значение одинаково для всех категорий.
Графики
Данные, расположенные в столбцах или строках листа, можно представить в виде графика. На графиках данные категорий равномерно распределяются вдоль горизонтальной оси, а все значения равномерно распределяются вдоль вертикальной оси. Графики позволяют отображать непрерывное изменение данных с течением времени на оси с равномерным распределением и идеально подходят для представления тенденций изменения данных с равными интервалами, такими как месяцы, кварталы или финансовые годы.
Типы графиков
-
Графики лучше всего подходят для вывода нескольких рядов данных- если нужно отобразить только один ряд данных, вместо графика рекомендуется использовать точечную диаграмму.
На графиках с накоплением данные суммируются, что может быть нежелательно. Увидеть накопление на графике бывает непросто, поэтому иногда вместо него стоит воспользоваться графиком другого вида либо диаграммой с областями с накоплением.
График и график с маркерами.
Графики с маркерами, отмечающими отдельные значения данных, или без маркеров можно использовать для отображения динамики изменения данных с течением времени или по категориям данных, разделенным равными интервалами, особенно когда точек данных много и порядок их представления существенен. Если категорий данных много или значения являются приблизительными, используйте график без маркеров.
График с накоплением и график с накоплением с маркерами.
Графики с накоплением, отображаемые как с маркерами для конкретных значений данных, так и без них, могут отображать динамику изменения вклада каждого значения с течением времени или по категориям данных, разделенным равными интервалами.
Нормированный график с накоплением и нормированный график с накоплением с маркерами.
Нормированные графики с накоплением с маркерами, отмечающими отдельные значения данных, или без маркеров могут отображать динамику вклада каждой величины в процентах с течением времени или по категориям данных, разделенным равными интервалами. Если категорий данных много или значения являются приблизительными, используйте нормированный график с накоплением без маркеров.
Примечания:
Круговые и кольцевые диаграммы
Данные в одном столбце или строке листа можно представить в виде круговой диаграммы. Круговая диаграмма отображает размер элементов одного ряд данных относительно суммы элементов. точки данных на круговой диаграмме выводятся как проценты от всего круга.
нужно отобразить только один ряд данных;
все значения ваших данных неотрицательны;
почти все значения данных больше нуля;
имеется не более семи категорий, каждой из которых соответствуют части общего круга.
Типы круговых диаграмм
Круговые диаграммы
Круговые диаграммы отображают вклад каждой величины в общую сумму в двухмерном виде.
Кольцевые диаграммы
Данные, расположенные только в столбцах или строках листа, можно представить в виде кольцевой диаграммы. Как и круговая диаграмма, кольцевая диаграмма отображает отношение частей к целому, но может содержать несколько ряд данных.
Типы кольцевых диаграмм
На диаграммах этого типа данные отображаются в виде колец, каждое из которых представляет ряд данных. Если в метках данных отображаются проценты, каждое кольцо в сумме должно давать 100 %.
Примечание:
Кольцевые диаграммы трудны для восприятия. Вместо них можно использовать линейчатые диаграммы с накоплением или гистограммы с накоплением.
Линейчатые диаграммы
Данные в столбцах или строках листа можно представить в виде линейчатой диаграммы. Линейчатые диаграммы используют для сравнения отдельных элементов. В диаграммах этого типа категории обычно располагаются по вертикальной оси, а величины — по горизонтальной.
метки осей имеют большую длину;
выводимые значения представляют собой длительности.
Типы линейчатых диаграмм
С группировкой
На линейчатой диаграмме с группировкой значения выводятся в виде плоских столбцов.
С накоплением
Линейчатая диаграмма с накоплением показывает вклад отдельных величин в общую сумму в виде плоских столбцов.
Нормированная
Этот тип диаграмм позволяет сравнить по категориям процентный вклад каждой величины в общую сумму. Значения отображаются в виде плоских столбцов.
Диаграммы с областями
Данные в столбцах или строках листа можно представить в виде диаграммы с областями. Диаграммы с областями могут использоваться для отображения изменений величин с течением времени и привлечения внимания к итоговому значению в соответствии с тенденцией. Отображая сумму значений рядов, такая диаграмма также наглядно показывает вклад каждого ряда.
Типы диаграмм с областями
С областями
Диаграммы с областями отображают изменение величин с течением времени или по категориям. Обычно вместо диаграмм с областями без накопления рекомендуется использовать графики, так как данные одного ряда могут быть скрыты за данными другого ряда.
С областями с накоплением
Диаграммы с областями с накоплением показывают изменения вклада каждой величины с течением времени или по категориям в двухмерном виде.
Нормированная
Нормированные диаграммы с областями с накоплением отображают изменения вклада каждой величины в процентах с течением времени или по категориям.
Точечные диаграммы
Данные в столбцах и строках листа можно представить в виде точечной диаграммы. Поместите данные по оси X в одну строку или столбец, а соответствующие данные по оси Y — в соседние строки или столбцы.
Точечная диаграмма имеет две оси значений: горизонтальную (X) и вертикальную (Y). На точечной диаграмме значения «x» и «y» объединяются в одну точку данных и выводятся через неравные интервалы или кластеры. Точечные диаграммы обычно используются для отображения и сравнения числовых значений, например научных, статистических или технических данных.
требуется изменять масштаб горизонтальной оси;
требуется использовать для горизонтальной оси логарифмическую шкалу;
значения расположены на горизонтальной оси неравномерно;
на горизонтальной оси имеется множество точек данных;
требуется настраивать независимые шкалы точечной диаграммы для отображения дополнительных сведений о данных, содержащих пары сгруппированных полей со значениями;
требуется отображать не различия между точками данных, а аналогии в больших наборах данных;
требуется сравнивать множество точек данных без учета времени; чем больше данных будет использовано для построения точечной диаграммы, тем точнее будет сравнение.
Типы точечных диаграмм
Диаграмма этого типа позволяет отображать точки данных без соединительных линий для сравнения пар значений.
Точечная диаграмма с плавными линиями и маркерами и точечная диаграмма с плавными линиями.
На этой диаграмме точки данных соединены сглаживающими линиями. Такие линии могут отображаться с маркерами или без них. Сглаживающую кривую без маркеров следует использовать, если точек данных достаточно много.
Точечная диаграмма с прямыми линиями и маркерами иточечная диаграмма с прямыми линиями.
На этой диаграмме точки данных соединяются прямыми линиями. Прямые могут отображаться с маркерами или без них.
Другие диаграммы
Данные в столбцах или строках листа можно представить в виде лепестковой диаграммы. Лепестковая диаграмма позволяет сравнить агрегированные значения нескольких ряд данных.
Типы лепестковых диаграмм
Лепестковая диаграмма и лепестковая диаграмма с маркерами.
Лепестковые диаграммы отображают изменения значений относительно центральной точки с маркерами для отдельных точек данных или без них.
Заполненная лепестковая диаграмма.
На такой диаграмме область, покрытая рядами данных, заполнена цветом.