| Раздел функций | ИНЖЕНЕРНЫЕ |
| Название на английском | DELTA |
| Волатильность | Не волатильная |
| Похожие функции | СОВПАД, ВПР |
Что делает эта функция?
Эта функция сравнивает два значения и проверяет, являются ли они абсолютно одинаковыми.
Если числа совпадают, результатом будет 1, в противном случае – 0.
Работает только с числами, текстовые значения на входе отдают результат #ЗНАЧ!
Форматирование числа не имеет существенного значения, поэтому числа, которые выглядят округленными из-за удаления десятичных разрядов, будут по-прежнему корректно соответствовать не округленным значениям.
Синтаксис
=ДЕЛЬТА(ПервоеЧисло;ВтороеЧисло)
Пример
Следующая таблица используется для определения того, сколько одинаковых пар чисел в списке.
Функция ДЕЛЬТА проверяет каждую пару, а затем функция СУММ суммирует их.

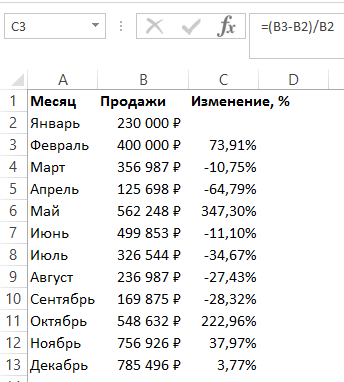
По иронии судьбы, функция ДЕЛЬТА не поможет посчитать дельту в Excel. Сравнивая данные в ячейках, функция лишь отвечает на вопрос, равна ли их дельта нулю или нет (иными словами, есть ли дельта).
А посчитать дельту между A и B можно без применения каких-либо функций вовсе, лишь зная две простые формулы ее подсчета:
Второй вариант в Excel использовать удобнее, т.к. первый требует использования скобок.
Не дайте буквам в формуле вас запутать – B обозначает первый замер (результат “до”), а A – второй (результат “после”). Иными словами, A случилось после B, их алфавитный порядок здесь не при чем.
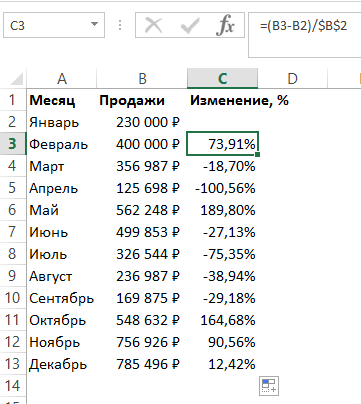
Чтобы полученный результат выражался в процентах, нужно изменить формат ячеек на процентный:

Другие инженерные функции
ДВ.В.ДЕС, ДЕС.В.ДВ, ДЕС.В.ШЕСТН, ПОРОГ, ПРЕОБР, ШЕСТН.В.ДЕС
Функция ДЕЛЬТА в Excel используется для проверки двух числовых значений и возвращает два возможных варианта:
- Числовое значение 1, если переданные в качестве первого и второго аргумента числа совпадают по значению.
- 0 (нуль), если переданные числа по значению не совпадают.
Примеры использования функции ДЕЛЬТА в Excel
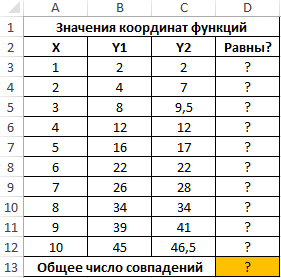
Пример 1. В таблице Excel указаны значения независимой координаты X и значения зависимых координат Y1 и Y2 для двух разных функций. Определить количество пар совпадающих значений.
Вид исходной таблицы данных:
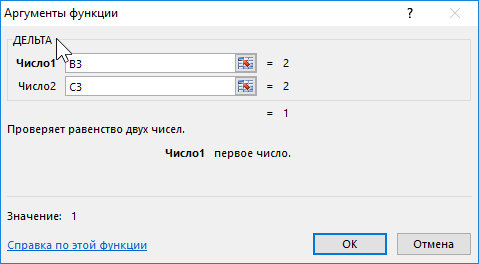
Для решения задачи сравним каждую пару значений зависимых координат Y1 и Y2 с помощью функции ДЕЛЬТА. В ячейке D3 запишем следующую формулу:
Описание аргументов:
- B3 – значение аргумента Y1 – сравниваемое число;
- C3 – значение аргумента Y2 – число, с которым сравнивается первое значение.
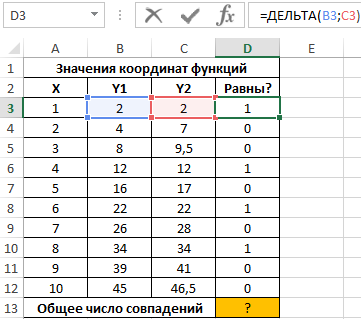
Полученное значение (1) свидетельствует о равенстве сравниваемых чисел. Протянем записанную в ячейке D3 формулу вниз до ячейки D12, чтобы автоматически рассчитать результаты для остальных значений Y1 и Y2:
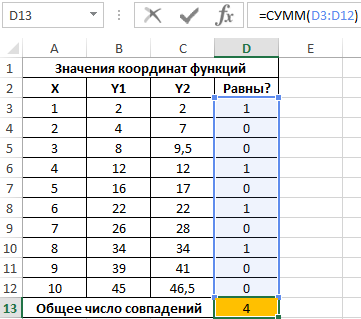
Для расчета числа пар совпадающих значений используем следующую функцию:
=СУММ(D3:D12)
Полученный результат:
Всего 4 пары совпадений в значениях функций координат.
Калькулятор сроков возврата инвестиций в банковские депозиты
Пример 2. Реализовать калькулятор, который рассчитывает, сколько времени потребуется на получение определенной прибыли от депозита при известной начальной сумме вклада и годовой процентной ставки. Предусмотреть вывод сообщения об ошибке в случае, если одно или несколько исходных данных не указаны.
Вид формы для расчета:
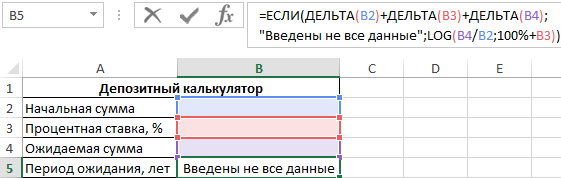
Поскольку для расчета используется логарифм из частного ожидаемой и начальной суммы с основанием в виде суммы депозита, выраженного в процентах (то есть 100%), и процентной ставки, то каждая ячейка из диапазона B2:B4 не должна являться пустой или принимать значение 0, поскольку логарифм нуля или логарифм с основанием 1 (100%) не может быть вычислен. Поэтому для расчетов используем следующую формулу:
В качестве проверочного выражения функции ЕСЛИ выступает значение, являющееся суммой возвращаемых результатов функциями ДЕЛЬТА. Последние сравнивают значения, содержащиеся в ячейках B2, B3 и B4 соответственно с 0 (второй аргумент явно не указан). Данный вариант записи соответствует логическому И (общий результат равен ИСТИНА, если все выражения, проверяемые функцией И, возвращают результат ИСТИНА). Полученное значение (0 или любое число от 1 до +∞) будет интерпретировано как ЛОЖЬ или ИСТИНА соответственно.
При незаполненных полях получим следующий результат:
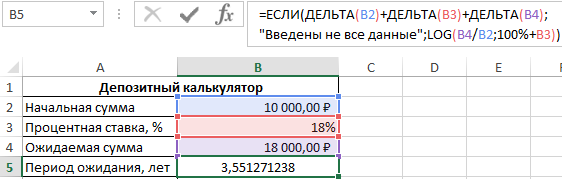
Пример расчета:
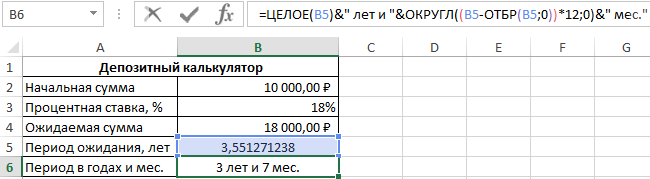
Напишем формулу для преобразования дробного числа в годы и месяцы:
В результате получим:
Расчет вероятности выпуска бракованной продукции на производстве в Excel
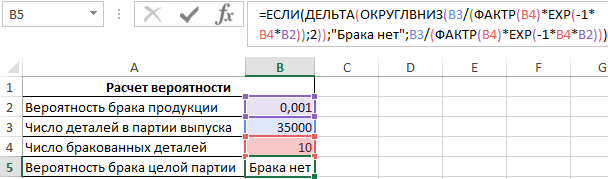
Пример 3. При изготовлении деталей на производственно-ремонтном заводе существует вероятность брака производимой продукции, которая равная коэффициенту 0,001. Определить, какая вероятность появления 10 выбракованных деталей (в этом случае вся партия считается браком) в партии из 35000 шт. Считается, что вероятностями ниже 10% можно пренебречь (то есть их приравнивают к нулю).
Вид исходной таблицы данных:
Для расчета используем следующую формулу:
Функция ОКРУГЛВНИЗ округляет до 0 все значения, которые меньше числа 0,01, то есть 10%-й вероятности. Функция ДЕЛЬТА принимает только один аргумент (выражение, полученное на основе формулы Пуассона для вычисления маловероятных случайных ситуаций), то есть сравнение выполняется с числом 0 (нуль).
Результат вычислений:
Если вычислять формулу поэтапно, будет видно, что вероятность по формуле Пуассона равна примерно 0,00974 < 0,01, поэтому результат округления равен 0. Тогда функция ДЕЛЬТА возвращает значение 1 (0=0), которое интерпретируется как логическое ИСТИНА.
Особенности использования функции ДЕЛЬТА в Excel
Функция имеет следующий синтаксис:
=ДЕЛЬТА(число1;[число2])
Описание аргументов:
- число1 – обязательный аргумент, принимающий данные числового типа, которые будут сравнены по значению с числом, переданным в качестве второго аргумента, или нулем, если последний опущен;
- [число2] – необязательный для заполнения аргумент, характеризующий числовое значение, с которым выполняется операция сравнения. Если явно не указан, принимает значение 0 (нуль).
Примечания:
- Рассматриваемая функция выполняет операцию сравнения только числовых значений. Если в качестве одного из аргументов было передано имя, текстовая строка или логические ИСТИНА и ЛОЖЬ, результатом выполнения функции ДЕЛЬТА будет код ошибки #ЗНАЧ!.
- Функция ДЕЛЬТА может быть использована для сравнения двух дат, которые являются результатами выполнения функции ДАТА или других функций, возвращающих данные формата Дата, поскольку Excel выполняет автоматическое преобразование в формат времени Excel (соответствующее числовое значение).
- Если в качестве первого аргумента функции ДЕЛЬТА было передано число 0, а в качестве второго – ссылка на пустую ячейку, результатом вычислений будет число 1, поскольку пустое значение интерпретируется как числовое значение 0.
- Рассматриваемая функция также имеет название дельта-функция Кронекера.
- Данную функцию можно использовать вместо логического знака равенства «=» в выражениях, которые используются как условия проверки в логических функциях. Например, функция =ЕСЛИ(ДЕЛЬТА(1;1);”равны”;”не равны”) вернет значение «равны». При этом преобразование чисел 1 и 0 в логические ИСТИНА и ЛОЖЬ выполняется автоматически.
- Функция ДЕЛЬТА не может быть использована в качестве формулы массива. Например, формула массива =ДЕЛЬТА (A1:A5;B1B5) вернет массив ошибок #ЗНАЧ!, даже если ячейки из диапазонов A1:A5 и B1:B5 содержат только числовые значения.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ДЕЛЬТА в Microsoft Excel.
Описание
Проверяет равенство двух значений. Возвращает 1, если число1 = число2, и 0 в противном случае. Эта функция используется для фильтрации множества значений. Например, суммируя несколько функций ДЕЛЬТА, можно подсчитать количество равных пар. Эту функцию также называют дельта-функцией Кронекера.
Синтаксис
ДЕЛЬТА(число1;[число2])
Аргументы функции ДЕЛЬТА описаны ниже.
-
Число1 — обязательный аргумент. Первое число.
-
Число2. Необязательный. Второе число. Если этот вопрос опущен, то число2 считается нулевым.
Замечания
-
Если число1 не является числом, delta возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если число2 не является числом, delta возвращает #VALUE! значение ошибки #ЗНАЧ!.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=ДЕЛЬТА(5;4) |
Проверяет, равно ли число 5 числу 4 |
0 |
|
=ДЕЛЬТА(5;5) |
Проверяет, равно ли число 5 числу 5 |
1 |
|
=ДЕЛЬТА(0,5;0) |
Проверяет, равно ли число 0,5 числу 0 |
0 |
Нужна дополнительная помощь?
Разница в процентах между двумя числами в Excel
Познакомимся с особенностями расчета разницы между двумя числами в процентах в Excel в зависимости от знаков рассматриваемых величин (обе величины положительные, обе отрицательные или разных знаков).
Приветствую всех, уважаемые читатели блога TutorExcel.Ru.
Кажется, что может быть проще, чем посчитать дельту в процентах между двумя числами — это несложная математическая операция.
Сначала вычислить разницу между двумя величинами в абсолютном выражении (разность первого и второго чисел), а затем полученный результат разделить на вторую величину.
Но все несколько сложнее, чем кажется на первый взгляд, и для некоторых случаев приведенная формула может дать неправильный результат. Поэтому давайте перейдем к рассмотрению особенностей вычислений.
Формула разницы между числами в процентах в Excel
Для удобства записи обозначим первую величину как A, а вторую как B.
Тогда процентный прирост первого числа ко второму, как уже писалось выше, будет считаться по следующей формуле:
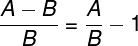
Теперь перейдем к проверке корректности формулы расчета и рассмотрим различные примеры в зависимости от знаков величин A и B.
Вариант 1: A и B одного знака (+ и +, или − и −)
Начнем со стандартного варианта, когда мы сравниваем друг с другом сопоставимые величины.
Предположим, что компания в этом году продала товаров на сумму 120 тысяч рублей, а в прошлом году — на сумму 100 тысяч рублей.
Вычислим темпы роста доходов компании год к году, т.е. посмотрим насколько компания в этом году заработала в процентах больше, чем в прошлом.
В данном случае, A это 120 тысяч рублей, а B, соответственно, 100 тысяч рублей, применим формулу и найдем соотношение между ними:
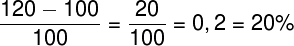
В итоге получаем, что 120 тысяч рублей больше, чем 100 тысяч рублей на 20%.
Действительно, все достаточно просто, но теперь рассмотрим те же самые величины, но с обратным знаком: -120 и -100.
И для лучшей наглядности расчета рассмотрим не доходы компании, а ее убытки, и представим, что убытки компании в этом году составили -120 тысяч рублей, когда в прошлом году составляли -100 тысяч рублей.
Логично предположить, что мы должны получить ответ -20%, так как на самом деле -120 меньше, чем -100 (с точки зрения математики, чем левее число на числовой оси, тем оно меньше) и, следовательно, в результате получить отрицательный процентный прирост.
Другими словами, убытки компании увеличились и результаты компании ухудшились, а значит прирост в процентах отрицательный.
Проверяем формулу и повторяем расчет:

Однако мы опять получаем результат 20%, который, как мы уже выяснили, является неправильным.
Поэтому отсюда делаем вывод, что наша формула для отрицательных чисел, к сожалению, не работает.
Скорректируем расчет, вместо величины B в знаменателе формулы поставим ее модуль.
Тогда формула расчета разницы в процентах примет окончательный вид:
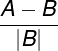
Пересчитаем пример и посмотрим какой ответ в итоге получится:
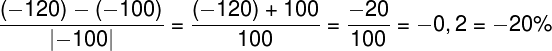
Отлично, все сошлось. При этом обратите внимание, что для положительных величин формула на самом деле осталась прежней и никак не поменялась, так как модуль положительные числа не изменяет.
Идем дальше и рассмотрим более сложный вариант.
Вариант 2: A и B разных знаков (+ и −, или − и +)
Теперь разберем нестандартный вариант, и от сравнения чисел одинаковых знаков (до этого мы сравнивали положительное с положительным и отрицательное с отрицательным) перейдем к сравнению чисел разных знаков.
Однако при попытке произвести такое сравнение, мы приходим к логическому несоответствию.
Например, давайте подумаем во сколько число 20 больше числа -5?
Предположим, что мы каким-то образом посчитали отношение и нашли численный ответ (предположу, что на предыдущий вопрос в качестве ответа хочется сказать, что в 5 раз больше):
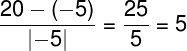
Однако точно такие же расчеты можно привести для чисел 20 и 4 (получается, что 20 одновременно в 5 раз больше, и чем 4 и чем -5).
Такого быть не может, в связи с чем получается, что посчитать разницу между двумя величинами с разными знаками в процентах корректно нельзя, так как сравниваются не сопоставимые друг с другом величины.
Поэтому в подобных случаях принято писать N/M — Not Meaningful (также встречаются обозначения N.M., NM), что можно перевести как не имеет смысла или не имеет значения.
В официальных пресс-релизах или презентациях крупных компаний это может обозначаться следующим образом (к примеру, результаты компании Thomson Reuters за 1 квартал 2017 г.):
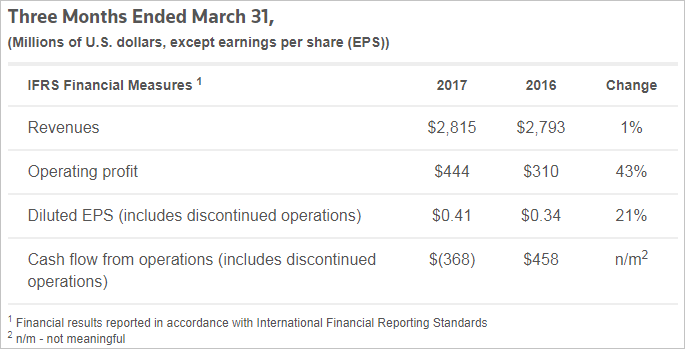
В результате, после всех рассуждений, мы можем вернуться в Excel и составить итоговую формулу расчета разницы в процентах между двумя числами.
Сначала с помощью функции ЕСЛИ проверим условие, что величины одного знака — это равносильно условию, что их произведение больше нуля. В том случае если условие выполняется, то считаем по формуле, если же не выполняется, то в качестве ответа возвращаем ошибку (обозначение NM):
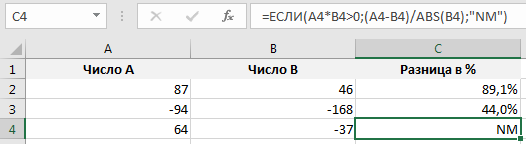
Спасибо за внимание!
Если у вас остались вопросы по методике расчета — спрашивайте в комментариях.
Примеры работы функции ДЕЛЬТА для сравнения двух чисел в Excel
Функция ДЕЛЬТА в Excel используется для проверки двух числовых значений и возвращает два возможных варианта:
- Числовое значение 1, если переданные в качестве первого и второго аргумента числа совпадают по значению.
- 0 (нуль), если переданные числа по значению не совпадают.
Примеры использования функции ДЕЛЬТА в Excel
Пример 1. В таблице Excel указаны значения независимой координаты X и значения зависимых координат Y1 и Y2 для двух разных функций. Определить количество пар совпадающих значений.
Вид исходной таблицы данных:
Для решения задачи сравним каждую пару значений зависимых координат Y1 и Y2 с помощью функции ДЕЛЬТА. В ячейке D3 запишем следующую формулу:
- B3 – значение аргумента Y1 – сравниваемое число;
- C3 – значение аргумента Y2 – число, с которым сравнивается первое значение.
Полученное значение (1) свидетельствует о равенстве сравниваемых чисел. Протянем записанную в ячейке D3 формулу вниз до ячейки D12, чтобы автоматически рассчитать результаты для остальных значений Y1 и Y2:
Для расчета числа пар совпадающих значений используем следующую функцию:
Всего 4 пары совпадений в значениях функций координат.
Калькулятор сроков возврата инвестиций в банковские депозиты
Пример 2. Реализовать калькулятор, который рассчитывает, сколько времени потребуется на получение определенной прибыли от депозита при известной начальной сумме вклада и годовой процентной ставки. Предусмотреть вывод сообщения об ошибке в случае, если одно или несколько исходных данных не указаны.
Вид формы для расчета:
Поскольку для расчета используется логарифм из частного ожидаемой и начальной суммы с основанием в виде суммы депозита, выраженного в процентах (то есть 100%), и процентной ставки, то каждая ячейка из диапазона B2:B4 не должна являться пустой или принимать значение 0, поскольку логарифм нуля или логарифм с основанием 1 (100%) не может быть вычислен. Поэтому для расчетов используем следующую формулу:
В качестве проверочного выражения функции ЕСЛИ выступает значение, являющееся суммой возвращаемых результатов функциями ДЕЛЬТА. Последние сравнивают значения, содержащиеся в ячейках B2, B3 и B4 соответственно с 0 (второй аргумент явно не указан). Данный вариант записи соответствует логическому И (общий результат равен ИСТИНА, если все выражения, проверяемые функцией И, возвращают результат ИСТИНА). Полученное значение (0 или любое число от 1 до +∞) будет интерпретировано как ЛОЖЬ или ИСТИНА соответственно.
При незаполненных полях получим следующий результат:
Напишем формулу для преобразования дробного числа в годы и месяцы:
В результате получим:
Расчет вероятности выпуска бракованной продукции на производстве в Excel
Пример 3. При изготовлении деталей на производственно-ремонтном заводе существует вероятность брака производимой продукции, которая равная коэффициенту 0,001. Определить, какая вероятность появления 10 выбракованных деталей (в этом случае вся партия считается браком) в партии из 35000 шт. Считается, что вероятностями ниже 10% можно пренебречь (то есть их приравнивают к нулю).
Вид исходной таблицы данных:
Для расчета используем следующую формулу:
Функция ОКРУГЛВНИЗ округляет до 0 все значения, которые меньше числа 0,01, то есть 10%-й вероятности. Функция ДЕЛЬТА принимает только один аргумент (выражение, полученное на основе формулы Пуассона для вычисления маловероятных случайных ситуаций), то есть сравнение выполняется с числом 0 (нуль).
Если вычислять формулу поэтапно, будет видно, что вероятность по формуле Пуассона равна примерно 0,00974 число1 ;[число2])
- число1 – обязательный аргумент, принимающий данные числового типа, которые будут сравнены по значению с числом, переданным в качестве второго аргумента, или нулем, если последний опущен;
- [число2] – необязательный для заполнения аргумент, характеризующий числовое значение, с которым выполняется операция сравнения. Если явно не указан, принимает значение 0 (нуль).
- Рассматриваемая функция выполняет операцию сравнения только числовых значений. Если в качестве одного из аргументов было передано имя, текстовая строка или логические ИСТИНА и ЛОЖЬ, результатом выполнения функции ДЕЛЬТА будет код ошибки #ЗНАЧ!.
- Функция ДЕЛЬТА может быть использована для сравнения двух дат, которые являются результатами выполнения функции ДАТА или других функций, возвращающих данные формата Дата, поскольку Excel выполняет автоматическое преобразование в формат времени Excel (соответствующее числовое значение).
- Если в качестве первого аргумента функции ДЕЛЬТА было передано число 0, а в качестве второго – ссылка на пустую ячейку, результатом вычислений будет число 1, поскольку пустое значение интерпретируется как числовое значение 0.
- Рассматриваемая функция также имеет название дельта-функция Кронекера.
- Данную функцию можно использовать вместо логического знака равенства «=» в выражениях, которые используются как условия проверки в логических функциях. Например, функция =ЕСЛИ(ДЕЛЬТА(1;1);”равны”;”не равны”) вернет значение «равны». При этом преобразование чисел 1 и 0 в логические ИСТИНА и ЛОЖЬ выполняется автоматически.
- Функция ДЕЛЬТА не может быть использована в качестве формулы массива. Например, формула массива =ДЕЛЬТА (A1:A5;B1B5) вернет массив ошибок #ЗНАЧ!, даже если ячейки из диапазонов A1:A5 и B1:B5 содержат только числовые значения.
Финансы в Excel+VBA. Калькулятор опционов по модели Блэка-Шоулза
Основы опционов
Для начала кратко о сути и ценообразовании опционов. Опцион имеет четыре основных параметра:
1. Базовый актив
2. Тип опциона (Колл или Пут)
3. Цена страйка (цена исполнения опциона)
4. Дата экспирации (истечения) опциона
Для покупателя опциона он представляет собой право купить (опцион Колл) или продать (опцион Пут) базовый актив по цене страйка в день экспирации. Для продавца опциона он представляет собой обязанность продать (опцион Колл) или купить (опцион Пут) базовый актив по цене страйка в день экспирации. Фактически опцион представляет собой страховку от изменения цены базового актива (БА) от момента сделки до даты экспирации — в роли страховщика выступает продавец (в случае неблагоприятного изменения цены БА он выплачивает страховку покупателю опциона), а страхователем является покупатель опциона (он платит за страховку продавцу).
Как и цена страховки цена опциона полностью определяется вероятностью «страхового случая», т.е. исполнения опциона (исполнения права покупателя опциона). Основные составляющие, которые влияют эту вероятность и на цену опциона, на стоимость страховки, которую платит покупатель и получает продавец:
- Разница между ценой страйка и ценой базового актива. Т.е. при покупке Колла, чем выше его страйк, тем он дешевле (т.к. снижается вероятность того, что на момент экспирации БА будет выше цены страйка)
- Волатильность базового актива. Чем выше волатильность (грубо размах колебаний цены) БА, тем выше вероятность достичь страйка до экспирации.
- Время до экспирации. Чем больше времени до экспирации опциона, тем при покупке Колла выше вероятность что за это время цена базового актива уйдёт выше страйка, соответственно цена опциона выше.
При этом зависимость цены опциона по каждой из этих трёх составляющих нелинейная. Ставшая общепринятой формула оценки опционов с учётом этих основных факторов была выведена Фишером Блэком и Майроном Шоулзом в 1973 году.
Формула Блэка-Шоулза имеет следующий вид (подробно можно посмотреть в Википедии):
Цена (европейского) опциона call: 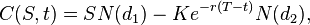


Цена (европейского) опциона put:
Обозначения:
C(S,t) — текущая стоимость опциона call в момент t до истечения срока опциона (до экспирации);
S — текущая цена базового актива;
N(x) — вероятность того, что отклонение будет меньше в условиях стандартного нормального распределения (таким образом, и ограничивают область значений для функции стандартного нормального распределения);
K — цена исполнения опциона;
r — безрисковая процентная ставка;
T — t — время до истечения срока опциона;

Греки опционов
Для оценки чувствительности цены опциона к цене БА, волатильности, и времени до экспирации, применяют коэффициенты, называемые Греками (коэффициенты в основном обозначаются греческими буквами, за исключением «веги»).
Греки в модели Блэка-Шоулза вычисляются следующим образом:
1. Дельта (
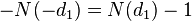
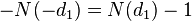
2. Гамма ( 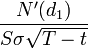
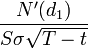
3. Вега ( 

4. Тета ( 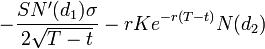
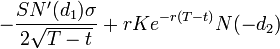
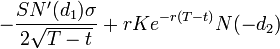
Вышеприведенные формулы верны для общего случая, в том числе для случая опционов на акции. Для расчёта опционов на фьючерсные контракты безрисковая ставка r не применяется. Т.к. на Московской бирже торгуются опционы на фьючерсы, далее в расчётах процентную ставку не учитываем.
Реализация модели в MS Excel
Итак, реализация модели Блэка-Шоулза в Excel+VBA.
Для удобства создадим функцию для каждой переменной из модели БШ. В каждой функции будут входные переменные:
S — цена БА
X — цена страйка
d — число дней до экспирации
y — число дней в году
v — волатильность
OptionType — тип опциона «Call» или «Put» (только для расчета цены и дельты)
Запись обычной функции в VBA выглядит следующим образом:
Function НазваниеФункции(входные переменные через запятую)
… вычисления…
НазваниеФункции =… вычисления…
End Function
Такую функцию можно вызывать как из других функций, так и из листа Excel.
Функции записываются в созданный Модуль (запускаем VBA в Excel, например нажатием Alt+F11, выбираем Insert -> Module):
T = d / y
d_1 = (Log(S / X) + (0.5 * (v ^ 2)) * T) / (v * (T ^ 0.5))
End Function
Function d_2(S, X, d, y, v)
T = d / y
d_2 = d_1(S, X, d, y, v) — v * (T ^ 0.5)
End Function
Function Nd_1(S, X, d, y, v)
Nd_1 = Application.NormSDist(d_1(S, X, d, y, v))
End Function
Function Nd_2(S, X, d, y, v)
Nd_2 = Application.NormSDist(d_2(S, X, d, y, v))
End Function
Function N_d_1(S, X, d, y, v)
N_d_1 = Application.NormSDist(-d_1(S, X, d, y, v))
End Function
Function N_d_2(S, X, d, y, v)
N_d_2 = Application.NormSDist(-d_2(S, X, d, y, v))
End Function
Function N1d_1(S, X, d, y, v)
T = d / y
N1d_1 = 1 / (2 * Application.Pi()) ^ 0.5 * (Exp(-0.5 * d_1(S, X, d, y, v) ^ 2))
End Function
Function OptionPrice(OptionType, S, X, d, y, v)
If OptionType = «Call» Then
OptionPrice = S * Nd_1(S, X, d, y, v) — X * Nd_2(S, X, d, y, v)
ElseIf OptionType = «Put» Then
OptionPrice = X * N_d_2(S, X, d, y, v) — S * N_d_1(S, X, d, y, v)
End If
End Function
Function Delta(OptionType, S, X, d, y, v)
If OptionType = «Call» Then
Delta = Application.NormSDist(d_1(S, X, d, y, v))
ElseIf OptionType = «Put» Then
Delta = Application.NormSDist(d_1(S, X, d, y, v)) — 1
End If
End Function
Function Theta(S, X, d, y, v)
T = d / y
Theta = -((S * v * N1d_1(S, X, d, y, v)) / (2 * (T ^ 0.5))) / y
End Function
Function Gamma(S, X, d, y, v)
T = d / y
Gamma = N1d_1(S, X, d, y, v) / (S * (v * (T ^ 0.5)))
End Function
Function Vega(S, X, d, y, v)
T = d / y
Vega = (S * (T ^ 0.5) * N1d_1(S, X, d, y, v)) / 100
End Function
Готовый Excel-файл можно скачать по ссылке.
Теперь в екселевской ячейке можем вызывать любую прописанную нами функцию, например введя в ячейке =OptionPrice(«Put»;76870;90000;13;365;0.47) мы получим теоретическую цену опциона Пут при цене базового актива 76870, страйке 90000, предполагаемой волатильности 45% и за 13 дней до экспирации.
Некоторые моменты, которые хотелось бы отметить
- Полученные в нашей программе значения теорцены практически идентичны тем, что транслирует Мосбиржа, это значит что биржа в своих расчётах использует именно модель БШ.
- На самом деле опцион (как и страховка) не имеет истинной справедливой стоимости — она для каждого своя, и зависит от того какая предполагается волатильность или например какое учитывать число дней (учитывать ли выходные, с каким весом учитывать разные дни недели, сколько дней в году использовать в формуле) и т.д.
- Греки обладают замечательным свойством — чтобы получить значение греков для портфеля фьючерсов и опционов нужно просто сложить соответствующие греки для отдельных активов портфеля. Т.е. мы легко можем рассчитать, например, сколько нужно купить/продать базовых фьючерсов чтобы общая стоимость портфеля не изменялась при изменении цены этого фьючерса (т.н. выравнивание Дельты или дельта-хеджирование).
- Не смотря на свою распространённость, модель БШ основана на допущении, что доходность актива имеет нормальное распределение, что на реальном рынке не выполняется никогда.
Как посчитать проценты в Excel
Почти в каждой сфере деятельности мы сталкиваемся с необходимостью уметь считать проценты. Чаще всего навыки вычисления процентов нам нужны при расчете НДС, маржи, наценки, процентов по кредиту, доходности вкладов и ценных бумаг, скидок. Все эти вычисления производятся как подсчет процента от суммы.
Кликните по кнопке ниже для загрузки Excel файла с примерами расчетов процентов в Excel:
Что такое процент?
Проце́нт (лат. per cent — на сотню) — одна сотая часть. Отмечается знаком «%». Обозначает долю чего-либо по отношению к целому. Например, 25 % от 500 руб. означает 25 частей по 5 руб. каждая, то есть 125 руб.
Базовая формула расчета процента от суммы выглядит так:
(Часть/Целое) * 100 = Процент (%)
Не существует универсальной формулы, подходящей для каждого сценария расчета процентов. Ниже вы узнаете о самых популярных способах расчета.
Как посчитать проценты от суммы в Excel
Видео урок:
Базово, рассчитать процент от суммы в Эксель можно по формуле:
(Часть/Целое) * 100 = Процент (%)
Но если использовать формат ячейки “Процентный”, то для вычисления процента от числа достаточно поделить одно число на другое. Например, у нас есть яблоки, которые мы купили по 100 руб. на оптовом складе, а розничную цену выставим 150 руб. Для того чтобы высчитать процент того, сколько составляет закупочная цена от розничной, нам потребуется:
- Составить таблицу с ценами и добавить колонку для вычисления величины процента:
- В ячейку D2 внести формулу, вычисляющую процент цены закупки от цены продажи:
- Применить формат ячейки D2 “Процентный”:
Как посчитать процент от суммы значений таблицы Excel
Видеоурок:
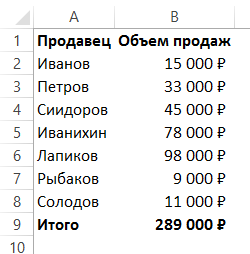
Представим, что у нас есть список продавцов с объемом продаж по каждому и общей суммой всех продаж по всем продавцам. Наша задача определить, какой процент составляет вклад каждого продавца в итоговый оборот:
Для этого нам нужно:
- Добавить колонку к таблице с расчетом процента;
- В ячейку C2 вставить формулу:
Значки $ фиксируют колонку “B” и ячейку “9” для того, чтобы при протягивании формулы на все строки таблицы, Excel автоматически подставлял объем продаж каждого продавца и высчитывал % от общего объема продаж. Если не поставить значки “$”, то при протягивании формулы, система будет смещать ячейку B9 на столько ячеек вниз, на сколько вы протяните формулу.
- Протянуть формулу на все ячейки таблицы, соответствующие строкам с фамилиями продавцов:
- На примере выше мы протянули формулу и получили значения в виде дробных чисел. Для того чтобы перевести полученные данные в проценты выделите данные левой клавишей мыши и смените формат ячеек на “Процентный”:
Как вычислить процент нескольких значений от суммы таблицы
Видеоурок:
На примере выше у нас был список продавцов и их объем продаж. Мы вычисляли какой вклад каждый из работников внес в итоговый объем продаж. Но что, если у нас есть список повторяющихся товаров с данными объема продаж и нам нужно вычислить какую часть конкретный товар составляет в процентах от всех продаж?
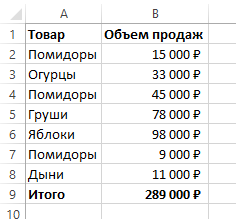
Из списка товаров выше мы хотим вычислить какой объем продаж составляют помидоры (они записаны в нескольких строках таблицы). Для этого:
- Справа от таблицы укажем товар (Помидоры), по которым хотим рассчитать долю в продажах:
- Сменим формат ячейки E2 на “Процентный”;
- В ячейку E2 вставим формулу с функцией СУММЕСЛИ, которая поможет вычислить из списка товаров Помидоры и суммировать их объем продаж, а затем поделить его на общий объем продаж товаров:
Как работает эта формула?
Для расчетов мы используем формулу СУММЕСЛИ. Эта функция возвращает сумму чисел, указанных в качестве аргументов и отвечающих заданным в формуле критериям.
Синтаксис функции СУММЕСЛИ:
=СУММЕСЛИ(диапазон; условие; [диапазон_суммирования])
- диапазон – диапазон ячеек, по которым оцениваются критерии. Аргументом могут быть числа, текст, массивы или ссылки, содержащие числа;
- условие – критерии, которые проверяются по указанному диапазону ячеек и определяют, какие ячейки суммировать;
- диапазон_суммирования – суммируемые ячейки. Если этот аргумент не указан, то функция использует аргумент диапазонв качестве диапазон_суммирования.
Таким образом, в формуле =СУММЕСЛИ($A$2:$A$8;$E$1;$B$2:$B$8)/B9 мы указали “ $A$2:$A$8 ” как диапазон товаров, среди которых функция будет искать нужный нам критерий (Помидоры). Ячейка “ $E$1 ” указана в качестве критерия и указывает что мы ищем “Помидоры”. Диапазон ячеек “ $B$2:$B$8 ” обозначает какие ячейки нужно суммировать, в случае если искомый критерий был найден.
Как посчитать разницу в процентах в Excel
При расчетах в Excel часто требуется посчитать разницу в процентах между двумя числами.
Например, для расчета разницы в процентах между двумя числами А и В используется формула:
(B-A)/A = Разница между двумя числами в процентах
На практике, при использовании этой формулы важно определить какое из нужных вам чисел является “А”, а какое “В”. Например, представим что вчера у вас было в наличии 8 яблок, а сегодня стало 10 яблок. Таким образом количество яблок относительно вчерашнего у вас изменилось на 25% в большую сторону. В том случае, если у вас вчера было 10 яблок, а сегодня стало 8 яблок, то количество яблок, относительно вчерашнего дня сократилось на 20%.
Таким образом, формула, позволяющая корректно вычислить изменения в процентах между двумя числами выглядит так:
Как найти процент между двумя числами из двух колонок в Excel
Видеоурок:
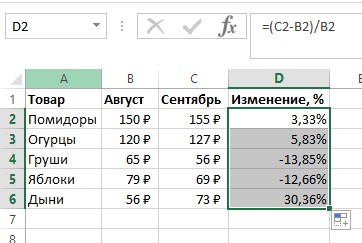
Предположим, что у нас есть цены прошлого и текущего месяца на товары. Наша задача вычислить изменение текущих цен по отношению предыдущим периодам.
Для расчетов нам потребуется формула:
- Протяните формулу на все строки со значениями;
- Измените формат ячейки для колонки “Изменение, %” на “Процентный”.
Как найти процент между двумя числами из двух строк в Excel
В том случае, если у нас есть список в котором в каждой строке указан период с данными продаж и нам нужно вычислить изменения от периода к периоду, то нам потребуется формула:
Где B2 это первая строчка, B3 вторая строчка с данными. После ввода формулы не забудьте отформатировать ячейки с вычислениями как “Процентные”. Выполнив все выше описанные действия, вы получите результат:
Если у вас есть необходимость вычислить изменения относительно какой-то конкретной ячейки, то важно зафиксировать ее значками “$”. Например, если перед нами стоит задача вычислить изменения объема продаж относительно Января, то формула будет такой:
На примере выше значения продаж каждого месяца сравниваются с данными продаж Января.
Как прибавить/вычесть процент к числу в Excel
При расчетах может понадобиться прибавить к какому-либо числу процент. Например, представим, что мы планируем расходы на отпуск. Для того чтобы рассчитать необходимую сумму денег на неделю отпуска, мы закладываем, что в отпуске будем тратить 30% больше чем в обычную рабочую неделю. Для такого расчета нам потребуется формула:
Например, мы хотим прибавить к числу “100” двадцать процентов, тогда формула будет следующая:
Если задача стоит вычесть 20% от числа “100”, то формула выглядит так:
Вернемся к нашей задаче. Запланируем, что на неделю отпуска мы будем тратить на 30% больше чем в регулярную неделю, а неделю после отпуска будем экономить и тратить на 30% меньше чем в неделю до отпуска. Тогда расчет нашего бюджета будет выглядеть так:
Что такое дельта-формула?
Формула дельты — это тип коэффициента, который сравнивает изменения цены актива с соответствующими изменениями цены его базового актива. Числитель — это изменение цены актива, которое отражает, как актив изменился с момента его последней цены. Активом может быть любой производный инструмент, такой как опцион колл или опцион пут. Опцион колл или опцион путВсе опционы колл предлагают право, но не обязательство купить базовый актив в определенную дату по заранее определенной цене исполнения. Напротив, опционы пут предлагают право, но не обязательство продать базовый актив в определенную дату по заранее установленной цене исполнения. Подробнее. В основе этих опционов лежат акции, и это ключевой аспект, влияющий на цены этих активов. На рынках капитала, на рынках капитала, рынок капитала — это место, где покупатели и продавцы взаимодействуют и торгуют финансовыми ценными бумагами, такими как долговые обязательства, акции, долговые инструменты, облигации и производные инструменты, такие как фьючерсы, опционы, свопы и биржевые фонды. (ETF). Есть два вида рынков: первичные рынки и вторичные рынки. Подробнее, эту дельту также называют коэффициентом хеджирования.
Оглавление
- Что такое дельта-формула?
- Примеры формулы дельты (с шаблоном Excel)
- Калькулятор формулы дельты
- Актуальность и использование
- Рекомендуемые статьи
Формула дельты:
Дельта = изменение цены актива / изменение цены базового актива.
Однако даже модель Блэка и Шоулза используется для определения значения дельты, где в ней есть переменная, которой является N(d1), которую можно рассчитать с помощью компьютерного программного обеспечения.
Примеры формулы дельты (с шаблоном Excel)
Давайте рассмотрим несколько простых и сложных примеров дельта-уравнения, чтобы лучше понять его.
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Delta Formula Excel здесь – Шаблон Excel с формулой дельты
Пример дельта-формулы #1
Предположим, что изменение цены актива составляет 0,6733, а изменение цены базового актива — 0,7788. Вам необходимо рассчитать дельту.
Решение:
Нам даны как цифры изменения цены актива, что составляет 0,6733, так и изменение цены базового актива, которое составляет 0,7788. Следовательно, мы можем использовать приведенное выше уравнение для расчета дельты.
Используйте приведенные ниже данные для расчета дельты.
- Изменение цены базового актива: 0,7788
- Изменение цены актива: 0,6733
Расчет дельты выглядит следующим образом:
Дельта = 0,6733 / 0,7788
Дельта будет –
Дельта = 0,8645
Следовательно, дельта будет 0,8645.
Пример дельта-формулы #2
Акции ABC торгуются в течение нескольких лет, но остаются весьма волатильными по своему характеру. Трейдеры и инвесторы несут убытки в связи с неестественным движением цены. Акции котируются уже пять лет, и теперь они имеют право выйти на рынок деривативов. Джон уже владеет этой акцией в своем портфеле.
Текущая цена акции составляет $88,92, а колл-опцион цены исполнения Цена исполнения или цена исполнения относится к цене, по которой базовая акция покупается или продается лицами, торгующими опционами колл и пут, доступными при торговле деривативами. . Таким образом, цена исполнения — это термин, используемый на рынке деривативов. Подробнее $87,95 торгуется по $1,35, срок экспирации которого составляет 1 месяц. Джон хочет хеджировать свою позицию, поэтому он хочет рассчитать дельту для этой акции. На следующий торговый день он замечает, что цена акций снизилась до 87,98 доллара, поэтому цена колл-опциона немного снизилась до 1,31 доллара.
На основе предоставленных данных вам необходимо рассчитать дельту, которая будет основой для коэффициента хеджирования Коэффициент хеджированияКоэффициент хеджирования представляет собой сравнительную величину коэффициента хеджирования открытой позиции с совокупным размером самой позиции. Кроме того, это может быть сравнительная стоимость купленных или проданных фьючерсных контрактов со стоимостью наличного товара, который хеджируется. Подробнее для трейдера.
Решение:
Используйте приведенные ниже данные для расчета дельты.
- Начальная цена колл-опциона: 1,35
- Цена опциона колл в конце: 1,31
- Цена акции в начале: 88,92
- Цена акции на конец: 87,98
Расчет дельты выглядит следующим образом:
Здесь активом является опцион колл, лежащий в основе акции. Итак, во-первых, мы узнаем изменение цены актива, то есть изменение цены колл-опциона, которое должно быть 1,35 доллара минус 1,31 доллара, что равно 0,04 доллара, и теперь изменение цены базового актива будет меньше 88,92 доллара. 87,98 долларов США, что равно 0,94 доллара США.
Мы можем использовать приведенное выше уравнение для расчета дельты (грубая цифра, истинная цифра может быть получена с помощью других сложных моделей, таких как Блэк и Шоулз)
Дельта = 0,04 00 долл. США/ 0,9400 долл. США
Дельта будет –
Дельта = 0,0426 доллара США
Следовательно, дельта будет равна 0,0426 доллара.
Пример дельта-формулы №3
JP Morgan — один из крупнейших инвестиционных банков. UBS.Подробнее в Соединенных Штатах Америки. У них есть несколько позиций по акциям, облигациям и производным инструментам, которые находятся в их балансе. Их балансовый отчет Балансовый отчет является одним из финансовых отчетов компании, в котором представлены акционерный капитал, обязательства и активы компании в определенный момент времени. Он основан на бухгалтерском уравнении, которое гласит, что сумма общих обязательств и собственного капитала равна общим активам компании. Подробнее. Одной из таких позиций являются акции WMD, которые торгуются по цене 52,67 доллара. У компании есть давняя подверженность этим акциям. На следующий торговый день акции торгуются по $51,78. Трейдер, действующий от имени компании, имеет возможность хеджировать убытки.
Цена исполнения опциона пут составляет 54,23 доллара, а в настоящее время он торгуется на уровне 3,92 доллара. Вчера цена опциона пут закрылась на уровне $3,75. Трейдер хочет узнать грубую дельту и просит вас рассчитать дельту пут-опциона WMD.
Решение:
Используйте приведенные ниже данные для расчета дельты.
- Опцион пут Начальная цена: 3,75
- Цена опциона пут в конце: 3,92
- Цена акции в начале: 52,67
- Цена акции на конец: 51,87
Расчет дельты выглядит следующим образом:
Здесь активом является опцион пут. Опцион пут Опцион пут — это финансовый инструмент, который дает покупателю право продать опцион в любое время до даты истечения контракта по заранее указанной цене, называемой ценой исполнения. Он защищает базовый актив от любого ожидаемого падения базового актива. Читать далее, и он лежит в основе акции. Итак, во-первых, мы узнаем изменение цены актива, то есть изменение цены опциона пут, которое должно быть 3,75 доллара минус 3,92 доллара, что равно -0,17 доллара, и теперь изменение базовой цены будет 52,67 доллара США минус 51,78 доллара США, что равно 0,99 доллара США.
Мы можем использовать приведенное выше уравнение для расчета дельты (грубая цифра, истинная цифра может быть получена с помощью других сложных моделей, таких как Блэк и Шоулз)
Дельта = -0,1700 долл. США / 0,8000 долл. США
Дельта будет –
Дельта =-0,2125$
Следовательно, дельта составит -0,2125 доллара.
Калькулятор формулы дельты
Вы можете использовать следующий калькулятор формулы дельты.
.cal-tbl td{ верхняя граница: 0 !важно; }.cal-tbl tr{ высота строки: 0.5em; } Только экран @media и (минимальная ширина устройства: 320 пикселей) и (максимальная ширина устройства: 480 пикселей) { .cal-tbl tr{ line-height: 1em !important; } } Изменение цены активаИзменение цены базовой дельты
Дельта = изменение цены актива = изменение цены базового актива 0 = 00
Актуальность и использование
Дельта — это жизненно важный расчет (в основном выполняемый с помощью программного обеспечения), так как это одна из ключевых причин того, что цены опциона движутся в определенном направлении, и это показатель того, как инвестировать. Поведение опциона пут и дельта опциона колл может быть в значительной степени предсказуемо и может быть очень полезным для трейдеров, портфельных менеджеров, индивидуальных инвесторов и менеджеров хедж-фондов.
Рекомендуемые статьи
Это было руководство по Формуле Дельта. Здесь мы предоставляем пошаговое руководство по расчету дельты, а также практические примеры и загружаемый шаблон Excel. Вы можете узнать больше о финансировании из следующих статей –
- Что делает портфельный менеджер?Что делает портфельный менеджер?Портфельный менеджер — это эксперт финансового рынка, который занимается стратегическим проектированием инвестиционных портфелей.Подробнее
- Формула альфаФормула альфаТермин альфа относится к индексу, который используется в различных финансовых моделях, включая модель ценообразования капитальных активов, для определения максимально возможного дохода от инвестиций с низким уровнем риска. Альфа портфеля = Фактическая доходность портфеля – Безрисковая доходность – β * (Рыночная доходность – Безрисковая доходность)Подробнее
- Гамма опционаГамма опционаГамма опциона – это диапазон изменения дельты опциона в ответ на единичное изменение цены базового актива. Гамма может быть выражена как вторая производная премии опциона по отношению к цене базового актива. читать далее
- Примеры производных инструментовПримеры производных инструментов Наиболее часто торгуемые производные инструменты — это форварды, фьючерсы, опционы и свопы. Их стоимость определяется другим базовым активом, которым могут быть товары, акции, облигации и т. д. Подробнее