e·qua·tion
(ĭ-kwā′zhən, -shən)
n.
1. The act or process of equating or of being equated.
2. The state of being equal.
3. Mathematics A statement asserting the equality of two expressions, usually written as a linear array of symbols that are separated into left and right sides and joined by an equal sign.
4. Chemistry A representation of a chemical reaction, usually written as a linear array in which the symbols and quantities of the reactants are separated from those of the products by an arrow or a set of opposing arrows.
5. A complex of variable elements or factors: «The world was full of equations … there must be an answer for everything, if only you knew how to set forth the questions» (Anne Tyler).
e·qua′tion·al adj.
e·qua′tion·al·ly adv.
American Heritage® Dictionary of the English Language, Fifth Edition. Copyright © 2016 by Houghton Mifflin Harcourt Publishing Company. Published by Houghton Mifflin Harcourt Publishing Company. All rights reserved.
equation
(ɪˈkweɪʒən; -ʃən)
n
1. (Mathematics) a mathematical statement that two expressions are equal: it is either an identity in which the variables can assume any value, or a conditional equation in which the variables have only certain values (roots)
2. the act of regarding as equal; equating
3. the act of making equal or balanced; equalization
4. a situation, esp one regarded as having a number of conflicting elements: what you want doesn’t come into the equation.
5. the state of being equal, equivalent, or equally balanced
6. a situation or problem in which a number of factors need to be considered
eˈquational adj
eˈquationally adv
Collins English Dictionary – Complete and Unabridged, 12th Edition 2014 © HarperCollins Publishers 1991, 1994, 1998, 2000, 2003, 2006, 2007, 2009, 2011, 2014
e•qua•tion
(ɪˈkweɪ ʒən, -ʃən)
n.
1. the act of equating or making equal.
2. the state of being equated or equal.
3. equally balanced state; equilibrium.
4. an expression or a proposition, often algebraic, asserting the equality of two quantities.
5. a symbolic representation in chemistry showing the kind and amount of the starting materials and products of a reaction.
[1350–1400; Middle English < Latin]
Random House Kernerman Webster’s College Dictionary, © 2010 K Dictionaries Ltd. Copyright 2005, 1997, 1991 by Random House, Inc. All rights reserved.
e·qua·tion
(ĭ-kwā′zhən)
1. Mathematics A written statement indicating the equality of two expressions. It consists of a sequence of symbols that is split into left and right sides joined by an equal sign. For example, 2 + 3 + 5 = 10 is an equation.
2. Chemistry A written representation of a chemical reaction, in which the symbols and amounts of the reactants are separated from those of the products by an equal sign, arrow, or a set of opposing arrows. For example, NaOH + HCl = NaCl + H2O is an equation.
The American Heritage® Student Science Dictionary, Second Edition. Copyright © 2014 by Houghton Mifflin Harcourt Publishing Company. Published by Houghton Mifflin Harcourt Publishing Company. All rights reserved.
ThesaurusAntonymsRelated WordsSynonymsLegend:
| Noun | 1. | math, mathematics, maths — a science (or group of related sciences) dealing with the logic of quantity and shape and arrangement regression equation, regression of y on x — the equation representing the relation between selected values of one variable (x) and observed values of the other (y); it permits the prediction of the most probable values of y simultaneous equations — a set of equations in two or more variables for which there are values that can satisfy all the equations simultaneously |
| 2. | equation — a state of being essentially equal or equivalent; equally balanced; «on a par with the best»
status, position — the relative position or standing of things or especially persons in a society; «he had the status of a minor»; «the novel attained the status of a classic»; «atheists do not enjoy a favorable position in American life» egalite, egality — social and political equality; «egality represents an extreme leveling of society» tie — equality of score in a contest |
|
| 3. | equation — the act of regarding as equal |
Based on WordNet 3.0, Farlex clipart collection. © 2003-2012 Princeton University, Farlex Inc.
equation
noun equating, match, agreement, balancing, pairing, comparison, parallel, equality, correspondence, likeness, equivalence, equalization the equation between higher spending and higher taxes
Collins Thesaurus of the English Language – Complete and Unabridged 2nd Edition. 2002 © HarperCollins Publishers 1995, 2002
equation
noun
The state of being equivalent:
The American Heritage® Roget’s Thesaurus. Copyright © 2013, 2014 by Houghton Mifflin Harcourt Publishing Company. Published by Houghton Mifflin Harcourt Publishing Company. All rights reserved.
Translations
rovnice
ligningregnestykke
yhtälö
jednadžba
egyenletkiegyenlítés
jafnaefnajafna
等しくすること
방정식
rovnica
enačba
ekvation
สมการ
phương trình
equation
[ɪˈkweɪʒən] N
2. (= linking) the equation of sth with sth → la identificación de algo con algo
Collins Spanish Dictionary — Complete and Unabridged 8th Edition 2005 © William Collins Sons & Co. Ltd. 1971, 1988 © HarperCollins Publishers 1992, 1993, 1996, 1997, 2000, 2003, 2005
Collins English/French Electronic Resource. © HarperCollins Publishers 2005
equation
Collins German Dictionary – Complete and Unabridged 7th Edition 2005. © William Collins Sons & Co. Ltd. 1980 © HarperCollins Publishers 1991, 1997, 1999, 2004, 2005, 2007
Collins Italian Dictionary 1st Edition © HarperCollins Publishers 1995
equate
(iˈkweit) verb
to regard as the same in some way. He equates money with happiness.
eˈquation (-ʒən) noun
1. a statement that two things are equal or the same. xy+xy=2xy is an equation.
2. a formula expressing the action of certain substances on others. 2H2 + O2 = 2 H2O is an equation.
Kernerman English Multilingual Dictionary © 2006-2013 K Dictionaries Ltd.
equation
→ مُعادَلة rovnice ligning Gleichung εξίσωση ecuación yhtälö équation jednadžba equazione 等しくすること 방정식 vergelijking likning równanie equação равенство ekvation สมการ eşitlik phương trình 等式
Multilingual Translator © HarperCollins Publishers 2009
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =.[2][3] The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.[4]
Solving an equation containing variables consists of determining which values of the variables make the equality true. The variables for which the equation has to be solved are also called unknowns, and the values of the unknowns that satisfy the equality are called solutions of the equation. There are two kinds of equations: identities and conditional equations. An identity is true for all values of the variables. A conditional equation is only true for particular values of the variables.[5][6]
An equation is written as two expressions, connected by an equals sign («=»).[2] The expressions on the two sides of the equals sign are called the «left-hand side» and «right-hand side» of the equation. Very often the right-hand side of an equation is assumed to be zero. This does not reduce the generality, as this can be realized by subtracting the right-hand side from both sides.
The most common type of equation is a polynomial equation (commonly called also an algebraic equation) in which the two sides are polynomials.
The sides of a polynomial equation contain one or more terms. For example, the equation
has left-hand side 

An equation is analogous to a scale into which weights are placed. When equal weights of something (e.g., grain) are placed into the two pans, the two weights cause the scale to be in balance and are said to be equal. If a quantity of grain is removed from one pan of the balance, an equal amount of grain must be removed from the other pan to keep the scale in balance. More generally, an equation remains in balance if the same operation is performed on its both sides.
In Cartesian geometry, equations are used to describe geometric figures. As the equations that are considered, such as implicit equations or parametric equations, have infinitely many solutions, the objective is now different: instead of giving the solutions explicitly or counting them, which is impossible, one uses equations for studying properties of figures. This is the starting idea of algebraic geometry, an important area of mathematics.
Algebra studies two main families of equations: polynomial equations and, among them, the special case of linear equations. When there is only one variable, polynomial equations have the form P(x) = 0, where P is a polynomial, and linear equations have the form ax + b = 0, where a and b are parameters. To solve equations from either family, one uses algorithmic or geometric techniques that originate from linear algebra or mathematical analysis. Algebra also studies Diophantine equations where the coefficients and solutions are integers. The techniques used are different and come from number theory. These equations are difficult in general; one often searches just to find the existence or absence of a solution, and, if they exist, to count the number of solutions.
Differential equations are equations that involve one or more functions and their derivatives. They are solved by finding an expression for the function that does not involve derivatives. Differential equations are used to model processes that involve the rates of change of the variable, and are used in areas such as physics, chemistry, biology, and economics.
The «=» symbol, which appears in every equation, was invented in 1557 by Robert Recorde, who considered that nothing could be more equal than parallel straight lines with the same length.[1]
Introduction[edit]
Analogous illustration[edit]
Illustration of a simple equation; x, y, z are real numbers, analogous to weights.
An equation is analogous to a weighing scale, balance, or seesaw.
Each side of the equation corresponds to one side of the balance. Different quantities can be placed on each side: if the weights on the two sides are equal, the scale balances, and in analogy, the equality that represents the balance is also balanced (if not, then the lack of balance corresponds to an inequality represented by an inequation).
In the illustration, x, y and z are all different quantities (in this case real numbers) represented as circular weights, and each of x, y, and z has a different weight. Addition corresponds to adding weight, while subtraction corresponds to removing weight from what is already there. When equality holds, the total weight on each side is the same.
Parameters and unknowns[edit]
Equations often contain terms other than the unknowns. These other terms, which are assumed to be known, are usually called constants, coefficients or parameters.
An example of an equation involving x and y as unknowns and the parameter R is
When R is chosen to have the value of 2 (R = 2), this equation would be recognized in Cartesian coordinates as the equation for the circle of radius of 2 around the origin. Hence, the equation with R unspecified is the general equation for the circle.
Usually, the unknowns are denoted by letters at the end of the alphabet, x, y, z, w, …, while coefficients (parameters) are denoted by letters at the beginning, a, b, c, d, … . For example, the general quadratic equation is usually written ax2 + bx + c = 0.
The process of finding the solutions, or, in case of parameters, expressing the unknowns in terms of the parameters, is called solving the equation. Such expressions of the solutions in terms of the parameters are also called solutions.
A system of equations is a set of simultaneous equations, usually in several unknowns for which the common solutions are sought. Thus, a solution to the system is a set of values for each of the unknowns, which together form a solution to each equation in the system. For example, the system
has the unique solution x = −1, y = 1.
Identities[edit]
An identity is an equation that is true for all possible values of the variable(s) it contains. Many identities are known in algebra and calculus. In the process of solving an equation, an identity is often used to simplify an equation, making it more easily solvable.
In algebra, an example of an identity is the difference of two squares:
which is true for all x and y.
Trigonometry is an area where many identities exist; these are useful in manipulating or solving trigonometric equations. Two of many that involve the sine and cosine functions are:
and
which are both true for all values of θ.
For example, to solve for the value of θ that satisfies the equation:
where θ is limited to between 0 and 45 degrees, one may use the above identity for the product to give:
yielding the following solution for θ:
Since the sine function is a periodic function, there are infinitely many solutions if there are no restrictions on θ. In this example, restricting θ to be between 0 and 45 degrees would restrict the solution to only one number.
Properties[edit]
Two equations or two systems of equations are equivalent, if they have the same set of solutions. The following operations transform an equation or a system of equations into an equivalent one – provided that the operations are meaningful for the expressions they are applied to:
- Adding or subtracting the same quantity to both sides of an equation. This shows that every equation is equivalent to an equation in which the right-hand side is zero.
- Multiplying or dividing both sides of an equation by a non-zero quantity.
- Applying an identity to transform one side of the equation. For example, expanding a product or factoring a sum.
- For a system: adding to both sides of an equation the corresponding side of another equation, multiplied by the same quantity.
If some function is applied to both sides of an equation, the resulting equation has the solutions of the initial equation among its solutions, but may have further solutions called extraneous solutions. For example, the equation 




The above transformations are the basis of most elementary methods for equation solving, as well as some less elementary ones, like Gaussian elimination.
Algebra[edit]
Polynomial equations[edit]
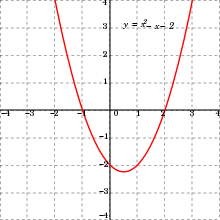
The solutions –1 and 2 of the polynomial equation x2 – x + 2 = 0 are the points where the graph of the quadratic function y = x2 – x + 2 cuts the x-axis.
In general, an algebraic equation or polynomial equation is an equation of the form
, or
[a]
where P and Q are polynomials with coefficients in some field (e.g., rational numbers, real numbers, complex numbers). An algebraic equation is univariate if it involves only one variable. On the other hand, a polynomial equation may involve several variables, in which case it is called multivariate (multiple variables, x, y, z, etc.).
For example,
is a univariate algebraic (polynomial) equation with integer coefficients and
is a multivariate polynomial equation over the rational numbers.
Some polynomial equations with rational coefficients have a solution that is an algebraic expression, with a finite number of operations involving just those coefficients (i.e., can be solved algebraically). This can be done for all such equations of degree one, two, three, or four; but equations of degree five or more cannot always be solved in this way, as the Abel–Ruffini theorem demonstrates.
A large amount of research has been devoted to compute efficiently accurate approximations of the real or complex solutions of a univariate algebraic equation (see Root finding of polynomials) and of the common solutions of several multivariate polynomial equations (see System of polynomial equations).
Systems of linear equations[edit]
A system of linear equations (or linear system) is a collection of linear equations involving one or more variables.[b] For example,
is a system of three equations in the three variables x, y, z. A solution to a linear system is an assignment of numbers to the variables such that all the equations are simultaneously satisfied. A solution to the system above is given by
since it makes all three equations valid. The word «system» indicates that the equations are to be considered collectively, rather than individually.
In mathematics, the theory of linear systems is a fundamental part of linear algebra, a subject which is used in many parts of modern mathematics. Computational algorithms for finding the solutions are an important part of numerical linear algebra, and play a prominent role in physics, engineering, chemistry, computer science, and economics. A system of non-linear equations can often be approximated by a linear system (see linearization), a helpful technique when making a mathematical model or computer simulation of a relatively complex system.
Geometry[edit]
Analytic geometry[edit]
The blue and red line is the set of all points (x,y) such that x+y=5 and —x+2y=4, respectively. Their intersection point, (2,3), satisfies both equations.
A conic section is the intersection of a plane and a cone of revolution.
In Euclidean geometry, it is possible to associate a set of coordinates to each point in space, for example by an orthogonal grid. This method allows one to characterize geometric figures by equations. A plane in three-dimensional space can be expressed as the solution set of an equation of the form 






A conic section is the intersection of a cone with equation 
The use of equations allows one to call on a large area of mathematics to solve geometric questions. The Cartesian coordinate system transforms a geometric problem into an analysis problem, once the figures are transformed into equations; thus the name analytic geometry. This point of view, outlined by Descartes, enriches and modifies the type of geometry conceived of by the ancient Greek mathematicians.
Currently, analytic geometry designates an active branch of mathematics. Although it still uses equations to characterize figures, it also uses other sophisticated techniques such as functional analysis and linear algebra.
Cartesian equations[edit]
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, that are marked using the same unit of length.
One can use the same principle to specify the position of any point in three-dimensional space by the use of three Cartesian coordinates, which are the signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines).
Cartesian coordinate system with a circle of radius 2 centered at the origin marked in red. The equation of a circle is (x − a)2 + (y − b)2 = r2 where a and b are the coordinates of the center (a, b) and r is the radius.
The invention of Cartesian coordinates in the 17th century by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra. Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by Cartesian equations: algebraic equations involving the coordinates of the points lying on the shape. For example, a circle of radius 2 in a plane, centered on a particular point called the origin, may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 4.
Parametric equations[edit]
A parametric equation for a curve expresses the coordinates of the points of the curve as functions of a variable, called a parameter.[7][8] For example,
are parametric equations for the unit circle, where t is the parameter. Together, these equations are called a parametric representation of the curve.
The notion of parametric equation has been generalized to surfaces, manifolds and algebraic varieties of higher dimension, with the number of parameters being equal to the dimension of the manifold or variety, and the number of equations being equal to the dimension of the space in which the manifold or variety is considered (for curves the dimension is one and one parameter is used, for surfaces dimension two and two parameters, etc.).
Number theory[edit]
Diophantine equations[edit]
A Diophantine equation is a polynomial equation in two or more unknowns for which only the integer solutions are sought (an integer solution is a solution such that all the unknowns take integer values). A linear Diophantine equation is an equation between two sums of monomials of degree zero or one. An example of linear Diophantine equation is ax + by = c where a, b, and c are constants. An exponential Diophantine equation is one for which exponents of the terms of the equation can be unknowns.
Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations. In more technical language, they define an algebraic curve, algebraic surface, or more general object, and ask about the lattice points on it.
The word Diophantine refers to the Hellenistic mathematician of the 3rd century, Diophantus of Alexandria, who made a study of such equations and was one of the first mathematicians to introduce symbolism into algebra. The mathematical study of Diophantine problems that Diophantus initiated is now called Diophantine analysis.
Algebraic and transcendental numbers[edit]
An algebraic number is a number that is a solution of a non-zero polynomial equation in one variable with rational coefficients (or equivalently — by clearing denominators — with integer coefficients). Numbers such as π that are not algebraic are said to be transcendental. Almost all real and complex numbers are transcendental.
Algebraic geometry[edit]
Algebraic geometry is a branch of mathematics, classically studying solutions of polynomial equations. Modern algebraic geometry is based on more abstract techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry.
The fundamental objects of study in algebraic geometry are algebraic varieties, which are geometric manifestations of solutions of systems of polynomial equations. Examples of the most studied classes of algebraic varieties are: plane algebraic curves, which include lines, circles, parabolas, ellipses, hyperbolas, cubic curves like elliptic curves and quartic curves like lemniscates, and Cassini ovals. A point of the plane belongs to an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve the study of the points of special interest like the singular points, the inflection points and the points at infinity. More advanced questions involve the topology of the curve and relations between the curves given by different equations.
Differential equations[edit]
A differential equation is a mathematical equation that relates some function with its derivatives. In applications, the functions usually represent physical quantities, the derivatives represent their rates of change, and the equation defines a relationship between the two. Because such relations are extremely common, differential equations play a prominent role in many disciplines including physics, engineering, economics, and biology.
In pure mathematics, differential equations are studied from several different perspectives, mostly concerned with their solutions — the set of functions that satisfy the equation. Only the simplest differential equations are solvable by explicit formulas; however, some properties of solutions of a given differential equation may be determined without finding their exact form.
If a self-contained formula for the solution is not available, the solution may be numerically approximated using computers. The theory of dynamical systems puts emphasis on qualitative analysis of systems described by differential equations, while many numerical methods have been developed to determine solutions with a given degree of accuracy.
Ordinary differential equations[edit]
An ordinary differential equation or ODE is an equation containing a function of one independent variable and its derivatives. The term «ordinary» is used in contrast with the term partial differential equation, which may be with respect to more than one independent variable.
Linear differential equations, which have solutions that can be added and multiplied by coefficients, are well-defined and understood, and exact closed-form solutions are obtained. By contrast, ODEs that lack additive solutions are nonlinear, and solving them is far more intricate, as one can rarely represent them by elementary functions in closed form: Instead, exact and analytic solutions of ODEs are in series or integral form. Graphical and numerical methods, applied by hand or by computer, may approximate solutions of ODEs and perhaps yield useful information, often sufficing in the absence of exact, analytic solutions.
Partial differential equations[edit]
A partial differential equation (PDE) is a differential equation that contains unknown multivariable functions and their partial derivatives. (This is in contrast to ordinary differential equations, which deal with functions of a single variable and their derivatives.) PDEs are used to formulate problems involving functions of several variables, and are either solved by hand, or used to create a relevant computer model.
PDEs can be used to describe a wide variety of phenomena such as sound, heat, electrostatics, electrodynamics, fluid flow, elasticity, or quantum mechanics. These seemingly distinct physical phenomena can be formalised similarly in terms of PDEs. Just as ordinary differential equations often model one-dimensional dynamical systems, partial differential equations often model multidimensional systems. PDEs find their generalisation in stochastic partial differential equations.
Types of equations[edit]
Equations can be classified according to the types of operations and quantities involved. Important types include:
- An algebraic equation or polynomial equation is an equation in which both sides are polynomials (see also system of polynomial equations). These are further classified by degree:
- linear equation for degree one
- quadratic equation for degree two
- cubic equation for degree three
- quartic equation for degree four
- quintic equation for degree five
- sextic equation for degree six
- septic equation for degree seven
- octic equation for degree eight
- A Diophantine equation is an equation where the unknowns are required to be integers
- A transcendental equation is an equation involving a transcendental function of its unknowns
- A parametric equation is an equation in which the solutions for the variables are expressed as functions of some other variables, called parameters appearing in the equations
- A functional equation is an equation in which the unknowns are functions rather than simple quantities
- Equations involving derivatives, integrals and finite differences:
- A differential equation is a functional equation involving derivatives of the unknown functions, where the function and its derivatives are evaluated at the same point, such as
. Differential equations are subdivided into ordinary differential equations for functions of a single variable and partial differential equations for functions of multiple variables
- An integral equation is a functional equation involving the antiderivatives of the unknown functions. For functions of one variable, such an equation differs from a differential equation primarily through a change of variable substituting the function by its derivative, however this is not the case when the integral is taken over an open surface
- An integro-differential equation is a functional equation involving both the derivatives and the antiderivatives of the unknown functions. For functions of one variable, such an equation differs from integral and differential equations through a similar change of variable.
- A functional differential equation of delay differential equation is a function equation involving derivatives of the unknown functions, evaluated at multiple points, such as
- A difference equation is an equation where the unknown is a function f that occurs in the equation through f(x), f(x−1), …, f(x−k), for some whole integer k called the order of the equation. If x is restricted to be an integer, a difference equation is the same as a recurrence relation
- A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process
- A differential equation is a functional equation involving derivatives of the unknown functions, where the function and its derivatives are evaluated at the same point, such as
See also[edit]
- Formula
- History of algebra
- Indeterminate equation
- List of equations
- List of scientific equations named after people
- Term (logic)
- Theory of equations
- Cancelling out
Notes[edit]
- ^ As such an equation can be rewritten P – Q = 0, many authors do not consider this case explicitly.
- ^ The subject of this article is basic in mathematics, and is treated in a lot of textbooks. Among them, Lay 2005, Meyer 2001, and Strang 2005 contain the material of this article.
References[edit]
- ^ a b Recorde, Robert, The Whetstone of Witte … (London, England: Jhon Kyngstone, 1557), the third page of the chapter «The rule of equation, commonly called Algebers Rule.»
- ^ a b «Equation — Math Open Reference». www.mathopenref.com. Retrieved 2020-09-01.
- ^ «Equations and Formulas». www.mathsisfun.com. Retrieved 2020-09-01.
- ^ Marcus, Solomon; Watt, Stephen M. «What is an Equation?». Retrieved 2019-02-27.
- ^ Lachaud, Gilles. «Équation, mathématique». Encyclopædia Universalis (in French).
- ^ «A statement of equality between two expressions. Equations are of two types, identities and conditional equations (or usually simply «equations»)». « Equation », in Mathematics Dictionary, Glenn James [de] et Robert C. James (éd.), Van Nostrand, 1968, 3 ed. 1st ed. 1948, p. 131.
- ^ Thomas, George B., and Finney, Ross L., Calculus and Analytic Geometry, Addison Wesley Publishing Co., fifth edition, 1979, p. 91.
- ^ Weisstein, Eric W. «Parametric Equations.» From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/ParametricEquations.html
External links[edit]
- Winplot: General Purpose plotter that can draw and animate 2D and 3D mathematical equations.
- Equation plotter: A web page for producing and downloading pdf or postscript plots of the solution sets to equations and inequations in two variables (x and y).
1
b(1)
: an element affecting a process : factor
(2)
: a complex of variable factors
c
: a state of being equated
specifically
: a state of close association or identification
bring governmental enterprises and payment for them into immediate equation —
2
a
: a usually formal statement of the equality or equivalence of mathematical or logical expressions
b
: an expression representing a chemical reaction quantitatively by means of chemical symbols
Example Sentences
the equation of material wealth with happiness
Recent Examples on the Web
Both sides of that equation have been overtaken by geopolitics.
—
As the bitter fight over President Emmanuel Macron’s hugely unpopular changes to the French pension system demonstrates, however, the French have to work hard to maintain the life side of that work-life equation.
—
Part of that equation changed Monday, when the district updated that figure to $5.12 billion — while also stating the system’s potential financial risk is unchanged and the available money for employee raises may be tighter than before.
—
The other part of that equation is the ease and honesty of all the controls.
—
And seventh grade is when her tell-tale red entered the equation.
—
How do the Mets move on? Oddly, Robertson is now part of that equation.
—
Fewer active workers pay the pensions of a growing number of retirees, who live longer: That equation does not work.
—
And while there is a glimmer of hope out there—avocados, chicken, bacon, and other favorites have dipped in price as of late—oranges are not a part of that economic equation.
—
See More
These examples are programmatically compiled from various online sources to illustrate current usage of the word ‘equation.’ Any opinions expressed in the examples do not represent those of Merriam-Webster or its editors. Send us feedback about these examples.
Word History
First Known Use
14th century, in the meaning defined at sense 1a
Time Traveler
The first known use of equation was
in the 14th century
Dictionary Entries Near equation
Cite this Entry
“Equation.” Merriam-Webster.com Dictionary, Merriam-Webster, https://www.merriam-webster.com/dictionary/equation. Accessed 13 Apr. 2023.
Share
More from Merriam-Webster on equation
Last Updated:
6 Apr 2023
— Updated example sentences
Subscribe to America’s largest dictionary and get thousands more definitions and advanced search—ad free!
Merriam-Webster unabridged
Educalingo cookies are used to personalize ads and get web traffic statistics. We also share information about the use of the site with our social media, advertising and analytics partners.
Download the app
educalingo

Risk and failure is a part of our equation, and if you are seeing too little failure, you are actually probably not taking enough risks.
Peter Barris
PRONUNCIATION OF EQUATION
GRAMMATICAL CATEGORY OF EQUATION
Equation is a noun.
A noun is a type of word the meaning of which determines reality. Nouns provide the names for all things: people, objects, sensations, feelings, etc.
WHAT DOES EQUATION MEAN IN ENGLISH?
Equation
In mathematics, an equation is a formula of the form A = B, where A and B are expressions that may contain one or several variables called unknowns, and «=» denotes the equality binary relation. Although written in the form of proposition, an equation is not a statement that is either true or false, but a problem consisting of finding the values, called solutions, that, when substituted for the unknowns, yield equal values of the expressions A and B. For example, 2 is the unique solution of the equation x + 2 = 4, in which the unknown is x. Historically, equations arose from the mathematical discipline of algebra, but later become ubiquitous. «Equations» should not be confused with «identities», which are presented with the same notation but have a different meaning: for example 2 + 2 = 4 and x + y = y + x are identities in arithmetic, and do not constitute a values-finding problem, even when variables are present as in the latter example.
Definition of equation in the English dictionary
The first definition of equation in the dictionary is a mathematical statement that two expressions are equal: it is either an identity in which the variables can assume any value, or a conditional equation in which the variables have only certain values. Other definition of equation is the act of regarding as equal; equating. Equation is also the act of making equal or balanced; equalization.
WORDS THAT RHYME WITH EQUATION
Synonyms and antonyms of equation in the English dictionary of synonyms
SYNONYMS OF «EQUATION»
The following words have a similar or identical meaning as «equation» and belong to the same grammatical category.
Translation of «equation» into 25 languages

TRANSLATION OF EQUATION
Find out the translation of equation to 25 languages with our English multilingual translator.
The translations of equation from English to other languages presented in this section have been obtained through automatic statistical translation; where the essential translation unit is the word «equation» in English.
Translator English — Chinese
等式
1,325 millions of speakers
Translator English — Spanish
ecuación
570 millions of speakers
English
equation
510 millions of speakers
Translator English — Hindi
समीकरण
380 millions of speakers
Translator English — Arabic
مُعادَلة
280 millions of speakers
Translator English — Russian
равенство
278 millions of speakers
Translator English — Portuguese
equação
270 millions of speakers
Translator English — Bengali
সমীকরণ
260 millions of speakers
Translator English — French
équation
220 millions of speakers
Translator English — Malay
Persamaan
190 millions of speakers
Translator English — German
Gleichung
180 millions of speakers
Translator English — Japanese
等しくすること
130 millions of speakers
Translator English — Korean
방정식
85 millions of speakers
Translator English — Javanese
Persamaan
85 millions of speakers
Translator English — Vietnamese
phương trình
80 millions of speakers
Translator English — Tamil
சமன்பாடு
75 millions of speakers
Translator English — Marathi
समीकरण
75 millions of speakers
Translator English — Turkish
denklem
70 millions of speakers
Translator English — Italian
equazione
65 millions of speakers
Translator English — Polish
równanie
50 millions of speakers
Translator English — Ukrainian
рівняння
40 millions of speakers
Translator English — Romanian
ecuație
30 millions of speakers
Translator English — Greek
εξίσωση
15 millions of speakers
Translator English — Afrikaans
vergelyking
14 millions of speakers
Translator English — Swedish
ekvation
10 millions of speakers
Translator English — Norwegian
likning
5 millions of speakers
Trends of use of equation
TENDENCIES OF USE OF THE TERM «EQUATION»
The term «equation» is very widely used and occupies the 9.733 position in our list of most widely used terms in the English dictionary.

FREQUENCY
Very widely used
The map shown above gives the frequency of use of the term «equation» in the different countries.
Principal search tendencies and common uses of equation
List of principal searches undertaken by users to access our English online dictionary and most widely used expressions with the word «equation».
FREQUENCY OF USE OF THE TERM «EQUATION» OVER TIME
The graph expresses the annual evolution of the frequency of use of the word «equation» during the past 500 years. Its implementation is based on analysing how often the term «equation» appears in digitalised printed sources in English between the year 1500 and the present day.
Examples of use in the English literature, quotes and news about equation
10 QUOTES WITH «EQUATION»
Famous quotes and sentences with the word equation.
I am much more wired to be an athlete than anything else. I understand the ‘hard work = payoff’ equation in sports. I run marathons and I box. And that’s my Puerto Rican flag hanging in Freddie Roach’s Wild Card Boxing gym. I gave it to him. My last N.Y.C. marathon time I ran in three hours flat.
If your DNA profile puts you at a higher risk of developing obesity, that doesn’t mean it’s your fate. You can take control of the environmental side of the equation and reduce your overall lifetime risk by a lot.
I have no hang-ups in life. I don’t care about groups and camps. I have been brought up with certain values and ethics. I have never been egoistic about my stardom and lineage. I don’t have any qualms about breaking the ice with my colleagues. I can walk up to any actor and greet him, irrespective of what kind of equation I share with him.
Risk and failure is a part of our equation, and if you are seeing too little failure, you are actually probably not taking enough risks.
In my experience, take the Holy Spirit out of the equation of your life and it spells boring. Add it into the equation of your life and you never know where you are going to go, what you are going to do, or who you are going to meet.
There’s no doubt that scientific training helps many authors to write better science fiction. And yet, several of the very best were English majors who could not parse a differential equation to save their lives.
Many people still believe that ‘green’ solutions are too expensive, but they are actually much cheaper when all of the costs to public health, social services, and waste handling are factored into the same equation.
Many training programs and often schools focus on just a skill or a kind of work competency. That’s only half the equation.
When you write, you take the ball and you hold it up to the light and you turn it slowly, and let people draw their own conclusions. And try to bring empathy to all sides of the equation.
The only difference was one of them was trying to make a perfect cake and one of them was trying to write a great book. But if we remove that from the equation, it’s the same impulse and they are equally entitled to their ecstasies and their despair.
10 ENGLISH BOOKS RELATING TO «EQUATION»
Discover the use of equation in the following bibliographical selection. Books relating to equation and brief extracts from same to provide context of its use in English literature.
1
The Human Equation: Building Profits by Putting People First
Criticizes many common personnel management practices, and argues that policies such as job security and fair compensation result in greater profits in the long run
2
The Procrastination Equation: How to Stop Putting Things Off …
Writing with a combination of humour, humanity and scientific research, Piers Steel explains why we procrastinate — why we knowingly and willingly put off a course of action despite recognising we’ll be worse off for it.
3
The Success Equation: Untangling Skill and Luck in Business, …
He offers concrete suggestions for how to put these insights to work to your advantage in business and other dimensions of life.
4
Parabolic Equation Methods for Electromagnetic Wave Propagation
This volume introduces the mathematical background to parabolic equation modelling and describes simple parabolic equation algorithms before progressing to more advanced topics, including domain truncation, impedance boundaries and the …
Mireille Levy, Institution of Electrical Engineers, 2000
5
Handbook of Structural Equation Modeling
«This handbook offers comprehensive coverage of structural equation modeling (SEM), beginning with background issues, continuing through statistical underpinnings and steps in implementation, then moving into basic and advanced applications …
6
The Duffing Equation: Nonlinear Oscillators and their Behaviour
The editors and the contributors explain the mathematical techniques required to study nonlinear dynamics, helping the reader with little mathematical background to understand the text.
Dr Ivana Kovacic, Michael J. Brennan, 2011
7
The One-Dimensional Heat Equation
This is a version of Gevrey’s classical treatise on the heat equations. Included in this volume are discussions of initial and/or boundary value problems, numerical methods, free boundary problems and parameter determination problems.
8
The Fokker-Planck Equation: Methods of Solution and Applications
The author of this book, Hannes Risken, has made substantial contributions to the development and application of such methods, e.g., to laser physics, diffusion in periodic potentials, and other problems.
9
Ordinary & Partial Diff.Equation
Tremendous response from teachers and students to the last edition of this book has necessiated the revision of the book in a very short span of time.The present edition has been throughly revised and enlarged.Many new important topics have …
10
Structural Equation Modeling: Applications Using Mplus
By following the examples provided in this book, readers will be able to build their own SEM models using Mplus. Teachers, graduate students, and researchers in social sciences and health studies will also benefit from this book.
Jichuan Wang, Xiaoqian Wang, 2012
10 NEWS ITEMS WHICH INCLUDE THE TERM «EQUATION»
Find out what the national and international press are talking about and how the term equation is used in the context of the following news items.
“Money” out of equation!
Floyd Mayweather Jr. poses during his weigh-in on Friday, May 1, 2015 in Las Vegas. The world weltherweight title fight between Mayweather … «Clitheroe Today, Jul 15»
Karan Johar’s equation with Kajol and her family
While Ajay Devgn’s equation with Shah Rukh seems to be getting bak on track, let’s take a look at Ajay Devgn and Kajol’s equation with Karan Johar. «Times of India, Jul 15»
FrancisChurch Doctrine In One Simple Equation
Why is it that Pope Francis seems to be deathly afraid of physical separation. To him, Heaven is like one enormous living pile. It doesn’t matter … «Pewsitter, Jul 15»
Food Brands Must Embrace New Value Equation To Win With …
The traditional food value equation is rapidly changing in order to keep up with the modern consumer. Millennials will only interact with brands … «Forbes, Jul 15»
Figuring Out Basware in the P2P and Trade Financing Equation
Basware doesn’t enjoy sitting still. When I first dove into the provider in the early days of Spend Matters, it was deeply rooted in the enterprise … «Spend Matters, Jul 15»
Schoolboy corrects mistake in equation at Boston’s Museum of …
A 15-year-old secondary school pupil corrected a mistake “which had been there for a very long time” in an equation at Boston’s venerable … «The Independent, Jul 15»
Perfect Equation
1990s megastar Nana Patekar (Tirangaa, Krantiveer, Agni Sakshi) is back. He takes on his comic-serious role from Welcome again in the … «The New Indian Express, Jul 15»
Waady enters Haydock equation
John Gosden feels the Sprint Cup at Haydock should be the major objective for the fast-improving Waady. The three-year-old overcame trouble … «Racinguk.com — pure racing entertainment, Jul 15»
Providers add population health management to chronic care equation
The Affordable Care Act (ACA) continues to drive changes in healthcare providers’ strategies for treating and managing chronic conditions … «FierceHealthcare, Jul 15»
New Studies Expand the BRCA Equation in Breast Cancer
Although BRCA1/2 mutations have been intensely studied in breast cancer for more than a decade, researchers are still seeking to determine … «OncLive, Jul 15»
REFERENCE
« EDUCALINGO. Equation [online]. Available <https://educalingo.com/en/dic-en/equation>. Apr 2023 ».
Download the educalingo app


Discover all that is hidden in the words on
- Top Definitions
- Quiz
- Related Content
- Examples
- British
- Scientific
- Cultural
This shows grade level based on the word’s complexity.
[ ih-kwey-zhuhn, -shuhn ]
/ ɪˈkweɪ ʒən, -ʃən /
This shows grade level based on the word’s complexity.
noun
the act of equating or making equal; equalization: the symbolic equation of darkness with death.
equally balanced state; equilibrium.
Mathematics. an expression or a proposition, often algebraic, asserting the equality of two quantities.
Also called chemical equation .Chemistry. a symbolic representation showing the kind and amount of the starting materials and products of a reaction.
QUIZ
CAN YOU ANSWER THESE COMMON GRAMMAR DEBATES?
There are grammar debates that never die; and the ones highlighted in the questions in this quiz are sure to rile everyone up once again. Do you know how to answer the questions that cause some of the greatest grammar debates?
Which sentence is correct?
Origin of equation
1350–1400; Middle English <Latin aequātiōn- (stem of aequātiō) an equalizing. See equate, -ion
OTHER WORDS FROM equation
non·e·qua·tion, noun
Words nearby equation
Equanil, equanimity, equanimous, equant, equate, equation, equational, equational verb, equation movement, equation of motion, equation of state
Dictionary.com Unabridged
Based on the Random House Unabridged Dictionary, © Random House, Inc. 2023
Words related to equation
How to use equation in a sentence
-
The right-hand side of the equations describes the contents of the universe — anything that has mass and energy.
-
In other words, machines that augment or supersede organic biology and change the equation limiting the scope of how, where, and when “genetic” information can be shared and transferred.
-
The scientists took this curve and developed a new mathematical equation to calculate a dog’s age.
-
Whatever the reason, once these individuals become infected and are removed from the equation through death or immunity, the effect on the pandemic is outsized.
-
The equations of general relativity let them evolve independently, and, crucially, you can flatten the universe by changing either.
-
Perhaps, like Hawking searching for his elegant equation, filmmakers will never find the answer.
-
But vibrant industry requires solid infrastructure, which is where the Chinese government enters the equation.
-
Until that equation tips, individual Republicans may break ranks on gay rights, but the party remains a countercultural bastion.
-
“We want to take out those biases, those prejudices, out of the equation, to remove those barriers,” says Halfteck.
-
Sadly, the “small room” part of that equation seems to have been a one-time thing.
-
Now the trouble with the main proposition just quoted is that each side of the equation is used as the measure of the other.
-
In other words, it is a truism, mere equation in terms, telling nothing whatever.
-
The fundamental equation of the economist, then, is that the value of everything is proportionate to its cost.
-
We are ourselves a term in the equation, a note of the chord, and make discord or harmony almost at will.
-
Inserting these values in our general equation and calculating the result, we obtain 18.1E6 as the value of the constant.
British Dictionary definitions for equation
noun
a mathematical statement that two expressions are equal: it is either an identity in which the variables can assume any value, or a conditional equation in which the variables have only certain values (roots)
the act of regarding as equal; equating
the act of making equal or balanced; equalization
a situation, esp one regarded as having a number of conflicting elementswhat you want doesn’t come into the equation
the state of being equal, equivalent, or equally balanced
a situation or problem in which a number of factors need to be considered
Derived forms of equation
equational, adjectiveequationally, adverb
Collins English Dictionary — Complete & Unabridged 2012 Digital Edition
© William Collins Sons & Co. Ltd. 1979, 1986 © HarperCollins
Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Scientific definitions for equation
Mathematics A written statement indicating the equality of two expressions. It consists of a sequence of symbols that is split into left and right sides joined by an equal sign. For example, 2 + 3 + 5 = 10 is an equation.
Chemistry A written representation of a chemical reaction, in which the symbols and amounts of the reactants are separated from those of the products by an equal sign, arrow, or a set of opposing arrows. For example, Ca(OH)2 + H2SO4 = CaSO4 + 2H2O, is an equation.
The American Heritage® Science Dictionary
Copyright © 2011. Published by Houghton Mifflin Harcourt Publishing Company. All rights reserved.
Cultural definitions for equation
An expression of equality between two formulas in mathematics. The two formulas are written with an equal sign between them: 2 + 2 = 4 is an equation, as is E = mc2.
The New Dictionary of Cultural Literacy, Third Edition
Copyright © 2005 by Houghton Mifflin Harcourt Publishing Company. Published by Houghton Mifflin Harcourt Publishing Company. All rights reserved.
Полезное
Смотреть что такое «equation» в других словарях:
-
Equation — Équation (mathématiques) Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
-
équation — [ ekwasjɔ̃ ] n. f. • 1613; h. XIIIe « égalité »; lat. æquatio 1 ♦ (1637) Math. Relation conditionnelle existant entre deux quantités et dépendant de certaines variables (ou inconnues). Poser une équation. Mettre en équation un phénomène complexe … Encyclopédie Universelle
-
Equation — E*qua tion, n. [L. aequatio an equalizing: cf. F. [ e]quation equation. See {Equate}.] 1. A making equal; equal division; equality; equilibrium. [1913 Webster] Again the golden day resumed its right, And ruled in just equation with the night.… … The Collaborative International Dictionary of English
-
equation — e‧qua‧tion [ɪˈkweɪʒn] noun [countable] a statement in mathematics, showing that two quantities are equal acˈcounting eˌquation one of the relationships between assets and liabilities used in accounting: • The accounting equation here is: assets… … Financial and business terms
-
equation — [ē kwā′zhən, ikwā′zhən] n. [ME equacioun < L aequatio] 1. the act of equating; equalization 2. the state of being equated; equality, equivalence, or balance; also, identification or association 3. a) a complex whole [the human equation] b) an… … English World dictionary
-
equation — index balance (equality), comparison, parity Burton s Legal Thesaurus. William C. Burton. 2006 … Law dictionary
-
equation — late 14c., a term in astrology; meaning “action of making equal” is from 1650s; mathematical sense is from 1560s, on notion of equalizing the expressions; from L. aequationem (nom. aequatio) an equal distribution, community, from pp. stem of… … Etymology dictionary
-
equation — ► NOUN 1) the process of equating one thing with another. 2) Mathematics a statement that the values of two mathematical expressions are equal (indicated by the sign =). 3) Chemistry a symbolic representation of the changes which occur in a… … English terms dictionary
-
Équation — Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
-
Equation — This article is about equations in mathematics. For the chemistry term, see chemical equation. The first use of an equals sign, equivalent to 14x+15=71 in modern notation. From The Whetstone of Witte by Robert Recorde (1557). An equation is a… … Wikipedia
-
equation — /i kway zheuhn, sheuhn/, n. 1. the act of equating or making equal; equalization: the symbolic equation of darkness with death. 2. equally balanced state; equilibrium. 3. Math. an expression or a proposition, often algebraic, asserting the… … Universalium
| Word | EQUATION |
| Character | 8 |
| Hyphenation | e qua tion |
| Pronunciations | /ɪˈkweɪʃən/ |
Sorry, your browser does not support the audio element!
What do we mean by equation?
The act or process of equating or of being equated. noun
The state of being equal. noun
A statement asserting the equality of two expressions, usually written as a linear array of symbols that are separated into left and right sides and joined by an equal sign. noun
A representation of a chemical reaction, usually written as a linear array in which the symbols and quantities of the reactants are separated from those of the products by an arrow or a set of opposing arrows. noun
A complex of variable elements or factors. noun
In the calculus, an equation which contains no differentials. noun
A making equal, or an equal division; equality. noun
In mathematics, a proposition asserting the equality of two quantities, and expressed by the sign = between them; or an expression of the same quantity in two terms dissimilar but of equal value: as, 3 lb. = 48 oz.; x = b + m − r. noun
In astronomy, the correction or quantity to be added to or subtracted from the mean position of a heavenly body to obtain the true position; also, in a more general sense, the correction arising from any erroneous supposition whatever. noun
In chem., a collection of symbols used to indicate that two or more definite bodies, simple or compound, having been brought within the sphere of chemical action, a reaction will take place, and new bodies be produced. noun
An equation for the steady motion of a liquid, namely, where p is the pressure, ρ the density, V the potential of the impressed forces, q the velocity, and C a constant for each stream-line and vortex-line, and in the case of irrotational motion a constant for all space. noun
With modern writers, a solution which is a particular case of the general solution; noun
With older writers, any solution not general. A singular solution is one which is neither general nor implied in the general solution. The complete integral of a partial differential equation is a solution containing the full number of arbitrary constants or functions. noun
In modern writings, the correction to be applied to the position of a planet or to the time of an eclipse, etc., owing to the finite velocity of light. noun
In modern astron., the excess of the true over the mean anomaly. (Gauss, Theoria Motus, I. 7.) noun
The equation of the argument. (Kepler, De Motibus Martis, I. iv.) noun
Any one of the usual equations of hydrodynamics, where the components of the velocity at fixed points of space are taken as variables: so called in contradistinction to the Lagrangian equations where the coordinates of a definite particle are taken as variables; these equations, though also discovered by Euler, having been used by Lagrauge. noun
A general equation of hydrodynamics, in which, instead of considering the velocity at each fixed point of space, the motion of each particle is followed out. This is called a Lagrangian equation because used by Lagrange in his “Méchanique Analitique,” though invented by Euler. noun
An equation of analytical geometry in which certain curves are represented by single letters. Thus, if U = 0, V = 0, W = 0, represent the equations of three circles, UV = W is the symbolic equation of a bicircular quartic noun
The act or process of equating two or more things, or the state of those things being equal (that is, identical).
An assertion that two expressions are equal, expressed by writing the two expressions separated by an equal sign; from which one is to determine a particular quantity.
A small correction to observed values to remove the effects of systematic errors in an observation.
The equator is like a hula hoop for the earth Urban Dictionary
When you are fucking a girl and when you are about to cum, pull out, tell the girl to spin like a top, and you leave a nice trail around her waist. Experts can attempt the prime meridian or the tropic of breast cancer. Urban Dictionary
Maths with fancy letters called pronumerals. It is useless shit that everyone forgets how to do after they graduate. Urban Dictionary
Eqaut is a spell to summon the legends of the equat havin azz darndiddly biddly doo of ur grandpa’s ashy pants from vietnam in the lost havin azz dumb cunt city of grU༼ ͡° ͜ʖ ͡° ༽. «god, 6969 b.c from the book of washing machine jorge» Urban Dictionary
Something too hard to solve,
takes too much time.
AIN’T NOBODY GOT TIME FO MATH. Urban Dictionary
A line on an globe that splits between continents and the north and the south . Urban Dictionary
The 0 degree line of latitude on a map or globe Urban Dictionary
A word that means nothing but you tell people it to make them confused Urban Dictionary
A word you say to people but it means nothing Urban Dictionary
The incorrect spelling of Ecuador Urban Dictionary
Other forms: equations
In an equation, the quantities on both sides of the equal sign are equal. That’s the mathematical meaning of equation, but equation can also be used in any number of situations, challenges, or efforts to solve a problem.
The «equa» at the beginning of equation will be familiar from other words such as «equal,» «equality,» and «equate.» All of these words have to do with making things balance out.
An equation is a statement of the equality of two quantities. If that equation is not a mathematical one but rather, say, an interpersonal one, it’s still a situation in which you might try to make the two sides equal. For example, taking marriage out of the equation might make it easier for two people to decide to stay together for a while.
Definitions of equation
-
noun
a mathematical statement that two expressions are equal
-
noun
the act of regarding as equal
-
noun
a state of being essentially equal or equivalent; equally balanced
-
synonyms:
equality, equivalence, par
see moresee less-
types:
-
egalite, egality
social and political equality
-
tie
equality of score in a contest
-
deuce
a tie in tennis or table tennis that requires winning two successive points to win the game
-
type of:
-
position, status
the relative position or standing of things or especially persons in a society
-
egalite, egality
DISCLAIMER: These example sentences appear in various news sources and books to reflect the usage of the word ‘equation’.
Views expressed in the examples do not represent the opinion of Vocabulary.com or its editors.
Send us feedback
EDITOR’S CHOICE
Look up equation for the last time
Close your vocabulary gaps with personalized learning that focuses on teaching the
words you need to know.
Sign up now (it’s free!)
Whether you’re a teacher or a learner, Vocabulary.com can put you or your class on the path to systematic vocabulary improvement.
Get started


- Entertainment & Pop Culture
- Geography & Travel
- Health & Medicine
- Lifestyles & Social Issues
- Literature
- Philosophy & Religion
- Politics, Law & Government
- Science
- Sports & Recreation
- Technology
- Visual Arts
- World History
- On This Day in History
- Quizzes
- Podcasts
- Dictionary
- Biographies
- Summaries
- Top Questions
- Infographics
- Demystified
- Lists
- #WTFact
- Companions
- Image Galleries
- Spotlight
- The Forum
- One Good Fact
- Entertainment & Pop Culture
- Geography & Travel
- Health & Medicine
- Lifestyles & Social Issues
- Literature
- Philosophy & Religion
- Politics, Law & Government
- Science
- Sports & Recreation
- Technology
- Visual Arts
- World History
- Britannica Explains
In these videos, Britannica explains a variety of topics and answers frequently asked questions. - Britannica Classics
Check out these retro videos from Encyclopedia Britannica’s archives. - Demystified Videos
In Demystified, Britannica has all the answers to your burning questions. - #WTFact Videos
In #WTFact Britannica shares some of the most bizarre facts we can find. - This Time in History
In these videos, find out what happened this month (or any month!) in history.
- Student Portal
Britannica is the ultimate student resource for key school subjects like history, government, literature, and more. - COVID-19 Portal
While this global health crisis continues to evolve, it can be useful to look to past pandemics to better understand how to respond today. - 100 Women
Britannica celebrates the centennial of the Nineteenth Amendment, highlighting suffragists and history-making politicians. - Saving Earth
Britannica Presents Earth’s To-Do List for the 21st Century. Learn about the major environmental problems facing our planet and what can be done about them! - SpaceNext50
Britannica presents SpaceNext50, From the race to the Moon to space stewardship, we explore a wide range of subjects that feed our curiosity about space!