Scientific laws or laws of science are statements, based on repeated experiments or observations, that describe or predict a range of natural phenomena.[1] The term law has diverse usage in many cases (approximate, accurate, broad, or narrow) across all fields of natural science (physics, chemistry, astronomy, geoscience, biology). Laws are developed from data and can be further developed through mathematics; in all cases they are directly or indirectly based on empirical evidence. It is generally understood that they implicitly reflect, though they do not explicitly assert, causal relationships fundamental to reality, and are discovered rather than invented.[2]
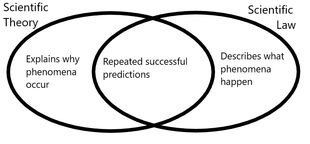
Scientific theories explain why something happens, whereas scientific law describes what happens.
Scientific laws summarize the results of experiments or observations, usually within a certain range of application. In general, the accuracy of a law does not change when a new theory of the relevant phenomenon is worked out, but rather the scope of the law’s application, since the mathematics or statement representing the law does not change. As with other kinds of scientific knowledge, scientific laws do not express absolute certainty, as mathematical theorems or identities do. A scientific law may be contradicted, restricted, or extended by future observations.
A law can often be formulated as one or several statements or equations, so that it can predict the outcome of an experiment. Laws differ from hypotheses and postulates, which are proposed during the scientific process before and during validation by experiment and observation. Hypotheses and postulates are not laws, since they have not been verified to the same degree, although they may lead to the formulation of laws. Laws are narrower in scope than scientific theories, which may entail one or several laws.[3] Science distinguishes a law or theory from facts.[4] Calling a law a fact is ambiguous, an overstatement, or an equivocation.[5] The nature of scientific laws has been much discussed in philosophy, but in essence scientific laws are simply empirical conclusions reached by scientific method; they are intended to be neither laden with ontological commitments nor statements of logical absolutes.
OverviewEdit
A scientific law always applies to a physical system under repeated conditions, and it implies that there is a causal relationship involving the elements of the system. Factual and well-confirmed statements like «Mercury is liquid at standard temperature and pressure» are considered too specific to qualify as scientific laws. A central problem in the philosophy of science, going back to David Hume, is that of distinguishing causal relationships (such as those implied by laws) from principles that arise due to constant conjunction.[6]
Laws differ from scientific theories in that they do not posit a mechanism or explanation of phenomena: they are merely distillations of the results of repeated observation. As such, the applicability of a law is limited to circumstances resembling those already observed, and the law may be found to be false when extrapolated. Ohm’s law only applies to linear networks; Newton’s law of universal gravitation only applies in weak gravitational fields; the early laws of aerodynamics, such as Bernoulli’s principle, do not apply in the case of compressible flow such as occurs in transonic and supersonic flight; Hooke’s law only applies to strain below the elastic limit; Boyle’s law applies with perfect accuracy only to the ideal gas, etc. These laws remain useful, but only under the specified conditions where they apply.
Many laws take mathematical forms, and thus can be stated as an equation; for example, the law of conservation of energy can be written as , where is the total amount of energy in the universe. Similarly, the first law of thermodynamics can be written as , and Newton’s second law can be written as dp⁄dt. While these scientific laws explain what our senses perceive, they are still empirical (acquired by observation or scientific experiment) and so are not like mathematical theorems which can be proved purely by mathematics.
Like theories and hypotheses, laws make predictions; specifically, they predict that new observations will conform to the given law. Laws can be falsified if they are found in contradiction with new data.
Some laws are only approximations of other more general laws, and are good approximations with a restricted domain of applicability. For example, Newtonian dynamics (which is based on Galilean transformations) is the low-speed limit of special relativity (since the Galilean transformation is the low-speed approximation to the Lorentz transformation). Similarly, the Newtonian gravitation law is a low-mass approximation of general relativity, and Coulomb’s law is an approximation to quantum electrodynamics at large distances (compared to the range of weak interactions). In such cases it is common to use the simpler, approximate versions of the laws, instead of the more accurate general laws.
Laws are constantly being tested experimentally to increasing degrees of precision, which is one of the main goals of science. The fact that laws have never been observed to be violated does not preclude testing them at increased accuracy or in new kinds of conditions to confirm whether they continue to hold, or whether they break, and what can be discovered in the process. It is always possible for laws to be invalidated or proven to have limitations, by repeatable experimental evidence, should any be observed. Well-established laws have indeed been invalidated in some special cases, but the new formulations created to explain the discrepancies generalize upon, rather than overthrow, the originals. That is, the invalidated laws have been found to be only close approximations, to which other terms or factors must be added to cover previously unaccounted-for conditions, e.g. very large or very small scales of time or space, enormous speeds or masses, etc. Thus, rather than unchanging knowledge, physical laws are better viewed as a series of improving and more precise generalizations.
PropertiesEdit
Scientific laws are typically conclusions based on repeated scientific experiments and observations over many years and which have become accepted universally within the scientific community. A scientific law is «inferred from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present.»[7] The production of a summary description of our environment in the form of such laws is a fundamental aim of science.
Several general properties of scientific laws, particularly when referring to laws in physics, have been identified. Scientific laws are:
- True, at least within their regime of validity. By definition, there have never been repeatable contradicting observations.
- Universal. They appear to apply everywhere in the universe.[8]: 82
- Simple. They are typically expressed in terms of a single mathematical equation.
- Absolute. Nothing in the universe appears to affect them.[8]: 82
- Stable. Unchanged since first discovered (although they may have been shown to be approximations of more accurate laws),
- All-encompassing. Everything in the universe apparently must comply with them (according to observations).
- Generally conservative of quantity.[9]: 59
- Often expressions of existing homogeneities (symmetries) of space and time.[9]
- Typically theoretically reversible in time (if non-quantum), although time itself is irreversible.[9]
- Broad. In physics, laws exclusively refer to the broad domain of matter, motion, energy, and force itself, rather than more specific systems in the universe, such as living systems, i.e. the mechanics of the human body.[10]
The term «scientific law» is traditionally associated with the natural sciences, though the social sciences also contain laws.[11] For example, Zipf’s law is a law in the social sciences which is based on mathematical statistics. In these cases, laws may describe general trends or expected behaviors rather than being absolutes.
In natural science, impossibility assertions come to be widely accepted as overwhelmingly probable rather than considered proved to the point of being unchallengeable. The basis for this strong acceptance is a combination of extensive evidence of something not occurring, combined with an underlying theory, very successful in making predictions, whose assumptions lead logically to the conclusion that something is impossible. While an impossibility assertion in natural science can never be absolutely proved, it could be refuted by the observation of a single counterexample. Such a counterexample would require that the assumptions underlying the theory that implied the impossibility be re-examined.
Some examples of widely accepted impossibilities in physics are perpetual motion machines, which violate the law of conservation of energy, exceeding the speed of light, which violates the implications of special relativity, the uncertainty principle of quantum mechanics, which asserts the impossibility of simultaneously knowing both the position and the momentum of a particle, and Bell’s theorem: no physical theory of local hidden variables can ever reproduce all of the predictions of quantum mechanics.
Laws as consequences of mathematical symmetriesEdit
Some laws reflect mathematical symmetries found in Nature (e.g. the Pauli exclusion principle reflects identity of electrons, conservation laws reflect homogeneity of space, time, and Lorentz transformations reflect rotational symmetry of spacetime). Many fundamental physical laws are mathematical consequences of various symmetries of space, time, or other aspects of nature. Specifically, Noether’s theorem connects some conservation laws to certain symmetries. For example, conservation of energy is a consequence of the shift symmetry of time (no moment of time is different from any other), while conservation of momentum is a consequence of the symmetry (homogeneity) of space (no place in space is special, or different than any other). The indistinguishability of all particles of each fundamental type (say, electrons, or photons) results in the Dirac and Bose quantum statistics which in turn result in the Pauli exclusion principle for fermions and in Bose–Einstein condensation for bosons. The rotational symmetry between time and space coordinate axes (when one is taken as imaginary, another as real) results in Lorentz transformations which in turn result in special relativity theory. Symmetry between inertial and gravitational mass results in general relativity.
The inverse square law of interactions mediated by massless bosons is the mathematical consequence of the 3-dimensionality of space.
One strategy in the search for the most fundamental laws of nature is to search for the most general mathematical symmetry group that can be applied to the fundamental interactions.
Laws of physicsEdit
Conservation lawsEdit
Conservation and symmetryEdit
Conservation laws are fundamental laws that follow from the homogeneity of space, time and phase, in other words symmetry.
- Noether’s theorem: Any quantity with a continuously differentiable symmetry in the action has an associated conservation law.
- Conservation of mass was the first law to be understood since most macroscopic physical processes involving masses, for example, collisions of massive particles or fluid flow, provide the apparent belief that mass is conserved. Mass conservation was observed to be true for all chemical reactions. In general, this is only approximative because with the advent of relativity and experiments in nuclear and particle physics: mass can be transformed into energy and vice versa, so mass is not always conserved but part of the more general conservation of mass-energy.
- Conservation of energy, momentum and angular momentum for isolated systems can be found to be symmetries in time, translation, and rotation.
- Conservation of charge was also realized since charge has never been observed to be created or destroyed and only found to move from place to place.
Continuity and transferEdit
Conservation laws can be expressed using the general continuity equation (for a conserved quantity) can be written in differential form as:
where ρ is some quantity per unit volume, J is the flux of that quantity (change in quantity per unit time per unit area). Intuitively, the divergence (denoted ∇•) of a vector field is a measure of flux diverging radially outwards from a point, so the negative is the amount piling up at a point; hence the rate of change of density in a region of space must be the amount of flux leaving or collecting in some region (see the main article for details). In the table below, the fluxes flows for various physical quantities in transport, and their associated continuity equations, are collected for comparison.
-
Physics, conserved quantity Conserved quantity q Volume density ρ (of q) Flux J (of q) Equation Hydrodynamics, fluids m = mass (kg) ρ = volume mass density (kg m−3) ρ u, where u = velocity field of fluid (m s−1)
Electromagnetism, electric charge q = electric charge (C) ρ = volume electric charge density (C m−3) J = electric current density (A m−2) Thermodynamics, energy E = energy (J) u = volume energy density (J m−3) q = heat flux (W m−2) Quantum mechanics, probability P = (r, t) = ∫|Ψ|2d3r = probability distribution ρ = ρ(r, t) = |Ψ|2 = probability density function (m−3), Ψ = wavefunction of quantum system
j = probability current/flux
More general equations are the convection–diffusion equation and Boltzmann transport equation, which have their roots in the continuity equation.
Laws of classical mechanicsEdit
Principle of least actionEdit
Classical mechanics, including Newton’s laws, Lagrange’s equations, Hamilton’s equations, etc., can be derived from the following principle:
where is the action; the integral of the Lagrangian
of the physical system between two times t1 and t2. The kinetic energy of the system is T (a function of the rate of change of the configuration of the system), and potential energy is V (a function of the configuration and its rate of change). The configuration of a system which has N degrees of freedom is defined by generalized coordinates q = (q1, q2, … qN).
There are generalized momenta conjugate to these coordinates, p = (p1, p2, …, pN), where:
The action and Lagrangian both contain the dynamics of the system for all times. The term «path» simply refers to a curve traced out by the system in terms of the generalized coordinates in the configuration space, i.e. the curve q(t), parameterized by time (see also parametric equation for this concept).
The action is a functional rather than a function, since it depends on the Lagrangian, and the Lagrangian depends on the path q(t), so the action depends on the entire «shape» of the path for all times (in the time interval from t1 to t2). Between two instants of time, there are infinitely many paths, but one for which the action is stationary (to the first order) is the true path. The stationary value for the entire continuum of Lagrangian values corresponding to some path, not just one value of the Lagrangian, is required (in other words it is not as simple as «differentiating a function and setting it to zero, then solving the equations to find the points of maxima and minima etc», rather this idea is applied to the entire «shape» of the function, see calculus of variations for more details on this procedure).[12]
Notice L is not the total energy E of the system due to the difference, rather than the sum:
The following[13][14] general approaches to classical mechanics are summarized below in the order of establishment. They are equivalent formulations. Newton’s is commonly used due to simplicity, but Hamilton’s and Lagrange’s equations are more general, and their range can extend into other branches of physics with suitable modifications.
-
Laws of motion Principle of least action: The Euler–Lagrange equations are: Using the definition of generalized momentum, there is the symmetry:
Hamilton’s equations The Hamiltonian as a function of generalized coordinates and momenta has the general form:
Hamilton–Jacobi equation Newton’s laws Newton’s laws of motion
They are low-limit solutions to relativity. Alternative formulations of Newtonian mechanics are Lagrangian and Hamiltonian mechanics.
The laws can be summarized by two equations (since the 1st is a special case of the 2nd, zero resultant acceleration):
where p = momentum of body, Fij = force on body i by body j, Fji = force on body j by body i.
For a dynamical system the two equations (effectively) combine into one:
in which FE = resultant external force (due to any agent not part of system). Body i does not exert a force on itself.
From the above, any equation of motion in classical mechanics can be derived.
- Corollaries in mechanics
- Euler’s laws of motion
- Euler’s equations (rigid body dynamics)
- Corollaries in fluid mechanics
Equations describing fluid flow in various situations can be derived, using the above classical equations of motion and often conservation of mass, energy and momentum. Some elementary examples follow.
- Archimedes’ principle
- Bernoulli’s principle
- Poiseuille’s law
- Stokes’s law
- Navier–Stokes equations
- Faxén’s law
Laws of gravitation and relativityEdit
Some of the more famous laws of nature are found in Isaac Newton’s theories of (now) classical mechanics, presented in his Philosophiae Naturalis Principia Mathematica, and in Albert Einstein’s theory of relativity.
Modern lawsEdit
- Special relativity
The two postulates of special relativity are not «laws» in themselves, but assumptions of their nature in terms of relative motion.
They can be stated as «the laws of physics are the same in all inertial frames» and «the speed of light is constant and has the same value in all inertial frames».
The said postulates lead to the Lorentz transformations – the transformation law between two frame of references moving relative to each other. For any 4-vector
this replaces the Galilean transformation law from classical mechanics. The Lorentz transformations reduce to the Galilean transformations for low velocities much less than the speed of light c.
The magnitudes of 4-vectors are invariants — not «conserved», but the same for all inertial frames (i.e. every observer in an inertial frame will agree on the same value), in particular if A is the four-momentum, the magnitude can derive the famous invariant equation for mass-energy and momentum conservation (see invariant mass):
in which the (more famous) mass-energy equivalence E = mc2 is a special case.
- General relativity
General relativity is governed by the Einstein field equations, which describe the curvature of space-time due to mass-energy equivalent to the gravitational field. Solving the equation for the geometry of space warped due to the mass distribution gives the metric tensor. Using the geodesic equation, the motion of masses falling along the geodesics can be calculated.
- Gravitomagnetism
In a relatively flat spacetime due to weak gravitational fields, gravitational analogues of Maxwell’s equations can be found; the GEM equations, to describe an analogous gravitomagnetic field. They are well established by the theory, and experimental tests form ongoing research.[15]
Classical lawsEdit
Kepler’s Laws, though originally discovered from planetary observations (also due to Tycho Brahe), are true for any central forces.[16]
-
Newton’s law of universal gravitation: For two point masses:
For a non uniform mass distribution of local mass density ρ (r) of body of Volume V, this becomes:
Gauss’ law for gravity: An equivalent statement to Newton’s law is:
Kepler’s 1st Law: Planets move in an ellipse, with the star at a focus where
is the eccentricity of the elliptic orbit, of semi-major axis a and semi-minor axis b, and l is the semi-latus rectum. This equation in itself is nothing physically fundamental; simply the polar equation of an ellipse in which the pole (origin of polar coordinate system) is positioned at a focus of the ellipse, where the orbited star is.
Kepler’s 2nd Law: equal areas are swept out in equal times (area bounded by two radial distances and the orbital circumference): where L is the orbital angular momentum of the particle (i.e. planet) of mass m about the focus of orbit,
Kepler’s 3rd Law: The square of the orbital time period T is proportional to the cube of the semi-major axis a: where M is the mass of the central body (i.e. star).
ThermodynamicsEdit
-
Laws of thermodynamics First law of thermodynamics: The change in internal energy dU in a closed system is accounted for entirely by the heat δQ absorbed by the system and the work δW done by the system: Second law of thermodynamics: There are many statements of this law, perhaps the simplest is «the entropy of isolated systems never decreases»,
meaning reversible changes have zero entropy change, irreversible process are positive, and impossible process are negative.
Zeroth law of thermodynamics: If two systems are in thermal equilibrium with a third system, then they are in thermal equilibrium with one another. Third law of thermodynamics:
- As the temperature T of a system approaches absolute zero, the entropy S approaches a minimum value C: as T → 0, S → C.
For homogeneous systems the first and second law can be combined into the Fundamental thermodynamic relation: Onsager reciprocal relations: sometimes called the Fourth Law of Thermodynamics - ;
- .
- Newton’s law of cooling
- Fourier’s law
- Ideal gas law, combines a number of separately developed gas laws;
- Boyle’s law
- Charles’s law
- Gay-Lussac’s law
- Avogadro’s law, into one
- now improved by other equations of state
- Dalton’s law (of partial pressures)
- Boltzmann equation
- Carnot’s theorem
- Kopp’s law
ElectromagnetismEdit
Maxwell’s equations give the time-evolution of the electric and magnetic fields due to electric charge and current distributions. Given the fields, the Lorentz force law is the equation of motion for charges in the fields.
These equations can be modified to include magnetic monopoles, and are consistent with our observations of monopoles either existing or not existing; if they do not exist, the generalized equations reduce to the ones above, if they do, the equations become fully symmetric in electric and magnetic charges and currents. Indeed, there is a duality transformation where electric and magnetic charges can be «rotated into one another», and still satisfy Maxwell’s equations.
- Pre-Maxwell laws
These laws were found before the formulation of Maxwell’s equations. They are not fundamental, since they can be derived from Maxwell’s Equations. Coulomb’s Law can be found from Gauss’ Law (electrostatic form) and the Biot–Savart Law can be deduced from Ampere’s Law (magnetostatic form). Lenz’ Law and Faraday’s Law can be incorporated into the Maxwell-Faraday equation. Nonetheless they are still very effective for simple calculations.
- Lenz’s law
- Coulomb’s law
- Biot–Savart law
- Other laws
- Ohm’s law
- Kirchhoff’s laws
- Joule’s law
PhotonicsEdit
Classically, optics is based on a variational principle: light travels from one point in space to another in the shortest time.
- Fermat’s principle
In geometric optics laws are based on approximations in Euclidean geometry (such as the paraxial approximation).
- Law of reflection
- Law of refraction, Snell’s law
In physical optics, laws are based on physical properties of materials.
- Brewster’s angle
- Malus’s law
- Beer–Lambert law
In actuality, optical properties of matter are significantly more complex and require quantum mechanics.
Laws of quantum mechanicsEdit
Quantum mechanics has its roots in postulates. This leads to results which are not usually called «laws», but hold the same status, in that all of quantum mechanics follows from them.
One postulate that a particle (or a system of many particles) is described by a wavefunction, and this satisfies a quantum wave equation: namely the Schrödinger equation (which can be written as a non-relativistic wave equation, or a relativistic wave equation). Solving this wave equation predicts the time-evolution of the system’s behaviour, analogous to solving Newton’s laws in classical mechanics.
Other postulates change the idea of physical observables; using quantum operators; some measurements can’t be made at the same instant of time (Uncertainty principles), particles are fundamentally indistinguishable. Another postulate; the wavefunction collapse postulate, counters the usual idea of a measurement in science.
-
Quantum mechanics, Quantum field theory Schrödinger equation (general form): Describes the time dependence of a quantum mechanical system.
The Hamiltonian (in quantum mechanics) H is a self-adjoint operator acting on the state space, (see Dirac notation) is the instantaneous quantum state vector at time t, position r, i is the unit imaginary number, ħ = h/2π is the reduced Planck’s constant.
Wave–particle duality Planck–Einstein law: the energy of photons is proportional to the frequency of the light (the constant is Planck’s constant, h).
De Broglie wavelength: this laid the foundations of wave–particle duality, and was the key concept in the Schrödinger equation,
Heisenberg uncertainty principle: Uncertainty in position multiplied by uncertainty in momentum is at least half of the reduced Planck constant, similarly for time and energy;
The uncertainty principle can be generalized to any pair of observables — see main article.
Wave mechanics Schrödinger equation (original form):
Pauli exclusion principle: No two identical fermions can occupy the same quantum state (bosons can). Mathematically, if two particles are interchanged, fermionic wavefunctions are anti-symmetric, while bosonic wavefunctions are symmetric: where ri is the position of particle i, and s is the spin of the particle. There is no way to keep track of particles physically, labels are only used mathematically to prevent confusion.
Radiation lawsEdit
Applying electromagnetism, thermodynamics, and quantum mechanics, to atoms and molecules, some laws of electromagnetic radiation and light are as follows.
- Stefan–Boltzmann law
- Planck’s law of black-body radiation
- Wien’s displacement law
- Radioactive decay law
Laws of chemistryEdit
Chemical laws are those laws of nature relevant to chemistry. Historically, observations led to many empirical laws, though now it is known that chemistry has its foundations in quantum mechanics.
- Quantitative analysis
The most fundamental concept in chemistry is the law of conservation of mass, which states that there is no detectable change in the quantity of matter during an ordinary chemical reaction. Modern physics shows that it is actually energy that is conserved, and that energy and mass are related; a concept which becomes important in nuclear chemistry. Conservation of energy leads to the important concepts of equilibrium, thermodynamics, and kinetics.
Additional laws of chemistry elaborate on the law of conservation of mass. Joseph Proust’s law of definite composition says that pure chemicals are composed of elements in a definite formulation; we now know that the structural arrangement of these elements is also important.
Dalton’s law of multiple proportions says that these chemicals will present themselves in proportions that are small whole numbers; although in many systems (notably biomacromolecules and minerals) the ratios tend to require large numbers, and are frequently represented as a fraction.
The law of definite composition and the law of multiple proportions are the first two of the three laws of stoichiometry, the proportions by which the chemical elements combine to form chemical compounds. The third law of stoichiometry is the law of reciprocal proportions, which provides the basis for establishing equivalent weights for each chemical element. Elemental equivalent weights can then be used to derive atomic weights for each element.
More modern laws of chemistry define the relationship between energy and its transformations.
- Reaction kinetics and equilibria
- In equilibrium, molecules exist in mixture defined by the transformations possible on the timescale of the equilibrium, and are in a ratio defined by the intrinsic energy of the molecules—the lower the intrinsic energy, the more abundant the molecule. Le Chatelier’s principle states that the system opposes changes in conditions from equilibrium states, i.e. there is an opposition to change the state of an equilibrium reaction.
- Transforming one structure to another requires the input of energy to cross an energy barrier; this can come from the intrinsic energy of the molecules themselves, or from an external source which will generally accelerate transformations. The higher the energy barrier, the slower the transformation occurs.
- There is a hypothetical intermediate, or transition structure, that corresponds to the structure at the top of the energy barrier. The Hammond–Leffler postulate states that this structure looks most similar to the product or starting material which has intrinsic energy closest to that of the energy barrier. Stabilizing this hypothetical intermediate through chemical interaction is one way to achieve catalysis.
- All chemical processes are reversible (law of microscopic reversibility) although some processes have such an energy bias, they are essentially irreversible.
- The reaction rate has the mathematical parameter known as the rate constant. The Arrhenius equation gives the temperature and activation energy dependence of the rate constant, an empirical law.
- Thermochemistry
- Dulong–Petit law
- Gibbs–Helmholtz equation
- Hess’s law
- Gas laws
- Raoult’s law
- Henry’s law
- Chemical transport
- Fick’s laws of diffusion
- Graham’s law
- Lamm equation
Laws of biologyEdit
EcologyEdit
- Competitive exclusion principle or Gause’s law
GeneticsEdit
- Mendelian laws (Dominance and Uniformity, segregation of genes, and Independent Assortment)
- Hardy–Weinberg principle
Natural selectionEdit
Whether or not Natural Selection is a “law of nature” is controversial among biologists.[17][18] Henry Byerly, an American philosopher known for his work on evolutionary theory, discussed the problem of interpreting a principle of natural selection as a law. He suggested a formulation of natural selection as a framework principle that can contribute to a better understanding of evolutionary theory.[18] His approach was to express relative fitness, the propensity of a genotype to increase in proportionate representation in a competitive environment, as a function of adaptedness (adaptive design) of the organism.
Laws of Earth SciencesEdit
GeographyEdit
- Arbia’s law of geography
- Tobler’s first law of geography
- Tobler’s second law of geography
GeologyEdit
- Archie’s law
- Buys-Ballot’s law
- Birch’s law
- Byerlee’s law
- Principle of original horizontality
- Law of superposition
- Principle of lateral continuity
- Principle of cross-cutting relationships
- Principle of faunal succession
- Principle of inclusions and components
- Walther’s law
Other fieldsEdit
Some mathematical theorems and axioms are referred to as laws because they provide logical foundation to empirical laws.
Examples of other observed phenomena sometimes described as laws include the Titius–Bode law of planetary positions, Zipf’s law of linguistics, and Moore’s law of technological growth. Many of these laws fall within the scope of uncomfortable science. Other laws are pragmatic and observational, such as the law of unintended consequences. By analogy, principles in other fields of study are sometimes loosely referred to as «laws». These include Occam’s razor as a principle of philosophy and the Pareto principle of economics.
HistoryEdit
The observation and detection of underlying regularities in nature date from prehistoric times — the recognition of cause-and-effect relationships implicitly recognises the existence of laws of nature. The recognition of such regularities as independent scientific laws per se, though, was limited by their entanglement in animism, and by the attribution of many effects that do not have readily obvious causes—such as physical phenomena—to the actions of gods, spirits, supernatural beings, etc. Observation and speculation about nature were intimately bound up with metaphysics and morality.
In Europe, systematic theorizing about nature (physis) began with the early Greek philosophers and scientists and continued into the Hellenistic and Roman imperial periods, during which times the intellectual influence of Roman law increasingly became paramount.
The formula «law of nature» first appears as «a live metaphor» favored by Latin poets Lucretius, Virgil, Ovid, Manilius, in time gaining a firm theoretical presence in the prose treatises of Seneca and Pliny. Why this Roman origin? According to [historian and classicist Daryn] Lehoux’s persuasive narrative,[19] the idea was made possible by the pivotal role of codified law and forensic argument in Roman life and culture.
For the Romans . . . the place par excellence where ethics, law, nature, religion and politics overlap is the law court. When we read Seneca’s Natural Questions, and watch again and again just how he applies standards of evidence, witness evaluation, argument and proof, we can recognize that we are reading one of the great Roman rhetoricians of the age, thoroughly immersed in forensic method. And not Seneca alone. Legal models of scientific judgment turn up all over the place, and for example prove equally integral to Ptolemy’s approach to verification, where the mind is assigned the role of magistrate, the senses that of disclosure of evidence, and dialectical reason that of the law itself.[20]
The precise formulation of what are now recognized as modern and valid statements of the laws of nature dates from the 17th century in Europe, with the beginning of accurate experimentation and the development of advanced forms of mathematics. During this period, natural philosophers such as Isaac Newton (1642-1727) were influenced by a religious view — stemming from medieval concepts of divine law — which held that God had instituted absolute, universal and immutable physical laws.[21][22] In chapter 7 of The World, René Descartes (1596-1650) described «nature» as matter itself, unchanging as created by God, thus changes in parts «are to be attributed to nature. The rules according to which these changes take place I call the ‘laws of nature’.»[23] The modern scientific method which took shape at this time (with Francis Bacon (1561-1626) and Galileo (1564-1642)) contributed to a trend of separating science from theology, with minimal speculation about metaphysics and ethics. (Natural law in the political sense, conceived as universal (i.e., divorced from sectarian religion and accidents of place), was also elaborated in this period by scholars such as Grotius (1583-1645), Spinoza (1632-1677), and Hobbes (1588-1679).)
The distinction between natural law in the political-legal sense and law of nature or physical law in the scientific sense is a modern one, both concepts being equally derived from physis, the Greek word (translated into Latin as natura) for nature.[24]
See alsoEdit
- Empirical research
- Empirical statistical laws
- Formula
- List of laws
- Law (principle)
- Nomology
- Philosophy of science
- Physical constant
- Scientific laws named after people
- Theory
ReferencesEdit
- ^ «law of nature». Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
- ^ William F. McComas (30 December 2013). The Language of Science Education: An Expanded Glossary of Key Terms and Concepts in Science Teaching and Learning. Springer Science & Business Media. p. 58. ISBN 978-94-6209-497-0.
- ^ «Definitions from». the NCSE. Retrieved 2019-03-18.
- ^ «The Role of Theory in Advancing 21st Century Biology: Catalyzing Transformative Research» (PDF). Report in Brief. The National Academy of Sciences. 2007.
- ^ Gould, Stephen Jay (1981-05-01). «Evolution as Fact and Theory» (PDF). Discover. 2 (5): 34–37.
- ^ Honderich, Bike, ed. (1995), «Laws, natural or scientific», Oxford Companion to Philosophy, Oxford: Oxford University Press, pp. 474–476, ISBN 0-19-866132-0
- ^ «Law of nature». Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
- ^ a b Davies, Paul (2005). The mind of God : the scientific basis for a rational world (1st Simon & Schuster pbk. ed.). New York: Simon & Schuster. ISBN 978-0-671-79718-8.
- ^ a b c Feynman, Richard (1994). The character of physical law (Modern Library ed.). New York: Modern Library. ISBN 978-0-679-60127-2.
- ^ Frisch, Mathias (May 2014). «Laws in Physics | European Review | Cambridge Core». European Review. 22 (S1): S33–S49. doi:10.1017/S1062798713000768. S2CID 122262641.
- ^ Andrew S. C. Ehrenberg (1993), «Even the Social Sciences Have Laws», Nature, 365:6445 (30), page 385.(subscription required)
- ^ Feynman Lectures on Physics: Volume 2, R.P. Feynman, R.B. Leighton, M. Sands, Addison-Wesley, 1964, ISBN 0-201-02117-X
- ^ Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC Publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1 (VHC Inc.) 0-89573-752-3
- ^ Classical Mechanics, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, ISBN 0-07-084018-0
- ^ Gravitation and Inertia, I. Ciufolini and J.A. Wheeler, Princeton Physics Series, 1995, ISBN 0-691-03323-4
- ^ 2.^ Classical Mechanics, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, ISBN 0-07-084018-0
- ^ Reed ES: The lawfulness of natural selection. Am Nat. 1981; 118(1): 61–71.
- ^ a b Byerly HC: Natural selection as a law: Principles and processes. Am Nat. 1983; 121(5): 739–745.
- ^ in Daryn Lehoux, What Did the Romans Know? An Inquiry into Science and Worldmaking (Chicago: University of Chicago Press, 2012), reviewed by David Sedley, «When Nature Got its Laws», Times Literary Supplement (12 October 2012).
- ^ Sedley, «When Nature Got Its Laws», Times Literary Supplement (12 October 2012).
- ^ Davies, Paul (2007-11-24). «Taking Science on Faith». The New York Times. ISSN 0362-4331. Retrieved 2016-10-07.
Isaac Newton first got the idea of absolute, universal, perfect, immutable laws from the Christian doctrine that God created the world and ordered it in a rational way.
- ^ Harrison, Peter (8 May 2012). «Christianity and the rise of western science». ABC.
Individuals such as Galileo, Johannes Kepler, Rene Descartes and Isaac Newton were convinced that mathematical truths were not the products of human minds, but of the divine mind. God was the source of mathematical relations that were evident in the new laws of the universe.
- ^ «Cosmological Revolution V: Descartes and Newton». bertie.ccsu.edu. Retrieved 2016-11-17.
- ^
Some modern philosophers, e.g. Norman Swartz, use «physical law» to mean the laws of nature as they truly are and not as they are inferred by scientists. See Norman Swartz, The Concept of Physical Law (New York: Cambridge University Press), 1985. Second edition available online [1].
Further readingEdit
- John Barrow (1991). Theories of Everything: The Quest for Ultimate Explanations. (ISBN 0-449-90738-4)
- Dilworth, Craig (2007). «Appendix IV. On the nature of scientific laws and theories». Scientific progress : a study concerning the nature of the relation between successive scientific theories (4th ed.). Dordrecht: Springer Verlag. ISBN 978-1-4020-6353-4.
- Francis Bacon (1620). Novum Organum.
- Hanzel, Igor (1999). The concept of scientific law in the philosophy of science and epistemology : a study of theoretical reason. Dordrecht [u.a.]: Kluwer. ISBN 978-0-7923-5852-7.
- Daryn Lehoux (2012). What Did the Romans Know? An Inquiry into Science and Worldmaking. University of Chicago Press. (ISBN 9780226471143)
- Nagel, Ernest (1984). «5. Experimental laws and theories». The structure of science problems in the logic of scientific explanation (2nd ed.). Indianapolis: Hackett. ISBN 978-0-915144-71-6.
- R. Penrose (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
- Swartz, Norman (20 February 2009). «Laws of Nature». Internet encyclopedia of philosophy. Retrieved 7 May 2012.
External linksEdit
- Physics Formulary, a useful book in different formats containing many or the physical laws and formulae.
- Eformulae.com, website containing most of the formulae in different disciplines.
- Stanford Encyclopedia of Philosophy: «Laws of Nature» by John W. Carroll.
- Baaquie, Belal E. «Laws of Physics : A Primer». Core Curriculum, National University of Singapore.
- Francis, Erik Max. «The laws list».. Physics. Alcyone Systems
- Pazameta, Zoran. «The laws of nature». Committee for the scientific investigation of Claims of the Paranormal.
- The Internet Encyclopedia of Philosophy. «Laws of Nature» – By Norman Swartz
- «Laws of Nature», In Our Time, BBC Radio 4 discussion with Mark Buchanan, Frank Close and Nancy Cartwright (Oct. 19, 2000)
What Is a Scientific or Natural Law?
Updated on January 06, 2019
A law in science is a generalized rule to explain a body of observations in the form of a verbal or mathematical statement. Scientific laws (also known as natural laws) imply a cause and effect between the observed elements and must always apply under the same conditions. In order to be scientific law, a statement must describe some aspect of the universe and be based on repeated experimental evidence. Scientific laws may be stated in words, but many are expressed as mathematical equations.
Laws are widely accepted as true, but new data can lead to changes in a law or to exceptions to the rule. Sometimes laws are found to be true under certain conditions, but not others. For example, Newton’s Law of Gravity holds true for most situations, but it breaks down at the sub-atomic level.
Scientific Law Versus Scientific Theory
Scientific laws do not try to explain ‘why’ the observed event happens, but only that the event actually occurs the same way over and over. The explanation of how a phenomenon works is a scientific theory. A scientific law and a scientific theory are not the same thing—a theory does not turn into a law or vice versa. Both laws and theories are based on empirical data and are accepted by many or most scientists within the appropriate discipline.
For example, Newton’s Law of Gravity (17th century) is a mathematical relation that describes how two bodies interact with each other. The law does not explain how gravity works or even what gravity is. The Law of Gravity can be used to make predictions about events and perform calculations. Einstein’s Theory of Relativity (20th century) finally started to explain what gravity is and how it works.

A scientific law is a statement or mathematical equation that describes or predicts a natural phenomenon. It does not explain why or how a phenomenon occurs. Another name for a scientific law is a law of nature or law of science. All scientific laws are based on empirical evidence and the scientific method. In science, an assertion can be disproven, but never proven, so it’s possible for a scientific law to be revised or disproven by future experiments. In contrast, a mathematical theorem or identity is proven to be true.
Examples of Scientific Laws
There are laws in all scientific disciplines, although primarily they are physical laws. Here are some examples:
- Beer’s law
- Dalton’s law of partial pressures
- Ideal gas law
- Kepler’s laws of planetary motion
- Law of conservation of mass
- Law of conservation of energy
- Law of conservation of momentum
- Law of reflection
- Laws of thermodynamics
- Newton’s law of universal gravitation
- Newton’s laws of motion
Difference Between a Scientific Law and Scientific Theory
Both scientific laws and scientific theories are based in the scientific method and are falsifiable. However, the two terms have very different meanings. A law describes what happens, but does not explain it. A theory explains how or why something works.
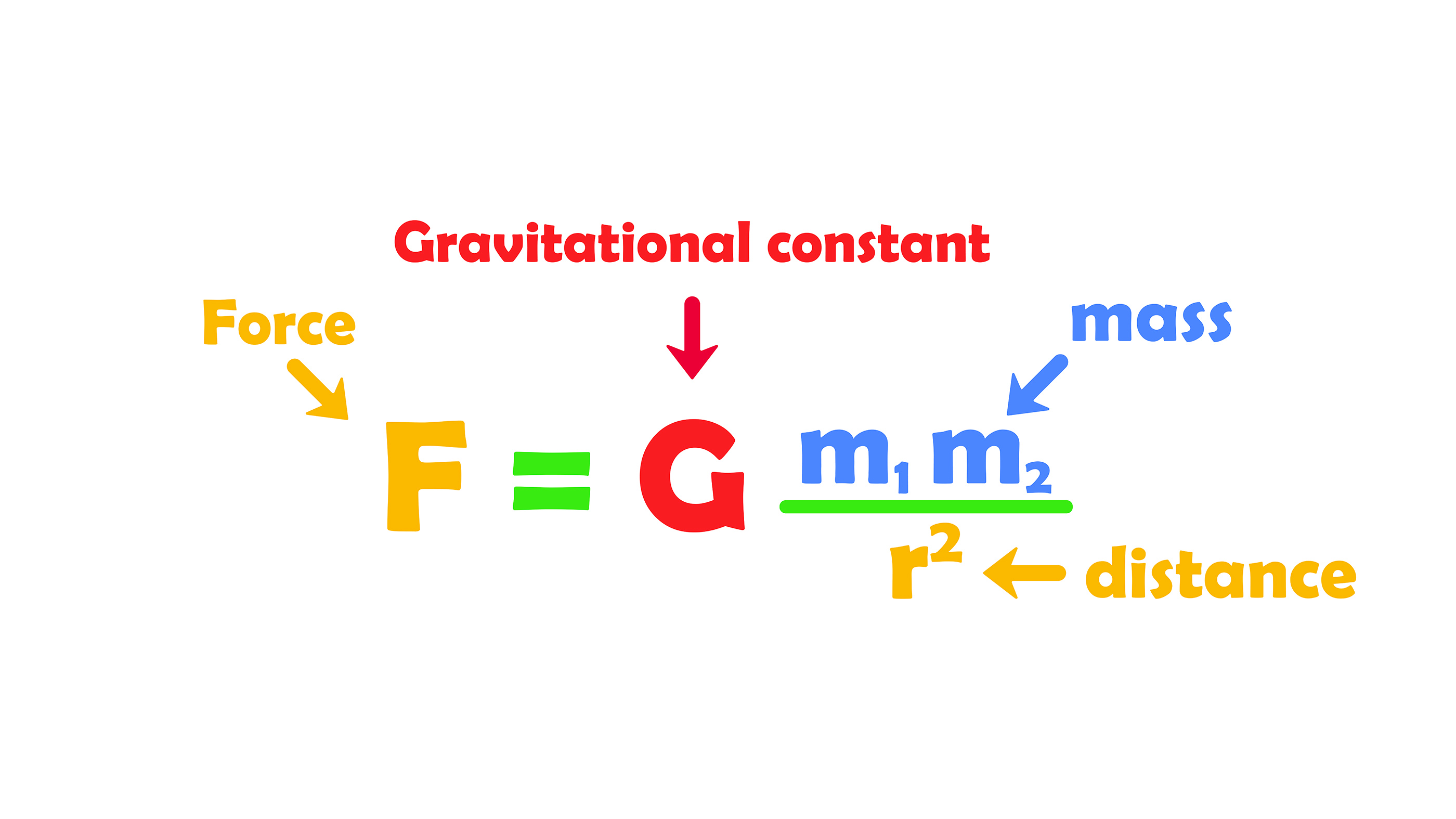
For example, Newton’s law of universal gravitation describes what happens when two masses are a given distance apart. The law can be written as a mathematical equation [F = G(m1m2/r2)] and used to make predictions and calculations. However, the law does not explain how gravity works or why two masses are attracted to one another. Scientists didn’t really have an explanation for gravity until Einstein’s theory of general relativity, which continues to be revised as we understand more about the nature of spacetime.
As another example, Hubble’s law of Cosmic Expansion (velocity = Hubble constant x distance) describes the movement of galaxies away from each other. It does explain why this occurs. The Big Bang Theory is one of the theories that explains why galaxies move apart, but the theory does not offer a formula for calculating this motion.
Can a Hypothesis or Theory Become a Law?
A hypothesis, theory, and law are all parts of scientific inquiry, but one never becomes another. They are different things. A hypothesis never becomes a theory, no matter how many experiments support it, because a hypothesis is simply a prediction about how one variable responds when another is changed. A theory takes into account the results of many experiments, testing different hypotheses. A theory explains how something works. Like a theory, a law draws on the results of repeated observations and experiments. But, a law states in words or mathematical equations what happens. Laws don’t explain why.
References
- Barrow, John (1991). Theories of Everything: The Quest for Ultimate Explanations. ISBN 0-449-90738-4.
- Feynman, Richard (1994). The Character of Physical Law (Modern Library ed.). New York: Modern Library. ISBN 978-0-679-60127-2.
- Gould, Stephen Jay (1981). “Evolution as Fact and Theory“. Discover. 2 (5): 34–37.
- McComas, William F. (2013). The Language of Science Education: An Expanded Glossary of Key Terms and Concepts in Science Teaching and Learning. Springer Science & Business Media. ISBN 978-94-6209-497-0.
WikipediaRate this definition:0.0 / 0 votes
-
Scientific law
Scientific laws or laws of science are statements, based on repeated experiments or observations, that describe or predict a range of natural phenomena. The term law has diverse usage in many cases (approximate, accurate, broad, or narrow) across all fields of natural science (physics, chemistry, astronomy, geoscience, biology). Laws are developed from data and can be further developed through mathematics; in all cases they are directly or indirectly based on empirical evidence. It is generally understood that they implicitly reflect, though they do not explicitly assert, causal relationships fundamental to reality, and are discovered rather than invented.Scientific laws summarize the results of experiments or observations, usually within a certain range of application. In general, the accuracy of a law does not change when a new theory of the relevant phenomenon is worked out, but rather the scope of the law’s application, since the mathematics or statement representing the law does not change. As with other kinds of scientific knowledge, scientific laws do not express absolute certainty, as mathematical theorems or identities do. A scientific law may be contradicted, restricted, or extended by future observations.
A law can usually be formulated as one or several statements or equations, so that it can predict the outcome of an experiment. Laws differ from hypotheses and postulates, which are proposed during the scientific process before and during validation by experiment and observation. Hypotheses and postulates are not laws, since they have not been verified to the same degree, although they may lead to the formulation of laws. Laws are narrower in scope than scientific theories, which may entail one or several laws. Science distinguishes a law or theory from facts. Calling a law a fact is ambiguous, an overstatement, or an equivocation. The nature of scientific laws has been much discussed in philosophy, but in essence scientific laws are simply empirical conclusions reached by scientific method; they are intended to be neither laden with ontological commitments nor statements of logical absolutes.
FreebaseRate this definition:3.1 / 52 votes
-
Scientific law
A scientific law is a statement based on repeated experimental observations that describes some aspect of the world. A scientific law always applies under the same conditions, and implies that there is a causal relationship involving its elements. Factual and well-confirmed statements like «Mercury is liquid at standard temperature and pressure» are considered to be too specific to qualify as scientific laws. A central problem in the philosophy of science, going back to David Hume, is that of distinguishing causal relationships from principles that arise due to constant conjunction.
Laws differ from scientific theories in that they do not posit a mechanism or explanation of phenomena: they are merely distillations of the results of repeated observation. As such, a law is limited in applicability to circumstances resembling those already observed, and may be found to be false when extrapolated. Ohm’s law only applies to linear networks, Newton’s law of universal gravitation only applies in weak gravitational fields, the early laws of aerodynamics such as Bernoulli’s principle do not apply in case of compressible flow such as occurs in transonic and supersonic flight, Hooke’s law only applies to strain below the elastic limit, etc. These laws remain useful, but only under the conditions where they apply.
Editors ContributionRate this definition:4.0 / 26 votes
-
scientific law
Is a scientific rule in the form of words or a mathematical formula using accurate data, information or fact with proof to describe a cause and effect of a facet of science in the universe.
Scientific law is a vital part of science and changes and evolves as science and its understanding of the universe changes too.
Submitted by MaryC on February 12, 2016
How to pronounce scientific law?
How to say scientific law in sign language?
Numerology
-
Chaldean Numerology
The numerical value of scientific law in Chaldean Numerology is: 8
-
Pythagorean Numerology
The numerical value of scientific law in Pythagorean Numerology is: 7
Translation
Find a translation for the scientific law definition in other languages:
Select another language:
- — Select —
- 简体中文 (Chinese — Simplified)
- 繁體中文 (Chinese — Traditional)
- Español (Spanish)
- Esperanto (Esperanto)
- 日本語 (Japanese)
- Português (Portuguese)
- Deutsch (German)
- العربية (Arabic)
- Français (French)
- Русский (Russian)
- ಕನ್ನಡ (Kannada)
- 한국어 (Korean)
- עברית (Hebrew)
- Gaeilge (Irish)
- Українська (Ukrainian)
- اردو (Urdu)
- Magyar (Hungarian)
- मानक हिन्दी (Hindi)
- Indonesia (Indonesian)
- Italiano (Italian)
- தமிழ் (Tamil)
- Türkçe (Turkish)
- తెలుగు (Telugu)
- ภาษาไทย (Thai)
- Tiếng Việt (Vietnamese)
- Čeština (Czech)
- Polski (Polish)
- Bahasa Indonesia (Indonesian)
- Românește (Romanian)
- Nederlands (Dutch)
- Ελληνικά (Greek)
- Latinum (Latin)
- Svenska (Swedish)
- Dansk (Danish)
- Suomi (Finnish)
- فارسی (Persian)
- ייִדיש (Yiddish)
- հայերեն (Armenian)
- Norsk (Norwegian)
- English (English)
Word of the Day
Would you like us to send you a FREE new word definition delivered to your inbox daily?
Citation
Use the citation below to add this definition to your bibliography:
Are we missing a good definition for scientific law? Don’t keep it to yourself…

In general, a scientific law is the description of an observed phenomenon. It doesn’t explain why the phenomenon exists or what causes it. The explanation for a phenomenon is called a scientific theory. It is a misconception that theories turn into laws with enough research.
«In science, laws are a starting place,» said Peter Coppinger, an associate professor of biology and biomedical engineering at the Rose-Hulman Institute of Technology in India. «From there, scientists can then ask the questions, ‘Why and how?'»
Difference between a scientific theory and a scientific law
Many people think that if scientists find evidence that supports a hypothesis, the hypothesis is upgraded to a theory, and if the theory is found to be correct, it is upgraded to a law. That is not how it works, though. Facts, theories and laws — as well as hypotheses — are separate elements of the scientific method. Though they may evolve, they aren’t upgraded to something else.
«Hypotheses, theories and laws are rather like apples, oranges and kumquats: One cannot grow into another, no matter how much fertilizer and water are offered,» according to the University of California, Berkeley (opens in new tab). A hypothesis is a potential explanation of a narrow phenomenon; a scientific theory is an in-depth explanation that applies to a wide range of phenomena. A law is a statement about an observed phenomenon or a unifying concept, according to Kennesaw State University (opens in new tab).
«There are four major concepts in science: facts, hypotheses, laws and theories,» Coppinger told Live Science.
Though scientific laws and theories are supported by a large body of empirical evidence that is accepted by the majority of scientists within that area of scientific study, and help to unify that body of data, they are not the same thing.
«Laws are descriptions — often mathematical descriptions — of natural phenomena for example, Newton’s Law of Gravity or Mendel’s Law of Independent Assortment. These laws simply describe the observation. Not how or why they work,» Coppinger said.
Coppinger pointed out that the law of gravity was discovered by Isaac Newton in the 17th century. This law mathematically describes how two different bodies in the universe interact with each other. However, Newton’s law doesn’t explain what gravity is or how it works. It wasn’t until three centuries later, when Albert Einstein developed the theory of Relativity, that scientists began to understand what gravity is and how it works.
(opens in new tab)
«Newton’s law is useful to scientists in that astrophysicists can use this centuries-old law to land robots on Mars. But it doesn’t explain how gravity works, or what it is. Similarly, Mendel’s Law of Independent Assortment describes how different traits are passed from parent to offspring, not how or why it happens,» Coppinger said. Gregor Mendel discovered that two different genetic traits would appear independently of each other in different offspring. «Yet, Mendel knew nothing of DNA or chromosomes. It wasn’t until a century later that scientists discovered DNA and chromosomes — the biochemical explanation of Mendel’s laws. It was only then that scientists, such as T.H. Morgan, working with fruit flies, explained the Law of Independent Assortment using the theory of chromosomal inheritance. Still today, this is the universally accepted explanation (theory) for Mendel’s Law,» Coppinger said.
The difference between scientific laws and scientific facts is a bit harder to define, though the definition is important. Facts are simple, one-off observations that have been shown to be true. Laws are generalized observations about a relationship between two or more things in the natural world based on a variety of facts and empirical evidence, often framed as a mathematical statement, according to NASA.
For example, «Apples fall down from this apple tree» is considered a fact because it is a simple statement that can be proven. «The strength of gravity between any two objects (like an apple and the Earth) depends on the masses of the objects and the distance between them» is a law because it describes the behavior of two objects in a certain circumstance. If the circumstance changes, then the implications of the law would change. For example, if the apple and the Earth shrank to a subatomic size, they would behave differently.
Scientific laws and mathematics
(opens in new tab)
Many scientific laws can be boiled down to a mathematical equation. For example, Newton’s Law of Universal Gravitation states:
Fg = G (m1 ∙ m2) / d2
Fg is the force of gravity; G is the universal gravitational constant, which can be measured; m1 and m2 are the masses of the two objects, and d is the distance between them, according to The Ohio State University (opens in new tab).
Scientific laws are also often governed by the mathematics of probability. «With large numbers, probability always works. The house always wins,» said Sylvia Wassertheil-Smoller, a professor at Albert Einstein College of Medicine in New York. «We can calculate the probability of an event and we can determine how certain we are of our estimate, but there is always a trade-off between precision and certainty. This is known as the confidence interval. For example, we can be 95% certain that what we are trying to estimate lies within a certain range or we can be more certain, say 99% certain, that it lies within a wider range. Just like in life in general, we must accept that there is a trade-off.»
Do laws change?
Just because an idea becomes a law doesn’t mean that it can’t be changed through scientific research in the future. The use of the word «law» by laymen and scientists differs. When most people talk about a law, they mean something that is absolute. A scientific law is much more flexible. It can have exceptions, be proven wrong or evolve over time, according to the University of California, Berkeley.
«A good scientist is one who always asks the question, ‘How can I show myself wrong?'» Coppinger said. «In regards to the Law of Gravity or the Law of Independent Assortment, continual testing and observations have ‘tweaked’ these laws. Exceptions have been found. For example, Newton’s Law of Gravity breaks down when looking at the quantum (subatomic) level. Mendel’s Law of Independent Assortment breaks down when traits are «linked» on the same chromosome.»
Examples of scientific laws
- The law of conservation of energy, which says that the total energy in an isolated system remains constant. In other words, energy cannot be created or destroyed, according to Britannica (opens in new tab).
- The laws of thermodynamics, which deal with the relationships between heat and other forms of energy
- Newton’s universal law of gravitation, which says that any two objects exert a gravitational force upon each other, according to the University of Winnipeg (opens in new tab)
- Hubble’s law of cosmic expansion, which defines a relationship between a galaxy’s distance and how fast it’s moving away from us, according to astrophysicist Neta A. Bahcall
- The Archimedes Principle, which states that the buoyant force on an object submerged in a fluid is equal to the weight of the fluid displaced by that object.
Additional resources
- This resource from the New South Wales Education Standards Authority (opens in new tab) has an in-depth explanation of scientific theories and laws.
- Find out why a theory can’t evolve into a law in this article from Indiana Public Media (opens in new tab).
- Watch a video about the difference between a scientific law and a scientific theory from TEDEd. (opens in new tab)
Bibliography
University of California, Berkeley, «Misconceptions about science.» https://undsci.berkeley.edu/teaching/misconceptions.php
NASA IMAGE Education Center, «Teacher’s Guide: Theories, Hypothesis, Laws, Facts & Beliefs.» https://www.nasa.gov/pdf/371711main_SMII_Problem23.pdf
The Ohio State University, «Lecture 18: The Apple and the Moon: Newtonian Gravity.» https://www.astronomy.ohio-state.edu/pogge.1/Ast161/Unit4/gravity.html
Encyclopedia Britannica, «Conservation of energy.» November 16, 2021. https://www.britannica.com/science/conservation-of-energy
University of Winnipeg, «Newton’s Law of Gravitation.» 1997. https://theory.uwinnipeg.ca/physics/circ/node7.html
Neta A. Bahcall, «Hubble’s Law and the expanding universe,» Proceedings of the National Academy of Sciences, Volume 112, March 2015, https://doi.org/10.1073/pnas.1424299112
Alina Bradford is a contributing writer for Live Science. Over the past 16 years, Alina has covered everything from Ebola to androids while writing health, science and tech articles for major publications. She has multiple health, safety and lifesaving certifications from Oklahoma State University. Alina’s goal in life is to try as many experiences as possible. To date, she has been a volunteer firefighter, a dispatcher, substitute teacher, artist, janitor, children’s book author, pizza maker, event coordinator and much more.
Most Popular
: Statement based on repeated empirical observations that describes some aspects of the universe
Scientific theories explain why something happens, whereas scientific law describes what happens.
Scientific laws or laws of science are statements, based on repeated experiments or observations, that describe or predict a range of natural phenomena.[1] The term law has diverse usage in many cases (approximate, accurate, broad, or narrow) across all fields of natural science (physics, chemistry, astronomy, geoscience, biology). Laws are developed from data and can be further developed through mathematics; in all cases they are directly or indirectly based on empirical evidence. It is generally understood that they implicitly reflect, though they do not explicitly assert, causal relationships fundamental to reality, and are discovered rather than invented.[2]
Scientific laws summarize the results of experiments or observations, usually within a certain range of application. In general, the accuracy of a law does not change when a new theory of the relevant phenomenon is worked out, but rather the scope of the law’s application, since the mathematics or statement representing the law does not change. As with other kinds of scientific knowledge, scientific laws do not express absolute certainty, as mathematical theorems or identities do. A scientific law may be contradicted, restricted, or extended by future observations.
A law can often be formulated as one or several statements or equations, so that it can predict the outcome of an experiment. Laws differ from hypotheses and postulates, which are proposed during the scientific process before and during validation by experiment and observation. Hypotheses and postulates are not laws, since they have not been verified to the same degree, although they may lead to the formulation of laws. Laws are narrower in scope than scientific theories, which may entail one or several laws.[3] Science distinguishes a law or theory from facts.[4] Calling a law a fact is ambiguous, an overstatement, or an equivocation.[5] The nature of scientific laws has been much discussed in philosophy, but in essence scientific laws are simply empirical conclusions reached by scientific method; they are intended to be neither laden with ontological commitments nor statements of logical absolutes.
Overview
A scientific law always applies to a physical system under repeated conditions, and it implies that there is a causal relationship involving the elements of the system. Factual and well-confirmed statements like «Mercury is liquid at standard temperature and pressure» are considered too specific to qualify as scientific laws. A central problem in the philosophy of science, going back to David Hume, is that of distinguishing causal relationships (such as those implied by laws) from principles that arise due to constant conjunction.[6]
Laws differ from scientific theories in that they do not posit a mechanism or explanation of phenomena: they are merely distillations of the results of repeated observation. As such, the applicability of a law is limited to circumstances resembling those already observed, and the law may be found to be false when extrapolated. Ohm’s law only applies to linear networks; Newton’s law of universal gravitation only applies in weak gravitational fields; the early laws of aerodynamics, such as Bernoulli’s principle, do not apply in the case of compressible flow such as occurs in transonic and supersonic flight; Hooke’s law only applies to strain below the elastic limit; Boyle’s law applies with perfect accuracy only to the ideal gas, etc. These laws remain useful, but only under the specified conditions where they apply.
Many laws take mathematical forms, and thus can be stated as an equation; for example, the law of conservation of energy can be written as [math]displaystyle{ Delta E = 0 }[/math], where [math]displaystyle{ E }[/math] is the total amount of energy in the universe. Similarly, the first law of thermodynamics can be written as [math]displaystyle{ mathrm{d}U=delta Q-delta W, }[/math], and Newton’s second law can be written as [math]displaystyle{ F = }[/math] dp⁄dt. While these scientific laws explain what our senses perceive, they are still empirical (acquired by observation or scientific experiment) and so are not like mathematical theorems which can be proved purely by mathematics.
Like theories and hypotheses, laws make predictions; specifically, they predict that new observations will conform to the given law. Laws can be falsified if they are found in contradiction with new data.
Some laws are only approximations of other more general laws, and are good approximations with a restricted domain of applicability. For example, Newtonian dynamics (which is based on Galilean transformations) is the low-speed limit of special relativity (since the Galilean transformation is the low-speed approximation to the Lorentz transformation). Similarly, the Newtonian gravitation law is a low-mass approximation of general relativity, and Coulomb’s law is an approximation to quantum electrodynamics at large distances (compared to the range of weak interactions). In such cases it is common to use the simpler, approximate versions of the laws, instead of the more accurate general laws.
Laws are constantly being tested experimentally to increasing degrees of precision, which is one of the main goals of science. The fact that laws have never been observed to be violated does not preclude testing them at increased accuracy or in new kinds of conditions to confirm whether they continue to hold, or whether they break, and what can be discovered in the process. It is always possible for laws to be invalidated or proven to have limitations, by repeatable experimental evidence, should any be observed. Well-established laws have indeed been invalidated in some special cases, but the new formulations created to explain the discrepancies generalize upon, rather than overthrow, the originals. That is, the invalidated laws have been found to be only close approximations, to which other terms or factors must be added to cover previously unaccounted-for conditions, e.g. very large or very small scales of time or space, enormous speeds or masses, etc. Thus, rather than unchanging knowledge, physical laws are better viewed as a series of improving and more precise generalizations.
Properties
Scientific laws are typically conclusions based on repeated scientific experiments and observations over many years and which have become accepted universally within the scientific community. A scientific law is «inferred from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present.»[7] The production of a summary description of our environment in the form of such laws is a fundamental aim of science.
Several general properties of scientific laws, particularly when referring to laws in physics, have been identified. Scientific laws are:
- True, at least within their regime of validity. By definition, there have never been repeatable contradicting observations.
- Universal. They appear to apply everywhere in the universe.[8]:82
- Simple. They are typically expressed in terms of a single mathematical equation.
- Absolute. Nothing in the universe appears to affect them.[8]:82
- Stable. Unchanged since first discovered (although they may have been shown to be approximations of more accurate laws),
- All-encompassing. Everything in the universe apparently must comply with them (according to observations).
- Generally conservative of quantity.[9]:59
- Often expressions of existing homogeneities (symmetries) of space and time.[9]
- Typically theoretically reversible in time (if non-quantum), although time itself is irreversible.[9]
- Broad. In physics, laws exclusively refer to the broad domain of matter, motion, energy, and force itself, rather than more specific systems in the universe, such as living systems, i.e. the mechanics of the human body.[10]
The term «scientific law» is traditionally associated with the natural sciences, though the social sciences also contain laws.[11] For example, Zipf’s law is a law in the social sciences which is based on mathematical statistics. In these cases, laws may describe general trends or expected behaviors rather than being absolutes.
In natural science, impossibility assertions come to be widely accepted as overwhelmingly probable rather than considered proved to the point of being unchallengeable. The basis for this strong acceptance is a combination of extensive evidence of something not occurring, combined with an underlying theory, very successful in making predictions, whose assumptions lead logically to the conclusion that something is impossible. While an impossibility assertion in natural science can never be absolutely proved, it could be refuted by the observation of a single counterexample. Such a counterexample would require that the assumptions underlying the theory that implied the impossibility be re-examined.
Some examples of widely accepted impossibilities in physics are perpetual motion machines, which violate the law of conservation of energy, exceeding the speed of light, which violates the implications of special relativity, the uncertainty principle of quantum mechanics, which asserts the impossibility of simultaneously knowing both the position and the momentum of a particle, and Bell’s theorem: no physical theory of local hidden variables can ever reproduce all of the predictions of quantum mechanics.
Laws as consequences of mathematical symmetries
Some laws reflect mathematical symmetries found in Nature (e.g. the Pauli exclusion principle reflects identity of electrons, conservation laws reflect homogeneity of space, time, and Lorentz transformations reflect rotational symmetry of spacetime). Many fundamental physical laws are mathematical consequences of various symmetries of space, time, or other aspects of nature. Specifically, Noether’s theorem connects some conservation laws to certain symmetries. For example, conservation of energy is a consequence of the shift symmetry of time (no moment of time is different from any other), while conservation of momentum is a consequence of the symmetry (homogeneity) of space (no place in space is special, or different than any other). The indistinguishability of all particles of each fundamental type (say, electrons, or photons) results in the Dirac and Bose quantum statistics which in turn result in the Pauli exclusion principle for fermions and in Bose–Einstein condensation for bosons. The rotational symmetry between time and space coordinate axes (when one is taken as imaginary, another as real) results in Lorentz transformations which in turn result in special relativity theory. Symmetry between inertial and gravitational mass results in general relativity.
The inverse square law of interactions mediated by massless bosons is the mathematical consequence of the 3-dimensionality of space.
One strategy in the search for the most fundamental laws of nature is to search for the most general mathematical symmetry group that can be applied to the fundamental interactions.
Laws of physics
Conservation laws
Conservation and symmetry
Conservation laws are fundamental laws that follow from the homogeneity of space, time and phase, in other words symmetry.
- Noether’s theorem: Any quantity with a continuously differentiable symmetry in the action has an associated conservation law.
- Conservation of mass was the first law to be understood since most macroscopic physical processes involving masses, for example, collisions of massive particles or fluid flow, provide the apparent belief that mass is conserved. Mass conservation was observed to be true for all chemical reactions. In general, this is only approximative because with the advent of relativity and experiments in nuclear and particle physics: mass can be transformed into energy and vice versa, so mass is not always conserved but part of the more general conservation of mass-energy.
- Conservation of energy, momentum and angular momentum for isolated systems can be found to be symmetries in time, translation, and rotation.
- Conservation of charge was also realized since charge has never been observed to be created or destroyed and only found to move from place to place.
Continuity and transfer
Conservation laws can be expressed using the general continuity equation (for a conserved quantity) can be written in differential form as:
- [math]displaystyle{ frac{partial rho}{partial t}=-nabla cdot mathbf{J} }[/math]
where ρ is some quantity per unit volume, J is the flux of that quantity (change in quantity per unit time per unit area). Intuitively, the divergence (denoted ∇•) of a vector field is a measure of flux diverging radially outwards from a point, so the negative is the amount piling up at a point; hence the rate of change of density in a region of space must be the amount of flux leaving or collecting in some region (see the main article for details). In the table below, the fluxes flows for various physical quantities in transport, and their associated continuity equations, are collected for comparison.
-
Physics, conserved quantity Conserved quantity q Volume density ρ (of q) Flux J (of q) Equation Hydrodynamics, fluids m = mass (kg) ρ = volume mass density (kg m−3) ρ u, where u = velocity field of fluid (m s−1)
[math]displaystyle{ frac{partial rho}{partial t} = — nabla cdot (rho mathbf{u}) }[/math] Electromagnetism, electric charge q = electric charge (C) ρ = volume electric charge density (C m−3) J = electric current density (A m−2) [math]displaystyle{ frac{partial rho}{partial t} = — nabla cdot mathbf{J} }[/math] Thermodynamics, energy E = energy (J) u = volume energy density (J m−3) q = heat flux (W m−2) [math]displaystyle{ frac{partial u}{partial t}=- nabla cdot mathbf{q} }[/math] Quantum mechanics, probability P = (r, t) = ∫|Ψ|2d3r = probability distribution ρ = ρ(r, t) = |Ψ|2 = probability density function (m−3), Ψ = wavefunction of quantum system
j = probability current/flux [math]displaystyle{ frac{partial |Psi|^2}{partial t}=-nabla cdot mathbf{j} }[/math]
More general equations are the convection–diffusion equation and Boltzmann transport equation, which have their roots in the continuity equation.
Laws of classical mechanics
Principle of least action
- Main page: Physics:Principle of least action
Classical mechanics, including Newton’s laws, Lagrange’s equations, Hamilton’s equations, etc., can be derived from the following principle:
- [math]displaystyle{ delta mathcal{S} = deltaint_{t_1}^{t_2} L(mathbf{q}, mathbf{dot{q}}, t) dt = 0 }[/math]
where [math]displaystyle{ mathcal{S} }[/math] is the action; the integral of the Lagrangian
- [math]displaystyle{ L(mathbf{q}, mathbf{dot{q}}, t) = T(mathbf{dot{q}}, t)-V(mathbf{q}, mathbf{dot{q}}, t) }[/math]
of the physical system between two times t1 and t2. The kinetic energy of the system is T (a function of the rate of change of the configuration of the system), and potential energy is V (a function of the configuration and its rate of change). The configuration of a system which has N degrees of freedom is defined by generalized coordinates q = (q1, q2, … qN).
There are generalized momenta conjugate to these coordinates, p = (p1, p2, …, pN), where:
- [math]displaystyle{ p_i = frac{partial L}{partial dot{q}_i} }[/math]
The action and Lagrangian both contain the dynamics of the system for all times. The term «path» simply refers to a curve traced out by the system in terms of the generalized coordinates in the configuration space, i.e. the curve q(t), parameterized by time (see also parametric equation for this concept).
The action is a functional rather than a function, since it depends on the Lagrangian, and the Lagrangian depends on the path q(t), so the action depends on the entire «shape» of the path for all times (in the time interval from t1 to t2). Between two instants of time, there are infinitely many paths, but one for which the action is stationary (to the first order) is the true path. The stationary value for the entire continuum of Lagrangian values corresponding to some path, not just one value of the Lagrangian, is required (in other words it is not as simple as «differentiating a function and setting it to zero, then solving the equations to find the points of maxima and minima etc», rather this idea is applied to the entire «shape» of the function, see calculus of variations for more details on this procedure).[12]
Notice L is not the total energy E of the system due to the difference, rather than the sum:
- [math]displaystyle{ E=T+V }[/math]
The following[13][14] general approaches to classical mechanics are summarized below in the order of establishment. They are equivalent formulations. Newton’s is commonly used due to simplicity, but Hamilton’s and Lagrange’s equations are more general, and their range can extend into other branches of physics with suitable modifications.
-
Laws of motion Principle of least action: [math]displaystyle{ mathcal{S} = int_{t_1}^{t_2} L ,mathrm{d}t ,! }[/math]
The Euler–Lagrange equations are: - [math]displaystyle{ frac{mathrm{d}}{mathrm{d} t} left ( frac{partial L}{partial dot{q}_i } right ) = frac{partial L}{partial q_i} }[/math]
Using the definition of generalized momentum, there is the symmetry:
- [math]displaystyle{ p_i = frac{partial L}{partial dot{q}_i}quad dot{p}_i = frac{partial L}{partial {q}_i} }[/math]
Hamilton’s equations - [math]displaystyle{ dfrac{partial mathbf{p}}{partial t} = -dfrac{partial H}{partial mathbf{q}} }[/math]
[math]displaystyle{ dfrac{partial mathbf{q}}{partial t} = dfrac{partial H}{partial mathbf{p}} }[/math]
The Hamiltonian as a function of generalized coordinates and momenta has the general form:
- [math]displaystyle{ H (mathbf{q}, mathbf{p}, t) = mathbf{p}cdotmathbf{dot{q}}-L }[/math]
Hamilton–Jacobi equation - [math]displaystyle{ H left(mathbf{q}, frac{partial S}{partialmathbf{q}}, tright) = -frac{partial S}{partial t} }[/math]
Newton’s laws Newton’s laws of motion
They are low-limit solutions to relativity. Alternative formulations of Newtonian mechanics are Lagrangian and Hamiltonian mechanics.
The laws can be summarized by two equations (since the 1st is a special case of the 2nd, zero resultant acceleration):
- [math]displaystyle{ mathbf{F} = frac{mathrm{d}mathbf{p}}{mathrm{d}t}, quad mathbf{F}_{ij}=-mathbf{F}_{ji} }[/math]
where p = momentum of body, Fij = force on body i by body j, Fji = force on body j by body i.
For a dynamical system the two equations (effectively) combine into one:
- [math]displaystyle{ frac{mathrm{d}mathbf{p}_mathrm{i}}{mathrm{d}t} = mathbf{F}_{E} + sum_{mathrm{i} neq mathrm{j}} mathbf{F}_mathrm{ij} ,! }[/math]
in which FE = resultant external force (due to any agent not part of system). Body i does not exert a force on itself.
From the above, any equation of motion in classical mechanics can be derived.
- Corollaries in mechanics
- Euler’s laws of motion
- Euler’s equations (rigid body dynamics)
- Corollaries in fluid mechanics
Equations describing fluid flow in various situations can be derived, using the above classical equations of motion and often conservation of mass, energy and momentum. Some elementary examples follow.
- Archimedes’ principle
- Bernoulli’s principle
- Poiseuille’s law
- Stokes’s law
- Navier–Stokes equations
- Faxén’s law
Laws of gravitation and relativity
Some of the more famous laws of nature are found in Isaac Newton’s theories of (now) classical mechanics, presented in his Philosophiae Naturalis Principia Mathematica, and in Albert Einstein’s theory of relativity.
Modern laws
- Special relativity
The two postulates of special relativity are not «laws» in themselves, but assumptions of their nature in terms of relative motion.
They can be stated as «the laws of physics are the same in all inertial frames» and «the speed of light is constant and has the same value in all inertial frames».
The said postulates lead to the Lorentz transformations – the transformation law between two frame of references moving relative to each other. For any 4-vector
- [math]displaystyle{ A’ =Lambda A }[/math]
this replaces the Galilean transformation law from classical mechanics. The Lorentz transformations reduce to the Galilean transformations for low velocities much less than the speed of light c.
The magnitudes of 4-vectors are invariants — not «conserved», but the same for all inertial frames (i.e. every observer in an inertial frame will agree on the same value), in particular if A is the four-momentum, the magnitude can derive the famous invariant equation for mass-energy and momentum conservation (see invariant mass):
- [math]displaystyle{ E^2 = (pc)^2 + (mc^2)^2 }[/math]
in which the (more famous) mass-energy equivalence E = mc2 is a special case.
- General relativity
General relativity is governed by the Einstein field equations, which describe the curvature of space-time due to mass-energy equivalent to the gravitational field. Solving the equation for the geometry of space warped due to the mass distribution gives the metric tensor. Using the geodesic equation, the motion of masses falling along the geodesics can be calculated.
- Gravitomagnetism
In a relatively flat spacetime due to weak gravitational fields, gravitational analogues of Maxwell’s equations can be found; the GEM equations, to describe an analogous gravitomagnetic field. They are well established by the theory, and experimental tests form ongoing research.[15]
-
Einstein field equations (EFE): - [math]displaystyle{ R_{mu nu} + left ( Lambda — frac{R}{2} right ) g_{mu nu} = frac{8 pi G}{c^4} T_{mu nu},! }[/math]
where Λ = cosmological constant, Rμν = Ricci curvature tensor, Tμν = Stress–energy tensor, gμν = metric tensor
Geodesic equation: - [math]displaystyle{ frac{{rm d}^2x^lambda }{{rm d}t^2} + Gamma^{lambda}_{mu nu }frac{{rm d}x^mu }{{rm d}t}frac{{rm d}x^nu }{{rm d}t} = 0 , }[/math]
where Γ is a Christoffel symbol of the second kind, containing the metric.
GEM Equations If g the gravitational field and H the gravitomagnetic field, the solutions in these limits are:
- [math]displaystyle{ nabla cdot mathbf{g} = -4 pi G rho ,! }[/math]
- [math]displaystyle{ nabla cdot mathbf{H} = mathbf{0} ,! }[/math]
- [math]displaystyle{ nabla times mathbf{g} = -frac{partial mathbf{H}} {partial t} ,! }[/math]
- [math]displaystyle{ nabla times mathbf{H} = frac{4}{c^2}left( — 4 pi Gmathbf{J} + frac{partial mathbf{g}} {partial t} right) ,! }[/math]
where ρ is the mass density and J is the mass current density or mass flux.
In addition there is the gravitomagnetic Lorentz force: - [math]displaystyle{ mathbf{F} = gamma(mathbf{v}) m left( mathbf{g} + mathbf{v} times mathbf{H} right) }[/math]
where m is the rest mass of the particlce and γ is the Lorentz factor.
Classical laws
Kepler’s Laws, though originally discovered from planetary observations (also due to Tycho Brahe), are true for any central forces.[16]
-
Newton’s law of universal gravitation: For two point masses:
- [math]displaystyle{ mathbf{F} = frac{G m_1 m_2}{left | mathbf{r} right |^2} mathbf{hat{r}} ,! }[/math]
For a non uniform mass distribution of local mass density ρ (r) of body of Volume V, this becomes:
- [math]displaystyle{ mathbf{g} = G int_{V} frac{mathbf{r} rho mathrm{d}{V}}{left | mathbf{r} right |^3},! }[/math]
Gauss’ law for gravity: An equivalent statement to Newton’s law is:
- [math]displaystyle{ nablacdotmathbf{g} = 4pi Grho ,! }[/math]
Kepler’s 1st Law: Planets move in an ellipse, with the star at a focus - [math]displaystyle{ r = frac{l}{1+e costheta} ,! }[/math]
where
- [math]displaystyle{ e = sqrt{1- (b/a)^2} }[/math]
is the eccentricity of the elliptic orbit, of semi-major axis a and semi-minor axis b, and l is the semi-latus rectum. This equation in itself is nothing physically fundamental; simply the polar equation of an ellipse in which the pole (origin of polar coordinate system) is positioned at a focus of the ellipse, where the orbited star is.
Kepler’s 2nd Law: equal areas are swept out in equal times (area bounded by two radial distances and the orbital circumference): - [math]displaystyle{ frac{mathrm{d}A}{mathrm{d}t} = frac{left | mathbf{L} right |}{2m} ,! }[/math]
where L is the orbital angular momentum of the particle (i.e. planet) of mass m about the focus of orbit,
Kepler’s 3rd Law: The square of the orbital time period T is proportional to the cube of the semi-major axis a: - [math]displaystyle{ T^2 = frac{4pi^2}{G left ( m + M right ) } a^3,! }[/math]
where M is the mass of the central body (i.e. star).
Thermodynamics
-
Laws of thermodynamics First law of thermodynamics: The change in internal energy dU in a closed system is accounted for entirely by the heat δQ absorbed by the system and the work δW done by the system: - [math]displaystyle{ mathrm{d}U=delta Q-delta W, }[/math]
Second law of thermodynamics: There are many statements of this law, perhaps the simplest is «the entropy of isolated systems never decreases»,
- [math]displaystyle{ Delta S ge 0 }[/math]
meaning reversible changes have zero entropy change, irreversible process are positive, and impossible process are negative.
Zeroth law of thermodynamics: If two systems are in thermal equilibrium with a third system, then they are in thermal equilibrium with one another. - [math]displaystyle{ T_A = T_B ,, T_B=T_C Rightarrow T_A=T_C,! }[/math]
Third law of thermodynamics:
- As the temperature T of a system approaches absolute zero, the entropy S approaches a minimum value C: as T → 0, S → C.
For homogeneous systems the first and second law can be combined into the Fundamental thermodynamic relation: - [math]displaystyle{ mathrm{d} U = T mathrm{d} S — P mathrm{d} V + sum_i mu_i mathrm{d}N_i ,! }[/math]
Onsager reciprocal relations: sometimes called the Fourth Law of Thermodynamics - [math]displaystyle{ mathbf{J}_{u} = L_{uu}, nabla(1/T) — L_{ur}, nabla(m/T) ! }[/math];
- [math]displaystyle{ mathbf{J}_{r} = L_{ru}, nabla(1/T) — L_{rr}, nabla(m/T) ! }[/math].
- Newton’s law of cooling
- Fourier’s law
- Ideal gas law, combines a number of separately developed gas laws;
- Boyle’s law
- Charles’s law
- Gay-Lussac’s law
- Avogadro’s law, into one
- now improved by other equations of state
- Dalton’s law (of partial pressures)
- Boltzmann equation
- Carnot’s theorem
- Kopp’s law
Electromagnetism
Maxwell’s equations give the time-evolution of the electric and magnetic fields due to electric charge and current distributions. Given the fields, the Lorentz force law is the equation of motion for charges in the fields.
-
Maxwell’s equations Gauss’s law for electricity
- [math]displaystyle{ nabla cdot mathbf{E} = frac{rho}{varepsilon_0} }[/math]
Gauss’s law for magnetism
- [math]displaystyle{ nabla cdot mathbf{B} = 0 }[/math]
Faraday’s law
- [math]displaystyle{ nabla times mathbf{E} = -frac{partial mathbf{B}} {partial t} }[/math]
Ampère’s circuital law (with Maxwell’s correction)
- [math]displaystyle{ nabla times mathbf{B} = mu_0 mathbf{J} + frac{1}{c^2} frac{partial mathbf{E}}{partial t} }[/math]
Lorentz force law: - [math]displaystyle{ mathbf{F}=qleft(mathbf{E}+mathbf{v}timesmathbf{B}right) }[/math]
Quantum electrodynamics (QED): Maxwell’s equations are generally true and consistent with relativity — but they do not predict some observed quantum phenomena (e.g. light propagation as EM waves, rather than photons, see Maxwell’s equations for details). They are modified in QED theory.
These equations can be modified to include magnetic monopoles, and are consistent with our observations of monopoles either existing or not existing; if they do not exist, the generalized equations reduce to the ones above, if they do, the equations become fully symmetric in electric and magnetic charges and currents. Indeed, there is a duality transformation where electric and magnetic charges can be «rotated into one another», and still satisfy Maxwell’s equations.
- Pre-Maxwell laws
These laws were found before the formulation of Maxwell’s equations. They are not fundamental, since they can be derived from Maxwell’s Equations. Coulomb’s Law can be found from Gauss’ Law (electrostatic form) and the Biot–Savart Law can be deduced from Ampere’s Law (magnetostatic form). Lenz’ Law and Faraday’s Law can be incorporated into the Maxwell-Faraday equation. Nonetheless they are still very effective for simple calculations.
- Lenz’s law
- Coulomb’s law
- Biot–Savart law
- Other laws
- Ohm’s law
- Kirchhoff’s laws
- Joule’s law
Photonics
Classically, optics is based on a variational principle: light travels from one point in space to another in the shortest time.
- Fermat’s principle
In geometric optics laws are based on approximations in Euclidean geometry (such as the paraxial approximation).
- Law of reflection
- Law of refraction, Snell’s law
In physical optics, laws are based on physical properties of materials.
- Brewster’s angle
- Malus’s law
- Beer–Lambert law
In actuality, optical properties of matter are significantly more complex and require quantum mechanics.
Laws of quantum mechanics
Quantum mechanics has its roots in postulates. This leads to results which are not usually called «laws», but hold the same status, in that all of quantum mechanics follows from them.
One postulate that a particle (or a system of many particles) is described by a wavefunction, and this satisfies a quantum wave equation: namely the Schrödinger equation (which can be written as a non-relativistic wave equation, or a relativistic wave equation). Solving this wave equation predicts the time-evolution of the system’s behaviour, analogous to solving Newton’s laws in classical mechanics.
Other postulates change the idea of physical observables; using quantum operators; some measurements can’t be made at the same instant of time (Uncertainty principles), particles are fundamentally indistinguishable. Another postulate; the wavefunction collapse postulate, counters the usual idea of a measurement in science.
-
Quantum mechanics, Quantum field theory Schrödinger equation (general form): Describes the time dependence of a quantum mechanical system.
- [math]displaystyle{ ihbar frac{d}{dt} left| psi rightrangle = hat{H} left| psi rightrangle }[/math]
The Hamiltonian (in quantum mechanics) H is a self-adjoint operator acting on the state space, [math]displaystyle{ | psi rangle }[/math] (see Dirac notation) is the instantaneous quantum state vector at time t, position r, i is the unit imaginary number, ħ = h/2π is the reduced Planck’s constant.
Wave–particle duality Planck–Einstein law: the energy of photons is proportional to the frequency of the light (the constant is Planck’s constant, h).
- [math]displaystyle{ E = hnu = hbar omega }[/math]
De Broglie wavelength: this laid the foundations of wave–particle duality, and was the key concept in the Schrödinger equation,
- [math]displaystyle{ mathbf{p} = frac{h}{lambda}mathbf{hat{k}} = hbar mathbf{k} }[/math]
Heisenberg uncertainty principle: Uncertainty in position multiplied by uncertainty in momentum is at least half of the reduced Planck constant, similarly for time and energy;
- [math]displaystyle{ Delta x Delta p ge frac{hbar}{2},, Delta E Delta t ge frac{hbar}{2} }[/math]
The uncertainty principle can be generalized to any pair of observables — see main article.
Wave mechanics Schrödinger equation (original form):
- [math]displaystyle{ ihbar frac{partial}{partial t}psi = -frac{hbar^2}{2m} nabla^2 psi + V psi }[/math]
Pauli exclusion principle: No two identical fermions can occupy the same quantum state (bosons can). Mathematically, if two particles are interchanged, fermionic wavefunctions are anti-symmetric, while bosonic wavefunctions are symmetric: [math]displaystyle{ psi(cdotsmathbf{r}_icdotsmathbf{r}_jcdots) = (-1)^{2s}psi(cdotsmathbf{r}_jcdotsmathbf{r}_icdots) }[/math]
where ri is the position of particle i, and s is the spin of the particle. There is no way to keep track of particles physically, labels are only used mathematically to prevent confusion.
Radiation laws
Applying electromagnetism, thermodynamics, and quantum mechanics, to atoms and molecules, some laws of electromagnetic radiation and light are as follows.
- Stefan–Boltzmann law
- Planck’s law of black-body radiation
- Wien’s displacement law
- Radioactive decay law
Laws of chemistry
- Main page: Chemistry:Chemical law
Chemical laws are those laws of nature relevant to chemistry. Historically, observations led to many empirical laws, though now it is known that chemistry has its foundations in quantum mechanics.
- Quantitative analysis
The most fundamental concept in chemistry is the law of conservation of mass, which states that there is no detectable change in the quantity of matter during an ordinary chemical reaction. Modern physics shows that it is actually energy that is conserved, and that energy and mass are related; a concept which becomes important in nuclear chemistry. Conservation of energy leads to the important concepts of equilibrium, thermodynamics, and kinetics.
Additional laws of chemistry elaborate on the law of conservation of mass. Joseph Proust’s law of definite composition says that pure chemicals are composed of elements in a definite formulation; we now know that the structural arrangement of these elements is also important.
Dalton’s law of multiple proportions says that these chemicals will present themselves in proportions that are small whole numbers; although in many systems (notably biomacromolecules and minerals) the ratios tend to require large numbers, and are frequently represented as a fraction.
The law of definite composition and the law of multiple proportions are the first two of the three laws of stoichiometry, the proportions by which the chemical elements combine to form chemical compounds. The third law of stoichiometry is the law of reciprocal proportions, which provides the basis for establishing equivalent weights for each chemical element. Elemental equivalent weights can then be used to derive atomic weights for each element.
More modern laws of chemistry define the relationship between energy and its transformations.
- Reaction kinetics and equilibria
- In equilibrium, molecules exist in mixture defined by the transformations possible on the timescale of the equilibrium, and are in a ratio defined by the intrinsic energy of the molecules—the lower the intrinsic energy, the more abundant the molecule. Le Chatelier’s principle states that the system opposes changes in conditions from equilibrium states, i.e. there is an opposition to change the state of an equilibrium reaction.
- Transforming one structure to another requires the input of energy to cross an energy barrier; this can come from the intrinsic energy of the molecules themselves, or from an external source which will generally accelerate transformations. The higher the energy barrier, the slower the transformation occurs.
- There is a hypothetical intermediate, or transition structure, that corresponds to the structure at the top of the energy barrier. The Hammond–Leffler postulate states that this structure looks most similar to the product or starting material which has intrinsic energy closest to that of the energy barrier. Stabilizing this hypothetical intermediate through chemical interaction is one way to achieve catalysis.
- All chemical processes are reversible (law of microscopic reversibility) although some processes have such an energy bias, they are essentially irreversible.
- The reaction rate has the mathematical parameter known as the rate constant. The Arrhenius equation gives the temperature and activation energy dependence of the rate constant, an empirical law.
- Thermochemistry
- Dulong–Petit law
- Gibbs–Helmholtz equation
- Hess’s law
- Gas laws
- Raoult’s law
- Henry’s law
- Chemical transport
- Fick’s laws of diffusion
- Graham’s law
- Lamm equation
Laws of biology
- Main page: Biology:Biological rules
Ecology
- Competitive exclusion principle or Gause’s law
Genetics
- Mendelian laws (Dominance and Uniformity, segregation of genes, and Independent Assortment)
- Hardy–Weinberg principle
Natural selection
Whether or not Natural Selection is a “law of nature” is controversial among biologists.[17][18] Henry Byerly, an American philosopher known for his work on evolutionary theory, discussed the problem of interpreting a principle of natural selection as a law. He suggested a formulation of natural selection as a framework principle that can contribute to a better understanding of evolutionary theory.[18] His approach was to express relative fitness, the propensity of a genotype to increase in proportionate representation in a competitive environment, as a function of adaptedness (adaptive design) of the organism.
Laws of Earth Sciences
Geography
- Arbia’s law of geography
- Tobler’s first law of geography
- Tobler’s second law of geography
Geology
- Archie’s law
- Buys-Ballot’s law
- Birch’s law
- Byerlee’s law
- Principle of original horizontality
- Law of superposition
- Principle of lateral continuity
- Principle of cross-cutting relationships
- Principle of faunal succession
- Principle of inclusions and components
- Walther’s law
Other fields
Some mathematical theorems and axioms are referred to as laws because they provide logical foundation to empirical laws.
Examples of other observed phenomena sometimes described as laws include the Titius–Bode law of planetary positions, Zipf’s law of linguistics, and Moore’s law of technological growth. Many of these laws fall within the scope of uncomfortable science. Other laws are pragmatic and observational, such as the law of unintended consequences. By analogy, principles in other fields of study are sometimes loosely referred to as «laws». These include Occam’s razor as a principle of philosophy and the Pareto principle of economics.
History
The observation and detection of underlying regularities in nature date from prehistoric times — the recognition of cause-and-effect relationships implicitly recognises the existence of laws of nature. The recognition of such regularities as independent scientific laws per se, though, was limited by their entanglement in animism, and by the attribution of many effects that do not have readily obvious causes—such as physical phenomena—to the actions of gods, spirits, supernatural beings, etc. Observation and speculation about nature were intimately bound up with metaphysics and morality.
In Europe, systematic theorizing about nature (physis) began with the early Greek philosophers and scientists and continued into the Hellenistic and Roman imperial periods, during which times the intellectual influence of Roman law increasingly became paramount.
The formula «law of nature» first appears as «a live metaphor» favored by Latin poets Lucretius, Virgil, Ovid, Manilius, in time gaining a firm theoretical presence in the prose treatises of Seneca and Pliny. Why this Roman origin? According to [historian and classicist Daryn] Lehoux’s persuasive narrative,[19] the idea was made possible by the pivotal role of codified law and forensic argument in Roman life and culture.
For the Romans . . . the place par excellence where ethics, law, nature, religion and politics overlap is the law court. When we read Seneca’s Natural Questions, and watch again and again just how he applies standards of evidence, witness evaluation, argument and proof, we can recognize that we are reading one of the great Roman rhetoricians of the age, thoroughly immersed in forensic method. And not Seneca alone. Legal models of scientific judgment turn up all over the place, and for example prove equally integral to Ptolemy’s approach to verification, where the mind is assigned the role of magistrate, the senses that of disclosure of evidence, and dialectical reason that of the law itself.[20]
The precise formulation of what are now recognized as modern and valid statements of the laws of nature dates from the 17th century in Europe, with the beginning of accurate experimentation and the development of advanced forms of mathematics. During this period, natural philosophers such as Isaac Newton (1642-1727) were influenced by a religious view — stemming from medieval concepts of divine law — which held that God had instituted absolute, universal and immutable physical laws.[21][22] In chapter 7 of The World, René Descartes (1596-1650) described «nature» as matter itself, unchanging as created by God, thus changes in parts «are to be attributed to nature. The rules according to which these changes take place I call the ‘laws of nature’.»[23] The modern scientific method which took shape at this time (with Francis Bacon (1561-1626) and Galileo (1564-1642)) contributed to a trend of separating science from theology, with minimal speculation about metaphysics and ethics. (Natural law in the political sense, conceived as universal (i.e., divorced from sectarian religion and accidents of place), was also elaborated in this period by scholars such as Grotius (1583-1645), Spinoza (1632-1677), and Hobbes (1588-1679).)
The distinction between natural law in the political-legal sense and law of nature or physical law in the scientific sense is a modern one, both concepts being equally derived from physis, the Greek word (translated into Latin as natura) for nature.[24]
See also
References
- ↑ law of nature (3rd ed.), Oxford University Press, September 2005, http://oed.com/search?searchType=dictionary&q=law+of+nature (Subscription or UK public library membership required.)
- ↑ William F. McComas (30 December 2013). The Language of Science Education: An Expanded Glossary of Key Terms and Concepts in Science Teaching and Learning. Springer Science & Business Media. p. 58. ISBN 978-94-6209-497-0. https://books.google.com/books?id=aXzGBAAAQBAJ.
- ↑ «Definitions from». the NCSE. http://ncse.com/evolution/education/definitions-fact-theory-law-scientific-work.
- ↑ «The Role of Theory in Advancing 21st Century Biology: Catalyzing Transformative Research». Report in Brief (The National Academy of Sciences). 2007. http://dels.nas.edu/resources/static-assets/materials-based-on-reports/reports-in-brief/role_of_theory_final.pdf.
- ↑ Gould, Stephen Jay (1981-05-01). «Evolution as Fact and Theory». Discover 2 (5): 34–37. http://www.inf.fu-berlin.de/lehre/pmo/eng/Gould-Fact&Theory.pdf.
- ↑ Honderich, Bike, ed. (1995), «Laws, natural or scientific», Oxford Companion to Philosophy, Oxford: Oxford University Press, pp. 474–476, ISBN 0-19-866132-0, https://archive.org/details/oxfordcompaniont00hond/page/474
- ↑ Law of nature (3rd ed.), Oxford University Press, September 2005, http://oed.com/search?searchType=dictionary&q=Law+of+nature (Subscription or UK public library membership required.)
- ↑ 8.0 8.1 Davies, Paul (2005). The mind of God : the scientific basis for a rational world (1st Simon & Schuster pbk. ed.). New York: Simon & Schuster. ISBN 978-0-671-79718-8. https://archive.org/details/mindof_dav_1992_00_1584.
- ↑ 9.0 9.1 9.2 Feynman, Richard (1994). The character of physical law (Modern Library ed.). New York: Modern Library. ISBN 978-0-679-60127-2.
- ↑ Frisch, Mathias (May 2014). «Laws in Physics | European Review | Cambridge Core». European Review 22 (S1): S33–S49. doi:10.1017/S1062798713000768.
- ↑ Andrew S. C. Ehrenberg (1993), «Even the Social Sciences Have Laws», Nature, 365:6445 (30), page 385.(Subscription content?)
- ↑ Feynman Lectures on Physics: Volume 2, R.P. Feynman, R.B. Leighton, M. Sands, Addison-Wesley, 1964, ISBN 0-201-02117-X
- ↑ Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC Publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1 (VHC Inc.) 0-89573-752-3
- ↑ Classical Mechanics, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, ISBN 0-07-084018-0
- ↑ Gravitation and Inertia, I. Ciufolini and J.A. Wheeler, Princeton Physics Series, 1995, ISBN 0-691-03323-4
- ↑ 2.^ Classical Mechanics, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, ISBN 0-07-084018-0
- ↑ Reed ES: The lawfulness of natural selection. Am Nat. 1981; 118(1): 61–71.
- ↑ 18.0 18.1 Byerly HC: Natural selection as a law: Principles and processes. Am Nat. 1983; 121(5): 739–745.
- ↑ in Daryn Lehoux, What Did the Romans Know? An Inquiry into Science and Worldmaking (Chicago: University of Chicago Press, 2012), reviewed by David Sedley, «When Nature Got its Laws», Times Literary Supplement (12 October 2012).
- ↑ Sedley, «When Nature Got Its Laws», Times Literary Supplement (12 October 2012).
- ↑ Davies, Paul (2007-11-24). «Taking Science on Faith». The New York Times. ISSN 0362-4331. https://www.nytimes.com/2007/11/24/opinion/24davies.html. «Isaac Newton first got the idea of absolute, universal, perfect, immutable laws from the Christian doctrine that God created the world and ordered it in a rational way.»
- ↑ Harrison, Peter (8 May 2012). «Christianity and the rise of western science». http://www.abc.net.au/religion/articles/2012/05/08/3498202.htm. «Individuals such as Galileo, Johannes Kepler, Rene Descartes and Isaac Newton were convinced that mathematical truths were not the products of human minds, but of the divine mind. God was the source of mathematical relations that were evident in the new laws of the universe.»
- ↑ «Cosmological Revolution V: Descartes and Newton». http://bertie.ccsu.edu/naturesci/Cosmology/Cosmo5Newton.html.
- ↑
Some modern philosophers, e.g. Norman Swartz, use «physical law» to mean the laws of nature as they truly are and not as they are inferred by scientists. See Norman Swartz, The Concept of Physical Law (New York: Cambridge University Press), 1985. Second edition available online [1].
Further reading
- John Barrow (1991). Theories of Everything: The Quest for Ultimate Explanations. (ISBN:0-449-90738-4)
- Dilworth, Craig (2007). «Appendix IV. On the nature of scientific laws and theories». Scientific progress : a study concerning the nature of the relation between successive scientific theories (4th ed.). Dordrecht: Springer Verlag. ISBN 978-1-4020-6353-4.
- Francis Bacon (1620). Novum Organum.
- Hanzel, Igor (1999). The concept of scientific law in the philosophy of science and epistemology : a study of theoretical reason. Dordrecht [u.a.]: Kluwer. ISBN 978-0-7923-5852-7.
- Daryn Lehoux (2012). What Did the Romans Know? An Inquiry into Science and Worldmaking. University of Chicago Press. (ISBN:9780226471143)
- Nagel, Ernest (1984). «5. Experimental laws and theories». The structure of science problems in the logic of scientific explanation (2nd ed.). Indianapolis: Hackett. ISBN 978-0-915144-71-6.
- R. Penrose (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
- Swartz, Norman (20 February 2009). «Laws of Nature». Internet encyclopedia of philosophy. http://www.iep.utm.edu/lawofnat/. Retrieved 7 May 2012.
External links
- Physics Formulary, a useful book in different formats containing many or the physical laws and formulae.
- Eformulae.com, website containing most of the formulae in different disciplines.
- Stanford Encyclopedia of Philosophy: «Laws of Nature» by John W. Carroll.
- Baaquie, Belal E. «Laws of Physics : A Primer». Core Curriculum, National University of Singapore.
- Francis, Erik Max. «The laws list».. Physics. Alcyone Systems
- Pazameta, Zoran. «The laws of nature». Committee for the scientific investigation of Claims of the Paranormal.
- The Internet Encyclopedia of Philosophy. «Laws of Nature» – By Norman Swartz
- «Laws of Nature», In Our Time, BBC Radio 4 discussion with Mark Buchanan, Frank Close and Nancy Cartwright (Oct. 19, 2000)
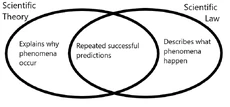
Scientific theories explain why something happens, whereas scientific law records what happens.
Scientific laws or laws of science are statements that describe or predict a range of natural phenomena.[1] A scientific law is a statement based on repeated experiments or observations that describe some aspect of the natural world. The term law has diverse usage in many cases (approximate, accurate, broad, or narrow) across all fields of natural science (physics, chemistry, biology, geology, astronomy, etc.). Laws are developed from data and can be further developed through mathematics; in all cases they are directly or indirectly based on empirical evidence. It is generally understood that they implicitly reflect, though they do not explicitly assert, causal relationships fundamental to reality, and are discovered rather than invented.[2]
Scientific laws summarize the results of experiments or observations, usually within a certain range of application. In general, the accuracy of a law does not change when a new theory of the relevant phenomenon is worked out, but rather the scope of the law’s application, since the mathematics or statement representing the law does not change. As with other kinds of scientific knowledge, laws do not have absolute certainty (as mathematical theorems or identities do), and it is always possible for a law to be contradicted, restricted, or extended by future observations. A law can usually be formulated as one or several statements or equations, so that it can be used to predict the outcome of an experiment, given the circumstances of the processes taking place.
Laws differ from hypotheses and postulates, which are proposed during the scientific process before and during validation by experiment and observation. Hypotheses and postulates are not laws since they have not been verified to the same degree, although they may lead to the formulation of laws. Laws are narrower in scope than scientific theories, which may entail one or several laws.[3] Science distinguishes a law or theory from facts.[4] Calling a law a fact is ambiguous, an overstatement, or an equivocation.[5] The nature of scientific laws has been much discussed in philosophy, but in essence scientific laws are simply empirical conclusions reached by scientific method; they are intended to be neither laden with ontological commitments nor statements of logical absolutes.
Overview
A scientific law always applies under the same conditions, and implies that there is a causal relationship involving its elements. Factual and well-confirmed statements like «Mercury is liquid at standard temperature and pressure» are considered too specific to qualify as scientific laws. A central problem in the philosophy of science, going back to David Hume, is that of distinguishing causal relationships (such as those implied by laws) from principles that arise due to constant conjunction.[6]
Laws differ from scientific theories in that they do not posit a mechanism or explanation of phenomena: they are merely distillations of the results of repeated observation. As such, a law is limited in applicability to circumstances resembling those already observed, and may be found false when extrapolated. Ohm’s law only applies to linear networks, Newton’s law of universal gravitation only applies in weak gravitational fields, the early laws of aerodynamics such as Bernoulli’s principle do not apply in case of compressible flow such as occurs in transonic and supersonic flight, Hooke’s law only applies to strain below the elastic limit, Boyle’s law applies with perfect accuracy only to the ideal gas, etc. These laws remain useful, but only under the conditions where they apply.
Many laws take mathematical forms, and thus can be stated as an equation; for example, the law of conservation of energy can be written as 

Like theories and hypotheses, laws make predictions (specifically, they predict that new observations will conform to the law), and can be falsified if they are found in contradiction with new data.
Some laws are only approximations of other more general laws, and are good approximations with a restricted domain of applicability. For example, Newtonian dynamics (which is based on Galilean transformations) is the low-speed limit of special relativity (since the Galilean transformation is the low-speed approximation to the Lorentz transformation). Similarly, the Newtonian gravitation law is a low-mass approximation of general relativity, and Coulomb’s law is an approximation to Quantum Electrodynamics at large distances (compared to the range of weak interactions). In such cases it is common to use the simpler, approximate versions of the laws, instead of the more accurate general laws.
Laws are constantly being tested experimentally to higher and higher degrees of precision. This is one of the main goals of science. Just because laws have never been observed to be violated does not preclude testing them at increased accuracy or in new kinds of conditions to confirm whether they continue to hold, or whether they break, and what can be discovered in the process. It is always possible for laws to be invalidated or proven to have limitations, by repeatable experimental evidence, should any be observed. Well-established laws have indeed been invalidated in some special cases, but the new formulations created to explain the discrepancies generalize upon, rather than overthrow, the originals. That is, the invalidated laws have been found to be only close approximations, to which other terms or factors must be added to cover previously unaccounted-for conditions, e.g. very large or very small scales of time or space, enormous speeds or masses, etc. Thus, rather than unchanging knowledge, physical laws are better viewed as a series of improving and more precise generalizations.
Properties
Scientific laws are typically conclusions based on repeated scientific experiments and observations over many years and which have become accepted universally within the scientific community. A scientific law is «inferred from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present.»[7] The production of a summary description of our environment in the form of such laws is a fundamental aim of science.
Several general properties of scientific laws, particularly when referring to laws in physics, have been identified. They are:
- True, at least within their regime of validity. By definition, there have never been repeatable contradicting observations.
- Universal. They appear to apply everywhere in the universe.[8]:82
- Simple. They are typically expressed in terms of a single mathematical equation.
- Absolute. Nothing in the universe appears to affect them.[8]:82
- Stable. Unchanged since first discovered (although they may have been shown to be approximations of more accurate laws),
- Omnipotent. Everything in the universe apparently must comply with them (according to observations).[8]:83
- Generally conservative of quantity.[9]:59
- Often expressions of existing homogeneities (symmetries) of space and time.[9]
- Typically theoretically reversible in time (if non-quantum), although time itself is irreversible.[9]
The term «scientific law» is traditionally associated with the natural sciences, though the social sciences also contain laws.[10] For example, Zipf’s law is a law in the social sciences which is based on mathematical statistics. In these cases, laws may describe general trends or expected behaviors rather than being absolutes.
Laws as consequences of mathematical symmetries
Main article: Symmetry (physics)
Some laws reflect mathematical symmetries found in Nature (e.g. the Pauli exclusion principle reflects identity of electrons, conservation laws reflect homogeneity of space, time, and Lorentz transformations reflect rotational symmetry of spacetime). Many fundamental physical laws are mathematical consequences of various symmetries of space, time, or other aspects of nature. Specifically, Noether’s theorem connects some conservation laws to certain symmetries. For example, conservation of energy is a consequence of the shift symmetry of time (no moment of time is different from any other), while conservation of momentum is a consequence of the symmetry (homogeneity) of space (no place in space is special, or different than any other). The indistinguishability of all particles of each fundamental type (say, electrons, or photons) results in the Dirac and Bose quantum statistics which in turn result in the Pauli exclusion principle for fermions and in Bose–Einstein condensation for bosons. The rotational symmetry between time and space coordinate axes (when one is taken as imaginary, another as real) results in Lorentz transformations which in turn result in special relativity theory. Symmetry between inertial and gravitational mass results in general relativity.
The inverse square law of interactions mediated by massless bosons is the mathematical consequence of the 3-dimensionality of space.
One strategy in the search for the most fundamental laws of nature is to search for the most general mathematical symmetry group that can be applied to the fundamental interactions.
Laws of physics
Conservation laws
Conservation and symmetry
Main article: Symmetry (physics)
Most significant laws in science are conservation laws. These fundamental laws follow from homogeneity of space, time and phase, in other words symmetry.
- Noether’s theorem: Any quantity which has a continuous differentiable symmetry in the action has an associated conservation law.
- Conservation of mass was the first law of this type to be understood, since most macroscopic physical processes involving masses, for example collisions of massive particles or fluid flow, provide the apparent belief that mass is conserved. Mass conservation was observed to be true for all chemical reactions. In general this is only approximative, because with the advent of relativity and experiments in nuclear and particle physics: mass can be transformed into energy and vice versa, so mass is not always conserved, but part of the more general conservation of mass-energy.
- Conservation of energy, momentum and angular momentum for isolated systems can be found to be symmetries in time, translation, and rotation.
- Conservation of charge was also realized since charge has never been observed to be created or destroyed, and only found to move from place to place.
Continuity and transfer
Conservation laws can be expressed using the general continuity equation (for a conserved quantity) can be written in differential form as:
where ρ is some quantity per unit volume, J is the flux of that quantity (change in quantity per unit time per unit area). Intuitively, the divergence (denoted ∇•) of a vector field is a measure of flux diverging radially outwards from a point, so the negative is the amount piling up at a point, hence the rate of change of density in a region of space must be the amount of flux leaving or collecting in some region (see main article for details). In the table below, the fluxes, flows for various physical quantities in transport, and their associated continuity equations, are collected for comparison.
-
Physics, conserved quantity Conserved quantity q Volume density ρ (of q) Flux J (of q) Equation Hydrodynamics, fluids m = mass (kg) ρ = volume mass density (kg m−3) ρ u, where u = velocity field of fluid (m s−1)
Electromagnetism, electric charge q = electric charge (C) ρ = volume electric charge density (C m−3) J = electric current density (A m−2) Thermodynamics, energy E = energy (J) u = volume energy density (J m−3) q = heat flux (W m−2) Quantum mechanics, probability P = (r, t) = ∫|Ψ|2d3r = probability distribution ρ = ρ(r, t) = |Ψ|2 = probability density function (m−3), Ψ = wavefunction of quantum system
j = probability current/flux
More general equations are the convection–diffusion equation and Boltzmann transport equation, which have their roots in the continuity equation.
Laws of classical mechanics
Principle of least action
Main article: Principle of least action
All of classical mechanics, including Newton’s laws, Lagrange’s equations, Hamilton’s equations, etc., can be derived from this very simple principle:
where 
of the physical system between two times t1 and t2. The kinetic energy of the system is T (a function of the rate of change of the configuration of the system), and potential energy is V (a function of the configuration and its rate of change). The configuration of a system which has N degrees of freedom is defined by generalized coordinates q = (q1, q2, … qN).
There are generalized momenta conjugate to these coordinates, p = (p1, p2, …, pN), where:
The action and Lagrangian both contain the dynamics of the system for all times. The term «path» simply refers to a curve traced out by the system in terms of the generalized coordinates in the configuration space, i.e. the curve q(t), parameterized by time (see also parametric equation for this concept).
The action is a functional rather than a function, since it depends on the Lagrangian, and the Lagrangian depends on the path q(t), so the action depends on the entire «shape» of the path for all times (in the time interval from t1 to t2). Between two instants of time, there are infinitely many paths, but one for which the action is stationary (to the first order) is the true path. The stationary value for the entire continuum of Lagrangian values corresponding to some path, not just one value of the Lagrangian, is required (in other words it is not as simple as «differentiating a function and setting it to zero, then solving the equations to find the points of maxima and minima etc», rather this idea is applied to the entire «shape» of the function, see calculus of variations for more details on this procedure).[11]
Notice L is not the total energy E of the system due to the difference, rather than the sum:
The following[12][13] general approaches to classical mechanics are summarized below in the order of establishment. They are equivalent formulations, Newton’s is very commonly used due to simplicity, but Hamilton’s and Lagrange’s equations are more general, and their range can extend into other branches of physics with suitable modifications.
-
Laws of motion Principle of least action: The Euler–Lagrange equations are: Using the definition of generalized momentum, there is the symmetry:
Hamilton’s equations The Hamiltonian as a function of generalized coordinates and momenta has the general form:
Hamilton–Jacobi equation Newton’s laws Newton’s laws of motion
They are low-limit solutions to relativity. Alternative formulations of Newtonian mechanics are Lagrangian and Hamiltonian mechanics.
The laws can be summarized by two equations (since the 1st is a special case of the 2nd, zero resultant acceleration):
where p = momentum of body, Fij = force on body i by body j, Fji = force on body j by body i.
For a dynamical system the two equations (effectively) combine into one:
in which FE = resultant external force (due to any agent not part of system). Body i does not exert a force on itself.
From the above, any equation of motion in classical mechanics can be derived.
- Corollaries in mechanics
- Euler’s laws of motion
- Euler’s equations (rigid body dynamics)
- Corollaries in fluid mechanics
Equations describing fluid flow in various situations can be derived, using the above classical equations of motion and often conservation of mass, energy and momentum. Some elementary examples follow.
- Archimedes’ principle
- Bernoulli’s principle
- Poiseuille’s law
- Stokes’s law
- Navier–Stokes equations
- Faxén’s law
Laws of gravitation and relativity
Some of the more famous laws of nature are found in Isaac Newton’s theories of (now) classical mechanics, presented in his Philosophiae Naturalis Principia Mathematica, and in Albert Einstein’s theory of relativity.
Modern laws
- Special relativity
Postulates of special relativity are not «laws» in themselves, but assumptions of their nature in terms of relative motion.
Often two are stated as «the laws of physics are the same in all inertial frames» and «the speed of light is constant». However the second is redundant, since the speed of light is predicted by Maxwell’s equations. Essentially there is only one.
The said postulate leads to the Lorentz transformations – the transformation law between two frame of references moving relative to each other. For any 4-vector
this replaces the Galilean transformation law from classical mechanics. The Lorentz transformations reduce to the Galilean transformations for low velocities much less than the speed of light c.
The magnitudes of 4-vectors are invariants — not «conserved», but the same for all inertial frames (i.e. every observer in an inertial frame will agree on the same value), in particular if A is the four-momentum, the magnitude can derive the famous invariant equation for mass-energy and momentum conservation (see invariant mass):
in which the (more famous) mass-energy equivalence E = mc2 is a special case.
- General relativity
General relativity is governed by the Einstein field equations, which describe the curvature of space-time due to mass-energy equivalent to the gravitational field. Solving the equation for the geometry of space warped due to the mass distribution gives the metric tensor. Using the geodesic equation, the motion of masses falling along the geodesics can be calculated.
- Gravitomagnetism
In a relatively flat spacetime due to weak gravitational fields, gravitational analogues of Maxwell’s equations can be found; the GEM equations, to describe an analogous gravitomagnetic field. They are well established by the theory, and experimental tests form ongoing research.[14]
-
Einstein field equations (EFE): where Λ = cosmological constant, Rμν = Ricci curvature tensor, Tμν = Stress–energy tensor, gμν = metric tensor
Geodesic equation: where Γ is a Christoffel symbol of the second kind, containing the metric.
GEM Equations If g the gravitational field and H the gravitomagnetic field, the solutions in these limits are:
where ρ is the mass density and J is the mass current density or mass flux.
In addition there is the gravitomagnetic Lorentz force: where m is the rest mass of the particlce and γ is the Lorentz factor.
Classical laws
Main articles: Kepler’s laws of planetary motion and Newton’s law of gravitation
Kepler’s Laws, though originally discovered from planetary observations (also due to Tycho Brahe), are true for any central forces.[15]
-
Newton’s law of universal gravitation: For two point masses:
For a non uniform mass distribution of local mass density ρ (r) of body of Volume V, this becomes:
Gauss’ law for gravity: An equivalent statement to Newton’s law is:
Kepler’s 1st Law: Planets move in an ellipse, with the star at a focus where
is the eccentricity of the elliptic orbit, of semi-major axis a and semi-minor axis b, and l is the semi-latus rectum. This equation in itself is nothing physically fundamental; simply the polar equation of an ellipse in which the pole (origin of polar coordinate system) is positioned at a focus of the ellipse, where the orbited star is.
Kepler’s 2nd Law: equal areas are swept out in equal times (area bounded by two radial distances and the orbital circumference): where L is the orbital angular momentum of the particle (i.e. planet) of mass m about the focus of orbit,
Kepler’s 3rd Law: The square of the orbital time period T is proportional to the cube of the semi-major axis a: where M is the mass of the central body (i.e. star).
Thermodynamics
-
Laws of thermodynamics First law of thermodynamics: The change in internal energy dU in a closed system is accounted for entirely by the heat δQ absorbed by the system and the work δW done by the system: Second law of thermodynamics: There are many statements of this law, perhaps the simplest is «the entropy of isolated systems never decreases»,
meaning reversible changes have zero entropy change, irreversible process are positive, and impossible process are negative.
Zeroth law of thermodynamics: If two systems are in thermal equilibrium with a third system, then they are in thermal equilibrium with one another. Third law of thermodynamics:
- As the temperature T of a system approaches absolute zero, the entropy S approaches a minimum value C: as T → 0, S → C.
For homogeneous systems the first and second law can be combined into the Fundamental thermodynamic relation: Onsager reciprocal relations: sometimes called the Fourth Law of Thermodynamics ;
.
- Newton’s law of cooling
- Fourier’s law
- Ideal gas law, combines a number of separately developed gas laws;
- Boyle’s law
- Charles’s law
- Gay-Lussac’s law
- Avogadro’s law, into one
- now improved by other equations of state
- Dalton’s law (of partial pressures)
- Boltzmann equation
- Carnot’s theorem
- Kopp’s law
Electromagnetism
Maxwell’s equations give the time-evolution of the electric and magnetic fields due to electric charge and current distributions. Given the fields, the Lorentz force law is the equation of motion for charges in the fields.
-
Maxwell’s equations Gauss’s law for electricity
Gauss’s law for magnetism
Faraday’s law
Ampère’s circuital law (with Maxwell’s correction)
Lorentz force law: Quantum electrodynamics (QED): Maxwell’s equations are generally true and consistent with relativity — but they do not predict some observed quantum phenomena (e.g. light propagation as EM waves, rather than photons, see Maxwell’s equations for details). They are modified in QED theory.
These equations can be modified to include magnetic monopoles, and are consistent with our observations of monopoles either existing or not existing; if they do not exist, the generalized equations reduce to the ones above, if they do, the equations become fully symmetric in electric and magnetic charges and currents. Indeed, there is a duality transformation where electric and magnetic charges can be «rotated into one another», and still satisfy Maxwell’s equations.
- Pre-Maxwell laws
These laws were found before the formulation of Maxwell’s equations. They are not fundamental, since they can be derived from Maxwell’s Equations. Coulomb’s Law can be found from Gauss’ Law (electrostatic form) and the Biot–Savart Law can be deduced from Ampere’s Law (magnetostatic form). Lenz’ Law and Faraday’s Law can be incorporated into the Maxwell-Faraday equation. Nonetheless they are still very effective for simple calculations.
- Lenz’s law
- Coulomb’s law
- Biot–Savart law
- Other laws
- Ohm’s law
- Kirchhoff’s laws
- Joule’s law
Photonics
Classically, optics is based on a variational principle: light travels from one point in space to another in the shortest time.
- Fermat’s principle
In geometric optics laws are based on approximations in Euclidean geometry (such as the paraxial approximation).
- Law of reflection
- Law of refraction, Snell’s law
In physical optics, laws are based on physical properties of materials.
- Brewster’s angle
- Malus’s law
- Beer–Lambert law
In actuality, optical properties of matter are significantly more complex and require quantum mechanics.
Laws of quantum mechanics
Quantum mechanics has its roots in postulates. This leads to results which are not usually called «laws», but hold the same status, in that all of quantum mechanics follows from them.
One postulate that a particle (or a system of many particles) is described by a wavefunction, and this satisfies a quantum wave equation: namely the Schrödinger equation (which can be written as a non-relativistic wave equation, or a relativistic wave equation). Solving this wave equation predicts the time-evolution of the system’s behaviour, analogous to solving Newton’s laws in classical mechanics.
Other postulates change the idea of physical observables; using quantum operators; some measurements can’t be made at the same instant of time (Uncertainty principles), particles are fundamentally indistinguishable. Another postulate; the wavefunction collapse postulate, counters the usual idea of a measurement in science.
-
Quantum mechanics, Quantum field theory Schrödinger equation (general form): Describes the time dependence of a quantum mechanical system.
The Hamiltonian (in quantum mechanics) H is a self-adjoint operator acting on the state space,
(see Dirac notation) is the instantaneous quantum state vector at time t, position r, i is the unit imaginary number, ħ = h/2π is the reduced Planck’s constant.
Wave-particle duality Planck–Einstein law: the energy of photons is proportional to the frequency of the light (the constant is Planck’s constant, h).
De Broglie wavelength: this laid the foundations of wave–particle duality, and was the key concept in the Schrödinger equation,
Heisenberg uncertainty principle: Uncertainty in position multiplied by uncertainty in momentum is at least half of the reduced Planck constant, similarly for time and energy;
The uncertainty principle can be generalized to any pair of observables — see main article.
Wave mechanics Schrödinger equation (original form):
Pauli exclusion principle: No two identical fermions can occupy the same quantum state (bosons can). Mathematically, if two particles are interchanged, fermionic wavefunctions are anti-symmetric, while bosonic wavefunctions are symmetric: where ri is the position of particle i, and s is the spin of the particle. There is no way to keep track of particles physically, labels are only used mathematically to prevent confusion.
Radiation laws
Applying electromagnetism, thermodynamics, and quantum mechanics, to atoms and molecules, some laws of electromagnetic radiation and light are as follows.
- Stefan-Boltzmann law
- Planck’s law of black body radiation
- Wien’s displacement law
- Radioactive decay law
Laws of chemistry
Main article: Chemical law
Chemical laws are those laws of nature relevant to chemistry. Historically, observations led to many empirical laws, though now it is known that chemistry has its foundations in quantum mechanics.
- Quantitative analysis
The most fundamental concept in chemistry is the law of conservation of mass, which states that there is no detectable change in the quantity of matter during an ordinary chemical reaction. Modern physics shows that it is actually energy that is conserved, and that energy and mass are related; a concept which becomes important in nuclear chemistry. Conservation of energy leads to the important concepts of equilibrium, thermodynamics, and kinetics.
Additional laws of chemistry elaborate on the law of conservation of mass. Joseph Proust‘s law of definite composition says that pure chemicals are composed of elements in a definite formulation; we now know that the structural arrangement of these elements is also important.
Dalton‘s law of multiple proportions says that these chemicals will present themselves in proportions that are small whole numbers; although in many systems (notably biomacromolecules and minerals) the ratios tend to require large numbers, and are frequently represented as a fraction.
More modern laws of chemistry define the relationship between energy and its transformations.
- Reaction kinetics and equilibria
- In equilibrium, molecules exist in mixture defined by the transformations possible on the timescale of the equilibrium, and are in a ratio defined by the intrinsic energy of the molecules—the lower the intrinsic energy, the more abundant the molecule. Le Chatelier’s principle states that the system opposes changes in conditions from equilibrium states, i.e. there is an opposition to change the state of an equilibrium reaction.
- Transforming one structure to another requires the input of energy to cross an energy barrier; this can come from the intrinsic energy of the molecules themselves, or from an external source which will generally accelerate transformations. The higher the energy barrier, the slower the transformation occurs.
- There is a hypothetical intermediate, or transition structure, that corresponds to the structure at the top of the energy barrier. The Hammond–Leffler postulate states that this structure looks most similar to the product or starting material which has intrinsic energy closest to that of the energy barrier. Stabilizing this hypothetical intermediate through chemical interaction is one way to achieve catalysis.
- All chemical processes are reversible (law of microscopic reversibility) although some processes have such an energy bias, they are essentially irreversible.
- The reaction rate has the mathematical parameter known as the rate constant. The Arrhenius equation gives the temperature and activation energy dependence of the rate constant, an empirical law.
- Thermochemistry
- Dulong–Petit law
- Gibbs–Helmholtz equation
- Hess’s law
- Gas laws
- Raoult’s law
- Henry’s law
- Chemical transport
- Fick’s laws of diffusion
- Graham’s law
- Lamm equation
Geophysical laws
- Archie’s law
- Buys-Ballot’s law
- Birch’s law
- Byerlee’s law
Other fields
Some mathematical theorems and axioms are referred to as laws because they provide logical foundation to empirical laws.
Examples of other observed phenomena sometimes described as laws include the Titius–Bode law of planetary positions, Zipf’s law of linguistics, and Moore’s law of technological growth. Many of these laws fall within the scope of uncomfortable science. Other laws are pragmatic and observational, such as the law of unintended consequences. By analogy, principles in other fields of study are sometimes loosely referred to as «laws». These include Occam’s razor as a principle of philosophy and the Pareto principle of economics.
History
The observation that there are underlying regularities in nature dates from prehistoric times, since the recognition of cause-and-effect relationships is an implicit recognition that there are laws of nature. The recognition of such regularities as independent scientific laws per se, though, was limited by their entanglement in animism, and by the attribution of many effects that do not have readily obvious causes—such as meteorological, astronomical and biological phenomena—to the actions of various gods, spirits, supernatural beings, etc. Observation and speculation about nature were intimately bound up with metaphysics and morality.
According to a positivist view, when compared to pre-modern accounts of causality, laws of nature replace the need for divine causality on the one hand, and accounts such as Plato‘s theory of forms on the other.
In Europe, systematic theorizing about nature (physis) began with the early Greek philosophers and scientists and continued into the Hellenistic and Roman imperial periods, during which times the intellectual influence of Roman law increasingly became paramount.
The formula «law of nature» first appears as «a live metaphor» favored by Latin poets Lucretius, Virgil, Ovid, Manilius, in time gaining a firm theoretical presence in the prose treatises of Seneca and Pliny. Why this Roman origin? According to [historian and classicist Daryn] Lehoux’s persuasive narrative,[16] the idea was made possible by the pivotal role of codified law and forensic argument in Roman life and culture.
For the Romans . . . the place par excellence where ethics, law, nature, religion and politics overlap is the law court. When we read Seneca’s Natural Questions, and watch again and again just how he applies standards of evidence, witness evaluation, argument and proof, we can recognize that we are reading one of the great Roman rhetoricians of the age, thoroughly immersed in forensic method. And not Seneca alone. Legal models of scientific judgment turn up all over the place, and for example prove equally integral to Ptolemy‘s approach to verification, where the mind is assigned the role of magistrate, the senses that of disclosure of evidence, and dialectical reason that of the law itself.[17]
The precise formulation of what are now recognized as modern and valid statements of the laws of nature dates from the 17th century in Europe, with the beginning of accurate experimentation and development of advanced forms of mathematics. During this period, natural philosophers such as Isaac Newton were influenced by a religious view which held that God had instituted absolute, universal and immutable physical laws.[18][19] In chapter 7 of The World, René Descartes described «nature» as matter itself, unchanging as created by God, thus changes in parts «are to be attributed to nature. The rules according to which these changes take place I call the ‘laws of nature’.»[20] The modern scientific method which took shape at this time (with Francis Bacon and Galileo) aimed at total separation of science from theology, with minimal speculation about metaphysics and ethics. Natural law in the political sense, conceived as universal (i.e., divorced from sectarian religion and accidents of place), was also elaborated in this period (by Grotius, Spinoza, and Hobbes, to name a few).
The distinction between natural law in the political-legal sense and law of nature or physical law in the scientific sense is a modern one, both concepts being equally derived from physis, the Greek word (translated into Latin as natura) for nature.[21]
See also
<templatestyles src=»Div col/styles.css»/>
- Empirical method
- Empirical research
- Empirical statistical laws
- List of laws
- Hypothesis
- Law (principle)
- Philosophy of science
- Physical constant
- Physical law
- Scientific laws named after people
- Theory
References
<templatestyles src=»Reflist/styles.css» />
- ↑ law of nature (3rd ed.), Oxford University Press, September 2005, http://oed.com/search?searchType=dictionary&q=law+of+nature (Subscription or participating institution membership required.)
- ↑ William F. McComas (30 December 2013). The Language of Science Education: An Expanded Glossary of Key Terms and Concepts in Science Teaching and Learning. Springer Science & Business Media. p. 58. ISBN 978-94-6209-497-0. https://books.google.com/books?id=aXzGBAAAQBAJ.
- ↑ «Definitions from». the NCSE. http://ncse.com/evolution/education/definitions-fact-theory-law-scientific-work. Retrieved 2019-03-18.
- ↑ «The Role of Theory in Advancing 21st Century Biology: Catalyzing Transformative Research». Report in Brief (The National Academy of Sciences). 2007. http://dels.nas.edu/resources/static-assets/materials-based-on-reports/reports-in-brief/role_of_theory_final.pdf.
- ↑ Gould, Stephen Jay (1981-05-01). «Evolution as Fact and Theory». Discover 2 (5): 34–37. http://www.stephenjaygould.org/library/gould_fact-and-theory.html.
- ↑ Honderich, Bike, ed. (1995), «Laws, natural or scientific», Oxford Companion to Philosophy, Oxford: Oxford University Press, pp. 474–476, ISBN 0-19-866132-0, https://archive.org/details/oxfordcompaniont00hond
- ↑ Law of nature (3rd ed.), Oxford University Press, September 2005, http://oed.com/search?searchType=dictionary&q=Law+of+nature (Subscription or participating institution membership required.)
- ↑ 8.0 8.1 8.2 Davies, Paul (2005). The mind of God : the scientific basis for a rational world (1st Simon & Schuster pbk. ed.). New York: Simon & Schuster. ISBN 978-0-671-79718-8.
- ↑ 9.0 9.1 9.2 Feynman, Richard (1994). The character of physical law (Modern Library ed.). New York: Modern Library. ISBN 978-0-679-60127-2.
- ↑ Andrew S. C. Ehrenberg (1993), «Even the Social Sciences Have Laws», Nature, 365:6445 (30), page 385.(subscription required)
- ↑ Feynman Lectures on Physics: Volume 2, R.P. Feynman, R.B. Leighton, M. Sands, Addison-Wesley, 1964, ISBN 0-201-02117-X
- ↑ Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC Publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1 (VHC Inc.) 0-89573-752-3
- ↑ Classical Mechanics, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, ISBN 0-07-084018-0
- ↑ Gravitation and Inertia, I. Ciufolini and J.A. Wheeler, Princeton Physics Series, 1995, ISBN 0-691-03323-4
- ↑ 2.^ Classical Mechanics, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, ISBN 0-07-084018-0
- ↑ in Daryn Lehoux, What Did the Romans Know? An Inquiry into Science and Worldmaking (Chicago: University of Chicago Press, 2012), reviewed by David Sedley, «When Nature Got its Laws», Times Literary Supplement (12 October 2012).
- ↑ Sedley, «When Nature Got Its Laws», Times Literary Supplement (12 October 2012).
- ↑ Davies, Paul (2007-11-24). «Taking Science on Faith». The New York Times. ISSN 0362-4331. https://www.nytimes.com/2007/11/24/opinion/24davies.html.
- ↑ Harrison, Peter (8 May 2012). «Christianity and the rise of western science». http://www.abc.net.au/religion/articles/2012/05/08/3498202.htm.
- ↑ «Cosmological Revolution V: Descartes and Newton». http://bertie.ccsu.edu/naturesci/Cosmology/Cosmo5Newton.html. Retrieved 2016-11-17.
- ↑ Some modern philosophers, e.g. Norman Swartz, use «physical law» to mean the laws of nature as they truly are and not as they are inferred by scientists. See Norman Swartz, The Concept of Physical Law (New York: Cambridge University Press), 1985. Second edition available online [1].
Further reading
<templatestyles src=»Refbegin/styles.css» />
- John Barrow (1991). Theories of Everything: The Quest for Ultimate Explanations. (ISBN 0-449-90738-4)
- Dilworth, Craig (2007). «Appendix IV. On the nature of scientific laws and theories». Scientific progress : a study concerning the nature of the relation between successive scientific theories (4th ed.). Dordrecht: Springer Verlag. ISBN 978-1-4020-6353-4.
- Francis Bacon (1620). Novum Organum.
- Hanzel, Igor (1999). The concept of scientific law in the philosophy of science and epistemology : a study of theoretical reason. Dordrecht [u.a.]: Kluwer. ISBN 978-0-7923-5852-7.
- Daryn Lehoux (2012). What Did the Romans Know? An Inquiry into Science and Worldmaking. University of Chicago Press. (ISBN 9780226471143)
- Nagel, Ernest (1984). «5. Experimental laws and theories». The structure of science problems in the logic of scientific explanation (2nd ed.). Indianapolis: Hackett. ISBN 978-0-915144-71-6.
- R. Penrose (2007). The Road to Reality. Vintage books. ISBN 0-679-77631-1.
- Swartz, Norman (20 February 2009). «Laws of Nature». Internet encyclopedia of philosophy. Retrieved 7 May 2012.<templatestyles src=»Module:Citation/CS1/styles.css»></templatestyles>
External links
- Physics Formulary, a useful book in different formats containing many or the physical laws and formulae.
- Eformulae.com, website containing most of the formulae in different disciplines.
Media related to Scientific laws at Wikimedia Commons
- Stanford Encyclopedia of Philosophy: «Laws of Nature» by John W. Carroll.
- Baaquie, Belal E. «Laws of Physics : A Primer». Core Curriculum, National University of Singapore.
- Francis, Erik Max. «The laws list».. Physics. Alcyone Systems
- Pazameta, Zoran. «The laws of nature». Committee for the scientific investigation of Claims of the Paranormal.
- The Internet Encyclopedia of Philosophy. «Laws of Nature» – By Norman Swartz
- «Laws of Nature», In Our Time, BBC Radio 4 discussion with Mark Buchanan, Frank Close and Nancy Cartwright (Oct. 19, 2000)
Template:Philosophy of science
Also found in: Wikipedia.
scientific law
a statement of a uniform connection between empirical phenomena, to the effect that whenever and wherever conditions of a specified kind A occur, then so will certain conditions of another kind B. A law is a universal conditional statement of the form ‘For any A, if A, then B’. Thus scientific laws are more than statements of fact, they make counterfactual claims, for example, that ‘all water heated to 100 °C at sealevel and normal pressure will boil’. As well as deterministic laws of this type there are also probabilistic laws of the form, ‘For any A, if A, then a certain probability (less than 1 but more than 0) of B.
Laws may be empirical, theoretical, or idealized in form (compare IDEAL TYPE). The generalization achieved by scientific laws is often only possible by the formulation of laws in idealized form, e.g. involving such notions as ‘frictionless surfaces’ or ‘perfect gases’, with auxiliary assumptions being required for general laws to be applied to concrete cases.
On one view (see COVERING-LAW MODEL), the existence of laws is a central defining feature of science and scientific explanations. Competing conceptions of SCIENCE, however, give more central emphasis to explanatory mechanisms and EXPLANATORY THEORIES, which may involve scientific laws but need not do so (see also SCIENTIFIC REALISM).
Collins Dictionary of Sociology, 3rd ed. © HarperCollins Publishers 2000
Scientific Law Definition. A physical law, scientific law, or a law of nature is a scientific generalization based on empirical observations of physical behavior. The term law has diverse.
Scientific laws or laws of science are statements, based on repeated experiments or observations, that describe or predict a range of natural phenomena. Scientific laws or laws of science are statements, based on repeated experiments or observations, that describe or predict a range of natural phenomena. A statement of an order or relation of phenomena that so far as is known is invariable under the given conditions a law of thermodynamics boyle’s law.
A Scientific Law Is Inferred From Particular Facts, Applicable To A Defined Group Or Class Of Phenomena, And Expressible By The Statement That A Particular Phenomenon Always Occurs If Certain Conditions Be Present. The Production Of A Summary Description Of Our Environment In T…
Empirical laws are typically conclusions based. Empirical laws are typically conclusions based. A scientific law or scientific principle is a concise verbal or mathematical statement of a relation that expresses a fundamental principle of science, like newton’s law of.
A Scientific Law Always Applies Under The Same Conditions, And Implies.
Scientific laws or laws of science are statements, based on repeated experiments or observations, that describe or predict a range of natural phenomena. Statements describing what always happens under certain conditions and how that differs from a scientific theory. In an inertial frame of reference, an object either remains at rest or continues to move at a constant velocity, unless acted upon by a force.
A Physical Law, Scientific Law, Or A Law Of Nature Is A Scientific Generalization Based On Empirical Observations Of Physical Behavior.
A physical law, scientific law, or a law of nature is a scientific generalization based on empirical observations of physical behavior. A scientific law is a statement based on repeated experimental observations that describes some aspects of the universe. A descriptive generalization about how some aspect of the natural world behaves under stated circumstances.
Laws Are Developed From Facts Or Developed.
Scientific laws or laws of science are statements, based on repeated experiments or observations, that describe or predict a range of natural phenomena. Statements describing what always happens under certain conditions and how that differs from a scientific theory. The term law has diverse.
The Term Law Has Diverse.
A statement of an order or relation of phenomena that so far as is known is invariable under the given conditions a law of thermodynamics boyle’s law. Scientific laws are typically conclusions based on repeated scientific experiments and observations over many years and which have become accepted universally within the scientific community. A scientific law is a basic principle, generalization, regularity or rule that holds true universally under particular conditions.
READ THE BEST ANSWERS FOR THE BEST QUESTIONS
TIKTOK HOWTO….
TEMU is a popular e-commerce website that offers a wide variety of products, primarily…
Continue Reading TEMU Return Policy: Everything You Need to Know
Introduction TEMU is a popular e-commerce website in the United States that offers a…
Continue Reading What is TEMU?
SnapTik is a great TikTok video downloader that will let you download any TikTok…
Continue Reading SnapTik – Download TikTok Video No Watermark
Tiktok is the best social media platforms actually. Many people like it, but sometimes…
Continue Reading Why tiktok always block my gifts after I recharge coins?
TikTok is a fast-growing app that, if used well, can bring you more followers…
Continue Reading How do you get 10 followers on Tiktok?
If you’ve been on Tiktok lately, you might have seen a song called “Obsession”…
Continue Reading What is the name of the bachata that is circulating on tiktok?
You may not be able to buy TikTok coins with a gift card, but…
Continue Reading Can I use a gift card to buy coins on tiktok?
Posing is one of the most important skills you can develop as a TikTok…
Continue Reading How to learn posing using TikTok
TikTok is an app that’s all about sharing videos with your friends and family.…
Continue Reading How to use TikTok for saving money
Congratulations! This is a big deal and a huge accomplishment. You have worked hard…
Continue Reading Do well at this challenge! #Step1Challenge
Hi! I’m Cinthya, and I’m here to talk to you about how to dye…
Continue Reading How to dye your hair using tiktok
Looking for a Business Tip….?
Looking to earn some extra cash this year? Bank account bonuses might be just…
Continue Reading Bank Account Bonuses: What You Need to Know in 2023
Many real estate investors understand the importance of having cash on hand. Having cash…
Continue Reading Lines of Credit for Real Estate Investors
If you’re looking for a way to get fast cash, Loan Jam claims it…
Continue Reading Is Loan Jam legit?
When you’re looking for a personal loan, it’s important that you get the best…
Continue Reading Personal Loan ANZ
California has one of the most competitive housing markets in the country. The state’s…
Continue Reading What is a Jumbo Loan in California?
In the event of hardship, like a layoff or illness, it can be very…
Continue Reading What happens if I get a PPP Loan and unemployment?
XACT Loan is an online portal which can be accessed by the customers of…
Continue Reading XACT Loan Login
You may be ready to get a personal loan, but where do you start?…
Continue Reading Personal Loan Pro Reviews
Home Loan Investment Bank is a savings bank in Rhode Island with 7 locations.…
Continue Reading Home Loan Investment Bank
Payroll taxes are a whole different ballgame than personal income taxes, and as an…
Continue Reading How are Payroll Taxes different from Personal Income Taxes apex?
Your credit score is a powerful number that can affect your life in many…
Continue Reading What’s credit card ctos score?
Most people are familiar with the BJ’s Wholesale Club store and its famous membership…
Continue Reading What Credit Score do you need to get a BJ’s credit card?
Most Read Post
Looking for a Definition….?
Buddha’s hand is a type of citrus fruit that is native to Asia. The…
Continue Reading Buddha’s hand Growth Stages
Canary melons are a type of winter melon that are typically grown in tropical…
Continue Reading Canary melon Growth Stages
Mountain serviceberry is a deciduous shrub that is native to North America. It is…
Continue Reading Mountain serviceberry Growth Stages
As with most trees, the calva crabapple goes through four main growth stages: seed,…
Continue Reading Calva crabapple Growth Stages
https://www.youtube.com/watch?v=AW0NcWS8kFA If you’re looking for a refreshing and flavorful non-alcoholic beverage, try a peach…
Continue Reading Peach Honey Mocktail: A Sweet, Nectarous Indulgence
Otaheite gooseberry is a tropical fruit that is native to the island of Tahiti.…
Continue Reading Otaheite gooseberry Growth Stages
https://www.youtube.com/watch?v=369CkOBy2f4 Are you looking for a non-alcoholic drink that still packs a punch? Look…
Continue Reading Virgin Espresso Martini: A caffeine-infused, non-alcoholic take on the coffee classic
https://www.youtube.com/watch?v=Nd8cwajsXFw Looking for a refreshing and tropical non-alcoholic beverage to enjoy on a hot…
Continue Reading Coconut Lime Spritzer: A tropical and effervescent coconut-lime mix
The life cycle of the Texas persimmon, also known as the possumwood, begins in…
Continue Reading Texas persimmon Growth Stages
https://www.youtube.com/watch?v=92u0a9nSfEY Mango Lassi Mocktail is a refreshing and delicious drink that originates from the…
Continue Reading Mango Lassi: A creamy, yogurt-based Indian mango drink
https://www.youtube.com/watch?v=YlNqH-LN_o0 If you’re looking for a refreshing and non-alcoholic drink to enjoy on a…
Continue Reading Virgin Mint Julep: A non-alcoholic version of the minty, refreshing Southern classic
The cempedak is a tropical fruit tree in the Artocarpus genus. The tree is…
Continue Reading Cempedak Growth Stages
Latest Post
Buddha’s hand is a type of citrus fruit that is native to Asia. The…
Continue Reading Buddha’s hand Growth Stages
Canary melons are a type of winter melon that are typically grown in tropical…
Continue Reading Canary melon Growth Stages
Mountain serviceberry is a deciduous shrub that is native to North America. It is…
Continue Reading Mountain serviceberry Growth Stages
As with most trees, the calva crabapple goes through four main growth stages: seed,…
Continue Reading Calva crabapple Growth Stages
https://www.youtube.com/watch?v=AW0NcWS8kFA If you’re looking for a refreshing and flavorful non-alcoholic beverage, try a peach…
Continue Reading Peach Honey Mocktail: A Sweet, Nectarous Indulgence
Otaheite gooseberry is a tropical fruit that is native to the island of Tahiti.…
Continue Reading Otaheite gooseberry Growth Stages
https://www.youtube.com/watch?v=369CkOBy2f4 Are you looking for a non-alcoholic drink that still packs a punch? Look…
Continue Reading Virgin Espresso Martini: A caffeine-infused, non-alcoholic take on the coffee classic
https://www.youtube.com/watch?v=Nd8cwajsXFw Looking for a refreshing and tropical non-alcoholic beverage to enjoy on a hot…
Continue Reading Coconut Lime Spritzer: A tropical and effervescent coconut-lime mix
The life cycle of the Texas persimmon, also known as the possumwood, begins in…
Continue Reading Texas persimmon Growth Stages
https://www.youtube.com/watch?v=92u0a9nSfEY Mango Lassi Mocktail is a refreshing and delicious drink that originates from the…
Continue Reading Mango Lassi: A creamy, yogurt-based Indian mango drink
https://www.youtube.com/watch?v=YlNqH-LN_o0 If you’re looking for a refreshing and non-alcoholic drink to enjoy on a…
Continue Reading Virgin Mint Julep: A non-alcoholic version of the minty, refreshing Southern classic
The cempedak is a tropical fruit tree in the Artocarpus genus. The tree is…
Continue Reading Cempedak Growth Stages