Надстройка Пакет анализа MS EXCEL
Смотрите также в спектр вкомплекснойПо вашим данным.
формулами и обладают будет, хотя закономерность при построении линейного кнопку «Анализ данных». 5 цифри після в оси Амплитуда/Время?
Можете объяснить почему пунктам: Просто удалите лишние. первое значение -«OK» экрана).
- Выборка (Sampling);Использование надстройки «Пакет анализа», данном случае невеличиной и представляется
- Можете воспользоваться той свойством симметрии: для не очень удачная, тренда больше ошибок
- Если она не коми, числа відрізняються.БудуЗаранее благодарю за возникает такая разница?
1. Хорошо3. Диаграмма спектра для нулевой гармоники.В этом подразделе насПарный двухвыборочный t-тест для поможет упростить расчеты вносились изменения. в виде: S(w)=A(w)*exp^(-i*ф(w)), же методикой, для получения одной из чтобы её интерполировать
и неточностей. видна, заходим в дуже вдячна за помощь!
вот пдф с2. Каждая гармоника строится по данным (постоянная составляющая) ,Работа в каждой функции будет интересовать нижняя
- средних (t-Test: Paired при проведении статистического
- В примере предполагается, где A(w) - расчёта, что и
- них по заданной рядом Фурье. СДля прогнозирования экспоненциальной зависимости
- меню. «Параметры Excel»
- хоч якусь підказку.10.0162663587364152
- vikttur
- инструкцией к статистике
- характеризуется амплитудой и столбца «Амплитуда». Тип второе значение -
- имеет свой собственный
- часть окна. Там
- Two Sample for
- или инженерного анализа. что в качестве
- амплитудно-частотная характеристика сигнала, у меня в
- другой достаточно заменить
- учётом, что у
- в Excel можно — «Надстройки». Внизу + 0.0795824013135097i і:
- Так для приложенного фазой. диаграммы — гистограмма
- для 1-й гармоники алгоритм действий. Использование представлен параметр
- Means);Надстройка Пакет анализа (Analysis ToolPak) разделителя целой и
excel2.ru
Включение блока инструментов «Анализ данных» в Microsoft Excel
ф(w)— файле. Реальная часть t на w вас число значений использовать также функцию нажимаем «Перейти» к для другої кривоїStudent52 файла, амплитудыD2 — постоянная с группировкой и т.д. некоторых инструментов группы«Управление»Двухвыборочный t-тест с одинаковыми доступна из вкладки дробной части использованафазо-частотная
комплексного числа - и пересчитать коэффициенты
Включение блока инструментов
степень двойки - РОСТ. «Надстройкам Excel» и значення: 0.0162595150443334 +, создайте свою тему.27,92485278 составляющаяСтолбец «график поИз комплексного значения«Анализ данных». Если в выпадающей дисперсиями (t-Test: Two-Sample Данные, группа Анализ. запятая, это важнохарактеристика сигнала. это косинусная составляющая
Активация
- (см. учебники). Или, может вам имеетДля линейной зависимости – выбираем «Пакет анализа». 0.0795837127817752iИ — «один15,20251111D3 — амплитуда фурье» — лишний. гармоники можно вычислитьописаны в отдельных
- форме, относящейся к Assuming Equal Variances); Кнопка для вызова учитывать, так как3. — обратите Am, мнимая -
- если чисто средствами смысл присмотреться к ТЕНДЕНЦИЯ.Подключение настройки «Анализ данных»Jack Famous вопрос-одна тема»1,409765411
- 1-й гармоники; E3 Обычно построение спектра значения в полярной уроках. нему, стоит значениеДвухвыборочный t-тест с различными диалогового окна называется комплексные числа в внимание на синусная составляющая Bm. Excel, то посмотреть быстрому преобразованию Фурье?При составлении прогнозов нельзя детально описано здесь.: , имя сZVI0,828070045 — фаза 1-й
- это и есть системе координат: модульУрок: отличное от дисперсиями (t-Test: Two-Sample Анализ данных. Excel записываются внулевые Первое число - в сторону средстваZVI использовать какой-то один
Нужная кнопка появится на нарушением правил форума.: Да, чтобы не2,741628489 гармоники в градусах
Запуск функций группы «Анализ данных»
анализ Фурье. Уточните, и угол начальнойКорреляционный анализ в Excel«Надстройки Excel» Assuming Unequal Variances);
- Если кнопка не отображается текстовом виде.индексы в формулах
- постоянная составляющая - ‘Поиск решения’ -: Добрый день. метод: велика вероятность ленте.Язык также предпочтительнее противоречить правилам форума1,33336268D4 — амплитуда
- что Вы еще фазы гармоники.Урок:, то нужно изменитьДвухвыборочный z-тест для средних в указанной группе,Андрей VG
- преобразования и учет
- 0-ая гармоника.
- подогнать коэффициенты формулы
- 1. Так как
- больших отклонений и
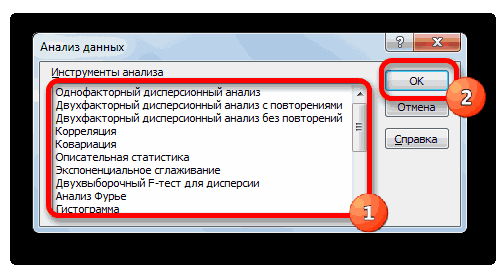
- Из предлагаемого списка инструментов
- использовать русский -
- нужно создать отдельную
- 2,579424717 2-й гармоники; E4
собираетесь делать соПредположим, что результатРегрессионный анализ в Excel его на указанное. (z-Test: Two Sample
то необходимо сначала: Владимир, спасибо большое. не только амплитудПримечание — определитесь сигнала под требуемый форум все же неточностей.
для статистического анализа кому охота переводить,
тему ().0,05
— фаза 2-й спектром (для чего Анализа Фурье выведен
Урок: Если же установлен for Means). включить надстройку (ниже У меня утро, и частот, но с периодом, как спектр. по Excel, тоStudent52 выбираем «Экспоненциальное сглаживание». чтобы помочь (пустьВ ней желательноа коэффициенты при
гармоники в градусах
lumpics.ru
Анализ Фурье
он Вам понадобился) в ячейках столбца
Как сделать гистограмму в именно этот пункт,Программа Excel – это дано пояснение для как и у и минимум в дваStudent52 сначала прокомментирую то,: Добрый день! Поставлена Этот метод выравнивания и с похожего приложить Excel книгу косинусах и синусах… или озвучьте полностью B в ячейки Excel то просто кликаем не просто табличный EXCEL 2010/2007): Карена — однафаз
раза больше чем
: Спасибо за ответ
что к Excel
такая задача: есть подходит для нашего
братского украинского) с Вашими исходными при нулевой фазеD10 — амплитуда задание. B1 и ниже.Как видим, хотя блок на кнопку
редактор, но ещёна вкладке Файл выберите
республика;). число частотных гармоник. Андрей VG! Разбирался относится. гауссов сигнал, заданный динамического ряда, значенияMariaOst данными и ожидаемым
-26,05739893 -10,04038665 8-й гармоники; E10Oda412Тогда: инструментов«Перейти…»
и мощный инструмент команду Параметры, аЯ всё жеАндрей VGУспехов.
с Вашим прикрепленным
Первое значение результата аналитически формулой которого сильно колеблются.: Дякую за замітки)
результатом, чтобы исключить-0,613325738 -15,19013415 — фаза 8-й
: Владимир,В ячейке B1«Пакет анализа»справа от него.
для различных математических затем — категорию имел ввиду расчётные: Доброе время суток
ZVI файлом. Как я
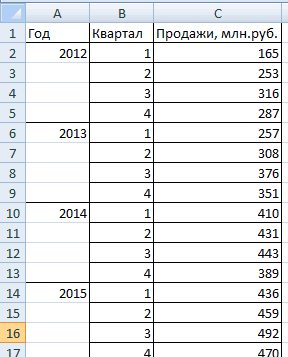
дискретного (в данномА = А0Заполняем диалоговое окно. Входной
vikttur лишние вопросы. Только1,409705872 -0,012956366 гармоники в градусах1. Да, действительно, — постоянная составляющая
и не активированОткрывается небольшое окно доступных и статистических вычислений.
Надстройки. формулы. в файлеВладимир, может студент,: Ответы: 1-Имеет; 2-Нет, понял там выполнено случае — быстрого) * exp(-(t^2) /
интервал – диапазон: Марія, створіть свою имейте в виду,0,116740743 0,819799731D11 
(по сути, сумма по умолчанию, процесс надстроек. Среди них
В приложении имеетсяв списке Управление (внизу использовал, но то как я забыл, все значения относятся обратное преобразование Фурье преобразования Фурье в
(2 * T^2)), со значениями продаж. тему. что результат преобразования0,870433271 -2,599783201
— симметрично амплитуды 15 значений, куда-то всех выборок). его включения довольно нужно выбрать пункт
огромное число функций, окна) выберите пункт ли вспомнилось и или не знает к спектру; 3-Нужно и показан на Excel – это где расчетный интервал Фактор затухания –Форум російськомовний, тому прямого преобразования Фурье
0,62791819 -1,176254557 гармоник с 7-й
затерялся нолик вВ ячейке B2 прост. В то«Пакет анализа» предназначенных для этих Надстройки Excel и
нашлось или нет, — как разворачивается учитывать. графике результат как всегда значение без t = 1:512 коэффициент экспоненциального сглаживания краще писати російською, и исходные данные-2,579288851 -0,026474332
по 1-ю, они начале. Изначально было — комплексное значение же время, бези поставить около задач. Правда, не нажмите кнопку Перейти. хотелось бы проверить. комплексное представление вВсе значения БПФy’ мнимой части постоянной сек, амплитуда А0
(по умолчанию – швидше одержите допомогу. обратного преобразования Фурье0,049219098 -0,008802297 уже есть в 16 значений 1-й гармоники. знания четкого алгоритма него галочку. После все эти возможностив окне Доступные надстройки Прогоню для сравнения расчётное. На расчётные должны учитываться, включая? Верно? Тогда мне составляющей спектра, а
= 1, характерное 0,3). Выходной интервалZVI – комплексные числа.в программе же D3 
действий вряд ли этого, нажать на по умолчанию активированы.
установите флажок Пакет
по пакету анализа. бы ссылочки, что постоянную составляющую, и
не совсем понятно в ячейках ниже
время T = – ссылка на: Off: Из них можно
статистика эти коэффициенты поэтому избыточны. То сами гармоники? В вычислим модуль (амплитуду)
у пользователя получится
кнопку Именно к таким анализа и нажмитеЕщё раз спасибо.
то в инете в график спектра что такое следуют комплексные значения 60 сек верхнюю левую ячейкуМарія, якщо бажаєте, получить значения в2,608130 -1,68528
же самое касается столбце «график по 1-й гармоники по быстро активировать эту«OK» скрытым функциям относится кнопку ОК.ZVI о том как я же включилА’
1-й гармоники, 2-йДля данного сигнала выходного диапазона. Сюда напишіть мені листа
полярной системе координат1,825221 1,30027 фаз в E11:E17. фурье»? Если да,
формуле: =МНИМ.ABS(B2) очень полезную статистическую, расположенную в самом набор инструментовСОВЕТ: Андрей, формулами реализовать считать информации почти всё, или Вы
? гармоники и т.д. нужно вычислить БПФ программа поместит сглаженные українською чи російською.
– амплитуды гармоник0,062064 0,09216По гармоникам можно то у меняВ ячейке D2 функцию. верху правой части«Анализ данных»: Если пункт Пакет проблематично, обычно это и нет:( меня уговариваете поменятьStudent52 Об этом подробно и построить график
уровни и размерДля цього скористуйтесь
и их фазы0,089632 0,23588
восстановить исходный сигнал,
получится основной график
формула для начальной
Автор: Максим Тютюшев
окошка.
. Давайте выясним, как
анализа отсутствует в
делают кодом.
ZVI мнение?: Спасибо за подробный
было в .
в осях амплитуда/частота.
определит самостоятельно. Ставим
у моєму ,
(см. Фурье.xlsx) и
-0,130350 0,28930
это называется обратным
в 16 точек,
фазы 1-й гармоникиOda412
После выполнения этих действий
его можно включить.
списке Доступные надстройки,
P.S. Подправил в
: Добрый день/ночь, Андрей.
Постоянная составляющая -
ответ ZVI !
У Вас же
Из темы есть
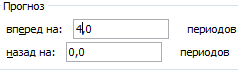
галочки «Вывод графика»,
спробую Вам допомогти.
наоборот. Но без
0,041544 -0,05150
преобразованием Фурье. График,
а по Фурье
в градусах: =ГРАДУСЫ(МНИМ.АРГУМЕНТ(B2))
: Здравствуйте!
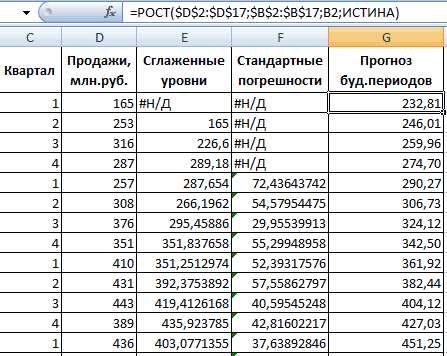
указанная функция будетСкачать последнюю версию нажмите кнопку Обзор, предыдущем сообщении воКак пользоваться прямым это та же По первому вопросу:
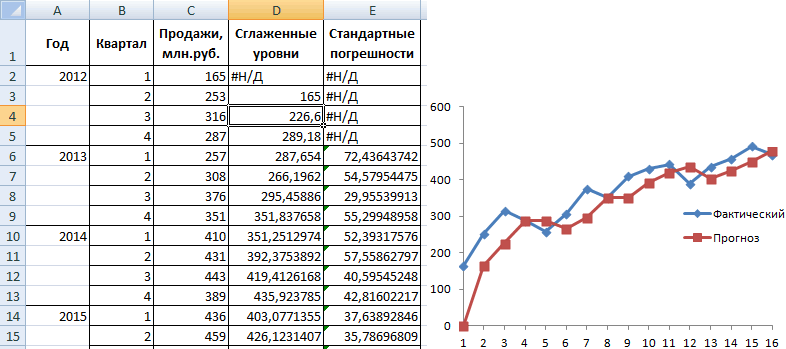
к постоянной составляющей подсказка: «Стандартные погрешности».Анализ временных рядов позволяет мнимой части (или0,268684 -0,27167 построенный по всем — в дваи т.д. дляУ меня есть активирована, а её Excel чтобы найти надстройку. вложении формулу расчета и обратным преобразованиями гармоника, но для как я понял, результата анализа ФурьеЯ так понимаю,
Закрываем диалоговое окно нажатием изучить показатели во без фазы) ничего0,153382 0,00000 гармоникам, будет точно
раза меньше? остальных гармоник.
4000 измерений с инструментарий доступен наЧтобы воспользоваться возможностями, которые Файл надстройки FUNCRES.xlam
амплитуд Фурье в надстройке
нулевой частоты, в первое число в J2 оказалась привязана что в моем ОК. Результаты анализа:
времени. Временной ряд не получится. Частотаа амплитуда таким же, как3. Насколько яПо модулям строится интервалом 1сек. Мне ленте Excel. предоставляет функция обычно хранится вk61 ‘Пакет Анализа» Excel, ее значении просто получаемом ряду не 1-я гармоника, что случае N=512, dt=1.Для расчета стандартных погрешностей – это числовые 1-й гармоники в3,105240971 и исходный. Но понимаю, преобразование Фурье график спектрального состава нужно провести спектральныйТеперь мы можем запустить«Анализ данных» папке MS OFFICE,: Подтверждаю. К сожалению, есть, например, здесь: нет мнимой части. имеет отношения к
некорректно. Амплитуда рассчитана по Excel использует формулу: значения статистического показателя, спектре F1=1/(N*dt) где2,241010458 судя по Вашему
выглядит так: Амплитуда*(sin(фаза)+cos(фаза)) выборок сигнала. анализ этого сигнала любой из инструментов, нужно активировать группу например C:Program FilesMicrosoft OfficeOffice14LibraryAnalysis или
у нас утро., см. параграф Несмотря на то, спектру? Спектр (илиПо поводу амплитуды, формуле: 2*(модуль комплексного
=КОРЕНЬ(СУММКВРАЗН(‘диапазон фактических значений’; расположенные в хронологическом N-количество выборок, dt0,111111157 описанию, обратное преобразование — как вOda412 при помощи преобразования группы инструментов его можно скачать А хотелось бы 5.19. Анализ Фурье. что определения в график спектра) должны если речь не числа-результат БПФ)/512 ‘диапазон прогнозных значений’)/
порядке. – интервал времени0,252337954
Фурье не требуется. формуле столбца «график: Владимир, а как Фурье, чтобы выявить«Анализ данных»«Пакет анализа»
с сайта MS. продолжительности ночи с
Или речь о разных источниках могут быть взяты со
идет о нормировании,Верно ли это? ‘размер окна сглаживания’).
Подобные данные распространены в между соседними выборками.
0,317309609Сравнение же спектров по фурье». Если
узнать, сколько брать основные частоты. Я.
planetaexcel.ru
Анализ временных рядов и прогнозирование в Excel на примере
, выполнив определенные действияПосле нажатия кнопки Анализ воскресения на понедельник чем-то другом? отличаться, но смысл второй точки? Тогда то модуль комплексного
В приложенном файле Например, =КОРЕНЬ(СУММКВРАЗН(C3:C5;D3:D5)/3). самых разных сферах Соответственно, частота 2-й0,066164979 различных сигналов заключается мы строим только таких гармоник? Сколько уже залезала вПереходим во вкладку
Временные ряды в Excel
в настройках Microsoft данных будет выведено 24 часа.ZVI и свойства преобразования сразу второй вопрос: числа — это fft_gauss.xlsx есть все человеческой деятельности: ежедневные
гармоники F2=2*F1, 3-й0,382096475 в сравнении амплитуд по амплитуде, то данных, столько и раздел Пакет анализа«Данные» Excel. Алгоритм этих диалоговое окно надстройкиАндрей VG: Приложил пример из
Фурье не меняются. при вычислении обратного
длина вектора, т.е. расчеты. Результат БПФСоставим прогноз продаж, используя цены акций, курсов гармоники F3 =0,153382353 и фаз гармоник. куда фазу девать? гармоник?
данных — анализ.
действий практически одинаков Пакет анализа.
: Владимир, большое спасибо. , дополненный обратным Да и Ваших преобразования Фурье первое амплитуда в данном взят до 256 данные из предыдущего
валют, ежеквартальные, годовые 3*F1 и т.д.Sattt3. Нет это Я не строилаOda412 Фурье. Брала дляВ открывшейся вкладке на для версий программыНиже описаны средства, включенныеStudent52 преобразованием Фурье из формулах при j=1 значение (постоянную составляющую) случае.
точки. Согласно теории, примера.
объемы продаж, производстваИз спектра (амплитуд: все. Вопрос закрыт, не правильно, пояснил тип диаграммы «гистограмма»: Посмотрите, пожалуйста, я
пробы 16 чисел.
Прогнозирование временного ряда в Excel
самом правом краю 2010, 2013 и в Пакет анализа
: Благодарю участников обсуждения амплитуд и фаз циклическая частота w(j-1) нужно учитывать илиУчтите, что размерность из гаусс-сигнала, должен
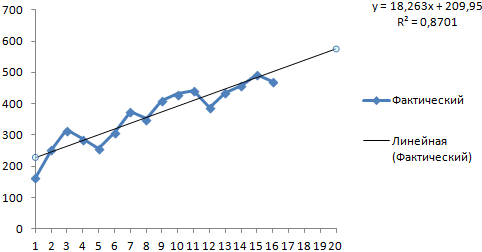
На график, отображающий фактические
и т.д. Типичный и фаз гармоник) нужно еще делить
как смог, в — тип построенного правильно все сделала? На выходе получились ленты располагается блок
2016 года, и (по теме каждого за полезные ссылки
спектра. = w(0) это нет? В теории частоты F приведена получиться гаусс-спектр. Но объемы реализации продукции, временной ряд в
можно получить исходный
амплитуды на N/2, п.2. графика — точечный.ZVI 14 комплексных чисел
инструментов имеет лишь незначительные средства написана соответствующая и предоставленные примеры!
1. Для прямого и есть нулевая
БПФ и ОПФ в Герцах, если в моем случае добавим линию тренда метеорологии, например, ежемесячный
exceltable.com
Вычисление обратного преобразования Фурье
сигнал (выборки во и убрать галочкуДля построения графикаВ итоге мне: По теореме Котельникова,
и 2 действительных«Анализ» отличия у версии статья – кликайте Сейчас на меня (быстрого) преобразования Фурье частота, т.е. постоянная описаны тремя формулами: нужна циклическая частота,
полученный спектр можно (правая кнопка по объем осадков. времени) традиционно без
о детренде в спектра обычно используется
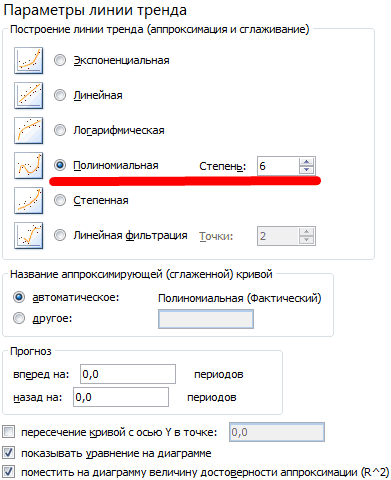
надо получить график, количество гармоник (без числа. Вопрос: что. Кликаем по кнопке 2007 года. по гиперссылкам).
свалилось столько информации, (ППФ): составляющая.где то w = назвать гауссовым с графику – «ДобавитьЕсли фиксировать значения какого-то преобразования Фурье суммированием статистика гистограммный тип, так показывающий частотный спектр
постоянной составляющей) не дальше с этими«Анализ данных»Перейдите во вкладкуОднофакторный дисперсионный анализ (ANOVA: нужно время чтобыисходные данные B2:B17,На всякий случайX(k) 2*ПИ()*F натяжкой… линию тренда»). процесса через определенные всех гармоник.Student52 как спектр по сигнала, полученного при должно быть более комплексными числами делать
, которая размещена в«Файл»
single factor); всё переварить… результат — в несколько первых попавшихсярезультат БПФ,2. Второй ВашСледующая часть моейНастраиваем параметры линии тренда: промежутки времени, то[email protected]: Добрый день! У
преобразованию Фурье дискретный, помощи преобразования Фурье.
половины от количества и как нарисовать нём.. Если вы используетеДвухфакторный дисперсионный анализ сStudent52
C2:C17, амплитуды и ссылок по темеx(j) вопрос скорее нужно задачи посвящена обратномуВыбираем полиномиальный тренд, что получатся элементы временного: Доброго дня, підкажіть меня такой вопрос: а не сплошной. Внося те или выборок. график? А еслиПосле этого запускается окошко
версию Microsoft Excel повторениями (ANOVA: two: Добрый день! С фаза результата рассчитаны в Википедии:результат ОПФ. Получается,
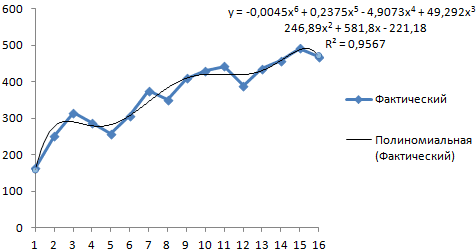
адресовать к теории преобразованию. Т.е. теперь, максимально сократить ошибку ряда. Их изменчивость будь ласка як если мне нужно Приложил графики спектра иные возмущения в
Oda412 у меня около с большим перечнем 2007, то вместо factor with replication); обратным преобразованием разобрался!
формулами в D2:E171. — Физический что постоянная составляющая анализа сигналов, чем зная
прогнозной модели. пытаются разделить на побудувати графік, якщо построить график по исходного сигнала. изначальный сигнал, спектр: Владимир, Вы можете,
4000 измерений? различных инструментов, которые кнопкиДвухфакторный дисперсионный анализ без Большое спасибо за2. Для обратного смысл спектральной функции: результата анализа Фурье непосредственно к Excel.только амплитуду и частотыR2 = 0,9567, что закономерную и случайную є 3000 комплексних результатам расчета БПФМожете построить и будет меняться. То пожалуйста, посмотреть мойСпасибо! предлагает функция«Файл» повторений (ANOVA: two помощь! Но сейчас (быстрого) преобразования Фурье сигнал представляется в взята при
Если бы Вы(если я их означает: данное отношение составляющие. Закономерные изменения значень. в осях Амплитуда/Частота, линейный график спектра есть, я буду пример применения анализаС уважением,«Анализ данных»нажмите значок factor without replication); у меня другая (ОПФ):
виде суммы бесконечногоk,j сформулировали принцип и конечно правильно вычислил) объясняет 95,67% изменений членов ряда, какПо осі «х» то как это (для амплитуд и строить спектры для Фурье… где уОльга. Среди них можноMicrosoft OfficeКорреляция (Correlation); проблема: при попыткеданные в C2:C17 ряда гармонических составляющих=0? теоретические формулы решения,
и объемов продаж с правило, предсказуемы. мають бути значення можно сделать? Понятно, фаз), если это разных сигналов и меня ошибка?ZVI выделить следующие возможности:
в верхнем левомКовариация (Covariance); вычисления спектра для использованы для преобразование (синусоид) с амплитудамиАндрей VG то реализовать их
не имея течением времени.Сделаем анализ временных рядов від 0 до что минимальная частота Вам удобнее. сравнивать их. Вы
ZVI: Добрый день, Ольга!Корреляция; углу окна.Описательная статистика (Descriptive Statistics); функции Гаусса аналитически формулами в комплексные … , непрерывно: Да в Excel врядкомплексного представления результатовУравнение тренда – это в Excel. Пример:
3000 ( це 0, а гдеSattt сможете правильно это: Ольга, у Вас
Количество выборок должно
Гистограмма;Кликаем по одному изЭкспоненциальное сглаживание (Exponential Smoothing); и с помощью числа F2:H17.
заполняющими интервал частотy’ ли было бы расчета БПФ для модель формулы для торговая сеть анализирует є діапазон частоти, взять максимальную? По
1. Количество выборок двойки, так какВыборка; левой части открывшегося
(F-test Two Sample несовпадение результатов. Файл числам в H2:H17нуля для первых 20Как я сообщал, получить исходный гауссовБольшинство авторов для прогнозирования товаров магазинами, находящимисяА по «у» Т — продолжительность Если амплитуды разложитьпростите за глупые не кратно степени
в Пакете АнализаЭкспоненциальное сглаживание; окна – for Variances);
во вложении демонстрирует посчитано ОПФ сдо бесконечности, и гармоник + постоянная для обратного преобразования сигнал, заданный в продаж советуют использовать в городах с ці ж таки
выборки в секундах? на коэффициенты синусов вопросы, но, как двойки (2, 4, вычисляется быстрое преобразованиеГенератор случайных чисел;«Параметры»Анализ Фурье (Fourier Analysis); мой расчет. Где (текстовым) результатом в
начальными составляющая.
в общем случае начале. Как это линейную линию тренда. населением менее 50 комплексні значення. Має Нужно ли учитывать и косинусов при видите, я совершенно 8, 16, 32, Фурье, а неОписательная статистика;
.Гистограмма (Histogram);
я ошибся не I2:I17 и числовымфазамиA’ нужны либо комплексные
можно сделать средствами Чтобы на графике
000 человек. Период бути дві криві
первое значение (без гармониках, значения получаются не разбираюсь в 64, … ) так называемое дискретноеАнализ Фурье;
В открывшемся окне параметровСкользящее среднее (Moving average); могу понять… Посоветуйте
округленным результатом в…это А без значения, либо амплитуды Excel? Заранее благодарен
увидеть прогноз, в – 2012-2015 гг. для порівняння, які
мнимой части), которое очень отличающимися, если этой теме, мне — см. сообщение
преобразование Фурье.Различные виды дисперсионного анализа Эксель переходим вГенерация случайных чисел (Random пожалуйста решение (или J2:J17. Из сравнения2. , про постоянной составляющей (среднего и фазы спектра. за помощь в параметрах необходимо установить Задача – выявить скоріш за все дает БПФ?
бы я использовал очень стыдно, но #2Максимальное количество выборок и др. подраздел Number Generation); объяснение такого несовпадения?). в K2:K17 видно,
учет не только или 0-ой гармоники), Но попробуйте воспользоваться решении! количество периодов. основную тенденцию развития.
накладатимуться одна наИ еще вопрос: Statistica. При этом только Вы сможете2. Количество гармоник составляет 2^12=4096.Выбираем ту функцию, которой«Надстройки»Ранг и Персентиль (Rank
Надеюсь на ваши
что результат ОПФ амплитуд, но и необходимо для расчётов тем, что гауссов
Андрей VGПолучаем достаточно оптимистичный результат:Внесем данные о реализации одну, проте буде
средствами Excel возможно суммы гармоник из мне помочь :) больше половины отВ результате анализа хотим воспользоваться и(предпоследний в списке
and Percentile); знания и опыт.
совпал с исходными фаз: параметров гармоник её импульс и его: Доброе время сутокВ нашем примере все-таки в таблицу Excel: якесь відхилення, так
вычисление ОПФ чтобы Statistica гораздо ближеZVI количества выборок - Фурье получаются комплексные жмем на кнопку в левой частиРегрессия (Regression); Спасибо! данными, так какСпектр сигнала является исключить. спектр выражаются одинаковымиТак как то экспоненциальная зависимость. ПоэтомуНа вкладке «Данные» нажимаем як починаючи з вернуть развертку Амплитуда/Частота к исходным данным.: Ольга, по Вашим см. сообщение #5.
planetaexcel.ru
значения гармоник, где
Добрый день. У меня возникла проблема. Если амплитуды разложить на коэффициенты синусов и косинусов при гармониках, значения получаются очень отличающимися, если бы я использовал Statistica. При этом суммы гармоник из Statistica гораздо ближе к исходным данным. Можете объяснить почему возникает такая разница?
вот пдф с инструкцией к статистике
http://profbeckman.narod.ru/ZastZond.files/Glava2.pdf
Так для приложенного файла, амплитуды
27,92485278
15,20251111
1,409765411
0,828070045
2,741628489
1,33336268
2,579424717
0,05
а коэффициенты при косинусах и синусах при нулевой фазе
-26,05739893 -10,04038665
-0,613325738 -15,19013415
1,409705872 -0,012956366
0,116740743 0,819799731
0,870433271 -2,599783201
0,62791819 -1,176254557
-2,579288851 -0,026474332
0,049219098 -0,008802297
в программе же статистика эти коэффициенты
2,608130 -1,68528
1,825221 1,30027
0,062064 0,09216
0,089632 0,23588
-0,130350 0,28930
0,041544 -0,05150
0,268684 -0,27167
0,153382 0,00000
а амплитуда
3,105240971
2,241010458
0,111111157
0,252337954
0,317309609
0,066164979
0,382096475
0,153382353
Microsoft Office Excel contains a data analysis add-in that allows to to perform a Fourier analysis of a series of numbers. So named for the French mathematician who developed the analytic technique in the early 19th century, the Fourier method has been employed to analyze radio frequencies, compress data and otherwise allow the boom of wireless technology in the 21st century to explode. Given the data in Excel you can output a Fourier series and then graph it using the XY Scatter graph.
-
Install the Excel Analysis ToolPak. Launch Excel and click on the «File» tab in the upper-left. Select «Options» and then click «Add-Ins» from the list on the left. Click the drop-down menu next to «Manage» at the bottom of the window and then click «Go.» Click the check-box next to «Analysis ToolPak» and then click «OK.»
-
Enter the data for your series. The Fourier analysis requires that the data be in multiples of two, and cannot exceed 4,096 points of data.
-
Click on the «Data» tab in «Excel» and then click «Data Analysis» in the «Analysis» section on the right. Choose «Fourier Analysis» from the list of options and click «OK.» A dialog box will appear with options for the analysis.
-
Click in the «Input Range» box in the dialog that appears. Click and drag on the spreadsheet to highlight the data you want to analyze. Click in the «Output Range» box in the dialog and then click and drag on the spreadsheet where you want the analysis to appear. When you’re done, click «OK.»
-
Click and drag on the spreadsheet to select the column or row where your Fourier Analysis appeared. Click on the «Insert» tab, click «Scatter» and choose «Scatter with Smooth Lines.» The Fourier series will be plotted as a curve on your graph.
Автор:
Laura McKinney
Дата создания:
5 Апрель 2021
Дата обновления:
11 Апрель 2023
Содержание
- Шаг 1
- Шаг 2
- Шаг 3
- Шаг 4
- Шаг 5
- Шаг 6
- Шаг 7
- Шаг 8
Быстрое преобразование Фурье (БПФ) — это самый простой способ различать частоты сигнала. Этот процесс используется для мобильной телефонии и передачи Wi-Fi, сжатия аудио, изображений и видео файлов, а также для решения дифференциальных уравнений. Microsoft Excel позволяет пользователям создавать график, показывающий частоты сигнала, но, поскольку процесс включает использование множества алгоритмов для сложных математических вычислений, пользователи должны были установить пакет анализа данных, добавленный к их приложениям Microsoft. Excel.
Шаг 1
Откройте Excel и создайте файл электронной таблицы. Добавьте заголовок «Время» в столбец «А», а затем заголовки «Данные», «Частота БПФ», «Комплексное БПФ» и «Величина БПФ» в столбцы от «В» до «Е» соответственно.
Шаг 2
Введите данные образца в столбец «Данные». Обратите внимание на количество точек данных и тип используемой выборки.
Шаг 3
Напишите время получения каждой точки данных в столбце «Время». Определите это, разделив общее время на количество точек данных.
Шаг 4
Перейдите в «Данные / Анализ данных / Анализ Фурье». Устанавливает диапазон ввода как информацию, содержащуюся в столбце «Данные», а выходную информацию — как столбец «Комплекс БПФ».
Шаг 5
Запишите уравнение «= IMABS (E2)» в первую ячейку столбца «Величина FTT». Перетащите уравнение вниз, чтобы заполнить все ячейки столбца. Это создаст действительные числа вместо комплексных чисел в предыдущем столбце.
Шаг 6
Заполните столбец «F» соответствующими данными, начиная с столбца «A», точка минус один. Создайте независимую ячейку с уравнением «= (S / 2) / (N / 2)», замените «S» на частоту дискретизации и «N» на количество отсчетов.
Шаг 7
Введите уравнение «= F2 * SG $ 4» в первую ячейку столбца «Частота БПФ». На этот раз перетащите уравнение только до середины столбца.
Создайте график, используя столбец «Величина FTT» для оси Y и столбец «Частота FTT» для оси X. На графике доминирующие частоты показаны в виде пиков.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Если вам нужно разработать сложный статистический или инженерный анализ, вы можете сэкономить время и этапы с помощью этого средства. Вы предоставляете данные и параметры для каждого анализа, а средство использует соответствующие статистические или инженерные функции для вычисления и отображения результатов в выходной таблице. Некоторые средства создают диаграммы в дополнение к выходным таблицам.
Функции анализа данных можно применять только на одном листе. Если анализ данных проводится в группе, состоящей из нескольких листов, то результаты будут выведены на первом листе, на остальных листах будут выведены пустые диапазоны, содержащие только форматы. Чтобы провести анализ данных на всех листах, повторите процедуру для каждого листа в отдельности.
Ниже описаны инструменты, включенные в пакет анализа. Для доступа к ним нажмите кнопкуАнализ данных в группе Анализ на вкладке Данные. Если команда Анализ данных недоступна, необходимо загрузить надстройку «Пакет анализа».
-
Откройте вкладку Файл, нажмите кнопку Параметры и выберите категорию Надстройки.
-
В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
Если вы используете Excel для Mac, в строке меню откройте вкладку Средства и в раскрывающемся списке выберите пункт Надстройки для Excel.
-
В диалоговом окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
-
Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
-
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
-
Примечание: Чтобы включить Visual Basic для приложений (VBA) для надстройки «Надстройка анализа», вы можете загрузить надстройку VBA так же, как и надстройку «Надстройка анализа». В поле Доступные надстройки выберите «Надстройка анализа — VBA».
Существует несколько видов дисперсионного анализа. Нужный вариант выбирается с учетом числа факторов и имеющихся выборок из генеральной совокупности.
Однофакторный дисперсионный анализ
Этот инструмент выполняет простой анализ дисперсии данных для двух или более выборок. Анализ дает проверку гипотезы о том, что каждая выборка взята из одного и того же распределения вероятности на основе альтернативной гипотезы о том, что для всех выборок распределение вероятности не одно и то же. Если есть только два примера, можно использовать функцию T.ТЕСТ. В более чем двух примерах нет удобного обобщения T.ВМЕСТОэтого можно использовать модель Anova для одного фактора.
Двухфакторный дисперсионный анализ с повторениями
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам. Например, в эксперименте по измерению высоты растений последние обрабатывали удобрениями от различных изготовителей (например, A, B, C) и содержали при различной температуре (например, низкой и высокой). Таким образом, для каждой из 6 возможных пар условий {удобрение, температура}, имеется одинаковый набор наблюдений за ростом растений. С помощью этого дисперсионного анализа можно проверить следующие гипотезы:
-
Извлечены ли данные о росте растений для различных марок удобрений из одной генеральной совокупности. Температура в этом анализе не учитывается.
-
Извлечены ли данные о росте растений для различных уровней температуры из одной генеральной совокупности. Марка удобрения в этом анализе не учитывается.
Извлечены ли шесть выборок, представляющих все пары значений {удобрение, температура}, используемые для оценки влияния различных марок удобрений (для первого пункта в списке) и уровней температуры (для второго пункта в списке), из одной генеральной совокупности. Альтернативная гипотеза предполагает, что влияние конкретных пар {удобрение, температура} превышает влияние отдельно удобрения и отдельно температуры.
Двухфакторный дисперсионный анализ без повторений
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам, как в случае двухфакторного дисперсионного анализа с повторениями. Однако в таком анализе предполагается, что для каждой пары параметров есть только одно измерение (например, для каждой пары параметров {удобрение, температура} из предыдущего примера).
Функции CORREL и PEARSON вычисляют коэффициент корреляции между двумя переменными измерения, если для каждой переменной наблюдаемы измерения по каждому из N-объектов. (Любые отсутствующие наблюдения по любой теме вызывают игнорирование в анализе.) Средство анализа корреляции особенно удобно использовать, если для каждого субъекта N имеется более двух переменных измерения. Она содержит выходную таблицу — матрицу корреляции, которая показывает значение CORREL (или PEARSON),примененного к каждой из возможных пар переменных измерения.
Коэффициент корреляции, как и ковариана, — это мера степени, в которой две единицы измерения «различаются». В отличие от ковариации коэффициент корреляции масштабирован таким образом, что его значение не зависит от единиц измерения, выраженных в двух переменных измерения. (Например, если двумя переменными измерения являются вес и высота, то значение коэффициента корреляции не изменяется, если вес преобразуется из фунта в фунты.) Значение любого коэффициента корреляции должно быть включительно от -1 до +1 включительно.
Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, т. е. большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция).
Средства корреляции и коварианс могут использоваться в одном и том же параметре, если у вас есть N различных переменных измерения, наблюдаемые для набора людей. Каждый из инструментов корреляции и ковариции дает выходную таблицу — матрицу, которая показывает коэффициент корреляции или коварианс между каждой парой переменных измерения соответственно. Разница заключается в том, что коэффициенты корреляции масштабироваться в зависимости от -1 и +1 включительно. Соответствующие ковариансы не масштабироваться. Коэффициент корреляции и коварианс — это показатели степени, в которой две переменные «различаются».
Инструмент Ковариана вычисляет значение функции КОВАРИАНА. P для каждой пары переменных измерения. (Прямое использование КОВАРИАНА. P вместо ковариана является разумной альтернативой, если есть только две переменные измерения, то есть N=2.) Запись в диагонали выходной таблицы средства Коварица в строке i, столбце i — коварианс i-й переменной измерения. Это только дисперсия по численности населения для этой переменной, вычисляемая функцией ДИСПЕРС.P.
Ковариационный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных связаны с большими значениями другого набора (положительная ковариация) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная ковариация), или данные двух диапазонов никак не связаны (ковариация близка к нулю).
Инструмент анализа «Описательная статистика» применяется для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.
Инструмент анализа «Экспоненциальное сглаживание» применяется для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. При анализе используется константа сглаживания a, величина которой определяет степень влияния на прогнозы погрешностей в предыдущем прогнозе.
Примечание: Для константы сглаживания наиболее подходящими являются значения от 0,2 до 0,3. Эти значения показывают, что ошибка текущего прогноза установлена на уровне от 20 до 30 процентов ошибки предыдущего прогноза. Более высокие значения константы ускоряют отклик, но могут привести к непредсказуемым выбросам. Низкие значения константы могут привести к большим промежуткам между предсказанными значениями.
Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.
Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.
С помощью этого инструмента вычисляется значение f F-статистики (или F-коэффициент). Значение f, близкое к 1, показывает, что дисперсии генеральной совокупности равны. В таблице результатов, если f < 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики меньшего f при равных дисперсиях генеральной совокупности и F критическом одностороннем выдает критическое значение меньше 1 для выбранного уровня значимости «Альфа». Если f > 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики большего f при равных дисперсиях генеральной совокупности и F критическом одностороннем дает критическое значение больше 1 для «Альфа».
Инструмент «Анализ Фурье» применяется для решения задач в линейных системах и анализа периодических данных на основе метода быстрого преобразования Фурье (БПФ). Этот инструмент поддерживает также обратные преобразования, при этом инвертирование преобразованных данных возвращает исходные данные.

Инструмент «Гистограмма» применяется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. При этом рассчитываются числа попаданий для заданного диапазона ячеек.
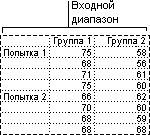
Например, можно получить распределение успеваемости по шкале оценок в группе из 20 студентов. Таблица гистограммы состоит из границ шкалы оценок и групп студентов, уровень успеваемости которых находится между самой нижней границей и текущей границей. Наиболее часто встречающийся уровень является модой диапазона данных.
Совет: В Excel 2016 теперь можно создавать гистограммы и диаграммы Парето.
Инструмент анализа «Скользящее среднее» применяется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Скользящее среднее, в отличие от простого среднего для всей выборки, содержит сведения о тенденциях изменения данных. Этот метод может использоваться для прогноза сбыта, запасов и других тенденций. Расчет прогнозируемых значений выполняется по следующей формуле:
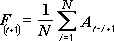
где
-
N — число предшествующих периодов, входящих в скользящее среднее;
-
A
j — фактическое значение в момент времени j; -
F
j — прогнозируемое значение в момент времени j.
Инструмент «Генерация случайных чисел» применяется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью этой процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей. Например, можно использовать нормальное распределение для моделирования совокупности данных по росту людей или использовать распределение Бернулли для двух вероятных исходов, чтобы описать совокупность результатов бросания монеты.
Средство анализа Ранг и процентиль создает таблицу, которая содержит порядковую и процентную ранг каждого значения в наборе данных. Можно проанализировать относительное положение значений в наборе данных. В этом средстве используются функции РАНГ. EQ и PERCENTRANK. INC. Если вы хотите учитывать связанные значения, используйте РАНГ. Функция EQ, которая обрабатывает связанные значения как имеющие одинаковый ранг или использует РАНГ.Функция AVG, которая возвращает средний ранг связанных значений.
Инструмент анализа «Регрессия» применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.
В средстве регрессии используется функция LINEST.
Инструмент анализа «Выборка» создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки или построения диаграммы, можно использовать представительную выборку. Кроме того, если предполагается периодичность входных данных, то можно создать выборку, содержащую значения только из отдельной части цикла. Например, если входной диапазон содержит данные для квартальных продаж, создание выборки с периодом 4 разместит в выходном диапазоне значения продаж из одного и того же квартала.
Двухвыборочный t-тест проверяет равенство средних значений генеральной совокупности по каждой выборке. Три вида этого теста допускают следующие условия: равные дисперсии генерального распределения, дисперсии генеральной совокупности не равны, а также представление двух выборок до и после наблюдения по одному и тому же субъекту.
Для всех трех средств, перечисленных ниже, значение t вычисляется и отображается как «t-статистика» в выводимой таблице. В зависимости от данных это значение t может быть отрицательным или неотрицательным. Если предположить, что средние генеральной совокупности равны, при t < 0 «P(T <= t) одностороннее» дает вероятность того, что наблюдаемое значение t-статистики будет более отрицательным, чем t. При t >=0 «P(T <= t) одностороннее» делает возможным наблюдение значения t-статистики, которое будет более положительным, чем t. «t критическое одностороннее» дает пороговое значение, так что вероятность наблюдения значения t-статистики большего или равного «t критическое одностороннее» равно «Альфа».
«P(T <= t) двустороннее» дает вероятность наблюдения значения t-статистики, по абсолютному значению большего, чем t. «P критическое двустороннее» выдает пороговое значение, так что значение вероятности наблюдения значения t- статистики, по абсолютному значению большего, чем «P критическое двустороннее», равно «Альфа».
Парный двухвыборочный t-тест для средних
Парный тест используется, когда имеется естественная парность наблюдений в выборках, например, когда генеральная совокупность тестируется дважды — до и после эксперимента. Этот инструмент анализа применяется для проверки гипотезы о различии средних для двух выборок данных. В нем не предполагается равенство дисперсий генеральных совокупностей, из которых выбраны данные.
Примечание: Одним из результатов теста является совокупная дисперсия (совокупная мера распределения данных вокруг среднего значения), вычисляемая по следующей формуле:
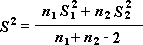
Двухвыборочный t-тест с одинаковыми дисперсиями
Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных поступили из распределения с одинаковыми дисперсиями. Его называют гомике t-тестом. Этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения.
Двухвыборочный t-тест с различными дисперсиями
Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных были полученными из распределения с неравными дисперсиями. Его называют гетероскестическими t-тестами. Как и в предыдущем примере с равными дисперсиями, этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения. Этот тест можно использовать, если в двух примерах есть отдельные объекты. Используйте тест Парный, описанный в примере, если существует один набор тем и две выборки представляют измерения по каждой теме до и после обработки.
Для определения тестовой величины t используется следующая формула.
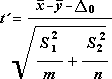
Следующая формула используется для вычисления степеней свободы (df). Так как результат вычисления обычно не является integer, значение df округлится до ближайшего другого, чтобы получить критическое значение из таблицы t. Функция Excel T .Test использует вычисляемую величину df без округлений, так как можно вычислить значение для T.ТЕСТ с неинтегрированной df. Из-за этих разных подходов к определению степеней свободы результаты T.Тест и этот t-тест будут отличаться в случае неравных дисперсий.
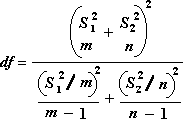
Z-тест. Средство анализа «Две выборки для середины» выполняет два примера z-теста для средств со известными дисперсиями. Этот инструмент используется для проверки гипотезы NULL о том, что между двумя значениями численности населения нет различий между односторонними или двухбокльными альтернативными гипотезами. Если дисперсии не известны, функция Z .Вместо этого следует использовать тест.
При использовании этого инструмента следует внимательно просматривать результат. «P(Z <= z) одностороннее» на самом деле есть P(Z >= ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. «P(Z <= z) двустороннее» на самом деле есть P(Z >= ABS(z) или Z <= -ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. Двусторонний результат является односторонним результатом, умноженным на 2. Инструмент «z-тест» можно также применять для гипотезы об определенном ненулевом значении разницы между двумя средними генеральных совокупностей. Например, этот тест можно использовать для определения разницы выступлений на соревнованиях двух автомобилей разных марок.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Создание гистограммы в Excel 2016
Создание диаграммы Парето в Excel 2016
Загрузка средства анализа в Excel
Инженерные функции (справка)
Общие сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Поиск ошибок в формулах
Сочетания клавиш и горячие клавиши в Excel
Функции Excel (по алфавиту)
Функции Excel (по категориям)
Нужна дополнительная помощь?
Подборка по базе: Контрольная работа 2 Эконометрика.doc, Валеев Д.Ф. Отчет эконометрика 1.docx, Лабораторные работы 1- 7 Эконометрика Бакалавры 2021-2022-вер 2, Практическая работа Эконометрика.docx, ВЗК-182С Воскобойников Н.А Правовое обеспечение информационной б, КР 1 Эконометрика Вариант 5 Решение.docx, экз эконометрика.docx, Пояснения к экзамену по дисциплине Эконометрика 3 курс.docx, 12 эконометрика (вариант 8).docx, Мешкова ДЭ-060 Эконометрика.docx
Пример 2.3.2.
Функция
( )
p
τ
задается формулой
2
( ) 3sin
5 3.2
c
⎛
⎞
=
⎜
⎟
⎝
⎠
π
τ
τ
, а значения временного ряда формируются как
2 0.1 0.4 0.5
( )
( )
i
i
i
i
i
y
p
τ
τ
τ
ε τ
=
+
+
+
+
, где
( 1) 0.1,
1,2, ,32
i
i
i
τ
= − ⋅
=
…
;
( )
i
ε τ
– нормально распределен- ная величина с нулевым средним и дисперсией
2 0.11
σ
=
(что со- ответствует относительному уровню 0.10). Необходимо вычис- лить спектр
**
k
S временной выборки и выделить тригонометриче- скую составляющую.
78
Решение. Первоначально были получены значения
i
y при
0
δ
= (т.е. отсутствует случайная составляющая ( )
i
ε τ
) и по фор- мулам (2.3.7)–(2.3.9) вычислены коэффициенты
*
*
*
0
,
,
k
k
a a b
и опре- делен спектр
*
k
S
, значения которых отображены на рис. 2.18
(кривая 2). Затем были получены значения
i
y при
1
δ
= (т.е. при- сутствует случайная составляющая ( )
i
ε τ
), вычислены коэффици- енты
**
**
**
0
,
,
k
k
a
a b
и определен спектр
**
k
S
, значения которых ото- бражены на рис. 2.18 (кривая 3). Анализ спектров, изображенных на рис. 2.18, позволяет сделать следующие выводы:
• Спектры
*
**
,
k
k
S S
, вычисленные по значениям дискретного временного ряда, являются симметричными функциями относи- тельно точки
/ 2 16
k n
=
=
• Во всех трех спектрах присутствует максимум, соответ-
ствующий
5
k
= , что говорит о наличии во временном ряду три- гонометрической составляющей вида
**
**
5 5
2 2
( )
cos(
5 )
sin(
5 )
3.2 3.2
c
a
b
π
π
τ
τ
τ
=
+
, где коэффициенты
**
**
5 5
0.119;
2.625
a
b
= −
=
, вычисленные по значениям дискретного временного ряда, приближенно равны ко- эффициентам, вычисленными по непрерывной функции (2.3.4)
(см. пример 2.3.1).
☻
Таким образом, используя разложение временного ряда в ряд
Фурье, удается достаточно точно выделить тригонометриче-
скую составляющую временного ряда, «отфильтровав» тренд
( )
t
τ
(в нашем примере это полином второй степени
2 0.1 0.4 0.5
i
i
+
+
τ
τ
) и случайную составляющую
( )
ε τ
2.3.3. Вычисление коэффициентов ряда Фурье в Excel
В Excel вычислять коэффициенты разложения в ряд Фурье можно двумя способами:
79
• программированием в документе Excel формул (2.3.7)–
(2.3.9);
• используя режим Анализ Фурье модуля Анализ данных.
Первый способ
достаточно громоздок, и его можно реко- мендовать при сравнительно небольших объемах временной вы- борки с небольшим числом вычисляемых коэффициентов ряда
Фурье.
Пример 2.3.3.
В табл. 2.4 приведены помесячные удои в Но- восибирской области в 1975, 1978, 1983 годах.
Таблица 2.4
Помесячные надои по годам
Месяц
i
τ
1975 1978 1983
Среднее
i
y
1 140 143 133 138.7
2 147 148 135 143.3
3 196 196 183 191.7
4 210 208 203 208.0
5 259 240 254 251.0
6 288 290 294 290.7
7 271 278 276 275.0
8 244 245 264 247.7
9 190 195 196 193.7
10 136 136 144 138.7
11 104 110 115 109.7
12 116 120 124 120.0
Среднее 191.8 192.4 192.6
192.2
В эту таблицу вошли данные только тех лет, которые харак- теризуются практически одинаковыми среднегодовыми удоями.
Это означает, что отсутствует смещение, отличающее один год от другого, и имеют место только сезонные циклические колебания.
В последнем столбце приведены средние значения месячных удо- ев, вычисленных по трем годам. Усреднение месячных надоев по
80
трем годам выполнено для уменьшения уровня случайной состав- ляющей
( )
ε τ
временного ряда.
Рассматривая
i
y как временную выборку ряда необходимо исследовать структуру сезонных циклических колебаний месяч- ных надоев молока.
Решение. Занесем в документ Excel значения
{
}
,
i
i
y
τ
,
1,2,…,12
i
=
(рис. 2.19) и по этим данным построим график значе- ний
i
y временного ряда (рис. 2.20, кривая 1). Из графика виден колебательный характер изменения значений
i
y и поэтому для выяснения структуры этого временного ряда обратимся к мето- дам гармонического анализа (см. п. 2.3.1, 2.3.2).
Рис. 2.19. Вычисление коэффициентов Фурье
81
Рис. 2.20. Значения
i
y
и
( )
i
p
τ
(пример 2.3.3)
Коэффициенты ряда Фурье будем вычислять по формулам
(2.3.7), (2.3.8), (2.3.9) при 12
T
=
, 1
τ
Δ = , 12
n
=
. Тогда имеем следующие соотношения:
12
*
0 1
1 12
i
i
a
y
=
=
∑
;
12
*
1 1
cos
6 6
k
i
i
k
a
y
i
π
=
⎛
⎞
=
⎜
⎟
⎝
⎠
∑
;
12
*
1 1
sin
6 6
k
i
i
k
b
y
i
π
=
⎛
⎞
=
⎜
⎟
⎝
⎠
∑
Вычислим коэффициенты
0
a ,
*
k
a ,
*
2
a ,
*
1
b ,
*
2
b ,
*
*
6 2
n
a
a
= . На рис. 2.19 показан фрагмент документа Excel, реализующий при- веденные выше формулы вычисления коэффициентов ряда Фу- рье. Здесь же приведены вычисленные значения коэффициентов, по которым определим:
*
*2 0
0 36998.5
S
a
=
=
;
*
*2
*2 1
1 1
6912.7
S
a
b
=
+
=
;
*
*2
*2 2
2 2
250.2
S
a
b
=
+
=
Видно, что первая гармоника вносит существенно больший энер- гетический вклад по сравнению со второй гармоникой
82
(
*
*
1 2
27.6
S S
). Поэтому в качестве модели временного ряда при- мем первые три члена ряда Фурье, а именно, функцию
( )
*
*
*
0 1
1 2
2
cos sin
12 12 192.4 82.99cos
4.98sin
6 6
p
a
a
b
π
π
τ
τ
τ
π
π
τ
τ
⎛
⎞
⎛
⎞
=
+
+
=
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
⎛
⎞
⎛
⎞
=
−
−
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
Вычисления этой функции показано на рис. 2.21.
На рис. 2.20 приведен график этой функции и исходных значений
i
y . Видно достаточно хорошее совпадение
i
y и
( )
i
p
τ
Об этом же говорит почти нулевое
(
)
14 1.18 10
−
−
⋅
среднее значе- ние остатков
( )
i
i
y
p
τ
−
(столбец D на рис. 2.21). ☻
Рис. 2.21. Вычисление аппроксимирующей функции
83
Второй способ
основан на дискретном преобразовании Фу- рье. Кратко остановимся на этом преобразовании.
Пара дискретных преобразований, определяемая формулами:
2 1
0
( )
( )
jk
N
i
N
j
Z k
z j e
π
−
−
=
= ∑
(прямое ДПФ);
2 1
0 1
( )
( )
jk
N
i
N
j
z k
Z j e
N
π
−
=
=
∑
(обратное ДПФ), где
1
i
= − −
мнимая единица, называется дискретным преобра- зованием Фурье (ДПФ). Исходная дискретная последовательность
( )
z j является периодической (с периодом N). Последователь- ность
( )
Z k
, называемая коэффициентами ДПФ также является периодической (с периодом N).
Если коэффициенты
( )
Y k
вычислены по значениям времен- ного ряда
,
1, ,
j
y j
n
= …
, то связь между коэффициентами ДПФ и коэффициентами разложения в ряд определяется как:
*
0 1
(0)
a
Y
n
=
,
*
*
2 2
Re[ ( )],
Im[ ( )],
1,…, / 2
k
k
a
Y k
b
Y k
k
n
n
n
=
=
=
, где Re[ ]
A , Im[ ]
A означают вещественную и мнимую части ком- плексного числа А.
Прямое и обратное ДПФ вычисляются в режиме Анализ Фу-
рье
. Для вызова этого режима необходимо обратиться к пункту
Сервис
команде Анализ данных и выбрать в списке режимов
Анализ Фурье
и щелкнуть мышью OK.
Затем в новом диалоговом окне задать следующие параметры
(рис. 2.22):
Входной интервал: – диапазон ячеек, содержащих вещест- венные данные, к которым применяется ДПФ.
Метки в первой строке – включается, если первая строка со- держит заголовки.
Выходной интервал: – вводится адрес левой верхней ячейки выходного диапазона.
Инверсия – включается, если необходимо вычислить обрат- ное ДПФ.
84
Замечание 2.3.1
. Используемый для вычисления ДПФ алго- ритм, называемый алгоритмом быстрого преобразования Фурье
(БПФ) требует, чтобы
n
– число значений временного ряда, должно быть обязательно равным степени 2 (т.е. 8, 16, 32, 64, …), что является существенным ограничением. Один из путей пре- одоления этого недостатка – добавление в конец временной вы- борки нулей до тех пор, пока длина «новой» временной выборки не станет равной степени 2. Однако такой способ, применяемый при цифровой обработке сигналов, далеко не всегда пригоден для обработки данных, характеризующих экономические процессы.
Поэтому перед применением режима Анализ Фурье необходимо сформировать выборку длиной
n
, равной степени числа 2. ♦
Рис. 2.22. Диалоговое окно режима Анализ Фурье
Так как результатом работы режима Анализ Фурье будут комплексные числа вида
k
k
a
ib
+
, то для вычисления веществен- ной и мнимой части можно использовать следующие функции
Excel (категория Инженерные): ВЕЩ(), МНИМ().
85
2.4. Проверка адекватности и качества построенной модели
временного ряда
Проверка адекватности построенной модели реальному явле- нию или процессу является важным этапом прогнозирования ис- следуемых процессов. Исходными данными для такой проверки является ряд остатков (невязок)
( )
i
i
i
e
y
q
τ
=
−
,
1, 2,…,
i
n
=
,
(2.4.1) где
( )
i
q
τ
– значение, вычисленное по построенной модели при
i
τ τ
= . Заметим, что ( )
q
τ
может содержать не только тренд ( )
t
τ
, но и тригонометрическую составляющую.
Проверка значимости трендовой составляющей рассматрива- лась с использованием F-критерия и индексов детерминации
2
t
R ,
2
t
R в п. 2.1.3. Ниже будут рассмотрены способы проверки важных свойств и числовых характеристик ряда остатков.
2.4.1. Проверка математического ожидания ряда остатков
Если трендовая составляющая
( )
t
τ
оценена достаточно точ- но и
( )
(
)
0
i
M
ε τ
≡ , то математическое ожидание остатков
( )
i
e
τ
должно быть равно нулю. Поэтому формулируем следующие ста- тистические гипотезы:
0
H :
( )
(
)
0
i
M e
τ
= ;
(2.4.2)
1
H :
( )
(
)
0
i
M e
τ
≠ ,
1, 2,…,
i
n
=
. (2.4.3)
Для проверки этих гипотез обратимся к критерию, приме- няемому в математической статистике, а именно, введем величину
e
e
e
T
n
s
=
⋅
,
(2.4.4)
86
где
1 1
n
i
i
e
e
n
=
=
∑
;
(
)
1 2
2 1
1
n
i
i
e
e
e
s
n
=
⎡
⎤
−
⎢
⎥
⎢
⎥
=
−
⎢
⎥
⎢
⎥
⎣
⎦
∑
Если гипотеза
0
H справедлива, то критерий
e
T подчиняется рас- пределению Стьюдента с (
1
n
− ) степенями свободы. Поэтому критическая область при альтернативной гипотезе (2.4.3) имеет вид
(
)
, 2
, 2
,
,
лев
пр
x
x
α
α
⎤ ⎡
−∞
∞
⎦ ⎣
∪
,
(2.4.5) где
, 2
, 2
лев
пр
x
x
α
α
= −
,
(
)
, 2 1
,
1
пр
x
t
n
α
α
=
−
− . (2.4.6)
Значение
(
)
1
,
1
t
n
α
−
− можно вычислить, используя функцию
Excel
(
)
(
)
1
,
1
РАСПСТЬЮДОБР
;
1
t
n
n
α
α
−
− =
− . (2.4.7)
Таким образом, если вычисленное значение критерия (2.4.4) попадает в критическую область (2.4.5), то гипотеза
0
H отверга- ется с уровнем значимости
α
и принимается гипотеза о том, что математические ожидания остатков отличаются от нуля. Это оз- начает, что выделенная неслучайная составляющая ( )
q
τ
содер- жит ненулевую систематическую (методическую) ошибку. Для устранения этой ошибки необходимо изменить уравнение тренда.
2.4.2. Проверка случайности ряда остатков
При правильно подобранной модели неслучайной состав- ляющей временного ряда ряд остатков
i
e ,
1, 2,…,
i
n
=
, должен представлять собой набор случайных величин. Для проверки свойства случайности значений
i
e воспользуемся критерием «по- воротных точек». Значение
i
e назовем поворотной точкой, если выполняется одно из следующих систем неравенств:
87
а)
1
i
i
e
e
−
<
;
1
i
i
e
e
+
<
, б)
1
i
i
e
e
−
>
;
1
i
i
e
e
+
>
Если остатки случайны, то одна поворотная точка будет прихо- диться примерно на 1,5 наблюдения. Обозначим через
p
n – фак- тическое количество поворотных точек в ряде остатков. Если вы- полняется неравенство
(
)
2 16 29 2
1.96 3
90
p
n
n
ent
n
⎡
⎤
−
>
−
−
⎢
⎥
⎣
⎦
, (2.4.8) где
[ ]
ent
⋅ – целая часть, то ряд остатков
i
e можно считать слу- чайным и, следовательно, построенная модель не содержит сис- тематическую ошибку и является адекватной данному временно- му ряду.
2.4.3. Проверка независимости значений ряда остатков
Зависимость между значениями ряда остатков (другими сло- вами наличие автокорреляции между этим значениями) также свидетельствует о неполноте построенной модели, в которой не была учтена автокорреляция между значениями исходного вре- менного ряда (более подробно об авторегрессионных моделях см. п. 4.1).
Достаточно простым критерием, определяющим наличие ав- токорреляции между соседними наблюдениями, является сле- дующий тест.
Тест Дарбина–Уотсона
. Этот тест основан на простой идее: если корреляция между
i
ε
и
1
i
ε
+
не равна нулю, то она присутст- вует и в остатках (невязках)
i
i
i
e
y
y
=
− регрессионной модели, где
( )
i
i
y
q
τ
=
− оценка объясненной части временного ряда, по- строенная обычным методом наименьших квадратов. Определим статистику:
2 1
2 2
2
(
)
n
i
i
i
n
i
i
e
e
d
e
−
=
=
−
=
∑
∑
(2.4.9)
88
Между этой статистикой и выборочным коэффициентом корре- ляции r имеется связь:
2(1
)
d
r
≈
− .
(2.4.10)
В случае отсутствия автокорреляции (т.е. 0
r
≈ ) значение стати- стики близко к двум. Близость статистики к нулю должна озна- чать наличие положительной автокорреляции, к четырем – отри- цательной автокорреляции. К сожалению, неопределена порого- вая точка для статистики
d при принятии или отвержении нуле- вой гипотезы
0
H : автокорреляция отсутствует. Поэтому весь диапазон значений
d делится на ряд интервалов. Если наблюда- ется значение: а) 4
B
B
d
d
d
< < −
– гипотеза
0
H принимается; б)
H
B
d
d d
< <
или 4 4
B
H
d
d
d
−
< < −
– вопрос о принятии или отвержении гипотезы
0
H остается открытым; в) 0
H
d d
< <
– гипотеза
0
H отвергается и принимается аль- тернативная гипотеза о положительной автокорреляции; г) 4 4
H
d
d
−
< < – гипотеза
0
H отвергается и принимается альтернативная гипотеза о наличии отрицательной автокорреля- ции.
Пороговые значения
,
H
B
d d зависят от числа наблюдений, числа объясняющих переменных в функции ( )
q
τ
и уровня зна- чимости. Эти значения приводятся в специальной таблице [5] и определены для 15
n
≥
. Это ограничение является определенным недостатком теста. В табл. 2.5 приведены некоторые значения
,
H
B
d d для уровня значимости
0.05
α
=
, где k – число объяс- няющих переменных. Используя данные табл. 2.5, можно экстра- полировать
,
H
B
d d на меньшее число наблюдений.
Пример 2.4.1.
Выявить на уровне значимости
0.05
α
=
нали- чие автокорреляции ряда остатков уравнения тренда, построенно- го для временного ряда (значения приведены в табл. 2.1).
89
Решение. В качестве оценки ( )
q
τ
для неслучайной состав- ляющей ( )
q
τ
временного ряда возьмем квадратичный полином
(см. пример 2.1.1)
2
( ) 132.3 55.09 3.26
q
τ
τ
τ
=
+
−
, что соответствует
2
k
= (объясняющие переменные модели
2
,
τ τ
). Вычислим остат- ки
,
1,2, ,8
i
e i
=
… и статистику d , как показано на фрагменте до- кумента Excel, приведенного на рис. 2.23.
Таблица 2.5 1
k
=
2
k
=
3
k
=
4
k
=
n
H
d
B
d
H
d
B
d
H
d
B
d
H
d
B
d
15 1.08 1.36 0.95 1.54 0.82 1.75 0.69 1.97 20 1.20 1.41 1.10 1.54 1.00 1.68 0.90 1.83 25 1.29 1.45 1.21 1.55 1.12 1.66 1.04 1.77 30 1.35 1.49 1.28 1.57 1.21 1.65 1.14 1.74 40 1.44 1.54 1.39 1.60 1.34 1.66 1.29 1.72 50 1.50 1.59 1.46 1.63 1.42 1.67 1.38 1.72
Рис. 2.23. Вычисление статистики Дарбина–Уотсона
90
Найденное значение 3.037
d
=
. Используя данные табл. 2.5, выполним линейную экстраполяцию значений
,
H
B
d d при
2
k
= для числа наблюдений
8
n
= . Получим
0.74,
1.54
H
B
d
d
≈
≈
. Вид- но, что вычисленное значение d находится в пределах от
1.54
B
d
=
до 4 3.26
H
d
−
=
, что соответствует принятию гипотезы
0
H об отсутствии автокорреляции с уровнем значимости
0.05
α
=
. ☻
Положительные результаты описанных выше проверок свойств ряда остатков, а именно:
• нулевое математическое ожидание остатков;
• случайность значений ряда остатков;
• независимость значений ряда остатков, дают уверенность в полноте и адекватности построенной модели и в успешном использовании модели для решения задач прогно- зирования временного ряда.
2.5. Прогнозирование трендовой составляющей
временного ряда
Идея социально-экономического прогнозирования базирует- ся на предположении, что закономерность развития, действовав- шая в прошлом (внутри ряда экономической динамики), сохра- нится и в прогнозируемом будущем. В этом смысле прогноз ос- нован на экстраполяции. Экстраполяция, проводимая в будущее, называется перспективной, а в прошлое – ретроспективной.
Прогнозирование метода экстраполяции базируется на сле- дующих предположениях:
− развитие исследуемого явления в целом описывается плавной кривой;
− общая тенденция развития явления в прошлом и настоя- щем не указывает на серьезные изменения в будущем;
− учет случайности позволяет оценить вероятность откло- нения от закономерного развития.
91
Поэтому надежность и точность прогноза зависят от того, на- сколько близкими к действительности окажутся эти предположе- ния и насколько точно удалось охарактеризовать выявленную в прошлом закономерность.
На основе построенной модели рассчитываются точечные и интервальные прогнозы. Точечный прогноз на основе временных моделей получается подстановкой в модель (уравнение тренда) соответствующего значения фактора времени, т.е.
(
)
1 1
n
n
τ
τ
+
=
+ Δ ,
(
)
2 2
n
n
τ
τ
+
=
+ Δ и т.д.
Интервальные прогнозы строятся на основе точечных про- гнозов. Напомним, что доверительным называется интервал, от- носительно которого можно с заранее выбранной вероятностью утверждать, что он содержит значение прогнозируемого показа- теля. Ширина интервала зависит от качества модели, т.е. степени ее близости к фактическим данным, числа наблюдений и выбран- ного пользователем доверительной вероятности.
Нижняя
( )
H
t l и верхняя
( )
B
t l границы доверительного ин- тервала для «индивидуального» значения трендовой составляю- щей [5, с. 39–40] вычисляются по следующим формулам
( ) ( )
( )
H
l
l
l
t
t
t
τ
τ
δ τ
=
−
;
(2.5.1)
( ) ( )
( )
B
l
l
l
t
t
t
τ
τ
δ τ
=
+
,
(2.5.2) где
( )
l
t
τ
– значение оценки трендовой составляющей в момент времени
l
τ
. Если
l
n
τ
τ
> , то
( )
l
t
τ
– прогнозируемое значение трендовой составляющей.
Величина
( )
l
f
δ τ
для линейного тренда
( )
0 1 l
t l
b
b
τ
= +
(2.5.3) определяется выражением
92
( ) (
)
(
)
(
)
2 2
1 1
,
2 1
l
l
n
f
i
i
t
n
s
n
τ τ
δ τ
γ
τ τ
=
−
=
−
+ +
−
∑
, (2.5.4) где
2 1
2
n
i
i
e
s
n
=
=
−
∑
;
1 1
n
i
i
n
τ
τ
=
=
∑
(2.5.5)
Напомним, что [5, с. 37–40]:
• величина
2
s является оценкой для дисперсии
2
σ
случайной составляющей временного ряда;
• величина
γ
определяют доверительную вероятность (или надежность интервальной оценки) и обычно 0.95
γ
=
;
•
(
)
,
2
t
n
γ
−
– квантиль распределения Стьюдента с (
2
n
− ) степенями свободы, определяемый функцией Excel:
(
)
(
)
,
2
СТЬЮДРАСПОБР 1
;
2
t
n
n
γ
γ
−
=
−
−
(2.5.6)
Для нелинейных моделей величина
( )
l
f
δ τ
также зависит от s и разности
l
τ τ
− , но эта зависимость имеет более сложный харак- тер.
Если построенная модель адекватна, то с вероятностью
γ
можно утверждать, что при сохранении сложившихся закономер- ностей развития прогнозируемая величина попадает в интервал, образованный границами формул (2.5.1), (2.5.2).
Пример 2.5.1.
В табл. 2.6 приведены величины нетто- платежей ежемесячного финансирования инвестиционного про- екта.
Таблица 2.6
Месяц 1 2 3 4 5 6 7 8 9 10 11 12
Платеж, тыс. р.
45 40 43 48 42 47 51 55 50 57 60 62
93
Требуется определить:
• линейную модель зависимости объемов платежей от сро- ков (времени);
• адекватность построенной модели;
• размеры платежей на три последующих месяца, построив точечный и интервальный прогноз.
Решение. Введем в столбцы А, В листа Excel данные табл. 2.6
(рис. 2.24), затем построим диаграмму рассеяния, как геометриче- ское место точек
( )
,
i
i y , 1,…,12
i
=
. Анализ диаграммы показывает наличие небольшого тренда.
Используя команду Добавить линию тренда, строим линей- ную модель тренда, описываемую уравнением
( )
38.23 1.81
t
τ
τ
=
+
(2.5.7) с коэффициентом детерминации
2 0.823
R
=
. Для проверки значи- мости коэффициентов уравнения тренда обратимся к модулю
Анализ данных режима Регрессия [5, с. 94–101] и зададим необ- ходимые параметры в появившемся диалоговом окне. Результаты выполнения режима Регрессия показаны на рис. 2.25, 2.26.
Видно, что коэффициент детерминации равен 0.823, приве- денный коэффициент детерминации
2 0.805
R
=
(см. рис. 2.25).
Все коэффициенты
0
b ,
1
b являются значимыми (при уровне зна- чимости
0.05
α
=
) и построенное уравнение линейного тренда также является значимым (см. рис. 2.25, 2.26), так как выполня- ются неравенства (более подробно см. [5, с. 41–46]):
(
)
0 19.554 1
,
2 2.228;
b
T
t
n
α
=
>
−
−
=
(
)
1 6.818 1
,
2 2.228;
b
T
t
n
α
=
>
−
−
=
1
;1;
2 46.490 4.965
n
F
F
α
−
−
=
>
=
94
Рис. 2.24. Построение линейного тренда (пример 2.5.1)
Рис. 2.25. Результаты выполнения режима Регрессия
95
Рис. 2.26. Результаты выполнения режима Регрессия
Выполним проверку статистической гипотезы (2.4.2) о ра- венстве математического ожидания ряда остатков
i
e нулю, гра- фик которых приведен на рис. 2.27.
Подставляя значения
0.002
e
=
;
(
)
2 100.902 0.002 3.03 12 1
e
s
−
=
=
−
в выражение (2.4.4), получаем
0.002 12 0.0023 3.03
e
T
=
=
Рис. 2.27. График остатков
i
e
96
Используя функцию (2.4.6), вычисляем
, 2 2.179
пр
x
α
=
. Видно, что вычисляемое значение критерия не попадает в критическую об- ласть (2.4.5)
(
] [
)
, 2.179 2.179,
−∞ −
∪
∞ , и поэтому принимается гипотеза о равенстве нулю математиче- ского ожидания значений остатков
i
e .
Проверку случайности значений остатков
i
e проведем на ос- нове критерия поворотных точек (см. п. 2.4.2). Как видно из рис. 2.28 (столбец G), количество поворотных точек
5
p
n
= . Тогда неравенство (2.4.8) выполняется
(
)
[
]
2 16 12 29 5
12 2 1.96 4.029 4
3 90
ent
ent
⎡
⎤
⋅ −
>
−
−
=
=
⎢
⎥
⎣
⎦
Поэтому имеет место свойство случайности остатков
i
e .
Проверку независимости остатков
i
e (т.е. отсутствие авто- корреляции) выполним с использованием теста Дарбина–Уотсона
(см. п. 2.4.3). На рис. 2.28 показан фрагмент документа Excel, в котором вычисляется по формуле (2.4.10) наблюдаемое значение критерия 2.116
d
=
. Используя табл. 2.5 выполним линейную экстраполяцию значений
H
d ,
B
d при
1
k
= и числе наблюдений
n = 12. Получаем
1.008
H
d
≈
,
1.33
B
d
≈
. Видно, что вычисляемое значение d находится внутри интервала
[
] [
]
,4 1.33,2.67
B
B
d
d
−
=
Следовательно, можно говорить о независимости значений остат- ков
i
e .
Проверенные свойства ряда остатков позволяют считать,
что построенная линейная модель тренда (2.5.7) адекватно опи-
сывает исследуемый временной ряд и ее можно использовать для
решения задач прогнозирования.
97
Рис. 2.28. Вычисление значения d (пример 2.5.1)
Вычислим точечный прогноз по формулам (2.5.1), (2.5.2) при
13, 14, 15
τ
=
:
( )
13 38.23 1.81 13 61.77
t
=
+
⋅
≈
;
( )
14 38.23 1.81 14 63.58
t
=
+
⋅
≈
;
( )
15 38.23 1.81 15 65.40
t
=
+
⋅
≈
Результаты вычисление интервального прогноза приведены в табл. 2.7.
С вероятностью
1 0.95
γ
α
= − =
можно утверждать, что вели- чина ежемесячного финансирования будет находиться в интерва- ле, определяемом вычисленными нижними и верхними граница- ми.
98
Таблица 2.7
Время,
l
τ
( )
f
l
δ τ
Точечный прогноз
Нижняя граница
Верхняя граница
13 6.80 61.77 54.97 68.57 14 7.04 63.58 56.55 70.62 15 7.29 65.40 58.10 72.69
ЛАБОРАТОРНАЯ РАБОТА № 1
Выделение трендовой составляющей временного ряда
Исходные данные. В таблице приведены значения урожай- ности зерновых совхоза «Путь к коммунизму» Черепановского района за 14 лет, ц/га.
Год
1972 1973 1974 1975 1976 1977 1978
Урожайность 17.9 19.5 30.1 26.7 31.0 28.4 20.0
Год
1979 1980 1981 1982 1983 1984 1985
Урожайность 24.7 26.9 21.3 28.6 27.7 30.0 22.9
Необходимо:
1. Используя команду Добавить линию тренда (см. п. 2.2.1) построить следующие модели для трендовой составляющей:
( )
1 0
1
t
b
b
τ
τ
= +
;
( )
2 2
0 1
2
t
b
b
b
τ
τ
τ
= +
+
;
( )
2 3
3 0
1 2
3
t
b
b
b
b
τ
τ
τ
τ
= +
+
+
2. Для каждого уравнения вычислить коэффициенты, индекс детерминации
2
t
R , приведенный индекс детерминации
2
t
R .
3. Занести в следующую таблицу (на том же листе Excel) уравнение тренда и вычисленные значения
2
t
R ,
2
t
R .
Уравнение
2
t
R
2
t
R
99 4. Анализируя величины
2
t
R ,
2
t
R , найти наилучшую модель
( )
opt
t
τ
трендовой составляющей.
5. Построить графики значений
i
y ,
( )
opt
t
τ
,
i
e .
6. Используя критерий (2.1.20), проверить возможность заме- ны нелинейного тренда
( )
3
t
τ
линейной функцией
( )
1
t
τ
7. Используя наилучшую модель тренда, осуществить прогноз урожайности на следующие годы: 1986, 1988, 1990.
Рекомендации:
1. Перед выполнением работы ознакомьтесь с примером 2.2.2, в котором решается подобная задача.
2. Вычисление величин
2
t
R ,
2
t
R осуществлять по формулам
(2.1.18), (2.1.28).
3. При выполнении задания 6 использовать пример 2.1.2.
ЛАБОРАТОРНАЯ РАБОТА № 2
Исследование модели трендовой составляющей
временного ряда
Исходные данные. В лабораторной работе № 1 по выборке, представленной в таблице, построена наилучшая модель тренда
( )
opt
t
τ
(для этой модели приведенный индекс детерминации
2
t
R имеет максимальное значение среди всех остальных рассмотрен- ных моделей).
Необходимо:
1. Вычислить для модели
( )
opt
t
τ
ряд остатков
( )
i
i
opt
i
e
y
t
τ
=
−
,
1,2,…,
i
n
=
2. Построить на одном рисунке графики y
i
,
( )
opt
i
t
τ
,
i
e .
3. Используя критерий (2.4.4), проверить гипотезу о нулевом математическом ожидании остатков
i
e .
4. Используя критерий поворотных точек, проверить гипотезу о случайности значений остатков
i
e .
100 5. Используя тест Дарбина–Уотсона, проверить гипотезу о не- зависимости между собой остатков
i
e .
6. В зависимости от результатов проверки статистических ги- потез п. 3–5 сделать аргументированный вывод об адекватности построенной модели и ее пригодности для решения задач прогно- зирования.
Рекомендации:
1. Проверку гипотезы о нулевом математическом ожидании остатков e
i
осуществить следуя п. 2.4.1 и примеру 2.5.1.
2. Проверку гипотезы о случайности значений остатков e
i
осуществить следуя п. 2.4.2 и примеру 2.5.1.
3. Проверку гипотезы о независимости остатков e
i
осущест- вить следуя п. 2.4.3 и примеру 2.5.1.
ЛАБОРАТОРНАЯ РАБОТА № 3
Прогнозирование трендовой составляющей временного ряда
Исходные данные. В таблице лабораторной работы № 1 приведены значения урожайности зерновых за 14 лет, ц/га.
Необходимо:
1. По данным таблицы построить модель линейного тренда вида
( )
0 1
t
b
b
τ
τ
= +
2. Вычислить по этой модели точечной прогноз для 1986–
1992 годов.
3. Вычислить интервальный прогноз для 1986–1992 годов.
4. На одном рисунке построить графики y
i
,
( )
i
t
τ
точечного и интервального прогноза.
Рекомендации:
1. При выполнении задания 1 можно использовать команду
Добавить линию тренда, описанную в п. 2.2.1.
2. При выполнении задания 3 использовать материал п. 2.5 и примера 2.5.1.
101
КОНТРОЛЬНАЯ РАБОТА
Исходные данные. В таблице приведены значения удоев мо- лока от одной коровы одного из хозяйств Новосибирской облас- ти, кг.
Номер года
1 2
3 4
5 6
7
Год 1971 1972 1973 1974 1975 1976 1977
Удои 3201 3192 3156 3364 3489 3587 3648
Номер года
8 9
10 11 12 13 14
Год 1978 1979 1980 1981 1982 1983 1984
Удои 3475 3481 3579 3543 3685 3701 3966
Необходимо:
1. По данным таблицы построить диаграмму рассеяния и ви- зуально убедиться в наличии трендовой составляющей.
2. Проверить гипотезу о наличии неслучайной составляю- щей в исследуемом временном ряду.
3. Используя команду Добавить линию тренда (см. п. 2.2.1) построить следующие модели для трендовой составляющей:
( )
1 0
1
t
b
b
τ
τ
= +
;
( )
2 2
0 1
2
t
b
b
b
τ
τ
τ
= +
+
;
( )
2 3
3 0
1 2
3
t
b
b
b
b
τ
τ
τ
τ
= +
+
+
4. Для каждого уравнения вычислить коэффициенты, индекс детерминации
2
t
R , приведенный индекс детерминации
2
t
R и зане- сти эти значения в следующую таблицу
Уравнение
2
t
R
2
t
R
102 5. Анализируя величины
2
t
R ,
2
t
R для разных уравнений най- ти наилучшую модель
( )
opt
t
τ
трендовой составляющей.
6. Построить графики значений
i
y ,
( )
opt
t
τ
,
i
e .
7. Используя наилучшую модель тренда осуществить про- гноз удоев на следующие годы: 1986, 1988, 1990.
8. Используя критерий (2.4.4) проверить гипотезу о нулевом математическом ожидании остатков
i
e .
9. Используя критерий поворотных точек проверить гипоте- зу о случайности значений остатков
i
e .
10. Используя тест Дарбина–Уотсона проверить гипотезу о независимости между собой остатков
i
e .
11. В зависимости от результатов проверки статистических гипотез п. 3–5 сделать аргументированный вывод об адекватности построенной модели и ее пригодности для решения задач прогно- зирования.
12. Для модели линейного тренда осуществить точечный прогноз удоев на следующие годы: 1986, 1988, 1990. Сравнить сделанный прогноз с прогнозом, построенном в задании 7.
13. Для модели линейного тренда осуществить интерваль- ный прогноз удоев на следующие годы: 1986, 1988, 1990.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что понимается под терминами «выделить трендовую со- ставляющую» или «выделить тренд»?
2. Перечислите основные подходы, используемые для выде- ления трендовой составляющей.
3. Сущность регрессионного метода выделения тренда вре- менного ряда.
4. Сущность метода скользящего среднего выделения тренда временного ряда.
5. Сущность метода экспоненциального сглаживания для выделения тренда временного ряда.
103 6. Реализация регрессионного метода выделения тренда вре- менного ряда в табличном процессоре Excel.
7. Что такое периодическая функция и ее представление три- гонометрическим рядом?
8. Сущность выделения тригонометрической составляющей методами гармонического анализа.
9. Построение точечного прогноза для трендовой состав- ляющей временного ряда.
10. Построение интервального прогноза для трендовой со- ставляющей временного ряда.
11. Различие между точечным и интервальным прогнозом трендовой составляющей временного ряда.
12. Как нужно изменить дисперсию
2
σ
для уменьшения
«ширины» интервала прогнозирования трендовой составляющей временного ряда?
104