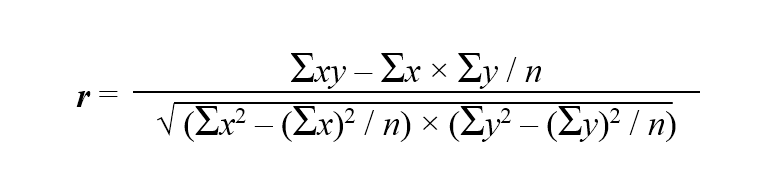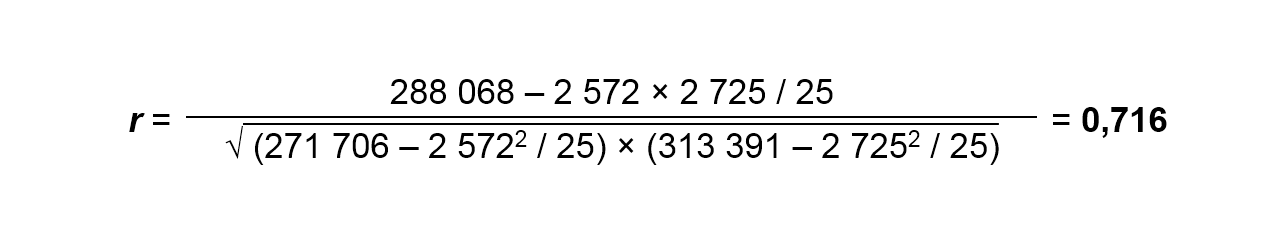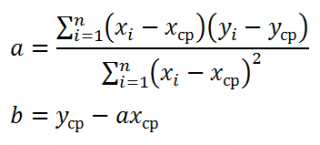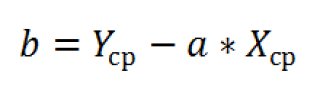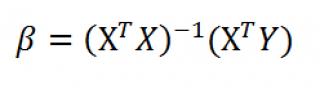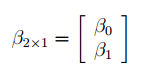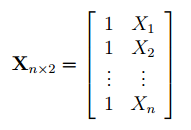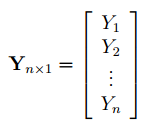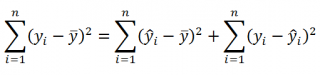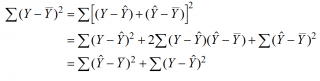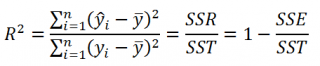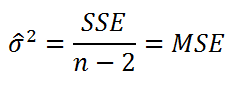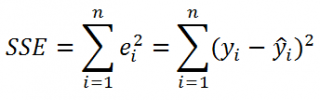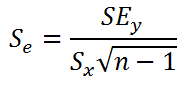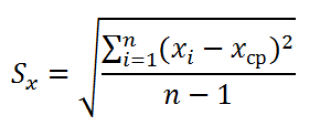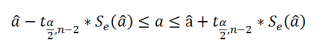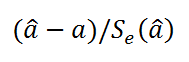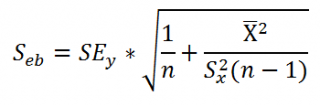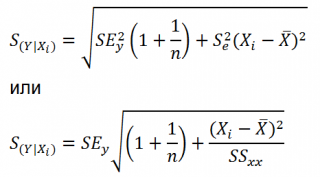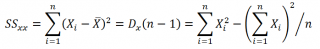В окружающем мире очень много взаимосвязей между объектами, предметами, событиями, отношениями и т.д. Например, между количеством заключенных контрактов и трудовыми затратами, между сбытом и доходами населения, между образованием и уровнем заработной платы, вмешательством государства и состоянием экономики. Каждое из измерений в этих парах можно изучать по отдельности. Как одномерную совокупность. Но реальный результат получается лишь при изучении обоих измерений, взаимосвязи между ними.
При работе с двумерными данными обычно рисуют диаграммы рассеяния. Другие названия – «диаграммы разброса», «точечные диаграммы». Подобные графики показывают значения двух переменных в виде точек. Если в двумерных данных содержатся какие-либо проблемы (выбросы), то их легко будет обнаружить с помощью соответствующей диаграммы разброса.
Что показывает диаграмма рассеяния
Диаграмма рассеяния – один из инструментов статистического контроля, анализа. С ее помощью выявляется зависимость и характер связи между двумя разными параметрами экономического явления, производственного процесса. Диаграмма разброса показывает вид и тесноту взаимосвязи между парами данных. К примеру, между:
- качеством продукта и влияющим фактором;
- двумя разными характеристиками качества;
- двумя обстоятельствами, влияющими на качество, и т.п.
Диаграммы рассеяния применяются для обнаружения корреляции между данными. Если корреляционная зависимость присутствует, то установить контроль над наблюдаемым явлением значительно проще.
Построение диаграммы рассеяния в Excel
Диаграмма разброса представляет наблюдаемое явление в пространстве двух измерений. Если одну величину рассматривать как «причину», влияющую на другую величину, то ей будет соответствовать ось Х (горизонтальная ось). Реагирующей на это влияние величине соответствует ось Y (вертикальная ось). Когда четко классифицировать переменные невозможно, распределение производится пользователем.
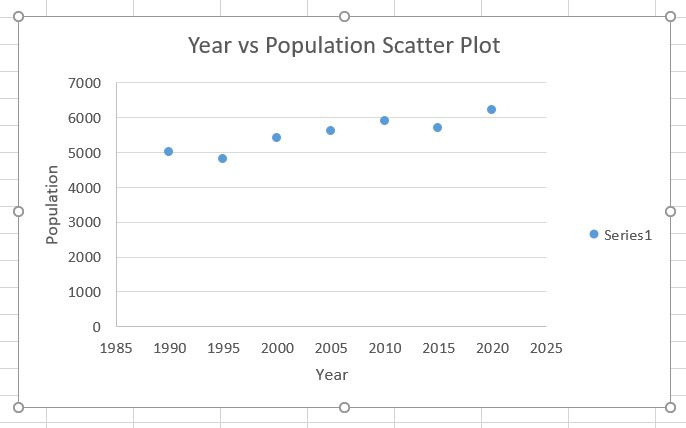
Построим диаграмму рассеяния для небольшой двумерной совокупности данных:
Предположим, что затраченные усилия каждого менеджера повлияли на результат его работы (так принято считать). Следовательно, число контактов необходимо показать на горизонтальной оси, а продажи (результат затраченных усилий) – на вертикальной.
Для построения диаграммы рассеяния в Excel выделим столбцы «Контакты», «Объем продаж» (включая заголовки). Перейдем на вкладку «Вставка» в группу «Диаграммы». Использование данного инструмента анализа возможно с помощью точечных диаграмм:
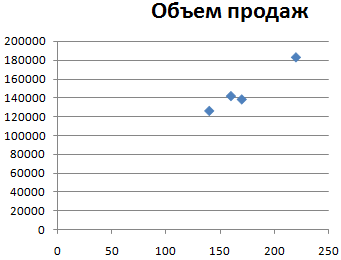
По умолчанию программа построила диаграмму разброса такого вида:
Изменим параметры горизонтальной и вертикальной оси, чтобы четыре пары показателей расположились более равномерно в области построения. Щелкнем сначала правой кнопкой мыши по вертикальной оси. Выберем «Формат оси»:
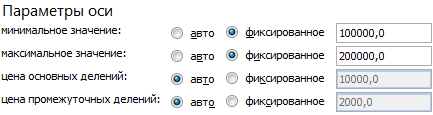
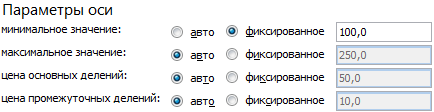
На вкладке «Параметры оси» установим минимальное значение 100 000, а максимальное – 200 000. Показатели объема продаж находятся в этих пределах:
Минимальное значение для горизонтальной оси Х – 100, т.к. ниже этого показателя данных в таблице нет.
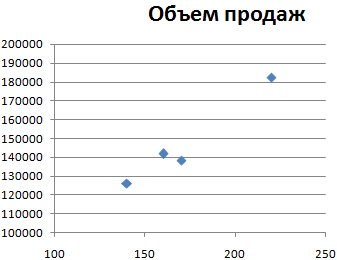
Диаграмма разброса приобрела следующий вид:
Какие можно сделать выводы по данной диаграмме рассеяния:
- Каждая точка дает представление об объеме продаж и контактах (как об одномерных совокупностях) и о взаимосвязи между этими параметрами.
- Количество контактов (горизонтальная ось) распределилось в диапазоне 140-220. Типичное значение равно примерно 170.
- Объемы продаж за анализируемый период (вертикальная ось) находятся в диапазоне примерно от 130 000 до 190 000. Типичное значение равняется приблизительно 150 000.
- Взаимосвязь между числом контактов и объемом сбыта является положительной, т.к. точки выстроились слева направо снизу вверх. Следовательно, чем больше у менеджера было контактов с клиентами (точки правее), тем больше прибыли организации он дал (точки выше).
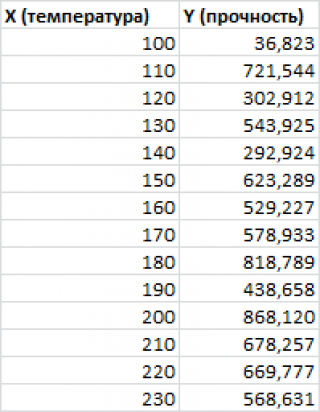
Построим диаграмму рассеяния для различных видов взаимосвязей двух переменных. Сгенерируем различные варианты трендов: линейный, квадратичный и затухающий синусоидальный.
Диаграмма рассеяния
(
scatter
plot
) используется для отображения возможной взаимосвязи между двумя переменными.
Диаграмма рассеяния
незаменима при проведении корреляционного и регрессионного анализа.
Возьмем 2 переменные
Х
и
Y
и, соответственно,
выборку
состоящую из нескольких пар значений (Х i ; Y i ). Для наглядности зададим различные типы зависимости между переменными: линейную, квадратичную и затухающую синусоидальную. Для этого сгенерируем соответствующие тренды и настроим случайный разброс переменной Y (по
нормальному закону
).
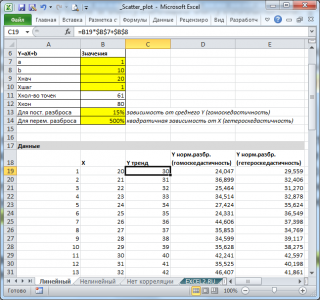
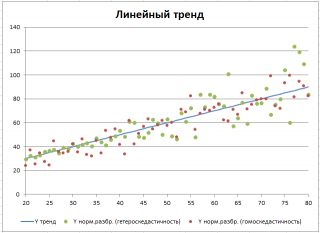
Сначала рассмотрим
линейный тренд
Y
=
aX
+
b
(см. Файл примера, лист Линейный ). Параметры тренда (прямой линии)
a
и
b
зададим в отдельной табличке, там же зададим параметры отвечающие за величину
дисперсии
переменной Y.
Величину постоянного разброса (отвечающую за
гомоскедастичность
модели) будем задавать в % от
среднего значения
Y. Иногда,
дисперсия
переменной Y не постоянна (имеется неоднородность наблюдений —
гетероскедастичность
). Поэтому, при построении формул учтем и такую возможность.
Для построения
диаграммы рассеяния
в файле примера использована
диаграмма График
, т.к. шаг по Х у нас задан постоянным. В случае реальных данных (переменная Х является случайной величиной, а не жестко заданной, как в нашем примере) используйте диаграмму типа Точечная. В файле примера реализовано оба варианта.
Примечание
: Подробнее о построении диаграмм см. статьи
Основы построения диаграмм
и
Основные типы диаграмм
.
Отображение информации о 3-х переменных на двухмерной диаграмме
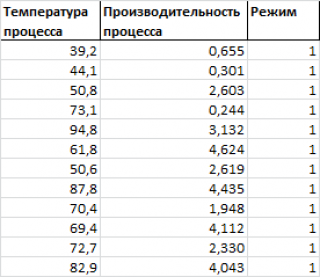
Предположим, что у нас имеются результаты измерения производительности некого непрерывного производственного процесса. Измерения проводились при различных рабочих температурах протекания процесса и в двух режимах.
Нам требуется построить двумерную
диаграмму рассеяния
(на плоскости), хотя у нас имеется 3 переменных:
производительность, температура
и
режим
.
Обратим внимание, что третья переменная
Режим
является категориальной (принимает только значения из ограниченного набора значений). В нашем случае переменная
Режим
принимает 2 значения:
Режим №1
и
Режим №2
(значения 1 и 2 присвоены номинально).
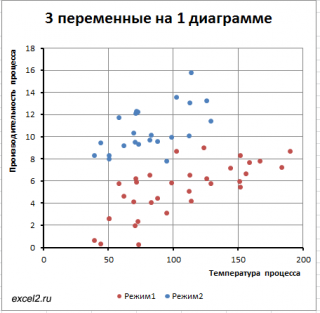
Пары значений (
производительность; температура
), относящиеся к
Режиму №1
будем на
диаграмме рассеяния
выводить красным цветом, а относящиеся к
Режиму №2
будем выводить синим ( файл примера лист 3-переменных ).
Такой же подход можно использовать для
дискретных переменных
, когда они принимают небольшое количество значений: 2-5.
Категоризованные диаграммы
Если третья переменная – непрерывная величина, то для отображения данных можно использовать так называемые
категоризованные диаграммы
(coplot = conditioning plot).
Теперь вместо категориальной переменной
Режим
у нас имеется
непрерывная переменная
Давление
, которая принимает значения от 10 до 20. Предположим, что значение переменной
Давление
= 15, является неким пороговым и протекание процесса значительно отличается, если оно протекает при давлении от 10 до 15 и от 15 до 20. Используя этот факт строят 2 диаграммы:
-
Пары значений (
производительность; температура
) при давлении от 10 до 15: -
Пары значений (
производительность; температура
) при давлении от 15 до 20.
Если пороговых значений 2, то понадобится 3 диаграммы и т.д. Эти диаграммы строятся аналогично диаграммам из предыдущего раздела.
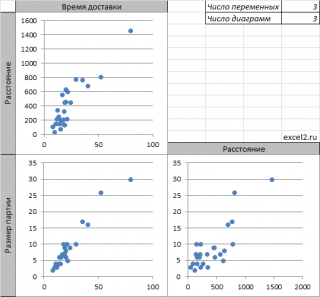
Матрица диаграмм рассеивания
Для множественной регрессии, когда имеется 3 или более переменных, часто строят
Матрицу диаграмм рассеивания
(Matrix Scatter Plot, Scatter Plot Matrix — SPM).
Если имеется 3 переменных (x 1 , x 2 , y), то строятся 3 обычные
диаграммы рассеяния
отображающие парные взаимосвязи переменных: (x 1 , x 2 ); (x 1 , y); (x 2 , y).
Примечание
: Чтобы найти количество
диаграмм рассеяния
в матрице, необходимо вычислить
число сочетаний
из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ЧИСЛКОМБ(4;2) =6.
Иногда строят не только диаграмму (x 1 , x 2 ), но и (x 2 , x 1 ). В этом случае матрица будет содержать в 2 раза больше диаграмм рассеяния (см. файл примера лист Matrix ).
Примечание
: Чтобы найти количество
диаграмм рассеяния
в такой (полной) матрице, необходимо вычислить
число перестановок
из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ПЕРЕСТ(4;2) =12.
«СЕМЬ ОСНОВНЫХ ИНСТРУМЕНТОВ КОНТРОЛЯ КАЧЕСТВА»
Диаграмма рассеяния
Что такое диаграмма рассеяния?
Очень часто в производственной, маркетинговой и иных видах деятельности необходимо понять, связаны ли между собой какие-либо явления, и если связаны, то насколько тесно.
Если вы, например, заметили увеличение объёма брака в какую-либо смену, вы вправе предположить, что это связано с трудовой деятельностью того или иного работника. Но как понять, так ли это на самом деле? Или вы считаете, что на тот или иной показатель качества выпускаемого изделия влияет некая технологическая операция, но хотите убедиться в этом и понять, насколько сильно данная операция оказывает влияние на интересующий вас показатель качества. А ваш маркетолог хочет выявить наличие и силу взаимосвязи между типом упаковки и её привлекательностью для потребителя. Директор же по информационным технологиям желает убедиться в том, что переход вашего предприятия на облачные технологии напрямую повлиял на снижение затрат в сфере ИТ, для чего хотел бы выявить связь между таким переходом и затратами, а также силу этой связи.
Практически любую такую связь или, более научно, корреляцию позволяет установить диаграмма рассеяния (другие названия – диаграмма разброса, диаграмма рассеивания, поле корреляции).
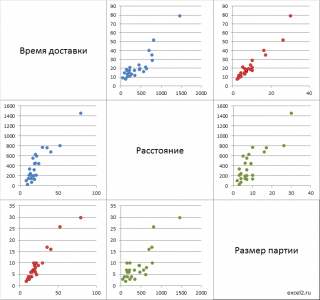
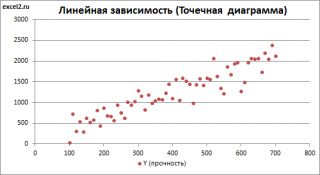
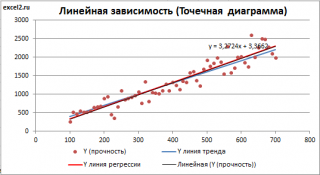
Типичный вид диаграммы рассеяния представлен на рисунке 1.
Диаграмма рассеяния – инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных.
В зависимости от наличия или отсутствия предполагаемых причинно-следственных связей при помощи диаграммы рассеяния можно анализировать зависимость:
- между влияющим фактором (причиной) и характеристикой (следствием);
- между двумя характеристиками;
- между двумя факторами.
Влияющий фактор (причину) иногда называют также факторным признаком, а характеристику (следствие) – результативным признаком.
Если говорить конкретно о качестве, то такие пары переменных чаще всего относятся [1, с. 144; 2, с. 125]:
- к характеристике качества и влияющему на неё фактору;
- к двум различным характеристикам качества;
- к двум факторам, влияющим на одну характеристику качества.
Все три категории анализа крайне важны, поскольку [4]:
- в первом случае, при наличии корреляционной зависимости, причинный фактор оказывает значительное влияние на характеристику качества, а потому если причинный фактор удерживать под контролем, то можно, во-первых, достичь стабильности характеристики качества, а во-вторых, определить уровень контроля, необходимый для требуемого показателя качества;
- во втором случае, при наличии корреляционной зависимости между двумя различными характеристиками качества, можно, например, осуществлять контроль только одной из них;
- в третьем случае наличие корреляционной зависимости между отдельными факторами значительно облегчает контроль процесса с технологической, временнóй и экономической точек зрения.
Если между сопоставляемыми парами переменных предполагается наличие причинно-следственной связи, то при построении диаграммы рассеяния причинные факторы, как правило, обозначаются переменной х и откладываются по горизонтальной оси (оси абсцисс); характеристики же, как правило, обозначаются переменной y и откладываются по вертикальной оси (оси ординат).
Построение диаграммы выполняется в следующей последовательности [1, с. 145–146; 2, с. 126]:
- Собираются парные данные (х, у), между которыми мы хотим исследовать зависимость, и заполняется таблица. Желательно собрать не менее 25–30 пар данных.
- Определяются максимальные и минимальные значения для х и y. Исходя из разницы между их максимальными и минимальными значениями устанавливаются размеры и шкалы осей, причём их лучше делать примерно одинаковыми, чтобы диаграмма легче читалась.
- Строится график, на который наносятся данные. Если на одну и ту же точку графика попадает несколько одинаковых значений, то соответствующие точки обозначаются при помощи концентрических кругов (точка в круге, в двух, трёх кругах) либо рядом с первой точкой наносится вторая, третья точка.
- На график наносятся все необходимые обозначения: название диаграммы, её составитель, дата, интервал времени, число пар данных, единицы измерения для каждой оси и т.д.
В зависимости от значений x и y графики могут иметь различный вид, при этом построенные графики надо уметь читать. Посмотрим, как это делается.
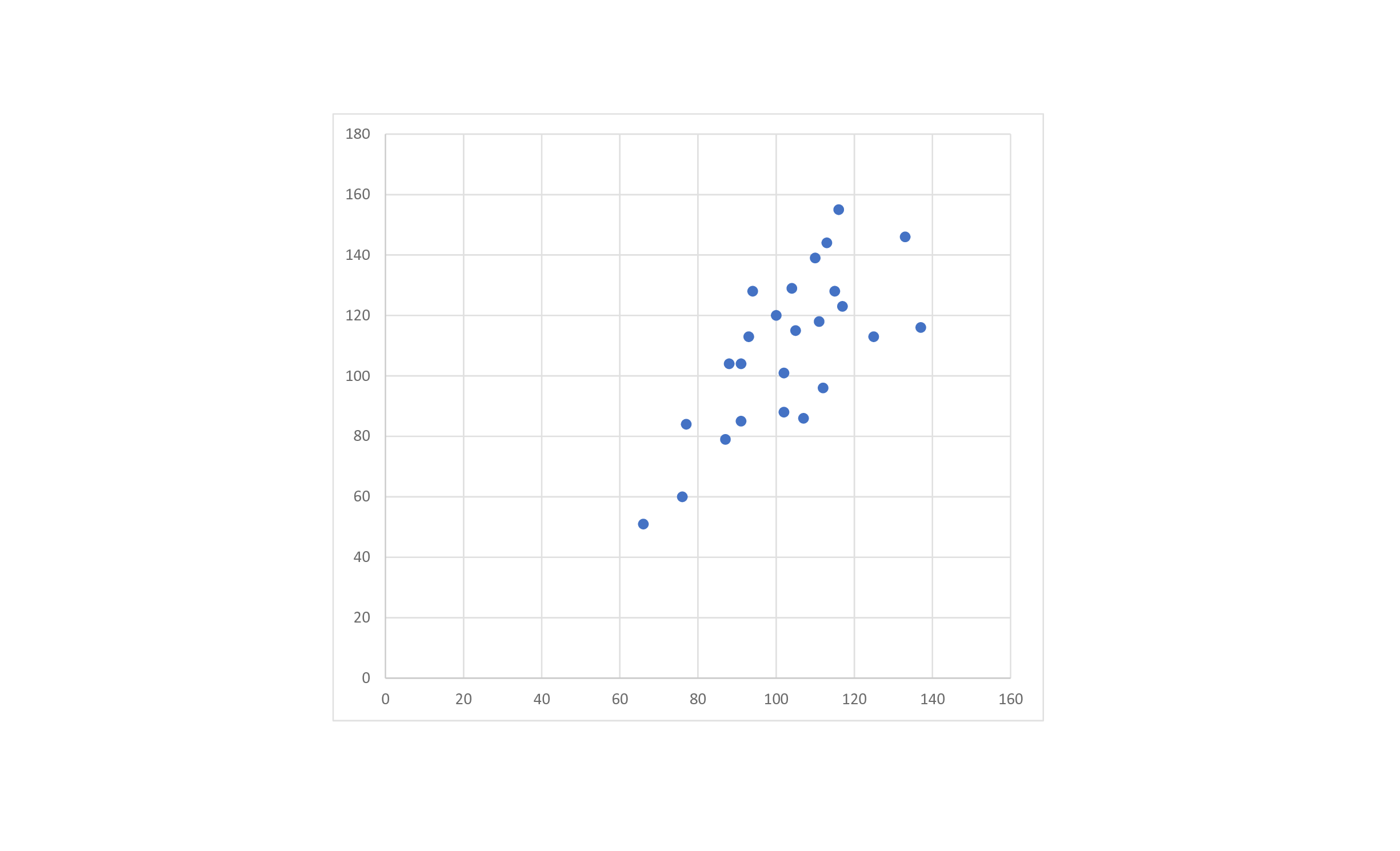
Ниже, на рисунке 2, представлены различные виды графиков. График позволяет нам воочию увидеть характер и тесноту связи между соответствующими переменными x и y. Ниже мы также научимся определять степень этой тесноты, называемую коэффициентом корреляции.
Коэффициент корреляции r может принимать значения от -1 до +1, т.е. -1 ≤ r ≤ 1. При этом чем ближе значение коэффициента к ±1, тем теснее связь. Чем ближе оно к нулю, тем связь меньше. В ±1 связь полная (её также называют функциональной, поскольку каждому значению x соответствует строго определённое значение y). В нуле связь отсутствует вообще.
Знак «плюс» или «минус» говорит о направлении связи – прямой или обратной: при плюсе значение y возрастает с возрастанием значения х; при минусе, наоборот, уменьшается.
Что касается оценки тесноты связи, то в разных источниках встречаются разные классификации (градации). Например, в источнике [3, с. 105] даётся следующая классификация:
- от ±0,81 до ±1,0 – сильная сила связи;
- от ±0,61 до ±0,8 – умеренная сила связи;
- от ±0,41 до ±0,6 – слабая сила связи;
- от ±0,21 до ±0,4 – очень слабая сила связи;
- от 0 до ±0,2 – связь отсутствует.
А теперь посмотрим на рисунок 2, на котором представлены различные виды диаграммы рассеяния, при этом сверху указаны соответствующие значения коэффициента корреляции r.
При отсутствии связи (корреляции) между исследуемыми параметрами точки на диаграмме расположены хаотично. Практически ту же самую картину мы видим и при слабой силе связи. Умеренная сила связи характеризуется большей степенью упорядоченности и достаточно равномерной удалённостью нанесённых точек от воображаемой средней линии. Сильная связь в большей степени стремится к такой воображаемой линии, а при r=1 график, собственно говоря, и представляет собой линию.
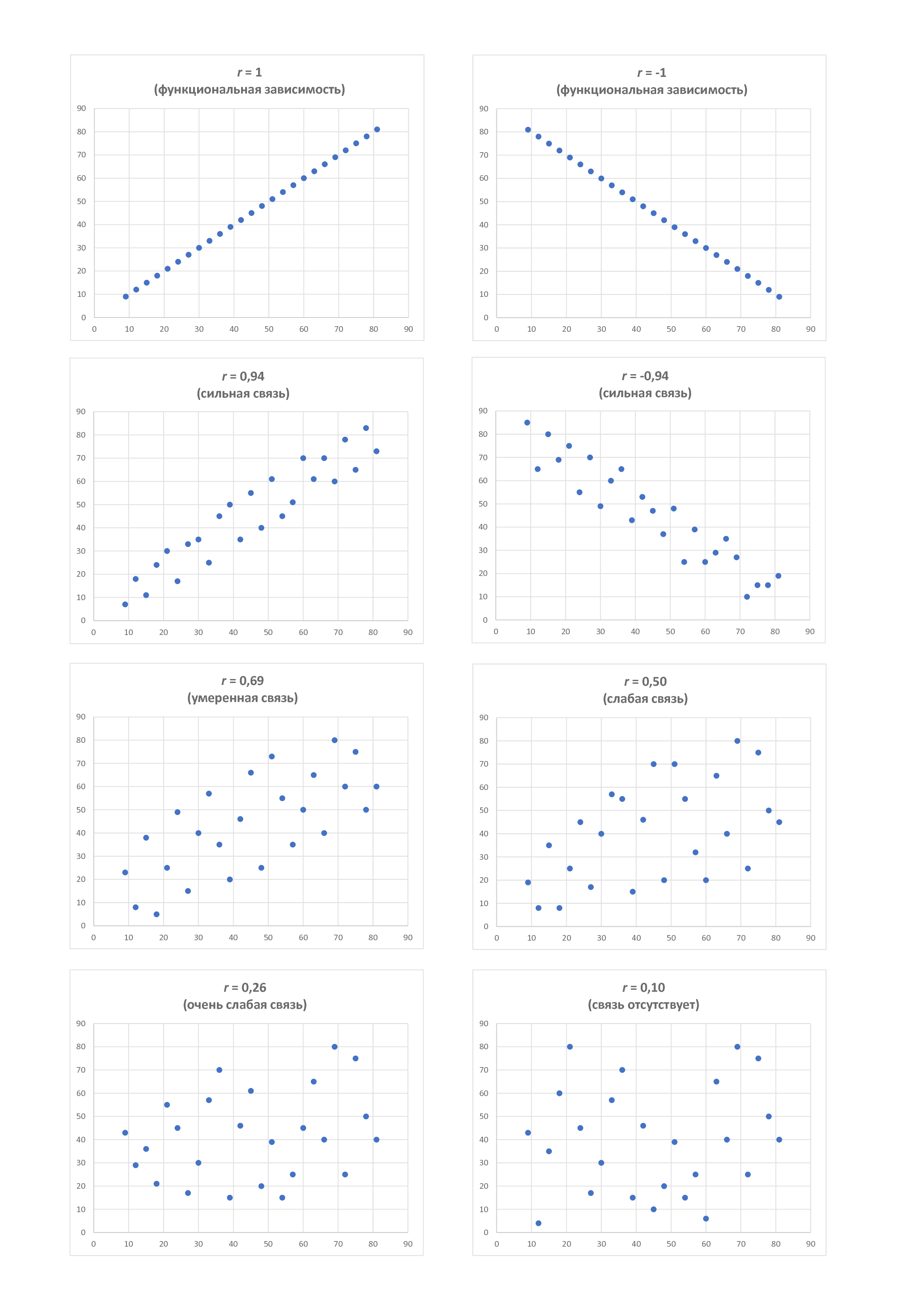
В случаях, представленных на рис. 2, корреляция носит линейный характер (воображаемая средняя линия – прямая), но в реальной жизни график может иметь иную, нелинейную (криволинейную) форму, например такую, как представлена на рис. 3.
Далее мы научимся рассчитывать коэффициент корреляции. Проще всего его рассчитать в программе MS Excel, и ниже мы покажем, как это делается, но прежде представим математическую формулу расчёта коэффициента корреляции и научимся рассчитывать его самостоятельно – без MS Excel или иной аналогичной программы. Все соответствующие расчёты делаются в рамках так называемого корреляционного анализа.
Корреляционный анализ
Коэффициент корреляции вычисляется по формуле:
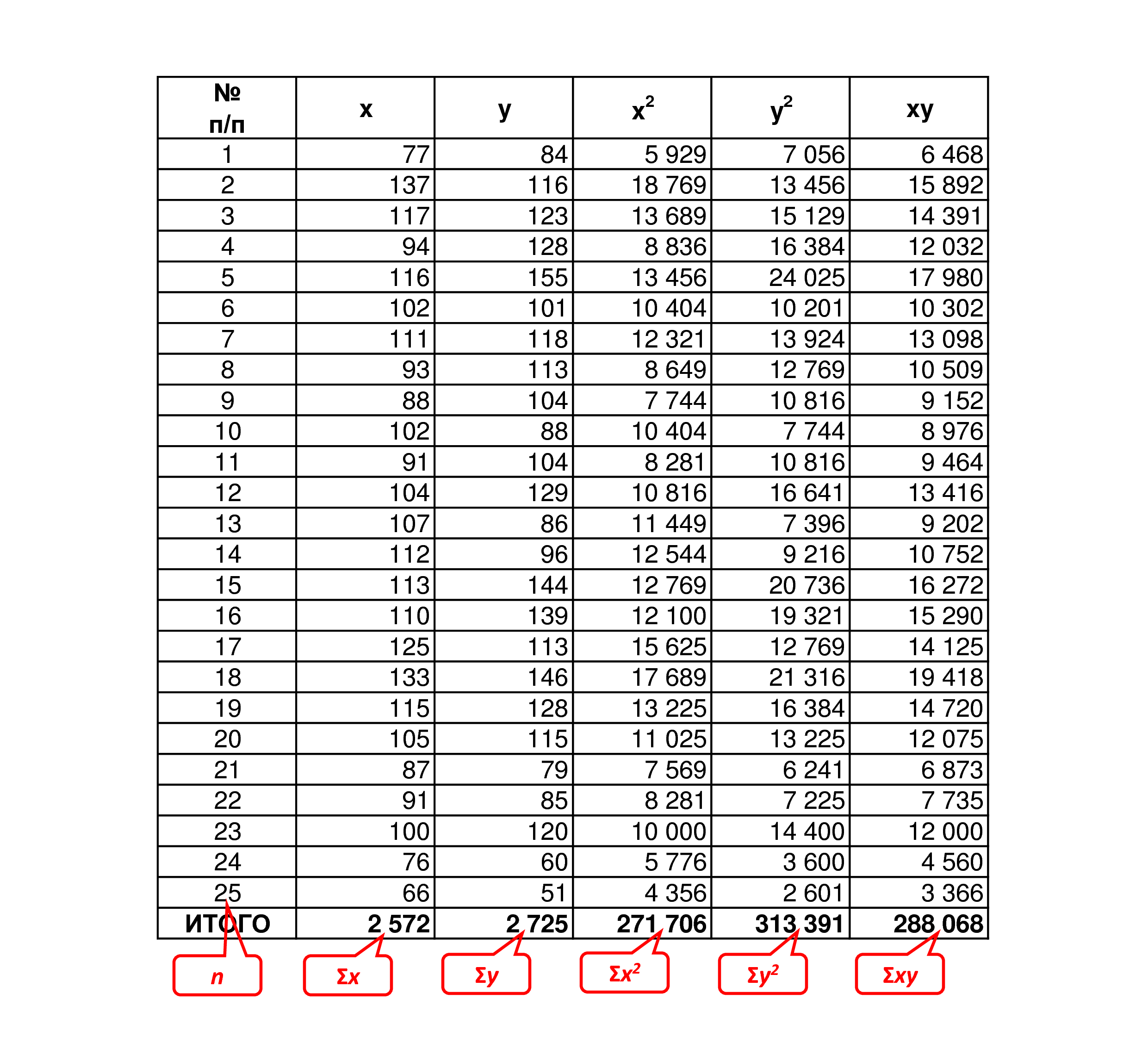
Допустим, мы собрали 25 (n=25) пар данных x и y и хотим определить коэффициент корреляции между ними. Разместим их в таблице и для удобства расчётов сразу определим значения x2, у2 и xy, чтобы затем просто подставить их в формулу:
Подставляем значения в указанную выше формулу и получаем коэффициент корреляции:
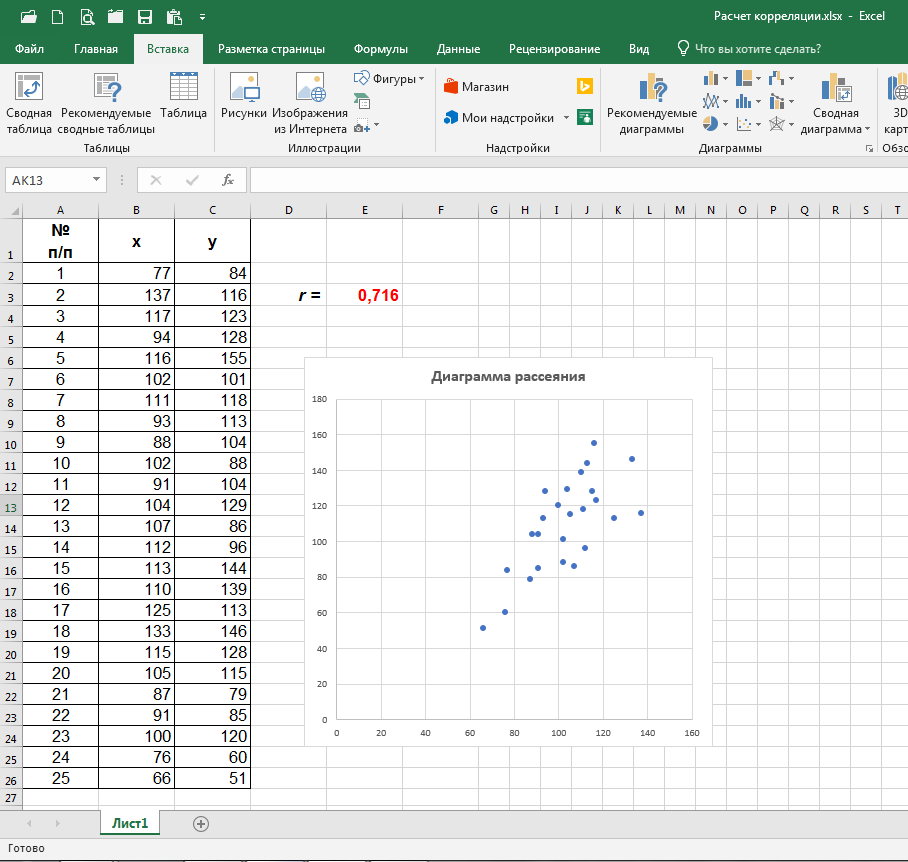
Диаграмма рассеяния, соответствующая этому массиву пар данных, была представлена выше – на рисунке 1.
Воспользуемся программой MS Excel
Всё сказанное выше, по сути, было теорией, призванной объяснить, что такое диаграмма рассеяния, как её читать и как рассчитать коэффициент корреляции.
В реальной жизни коэффициент корреляции рассчитывается, а диаграмма рассеяния – строится значительно проще и быстрее. Для наглядности будем использовать те же самые значения, что и выше.
Шаг 1 – Составление таблицы и расчёт коэффициента корреляции
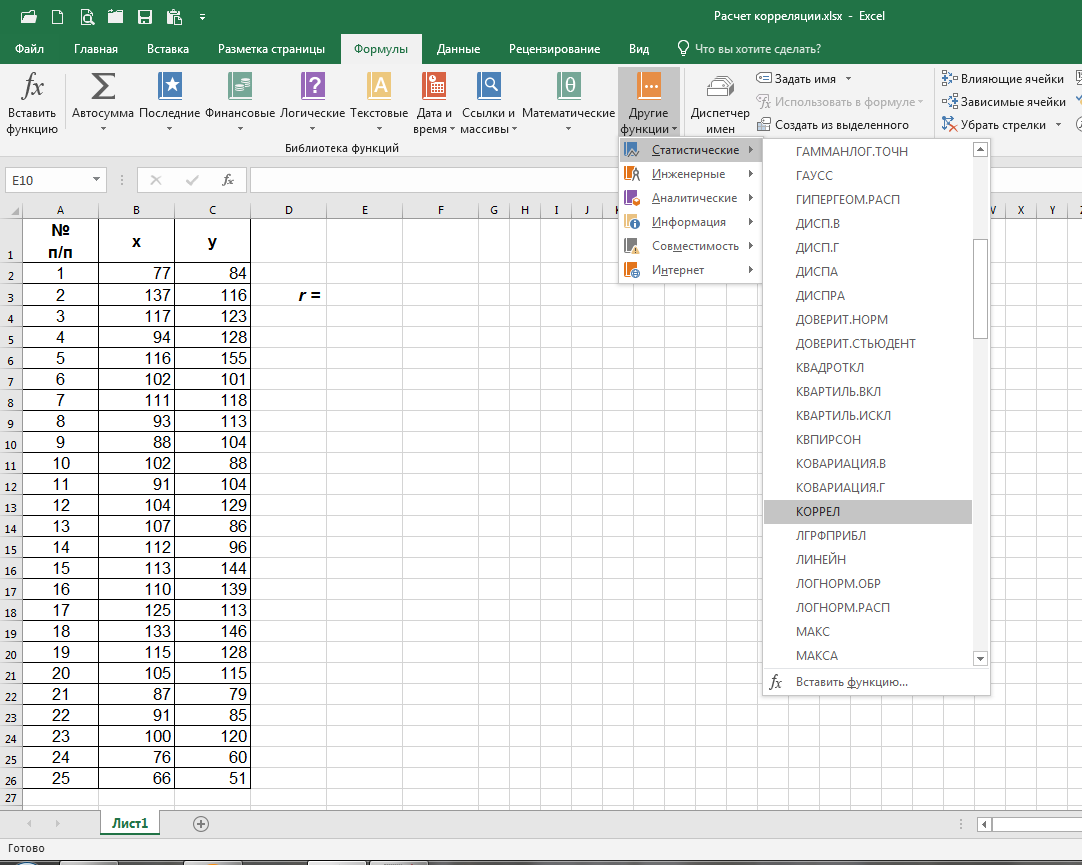
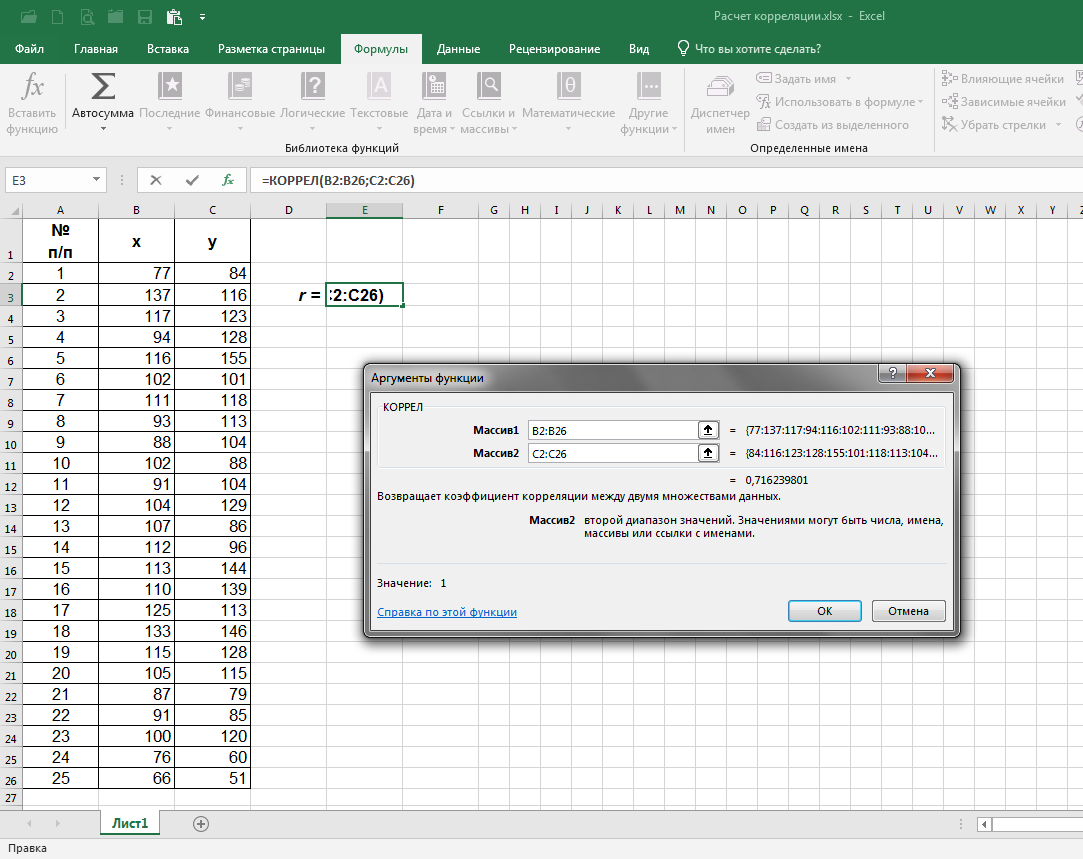
В программе Excel составляем таблицу и в любой удобной нам ячейке за пределами таблицы вводим формулу расчёта коэффициента корреляции (Формулы => Другие функции => Статистические => КОРРЕЛ):
При нажатии на «КОРРЕЛ» в открывающемся окне в качестве значений «Массив1» и «Массив2» через двоеточие ставим верхнюю и нижнюю ячейки соответствующих колонок х и y (в нашем случае – B2:B26 и C2:C26) и нажимаем на ОК:
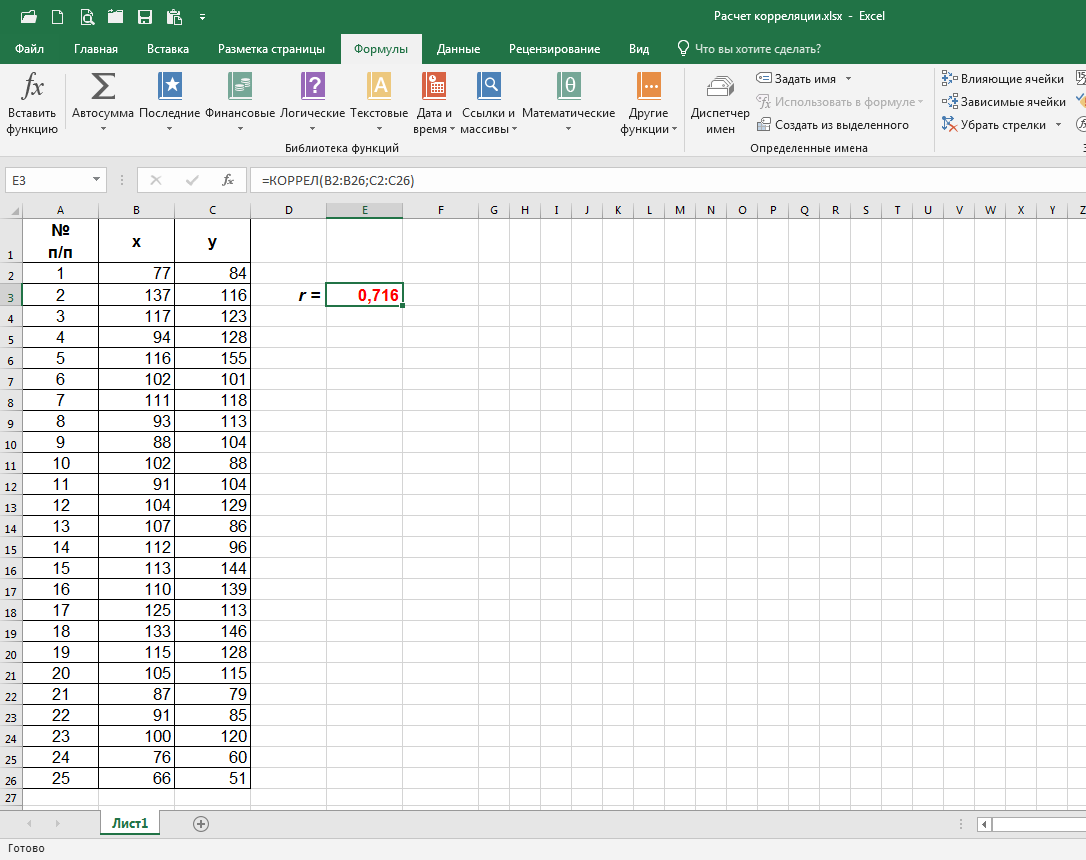
Итак, коэффициент корреляции рассчитан! Как и при расчётах выше, он равен 0,716. (Если необходимо, измените числовой формат в соответствующей ячейке, а иначе коэффициент может быть округлён до единицы.)
В принципе, коль скоро коэффициент корреляции нам уже известен, диаграмма рассеяния не очень-то и нужна. И всё же её иногда полезно построить, чтобы воочию увидеть, как соответствующие точки располагаются.
Шаг 2 – Построение диаграммы рассеяния
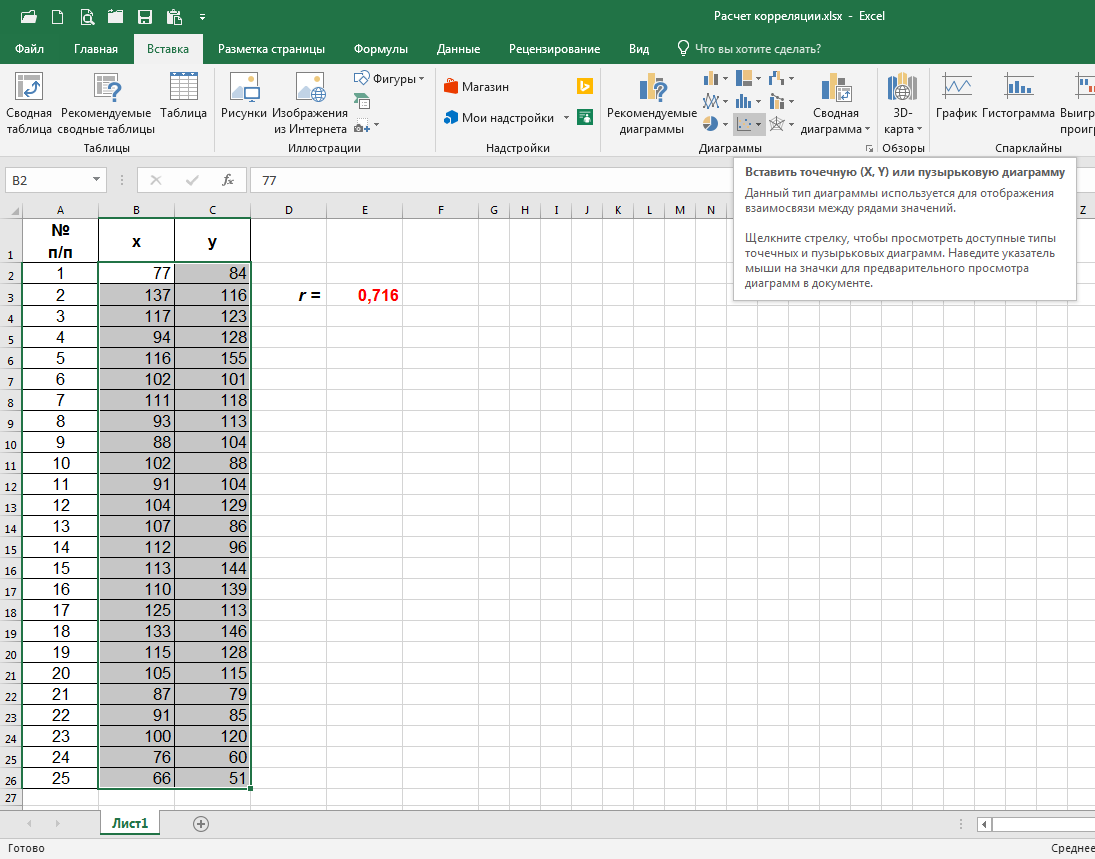
Чтобы построить диаграмму рассеяния, открываем вкладку «Вставка», выделяем мышкой ячейки от B2 до С26 в нашем случае (т.е. от верхней ячейки столбца x до нижней столбца y) и нажимаем на значок «Точечная» в разделе «Диаграммы»:
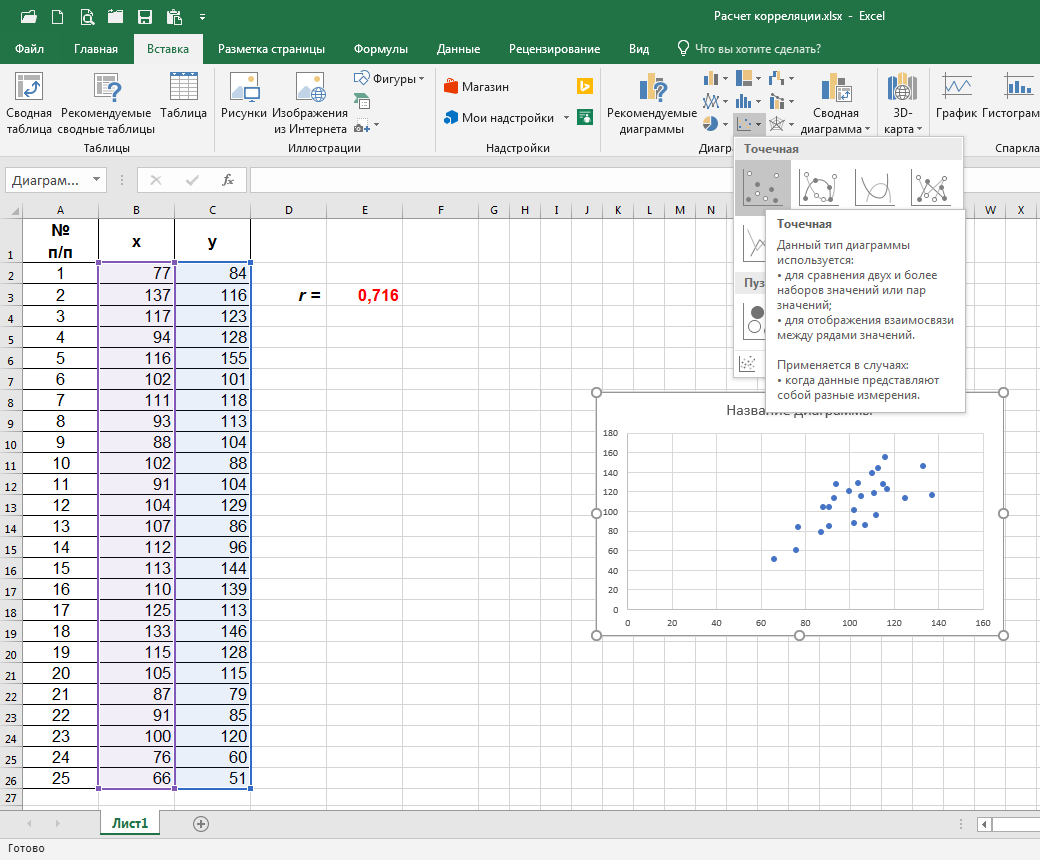
Далее, при нажатии на верхний левый значок в выпадающем окне, мы получаем необходимую нам диаграмму рассеяния:
Если необходимо, мышкой выравниваем диаграмму (меняем размеры её сторон), перемещаем в нужное нам место на листе и вставляем название диаграммы:
Итак, коэффициент корреляции определён, диаграмма рассеяния построена. Поставленная задача нами выполнена.
Что ещё важно знать
Следует учесть, что данный инструмент (диаграмма рассеяния и расчёт коэффициента корреляции) не является стопроцентной гарантией того, что две переменные, имеющие высокий коэффициент корреляции, действительно связаны между собой: существуют так называемые ложные корреляции, при которых расчётное значение коэффициента корреляции высоко, но при этом зависимости одного признака от другого нет. Причины возникновения ложных корреляций могут быть самыми разнообразными, например наличие какого-либо другого, скрытого от нас признака, который влияет одновременно на оба исследуемых нами признака. Так, цена продуктов питания и стоимость жилья могут показывать высокий коэффициент корреляции, но на самом деле эти величины связаны не между собой, а с инфляцией или с ростом стоимости производства. Подобные ситуации – ловушка для исследователей [2, с. 128].
Возможны и обратные ситуации: связь реально существует, но установить её данным инструментом не удалось. Причины этого опять-таки могут быть самыми разными – от недостаточного числа собранных данных до чрезмерно большой ошибки измерения [2, с. 128–129].
Но это не значит, что данным инструментом нельзя пользоваться! Наоборот, это достаточно простое, но эффективное средство статистического анализа. Необходимо всего лишь учитывать, что, во-первых, правильно диаграмму рассеяния и коэффициент корреляции могут оценить только те, кто хорошо знаком с исследуемым процессом; во-вторых, полученный таким образом коэффициент корреляции – это величина случайная и физической константой не является [2, с. 129].
Иными словами, применение данного инструмента требует известной доли осторожности, внимания к деталям и знания сути вопроса.
А что дальше?
Ещё одним важным моментом является то, что коэффициент корреляции позволяет оценить степень тесноты связи между результативным признаком (y) и воздействующим на него фактором (х), но не даёт ответа на вопрос: на сколько единиц изменится результативный признак при изменении фактора на одну единицу? [3, с. 108].
Ответ на этот вопрос можно получить при помощи другого инструмента – регрессионного анализа. Объяснение сути данного анализа выходит за рамки настоящей темы, но с ней можно самостоятельно ознакомиться по различным источникам, например по источнику [3, с. 108].
Вместе с тем один сугубо практический совет на этот счёт мы дадим.
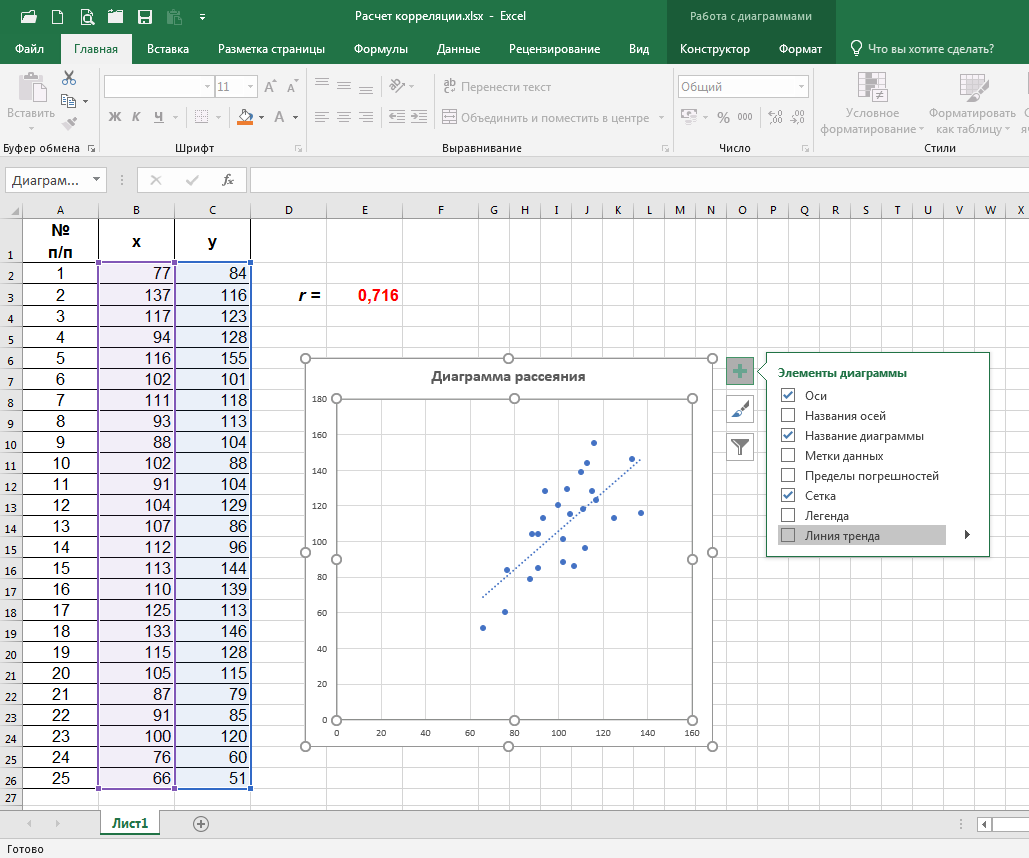
В любой диаграмме рассеяния, построенной в последних версиях программы Excel, можно мгновенно, путём нажатия мышкой на соответствующее поле, как показано на рисунке ниже, построить «линию тренда», т.е. ту самую воображаемую среднюю линию, о который мы говорили выше. Она и даст нам общее представление о характере и величине изменения результативного признака y при изменении воздействующего на него фактора х:
Описание представленного инструмента контроля качества мы постарались изложить в максимально простой и доступной форме – в расчёте на то, что его будут читать и, надеемся, применять в работе в том числе и далёкие от математики люди.
Источники:
- Васин С.Г. Управление качеством. Всеобщий подход : учебник для бакалавриата и магистратуры / С.Г. Васин. – М. : Издательство Юрайт, 2016.
- Гродзенский С.Я. Управление качеством : учебник. – Москва : Проспект, 2017.
- Маркетинг: теория и практика : учеб. пособие для бакалавров / под общ. ред. С.В. Карповой. – М. : Издательство Юрайт, 2016.
- Диаграмма разброса. / Сайт studfiles.net [Электронный ресурс]. Режим доступа: https://studfiles.net/preview/4499997 (дата обращения: 25.12.2018).
Если вы считаете, что при публикации настоящего материала нарушены ваши авторские права, напишите нам.
If you believe that the publication of this material infringes your copyright, please let us know.
17 авг. 2022 г.
читать 2 мин
Матрица диаграммы рассеяния — это матрица диаграмм рассеяния, которая позволяет понять попарные отношения между различными переменными в наборе данных.
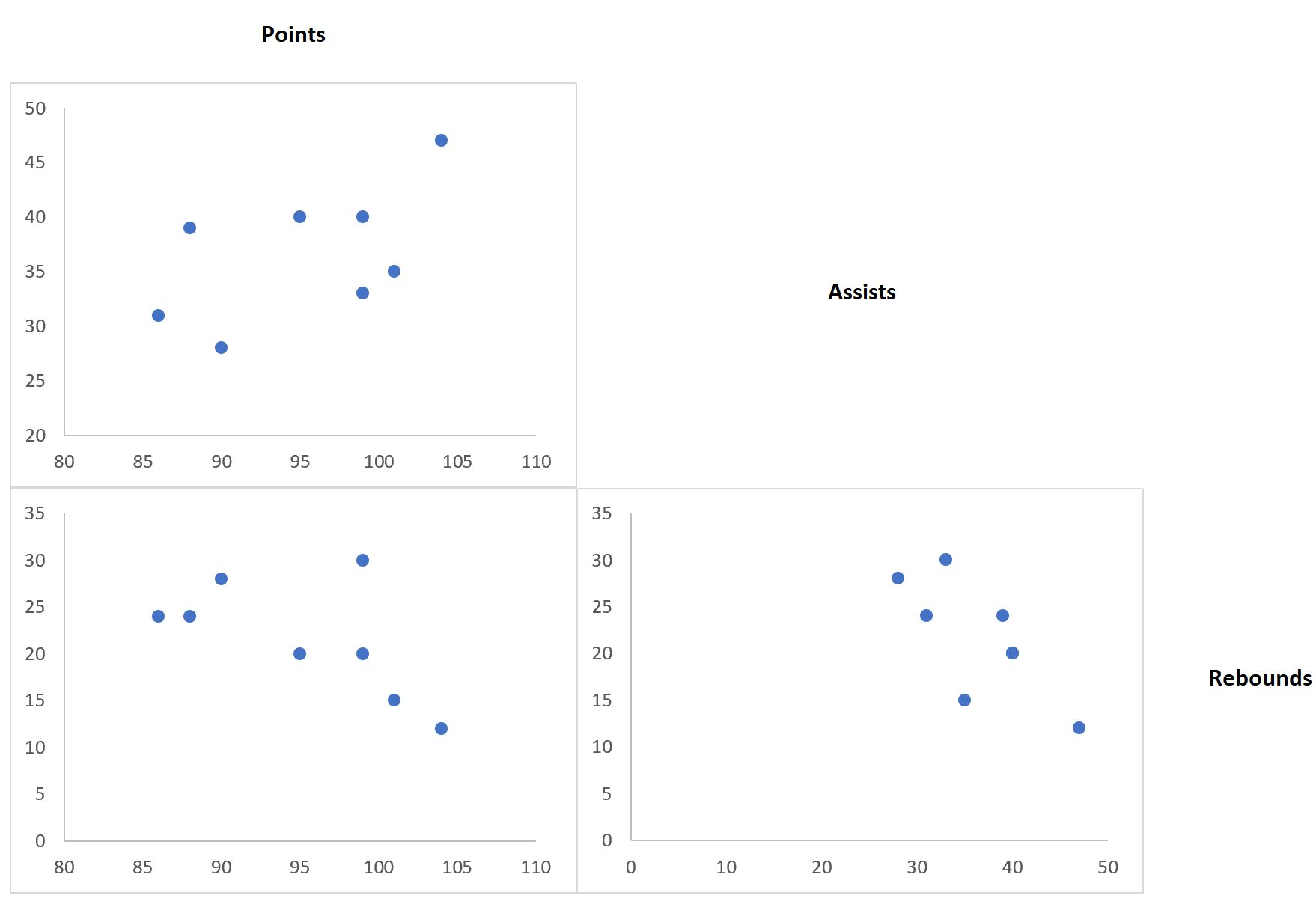
В этом руководстве объясняется, как создать следующую матрицу диаграммы рассеяния в Excel:
Давайте прыгать!
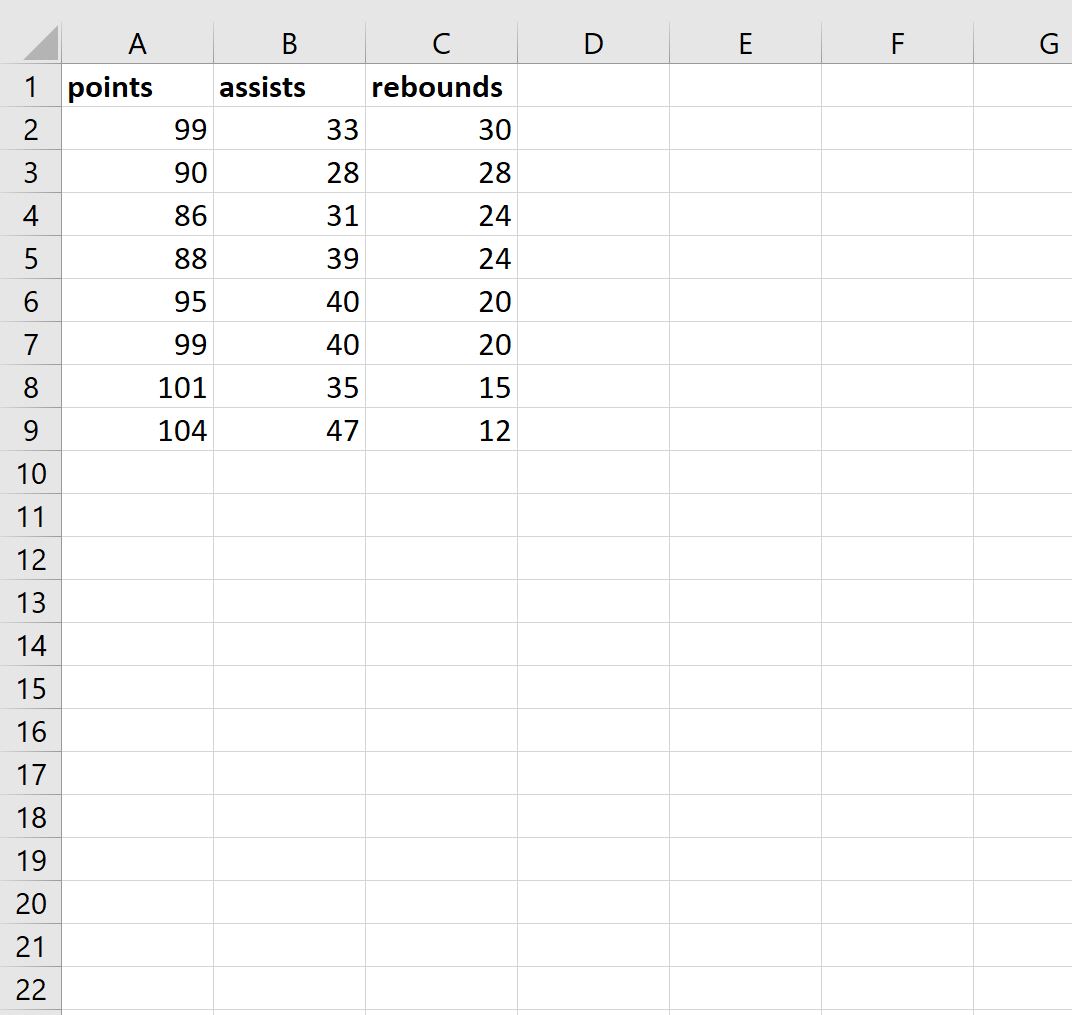
Шаг 1: введите данные
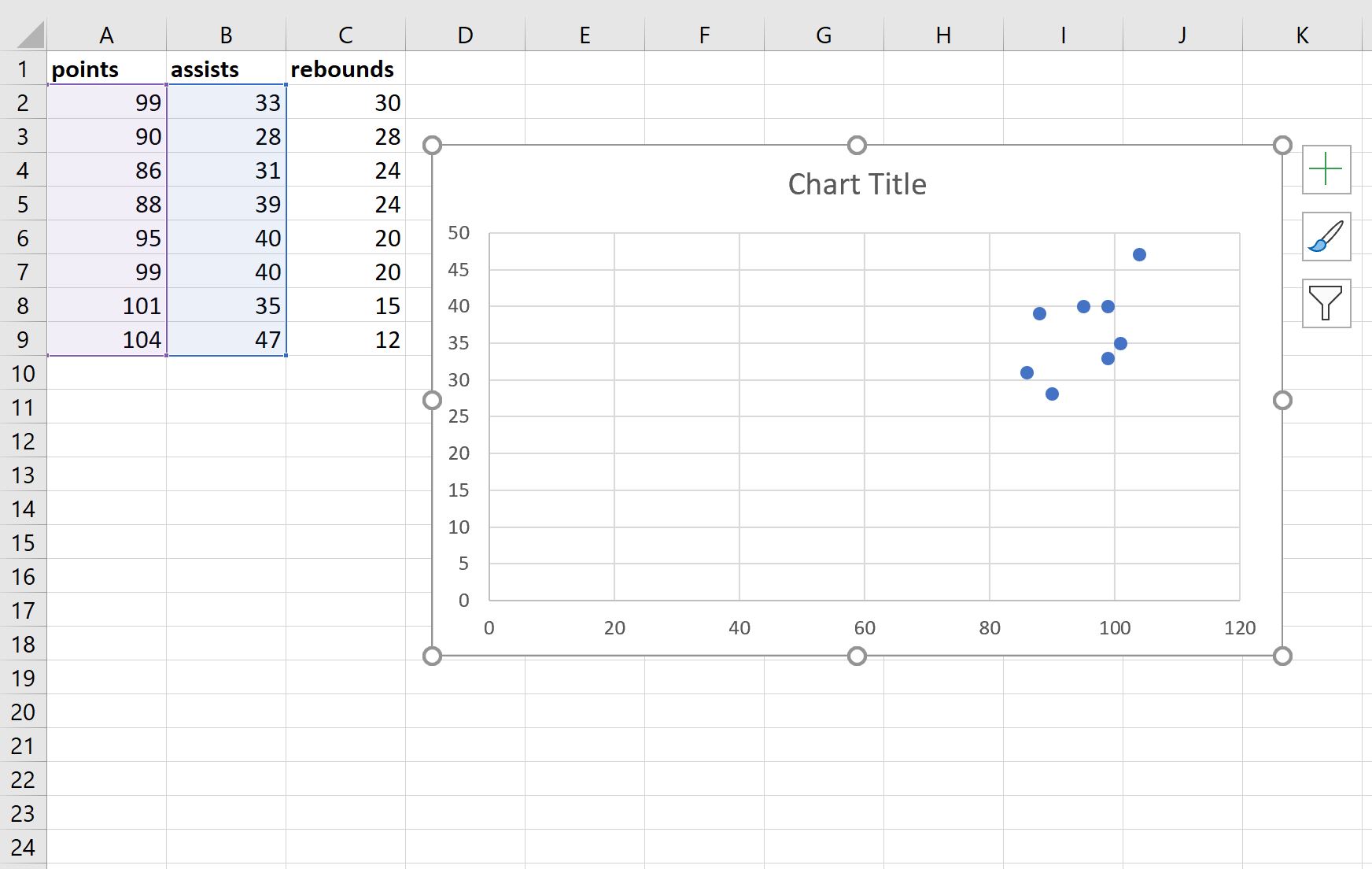
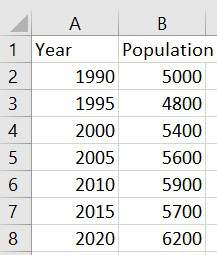
Во-первых, давайте введем следующие значения для набора данных, который содержит три переменные: очки, передачи и подборы.
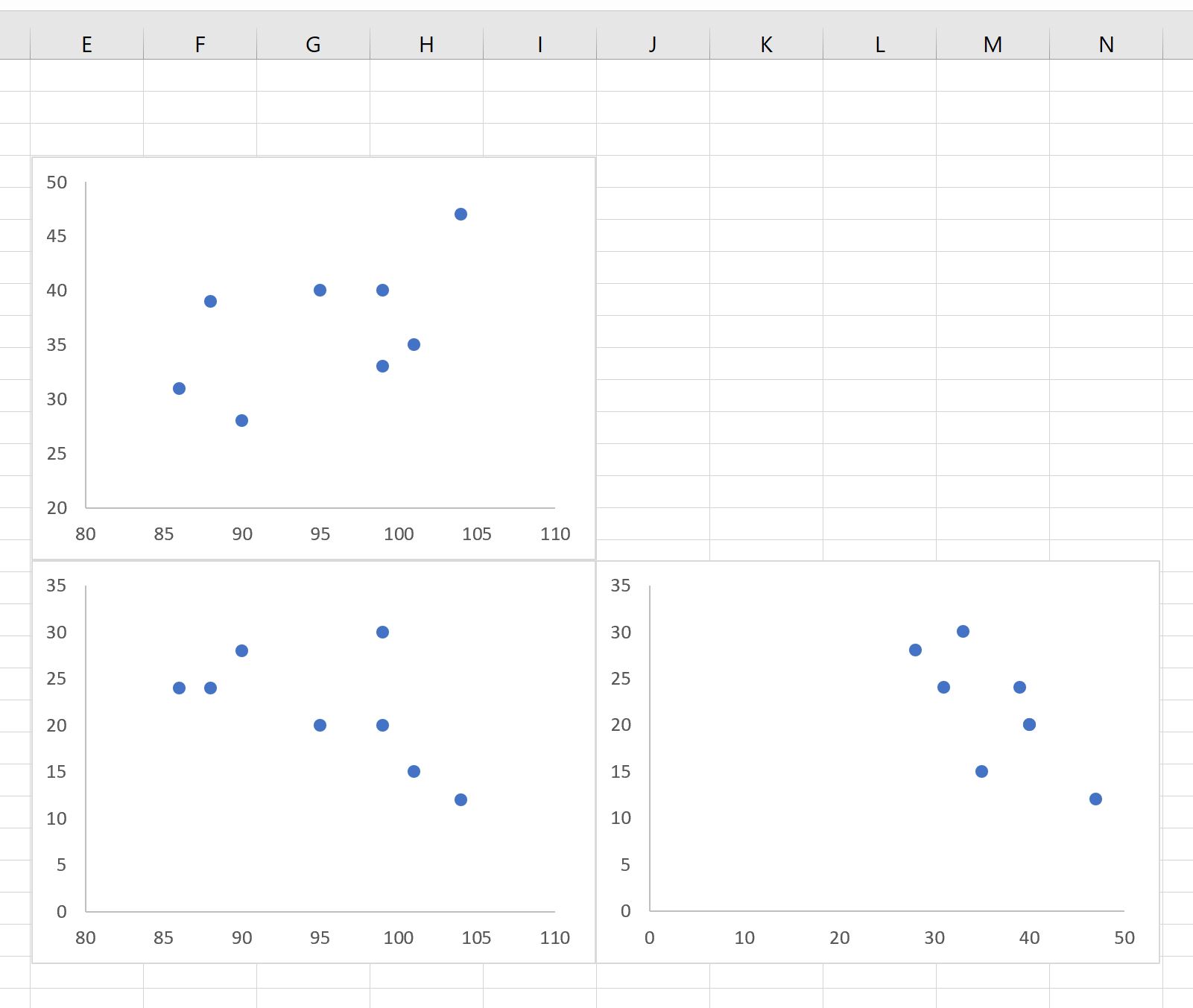
Шаг 2: Создайте диаграммы рассеяния
Затем выделим диапазон ячеек A2:B9 , затем щелкните вкладку « Вставка », затем нажмите кнопку « Разброс » в группе « Диаграммы ».
Автоматически будет создана следующая диаграмма рассеяния очков и передач:
Далее выполните следующие шаги:
- Нажмите на значения на оси X и измените минимальную ось, привязанную к 80.
- Щелкните ось Y и измените минимальное значение оси на 20.
- Щелкните заголовок диаграммы и удалите его.
- Нажмите на линии сетки на диаграмме и удалите их.
- Наконец, измените размер диаграммы, чтобы сделать ее меньше.
Конечный результат должен выглядеть примерно так:
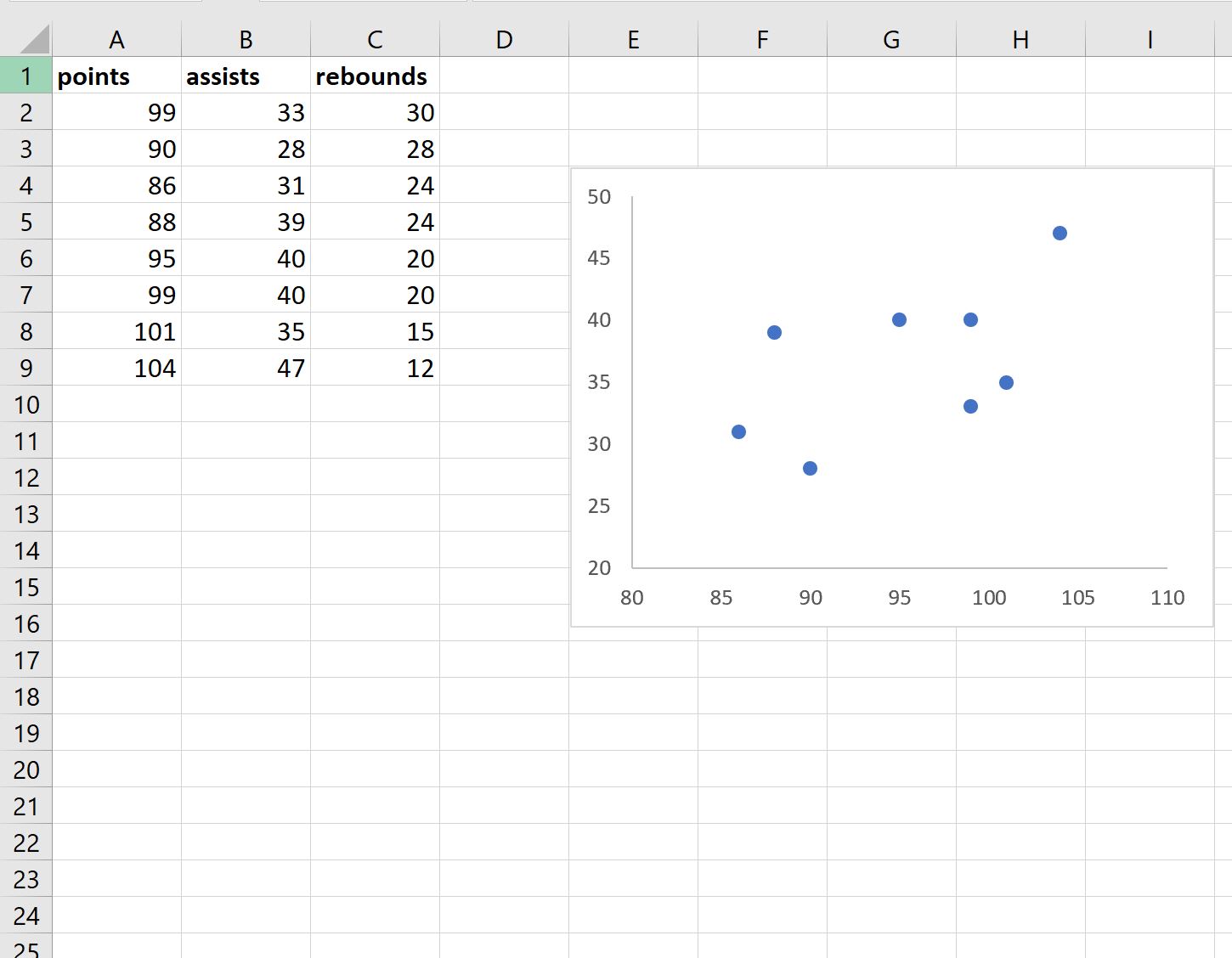
Затем повторите те же самые шаги для переменных очков и подборов и поместите диаграмму рассеяния под существующую диаграмму рассеяния:
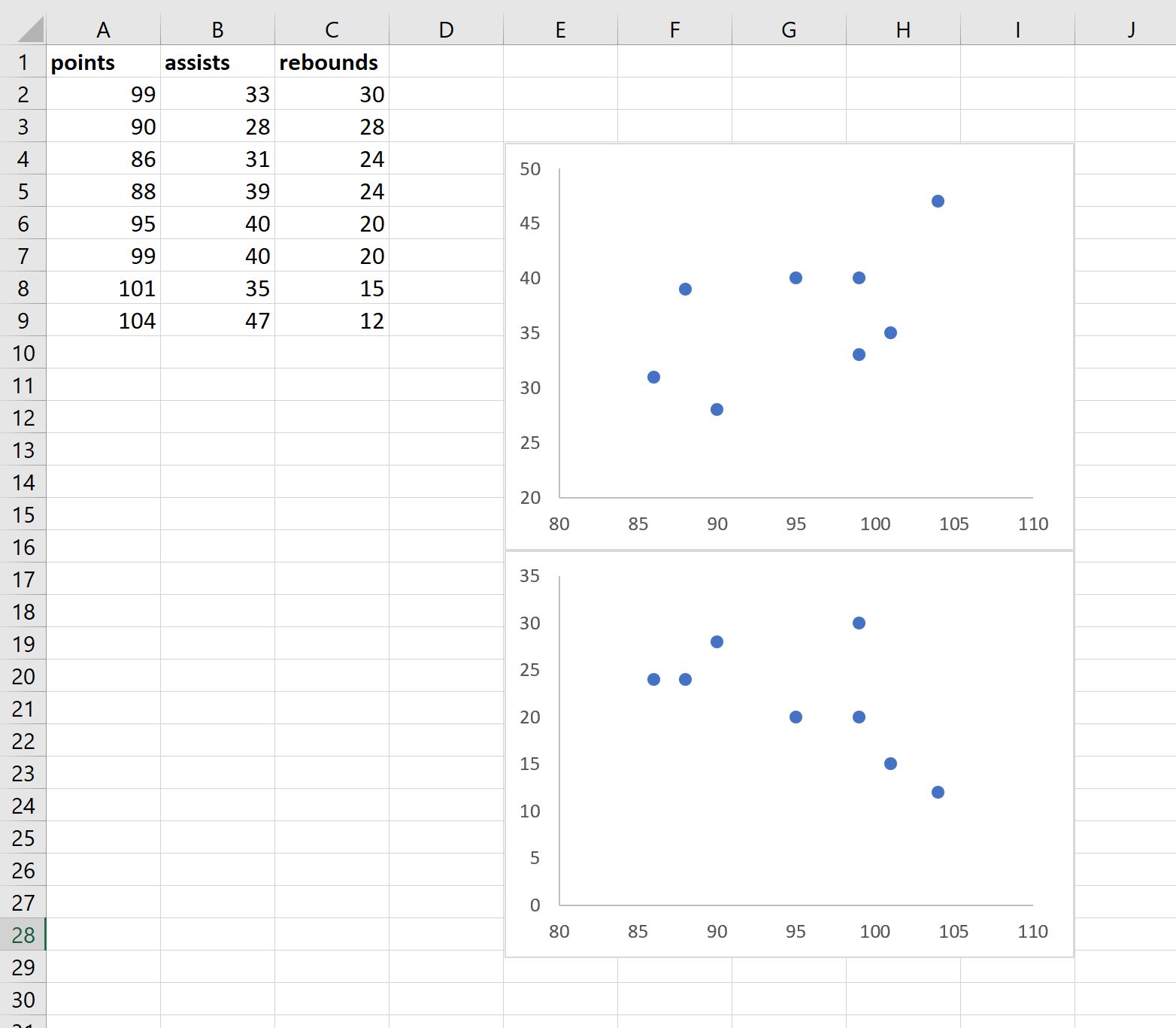
Наконец, повторите эти шаги для переменных передач и подборов и поместите диаграмму рассеяния в нижний правый угол:
Шаг 3: Пометьте диаграммы рассеяния
Наконец, введите имена переменных рядом с диаграммами рассеяния, чтобы было легко понять, какие диаграммы рассеяния представляют какие переменные:
Вот как интерпретировать сюжеты:
- Диаграмма рассеяния в верхнем левом углу представляет соотношение между очками и передачами.
- Диаграмма рассеяния в левом нижнем углу представляет соотношение между очками и подборами.
- Диаграмма рассеяния в правом нижнем углу представляет соотношение между передачами и подборами.
Примечание.Не стесняйтесь изменять цвет и размер точек на диаграммах рассеяния, чтобы они выглядели так, как вам нравится.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как создать диаграмму рассеяния с несколькими рядами в Excel
Как создать корреляционную матрицу в Excel
Как выполнить корреляционный тест в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
A scatter plot is a mathematical diagram made using the Cartesian coordinates which are used to display typically 2D-data sets. These are also known as scatterplot, scatter graph, scatter chart, scatter gram, or scatter diagram.
In this article we will look into how we can create scatter plot in Excel. To do so follow the below steps:
Step 1: Formatting data for Scatter Plot.
We have to make sure that there should be two variables for a set of data.
Step 2: Converting data into Scatter Plot.
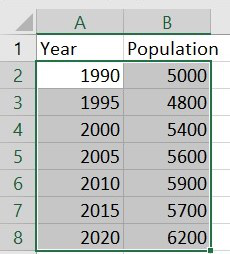
First, highlight the data which we want in the scatter plot.
Step 3: Then, click to the Insert tab on the Ribbon. In the Charts group, click Insert Scatter(X, Y) or Bubble Chart.
Step 4: In the resulting menu, click Scatter.
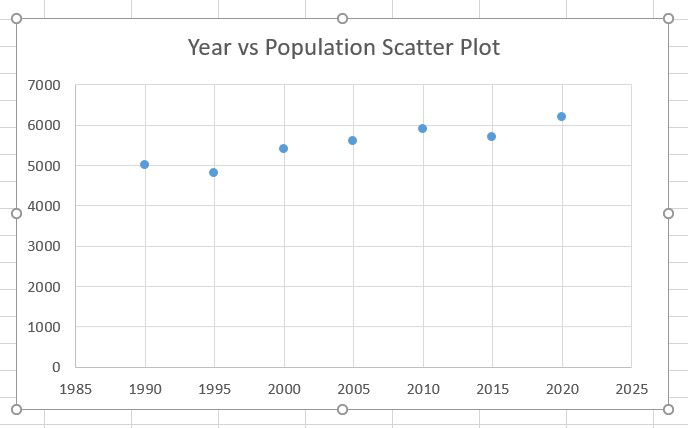
Once we have clicked that, our Scatter Plot will appear.
Step 5: Now, to add label on x-axis and y-axis we have to click to the Design tab on the Ribbon. In the Chart Layouts group, click Quick Layout.
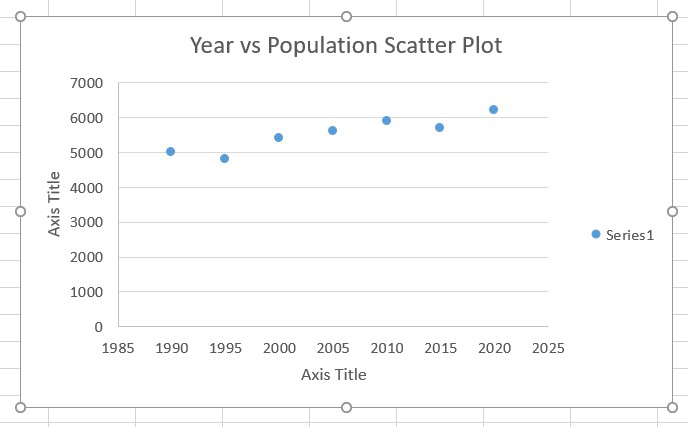
Step 6: In the resulting menu, click Layout 1.
Step 7: Then change the label name of X axis from Axis Title to Year and Y axis from Axis Title to Population.
Когда вам нужно визуализировать взаимосвязь между двумя наборами количественных данных, Microsoft Excel позволяет создать диаграмму рассеяния XY.
Для регрессионного анализа графики точечной диаграммы являются наиболее важным инструментом визуализации данных. Однако вам может быть интересно, как построить диаграмму рассеяния в Excel. Продолжайте читать эту основанную на данных статью, чтобы узнать, как это сделать.
В Microsoft Excel вы можете запутаться, является ли график XY диаграммой рассеяния или линейной диаграммой. Оба аналогичны, за исключением представления данных по горизонтальной оси (X).
Точечная диаграмма состоит из двух осей значений для визуализации количественных данных. Горизонтальная ось (X) представляет один набор числовых данных, а вертикальная ось (Y) указывает другой набор данных.
Но линейный график Excel визуализирует все данные категории по горизонтальной оси (X) и числовые значения по вертикальной оси (Y).
В Excel вы можете создать диаграмму рассеяния для визуализации и сравнения числовых значений, полученных в результате научного и статистического анализа. В следующих сценариях вместо линейного графика следует использовать точечную диаграмму:
- Чтобы проанализировать, есть ли корреляция между двумя наборами количественно измеримых значений. Внешний вид диаграммы X и Y будет очень похож на диагональное расположение.
- Чтобы изучить положительные или отрицательные тенденции в переменных.
- Чтобы увеличить горизонтальную ось (X).
- Для визуализации выбросов, кластеров, нелинейных трендов и линейных трендов в большом наборе данных.
- Для сравнения большого количества независимых от времени точек данных.
Как сделать точечную диаграмму в Excel
Вот шаги для создания диаграммы рассеяния с использованием шаблона графика XY в Microsoft Excel. Вы можете использовать следующие наборы данных в качестве примера для создания диаграммы рассеяния.
1. Для начала отформатируйте наборы данных так, чтобы независимые переменные помещались в левый столбец, а зависимые переменные – в правый столбец. В приведенных выше наборах данных рекламные бюджеты являются независимыми переменными, а проданные товары – зависимыми переменными.
2. Вам нужно выбрать в Microsoft Excel два столбца с числовыми данными. Не забудьте также включить заголовки столбцов. В данном случае это диапазон B1: C13 .
3. Теперь щелкните вкладку « Вставка » на ленте и выберите нужный шаблон точечной диаграммы в разделе « Графики ». В этом уроке это первая миниатюра, которая представляет собой классическую диаграмму рассеяния.
4. Классическая точечная диаграмма XY-графика появится в рабочем листе Microsoft Excel. Это наиболее простая форма диаграммы рассеяния. Вы также можете настроить четкую и профессиональную визуализацию корреляции.
Разная оптимизация для визуализации точечных диаграмм
Excel позволяет настраивать диаграмму рассеяния несколькими способами. Вот некоторые из возможных модификаций, которые вы можете внести:
Типы точечных диаграмм
Диаграмма рассеяния XY является наиболее распространенным типом графика рассеяния. Другие включают:
- Скаттер с плавными линиями и маркерами.
- Скаттер с плавными линиями.
- Скаттер с прямыми линиями и маркерами.
- Скаттер с прямыми линиями.
- Пузырьковый разброс XY.
- 3-D пузырьковый XY-разброс.
Настройка точечной диаграммы XY Graph
Создавая диаграмму рассеяния в Microsoft Excel, вы можете настроить практически каждый ее элемент. Вы можете изменять такие разделы, как заголовки осей, заголовки диаграмм, цвета диаграмм, легенды и даже скрывать линии сетки.
Если вы хотите уменьшить область построения, выполните следующие действия:
- Дважды щелкните горизонтальную (X) или вертикальную (Y) ось, чтобы открыть « Ось формата» .
- В меню « Параметры оси» установите минимальные и максимальные границы в соответствии с наборами данных.
- График точечной диаграммы изменится соответственно.
Если вы хотите удалить линии сетки, выполните следующие действия:
- Дважды щелкните любую из горизонтальных линий сетки в области построения графика XY.
- В меню « Формат основных линий сетки» на боковой панели выберите « Нет линии» .
- Теперь щелкните любую из оставшихся вертикальных линий сетки и выберите Нет линии .
- Линии сетки исчезнут с точечной диаграммы.
Microsoft Excel также предлагает профессиональные шаблоны точечной диаграммы. Вот как вы можете это проверить:
- Дважды щелкните пустую область диаграммы.
- На ленте найдите « Быстрый макет» в разделе « Макеты диаграмм ».
- Нажмите « Быстрый макет» , и вы увидите 11 предустановленных макетов для создания точечной диаграммы.
- Наведите указатель на каждую из них, чтобы узнать о функциях, и выберите ту, которая подходит для ваших наборов данных.
Добавьте профессиональный вид своему точечному графику, выполнив следующие действия:
- Щелкните любое пустое место диаграммы, чтобы открыть Инструменты диаграммы на ленте .
- На вкладке « Дизайн » вы увидите 12 стилей для диаграммы X и Y.
- Выберите любой, чтобы мгновенно превратить классический график точечной диаграммы в стильный.
Добавление меток к точкам данных Excel на точечной диаграмме
Вы можете пометить точки данных на диаграмме X и Y в Microsoft Excel, выполнив следующие действия:
- Щелкните любое пустое место на диаграмме, а затем выберите элементы диаграммы (выглядит как значок плюса).
- Затем выберите метки данных и щелкните черную стрелку, чтобы открыть дополнительные параметры .
- Теперь нажмите « Дополнительные параметры», чтобы открыть « Параметры метки» .
- Щелкните Выбрать диапазон, чтобы определить более короткий диапазон из наборов данных.
- Теперь для точек будут отображаться метки из столбца A2: A6 .
- Для четкой визуализации метки при необходимости перетащите метки.
Добавьте линию тренда и уравнение в точечный график
Вы можете добавить в точечную диаграмму линию наилучшего соответствия или линию тренда, чтобы визуализировать взаимосвязь между переменными.
- Чтобы добавить линию тренда , щелкните любое пустое место на диаграмме разброса.
- На ленте появится раздел « Макеты диаграмм» .
- Теперь нажмите « Добавить элемент диаграммы», чтобы открыть раскрывающееся меню.
- В этом меню нажмите « Линия тренда», а затем выберите стиль линии тренда, соответствующий наборам данных.
Чтобы визуализировать математическую связь между переменными данных, активируйте отображение уравнения на графике точечной диаграммы.
- Дважды щелкните линию тренда .
- Откроется боковая панель Format Trendline .
- На этой боковой панели нажмите Параметры линии тренда .
- Теперь установите флажок Отображать уравнение на диаграмме .
Диаграмма рассеяния и переменная корреляция
Диаграмма разброса диаграммы X и Y может визуализировать три типа корреляции между переменными в наборах данных для значимого представления данных. Эти корреляции следующие:
- Отрицательная корреляция: при отрицательной корреляции значение одной переменной увеличивается, а значение другой уменьшается.
- Положительная корреляция: Ярким примером положительной корреляции является увеличение значений переменных по вертикальной (Y) оси, увеличение и для переменных по горизонтальной (X) оси.
- Нет корреляции: корреляции не будет, если точки разбросаны по всей области диаграммы разброса.
Произведите впечатление на аудиторию, создав точечную диаграмму в Excel
Microsoft Excel – это надежное приложение, которое позволяет создавать диаграмму рассеяния следующего поколения. Узнав, как создать диаграмму рассеяния в Excel, вы также можете создавать в программе интеллектуальные диаграммы, которые обновляются автоматически.
history 25 ноября 2018 г.
- Группы статей
- Статистический анализ
- Случайные ЧИСЛА
Построим диаграмму рассеяния для различных видов взаимосвязей двух переменных. Сгенерируем различные варианты трендов: линейный, квадратичный и затухающий синусоидальный.
Диаграмма рассеяния ( scatter plot ) используется для отображения возможной взаимосвязи между двумя переменными. Диаграмма рассеяния незаменима при проведении корреляционного и регрессионного анализа.
Возьмем 2 переменные Х и Y и, соответственно, выборку состоящую из нескольких пар значений (Х i ; Y i ). Для наглядности зададим различные типы зависимости между переменными: линейную, квадратичную и затухающую синусоидальную. Для этого сгенерируем соответствующие тренды и настроим случайный разброс переменной Y (по нормальному закону ).
Сначала рассмотрим линейный тренд Y = aX + b (см. Файл примера, лист Линейный ). Параметры тренда (прямой линии) a и b зададим в отдельной табличке, там же зададим параметры отвечающие за величину дисперсии переменной Y.
Величину постоянного разброса (отвечающую за гомоскедастичность модели) будем задавать в % от среднего значения Y. Иногда, дисперсия переменной Y не постоянна (имеется неоднородность наблюдений — гетероскедастичность ). Поэтому, при построении формул учтем и такую возможность.
Для построения диаграммы рассеяния в файле примера использована диаграмма График , т.к. шаг по Х у нас задан постоянным. В случае реальных данных (переменная Х является случайной величиной, а не жестко заданной, как в нашем примере) используйте диаграмму типа Точечная. В файле примера реализовано оба варианта.
Примечание : Подробнее о построении диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Отображение информации о 3-х переменных на двухмерной диаграмме
Предположим, что у нас имеются результаты измерения производительности некого непрерывного производственного процесса. Измерения проводились при различных рабочих температурах протекания процесса и в двух режимах.
Нам требуется построить двумерную диаграмму рассеяния (на плоскости), хотя у нас имеется 3 переменных: производительность, температура и режим .
Обратим внимание, что третья переменная Режим является категориальной (принимает только значения из ограниченного набора значений). В нашем случае переменная Режим принимает 2 значения: Режим №1 и Режим №2 (значения 1 и 2 присвоены номинально).
Пары значений ( производительность; температура ), относящиеся к Режиму №1 будем на диаграмме рассеяния выводить красным цветом, а относящиеся к Режиму №2 будем выводить синим ( файл примера лист 3-переменных ).
Такой же подход можно использовать для дискретных переменных , когда они принимают небольшое количество значений: 2-5.
Категоризованные диаграммы
Если третья переменная – непрерывная величина, то для отображения данных можно использовать так называемые категоризованные диаграммы (coplot = conditioning plot).
Теперь вместо категориальной переменной Режим у нас имеется непрерывная переменная Давление , которая принимает значения от 10 до 20. Предположим, что значение переменной Давление = 15, является неким пороговым и протекание процесса значительно отличается, если оно протекает при давлении от 10 до 15 и от 15 до 20. Используя этот факт строят 2 диаграммы:
- Пары значений ( производительность; температура ) при давлении от 10 до 15:
- Пары значений ( производительность; температура ) при давлении от 15 до 20.
Если пороговых значений 2, то понадобится 3 диаграммы и т.д. Эти диаграммы строятся аналогично диаграммам из предыдущего раздела.
Матрица диаграмм рассеивания
Для множественной регрессии, когда имеется 3 или более переменных, часто строят Матрицу диаграмм рассеивания (Matrix Scatter Plot, Scatter Plot Matrix — SPM).
Если имеется 3 переменных (x 1 , x 2 , y), то строятся 3 обычные диаграммы рассеяния отображающие парные взаимосвязи переменных: (x 1 , x 2 ); (x 1 , y); (x 2 , y).
Примечание : Чтобы найти количество диаграмм рассеяния в матрице, необходимо вычислить число сочетаний из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ЧИСЛКОМБ(4;2) =6.
Иногда строят не только диаграмму (x 1 , x 2 ), но и (x 2 , x 1 ). В этом случае матрица будет содержать в 2 раза больше диаграмм рассеяния (см. файл примера лист Matrix ).
Примечание : Чтобы найти количество диаграмм рассеяния в такой (полной) матрице, необходимо вычислить число перестановок из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ПЕРЕСТ(4;2) =12.
ПОСТРОЕНИЕ ДИАГРАММЫ РАЗБРОСА
В ПРОГРАММЕ EXCEL
Цель работы: ознакомиться с методикой оценки связей между двумя и более показателями и построения диаграммы разброса в программе Excel.
Задание:1. Определить вид корреляционной связи между двумя переменными.
2. Построить диаграмму разброса в программе Excel.
Основные сведения
Диаграмма разброса (рассеяния) показывает взаимосвязь между двумя видами связанных данных и подтверждает их зависимость. Такими двумя видами данных могут быть характеристика качества и фактор, влияющий на нее, две разные характеристики качества одной продукции, два фактора, влияющих на одну характеристику качества, и т. д.
Для построения диаграммы рассеяния требуется не менее 30 пар данных (x, y).
Этапы построения диаграммы разброса:
1. Собрать парные данные (x, y), между которыми необходимо исследовать зависимость.
2. Найти минимальное и максимальное значения для x и y. Выбрать шкалу для горизонтальной и вертикальной осей так, чтобы длины рабочих частей осей x и y были приблизительно равны.
3. На диаграмму наносят точки (x, y), название диаграммы, интервал времени, число пар данных, названия осей, ФИО, должность исполнителя, и т. д.
Точки, которые далеко отстоят от основной группы распределения точек, является выбросами, и их исключают.
Возможны различные варианты скоплений точек. Для установления силы связи необходимо вычислить коэффициент корреляции r по формуле:
где n – число пар данных;
xi, yi — собранные статистические данные;
, — средние арифметические значения x и y;
r – коэффициент корреляции (множественный R ).
Коэффициент корреляции r используют только при линейной связи между величинами. Значение r находится в пределах от -1 до +1. Если r по модулю в диапазоне от 0,7 до 1, то проявляется сильная связь между рядами данных. Если коэффициент корреляции по модулю меньше 0,7, но больше 0,5 – говорят о связи средней силы; меньше 0,5 – говорят о слабой связи х и у. Если r, близко к нулю, корреляция слабая, а при нуле — отсутствует.
Можно оценить вероятность коэффициента корреляции mr. Для этого вычисляют его среднюю ошибку по формуле
При r/mr > 3 коэффициент корреляции считается достоверным, то есть связь доказана. При r/mr
В пакете Анализ данных инструмент Корреляция используется для количественной оценки взаимосвязи между двумя диапазонами данных, представленных в безразмерном виде. Коэффициент корреляции выборки представляет собой ковариацию двух наборов данных, деленную на произведение их стандартных отклонений.
Таблица 3.1. Экспериментальные данные
| № | ||||||||||
| X | 0,20 | 0,19 | 0,28 | 0,26 | 0,23 | 0,21 | 0,24 | 0,26 | 0,28 | 0,25 |
| Y | ||||||||||
| № | ||||||||||
| X | 0.25 | 0.22 | 0.18 | 0.26 | 0.17 | 0.30 | 0.19 | 0.25 | 0.29 | 0.27 |
| Y | ||||||||||
| № | ||||||||||
| X | 0,20 | 0,19 | 0,29 | 0,31 | 0,24 | 0,22 | 0,27 | 0,23 | 0,25 | 0,17 |
| Y |
Алгоритм действий следующий:
Формируют таблицу исходных данных в программе Excel. В ячейки А1 внести Х и В1- У.
Далее в ячейки А2:А31 располагаем значения Х. В ячейки В2:В31- значения У.
Открыть пакет Данные / Анализ / Анализ данных/ Корреляция / ОК.
Входной интервал: $А$1: $В$31 (или выделить диапазон данных ХУ).
Поставить галочку: метка в первой строке.
Выходной интервал: $D$1.
Нажать кнопкуОК.
Excel представит результаты решения в виде (табл. 3.2).
Таблица 3.2. Данные связи двух переменных Х и У (данные Корреляции)
| Столбец Х | Столбец У |
| Столбец Х | |
| Столбец У | 0,683269863 |
Полученные результаты свидетельствуют о сильной связи между данными х и у , т.к. коэффициент корреляции r ≈0,7.
Чтобы построить диаграмму разброса и получить его статистические характеристики воспользуемся инструментом Регрессия.Этот инструмент используется для анализа воздействия на зависимую переменную у одного или несколько независимых переменных х.
Алгоритм действий следующий:
Открыть пакет Данные / Анализ / Анализ данных / Регрессия / ОК.
Входной интервал У: $А$1: $А$31 (или выделить диапазон данных У).
Входной интервал Х: $В$1: $В$31 (или выделить диапазон данных Х).
Поставить галочки: константа-ноль, метка, уровень надежности (95%), график подбора, график нормальной вероятности.
Выходной интервал: $Е$6.Нажать кнопкуОК.
Excel представит результаты решения в виде (табл. 3.3 и 3.4, рис. 3.1 и 3.2).
Таблица 3.3. Данные регрессионной статистики
связи толщины и прочности ткани
| Регрессионная статистика | |
| Множественный R (коэффициент корреляции) | 0,683269863 |
| R-квадрат | 0,466857706 |
| Нормированный R-квадрат | 0,44781691 |
| Стандартная ошибка | 1,972317081 |
| Наблюдения |
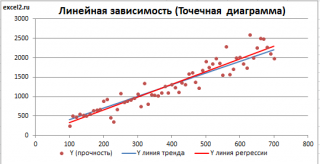
Рис. 3.1. Диаграмма разброса парных данных двух переменных Х и У
Таблица 3.4. Статистические данные дисперсионного анализа
связи толщины и прочности ткани
| Дисперсионный анализ | ||||
| df | SS — суммы квадратов разностей | MS – оценки дисперсий | F –Расчетное значение критерия Фишера | Значимость F (табличное) |
| Регрес-сия | 95,37902934 | 95,37902934 | 24,51881217 | 3,16536 α=E=0,5 |
| Остаток | 108,9209707 | 3,890034667 | ||
| Итого | 204,3 |
Рис. 3.2. График нормального распределения взаимосвязанных парных данных
Учитывая, что расчетное значение коэффициента Фишера больше чем табличное (табл. 3.4), то можно с 95 % уверенность утверждать, что прочность ткани зависит от её толщины, а коэффициенты корреляции значимы.
График нормального распределения (рис. 3.2) позволяет оценить сорт и качество ткани. График свидетельствует, что более 20% проб имеют стабильные значения, многократно повторяющиеся, что свидетельствует о высоком качестве ткани.
Персентиль – рассчитывается для каждого значения У, как сумма предшествующего вычисленного значения персентиля и h=(100% / наблюдения).
Начальное и конечное значение персентиля рассчитывается как (0+ h/2) и (100- h/2), соответственно.
Задание для самостоятельной работы 3.1.
В таблице 3.5 представлены данные испытания пальтовой ткани и содержания аппрета. Х — содержание аппрета, %, а У — воздухопроницаемость, дм 3 /м 2 ·с. Рассмотреть корреляционную взаимозависимость между процентным содержанием аппрета- x и воздухопроницаемостью ткани — y. Построить диаграмму разброса данных. Сделать выводы по результатам анализа о достоверности оценки показателей дисперсии испытываемых материалов и качестве ткани.
Перенести данные в документ Word, оформить результаты как лабораторную работу №3, задание 3.1.
Таблица 3.5. Данные измерения количества аппрета и воздухопроницаемости пальтовой ткани
| № | ||||||||||||
| X | 3,9 | 6,5 | 3,7 | 4,5 | 5,0 | 5,8 | 3,3 | 6,2 | 3,6 | 3,9 | 5,1 | 6,4 |
| Y | ||||||||||||
| № | ||||||||||||
| X | 4,2 | 4,9 | 6,0 | 5,4 | 4,4 | 3,8 | 6,7 | 4,6 | 4,3 | 6,3 | 5,2 | 6,4 |
| Y | ||||||||||||
| № | ||||||||||||
| X | 6,2 | 5,5 | 2,7 | 2,8 | 5,4 | 5,8 | 6,6 | 5,3 | 4,2 | 4,3 | 4,0 | 5,4 |
| Y |
Задание для самостоятельной работы 3.2.
В таблице 3.6 представлены данные испытания плащевой хлопколавсановой ткани: Х — содержание лавсановых волокон, %; У – разрывная нагрузка, даН. Рассмотреть корреляционную взаимозависимость между процентным содержанием лавсановых волокон — x и прочностью ткани — y. Построить диаграмму разброса данных. Сделать выводы по результатам анализа о достоверности оценки показателей дисперсии испытываемых материалов и качестве продукции.
Таблица 3.6. Экспериментальные данные
Перенести данные в документ Word, оформить результаты как лабораторную работу №3, задание 3.2.
Лабораторная работа №4
КОНТРОЛЬНЫЕ КАРТЫ (КАРТЫ ШУХАРТА) ПО КОЛИЧЕСТВЕННЫМ ПРИЗНАКАМ В ПРОГРАММЕ EXCEL
Цель работы: ознакомиться с методикой построения контрольных карт по количественным признакам с помощью программы Excel.
Задание:1. Построить контрольные карты по количественным признакам в программе Excel.
2. Определить причины появления дефектов и разработать рекомендации по устранению брака.
Основные сведения
Контрольные карты представляют собой разновидности графиков, но отличаются тем, что имеют контрольные границы (границы регулирования). Если все значения (точки) окажутся внутри контрольных границ (рис. 4.1 а), то процесс рассматривается как управляемый (стабильный).
Рис. 4.1. Контрольные карты и контрольные границы
Если на графике есть точки, выходящие за пределы контрольных границ (рис. 4.1 б), то это свидетельствует о наличии погрешности и неуправляемости процесса. Различают контрольные карты двух типов: — для непрерывных и дискретных значений или по качественным и количественным признакам.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Регрессионный анализ в Microsoft Excel
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
-
Перемещаемся во вкладку «Файл».
Переходим в раздел «Параметры».
В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк . В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Помимо этой статьи, на сайте еще 12765 полезных инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Простая линейная регрессия в EXCEL
history 26 января 2019 г.
-
Группы статей
- Статистический анализ
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В MS EXCEL имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Примечание : Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место множественная регрессия .
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Примечание : Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части — оценке неизвестных параметров линейной модели .
Немного теории и основные понятия
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем прочность этого волокна (Y) зависит только от рабочей температуры процесса в реакторе (Х), которая задается оператором.
Построим диаграмму рассеяния (см. файл примера лист Линейный ), созданию которой посвящена отдельная статья . Вообще, построение диаграммы рассеяния для целей регрессионного анализа де-факто является стандартом.
СОВЕТ : Подробнее о построении различных типов диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Приведенная выше диаграмма рассеяния свидетельствует о возможной линейной взаимосвязи между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание : Наличие даже такой очевидной линейной взаимосвязи не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие причинной взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Примечание : Как известно, уравнение прямой линии имеет вид Y = m * X + k , где коэффициент m отвечает за наклон линии ( slope ), k – за сдвиг линии по вертикали ( intercept ), k равно значению Y при Х=0.
Предположим, что мы можем зафиксировать переменную Х ( рабочую температуру процесса ) при некотором значении Х i и произвести несколько наблюдений переменной Y ( прочность нити ). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого значения . При увеличении количества измерений, среднее этих измерений, будет стремиться к математическому ожиданию случайной величины Y (при Х i ) равному μy(i)=Е(Y i ).
Подобные рассуждения можно привести для любого значения Хi.
Чтобы двинуться дальше, воспользуемся материалом из раздела Проверка статистических гипотез . В статье о проверке гипотезы о среднем значении генеральной совокупности в качестве нулевой гипотезы предполагалось равенство неизвестного значения μ заданному μ0.
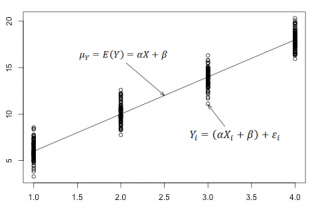
В нашем случае простой линейной регрессии в качестве нулевой гипотезы предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ y(i) =α* Х i +β. Уравнение μ y(i) =α* Х i +β можно переписать в обобщенном виде (для всех Х и μ y ) как μ y =α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Данная линия называется регрессионной линией генеральной совокупности (population regression line), параметры которой ( наклон a и сдвиг β ) нам не известны (по аналогии с гипотезой о среднем значении генеральной совокупности , где нам было неизвестно истинное значение μ).
Теперь сделаем переход от нашего предположения, что μy=a* Х + β , к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.
Уравнение Y=a*X+b+ε называют линейной регрессионной моделью . Часто Х еще называют независимой переменной (еще предиктором и регрессором , английский термин predictor , regressor ), а Y – зависимой (или объясняемой , response variable ). Так как регрессор у нас один, то такая модель называется простой линейной регрессионной моделью ( simple linear regression model ). α часто называют коэффициентом регрессии.
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Чтобы модель линейной регрессии Yi=a*Xi+β+ε i была адекватной — требуется:
- Ошибки ε i должны быть независимыми переменными;
- При каждом значении Xi ошибки ε i должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε i ]=0);
- При каждом значении Xi ошибки ε i должны иметь равные дисперсии (обозначим ее σ 2 ).
Примечание : Последнее условие называется гомоскедастичность — стабильность, гомогенность дисперсии случайной ошибки e. Т.е. дисперсия ошибки σ 2 не должна зависеть от значения Xi.
Используя предположение о равенстве математического ожидания Е[ε i ]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε i ]= Е[a*Xi+β]+ Е[ε i ]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Дисперсия случайной переменной Y равна дисперсии ошибки ε, т.е. VAR(Y)= VAR(ε)=σ 2 . Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε i ).
Задачи регрессионного анализа
Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует регрессионная линия генеральной совокупности , т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений .
На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно a и b . Также часто используются обозначения â и b̂.
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Первая задача регрессионного анализа – оценка неизвестных параметров ( estimation of the unknown parameters ). Подробнее см. раздел Оценки неизвестных параметров модели .
Вторая задача регрессионного анализа – Проверка адекватности модели ( model adequacy checking ).
Примечание : Оценки параметров модели обычно вычисляются методом наименьших квадратов (МНК), которому посвящена отдельная статья .
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры простой линейной регрессионной модели Y=a*X+β+ε оценим с помощью метода наименьших квадратов (в статье про МНК подробно описано этот метод ).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Таким образом, мы получим уравнение прямой линии Y= a *X+ b , которая наилучшим образом аппроксимирует имеющиеся данные.
Примечание : В статье про метод наименьших квадратов рассмотрены случаи аппроксимации линейной и квадратичной функцией , а также степенной , логарифмической и экспоненциальной функцией .
Оценку параметров в MS EXCEL можно выполнить различными способами:
Сначала рассмотрим функции НАКЛОН() , ОТРЕЗОК() и ЛИНЕЙН() .
Пусть значения Х и Y находятся соответственно в диапазонах C 23: C 83 и B 23: B 83 (см. файл примера внизу статьи).
Примечание : Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью Генерация данных для линейной регрессии в MS EXCEL ).
В MS EXCEL наклон прямой линии а ( оценку коэффициента регрессии ), можно найти по методу МНК с помощью функции НАКЛОН() , а сдвиг b ( оценку постоянного члена или константы регрессии ), с помощью функции ОТРЕЗОК() . В английской версии это функции SLOPE и INTERCEPT соответственно.
Аналогичный результат можно получить с помощью функции ЛИНЕЙН() , английская версия LINEST (см. статью об этой функции ).
Формула =ЛИНЕЙН(C23:C83;B23:B83) вернет наклон а . А формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) — сдвиг b . Здесь требуются пояснения.
Функция ЛИНЕЙН() имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Если 4-й аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН() возвращает только оценки параметров модели: a и b .
Примечание : Остальные значения, возвращаемые функцией ЛИНЕЙН() , нам потребуются при вычислении стандартных ошибок и для проверки значимости регрессии . В этом случае аргумент статистика должен иметь значение ИСТИНА.
Чтобы вывести сразу обе оценки:
- в одной строке необходимо выделить 2 ячейки,
- ввести формулу в Строке формул
- нажать CTRL+SHIFT+ENTER (см. статью про формулы массива ).
Если в Строке формул выделить формулу = ЛИНЕЙН(C23:C83;B23:B83) и нажать клавишу F9 , то мы увидим что-то типа <3,01279389265416;154,240057900613>. Это как раз значения a и b . Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».
Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу = ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83)) . При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция ТРАНСП() транспонировала строку в столбец ).
Чтобы разобраться в этом подробнее необходимо ознакомиться с формулами массива .
Чтобы не связываться с вводом формул массива , можно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1) или просто ЛИНЕЙН(C23:C83;B23:B83) вернет параметр, отвечающий за наклон линии, т.е. а . Формула =ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) вернет параметр b .
Оценка неизвестных параметров линейной модели (через статистики выборок)
Наклон линии, т.е. коэффициент а , можно также вычислить через коэффициент корреляции и стандартные отклонения выборок :
= КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению ковариации выборок Х и Y и дисперсии выборки Х:
И, наконец, запишем еще одну формулу для нахождения сдвига b . Воспользуемся тем фактом, что линия регрессии проходит через точку средних значений переменных Х и Y.
Вычислив средние значения и подставив в формулу ранее найденный наклон а , получим сдвиг b .
Оценка неизвестных параметров линейной модели (матричная форма)
Также параметры линии регрессии можно найти в матричной форме (см. файл примера лист Матричная форма ).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг b ), β1 (наклон a ).
Матрица Х равна:
Матрица Х называется регрессионной матрицей или матрицей плана . Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.
Матрица Х T – это транспонированная матрица Х . Она состоит соответственно из n столбцов и 2-х строк.
В формуле символом Y обозначен столбец значений переменной Y.
Чтобы перемножить матрицы используйте функцию МУМНОЖ() . Чтобы найти обратную матрицу используйте функцию МОБР() .
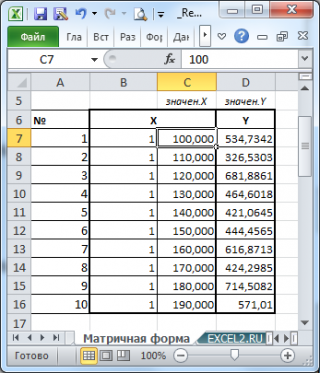
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
и введя ее как формулу массива в 2 ячейки, получим оценку параметров модели.
Красота применения матричной формы полностью раскрывается в случае множественной регрессии .
Построение линии регрессии
Для отображения линии регрессии построим сначала диаграмму рассеяния , на которой отобразим все точки (см. начало статьи ).
Для построения прямой линии используйте вычисленные выше оценки параметров модели a и b (т.е. вычислите у по формуле y = a * x + b ) или функцию ТЕНДЕНЦИЯ() .
Формула = ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23) возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца В2 .
Примечание : Линию регрессии можно также построить с помощью функции ПРЕДСКАЗ() . Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции ТЕНДЕНЦИЯ() работает только в случае одного регрессора. Функция ТЕНДЕНЦИЯ() может быть использована и в случае множественной регрессии (в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).
Как видно из диаграммы выше линия тренда и линия регрессии не обязательно совпадают: отклонения точек от линии тренда случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
Линию регрессии можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента Линия тренда. Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение. В диалоговом окне установите галочку Показывать уравнение на диаграмме (подробнее см. в статье про МНК ).
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами линией регрессии, а параметры уравнения a и b должны совпасть с параметрами уравнения отображенными на диаграмме.
Примечание: Для того, чтобы вычисленные параметры уравнения a и b совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был Точечная, а не График , т.к. тип диаграммы График не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; . Именно эти значения и берутся при расчете параметров линии тренда . Убедиться в этом можно если построить диаграмму График (см. файл примера ), а значения Хнач и Хшаг установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с a и b .
Коэффициент детерминации R 2
Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения регрессионной модели ). Очевидно, что лучшей оценкой для yi будет среднее значение ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).
Примечание : Далее будет использована терминология и обозначения дисперсионного анализа .
После построения регрессионной модели для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).
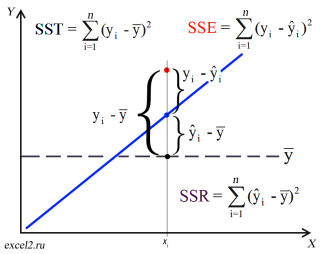
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
Очевидно, что используя регрессионную модель мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).
(yi — ŷi) – это оставшаяся, необъясненная ошибка.
Очевидно, что все три ошибки связаны выражением:
(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)
Можно показать, что в общем виде справедливо следующее выражение:
или в других, общепринятых в зарубежной литературе, обозначениях:
Total Sum of Squares = Regression Sum of Squares + Error Sum of Squares
Примечание : SS — Sum of Squares — Сумма Квадратов.
Как видно из формулы величины SST, SSR, SSE имеют размерность дисперсии (вариации) и соответственно описывают разброс (изменчивость): Общую изменчивость (Total variation), Изменчивость объясненную моделью (Explained variation) и Необъясненную изменчивость (Unexplained variation).
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату коэффициента корреляции и в MS EXCEL его можно вычислить с помощью функции КВПИРСОН() или ЛИНЕЙН() :
R 2 принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии ( Standard Error of a regression ) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Теперь вспомним уравнение линейной регрессионной модели Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со средним значением μ и дисперсией σ 2 .
Оценив значение дисперсии σ 2 и вычислив из нее квадратный корень – получим Стандартную ошибку регрессии. Чем точки наблюдений на диаграмме рассеяния ближе находятся к прямой линии, тем меньше Стандартная ошибка.
Примечание : Вспомним , что при построении модели предполагается, что среднее значение ошибки ε равно 0, т.е. E[ε]=0.
Оценим дисперсию σ 2 . Помимо вычисления Стандартной ошибки регрессии эта оценка нам потребуется в дальнейшем еще и при построении доверительных интервалов для оценки параметров регрессии a и b .
Для оценки дисперсии ошибки ε используем остатки регрессии — разности между имеющимися значениями yi и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.
Для оценки дисперсии σ 2 используют следующую формулу:
где SSE – сумма квадратов значений ошибок модели ε i =yi — ŷi ( Sum of Squared Errors ).
SSE часто обозначают и как SSres – сумма квадратов остатков ( Sum of Squared residuals ).
Оценка дисперсии s 2 также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов ошибок или MSRES (Mean Square of Residuals), т.е. среднее квадратов остатков . Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.
Примечание : Напомним, что когда мы использовали МНК для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на линии регрессии.
Математическое ожидание случайной величины MSE равно дисперсии ошибки ε, т.е. σ 2 .
Чтобы понять почему SSE выбрана в качестве основы для оценки дисперсии ошибки ε, вспомним, что σ 2 является также дисперсией случайной величины Y (относительно среднего значения μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi = a * Хi + b (значение уравнения регрессии при Х= Хi), то логично использовать именно SSE в качестве основы для оценки дисперсии σ 2 . Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае простой линейной регрессии число степеней свободы равно n-2, т.к. при построении линии регрессии было оценено 2 параметра модели (на это было «потрачено» 2 степени свободы ).
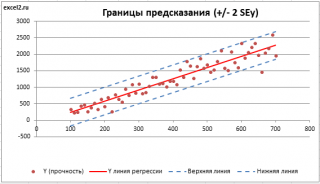
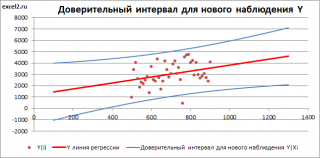
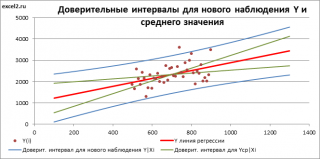
Итак, как сказано было выше, квадратный корень из s 2 имеет специальное название Стандартная ошибка регрессии ( Standard Error of a regression ) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см. этот раздел ). Если ошибки предсказания ε имеют нормальное распределение , то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от линии регрессии . SEy имеет размерность переменной Y и откладывается по вертикали. Часто на диаграмме рассеяния строят границы предсказания соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).
В MS EXCEL стандартную ошибку SEy можно вычислить непосредственно по формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))
или с помощью функции ЛИНЕЙН() :
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
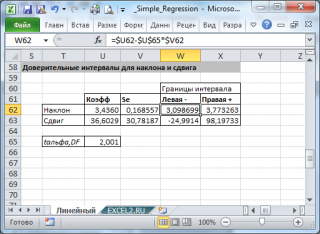
Стандартные ошибки и доверительные интервалы для наклона и сдвига
В разделе Оценка неизвестных параметров линейной модели мы получили точечные оценки наклона а и сдвига b . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ).
Стандартная ошибка коэффициента регрессии a вычисляется на основании стандартной ошибки регрессии по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey – стандартная ошибка регрессии, т.е. ошибка предсказания значения переменой Y ( см. выше ).
В MS EXCEL стандартную ошибку коэффициента регрессии Se можно вычислить впрямую по вышеуказанной формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)
или с помощью функции ЛИНЕЙН() :
Формулы приведены в файле примера на листе Линейный в разделе Регрессионная статистика .
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
где — квантиль распределения Стьюдента с n-2 степенями свободы. Величина а с «крышкой» является другим обозначением наклона а .
Например для уровня значимости альфа=0,05, можно вычислить с помощью формулы =СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является t-распределением Стьюдента с n-2 степенью свободы (то же справедливо и для наклона b ).
Примечание : Подробнее о построении доверительных интервалов в MS EXCEL можно прочитать в этой статье Доверительные интервалы в MS EXCEL .
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии. Здесь мы считаем, что коэффициент регрессии a имеет распределение Стьюдента с n-2 степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Примечание : Подробнее о построении доверительных интервалов с использованием t-распределения см. статью про построение доверительных интервалов для среднего .
Стандартная ошибка сдвига b вычисляется по следующей формуле:
В MS EXCEL стандартную ошибку сдвига Seb можно вычислить с помощью функции ЛИНЕЙН() :
При построении двухстороннего доверительного интервала для сдвига его границы определяются аналогичным образом как для наклона : b +/- t*Seb.
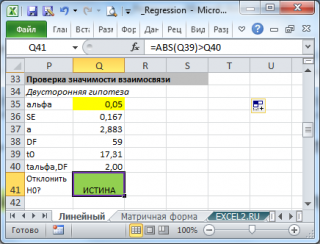
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда коэффициент регрессии a равен 0.
Чтобы убедиться, что вычисленная нами оценка наклона прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют проверку гипотез . В качестве нулевой гипотезы Н 0 принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы Н 1 принимают, что a <>0.
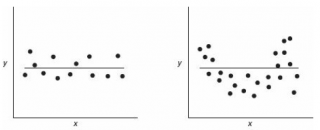
Ниже на рисунках показаны 2 ситуации, когда нулевую гипотезу Н 0 не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом коэффициент линейной корреляции равен 0.
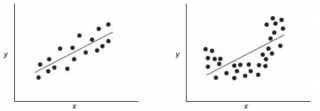
Ниже — 2 ситуации, когда нулевая гипотеза Н 0 отвергается.
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).
Для проверки гипотезы нам потребуется:
- Установить уровень значимости , пусть альфа=0,05;
- Рассчитать с помощью функции ЛИНЕЙН() стандартное отклонение Se для коэффициента регрессии (см. предыдущий раздел );
- Рассчитать число степеней свободы: DF=n-2 или по формуле = ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
- Вычислить значение тестовой статистики t 0 =a/S e , которая имеет распределение Стьюдента с числом степеней свободы DF=n-2;
- Сравнить значение тестовой статистики |t0| с пороговым значением t альфа ,n-2. Если значение тестовой статистики больше порогового значения, то нулевая гипотеза отвергается ( наклон не может быть объяснен лишь случайностью при заданном уровне альфа) либо
- вычислить p-значение и сравнить его с уровнем значимости .
В файле примера приведен пример проверки гипотезы:
Изменяя наклон тренда k (ячейка В8 ) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
Примечание : Проверка значимости взаимосвязи эквивалентна проверке статистической значимости коэффициента корреляции . В файле примера показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью процедуры F-тест .
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры простой линейной регрессионной модели Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ= a * Хi + b
Ŷ также является точечной оценкой для среднего значения Yi при заданном Хi. Но, при построении доверительных интервалов используются различные стандартные ошибки .
Стандартная ошибка нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
- неопределенность связанную со случайностью оценок параметров модели a и b ;
- случайность ошибки модели ε.
Учет этих неопределенностей приводит к стандартной ошибке S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS xx – сумма квадратов отклонений от среднего значений переменной Х:
В MS EXCEL 2010 нет функции, которая бы рассчитывала эту стандартную ошибку , поэтому ее необходимо рассчитывать по вышеуказанным формулам.
Доверительный интервал или Интервал предсказания для нового наблюдения (Prediction Interval for a New Observation) построим по схеме показанной в разделе Проверка значимости взаимосвязи переменных (см. файл примера лист Интервалы ). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х ср ), то интервал будет постепенно расширяться при удалении от Х ср .
Границы доверительного интервала для нового наблюдения рассчитываются по формуле:
Аналогичным образом построим доверительный интервал для среднего значения Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае доверительный интервал будет уже, т.к. средние значения имеют меньшую изменчивость по сравнению с отдельными наблюдениями ( средние значения, в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка S(Yср|Xi) вычисляется по практически аналогичным формулам как и стандартная ошибка для нового наблюдения:
Как видно из формул, стандартная ошибка S(Yср|Xi) меньше стандартной ошибки S(Y|Xi) для индивидуального значения .
Границы доверительного интервала для среднего значения рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел Предположения линейной регрессионной модели ).
Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках простой линейной модели n остатков имеют только n-2 связанных с ними степеней свободы . Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.
Чтобы проверить предположение о нормальности распределения ошибок строят график проверки на нормальность (Normal probability Plot).
В файле примера на листе Адекватность построен график проверки на нормальность . В случае нормального распределения значения остатков должны быть близки к прямой линии.
Так как значения переменной Y мы генерировали с помощью тренда , вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор о нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе Стандартная ошибка регрессии оценкой стандартного отклонения ошибок является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции ЛИНЕЙН() :
Иногда нормирование остатков производится на величину стандартного отклонения остатков (это мы увидим в статье об инструменте Регрессия , доступного в надстройке MS EXCEL Пакет анализа ), т.е. по формуле:
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
источники:
http://excel2.ru/articles/prostaya-lineynaya-regressiya-v-ms-excel
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/