Целочисленная оптимальность в excel это - Word и Excel - помощь в работе с программами

Оптимизация значений таблицы Excel, удовлетворяющих определенным критериям, может быть сложным процессом. К счастью, Microsoft предлагает надстройку Решение проблем для численной оптимизации. Хотя данный сервис не может решить всех проблем, он может быть полезным в качестве инструмента что-если. Данный пост посвящен надстройке Решение проблем в Excel.

Надстройка Решение проблем доступна во всех версиях Excel. Обратите внимание, что скриншоты могут не соответствовать вашей версии. Несмотря на то, что некоторые функции могут менять свое местоположение в зависимости от версии надстройки, функционал остается практически неизменным.

Что такое Поиск решений

Поиск решений – надстройка Excel, которая помогает найти решение с помощью изменения значений целевых ячеек. Целью может быть минимизация, максимизация или достижение некоторого целевого значения. Проблема решается путем регулировки входных критериев или ограничений, определенных пользователем.

Где в Excel поиск решений

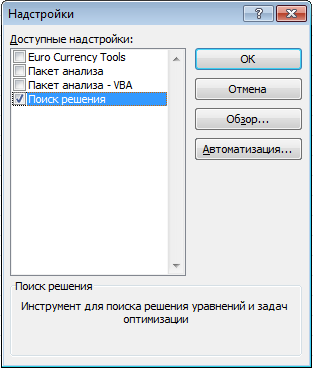
Надстройка Поиск решений поставляется вместе с Excel, но по умолчанию отключена. Чтобы включить его, перейдите по вкладке Файл в группу Параметры. В появившемся диалоговом окне Параметры, выберите Надстройки -> Управление: Надстройки Excel -> Перейти. В окне Надстройки устанавливаем галочку напротив поля Поиск решения, жмем ОК.

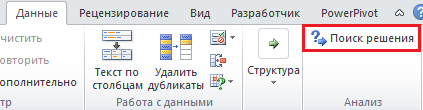
Теперь во вкладке Данные появилась новая группа Анализ с кнопкой Поиск решения.

Пример использования Поиска решения

Данный пост основан на примере использования Надстройки Поиск решения. Файл совместим со всеми версиями Excel.

Определение проблемы

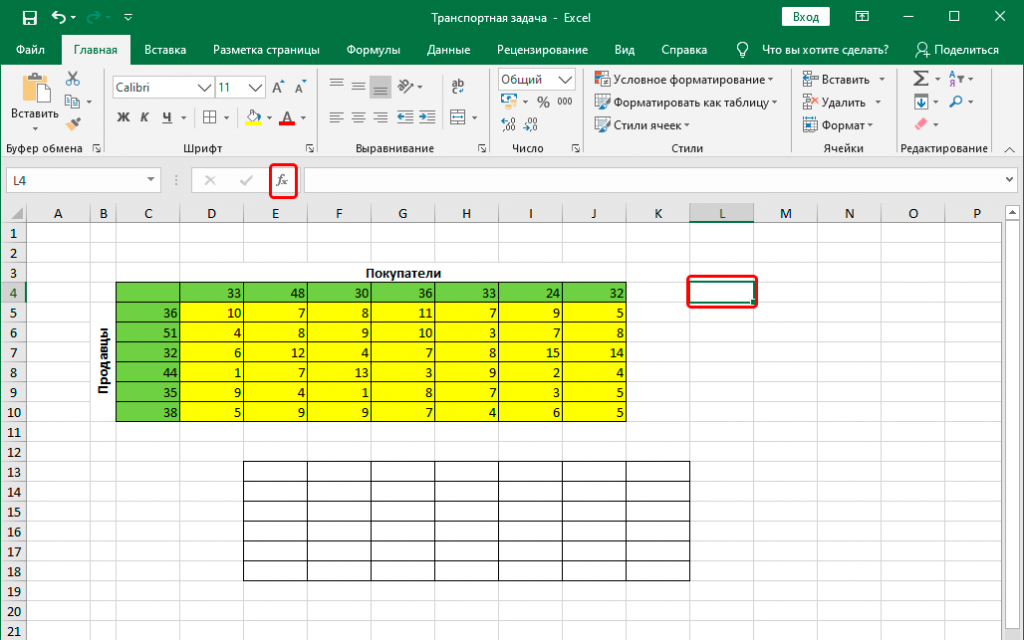
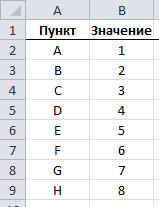
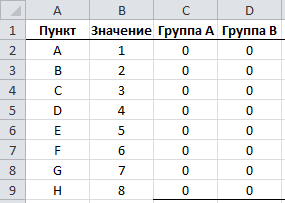
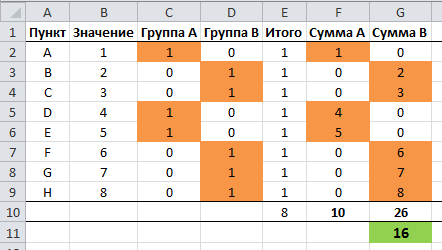
Предположим, что у нас есть набор данных, состоящий из 8 пунктов, каждому из которых соответствует свое значение.

… и нам необходимо скомбинировать значения в две группы так, чтобы суммы значений этих групп примерно совпадали.

Для начала требуется определить каждый пункт к какой-нибудь группе.

Чтобы указать привязанность пункта к группе, будем помечать их единицей (1), в противном случае нулем (0).

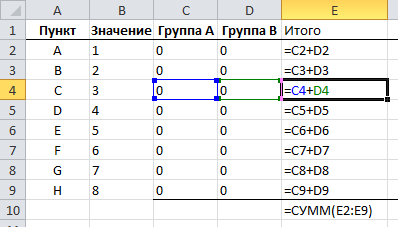
В следующем столбце мы будем суммировать значения каждого пункта в группе, и затем подведем итог в конце столбца.

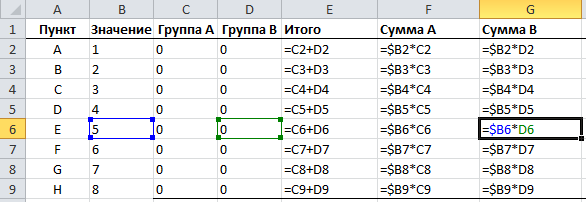
Нам также необходимо обработать значение каждого пункта в каждой группе, для этого умножаем значение пункта на значение группы, соответствующее этому пункту.

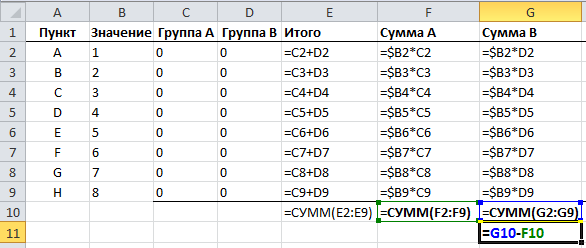
Наконец, нам необходимо свести сумму групп и работать с разницей между ними.

Наша задача минимизировать разницу между суммами групп.

Теперь мы можем присвоить каждой группе пункты, для этого вручную проставляем единицы в столбцах С и D. Excel отобразит разницу сумм групп в ячейке G11.

Для большей наглядности я добавил условное форматирование для ячеек, имеющих значение >0.

Проблема в том, что количество возможных комбинаций 2⁸, т.е. 256 вероятных ответов на вопрос. Если на каждый из них тратить по 5 секунд, это займет у нас 21,3 минуты, предполагая, что мы сможем выдержать темп и запомнить лучшую комбинацию.

Вот где Поиск решения находит применение.

Поиск оптимального решения в Excel

Чтобы применить сервис Поиск решения, нам необходимо определить ряд требований, правил и ограничений, которые позволят надстройке найти правильный ответ.

Наши правила

Наше основное требование – это минимизировать разницу между двумя группами. В нашем примере она находится в ячейке G11 – Группа B минус Группа A. Нам нужно, чтобы значение в ячейке G11 было настолько малым насколько это возможно, но больше или равно 0.

Мы также знаем, что пункт может находиться либо в Группе A, либо в Группе B, к тому он не может быть дробным. Таким образом у нас два ограничения для каждого элемента:

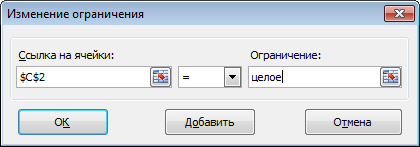
Во-первых: Значение элемента в колонке Итог должна равняться единице.

Во-вторых: Значения элементов в группах должны быть целыми.

Мы также знаем, что общее количество элементов 8, это еще одно ограничение. Как использовать эти ограничения мы обсудим в следующем разделе.

Диалоговое окно Поиска решения

В этом разделе описано окно надстройки Поиск решения и его использования для определения проблемы.

Пустое окно Поиска решения

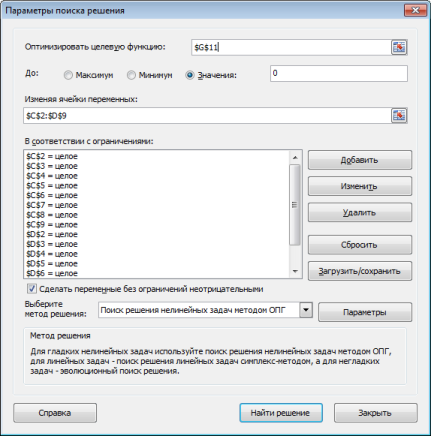
Заполненное окно Поиска решения

Оптимизировать целевую функцию

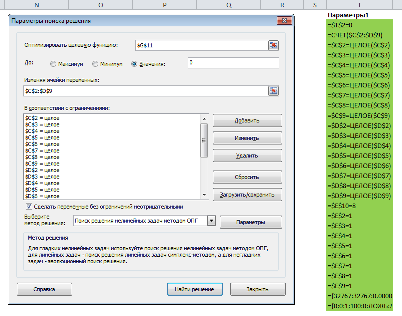
Это целевая ячейка, в которой мы пытаемся решить проблему. Наша целевая ячейка G11 – разница в группах.

До

Здесь мы указываем, каких результатов хотим добиться от целевой функции.

Мы хотим, чтобы суммы обоих групп совпадали, т.е. чтобы разница сумм была равна 0. Это может показаться странным, но нам не требуется минимизировать разницу, потому что при этом все элементы будут помещены в Группу A, что приведет к значению ячейки G11 меньше нуля.

Другой способ наложения ограничения – изменить G11 на =ABS(G10-F10). При этом мы сможем установить маркер на Минимум, как результат достижения целевой функции.

Но пока мы остановимся на формуле =G10-F10 и установим маркер в значение равным 0.

Изменяя ячейки переменных

Изменяемые ячейки – ячейки, которые надстройка попытается изменить, чтобы решить задачу. В нашем случае это привязка элемента к конкретной группе: $C$2:$D$9.

В соответствии с ограничениями

Ограничения – это правила, которые лимитируют возможные решения проблемы.

Нам необходимо добавить несколько ограничений в наш список:

В колонке Итого каждый элемент должен равняться 1
Элементы групп должны быть целым числом
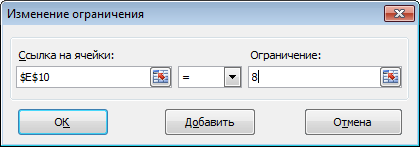
Сумма значений столбца Итого должна равняться 8

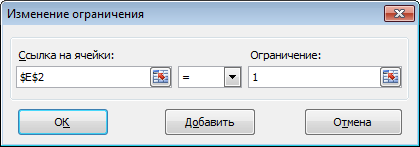
Чтобы наложить ограничения, жмем кнопку Добавить

Для каждой ячейки диапазона E2:E9 устанавливаем ограничение значения равным 1
Для каждой ячейки диапазона C2:D9 устанавливаем ограничение значение целое число.
Необходимо добавить ограничение на сумму обоих групп, ячейка E10 = 8.

Вы можете Изменить или Удалить ограничение, если допустили ошибку, выбрав конкретное ограничение и нажав соответствующие кнопки в диалоговом окне.

Загрузить/сохранить параметры поиска решений

Сервис поиска решений позволяет сохранять и загружать параметры надстройки. Для этого в окне существует кнопка Загрузить/сохранить. Параметры модели сохраняются в диапазон, который вы указали ранее. Данный подход позволяет быстро настраивать и изменять параметры Поиска решения.

Запуск поиска оптимального решения в Excel

Предупреждение!!! Надстройка поиск решения является сложной вычислительной надстройкой, поэтому перед запуском сохраните рабочую книгу.

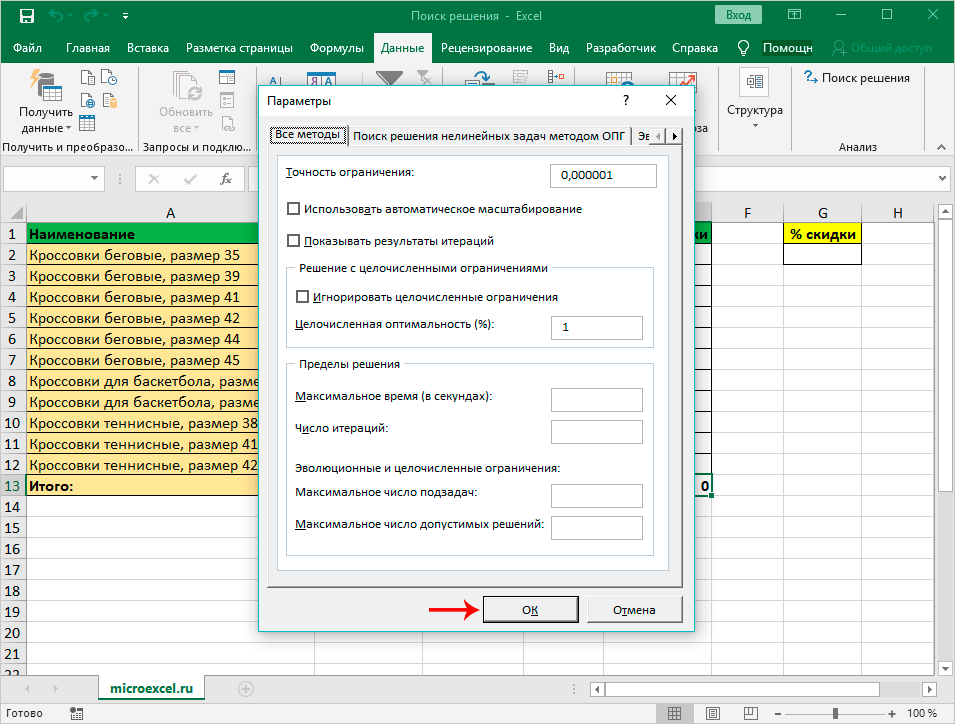
Прежде чем запустить модель, необходимо задать еще несколько параметров, чтобы убедиться, что сервис отработает корректно. В основном диалоговом окне убедитесь, что стоит маркер напротив поля Сделать переменные без ограничений неотрицательными. В этом же окне нажмите кнопку Параметры.

Два параметра, которые необходимо будет менять время от времени:

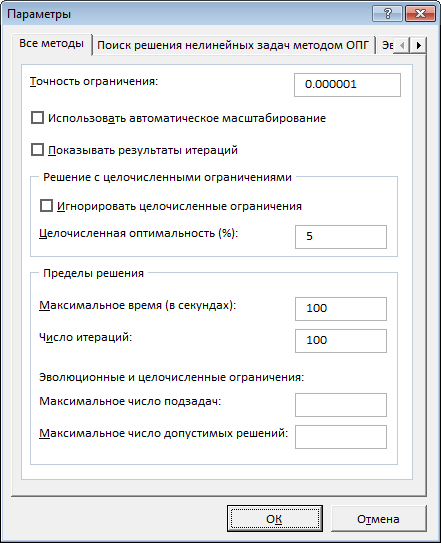
Точность ограничения: значение от 0 до 1, где, чем больше цифра, тем больше ограничение

Целочисленная оптимальность: показывает насколько далеко от целого числа ограничение имеет право быть.

Запуск модели

Чтобы запустить надстройку нажмите кнопку Найти решение в основном окне.

В строке состояния вы увидите ряд статических данных, которые будут отображать внутреннюю работу надстройки. Как правило, они быстро меняются, и читать их сложно. Если модель сложная, то работа может остановится на некоторое время, надстройка обычно восстанавливается от этих проблем сама.

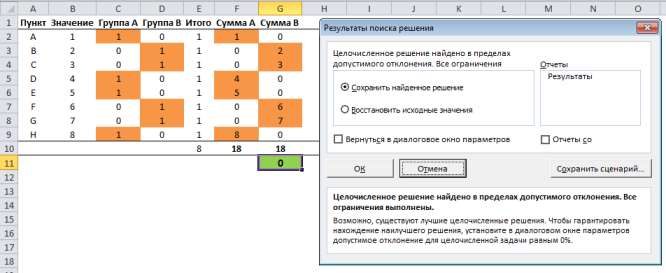
После того, как Поиск решения закончит свою работу, Excel отобразит диалоговое окно Результаты поиска решения с некоторой информацией. Первое, на что стоит обратить внимание – это надпись Решение найдено в пределах допустимого отклонения. Если решение найдено, ячейки рабочей книги изменятся с предложенным решением.

Теперь у вас есть 4 варианта на выбор:

— Запустить отчет

— Сохранить сценарий

— Восстановить исходные значения

— Сохранить найденное решение

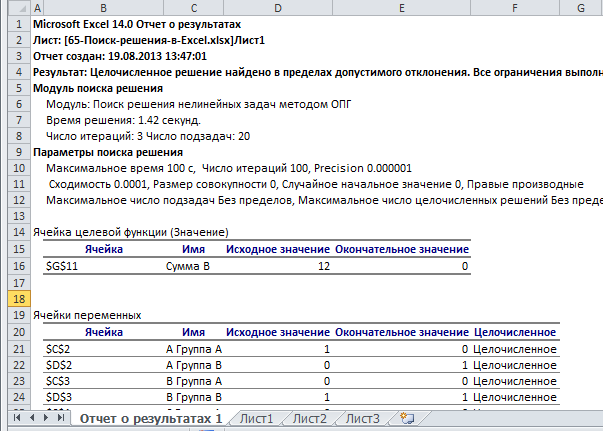
Запустить отчет

Вы можете создать отчет, выбрав доступные из списка отчетов. Будет создан новый лист Отчет о результатах1.

Обратите внимание, что в зависимости от установленных вами ограничений, будут доступны различные отчеты.

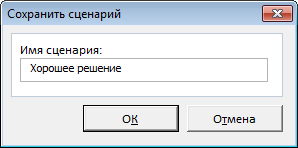
Сохранить сценарий

Если вы нажмете кнопку Сохранить сценарий, Excel откроет следующее диалоговое окно:

Где необходимо ввести название вашего сценария модели и нажать кнопку ОК.

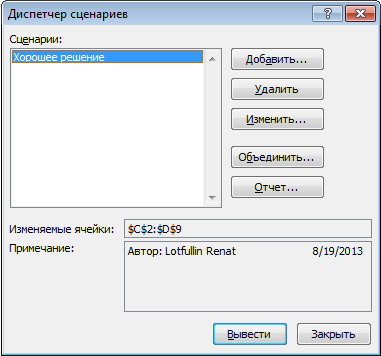
Все сценарии доступны в Диспетчере сценариев, который находится во вкладке Данные в группе Работа с данными –> Анализ что-если -> Диспетчер сценариев.

Вернуться к модели

К тому же, вы можете вернуться к модели и:

— Восстановить исходные значения

— Сохранить найденное решение

Проверка результатов

Сервис Поиск решения, вероятно, самая непредсказуемая система в Excel. Таким образом, все найденные решения, которые он выдает необходимо перепроверять вручную, для дальнейшего использования.

Данная проверка на реалистичность должна начинаться с подтверждения, что все результаты удовлетворяют заданным критериям:

— Являются ли результаты примерно похожими на ваши ожидания?

— Не нарушены ли максимумы и минимумы?

Источник

Чтобы
получить целочисленное решение задачи
линейного программирования с помощью
программы Excel,
к
обычным ограничениям задачи добавляются
условия целочнсленности. Это можно
сделать в окне Добавление
ограничения, вид
которого для нашего примера (см. раздел
1.1) показан на рис. 2.2.

В
поле
Ссылка
на ячейки (Ссылка на ячейку) задается
диапазон ячеек содержащих значения
переменных, а в раскрывающемся списке
вместо знака выбирается один из следующих
пунктов:

цел
—
целое число;

в
бин в
Excel
2010
(или двоич
в
предыдущих версиях)—
бинарное
(двоичное) число 0 или 1;

раз
(только
в Excel
2010)
— разные целые числа от 1 до N
(где
N
—
число переменных).

При
этом в поле Ограничение
автоматически
появляется слова: целое,
бинарное
(двоичное) или
Все
разные.

Если
переменные в модели — разных типов
(целые, бинарные, разные целые,
вещественные), можно задать несколько
условий целочнсленности, для каждого
типа переменных в отдельности.

Поскольку
нахождение целочисленного решения
зачастую является довольно длительной
процедурой, предусмотрена возможность
ее ускорения. Для этого используются
следующие параметры, задаваемые в Excel
2010
в окне Параметры
(см.
рис. 1.26), а в предыдущих версиях — в окне
Параметры
поиска решения (см.
рис. 1.27) (названия параметров, используемые
в предыдущих версиях, даны в скобках):

Игнорировать
целочисленные ограничения (только
в Excel
2010)
—

Добавление
ограничения

Ссылка
на ячеикм:

ГШ

Ограничение:

ок

Отмена

Добавить

Рис.
2.2. Добавление требования целочнсленности
переменных

флажок,
установка которого приводит к решению
задачи без учета условий целочисленное™.

Целочисленная
оптимальность (Допустимое отклонение)—
указывает, на сколько процентов
полученное значение целевой функции
может отличаться от оптимального
(по умолчанию в Excel
2010
— 1%, а в предыдущих версиях — 5% ). Для
ускорения можно увеличить это значение.
Если же необходимо получить точное
решение, то следует установить этот
параметр равным 0%, но это может значительно
увеличить время оптимизации,
Максимальное
время —
позволяет задать в секундах максимальное
время, которое отводится на поиск
решения (значение по умолчанию в Excel
2010
не задано, а в предыдущих версиях— 100
секунд).
Число
итераций (Предельное число итераций)
—
позволяет определить максимальное
количество итераций при поиске решения
(значение по умолчанию в Excel
2010
не задано, а в предыдущих версиях—
100). Для целочисленных моделей данный
параметр указывает максимальное
количество итераций для каждой
подзадачи.
Максимальное
число подзадач (только
в Excel
2010)—
позволяет задать максимальное количество
подзадач при целочисленном решении.
Максимальное
число допустимых решений (только
в Excel
2010)
— позволяет определить максимальное
количество рассматриваемых допустимых
целочисленных решений.

Если
вы задали некоторые из перечисленных
предельных значений, то поиск решения
будет продолжаться до тех пор, пока
какое-нибудь нз них не будет достигнуто.
Тогда появится окно с предложением
остановить вычисления или продолжить.
Если вы решили продолжить вычисления,
достигнутое предельное значение
отменяется н расчеты продолжаются до
достижения следующего нз заданных
предельных значений. Если вы выбрали
вариант остановки вычислений, появится
окно с сообщением о том, что решение
остановлено по запросу пользователя и
на листе окажутся результаты, достигнутые
на этот момент. Прервать вычисления
можно также нажатием клавиши Esc.
При
этом также появляется окно с предложением
остановить пли продолжить вычисления.

Остальные
ограничения и параметры поиска решения
— те же, что и для обычной задачи линейного
программирования (см. раздел 1.3). Выполнив
вычисления с условием целочнсленности,
показанным на рис. 2.2, вы получите
целочисленное решение нашей задачи (5;
1; 3, 4).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
21.03.201614.11 Mб13МЕТОДИЧКА ЭТМ №2.rtf
#
#
#
#
#
#
#
#

Источник

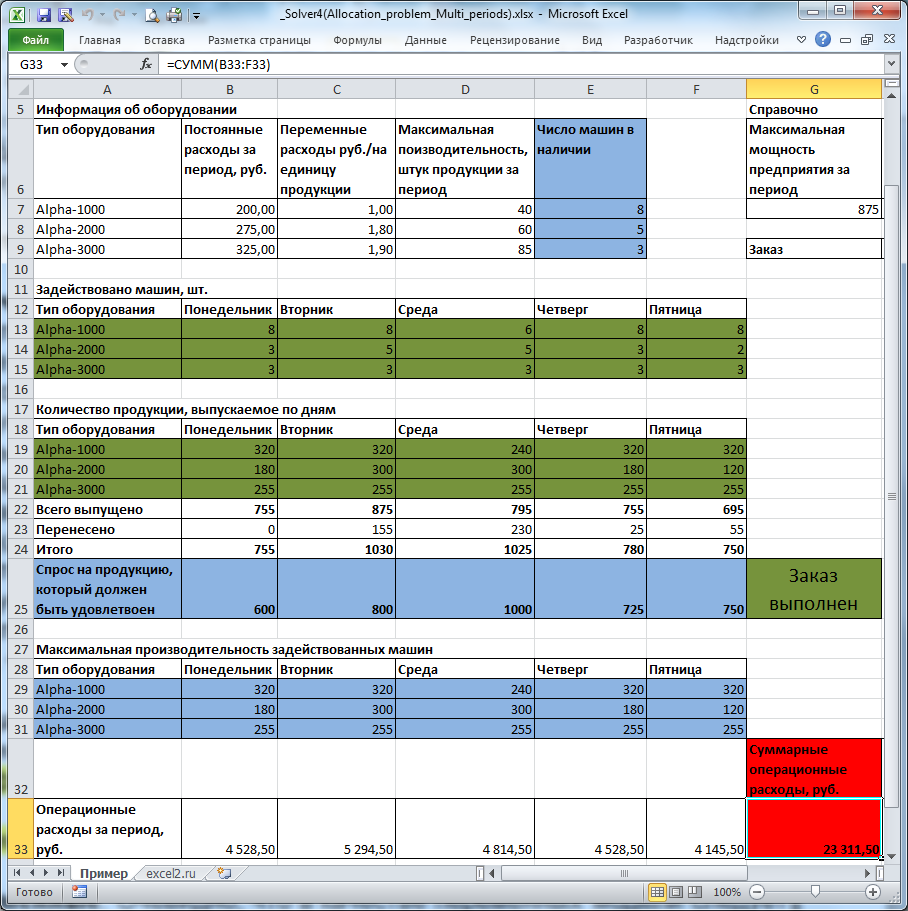
Создадим модель для нахождения наилучшего распределения ресурсов, при котором минимизируются затраты, понесенные за несколько периодов (Allocation Problem). Расчет будем проводить с помощью надстройки Поиск решения.

Задача оптимального распределения ресурсов (распределительная задача) заключается в отыскании наилучшего распределения ресурсов, при котором либо максимизируется результат, либо минимизируются затраты. Задача, в которой минимизируются затраты, понесенные в одном периоде решена в статье

Поиск решения MS EXCEL (1.2). Распределение ресурсов (ограничение по количеству оборудования)

, и имеет смысл предварительно познакомиться с изложенным там материалом. В этой статье мы решим аналогичную задачу, но для случая работы оборудования в нескольких периодах (пример с сайта

www.solver.com

Вводная статья про

Поиск решения

в MS EXCEL 2010

находится здесь

Задача

Предприятие выпускает монопродукт (только один вид изделия и ничего более) и ему необходимо выполнить заказ клиента. Выпуск продукции осуществляется в течение 5 дней. Отгрузка заказа ежедневная. На предприятии 3 типа оборудования. Каждый тип оборудования выпускает один и тот же продукт. Производительность каждого типа оборудования разная. Каждый тип оборудования имеет постоянную и переменную часть расходов. Переменная часть расходов пропорциональна количеству произведенных изделий. Имеется ограниченное количество единиц оборудования каждого типа (но общее количество оборудования избыточно для выполнения заказа). Требуется минимизировать расходы на оборудование при условии выполнения заказа.

Создание модели

На рисунке ниже приведена модель, созданная для решения задачи (см.

файл примера

).

Предприятие несет расходы в зависимости от типа оборудования: использование оборудования типа Alpha-3000 самое дорогое в эксплуатации, но оно и самое производительное. Оборудование типа Alpha-1000 самое дешевое в эксплуатации, но оно и менее производительное. Задача

Поиска решения

выбрать наиболее дешевое оборудование, так чтобы заказ был выполнен (мощностей Alpha-1000 не хватит для выполнения заказа). Казалось бы, решение очевидно (взять по максимуму дешевое оборудование, остальную производительность обеспечить более дорогим). Однако, если учесть, что из-за низкой производительности дешевых машин приходится их брать больше, неся существенные постоянные расходы, то решение уже не кажется очевидным.

Переменные (выделено зеленым)

. В качестве переменных модели следует взять количество задействованных единиц оборудования каждого типа и суммарное количество продукции, выпущенное на каждом типе оборудования (производительность задается не для каждой единицы, а для типа в целом). Для наглядности диапазонам ячеек, содержащих переменные, присвоены

имена

Машин_Задействовано

и

Продукции_выпущено.

Ограничения (выделено синим)

. Количество задействованных машин должно быть целым числом. Количество задействованных машин каждого типа должно быть не больше, чем имеется в наличии (используются

именованные диапазоны

Alpha

XXXX

_Задействовано

и

Alpha

XXXX

_в_наличии

). Всего должно быть выпущено продукции не меньше чем величина заказа (используется

именованный диапазон

Продукции выпущено_Итого

). В день возможно производить больше продукции, чем требуется в день заказа, излишек переносится на следующий день. Также необходимо ограничить производительность задействованного оборудования. Производительность задается не для каждой единицы, а для типа в целом (используются

именованные диапазоны

Продукции выпущено

и

Макс_производительность_задейств_машин

).

Целевая функция (выделено красным)

. Целевая функция – это сумма операционных расходов за 5 дней. Операционные расходы, понесенные за день, задается формулой

=СУММПРОИЗВ(B19:B21; Расходы_переменные)+ СУММПРОИЗВ(B13:B15; Расходы_постоянные)

B19:B21

– количество продукции, выпущенной в определенный день.

B13:B15

— количество задействованных машин в определенный день.

Это суммарные операционные расходы (переменная и постоянные части). Сумма операционных расходов за 5 дней должна быть минимизирована.

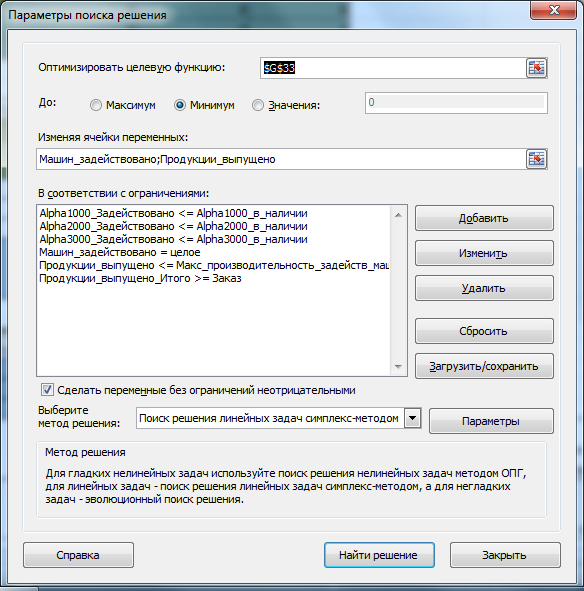
Убедитесь, что метод решения соответствует линейной задаче. Параметры

Поиска решения

были выбраны следующие:

Теперь в диалоговом окне можно нажать кнопку

Найти решение

.

Результаты расчетов

Поиск решения

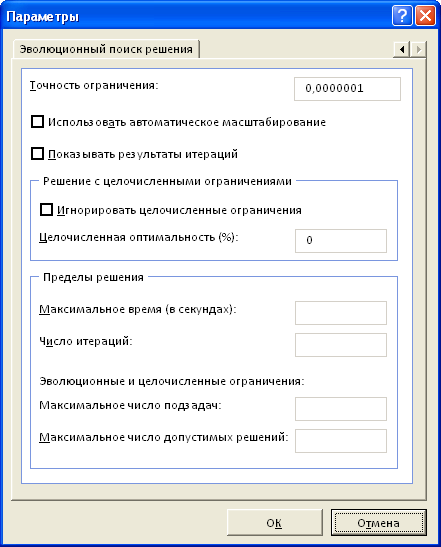
подберет оптимальный набор единиц оборудования по типам и их производительность, при котором операционные расходы будут минимальные, а заказ выполнен. В нашей задаче было установлено целочисленное ограничение, что существенно усложняет задачу поиска и, соответственно, сказывается на скорости расчета. Как показано на рисунке выше,

Целочисленная оптимальность

была выбрана 0% (

Целочисленная оптимальность

(Integer Optimality) позволяет

Поиску решения

остановить поиск, в случае, если он найдет целочисленное решение, в пределах указанного процента от оптимального). В нашем случае (0%), требуется найти лучшее из известных

Поиску решения

решений. Поиск в этом случае занял 8 секунд, результат 23 311,50. Установив

Целочисленную оптимальность

1%, поиск займет 0,2 сек, результат 23 370,50 (отличие на 0,3%). Это информация к размышлению: стоит ли увеличение точности на 0,3% уменьшения скорости расчетов более чем на порядок? Решать Вам. В любом случае, первые расчеты модели лучше проводить при

Целочисленной оптимальности

не равной 0%.

Источник

У меня есть упражнение по производственному программированию, которое я должен решить с помощью решателя Excel. Однако я не могу установить целочисленное ограничение для определенной ячейки, которая должна быть только целой.

Я приложил минимальный пример к этому посту, структура выглядит следующим образом:
Существует 6 продуктов, в каждом из которых есть количество для изготовления на заказ и для производства, сумма этих двух и соответствующая маржинальная прибыль. Общая маржинальная прибыль рассчитывается как произведение общего количества каждого продукта на сумму его маржинальной прибыли.
Теперь для решателя я хочу максимизировать общую маржу вклада, изменяя значения для каждого продукта на складе и значения для некоторых продуктов (есть еще некоторые ограничения, которые не относятся к этой проблеме). ).

Теперь я уже установил решатель на место возникновения проблемы, и как только я пытаюсь добавить целочисленное ограничение в ячейку «сделать на склад», где ячейка «сделать на заказ» над ней должна измениться, я получаю ошибку Msgstr «Ссылка на ячейку целочисленного ограничения должна включать только переменные ячейки.» Я не понимаю почему, потому что ячейка (в данном случае F3) помечена как переменная ячейка. Это ошибка в Солвере, или я что-то упустил?

Минимальный пример: ссылка

I recently encountered the same problem. Even without having the FormulaText at the end of the integer constraint.

This should work:

Sub Solve()
   SolverReset
   SolverOk SetCell:="$N$95", MaxMinVal:=1, ValueOf:="0", ByChange:="$C$87:$K$93"
   SolverAdd CellRef:="$C$87:$K$93", Relation:=4
   SolverAdd CellRef:="$C$87:$K$93", Relation:=1, FormulaText:="$C$48:$K$54"
   SolverAdd CellRef:="$L$87:$L$93", Relation:=1, FormulaText:="$M$87:$M$93"
   SolverAdd CellRef:="$C$87:$K$93", Relation:=3, FormulaText:="0"

   SolverSolve UserFinish:=True
End Sub

When applying an integer constraint (SolverAdd) to cells that are not part of the decision variables (ByChange), the solver prompts:

«Integer Constraint Cell Reference must include only Variable Cells.»

This is not the case in your example, but the setting the objective function still plays a role. I assume that if you add the integer constraint before you add the SolverOk, the solver does not know the decision variables (ByChange) yet and therefore does not include the integer constraint.

I recently encountered the same problem. Even without having the FormulaText at the end of the integer constraint.

This should work:

Sub Solve()
   SolverReset
   SolverOk SetCell:="$N$95", MaxMinVal:=1, ValueOf:="0", ByChange:="$C$87:$K$93"
   SolverAdd CellRef:="$C$87:$K$93", Relation:=4
   SolverAdd CellRef:="$C$87:$K$93", Relation:=1, FormulaText:="$C$48:$K$54"
   SolverAdd CellRef:="$L$87:$L$93", Relation:=1, FormulaText:="$M$87:$M$93"
   SolverAdd CellRef:="$C$87:$K$93", Relation:=3, FormulaText:="0"

   SolverSolve UserFinish:=True
End Sub

When applying an integer constraint (SolverAdd) to cells that are not part of the decision variables (ByChange), the solver prompts:

«Integer Constraint Cell Reference must include only Variable Cells.»

I would like a constraint for a formula so it can only return an even number.

For example:

A formula in cell A1, *SUM(A2+A3)/2* should only return a even number.

MDaniyal

1,0973 gold badges13 silver badges29 bronze badges

asked Apr 1, 2016 at 11:09

You can use the MOD function:

In another cell, say A2 have the formula =MOD(A1,2) and constrain it to be 0.

Another possibility is to create a new changing cell (say B1) and constrain it to be an integer, and then add a constraint that forces A1 = 2*B1. The new changing cell will have no other role to play in the model.

answered Apr 1, 2016 at 11:19

John ColemanJohn Coleman

51.1k7 gold badges51 silver badges116 bronze badges

I would like a constraint for a formula so it can only return an even number.

For example:

A formula in cell A1, *SUM(A2+A3)/2* should only return a even number.

MDaniyal

1,0973 gold badges13 silver badges29 bronze badges

asked Apr 1, 2016 at 11:09

You can use the MOD function:

In another cell, say A2 have the formula =MOD(A1,2) and constrain it to be 0.

answered Apr 1, 2016 at 11:19

John ColemanJohn Coleman

51.1k7 gold badges51 silver badges116 bronze badges

цел
—
целое число;

в
бин в
Excel
2010
(или двоич
в
предыдущих версиях)—
бинарное
(двоичное) число 0 или 1;

раз
(только
в Excel
2010)
— разные целые числа от 1 до N
(где
N
—
число переменных).

При
этом в поле Ограничение
автоматически
появляется слова: целое,
бинарное
(двоичное) или
Все
разные.

Игнорировать
целочисленные ограничения (только
в Excel
2010)
—

Добавление
ограничения

Ссылка
на ячеикм:

ГШ

Ограничение:

ок

Отмена

Добавить

Рис.
2.2. Добавление требования целочнсленности
переменных

флажок,
установка которого приводит к решению
задачи без учета условий целочисленное™.

Целочисленная
оптимальность (Допустимое отклонение)—
указывает, на сколько процентов
полученное значение целевой функции
может отличаться от оптимального
(по умолчанию в Excel
2010
— 1%, а в предыдущих версиях — 5% ). Для
ускорения можно увеличить это значение.
Если же необходимо получить точное
решение, то следует установить этот
параметр равным 0%, но это может значительно
увеличить время оптимизации,
Максимальное
время —
позволяет задать в секундах максимальное
время, которое отводится на поиск
решения (значение по умолчанию в Excel
2010
не задано, а в предыдущих версиях— 100
секунд).
Число
итераций (Предельное число итераций)
—
позволяет определить максимальное
количество итераций при поиске решения
(значение по умолчанию в Excel
2010
не задано, а в предыдущих версиях—
100). Для целочисленных моделей данный
параметр указывает максимальное
количество итераций для каждой
подзадачи.
Максимальное
число подзадач (только
в Excel
2010)—
позволяет задать максимальное количество
подзадач при целочисленном решении.
Максимальное
число допустимых решений (только
в Excel
2010)
— позволяет определить максимальное
количество рассматриваемых допустимых
целочисленных решений.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
21.03.201614.11 Mб12МЕТОДИЧКА ЭТМ №2.rtf
#
#
#
#
#
#
#
#

0 / 0 / 0

Регистрация: 22.05.2012

Сообщений: 5

22.05.2012, 14:43

[ТС]

Суть задачи — составление модели управления активами и пассивами по срокам погашения. Целевая функция: F(x)=0,2*X11+0,46*X12+0,06*X13+0,16*X14+0,1*X15+0, 02*X16 28310859 , где X12,13…16 -активы с разными сроками погашения, а коэффициенты — это удельные веса активов. имеются ограничения:
1) 0,27*X21+0,26*X22+0,03*X23+0,09*X24+0,03*X25+0,32* X26=28310859, где X21…26, пассивы с соответствующими сроками погашения.
2)0,2*X11/(0,27*X21)0.2
3) (0,2*X11+0,46*X12)/(0,27*X21+0,26*X22)0.7
4) Хij 0
деление заменил на умножение, Поиск решения стал работать, указал показывать итерации, но найдя первые три переменные, поиск решения останавливается и остальные оставляет равными 0. В итоге задачу решить не получается.

Поиск решения, бинарные значения

exek

Дата: Четверг, 17.10.2013, 16:48 |
Сообщение № 1

Группа: Пользователи

Ранг: Прохожий

Сообщений: 3

Репутация:
0
±

Замечаний:
0% ±

Excel 2010

Здравствуйте, при добавлении ограничения «бинарное» вылазит следующая ошибка:

В первом варианте все работает, но при добавлении техники ограничение не задается.
Помогите разобраться в проблеме.

Сообщение отредактировал exek — Четверг, 17.10.2013, 20:17

Ответить

Pelena

Дата: Четверг, 17.10.2013, 17:01 |
Сообщение № 2

Группа: Админы

Ранг: Местный житель

Сообщений: 18697

Репутация:
4254
±

Замечаний:
±

Excel 2016 & Mac Excel

Если Вы добавляете технику, то диапазон ячеек переменных тоже надо увеличить $C$25:$K$32

[p.s.]При таком количестве данных минут пять считал [/p.s.]

«Черт возьми, Холмс! Но как??!!»
Ю-money 41001765434816

Ответить

exek

Дата: Четверг, 17.10.2013, 17:12 |
Сообщение № 3

Группа: Пользователи

Ранг: Прохожий

Сообщений: 3

Репутация:
0
±

Замечаний:
0% ±

Excel 2010

Этот момент как раз и не выходит, если я правильно Вас понял.

Ответить

Pelena

Дата: Четверг, 17.10.2013, 17:19 |
Сообщение № 4

Группа: Админы

Ранг: Местный житель

Сообщений: 18697

Репутация:
4254
±

Замечаний:
±

Excel 2016 & Mac Excel

если я правильно Вас понял

Неправильно поняли

К сообщению приложен файл: 6188203.jpg(23.6 Kb)

«Черт возьми, Холмс! Но как??!!»
Ю-money 41001765434816

Ответить

exek

Дата: Четверг, 17.10.2013, 17:22 |
Сообщение № 5

Группа: Пользователи

Ранг: Прохожий

Сообщений: 3

Репутация:
0
±

Замечаний:
0% ±

Excel 2010

Спасибо!

Ответить

Источник

«Поиск решения» в Excel 2007, 2010, 2013, 2016 (и других) – где находится функция, как включить подбор решений, возможности надстройки
- Обзор и возможности функции
- Включение возможности
- Подготовка таблицы
- Конкретные примеры использования
  - Изготовление йогурта
  - Затраты на рекламу
  - Оптимизация игрового процесса
- Установка ограничений
Курс Microsoft Excel 2019/2016. Уровень 3. Анализ и визуализация данных в Екатеринбурге
- - Стоимость курса
  - Вы научитесь:
  - Аудитория:
  - Требования к предварительной подготовке слушателя:
- Содержание курса
- Другие курсы данной тематики
Как использовать Solver в Excel для оптимизации вашего решения?
- Что такое решатель в Excel?
- Как включить решатель в Excel?
- Как использовать решатель в Excel?
  - 1. Сформулируйте модель
    - Постановка проблемы
    - Цель
  - 2. Метод проб и ошибок
  - 3. Решите модель
    - 1. Объективные клетки
    - 2. Переменные ячейки
    - 3. Ограничения
- Опции решателя
  - - 1. Точность ограничения
    - 2. Используйте автоматическое масштабирование
    - 3. Показать результаты итерации
    - 4. Игнорировать целочисленные ограничения
    - 5. Целочисленная оптимальность (%)
    - 6. Максимальное время (секунды)
    - 7. Итерации
    - 8. Максимальное количество подзадач
    - 9. Максимально возможные решения
- Заключение
Поиск и анализ информации с помощью формул в Excel 2019 для Windows — Excel 2019 (Windows) — ПРОМЕЖУТОЧНЫЙ

«Поиск решения» в Excel 2007, 2010, 2013, 2016 (и других) – где находится функция, как включить подбор решений, возможности надстройки

Работа с табличным редактором Эксель включает в себя различные функции. Одной из таких возможностей Excel является «поиск решений», которая позволяет пользователь значительно упростить работу в табличном процессоре.

Обзор и возможности функции

Надстройка «Поиск решений» — специфическая возможность Excel 2007, 2010, 2013, 2016, которая предназначена для работы с формулой при наличии определённых условий. Описать её логику можно следуя принципу «что если?». То есть, просчитать изменение конечной ячейки при условии изменения других. Хотя и звучит это сложно, но описать данный принцип удобнее на конкретном примере: как будет изменяться остаток средств в конце месяца, если изменить разные статьи расходов.

Ожидать, что функция сработает в обратном порядке можно, но для этого потребуется изменять формулу и вводные данные для этой формулы. Фактически Excel следует строгой логике и сама по себе функция не решит проблему, но поможет прийти к корректному решению подбором или перебором вводных данных.

Включение возможности

Функция поиска решений является надстройкой Excel. Для версий Excel ниже 2010 её потребуется запускать следующим образом:

Открыть «Параметры» программы.
Перейти в раздел «Надстройки».
Найти «поиск решений» и клацнуть по нему дважды. В случае если пакет не установлен Office предложит загрузить его. С таким предложением потребуется согласиться.

Теперь возможность можно будет найти в разделе «Данные». Отмечена она названием «Поиск решений».

Подготовка таблицы

Текущий раздел будет выглядеть сложным, поскольку без конкретного примера разобраться в таблице будет проблематично. Следует сразу оговориться, что в конкретных примерах будет проще разобраться, чем в имеющейся таблице, но в этом разделе объясняется какие предусловия используются для работы с функцией:

Представим, что в таблице имеются пункты, которые имеют какое-то значение.
Осложним задачу введением двух виртуальных групп, которые могут соответствовать пунктам (это могут быть статьи расходов).

В случае соответствия группы пункту она получает «вес» равный «1». В противном случае – «0». Это потребуется для дальнейших операций.

Теперь добавим 2 группы формул, которые выражают взаимодействие между группами, «весомостью» (значение) и пунктами. Пускай это будет сложение и умножение, для простоты. Таким образом мы получим сумму важности пунктов (итоговое значение для каждой из групп) и что-то вроде важности затрат для каждого из пунктов.
Теперь постараемся прийти к конечным решениям по затратам и итогам. Сделаем это при помощи операций сложения в соответствующих столбцах.
Последним действием будет сведений разницы между затратами групп.

Теперь таблицу можно считать сведённой и подготовленной. Требуется только завершить работу с функцией и настроить формулы для её эффективного срабатывания. Предположим, что нас интересует результат, при котором разница между затратами групп будет минимизирована или сравняется с нулём (ячейка «Разница»).

Запускаем функцию подбора решений и начинаем задавать ей необходимые переменные и значения:

Указывается, в какой ячейке находится формула, результат которой интересует пользователя.
Указывается результат, к которому должно привести изменений значений. Если указать в качестве значения 0, то, вероятнее всего, таблица будет заполнена нулями. Чтобы избежать подобного требуется выставить хотя-бы «1».
Диапазон ячеек, подлежащих изменению.
Ограничения, которые можно логически вписать в переменные. В указанном случае это должны быть целые числа 0 или 1.
Метод решения. Лучше оставить без изменений, если ранее не было произведено знакомство с алгоритмами работы.
Запуск поиска решений.

Получаем следующее заполнение:

Получаем решение в течении нескольких секунд. Для сравнения, по самым оптимистичным прикидкам, человек потратил бы на аналогичное действие около 5 минут.

Конкретные примеры использования

Закончив с виртуальным примером, который помог разобраться с особенностями построения таблицы и задачи условий перейдём к более приземлённым и конкретным примерам. С их помощью в задаче будет разобраться немного проще.

Изготовление йогурта

Попробуем рассчитать какой из видов йогурта при разной концентрации компонентов производить лучше, чем остальные. Для этого определим компоненты, их соотношение и стоимость конечного продукта, при условии ограниченности запасов:

В раздел «Расход сырья» внесены формулы, которые опираются на «количество» и нормы расхода. Прибыль является произведением стоимости и количества. Количество и будет переменной, которая будет изменяться в пределах «запасы». Для этого формируется следующий набор условий:

В результате вычислений (с учётом дробного остатка, поскольку условие работы только с целыми числами добавлено не было), получилось, что эффективнее всего производить 1 и 3 йогурты, а второй полностью игнорировать.

Затраты на рекламу

Другим вопросом, с которым поможет эта функция будет «оптимизация расходов на рекламу». В этом случае перед пользователем стоит задача: повысить возможную прибыль посредством изменения рекламных вложений в определённые месяцы.

Итак, прибыль является целевой ячейкой (выделена изумрудным цветом). Зелёным выделены расходы на рекламу, а красным максимальные затраты. При поиске решения ограничиваем подстановку переменных в значениях рекламы максимумом, а в качестве цели ставим максимизацию прибыли.

В результате получаем максимизированную прибыль в указанном месяце, посредством грамотного распределения рекламного бюджета между остальными месяцами.

Отсюда и вытекает главный недостаток «поиска решений». Он оперирует лишь конечной (одной) ячейкой. Чтобы максимизировать прибыль требуется работать с последней ячейкой (прибыль – всего), что сопряжено с вероятностью появления ошибки в программе, если формулы настроены неверно.

Оптимизация игрового процесса

Данный пример будет выглядеть сложнее. Не вдаваясь в подробности предположим, что в компьютерной игре имеется несколько комплектов (перечислены в соответствующей графе), которые могут быть проданы за некоторую сумму денег (цифры не соответствуют реальным) и для сбора которых требуется определённое время (откинем случайность выпадения и предположим, что за указанное время можно собрать весь комплект целиком). Наша задача определить максимальную выгоду от сбора комплекта с учётом ограничения времени в игре (говоря геймерским языком «определиться, что гриндить на продажу»).

Итоговое доступное время по условиям подбора решения ограничено 4 единицами (время устанавливаем условно, не важно будут это часы, дни или месяцы). Графа «выгода» представляет собой формулу, говорящую, что будет если выделить «х» времени на сбор определённого комплекта. Задачей Excel является оптимизация максимальной (суммарной) выгоды.

В условиях имеем: требуется получить максимальную выгоду при лимите времени. Следовательно, программа определяет на каком комплекте сфокусировать внимание. Результат предсказуем: самый дорогой комплект достоин 100% временных затрат.

Установка ограничений

При работе с функцией, как упоминалось выше, можно установить ограничения. Они выставляются в поле «В соответствии с ограничениями». Их можно устанавливать, убирать или редактировать. Главное понимать какая цель ставится перед программой и какими способами Excel может её добиться.

Например, программа может использовать дробные числа там, где это выгоднее, хотя это физически невозможно (эффект «полтора землекопа») или уходить в отрицательные значения. Поэтому прежде чем ставить перед Excel задачу нужно сориентироваться в ней самому. Повторять постановку задачи с разными условиями тоже можно, особенно когда результаты получаются уж очень фантастическими.

Курс Microsoft Excel 2019/2016. Уровень 3. Анализ и визуализация данных в Екатеринбурге

Код: ITCloud-DAVS

Курс нацелен на расширение знаний встроенных функций MS Excel в рамках категории «Ссылки и массивы», чтобы научиться новым возможностям обработки данных. Программа курса поможет научиться создавать нестандартные сложные диаграммы, которые помогут визуализировать данные, сделать их запоминающимися и легкими в управлении.

В курсе изучаются компоненты группы «Анализ «Что если», новые возможности 2019 версии — быстрый прогноз с использованием листа прогноза, а также «Подбор параметра» и «Поиск решения», чтобы подобрать оптимальные исходные данные для получения результата.
Курс позволит научиться не только импортировать данные, но и создавать запросы с использованием Microsoft Query, строить отчеты по данным OLAP-куба.

Стоимость курса

14 998 руб

Заказать

Вы научитесь:

Создавать формулы массивов для обработки данных с использованием встроенных функций разных категорий
Строить нестандартные типы диаграмм для наглядного сравнения и анализа числовых данных
Использовать новые типы диаграмм: воронкообразная и картограмма
Управлять данными диаграммы с помощью пользовательских элементов управления
Прогнозировать развитие ситуаций разными способами, в том числе с учетом сезонности
Выбирать оптимальные стратегии решений с помощью Сценариев и Таблиц данных
Решать задачи одно- и многокритериальной оптимизации
Использовать быстрый прогноз с использованием листа прогноза
Импортировать данные из внешних источников: web, текстовых файлов (*.txt, *.csv), баз данных Access.
Создавать запросы к внешним данным с использованием надстройки PowerQuery
Строить отчеты сводных таблиц по данным OLAP-куба

Аудитория:

Для опытных, уверенных пользователей MS Excel, которые по роду своей деятельности часто сталкиваются с задачами анализа и прогнозирования в Excel

Требования к предварительной подготовке слушателя:

Знания в объеме курса Электронные таблицы Microsoft Excel. Углубленный курс: фильтрация, подведение итогов, консолидация данных, построение сводных таблиц и диаграмм.

Содержание курса

Модуль 1. Применение категории встроенных функций «Ссылки и Массивы» и формул массивов

1. Формулы массивов

Использование в простых расчетах
Применение функций в формулах массивов

2. Использование именованных диапазонов в расчетах

3. Решение задач по извлечению данных из массива данных:

Двусторонний поиск
Поиск по нескольким критериям
Двусторонний многокритериальный поиск
С применением функций СТРОКА, СТОЛБЕЦ

4. Применение функции ДВССЫЛ в решении задач:

Обработка данных с одного или нескольких листов
Создание зависимых списков с постоянным источником

5. Работа с функцией СМЕЩ

Модуль 2. Пользовательские форматы

1. Создание пользовательских форматов:

Числовые форматы
Форматы даты и времени
Группы пользовательских форматов

2. Редактирование, применение и удаление форматов

Модуль 3. Диаграммы

1. Спарклайны
2. Комбинированные диаграммы
3. Гистограмма с отображением итогов
4. Проектная диаграмма Ганта
5. Диаграмма сравнений Торнадо

6. Воронкообразная диаграмма
7. Каскадная диаграмма
8. Картограмма
9. Иерархические диаграммы:

Солнечные лучи
Иерархическая

10. Статистические диаграммы:

Диаграмма Парето
Ящик с усами
Частотная диаграмма

11. Термометр
12. Диаграммы с пользовательскими элементами управления:

Диаграмма с включением/выключением рядов данных
Диаграмма с выбором значений и отображением средних, минимальных и максимальных значений

Модуль 4. Прогнозирование данных

1. Выделение тренда:

Скользящее среднее
Функции регрессионного анализа: ПРЕДСКАЗ, ТЕНДЕНЦИЯ, РОСТ

Построение линий тренда
3. Учет сезонности в прогнозах
4. Быстрый прогноз с использованием листа прогноза

Модуль 5. Вариативный анализ «Что Если» и Оптимизация

1. Использование инструмента Таблица данных для анализа развития ситуации при 2-х переменных
2. Оценка развития ситуации и выбор оптимальной стратегии с помощью Сценариев
3. Решение однокритериальной задачи оптимизации с помощью Подбора параметра
4. Решение многокритериальных задач оптимизации с использованием надстройки Поиск решения

Модуль 6. Обработка внешних Баз Данных

1. Импорт данных с использованием PowerQuery из текстового файла, базы данных Access и Web-страницы
2. Запрос к файлу Excel
3. Особенности анализа куба данных OLAP в сводных таблицах Excel

Другие курсы данной тематики

Основы анализа данных с использованием Excel / Data Analysis Fundamentals using Excel
Анализ данных в PowerBI / Analyzing Data with Power BI
Oracle BI(Business Intelligence Suite Enterprise Edition) Сервер — версия 12. Создание, организация совместного использования аналитических WEB витрин и отчетов во всех стандартных форматах
Анализ данных с использованием Excel / Analyzing Data with Excel
Электронные таблицы Microsoft Excel и анализ данных. Углубленный курс
Бизнес-анализ в области разработки ПО
Унифицированный язык моделирования UML
Углублённое изучение языка DAX для Excel PowerPivotExcel PowerPivot DAX in Depth
Microsoft Excel 2019/2016. Power Query в Microsoft Excel
OBI11gBR — Oracle BI 11g R1: Build Repositories/Создание репозиториев

Как использовать Solver в Excel для оптимизации вашего решения?

Microsoft Excel — это популярный инструмент анализа данных, повышающий производительность пользователя при работе с данными. Когда дело доходит до принятия важных решений, таких как составление бюджета, аутсорсинг, добавление или удаление линейки продуктов, нам необходимо учитывать общие затраты. Эти решения требуют знаний бухгалтеров, чтобы определить, какие действия необходимо предпринять, чтобы максимизировать результат. Таким образом, помогая нам решать бизнес-задачи наиболее эффективным способом. Вот где Солвер вступает в действие.

В этой статье представлено простое введение в Solver в Excel, которое позволяет выполнять линейное программирование и получать наилучшие возможные результаты.

Что такое решатель в Excel?

Solver в Excel — это инструмент, который помогает нам решать проблемы принятия решений, находя соответствующие оптимальные решения. Этот Решатель относится к набору инструментов анализа «что, если», которые помогают нам тестировать различные сценарии в Excel. Они также определяют, как каждый сценарий влияет на результат на рабочем листе.

Эта тема может показаться немного сложной для новичков, но пошаговое руководство, описанное в этой статье, даст вам представление о том, как можно использовать инструмент «Решатель» для принятия решений. Но сначала давайте посмотрим, как включить Solver в Excel.

Как включить решатель в Excel?

Решатель — это надстройка, доступная в Excel. Теперь давайте посмотрим, как добавить этот инструмент.

Если у вас есть версии Excel: — 2010, 2013, 2016 или 2019, вы должны сначала перейти на вкладку «Файл» → «ОПЦИИ», как показано.

Примечание. Если у вас Excel 2007, нажмите кнопку Microsoft Office → Параметры.

Откроется окно параметров Excel. Нажмите на опцию «Надстройки», а затем нажмите «Перейти».

Откроется окно надстройки с различными инструментами, которые вы можете выбрать. Отметьте опцию надстройки Solver из списка. Нажмите «ОК».

В версии Excel 2003 мы можем добавить Solver из меню Tools, чтобы найти надстройки. При нажатии на нее откроется список надстроек, из которых вы должны выбрать Solver и нажать OK.

Теперь вы найдете Решатель в разделе «Анализ» на вкладке «Данные».

Недавно добавленный Решатель можно найти в меню «Инструменты» для версии Excel 2003 года.

Двигаясь вперед, давайте разберемся, как использовать инструмент «Решатель».

Как использовать решатель в Excel?

Давайте узнаем, как мы можем использовать решатель на примере. Необходимо выполнить три основных шага:

Формулировка модели
Метод проб и ошибок
Решите модель

Мы подробно обсудим их вместе с пошаговым руководством.

1. Сформулируйте модель

Мы будем использовать следующий набор данных хранилища для демонстрации Solver в Excel.

Этот набор данных состоит из столбцов с названиями продуктов, общим количеством единиц, продажной ценой, себестоимостью каждой единицы, прибылью и общим доходом. Ячейка B5 содержит общее количество доступных единиц, а ячейка F5 содержит общий полученный доход.

Теперь давайте посмотрим на постановку задачи.

Постановка проблемы

Максимальное количество единиц, которое можно заказать, равно 150. Прибыль, полученная от продажи каждой единицы, указана в таблице. Нам нужно максимизировать общую прибыль, полученную от продажи продуктов: телевизора, стереосистемы и динамиков.

Цель

Найти, сколько единиц каждого продукта требуется, чтобы прибыль была максимальной?

2. Метод проб и ошибок

С помощью этой концепции пользователь может легко проанализировать любое пробное решение.

Предположим, мы заказываем 50 единиц телевизоров, 50 единиц стереосистем и 50 единиц динамиков, причем максимальное количество единиц, которые можно заказать, равно 150, мы получим общий доход в размере 1 25 000 рупий. Однако, чтобы максимизировать прибыль, давайте продвинемся вперед и добавим необходимые входные данные в инструмент решателя.

3. Решите модель

Для решения этой задачи мы используем Solver в Excel. Теперь мы выполним следующие шаги, чтобы найти оптимальное решение.

Нажмите на инструмент «Решатель», который теперь добавлен в раздел «Анализ» на вкладке «Данные». Это откроет вкладку Solver Parameters.
Далее нам нужно сформулировать модель. Для этого необходимо указать три основных параметра, т. е.

1. Ячейка объектива
2. Переменные ячейки
3. Ограничения

Excel находит оптимальное значение (минимальное, максимальное, заданное) для формулы, представленной в ячейке «Цель». Это делается путем изменения значений в ячейках Variable в зависимости от ограничений, указанных в ячейках Constraint.

Теперь давайте сопоставим каждый параметр с ячейками в наборе данных, введя значения ячеек в диалоговом окне «Параметры решателя».

1. Объективные клетки

Целевая ячейка содержит формулу, определяющую цель постановки задачи. Здесь ячейка F5 указана как целевая ячейка. Цель может состоять в том, чтобы найти минимальное, максимальное или точное значение.

Здесь цель состоит в том, чтобы найти максимальное значение, так как мы максимизируем прибыль. Итак, мы устанавливаем значение целевой ячейки как ячейку F5 и выбираем опцию MAX.

2. Переменные ячейки

Переменные ячейки состоят из переменных данных, которые модифицируются Солвером для достижения цели.

Это ячейки, содержащие переменные данные. Значение этих ячеек необходимо изменить для оптимизации прибыли. В этом примере мы указываем ячейки с количеством единиц/продукта как ячейки переменной, которые находятся в диапазоне B2: B4.

3. Ограничения

Ограничения — это ограничения, накладываемые на Решатель. Эти ограничения аналогичны ограничениям реального мира на общую производительность продукта, требования рынка и т. д. Решение, предоставляемое Солвером, должно удовлетворять этим ограничениям. Для получения оптимального решения эти условия должны быть соблюдены.

В этом примере мы можем указать следующие ограничения:

Количество единиц для каждого продукта должно быть больше или равно нулю. Следовательно, мы можем установить ограничение как $B$2 >= 0, $B$3 >= 0 и $B$4 >=0.
Количество продаваемых единиц не может превышать общее количество единиц. Итак, $B$5 <=150.

Чтобы добавить эти ограничения, нажмите кнопку «Добавить».

Далее открывается диалоговое окно «Добавить ограничение». Теперь введите ссылку на ячейку. Укажите необходимое значение ограничения и нажмите «Добавить».

После добавления всех ограничений закройте диалоговое окно «Добавить ограничение».

Давайте продолжим и разберемся с параметрами, доступными в разделе «Поиск решения» в Excel, которые изменяют то, как «Поиск решения» находит решения.

Опции решателя

Для большинства задач нет необходимости изменять параметры Решателя по умолчанию. Однако если вы хотите изменить некоторые параметры, выполните следующие действия:

В диалоговом окне «Параметры решения» нажмите «Параметры».
Появится диалоговое окно «Параметры решения».
На вкладке «Все методы» выберите один или несколько вариантов:

1. Точность ограничения

Введите требуемую степень точности в поле Constraint Precision Box. Это определяет точность ограничений. Вы можете указать более низкое значение (от 0 до 1), чтобы сократить время, необходимое Солверу для возврата решения.

2. Используйте автоматическое масштабирование

Установка этого флажка автоматически масштабирует результаты при решении задачи.

3. Показать результаты итерации

При установке этого флажка отображаются результаты итераций, использованных при решении задачи.

4. Игнорировать целочисленные ограничения

Установка этого флажка игнорирует все ограничения, указанные для целых чисел.

5. Целочисленная оптимальность (%)

Указывает процент целочисленных критериев оптимальности, используемых решателем для решения проблемы.

6. Максимальное время (секунды)

Указывает максимальное количество секунд, которое потребуется Солверу для поиска решения.

7. Итерации

Указывает, сколько раз Солвер будет пересчитывать проблему при поиске решения.

8. Максимальное количество подзадач

Указывает максимальное количество подзадач, разрешенных для Решателя.

9. Максимально возможные решения

Указывает максимальное количество необходимых возможных решений.

Нажмите OK после изменения необходимых параметров.

Наконец, нажмите кнопку «Решить» в диалоговом окне «Параметры решателя», чтобы найти оптимальное решение.

Excel найдет решение, максимизирующее прибыль. Откроется диалоговое окно «Результаты решения», в котором говорится: «Решатель нашел решение». Вы можете выбрать отчеты, необходимые для создания отчета Solver. Затем выберите опцию «Сохранить результаты решателя» и нажмите «ОК».

Оптимизированное решение будет отображаться на вашем рабочем листе. Наша цель оптимизировать решение, которое было достигнуто, и Решатель пришел к решению, указанному ниже.

Оптимальным решением будет заказать 100 единиц телевизоров и 50 единиц стереосистем. Это решение дает максимальную прибыль в размере 1 50 000 рупий.

Будет создан следующий отчет. В этом отчете упоминаются исходные и окончательные значения ячеек Целевая ячейка и Переменная, а также статус каждого ограничения в оптимальном решении.

Это основы для понимания того, как использовать Solver в Excel, чтобы найти оптимальные решения для ваших проблем принятия решений.

Получите опыт работы с новейшими инструментами и методами бизнес-аналитики с помощью магистерской программы для бизнес-аналитиков. Зарегистрируйтесь сейчас!

Заключение

В этой статье вы узнали, как использовать Решатель в Excel для решения проблемы принятия решения, указав Целевые ячейки, Переменные ячейки и Ограничения на примере.

Если у вас есть какие-либо вопросы по этой статье, укажите их в разделе комментариев, и наши специалисты свяжутся с вами в ближайшее время.

Вы можете улучшить свои навыки работы с Excel, записавшись на бесплатный курс Business Analytics with Excel, предлагаемый Simplilearn.

Поиск и анализ информации с помощью формул в Excel 2019 для Windows — Excel 2019 (Windows) — ПРОМЕЖУТОЧНЫЙ

Excel 2019 (Windows)
| Средний

9 видео | 36м 41с
Включает оценку
Получает значок
СертификацияCPE

Для извлечения, возврата и расчета данных можно использовать широкий спектр инструментов Excel. В этом курсе из 9 видео учащиеся увидят, как извлекать информацию о датах и значениях рангов, объединять и разделять уже имеющиеся данные, а также автоматизировать и упрощать вычисления с помощью инструментов поиска и СУММПРОИЗВ. Ключевые понятия, описываемые здесь, включают в себя извлечение значений дат и выполнение вычислений с использованием дат; как получить информацию о датах в прошлом, настоящем и будущем; и как использовать формулы ранжирования для поиска наименьшего и наибольшего значений в списке. Затем узнайте, как извлекать данные и разделять значения по отдельным ячейкам; как объединить существующие значения данных в одной ячейке; и как анализировать сложные таблицы с несколькими массивами для получения сводных результатов. Продолжайте, наблюдая за тем, как использовать формулы ВПР и ГПР для перекрестных ссылок на списки данных и проверки отсутствующих значений; как использовать условные формулы для поиска по нескольким таблицам и автоматической вставки данных; и как использовать формулу ВПР для сопоставления списков данных и извлечения соответствующих значений. Чтобы попрактиковаться в том, что вы узнали, вы найдете документ Word с именем Excel 2019для Windows: поиск и анализ информации с помощью упражнения «Формулы», а также сопутствующие материалы в разделе «Ресурсы».

ЧТО ВЫ УЗНАЕТЕ

использовать даты для получения информации

найти дату автоматически

найти наибольшее и наименьшее значения в списке

разделить данные на несколько ячеек

объединить значения данных в одной ячейке
создавать автоматические отчеты

данные перекрестных ссылок с формулами

выполнить поиск по таблицам

использовать формулы для автоматической вставки данных

В ЭТОМ КУРСЕ

Playable

1.

Получение информации с датами в Excel 2019 для Windows

4м 56с

ВВЕРХ СЛЕДУЮЩИЙ
Играбельно

2.

Автоматический поиск даты в Excel 2019 для Windows

3 м 17 с
Заблокировано

3.

Поиск наибольшего и наименьшего значений в списке в Excel 2019 для Windows

4м 1с
Заблокировано

4.

Разделение данных на несколько ячеек в Excel 2019 для Windows

6м 23с
Заблокировано

5.

Объединение значений данных в одной ячейке в Excel 2019 для Windows

3 м 22 с
Заблокировано

6.

Создание автоматических отчетов в Excel 2019 для Windows

2м 56с
Заблокировано

7.

Перекрестные ссылки на данные с формулами в Excel 2019 для Windows

3 м 16 с
Заблокировано

8.

Выполнение поиска по двум таблицам в Excel 2019 для Windows

4м 4с
Заблокировано

9.

Автоматическая вставка данных с формулами в Excel 2019 для Windows

4 м 26 с

ПОЛУЧИТЕ ЦИФРОВОЙ БЕЙДЖ ПО ЗАВЕРШЕНИИ ЭТОГО КУРСА

Skillsoft предоставляет вам возможность заработать цифровой значок после успешного завершения некоторых из наших курсов, которым можно поделиться в любой социальной сети или бизнес-платформе.

Источник