This tutorial will help you set up and interpret a Cubic Spline in Excel using the XLSTAT software.
Not sure this is the modeling feature you are looking for? Check out this guide.
Dataset for running a Cubic Spline
The data that we use are the speed of numerous cars and the distance they need to stop [Ezekiel, M. (1930)]. Note that the data were recorded in the 1920s.
The goal is to fit those data using a cubic spline.
Setting up a cubic spline in XLSTAT
After opening XLSTAT, select the XLSTAT / Modeling data/ Cubic splines command, or click on the matching button of the toolbar.
Once you’ve clicked on the button, the dialog box appears.
The data are presented in a table of 50 observations and 2 variables. Speed is the X variable and Distance the Y variable. As we select the column title for the variables, we leave the option Variable labels activated.
In the Options tab**,** three approaches are proposed to defined the spline nodes. Here we choose to fix the number of nodes to 10.
The computations begin once you have clicked on OK. The results will then be displayed in a new sheet.
Interpreting the results
The first results being displayed are the statistics and the correlation matrix for the 2 variables. Next, we get the table of the coefficients of the polynomials for each interval.
The cubic spline is then displayed on graph.
Finally, table and graphs enable us to take a closer look at each of the residuals.
Was this article useful?
- Yes
- No
Cubic splines are used to fit a smooth curve to a series of points with a piecewise series of cubic polynomial curves. In addition to their use in interpolation, they are of particular interest to engineers because the spline is defined as the shape that a thin flexible beam (of constant flexural stiffness) would take up if it was constrained to pass through the defined points. This post will present an Excel User Defined Function (UDF) to generate a “natural” cubic spline for any series of 3 or more points. Later posts will look at alternative spline formulations, and applications of the cubic spline to structural analysis.
A cubic spline is defined as the curve that for any two adjacent internal points:
- The curve passes exactly through both points
- The slope of the curve at the end points is equal to the slope of the adjacent segments
- The curvature of the curve at the end points is equal to the curvature of the adjacent segments
Alternative provisions for the end segments will generate different spline curves over the full extent of the curve. The most common provision for the ends is that the curvature is zero at both ends. This is known as a “natural cubic spline”. In a structural analysis context this corresponds to a beam that is free to rotate at both ends, but is constrained in position at the ends and a number of internal points.
Further details of the theory of cubic splines, and an algorithm for generating natural cubic splines are given in this Wikipedia article.
An excel spreadsheet with a UDF for generating cubic splines, based on the algorithm in the Wikipedia article, can be downloaded from: CSpline2.zip
The download is open source, and full VBA code for the UDF is freely accessible.
Example screen shots from this file are shown below:
Csplinea Function
Example 1; Fit spline to 5 data points
Example 1; Fit spline to 5 data points
Example 2; Fit spline to 9 data points on a circular arc
Example 2; Fit spline to 9 data points on a circular arc
“Dummy” data points at each end allow the curvature at the start and end points to be adjusted to the required value.
Example 2; Fit spline to 9 data points on a circular arc
Example 3; Fit spline to the deflected shape of a 3 span beam
Example 3; Fit spline to the deflected shape of a 3 span beam
Polynomial coefficients from example 3
Example 3; Bending Moments
Bending moments are calculated by multiplying the curvature at each point by the beam flexural stiffness, EI.
MS Excel VBA code to be put in a module — array functions
In MS Excel, press Alt+F11 to open the Visual Basic Editor (Windows). Via top menu: Insert → Module. Copy the MS Excel VBA code of the functions into the module.
Generic helper function to read range data into single dimensional array.
Your input data can now be column organized (default table) or row organized (transposed default table).
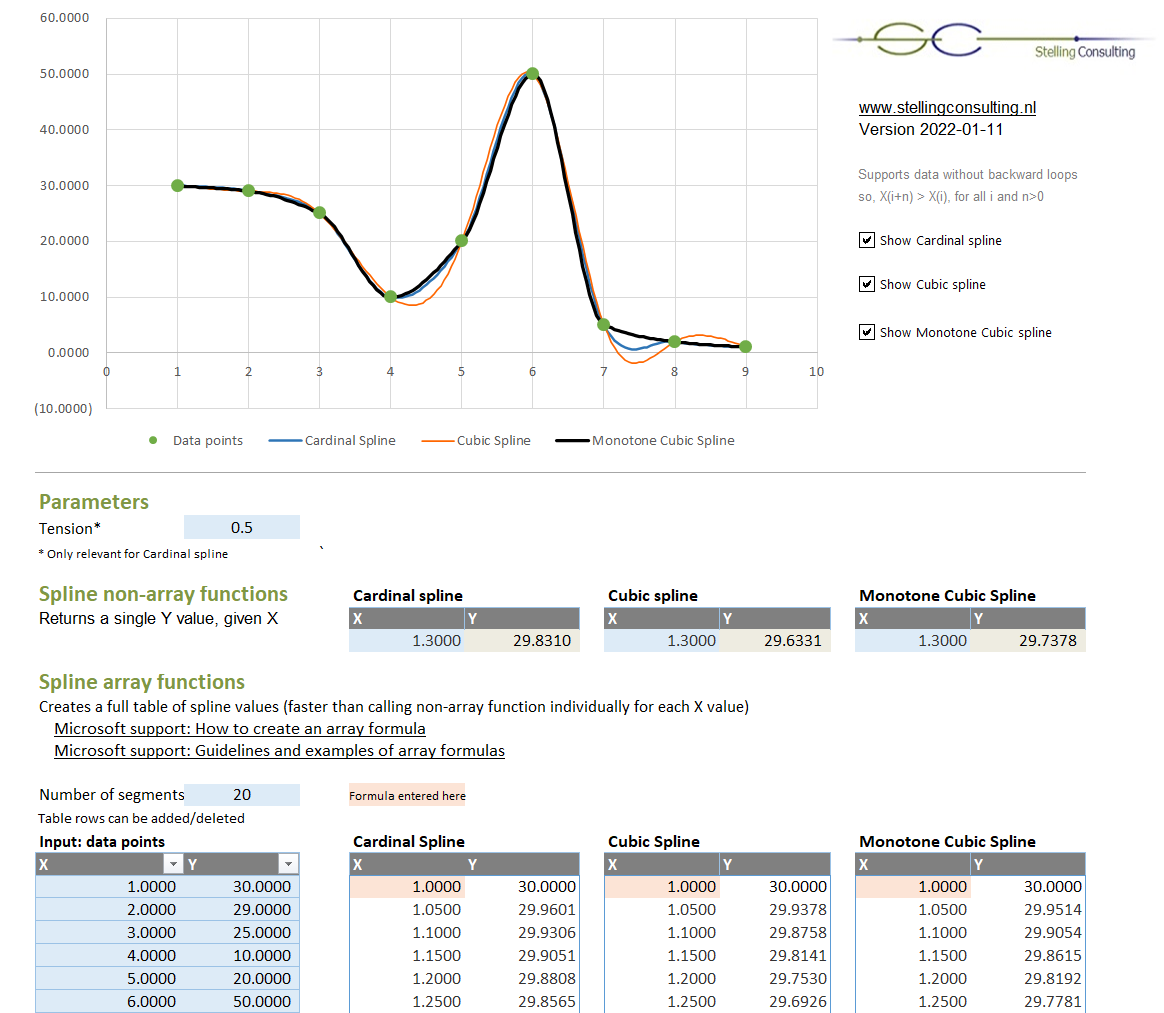
Cardinal spline
Cubic spline
Monotone cubic spline
Regular function — Single Y value output only, given X value
In MS Excel, press Alt+F11 to open the Visual Basic Editor (Windows). Via top menu: Insert → Module. Copy the MS Excel VBA code of the functions into the module.
Cardinal spline
Cubic spline
Monotone cubic spline