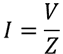Complex numbers with excel - Word и Excel - помощь в работе с программами

Excel for Microsoft 365 Excel for Microsoft 365 for Mac Excel for the web Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 for Mac Excel 2016 Excel 2016 for Mac Excel 2013 Excel 2010 Excel 2007 Excel for Mac 2011 Excel Starter 2010 More…Less

This article describes the formula syntax and usage of the COMPLEX
function in Microsoft Excel.

Description

Converts real and imaginary coefficients into a complex number of the form x + yi or x + yj.

Syntax

COMPLEX(real_num, i_num, [suffix])

The COMPLEX function syntax has the following arguments:

Real_num Required. The real coefficient of the complex number.
I_num Required. The imaginary coefficient of the complex number.
Suffix Optional. The suffix for the imaginary component of the complex number. If omitted, suffix is assumed to be «i».

Note: All complex number functions accept «i» and «j» for suffix, but neither «I» nor «J». Using uppercase results in the #VALUE! error value. All functions that accept two or more complex numbers require that all suffixes match.

Remarks

If real_num is nonnumeric, COMPLEX returns the #VALUE! error value.
If i_num is nonnumeric, COMPLEX returns the #VALUE! error value.
If suffix is neither «i» nor «j», COMPLEX returns the #VALUE! error value.

Example

Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.

Formula	Description	Result
=COMPLEX(3,4)	Complex number with 3 and 4 as the real and imaginary coefficients	3+4i
=COMPLEX(3,4,»j»)	Complex number with 3 and 4 as the real and imaginary coefficients, and j as the suffix	3+4j
=COMPLEX(0,1)	Complex number with 0 and 1 as the real and imaginary coefficients	i
=COMPLEX(1,0)	Complex number with 1 and 0 as the real and imaginary coefficients	1

Need more help?

Источник

In some branches of engineering, it’s inevitable that you’re going to end up working with complex numbers. Fortunately, though, you don’t have to run to another piece of software to perform calculations with these numbers. There is built-in capability to work directly with complex numbers in Excel.

How to Enable Complex Number Calculations in Excel

Microsoft does not automatically expose the complex number functions in default Excel installations.

Why? I don’t know. Maybe to reduce the “complex”-ity?

Sorry – couldn’t help it. J

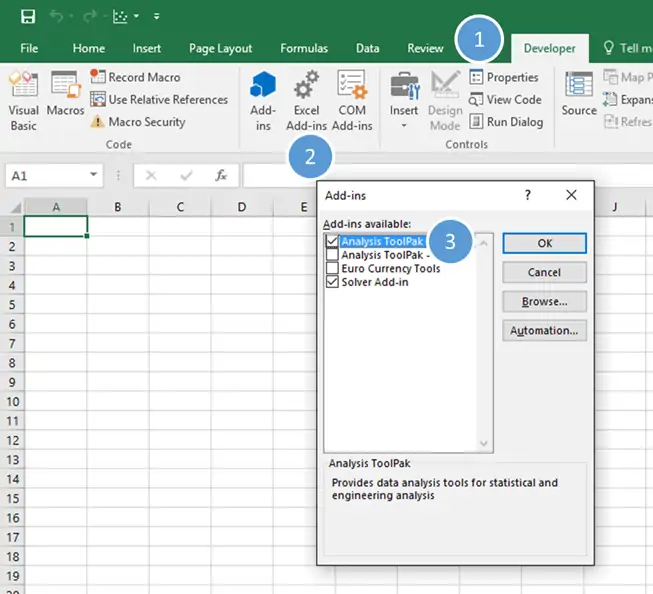
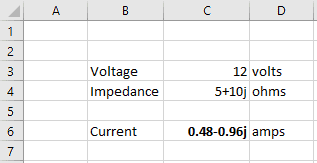
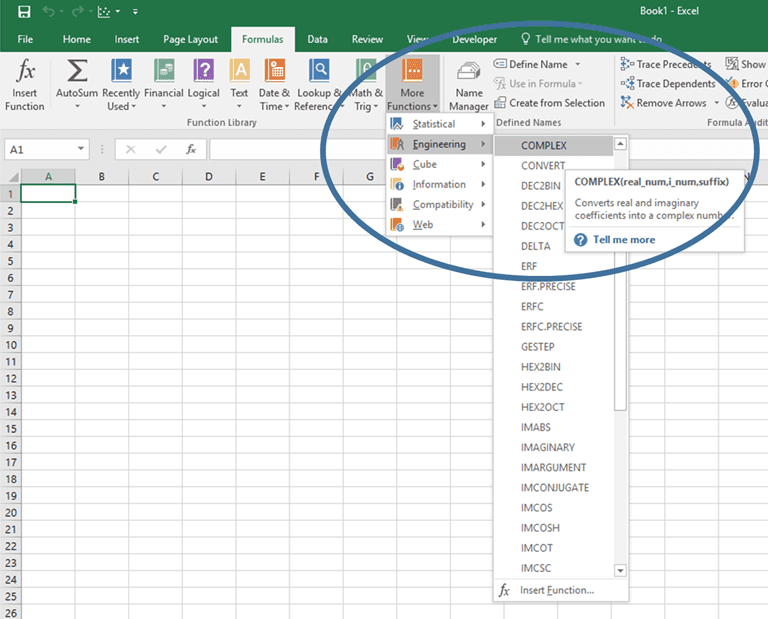
To gain access to them, first enable the Analysis Toolpak Add-In.

Navigate to the Developer Tab
Click “Excel Add-Ins”
Select “Analysis Toolpak”

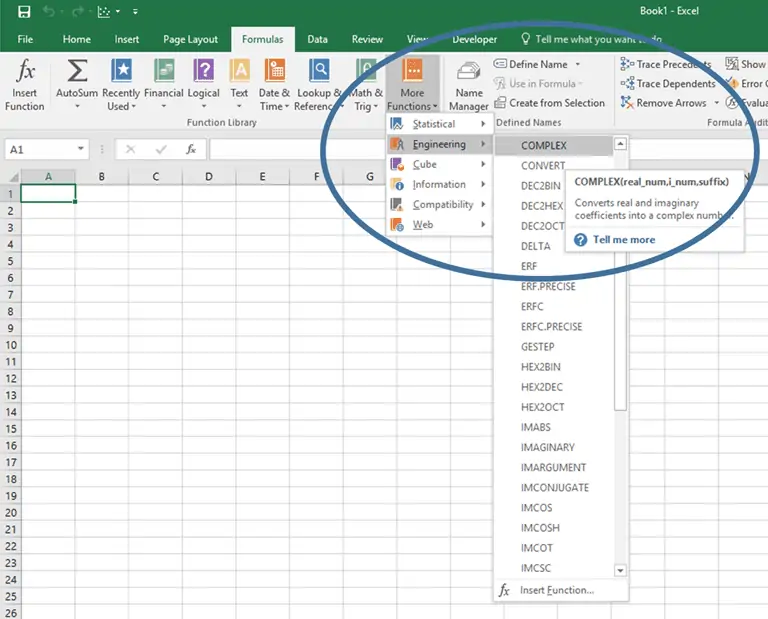
Once turned on, these functions reside in the “Engineering” category of Excel functions.

Complex Number Functions in Excel

The first, and most fundamental, complex number function in Excel converts two components (one real and one imaginary) into a single complex number represented as a+bi. The function is “COMPLEX” and its syntax is as follows:

COMPLEX(real_num, i_num, [suffix])

Where:

real_num is the real part of the complex number

i_num is the imaginary part of the complex number

[suffix] is the letter appended to the imaginary component of the complex number. You can use this optional argument to change the suffix from “i” to “j” if you wish. However, for most of us this can be omitted and the suffix will default to “i”.

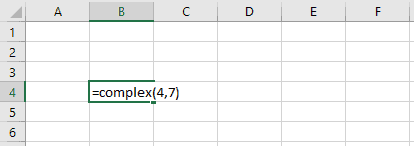
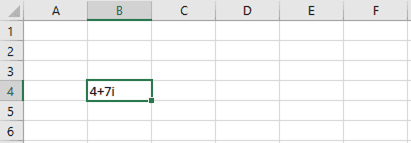
As an example, entering the following equation in Excel:

yields this result:

Conversely, the real and imaginary components of a complex number can be extracted using the IMREAL and IMAGINARY functions, respectively:

If this is where Excel’s complex number capability stopped, it would be a huge disappointment. But Microsoft includes many more useful functions for complex number calculations:

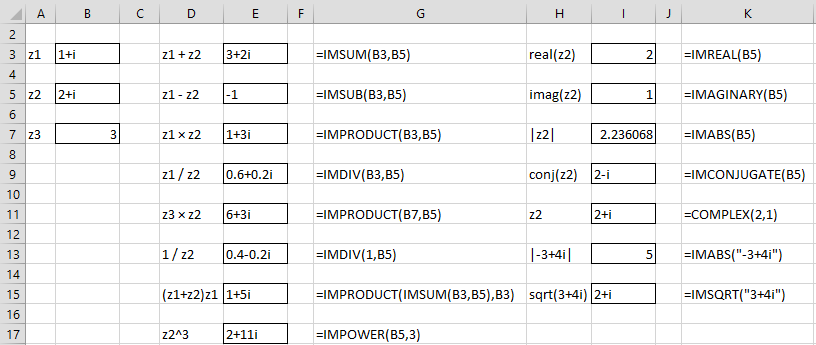
IMABS: Returns the absolute value of a complex number. This is equivalent to the magnitude of the vector.
IMSUM, IMSUB, IMPRODUCT, IMDIV: Return the results of complex number addition, subtraction, multiplication, and division
IMSIN, IMCOS, IMTAN, etc.: Return the sine, cosine, tangent, etc. of a complex number.
IMEXP, IMLN, IMLOG10, IMLOG2: Return the exponential, natural log, log (base 10) and log (base 2) of a complex number

These functions enable many different engineering calculations in Excel, such as analyzing current in an RLC circuit or describing the motion of a damped harmonic oscillator.

Let’s take a look at one of the calculations that Excel’s complex number functions enable: an RLC circuit.

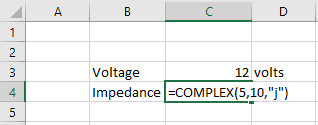
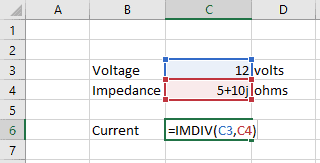
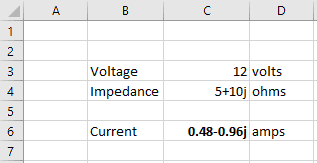
Suppose we have a circuit with a voltage of 12 volts and an impedance (Z) of 5+10j ohms. What is the current in the circuit?

From circuits, we remember that:

As you’ve seen, we can use Excel to handle the complex number calculations.

First, I enter the input values for voltage and impedance.

Since the impedance is a complex number, I use the COMPLEX function in Excel.

In this case, I’ve used the suffix “j” to avoid confusion between the imaginary number “i” and the current “I”.

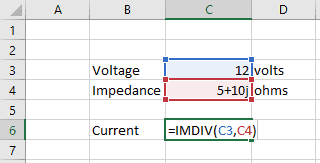
Next, to calculate the current, I divide the voltage by the complex impedance using the function IMDIV.

Finally, we have our result:

Wrap-Up

Complex numbers will always be…umm…complex, I guess. But they don’t have to be difficult. J We can handle calculations involving complex numbers in Excel with a few simple functions.

Источник

Содержание

COMPLEX function
Description
Syntax
Remarks
Example
Функция КОМПЛЕКСН
Описание
Синтаксис
Замечания
Пример
Complex Numbers in Excel
How to Enable Complex Number Calculations in Excel
Complex Number Functions in Excel
Example: Complex Numbers in Excel
Wrap-Up
How to Calculate Complex Numbers in Excel
How to insert a complex number
How to find the real part of a complex number
How to find the imaginary part of a complex number
How to sum complex numbers
Complex number subtraction
How to find the product of complex numbers
How to find the quotient of complex numbers
How to find the absolute value of a complex number
How to find the argument of a complex number
How to find the conjugate of a complex number
How to find the natural logarithm of a complex number
How to find the square root of a complex number
How to find the exponential of a complex number

COMPLEX function

This article describes the formula syntax and usage of the COMPLEX function in Microsoft Excel.

Description

Converts real and imaginary coefficients into a complex number of the form x + yi or x + yj.

Syntax

COMPLEX(real_num, i_num, [suffix])

The COMPLEX function syntax has the following arguments:

Real_num Required. The real coefficient of the complex number.

I_num Required. The imaginary coefficient of the complex number.

Suffix Optional. The suffix for the imaginary component of the complex number. If omitted, suffix is assumed to be «i».

Note: All complex number functions accept «i» and «j» for suffix, but neither «I» nor «J». Using uppercase results in the #VALUE! error value. All functions that accept two or more complex numbers require that all suffixes match.

If real_num is nonnumeric, COMPLEX returns the #VALUE! error value.

If i_num is nonnumeric, COMPLEX returns the #VALUE! error value.

If suffix is neither «i» nor «j», COMPLEX returns the #VALUE! error value.

Example

Complex number with 3 and 4 as the real and imaginary coefficients

Complex number with 3 and 4 as the real and imaginary coefficients, and j as the suffix

Complex number with 0 and 1 as the real and imaginary coefficients

Complex number with 1 and 0 as the real and imaginary coefficients

Источник

Функция КОМПЛЕКСН

В этой статье описаны синтаксис формулы и использование комплексного в Microsoft Excel.

Описание

Преобразует коэффициенты при вещественной и мнимой частях комплексного числа в комплексное число в форме x + yi или x + yj.

Синтаксис

Аргументы функции КОМПЛЕКСН описаны ниже.

Действительная_часть — обязательный аргумент. Действительная часть комплексного числа.

Мнимая_часть — обязательный аргумент. Мнимая часть комплексного числа.

Мнимая_единица — необязательный аргумент. Обозначение мнимой единицы в комплексном числе. Если аргумент «мнимая_единица» опущен, используется суффикс «i».

Примечание: Все функции с комплексными числами принимают суффиксы «i» и «j», но не «I» и «J». Использование верхнего регистра результатов в #VALUE! значение ошибки #ЗНАЧ!. Для всех функций, которые принимают два или более сложных числа, требуется, чтобы все суффиксы совпадали.

Замечания

Если real_num не является числом, то #VALUE! значение ошибки #ЗНАЧ!.

Если i_num не является числом, то #VALUE! значение ошибки #ЗНАЧ!.

Если суффикс не является ни «i», ни «j», то #VALUE! значение ошибки #ЗНАЧ!.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Комплексное число с действительным и мнимым коэффициентами 3 и 4 соответственно

Комплексное число с действительным и мнимым коэффициентами 3 и 4 соответственно и мнимой единицей j

Комплексное число с действительным и мнимым коэффициентами 0 и 1 соответственно

Комплексное число с действительным и мнимым коэффициентами 1 и 0 соответственно

Источник

Complex Numbers in Excel

How to Enable Complex Number Calculations in Excel

Microsoft does not automatically expose the complex number functions in default Excel installations.

Why? I don’t know. Maybe to reduce the “complex”-ity?

Sorry – couldn’t help it. J

To gain access to them, first enable the Analysis Toolpak Add-In.

Navigate to the Developer Tab
Click “Excel Add-Ins”
Select “Analysis Toolpak”

Complex Number Functions in Excel

COMPLEX(real_num, i_num, [suffix])

real_num is the real part of the complex number

i_num is the imaginary part of the complex number

As an example, entering the following equation in Excel:

yields this result:

Conversely, the real and imaginary components of a complex number can be extracted using the IMREAL and IMAGINARY functions, respectively:

If this is where Excel’s complex number capability stopped, it would be a huge disappointment. But Microsoft includes many more useful functions for complex number calculations:

IMABS: Returns the absolute value of a complex number. This is equivalent to the magnitude of the vector.
IMSUM, IMSUB, IMPRODUCT, IMDIV: Return the results of complex number addition, subtraction, multiplication, and division
IMSIN, IMCOS, IMTAN, etc.: Return the sine, cosine, tangent, etc. of a complex number.
IMEXP, IMLN, IMLOG10, IMLOG2: Return the exponential, natural log, log (base 10) and log (base 2) of a complex number

These functions enable many different engineering calculations in Excel, such as analyzing current in an RLC circuit or describing the motion of a damped harmonic oscillator.

Example: Complex Numbers in Excel

Let’s take a look at one of the calculations that Excel’s complex number functions enable: an RLC circuit.

Suppose we have a circuit with a voltage of 12 volts and an impedance (Z) of 5+10j ohms. What is the current in the circuit?

From circuits, we remember that:

As you’ve seen, we can use Excel to handle the complex number calculations.

First, I enter the input values for voltage and impedance.

Since the impedance is a complex number, I use the COMPLEX function in Excel.

In this case, I’ve used the suffix “j” to avoid confusion between the imaginary number “i” and the current “I”.

Next, to calculate the current, I divide the voltage by the complex impedance using the function IMDIV.

Finally, we have our result:

Wrap-Up

Complex numbers will always be…umm…complex, I guess. But they don’t have to be difficult. J We can handle calculations involving complex numbers in Excel with a few simple functions.

Are you struggling to the find the right solutions to your engineering problems in Excel?

In Engineering with Excel, you’ll learn Excel for advanced engineering calculations through a step-by-step system that helps engineers solve difficult problems quickly and accurately.

Источник

How to Calculate Complex Numbers in Excel

Performing calculations on complex numbers in Excel is not difficult because Excel has a set of functions that allow many different calculations of complex numbers.

Complex numbers consist of a real part and an imaginary part. You can perform arithmetic operations on complex numbers. Excel has built-in functions that will make it easier for you to perform complex calculations.

You can use a spreadsheet to perform operations with complex numbers. To use the complex number functions, you must first install the Analysis Toolpak.

The functions that enable this are included in the group of engineering functions. Below we present the most important of them.

Wherever the argument is a complex number, enter it in the form «a + bi» or «a + bj», where i and j denote the imaginary unit. This form can also be obtained in place of the argument by inserting the formula COMPLEX (a; b; «i») or COMPLEX (a; b; «j»).

How to insert a complex number

Use the COMPLEX function to create a complex number. The complex function has three arguments:

real_num — this is the real part of a complex number
i_num — imaginary part
[suffix] — This is an optional argument. If it isn’t fixed, Excel will type i. Sometimes you may want to change to j.

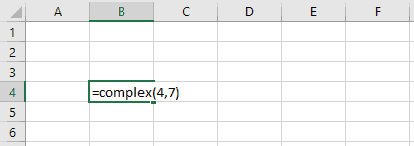
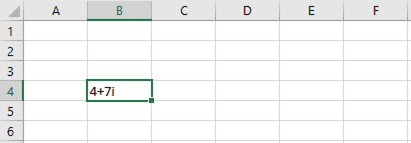
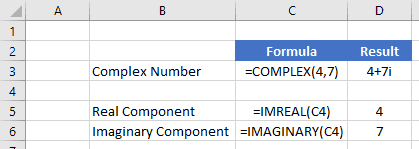
The Complex formula =COMPLEX (5,7) creates a complex number 5 + 7i. 5 is the real part and 7 is the imaginary part.

How to find the real part of a complex number

To find the real part of a complex number use the IMREAL function. The IMREAL function only takes one argument, which is inumber. In my case, using the formula = IMREAL (B3) will return 5 because 5 is the real part of the complex number 5 + 7i

How to find the imaginary part of a complex number

Similarly, to find the imaginary part of a complex number, use the IMAGINARY function. The IMAGINARY function also takes only one argument to inumber. The formula = IMAGINARY (B3) will return 7.

How to sum complex numbers

Use the IMSUM function to sum complex numbers. The syntax for the IMSUM function is = IMSUM (inumber1, inumber2, . ). You must enter a minimum of two complex numbers that you want to add together.

The formula for adding complex numbers in my example is =IMSUM(B3,C3)

Complex number subtraction

Use the IMSUB function to find the difference of complex numbers. The syntax for the IMSUB function is =IMSUB(inumber1, inumber2, . ).

The IMSUB formula I used: =IMSUB(B3,C3)

How to find the product of complex numbers

Use the IMPRODUCT function to find the product of complex numbers.

In my case, the formula product to =IMPRODUCT(B3, C3) i gave the result 2 + 62i.

How to find the quotient of complex numbers

Use the IMDIV function to find the quotient of complex numbers. The imdiv function returns the quotient of two complex numbers.

In my case, the formula quotient is =IMDIV(B3, C3).

How to find the absolute value of a complex number

Use the IMABS function to find the modulus of a complex number. The imabs function returns the absolute value of a complex number.

In my case, the formula imabs is =IMABS(B3).

How to find the argument of a complex number

To find the argument of a complex number, use the IMARGUMENT function. The imargument function returns the argument q of a complex number expressed in radians.

In my case, the formula imabs is =IMARGUMENT(B3).

How to find the conjugate of a complex number

Use the IMCONJUGATE function to find the conjugate of a complex number. The imargument function returns the conjugate of a complex number.

In my case, the formula for imconjugate is =IMCONJUGATE(B3).

IMPOWER (team_number, integer_number) — returns a complex number raised to the power of a given integer.

How to find the natural logarithm of a complex number

Use the IMLN function to find the natural logarithm of a complex number. The imargument function returns the natural logarithm of a complex number.

In my case, the formula imln is =IMLN(B3).

Likewise, you can also calculate:

base-10 logarithm of a complex number using the IMLOG10 function
base-2 logarithm of a complex number using the IMLOG2 function

How to find the square root of a complex number

Use the IMSQRT function to find the square root of a complex number. The imargument function returns the exp of a complex number.

In my case, the formula imexp is =IMSQRT(B3).

How to find the exponential of a complex number

In order to find the exponents of a complex number use the IMEXP function. The imargument function returns the exp of a complex number.

In my case, the formula imexp is =IMEXP(B3).

The other complex functions:

IMCOS function to calculate the cosine of a complex number
IMCOSH function to calculate the hyperbolic cosine of a complex number
IMCOT function to calculate the cotangent of a complex number
IMCSC function to calculate the cosecant of a complex number
IMCSCH function to calculate the hyperbolic cosecant of a complex number
IMSEC function to calculate the secant of a complex number
IMSECH function to calculate the hyperbolic secant of a complex number
IMSIN function to calculate the sine of a complex number
IMSINH function to calculate the hyperbolic sine of a complex number
IMTAN function to calculate the tangent of a complex number

Hope the Excel tutorial of complex number calculator above helped you. I believe that thanks to this knowledge, no complex number calculations will be difficult for you.

Источник

The set of complex numbers consists of all numbers of the form a + bi where a and b are real numbers and i = . We call a the real part of the complex number and b the imaginary part. We define the absolute value of the complex number to be |a + bi| = $sqrt{a^2+b^2}$ . The conjugate of the complex number a + bi is a – bi.

Excel Format

In Excel, complex numbers are represented as text of the form “a + bi”. Excel provides a variety of worksheet functions to deal with complex numbers. Most of these begin with the letters “IM”. Some examples are shown in Figure 1. Note that values that are left-justified are text, while values that are right justified are real numbers.

Figure 1 – Complex number operations in Excel

Excel also provides functions for log (IMLN, IMLOG10, IMLOG2), exponential (IMEXP), various trigonometric functions (IMSIN, IMCOS) square root (IMSQRT) and angle in radians (IMARGUMENT). Additional trigonometric functions are available in Excel 2011, 2013, 2016, 2019 and 365.

Real Statistics Functions: The Real Statistics Resource Pack supplies the following two additional complex number functions:

IMROOTS(z, n) = column array containing the n unique nth roots of the complex number z

IMROUND(z, n) = the complex number equivalent to z with the real and imaginary parts rounded to n decimal places

Real Statistics Format

Excel does not support complex numbers as numeric values, but we can use a 1 × 2 range to represent the complex number a + bi, where the first cell contains the value for a and the second cell contains the value for b.

We now show how to perform the usual operations on complex numbers and define Real Statistics functions that perform the same operations in Excel.

Addition and subtraction are performed using the usual rules from algebra, as is multiplication where we need to use the fact that i² = -1.

Addition	(a + bi) + (c + di) = (a+c) + (b+d)i
Subtraction	(a + bi) – (c + di) = (a–c) + (b–d)i
Multiplication	(a + bi) · (c + di) = (ac–bd) + (ad+bc)i

Note using the fact that a real number c can be expressed as c + 0i, we see that the multiplication of a complex number by a real number can be expressed as

c · (a + bi) = ac + (bc)i

Note too that

i · (a + bi) = –b + ai

The reciprocal of a complex number is equal to its conjugate divided by the square of its absolute value, as shown by the following

Thus, division of c + di by a + bi can be accomplished by first expressing the reciprocal of c + di as described above and then multiplying by a + bi.

We can also express raising a complex number z to a positive integer power recursively by performing repeated multiplications: z¹ = z and zⁿ⁺¹ = z · zⁿ. If n is not an integer, then things get a bit more complicated, but we won’t get into that here.

Worksheet Functions

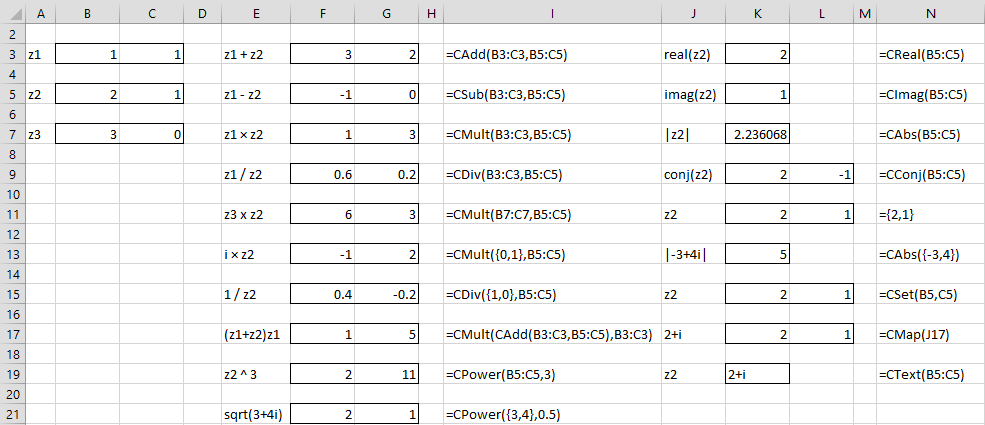
Real Statistics Functions: The Real Statistics Resource Pack supplies the following array functions, where z1, z2 are 1 × 2 ranges which represent complex numbers and a and b are real numbers. We also suppose that z1 represents the complex number c+di.

CReal(z1) = c	CImag(z1) = d
CAdd(z1, z2) = z1 + z2	CSub(z1, z2) = z1 – z2
CMult(z1, z2) = z1 * z2	CDiv(z1, z2) = z1 / z2
CExp(z1) = exp(z1) = e^z1	CLn(z1) = ln(z1)
CAbs(z1) = \|z1\|	CConj(z1) = c – di
CSet(a,b) = a + bi	CMap(“a+bi”) = a + bi
CPower(z1, n) = z1ⁿ	CText(z1) = “c+di”

Here c–di and a+bi are the 1 × 2 range representations of the corresponding complex number. Note that CReal, CImag, CAbs, CConj and CText are ordinary functions, while the others are array functions.

A constant complex number can be represented in the form {a, b}. Thus the complex number 3–4i can be represented by {3,-4}. The complex number i can be represented by {0,1} and the complex number 5.2+0i can be represented by {5.2,0} or simply by 5.2.

In Figure 2, we show the results of various complex number operations.

Figure 2 – Complex number operations

Observations

CAdd can be used with up to 5 arguments; these arguments can be real or complex numbers: e.g. CAdd(B3:C3, B5:C5, B7:C7) or CAdd(B3:C3, B5, B7:C7,-3). The arguments in CSub can be either complex numbers or real numbers: e.g. CSub(B3:C3, 3) or CSub(F3, B5:C5). The first argument in CDiv can be a complex or real number: e.g. CDiv(1,B5:C5).

Multiplication of a complex number z by a real number a can be accomplished by z * a or CMULT(z, CSet(a,0)). Similarly, division of a complex number by a real number can be accomplished by z/a or CDiv(z, CSet(a,0)).

You can convert a complex number in Real Statistics format to one in Excel format via the formula =CText(z1), which is equivalent to the formula

=COMPLEX(CReal(z1),CImag(z1))

You can convert from Excel format to Real Statistics format using the array formula =CMap(z1).

Note that for the complex operations not supported by Real Statistics, you can use the Excel functions (when available). E.g. to get the sine of z1 you can use the formula

=CMap(IMSIN(CText(z1))

References

Lokken, R. (2009) Complex functions in Excel
http://ecampus.matc.edu/lokkenr/pdfs/complex%20numbers.pdf

Varsity Tutors (2021) Operations with complex numbers
https://www.varsitytutors.com/hotmath/hotmath_help/topics/operations-with-complex-numbers

Источник

Performing calculations on complex numbers in Excel is not difficult because Excel has a set of functions that allow many different calculations of complex numbers.

You can use a spreadsheet to perform operations with complex numbers. To use the complex number functions, you must first install the Analysis Toolpak.

At this link you can learn how to add the Analysis Toolpak add-in.

The functions that enable this are included in the group of engineering functions. Below we present the most important of them.

How to insert a complex number

Use the COMPLEX function to create a complex number. The complex function has three arguments:

real_num — this is the real part of a complex number
i_num — imaginary part
[suffix] — This is an optional argument. If it isn’t fixed, Excel will type i. Sometimes you may want to change to j.

The Complex formula =COMPLEX (5,7) creates a complex number 5 + 7i. 5 is the real part and 7 is the imaginary part.

How to find the real part of a complex number

How to find the imaginary part of a complex number

Similarly, to find the imaginary part of a complex number, use the IMAGINARY function. The IMAGINARY function also takes only one argument to inumber. The formula = IMAGINARY (B3) will return 7.

How to sum complex numbers

Use the IMSUM function to sum complex numbers. The syntax for the IMSUM function is = IMSUM (inumber1, inumber2, …). You must enter a minimum of two complex numbers that you want to add together.

The formula for adding complex numbers in my example is =IMSUM(B3,C3)

Complex number subtraction

Use the IMSUB function to find the difference of complex numbers. The syntax for the IMSUB function is =IMSUB(inumber1, inumber2, …).

The IMSUB formula I used: =IMSUB(B3,C3)

How to find the product of complex numbers

Use the IMPRODUCT function to find the product of complex numbers.

In my case, the formula product to =IMPRODUCT(B3, C3) i gave the result 2 + 62i.

How to find the quotient of complex numbers

Use the IMDIV function to find the quotient of complex numbers. The imdiv function returns the quotient of two complex numbers.

In my case, the formula quotient is =IMDIV(B3, C3).

How to find the absolute value of a complex number

Use the IMABS function to find the modulus of a complex number. The imabs function returns the absolute value of a complex number.

In my case, the formula imabs is =IMABS(B3).

How to find the argument of a complex number

To find the argument of a complex number, use the IMARGUMENT function. The imargument function returns the argument q of a complex number expressed in radians.

In my case, the formula imabs is =IMARGUMENT(B3).

How to find the conjugate of a complex number

Use the IMCONJUGATE function to find the conjugate of a complex number. The imargument function returns the conjugate of a complex number.

In my case, the formula for imconjugate is =IMCONJUGATE(B3).

IMPOWER (team_number, integer_number) — returns a complex number raised to the power of a given integer.

How to find the natural logarithm of a complex number

Use the IMLN function to find the natural logarithm of a complex number. The imargument function returns the natural logarithm of a complex number.

In my case, the formula imln is =IMLN(B3).

Likewise, you can also calculate:

base-10 logarithm of a complex number using the IMLOG10 function
base-2 logarithm of a complex number using the IMLOG2 function

How to find the square root of a complex number

Use the IMSQRT function to find the square root of a complex number. The imargument function returns the exp of a complex number.

In my case, the formula imexp is =IMSQRT(B3).

How to find the exponential of a complex number

In order to find the exponents of a complex number use the IMEXP function. The imargument function returns the exp of a complex number.

In my case, the formula imexp is =IMEXP(B3).

The other complex functions:

IMCOS function to calculate the cosine of a complex number
IMCOSH function to calculate the hyperbolic cosine of a complex number
IMCOT function to calculate the cotangent of a complex number
IMCSC function to calculate the cosecant of a complex number
IMCSCH function to calculate the hyperbolic cosecant of a complex number
IMSEC function to calculate the secant of a complex number
IMSECH function to calculate the hyperbolic secant of a complex number
IMSIN function to calculate the sine of a complex number
IMSINH function to calculate the hyperbolic sine of a complex number
IMTAN function to calculate the tangent of a complex number

Hope the Excel tutorial of complex number calculator above helped you. I believe that thanks to this knowledge, no complex number calculations will be difficult for you.

Источник

Summary

The Excel COMPLEX function creates a complex number with given real and imaginary coefficients. COMPLEX returns a text result in the form x + yi or x + yj.

Purpose

Convert coefficients to complex number

Return value

Arguments

real_num — The real number.
i_num — The imaginary number.
suffix — [optional] The suffix, either «i» or «j».

Syntax

=COMPLEX(real_num, i_num, [suffix])

Usage notes

A complex number has two parts: a real number and an imaginary number. The COMPLEX function converts real and imaginary coefficients into a complex number of the form x + yi or x + yj, where x represents the real number and y represents the imaginary number. For example:

=COMPLEX(5,3) // returns 5+3i

To use the «j» instead of «i»:

=COMPLEX(5,3,"j") // returns 5+3j

In the example shown, the formula in E6 is:

=COMPLEX(B6,C6)

Notes:

If omitted, suffix defaults to «i».
suffix must be lowercase «i» or «j»; other values result in a #VALUE error.
If real_num or i_num are nonnumeric, COMPLEX returns the #VALUE! error.

Author

Dave Bruns

Hi — I’m Dave Bruns, and I run Exceljet with my wife, Lisa. Our goal is to help you work faster in Excel. We create short videos, and clear examples of formulas, functions, pivot tables, conditional formatting, and charts.

Great site — amazingly clear but with a lot of depth in terms of the explanations.

Get Training

Quick, clean, and to the point training

Learn Excel with high quality video training. Our videos are quick, clean, and to the point, so you can learn Excel in less time, and easily review key topics when needed. Each video comes with its own practice worksheet.

View Paid Training & Bundles

Help us improve Exceljet

Источник

This Excel tutorial explains how to use the Excel COMPLEX function with syntax and examples.

Description

The Microsoft Excel COMPLEX function converts coefficients (real and imaginary) into a complex number. The complex number can be in either form, x + yi or x + yj.

The COMPLEX function is a built-in function in Excel that is categorized as an Engineering Function. It can be used as a worksheet function (WS) in Excel. As a worksheet function, the COMPLEX function can be entered as part of a formula in a cell of a worksheet.

Syntax

The syntax for the COMPLEX function in Microsoft Excel is:

COMPLEX( real_coefficient, imaginary_coefficient, [suffix] )

Parameters or Arguments

real_coefficient: The real coefficient of the complex number.
imaginary_coefficient: The imaginary coefficient of the complex number.
suffix: Optional. It is either «i» or «j» which is to represent the suffix for the imaginary component of the complex number. If suffix is omitted, it assumes that suffix is «i».

Returns

The COMPLEX function returns a string/text value.
If real_coefficient is not a numeric value, the COMPLEX function will return a #VALUE! error.
If imaginary_coefficient is not a numeric value, the COMPLEX function will return a #VALUE! error.
If suffix is not either «i» or «j», the COMPLEX function will return a #VALUE! error.
If suffix is entered in uppercase (ie «I» or «J» instead of «i» or «j»), the COMPLEX function will return a #VALUE! error.

Applies To

Excel for Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2011 for Mac, Excel 2010, Excel 2007

Type of Function

Worksheet function (WS)

Example (as Worksheet Function)

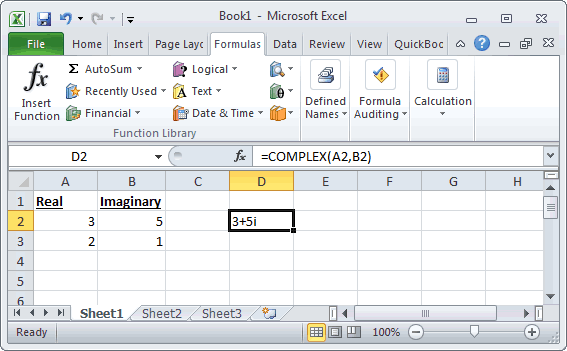
Let’s look at some Excel COMPLEX function examples and explore how to use the COMPLEX function as a worksheet function in Microsoft Excel:

Based on the Excel spreadsheet above, the following COMPLEX examples would return:

=COMPLEX(A2,B2)
Result: "3+5i"

=COMPLEX(A2,B2,"i")
Result: "3+5i"

=COMPLEX(A2,B2,"j")
Result: "3+5j"

=COMPLEX(A3,B3)
Result: "2+i"

=COMPLEX(A3,B3,"i")
Result: "2+i"

=COMPLEX(A3,B3,"j")
Result: "2+j"

Источник