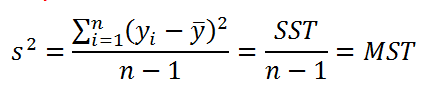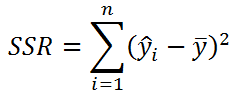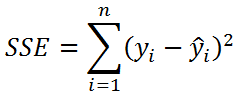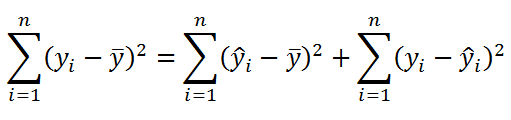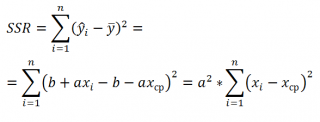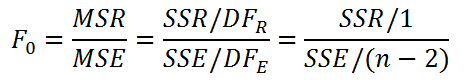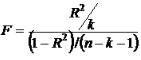- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Курзаева Л.В.
1
1 ФГБОУ ВО «Магнитогорский государственный технический университет им. Г.И. Носова»
Аналитическая статистика – одиниз самых сложных разделов анализа данных в плане изучения, при этом регрессионный анализ является одним из самых информативных. Такой анализ производится при решения следующих задач: установление и оценка взаимосвязи признаков; прогнозирование и предсказание; управление процессами. Существует два вида анализа двумерных данных, представленных переменными: корреляционный и регрессионныйанализ, последнийпозволяет определить форму взаимосвязи между признаками. В статье описывается простой способ проведения регрессионного анализа в MicrosoftExcel. Материалы данной статьи представляют методическую и практическую ценность для преподавателей, занимающихся вопросами повышения эффективности обучения в области основ анализа данных с информационных технологий, и осуществляющие реализацию образовательного процесса в вузах и на курсах повышения квалификаций.
Ключевыеслова: анализ данных
электронные таблицы
1. Овчинникова И.Г., Варфоломеева Т.Н., Гусева Е.Н. Учебно-методическое пособие для подготовки к вступительным экзаменам по информатике. -Магнитогорск, 2002. -С. 119
2. Овчинникова И.Г., Варфоломеева Т.Н., Корнещук Н.Г. Учебное пособие для подготовки к централизованному тестированию по информатике. -Магнитогорск, 2002. -С.205
3. Курзаева Л.В. Дистанционный курс «Основы математической обработки информации»: электронный учебно-методический комплекс // Хроники объединенного фонда электронных ресурсов Наука и образование. — 2014. -Т. 1. — № 12 (67). — С. 117
4. Курзаева Л.В. Введение в теорию систем и системный анализ: учеб. пособие/Л.В. Курзаева. -Магнитогорск: МаГУ, 2015. -211 с.
5. Курзаева Л.В. Введение в методы и средства получения и обработки информации для задач управления социальными и экономическими системами: учеб. пособие/Л.В. Курзаева, И.Г. Овчинникова, Г.Н. Чусавитина. -Магнитогорск:Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2016. -118 с.
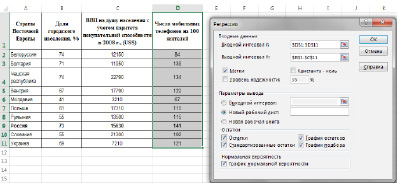
Для реализации процедуры Регрессия необходимо: выбрать в меню Сервис команду Анализ данных. В появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать строку Регрессия.
Рис.1. Окно «Регрессия»
В появившемся диалоговом окне (рис.1) задать:
Входной интервал Y– диапазон (столбец), содержащий данные со значениями объясняемой переменной;
Входной интервал Х– диапазон (столбцы), содержащий данные с заголовками.
Метки – флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет;
Константа-ноль– флажок, указывающий на наличие или отсутствие свободного члена в уравнении (а);
Уровень надежности– уровень значимости, (например, 0,05);
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет по построению модели;
Новый рабочий лист– поставить значок и задать имя нового листа (Отчет – регрессия), в котором будет сохранен отчет.
Если необходимо получить значения и график остатков, а также график подбора (чтобы визуально проверить отличие экспериментальных точек от предсказанных по регрессионной модели), установите соответствующие флажки в диалоговом окне.
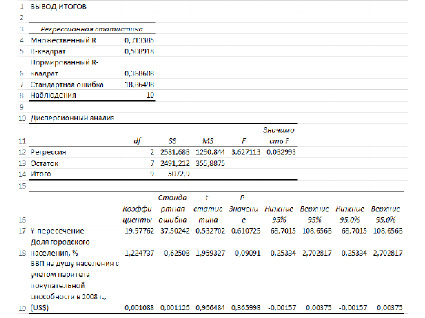
Рассмотрим результаты регрессионного анализа (рис. 2, 3).
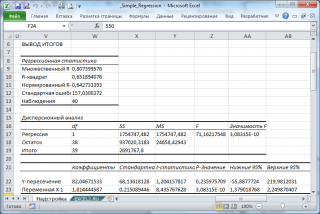
Рис. 2. Вывод итогов регрессионного анализа
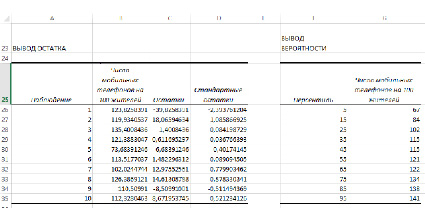
Рис. 3. Вывод остатков и вероятности по результатам регрессионного анализа
Множественный R – коэффициент корреляции
R-квадрат – это коэффициент линейной детерминации. Коэффициент является одной из наиболее эффективных оценок адекватности регрессионной R2модели, мерой качества уравнения регрессии в целом (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям.
Если R-квадрат > 0,95, говорят о высокой точности аппроксимации (модель хорошо описывает явление). Если R-квадрат лежит в диапазоне от 0,8 до 0,95, говорят об удовлетворительной аппроксимации (модель в целом адекватна описываемому явлению). Если R-квадрат < 0,6, принято считать, что точность аппроксимации недостаточна и модель требует улучшения (введения новых независимых переменных, учета нелинейностей и т. д.).
Нормированный R-квадрат – скорректированный (адаптированный, поправленный) коэффициент детерминации.
Недостатком коэффициента детерминации R-квадратявляется то, что он увеличивается при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. В этом смысле предпочтительнее использовать нормированный, который в отличие от R-квадрат может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенное влияние на зависимую переменную.
Наблюдения – число наблюдений (в нашем случае 10 стран).
Df– число степеней свободы связано с числом единиц совокупности и с числом определяемых по ней констант.
F и Значимость F позволяют проверить значимость уравнения регрессии, т.е. установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
SS – Сумма квадратов отклонений значений признака Y.
MS – Дисперсия на одну степень свободы.
F – Наблюдаемое (эмпирическое) значение статистики F, по которой проверяется гипотеза равенства нулю одновременно всех коэффициентов модели. Значимость F – теоретическая вероятность того, что при гипотезе равенства нулю одновременно всех коэффициентов модели F-статистика больше эмпирического значения F.
На уровне значимости α=0,05 гипотеза H0:b1=0отвергается, если Значимость F<0.05, и принимается, если Значимость F
Значения коэффициентов регрессии находятся в столбце Коэффициенты и соответствуют:
У-пересечение – a;
переменная XI – b1;
переменная Х2 – b2 и т. Д.
Таким образом, получена следующая модель регрессии:
Y=1.2247X1+0.00108X2+19.9776
t-статистика соответствующего коэффициента.
P-Значение – вероятность, позволяющая определить значимость коэффициента регрессии. В случаях, когда Р-Значение>0,05, коэффициент может считаться нулевым, что означает, что соответствующая независимая переменная практически не влияет на зависимую переменную.
В нашем случае оба коэффициента оказались «нулевыми», а значит обе независимые переменные не влияют на модель.
Нижние 95% – Верхние 95% – доверительный интервал для параметра , т.е. с надежностью 0.95 этот коэффициент лежит в данном интервале. Поскольку коэффициент регрессии в исследованиях имеют четкую интерпретацию, то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов. Так, например, «Доля городского населения, в %» не может лежать в интервале -0,25≥b1≥2,7. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
Предсказанное Y — теоретические (расчетные) значения результативного признака.
Остатки – остатки по модели регрессии.
На основе данных об остатках модели регрессии был построен график остатков (рис. 4) и график подбора – поле корреляции фактических и теоретических (расчетных) значений результативной переменной (рис.5).
Рис. 4. График остатков по значениям признака «Доля городского населения, %»
Рис. 5. График подбора для признаков «Доля городского населения, %» и «Число мобильных телефонов на 100 жителей»
Рассмотрение графиков подбора позволяет предположить, что, возможно, качество модели можно усовершенствовать, исключив данные по Белоруссии как аномальные значения.
Библиографическая ссылка
Курзаева Л.В. РЕГРЕССИОННЫЙ АНАЛИЗ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 12-7.
– С. 1234-1238;
URL: https://applied-research.ru/ru/article/view?id=11019 (дата обращения: 17.04.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Проведем проверку значимости простой линейной регрессии с помощью процедуры
F
-тест.
Disclaimer
: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей
Регрессионного анализа.
Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения
Регрессии
– плохая идея.
Проверку значимости взаимосвязи переменных в рамках модели
простой линейной регрессии
можно провести разными, но эквивалентными между собой, способами:
Проверку значимости взаимосвязи переменных в рамках модели простой линейной регрессии можно провести разными, но эквивалентными между собой, способами:
-
проверка гипотезы о равенстве 0 коэффициента регрессии
, т.е. наклона;
-
проверка статистической значимости коэффициента корреляции
;
-
с использованием дисперсионного анализа (процедура
F
-тест
).
Процедуру
F
-теста
рассмотрим на примере
простой линейной регрессии
, когда прогнозируемая переменная Y зависит только от одной переменной Х.
Чтобы определить может ли предложенная модель
линейной регрессии
быть использована для адекватного описания значений переменной Y,
дисперсию
наблюдаемых данных анализируют методом
Дисперсионного анализа (ANOVA for Simple Regression)
.
Дисперсия
данных разбивается на компоненты, которые затем используются в
F
-тесте
для определения значимости регрессии.
F
-тест для проверки значимости регрессии
НЕ относится к простым и интуитивно понятным процедурам. Вероятно, это связано с тем, что для проведения
F
-теста
требуется быть знакомым с определенным количеством статистических понятий и нужно неплохо разбираться в связанных с ними статистических методах. Нам потребуются понятия из следующих разделов статистики:
-
регрессионный анализ
;
-
процедура проверки гипотез
;
-
статистики и выборочные распределения
;
-
распределение Фишера
;
-
уровень значимости
.
Можно, конечно, рассмотреть
F
-тест
формально:
-
вычислить на основании выборки значение
тестовой
F
статистики;
-
сравнить полученное значение со значением, соответствующему заданному
уровню значимости
;
-
в зависимости от соотношения этих величин принять решение о значимости вычисленной
линейной регрессии
В этой статье ставится более амбициозная задача – разобраться в самом подходе, на котором основан
F
-тест
. Сначала введем несколько определений, которые используются в процедуре
F
-теста
, затем рассмотрим саму процедуру.
Примечание
: Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к
вычислительной части
.
Определения, необходимые для
F
-теста
Согласно
определению дисперсии
,
дисперсия выборки
прогнозируемой переменной Y определяется формулой:
В формуле используется ряд сокращений:
- SST (Total Sum of Squares) – это просто компактное обозначение Суммы Квадратов отклонений от среднего (такое сокращение часто используется в зарубежной литературе).
- MST (Total Mean Square) – Среднее Суммы Квадратов отклонений (еще одно общеупотребительное сокращение).
Примечание
: Необходимо иметь в виду, что с одной стороны величины MST и SST являются случайными величинами, вычисленными на основании выборки, т.е.
статистиками
. Однако с другой стороны, при проведении
регрессионного анализа
по данным имеющейся выборки вычисляются их конкретные значения. В этом случае величины MST и SST являются просто числами.
Значение n-1 в вышеуказанной формуле равно
числу степеней свободы (
DF
)
, которое относится к
дисперсии выборки
(одна
степень свободы
у
n
величин yi потеряна в результате наличия ограничения
, связывающего все значения выборки). Число
степеней свободы
у величины SST также имеет специальное обозначение: DFT (DF Total).
Как видно из формулы, отношение величин SST и DFT обозначается как MST. Эти 3 величины обычно выдаются в таблице результатов
дисперсионного анализа
в различных прикладных статистических программах (в том числе и в
надстройке Пакет анализа, инструмент Регрессия
).
Значение SST, характеризующую
общую
изменчивость переменной
Y, можно разбить на 2 компоненты:
Изменчивость объясненную моделью
(Explained variation), обозначается SSR
Необъясненную изменчивость
(Unexplained variation), обозначается SSЕ
Известно
, что справедливо равенство:
SST
=
SSR
+
SSE
Величинам
SSR
и
SSE
также сопоставлены
степени свободы
. У
SSR
одна
степень свободы
, т.к. она однозначно определяется одним параметром – наклоном
линии регрессии
a
(напомним, что мы рассматриваем
простую линейную регрессию
). Это очевидно из формулы:
Примечание:
Очевидность наличия только одной
степени свободы
проистекает из факта, что переменная Х – контролируемая (не является случайной величиной).
Число степеней свободы
величины
SSR
имеет специальное обозначение:
DFR
(для простой регрессии DFR=1, т.к. число независимых переменных Х равно 1)
.
По аналогии с MST, отношение этих величин также часто обозначают
MSR
=
SSR
/
DFR
.
У
SSE
число степеней свободы
равно
n
-2
, которое обозначается как
DFE
(или
DFRES
— residual degrees of freedom).
Двойка вычитается, т.к. изменчивость переменной yi имеет 2 ограничения, связанные с оценкой 2-х параметров линейной модели (
а
и
b
): ŷi=a*xi+b
Отношение этих величин также часто обозначают
MSE
=
SSE
/
DFE
.
MSR и MSE имеют размерность дисперсий, хотя корректней их называть средними значениями квадратов отклонений. Тем не менее, ниже мы их будем «дисперсиями», т.к. они отображают меру разброса: MSE – меру разброса точек наблюдений относительно линии регрессии, MSR показывает насколько линия регрессии совпадает с горизонтальной линией среднего значения Y.
Примечание
: Напомним, что MSE (Mean Square of Errors) является оценкой
дисперсии
s
2
ошибки, подробнее см. статью про
линейную регрессию
, раздел
Стандартная ошибка регрессии
.
Число степеней свободы
обладает свойством аддитивности:
DFT
=
DFR
+
DFE
.
В этом можно убедиться, составив соответствующее равенство
n
-1=1+(
n
-2)
Наконец, определившись с определениями, переходим к рассмотрению самой процедуры
F
-тест
.
Процедура
F
-теста
Сущность
F
-теста
при проверке значимости регрессии заключается в том, чтобы сравнить 2
дисперсии
:
объясненную
моделью (MSR) и
необъясненную
(MSE). Если эти
дисперсии
«примерно равны», то
регрессия незначима
(построенная модель не позволяет объяснить поведение прогнозируемой Y в зависимости от значений переменной Х). Если
дисперсия,
объясненная
моделью (MSR) «существенно больше», чем необъясненная, то
регрессия значимая
.
Примечание
: Чтобы быстрее разобраться с процедурой
F
-теста
рекомендуется вспомнить процедуру проверки статистических гипотез о равенстве дисперсий 2-х
нормальных распределений
(т.е.
двухвыборочный F-тест для дисперсий
).
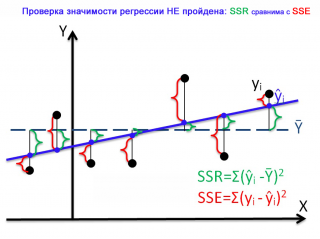
Чтобы пояснить вышесказанное изобразим на
диаграммах рассеяния
2 случая:
- регрессия значима (в этом случае имеем значительный наклон прямой) и
- регрессия незначима (линия регрессии близка к горизонтальной прямой).
На первой диаграмме показан случай, когда регрессия значима:
- Зеленым цветом выделены расстояния от среднего значения до линии регрессии , вычисленные для каждого хi. Сумма квадратов этих расстояний равна SSR;
- Красным цветом выделены расстояния от линии регрессии до соответствующих точек наблюдений . Сумма квадратов этих расстояний равна SSЕ.
Из диаграммы видно, что в случае значимой регрессии, сумма квадратов «зеленых» расстояний, гораздо больше суммы квадратов «красных». Понятно, что их отношение будет гораздо больше 1. Следовательно, и отношение дисперсий MSR и MSE будет гораздо больше 1 (не забываем, что SSE нужно разделить еще на соответствующее количество степеней свободы n-2).
В случае значимой регрессии точки наблюдений будут находиться вдоль линии регрессии. Их разброс вокруг этой линии описываются ошибками регрессии, которые были минимизированы посредством
процедуры МНК
. Очевидно, что разброс точек относительно линии регрессии значительно меньше, чем относительно горизонтальной линии, соответствующей среднему значению Y.
Совершенно другую картину мы можем наблюдать в случае незначимой регрессии.
Очевидно, что в этом случае, сумма квадратов «зеленых» расстояний, примерно соответствует сумме квадратов «красных». Это означает, что объясненная дисперсия примерно соответствует величине необъясненной дисперсии (MSR/MSE будет близко к 1).
Если ответ о значимости регрессии практически очевиден для 2-х вышеуказанных крайних ситуаций, то как сделать правильное заключение для промежуточных углов наклона линии регрессии?
Понятно, что если вычисленное на основании выборки значение MSR/MSE будет существенно больше некоторого критического значения, то регрессия значима, если нет, то не значима. Очевидно, что это значение должно быть больше 1, но
как определить это критическое значение статистически обоснованным методом
?
Вспомним, что для формулирования статистического вывода (т.е. значима регрессия или нет) используют
проверку гипотез
. Для этого формулируют 2 гипотезы: нулевую
Н
0
и альтернативную
Н
1
. Для проверки значимости регрессии в качестве
нулевой гипотезы
Н
0
принимают, что связи нет, т.е. наклон прямой a=0. В качестве альтернативной гипотезы
Н
1
принимают, что a <>0.
Примечание
: Даже если связи между переменными нет (a=0), то вычисленная на основании данных выборки оценка
наклона
— величина
а
, из-за случайности выборки будет близка, но все же отлична от 0.
По умолчанию принимается, что нулевая гипотеза верна – связи между переменными нет. Если это так, то:
- MSR/MSE будет близко к 1;
-
Случайная величина F = MSR/MSE будет иметь
F-распределение
со степенями свободы
1 (в числителе) и n-2 (знаменателе). F является
тестовой статистикой
для проверки значимости регрессии.
Примечание
: MSR и MSE являются случайными величинами (т.к. они получены на основе случайной выборки). Соответственно, выражение F=MSR/MSE, также является случайной величиной, которая имеет свое распределение,
среднее значение
и
дисперсию
.
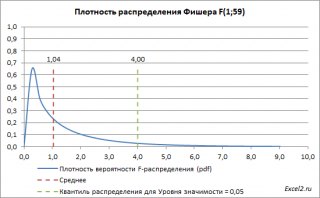
Ниже приведен
график плотности вероятности F-распределения
со степенями свободы
1 (в числителе) и 59 (знаменателе). 59=61-2, 61 наблюдение минус 2 степени свободы.
Если нулевая гипотеза верна, то значение F
0
=MSR/MSE, вычисленное на основании выборки, должно быть около ее
среднего значения
(т.е. около 1,04). Если F
0
будет существенно больше 1 (чем больше F0 отклоняется в сторону больших значений, тем это маловероятней), то это будет означать, что F не имеет
F-распределение
, а, следовательно, нулевую гипотезу нужно отклонить и принять альтернативную, утверждающую, что связь между переменными есть (значима).
Обычно предполагают, что если вероятность, того что
F
-статистика
приняла значение F0 составляет менее 5%, то это событие маловероятно и нулевую гипотезу необходимо отклонить. 5% — это
заданный
исследователем
уровень значимости
, который может быть, например, 1% или 10%.
Значение статистики F0 может быть вычислено на основании выборки:
Вычисления в
MS
EXCEL
В MS EXCEL критическое значение для заданного
уровня значимости
F1-альфа, 1, n-2 можно вычислить по формуле =
F.ОБР(1- альфа;1; n-2)
или =
F.ОБР.ПХ(альфа;1; n-2)
. Другими словами требуется вычислить
верхний альфа-квантиль F-распределения
с соответствующими
степенями свободы
.
Таким образом, при значении статистики F0> F1-альфа, 1, n-2 мы имеем основание для отклонения нулевой гипотезы.
Значение F
0
можно вычислить на основании значений выборки по вышеуказанной формуле или с
помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН($C$23:$C$83;$B$23:$B$83;;ИСТИНА);4;1)
В случае простой регрессии значение F0 также равно квадрату t-статистики, которую мы использовали при проверке двусторонней гипотезе
о равенстве 0 коэффициента регрессии
.
Проверку значимости регрессии можно также осуществить через вычисление p-значения. В этом случае вычисляют вероятность того, что случайная величина F примет значение F0 (это и есть p-значение), затем сравнивают p-значение с заданным
уровнем значимости
. Если p-значение больше
уровня значимости,
то нулевую гипотезу нет оснований отклонить, и регрессия незначима.
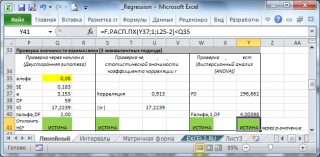
В MS EXCEL для проверки гипотезы используя
p
-значение
используйте формулу =
F.РАСП.ПХ(F0;1;n-2)
< альфа
Если формула вернет ИСТИНА, то регрессия значима. Если формула вернет ЛОЖЬ, то у нас нет оснований отклонить нулевую гипотезу, т.е. «скорее всего» параметр модели a равен 0 (см.
файл примера
, где показано эквивалентность всех подходов проверки значимости регрессии).
В программах статистики результаты процедуры
F
-теста
выводят с помощью стандартной таблицы
дисперсионного анализа
. В
файле примера
такая таблица приведена на листе Таблица, которая построена на основе результатов, возвращаемых
инструментом Регрессия надстройки Пакета анализа MS EXCEL
.
Для
оценки существенности, значимости
коэффициента корреляции используется
t-критерий
Стьюдента.
Находится средняя
ошибка коэффициента корреляции по
формуле:
На
основе ошибки рассчитываетсяt-критерий:
Рассчитанное
значение t-критерия
сравнивают с табличным, найденным в
таблице распределения Стьюдента при
уровне значимости 0,05 или 0,01 и числе
степеней свободы n-1.
Если расчетное значение t-критерия
больше табличного, то коэффициент
корреляции признается значимым.
При
криволинейной связи для оценки значимости
корреляционного отношения и уравнения
регрессии применяется F-критерий.
Он вычисляется по формуле:
или
где
η – корреляционное отношение; n
– число наблюдений; m
– число параметров в уравнении регрессии.
Рассчитанное
значение F
сравнивается с табличным для принятого
уровня значимости α (0,05 или 0,01) и чисел
степеней свободы к1=m-1
и k2=n-m.
Если расчетное значение F
превышает табличное, связь признается
существенной.
Значимость
коэффициента регрессии устанавливается
с помощью t-критерия Стьюдента,
который вычисляется по формуле:
где
σ2аi
— дисперсия коэффициента регрессии.
Она
вычисляется по формуле:
где
к – число факторных признаков в уравнении
регрессии.
Коэффициент
регрессии признается значимым, если
ta1≥tкр.
tкр
отыскивается в таблице критических
точек распределения Стьюдента при
принятом уровне значимости и числе
степеней свободы k=n-1.
4.3.Корреляционно-регрессионный анализ в Excel
Проведём
корреляционно-регрессионный анализ
взаимосвязи урожайности и затрат труда
на 1 ц зерна. Для этого открываем лист
Excel,
в ячейки А1:А30 вводим значения факторного
признака –
урожайности зерновых культур, в ячейки
В1:В30 значения результативного признака
– затрат труда
на 1 ц зерна. В меню Сервис выберем опцию
Анализ данных. Щелкнув левой кнопкой
мыши по этому пункту, откроем инструмент
Регрессия. Щелкаем по кнопке OK,
на экране появляется диалоговое окно
Регрессия. В поле Входной интервал У
вводим значения результативного признака
(выделяя ячейки В1:В30), в поле Входной
интервал Х вводим значения факторного
признака (выделяя ячейки А1:А30). Отмечаем
уровень вероятности 95%, выбираем Новый
рабочий лист. Щелкаем по кнопке OK.
На рабочем листе появляется таблица
«ВЫВОД ИТОГОВ», в которой даны результаты
вычисления параметров уравнения
регрессии, коэффициента корреляции и
другие показатели, позволяющие определить
значимость коэффициента корреляции и
параметров уравнения регрессии.
|
ВЫВОД |
||||||||
|
Регрессионная |
||||||||
|
Множественный |
0,853301 |
|||||||
|
R-квадрат |
0,728123 |
|||||||
|
Нормированный |
0,718413 |
|||||||
|
Стандартная |
0,112121 |
|||||||
|
Наблюдения |
30 |
|||||||
|
Дисперсионный |
||||||||
|
df |
SS |
MS |
F |
Значимость |
||||
|
Регрессия |
1 |
0,942676 |
0,942676 |
74,9876 |
2,09E-09 |
|||
|
Остаток |
28 |
0,351991 |
0,012571 |
|||||
|
Итого |
29 |
1,294667 |
||||||
|
Коэффициенты |
Стандартная |
t-статистика |
P-Значение |
Нижние |
Верхние |
Нижние |
Верхние |
|
|
Y-пересечение |
2,836242 |
0,200011 |
14,18042 |
2,64E-14 |
2,426538 |
3,245947 |
2,426538 |
3,245947 |
|
Переменная |
-0,06654 |
0,007684 |
-8,65954 |
2,09E-09 |
-0,08228 |
-0,0508 |
-0,08228 |
-0,0508 |
В
данной таблице «Множественный R»
— это коэффициент корреляции, «R-квадрат»
— коэффициент детерминации. «Коэффициенты:
Y-пересечение»
— свободный член уравнения регрессии
2,836242; «Переменная Х1» – коэффициент
регрессии -0,06654. Здесь имеются также
значения F-критерия
Фишера 74,9876, t-критерия
Стьюдента 14,18042, «Стандартная ошибка
0,112121», которые необходимы для оценки
значимости коэффициента корреляции,
параметров уравнения регрессии и всего
уравнения.
На
основе данных таблицы построим уравнение
регрессии: ух=2,836-0,067х.
Коэффициент регрессии а1=-0,067
означает, что с повышением урожайности
зерновых на 1 ц/га затраты труда на 1 ц
зерна уменьшаются на 0,067 чел.-ч.
Коэффициент
корреляции r=0,85>0,7,
следовательно, связь между изучаемыми
признаками в данной совокупности тесная.
Коэффициент детерминации r2=0,73
показывает, что 73% вариации результативного
признака (затрат труда на 1 ц зерна)
вызвано действием факторного признака
(урожайности зерновых).
В
таблице критических точек распределения
Фишера — Снедекора найдём критическое
значение F-критерия
при уровне значимости 0,05 и числе степеней
свободы к1=m-1=2-1=1
и k2=n-m=30-2=28,
оно равно 4,21. Так как рассчитанное
значение критерия больше табличного
(F=74.9896>4,21),
то уравнение регрессии признаётся
значимым.
Для
оценки значимости коэффициента корреляции
рассчитаем t-критерий
Стьюдента:
Втаблице критических точек распределения
Стьюдента найдём критическое значениеt-критерия
при уровне значимости 0,05 и числе степеней
свободы n-1=30-1=29,
оно равно 2,0452. Так как расчётное значение
больше табличного, то коэффициент
корреляции является значимым.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В таблице Дисперсионный анализ оценивается общее качество полученной модели:
ее достоверность по уровню значимости критерия Фишера — р, который должен быть
меньше, чем 0,05 (строка Регрессия, столбец Значимость F).
Значение R-квадрат описывает степень точности описания моделью процесса
(вторая строка сверху в таблице Регрессионная статистика).
Далее определяем значения коэффициентов модели.
Они определяютя из таблицы в столбце Коэффициенты — в строке Y-пересечение — свободный член,
в строках соответствующих переменных — значения коэффициентов при этих переменных.
В столбце р-значение приводится достоверность отличия соответствующих коэффициентов от нуля.
В случае, когда р>0,05, коэффициент может считаться нулевым.
Это означает, что соответствующая независимая переменная практически не влияет на зависимую
переменную и коэффициент может быть убран из уравнения.
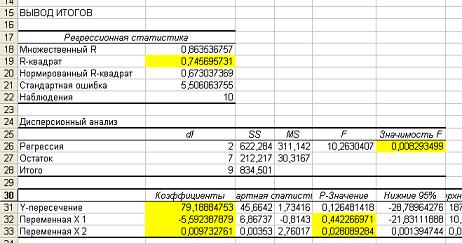
Именно поэтому в данной задаче дается такая интерпретация:
Достоверность по уровню значимости критерия Фишера (Значимость F) значительно меньше 0,05, значит модель значима.
Степень точности описания моделью процесса R-квадрат равен 0,75, что говорит о высокой точности аппроксимации (модель хорошо описывает процесс).
p-значение для коэффициента х1 больше 0,05, значит этот коэффициент может считаться нулевым.
p-значение для коэффициента х2 меньше 0,05, значит этот коэффициент может считаться не нулевым.
Значение свободного члена (Y-пересечение) 79,19.
Отсюда уравнение для расчета выхода телят на 100 коров (y) от среднегодового потребления кормовых единиц (x2) и среднего возраста стада (x1) будет иметь вид y=0,0097x2+79,19 с достоверностью R2=75%.
Функция FПАСПОБР в Excel используется для проверки значимости модели регрессии с применением F-критерия (критерий Фишера), и возвращает числовое значение, соответствующее обратному значению для F-распределения вероятностей (верхнему квантилю). Например, если в качестве вероятности (первый аргумент функции) было введено значение уровня значимости, к примеру, 0,08, то FПАСПОБР вычислит значение случайной величины x, для которой выполняется следующее условие – P(X>x) = 0,08.
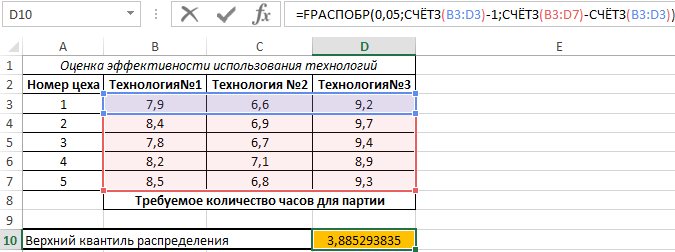
Функция FРАСПОБР для оценки значимости параметров модели регрессии
Критическое значения F может быть определено в случае, если в качестве первого аргумента рассматриваемой функции будет введено значение уровня значимости.
Для расчета F используется следующая формула:
Функция оперирует двумя дополнительными критериями:
- Числитель степеней свободы: n1 = k.
- Знаменатель степеней свободы: n2 = (n – k – 1).
Через переменную k обозначают число факторов, которые были включены в исследуемую модель регрессии.
В Excel предусмотрена функция для расчета вероятности для распределения Фишера – FРАСП. Между данной и рассматриваемой функциями существует следующая взаимосвязь: =FРАСПОБР(FРАСП(x;n1;n2);n1;n2)=x.
Примечание:
В MS Office 2007 и более поздних версиях была введена функция F.ОБР.ПХ, которая заменила рассматриваемую функцию. FПАСПОБР была оставлена для обеспечения совместимости с документами, созданными в более старых версиях Excel.
Определение верхнего квартиля F-распределения Фишера в Excel
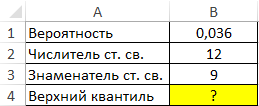
Пример 1. В таблице указаны вероятность, связанная с распределением Фишера, а также числитель и знаменатель степеней свободы соответственно. Определить верхний квантиль данного F-распределения.
Вид таблицы данных:
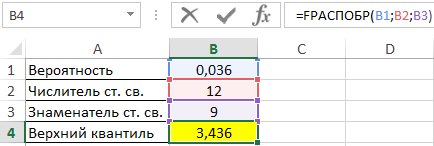
Вычислим искомое значение с помощью функции:
=FРАСПОБР(B1;B2;B3)
Полученное число:
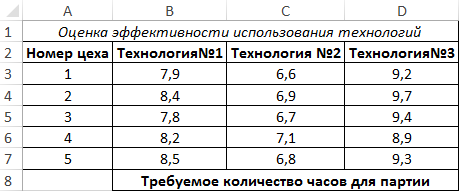
Оценка в Excel эффективности использования технологий на производстве
Пример 2. На заводе есть несколько цехов по производству одного типа продукции. Существует 3 различные технологии изготовления данной продукции. Для оценки были записаны данные о количестве часов, необходимых для производства одной партии продукции каждым цехом с использованием каждой из трех технологий. Оценить эффективность использования технологий, проанализировать полученные значения.
Вид таблицы данных:
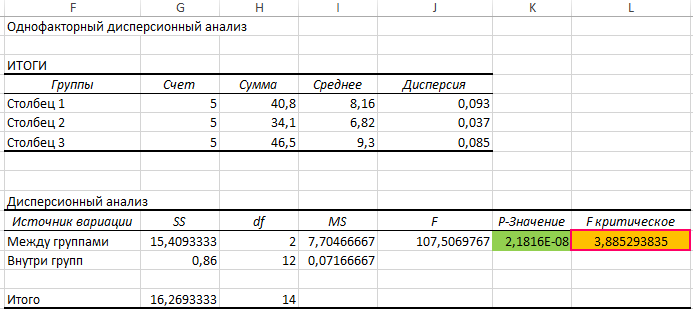
Проведем однофакторный дисперсионный анализ для данных, находящихся в диапазоне ячеек B3:D7, используя соответствующую надстройку Excel. Полученная таблица результатов:
По условия поставленной задачи нас интересует выделенное значение. Поскольку оно <0,05, между данными существует линейная зависимость. В результате анализа уже было определено значение, возвращаемое функцией FРАСПОБР (F критическое). Для расчета можно было использовать функцию:
Здесь СЧЁТЗ(B3:D3) определяет число полей данных, а СЧЁТЗ(B3:D7) – количество исследуемых числовых значений.
Полученное число:
Особенности использования функции FРАСПОБР в Excel
Функция имеет следующую синтаксическую запись:
=FРАСПОБР(вероятность;степени_свободы1;степени_свободы2)
Описание аргументов:
- вероятность – обязательный, принимает числовое значение, характеризующее вероятность, которая связана с распределением Фишера;
- степени_свободы1 – обязательный, принимает числовое значение, соответствующее числителю степеней свободы (равно числу факторов исследуемой регрессии);
- степени_свободы2 – обязательный, принимает числовое значение, соответствующее знаменателю степеней свободы.
Примечания:
- Рассматриваемая функция принимает в качестве любого из аргументов только числовые значения и данные, которые могут быть преобразованы к числам. Если любой из аргументов принимает данные недопустимого типа, будет сгенерирован код ошибки #ЗНАЧ!
- Первый аргумент должен быть задан числом из диапазона от 0 до 1. В противном случае функция FПАСПОБР вернет код ошибки #ЧИСЛО!
- Второй и третий аргумент функции должны быть заданы числами из диапазона от 1 до 10^10. При вводе значений, находящихся вне допустимого диапазона, будет сгенерирован код ошибки #ЧИСЛО!
- Рассматриваемая функция использует итеративный подход к вычислениям (последовательный подбор приближенного значения в циклах). Если спустя 100 итераций решение не было найдено, результатом выполнения функции FПАСПОБР будет код ошибки #Н/Д.