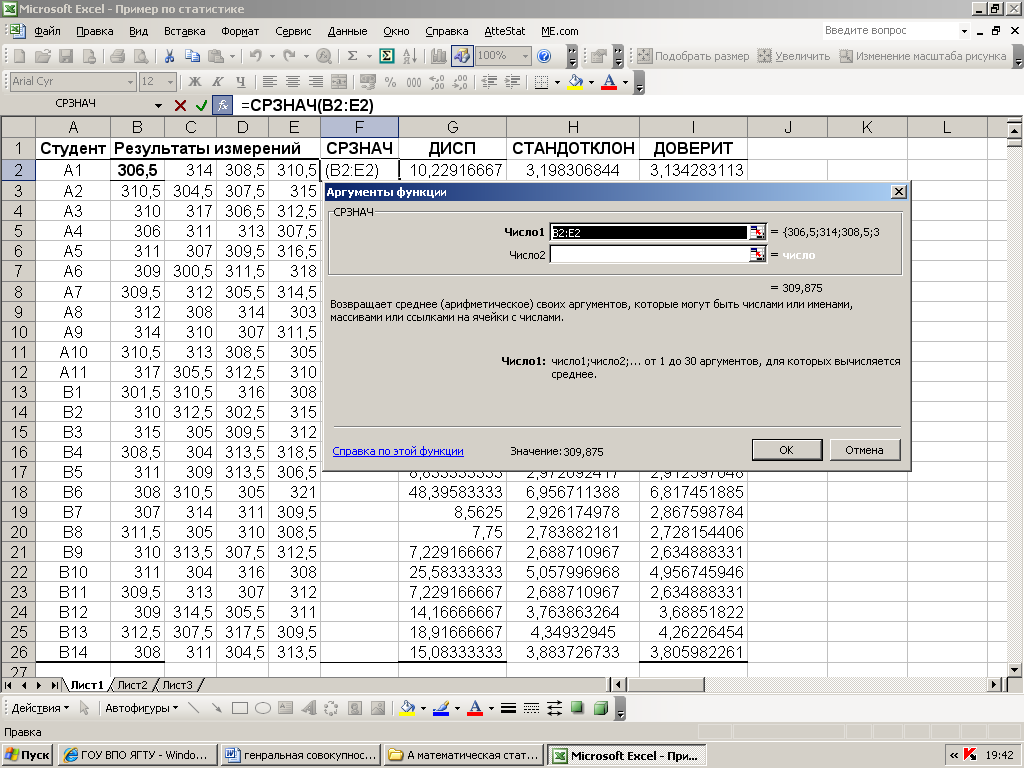
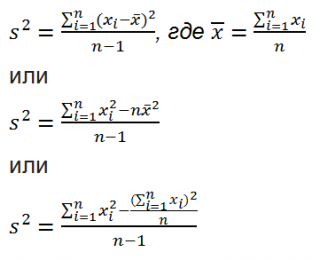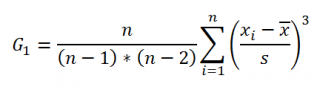Что такое входной интервал в excel - Word и Excel - помощь в работе с программами

Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.

Задача

описательной статистики

(descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений

выборки

к нескольким итоговым показателям, которые дают представление о

выборке

.В качестве таких статистических показателей используются:

среднее

медиана

мода

дисперсия, стандартное отклонение

и др.

Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные

статистические выводы о распределении

, из которого была взята

выборка

. Например, если у нас есть

выборка

значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой

выборки

мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.

Содержание статьи:

Надстройка Пакет анализа;
Среднее выборки

;
Медиана выборки

;
Мода выборки

;
Мода и среднее значение

;
Дисперсия выборки

;
Стандартное отклонение выборки

;
Стандартная ошибка

;
Ассиметричность

;
Эксцесс выборки

;
Уровень надежности

.

Надстройка Пакет анализа

Для вычисления статистических показателей одномерных

выборок

, используем

надстройку Пакет анализа

. Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.

СОВЕТ

: Подробнее о других инструментах надстройки

Пакет анализа

и ее подключении – читайте в статье

Надстройка Пакет анализа MS EXCEL

Выборку

разместим на

листе

Пример

в файле примера

в диапазоне

А6:А55

(50 значений).

Примечание

: Для удобства написания формул для диапазона

А6:А55

создан

Именованный диапазон

Выборка.

В диалоговом окне

Анализ данных

выберите инструмент

Описательная статистика

.

После нажатия кнопки

ОК

будет выведено другое диалоговое окно,

в котором нужно указать:

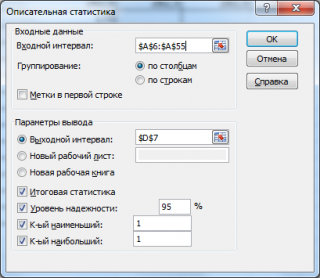
входной интервал

(Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле

Метки в первой строке (

Labels

in

first

row

).

В этом случае заголовок будет выведен в

Выходном интервале.

Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
выходной интервал

(Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
Итоговая статистика (

Summary

Statistics

)

. Поставьте галочку напротив этого поля – будут выведены основные показатели выборки:

среднее, медиана, мода, стандартное отклонение

и др.;
Также можно поставить галочки напротив полей

Уровень надежности (

Confidence

Level

for

Mean

)

,

К-й наименьший

(Kth Largest) и

К-й наибольший

(Kth Smallest).

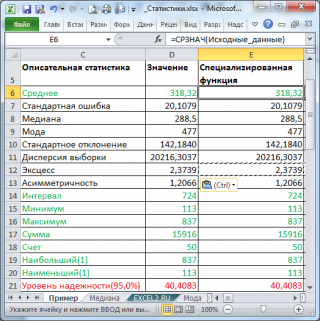
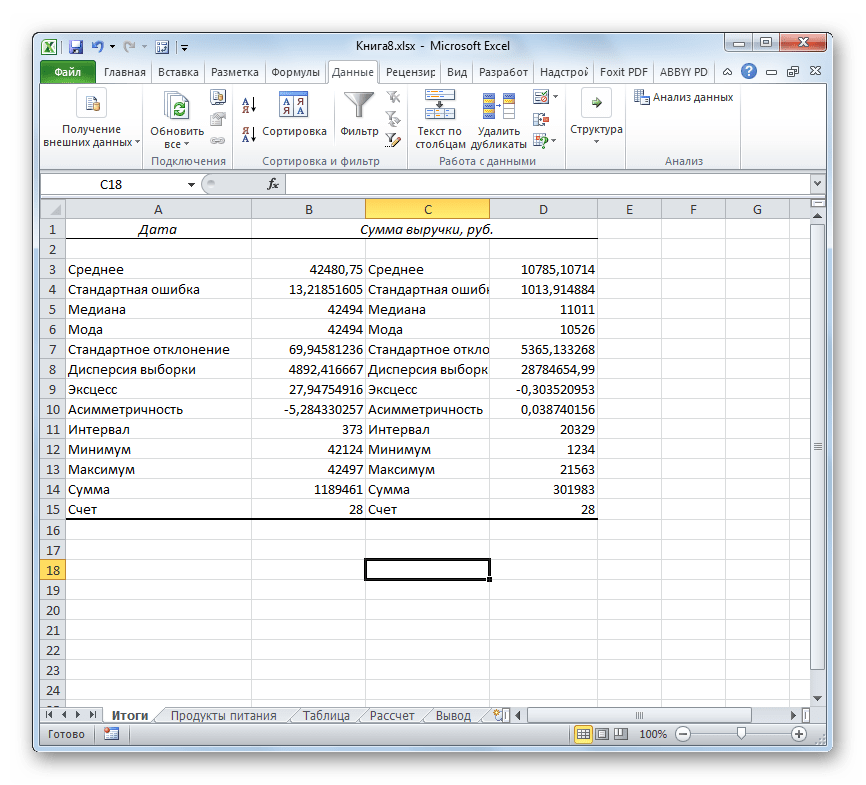
В результате будут выведены следующие статистические показатели:

Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.

Если во

входном интервале

указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во

Входной интервал

и установите галочку в поле

Метки в первой строке

). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.

Зеленым цветом на картинке выше и в

файле примера

выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:

Интервал

(Range) — разница между максимальным и минимальным значениями;
Минимум

(Minimum) – минимальное значение в диапазоне ячеек, указанном во

Входном интервале

(см.

статью про функцию

МИН()

);
Максимум

(Maximum)– максимальное значение (см.

статью про функцию

МАКС()

);
Сумма

(Sum) – сумма всех значений (см.

статью про функцию

СУММ()

);
Счет

(Count) – количество значений во

Входном интервале

(пустые ячейки игнорируются, см.

статью про функцию

СЧЁТ()

);
Наибольший

(Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см.

статью про функцию

НАИБОЛЬШИЙ()

);
Наименьший

(Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см.

статью про функцию

НАИМЕНЬШИЙ()

).

Ниже даны подробные описания остальных показателей.

Среднее выборки

Среднее

(mean, average) или

выборочное среднее

или

среднее выборки

(sample average) представляет собой

арифметическое среднее

всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция

СРЗНАЧ()

.

Выборочное среднее

является «хорошей» (несмещенной и эффективной) оценкой

математического ожидания

случайной величины (подробнее см. статью

Среднее и Математическое ожидание в MS EXCEL

Медиана выборки

Медиана

(Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем

медиана

, а половина чисел меньше, чем

медиана

. Для определения

медианы

необходимо сначала

отсортировать множество чисел

. Например,

медианой

для чисел 2, 3, 3,

4

, 5, 7, 10 будет 4.

Если множество содержит четное количество чисел, то вычисляется

среднее

для двух чисел, находящихся в середине множества. Например,

медианой

для чисел 2, 3,

3

,

5

, 7, 10 будет 4, т.к. (3+5)/2.

Если имеется длинный хвост распределения, то

Медиана

лучше, чем

среднее значение

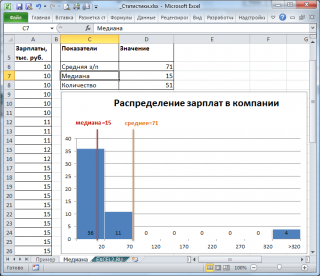
, отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.

Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что

как минимум

у 50% сотрудников зарплата меньше или равна 15 тыс. руб.

Для определения

медианы

в MS EXCEL существует одноименная функция

МЕДИАНА()

, английский вариант — MEDIAN().

Медиану

также можно вычислить с помощью формул

=КВАРТИЛЬ.ВКЛ(Выборка;2) =ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).

Подробнее о

медиане

см. специальную статью

Медиана в MS EXCEL

СОВЕТ

: Подробнее про

квартили

см. статью, про

перцентили (процентили)

см. статью.

Мода выборки

Мода

(Mode) – это наиболее часто встречающееся (повторяющееся) значение в

выборке

. Например, в массиве (1; 1;

2

;

2

;

2

; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это

мода

. Для вычисления

моды

используется функция

МОДА()

, английский вариант MODE().

Примечание

: Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье

Есть ли повторы в списке?

Начиная с

MS EXCEL 2010

вместо функции

МОДА()

рекомендуется использовать функцию

МОДА.ОДН()

, которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция

МОДА.НСК()

, которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.

Например, в массиве (1; 1;

2

;

2

;

2

; 3;

4

;

4

;

4

; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются

модами

. Функции

МОДА.ОДН()

и

МОДА()

вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см.

файл примера

, лист

Мода

).

Чтобы исправить эту несправедливость и была введена функция

МОДА.НСК()

, которая выводит все

моды

. Для этого ее нужно ввести как

формулу массива

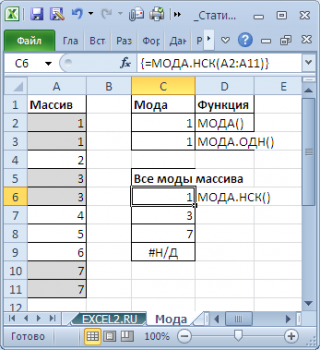
Как видно из картинки выше, функция

МОДА.НСК()

вернула все три

моды

из массива чисел в диапазоне

A2:A11

: 1; 3 и 7. Для этого, выделите диапазон

C6:C9

, в

Строку формул

введите формулу

=МОДА.НСК(A2:A11)

и нажмите

CTRL+SHIFT+ENTER

. Диапазон

C

6:

C

9

охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству

мод

. Если ячеек больше чем м

о

д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если

мода

только одна, то все выделенные ячейки будут заполнены значением этой

моды

.

Теперь вспомним, что мы определили

моду

для выборки, т.е. для конечного множества значений, взятых из

генеральной совокупности

. Для

непрерывных случайных величин

вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция

МОДА()

вернет ошибку.

Даже в нашем массиве с

модой

, которая была определена с помощью

надстройки Пакет анализа

, творится, что-то не то. Действительно,

модой

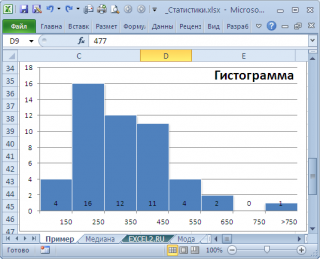
нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на

гистограмму распределения

, построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).

Проблема в том, что мы определили

моду

как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому,

моду

в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для

логнормального распределения

мода

(наиболее вероятное значение непрерывной случайной величины х), вычисляется как

exp

(

m

—

s
²
)

, где m и s параметры этого распределения.

Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для

моды

распределения, из которого взята

выборка

(наиболее вероятного значения или для которого плотность вероятности распределения максимальна).

Для того, чтобы получить оценку

моды

распределения, из

генеральной совокупности

которого взята

выборка

, можно, например, построить

гистограмму

. Оценкой для

моды

может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.

Вывод

: Значение

моды

для

выборки

, рассчитанное с помощью функции

МОДА()

, может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер

выборки

существенно превышает количество этих значений.

Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане),

модой

является число 15 (17 значений из 51, т.е. 33%). В этом случае функция

МОДА()

дает хорошую оценку «наиболее вероятного» значения зарплаты.

Примечание

: Строго говоря, в примере с зарплатой мы имеем дело скорее с

генеральной совокупностью

, чем с

выборкой

. Т.к. других зарплат в компании просто нет.

О вычислении

моды

для распределения

непрерывной случайной величины

читайте статью

Мода в MS EXCEL

Мода и среднее значение

Не смотря на то, что

мода

– это наиболее вероятное значение случайной величины (вероятность выбрать это значение из

Генеральной совокупности

максимальна), не следует ожидать, что

среднее значение

обязательно будет близко к

моде

.

Примечание

:

Мода

и

среднее

симметричных распределений совпадает (имеется ввиду симметричность

плотности распределения

Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6.

Модой

является 6, а среднее значение – 3,6666.

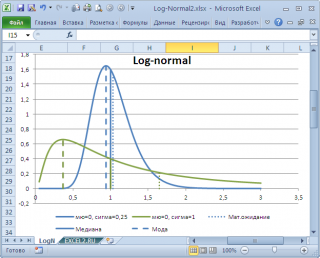
Другой пример. Для

Логнормального распределения

LnN(0;1)

мода

равна =EXP(m-s2)= EXP(0-1*1)=0,368, а

среднее значение

1,649.

Дисперсия выборки

Дисперсия выборки

или

выборочная дисперсия (

sample

variance

) характеризует разброс значений в массиве, отклонение от

среднего

.

Из формулы №1 видно, что

дисперсия выборки

это сумма квадратов отклонений каждого значения в массиве

от среднего

, деленная на размер выборки минус 1.

В MS EXCEL 2007 и более ранних версиях для вычисления

дисперсии выборки

используется функция

ДИСП()

. С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию

ДИСП.В()

.

Дисперсию

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

):

=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)

– обычная формула

=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)

–

формула массива

Дисперсия выборки

равна 0, только в том случае, если все значения равны между собой и, соответственно, равны

среднему значению

.

Чем больше величина

дисперсии

, тем больше разброс значений в массиве относительно

среднего

.

Размерность

дисперсии

соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность

дисперсии

будет кг
²
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из

дисперсии – стандартное отклонение

.

Подробнее о

дисперсии

см. статью

Дисперсия и стандартное отклонение в MS EXCEL

Стандартное отклонение выборки

Стандартное отклонение выборки

(Standard Deviation), как и

дисперсия

, — это мера того, насколько широко разбросаны значения в выборке

относительно их среднего

.

По определению,

стандартное отклонение

равно квадратному корню из

дисперсии

:

Стандартное отклонение

не учитывает величину значений в

выборке

, а только степень рассеивания значений вокруг их

среднего

. Чтобы проиллюстрировать это приведем пример.

Вычислим стандартное отклонение для 2-х

выборок

: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у

выборок

существенно отличается.

В MS EXCEL 2007 и более ранних версиях для вычисления

Стандартного отклонения выборки

используется функция

СТАНДОТКЛОН()

. С версии MS EXCEL 2010 рекомендуется использовать ее аналог

СТАНДОТКЛОН.В()

.

Стандартное отклонение

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

):

=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))

Подробнее о

стандартном отклонении

см. статью

Дисперсия и стандартное отклонение в MS EXCEL

Стандартная ошибка

В

Пакете анализа

под термином

стандартная ошибка

имеется ввиду

Стандартная ошибка среднего

(Standard Error of the Mean, SEM).

Стандартная ошибка среднего

— это оценка

стандартного отклонения

распределения

выборочного среднего

Примечание

: Чтобы разобраться с понятием

Стандартная ошибка среднего

необходимо прочитать о

выборочном распределении

(см. статью

Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL

) и статью про

Центральную предельную теорему

.

Стандартное отклонение распределения выборочного среднего

вычисляется по формуле σ/√n, где n — объём

выборки, σ — стандартное отклонение исходного

распределения, из которого взята

выборка

. Т.к. обычно

стандартное отклонение

исходного распределения неизвестно, то в расчетах вместо

σ

используют ее оценку

s

—

стандартное отклонение выборки

. А соответствующая величина s/√n имеет специальное название —

Стандартная ошибка среднего.

Именно эта величина вычисляется в

Пакете анализа.

В MS EXCEL

стандартную ошибку среднего

можно также вычислить по формуле

=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))

Асимметричность

Асимметричность

или

коэффициент асимметрии

(skewness) характеризует степень несимметричности распределения (

плотности распределения

) относительно его

среднего

.

Положительное значение

коэффициента асимметрии

указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого.

Коэффициент асимметрии

идеально симметричного распределения или выборки равно 0.

Примечание

:

Асимметрия выборки

может отличаться расчетного значения асимметрии теоретического распределения. Например,

Нормальное распределение

является симметричным распределением (

плотность его распределения

симметрична относительно

среднего

) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в

выборке

из соответствующей

генеральной совокупности

не обязательно должны располагаться совершенно симметрично относительно

среднего

. Поэтому,

асимметрия выборки

, являющейся оценкой

асимметрии распределения

, может отличаться от 0.

Функция

СКОС()

, английский вариант SKEW(), возвращает коэффициент

асимметрии выборки

, являющейся оценкой

асимметрии

соответствующего распределения, и определяется следующим образом:

где n – размер

выборки

, s –

стандартное отклонение выборки

.

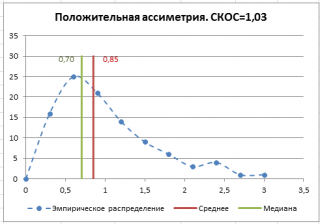
В

файле примера на листе СКОС

приведен расчет коэффициента

асимметрии

на примере случайной выборки из

распределения Вейбулла

, которое имеет значительную положительную

асимметрию

при параметрах распределения W(1,5; 1).

Эксцесс выборки

Эксцесс

показывает относительный вес «хвостов» распределения относительно его центральной части.

Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/-

σ

.

Примечание

: Не смотря на старания профессиональных статистиков, в литературе еще попадается определение

Эксцесса

как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение

Эксцесса

ничего не говорит о форме пика распределения.

Согласно определения,

Эксцесс

равен четвертому

стандартизированному моменту:

Для

нормального распределения

четвертый момент равен 3*σ
⁴
, следовательно,

Эксцесс

равен 3. Многие компьютерные программы используют для расчетов не сам

Эксцесс

, а так называемый Kurtosis excess, который меньше на 3. Т.е. для

нормального распределения

Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.

Примечание

: Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как

Эксцесс

(от англ. excess — «излишек»). Например, функция MS EXCEL

ЭКСЦЕСС()

на самом деле вычисляет Kurtosis excess.

Функция

ЭКСЦЕСС()

, английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку

эксцесса распределения

случайной величины и определяется следующим образом:

Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из

нормального распределения

формула вернет близкое к 0 значение.

Если задано менее четырех точек данных, то функция

ЭКСЦЕСС()

возвращает значение ошибки #ДЕЛ/0!

Вернемся к

распределениям случайной величины

.

Эксцесс

(Kurtosis excess) для

нормального распределения

всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений

Эксцесс

зависит от параметров распределения: см., например,

распределение Вейбулла

или

распределение Пуассона

, для котрого

Эксцесс

= 1/λ.

Уровень надежности

Уровень

надежности

— означает вероятность того, что

доверительный интервал

содержит истинное значение оцениваемого параметра распределения.

Вместо термина

Уровень

надежности

часто используется термин

Уровень доверия

. Про

Уровень надежности

(Confidence Level for Mean) читайте статью

Уровень значимости и уровень надежности в MS EXCEL

Задав значение

Уровня

надежности

в окне

надстройки Пакет анализа

, MS EXCEL вычислит половину ширины

доверительного интервала для оценки среднего (дисперсия неизвестна)

Тот же результат можно получить по формуле (см.

файл примера

):

=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n)

s —

стандартное отклонение выборки

, n – объем

выборки

.

Подробнее см. статью про

построение доверительного интервала для оценки среднего (дисперсия неизвестна)

Источник

Содержание

1 Использование описательной статистики
- 1.1 Подключение «Пакета анализа»
- 1.2 Применение инструмента «Описательная статистика»
- 1.3 Помогла ли вам эта статья?
- 1.4 Статистические процедуры Пакета анализа
- 1.5 Статистические функции библиотеки встроенных функций Excel

Пользователи Эксель знают, что данная программа имеет очень широкий набор статистических функций, по уровню которых она вполне может потягаться со специализированными приложениями. Но кроме того, у Excel имеется инструмент, с помощью которого производится обработка данных по целому ряду основных статистических показателей буквально в один клик.

Этот инструмент называется «Описательная статистика». С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Давайте взглянем, как работает данный инструмент, и остановимся на некоторых нюансах работы с ним.

Использование описательной статистики

Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.

В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:

Медиана;
Мода;
Дисперсия;
Среднее;
Стандартное отклонение;
Стандартная ошибка;
Асимметричность и др.

Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.

Подключение «Пакета анализа»

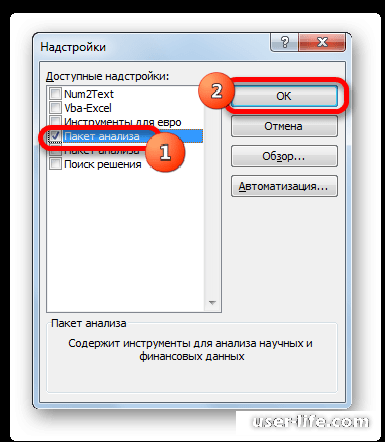
Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.

Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
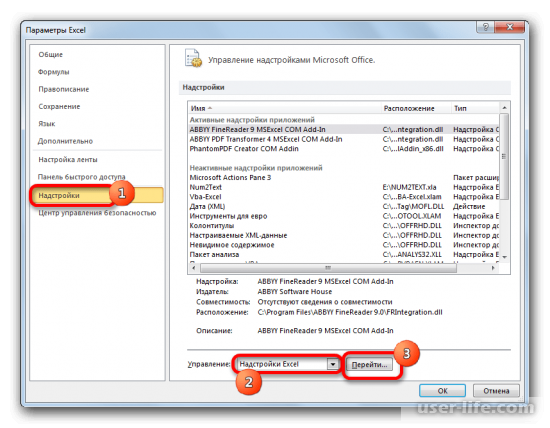
В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
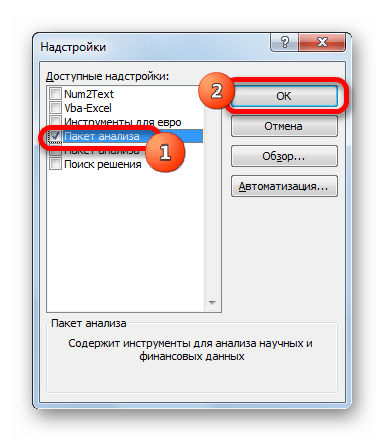
Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.

Применение инструмента «Описательная статистика»

Теперь посмотрим, как инструмент описательная статистика можно применить на практике. Для этих целей используем готовую таблицу.

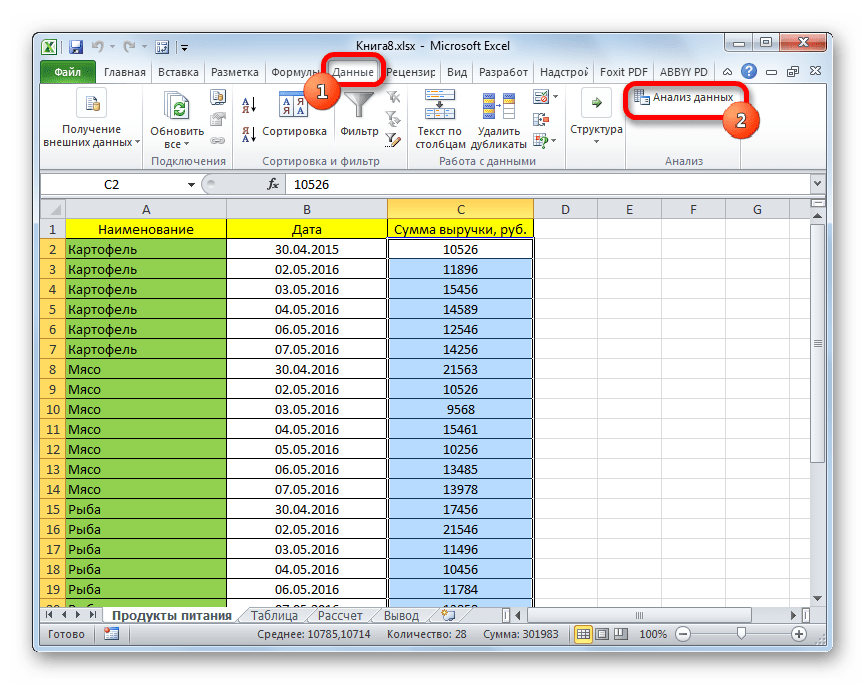
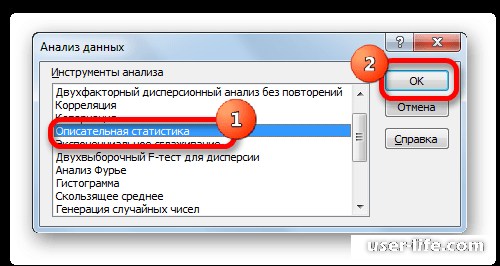
Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ».
Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK».
После выполнения данных действий непосредственно запускается окно «Описательная статистика».
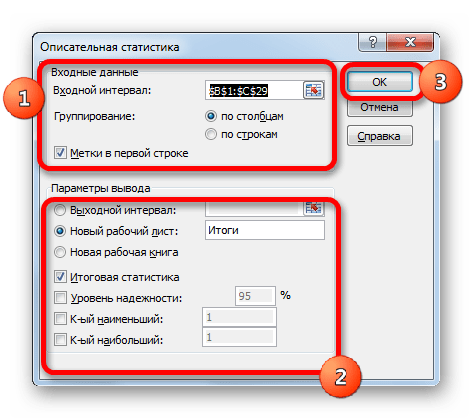
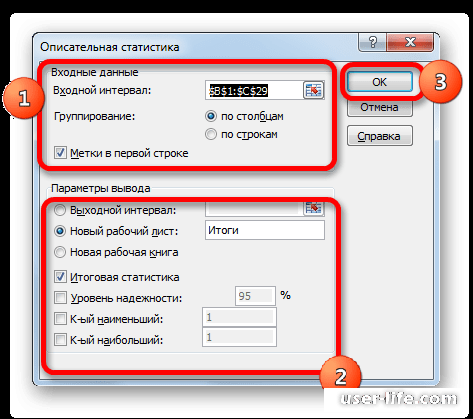
В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Для того, чтобы внести нужные нам координаты, устанавливаем курсор в указанное поле. Затем, зажав левую кнопку мыши, выделяем на листе соответствующую табличную область. Как видим, её координаты тут же отобразятся в поле. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.

Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:
- Выходной интервал;
- Новый рабочий лист;
- Новая рабочая книга.
В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на новом рабочем листе под названием «Итоги».

Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.

Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Но в нашем случае этот параметр так же, как и предыдущий, не является обязательным, поэтому флажки мы не ставим.

После того, как все указанные данные внесены, жмем на кнопку «OK».
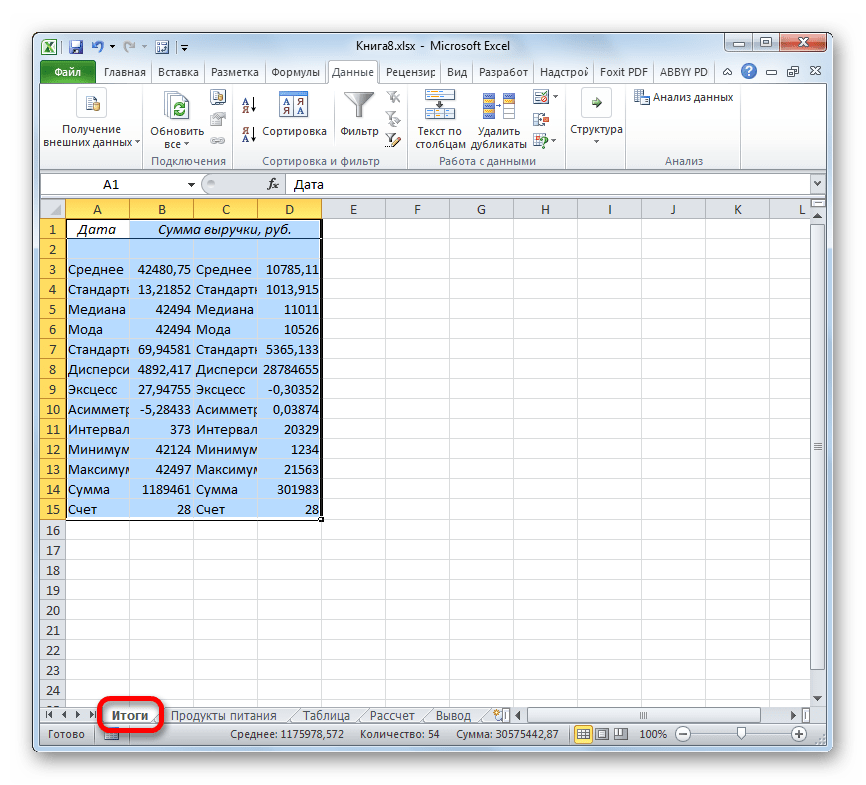
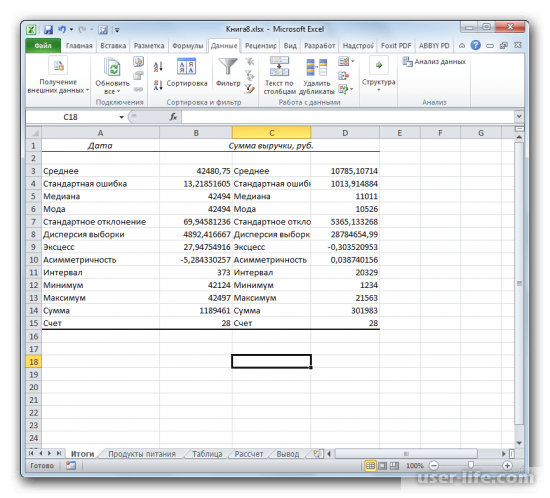
После выполнения этих действий таблица с описательной статистикой выводится на отдельном листе, который был нами назван «Итоги». Как видим, данные представлены сумбурно, поэтому их следует отредактировать, расширив соответствующие колонки для более удобного просмотра.
После того, как данные «причесаны» можно приступать к их непосредственному анализу. Как видим, при помощи инструмента описательной статистики были рассчитаны следующие показатели:
- Асимметричность;
- Интервал;
- Минимум;
- Стандартное отклонение;
- Дисперсия выборки;
- Максимум;
- Сумма;
- Эксцесс;
- Среднее;
- Стандартная ошибка;
- Медиана;
- Мода;
- Счет.

Если какие-то из вышеуказанных данных для конкретного вида анализа не нужны, то их можно удалить, чтобы они не мешали. Далее производится анализ с учетом статистических закономерностей.

Урок: Статистические функции в Excel

Как видим, с помощью инструмента «Описательная статистика» можно сразу получить результат по целому ряду критериев, которые в ином случае рассчитывались с применением отдельно предназначенной для каждого расчета функцией, что заняло бы значительное время у пользователя. А так, все эти расчеты можно получить практически в один клик, использовав соответствующий инструмент — Пакета анализа.

Мы рады, что смогли помочь Вам в решении проблемы.

Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

Да Нет

Описательная статистика в Эксель. Описательная статистика в MS Excel позволяет представить статистическую информацию как совокупность данных, для характеристики которых могут быть использованы различные показатели.

Использование инструмента «Описательная статистика» рассмотрим на примере MS Excel 2010, а в качестве данных для анализа возьмем статистическую информацию по изменению курса доллара за месяц:

Для начала на вкладке «Данные» в группе «Анализ» выбрать пункт «Анализ данных»:

В открывшемся окне «Анализ данных» выбрать инструмент для анализа «Описательная статистика»:

В новом окне «Описательная статистика»,

следует выбрать исходные данные для анализа:

• Входной интервал – это диапазон ячеек с исходными данными для анализа. В случае, если в исходный диапазон входит текстовый заголовок, тогда следует поставить галочку в поле «Метки в первой строке»

• Выходной интервал – это адрес верхней левой ячейки диапазона, в котором будут представлены результаты статистического анализа.

• Итоговая статистика – позволяет вывести дополнительные расширенные результаты анализа исходных данных.

• Уровень надежности – показывает вероятность того, что исследуемый исходный интервал содержит истинное значение оцениваемого параметра. В математической статистике обычно используют значения: 90%, 95%, 99%. В нашем случае, по умолчанию установлено значение 95%.

• К-ый наименьший – показывает наименьшее значение из исследуемого исходного интервала.

• К-ый наибольший – показывает наибольшее значение из исследуемого исходного интервала.

В результате использования инструмента «Описательная статистика», на основании наших исходных данных, получим:

Таким образом, для проведения сложного статистического или инженерного анализа, чтобы упростить процесс и сэкономить время, следует использовать инструмент «Описательная статистика» MS Exсel.

Основными средствами анализа статистических данных в Excel являются статистические процедуры надстройки Пакет анализа (Analysis ToolРак) и статистические функции библиотеки встроенных функций. Основные сведения обо всех этих средствах имеются в электронной справочной системе Excel.

Однако качество описаний статистических процедур и функций, приведенных в этой системе, заставляет желать лучшего. Некоторые из этих описаний не очень понятны, в них имеются неточности, а подчас и просто ошибки (это относится как к англоязычному оригиналу, так и к русскому переводу). Эти недостатки с завидным постоянством повторяются и во многих пособиях по Excel. Найти необходимые пособия в интернете можно быстро если скачать бесплатно Амиго браузер с усовершенствованным поисковым алгоритмом.

Статистические процедуры Пакета анализа

Наиболее развитыми средствами анализа данных являются статистические процедуры Пакета анализа. Они обладают большими возможностями, чем статистические функции. С их помощью можно решать более сложные задачи обработки статистических данных и выполнять более тонкий анализ этих данных.

В Пакет анализа входят следующие статистические процедуры:

генерация случайных чисел (Random number generation);
выборка (Sampling);
гистограмма (Histogram);
описательная статистика (Descriptive statistics);
ранги персентиль (Rank and percentile);
двухвыборочный z-тест для средних (z-Test: Two Sample for Means);
двухвыборочный t-тест для средних с одинаковыми дисперсиями (t-Test: Two-Sample Assuming Equal Variances);
двухвыборочный t-тест для средних с различными дисперсиями (t-Test: Two-Sample Assuming Unequal Variances);
парный двухвыборочный t-тест для средних (t-Test: Paired Two Sample for Means);
двухвыборочный F-тест да я дисперсий (F-Test: Two Sample for Variances);
коварнация (Covariance);
корреляция (Correlation);
рецессия (Regression);
однофакторный дисперсионный анализ (ANOVA: Single Factor);
двухфакторный дисперсионный анализ без повторений (ANOVA: Two Factor Without Replication);
двухфакторный дисперсионный анализ с повторениями (ANOVA: Two Factor With Replication);
скользящее среднее (Moving Average);
экспоненциальное сглаживание (Exponential Smoothing);
анализ Фурье (Fourier Analysis).

Для доступа к процедурам Пакета анализа необходимо в меню Сервис (Tools) щелкнуть указателем мыши на строке Анализ данных (Data Analysis). Откроется диалоговое окно с соответствующим названием, в котором перечислены процедуры статистического анализа данных (рис. 1).

Рис.1. Диалоговое окно Анализ данных

Для того чтобы запустить в работу нужную статистическую процедуру, нужно выделить ее указателем мыши и щелкнуть на кнопке ОК. На экране появится диалоговое окно вызванной процедуры. На рис. 2 для примера показано диалоговое окно процедуры Описательная статистика (Descriptive statistics).

Рис.2. Диалоговое окно процедуры Описательная статистика

Диалоговое окно каждой процедуры содержит элементы управления: поля ввода, раскрывающиеся списки, переключатели, флажки и т. п. Эти элементы позволяют задать нужные параметры используемой процедуры. Некоторые элементы управления имеют специфический характер, присущий одной процедуре или небольшой группе процедур. Назначение таких элементов управления будет рассмотрено при описании соответствующих процедур. Другие элементы управления присутствуют в диалоговых окнах почти всех статистических процедур.

К числу общих для большинства процедур элементов управления относятся:

поле ввода Входной интервал (Input Range). В это поле вводится ссылка на диапазон, содержащий статистические данные, подлежащие обработке. Входной диапазон может быть столбцом пли группой столбцов (строкой или группой строк);
переключатель Группирование (Grouped By). В том случае, когда входной диапазон представляет собой столбец или группу столбцов, переключатель устанавливается в положение по столбцам (Columns). Если же входной диапазон представляет собой строку или группу строк, то переключатель устанавливается в положение по строкам (Rows). Более точным названием этого переключателя было бы название Расположение;
флажок Метки (Labels in First Row). Флажок устанавливается в тех случаях, когда первая строка (первый столбец) входного диапазона содержит заголовки. Если такие заголовки отсутствуют, флажок Метки не устанавливают. При этом Excel автоматически создает и выводит на экран стандартные названия для данных выходного диапазона (Столбец1, Столбец2,… или Строка 1. Строка2,…);
переключатели Выходной интервал/Новый рабочий лист/Новая книга (Output Range/New Worksheet/New Workbook). Эти переключатели определяют место вывода таблицы, содержащей результаты реализации статистической процедуры. В группе может быть выбран только одни переключатель.

При выборе переключателя Выходной интервал таблица результатов решения выводится на тот же рабочий лист, на котором находятся исходные данные. Справа от переключателя открывается поле ввода, в которое надо ввести ссылку на левую верхнюю ячейку таблицы результатов. Если возникает опасность наложения таблицы результатов на уже заполненные ячейки, на экране появляется сообщение о такой опасности. В ответ на это сообщение пользователь должен разрешить удаление старых данных и вывод на их место новых.

В положении Новый рабочий лист открывается новый лист рабочей книги. На этот лист, начиная с ячейки А1, и выводится таблица результатов решения. Справа от переключателя имеется поле ввода, в которое в случае необходимости можно ввести имя нового рабочего листа. При выборе переключателя Новая рабочая книга открывается новая рабочая книга. На первый лист этой новой книги, начиная с ячейки А1, выводится таблица результатов решения.

Следует заметить, что результаты;, получаемые с помощью статистических процедур Пакета анализа, не имеют постоянной связи с исходными данными — в случае изменения исходных данных результаты решения автоматически не изменяются. В том случае, когда необходимо получить результаты, автоматически изменяющиеся вместе с исходными данными, нужно использовать подходящие статистические функции библиотеки встроенных функций.

Эффективным и очень удобным в использовании средством парного регрессионного анализа и анализа временных рядов является процедура Добавить линию тренда (Add Trendline), входящая в комплекс графических средств Excel.

Статистические функции библиотеки встроенных функций Excel

Табличный процессор Excel имеет библиотеку встроенных функции рабочего листа (Worksheet function). Одним из разделов этой библиотеки является раздел Статистические функции. В этот раздел входят 83 функции, предназначенные для решения некоторых наиболее востребованных задач теории вероятностей и математической статистики.

Аргументы статистических функций должны быть числами или ссылками на диапазоны, которые содержат числа Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются, однако ячейки с нулевыми значениями учитываются.

Когда в качестве какого-либо аргумента встроенной статистической функции введен текст, функция выдает сообщение об ошибке #ЗНАЧ! (#VALUE!). Если в качестве аргумента, который по определению должен быть целым числом, введено число не целое, Excel использует в качестве аргумента целую часть этот числа. Никакие сообщения об этом «несанкционированном округлении» на экран не выводятся.

Источник

Сегодня практически каждый понимает, что нет таких данных, которые было бы невозможно получить. Чтобы получить данные по сайту, используются бесплатные инструменты или тратятся огромные суммы денег на платные инструменты, чтобы получить еще больше информации. Неважно какую информацию вы ищите, вы точно ее найдете и вопрос лишь в том — бесплатно или за деньги.

У всех инструментов есть кое-что общее — это кнопка «Экспорт». Возможно, это самое важное свойство всех инструментов. Сэкспортировав данные в Excel, специалист может сортировать и фильтровать их так, как ему нужно. Большинство из нас регулярно пользуется Excel, но только его стандартными функциями. Однако Excel может гораздо больше!

Виргил Гик (Virgil Ghic) рассказал о наиболее распространенных приемах обработки статистических данных. И самое главное — вам не придется их запоминать, все они встроены в Excel.

Статистика — это сбор, анализ и интерпретация данных. Она помогает в тех ситуациях, когда принятию решения мешает некоторая неопределенность. Используя статистику, мы избежим неопределенность и получим действенный анализ.

В статистике можно выделить два главных направления: описательная статистика и логически выведенная статистика.

Описательная (дескриптивная) статистика используется в том случае, когда вам известны все значения в наборе данных. Например, вы задаете 1000 респондентов вопрос, любят ли они апельсины, и предоставляете им два варианта ответа: Да и Нет. Затем собираете данные и выясняете, что 900 человек ответили Да и 100 — Нет. Пропорция будет следующей: 90% составил ответ Да и 10% — ответ Нет. Достаточно легко, не правда ли?

Но как быть в том случае, когда у нас нет всех данных?

В случае когда у вас только часть данных на помощь придет логически выведенная статистика. Она используется тогда, когда вы знаете только небольшую часть всех данных и вам необходимо сделать предположение о всем объеме данных.

Давайте предположим, что вы хотите рассчитать количество просмотров email за последние два года, но вы располагаете данными только за последние шесть месяцев. Предположим, что из 1000 email-адресов письма открыли только 200 получателей, значит остальные 800 — не открывали. Следовательно мы имеем соотношение 20% открывших к 80% неоткрывших. Эти данные верны для периода в шесть месяцев, но они также могут быть верны и для периода в два года. Логически выведенная статистика поможет нам понять, насколько верно наше предположение.

Доля открытых писем может составлять 20%, а может немного отличаться. Допустим, она варьируется +/-3%, тогда доля открытых писем будет составлять от 17% до 23%. Но насколько мы уверены в этих данных? Кроме того, какой процент случайной выборки из всего набора данных будет находиться в диапазоне от 17% −23%?

В статистике считается приемлемым уровень достоверности в 95%. Это означает, что 95% выборочных данных, взятых из всего набора данных, будет соответствовать 17-23%, оставшиеся 5% будут либо выше 23%, либо ниже 17%. Но мы уверены в том, что для 95% доля открытых писем составляет 20% +/- 3%.

Термин данные (data) предполагает любую величину, обозначающую объект или событие, например, посетители, исследования, письма.

Термин набор данных (data set) состоит из двух компонентов: Единица наблюдения (observation unit) может означать посетителей и переменные, представляющие демографические данные ваших посетителей (возраст, зарплата, образование). Совокупность (population) предполагает каждого члена вашей группы, а в веб-аналитике — всех посетителей. Предположим, посетителей 10 000.

Выборка (sample) — часть вашей совокупности, представленная на основе определенной даты или сконвертированных посетителей и т.д. В статистике наиболее ценной является случайная выборка (random sample).

Распределение данных (data distribution) определяется частотой, согласно которой представлены значения в наборе данных. Представив частоту на графике с диапазоном значений на горизонтальной оси и частотой по вертикальной оси, мы получим кривую распределения. Наиболее распространенным является нормальное распределение или колоколообразная кривая.

Самый простой способ понять это — представить на количестве посетителей веб-сайта. Например, в среднем ежедневное количество посещений сайта составляет 2000, иногда бывает больше — 3000 посещений или меньше — 1000.

Здесь пригодится теория вероятности (probability theory).

Вероятность означает вероятность события, которое происходит, например, при наличии 3000 посетителей в день и выражается в процентах.

Самым распространенным примером вероятности, известным многим, является подбрасывание монеты. У монеты две стороны: орел и решка. Какова вероятность того, что монета ляжет той или другой стороной? Существует две возможности, таким образом 100%/2=50%

Достаточно теории, перейдет к практике.

Excel — прекрасный инструмент, который поможет нам в работе со статистикой. Отметим, что это не лучший инструмент, но зато все знают, как им пользоваться, поэтому рассмотрим именно Excel.

Во-первых, установите надсройку Analysis ToolPack.

Откройте Excel, перейдите в Опции -> Add-ins->внизу списка вы найдёте

Нажимайте Go ->выберите Analysis ToolPack->и нажимайте OK.

Теперь в панеле выберите опцию Данные и найдите там Анализ данных.

Инструмент Анализ данных может предоставить вам невероятную статистическую информацию, но давайте начнем с чего-нибудь попроще.

Среднее (mean) это статистическое значение среднего значения, например, средним для 4,5,6 будет 5. Как рассчитать среднее значение в Excel? =average(число1,число2 и т.д.)

Mean=AVERAGE(AC16:AC21)

Путем вычисления среднего мы определяем, сколько мы продали в среднем. Эта информация полезна, если нет экстремальных значений (или выбросов). Почему?

Например, мы продали в среднем товаров на $3000, но на самом деле нам повезло, т.к. 6 сентября покупатели потратили больше. В предыдущие шесть дней товара было куплено в среднем лишь на $618. Исключив крайние значения от среднего, можно получить более репрезентативные даные.

Медиана (median) это значение, которое делит набор данных на две равные части. Например, для набора данных 224, 298, 304 медианой является — 298. Для того чтобы вычислить среднее для большого набора данных, можно использовать следующую формулу =MEDIAN(224,298,304).

Когда может пригодиться медиана? Медиана полезна, когда у вас есть неравномерное распределение, например, цена ваших конфет варьируется от $3 до $15 за упаковку, но также у вас есть очень дорогие конфеты за $100, которые покупают редко. В конце месяца вы делаете отчет, и вы видите, что вы продали в основном дешевые конфеты и только пару упаковок за $100. В этом случае вам будет полезен расчет медианы.

Самый простой способ понять, когда лучше использовать медиану и среднее, это построение гистограммы. Если ваша гистограмма сильно смещена до экстримальных значений, значит нужно рассчитывать медиану.

Мода (mode) самое распространенное значение, например, мода для: 4,6,7,7,7,7,9,10 это 7.

Рассчитать моду в Excel вы можете с помощью формулы =MODE(4,6,7,7,7,7,9,10).

Но имейте в виду, что Excel выдает за моду наименьшее значение из возможных. Например, вы рассчитываете моду для следующего набора данных: 2,2,2,4,5,6,7,7,7,8,9, сразу отметим, что здесь две моды — 2 и 7, но Excel покажет вам только наименьшее значение — 2.

Когда можно использовать функцию моды? Расчет моды полезен только для целых чисел, например 1, 2 и 3. И нежелателен для дробных чисел, таких как 1,744; 2,443; 3,323, т.к. числа могут дублироваться.

Гистограммы

Предположим, недавно в вашем блоге была опубликована сотня гостевых постов, некоторые из них хорошего качества, другие не очень. Возможно, вы захотели узнать, какие из постов получили по 10, 20, 30 обратных ссылок или вам интересны твиты, лайки, расшаривания, а может и просто посещения.

Мы разделили все это на группы с помощью графического представления данных под названием гистограмма. Виргил Гик (Virgil Ghic) приводит пример с посещениями и постами, как один из менее сложных. Он настроил свой аккаунт в Google Analytics следующим образом: у него есть профиль, в который собирается статистика только по его блогу, ничего больше. Если у вас нет такого же профиля, тогда вы можете использовать сегменты.

Это несложно.

Далее идем в экспорт ->CSV

Открываем Excel и создаем два столбца: Целевая страница и Посещения. Также создаем список, в соответствии с которым будем категоризировать данные. В данном случае мы определяем, сколько статей имеют 100, 300, 500 и т.д. посещений.

Данные -> Анализ данных->Гистограммы->OK

Входной интервал (input range) будет столбец с посещениями.
Интервал карманов (bin range) — это группы.
Выходной интервал (output range), кликните на ячейку, где вы хотите создать гистограмму.
Проверьте график выхода (chart output).
Нажимаем OK.

Вы получили гистограмму, которая отражает количество статей, сгруппированных по посещениям. Чтобы лучше разобраться в гистограмме, нужно кликнуть на любую ячейку в столбцах Bin и Frequency и отфильтровать частоту от меньшего к большему.

Анализировать данные теперь еще проще. Возвращаемся и фильтруем все статьи от меньшего или равного 100 посещениям (Визиты, выпадающее меню->Числовые фильтры->Между…0-100->Ok) в прошлом месяце и обновляем.

Источники посещений

Насколько значим данный отчет для вас?

Он достаточно хорош, но не более того. Мы можем проанализировать рост и снижение посещений, но … какова доля посещений с YouTube в общей статистике посещений за февраль? Конечно, можно разбираться, но это дополнительная работа, и это очень неудобно, когда этот вопрос вам задает клиент по телефону. Чтобы ваши графики были максимально полезны, создавайте описательные отчеты.

В вышеупомянутом отчете просто разобраться, сложнее его создать. Но зато он вам очень пригодится.

Что мы видим в мае: доля переходов с Facebook в общей статистике посещений больше обычного. Почему? Возможно, в мае рекламная кампания оказалась более эффективной, чем в другие месяцы, это и привело к росту трафика с Facebook. Если дело в рекламной кампании, давайте повторим ее.

Однако правильней будет провести хи-квадрат тест (Chi-Square Test), который позволит нам понять была ли это счастливая случайность или эффективная маркетинговая кампания.

Фактический столбец — количество посещений, Ожидаемый столбец — среднее из «фактического» столбца. Формула хи-квадрат теста следующая: =1-CHITEST(N10:N16,O10:O16), где N10:N16 — это значения из Актуального столбца, а O10:O16 — значения из Ожидаемого.

Результат в 100% является уровнем достоверности, свидетельствующий о вероятности того, что рост посещений с Facebook является результатом маркетинговых кампаний.

Создавая метрики, помните, они должны быть максимально понятными и релевантными вашей бизнес-модели.

В данном видео вы найдете еще один пример использования хи-квадрат теста.

Скользящее среднее (moving average) и линейная регрессия (linear regression) для прогнозирования

Мы часто встречаем такие графики, как расположенный выше. На них могут быть представлены продажи, посещения и т.д. И они всегда выглядят именно так: прямая, идущая вверх-вниз. В такой картине данных присутствует много шума, который мы хотим сгладить для лучшего понимания данных.

Решением является скользящее среднее! Данный метод обычно используется трейдерами для прогнозирования цен акций, которые сегодня могут взлететь вверх, а уже завтра обвалиться.

Давайте разберемся, как мы можем использовать данный метод.

Шаг 1:

Экспортируйте в Excel число посещений/продаж за долгий период времени, например, один-два года.

Шаг 2:

Данные-> Анализ данных -> Скользящее среднее ->OK

Входной интервал — это столбец с числом посещений.

Интервал — это количество дней для которых вычисляется среднее. Вам нужно создать одно скользящее среднее с большим числом, например, 30 и одно с меньшим числом, например, 7.

Выходной интервал — это столбец справа от столбца посещений.

Повторите данные шаги для интервала в 7 дней.

Теперь ваши данные выглядят примерно так:

Если вы выберете все столбцы и построите линейный график, вы получите следующее:

В таком представлении данных меньше шума, их легче анализировать и можно увидеть некоторые тренды. Зеленая линия визуально немного облегчает график, но она реагирует на почти каждое крупное событие. Тогда как красная линия является более стабильной, она отражает реальный тренд.

В конце линейного графика вы увидите такие значения, как Прогноз. Это прогнозируемые данные, выведенные на основе предыдущих трендов.

В Excel есть два способа создать линейную регрессию, используя формулу =FORECAST(x,known_y’s, known_x’s), где «x» означает дату, для которой вы создаете прогноз; «known_y’s» — это столбец посещений, «known_x’s» — столбец с датами. Данный метод не так уж сложен, но есть более простой способ сделать то же самое.

Выделив весь столбец посещений и потянув вниз за край, автоматически сгенерируется прогноз на следующие даты.

Убедитесь в том, что вы выбрали весь набор данных для того, чтобы результат был точный.

Существует теория при сравнении скользящего среднего для 7дней и 30дней. Как было сказано выше линия 7дней реагирует практически на все основные изменения, в то время как линии 30дней требуется больше времени, чтобы изменить свое направление. Как правило, когда скользящее среднее 7дней пересекает скользящее среднее 30дней, вы можете рассчитывать на существенное изменение, которое будет длиться дольше, чем день или два. Как можно увидеть выше, 6 апреля скользящее среднее 7дней пересекает скользящее среднее 30дней, число посещений снижается, у 6 июня линии снова пересекаются и тренды идут вверх. Этот метод полезен, когда вы теряете трафик и не уверены, тренд ли это или всего лишь суточные колебания.

Линия Тренда (trendline)

Те же результаты могут быть получены с помощью линии тренда в Excel: щелкните правой кнопкой мыши по движущейся линии -> выберите: Добавить линию тренда (Add Trendline).

Теперь вы можете выбрать Тип Регрессии (Regression Type) и использовать функцию Прогноз. Линия тренда, возможно, наиболее полезный инструмент, помогающий разобраться почему ваш трафик/продажи растут, сокращаются или остаются неизменными.

Без линейной функции мы не сможем уверенно говорить о том, что мы делаем правильно, а что нет. Добавляя линейный тренд мы видим, что наклон положительный, уравнение линии тренда объясняет, как движется наш тренд.

y=0.5516x-9541.2

X — это количество дней. Коэффициент Х — 0.5516 — положительное число. Это означает, что линия тренда идет вверх. Т.е. ежедневно мы увеличиваем количество посетителей на 0,5, это является трендом.

R^2 — это уровень точности модели. Наше число R^2 = 0,26 означает, что наша модель объясняет 26% вариаций. Проще говоря, мы уверены на 26%, что ежедневно количество посетителей увеличивается на одного.

Сезонное прогнозирование

Предположим, скоро Рождество. Прогнозирование на зимний сезон будет весьма полезно, особенно когда с этим периодом вы связываете большие надежды.

Если вы не попали под Google-фильтры Panda или Penguin и ваши продажи/посетители соответствуют сезонным тенденциям, вы можете спрогнозировать характер продаж или посещений.

Сезонное прогнозирование — это метод, который позволяем нам оценить будущие значения набора данных на основе сезонных колебаний. Сезонные наборы данных есть везде, например, магазин мороженого будет очень востребован во время летнего сезона, а сувенирный магазин может достичь максимальных продаж во время зимних праздников.

Прогнозирование данных на ближайшее будущее может быть очень полезно, особенно когда мы планируем вкладывать деньги в маркетинговые кампании для таких сезонов.

Следующий пример представляет собой базовую модель, но она может быть расширена до более сложных, чтобы отвечать вашей бизнес-модели.

Загрузите Пример прогнозирования в Excel

Для удобства восприятия я разобью весь процесс на этапы. Вам нужно загрузить таблицу Excel и выполнить следующие шаги:

Экспортируйте ваши данные; чем больше данных, тем более точным будет прогноз! Укажите даты в столбце А, а продажи в столбце В.
Рассчитайте индекс для каждого месяца и добавьте полученные данные в столбец С.

Для расчета индекса прокрутите вниз, справа вы найдете таблицу под названием Индекс (Index). Индекс за январь 2009 рассчитывается путем деления продаж за январь 2009 г. на среднее значение продаж за весь 2009 год.

Таким же образом рассчитайте индекс для каждого месяца каждого года.

В столбце S с 38 по 51 строки мы рассчитали средний индекс для каждого месяца.

Т.к. сезонность повторяется каждые 12 месяцев, мы скопировали значения индекса в столбец C, т.к. они остаются актуальными. Вы можете заметить, что индекс января 2009 такой же как и в январе 2010 и 2011 годов.

В столбце D рассчитайте Скорректированные данные (Adjusted data) путем деления ежемесячных продаж на индекс =B10/C10.
Выберите значения из столбцов A, B и D и постройте линейный график.
Выберите скорректированную линию (в моем случае это красная линия) и добавьте линейный тренд, проверьте окошко «Показать уравнение на графике».

Рассчитайте несезонные значения для прошлого периода путем умножения ежемесячных продаж на коэффициент из уравнения линии тренда и добавьте константу из уравнения (столбец Е).

После создания линии тренда и представления Уравнения на графике, мы принимаем во внимание Коэффициент — число, которое умножается на X, и константу — число, которое, как правило, является отрицательным.

Проставляем коэффициент в ячейку E2, а Константу — в ячейку F2.

Рассчитайте Сезонные значения для прошлого периода путем умножения индекса (столбец С) на ранее рассчитанные данные (столбец Е).
Рассчитайте средний процент ошибки (MPE — mean percentage error) путем деления продаж на Сезонные значения для прошлого периода минус 1 (=B10/F10-1).
Рассчитайте средний абсолютный процент ошибки (MAPE — mean adjusted percentage error) путем возведения в квадрат данные в стобце MPE (=G10^2).

В моих ячейках F50 и F51 представлены спрогнизованные данные для ноября 2012 и декабря 2012. Ячейка H52 демонстрирует погрешность.

С помощью данного метода мы можем определить, что в декабре 2012 мы заработаем $22,022 ± 3.11%. Теперь идем к боссу и рассказываем о своих предположениях.

Стандартное отклонение

Стандартное отклонение (standard deviation) говорит о том, насколько наши значения отклоняться от среднего значения, мы можем назвать его уровнем доверия. Например, у вас есть данные по продажам за месяц и данные по ежедневным продажам, причем каждый день объем продаж разный. Вы можете использовать стандартное отклонение чтобы рассчитать, насколько вы отклонились от среднемесячного показателя.

Вот две формулы Стандартного отклонения в Excel, которые вы можете использовать

=stdev — когда у вас есть выборочные данные -> Авинаш Кошик подробно рассказывает, как работает выборка

или

=stdevp — когда у вас полная совокупность данных, т.е. когда вы анализируете каждого посетителя. Я предпочитаю именно =stdev, потому что бывают случаи, когда код отслеживания JS не работает.

Давайте посмотрим, как мы можем применить стандартное отклонение в нашей повседневной жизни.

Используя стандартное отклонение в Excel, данные можно представить более наглядным и понятным образом. Как вы видеть на графике выше, средняя ежедневная посещаемость равна 501 со стандартным отклонением 53. Но самое главное на таком графике вы видите, где вы превысили свои обычные показатели. Это позволит выделить те маркетинговые кампании, которые привели к такому всплеску, и применить/проверить их еще раз.

Для работы используйте данную ссылку: http://blog.instantcognition.com/wp-content/uploads/2007/01/controllimits_final.xls

Корреляция

Корреляция — это статистическая взаимосвязь двух или нескольких (случайных) переменных. Типичным примером корреляции в веб-аналитики может быть количество посетителей и количество продаж. Чем больше у вас целевых посетителей, тем больше будет продаж. У доктора Пита (Dr Pete) есть хорошая инфографика, посвященная корреляции vs. причинности.

В Excel мы используем следующую формулу для определения корреляции:

=correl(x,y)

Как вы видит на картинке выше, корреляция между Посещениями и Продажами равна 0.1. Что это значит?

от 0 до 0,3 считается слабой корреляцией
от 0.3 до 0,7 — нормальная
более 0,7 — сильная

Заключение следующее: ежедневные посещения не влияют на ежедневные продажи, что также означает, что посетители, которых вы привлекли, не являются целевыми. При принятии решения полагайтесь на ваше деловое чутье, но не игнорируйте корреляцию в 0,1.

Если вы хотите определить корреляцию между тремя и более переменными, используйте функцию корреляции в разделе Анализ данных.

Данные->Анализ данных->Корреляция

Ваш результат будет похож на один из этих:

Здесь мы видим, что ни один из элементов не коррелируют друг с другом:

Продажи и посетители = корреляция 0,1.
Продажи и расшаривания = корреляция 0,23.
Описательная статистика для быстрого анализа.

Теперь у вас есть довольно хорошее представление о среднем, стандартных отклонениях и т.д., но расчет каждого статистического элемента требует дополнительного времени. В разделе Анализ данных вы найдете краткий обзор наиболее распространенных элементов.

Данные->Анализ данных-> Описательная статистика.
Входной интервал — выбираем данные для анализа.
Выходной интервал — выбираем ячейку, где отобразится таблица.
Проверяем Сводную статистику.

Достаточно хороший результат:

Нам осталось разобраться с тем, что такое Эксцесс (kurtosis) и Асимметрия (skewness).

Эксцесс — это мера остроты пика распределения случайной величины, как далеко пик кривой находится от среднего значения. Чем выше значение эксцесса, тем острее пики по бокам. В нашем случае эксцесс является очень низким, это означает, что значения распределены равномерно.

Асимметрия показывает, насколько искажены ваши данные — негативно или позитивно, по сравнению с нормальным распределением. Теперь представим асимметрию более наглядно:

Асимметрия: −0.28 (распределение, скорее всего, ориентировано на более высоких значений 2500 и 3000).

Эксцесс: −0.47 (небольшое пиковое отклонение от центра).

Все эти методы можно использовать при анализе данных. Самой большой сложностью со статистическими данными и Excel является возможность применения этих методов в самых различных ситуациях, не ограничиваясь посещениями или продажами. Отличный пример использования нескольких статистических подходов представил Том Энтони в своем посте об инструменте для определения ссылочного профиля (Link Profile Tool).

Приведенные выше примеры являются лишь малой частью того, что можно сделать с помощью статистики и Excel. Если вы используете другие методы, поделитесь ими в комментариях.

Источник

Содержание

Использование описательной статистики
- Подключение «Пакета анализа»
- Применение инструмента «Описательная статистика»
Вопросы и ответы

Этот инструмент называется «Описательная статистика». С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Давайте взглянем, как работает данный инструмент, и остановимся на некоторых нюансах работы с ним.

Использование описательной статистики

В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:

Медиана;
Мода;
Дисперсия;
Среднее;
Стандартное отклонение;
Стандартная ошибка;
Асимметричность и др.

Подключение «Пакета анализа»

Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.

Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».

В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».

Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.

Применение инструмента «Описательная статистика»

Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ».

Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK».

После выполнения данных действий непосредственно запускается окно «Описательная статистика».
В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Для того, чтобы внести нужные нам координаты, устанавливаем курсор в указанное поле. Затем, зажав левую кнопку мыши, выделяем на листе соответствующую табличную область. Как видим, её координаты тут же отобразятся в поле. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.

Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:
- Выходной интервал;
- Новый рабочий лист;
- Новая рабочая книга.
В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на новом рабочем листе под названием «Итоги».

Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.

Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Но в нашем случае этот параметр так же, как и предыдущий, не является обязательным, поэтому флажки мы не ставим.

После того, как все указанные данные внесены, жмем на кнопку «OK».

После выполнения этих действий таблица с описательной статистикой выводится на отдельном листе, который был нами назван «Итоги». Как видим, данные представлены сумбурно, поэтому их следует отредактировать, расширив соответствующие колонки для более удобного просмотра.

После того, как данные «причесаны» можно приступать к их непосредственному анализу. Как видим, при помощи инструмента описательной статистики были рассчитаны следующие показатели:
- Асимметричность;
- Интервал;
- Минимум;
- Стандартное отклонение;
- Дисперсия выборки;
- Максимум;
- Сумма;
- Эксцесс;
- Среднее;
- Стандартная ошибка;
- Медиана;
- Мода;
- Счет.

Урок: Статистические функции в Excel

Как видим, с помощью инструмента «Описательная статистика» можно сразу получить результат по целому ряду критериев, которые в ином случае рассчитывались с применением отдельно предназначенной для каждого расчета функцией, что заняло бы значительное время у пользователя. А так, все эти расчеты можно получить практически в один клик, использовав соответствующий инструмент — Пакета анализа.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Описательная статистика Excel позволяет за несколько минут обработать достаточно большое количество информации и найти необходимые значения, учитывая определенный набор условий и критерий. Обработка данных большого ряда значений согласно всем законам статистики – нет проблем, Microsoft Excel справиться со всем.

Для того чтобы сформировать вывод о результатах полученных данных с целого ряда массива значений можно использовать достаточно простую функцию из «Пакета анализа», которая позволит систематизировать эмпирические значения согласно определенным критериям.

Эта функция можем высчитывать большинство критериев, среди которых:

• Отклонение и стандартное отклонение;
• Ошибка и стандартная ошибка;
• Асимметричность значений;
• Мода;
• Дисперсия;
• Медиана;
• Другие значения.

По умолчанию, возможность работы с «Относительной статистикой» скрыта от большинства пользователей. Для того чтобы активировать данную панель, необходимо включить ее в параметрах документа.

Для этого нажмем на вкладку «Файл» — «Параметры».

В появившемся диалоговом окне перейдем в меню «Надстройки», где внизу в подменю «Управление» нужно выбрать «Надстройки Excel» и перейти к последующим настройкам.

В новом окне ставим галочку напротив «Пакет анализа» и применяем операцию.

Весь функционал «Пакета анализа» был добавлен в рабочую область и появился во вкладке «Данные». Приступим непосредственно к «Описательной статистике» и попробуем на практике данный инструмент.

Перейдем во вкладку «Анализ данных», которая размещена в «Данных» и выбираем функцию «Описательная статистика».

Теперь необходимо заполнить все поля и ввести аргументы функции.

• «Входной интервал» — укажем весь диапазон данных, для которых необходимо применить функцию «Описательной статистики» — выделяем весь столбец вместе с названием с включением функции «Метки в первой строке».
• Включим группирование «По строкам» и «По столбцам».
• Выберем место, куда будут сохраняться результаты работы функции, это могут быть и новая книга, новый лист либо просто выбранный интервал.

Теперь можно анализировать результаты работы функции. «Описательная статистика» рассчитала сразу несколько показателей, которые дают более четкое представление о выполненной работе: интервал, минимум и максимум, общую сумму и среднее значение и так далее.

Пакет анализа предлагает пользователю результаты сразу по нескольким критериям. Это экономит большое количество времени, которое ушло бы на отдельный расчет по каждому показателю.

Описательная статистика в excel

Инструмент Описательная статистика входит в Пакет анализа (активация Пакета анализа смотри п.2.7.2). С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Среди критериев, которые высчитывает данный инструмент следующие показатели:

Медиана;
Мода;
Дисперсия;
Среднее;
Стандартное отклонение;
Стандартная ошибка;
Асимметричность и др.

Рассмотрим работу данного инструмента на примере задачи 4.2.

Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ». Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK» (рис. 4.1).

Рис. 4.1. Описательная статистика

После выполнения данных действий непосредственно запускается окно «Описательная статистика».

В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.

Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:

Выходной интервал;
Новый рабочий лист;
Новая рабочая книга.

В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на этом же рабочем листе (рис.4.2).

Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.

Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Этот параметр, также как и предыдущий, не является обязательным, поэтому флажки можно не ставить.

После того, как все указанные данные внесены, жмем на кнопку «OK».

Среди множества показателей Описательной статистики есть те, которые нас интересуют, они выделены цветом (рис. 4.3).

ВОПРОСЫ И УПРАЖНЕНИЯ

1. Дайте определение размаху, выборочной дисперсии, генеральной дисперсии, стандартному отклонению. Воспроизведите формулы для их нахождения.

2. Что характеризует выборочная дисперсия.

3. Вычислите для множества: 22, 15, 16, 21, 24, 24, 27, 28, 30, 30, 31, 31, 31, 34, 36 размах, дисперсию, стандартное отклонение.

4. В каких случаях можно проводить сравнение разных выборок по дисперсиям?

5. Выборочные дисперсии результатов контрольной работы в классе 7«А» и 7«Б» соответственно равны 0,44 и 1,38. Какой вывод можно сделать при сравнении результатов контрольной работы в двух классах?

6. Дисперсия каждой из групп A и В равна 5. Будет ли дисперсия 10 значений, полученных путем объединения групп, меньше, больше или равна 5?

Группа А: 13, 11, 10, 9, 7

Группа В: 28, 26, 25, 24, 22

Лабораторная работа №2

Описательная статистика

Этапы обработки данных:

1. Занести данные в таблицу Excel (две выборки).

2. Упорядочить данные (по возрастанию) в каждой выборке.

3. Рассчитать моду, медиану и среднее.

4. Посчитать дисперсию, стандартное отклонение.

5. Посчитать коэффициент вариации.

6. Сделать сравнительный анализ, полученных результатов.

Задания для вариантов 1 – 5

При определении степени выраженности некоторого психического свойства в двух группах, опытной и контрольной, баллы распределились следующим образом.

Дать сравнительную характеристику степени выраженности этого свойства в данных группах.

Вариант 1.

Опытная	18, 15, 16, 11, 14,15, 16, 16, 20, 22, 17, 12, 11, 12, 18, 19, 20
Контрольная	26, 8, 11, 12, 25, 22, 13, 14, 21, 20, 15, 16, 17, 16, 9, 11, 16

Вариант 2

Опытная	19, 16, 17, 12, 15,16, 17,17, 21, 23, 18, 13, 12, 13, 19, 20, 21
Контрольная	27, 9, 12, 13, 26, 23, 14, 15, 22, 21, 16, 16, 18, 17, 10, 12, 17

Вариант 3.

Опытная	16, 13, 14, 9, 10,13, 14,14, 18, 20, 15, 10, 9, 10, 16, 17, 18
Контрольная	24, 6, 9, 10, 23, 20, 11, 12, 19, 18, 13, 14, 12, 14, 7, 9, 14

Опытная	15, 12, 13, 8, 11,12, 13,13, 17, 19, 14, 9, 8, 9, 15, 16, 17
Контрольная	23, 5, 9, 9, 22, 19, 10, 11, 18, 17, 12, 13, 14, 13, 6, 8, 13

Опытная	15, 12, 13, 8, 11,12, 13,13, 17, 19, 14, 9, 8, 9, 15, 16, 17
Контрольная	24, 6, 9, 10, 23, 20, 11, 12, 19, 18, 13, 14, 12, 14, 7, 9, 14

Задания для вариантов 6 – 10

Была исследована группа детей с заболеванием крови до лечения препаратами и после лечения. В таблицу занесены показатели крови по результатам медицинского обследования. Сделать сравнительный анализ результативности лечения данным препаратом, используя методы описательной статистики.

до лечения	20,5 12,1 13,6 40,5 9,6 33 77,2 8,7 3,5 13,8 7,4 29,4 116 21,9
после лечения	2,3 7,5 3,8 3,8 8,8 13 4,7 3,9 4,8 5,7 9 13 0,9

до лечения	280 230 100 60 90 80 8 36 50 90 17 42 42 30
после лечения	86 280 30 170 210 230 230 156 102 161 15 60 20

до лечения	112 60 84 60 60 40 76 60 84 40 112 46 64 70
после лечения	82 78 110 130 130 104 108 129 110 88 105 73 85 80

до лечения	113 61 85 61 61 41 77 61 85 41 113 47 65 71
после лечения	81 77 109 129 129 103 107 128 109 87 104 72 84 79

до лечения	111 59 83 59 59 39 75 59 83 39 111 45 63 69
после лечения	83 79 111 131 131 105 109 130 111 89 106 74 86 81

Задания для вариантов 11 – 15

Для проверки эффективности новой развивающей программы были созданы две группы детей шестилетнего возраста. На первом этапе дети обеих групп были протестированы по методике Керна-Йерасика (школьная зрелость). Результаты тестирования по невербальной шкале занесены в таблицу. Сделать сравнительный анализ школьной зрелости детей этих групп.

Эксперимент.	29 31 31 25 25 19 22 20 14 16 27 24 32 27 14 24
Контроль	34 31 28 27 30 23 21 28 29 31 17 22 21 15 33 29

Эксперимент.	14 13 11 8 12 13 13 13 11 12 14 13 12 14 10 13
Контроль	13 13 14 12 14 14 12 13 15 13 11 12 14 9 14 13

Эксперимент.	33 33 37 33 34 33 31 29 29 35 31 29 31 34 26 26
Контроль	39 30 38 36 31 37 35 32 39 34 30 32 36 29 39 36

Эксперимент.	13 12 10 7 11 12 12 12 10 11 13 12 11 13 9 12
Контроль	12 12 13 11 13 13 11 12 14 12 10 11 13 8 13 12

Эксперимент.	30 32 32 26 26 20 23 21 15 17 28 25 33 28 15 25
Контроль	35 32 29 28 31 24 22 29 30 32 18 24 22 16 34 30

Задания для вариантов 16 – 20

У участников психологического исследования, в число которых входила группа педагогов и группа непедагогов, был исследован уровень конфликтности. Полученные данные занесены в таблицу. Можно ли утверждать, что уровень конфликтности педагогов выше, чем у непедагогов?

Использование пакета анализа

Если вам нужно провести сложный статистический или инженерный анализ, можно сэкономить время и этапы с помощью «Pak анализа». Вы предоставляете данные и параметры для каждого анализа, а средство использует соответствующие статистические или инженерные функции для вычисления и отображения результатов в выходной таблице. Некоторые средства создают диаграммы в дополнение к выходным таблицам.

Функции анализа данных можно применять только на одном листе. Если анализ данных проводится в группе, состоящей из нескольких листов, то результаты будут выведены на первом листе, на остальных листах будут выведены пустые диапазоны, содержащие только форматы. Чтобы провести анализ данных на всех листах, повторите процедуру для каждого листа в отдельности.

Ниже описаны инструменты, включенные в пакет анализа. Для доступа к ним нажмите кнопку Анализ данных в группе Анализ на вкладке Данные. Если команда Анализ данных недоступна, необходимо загрузить надстройку «Пакет анализа».

Откройте вкладку Файл, нажмите кнопку Параметры и выберите категорию Надстройки.

Если вы используете Excel 2007, нажмите Microsoft Office кнопку и выберите «Параметры Excel»

В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.

Если вы используете Excel для Mac, в строке меню откройте вкладку Средства и в раскрывающемся списке выберите пункт Надстройки для Excel.

В диалоговом окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.

Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.

Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.

Примечание: Чтобы включить Visual Basic для приложений (VBA) в надстройку «Надстройка «Анализ», можно загрузить его так же, как и надстройку «Надстройка «Анализ». В поле «Доступные надстройки» выберите «Надстройка анализа — VBA».

Существует несколько видов дисперсионного анализа. Нужный вариант выбирается с учетом числа факторов и имеющихся выборок из генеральной совокупности.

Однофакторный дисперсионный анализ

Этот инструмент выполняет простой анализ дисперсии данных для двух или более выборок. Анализ предоставляет проверку гипотезы о том, что все выборки взяты из одного и того же распределения вероятности относительно альтернативной гипотезы о том, что распределение вероятностей не одинаково для всех выборок. Если выборок всего два, можно использовать функцию T. ТЕСТ. В более чем двух примерах не существует удобного обобщения T. Ивместо нее можно использовать модель однофакторного коэффициента.

Двухфакторный дисперсионный анализ с повторениями

Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам. Например, в эксперименте по измерению высоты растений последние обрабатывали удобрениями от различных изготовителей (например, A, B, C) и содержали при различной температуре (например, низкой и высокой). Таким образом, для каждой из 6 возможных пар условий <удобрение, температура>, имеется одинаковый набор наблюдений за ростом растений. С помощью этого дисперсионного анализа можно проверить следующие гипотезы:

Извлечены ли данные о росте растений для различных марок удобрений из одной генеральной совокупности. Температура в этом анализе не учитывается.

Извлечены ли данные о росте растений для различных уровней температуры из одной генеральной совокупности. Марка удобрения в этом анализе не учитывается.

Извлечены ли шесть выборок, представляющих все пары значений <удобрение, температура>, используемые для оценки влияния различных марок удобрений (для первого пункта в списке) и уровней температуры (для второго пункта в списке), из одной генеральной совокупности. Альтернативная гипотеза предполагает, что влияние конкретных пар <удобрение, температура>превышает влияние отдельно удобрения и отдельно температуры.

Двухфакторный дисперсионный анализ без повторений

Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам, как в случае двухфакторного дисперсионного анализа с повторениями. Однако в таком анализе предполагается, что для каждой пары параметров есть только одно измерение (например, для каждой пары параметров <удобрение, температура>из предыдущего примера).

Функции КОРРЕЛ и PEARSON рассчитывают коэффициент корреляции между двумя переменными измерения, если измерения по каждой переменной наблюдались для каждого из N-объектов. (Отсутствуют результаты наблюдений по любой теме, которые при анализе игнорируются.) Инструмент анализа корреляции особенно удобен, если для каждого субъекта N существует более двух переменных измерения. Она содержит выходную таблицу — матрицу корреляции, которая показывает значение КОРРЕЛ (или PEARSON),примененного к каждой из возможных пар переменных измерения.

Коэффициент корреляции, как и ковариана, — это мера степени, в которой две переменные измерения «различаются». В отличие от ковариации коэффициент корреляции масштабирован таким образом, что его значение не зависит от единиц, в которых выражены две переменные измерения. (Например, если двумя переменными измерения являются вес и высота, коэффициент корреляции не изменяется, если вес преобразуется из фунта в фунты.) Значение любого коэффициента корреляции должно быть включительно (от -1 до +1).

Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, т. е. большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция).

Средства корреляции и ковариатора можно использовать в одном и том же параметре, если у вас есть N различных переменных измерения для набора людей. Каждый из инструментов корреляции и ковариции дает выходную таблицу — матрицу, в которую указывается коэффициент корреляции или коварианс между каждой парой переменных измерения. Разница заключается в том, что коэффициенты корреляции масштабироваться в зависимости от -1 и +1 включительно. Соответствующие ковариансии не масштабироваться. Коэффициент корреляции и ковариатор — это меры, в которых две переменные «различаются».

Инструмент «Ковариана» вычисляет значение функции КОВАРИАНАС на этом компьютере. P для каждой пары переменных измерения. (Непосредственное использование КОВАРИАНС. Вместо ковариатора P лучше использовать ковариативную единицу, если имеется только две переменных измерения, то есть N=2.) Запись на диагонали выходной таблицы инструмента «Ковариальная» в строке i, столбце i — ковариальная величина i-й переменной. Это только дисперсия по численности населения для этой переменной, вычисляемая функцией ДИСПЕ. P.

Ковариационный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных связаны с большими значениями другого набора (положительная ковариация) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная ковариация), или данные двух диапазонов никак не связаны (ковариация близка к нулю).

Инструмент анализа «Описательная статистика» применяется для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.

Инструмент анализа «Экспоненциальное сглаживание» применяется для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. При анализе используется константа сглаживания a, величина которой определяет степень влияния на прогнозы погрешностей в предыдущем прогнозе.

Примечание: Для константы сглаживания наиболее подходящими являются значения от 0,2 до 0,3. Эти значения показывают, что ошибка текущего прогноза установлена на уровне от 20 до 30 процентов ошибки предыдущего прогноза. Более высокие значения константы ускоряют отклик, но могут привести к непредсказуемым выбросам. Низкие значения константы могут привести к большим промежуткам между предсказанными значениями.

Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.

Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.

С помощью этого инструмента вычисляется значение f F-статистики (или F-коэффициент). Значение f, близкое к 1, показывает, что дисперсии генеральной совокупности равны. В таблице результатов, если f 1, «P(F

Инструмент «Анализ Фурье» применяется для решения задач в линейных системах и анализа периодических данных на основе метода быстрого преобразования Фурье (БПФ). Этот инструмент поддерживает также обратные преобразования, при этом инвертирование преобразованных данных возвращает исходные данные.

Инструмент «Гистограмма» применяется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. При этом рассчитываются числа попаданий для заданного диапазона ячеек.

Например, можно получить распределение успеваемости по шкале оценок в группе из 20 студентов. Таблица гистограммы состоит из границ шкалы оценок и групп студентов, уровень успеваемости которых находится между самой нижней границей и текущей границей. Наиболее часто встречающийся уровень является модой диапазона данных.

Совет: В Excel 2016 теперь можно создавать гистограммы и диаграммы Парето.

Инструмент анализа «Скользящее среднее» применяется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Скользящее среднее, в отличие от простого среднего для всей выборки, содержит сведения о тенденциях изменения данных. Этот метод может использоваться для прогноза сбыта, запасов и других тенденций. Расчет прогнозируемых значений выполняется по следующей формуле:

N — число предшествующих периодов, входящих в скользящее среднее;

A j — фактическое значение в момент времени j;

F j — прогнозируемое значение в момент времени j.

Инструмент «Генерация случайных чисел» применяется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью этой процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей. Например, можно использовать нормальное распределение для моделирования совокупности данных по росту людей или использовать распределение Бернулли для двух вероятных исходов, чтобы описать совокупность результатов бросания монеты.

Инструмент анализа «Ранг» и «Процентиль» создает таблицу, которая содержит порядкованный и процентный ранг каждого значения в наборе данных. Можно проанализировать относительное положение значений в наборе данных. В этом средстве используются функции РАНГ. EQ и PERCENTRANK. INC. Если вы хотите учитывать связанные значения, используйте РАНГ. Функция EQ, которая рассматривает связанные значения как связанные значения с одинаковым рангом, или использует РАНГ. Функция AVG, которая возвращает среднее ранг для связанных значений.

Инструмент анализа «Регрессия» применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.

Инструмент «Регрессия» использует функцию LINEST.

Инструмент анализа «Выборка» создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки или построения диаграммы, можно использовать представительную выборку. Кроме того, если предполагается периодичность входных данных, то можно создать выборку, содержащую значения только из отдельной части цикла. Например, если входной диапазон содержит данные для квартальных продаж, создание выборки с периодом 4 разместит в выходном диапазоне значения продаж из одного и того же квартала.

Двухвыборочный t-тест проверяет равенство средних значений генеральной совокупности по каждой выборке. Три вида этого теста допускают следующие условия: равные дисперсии генерального распределения, дисперсии генеральной совокупности не равны, а также представление двух выборок до и после наблюдения по одному и тому же субъекту.

Для всех трех средств, перечисленных ниже, значение t вычисляется и отображается как «t-статистика» в выводимой таблице. В зависимости от данных это значение t может быть отрицательным или неотрицательным. Если предположить, что средние генеральной совокупности равны, при t =0 «P(T Парный двухвыборочный t-тест для средних

Парный тест используется, когда имеется естественная парность наблюдений в выборках, например, когда генеральная совокупность тестируется дважды — до и после эксперимента. Этот инструмент анализа применяется для проверки гипотезы о различии средних для двух выборок данных. В нем не предполагается равенство дисперсий генеральных совокупностей, из которых выбраны данные.

Примечание: Одним из результатов теста является совокупная дисперсия (совокупная мера распределения данных вокруг среднего значения), вычисляемая по следующей формуле:

Двухвыборочный t-тест с одинаковыми дисперсиями

Этот инструмент анализа выполняет двухуголовый t-тест учащегося. В этой форме t-теста предполагается, что два набора данных поступили из распределения с одинаковыми дисперсиями. Этот тест называется гомомоcedastic t-test. Этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами.

Двухвыборочный t-тест с различными дисперсиями

Этот инструмент анализа выполняет двухуголовый t-тест учащегося. В этой форме t-теста предполагается, что два набора данных поступили из распределений с неравными дисперсиями. Это называется гетероскестический t-тест. Как и в предыдущем случае с равными дисперсиями, этот t-тест можно использовать для определения вероятности того, что две выборки взяты из распределения с равными средствами. Этот тест можно использовать, если в двух примерах есть различные темы. Используйте парный тест, описанный в примере, если существует один набор субъектов и два примера представляют измерения для каждой темы до и после обработки.

Для определения тестовой величины t используется следующая формула.

Для вычисления степеней свободы (df) используется следующая формула: Так как результат вычисления обычно не является integer, значение df округлится до ближайшего ближайшего другого для получения критического значения из таблицы t. Функция листа Excel T. В этой проверке используется вычисляемая величина df без округления, так как ее можно вычислить для значения T. ТЕСТ с неинтегрным df. Из-за таких разных подходов к определению степеней свободы результаты T. Тест и этот t-тест различаются в случае неравных дисперсий.

Z-тест. Средство анализа «Две выборки для средств» выполняет два примера z-теста для средств со известными дисперсиями. Это средство используется для проверки гипотезы null о том, что между двумя значениями населения нет различий между односторонними или двухбокльными гипотезами. Если дисперсии не известны, функция Z. Вместо нее следует использовать тест.

При использовании этого инструмента следует внимательно просматривать результат. «P(Z = ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. «P(Z = ABS(z) или Z

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.

ОПИСАТЕЛЬНАЯ СТАТИСТИКА

Первичный анализ скалярных экспериментальных данных начинается с вычисления описательных статистик. Добавив к этому графические характеристики, получим некоторые основания для выводов о характере распределения данных исследуемой совокупности. К тому же базовый анализ дает основу для дальнейшего проведения более сложного анализа данных.

Из множества инструментов надстройки «Анализ данных» будем использовать «Описательную статистику» для получения числовых характеристик и «Гистограмму» — для графических. Заметим, что наряду с этим можно использовать также встроенные «Статистические функции», которые дублируют возможности надстройки.

Рассмотрим работу с описательной статистикой на примере.

Пример 4.1. Имеются некоторые данные о стоимости новогодних туров (рис. 4.2). Каждый из столбцов можно рассматривать как отдельный признак или переменную. Требуется провести анализ данных о продолжительности туров.

Таблица исходных данных

Исходные данные содержат несколько переменных, характеризующих тур. «Название фирмы», «Страна», «Транспорт» — качественные переменные, которые относятся к номинальной шкале. «Отель» —качественная переменная, которую можно отнести к порядковой шкале, так как количество звездочек отражает уровень обслуживания в отеле. «Количество дней» и «Стоимость» —количественные данные, которые относятся к метрической шкале.

Вычислим основные описательные статистики для переменной «Количество дней», которая является числовой переменной, принимающей дискретные значения. Для этого используем инструмент «Описательная статистика», входящий в «Пакет анализа».

Для перехода к описательной статистике выполните: «Данные» —» «Анализ» —> «Анализ данных» —» «Описательная статистика» -> «Ок». В открывшемся диалоговом окне «Описательная статистика» (рис. 4.3) укажите «Входной интервал», диапазон В2:Б16, выберите «Труп-

Диалоговое окно «Описательной статистики»

иирование по столбцам», установите «Метки в первой строке», так как входной интервал содержит наименование столбца. Для «Выходного интервала» достаточно указать одну, первую, ячейку на текущем листе, как альтернативу можно выбрать «Новый рабочий лист» или «Новую рабочую книгу». И наконец, укажите хотя бы одну из выводимых статистик: «Итоговая статистика», «Уровень надежности», «К-й наименьший», «К-й наибольший».

В большинстве случаев достаточно выбрать «Итоговую статистику», которая рассчитывает основные числовые характеристики исследуемой совокупности. Три последних значения рассчитывают, только когда они действительно нужны.

«Описательная статистика» вычисляет 16 значений, из них 13 относятся к «Итоговой статистике», еще три определяют доверительный интервал и два выборочных значения.

Отметим главное — «Описательная статистка» надстройки «Анализ данных» предназначена для вычислений статистических характеристик, или статистик, одномерной выборки или нескольких выборок.

В литературе по статистике часто используют термин «генеральная совокупность». Обычно имеется в виду, что это множество всех доступных для наблюдения данных в противоположность «выборки» — которая подразумевает, что исследуется лишь часть данных выбранных из генеральной совокупности (может быть с помощью случайного отбора).

Обычно числовые характеристики генеральной совокупности называют параметрами, а числовые характеристики выборки — статистиками, или выборочными характеристиками, которые являются оценками параметров генеральной совокупности. Для более полного понимания выборочного метода следует обратиться к специальной литературе.

Результаты расчетов «Итоговой статистики» для переменной «Количество дней» приведены на рисунке 4.4. На этом же рисунке приведены альтернативные расчеты этих числовых характеристик с использованием встроенных функций категории «Статистические». Аргументом статистических функций является диапазон исходных данных, в данном случае D3:D16.

Таким образом, практически все расчеты «Описательной статистики» дублируются «Статистическими» функциями. Остальные характеристики можно посчитать, используя формулы. Для того чтобы на рабочем листе Excel отобразились не результаты, а формулы, следует выполнить: «Формулы» -» «Зависимости формул» -» «Показать формулы».

Отметим некоторое отличие в применении инструментов «Анализа данных» и использовании статистических функций. При изменении значений исходных данных формулы пересчитываются, в то время как результаты, полученные с помощью инструментов «Анализа данных»,

«Итоговая статистика» и «Статистические функции»

не изменяются. Чтобы обновить результаты, потребуется вызывать «Анализ данных» снова.

Числовые характеристики «Итоговой статистики» описывают средние, вариацию и форму распределения, всего 13 параметров:

• среднее, или выборочное среднее, вычисляется как среднее арифметическое наблюдаемых значений выборки;
• медиана определяется как значение, находящееся в середине распределения, полученного из исходного путем упорядочивания по возрастанию;
• мода равна наиболее часто встречающемуся значению. Кроме того, выделяют две величины, характеризующие изменчивость, или разброс, значений распределения относительно среднего:
- 1) дисперсию выборки, или выборочную дисперсию, равную сумме квадратов отклонений каждого значения от среднего, деленной на (А — 1), где N — число значений в распределении, или объем выборки;

2) стандартное отклонение, или выборочное среднеквадратическое отклонение, равное квадратному корню из выборочной дисперсии.

Дополнительными мерами изменчивости являются три простые характеристики, отражающие границы распределения данных и его размах:

• минимум равен наименьшему из выборочных значений;
• максимум равен наибольшему из выборочных значений;
• интервал составляет разность между максимумом и

минимумом, этот параметр называют также размахом.

Если набор данных рассматривается как множество

независимых реализаций случайной величины, то возникает вопрос, что можно сказать о функции распределения этой величины на основании выборки. Очень часто распределение оказывается нормальным или близким к нему.

Для отражения близости формы распределения к нормальному виду существует две основные характеристики:

1) эксцесс, или выборочный коэффициент эксцесса, который является мерой «сглаженности» распределения;
2) асимметричность, или выборочный коэффициент асимметрии, показывает, в какую сторону относительно среднего сдвинуто большинство значений выборки.

И наконец, сумма равна сумме всех выборочных значений, счет вычисляет объем выборки, стандартная ошибка равна выборочному стандартному отклонению, деленному на квадратный корень из объема выборки.

При необходимости можно вычислить три дополнительные характеристики (рис. 4.5). Результаты расчетов этих характеристик приведены на рисунке 4.6.

«К-й наибольший» выдает К-е выборочное значение, если бы выборка была отсортирована по убыванию. В рассматриваемом примере сортировка по убыванию имеет вид 14,12,12,12, 11, Юит. д., третье значение равно 12. «К-й наименьший» выдает К-е выборочное значение, если бы выборка была отсортирована по возрастанию, это значение равно 5.

Задав «Уровень надежности», например 95%, получим значение для построения доверительного интервала для

Описательная статистика, дополнительные параметры

Результаты расчетов дополнительных параметров

неизвестного математического ожидания генеральной средней с доверительным уровнем 95%. Доверительный интервал строится как выборочное среднее плюс-минус полученное значение. Обратим внимание, что граница здесь вычисляется с помощью распределения Стьюдента, что требует достаточного количества наблюдений на каждую степень свободы.

Таким образом, к вычислению доверительных интервалов нужно относиться с осторожностью, особенно при малых выборках. Использование функции расчета доверительного интервала без понимания статистического смысла может привести к ошибкам. Начинающим исследователям посоветуем обратиться к специальной литературе.

Например, для рассматриваемого примера полученный доверительный интервал не несет смыслового содержания.

Итак, на этапе проведения описательной статистики исследуемый ряд данных может быть как генеральной совокупностью, так и выборкой. Если для генеральной совокупности вычисляются значения параметров распределения, то для выборки находят оценки этих параметров. Рассмотрим ниже подробнее вычисление некоторых числовых характеристик в пакете Excel.

Построение доверительных интервалов для среднего. Описательная статистика в Excel

2015-03-22
2255

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3

Описательная статистика в Excel

Вычисление границ доверительных интервалов в Excel

Использование инструмента Пакета анализа Описательная статистика.

Построение доверительных интервалов для среднего.

В пакете Excel помимо мастера функций имеется набор более мощных инструментов для работы с несколькими выборками углубленного анализа данных, называемый Пакет анализа, который может быть использован для решения задач статистической обработки выборочных данных.

Для установки раздела Анализ данных в пакете Excel сделайте следующее:

— в меню Сервис выберите команду Надстройки;

— в появившемся списке установите флажок Пакет анализа.

Ввод данных. Исследуемые данные следует представить в виде таблицы, где столбцами являются соответствующие показатели. При создании таблицы Excel информация вводится в отдельные ячейки. Совокупность ячеек, содержащих анализируемые данные, называется входным диапазоном.

Последовательность обработки данных. Для использования статистического пакета анализа данных необходимо:

— указать курсором мыши на пункт меню Сервис и щелкнуть левой кнопкой мыши;

— в раскрывающемся списке выбрать команду Анализ данных (если команда Анализ данных отсутствует в меню Сервис, то необходимо установить в Excel пакет анализа данных);

— выбрать необходимую строку в появившемся списке Инструменты анализа;

— ввести входной и выходной диапазоны и выбрать необходимые параметры.

Нахождение основных выборочных характеристик. Для определения характеристик выборки используется процедура Описательная статистика. Процедура позволяет получить статистический отчет, содержащий информацию о центральной тенденции и изменчивости входных данных. Для выполнения процедуры необходимо:

— выполнить команду Сервис > Анализ данных;

— в появившемся списке Инструменты анализа выбрать строку Описательная статистика и нажать кнопку ОК (рис. 1);

— в появившемся диалоговом окне указать входной диапазон, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Для этого следует навести указатель мыши на левую верхнюю ячейку данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

Рис. 1. Окно выбора метода обработки данных

— указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной диапазон (навести указатель мыши и щелкнуть левой клавишей), далее навести указатель мыши в поле ввода Выходной диапазон и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши;

— в разделе Группировка переключатель установить в положение по столбцам; о установить флажок в поле Итоговая статистика;

— нажать кнопку ОК.

В результате анализа в указанном выходном диапазоне для каждого столбца данных выводятся следующие статистические характеристики: среднее, стандартная ошибка (среднего), медиана, мода, стандартное отклонение, дисперсия выборки, эксцесс, асимметричность, интервал, минимум, максимум, сумма, счет, наибольшее, наименьшее, уровень надежности.

Пример 1. Рассматривается зарплата основных групп работников гостиницы: администрации, обслуживающего персонала и работников ресторана. Были получены следующие данные:

Необходимо определить основные статистические характеристики в группах данных.

1. Для использования инструментов анализа исследуемые данные следует представить в виде таблицы, где столбцами являются соответствующие показатели. Значения зарплат сотрудников администрации введите в диапазон А1:А5, обслуживающего персонала— в диапазон В1:В8 и т. д. В результате получится таблица, представленная на рис. 2.

Рис. 2. Таблица из примера

2. Далее необходимо провести элементарную статистическую обработку. Для этого, указав курсором мыши на пункт меню Сервис, выберите команду Анализ данных. Затем в появившемся списке Инструменты анализа выберите строку Описательная статистика.

Рис. 3. Пример заполнения диалогового окна Описательная статистика

3. В появившемся диалоговом окне (рис. 3) в рабочем поле Входной интервал укажите входной диапазон —А1:С8. Активировав переключателем рабочее поле Выходной интервал, укажите выходной диапазон — ячейку А9. В разделе Группировка переключатель установите в положение по столбцам. Установите флажок в поле Итоговая статистика и нажмите кнопку ОК. В результате анализа (рис. 4) в указанном выходном диапазоне для каждого столбца данных получим соответствующие результаты.

Рис. 4. Результаты работы инструмента Описательная статистика.

1. Найдите наиболее популярный туристический маршрут из четырех реализуемых фирмой (моду), если за неделю последовательно были реализованы следующие маршруты (приводятся номера маршрутов): 1, 3, 3, 2, 1, 1, 4, 4, 2, 4, 1, 3, 2, 4, 1, 4, 4, 3, 1, 2, 3, 4, 1, 1, 3.

2. В рабочей зоне производились замеры концентрации вредного вещества. Получен ряд значений (в мг/м3): 12, 16, 15, 14, 10, 20, 16, 14, 18, 14, 15, 17, 23, 16. Необходимо определить основные выборочные характеристики.

Источник

При
большом объёме выборки её анализ требует
большого объёма вычислений, поэтому
естественно проводить его за компьютером.
Имеется большое число программных
средств, как специально предназначенных
для статистического анализа, так и
содержащихся в универсальных
программах в качестве подпрограмм и
опций. Достаточно возможностей для
этого предоставляет, в частности,
доступная всем программаExcel.
Команды для
проведения статистического анализа
можно найти в меню «СервисАнализ
данных» и в меню «ФункцииСтатистические»
и «ФункцииРабота
с базами данных».

Таблица
1.

Рассмотрим
работу в этой среде на следующем примере.
В лабораторном практикуме группа из 25
студентов определяла концентрацию
некоторого вещества в выданном им
растворе. Каждый из них сделал по 4
параллельных определения. Их результаты,
округлённые до 0,5 г/л я занёс в таблицу
Excel
(табл.1).У
меня образовался массив, содержащий 4
столбца B,C,D
и E,
и 25 строк с №2 до №26. Далее я хочу найти
минимальное число из этого массива –
нижнюю границу выборки. Я щёлкаю по
пустой ячейке, в которой хочу найти
ответ, затем навожу курсор на «»,
и нажимаю левую клавишу мыши. Открывается
окно выбора функций – «Мастер функций».
В разделе «Категории» я открываю
«статистические» и нахожу тамМИН.

После
щелчка мышью по этому названию и “OK”
открывается диалоговое окно «Аргументы
функции» с пометкой МИН.
В окошко,
помеченное «Число 1», можно ввести сами
числа, что, конечно, неудобно. Вместо
этого я щёлкаю мышью по крайней левой
верхней клетке массива, затем нажимаю
“Shift”
и одновременно щёлкаю по крайней правой
нижней клетке. При этом в вышеуказанном
окошке появляются границы массива в
виде “$B$2:$E$26.
Ответ «300,5» появляется сразу, а при
щелчке «OK»
— в заготовленной клетке. Точно так же
я могу применить эту функцию к любой
прямоугольной части этого массива,
вызвав саму функцию МИН
(теперь её
позывной можно найти в категории
«Последние») и отметив, как описано
выше, щелчками мыши, клетки в начале и
конце выбранной части массива. Впрочем,
выделять массив можно и движением мыши,
если сначала навести курсор на начало
массива, нажать левую клавишу мыши, и,
не снимая нажатия, провести курсор до
конечной точки массива.

Конечно,
такое подробное описание вызовет улыбку
у продвинутого пользователя, но, возможно,
среди читателей есть и такие, которые
впервые в жизни откроют документ Excel.

Для
краткого описания действий при
использовании других функций будем
использовать следующие обозначения:

ЩАа
– щелчок по клетке начала диапазона,

ЪЩЯя
— щелчок по клетке конца диапазона с
одновременным нажатием Shift,

ЩСс
– щелчок по свободной ячейке, в которой
будет указан результат.

,
серв., дигр., адат, стат. – щелчки по
значкам
,
«сервис», «диаграмма», «анализ данных»,
«статистические» соответственно.
Напомним, что если какая-либо функция
используется повторно, то быстрее найти
её не через «статистические», а через
«последние».

Итак,
считаем, что в таблицу Excel
внесены
данные выборки в виде строки, столбца,
или двумерного массива. Цели и действия
представлены в таблице 2.

Таблица
2.

Что требуется найти	Действия
Объём выборки	ЩСс,, стат.,СЧЕТ, ЩАа, ЪЩЯя,
Нижнюю границу	ЩСс,, стат.,МИН, ЩАа, ЪЩЯя,
Верхнюю границу	ЩСс,, стат.,МАКС, ЩАа, ЪЩЯя,
Среднее арифметическое	ЩСс,, стат.,СРЗНАЧ, ЩАа, ЪЩЯя,
Моду	ЩСс,, стат.,МОДА, ЩАа, ЪЩЯя,
Медиану	ЩСс,, стат.,МЕДИАНА, ЩАа, ЪЩЯя,
Нижний квартиль	ЩСс,, стат.,КВАРТИЛЬ, ЩАа, ЪЩЯя, затем щёлкнуть по окну «значение» и ввести число «1»,
Верхний квартиль	ЩСс,, стат.,КВАРТИЛЬ, ЩАа, ЪЩЯя, затем щёлкнуть по окну «значение» и ввести число «3»,
Выборочную дисперсию	ЩСс,, стат.,ДИСП, ЩАа, ЪЩЯя,
	ЩСс,, стат.,СТАНДОТКЛОН, ЩАа, ЪЩЯя,
Доверительный интервал для среднего	ЩСс,, стат.,ДОВЕРИТ, ЩАа, ЪЩЯя,
Асимметрию	ЩСс,, стат.,СКОС, ЩАа, ЪЩЯя,
Эксцесс	ЩСс,, стат.,ЭКСЦЕСС, ЩАа, ЪЩЯя,

В
таблице 1 в столбцах F—I
вы видите результаты выполнения
соответствующих функций для каждой из
25 строк массива. При этом нет необходимости
вводить формулу функции в каждую строку
отдельно – достаточно ввести её в первую
строку, а в окошко аргументов ввести
координаты начала и конца этой строки:

После
нажатия «»
в ячейке, в которую введена данная
формула, появляется соответствующий
результат:

Если
теперь навести курсор на чёрный квадратик
в нижнем правом углу этой ячейки, и при
нажатой левой клавише мыши провести
его вдоль столбца до последней строки
массива данных, то после отпускания
клавиши весь столбец заполнится
результатами, полученными для всех
остальных строк по той же формуле.

Для
группировки данных и получения
интервального ряда можно использовать
функцию ЧАСТОТА.
Для её
применения
сначала
формируем столбец интервалов. Для нашего
примера, в котором объём выборки
,,
удобно выборку разбить на 7 равных
интервалов шириной 3 . При этом в ячейки
для массива интервалов вводим только
значения верхних границ интервалов.
Так, в ячейкуя внёс число 303 для интервала,
в— число 306 для интервала,
…, в— 321 для интервала.
Затем я выделяю свободную ячейку,
и щёлкаю по.
Появляется мастер функций, в котором я
нахожуЧАСТОТА
и раскрываю
шаблон для ввода аргументов. После
ввода вышеописанным способом границ
массива данных щёлкаем по окну массив
интервалов и
выделяем для ввода ячейки
.
Обратите внимание, что выделена одна
дополнительная ячейка, как этого требует
синтаксис функции.

После
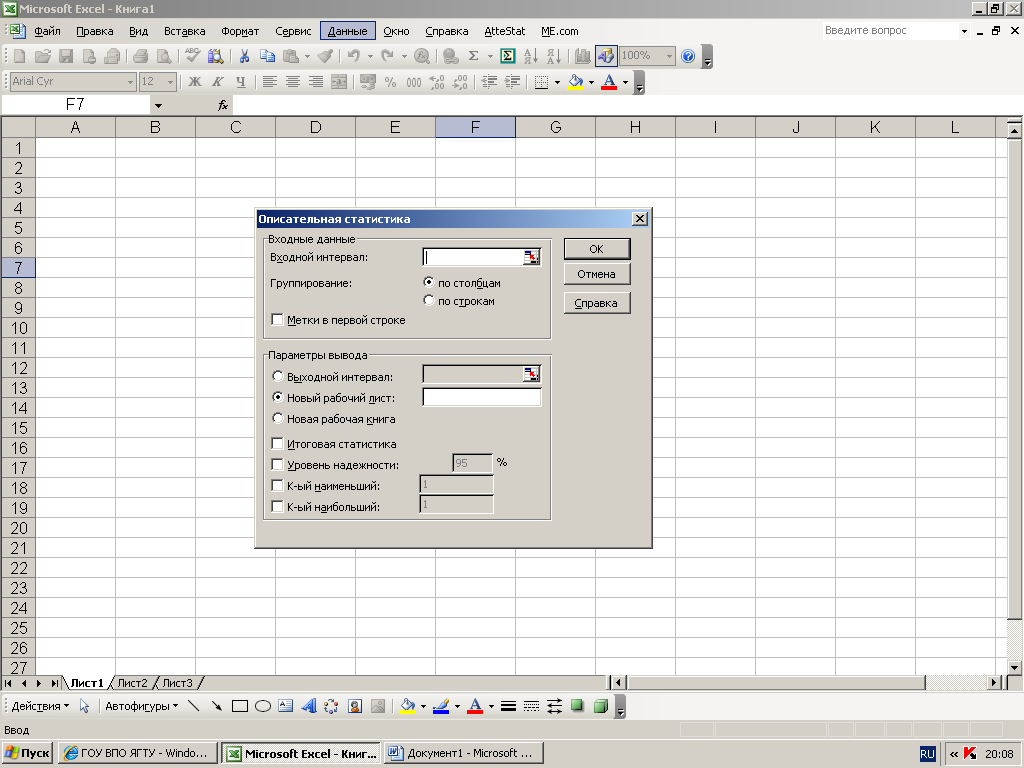
нажатия
в ячейкепоявляется число вариант со значением,.
Для вывода остальных значенийнадо выделить ячейки,
после чего нажать клавишу,
а затем.
В результате в столбцеи появятся все компоненты вектора
частот.

ЧАСТОТА
303	4
306	12
309	23
312	31
315	21
318	7
321	2

Рассмотрим
теперь, какие возможности для первичной
обработки выборки имеются в меню
«сервис
анализ данных». Раскроем диалоговое
окно«описательная
статистика».

Первая
строка «Входной
интервал»
нам уже знакома: данные в неё можно
внести действиями ЩАа, ЪЩЯя, или
движениями мыши с нажатой правой кнопкой,
или непосредственно введя в окошко
номера левой верхней и правой нижней
ячеек массива, разделённые двоеточием
Аа:Яя. Далее предлагается выбрать
группировку – «По
строкам»
или «По
столбцам».
Дело в том, что эта «описательная
статистика»
может обрабатывать одновременно большое
количество выборок, каждая из которых
может быть введена либо в виде строки,
либо в виде столбца. Поэтому, если мы
выделим массив, содержащий 25 строк и 4
столбца, то программа не
будет рассматривать его как одну выборку,
содержащую 100 вариант. Если мы пометим
окошко «По
столбцам», то
программа будет обрабатывать массив
как 4 выборки по 25 вариант в каждой.
Соответственно, при флажке «По
строкам» мы
получим обработку 25 выборок по 4 варианта.
Далее следует окошко
«Метки в первой строке/столбце». Если
его не помечать, то результаты обработки
каждой из выборок будут помечены
надписями «Строка (Столбец) 1», «Строка
(Столбец) 2», «Строка (Столбец)3»… .Если
же мы хотим , чтобы результаты были
обозначены иначе, (например, фамилиями
студентов), то мы при вводе указаний
массива данных в строку Входной
диапазон должны
захватить и стоящий перед ним столбец
(строку) меток (фамилий или номеров
опытов в данном примере). На этом ввод
данных завершается.

Куда
выводить результаты:

Строка1
Среднее	309,875
Стандартная ошибка	1,599153422
Медиана	309,5
Мода	#Н/Д
Стандартное отклонение	3,198306844
Дисперсия выборки	10,22916667
Эксцесс	-0,02453947
Асимметричность	0,598903954
Интервал	7,5
Минимум	306,5
Максимум	314
Сумма	1239,5
Счет	4

Параметры
вывода. Обычно при открытии
диалогового окна активизировано окошко
Новый рабочий лист.
Это означает, что результаты будут
выведены на новом листе, номер которого
при желании можно задать, так же как и
номер новой книги в окошке Новая
рабочая книга. Если же
надо поместить результаты на исходном
листе, то надо активизировать окошко
Выходной интервал,
после чего щёлкнуть по свободной ячейке,
которая будет левой верхней ячейкой
выходного массива.

Что
выводить.

При
установке флажка
«Итоговая статистика» для
каждой выборки будет выведена таблица
такого вида:

В
этой таблице под стандартным отклонением
понимается величина выборочного
стандарта
,
под стандартной ошибкой – выборочный
стандарт среднего,
интервал – разность между максимальным
и минимальным значениями выборки, сумма
– сумма всех значений выборки, счёт –
объём выборки. Остальные термины
пояснения не требуют.

Если
активизировать окошко «Уровень
надёжности»,
то выводится строка со значением
полуширины симметричного доверительного
интервала, соответствующим указанной
в этом окошке доверительной вероятности
и равным произведению
на соответствующий квантиль распределения
Стьюдента:

Уровень
надежности(95,0%)

5,089219898

Активизация
окошек К-ый
наименьший и
К-ый наибольший позволяет
выводить к-ое в порядке возрастания и
(или) к-ое в порядке убывания значения
в выборке, соответствующие указанным
номерам. Значениям к=1 соответствуют
минимальное и максимальное значения
вариант.

Обратимся
теперь к графическому изображению
данных. Для этого в меню Анализ
данных есть
функция Гистограмма,
в диалоговом окне которой в окошко
Входной
интервал вводим
одним из описанных ранее способов номера
ячеек начала и конца массива данных.
Затем в окошко Интервал
карманов вводим
таким же образом номера массива, в
котором указаны верхние границы
интервалов, на которые мы решили разбить
выборку (см. выше описание функции
Частота).
Флажок Метки
надо устанавливать только в том случае,
если в массив данных включён и столбец
меток. Как и в вышеописанных функциях
ставим флажок Новый
лист или
Новая книга (с
указанием номера или без), или Выходной
интервал. В
последнем случае в активизированное
окошко вводим номер левой верхней ячейки
диапазона вывода результата. Игнорируя
надпись Парето,
помечаем
Интегральный процент и
Вывод графика.
выводит нам
во-первых,
таблицу, два первых столбца, как и после
исполнения функции Частота
представляют
интервальный вариационный ряд, а третий
столбец – аналог интегральной функции
распределения, показывает долю вариант
в выборки, имеющих значение меньшее или
равное указанного в первом столбце.
Кроме этого, появляется и графическое
изображение – гистограмма и график
интегрального процента. Можно редактировать
это изображение, но здесь мы не будем
рассматривать все многочисленные
возможности этого.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Дмитрий Михайлович Беляев

Эксперт по предмету «Информатика»

Задать вопрос автору статьи

Замечание 1

Статистическая обработка данных — это выполнение сбора, упорядочивания, обобщения и анализа информации с возможностью определить тенденции и сделать прогноз развития исследуемого явления.

Введение

Главными средствами, которые предназначены для выполнения операций по анализу статистических данных в программном приложении Excel, являются статистические операции надстройки «Пакет анализа» (Analysis ToolРак) и статистические функции, расположенные в библиотеке встроенных функций. Основная совокупность сведений обо всех названных выше средствах содержится в электронной справочной системе Excel. Однако необходимо подчеркнуть, что уровень качества описания статистических операций и функций, приводимых в этой системе, является довольно низким. Некоторые описания воспринимаются недостаточно ясно, в них могут присутствовать некоторые неточности, а иногда и просто ошибки, причем эти недостатки присущи как англоязычному варианту, так и варианту на русском языке.

Статистическая обработка данных в Excel

Наиболее эффективными средствами, которые предназначены для выполнения анализа информации, могут считаться статистические операции «Пакета анализа» в программном приложении Excel. Они обладают большой совокупностью возможностей, гораздо большей, чем статистические функции. С помощью «Пакета анализа» можно решать очень сложные задачи, связанные с обработкой статистической информации, а также выполнять расширенный анализ этих данных.

«Пакет анализа» имеет в своем составе следующие статистические операции:

Операция, реализующая генерацию случайных чисел (Random number generation).
Операция, предназначенная для осуществления выборки (Sampling).
Операция построения гистограмм (Histogram).
Операция, осуществляющая описательную статистику (Descriptive statistics).
Операция по назначению рангов персентиль (Rank and percentile).
Операция, реализующая двухвыборочный Z-тест для средних (z-Test: Two Sample for Means).
Операция двухвыборочного T-теста для средних, имеющих одинаковую дисперсию (T-Test: Two-Sample Assuming Equal Variances).
Операция двухвыборочного T-теста для средних, имеющих разную дисперсию (t-Test: Two-Sample Assuming Unequal Variances).
Операция парного двухвыборочного T-теста для средних (t-Test: Paired Two Sample for Means).
Операция двухвыборочного F-теста для дисперсий (F-Test: Two Sample for Variances).
Операция коварнации (Covariance).
Операция корреляции (Correlation).
Операция рецессии (Regression).
Операция однофакторного дисперсионного анализа (ANOVA: Single Factor).
Операция двухфакторного дисперсионного анализа без присутствия повторений (ANOVA: Two Factor Without Replication).
Операция двухфакторного дисперсионного анализа с наличием повторений (ANOVA: Two Factor With Replication).
Операция скользящего среднего (Moving Average).
Операция экспоненциального сглаживания (Exponential Smoothing).
Операция анализа Фурье (Fourier Analysis).

«Статистическая обработка данных в Excel» 👇

Для получения доступа к операциям «Пакета анализа», необходимо в меню «Инструменты» (Tools) осуществить щелчок указателем мыши по строчке «Анализ данных» (Data Analysis). После этого открывается диалоговое окно, имеющее такое же название, в котором отображается весь перечень операций статистического информационного анализа. Вид данного окна показан на рисунке ниже.

Рисунок 1. Окно программы. Автор24 — интернет-биржа студенческих работ

Для того чтобы запустить выполнение необходимой статистической операции, необходимо выделить с помощью указателя мышки и осуществить щелчок по клавише ОК. На экране монитора появится диалоговое окно выбранной операции.

Диалоговое окно любой из возможных операций должно содержать следующий набор элементов управления:

Совокупность полей ввода.
Списки, которые можно раскрывать.
Совокупность переключателей.
Совокупность флажков и так далее.

Эти элементы могут предоставить возможность задания необходимых параметров исполняемой операции. Некоторые элементы управления обладают специфическим характером, который может быть присущ одной из операций или же их набору. Остальные элементы управления присутствуют в диалоговом окне фактически любой статистической процедуры. В качестве общих элементов управления для практически всех операций выступают следующие элементы:

Элемент поля ввода, который обозначается как «Входной интервал» (Input Range). В этом поле следует вводить ссылку на диапазон, содержащий статистическую информацию, которая нуждается в обработке. Входной диапазон может быть в виде столбца или их совокупности, а также в виде строки или совокупности строк.
Элемент переключатель «Группирование» (Grouped By). Когда входной диапазон задан в виде столбца или совокупности столбцов, то переключатель следует поставить в положение по столбцам (Columns). А если входной диапазон задан строкой или совокупностью строк, то переключатель следует поставить в положение по строкам (Rows). Некоторые специалисты полагают, что наиболее правильным наименованием этого переключателя было бы «Расположение».
Элемент «флажок Метки» (Labels in First Row). Флажок необходимо установить в том случае, если первая строка или первый столбик входного диапазона состоят из заголовков. А если такие заголовки отсутствуют, то флажок Метки не устанавливается. При этом программа Excel может автоматически создать и вывести на экран монитора стандартные наименования для информации выходного диапазона, а именно, Столбец1, столбец 2, … или Строка1, Строка2, … .
Элемент «Переключатели Выходной интервал/Новый рабочий лист/Новая книга (Output Range/New Worksheet/New Workbook). Эти переключатели способны задавать место для вывода таблицы, содержащей итоговые результаты исполнения статистической операции. В группе можно выбрать только один переключатель.

Если выбран переключатель «Выходной интервал», то таблица итогов решения будет отображаться на этом же рабочем листе, на котором расположены исходные данные.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник