Содержание
- Вычисление коэффициента детерминации
- Способ 1: вычисление коэффициента детерминации при линейной функции
- Способ 2: вычисление коэффициента детерминации в нелинейных функциях
- Способ 3: коэффициент детерминации для линии тренда
- Вопросы и ответы
Одним из показателей, описывающих качество построенной модели в статистике, является коэффициент детерминации (R^2), который ещё называют величиной достоверности аппроксимации. С его помощью можно определить уровень точности прогноза. Давайте узнаем, как можно произвести расчет данного показателя с помощью различных инструментов программы Excel.
Вычисление коэффициента детерминации
В зависимости от уровня коэффициента детерминации, принято разделять модели на три группы:
- 0,8 – 1 — модель хорошего качества;
- 0,5 – 0,8 — модель приемлемого качества;
- 0 – 0,5 — модель плохого качества.
В последнем случае качество модели говорит о невозможности её использования для прогноза.
Выбор способа вычисления указанного значения в Excel зависит от того, является ли регрессия линейной или нет. В первом случае можно использовать функцию КВПИРСОН, а во втором придется воспользоваться специальным инструментом из пакета анализа.
Способ 1: вычисление коэффициента детерминации при линейной функции
Прежде всего, выясним, как найти коэффициент детерминации при линейной функции. В этом случае данный показатель будет равняться квадрату коэффициента корреляции. Произведем его расчет с помощью встроенной функции Excel на примере конкретной таблицы, которая приведена ниже.
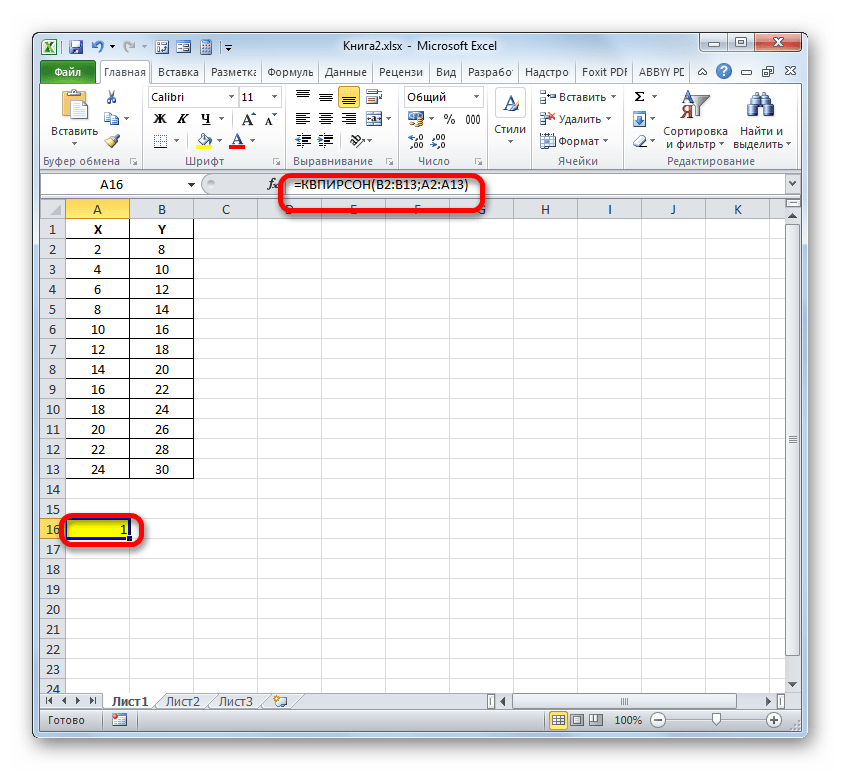
- Выделяем ячейку, где будет произведен вывод коэффициента детерминации после его расчета, и щелкаем по пиктограмме «Вставить функцию».
- Запускается Мастер функций. Перемещаемся в его категорию «Статистические» и отмечаем наименование «КВПИРСОН». Далее клацаем по кнопке «OK».
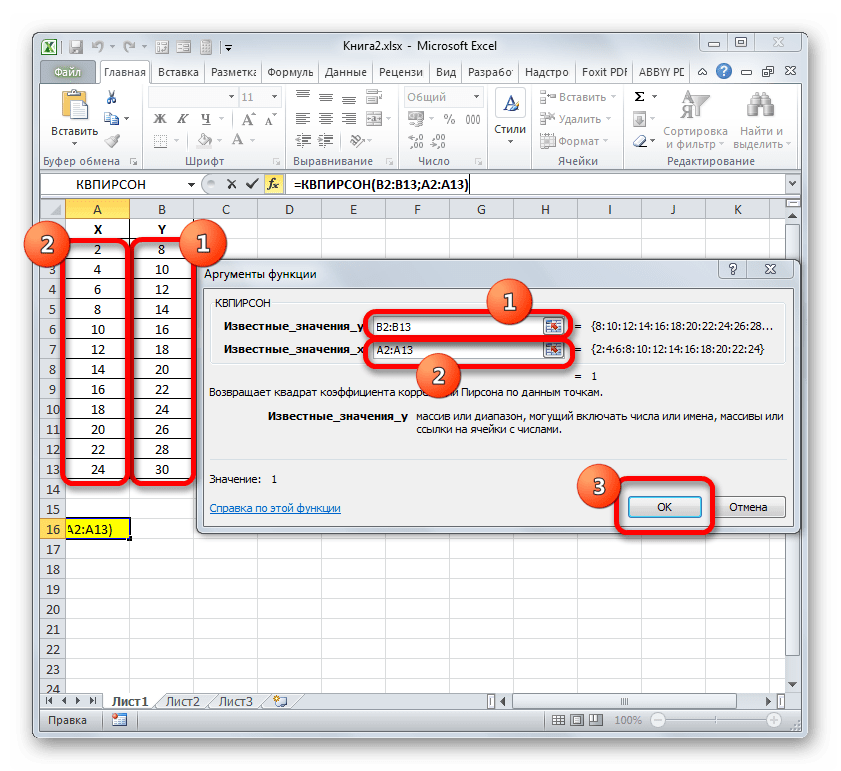
- Происходит запуск окна аргументов функции КВПИРСОН. Данный оператор из статистической группы предназначен для вычисления квадрата коэффициента корреляции функции Пирсона, то есть, линейной функции. А как мы помним, при линейной функции коэффициент детерминации как раз равен квадрату коэффициента корреляции.
Синтаксис этого оператора такой:
=КВПИРСОН(известные_значения_y;известные_значения_x)Таким образом, функция имеет два оператора, один из которых представляет собой перечень значений функции, а второй – аргументов. Операторы могут быть представлены, как непосредственно в виде значений, перечисленных через точку с запятой (;), так и в виде ссылок на диапазоны, где они расположены. Именно последний вариант и будет использован нами в данном примере.
Устанавливаем курсор в поле «Известные значения y». Выполняем зажим левой кнопки мышки и производим выделение содержимого столбца «Y» таблицы. Как видим, адрес указанного массива данных тут же отображается в окне.
Аналогичным образом заполняем поле «Известные значения x». Ставим курсор в данное поле, но на этот раз выделяем значения столбца «X».
После того, как все данные были отображены в окне аргументов КВПИРСОН, клацаем по кнопке «OK», расположенной в самом его низу.
- Как видим, вслед за этим программа производит расчет коэффициента детерминации и выдает результат в ту ячейку, которая была выделена ещё перед вызовом Мастера функций. В нашем примере значение вычисляемого показателя получилось равным 1. Это значит, что представленная модель абсолютно достоверная, то есть, исключает погрешность.
Урок: Мастер функций в Microsoft Excel
Способ 2: вычисление коэффициента детерминации в нелинейных функциях
Но указанный выше вариант расчета искомого значения можно применять только к линейным функциям. Что же делать, чтобы произвести его расчет в нелинейной функции? В Экселе имеется и такая возможность. Её можно осуществить с помощью инструмента «Регрессия», который является составной частью пакета «Анализ данных».
- Но прежде, чем воспользоваться указанным инструментом, следует активировать сам «Пакет анализа», который по умолчанию в Экселе отключен. Перемещаемся во вкладку «Файл», а затем переходим по пункту «Параметры».
- В открывшемся окне производим перемещение в раздел «Надстройки» при помощи навигации по левому вертикальному меню. В нижней части правой области окна располагается поле «Управление». Из списка доступных там подразделов выбираем наименование «Надстройки Excel…», а затем щелкаем по кнопке «Перейти…», расположенной справа от поля.
- Производится запуск окна надстроек. В центральной его части расположен список доступных надстроек. Устанавливаем флажок около позиции «Пакет анализа». Вслед за этим требуется щелкнуть по кнопке «OK» в правой части интерфейса окна.
- Пакет инструментов «Анализ данных» в текущем экземпляре Excel будет активирован. Доступ к нему располагается на ленте во вкладке «Данные». Перемещаемся в указанную вкладку и клацаем по кнопке «Анализ данных» в группе настроек «Анализ».
- Активируется окошко «Анализ данных» со списком профильных инструментов обработки информации. Выделяем из этого перечня пункт «Регрессия» и клацаем по кнопке «OK».
- Затем открывается окно инструмента «Регрессия». Первый блок настроек – «Входные данные». Тут в двух полях нужно указать адреса диапазонов, где находятся значения аргумента и функции. Ставим курсор в поле «Входной интервал Y» и выделяем на листе содержимое колонки «Y». После того, как адрес массива отобразился в окне «Регрессия», ставим курсор в поле «Входной интервал Y» и точно таким же образом выделяем ячейки столбца «X».
Около параметров «Метка» и «Константа-ноль» флажки не ставим. Флажок можно установить около параметра «Уровень надежности» и в поле напротив указать желаемую величину соответствующего показателя (по умолчанию 95%).
В группе «Параметры вывода» нужно указать, в какой области будет отображаться результат вычисления. Существует три варианта:
- Область на текущем листе;
- Другой лист;
- Другая книга (новый файл).
Остановим свой выбор на первом варианте, чтобы исходные данные и результат размещались на одном рабочем листе. Ставим переключатель около параметра «Выходной интервал». В поле напротив данного пункта ставим курсор. Щелкаем левой кнопкой мыши по пустому элементу на листе, который призван стать левой верхней ячейкой таблицы вывода итогов расчета. Адрес данного элемента должен высветиться в поле окна «Регрессия».
Группы параметров «Остатки» и «Нормальная вероятность» игнорируем, так как для решения поставленной задачи они не важны. После этого клацаем по кнопке «OK», которая размещена в правом верхнем углу окна «Регрессия».
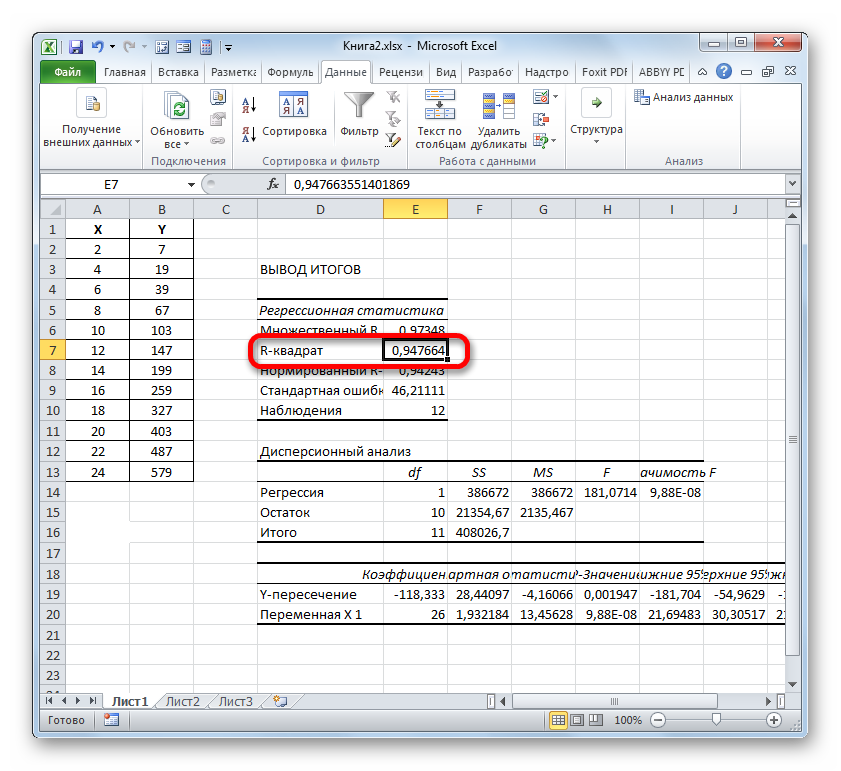
- Программа производит расчет на основе ранее введенных данных и выводит результат в указанный диапазон. Как видим, данный инструмент выводит на лист довольно большое количество результатов по различным параметрам. Но в контексте текущего урока нас интересует показатель «R-квадрат». В данном случае он равен 0,947664, что характеризует выбранную модель, как модель хорошего качества.
Способ 3: коэффициент детерминации для линии тренда
Кроме указанных выше вариантов, коэффициент детерминации можно отобразить непосредственно для линии тренда в графике, построенном на листе Excel. Выясним, как это можно сделать на конкретном примере.
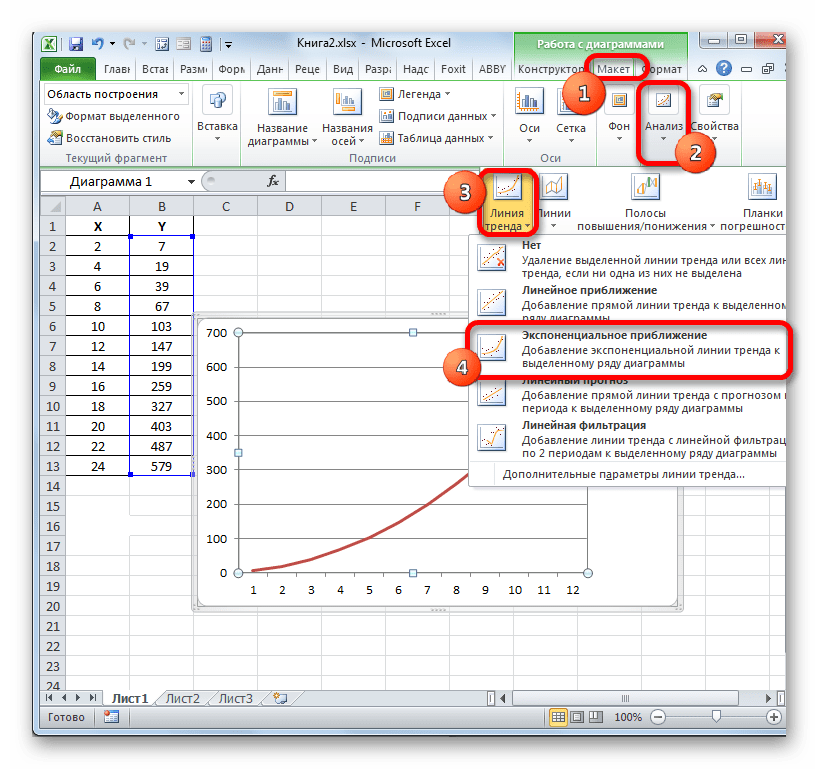
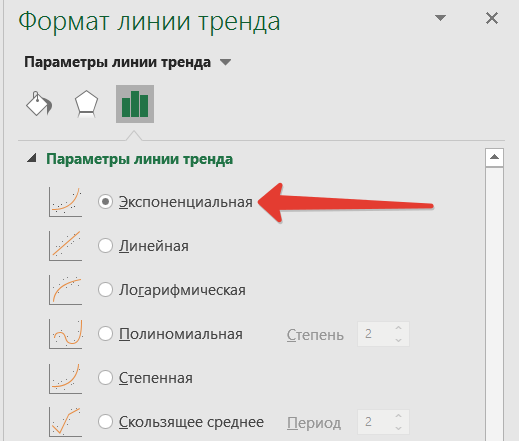
- Мы имеем график, построенный на основе таблицы аргументов и значений функции, которая была использована для предыдущего примера. Произведем построение к нему линии тренда. Кликаем по любому месту области построения, на которой размещен график, левой кнопкой мыши. При этом на ленте появляется дополнительный набор вкладок – «Работа с диаграммами». Переходим во вкладку «Макет». Клацаем по кнопке «Линия тренда», которая размещена в блоке инструментов «Анализ». Появляется меню с выбором типа линии тренда. Останавливаем выбор на том типе, который соответствует конкретной задаче. Давайте для нашего примера выберем вариант «Экспоненциальное приближение».
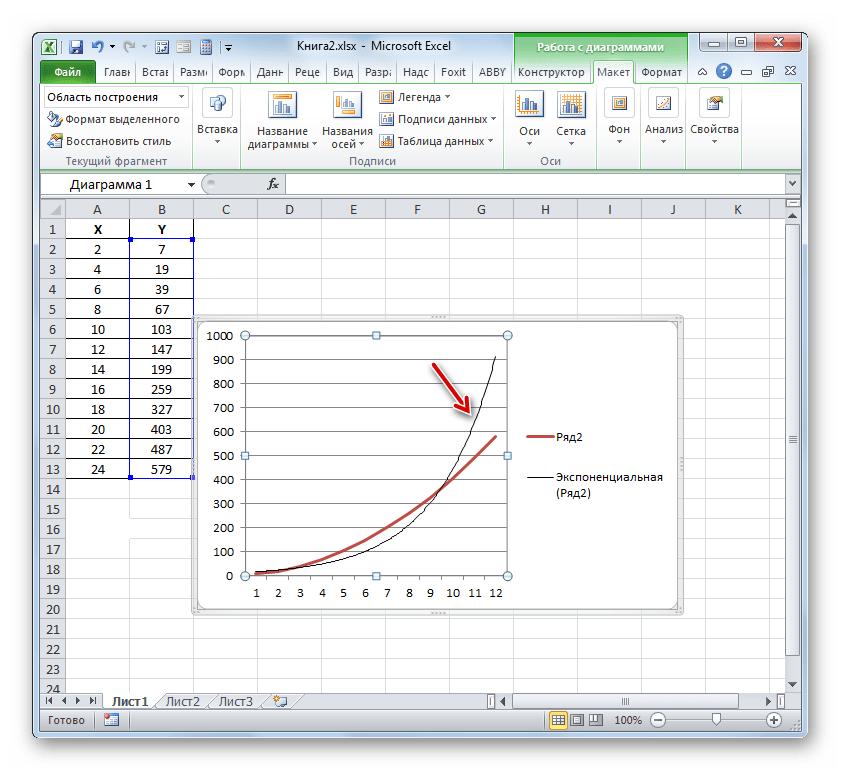
- Эксель строит прямо на плоскости построения графика линию тренда в виде дополнительной черной кривой.
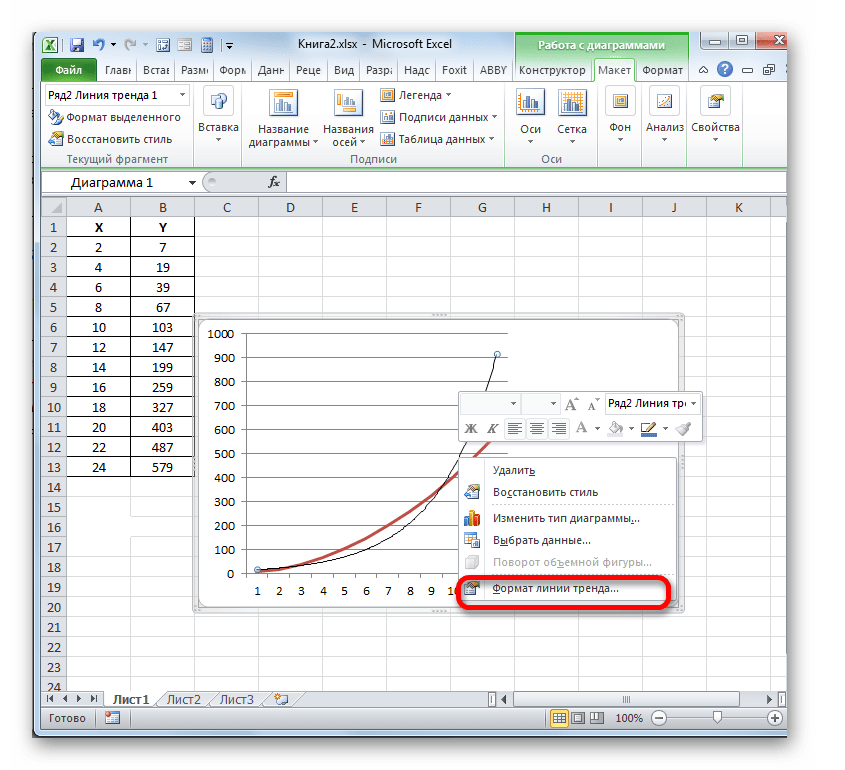
- Теперь нашей задачей является отобразить собственно коэффициент детерминации. Кликаем правой кнопкой мыши по линии тренда. Активируется контекстное меню. Останавливаем выбор в нем на пункте «Формат линии тренда…».
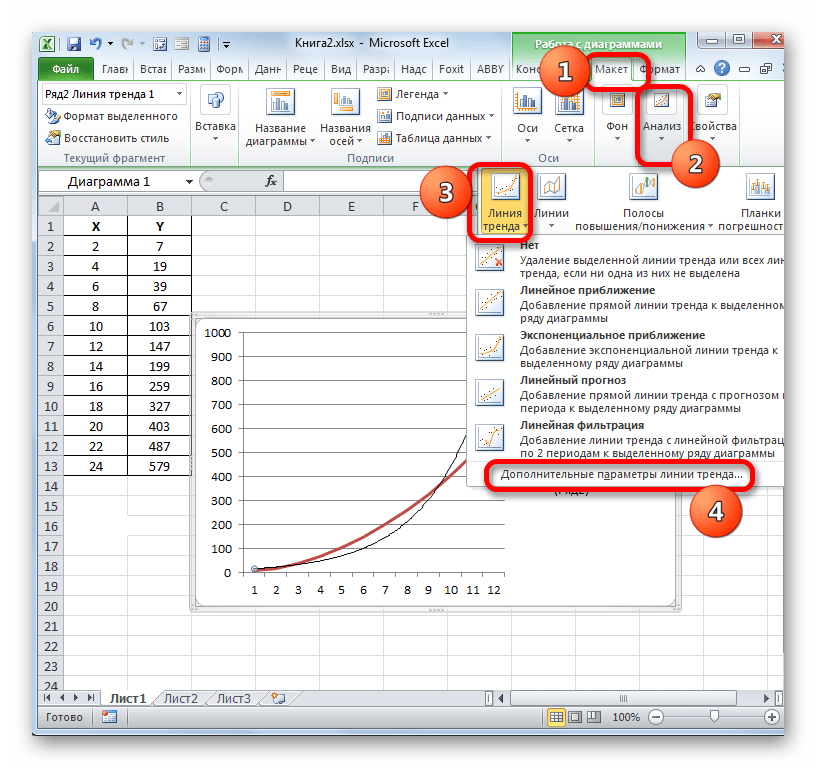
Для выполнения перехода в окно формата линии тренда можно выполнить альтернативное действие. Выделяем линию тренда кликом по ней левой кнопки мыши. Перемещаемся во вкладку «Макет». Клацаем по кнопке «Линия тренда» в блоке «Анализ». В открывшемся списке клацаем по самому последнему пункту перечня действий – «Дополнительные параметры линии тренда…».
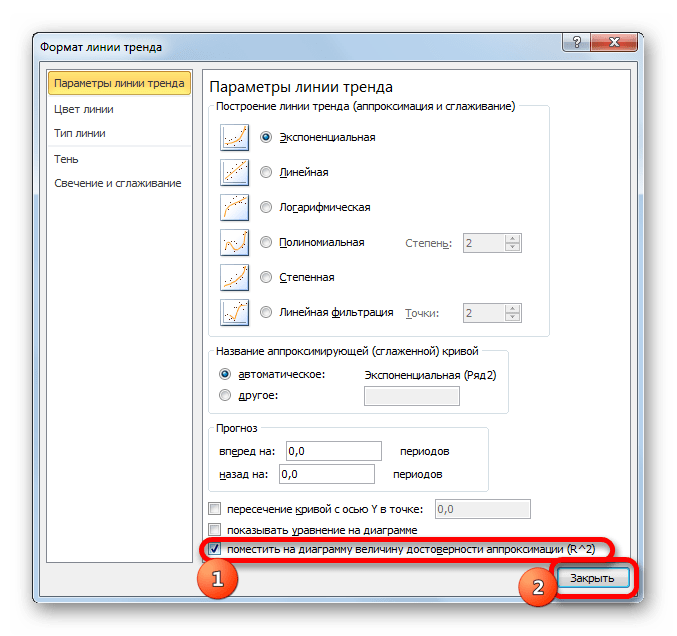
- После любого из двух вышеуказанных действий запускается окошко формата, в котором можно произвести дополнительные настройки. В частности, для выполнения нашей задачи необходимо установить флажок напротив пункта «Поместить на диаграмму величину достоверности аппроксимации (R^2)». Он размещен в самом низу окна. То есть, таким образом мы включаем отображение коэффициента детерминации на области построения. Затем не забываем нажать на кнопку «Закрыть» внизу текущего окна.
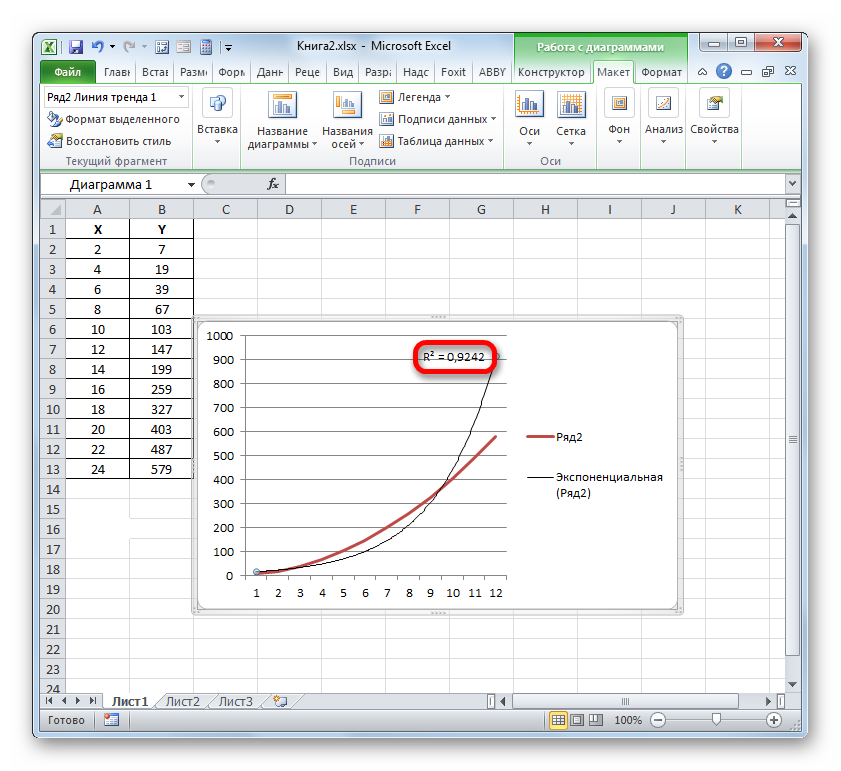
- Значение достоверности аппроксимации, то есть, величина коэффициента детерминации, будет отображено на листе в области построения. В данном случае эта величина, как видим, равна 0,9242, что характеризует аппроксимацию, как модель хорошего качества.
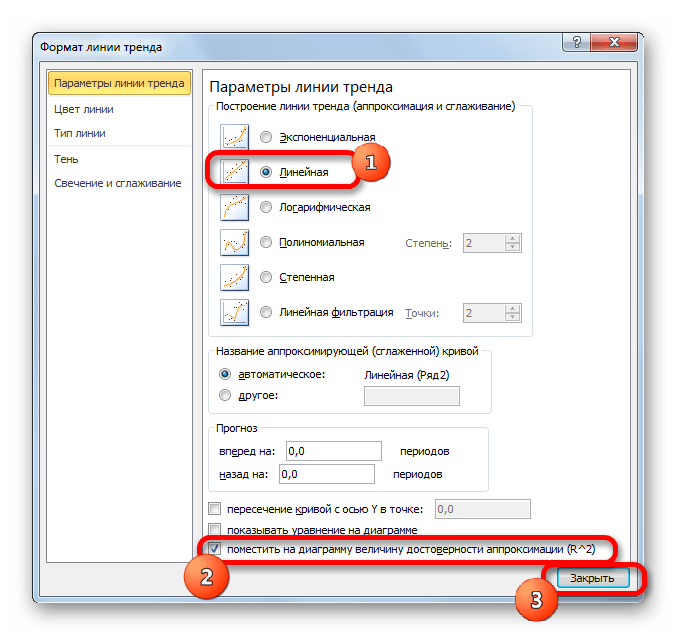
- Абсолютно точно таким образом можно устанавливать показ коэффициента детерминации для любого другого типа линии тренда. Можно менять тип линии тренда, произведя переход через кнопку на ленте или контекстное меню в окно её параметров, как было показано выше. Затем уже в самом окне в группе «Построение линии тренда» можно переключиться на другой тип. Не забываем при этом контролировать, чтобы около пункта «Поместить на диаграмму величину достоверности аппроксимации» был установлен флажок. Завершив вышеуказанные действия, щелкаем по кнопке «Закрыть» в нижнем правом углу окна.
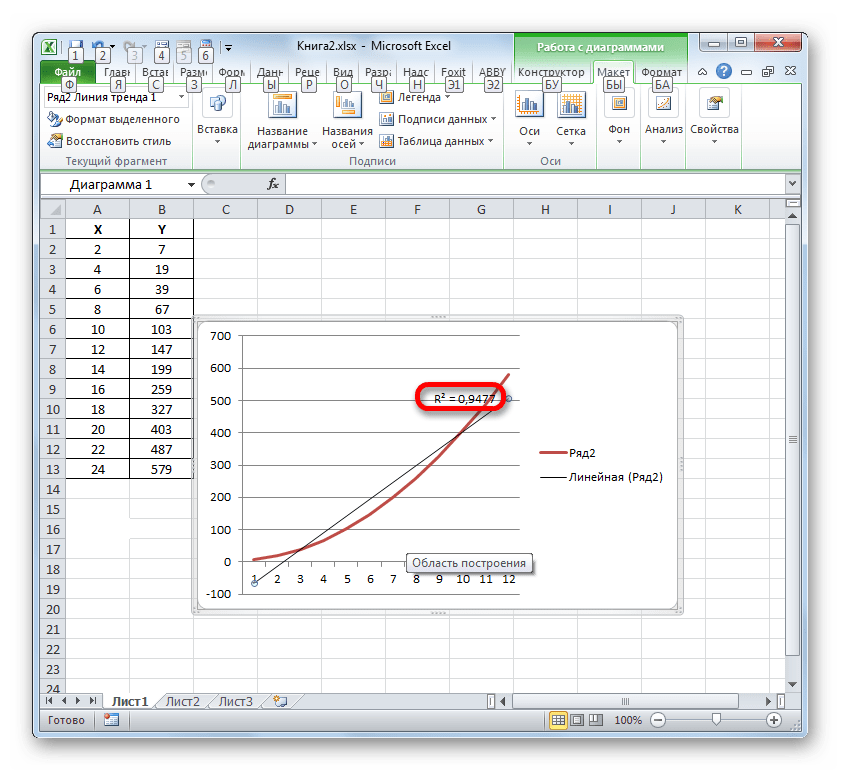
- При линейном типе линия тренда уже имеет значение достоверности аппроксимации равное 0,9477, что характеризует эту модель, как ещё более достоверную, чем рассматриваемую нами ранее линию тренда экспоненциального типа.
- Таким образом, переключаясь между разными типами линии тренда и сравнивая их значения достоверности аппроксимации (коэффициент детерминации), можно найти тот вариант, модель которого наиболее точно описывает представленный график. Вариант с самым высоким показателем коэффициента детерминации будет наиболее достоверным. На его основе можно строить самый точный прогноз.
Например, для нашего случая опытным путем удалось установить, что самый высокий уровень достоверности имеет полиномиальный тип линии тренда второй степени. Коэффициент детерминации в данном случае равен 1. Это говорит о том, что указанная модель абсолютно достоверная, что означает полное исключение погрешностей.
Но, в то же время, это совсем не значит, что для другого графика тоже наиболее достоверным окажется именно этот тип линии тренда. Оптимальный выбор типа линии тренда зависит от типа функции, на основании которой был построен график. Если пользователь не обладает достаточным объемом знаний, чтобы «на глаз» прикинуть наиболее качественный вариант, то единственным выходом определения лучшего прогноза является как раз сравнение коэффициентов детерминации, как было показано на примере выше.
Читайте также:
Построение линии тренда в Excel
Аппроксимация в Excel
В Экселе существуют два основных варианта вычисления коэффициента детерминации: использование оператора КВПИРСОН и применение инструмента «Регрессия» из пакета инструментов «Анализ данных». При этом первый из этих вариантов предназначен для использования только в процессе обработки линейной функции, а другой вариант можно использовать практически во всех ситуациях. Кроме того, существует возможность отображения коэффициента детерминации для линии трендов графиков в качестве величины достоверности аппроксимации. С помощью данного показателя имеется возможность определить тип линии тренда, который располагает самым высоким уровнем достоверности для конкретной функции.
Еще статьи по данной теме:
Помогла ли Вам статья?
17 авг. 2022 г.
читать 2 мин
R-квадрат , часто обозначаемый как r 2 , является мерой того, насколько хорошо модель линейной регрессии соответствует набору данных.
С технической точки зрения, это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной.
Значение для r 2 может варьироваться от 0 до 1:
- Значение 0 указывает, что переменная отклика вообще не может быть объяснена предикторной переменной.
- Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.
Связанный: Что такое хорошее значение R-квадрата?
В этом руководстве объясняется, как рассчитать r 2 для двух переменных в Excel.
Пример: расчет R-квадрата в Excel
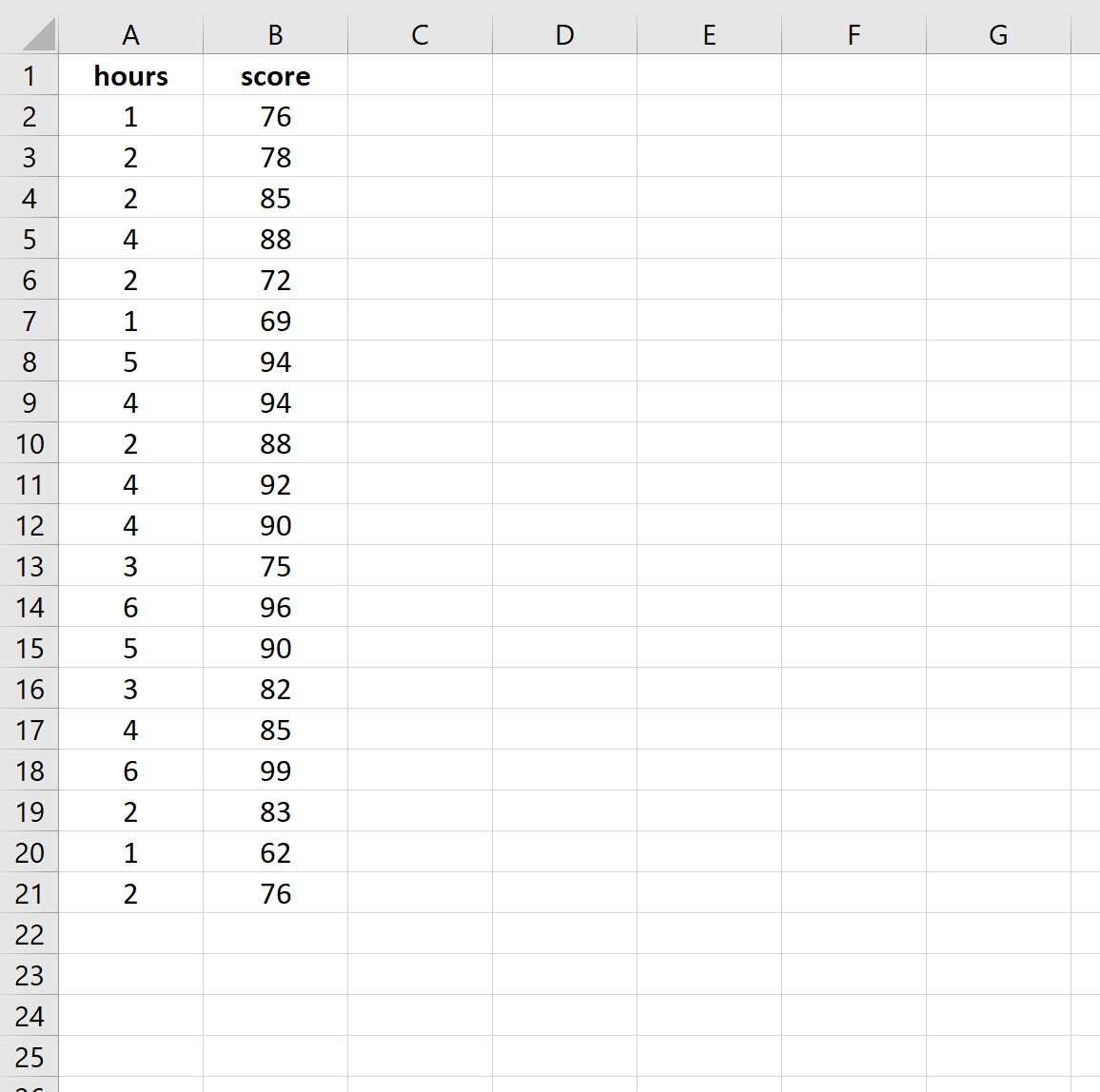
Предположим, у нас есть следующие данные о количестве часов обучения и экзаменационном балле, полученном для 20 студентов:
Теперь предположим, что мы заинтересованы в подгонке к этим данным простой модели линейной регрессии, используя «часы» в качестве переменной-предиктора и «оценку» в качестве переменной-ответа.
Чтобы найти r 2 для этих данных, мы можем использовать функцию RSQ() в Excel, которая использует следующий синтаксис:
=RSQ(известный_ys, известный_xs)
куда:
- known_ys: значения для переменной ответа
- known_xs: значения для переменной-предиктора
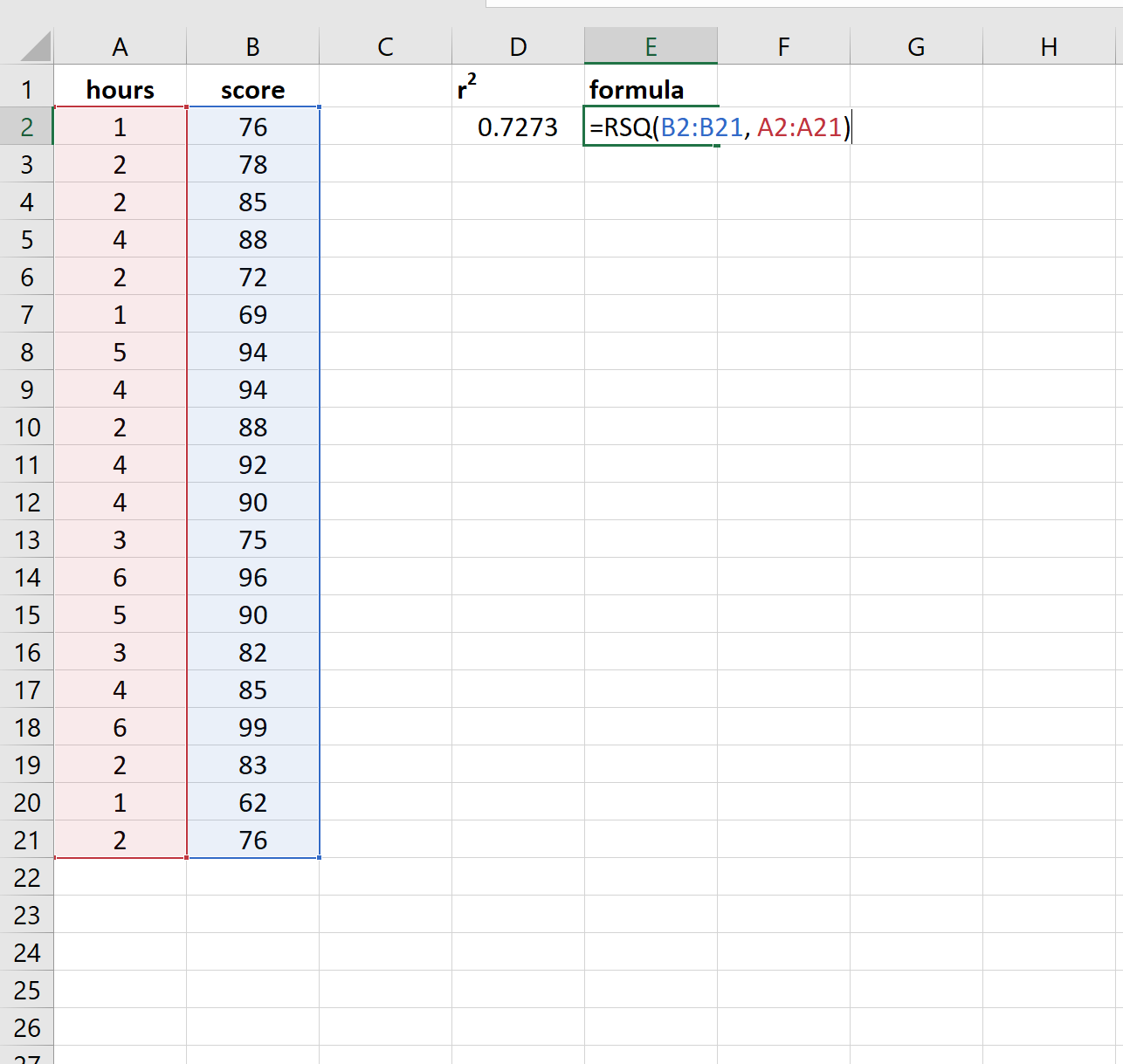
Вот как эта формула выглядит в нашем примере:
В этом примере 72,73 % различий в баллах за экзамены можно объяснить количеством часов обучения.
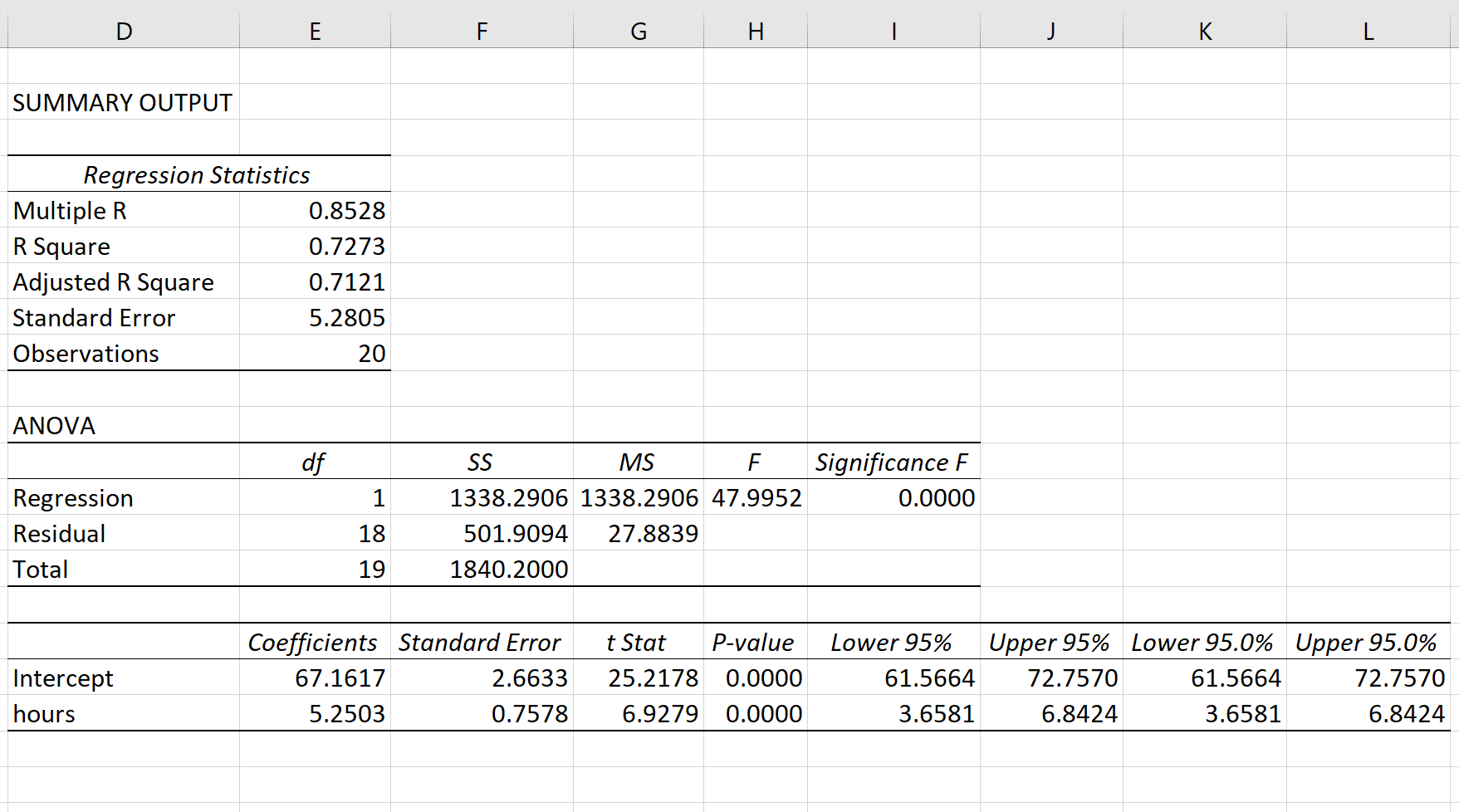
Обратите внимание, что если мы подгоним к этим данным простую модель линейной регрессии , результат будет выглядеть следующим образом:
Обратите внимание, что значение R Square в первой таблице равно 0,7273 , что соответствует результату, полученному с помощью функции RSQ().
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Когда научный руководитель сказал мне о необходимости указать на графике R² (р квадрат), я растерялся. В тот момент я не знал о трендах в диаграммах и графиках Excel. Этот материал поможет сориентироваться начинающим.
Что такое R² в Экселе
Для примера возьмем данные о продажах умных часов по брендам. Саму таблицу и график можно найти по этой ссылке на сайте CounterPointResearch. Там много подобной информации.
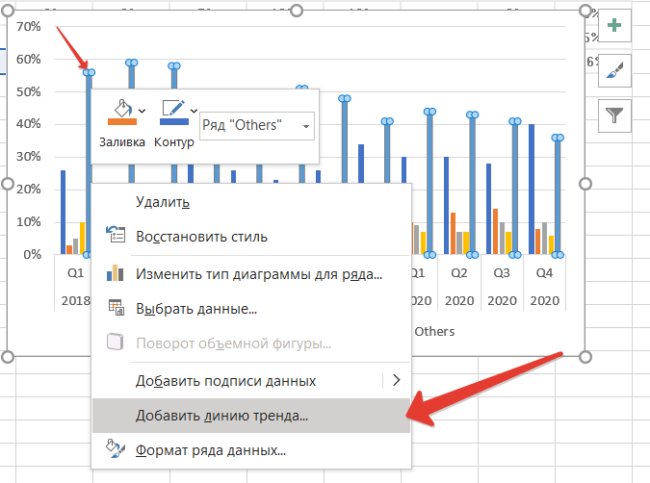
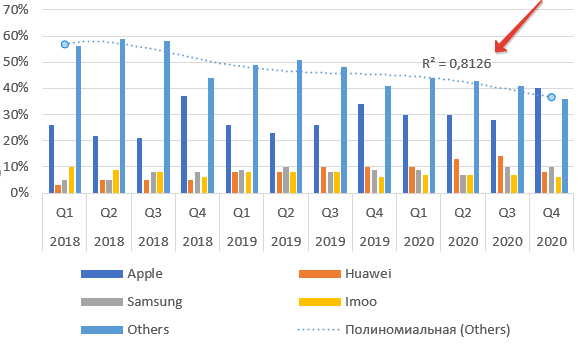
Выделяем диапазон данных и добавляем диаграмму. Теперь наводим мышь на столбцы бренда Others — «остальные», нажимаем правую клавишу мыши. Выбираем пункт Добавить линию тренда.
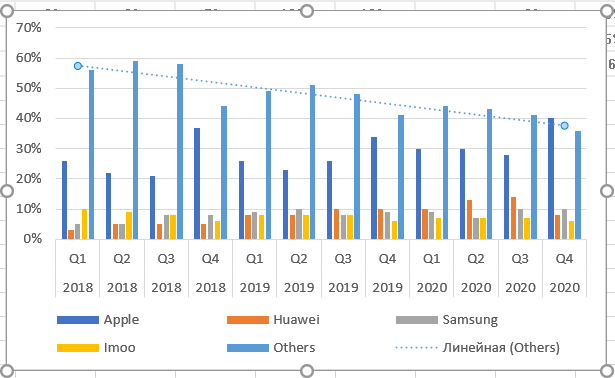
По умолчанию тренд линейный. Чуть позднее расскажу, как выбрать иную функцию, и стоит ли это делать. Теперь подводим курсор мыши к тренду и снова нажимаем правую кнопку.
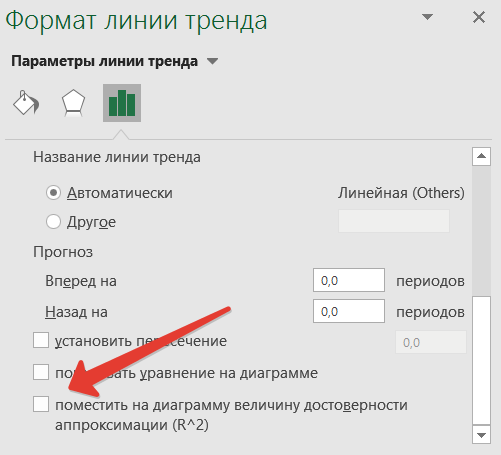
Добавляем на график R².
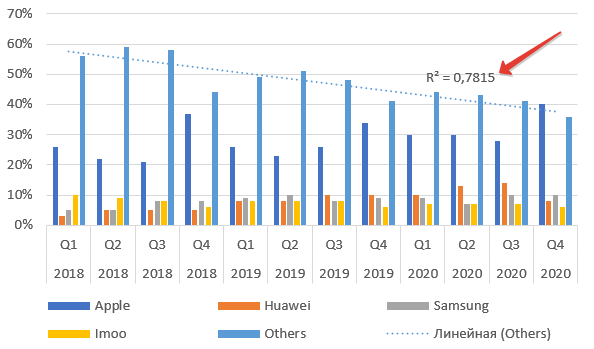
Как видим из названия пункта, это величина достоверности апроксимации. Максимальное значение параметра Р-квадрат единица. Но получить ее можно только на специально подогнанных данных в реальной жизни приемлемое значение 0,8-0,9. В нашем случае — 0,78, что неплохо.
Стоит ли добиваться максимального значения R²
Улучшить достоверность апроксимации можно меняя вид кривой. Это можно сделать в открывающемся справа окошке Формат линии тренда.
Если использовать полиноминальную функцию, то апроксимацию можно улучшить значительно. Но вот смысла это не имеет. Экономические показатели обычно укладываются в линейный (рост/падение) или экспоненциальный тренд. Экспоненциально, например, растет число клиентов быстрорастущей фирмы.
Выбор полиноминальной функции может и улучшит показатель достоверности, а вот прогноз сделает менее точным.
Как использовать тренд для прогноза
Кроме определения общего положения дел (рост/снижение), тренд может предсказать значения показателей в будущем. Это делается в окошке Формата линии тренда.
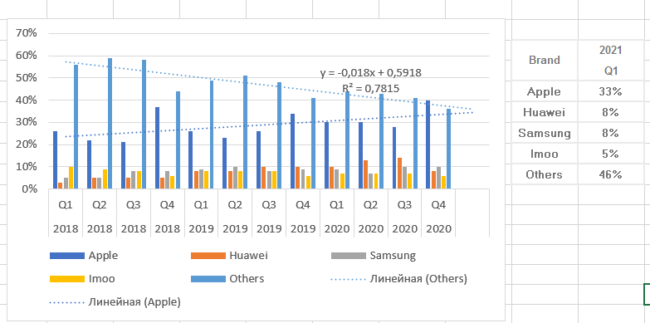
Попробуем предсказать продажи умных часов в первом квартале 2021 году и сравним их с фактом. Добавим два линейных тренда для Apple и Остальных.
Как видим, по яблочным часа прогноз построен верно, по остальным функция прогнозирует значение около 35%, а в реальности 46%. Возможно, это связано с выходом новых игроков на рынок или снижением доли Huawei. Мы имеем дело с относительными показателями (доля), а не с натуральными. Кстати, полиноминальный прогноз для категории Остальные дал бы еще менее точный прогноз, хотя R² и выше, что подтверждает необходимость осторожно выбирать функцию.
Почитайте и другие статьи про работу с таблицами Excel на нашем сайте. Например, у нас есть полезный материал об условном оформлении ячеек в таблице.
Понравилась статья? Поделитесь!
What Is R-Squared?
In the financial world, R-squared is a statistical measure that represents the percentage of a fund’s or a security’s movements that can be explained by movements in a benchmark index. In this field, R-squared typically ranges from 1% to 100%.
Where correlation explains the strength of the relationship between an independent and dependent variable, R-squared explains to what extent the variance of one variable explains the variance of the second variable.
Continue reading to learn more about R-squared, including how to automate its calculation in Excel.
Key Takeaways
- R-squared, or the coefficient of determination, is a statistical measure that uses the variance of one variable to explain the variance of another.
- Further testing is required to determine if R-squared approaching +/- 1 is statistically significant.
- Variables must be independent and their relationship linear for correlation to exist.
- When calculating a correlation, it is important to normalize data into a common unit.
- To correlate stocks, normalize their data into percent return.
Formula for R-Squared
R
2
=
1
−
R
S
S
T
S
S
where:
R
2
=
Coefficient of determination
R
S
S
=
Sum of squares of residuals
T
S
S
=
Total sum of squares
begin{aligned}&R^2=1-frac{RSS}{TSS}\&textbf{where:}\&R^2=text{Coefficient of determination}\&RSS=text{Sum of squares of residuals}\&TSS=text{Total sum of squares}end{aligned}
R2=1−TSSRSSwhere:R2=Coefficient of determinationRSS=Sum of squares of residualsTSS=Total sum of squares
Common Mistakes With R-Squared
The first most common mistake is assuming an R-squared approaching +/- 1 is statistically significant. A reading approaching +/- 1 increases the chances of actual statistical significance, but without further testing, it’s impossible to know based on the result alone.
Statistical testing is not completely straightforward; it can get complicated for several reasons. To touch on this briefly, a critical assumption of correlation (and thus R-squared) is that the variables are independent and that the relationship between them is linear. In theory, you would test these claims to determine if a correlation calculation is appropriate.
Investors often use R-squared with beta to more accurately assess asset managers’ performance.
The second most common mistake is forgetting to normalize the data into a common unit. If you are calculating a correlation (or R-squared) on two betas, then the units are already normalized: The unit is beta.
If you want to correlate stocks, it’s critical you normalize them into percent return and not share price changes. This happens frequently, even among investment professionals.
For stock price correlation (or R-squared), you are essentially asking two questions: What is the return over a certain number of periods, and how does that variance relate to another securities variance over the same period? Two securities might have a high correlation (or R-squared) if the return is daily percent changes over the past 52 weeks but a low correlation if the return is monthly changes over the past 52 weeks.
Which one is «better»? There is no perfect answer, and it depends on the purpose of the test.
How to Calculate R-Squared in Excel
There are several methods for calculating R-squared in Excel.
The simplest way is to get two data sets and use the built-in R-squared formula. The other alternative is to find a correlation and then square it. Both are shown below:
Frequently Asked Questions
How Do I Find R-Squared in Excel?
To find R-squared in Excel, enter the following formula into an empty cell:=RSQ([Data set 1], [Data set 2]). Data sets are ranges of data, most often arranged in a column or row. To select a group or set of data, select a cell and drag the cursor to highlight the other cells.
How Can You Find Adjusted R-Squared in Excel?
When a variable is added, R-squared will increase. However, the adjusted R-squared may increase or decrease depending on the explanatory power of the added variable. To calculate adjusted R-squared in Excel, enter the following formula into an empty cell: = 1 — (1 — R^2)(n-1/n-k-1), where k is the number of variables, and n is the number of data points.
How Can I Add R-Squared Value in Excel?
Adding an R-squared value in Excel can be done by using the formula to find the correlation of variables and then squaring the result, or by using the R-squared formula. The Excel formula for finding the correlation is «= CORREL([Data set 1], [Data set 2]).
To find R-squared, select the cell with the correlation formula and square the result (=[correlation cell] ^2). To find R-squared using a single formula, enter the following in an empty cell: =RSQ([Data set 1],[Data set 2]).
R-squared, often written as r2, is a measure of how well a linear regression model fits a dataset.
In technical terms, it is the proportion of the variance in the response variable that can be explained by the predictor variable.
The value for r2 can range from 0 to 1:
- A value of 0 indicates that the response variable cannot be explained by the predictor variable at all.
- A value of 1 indicates that the response variable can be perfectly explained without error by the predictor variable.
Related: What is a Good R-squared Value?
This tutorial explains how to calculate r2 for two variables in Excel.
Example: Calculating R-Squared in Excel
Suppose we have the following data for the number of hours studied and the exam score received for 20 students:
Now suppose we are interested in fitting a simple linear regression model to this data, using “hours” as the predictor variable and “score” as the response variable.
To find the r2 for this data, we can use the RSQ() function in Excel, which uses the following syntax:
=RSQ(known_ys, known_xs)
where:
- known_ys: the values for the response variable
- known_xs: the values for the predictor variable
Here’s what that formula looks like in our example:
In this example, 72.73% of the variation in the exam scores can be explained by the number of hours studied.
Note that if we fit a simple linear regression model to this data, the output would look like this:
Notice that the R Square value in the first table is 0.7273, which matches the result that we got using the RSQ() function.
Additional Resources
The following tutorials explain how to perform other common tasks in Excel:
How to Calculate Adjusted R-Squared in Excel
How to Calculate SST, SSR, and SSE in Excel
How to Create a Residual Plot in Excel
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.