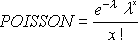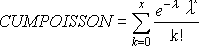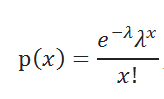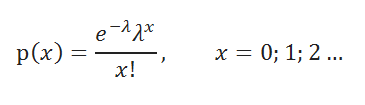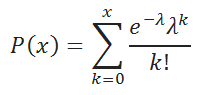Что такое пуассон в excel - Word и Excel - помощь в работе с программами

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

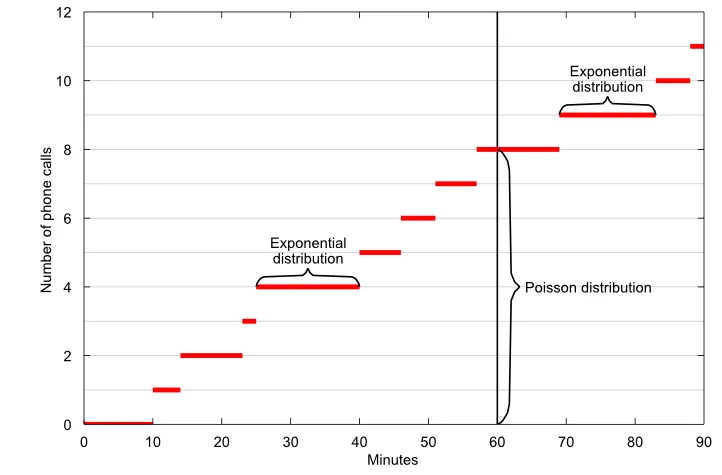
Возвращает распределение Пуассона. Обычное применение распределения Пуассона состоит в предсказании количества событий, происходящих за определенное время, например количества машин, появляющихся на площади за одну минуту.

Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.

Дополнительные сведения о новом варианте этой функции см. в статье Функция ПУАССОН.РАСП.

Синтаксис

ПУАССОН(x;среднее;интегральная)

Аргументы функции ПУАССОН описаны ниже.

X Обязательный. Количество событий.
Среднее Обязательный. Ожидаемое числовое значение.
Интегральная — обязательный аргумент. Логическое значение, определя которое определяет форму возвращаемого распределения вероятности. Если значение «совокупное» имеет значение ИСТИНА, то пуассон возвращает совокупное значение вероятности того, что число случайных событий включительно будет от нуля до x. Если этот ложь, возвращается функция массовой вероятности Пуассона, которая вероятность того, что количество произошедших событий будет точно x.

Замечания

Если x не является целым числом, оно усекается.
Если x или «число» не является числом, то пуАССОН возвращает #VALUE! значение ошибки #ЗНАЧ!.
Если x < 0, то пуассон возвращает #NUM! значение ошибки #ЗНАЧ!.
Если в < 0, то пуассон возвращает #NUM! значение ошибки #ЗНАЧ!.
Функция ПУАССОН вычисляется следующим образом.

Если интегральная = ЛОЖЬ:

Если интегральная = ИСТИНА:

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
2	Число событий
5	Ожидаемое среднее
Формула	Описание (результат)	Результат
=ПУАССОН(A2;A3;ИСТИНА)	Интегральное распределение Пуассона для приведенных выше условий (0,124652)	0,124652
=ПУАССОН(A2;A3;ЛОЖЬ)	Функция плотности распределения Пуассона для приведенных выше условий (0,084224)	0,084224

Нужна дополнительная помощь?

Источник

Функция ПУАССОН.РАСП в Excel используется для получения распределения Пуассона для случайных событий, происходящих за определенный промежуток времени с известной средней частотой.

Закон Пуассона распределения вероятностей случайной величины в Excel

Функция ПУАССОН.РАСП возвращает два варианта значений (в зависимости от значения, переданного в качестве третьего аргумента):

Интегральное распределение Пуассона – числовое значение вероятности того, что известное количество случайных событий принадлежит диапазону 0;[x] (то есть, от 0 до x включительно).
Функция весовых коэффициентов – числовое значение вероятности того, что количество произошедших событий точно равно числу x.

Для расчета плотности вероятности используется следующая формула:

Здесь x находится в диапазоне от 0 до бесконечности со знаком плюс.

Примечания:

Функция распределения вероятностей (в целом) – зависимость F(x), которая в точке x принимает значение, соответствующее вероятности того, что некоторая случайная величина X будет меньше значения x), то есть F(x)=P(X<x).
Для понимания функций распределения вероятности рассмотрим пример о заводе по производству соков. При расфасовке тар емкостью 1000 г возможны отклонения от заявленного объема, поскольку дозирующее устройство работает с погрешностью. То есть, может быть емкость, содержащая 1000 г сока, и емкость с 980 г сока. Вероятность того, что в одной из тар будет 980 г напитка составляет 0, а 1000г – 1. Для нахождения промежуточных значений объемов используют функции распределения. К примеру, если настроить дозирующее устройство на наполнение емкостей по 990 г сока, вероятность нахождения тары с меньшим объемом напитка составляет 0,5.
Функция ПУАССОН использовалась в более старых версиях Excel до 2010 года. Она была оставлена для обеспечения совместимости. В более новых версиях следует использовать функцию ПУАССОН.РАСП.
Распределение Пуассона – один из видов функций распределения величин. Ее рационально использовать, если исследуемая математическая модель удовлетворяет следующим условиям:

Вероятность каждого последующего события не связана с предыдущим, то есть каждое событие является независимым;
События характеризуются средней частотой, которая является константой;
Вероятность события и длина периода наблюдения являются пропорциональными величинами;
Вероятность происхождения двух событий одновременна равна нулю;
Отсчет количества событий начинается от 0 до бесконечности (0, 1, 2,…);
Среднее значение выборки является величиной, близкой по значению к значению дисперсии.

Примечание: Распределение Пуассона неприменимо в следующих случаях:

события являются зависимыми;
непостоянство средней величины;
минимальная величина превышает значение 0.

Решение задачи на распределение Пуассона в Excel

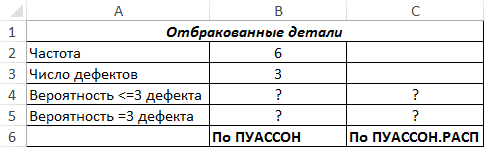
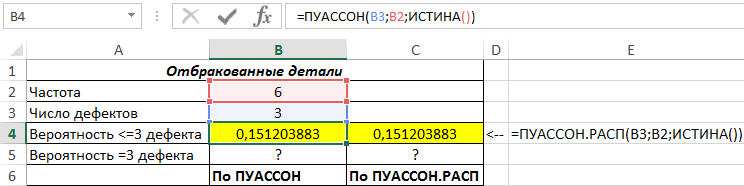
Пример 1. Отдел технического контроля определил, что среднее число не соблюденных допусков в размерах производимых деталей составляет 6. Определить вероятности следующих событий обеими рассматриваемыми функциями (для сравнения результатов вычислений):

Вероятность наличия 3 и менее погрешностей в случайно отобранной детали.
Вероятность наличия ровно 3 погрешностей в случайно выбранной детали.

Вид таблицы данных:

Рассчитаем вероятность наличия трех и менее дефектов с помощью функций:

=ПУАССОН(B3;B2;ИСТИНА())

=ПУАССОН.РАСП(B3;B2;ИСТИНА())

Описание аргументов:

B3 – среднее значение;
B2 – предполагаемое значение, для которого рассчитывается вероятность;
ИСТИНА – указатель на интегральный тип функции.

Полученные результаты:

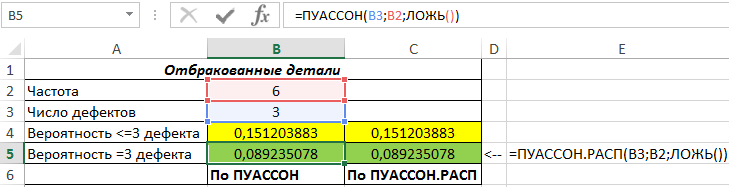
Для нахождения вероятности выбора детали с наличием ровно трех дефектов используем функции:

=ПУАССОН(B3;B2;ЛОЖЬ())

=ПУАССОН.РАСП(B3;B2;ЛОЖЬ())

Для расчета вероятности точного совпадения третий аргумент задан в качестве логического ЛОЖЬ.

Результаты вычислений:

Как видно, результаты вычислений обеих функций идентичны.

Биномиальное распределение Пуассона в Excel

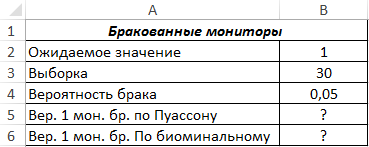
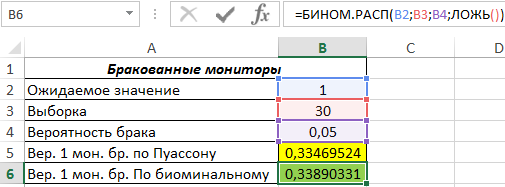
Пример 2. На заводе по производству мониторов ожидается, что 5% изделий будут бракованными. Была взята выборка из 30 мониторов. Определить вероятность того, что 1 монитор из 30 окажется бракованным. Для решения использовать распределение Пуассона и биномиальное распределение, полученные результаты сравнить.

Вид таблицы данных:

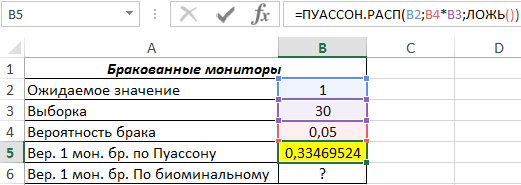
Для определения вероятности события, при котором в выборке будет найден один бракованный монитор с использованием распределения Пуассона запишем функцию:

=ПУАССОН.РАСП(B2;B4*B3;ЛОЖЬ())

Произведение B4*B3 соответствует среднему ожидаемому значению (1,5). Полученный результат:

Для расчета с использованием биномиального распределения запишем функцию:

=БИНОМ.РАСП(B2;B3;B4;ЛОЖЬ())

Результат вычислений:

Как видно, для данной математической модели подходят оба метода определения вероятностей, поскольку полученные значения отличаются незначительно.

Источник

Распределение Пуассона является одним из наиболее часто используемых распределений в статистике.

В Excel мы можем использовать функцию ПУАССОН.РАСП() , чтобы найти вероятность того, что событие произойдет определенное количество раз в течение заданного интервала, на основе знания среднего количества раз, когда событие происходит в течение заданного интервала.

Синтаксис POISSON.DIST следующий:

ПУАССОНА.РАСП (x, среднее, кумулятивное)

x: количество вхождений в течение заданного интервала
среднее значение: среднее количество вхождений в течение заданного интервала
кумулятивный: TRUE возвращает кумулятивную вероятность; FALSE возвращает точную вероятность

В следующих примерах показано, как решать вопросы вероятности Пуассона с помощью POISSON.DIST .

Пример 1

Хозяйственный магазин продает в среднем 3 молотка в день. Какова вероятность того, что они продадут 5 молотков в данный день?

В этом примере мы можем подключить следующие числа к функции POISSON.DIST :

x: количество вхождений в течение заданного интервала (продажа 5 молотков)
среднее значение: среднее количество вхождений в течение заданного интервала (в среднем они продают 3 )
кумулятивный: ЛОЖЬ (нам нужна точная вероятность, а не кумулятивная вероятность)

Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Excel: ПУАССОН.РАСП(5, 3, ЛОЖЬ)

Вероятность того, что магазин продаст 5 молотков в данный день, равна 0,100819 .

Пример 2

Один магазин продает в среднем 15 банок тунца в день. Какова вероятность того, что этот магазин продаст более 20 банок тунца в данный день?

В этом примере мы можем подключить следующие числа к функции POISSON.DIST :

x: количество вхождений в течение заданного интервала (продажа 20 банок)
среднее: среднее количество вхождений в течение заданного интервала (в среднем они продают 15 банок)
кумулятивный: ИСТИНА (нам нужна кумулятивная вероятность, а не точная вероятность)

Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Excel: 1 – ПУАССОН.РАСП(20, 15, ИСТИНА)

Вероятность того, что магазин продаст более 20 банок тунца в данный день, равна 0,082971 .

Примечание. В этом примере функция ПУАССОН.РАСП(20, 15, ИСТИНА) возвращает вероятность того, что магазин продаст 20 или менее банок тунца. Итак, чтобы найти вероятность того, что магазин продаст более 20 банок, мы просто используем 1 — ПУАССОН.РАСП(20, 15, ИСТИНА).

Пример 3

Один магазин спортивных товаров продает в среднем семь баскетбольных мячей в день. Какова вероятность того, что этот магазин продаст четыре или меньше баскетбольных мячей в данный день?

В этом примере мы можем подключить следующие числа к функции POISSON.DIST :

x: количество событий в течение заданного интервала (продажа 4 баскетбольных мячей)
среднее значение: среднее количество вхождений в течение заданного интервала (в среднем они продают 7 )
кумулятивный: ИСТИНА (нам нужна кумулятивная вероятность, а не точная вероятность)

Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Excel: ПУАССОН.РАСП(4, 7, ИСТИНА)

Вероятность того, что магазин продаст 4 или меньше баскетбольных мячей в данный день, равна 0,172992 .

Пример 4

Один магазин продает в среднем двенадцать ананасов в день. Какова вероятность того, что в данном магазине в данный день продается от 12 до 14 ананасов?

В этом примере мы можем подключить следующие числа к функции POISSON.DIST :

x: количество случаев в течение заданного интервала (продажа от 12 до 14 ананасов)
среднее значение: среднее количество вхождений в течение заданного интервала (в среднем они продают 12 )
кумулятивный: ИСТИНА (нам нужна кумулятивная вероятность, а не точная вероятность)

Чтобы ответить на этот вопрос, мы можем использовать следующую формулу в Excel:

ПУАССОНА.РАСП(14, 12, ИСТИНА) – ПУАССОНА.РАСП(11, 12, ИСТИНА)

Вероятность того, что магазин продаст от 12 до 14 ананасов в данный день, равна 0,310427 .

Примечание. В этом примере функция ПУАССОН.РАСП(14, 12, ИСТИНА) возвращает вероятность того, что в магазине будет продано 14 или меньше ананасов, а ПУАССОН.РАСП(11, 12, ИСТИНА) возвращает вероятность того, что в магазине будет продано 11 или меньше ананасов. Итак, чтобы найти вероятность того, что в магазине продается от 12 до 14 наименований, мы вычитаем разницу, так что мы фактически находим вероятность того, что в магазине продается 12, 13 или 14 ананасов.

Альтернативный способ решить эту задачу — просто найти отдельные вероятности продажи 12, 13 и 14 ананасов, а затем сложить эти вероятности:

Это дает нам ту же вероятность, что и предыдущий метод.

Источник

Рассмотрим распределение Пуассона, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL

ПУАССОН.РАСП()

построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения, его математического ожидания и стандартного отклонения.

Сначала дадим сухое формальное определение распределения, затем приведем примеры ситуаций, когда

распределение Пуассона

(англ.

Poisson

distribution

) является адекватной моделью для описания случайной величины.

Если случайные события происходят в заданный период времени (или в определенном объеме вещества) со средней частотой λ(

лямбда

), то число событий

x

,

произошедших за этот период времени, будет иметь

распределение Пуассона

.

Плотность вероятности

распределения Пуассона

задается следующей формулой:

λ – единственный параметр

распределения Пуассона

.

СОВЕТ

: подробнее о

Функции распределения

и

Плотности вероятности

см. статью

Функция распределения и плотность вероятности в MS EXCEL

Применение распределения Пуассона

Примеры, когда

Распределение Пуассона

является адекватной моделью:

число вызовов, поступивших на телефонную станцию за определенный период времени;
число частиц, подвергнувшихся радиоактивному распаду за определенный период времени;
число дефектов в куске ткани фиксированной длины.

Распределение Пуассона

является адекватной моделью, если выполняются следующие условия:

события происходят независимо друг от друга, т.е. вероятность последующего события не зависит от предыдущего;
средняя частота событий постоянна. Как следствие, вероятность события пропорциональна длине интервала наблюдения;
два события не могут произойти одновременно;
число событий должно принимать значения 0; 1; 2…

Примечание

: Хорошей подсказкой, что наблюдаемая случайная величина имеет

распределение Пуассона,

является тот факт, что

среднее значение выборки

приблизительно равно

дисперсии

(см. ниже).

Ниже представлены примеры ситуаций, когда

Распределение Пуассона

не может

быть применено:

число студентов, которые выходят из университета в течение часа (т.к. средний поток студентов не постоянен: во время занятий студентов мало, а в перерыве между занятиями число студентов резко возрастает);
число землетрясений амплитудой 5 баллов в год в Калифорнии (т.к. одно землетрясение может вызвать повторные толчки сходной амплитуды – события не независимы);
число дней, которые пациенты проводят в отделении интенсивной терапии (т.к. число дней, которое пациенты проводят в отделении интенсивной терапии всегда больше 0).

Примечание

:

Распределение Пуассона

является приближением более точных дискретных распределений:

Гипергеометрического

Биномиального

Примечание

: О взаимосвязи

распределения Пуассона

и

Биномиального распределения

можно прочитать в статье

Взаимосвязь некоторых распределений в MS EXCEL

. О взаимосвязи

распределения Пуассона

и

Экспоненциального распределения

можно прочитать в статье про

Экспоненциальное распределение

Распределение Пуассона в MS EXCEL

В MS EXCEL, начиная с версии 2010, для

Распределения

Пуассона

имеется функция

ПУАССОН.РАСП()

, английское название — POISSON.DIST(), которая позволяет вычислить не только вероятность того, что за заданный период времени произойдет

х

событий (функцию

плотности вероятности

p(x), см. формулу выше), но и

интегральную функцию распределения

(вероятность того, что за заданный период времени произойдет не меньше

x

событий).

До MS EXCEL 2010 в EXCEL была функция

ПУАССОН()

, которая также позволяет вычислить

функцию распределения

и

плотность вероятности

p(x).

ПУАССОН()

оставлена в MS EXCEL 2010 для совместимости.

В

файле примера

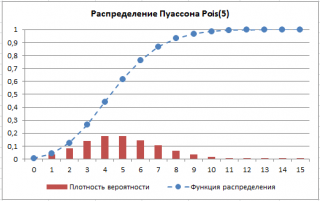
приведены графики

плотности распределения вероятности

и

интегральной функции распределения

.

Распределение Пуассона

имеет скошенную форму (длинный хвост справа у функции вероятности), но при увеличении параметра λ становится все более симметричным.

Примечание

: Для построения

интегральной функции распределения

идеально подходит диаграмма типа

График

, для

плотности распределения

–

Гистограмма с группировкой

. Подробнее о построении диаграмм читайте статью

Основные типы диаграмм

Примечание

:

Среднее

и

дисперсия

(квадрат

стандартного отклонения

) равны параметру

распределения Пуассона

– λ (см.

файл примера лист Пример

).

Задача

Типичным применением

Распределения Пуассона

в контроле качества является модель количества дефектов, которые могут появиться в приборе или устройстве.

Например, при среднем количестве дефектов в микросхеме λ (лямбда) равном 4, вероятность, что случайно выбранная микросхема будет иметь 2 или меньше дефектов, равна: =

ПУАССОН.РАСП(2;4;ИСТИНА)=0,2381

Третий параметр в функции установлен = ИСТИНА, поэтому функция вернет

интегральную функцию распределения

, то есть вероятность того, что число случайных событий окажется в диапазоне от 0 до 4 включительно.

Вычисления в этом случае производятся по формуле:

Вероятность того, что случайно выбранная микросхема будет иметь ровно 2 дефекта, равна: =

ПУАССОН.РАСП(2;4;ЛОЖЬ)=0,1465

Третий параметр в функции установлен = ЛОЖЬ, поэтому функция вернет плотность вероятности.

Вероятность того, что случайно выбранная микросхема будет иметь больше 2-х дефектов, равна:

=1-ПУАССОН.РАСП(2;4;ИСТИНА) =0,8535

Примечание

: Если

x

не является целым числом, то при вычислении формулы

дробная часть числа отбрасывается

. Формулы

=ПУАССОН.РАСП(

2

; 4; ЛОЖЬ)

и

=ПУАССОН.РАСП(

2,9

; 4; ЛОЖЬ)

вернут одинаковый результат.

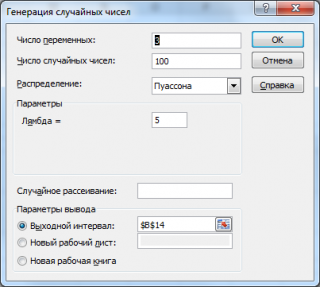
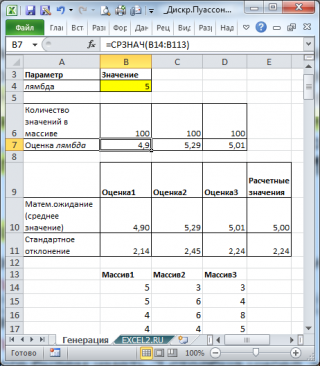
Генерация случайных чисел и оценка λ

С помощью надстройки

Пакет анализа

можно сгенерировать случайные числа, извлеченные из

распределения Пуассона

.

Сгенерируем 3 массива по 100 чисел с параметром λ=5. Для этого в окне

Генерация случайных чисел

установим следующие параметры:

В итоге будем иметь 3 столбца чисел, на основании которых можно оценить параметр λ для каждого массива с помощью функции

СРЗНАЧ()

, см.

файл примера лист Генерация

.

Связь Распределения Пуассона с Биномиальным и Нормальным распределением

Распределение Пуассона

является предельным случаем

Биномиального распределения

, при условии, если параметр

n

Биномиального распределения

стремится к бесконечности, а

p

– к 0.

Можно сформулировать условия, когда приближение

распределением Пуассона

работает хорошо:

p
<0,1

(чем меньше p и больше n, тем приближение точнее);
p

>0,9

(учитывая, что

q

=1-

p

, вычисления в этом случае необходимо производить через

q

(а

х

нужно заменить на

n

—

x

). Следовательно, чем меньше

q

и больше

n

, тем приближение точнее).

Примечание

: Если 0,1<=p<=0,9, а n*p>10, то

Биномиальное распределение

можно аппроксимировать

Нормальным распределением

При значениях λ

>15

,

Распределение Пуассона

хорошо аппроксимируется

Нормальным распределением

со следующими параметрами: μ

=λ

, σ
²
=λ

.

Подробнее о связи этих распределений, можно прочитать в статье

Взаимосвязь некоторых распределений в MS EXCEL

. Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.

СОВЕТ

: О других распределениях MS EXCEL можно прочитать в статье

Распределения случайной величины в MS EXCEL

Источник

The Poisson distribution is one of the most commonly used distributions in statistics.

In Excel, we can use the POISSON.DIST() function to find the probability that an event occurs a certain number of times during a given interval, based on knowing the mean number of times the event occurs during the given interval.

The syntax for POISSON.DIST is as follows:

POISSON.DIST(x, mean, cumulative)

x: number of occurrences during a given interval
mean: mean number of occurrences during a given interval
cumulative: TRUE returns the cumulative probability; FALSE returns the exact probability

The following examples illustrate how to solve Poisson probability questions using POISSON.DIST.

Example 1

A hardware store sells 3 hammers per day on average. What is the probability that they will sell 5 hammers on a given day?

In this example, we can plug in the following numbers to the POISSON.DIST function:

x: number of occurrences during a given interval (selling 5 hammers)
mean: mean number of occurrences during a given interval (they sell 3 on average)
cumulative: FALSE (we want an exact probability, not a cumulative probability)

To answer this question, we can use the following formula in Excel: POISSON.DIST(5, 3, FALSE)

The probability that the store sells 5 hammers in a given day is 0.100819.

Example 2

A certain store sells 15 cans of tuna per day on average. What is the probability that this store sells more than 20 cans of tuna in a given day?

In this example, we can plug in the following numbers to the POISSON.DIST function:

x: number of occurrences during a given interval (selling 20 cans)
mean: mean number of occurrences during a given interval (they sell 15 cans on average)
cumulative: TRUE (we want a cumulative probability, not an exact probability)

To answer this question, we can use the following formula in Excel: 1 – POISSON.DIST(20, 15, TRUE)

The probability that the store sells more than 20 cans of tuna in a given day is 0.082971.

Note: In this example, POISSON.DIST(20, 15, TRUE) returns the probability that the store sells 20 or fewer cans of tuna. So, to find the probability that the store sells more than 20 cans, we simply use 1 – POISSON.DIST(20, 15, TRUE).

Example 3

A certain sporting goods store sells seven basketballs per day on average. What is the probability that this store sells four or less basketballs in a given day?

In this example, we can plug in the following numbers to the POISSON.DIST function:

x: number of occurrences during a given interval (selling 4 basketballs)
mean: mean number of occurrences during a given interval (they sell 7 on average)
cumulative: TRUE (we want a cumulative probability, not an exact probability)

To answer this question, we can use the following formula in Excel: POISSON.DIST(4, 7, TRUE)

The probability that the store sells 4 or fewer basketballs in a given day is 0.172992.

Example 4

A certain store sells twelve pineapples per day on average. What is the probability that this store sells between 12 and 14 pineapples in a given day?

In this example, we can plug in the following numbers to the POISSON.DIST function:

x: number of occurrences during a given interval (selling between 12 and 14 pineapples)
mean: mean number of occurrences during a given interval (they sell 12 on average)
cumulative: TRUE (we want a cumulative probability, not an exact probability)

To answer this question, we can use the following formula in Excel:

POISSON.DIST(14, 12, TRUE) – POISSON.DIST(11, 12, TRUE)

The probability that the store sells between 12 and 14 pineapples in a given day is 0.310427.

Note: In this example, POISSON.DIST(14, 12, TRUE) returns the probability that the store sells 14 or fewer pineapples and POISSON.DIST(11, 12, TRUE) returns the probability that the store sells 11 or fewer pineapples . So, to find the probability that the store sells between 12 and 14 titles, we subtract the difference so that we are actually finding the probability that the store sells either 12, 13, or 14 pineapples.

An alternative way to solve this problem is to simply find the individual probabilities of selling 12, 13, and 14 pineapples, and then add up these probabilities:

This gives us the same probability as the previous method.

Источник

Описание

Excel POISSON Функция возвращает распределение Пуассона, которое используется для прогнозирования количества событий, происходящих за определенное время, например, количества людей, прибывающих на рынок за 10 минут.

Примечание. Эта функция была заменена функцией ПУАССОН.РАСП, которая может обеспечивать повышенную точность после версии Excel 2010. Эта функция по-прежнему может быть доступна, но, учитывая, что она может быть недоступна в будущем, вам следует изучить возможность использования новой функции прямо сейчас.

Синтаксис формулы

ПУАССОН(x,значить,кумулятивный)

аргументы

X: Обязательное количество событий.

Mean: Обязательное, ожидаемое числовое значение.

Cumulative: Обязательное логическое значение, определяющее форму возвращаемого распределения вероятностей.
TRUE: возвращает кумулятивную пуассоновскую вероятность того, что количество случайных событий будет находиться в диапазоне от 0 до x включительно;
ЛОЖЬ: возвращает функцию массы вероятности Пуассона, согласно которой число происходящих событий будет равно x.

Условия возврата товара

Функция ПУАССОН возвращает числовое значение.

Замечания

1. Если x не является целым числом, оно будет усечено.

2. Если x или среднее значение не являются числовыми, #VALUE! будет возвращено значение ошибки.

3. Если x < 0 или среднее значение < 0, функция #ЧИСЛО! будет возвращено значение ошибки.

4. ПУАССОН.РАСП рассчитывается по следующим уравнениям:

Для кумулятивного = ИСТИНА

для кумулятивного = ЛОЖЬ

Версия

Excel 2007

Использование и примеры

Основное использование

Основываясь на заданном количестве событий и ожидаемом среднем значении в ячейках B3 и B5, вы можете получить кумулятивную вероятность Пуассона (кумулятивная как ИСТИНА) и массовую функцию вероятности Пуассона (кумулятивную как ЛОЖЬ) с помощью функции ПУАССОНА, как показано ниже:

=POISSON (B3,B5,TRUE)

Или напрямую используйте числа в функции

=POISSON (5,10,TRUE)

=POISSON (B3,B5,FALSE)

Или напрямую используйте числа в функции

=POISSON (5,10,FALSE)

Нажмите Enter ключ к результату.

Другие функции:

Excel F.INV Функция
Функция Excel F.ОБР возвращает обратное F-распределение вероятностей. Если p (вероятность) = F.РАСП(x,…), то F.ОБР(p,…)= x.

Excel FDIST Функция
Функция Excel FDIST возвращает (правостороннее) распределение вероятностей F, которое обычно используется для измерения степени разнообразия между двумя наборами данных.

Excel EXPON.DIST Функция
Функция EXPON.DIST, используемая в Excel 2010, возвращает экспоненциальное распределение на основе заданного значения x и параметра распределения.

Excel F.DIST Функция
Функция Excel F.РАСП возвращает F-распределение вероятностей, которое обычно используется для измерения степени разнообразия между двумя наборами данных.

Лучшие инструменты для работы в офисе

Kutools for Excel — Помогает вам выделиться из толпы

Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает 300 мощных расширенных функций (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80 % времени.

Разработан для 1500 рабочих сценариев, помогает решить 80% проблем с Excel.
Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
Станьте экспертом по Excel за 3 минуты. Больше не нужно запоминать какие-либо болезненные формулы и коды VBA.
30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.

Вкладка Office — включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)

Одна секунда для переключения между десятками открытых документов!
Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
Добавляет эффективные вкладки в Office (включая Excel), точно так же, как Chrome, Firefox и новый Internet Explorer.

Комментарии (0)

Оценок пока нет. Оцените первым!

Источник

Обзор распределения Пуассона в Excel

Распределение Пуассона в Excel (Содержание)

Обзор функции распределения Пуассона в Excel
Как использовать функцию распределения Пуассона в Excel?

Обзор распределения Пуассона в Excel

В следующем разделе «Распределение Пуассона в Excel» представлен обзор наиболее часто используемых функций в Excel. Это предварительно встроенная интегрированная функция распределения вероятностей (pdf) в Excel, которая классифицируется как Статистические функции.

Используется для расчета прогноза выручки.

Это связано с экспоненциальным распределением. Это число событий, произошедших в данной единице времени или расстояния, области или объема, например

а) Нет случаев несчастных случаев на велосипеде в день. Здесь число появлений события является случайной величиной Пуассона, оно непредсказуемо и неизвестно, события происходят случайным образом и независимо.

б) Количество телефонных звонков, полученных агентом колл-центра за 60 минут.

в) Количество недостатков в болте ткани.

d) Количество ошибок на каждой странице документа, которые могут быть орфографическими или другими ошибками.

Массовая функция вероятности Пуассона вычисляет вероятность появления x и рассчитывается по нижеприведенной статистической формуле:
P (x, λ) = ((e ^−λ ) * λ ^x ) / x!

Вот,

λ (лямбда) — ожидаемое количество вхождений за указанный период времени.
X (случайная величина) называется пуассоновской случайной величиной с параметром λ.
е аналогичен пи, является математической константой, базой натуральных логарифмов, которая приблизительно равна 2, 71828.
Икс! который называется х факториал, например, 5 факториалов будет 120, который рассчитывается как

5! = 5x4x3x2x1 = 120

Примечание. Здесь значение случайной величины равно лямбде, лямбда часто используется в распределении Пуассона.

Кривые распределения Пуассона для вероятности массы и кумулятивного

Объяснение функции распределения Пуассона в Excel

Он используется для оценки или прогнозирования вероятности определенного числа событий в течение определенного интервала времени или пространства.

Синтаксис или формула для функции распределения Пуассона в Microsoft Excel:

Синтаксис или формула функции POISSON.DIST имеет нижеприведенный аргумент:

x: это общее количество событий, вероятность которых будет рассчитана.

Примечание: оно не должно быть отрицательным значением, оно должно быть ≥ 0).

Это значение должно быть целым числом; Если указан десятичный знак, он будет сокращен до целого числа в Excel.

Среднее значение : ожидаемое количество событий (Примечание: оно должно быть ≥ 0).
Накопительный : логический аргумент, который указывает тип распределения, которое будет рассчитано.

Здесь тип распространения может быть или может быть одним из следующих:

ИСТИНА или 1 — использовать накопительную функцию распределения или

Он вернет совокупную вероятность того, что событие x или меньше произойдет.

FALSE или 0 — использовать функцию вероятности массы или плотности.

то есть Excel вернет вероятность только x количества событий.

Как использовать функцию распределения Пуассона в Excel?

Давайте посмотрим, как работает функция распределения Пуассона в Excel, с примерами.

Вы можете скачать этот шаблон Excel по распределению Пуассона здесь — Шаблон Excel по распределению Пуассона

Пример № 1 — Расчет вероятности массы или функции плотности

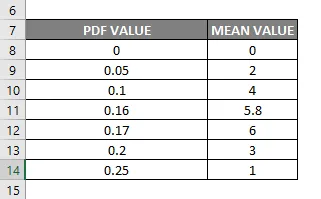
Предположим, что агент исходящих звонков совершил 5, 8 телефонных звонков в минуту, и в этом случае возникновение звонков можно прогнозировать с помощью или посредством распределения POISSON. Давайте проверим, как рассчитать как интегральную функцию распределения, так и функцию вероятности или плотности.

Теперь мы можем вычислить массу вероятности или функцию плотности, используя функцию распределения Пуассона.

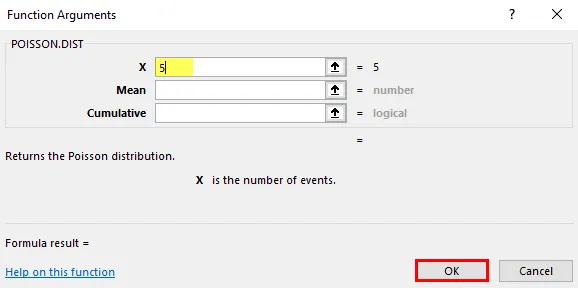
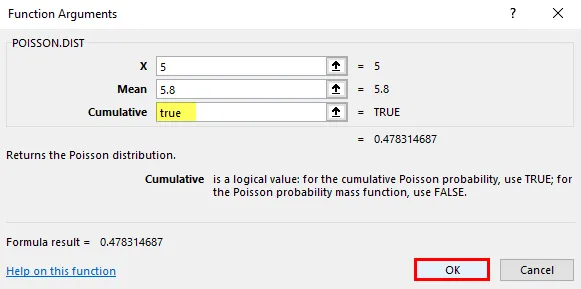
Выберите ячейку, в которой необходимо применить функцию распределения Пуассона для расчета кумулятивного распределения , т.е. «A2»
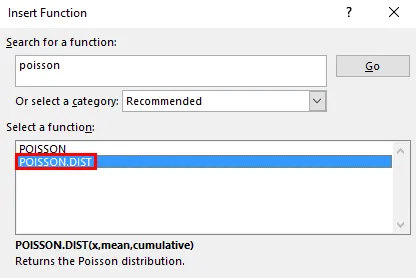
Теперь нажмите кнопку «Вставить функцию» (fx) под панелью инструментов формул в верхней части листа Excel. Появится диалоговое окно, в котором необходимо ввести ключевое слово «POISSON» в поиске функционального окна, появятся два типа уравнений Пуассона. Для этого вам нужно выбрать функцию распределения Пуассона.

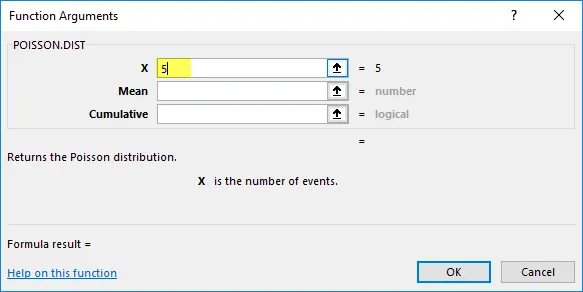
Предположим, агент колл-центра совершил ровно 5 телефонных звонков за 1 минуту.

X = 5, это общее количество событий, вероятность которых будет рассчитана.

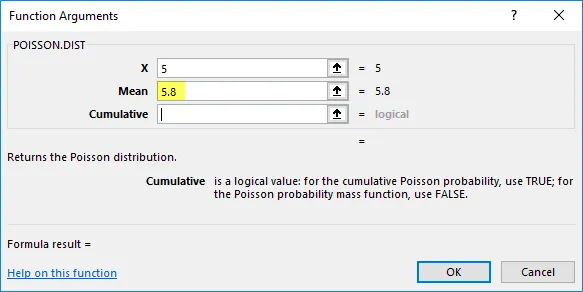
Среднее значение = 5, 8, это ожидаемое количество событий, которые должны произойти.

Накопительный : логический аргумент, который указывает тип распределения, которое будет рассчитано.

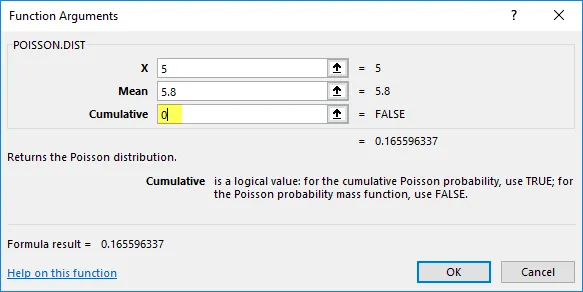
Здесь тип распределения, который нужно выяснить, — это вероятность или функция плотности. следовательно, кумулятивный = ложь или 0 (функция плотности вероятности). Он вернёт вероятность только x количества событий.

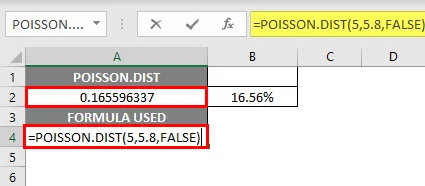
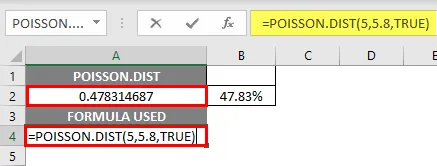
Функция распределения Пуассона возвращает значение вероятностной массы или функции плотности, т. Е. 0, 165596337, где вам нужно преобразовать его в процент, что дает 16, 55%.

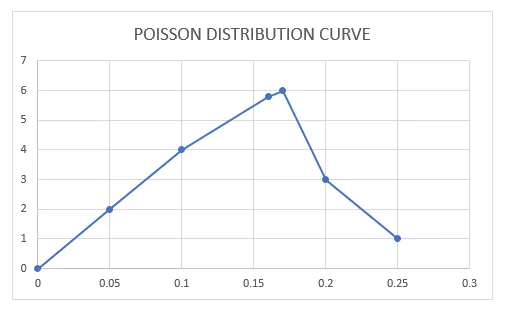
При указанном выше значении, если я строю график для вероятности массы или функции плотности, то есть телефонных звонков в минуту по оси Y (средние значения) и вероятности массы или плотности по оси X (значения в формате PDF), он выглядит как упомянуто ниже.

Кривая распределения Пуассона для функции вероятности массы или плотности

Аналогично, мы можем вычислить кумулятивное распределение с помощью функции распределения Пуассона.

Пример № 2 — Расчет совокупного распределения

Предположим, колл-центр совершил до 5 звонков в минуту.

Чтобы рассчитать совокупное распределение с помощью функции распределения Пуассона, единственное изменение, которое необходимо сделать, — это кумулятивный аргумент в функции распределения Пуассона, установленный как значение ИСТИНА, а не ложь.

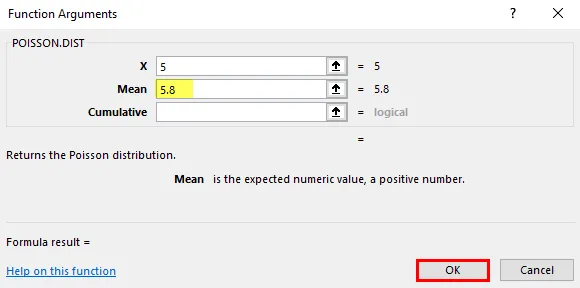
Выберите ячейку, в которой необходимо применить функцию распределения Пуассона для расчета кумулятивного распределения, т.е. «D6»
Теперь нажмите кнопку «Вставить функцию» (fx) под панелью инструментов формул в верхней части листа Excel. Появится диалоговое окно, в котором необходимо ввести ключевое слово «POISSON» в поиске функционального окна, появятся два типа уравнений Пуассона. Для этого вам нужно выбрать функцию распределения Пуассона.

Предположим, агент колл-центра совершил ровно 5 телефонных звонков за 1 минуту.

X = 5, это общее количество событий, вероятность возникновения которых будет рассчитана

Среднее значение = 5, 8, это ожидаемое количество событий, которые должны произойти.

Накопительный : логический аргумент, который указывает тип распределения, которое будет рассчитано.

Здесь тип распределения, чтобы узнать, является кумулятивным. Следовательно, кумулятивный = ИСТИНА или 1 Кумулятивная функция плотности (CDF).

Excel вернет совокупную вероятность события x или меньше.

Функция распределения Пуассона возвращает значение кумулятивного распределения, то есть 0, 478314687, где вам нужно преобразовать его в процент, что дает 47, 83%.

То, что нужно запомнить

Если значение X или среднее значение меньше нуля в функции распределения Пуассона, возникает ошибка #NUM.

Если какой-либо аргумент в функции распределения Пуассона не является числовым, тогда #VALUE! ошибка

Значение X в функции распределения Пуассона всегда должно быть целым числом, если вы введете десятичное значение, оно будет усечено до целого числа в Excel

Определение распределения Пуассона

Распределение Пуассона относится к процессу определения вероятности повторения событий в течение определенного периода времени. Переменные для этого распределения вероятностей должны быть счетными, случайными и независимыми.

Этот статистический инструмент используется для понимания будущих возможностей и тенденций. Он используется бизнес-организациями, финансовыми аналитиками. Финансовые аналитики. Финансовый аналитик анализирует проект или компанию с основной целью консультировать руководство / клиентов по поводу жизнеспособных инвестиционных решений. Они проводят тщательный финансовый анализ и делают подходящие объективные прогнозы, чтобы прийти к своим выводам. Читать далее, исследователи рынка, астрономы, ученые, физиологи, спортивные власти и правительственные учреждения. Впервые он был введен Симеоном Дени Пуассоном в 1830 году. Используя этот метод, французский математик рассчитал вероятность успеха в азартных играх.

Оглавление

Определение распределения Пуассона
- Как работает распределение Пуассона?
- Формула распределения Пуассона
- Расчет с графиком
- Примеры распределения Пуассона в Excel
  - Пример №1
  - Пример #2
- Приложения распределения Пуассона
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи

Распределение Пуассона — это однопараметрический вероятностный инструмент, используемый для определения шансов на успех, т. е. для определения того, сколько раз событие происходит в течение определенного периода времени.
Формула распределения Пуассона: P(x;µ)=(e^(-µ) µ^x)/x!.
Распределение считается моделью Пуассона, когда количество вхождений является счетным (в целых числах), случайным и независимым. Другими словами, оно должно быть независимым от других событий и их возникновения.
Кроме того, среднее значение X ∼P(µ) = µ; Дисперсия X ∼P(µ) = µ; и стандартное отклонение X ∼P(µ) = +√µ.

Как работает распределение Пуассона?

Распределение Пуассона есть не что иное, как прогноз события, происходящего в определенный период. Устанавливается возможность возникновения события заданное количество раз для заданного периода времени. Например, шансы получить определенное количество ударов сердца в течение минуты — это распределение вероятностей. Рассмотрим другой пример, предположим, что больница хочет реструктурировать персонал своего отделения неотложной помощи. Скажем, больница ежедневно принимает три неотложных случая. Администрация использует распределение Пуассона, чтобы определить возможность приема пяти экстренных случаев в день для найма резервного персонала.

Этот статистический инструмент является однопараметрическим. В результате знание средней переменной возникновения события можно использовать для определения других возможностей. Распределение ПуассонаРаспределение ПуассонаРаспределение Пуассона относится к процессу определения вероятности повторения событий в течение определенного периода времени. X ∼ P(μ). Более того, мы также можем найти его среднее значение, дисперсию и стандартное отклонение, используя следующие уравнения:

Среднее значение X ∼P(µ) = µ
Дисперсия X ∼P(µ) = µ
Стандартное отклонениеСтандартное отклонениеСтандартное отклонение (SD) — это популярный статистический инструмент, обозначаемый греческой буквой «σ», для измерения вариации или дисперсии набора значений данных относительно их среднего (среднего) значения, таким образом интерпретируя надежность данных.Подробнее о X ∼P(μ) = +√μ

Результаты двух распределений Пуассона можно суммировать, чтобы получить вероятность более широкой случайной величины. То есть X1∼P(µ1) и X2∼P(µ2) могут предоставить значение третьей переменной Y. Здесь Y = X1+X2∼P (µ1+ µ2). Например, предположим, что хоккейная команда выигрывает в среднем два матча на каждые пять сыгранных игр. Какова вероятность выиграть одно соревнование в этом году? Команда может выиграть 0 или 1 матч. Таким образом, чтобы вычислить желаемые результаты, сложите обе вероятности. То есть сложите вероятность выигрыша нулевого матча и вероятность выигрыша одного матча.

В 1830 году Симеон Дени Пуассон представил модель распределения Пуассона. Он был французским математиком, который вычислил шансы на успех в азартных играх, используя этот метод. Однако это был непопулярный инструмент среди игроков. Тем не менее, концепция приобрела значение в области статистики после Второй мировой войны. Британский статистик Р. Д. Кларк использовал этот инструмент, чтобы помочь британскому правительству получить представление о немецких бомбардировках Лондона. Кларк проанализировал, что немцы сбросили бомбы случайным образом. Кларк пришел к выводу, что в атаках не указан регион или город.

Формула распределения Пуассона

Это распределение вероятности определяет вероятность повторения события в течение заданного интервала времени. Формула выглядит следующим образом:

Здесь P(x; µ) — вероятность того, что событие произойдет определенное число раз за определенный период;

e обозначает число Эйлера, основное значение которого равно 2,72;

µ — среднее количество вхождений за определенный период; и

Икс! является факториалом числа событий, для которых определяется вероятность.

Расчет с графиком

Рассмотрим следующее числовое значение, чтобы лучше понять вычисления, используемые в этом математическом инструменте.

Компания-производитель часов хочет сократить количество бракованных изделий. Было отобрано в среднем 100 партий, и было обнаружено, что 7 часов из каждой партии были бракованными. Какова вероятность того, что 10 часов будут бракованными в одной партии?

Решение:

Данный:

Среднее количество бракованных часов в партии (µ) = 7

Ожидаемое количество бракованных часов в конкретной партии (x) = 10

Р (х; мк) = [e^(-μ) μ^x]/Икс!

Р (10;7) = [e^ (-7) 7^10]/10!

Р (10;7) = 0,07098 или 7,098%

Таким образом, вероятность того, что в данной партии будет 10 бракованных часов, составляет 7,098%.

График распределения Пуассона

На том же примере изобразим на графике вероятность наличия 0,1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 бракованных часов.

Примеры распределения Пуассона в Excel

Рассмотрим этот простой пример Excel, чтобы лучше понять, как применяется формула распределения Пуассона.

Пример №1

Среднее количество событий в заданном временном интервале равно 10. Какова вероятность того, что это событие произойдет 15 раз?

В этом примере u = среднее количество появлений события = 10

И х = 15

Следовательно, расчет распределения Пуассона можно выполнить следующим образом:

P (15;10) = e^(-10)*10^15/15!

Р (15; 10) = 0,0347 = 3,47%

Следовательно, вероятность того, что это событие произойдет 15 раз, составляет 3,47%.

Пример #2

Другое использование формулы Пуассона в страховой отрасли. Компания, занимающаяся страховым бизнесом, определяет размер страховой премии на основе количества исков и суммы требований в год. Так, для оценки суммы своей премии страховая компания будет определять среднее количество заявленной суммы в год. Затем, основываясь на этом среднем, он также определит минимальное и максимальное количество исков, которые можно обоснованно подать в год. Основываясь на максимальном количестве суммы претензии, а также стоимости и прибыли от премии, страховая компания определит, какая сумма премии будет хорошей для безубыточности.

Скажем, среднее количество претензий, обрабатываемых страховой компанией в день, равно 5. Она выяснит, какова вероятность 10 претензий в день.

Следовательно, расчет можно провести следующим образом:

Р(10;5) = е^(-5). 5^10/10!

Р(10;5) = 1,81%

Следовательно, вероятность того, что компания будет иметь 10 претензий в день, очень мала. На основании этих данных компания может принять решение о размере премии.

Приложения распределения Пуассона

Распределение Пуассона полезно для прогнозирования, отслеживания и повышения эффективности компании. Он часто применяется для оценки эффективности бизнеса и направления организационных усилий для достижения операционной эффективности. Например, руководство может определить пиковые часы продаж и эффективности обслуживания клиентов, чтобы спланировать потребности в рабочей силе. Таким образом, можно комфортно переносить периоды спешки и суеты.

Этот статистический инструмент очень эффективен для проверки осуществимости и жизнеспособности страхового покрытия. Он включает в себя анализ различных факторов, таких как вероятность несчастных случаев, стоимость страхового покрытия, количество раз, когда может быть предъявлен иск, является ли компания чрезмерно застрахованной или недостаточно застрахованной. Кроме того, используя этот метод, менеджеры по производству контролируют потери, отслеживая количество бракованных изделий в каждом цикле производства.

Это одинаково важный инструмент в области финансов для фондовых аналитиков и рыночных прогнозов. Это помогает определить уровень риска, связанный с инвестициями в ценные бумаги. Это достигается путем установления возможности падения рынка в определенный период. Этот метод даже облегчает анализ поведения инвесторов и частоты инвестиций.

Часто задаваемые вопросы (FAQ)

Что такое распределение Пуассона в статистике?

Распределение Пуассона — это не что иное, как предсказание события, происходящего в течение заданного периода времени. Устанавливается возможность возникновения события заданное количество раз для заданного периода времени.

Какими свойствами обладает распределение Пуассона?

Модель называется распределением Пуассона, если она обладает следующими свойствами:

• Возможность успеха в конкретный период времени не зависит от его более раннего наступления.
• Переменные или количество вхождений должны быть целыми числами, т. е. быть исчисляемыми.
• Шансы на успешный исход более одного раза за данный период ничтожны.
• Следует указать значение µ, т. е. среднее количество событий за определенный период.

В чем разница между процессом Пуассона и распределением Пуассона?

Процесс Пуассона — это непрерывное возникновение независимых событий, подобных безостановочному сердцебиению человека. В то время как распределение Пуассона — это средство нахождения возможности повторения события несколько раз за определенный период, т. е. количества повторений события в процессе Пуассона. Например, шансы получить определенное количество ударов сердца в течение минуты — это распределение вероятностей.

Описание функции ПУАССОН.РАСП

Синтаксис

=ПУАССОН.РАСП(x; среднее; интегральная)

Аргументы

xсреднееинтегральная

Обязательный. Количество событий.

Обязательный. Ожидаемое числовое значение.

Обязательный. Логическое значение, определяющее форму возвращаемого распределения вероятностей. Если аргумент «интегральная» имеет значение ИСТИНА, то функция ПУАССОН.РАСП возвращает интегральное распределение Пуассона, то есть вероятность того, что число случайных событий окажется в диапазоне от 0 до x включительно. Если этот аргумент имеет значение ЛОЖЬ, то возвращается весовая функция распределения Пуассона, то есть вероятность точного равенства числа произошедших событий значению x.

Замечания

Пример

Источник

Синтаксис

Замечания

Пример

Нужна дополнительная помощь?

Закон Пуассона распределения вероятностей случайной величины в Excel

Решение задачи на распределение Пуассона в Excel

Биномиальное распределение Пуассона в Excel

Пример 1

Пример 2

Пример 3

Пример 4

Применение распределения Пуассона

Распределение Пуассона в MS EXCEL

Задача

Генерация случайных чисел и оценка λ

Связь Распределения Пуассона с Биномиальным и Нормальным распределением

Example 1

Example 2

Example 3

Example 4

Описание

Условия возврата товара

Замечания

Версия

Использование и примеры

Другие функции:

Лучшие инструменты для работы в офисе

Kutools for Excel — Помогает вам выделиться из толпы

Вкладка Office — включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)

Обзор распределения Пуассона в Excel

Объяснение функции распределения Пуассона в Excel

Как использовать функцию распределения Пуассона в Excel?

Пример № 1 — Расчет вероятности массы или функции плотности

Пример № 2 — Расчет совокупного распределения

То, что нужно запомнить

Рекомендуемые статьи

Определение распределения Пуассона

Как работает распределение Пуассона?

Формула распределения Пуассона

Расчет с графиком

Примеры распределения Пуассона в Excel

Приложения распределения Пуассона

Часто задаваемые вопросы (FAQ)

Рекомендуемые статьи

Описание функции ПУАССОН.РАСП

Синтаксис

Аргументы

Замечания

Пример