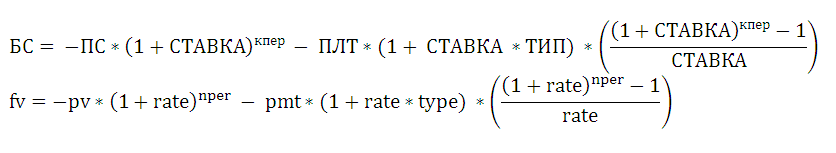Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ПРПЛТ в Microsoft Excel.
Описание
Возвращает сумму платежей по процентам для инвестиции за данный период на основе постоянства сумм периодических платежей и постоянства процентной ставки.
Синтаксис
ПРПЛТ(ставка;период;кпер;пс;[бс];[тип])
Аргументы функции ПРПЛТ описаны ниже.
-
Ставка — обязательный аргумент. Процентная ставка за период.
-
Период — обязательный аргумент. Период, для которого требуется найти платежи по процентам; число в интервале от 1 до «кпер».
-
Кпер — обязательный аргумент. Общее количество периодов платежей по аннуитету.
-
Пс — обязательный аргумент. Приведенная к текущему моменту стоимость, т. е. общая сумма, которая на текущий момент равноценна ряду будущих платежей.
-
Fv Необязательный. Будущая стоимость или баланс, который вы хотите достичь после последнего платежа. Если значение «ок» опущено, предполагается значение 0 (например, будущая стоимость займа — 0).
-
Тип Необязательный. Число 0 или 1, обозначающее срок выплаты. Если аргумент «тип» опущен, предполагается значение 0.
|
Тип |
Выплата |
|
0 |
В конце периода |
|
1 |
В начале периода |
Замечания
-
Убедитесь, что единицы измерения аргументов «ставка» и «кпер» используются согласованно. При ежемесячных выплатах по четырехгодичному займу из расчета 12 процентов годовых используйте значение 12%/12 в качестве аргумента «ставка» и 4*12 — в качестве аргумента «кпер». При ежегодных платежах по тому же займу используйте значение 12% в качестве аргумента «ставка» и 4 — в качестве аргумента «кпер».
-
Все аргументы, которым соответствуют выплачиваемые денежные средства (например, сберегательные вклады), представляются отрицательными числами, а получаемые (например, дивиденды) — положительными.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
10,00 % |
Годовая процентная ставка |
|
|
1 |
Период, для которого требуется найти выплаты. |
|
|
3 |
Срок займа (в годах) |
|
|
8 000р. |
Стоимость займа на текущий момент |
|
|
Формула |
Описание |
Оперативные результаты |
|
=ПРПЛТ(A2/12; A3; A4*12; A5) |
Выплаты по процентам за первый месяц в соответствии с условиями, указанными в диапазоне A2:A5. |
(66,67р.) |
|
=ПРПЛТ(A2; 3; A4; A5) |
Выплаты по процентам за последний год в соответствии с теми же условиями (начисление процентов производится ежегодно). |
(292,45 ₽) |
Нужна дополнительная помощь?
Функция ПРПЛТ в Excel используется для определения части суммы регулярного платежа, определенного для использования финансового продукта (например, кредита) с целью его погашения, которая направлена на погашение процентной части имеющейся задолженности.
Примеры использования функции ПРПЛТ в Excel
Функция ПРПЛТ используется для расчета финансовых продуктов, для погашения задолженности в отношении которых используется аннуитетная схема. Она предусматривает разделение общей суммы задолженности на равные суммы платежей, вносимые через определенные промежутки времени.
Например, кредит на сумму 10000 рублей взят на срок 1 год (12 месяцев) под 20% годовых. При погашении по аннуитету, сумма каждого платежа примерно равна 936 рублей. Часть этого значения составляет тело кредита (основная задолженность), остальная – насчитанные проценты за период выплат.
Для расчета полной суммы платежа в Excel используют формулу ПЛТ. Для расчета части суммы платежа, идущей на оплату основной задолженности – ОСПЛТ. Таким образом, между перечисленными и рассматриваемой функциями существует следующая взаимосвязь: ПЛТ = ОСПЛТ + ПРПЛТ. Главная особенность состоит в том, что соотношение между ОСПЛТ и ПРПЛТ (при ПЛТ = const) меняется от периода к периоду. Поэтому в Excel введена функция ПРПЛТ, учитывающая номер периода платежа, для которого производится расчет процентной части этого платежа.
Расчет кредита процентов ежемесячно в Excel
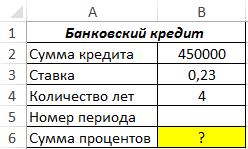
Пример 1. Клиент получил кредит 450000 руб. со ставкой 23% годовых на 4 года. Определить сумму процентов, которую он выплатит за любой период.
Вид таблицы данных:
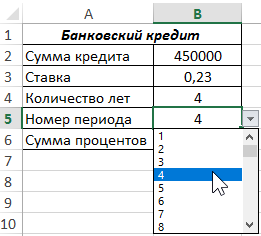
С помощью инструмента «ДАННЫЕ»-«Проверка данных» создадим выпадающий список в ячейке B5. В отдельном месте на листе заполним ряд ячеек числами от 1 до 48 (4*12=48 – общее число периодов выплат по кредиту) и используем полученный ряд в качестве источника для списка. Получим следующее:
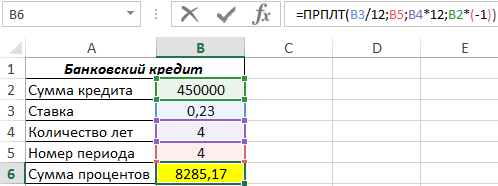
Для расчета значения, например, для 4-го периода выплат выберем значение 4 из созданного списка. В ячейке запишем следующую формулу:
Описание аргументов:
- B3/12 – приведенное значение ставки к числу периодов в году;
- B5 – номер периода из списка;
- B4*12 – общее число периодов выплат;
- B2*(-1) – приведенная стоимость финансового продукта.
Результат вычислений:
В результате вычисления формулы получаем сумму для ежемесячного погашения процентов по кредиту.
Расчет суммы годовых процентов по кредиту в Excel
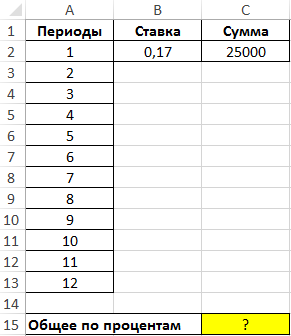
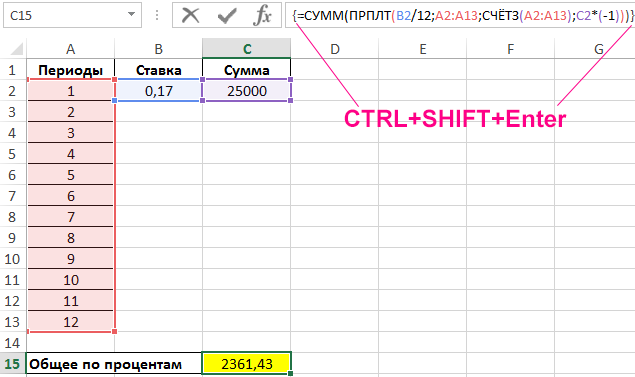
Пример 2. Рассчитать общую сумму процентов, которые заплатит клиент за все периоды выплат по кредиту на 25000 рублей сроком на 12 месяцев, используя функцию ПРПЛТ. Годовая процентная ставка – 17%.
Вид таблицы данных:
Для расчета используем следующую формулу массива CTRL+SHIFT+Enter:
Функция ПРПЛТ возвращает массив значений сумм, потраченных на оплату процентной части, которые суммируются с помощью функции СУММ. Для определения числа периодов выплат используется функция СЧЁТЗ.
Результат вычислений:
То есть, заемщик переплатит около 2360 рублей за год использования финансового продукта.
Правила использования функции ПРПЛТ в Excel
Функция имеет следующий синтаксис:
= ПРПЛТ(ставка;период;кпер;пс;[бс];[тип])
Описание аргументов:
- ставка – обязательный, принимает числовое значение ставки за конкретный период выплат. То есть, при расчетах необходимо использовать приведенное значение. Если финансовый продукт выдан под 24% годовых с 12-ю периодами выплат, вводят значение 0,24/12.
- период – обязательный, принимает числовое значение из диапазона от 1 (первый период) до числа периодов выплат, указанных следующим аргументом.
- кпер – обязательный, указывается в виде числа, соответствующего количеству периодов выплат, например, по банковскому кредиту.
- пс – обязательный, указывается в виде числа, характеризующего приведенную стоимость финансового продукта (средства, которые банк выдает клиенту в момент оформления займа).
- [бс] – необаятельный для заполнения, принимает числовое значение будущей стоимости финансового продукта. Для расчета банковского кредита обычно указывают значение 0, поскольку последний платеж (за последний период выплат) должен погашать всю задолженность перед кредитной организацией. Если явно не указан, принимается значение 0 по умолчанию.
- [тип] – необязательный, может иметь только два значения: 0 (выплаты в конце периода) и 1 (выплаты в начале периода). Если не указан, по умолчанию принимается значение 0.
Примечания:
- Если один или несколько аргументов функции ПРПЛТ указаны в виде данных недопустимого типа (например, не преобразуемой к числовому значению текстовой строкой), результатом расчетов будет код ошибки #ЗНАЧ!
- Для обозначения выплачиваемых средств (например, при использовании формулы для расчетов банковских депозитов) необходимо указывать отрицательные значения сумм. Получаемые средства указывают в виде положительных чисел.
Функция ПРПЛТ возвращает сумму платежей по процентам для инвестиции за данный период на основе постоянства сумм периодических платежей и постоянства процентной ставки.
Описание функции ПРПЛТ
Возвращает сумму платежей по процентам для инвестиции за данный период на основе постоянства сумм периодических платежей и постоянства процентной ставки.
Синтаксис
=ПРПЛТ(ставка; период; кпер; пс; [бс]; [тип])Аргументы
ставкапериодкперпсбстип
Обязательный. Процентная ставка за период.
Обязательный. Период: значение должно находиться в диапазоне от 1 до «кпер».
Обязательный. Общее число периодов платежей для ежегодного платежа.
Обязательный. Приведенная (текущая) стоимость, т. е. общая сумма, которая на данный момент равноценна ряду будущих платежей.
Необязательный. Значение будущей стоимости, т. е. желаемого остатка средств после последнего платежа. Если аргумент «бс» опущен, предполагается, что он равен 0 (например, будущая стоимость для займа равна 0).
Необязательный. Число 0 или 1, обозначающее, когда должна производиться выплата.
| Тип | Когда нужно платить |
|---|---|
| 0 или опущен | В конце периода |
| 1 | В начале периода |
Замечания
- Убедитесь, что единицы измерения аргументов «ставка» и «кпер» используются согласованно. При ежемесячных выплатах по четырехгодичному займу из расчета 12 процентов годовых используйте значение 12%/12 в качестве аргумента «ставка» и 4*12 — в качестве аргумента «кпер». При ежегодных платежах по тому же займу используйте значение 12% в качестве аргумента «ставка» и 4 — в качестве аргумента «кпер».
- Все аргументы, которым соответствуют выплачиваемые денежные средства (например, сберегательные вклады), представляются отрицательными числами, а получаемые (например, дивиденды) — положительными.
Примеры
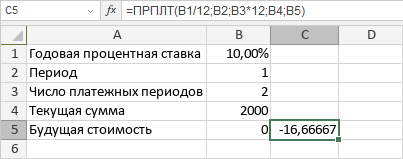
Пример1Пример задачи1
Задача
Определить платежи по процентам за первый месяц от трехгодичного займа в 100 000 руб. из расчета 10% годовых.
Решение
Введем первоначальные данные:

Заполним поля функции:
Ответ: -833,33 руб. Знак «минус» означает, что платеж необходимо внести.
Файл с решением
В статье рассмотрены финансовые функции
ПЛТ()
,
ОСПЛТ()
,
ПРПЛТ()
,
КПЕР()
,
СТАВКА()
,
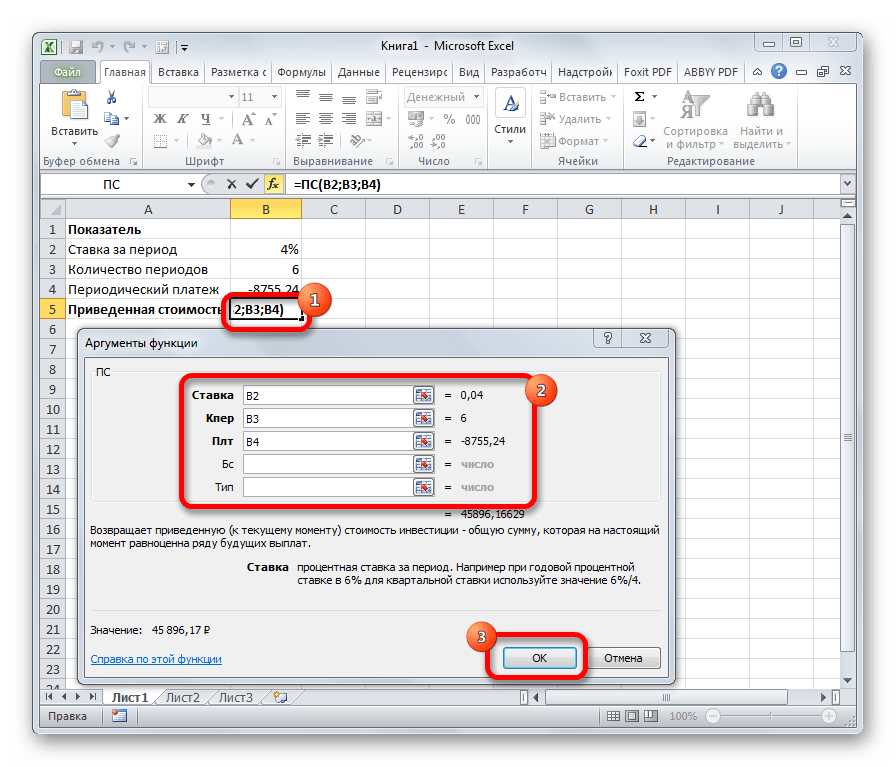
ПС()
,
БС()
, а также
ОБЩДОХОД()
и
ОБЩПЛАТ()
, которые используются для расчетов параметров аннуитетной схемы.
Данная статья входит в цикл статей о расчете параметров аннуитета. Перечень всех статей на нашем сайте об аннуитете
размещен здесь
.
В этой статье содержится небольшой раздел о теории аннуитета, краткое описание функций аннуитета и их аргументов, а также ссылки на статьи с примерами использования этих функций.
Немного теории
Аннуитет (иногда используются термины «рента», «финансовая рента») представляет собой
однонаправленный
денежный поток, элементы которого
одинаковы
по величине
и производятся через
равные периоды времени
(например, когда платежи производятся ежегодно равными суммами).
Каждый элемент такого денежного потока называется
членом аннуитета
, а величина постоянного временного интервала между двумя его последовательными элементами называется
периодом аннуитета
. В широком смысле, аннуитетом может называться как сам финансовый инструмент, так и сумма периодического платежа. Исторически вначале рассматривались равные ежегодные денежные поступления (период между платежами принимался равным одному году), что и послужило основой для именования денежного потока аннуитетом («год» на латинском языке — anno). В дальнейшем, в качестве периода стал выступать любой промежуток времени, но прежнее название сохранилось. Сейчас
период аннуитета
чаще всего равен одному месяцу.
Аннуитетную схему банки часто используют при кредитовании
. Эта схема предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), т.е.
равными суммами через равные промежутки времени
, которые включают как выплату основного долга, так и процентный платеж за пользование кредитом.
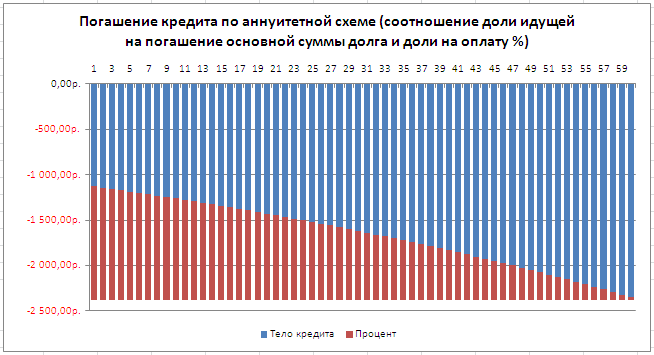
На картинке ниже приведен пример погашения кредита (100 000 руб.) ежемесячными платежами в течение 5 лет при ставке 15%. Для погашения тела кредита и начисленных процентов потребуется произвести 60 платежей (5 лет*12мес в году). Сумма ежемесячного платежа = 2378,99руб. См.
файл примера Лист Аннуитет (ПЛТ)
. Как видно из графика платежей, банк в первые периоды получает платежи, идущие на погашение %, а тело кредита сокращается медленно (см. статью
Сравнение графиков погашения кредита дифференцированными и аннуитетными платежами в MS EXCEL
).
Если каждый элемент аннуитета имеет место в конце соответствующего периода, аннуитет называется аннуитетом постнумерандо (Ordinary Annuity); если в начале периода — аннуитетом пренумерандо (Annuity Due). Обычно используется аннуитет постнумерандо.
Примечание
. В функциях MS EXCEL для указания типа аннуитета предусмотрен специальный необязательный параметр
[тип]
. По умолчанию
тип
=0 (выплаты в конце периода), что соответствует аннуитету постнумерандо. Если
тип
=1, то предполагается аннуитет пренумерандо (выплаты в начале периода).
Часто в расчетах используют понятие
аннуитетный коэффициент
(А):
A = -Ставка * (1+ Ставка)^Кпер / (1-(1+ Ставка)^ Кпер ) / (1+ Ставка*Тип)
где: Ставка — процентная ставка за период; Кпер — общее количество периодов выплаты; Тип – для аннуитета постнумерандо Тип=0, для пренумерандо Тип=1.
Чтобы вычислить
член аннуитета
(величину регулярного платежа) нужно использовать формулу =А*ПС, где ПС – это начальная сумма кредита. Специфика аннуитета (равенство денежных поступлений) позволяет вывести стандартизованные формулы, существенно упрощающие счетные процедуры. Об этих формулах и об их использовании в MS EXCEL и пойдет речь ниже.
Параметры функций аннуитета
Финансовые функции
ПЛТ()
,
ОСПЛТ()
,
ПРПЛТ()
,
КПЕР()
,
СТАВКА()
,
БС()
,
ПС()
, а также
ОБЩДОХОД()
и
ОБЩПЛАТ()
тесно связаны между собой, т.к. все они вычисляют параметры аннуитета и, соответственно, используют один и тот же набор аргументов. В этом можно убедиться, перечислив все функции вместе с аргументами:
ПЛТ(ставка; кпер; пс; [бс]; [тип]) ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип]) ПРПЛТ(ставка; период; кпер; пс; [бс]; [тип]) КПЕР(ставка; плт; пс; [бс]; [тип]) СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение]) БС(ставка; кпер; плт; [пс]; [тип]) ПС(ставка; кпер; плт; [бс]; [тип])
ПЛТ
(английское название функции: PMT, от слова
payment
). Регулярный платеж, осуществляемый каждый период. Платеж – постоянная величина, она не меняется в течение всего срока аннуитета.
Ставка
(англ.: RATE, interest).
Процентная ставка за период
, чаще всего за год или за месяц. Обычно задается через годовую ставку, деленную на количество периодов в году. При годовой ставке 10% месячная ставка составит 10%/12. Ставка не изменяется в течение всего срока аннуитета.
Кпер
(англ.: NPER).
Общее число периодов платежей по аннуитету
. Если кредит взят на 5 лет, а выплаты производятся ежемесячно, то всего 60 периодов (12 мес. в году * 5 лет)
Бс
(англ.: FV, future value).
Будущая стоимость
в конце срока аннуитета (по истечении числа периодов Кпер). Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты. Например, в случае расчета аннуитетного платежа для полной выплаты ссуды к концу срока Бс = 0, т.к. ссуда в конце срока должна быть полностью погашена.
Пс
(англ.: PV, present value).
Приведенная стоимость
, т.е. стоимость приведенная к определенному моменту (часто к текущему, т.е. настоящему времени). Если взят кредит и производятся регулярные выплаты по аннуитетной схеме, то Приведенная стоимость – это сумма кредита. Если планируется регулярно вносить равновеликие платежи на счет в банке (и период начисления % совпадает с периодом платежей), то Приведенную стоимость также нужно указывать = 0.
Тип
(англ.: type). Число 0 или 1, обозначающее, когда должна производиться выплата (и соответственно начисление процентов). 0 – в конце периода, 1 – в начале. Подробнее см. раздел
Немного теории
в начале статьи о постнумерандо и пренумерандо или статьи с примерами, указанные выше.
Все 6 аргументов (параметров аннуитета) связаны между собой выражением:
поэтому каждый из них может быть вычислен при условии, если заданы остальные параметры. Функции аннуитета помогают пользователю упростить вычисления, но все они основаны на Формуле 1.
Примечание
. Формула 1 работает, если Ставка не равна 0. Если ставка равна 0, то вместо Формулы 1 действует гораздо более простое выражение: ПЛТ * Кпер + ПС + БС = 0 (в этом случае схема платежей перестает быть аннуитетом и превращается в беспроцентную ссуду).
О направлениях денежных потоков и знаках ПС, БС и ПЛТ
Вышеуказанная Формула 1 предполагает, что знаки денежных потоков (+/-) указываются с учетом их направления. Например, банк выдал кредит (ПС>0), клиент банка ежемесячно вносит одинаковый платеж (ПЛТ<0). Т.е. имеет место 2 направления движения денег:
от
банка к клиенту
(ПС) и
в банк от клиента
(ПЛТ). Если схема погашения кредита учитывает единовременную выплату в конце погашения, то БС<0, т.к. этот платеж, как и ПЛТ направлен
в банк от клиента
. Функции MS EXCEL также учитывают направления платежей, поэтому функция
ПЛТ()
возвращает отрицательные значения, если ПС>0.
Тождество аннуитета
Если Тип=0, то для функций MS EXCEL справедливо тождество: ОБЩДОХОД(за все периоды) + ПС + БС = 0
Это тождество можно переписать в другом виде: СУММ(ОСПЛТ()) + ПС + БС = 0. В случае использования
аннуитетной схемы погашения кредита
(сумма кредита =ПС), выражение СУММ(ОСПЛТ()) вычисляет общую сумму платежей, идущих на оплату основной суммы долга (тело кредита). В случае полного погашения кредита БС=0, а тождество превращается в ПС=-СУММ(ОСПЛТ()).
Функции
MS
EXCEL
для расчета параметров аннуитета
Теперь кратко рассмотрим функции MS EXCEL. Для того, чтобы нижесказанное было понятным, необходимо предварительно ознакомиться с теорией аннуитета, понятиями
Будущая
и
Приведенная
стоимость.
Функция ПЛТ(ставка; кпер; пс; [бс]; [тип])
рассчитывает величину регулярного платежа на основе заданных 5 аргументов.
Примечание
.
Английский вариант функции: PMT(rate, nper, pv, [fv], [type]), т.е. PayMenT – платеж.
Примечание
.
Вышеуказанные функции входят в надстройку «Пакет анализа». Если функция недоступна или возвращает ошибку #ИМЯ?, то включите или установите и загрузите эту надстройку (с версии MS EXCEL 2007 надстройка «Пакет анализа» включена по умолчанию).
Для понимания работы формулы приведем эквивалентное ей выражение для расчета платежа:
Формула 2 есть не что иное, как решение Формулы 1 относительно параметра ПЛТ.
Примечание.
В
файле примера на листе Аннуитет (без ПЛТ)
приведен расчет ежемесячных платежей без использования финансовых функций EXCEL.
Если процентная ставка = 0, то Формула 2 упростится до
=(ПС + БС)/Кпер
Если Тип=0 (выплата в конце периода) и БС =0, то Формула 2 заметно упрощается:
В случае применения схемы аннуитета для выплаты ссуды платеж включает денежную сумму в счет погашения части ссуды и сумму для оплаты начисленных за прошедший период процентов, поэтому функция
ПЛТ()
связана с
ОСПЛТ()
и
ПРПЛТ()
соотношением ПЛТ = ОСПЛТ + ПРПЛТ (для каждого периода).
Примечание
.
В
файле примера на листе Зависимости ПЛТ()
приведены графики: Зависимость суммы платежа от размера ссуды, Зависимость суммы платежа от ставки, Зависимость суммы платежа от срока ссуды. Также в файле примера приведены некоторые задачи.
Функция ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип])
используется для вычисления регулярных сумм идущих на погашение основной суммы долга практически с теми же аргументами, что и
ПЛТ()
. Т.к. сумма идущая на погашение основной суммы долга изменяется от периода к периоду, то необходим еще один аргумент
период
, который определяет к какому периоду относится сумма.
Примечание
.
Английский вариант функции: PPMT(rate, per, nper, pv, [fv], [type]), т.е. Principal Payment – платеж основной части долга.
В случае
применения схемы аннуитета для выплаты ссуды
для каждого периода действует равенство: ОСПЛТ =ПЛТ – ПРПЛТ, т.к. платеж включает сумму в счет погашения части ссуды (ОСПЛТ) и сумму для оплаты начисленных за прошедший период процентов (ПРПЛТ). Сумму, идущую на погашение основной суммы долга также можно вычислить, зная величину платежа (ПЛТ), период (Период), общее количество периодов (Кпер) и ставку (СТАВКА):
ОСПЛТ=ПЛТ*(1+СТАВКА)^(Период-Кпер-1)
Вышеуказанная формула работает при БС=0. При ТИП=1 (платеж в начале периода) и n=1 (первый платеж), ПРПЛТ=ПЛТ Если БС<>0, то формула усложнится:
Функцию
ОСПЛТ()
часто применяют при составлении графика платежей по аннуитетной схеме (см.
Выплата основной суммы долга в аннуитетной схеме. Расчет в MS EXCEL
)
Примечание
.
В
файле примера на листе Аннуитет (без ПЛТ)
определена аналитическая зависимость суммы идущей на погашение долга от номера периода.
Функция ПРПЛТ (ставка; период; кпер; пс; [бс]; [тип])
используется для вычисления регулярных сумм идущих на погашение процентов за ссуду используется с теми же аргументами, что и
ОСПЛТ()
.
Примечание.
Английский вариант функции: IPMT(rate, per, nper, pv, [fv], [type]), т.е. Interest Payment – выплата процентов.
В случае применения схемы аннуитета для выплаты ссуды для каждого периода действует равенство: ПРПЛТ =ПЛТ – ОСПЛТ
Сумму, идущую на погашение процентов за ссуду, можно вычислить зная: величину платежа (ПЛТ), период (Период), общее количество периодов (Кпер) и ставку (СТАВКА):
ПРПЛТ =ПЛТ*(1-(1+СТАВКА)^(Период-Кпер-1))
Вышеуказанная формула работает при БС=0. При ТИП=1 (платеж в начале периода) и n=1 (первый платеж), ПРПЛТ=0 Если БС<>0, то формула усложнится:
Соотношение выплат основной суммы долга и на погашение начисленных процентов за период хорошо демонстрирует график, приведенный в
файле примера
.
Функцию
ПРПЛТ()
часто применяют при составлении графика платежей по аннуитетной схеме (см.
Аннуитет. Расчет в MS EXCEL выплаченных процентов за период
).
Функция КПЕР(ставка; плт; пс; [бс]; [тип])
позволяет вычислить количество периодов, через которое текущая сумма вклада (пс) станет равной заданной сумме (бс) при известной процентной ставке за период (ставка) и известной величине пополнения вклада (плт). При этом предполагается, сумма пополнения вклада вносится регулярно в каждый период, тогда же происходит и начисление процентов. Сумма пополнения вклада может быть равна 0 (вклад не пополняется, рост вклада осуществляет только за счет капитализации процентов). Бс (будущая стоимость) может быть =0 или опущена. Также функцию
КПЕР()
можно использовать для определения количества периодов, необходимых для погашения долга по ссуде (погашение осуществляется регулярно равными платежами, ставка не изменяется весь срок, на который выдана ссуда, процент начисляется каждый период на остаток ссуды).
Примечание
.
Английский вариант функции: NPER(rate, pmt, pv, [fv], [type]), т.е. Number of Periods – число периодов.
Эквивалентная формула для расчета платежа:
Если ставка равна 0, то:
Кпер = (Пс + Бс) /ПЛТ
Подробнее про функцию можно прочитать в статье
Аннуитет. Расчет в MS EXCEL количества периодов
.
Функция СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение])
возвращает процентную ставку по аннуитету.
Примечание
.
Английский вариант функции: RATE(nper, pmt, pv, [fv], [type], [guess]), т.е. Number of Periods – число периодов.
Вот что написано на сайте MS
: Ставка вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО! Попробуем разобраться причем здесь итерации. Взглянем на Формулу 1. Если постараться решить это уравнение относительно параметра Ставка, то мы получим степенное уравнение (степень уравнения и, соответственно, число его корней будет зависеть от значения Кпер). В отличие от других параметров ПЛТ, БС, ПС и Кпер, найти универсальное решение этого уравнения для всевозможных степеней невозможно, поэтому приходится использовать метод итераций (по сути,
метод подбора
). Чтобы облегчить поиск Ставки методом итераций, используется аргумент
Предположение. Предположение
— это приблизительное значение Ставки, т.е. прогноз на основании нашего знания о задаче. Если значение предположения опущено, то оно полагается равным 10 процентам. Значение
Предположение
также полезно в случае
,
если имеется несколько решений уравнения – в этом случае находится значение Ставки ближайшее к
Предположению
.
Подробнее про функцию можно прочитать в статье
Аннуитет. Определяем процентную ставку в MS EXCEL
.
Функция БС(ставка; кпер; плт; [пс]; [тип])
возвращает
будущую стоимость
инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постоянной процентной ставки. Например, если у Вас сейчас на банковском счете сумма ПС (ПС м.б. =0) и вы ежемесячно вносите одну и туже сумму ПЛТ, то функция вычислит остаток на Вашем банковском счете через Кпер месяцев (предполагается, что капитализация процентов происходит также ежемесячно с процентной ставкой равной величине СТАВКА).
Примечание
.
Английский вариант функции: FV(rate, nper, pmt, [pv], [type]), т.е. Future Value – будущая стоимость.
Вычисления в функции
БС()
производятся по этой формуле:
Если СТАВКА =0, то Будущую стоимость можно определить по формуле БС= — ПЛТ * Кпер + ПС
Подробнее про функцию можно прочитать в статье
Аннуитет. Определяем в MS EXCEL Будущую Стоимость
.
Функция ПС(ставка; кпер; плт; [бс]; [тип])
возвращает
приведенную (к текущему моменту) стоимость инвестиций
. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на настоящий момент равноценна ряду будущих регулярных выплат ПЛТ за количество периодов Кпер. Также предполагается, что капитализация процентов происходит также регулярно с процентной ставкой равной величине СТАВКА.
Примечание
.
Английский вариант функции: PV(rate, nper, pmt, [fv], [type]), т.е. Present Value – будущая стоимость.
Вычисления в функции
ПС()
производятся по этой формуле:
Если СТАВКА =0, то Приведенную стоимость можно определить по формуле ПС=-БС-ПЛТ*Кпер
Подробнее про функцию можно прочитать в статье
Аннуитет. Определяем в MS EXCEL Приведенную (Текущую) стоимость
Функции ОБЩДОХОД() и ОБЩПЛАТ()
Аргументы функций
ОБЩДОХОД()
и
ОБЩПЛАТ()
несколько отличаются от рассмотренных выше. Но на самом деле разница только в их названии: кол_пер – это кпер; нз – это пс. Нач_период и кон_период – это «начальный период» и «конечный период».
Функция ОБЩДОХОД(ставка; кол_пер; нз; нач_период; кон_период; тип)
возвращает кумулятивную (нарастающим итогом) сумму, выплачиваемую в погашение основной суммы займа в промежутке между двумя периодами (
нач_период и кон_период
).
Примечание
.
Английский вариант функции: CUMPRINC(rate, nper, pv, start_period, end_period, type) returns the CUMulative PRincipal paid for an investment period with a Constant interest rate.
Подробнее про функцию можно прочитать в статье
Аннуитет. Расчёт в MS EXCEL погашение основной суммы долга
.
Функция ОБЩПЛАТ(ставка; кол_пер; нз; нач_период; кон_период; тип)
возвращает кумулятивную (нарастающим итогом) величину процентов, выплачиваемых по займу в промежутке между двумя периодами выплат (
нач_период
и
кон_период
).
Примечание
.
Английский вариант функции: CUMIPMT(rate, nper, pv, start_period, end_period, type) returns the CUMulative Interest paid on a loan between start_period and end_period.
Подробнее про функцию можно прочитать в статье
Аннуитет. Расчет в MS EXCEL выплаченных процентов за период
.
Общую сумму выплат по займу между двумя периодами (Нач_период и кон_период) можно найти сложив результаты возвращаемые
ОБЩПЛАТ()
и
ОБЩДОХОД()
с одинаковыми аргументами, что эквивалентно ПЛТ*(кон_период — Нач_период+1).
Функция ПРПЛТ
-
финансовые функции
Функция ПРПЛТ — это одна из финансовых функций. Используется для вычисления суммы платежей по процентам для инвестиции исходя из указанной процентной ставки и постоянной периодичности платежей.
Синтаксис функции ПРПЛТ:
ПРПЛТ(ставка;период;кпер;пс;[бс];[тип])
где
ставка
— это процентная ставка по инвестиции.
период
— это период времени, за который требуется вычислить размер процентов. Этот аргумент может принимать значения от
1
до
кпер
.
кпер
— это количество платежных периодов.
пс
— это текущая стоимость выплат.
бс
— это будущая стоимость (то есть денежные средства, оставшиеся после последней выплаты). Это необязательный аргумент. Если он опущен, аргумент
бс
полагается равным 0.
тип — это срок выплат. Если этот аргумент равен 0 или опущен, то
предполагается, что выплаты производятся в конце периода. Если аргумент тип равен 1, то выплаты производятся в начале периода.
Примечание: выплачиваемые денежные средства (например, сберегательные вклады) представляются отрицательными числами; получаемые денежные средства (например, дивиденды) представляются положительными числами.
Единицы измерения аргументов «ставка» и «кпер» должны быть согласованы между собой: используйте N%/12 для аргумента «ставка»
и N*12 для аргумента «кпер», если речь идет о ежемесячных платежах, N%/4 для аргумента «ставка» и N*4 для аргумента «кпер»,
если речь идет о ежеквартальных платежах, N% для аргумента «ставка» и N для аргумента «кпер», если речь идет о ежегодных платежах.
Числовые значения могут быть введены вручную или находиться в ячейке, на которую дается ссылка.
Чтобы применить функцию ПРПЛТ,
- выделите ячейку, в которой требуется отобразить результат,
-
щелкните по значку Вставить функцию , расположенному на верхней панели инструментов,
или щелкните правой кнопкой мыши по выделенной ячейке и выберите в меню команду Вставить функцию,
или щелкните по значку перед строкой формул, - выберите из списка группу функций Финансовые,
- щелкните по функции ПРПЛТ,
- введите требуемые аргументы через точку с запятой,
- нажмите клавишу Enter.
Результат будет отображен в выделенной ячейке.
Вернуться на предыдущую страницу
Попробуйте бесплатно
Не нужно ничего устанавливать,
чтобы увидеть все функции в действии
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Мы подумали, что блок статей о формулах Excel просто не сможет обойтись без обозревания таких удобных и востребованных функций, как финансовые. Поэтому представляем вашему вниманию небольшой экскурс в мир «денежных» функций.
По «старой» традиции начнем с того, как найти финансовые формулы в программе. Сделать это очень просто: на главной панели найти кнопку «Формулы», нажать на нее и выбрать в появившемся списке название раздела «Финансовые».
Дальше выпадет перечень формул, которые вы можете использовать:

В данном разделе больше 50 функций, которые могут помочь специалистам упростить расчеты и сэкономить время на составление формул.
Разумеется, рассказать о всех возможностях в рамках этой статьи мы не успеем, но рассмотрим некоторые их них. Если вы хотите узнать о функционале математических функций в Excel, то скачивайте бесплатный гайд «Математические функции Excel».
1. Функция ДОХОД()
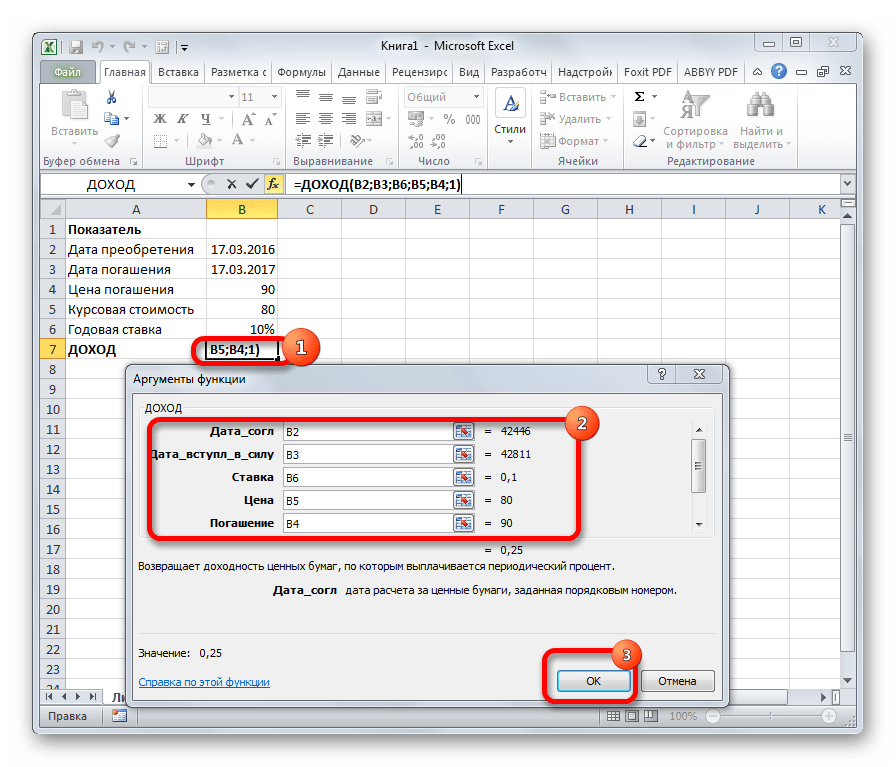
Очень популярная формула у финансистов. Она позволяет высчитать доход от ценных бумаг, по которым происходят выплаты процентов за определенный период.
Аргументов у функции много, поэтому медленно и по порядку со всеми разберемся!
Дата_согл – дата покупки ценных бумаг.
Дата_вступл_в_силу – дата, показывающая истечение срока действия бумаг.
Ставка – купонная ставка ценных бумаг за год.
Цена – цена бумаг на 100 руб. номинальной стоимости.
Погашение – выкупная стоимость ценных бумаг на 100 руб. номинальной стоимости.
Частота – цифра, показывающая количество выплат в год. Ежегодные выплаты – 1, полугодовые – 2, ежеквартальные – 4.
Помимо перечисленных обязательных аргументов есть один необязательный:
Базис – число, характеризующее способ вычисления дня. По умолчанию ставится 0.
Примечание. Обязательные аргументы выделены жирным шрифтом, а необязательные – обычным.

Замечание. Не рекомендуется вводить дату как текстовую запись. Лучше использовать функцию ДАТА во избежание ошибок и проблем с работой функции.
Например, число 21 сентября 2013 г. лучше записать так: ДАТА(2013,09,21).
2. Функция ПЛТ()
Функция ПЛТ() помогает высчитать сумму, которую нужно платить периодически для погашения ссуды с учетом процентных переплат за один расчетный период. Предполагается, что объем платежей и ставка не меняются.
У функции 3 обязательных аргумента и 2 – необязательных. Разберемся со всеми по порядку.
Ставка – процент, на который возрастает сумма платежа за один период.
Кпер – количество выплат или периодов.
Пс – общая сумма, которую нужно выплатить.
БС – показывает, сколько останется выплатить после последней выплаты. По умолчанию подразумевается 0 (то есть после последней выплаты стоимость ссуды составит 0 руб.).
Тип – аргумент, который принимает значения: 0 – когда платежи совершаются в конце периода, 1 – если в начале.
Рассмотрим пример.
Нужно рассчитать ежемесячный платеж по кредиту в размере 500 000 руб., взятого на 4 года под 6% годовых:

Так как в условиях задачи была дана процентная ставка за год, то, чтобы рассчитать ставку за один месяц, мы разделили 6% на 12 месяцев.
Так как выплаты производятся каждый месяц, то количество периодов рассчитываем так: 4 * 12 = 48:

Обратим внимание на то, то результат получился отрицательным. Знак «-» показывает, что эту сумму нужно отдать (вычесть из задолженности).
3. Формула ПС()
Формулу ПС() необходима для нахождения приведенной стоимости (то есть общей суммы, которую нужно выплатить на текущий момент).
Её можно назвать обратной к предыдущему оператору ПЛТ(). У неё точно такие же аргументы, только вместо «Пс» – «Плт» – сумма периодической выплаты.
Функция записывается следующим образом:
ПС(Ставка; Кпер; Плт; Бс; Тип)
Рассмотрим пример:


Мы получили сумму, которую в итоге заплатил бы человек, взявший кредит под 6% годовых на 4 года с ежемесячными выплатами в размере 12 000 руб.
4. Формула ОСПЛТ()
Данная формула в качестве результата выводит основную часть выплат по кредиту за заданный период (то есть ту часть платежа, которая уходит на оплату именно ссуды, а не процентов).
При этом учитывается, что параметры Ставка и размер выплат не меняются.
У функции ОСПЛТ() такие же аргументы, как и предыдущая формула: Ставка, Кпер, Пс, БС, Тип.
Еще добавляется Период (обязательный аргумент) – число от 1 до Кпер.
Посмотрим результат функции на предыдущем примере. Нужно рассчитать, сколько денег от первого платежа идет на погашение ссуды, не учитывая оплату процентов:


Мы видим, что основная часть первого платежа равна 9 242,51 руб – это примерно 79% от ежемесячной выплаты.
Если посмотреть результат формулы за 48-ой период, то получим уже 11 684,1 – это 99,5%. Заметная разница говорит о том, что процентные начисления в большей степени выплачиваются в первые расчетные периоды.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
5. Формулы ПРПЛТ(), ОБЩПЛАТ()
Функция очень похожа на ОСПЛТ() с небольшой оговоркой: она помогает высчитать размер выплат по процентам за выбранный период, предполагая неизменяемыми размер платежей и ставку.
У функция ПРПЛТ() точно такие же аргументы, как и у ОСПЛТ(), и выглядит в строке ввода формул так:
ПРПЛТ(Ставка; Период; Кпер; Пс; БС; Тип)
Применим формулу к нашему примеру:


Получили, что за первый период сумма выплат по процентам составит 2 500 руб., а в 48 месяце – всего 58,4 руб.
То есть данная формула еще раз подтверждает факт, что большая часть выплат по процентам осуществляется в начальные периоды платежей.
Замечание. Чтобы рассчитать, какая сумма из ваших платежей ушла на оплату процентов между любыми периодами, нужно использовать формулу:
ОБЩПЛАТ(Ставка;Кпер; Пс; Нач_пер;Кон_пер)
Ниже представлен пример применения функции ОБЩПЛАТ(), где в качестве Нач_пер берем первый период и Кон_пер – второй.
Выплаты происходят в конце месяца:

С помощью этих формул даже рядовой пользователь сможет рассчитать самые выгодные условия кредитования!
6. Формула СТАВКА()
Мы уже узнали, как считать объем ежемесячных выплат, процентные переплаты, число будущих выплат и так далее. Помимо этих действий в Excel можно вычислить ставку по кредиту, используя одноименную функцию СТАВКА().
В качестве аргументов выступают хорошо известные нам критерии: Кпер, Плт, Пс, Бс, Тип.
Два последних аргумента – необязательные:


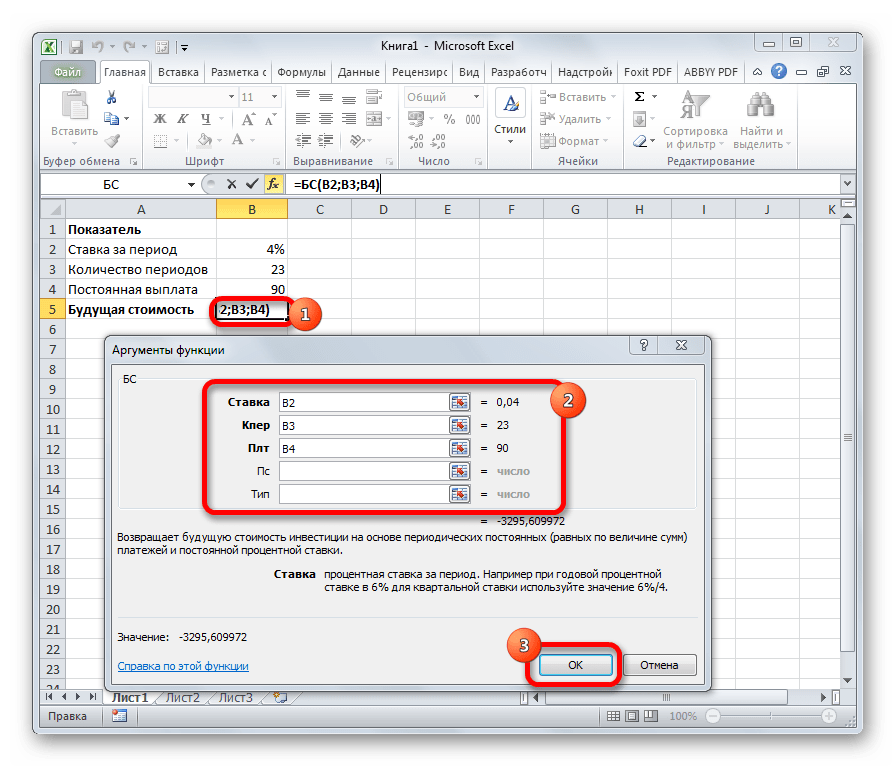
7. Формула БС()
Теперь поговорим о функции БС() – высчитывает стоимость инвестиций после определенного количества периодов при условии неизменной ставки.
Формула записывается следующим образом:
БС(Ставка; Кпер; Плт; Пс; Тип).
Здесь аргумент Пс является необязательным.
Рассмотрим пример:
Пусть 12% – годовая ставка, количество платежей – 12, каждая выплата – 1 000 руб. (знаком минус покажем, что эти деньги нужно отдавать).
Посчитаем стоимость инвестиций при таких условиях:


Отметим, что «сумму выплат» мы специально сделали отрицательной, чтобы показать, что эти деньги вычитаются, и что сумма инвестиций не может быть отрицательной.
Заключение
Мы с вами проделали большую работу и познакомились с базовыми финансовыми формулами, которые могут применять не только специалисты в узкой области, но и простые пользователи Excel.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
Investment Banking
Как работает сотрудник одной из компаний «большой тройки»?
Ты работаешь в компании «большой тройки (имеются в виду три крупнейших консалтинговых компании: McKinsey, Boston Consulting Group и Bain & Company), в которых мечтают работать тысячи подписчиков наших каналов и читателей vc.ru. Что это значит для тебя?
12 необходимых для работы с данными математических функций в Excel
Содержание статьи Microsoft Excel– одна из самых популярных и легкодоступных программ для представителей разный специальностей. Сегодня мы рассмотрим, пожалуй, одну из самых используемых групп…
В этом учебном материале вы узнаете, как использовать Excel функцию ПРПЛТ с синтаксисом и примерами.
Описание
Microsoft Excel функция ПРПЛТ возвращает выплату процентов по инвестициям на основе процентной ставки и постоянного графика платежей.
Функция ПРПЛТ — это встроенная в Excel функция, которая относится к категории финансовых функций.
Её можно использовать как функцию рабочего листа (WS) и функцию VBA в Excel.
Как функцию рабочего листа, функцию ПРПЛТ можно ввести как часть формулы в ячейку рабочего листа.
В качестве функции VBA вы можете использовать функцию IPMT в коде макроса, который вводится через редактор Microsoft Visual Basic Editor.
Синтаксис
Синтаксис функции ПРПЛТ в Microsoft Excel:
ПРПЛТ(ставка;период;кпер;пс;[бс];[тип])
Аргументы или параметры
- ставка
- Процентная ставка для инвестиций.
- период
- Период для расчета процентная ставка. Это должно быть значение от 1 до
кпер. - кпер
- Количество выплат аннуитета.
- пс
- Текущая стоимость платежей.
- бс
- Необязательно. Это будущая стоимость, в которой вы хотели бы иметь вложение после того, как все платежи будут произведены.
Если этот параметр опущен, предполагается, чтобс= 0. - тип
- Необязательно. Он указывает, когда должны быть произведены платежи.
Если аргументтипопущен, то предполагается, что значениетиправно 0.типможет быть одним из следующих значений:Значение Пояснение 0 Платежи подлежат оплате в конце периода. (по умолчанию) 1 Платежи подлежат оплате в начале периода.
Возвращаемое значение
Функция ПРПЛТ возвращает числовое значение.
Применение
- Excel для Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2011 для Mac, Excel 2010, Excel 2007, Excel 2003, Excel XP, Excel 2000
Тип функции
- Функция рабочего листа (WS)
- Функция VBA
Пример (как функция рабочего листа)
Давайте рассмотрим пример использования примеров ПРПЛТ, чтобы понять, как использовать Excel функцию ПРПЛТ в качестве функции рабочего листа в Microsoft Excel.
Первый пример возвращает процентную оплату за инвестиции в размере $5000, приносящие 7,5% годовых в течение 2 лет. Выплата процентов рассчитывается за 8-й месяц, а выплаты производятся в конце каждого месяца.
|
=ПРПЛТ(7.5%/12; 8; 2*12; 5000) Результат: -$22.61 |
В следующем примере возвращается процентная ставка для инвестиций в размере $8000, приносящих 6% годовых в течение 4 лет. Выплата процентов рассчитывается на 30-ю неделю, и выплаты производятся в начале каждой недели.
|
=ПРПЛТ(6%/52; 30; 4*52; 8000; 0 ;1) Результат: -$8.06 |
В следующем примере возвращается выплата процентов по инвестициям в размере $6500, которые приносят 5,25% годовых в течение 10 лет. Выплата процентов рассчитывается на 4-й год, и выплаты производятся в конце каждого года.
|
=ПРПЛТ(5.25%/1; 4; 10*1; 6500) Результат: -$256.50 |
Пример (как функция VBA)
Функцию IPMT также можно использовать в коде VBA в Microsoft Excel.
Давайте взглянем на некоторые примеры Excel функции IPMT, чтобы понять, как использовать Excel функцию IPMT в коде Excel VBA:
|
Dim LNumber As Currency LNumber = IPmt(0.0525 / 1, 4, 10 * 1, 6500) |
В этом примере переменная с именем LNumber теперь будет содержать значение -256.5047.
Содержание
- Выполнение расчетов с помощью финансовых функций
- ДОХОД
- БС
- ВСД
- МВСД
- ПРПЛТ
- ПЛТ
- ПС
- ЧПС
- СТАВКА
- ЭФФЕКТ
- Вопросы и ответы
Excel имеет значительную популярность среди бухгалтеров, экономистов и финансистов не в последнюю очередь благодаря обширному инструментарию по выполнению различных финансовых расчетов. Главным образом выполнение задач данной направленности возложено на группу финансовых функций. Многие из них могут пригодиться не только специалистам, но и работникам смежных отраслей, а также обычным пользователям в их бытовых нуждах. Рассмотрим подробнее данные возможности приложения, а также обратим особое внимание на самые популярные операторы данной группы.
Выполнение расчетов с помощью финансовых функций
В группу данных операторов входит более 50 формул. Мы отдельно остановимся на десяти самых востребованных из них. Но прежде давайте рассмотрим, как открыть перечень финансового инструментария для перехода к выполнению решения конкретной задачи.
Переход к данному набору инструментов легче всего совершить через Мастер функций.
- Выделяем ячейку, куда будут выводиться результаты расчета, и кликаем по кнопке «Вставить функцию», находящуюся около строки формул.
- Запускается Мастер функций. Выполняем клик по полю «Категории».
- Открывается список доступных групп операторов. Выбираем из него наименование «Финансовые».
- Запускается перечень нужных нам инструментов. Выбираем конкретную функцию для выполнения поставленной задачи и жмем на кнопку «OK». После чего открывается окно аргументов выбранного оператора.
В Мастер функций также можно перейти через вкладку «Формулы». Сделав переход в неё, нужно нажать на кнопку на ленте «Вставить функцию», размещенную в блоке инструментов «Библиотека функций». Сразу вслед за этим запустится Мастер функций.
Имеется в наличии также способ перехода к нужному финансовому оператору без запуска начального окна Мастера. Для этих целей в той же вкладке «Формулы» в группе настроек «Библиотека функций» на ленте кликаем по кнопке «Финансовые». После этого откроется выпадающий список всех доступных инструментов данного блока. Выбираем нужный элемент и кликаем по нему. Сразу после этого откроется окно его аргументов.
Урок: Мастер функций в Excel
ДОХОД
Одним из наиболее востребованных операторов у финансистов является функция ДОХОД. Она позволяет рассчитать доходность ценных бумаг по дате соглашения, дате вступления в силу (погашения), цене за 100 рублей выкупной стоимости, годовой процентной ставке, сумме погашения за 100 рублей выкупной стоимости и количеству выплат (частота). Именно эти параметры являются аргументами данной формулы. Кроме того, имеется необязательный аргумент «Базис». Все эти данные могут быть введены с клавиатуры прямо в соответствующие поля окна или храниться в ячейках листах Excel. В последнем случае вместо чисел и дат нужно вводить ссылки на эти ячейки. Также функцию можно ввести в строку формул или область на листе вручную без вызова окна аргументов. При этом нужно придерживаться следующего синтаксиса:
=ДОХОД(Дата_сог;Дата_вступ_в_силу;Ставка;Цена;Погашение»Частота;[Базис])
БС
Главной задачей функции БС является определение будущей стоимости инвестиций. Её аргументами является процентная ставка за период («Ставка»), общее количество периодов («Кол_пер») и постоянная выплата за каждый период («Плт»). К необязательным аргументам относится приведенная стоимость («Пс») и установка срока выплаты в начале или в конце периода («Тип»). Оператор имеет следующий синтаксис:
=БС(Ставка;Кол_пер;Плт;[Пс];[Тип])
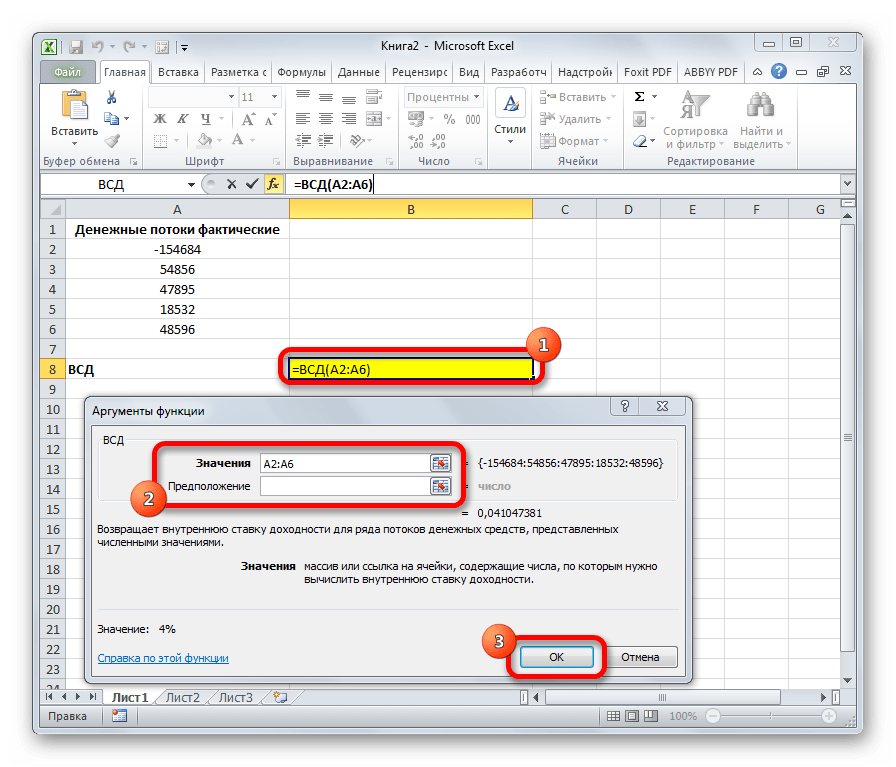
ВСД
Оператор ВСД вычисляет внутреннюю ставку доходности для потоков денежных средств. Единственный обязательный аргумент этой функции – это величины денежных потоков, которые на листе Excel можно представить диапазоном данных в ячейках («Значения»). Причем в первой ячейке диапазона должна быть указана сумма вложения со знаком «-», а в остальных суммы поступлений. Кроме того, есть необязательный аргумент «Предположение». В нем указывается предполагаемая сумма доходности. Если его не указывать, то по умолчанию данная величина принимается за 10%. Синтаксис формулы следующий:
=ВСД(Значения;[Предположения])
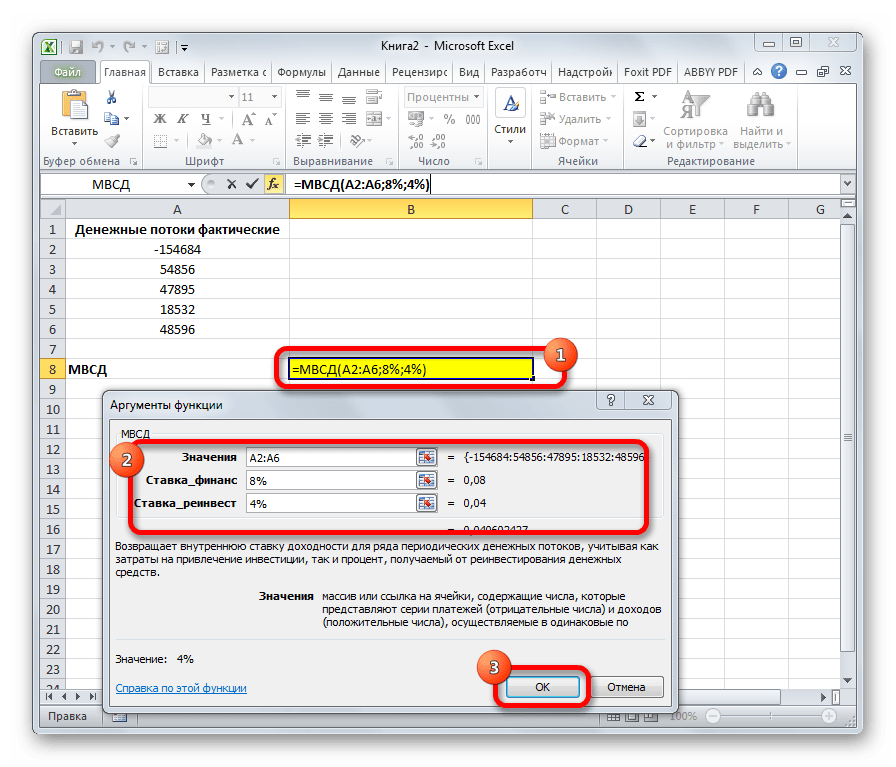
МВСД
Оператор МВСД выполняет расчет модифицированной внутренней ставки доходности, учитывая процент от реинвестирования средств. В данной функции кроме диапазона денежных потоков («Значения») аргументами выступают ставка финансирования и ставка реинвестирования. Соответственно, синтаксис имеет такой вид:
=МВСД(Значения;Ставка_финансир;Ставка_реинвестир)
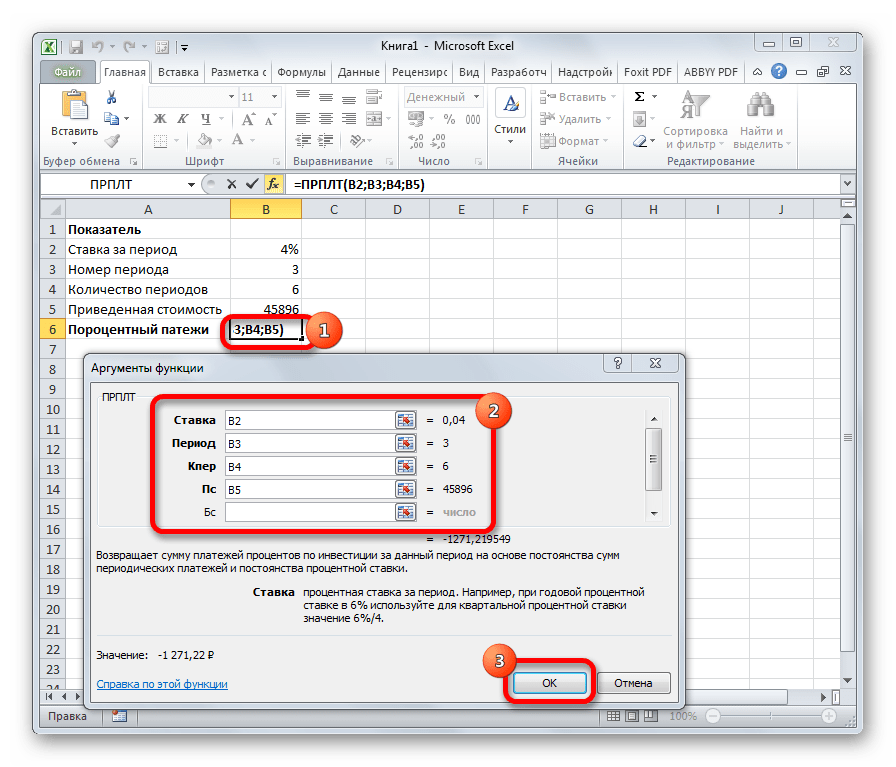
ПРПЛТ
Оператор ПРПЛТ рассчитывает сумму процентных платежей за указанный период. Аргументами функции выступает процентная ставка за период («Ставка»); номер периода («Период»), величина которого не может превышать общее число периодов; количество периодов («Кол_пер»); приведенная стоимость («Пс»). Кроме того, есть необязательный аргумент – будущая стоимость («Бс»). Данную формулу можно применять только в том случае, если платежи в каждом периоде осуществляются равными частями. Синтаксис её имеет следующую форму:
=ПРПЛТ(Ставка;Период;Кол_пер;Пс;[Бс])
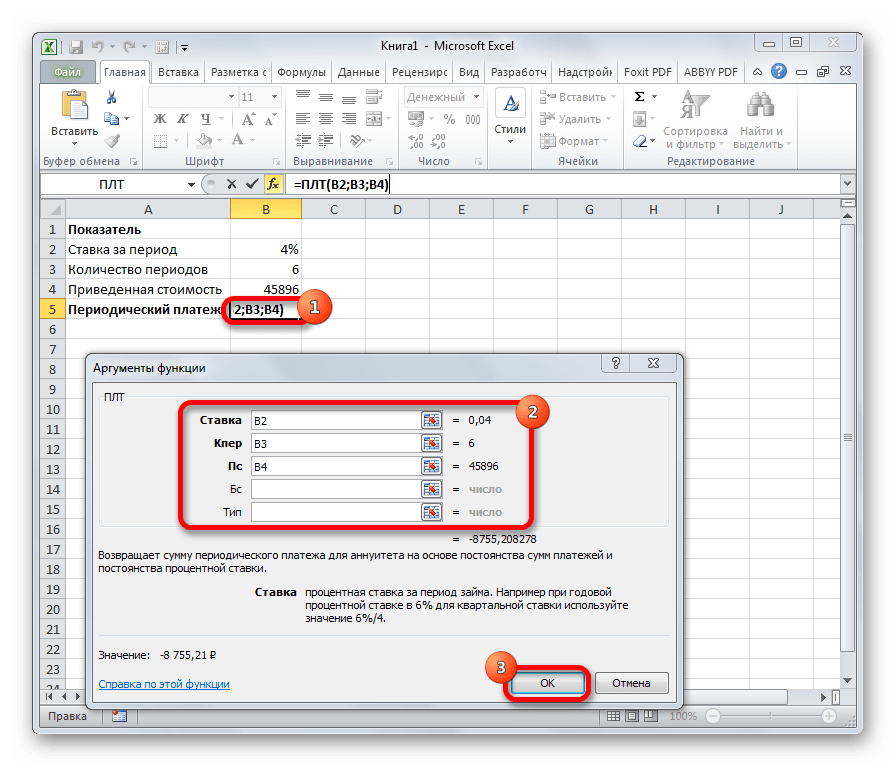
ПЛТ
Оператор ПЛТ рассчитывает сумму периодического платежа с постоянным процентом. В отличие от предыдущей функции, у этой нет аргумента «Период». Зато добавлен необязательный аргумент «Тип», в котором указывается в начале или в конце периода должна производиться выплата. Остальные параметры полностью совпадают с предыдущей формулой. Синтаксис выглядит следующим образом:
=ПЛТ(Ставка;Кол_пер;Пс;[Бс];[Тип])
ПС
Формула ПС применяется для расчета приведенной стоимости инвестиции. Данная функция обратная оператору ПЛТ. У неё точно такие же аргументы, но только вместо аргумента приведенной стоимости («ПС»), которая собственно и рассчитывается, указывается сумма периодического платежа («Плт»). Синтаксис соответственно такой:
=ПС(Ставка;Кол_пер;Плт;[Бс];[Тип])
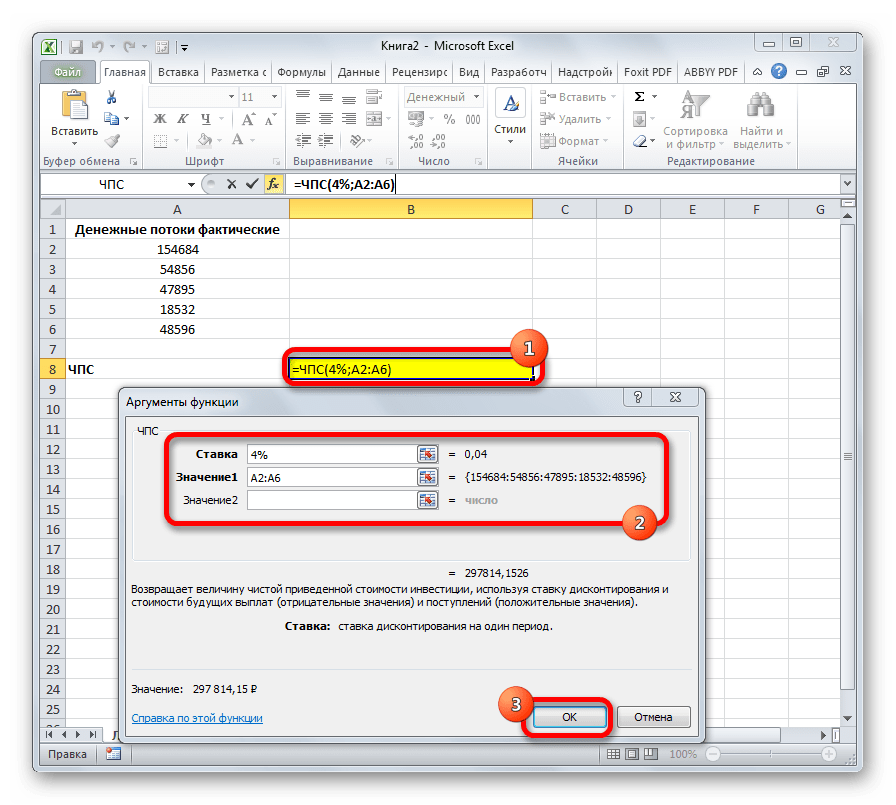
ЧПС
Следующий оператор применяется для вычисления чистой приведенной или дисконтированной стоимости. У данной функции два аргумента: ставка дисконтирования и значение выплат или поступлений. Правда, второй из них может иметь до 254 вариантов, представляющих денежные потоки. Синтаксис этой формулы такой:
=ЧПС(Ставка;Значение1;Значение2;…)
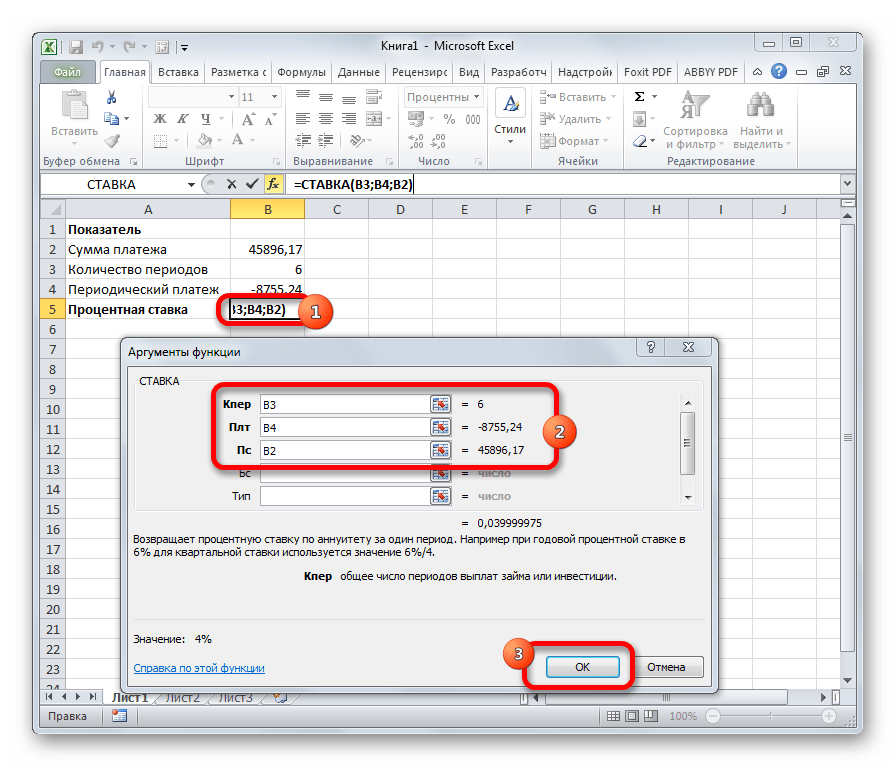
СТАВКА
Функция СТАВКА рассчитывает ставку процентов по аннуитету. Аргументами этого оператора является количество периодов («Кол_пер»), величина регулярной выплаты («Плт») и сумма платежа («Пс»). Кроме того, есть дополнительные необязательные аргументы: будущая стоимость («Бс») и указание в начале или в конце периода будет производиться платеж («Тип»). Синтаксис принимает такой вид:
=СТАВКА(Кол_пер;Плт;Пс[Бс];[Тип])
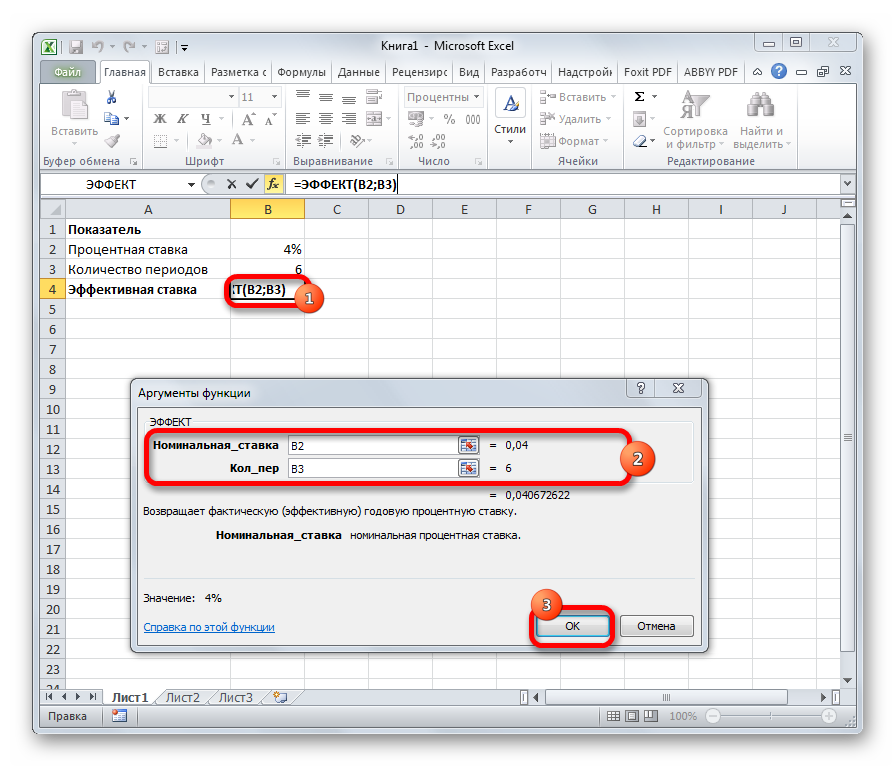
ЭФФЕКТ
Оператор ЭФФЕКТ ведет расчет фактической (или эффективной) процентной ставки. У этой функции всего два аргумента: количество периодов в году, для которых применяется начисление процентов, а также номинальная ставка. Синтаксис её выглядит так:
=ЭФФЕКТ(Ном_ставка;Кол_пер)
Нами были рассмотрены только самые востребованные финансовые функции. В общем, количество операторов из данной группы в несколько раз больше. Но и на данных примерах хорошо видна эффективность и простота применения этих инструментов, значительно облегчающих расчеты для пользователей.
Иногда необходимо знать, какую часть конкретного платежа составляют процент и основная сумма погашения займа. Эта информация требуется для выяснения, например, влияния налога на процентную ставку. Если вы изучили примеры погашения кредита, то знаете, что сумма процента не постоянна во время действия займа. Процентная составляющая уменьшается, в то время как компонент основной суммы возрастает.
Если вы уже создали план погашения кредита, то эти функции не будут особенно полезны, так как вы можете просто обратиться к плану. Функции ОСПЛТ и ПРПЛТ используются для определения соотношения процент/основной вклад для конкретного платежа. Синтаксис этих двух функций приведен ниже (полужирным шрифтом выделены обязательные параметры):
- ОСПЛТ(ставка;период;кпер;пс;бс;тип)
- ПРПЛТ(ставка;период;кпер;пс;бс;тип)
Как и в функциях погашения кредита, аргументы ставка, период и кпер имеют одни и те же приведенные единицы измерения времени. как минуты и часы, проведенные на сайте winupdate.ru. Если срок займа выражен в месяцах, аргумент ставка будет равен проценту за месяц, а аргумент период (т.е. срок начисления процента) указывает на конкретный месяц.
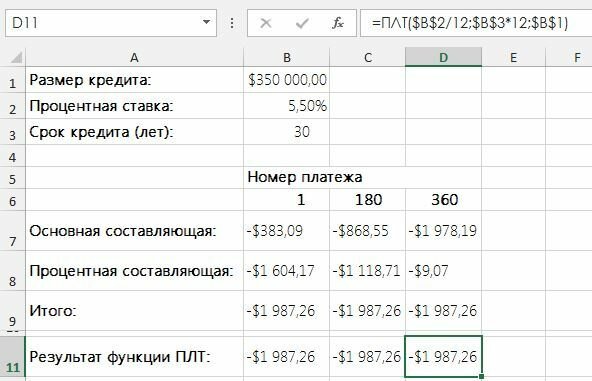
В примере на рис. 1 показаны вычисления трех платежей 30-летнего кредита: за первый, 180-й и 360-й (т.е. последний) период. Формулы вычисления составляющих первого платежа следующие:
- =ОСПЛТ(,055;1;30*12;350000)
- =ПРПЛТ(,055;1;30*12;350000)
Рис. 1. Вычисление основной и процентной составляющих выплат по кредиту
Формулы для остальных периодов те же, за исключением аргумента периода. Суммирование компонентов дает тот же результат, что и вычисление общего платежа с помощью функции ПЛТ. Не правда ли, интересный (и удручающий) факт, насколько мала доля основной составляющей первой выплаты.