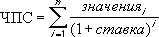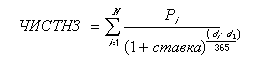Что такое приведенная стоимость в excel

Рассчитаем

Приведенную (к текущему моменту) стоимость

инвестиции при различных способах начисления процента: по формуле простых процентов, сложных процентов, аннуитете и в случае платежей произвольной величины.

Текущая стоимость (Present Value) рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Текущей стоимости, также как и

Будущей стоимости

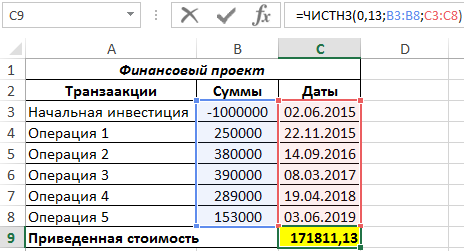
важен, так как, платежи, осуществленные в различные моменты времени, можно сравнивать лишь после приведения их к одному временному моменту. Текущая стоимость получается как результат приведения Будущих доходов и расходов к начальному периоду времени и зависит от того, каким методом начисляются проценты:

простые проценты

,

сложные проценты

или

аннуитет

(в

файле примера

приведено решение задачи для каждого из методов).

Простые проценты

Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты начисленные  за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).

В MS EXCEL для обозначения Приведенной стоимости используется аббревиатура ПС (ПС фигурирует как аргумент в многочисленных финансовых функциях MS EXCEL).

Примечание

. В MS EXCEL нет отдельной функции для расчета Приведенной стоимости по методу Простых процентов. Функция

ПС()

используется для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить

ПС()

рассчитать Приведенную стоимость и по методу простых процентов (см.

файл примера

).

Для определения Приведенной стоимости при начислении простых процентов воспользуемся формулой для расчета

Будущей стоимости

(FV): FV = PV * (1+i*n) где PV — Приведенная стоимость (сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка

за период

начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц); n – количество периодов времени, в течение которых начисляются проценты.

Из этой формулы получим, что:

PV = FV / (1+i*n)

Таким образом, процедура расчета Приведенной стоимости противоположна вычислению Будущей стоимости. Иными словами, с ее помощью мы можем выяснить, какую сумму нам необходимо вложить сегодня для того, чтобы получить определенную сумму в будущем. Например, мы хотим знать, на какую сумму нам сегодня нужно открыть вклад, чтобы накопить через 3 года сумму 100 000р. Пусть в банке действует ставка по вкладам 15% годовых, а процент начисляется только основную сумму вклада (простые проценты). Для того чтобы найти ответ на этот вопрос, нам необходимо рассчитать Приведенную стоимость этой будущей суммы по формуле PV = FV / (1+i*n) = 100000 / (1+0,15*3) = 68 965,52р. Мы получили, что сегодняшняя (текущая, настоящая) сумма 68 965,52р. эквивалентна сумме через 3 года в размере 100 000,00р. (при действующей ставке 15% и начислении по методу простых процентов).

Конечно, метод Приведенной стоимости не учитывает инфляции, рисков банкротства банка и пр. Этот метод эффективно работает для сравнения сумм «при прочих равных условиях». Например, что с помощью него можно ответить на вопрос «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? Чтобы ответить на этот вопрос рассмотрим расчет Приведенной стоимости при начислении сложных процентов.

Сложные проценты

При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования

простых процентов

изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».

Приведенную стоимость PV (или ПС) в этом случае можно рассчитать, используя

формулу наращения для сложных процентов

.

FV = РV*(1+i)^n где FV (или S) – будущая (или наращенная сумма), i — годовая ставка, n — срок ссуды в годах,

т.е. PV = FV / (1+i)^n

При капитализации m раз в год формула Приведенной стоимости выглядит так: PV = FV / (1+i/m)^(n*m) i/m – это ставка за период.

Например, сумма 100 000р. на расчетном счету через 3 года эквивалентна сегодняшней сумме 69 892,49р. при действующей процентной ставке 12% (начисление % ежемесячное; пополнения нет). Результат получен по формуле =100000 / (1+12%/12)^(3*12) или по формуле =ПС(12%/12;3*12;0;-100000).

Отвечая на вопрос из предыдущего раздела «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? нам нужно сравнить две Приведенные стоимости: 69 892,49р. (сложные проценты) и 68 965,52р. (простые проценты). Т.к. Приведенная стоимость, рассчитанная по предложению банка для вклада с простыми процентами, меньше, то это предложение выгоднее (сегодня нужно вложить денег меньше, чтобы через 3 года получить ту же сумму 100 000,00р.)

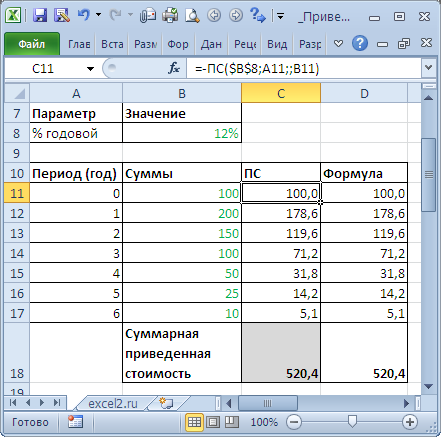
Сложные проценты (несколько сумм)

Определим приведенную стоимость нескольких сумм, которые принадлежат разным периодам. Это можно сделать с помощью функции

ПС()

или альтернативной формулы PV = FV / (1+i)^n

Установив значение ставки дисконтирования равной 0%, получим просто сумму денежных потоков (см.

файл примера

).

Аннуитет

Если, помимо начальной инвестиции, через равные периоды времени производятся дополнительные равновеликие платежи (дополнительные инвестиции), то расчет Приведенной стоимости существенно усложняется (см. статью

Аннуитет. Определяем в MS EXCEL Приведенную (Текущую) стоимость

, где приведен расчет с помощью функции

ПС()

, а также вывод альтернативной формулы).

Здесь разберем другую задачу (см.

файл примера

):

Клиент открыл вклад на срок 1 год под ставку 12% годовых с ежемесячным начислением процентов в конце месяца. Клиент также в конце каждого месяца вносит дополнительные взносы в размере 20000р. Стоимость вклада в конце срока достигла 1000000р. Какова первоначальная сумма вклада?

Решение может быть найдено с помощью функции

ПС()

:

=ПС(12%/12;12;20000;-1000000;0)

= 662 347,68р.

Аргумент

Ставка

указан за период начисления процентов (и, соответственно, дополнительных взносов), т.е. за месяц. Аргумент

Кпер

– это количество периодов, т.е. 12 (месяцев), т.к. клиент открыл вклад на 1 год. Аргумент

Плт

— это 20000р., т.е. величина дополнительных взносов. Аргумент

Бс

— это -1000000р., т.е. будущая стоимость вклада. Знак минус указывает на направление денежных потоков: дополнительные взносы и первоначальная сумма вклада одного знака, т.к. клиент

перечисляет

эти средства банку, а будущую сумму вклада клиент

получит

от банка. Это очень важное замечание касается всех

функций аннуитета

, т.к. в противном случае можно получить некорректный результат. Результат функции

ПС()

– это первоначальная сумма вклада, она не включает Приведенную стоимость всех дополнительных взносов по 20000р. В этом можно убедиться подсчитав Приведенную стоимость дополнительных взносов. Всего дополнительных взносов было 12, общая сумма 20000р.*12=240000р. Понятно, что при действующей ставке 12% их Приведенная стоимость будет меньше

=ПС(12%/12;12;20000)

= -225 101,55р. (с точностью до знака). Т.к. эти 12 платежей, сделанные в разные периоды времени, эквивалентны 225 101,55р. на момент открытия вклада, то их можно прибавить к рассчитанной нами первоначальной сумме вклада 662 347,68р. и подсчитать их общую Будущую стоимость

= БС(12%/12;12;; 225 101,55+662 347,68)

= -1000000,0р., что и требовалось доказать.

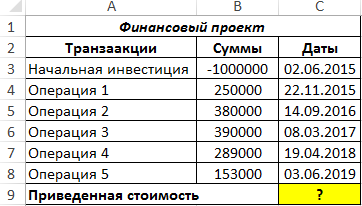
Определение Приведенной стоимости в случае платежей произвольной величины

Если денежные потоки представлены в виде платежей произвольной величины, осуществляемые через равные промежутки времени, то для нахождения Текущей (приведенной) стоимости по методу сложных процентов используется функция

ЧПС()

. Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция

ЧИСТНЗ()

. Об этих расчетах читайте в статье

Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в MS EXCEL

.

Расчет приведенной или дисконтированной стоимости может потребоваться в различных случаях. В том числе с 2022 года выполнять его придется всем бухгалтерам, у кого есть договоры аренды, признаваемой неоперационной, и лизинга. Постараемся рассказать простыми словами, что такое приведенная стоимость и как и зачем ее вычислять.

Дисконтирование простыми словами

Рассмотрим пример

Банк сделал Васе персональное предложение по кредиту на сумму 200 тыс. руб. по ставке 10% годовых, сроком на год. Причем вернуть сумму с процентами можно всю сразу по завершении этого года.

Вася рассказал об этом своему другу Пете. И заметил, что все 200 тыс. руб. ему не нужны, но некоторой суммой он бы воспользовался. Петя предложил Васе взять весь кредит и ссудить часть суммы ему, а он, по прошествии года, вернет ее с такими же процентами.

Вася прикинул свои возможности и понял, что на возврат кредита он сможет набрать через год порядка 120 тыс. руб. Значит, вторую часть – еще 100 тысяч – должен к тому моменту вернуть Петя.

Сколько же нужно сегодня ссудить Пете под 10% годовых, чтобы через год он вернул 100 тысяч?

Считать нужно, исходя из формулы банковского (сложного) процента.

Например, общая сумма к возврату по Васиному кредиту:

S=200*(1+0,10)¹ = 220

Степень 1 в формуле означает, что у кредита только один период выплаты – через год. Если бы срок был 2 года – в степень в формулу следовало бы поставить 2. И так далее.

Чтобы узнать, какая сумма, выданная под 10% годовых, через год превратиться в 220, нужно принять 200 тыс. руб. за Х и решить получившееся уравнение.

Х = 220/(1+0,10)¹ = 200

А теперь Вася по той же методике посчитает, какая сумма превратится в 100 тыс. руб.

100/(1+0,10)¹ = 90,91 тыс. руб.

Вася произвел дисконтирование и получил приведенную стоимость Петиной ссуды к возврату.

А мы запомним формулу дисконтирования:

   К

ПС = ————-

        (1+ r) ^t

ПС – приведенная (дисконтированная) стоимость

К – дисконтируемая сумма

r – процентная ставка

t – период кредитования

Зачем вообще это нужно

Продолжим пример

О том, что у Васи есть свободные средства, узнал Федя. Пришел к Васе и сказал:

— Инвестируй в мой бизнес свободные 100 тысяч и через 2 года я выплачу тебе 120 тысяч. Ты компенсируешь проценты, которые заплатишь банку по всему кредиту.

— Я подумаю, — сказал Вася и снова занялся подсчетами.

Потенциальный доход от вложения в бизнес Феди получится:

S=100*(1+ r)² = 120

Решив уравнение, Вася выяснил, что на таких условиях он выдаст Феде деньги под 9,5% годовых. В то время как сам получит их под 10%. Да и воспользоваться ими сможет только через 2 года.

А вот, если Петя согласится взять еще 100 тысяч и вернуть через 2 года по ставке 10% годовых, то Вася получит:

S=100*(1+ 0,1)² = 121 (побольше, чем от Феди).

В бытовых ситуациях, как у Васи из примера, можно обойтись базовыми формулами и не долгими подсчетами. Но что делать, если обсчитать надо большой и долгосрочный проект? Где много денежных потоков и двигаться они будут на отрезке времени длиннее, чем 1-2 года?

Есть два способа привести все потоки инвестпроекта к общему знаменателю, чтобы можно было сравнить разные проекты:

1. Рассчитать будущую доходность от инвестируемой суммы и сравнить результат по разным проектам. Это будет процесс обратный дисконтированию и называется он компаундинг. (Примерно то, что сделал Вася, оценивая предложение Феди).
2. Взять за основу прогнозные данные по получаемым в результате инвестирования денежным поступлениям и дисконтировать на текущий момент. Если, например, два проекта обещают поступления 1 миллион рублей через 3 года, но в результате приведения вложений оказалось, что в первый надо вложить 900 тысяч, а во второй 850, то второй проект можно рассматривать как более предпочтительный.

Зачем берется банковская ставка

Снова приведем пример

Костя выиграл в лотерею. После уплаты налогов у него остался 1 миллион рублей. Костя решил открыть свой бизнес – небольшое кафе. Арендовал помещение, купил оборудование, нанял персонал, сам за всем следил, практически в своем кафе поселился… Через год получил первую чистую прибыль – 50 тысяч рублей.

В то время как на момент открытия кафе можно было положить деньги в банк на депозит по 6% годовых. И получить по окончании года доход в 60 тысяч рублей, миллион обратно в свое распоряжение и все это не особо напрягаясь и с минимальными рисками.

С этим примером мы вплотную подошли к тому, для кого в идеале делается бухгалтерская отчетность по МСФО. А делается она для потенциальных инвесторов, которые, посмотрев на нее, должны принять решение: вложить свои деньги в эту компанию или проще отнести их в банк на депозит?

То есть инвестор, анализируя состояние дел компании по отчетности, подготовленной по принципам МСФО, оценивает выбор между двумя инвестиционными проектами – с компанией и с банком.

А, поскольку, в бухотчетности мы отражаем то, что есть именно на текущий момент, то для информативного отражения, например, расчетов по аренде и лизингу, мы пользуемся вторым способом, позволяющим сравнить разные проекты – дисконтированием. И из этих же соображений часто подставляем в формулу ставку дисконтирования – величину банковского процента.

Как определить ставку дисконтирования

Отметим, что в случае с долгосрочной арендой или лизингом у сторон сделки будет немного разный подход к оценке.

Арендатор (или лизингополучатель) должен показать, что для него взять объект в аренду или лизинг выгоднее, чем взять кредит и купить такой же объект. (Ну, или не выгоднее, и тогда отражение по приведенной стоимости даст убыток). Поэтому арендатор в качестве ставки для подстановки в формулу дисконтирования берет ставку, по которой он мог бы взять кредит на приобретение аналогичного объекта.

Если у арендатора уже есть подобные кредиты – можно опираться на ставку по ним. Если нет – нужно определять по какой ставке арендатор, на дату получения объекта,  мог бы взять кредит с аналогичным сроком и обеспечением для приобретения примерно такого же.

Важно! В МСФО процесс выбора ставки дисконтирования гораздо более обусловлен и имеет несколько вариантов расчета. Причем выбранный вариант еще надо обосновать аудиторам. Российские ФСБУ, дублируя необходимость применения дисконтирования, пока не настолько усложнены и можно следовать общим предписаниям стандарта и логике.

У арендо- и лизингодателя ситуация больше похожа на ситуацию Кости, получившего миллион. У Кости заключен договор аренды, куплено оборудование и мебель. Как отбить обратно свой миллион, чтобы подумать, куда его дальше лучше вложить?

Продолжим пример

Костя нашел арендатора, который готов арендовать его кафе. Помещение, соответственно, пойдет в субаренду, а оборудование и мебель – в аренду от самого Кости. Договор заключен на 4 года, для упрощения расчетов примем, что арендатор рассчитывается сразу за год по 250 000 рублей. То есть, через 4 года Костя вернет свой миллион.

При этом у Кости уже есть вложения по объекту аренды:

480 000 – аренда (опять же, чтобы не перегружать пример, будем считать, что Костя оплатил всю сумму на 5 лет авансом);

280 000 – затраты на покупку оборудования и мебели;

40 000 – расходы на монтаж и обслуживание оборудования.

Итого можно определить стоимость инвестиционного вложения Кости – 800 тыс. руб.

То есть, следуя все тем же формулам, выполняется равенство:

800*(1+ r)⁴ = 1 000 000

Вот эта ставка r, при которой валовая стоимость инвестиции в аренду (будущий 1 миллион) равна справедливой стоимости вложений арендодателя (800 тысяч) и будет ставкой дисконтирования, которая нужна арендодателю. Зависящей от условий конкретного договора и позволяющей сравнивать его с другими подобными договорами.

Для полноты картины следует учесть, что оборудование и мебель, которые вернутся к Косте по окончании срока аренды, возможно, еще будут иметь какую-то ценность. Например, их можно будет продать как б/у, но еще годные к использованию. Поэтому, на практике, нужно эту ценность, называемую негарантированной ликвидационной стоимостью, оценить и добавить в равенство, приплюсовав к поступлениям от аренды.

Допустим, Костя договорился по окончании срока аренды помещения продать оптом находящееся в нем к тому моменту имущество (мебель и оборудование) за 50 000 рублей.

Тогда равенство для вычисления ставки дисконтирования примет вид

800*(1+ r)⁴ = 1 050 000 (1 000 000 + 50 000)

Отметим также, что на практике решить как уравнение подобное равенство для большого временного отрезка, а потом вычислить дисконтированные величины арендных платежей не так просто. Не всякий и не со всяким калькулятором справится. Поэтому далее мы поговорим о том, какие есть способы упростить расчеты.

Как считать показатели для приведенной стоимости в Excel

Традиционной палочкой-выручалочкой для бухгалтеров в случаях, когда надо дисконтировать, является Excel. В нем имеются функции как для расчета, например, ставки дисконтирования для арендодателя, так и для вычисления самих приведенных сумм.

Функция ЧИСТВНДОХ

С помощью этого средства как раз можно вычислить ставку внутренней доходности для арендодателя (лизингодателя).

Чтобы воспользоваться данным инструментом, нужно внести в лист Excel данные по датам и платежам договора. А в первой строке отразить величину инвестиционных вложений со знаком «-».

Возьмем данные из примера про сдачу в аренду Костиного кафе. Пусть кафе он передал арендатору 01.01.2022, а платит арендатор по истечении года. Для упрощения не станем учитывать негарантированную ликвидационную стоимость.

Далее ставим курсор в свободную ячейку и нажимаем на значок формул. Формула ЧИСТВНДОХ находится в разделе Финансовые. В англоязычном Excel она же называется XIRR.

Вносим данные для расчета, выделяя нужные области. На первое место ставим суммовые значения, на второе – даты

Далее жмем ОК и получаем ставку дисконтирования, с помощью которой арендодателю надо производить вычисления для отражения в отчетности договоров по ФСБУ 25/2018.

Важно!

Переписывать по датам обязательно нужно все платежи по условиям договора. Если у вас, к примеру, договор заключен на 5 лет с платежами ежемесячно, то придется заполнить 60 строк под каждый платеж.

А вот такие параметры как периодичность, аннуитетность – на точность вычислений не влияют. С помощью формулы можно рассчитывать ставку внутренней доходности и в случае, если платежи идут произвольно, и в случае, если их суммы не равные.

Функция ЧИСТНЗ

С помощью этой формулы, зная ставку дисконтирования, можно быстро вычислить чистую стоимость инвестиций в аренду на дату отражения в отчетности. Английская аббревиатура функции XNPV. Эта формула тоже больше подойдет для арендодателя (лизингодателя).

Для вычислений можно завести еще один столбец в табличке, которая получилась из платежей и их дат.

На момент передачи стоимость инвестиций принимаем равной справедливой стоимости вложений в объект аренды или лизинг. Скажем по секрету, что если объект ОС, передаваемый в аренду, учитывался с соблюдением правил приема на баланс, оценки и тестирования на обесценение, то его стоимость при  передаче вполне можно считать справедливой.

А далее начинаем вычислять чистую стоимость инвестиций для каждого последнего дня года.

Важно! Если на дату, на которую определяется приведенная чистая стоимость инвестиций, приходится и дата платежа по договору, то сумму платежа нужно вычесть из значения, получившегося по формуле ЧИСТНЗ.

Выбираем значения, начиная от того, на дату которого считаем и далее до конца договора. Даты выбираем соответственно.

Вычитаем из получившегося по формуле значения сумму платежа по договору, чтобы получить справедливое значение на конец дня 31 декабря.

При наступлении следующей даты поступаем так же. Расчеты рекомендуется сохранить для каждого договора.

Дальнейшие вычисления для арендодателя

Используя полученные значения, арендодатель  может определить величину дохода по процентам для отражения в учете по правилам ФСБУ 25/2018.

И получившаяся расчетная табличка целиком, на всякий случай.

Приведенная стоимость у арендатора

Описанный далее функционал больше подойдет арендаторам. Например, для вычисления приведенной стоимости платежей по договору.

В принципе, определив ставку дисконтирования, с помощью Excel можно производить расчеты и просто через формулы. Напомним, что значок степени в формуле Excel выставляется как комбинация «^число», например, чтобы возвести в 3-ю степень нужно ввести в формулу «^3».

Например, покажем, какая приведенная стоимость получится у платежей по договору у арендатора Костиного кафе. Допустим, что для покупки всего того, что он арендует у Кости, ему бы понадобилось взять кредит в банке по ставке 11,5% годовых.

Помним, что в данном случае дисконтируется каждый платеж. А t принимает значение количества периодов, оставшихся до платежа.

Если t выражено не в годах, а в более мелких периодах: кварталах или месяцах, то для подстановки в формулу дисконтирования нужно вычислить соответствующую периоду ставку исходя из годовой.

r = ((1 + годовая ставка/100)^{1/число периодов в году} Х 100%

Например, при ежеквартальных платежах в степени будет 1/4

r = ((1 + годовая ставка/100)^1/4 Х 100%

Также можно воспользоваться функцией ПС (приведенная стоимость, в английском PV). Помните, что она корректно работает только для единой процентной ставки и фиксированного размера периодического платежа.

Попробуем вычислить приведенную стоимость платежей по договору с помощью функции ПС

Ставка – указываем значение ставки за период платежа. Например, за квартал квартальную, рассчитав ее по предложенной выше формуле.

Кпер – количество периодов, за которые будут производятся платежи до конца договора. Мы вычисляем для всех платежей, поэтому ставим 4.

Плт – фиксированная сумма платежа за период. Если считаем поступления (например, от инвестиций), ставим значение с плюсом. Если считаем выплаты – ставим с минусом.

Бс – будущая стоимость. Желаемый остаток средств  после завершения платежей. В данном случае он не нужен. Если ячейка не заполнена, программа автоматом считает 0.

Тип – характеристика выплаты: в начале периода – 1, в конце периода – 0. Если не заполнено, автоматически считается 0 (конец периода). У нас как раз конец периода, поэтому не заполняем.

Когда все внесено, нажимаем Ок.

Как видим, общая сумма дисконтированных платежей, рассчитанная по периодам, и сумма, полученная с помощью функции ПС одинаковы.

ЧПС – еще одна похожая функция. Удобна тем, что можно выбирать любые значения размера платежа из уже внесенных в таблицу.

Полученный результат совпадет с полученным по ПС и из сложения дисконтированных сумм каждого платежа.

Таблицы дисконтирования

Как вы, должно быть, уже успели заметить, дисконтированная сумма всегда меньше приводимой. И чем больше периодов дисконтирования, тем меньше итоговый результат.

То есть, можно сказать, что величина, которую мы дисконтируем, уменьшается в пропорции к количеству периодов и зависит от значения ставки.

Это давно подметили финансисты и высчитали закономерности для разных значений периодов и ставок. В результате мы можем пользоваться таблицами дисконтирования, которые есть в свободном доступе.

По вертикали в таких таблицах обычно идут периоды, а по горизонтали ставки. Единственный минус – ставки, как правило, выражены только в целых числах.

В остальном же работа с таблицами очень проста. Достаточно выбрать строку с нужным количеством периодов и столбец с нужным процентом, а на их пересечении будет ячейка с коэффициентом, на который надо умножить сумму, чтобы получить ее приведенное значение.

Вспомним Васю, который прикидывал, сколько денег дать Пете на 1 год под 10%, чтобы Петя вернул 100 тыс. руб.

Вася мог бы не проводить расчеты, а взять коэффициент из таблицы и умножить на него 100 000.

Бухгалтерские программы

На текущий момент (осень 2021 года) можно найти отдельно написанные программки, предназначенные для проведения вычислений, которые мы описали выше. Сделали их после появления ФСБУ 25/2018 для тех, кто хотел перейти на стандарт раньше установленного срока. Как вы понимаете, особенной популярностью это ПО не пользовалось. Даже то, которое коннектилось с 1С.

Что же касается 1С, то корректно работающий функционал для расчетов с приведенной стоимостью есть в 1С МСФО (там все настроено на МСФО и даже после внедрения ФСБУ логика расчетов все равно может отличаться) и в 1С Управление предприятием 2 (Бюджетирование лизинговых платежей).

Следует ожидать, что разработчики 1С отреагируют на необходимость ведения учета по ФСБУ 25/2018 и к 01.01.2022 появится необходимый функционал и в Бухгалтерии. Как только он появится – мы сразу же подготовим подробную инструкцию со скриншотами по работе с ним.

---

Автор материала:
Оксана Лим

В этой статье описаны синтаксис формулы и использование функции ЧПС в Microsoft Excel.

Описание

Возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также последовательность будущих выплат (отрицательные значения) и поступлений (положительные значения).

Синтаксис

ЧПС(ставка; значение1; [значение2],…)

Аргументы функции ЧПС описаны ниже.

• Ставка    Обязательный аргумент. Ставка дисконтирования за один период.

• Значение1, значение2,…    Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 254 аргументов, представляющих выплаты и поступления.

  • Аргументы «значение1, значение2, …» должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.

  • Функция ЧПС использует порядок аргументов «значение1, значение2, …» для определения порядка поступлений и платежей. Убедитесь в том, что ваши платежи и поступления введены в правильном порядке.

  • Аргументы, которые являются пустыми ячейками, логическими значениями или текстовыми представлениями чисел, значениями ошибок или текстом, который невозможно преобразовать в числа, игнорируются.

  • Если аргумент является массивом или ссылкой, то учитываются только числа в массиве или ссылке. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.

Замечания

• Считается, что инвестиция, значение которой вычисляет функция ЧПС, начинается за один период до даты денежного взноса «значение1» и заканчивается с последним денежным взносом в списке. Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС, но не включать в список аргументов. Дополнительные сведения см. в приведенных ниже примерах.

• Если n — количество денежных потоков в списке значений, формула для функции ЧПС имеет следующий вид:

  

• ЧПС аналогична функции ПС (текущее значение). Основное различие между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В функции ЧПС денежные взносы могут быть переменной величиной, тогда как в функции ПС они должны быть постоянными на протяжении всего периода инвестиции. Сведения о функциях платежей по ссуде и финансовых функциях см. в описании функции ПС.

• ЧПС связана также с функцией ВСД (внутренняя ставка доходности). ВСД — это ставка, для которой ЧПС равняется нулю: ЧПС(ВСД(…); …) = 0.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
0,1	Годовая ставка дисконтирования
-10 000	Начальная стоимость инвестиции через один год
3000	Доход за первый год
4200	Доход за второй год
6800	Доход за третий год
Формула	Описание	Результат
=ЧПС(A2; A3; A4; A5; A6)	Чистая приведенная стоимость данной инвестиции	1 188,44 ₽

Пример 2

Данные	Описание
0,08	Годовая ставка дисконтирования. Она может представлять показатель инфляции или процентную ставку по конкурирующим инвестициям.
-40 000	Начальная стоимость инвестиции
8000	Доход за первый год
9200	Доход за второй год
10000	Доход за третий год
12000	Доход за четвертый год
14500	Доход за пятый год
Формула	Описание	Результат
=ЧПС(A2; A4:A8)+A3	Чистая приведенная стоимость данной инвестиции	1 922,06 ₽
=ЧПС(A2; A4:A8; -9000)+A3	Чистая приведенная стоимость данной инвестиции с учетом убытка (9000) на шестом году	(3 749,47 ₽)

К началу страницы

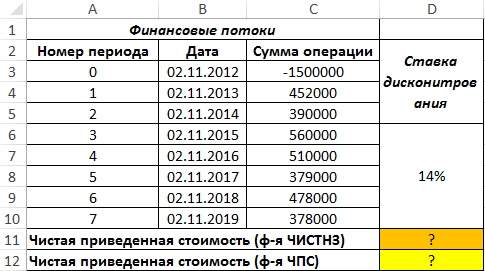
Функция ЧИСТНЗ предназначена для расчета приведенной стоимости на основе данных о имеющихся денежных потоках и датах проведения этих платежей (непериодические платежи), и возвращает соответствующее числовое значение.

Функции ЧИСТНЗ и ЧПС рассчитывают один и тот же экономический параметр, однако вторая может быть использована только для определения приведенной стоимости для ряда периодических финансовых потоков (проводимых через определенные промежутки времени, например, через 365 дней).

Пример расчета приведенной стоимости проекта в Excel

Пример 1. Определить значение чистой приведенной стоимости для проекта, начальные затраты на реализацию которого составили 1 млн у. е. Длительность проекта составила 5 лет, ставка дисконтирования – 13%.

Вид таблицы данных:

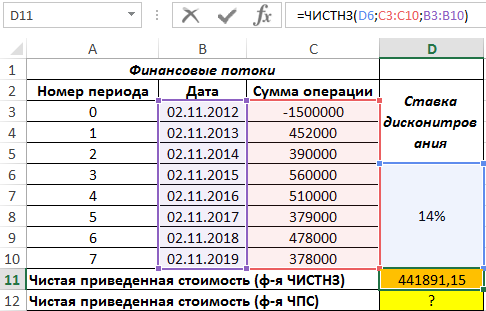
Для определения искомого значения используем функцию:

Описание аргументов:

• 0,13 – числовое значение ставки дисконтирования (13%);
• B3:B8 – диапазон ячеек с числовыми данными о денежных потоках;
• C3:C8 – диапазон ячеек с датами совершения финансовых операций.

Результат:

Это был базовый пример использования функции ЧИСТНЗ в Excel



Расчет приведенной стоимости денежного потока в Excel

Пример 2. Рассчитать значение чистой приведенной стоимости для финансовых потоков, представленных в таблице, с использованием функции ЧПС, сравнить данные, применив функцию ЧИСТНЗ, объяснить расхождения в полученных результатах.

Вид таблицы данных:

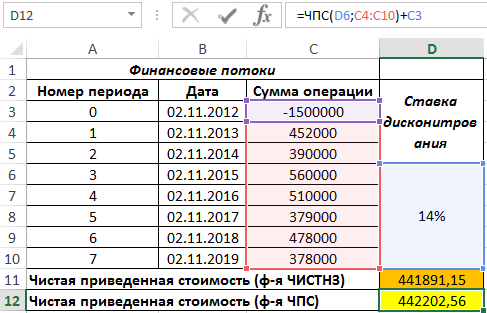
Вначале рассчитаем значение приведенной стоимости с использованием рассматриваемой функции:

В результате получим:

Если бы в табличном редакторе Excel отсутствовала формула ЧИСТНЗ, кроме ручного способа можно было бы рассчитать приведенную стоимость с помощью функции ЧПС следующим образом:

Поскольку функция ЧПС учитывает только платежи, к результатам ее вычислений добавлено значение первоначальных затрат (+C3).

Результат вычислений:

Как видно, результаты немного различны. Это обусловлено тем, что функция ЧИСТНЗ учитывает реальное количество дней в году (в високосном году дней больше на 1). Несмотря на то, что все платежи производились 2-го числа 11 месяца ежегодно, их нельзя считать периодичными, поскольку в списке дат есть високосный год и реальное число дней между 2.11.2016 и 2.11.2017 равен 366 дней. Функция ЧИСТНЗ в подобных расчетах дает более точный результат.

Правила использования функции ЧИСТНЗ в Excel

Функция имеет следующую синтаксическую запись:

=ЧИСТНЗ(ставка;значения;даты)

Описание аргументов:

• ставка – обязательный для заполнения, принимает числовое значение ставки дисконтирования для исследуемого потока финансовых движений.
• значения – обязательный для заполнения, принимает ссылку на диапазон ячеек, содержащих данные о денежных потоках. Фактически, это столбец, в котором приведен график платежей. Указанные значения могут быть как затратами, так и поступлениями. Любая затрата указывается в виде отрицательного числового значения (например, — 10000). Для корректных расчетов хотя бы одно число в графике платежей должно быть отрицательным. Дисконтирование выплат осуществляется на основе года длительностью в 365 дней.
• даты – обязательный для заполнения, принимает ссылку на ячейки с датами, соответствующим моментам совершения финансовых операций (расходы или получение прибыли). Первая дата соответствует началу графика платежей. Последующие должны являться более поздними датами относительно первой. Периодичность дат – необязательное условие. Например, 1-й платеж может быть совершен 1.01.2018, 2-й – 3.07.2018, 3-й – 14.09.2018 и т. д.

Примечания:

1. Для корректных расчетов значения в столбце, передаваемые в качестве аргумента даты, должны быть записаны с использованием функции ДАТА. Если они указаны в виде числовых значений (например, записанная в Excel дата 03.06.2019 соответствует числу 43619), дробные части таких чисел будут усечены (например, 43619,3 будет считаться равным 43619).
2. Любое значение, переданное в качестве любого из трех аргументов, должно являться числом (или данными типа ДАТА – аргумент даты). Если этой условие не соблюдено, функция ЧИСТНЗ вернет код ошибки #ЧИСЛО!
3. Если любая из дат, содержащихся в столбце с датами совершения платежей, является более ранней датой, чем момент осуществления первого платежа, функция ЧИСТНЗ вернет код ошибки #ЧИСЛО!
4. Если число ячеек в столбцах с данными о платежах и соответствующими им датами различны, функция ЧИСТНЗ вернет ошибку #ЧИСЛО!

Для проверки значений, вычисленных с использованием функции ЧИСТНЗ, можно использовать формулу:

Эта формула положена в основу алгоритма расчета рассматриваемой функции. Аргументы:

• d0 – дата начальной выплаты (принимается как нулевая выплата, в отличие от функции ЧПС, где начальная выплата является 1-й, чем в первую очередь и обуславливаются различия в результатах вычислений);
• di – дата, соответствующая последней финансовой операции по графику;
• Pi – сумма платежа последней финансовой операции по графику.

Present value (PV) is the current value of an expected future stream of cash flow. Present value can be calculated relatively quickly using Microsoft Excel.

The formula for calculating PV in Excel is =PV(rate, nper, pmt, [fv], [type]).

Formula for PV in Excel 

Again, the formula for calculating PV in Excel is

=PV(rate, nper, pmt, [fv], [type]).

The inputs for the present value (PV) formula in excel includes the following:

• RATE = Interest rate per period 
• NPER = Number of payment periods
• PMT = Amount paid each period (if omitted—it’s assumed to be 0 and FV must be included)
• [FV] = Future value of the investment (if omitted—it’s assumed to be 0 and PMT must be included)
• [TYPE] = When payments are made (0, or if omitted—assumed to be at the end of the period, or 1—assumed to be at the beginning of the period) 

 Some keys to remember for PV formulas is that any money paid out (outflows) should be a negative number. Money in (inflows) are positive numbers. 

NPV vs. PV Formula in Excel 

While you can calculate PV in Excel, you can also calculate net present value (NPV). Present value is discounted future cash flows. Net present value is the difference between PV of cash flows and PV of cash outflows. 

The big difference between PV and NPV is that NPV takes into account the initial investment. The NPV formula for Excel uses the discount rate and series of cash outflows and inflows. 

Key differences between NPV and PV:

• The PV formula in Excel can only be used with constant cash flows that don’t change. 
• NPV can be used with variable cash flows.  
• PV can be used for regular annuities (payments at the end of the period) and annuities due (payments at the beginning of the period). 
• NPVs can only be used for payments or cash flows at the end of the period.

Example of PV Formula in Excel 

 If you expect to have $50,000 in your banking account 10 years from now, with the interest rate at 5%, you can figure out the amount that would be invested today to achieve this. 

You can label cell A1 in Excel «Years.» Besides that, in cell B1, enter the number of years (in this case 10). Label cell A2 «Interest Rate» and enter 5% in cell B2 (0.05). Now in cell A3, label it “Future Value” and put $50,000 into cell B3.  

The built-in function PV can easily calculate the present value with the given information. Enter «Present Value» into cell A4, and then enter the PV formula in B4, =PV(rate, nper, pmt, [fv], [type], which, in our example, is «=PV(B2,B1,0,B3).» 

Since there are no intervening payments, 0 is used for the «PMT» argument. The present value is calculated to be ($30,695.66), since you would need to put this amount into your account; it is considered to be a cash outflow, and so shows as a negative. If the future value was shown as an outflow, then Excel will show the present value as an inflow.

Special Considerations 

For the PV formula in Excel, if the interest rate and payment amount are based on different periods, adjustments must be made. A popular change that’s needed to make the PV formula in Excel work is changing the annual interest rate to a period rate. That’s done by dividing the annual rate by the number of periods per year. 

For example, if your payment for the PV formula is made monthly then you’ll need to convert your annual interest rate to monthly by dividing by 12. As well, for NPER, which is the number of periods, if you’re collecting an annuity payment monthly for four years, the NPER is 12 times 4, or 48.