Что такое оптимизация данных ms excel

What Is Excel Solver?

Solve your programming woes with this popular Excel add-in

Updated on December 2, 2020

The Excel Solver add-in performs mathematical optimization. This is typically used to fit complex models to data or find iterative solutions to problems. For example, you might want to fit a curve through some data points, using an equation. Solver can find the constants in the equation that give the best fit to the data. Another application is where it is difficult to rearrange a model to make the required output the subject of an equation. 

Where Is Solver in Excel?

The Solver add-in is included with Excel but it isn’t always loaded as part of a default installation. To check if it’s loaded, select the DATA tab and look for the Solver icon in the Analysis section.

If you can’t find Solver under the DATA tab then you will need to load the add-in:

1. Select the FILE tab and then select Options.

2. In the Options dialogue box select Add-Ins from the tabs on the left-hand side.

3. At the bottom of the window, select Excel Add-ins from the Manage dropdown and select Go…

4. Check the check-box next to Solver Add-in and select OK. 

5. The Solver command should now appear on the DATA tab. You’re ready to use Solver.

Using Solver in Excel

Let’s start with a simple example to understand what the Solver does. Imagine that we want to know what radius will give a circle with an area of 50 square units. We know the equation for the area of a circle (A=pi r²). We could, of course, rearrange this equation to give the radius required for a given area, but for the sake of example let’s pretend we don’t know how to do that.

Create a spreadsheet with the radius in B1 and calculate the area in B2 using the equation =pi()*B1^2.

We could manually adjust the value in B1 until B2 shows a value that is close enough to 50. Depending on how accurate we need to be, this might be a practical approach. However, if we need to be very exact, it will take a long time to make the required adjustments. Actually, this is essentially what Solver does. It makes adjustments to values in certain cells, and checks the value in a target cell:

1. Select DATA tab and Solver, to load the Solver Parameters dialogue box

2. Set Objective cell to be the Area, B2. This is the value that will be checked, adjusting other cells until this one reaches the correct value.

3. Select the button for Value of: and set a value of 50. This is the value that B2 should achieve.

4. In the box titled By Changing Variable Cells: enter the cell containing the radius, B1.

5. Leave the other options as they are by default and select Solve. The optimization is carried out, the value of B1 is adjusted until B2 is 50 and the Solver Results dialogue is displayed.

6. Select OK to keep the solution.

This simple example showed how the solver works. In this case, we could have more easily got the solution in other ways. Next we will look at some examples where Solver gives solutions that would be difficult to find any other way.

Fitting a Complex Model Using the Excel Solver Add-In

Excel has a built-in function to perform linear regression, fitting a straight line through a set of data. Many common non-linear functions can be linearized meaning that linear regression can be used to fit functions such as exponentials. For more complex functions the Solver can be used to perform a ‘least squares minimization’. In this example, we will consider fitting an equation of the form ax^b+cx^d to the data shown below.

This involves the following steps:

1. Arrange the dataset with the x values in column A and the y-values in column B.

2. Create the 4 coefficient values (a, b, c, and d) somewhere on the spreadsheet, these can be given arbitrary starting values.

3. Create a column of fitted Y values, using an equation of form ax^b+cx^d which references the coefficients created in step 2 and the x values in column A. Note that in order to copy the formula down the column, the references to the coefficients must be absolute while the references to x values must be relative.

4. Although not essential, you can get a visual indication of how good a fit the equation is by plotting both y columns against the x values on a single XY scatter chart. It makes sense to use markers for the original data points, since these are discrete values with noise, and to use a line for the fitted equation.

5. Next, we need a way of quantifying the difference between the data and our fitted equation. The standard way to do this is to calculate the sum of the squared differences. In a third column, for each row, the original data value for Y is subtracted from the fitted equation value, and the result is squared. So, in D2, the value is given by =(C2-B2)^2. The sum of all these squared values is then calculated. Since the values are squared they can only be positive.

6. You are now ready to perform the optimization using Solver. There are four coefficients that need to be adjusted (a, b, c and d). You also have a single objective value to minimize, the sum of the squared differences. Launch the solver, as above, and set the solver parameters to reference these values, as shown below.

7. Uncheck the option to Make Unconstrained Variables Non-Negative, this would force all coefficients to take positive values.

8. Select Solve and review the results. The chart will update giving a good indication of the goodness of fit. If the solver doesn’t produce a good fit on the first attempt you could try running it again. If the fit has improved, try resolving from the current values. Otherwise, you could try manually improving the fit before resolving.

9. Once a good fit has been obtained you can exit the solver.

Solving a Model Iteratively

Sometimes there is a relatively simple equation which gives an output in terms of some input. However, when we try to invert the problem it is not possible to find a simple solution. For example, the power consumed by a vehicle is approximately given by P = av + bv^3 where v is the velocity, a is a coefficient for the rolling resistance and b is a coefficient for aerodynamic drag. Although this is quite a simple equation, it is not easy to rearrange to give an equation of the velocity the vehicle will reach for a given power input. We can, however, use Solver to iteratively find this velocity. For example, find the velocity attained with a power input of 740 W.

1. Set up a simple spreadsheet with the velocity, the coefficients a and b, and the power calculated from them.

2. Launch the Solver and enter the power, B5, as the objective. Set an objective value of 740 and select the velocity, B2, as the variable cells to change. Select solve to start the solution.

3. The solver adjusts the value of the velocity until the power is very close to 740, providing the velocity we require.

4. Solving models in this way can often be faster and less error-prone than inverting complex models.

Understanding the different options available in the solver can be quite difficult. If you’re having difficulty obtaining a sensible solution then it’s often useful to apply boundary conditions to the changeable cells. These are limiting values beyond which they should not be adjusted. For example, in the previous example, the velocity should not be less than zero and it would also be possible to set an upper bound. This would be a speed you’re pretty sure the vehicle cannot go faster than. If you are able to set bounds for the changeable variable cells, then it also makes other more advanced options work better, such as multistart. This will run a number of different solutions, starting at different initial values for variables.

Choosing the Solving Method can also be difficult. Simplex LP is only suitable for linear models, if the problem isn’t linear it will fail with a message that this condition was not met. The other two methods are both suited to non-linear methods. GRG Nonlinear is the fastest but it’s solution can be highly dependent on the initial starting conditions. It does have the flexibility that it doesn’t require variables to have bounds set. The Evolutionary solver is often the most reliable but it requires all variables to have both upper and lower bounds, which may be difficult to work out in advance.

The Excel Solver add-in is a very powerful tool which can be applied to many practical problems. To fully access the power of Excel, try combining Solver with Excel macros.

Thanks for letting us know!

Get the Latest Tech News Delivered Every Day

Subscribe

В данной статье рассматривается расчет инструмента Excel «Поиск решений». Освоение работы с надстройкой «Поиск решений» даст преимущество в решении многих экономических задач: минимизация расходов при формировании состава сырья и штатного расписания, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы.

Зачастую экономисты в своей практике встречаются с вопросами оптимизации расходов.

Рассмотрим пример оптимизации транспортных расходов с помощью инструмента Excel «Поиск решений».

Пример 1

На предприятии X осуществляются транспортные перевозки с помощью четырех компаний до пяти населенных пунктов. Руководство компании решило распределить все количество перевозок между поставщиками транспортных услуг (транспортными компаниями) в определенной пропорции, выраженной в процентном соотношении — удельный вес в общем количестве перевозок. Известны также тарифы транспортных компаний за одну ездку и количество плановых перевозок до каждого населенного пункта в планируемом периоде .

Необходимо оптимально распределить ездки в населенные пункты между транспортными компаниями таким образом, чтобы транспортные расходы были минимальными.

Для успешного решения этой задачи необходимо выбрать минимизируемую ячейку, определить ограничения, а также правильно сформировать таблицы с исходными и расчетными данными (рис. 1). 

 

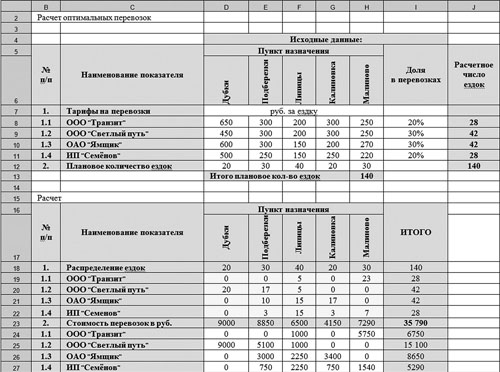
 Рис. 1. Расчет оптимальных перевозок

На рис. 1 расположены две таблицы: с исходными данными и расчетными данными. В ячейках D8:H11 расположены тарифы за 1 ездку в разрезе транспортных компаний до пунктов назначения, в ячейках D12:H12 — плановое количество ездок за период до пунктов назначения, в ячейках I8:I11 — удельный вес перевозок каждой транспортной компании в общем количестве планируемых перевозок за период. Эти ячейки для удобства не раскрашены. В ячейках J8:J12 и Н13 рассчитано число ездок по каждой транспортной компании и в целом за период. Формулы в этих ячейках выглядят следующим образом:

Ячейка Н13: =СУММ(D12:H12),

Ячейка J8: =I8*$H$13.

Данную формулу из ячейки J8 протаскиваем (копируем) в ячейки J9, J10, J11.

Ячейка J12: =СУММ(J8:J11).

Следующая таблица на листе посвящена расчету и называется «Расчет». Ячейки D19:Н22 предназначены для распределения количества ездок до пунктов назначения между транспортными компаниями. На рис. 1 в ячейках дано такое распределение, заполненное вручную. В ячейках D23:I27 рассчитаны суммы расходов на транспортные перевозки в разрезе транспортных компаний, оказывающих транспортные услуги, и пунктов назначений, а также итоги.

Приведем формулы, представленные в этих ячейках.

Значения в ячейках D24:Н27 получены перемножением количества ездок (ячейки D19:Н22) на тарифы (ячейки D8:Н12). В ячейку D24 запишем формулу:

=D19*D8.

Протащим (скопируем) формулу в ячейки D25:D27 и E24:Н27.

В ячейках D23:I23 формируются итоговые суммы транспортных услуг в разрезе пунктов назначения. Запишем в ячейку D23 формулу:

=СУММ(D24:D27).

Протащим (скопируем) эту формулу в ячейки Е23:I23.

В ячейках I24:I27 формируются итоговые суммы транспортных услуг в разрезе компаний, оказывающих эти услуги. Запишем в ячейку I24 формулу:

=СУММ(D24:H24).

Протащим (скопируем) ее в ячейки I25:I27.

Таким образом, стоимость транспортных расходов по компании в целом формируется в ячейке I23. В первоначальном расчете, представленном на рис. 1, данная сумма равна 35 790 руб.

Скопируем данный лист в эту же книгу. Далее необходимо приступить непосредственно к оптимизации. Задача — подобрать в ячейках D19:Н22 такие значения, чтобы в ячейке I23 была рассчитана минимальная сумма расходов на транспорт. Для этого воспользуемся инструментом «Поиск решений».

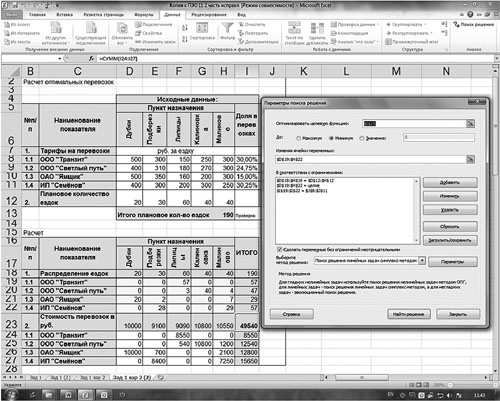
Для начала надо выбрать оптимизируемую ячейку (I23). Затем вызовем диалоговое окно «Поиск решений», представленное на рис. 2.

Это важно. Надстройку «Поиск решений» не всегда можно обнаружить в меню рабочего стола компьютера, так как она может быть не подключена. Для ее подключения необходимо выполнить ряд действий, которые аналогичны во всех версиях MS Office: «Сервис — Надстройки — Поиск решений (установить флажок)». Теперь данный инструмент можно будет найти на панели инструментов рабочего стола.

 

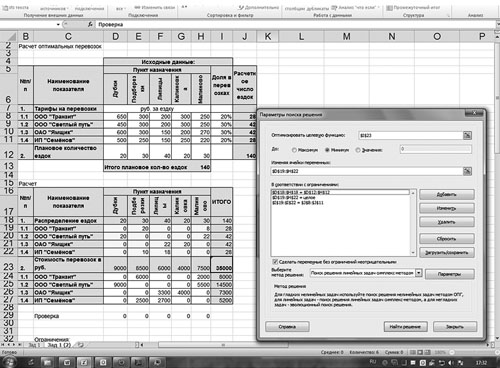
Рис. 2. Использование надстройки «Поиск решений»

В строке «Оптимизировать целевую функцию» будет стоять адрес оптимизируемой ячейки, в данном случае — $I$23. Выберем цель, поставив флажок «Минимум». В строке «Изменяя ячейки переменных» помещаются адреса ячеек, которые необходимо будет подобрать для достижения желаемого результата ($D$19:$Н$22).

В поле запишем ограничения в соответствии с ограничениями. Для этого воспользуемся кнопкой «Добавить», которая откроет окно «Добавить ограничения». Введем одно из ограничений:

$D$19:$H$22 = целое,

$D$12:$H$12 = $D$18:$H$18,

$J$8:$J$11 = $I$19:$I22.

Чтобы добавить следующее ограничение, в этом же окне нажмите на кнопку «Добавить». Результатом этого действия будет добавление текущего ограничения в список ограничений, а поля окна «Добавить ограничения» будут очищены для ввода следующего ограничения. После того как введено последнее из ограничений, необходимо нажать на кнопку «ОК».

Порядок ввода ограничений не имеет значения. Главное — не забыть ни одно из ограничений.

В данном примере все ограничения представлены в виде равенств. Но существуют задачи, в которых требуются ввести ограничения в виде неравенств. Например, в транспортных компаниях объем перевозимого груза не может превышать грузоподъемности автомобиля (или время работы автотранспортного средства не может превышать количества часов в сутки за вычетом нормативных простоев).

Очень важно правильно сформулировать ограничения. Для того чтобы не забыть ни одно из ограничений, необходимо правильно поставить задачу и определить ее цели. Не бывает мелочей в постановке задачи. В задаче о поставке деталей необходимо учесть, что количество деталей на складе на начало периода плюс количество поступивших за планируемый период деталей должно равняться сумме их остатка на складе на конец периода плюс количество отгруженных деталей за планируемый период. Или, например, количество деталей на начало планируемого периода должно равняться количеству деталей на конец периода, предшествующему планируемому.

Необходимо также помнить о том, что некоторые показатели могут быть только положительными значениями (например, сумма поступления от покупателя на расчетный счет поставщик). В данном случае в ограничениях целесообразно указать, что эта величина не может быть отрицательной, иначе надстройка «Поиск решений», вполне возможно, предложит в качестве решения отрицательное число.

Далее следует выбрать метод решения. Для этого необходимо определить, является модель линейной или нелинейной. Напомним, что линейной моделью является такая модель, связи в которой между данными для расчета и результирующим показателем можно описать линейными функциями. Линейная функция имеет следующий вид:

F(x) = a1 × x1 + а2 × x2 + … + аn × xn,

где a1, а2, …, аn — константы;

x1, x2, …, xn — переменные.

Данная модель является линейной.

Примером нелинейной модели является оптимизация перевозок с целью минимизации расходов, когда тарифы на перевозки распределены по интервалам:

• от 0 до 10 км — стоимость перевозки 200 руб.;
• от 11 до 20 км — стоимость перевозки 250 руб.;
• от 21 до 50 км — стоимость перевозки 500 руб. и т. д.

Вернемся к диалоговому окну «Параметры поиска решений». Далее нажимаем кнопку «Найти решение», в результате чего появится окно с результатом поиска решения. Так как нам необходимо сохранить найденный результат, то ставим флажок «Сохранить найденное решение», в результате чего на нашем листе сохранится найденное решение. Нажмем кнопку «ОК».

В ячейках $D$19:$Н$22 появляются подобранные системой значения, при которых в ячейке I23 формируется минимальное значение стоимости транспортных услуг — 35 000 руб.

В данном случае отклонения от подобранного нами вручную результата составляют лишь 2,2 %, или 790 руб., но это означает лишь то, что мы вручную удачно подобрали решение.

На рис. 3 представлены полученные при оптимизации данные.

Рис. 3. Результаты оптимизации

Для того чтобы использовать ссылки на ячейки в составе сценария, необходимо сохранить этот сценарий, нажав на кнопку «Сохранить сценарий» в окне «Результат поиска решения», введя имя сценария и нажав кнопку «ОК». При этом исходные данные сохраняются.

Таким образом, предоставлена возможность сохранить все варианты решений при изменении исходных данных. Затем можно создавать отчеты, по которым можно сравнивать влияние изменений исходных данных и ограничений на результат решения.

Существует одна важная деталь: при расчетах количества ездок лучше всего в ячейках J8:J11 использовать функцию округления, чтобы значения были целыми числами.

По этому случаю рассмотрим пример с другими исходными данными.

Пример 2

В ячейках J8:J11 запишем формулу, позволяющую округлить вычисляемые значения до целого числа, которая имеет вид:

Ячейка J8: =ОКРУГЛ(I8*$H$13;0).

Протащим (скопируем) эту формулу в ячейки J9:J11.

Как видим (рис. 4) плановое количество ездок в ячейке Н13 отличается от суммы в ячейках J8:J11, записанной в ячейке J12: значение в ячейке J12, полученное в результате суммирования округленных результатов расчетов числа ездок в ячейках J8:J11, не равно значению в ячейке Н13, полученному суммированием планового числа ездок до пунктов назначения. Это издержки примененной функции округления. Для того чтобы избежать данной ошибки, проделаем следующую процедуру. Для контроля и удобства вычислений введем проверочную ячейку J13. Формула в этой ячейке будет представлять собой разницу полученных значений в ячейках J12 и H13. Ячейка понадобится нам для коррекции вычислений.

 

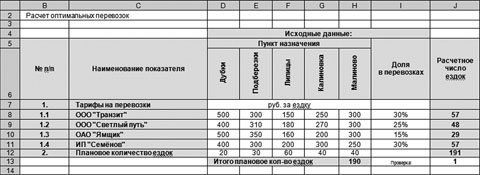
Рис. 4. Пример с функцией округления расчетного числа ездок до целого числа

Используем для коррекции инструмент «Подбор параметра». Процедура подбора иллюстрируется на рис. 5.

 

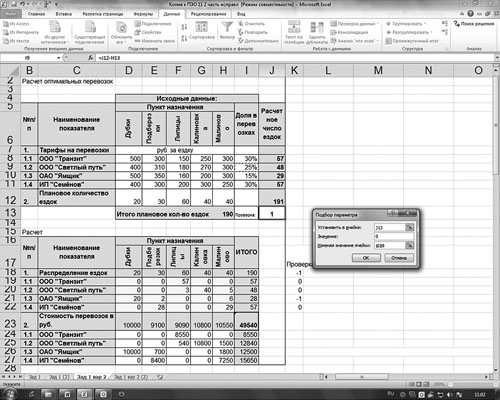
Рис. 5. Использование инструмента «Подбор параметра»

Здесь необходимо применить следующую схему: подобрать в ячейке J13 значение равное 0, изменяя значение в ячейке I9 (доля в перевозках). Предварительно в ячейку I11 целесообразно ввести следующую формулу:

=100 % – I8 – I9 – I10.

Тогда при изменении значения в ячейке I9 в результате применения инструмента «Подбор параметра» автоматически изменится и значение в ячейке I11.

Так как в ячейках I8:I11 применено округление до целого значения, изменения в ячейках I9 и I11 на 0,25 % не обнаруживаются. Эти изменения будут видны, если мы добавим знаки после запятой.

Результат применения инструмента «Подбор параметра» приведен на рис. 6 (на с. …).

Необходимо проделать процедуры, что и в предыдущем примере (см. рис. 1, 2, 3). В ячейках D19:H22 распределим количество ездок для каждой транспортной компании до каждого пункта назначения, используя следующие ограничения:

D19:H22 = целое,

D12:H12 = D18:H18,

J8:J11 = I19:I22.

Сумма транспортных расходов в ячейке I23 на рис. 6 рассчиталась равной 49 540 руб., а наша задача — минимизировать ее.

 

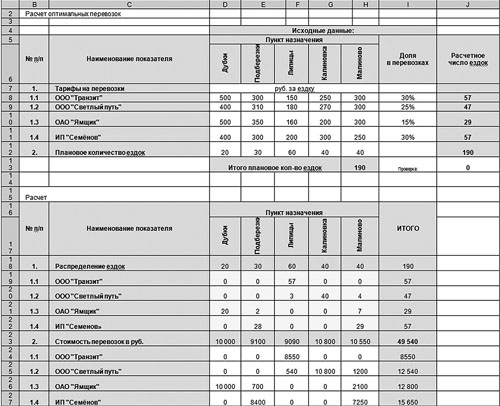
Рис. 6. Скорректированный вариант

На рис. 7 представлена демонстрация использования инструмента «Поиск решений» для оптимизации результата.

 

Рис. 7. Минимизация значения в ячейке I23 с помощью надстройки «Поиск решения»

На рис. 8 в ячейках D19:Н22 представлены данные, полученные в ходе оптимизации с помощью инструмента «Поиск решений». В результате минимизации в ячейке I23 получено значение 44 990 руб. Отклонения от достигнутого при первоначальном распределении результата составило 9 %, или 4550 руб.

Возможно, имеет право на существование такой вопрос: «Для чего нужна табличная часть со стоимостями перевозок в разрезе транспортных компаний и пунктов назначений?». Ведь можно было бы просто в итоговую ячейку I23 ввести формулу:

=СУММПРОИЗВ(D8:D11;D19:D22)+СУММПРОИЗВ(E8:E11;E19:E22)+СУММПРОИЗВ(F8:F11;F19:F22)+СУММПРОИЗВ(G8:G11;G19:G22)+СУММПРОИЗВ(H8:H11;H19:H22).

Следует помнить следующее:

• строк и столбцов может быть достаточно большое количество. Это значит, что написание самой формулы в ячейках будет слишком трудоемкой задачей;
• потеряется возможность анализа данных по компаниям и пунктам назначения. Значит, целесообразнее использовать вспомогательную таблицу (в нашем примере это ячейки B23:I27), которая содержала бы множество простых формул. Эти формулы записываются всего в два мгновения: запись в одной из ячеек и копирование или протаскивание в остальные ячейки. Такая таблица несет в себе полезную для анализа информацию о стоимости транспортных услуг в разрезе перевозчиков и пунктов назначения.

 

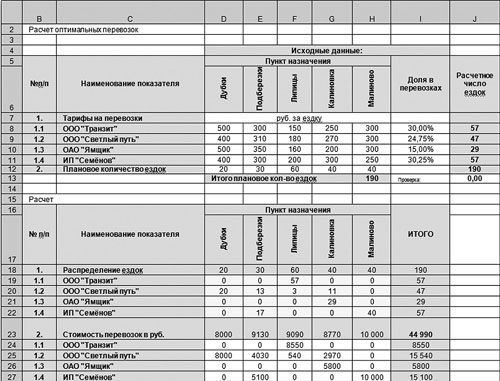
Рис. 8. Результат оптимизации примера с округлением

Заключение

В данной статье рассмотрена простейшая задача, цель статьи — побудить экономистов использовать в расчетах инструмент Excel «Поиск решений», который удобен и прост в применении. Освоив и поняв данный инструмент, можно будет переходить к более сложным задачам.

Освоение работы с надстройкой «Поиск решений» даст преимущество в решении многих экономических задач: минимизация расходов при формировании состава сырья (например, на текстильных предприятиях), оптимизация раскроя (например, на швейных производствах), минимизация расходов при формировании штатного расписания, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы и др.

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.



Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Microsoft
Excel – это программа управления электронными
таблицами, которая используется для
вычислений, организации и анализа
деловых данных.

Оптимизация
— модификация системы для улучшения
её эффективности.

Оптимизационные
модели применяются в экономической и
технической сфере. Их цель – подобрать
сбалансированное решение, оптимальное
в конкретных условиях (количество продаж
для получения определенной выручки,
лучшее меню, число рейсов и т.п.).

В
Excel для решения задач оптимизации
используются следующие команды:

Подбор
параметров («Данные» — «Работа с данными»
— «Анализ «что-если»» —

«Подбор
параметра») – находит значения, которые
обеспечат нужный результат.

Поиск
решения (надстройка Microsoft Excel; «Данные»
— «Анализ») – рассчитывает оптимальную
величину, учитывая переменные и
ограничения.

Диспетчер
сценариев («Данные» — «Работа с данными»
— «Анализ «что-если»» — «Диспетчер
сценариев») – анализирует несколько
вариантов исходных значений, создает
и оценивает наборы сценариев.

Для
решения простейших задач применяется
команда «Подбор параметра». Самых
сложных – «Диспетчер сценариев».

Итоговые
вычисления предполагают получение
числовых характеристик, описывающих
определенный набор данных в целом.
Например, возможно вычисление суммы
значений, входящих в набор, среднего
значения и других статистических
характеристик, количества или доли
элементов набора, удовлетворяющих
определенных условиям. Проведение
итоговых вычислений в программе Excel
выполняется при помощи встроенных
функций.

Встроенная
функция – это специальные тематические
формулы, дающие возможность быстро и
качественно выполнить любое вычисление.

Сама
функция состоит из двух компонентов:
имя функции (например, СУММ, ЕСЛИ, ИЛИ),
которое указывает на то, что делает
данная операция; аргумент функции — он
заключен в скобках и указывает, в каком
диапазоне действует формула, и какие
действия будут выполнены.

С
помощью аппроксимаций данных можно
производить приблизительные подсчеты
и вычислять планируемые показатели,
путем замены исходных объектов на более
простые. Но данный метод можно использовать
не только для прогнозирования, но и для
исследования уже имеющихся результатов.

Главный
инструмент, с помощью которого проводится
сглаживания в Excel – это построение линии
тренда. Суть состоит в том, что на основе
уже имеющихся показателей достраивается
график функции на будущие периоды.
Основное предназначение линии тренда,
как не трудно догадаться, это составление
прогнозов или выявление общей тенденции.

Но
она может быть построена с применением
одного из пяти видов аппроксимации:
линейной; экспоненциальной; логарифмической;
полиномиальной; степенной.

16. Информационные системы, понятие, примеры. Основные функции и назначения информационных систем. Базы данных, понятие. Базы данных в структуре информационных систем.

Информационная
система
– это взаимосвязанная совокупность
средств, методов и персонала, используемых
для хранения, обработки и выдачи
информации в интересах достижения
поставленной цели.

Главная
цель
информационной системы – это производство
и распространение профессиональной
информации.

Информационные
системы обеспечивают
сбор, хранение, обработку, поиск, выдачу
информации, необходимой в процессе
принятия решений задач из любой области.

Информационные
системы помогают
анализировать проблемы и создавать
новые продукты, а так же предназначены
для долговременного хранения, обеспечения
эффективного поиска и передачи информации
по соответствующим запросам. В этом
смысле их обычно называют системами
обработки и хранения информации.

Информационная
система является
системой
информационного обслуживания пользователей
и выполняет технологические функции
по накоплению, хранению, передаче и
обработке информации. Она формируется
и функционирует в регламенте, определённом
методами и структурой, принятыми в
конкретной предметной области и даже
на конкретном объекте, реализуя цели и
задачи, стоящие перед ним.

Свойства
информационных систем:

1)
любая информационная система может
быть подвергнута анализу, построена и
управляема на основе общих принципов
построения систем;

2)
информационная система является
динамичной и развивающейся;

3)
при построении информационной системы
необходимо использовать системный
подход;

4)
выходной продукцией информационной
системы является информация, на основе
которой принимаются решения;

5)
информационную систему следует
воспринимать как человеко-машинную
систему обработки информации.

Классификация
информационных систем.

По
характеру представления и логической
организации хранимой информации

Фактографические
информационные системы накапливают и
хранят данные в виде множества экземпляров
одного или нескольких типов структурных
элементов (информационных объектов).
Каждый из таких экземпляров или некоторая
их совокупность отражают сведения по
какому-либо факту, событию отдельно от
всех прочих сведений и фактов.

В
документальных
(документированных) информационных
системах единичным элементом информации
является нерасчлененный на более мелкие
элементы документ и информация при
вводе (входной документ), как правило,
не структурируется, или структурируется
в ограниченном виде. Для вводимого
документа могут устанавливаться
некоторые формализованные позиции
(дата изготовления, исполнитель,
тематика).

В
геоинформационных
системах данные организованы в виде
отдельных информационных объектов (с
определенным набором реквизитов),
привязанных к общей электронной
топографической основе (электронной
карте). Геоинформационные системы
применяются для информационного
обеспечения в тех предметных областях,
структура информационных объектов и
процессов в которых имеет
пространственно-географический компонент
(маршруты транспорта, коммунальное
хозяйство).

1)
по масштабам применения — настольные и
офисные.

2)
по признаку структурированности задач
структурированные (формализуемые), не
структурируемые (не формализуемые),
частично структурируемые.

3)
по функциональному признаку –
производственные, маркетинговые (анализа
рынка, рекламные, снабженческие и т.п.),
финансовые (бухгалтерские, статистические,
и т.п.), кадровые.

4)
по квалификации персонала и уровням
управления – стратегические
(топ-менеджеров), функциональные
(менеджеров среднего звена) и оперативные
(специалистов).

5)
по характеру обработки информации:
системы обработки данных, системы
управления, система поддержки принятия
решений.

6)
по оперативности обработки данных –
пакетной обработки и оперативные.

7)
по степени автоматизации -ручные,
автоматические, автоматизированные.

по характеру использования информации
— наинформационно-поисковые,
информационно-справочные,информационно-решающие,управляющие,
советующие и т.п..

9)
по степени централизации обработки
информации — на централизованные,
децентрализованные, информационные
системы коллективного использования.

10)
по характеру использования вычислительных
ресурсов –локальные и распределенные;

11)
по сфере деятельности – на государственные,
территориальные (региональные),
отраслевые, объединений, предприятий
или учреждений, технологических процессов

12)
по классу реализуемых технологических
операций-на системы с текстовыми
редакторами, системы с табличными
редакторами, СУБД, СУБЗ, системы с
графикой, мультимедиа, гипертекстом

13)
по месту в процессе управления
предприятия–на АРМ специалиста, ИС
руководителя, ИС внешнего контролера,
интегрированные системы, объединяющие
в себе часть или все из этих функций.

14)
по концепции построения – файловые,
автоматизированные банки данных, банки
знаний.

15)
по режиму работы — пакетные, диалоговые
и смешанные.

Совокупность
информации по какому-либо объекту
называется информационной
базой. Информационная
база присуща любому объекту независимо
от уровня управленческой техники. Она
делится на подсистемы, массивы, показатели,
реквизиты.

Информационная
база, записанная на машинные (электронные)
носители информации и используемая для
решения задач на ЭВМ, называется базой
данных.

Понятие
и назначение базы данных.

Понятие
«база данных» возникло в результате
стандартизации и унификации данных,
универсально организованных и хранящихся
с помощью ЭВМ с целью использования для
многих приложений.

Структурирование
данных
– объединение данных по определенным
параметрам.

База
данных
– это реализованная с помощью компьютера
информационная структура (модель),
отражающая состояние объектов и их
отношения.

База
данных
– структурная совокупность данных,
поддерживаемых в актуальном состоянии
(в соответствии объектам некоторой
предметной области) и служащая для
удовлетворения информационных
потребностей пользователей.

Существенные
различия между БД и ИС
– для хранения БД используется
персональный компьютер, совокупность
БД образует уже информационную систему,
распределенную на несколько компьютеров.

Виды
информационных систем относительно
вида деятельности: производственные
системы, системы маркетинга, системы
учета и бухгалтерии, системы кадров и
т.д.

Требования
к информационной системе:
1) требование к назначению (сбор, хранение
и обработка информации); 2) требование
к среде хранения и доступу к данным; 3)
(самое главное) удобный и понятный
интерфейс для конечного пользователя.

Характеристики
базы данных

полнота
– чем полнее база данных, тем вероятнее,
что она содержит нужную информацию
(однако не должно быть избыточной
информации);

правильная
организация
– чем лучше структурирована, тем легче
в ней найти необходимые сведения;

актуальность–любая
база данных может быть точной и полной,
если она постоянно обновляется, т. е.
необходимо, чтобы база данных в каждый
момент времени полностью соответствовала
состоянию отображаемого ею объекта;

удобство
для использования
– база данных должна быть проста и
удобна в использовании и иметь развитые
методы доступа к любой части информации.

Требования
к базе данных

адекватность
базы данных предметной области;

интегрированность
данных;

независимость
данных;

минимальная
избыточность хранимых данных;

целостность
базы данных;

обеспечение
защиты от несанкционированного доступа
или случайного уничтожения данных;

гибкость
и адаптивность структуры базы данных;

динамичность
данных и способность к расширению;

возможность
поиска по многим ключам.

Классификация
баз данных

1.По
характеру хранимой информации:
фактографические (база данных, содержащая
информацию, относящуюся непосредственно
к предметной области) и документальные
(база, в которой каждый элемент представлен
только в объёме поискового образа
адресата. Такой элемент содержит
совокупность признаков, характеризующих
адресата (полный почтовый адрес,
банковские реквизиты, фамилии – имена
— отчества нужных лиц, профиль деятельности
и т.д.)).

2.По
способу хранения данных:
централизованные (база данных, размещенная
в виде единого информационного массива
на одном или нескольких носителях в
одной ЭВМ)и распределенные (совокупность
логически взаимосвязанных баз данных,
распределённых в компьютерной сети).

3.По
структуре организации данных:
реляционные (табличные БД), иерархические
и сетевые БД.

Соседние файлы в предмете Медицинская информатика

• #
• #