Что такое оптимальное планирование в excel - Word и Excel

Описание презентации по отдельным слайдам:

1 слайд

Оптимальное планирование
Решение задачи оптимального планирования в MS Excel
2 слайд

Определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения цели — оптимальный план.
Пример.
3 слайд

Пример:
Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности емкости склада за день можно приготовить в совокупности не более 700 изделий. Рабочий день в кондитерском цехе длится 8 часов. Если выпускать только пирожные, за день можно произвести не более 250 штук, пирожков же можно произвести 1000, если при этом не выпускать пирожных. Стоимость пирожного вдвое выше, чем пирожка. Требуется составить дневной план производства, обеспечивающий кондитерскому цеху наибольшую выручку.
4 слайд

математическая модель:
Плановый показатель:

х – дневной план выпуска пирожков;
у – дневной план выпуска пирожных.

Ресурсы деятельности:

длительность рабочего дня – 8 часов;
вместимость склада – 700 мест.

Цель:

достижение максимальной выручки цеха.
5 слайд

Математические соотношения:
Обозначим время изготовления пирожка
– t мин. (из условия t = 8 · 60 / 1000 = 0,48 мин.)
Время для пирожного(см.условие)
– 4t мин.
Суммарное время для изготовления х пирожков и у пирожных:
tx + 4ty = (x + 4y) t.
Но оно не может быть больше 8 часов:
(x + 4y) t ≤ 8 · 60
Подставив t, получим:
(x + 4y) · 0,48 ≤ 480
или
x + 4y ≤ 1000
6 слайд

Ограничение на общее число изделий :
x + y ≤ 700
Добавив условие положительности х и у получаем систему неравенств:

x + 4y ≤ 1000
x + y ≤ 700
х ≥ 0
у ≥ 0
7 слайд

Максимальная выручка.
Выручка – стоимость всей проданной продукции.
Пусть цена одного пирожка – r рублей.
Тогда, из условия, цена одного пирожного – 2r рублей.
Отсюда стоимость всей произведенной продукции:
rx + 2ry = r (x + 2y)
Будем рассматривать данное выражение
как функцию от х, у :
f (x,y) = r (x + 2y)
– целевая функция
r – константа, то максимум выручки зависит от
выражения (x + 2y) и целевую функцию можно
записать как:
f(x,y) = (x + 2y)
8 слайд

Итак, математическая задача:
найти значение плановых показателей х, у, удовлетворяющих
системе неравенств, при которых целевая функция
принимает максимальное значение.

Решает такие задачи — математическое программирование
в нашем случае – линейное программирование.

Система неравенств представляет на координатной плоскости четырехугольник, ограниченный четырьмя прямыми:

x + 4y = 1000
x + y = 700
х = 0
у = 0

Любая точка четырехугольника ABCD является решением системы неравенств. Но решением является та точка, в которой целевая функция максимальна.
Чтобы ее найти воспользуемся функциями MS Excel.
9 слайд

Электронная таблица с нашими данными

Источник

Урок № Класс 11 предмет информатика дата 19.04.2021

Тема: Модели оптимального планирования

Цели урока: изучить задачи оптимизационного моделирования на базовом уровне

Образовательная — познакомить учащихся с понятием «Оптимальное

планирование», получить представление о решении задач оптимального

планирования, получить и закрепить на практике знания и навыки работы

с надстройкой «Поиск решения» в MS Excel, выработать навыки работы

с задачами оптимального планирования в MS Excel.

Развивающая — продолжить развитие познавательных психических и

эмоционально-волевых процессов: внимание, память, воображение;

алгоритмического мышления;

Воспитательная — воспитать у учащихся дисциплинированность,

аккуратность при выполнении лабораторной работы, собранность, стимулировать интерес обучающихся к информационным технологиям, побудить интерес к самостоятельному решению задач

Тип урока:

Техническое обеспечение урока: компьютерный класс с установленным ПО (MS Power Point, MS Excel), проектор, экран.

План-конспект урока:

Этапы урока/время

Содержание урока /Деятельность учителя

Деятельность учащихся

1. Организационный

этап (1 мин.)

Учитель: приветствует учащихся, проверяет отсутствующих.

Учащиеся: приветствуют учителя.

2. Постановка целей

урока (2 мин.)

Учитель: на экране (слайд 1) представлена тема урока «Модели

оптимального планирования», вы знакомы с данным понятием?

Учащиеся: нет, не знакомы.

Учитель: значит, это понятие для вас новое и сегодня на уроке мы должны…

Учащиеся: узнать, что такое модели оптимального планирования;

Учитель: Человек, в течение всей своей жизни, совершая те или иные действия, старался вести себя таким образом, чтобы результат, достигаемый как следствие некоего действия, оказался наилучшим или более успешным. Чтобы переместиться из одного места в другое, человек пытался найти самый короткий путь. В строительстве домов пытался снизить затраты, но в тоже время обеспечить комфортные условия существования. Таких примеров можно привести безграничное множество. Решения данных задач принято называть оптимальными. Оптимальное (от лат. optimus — наилучшее) решение — «решение, которое по тем или иным признакам предпочтительнее других».

Сегодня предметом изучения будет задача выбора какого решения?

Учащиеся: оптимального

Учитель: Верно! Молодцы! Сегодня на уроке мы с вами

познакомимся с понятием «оптимальное планирование», разберем и решим задачу оптимального планирования, запишем ее математическую формулировку в тетради и вместе решим ее на компьютере, а дома вы выполните задание уже самостоятельно.

3. Изучение нового

материала (20

мин.)

Учитель: Объектами оптимального планирования могут служить различные системы: отрасли сельского хозяйства, региона, государства, деятельность предприятия. Слайд2.

Процесс постановки и решения задач оптимизации можно представить в виде взаимосвязанных этапов, на которых выполняются определенные действия, направленные на построение и использование оптимизационного моделирования.

осмысление задачи, выделение наиболее важных качеств, свойств, величин, параметров;
введение неизвестных;
создание целевой функции;
составление системы ограничений;
решение задачи на компьютере.

Построим изучение данной темы на разборе конкретной задачи «Оптимизация перевозки компьютерного класса».

Постановка задачи: Слайд3. «Оптимизация перевозки». Построить формальную модель «Оптимизация перевозки» перевозки компьютерного класса, состоящего из 15 компьютеров, с использованием единственного легкового автомобиля. Каждый компьютер упакован в две коробки (монитор и системный блок) и существует три варианта погрузки коробок в автомобиль:

Тип коробки	Варианты погрузки
1	2	3
Монитор	3	2	1
Системный блок	1	2	4

Необходимо выбрать оптимальное сочетание вариантов погрузки, для того чтобы перевести 15 коробок с мониторами и 15 коробок с системными блоками за минимальное количество рейсов автомобиля.

–Решить задачу значит найти оптимальный план решения.

Учащиеся: записывают в тетрадь.

Формальная модель. Слайд4. Параметрами, значения которых требуется определить, являются количества рейсов автомобиля, загруженного различными способами:

Х₁ – количество рейсов автомобиля, загруженного по варианту1;

Х₂ – количество рейсов автомобиля, загруженного по

варианту 2;

Х₃ – количество рейсов автомобиля, загруженного по

варианту 3;

Тогда целевая функция, равная количеству рейсов автомобиля, примет вид:

F = Х₁+ Х₂ + Х₃

Оптимальным планом будет определение значений параметров с учетом ограниченности ресурсов при достижении стратегической цели.

Цель – минимальное количество рейсов автомобиля.

Учащиеся: записывают определение в тетрадь.

Учитель: Ограничения накладываются количествами коробок с мониторами и системными блоками, которые необходимо перевести. За один рейс можно перевести: 3 монитора и один системный блок или …

Должны выполняться два равенства: какие? Если существует 3 варианта погрузки (смотрим таблицу слайд4) 15 мониторов и 15 системных блоков

Учащиеся: 3∙Х₁+ 2∙Х₂ + 1∙Х₃= 15

1∙Х₁+ 2∙Х₂ + 4∙Х₃= 15

Учитель: Верно! Молодцы Слайд5

Учитель: Кроме того, количества рейсов не могут быть отрицательными, поэтому должны выполняться неравенства:

Какие?

Ученики: Х₁³ 0; Х₂³ 0; Х₃³ 0

Учащиеся: учащиеся записывают все формулы в тетрадь с пояснением.

Физкультминутка.

4.Закрепление и

применение

знаний на

практике (20 мин.)

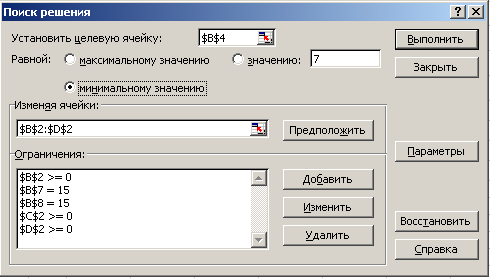
Учитель: математическая формулировка задачи готова.

Учитель: Для того, чтобы найти оптимальное решение задачи с

помощью надстройки «Поиск решения», сначала в MS Excel нужно построить таблицу, куда требуется внести плановые показатели, ресурсы и цель задачи (слайд7). На слайде представлена таблица перед нахождением оптимального решения, Теперь следует решить задачу на компьютере с помощью табличного процессора MS Excel. Табличный процессор MS Excel предоставляет большие возможности при решении различных задач. В нем имеется надстройка «Поиск решения», которая дает возможность решать задачи для нахождения оптимального значения наибольших и наименьших значений (наилучших) при заданных ограничениях. В окне «Поиск решения» требуется указать (слайд 8):

 В поле «Установить целевую ячейку» указать ячейку,

содержащую оптимизируемое решение – целевую функцию;

 В поле «Равной» требуется установить переключатель,

выбрав вариант оптимизации (максимальное, минимальное

или значение равное какому-либо числу);

 В поле «Изменяя ячейки» задать диапазон подбираемых

параметров (неизвестных);

 В поле «Ограничения» указать получившиеся ограничения.

После того, как всё заполнено, нажать кнопку «Выполнить».

Откроется диалоговое окно «Результаты поиска решения», где

требуется установить переключатель в положение «Сохранить

найденное решение», после чего нажать кнопку «Ок».

Учащиеся: Внимательно слушают учителя, делают записи в

тетради, после пересаживаются за компьютеры.

Учитель: раздает описание работы – приложение№1.

Учащиеся: самостоятельно строят таблицу за компьютерами.

Учитель: После того, как вы построили таблицу, нужно процедуру «Поиск решения» (Данные — Анализ — Поиск

решения). Далее в диалоговом окне установить целевую ячейку,

выбрать параметр оптимизации, задать диапазон изменяемых

параметров (количества рейсов автомобиля, загруженного различными способами) и установить ограничения.

Учащиеся: самостоятельно заполняют окно «Поиск решения».

Учитель: Процедура заполнения окна «Поиск решения» выполнена, какой получился у вас результат?

Учащиеся: 3 рейса должны быть загружены по первому, 2 рейса по второму и 2 рейса по третьему варианту. А минимальное количество рейсов -7.

Учитель: Верно! Молодцы! У кого получился такой же результатов? (обсуждение полученных результатов, исправление ошибок).

5. Подведение

итогов и

результатов урока

и выдача

домашнего

задания (2 мин.)

Учитель: Таким образом, мы нашли оптимальный план перевозки 15 компьютеров одной легковой машиной.

Дома вам нужно будет решить задачу на компьютере описанную в учебнике §39 . Требуется найти число пирожков и пирожных, чтобы обеспечить максимальную выручку кондитерскому цеху, только с немного

измененным условием : число пирожных должно быть не меньше числа пирожков.

Сегодня мы с вами узнали, что такое оптимальное планирование, получили представление о решении задач оптимального планирования, закрепили на практике знания и навыки работы с надстройкой «Поиск решения» в MS Excel, выработали навыки работы с задачами оптимального планирования в MS Excel.

Спасибо за урок!

Приложене№1

Практикум: компьютерная модель «Оптимизация перевозки» в электронных таблицах Microsoft Excel.

1.Ячейки B2, C2 и D2 выделить для хранения значений параметров X1, X2 и X3.

В ячейку B4 ввести формулу вычисления целевой функции: =B2+C2+D2.

В ячейку B7 ввести формулу вычисления количества коробок с мониторами:

=3*B2+ 2*C2 + 1*D2

В ячейку B8 ввести формулу вычисления количества коробок с системными блоками:

=1*B2+ 2*C2 + 4*D2

2.Ввести команду [Данные-Поиск решений…]. На появившейся диалоговой панели Поиск решения установить:

 адрес целевой ячейки;

 вариант оптимизации значения целевой ячейки (максимизация, минимизация или подбор значения);

 адреса ячеек, значения которых изменяются в процессе поиска решения (в которых хранятся значения параметров);

 ограничения (типа равно для ячеек, хранящих количество деталей, и типа больше равно для параметров).

3.Щелкнуть по кнопке Выполнить.

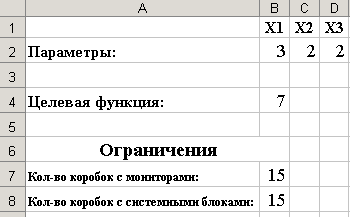
В ячейке целевой функции появится значение 7, а в ячейках параметров значения 3, 2, 2.

Таким образом, для перевозки 15 коробок с мониторами и 15 коробок с системными блоками потребуется 7 рейсов автомобиля, при этом 3 рейса должны быть загружены по первому, 2 рейса по второму и 2 рейса по третьему варианту.

Источник

Слайд 1

11 класс Учитель: Куляпина Елизавета Сергеевна

Слайд 2

Объекты планирования : деятельность отдельного предприятия, деятельность отрасли промышленности или сельского хозяйства, деятельность региона, деятельность государства.

Слайд 3

Имеются некоторые плановые показатели: х, у и др.; Имеются некоторые ресурсы: R1 , R2 и др., за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены.; Имеется определенная стратегическая цель , зависящая от значений х, у и других плановых показателей, на которую следует ориентировать планирование. Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.

Слайд 4

Объект : детский сад, Плановые показатели : 1) число детей, 2) число воспитателей Основные ресурсы деятельности детского сада: 1) размер финансирования, 2) площадь помещения Стратегические цели : сохранение и укрепление здоровья детей (минимизация заболеваемости воспитанников детского сада)

Слайд 5

Оптимальное планирование заключается в определении значений плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Условия ограниченности ресурсов математически представляются в виде системы неравенств. Решение задачи оптимального планирования сводится к построению целевой функции и назначению определенных условий для ее величины: чаще всего максимума или минимума.

Слайд 6

Задача 2: Кондитерский цех готовит пирожки и пирожные. Ограниченность емкости склада – за день можно приготовить не более 700 изделий. Рабочий день – 8 часов.. Если выпускать только пирожные, за день можно произвести не более 250 штук, пирожков можно произвести 1000 штук (без пирожных). Стоимость пирожного вдвое выше, чем стоимость пирожка. Требуется составить дневной план производства, обеспечивающий наибольшую выручку.

Слайд 7

Плановые показатели: Х – дневной план выпуска пирожков; У — дневной план выпуска пирожных. Ресурсы производства: Длительность рабочего дня – 8 часов, Вместимость склада – 700 мест. Время изготовления пирожка – t мин, Время изготовления пирожного — 4 t мин Суммарное время на изготовление х пирожков и у пирожных равно t х + 4 t х = (х + 4у) t . По условию задачи (х + 4у) t < 8*60 или (х + 4у) t < 480 Вычислим t ( время изготовления одного пирожка): t = 480/1000 = 0,48 мин Получаем (х + 4у)*0,48 < 480 или х + 4у < 1000 ограничение на общее число изделий дает неравенство х + у < 700 . Добавим условие положительности значений величин х и у

Слайд 8

х + 4у < 1000 х + у < 700 х > 0 у > 0

Слайд 9

Пусть цена одного пирожка – r рублей, тогда цена пирожного – 2 r рублей, а стоимость всей произведенной за день продукции равна rx + 2ry = r(x + 2y) . Запишем полученное выражение как функцию f(x,y) = r(x + 2y) . Она называется целевой функцией. Так как r – константа, в качестве целевой функции можно принять f(x,y) = (x + 2y)

Слайд 10

найти значения плановых показателей х и у, удовлетворяющих системе неравенств при которых целевая функция f(x,y) = (x + 2y) принимает максимальное значение х + 4у < 1000 х + у < 700 х > 0 у > 0

Слайд 11

Система неравенств представляется на координатной плоскости четырехугольником, ограниченным прямыми, соответствующим линейным уравнениям х + 4у = 1000 х + у = 700 х = 0 у = 0 Любая точка четырехугольника является решением системы неравенств. Но, искомым решением задачи будет та точка, в которой целевая функция максимальна.

Слайд 13

Нахождение точки в которой целевая функция максимальна производится с помощью методов линейного программирования. Эти методы имеются в математическом арсенале MS Excel . Осуществляется это с помощью средства «Поиск решения». Команда находится на вкладке Данные в группе Анализ .

Слайд 15

Рис. 3. Начальное состояние формы «Поиск решения»

Слайд 16

Рис. 4. Форма «Поиск решения» после ввода информации

Слайд 17

Рис. 5. Форма «Параметры поиска решения» Нажать!

Слайд 18

Рис. 6. Результаты решения задачи ( соответствует точке В рис. 1.) Решение : f(x,y)=800

Слайд 19

Рис. 7. Нажать!

Слайд 20

Рис. 8. Результат решения задачи 2 Решение: f(x,y)=600

Источник

В программу Excel встроены возможности
решения задач математического
программирования.

Средство «Поиск решения» реализовано
в форме надстройки. Соответствующая
команда находится в меню Сервис (MS
Excel 97-2003) или в группе
Анализ вкладки Данные.

Замечание. Средство поиска решения
является надстройкой — вспомогательной
программой, служащая для добавления в
Microsoft Office специальных команд или
возможностей. Чтобы использовать эту
надстройку в Excel, необходимо сначала
загрузить ее. Для этого в MS
Excel 7 нажмите кнопку MS
Office

,
а затем щелкните Параметры Excel.
Выберите команду Надстройки, а затем
в окне Управление выберите пункт
Надстройки Excel. Нажмите кнопку
Перейти. В окне Доступные надстройки
установите флажок Поиск решения и
нажмите кнопку ОК.

В случае появления сообщения о том, что
надстройка для поиска решения не
установлена на компьютере, нажмите
кнопку Да, чтобы установить ее.

Покажем на рассмотренном нами простейшем
примере («пирожки и пирожные»), как
воспользоваться средством Поиск Решения.

Вначале надо подготовить электронную
таблицу к решению задачи оптимального
планирования. В режиме отображения
формул таблица показана на рис. 2.20.
Ячейки В5 и С5 зарезервированы соответственно
для значений х (план по изготовлению
пирожков) и у (план по изготовлению
пирожных). Ниже этих ячеек представлена
система неравенств (а), определяющая
ограничения на искомые решения.
Неравенства разделены на левую часть
(столбец В) и правую часть (столбец D).
Знаки неравенств в столбце С имеют чисто
оформительское значение. Целевая функция
(p) занесена в ячейку В15.

	А	В	С	D
1	Оптимальное планирование
2
3	Плановые показатели
4		X (пирожки)	У (пирожные)^
5
6
7	Ограничения
8
9		Левая часть	Знак	Правая часть
10	Время производства:	=В5+4*С5	<=	1000
11	Общее количество:	=В5+С5	<=	700
12	Положительность X:	=В5	>=	0
13	Положительность Y:	=С5	>=	0
14
15	Целевая функция	=В5+2*С5
16

Рис. 2.20. Таблица, подготовленная к
вычислению оптимального плана

Теперь следует вызвать программу
оптимизации «Поиск решения» и сообщить
ей, где расположены данные. Для этого
надо выполнить команду => Сервис =>
Поиск решения. На экране откроется
соответствующая форма (рис. 2.21).

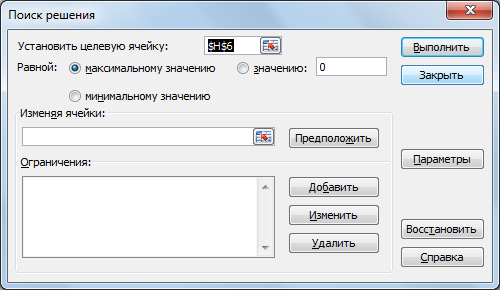
Рис. 2.21. Начальное состояние формы «Поиск
решения»

Далее надо выполнить следующий алгоритм:

Ввести координату ячейки с целевой
функцией. В нашем случае это В15. (Заметим,
что если перед этим установить курсор
на ячейку В15, то ввод произойдет
автоматически).

Поставить отметку «максимальному
значению», то есть сообщить программе,
что нас интересует нахождение максимума
целевой функции.

В поле «Изменяя ячейки» ввести В5:С5, то
есть сообщить, какое место отведено под
значения переменных — плановых показателей.

В поле «Ограничения» надо ввести
информацию о неравенствах-ограничениях,
которые имеют вид B10<=D10;

B1K=D11;

B12>=D12;

B13>=D13.

Ограничения вводятся следующим образом:

=> щелкнуть по кнопке «Добавить»;

в появившемся диалоговом окне «Добавление
ограничения» ввести ссылку на ячейку
В10, выбрать из меню знак неравенства <=
и ввести ссылку на ячейку D10; снова
щелкнуть по кнопке «добавить» и аналогично
ввести второе ограничение B11<=D11 и так
далее. В конце надо щелкнуть на кнопке
ОК.

Закрыть диалоговое окно «Добавление
ограничения».Снова появится форма
«Поиск решения» (рис. 2.22).

Теперь надо дать последние указания:
задача является линейной (это многократно
облегчит программе ее решение). Для
этого следует щелкнуть по кнопке
«Параметры» — появится форма «Параметры
поиска решения» (рис. 2.23).

Рис. 2.23. Форма «Параметры поиска решения»

Надо выставить флажок на переключателе
«Линейная модель» Остальная информация
в форме «Параметры поиска решения»
служебная, автоматически устанавливаемые
значения нас устраивают . Следует
щелкнуть по кнопке ОК, что возвратит
нас в форму «Поиск решения».

Вся информация введена. Далее надо
щелкнуть по кнопке «Выполнить» —
мгновенно в ячейках В5 и С5 появится
оптимальное решение (числа 600 и 100), а
также число 800 в ячейке В15 — максимальное
значение целевой функции (рис. 2.24).

	А	В	С	D
1	Оптимальное планирование
2
3	Плановые показатели
4		X (пирожки)	Y (пирожные)
5		600	100
в
7	Ограничения
8
9		Левая часть	Знак	Правая часть
10	Время производства:	1000	<=	1000
11	Общее количество:	700	<=	700
12	Положительность X:	600	>=	0
13	Положительность Y:	100	>=	0
14
15	Целевая функция	800
16

Рис. 2.24. Результаты решения задачи

Кроме того, на экране появилась еще одна
форма — «Результаты поиска решения».

На первом этапе освоения возможностей
программы на эту форму можно не обращать
внимания (хотя в принципе в ней может
оказаться очень полезная информация).

Итак, в результате применения инструмента
«Поиск решения», мы получим следующий
оптимальный план дневного производства
кондитерского цеха: нужно выпускать
600 пирожков и 100 пирожных. В этой точке
значение целевой функции f(600,100)
= 800. Если один пирожок стоит 2 рубля, то
полученная выручка составит 1600 рублей.

Решение, которое мы получили, вполне
разумно как с экономической точки
зрения, так и с медицинской. Много
сладкого — вредно для здоровья, а пирожки
и сытнее и полезнее.

Полученная электронная таблица и
настроенная на нее сервисная функция
«Поиск решения» являются средством, с
помощью которого можно решать задачу
оптимального планирования при меняющихся
условиях. Например, может измениться
длина рабочего дня. Тогда надо внести
новое значение в ячейку D10 и оптимальный
план автоматически пересчитается. Так
же может измениться допустимое суммарное
число изделий в ячейке D11.

Представьте себе, что в вашей школе
учатся неисправимые сладкоежки. И,
кроме всех прочих ограничений, перед
кондитерским цехом ставится обязательное
условие: число пирожных должно быть не
меньше числа пирожков. При такой
постановке задачи система неравенств
(а) примет вид:

х + 4у < 1000;

х + у < 700;

х >0; у>х.

Соответствующее изменение легко внести
в электронную таблицу. Для этого
достаточно в ячейке D13 вместо 0 записать
В5. Результаты поиска решения будут
следующими: х = 200, у = 200, f(x,y) = 600. Таким
планом вряд ли будет доволен директор
кондитерского цеха, поскольку потери
прибыли окажутся очень существенными.

Следует иметь в виду, что при решении
подобных задач могут возникнуть проблемы,
о которых мы здесь не говорили.
Например, искомого оптимального решения
может вовсе не существовать — тогда
программа об этом сообщит

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Решение задачи оптимального планирования в

Решение задачи оптимального планирования в MS Excel

R1, R2 и другие, за счет которых эти плановые показатели могут быть достигнуты

имеются некоторые плановые показатели: х, у и другие;
имеются некоторые ресурсы: R1, R2 и другие, за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены;
имеется определенная стратегическая цель, зависящая от значений х, у и других плановых показателей, на которую следует ориентировать планирование.

Постановка задачи планирования

Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели

Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.

Пусть совхоз занимается возделыванием только двух культур — зерновых и картофеля — и располагает следующими ресурсами: пашня — 5000 га, труд — 300 тыс

Пусть совхоз занимается возделыванием только двух культур — зерновых и картофеля — и располагает следующими ресурсами:
пашня — 5000 га,
труд — 300 тыс. чел.-ч,
возможный объем тракторных работ — 28 000 условных га.
Цель производства—получение максимального объема валовой продукции (в стоимостном выражении).
Найдите оптимальное сочетание посевных площадей культур.

Рассмотрим пример

Этап I. Решение. культуры Затраты на 1 га посева

Этап I.

Решение.

культуры	Затраты на 1 га посева	Стоимость валовой продукции с 1 га, р.
труда, чел.-ч	тракторных работ, усл. га
Зерновые	30	4	400
Картофель	150	12	1000

Для поиска оптимального решения задачи обозначим через х1 -га площадь, отводимую под зерновые, х2 га — площадь, отводимую под картофель

Для поиска оптимального решения задачи обозначим через
х1 -га площадь, отводимую под зерновые,
х2 га — площадь, отводимую под картофель. Тогда стоимость зерновых составит 400 х1 р.,
а стоимость картофеля — 1000 х2 р.
Отсюда стоимость всей валовой продукции составит ( 400 х1 + 1000 х2) р.
Обозначим это выражение через у и назовем его целевой функцией:
у = 400 х1 + 1000 х2

Нам надо найти максимум этой целевой функции при соблюдении следующих условий: а) общая площадь зерновых и картофеля не должна превышать 5000 га, т

Нам надо найти максимум этой целевой функции при соблюдении следующих условий:
а) общая площадь зерновых и картофеля не должна превышать 5000 га, т. е. х1 + х2≤5000;
б) общие затраты труда не должны превосходить 300 тыс. человеко-часов, т. е. 30 х1 + 150 х2≤ 300 000;
в) общий объем механизированных работ не должен превосходить 28 000 усл. га, т. е. 4 х1 + 12 х2≤28 000;
г) площади, отводимые под зерновые и картофель, могут принимать только неотрицательные значения: х1≥0 и х2 ≥0.

Таким образом, условия задачи выражаются следующей системой неравенств

Требуется найти такие значения х1 и х2, при которых целевая функция у = 400 х1 + 1000 х2 принимает наибольшее значение.

Этап II. Решим задачу графически

Этап II. Решим задачу графически.

Построим прямую х1 + х2=5000.

Построим прямую х1 + х2=5000.

Построим прямую 30 х1 + 150 х2=300 000.

Построим прямую 4 х1 + 12 х2=28 000.

Таким образом, наибольшее значение целевой функции достигается в вершине

Таким образом, наибольшее значение целевой функции достигается в вершине М, что соответствует варианту плана, по которому под зерновые отводится 4000 га, а под картофель — 1000 га.

Решение задачи оптимального планирования в

Решение задачи оптимального планирования в MS Excel

Поиск решения». Для этого надо выполнить команду =>

программа оптимизации «Поиск решения». Для этого надо выполнить команду => Сервис => Поиск решения. На экране откроется соответствующая форма

Далее надо выполнить следующий алгоритм:

Далее надо выполнить следующий алгоритм:
Ввести координату ячейки с целевой функцией. В нашем случае это В15. (Заметим, что если перед этим установить курсор на ячейку В15, то ввод произойдет автоматически).
Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции.
В поле «Изменяя ячейки» ввести В5:С5, то есть сообщить, какое место отведено под значения переменных -плановых показателей.
В поле «Ограничения» надо ввести информацию о неравенствах-ограничениях, которые имеют вид B10<=D10; B1K=D11; B12>=D12; B13>=D13.

Закрыть диалоговое окно «Добавление ограничения»

Закрыть диалоговое окно «Добавление ограничения». Снова появится форма «Поиск решения»

Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение)

6. Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение). Для этого следует щелкнуть по кнопке «Параметры» — появится форма «Параметры поиска решения»

Вся информация введена. Далее надо щелкнуть по кнопке «Выполнить» — мгновенно в ячейках

Вся информация введена. Далее надо щелкнуть по кнопке «Выполнить» — мгновенно в ячейках В5 и С5 появится оптимальное решение

Практическая работа в парах (делятся на пары, каждая пара вытягивает задачу

Практическая работа в парах (делятся на пары, каждая пара вытягивает задачу. Приступают к решению)
Итоги (что получилось в решении, мнение о работе)

Спасибо за урок!

Источник