Что такое математическая модель в excel - Word и Excel - помощь в работе с программами

Цели урока:

Обучающие: Повторить и закрепить навыки
работы в MS Excel; научить применять современное
программное обеспечение в решении
математических задач, строить математические
модели в среде MS Excel.

Развивающие: Развивать: практические и
исследовательские навыки по составлению моделей
в электронных таблицах, научное мировоззрение
через связь информационных технологий с другими
школьными предметами, логическое и
алгоритмическое мышление, аналитические
способности, внимание, память.

Воспитательные: Воспитание общей и
информационной культуры, творческого подхода к
работе, желания экспериментировать,
самостоятельности в учебном труде.

Тип урока: Комплексного применения
знаний, обобщения и систематизации.

Программное и техническое обеспечение
урока:

компьютеры с ОС MS Windows XP;

пакет Microsoft Office;

мультимедийный проектор

Время проведения урока: один из
последних уроков в разделе «Информационное
моделирование».

План урока: (40 минут)

Орг. момент. (1 мин)
Проверка и актуализация знаний. / Тестирование
по теме (4 мин)./ Разминка (5 мин)
Теоретическая часть. (10 мин)
Практическая часть. (10 мин)
Самостоятельная работа. (8 мин)
Подведение итогов. Д/з (2 мин)

Ход урока:

1. Организационный момент.

Приветствие, проверка присутствующих.

С помощью проектора демонстрируется
на экране первый слайд презентации. Приложение 1

Сообщается тема урока: «Математическое
моделирование в среде электронных таблиц MS Excel
«.Озвучить цели и план урока.

2. Актуализация опорных знаний.

Пройденная нами тема «Электронные
таблицы»– одна из наиболее практически
значимых, востребованных, после текстового
редактора Word и его возможностей. Но электронные
таблицы не только позволяют автоматизировать
расчеты, но и являются эффективным средством
моделирования различных вариантов и ситуаций.
Меняя значения исходных данных, можно проследить
за изменением получаемых результатов и из
множества вариантов решения задачи выбрать
наиболее подходящий.

Перечислите, что вы научились делать,
изучая табличный процессор MS Excel?

– выполнять вычислительные операции
при помощи формул;

– составлять таблицы;

– строить графики и диаграммы.

Тестирование по теме «Электронные
таблицы».

Домашним заданием было повторить весь
изученный материал по теме «Электронные
таблицы». Чтобы проверить домашнее задание, я
предлагаю Вам ответить на вопросы электронного
теста. (Дети уже знакомы с работой системы
дистанционного обучения MyTestServer 1.1) Приложение 2

Перед началом работы учащиеся
прослушивают инструкцию по выполнению теста.

Тест состоит из 5 вопросов. Дается
только одна попытка, будьте внимательны, не
торопитесь. Время на тест 3 минуты.

После завершения тестирования каждому
ученику системой выставляется оценка, которую он
видит на экране своего монитора.

Сегодня на уроке мы будем использовать
электронные таблицы с их мощным вычислительным
потенциалом для решения математических задач –
построим математическую модель в среде MS Excel и
проведем небольшое исследование.

А для этого вспомним основные понятия
по теме “моделирование” (проводим устную разминку).

Вопросы разминки: Приложение 1

Моделирование – метод познания
окружающего мира, состоящий..

Модель – это объект, который
используется в качестве..

Различают ____________и ___________модели.

Натурные модели – это…

Информационные модели – это…

Основными видами информационных
моделей являются:_________ ,_________, __________.

А как вы думаете, математическая
модель к какому виду принадлежит?

Математическая модель – это модель,
построенная с использованием…

Приведите пример знаковой
информационной модели, рассматриваемой на
уроках математики.

Основным языком информационного
моделирования в науке является язык математики.

3. Теоретическая часть.

Какую бы жизненную задачу ни взялся
решать человек, первым делом он строит модель
заданного объекта. Очень часто задачи связаны с
потребностями человека.

Сегодня нам предстоит решить
следующую задачу:

Задача 1: Приложение
1

У маленького Васи есть небольшой
бассейн во дворе. Иногда Вася ходит к речке и
приносит воду в бассейн в небольшой цистерне
цилиндрической формы. Известны ширина ШБ, высота
ВБ, ДБ бассейна и объем цистерны Об Ц. Сколько раз
Васе нужно сходить к речке за водой, чтобы
наполнить бассейн наполовину?

Этот текст можно рассматривать как
словесную модель бассейна.

Постановка задачи: выяснение
условий

Какую форму может иметь бассейн?
(ответы детей).

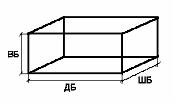
А какой формы он в нашей задаче?– В
форме куба или параллелепипеда, потому, что даны
его параметры: ширина, высота, длина. А что еще нам
известно?

– объем цистерны.

Давайте попробуем решить задачу:
узнаем сколько раз (N) Васе нужно сходить к речке
за водой, чтобы наполнить бассейн наполовину.

Что для этого нужно знать?

– сколько цистерн воды помещается в
бассейн.

А как это узнать?

– определить объем бассейна (Об Б)

– сравнить половину объема бассейна и
объем цистерны (Об Б / Об Ц / 2).

4. Практическая часть.

Карточка – задание №1 Приложение 3

Задание для практической работы: Скопировать
в свою папку файл – шаблон Excel Приложение 4

Назвать лист номером задачи «Задача
1» (редактирование названия – двойной щелчок
мыши на «Лист 1»).

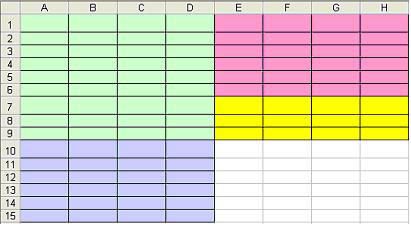
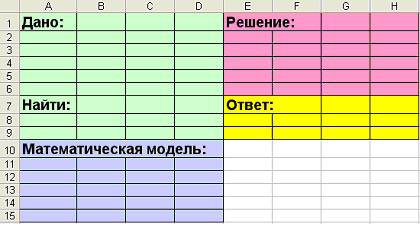
Оформить на листе решения разделы «Дано«,
«Найти«, «Математическая модель«,
«Решение«, «Ответ» (по образцу):

В ячейках А1и А7 напечатать
слова «Дано» и «Найти«.

Объединить ячейки А10, В10 и С10,
ввести текст: «Математическая модель«

Объединить ячейки Е1 и F1,
напечатать слово «Решение«.

В ячейку Е7 – «Ответ«.

Заполнить таблицу начальными
данными.

В ячейки В1:В4 ввести текст: ШБ=;
ДБ=; ВБ=; Об Ц=.

В ячейки С1:С4; ввести
соответствующие значения параметров: 4,3; 5,8; 2; 4,5.

Для наглядности, если есть
возможность, можно построить графическую модель
(рисунок задаче) в Painte и скопировать ее в
электронную таблицу или нарисовать бассейн
непосредственно в Excel.

Далее заполнить раздел таблицы
«Математическая модель».

Объединить ячейки А11, В11 и С11,
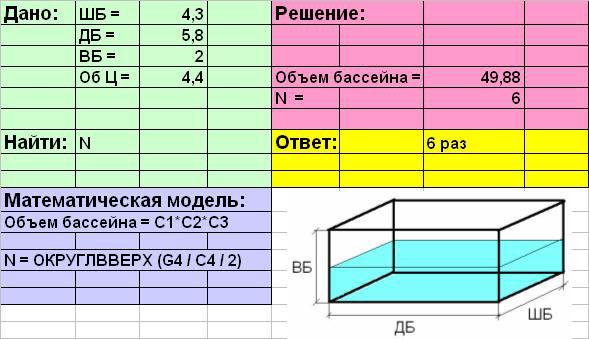
ввести формулы (тип данных – текст) в раздел
(пробел перед знаком «=»). «Объем бассейна
=С1*С2*С3«

Объединить ячейки А13, В13 и С13
и ввести текст «N = ОКРУГЛВВЕРХ(G4 / C4 / 2)«.
(для получения целого числа используем функцию
округления ОКРУГЛВВЕРХ)

В разделе «Решение»
создать сетку вычислений:

– Обозначить искомые и промежуточные
величины.

– Объединить ячейки Е4 и F4,
ввести текст: «Объем бассейна =«. В ячейку
Е5 – «N =«(тип данных – текст).

В ячейки G4 и G5; ввести
соответствующие формулы (тип данных – формулы):
=С1*С2*С3;

Используем функцию округления
дробного числа до целого:

Вставка-функция – математические –
ОКРУГЛВВЕРХ – число разрядов выбираем «0«.

=ОКРУГЛВВЕРХ(G4 / C4 / 2)

В разделе «Ответ» запишем
искомый результат в ячейку G7 (тип данных –
текст).

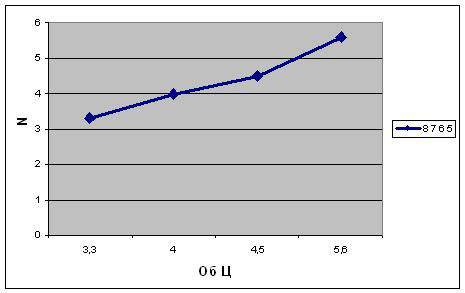
Проведем небольшое исследование:

Вопрос: Сколько раз Васе нужно будет
сходить к речке за водой, если он возьмет
цистерну емкостью 5,6 литров; 4 литра; 3,3
литра?

Меняем в ячейке С4 значение на 5,6
и электронные таблицы автоматически производят
пересчет.

Создадим таблицу значений Об Ц и
будем заносить в нее результаты вычислений N.

Введем в ячейку А20 и В2 текст
«Об Ц» и » N«. Заполним таблицу
данными.

Об Ц	N
3,3	8
4	7
4,5	6
5,6	5

Для графического представления
результатов выделить диапазон А21: В24,
построить график функции, отредактировать его.

Анализ полученных результатов.

5. Самостоятельная работа.

Задание для самостоятельной разработки:

Карточка – задание №2 Приложение
3

Задача 2. Пешеход начал движение из
начала координат со скоростью V=0,6 м/с.
Найдите, какой путь S прошел пешеход за одну
минуту t после начала движения, если он
двигался равномерно.

Постановка задачи: выяснение
условий

Скажите, что мы будем моделировать? –

– движение

Какие виды движения вы знаете? (ответы
детей)

Какое движение рассматривается в
нашей задаче?

– равномерное. Приложение 1

Давайте вспомним формулу расчета
скорости: V=s/t– отсюда s=V*t

Технология моделирования:

Назвать лист номером задачи «Задача 2»
(редактирование названия – двойной щелчок мыши
на «Лист 2»).
Выделить расчетную таблицу на листе «Задача1»
и скопировать ее на лист «Задача 2«.
Заполнить таблицу новыми начальными данными.
Ввести формулу (тип данных – текст) в раздел
«Математическая модель» (пробел перед
знаком «=»).
Ввести фоpмулу (тип данных – формулы) в
раздел «Решение«.
В разделе «Ответ» записать искомый
результат (тип данных – текст).

Создать таблицу значений t и занести в нее
результаты вычислений S. Заполнить таблицу
данными.
Для графического представления результатов
выделить область аргументов и функций, построить
график зависимости пути S от времени при t=40;60;90,
отредактировать график.

6. Итог урока.

Сегодня на уроке мы узнали, как можно
использовать электронные таблицы в решении
математических задач, научились строить
математические модели в. среде MS Excel

Домашним заданием будет: самим
придумать задачу, разработать ее математическую
модель.

У кого есть вопросы по пройденному материалу?

Спасибо за работу. Вы сегодня молодцы. Можете
быть свободны.

Источник

Федеральное
агентство по образованию

ГОУ ВПО «Российский
государственный профессионально–педагогический

университет»

Уральское отделение
Российской академии образования

Академия
профессионального образования

Екатеринбург

2007

УДК

ББК

Городецкая
Н.В.
Математическое моделирование в MS
Excel:
Учеб. пособие. Екатеринбург: Изд-во ГОУ
ВПО «Рос. гос. проф.-пед. ун-т», 2007. 64 с.

Учебное пособие
содержит лабораторные работы,
ориентированные на знакомство с одной
из технологий – математическое
моделирование на основе среды Microsoft
Excel.

Лабораторные
работы включают необходимый теоретический
материал и непосредственные инструкции
по освоению математического моделирования
в среде Microsoft
Excel.

Пособие может быть
использовано для преподавания дисциплины
«Математическое моделирование» у
студентов специальности
050501 Профессиональное обучение
(информатика, вычислительная техника
и компьютерные технологии) (030500.06),
специализации «Компьютерные технологии».

Практикум подготовлен
при финансовой поддержке Российского
гуманитарного научного фонда в рамках
научно–исследовательского проекта
«Психолого–педагогические и
технологические условия применения
адаптивных методических систем в
дистанционных образовательных
технологиях» (№ 06−06−00475а).

Рецензенты: д-р
физ.-мат. наук, проф. В.Е. Третьяков
(ГОУ ВПО «Уральский государственный
университет»); д-р пед. наук, проф. Л.И.
Долинер (ГОУ ВПО «Российский
государственный профессионально-педагогический
университет»)

государственный
профессионально-

педагогический
университет», 2007

Преподавателю: как использовать это пособие

Данная
серия лабораторных работ предназначена
для знакомства обучаемых с технологией
использования математического
моделирования для решения задач. В
качестве конкретного инструментального
средства выбрана среда MicrosoftExcel.

Для
использования данного пособия в обучении
необходимо:

иметь
дискету, прилагаемую к пособию, для
установки рабочих файлов (без них работа
с пособием невозможна);
установить
на компьютере полную версию MicrosoftExcel(с возможностью
осуществлятьПоиск решения);
создать
(в случае отсутствия) в корневом каталоге
одного из дисков папку Учебнаяи
скопировать в папкуУчебнаяпапкуМАТ_МОД, содержащую учебные файлы
с прилагаемой дискеты.

Тому, кто хочет научиться

Если
Вы решили с помощью этого пособия
познакомиться с технологией использования
математического моделирования в среде
MicrosoftExcel,
рекомендуется:

расположиться
перед включенным компьютером с
установленной полной версией MicrosoftExcel;
выполнять
лабораторные работы как можно более
точно, поскольку тексты лабораторных
работ представляют собой в некотором
роде инструкции, соблюдение которых
обеспечит Вам успешную и комфортную
работу;
соблюдать
следует следующие правила:

текст,
который никак не выделен, следует только
читать;
определения,
отмеченные значком
,
необходимо запомнить;
обращать
внимание на текст, помеченный значком
;
практические
задания, отмеченные словом «Задание»,
следует обязательно и в полном объеме
выполнять на компьютере;
контрольные
задания следует также выполнять
самостоятельно; если Вы справитесь с
ними без помощи преподавателя, это
означает, что Вы усвоили материал;
на
контрольные вопросы нужно отвечать
устно – они подготовят Вас к компьютерным
тестовым вопросам;
для
повторения пройденного материала
следует использовать резюме;

делать
краткий конспект — это поможет Вам
ускорить усвоение материала;
отвечать
на все вопросы, приведенные в конце
каждой лабораторной работы;
приглашать
преподавателя тогда, когда это
предлагается сделать в тексте лабораторной
работы;
если
Вы занимаетесь без преподавателя,
выполняйте полностью все задания
лабораторных работ, отвечайте устно
на вопросы.

В книге
приняты следующие обозначения:

—
этот символ используется для выделения
определений;

—
так помечаются важные замечания;

—
резюме;

—
при встрече с таким символом следует
пригласить преподавателя (консультанта)
и показать ему результаты выполнения
заданий. Если Вы работаете самостоятельно,
просто пропустите текст, помеченный
этим символом;

ЛП– линейное программирование; ЦФ–
целевая функция;

РЗ– распределительная задача; ТЗ–
транспортная задача.

Соседние файлы в папке Исслед_опер

#
24.04.201517.92 Кб149lab_3(b).xls
#
24.04.201517.92 Кб88lab_3(а).xls
#
24.04.201527.14 Кб114lab_4(a).xls
#
24.04.201523.04 Кб91lab_4(b).xls
#
24.04.201519.97 Кб143lab_5.xls
#

Источник

Реферат на тему:

Использование табличного процессора MS Excel и математического моделирования для решения математических задач

Выполнила: Миняева Анна

студентка группы МДИ-114

2012

Содержание:

1.
Введение ……………………………………………………………………………….3

2.
Моделирование и решение математических задач……………………………………4

3.
Моделирование и решение задач оптимизации……………………………………….8

4.
Заключение………………………………………………………………………………26

5.
Литература………………………………………………………………………………………………………..27

Введение

Microsoft Excel (также иногда называется Microsoft
Office Excel) — программа для работы с электронными таблицами, созданная
корпорацией Microsoft для Microsoft Windows, Windows NT и Mac OS.

Она предоставляет
возможности экономико-статистических расчетов, графические инструменты и язык
макропрограммирования VBA (Visual Basic for Application). Microsoft Excel
входит в состав Microsoft Office и на сегодняшний день Excel является одним из
наиболее популярных приложений в мире.

Моделирование
и решение математических задач

С середины XX века в самых различных областях человеческой
деятельности стали широко применять математические методы и ЭВМ. Возникли такие
новые дисциплины, как «математическая экономика», «математическая химия»,
«математическая лингвистика» и т.д., изучающие математические модели
соответствующих объектов и явлений, а также методы исследования этих моделей.

Под моделью (от лат. modulus — мера, образец, норма)
понимают такой материальный или мысленно представляемый объект, который в
процессе познания (изучения) замещает объект — оригинал, сохраняя некоторые
важные для данного исследования типичные черты. Процесс построения и
использования модели, называется моделированием.

Во всех науках модели выступают как мощное орудие познания.

Например:
Люди издавна интересуются, как устроена наша Вселенная. Этот интерес не только
познавательный, но и сугубо практический, так как люди хотели научиться
предсказывать периодические явления, связанные с устройством Вселенной, такие,
как: затмение солнца и луны, наступление времен года.

Для решения этих задач, ученые строили свои представления о
Вселенной в виде схемы картины мира, в которой объекты (планеты, Солнце,
звезды, Земля и Луна) изображались точками, движущимся по каким-то кривым —
траекториям их движения. Таковы, например, схемы, построенные Птолемеем, в
которых центральное место занимала наша Земля, или схема Коперника, в которой
центральное место занимало Солнце.

С
помощью этих схем ученые решали задачи предсказания отдельных астрономических
явлений. Эти схемы или картины мира — суть модели Вселенной, а метод
исследования Вселенной, нахождение законов и решения задач, связанных с помощью
этих моделей, является методом моделирования. В математике широко используется
метод моделирования при решении задач.

В процессе математического моделирования выделяют три
этапа:

1. Формализация —
перевод предложенной задачи (ситуации) на язык

математической
теории (построение математической модели задачи).

2. Решение задачи
в рамках математической теории (говорят: решение внутри модели).

3.Перевод результата математического решения задачи на тот язык, на котором
была

сформулирована исходная задача (интерпретация решения).

Умение строить учебные модели и работать с ними является
одним из компонентов общего приема решения задач. С помощью модели словесно
заданный текст можно перевести на математический язык и увидеть структуру
математических отношений, скрытую в тексте. Использование одних и тех же
знаково-символических средств при построении модели для математических задач с
разными сюжетами и разных типов способствует формированию обобщенного способа
анализа задачи, выделению составляющих ее компонентов и нахождению путей
решения.

Моделирование числовых рядов и их применение при решении математических
задач

При решении некоторых задач часто возникает необходимость
использования последовательности чисел.

Числовые ряды, их моделирование и применение в математических задачах

Рядом
называется бесконечная последовательность чисел, элементы которой объединены
попарно арифметическими операциями сложения или вычитания.

Ряд
считается заданным, если известно выражение его общего элемента.

Сумма
конечного числа бесконечной последовательности ряда называется частичной суммой
ряда.

Для
вычисления частичной суммы нужно вычислить определенное число членов ряда и
затем найти их сумму. Для этого должны быть заданы: 1) количество суммируемых
элементов; 2) формула для вычисления элементов ряда.

Создание числовых последовательностей в табличном процессоре

В общем
случае для создания числовой последовательности в табличном процессоре нужно:

—
задать номера элементов последовательности в виде массива натуральных чисел,
расположенных либо в столбце, либо в строке таблицы в листе;

—
ввести в ячейку, соответствующую первому номеру элемента, формулу (выражение)
для его вычисления;

—
скопировать с помощью маркера автозаполнения в следующие ячейки столбца или
строки, где будет формироваться числовая последовательность.

Задание 1. Создать в листе табличного процессора
числовую последовательность, которая задана формулой общего элемента {n/(n+1)}.

Порядок реализации задания 1 в табличном процессоре

1)
Объединить ячейки А1:В1 и записать в них текст: Последовательность (n/(n+1));

2)
Отформатировать ячейки А2:В2 (перенос по словам) и записать в ячейке А2 текст «Номер
элемента», в ячейке В2 – «Значение элемента»;

3)
задать номера элементов последовательности в виде массива натуральных чисел в
ячейках столбца А, начиная с ячейки А3 (не менее 10);

4)
В ячейку В3 ввести формулу для вычисления первого элемента последовательности:
=А3/(А3+1);

5)
С помощью маркера автозаполнения скопировать формулу в следующие ячейки столбца
В, чтобы получить значения всех элементов последовательности.

Для
создания наиболее известных в математике последовательностей (арифметической,
геометрической и т.д.) в табличном процессоре имеет специальный инструмент Прогрессия,
который находится в процессоре на вкладке Главная в группе Редактирование,
где находится кнопка Заполнить. Данная кнопка открывает меню с выбором
метода заполнения. В списке вариантов есть вариант Прогрессия.
После его выбора откроется диалоговое окно, в котором требуется ввести тип и
параметры создаваемой последовательности. ( В Microsoft Excel 2003 – Правка, Заполнить,
Прогрессия)

При
исследовании последовательностей чисел требуется вычислить ее предел или
другие числовые характеристики.

Задание 2. Найти предел числовой
последовательности .

Математическое решение

Порядок реализации в табличном процессоре

1)
В ячейку А1 внести текст: Предел последовательности n/(n+1);

2)
Полагая, что в ячейке А2 будет находиться число n,
в ячейку В2 введите формулу: =А2/(А2+1);

3)
В ячейку А2 введите достаточно большое число, примерно равное 1*10¹²;
если будет введено число, превышающее данную величину, то может наступить
переполнение ячейки и результат вычисления будет неправильным;

4)
После заполнения ячейки А2 в ячейке В2 появится приближенное значение предела
исследуемой числовой последовательности.

Функция – это модель, устанавливающая зависимость
какой-либо одной величины (переменной) от другой величины или нескольких
величин (аргументов).

Одни
из способов задания функции – табличный – имеет широкое распространение
в различных областях исследований: экспериментальных измерениях, таблицах
бухгалтерской отчетности, банковской деятельности, статистических исследованиях
и измерениях и т.д.

При
табличном задании функции один ряд данных представлен как значения
функции, другой (или другие) – как значения аргумента.

Каждому
значению аргумента соответствует значение функции, находящееся в той же строке
таблицы, что и аргумент.

Формула
функции даст также возможность найти значения функции, не отраженные в ее табличном
представлении. При выборе функции должны быть рассмотрены следующие вопросы:

1)
Выбор типа функции (линейная, показательная, логарифмическая и т.д.).

2)
Оценка погрешности приближения.

Виды функций, из которых производится
выбор зависимости, могут быть следующими:

—
линейная у=ах+в; применяется в случае постоянного изменения данных на
определенную величину;

—
полиномиальная – для данных, которые попеременно возрастают и убывают;

—
логарифмическая y=a*lnx+b; применяется для описания данных, которые
вначале быстро убывают и возрастают, а затем стабилизируются;

—
степенная у=в*х^а; используется для аппроксимации данных,
скорость изменения которых быстро увеличивается или уменьшается;

—
экспоненциальная у=в*е^х; применяется для описания данных,
которые быстро убывают и возрастают, а затем стабилизируются.

Мощным средством анализа данных Excel является
надстройка Solver (Поиск решения). С ее помощью можно определить, при
каких значениях указанных влияющих ячеек формула в целевой ячейке принимает
нужное значение (минимальное, максимальное или равное какой-либо величине). Для
процедуры поиска решения можно задать ограничения, причем не обязательно, чтобы
при этом использовались те же влияющие ячейки. Для расчета заданного значения
применяются различные математические методы поиска по умолчанию в Excel
надстройка Поиск решения отключена. Чтобы активизировать ее в Excel 2007,
щелкните значок Кнопка Microsoft Office , щелкните Параметры Excel,
а затем выберите категорию Надстройки. В поле Управление
выберите значение Надстройки Excel и нажмите кнопку Перейти.
В поле Доступные надстройки установите флажок рядом с пунктом Поиск
решения и нажмите кнопку ОК. В Excel 2003
и ниже выберите команду Сервис/Надстройки, в появившемся диалоговом
окне Надстройки установите флажок Поиск решения и щелкните на
кнопке ОК.

Моделирование
и решение задач оптимизации

Оптимизацией
называется процесс выбора наилучшего варианта решения из множества возможных
решений.

При решении
оптимизационных задач с помощью надстройки «Поиск решения» целесообразно
различать линейные и нелинейные модели.

Под линейными
понимаются модели, в которых связь между входными значениями переменных и
результирующими значениями описывается линейными функциями.

Для использования
линейных методов следует установить параметр «Линейная модель» в окне «Параметры
поиска решения». Если этот параметр не установить, то даже для линейной
задачи будут использоваться общие более медленные методы.

Чтобы использовать надстройку «Поиск решения»
не обязательно знать методы программирования и исследования операций, но
необходимо определять, какие задачи можно решать этими методами.

Задание 3: Решите систему уравнений.

Математическое решение

Выразим
в каждом уравнении х относительно у, получим:

Можно
заметить, что все эти функции имеют общую точку (0;2). Это и есть их общее
решение.

Порядок реализации в табличном процессоре.

Для
реализации решения в табличном процессоре следует преобразовать систему
уравнений, выразив в каждом уравнении х относительно y.

Получить
таблицу значений х в указанном диапазоне с определенным шагом (инструмент
Прогрессия) в столбце А.

Получить
таблицу значений функции у₁ для каждого значения х в столбце В.

Получить
таблицу значений функции у₂ для кадого значения х в столбце С.

Получить
таблицу значений функции у₃ для кадого значения х в столбце D.

Построить
графики всех функций в одной области построения диаграммы (тип – ТОЧЕЧНАЯ, вид
– точки, соединенные линией).

Задать
подписи рядов и заголовок диаграммы (в соответствии с темой задания).

Построение графиков и нахождение пары приближенных значений

При построении графиков функций и нахождении их общей
точки – точки пересечения, наводим указатель мыши на точку пересечения, при
этом всплывает подсказка, что точка пересечения с координатой (0; 2).

Уточним найденное решение, для этого ниже, например в ячейку
А25 внесем текст – уточнение решения, и ниже запишем неизвестные – х и у, в
ячейки А26, В26, С26. далее в ячейки А27-С27 внесем соответственно решение и
наши полученные ответы 0 и 2.

Еще ниже, например в ячейку А29 запишем текст- Формулы
уравнений, в ячейки А30-А32- тексты первое уравнение, второе уравнение, третье
уравнение. В ячейки В30-В32 внесем формулы наших функций с ссылками на ячейки
где у нас стоят наши ответы, это адреса ячеек В27 и С27. Следовательно, в
ячейке В30 будет стоять формула =-1,6*В27+2-С27, аналогично в ячейке В31 будет
стоять формула =-2,5*В27+2-С27, и в ячейке В32 формула =-1,75*В27+2-С27.

Выбираем для уточнения Сервис, Поиск решения, в диалоговом
окне указываем целевую ячейку $B$30, равной значению 0.
Так как это разница левой и правой части функции. Указать, какие изменять
ячейки, мы проверяем ответы ячеек В27:С27, и указываем ограничения, что ячейки
с адресами В31=0 и В32=0. Выполняем поиск решения, сохраняем, получившиеся
значения.

Вычисление корней функции одной переменной.

Как известно из математики, корнями функции Y=f(x) называют такие значения
х, при которых функция принимает значение 0.

Процесс
нахождения корней функции осуществляется в два этапа.

Этап 1. Требуется определить, есть ли у
функции корни. Для этого нужно построить график функции для какого-то интервала
значений аргумента и визуально определить, имеет ли функция точки пересечения с
осью ОХ (осью абсцисс).

Этап 2. Требуется уточнить значения корней,
т.е. найти значения корней с заданной точностью.

При решении практических задач аргументом
функции обычно является значение какого-то ресурса, величина которого
ограничена и лежит в области допустимого диапазона значений. Поэтому при
решении задачи интерес представляют только те корни, которые находятся в
области возможных значений х.

Задача 4: Найти корни функции в диапазоне значений аргумента [-1;1] с
точностью 0,1.

Математическое решение

1.
Заданная функция представлена уравнением третьей степени, следовательно, она
может иметь не более трех корней.

2.
Функция непрерывна, поэтому достаточно найти отрезок длиной 0,2 на концах
которого функция имеет значения разных знаков. Имеем f(-1)=-0,1665
<0; f(-0,9)=0,035964 значит один корень уравнения
существует и он принадлежит отрезку [-1;-0,9], х ≈ -0,9
f(0)=0,139104>0; f(0,2)=0,005824>0;
f(0.3)=-0,04612<0; f(0,7)=-0,01588<0;
f(0,8)=0,081184>0, значит два других корня будут
принадлежать отрезкам [0,2;0,3] и [0,7;0.8], х ≈ 0,2 и х ≈ 0,7

2.
Для определения локализации корней функции требуется построить ее график на
указанном диапазоне значений аргумента. Для этого следует получить таблицу значений переменной х в
диапазоне [-1;1]. Для этого следует выбрать шаг изменения аргумента на
заданном отрезке, например, 0,1. Затем нужно вычислить все значения
аргумента на указанном отрезке с выбранным шагом изменения.

3.
Вычислить значения заданной функции для всех значений таблицы значений
аргумента. Таким образом, получится таблица
значений функции.

4.
По таблице значений аргумента и функции построить график и найти точки пересечения графика с осью абсцисс.
Так определяется количество и приближенное значение корней (интервалы,
содержащие корни функции).

5.
Интервалы, содержащие корни функции, дают возможность выбрать приближенное
значение каждого корня, далее требуется уточнить значение с заданной точностью.

Порядок реализации в табличном процессоре

1.
Объединить ячейки А1:С1 и внести в них текст:

2.
В ячейку А2 внести имя аргумента х, в ячейку В2 внести имя функции у.

3.
В ячейку А3 внести первое значение аргумента: -1.

4.
Выделить ячейку А3, затем вызвать команду Заполнить «Прогрессия…(вкладка Главная, группа Редактирование). В диалоговом окне
задать параметры прогрессии.

В
результате заполнения у вас должен появиться столбец значений аргумента.

5.
В ячейку В3 ввести выражение для вычисления значения функции для первого
значения аргумента:

6.
Выделив ячейку В3, за маркер автозаполнения скопировать формулу функции для
всех следующих значений аргумента. Получится столбец значений функции.

7.
По таблице значений аргумента и функции строим график функции. Для этого
выделяем два столбца значений (аргумент и функция), строим диаграмму (тип –
ТОЧЕЧНАЯ, вид – точки, соединенные линией). Подпись ряда – у=х^3-0,01*x^2-0,7044*x+0,139104, заголовок диаграммы – График функции.

Из
графика видно, что функция пересекает ось абсцисс на указанном отрезке три
раза. Следовательно, она имеет три корня.

8.
Чтобы определиться со значениями начальных приближений корней функции,
проанализируйте таблицу значений функции (столбец В). В ней нужно найти ячейки,
которые содержат значения, меняющие знак (например, с – на +, или наоборот).

а)
функция меняет знак на отрезке [-1;-0,9];

б)
функция меняет знак на отрезке [0,2;0,3];

в)
функция меняет знак на отрезке [0,7;0,8].

Следовательно,
точные значения корней функции находятся внутри этих интервалов.

9.
В качестве начальных приближений корней функции нужно выбрать значения
аргумента в ячейках А4 (-0,9), А15 (0,2), А20 (0,7).

На
свободном участке листа, в ячейках А25:С25 (объединив их) разместить текст: .

10.
В ячейки А26:А28 ввести значения выбранных приближений Для каждого значения
ячеек А26:А28 в ячейки В26:В28 нужно ввести формулу функции из пункта 5.

11.
Нажмите на копку Файл. В меню выберите пункт Параметры, в диалоговом
окне выберите пункт Формулы и в разделе Параметры вычислений
установите переключатель рядом с параметром Включить итеративные вычисления,
и укажите предельное число итераций 1000, а значение относительной погрешности
установите равным 0,000001.

(Или
для версии 2003, Сервис Параметры, Вычисления, указать число итераций
1000, относительная погрешность 0,000001.

12.
После установки параметров вычислений выделите ячейку В26, нужно перейти на
вкладку Данные, в группе Работа с данными выбрать кнопку
Анализ «что если».

В
открывшемся списке вариантов выбрать Подбор параметра… Откроется
диалоговое окно, в котором требуется заполнить три поля. (Или Сервис, Подбор
параметра, в версии 2003)

В
поле Установить в ячейке нужно указать адрес ячейки, в которой будет
получено точное значение первого корня уравнения: В26.

В
поле Значение указывается значение функции для данного корня, т.е. 0.

В
поле Изменяя значений ячейки указывается адрес ячейки, содержащей
приближенное значение корня функции (ссылка на ячейку указывается в абсолютном
формате): $A$26.

После
нажатия на кнопку ОК в ячейке А26 появится точное значение корня
функции.

Нажмите
ОК в окне результата подбора параметра.

13.
Повторяя действия из п. 12 для каждого приближенного значения корня, нужно
получить точные значения второго и третьего корней функции.

Для решения практических задач часто требуется найти экстремум.
Экстремумом является минимальное или максимальное значение функции.

Задача 3: Задана неразрывная функция . Требуется найти ее экстремум
(минимальное значение) на отрезке [-2;2].

Порядок реализации в табличном процессоре

1.
Объедините ячейки А1:С1 и введите текст задания: .

2.
В ячейку А2 введите имя аргумента х. В ячейку В2 введите имя функции у.

3.
В ячейку А3 введите любое значение аргумента, принадлежащее отрезку,
указанному в условии, например: -0,8.

4.
В ячейку В3 введите формулу для нахождения значения функции для значения
аргумента, заданного в ячейке А3: .

5.
Перейдите на вкладку Данные, в группе Анализ выберите кнопку Поиск
решения.

(Или в в версии 2003- Сервис, Поиск решения)

6.
В открывшемся диалоговом окне требуется задать все нужные параметры.

а)
в поле Оптимизировать целевую функцию указана ссылка на ячейку В3 (в
абсолютном формате);

б)
в строке До переключатель должент быть установлен рядом с параметром Минимум;

в)
в поле Изменяя ячейки переменных должна быть указана ссылка на ячеку А3
(в абсолютном формате);

г)
в области с названием В соответствии с ограничениями должны быть указаны
огранияения на значения переменной. Для этого нажмите справа на кнопку Добавить и
запишите первое условие:

Нажмите
кнопку Добавить в окне, указанном выше, и запишите второе условие:

После
чего нажмите кнопку ОК.

Окно
Параметры поиска решения примет вид:

Нажмите
на кнопку Найти решение, после чего в ячейке А3 появится значение
аргумента, при котором функция (формула в ячейке В3) принимает минимальное
значение. Так же будет выведено диалоговое окно с дополнительными сведениями о
полученном результате.

Нажмите
в окне Результаты поиска решения кнопку ОК, чтобы сохранить найденное
решение.

7.
Проверим правильно ли найдено решение задания.

8.
Построим график функции.

С
помощью Правка, Заполнить, Прогрессия , указать шаг, например 0,2, предельное
значение 2 (так как отрезок от -2 до 2) зададим значения х., в ячейке А7,

В
ячейку В7 внесем формулу =степень(А7;2)+А7+2 и скопировать формулу в ячейки
В8:В27

Построим
с помощью мастера диаграмм график функции

9.
Определите с помощью функции МИН минимум в столбце значений функции, и
определите значение аргумента для этого значения функции.

10.
В частном случае при нахождении экстремума на указанном отрезке,
найденное значение может быть не минимумом (максимумом) функции, а просто минимальным
(максимальным) значением на указанном отрезке, т.е. экстремумом являться
не будет. Чтобы проверить, является ли найденное решение экстремумом
функции, необходима дополнительная проверка с помощью вычисления производной
функции. Если производная функции для найденного решения равна нулю, то точка
является экстремумом, а не точкой перегиба функции.

Производная – это отношение малого приращения функции к
малому приращению аргумента. Для вычисления производной нашей функции , выполните следующие шаги:

1)
В ячейку Е2 (лист с поиском экстремума, где
находится значение -0,5) введите значение переменной, отличающееся от
найденного на очень малую величину. Для этого введите в ячейку Е2
формулу: . В ячейку Е3 введите
формулу: . Задайте формат ячеек Е2:Е3
– числовой, число разрядов после запятой: 9.

2)
В ячейку F2 введите формулу . Скопируйте формулу в ячейку F3. Отформатируйте ячейки F2:F3
аналогично тому, как отоформатированы ячейки Е2:Е3.

3)
В ячейку G2 записываем формулу для вычисления производной:

Отформатируйте
ячейку аналогично формату предыдущих: с количеством знаков после запятой 9.

Вывод: производная в указанной точке равна
0, следовательно, найденное значение является экстремальным.

Задача 4: Требуется найти значения аргумента в
диапазоне [-1;1], при которых функция имеет экстремумы.

Математическое решение

— +

-0,5

Уَ(-0,6)=2*(-0,6)+1=-0,2

Уَ(0,5)=2*0,5+1=2

Производная
меняет знак с минуса на плюс, следовательно х=-0,5 у=1,75 – точка минимума

Порядок реализации в табличном процессоре.

.1.Получить
таблицу значений аргумента с шагом 0,1 с помощью Прогрессии .

В ячейки
А1 и В1 внести х и у. В ячейки А2:А22 с помощью Правка, Заполнить,
Прогрессия, с шагом 0,1 заполнить значения х.

2.
Получить таблицу значений функции для всех значений аргумента .

В
ячейку В2 внести формулу =СТЕПЕНЬ(A2;2)+A2+2. С помощью копирования формул
заполнить ячейки В3:В22

3.
Получить таблицу значений функции для всех значений (аргумент+dx) (dx = 0,00000001 – малое приращение
аргумента функции). Для этого в формуле функции вместо значения
аргумента записать аргумент+малое приращение.

В
ячейку С1 внесем обозначение у(х+∆х). В ячейку С2 внесем формулу нахождения
значения функции с приращением 0,00000001. Формула-
=степень(А2+1Е-8;2)+(А2+1Е-8)+2. Ячейки С3:С22 заполним с помощью копирования
формул.

4.
Вычислить значения производной функции как отношение малого приращения
функции к малому приращению аргумента: =(второе значение
функции – первое значение функции)/приращение аргумента.

В
ячейку D1 введем обозначение уَ. В ячейку D2 введем формулу =(C2-B2)/0,00000001- отношение малого приращения
функции к малому приращению аргумента.

5.Анализируя
полученные значения производной функции в точках сетки аргумента, определить, на
каком интервале функция меняет знак. В этом интервале может находиться
точка экстремума. Если производная меняет знак с минуса на плюс, то точка
экстремума является минимумом функции (и наоборот).

При
х=-0,5 и у=1,75 производная равна нулю, следовательно это критическая точка, а
производная меняет знак с “-“ на “+” , следовательно это минимум.

6.
Уточните значение аргумента, при котором производная равна 0, используя
интсрументы MS Excel Подбор параметра или Поиск решения В указанной точке функция принимает
минимальное значение (экстремальное значение).

Уточним
наш ответ с помощью Сервис, Поиск решения, для этого в ячейку А25 внесем любое
значение из отрезка [-1;1], например 0,2, а в ячейку В25 формулу нашей функции

=
степень(А25;2)+А25+2. Выделим ячейку В25 и через Поиск решения установить
целевую ячейку В25, равной минимальному значению, изменяя ячейку А25, с
ограничениями ячека А25<=1 и А25>=1 и выполнить.

сохранить
полученный результат

Построим
график функции и график ее производной

Заключение
            В настоящее время получило всеобщее признание то, что успех
развития многих областей науки и техники существенно зависит от развития многих
направлений математики. Математика становится средством решения проблем
организации производства, поисков оптимальных решений.

Программа

Microsoft Excel – одна из наиболее
практически значимых, востребованных. Электронные таблицы не только позволяют
автоматизировать расчеты, но и являются эффективным средством моделирования
различных вариантов и ситуаций. Меняя значения исходных данных, можно
проследить за изменением получаемых результатов и из множества вариантов
решения задачи выбрать наиболее подходящий.

Литература:
1. Мордкович А.Г . Алгебра и начала анализа 10-11.
М.: Просвещение, 2005

2.Виленкин Н. Л. Функции в природе и технике. – М.: Просвещение,
1978

3. Возняк Г. М., Гусев В. А. Прикладные задачи на экстремумы. М.:
Просвещение, 1985.

4. Информатика и информационные технологии, 10-11 класс. –
Бином Лаборатория знаний, 2005.

Источник

Создание простых

математических моделей с

помощью электронных таблиц

Выполнила:

Мальчук Светлана Викторовна

Оглавление

Введение

1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНФОРМАЦИОННОГО МОДЕЛИРОВАНИЯ

1.1. Классификация моделей.

1.2. Математические модели.

1.3. Основные этапы моделирования.

2. СОЗДАНИЕ ПРОСТЫХ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ С ПОМОЩЬЮ ЭЛЕКТРОННЫХ ТАБЛИЦ

2.1. Общая характеристика электронных таблиц.

2.2. Исследование математических моделей в электронных таблицах.

Заключение

СПИСОК ЛИТЕРАТУРЫ

Введение

Человек издавна использует моделирование для исследования объектов, процессов, явлений в различных областях. Результаты этих исследований служат для определения и улучшения характеристик реальных объектов и процессов; для понимания сути явлений и выработки умения приспосабливаться или управлять ими; для конструирования новых объектов или модернизации старых. Моделирование помогает человеку принимать обоснованные и продуманные решения, предвидеть последствия своей деятельности.

Применение компьютера в качестве нового динамичного, развивающего средства обучения — главная отличительная особенность компьютерного моделирования. Для осуществления математических расчётов и моделирования, как в практической, так и в научной деятельности, используются различные компьютерные программы. Наиболее широко распространены электронные таблицы и такие программы для работы с ними, как MS Excel и OpenOffice.org Calc. Данные программы являются многофункциональными и в то же время довольно простыми для изучения. Хотя на самом деле, в данных программ легко начать работать, а уметь использовать все возможности не так просто. Поэтому целью данной работы является изучение теоретических основ информационного моделирования, создание различных математических моделей и исследование их поведения с помощью электронных таблиц. Исходя из цели работы, были определены следующие задачи:

— Определить понятие модели и познакомиться с основными типами информационных моделей.

— Рассмотреть математические модели объектов или процессов

— Исследовать основные возможности программ MS Excel и OpenOffice.org Calc;

— Строить компьютерные модели в среде электронных таблиц.

1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНФОРМАЦИОННОГО МОДЕЛИРОВАНИЯ

Слово «модель» произошло от латинского слова «modulus», означает «мера», «образец». Его первоначальное значение было связано со строительным искусством и почти во всех европейских языках оно употреблялось для обозначения образа или прообраза, или вещи, сходной в каком-то отношении с другой вещью.

Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области научных знаний: техническое конструирование, строительство и архитектуру, астрономию, физику, химию, биологию и, наконец, общественные науки. Большие успехи и признание практически во всех отраслях современной науки принес методу моделирования XX век. Постепенно стала осознаваться роль моделирования как универсального метода научного познания.

Термин «модель» широко используется различных сферах человеческой деятельности и имеет множество смысловых значений.

Модель — это такой материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале. [2]

Под моделированием понимается процесс построения, изучения и применения моделей. Оно тесно связано с такими категориями, как абстракция, аналогия, гипотеза и др. Процесс моделирования обязательно включает и построение абстракций, и умозаключения по аналогии, и конструирование научных гипотез.

Главная особенность моделирования в том, что это метод опосредованного познания с помощью объектов-заместителей. Модель выступает как своеобразный инструмент познания, который исследователь ставит между собой и объектом, и с помощью которого изучает интересующий его объект. Именно эта особенность метода моделирования определяет специфические формы использования абстракций, аналогий, гипотез, других категорий и методов познания.[2]

В самом общем случае при построении модели исследователь отбрасывает те характеристики, параметры объекта-оригинала, которые несущественны для изучения объекта. Выбор характеристик объекта-оригинала, которые при этом сохраняются и войдут в модель, определяется целями моделирования. Обычно такой процесс абстрагирования от несущественных параметров объекта называют формализацией. Более точно, формализация — это замена реального объекта или процесса его формальным описанием.

Практически во всех науках о природе, живой и неживой, об обществе, построение и использование моделей является мощным орудием познания. Реальные объекты и процессы бывают столь многогранны и сложны, что лучшим (а иногда и единственным) способом их изучения часто является построение и исследование модели, отображающей лишь какую-то грань реальности и потому многократно более простой, чем эта реальность.[5]

1.1. Классификация моделей.

Границы между моделями различных типов или классов, а также отнесение модели к какому-то типу или классу чаще всего условны. Рассмотрим наиболее распространенные признаки, по которым классифицируются модели.

1) Классификация моделей по области использования:

Учебные модели – используются при обучении.

Опытные – это уменьшенные или увеличенные копии проектируемого объекта. Используют для исследования и прогнозирования его будущих характеристик.

Научно-технические — создаются для исследования процессов и явлений.

Игровые – репетиция поведения объекта в различных условиях

Имитационные – отражение реальности в той или иной степени (это метод проб и ошибок).

2) Классификация моделей по фактору времени:

Статические — модели, описывающие состояние системы в определенный момент времени (единовременный срез информации по данному объекту). Примеры моделей: классификация животных, строение молекул, список посаженных деревьев, отчет об обследовании состояния зубов в школе и тд..

Динамические – модели, описывающие процессы изменения и развития системы (изменения объекта во времени). Примеры: описание движения тел, развития организмов, процесс химических реакций.

3) Классификация моделей по отрасли знаний — это классификация по отрасли деятельности человека:

Математические, биологические, химические, социальные, экономические, исторические и т.д..

4) Классификация моделей по форме представления:

Материальные – это предметные (физические) модели. Они всегда имеют реальное воплощение. Отражают внешнее свойство и внутреннее устройство исходных объектов, суть процессов и явлений объекта-оригинала. Это экспериментальный метод познания окружающей среды. Примеры: детские игрушки, скелет человека, чучело, макет солнечной системы, школьные пособия, физические и химические опыты

Абстрактные (нематериальные) – не имеют реального воплощения. Их основу составляет информация. Это теоретический метод познания окружающей среды. По признаку реализации они бывают: мысленные и вербальные; информационные.

Мысленные модели формируются в воображении человека в результате раздумий, умозаключений, иногда в виде некоторого образа. Это модель сопутствует сознательной деятельности человека.

Вербальные – мысленные модели, выраженные в разговорной форме. Используются для передачи мыслей.

Информационные модели – целенаправленно отобранная информация об объекте, которая отражает наиболее существенные для исследователя свойств этого объекта.

По степени формализации информационные модели бывают:

Образно-знаковые: геометрические (рисунок, пиктограмма, чертеж, карта, план, объемное изображение); структурные (таблица, граф, схема, диаграмма); словесные (описание естественными языками); алгоритмические (нумерованный список, пошаговое перечисление, блок-схема).

Знаковые модели: математические – представлены математическими формулами, отображающими связь параметров; специальные – представлены на спец. языках (ноты, химические формулы); алгоритмические – программы.[2]

1.2. Математические модели.

Широко распространенным видом моделирования является математическое моделирование. Математическая модель отражает существенные свойства объекта или процесса языком уравнений и других математических средств. Математическое моделирование стало чрезвычайно мощным средством познания в естественных, технических и социальных науках, экономике, многих видах практической деятельности, и заслуживает углубленного изучения.

Нужно отметить, что математическое моделирование, являющееся основой компьютерного моделирования, появилось задолго до создания компьютеров. Однако возможности компьютеров позволили ученым моделировать сложные динамические явления природы, а также сложные экономические и социальные процессы. Цель создания компьютерной математической модели — проведение численного эксперимента, позволяющего исследовать моделируемую систему, спрогнозировать ее поведение, подобрать оптимальные параметры и пр.[7]

Характерные признаки компьютерной математической модели:

• наличие реального объекта моделирования;

• наличие количественных характеристик объекта: входных и выходных параметров;

• наличие математической связи между входными и выходными параметрами;

• реализация модели с помощью определенных компьютерных средств.

1.3. Основные этапы моделирования.

Моделирование — творческий процесс. Заключить его в формальные рамки очень трудно. В наиболее общем виде его можно представить поэтапно в следующем виде.

рис. 1 Этапы моделирования

Каждый раз при решении конкретной задачи такая схема может подвергаться некоторым изменениям: какой-то блок может быть убран или усовершенствован. Все этапы определяются поставленной задачей и целями моделирования.[3]

I этап. Постановка задачи

Под задачей в самом общем смысле понимается некая проблема, которую надо решить. Главное — определить объект моделирования и понять, что собой должен представлять результат.

По характеру постановки все задачи можно разделить на две основные группы. К первой группе можно отнести задачи, в которых требуется исследовать, как изменяется характеристика объекта при некотором воздействии на него. Такую постановку задачи принято называть “что будет, если…”. Вторая группа задач имеет такую обобщенную формулировку: какое надо произвести воздействие на объект, чтобы его параметры удовлетворяли некоторому заданному условию? Такая постановка задачи часто называется “как сделать, чтобы…”.

Цели моделирования определяются расчетными параметрами модели. Чаще всего это поиск ответа на вопрос, поставленный в формулировке задачи.

Далее переходят к описанию объекта или процесса. Иногда задача может быть уже сформулирована в упрощенном виде, и в ней четко поставлены цели и определены параметры модели, которые надо учесть.

При анализе объекта необходимо ответить на следующий вопрос: можно ли исследуемый объект или процесс рассматривать как единое целое или же это система, состоящая из более простых объектов? Если это единое целое, то можно перейти к построению информационной модели. Если система — надо перейти к анализу объектов, ее составляющих, определить связи между ними.

II этап. Разработка модели

По результатам анализа объекта составляется информационная модель. В ней детально описываются все свойства объекта, их параметры, действия и взаимосвязи.

Далее информационная модель должна быть выражена в одной из знаковых форм. Учитывая, что мы будем работать в среде электронных таблиц, то информационную модель необходимо преобразовать в математическую. На основе информационной и математической моделей составляется компьютерная модель в форме таблиц, в которой выделяются три области данных: исходные данные, промежуточные расчеты, результаты. Исходные данные вводятся “вручную”. Расчеты, как промежуточные, так и окончательные, проводятся по формулам, записанным по правилам электронных таблиц.

III этап. Компьютерный эксперимент

Чтобы дать жизнь новым конструкторским разработкам, внедрить новые технические решения в производство или проверить новые идеи, нужен эксперимент. В недалеком прошлом такой эксперимент можно было провести либо в лабораторных условиях на специально создаваемых для него установках, либо на натуре, т.е. на настоящем образце изделия, подвергая его всяческим испытаниям. Это требует больших материальных затрат и времени. В помощь пришли компьютерные исследования моделей. При проведении компьютерного эксперимента проверяют правильность построения моделей. Изучают поведение модели при различных параметрах объекта. Каждый эксперимент сопровождается осмыслением результатов. Если результаты компьютерного эксперимента противоречат смыслу решаемой задачи, то ошибку надо искать в неправильно выбранной модели или в алгоритме и методе ее решения. После выявления и устранения ошибок компьютерный эксперимент повторяется.

IV этап. Анализ результатов моделирования

Заключительный этап моделирования — анализ модели. По полученным расчетным данным проверяется, насколько расчеты отвечают нашему представлению и целям моделирования. На этом этапе определяются рекомендации по совершенствованию принятой модели и, если возможно, объекта или процесса.[4]

2. СОЗДАНИЕ ПРОСТЫХ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ С ПОМОЩЬЮ ЭЛЕКТРОННЫХ ТАБЛИЦ

Электронные таблицы (или табличные процессоры) — это прикладные программы, предназначенные для проведения табличных расчётов. Данное средство информационных технологий, позволяет решать целый комплекс задач, и прежде всего, выполнение вычислений. Многие расчёты выполняются в табличной форме, особенно в области делопроизводства: многочисленные расчётные ведомости, сметы расходов и т. д. Кроме того, в табличной форме удобно выполнять решение численными методами целого ряда математических задач. Электронные таблицы (ЭТ) являются удобным инструментом для автоматизации таких вычислений. Решения многих вычислительных задач на ЭВМ, которые раньше можно было осуществить только путём программирования, стало возможным осуществлять с помощью электронных таблиц. Использование математических формул в ЭТ позволяет представить взаимосвязь между различными параметрами некоторой реальной системы. Основное свойство ЭТ — мгновенный пересчёт значений рассчитываемых показателей при изменении входящих данных. Благодаря этому свойству, таблица представляет собой удобный инструмент для организации численного эксперимента.[7]

Дополнительные удобства для моделирования даёт возможность графического представления данных (диаграммы), а также возможность использования электронной таблицы в качестве базы данных. Электронные таблицы просты в обращении, значительно упрощают и ускоряют работу.

2.1. Общая характеристика электронных таблиц.

В настоящее время наиболее распространённая программа для работы с электронными таблицами — MS Excel, которая является составной частью пакета MS Office. Широкое распространение получил и пакет OpenOffice.org, в том числе и его составляющая для работы с электронными таблицами Calc. Данные пакеты программ, в том числе и для работы с электронными таблицами, имеют схожие возможности. [1]

Электронная таблица в MS Excel и OpenOffice.org Calc (рабочий лист) — это множество элементарных ячеек, каждая из которых имеет адрес, определяемый координатами по вертикали (столбцы) и горизонтали (строки). Столбцы рабочего листа именуются, а строки нумеруются. (рис.2)

Каждый документ в MS Excel называется рабочей книгой и состоит из нескольких рабочих листов. Книга в MS Excel представляет собой файл с расширением .xls (и xlsx в версии 2007 года), предназначенный для хранения и обработки данных. В OpenOffice.org Calc рабочие книги можно сохранять в виде файлов с различными расширениями (основным расширением файла является .ods). Данная программа открывает файлы созданные в MS Excel (с расширениями .xls и .xlsx) и возможно сохранение файлов с расширением .xls, то есть такие файлы можно открывать и редактировать в MS Excel. В свою очередь, файлы с расширением .ods в программе MS Excel открывать и редактировать нельзя. [6].

Рис. 2 Внешний вид главного окна OOCalc

Для ввода данных в программах MS Excel и OpenOffice.org Calc нужно выбрать ячейку и ввести то, что требуется. Набираемые данные отображаются в ячейке и в строке ввода, которая особенно полезна с учётом того, что ячейка может содержать больше символов, чем позволяет отобразить её текущая ширина. В ячейку можно вводить числовые значения, текст, а также дату и время. Причём можно выбирать формат ячеек (числовой, текстовой, формат даты и времени). Если текст начинается со знака «=», то он не отображается в ячейке, поскольку эти программы считают такой текст формулой. Если нужно напечатать текст, начинающийся со знака «=», то необходимо самым первым символом поставить знак одинарной кавычки. Если есть необходимость начать строку со знака кавычки, то необходимо напечатать кавычку два раза.

Основными возможностями программ MS Excel и OpenOffice.org Calc являются: вычисления с помощью формул, вводимых в ячейки; использование встроенных функций, построение диаграмм и графиков.[1]

В OOCalc и MS Excel доступны следующие основные арифметические операции:

«+» – сложение;

«-» – вычитание;

«*» – умножение;

«/» – деление;

«^» – возведение в степень;

«:» – задание диапазона.

Кроме этих операций, в этих программах доступен обширный набор функций следующих категорий:

● работа с базами данных;

● обработка времени и дат;

● финансовые;

● информационные;

● логические;

● математические;

● работа с массивами;

● статистические;

● текстовые;

● дополнительные [5].

Для удобства написания формул в OOCalc и MS Excel используется Мастер функций. В OOCalc кнопка «Мастер функций» находится слева от строки ввода.

Рис. 3 Мастер функций в программе OOCalc

В программах OOCalc и MS Excel можно вставлять диаграммы и графики вычислений. Для этого надо выделить столбцы со значениями, например, выделяются два столбца A и B. В программе в программе OOCalc из меню (или панели инструментов) выбирается пункт «Вставка — Диаграмма». Необходимо выбрать тип диаграммы:

Двумерные диаграммы:

● линии;

● с областями;

● гистограмма;

● линейчатая;

● круговая;

● диаграмма XY;

● сетчатая;

● биржевая.

Трехмерные диаграммы

● график 3М;

● с областями 3М;

● гистограмма 3М;

● линейчатая 3М;

● круговая 3М.

Перечисленные возможности программ OOCalc и MS Excel являются востребованными и часто используются при математическом моделировании.

2.2. Исследование математических моделей в электронных таблицах.

Задача 1. Необходимо покрасить краской стены кухни. Сколько потребуется банок краски, если известно, что размеры кухни 405 × 310 × 285 см; 88% площади стен занимает кафельная плитка; 1 банка краски предназначена для покраски площади 5 м2?

I этап. Постановка задачи.

Описание задачи.

a = 405 см – длина комнаты,
b = 310 см – ширина комнаты,
c = 285 см – высота комнаты,
1 – 0,88 = 0,12 – часть комнаты для покраски (без кафеля),
5 м2 – площадь покраски при использовании 1 банки краски.

Цель моделирования. Определить необходимое количество краски.

Формализация задачи в виде поиска ответов на вопросы.

Таблица 1. Формализация задачи 1

Что моделируется?

Система, состоящая из двух объектов: комнаты и краски.

Форма комнаты?

Прямоугольная.

Что известно о комнате?

Размеры задаются длиной (а), шириной (b), высотой (с).

Как учитывается окрашиваемая поверхность?

88% не окрашивается, следовательно, можно рассчитать процент окрашиваемой поверхности.

Что известно о краске?

1 банка предназначена для покраски 5 м2.

Можно ли купить часть банки с краской?

Нет. Количество банок с краской должно быть целым.

Что надо определить?

Необходимое количество банок с краской.

II этап. Разработка модели.

Информационная модель.

Таблица 2. Информационная модель задачи 1

Краска

Наименование образцов

Площадь покраски при использовании 1 банки (S1 банка)

Исходные данные

Расчетные данные

Комната

Длина (а)

Ширина (b)

Высота (с)

Неокрашиваемая поверхность (Sстен с кафелем)

Площадь стен (Sстен для покраски.)

Исходные данные

Рекомендуется 88%

Расчетные данные

Система

Количество банок (К)

Результаты

Дополним информационную модель в табличной форме математической моделью. Sстен с кафелем =2(a + b)c; Sстен для покраски = 2(a + b)c * 0,12.

Чтобы определить, сколько потребуется банок краски, надо площадь для покраски разделить на 5 м2, т. е. Sстен для покраски /5 и результат округлить до целых.

На основе информационной и математической моделей составляется компьютерная модель. Заносим данные задачи в электронную таблицу, вводим формулы.

Рис. 4 Электронная таблица в режиме отображения формул

Рис. 5 Электронная таблица в режиме отображения значений

III этап. Компьютерный эксперимент.

Проведем расчет количества банок краски, необходимых для покраски стен кухни.
Изменим данные (1 банку краски хватит на 2 м2, 1 м2, 3 м2, 0,5 м2) и проследим за пересчетом результатов.

IV этап. Анализ результатов. С помощью MS Excel мы определили, что для покраски стен кухни необходима 1 банка краски. Можно также определить, сколько краски понадобится, если размер кухни будет иным или 1 банку краски хватит на иную площадь.

Задача 2. Площадь прямоугольника 64 см2. Какую длину должны иметь его стороны, чтобы периметр был наименьшим?

I этап. Постановка задачи.

Описание задачи.

a – длина прямоугольника,
b – ширина прямоугольника,
S=64 см2 — площадь прямоугольника,
P – периметр прямоугольника.
Цель моделирования. Определить длину каждой стороны прямоугольника, чтобы периметр был наименьшим.

Формализация задачи в виде поиска ответов на вопросы.

Таблица 3. Формализация задачи 2

Что моделируется?

Фигура, состоящая из двух объектов: ширины и длины.

Форма фигуры?

Прямоугольная.

Что известно о фигуре?

Размеры задаются длиной (а), шириной (b), площадью (S), периметром (Р).

В какой зависимости находятся объекты в фигуре?

Площадь равна произведению длины и ширины.

Периметр – сумма длин всех сторон.

Что известно о площади?

Площадь – величина постоянная, S=64см2.

Что известно о периметре?

Периметр должен быть наименьшим возможным.

Что надо определить?

Длины сторон прямоугольника при наименьшем периметре.

II этап. Разработка модели.

Информационная модель.

Таблица 4. Информационная модель задачи 2

Длина

Размер (a)

Результаты

Ширина

Размер (b)

Расчетные данные

Площадь

Произведение длины и ширины (S)

Исходные данные, в задаче константа

Периметр

Периметр – сумма длин всех сторон.

Расчетные данные

Дополним информационную модель в табличной форме математической моделью. Sпрям. =a*b; Pпрям.= 2(a + b). Чтобы определить размер длины, нужно площадь прямоугольника разделить на размер ширины, т. е. b=S/a.

На основе информационной и математической моделей составляется компьютерная модель. Заносим данные задачи в электронную таблицу, вводим формулы. В ячейке B3 (значение длины) будет подбираться значение, поэтому ничего не вводим. В ячейку B4 вводим формулу для вычисления ширины, в ячейку B5 – для вычисления площади, в ячейку B6 – для вычисления периметра.

Рис. 6 Электронная таблица в режиме отображения формул

III этап. Компьютерный эксперимент.

Установив курсор в ячейке со значением периметра B6, который по условию должен быть наименьшим, в «Сервис – Поиск решений», установим целевую ячейку $B$6 равной минимальному значению, изменяя ячейки $B$3
Изменим данные (пусть площадь будет равна 36 см2, 100 см2, 150 см2) и проследим за пересчетом результатов.

IV этап. Анализ результатов. С помощью MS Excel мы определили, что, если площадь прямоугольника равна 64 см2, стороны будут равны 8 см, периметр в этом случае будет наименьшим.

Задача 3. У маленького Васи есть небольшой бассейн во дворе. Иногда Вася ходит к речке и приносит воду в бассейн в небольшой цистерне цилиндрической формы. Известны ширина — 4,3 м, высота – 2 м, длина — 5,8 м бассейна и объем цистерны 4,5 м3. Сколько раз Васе нужно сходить к речке за водой, чтобы наполнить бассейн наполовину?

I этап. Постановка задачи.

Описание задачи.

ДБ – длина бассейна,
ШБ – ширина бассейна,

ВБ – высота бассейна,
ОбЦ – объём цистерны.
Цель моделирования. Определить количество походов к реке за водой, чтобы наполнить бассейн наполовину.

Формализация задачи в виде поиска ответов на вопросы.

Таблица 5. Формализация задачи 3

Что моделируется?

Система, состоящая из бассейна и воды.

Форма бассейна?

Параллелепипед.

Что известно о бассейне?

Размеры бассейна задаются длиной (ДБ), шириной (ШБ), высотой (ВБ).

Как учитывается заполняемое водой пространство?

Бассейн должен быть заполнен наполовину.

Что надо знать о воде?

Ее приносят в бассейн цистерной в форме цилиндра.

Что надо определить?

Сколько раз (N) нужно сходить к речке за водой, чтобы наполнить бассейн наполовину?

II этап. Разработка модели.

Информационная модель.

Таблица 6. Информационная модель задачи 3

Вода

Объем цистерны (ОбЦ)

Исходные данные

Расчетные данные

Бассейн

Длина (ДБ)

Ширина (ШБ)

Высота (ВБ)

Объем бассейна (ОБ)

Исходные данные

Расчетные данные

Система

Количество походов за водой (N)

Результаты

Дополним информационную модель в табличной форме математической моделью. ОБб=ДБ*ВБ*ШБ. Чтобы определить, сколько раз нужно сходить к речке за водой, чтобы наполнить бассейн наполовину, нужно объем бассейна разделить на объем цистерны и разделить на 2, т. е. N= ОБб/ОБЦ/2. Данный результат, скорее всего, будет представлен десятичной дробью. Округляем его до целых. На основе информационной и математической моделей составляется компьютерная модель. Заносим данные задачи в электронную таблицу, вводим формулы.

Рис. 7 Электронная таблица в режиме отображения формул

III этап. Компьютерный эксперимент.

Изменим данные, проследим за пересчетом результатов.

Таблица 7. Изменение параметров задачи 3

№ эксперимента

Длина бассейна

Ширина бассейна

Высота бассейна

Объем цистерны

Объем бассейна

Количество походов за водой

5,8 м

4,3 м

2 м

4,5 м3

49,88 м3

6 раз

5,8 м

3 м

2 м

4,5 м3

34,8 м3

4 раза

5,8 м

3 м

1 м

4,5 м3

17,4 м3

2 раза

4 м

3 м

1 м

4,5 м3

12 м3

2 раза

4 м

3 м

1 м

3 м3

12 м3

2 раза

IV этап. Анализ результатов. Полученная модель позволяет пересчитывать количество походов за водой для наполнения бассейна при изменении каких-либо параметров (ширина, длина, высота бассейна, объем цистерны).

Заключение

В процессе написания курсовой работы была изучена литература, связанная с теоретическими основами моделирования. Дано определение понятию модели, приведена классификация различных моделей, исследованы основные возможности программ MS Excel и OpenOffice.org Calc. Также рассмотрены математические модели и исследовано их поведения с помощью электронных таблиц.

Тема, освещённая в данной работе, актуальна, т.к. понятие модели – фундаментальное понятие информатики. Оно проходит через весь курс информатики, изучаемой в школе. В процессе познания окружающего мира человечество постоянно использует моделирование и формализацию. Очень часто формализованная модель выражается с помощью математических формул, т.е. математическая модель – одна из наиболее используемых.
Основной инструмент при создании и исследовании моделей – компьютер. Прикладные программы помогают быстро и надёжно исследовать созданные модели и представлять наглядный результат.

Работа может быть использована на уроках информатики. Модели и методы их обработки создаются новые, поэтому тема в дальнейшем может быть дополнена.

СПИСОК ЛИТЕРАТУРЫ

Microsoft Excel. [Википедия] (01.12.12), /http://ru.wikipedia.org/wiki/Microsoft_Excel
Гейн А. Г., Информатика. 7-9 класс: Учебник для общеобразовательных учреждений. — 8-е изд., стер. — М.: Дрофа, 2005. — 240с.: ил.
Макарова Н. В. Информатика. 7-9 класс. Базовый курс. Задачник по моделированию. – СПб.: Питер, 2007. – 176 с.: ил.
Макарова Н. В. Информатика. 7–9 класс. Базовый курс. Учебник. – СПб.: Питер, 2008. — 288с.: ил.
Семакин И. Г, Залогова Л. А, Русаков С. В, Шестакова Л. В. Информатика. Базовый курс. 7–9 классы– 4-е издание. М.:БИНОМ. Лаборатория знаний, 2009. – 390 с.: ил.

Табличный процессор. [Википедия] (01.12.12), /http://ru.wikipedia.org/wiki/Табличный_ процессор
Церенова О. А. Математическое моделирование: Пособие для учителя. — Пермь: Перм. гос. пед. ун-т, 1995. — 259с.

Источник