Содержание
- Применение математических функций
- СУММ
- СУММЕСЛИ
- ОКРУГЛ
- ПРОИЗВЕД
- ABS
- СТЕПЕНЬ
- КОРЕНЬ
- СЛУЧМЕЖДУ
- ЧАСТНОЕ
- РИМСКОЕ
- Вопросы и ответы
Чаще всего среди доступных групп функций пользователи Экселя обращаются к математическим. С помощью них можно производить различные арифметические и алгебраические действия. Их часто используют при планировании и научных вычислениях. Узнаем, что представляет собой данная группа операторов в целом, и более подробно остановимся на самых популярных из них.
Применение математических функций
С помощью математических функций можно проводить различные расчеты. Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.
Открыть список математических формул можно несколькими путями. Проще всего запустить Мастер функций, нажав на кнопку «Вставить функцию», которая размещена слева от строки формул. При этом нужно предварительно выделить ячейку, куда будет выводиться результат обработки данных. Этот метод хорош тем, что его можно реализовать, находясь в любой вкладке.
Также можно запустить Мастер функций, перейдя во вкладку «Формулы». Там нужно нажать на кнопку «Вставить функцию», расположенную на самом левом краю ленты в блоке инструментов «Библиотека функций».
Существует и третий способ активации Мастера функций. Он осуществляется с помощью нажатия комбинации клавиш на клавиатуре Shift+F3.
После того, как пользователь произвел любое из вышеуказанных действий, открывается Мастер функций. Кликаем по окну в поле «Категория».
Открывается выпадающий список. Выбираем в нем позицию «Математические».
После этого в окне появляется список всех математических функций в Excel. Чтобы перейти к введению аргументов, выделяем конкретную из них и жмем на кнопку «OK».
Существует также способ выбора конкретного математического оператора без открытия главного окна Мастера функций. Для этого переходим в уже знакомую для нас вкладку «Формулы» и жмем на кнопку «Математические», расположенную на ленте в группе инструментов «Библиотека функций». Открывается список, из которого нужно выбрать требуемую формулу для решения конкретной задачи, после чего откроется окно её аргументов.
Правда, нужно заметить, что в этом списке представлены не все формулы математической группы, хотя и большинство из них. Если вы не найдете нужного оператора, то следует кликнуть по пункту «Вставить функцию…» в самом низу списка, после чего откроется уже знакомый нам Мастер функций.
Урок: Мастер функций в Excel
СУММ
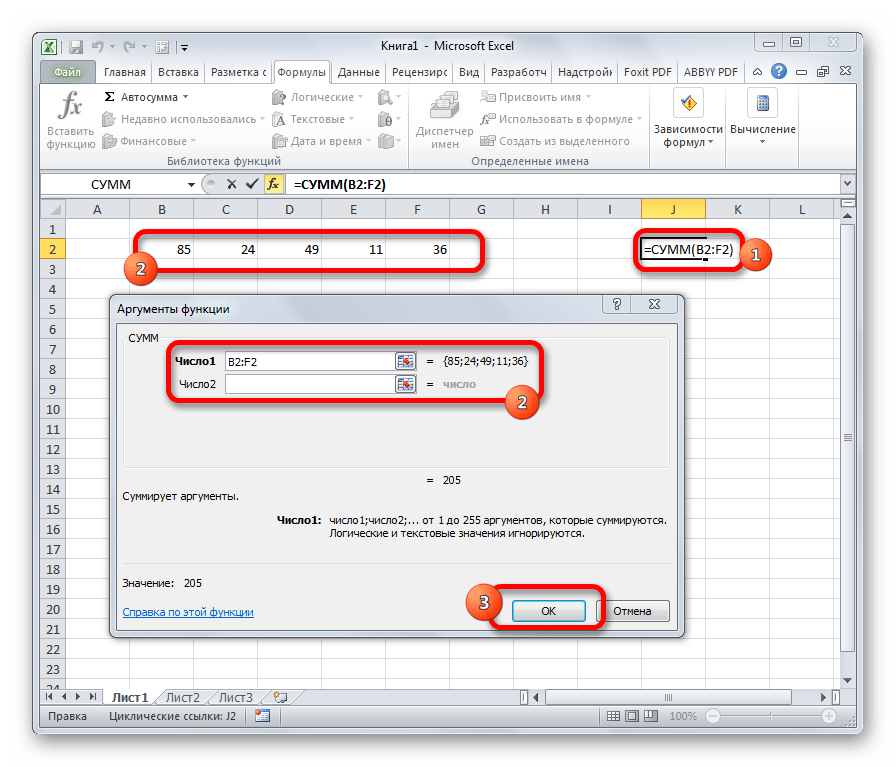
Наиболее часто используется функция СУММ. Этот оператор предназначен для сложения данных в нескольких ячейках. Хотя его можно использовать и для обычного суммирования чисел. Синтаксис, который можно применять при ручном вводе, выглядит следующим образом:
=СУММ(число1;число2;…)
В окне аргументов в поля следует вводить ссылки на ячейки с данными или на диапазоны. Оператор складывает содержимое и выводит общую сумму в отдельную ячейку.
Урок: Как посчитать сумму в Экселе
СУММЕСЛИ
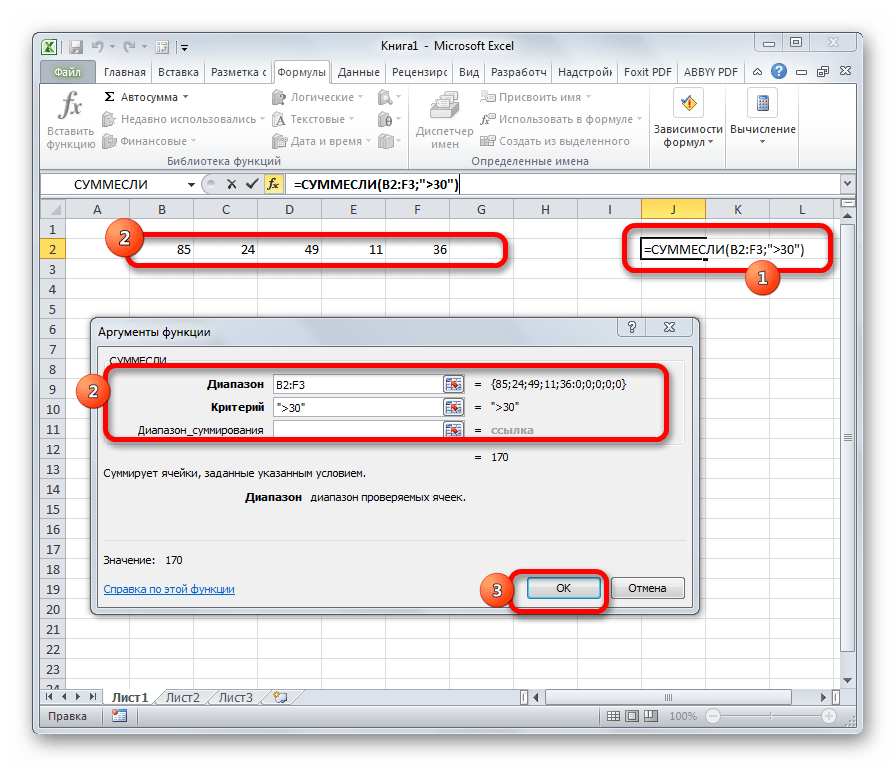
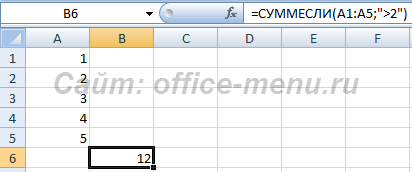
Оператор СУММЕСЛИ также подсчитывает общую сумму чисел в ячейках. Но, в отличие от предыдущей функции, в данном операторе можно задать условие, которое будет определять, какие именно значения участвуют в расчете, а какие нет. При указании условия можно использовать знаки «>» («больше»), «<» («меньше»), «< >» («не равно»). То есть, число, которое не соответствует заданному условию, во втором аргументе при подсчете суммы в расчет не берется. Кроме того, существует дополнительный аргумент «Диапазон суммирования», но он не является обязательным. Данная операция имеет следующий синтаксис:
=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)
ОКРУГЛ
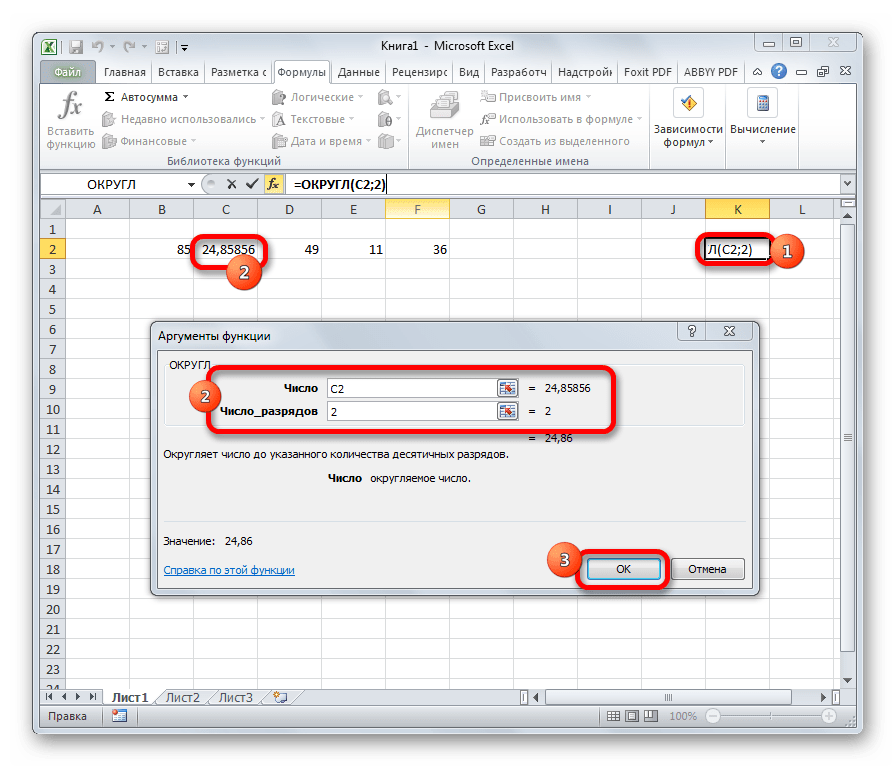
Как можно понять из названия функции ОКРУГЛ, служит она для округления чисел. Первым аргументом данного оператора является число или ссылка на ячейку, в которой содержится числовой элемент. В отличие от большинства других функций, у этой диапазон значением выступать не может. Вторым аргументом является количество десятичных знаков, до которых нужно произвести округление. Округления проводится по общематематическим правилам, то есть, к ближайшему по модулю числу. Синтаксис у этой формулы такой:
=ОКРУГЛ(число;число_разрядов)
Кроме того, в Экселе существуют такие функции, как ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые соответственно округляют числа до ближайшего большего и меньшего по модулю.
Урок: Округление чисел в Excel
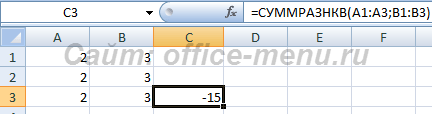
ПРОИЗВЕД
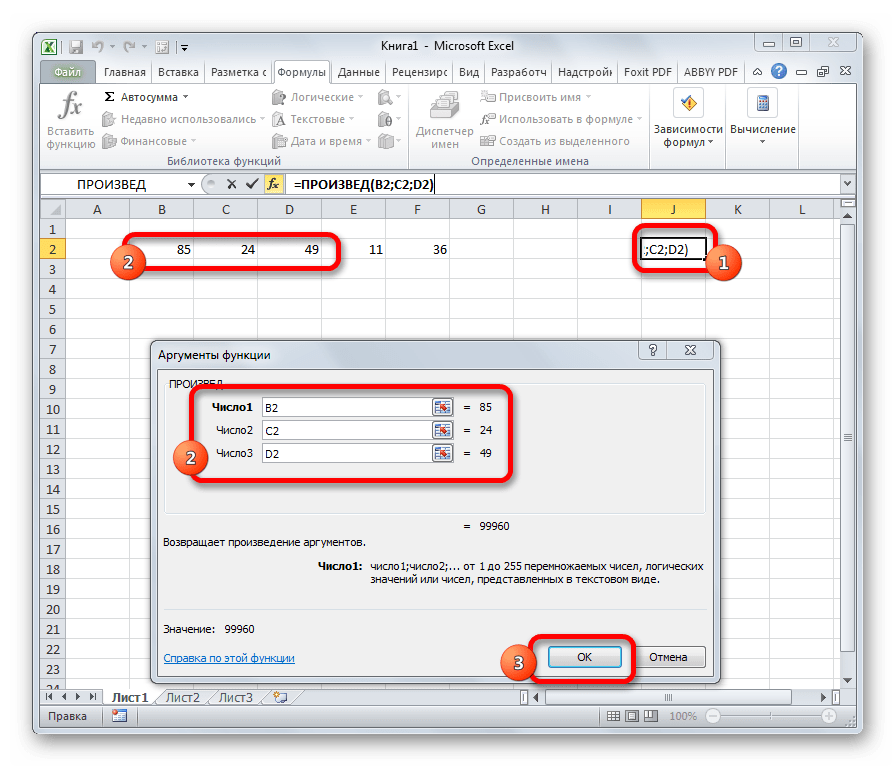
Задачей оператора ПРИЗВЕД является умножение отдельных чисел или тех, которые расположены в ячейках листа. Аргументами этой функции являются ссылки на ячейки, в которых содержатся данные для перемножения. Всего может быть использовано до 255 таких ссылок. Результат умножения выводится в отдельную ячейку. Синтаксис данного оператора выглядит так:
=ПРОИЗВЕД(число;число;…)
Урок: Как правильно умножать в Excel
ABS
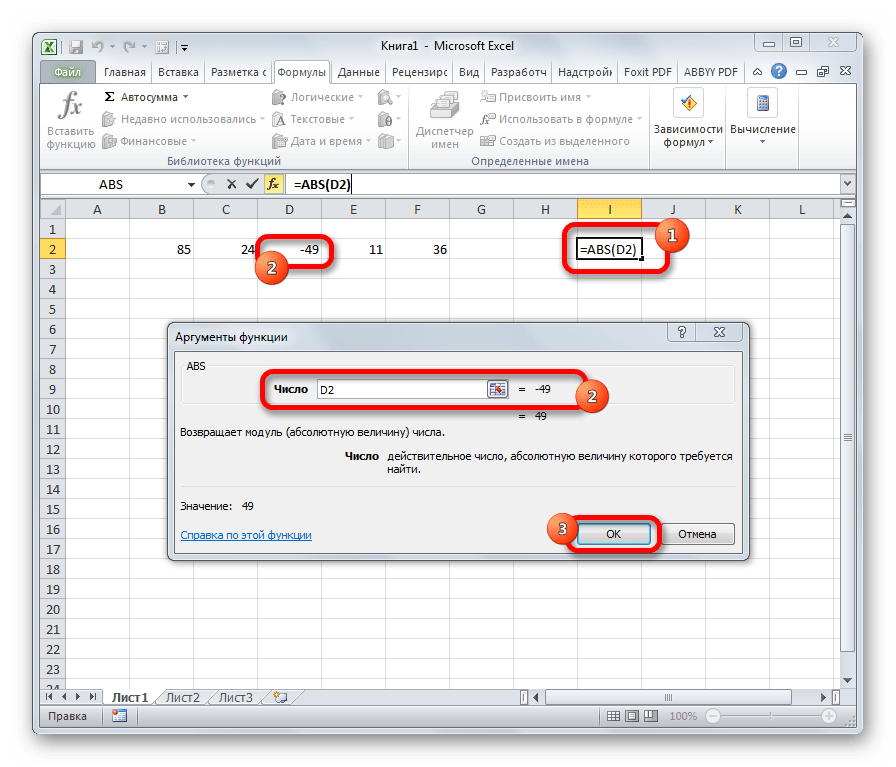
С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:
=ABS(число)
Урок: Функция модуля в Excel
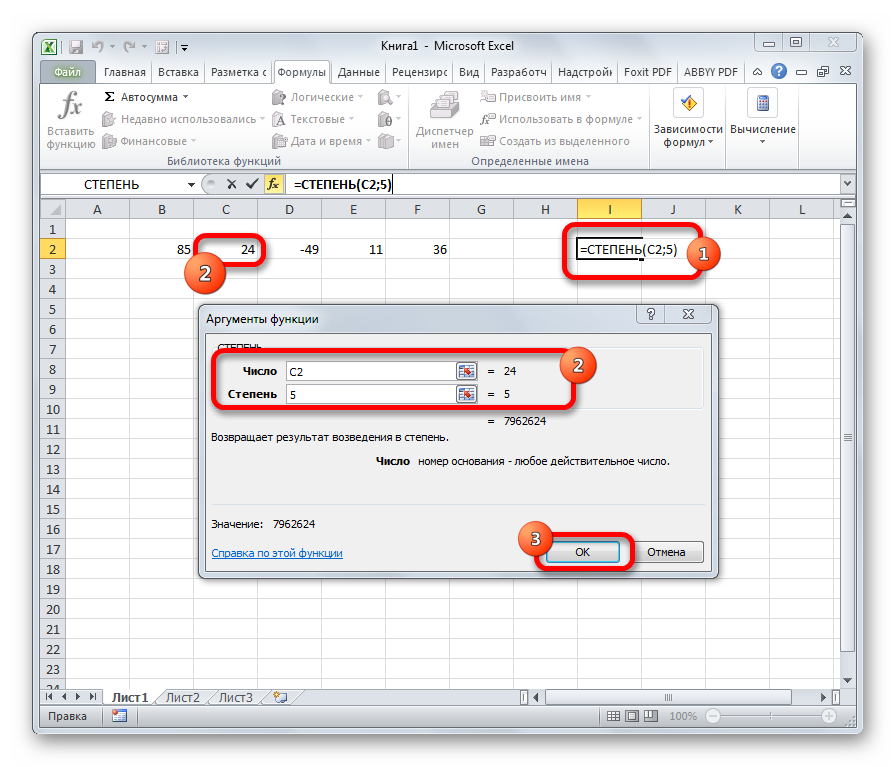
СТЕПЕНЬ
Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:
=СТЕПЕНЬ(число;степень)
Урок: Как возводить в степень в Экселе
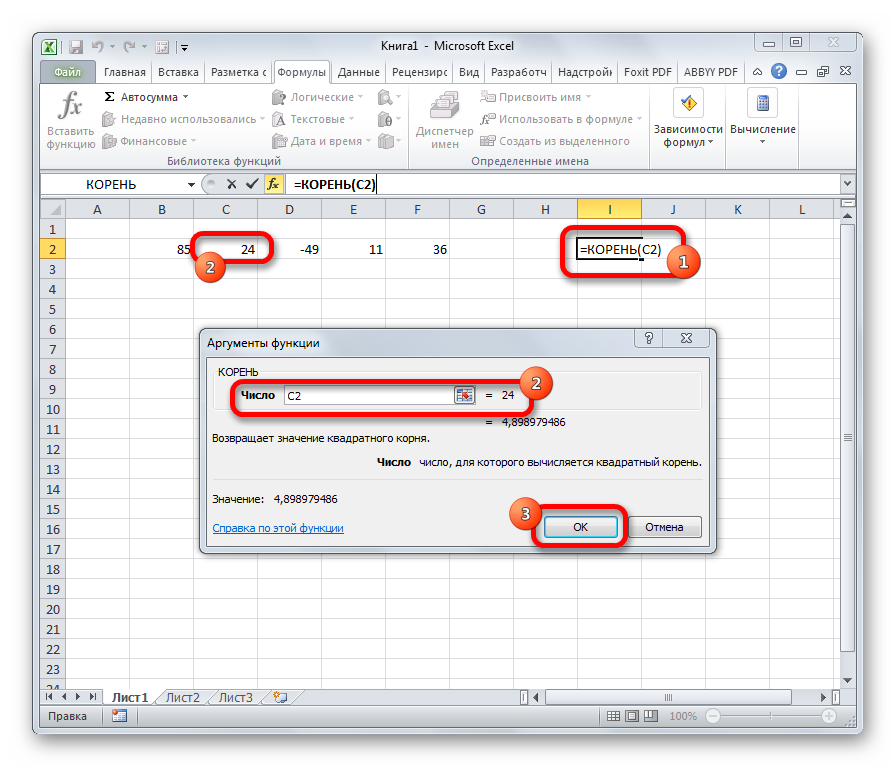
КОРЕНЬ
Задачей функции КОРЕНЬ является извлечение квадратного корня. Данный оператор имеет только один аргумент – «Число». В его роли может выступать ссылка на ячейку, содержащую данные. Синтаксис принимает такую форму:
=КОРЕНЬ(число)
Урок: Как посчитать корень в Экселе
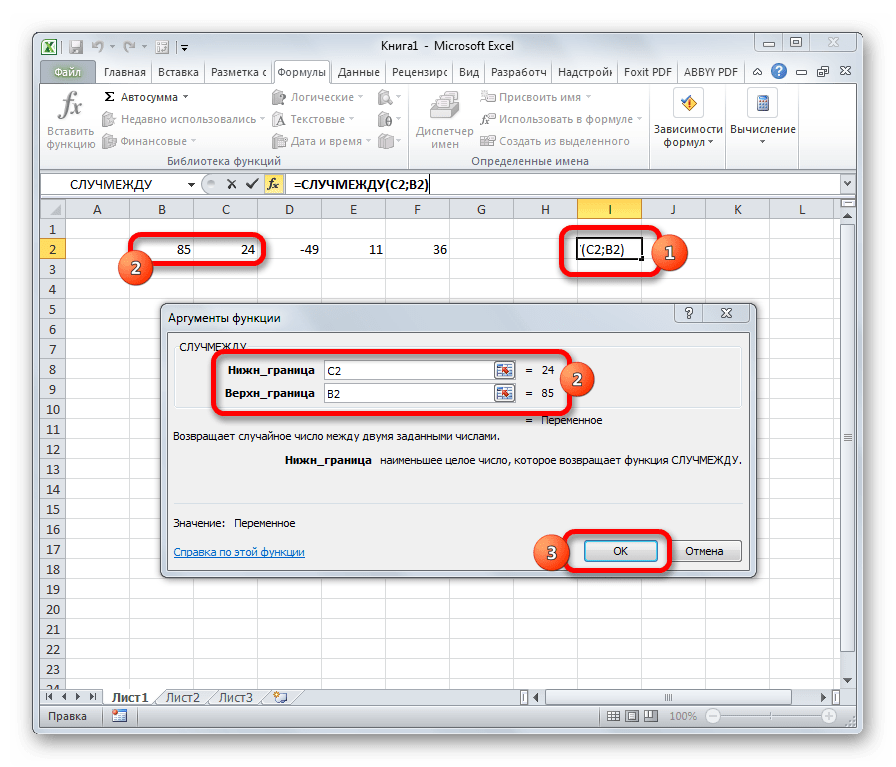
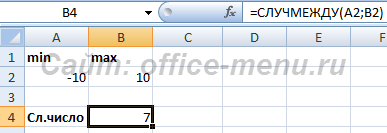
СЛУЧМЕЖДУ
Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:
=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)
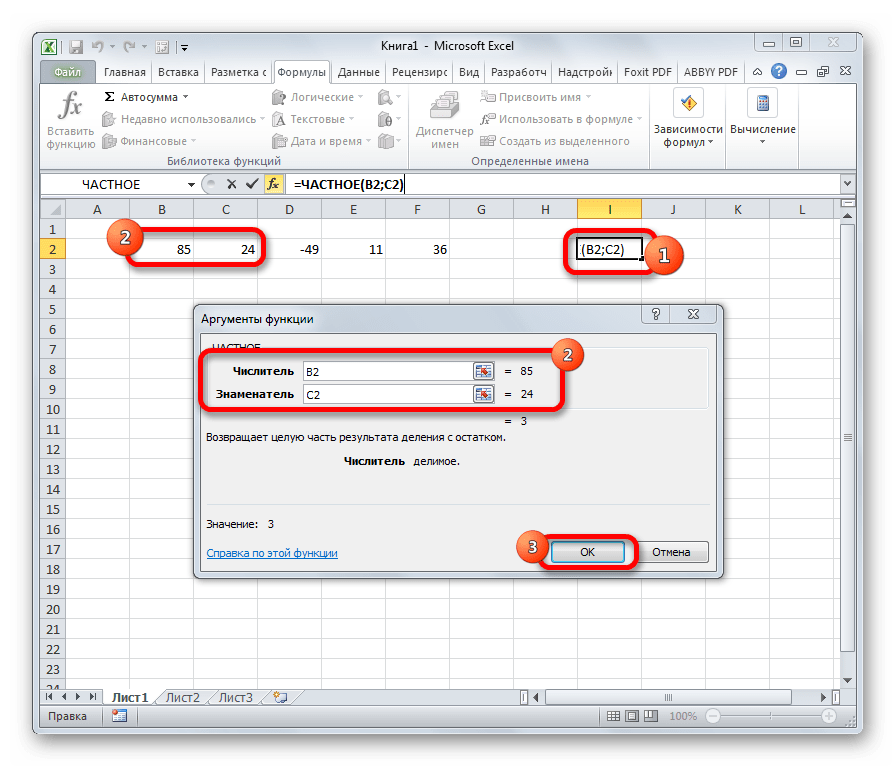
ЧАСТНОЕ
Оператор ЧАСТНОЕ применяется для деления чисел. Но в результатах деления он выводит только четное число, округленное к меньшему по модулю. Аргументами этой формулы являются ссылки на ячейки, содержащие делимое и делитель. Синтаксис следующий:
=ЧАСТНОЕ(Числитель;Знаменатель)
Урок: Формула деления в Экселе
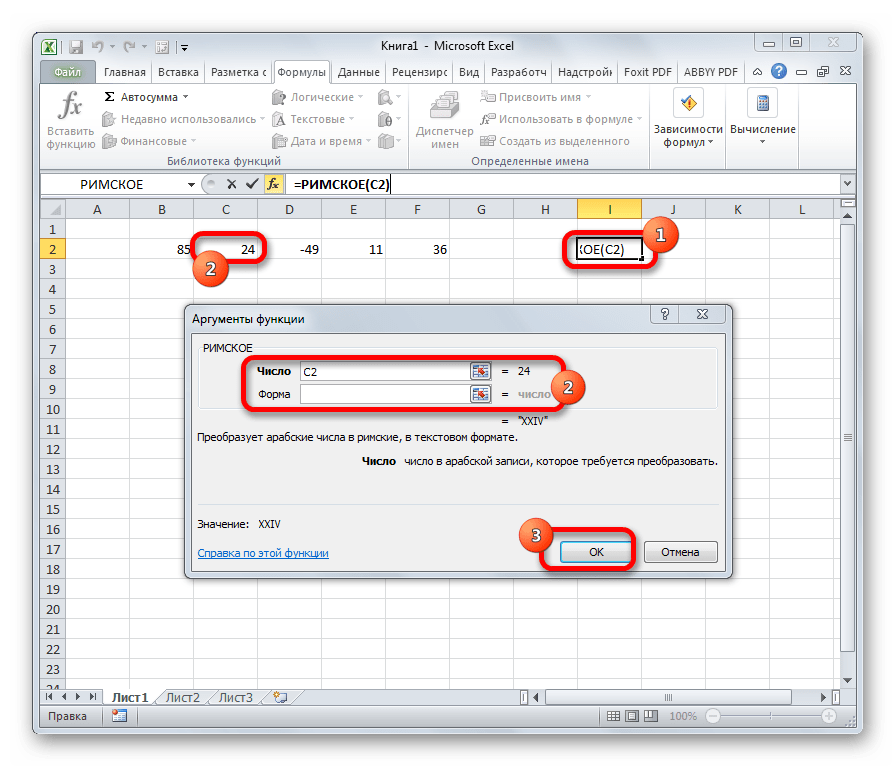
РИМСКОЕ
Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:
=РИМСКОЕ(Число;Форма)
Выше были описаны только наиболее популярные математические функции Эксель. Они помогают в значительной мере упростить различные вычисления в данной программе. При помощи этих формул можно выполнять как простейшие арифметические действия, так и более сложные вычисления. Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.
Если вы не знакомы с Excel в Интернете, скоро вы обнаружите, что это не просто сетка, в которую вы вводите числа в столбцах или строках. Да, можно использовать Excel в Интернете для поиска итогов по столбцу или строке чисел, но можно также вычислить платеж по кредиту, решить математические или технические задачи или найти оптимальный сценарий на основе переменных чисел, которые вы подключали.
Excel в Интернете делает это с помощью формул в ячейках. Формула выполняет вычисления или другие действия с данными на листе. Формула всегда начинается со знака равенства (=), за которым могут следовать числа, математические операторы (например, знак «плюс» или «минус») и функции, которые значительно расширяют возможности формулы.
Ниже приведен пример формулы, умножающей 2 на 3 и прибавляющей к результату 5, чтобы получить 11.
=2*3+5
Следующая формула использует функцию ПЛТ для вычисления платежа по ипотеке (1 073,64 долларов США) с 5% ставкой (5% разделить на 12 месяцев равняется ежемесячному проценту) на период в 30 лет (360 месяцев) с займом на сумму 200 000 долларов:
=ПЛТ(0,05/12;360;200000)
Ниже приведены примеры формул, которые можно использовать на листах.
-
=A1+A2+A3 Вычисляет сумму значений в ячейках A1, A2 и A3.
-
=КОРЕНЬ(A1) Использует функцию КОРЕНЬ для возврата значения квадратного корня числа в ячейке A1.
-
=СЕГОДНЯ() Возвращает текущую дату.
-
=ПРОПИСН(«привет») Преобразует текст «привет» в «ПРИВЕТ» с помощью функции ПРОПИСН.
-
=ЕСЛИ(A1>0) Анализирует ячейку A1 и проверяет, превышает ли значение в ней нуль.
Элементы формулы
Формула также может содержать один или несколько из таких элементов: функции, ссылки, операторы и константы.
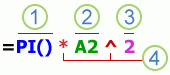
1. Функции. Функция ПИ() возвращает значение числа Пи: 3,142…
2. Ссылки. A2 возвращает значение ячейки A2.
3. Константы. Числа или текстовые значения, введенные непосредственно в формулу, например 2.
4. Операторы. Оператор ^ («крышка») применяется для возведения числа в степень, а оператор * («звездочка») — для умножения.
Использование констант в формулах
Константа представляет собой готовое (не вычисляемое) значение, которое всегда остается неизменным. Например, дата 09.10.2008, число 210 и текст «Прибыль за квартал» являются константами. выражение или его значение константами не являются. Если формула в ячейке содержит константы, но не ссылки на другие ячейки (например, имеет вид =30+70+110), значение в такой ячейке изменяется только после изменения формулы.
Использование операторов в формулах
Операторы определяют операции, которые необходимо выполнить над элементами формулы. Вычисления выполняются в стандартном порядке (соответствующем основным правилам арифметики), однако его можно изменить с помощью скобок.
Типы операторов
Приложение Microsoft Excel поддерживает четыре типа операторов: арифметические, текстовые, операторы сравнения и операторы ссылок.
Арифметические операторы
Арифметические операторы служат для выполнения базовых арифметических операций, таких как сложение, вычитание, умножение, деление или объединение чисел. Результатом операций являются числа. Арифметические операторы приведены ниже.
|
Арифметический оператор |
Значение |
Пример |
|
+ (знак «плюс») |
Сложение |
3+3 |
|
– (знак «минус») |
Вычитание |
3–1 |
|
* (звездочка) |
Умножение |
3*3 |
|
/ (косая черта) |
Деление |
3/3 |
|
% (знак процента) |
Доля |
20% |
|
^ (крышка) |
Возведение в степень |
3^2 |
Операторы сравнения
Операторы сравнения используются для сравнения двух значений. Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.
|
Оператор сравнения |
Значение |
Пример |
|
= (знак равенства) |
Равно |
A1=B1 |
|
> (знак «больше») |
Больше |
A1>B1 |
|
< (знак «меньше») |
Меньше |
A1<B1 |
|
>= (знак «больше или равно») |
Больше или равно |
A1>=B1 |
|
<= (знак «меньше или равно») |
Меньше или равно |
A1<=B1 |
|
<> (знак «не равно») |
Не равно |
A1<>B1 |
Текстовый оператор конкатенации
Амперсанд (&) используется для объединения (соединения) одной или нескольких текстовых строк в одну.
|
Текстовый оператор |
Значение |
Пример |
|
& (амперсанд) |
Соединение или объединение последовательностей знаков в одну последовательность |
Выражение «Северный»&«ветер» дает результат «Северный ветер». |
Операторы ссылок
Для определения ссылок на диапазоны ячеек можно использовать операторы, указанные ниже.
|
Оператор ссылки |
Значение |
Пример |
|
: (двоеточие) |
Оператор диапазона, который образует одну ссылку на все ячейки, находящиеся между первой и последней ячейками диапазона, включая эти ячейки. |
B5:B15 |
|
; (точка с запятой) |
Оператор объединения. Объединяет несколько ссылок в одну ссылку. |
СУММ(B5:B15,D5:D15) |
|
(пробел) |
Оператор пересечения множеств, используется для ссылки на общие ячейки двух диапазонов. |
B7:D7 C6:C8 |
Порядок выполнения Excel в Интернете в формулах
В некоторых случаях порядок вычисления может повлиять на возвращаемое формулой значение, поэтому для получения нужных результатов важно понимать стандартный порядок вычислений и знать, как можно его изменить.
Порядок вычислений
Формулы вычисляют значения в определенном порядке. Формула всегда начинается со знака равенства (=). Excel в Интернете интерпретирует символы, которые следуют знаку равенства, как формулу. После знака равенства вычисляются элементы (операнды), такие как константы или ссылки на ячейки. Они разделяются операторами вычислений. Excel в Интернете вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.
Приоритет операторов
Если объединить несколько операторов в одну формулу, Excel в Интернете выполняет операции в порядке, показанном в следующей таблице. Если формула содержит операторы с одинаковым приоритетом (например, если формула содержит оператор умножения и деления), Excel в Интернете вычисляет операторы слева направо.
|
Оператор |
Описание |
|
: (двоеточие) (один пробел) , (запятая) |
Операторы ссылок |
|
– |
Знак «минус» |
|
% |
Процент |
|
^ |
Возведение в степень |
|
* и / |
Умножение и деление |
|
+ и — |
Сложение и вычитание |
|
& |
Объединение двух текстовых строк в одну |
|
= |
Сравнение |
Использование круглых скобок
Чтобы изменить порядок вычисления формулы, заключите ее часть, которая должна быть выполнена первой, в скобки. Например, приведенная ниже формула возвращает значение 11, так как Excel в Интернете выполняет умножение перед добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.
=5+2*3
В отличие от этого, если для изменения синтаксиса используются круглые скобки, Excel в Интернете 5 и 2, а затем умножает результат на 3, чтобы получить 21.
=(5+2)*3
В следующем примере скобки, которые заключают первую часть формулы, принудительно Excel в Интернете сначала вычислить B4+25, а затем разделить результат на сумму значений в ячейках D5, E5 и F5.
=(B4+25)/СУММ(D5:F5)
Использование функций и вложенных функций в формулах
Функции — это заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. Эти функции позволяют выполнять как простые, так и сложные вычисления.
Синтаксис функций
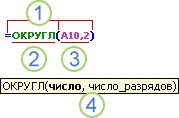
Приведенный ниже пример функции ОКРУГЛ, округляющей число в ячейке A10, демонстрирует синтаксис функции.
1. Структура. Структура функции начинается со знака равенства (=), за которым следует имя функции, открывающая скобка, аргументы функции, разделенные запятыми, и закрывающая скобка.
2. Имя функции. Чтобы отобразить список доступных функций, щелкните любую ячейку и нажмите клавиши SHIFT+F3.
3. Аргументы. Существуют различные типы аргументов: числа, текст, логические значения (ИСТИНА и ЛОЖЬ), массивы, значения ошибок (например #Н/Д) или ссылки на ячейки. Используемый аргумент должен возвращать значение, допустимое для данного аргумента. В качестве аргументов также используются константы, формулы и другие функции.
4. Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Ввод функций
Диалоговое окно Вставить функцию упрощает ввод функций при создании формул, в которых они содержатся. При вводе функции в формулу в диалоговом окне Вставить функцию отображаются имя функции, все ее аргументы, описание функции и каждого из аргументов, текущий результат функции и всей формулы.
Чтобы упростить создание и редактирование формул и свести к минимуму количество опечаток и синтаксических ошибок, пользуйтесь автозавершением формул. После ввода знака = (знак равенства) и начальных букв или триггера отображения Excel в Интернете под ячейкой отображается динамический раскрывающийся список допустимых функций, аргументов и имен, соответствующих буквам или триггеру. После этого элемент из раскрывающегося списка можно вставить в формулу.
Вложенные функции
В некоторых случаях может потребоваться использовать функцию в качестве одного из аргументов другой функции. Например, в приведенной ниже формуле для сравнения результата со значением 50 используется вложенная функция СРЗНАЧ.
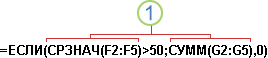
1. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.
Допустимые типы вычисляемых значений Вложенная функция, используемая в качестве аргумента, должна возвращать соответствующий ему тип данных. Например, если аргумент должен быть логическим, т. е. Если это не так, Excel в Интернете отображает #VALUE! В противном случае TE102825393 выдаст ошибку «#ЗНАЧ!».
<c0>Предельное количество уровней вложенности функций</c0>. В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, в приведенном выше примере функции СРЗНАЧ и СУММ являются функциями второго уровня, поскольку обе они являются аргументами функции ЕСЛИ. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.
Использование ссылок в формулах
Ссылка определяет ячейку или диапазон ячеек на листе и сообщает Excel в Интернете где искать значения или данные, которые нужно использовать в формуле. С помощью ссылок можно использовать в одной формуле данные, находящиеся в разных частях листа, а также использовать значение одной ячейки в нескольких формулах. Вы также можете задавать ссылки на ячейки разных листов одной книги либо на ячейки из других книг. Ссылки на ячейки других книг называются связями или внешними ссылками.
Стиль ссылок A1
Стиль ссылок по умолчанию По умолчанию в Excel в Интернете используется ссылочный стиль A1, который ссылается на столбцы с буквами (A–XFD, всего 16 384 столбца) и ссылается на строки с числами (от 1 до 1 048 576). Эти буквы и номера называются заголовками строк и столбцов. Для ссылки на ячейку введите букву столбца, и затем — номер строки. Например, ссылка B2 указывает на ячейку, расположенную на пересечении столбца B и строки 2.
|
Ячейка или диапазон |
Использование |
|
Ячейка на пересечении столбца A и строки 10 |
A10 |
|
Диапазон ячеек: столбец А, строки 10-20. |
A10:A20 |
|
Диапазон ячеек: строка 15, столбцы B-E |
B15:E15 |
|
Все ячейки в строке 5 |
5:5 |
|
Все ячейки в строках с 5 по 10 |
5:10 |
|
Все ячейки в столбце H |
H:H |
|
Все ячейки в столбцах с H по J |
H:J |
|
Диапазон ячеек: столбцы А-E, строки 10-20 |
A10:E20 |
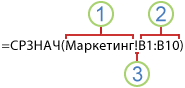
<c0>Ссылка на другой лист</c0>. В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.
1. Ссылка на лист «Маркетинг».
2. Ссылка на диапазон ячеек с B1 по B10 включительно.
3. Ссылка на лист, отделенная от ссылки на диапазон значений.
Различия между абсолютными, относительными и смешанными ссылками
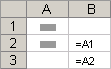
Относительные ссылки . Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейки, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании или заполнении формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании или заполнении относительной ссылки из ячейки B2 в ячейку B3 она автоматически изменяется с =A1 на =A2.
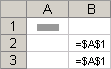
Абсолютные ссылки . Абсолютная ссылка на ячейку в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам и столбцам абсолютная ссылка не корректируется. По умолчанию в новых формулах используются относительные ссылки, а для использования абсолютных ссылок надо активировать соответствующий параметр. Например, при копировании или заполнении абсолютной ссылки из ячейки B2 в ячейку B3 она остается прежней в обеих ячейках: =$A$1.
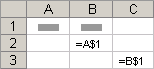
Смешанные ссылки . Смешанная ссылка содержит либо абсолютный столбец и относительную строку, либо абсолютную строку и относительный столбец. Абсолютная ссылка на столбец имеет вид $A1, $B1 и т. д. Абсолютная ссылка на строку имеет вид A$1, B$1 и т. д. Если положение ячейки с формулой изменяется, относительная ссылка меняется, а абсолютная — нет. При копировании или заполнении формулы по строкам и столбцам относительная ссылка автоматически изменяется, а абсолютная ссылка не корректируется. Например, при копировании или заполнении смешанной ссылки из ячейки A2 в ячейку B3 она автоматически изменяется с =A$1 на =B$1.
Стиль трехмерных ссылок
Удобный способ для ссылки на несколько листов . Трехмерные ссылки используются для анализа данных из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка содержит ссылку на ячейку или диапазон, перед которой указываются имена листов. Excel в Интернете использует все листы, хранящиеся между начальным и конечным именами ссылки. Например, формула =СУММ(Лист2:Лист13!B5) суммирует все значения, содержащиеся в ячейке B5 на всех листах в диапазоне от Лист2 до Лист13 включительно.
-
При помощи трехмерных ссылок можно создавать ссылки на ячейки на других листах, определять имена и создавать формулы с использованием следующих функций: СУММ, СРЗНАЧ, СРЗНАЧА, СЧЁТ, СЧЁТЗ, МАКС, МАКСА, МИН, МИНА, ПРОИЗВЕД, СТАНДОТКЛОН.Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.
-
Трехмерные ссылки нельзя использовать в формулах массива.
-
Трехмерные ссылки нельзя использовать вместе с оператор пересечения (один пробел), а также в формулах с неявное пересечение.
Что происходит при перемещении, копировании, вставке или удалении листов . Нижеследующие примеры поясняют, какие изменения происходят в трехмерных ссылках при перемещении, копировании, вставке и удалении листов, на которые такие ссылки указывают. В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для суммирования значений в ячейках с A2 по A5 на листах со второго по шестой.
-
Вставка или копирование . Если вставить или скопировать листы между листами 2 и 6 (в этом примере это конечные точки), Excel в Интернете содержит все значения в ячейках A2–A5 из добавленных листов в вычислениях.
-
Удаление . При удалении листов между листами 2 и 6 Excel в Интернете удаляет их значения из вычисления.
-
Перемещение . При перемещении листов между листами 2 и 6 в расположение за пределами указанного диапазона листов Excel в Интернете удаляет их значения из вычисления.
-
Перемещение конечного листа . При перемещении листа 2 или листа 6 в другое место в той же книге Excel в Интернете корректирует вычисление в соответствии с новым диапазоном листов между ними.
-
Удаление конечного листа . При удалении sheet2 или Sheet6 Excel в Интернете корректирует вычисление в соответствии с диапазоном листов между ними.
Стиль ссылок R1C1
Можно использовать такой стиль ссылок, при котором нумеруются и строки, и столбцы. Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает расположение ячейки с «R», за которым следует номер строки и «C», за которым следует номер столбца.
|
Ссылка |
Значение |
|
R[-2]C |
относительная ссылка на ячейку, расположенную на две строки выше в том же столбце |
|
R[2]C[2] |
Относительная ссылка на ячейку, расположенную на две строки ниже и на два столбца правее |
|
R2C2 |
Абсолютная ссылка на ячейку, расположенную во второй строке второго столбца |
|
R[-1] |
Относительная ссылка на строку, расположенную выше текущей ячейки |
|
R |
Абсолютная ссылка на текущую строку |
При записи макроса Excel в Интернете некоторые команды с помощью ссылочного стиля R1C1. Например, если вы записываете команду, например нажатие кнопки « Автосчет», чтобы вставить формулу, которая добавляет диапазон ячеек, Excel в Интернете формулу с помощью стиля R1C1, а не стиля A1, ссылок.
Использование имен в формулах
Можно создать определенные имена для представления ячеек, диапазонов ячеек, формул, констант или Excel в Интернете таблиц. Имя — это значимое краткое обозначение, поясняющее предназначение ссылки на ячейку, константы, формулы или таблицы, так как понять их суть с первого взгляда бывает непросто. Ниже приведены примеры имен и показано, как их использование упрощает понимание формул.
|
Тип примера |
Пример использования диапазонов вместо имен |
Пример с использованием имен |
|
Ссылка |
=СУММ(A16:A20) |
=СУММ(Продажи) |
|
Константа |
=ПРОИЗВЕД(A12,9.5%) |
=ПРОИЗВЕД(Цена,НСП) |
|
Формула |
=ТЕКСТ(ВПР(MAX(A16,A20),A16:B20,2,FALSE),»дд.мм.гггг») |
=ТЕКСТ(ВПР(МАКС(Продажи),ИнформацияОПродажах,2,ЛОЖЬ),»дд.мм.гггг») |
|
Таблица |
A22:B25 |
=ПРОИЗВЕД(Price,Table1[@Tax Rate]) |
Типы имен
Существует несколько типов имен, которые можно создавать и использовать.
Определенное имя Имя, используемое для представления ячейки, диапазона ячеек, формулы или константы. Вы можете создавать собственные определенные имена. Кроме того, Excel в Интернете иногда создает определенное имя, например при настройке области печати.
Имя таблицы Имя таблицы Excel в Интернете, которая представляет собой коллекцию данных об определенной теме, которая хранится в записях (строках) и полях (столбцах). Excel в Интернете создает имя таблицы Excel в Интернете «Table1», «Table2» и т. д. при каждой вставке таблицы Excel в Интернете, но вы можете изменить эти имена, чтобы сделать их более значимыми.
Создание и ввод имен
Имя создается с помощью команды «Создать имя» из выделенного фрагмента. Можно удобно создавать имена из существующих имен строк и столбцов с помощью фрагмента, выделенного на листе.
Примечание: По умолчанию в именах используются абсолютные ссылки на ячейки.
Имя можно ввести указанными ниже способами.
-
Ввода Введите имя, например, в качестве аргумента формулы.
-
<c0>Автозавершение формул</c0>. Используйте раскрывающийся список автозавершения формул, в котором автоматически выводятся допустимые имена.
Использование формул массива и констант массива
Excel в Интернете не поддерживает создание формул массива. Вы можете просматривать результаты формул массива, созданных в классическом приложении Excel, но не сможете изменить или пересчитать их. Если на вашем компьютере установлено классическое приложение Excel, нажмите кнопку Открыть в Excel, чтобы перейти к работе с массивами.
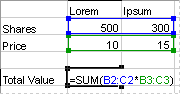
В примере формулы массива ниже вычисляется итоговое значение цен на акции; строки ячеек не используются при вычислении и отображении отдельных значений для каждой акции.
При вводе формулы «={СУММ(B2:D2*B3:D3)}» в качестве формулы массива сначала вычисляется значение «Акции» и «Цена» для каждой биржи, а затем — сумма всех результатов.
<c0>Вычисление нескольких значений</c0>. Некоторые функции возвращают массивы значений или требуют массив значений в качестве аргумента. Для вычисления нескольких значений с помощью формулы массива необходимо ввести массив в диапазон ячеек, состоящий из того же числа строк или столбцов, что и аргументы массива.
Например, по заданному ряду из трех значений продаж (в столбце B) для трех месяцев (в столбце A) функция ТЕНДЕНЦИЯ определяет продолжение линейного ряда объемов продаж. Чтобы можно было отобразить все результаты формулы, она вводится в три ячейки столбца C (C1:C3).
Формула «=ТЕНДЕНЦИЯ(B1:B3;A1:A3)», введенная как формула массива, возвращает три значения (22 196, 17 079 и 11 962), вычисленные по трем объемам продаж за три месяца.
Использование констант массива
В обычную формулу можно ввести ссылку на ячейку со значением или на само значение, также называемое константой. Подобным образом в формулу массива можно ввести ссылку на массив либо массив значений, содержащихся в ячейках (его иногда называют константой массива). Формулы массива принимают константы так же, как и другие формулы, однако константы массива необходимо вводить в определенном формате.
Константы массива могут содержать числа, текст, логические значения, например ИСТИНА или ЛОЖЬ, либо значения ошибок, такие как «#Н/Д». В одной константе массива могут присутствовать значения различных типов, например {1,3,4;ИСТИНА,ЛОЖЬ,ИСТИНА}. Числа в константах массива могут быть целыми, десятичными или иметь экспоненциальный формат. Текст должен быть заключен в двойные кавычки, например «Вторник».
Константы массива не могут содержать ссылки на ячейку, столбцы или строки разной длины, формулы и специальные знаки: $ (знак доллара), круглые скобки или % (знак процента).
При форматировании констант массива убедитесь, что выполняются указанные ниже требования.
-
Константы заключены в фигурные скобки ( { } ).
-
Столбцы разделены запятыми (,). Например, чтобы представить значения 10, 20, 30 и 40, введите {10,20,30,40}. Эта константа массива является матрицей размерности 1 на 4 и соответствует ссылке на одну строку и четыре столбца.
-
Значения ячеек из разных строк разделены точками с запятой (;). Например, чтобы представить значения 10, 20, 30, 40 и 50, 60, 70, 80, находящиеся в расположенных друг под другом ячейках, можно создать константу массива с размерностью 2 на 4: {10,20,30,40;50,60,70,80}.
В программе Excel разработчиками заложено огромное количество различных функций, но, пользователи чаще всего пользуются математическими. Давайте рассмотрим их и подробнее остановимся на самых популярных.
-
Использование математических функций в программе
- СУММ
- СУММЕСЛИ
- ПРОИЗВЕД
- ЧАСТНОЕ
- СТЕПЕНЬ
- КОРЕНЬ
- ОКРУГЛ
- ABS
- LOG
- ОСТАТОК
- Заключение
Использование математических функций в программе
В категорию математических функций входит более 60 различных операторов, которые позволяют выполнять различные вычисления.
Вставить функцию в свободную ячейку таблицы можно по-разному:
- Жмем кнопку “Вставить функцию” (fx) слева от строки формул. Выполнить данное действие можно, находясь в любой вкладке.
- Переключаемся во вкладку “Формулы”. Здесь также представлена кнопка “Вставить функцию” – в левом углу ленты инструментов.
- Нажимаем комбинацию клавиш Shift+F3, чтобы вызвать Мастер функций.
Результатом любого из вышеописанных способов будет открытие окна вставки функции. Здесь мы выбираем категорию “Математические”.
Теперь, когда категория выбрана, в поле ниже отмечаем требуемую функцию и щелкаем OK.
После этого откроется окно с аргументами для заполнения.
Примечание: Если мы, находясь во вкладке “Формулы”, в группе инструментов “Библиотека функций” нажмем по значку математических функций, сразу откроется список операторов, которые мы можем выбрать, минуя окно вставки функции.
Стоит учитывать, что в предлагаемом перечне присутствуют не все операторы, но самые необходимые здесь все же есть, и в большинстве случаев их достаточно.
Теперь перейдем к детальному рассмотрению самых популярных функций.
СУММ
Пожалуй, это самая популярная функция, которая используется в Эксель. С помощью нее выполняется суммирование числовых данных. Формула функции:
=СУММ(число1;число2;...)
В аргументах можно указать как конкретные числа, так и ссылки на ячейки, содержащие числовые значения. Причем указать координаты можно вручную (с помощью клавиш клавиатуры) или методом клика/выделения непосредственно в самой таблице.
Для перехода к заполнению следующего аргумента достаточно кликнуть по полю напротив него или нажать клавишу Tab.
СУММЕСЛИ
Данная функция позволяет считать сумму чисел с заданным условиями, с помощью которых будет выполняться отбор значений, учитывающихся в суммировании. Формула выглядит следующим образом:
=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)
В аргументах функции указывается диапазон ячеек (вручную или путем выделения в таблице), значения которых нужно просуммировать. В качестве критерия можно задать следующие условия (в кавычках):
- больше (“>”)
- меньше (“<“)
- не равно (“<>”)
Аргумент “Диапазон_сумирования” заполнять не обязательно.
ПРОИЗВЕД
С помощью данного оператора выполняется умножение чисел. Синтаксис выглядит следующим образом:
=ПРОИЗВЕД(число;число;…)
В аргументах функции, как и в СУММ, можно указывать как конкретные числа, так и адреса ячеек (диапазоны ячеек), которые содержат числовые значения.
ЧАСТНОЕ
Чаще всего для деления используется формула со знаком “/” между делимым и делителем: =Число1/Число2.
Однако в программе также есть отдельная функция для выполнения деления, синтаксис которой представлен ниже:
=ЧАСТНОЕ(Числитель;Знаменатель)
Заполнить нужно два аргумента: Числитель (Делимое) и Знаменатель (Делитель).
СТЕПЕНЬ
Оператор позволяет возвести число в указанную степень. Формула выглядит так:
=СТЕПЕНЬ(число;степень)
В аргументах функции указывается само число, а также, степень, в которую нужно его возвести.
КОРЕНЬ
С помощью данного оператора можно извлечь квадратный корень из числа. Синтаксис выглядит следующим образом:
=КОРЕНЬ(число)
Заполнить требуется только один аргумент – “Число”.
ОКРУГЛ
Функция применяется для выполнения еще одного распространенного математического действия – округления чисел (по общематематическим правилам, т.е., к ближайшему по модулю значению). Синтаксис функции представлен ниже:
=ОКРУГЛ(число;число_разрядов)
В аргументе “Число” указывается значение, которое требуется округлить. В числе разрядов, соответственно, пишем количество цифр, которые хотим оставить после запятой.
Также, в Excel доступны операторы ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые, как следует из их названий, используются для округления до ближайшего верхнего и нижнего числа, соответственно (по модулю).
ABS
Позволяет получить модуль числа. Формула функции представлена ниже:
=ABS(число)
Заполнить нужно всего один аргумент – “Число”, модуль которого требуется найти.
LOG
С помощью этого оператора определяется логарифм числа по заданному основанию. Синтаксис функции представлен в виде:
=LOG(Число;Основание)
Необходимо заполнить два аргумента: Число и Основание логарифма (если его не указать, программа примет значение по умолчанию, равное 10).
Также для десятичного логарифма предусмотрена отдельная функция – LOG10.
ОСТАТОК
Применяется для получения остатка от деления чисел. Формула оператора выглядит следующим образом:
=ОСТАТ(чило;делитель)
Для того, чтобы получить результат, требуется заполнить значения двух аргументов: Число и Делитель.
Заключение
Таким образом, мы разобрали самые популярные математические функции, которые используются в Excel. Однако возможности программы гораздо шире, и в ее инструментарии можно найти функцию для успешного выполнения практически любой задачи.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Microsoft Excel – одна из самых популярных и легкодоступных программ для представителей разный специальностей. Сегодня мы рассмотрим, пожалуй, одну из самых используемых групп формул – математические формулы.
Начнем с того, как найти их среди прочего функционала. Есть несколько путей того, как открыть список математических формул.
Самый простой способ – нажать на кнопку «Формулы» на панели управления. Затем выбрать из перечня тип функций: «Математические».
Перед вами появится выпадающий длинный список всех существующих операторов:

Всего в Excel около 80 математических и тригонометрических функций. Мы рассмотрим не все, только самые распространенные из них, а также обратим внимание на некоторые нюансы, о которых вы, возможно, не знали. Если в статье вы не нашли нужную вам функцию, то скачивайте наш бесплатный гайд «Математические функции в Excel».
Для разминки вспомним самые простые формулы.
1. Формулы СУММ(), ПРОИЗВЕД()
Эти операции имеют схожую структуру и одинаковый тип аргументов, поэтому мы их объединили в один блок. СУММ() служит для сложения данных в нескольких ячейках, ПРОИЗВЕД() – очевидно, для нахождения произведения.
Аргументами этих функций могут быть числа, диапазоны, ссылки на ячейку, в которой содержится числовое значение. Количество элементов не может быть больше 30.
СУММ() и ПРОИЗВЕД() пропускают пустые ячейки, ячейки текстового формата и логические значения. Операторы вносят результат вычислений в отдельную, ранее выделенную курсором ячейку:

Аналогично для формулы ПРОИЗВЕД():

2. Формула ЧАСТНОЕ()
Тоже одна из простых операций в математике. В Excel выполняется тоже несложно: у функции ЧАСТНОЕ() есть два аргумента: делимое и делитель.
В выделенной ячейке выводится частное:

3. Формула СУММЕСЛИ()
Оператор СУММЕСЛИ() находит сумму чисел. Главное отличие этой функции от СУММ() в том, что здесь в качестве аргумента можно задавать условие (только одно), которое будет показывать, какие значения будут использованы в расчетах, а какие – нет.
В качестве условий могут выступать неравенства со знаками больше, меньше или не равно («>», «<», «< >»). Число, которое не соответствует введенному условию, не будет включен в суммирование.
На рисунке 5 изображено суммирование всех чисел, которые больше 0.
Оранжевым выделены те числа, которые будут включены в расчет функцией СУММЕСЛИ().
Остальные числа просто будут игнорироваться:

Кроме постоянных аргументов, существует еще и дополнительный – «Диапазон суммирования». Он добавляется тогда, когда необходимо просуммировать один диапазон, а условия выбирать по другому диапазону.
Например, нужно посчитать общую стоимость всех проданных фруктов.
Для этого воспользуемся следующей формулой:

То есть сначала пишем диапазон, по которому проверяем условие, затем само ограничение и в конце диапазон чисел, которые надо суммировать. В примере на рисунке 6 выше, соответственно, все строки из категории «Овощи» в расчет включены не будут.
4. Формулы ОКРУГЛ(), ОКРУГЛВВЕРХ(), ОКРУГЛВНИЗ()
Функция ОКРУГЛ() предназначена для округления значения до заданного количества знаков после запятой. В качестве первого аргумента выступают, как обычно, числа или диапазон ячеек, второго – разряд, до которого нужно округлить число.
Например, округление значения до второго знака после запятой:

Если в качестве второго аргумента выступает 0, то число будет округляться до ближайшего целого:

Второй аргумент может быть и отрицательным, тогда округление будет происходить до требуемого знака перед запятой:

Если необходимо округлить в сторону меньшего или большего по модулю числа используют функции ОКРУГЛВНИЗ(), ОКРУГЛВВЕРХ(), соответственно:


Замечание: многие могут решить, что функции округления бесполезны, так как можно просто убрать/добавить дополнительный знак после запятой с помощью кнопок увеличить/уменьшить разрядность.
На самом деле, это не так.
Дело в том, что увеличение или уменьшение разрядности влияет только на «внешний вид» ячейки, то есть на то, как мы число видим.
Само число, при этом, не меняется. Функции округления же полностью меняют вид числа, убирая лишние разряды.
5. Формулы ОТБР(), ЦЕЛОЕ()
Эти функции очень похожи на предыдущие, но работают немного по-другому.
ОТБР() убирает все цифры справа от запятой и у положительных, и у отрицательных чисел. На первом месте в скобках после оператора пишется значение, а на втором – разряд, после которого удалятся все знаки.
Если второй аргумент пропущен, то по умолчанию ставится 0:

ЦЕЛОЕ() – функция, которая выдает в качестве результата наименьшее целое число, стоящее перед аргументом:

На положительные числа операторы влияют почти одинаково, а вот на отрицательные – нет.
Функция ЦЕЛОЕ(-5,6) выдаст результат (-6), а ОТБР(-5,6;0) выдаст (-5), хотя в то же время для числа 5,3 результат обеих функций будет одинаковый – число (5).
6. Формула ABS()
Математическая формула ABS() позволяет получить число по модулю. Как обычно, аргументами оператора является число или ссылка на ячейку.

Эту функцию удобно использовать, например, когда необходимо найти количество дней между датами. Из школьной программы многие знают, что нужно из большего вычитать меньшее.
Но что делать если дана огромная таблица, где трудно определить, где какое значение? Здесь нам помогает оператор ABS(), который переводит отрицательное число в положительное.

7. Формула КОРЕНЬ()
КОРЕНЬ() – довольно легкая функция с одним аргументом (числом или ссылкой на ячейку), которая находит квадратный корень числа:

Замечание. Для извлечения корня другой степени (не квадратного) можно пользоваться функцией СТЕПЕНЬ().
8. Формула СТЕПЕНЬ()
Функция СТЕПЕНЬ() позволяет возвести число в любую степень, в том числе извлечь корень (то есть возвести число в дробную степень).
Например, чтобы извлечь кубический корень из числа 8, необходимо воспользоваться формулой, как на рисунке 17.1.


Помимо математической функции СТЕПЕНЬ(), можно пользоваться оператором “^”, но он выглядит менее опрятно в формулах.
Если вам интересно узнать больше о других математических функциях, напишите об этом ниже в комментариях. Записывайтесь на открытый онлайн-курс «Аналитика в Excel», если хотите научиться выполнять рутинную работу в программе быстрее.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
Investment Banking
5 примеров экономии времени в Excel
Содержание статьи Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на…
Как работает сотрудник одной из компаний «большой тройки»?
Ты работаешь в компании «большой тройки (имеются в виду три крупнейших консалтинговых компании: McKinsey, Boston Consulting Group и Bain & Company), в которых мечтают работать тысячи подписчиков наших каналов и читателей vc.ru. Что это значит для тебя?
Содержание
- Математические функции Excel
- Функции, связанные с округлением
- Функция ОКРУГЛ
- Функция ОТБР
- Функция ОКРУГЛВВЕРХ
- Функция ОКРУГЛВНИЗ
- Функция ОКРУГЛТ
- Функция ОКРВВЕРХ.МАТ
- Функция ОКРВНИЗ.МАТ
- Функция ЦЕЛОЕ
- Функция ЧЁТН
- Функция НЕЧЁТ
- Суммирование и условное суммирование
- Функция СУММ
- Функция СУММПРОИЗВ
- Функция СУММЕСЛИ
- Функция СУММЕСЛИМН
- Функции, связанные с возведением в степень и извлечением корня
- Функция КОРЕНЬ
- Функция СУММКВРАЗН
- Функция СУММКВ
- Функция СУММСУММКВ
- Функция СУММРАЗНКВ
- Функции случайных чисел и возможных комбинаций
- Функция СЛЧИС
- Функция СЛУЧМЕЖДУ
- Функция ЧИСЛКОМБ
- Функция ФАКТР
- Функции, связанные с делением
- Функция ЧАСТНОЕ
- Функция ОСТАТ
- Функция НОД
- Функция НОК
- Преобразование чисел
- Функция ABS
- Функция РИМСКОЕ
- Иные функции
- Функция ЗНАК
- Функция ПИ
- Функция ПРОИЗВЕД
- Функция ПРОМЕЖУТОЧНЫЕ.ИТОГИ()
Математические функции Excel
В данной статье будет рассмотрена та часть математических функций, которая наиболее часто применяется в решении различных задач. С полным перечнем можно ознакомиться на вкладке «Формулы» => выпадающий список «Математические»:
Какие функции затронет статья:
Функции, связанные с округлением
Функция ОКРУГЛ
Осуществляет стандартное округление, а именно округляет число до ближайшего разряда с указанной точностью.
Синтаксис: =ОКРУГЛ(число; число_разрядов), где
- Число – обязательный аргумент. Число либо ссылка на ячейку, его содержащую;
- Число_разрядов – обязательный аргумент. Указывает, какое количество знаков после запятой необходимо оставить:
- 0 – округление до целого числа;
- 1 – округление до десятых долей;
- 2 – округление до сотых долей;
- И т.д.
Аргумент может также принимать отрицательные числа:
- -1 – округление до десятков;
- -2 – округление до сотен;
- И т.д.
=ОКРУГЛ(5,45;0) – формула возвращает значение 5.
=ОКРУГЛ(5,45;1) – формула возвращает значение 5,5.
=ОКРУГЛ(5,45;3) – не меняет число, т.к. указанное число разрядов превышает его точность.
=ОКРУГЛ(5,45;-1) – формула возвращает значение 10.
Функция ОТБР
Отбрасывает дробную часть числа. Отличие от предыдущей функции заключается в том, что число по факту не округляется, а только усекается до указанного разряда.
Синтаксис: =ОТБР(число; [число_разрядов]), где
- Число – обязательный аргумент. Число либо ссылка на ячейку с числом;
- Число_разрядов – необязательный аргумент. Указывает, какое количество знаков после запятой необходимо оставить:
- 0 – точность до целого числа;
- 1 – точность до десятых долей;
- 2 – точность до сотых долей;
- И т.д.
=ОТБР(5,45;0) – формула возвращает значение 5.
=ОТБР(5,85;0) – так же возвращает значение 5.
=ОТБР(5,45;1) – возвращает значение 5,4.
=ОТБР(5,45;3) – формула не меняет число, т.к. указанное количество разрядов превышает его точность.
Функция ОКРУГЛВВЕРХ
Производит округление до ближайшего большего по модулю числа с указанной точностью.
Синтаксис: =ОКРУГЛВВЕРХ(число; число_разрядов), где
- Число – обязательный аргумент. Число либо ссылка на ячейку, содержащую число;
- Число_разрядов – обязательный аргумент. Указывает, какое количество знаков после запятой необходимо оставить:
- 0 – округление до целого числа;
- 1 – округление до десятых долей;
- 2 – округление до сотых долей;
- И т.д.
Аргумент может также принимать отрицательные числа:
- -1 – округление до десятков;
- -2 – округление до сотен;
- И т.д.
=ОКРУГЛВВЕРХ(5,001;0) – формула возвращает значение 6.
=ОКРУГЛВВЕРХ(-5,001;0) – формула возвращает значение -6, т.к. -6 по модулю больше, чем -5,001 по модулю.
=ОКРУГЛВВЕРХ(5,45;1) – возвращает значение 5,5.
=ОКРУГЛВВЕРХ(5,45;3) – функция не изменяет число, т.к. требуемая разрядность превышает его точность.
=ОКРУГЛВВЕРХ(5,45;-1) – формула возвращает значение 10.
Функция ОКРУГЛВНИЗ
Аналогична предыдущей функции, за исключением того, то округляет число в меньшую сторону по модулю с указанной точностью.
=ОКРУГЛВНИЗ(5,99;0) – формула возвращает значение 5.
=ОКРУГЛВНИЗ(-5,99;0) – формула возвращает значение -5, т.к. -5 по модулю меньше, чем -5,99 по модулю.
=ОКРУГЛВНИЗ(5,45;1) – функция возвращает значение 5,4.
=ОКРУГЛВНИЗ(5,45;3) – не меняет число, т.к. указанная разрядность превышает его точность.
=ОКРУГЛВНИЗ(5,45;-1) – формула возвращает значение 0.
Функция ОКРУГЛТ
Округляет число до ближайшего кратного числу, заданного вторым аргументом.
Синтаксис: =ОКРУГЛТ(число; точность), где
- Число – обязательный аргумент. Число либо ссылка на ячейку, содержащую число;
- Точность – обязательный аргумент. Число, для которого необходимо найти кратное ближайшее к первому аргументу. В случае задания нулевого значения, функция всегда будет возвращать 0.
Знаки двух аргументов должны совпадать, иначе функция вернем ошибку.
=ОКРУГЛТ(5,45;0) – формула возвращает значение 0.
=ОКРУГЛТ(5,45; 1,45) – возвращает значение 5,8, т.к. 5,8/1,45=4 и это ближе, чем 7,25/1,45=5.
=ОКРУГЛТ(5,45;3) – формула возвращает значение 6, т.к. 6/3=2, ближе, чем 3/3=1.
Функция ОКРВВЕРХ.МАТ
Появилась в Microsoft Excel 2013. Она округляет число до ближайшего большего кратного числу, заданного вторым аргументом.
Синтаксис: =ОКРВВЕРХ.МАТ(число; [точность]; [режим]), где
- Число – обязательный аргумент. Число либо ссылка на ячейку, содержащую числовое значение;
- Точность – необязательный аргумент. Число, для которого необходимо найти большее кратное, наиболее приближенное к заданному числу. В случае задания данному аргументу нулевого значения, функция всегда будет возвращать 0.
- Режим – необязательный аргумент. Принимает число. Если режим не задан либо равно нулю, то округление будет производиться до большего кратного не по модулю. Если же аргумент отличается от 0, то при округлении отрицательных чисел, большим будет считаться кратное наиболее отдаленное от нуля, т.е. по модулю.
=ОКРВВЕРХ.МАТ(5,45;0) – формула возвращает значение 0.
=ОКРВВЕРХ.МАТ(5,45;4) – формула возвращает значение 8, несмотря на то, что кратное 4 ближе к 5,45.
=ОКРВВЕРХ.МАТ(-5,45;4) – формула возвращает значение -4, т.к. режим не задан, то округление производиться не по модулю.
=ОКРВВЕРХ.МАТ(-5,45;4;1) – формула возвращает значение -8, т.к. аргумент режим отличается от нуля, то округление производиться по модулю.
Функция ОКРВНИЗ.МАТ
Появилась в Microsoft Excel 2013. Она округляет число до ближайшего меньшего кратного числу, заданного вторым аргументом.
Синтаксис: =ОКРВНИЗ.МАТ(число; [точность]; [режим]), где
- Число – обязательный аргумент. Число либо ссылка на ячейку, содержащую число;
- Точность – необязательный аргумент. Число, для которого необходимо найти меньшее кратное, наиболее приближенное к первому аргументу. В случае задания нулевого значения, функция всегда будет возвращать 0.
- Режим – необязательный аргумент. Принимает число. Если данное число отсутствует либо равно нулю, то округление будет производиться до меньшего кратного не по модулю. Если же аргумент отличается от 0, то при округлении отрицательных чисел, меньшим будет считаться кратное наиболее приближенное к нулю, т.е. по модулю.
Обращаем внимание на то, что третьи аргументы функций ОКРВВЕРХ.МАТ и ОКРВНИЗ.МАТ, не смотря на то, что очень похожи, все же отличаются, т.к. имеют противоположный эффект. Для избавления от путаницы можно прибегать к следующей ассоциации:
- Если режим для функции ОКРВВЕРХ.МАТ равен 0, то направление округления к нулю, т.к. аргумент действует только на отрицательные числа;
- Если режим для функции ОКРВНИЗ.МАТ равен 0, то направление округления от нуля.
=ОКРВНИЗ.МАТ(5,45;0) – формула возвращает значение 0.
=ОКРВНИЗ.МАТ(5,45;3) – формула возвращает значение 3, несмотря на то, что кратное 6 ближе к 5,45.
=ОКРВНИЗ.МАТ(-5,45;3) – возвращает значение -6, т.к. режим не задан, то округление производиться не по модулю.
=ОКРВНИЗ.МАТ(-5,45;4;1) – функция возвращает значение -4, т.к. аргумент режим принимает не равен 0, то округление производиться по модулю.
Функция ЦЕЛОЕ
Округляет число до целого в меньшую сторону.
Синтаксис: =ЦЕЛОЕ(число), где число – обязательный аргумент, принимающий числовое значение либо ссылку на ячейку с числовым значением.
=ЦЕЛОЕ(5,85) – формула вернет значение 5.
=ЦЕЛОЕ(-5,85) – вернет значение -6.
Функция ЧЁТН
Округляет число до ближайшего большего по модулю четного числа.
Синтаксис: =ЧЁТН(число), где число – обязательный аргумент. Принимает числовое значение либо ссылку на ячейку, содержащую число.
=ЧЁТН(6,85) – вернет значение 8.
=ЧЁТН(-6,85) – вернет значение -8.
Функция НЕЧЁТ
Аналогична функции ЧЁТН за исключением того, что числа округляются до нечетных.
=НЕЧЁТ(5,85) – вернет значение 7.
=НЕЧЁТ(-5,85) – вернет значение -7.
Суммирование и условное суммирование
Функция СУММ
Суммирует свои аргументы. Максимальное число аргументов 255.
Если функция ссылается на ячейку, диапазон ячеек или массив, содержащий текстовые либо логические значения, то такие значения игнорируются. Если какой-либо аргумент принимает константу (значение введенное руками), содержащую текстовое значение, то такой аргумент возвращает ошибку, в результате чего вся формула вернет ошибку.
Если же в качестве аргумента функции принимается константа с логическим значением, то ЛОЖЬ приравнивается к нулю, а ИСТИНА к единице.
Синтаксис: =СУММ(число1; [число2]; …), где
- Число1 – обязательный аргумент, являющийся числом либо ссылкой на ячейку или диапазон ячеек, содержащих число;
- Число2 и последующие аргументы – необязательные аргументы, аналогичные первому.
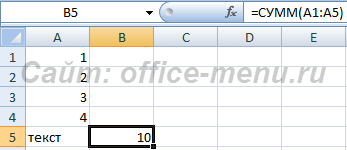
- В данном примере значение ячейки A5 игнорируется.
- =СУММ(1;2;3;4;»текст») – данный вариант вернет ошибку #ЗНАЧ!, т.к. последний аргумент явно принимает текстовое значение.
- =СУММ(ИСТИНА;ЛОЖЬ) – формула вернет значение 1.
Функция СУММПРОИЗВ
Производит суммирование произведений массивов либо диапазонов.
Если аргументы принимают диапазоны либо массивы, содержащие текстовые или логические значения, то такие значения игнорируются.
Если в аргументе явно задать логическое либо текстовое значение или ссылку на одну ячейку, содержащую такое значение, то вся формула вернет ошибку.
Синтаксис: =СУММПРОИЗВ(массив1; [массив2]; …), где
- Массив1 – обязательный аргумент, являющийся числом либо ссылкой на ячейку, диапазон ячеек или массив, содержащих числовое значение;
- Массив2 и последующие аргументы – необязательные аргументы, аналогичные первому.
Все аргументы функции должны иметь одинаковую размерность, т.е. если один аргумент ссылается на диапазон с 5 ячейками, то и остальные аргументы должны иметь по 5 элементов. Также должны использоваться диапазоны и массивы одних типов, т.е. горизонтальные и вертикальные массивы и диапазоны либо двумерные и одномерные массивы не могут использоваться одновременно в данной функции, иначе она возвратит ошибку. Чтобы лучше понять этот абзац, ознакомьтесь со статьей «Массивы Excel».
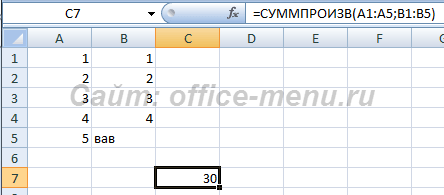
- В данном примере один диапазон содержит текст, но функция игнорирует данное значение и возвращает сумму произведений остальных элементов.
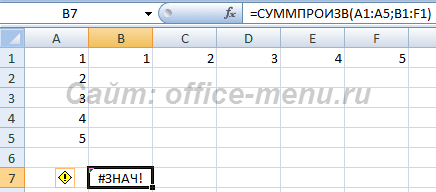
- В данном случае формула возвращает ошибку, потому что, не смотря на одинаковое количество элементов в двух диапазонах, они имеют разные типы, т.е. A1:A5 – вертикальный диапазон, а B1:F1 – горизонтальный диапазон.
Функция СУММЕСЛИ
Возможно, одна из самых полезных функций, по мнению office-menu. Она производит суммирование элементов, которые соответствуют заданным условиям.
Синтаксис: =СУММЕСЛИ(диапазон_условия; критерий;[диапазон_суммирования]), где
- диапазон_условия – обязательный атрибут. Ссылка на ячейку или диапазон ячеек, которые необходимо проверить на совпадение с условием;
- критерий – обязательный атрибут. Содержит в себе конкретное значение либо условие для проверки. Условия типа больше, меньше, равно либо их комбинации всегда заключаются в кавычки.
- диапазон_суммирования – необязательный атрибут. Ссылка на ячейку либо диапазон ячеек, которые необходимо просуммировать в случае, если элемент диапазона условия подходит под критерий. Если аргумент не указан, то по умолчанию он принимает значение первого аргумента. Также, если диапазон указан не правильно, т.е. для вертикального диапазона условия, указан горизонтальный диапазон суммирования, то последний заменяется на вертикальный, не меняя своего первого элемента, т.е. претерпевает транспонирование.
- В данном примере производится суммирование чисел, которые больше 2. Так как диапазон суммирования не указан, то по умолчанию принимает диапазон условия.
- В следующем примере используются разные типы диапазонов, поэтому 3 аргумент меняет ссылку с A1:B1 на A1:A2, и функция возвращает значение 2.
- При совместном использовании текстовых и числовых значений в диапазоне условия, проверяться будут либо те, либо другие. Рассмотрите последние два примера.
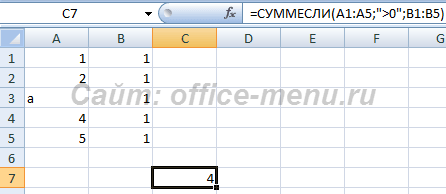
В первом случае, необходимо произвести суммирование по B1:B5, если элемент из A1:A5 больше нуля. Возвращаемое значение 4, так как текстовый элемент A3 игнорируется.
Теперь изменим условие и найдем сумму, если элементы для условия больше или равняются «а». По условиям сортировки все числа являются меньшими любым буквам, поэтому результат должен быть 5. Но так как в условии задано сравнение с текстовой строкой, то все числовые значения отбрасываются. Чтобы они учитывались, их необходимо перевести в текстовый формат. Также можно использовать массивы, для лучшего контроля перевода чисел в текст – <=СУММ(ЕСЛИ(ТЕКСТ(A1:A5;0)
Функция СУММЕСЛИМН
Выполняет те же действия, что и СУММЕСЛИ, но может проверять различные условия по нескольким диапазонам.
Синтаксис: =СУММЕСЛИМН(диапазон_суммирования; диапазон_условия1; критерий1; [диапазон_условия2]; [критерий2]; …), где аргументы в точности совпадают с аргументами функции СУММЕСЛИ, за исключением того, что диапазон суммирования и первая пара диапазон условия — критерий являются обязательными аргументами. Все последующие пары (от диапазон_условия2; критерий2 до диапазон_условия127; критерий127) необязательны.
Также в данной функции не происходит никаких подмен диапазонов, поэтому все заданные в функции диапазоны должны быть равны по размерности и иметь один тип, т.е. только горизонтальные либо только вертикальные.
Необходимо узнать сумму ячеек, удовлетворяющих условиям:
- По A1:A5 больше 2;
- По B1:B5 меньше или равно “г”.
Таким образом, по первому критерию подходят 3 ячейки, по второму 4, но ячеек, которые подходят под оба условия две – C3 и C4. Поэтому формула вернет значение 2.
Функции, связанные с возведением в степень и извлечением корня
Функция КОРЕНЬ
Извлекает квадратный корень из числа.
Синтаксис: =КОРЕНЬ(число), где аргумент число – является числом, либо ссылкой на ячейку с числовым значением.
=КОРЕНЬ(4) – функция вернет значение 2.
Если возникает необходимость извлечь из числа корень со степенью больше 2, данное число необходимо возвести в степень 1/(показатель корня). Например, для извлечения кубического корня из числа 27 необходимо применить следующую формулу: =27^(1/3) – результат 3.
Функция СУММКВРАЗН
Производит суммирование возведенных в квадрат разностей между элементами двух диапазонов либо массивов.
Синтаксис: =СУММКВРАЗН(диапазон1; диапазон2), где первый и второй аргументы являются обязательными и содержать ссылки на диапазоны либо массивы с числовыми значениями. Текстовые и логические значения игнорируются.
Вертикальные и горизонтальные диапазоны и массивы в данной функции не различаются, но должны иметь одинаковую размерность.
=СУММКВРАЗН(<1;2>;<0;4>) – функция вернет значение 5. Альтернативное решение =(1-0)^2+(2-4)^2.
Функция СУММКВ
Воспроизводит числа, заданные ее аргументами, в квадрат, после чего их суммирует.
Синтаксис: =СУММКВ(число1; [число2]), где число1 … число255, число, либо ссылки на ячейки и диапазоны, содержащие числовые значения. Максимальное число аргументов 255, минимальное 1. Все текстовые и логические значения игнорируются, за исключением случаев, когда они заданы явно. В последнем случае текстовые значения возвращают ошибку, логические 1 для ИСТИНА, 0 для ЛОЖЬ.
=СУММКВ(2;2) – функция вернет значение 8.
=СУММКВ(2;ИСТИНА) – возвращает значение 5, так как ИСТИНА приравнивается к единице.
В данном примере текстовое значение игнорируется, так как оно задано через ссылку на диапазон.
Функция СУММСУММКВ
Возводит все элементы указанных диапазонов либо массивов в квадрат, суммирует их пары, затем выводит общую сумму.
Синтаксис: =СУММСУММКВ(диапазон1; диапазон2), где аргументы являются числами, либо ссылками на диапазоны или массивы.
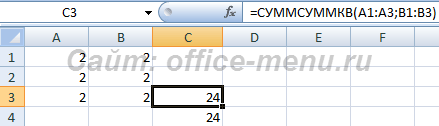
Функция при обычных условиях возвращает точно такой же результат, как и функция СУММКВ. Но если в качестве элемента одного из аргументов будет указано текстовое или логическое значение, то проигнорирована будет вся пара элементов, а не только сам элемент.
Рассмотрим применение функции СУММСУММКВ и СУММКВ к одним и тем же данным.
В первом случае функции возвращают один и тот же результат:
- Алгоритм для СУММСУММКВ =(2^2+2^2) + (2^2+2^2) + (2^2+2^2);
- Алгоритм для СУММКВ =2^2 +2 ^2 + 2^2 + 2^2 + 2^2 + 2^2.
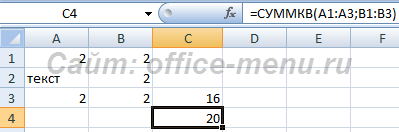
Во втором случае функции вернут разные результаты из-за несущественных различий в алгоритме вычисления (части выделенные красным игнорируются, т.к. возвращают ошибку):
- Алгоритм для СУММСУММКВ =(2^2+2^2) + (текст^2+2^2) + (2^2+2^2);
- Алгоритм для СУММКВ =2^2 +2 ^2 + «текст»^2 + 2^2 + 2^2 + 2^2.
Функция СУММРАЗНКВ
Аналогична во всем функции СУММСУММКВ за исключение того, что для пар соответствующих элементов находится не сумма, а их разница.
Синтаксис: =СУММРАЗНКВ(диапазон1; диапазон2), где аргументы являются числами, либо ссылками на диапазоны или массивы.
Функции случайных чисел и возможных комбинаций
Функция СЛЧИС
Возвращает случайно сгенерированное число в пределах: >=0 и
Функция СЛУЧМЕЖДУ
Возвращает случайно сгенерированное целое число в пределах указанных границ. При использовании нескольких таких функций, возвращаемые значения могут повторяться.
Синтаксис: =СЛУЧМЕЖДУ(нижняя_граница; верхняя_граница), где аргументы являются числами, либо ссылками на ячейки, содержащие числа. Все аргументы обязательны, и представляют собой минимальное и максимальное возможные значения соответственно. Аргументы могут быть равны друг другу, но минимальная граница не может быть больше максимальной.
Значение возвращаемое функцией меняется каждый раз, когда происходит изменение книги.
Если вдруг возникнет необходимость возвращать дробные числа, то это можно сделать с использованием функции СЛЧИС по следующей формуле:
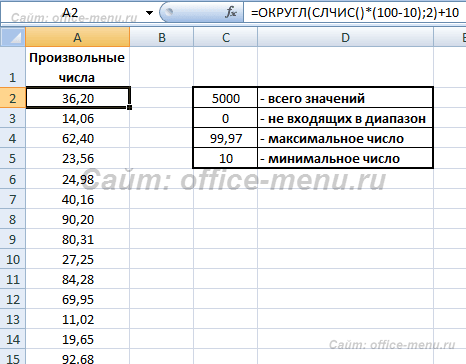
В следующем примере возвращаются 5000 произвольных значений, лежащих в диапазоне от 10 до 100. В дополнительно приведенной таблице можно посмотреть минимальные и максимальные возвращенные значения. Также для части формулы используется округление. Оно использовано для того, чтобы увеличить вероятность возврата крайних значений диапазона.
Функция ЧИСЛКОМБ
Возвращает возможное число уникальных комбинаций для определенного количества элементов из общего набора элементов.
Синтаксис: =ЧИСЛКОМБ(размер_набора; колво_элементов), где
- размер_набора – обязательный аргумент. Число либо ссылка на ячейку, содержащую число, которое указывает, сколько элементов всего находится в наборе;
- колво_элементов – обязательный аргумент. Число либо ссылка на ячейку, содержащую число, которое указывает, какое количество элементов из общего набора должно присутствовать в одной комбинации. Данный аргумент должен равняться либо не превышать первый.
Все аргументы должны содержать целые положительные числа.
Имеется набор из 4 элементов – ABCD. Из него необходимо составить уникальные комбинации по 2 элемента, при условии что в комбинации элементы не повторяются и их расположение не имеет значения, т.е. пары AB и BA являются равнозначными.
=ЧИСЛКОМБ(4;2) – возвращаемый результат 6:
Функция ФАКТР
Возвращает факториал числа, что соответствует числу возможных вариаций упорядочивания элементов группы.
Синтаксис: =ФАКТР(число), где число – обязательный аргумент, являющийся числом либо ссылкой на ячейку, содержащую числовое значение.
Имеется набор из 3 элементов – ABC, который можно упорядочить 6 разными способами:
Используем функцию, чтобы подтвердить данное количество: =ФАКТР(3) – формула возвращает значение 6.
Функции, связанные с делением
Функция ЧАСТНОЕ
Выполняет самое простое деление.
Синтаксис: =ЧАСТНОЕ(делимое; делитель), где все аргументы являются обязательными и должны представляться числами.
=ЧАСТНОЕ(8;4) – возвращаемое значение 2.
Можно воспользоваться альтернативой функции: =8/2.
Функция ОСТАТ
Возвращает остаток от деления двух чисел.
Синтаксис: =ОСТАТ(делимое; делитель), где все аргументы являются обязательными и должны иметь числовое значение.
Знак остатка всегда совпадает со знаком делителя.
Сама функция из-за алгоритма своего вычисления выдает результат обработки чисел с разными знаками, который возможно Вы от нее ожидать не будете. Подробнее:
=ОСТАТ(8;3) – результат выполнения функции 2.
=ОСТАТ(-8;3) – результат выполнения функции 1. Хотя скорее всего Вы будете ожидать результат 2. Так происходит из-за алгоритма функции: =делимое – делитель*ЦЕЛОЕ(делимое/делитель). В связи с тем, что ЦЕЛОЕ округляет дробные значения до меньшего целого, то результат деления (-8/3) равняется -2,6666 и, соответственно, будет округлен до -3, а не до 2, как в случае с положительными числами. Чтобы избавиться от такого эффекта необходимо не округлять число, а просто отбрасывать дробную часть: =делимое – делитель*ОТБР(делимое/делитель).
=-8-3*ОТБР(-8/3) – результат -2.
=ОСТАТ(-8;-3) – функция вернет результат -2.
Функция НОД
Вычисляет наибольший общий делитель для всех аргументов, на который они делятся без остатка. Наибольший делитель всегда целое число.
=НОД(число1; [число2]; …). Максимальное число аргументов 255, минимальное 1. Аргументы являются числами, ссылками на ячейки или диапазонами ячеек, которые содержат числа. Значения аргументов должны быть всегда положительными числами.
=НОД(8;4) – результат выполнения 4.
=НОД(6;4) – результат выполнения 2.
Функция НОК
Вычисляет наименьшее общее кратное для всех аргументов.
Синтаксис и описание аргументов аналогичны функции НОД.
=НОК(8;4) – результат выполнения 8.
=НОК(6;4) – результат выполнения 12.
Преобразование чисел
Функция ABS
Возвращает модуль числа.
=ABS(число), где число обязательный аргумент, являющийся числом либо ссылкой на ячейку, содержащую число.
=ABS(-4) – результат 4.
Функция РИМСКОЕ
Преобразует число в строку, представляющую римское число.
Синтаксис: =РИМСКОЕ(число; [формат]), где
- Число – обязательный аргумент. Положительное число либо ссылка на ячейку с положительным числом. Если число дробное, то дробная часть отсекается;
- Формат – необязательный аргумент. По умолчанию принимает значение 0. Возможные значения:
- 0 – классическое представление римских чисел;
- От 1 до 3 – наглядные форматы представления длинных римских чисел;
- 4 – упрощенный вариант представления длинных римских чисел;
- ИСТИНА — аналогично 0;
- ЛОЖЬ – аналогично 4.
=РИМСКОЕ(999;0) – результат «CMXCIX»;
=РИМСКОЕ(999;1) – результат «LMVLIV»;
=РИМСКОЕ(999;2) – возвращает «XMIX»;
=РИМСКОЕ(999;3) – результат «VMIV»;
=РИМСКОЕ(999;4) – результат «IM»;
=РИМСКОЕ(999;ИСТИНА) – результат «CMXCIX»;
=РИМСКОЕ(999;ЛОЖЬ) – результат «IM».
Иные функции
Функция ЗНАК
Проверяет знак числа и возвращает значение:
- -1 – для отрицательных чисел;
- 0 – если число равняется 0;
- 1 – для положительных чисел.
Синтаксис: =ЗНАК(число), где число – обязательный аргумент, являющийся числом либо ссылкой на ячейку, содержащую числовое значение.
=ЗНАК(-14) – возвращается значение -1.
Функция ПИ
Возвращает значение числа пи, округленное до 14 знаков после запятой – 3,14159265358979.
Синтаксис: =ПИ().
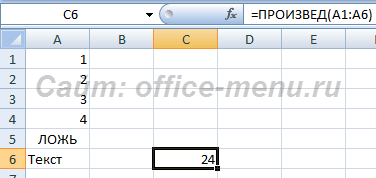
Функция ПРОИЗВЕД
Вычисляет произведение всех своих аргументов. Максимальное число аргументов 255.
Если функция ссылается на ячейку, диапазон ячеек или массив, содержащий текстовые либо логические значения, то такие значения игнорируются. Если какой-либо аргумент явно принимает текстовое значение, то он вызывает ошибку. Если же аргумент явно принимает логическое значением, то ЛОЖЬ приравнивается к нулю, а ИСТИНА к единице.
Синтаксис: =ПРОИЗВЕД(число1; [число2]; …), где
- Число1 – обязательный аргумент, являющийся числом либо ссылкой на ячейку или диапазон ячеек, содержащих число;
- Число2 и последующие аргументы – необязательные аргументы, аналогичные первому.
В данном примере видно, что текстовые и логические значения никак не влияют на конечный результат формулы.
Альтернатива использования данной функции — символ звездочки: =2*3*4
Функция ПРОМЕЖУТОЧНЫЕ.ИТОГИ()
Данная функция предназначена для работы со структурой промежуточных итогов. Ознакомиться с применением такой структуры можно в соответствующей статье категории Уверенное использование Excel на нашем сайте.
Во время задания подобной структуры, рассматриваемая функция создается автоматически. Смысл ее использования таков, что она игнорирует значения в ячейках, высчитанные с использованием промежуточных итогов. Рассмотрим синтаксис и пример использования.
Синтаксис: =ПРОМЕЖУТОЧНЫЕ.ИТОГИ(номер_функции; ссылка1; [ссылка2]; . ), где
- номер_функции – обязательный аргумент. Число от 1 до 11 либо от 101 до 111, указывающее на то, какую функцию использовать для расчета и в каком режиме (подробнее читайте ниже);
- ссылка1 и последующие ссылки – ссылки на ячейки или диапазоны ячеек, содержащие значения для расчета. Минимальное количество ссылок — 1, максимальное — 254.
Соотношение номера функции с конкретной функцией:
- 1 – СРЗНАЧ;
- 2 – СЧЁТ;
- 3 – СЧЁТЗ;
- 4 – МАКС;
- 5 – МИН;
- 6 – ПРОИЗВЕД;
- 7 – СТАНДОТКЛОН;
- 8 – СТАНДОТКЛОНП;
- 9 – СУММ;
- 10 – ДИСП;
- 11 – ДИСПР.
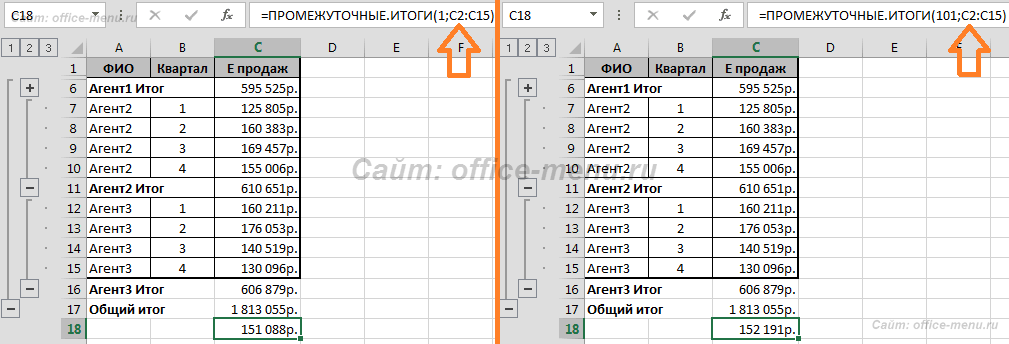
Если к описанным номерам прибавить 100 (т.е. вместо 1 указать 101 и т.д.), то они все равно будут указывать на те же функции. Но отличие заключается в том, что во втором варианте, при скрытие строк, те ячейки, указанные в ссылках, которые будут находится в скрытых строках, участвовать в подсчете не будут.
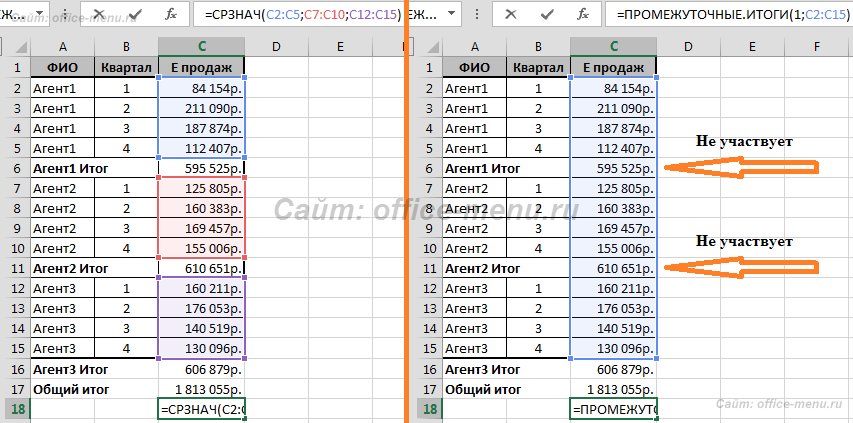
Используем структуру промежуточных итогов, которую мы применяли в одноименной статье. Добавим к ней средний результат по всем агентам за каждый квартал. Для того, чтобы корректно применить функцию СРЗНАЧ для имеющихся значений, нам пришлось бы указать 3 отдельных диапазона, чтобы не принимать в расчет промежуточные значение. Это не составить проблем, если данных не много, но если таблица большая, то выделять каждый диапазон будет проблематично. В данной ситуации лучше применить функцию ПРОМЕЖУТОЧНЫЕ.ИТОГИ, т.к она проигнорирует все ненужные ячейки. Обратите внимание на изображение. Разница очевидна, что второй пример использовать гораздо удобнее при одинаковых результатах функций. Также можно не беспокоиться о добавлении в будущем других строк с итогами.
Теперь продемонстрируем различия в использовании режимов функций. В качестве примера используем только что созданную формулу и изменим значение первого аргумента на 101 вместо 1. Возвращаемый результат не измениться до тех пор, пока мы не скроем строки структуры.
Информация продаж по Агенту1 во втором случае не учитывается.
Источник