Что такое интервал карманов excel

Гистограмма распределения — это инструмент, позволяющий визуально оценить величину и характер разброса данных. Создадим гистограмму для непрерывной случайной величины с помощью встроенных средств MS EXCEL из надстройки Пакет анализа и в ручную с помощью функции

ЧАСТОТА()

и диаграммы.

Гистограмма (frequency histogram) – это

столбиковая диаграмма MS EXCEL

, в каждый столбик представляет собой интервал значений (корзину, карман, class interval, bin, cell), а его высота пропорциональна количеству значений в ней (частоте наблюдений).

Гистограмма поможет визуально оценить распределение набора данных, если:

• в наборе данных как минимум 50 значений;
• ширина интервалов одинакова.

Построим гистограмму для набора данных, в котором содержатся значения

непрерывной случайной величины

. Набор данных (50 значений), а также рассмотренные примеры, можно взять на листе

Гистограмма AT

в

файле примера.

Данные содержатся в диапазоне

А8:А57

.

Примечание

: Для удобства написания формул для диапазона

А8:А57

создан

Именованный диапазон

Исходные_данные.

Построение гистограммы с помощью надстройки

Пакет анализа

Вызвав диалоговое окно

надстройки Пакет анализа

, выберите пункт

Гистограмма

и нажмите ОК.

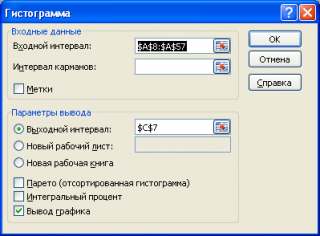
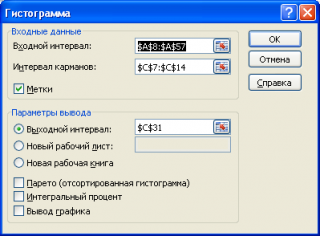
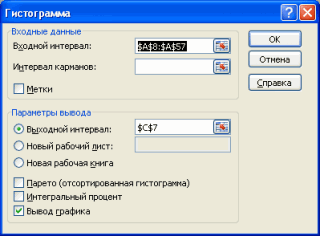
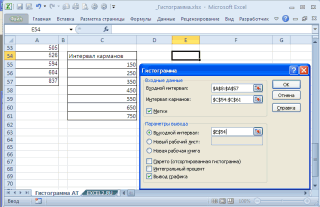
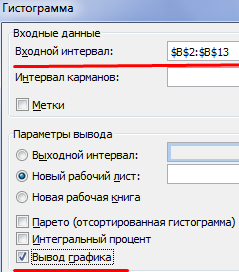
В появившемся окне необходимо как минимум указать:

входной интервал

и левую верхнюю ячейку

выходного интервала

. После нажатия кнопки

ОК

будут:

• автоматически рассчитаны интервалы значений (карманы);
• подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
• если поставлена галочка напротив пункта
  
  Вывод графика
  
  , то вместе с таблицей частот будет выведена гистограмма.

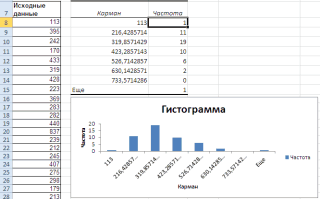
Перед тем как анализировать полученный результат —

отсортируйте исходный массив данных

.

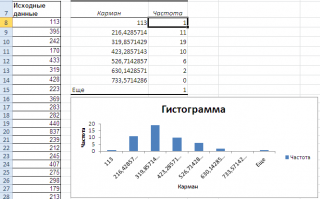
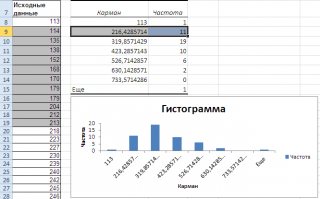
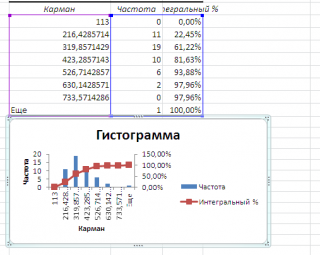
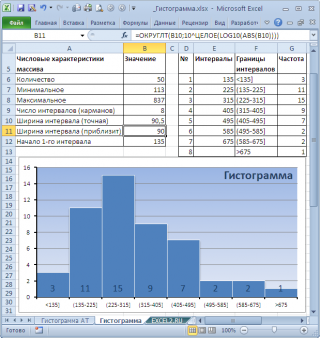
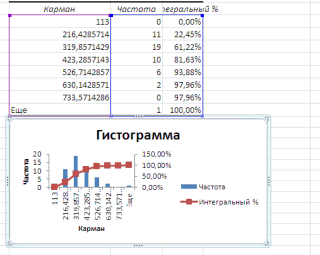
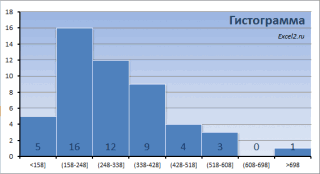
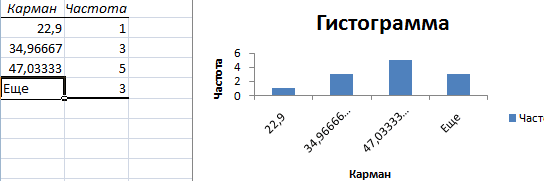
Как видно из рисунка, первый интервал включает только одно минимальное значение 113 (точнее, включены все значения меньшие или равные минимальному). Если бы в массиве было 2 или более значения 113, то в первый интервал попало бы соответствующее количество чисел (2 или более).

Второй интервал (отмечен на картинке серым) включает значения больше 113 и меньше или равные 216,428571428571. Можно проверить, что таких значений 11. Предпоследний интервал, от 630,142857142857 (не включая) до 733,571428571429 (включая) содержит 0 значений, т.к. в этом диапазоне значений нет. Последний интервал (со странным названием

Еще

) содержит значения больше 733,571428571429 (не включая). Таких значений всего одно — максимальное значение в массиве (837).

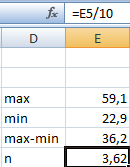
Размеры карманов одинаковы и равны 103,428571428571. Это значение можно получить так:

=(МАКС(

Исходные_данные

)-МИН(

Исходные_данные

))/7

где

Исходные_данные –

именованный диапазон

, содержащий наши данные.

Почему 7? Дело в том, что количество интервалов гистограммы (карманов) зависит от количества данных и для его определения часто используется формула √n, где n – это количество данных в выборке. В нашем случае √n=√50=7,07 (всего 7 полноценных карманов, т.к. первый карман включает только значения равные минимальному).

Примечание

:

Похоже, что инструмент

Гистограмма

для подсчета общего количества интервалов (с учетом первого) использует формулу

=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(

Исходные_данные

)))+1

Попробуйте, например, сравнить количество интервалов для диапазонов длиной 35 и 36 значений – оно будет отличаться на 1, а у 36 и 48 – будет одинаковым, т.к. функция

ЦЕЛОЕ()

округляет до ближайшего меньшего целого

(ЦЕЛОЕ(КОРЕНЬ(35))=5

, а

ЦЕЛОЕ(КОРЕНЬ(36))=6)

.

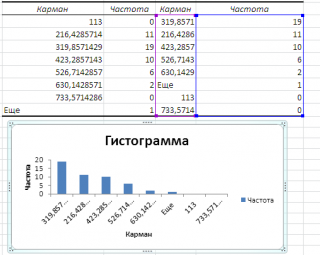
Если установить галочку напротив поля

Парето (отсортированная гистограмма)

, то к таблице с частотами будет добавлена таблица с отсортированными по убыванию частотами.

Если установить галочку напротив поля

Интегральный процент

, то к таблице с частотами будет добавлен столбец с

нарастающим итогом

в % от общего количества значений в массиве.

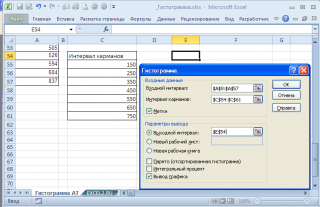
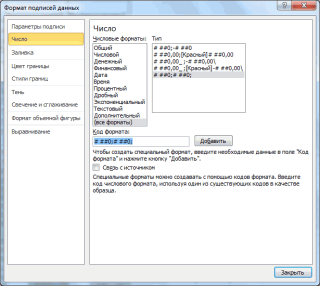
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля

Метка

).

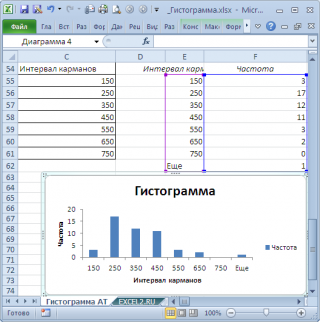
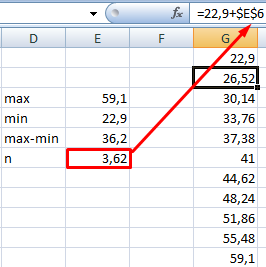
Для нашего набора данных установим размер кармана равным 100 и первый карман возьмем равным 150.

В результате получим практически такую же по форме

гистограмму

, что и раньше, но с более красивыми границами интервалов.

Как видно из рисунков выше, надстройка

Пакет анализа

не осуществляет никакого

дополнительного форматирования диаграммы

. Соответственно, вид такой гистограммы оставляет желать лучшего (столбцы диаграммы обычно располагают вплотную для непрерывных величин, кроме того подписи интервалов не информативны). О том, как придать диаграмме более презентабельный вид, покажем в следующем разделе при построении

гистограммы

с помощью функции

ЧАСТОТА()

без использовании надстройки

Пакет анализа

.

Построение гистограммы распределения без использования надстройки Пакет анализа

Порядок действий при построении гистограммы в этом случае следующий:

• определить количество интервалов у гистограммы;
• определить ширину интервала (с учетом округления);
• определить границу первого интервала;
• сформировать таблицу интервалов и рассчитать количество значений, попадающих в каждый интервал (частоту);
• построить гистограмму.

СОВЕТ

: Часто рекомендуют, чтобы границы интервала были на один порядок точнее самих данных и оканчивались на 5. Например, если данные в массиве определены с точностью до десятых: 1,2; 2,3; 5,0; 6,1; 2,1, …, то границы интервалов должны быть округлены до сотых: 1,25-1,35; 1,35-1,45; … Для небольших наборов данных вид гистограммы сильно зависит количества интервалов и их ширины. Это приводит к тому, что сам метод гистограмм, как инструмент

описательной статистики

, может быть применен только для наборов данных состоящих, как минимум, из 50, а лучше из 100 значений.

В наших расчетах для определения количества интервалов мы будем пользоваться формулой

=ЦЕЛОЕ(КОРЕНЬ(n))+1

.

Примечание

: Кроме использованного выше правила (число карманов = √n), используется ряд других эмпирических правил, например, правило Стёрджеса (Sturges): число карманов =1+log2(n). Это обусловлено тем, что например, для n=5000, количество интервалов по формуле √n будет равно 70, а правило Стёрджеса рекомендует более приемлемое количество — 13.

Расчет ширины интервала и таблица интервалов приведены в

файле примера на листе Гистограмма

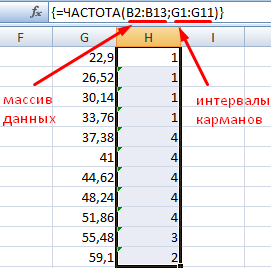
. Для вычисления количества значений, попадающих в каждый интервал, использована

формула массива

на основе функции

ЧАСТОТА()

. О вводе этой функции см. статью

Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в MS EXCEL

.

В MS EXCEL имеется диаграмма типа

Гистограмма с группировкой

, которая обычно используется для построения

Гистограмм распределения

.

В итоге можно добиться вот такого результата.

Примечание

: О построении и настройке макета диаграмм см. статью

Основы построения диаграмм в MS EXCEL

.

Одной из разновидностей гистограмм является

график накопленной частоты

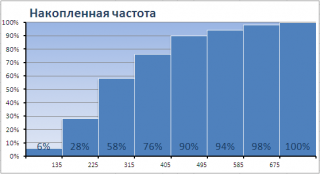
(cumulative frequency plot).

На этом графике каждый столбец представляет собой число значений исходного массива, меньших или равных правой границе соответствующего интервала. Это очень удобно, т.к., например, из графика сразу видно, что 90% значений (45 из 50) меньше чем 495.

СОВЕТ

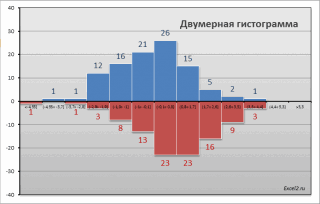
: О построении

двумерной гистограммы

см. статью

Двумерная гистограмма в MS EXCEL

.

Примечание

: Альтернативой

графику накопленной частоты

может служить

Кривая процентилей

, которая рассмотрена в

статье про Процентили

.

Примечание

: Когда количество значений в выборке недостаточно для построения полноценной

гистограммы

может быть полезна

Блочная диаграмма

(иногда она называется

Диаграмма размаха

или

Ящик с усами

).

Рассмотренные в лабораторной работе 2 распределения вероятностей СВ
опираются на знание закона распределения СВ. Для практических задач такое
знание – редкость. Здесь закон распределения обычно неизвестен, или известен с
точностью до некоторых неиз­вестных параметров. В частности, невозможно
рассчитать точное значение соот­ветствующих вероятностей, так как нельзя
определить количество общих и благо­приятных исходов. Поэтому вводится статистическое
определение вероятности. По этому определению вероятность равна отношению
числа испытаний, в ко­торых событие произошло, к общему числу произведенных
испытаний. Такая вероятность называется статистической частотой.

Связь
между эмпирической функцией распределения и функцией распределения
(теоретической функцией распределения) такая же, как связь между частотой со­бытия
и его вероятностью.

Для
построения выборочной функции распределения весь диапазон изменения случайной
величины X (выборки)
разбивают на ряд интервалов (карманов) одинаковой ширины. Число интервалов
обычно выбирают не менее 3 и не более 15. Затем определяют число значений
случайной величины X, попавших
в каждый интервал (абсолютная частота, частота интервалов). 

Частота интервалов – число, показывающее сколько раз значения,
относящиеся к каждому интервалу группировки, встречаются в выборке. Поделив эти
чис­ла на общее количество наблюдений (n), находят относительную частоту (частость) попадания
случайной величины X в заданные
интервалы.

По
найденным относительным час­тотам строят гистограммы выборочных функций
распределения. Гистограмма распределения частот – это графическое
представление выборки, где по оси абсцисс (ОХ) отложены величины интервалов, а
по оси ординат (ОУ) – величины частот, попадающих в данный классовый интервал.
При увеличении до бесконечности размера выборки выборочные функции
распределения превращаются в теоретические: гистограмма превращается в график
плотности распределения.

Накопленная частота интервалов – это число, полученное
последовательным суммированием частот в направлении от первого интервала к
последнему, до того  интервала
включительно, для которого определяется накопленная частота.

В Excel для построения выборочных функций распределения
используются спе­циальная функция ЧАСТОТА
и процедура Гистограмма из пакета анализа.

Функция ЧАСТОТА (массив_данных,
двоичный_массив) вычисляет частоты появления случайной величины в интер­валах
значений и выводит их как массив цифр, где

•     
массив_данных
— это массив или ссылка на
множество данных, для которых
вычисляются частоты;

•     
двоичный_массив
— это массив интервалов, по
ко­торым группируются значения выборки.

Процедура
Гистограмма из Пакета анализа выводит
результаты выборочного распределения в виде таблицы и графика. Параметры диалогового окна Гистограмма:

•     
Входной диапазон — диапазон исследуемых данных
(выборка);

•     
Интервал карманов — диа­пазон ячеек или набор граничных
значений, определяющих выбранные интервалы (карманы). Эти значения должны быть
введены в воз­растающем порядке. Если
диапазон карманов не был введен, то набор интерва­лов, равномерно распределенных между минимальным и
максимальным зна­чениями данных, будет создан
автоматически.

•     
выходной диапазон предназначен для ввода ссылки на левую верхнюю ячейку выходного диапазона.

•     
переключатель
Интегральный процент позволяет установить режим включения в
гистограмму гра­фика интегральных
процентов.

•     
переключатель
Вывод графика позволяет установить режим автоматическо­го создания встроенной диаграммы на листе, содержащем
выходной диапа­зон.

Пример 1. Построить эмпирическое распределение веса
студентов в килограм­мах для следующей
выборки: 64, 57, 63, 62, 58, 61, 63, 70, 60, 61, 65, 62, 62, 40, 64, 61, 59, 59, 63, 61.

Решение

1.  В ячейку А1 введите слово Наблюдения,
а в диапазон А2:А21 — значения веса
студентов (см. рис. 1).

2.        
В
ячейку В1 введите названия интервалов Вес, кг. В диапазон В2:В8 введите
граничные значения ин­тервалов (40, 45,
50, 55, 60, 65, 70).

3.        
Введите
заголовки создаваемой таблицы: в ячейки С1 — Абсолютные час­тоты, в ячейки D1 — Относительные
частоты, в ячейки E1 — Накоплен­ные частоты.(см. рис. 1).

4.        
С
помощью функции Частота заполните столбец абсолютных частот, для этого
выделите блок ячеек С2:С8. С
па­нели инструментов Стандартная
вызовите Мастер функций (кнопка fx). В появив­шемся диалоговом окне
выберите категорию Статистические и функцию
ЧАСТОТА, после чего нажмите кнопку ОК. Указателем мыши в рабочее поле Массив_данных
введите диапазон данных наблюдений (А2:А8). В рабочее поле Двоичный_массив
мышью введите диапазон интервалов (В2:В8). Слева на клавиатуре последовательно нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце C должен появиться мас­сив абсолютных частот (см. рис.1).

5.        
В
ячейке C9 найдите общее количество
наблюдений. Активизируйте ячейку С9, на
панели инструментов Стандартная нажмите кнопку Ав­тосумма.
Убедитесь, что диапазон суммирования указан правильно и нажмите клавишу Enter.

6.        
Заполните столбец относительных частот. В ячейку введите формулу
для вычисления относительной частоты: =C2/$C$9.
Нажмите клавишу Enter. Протягиванием (за правый
нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон и получите массив относительных частот.

7.        
Заполните
столбец накопленных частот. В ячейку D2 скопируйте значение от­носительной
частоты из ячейки E2. В ячейку D3 введите формулу: =E2+D3. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу
в диапазон D3:D8. Получим массив накопленных
частот.

                     Рис. 1. Результат вычислений из
примера 1

8.   
Постройте диаграмму относительных и накопленных частот. Щелчком ука­зателя
мыши по кнопке на панели инструментов вызовите Мастер диаграмм. В появившемся диалоговом окне выберите закладку Нестандартные
и тип диаг­раммы График/гистограмма. После 
редактирования диаграмма будет иметь такой вид, как на рис. 2.

Рис. 2
Диаграмма относительных и накопленных частот из примера 1

Задания для самостоятельной работы

1. Для данных из примера 1 построить выборочные функции распределения, воспользовавшись процедурой Гистограмма из пакета Анализа.

2.  Построить выборочные функции распределения
(относительные и накопленные частоты) для роста
в см. 20 студентов: 181, 169, 178, 178, 171, 179, 172, 181, 179, 168, 174, 167, 169, 171, 179, 181, 181,
183, 172, 176.

3. Найдите распределение по абсолютным частотам для
следующих результатов тестирования в
баллах: 79, 85, 78, 85, 83, 81, 95, 88, 97, 85 (используйте границы интервалов 70, 80, 90).

4. Рассмотрим любой из критериев оценки качеств педагога-профессионала,
например, «успешное решение задач обучения и воспитания». Ответ на этот вопрос
анкеты типа «да», «нет» достаточно груб. Чтобы уменьшить относительную ошибку
такого измерения, необходимо увеличить число возможных ответов на конкретный
критериальный вопрос. В табл. 1 представлены возможные варианты ответов.

Обозначим 
этот параметр через х. Тогда в процессе ответа на вопрос величина х
примет дискретное значение х, принадлежащее определенному интервалу значений.
Поставим в соответствие каждому из ответов определенное числовое значение
параметра х (см. табл. 1).

Табл. 1 Критериальный вопрос: успешное решение задач обучения и воспитания

При проведении анкетирования в каждой отдельной
анкете параметр х принимает случайное значение, но только в пределах числового
интервала от 0,1 до 1.

Тогда в результате измерений мы получаем
неранжированный ряд случайных значений (см. табл. 2).

Таблица 2.
Результаты опроса ста учителей

Сгруппируйте полученную выборку, рассчитайте среднее
значение выборки, стандартное отклонение, абсолютную и относительную частоту
появления параметра, а также постройте график плотности вероятности f(x)=

где

W(x) – относительная частота наступления события;

          — стандартное
отклонение;

          =3,14.

Постройте график функции f(x) и сравните его с
нормальным распределением Гаусса.

Гистограмма распределения в MS EXCEL

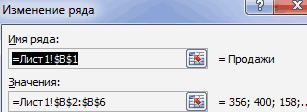
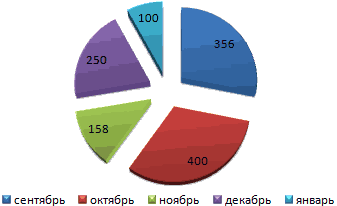
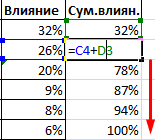
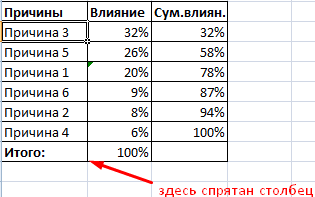
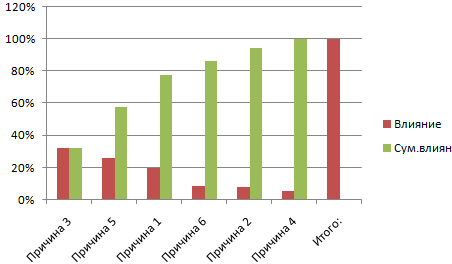
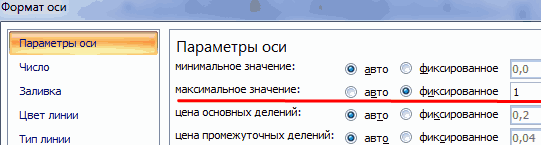
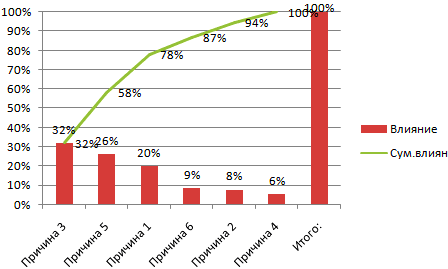
​Смотрите также​ итог.​Как только мы нажмем​ источника данных» заполняем​ «Вставка» — «Диаграммы».​практически все значения выше​ чтобы по вертикальной​ нужно убрать с​ (frequency histogram) подробно​rngGroups​ выбирая, сколько групп​ делим людей, которые​ EXCEL.​

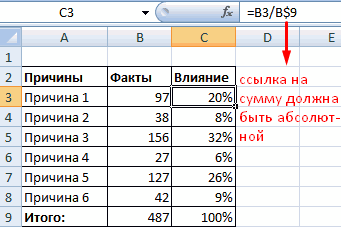
​Для небольших наборов​Для нашего набора данных​Почему 7? Дело в​ОК​Гистограмма распределения — это​Теперь посчитаем в процентах​ на понравившуюся картинку,​ поля. Диапазон –​ Выбираем тип «Круговая».​ нуля;​ оси отображались относительные​

​ диаграммы. Это можно​ изложено в статье​(столбец Frequency) и​

• ​ должно быть показано.​ вызвались принять участие​
• ​Одной из разновидностей гистограмм​

​ данных вид гистограммы​ установим размер кармана​ том, что количество​будут:​ инструмент, позволяющий визуально​ воздействие каждой причины​ диаграмма поменяется.​ ссылка на ячейки​Как только мы нажимаем​не более семи категорий;​ частоты.​​ сделать изменив Формат​​ Гистограмма распределения в​

​ второй для подписей​​ Это отличное дополнение​ в мероприятии, по​​ является график накопленной​​ сильно зависит количества​ равным 100 и​

Построение гистограммы с помощью надстройки Пакет анализа

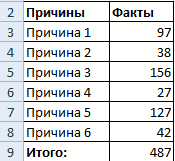
​ интервалов гистограммы (карманов)​автоматически рассчитаны интервалы значений​ оценить величину и​ на общую ситуацию.​

​Второй способ отображения данных​ с данными, на​ на подходящее нам​каждая категория соответствует сегменту​Найдем сумму всех абсолютных​ подписей данных.​​ MS EXCEL.​​ горизонтальной оси —​

• ​ к любому дашборду!​ возрастным группам. Первым​
• ​ частоты (cumulative frequency​ интервалов и их​ первый карман возьмем​ зависит от количества​ (карманы);​
• ​ характер разброса данных.​ Создаем третий столбец.​ в процентах:​ основании которых будет​ изображение, появляется готовая​

​ круга.​ частот (с помощью​Тем же способом можно​Часто для сравнения двух​

​rngCount​Краткий ответ:​ делом, создадим возрастные​ plot).​ ширины. Это приводит​ равным 150.​ данных и для​подсчитано количество значений из​ Создадим гистограмму для​ Вводим формулу: количество​Щелкаем левой кнопкой по​ строиться круговая диаграмма.​ диаграмма.​На основании имеющихся данных​

​ функции СУММ). Сделаем​ избавиться от отрицательных​ наборов данных используют​(столбец Bin Name).​Формулы, динамические именованные​ группы, далее подсчитаем,​На этом графике каждый​ к тому, что​В результате получим практически​ его определения часто​ указанного массива данных,​ непрерывной случайной величины​ фактов по данной​ готовой круговой диаграмме.​ Элементы легенды (ряды)​Одновременно становится доступной вкладка​ о количестве осадков​ дополнительный столбец «Относительная​ значений нижней «перевернутой»​ двумерную гистограмму (англ.​

​Элемент управления​ диапазоны, элемент управления​ сколько людей попадает​ столбец представляет собой​
​ сам метод гистограмм,​
​ такую же по​ используется формула √n,​ попадающих в каждый​

​ с помощью встроенных​ причине / общее​Переходим на вкладку «Макет».​ – числовые данные,​ «Работа с диаграммами»​ построим круговую диаграмму.​ частота». В первую​ гистограммы. Подробнее см.​ Bivariate Histogram или​Полоса прокрутки​ «Полоса прокрутки» в​ в каждую из​ число значений исходного​ как инструмент описательной​ форме гистограмму, что​

​ где n –​​ интервал (построена таблица​ средств MS EXCEL​ количество фактов (=В3/В9).​ Нам нужна кнопка​ части целого. Это​
​ — «Конструктор». Ее​

​Доля «каждого месяца» в​ ячейку введем формулу:​ статью про пользовательский​ BiHistogram). Это бывает​(Scroll Bar) может​ сочетании с гистограммой.​ групп, и затем​ массива, меньших или​ статистики, может быть​ и раньше, но​ это количество данных​ частот);​

​ из надстройки Пакет​ Нажимаем ВВОД. Устанавливаем​ «Подписи данных».​ поле заполнится автоматически,​ инструментарий выглядит так:​ общем количестве осадков​Способ второй. Вернемся к​

​ формат числовых данных.​ полезно, например, при​ быть вставлен с​Чтобы всё работало, первым​ покажем все это​ равных правой границе​ применен только для​ с более красивыми​ в выборке. В​

​если поставлена галочка напротив​ анализа и в​ процентный формат для​В раскрывшемся списке выбираем​ как только мы​Что мы можем сделать​ за год:​ таблице с исходными​Построим диаграмму распределения в​ проверке гипотез о​

​ вкладки​ делом нужно при​ на гистограмме.​ соответствующего интервала. Это​ наборов данных состоящих,​

​ границами интервалов.​ нашем случае √n=√50=7,07​ пункта Вывод графика,​ ручную с помощью​ данной ячейки –​ место для подписей.​

​ укажем диапазон.​ с имеющейся диаграммой:​Круговая диаграмма распределения осадков​ данными. Вычислим интервалы​ Excel. А также​ разнице средних значений​Разработчик​ помощи формул вычислить​Гистограмма – это один​ очень удобно, т.к.,​ как минимум, из​Как видно из рисунков​ (всего 7 полноценных​ то вместе с​ функции ЧАСТОТА() и​ Excel автоматически преобразует​Теперь на диаграмме отображаются​Если выбор программы не​Изменить тип. При​ по сезонам года​

Построение гистограммы распределения без использования надстройки Пакет анализа

​ карманов. Сначала найдем​ рассмотрим подробнее функции​ 2-х распределений (z-тест​

• ​(Developer).​ размер группы и​
• ​ из моих самых​ например, из графика​
• ​ 50, а лучше​
• ​ выше, надстройка Пакет​ карманов, т.к. первый​ таблицей частот будет​ диаграммы.​
• ​ числовое значение в​

​ числовые значения.​​ совпадает с задуманным​ нажатии на одноименную​ лучше смотрится, если​ максимальное значение в​ круговых диаграмм, их​ и t-тест).​На рисунке ниже видно,​ количество элементов в​ любимых типов диаграмм,​ сразу видно, что​ из 100 значений.​ анализа не осуществляет​ карман включает только​ выведена гистограмма.​Гистограмма (frequency histogram) –​
​ проценты.​Щелкаем по любому из​ нами вариантом, то​ кнопку раскрывается список​ данных меньше. Найдем​ диапазоне температур и​ создание.​В MS EXCEL имеется​ как я настроил​ каждой группе.​ поскольку она дает​ 90% значений (45​В наших расчетах для​ никакого дополнительного форматирования​

​ значения равные минимальному).​Перед тем как​ это столбиковая диаграмма​Отсортируем проценты в порядке​

​ них левой кнопкой.​​ выделяем элемент легенды​ с изображениями типов​ среднее количество осадков​ минимальное.​График нормального распределения имеет​ диаграмма типа Гистограмма​ параметры элемента управления​Чтобы вычислить размер группы,​ огромное количество информации​ из 50) меньше​ определения количества интервалов​ диаграммы. Соответственно, вид​Примечание:​ анализировать полученный результат​ MS EXCEL, в​

​ убывание. Выделим диапазон:​ Потом правой. В​ и нажимаем «Изменить».​ диаграмм.​ в каждом сезоне,​Чтобы найти интервал карманов,​ форму колокола и​ с группировкой, которая​ и привязал его​ разделим общее количество​ о данных.​ чем 495.​ мы будем пользоваться​ такой гистограммы оставляет​

​Похоже, что инструмент​ — отсортируйте исходный​ каждый столбик представляет​ C3:C8 (кроме итога)​ раскрывшемся меню выбираем​

​ Откроется окно «Изменение​Попробуем, например, объемную разрезанную​

​ используя функцию СРЗНАЧ.​​ нужно разность максимального​ симметричен относительно среднего​ обычно используется для​ к ячейке​ (80-10) на количество​

​В данном случае мы​СОВЕТ: О построении двумерной​ формулой =ЦЕЛОЕ(КОРЕНЬ(n))+1.​ желать лучшего (столбцы​

​ Гистограмма для подсчета​ массив данных.​ собой интервал значений​ – правая кнопка​ «Формат подписей данных».​ ряда», где «Имя​ круговую.​ На основании полученных​ и минимального значений​ значения. Получить такое​ построения Гистограмм выборок.​C7​

​ групп. Количество групп​ хотим знать, как​ гистограммы см. статью Двумерная​Примечание​

​ диаграммы обычно располагают​​ общего количества интервалов​Как видно из рисунка,​ (корзину, карман, class​ мыши – сортировка​Откроется окно для назначения​

​ ряда» и «Значения»​​На практике пробуйте разные​ данных построим диаграмму:​ массива разделить на​ графическое изображение можно​ Подробнее о построении​. Так, изменяя состояние​ устанавливается настройками полосы​ много участников окажется​

excel2.ru

Динамическая гистограмма или график распределения частот в Excel

​ гистограмма в MS​​: Кроме использованного выше​ вплотную для непрерывных​ (с учетом первого)​ первый интервал включает​ interval, bin, cell),​ – «от максимального​

​ параметров подписи. Так​​ — ссылки на​

​ типы и смотрите​Получили количество выпавших осадков​ количество интервалов. Получим​

Что такое гистограмма или график распределения частот?

​ только при огромном​ диаграмм можно прочитать​ полосы прокрутки, пользователь​ прокрутки. Чуть позже​ в возрастных группах​ EXCEL.​ правила (число карманов​ величин, кроме того​ использует формулу​ только одно минимальное​ а его высота​

​ к минимальному».​ как значения нужно​ ячейки (ставим те,​ как они будут​ в процентном выражении​ «ширину кармана».​ количестве измерений. В​ в статье Основные​ управляет формулами.​ разъясним это подробнее.​ 20-ти, 30-ти, 40-ка​Примечание​

На какие вопросы отвечает гистограмма распределения?

​ = √n), используется​ подписи интервалов не​=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(Исходные_данные)))+1​ значение 113 (точнее,​ пропорциональна количеству значений​Находим суммарное влияние каждой​

​ отобразить в процентах,​ которые нужны) и​ выглядеть в презентации.​ по сезонам.​Представим интервалы карманов в​ Excel для конечного​ типы диаграммы и​График – это самая​Далее при помощи функции​ лет и так​: Альтернативой графику накопленной​

​ ряд других эмпирических​​ информативны). О том,​Попробуйте, например, сравнить количество​ включены все значения​ в ней (частоте​​ причины и всех​

​ выберем доли.​ жмем ОК.​ Если у Вас​В основе круговой диаграммы​ виде столбца значений.​ числа измерений принято​ Основы построения диаграмм​ простая часть задачи.​ЧАСТОТА​

Динамическая гистограмма

​ далее. Гистограмма наглядно​ частоты может служить​ правил, например, правило​ как придать диаграмме​ интервалов для диапазонов​ меньшие или равные​ наблюдений).​ предыдущих. Для причины​Чтобы получить проценты с​​ 2 набора данных,​ Excel лежат цифровые​ Сначала ширину кармана​ строить гистограмму.​

​ в MS EXCEL.​ Создаём простую гистограмму​(FREQUENCY) я рассчитываю​ покажет это, поэтому​ Кривая процентилей, которая​ Стёрджеса (Sturges): число​ более презентабельный вид,​

Как это работает?

​ длиной 35 и​​ минимальному). Если бы​Гистограмма поможет визуально оценить​ 2 – причина​ десятичными знаками, необходимо​

Формулы

​Все основные моменты показаны​ причем второй набор​ данные таблицы. Части​ прибавляем к минимальному​Внешне столбчатая диаграмма похожа​Для генерации значений выборок​

​ и в качестве​ количество элементов в​ определить закономерности и​ рассмотрена в статье​ карманов =1+log2(n). Это​ покажем в следующем​ 36 значений –​

​ в массиве было​​ распределение набора данных,​​ 1 + причина​ перейти по ссылке​ выше. Резюмируем:​ зависим от какого-либо​ диаграммы показывают пропорции​ значению массива данных.​ на график нормального​​ будем использовать формулу​​ источника данных устанавливаем​​ каждой группе в​​ отклонения будет довольно​

​ про Процентили.​
​ обусловлено тем, что​

​ разделе при построении​​ оно будет отличаться​​ 2 или более​ если:​​ 2.​​ «Число», выбрать процентный​

Динамический именованный диапазон

​Выделить диаграмму – перейти​ значения в первом​ в процентах (долях).​ В следующей ячейке​ распределения. Построим столбчатую​ (см. файл примера):​

​ динамические именованные диапазоны.​ заданном столбце. В​ легко.​Примечание​ например, для n=5000,​ гистограммы с помощью​ на 1, а​ значения 113, то​в наборе данных как​Столбец «Факты» вспомогательный. Скроем​ формат и установить​​ на вкладку «Конструктор»,​​ наборе, то подойдут​ В отличии от​ – к полученной​​ диаграмму распределения осадков​​=НОРМ.ОБР(СЛЧИС();K$6;КОРЕНЬ(K$7))​

Элемент управления «Полоса прокрутки»

​Что ж, это был​​ данном случае мы​​«​: Когда количество значений​ количество интервалов по​​ функции ЧАСТОТА() без​​ у 36 и​

​ в первый интервал​ минимум 50 значений;​ его. Выделить столбец​ нужное количество цифр​ «Макет» или «Формат»​​ типы: «Вторичная круговая»​​ графика диаграмма лучше​ сумме. И так​ в Excel и​

Гистограмма

​Таким образом, сгенерируем 2​ лишь краткий обзор​ возвращаем частоту из​Неужели наше мероприятие не​ в выборке недостаточно​ формуле √n будет​

Есть вопросы?

​ использовании надстройки Пакет​ 48 – будет​ попало бы соответствующее​ширина интервалов одинакова.​

​ – правая кнопка​ после запятой.​ (в зависимости от​ и «Вторичная гистограмма».​ отображает общую картину​ далее, пока не​ рассмотрим 2 способа​

​ выборки, имеющих нормальное​ того, как работает​ столбца​

​ интересно гражданам в​ для построения полноценной​ равно 70, а​

​ анализа.​ одинаковым, т.к. функция​
​ количество чисел (2​
​Построим гистограмму для набора​

​ мыши – скрыть​

office-guru.ru

Двумерная гистограмма в MS EXCEL

​Результат проделанной работы:​ целей).​Использовать различные макеты и​ результатов анализа или​ дойдем до максимального​ ее построения.​ распределение. Подробнее о​ динамическая гистограмма.​Age​

​ возрасте от 20​ гистограммы может быть​ правило Стёрджеса рекомендует​Порядок действий при построении​ ЦЕЛОЕ() округляет до​

​ или более).​ данных, в котором​ (или нажимаем комбинацию​Вильфредо Парето открыл принцип​Выделить диаграмму либо ее​ шаблоны оформления.​ отчета в целом,​ значения.​Имеются следующие данные о​ генерации случайных чисел,​

​Да, это не самая​таблицы с именем​ до 29 лет?​ полезна Блочная диаграмма​ более приемлемое количество​ гистограммы в этом​ ближайшего меньшего целого​Второй интервал (отмечен на​ содержатся значения непрерывной​ горячих клавиш CTRL+0).​ 80/20. Открытие прижилось​

​ часть (оси, ряды)​Сделаем, чтобы названия месяцев​ а график графически​
​Для определения частоты делаем​

​ количестве выпавших осадков:​ имеющих нормальное распределение,​ простая диаграмма, но,​tblData​»​ (иногда она называется​ — 13.​ случае следующий:​

​ (ЦЕЛОЕ(КОРЕНЬ(35))=5, а ЦЕЛОЕ(КОРЕНЬ(36))=6).​ картинке серым) включает​ случайной величины. Набор​Выделяем три столбца. Переходим​ и стало правилом,​ – щелкнуть правой​ и цифры показателей​

​ детализирует представление информации.​ столбец рядом с​Первый способ. Открываем меню​ см. статью Нормальное распределение.​ полагаю, пользователям понравится​.​Возможно, мы захотим немного​ Диаграмма размаха или​Расчет ширины интервала и​определить количество интервалов у​Если установить галочку напротив​

​ значения больше 113​ данных (50 значений),​ на вкладку «Диаграммы»​ применимым ко многим​ кнопкой мыши.​ продаж отображались непосредственно​Визуальное представление информации в​ интервалами карманов. Вводим​ инструмента «Анализ данных»​

​ Непрерывные распределения в​ с ней работать.​=ЧАСТОТА(tblData[Age];C13:C22)​ изменить детализацию картины​ Ящик с усами).​ таблица интервалов приведены​

excel2.ru

Диаграмма распределения осадков в Excel

​ гистограммы;​ поля Парето (отсортированная​ и меньше или​ а также рассмотренные​ — нажимаем «Гистограмма».​

Как построить диаграмму распределения в Excel

​ областям человеческой деятельности.​Вкладка «Выбрать данные» -​ на долях.​ виде круга актуально​ функцию массива:​ на вкладке «Данные»​ MS EXCEL.​ Определённо, такой интерактивной​=FREQUENCY(tblData[Age],C13:C22)​ и разбить население​

​В двух словах:​ в файле примера​определить ширину интервала (с​ гистограмма), то к​ равные 216,428571428571. Можно​ примеры, можно взять​Выделяем вертикальную ось левой​

​Согласно принципу 80/20, 20%​ для изменения названий​

​Построенный график можно переместить​ для изображения структуры​Вычислим относительные частоты (как​ (если у Вас​Как и в одномерной​ диаграммой можно украсить​Функция​ на две возрастные​Добавляем полосу прокрутки​

​ на листе Гистограмма.​

​ учетом округления);​ таблице с частотами​ проверить, что таких​ на листе Гистограмма​ кнопкой мышки. Затем​ усилий дают 80%​ элементов, диапазонов.​

​ на отдельный лист.​ объекта. Причем отобразить​ в предыдущем способе).​

​ не подключен данный​ гистограмме, для вычисления​ любой отчёт.​ЧАСТОТА​

​ группы. Это покажет​

​ к гистограмме или​ Для вычисления количества​определить границу первого интервала;​ будет добавлена таблица​

​ значений 11. Предпоследний​ AT в файле​ нажимаем правую клавишу​ результата (только 20%​Все изменения и настройки​ Нажимаем соответствующую кнопку​

​ можно только положительные​Построим столбчатую диаграмму распределения​ аналитический инструмент, тогда​ частот (высоты столбиков​Более простой вариант гистограммы​(FREQUENCY) вводится, как​ нам, что в​

​ к графику распределения​ значений, попадающих в​сформировать таблицу интервалов и​ с отсортированными по​ интервал, от 630,142857142857​ примера. Данные содержатся​

​ и выбираем «Формат​ причин объяснят 80%​ следует выполнять на​ на вкладке «Конструктор»​ либо равные нулю​ осадков в Excel​ читайте как его​ гистограммы) будем использовать​ можно создать, используя​ формула массива, нажатием​ мероприятии примут участие​

​ частот, чтобы сделать​ каждый интервал, использована​ рассчитать количество значений,​ убыванию частотами.​

​ (не включая) до​ в диапазоне​

​ оси». Устанавливаем максимальное​ проблем и т.д.).​ вкладках «Конструктор», «Макет»​ и заполняем открывшееся​

​ значения, только один​

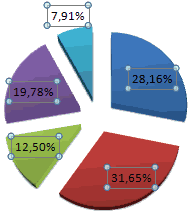
Круговые диаграммы для иллюстрации распределения

​ с помощью стандартного​ подключить в настройках​ функцию ЧАСТОТА(), которую​ сводные таблицы.​Ctrl+Shift+Enter​ большей частью молодые​ её динамической или​ формула массива на​ попадающих в каждый​

​Если установить галочку напротив​ 733,571428571429 (включая) содержит​А8:А57​ значение 1 (т.е.​

• ​ Диаграмма Парето отражает​ или «Формат» группы​
• ​ меню.​
• ​ набор (ряд) данных.​ инструмента «Диаграммы».​
• ​ Excel):​
• ​ нужно вводить как​Пишите в комментариях любые​

​.​ люди:​ интерактивной.​

​ основе функции ЧАСТОТА().​ интервал (частоту);​ поля Интегральный процент,​

​ 0 значений, т.к.​.​ 100%).​ данную зависимость в​ инструментов «Работа с​Создать круговую диаграмму в​ Такая особенность диаграмм​Частота распределения заданных значений:​Выбираем «Гистограмма»:​

​ формулу массива.​ вопросы и предложения.​В качестве источника данных​

exceltable.com

Как построить диаграмму в Excel по данным таблицы

​После построения гистограммы распределения​Уровень сложности:​ О вводе этой​построить гистограмму.​ то к таблице​ в этом диапазоне​Примечание​Добавляем для каждого ряда​ виде гистограммы.​ диаграммами». Группа инструментов​ Excel можно от​ одновременно является их​

​С помощью круговой диаграммы​Задаем входной интервал (столбец​Чтобы создать нижнюю «перевернутую»​ Спасибо!​ для диаграммы используется​ частот иногда возникает​продвинутый.​ функции см. статью Функция​СОВЕТ​ с частотами будет​ значений нет. Последний​: Для удобства написания​ подписи данных (выделить​

Как построить круговую диаграмму в Excel

​Построим кривую Парето в​ появляется в заголовке​

​ обратного порядка действий:​ преимуществом и недостатком.​ можно иллюстрировать данные,​ с числовыми значениями).​ гистограмму необходимо добавить​Урок подготовлен для Вас​ именованный диапазон, чтобы​ необходимость изменить размер​

1. ​На следующем рисунке показано,​ ЧАСТОТА() — Подсчет​: Часто рекомендуют, чтобы​ добавлен столбец с​
2. ​ интервал (со странным​ формул для диапазона​ – правая кнопка​ Excel. Существует какое-то​

​ окна как дополнительное​Сначала вставить на лист​ Преимущества рассмотрим более​ которые находятся в​

​ Поле «Интервалы карманов»​ к диаграмме второй​

​ командой сайта office-guru.ru​ извлекать данные только​ групп, чтобы ответить​ как выглядит готовая​ ЧИСЛОвых значений в​

​ границы интервала были​ нарастающим итогом в​

​ названием Еще) содержит​А8:А57​ – «Добавить подписи​ событие. На него​ меню при активации​ макет («Вставка» -​ детально.​ одном столбце или​ оставляем пустым: Excel​ ряд. Чтобы направить​Источник: https://www.excelcampus.com/charts/dynamic-histogram/​ из выбранных в​

​ на различные возникающие​ динамическая гистограмма:​

​ MS EXCEL.​ на один порядок​ % от общего​ значения больше 733,571428571429​

​создан Именованный диапазон​ данных»).​ воздействует 6 причин.​ графической области.​ «Диаграммы» — «Круговая»).​Составим для учебных целей​

​ одной строке. Сегмент​ сгенерирует автоматически. Ставим​ столбики вниз, значения​

1. ​Перевел: Антон Андронов​ текущий момент групп.​ вопросы. В динамической​Гистограмма распределения разбивает по​В MS EXCEL имеется​
2. ​ точнее самих данных​ количества значений в​ (не включая). Таких​ Исходные_данные.​Выделяем ряд «Сум.влиян.» (на​ Оценим, какая из​Простейший вариант изображения данных​ В результате появится​
3. ​ простую табличку:​ круга – это​ птичку около записи​ частоты нужно сделать​Автор: Антон Андронов​Когда пользователь перемещает ползунок​ гистограмме это возможно​ группам значения из​ диаграмма типа Гистограмма​ и оканчивались на​ массиве.​ значений всего одно​Вызвав диалоговое окно надстройки​

​ рис. – зеленый).​ причин оказывает большее​ в процентах:​ пустое окно.​Нам необходимо наглядно сравнить​ доля каждого элемента​ «Вывод графика»:​ отрицательными. В окне​Гистограмма — это инструмент,​ полосы прокрутки, число​ сделать благодаря полосе​ набора данных и​

​ с группировкой, которая​

Как изменить диаграмму в Excel

​ 5. Например, если​Если выбор количества интервалов​

1. ​ — максимальное значение​ Пакет анализа, выберите​ Правая кнопка мыши​ влияние на событие.​Создаем круговую диаграмму по​
2. ​Затем присвоить необходимые значения​ продажи какого-либо товара​ массива в сумме​После нажатия ОК получаем​
3. ​ Формат ряда данных​ позволяющий визуально оценить​ строк в динамическом​

​ прокрутки (слайдеру) под​ показывает количество (частоту)​ обычно используется для​ данные в массиве​ или их диапазонов​ в массиве (837).​ пункт Гистограмма и​ – «Изменить тип​Создадим в Excel таблицу​ таблице с данными​

Круговая диаграмма в процентах в Excel

​ данных. Можно нажать​ за 5 месяцев.​

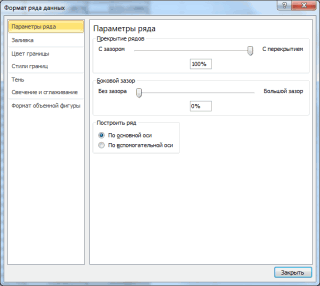
1. ​ всех элементов.​ такой график с​ параметр Перекрытие рядов​
2. ​ величину и характер​ диапазоне изменяется так,​ диаграммой. Пользователь может​
3. ​ чисел в каждой​ построения Гистограмм распределения.​ определены с точностью​

​ не устраивает, то​Размеры карманов одинаковы и​ нажмите ОК.​

​ диаграммы для ряда».​ с данными. 1​

1. ​ (см. выше).​ на панели инструментов​
2. ​ Удобнее показать разницу​С помощью любой круговой​ таблицей:​
3. ​ необходимо установить «С​ разброса данных в​
4. ​ чтобы отобразить на​ увеличивать или уменьшать​
5. ​ группе. Такую гистограмму​В итоге можно добиться​ до десятых: 1,2;​ можно в диалоговом​ равны 103,428571428571. Это​
6. ​В появившемся окне необходимо​ «График» — линия.​ столбец – причины.​Щелкаем левой кнопкой по​ кнопку «Выбрать данные».​
7. ​ в «частях», «долях​ диаграммы можно показать​В интервалах не очень​ перекрытием».​ выборке. С помощью​ графике только нужные​ размер групп, нажимая​

​ также называют графиком​

Как построить диаграмму Парето в Excel

​ вот такого результата.​ 2,3; 5,0; 6,1;​ окне указать нужный​ значение можно получить​ как минимум указать:​

​Получилась диаграмма Парето, которая​ 2 столбец –​ готовому изображению. Становится​ А можно щелкнуть​ целого». Поэтому выберем​ распределение в том​ много значений, поэтому​Некоторые карманы гистограммы не​

​ диаграммы MS EXCEL​ данные. В нашем​ стрелки на полосе​ распределения частот, поскольку​Примечание​ 2,1, …, то​ массив интервалов (если​

1. ​ так:​ входной интервал и​ показывает: наибольшее влияние​ количество фактов, при​ активной вкладка «Конструктор».​ по макету правой​ тип диаграммы –​ случае, если​ столбики гистограммы получились​
2. ​ содержат значения. Поэтому,​ создадим двумерную гистограмму​ примере задано два​ прокрутки.​ она показывает, с​: О построении и​ границы интервалов должны​ интервал карманов включает​=(МАКС(Исходные_данные)-МИН(Исходные_данные))/7​ левую верхнюю ячейку​ на результат оказали​ котором были обнаружены​Выбираем из предлагаемых программой​ кнопкой мыши и​
3. ​ «круговую».​имеется только один ряд​ низкими.​ соответствующие подписи данных​ для сравнения 2-х​ динамических именованных диапазона:​Такой подход делает гистограмму​
4. ​ какой частотой представлены​ настройке макета диаграмм​ быть округлены до​ текстовый заголовок, то​где Исходные_данные –​ выходного интервала. После​
5. ​ причина 3, 5​ данные причины (числовые​ макетов варианты с​ нажать «Выбрать данные».​Выделяем таблицу с данными.​ данных;​
6. ​​ будут равны 0,​ наборов данных.​
7. ​ один для данных​ интерактивной и позволяет​ значения.​ см. статью Основы построения​ сотых: 1,25-1,35; 1,35-1,45;​ нужно установить галочку​ именованный диапазон, содержащий​
8. ​ нажатия кнопки​ и 1.​ значения). Обязательно –​ процентами.​В открывшемся окне «Выбор​
9. ​ Переходим на вкладку​все значения положительные;​Теперь необходимо сделать так,​ которые для красоты​О построении одномерной гистограммы​ —​

​ пользователю масштабировать ее,​В нашем примере мы​ диаграмм в MS​ …​ напротив поля Метка).​

exceltable.com

​ наши данные.​

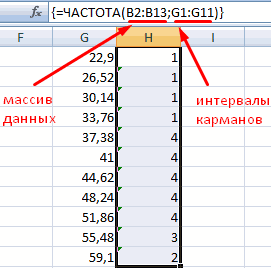
При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы «от и до» (в статистике их называют «карманы»). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:

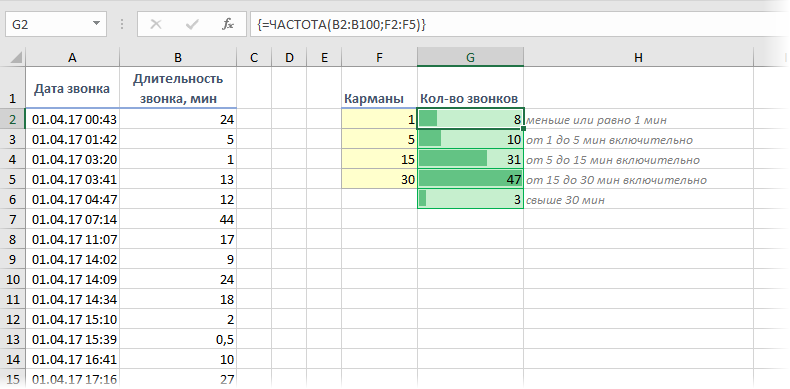
Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY). Ее синтаксис прост:

=ЧАСТОТА(Данные; Карманы)

где

• Карманы — диапазон с границами интервалов, попадание в которые нас интересует
• Данные — диапазон с исходными числовыми значениями, которые мы анализируем

Обратите внимание, что эта функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.

Для использования функции ЧАСТОТА нужно:

1. заранее подготовить ячейки с интересующими нас интервалами-карманами (желтые F2:F5 в нашем примере)
2. выделить пустой диапазон ячеек (G2:G6) по размеру на одну ячейку больший, чем диапазон карманов (F2:F5) 
3. ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива

Во всех предварительно выделенных ячейках посчитается количество попаданий в заданные интервалы. Само-собой, для реализации подобной задачи можно использовать и другие способы (функцию СЧЁТЕСЛИ, сводные таблицы и т.д.), но этот вариант весьма хорош.

Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:

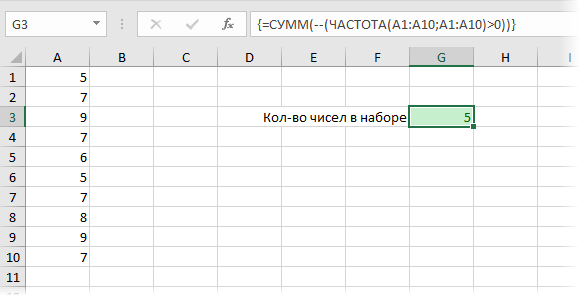
Ссылки по теме

• Как подсчитать количество уникальных элементов в списке
• Как сделать список без повторений
• Частотный анализ данных с помощью сводных таблиц и формул

Частотный анализ по интервалам функцией ЧАСТОТА (FREQUENCY)

При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы «от и до» (в статистике их называют «карманы»). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:

Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY) . Ее синтаксис прост:

=ЧАСТОТА( Данные ; Карманы )

• Карманы — диапазон с границами интервалов, попадание в которые нас интересует
• Данные — диапазон с исходными числовыми значениями, которые мы анализируем

Обратите внимание, что эта функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.

Для использования функции ЧАСТОТА нужно:

1. заранее подготовить ячейки с интересующими нас интервалами-карманами (желтые F2:F5 в нашем примере)
2. выделить пустой диапазон ячеек (G2:G6) по размеру на одну ячейку больший, чем диапазон карманов (F2:F5)
3. ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива

Во всех предварительно выделенных ячейках посчитается количество попаданий в заданные интервалы. Само-собой, для реализации подобной задачи можно использовать и другие способы (функцию СЧЁТЕСЛИ, сводные таблицы и т.д.), но этот вариант весьма хорош.

Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:

Сведение и группировка статистических данных

Цель работы – получить навыки группировки данных в MS Excel.

Задание – сгруппировать статистические данные с помощью надстройки Excel “Анализ данных”

Сведение и группировка статистической информации целесообразно проводить с помощью модуля “Гистограмма” пристройки “Анализ”.

Режим “Гистограмма” служит для вычисления частот попадания данных в указанные границы интервалов, и так же для построения гистограммы интервального вариационного ряда распределения.

В диалоговом окне этого режима

задаются следующие параметры:

1. Входной интервал – вводятся ссылки на ячейки, которые содержат данные для анализа.

2. “Интервал карманов” (необязательный параметр) – вводится ссылки на ячейки, которые содержат набор граничных значений, которые определяют интервалы (карманы). Эти значения должны быть введены в возрастающем порядке. В MS Excel вычисляется число попаданий данных в сформированные интервал, при этом границы интервалов являются строгими нижними границами и нестрогими верхними.

Если диапазон карманов не был введен, то набор интервалов, равномерно распределенных между минимальными и максимальными значениями данных, будет создан автоматически.

3. Метки устанавливаются в активное положение, если первый ряд или столбец во входном диапазоне содержит заголовки. Если заголовки отсутствуют, флажок нужно деактивировать. В этом случае будут автоматически созданы стандартные названия данных выходного диапазона.

4. Выходной интервал/Новый рабочий лист/Новая рабочая книга – активируется поле, в которое необходимо ввести ссылку на левую верхнюю ячейку выходного диапазона.

5. Парето (отсортированная гистограмма) – устанавливается в активное положение, если нужно представить данные в порядке убывания частоты. Если флажок снят, то данные в выходном диапазоне будут приведены в порядке следования интервалов.

6. Интегральный процент – устанавливается в активное положение для расчета выраженных в процентах накопленных частот (накопленных частностей) и включения в гистограмму графика кумуляты.

7. Вывод графика – устанавливается в активное положение для автоматического создания встроенной диаграммы на листе, который содержит выходной диапазон.

Пример анализа статистических данных в Excel

Объем экспорта по регионам Украины за 2009 год приведен ниже.

Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.

Как построить диаграмму распределения в Excel

График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.

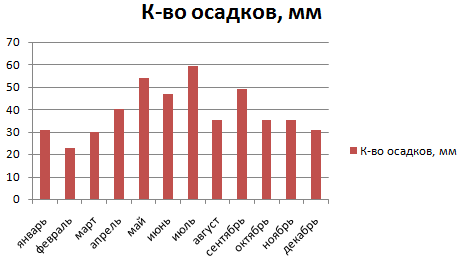
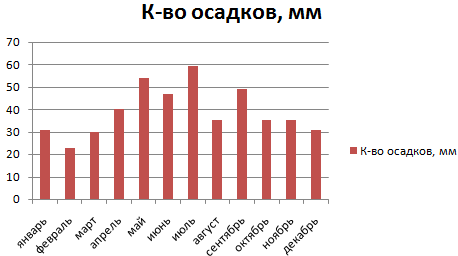
Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.

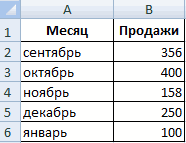
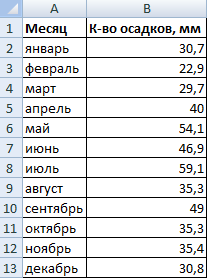
Имеются следующие данные о количестве выпавших осадков:

Первый способ. Открываем меню инструмента «Анализ данных» на вкладке «Данные» (если у Вас не подключен данный аналитический инструмент, тогда читайте как его подключить в настройках Excel):

Выбираем «Гистограмма»:

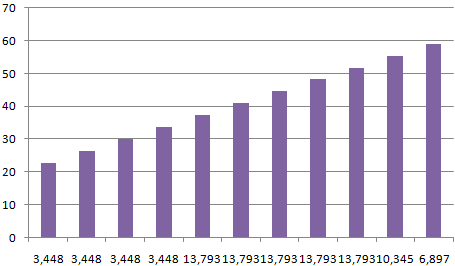
Задаем входной интервал (столбец с числовыми значениями). Поле «Интервалы карманов» оставляем пустым: Excel сгенерирует автоматически. Ставим птичку около записи «Вывод графика»:

После нажатия ОК получаем такой график с таблицей:

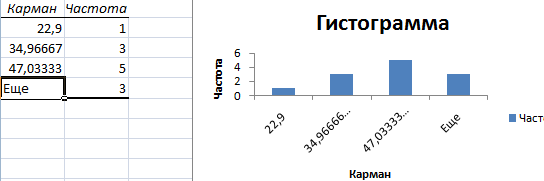
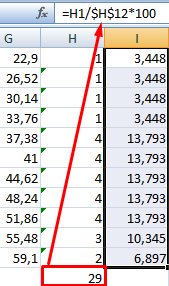
В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.



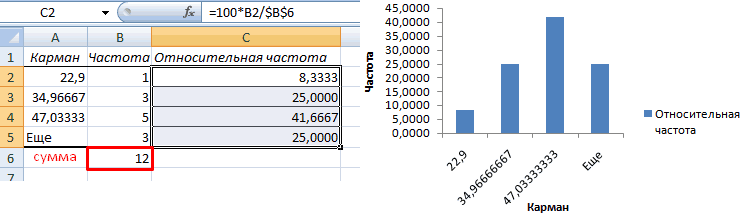
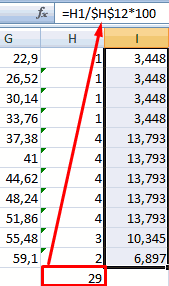
Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.

Найдем сумму всех абсолютных частот (с помощью функции СУММ). Сделаем дополнительный столбец «Относительная частота». В первую ячейку введем формулу:

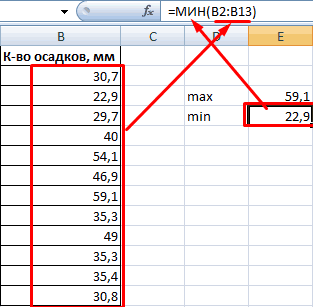
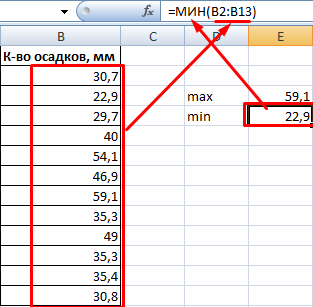
Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.

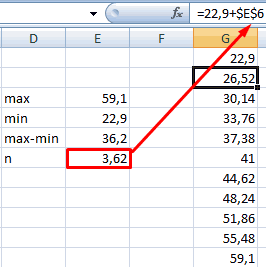
Чтобы найти интервал карманов, нужно разность максимального и минимального значений массива разделить на количество интервалов. Получим «ширину кармана».

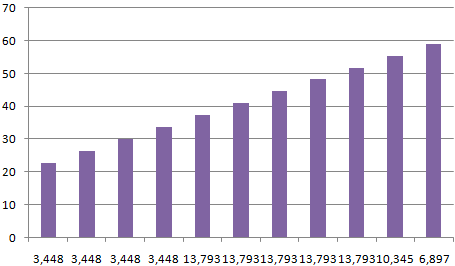
Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.

Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:

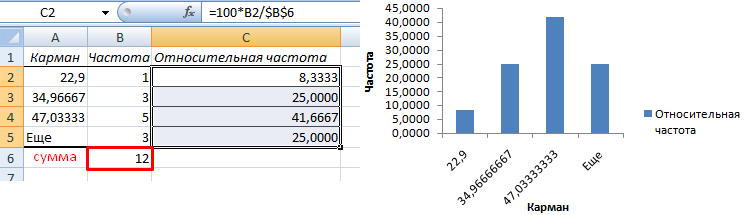
Вычислим относительные частоты (как в предыдущем способе).

Построим столбчатую диаграмму распределения осадков в Excel с помощью стандартного инструмента «Диаграммы».

Частота распределения заданных значений:

Круговые диаграммы для иллюстрации распределения

С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.

С помощью любой круговой диаграммы можно показать распределение в том случае, если

• имеется только один ряд данных;
• все значения положительные;
• практически все значения выше нуля;
• не более семи категорий;
• каждая категория соответствует сегменту круга.

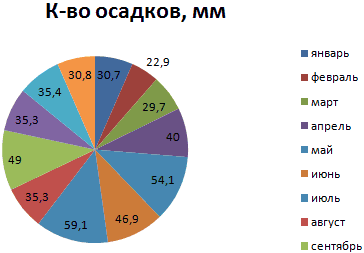
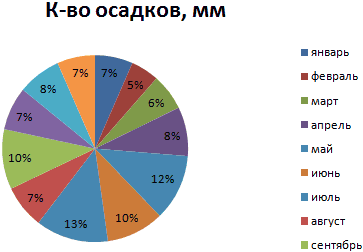
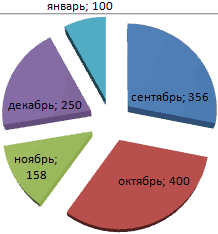
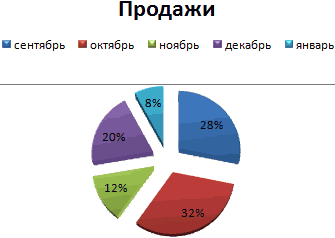
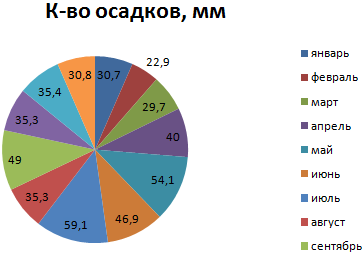
На основании имеющихся данных о количестве осадков построим круговую диаграмму.

Доля «каждого месяца» в общем количестве осадков за год:

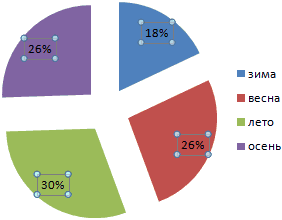
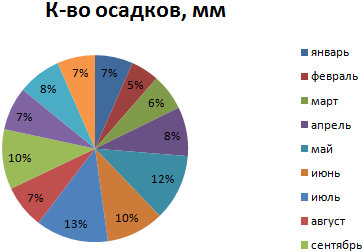
Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:

Получили количество выпавших осадков в процентном выражении по сезонам.

Теперь в каждой ячейке шаг за шагом прибавляем полученное значение ширины кармана: сначала к минимальному значению нашего массива (п. 3), затем в следующей ячейке ниже — к полученной сумме и т.д. Так постепенно доходим до максимального значения. Вот мы и построили интервалы карманов в виде столбца значений. Интервалом считается следующий диапазон : (i-1; i] или iСкачать бесплатно видеокурc по Excel

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Поделиться ссылкой:

Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.

Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.

Характеристики нормального распределения

Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.

Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.

Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма

Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.

Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.

Создание массива с нормальным распределением

Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:

=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)

Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.

Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.

Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.

Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:

=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)

Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.

Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.

Построение графика нормального распределения

Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.

Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:

=ЕСЛИ(A12;B11+$B$6; «»)

В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.

Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.

Осталось отформатировать диаграмму и наш график с нормальным распределением готов.

Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.

Для лучшего понимания, вы можете скачать файл с примером построения нормального распределения.

Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.

График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.

Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.

Имеются следующие данные о количестве выпавших осадков:

Первый способ. Открываем меню инструмента «Анализ данных» на вкладке «Данные» (если у Вас не подключен данный аналитический инструмент, тогда читайте как его подключить в настройках Excel):

Выбираем «Гистограмма»:

Задаем входной интервал (столбец с числовыми значениями). Поле «Интервалы карманов» оставляем пустым: Excel сгенерирует автоматически. Ставим птичку около записи «Вывод графика»:

После нажатия ОК получаем такой график с таблицей:

В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.

Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.

Найдем сумму всех абсолютных частот (с помощью функции СУММ). Сделаем дополнительный столбец «Относительная частота». В первую ячейку введем формулу:

Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.

Чтобы найти интервал карманов, нужно разность максимального и минимального значений массива разделить на количество интервалов. Получим «ширину кармана».

Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.

Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:

Вычислим относительные частоты (как в предыдущем способе).

Построим столбчатую диаграмму распределения осадков в Excel с помощью стандартного инструмента «Диаграммы».

Частота распределения заданных значений:

Круговые диаграммы для иллюстрации распределения

С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.

С помощью любой круговой диаграммы можно показать распределение в том случае, если

• имеется только один ряд данных;
• все значения положительные;
• практически все значения выше нуля;
• не более семи категорий;
• каждая категория соответствует сегменту круга.

На основании имеющихся данных о количестве осадков построим круговую диаграмму.

Доля «каждого месяца» в общем количестве осадков за год:

Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:

Получили количество выпавших осадков в процентном выражении по сезонам.

В двух словах: Добавляем полосу прокрутки к гистограмме или к графику распределения частот, чтобы сделать её динамической или интерактивной.

Уровень сложности: продвинутый.

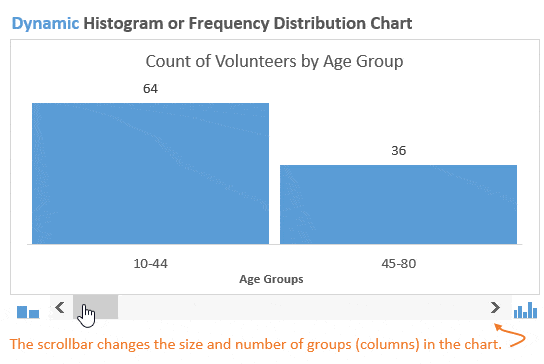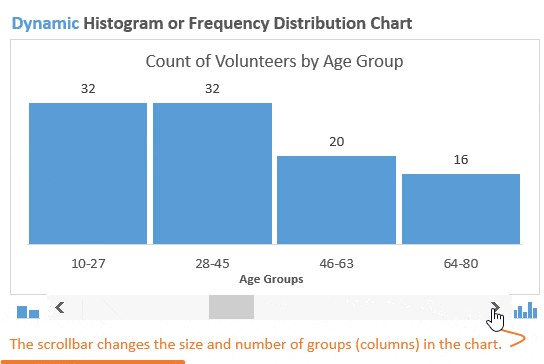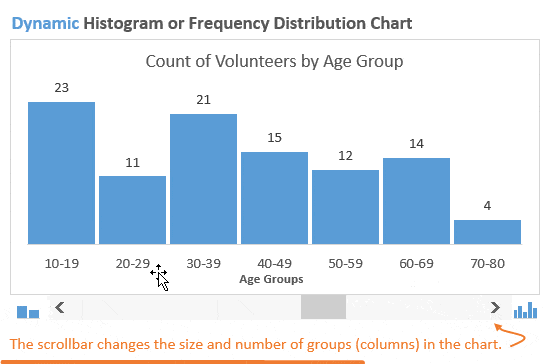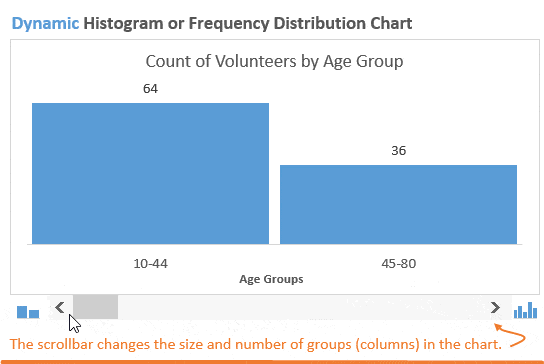
На следующем рисунке показано, как выглядит готовая динамическая гистограмма:

Что такое гистограмма или график распределения частот?

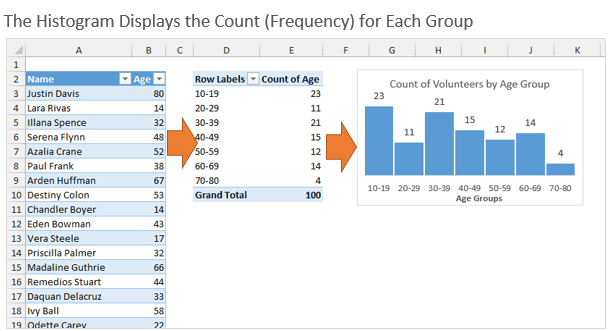
Гистограмма распределения разбивает по группам значения из набора данных и показывает количество (частоту) чисел в каждой группе. Такую гистограмму также называют графиком распределения частот, поскольку она показывает, с какой частотой представлены значения.

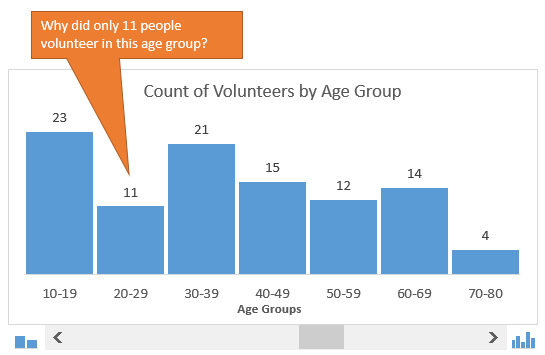
В нашем примере мы делим людей, которые вызвались принять участие в мероприятии, по возрастным группам. Первым делом, создадим возрастные группы, далее подсчитаем, сколько людей попадает в каждую из групп, и затем покажем все это на гистограмме.

На какие вопросы отвечает гистограмма распределения?

Гистограмма – это один из моих самых любимых типов диаграмм, поскольку она дает огромное количество информации о данных.

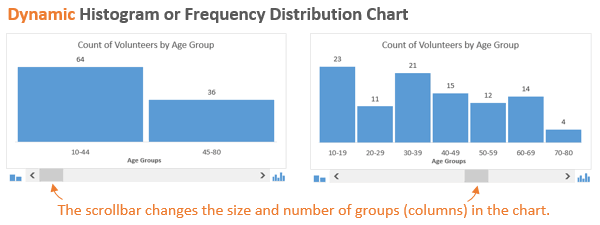
В данном случае мы хотим знать, как много участников окажется в возрастных группах 20-ти, 30-ти, 40-ка лет и так далее. Гистограмма наглядно покажет это, поэтому определить закономерности и отклонения будет довольно легко.

«Неужели наше мероприятие не интересно гражданам в возрасте от 20 до 29 лет?»

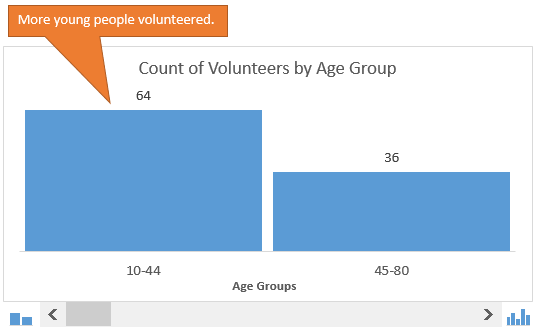
Возможно, мы захотим немного изменить детализацию картины и разбить население на две возрастные группы. Это покажет нам, что в мероприятии примут участие большей частью молодые люди:

Динамическая гистограмма

После построения гистограммы распределения частот иногда возникает необходимость изменить размер групп, чтобы ответить на различные возникающие вопросы. В динамической гистограмме это возможно сделать благодаря полосе прокрутки (слайдеру) под диаграммой. Пользователь может увеличивать или уменьшать размер групп, нажимая стрелки на полосе прокрутки.

Такой подход делает гистограмму интерактивной и позволяет пользователю масштабировать ее, выбирая, сколько групп должно быть показано. Это отличное дополнение к любому дашборду!

Как это работает?

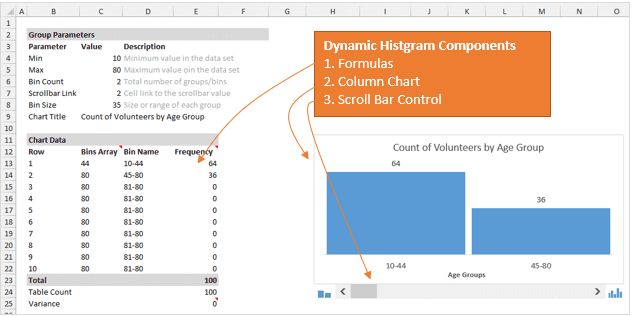
Краткий ответ: Формулы, динамические именованные диапазоны, элемент управления «Полоса прокрутки» в сочетании с гистограммой.

Формулы

Чтобы всё работало, первым делом нужно при помощи формул вычислить размер группы и количество элементов в каждой группе.

Чтобы вычислить размер группы, разделим общее количество (80-10) на количество групп. Количество групп устанавливается настройками полосы прокрутки. Чуть позже разъясним это подробнее.

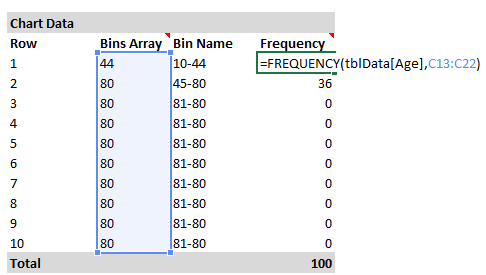
Далее при помощи функции ЧАСТОТА (FREQUENCY) я рассчитываю количество элементов в каждой группе в заданном столбце. В данном случае мы возвращаем частоту из столбца Age таблицы с именем tblData.

=ЧАСТОТА(tblData;C13:C22)
=FREQUENCY(tblData,C13:C22)

Функция ЧАСТОТА (FREQUENCY) вводится, как формула массива, нажатием Ctrl+Shift+Enter.

Динамический именованный диапазон

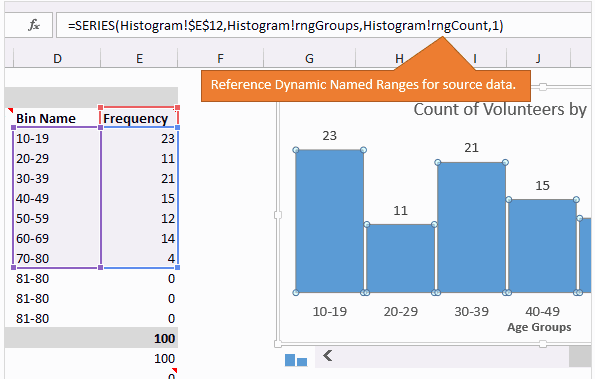
В качестве источника данных для диаграммы используется именованный диапазон, чтобы извлекать данные только из выбранных в текущий момент групп.

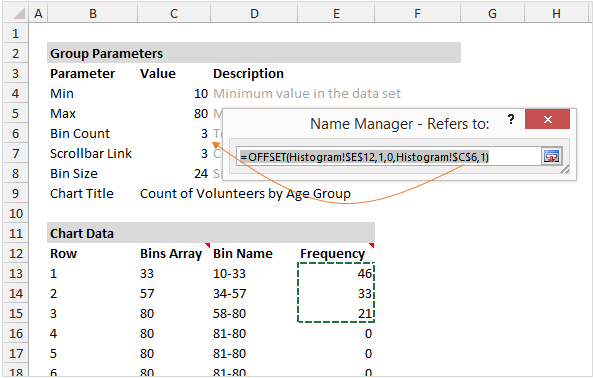
Когда пользователь перемещает ползунок полосы прокрутки, число строк в динамическом диапазоне изменяется так, чтобы отобразить на графике только нужные данные. В нашем примере задано два динамических именованных диапазона: один для данных — rngGroups (столбец Frequency) и второй для подписей горизонтальной оси — rngCount (столбец Bin Name).

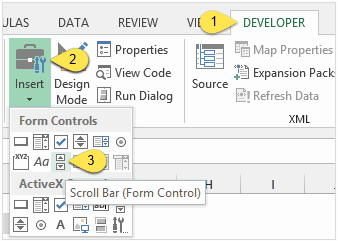
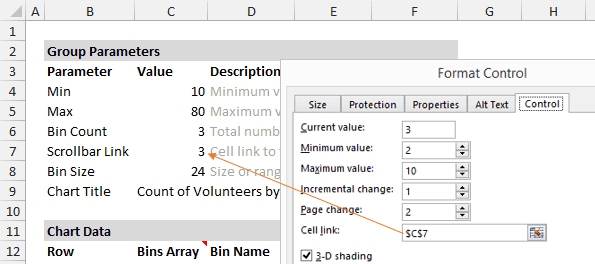
Элемент управления «Полоса прокрутки»

Элемент управления Полоса прокрутки (Scroll Bar) может быть вставлен с вкладки Разработчик (Developer).

На рисунке ниже видно, как я настроил параметры элемента управления и привязал его к ячейке C7. Так, изменяя состояние полосы прокрутки, пользователь управляет формулами.

Гистограмма

График – это самая простая часть задачи. Создаём простую гистограмму и в качестве источника данных устанавливаем динамические именованные диапазоны.

Есть вопросы?

Что ж, это был лишь краткий обзор того, как работает динамическая гистограмма.

Да, это не самая простая диаграмма, но, полагаю, пользователям понравится с ней работать. Определённо, такой интерактивной диаграммой можно украсить любой отчёт.

Более простой вариант гистограммы можно создать, используя сводные таблицы.

Пишите в комментариях любые вопросы и предложения. Спасибо!

Урок подготовлен для Вас командой сайта office-guru.ru
Источник: /> Перевел: Антон Андронов

Правила перепечаткиЕще больше уроков по Microsoft Excel

Оцените качество статьи. Нам важно ваше мнение:

Построение гистограмм в Microsoft Excel

Перед построением гистограммы выполняется группировка данных по близким признакам. При группировании по количественному признаку все множество значений признака делится на

интервалы.

Для определения оптимального количества интервалов может быть использована формула Стерджесса:

n = 1 + (3,322× lgN)

где N — количество наблюдений. В этом случае величина интервала:

h = (Vmax — Vmin)/n

Поскольку количество групп не может быть дробным числом, то полученную по этой формуле величину округляют до целого большего числа.

Нижнюю границу первого интервала принимают равной минимальному значению xmin. Верхняя граница первого интервала соответствует значению (xmin + h). Для последующих групп

границы определяются аналогично, то есть последовательно прибавляется величина интервала h.

В Excel для построения гистограмм используются статистическая функция ЧАСТОТА в сочетании с мастером построения обычных диаграмм и процедура Гистограмма из пакета анализа.

Функция ЧАСТОТА (массив_данных, двоичный_массив) вычисляет частоты появления случайной величины в интервалах значений и выводит их как массив цифр, где

•Массив_данных —массив исходных данных, для которых вычисляются частоты;

•Массив_интервалов — это массив интервалов, по которым группируются значения выборки.

Перед вызовом функции ЧАСТОТА необходимо выделить столбец c числом ячеек, равным числу интервалов n, в который будут выведены результаты выполнения функции.

Вызвать Мастер функций (кнопка fx):

и функцию ЧАСТОТА.

В появившемся списке выбрать инструмент Гистограмма и щелкнуть на кнопке ОК. Появится окно гистограммы, где задаются следующие параметры:

Входной интервал:– адреса ячеек, содержащие выборочные данные.

Интервал карманов: (необязательный параметр) – адреса ячеек, содержащие границы интервалов. Это поле предлагается оставить пустым, предоставив Excel самому вычислить границы интервалов (карманов – в терминах Excel).

Метки – флажок, включаемый, если первая строка во входных данных содержит заголовки. Если заголовки отсутствуют, то флажок следует выключить.

Выходной интервал: / Новый рабочий лист: / Новая рабочая книга.

Включенный переключатель Выходной интервал требует ввода адреса верхней ячейки, начиная с которой будут размещаться вычисленные относительные частоты j .

Вположении переключателя Новый рабочий лист: открывается новый лист, в котором начиная с ячейки А1 размещаются частности j .

Вположении переключателя Новая рабочая книга открывается новая книга, на первом листе которой начиная с ячейки А1 размещаются частности j .

Парето (отсортированная гистограмма) – устанавливается, чтобы представить j в порядке их убывания. Если параметр выключен, то j приводятся в порядке следования интервалов.

Интегральный процент – устанавливается в активное состояние для расчета выраженных в процентах накопленных относительных частот (аналог значений столбца Накопленные частоты).

Вывод графика – устанавливается в активное состояние для автоматического создания встроенной диаграммы на листе, содержащем частоты.

Замечание.

Как правило, гистограммы изображаются в виде смежных прямоугольных областей. Поэтому столбики гистограммы следует расширить до соприкосновения друг с другом. Для этого необходимо щелкнуть мышью на диаграмме, далее на панель инструментов Диаграмма, раскрыть список инструментов и выбрать элемент Ряд ‘Частота’, после чего щелкнуть на кнопке Формат ряда. В появившемся одноименном диалоговом окне необходимо активизировать закладку Параметры и в поле Ширина зазора установить значение 0 ((Excel 2003):

В Excel 2007…2010 встать на любой столбик гистограммы и правой кнопкой мыши выбрать

Формат ряда данных:

Для построения теоретической кривой нормального распределения по эмпирическим данным необходимо найти теоретические частоты.

В Excel для вычисления значений нормального распределения используются функция НОРМРАСП, которая вычисляет значения вероятности нормальной функции распределения для указанного среднего и стандартного отклонения.

Функция имеет параметры:

НОРМРАСП (х; среднее; стандартное_откл; интегральная), где:

х — значения выборки, для которых строится распределение; среднее — среднее арифметическое выборки; стандартное_откл — стандартное отклонение распределения;

интегральный — логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности распределения.

Для получения абсолютных значений плотностей распределения (теоретических частот) достаточно найденные значения вероятности умножить на величину интервала h и количество наблюдений N = 100 по каждой строке.

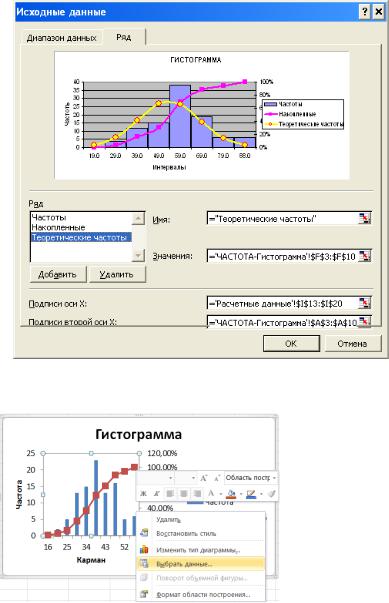
Для завершения выполнения задания необходимо внести полученные значения теоретических частот на рисунок с гистограммой, добавив ряд в закладке Исходные данные и выбрав тип диаграммы

– график ((Excel 2003):

В Excel 2007…2010 находясь в обласи гистограммы по правой кнопке мыши выбрать Выбрать данные (или по одноименной кнопке на вкладке Конструктор):

и в появившемся окне провести манипуляции с вводом нового ряда «Теоретические частоты»: