Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel для iPad Excel для iPhone Excel для планшетов с Android Excel 2010 Excel 2007 Excel для Mac 2011 Excel для телефонов с Android Еще…Меньше
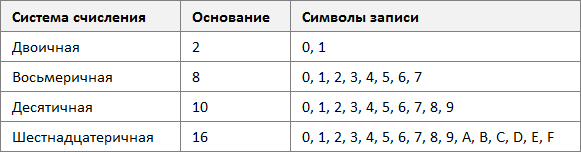
Система чисел является систематическим способом представления чисел символьными символами и использует базовое значение для удобной группировки чисел в сжатой форме. Самая распространенная система числов — десятичная, которая имеет базовое значение 10, и набор символов 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Однако существуют и другие числовые системы, которые могут быть более эффективными для определенной цели. Например, так как на компьютерах используется логическое значение для вычислений и операций, для выполнения вычислений и операций используется двоичная числовая система, которая имеет базовое значение 2.
Microsoft Office Excel есть несколько функций, которые можно использовать для преобразования чисел в числовые системы и из них:
|
Система номеров |
Базовое значение |
Набор символьных знаков |
|
Двоичный |
2 |
0,1 |
|
Восьмеричном |
8 |
0, 1, 2, 3, 4, 5, 6, 7 |
|
Действительное. |
10 |
0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 |
|
Шестнадцатеричный |
16 |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Для этого используйте функцию ДВ.В.Е.
|
|
Для этого используйте функцию ДВ.В.EX.
|
|
Для этого используйте функцию ДВ.В.ВЕХ.
|
|
Для этого используйте функцию DEC2BIN.
|
|
Для этого используйте функцию DEC2HEX.
|
|
Для этого используйте функцию DEC2OCT.
|
|
Для этого используйте функцию HEX2BIN.
|
|
Для этого используйте функцию HEX2DEC.
|
|
Для этого используйте функцию HEX2OCT.
|
|
Для этого используйте функцию ВОСЬМ.В.ДВ.
|
|
Для этого используйте функцию ВОСЬМ.В.Е.
|
|
Для этого используйте функцию ВОСЬМ.В.EX.
|
|
Нужна дополнительная помощь?
Изучим стандартные способы перевода чисел в различные системы счисления в Excel: двоичную, восьмеричную, десятичную и шестнадцатеричную.
Помимо повсеместно распространенной и всем нам хорошо известной десятичной системы счисления также используются и системы с другими основаниями (отличными от 10), например, двоичная, троичная, восьмеричная и т.д.
Большинство из них имеют достаточно широкое применение практически во всех современных электронных устройствах, в программировании или компьютерной документации.
В Excel есть возможность стандартными средствами переводить данные в четырех системах счисления:
Давайте подробно остановимся на основных вариантах преобразования данных.
Перевод числа из десятичной в двоичную систему в Excel
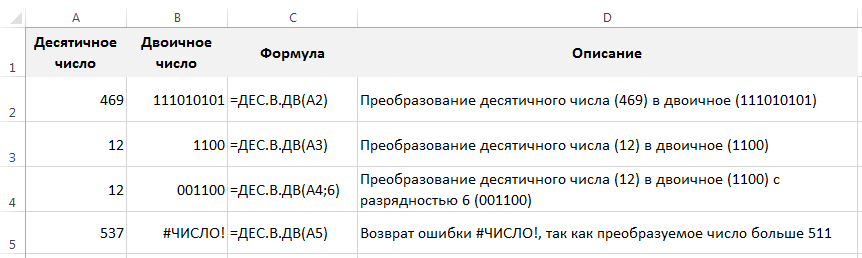
Для преобразования данных в двоичную запись в Excel существует стандартная функция ДЕС.В.ДВ (имя функции получается как первые буквы от слов ДЕСятичное В ДВоичное, дополнительно разделенное точками):
ДЕС.В.ДВ(число; [разрядность])
Преобразует десятичное число в двоичное.
- Число (обязательный аргумент) — десятичное целое число, которое требуется преобразовать;
- Разрядность (необязательный аргумент) — количество знаков для использования в записи.
Данный аргумент необходим если нужно приписать к двоичной записи данных ведущие нули. К примеру, число 1101 с разрядностью 7 будет иметь вид 0001101.
Обратите внимание, что Excel накладывает определенные ограничения на размер преобразуемых данных.
Двоичная запись не должна занимать более 10 знаков, поэтому десятичное число, соответственно, не должно быть больше 511 или меньше -512, иначе в качестве значения функция ДЕС.В.ДВ вернет ошибку.
Перевод числа из двоичной в десятичную систему в Excel
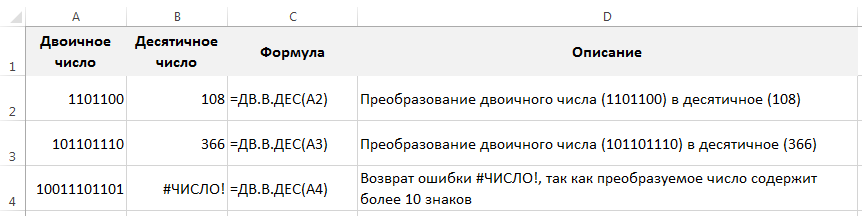
Для осуществления обратного перевода можно воспользоваться функцией ДВ.В.ДЕС:
ДВ.В.ДЕС(число)
Преобразует двоичное число в десятичное.
- Число (обязательный аргумент) — двоичное число, которое требуется преобразовать.
При этом разрядность в качестве аргумента функции для десятичной записи не используется.
Как и в случае с функцией ДЕС.В.ДВ при использовании ДВ.В.ДЕС существует ограничение на размер преобразуемых данных — не более 10 знаков в записи, в ином случае функция вернет значение ошибки.
Перевод в других системах счисления
Для других систем счисления (восьмеричной, шестнадцатеричной) также определен набор стандартных формул.
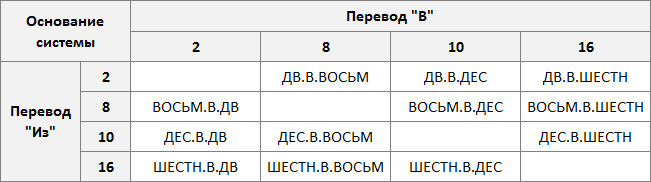
Для удобства мы составили таблицу со схемой выбора формулы для преобразования данных (в левом столбце указано откуда переводим данные, в верхней строчке — куда переводим):
Как и в примерах выше имена функций образуются по достаточно простому правилу — берутся первые буквы от названий систем в которых преобразуются данные и разделяются точками (ВОСЬМеричное В ШЕСТНадцатеричное и пр.)
Арифметические операции с данными
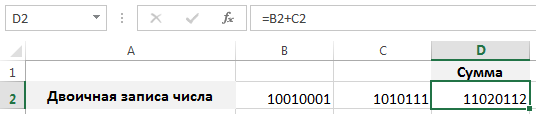
Операции в Excel осуществляются в десятичной системе счисления, поэтому при применении арифметических действий (сложение, вычитание и т.д.) для преобразованных данных учитывайте, что конечный результат также будет записан в десятичной записи:
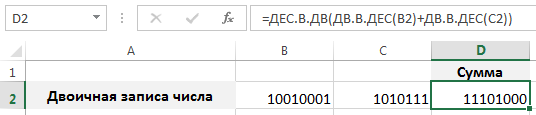
Чтобы избежать подобной проблемы, необходимо сначала перевести все данные в десятичный вид, произвести требуемые вычисления, а уже затем вновь преобразовать полученный результат в исходную систему счисления:
Удачи вам и до скорых встреч на страницах блога Tutorexcel.ru!
Поделиться с друзьями:
Поиск по сайту:
Перейти к содержимому
Системы исчисления в программе «Эксель».
В мире существует множество различных способов записи чисел и систем исчисления. В текущем столетии самыми популярными являются системы исчисления:
• Двоичная;
• Восьмеричная;
• Десятеричная;
• Шестнадцатеричная.

Для удобства перевода чисел из различных систем в привычную большинству пользователей десятеричную систему, а так же перевода чисел между восьмеричной, двоичной, шестнадцатеричной системами существует целый ряд функций. Эти функции позволяют произвести перевод чисел из одной системы в другую.
Рассмотрим эти функции:
• ДЕС.В.ДВ( ) – переводит десятичные числа в двоичные;
• ДЕС.В.ВОСЬМ( ) – переводит десятичные числа в восьмеричные;
• ДЕС.В.ШЕСТН( ) – переводит десятичные числа в шестнадцатеричные;
• ВОСЬМ.В.ДВ() – переводит восьмеричные в двоичные;
• ВОСЬМ.В.ДЕС() – переводит восьмеричные десятичные;
• ВОСЬМ.В.ШЕСТН() – переводит восьмеричные в шестнадцатеричные;
• ШЕСТН.В.ВОСЬМ() – переводит шестнадцатеричные в восьмеричные;
• ШЕСТН.В.ДВ() – переводит шестнадцатеричные в двоичные;
• ШЕСТН.В.ДЕС() – переводит шестнадцатеричные в десятичные;
• ДВ.В.ВОСЬМ() – переводит двоичные в восьмеричные;
• ДВ.В.ДЕС() – переводит двоичные в десятичные;
• ДВ.В. ШЕСТН() – переводит двоичные в шестнадцатеричные.
Пример использования:
• Установить курсор в ячейку, которой будет присвоено значение;
• Выбрать необходимую функцию при помощи мастера функций в зависимости от того в какую систему исчисления вы хотите перевести число;
• В появившемся окне указать ячейку с переводимым числом или прописать само число;
• Указать количество разрядов – количество знаков в написании числа при необходимости (для функций перевода в десятичную систему количество разрядов не указывается).
• Нажать «Enter» или «Ok».
Скачать таблицу перевода чисел между двоичной, восьмеричной, десятеричной и шестнадцатеричной системами исчисления.
Функция ОСНОВАНИЕ выполняет преобразование числового значение в указанную систему счисления (двоичная, восьмеричная, шестнадцатеричная и т. д.) и возвращает соответствующий результат в виде текстовой строки.
Примеры использования функции ОСНОВАНИЕ в Excel
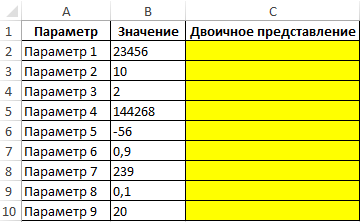
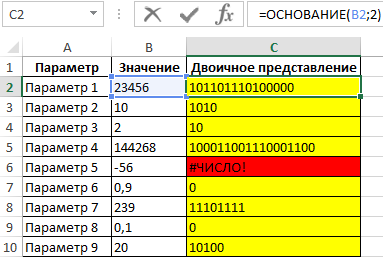
Пример 1. Для хранения чисел в БД удобно использовать их представление в двоичной системе счисления. Выполнить преобразование представленных значений.
Исходная таблица:
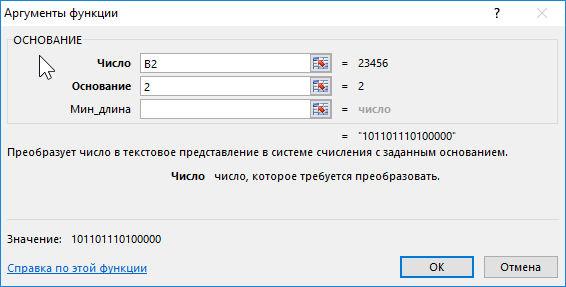
Для преобразования используем формулу:
Описание аргументов:
- B2 – число, которое требуется преобразовать;
- 2 – указатель вида системы счисления.
Выполним преобразование для всех чисел. Полученный результат:
Ошибка #ЧИСЛО! Возникла потому, что -56 находится вне диапазона допустимых значений (отрицательное число). Результат вычисления формулы =ОСНОВАНИЕ(0,9;2) эквивалентен результату =ОСНОВАНИЕ(0;2), поскольку рассматриваемая функция усекает дробные значения аргумента число до целых значений.
Перевод числа из одной системы счисления в другую в Excel
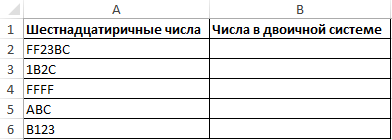
Пример 2. Преобразовать числа, записанные в шестнадцатеричной системе счисления в двоичную систему с длиной полученной строки не менее 20 символов.
Таблица значений:
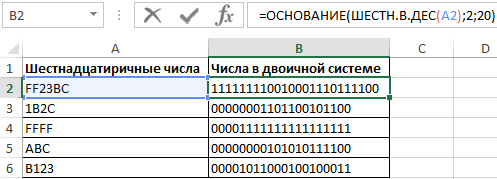
В Excel предусмотрена формула ШЕСТН.В.ДВ, однако она поддерживает значения из диапазона от FFFFFFFE00 до 1FF. Поэтому выполним промежуточное преобразование в десятичную систему и воспользуемся функцией ОСНОВАНИЕ для перевода в двоичную:
Описание аргументов:
- ШЕСТН.В.ДЕС(A2) – исходное число, преобразованное в десятичную систему счисления;
- 2 – указание на вид системы счисления;
- 20 – минимальное количество символов в возвращаемой строке.
Результаты расчетов:
Сложение чисел в разных системах счисления в Excel
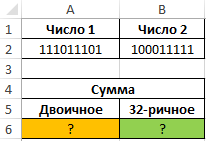
Пример 3. Отобразить результаты сложения двух чисел, записанных в двоичной системе, в виде чисел в десяти- и тридцатидвухричных системах счисления.
Исходная таблица:
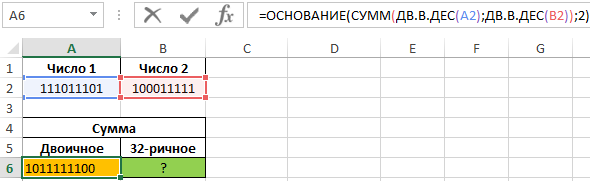
В ячейке A6 запишем следующую формулу:
Функция ДВ.В.ДЕС преобразует числа из двоичной в десятеричную систему.
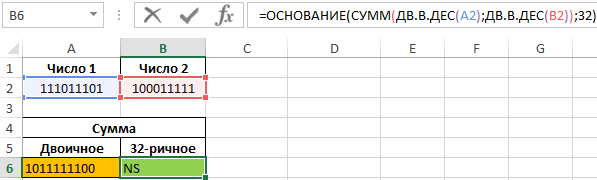
В ячейке B6 запишем формулу:
В данном способе выполняется преобразование в понятную многим десятичную систему счисления, в которой и выполняется операция сложения чисел (вместо, например, алгоритма сложения в столбик в двоичной системе, где необходимо учитывать правила: 0+0=0, 1+1=10 и т. д.). Функцией ОСНОВАНИЕ выполняется преобразование результата в требуемые системы исчисления. Пример расчета:
Особенности использования функции ОСНОВАНИЕ в Excel
Функция имеет следующую синтаксическую запись:
=ОСНОВАНИЕ(число;основание;[минимальная_длина])
Описание аргументов:
- число – обязательный аргумент, характеризующий числовое значение из диапазона целых чисел от 0 до 253, которое требуется преобразовать к указанной системе счисления.
- основание – обязательный аргумент, характеризующий числовое значение из диапазона целых чисел от 2 до 36, которое является основанием требуемой системы исчисления.
- [минимальная_длина] – необязательный аргумент, характеризующий числовое значение из диапазона от 0 до 255, определяющее минимальную длину в символах возвращаемой текстовой строки.
Примечания:
- Функция возвращает код ошибки #ЧИСЛО!, если любой из ее аргументов является числовым значением, выходящим за пределы допустимых для данного аргумента значений.
- Если один или несколько аргументов являются текстовой строкой, рассматриваемая функция вернет код ошибки #ЗНАЧ!.
- Функция доступна только в новых версиях программы (Excel 2013 и более поздних).
- В отличие, например, от функции ДЕС.В.ДВ, которая выполняет преобразование чисел из диапазона от -512 до 511, функция ОСНОВАНИЕ выполняет преобразование чисел от 0 до 253.
- При явном указании аргумента [минимальная_длина] возможны следующие ситуации:
- длина полученного значения меньше, чем регламентируется аргументом [минимальная_длина]. В этом случае в начале возвращаемой строки слева будет добавлено определенное количество нулей для достижения требуемой длины;
- длина рассчитанного значения больше, чем регламентируемая. Функция ОСНОВАНИЕ вернет полученный результат, не урезая его. Например, функция с аргументами (12345;2;20) вернет значение «00000011000000111001», а функция с аргументами (12345;2;2) вернет «11000000111001».
Учитель информатики
§11. Перевод чисел из одной позиционной системы счисления в другую
Для перевода целого десятичного числа в систему счисления с основанием q следует:
Рассмотрим примеры перевода целых десятичных чисел в 2-ичную, 8-ричную и 16-ричную системы счисления.
Пример 4. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись десятичного числа 22 оканчивается на 4.
Поскольку запись числа в системе счисления с основанием q заканчивается на 4, остаток от деления числа 22 на q равен 4: 22 mod q = 4 1) . Следовательно, 18 mod q = 0. Это верно для q ? .
1) Операция mod — вычисление остатка от целочисленного деления.
Так как в новой системе счисления запись числа оканчивается на 4, то q > 4. Следовательно, условию задачи удовлетворяют основания: 18, 9 и 6.
Перевод чисел из одной позиционной системы счисления в другую
Например, перевести число 528 из десятичной системы. 528=512+16. Переводим отдельно 512 и 16.
512=2 9 . 51210=1 000000000 2.
16=2 4 . 1610=1 0000 2.
Теперь сложим столбиком:
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
В компьютерных науках широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления, благодаря чему их называют компьютерными. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).
Перевод чисел из одной системы счисления в другую
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
infoegehelp.ru
Чтобы быстро переводить числа из десятичной системы счисления в двоичную, нужно хорошо знать числа «2 в степени». Например, 2 10 =1024 и т.д. Это позволит решать некоторые примеры на перевод буквально за секунды. Одной из таких задач является задача A1 из демо ЕГЭ 2012 года. Можно, конечно, долго и нудно делить число на «2». Но лучше решать по-другому, экономя драгоценное время на экзамене.
Метод очень простой. Суть его такая: если число, которое нужно перевести из десятичной системы, равно числу «2 в степени», то это число в двоичной системе содержит количество нулей, равное степени. Впереди этих нулей добавляем «1».
- Переведем число 2 из десятичной системы. 2=2 1 . Поэтому в двоичной системе число содержит 1 нуль . Впереди ставим «1» и получаем 1 0 2.
- Переведем 4 из десятичной системы. 4=2 2 . Поэтому в двоичной системе число содержит 2 нуля . Впереди ставим «1» и получаем 1 00 2.
- Переведем 8 из десятичной системы. 8=2 3 . Поэтому в двоичной системе число содержит 3 нуля . Впереди ставим «1» и получаем 1 000 2.
На рисунке квадратиками обозначено двоичное представление числа, а слева розовым цветом-десятичное.
Если число, которое нужно перевести, меньше числа «2 в степени» на 1, то в двоичной системе это число состоит только из единиц, количество которых равно степени.
- Переведем 3 из десятичной системы. 3=2 2 -1. Поэтому в двоичной системе число содержит 2 единицы . Получаем 11 2.
- Переведем 7 из десятичной системы. 7=2 3 -1. Поэтому в двоичной системе число содержит 3 единицы . Получаем 111 2.
На рисунке квадратиками обозначено двоичное представление числа, а слева розовым цветом-десятичное.
Аналогичен перевод и для других чисел «2 в степени-1».
Понятно, что перевод чисел от 0 до 8 можно сделать быстро или делением, или просто знать наизусть их представление в двоичной системе. Я привела эти примеры, чтобы Вы поняли принцип данного метода и использовали его для перевода более «внушительных чисел», например, для перевода чисел 127,128, 255, 256, 511, 512 и т.д.
Можно встретить такие задачи, когда нужно перевести число, не равное числу «2 в степени», но близкое к нему. Оно может быть больше или меньше числа «2 в степени». Разница между переводимым числом и числом «2 в степени» должна быть небольшая. Например, до 3. Представление чисел от 0 до 3 в двоичной системе надо просто знать без перевода.
Переводим сначала число «2 в степени» в двоичную систему. А потом прибавляем к нему разницу между числом «2 в степени» и переводимым числом.
Например, переведем 19 из десятичной системы. Оно больше числа «2 в степени» на 3.
Если число меньше числа «2 в степени», то удобнее пользоваться числом «2 в степени-1». Решаем так:
Переводим сначала число «2 в степени-1» в двоичную систему. А потом вычитаем из него разницу между числом «2 в степени-1» и переводимым числом.
Например, переведем 29 из десятичной системы. Оно больше числа «2 в степени-1» на 2. 29=31-2.
Если разница между переводимым числом и числом «2 в степени» больше трех , то можно разбить число на составляющие, перевести каждую часть в двоичную систему и сложить.
Например, перевести число 528 из десятичной системы. 528=512+16. Переводим отдельно 512 и 16.
512=2 9 . 51210=1 000000000 2.
16=2 4 . 1610=1 0000 2.
Теперь сложим столбиком:
Данная методика позволяет тратить минимум времени на перевод чисел из десятичной системы в двоичную, но при условии, что Вы прекрасно знаете числа «2 в степени». Если это не так, то заучите эти числа. Тем более, что в задачах по информатике они активно используются.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Число в двоичной системе представить как последовательность последнего результата деления и остатков от деления в обратном порядке. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
3.3. Правила перевода чисел из одной системы счисления в другую
1. Перевести число 1001101.11012 в десятичную систему счисления.
Решение: 1001101.11012 = 1·2 6 +0·2 5 +0·2 4 +1·2 3 +1·2 2 +0·2 1 +1·2 0 +1·2 -1 +1·2 -2 +0·2 -3 +1·2 -4 = 64+8++4+1+0.5+0.25+0.0625 = 77.812510
Ответ: 1001101.11012 = 77.812510