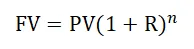Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
БС — одна из финансовых функций, возвращающая будущую стоимость инвестиции на основе постоянной процентной ставки. В функции БС можно использовать как периодические постоянные платежи, так и единый общий платеж.

Воспользуйтесь средством Excel Formula Coach для расчета будущей стоимости серии платежей. При этом вы узнаете, как использовать функцию БС в формуле.
Excel Formula Coach также можно использовать для расчета будущей стоимости единого общего платежа.
Синтаксис
БС(ставка;кпер;плт;[пс];[тип])
Дополнительные сведения об аргументах функции БС и других функциях, связанных с аннуитетами, см. в описании функции ПС.
Аргументы функции БС описаны ниже.
-
Ставка — обязательный аргумент. Процентная ставка за период.
-
Кпер — обязательный аргумент. Общее количество периодов платежей по аннуитету.
-
Плт — обязательный аргумент. Выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно аргумент «плт» состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если он опущен, аргумент «пс» является обязательным.
-
Пс — необязательный аргумент. Приведенная к текущему моменту стоимость, т. е. общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент «пс» опущен, предполагается значение 0. В этом случае аргумент «плт» является обязательным.
-
Тип Необязательный. Число 0 или 1, обозначающее срок выплаты. Если аргумент «тип» опущен, предполагается значение 0.
|
Тип |
Выплата |
|---|---|
|
0 |
В конце периода |
|
1 |
В начале периода |
Замечания
-
Убедитесь, что единицы измерения аргументов «ставка» и «кпер» используются согласованно. При ежемесячных выплатах по четырехгодичному займу из расчета 12 процентов годовых используйте значение 12%/12 в качестве аргумента «ставка» и 4*12 — в качестве аргумента «кпер». При ежегодных платежах по тому же займу используйте значение 12% в качестве аргумента «ставка» и 4 — в качестве аргумента «кпер».
-
Все аргументы, которым соответствуют выплачиваемые денежные средства (например, сберегательные вклады), представляются отрицательными числами, а получаемые (например, дивиденды) — положительными.
Примеры
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|---|---|---|
|
0,06 |
Годовая процентная ставка |
|
|
10 |
Количество платежей |
|
|
-200 |
Объем платежей |
|
|
-500 |
Стоимость на текущий момент |
|
|
1 |
Платежи осуществляются в начале периода (0 означает, что платежи осуществляются в конце периода) |
|
|
Формула |
Описание |
Результат |
|
=БС(A2/12; A3; A4; A5; A6) |
Будущая стоимость инвестиций при условиях, указанных в ячейках A2:A5. |
2 581,40 ₽ |
Пример 2
|
Данные |
Описание |
|
|---|---|---|
|
0,12 |
Годовая процентная ставка |
|
|
12 |
Количество платежей |
|
|
-1000 |
Объем платежей |
|
|
Формула |
Описание |
Результат |
|
=БС(A2/12; A3; A4) |
Будущая стоимость инвестиций при условиях, указанных в ячейках A2:A4. |
12 682,50 ₽ |
Пример 3
|
Данные |
Описание |
|
|---|---|---|
|
0,11 |
Годовая процентная ставка |
|
|
35 |
Количество платежей |
|
|
-2000 |
Объем платежей |
|
|
1 |
Платежи осуществляются в начале года (0 означает конец года) |
|
|
Формула |
Описание |
Результат |
|
=БС(A2/12; A3; A4;; A5) |
Будущая стоимость инвестиций с условиями, указанными в ячейках A2:A4. |
82 846,25 ₽ |
Пример 4
|
Данные |
Описание |
|
|---|---|---|
|
0,06 |
Годовая процентная ставка |
|
|
12 |
Количество платежей |
|
|
-100 |
Объем платежей |
|
|
-1000 |
Стоимость на текущий момент |
|
|
1 |
Платежи осуществляются в начале года (0 означает конец года) |
|
|
Формула |
Описание |
Результат |
|
=БС(A2/12; A3; A4; A5; A6) |
Будущая стоимость инвестиций при условиях, указанных в ячейках A2:A5. |
2 301,40 ₽ |
Нужна дополнительная помощь?
Функция БС в Excel рассчитывает будущую стоимость инвестиции при условии, что процентная ставка является константой (не меняется с течением времени), и возвращает соответствующее значение. Функцию можно использовать в случаях, когда по окончанию срока выполняется единый платеж, а также при разбиении общей суммы на несколько фиксированных платежей.
Примеры использования финансовой функции БС в Excel
Пример 1. Вкладчик сделал депозит с ежемесячной капитализацией на сумму 100 000 рублей под 13% годовых сроком на 4 года. Какую сумму средств он сможет снять со своего депозитного счета по окончанию действия договора с банком?
Исходные данные:
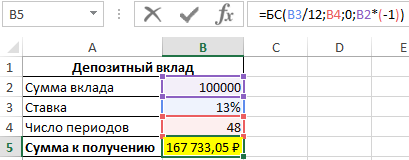
Формула для расчета:
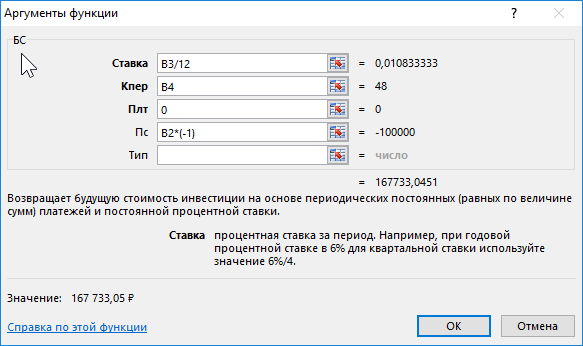
Описание аргументов:
- B3/12 – ставка за период (капитализация выполняется ежемесячно);
- B4 – число периодов капитализации вклада;
- 0 – сумма выплаты за период капитализации (неизвестная величина в рамках данной задачи, поэтому значение 0);
- B2*(-1) – начальная сумма вклада (инвестиция, которая должна являться отрицательным числом).
Результаты расчета:
Спустя 4 года вкладчик получит 167 733 рубля.
Расчет суммы долга по кредиту по состоянию на 30-й период погашения
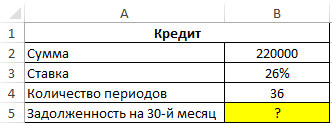
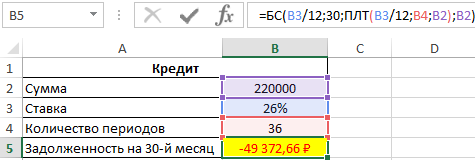
Пример 2. Заемщик взял кредит в банке под 26% годовых на сумму 220 000 рублей сроком на 3 года с ежемесячным фиксированным платежом. Какой будет сумма задолженности заемщика по окончанию 30-го периода выплат?
Исходные данные:
Формула для расчета:
=БС(B3/12;30;ПЛТ(B3/12;B4;B2);B2)
Описание аргументов:
- B3/12 – месячная процентная ставка;
- 30 – номер периода для расчета остатка задолженности;
- ПЛТ(B3/12;B4;B2) – функция, возвращающая сумму ежемесячного платежа;
- B2 – тело кредита.
Полученный результат:
Фактическая задолженность за кредит по окончанию 30-го месяца составит примерно 49372 рубля.
Сравнительный инвестиционный анализ условий депозита в банке
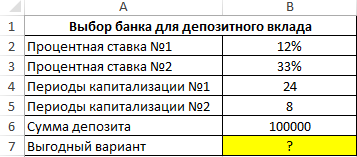
Пример 3. Вкладчик получил предложения по депозитному вкладу от двух банков с различными условиями:
- Ставка – 12% годовых, капитализация – ежемесячная.
- Ставка – 33% годовых, капитализация – ежеквартальная.
Определить, какое из предложений является более выгодным, если сумма вклада – 100000 рублей, срок действия договора – 2 года.
Исходные данные:
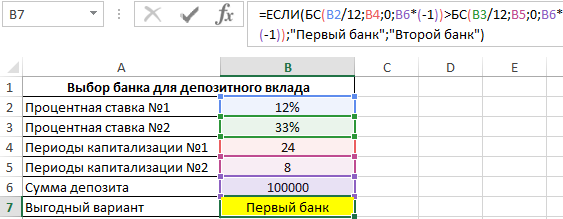
Формула для расчета:
С помощью функции ЕСЛИ определяем, в каком случае будущая стоимость окажется больше и возвращаем соответствующее значение. Полученный результат:
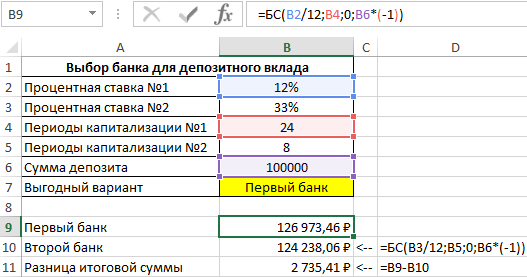
Выведем результаты расчетов функций БС и разницу сумм:
Как видно, несмотря на высокую годовую ставку, первый банк сделал более выгодное предложение, поскольку по условиям предложенного договора капитализация является ежемесячной. То есть, чем чаще происходит капитализация, тем быстрее увеличивается сумма вклада.
Особенности использования финансовой функции БС в Excel
Функция БС используется наряду с прочими финансовыми функциями (ПС, ПЛТ, КПЕР и другими) и имеет следующий синтаксис:
=БС(ставка;кпер;плт;[пс];[тип])
Описание аргументов:
- ставка – аргумент, принимающий числовое или процентное значение ставки за указанный период. Обязательный для заполнения. Если по условию используется годовая ставка, необходимо выполнить пересчет по следующей формуле: R=Rg/n, где Rg – годовая ставка, n – число периодов.
- кпер – числовое значение, характеризующее число периодов оплаты. Аргумент обязателен для заполнения. Если кредит был взят на период 3 года, выплаты по которому должны производиться каждый месяц, аргумент кпер должен принять значение 3*12=36 (12 – месяцы в году).
- плт – числовое значение, характеризующее фиксированную сумму выплаты за каждый период. Аргумент обязателен для заполнения. Если выплата за период является неизвестной величиной, аргумент плт может принимать значение 0, но при этом следующий аргумент задается явно.
- [пс] – приведенная стоимость на данный момент. Например, когда заемщик берет кредит у финансовой организации, тело кредита является приведенной на текущий момент стоимостью. По умолчанию аргумент [пс] принимает значение 0, а плт должен иметь отличное от нуля значение.
- [тип] – числовое значение, характеризующее тип выплат: в конце или начале периода. Принимает только два значения: 0 (если явно не указан) и 1.
Примечание 1:
- При указании аргумента ставка можно использовать процентный формат данных (например 17%) и числовой аналог (0,17).
- Расходные операции (текущая стоимость, выплата за период) должны быть указаны со знаком «-», то есть являться отрицательными числами.
- Функция БС использует в расчетах следующую формулу:
- Данная функция может быть использована для расчета баланса на конец периода и остаточной суммы задолженности по кредиту на текущий момент.
- Если процентная ставка меняется со временем, для расчетов следует использовать формулу БЗРАСПИС.
- Аргументы функции могут являться числовыми значениями или текстовыми данными, которые могут быть преобразованы в числа. Если один или несколько аргументов функции БС принимают текстовые строки, не содержащие числовые значения, будет возвращен код ошибки #ЗНАЧ!.
Примечание 2: функция БС также применяется для определения остатка задолженности по кредиту с аннуитетным графиком выплат, при этом дополнительные проценты и комиссии учтены не будут. Аннуитетный график предполагает фиксированную сумму погашения для каждого периода выплат (состоит из процентов и тела кредита).
Рассчитаем Будущую стоимость инвестиции для различных способов начисления процента: по формуле простых процентов, сложных процентов и формуле аннуитета.
Будущая стоимость (Future Value), является суммой, в которую в будущем превратится определенная сумма денег, инвестированная ранее под известную процентную ставку. Она рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Будущей стоимости, также как и
Приведенной (Текущей) стоимости
важен, так как, платежи, осуществленные в различные моменты времени, можно сопоставлять (сравнивать, складывать, вычитать) лишь после приведения их к одному временному моменту.
Будущая стоимость инвестиций зависит от того, каким методом начисляются проценты:
простые проценты
,
сложные проценты
или
аннуитет
(в
файле примера
приведено решение задачи для каждого из методов).
Простые проценты
Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты, начисленные за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).
При начислении простых процентов формула для расчета будущей стоимости (FV) инвестиций имеет следующий вид:
FV = PV * (1+i*n)
где PV —
настоящая (приведенная) стоимость
(сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка
за период
начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц (=годовая ставка/12)); n – количество периодов времени, в течение которых начисляются проценты.
Как видно из формулы FV (в MS EXCEL используется аббревиатура БС) это ни что иное, как
наращенная сумма
с использованием простых процентов. Про вычисление наращенной суммы при постоянной и переменной ставке можно прочитать в статье
Простые проценты в MS EXCEL
.
Примечание
. В MS EXCEL нет отдельной функции для расчета Будущей стоимости по методу Простых процентов. Функция
БС()
используется только для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить
БС()
рассчитать Будущую стоимость и по методу простых процентов (см.
файл примера
).
Сложные проценты
При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования
простых процентов
изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент» (см.
файл примера
). Формула для расчета Будущей стоимости в случае начисления по сложным процентам имеет следующий вид:
FV = PV * (1+i)^n
где PV —
настоящая (приведенная) стоимость
(сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка
за период
начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц). Предполагается, что процентная ставка не изменяется в течение всего срока инвестирования; n – количество периодов времени, в течение которого начисляются проценты.
Про вычисление Будущей стоимости по сложным процентам можно прочитать в статье
Сложные проценты в MS EXCEL
. В этой статье разобраны случаи применения функции
БС()
и формула капитализации m раз в год. В статье
Сложные проценты в MS EXCEL. Переменная ставка
разобраны случаи применения функции
БЗРАСПИС()
для расчета будущей стоимости при переменной ставке. В статье
Непрерывные проценты
Будущая стоимость рассчитывается при непрерывном начислении процентов.
Аннуитет
Если, помимо начальной инвестиции, через равные периоды времени производятся дополнительные равновеликие платежи (дополнительные инвестиции), то расчет Будущей стоимости существенно усложняется См. статью
Аннуитет. Определяем в MS EXCEL Будущую Стоимость
.
В случае, если сумма начальной инвестиции =0 и нужно определить Будущую стоимость периодических равновеликих платежей, то это можно сделать по формуле (см.
файл примера
):
FV = PMT * (((1+i)^n)-1) / i
где PMT – размер платежа при аннуитете; i — процентная ставка
за период
начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц). В формуле предполагается, что проценты начисляются в конце периода; n – количество периодов времени, в течение которых начисляются проценты (и делаются платежи).
В этом учебном материале вы узнаете, как использовать Excel функцию БС с синтаксисом и примерами.
Описание
Microsoft Excel функция БС возвращает будущую стоимость инвестиции на основе процентной ставки и постоянного графика платежей.
Функция БС — это встроенная в Excel функция, которая относится к категории финансовых функций.
Её можно использовать как функцию рабочего листа (WS) и функцию VBA в Excel.
Как функцию рабочего листа, функцию БС можно ввести как часть формулы в ячейку рабочего листа.
В качестве функции VBA вы можете использовать функцию FV в коде макроса, который вводится через редактор Microsoft Visual Basic Editor.
Синтаксис
Синтаксис функции БС в Microsoft Excel:
БС(ставка;кпер;плт;[пс];[тип])
Аргументы или параметры
- ставка
- Процентная ставка для инвестиции.
- кпер
- Количество платежей для аннуитета.
- плт
- Сумма платежа за каждый период.
- пс
- Необязательно. Это текущая стоимость платежей.
Если этот параметр опущен, предполагается, чтопсравно 0. - тип
- Необязательно. Он указывает, когда должны быть произведены выплаты.
Если аргументтипопущен, то предполагается, что значениетиправно 0.типможет быть одним из следующих значений:Значение Пояснение 0 Платежи подлежат оплате в конце периода. (по умолчанию) 1 Платежи подлежат оплате в начале периода.
Возвращаемое значение
Функция БС возвращает числовое значение.
Применение
- Excel для Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2011 для Mac, Excel 2010, Excel 2007, Excel 2003, Excel XP, Excel 2000
Тип функции
- Функция рабочего листа (WS)
- Функция VBA
Пример (как функция рабочего листа)
Рассмотрим несколько примеров Excel БС, чтобы понять, как использовать Excel функцию БС как функцию рабочего листа в Microsoft Excel.
Первый пример возвращает будущую стоимость инвестиции, в которую вы вносите $5000 на сберегательный счет, приносящий 7,5% годовых. Вы собираетесь вносить $250 в начале месяца каждый месяц на 2 года.
|
=БС(7.5%/12; 2*12; —250; —5000; 1) Результат: $12,298.46 |
В следующем примере возвращается будущая стоимость инвестиции, когда вы вносите $8000 на сберегательный счет, приносящий 6% годовых. Вы собираетесь вносить $50 в конце недели каждую неделю в течение 4 лет.
|
=БС(6%/52; 4*52; —50; —8000; 0) Результат: $21,915.09 |
В следующем примере возвращается будущая стоимость инвестиции, когда вы вносите $6500 на сберегательный счет, приносящий 5,25% годовых. Вы собираетесь вносить $100 в конце года каждый год на 10 лет.
|
=БС(5.25%/1; 10*1; —100; —6500; 0) Результат: $12,115.19 |
Пример (как функция VBA)
Функцию FV также можно использовать в коде VBA в Microsoft Excel.
Рассмотрим несколько примеров функции Excel FV, чтобы понять, как использовать Excel функцию FV в коде Excel VBA:
|
Dim LValue As Currency LValue = FV(0.0525 / 1; 10*1; —100; —6500; 0) |
В этом примере переменная LValue теперь будет содержать значение $12,115.19.
Аннотация:
Цель работы: научиться работать с финансовыми функциями Excel и выполнять анализ «Что-если» при варьировании данных.
Содержание работы:
Использование финансовых функций при экономических расчётах.
Способы прогнозирования значений с помощью анализа «Что – если».
Таблицы подстановки данных, создание сценариев, подбор параметра.
Порядок выполнения работы:
Изучить методические указания.
Выполнить задания.
Оформить отчет и ответить на контрольные вопросы.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Использование финансовых функций при экономических расчётах
Функция ПЛТ
Функция ПЛТ (PMT) – возвращает сумму периодического платежа на основе постоянства сумм платежей и постоянства процентной ставки.
Синтаксис:
ПЛТ(СТАВКА;КПЕР;ПС;[БС];ТИП)
- СТАВКА – Удельная ставка за период займа.
- КПЕР– общее число периодов выплат.
- ПС– текущая стоимость: общая сумма всех будущих платежей с настоящего момента.
- БС – будущая стоимость или баланс наличности, которую нужно достичь после последней выплаты.Если аргумент БС опущен, то он полагается равным 0 (нулю), т. е. для займа, например, значение БС равно 0.
- ТИП– логическое значение (0 или 1), обозначающее, должна ли производиться выплата в конце периода (0) или в начале периода (1).
Функция ПЛТ может быть использована для анализа всевозможных ссуд. Необходимым условием является непротиворечивость аргументов функции.
Пример 1. Предположим, что нужно воспользоваться 9-процентной 15-летней ссудой. Объем ссуды составляет 150 000 000 рублей. C помощью Мастера функций можно определить величины ежемесячных выплат. Предварительно следует привести все другие значения к месячной норме.
Ввести таблицу (рис. 9.1
рис.
9.1 ), начиная с ячейки А1:
Рис.
9.1.
Определение величины ежемесячных выплат
В ячейки В 3 и В 4 ввести соответствующие формулы.
Процентная ставка (СТАВКА) – годовая, поэтому для получения месячной ставки (Удельная ставка) соответствующее значение делится на 12 (0,09/12).
Срок действия ссуды – 15 лет, поэтому с учетом 12 платежей год общее количество месячных выплат (КПЕР) составит 12х15.
Для ячейки В6 пошаговыми действиями Мастера функций выполните настройку функции ПЛТ. Для вызова Мастера функций необходимо выбрать команду Вставить функцию (значок fx) в меню Формулы.
После этого в поле Значение диалогового окна Мастера функций вы увидите сумму ежемесячного взноса. А после нажатия на кнопку Готово результат отобразится в ячейке.
Примечание. Необходимо исходные данные заносить в ячейки на рабочий лист Excel, давая им в левом столбце соответствующие названия параметров, а для рассчитываемых параметров использовать формулы. Тогда при изменении исходных данных будет автоматически выполнен перерасчет по формулам.
Функция БС
Функция БС(FV) предназначена для расчета будущей стоимости периодических постоянных платежей и единой суммы вклада или займа на основе постоянной процентной ставки.
БС – будущее значение, возвращает будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки.
Синтаксис:
БС (СТАВКА; КПЕР; ПЛТ; ПС; ТИП).
- СТАВКА – это процентная ставка за период.
- КПЕР– это общее число периодов платежей.
- ПЛТ– это выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно ПЛТ состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов.
- ПС – это текущая стоимость, или общая сумма всех будущих платежей с настоящего момента. Если аргумент ПС опущен, то он полагается равным 0. В этом случае должно быть указано значение аргумента ПЛТ.
- ТИП– это число 0 или 1, обозначающее, когда должна производиться выплата: 0 – в конце периода, 1 – в начале периода. Если аргумент опущен, то он полагается равным 0.
Для аргументов СТАВКА и КПЕР используются согласованные единицы измерения. Если производятся ежемесячные платежи по четырехгодичному займу из расчета 12% годовых, то СТАВКА должна быть 12%/12, а КПЕР должно быть 4*12. Если производятся ежегодные платежи по тому же займу, то СТАВКА должна быть 12%, а КПЕР должно быть 4.
Все аргументы, означающие деньги, которые вы платите (например, депозитные вклады), представляются отрицательными числами; деньги, которые вы получаете (например, дивиденды), представляются положительными числами.
Например, вы собираетесь вложить под 12% годовых (что составит в месяц 12%/12 или 1%). Вы собираетесь вкладывать по 1000 руб. в конце каждого следующего месяца в течении следующих 12 месяцев. Сколько денег будет на счету в конце12 месяцев?
Результат 12682,50 руб.
Для выполнения расчета вызывается Мастер функций, в поле Категории выбираются финансовые функции и в поле Функция выбирается функция БС. В появившемся окне заполняются соответствующие поля путем подстановки значений аргументов, а если данная функция вычисляется в расчете, то вместо этого указываются адреса исходных данных из таблицы расчета.
Функция ПС
Функция ПС (PV) предназначена для расчета текущей стоимости как единой суммы вклада (займа), так и будущих фиксированных периодических платежей. Этот расчет является обратным по отношению к будущей стоимости (БС).
ПС (PV )– возвращает текущий объем вклада. Текущий объем -это общая сумма, которую составят будущие платежи. Например, когда вы берете взаймы деньги, заимствованная сумма и есть текущий объем для заимодавца.
Синтаксис:
ПС (СТАВКА; КПЕР; ПЛТ; БС; ТИП).
Например, определите необходимую сумму текущего вклада в банк, чтобы через пять лет он достиг 5000 руб. при 20% годовых и ежегодном начислении процентов в конце года. Синтаксис: ПС (20%, 5, 5000). Результат 2009,39.
Функция КПЕР
Для определения срока платежа и процентной ставки используются функции КПЕР (NPER) и СТАВКА (RATE).
Функция КПЕР вычисляет общее число периодов выплат как для единой суммы вклада (займа), так и для периодических постоянных выплат на основе постоянной процентной ставки. Если платежи производятся несколько раз в год, то для того, чтобы найти число лет выплат, общее число периодов надо разделить на число периодов в году.
Синтаксис:
КПЕР (СТАВКА; ПЛТ; ПС; БС; ТИП).
- СТАВКА– это процентная ставка за период.
- ПЛТ– это выплата, производимая в каждый период; он не может меняться в течение всего периода выплат. Обычно платеж состоит из основного платежа и платежа по процентам, никакие другие сборы или налоги не учитываются.
- ПС– это текущая стоимость, или общая сумма всех будущих платежей с настоящего момента.
- БС– это будущая стоимость, или баланс наличности, который должен быть достигнут после последней выплаты. Если аргумент БС опущен, то предполагается, что он равен 0 (будущая стоимость займа, например, равна 0).
- ТИП– это число 0 или 1, обозначающее, когда должна производиться выплата.
Например, рассчитаем срок погашения ссуды размером 5000 руб., выданной под 20% годовых при погашении ежемесячными платежами по 200 руб.
КПЕР (20%/12; -200; 5000).
Результат 32,6 месяца или 2,7 года.
Функция СТАВКА
Функция СТАВКА (RATE) определяет значение процентной ставки за один расчетный период. Для нахождения годовой процентной ставки полученное значение необходимо умножить на число расчетных периодов в году.
СТАВКА вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО!.
Синтаксис:
СТАВКА (кпер; плт; пс; бс; тип; предположение).
- Кпер– общее число периодов платежей по аннуитету.
- Плт– регулярный платеж (один раз в период), величина которого остается постоянной в течение всего срока аннуитета. Обычно плт состоит из платежа основной суммы и платежа процентов, но не включает других сборов или налогов. Если аргумент опущен, должно быть указано значение аргумента БС.
- Пс– приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей.
- Бс– требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (например, бс для займа равно 0).
- Тип– число 0 или 1, обозначающее, когда должна производиться выплата.
- Предположение – предполагаемая величина ставки. Если значение предположения опущено, то оно полагается равным 10 процентам.
Если функция СТАВКА не сходится, попробуйте подставить различные значения для предположения. СТАВКА обычно сходится, если величина предположения находится между числами 0 и 1.
Например, надо определить процентную ставку для четырёхлетнего займа в 8000 руб. с ежемесячной выплатой в 200 руб.
Результат 0,008, или 0,8 в месяц или 9,6% годовых.
Функции по расчету амортизации: AПЛ, АСЧ и ДДОБ
Под амортизацией подразумевается уменьшение стоимости имущества в процессе эксплуатации. Обычно оценивают величину этого уменьшения на единицу времени.
Функция АПЛ (SLN) возвращает величину амортизации имущества за один период времени, используя метод равномерной амортизации.
Синтаксис:
АПЛ (нач_стоимость;ост_стоимость;время_эксплуатации).
- нач_стоимость – начальная стоимость имущества;
- ост_стоимость –остаточная стоимость в конце периода амортизации;
- время_эксплуатации – количество периодов, за которые собственность амортизируется (иногда называется временем полной амортизации).
Предположим, вы купили за 6000 руб. компьютер, который имеет срок эксплуатации 5 лет, после чего оценивается в 1000 руб. Снижение стоимости для каждого года эксплуатации вычисляется формулой
которая возвращает значение 1000 р.
Функция АСЧ(SYD) возвращает годовую амортизацию имущества для указанного периода.
АСЧ (нач_стоимость; ост_стоимость; время_эксплуатации; период)
- нач_стоимость – начальная стоимость имущества;
- ост_стоимость – остаточная стоимость в конце периода амортизации;
- время_эксплуатации – количество периодов, за которые собственность амортизируется (иногда называется временем полной амортизации);
- период – номер периода для вычисления амортизации (должен быть измерен в тех же единицах, что и время полной амортизации).
При расчете предыдущего примера получим:
- за первый год эксплуатации компьютера амортизация вычисляется формулой
которая возвращает значение 1666.67р.
- за последний – формулой
которая возвращает 333. 33 р.
Функция ДДОБ (DDB) возвращает величину амортизации имущества для указанного периода, используя метод двукратного (или k-кратного) учета амортизации.
Синтаксис:
ДДОБ (стоимость; остаточная_стоимость; время_эксплуатации; период; k-коэффициент).
- стоимость–начальная стоимость имущества;
- остаточная_стоимость– остаточная стоимость в конце периода;
- время_эксллуатадии– количество периодов, за которые собственность амортизируется (иногда называется временем полной амортизации);
- период – номер периода для вычисления амортизации (должен быть измерен в тех же единицах, что и время полной амортизации);
- коэффициент– норма снижения балансовой стоимости (амортизации). Если коэффициент опущен, то предполагается, что он равен 2 (методдвукратного учета амортизации).
Метод двукратного учета амортизации предполагает ускоренную амортизацию имущества. При этом амортизация максимальна в первый период и снижается в последующие периоды.
В примере с компьютером по методу двукратной амортизации она составит:
- =ДДОБ (6000; 1000; 5; 1) возвращает 2400.00р.
- =ДДОБ (6000; 1000; 5; 2) возвращает 1440.00р.
- =ДДОБ (6000; 1000; 5; 3) возвращает 864.00р.
- =ДДОБ (6000; 1000; 5; 4) возвращает 296.00р.
- =ДДОБ (6000; 1000; 5; 5) возвращает 0.00р.
Примечание
В заключение попытаемся разобраться, как работают функции АПЛ, АСЧ, ДОБ и ДДОБ.
Проще всего дело обстоит с функцией АПЛ. Она возвращает одну и ту же амортизацию за каждый период.
Значения функции АСЧ изменяются по линейному закону. Разность любых двух ее значений за последовательные периоды постоянна. Таким образом значения за последовательные периоды образуют убывающую арифметическую прогрессию, подобранную таким образом, чтобы суммарная амортизация равнялась разности между начальной и остаточной стоимостью.
Значения функции ДДОБ изменяются также по экспоненциальному закону. Но коэффициент этой геометрической прогрессии не вычисляется, а является параметром.
Анализ «Что-если»
Анализ «Что-если» позволяет прогнозировать значение какой-либо функции (математической, финансовой, статистической и др.) при изменении её аргументов.
Существует четыре способа прогнозирования значений с помощью:
- таблиц подстановки данных,
- сценариев
- подбора параметров
- поиска решения.
1 способ. Таблица подстановки данных
Таблица подстановки данных представляет собой блок ячеек, в котором выводятся результаты подстановки различных значений переменных в одну или несколько формул.
Анализ может проводиться для функций с одной переменной или для функций с двумя переменными. Причем в случае одной переменной можно табулировать сразу несколько функций, зависящих от этой переменной.
Анализ формулы начинается с подготовки таблицы подстановки:
- Левую верхнюю ячейку блока, отведенного под таблицу, оставить пустой.
- В левый столбец блока, начиная со второй ячейки, последовательно ввести значения варьируемой переменной.
- В верхнюю строку блока, начиная со второй ячейки, ввести ссылки на ячейки с анализируемыми формулами.
Допускается и другая ориентация таблицы, когда значения варьируемой переменной вводятся в первую строку, а анализируемые форму-лы – в первый столбец блока.
- Выделить таблицу подстановки (в ячейки, расположенные рядом с таблицей, можно ввести пояснительные надписи, но эти ячейки не входят в таблицу подстановки данных и, следовательно, не выделяются).
- В меню Данные выбрать Анализ «Что-если» и выбрать команду Таблица данных.
- Если значения варьируемой переменной расположены в столбце, то надо щелкнуть по полю Подставлять значения по строкам и ввести в это поле адрес изменяемой ячейки (т.е. ячейки, которая играет роль варьируемой переменной в формуле). Если значения варьируемой переменной расположены в строке, то адрес изменяемой ячейки вводится в поле Подставлять значения по столбцам.
- Щелкнуть по кнопке ОК. Таблица будет заполнена значениями.
В случае анализа зависимости формулы от двух переменных таблица подстановки подготавливается по-другому:
- В левую верхнюю ячейку блока, отведенного под таблицу, ввести ссылку на ячейку с анализируемой формулой.
- В левый столбец блока, начиная со второй ячейки, последовательно ввести значения одной из варьируемых переменных.
- В верхнюю строку блока, начиная со второй ячейки, ввести значения другой варьируемой переменной.
- Выделить таблицу подстановки.
- В меню Данные выбрать Анализ «Что-если» и выбрать команду Таблица данных.
- В поле Подставлять значения по строкам в ввести ссылку на ячейку с переменной, значения для которой расположены в левом столбце таблицы подстановки.
- В поле Подставлять значения по столбцам ввести ссылку на ячейку с переменной, значения для которой расположены в первой строке таблицы подстановки.
- Щелкнуть по кнопке ОК. Таблица будет заполнена значениями.
Если в какой-либо ячейке записана формула, содержащая элементы из других ячеек, то при изменении значения в какой-нибудь или нескольких ячейках изменится результат в ячейке, содержащей формулу.
Пример 2.
Определить какими будут выплаты по ссуде при меняющейся процентной ставке (для примера 1)
В ячейки А9:В13 введите следующие значения, оставив пустой строку перед числовыми значениями (рис. 9.2
рис.
9.2 ):
Рис.
9.2.
Определение величины ежемесячных выплат с использованием таблицы подстановки
В ячейку В10 скопировать ссылку на ячейку с формулой для расчета ежемесячных выплат.
Для расчета выплат по каждой из ставок воспользуйтесь возможностью автоматической подстановки значений в нужную ячейку (в нашем случае в В1).
Для этого нужно:
- Выделить диапазон А10:В13, включив в него значения процентных ставок и расчетную формулу (формула должна находиться в ячейке, расположенной правее и выше заданных значений).
- В меню Данные выбрать Анализ «Что-если» и выбрать команду Таблица данных.
- В поле «Подставлять значения по строкам в:» указать ячейку В1 (рис.9.3 ).
Рис.
9.3.
Таблица подстановки
Рядом с каждой процентной ставкой появится соответствующий результат.
Измените значения процентных ставок или расширьте предлагаемый диапазон и вновь воспользуйтесь таблицей подстановки значений.
2 способ. Диспетчер сценариев
Средства Microsoft Excel позволяют создавать и сохранять в виде сценариев наборы входных значений, приводящих к различным результатам.
Сценарий – это множество входных значений, называемых изменяемыми ячейками, которое можно сохранить под указанным именем, а затем применить к модели рабочего листа, чтобы проследить, как значения изменяемых ячеек влияют на другие значения модели. Для каждого сценария можно определить до 32 изменяемых ячеек.
Чтобы создать сценарий, следует:
1. В меню Данные выбрать команду Анализ «Что-если», указав Диспетчер сценариев (рис. 9.4
рис.
9.4 ).
Появится окно «Диспетчер сценариев» (рис. 9.5
рис.
9.5)
Рис.
9.5.
Диспетчер сценариев
2. Щелкнуть по кнопке Добавить. Откроется окно Добавление сценария (рис. 9.6
рис.
9.6).
Рис.
9.6.
Диалоговое окно Добавление сценария
3. В поле Название сценария ввести имя сценария.
4. В поле Изменяемые ячейки ввести ссылки на изменяемые ячейки. Несколько ссылок отделяются друг от друга точками с запятыми. Ссылки можно ввести с клавиатуры или выделить их на рабочем листе. Несмежные ячейки добавляются при нажатой клавише <Ctrl>.
5. Щелкнуть по кнопке ОК.
6. В открывшемся диалоговом окне Значения ячеек сценария ввести значения каждой изменяемой ячейки (рис. 9.7
рис.
9.7).
Рис.
9.7.
Диалоговое окно Значения ячеек сценария
7. Для создания других сценариев щелкнуть по кнопке Добавить (откроется диалоговое окно Добавление сценария) и повторить пункты 3 – 6.
Для завершения работы с Диспетчером сценариев щелкнуть по кнопке ОК, а затем – по кнопке Закрыть.
Рекомендуется сохранить в качестве сценария первоначальные значения изменяемых ячеек, чтобы потом можно было быстро восстановить эти значения.
Для просмотра сценария нужно:
- В меню Данные выбрать команду Анализ данных и указать Диспетчер сценариев.
- В поле Сценарии выделить имя сценария, который необходимо просмотреть.
- Щелкнуть по кнопке Вывести.
Вместо пунктов 2 и 3 можно дважды щелкнуть по имени нужного сценария.
Чтобы отредактировать сценарий, надо:
- В меню Данные выбрать команду Анализ данных и указать Диспетчер сценариев.
- В поле Сценарии выделить имя сценария, который необходимо отредактировать.
- Щелкнуть по кнопке Изменить.
- Внести необходимые изменения: можно изменить имя сценария, изменяемые ячейки, значения изменяемых ячеек.
- Для завершения работы с Диспетчером сценариев щелкнуть по кнопке ОК, а затем – по кнопке Закрыть.
Для создания итогового отчета по сценариям следует:
- В меню Данные выбрать команду Анализ данных и указать Диспетчер сценариев.
- Щелкнуть по кнопке Отчет.
- Выбрать тип отчета: Структура или Сводная таблица.
В отчете типа Структура перечислены все сценарии с определенными для них значениями ячеек. Этот тип отчета полезен тогда, когда каждый пользователь определяет сценарий со своими данными.
Отчет типа Сводная таблица предоставляет возможность эмпирического анализа сценариев. Этот тип отчета полезен тогда, когда сценарий имеет несколько наборов значений изменяющихся ячеек, заданных различными пользователями; с помощью сводных таблиц можно выполнить анализ для разных комбинаций сценариев.
- В поле Ячейки результата ввести ссылки на ячейки, значения которых надо представить в отчете. В качестве разделителя ссылок используется запятая. Ссылки можно ввести с клавиатуры или выделить их на рабочем листе. Несмежные ячейки добавляются при нажатой клавише <Ctrl>. Итоговые отчеты создаются на отдельных листах.
3 способ. Подбор параметра
Пусть имеется формула, которая прямо или косвенно зависит от некоторого параметра. Задача состоит в определении такого значения этого параметра, которое позволяет получить нужный результат формулы. При подборе параметра значение влияющей ячейки (параметра) изменяется до тех пор, пока формула, зависящая от этой ячейки не возвратит заданное значение.
Математическая суть задачи состоит в решении уравнения X = a, где функция х описывается заданной формулой, х – искомый параметр, а – требуемый результат формулы.
Для решения этой задачи необходимо выполнить следующие действия:
- Выделить ячейку, содержащую формулу, для которой нужно найти определенное решение.
- В меню Данные > Анализ «что-если» выбрать команду Подбор параметра. В поле Установить в ячейке ввести ссылку на ячейку, содержащую формулу (по умолчанию в это поле вводится адрес текущей ячейки).
- В поле Значение ввести значение, которое нужно получить по заданной формуле.
- В поле Изменяя ячейку ввести ссылку на ячейку, содержащую значение изменяемого параметра (эта ячейка называется изменяемой).
- Щелкнуть по кнопке ОК.
Пример 3.
Дано уравнение: 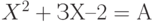
где: А – требуемый результат формулы; Х – искомый параметр.
Определить такое значение параметра X, при котором А будет равно 20.
- Занести в ячейку A1 любое значение, например, 1.
- Ввести в ячейку А2 указанную формулу, которая примет следующий вид: =A1^2+3*A1-2. В формуле указана ссылка на ячейку А1, в которой условно находится параметр X.
- Задать команду Данные > Анализ «что-если» > Подбор параметра (рис. 9.8
рис.
9.8 ). - В поле Установить в ячейке указать А2 (по умолчанию в это поле вводится адрес текущей ячейки).
- В поле Значение ввести – 20.
- В поле Изменяя значение ячейки указать адрес ячейки, в которой должен находиться параметр X, т.е. А1.
Рис.
9.8.
Окно Подбор параметра
После выполнения команды в изменяемой ячейке появится значение параметра X, при котором результат формулы равняется заданной величине. При этом будет пересчитана вся таблица, т.е. изменятся значения, прямо или косвенно зависящие от изменяемого параметра.
Подбор параметра можно выполнять графически, перетаскивая точки данных на диаграмме.
При подборе параметра одна из ячеек обязательно должна содержать формулу.
ЗАДАНИЯ
- Используя соответствующие финансовые функции, решите следующие задачи, (номер варианта задания – номер компьютера в учебной аудитории).
- Для созданной задачи изменить величины ее параметров так, чтобы (не меняя формулы) результат вычислений тоже изменился.
- Выполнить анализ данных «Что – если», используя таблицу подстановок.
- Изменить результат вычислений задачи с помощью Сценария. Вывести итоговый отчет типа структура.
- Изменить результат вычисления при помощи Подбора параметров.
Вариант 1.
- Определить величину ежемесячной амортизации имущества (АПЛ (SLN)) при условии, что начальная стоимость его 10000р., а остаточная (в конце периода амортизации) 2000р.; амортизация имущества занимает период 10 месяцев.
- Затем вычислить эту величину (не меняя формулу) при условии, что остаточная амортизация равна 1500р..
- Определить величину ежемесячной амортизации имущества (АПЛ), используя таблицу подстановок:
- при различных периодах: 5, 7, 8, 9, 10, 12 месяцев;
- при различных периодах: 5, 7, 8, 9, 10, 12 месяцев, а также при остаточных стоимостях 5000, 4500, 4000, 3000, 2000, 1000 соответственно.
- Составить сценарий, если начальная стоимость имущества изменится на 15000р.
- Подобрать параметр срока полной амортизации при условии, что ежемесячные отчисления составят 1500р.
Вариант 2.
- Вычислить, на сколько снизится стоимость основных фондов, рассчитанная по методу двойной амортизации (ДДОБ), если начальная стоимость имущества 30000р., а в конце периода эксплуатации 4000р. Время эксплуатации считать равным 3 года, период, для которого вычисляется амортизация, равным 2,5 года.
- Вычислить эту величину (не меняя формулу) при условии, что остаточная стоимость имущества равна 5000р..
- Определить величину ДДОБ используя таблицу подстановок:
- при изменении времени эксплуатации: 7, 6, 5, 4, 3 года;
- при изменении времени эксплуатации: 7, 6, 5, 4, 3 года; и начальной стоимости 70000, 60000, 50000, 40000, 30000 руб. соответственно.
- Составить сценарий, если величина начальной стоимости изменится на 35000р.
- Подобрать параметр срока эксплуатации, если стоимость основных фондов снизится на 1000р.
Вариант 3.
- Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 50000р. со ставкой 5% годовых сроком на 4 года и будущей стоимостью 5000р.
- Вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 7%.
- Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
- при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
- при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и сроком на 5, 7, 8, 9, 10 лет соответственно.
- Составить сценарий, если величина кредита изменится на 60000р, а срок на 5 лет.
- Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 7000р.
Вариант 4.
- Вычислить величину всех выплат (БС) фирмой, взявшей кредит в размере 45000р., сроком на год, с ежемесячной выплатой 3000р. и годовой ставкой процента, равной 5%.
- Затем, вычислить эту величину (не меняя формулу) при условии, что величина процентной ставки изменится на 3%.
- Определить величину всех выплат (БС) используя таблицу подстановок:
- при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
- при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 50000, 60000, 70000, 80000, 90000, 100000 руб. соответственно.
- Составить сценарий, если величина кредита изменится на 50000р.
- Подобрать параметр ежемесячной выплаты, если величина всех выплат составит 85000р.
Вариант 5.
- Вычислить общее количество периодов выплаты (КПЕР) фирмой, взявшей кредит в размере 73000р. Ставка процента постоянна и равна 6%. Ежемесячные выплаты фирмой также постоянны и равны 5500р.
- Вычислить эту величину (не меняя формулу) при условии, что величина кредита изменится на 60000р.
- Определить величину КПЕР используя таблицу подстановок:
- при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
- при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 50000, 60000, 70000, 80000, 90000, 100000 руб. соответственно.
- Затем составить сценарий, если величина процентной ставки изменится на 12%.
- Подобрать параметр величины кредита, если выплата будет производиться 19 месяцев.
Вариант 6.
- Определить величину ежемесячной амортизации имущества (АПЛ) при условии, что начальная стоимость его 40000р., а остаточная (в конце периода амортизации) 9000р.; амортизация имущества занимает период 2 года.
- Вычислить эту величину (не меняя формулу) при условии, что остаточная амортизация равна 7000р.
- Определить величину АПЛ используя таблицу подстановок:
- при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 9000 и том же периоде;
- при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 9000 и периоде 0,5; 1, 1,5; 2, 3 года соответственно.
- Составить сценарий, если начальная стоимость имущества изменится на 55000р.
- Подобрать параметр срока полной амортизации при условии, что ежемесячные отчисления составят 3500р.
Вариант 7.
- Вычислить, на сколько снизится стоимость основных фондов, рассчитанная по методу двойной амортизации (ДДОБ), если начальная стоимость имущества 80000р., а в конце периода эксплуатации 10000р. Время эксплуатации считать равным 17 месяцев, период, для которого вычисляется амортизация, равным10 месяцев.
- Вычислить эту величину (не меняя формулу) при условии, что остаточная стоимость имущества равна 7000р.
- Определить величину ДДОБ спользуя таблицу подстановок:
- при варьировании начальной стоимости: 50000, 60000, 70000, 90000, 110000 и том же периоде амортизации;
- при варьировании начальной стоимости: 50000, 60000, 70000, 90000, 110000 и периоде 5; 6, 7, 8, 9 месяцев соответственно.
- Составить сценарий, если величина начальной стоимости изменится на 75000р.
- Подобрать параметр срока эксплуатации, если стоимость основных фондов снизится на 2500р.
Вариант 8.
- Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 90000р. со ставкой 7% на период, равный 1 году и будущей стоимостью 9000р.
- После, вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 10%.
- Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
- при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
- при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 70000, 80000, 90000, 100000, 120000 руб. соответственно.
- Составить сценарий, если величина кредита изменится на 80000р., а срок на 2 года.
- Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 5000р.
Вариант 9.
- Вычислить величину всех выплат (БС) фирмой, взявшей кредит в размере 67000р., сроком на 3 года, с ежемесячной выплатой 7000р. и годовой ставкой процента, равной 4,5%.
- Вычислить эту величину (не меняя формулу) при условии, что величина процентной ставки изменится на 6%.
- Определить величину БС используя таблицу подстановок:
- при процентных ставках 5%, 6%, 7% , 8% и 9% годовых;
- при процентной ставке 5%, 6%, 7% , 8% и 9% годовых, и суммах кредита 70000, 80000, 90000, 100000, 120000 руб. соответственно.
- После, составить сценарий, если величина кредита изменится на 59000р.
- Подобрать параметр ежемесячной выплаты, если величина всех выплат составит 103000р.
Вариант 10.
- Вычислить общее количество периодов выплаты (КПЕР) фирмой, взявшей кредит в размере 93000р. Ставка процента постоянна и равна 6,5%. Ежемесячные выплаты фирмой также постоянны и равны 6500р.
- Вычислить эту величину (не меняя формулу) при условии, что величина кредита изменится на 80000р.
- Определить величину КПЕР используя таблицу подстановок:
- при процентных ставках 5%, 6%,7%, 8% , 9% и 10% годовых;
- при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 100000,90000, 80000, 70000, 60000, 50000 руб. соответственно.
- Затем составить сценарий (условие п.1), если величина процентной ставки изменится на 9%, а ежемесячная выплата 4500р.
- Подобрать параметр величины кредита, если выплата будет производиться 2 года.
Вариант 11.
- Определить величину ежемесячной амортизации имущества (АПЛ) при условии, что начальная стоимость его 100000р., а остаточная (в конце периода амортизации) 10000р.; амортизация имущества занимает период 4 года.
- Затем вычислить эту величину (не меняя формулу) при условии, что остаточная амортизация равна 12000р.
- Определить величину АПЛ используя таблицу подстановок:
- при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 9000 и том же периоде;
- при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 10000 и периоде 1, 2, 3, 3,5 и 4 года соответственно.
- После, составить сценарий, если начальная стоимость имущества изменится на 97000р.
- Подобрать параметр срока полной амортизации при условии, что ежемесячные отчисления составят 7500р.
Вариант 12.
- Вычислить, на сколько снизится стоимость основных фондов, рассчитанная по методу двойной амортизации (ДДОБ), если начальная стоимость имущества 123000р., а в конце периода эксплуатации 9000р. Время эксплуатации считать равным 13 месяцев, период, для которого вычисляется амортизация, равным8 месяцев.
- После, вычислить эту величину (не меняя формулу) при условии, что остаточная стоимость имущества равна 9500р.
- Определить величину ДДОБ используя таблицу подстановок:
- при изменении времени эксплуатации: 7, 6, 5, 4, 3 года;
- при изменении времени эксплуатации: 7, 6, 5, 4, 3 года; и начальной стоимости 70000, 60000, 50000, 40000, 30000 руб. соответственно.
- Затем составить сценарий, если величина начальной стоимости изменится на 115000р.
- Подобрать параметр срока эксплуатации, если стоимость основных фондов снизится на 5500р.
Вариант 13.
- Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 74000р. со ставкой 8% годовых на период, равный 5 лет и будущей стоимостью 5000р.
- После, вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 14%.
- Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
- при процентных ставках 5%, 7%, 8% , 9% ,10%, 12% годовых;
- при процентной ставке 5%, 7%, 8%, 9%, 10%, 12% годовых, и сроке кредита 3, 4, 5, 6, 7, 8 лет соответственно.
- Затем составить сценарий, если величина кредита изменится на 87000р.
- Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 7500р.
Вариант 14.
- Вычислить величину всех выплат (БС) фирмой, взявшей кредит в размере 77000р., сроком на 2 года, с ежемесячной выплатой 9000р. и годовой ставкой процента, равной 7,5%.
- Затем, вычислить эту величину (не меняя формулу) при условии, что величина процентной ставки изменится на 9%.
- Определить, используя таблицу подстановок:
- величину всех выплат (БС) при процентных ставках 7%, 8% , 9% и 10% годовых;
- величину всех выплат (БС) при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, а сроке займа 5, 7, 8, 9, 10 лет соответственно.
- Составить сценарий, если величина кредита изменится на 86000р.
- Подобрать параметр ежемесячной выплаты, если величина всех выплат составит 120000р.
Вариант 15.
- Вычислить общее количество периодов выплаты (КПЕР) фирмой, взявшей кредит в размере 113000р. Ставка процента постоянна и равна 10%. Ежемесячные выплаты фирмой также постоянны и равны 8500р.
- Вычислить эту величину (не меняя формулу) при условии, что величина кредита изменится на 100000р.
- Определить общее количество периодов выплаты (КПЕР), используя таблицу подстановок:
- при процентных ставках 7%, 8% , 9% и 10% годовых;
- при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и сумме кредита 50000, 70000, 80000, 90000, и 100000 руб. соответственно.
- Составить сценарий, если величина процентной ставки изменится на 8,5%, а сумма кредита на 85000 руб. Сохранить отчет типа структура.
- Подобрать параметр величины кредита, если выплата будет производиться 4 года.
Вариант 16.
- Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 80000р. со ставкой 8% годовых сроком на 6 лет и будущей стоимостью 8000р.
- Вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 12%.
- Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
- при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
- при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и сроком на 5, 7, 8, 9, 10 лет соответственно.
- Составить сценарий, если величина кредита изменится на 120000р, а срок на 10 лет.
- Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 7000р.
Вариант 17.
- Вычислить величину всех выплат (БС) фирмой, взявшей кредит в размере 65000р., сроком на 3 года, с ежемесячной выплатой 4000р. и годовой ставкой процента, равной 6,5%.
- Затем, вычислить эту величину (не меняя формулу) при условии, что величина процентной ставки изменится на 5%.
- Определить величину всех выплат (БС) используя таблицу подстановок:
- при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
- при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 50000, 60000, 70000, 80000, 90000, 100000 руб. соответственно.
- Составить сценарий, если величина кредита изменится на 70000р., а срок на 5 лет.
- Подобрать параметр ежемесячной выплаты, если величина всех выплат составит 95000р.
Вариант 18.
- Определить величину ежемесячной амортизации имущества (АПЛ) при условии, что начальная стоимость его 90000р., а остаточная (в конце периода амортизации) 9000р.; амортизация имущества занимает период 5 лет.
- Затем вычислить эту величину (не меняя формулу) при условии, что остаточная амортизация равна 10000р.
- Определить величину АПЛ используя таблицу подстановок:
- при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 9000 и том же периоде;
- при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 10000 и периоде 1, 2, 3, 3,5 и 4 года соответственно.
- После, составить сценарий, если начальная стоимость имущества изменится на 127000р., а период на 7 лет
- Подобрать параметр срока полной амортизации при условии, что ежемесячные отчисления составят 7500р.
Вариант 19.
- Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 60000р. со ставкой 6% годовых сроком на 4 года и будущей стоимостью 6000р.
- Вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 7%.
- Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
- при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
- при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и сроком на 5, 7, 8, 9, 10 лет соответственно.
- Составить сценарий, если величина кредита изменится на 80000р, а срок на 5 лет.
- Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 2000р.
Вариант 20.
- Определить, на сколько снизится стоимость имущества (ДДОБ) на заданный период, используя метод двойной амортизации,если начальная стоимость имущества 120000р., а в конце периода эксплуатации 12000р. Время эксплуатации считать равным 26 месяцев, период, для которого вычисляется амортизация, равным 12 месяцев.
- Вычислить эту величину (не меняя формулу) при условии, что остаточная стоимость имущества равна 9000р.
- Определить величину ДДОБ используя таблицу подстановок:
- при изменении времени эксплуатации: 7, 6, 5, 4, 3 года;
- при изменении времени эксплуатации: 7, 6, 5, 4, 3 года и варьировании начальной стоимости: 70000, 80000, 90000, 100000, 110000 соответственно.
- Составить сценарий, если величина начальной стоимости изменится на 95000р.
- Подобрать параметр срока эксплуатации, если стоимость имущества снизится до 7000р.
КОНТРОЛЬНЫЕ ВОПРОСЫ
- Для чего предназначены функции: ПЛТ; БС; ПС; КПЕР и СТАВКА? Поясните синтаксис перечисленных функций.
- Назначение и способы анализа «Что если»?
- Для чего предназначена «Таблица подстановок», опишите технологию ее применение для функций с одной переменной и для функций с двумя переменными?
- Что такое сценарий, как его создать, просмотреть, изменить, получить итоговый отчет на отдельном листе?
- Сущность операции Подбор параметра, как она выполняется?
- Формула будущей стоимости
Формула будущей стоимости (Содержание)
- Формула будущей стоимости
- Калькулятор будущей стоимости
- Формула будущей стоимости в Excel (с шаблоном Excel)
Формула будущей стоимости
Ценность денег не остается прежней, она уменьшается или увеличивается из-за процентных ставок и состояния инфляции, дефляция, которая делает ценность денег менее ценной или более ценной в будущем. Но для финансового планирования того, что мы ожидаем денег для наших будущих целей, мы рассчитываем будущую стоимость денег, используя соответствующий коэффициент в будущей формуле.
Формула будущей стоимости дает нам будущую стоимость денег для принципа или денежного потока в данный период.
FV — будущая стоимость суммы, PV — текущая стоимость суммы,
r — показатель, взятый для расчета с учетом всего, что есть в нем, n — количество лет.
Пример формулы будущей стоимости
Чтобы лучше понять концепцию, мы рассчитаем будущую стоимость, используя вышеупомянутую формулу.
Вы можете скачать этот шаблон будущей стоимости здесь — Шаблон будущей стоимости
Рассчитайте будущую стоимость 15 000 рупий, одолженных по ставке 12 процентов годовых на 10 лет.
Чтобы рассчитать будущую стоимость,
PV = 15000
R = 12%
N = 10
- FV = PV (1 + R) n
- FV = 15000 (1 + 0, 12) 10
- FV = 46587, 72
Здесь мы указали текущую стоимость как 15000
Показатель периода в годах как 0, 12
Количество периодов, который год 10 лет
Здесь показатель 1.12 повышается до степени 10, которая в годах умножается на принцип 15000.
объяснение
Формула будущей стоимости очень широко используется во всех аспектах финансов, будь то инвестиции, корпоративные финансы, личные финансы, бухгалтерский учет и т. Д.
Будущая стоимость инвестиции зависит от покупательной способности, которую она будет иметь, и возврата инвестиций на капитал.
Теперь этот кумулятивный показатель инфляции и доходности инвестиций в одном выражении учитывается как норма доходности за период.
Следовательно,
БУДУЩЕЕ ЗНАЧЕНИЕ = НАСТОЯЩЕЕ ЗНАЧЕНИЕ + ПОЛУЧЕННЫЙ ВОЗВРАТ НА ИНВЕСТИЦИИ
Теперь, чтобы вычислить эту будущую стоимость, нам нужно понять, что рассчитанная стоимость будет использоваться с совокупной нормой доходности по годам текущей стоимости капитала.
Это можно объяснить: беру пример.
Позвольте представить пример
10 процентов
И капитал равен 1000, поэтому будущая стоимость будет равна 1000 + 100 = 1100.
Теперь для расчета за 2 года мы можем рассчитать, используя 1100 + 110 = 1210
Который также может быть записан как 1000 (1.1) 2, что сделает вычисление до 1.21 * 1000 = 1210
Таким образом, мы можем рассчитать будущие значения любой суммы, когда указана процентная ставка.
Значение и использование формулы будущей стоимости
Использование формулы будущей стоимости огромно и помогает нам быть очень информативными и иметь перспективу:
- Лучшее использование формулы будущей стоимости заключается в том, чтобы узнать, какая стоимость инвестиций будет стоить после определенного периода.
- Корпоративные финансы используют формулу будущей стоимости, чтобы принимать эффективные решения для оценки капитальных затрат
- Вы можете рассчитать количество взносов на сумму кредита
- Вы можете рассчитать количество сбережений, необходимых для достижения финансовой цели, когда на вас работают годы сложного возврата.
- Расчет аннуитета, дохода от инвестиций с течением времени.
Калькулятор будущей стоимости
Вы можете использовать следующий калькулятор стоимости в будущем
| PV | |
| р | |
| N | |
| Формула будущей стоимости | |
| Формула будущей стоимости | знак равно | PV x (1 + r) n |
| знак равно | 0 х (1 + 0) 0 = 0 |
Формула будущей стоимости в Excel (с шаблоном Excel)
Вычисление будущей стоимости в Excel очень простое и может принимать множество переменных, которые в противном случае очень сложно вычислить без использования электронной таблицы.
Здесь мы возьмем пример, и я решу его в электронной таблице:
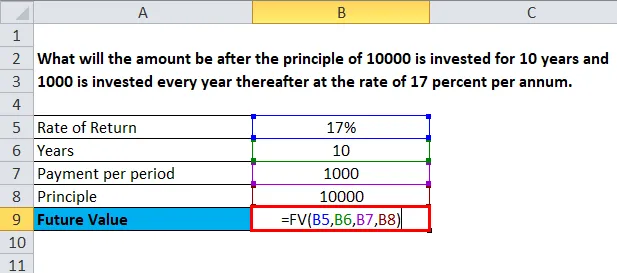
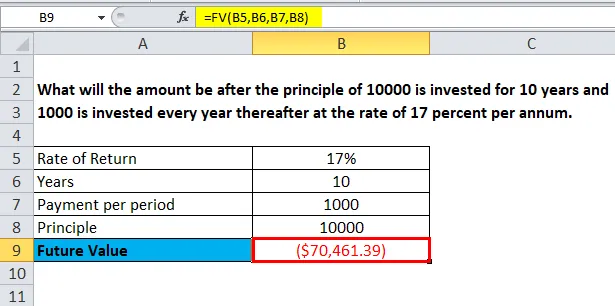
Какова будет сумма после того, как принцип 10000 будет инвестирован в течение 10 лет, а затем 1000 будет инвестироваться каждый год по ставке 17 процентов в год.
Теперь то, что мы видим здесь, это то, что мы должны быть очень конкретными относительно функции, используемой для вычисления будущей стоимости, обозначаемой как FV
Теперь, как только вы включите функцию FV и начнете скобку, Excel попросит вас открыть скобку и указать ставку (курс), количество периодов (nper), платеж за термин (pmt), текущую стоимость (PV) закройте скобки.
Теперь следуя вышеописанной проблеме:
Ставка = B5 = 17%
Nper = B6 = 10
PMT = B7 = 1000
PV = B8 = 10000
Будущая стоимость = FV (B5, B6, B7, B8)
Теперь, когда мы нажмем Enter в B6, мы получим нашу будущую стоимость.
Эту иллюстрацию Excel также можно использовать в листах Google. Нам просто нужно четко понимать функции и входные данные.
Рекомендуемые статьи
Это было руководство к формуле будущей стоимости. Здесь мы обсуждаем его использование вместе с практическими примерами. Мы также предоставляем калькулятор стоимости будущего с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше —
- Основные отличия — будущее против варианта
- Рост запасов против стоимости акций — сравнение
- Стратегии биржевой торговли фьючерсами
- Акции и паевые инвестиционные фонды
В Microsoft Excel предусмотрено огромное количество разнообразных функций, позволяющих справляться с математическими, экономическими, финансовыми и другими задачами. Программа является одним из основных инструментов, использующихся в малых, средних и больших организациях для ведения различных видов учета, выполнения расчетов и т.д. Ниже мы рассмотрим финансовые функции, которые наиболее востребованы в Экселе.
- Вставка функции
-
Популярные финансовые функции
- БС
- ВСД
- ДОХОД
- МВСД
- ИНОРМА
- ПЛТ
- ПОЛУЧЕНО
- ПС
- СТАВКА
- ЦЕНА
- ЧПС
- Заключение
Вставка функции
Для начала вспомним, как вставить функцию в ячейку таблицы. Сделать это можно по-разному:
- Выбрав нужную ячейку щелкаем по значку “fx (Вставить функцию)” слева от строки формул.
- Или переключаемся во вкладку “Формулы” и жмем аналогичную кнопку, расположенную в левом углу ленты программы.
Независимо от выбранного варианта, откроется окно вставки функции, в котором требуется выбрать категорию “Финансовые”, определиться с нужным оператором (например, ДОХОД), после чего нажать кнопку OK.
На экране отобразится окно с аргументами функции, которые требуется заполнить, после чего нажать кнопку OK, чтобы добавить ее в выбранную ячейку и получить результат.
Указывать данные можно вручную, используя клавиши клавиатуры (конкретные значения или ссылки на ячейки), либо встав в поле напротив нужного аргумента, выбирать соответствующие элементы в самой таблице (ячейки, диапазон ячеек) с помощью левой кнопки мыши (если это допустимо).
Обратите внимание, что некоторые аргументы могут не показываться и необходимо пролистать область вниз для получения доступа к ним (с помощью вертикального ползункам справа).
Альтернативный способ
Находясь во вкладке “Формулы” можно нажать кнопку “Финансовые” в группе “Библиотека функций”. Раскроется список доступных вариантов, среди которых просто кликаем по нужному.
После этого сразу же откроется окно с аргументами функции для заполнения.
Популярные финансовые функции
Теперь, когда мы разобрались с тем, каким образом функция вставляется в ячейку таблицы Excel, давайте перейдем к перечню финансовых операторов (представлены в алфавитном порядке).
БС
Данный оператор применяется для вычисления будущей стоимости инвестиции исходя из периодических равных платежей (постоянных) и размера процентной ставки (постоянной).
Обязательными аргументами (параметрами) для заполнения являются:
- Ставка – процентная ставка за период;
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период.
Необязательные аргументы:
- Пс – приведенная (нынешняя) стоимость. Если не заполнять, будет принято значение, равное “0”;
- Тип – здесь указывается:
- 0 – выплата в конце периода;
- 1 – выплата в начале периода
- если поле оставить пустым, по умолчанию будет принято нулевое значение.
Также есть возможность вручную ввести формулу функции сразу в выбранной ячейке, минуя окна вставки функции и аргументов.
Синтаксис функции:
=БС(ставка;кпер;плт;[пс];[тип])
Результат в ячейке и выражение в строке формул:
ВСД
Функция позволяет вычислить внутреннюю ставку доходности для ряда денежных потоков, выраженных числами.
Обязательный аргумент всего один – “Значения”, в котором нужно указать массив или координаты диапазона ячеек с числовыми значениями (по крайней мере, одно отрицательное и одно положительное число), по которым будет выполняться расчет.
Необязательный аргумент – “Предположение”. Здесь указывается предполагаемая величина, которая близка к результату ВСД. Если не заполнять данное поле, по умолчанию будет принято значение, равное 10% (или 0,1).
Синтаксис функции:
=ВСД(значения;[предположение])
Результат в ячейке и выражение в строке формул:
ДОХОД
С помощью данного оператора можно посчитать доходность ценных бумаг, по которым производится выплата периодического процента.
Обязательные аргументы:
- Дата_согл – дата соглашения/расчета по ценным бумагам (далее – ц.б.);
- Дата_вступл_в_силу – дата вступления в силу/погашения ц.б.;
- Ставка – годовая купонная ставка ц.б.;
- Цена – цена ц.б. за 100 рублей номинальной стоимости;
- Погашение – суммы погашения или выкупная стоимость ц.б. за 100 руб. номинальной стоимости;
- Частота – количество выплат за год.
Аргумент “Базис” является необязательным, в нем задается способ вычисления дня:
- 0 или не заполнен – армериканский (NASD) 30/360;
- 1 – фактический/фактический;
- 2 – фактический/360;
- 3 – фактический/365;
- 4 – европейский 30/360.
Синтаксис функции:
=ДОХОД(дата_согл;дата_вступл_в_силу;ставка;цена;погашение;частота;[базис])
Результат в ячейке и выражение в строке формул:
МВСД
Оператор используется для расчета внутренней ставки доходности для ряда периодических потоков денежных средств исходя из затрат на привлечение инвестиций, а также процента от реинвестирования денег.
У функции только обязательные аргументы, к которым относятся:
- Значения – указываются отрицательные (платежи) и положительные числа (поступления), представленные в виде массива или ссылок на ячейки. Соответственно, здесь должно быть указано, как минимум, одно положительное и одно отрицательное числовое значение;
- Ставка_финанс – выплачиваемая процентная ставка за оборачиваемые средства;
- Ставка _реинвест – процентная ставка при реинвестировании за оборачиваемые средства.
Синтаксис функции:
=МВСД(значения;ставка_финанс;ставка_реинвест)
Результат в ячейке и выражение в строке формул:
ИНОРМА
Оператор позволяет вычислить процентную ставку для полностью инвестированных ц.б.
Аргументы функции:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Инвестиция – сумма, вложенная в ц.б.;
- Погашение – сумма к получению при погашении ц.б.;
- аргумент “Базис” как и для функции ДОХОД является необязательным.
Синтаксис функции:
=ИНОРМА(дата_согл;дата_вступл_в_силу;инвестиция;погашение;[базис])
Результат в ячейке и выражение в строке формул:
ПЛТ
С помощью этой функции рассчитывается сумма периодического платежа по займу исходя из постоянства платежей и процентной ставки.
Обязательные аргументы:
- Ставка – процентная ставка за период займа;
- Кпер – общее количество периодов выплат;
- Пс – приведенная (нынешняя) стоимость.
Необязательные аргументы:
- Бс – будущая стоимость (баланс после последней выплаты). Если поле оставить незаполненным, по умолчанию будет принято значение, равное “0”.
- Тип – здесь указывается, как будет производиться выплата:
- “0” или не указано – в конце периода;
- “1” – в начале периода.
Синтаксис функции:
=ПЛТ(ставка;кпер;пс;[бс];[тип])
Результат в ячейке и выражение в строке формул:
ПОЛУЧЕНО
Применяется для нахождения суммы, которая будет получена к сроку погашения инвестированных ц.б.
Аргументы функции:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Инвестиция – сумма, инвестированная в ц.б.;
- Дисконт – ставка дисконтирования ц.б.;
- “Базис” – необязательный аргумент (см. функцию ДОХОД).
Синтаксис функции:
=ПОЛУЧЕНО(дата_согл;дата_вступл_в_силу;инвестиция;дисконт;[базис])
Результат в ячейке и выражение в строке формул:
ПС
Оператор используется для нахождения приведенной (т.е. к настоящему моменту) стоимости инвестиции, которая соответствует ряду будущих выплат.
Обязательные аргументы:
- Ставка – процентная ставка за период;
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период.
Необязательные аргументы – такие же как и для функции “ПЛТ”:
- Бс – будущая стоимость;
- Тип.
Синтаксис функции:
=ПС(ставка;кпер;плт;[бс];[тип])
Результат в ячейке и выражение в строке формул:
СТАВКА
Оператор поможет найти процентную ставку по аннуитету (финансовой ренте) за 1 период.
Обязательные аргументы:
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период;
- Пс – приведенная стоимость.
Необязательные аргументы:
- Бс – будущая стоимость (см. функцию ПЛТ);
- Тип (см. функцию ПЛТ);
- Предположение – предполагаемая величина ставки. Если не указывать, будет принято значение по умолчанию – 10% (или 0,1).
Синтаксис функции:
=СТАВКА(кпер;;плт;пс;[бс];[тип];[предположение])
Результат в ячейке и выражение в строке формул:
ЦЕНА
Оператор позволяет найти цену за 100 рублей номинальной стоимости ц.б., по которым производится выплата периодического процента.
Обязательные аргументы:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Ставка – годовая купонная ставка ц.б.;
- Доход – годовой доход по ц.б.;
- Погашение – выкупная стоимость ц.б. за 100 руб. номинальной стоимости;
- Частота – количество выплат за год.
Аргумент “Базис” как и для оператора ДОХОД является необязательным.
Синтаксис функции:
=ЦЕНА(дата_согл;дата_вступл_в_силу;ставка;доход;погашение;частота;[базис])
Результат в ячейке и выражение в строке формул:
ЧПС
С помощью данной функции можно определить чистую приведенную стоимость инвестиции исходя из ставки дисконтирования, а также размера будущих поступлений и платежей.
Аргументы функции:
- Ставка – ставка дисконтирования за 1 период;
- Значение1 – здесь указываются выплаты (отрицательные значения) и поступления (положительные значения) в конце каждого периода. Поле может содержать до 254 значений.
- Если лимит аргумента “Значение 1” исчерпан, можно перейти к заполнению следующих – “Значение2”, “Значение3” и т.д.
Синтаксис функции:
=ЧПС(ставка;значение1;[значение2];...)
Результат в ячейке и выражение в строке формул:
Заключение
Категория “Финансовые” в программе Excel насчитывает свыше 50 различных функций, но многие из них специфичны и узконаправлены, из-за чего используются редко. Мы же рассмотрели 11 самых востребованных, по нашему мнению.
Функция БС возвращает будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки.
Описание функции БС
Возвращает будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки.
Синтаксис
=БС(ставка;кпер;плт;[пс];[тип])Аргументы
ставкакперплтпстип
Обязательный аргумент. Процентная ставка за период.
Обязательный аргумент. Общее количество периодов платежей по аннуитету.
Обязательный аргумент. Выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно аргумент «плт» состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если он опущен, аргумент «пс» является обязательным.
Обязательный аргумент. Приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент «пс» опущен, предполагается значение 0. В этом случае аргумент «плт» является обязательным.
Необязательный аргумент. Число 0 или 1, обозначающее срок выплаты. Если аргумент «тип» опущен, предполагается значение 0.
| Тип | Выплата |
|---|---|
| 0 | В конце периода |
| 1 | В начале периода |
Замечания
- Убедитесь, что единицы измерения аргументов «ставка» и «кпер» используются согласованно. При ежемесячных выплатах по четырехгодичному займу из расчета 12 процентов годовых используйте значение 12%/12 в качестве аргумента «ставка» и 4*12 — в качестве аргумента «кпер». При ежегодных платежах по тому же займу используйте значение 12% в качестве аргумента «ставка» и 4 — в качестве аргумента «кпер».
- Все аргументы, которым соответствуют выплачиваемые денежные средства (например, сберегательные вклады), представляются отрицательными числами, а получаемые (например, дивиденды) — положительными.
Примеры
Пример1Пример задачи1Пример задачи2
Задача
На банковский счет под 11,5% годовых внесли 37000 руб. Определить размер вклада по истечении 3 лет, если проценты начисляются каждые полгода.
Решение
Согласно условиям задачи, имеем следующие аргументы функции:
- Ставка: 11,5%/2 (так, как проценты будут начисляться каждые полгода)
- Кпер: 3*2 лет (количество производимых начислений за весь период).
- Плт: — не заполняем, т.к. у нас нет суммы обязательных платежей
- Пс: -37000 (стоимость наших активов на текущий момент с минусом, т.к. счет сберегательный)
- Тип: 0 (выплаты в конце периода)
Ответ: размер вклада составит 51746,86 руб.
Задача
На счет в банке в течении пяти лет в конце каждого года будут вноситься суммы в размере 500 руб., на которые будут начисляться проценты по ставке 30%. Определить сумму, которую банк выплатит владельцу счета.
Решение
Введем первоначальные данные:
Заполним поля функции:
Ответ: сумма всех взносов с начисленными процентами будет равна 4521,55 руб.
Файл с решением