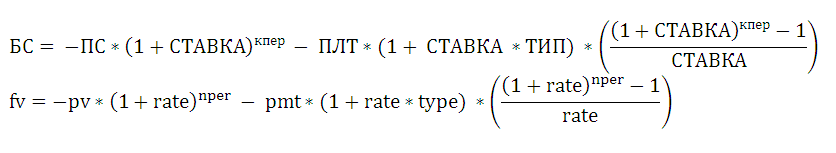Что такое аннуитет excel

ПЛТ — одна из финансовых функций, возвращающая сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянной процентной ставки.

Воспользуйтесь средством Excel Formula Coach для расчета ежемесячных выплат по ссуде. При этом вы узнаете, как использовать функцию ПЛТ в формуле.

Синтаксис

ПЛТ(ставка; кпер; пс; [бс]; [тип])

Примечание: Более подробное описание аргументов функции ПЛТ см. в описании функции ПС.

Аргументы функции ПЛТ описаны ниже.

• Ставка    Обязательный аргумент. Процентная ставка по ссуде.

• Кпер    Обязательный аргумент. Общее число выплат по ссуде.

• Пс    Обязательный аргумент. Приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой.

• Бс    Необязательный. Значение будущей стоимости, то есть желаемого остатка средств после последней выплаты. Если аргумент «бс» опущен, предполагается значение 0 (например, значение будущей стоимости для займа равно 0).

• Тип    Необязательный аргумент. Число 0 (нуль) или 1, обозначающее, когда должна производиться выплата.

Тип	Когда нужно платить
0 или опущен	В конце периода
1	В начале периода

Замечания

• Выплаты, возвращаемые функцией ПЛТ, включают основные платежи и платежи по процентам, но не включают налогов, резервных платежей или комиссий, иногда связываемых со ссудой.

• Убедитесь, что вы последовательны в выборе единиц измерения для задания аргументов «ставка» и «кпер». Если вы делаете ежемесячные выплаты по четырехгодичному займу из расчета 12 процентов годовых, то используйте значения 12%/12 для задания аргумента «ставка» и 4*12 для задания аргумента «кпер». Если вы делаете ежегодные платежи по тому же займу, то используйте 12 процентов для задания аргумента «ставка» и 4 для задания аргумента «кпер».

Совет    Для нахождения общей суммы, выплачиваемой на протяжении интервала выплат, умножьте возвращаемое функцией ПЛТ значение на «кпер».

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу Enter. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
8 %	Годовая процентная ставка
10	Количество месяцев платежей
10 000р.	Сумма займа
Формула	Описание	Результат
=ПЛТ(A2/12;A3;A4)	Ежемесячный платеж по займу в соответствии с условиями, указанными в качестве аргументов в диапазоне A2:A4.	(1 037,03р.)
=ПЛТ(A2/12;A3;A4;;1)	Ежемесячный платеж по займу в соответствии с условиями, указанными в качестве аргументов в диапазоне A2:A4, за исключением платежей, подлежащих оплате в начале периода.	(1 030,16р.)
Данные	Описание
6 %	Годовая процентная ставка
18	Количество месяцев платежей
50 000р.	Сумма займа
Формула	Описание	Оперативный результат
ПЛТ(A9/12;A10*12; 0;A11)	Необходимая сумма ежемесячных платежей для выплаты 50 000р. за 18 лет.	(129,08 ₽)

Платежи по кредитам удобнее и быстрее рассчитывать с Microsoft Office Excel. На ручное вычисление уходит гораздо больше времени. В данной статье речь пойдет об аннуитетных платежах, особенностях их расчета, преимуществах и недостатках.

Что такое аннуитетный платеж

Способ ежемесячного погашения кредита, при котором вносимая сумма не меняется в течение всего времени кредитования. Т.е. человек по определенным числам каждого месяца вносит конкретную сумму денег до тех пор, пока полностью не погасит кредит.

Причем проценты по кредиту уже включены в общую сумму, вносимую в банк.

Классификация аннуитета

Аннуитетные платежи можно разделить на следующие виды:

1. Фиксированные. Платежи, которые не меняются, имеют фиксированную ставку вне зависимости от внешних условий.
2. Валютные. Возможность смены размера платежа при падении или росте курса валют.
3. Индексируемые. Платежи, зависящие от уровня, показателя инфляции. В период кредитования их размер часто меняется.
4. Переменные. Аннуитет, который может смениться в зависимости от состояния финансовой системы, инструментов.

Обратите внимание! Фиксируемые платежи предпочтительнее для всех заемщиков, т.к. имеют небольшой риск.

Преимущества и недостатки аннуитетных платежей

Чтобы лучше разбираться в теме, необходимо изучить ключевые особенности данного типа кредитных платежей. Он имеет следующие преимущества:

• Установление конкретной суммы платежа и даты ее взноса.
• Высокая доступность для заемщиков. Практически любой человек сможет оформить аннуитет, независимо от своего финансового положения.
• Возможность понижения суммы ежемесячного взноса с повышением уровня инфляции.

Без недостатков не обошлось:

• Высокая ставка. Заемщик переплатит большую сумму денег по сравнению с дифференциальным платежом.
• Проблемы, возникающие при желании досрочно погасить долг.
• Отсутствие перерасчетов при досрочных выплатах.

Из чего состоит платеж по кредиту?

Аннуитетный платеж имеет следующие составляющие части:

• Проценты, переплачиваемые человеком при погашении ссуды.
• Часть суммы основной задолженности.

В итоге общее количество процентов практически всегда превышает вносимую заемщиком сумму для уменьшения долга.

Основная формула аннуитетного платежа в Excel

Как и говорилось выше, в Microsoft Office Excel можно работать с различными типами платежей по кредитам и ссудам. Аннуитет не является исключением. В общем виде формула, с помощью которой можно быстро вычислить аннуитетные взносы, выглядит следующим образом:  

Важно! Раскрывать скобки в знаменателе данного выражения для его упрощения нельзя.

Основные значения формулы расшифровываются так:

• АП – аннуитетный платеж (название сокращено).
• О – размер основного долга заемщика.
• ПС – процентная ставка, выдвигаемая ежемесячно конкретным банком.
• С – число месяцев, на протяжении которых длится кредитование.

Для усвоения информации достаточно привести несколько примеров использования данной формулы. О них пойдет речь далее.

Примеры использования функции ПЛТ в Excel

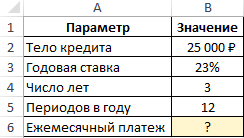
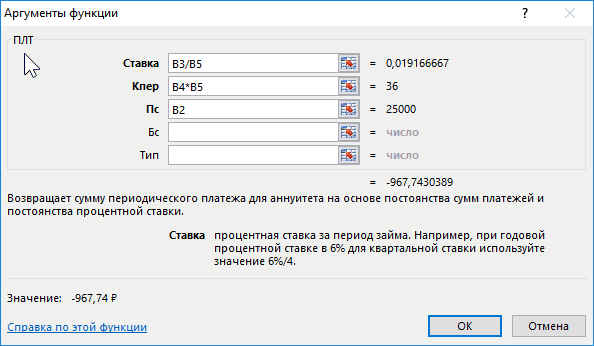
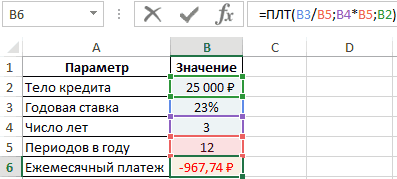
Приведем простое условие задачи. Необходимо посчитать ежемесячный кредитный платеж, если банк выдвигает процент в размере 23%, а общая сумма составляет 25000 рублей. Кредитование продлится на протяжении 3-х лет. Задача решается по алгоритму:

1. Составить общую таблицу в Excel по исходным данным.

1. Активировать функцию ПЛТ и ввести для нее аргументы в соответствующее окошко.
2. В поле «Ставка» прописать формулу «В3/В5». Это и будет процентная ставка по взятому кредиту.
3. В строке «Кпер» написать значение в виде «В4*В5». Это будет общее количество выплат за весь срок кредитования.
4. Заполнить поле «Пс». Здесь нужно указать первоначальную сумму, взятую в банке, прописав значение «В2».

1. Удостовериться, что после нажать «ОК» в исходной таблице посчиталось значение «Ежемесячный платеж».

Дополнительная информация! Отрицательное число свидетельствует о том, что заемщик расходует деньги.

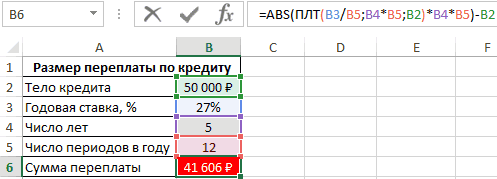
Пример расчета суммы переплаты по кредиту в Excel

В этой задаче надо подсчитать сумму, которую переплатит человек, взявший кредит 50000 рублей по процентной ставке 27% на 5 лет. Всего в год заемщик производит 12 выплат. Решение:

1. Составить исходную таблицу данных.

1. Из общей суммы выплат отнять первоначальный размер суммы по формуле «=ABS(ПЛТ(B3/B5;B4*B5;B2)*B4*B5)-B2». Ее надо вставить в строку формул сверху главного меню программы.
2. В итоге в последней строке созданной таблички появится сумма переплат. Заемщик переплатит 41606 рублей сверху.

Формула вычисления оптимального ежемесячного платежа по кредиту в Excel

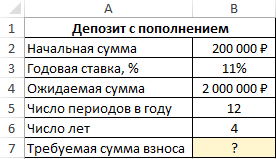
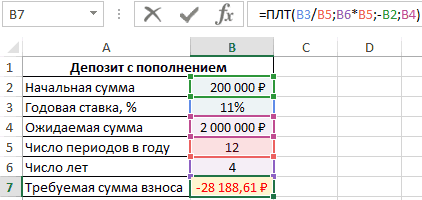
Задача с таким условием: клиент зарегистрировал счет в банке на 200000 рублей с возможностью ежемесячного пополнения. Нужно посчитать количество платежа, который человек должен вносить каждый месяц, чтобы через 4 года на его счету оказалось 2000000 рублей. Ставка составляет 11%. Решение:

1. Составить табличку по исходным данным.

1. В строку ввода Эксель ввести формулу «=ПЛТ(B3/B5;B6*B5;-B2;B4)» и нажать «Enter» с клавиатуры. Буквы будут отличаться в зависимости от ячеек, в которых размещена таблица.
2. Проверить, что сумма взноса автоматически посчиталась в последней строке таблицы.

Обратите внимание! Таким образом, чтобы на счету клиенту через 4 года накопилось 2000000 рублей по ставке 11%, ему нужно каждый месяц вносить по 28188 рублей. Минус в сумме свидетельствует о том, что клиент несет убытки, отдавая деньги в банк.

Особенности использования функции ПЛТ в Excel

В общем виде данная формула записывается следующим образом: =ПЛТ(ставка; кпер; пс; [бс]; [тип]). У функции есть следующие особенности:

1. Когда рассчитываются ежемесячные взносы, в рассмотрение берется исключительно годовая ставка.
2. Указывая размер процентной ставки, важно сделать перерасчет, опираясь на число взносов за год.
3. Вместо аргумента «Кпер» в формуле указывается конкретное число. Это период выплат по задолженности.

Расчет оплаты

В общем виде оплата по аннуитету рассчитывается в два этапа. Чтобы разбираться в теме, каждый из этапов необходимо рассмотреть по отдельности. Об этом пойдет речь далее.

Этап 1: расчет ежемесячного взноса

Чтобы в Excel посчитать сумму, которую нужно вносить каждый месяц по кредиту с фиксируемой ставкой, необходимо:

1. Составить исходную таблицу и выделить ячейку, в которую надо выводить результат и нажать по кнопке «Вставить функцию» сверху.

1. В списке функций выбрать «ПЛТ» и нажать «ОК».

1. В следующем окне задать аргументы для функции, указывая соответствующие строки в составленной таблице. В конце каждой строчки надо нажимать на пиктограмму, а затем выделять нужную ячейку в массиве.

1. Когда все аргументы будут заполнены, в строке для ввода значений пропишется соответствующая формула, а в поле таблицы «Ежемесячный платеж» появится результат вычислений со знаком минус.

Важно! После расчета взноса можно будет рассчитать сумму, которую переплатит заемщик за весь период кредитования.

Этап 2: детализация платежей

Сумму переплаты можно посчитать помесячно. В итоге человек поймет, сколько денег каждый месяц он будет тратить на кредит. Расчет по детализации выполняется следующим образом:

1. Составить исходную таблицу на 24 месяца.

1. Поставить курсор в первую ячейку таблицы и вставить функцию «ОСПЛТ».

1. Заполнить аргументы функции аналогичным образом.

1. При заполнении поля «Период» нужно сослаться на первый месяц в табличке, указав ячейку 1.

1. Проверить, что первая ячейка в графе «Выплата по телу кредита» заполнилась.
2. Чтобы заполнить все строки первого столбца, необходимо растянуть ячейку до конца таблицы

1. Выбрать функцию «ПРПЛТ» для заполнения второго столбца таблицы.
2. Заполнить все аргументы в открывшемся окошке в соответствии со скриншотом ниже.

1. Рассчитать общую ежемесячную выплату, сложив значения в двух предыдущих столбиках.

1. Чтобы посчитать «Остаток к выплате», надо сложить процентную ставку с выплатой по телу кредита и растянуть до конца таблички, чтобы заполнить все месяцы кредитования.

Дополнительная информация! При расчете остатка на формулу надо навешивать знаки долларов, чтобы она не съехала при растягивании.

Расчет аннуитетных платежей по кредиту в Excel

За вычисление аннуитета в Excel отвечает функция ПЛТ. Принцип вычисления в общем виде заключается в выполнении следующих шагов:

1. Составить исходную таблицу данных.
2. Построить график погашения долга для каждого месяца.
3. Выделить первую ячейку в столбике «Платежи по кредиту» и ввести формулу расчета «ПЛТ ($В3/12;$В$4;$В$2)».
4. Получившееся значение растянуть для всех столбцов таблички.

Расчет в MS Excel погашение основной суммы долга

Аннуитетные платежи должны вноситься ежемесячно определенными суммами. Причем процентная ставка не изменяется.

Вычисление остатка суммы основного долга (при БС=0, тип=0)

Предположим, что кредит на 100000 рублей берется на 10 лет под 9%. Необходимо рассчитать сумму основного долга в 1 месяце 3-го года. Решение:

1. Составить таблицу данных и вычислить ежемесячный платеж по приведенной выше формуле ПС.
2. Рассчитать долю платежа, необходимую для погашения части долга, по формуле «=-ПМТ-(ПС-ПС1)*ставка=-ПМТ-(ПС +ПМТ+ПС*ставка)».
3. Посчитать сумму основного долга за 120 периодов по известной формуле.
4. Используя оператор ПРПЛТ найти количество процентов, выплаченных за 25 месяц.
5. Проверить результат.

Вычисление суммы основного долга, которая была выплачена в промежутке между двумя периодами

Такой расчет лучше сделать простым способом. Нужно использовать следующие формулы для вычисления суммы в промежутке за два периода:

• =«-БС(ставка; кон_период; плт; [пс]; [тип]) /(1+тип *ставка)».
• = «+ БС(ставка; нач_период-1; плт; [пс]; [тип]) /ЕСЛИ(нач_период =1;1; 1+тип *ставка)».

Обратите внимание! Буквы в скобках заменяются конкретными значениями.

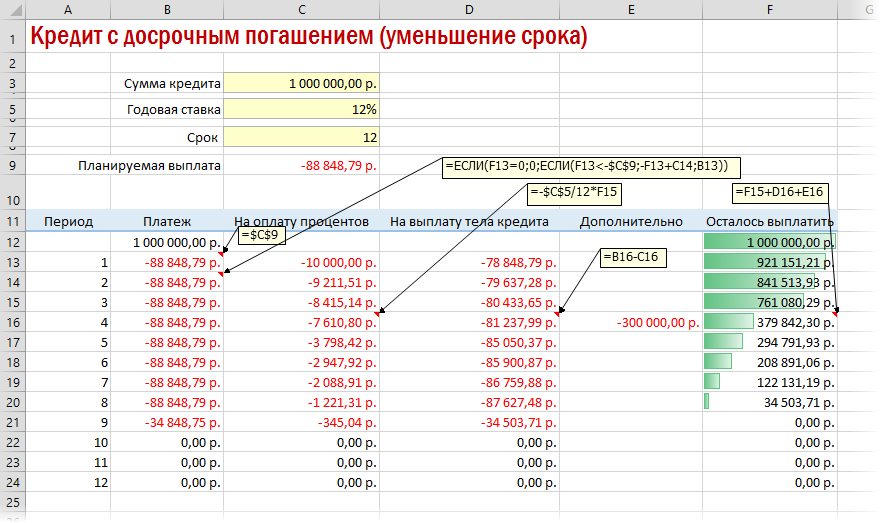
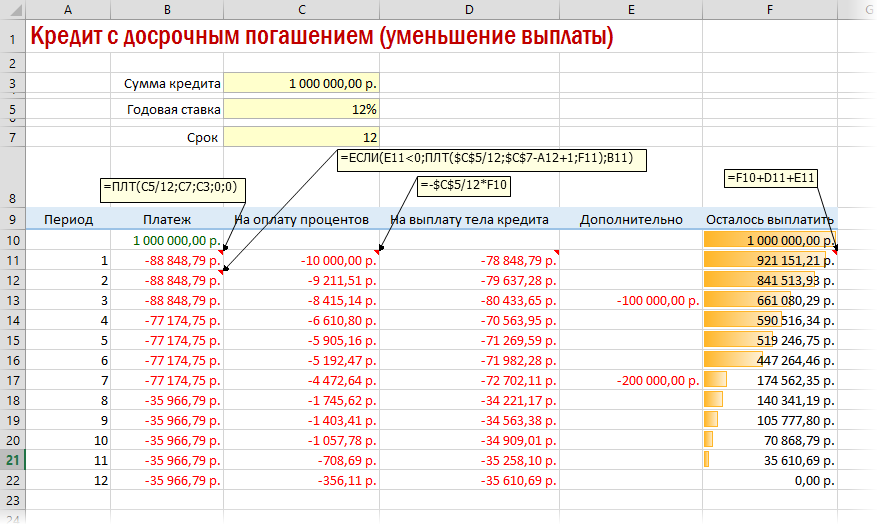
Досрочное погашение с уменьшением срока или выплаты

Если потребуется уменьшить срок кредитования, то придется производить дополнительные вычисления с помощью оператора ЕСЛИ. Так можно будет контролировать нулевой баланс, который не должен быть достигнут раньше окончания сроков выплаты.

Чтобы снизить выплаты, нужно пересчитывать взнос за каждый предыдущий месяц.

Кредитный калькулятор с нерегулярными выплатами

Есть несколько вариантов аннуитета, когда заемщик может вносить нефиксированные суммы в любой день месяца. В такой ситуации остаток долга и проценты считаются за каждый день. При этом в Экселе надо:

1. Ввести числа месяца, по которым вносятся платежи, и указать их количество.
2. Проконтролировать отрицательные и положительные суммы. Отрицательные предпочтительнее.
3. Посчитать дни между двумя датами, в которые вносились деньги.

Расчет периодического платежа в MS Excel. Срочный вклад

В Excel можно быстро посчитать размер регулярных выплат при условии, что уже накопилась фиксированная сумма. Данное действие выполняется с использованием функции ПЛТ после составления исходной таблицы.

Заключение

Таким образом, аннуитетные платежи проще, быстрее и эффективнее рассчитывать именно в Эксель. За их вычисление отвечает оператор ПЛТ. С подробными примерами можно ознакомиться выше.

В статье рассмотрены финансовые функции

ПЛТ()

,

ОСПЛТ()

,

ПРПЛТ()

,

КПЕР()

,

СТАВКА()

,

ПС()

,

БС()

, а также

ОБЩДОХОД()

и

ОБЩПЛАТ()

, которые используются для расчетов параметров аннуитетной схемы.

Данная статья входит в цикл статей о расчете параметров аннуитета. Перечень всех статей на нашем сайте об аннуитете

размещен здесь

.

В этой статье содержится небольшой раздел о теории аннуитета, краткое описание функций аннуитета и их аргументов, а также ссылки на статьи с примерами использования этих функций.

Немного теории

Аннуитет (иногда используются термины «рента», «финансовая рента») представляет собой

однонаправленный

денежный поток, элементы которого

одинаковы

по величине

и производятся через

равные периоды времени

(например, когда платежи производятся ежегодно равными суммами).

Каждый элемент такого денежного потока называется

членом аннуитета

, а величина постоянного временного интервала между двумя его последовательными элементами называется

периодом аннуитета

. В широком смысле, аннуитетом может называться как сам финансовый инструмент, так и сумма периодического платежа. Исторически вначале рассматривались равные ежегодные денежные поступления (период между платежами принимался равным одному году), что и послужило основой для именования денежного потока аннуитетом («год» на латинском языке — anno). В дальнейшем, в качестве периода стал выступать любой промежуток времени, но прежнее название сохранилось. Сейчас

период аннуитета

чаще всего равен одному месяцу.

Аннуитетную схему банки часто используют при кредитовании

. Эта схема предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), т.е.

равными суммами через равные промежутки времени

, которые включают как выплату основного долга, так и процентный платеж за пользование кредитом.

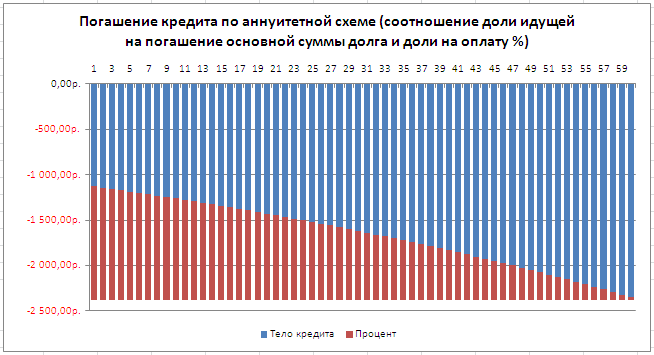
На картинке ниже приведен пример погашения кредита (100 000 руб.) ежемесячными платежами в течение 5 лет при ставке 15%. Для погашения тела кредита и начисленных процентов потребуется произвести 60 платежей (5 лет*12мес в году). Сумма ежемесячного платежа = 2378,99руб. См.

файл примера Лист Аннуитет (ПЛТ)

. Как видно из графика платежей, банк в первые периоды получает платежи, идущие на погашение %, а тело кредита сокращается медленно (см. статью

Сравнение графиков погашения кредита дифференцированными и аннуитетными платежами в MS EXCEL

).

Если каждый элемент аннуитета имеет место в конце соответствующего периода, аннуитет называется аннуитетом постнумерандо (Ordinary Annuity); если в начале периода — аннуитетом пренумерандо (Annuity Due). Обычно используется аннуитет постнумерандо.

Примечание

. В функциях MS EXCEL для указания типа аннуитета предусмотрен специальный необязательный параметр

[тип]

. По умолчанию

тип

=0  (выплаты в конце периода), что соответствует аннуитету постнумерандо. Если

тип

=1, то предполагается аннуитет пренумерандо (выплаты в начале периода).

Часто в расчетах используют понятие

аннуитетный коэффициент

(А):

A = -Ставка * (1+ Ставка)^Кпер / (1-(1+ Ставка)^ Кпер ) / (1+ Ставка*Тип)

где: Ставка — процентная ставка за период; Кпер — общее количество периодов выплаты; Тип – для аннуитета постнумерандо Тип=0, для пренумерандо Тип=1.

Чтобы вычислить

член аннуитета

(величину регулярного платежа) нужно использовать формулу =А*ПС, где ПС – это начальная сумма кредита. Специфика аннуитета (равенство денежных поступлений) позволяет вывести стандартизованные формулы, существенно упрощающие счетные процедуры. Об этих формулах и об их использовании в MS EXCEL и пойдет речь ниже.

Параметры функций аннуитета

Финансовые функции

ПЛТ()

,

ОСПЛТ()

,

ПРПЛТ()

,

КПЕР()

,

СТАВКА()

,

БС()

,

ПС()

, а также

ОБЩДОХОД()

и

ОБЩПЛАТ()

тесно связаны между собой, т.к. все они вычисляют параметры аннуитета и, соответственно, используют один и тот же набор аргументов. В этом можно убедиться, перечислив все функции вместе с аргументами:

ПЛТ(ставка; кпер; пс; [бс]; [тип]) ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип]) ПРПЛТ(ставка; период; кпер; пс; [бс]; [тип]) КПЕР(ставка; плт; пс; [бс]; [тип]) СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение]) БС(ставка; кпер; плт; [пс]; [тип]) ПС(ставка; кпер; плт; [бс]; [тип])

ПЛТ

(английское название функции: PMT, от слова

payment

). Регулярный платеж, осуществляемый каждый период. Платеж – постоянная величина, она не меняется в течение всего срока аннуитета.

Ставка

(англ.: RATE, interest).

Процентная ставка за период

, чаще всего за год или за месяц. Обычно задается через годовую ставку, деленную на количество периодов в году. При годовой ставке 10% месячная ставка составит 10%/12. Ставка не изменяется в течение всего срока аннуитета.

Кпер

(англ.: NPER).

Общее число периодов платежей по аннуитету

. Если кредит взят на 5 лет, а выплаты производятся ежемесячно, то всего 60 периодов (12 мес. в году * 5 лет)

Бс

(англ.: FV, future value).

Будущая стоимость

в конце срока аннуитета (по истечении числа периодов Кпер). Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты. Например, в случае расчета аннуитетного платежа для полной выплаты ссуды к концу срока Бс = 0, т.к. ссуда в конце срока должна быть полностью погашена.

Пс

(англ.: PV, present value).

Приведенная стоимость

, т.е. стоимость приведенная к определенному моменту (часто к текущему, т.е. настоящему времени). Если взят кредит и производятся регулярные выплаты по аннуитетной схеме, то Приведенная стоимость – это сумма кредита. Если планируется регулярно вносить равновеликие платежи на счет в банке (и период начисления % совпадает с периодом платежей), то Приведенную стоимость также нужно указывать = 0.

Тип

(англ.: type). Число 0 или 1, обозначающее, когда должна производиться выплата (и соответственно начисление процентов). 0 – в конце периода, 1 – в начале. Подробнее см. раздел

Немного теории

в начале статьи о постнумерандо и пренумерандо или статьи с примерами, указанные выше.

Все 6 аргументов (параметров аннуитета) связаны между собой выражением:

поэтому каждый из них может быть вычислен при условии, если заданы остальные параметры. Функции аннуитета помогают пользователю упростить вычисления, но все они основаны на Формуле 1.

Примечание

. Формула 1 работает, если Ставка не равна 0. Если ставка равна 0, то вместо Формулы 1 действует гораздо более простое выражение: ПЛТ * Кпер + ПС + БС = 0 (в этом случае схема платежей перестает быть аннуитетом и превращается в беспроцентную ссуду).

О направлениях денежных потоков и знаках ПС, БС и ПЛТ

Вышеуказанная Формула 1 предполагает, что знаки денежных потоков (+/-) указываются с учетом их направления. Например, банк выдал кредит (ПС>0), клиент банка ежемесячно вносит одинаковый платеж (ПЛТ<0). Т.е. имеет место 2 направления движения денег:

от

банка к клиенту

(ПС) и

в банк от клиента

(ПЛТ). Если схема погашения кредита учитывает единовременную выплату в конце погашения, то БС<0, т.к. этот платеж, как и ПЛТ направлен

в банк от клиента

. Функции MS EXCEL также учитывают направления платежей, поэтому функция

ПЛТ()

возвращает отрицательные значения, если ПС>0.

Тождество аннуитета

Если Тип=0, то для функций MS EXCEL справедливо тождество: ОБЩДОХОД(за все периоды) + ПС + БС = 0

Это тождество можно переписать в другом виде: СУММ(ОСПЛТ()) + ПС + БС = 0. В случае использования

аннуитетной схемы погашения кредита

(сумма кредита =ПС), выражение СУММ(ОСПЛТ()) вычисляет общую сумму платежей, идущих на оплату основной суммы долга (тело кредита). В случае полного погашения кредита БС=0, а тождество превращается в ПС=-СУММ(ОСПЛТ()).

Функции

MS

EXCEL

для расчета параметров аннуитета

Теперь кратко рассмотрим функции MS EXCEL. Для того, чтобы нижесказанное было понятным, необходимо предварительно ознакомиться с теорией аннуитета, понятиями

Будущая

и

Приведенная

стоимость.

Функция ПЛТ(ставка; кпер; пс; [бс]; [тип])

рассчитывает величину регулярного платежа на основе заданных 5 аргументов.

Примечание

.

Английский вариант функции: PMT(rate, nper, pv, [fv], [type]), т.е. PayMenT – платеж.

Примечание

.

Вышеуказанные функции входят в надстройку «Пакет анализа». Если функция недоступна или возвращает ошибку #ИМЯ?, то включите или установите и загрузите эту надстройку (с версии MS EXCEL 2007 надстройка «Пакет анализа» включена по умолчанию).

Для понимания работы формулы приведем эквивалентное ей выражение для расчета платежа:

Формула 2 есть не что иное, как решение Формулы 1 относительно параметра ПЛТ.

Примечание.

В

файле примера на листе Аннуитет (без ПЛТ)

приведен расчет ежемесячных платежей без использования финансовых функций EXCEL.

Если процентная ставка = 0, то Формула 2 упростится до

=(ПС + БС)/Кпер

Если Тип=0 (выплата в конце периода) и БС =0, то Формула 2 заметно упрощается:

В случае применения схемы аннуитета для выплаты ссуды платеж включает денежную сумму в счет погашения части ссуды и сумму для оплаты начисленных за прошедший период процентов, поэтому функция

ПЛТ()

связана с

ОСПЛТ()

и

ПРПЛТ()

соотношением ПЛТ = ОСПЛТ + ПРПЛТ (для каждого периода).

Примечание

.

В

файле примера на листе Зависимости ПЛТ()

приведены графики: Зависимость суммы платежа от размера ссуды, Зависимость суммы платежа от ставки, Зависимость суммы платежа от срока ссуды. Также в файле примера приведены некоторые задачи.

Функция ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип])

используется для вычисления регулярных сумм идущих на погашение основной суммы долга практически с теми же аргументами, что и

ПЛТ()

. Т.к. сумма идущая на погашение основной суммы долга изменяется от периода к периоду, то необходим еще один аргумент

период

, который определяет к какому периоду относится сумма.

Примечание

.

Английский вариант функции: PPMT(rate, per, nper, pv, [fv], [type]), т.е. Principal Payment – платеж основной части долга.

В случае

применения схемы аннуитета для выплаты ссуды

для каждого периода действует равенство: ОСПЛТ =ПЛТ – ПРПЛТ, т.к. платеж включает сумму в счет погашения части ссуды (ОСПЛТ) и сумму для оплаты начисленных за прошедший период процентов (ПРПЛТ). Сумму, идущую на погашение основной суммы долга также можно вычислить, зная  величину платежа (ПЛТ), период (Период), общее количество периодов (Кпер) и ставку (СТАВКА):

ОСПЛТ=ПЛТ*(1+СТАВКА)^(Период-Кпер-1)

Вышеуказанная формула работает при БС=0. При ТИП=1 (платеж в начале периода) и n=1 (первый платеж), ПРПЛТ=ПЛТ Если БС<>0, то формула усложнится:

Функцию

ОСПЛТ()

часто применяют при составлении графика платежей по аннуитетной схеме (см.

Выплата основной суммы долга в аннуитетной схеме. Расчет в MS EXCEL

)

Примечание

.

В

файле примера на листе Аннуитет (без ПЛТ)

определена аналитическая зависимость суммы идущей на погашение долга от номера периода.

Функция ПРПЛТ (ставка; период; кпер; пс; [бс]; [тип])

используется для вычисления регулярных сумм идущих на погашение процентов за ссуду используется с теми же аргументами, что и

ОСПЛТ()

.

Примечание.

Английский вариант функции: IPMT(rate, per, nper, pv, [fv], [type]), т.е. Interest Payment – выплата процентов.

В случае применения схемы аннуитета для выплаты ссуды для каждого периода действует равенство: ПРПЛТ =ПЛТ – ОСПЛТ

Сумму, идущую на погашение процентов за ссуду, можно вычислить зная: величину платежа (ПЛТ), период (Период), общее количество периодов (Кпер) и ставку (СТАВКА):

ПРПЛТ =ПЛТ*(1-(1+СТАВКА)^(Период-Кпер-1))

Вышеуказанная формула работает при БС=0. При ТИП=1 (платеж в начале периода) и n=1 (первый платеж), ПРПЛТ=0 Если БС<>0, то формула усложнится:

Соотношение выплат основной суммы долга и на погашение начисленных процентов за период хорошо демонстрирует график, приведенный в

файле примера

.

Функцию

ПРПЛТ()

часто применяют при составлении графика платежей по аннуитетной схеме (см.

Аннуитет. Расчет в MS EXCEL выплаченных процентов за период

).

Функция КПЕР(ставка; плт; пс; [бс]; [тип])

позволяет вычислить количество периодов, через которое текущая сумма вклада (пс) станет равной заданной сумме (бс) при известной процентной ставке за период (ставка) и известной величине пополнения вклада (плт). При этом предполагается, сумма пополнения вклада вносится регулярно в каждый период, тогда же происходит и начисление процентов. Сумма пополнения вклада может быть равна 0 (вклад не пополняется, рост вклада осуществляет только за счет капитализации процентов). Бс (будущая стоимость) может быть =0 или опущена. Также функцию

КПЕР()

можно использовать для определения количества периодов, необходимых для погашения долга по ссуде (погашение осуществляется регулярно равными платежами, ставка не изменяется весь срок, на который выдана ссуда, процент начисляется каждый период на остаток ссуды).

Примечание

.

Английский вариант функции: NPER(rate, pmt, pv, [fv], [type]), т.е. Number of Periods – число периодов.

Эквивалентная формула для расчета платежа:

Если ставка равна 0, то:

Кпер = (Пс + Бс) /ПЛТ

Подробнее про функцию можно прочитать в статье

Аннуитет. Расчет в MS EXCEL количества периодов

.

Функция СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение])

возвращает процентную ставку по аннуитету.

Примечание

.

Английский вариант функции: RATE(nper, pmt, pv, [fv], [type], [guess]), т.е. Number of Periods – число периодов.

Вот что написано на сайте MS

: Ставка вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО! Попробуем разобраться причем здесь итерации. Взглянем на Формулу 1. Если постараться решить это уравнение относительно параметра Ставка, то мы получим степенное уравнение (степень уравнения и, соответственно, число его корней будет зависеть от значения Кпер). В отличие от других параметров ПЛТ, БС, ПС и Кпер, найти универсальное решение этого уравнения для всевозможных степеней невозможно, поэтому приходится использовать метод итераций (по сути,

метод подбора

). Чтобы облегчить поиск Ставки методом итераций, используется аргумент

Предположение. Предположение

— это приблизительное значение Ставки, т.е. прогноз на основании нашего знания о задаче. Если значение предположения опущено, то оно полагается равным 10 процентам. Значение

Предположение

также полезно в случае

,

если имеется несколько решений уравнения – в этом случае находится значение Ставки ближайшее к

Предположению

.

Подробнее про функцию можно прочитать в статье

Аннуитет. Определяем процентную ставку в MS EXCEL

.

Функция БС(ставка; кпер; плт; [пс]; [тип])

возвращает

будущую стоимость

инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постоянной процентной ставки. Например, если у Вас сейчас на банковском счете сумма ПС (ПС м.б. =0) и вы ежемесячно вносите одну и туже сумму ПЛТ, то функция вычислит остаток на Вашем банковском счете через Кпер месяцев (предполагается, что капитализация процентов происходит также ежемесячно с процентной ставкой равной величине СТАВКА).

Примечание

.

Английский вариант функции: FV(rate, nper, pmt, [pv], [type]), т.е. Future Value – будущая стоимость.

Вычисления в функции

БС()

производятся по этой формуле:

Если СТАВКА =0, то Будущую стоимость можно определить по формуле БС= — ПЛТ * Кпер + ПС

Подробнее про функцию можно прочитать в статье

Аннуитет. Определяем в MS EXCEL Будущую Стоимость

.

Функция ПС(ставка; кпер; плт; [бс]; [тип])

возвращает

приведенную (к текущему моменту) стоимость инвестиций

. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на настоящий момент равноценна ряду будущих регулярных выплат ПЛТ за количество периодов Кпер. Также предполагается, что капитализация процентов происходит также регулярно с процентной ставкой равной величине СТАВКА.

Примечание

.

Английский вариант функции: PV(rate, nper, pmt, [fv], [type]), т.е. Present Value – будущая стоимость.

Вычисления в функции

ПС()

производятся по этой формуле:

Если СТАВКА =0, то Приведенную стоимость можно определить по формуле ПС=-БС-ПЛТ*Кпер

Подробнее про функцию можно прочитать в статье

Аннуитет. Определяем в MS EXCEL Приведенную (Текущую) стоимость

Функции ОБЩДОХОД() и ОБЩПЛАТ()

Аргументы функций

ОБЩДОХОД()

и

ОБЩПЛАТ()

несколько отличаются от рассмотренных выше. Но на самом деле разница только в их названии: кол_пер – это кпер; нз – это пс. Нач_период и кон_период – это «начальный период» и «конечный период».

Функция ОБЩДОХОД(ставка; кол_пер; нз; нач_период; кон_период; тип)

возвращает кумулятивную (нарастающим итогом) сумму, выплачиваемую в погашение основной суммы займа в промежутке между двумя периодами (

нач_период и кон_период

).

Примечание

.

Английский вариант функции:  CUMPRINC(rate, nper, pv, start_period, end_period, type) returns the CUMulative PRincipal paid for an investment period with a Constant interest rate.

Подробнее про функцию можно прочитать в статье

Аннуитет. Расчёт в MS EXCEL погашение основной суммы долга

.

Функция ОБЩПЛАТ(ставка; кол_пер; нз; нач_период; кон_период; тип)

возвращает кумулятивную (нарастающим итогом) величину процентов, выплачиваемых по займу в промежутке между двумя периодами выплат (

нач_период

и

кон_период

).

Примечание

.

Английский вариант функции: CUMIPMT(rate, nper, pv, start_period, end_period, type) returns the CUMulative Interest paid on a loan between start_period and end_period.

Подробнее про функцию можно прочитать в статье

Аннуитет. Расчет в MS EXCEL выплаченных процентов за период

.

Общую сумму выплат по займу между двумя периодами (Нач_период и кон_период) можно найти сложив результаты возвращаемые

ОБЩПЛАТ()

и

ОБЩДОХОД()

с одинаковыми аргументами, что эквивалентно ПЛТ*(кон_период — Нач_период+1).

Прежде, чем брать заем, неплохо было бы рассчитать все платежи по нему. Это убережет заёмщика в будущем от различных неожиданных неприятностей и разочарований, когда выяснится, что переплата слишком большая. Помочь в данном расчете могут инструменты программы Excel. Давайте выясним, как рассчитать аннуитетные платежи по кредиту в этой программе.

Расчет оплаты

Прежде всего, нужно сказать, что существует два вида кредитных платежей:

• Дифференцированные;
• Аннуитетные.

При дифференцированной схеме клиент вносит в банк ежемесячно равную долю выплат по телу кредита плюс платежи по процентам. Величина процентных выплат каждый месяц уменьшается, так как уменьшается тело займа, с которого они рассчитываются. Таким образом и общий ежемесячный платеж тоже уменьшается.

При аннуитетной схеме используется несколько другой подход. Клиент ежемесячно вносит одинаковую сумму общего платежа, который состоит из выплат по телу кредита и оплаты процентов. Изначально процентные взносы насчитываются на всю сумму займа, но по мере того, как тело уменьшается, сокращается и начисление процентов. Но общая сумма оплаты остается неизменной за счет ежемесячного увеличения величины выплат по телу кредита. Таким образом, с течением времени удельный вес процентов в общем ежемесячном платеже падает, а удельный вес оплаты по телу растет. При этом сам общий ежемесячный платеж на протяжении всего срока кредитования не меняется.

Как раз на расчете аннуитетного платежа мы и остановимся. Тем более, это актуально, так как в настоящее время большинство банков используют именно эту схему. Она удобна и для клиентов, ведь в этом случае общая сумма оплаты не меняется, оставаясь фиксированной. Клиенты всегда знают сколько нужно заплатить.

Этап 1: расчет ежемесячного взноса

Для расчета ежемесячного взноса при использовании аннуитетной схемы в Экселе существует специальная функция – ПЛТ. Она относится к категории финансовых операторов. Формула этой функции выглядит следующим образом:

=ПЛТ(ставка;кпер;пс;бс;тип)

Как видим, указанная функция обладает довольно большим количеством аргументов. Правда, последние два из них не являются обязательными.

Аргумент «Ставка» указывает на процентную ставку за конкретный период. Если, например, используется годовая ставка, но платеж по займу производится ежемесячно, то годовую ставку нужно разделить на 12 и полученный результат использовать в качестве аргумента. Если применяется ежеквартальный вид оплаты, то в этом случае годовую ставку нужно разделить на 4 и т.д.

«Кпер» обозначает общее количество периодов выплат по кредиту. То есть, если заём берется на один год с ежемесячной оплатой, то число периодов считается 12, если на два года, то число периодов – 24. Если кредит берется на два года с ежеквартальной оплатой, то число периодов равно 8.

«Пс» указывает приведенную стоимость на настоящий момент. Говоря простыми словами, это общая величина займа на начало кредитования, то есть, та сумма, которую вы берете взаймы, без учета процентов и других дополнительных выплат.

«Бс» — это будущая стоимость. Эта величина, которую будет составлять тело займа на момент завершения кредитного договора. В большинстве случаев данный аргумент равен «0», так как заемщик на конец срока кредитования должен полностью рассчитаться с кредитором. Указанный аргумент не является обязательным. Поэтому, если он опускается, то считается равным нулю.

Аргумент «Тип» определяет время расчета: в конце или в начале периода. В первом случае он принимает значение «0», а во втором – «1». Большинство банковских учреждений используют именно вариант с оплатой в конце периода. Этот аргумент тоже является необязательным, и если его опустить считается, что он равен нулю.

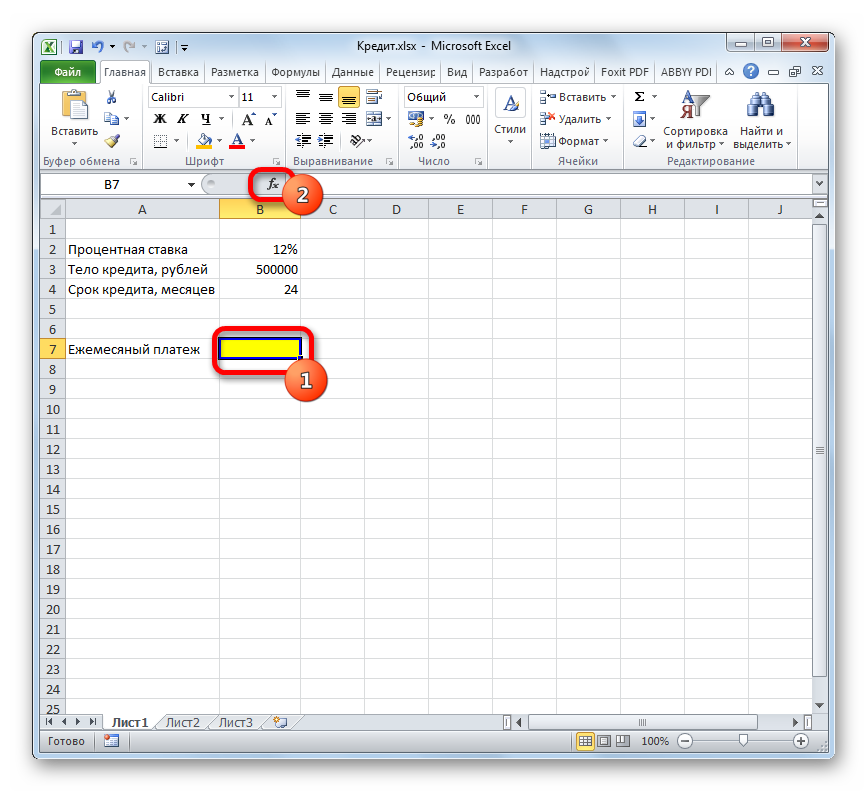
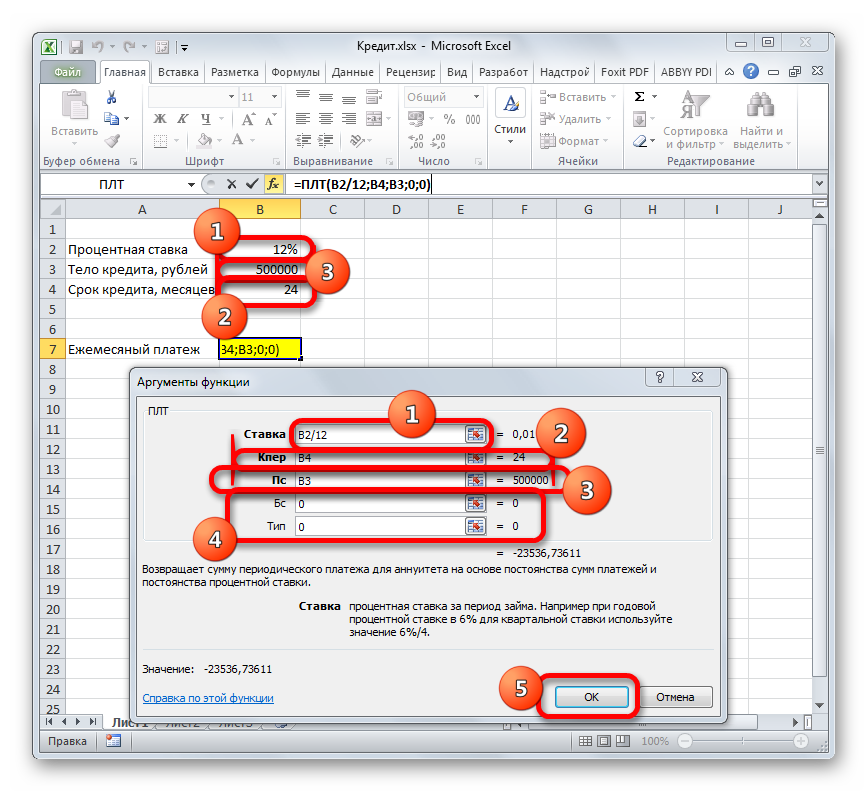
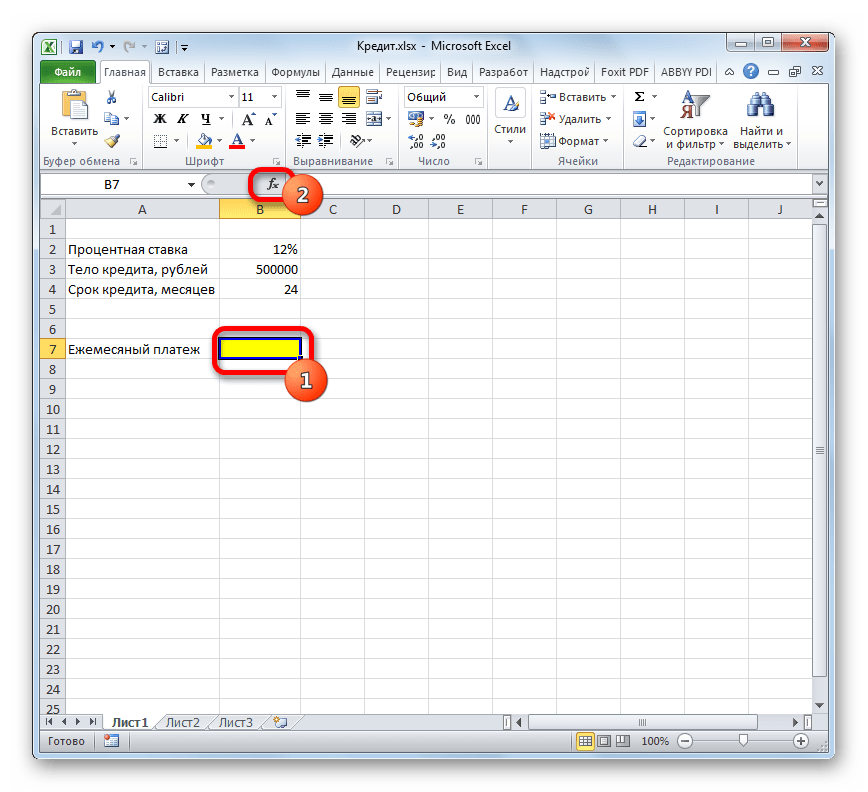
Теперь настало время перейти к конкретному примеру расчета ежемесячного взноса при помощи функции ПЛТ. Для расчета используем таблицу с исходными данными, где указана процентная ставка по кредиту (12%), величина займа (500000 рублей) и срок кредита (24 месяца). При этом оплата производится ежемесячно в конце каждого периода.

1. Выделяем элемент на листе, в который будет выводиться результат расчета, и щелкаем по пиктограмме «Вставить функцию», размещенную около строки формул.



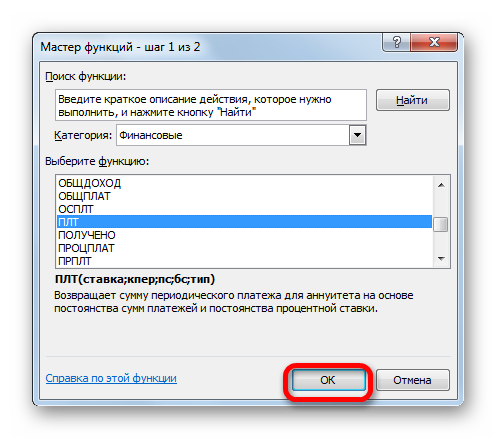
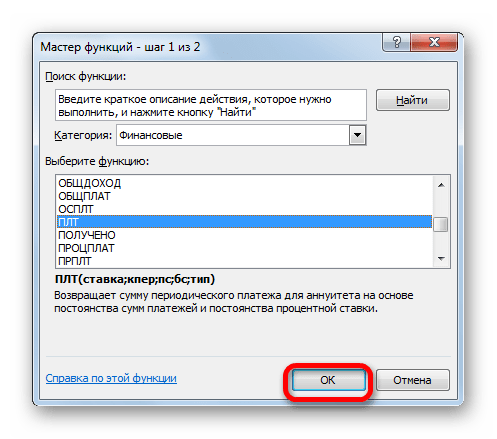
2. Производится запуск окошка Мастера функций. В категории «Финансовые» выделяем наименование «ПЛТ» и жмем на кнопку «OK».



3. После этого открывается окно аргументов оператора ПЛТ.

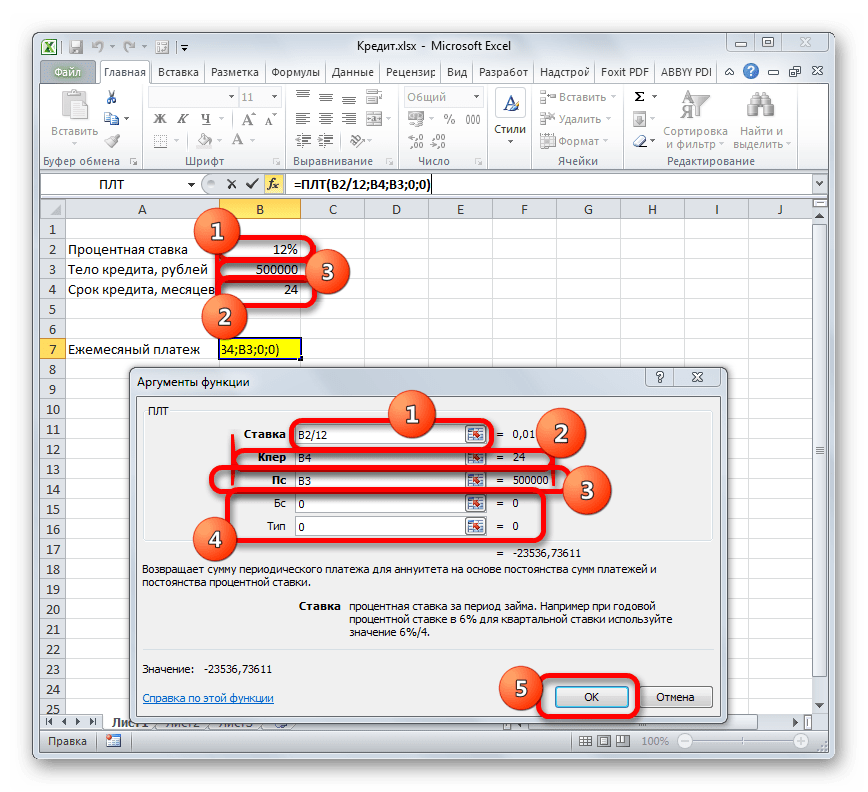
   В поле «Ставка» следует вписать величину процентов за период. Это можно сделать вручную, просто поставив процент, но у нас он указан в отдельной ячейке на листе, поэтому дадим на неё ссылку. Устанавливаем курсор в поле, а затем кликаем по соответствующей ячейке. Но, как мы помним, у нас в таблице задана годовая процентная ставка, а период оплаты равен месяцу. Поэтому делим годовую ставку, а вернее ссылку на ячейку, в которой она содержится, на число 12, соответствующее количеству месяцев в году. Деление выполняем прямо в поле окна аргументов.

   В поле «Кпер» устанавливается срок кредитования. Он у нас равен 24 месяцам. Можно занести в поле число 24 вручную, но мы, как и в предыдущем случае, указываем ссылку на месторасположение данного показателя в исходной таблице.

   В поле «Пс» указывается первоначальная величина займа. Она равна 500000 рублей. Как и в предыдущих случаях, указываем ссылку на элемент листа, в котором содержится данный показатель.

   В поле «Бс» указывается величина займа, после полной его оплаты. Как помним, это значение практически всегда равно нулю. Устанавливаем в данном поле число «0». Хотя этот аргумент можно вообще опустить.

   В поле «Тип» указываем в начале или в конце месяца производится оплата. У нас, как и в большинстве случаев, она производится в конце месяца. Поэтому устанавливаем число «0». Как и в случае с предыдущим аргументом, в данное поле можно ничего не вводить, тогда программа по умолчанию будет считать, что в нем расположено значение равное нулю.

   После того, как все данные введены, жмем на кнопку «OK».



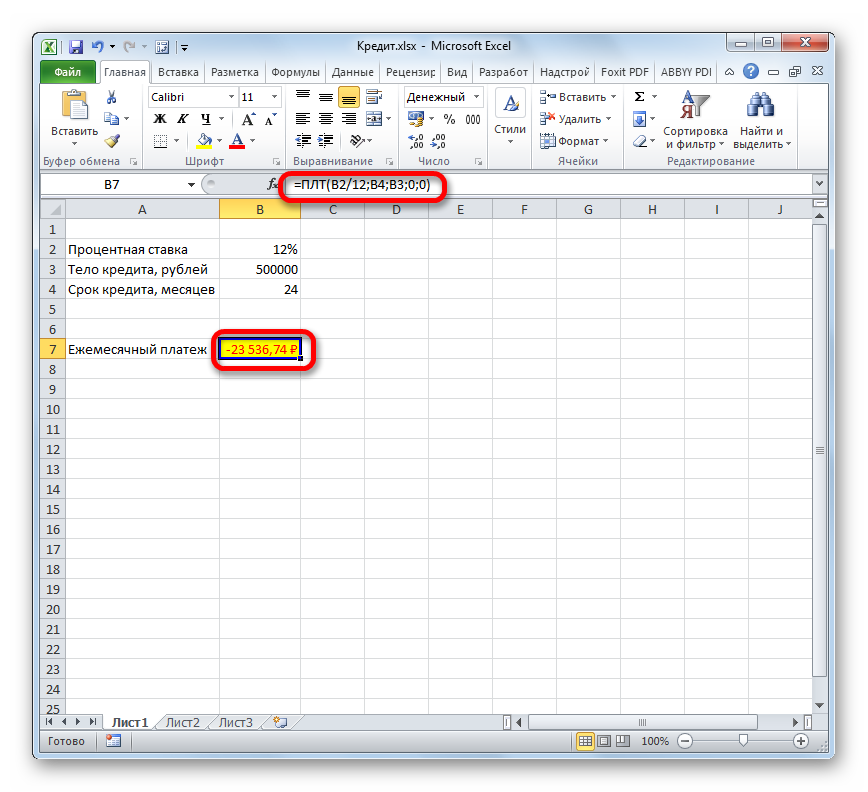
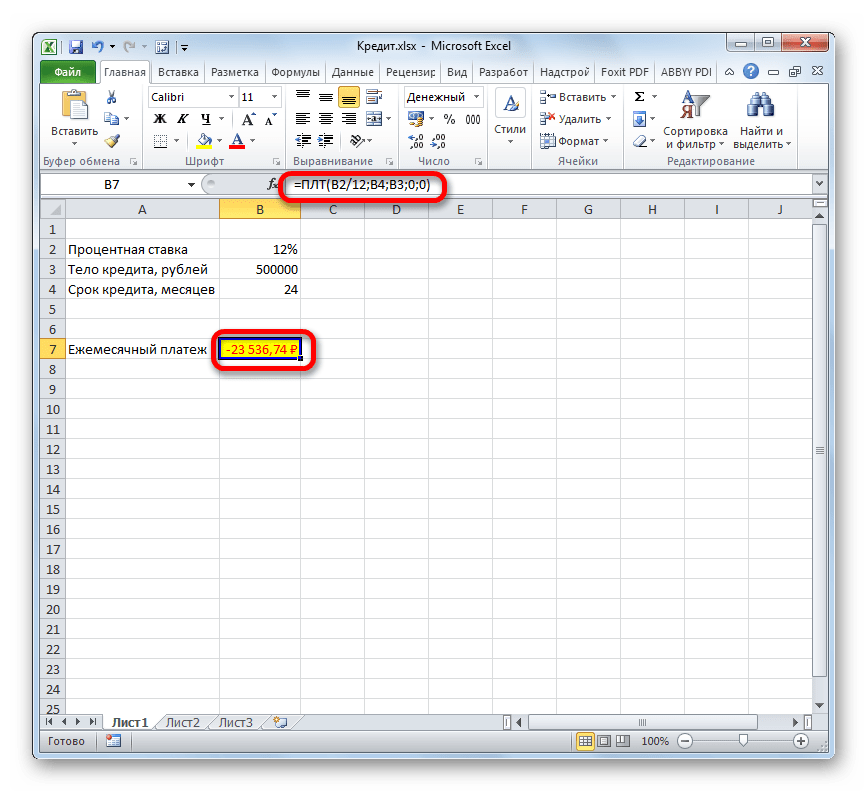
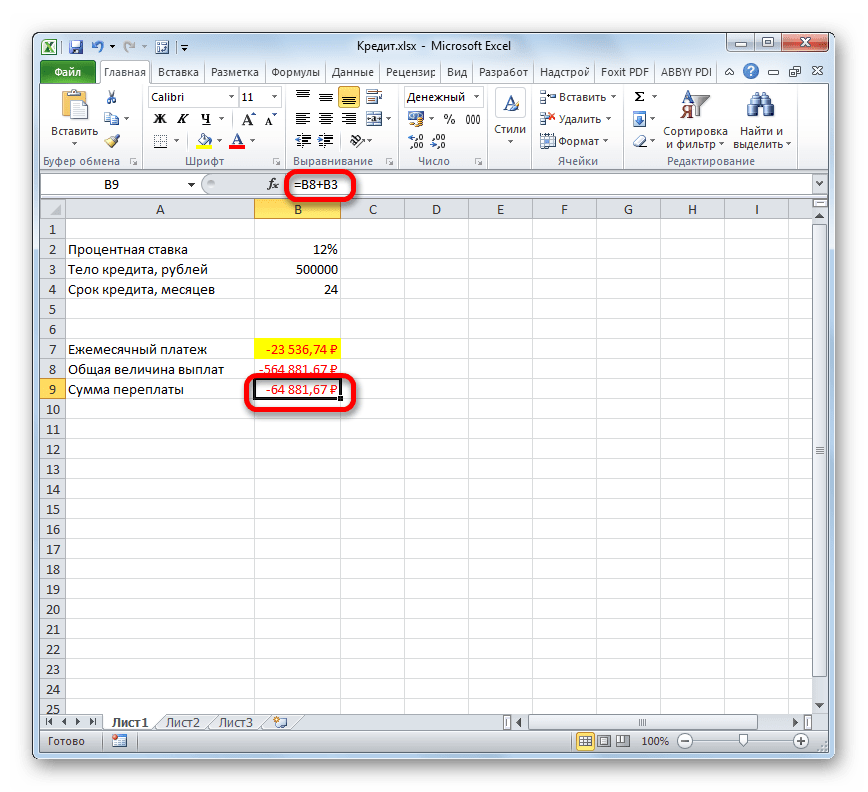
4. После этого в ячейку, которую мы выделили в первом пункте данного руководства, выводится результат вычисления. Как видим, величина ежемесячного общего платежа по займу составляет 23536,74 рубля. Пусть вас не смущает знак «-» перед данной суммой. Так Эксель указывает на то, что это расход денежных средств, то есть, убыток.



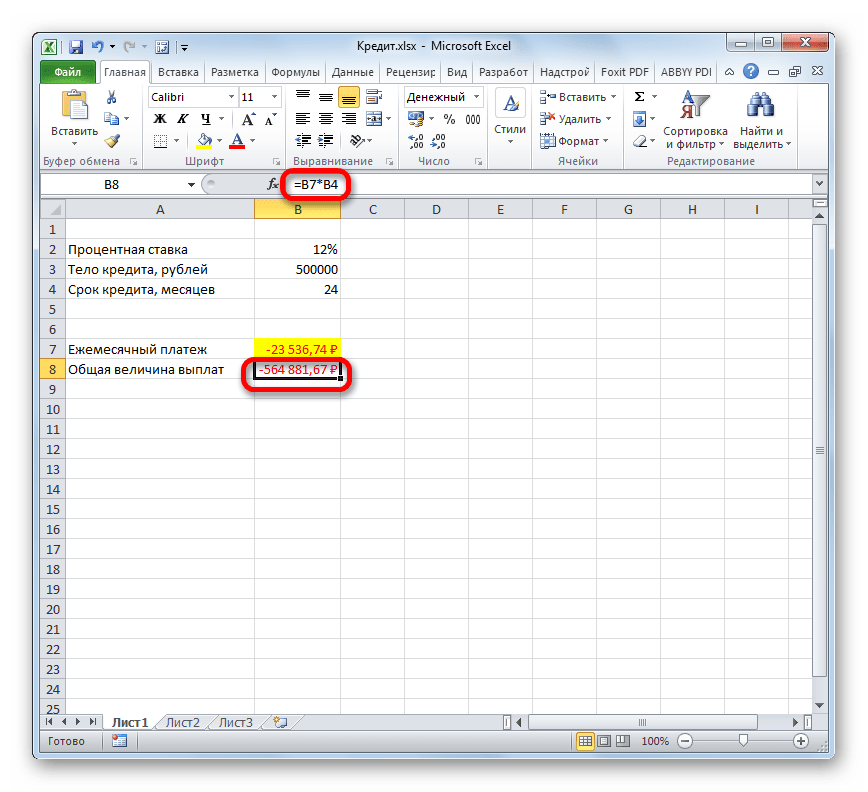
5. Для того, чтобы рассчитать общую сумму оплаты за весь срок кредитования с учетом погашения тела займа и ежемесячных процентов, достаточно перемножить величину ежемесячного платежа (23536,74 рубля) на количество месяцев (24 месяца). Как видим, общая сумма платежей за весь срок кредитования в нашем случае составила 564881,67 рубля.



6. Теперь можно подсчитать сумму переплаты по кредиту. Для этого нужно отнять от общей величины выплат по кредиту, включая проценты и тело займа, начальную сумму, взятую в долг. Но мы помним, что первое из этих значений уже со знаком «-». Поэтому в конкретно нашем случае получается, что их нужно сложить. Как видим, общая сумма переплаты по кредиту за весь срок составила 64881,67 рубля.

Урок: Мастер функций в Эксель

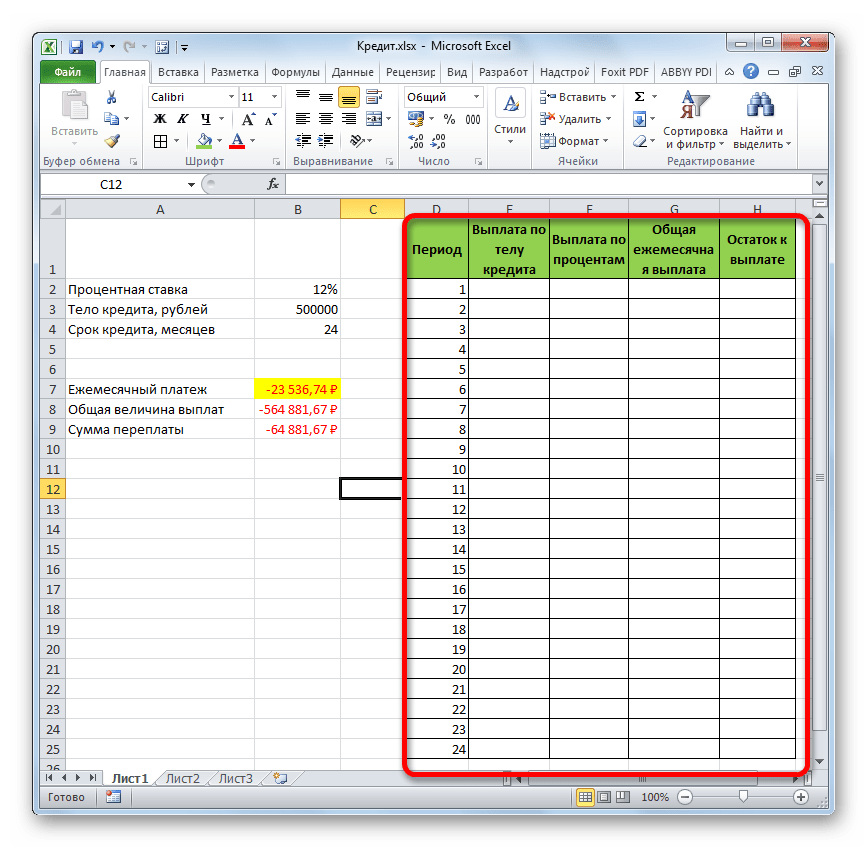
Этап 2: детализация платежей

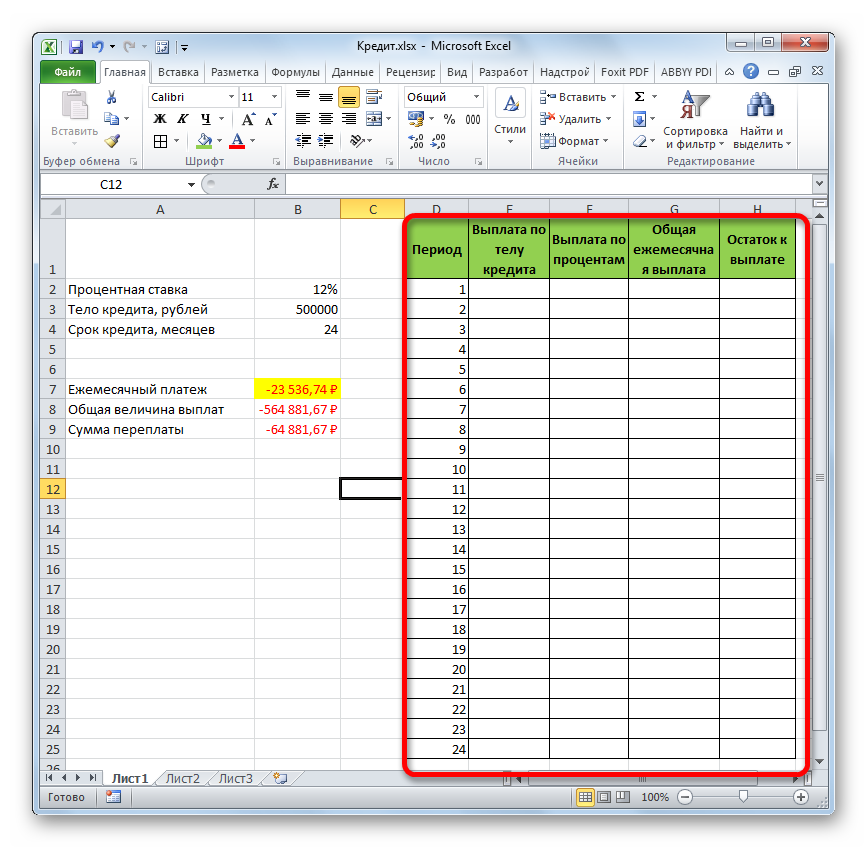
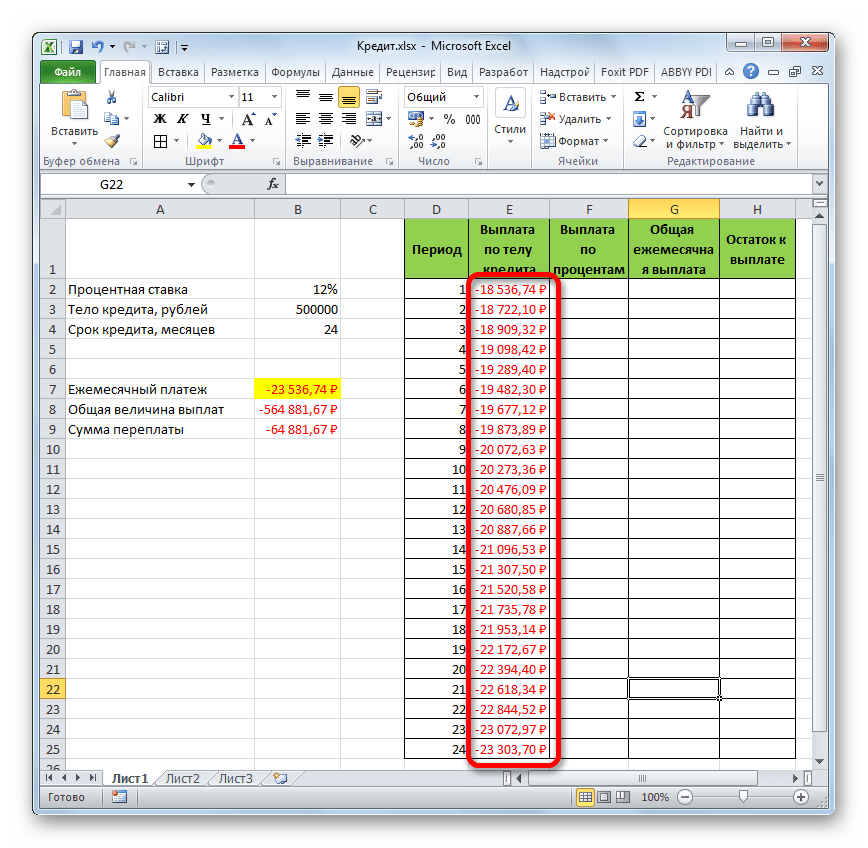
А теперь с помощью других операторов Эксель сделаем помесячную детализацию выплат, чтобы видеть, сколько в конкретном месяце мы платим по телу займа, а сколько составляет величина процентов. Для этих целей чертим в Экселе таблицу, которую будем заполнять данными. Строки этой таблицы будут отвечать соответствующему периоду, то есть, месяцу. Учитывая, что период кредитования у нас составляет 24 месяца, то и количество строк тоже будет соответствующим. В столбцах указана выплата тела займа, выплата процентов, общий ежемесячный платеж, который является суммой предыдущих двух колонок, а также оставшаяся сумма к выплате.

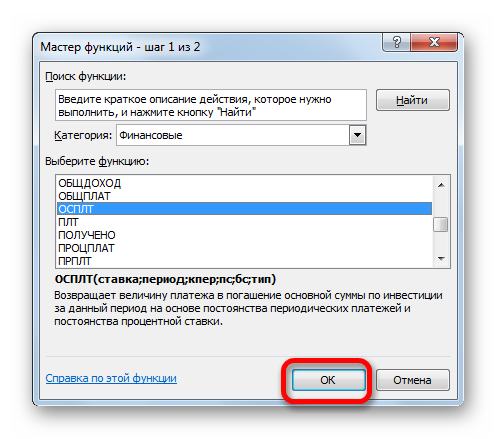
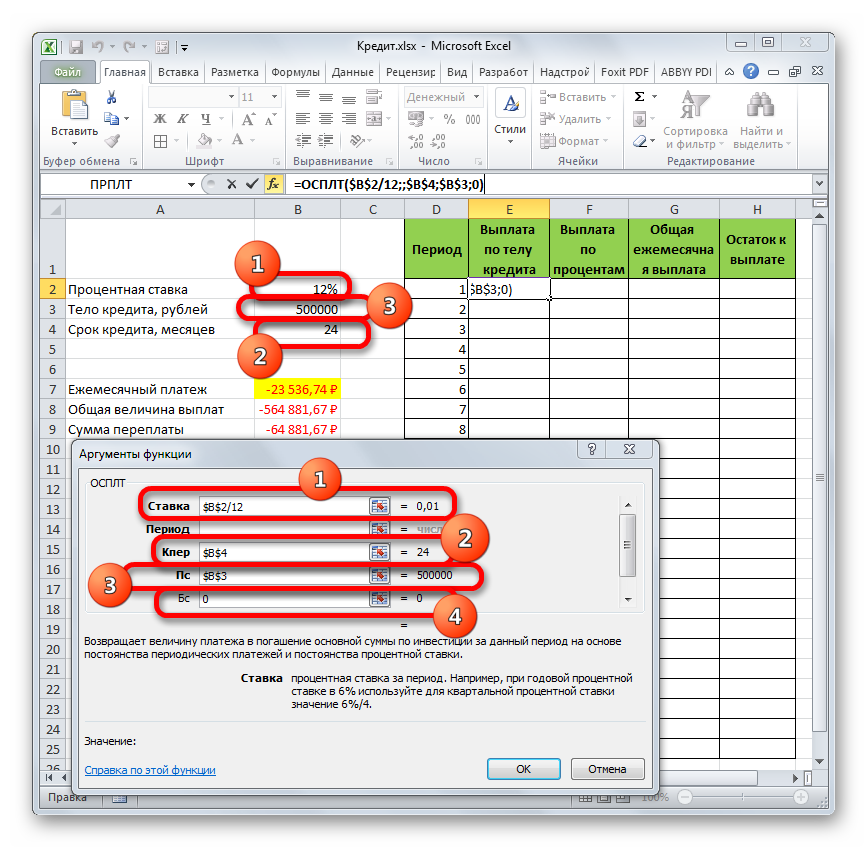
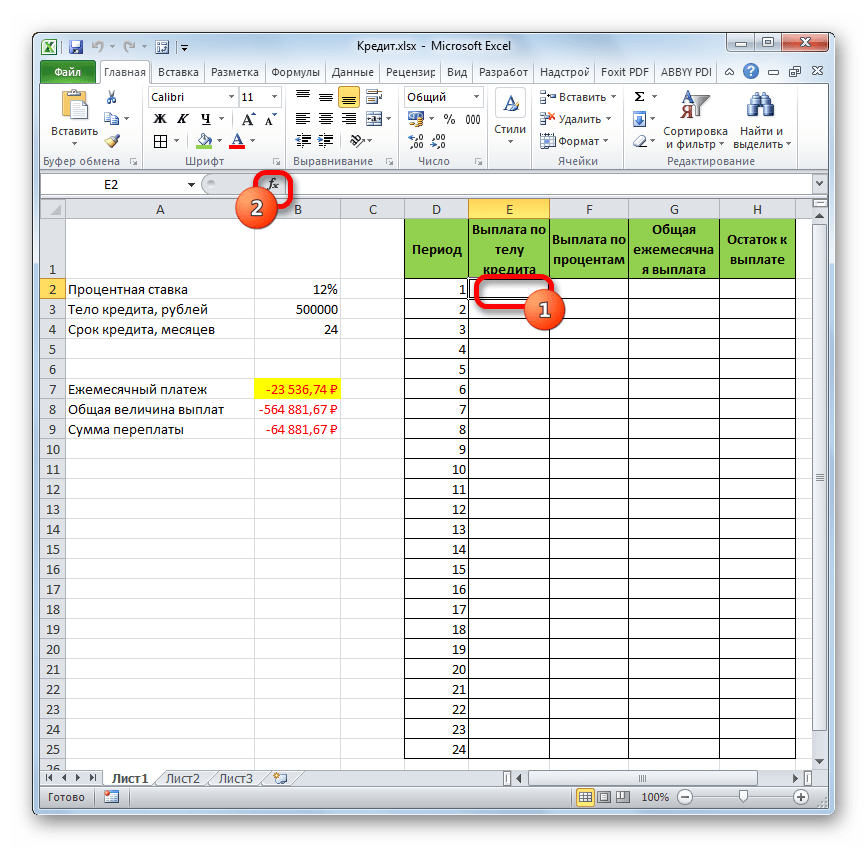
1. Для определения величины оплаты по телу займа используем функцию ОСПЛТ, которая как раз предназначена для этих целей. Устанавливаем курсор в ячейку, которая находится в строке «1» и в столбце «Выплата по телу кредита». Жмем на кнопку «Вставить функцию».



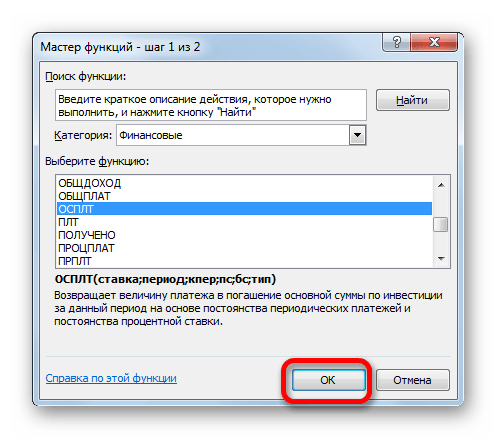
2. Переходим в Мастер функций. В категории «Финансовые» отмечаем наименование «ОСПЛТ» и жмем кнопку «OK».



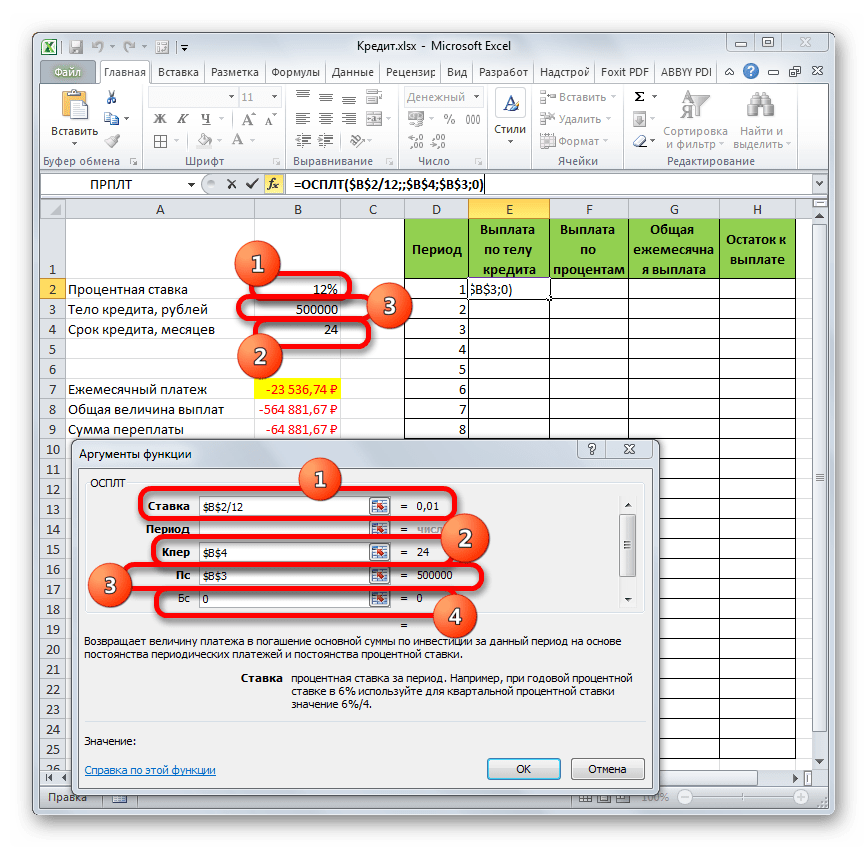
3. Запускается окно аргументов оператора ОСПЛТ. Он имеет следующий синтаксис:

   =ОСПЛТ(Ставка;Период;Кпер;Пс;Бс)

   Как видим, аргументы данной функции почти полностью совпадают с аргументами оператора ПЛТ, только вместо необязательного аргумента «Тип» добавлен обязательный аргумент «Период». Он указывает на номер периода выплаты, а в нашем конкретном случае на номер месяца.

   Заполняем уже знакомые нам поля окна аргументов функции ОСПЛТ теми самыми данными, что были использованы для функции ПЛТ. Только учитывая тот факт, что в будущем будет применяться копирование формулы посредством маркера заполнения, нужно сделать все ссылки в полях абсолютными, чтобы они не менялись. Для этого требуется поставить знак доллара перед каждым значением координат по вертикали и горизонтали. Но легче это сделать, просто выделив координаты и нажав на функциональную клавишу F4. Знак доллара будет расставлен в нужных местах автоматически. Также не забываем, что годовую ставку нужно разделить на 12.



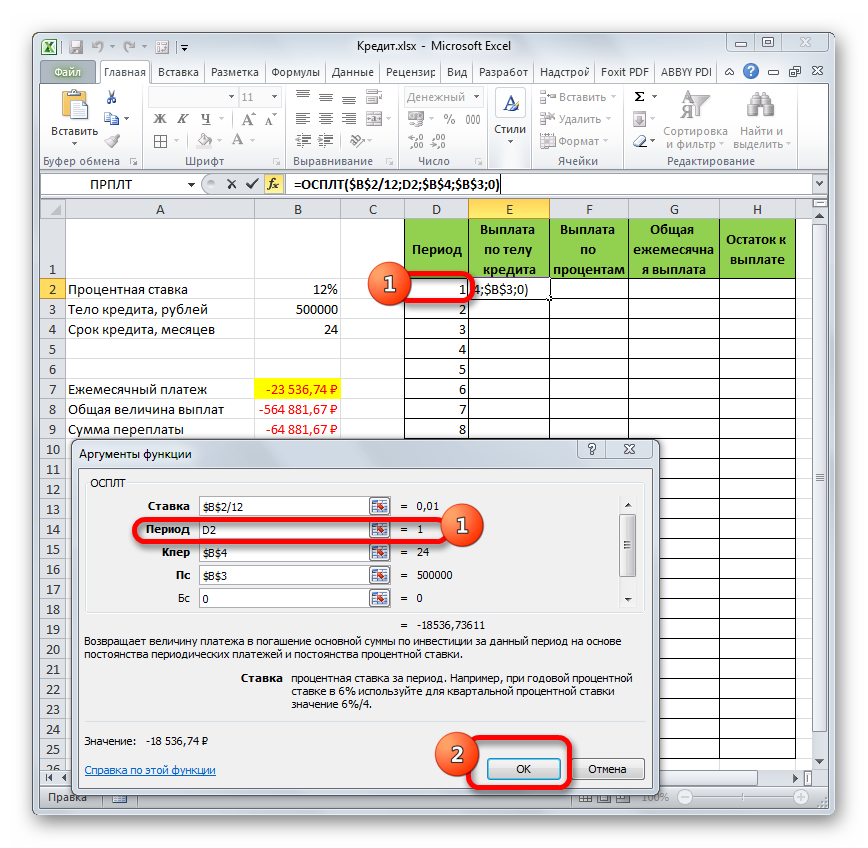
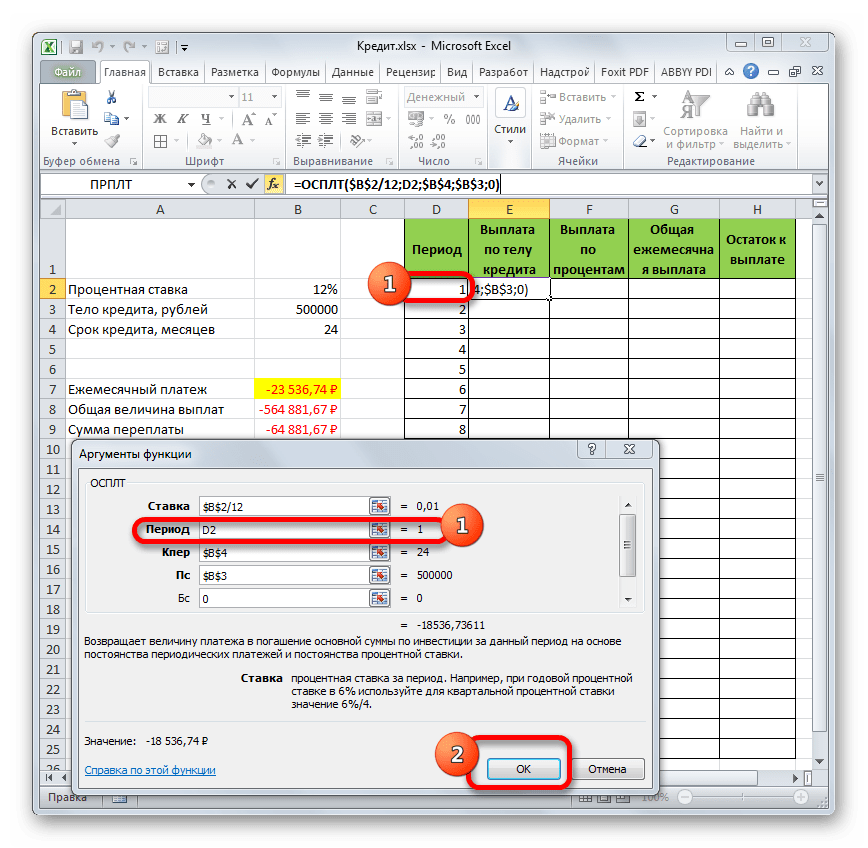
4. Но у нас остается ещё один новый аргумент, которого не было у функции ПЛТ. Этот аргумент «Период». В соответствующее поле устанавливаем ссылку на первую ячейку столбца «Период». Данный элемент листа содержит в себе число «1», которое обозначает номер первого месяца кредитования. Но в отличие от предыдущих полей, в указанном поле мы оставляем ссылку относительной, а не делаем из неё абсолютную.

   После того, как все данные, о которых мы говорили выше, введены, жмем на кнопку «OK».



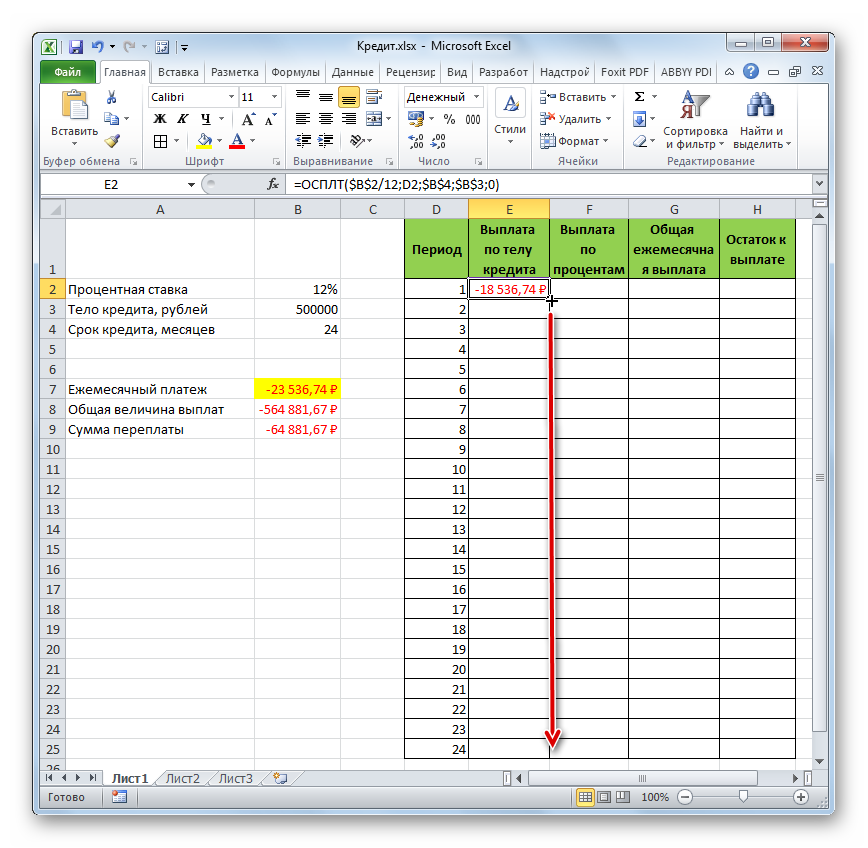
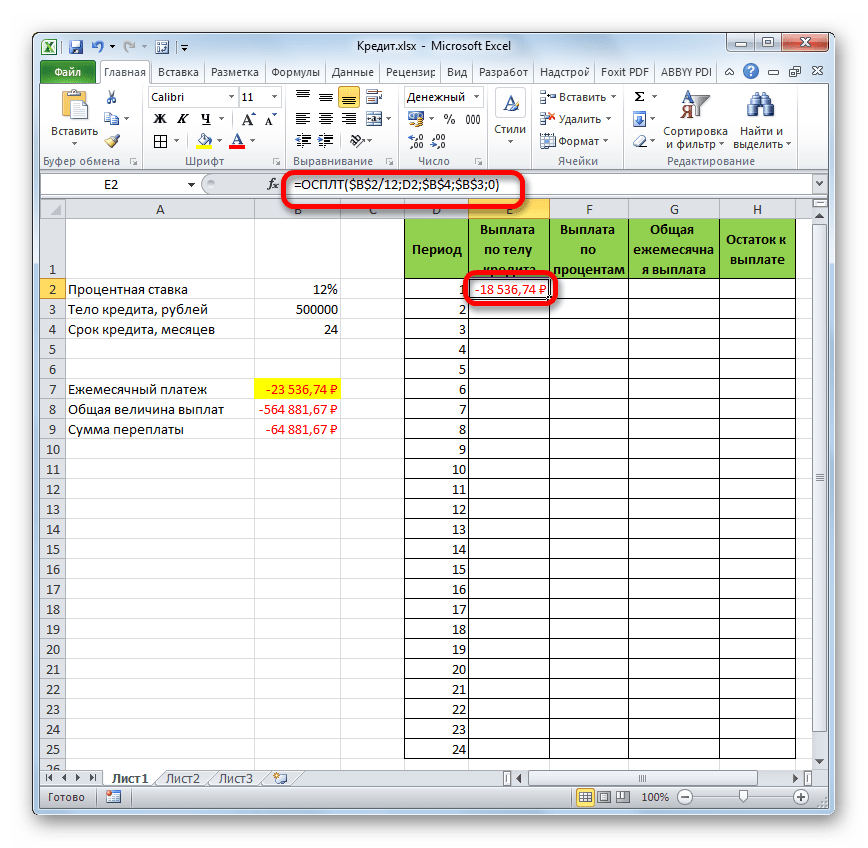
5. После этого в ячейке, которую мы ранее выделили, отобразится величина выплаты по телу займа за первый месяц. Она составит 18536,74 рубля.



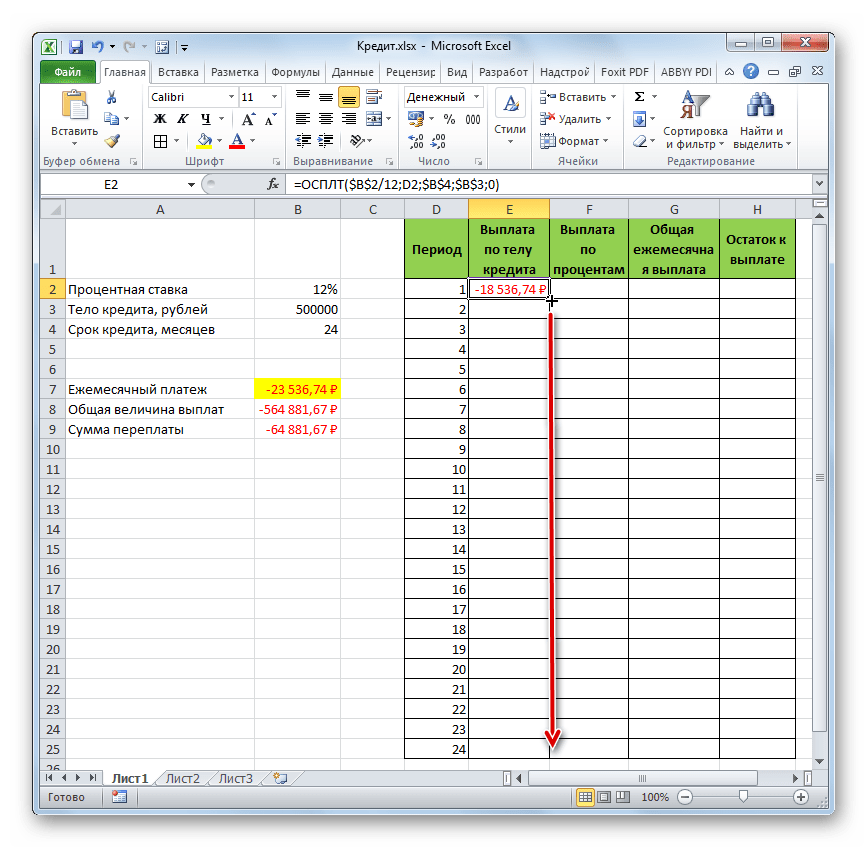
6. Затем, как уже говорилось выше, нам следует скопировать данную формулу на остальные ячейки столбца с помощью маркера заполнения. Для этого устанавливаем курсор в нижний правый угол ячейки, в которой содержится формула. Курсор преобразуется при этом в крестик, который называется маркером заполнения. Зажимаем левую кнопку мыши и тянем его вниз до конца таблицы.



7. В итоге все ячейки столбца заполнены. Теперь мы имеем график выплаты тела займа помесячно. Как и говорилось уже выше, величина оплаты по данной статье с каждым новым периодом увеличивается.



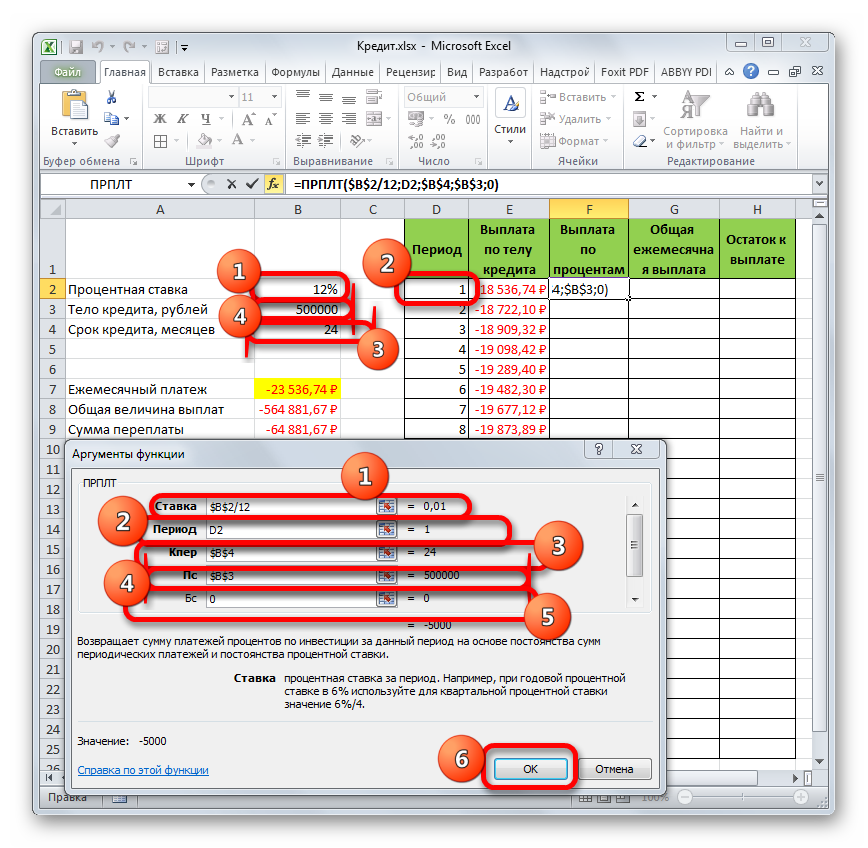
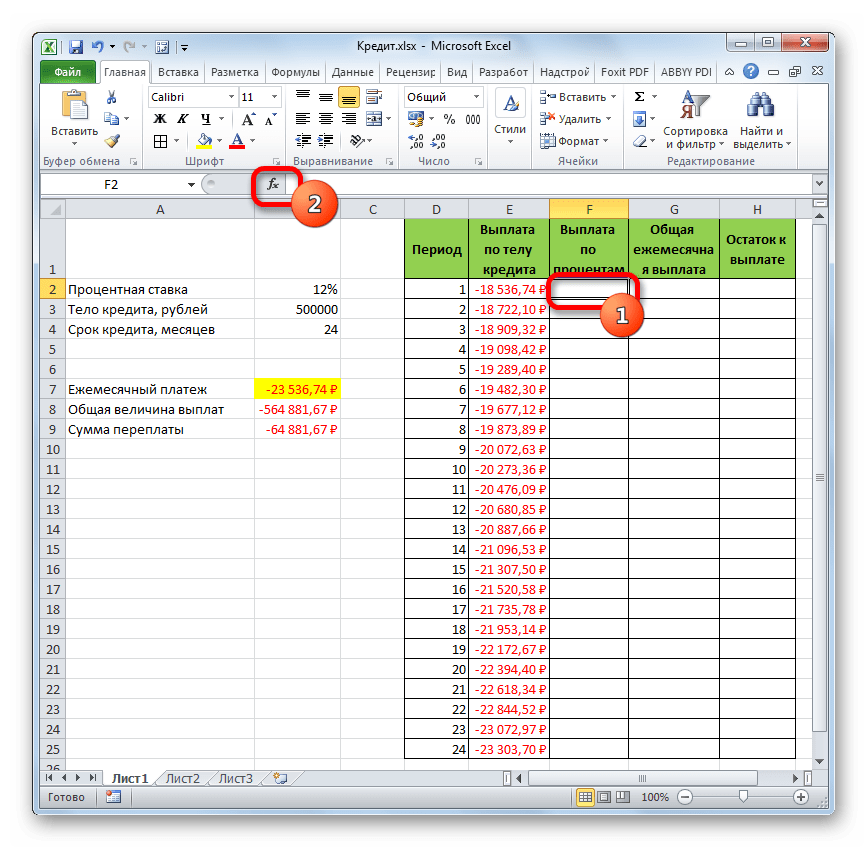
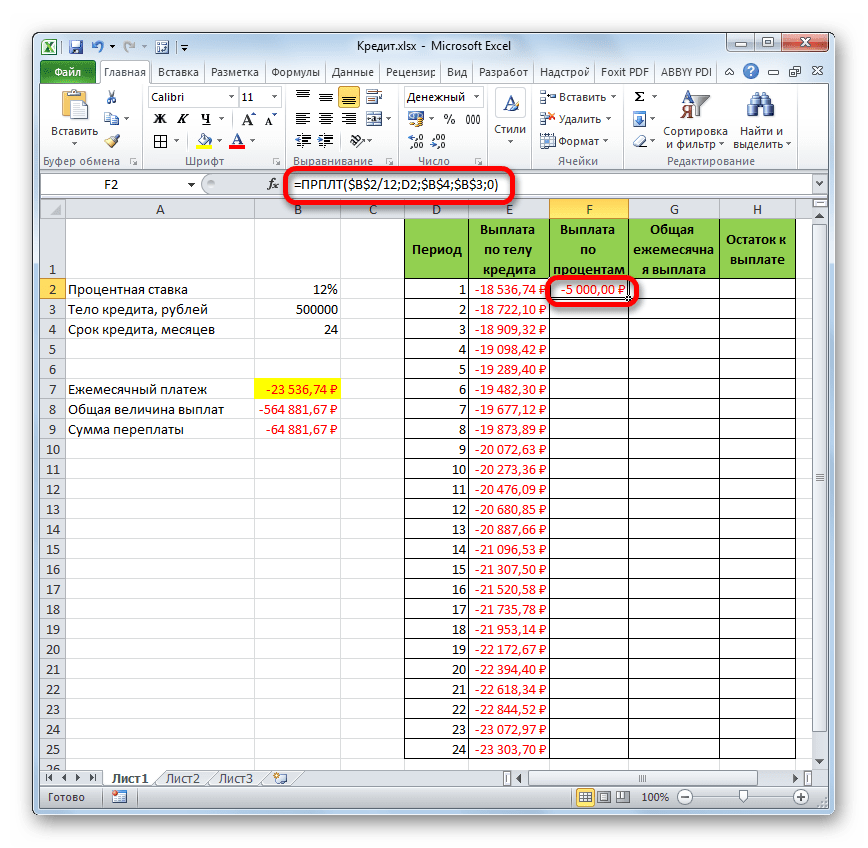
8. Теперь нам нужно сделать месячный расчет оплаты по процентам. Для этих целей будем использовать оператор ПРПЛТ. Выделяем первую пустую ячейку в столбце «Выплата по процентам». Жмем на кнопку «Вставить функцию».



9. В запустившемся окне Мастера функций в категории «Финансовые» производим выделение наименования ПРПЛТ. Выполняем щелчок по кнопке «OK».



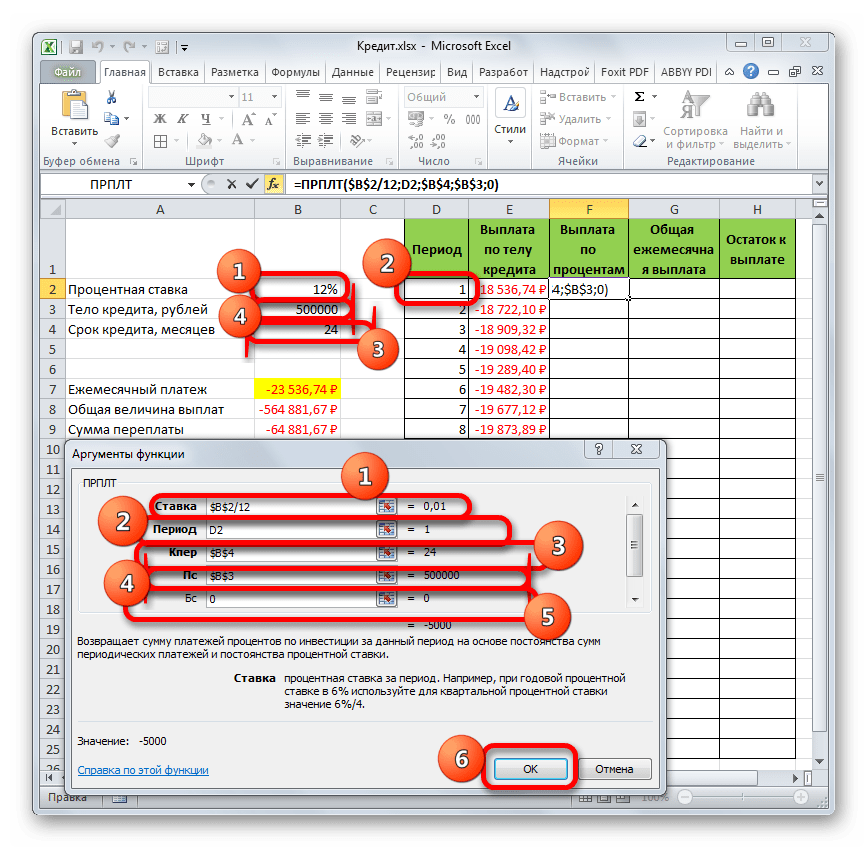
10. Происходит запуск окна аргументов функции ПРПЛТ. Её синтаксис выглядит следующим образом:

    =ПРПЛТ(Ставка;Период;Кпер;Пс;Бс)

    Как видим, аргументы данной функции абсолютно идентичны аналогичным элементам оператора ОСПЛТ. Поэтому просто заносим в окно те же данные, которые мы вводили в предыдущем окне аргументов. Не забываем при этом, что ссылка в поле «Период» должна быть относительной, а во всех других полях координаты нужно привести к абсолютному виду. После этого щелкаем по кнопке «OK».



11. Затем результат расчета суммы оплаты по процентам за кредит за первый месяц выводится в соответствующую ячейку.



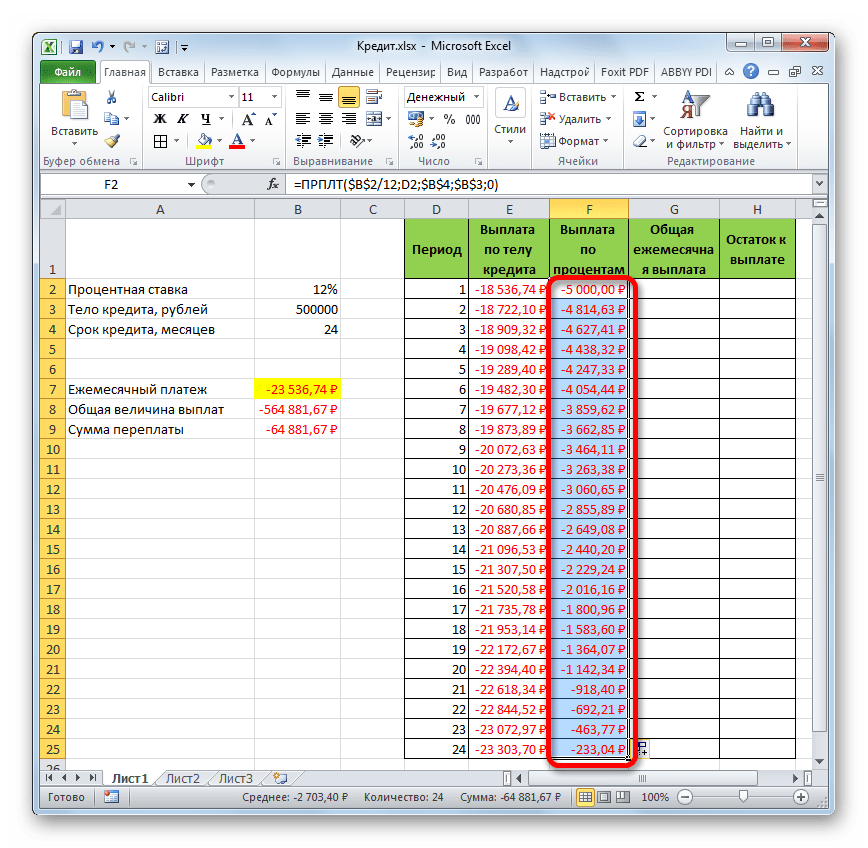
12. Применив маркер заполнения, производим копирование формулы в остальные элементы столбца, таким способом получив помесячный график оплат по процентам за заём. Как видим, как и было сказано ранее, из месяца в месяц величина данного вида платежа уменьшается.



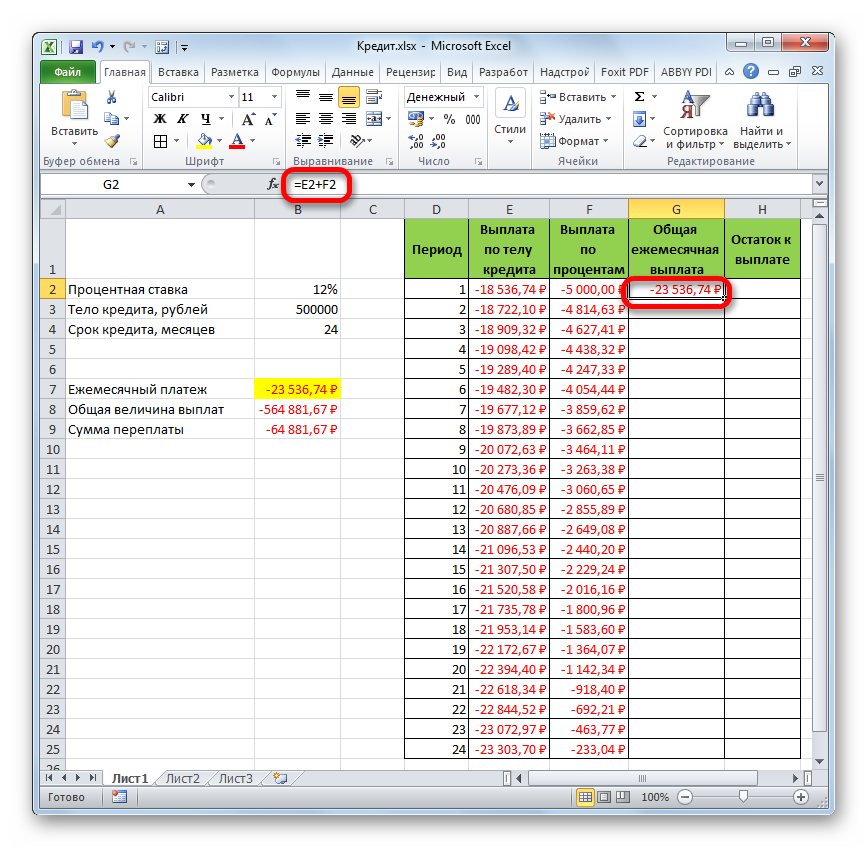
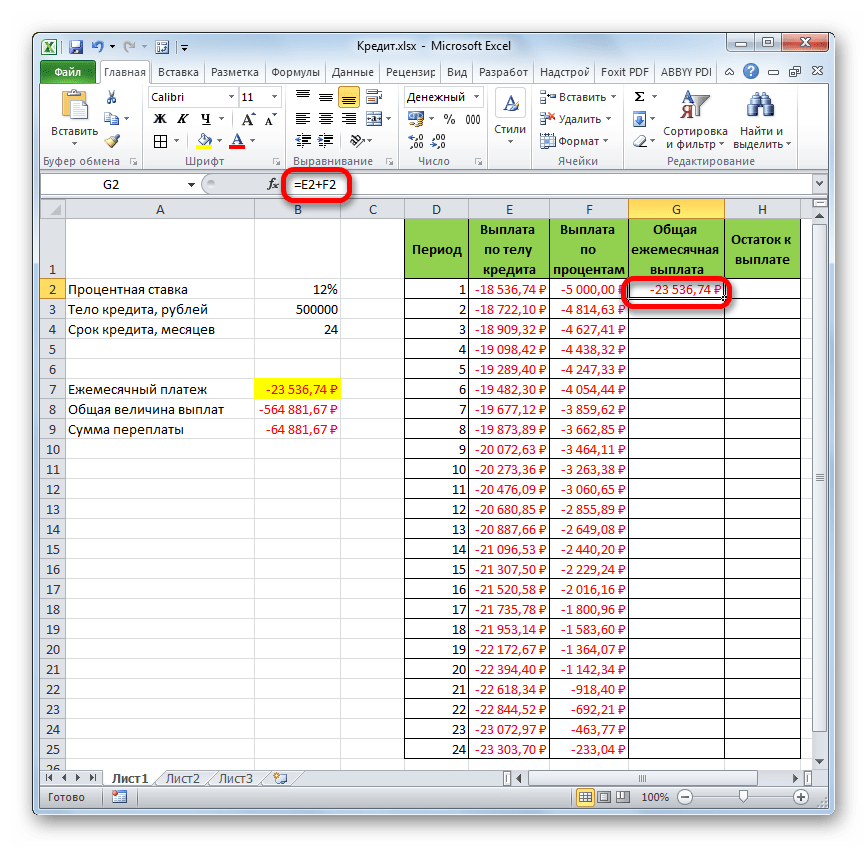
13. Теперь нам предстоит рассчитать общий ежемесячный платеж. Для этого вычисления не следует прибегать к какому-либо оператору, так как можно воспользоваться простой арифметической формулой. Складываем содержимое ячеек первого месяца столбцов «Выплата по телу кредита» и «Выплата по процентам». Для этого устанавливаем знак «=» в первую пустую ячейку столбца «Общая ежемесячная выплата». Затем кликаем по двум вышеуказанным элементам, установив между ними знак «+». Жмем на клавишу Enter.



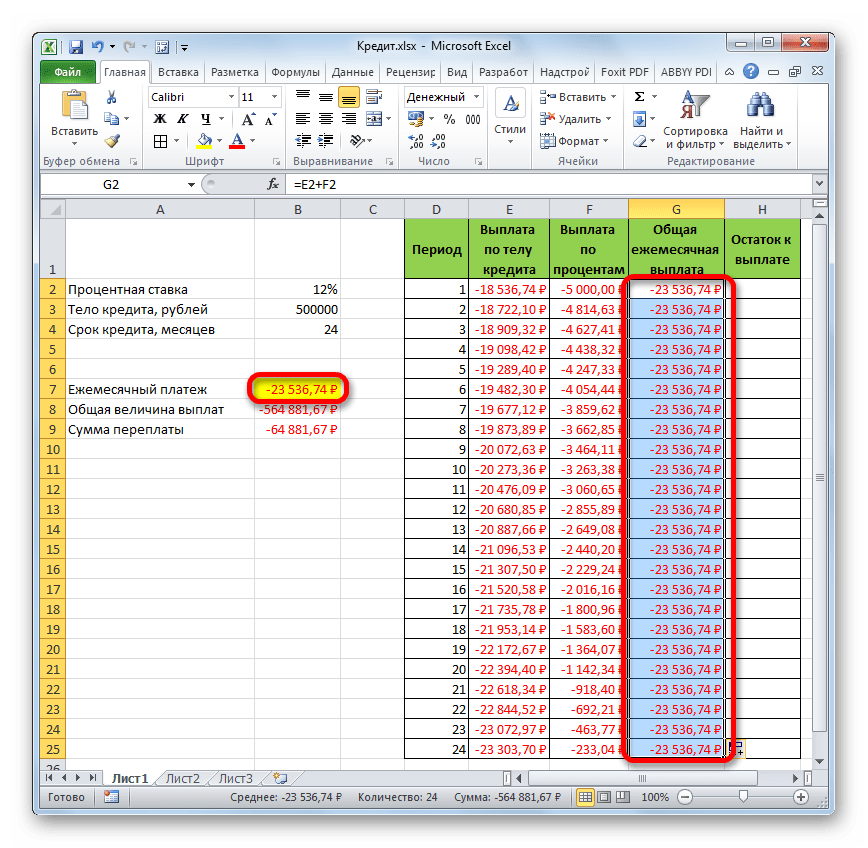
14. Далее с помощью маркера заполнения, как и в предыдущих случаях, заполняем колонку данными. Как видим, на протяжении всего действия договора сумма общего ежемесячного платежа, включающего платеж по телу займа и оплату процентов, составит 23536,74 рубля. Собственно этот показатель мы уже рассчитывали ранее при помощи ПЛТ. Но в данном случае это представлено более наглядно, именно как сумма оплаты по телу займа и процентам.



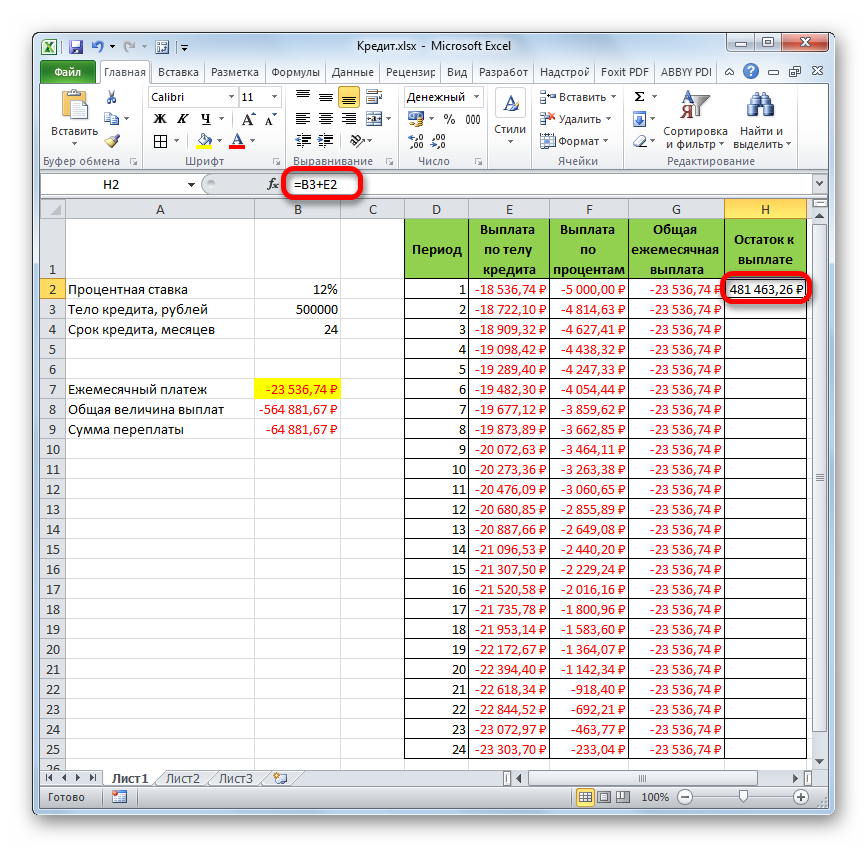
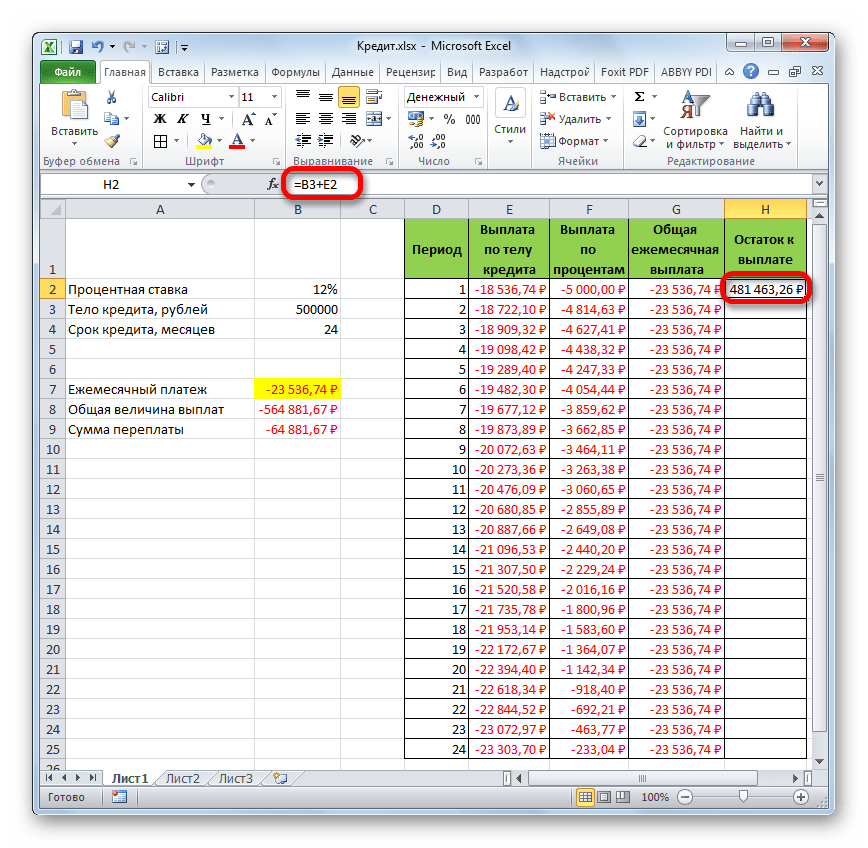
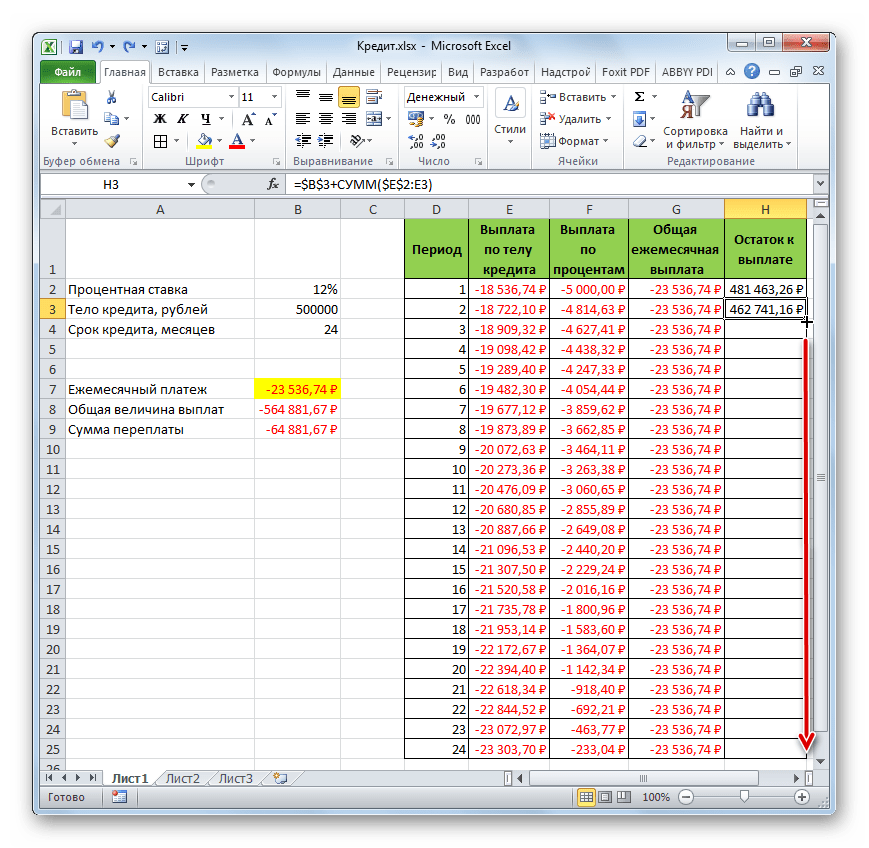
15. Теперь нужно добавить данные в столбец, где будет ежемесячно отображаться остаток суммы по кредиту, который ещё требуется заплатить. В первой ячейке столбца «Остаток к выплате» расчет будет самый простой. Нам нужно отнять от первоначальной величины займа, которая указана в таблице с первичными данными, платеж по телу кредита за первый месяц в расчетной таблице. Но, учитывая тот факт, что одно из чисел у нас уже идет со знаком «-», то их следует не отнять, а сложить. Делаем это и жмем на кнопку Enter.



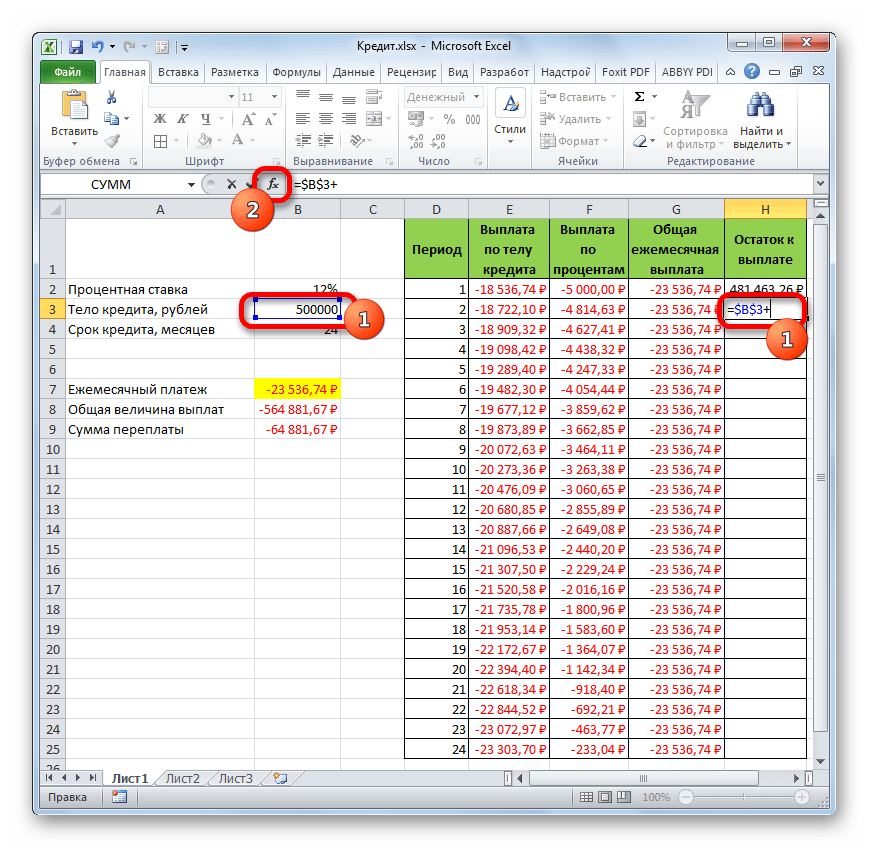
16. А вот вычисление остатка к выплате после второго и последующих месяцев будет несколько сложнее. Для этого нам нужно отнять от тела кредита на начало кредитования общую сумму платежей по телу займа за предыдущий период. Устанавливаем знак «=» во второй ячейке столбца «Остаток к выплате». Далее указываем ссылку на ячейку, в которой содержится первоначальная сумма кредита. Делаем её абсолютной, выделив и нажав на клавишу F4. Затем ставим знак «+», так как второе значение у нас и так будет отрицательным. После этого кликаем по кнопке «Вставить функцию».



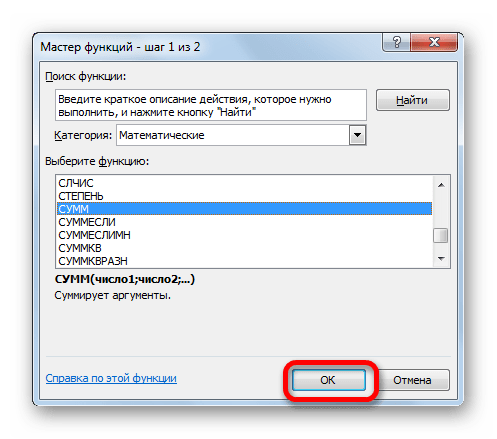
17. Запускается Мастер функций, в котором нужно переместиться в категорию «Математические». Там выделяем надпись «СУММ» и жмем на кнопку «OK».



18. Запускается окно аргументов функции СУММ. Указанный оператор служит для того, чтобы суммировать данные в ячейках, что нам и нужно выполнить в столбце «Выплата по телу кредита». Он имеет следующий синтаксис:

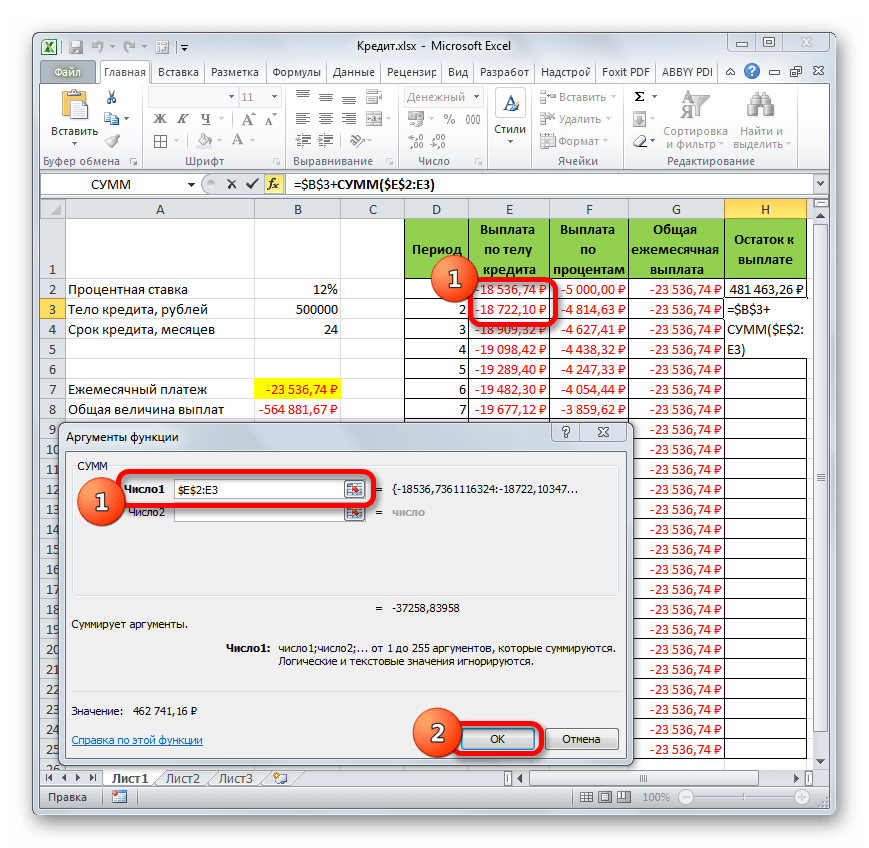
    =СУММ(число1;число2;…)

    В качестве аргументов выступают ссылки на ячейки, в которых содержатся числа. Мы устанавливаем курсор в поле «Число1». Затем зажимаем левую кнопку мыши и выделяем на листе первые две ячейки столбца «Выплата по телу кредита». В поле, как видим, отобразилась ссылка на диапазон. Она состоит из двух частей, разделенных двоеточием: ссылки на первую ячейку диапазона и на последнюю. Для того, чтобы в будущем иметь возможность скопировать указанную формулу посредством маркера заполнения, делаем первую часть ссылки на диапазон абсолютной. Выделяем её и жмем на функциональную клавишу F4. Вторую часть ссылки так и оставляем относительной. Теперь при использовании маркера заполнения первая ячейка диапазона будет закреплена, а последняя будет растягиваться по мере продвижения вниз. Это нам и нужно для выполнения поставленных целей. Далее жмем на кнопку «OK».



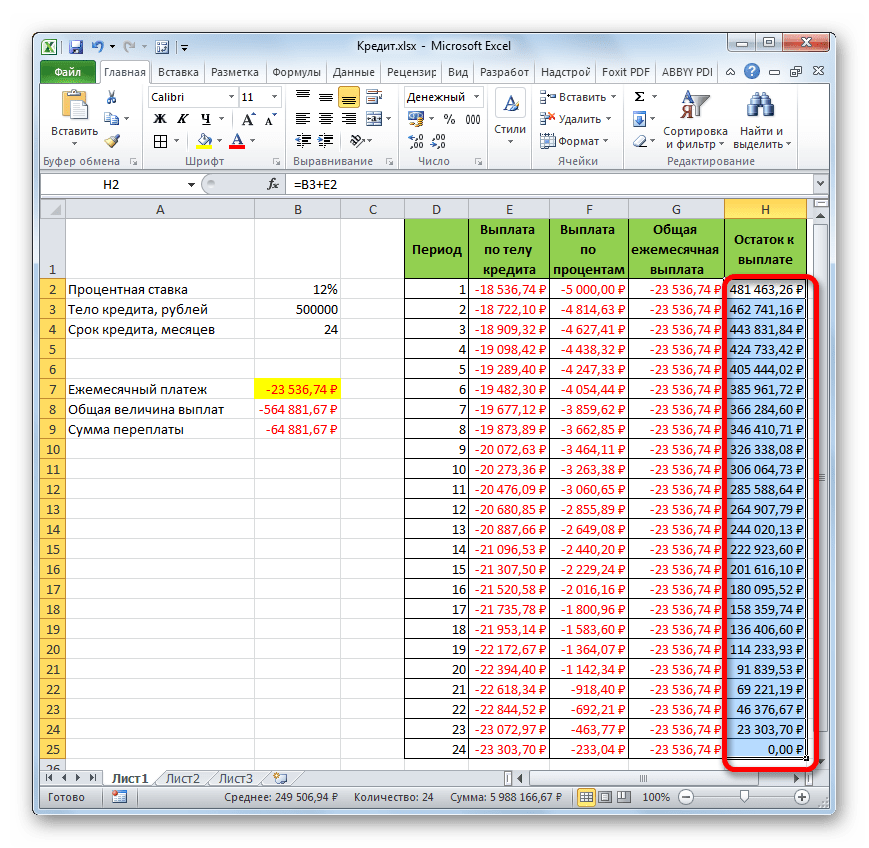
19. Итак, результат остатка кредитной задолженности после второго месяца выводится в ячейку. Теперь, начиная с данной ячейки, производим копирование формулы в пустые элементы столбца с помощью маркера заполнения.



20. Помесячный расчет остатков к оплате по кредиту сделан за весь кредитный период. Как и положено, на конец срока эта сумма равна нулю.

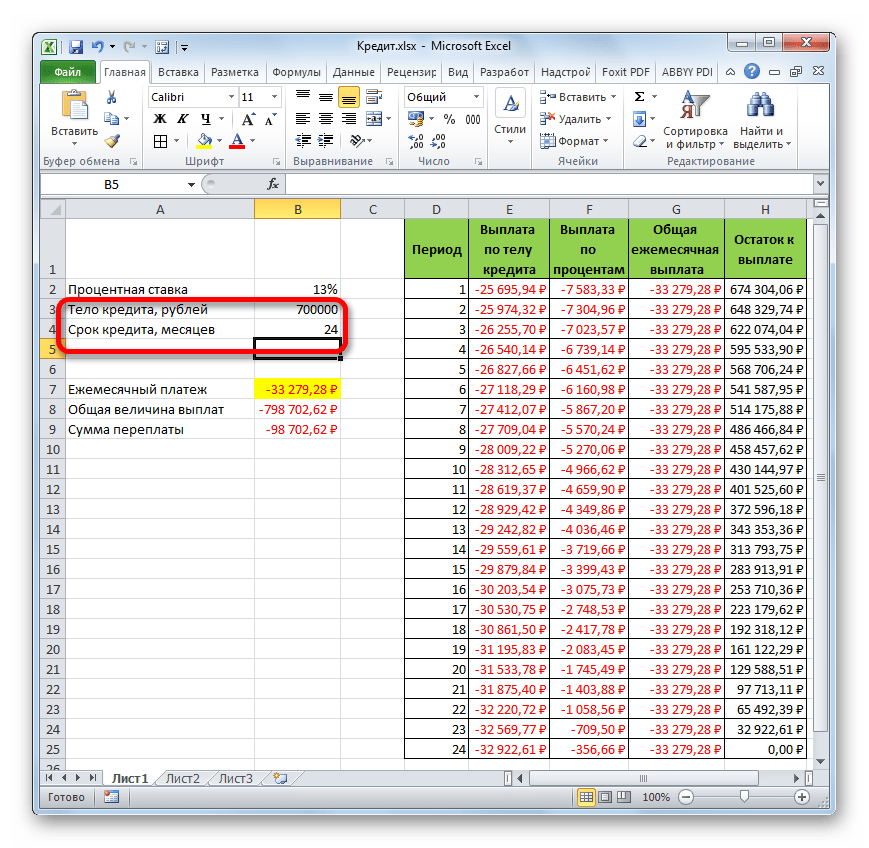
Таким образом, мы произвели не просто расчет оплаты по кредиту, а организовали своеобразный кредитный калькулятор. Который будет действовать по аннуитетной схеме. Если в исходной таблице мы, например, поменяем величину займа и годовой процентной ставки, то в итоговой таблице произойдет автоматический пересчет данных. Поэтому её можно использовать не только один раз для конкретного случая, а применять в различных ситуациях для расчета кредитных вариантов по аннуитетной схеме.

Урок: Финансовые функции в Excel

Как видим, при помощи программы Excel в домашних условиях можно без проблем рассчитать общий ежемесячный кредитный платеж по аннуитетной схеме, используя для этих целей оператор ПЛТ. Кроме того, при помощи функций ОСПЛТ и ПРПЛТ можно произвести расчет величины платежей по телу кредита и по процентам за указанный период. Применяя весь этот багаж функций вместе, существует возможность создать мощный кредитный калькулятор, который можно будет использовать не один раз для вычисления аннуитетного платежа.

Excel – это универсальный аналитическо-вычислительный инструмент, который часто используют кредиторы (банки, инвесторы и т.п.) и заемщики (предприниматели, компании, частные лица и т.д.).

Быстро сориентироваться в мудреных формулах, рассчитать проценты, суммы выплат, переплату позволяют функции программы Microsoft Excel.

Как рассчитать платежи по кредиту в Excel

Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:

1. Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.

Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.

Расчет аннуитетных платежей по кредиту в Excel

Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:

А = К * S

где:

• А – сумма платежа по кредиту;
• К – коэффициент аннуитетного платежа;
• S – величина займа.

Формула коэффициента аннуитета:

К = (i * (1 + i)^n) / ((1+i)^n-1)

• где i – процентная ставка за месяц, результат деления годовой ставки на 12;
• n – срок кредита в месяцах.

В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:

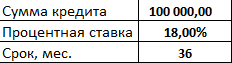
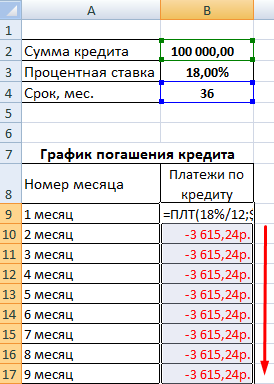
1. Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.



2. Составим график погашения кредита. Пока пустой.



3. В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).

Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.



Расчет платежей в Excel по дифференцированной схеме погашения

Дифференцированный способ оплаты предполагает, что:

• сумма основного долга распределена по периодам выплат равными долями;
• проценты по кредиту начисляются на остаток.

Формула расчета дифференцированного платежа:

ДП = ОСЗ / (ПП + ОСЗ * ПС)

где:

• ДП – ежемесячный платеж по кредиту;
• ОСЗ – остаток займа;
• ПП – число оставшихся до конца срока погашения периодов;
• ПС – процентная ставка за месяц (годовую ставку делим на 12).

Составим график погашения предыдущего кредита по дифференцированной схеме.

Входные данные те же:

Составим график погашения займа:

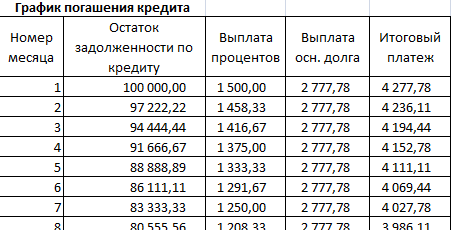
Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.

Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).

Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9<=$B$4;$B$2/$B$4;0).

Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.

Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.

Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:

Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.

Формула расчета процентов по кредиту в Excel

Проведем расчет процентов по кредиту в Excel и вычислим эффективную процентную ставку, имея следующую информацию по предлагаемому банком кредиту:

Рассчитаем ежемесячную процентную ставку и платежи по кредиту:

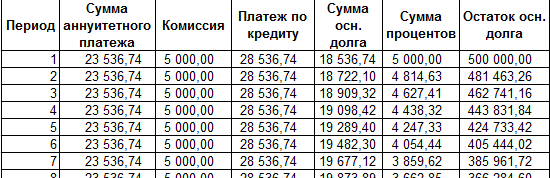
Заполним таблицу вида:

Комиссия берется ежемесячно со всей суммы. Общий платеж по кредиту – это аннуитетный платеж плюс комиссия. Сумма основного долга и сумма процентов – составляющие части аннуитетного платежа.

Сумма основного долга = аннуитетный платеж – проценты.

Сумма процентов = остаток долга * месячную процентную ставку.

Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.

Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:

• взяли кредит 500 000 руб.;
• вернули в банк – 684 881,67 руб. (сумма всех платежей по кредиту);
• переплата составила 184 881, 67 руб.;
• процентная ставка – 184 881, 67 / 500 000 * 100, или 37%.
• Безобидная комиссия в 1 % обошлась кредитополучателю очень дорого.

Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.

Расчет полной стоимости кредита в Excel

Согласно Закону о потребительском кредите для расчета полной стоимости кредита (ПСК) теперь применяется новая формула. ПСК определяется в процентах с точностью до третьего знака после запятой по следующей формуле:

• ПСК = i * ЧБП * 100;
• где i – процентная ставка базового периода;
• ЧБП – число базовых периодов в календарном году.

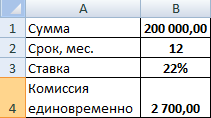
Возьмем для примера следующие данные по кредиту:

Для расчета полной стоимости кредита нужно составить график платежей (порядок см. выше).

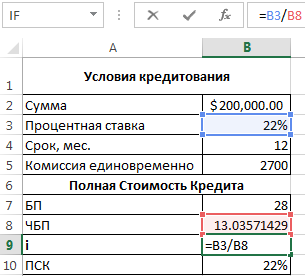
Нужно определить базовый период (БП). В законе сказано, что это стандартный временной интервал, который встречается в графике погашения чаще всего. В примере БП = 28 дней.

Далее находим ЧБП: 365 / 28 = 13.

Теперь можно найти процентную ставку базового периода:

У нас имеются все необходимые данные – подставляем их в формулу ПСК: =B9*B8

Примечание. Чтобы получить проценты в Excel, не нужно умножать на 100. Достаточно выставить для ячейки с результатом процентный формат.

ПСК по новой формуле совпала с годовой процентной ставкой по кредиту.

Скачать кредитный калькулятор в Excel

Таким образом, для расчета аннуитетных платежей по кредиту используется простейшая функция ПЛТ. Как видите, дифференцированный способ погашения несколько сложнее.