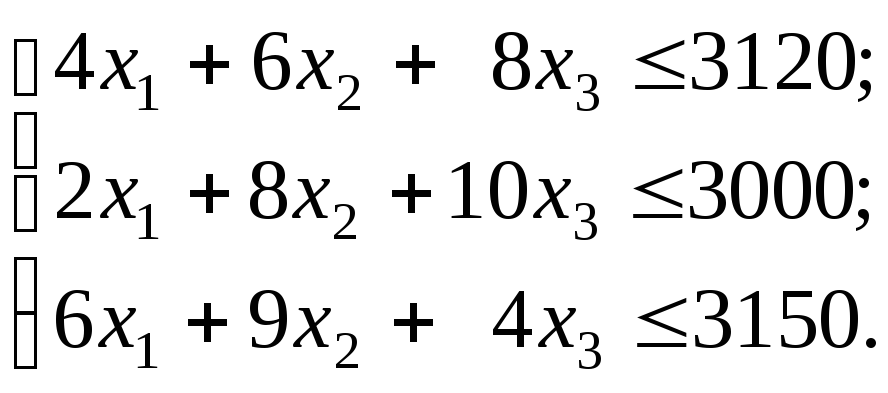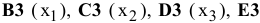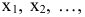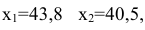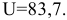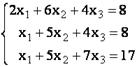15
Лабораторная
работа № 1
Цель работы:изучение современных программных
средств решения задачи линейного
программирования; практическое решение
задач линейного программирования
графическим методом, симплекс-методом
и средствами программыMicrosoftExcel; программная реализация
симплекс-метода на языке программирования
высокого уровня.
1. Теоретическая часть
Для решения задач
линейного программирования в программе
Microsoft
Excel
имеется надстройка Поиск
решения,
обращение
к которой производится из меню Сервис.
Если команда
Поиск решения
отсутствует в меню Сервис,
то требуется установить надстройку
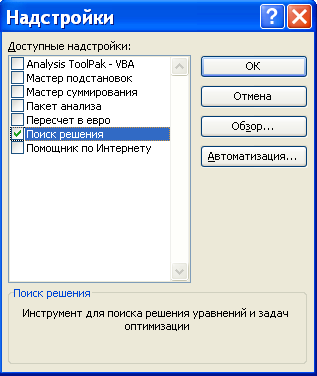
«Поиск решения». Для этого в меню Сервис
выбирается команда Надстройки,
которая открывает диалоговое окно,
показанное на рис. 1.
Рис. 1
Далее в этом окне
устанавливается флажок той надстройки,
которую необходимо загрузить, и нажимается
кнопка OK.
Покажем использование
надстройки
«Поиск решения» на примере решения
следующей задачи.
Постановка задачи
Предприятие
изготавливает и реализует три вида
продукции – P1,
Р2
и Р3.
Для производства продукции используются
три вида ресурсов – комплектующие
изделия, сырье и материалы. Запасы
ресурсов и их расход на изготовление
единицы продукции каждого вида приведены
в табл. 1.
Таблица 1
|
Виды |
Расходы |
Запасы ресурсов, |
||
|
P1 |
P2 |
P3 |
||
|
Комплектующие |
4 |
6 |
8 |
3120 |
|
Сырье |
2 |
8 |
10 |
3000 |
|
Материалы |
6 |
9 |
4 |
3150 |
Прибыль от реализации
единицы продукции каждого вида составляет
240, 210 и 180 денежных единиц для P1,
Р2
и Р3
соответственно.
Требуется определить
производственную программу предприятия
таким образом, чтобы прибыль от реализации
продукции была максимальной.
Математическая модель задачи
Обозначим переменными
x1,
x2
и x3
искомые объемы производства продукции
видов P1,
Р2
и Р2,
а через F
– прибыль предприятия. Тогда математическая
постановка представленной задачи
принимает следующий вид.
Определить значения
переменных x1,
x2
и x3,
для которых достигается максимум целевой
функции
F
=
240 x1
+ 210 х2
+ 180 x3
при ограничениях:
Целевая функция
описывает суммарную прибыль от реализации
произведенной продукции всех трех
видов. Ограничения (1), (2) и (3) учитывают
расход и запасы комплектующих изделий,
сырья и материалов соответственно.
Поскольку объемы производства продукции
не могут быть отрицательными, добавляются
условия
x1
≥ 0; x2
≥ 0; x3
≥ 0.
Порядок оптимального решения задачи
Примерные действия,
необходимые для решения задачи линейного
программирования средствами программы
Excel,
представим в виде последовательности
шагов.
Шаг 1.
Исходные данные задачи записываются
на рабочем листе электронной таблицы.
Один из вариантов показан на рис. 2.
Рис. 2
Замечание.
Если известно исходное допустимое
базисное решение, то можно несколько
ускорить процесс поиска оптимального
решения. Для этого начальные значения
некоторых или всех переменных могут
быть заданы вручную. В данном примере
для их хранения используются ячейки
$B$2,
$C$2
и $D$2.
Если допустимое базисное решение не
задано, то программа Excel
автоматически определяет начальные
значения переменных задачи.
Шаг 2.
В ячейку E3
вводится формула
=СУММПРОИЗВ(В3:D3;
$B$2:$D$2)
для вычисления
текущего значения целевой функции,
которая находит сумму попарных
произведений ячеек (В3:D3)
с коэффициентами при переменных в
выражении целевой функции на ячейки
($B$2:$D$2)
с текущими значениями переменных.
Шаг 3.
Чтобы задать ограничения решаемой
задачи, в ячейки E5,
E6
и E7
копируется формула из ячейки E3.
После этого в указанных ячейках должны
быть получены формулы, представленные
в табл. 2.
Таблица
2
-
Ячейка
Содержание
(формула)E5
=СУММПРОИЗВ(В5:D5;
$B$2:$D$2)E6
=СУММПРОИЗВ(В6:D6;
$B$2:$D$2)E7
=СУММПРОИЗВ(В7:D7;
$B$2:$D$2)
Шаг 4.
После создания таблицы с исходными
данными курсор устанавливается в ячейку
E3,
содержащую формулу для вычисления
целевой функции. Далее в меню Сервис
выбирается
команда Поиск
решения,
которая открывает диалоговое окно,
приведенное на рис. 3.
Рис. 3
В поле Установить
целевую ячейку
окна «Поиск решения», показанного на
рис. 3, должен
появиться адрес ячейки с формулой
целевой функции (в данном примере это
ячейка $E$3).
Затем в этом окне
(рис. 3) заполняются следующие поля этого
окна:
— в поле Равной
переключатель вида экстремума целевой
функции устанавливается в положение
максимальное
значение
(или минимальное
значение
при
соответствующей постановке задачи);
— в поле Изменяя
ячейки
указывается
диапазон ячеек со значениями переменных
задачи, выделяемый на рабочем листе
электронной таблицы (в примере это
ячейки $B$2:$D$2);
— в поле Ограничения
задаются
ограничения исходной задачи. Для этого
курсор устанавливается в поле ввода
ограничений и нажимается кнопка Добавить.
В результате
выводится диалоговое окно «Добавление
ограничения», показанное на рис. 4.
Рис. 4
В этом окне в поле
Ссылка на
ячейку
вводится
адрес ячейки
с формулой соответствующего ограничения
(например, для ограничения (1) это будет
ячейка E5),
а в поле Ограничение
указывается
предельное значение, которое может
принимать выбранное ограничение (в
данном примере правая часть ограничения
(1) находится в ячейке G5).
Следует заметить,
что заполнение полей Ссылка
на ячейку
и Ограничение
в окне «Добавление
ограничения» можно выполнить выделением
соответствующих ячеек рабочего листа
электронной таблицы.
Затем выбирается
вид отношения, связывающего левую и
правую части ограничения, что показано
на рис. 5.
Рис. 5
После нажатия
кнопки Добавить
в окне
«Добавление ограничения»
(или кнопки
ОК
для ввода
последнего ограничения) данное ограничение
попадает в список ограничений решаемой
задачи. С помощью кнопок Удалить
и Изменить
можно удалять
выделенные в списке ограничения или
вносить в них исправления.
Замечание.
В окне «Добавление
ограничения» можно указать, что все или
некоторые переменные должны принимать
только целые значения (рис. 5). Это
позволяет получать решения задач
целочисленного линейного программирования
(полностью или частично целочисленных).
Шаг 5.
После заполнения всех полей окна «Поиск
решения» нажимается кнопка Параметры
(рис. 3),
которая открывает диалоговое окно
«Параметры поиска решения», показанное
на рис. 6.
Рис. 6
В этом окне требуется
установить флажки Линейная
модель
для решения
задачи линейного программирования и
Неотрицательные
значения,
если такое
условие накладываются на все переменные
задачи.
Здесь (рис. 6) также
можно определить параметры процесса
решения: предельное время поиска решения,
максимальное количество итераций,
точность и т.п. Флажок Показывать
результаты
итераций
позволяет по шагам следить за поиском
решения. Флажок Автоматическое
масштабирование
включается
в том случае, когда разброс значений
переменных очень велик.
Шаг 6.
Задав необходимые параметры в окне
«Параметры
поиска решения»,
следует нажать на кнопку Выполнить
для поиска
решения задачи (рис. 3) в
окне «Поиск решения».
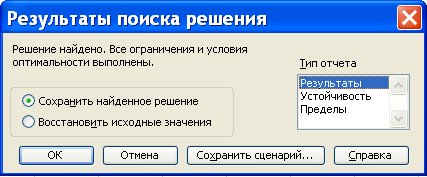
Если решение найдено, то на экран
выводится окно с соответствующим
сообщением (рис. 7).
Рис. 7
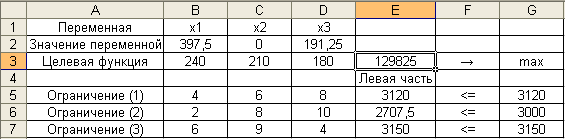
Полученные
результаты отображаются на рабочем
листе электронной таблицы, как это
показано на рис. 8. В частности, значения
переменных — в ячейках $B$2:$D$2,
значение целевой функции – в ячейке
E3.
Рис. 8
Таким образом,
получено оптимальное решение исходной
задачи в виде вектора
,
где,
и
,
для которого значение целевой функцииF
максимально и составляет F*
= 129825.
Результаты решения
задачи линейного программирования
также можно сохранить в виде отдельных
рабочих листов с именами Отчет
по результатам,
Отчет
по устойчивости
и Отчет
по пределам.
Для сохранения
результатов в виде отчетов необходимо
предварительно в поле Тип
отчета
выделить
требуемые типы отчетов (рис. 7). В этом
же окне можно отказаться от полученных
решений и восстановить исходные значения
переменных.
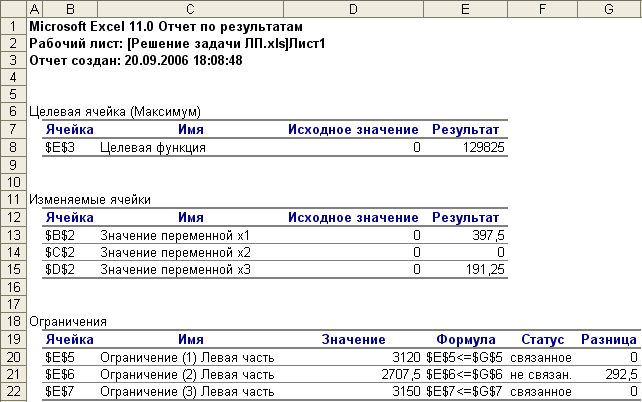
Отчет по результатам
для рассмотренной задачи показан
на рис. 9.
Рис. 9
В данном отчете
представлены оптимальное решение задачи
линейного программирования и его
расположение в области допустимых
решений. В графах Результат
выводятся
оптимальные значения целевой функции
F*
и переменных задачи
,
а также их значения для исходного
базисного решения, с которого начинался
поиск оптимального решения (графаИсходное
значение).
Состояние
ограничений (графа Статус)
характеризует расположение точки
в области допустимых решений. ГрафаРазница
показывает разности между значениями
левых и правых частей ограничений
(невязки). Для связанного ограничения
невязка равна нулю, что свидетельствует
о расположение точки
на границе области допустимых решений,
которая задается этим ограничением.
Если ограничение являются не связанным,
то оно не влияет на оптимальное решение.
Замечание.
В экономической интерпретации связанные
ограничения соответствуют дефицитным
ресурсам. Для не связанных ограничений
графа Разница
показывает оставшиеся объемы
неиспользованных не дефицитных ресурсов.
В рассмотренной задаче ограничения (1)
и (3) соответствуют комплектующим изделиям
и материалам, которые являются дефицитными
ресурсами. Ограничение (2) является не
связанным, т.е. не влияет на оптимальный
план производства продукции по критерию
максимальной прибыли. Это означает, что
второй ресурс (сырье) не использован в
объеме 292,5 ед.
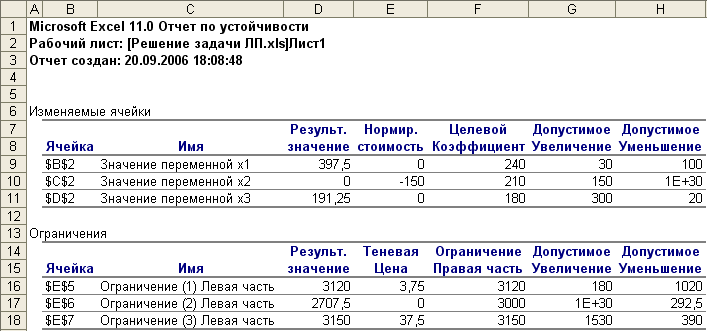
В
отчете по устойчивости (рис.
10) приведены
границы устойчивости переменных задачи
(графы Допустимое
увеличение
и Допустимое
уменьшение
коэффициентов целевой функции), а также
границы устойчивости теневых цен (т.е.
переменных двойственной задачи), в
пределах которых оптимальное решение
не изменяется. Большие
значения пределов (1Е+30)
означают фактическое
отсутствие соответствующих границ,
т.е. переменная может изменяться до
бесконечности.
Рис. 10
В графе Нормированная
стоимость
элемент во второй строке
(-150) показывает,
на сколько уменьшится значение функции,
если в решении переменную x2
увеличить на единицу. С другой стороны,
при допустимом увеличении коэффициента
функции при неизвестной x2
на 150 единиц значение этой переменной
не изменится, т.е. неизвестная x2
будет равна нулю, а если выйти за пределы
допустимого увеличения (коэффициент
при x2
увеличить более чем на 150), то неизвестная
x2
в решении будет больше нуля.
В
отчете
по пределам
(рис. 11) показаны нижние и верхние пределы
возможного изменения переменных (в
пределах области допустимых решений)
и соответствующие значения целевой
функции (графа Целевой
результат)
при этих изменениях. В частности, если
x1
= 0, а x2
и x3
остаются без изменений, то F
= 2400
+ 2100
+ 180191,25
= 34425; при x3
= 0 и неизменных x1
и x2
получим F
= 240397,5
+ 2100
+ 1800
= 95400.
Рис. 11
Соседние файлы в папке 3922
- #
- #
- #
- #
- #
- #
Задачи линейного программирования относятся к широко распространённому классу задач, встречающихся в различных сферах деятельности: в бизнесе, на производстве, в быту. Как оптимально распорядиться бюджетом или за минимальное время добраться до нужного места в городе, как наилучшим образом спланировать деловые встречи, минимизировать риски капитальных вложений, определить оптимальные запасы сырья на складе – это те задачи, в которых нужно найти наилучшее из всех возможных решений.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Линейное программирование
Линейное программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Слово «программирование» заимствовано из зарубежной литературы, где оно используется в смысле «планирование».
Решение задач линейного программирования с использованием microsoft excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.
Порядок выполнения работы
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить задачу линейного программирования в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- переменных,
- целевой функции (ЦФ),
- ограничений,
- граничных условий;
b) ввести исходные данные в экранную форму:
- коэффициенты ЦФ,
- коэффициенты при переменных в ограничениях,
- правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- формулу для расчета ЦФ,
- формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне «Поиск решения»):
- целевую ячейку,
- направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне «Поиск решения»):
- ячейки со значениями переменных,
- граничные условия для допустимых значений переменных,
- соотношения между правыми и левыми частями ограничений.
Решить задачу:
a) установить параметры решения задачи (в окне «Поиск решения»);
b) запустить задачу на решение (в окне «Поиск решения»);
с) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Возможно эта страница вам будет полезна:
Одноиндексные задачи линейного программирования
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
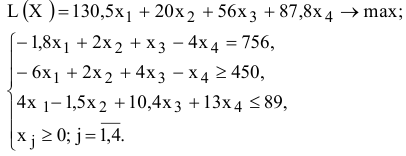
Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
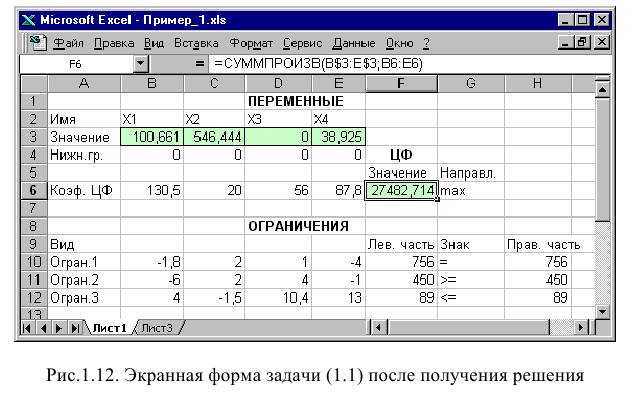
Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис. 1.1.
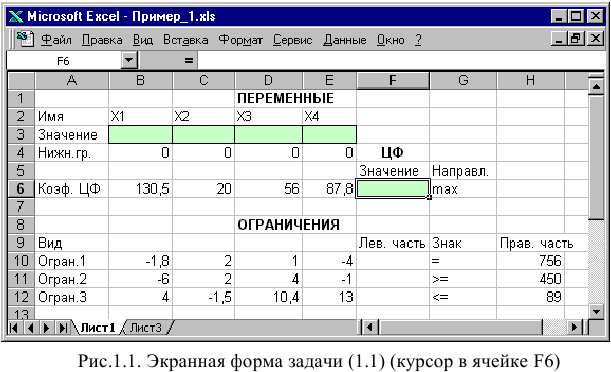
В экранной форме на рис. 1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи линейного программирования. Так, например, переменным задачи (1.1) соответствуют ячейки 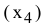
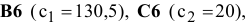
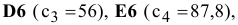
правым частям ограничений соответствуют ячейки
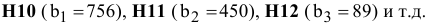
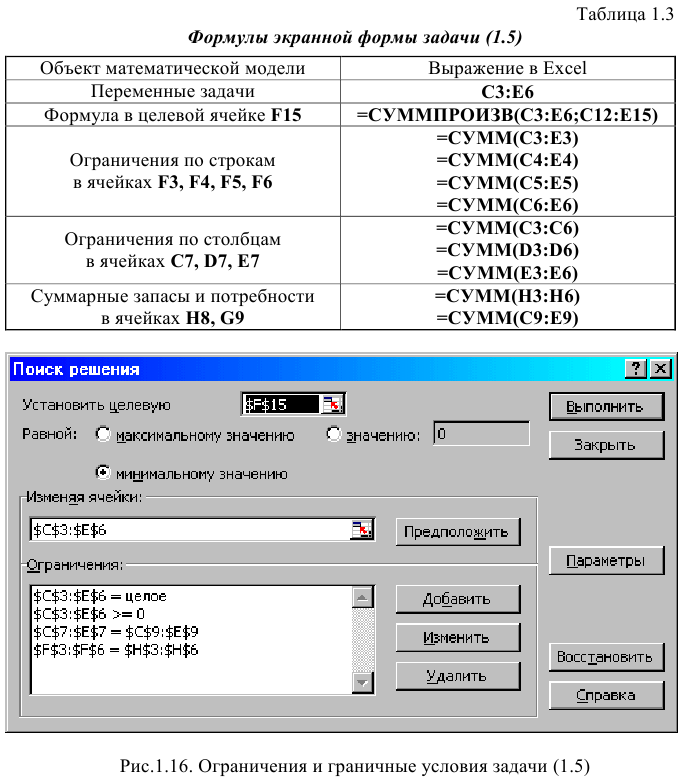
Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ
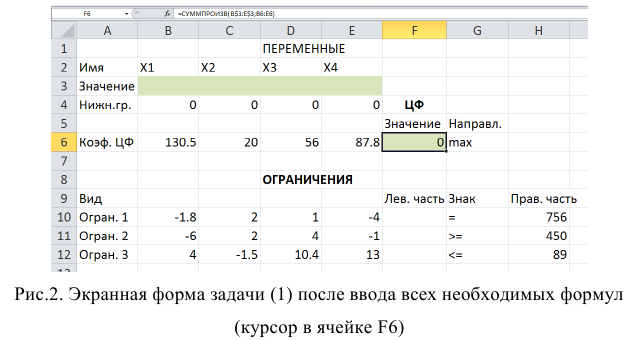
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением
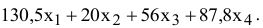
Используя обозначения соответствующих ячеек в Excel (см. рис. 1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6, Е6), то есть
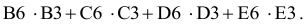
Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу «Enter»
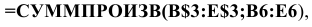
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;
символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись В6:Е6 указывает на ячейки В6, С6, D6 и Е6). После этого в целевой ячейке появится 0 (нулевое значение) (рис. 1.2).
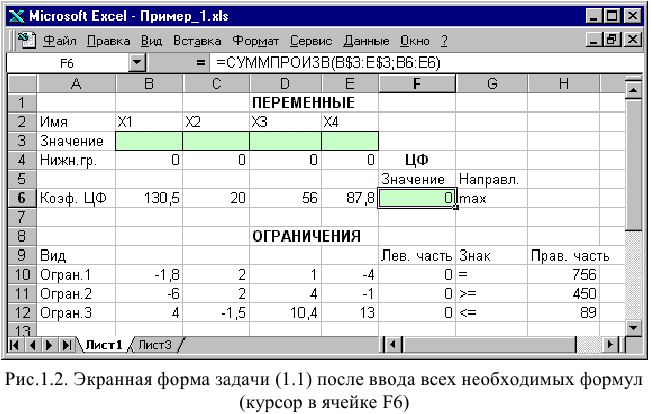
Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима «Вставка функций», который можно вызвать из меню «Вставка» или при нажатии кнопки «
• курсор в поле F6;
• нажав кнопку «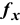
• выберите в окне «Категория» категорию «Математические»;
• в окне «Функция» выберите функцию СУММПРОИЗВ;
• в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение В$3:Е$3, а в строку «Массив 2» — выражение В6:Е6 (рис. 1.3);
• после ввода ячеек в строки «Массив 1» и «Массив 2» в окне «СУММПРОИЗВ» появятся числовые значения введенных массивов (см. рис. 1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
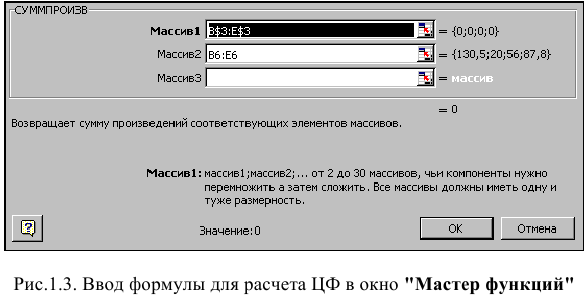
Зависимости для левых частей ограничений
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (В 10, СЮ, D10, ЕЮ — 1-е ограничение; В11, С11, D11, El 1 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл. 1.1.

Как видно из табл. 1.1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:
• поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами «Ctrl-Insert»);
• помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11 и F12, и вставлять в эти поля содержимое буфера (клавишами «Shift-Insert») (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера);
• на экране в полях F10, F11 и F12 появится 0 (нулевое значение) (см. рис. 1.2).
Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле (рис. 1.4 и 1.5).

Задание ЦФ
Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис» (рис. 1.6):
• поставьте курсор в поле «Установить целевую ячейку»;
• введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме — это будет равносильно вводу адреса с клавиатуры;
• введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению».
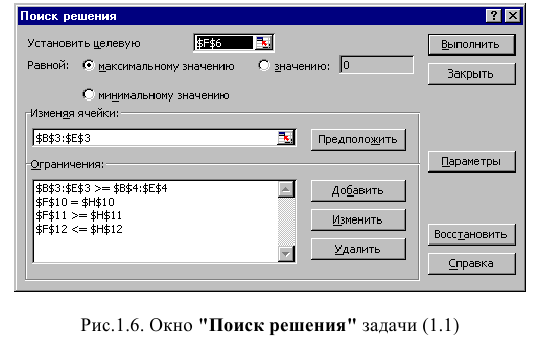
Ввод ограничений и граничных условий
Задание ячеек переменных
В окно «Поиск решения» в поле «Изменяя ячейки» впишите адреса $BS3:$E$3. Необходимые адреса можно вносить в поле «Изменяя ячейки» и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных
В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1.1).
• Нажмите кнопку «Добавить», после чего появится окно «Добавление ограничения» (рис. 1.7).
• В поле «Ссылка на ячейку» введите адреса ячеек переменных $BS3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.
• В поле знака откройте список предлагаемых знаков и выберите >.
• В поле «Ограничение» введите адреса ячеек нижней границы значений переменных, то есть $В$4:$Е$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.
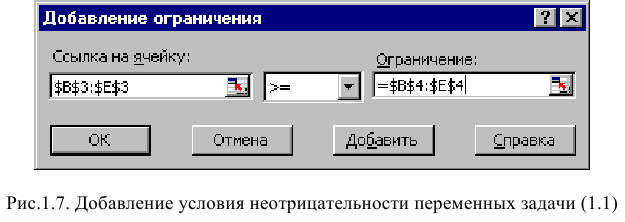
Задание знаков ограничений <. >, =
• Нажмите кнопку «Добавить» в окне «Добавление ограничения».
• В поле «Ссылка на ячейку» введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.
• В соответствии с условием задачи (1.1) выбрать в поле знака необходимый знак, например =.
• В поле «Ограничение» введите адрес ячейки правой части рассматриваемого ограничения, например $Н$10.
• Аналогично введите ограничения: $F$11>=$Н$11, $F$12<=$H$12.
• Подтвердите ввод всех перечисленных выше условий нажатием кнопки ОК.
Окно «Поиск решения» после ввода всех необходимых данных задачи (1.1) представлено на рис. 1.6.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить» или «Удалить» (см. рис. 1.6).
Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры» и заполнить некоторые поля окна «Параметры поиска решения» (рис. 1.8).
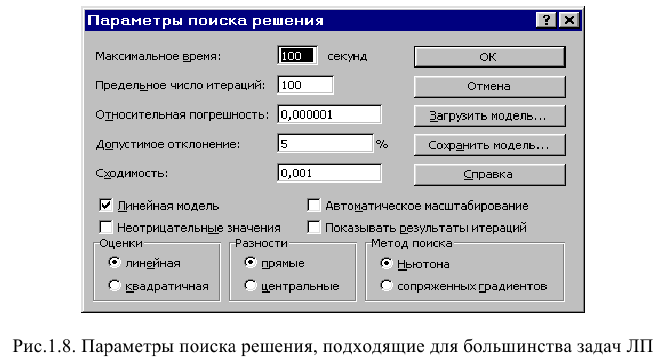
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр «Сходимость» применяется только при решении нелинейных задач.
Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки «ОК».
Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений, представленных на рис. 1.9, 1.10 и 1.11.

Иногда сообщения, представленные на рис. 1.10 и 1.11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует (см. ниже подразд.1.3.5).
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (см. ниже подразд.3.3). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис. 1.12).
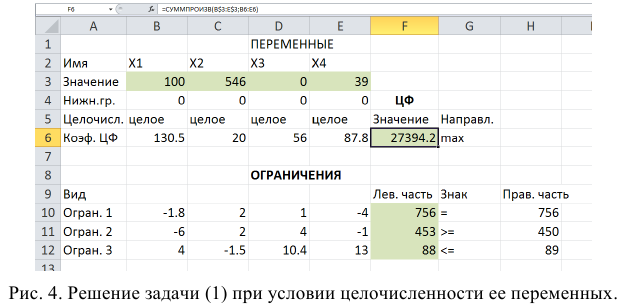
Целочисленное программирование
Допустим, что к условию задачи (1.1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 1.13).
• В окне «Поиск решения» (меню «Сервис»—>»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения следующим образом (рис.1.14):
- в поле «Ссылка на ячейку» введите адреса ячеек переменных задачи, то есть $В$3:$Е$3;
- в поле ввода знака ограничения установите «целое»;
- подтвердите ввод ограничения нажатием кнопки «ОК».
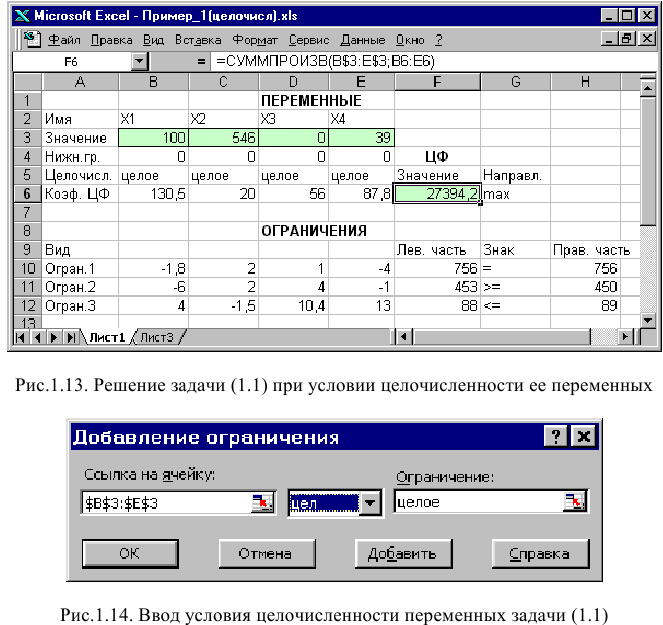
На рис. 1.13 представлено решение задачи (1.1), к ограничениям которой добавлено условие целочисленности значений ее переменных.
Двухиндексные задачи линейного программирования
Двухиндексные задачи линейного программирования вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ.
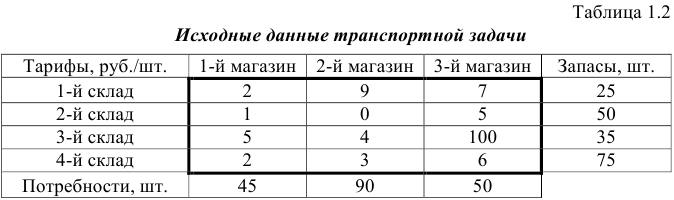
Рассмотрим решение двухиндексной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара со складов в магазины (табл. 1.2).
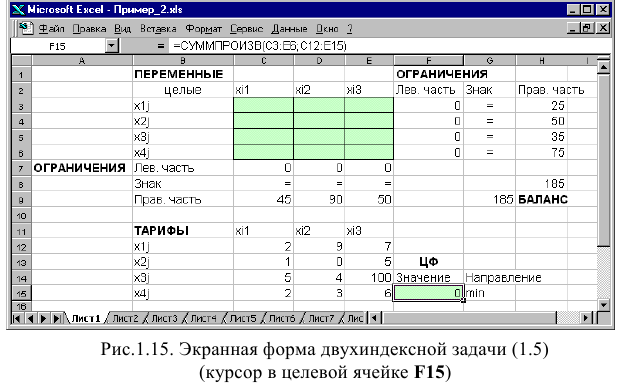
Целевая функция и ограничения данной задачи имеют вид
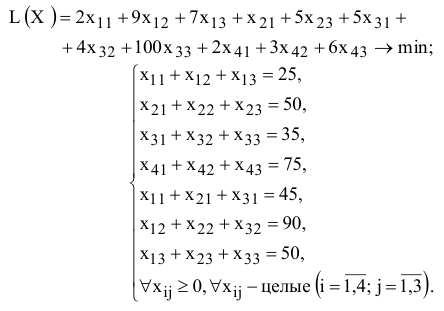
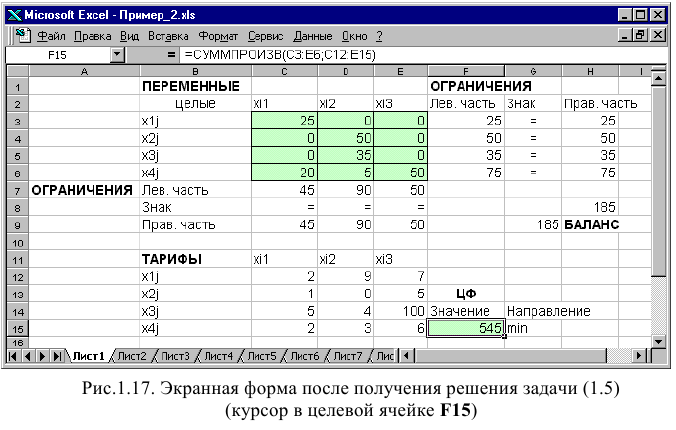
Экранные формы, задание переменных, целевой функции, ограничений и граничных условий двухиндексной задачи (1.5) и ее решение представлены на рис. 1.15, 1.16, 1.17 и в табл. 1.3.
Задачи с булевыми переменными
Частным случаем задач с целочисленными переменными являются задачи, в результате решения которых искомые переменные 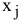
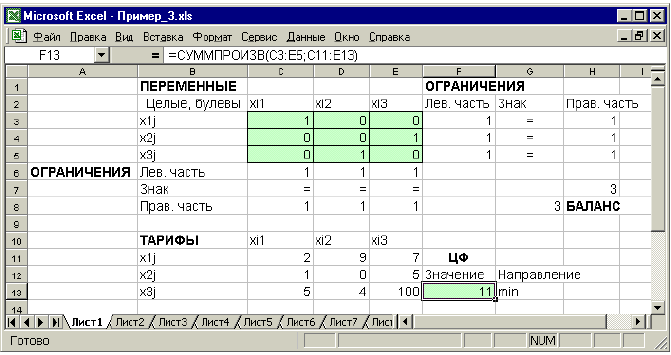
Рис. 1.18. Решение двухиндексной задачи с булевыми переменными
Помимо задания требования целочисленности (см. подразд.1.3.2) при вводе условия задач с булевыми переменными необходимо:
• для наглядности восприятия ввести в экранную форму слово «булевы» в качестве характеристики переменных (см. рис. 1.18);
• в окне «Поиск решения» добавить граничные условия, имеющие смысл ограничения значений переменных по их единичной верхней границе (рис. 1.19).
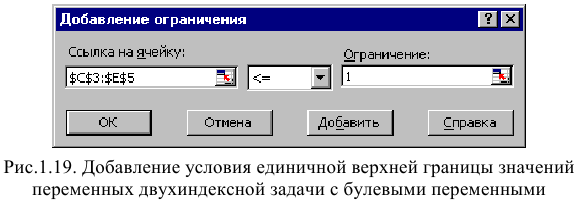
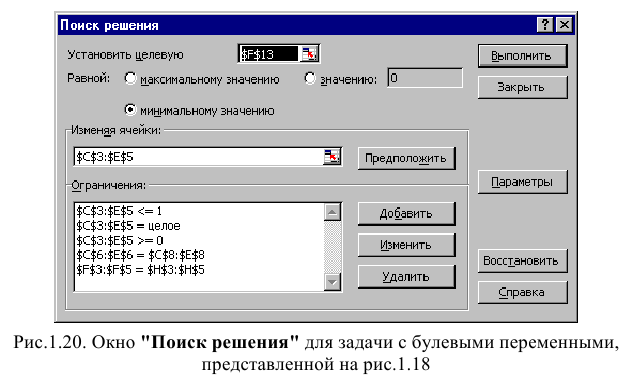
Вид окна «Поиск решения» для задачи с булевыми переменными, представленной на рис. 1.18, приведен на рис. 1.20.
Возможные ошибки при вводе условий задач линейного программирования
Если при решении задачи линейного программирования выдается сообщение о невозможности нахождения решения, то возможно, что причина заключается в ошибках ввода условия задачи в Excel.
Как решить задачу линейного программирования в excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЗЛП) в табличном редакторе Microsoft Excel. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить ЗЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия. 1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- • переменных,
- • целевой функции (ЦФ),
- • ограничений,
- • граничных условий;
b) ввести исходные данные в экранную форму:
- • коэффициенты ЦФ,
- • коэффициенты при переменных в ограничениях,
- • правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- • формулу для расчета ЦФ,
- • формулы для расчета значений левых частей ограничений; с!) задать ЦФ (в окне «Поиск решения»):
- • целевую ячейку,
- • направление оптимизации ЦФ;
е) ввести ограничения и граничные условия (в окне «Поиск решения»):
- • ячейки со значениями переменных,
- • граничные условия для допустимых значений переменных,
- • соотношения между правыми и левыми частями ограничений. 2. Решить задачу:
a)установить параметры решения задачи (в окне «Поиск решения»,);
b) запустить задачу на решение (в окне «Поиск решения»,);
c) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Одноиндексные ЗЛП
Рассмотрим пример нахождения решения для следующей одноиндексной ЗЛП:
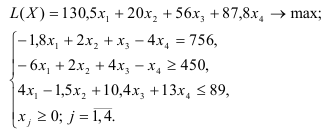
- Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1) вместе с введенными в нее исходными данными представлена на рис.1.
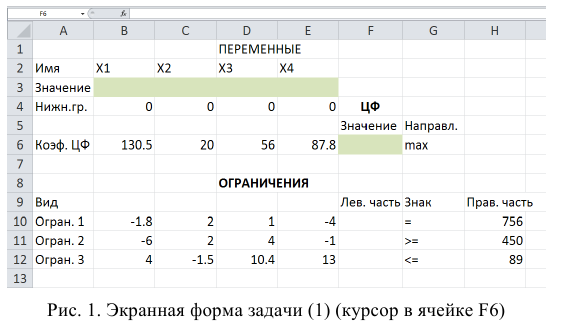
В экранной форме на рис. 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Так, например, переменным задачи (1) соответствуют ячейки
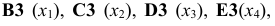
коэффициентам ЦФ соответствуют ячейки
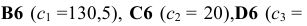
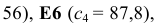
правым частям ограничений соответствуют ячейки
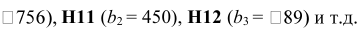
- Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ.
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1 (значение ЦФ определяется выражением
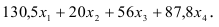
Используя обозначения соответствующих ячеек в Excel (см. рис. 1), формулу для расчета ЦФ (2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6,E6):
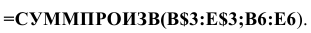
После этого в целевой ячейке появится 0 (нулевое значение) (рис. 2).
Зависимости для левых частей ограничений
Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи(ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, С10, D10, Е10 — 1-е ограничение; В11, C11,D11, Е11 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, записать самостоятельно. Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле. Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис». Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры»и заполнить некоторые поля окна «Параметры поиска решения».
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее32 767. Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее. Параметр «Сходимость» применяется только при решении нелинейных задач. Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода. Подтвердите установленные параметры нажатием кнопки «ОК». Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений:
• Сообщение об успешном решении задачи
• Сообщение при несовместной системе ограничений задачи
• Сообщение при неограниченности ЦФ в требуемом направлении Иногда второе и третье сообщения свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условийзадачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра»Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (будет рассмотрено позже). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис.3).
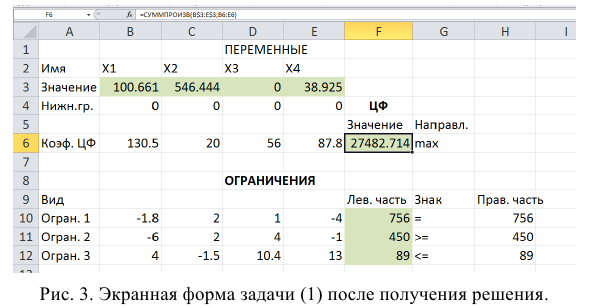
Целочисленное программирование
Допустим, что к условию задачи (1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 4).
• В окне «Поиск решения» (меню «Сервис»—►»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения целочисленности. Сравните результаты.
Получите у преподавателя индивидуальные задания.
Примеры решения экономических задач Задача 1.
Средства очистки пола оценивают по следующим трем показателям:
- • очищающие свойства;
- • дезинфицирующие свойства;
- • раздражающее воздействие на кожу.
Каждый из этих показателей измеряется по линейной шкале от 0 до 100. Продукт на рынке должен иметь по крайней мере 60 ед. очищающих свойств и по крайней мере 60 ед. дезинфицирующих свойств по соответствующей шкале. При этом раздражающее воздействие на кожу должно быть минимальным. Конечный продукт должен быть смесью трех основных очистителей, характеристики которых приведены в таблице.
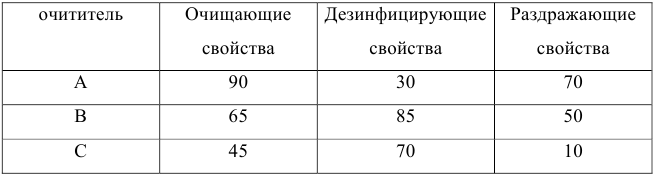
Составим математическую модель задачи. Пусть 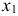
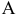
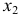
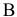
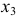
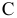
Целевая функция: 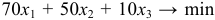
Ограничения:
Решение задачи с помощью MS Excel.
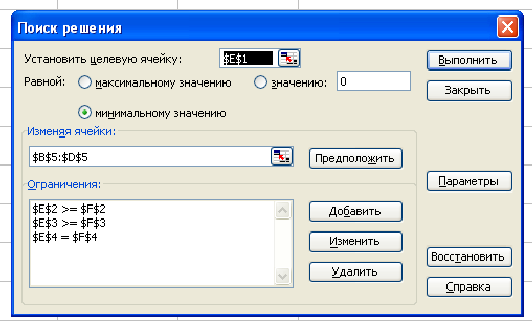
Заполним таблицу, содержащую исходные данные. Заполним диалоговое окно
«Поиск решения».
Щелкнув по кнопке ОК, мы получаем на месте исходной таблицы — таблицу с найденными оптимальными значениями. В результате в таблице получим значение целевой функции — 31,4 ед. раздражающего воздействия на кожу при
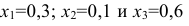
(т.е. очистители 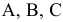
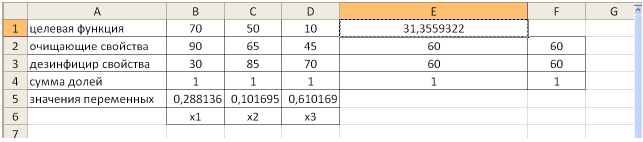
Задача 2.
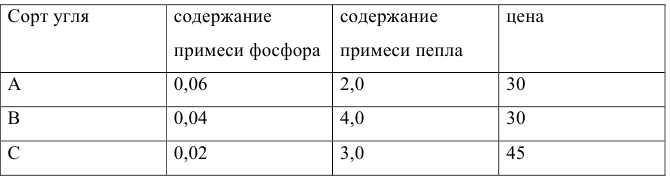
Фирме требуется уголь с содержанием фосфора не более 0,03% и с примесью пепла не более 3,25%. Доступны 3 сорта угля 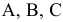
Как следует их смешать, чтобы удовлетворить ограничениям на примеси и минимизировать цену?
Решение задач математического программирования с помощью надстройки «Поиск решения» ЭТ Excel
Задачи линейного программирования, целочисленного программирования и ряд задач нелинейного программирования могут быть решены с помощью стандартного прикладного программного обеспечения. Например, в ЭТ MS Excel для этого имеется модуль «Поиск решения», вызываемый командой меню «Сервис/Поиск решения». Для активизации данного модуля необходимо выполнить команду «Сервис/Надстройки» и установить флажок напротив строки меню «Поиск решения».
Рассмотрим пример применения «Поиска решения» на основе решения задачи оптимизации портфеля ценных бумаг — одной из классических задач управления финансовыми средствами.
Постановка задачи. Перед инвестором стоит задача на основе информации, представленной в таблице 1, разместить имеющиеся средства так, чтобы получить максимальную прибыль за 1 период планирования (1 год), при этом должны быть выполнены следующие условия:
- Суммарный объем капитала составляет 100 000 $;
- доля средств, вложенная в один из объектов, не может превышать 25%;
- более 40% всех средств должны быть вложены в долгосрочные активы;
- доля высокорисковых активов не может превышать трети от суммарного объема.
Таблица 1 — Информация об объектах инвестирования
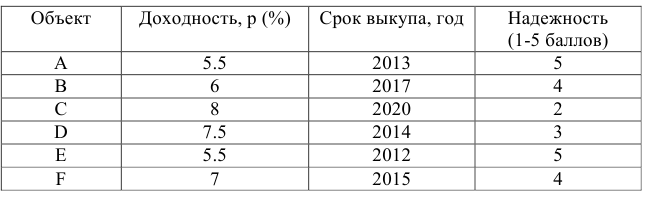
Построим экономико-математическую модель задачи.
Искомые переменные — объемы средств, вложенные в активы: 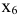
Прибыль, которую получит инвестор, задается целевой функцией:
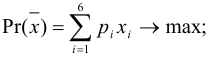
Сформируем ограничения:
Ограничения на суммарный объем активов —
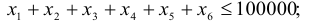
Ограничение на размер доли каждого актива
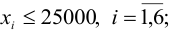
Необходимость долгосрочного инвестирования (например, более 3 лет)
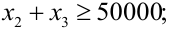
Учет необходимости снижения риска —
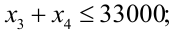
Естественное экономическое ограничение — неотрицательность искомых переменных —
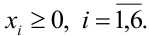
Для решения задачи выполним следующие шаги.
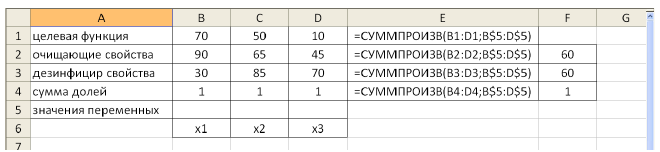
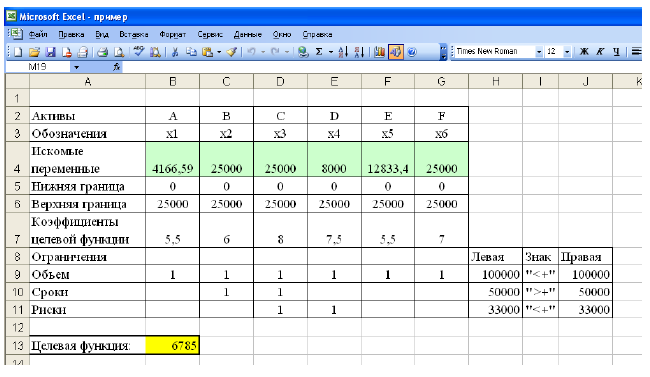
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 1.
Ячейки В13, Н9-Н11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Суммпроизв(…), аргументами которой являются диапазоны B4-G4 и диапазоны соответствующих параметров.
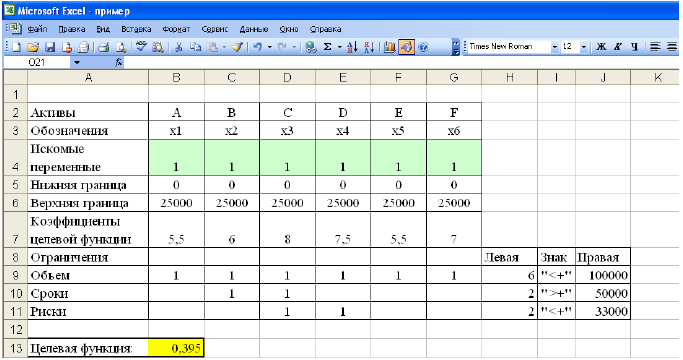
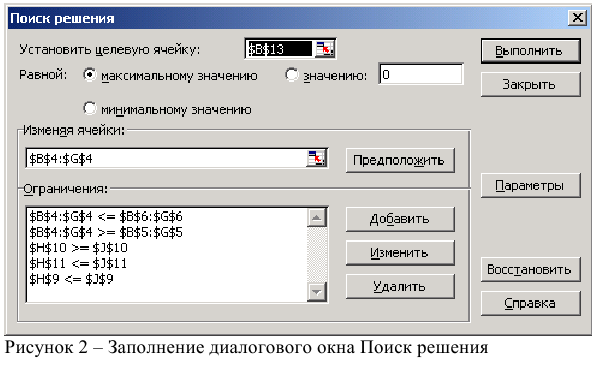
Рисунок 1 — Исходные данные для решения ЗЛП
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 13), содержащей целевую функцию, указать тип целевой функции,
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В4 до G4).
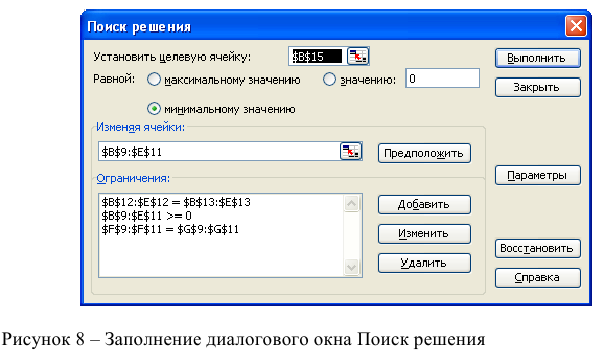
Затем последовательно заполнить все ограничения (Пример на рисунке 2.)
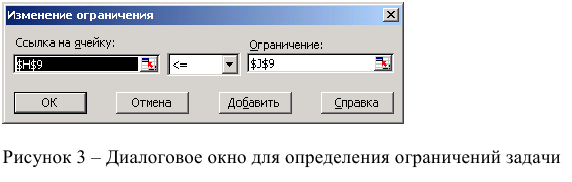
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить».
Далее, если это необходимо, устанавливаются особые значения параметров (кнопка «Параметры»).
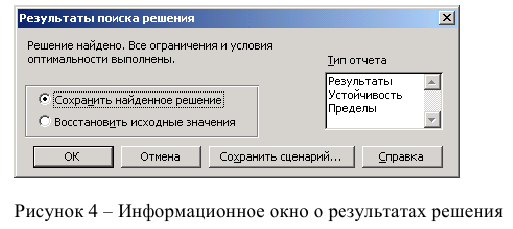
Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 5.
Рисунок 5 — Результаты решения задачи
На рисунке 6 представлена структура инвестиционного портфеля.
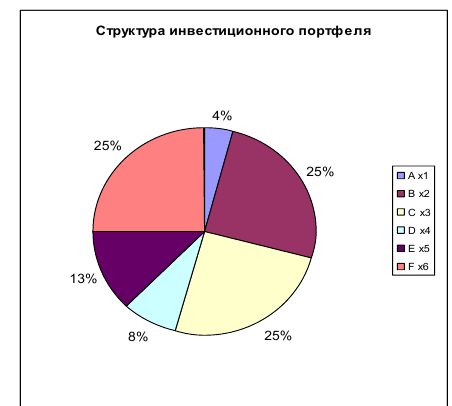
На основе решения проводится анализ, и принимаются соответствующие управленческие решения.
Технология решения транспортной задачи
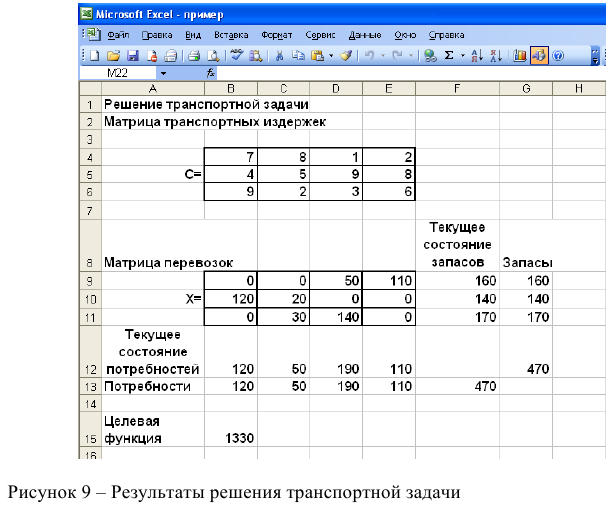
1. На рабочем листе представим необходимую для решения информацию, согласно рисунку 7.
Ячейки В15 содержит формулу Суммпроизв(…), аргументами которой являются диапазоны В4-Е6 и В9-Е11. Ячейки F9-F11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Сумм(…), аргументами которой являются диапазоны В9-Е9, В10-Е 10 и В11 -Е11. Аналогично определяются формулы в В12-Е 12.
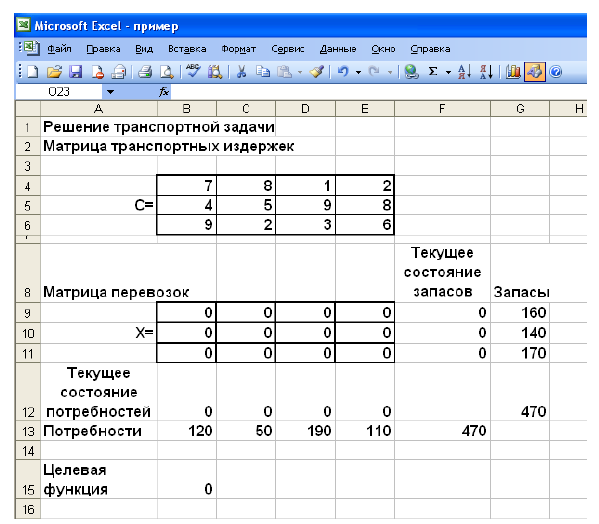
Рисунок 7 — Исходные данные для решения ЗЛП
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 15), содержащей целевую функцию, указать тип целевой функции (минимум),
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В9 до Е11).
Затем последовательно заполнить все ограничения (Пример на рисунке 8.)
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить». Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 9.
Технология решения задачи нелинейного программирования
Построить математическую модель и решить задачу потребительского выбора для заданной функции полезности 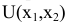
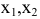
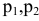
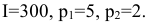
доходе I. Найти максимальное значение функции полезности.
Построим математическую модель задачи потребительского выбора:
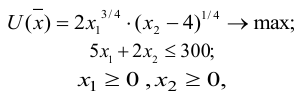
где 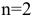
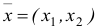
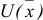
Набор, который является решением задачи потребительского выбора, называется оптимальным потребительским набором, или точкой локального рыночного равновесия потребителя. Поставленная задача — задача потребительского выбора — является задачей нелинейного программирования.
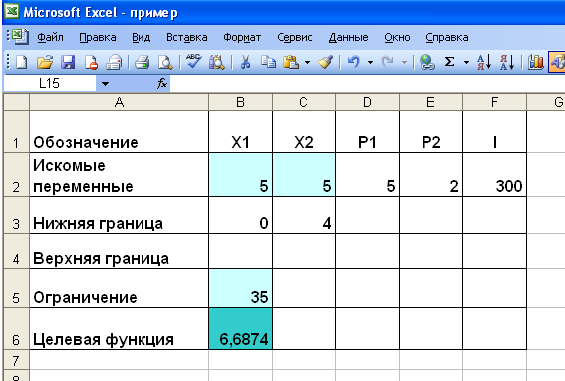
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 10.
Ячейки В5, В6 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае ячейка В5 содержит формулу «=D2B2+E2C2», а ячейка В6 содержит формулу «=2В2Л(3/4)(С2-4)А(1/4)».
Рисунок 10 — Исходные данные для решения ЗНП
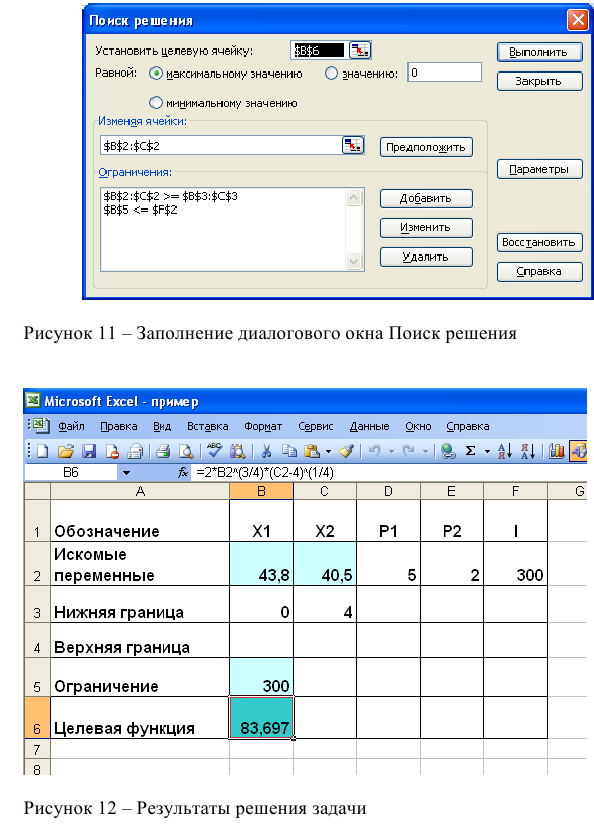
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Аналитическое решение задачи нелинейного программирования.
В рассматриваемом случае ограничение можно записать в виде строгого равенства, так как оптимальное решение достигается при полном использовании имеющихся средств.
Для решения классической задачи нелинейного программирования применим метод множителей Лагранжа, для этого составим функцию Лагранжа:
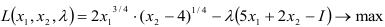
Найдем точки экстремума функции Лагранжа.
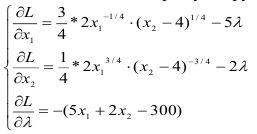
Приравняем каждое уравнение к 0:
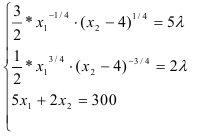
С помощью преобразований — разделим первое уравнение системы на второе, перейдем к системе:
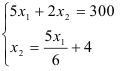
Подставим второе уравнение в первое и построим аналитические функции спроса:
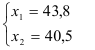
Максимальное значение функции полезности-
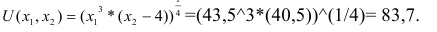
Решением задачи потребительского выбора будет набор
Возможно эти страницы вам будут полезны:
- Решение задач по математическому программированиюПримеры решения задач по математическому программированиюЗаказать работу по математическому программированиюПомощь по математическому программированиюЗадачи математического программированияЗадача линейного программированияРешение задач по линейному программированиюМетоды решения задач линейного программированияГрафическое решение задач линейного программированияГрафический метод решения задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа по линейному программированиюКурсовая работа по линейному программированию
Ранее я писал, что для принятия решений с учетом ограничивающих факторов может использоваться линейное программирование. Напомню, что этот метод решает проблему распределения ограниченных ресурсов между конкурирующими видами деятельности с тем, чтобы максимизировать или минимизировать некоторые численные величины, такие как маржинальная прибыль или расходы.
При решении задач линейного программирования, во-первых, необходимо составить модель, то есть сформулировать условия на математическом языке. После этого решение может быть найдено графически (см., например, здесь), с использованием надстройки Excel «Поиск решения» (рассмотрено в настоящей заметке) или с помощью специализированных компьютерных программ (см., например, здесь).
Рассмотрим линейное программирование в Excel на примере задачи, ранее решенной графическим методом.
Задача. Николай Кузнецов управляет небольшим механическим заводом. В будущем месяце он планирует изготавливать два продукта (А и В), по которым удельная маржинальная прибыль оценивается в 2500 и 3500 руб., соответственно. Изготовление обоих продуктов требует затрат на машинную обработку, сырье и труд. На изготовление каждой единицы продукта А отводится 3 часа машинной обработки, 16 единиц сырья и 6 единиц труда. Соответствующие требования к единице продукта В составляют 10, 4 и 6. Николай прогнозирует, что в следующем месяце он может предоставить 330 часов машинной обработки, 400 единиц сырья и 240 единиц труда. Технология производственного процесса такова, что не менее 12 единиц продукта В необходимо изготавливать в каждый конкретный месяц. Необходимо определить количество единиц продуктов А и В, которые Николай доложен производить в следующем месяце для максимизации маржинальной прибыли.
Скачать заметку в формате Word, пример в формате Excel
1. Воспользуемся математической моделью построенной в упомянутой заметке. Вот эта модель:
Максимизировать: Z = 2500 * х1 + 3500 *х2
При условии, что: 3 * х1 + 10 * х2 ≤ 330
16 * х1 + 4 * х2 ≤ 400
6 * х1 + 6 * х2 ≤ 240
х2 ≥ 12
х1 ≥ 0
2. Создадим экранную форму и введем в нее исходные данные (рис. 1).
Рис. 1. Экранная форма для ввода данных задачи линейного программирования
Обратите внимание на формулу в ячейке С7. Это формула целевой функции. Аналогично, в ячейки С16:С18 введены формулы для расчета левой части ограничений.
3. Проверьте, если у вас установлена надстройка «Поиск решения» (рис. 2), пропустите этот пункт.
Рис. 2. Надстройка Поиск решения установлена; вкладка «Данные», группа «Анализ»
Если надстройки «Поиск решения» вы на ленте Excel не обнаружили, щелкните на кнопку Microsoft Office, а затем Параметры Excel (рис. 3).
Рис. 3. Параметры Excel
Выберите строку Надстройки, а затем в самом низу окна «Управление надстройками Microsoft Excel» выберите «Перейти» (рис. 4).
Рис. 4. Надстройки Excel
В окне «Надстройки» установите флажок «Поиск решения» и нажмите Ok (рис. 5). (Если «Поиск решения» отсутствует в списке поля «Надстройки», чтобы найти надстройку, нажмите кнопку Обзор. В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.)
Рис. 5. Активация надстройки «Поиск решения»
После загрузки надстройки для поиска решения в группе Анализ на вкладке Данные становится доступна команда Поиск решения (рис. 2).
4. Следующим этапом заполняем окно Excel «Поиск решения» (рис. 6)
Рис. 6. Заполнение окна «Поиск решения»
В поле «Установить целевую ячейку» выбираем ячейку со значением целевой функции – $C$7. Выбираем, максимизировать или минимизировать целевую функцию. В поле «Изменяя ячейки» выбираем ячейки со значениями искомых переменных $C$4:$D$4 (пока в них нули или пусто). В области «Ограничения» с помощью кнопки «Добавить» размещаем все ограничения нашей модели. Жмем «Выполнить». В появившемся окне «Результат поиска решения» выбираем все три типа отчета (рис. 7) и жмем Ok. Эти отчеты нужны для анализа полученного решения. Подробнее о данных, представленных в отчетах, можно почитать здесь.
Рис. 7. Выбор типов отчета
На основном листе появились значения максимизированной целевой функции – 130 000 руб. и изменяемых параметров х1 = 10 и х2 = 30. Таким образом, для максимизации маржинального дохода Николаю в следующем месяце следует произвести 10 единиц продукта А и 30 единиц продукта В.
Если вместо окна «Результат поиска решения» появилось что-то иное, Excel`ю найти решение не удалось. Проверьте правильность заполнения окна «Поиск решения». И еще одна маленькая хитрость. Попробуйте уменьшить точность поиска решения. Для этого в окне «Поиск решения» щелкните на Параметры (рис. 8.) и увеличьте погрешность вычисления, например, до 0,001. Иногда из-за высокой точности Excel не успевает за 100 итераций найти решение. Подробнее о параметрах поиска решения можно почитать здесь.
Рис. 8. Увеличение погрешности вычислений
Изучив алгоритмы «ручного» решения задач линейного программирования, полезно познакомиться и со способом упростить этот процесс. Ясно, что чем сложнее задача, чем больше в ней переменных и условий, тем утомительнее и дольше ее решать. В таких случаях удобно использовать специальные математические пакеты, или доступную многим программу MS Excel (версии 2003, 2007, 2010, 2013 и др.).
Решить задачи линейного программирования в Excel достаточно просто:
- составить математическую модель задачи,
- внести исходные данные задачи и ограничения,
- выделить место под ячейки решения и целевую функцию, ввести ее формулу,
- запустить надстройку Поиск решения,
- установить нужные параметры решения и запустить выполнение.
Программа подберёт оптимальное решение и покажет его в нужных ячейках, вычислит значение целевой функции. При необходимости можно построить отчеты для анализа решения задачи.
Подробнее все эти этапы с пояснениями и скриншотами разобраны ниже в примерах на разных задачах линейного программирования — изучайте, ищите похожие, решайте.
Помогаем студентам: Работы по линейному программированию на заказ
Спасибо за ваши закладки и рекомендации
Линейное программирование: примеры в Excel
Задача 1. Построить математическую модель задачи и решить её средствами Excel. Записать сопряжённую задачу. Провести анализ и сделать выводы по полученным результатам.
Для производства столов и шкафов мебельная фабрика использует различные ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в таблице.
Определить, сколько столов и шкафов фабрике следует выпускать, чтобы прибыль от реализации была максимальной.
Задача 2. Цех производит 8 различных видов деталей для двигателей A, B, C1, C2, C3, D, E6, F имея в своем распоряжении перечисленный ниже парк из 7 видов универсальных станков: 2 шт. -ADF, 3 шт. -SHG, 3 шт. -BSD, 1 шт. -AVP, 1 шт. -BFG, 3 шт. -ABM, 2 шт. -RL.
Время, требуемое для обработки единицы каждого продукта на каждом станке, вклад в прибыль от производства единицы каждого продукта и рыночный спрос на каждый продукт за месяц даны в таблице.
Цех работает 12 часов в день. Каждый месяц содержит 26 рабочих дней. Для упрощения задачи считаем, что возможен произвольный порядок обработки деталей на различных станках.
Составьте оптимальный план производства.
Определите, производство каких продуктов лимитировано рынком, и каких – техническими возможностями цеха. Какие машинные ресурсы должны быть увеличены в первую очередь, чтобы добиться максимального увеличения прибыли (при заданных потребностях рынка)?
Есть ли продукт, который невыгодно производить? Почему? Что нужно изменить, чтобы все продукты стало выгодно производить?
Может пригодиться: транспортные задачи в Excel
Задача 3. Необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ тиамина Т и ниацина Н. Пищевая ценность рациона (в калориях) должна быть не менее заданной. Смесь для цыплят изготавливается из двух продуктов — К и С. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в таблице.
Задача 4. Фирма «Компьютер-сервис» поставляет компьютеры под ключ четырех базовых комплектаций: «домашний», «игровой», «офисный» и «экстрим». Известны средние затраты времени на сборку, проверку и подключение компьютеров. Каждый компьютер приносит определенный уровень прибыли, но спрос ограничен. Кроме того, в плановом периоде ограничен ресурс человеко-часов, отведенных на выполнение каждой производственной операции. Определить, сколько компьютеров каждого типа необходимо произвести в плановом периоде, имея целью максимизировать прибыль.
Задача 5. На лесопилку поступают доски длиной 10 м. По контракту лесопилка должна поставить клиенту не менее 100 досок длиной 5 м, не менее 200 досок длиной 4 м и не менее 300 досок длиной 3 м. Как работникам лесопилки выполнить условия контракта, разрезав наименьшее количество досок?
Помогаем с контрольными по линейному программированию
Задача 6. Компания «Евростройтур» организует экскурсионные автобусные туры по странам Европы. Компания получила 4 новых автобуса и предполагает направить их на маршруты во Францию, Италию, Чехию и Испанию.
Каждый автобус обслуживают 2 водителя. Компанией приглашены 8 водителей, в различной степени знакомых с дорогами европейских стран (в % от экскурсионного маршрута).
Необходимо распределить водителей так, чтобы общий показатель освоения маршрутов был максимальным.
Задача 7. Решить задачу методом ветвей и границ, решая отдельные задачи линейного нецелочисленного программирования с помощью функции «Поиск решения» в Microsoft Excel (в случае, если первая же задача ЛП выдает целочисленное решение, не позволяя ветвить задачу, немного изменить начальные условия).
Состав еды рядовых регламентируется верховной ставкой главнокомандующего, которая устанавливает нижние нормы питания в сутки по основным компонентам: 1500 килокалорий, 100 г белков, 280 г углеводов, 90 г жиров, 1 кг воды. На складах есть 4 вида продуктов, которые выдают защитникам Родины сухим пайком: лимонад, тушенка в маленьких банках, унифицированные наборы горбушек и пирожки с ежевикой. Стоимость этих четырех продуктов соответственно 12 руб., 34 руб., 3 руб. и 20 руб. Какова минимальная сумма, которую должен затратить прапорщик на питание одного солдата?
Задача 8. Предприятие выпускает два вида продукции: Изделие 1 и Изделие 2. На изготовление единицы Изделия 1 требуется затратить a11 кг сырья первого типа, a21 кг сырья второго типа, a31 кг сырья третьего типа.
На изготовление единицы Изделия 2 требуется затратить a12 кг сырья первого типа, a22 кг сырья второго типа, a32 кг сырья третьего типа.
Производство обеспечено сырьем каждого типа в количестве b1 кг, b2 кг, b3 кг соответственно.
Рыночная цена единицы Изделия 1 составляет c1 тыс. руб., а единицы Изделия 2 — c2 тыс.руб.
Требуется:
1) построить экономико – математическую модель задачи;
2) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи графического метода решения задачи линейного программирования.
3) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи табличного симплекс – метода решения задачи линейного программирования.
4) составить план производства изделий, обеспечивающий максимальную выручку от их реализации, используя надстройку «Поиск решения» в среде MS EXCEL.
Полезные ссылки
|
|
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12701 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в EXCEL
history 12 ноября 2015 г.
-
Группы статей
- Системы линейных уравнений
Решим Систему Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL. В этой статье нет теории, объяснено только как выполнить расчеты, используя MS EXCEL.
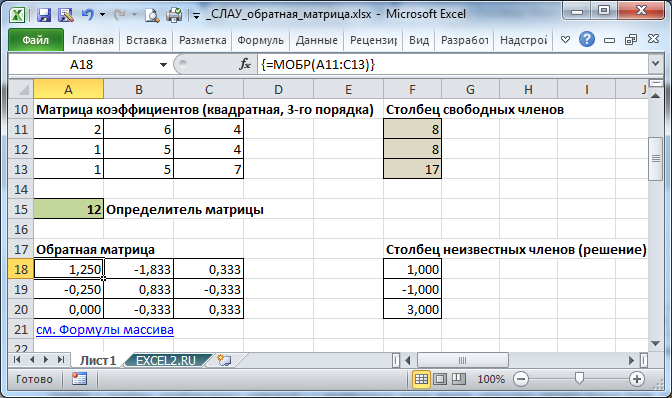
Решим систему из 3-х линейных алгебраических уравнений с помощью обратной матрицы (матричным методом).
Запишем в ячейки основную матрицу системы и столбец свободных членов.
Систему n линейных алгебраических уравнений с n неизвестными можно решать матричным методом только тогда, когда определитель основной матрицы системы отличен от нуля (в противном случае мы имеем линейно зависимые уравнения и соответственно решение систем не единственное). В нашем случае определитель =12.
Для этого выделите ячейки A18:C20 , а в Строке формул введите =МОБР(A11:C13) , затем нажмите CTRL+SHIFT+ENTER .
Решение системы уравнений получим умножением обратной матрицы и столбца свободных членов. Перемножить матрицы можно с помощью формулы массива =МУМНОЖ() .
Для этого выделите ячейки F18:F20 , а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13) , затем нажмите CTRL+SHIFT+ENTER .
В файле примера также приведено решение системы 4-х и 5-и уравнений.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
источники:
http://excel2.ru/articles/reshenie-sistemy-lineynyh-algebraicheskih-uravneniy-slau-metodom-obratnoy-matricy-v-ms-excel
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/