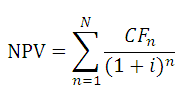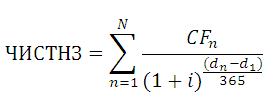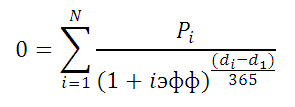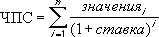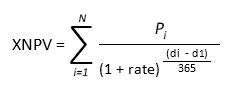Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул
MS
EXCEL.
Начнем с определения, точнее с определений.
Чистой приведённой стоимостью (Net present value, NPV) называют
сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню
(взято из Википедии). Или так:
Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт
cfin.
ru)
Или так:
Текущая
стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика
.
Толковыйсловарь
. —
М
.
:
»
ИНФРА
—
М
«,
Издательство
»
ВесьМир
«.
Дж
.
Блэк
.)
Примечание1
. Чистую приведённую стоимость также часто называют Чистой текущей стоимостью, Чистым дисконтированным доходом (ЧДД). Но, т.к. соответствующая функция MS EXCEL называется
ЧПС()
, то и мы будем придерживаться этой терминологии. Кроме того, термин Чистая Приведённая Стоимость (ЧПС) явно указывает на связь с
Приведенной стоимостью
.
Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма
Приведенных стоимостей
денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.
Совет
: при первом знакомстве с понятием Чистой приведённой стоимости имеет смысл познакомиться с материалами статьи
Приведенная стоимость
.
Это более формализованное определение без ссылок на проекты, инвестиции и ценные бумаги, т.к. этот метод может применяться для оценки денежных потоков любой природы (хотя, действительно, метод NPV часто применяется для оценки эффективности проектов, в том числе для сравнения проектов с различными денежными потоками). Также в определении отсутствует понятие дисконтирование, т.к. процедура дисконтирования – это, по сути, вычисление приведенной стоимости по методу
сложных процентов
.
Как было сказано, в MS EXCEL для вычисления Чистой приведённой стоимости используется функция
ЧПС()
(английский вариант — NPV()). В ее основе используется формула:
CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).
Примечание2
. Т.к. денежный поток может присутствовать не в каждый период, то определение NPV можно уточнить:
Чистая приведённая стоимость — это Приведенная стоимость денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через промежутки времени, кратные определенному периоду (месяц, квартал или год)
. Например, начальные инвестиции были сделаны в 1-м и 2-м квартале (указываются со знаком минус), в 3-м, 4-м и 7-м квартале денежных потоков не было, а в 5-6 и 9-м квартале поступила выручка по проекту (указываются со знаком плюс). Для этого случая NPV считается точно также, как и для регулярных платежей (суммы в 3-м, 4-м и 7-м квартале нужно указать =0).
Если сумма приведенных денежных потоков представляющих собой доходы (те, что со знаком +) больше, чем сумма приведенных денежных потоков представляющих собой инвестиции (расходы, со знаком минус), то NPV >0 (проект/ инвестиция окупается). В противном случае NPV <0 и проект убыточен.
Выбор периода дисконтирования для функции ЧПС()
При выборе периода дисконтирования нужно задать себе вопрос: «Если мы прогнозируем на 5 лет вперед, то можем ли мы предсказать денежные потоки с точностью до месяца/ до квартала/ до года?». На практике, как правило, первые 1-2 года поступления и выплаты можно спрогнозировать более точно, скажем ежемесячно, а в последующие года сроки денежных потоков могут быть определены, скажем, один раз в квартал.
Примечание3
. Естественно, все проекты индивидуальны и никакого единого правила для определения периода существовать не может. Управляющий проекта должен определить наиболее вероятные даты поступления сумм исходя из действующих реалий.
Определившись со сроками денежных потоков, для функции
ЧПС()
нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см.
файл примера, лист NPV
).
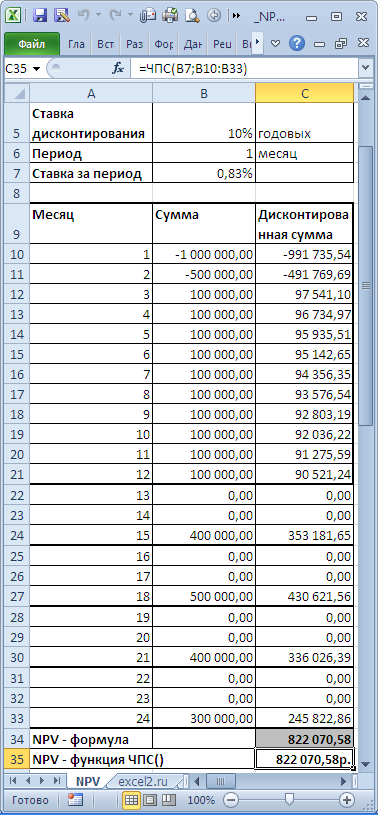
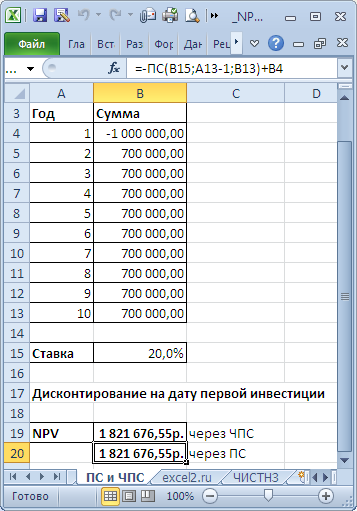
В таблице NPV подсчитан двумя способами: через функцию
ЧПС()
и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.) Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода. Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции
ЧПС()
, а нужно просто прибавить к получившемуся результату (см.
файл примера
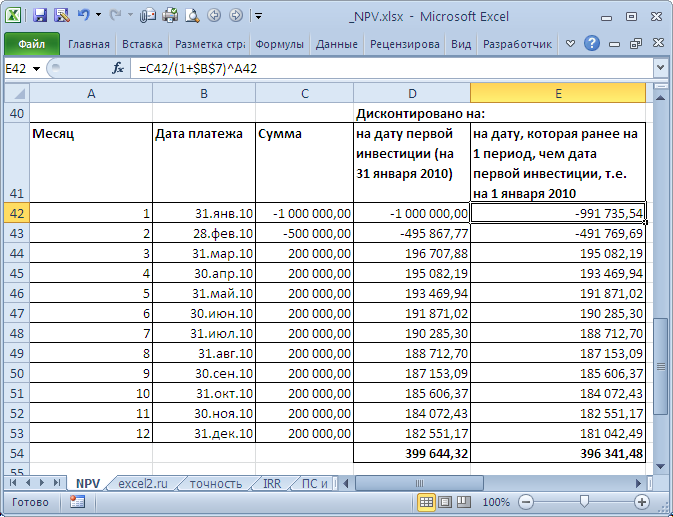
). Сравнение 2-х вариантов дисконтирования приведено в
файле примера
, лист NPV:
О точности расчета ставки дисконтирования
Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см.
файл примера, лист Точность
).
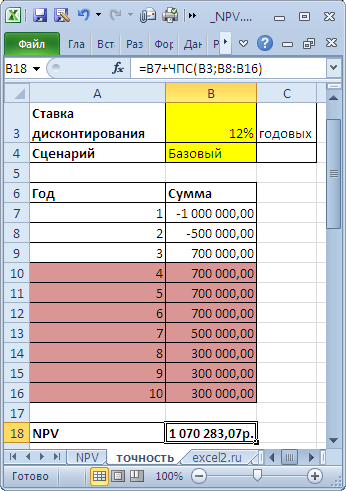
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.
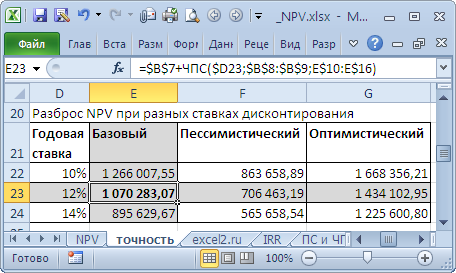
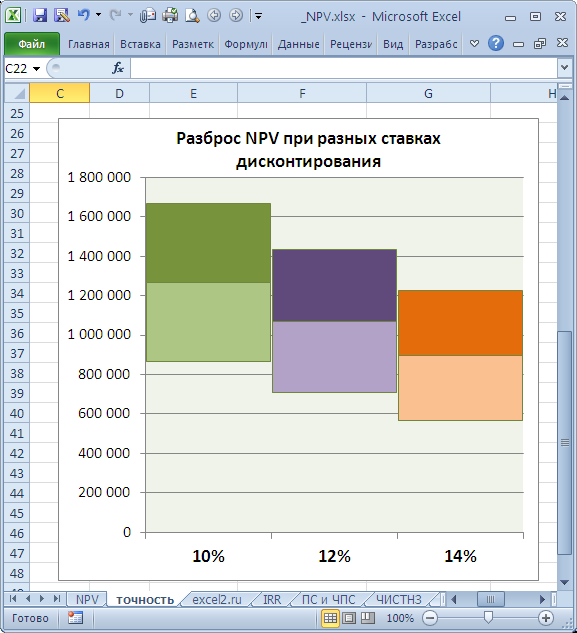
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):
Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.
Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.
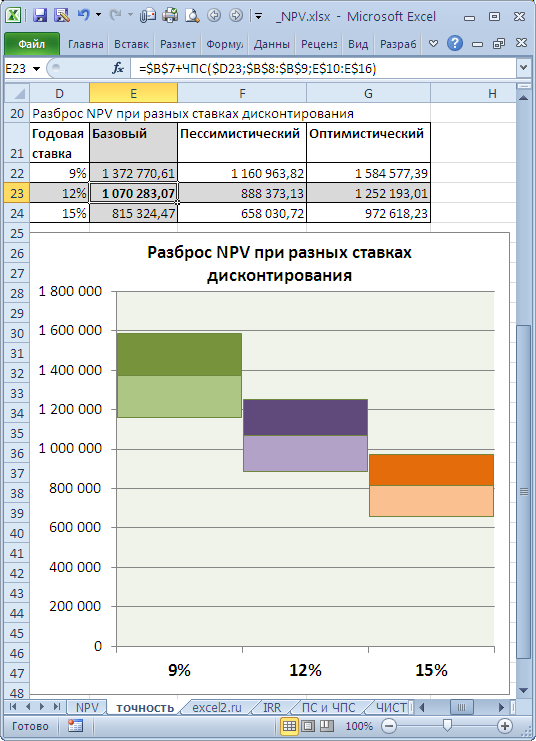
Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0
Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.
Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.
После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.
Внутренняя ставка доходности
IRR
(ВСД)
Внутренняя ставка доходности (англ.
internal rate of return
, IRR (ВСД)) — это ставка дисконтирования, при которой Чистая приведённая стоимость (NPV) равна 0. Также используется термин Внутренняя норма доходности (ВНД) (см.
файл примера, лист IRR
).
Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.
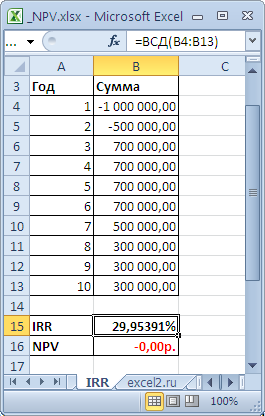
Для расчета IRR используется функция
ВСД()
(английский вариант – IRR()). Эта функция тесно связана с функцией
ЧПС()
. Для одних и тех же денежных потоков (B5:B14) Ставка доходности, вычисляемая функцией
ВСД()
, всегда приводит к нулевой Чистой приведённой стоимости. Взаимосвязь функций отражена в следующей формуле:
=ЧПС(ВСД(B5:B14);B5:B14)
Примечание4
. IRR можно рассчитать и без функции
ВСД()
: достаточно иметь функцию
ЧПС()
. Для этого нужно использовать инструмент
Подбор параметра
(поле «Установить в ячейке» должно ссылаться на формулу с
ЧПС()
, в поле «Значение» установите 0, поле «Изменяя значение ячейки» должно содержать ссылку на ячейку со ставкой).
Расчет NPV при постоянных денежных потоках с помощью функции ПС()
Напомним, что
аннуитет
представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию
ПС()
(см.
файл примера, лист ПС и ЧПС
).
В этом случае все денежные потоки (диапазон
В5:В13
, 9 одинаковых платежей) дисконтируются на дату первой (и единственной) суммы инвестиции, расположенной в ячейке
В4
. Ставка дисконтирования расположена в ячейке
В15
со знаком минус. В этом случае формула
=B4+ЧПС(B15;B5:B13)
дает тот же результат, что и
= B4-ПС(B15;9;B13)
Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за
любые
промежутки времени, то используется функция
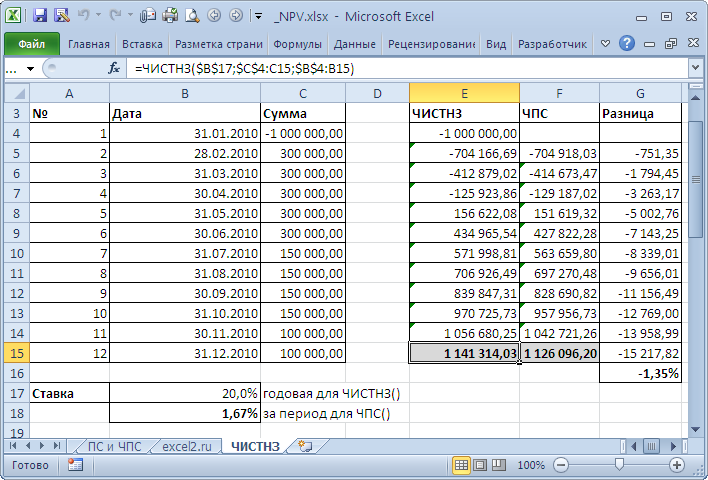
ЧИСТНЗ()
(английский вариант – XNPV()).
Функция
ЧИСТНЗ()
возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:
Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.
Принципиальным отличием от
ЧПС()
является то, что денежный поток привязан не к конкретным периодам, а к датам. Другое отличие: ставка у
ЧИСТНЗ()
всегда годовая, т.к. указана база 365 дней, а не за период, как у
ЧПС()
. Еще отличие от
ЧПС()
: все денежные потоки всегда дисконтируются на дату первого платежа.
В случае, когда платежи осуществляются регулярно можно сравнить вычисления функций
ЧИСТНЗ()
и
ЧПС()
. Эти функции возвращают несколько отличающиеся результаты. Для задачи из
файла примера, Лист ЧИСТНЗ
разница составила порядка 1% (период = 1 месяцу).
Это связано с тем, что у
ЧИСТНЗ()
длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у
ЧПС()
указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет
високосного
года).
Внутренняя ставка доходности ЧИСТВНДОХ()
По аналогии с
ЧПС()
, у которой имеется родственная ей функция
ВСД()
, у
ЧИСТНЗ()
есть функция
ЧИСТВНДОХ()
, которая вычисляет годовую ставку дисконтирования, при которой
ЧИСТНЗ()
возвращает 0.
Расчеты в функции
ЧИСТВНДОХ()
производятся по формуле:
Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).
Примечание5
. Функция
ЧИСТВНДОХ()
используется для
расчета эффективной ставки по потребительским кредитам
.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ЧПС в Microsoft Excel.
Описание
Возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также последовательность будущих выплат (отрицательные значения) и поступлений (положительные значения).
Синтаксис
ЧПС(ставка; значение1; [значение2],…)
Аргументы функции ЧПС описаны ниже.
-
Ставка Обязательный аргумент. Ставка дисконтирования за один период.
-
Значение1, значение2,… Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 254 аргументов, представляющих выплаты и поступления.
-
Аргументы «значение1, значение2, …» должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.
-
Функция ЧПС использует порядок аргументов «значение1, значение2, …» для определения порядка поступлений и платежей. Убедитесь в том, что ваши платежи и поступления введены в правильном порядке.
-
Аргументы, которые являются пустыми ячейками, логическими значениями или текстовыми представлениями чисел, значениями ошибок или текстом, который невозможно преобразовать в числа, игнорируются.
-
Если аргумент является массивом или ссылкой, то учитываются только числа в массиве или ссылке. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Замечания
-
Считается, что инвестиция, значение которой вычисляет функция ЧПС, начинается за один период до даты денежного взноса «значение1» и заканчивается с последним денежным взносом в списке. Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС, но не включать в список аргументов. Дополнительные сведения см. в приведенных ниже примерах.
-
Если n — количество денежных потоков в списке значений, формула для функции ЧПС имеет следующий вид:
-
ЧПС аналогична функции ПС (текущее значение). Основное различие между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В функции ЧПС денежные взносы могут быть переменной величиной, тогда как в функции ПС они должны быть постоянными на протяжении всего периода инвестиции. Сведения о функциях платежей по ссуде и финансовых функциях см. в описании функции ПС.
-
ЧПС связана также с функцией ВСД (внутренняя ставка доходности). ВСД — это ставка, для которой ЧПС равняется нулю: ЧПС(ВСД(…); …) = 0.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|---|---|---|
|
0,1 |
Годовая ставка дисконтирования |
|
|
-10 000 |
Начальная стоимость инвестиции через один год |
|
|
3000 |
Доход за первый год |
|
|
4200 |
Доход за второй год |
|
|
6800 |
Доход за третий год |
|
|
Формула |
Описание |
Результат |
|
=ЧПС(A2; A3; A4; A5; A6) |
Чистая приведенная стоимость данной инвестиции |
1 188,44 ₽ |
Пример 2
|
Данные |
Описание |
|
|---|---|---|
|
0,08 |
Годовая ставка дисконтирования. Она может представлять показатель инфляции или процентную ставку по конкурирующим инвестициям. |
|
|
-40 000 |
Начальная стоимость инвестиции |
|
|
8000 |
Доход за первый год |
|
|
9200 |
Доход за второй год |
|
|
10000 |
Доход за третий год |
|
|
12000 |
Доход за четвертый год |
|
|
14500 |
Доход за пятый год |
|
|
Формула |
Описание |
Результат |
|
=ЧПС(A2; A4:A8)+A3 |
Чистая приведенная стоимость данной инвестиции |
1 922,06 ₽ |
|
=ЧПС(A2; A4:A8; -9000)+A3 |
Чистая приведенная стоимость данной инвестиции с учетом убытка (9000) на шестом году |
(3 749,47 ₽) |
К началу страницы
Нужна дополнительная помощь?
Что такое PV в Excel? Это функция для расчета текущей стоимости. В этом руководстве объясняется его синтаксис, показано, как построить правильную формулу PV для серии денежных потоков и одного платежа, описаны подводные камни, с которыми вы можете столкнуться, и способы их преодоления.
Предположим, вы думаете о покупке страхового аннуитета, чтобы обеспечить стабильный денежный поток в течение пенсионных лет. Или, может быть, вы думаете о том, чтобы положить немного денег на сберегательный счет с приличной годовой процентной ставкой. Что бы это ни было, вы задаетесь вопросом — это хорошая сделка? Чтобы узнать это наверняка, вам нужно найти текущую стоимость инвестиций. Для этого Microsoft Excel предоставляет функцию PV, которая означает «текущая стоимость».
PV — это финансовая функция Excel, которая возвращает текущую стоимость аннуитета, кредита или инвестиции на основе постоянной процентной ставки. Его можно использовать для серии периодических денежных потоков или одного единовременного платежа.
Функция PV доступна во всех версиях Excel 365, Excel 2019, Excel 2016, Excel 2013, Excel 2010 и Excel 2007.
Синтаксис следующий:
PV(скорость, кпер, плт, [fv], [type])
Где:
- Ставка (обязательно) — процентная ставка за период. Если вы производите ежегодные платежи, укажите годовую процентную ставку; если вы платите ежемесячно, укажите ежемесячную процентную ставку и так далее.
- Кпер (обязательно) — общее количество периодов выплат на протяжении аннуитета.
- Pmt (необязательно) — сумма, выплачиваемая за каждый период. Если он опущен, предполагается, что он равен 0, а фв аргумент должен быть включен.
- Fv (необязательно) — будущая стоимость аннуитета после последнего платежа. Если он опущен, предполагается, что он равен 0, а пмт аргумент должен быть включен.
- Тип (необязательно) — когда будут производиться платежи:
- 0 или опущен (по умолчанию) — в конце периода (обычный аннуитет)
- 1 — на начало периода (аннуитетный платеж)
5 вещей, которые вы должны знать о функции PV
Чтобы функция Excel PV правильно работала на ваших листах, примите во внимание следующие примечания по использованию:
- Если фв аргумент равен нулю или опущен, пмт должны быть включены, и наоборот.
- оценивать Аргумент может быть представлен в виде процента или десятичного числа, например, 10% или 0,1.
- Любые деньги, которые вы выплачиваете (отток), должны быть представлены отрицательным числом. Любые деньги, которые вы получаете (приток), должны быть представлены положительным числом. Например, когда вы инвестируете деньги в страховой аннуитет, используйте отрицательное число для пмт. Когда страховая компания начнет выплачивать вам выплаты, выражайте платежи в виде положительных чисел.
- При расчете периодических денежных потоков соблюдайте оценивать а также Например единицы. Например, если вы делаете 5 ежегодных платежей по годовой процентной ставке 7%, используйте 5 для Например и 7% или 0,07 для оценивать. Если вы делаете ежемесячные платежи сроком на 5 лет, то используйте 5*12 (всего 60 периодов) для Например и 7%/12 для оценивать.
- Все аргументы должны быть числовыми, в противном случае функция PV возвращает ошибку #ЗНАЧ! ошибка.
Базовая формула PV в Excel
Чтобы получить общее представление о том, как использовать функцию PV в Excel, давайте создадим формулу приведенной стоимости в ее простейшей форме.
Предположим, вы делаете регулярные взносы для накопления пенсионных сбережений. Вы вносите 500 долларов на период по ставке 7% и делаете 50 таких платежей через равные промежутки времени.
Чтобы найти текущую стоимость аннуитета, настройте свой рабочий лист таким образом:
- Периодическая процентная ставка (C2): 7%
- Количество периодов (C3): 100
- Сумма платежа (С4): -500
- Тип аннуитета (C5): 0 (обычный аннуитет) или 1 (аннуитетный платеж)
Формула для расчета PV инвестиций выглядит следующим образом:
=PV(С2, С3, С4, ,С5)
Если вы сравните результаты порядкового аннуитета (платежи производятся в конце периода) и аннуитета к оплате (платежи производятся в начале периода), вы заметите, что в последнем случае текущая стоимость равна выше.
PV регулярного аннуитета:
PV аннуитета:
И вот еще несколько вещей, на которые стоит обратить внимание:
- В этом примере пмт аргумент является отрицательным числом, потому что мы вкладываем деньги. Если вы рассчитываете PV аннуитета, который выплачивается вам, введите пмт как положительное число, и в результате вы получите отрицательный PV.
- Будущая стоимость в данном расчете не используется, поэтому фв аргумент опущен.
- При составлении формулы PV для ежемесячных денежных потоков (или других периодических платежей, таких как еженедельные, ежеквартальные и т. д.) не забудьте преобразовать годовую процентную ставку в периодическую ставку, как показано на рис. этот пример.
Можно также посмотреть на проблему под другим углом. Чтобы найти процентную ставку, при которой PV равен 0, используйте функцию IRR.
Как использовать функцию PV в Excel — примеры формул
Следующие примеры дадут вам представление о том, как функция Excel PV работает в различных сценариях, чтобы вы могли настроить базовую формулу для своей конкретной задачи.
Рассчитать PV аннуитета
Допустим, вы купили аннуитет, по которому регулярный платеж в размере 200 долларов США должен производиться страховой компании в начале каждого месяца в течение следующих 10 лет. По аннуитету ежемесячно начисляются проценты по ставке 9% годовых. Вопрос — сколько сейчас стоит эта рента?
Для начала введите все данные в отдельные ячейки:
- Годовая процентная ставка (B2): 9%
- Количество лет (B3): 10
- Ежемесячный платеж (В4): -200
- Аннуитетный тип (B5): 1
- Количество периодов в году (B6): 12
В этом случае процентная ставка (оценивать) и оплата (пмт) относятся к разным периодам. Чтобы сделать PV правильно, нам нужно сделать пару преобразований:
Чтобы преобразовать годовую процентную ставку в периодическую, разделите годовую ставку на количество периодов в году:
оценивать = годовая процентная ставка / кол. периодов в год
Чтобы получить общее количество периодов, умножьте срок аннуитета в годах на количество периодов в году:
Например = нет. лет * нет. периодов в год
Так как у нас ежемесячная рента, мы можем делить и умножать на 12 или на ячейку В6, в которую вписано это число.
Полная формула PV в B8:
=PV(B2/B6, B3*B6, B4,, B5)
Аналогичным образом можно рассчитать текущую стоимость еженедельной, квартальной или полугодовой ренты. Для этого просто измените количество периодов в году в соответствующей ячейке:
- Еженедельно: 52
- Ежемесячно: 12
- Ежеквартально: 4
- Полугодовой: 2
- Годовой: 1
Рассчитать PV инвестиций на основе их будущей стоимости
В этом примере мы собираемся найти текущую стоимость инвестиции, которая принесет 50 000 долларов через 5 лет при годовой процентной ставке 7%. Цель состоит в том, чтобы выяснить, сколько денег нам нужно инвестировать сегодня, чтобы достичь целевой суммы в конце инвестиционного периода.
Как обычно, мы вводим данные аннуитета в отдельные ячейки:
- Годовая процентная ставка (B2): 7%
- Количество лет (B3): 5
- Будущая стоимость (B4): 50 000
- Тип аннуитета (B5): 0
Предполагая, что процентная ставка начисляется ежегодно, формула приведенной стоимости проста:
=PV(B2, B3, , B4, B5)
Пожалуйста, обратите внимание, что пмт аргумент в данном случае опущен, поскольку предполагается единовременное вложение без дополнительных периодических платежей.
Как показано на снимке экрана ниже, результат формулы PV отрицательный, потому что это отток, то есть деньги, которые вы инвестируете сейчас, чтобы заработать целевую сумму в будущем.
Но что, если у нас есть несколько предложений от разных инвестиционных компаний и мы хотим сравнить эффект разных периодов начисления процентов?
В этом случае мы вводим количество периодов начисления процентов в год в ячейки E2:E6, как показано на рисунке ниже. Затем мы вводим приведенную ниже формулу в F2 и перетаскиваем ее вниз через F6:
=PV($B$2/E2, $B$3* E2, ,$B$4)
Постоянные данные, такие как процентная ставка ($B$2), срок аннуитета ($B$3), будущая стоимость ($B$4) и тип ($B$5), должны быть указаны как абсолютные ссылки, чтобы формула копировала правильно. к нижним ячейкам.
Присмотревшись к результатам, вы можете заметить обратную зависимость между рассчитанным PV (абсолютное значение без учета знака) и количеством периодов начисления сложных процентов. Лучшее предложение для нас — это еженедельное начисление процентов — вложив сейчас наименьшую сумму денег, мы получим те же $50 000 через 5 лет.
Дополнительные примеры формул см. в разделе Как рассчитать текущую стоимость ренты в Excel.
Разница между формулой NPV и PV в Excel
Помимо PV, в финансах есть еще один термин, называемый NPV, который дисконтирует будущие денежные потоки по ожидаемой норме прибыли для оценки их текущей стоимости. Хотя эти два термина имеют много общего, они существенно различаются.
Текущая стоимость (PV) — относится к будущим поступлениям денежных средств в данный период.
Чистая приведенная стоимость (NPV) – это разница между приведенной стоимостью притока денежных средств и приведенной стоимостью оттока денежных средств. Другими словами, NPV учитывает первоначальные инвестиции, что делает текущую стоимость чистой величиной.
В Microsoft Excel есть два основных различия между функциями PV и NPV:
- Функция PV может рассчитывать только постоянные денежные потоки, которые не меняются в течение всего срока действия аннуитета. Функция NPV может рассчитывать переменные денежные потоки.
- PV работает как для обычного аннуитета, так и для аннуитета. NPV может обрабатывать только денежные потоки, возникающие в конце каждого периода.
Для получения дополнительной информации см. функцию Excel NPV с примерами формул.
Вот как рассчитать PV в Excel. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Практическая рабочая тетрадь для скачивания
Использование формулы PV в Excel (файл .xlsx)
Вас также могут заинтересовать:
NPV (аббревиатура, на английском языке — Net Present Value), по-русски этот показатель имеет несколько вариаций названия, среди них:
- чистая приведенная стоимость (сокращенно ЧПС) — наиболее часто встречающееся название и аббревиатура, даже формула в Excel именно так и называется;
- чистый дисконтированный доход (сокращенно ЧДС) — название связано с тем, что денежный потоки дисконтируются и только потом суммируются;
- чистая текущая стоимость (сокращенно ЧТС) — название связано с тем, что все доходы и убытки от деятельности за счет дисконтирования как бы приводятся к текущей стоимости денег (ведь с точки зрения экономики, если мы заработаем 1 000 руб. и получим потом на самом деле меньше, чем если бы мы получили ту же сумму, но сейчас).
NPV — это показатель прибыли, которую получат участники инвестиционного проекта. Математически этот показатель находится путем дисконтирования значений чистого денежного потока (вне зависимости от того отрицательный он или положительный).
Чистый дисконтированный доход может быть найден за любой период времени проекта начиная с его начала (за 5 лет, за 7 лет, за 10 лет и так далее) в зависимости от потребности расчета.
Для чего нужен
NPV — один из показателей эффективности проекта, наряду с IRR, простым и дисконтированным сроком окупаемости. Он нужен, чтобы:
- понимать какой доход принесет проект, окупится ли он в принципе или он убыточен, когда он сможет окупиться и сколько денег принесет в конкретный момент времени;
- для сравнения инвестиционных проектов (если имеется ряд проектов, но денег на всех не хватает, то берутся проекты с наибольшей возможностью заработать, т.е. наибольшим NPV).
Формула расчета
Для расчета показателя используется следующая формула:

- CF — сумма чистого денежного потока в период времени (месяц, квартал, год и т.д.);
- t — период времени, за который берется чистый денежный поток;
- N — количество периодов, за который рассчитывается инвестиционный проект;
- i — ставка дисконтирования, принятая в расчет в этом проекте.
Пример расчета
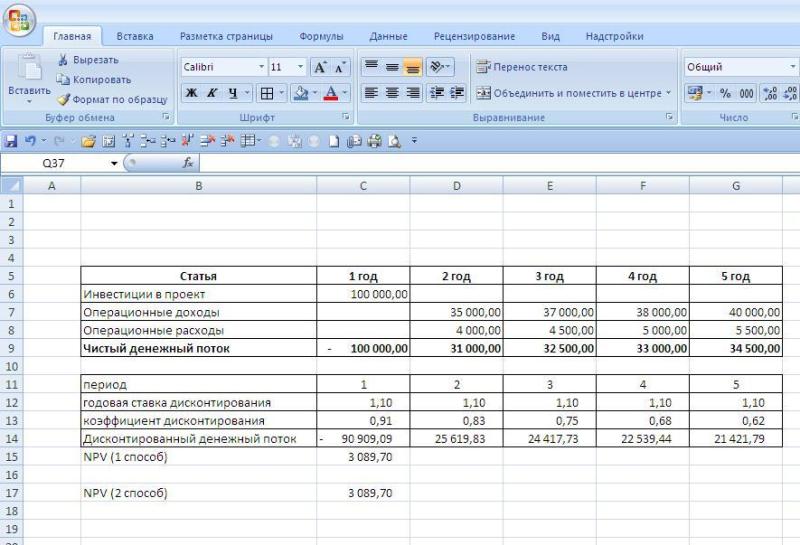
Для рассмотрения примера расчета показателя NPV возьмем упрощенный проект по строительству небольшого офисного здания. Согласно проекту инвестиций планируются следующие денежные потоки (тыс. руб.):
| Статья | 1 год | 2 год | 3 год | 4 год | 5 год |
| Инвестиции в проект | 100 000 | ||||
| Операционные доходы | 35 000 | 37 000 | 38 000 | 40 000 | |
| Операционные расходы | 4 000 | 4 500 | 5 000 | 5 500 | |
| Чистый денежный поток | — 100 000 | 31 000 | 32 500 | 33 000 | 34 500 |
Коэффициент дисконтирования проекта — 10%.
Подставляя в формулу значения чистого денежного потока за каждый период (там где получается отрицательный денежный поток ставим со знаком минус) и корректируя их с учетом ставки дисконтирования получим следующий результат:
NPV = — 100 000 / 1.1 + 31 000 / 1.12 + 32 500 / 1.13 + 33 000 / 1.14 + 34 500 / 1.15 = 3 089.70
Чтобы проиллюстрировать как рассчитывается NPV в Excel, рассмотрим предыдущий пример заведя его в таблицы. Расчет можно произвести двумя способами
- В Excel имеется формула ЧПС, которая рассчитывает чистую приведенную стоимость, для этого вам необходимо указать ставку дисконтирования (без знака проценты) и выделить диапазон чистого денежного потока. Вид формулы такой: = ЧПС (процент; диапазон чистого денежного потока).
- Можно самим составить дополнительную таблицу, где продисконтировать денежный поток и просуммировать его.
Ниже на рисунке мы привели оба расчета (первый показывает формулы, второй результаты вычислений):
Как вы видите, оба метода вычисления приводят к одному и тому же результату, что говорит о том, что в зависимости от того, чем вам удобнее пользоваться вы можете использовать любой из представленных вариантов расчета.
Примеры расчета NPV в бизнес-планах
Увидеть как рассчитан показатель на конкретном примере бизнес-плана вы можете выбрав соответствующий документ в форме поиска или перейдя по ссылке ниже:
Функция XNPV вычисляет чистую текущую стоимость (NPV) для ряда денежных потоков, которые могут быть или не быть периодическими.
Синтаксис
XNPV(rate, values, dates)
аргументы
- Обменный курс (обязательно): ставка дисконтирования, применяемая к денежным потокам.
- Ценности(обязательно): массив или диапазон ячеек, представляющий серию денежных потоков.
Ряд значений должен содержать как минимум одно положительное и одно отрицательное значение:
— Отрицательное значение: представляет стоимость или оплату;
— Положительное значение: представляет доход.
- Даты (обязательно): ряд дат, соответствующий значениям.
- Дата первоначальных инвестиций должна быть первой в массиве;
- Все остальные даты должны быть позже начальной даты и могут быть в любом порядке;
- Необходимо ввести даты:
— Используя функцию DATE;
— Как ссылки на ячейки, содержащие даты;
— Как результаты возвращаются из других формул.
Замечания
1. В Excel даты можно использовать в расчетах, поскольку они хранятся в виде последовательных чисел. По умолчанию 1 — это порядковый номер 1, поэтому 1900 — порядковый номер 1, поскольку это 12 дней после 1;
2. Даты усекаются до целых чисел, если они содержат время;
3. #NUM! ошибка возникает при выполнении любого из следующих условий:
— Аргументы «ценности(Основной ключ) и даты” массивы имеют разную размерность;
— Любой из указанных “даты” предшествует дате начала.
4. #СТОИМОСТЬ! ошибка возникает при выполнении одного из следующих условий:
— Любая из предоставленных дат является недопустимой датой;
— Любой из поставляемых “скорость«,»ценности(Основной ключ) и даты” не является числовым.
5. XNPV рассчитывается по следующему уравнению:
Где:
— Pi — i-й или последний денежный поток (платеж);
— di — i-я или последняя дата платежа;
— d1 — 0-я дата платежа.
Возвращаемое значение
Возвращает числовое значение.
Пример
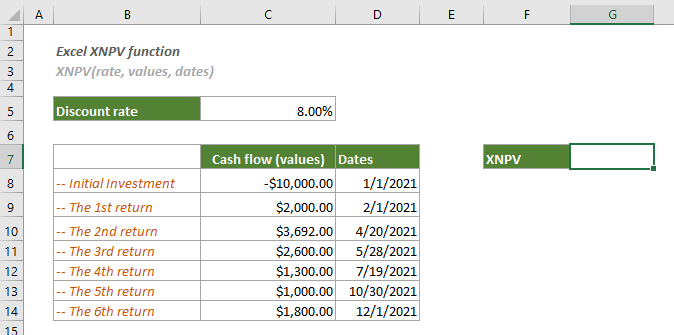
Как показано на снимке экрана ниже, существует инвестиционный проект сроком на 1 год, который, как ожидается, будет генерировать следующие денежные потоки на основе ставки дисконтирования 8%. Чтобы рассчитать чистую приведенную стоимость с помощью функции XNPV, вы можете сделать следующее.
1. Выберите пустую ячейку, скопируйте или введите формулу ниже и нажмите Enter ключ для получения результата.
=XNPV(C5,C8:C14,D8:D14)
Затем вы можете изменить формат ячейки на валюту, если вам нужно.
Примечание: Если функция возвращает положительное число, инвестиции осуществимы. В противном случае инвестиции нецелесообразны.
Связанные функции
Функция ЧПС Excel
Функция NPV возвращает чистую текущую стоимость инвестиции на основе дисконтной или процентной ставки и ряда будущих денежных потоков: платежи (отрицательные значения) и доход (положительные значения).
Лучшие инструменты для работы в офисе
Kutools for Excel — Помогает вам выделиться из толпы
Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает 300 мощных расширенных функций (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80 % времени.
- Разработан для 1500 рабочих сценариев, помогает решить 80% проблем с Excel.
- Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
- Станьте экспертом по Excel за 3 минуты. Больше не нужно запоминать какие-либо болезненные формулы и коды VBA.
- 30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.
Вкладка Office — включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)
- Одна секунда для переключения между десятками открытых документов!
- Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
- Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
- Добавляет эффективные вкладки в Office (включая Excel), точно так же, как Chrome, Firefox и новый Internet Explorer.
Комментарии (0)
Оценок пока нет. Оцените первым!