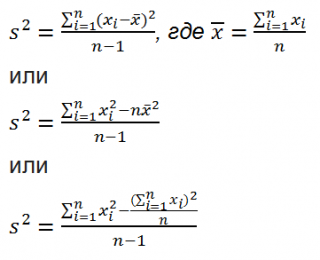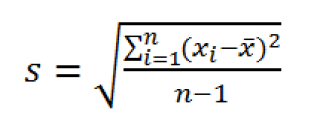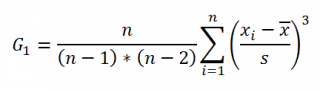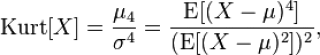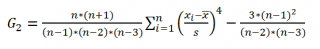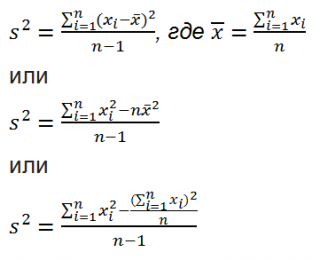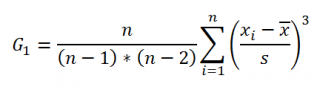Цель:
- Совершенствование умений и навыков нахождения статистических
характеристик случайной величины, работа с расчетами в Excel; - применение информационно коммутативных технологий для анализа данных;
работа с различными информационными носителями.
Ход урока
- Сегодня на уроке мы научимся рассчитывать статистические характеристики
для больших по объему выборок, используя возможности современных
компьютерных технологий. - Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют
переменную величину, которая в зависимости от исхода испытания принимает одно
значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных
случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода,
медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических
характеристик случайной величины (полигон частот, круговые и столбчатые
диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических
задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества
работающих в компании (чел.):
| 23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28 |
рассчитать числовые характеристики:
|
Ход работы.
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
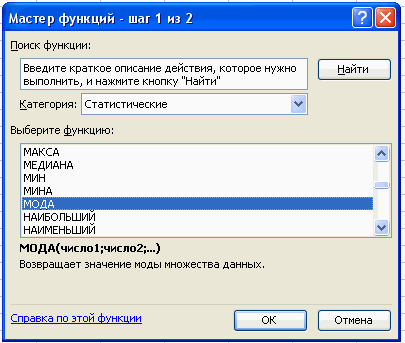
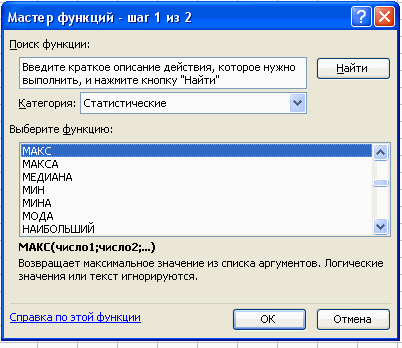
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в
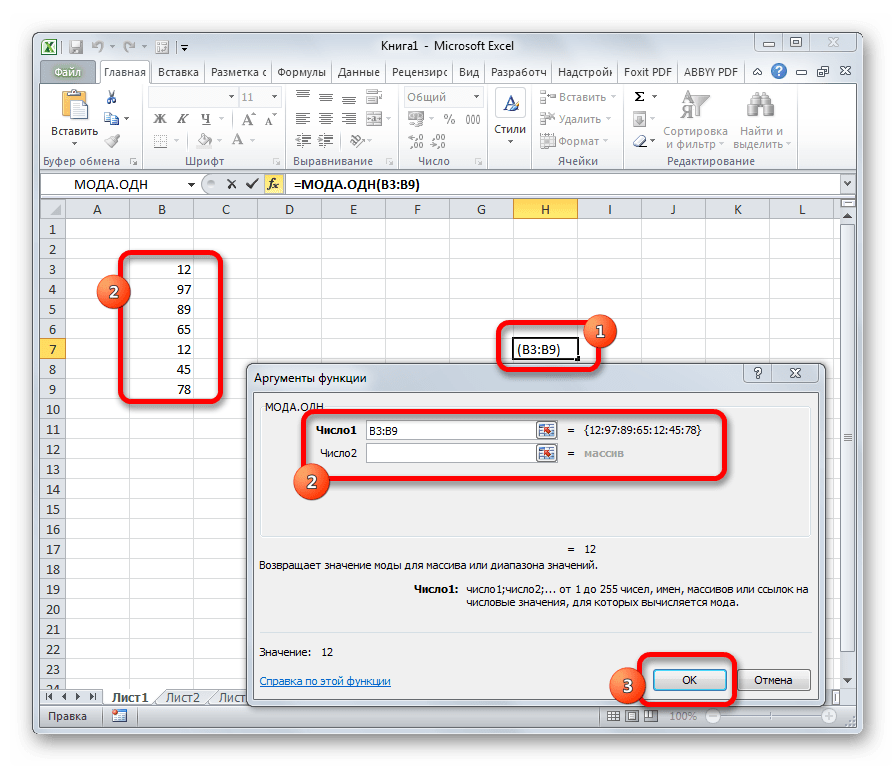
появившемся окне в строке категория выберем — статистические, в списке: МОДА
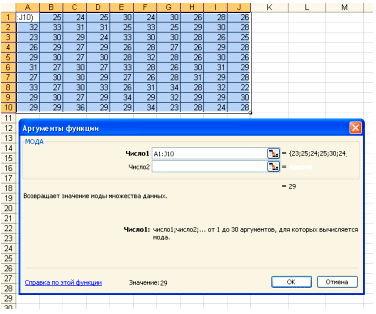
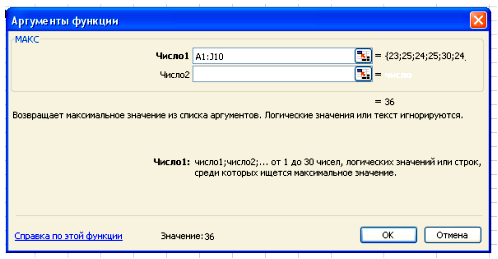
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в
штате 29 человек больше всего.
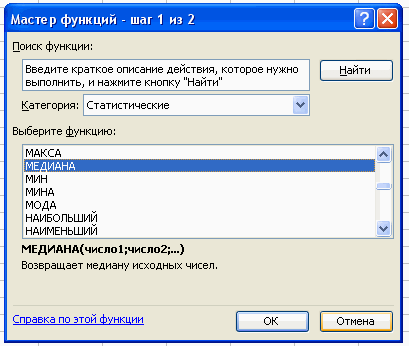
Используя тот же путь вычисляем медиану.
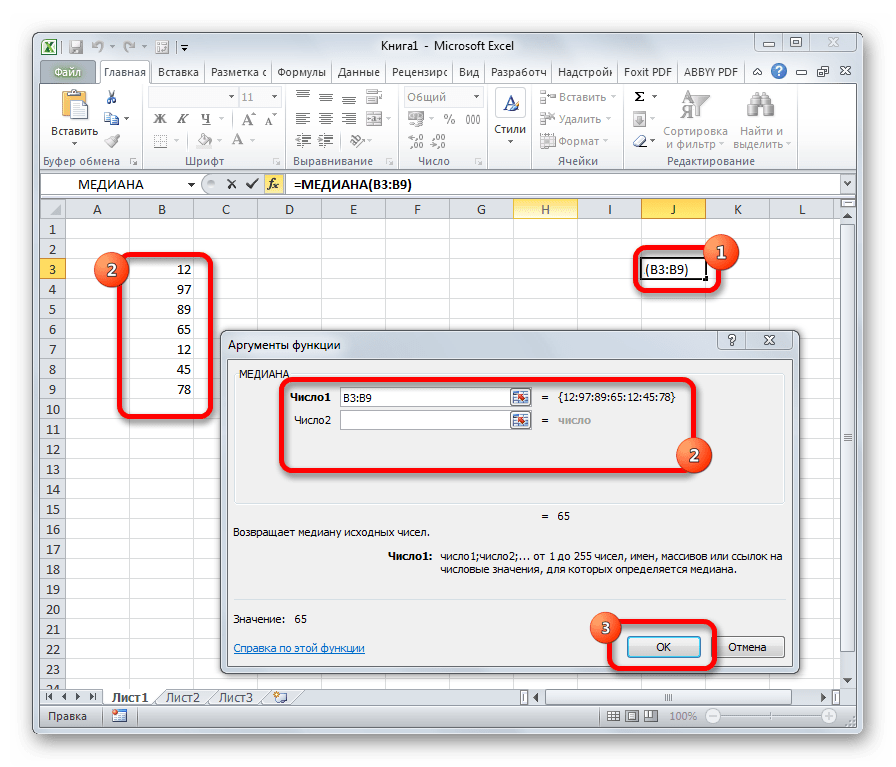
Вставка – Функция – Статистические – Медиана.
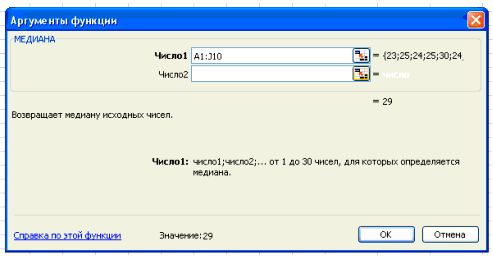
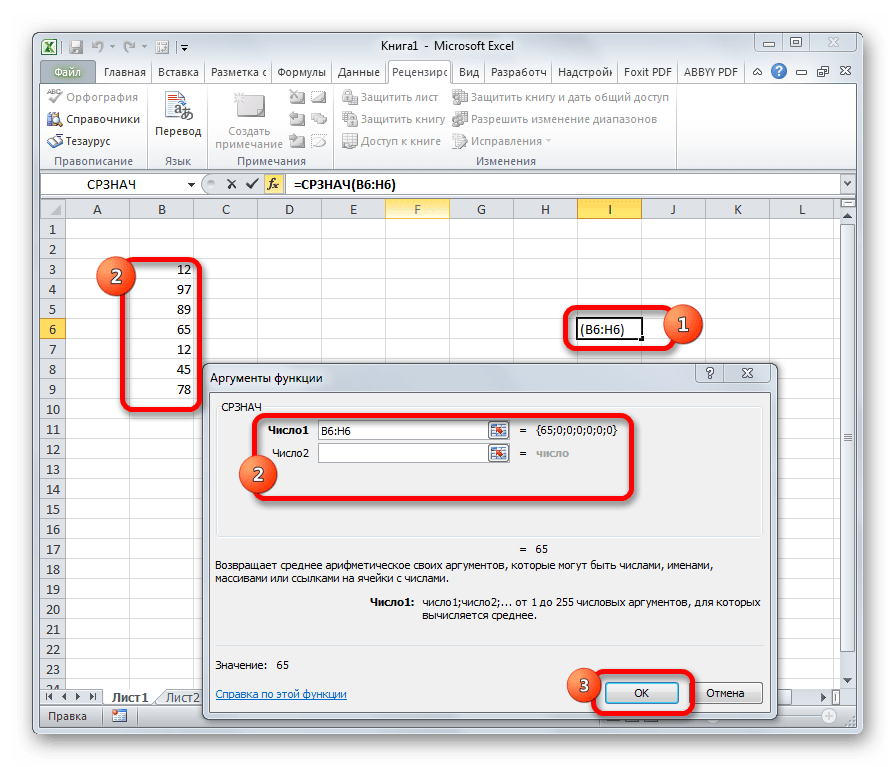
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение
сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением
случайной величины. Для вычисления размаха ряда нужно найти наибольшее и
наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
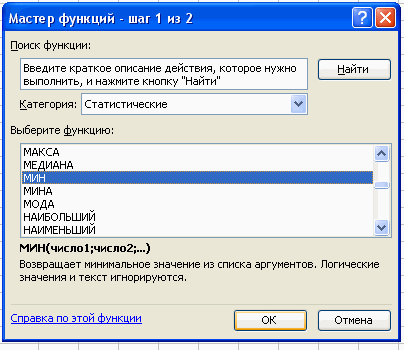
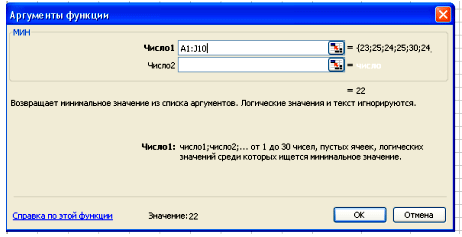
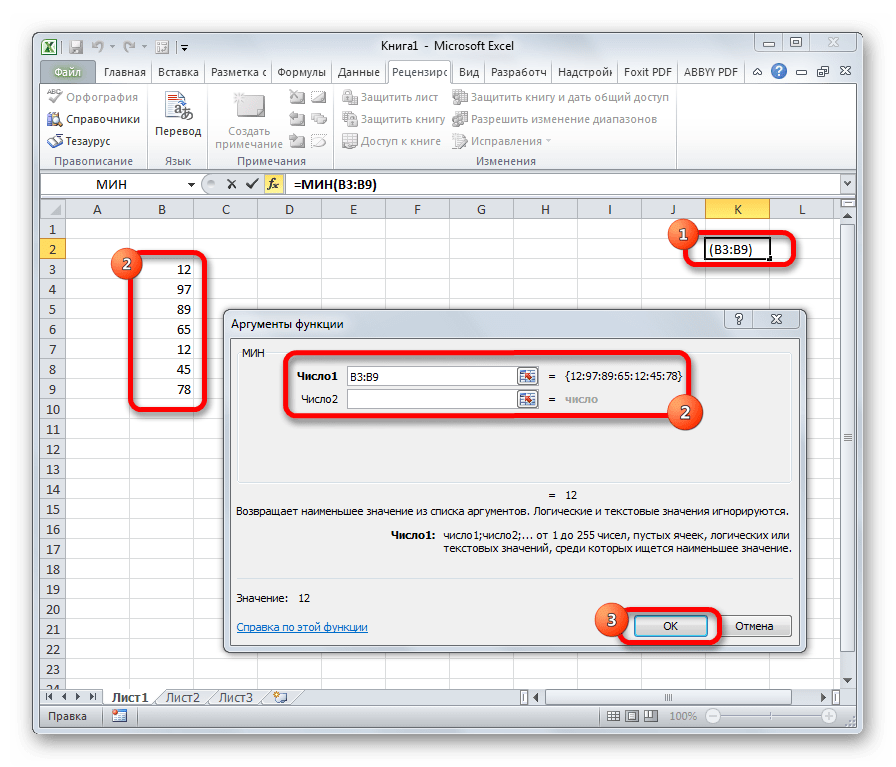
Вставка – Функция – Статистические – МИН.
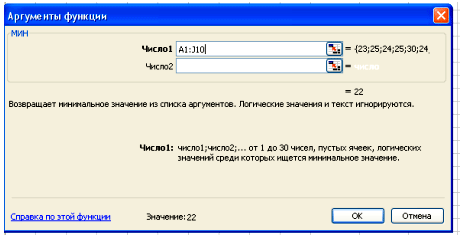
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и
фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон
распределения, т.е. составить таблицу значений случайной величины и
соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в
фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi
случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
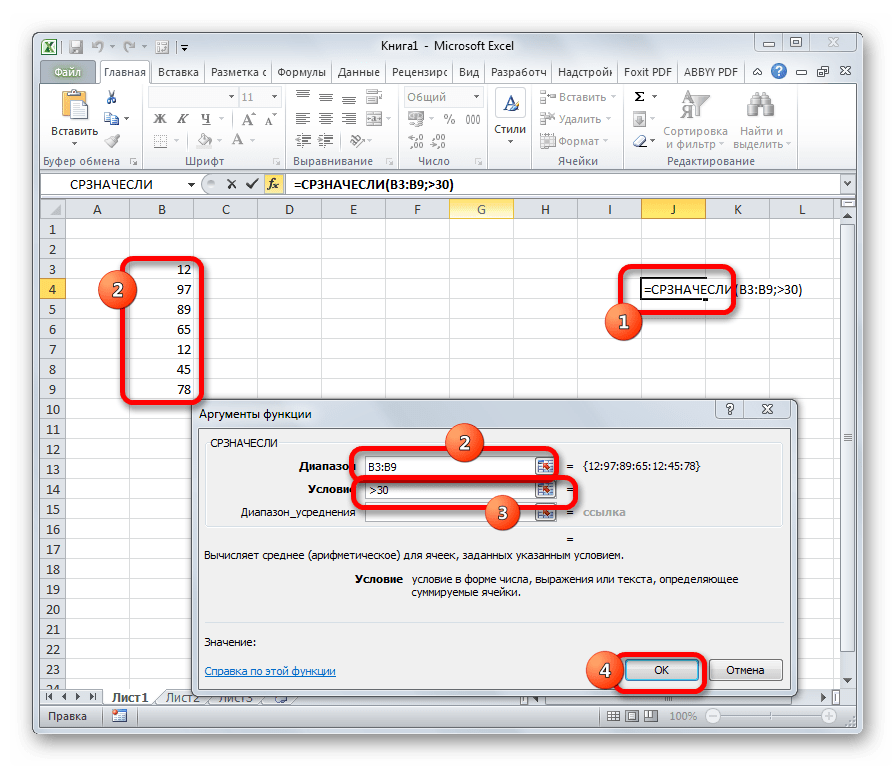
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий
ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке
встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция –
Математические — СУММА). Должно получиться 100 (количество всех фирм).
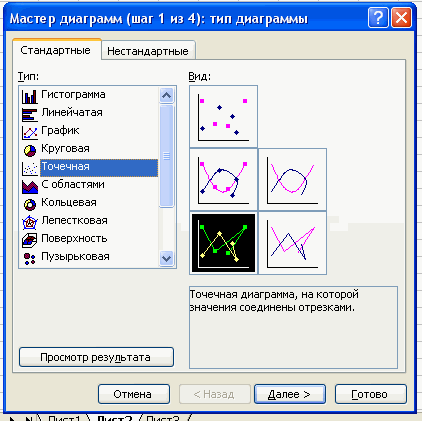
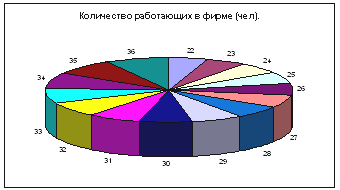
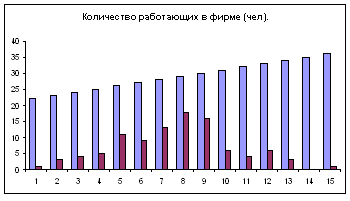
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма –
Стандартные – Точечная (точечная диаграмма на которой значения соединены
отрезками)
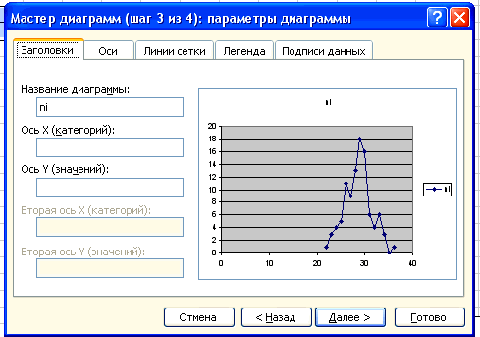
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы
(Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы
для наибольшей наглядности.
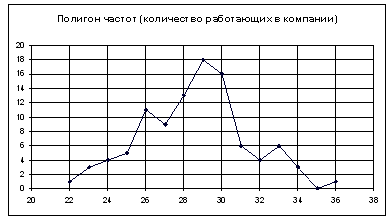
Получаем:
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая
нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для
анализа и обработки статистической информации.
- Авторы
- Файлы работы
- Сертификаты
Коваль О.В. 1, Аверьянова С.Ю. 2
1Филиал Южного федерального универстета в г.Новошахтинске
2Филиал Южного федерального университета в г.Новошахтинске Ростовской области
Комментарии
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
овладеть навыками расчета числовых характеристик выборки с помощью Надстройки Пакет Анализа ЭТ MS Excel.
Краткая теория
В ЭТ MS Excel имеется набор мощных инструментов для работы с выборками и углубленного статистического анализа данных, называемый Пакет анализа, который может быть использован для решения задач статистической обработки выборочных данных.
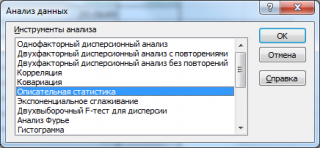
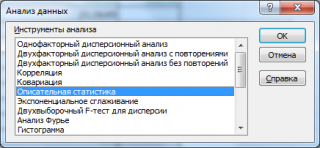
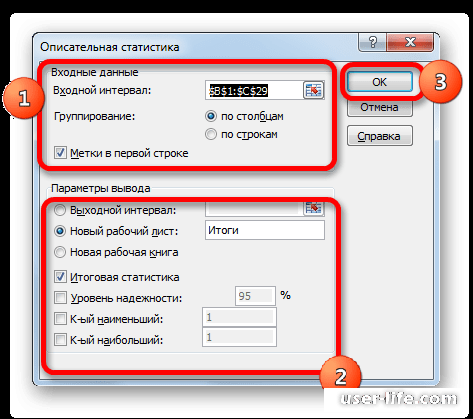
Надстройка Пакет анализа вызывается командой главного меню Данные → Анализ данных. В появившемся окне Анализ данных выбираем пункт Описательная статистика.
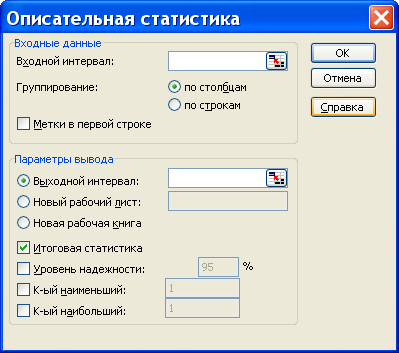
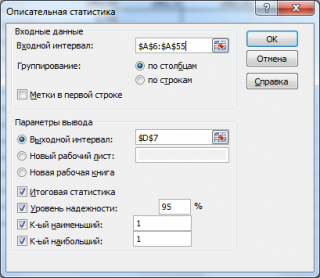
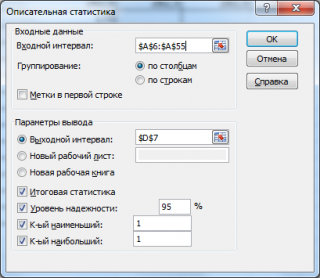
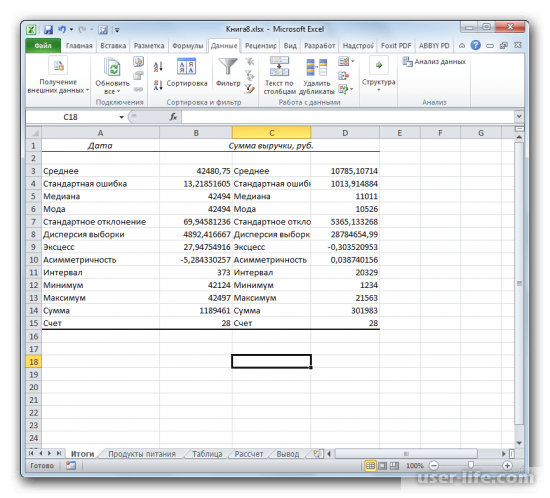
Далее откроется окно Описательная статистика, в котором необходимо сделать нужные установки.
Входной диапазон. Ссылка на диапазон, содержащий анализируемые данные. Ссылка должна состоять не менее чем из двух смежных диапазонов данных, данные в которых расположены по строкам или столбцам.
Группирование. Установите переключатель в положение «По столбцам» или «По строкам» в зависимости от расположения данных во входном диапазоне.
Метки в первой строке/Метки в первом столбце. Если первая строка исходного диапазона содержит названия столбцов, установите переключатель в положение Метки в первой строке. Если названия строк находятся в первом столбце входного диапазона, установите переключатель в положение Метки в первом столбце. Если входной диапазон не содержит меток, то необходимые заголовки в выходном диапазоне будут созданы автоматически.
Уровень надежности. Установите флажок, если в выходную таблицу необходимо вывести границу доверительного интервала для среднего. В поле введите требуемое значение в процентах. Например, значение 95% вычисляет уровень надежности среднего с уровнем значимости 0,05.
К-ый наибольший. Установите флажок, если в выходную таблицу необходимо включить строку для k-го наибольшего значения для каждого диапазона данных. В соответствующем окне введите число k. Если k равно 1, эта строка будет содержать максимальное значение выборки.
К-ый наименьший. Установите флажок, если в выходную таблицу необходимо включить строку для k-го наименьшего значения для каждого диапазона данных. В соответствующем окне введите число k. Если k равно 1, эта строка будет содержать минимальное значение выборки.
Выходной диапазон. Введите ссылку на левую верхнюю ячейку выходного диапазона. Этот инструмент анализа выводит два столбца сведений для каждого набора данных. Левый столбец содержит метки статистических данных; правый столбец содержит статистические данные. Состоящий их двух столбцов диапазон статистических данных будет выведен для каждого столбца или для каждой строки входного диапазона в зависимости от положения переключателя Группирование.
Если хотим вывести результаты расчета на новый лист, то установите переключатель, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. Если в этом есть необходимость, введите имя нового листа в поле, расположенном напротив соответствующего положения переключателя.
Если хотим вывести результаты расчета в новой книге, то установите переключатель, чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге.
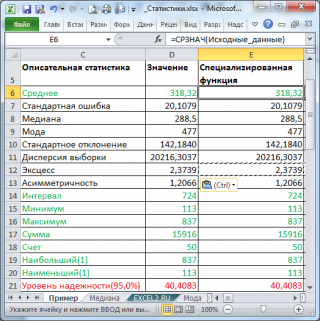
Итоговая статистика. Установите флажок, если в выходном диапазоне необходимо получить по одному полю для каждого из следующих видов статистических данных, представленных в таблице 2.
Таблица 2.
|
Значение |
Примечания |
|
Среднее |
Выборочное среднее х=1n∙i=1nxi. Функция СРЗНАЧ. |
|
Стандартная ошибка |
Оценка среднеквадратичного отклонения выборочного среднего. Вычисляется по формуле 1n∙(n-1)∙i=1n(xi-x)2 |
|
Медиана |
Число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Функция МЕДИАНА. |
|
Мода |
Наиболее часто встречающееся значение в выборке. Если нет одинаковых значений, то возвращается значение ошибки #Н/Д. Функция МОДА.ОДН. |
|
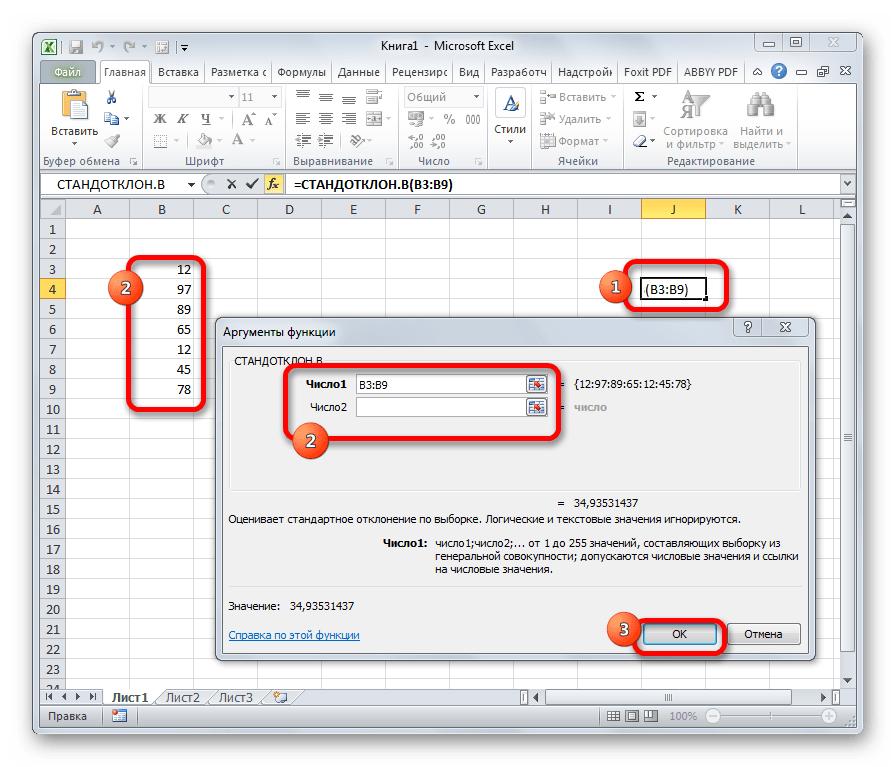
Стандартное отклонение |
Оценка среднеквадратичного отклонения генеральной совокупности S=1n-1∙i=1n(xi-x)2. Функция СТАНДОТКЛОН.В. |
|
Дисперсия выборки |
Оценка дисперсии генеральной совокупности . Функция ДИСП.В. |
|
Эксцесс |
Выборочный эксцесс. Функция ЭКСЦЕСС. |
|
Асимметрич-ность |
Коэффициент асимметрии. Функция СКОС. |
|
Интервал |
Размах варьирования R = xmax ‒ xmin . |
|
Минимум |
Минимальное значение в выборке. Функция МИН. |
|
Максимум |
Максимальное значение в выборке. Функция МАКС. |
|
Сумма |
Сумма всех значений в выборке. Функция СУММ. |
|
Счет |
Объем выборки. Функция СЧЕТ. |
|
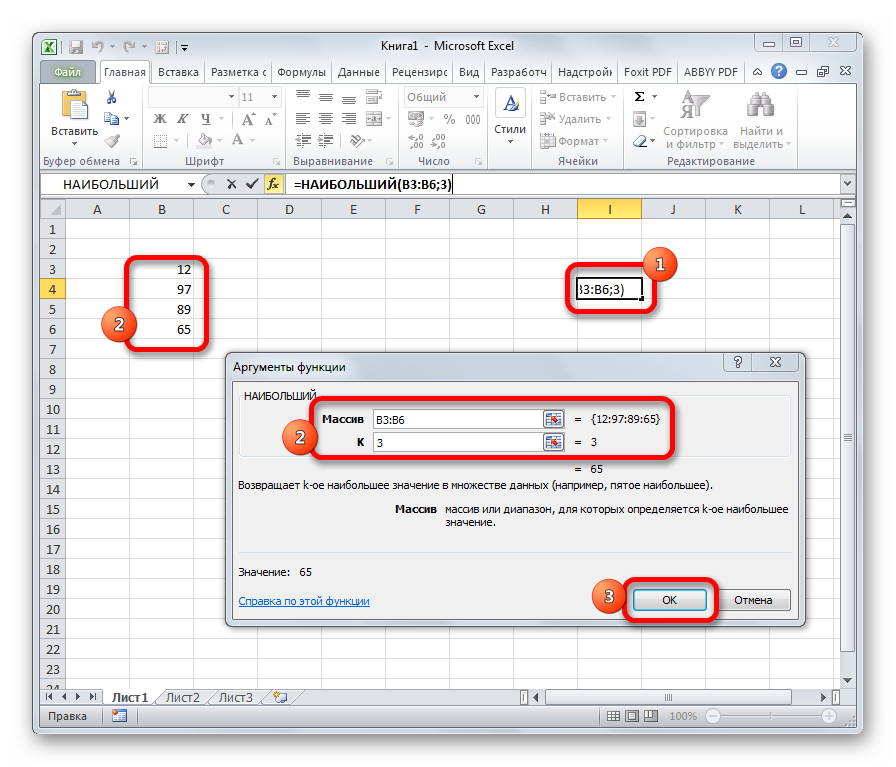
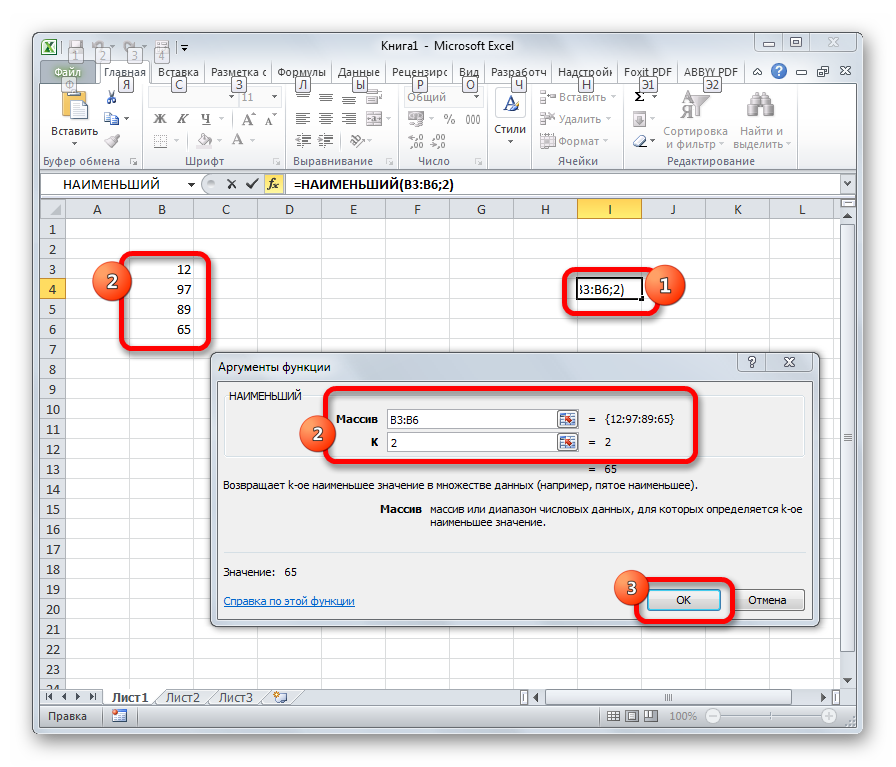
Наибольший |
k-тое наибольшее значение выборки. Если k=1, то выводится максимальное значение. Функция НАИБОЛЬШИЙ. |
|
Наименьший |
k-тое наименьшее значение выборки. Если k=1, то выводится минимальное значение. Функция НАИМЕНЬШИЙ |
|
Уровень надежности |
Параметр показывает возможность отклонения среднего по выборке, от среднего для генеральной совокупности, при заданном уровне надежности. |
Замечание. Следует обратить внимание на то, что расчет параметров в режиме Описательная статистика имеет ряд важных особенностей:
1. В качестве значений параметров: Стандартное отклонение, Дисперсия выборки, Эксцесс, Асимметричность – Excel генерирует оценки соответствующих параметров для генеральной совокупности, а не для выборки.
2. Для применения Описательной статистики предварительное ранжирование исходных данных не требуется: при вычислении показателей ранжирование выполняется автоматически.
3. Появление в ячейке Мода индикатора ошибки #Н/Д указывает на то, что в анализируемых данных нет одинаковых значений признака. В этом случае в качестве моды Мо выбирается то значение признака, которое соответствует максимальной ординате теоретической кривой распределения.
4. Индикатор ошибки #ДЕЛ/0! В ячейке Эксцесс и/или Асимметричность означает, что в результативной таблице стандартное отклонение является нулевым или же заданный входной диапазон данных содержит менее четырех элементов данных
5. Стандартная ошибка ‒ это разность между ожидаемыми и наблюдаемыми значениями исследуемого признака.
Стандартная ошибка или ошибка среднегонаходится из выражения
m=Sn .
Стандартная ошибка – это параметр, характеризующий степень возможного отклонения среднего значения, полученного на исследуемой ограниченной выборке, от истинного среднего значения, полученного на всей совокупности элементов. С помощью стандартной ошибки задается так называемый доверительный интервал. 95%-ый доверительный интервал, равный х ± 2т , обозначает диапазон, в который с вероятностью р = 0,95 (при достаточно большом числе наблюдений п>30) попадает среднее значение генеральной совокупности.
Пример выполнения
Постановка задачи. Приведены объемы дневной выручки (в тыс. руб.) 24 продавцов колбасных изделий, работающих в разных районах города (см. табл.1).
Таблица 1.
|
20,2 |
19,3 |
19,9 |
23,1 |
18,8 |
17,4 |
|
19,9 |
18,3 |
16,4 |
17,3 |
18,3 |
15,8 |
|
20,5 |
20,6 |
19,4 |
18,7 |
16,3 |
18,4 |
|
21,6 |
21,2 |
19,3 |
19,1 |
19,3 |
18,8 |
Требуется: выполнить описательную статистику выборки с помощью Надстройки Пакет Анализа ЭТ MS Excel.
Решение задачи в среде ЭТ MSExcel. Для решения задачи в среде ЭТ MS Excel необходимо выполнить следующие действия:
1. Идентифицируйте свою работу, переименовав Лист1 в Титульный лист и записав номер лабораторной работы, ее название, кто выполнил и проверил.
2. Переименуйте Лист 2 в Исходные данные и наберите столбец исходных данных.
3. Вычислите величины хmax, хmin, R, n, N, Nокругл., Δ и Δокругл. , используя встроенные функции Excel МАКС, МИН, СЧЕТ, КОРЕНЬ и ОКРУГЛ.
4. Сформируйте столбец интервалов группировки. Наберите команду Данные → Анализ данных → Гистограмма и в появившемся диалоговом окне выполните нужные установки. Отформатируйте полученную таблицу и построенную гистограмму выборки.
5. Наберите команду Данные → Анализ данных → Описательная статистика и в появившемся диалоговом окне выполните нужные установки.
6. Щелчок по кнопке «ОК» приводит к появлению результирующей таблицы статистических характеристик выборки.
7. Повторно вычислим найденные характеристики с помощью встроенных функций MS Excel или формул. Сравним полученные результаты.
8. Сделайте выводы и сохраните работу в вашем каталоге.
Исходные данные для самостоятельного решения
Задание. Имеется выборка объема n = 27 (табл. 2).
Требуется: выполнить описательную статистику выборки с помощью Надстройки Пакет Анализа ЭТ MS Excel.
Таблица 2.
|
№ варианта |
Выборка |
||||||||
|
1 |
22,5 |
20,2 |
19,3 |
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
|
21,6 |
19,9 |
18,3 |
16,4 |
17,3 |
18,3 |
15,8 |
21,2 |
19,3 |
|
|
17,8 |
20,5 |
20,6 |
19,4 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
|
|
2 |
18,8 |
20,2 |
19,3 |
19,9 |
23,2 |
22,5 |
17,4 |
21,8 |
19,2 |
|
19,4 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
19,4 |
18,7 |
16,3 |
|
|
20,5 |
20,6 |
19,4 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
17,8 |
|
|
2 |
20,2 |
19,3 |
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
22,4 |
|
18,7 |
20,2 |
19,3 |
19,9 |
23,2 |
22,5 |
17,4 |
21,8 |
19,2 |
|
|
18,1 |
19,8 |
18,2 |
16,4 |
17,2 |
21,8 |
15,8 |
21,2 |
19,2 |
|
|
3 |
19,4 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
19,4 |
18,7 |
16,3 |
|
18,5 |
20,6 |
19,4 |
20,7 |
16,3 |
18,4 |
19,3 |
18,8 |
17,8 |
|
|
20,1 |
19,3 |
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
22,4 |
|
|
4 |
19,7 |
20,2 |
19,3 |
18,9 |
23,2 |
22,5 |
17,4 |
21,8 |
19,2 |
|
18,3 |
19,8 |
18,2 |
16,4 |
17,2 |
21,8 |
15,8 |
21,2 |
19,2 |
|
|
19,7 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
19,4 |
18,7 |
16,3 |
|
|
5 |
19,4 |
20,7 |
16,3 |
18,4 |
19,3 |
18,8 |
17,8 |
18,7 |
20,2 |
|
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
22,4 |
18,1 |
19,8 |
|
|
19,3 |
18,9 |
23,2 |
22,5 |
17,4 |
21,8 |
19,2 |
19,4 |
18,7 |
|
|
6 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
19,4 |
18,7 |
18,5 |
20,6 |
|
20,6 |
19,4 |
20,7 |
16,3 |
18,4 |
19,3 |
18,8 |
18,4 |
19,3 |
|
|
19,3 |
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
18,4 |
19,3 |
|
|
7 |
16,3 |
18,4 |
19,3 |
18,8 |
19,4 |
18,7 |
18,5 |
20,6 |
18,7 |
|
19,4 |
20,7 |
16,3 |
18,4 |
19,3 |
18,8 |
18,4 |
19,3 |
20,6 |
|
|
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
18,4 |
19,3 |
19,3 |
|
|
8 |
19,3 |
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
22,5 |
20,2 |
|
18,3 |
16,4 |
17,3 |
18,3 |
15,8 |
21,2 |
19,3 |
21,6 |
19,9 |
|
|
20,6 |
19,4 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
17,8 |
20,5 |
|
|
9 |
19,4 |
20,7 |
16,3 |
18,4 |
19,3 |
18,8 |
17,8 |
18,7 |
20,2 |
|
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
22,4 |
18,1 |
19,8 |
|
|
19,3 |
18,9 |
23,2 |
22,5 |
17,4 |
21,8 |
19,2 |
19,4 |
18,7 |
|
|
10 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
19,4 |
18,7 |
18,5 |
20,6 |
|
20,6 |
19,4 |
20,7 |
16,3 |
18,4 |
19,3 |
18,8 |
18,4 |
19,3 |
|
|
16,4 |
20,4 |
20,8 |
19,4 |
18,7 |
17,8 |
18,4 |
19,4 |
18,8 |
Просмотров работы: 3443
Код для цитирования:
Содержание
- Инструменты Excel для вычисления числовых характеристик выборки
- Практическая работа № 1-2 Вычисления выборочных характеристик данных
- 1.1 Характеристика пакета Excel
- 1.2 Использование специальных функций
- Выборочные числовые характеристики excel
- 1. Характеристика пакета Excel
- 2 Использование специальных функций
- Задания для самостоятельной работы
- 3. Использование инструмента Пакет анализа
- Задание для самостоятельной работы
- Описательная статистика в EXCEL
- Надстройка Пакет анализа
- Среднее выборки
- Медиана выборки
- Мода выборки
- Мода и среднее значение
- Дисперсия выборки
- Стандартное отклонение выборки
- Стандартная ошибка
- Асимметричность
- Эксцесс выборки
- Уровень надежности
Инструменты Excel для вычисления числовых характеристик выборки
Процедура «Описательные статистики » пакета «Анализ данных.
В процедуре автоматически вычисляются следующие числовые характеристики выборки:
Для того чтобы выполнить вычисления, вводим в поле «Водной интервал» адреса ячеек, в которых записаны выборочные значения;
помечаем «Выходной интервал» и вводим в поле адрес первой ячейки, начиная с которой в листе Excel будет отображён резгультат; помечаем «Итоговая статистика»:
Результаты вычислений процедуры представлены в виде таблицы:
Источник
Практическая работа № 1-2 Вычисления выборочных характеристик данных
Цель работы: научиться использовать специальные функции и инструменты Пакета анализа Microsoft Excel для расчета выборочных характеристик данных.
Задание. Прочитайте теоретические сведения, выполните примеры и задания для самостоятельного решения.
Математическая статистика подразделяется на две основные области: описательную и аналитическую статистику. Описательная статистика охватывает методы описания статистических данных, представления их в форме таблиц, распределений.
Аналитическая статистика или теория статистических выводов ориентирована на обработку данных, полученных в ходе эксперимента, с целью формулировки выводов, имеющих прикладное значение для самых различных областей человеческой деятельности.
1.1 Характеристика пакета Excel
Пакет Excel оснащен средствами статистической обработки данных. И хотя Excel существенно уступает специализированным статистическим пакетам обработки данных, тем не менее этот раздел математики представлен в Excel наиболее полно. В него включены основные, наиболее часто используемые статистические процедуры: средства описательной статистики, критерии различия, корреляционные и другие методы, позволяющие проводить необходимый статистический анализ экономических, психологических, педагогических и медико-биологических типов данных.
При рассмотрении применения методов обработки статистических данных в данной практической работе ограничимся только простейшими и наиболее часто описательными статистиками, реализованными в мастере функций Excel.
1.2 Использование специальных функций
В мастере функций Excel имеется ряд специальных функций, предназначенных для вычисления выборочных характеристик.
Функция СРЗНАЧ(число1; число2; . ) вычисляет среднее арифметическое из нескольких аргументов (массивов) чисел.
Функция МЕДИАНА(число1;число2;. ) позволяет получать медиану заданной выборки. Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана.
Пример. Найти медиану для ряда с нечетным и четным числом элементов.
В первом случае медиана вычисляется по формуле =МЕДИАНА(b4:b8) и является серединным значением упорядоченного ряда. Во втором случае медиана вычисляется по формуле =МЕДИАНА(b4:b7) и является средним арифметическим двух срединных значений.
Функция МОДА(число1;число2; . ) возвращает наиболее часто встречающееся или повторяющееся значение в массиве или интервале данных. Как и функция МЕДИАНА, функция МОДА является мерой взаимного расположения значений.
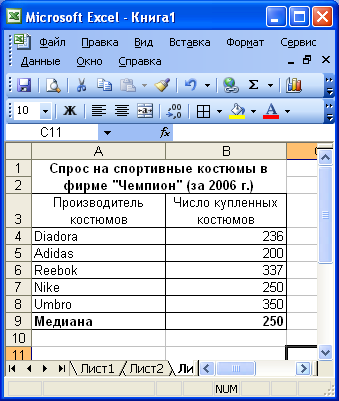
Пример. Определить костюмы какого размера пользуются наибольшим спросом
В данном примере не используется функция МОДА, т.к. таблица представлена двумя рядами данных. Чтобы определить модальное значение, определяется наибольшее количество купленных костюмов =МАКС(C4:C8), а затем данное значение индексируется с размером костюма =ИНДЕКС(B4:B8;ПОИСКПОЗ(C9;C4:C8)).
Функция ДИСП(число1; число2; . ) позволяет оценить дисперсию по выборочным данным. Дисперсия (от лат. dispersion – рассеяние) – числовая характеристика случайной величины, характеризующая рассеяние ее возможных значений около математического ожидания.
Функция СТАНДОТКЛОН(число1; число2; . ) вычисляет стандартное отклонение. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.
Функция ЭКСЦЕСС(число1;число2; . ) вычисляет оценку эксцесса по выборочным данным. Эксцесс (Ek) характеризует так называемую «крутость», т.е. островершинность или плосковершинность распределения. Если Ek >0, распределение островершинное, если Ek 0 — асимметрия правосторонняя, т.е. распределение скошено вправо, т.е. его более длинная часть лежит правее центра (математического ожидания), если As
Источник
Выборочные числовые характеристики excel
Математическая статистика подразделяется на две основные области: описательную и аналитическую статистику. Описательная статистика охватывает методы описания статистических данных, представления их в форме таблиц, распределений.
Аналитическая статистика или теория статистических выводов ориентирована на обработку данных, полученных в ходе эксперимента, с целью формулировки выводов, имеющих прикладное значение для самых различных областей человеческой деятельности.
1. Характеристика пакета Excel
Пакет Excel оснащен средствами статистической обработки данных. И хотя Excel существенно уступает специализированным статистическим пакетам обработки данных, тем не менее этот раздел математики представлен в Excel наиболее полно. В него включены основные, наиболее часто используемые статистические процедуры: средства описательной статистики, критерии различия, корреляционные и другие методы, позволяющие проводить необходимый статистический анализ экономических, психологических, педагогических и медико-биологических типов данных.
Каждая единица информации занимает свою собственную ячейку (клетку) в создаваемой рабочей таблице. В каждой рабочей таблице 256 столбцов (из которых в новой рабочей таблице на экране видны, как правило, только первые 10 или 11 (от А до J или К) и 65 536 строк (из которых обычно видны только первые 15-20). Каждая новая рабочая книга содержит три чистых листа рабочих таблиц.
Вся помещаемая в электронную таблицу информация хранится в отдельных клетках рабочей таблицы. Но ввести информацию можно только в текущую клетку. С помощью адреса в строке формул и табличного курсора Excel указывает, какая из клеток рабочей таблицы является текущей. В основе системы адресации клеток рабочей таблицы лежит комбинация буквы (или букв) столбца и номера строки, например A 2, B 12.
При рассмотрении применения методов обработки статистических данных в данной лабораторной работе ограничимся только простейшими и наиболее часто описательными статистиками, реализованными в мастере функций Excel .
2 Использование специальных функций
В мастере функций Excel имеется ряд специальных функций, предназначенных для вычисления выборочных характеристик.
Функция СРЗНАЧ вычисляет среднее арифметическое из нескольких массивов (аргументов) чисел. Аргументы число1, число2, . — это от 1 до 30 массивов для которых вычисляется среднее.
Функция МЕДИАНА позволяет получать медиану заданной выборки. Медиана — это элемент выборки, число элементов выборки со значениями больше которого и меньше которого равно.
Функция МОДА вычисляет наиболее часто встречающееся значение в выборке.
Функция ДИСП позволяет оценить дисперсию по выборочным данным.
Функция СТАНДОТКЛОН вычисляет стандартное отклонение.
Функция ЭКСЦЕСС вычисляет оценку эксцесса по выборочным данным.
Функция СКОС позволяет оценить асимметрию выборочного распределения.
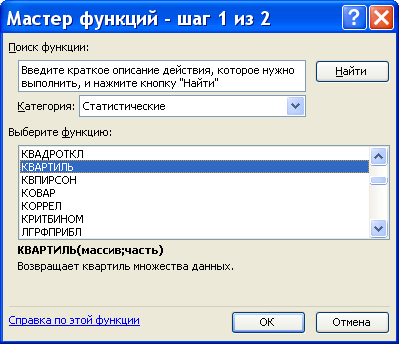
Функция КВАРТИЛЬ вычисляет квартили распределения. Функция имеет формат КВАРТИЛЬ(массив, значение), где массив – интервал ячеек, содержащих значения СВ; значение определяет какая квартиль должна быть найдена (0 – минимальное значение, 1 – нижняя квартиль, 2 – медиана, 3 – верхняя квартиль, 4 – максимальное значение распределения).
Пример 1. Провести статистический анализ методом описательной статистики доходов населения в регионе 1 и регионе 2.
Задания для самостоятельной работы
1. Наблюдение посещаемости четырех внеклассных мероприятий в экспериментальном (20 человек) и контрольном (30 человек) классах дали значения (соответственно): 18, 20, 20, 18 и 15, 23, 10, 28. Требуется найти среднее значение, стандартное отклонение, медиану и квартили этих данных.
2. Найти среднее значение, медиану, стандартное отклонение и квартили результатов бега на дистанцию 100 м у группы студентов (с): 12,8; 13,2; 13,0; 12,9; 13,5; 13,1.
3. Определите верхнюю и нижнюю квартиль, выборочную асимметрию и эксцесс для данных измерений роста групп студенток: 164, 160, 157, 166, 162, 160, 161, 159, 160, 163, 170, 171.
4. Найти наиболее популярный туристический маршрут из четырех реализуемых фирмой, если за неделю последовательно были реализованы следующие маршруты: 1, 3, 3, 2, 1, 1, 4, 4, 2, 4, 1, 3, 2, 4, 1, 4, 4, 3, 1, 2, 3, 4, 1, 1, 3.
3. Использование инструмента Пакет анализа
В пакете Excel помимо мастера функций имеется набор более мощных инструментов для работы с несколькими выборками и углубленного анализа данных, называемый Пакет анализа, который может быть использован для решения задач статистической обработки выборочных данных.
Для установки пакета Анализ данных в Excel сделайте следующее:
— в меню Сервис выберите команду Надстройки;
— в появившемся списке установите флажок Пакет анализа.
Для использования статистического пакета анализа данных необходимо:
- указать курсором мыши на пункт меню Сервис и щелкнуть левой кнопкой мыши;
- в раскрывающемся списке выбрать команду Анализданных (если команда Анализ данных отсутствует в меню Сервис, то необходимо установить в Excel пакет анализа данных);
- выбрать строку Описательнаястатистика и нажать кнопку Оk
- в появившемся диалоговом окне указать входной интервал, то есть ввести ссылки на ячейки, содержащие анализируемые данные;
- указать выходной интервал, то есть ввести ссылку на ячейку, в которую будут выведены результаты анализа;
- в разделе Группирование переключатель установить в положение по столбцам или по строкам;
- установить флажок в поле Итоговая статистика и нажать Ок.
Задание для самостоятельной работы
1. В рабочей зоне производились замеры концентрации вредного вещества. Получен ряд значений (в мг./м 3 ): 12, 16, 15, 14, 10, 20, 16, 14, 18, 14, 15, 17, 23, 16. Необходимо определить основные выборочные характеристики.
Источник
Описательная статистика в EXCEL
history 17 ноября 2016 г.
Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.
Задача описательной статистики (descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений выборки к нескольким итоговым показателям, которые дают представление о выборке .В качестве таких статистических показателей используются: среднее , медиана , мода , дисперсия, стандартное отклонение и др.
Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные статистические выводы о распределении , из которого была взята выборка . Например, если у нас есть выборка значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой выборки мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.
Надстройка Пакет анализа
Для вычисления статистических показателей одномерных выборок , используем надстройку Пакет анализа . Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.
СОВЕТ : Подробнее о других инструментах надстройки Пакет анализа и ее подключении – читайте в статье Надстройка Пакет анализа MS EXCEL .
Выборку разместим на листе Пример в файле примера в диапазоне А6:А55 (50 значений).
Примечание : Для удобства написания формул для диапазона А6:А55 создан Именованный диапазон Выборка.
В диалоговом окне Анализ данных выберите инструмент Описательная статистика .
После нажатия кнопки ОК будет выведено другое диалоговое окно,
в котором нужно указать:
- входной интервал (Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле Метки в первой строке (Labelsinfirstrow). В этом случае заголовок будет выведен в Выходном интервале. Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
- выходной интервал (Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
- Итоговая статистика (SummaryStatistics) . Поставьте галочку напротив этого поля – будут выведены основные показатели выборки: среднее, медиана, мода, стандартное отклонение и др.;
- Также можно поставить галочки напротив полей Уровень надежности (ConfidenceLevelforMean) , К-й наименьший (Kth Largest) и К-й наибольший (Kth Smallest).
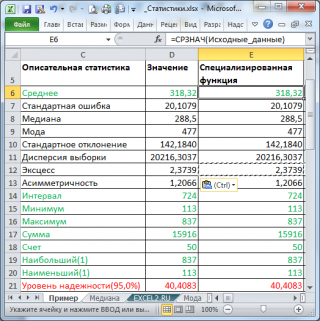
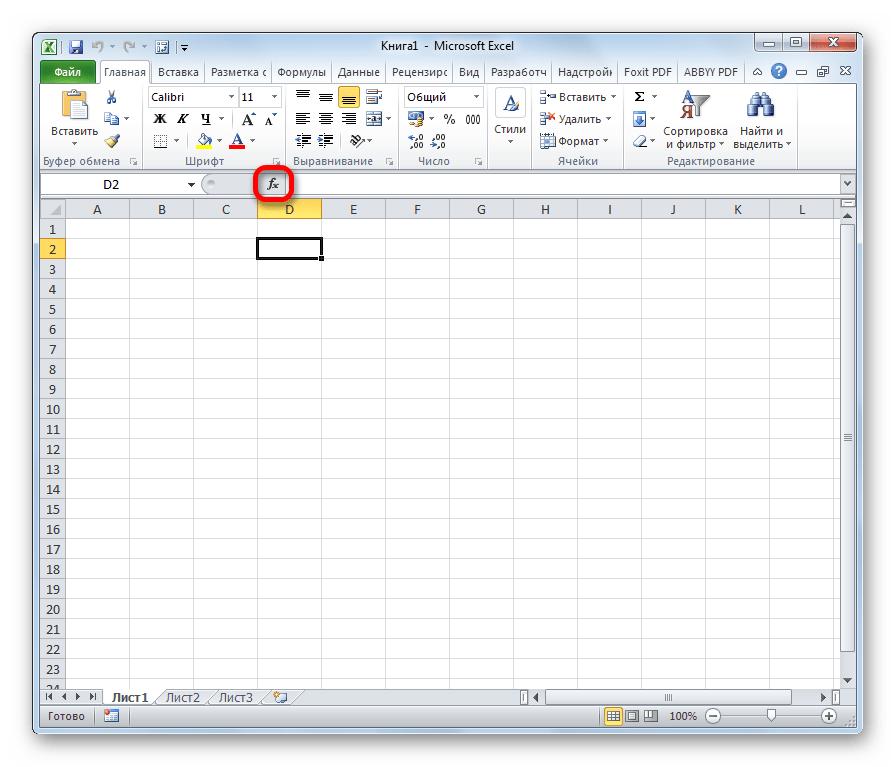
В результате будут выведены следующие статистические показатели:
Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.
Если во входном интервале указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во Входной интервал и установите галочку в поле Метки в первой строке ). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.
Зеленым цветом на картинке выше и в файле примера выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:
- Интервал (Range) — разница между максимальным и минимальным значениями;
- Минимум (Minimum) – минимальное значение в диапазоне ячеек, указанном во Входном интервале (см. статью про функцию МИН() );
- Максимум (Maximum)– максимальное значение (см. статью про функцию МАКС() );
- Сумма (Sum) – сумма всех значений (см. статью про функцию СУММ() );
- Счет (Count) – количество значений во Входном интервале (пустые ячейки игнорируются, см. статью про функцию СЧЁТ() );
- Наибольший (Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см. статью про функцию НАИБОЛЬШИЙ() );
- Наименьший (Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см. статью про функцию НАИМЕНЬШИЙ() ).
Ниже даны подробные описания остальных показателей.
Среднее выборки
Среднее (mean, average) или выборочное среднее или среднее выборки (sample average) представляет собой арифметическое среднее всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция СРЗНАЧ() . Выборочное среднее является «хорошей» (несмещенной и эффективной) оценкой математического ожидания случайной величины (подробнее см. статью Среднее и Математическое ожидание в MS EXCEL ).
Медиана (Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем медиана , а половина чисел меньше, чем медиана . Для определения медианы необходимо сначала отсортировать множество чисел . Например, медианой для чисел 2, 3, 3, 4 , 5, 7, 10 будет 4.
Если множество содержит четное количество чисел, то вычисляется среднее для двух чисел, находящихся в середине множества. Например, медианой для чисел 2, 3, 3 , 5 , 7, 10 будет 4, т.к. (3+5)/2.
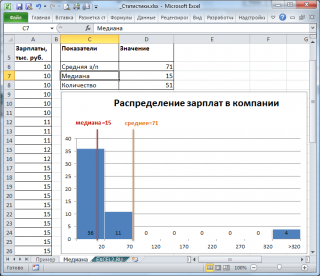
Если имеется длинный хвост распределения, то Медиана лучше, чем среднее значение , отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.
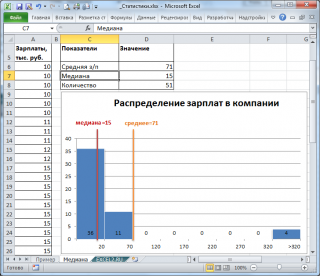
Для определения медианы в MS EXCEL существует одноименная функция МЕДИАНА() , английский вариант — MEDIAN().
Медиану также можно вычислить с помощью формул
Подробнее о медиане см. специальную статью Медиана в MS EXCEL .
СОВЕТ : Подробнее про квартили см. статью, про перцентили (процентили) см. статью.
Мода выборки
Мода (Mode) – это наиболее часто встречающееся (повторяющееся) значение в выборке . Например, в массиве (1; 1; 2 ; 2 ; 2 ; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это мода . Для вычисления моды используется функция МОДА() , английский вариант MODE().
Примечание : Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье Есть ли повторы в списке?
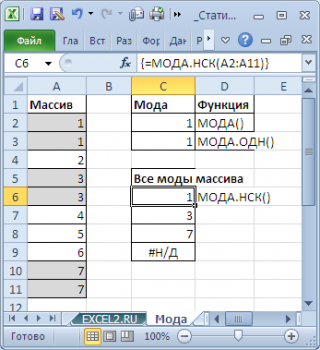
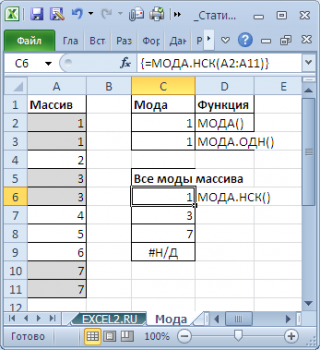
Начиная с MS EXCEL 2010 вместо функции МОДА() рекомендуется использовать функцию МОДА.ОДН() , которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция МОДА.НСК() , которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.
Например, в массиве (1; 1; 2 ; 2 ; 2 ; 3; 4 ; 4 ; 4 ; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются модами . Функции МОДА.ОДН() и МОДА() вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см. файл примера , лист Мода ).
Чтобы исправить эту несправедливость и была введена функция МОДА.НСК() , которая выводит все моды . Для этого ее нужно ввести как формулу массива .
Как видно из картинки выше, функция МОДА.НСК() вернула все три моды из массива чисел в диапазоне A2:A11 : 1; 3 и 7. Для этого, выделите диапазон C6:C9 , в Строку формул введите формулу =МОДА.НСК(A2:A11) и нажмите CTRL+SHIFT+ENTER . Диапазон C 6: C 9 охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству мод . Если ячеек больше чем м о д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если мода только одна, то все выделенные ячейки будут заполнены значением этой моды .
Теперь вспомним, что мы определили моду для выборки, т.е. для конечного множества значений, взятых из генеральной совокупности . Для непрерывных случайных величин вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция МОДА() вернет ошибку.
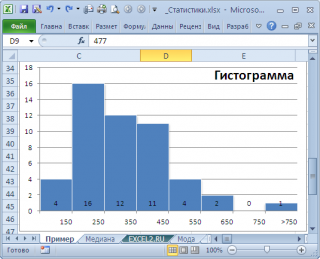
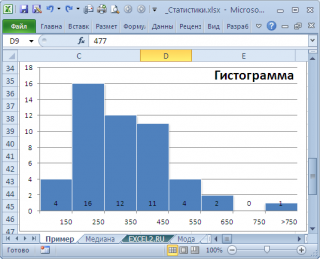
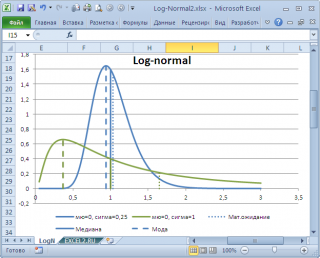
Даже в нашем массиве с модой , которая была определена с помощью надстройки Пакет анализа , творится, что-то не то. Действительно, модой нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на гистограмму распределения , построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).
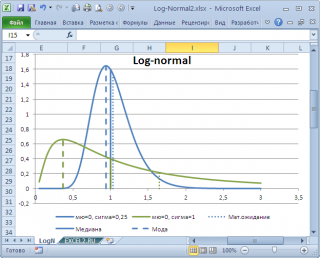
Проблема в том, что мы определили моду как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому, моду в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для логнормального распределения мода (наиболее вероятное значение непрерывной случайной величины х), вычисляется как exp ( m — s 2 ) , где m и s параметры этого распределения.
Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для моды распределения, из которого взята выборка (наиболее вероятного значения или для которого плотность вероятности распределения максимальна).
Для того, чтобы получить оценку моды распределения, из генеральной совокупности которого взята выборка , можно, например, построить гистограмму . Оценкой для моды может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.
Вывод : Значение моды для выборки , рассчитанное с помощью функции МОДА() , может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер выборки существенно превышает количество этих значений.
Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане), модой является число 15 (17 значений из 51, т.е. 33%). В этом случае функция МОДА() дает хорошую оценку «наиболее вероятного» значения зарплаты.
Примечание : Строго говоря, в примере с зарплатой мы имеем дело скорее с генеральной совокупностью , чем с выборкой . Т.к. других зарплат в компании просто нет.
О вычислении моды для распределения непрерывной случайной величины читайте статью Мода в MS EXCEL .
Мода и среднее значение
Не смотря на то, что мода – это наиболее вероятное значение случайной величины (вероятность выбрать это значение из Генеральной совокупности максимальна), не следует ожидать, что среднее значение обязательно будет близко к моде .
Примечание : Мода и среднее симметричных распределений совпадает (имеется ввиду симметричность плотности распределения ).
Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6. Модой является 6, а среднее значение – 3,6666.
Другой пример. Для Логнормального распределения LnN(0;1) мода равна =EXP(m-s2)= EXP(0-1*1)=0,368, а среднее значение 1,649.
Дисперсия выборки
Дисперсия выборки или выборочная дисперсия ( sample variance ) характеризует разброс значений в массиве, отклонение от среднего .
Из формулы №1 видно, что дисперсия выборки это сумма квадратов отклонений каждого значения в массиве от среднего , деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления дисперсии выборки используется функция ДИСП() . С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию ДИСП.В() .
Дисперсию можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ): =КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) – обычная формула =СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1) – формула массива
Дисперсия выборки равна 0, только в том случае, если все значения равны между собой и, соответственно, равны среднему значению .
Чем больше величина дисперсии , тем больше разброс значений в массиве относительно среднего .
Размерность дисперсии соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг 2 . Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из дисперсии – стандартное отклонение .
Стандартное отклонение выборки
Стандартное отклонение выборки (Standard Deviation), как и дисперсия , — это мера того, насколько широко разбросаны значения в выборке относительно их среднего .
По определению, стандартное отклонение равно квадратному корню из дисперсии :
Стандартное отклонение не учитывает величину значений в выборке , а только степень рассеивания значений вокруг их среднего . Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок : (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается.
В MS EXCEL 2007 и более ранних версиях для вычисления Стандартного отклонения выборки используется функция СТАНДОТКЛОН() . С версии MS EXCEL 2010 рекомендуется использовать ее аналог СТАНДОТКЛОН.В() .
Стандартное отклонение можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ): =КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Стандартная ошибка
В Пакете анализа под термином стандартная ошибка имеется ввиду Стандартная ошибка среднего (Standard Error of the Mean, SEM). Стандартная ошибка среднего — это оценка стандартного отклонения распределения выборочного среднего .
Примечание : Чтобы разобраться с понятием Стандартная ошибка среднего необходимо прочитать о выборочном распределении (см. статью Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL ) и статью про Центральную предельную теорему .
Стандартное отклонение распределения выборочного среднего вычисляется по формуле σ/√n, где n — объём выборки, σ — стандартное отклонение исходного распределения, из которого взята выборка . Т.к. обычно стандартное отклонение исходного распределения неизвестно, то в расчетах вместо σ используют ее оценку s — стандартное отклонение выборки . А соответствующая величина s/√n имеет специальное название — Стандартная ошибка среднего. Именно эта величина вычисляется в Пакете анализа.
В MS EXCEL стандартную ошибку среднего можно также вычислить по формуле =СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))
Асимметричность
Асимметричность или коэффициент асимметрии (skewness) характеризует степень несимметричности распределения ( плотности распределения ) относительно его среднего .
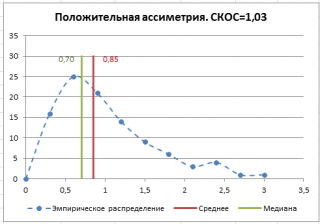
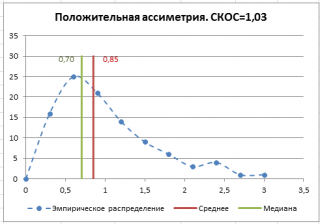
Положительное значение коэффициента асимметрии указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого. Коэффициент асимметрии идеально симметричного распределения или выборки равно 0.
Примечание : Асимметрия выборки может отличаться расчетного значения асимметрии теоретического распределения. Например, Нормальное распределение является симметричным распределением ( плотность его распределения симметрична относительно среднего ) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в выборке из соответствующей генеральной совокупности не обязательно должны располагаться совершенно симметрично относительно среднего . Поэтому, асимметрия выборки , являющейся оценкой асимметрии распределения , может отличаться от 0.
Функция СКОС() , английский вариант SKEW(), возвращает коэффициент асимметрии выборки , являющейся оценкой асимметрии соответствующего распределения, и определяется следующим образом:
где n – размер выборки , s – стандартное отклонение выборки .
В файле примера на листе СКОС приведен расчет коэффициента асимметрии на примере случайной выборки из распределения Вейбулла , которое имеет значительную положительную асимметрию при параметрах распределения W(1,5; 1).
Эксцесс выборки
Эксцесс показывает относительный вес «хвостов» распределения относительно его центральной части.
Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/- σ .
Примечание : Не смотря на старания профессиональных статистиков, в литературе еще попадается определение Эксцесса как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение Эксцесса ничего не говорит о форме пика распределения.
Согласно определения, Эксцесс равен четвертому стандартизированному моменту:
Для нормального распределения четвертый момент равен 3*σ 4 , следовательно, Эксцесс равен 3. Многие компьютерные программы используют для расчетов не сам Эксцесс , а так называемый Kurtosis excess, который меньше на 3. Т.е. для нормального распределения Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.
Примечание : Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как Эксцесс (от англ. excess — «излишек»). Например, функция MS EXCEL ЭКСЦЕСС() на самом деле вычисляет Kurtosis excess.
Функция ЭКСЦЕСС() , английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку эксцесса распределения случайной величины и определяется следующим образом:
Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из нормального распределения формула вернет близкое к 0 значение.
Если задано менее четырех точек данных, то функция ЭКСЦЕСС() возвращает значение ошибки #ДЕЛ/0!
Вернемся к распределениям случайной величины . Эксцесс (Kurtosis excess) для нормального распределения всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений Эксцесс зависит от параметров распределения: см., например, распределение Вейбулла или распределение Пуассона , для котрого Эксцесс = 1/λ.
Уровень надежности
Уровень надежности — означает вероятность того, что доверительный интервал содержит истинное значение оцениваемого параметра распределения.
Вместо термина Уровень надежности часто используется термин Уровень доверия . Про Уровень надежности (Confidence Level for Mean) читайте статью Уровень значимости и уровень надежности в MS EXCEL .
Задав значение Уровня надежности в окне надстройки Пакет анализа , MS EXCEL вычислит половину ширины доверительного интервала для оценки среднего (дисперсия неизвестна) .
Тот же результат можно получить по формуле (см. файл примера ): =ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n) s — стандартное отклонение выборки , n – объем выборки .
Источник
Содержание
- Использование описательной статистики
- Подключение «Пакета анализа»
- Размах вариации
- Вычисление коэффициента вариации
- Шаг 1: расчет стандартного отклонения
- Шаг 2: расчет среднего арифметического
- Шаг 3: нахождение коэффициента вариации
- Простая формула для расчета объема выборки
- Пример расчета объема выборки
- Задачи о генеральной доле
- По части судить о целом
- Как рассчитать объем выборки
- Как определить статистические выбросы и сделать выборку для их удаления в Excel
- Способ 1: применение расширенного автофильтра
- Способ 2: применение формулы массива
- СРЗНАЧ()
- СРЗНАЧЕСЛИ()
- МАКС()
- МИН()
Использование описательной статистики
Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.
В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.
Подключение «Пакета анализа»
Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.
- Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
- В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
- Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».
После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».
Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».
Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Разделы: Математика
- Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
- применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.
- Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
- Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
| 23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28 |
рассчитать числовые характеристики:
|
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Простая формула для расчета объема выборки
где: n – объем выборки;
z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;
p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;
q = (1 – p);
e – допустимая ошибка, в долях.
Пример расчета объема выборки
Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».
Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.
Подставляем эти данные в формулу и считаем:
Получаем объем выборки n = 96 человек.
Задачи о генеральной доле
На вопрос «Накрывает ли доверительный интервал заданное значение p0?» — можно ответить, проверив статистическую гипотезу H0:p=p0. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p* появления события A: где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H0 используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле
|
Гипотеза |
H0:p=p0 | H0:p1=p2 |
| Предположения | Схема испытаний Бернулли | Схема испытаний Бернулли |
| Оценки по выборке |  |
|
| Статистика K |  |
 |
| Распределение статистики K | Стандартное нормальное N(0,1) | Стандартное нормальное N(0,1) |
Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
Значение uкр находим по таблице функции Лапласа из соотношения 2Ф(uкр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка
Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.
Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
Ф(2.23) = 0.49, uкр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
где n=40, N = 365 (дней). Отсюда
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.
Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.
Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01
Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H0:p=p0=0,97 — неизвестная генеральная доля p равна заданному значению p0=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H1:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p0=0,97, n=200, m=193

Критическое значение находим по таблице функции Лапласа из равенства
По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-Kkp)= (-∞;-2,05). Наблюдаемое значение Кнабл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.
Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H0:p1=p2 — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H0:p1≠p2 — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.
Наблюдаемое значение равно

Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение Kнабл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.
По части судить о целом
О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при
достаточном числе наблюдений
. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:
С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.
Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.
Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.
Как рассчитать объем выборки
Достаточный размер выборки зависит от следующих составляющих:
- изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
- размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
- уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)
ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента
Формулы для расчета объема выборки:
Формулы расчета объема выборки
Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.
График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.
Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.
Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.
Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.
Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.
В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:

Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.
В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:
- Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
- Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.
Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.
Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.
Способ 1: применение расширенного автофильтра
Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.
- Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».
Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».
- После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».
- Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».
- Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.
- Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».
- Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.
- Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».
- Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».
- Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.
- Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».
- Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).
- В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».
- Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».
- Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.
- Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».
Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».
При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.
Способ 2: применение формулы массива
Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.
- На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.
- Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.
- Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.
- Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Жмем сочетание клавиш Ctrl+Shift+Enter.
- Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Опять набираем сочетание клавиш Ctrl+Shift+Enter.
Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.
- Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».
- В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».
- Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».
- В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».
- В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».
- На кнопку с точно таким же названием жмем после возвращения в окно создания условий.
Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.
СРЗНАЧ()
Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.
Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:
Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13
Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).
Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:
СРЗНАЧЕСЛИ()
Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:
В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.
Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:
Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.
МАКС()
Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:
МИН()
Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:
Источники
- https://lumpics.ru/descriptive-statistics-in-excel/
- https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
- https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
- http://galyautdinov.ru/post/formula-vyborki-prostaya
- https://math.semestr.ru/group/interval-estimation-share.php
- https://tidydata.ru/sample-size
- https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
- https://lumpics.ru/how-to-make-a-sample-in-excel/
- https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html
Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.
Задача
описательной статистики
(descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений
выборки
к нескольким итоговым показателям, которые дают представление о
выборке
.В качестве таких статистических показателей используются:
среднее
,
медиана
,
мода
,
дисперсия, стандартное отклонение
и др.
Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные
статистические выводы о распределении
, из которого была взята
выборка
. Например, если у нас есть
выборка
значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой
выборки
мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.
Содержание статьи:
- Надстройка Пакет анализа;
-
Среднее выборки
;
-
Медиана выборки
;
-
Мода выборки
;
-
Мода и среднее значение
;
-
Дисперсия выборки
;
-
Стандартное отклонение выборки
;
-
Стандартная ошибка
;
-
Ассиметричность
;
-
Эксцесс выборки
;
-
Уровень надежности
.
Надстройка Пакет анализа
Для вычисления статистических показателей одномерных
выборок
, используем
надстройку Пакет анализа
. Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.
СОВЕТ
: Подробнее о других инструментах надстройки
Пакет анализа
и ее подключении – читайте в статье
Надстройка Пакет анализа MS EXCEL
.
Выборку
разместим на
листе
Пример
в файле примера
в диапазоне
А6:А55
(50 значений).
Примечание
: Для удобства написания формул для диапазона
А6:А55
создан
Именованный диапазон
Выборка.
В диалоговом окне
Анализ данных
выберите инструмент
Описательная статистика
.
После нажатия кнопки
ОК
будет выведено другое диалоговое окно,
в котором нужно указать:
входной интервал
(Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле
Метки в первой строке (
Labels
in
first
row
).
В этом случае заголовок будет выведен в
Выходном интервале.
Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
выходной интервал
(Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
Итоговая статистика (
Summary
Statistics
)
. Поставьте галочку напротив этого поля – будут выведены основные показатели выборки:
среднее, медиана, мода, стандартное отклонение
и др.;-
Также можно поставить галочки напротив полей
Уровень надежности (
Confidence
Level
for
Mean
)
,
К-й наименьший
(Kth Largest) и
К-й наибольший
(Kth Smallest).
В результате будут выведены следующие статистические показатели:
Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.
Если во
входном интервале
указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во
Входной интервал
и установите галочку в поле
Метки в первой строке
). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.
Зеленым цветом на картинке выше и в
файле примера
выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:
Интервал
(Range) — разница между максимальным и минимальным значениями;
Минимум
(Minimum) – минимальное значение в диапазоне ячеек, указанном во
Входном интервале
(см.статью про функцию
МИН()
);
Максимум
(Maximum)– максимальное значение (см.статью про функцию
МАКС()
);
Сумма
(Sum) – сумма всех значений (см.статью про функцию
СУММ()
);
Счет
(Count) – количество значений во
Входном интервале
(пустые ячейки игнорируются, см.статью про функцию
СЧЁТ()
);
Наибольший
(Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см.статью про функцию
НАИБОЛЬШИЙ()
);
Наименьший
(Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см.статью про функцию
НАИМЕНЬШИЙ()
).
Ниже даны подробные описания остальных показателей.
Среднее выборки
Среднее
(mean, average) или
выборочное среднее
или
среднее выборки
(sample average) представляет собой
арифметическое среднее
всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция
СРЗНАЧ()
.
Выборочное среднее
является «хорошей» (несмещенной и эффективной) оценкой
математического ожидания
случайной величины (подробнее см. статью
Среднее и Математическое ожидание в MS EXCEL
).
Медиана выборки
Медиана
(Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем
медиана
, а половина чисел меньше, чем
медиана
. Для определения
медианы
необходимо сначала
отсортировать множество чисел
. Например,
медианой
для чисел 2, 3, 3,
4
, 5, 7, 10 будет 4.
Если множество содержит четное количество чисел, то вычисляется
среднее
для двух чисел, находящихся в середине множества. Например,
медианой
для чисел 2, 3,
3
,
5
, 7, 10 будет 4, т.к. (3+5)/2.
Если имеется длинный хвост распределения, то
Медиана
лучше, чем
среднее значение
, отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.
Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что
как минимум
у 50% сотрудников зарплата меньше или равна 15 тыс. руб.
Для определения
медианы
в MS EXCEL существует одноименная функция
МЕДИАНА()
, английский вариант — MEDIAN().
Медиану
также можно вычислить с помощью формул
=КВАРТИЛЬ.ВКЛ(Выборка;2) =ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).
Подробнее о
медиане
см. специальную статью
Медиана в MS EXCEL
.
СОВЕТ
: Подробнее про
квартили
см. статью, про
перцентили (процентили)
см. статью.
Мода выборки
Мода
(Mode) – это наиболее часто встречающееся (повторяющееся) значение в
выборке
. Например, в массиве (1; 1;
2
;
2
;
2
; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это
мода
. Для вычисления
моды
используется функция
МОДА()
, английский вариант MODE().
Примечание
: Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье
Есть ли повторы в списке?
Начиная с
MS EXCEL 2010
вместо функции
МОДА()
рекомендуется использовать функцию
МОДА.ОДН()
, которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция
МОДА.НСК()
, которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.
Например, в массиве (1; 1;
2
;
2
;
2
; 3;
4
;
4
;
4
; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются
модами
. Функции
МОДА.ОДН()
и
МОДА()
вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см.
файл примера
, лист
Мода
).
Чтобы исправить эту несправедливость и была введена функция
МОДА.НСК()
, которая выводит все
моды
. Для этого ее нужно ввести как
формулу массива
.
Как видно из картинки выше, функция
МОДА.НСК()
вернула все три
моды
из массива чисел в диапазоне
A2:A11
: 1; 3 и 7. Для этого, выделите диапазон
C6:C9
, в
Строку формул
введите формулу
=МОДА.НСК(A2:A11)
и нажмите
CTRL+SHIFT+ENTER
. Диапазон
C
6:
C
9
охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству
мод
. Если ячеек больше чем м
о
д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если
мода
только одна, то все выделенные ячейки будут заполнены значением этой
моды
.
Теперь вспомним, что мы определили
моду
для выборки, т.е. для конечного множества значений, взятых из
генеральной совокупности
. Для
непрерывных случайных величин
вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция
МОДА()
вернет ошибку.
Даже в нашем массиве с
модой
, которая была определена с помощью
надстройки Пакет анализа
, творится, что-то не то. Действительно,
модой
нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на
гистограмму распределения
, построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).
Проблема в том, что мы определили
моду
как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому,
моду
в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для
логнормального распределения
мода
(наиболее вероятное значение непрерывной случайной величины х), вычисляется как
exp
(
m
—
s
2
)
, где m и s параметры этого распределения.
Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для
моды
распределения, из которого взята
выборка
(наиболее вероятного значения или для которого плотность вероятности распределения максимальна).
Для того, чтобы получить оценку
моды
распределения, из
генеральной совокупности
которого взята
выборка
, можно, например, построить
гистограмму
. Оценкой для
моды
может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.
Вывод
: Значение
моды
для
выборки
, рассчитанное с помощью функции
МОДА()
, может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер
выборки
существенно превышает количество этих значений.
Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане),
модой
является число 15 (17 значений из 51, т.е. 33%). В этом случае функция
МОДА()
дает хорошую оценку «наиболее вероятного» значения зарплаты.
Примечание
: Строго говоря, в примере с зарплатой мы имеем дело скорее с
генеральной совокупностью
, чем с
выборкой
. Т.к. других зарплат в компании просто нет.
О вычислении
моды
для распределения
непрерывной случайной величины
читайте статью
Мода в MS EXCEL
.
Мода и среднее значение
Не смотря на то, что
мода
– это наиболее вероятное значение случайной величины (вероятность выбрать это значение из
Генеральной совокупности
максимальна), не следует ожидать, что
среднее значение
обязательно будет близко к
моде
.
Примечание
:
Мода
и
среднее
симметричных распределений совпадает (имеется ввиду симметричность
плотности распределения
).
Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6.
Модой
является 6, а среднее значение – 3,6666.
Другой пример. Для
Логнормального распределения
LnN(0;1)
мода
равна =EXP(m-s2)= EXP(0-1*1)=0,368, а
среднее значение
1,649.
Дисперсия выборки
Дисперсия выборки
или
выборочная дисперсия (
sample
variance
) характеризует разброс значений в массиве, отклонение от
среднего
.
Из формулы №1 видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии выборки
используется функция
ДИСП()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию
ДИСП.В()
.
Дисперсию
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)
–
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
.
Чем больше величина
дисперсии
, тем больше разброс значений в массиве относительно
среднего
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность
дисперсии
будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии – стандартное отклонение
.
Подробнее о
дисперсии
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартное отклонение выборки
Стандартное отклонение выборки
(Standard Deviation), как и
дисперсия
, — это мера того, насколько широко разбросаны значения в выборке
относительно их среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х
выборок
: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у
выборок
существенно отличается.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
СТАНДОТКЛОН()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
СТАНДОТКЛОН.В()
.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Подробнее о
стандартном отклонении
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартная ошибка
В
Пакете анализа
под термином
стандартная ошибка
имеется ввиду
Стандартная ошибка среднего
(Standard Error of the Mean, SEM).
Стандартная ошибка среднего
— это оценка
стандартного отклонения
распределения
выборочного среднего
.
Примечание
: Чтобы разобраться с понятием
Стандартная ошибка среднего
необходимо прочитать о
выборочном распределении
(см. статью
Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL
) и статью про
Центральную предельную теорему
.
Стандартное отклонение распределения выборочного среднего
вычисляется по формуле σ/√n, где n — объём
выборки, σ — стандартное отклонение исходного
распределения, из которого взята
выборка
. Т.к. обычно
стандартное отклонение
исходного распределения неизвестно, то в расчетах вместо
σ
используют ее оценку
s
—
стандартное отклонение выборки
. А соответствующая величина s/√n имеет специальное название —
Стандартная ошибка среднего.
Именно эта величина вычисляется в
Пакете анализа.
В MS EXCEL
стандартную ошибку среднего
можно также вычислить по формуле
=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))
Асимметричность
Асимметричность
или
коэффициент асимметрии
(skewness) характеризует степень несимметричности распределения (
плотности распределения
) относительно его
среднего
.
Положительное значение
коэффициента асимметрии
указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого.
Коэффициент асимметрии
идеально симметричного распределения или выборки равно 0.
Примечание
:
Асимметрия выборки
может отличаться расчетного значения асимметрии теоретического распределения. Например,
Нормальное распределение
является симметричным распределением (
плотность его распределения
симметрична относительно
среднего
) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в
выборке
из соответствующей
генеральной совокупности
не обязательно должны располагаться совершенно симметрично относительно
среднего
. Поэтому,
асимметрия выборки
, являющейся оценкой
асимметрии распределения
, может отличаться от 0.
Функция
СКОС()
, английский вариант SKEW(), возвращает коэффициент
асимметрии выборки
, являющейся оценкой
асимметрии
соответствующего распределения, и определяется следующим образом:
где n – размер
выборки
, s –
стандартное отклонение выборки
.
В
файле примера на листе СКОС
приведен расчет коэффициента
асимметрии
на примере случайной выборки из
распределения Вейбулла
, которое имеет значительную положительную
асимметрию
при параметрах распределения W(1,5; 1).
Эксцесс выборки
Эксцесс
показывает относительный вес «хвостов» распределения относительно его центральной части.
Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/-
σ
.
Примечание
: Не смотря на старания профессиональных статистиков, в литературе еще попадается определение
Эксцесса
как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение
Эксцесса
ничего не говорит о форме пика распределения.
Согласно определения,
Эксцесс
равен четвертому
стандартизированному моменту:
Для
нормального распределения
четвертый момент равен 3*σ
4
, следовательно,
Эксцесс
равен 3. Многие компьютерные программы используют для расчетов не сам
Эксцесс
, а так называемый Kurtosis excess, который меньше на 3. Т.е. для
нормального распределения
Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.
Примечание
: Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как
Эксцесс
(от англ. excess — «излишек»). Например, функция MS EXCEL
ЭКСЦЕСС()
на самом деле вычисляет Kurtosis excess.
Функция
ЭКСЦЕСС()
, английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку
эксцесса распределения
случайной величины и определяется следующим образом:
Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из
нормального распределения
формула вернет близкое к 0 значение.
Если задано менее четырех точек данных, то функция
ЭКСЦЕСС()
возвращает значение ошибки #ДЕЛ/0!
Вернемся к
распределениям случайной величины
.
Эксцесс
(Kurtosis excess) для
нормального распределения
всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений
Эксцесс
зависит от параметров распределения: см., например,
распределение Вейбулла
или
распределение Пуассона
, для котрого
Эксцесс
= 1/λ.
Уровень надежности
Уровень
надежности
— означает вероятность того, что
доверительный интервал
содержит истинное значение оцениваемого параметра распределения.
Вместо термина
Уровень
надежности
часто используется термин
Уровень доверия
. Про
Уровень надежности
(Confidence Level for Mean) читайте статью
Уровень значимости и уровень надежности в MS EXCEL
.
Задав значение
Уровня
надежности
в окне
надстройки Пакет анализа
, MS EXCEL вычислит половину ширины
доверительного интервала для оценки среднего (дисперсия неизвестна)
.
Тот же результат можно получить по формуле (см.
файл примера
):
=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n)
s —
стандартное отклонение выборки
, n – объем
выборки
.
Подробнее см. статью про
построение доверительного интервала для оценки среднего (дисперсия неизвестна)
.
Описательная статистика Excel позволяет за несколько минут обработать достаточно большое количество информации и найти необходимые значения, учитывая определенный набор условий и критерий. Обработка данных большого ряда значений согласно всем законам статистики – нет проблем, Microsoft Excel справиться со всем.
Для того чтобы сформировать вывод о результатах полученных данных с целого ряда массива значений можно использовать достаточно простую функцию из «Пакета анализа», которая позволит систематизировать эмпирические значения согласно определенным критериям.
Эта функция можем высчитывать большинство критериев, среди которых:
• Отклонение и стандартное отклонение;
• Ошибка и стандартная ошибка;
• Асимметричность значений;
• Мода;
• Дисперсия;
• Медиана;
• Другие значения.
По умолчанию, возможность работы с «Относительной статистикой» скрыта от большинства пользователей. Для того чтобы активировать данную панель, необходимо включить ее в параметрах документа.
Для этого нажмем на вкладку «Файл» — «Параметры».
В появившемся диалоговом окне перейдем в меню «Надстройки», где внизу в подменю «Управление» нужно выбрать «Надстройки Excel» и перейти к последующим настройкам.
В новом окне ставим галочку напротив «Пакет анализа» и применяем операцию.
Весь функционал «Пакета анализа» был добавлен в рабочую область и появился во вкладке «Данные». Приступим непосредственно к «Описательной статистике» и попробуем на практике данный инструмент.
Перейдем во вкладку «Анализ данных», которая размещена в «Данных» и выбираем функцию «Описательная статистика».
Теперь необходимо заполнить все поля и ввести аргументы функции.
• «Входной интервал» — укажем весь диапазон данных, для которых необходимо применить функцию «Описательной статистики» — выделяем весь столбец вместе с названием с включением функции «Метки в первой строке».
• Включим группирование «По строкам» и «По столбцам».
• Выберем место, куда будут сохраняться результаты работы функции, это могут быть и новая книга, новый лист либо просто выбранный интервал.
Теперь можно анализировать результаты работы функции. «Описательная статистика» рассчитала сразу несколько показателей, которые дают более четкое представление о выполненной работе: интервал, минимум и максимум, общую сумму и среднее значение и так далее.
Пакет анализа предлагает пользователю результаты сразу по нескольким критериям. Это экономит большое количество времени, которое ушло бы на отдельный расчет по каждому показателю.
Описательная статистика в excel
Инструмент Описательная статистика входит в Пакет анализа (активация Пакета анализа смотри п.2.7.2). С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим работу данного инструмента на примере задачи 4.2.
Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ». Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK» (рис. 4.1).
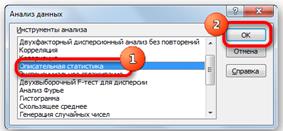 |
| Рис. 4.1. Описательная статистика |
После выполнения данных действий непосредственно запускается окно «Описательная статистика».
В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.
Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:
- Выходной интервал;
- Новый рабочий лист;
- Новая рабочая книга.
В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на этом же рабочем листе (рис.4.2).
Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.
Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Этот параметр, также как и предыдущий, не является обязательным, поэтому флажки можно не ставить.
После того, как все указанные данные внесены, жмем на кнопку «OK».
Среди множества показателей Описательной статистики есть те, которые нас интересуют, они выделены цветом (рис. 4.3).
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Дайте определение размаху, выборочной дисперсии, генеральной дисперсии, стандартному отклонению. Воспроизведите формулы для их нахождения.
2. Что характеризует выборочная дисперсия.
3. Вычислите для множества: 22, 15, 16, 21, 24, 24, 27, 28, 30, 30, 31, 31, 31, 34, 36 размах, дисперсию, стандартное отклонение.
4. В каких случаях можно проводить сравнение разных выборок по дисперсиям?
5. Выборочные дисперсии результатов контрольной работы в классе 7«А» и 7«Б» соответственно равны 0,44 и 1,38. Какой вывод можно сделать при сравнении результатов контрольной работы в двух классах?
6. Дисперсия каждой из групп A и В равна 5. Будет ли дисперсия 10 значений, полученных путем объединения групп, меньше, больше или равна 5?
Группа А: 13, 11, 10, 9, 7
Группа В: 28, 26, 25, 24, 22
Лабораторная работа №2
Описательная статистика
Этапы обработки данных:
1. Занести данные в таблицу Excel (две выборки).
2. Упорядочить данные (по возрастанию) в каждой выборке.
3. Рассчитать моду, медиану и среднее.
4. Посчитать дисперсию, стандартное отклонение.
5. Посчитать коэффициент вариации.
6. Сделать сравнительный анализ, полученных результатов.
Задания для вариантов 1 – 5
При определении степени выраженности некоторого психического свойства в двух группах, опытной и контрольной, баллы распределились следующим образом.
Дать сравнительную характеристику степени выраженности этого свойства в данных группах.
Вариант 1.
| Опытная | 18, 15, 16, 11, 14,15, 16, 16, 20, 22, 17, 12, 11, 12, 18, 19, 20 |
| Контрольная | 26, 8, 11, 12, 25, 22, 13, 14, 21, 20, 15, 16, 17, 16, 9, 11, 16 |
Вариант 2
| Опытная | 19, 16, 17, 12, 15,16, 17,17, 21, 23, 18, 13, 12, 13, 19, 20, 21 |
| Контрольная | 27, 9, 12, 13, 26, 23, 14, 15, 22, 21, 16, 16, 18, 17, 10, 12, 17 |
Вариант 3.
| Опытная | 16, 13, 14, 9, 10,13, 14,14, 18, 20, 15, 10, 9, 10, 16, 17, 18 |
| Контрольная | 24, 6, 9, 10, 23, 20, 11, 12, 19, 18, 13, 14, 12, 14, 7, 9, 14 |
| Опытная | 15, 12, 13, 8, 11,12, 13,13, 17, 19, 14, 9, 8, 9, 15, 16, 17 |
| Контрольная | 23, 5, 9, 9, 22, 19, 10, 11, 18, 17, 12, 13, 14, 13, 6, 8, 13 |
| Опытная | 15, 12, 13, 8, 11,12, 13,13, 17, 19, 14, 9, 8, 9, 15, 16, 17 |
| Контрольная | 24, 6, 9, 10, 23, 20, 11, 12, 19, 18, 13, 14, 12, 14, 7, 9, 14 |
Задания для вариантов 6 – 10
Была исследована группа детей с заболеванием крови до лечения препаратами и после лечения. В таблицу занесены показатели крови по результатам медицинского обследования. Сделать сравнительный анализ результативности лечения данным препаратом, используя методы описательной статистики.
| до лечения | 20,5 12,1 13,6 40,5 9,6 33 77,2 8,7 3,5 13,8 7,4 29,4 116 21,9 |
| после лечения | 2,3 7,5 3,8 3,8 8,8 13 4,7 3,9 4,8 5,7 9 13 0,9 |
| до лечения | 280 230 100 60 90 80 8 36 50 90 17 42 42 30 |
| после лечения | 86 280 30 170 210 230 230 156 102 161 15 60 20 |
| до лечения | 112 60 84 60 60 40 76 60 84 40 112 46 64 70 |
| после лечения | 82 78 110 130 130 104 108 129 110 88 105 73 85 80 |
| до лечения | 113 61 85 61 61 41 77 61 85 41 113 47 65 71 |
| после лечения | 81 77 109 129 129 103 107 128 109 87 104 72 84 79 |
| до лечения | 111 59 83 59 59 39 75 59 83 39 111 45 63 69 |
| после лечения | 83 79 111 131 131 105 109 130 111 89 106 74 86 81 |
Задания для вариантов 11 – 15
Для проверки эффективности новой развивающей программы были созданы две группы детей шестилетнего возраста. На первом этапе дети обеих групп были протестированы по методике Керна-Йерасика (школьная зрелость). Результаты тестирования по невербальной шкале занесены в таблицу. Сделать сравнительный анализ школьной зрелости детей этих групп.
| Эксперимент. | 29 31 31 25 25 19 22 20 14 16 27 24 32 27 14 24 |
| Контроль | 34 31 28 27 30 23 21 28 29 31 17 22 21 15 33 29 |
| Эксперимент. | 14 13 11 8 12 13 13 13 11 12 14 13 12 14 10 13 |
| Контроль | 13 13 14 12 14 14 12 13 15 13 11 12 14 9 14 13 |
| Эксперимент. | 33 33 37 33 34 33 31 29 29 35 31 29 31 34 26 26 |
| Контроль | 39 30 38 36 31 37 35 32 39 34 30 32 36 29 39 36 |
| Эксперимент. | 13 12 10 7 11 12 12 12 10 11 13 12 11 13 9 12 |
| Контроль | 12 12 13 11 13 13 11 12 14 12 10 11 13 8 13 12 |
| Эксперимент. | 30 32 32 26 26 20 23 21 15 17 28 25 33 28 15 25 |
| Контроль | 35 32 29 28 31 24 22 29 30 32 18 24 22 16 34 30 |
Задания для вариантов 16 – 20
У участников психологического исследования, в число которых входила группа педагогов и группа непедагогов, был исследован уровень конфликтности. Полученные данные занесены в таблицу. Можно ли утверждать, что уровень конфликтности педагогов выше, чем у непедагогов?
Использование пакета анализа
Если вам нужно провести сложный статистический или инженерный анализ, можно сэкономить время и этапы с помощью «Pak анализа». Вы предоставляете данные и параметры для каждого анализа, а средство использует соответствующие статистические или инженерные функции для вычисления и отображения результатов в выходной таблице. Некоторые средства создают диаграммы в дополнение к выходным таблицам.
Функции анализа данных можно применять только на одном листе. Если анализ данных проводится в группе, состоящей из нескольких листов, то результаты будут выведены на первом листе, на остальных листах будут выведены пустые диапазоны, содержащие только форматы. Чтобы провести анализ данных на всех листах, повторите процедуру для каждого листа в отдельности.
Ниже описаны инструменты, включенные в пакет анализа. Для доступа к ним нажмите кнопку Анализ данных в группе Анализ на вкладке Данные. Если команда Анализ данных недоступна, необходимо загрузить надстройку «Пакет анализа».
Откройте вкладку Файл, нажмите кнопку Параметры и выберите категорию Надстройки.
Если вы используете Excel 2007, нажмите Microsoft Office кнопку и выберите «Параметры Excel»
В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
Если вы используете Excel для Mac, в строке меню откройте вкладку Средства и в раскрывающемся списке выберите пункт Надстройки для Excel.
В диалоговом окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
Примечание: Чтобы включить Visual Basic для приложений (VBA) в надстройку «Надстройка «Анализ», можно загрузить его так же, как и надстройку «Надстройка «Анализ». В поле «Доступные надстройки» выберите «Надстройка анализа — VBA».
Существует несколько видов дисперсионного анализа. Нужный вариант выбирается с учетом числа факторов и имеющихся выборок из генеральной совокупности.
Однофакторный дисперсионный анализ
Этот инструмент выполняет простой анализ дисперсии данных для двух или более выборок. Анализ предоставляет проверку гипотезы о том, что все выборки взяты из одного и того же распределения вероятности относительно альтернативной гипотезы о том, что распределение вероятностей не одинаково для всех выборок. Если выборок всего два, можно использовать функцию T. ТЕСТ. В более чем двух примерах не существует удобного обобщения T. Ивместо нее можно использовать модель однофакторного коэффициента.
Двухфакторный дисперсионный анализ с повторениями
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам. Например, в эксперименте по измерению высоты растений последние обрабатывали удобрениями от различных изготовителей (например, A, B, C) и содержали при различной температуре (например, низкой и высокой). Таким образом, для каждой из 6 возможных пар условий <удобрение, температура>, имеется одинаковый набор наблюдений за ростом растений. С помощью этого дисперсионного анализа можно проверить следующие гипотезы:
Извлечены ли данные о росте растений для различных марок удобрений из одной генеральной совокупности. Температура в этом анализе не учитывается.
Извлечены ли данные о росте растений для различных уровней температуры из одной генеральной совокупности. Марка удобрения в этом анализе не учитывается.
Извлечены ли шесть выборок, представляющих все пары значений <удобрение, температура>, используемые для оценки влияния различных марок удобрений (для первого пункта в списке) и уровней температуры (для второго пункта в списке), из одной генеральной совокупности. Альтернативная гипотеза предполагает, что влияние конкретных пар <удобрение, температура>превышает влияние отдельно удобрения и отдельно температуры.
Двухфакторный дисперсионный анализ без повторений
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам, как в случае двухфакторного дисперсионного анализа с повторениями. Однако в таком анализе предполагается, что для каждой пары параметров есть только одно измерение (например, для каждой пары параметров <удобрение, температура>из предыдущего примера).
Функции КОРРЕЛ и PEARSON рассчитывают коэффициент корреляции между двумя переменными измерения, если измерения по каждой переменной наблюдались для каждого из N-объектов. (Отсутствуют результаты наблюдений по любой теме, которые при анализе игнорируются.) Инструмент анализа корреляции особенно удобен, если для каждого субъекта N существует более двух переменных измерения. Она содержит выходную таблицу — матрицу корреляции, которая показывает значение КОРРЕЛ (или PEARSON),примененного к каждой из возможных пар переменных измерения.
Коэффициент корреляции, как и ковариана, — это мера степени, в которой две переменные измерения «различаются». В отличие от ковариации коэффициент корреляции масштабирован таким образом, что его значение не зависит от единиц, в которых выражены две переменные измерения. (Например, если двумя переменными измерения являются вес и высота, коэффициент корреляции не изменяется, если вес преобразуется из фунта в фунты.) Значение любого коэффициента корреляции должно быть включительно (от -1 до +1).
Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, т. е. большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция).
Средства корреляции и ковариатора можно использовать в одном и том же параметре, если у вас есть N различных переменных измерения для набора людей. Каждый из инструментов корреляции и ковариции дает выходную таблицу — матрицу, в которую указывается коэффициент корреляции или коварианс между каждой парой переменных измерения. Разница заключается в том, что коэффициенты корреляции масштабироваться в зависимости от -1 и +1 включительно. Соответствующие ковариансии не масштабироваться. Коэффициент корреляции и ковариатор — это меры, в которых две переменные «различаются».
Инструмент «Ковариана» вычисляет значение функции КОВАРИАНАС на этом компьютере. P для каждой пары переменных измерения. (Непосредственное использование КОВАРИАНС. Вместо ковариатора P лучше использовать ковариативную единицу, если имеется только две переменных измерения, то есть N=2.) Запись на диагонали выходной таблицы инструмента «Ковариальная» в строке i, столбце i — ковариальная величина i-й переменной. Это только дисперсия по численности населения для этой переменной, вычисляемая функцией ДИСПЕ. P.
Ковариационный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных связаны с большими значениями другого набора (положительная ковариация) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная ковариация), или данные двух диапазонов никак не связаны (ковариация близка к нулю).
Инструмент анализа «Описательная статистика» применяется для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.
Инструмент анализа «Экспоненциальное сглаживание» применяется для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. При анализе используется константа сглаживания a, величина которой определяет степень влияния на прогнозы погрешностей в предыдущем прогнозе.
Примечание: Для константы сглаживания наиболее подходящими являются значения от 0,2 до 0,3. Эти значения показывают, что ошибка текущего прогноза установлена на уровне от 20 до 30 процентов ошибки предыдущего прогноза. Более высокие значения константы ускоряют отклик, но могут привести к непредсказуемым выбросам. Низкие значения константы могут привести к большим промежуткам между предсказанными значениями.
Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.
Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.
С помощью этого инструмента вычисляется значение f F-статистики (или F-коэффициент). Значение f, близкое к 1, показывает, что дисперсии генеральной совокупности равны. В таблице результатов, если f 1, «P(F
Инструмент «Анализ Фурье» применяется для решения задач в линейных системах и анализа периодических данных на основе метода быстрого преобразования Фурье (БПФ). Этот инструмент поддерживает также обратные преобразования, при этом инвертирование преобразованных данных возвращает исходные данные.
Инструмент «Гистограмма» применяется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. При этом рассчитываются числа попаданий для заданного диапазона ячеек.
Например, можно получить распределение успеваемости по шкале оценок в группе из 20 студентов. Таблица гистограммы состоит из границ шкалы оценок и групп студентов, уровень успеваемости которых находится между самой нижней границей и текущей границей. Наиболее часто встречающийся уровень является модой диапазона данных.
Совет: В Excel 2016 теперь можно создавать гистограммы и диаграммы Парето.
Инструмент анализа «Скользящее среднее» применяется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Скользящее среднее, в отличие от простого среднего для всей выборки, содержит сведения о тенденциях изменения данных. Этот метод может использоваться для прогноза сбыта, запасов и других тенденций. Расчет прогнозируемых значений выполняется по следующей формуле:
N — число предшествующих периодов, входящих в скользящее среднее;
A j — фактическое значение в момент времени j;
F j — прогнозируемое значение в момент времени j.
Инструмент «Генерация случайных чисел» применяется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью этой процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей. Например, можно использовать нормальное распределение для моделирования совокупности данных по росту людей или использовать распределение Бернулли для двух вероятных исходов, чтобы описать совокупность результатов бросания монеты.
Инструмент анализа «Ранг» и «Процентиль» создает таблицу, которая содержит порядкованный и процентный ранг каждого значения в наборе данных. Можно проанализировать относительное положение значений в наборе данных. В этом средстве используются функции РАНГ. EQ и PERCENTRANK. INC. Если вы хотите учитывать связанные значения, используйте РАНГ. Функция EQ, которая рассматривает связанные значения как связанные значения с одинаковым рангом, или использует РАНГ. Функция AVG, которая возвращает среднее ранг для связанных значений.
Инструмент анализа «Регрессия» применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.
Инструмент «Регрессия» использует функцию LINEST.
Инструмент анализа «Выборка» создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки или построения диаграммы, можно использовать представительную выборку. Кроме того, если предполагается периодичность входных данных, то можно создать выборку, содержащую значения только из отдельной части цикла. Например, если входной диапазон содержит данные для квартальных продаж, создание выборки с периодом 4 разместит в выходном диапазоне значения продаж из одного и того же квартала.
Двухвыборочный t-тест проверяет равенство средних значений генеральной совокупности по каждой выборке. Три вида этого теста допускают следующие условия: равные дисперсии генерального распределения, дисперсии генеральной совокупности не равны, а также представление двух выборок до и после наблюдения по одному и тому же субъекту.
Для всех трех средств, перечисленных ниже, значение t вычисляется и отображается как «t-статистика» в выводимой таблице. В зависимости от данных это значение t может быть отрицательным или неотрицательным. Если предположить, что средние генеральной совокупности равны, при t =0 «P(T Парный двухвыборочный t-тест для средних
Парный тест используется, когда имеется естественная парность наблюдений в выборках, например, когда генеральная совокупность тестируется дважды — до и после эксперимента. Этот инструмент анализа применяется для проверки гипотезы о различии средних для двух выборок данных. В нем не предполагается равенство дисперсий генеральных совокупностей, из которых выбраны данные.
Примечание: Одним из результатов теста является совокупная дисперсия (совокупная мера распределения данных вокруг среднего значения), вычисляемая по следующей формуле:
Двухвыборочный t-тест с одинаковыми дисперсиями
Этот инструмент анализа выполняет двухуголовый t-тест учащегося. В этой форме t-теста предполагается, что два набора данных поступили из распределения с одинаковыми дисперсиями. Этот тест называется гомомоcedastic t-test. Этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами.
Двухвыборочный t-тест с различными дисперсиями
Этот инструмент анализа выполняет двухуголовый t-тест учащегося. В этой форме t-теста предполагается, что два набора данных поступили из распределений с неравными дисперсиями. Это называется гетероскестический t-тест. Как и в предыдущем случае с равными дисперсиями, этот t-тест можно использовать для определения вероятности того, что две выборки взяты из распределения с равными средствами. Этот тест можно использовать, если в двух примерах есть различные темы. Используйте парный тест, описанный в примере, если существует один набор субъектов и два примера представляют измерения для каждой темы до и после обработки.
Для определения тестовой величины t используется следующая формула.
Для вычисления степеней свободы (df) используется следующая формула: Так как результат вычисления обычно не является integer, значение df округлится до ближайшего ближайшего другого для получения критического значения из таблицы t. Функция листа Excel T. В этой проверке используется вычисляемая величина df без округления, так как ее можно вычислить для значения T. ТЕСТ с неинтегрным df. Из-за таких разных подходов к определению степеней свободы результаты T. Тест и этот t-тест различаются в случае неравных дисперсий.
Z-тест. Средство анализа «Две выборки для средств» выполняет два примера z-теста для средств со известными дисперсиями. Это средство используется для проверки гипотезы null о том, что между двумя значениями населения нет различий между односторонними или двухбокльными гипотезами. Если дисперсии не известны, функция Z. Вместо нее следует использовать тест.
При использовании этого инструмента следует внимательно просматривать результат. «P(Z = ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. «P(Z = ABS(z) или Z
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА
Первичный анализ скалярных экспериментальных данных начинается с вычисления описательных статистик. Добавив к этому графические характеристики, получим некоторые основания для выводов о характере распределения данных исследуемой совокупности. К тому же базовый анализ дает основу для дальнейшего проведения более сложного анализа данных.
Из множества инструментов надстройки «Анализ данных» будем использовать «Описательную статистику» для получения числовых характеристик и «Гистограмму» — для графических. Заметим, что наряду с этим можно использовать также встроенные «Статистические функции», которые дублируют возможности надстройки.
Рассмотрим работу с описательной статистикой на примере.
Пример 4.1. Имеются некоторые данные о стоимости новогодних туров (рис. 4.2). Каждый из столбцов можно рассматривать как отдельный признак или переменную. Требуется провести анализ данных о продолжительности туров.
Таблица исходных данных
Исходные данные содержат несколько переменных, характеризующих тур. «Название фирмы», «Страна», «Транспорт» — качественные переменные, которые относятся к номинальной шкале. «Отель» —качественная переменная, которую можно отнести к порядковой шкале, так как количество звездочек отражает уровень обслуживания в отеле. «Количество дней» и «Стоимость» —количественные данные, которые относятся к метрической шкале.
Вычислим основные описательные статистики для переменной «Количество дней», которая является числовой переменной, принимающей дискретные значения. Для этого используем инструмент «Описательная статистика», входящий в «Пакет анализа».
Для перехода к описательной статистике выполните: «Данные» —» «Анализ» —> «Анализ данных» —» «Описательная статистика» -> «Ок». В открывшемся диалоговом окне «Описательная статистика» (рис. 4.3) укажите «Входной интервал», диапазон В2:Б16, выберите «Труп-
Диалоговое окно «Описательной статистики»
иирование по столбцам», установите «Метки в первой строке», так как входной интервал содержит наименование столбца. Для «Выходного интервала» достаточно указать одну, первую, ячейку на текущем листе, как альтернативу можно выбрать «Новый рабочий лист» или «Новую рабочую книгу». И наконец, укажите хотя бы одну из выводимых статистик: «Итоговая статистика», «Уровень надежности», «К-й наименьший», «К-й наибольший».
В большинстве случаев достаточно выбрать «Итоговую статистику», которая рассчитывает основные числовые характеристики исследуемой совокупности. Три последних значения рассчитывают, только когда они действительно нужны.
«Описательная статистика» вычисляет 16 значений, из них 13 относятся к «Итоговой статистике», еще три определяют доверительный интервал и два выборочных значения.
Отметим главное — «Описательная статистка» надстройки «Анализ данных» предназначена для вычислений статистических характеристик, или статистик, одномерной выборки или нескольких выборок.
В литературе по статистике часто используют термин «генеральная совокупность». Обычно имеется в виду, что это множество всех доступных для наблюдения данных в противоположность «выборки» — которая подразумевает, что исследуется лишь часть данных выбранных из генеральной совокупности (может быть с помощью случайного отбора).
Обычно числовые характеристики генеральной совокупности называют параметрами, а числовые характеристики выборки — статистиками, или выборочными характеристиками, которые являются оценками параметров генеральной совокупности. Для более полного понимания выборочного метода следует обратиться к специальной литературе.
Результаты расчетов «Итоговой статистики» для переменной «Количество дней» приведены на рисунке 4.4. На этом же рисунке приведены альтернативные расчеты этих числовых характеристик с использованием встроенных функций категории «Статистические». Аргументом статистических функций является диапазон исходных данных, в данном случае D3:D16.
Таким образом, практически все расчеты «Описательной статистики» дублируются «Статистическими» функциями. Остальные характеристики можно посчитать, используя формулы. Для того чтобы на рабочем листе Excel отобразились не результаты, а формулы, следует выполнить: «Формулы» -» «Зависимости формул» -» «Показать формулы».
Отметим некоторое отличие в применении инструментов «Анализа данных» и использовании статистических функций. При изменении значений исходных данных формулы пересчитываются, в то время как результаты, полученные с помощью инструментов «Анализа данных»,
«Итоговая статистика» и «Статистические функции»
не изменяются. Чтобы обновить результаты, потребуется вызывать «Анализ данных» снова.
Числовые характеристики «Итоговой статистики» описывают средние, вариацию и форму распределения, всего 13 параметров:
- • среднее, или выборочное среднее, вычисляется как среднее арифметическое наблюдаемых значений выборки;
- • медиана определяется как значение, находящееся в середине распределения, полученного из исходного путем упорядочивания по возрастанию;
- • мода равна наиболее часто встречающемуся значению. Кроме того, выделяют две величины, характеризующие изменчивость, или разброс, значений распределения относительно среднего:
- 1) дисперсию выборки, или выборочную дисперсию, равную сумме квадратов отклонений каждого значения от среднего, деленной на (А — 1), где N — число значений в распределении, или объем выборки;
2) стандартное отклонение, или выборочное среднеквадратическое отклонение, равное квадратному корню из выборочной дисперсии.
Дополнительными мерами изменчивости являются три простые характеристики, отражающие границы распределения данных и его размах:
- • минимум равен наименьшему из выборочных значений;
- • максимум равен наибольшему из выборочных значений;
- • интервал составляет разность между максимумом и
минимумом, этот параметр называют также размахом.
Если набор данных рассматривается как множество
независимых реализаций случайной величины, то возникает вопрос, что можно сказать о функции распределения этой величины на основании выборки. Очень часто распределение оказывается нормальным или близким к нему.
Для отражения близости формы распределения к нормальному виду существует две основные характеристики:
- 1) эксцесс, или выборочный коэффициент эксцесса, который является мерой «сглаженности» распределения;
- 2) асимметричность, или выборочный коэффициент асимметрии, показывает, в какую сторону относительно среднего сдвинуто большинство значений выборки.
И наконец, сумма равна сумме всех выборочных значений, счет вычисляет объем выборки, стандартная ошибка равна выборочному стандартному отклонению, деленному на квадратный корень из объема выборки.
При необходимости можно вычислить три дополнительные характеристики (рис. 4.5). Результаты расчетов этих характеристик приведены на рисунке 4.6.
«К-й наибольший» выдает К-е выборочное значение, если бы выборка была отсортирована по убыванию. В рассматриваемом примере сортировка по убыванию имеет вид 14,12,12,12, 11, Юит. д., третье значение равно 12. «К-й наименьший» выдает К-е выборочное значение, если бы выборка была отсортирована по возрастанию, это значение равно 5.
Задав «Уровень надежности», например 95%, получим значение для построения доверительного интервала для
Описательная статистика, дополнительные параметры
Результаты расчетов дополнительных параметров
неизвестного математического ожидания генеральной средней с доверительным уровнем 95%. Доверительный интервал строится как выборочное среднее плюс-минус полученное значение. Обратим внимание, что граница здесь вычисляется с помощью распределения Стьюдента, что требует достаточного количества наблюдений на каждую степень свободы.
Таким образом, к вычислению доверительных интервалов нужно относиться с осторожностью, особенно при малых выборках. Использование функции расчета доверительного интервала без понимания статистического смысла может привести к ошибкам. Начинающим исследователям посоветуем обратиться к специальной литературе.
Например, для рассматриваемого примера полученный доверительный интервал не несет смыслового содержания.
Итак, на этапе проведения описательной статистики исследуемый ряд данных может быть как генеральной совокупностью, так и выборкой. Если для генеральной совокупности вычисляются значения параметров распределения, то для выборки находят оценки этих параметров. Рассмотрим ниже подробнее вычисление некоторых числовых характеристик в пакете Excel.
Построение доверительных интервалов для среднего. Описательная статистика в Excel





ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3
Описательная статистика в Excel
Вычисление границ доверительных интервалов в Excel
Использование инструмента Пакета анализа Описательная статистика.
Построение доверительных интервалов для среднего.
В пакете Excel помимо мастера функций имеется набор более мощных инструментов для работы с несколькими выборками углубленного анализа данных, называемый Пакет анализа, который может быть использован для решения задач статистической обработки выборочных данных.
Для установки раздела Анализ данных в пакете Excel сделайте следующее:
— в меню Сервис выберите команду Надстройки;
— в появившемся списке установите флажок Пакет анализа.
Ввод данных. Исследуемые данные следует представить в виде таблицы, где столбцами являются соответствующие показатели. При создании таблицы Excel информация вводится в отдельные ячейки. Совокупность ячеек, содержащих анализируемые данные, называется входным диапазоном.
Последовательность обработки данных. Для использования статистического пакета анализа данных необходимо:
— указать курсором мыши на пункт меню Сервис и щелкнуть левой кнопкой мыши;
— в раскрывающемся списке выбрать команду Анализ данных (если команда Анализ данных отсутствует в меню Сервис, то необходимо установить в Excel пакет анализа данных);
— выбрать необходимую строку в появившемся списке Инструменты анализа;
— ввести входной и выходной диапазоны и выбрать необходимые параметры.
Нахождение основных выборочных характеристик. Для определения характеристик выборки используется процедура Описательная статистика. Процедура позволяет получить статистический отчет, содержащий информацию о центральной тенденции и изменчивости входных данных. Для выполнения процедуры необходимо:
— выполнить команду Сервис > Анализ данных;
— в появившемся списке Инструменты анализа выбрать строку Описательная статистика и нажать кнопку ОК (рис. 1);
— в появившемся диалоговом окне указать входной диапазон, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Для этого следует навести указатель мыши на левую верхнюю ячейку данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;
Рис. 1. Окно выбора метода обработки данных
— указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной диапазон (навести указатель мыши и щелкнуть левой клавишей), далее навести указатель мыши в поле ввода Выходной диапазон и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши;
— в разделе Группировка переключатель установить в положение по столбцам; о установить флажок в поле Итоговая статистика;
— нажать кнопку ОК.
В результате анализа в указанном выходном диапазоне для каждого столбца данных выводятся следующие статистические характеристики: среднее, стандартная ошибка (среднего), медиана, мода, стандартное отклонение, дисперсия выборки, эксцесс, асимметричность, интервал, минимум, максимум, сумма, счет, наибольшее, наименьшее, уровень надежности.
Пример 1. Рассматривается зарплата основных групп работников гостиницы: администрации, обслуживающего персонала и работников ресторана. Были получены следующие данные:
Необходимо определить основные статистические характеристики в группах данных.
1. Для использования инструментов анализа исследуемые данные следует представить в виде таблицы, где столбцами являются соответствующие показатели. Значения зарплат сотрудников администрации введите в диапазон А1:А5, обслуживающего персонала— в диапазон В1:В8 и т. д. В результате получится таблица, представленная на рис. 2.

Рис. 2. Таблица из примера
2. Далее необходимо провести элементарную статистическую обработку. Для этого, указав курсором мыши на пункт меню Сервис, выберите команду Анализ данных. Затем в появившемся списке Инструменты анализа выберите строку Описательная статистика.
Рис. 3. Пример заполнения диалогового окна Описательная статистика
3. В появившемся диалоговом окне (рис. 3) в рабочем поле Входной интервал укажите входной диапазон —А1:С8. Активировав переключателем рабочее поле Выходной интервал, укажите выходной диапазон — ячейку А9. В разделе Группировка переключатель установите в положение по столбцам. Установите флажок в поле Итоговая статистика и нажмите кнопку ОК. В результате анализа (рис. 4) в указанном выходном диапазоне для каждого столбца данных получим соответствующие результаты.
Рис. 4. Результаты работы инструмента Описательная статистика.
1. Найдите наиболее популярный туристический маршрут из четырех реализуемых фирмой (моду), если за неделю последовательно были реализованы следующие маршруты (приводятся номера маршрутов): 1, 3, 3, 2, 1, 1, 4, 4, 2, 4, 1, 3, 2, 4, 1, 4, 4, 3, 1, 2, 3, 4, 1, 1, 3.
2. В рабочей зоне производились замеры концентрации вредного вещества. Получен ряд значений (в мг/м3): 12, 16, 15, 14, 10, 20, 16, 14, 18, 14, 15, 17, 23, 16. Необходимо определить основные выборочные характеристики.
Содержание
- Статистические функции
- МАКС
- МИН
- СРЗНАЧ
- СРЗНАЧЕСЛИ
- МОДА.ОДН
- МЕДИАНА
- СТАНДОТКЛОН
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- РАНГ.СР
- Вопросы и ответы
Статистическая обработка данных – это сбор, упорядочивание, обобщение и анализ информации с возможностью определения тенденции и прогноза по изучаемому явлению. В Excel есть огромное количество инструментов, которые помогают проводить исследования в данной области. Последние версии этой программы в плане возможностей практически ничем не уступают специализированным приложениям в области статистики. Главными инструментами для выполнения расчетов и анализа являются функции. Давайте изучим общие особенности работы с ними, а также подробнее остановимся на отдельных наиболее полезных инструментах.
Статистические функции
Как и любые другие функции в Экселе, статистические функции оперируют аргументами, которые могут иметь вид постоянных чисел, ссылок на ячейки или массивы.
Выражения можно вводить вручную в определенную ячейку или в строку формул, если хорошо знать синтаксис конкретного из них. Но намного удобнее воспользоваться специальным окном аргументов, которое содержит подсказки и уже готовые поля для ввода данных. Перейти в окно аргумента статистических выражений можно через «Мастер функций» или с помощью кнопок «Библиотеки функций» на ленте.
Запустить Мастер функций можно тремя способами:
- Кликнуть по пиктограмме «Вставить функцию» слева от строки формул.
- Находясь во вкладке «Формулы», кликнуть на ленте по кнопке «Вставить функцию» в блоке инструментов «Библиотека функций».
- Набрать на клавиатуре сочетание клавиш Shift+F3.
При выполнении любого из вышеперечисленных вариантов откроется окно «Мастера функций».
Затем нужно кликнуть по полю «Категория» и выбрать значение «Статистические».
После этого откроется список статистических выражений. Всего их насчитывается более сотни. Чтобы перейти в окно аргументов любого из них, нужно просто выделить его и нажать на кнопку «OK».
Для того, чтобы перейти к нужным нам элементам через ленту, перемещаемся во вкладку «Формулы». В группе инструментов на ленте «Библиотека функций» кликаем по кнопке «Другие функции». В открывшемся списке выбираем категорию «Статистические». Откроется перечень доступных элементов нужной нам направленности. Для перехода в окно аргументов достаточно кликнуть по одному из них.
Урок: Мастер функций в Excel
МАКС
Оператор МАКС предназначен для определения максимального числа из выборки. Он имеет следующий синтаксис:
=МАКС(число1;число2;…)
В поля аргументов нужно ввести диапазоны ячеек, в которых находится числовой ряд. Наибольшее число из него эта формула выводит в ту ячейку, в которой находится сама.
МИН
По названию функции МИН понятно, что её задачи прямо противоположны предыдущей формуле – она ищет из множества чисел наименьшее и выводит его в заданную ячейку. Имеет такой синтаксис:
=МИН(число1;число2;…)
СРЗНАЧ
Функция СРЗНАЧ ищет число в указанном диапазоне, которое ближе всего находится к среднему арифметическому значению. Результат этого расчета выводится в отдельную ячейку, в которой и содержится формула. Шаблон у неё следующий:
=СРЗНАЧ(число1;число2;…)
СРЗНАЧЕСЛИ
Функция СРЗНАЧЕСЛИ имеет те же задачи, что и предыдущая, но в ней существует возможность задать дополнительное условие. Например, больше, меньше, не равно определенному числу. Оно задается в отдельном поле для аргумента. Кроме того, в качестве необязательного аргумента может быть добавлен диапазон усреднения. Синтаксис следующий:
=СРЗНАЧЕСЛИ(число1;число2;…;условие;[диапазон_усреднения])
МОДА.ОДН
Формула МОДА.ОДН выводит в ячейку то число из набора, которое встречается чаще всего. В старых версиях Эксель существовала функция МОДА, но в более поздних она была разбита на две: МОДА.ОДН (для отдельных чисел) и МОДА.НСК(для массивов). Впрочем, старый вариант тоже остался в отдельной группе, в которой собраны элементы из прошлых версий программы для обеспечения совместимости документов.
=МОДА.ОДН(число1;число2;…)
=МОДА.НСК(число1;число2;…)
МЕДИАНА
Оператор МЕДИАНА определяет среднее значение в диапазоне чисел. То есть, устанавливает не среднее арифметическое, а просто среднюю величину между наибольшим и наименьшим числом области значений. Синтаксис выглядит так:
=МЕДИАНА(число1;число2;…)
СТАНДОТКЛОН
Формула СТАНДОТКЛОН так же, как и МОДА является пережитком старых версий программы. Сейчас используются современные её подвиды – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Первая из них предназначена для вычисления стандартного отклонения выборки, а вторая – генеральной совокупности. Данные функции используются также для расчета среднего квадратичного отклонения. Синтаксис их следующий:
=СТАНДОТКЛОН.В(число1;число2;…)
=СТАНДОТКЛОН.Г(число1;число2;…)
Урок: Формула среднего квадратичного отклонения в Excel
НАИБОЛЬШИЙ
Данный оператор показывает в выбранной ячейке указанное в порядке убывания число из совокупности. То есть, если мы имеем совокупность 12,97,89,65, а аргументом позиции укажем 3, то функция в ячейку вернет третье по величине число. В данном случае, это 65. Синтаксис оператора такой:
=НАИБОЛЬШИЙ(массив;k)
В данном случае, k — это порядковый номер величины.
НАИМЕНЬШИЙ
Данная функция является зеркальным отражением предыдущего оператора. В ней также вторым аргументом является порядковый номер числа. Вот только в данном случае порядок считается от меньшего. Синтаксис такой:
=НАИМЕНЬШИЙ(массив;k)
РАНГ.СР
Эта функция имеет действие, обратное предыдущим. В указанную ячейку она выдает порядковый номер конкретного числа в выборке по условию, которое указано в отдельном аргументе. Это может быть порядок по возрастанию или по убыванию. Последний установлен по умолчанию, если поле «Порядок» оставить пустым или поставить туда цифру 0. Синтаксис этого выражения выглядит следующим образом:
=РАНГ.СР(число;массив;порядок)
Выше были описаны только самые популярные и востребованные статистические функции в Экселе. На самом деле их в разы больше. Тем не менее, основной принцип действий у них похожий: обработка массива данных и возврат в указанную ячейку результата вычислительных действий.
В Excel
имеется специальное средство– Мастер
диаграмм,
под руководством которого пользователь
может осуществить процесс графического
изображения статистических данных в
виде диаграмм различных типов. В Excel
предусмотрены 34 типа диаграмм: 14
стандартных и 20 нестандартных. Из них
только единственным типом диаграммы,
оси которой могут быть и линейными, и
логарифмическими, является Точечная.
В остальных типах диаграмм масштаб
оси абсцисс всегда равномерен, независимо
от «равномерности» фактических значений
аргумента функции, график которой надо
построить. То есть такие диаграммы
применимы только в тех случаях, когда
значения аргумента имеют постоянный
шаг.
Построение графика
осуществляется следующим образом:
-
Выделяется
диапазон, содержащий данные, по которым
должен быть построен график. -
Нажимается кнопка
Мастер
диаграмм,
расположенная на панели инструментов
Стандартная.
На экране появится диалоговое окно
Мастер
диаграмм (шаг 1 из 4): тип диаграммы.
В нем выбирается Тип
диаграммы. При построении диаграммы
типа Точечная
Excel
воспринимает первый ряд выделенного
диапазона исходных данных как набор
значений аргумента функций, графики
которых нужно построить (один и тот же
набор для всех функций). Следующие ряды
воспринимаются как наборы значений
самих функций (каждый ряд содержит
значения одной из функций, соответствующие
заданным значениям аргумента, находящимся
в первом ряду выделенного диапазона). -
У каждого
стандартного типа диаграммы есть
несколько видов. Их образцы представлены
в палитре Вид.
Выбрав тип диаграммы, нужно щёлкнуть
на том виде диаграммы, который лучше
всего подходит для целей исследования.
Под палитрой Вид
находится информационное окно с краткими
сведениями о выбранной диаграмме. Для
того чтобы посмотреть, как будет
выглядеть выбранная диаграмма,
построенная по данным, выделенным на
первом шаге, нажимается кнопка Просмотр
результата,
расположенная под списком типов
диаграмм. -
После выбора вида
диаграммы в левом верхнем углу палитры,
нажимается кнопка Далее,
расположенная в нижней части окна.
Открывается диалоговое окно Мастер
диаграмм (шаг 2 из 4): источник данных
диаграммы,
в верхней части которого находится
«эскиз» будущего графика.
Это диалоговое
окно имеет две вкладки: Диапазон
данных и
Ряд.
Вкладка Диапазон
данных
позволяет:
– выделить диапазон
исходных данных, по которым должна быть
построена диаграмма, если это не было
сделано до обращения к Мастеру
Диаграмм;
– исправить
неверное выделение исходных данных,
сделанное до обращения к Мастеру
Диаграмм.
На этой же вкладке
определяется ориентация рядов данных.
Делается это с помощью переключателей
Ряды в строках
и Ряды в
столбцах.
Выделение исходных
данных, по которым будет строиться
график, и исправление неверного выделения
выполняются с помощью поля ввода Диапазон
следующим образом:
–щелчком на
красно-белой кнопке минимизации,
расположенной в конце поля ввода
Диапазон,
сворачивается диалоговое окно Мастер
диаграмм (шаг 2 из 4)
в одну строку;
–с помощью мыши
выделяется нужный диапазон данных;
-щелчком на кнопке
минимизации в конце поля ввода Диапазон,
свёрнутого в строку, осуществляется
возвращение свёрнутого диалогового
окна в первоначальный вид.
Вкладка Ряд
служит для ввода названий рядов исходных
данных.
-
После проверки
правильности данных, отображённых в
окне Мастер
диаграмм (шаг 2 из 4),
нажимается кнопка Далее.
Откроется диалоговое окно Мастер
диаграмм (шаг 3 из 4: параметры диаграммы.
С помощью этого окна вводятся названия
диаграммы и осей координат, включается
или выключаются линии координатной
сетки, вводится или убирается легенда,
определяется место расположения
диаграммы и т.д. Для этого предусмотрены
вкладки Заголовки,
Оси,
Линии сетки,
Легенда.
Вводя соответствующий текст в поля
ввода и расставляя или убирая нужные
пользователю флажки в этих вкладках
формируется экспликация графика. -
Нажимается кнопка
Далее. Откроется диалоговое окно Мастер
диаграмм (шаг 4 из 4): размещение диаграммы.
В этом окне определяется вариант
размещения диаграммы в рабочей книге–
создать для неё персональный рабочий
лист или расположить на том же рабочем
листе, на котором находятся данные,
использованные для её построения.
Для перемещения
диаграммы на рабочем листе, надо щёлкнуть
в любой её точке, находящейся вне области
построения графика, и, удерживая нажатой
левую клавишу мыши, передвинуть диаграмму
в нужное место.
Для изменения
размера
диаграммы, надо «ухватиться» за один
из угловых или боковых манипуляторов
и передвинуть его в нужную сторону и на
нужное расстояние.
Для редактирования
существующей
диаграммы нужно щёлкнуть в любой её
точке. Это активизирует диаграмму и
сделает её элементы доступными для
изменения. В частности, можно более
рационально расположить заголовок
диаграммы и названия осей. Для этого
следует щёлкнуть по элементу диаграммы,
который нужно перемесить, и передвинуть
его в нужное место. Щелчком сначала
правой, а затем левой клавишей мыши по
любому элементы диаграммы можно открыть
диалоговое окно редактирования этого
элемента и внести в него нужные изменения.
При активизации
диаграммы на панели меню вместо меню
Данные
появляется
меню Диаграмма.
Используя команды этого меню, можно
более «тонко» отредактировать диаграмму.
Числовые характеристики результатов наблюдения
Следующим этапом
статистического анализа данных после
построения вариационного ряда является
характеристика отдельных свойств
распределения данных наблюдения. С этой
целью в статистике используются
специальные числовые параметры, найденные
по результатам наблюдения и отражающие
в сжатом виде основные, существенные
черты распределения данных. Эти числовые
параметры называются эмпирическими
числовыми характеристиками.
Наиболее важными числовыми характеристиками
являются характеристики положения,
вариации, асимметрии и эксцесса.
Для характеристики
положения
используются показатели
центра распределения
данных наблюдения–
средняя
арифметическая, мода и медиана.
Средняя
арифметическая для
дискретного ряда распределения
рассчитывается по формуле:
,
где
–варианты значений
признака;
–
частота повторения
данного варианта.
В интервальном
вариационном ряду
средняя арифметическая определяется
по формуле:
,
где
– середина
соответствующего интервала;
–
частота интервала.
Мода распределения–
это наиболее часто встречающееся
значение признака в совокупности. В
дискретном ряду
определение моды не требует специальных
расчётов. Мода соответствует варианту
с наибольшей частотой. В
интервальном вариационном ряду
в отличие от дискретного ряда определение
моды требует определённых расчётов на
основе специальной формулы.
Модальный интервал
(то есть содержащий моду) при интервальном
распределении с равными интервалами
определяется по наибольшей частоте, а
с неравными интервалами– по наибольшей
плотности. В первом случае мода
рассчитывается по следующей формуле:

–
нижняя граница
модального интервала;
–
величина модального
интервала;
–
частота модального
интервала;
–
частота интервала,
предшествующего модальному;
–
частота интервала,
следующего за модальным.
Во втором случае
в формуле моды вместо частот
используется
соответствующая плотность
.
Медиана
–
это значение признака, расположенное
в середине (в центре) ранжированного
ряда. Медиана делит совокупность на две
равные части– со значениями признака
меньше медианы и со значениями признака
больше медианы.
В дискретном
ряду для
вычисления медианного значения признака
сначала находят его порядковый номер:
,
где
–
число единиц
совокупности.
Полученное значение
указывает, что середина приходится на
данный номер единицы совокупности.
Необходимо определить, к какой группе
относится единица с этим порядковым
номером. Это можно сделать, рассчитав
накопленные частоты.
В интервальном
вариационном ряду
медиана определяется по формуле:
,
где
–
нижняя граница
медианного интервала;
–
величина медианного
интервала;
–
сумма всех частот
ряда;
–
накопленная частота
интервала, предшествующего медианному;
–
частота медианного
интервала.
Медианным
является интервал,
в котором сумма накопленных частот
равна или превышает полусумму частот
ряда.
Основными
характеристики вариации
признака
являются дисперсия, среднее квадратическое
(стандартное) отклонение и коэффициент
вариации. Они характеризуют степень
рассеивания данных наблюдения относительно
центра распределения.
Дисперсия
рассчитывается по формуле:
.
Среднее
квадратическое (стандартное)
отклонение
равно корню квадратному из дисперсии.
Коэффициент
вариации равен:
.
Для оценки степени
отклонения распределения исследуемой
величины от нормального распределения
используется коэффициент
асимметрии,
основанный на определении центрального
момента третьего порядка
(в
нормальном распределении его величина
равна нулю):
.
В Excel
вычисляется несмещённая состоятельная
оценка коэффициента асимметрии:
,
.
Стандартизированный
коэффициент асимметрии
имеет приближённое стандартное нормальное
распределение.
Эксцесс
представляет собой выпад вершины
эмпирического распределения вверх или
вниз от вершины кривой нормального
распределения, имеющей куполообразную
форму.
Наиболее точным
является коэффициент
эксцесса,
основанный на использовании центрального
момента четвёртого порядка:
.
Для нормального распределения
равен нулю, так как
.
В Excel
вычисляется несмещённая состоятельная
оценка коэффициента:
;
.
Стандартизированный
выборочный коэффициент эксцесса
используется при оценке степени
отклонения распределения исследуемой
случайной величины от нормального
распределения.
В Excel
числовые характеристики вычисляются
с помощью процедуры Описательная
статистика,
входящей в Пакет
анализа, и
соответствующих встроенных статистических
функций СРЗНАЧ,
МЕДИАНА, МОДА, ДИСП, ДИСПР, СТАНДОТКЛОН,
СТАНДОТКЛОНП, СРОТКЛ, КВАДРОТКЛ, СКОС
и ЭКСЦЕСС.
Для доступа к
процедуре Описательная
статистика
необходимо:
-
В меню Сервис
выделить строку Анализ
данных. -
В открывшемся
окне Анализ
данных
выделить процедуру Описательная
статистика
и щёлкнуть на кнопке ОК. На экране
появится диалоговое окно Описательная
статистика,
которое содержит следующие элементы
управления:-
поле ввода Входной
интервал.
В это поле вводится ссылка на диапазон
ячеек (входной диапазон), содержащий
статистические данные, подлежащие
обработке. Входной диапазон может быть
столбцом или группой смежных столбцов
(строкой или группой смежных строк).
Если входной диапазон представляет
собой группу столбцов (строк), то
процедура воспринимает каждый столбец
(строку) как отдельную совокупность; -
флажок Итоговая
статистика.
Если этот флажок установлен, процедура
вычисляет и помещает в таблицу
результатов решения следующие числовые
характеристики: среднюю, стандартную
ошибку средней, медиану, моду, стандартное
отклонение, дисперсию, эксцесс,
асимметрию, размах вариации, минимальное
и максимальное значение изучаемого
признака, сумму всех значений признака
и объём совокупности. Если совокупность
не имеет повторяющихся значений
признака, в строке Мода
появляется сообщение #
Н/Д!–
неопределённые данные; -
флажок Уровень
надёжности.
Флажок устанавливается в том случае,
когда необходимо вычислить доверительный
интервал для средней, соответствующий
заданной доверительной вероятности.
При этом справа от флажка открывается
поле для ввода доверительной вероятности,
выраженной в процентах. Если этот
флажок установлен, то в последней
строке таблицы результатов решения
появляется число, равное половине
длины доверительного интервала; -
флажки К-й
наименьший/К-й наибольший.
Если эти флажки установлены. то в
таблице результатов решения появляются-й
и
-й
элементы упорядоченной совокупности
(то есть единицы совокупности,
расположенные на-м
месте от её начала и от конца).
-
Назначение
переключателей Группирование
по столбцам/по строкам,
флажка Метки
в первой строке/Метки в первом столбце
и группы переключателей Выходной
интервал/Новый рабочий лист/Новая книга
рассмотрено на стр. 8-9.
Результаты решения
выводятся на экран в виде набора таблиц–
по одной таблице на каждый столбец
входного интервала (на каждую обработанную
совокупность). Каждая выходная таблица
состоит из двух столбцов. В первом
столбце указывается названия числовых
характеристик, во втором– их значения.
В заголовке указывается номер совокупности,
к которой относится данная таблица
(например, Столбец
1).
Свой наибольший
размер (18×2) таблица принимает при
установке всех четырёх флажков,
расположенных в нижней части диалогового
окна процедуры. В случае возникновения
опасности того, что таблица результатов
наложится на уже заполненные ячейки,
на экран выводится сообщение о такой
опасности. В ответ на это сообщение
пользователь должен разрешить удаление
старых данных и вывод на их место новых
(для этого надо щёлкнуть на кнопке ОК).
Формирование выборки
Метод статистического
исследования, при котором обобщающие
показатели изучаемой совокупности
устанавливаются по некоторой её части
на основе положений случайного отбора,
называется выборочным
методом.
Подлежащая изучению
по определённым признакам статистическая
совокупность, из которой производится
отбор единиц, называется генеральной.
Отобранная из генеральной совокупности
в случайном порядке некоторая часть
единиц, подвергающаяся обследованию,
называется выборочной
совокупностью
или просто выборкой.
В теории выборочного
метода разработаны и в практике
статистико-экономических исследований
применяются различные способы
формирования
выборочных совокупностей, обеспечивающие
репрезентативность. Организация
выборочного наблюдения заключается в
определении способа
и вида отбора
единиц.
Под способом
отбора
понимают порядок отбора единиц из
генеральной совокупности. Различают
два способа
отбора:
повторный и бесповторный.
При повторном
способе
каждая отобранная в случайном порядке
единица после её обследования возвращается
в генеральную совокупность и при
последующем отборе может снова попасть
в выборку. Вероятность попадания любой
единицы в выборку равна
,
и она остаётся той же самой на протяжении
всей процедуры отбора.
При бесповторном
способе
отбора попавшая в выборочную совокупность
единица после регистрации значений
наблюдаемых признаков не
возвращается в совокупность, из которой
осуществляется дальнейший отбор.
Вероятность попадания единицы в выборку
изменяется от
– для первой отбираемой единицы до
–
для последней единицы, то есть по мере
производства отбора вероятность попасть
в выборку для каждой единицы генеральной
совокупности увеличивается, тем самым
повышается репрезентативность выборки.
В зависимости
от методики формирования
выборочной совокупности различают
следующие основные
виды выборки:
-
собственно–
случайная; -
механическая;
-
типическая
(стратифицированная, расслоенная,
районированная); -
серийная (гнездовая);
-
многоступенчатая;
-
многофазная;
-
комбинированная;
-
взаимопроникающая.
В Пакете
анализа
табличного процессора Excel
имеется процедура Выборка,
реализующая повторную собственно-случайную
выборку и механическую выборку с заданным
пользователем шагом (периодом) отбора.
Формирование
выборки в Excel
осуществляется следующим образом:
-
Единицам генеральной
совокупности присваиваются порядковые
номера. Для проведения механической
выборки генеральная совокупность
должна быть каким-либо образом
упорядочена,
то есть должна быть определённая
последовательность в расположении её
единиц. Для получения результатов, не
содержащих систематическую ошибку
выборки, упорядочение необходимо
произвести по нейтральному признаку
по отношению к изучаемому. -
Порядковые номера
единиц исходной совокупности вводятся
в диапазон ячеек (входной диапазон).
Эти номера могут находиться в одном
столбце или группе смежных столбцов
одинаковой «высоты». При этом число
всех ячеек входного диапазона должно
равняться числу единиц исходной
совокупности. Если среди элементов
входного интервала имеются нечисловые
данные, то отбор не состоится, а на
экране появится сообщение «Выборка–
входной интервал содержит нечисловые
данные». -
В меню Сервис
выделяется строка Анализ
данных. -
В открывшемся
диалоговом окне Анализ
данных
выделяется процедура Выборка
и нажимается кнопка ОК. На экране
появится диалоговое окно Выборка,
которое содержит следующие элементы
управления:-
поле ввода Входной
интервал.
В это поле вводится ссылка на диапазон,
в котором хранятся номера всех единиц
генеральной совокупности, из которой
осуществляется выборка. -
Метод выборки
устанавливается с помощью переключателей
Периодический
и Случайный.
При активизации переключателя Случайный
процедура «настраивается» на выполнение
случайной выборки с повторением. Нужный
объёмвыборки вводится в поле Число
выборок.
Единицы генеральной совокупности
отбираются случайным образом. Каждая
единица исходной совокупности имеет
равную со всеми остальными единицами
возможность быть включённой в выборку.
Любая единица генеральной совокупности
может попасть в выборку более одного
раза.
-
При необходимости
реализовать механическую выборку
активизируется переключатель
Периодический.
Шаг выборки вводится в поле Период,
находящееся справа от переключателя.
В выборку войдут элементы исходной
совокупности с номерами, кратными
заданному периоду. Если входной диапазон
состоит из нескольких столбцов, то
отбираемые значения будут извлекаться
сначала из первого столбца, затем из
второго и т.д. Формирование выборки
прекращается по достижении конца
исходной совокупности.
При формировании
случайной выборки выходной интервал
представляет собой столбец с числом
ячеек, равным заданному объёму
выборки. В случае механической выборки
число ячеек выходного интервала равно
целой части результата деления объёма
исходной совокупности на шаг выборки.
Для получения
упорядоченной копии номеров единиц
совокупности, подлежащих включению в
выборку, необходимо щелчком на кнопке
Сортировка
по возрастанию,
расположенной на панели инструментов
Стандартная,
упорядочить полученный набор номеров.
Корреляционный анализ
В статистике
различают две категории зависимостей
между признаками:
1) функциональная;
2) стохастическая,
частным случаем которой является
корреляционная.
При этом признаки
для изучения взаимосвязи по их значению
делятся на два класса. Признаки,
обуславливающие изменение других,
связанных с ними признаков, называются
факторными
(х). Признаки,
изменяющиеся под действием факторных
признаков, являются результативными
(у).
Функциональной
называется связь, при которой каждому
значению факторного признака соответствует
вполне определённое значение
результативного признака. Функциональная
связь является строгой, точной, полной
зависимостью; проявляется и для каждой
единицы совокупности, и во всех случаях
наблюдения. Характерной особенностью
функциональной связи является то, что
в каждом отдельном случае известен
полный перечень факторов, влияющих на
результативный признак, а также механизм
этого влияния, выраженный определённым
уравнением.
Стохастическая
(вероятностная)
связь не проявляется в каждом отдельном
случае, а лишь в общем, среднем, при
большом числе наблюдений.
Корреляционной
называется
связь, при которой каждому значению
факторного признака может соответствовать
несколько значений результативного
признака.
Корреляционные
связи имеют ряд характеристик:
По форме
(аналитическому
выражению)
корреляционные связи между признаками
могут быть линейными (прямолинейными)
и нелинейными (криволинейными). При
линейной
форме
равномерное изменение значений одного
признака сопровождается более или менее
равномерным изменением значений другого
признака. Математически она выражается
уравнением прямой ух
= а + вх, графически — прямой линией.
При нелинейной
форме
равномерному изменению значений одного
признака соответствует неравномерное
изменение значений другого. Выражается
уравнением какой- либо кривой линии:
параболы, гиперболы, показательной,
степенной, логарифмической, логической
функции и др.
По направлению
(характеру изменения)
корреляционные связи бывают прямыми и
обратными. Прямой
(положительной)
является зависимость, при которой
направление изменения значений факторного
и результативного признаков совпадает,
то есть с увеличением факторного
признака, результативный также возрастает,
и, наоборот, при уменьшении факторного
признака результативный тоже убывает.
Обратной
(отрицательной)
называется связь, при которой изменение
значений факторного и результативного
признаков осуществляется в разных
направлениях, то есть с ростом факторного
результативный признак убывает или при
убывании факторного признака результативный
возрастает.
Степень тесноты
корреляционной связи оценивается по
специальным шкалам, например, по шкале
Чеддока.
Количественный критерий оценки тесноты
связи по шкале Чеддока
|
Величина |
Характер связи |
|
до |0,3| |
слабая |
|
|0,3|-|0,5| |
умеренная |
|
|0,5|-|0,7| |
заметная |
|
|0,7|-|0,9| |
высокая |
|
|0,9|-|1| |
весьма высокая |
|
|1| |
функциональная |
|
0 |
отсутствие связи |
Существуют и другие
менее детальные шкалы.
В статистике
различают следующие варианты зависимостей:
1) парная
корреляция
– связь между двумя признаками
(результативным и факторным);
2) частная
корреляция
– зависимость между результативным и
одним факторным признаком при
фиксированном значении других факторных
признаков;
3) множественная
корреляция
– зависимость результативного от двух
или более факторных признаков.
В практике
статистических исследований выделяют:
-
корреляционный
анализ,
который
имеет своей задачей количественное
измерение тесноты связи между признаками; -
регрессионный
анализ,
который заключается в определении
формы связи, построении одно- или
многофакторных моделей (уравнений)
регрессии; -
корреляционно-регрессионный
анализ, который
включает в себя установление аналитического
выражения (формы) и измерение степени
тесноты связи.
Следует также
различать собственно-корреляционные
(параметрические)
и непараметрические
методы
изучения взаимосвязей между признаками.
Основу применения собственно-корреляционных
методов составляют однородность и
необходимость подчинения распределения
совокупности по факторным и результативному
признаку закону нормального распределения
вероятностей. Несоблюдение этих условий
обуславливает необходимость применения
при изучении взаимосвязей непараметрических
методов.
В связи с этим
первым этапом изучения зависимостей
является установление подчинения
распределения результатов наблюдения
по изучаемым признакам закону нормального
распределения.
На соответствие
изучаемого эмпирического распределения
нормальному закону указывает близость
значений показателей центра распределения
– средней арифметической, моды и медианы.
С этой целью производится также расчёт
и оценка степени существенности
показателей асимметрии и эксцесса. В
Excel
выборочные числовые характеристики
вычисляются с помощью процедуры
Описательная
статистика,
входящей в Пакет
анализа, и
соответствующих встроенных статистических
функций (см. раздел 4).
Для проверки
гипотезы о законе распределения
изучаемого признака используются также
специальные статистические критерии.
При этом выдвигается гипотеза
о
том, что истинной функцией распределения
признака является некоторая заданная
функция
(для
нашей задачи– функция нормального
распределения). Если гипотеза
верна
(то есть, если значения признака
действительно имеют функцию распределения
),
то найденная по данным наблюдения
эмпирическая функция распределения
не
должна сильно отличаться от гипотетической
функции распределения
,
и с увеличением объёма
совокупности
различие между ними должно уменьшаться.
В связи с этим вопрос о принятии или
отклонении проверяемой гипотезы решается
в зависимости от того, насколько хорошо
согласуются эмпирическая
и гипотетическая
функции
распределения. Статистические критерии,
базирующиеся на таком подходе, называются
критериями согласия или соответствия.
В основе этих критериев лежит выбранная
статистика, которая служит мерой
расхождения между эмпирическим и
гипотетическим законами распределения
исследуемого признака.
Известны критерии К. Пирсона (хи-
квадрат), В.И. Романовского, А.Н. Колмогорова,
Б.С. Ястремского, омега-квадрат,
Крамера-Мизеса-Смирнова и др.
Excel
позволяет реализовать проверку
статистических гипотез о соответствии
эмпирических результатов наблюдения
закону нормального распределения на
основу вышеуказанных критериев согласия.
Последующий
собственно-корреляционный
анализ
статистических данных, полученных в
результате наблюдения, включает в себя:
-
построение
корреляционного поля и корреляционной
таблицы; -
вычисление
выборочных коэффициентов корреляции
и корреляционных отношений; -
проверка
статистических гипотез о значимости
корреляционной зависимости.
Корреляционное
поле и
корреляционная
таблица
служат для установления наличия и
направления зависимости между изучаемыми
признаками, дают общее представление
об этой зависимости.
В Excel
построение поля корреляции (диаграммы
рассеивания) между изучаемыми признаками
осуществляется при помощи специального
средства, служащего для графического
изображения статистических данных–
Мастера
диаграмм
(см. 19). Для построения корреляционного
поля используется тип Точечная.
На палитре Вид
выделяется диаграмма в виде изолированных
точек, находящаяся в левом верхнем углу
палитры.
Расположение точек
на графике позволяет в ряде случаев
сделать предположение о наличии,
направлении и форме взаимосвязи между
изучаемыми признаками. Так, линейное
расположение точек даёт серьёзное
основание для выбора линейной модели,
сравнительно небольшой разброс точек
относительно воображаемой кривой,
проходящей «наилучшим образом» через
эти точки, говорит о довольно сильной
зависимости между признаками, и наоборот.
Расположение точек слева на право
свидетельствует о прямой корреляции,
а справа налево– об обратной корреляции.
Для подтверждения
выводов, сделанных в результате анализа
корреляционного поля и в тех случаях,
когда корреляция между признаками имеет
явно выраженный нелинейный характер и
объём выборки велик, данные наблюдения
группируют и представляют их в виде
корреляционной таблицы, состоящей из
строк и
столбцов, где
–число
интервалов группировки по факторному
признаку и
–
число интервалов группировки по
результативному признаку. Это обусловлено
тем, что при нелинейной зависимости
вычисляются корреляционные отношения,
которые могут быть определены только
по сгруппированным данным.
Построение
корреляционной таблицы начинают с
группировки значений факторного и
результативного признаков. В Excel
для группировки данных способом равных
интервалов используются процедура
Гистограмма,
входящая в Пакет анализа (см стр.14).
Корреляционная таблица
|
Х |
Y 8640 9600 10561 11521 |
|
||||
|
|
… |
|
… |
|
||
|
|
|
… |
|
… |
|
|
|
… |
… |
… |
… |
… |
… |
… |
|
|
|
… |
|
… |
|
|
|
… |
… |
… |
… |
… |
… |
… |
|
|
|
… |
|
… |
|
|
|
|
|
… |
… |
|
–
середина
-го
интервала группировки по факторному
признаку;
–
середина
-го
интервала группировки по результативному
признаку;
–
групповая частота
«клетки», находящейся на пересечении
строки
и столбца
корреляционной таблицы;
–
групповая частота
-го
интервала группировки по факторному
признаку (число наблюдений в
-й
строке);
–групповая частота
-го
интервала группировки по результативному
признаку (число наблюдений в
-м
столбце);
–объём
изучаемой совокупности (общее число
наблюдений).
Заполнение
корреляционной таблицы даёт довольно
наглядное представление о характере
зависимости между изучаемыми признаками.
Для количественного
измерения степени тесноты связи служат
выборочные коэффициенты
корреляции
и корреляционные
отношения.
Линейный
коэффициент корреляции
рассчитывается для определения тесноты
и направления связи между двумя
корреляционными признаками в случае
наличия между ними линейной
зависимости и распределения значений
признаков близкого к нормальному.
Линейный коэффициент корреляции может
принимать значение от -1 до +1. Чем ближе
коэффициент корреляции к 1, тем сильнее
(теснее) связь между признаками. Для
определения характера связи используют
шкалу Чеддока.
В теории разработаны
и на практике применяются различные
модификации формулы расчёта данного
коэффициента:
;
;
;
;
,
где
–ковариация
факторного и результативного признаков;
,
–
среднее квадратическое (стандартное)
отклонение соответственно факторного
и результативного признака;
n
– число наблюдений.
Квадрат коэффициента
корреляции (r2)
носит название коэффициента
детерминации. Он
показывает долю вариации результативного
признака, обусловленную влиянием
вариации факторного признака.
При наличии
нелинейной
зависимости
используется более универсальный
показатель измерения тесноты связи:
корреляционное
отношение.
Различают эмпирическое и теоретическое
корреляционное отношение.
Расчет эмпирического
корреляционного отношения осуществляется
по сгруппированным данным наблюдения
и основан на использовании теоремы
(правила) сложения дисперсий:
Эмпирическое
корреляционное отношение
определяется
по формуле:
Межгрупповая
дисперсия характеризует ту часть
колеблемости результативного признака,
которая складывается под влиянием
изменения факторного признака, положенного
в основание группировки:
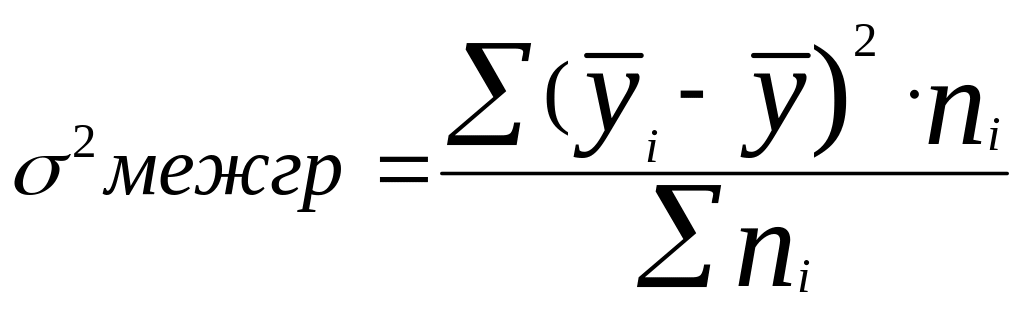
Средняя из
внутригрупповых дисперсий оценивает
ту часть вариации результативного
признака, которая обусловлена действием
других, прочих, «случайных» причин:
,
где
-дисперсия
результативного признака в соответствующей
группе.
Общая дисперсия
характеризует вариацию результативного
признака, обусловленную влиянием всех
факторов:
Расчёт теоретического
корреляционного отношения в Excel
осуществляется в рамках регрессионного
анализа, поэтому будет рассмотрен в
следующем разделе.
В Excel
вычисление выборочного коэффициента
корреляции осуществляется с помощью
процедуры Корреляция,
входящей в Пакет анализа, и встроенных
статистических функций КОРРЕЛ,
ПИРСОН
и КВПИРСОН.
При применении
процедуры Корреляция
в поле Входной
интервал
диалогового окна этой процедуры вводится
ссылка на входной диапазон (на диапазон,
содержащий данные наблюдения, подлежащие
обработке). Входной диапазон должен
содержать
смежных столбцов по
ячеек в каждом столбце или
смежных
строк по
ячеек в каждой строке.
Назначение
переключателя Группирование,
флажка Метки
и группы переключателей Выходной
интервал/Новый
рабочий лист/
Новая книга
рассмотрено в первом разделе на стр.8-9.
Статистические
функции КОРРЕЛ
и ПИРСОН
вычисляют выборочную оценку линейного
коэффициента корреляции по первой
формуле, представленной на стр. 34, и
дублируют друг друга. Синтаксис функции
КОРРЕЛ
(массив 1;
массив 2),
где массив
1– диапазон
ячеек, в который введены значения
факторного признака (например, А1:А25), а
массив 2–
диапазон ячеек, в который введены
значения результативного признака
(например, В1:В25). Статистическая функция
КВПИРСОН
вычисляет квадрат выборочного коэффициента
корреляции.
Для вычисление
эмпирического корреляционного отношения
в Excel
не предусмотрено специальных статистических
процедур и встроенных функций. Вычисление
корреляционного отношения осуществляется
по представленным выше формулам и
требует предварительного построения
корреляционной таблицы и ряда
вспомогательных расчётов.
Значимость
линейного коэффициента корреляции
проверяется на основе t
– критерия Стьюдента. При этом выдвигается
и проверяется гипотеза (
)
о равенстве коэффициента корреляции в
генеральной совокупности нулю (то есть
в действительности связь между изучаемыми
признаками отсутствует, а эмпирическое
значение выборочного коэффициента
корреляции обусловлено только случайными
совпадениями
и
в
выборке).
Фактическое
значение t
— критерия рассчитывается по формуле
— для совокупностей n<50
по формуле:
;
(*)
при большом числе
наблюдений (n>100):
.
Вычисленное
значение t
– критерия сравнивается с критическим
его значением при принятом уровне
занятости α
и числе степеней свободы k
= n-2.
В социально-экономических исследованиях
уровень значимости α
обычно принимается равным 0,05.
При «ручной»
проверке гипотезы критические значения
t
находятся по таблице распределения
Стьюдента. Если расчётное значение t
– критерия больше критического, то
гипотеза о том, что линейный коэффициент
корреляции в генеральной совокупности
равен нулю и лишь в силу случайных
обстоятельств оказался равен проверяемому
значению, отклоняется, то есть коэффициент
корреляции признаётся значимым, а связь
между признаками – статистически
существенной. Если расчётное значение
t
– критерия меньше критического, то
нулевая гипотеза принимается, что
означает, что коэффициент корреляции
в генеральной совокупности в
действительности равен нулю и
соответственно эмпирический коэффициент
корреляции существенно не отличается
от нуля.
В Excel
проверка гипотезы
об отсутствии корреляции между изучаемыми
признаками осуществляется следующим
образом:
-
В ячейку (например,
В1) вводится значение выборочного
коэффициента корреляции
; -
В ячейку В2 для
определения расчётного значения t
– критерия вводится формула (*): =
В1*КОРЕНЬ (115/(1-В1^2)) (
=
117); -
В ячейку В3 для
нахождения критического значения t
– критерия Стьюдента при уровне
значимости α=
0,05 и числе степеней свободы k
=115 вводится формула: =
СТЬЮДРАСПОБР (0.05;115); -
Полученные
расчётное и критическое значения t
– критерия Стьюдента сравниваются, и
делается вывод об отклонении или
принятии нулевой гипотезы на уровне
значимости
=0,025
. Если гипотезапротиворечит реальным данным наблюдения
(отклоняется), то выборочный коэффициент
корреляции признаётся значимым и между
изучаемыми признаками существует
соответствующая по степени тесноты
корреляционная зависимость. Если
гипотеза принимается, коэффициент
корреляции признаётся незначимым.
Для оценки
значимости корреляционного отношения
используется
F
– критерий Фишера–Снедекора, вычисленный
по формуле:
,
(**)
где n
— число наблюдений; m
– число интервалов группировки или
параметров в уравнении регрессии.
При этом проверяется
гипотеза
об отсутствии корреляционной зависимости
между изучаемыми признаками. Проверяемая
гипотеза отклоняется на уровне значимости
,
если расчётное значение F
– критерия превышает его критическое
значение для принятого уровня значимости
и чисел степеней свободы k1=m-1
и k2=m-n.
В этом случае величина корреляционного
отношения признаётся значимой, а связь
между признаками существенной.
При «ручной»
проверке гипотезы используются
специальные таблицы F
– распределения. В них указывается
предельные (критические) значения F
– критерия для различных степеней
свободы k1
и k2,
которые могут быть превзойдены с
вероятностью α = 0,05.
В Excel
проверка гипотезы
об отсутствии корреляции между изучаемыми
признаками осуществляется следующим
образом:
-
В ячейку В1 вводится
объём совокупности(например, 132) в ячейку В2– число интервалов
группировки или параметров в уравнении
регрессии (например, 12); в ячейку В3–
значение выборочного корреляционного
отношения; -
В ячейку Е1 для
нахождения расчётного значения F
– критерий Фишера вводится формула
(**): =
В3^2*120/(1-В3^2)*11; -
В ячейку Е2 для
определения критического значения F
– критерий Фишера для принятого уровня
значимости=0,05
и чисел степеней свободы k1=m-1
(11) и k2=m-n
(120) вводится формула: = FРАСПОБР
(0.05;11;120). -
Полученные
расчётное и критическое значения F
– критерий Фишера сравниваются, и
делается вывод об отклонении или
принятии нулевой гипотезыи соответственно о значимости или
незначимости корреляционного отношения.
Множественный
коэффициент корреляции вычисляется
статистической процедурой Регрессия
(см. следующий раздел).
Рассмотренные
выше вычисления относятся к
собственно-корреляционным, параметрическим
методам изучения связей.
В случаях, когда
анализируется взаимосвязь между
количественными признаками, форма
распределения которых отличается от
нормальной, а также между качественными
признаками, используются так называемые
непараметрические
методы.
В основу этих методов положен принцип
нумерации значений признаков
статистического ряда.
Значения факторного
признака записываются в возрастающем
или убывающем порядке, а затем ранжируются
соответствующие им значения результативного
признака. При этом каждой единице в
упорядоченном ряду присваивается
порядковый номер, который будет её
рангом.
В случаях наличия одинаковых вариантов
каждому из них присваивается среднее
арифметическое значение их рангов.
Для определения
рангов в Excel
предусмотрены статистическая процедура
Ранг и
персентиль
и статистическая функция РАНГ.
Использование
процедуры Ранг
и персентиль
заключается в следующем:
-
В меню Сервис
выделяется строка Анализ
данных. -
В открывшемся
окне Анализ
данных
выделяется процедура Ранг
и персентиль,
нажимается кнопка ОК. На экране появляется
диалоговое окно Ранг
и персентиль. -
В поле Входной
интервал
вводится ссылка на диапазон ячеек,
содержащий данные, подлежащие
ранжированию. Входной диапазон может
быть столбцом или группой смежных
столбцов (строкой или группой смежных
строк). Если входной диапазон представляет
собой группу столбцов (строк), то
процедура воспринимает каждый столбец
(строку) как отдельную выборку. -
Устанавливается
переключатель Группирование
в нужное положение (по столбцам или
строкам). -
Флажок Метки
устанавливается, если первая строка
(столбец) входного диапазона содержит
заголовки. Если такие заголовки
отсутствуют, флажок не устанавливается. -
Щелчком на
переключателе Выходной
интервал
активизируется поле ввода, находящее
справа от этого переключателя и вводится
в него ссылка на левую верхнюю ячейку
таблицы результатов решения. В случае
необходимости результаты выводятся
на Новый
рабочий лист
или Новую
рабочую книгу.
Нажимается кнопка ОК.
Статистическая
функция РАНГ
имеет следующий синтаксис: РАНГ
(число; массив; порядок):
-
число–
номер единицы совокупности, ранг
которой надо определить. Если необходимо
осуществить ранжирование всей
совокупности сразу, то вводится диапазон
ячеек, в котором находятся данные,
подлежащие обработке; -
массив–
массив или диапазон ячеек, содержащий
единицы исследуемой совокупности
(неупорядоченные данные наблюдения); -
порядок–
величина, определяющая, как упорядочивать
(ранжировать) массив:
– если порядок
равен 0 или пропущен, массив упорядочивается
в порядке убывания;
– если порядок–
любое число, не равное нулю, то массив
упорядочивается по возрастанию.
Среди непараметрических
методов оценки тесноты связи наибольшее
значение имеют коэффициенты ранговой
корреляции Спирмена и Кендалла.
Коэффициент
корреляции рангов (Спирмена)
определяется по формуле:
r
=
,
где
d
– разность между рангами соответствующих
величин двух признаков;
n
– число единиц в ряду (число пар рангов).
Коэффициент
корреляции рангов принимает любые
значения от -1 до +1. Если все ранги строго
изменяются в одном и том же порядке, то
d=0,
а r=1.
Если же ранги изменяются строго в
противоположных направлениях, то r=
-1. Значение r=0
характеризует отсутствие связи.
В Excel
вычисление коэффициента ранговой
корреляции Спирмена осуществляется
следующим образом:
1. Вводятся заголовки
исходных и расчётных данных, необходимых
для расчёта коэффициента корреляции
рангов: в ячейку А1– названия единиц
изучаемой совокупности, в ячейку В1–
название факторного признака, в ячейку
С1– названия результативного признака,
в ячейку D1–
символ
,
обозначающий ранг по факторному признаку,
в ячейку Е1– символ
,
обозначающий ранг по результативному
признаку, в ячейку– F–
символ
,
обозначающий квадрат разности между
рангами соответствующих величин двух
признаков.
2. Производится
ввод исходных данных: в диапазон ячеек
столбца А вводятся названия или номера
единиц изучаемой совокупности; в диапазон
ячеек столбца В (например, В2:В11)–
значения факторного признака, в диапазон
ячеек столбца С (С2:С11)– значения
результативного признака.
3. В диапазонах
ячеек D2:D11
и Е2:Е11 определяются соответственно
ранги по факторному и результативному
признаку с помощью описанной выше
процедуры
Ранг и персентиль
или функции РАНГ,
для чего вводятся формулы массива =
РАНГ (В2:В11; В2:В11;1)
и = РАНГ
(С2:С11; С2:С11;1).
4. В диапазоне
F2:F11
вычислить квадраты разности рангов с
помощью формулы массива: = (D2:D11-E2:E11)^2.
5. В ячейках D12,
E12
и F12
с помощью кнопки Автосуммирование
определить суммы рангов по факторному
и результативному признакам и сумму
квадрата разности рангов.
6. По формуле
рассчитывается выборочная оценка
коэффициента ранговой корреляции
Спирмена.
Значимость
коэффициента корреляции рангов для
совокупностей небольшого объёма (n£30)
проверяется по таблице предельных
значений коэффициента корреляции рангов
Спирмена при заданном уровне значимости
a
и определённом объёме совокупности.
Значимость r
может быть проверена также на основе t
– критерия Стьюдента. Расчётное значение
критерия определяется по формуле:
tрасч=
r×
Значение коэффициента
корреляции считается статистически
существенным, если расчётное значение
t
– критерия Стьюдента превосходит его
критическое значение при заданном
уровне значимости a
и числе степеней свободы k=n-2.
Критическое значение t
– критерия может быть определено по
таблице распределения Стьюдента или
в Excel
по представленному выше в данном разделе
порядку.
Коэффициент
корреляции рангов Кендалла
рассчитывается
по формуле:
t=
,
S=P+Q
n
– число наблюдений;
S
– сумма разностей между числом
последовательностей и числом инверсий
по результативному признаку.
Расчёт данного
коэффициента выполняется в следующей
последовательности:
-
ранги факторного
признака располагаются в порядке
возрастания; -
ранги результативного
признака располагаются в порядке,
соответствующем рангам признака х; -
для каждого ранга
результативного признака определяется
сколько чисел, находящихся справа от
него (следующих за ним) имеют величину
ранга, превышающую его величину. Суммируя
полученные таким образом числа, получаем
слагаемое P,
которое можно рассматривать как меру
соответствия последовательностей
рангов по x
и y,
и которое учитывается со знаком «+»; -
для каждого ранга
y
определяется число, следующих за ним
рангов, меньших его величины. Суммарная
величина обозначается через Q
и фиксируется со знаком «-»; -
определяется
сумма баллов S=P+Q
Коэффициент
Кендалла также изменяется в пределах
от -1 до +1. При достаточно большом числе
наблюдений между коэффициентами
корреляции рангов Спирмена и Кендалла
существует следующее соотношение: r»
.
Вычисления,
связанные с коэффициентом ранговой
корреляции
,
заметно упрощаются, если результаты
ранжировки представить в виде:
,
(***)
где
–
ранг по результативному признаку той
единицы совокупности, которая по
факторному признаку имеет ранг
.
При таком
представлении ранжировки формула
коэффициента корреляции рангов Кендалла
имеет вид:
,
(****)
где
–число
единиц совокупности, для которых
и
одновременно
.
На практике
вычисляют
по формуле
,
где –
–
число рангов
в ранжировке (***), для которых для которых
и
одновременно
.
В Excel
вычисление коэффициента ранговой
корреляции Кендалла осуществляется по
формуле (****) следующим образом:
1. Вводятся заголовки
исходных и расчётных данных, необходимых
для расчёта коэффициента корреляции
рангов: в ячейку А1– названия единиц
изучаемой совокупности, в ячейку В1–
название факторного признака, в ячейку
С1– названия результативного признака,
в ячейку D1–
символ
,
обозначающий ранг по факторному признаку,
в ячейку Е1– символ
,
обозначающий ранг по результативному
признаку, в ячейку– F–
символ
,
обозначающий квадрат разности между
рангами соответствующих величин двух
признаков.
2. Производится
ввод исходных данных: в диапазон ячеек
столбца А вводятся названия или номера
единиц изучаемой совокупности; в диапазон
ячеек столбца В (например, В2:В11)–
значения факторного признака, в диапазон
ячеек столбца С (С2:С11)– значения
результативного признака.
3. В диапазонах
ячеек D2:D11
и Е2:Е11 определяются соответственно
ранги по факторному и результативному
признаку с помощью описанной выше
процедуры
Ранг и персентиль
или функции РАНГ,
для чего вводятся формулы массива =
РАНГ (В2:В11; В2:В11;1)
и = РАНГ
(С2:С11; С2:С11;1).
4. Выделяется
диапазон D1:E11,
в котором находятся ранги по факторному
и результативному признакам, нажимается
кнопка Копировать
на панели инструментов Стандартная.
5. Выделяется ячейка
F1.
В меню Правка
выделяется команда Специальная
вставка.
6. В открывшемся
диалоговом окне Специальная
вставка в
группе переключателей Вставить
установливается
переключатель Значения
и нажимается
кнопка ОК. В диапазоне F2:G11
появятся «копии» рангов.
7. Выделяется
диапазон F1:G11.
В меню Данные
выделяется команда Сортировка.
8. В открывшемся
окне Сортировка
диапазона
в раскрывшемся списке Сортировать
по выбирается
поле
,
по которому надо выполнить сортировку,
и установливается переключатель по
возрастанию;
в группе переключателей Идентифицировать
поля по
установливатся
переключатель подписям
(первая строка диапазона)
и нажимается кнопка ОК.
В диапазоне F2:G11
появятся ранги по факторному и
результативному признакам, отсортированные
в порядке возрастания рангов факторного
признака.
9. В ячейку Н2
вводится формула массива =
СУММ (ЕСЛИ ($G3:$G11>G2;1;0)),
нажимаются клавиши Ctrl+Shift+
Enter
и затем эта формула копируется в ячейки
Н3:Н11. В диапазоне Н2:Н11 появятся числа
.
10. Суммируя эти
числа в ячейке Н12, находится выборочное
значение
.
11. Используя формулу
= 4* Н12/(10^2-10)-1 (машинный аналог формулы
(****)), находится выборочное значение
.
Существенность
коэффициента корреляции рангов Кендалла
проверяется
–при малом объёме
совокупности (
)
с помощью таблиц точного распределения
статистики
;
– при больших n
для заданного уровня значимости a
по формуле:
t>ta×
,
где
ta
– коэффициент, определяемый по таблице
нормального распределения.
Регрессионный анализ
Регрессионным
анализом называется
раздел статистики, объединяющий
практические методы исследования формы
корреляционной зависимости между
изучаемыми признаками единиц исследуемой
совокупности.
В регрессионном
анализе различают парную и множественную
регрессию. Парная
регрессия
описывает связь между двумя признаками:
факторным и результативным. Множественная
регрессия
описывает зависимость результативного
признака от нескольких факторных
признаков.
Регрессионной
моделью
системы взаимосвязанных признаков
принято считать такое уравнение
регрессии, которое включает основные
факторы, влияющие на вариацию
результативного признака, обладает
высоким (не ниже 0,5) коэффициентом
детерминации и коэффициентами регрессии,
интерпретируемыми в соответствии с
теоретическим знанием о природе связей
в изучаемой системе. Приведённое
определение включает достаточно строгие
условия: не всякое уравнение регрессии
можно считать моделью.
Регрессионный
анализ включает в себя следующие основные
этапы:
-
выбор модели
регрессии; -
оценка параметров
выбранной модели регрессии; -
проверка значимости
параметров модели регрессии и их
интерпретация; -
проверка адекватности
построенной модели регрессии.
Выбор аналитической
формы связи
осуществляется на основе:
-
логического
теоретического анализа; -
графического
изображения зависимости в виде
эмпирической линии регрессии; -
опыта предыдущих
исследований, где выбранные формы связи
давали удовлетворительные результаты; -
различных
статистико-математических критериев
адекватности конкурирующих уравнений
регрессии (остаточных дисперсий, ошибок
аппроксимации и др.).
Наиболее разработанной
в теории статистики является методология
парной регрессии. При этом для изучения
связи между изучаемыми признаками
применяются различного вида уравнения
(типы математических функций) линейной
и нелинейной зависимостей.
При анализе
линейной связи
применяется прямолинейная функция,
математическим выражением которой
является уравнение прямой линии:
yx=a+bx.
При анализе
нелинейных связей
используются следующие функции:
параболическая
yx=a+bx+cx2
гиперболическая
yx=a+
показательная
yx=abx
степенная yx=axb
логарифмическая
yx=a+blgx
логистическая
yx=
и др.
Решение математических
уравнений связи предполагает вычисление
по исходным данным их параметров a
и b.
Это осуществляется способом выравнивания
эмпирических (фактических) данных
методом
наименьших квадратов (МНК).
В основу этого метода положено требование
минимальности суммы разности квадрата
отклонений эмпирических значений
результативного признака от его
выровненных (теоретических) значений
yxi,
полученных по выбранному уравнению
регрессии:
.
Параметры b1,…
bn
в уравнении регрессии называют
коэффициентами
регрессии.
Если связь по направлению прямая – он
имеет положительное значение, если
обратная – отрицательное. При линейной
связи коэффициент регрессии показывает
на сколько единиц своего измерения в
среднем изменяется величина результативного
признака при изменении факторного
признака на единицу своего измерения.
В Excel
имеется две процедуры и восемь встроенных
функций для регрессионного анализа.
Они вычисляют не только выборочные
параметры регрессии, но и ещё ряд
дополнительных выборочных характеристик
исследуемой регрессионной зависимости.
К числу таких характеристик относятся:
-
общая сумма
квадратов=
–
сумма квадратов отклонений
фактических(эмпирических) значений
результативного признака
от его среднего значения
; -
сумма квадратов,
обусловленная регрессией
=
–сумма
квадратов отклонений теоретических
(расчётных, выровненных) значений
результативного признака
от его среднего значения
;
-
сумма квадратов
остатков
=
–сумма
квадратов отклонений фактических
значений результативного признакаот его теоретических значений
;
-
числа степеней
свободы этих сумм
. -
средний квадрат
регрессии или
факторная
(систематическая) дисперсия–
–
характеризует колеблемость результативного
признака под влиянием только фактора
х, входящего в уравнение регрессии; -
средний квадрат
остатков или
остаточная
(случайная) дисперсия–
–характеризует
колеблемость результативного признака
под влиянием прочих факторов, не входящих
в уравнение регрессия.
Эти дисперсии
связаны между собой равенством, носящим
название «правило сложения дисперсий»–
;
;
-
множественный
коэффициент (индекс) корреляции
;
в случае парной линейной регрессии
этот показатель совпадает с коэффициентом
корреляции,
а в случае парной нелинейной регрессии
носит название теоретического
корреляционного отношения; -
коэффициент
детерминации–
;
показывает вариацию результативного
признака, обусловленную вариацией
факторов, входящих в регрессионную
модель; -
нормированный
(скорректированный) коэффициент
детерминации
–
.
где–число
факторов, включённых в регрессионную
модель. Корректировка не производится
при условии, если
; -
стандартная
ошибка аппроксимации
(средняя
квадратическая ошибка) уравнения
регрессии:
;
где
-число
параметров в уравнении регрессии.
-
стандартное
отклонение параметров регрессии–
.
Наиболее точно эта величина может
быть определена по формуле:
,
где
–
среднее квадратическое отклонение
результативного признака (корень
квадратный из общей дисперсии);
–среднее
квадратическое отклонение
—
го факторного признака;
–величина
множественного коэффициента корреляции
по фактору
с остальными факторами.
Выборочный
коэффициент детерминации и выборочные
параметры регрессии, вычисленные по
ограниченному числу единиц изучаемой
совокупности, всегда содержат элемент
случайности, в связи, с чем возникает
необходимость проверки значимости этих
выборочных характеристик.
При проверке
значимости параметра регрессии
,
выдвигается гипотеза
о том, что фактор
не
оказывает заметного влияния на
результативный признак. Значимость
параметров
регрессии
проверяется на основе t
– критерия Стьюдента:
.
Параметр признаётся
статистически значимым, если расчётное
значение t
– критерия Стьюдента превосходит его
критическое значение, определяемое при
заданном уровне значимости α и числе
степеней свободы
.
Критическое значение t
– критерия может быть определено по
таблице распределения Стьюдента или
в Excel
по представленному в предыдущем разделе
порядку.
При проверке
значимости коэффициента детерминации
выдвигается гипотеза
о том, что коэффициент детерминации
генеральной совокупности, из которой
извлечена исследуемая выборка, равен
нулю. Эта гипотеза равносильна гипотезе
о том, что ни один из факторов, включённых
в регрессию, не оказывает существенного
влияния на результативный признак.
Поэтому проверка значимости коэффициента
детерминации является проверкой
адекватности (соответствия) выбранной
модели регрессии реальным
данным наблюдения. Значимость
коэффициента детерминации осуществляется
с помощью F-критерия.
Расчётное значение
критерия Фишера–Снедекора,
вычисляется по формуле:
,
Если
,
то гипотеза о равенстве коэффициента
детерминации нулю и несоответствии
заложенных в модели связей реально
существующим отклоняется на уровне
значимости
,
то есть коэффициент детерминации
признаётся статистически значимым, а
модель регрессии – адекватной. Величина
определяется по специальным таблицам
и зависит от заданного уровня значимости
и числа степеней свободы:
и
,
где
–
число наблюдений;
–
число факторных признаков в модели.
В качестве меры
адекватности модели регрессии
используется также процентное отношение
стандартной ошибки
к
среднему уровню результативного признака
–
относительная
ошибка аппроксимации:
, где
Если
,
то точность модели регрессии высокая,
если 10-20% – точность модели регрессии
хорошая (то есть уравнение достаточно
хорошо описывает взаимосвязь между
изучаемыми признаками), если 20-50% –
точность модели регрессии удовлетворительная.
В Excel
для проведения регрессионного анализа
существует статистическая процедура
Регрессия,
позволяющая осуществлять парную
линейную, параболическую (полиноминальную)
и множественную регрессии. Для выбора
формы связи целесообразно построить
корреляционное поле, воспользовавшись
специальным средством Мастер
диаграмм,
выбрав тип Точечная
(см. предыдущий раздел).
Парная линейная
регрессия
в Excel
осуществляется следующим образом:
-
Осуществляется
ввод исходных данных, т.е. значений
факторного и результативного признака. -
В меню Сервис
выделяется строка Анализ
Данных. -
В открывшемся
окне Анализ
данных
выделяется процедура Регрессия
и нажимается кнопка ОК. Откроется
диалоговое окно Регрессия
с пульсирующим курсором в поле ввода
Входной
интервал Y. -
С помощью мыши
выделяется диапазон ячеек, в котором
находятся эмпирические значения
результативного признака Y.
В поле ввода Входной
интервал Y
появится соответствующая ссылка. -
Нажатием клавиши
Tab
осуществляется переход в поле ввода
Входной
интервал Х.
С помощью мыши выделяется диапазон
ячеек, в котором находятся эмпирические
значения факторного признака Х. В поле
ввода Входной
интервал Х
появится соответствующая ссылка. -
Устанавливается
флажок в группе флажков Остатки.
В данную группу входят следующие
флажки:
– флажок Остатки.
При его установке на экран выводится
таблица ВЫВОД
ОСТАТКОВ, в
состав которой входит столбец Остатки;
– флажок График
остатков.
При активизации этого флажка на экран
выводятся графики зависимости остатков
от регрессионных переменных (по одному
графику на каждую переменную);
– флажок
Стандартизированные
остатки. При
установке данного флажка в таблицу
ВЫВОД ОСТАТКОВ
добавляется столбец центрированных
нормированных (стандартизированных),
которые получаются из остатков
делением их на
;
– флажок График
подбора. При
установке этого флажка на рабочий лист
выводятся
точечных графиков (по числу контролируемых
переменных). На графике, связанном с
-й
контролируемой переменной
,
=1,
2….,
,
каждому значению
этой переменной поставлены в соответствие
две точки
и
;
– флажок График
нормальной вероятности. При активизации
этого флажка на экран выводятся таблица
ВЫВОД ВЕРОЯТНОСТИ и график функции,
обратной эмпирической функции
распределения результативного признака,
выполненный на «вероятностной нормальной
бумаге».
-
Щелчком на кнопке
ОК запускается процедура Регрессия.
Помимо этого
процедура содержит также следующие
элементы управления:
-
Флажок Константа-ноль.
Устанавливается
в том случае, когда необходимо, чтобы
линия регрессии проходила через начало
координат. При этом параметрравен нулю и число параметров регрессии
равно числу факторов. -
флажок Уровень
надёжности.
Устанавливается в том случае, когда
помимо доверительных интервалов для
параметров регрессии, соответствующих
используемой по умолчанию «стандартной»
доверительной вероятности 95%, необходимо
вычислить доверительные интервалы,
доверительная вероятность которых
отличается от «стандартной».
«Нестандартная» вероятность, выраженная
в процентах, вводится в поле, расположенное
справа от рассматриваемого флажка.
Если этот флажок не установлен, то
выходной таблице параметров регрессии
будут одинаковые пары столбцов,
содержащие доверительные границы для
параметров регрессии, соответствующие
одной и той же доверительной вероятности
95% (при редактировании таблицы их можно
убрать).
Назначение флажка
Метки
и переключателей Выходной
интервал/Новый рабочий лист/ Новая книга
рассмотрено в 1 разделе.
После запуска
процедуры Регрессия
на рабочем листе появляются три таблицы
результатов этой процедуры. В первой
таблице «Регрессионная статистика»
содержатся значения множественного
коэффициента корреляции, коэффициента
детерминации, нормированного коэффициента
детерминации, стандартная ошибка
уравнения регрессии и число наблюдений.
Во второй таблице «Дисперсионный анализ»
содержатся значения сумм квадратов и
среднего квадрата регрессии, остатков
и общие., а также расчётное значение
критерия Фишера–Снедекора. В третьей
таблице в графе «Коэффициенты» по строке
«Y-
пересечение» находится значение
свободного члена уравнения регрессии
,
а по строке Х – значение параметра
.
Далее по графам расположены стандартная
ошибка, расчётное значение t
– критерия Стьюдента, доверительные
интервалы для этих параметров.
Полиноминальная
(параболическая)
регрессия
в Excel
осуществляется следующим образом:
1. В ячейки А1, В1 и
С1 вводятся метки Y,
X
и X2.
2. В диапазон А2 и
далее (например, А2: А15) вводятся значения
результативного признака, в диапазон
В2 и далее (соответственно В2:В15)– значения
факторного признака.
3.В диапазон С2 и
далее (С2: С15) вводится формула массива
= В2:В15^2
и нажимается комбинация клавиш Ctrl+Shift+
Enter.
В диапазоне
С2:С15 появится столбец квадратов значений
факторного признака.
4. В открывшемся
окне Анализ
данных
выделяется процедура Регрессия
и нажимается кнопка ОК. Откроется
диалоговое окно Регрессия
с пульсирующим курсором в поле ввода
Входной
интервал Y.
5. С помощью мыши
выделяется диапазон ячеек, в котором
находятся эмпирические значения
результативного признака Y.
В поле ввода Входной
интервал Y
появится соответствующая ссылка.
6. Осуществляется
переход в поле ввода Входной
интервал Х.
С помощью мыши выделяется диапазон
ячеек, в котором находятся эмпирические
значения факторного признака. В поле
ввода Входной
интервал Х
появится соответствующая ссылка.
7. Устанавливается
флажок в группе флажков Остатки.
8. Щелчком на кнопке
ОК запускается процедура Регрессия.
После запуска
процедуры Регрессия
на рабочем листе появляются три таблицы
результатов этой процедуры.
Множественная
линейная регрессия
в Excel
осуществляется аналогичным образом.
При этом в качестве исходных данных
вводятся значения результативного и
нескольких (
)
факторных признаков.
К статистическим
функциям, предназначенным для
регрессионного анализа в Excel,
относятся ЛИНЕЙН,
НАКЛОН,
ОТРЕЗОК,
ТЕНДЕНЦИЯ,
ПРЕДСКАЗ,
СТОШYХ,
ЛГРФПРИБЛ,
РОСТ.
Из этих функций
интерес представляют функции ЛГРФПРИБЛ,
ТЕНДЕНЦИЯ
и РОСТ,
так как другие функции вычисляют
некоторые характеристики, определяемые
статистической процедурой РЕГРЕССИЯ,
а также дублируют друг друга. Эти же три
функции производят вычисления, не
предусмотренные статистической
процедурой РЕГРЕССИЯ.
Функция ЛГРФПРИБЛ
вычисляет
выборочные оценки параметров показательной
(экспоненциальной) регрессии.
Синтаксис данной
функции: ЛГРФПРИБЛ
(известные
значения у; известные значения х;, конст;
стат):
-
известные
значения у–
множество значений результативного
признака. Данный массив представляет
собой вектор-столбец размером
; -
известные
значения х–множество
значений факторных признаков.
– Если в случае
парной регрессии этот аргумент опущен,
то при вычислениях в качестве массива
известные
значения х
используется массив натуральных чисел
1,2…и
т.д. такого же размера, как и массив
известные
значения у;
– В случае
множественной регрессии, если массив
известные
значения у
представляет собой вектор-столбец, то
массив известные
значения х
должен иметь
строк и
столбцов. При этом каждый столбец этого
массива содержит
значений определённого факторного
признака;
– При вводе массива
чисел известные
значения х
с клавиатуры для разделения значений
в одной строке используют точку с
запятой, а для разделения строк–
двоеточие.
-
конст–логическая
переменная, определяющая, следует ли
включать в уравнение регрессии свободный
член.
– Если конст=1
(ИСТИНА) или опущен, то вычисляются и
коэффициенты регрессии, и свободный
член.
– Если конст=
0 (ЛОЖЬ), то предполагается, что свободный
член равен единице.
-
стат–
логическая переменная, определяющая
объём выходной информации.
– Если аргумент
стат =0
(ЛОЖЬ) или опущен, то функция выдаёт
только параметры уравнения регрессии.
При этом для вывода результатов решения
надо заранее выделить диапазон ячеек
размером
,
где
–
число факторов, включённых анализ.
– Если аргумент
стат =1
(ИСТИНА), то помимо функция выдаёт
дополнительную информацию об исследуемой
регрессионной зависимости. В этом случае
для вывода результатов решения надо
выделить диапазон ячеек размером
.
В первом столбце выделенного диапазона
находятся следующие характеристики
коэффициенты регрессии, стандартная
ошибка коэффициента регрессии, коэффициент
детерминации, расчётное значение F-
критерия Фишера, сумма квадратов,
обусловленная регрессией. Во втором
столбце находятся значения свободного
члена, его стандартная ошибка, стандартная
ошибка уравнения регрессии, число
степеней свободы, сумма квадратов
остатков.
Так как результатом
реализации функции является массив
чисел, содержащий выборочные характеристики
исследуемой регрессионной зависимости,
то функция вводится как формула массива
Ctrl+Shift+
Enter.
Например, = ЛГРФПРИБЛ
(А1:А6;В1:В6;1;1).
Функции ТЕНДЕНЦИЯ
и РОСТ
используются для вычисления расчётных
значений результативного признака,
соответствующих заданным пользователем
значениям факторных признаков, хранящимся
в массиве новые
значения х.
При этом функция ТЕНДЕНЦИЯ
вычисляет параметры линейной и других
видов регрессии, линейных относительно
входящих в них коэффициентов, таких,
например, как полиноминальная
(параболическая) регрессия
,
а функция РОСТ–
параметры экспоненциальной регрессии.
Функции вводится
как формула массива Ctrl+Shift+
Enter.
Синтаксис данных
функций идентичен: ТЕНДЕНЦИЯ
(известные значения у; известные значения
х;, новые значения х,; конст)
и РОСТ
(известные значения у; известные значения
х;, новые значения х,; конст):
-
известные
значения у–
множество значений результативного
признака. Данный массив представляет
собой вектор-столбец размером;
-
известные
значения х–множество
значений факторных признаков.
– Если в случае
парной регрессии этот аргумент опущен,
то при вычислениях в качестве массива
известные
значения х
используется массив натуральных чисел
1,2…и
т.д. такого же размера, как и массив
известные
значения у;
– В случае
множественной регрессии, если массив
известные
значения у
представляет собой вектор-столбец, то
массив известные
значения х
должен иметь
строк и
столбцов. При этом каждый столбец этого
массива содержит
значений определённого факторного
признака;
– При вводе массива
чисел известные
значения х
с клавиатуры для разделения значений
в одной строке используют точку с
запятой, а для разделения строк–
двоеточие.
-
новые значения
х– новые
значения факторных признаков, для
которых функция должна вычислить
расчётные значения результативного
признака;
– В случае
множественной регрессии, если массив
известные
значения у
представляет собой вектор-столбец, то
массив новые
значения х
должен иметь
столбцов и столько строк, сколько
расчётных значений у надо вычислить.
–Массив новые
значения х,
так же как и массив
известные значения х,
должен содержать столбец для каждого
факторного признака. Число столбцов
этих массивов должно быть одинаково.
– Если аргумент
новые значения
х опущен, то
предполагается, что он совпадает с
аргументом известные
значения х.
-
конст–логическая
переменная, определяющая, следует ли
включать в уравнение регрессии свободный
член.
– Если конст=1
(ИСТИНА) или опущен, то вычисляются и
коэффициенты регрессии, и свободный
член.
– Если конст=
0 (ЛОЖЬ), то предполагается, что свободный
член равен нулю (в случае линейной
регрессии) и единице (в случае
экспоненциальной регрессии).
Ряды динамики
Ряд
динамики–
это ряд числовых значений статистических
показателей, расположенных в хронологической
последовательности и характеризующих
изменение явления во времени.
Ряд динамики
состоит из двух
элементов:
-
уровней динамического
ряда– числовых значений статистических
показателей, характеризующих величину
изучаемого явления–
;
-
периодов (или
моментов) времени, к которым относятся
данные уровни –
.
Одной из основных
задач в процессе анализа уровней
динамического ряда является определение
основной закономерности (тенденции) их
изменений
во времени.
При этом выделяются
следующие основные
компоненты динамического ряда:
-
основная тенденция
(тренд) (Т); -
циклическая (Ц);
-
сезонная (S);
-
случайная (Е).
Первые три компоненты
формируют систематическую
составляющую
динамического ряда.
Тренд
характеризует устойчивое систематическое
изменение динамического ряда, происходящее
в течение длительного времени и
обусловленное влиянием медленно
развивающихся долговременных факторов.
Сезонная
компонента–
это колебания, периодически повторяющиеся
в некоторое определённое время каждого
года, дня месяца или часа дня.
Циклическая
(периодическая) компонента
проявляется
в том, что значение изучаемого показателя
в течение какого-то времени возрастает,
достигает определённого максимума,
затем понижается, достигает определённого
минимума, вновь возрастает до прежнего
значения и т.д.
Четвёртую компоненту
формируют случайные
колебания,
которые являются результатом действия
большого количества относительно слабых
второстепенных факторов.
Для выявления
и характеристики
основной закономерности развития
явления необходимо выявить первую
компоненту динамического ряда – тренд,
и погасить влияние других типов колебаний
на изменение уровней ряда.
С этой целью
проводят выравнивание динамических
рядов. Различают два вида выравнивания:
механическое (или сглаживание) и
аналитическое.
К приёмам
механического выравнивания
относятся:
-
усреднение левой
и правой половины ряда; -
укрупнение
периодов; -
скользящая средняя:
простая, взвешенная; -
экспоненциальное
сглаживание.
Выбор приема
выравнивания зависит от исходной
информации и задач исследования.
В среде Excel
для выравнивания динамических рядов
используются процедуры Скользящее
среднее и
Экспоненциальное
сглаживание,
входящие в Пакет анализа.
Сущность метода
скользящей средней
заключается в том, что вычисляется
средний уровень из определенного числа
первых по порядку уровней ряда, затем
– средний уровень из такого же числа
уровней, начиная со второго, затем,
начиная с третьего и т.д. Таким образом,
при расчётах среднего уровня как бы
«скользят» по ряду динамики от его
начала к концу, каждый раз отбрасывая
один уровень вначале и добавляя один
следующий. Этим объясняется название
– скользящая средняя.
;
;
и т.д.
Следует
отметить, что при использовании метода
скользящей средней «теряются»
членов в начале и в конце динамического
ряда (где
–размер
интервала (окна) сглаживания). Для
восстановления «потерянных» уровней
в начале и в конце сглаженного ряда для
=3
и
=5
могут быть использованы следующие
формулы:
-
=3
(
):
;
;
-
=5(
):
;
;
;
.
Для получения
количественной модели, выражающей
основную тенденцию изменения уровней
динамического ряда во времени, используется
приём
аналитического выравнивания.
Сущность
его состоит в том, что основная тенденция
развития
рассчитывается как функция времени. В
этом случае фактические (эмпирические)
уровни заменяются теоретическими,
вычисленными по соответствующему
аналитическому уравнению.
Аналитическое
выравнивание производится в следующей
последовательности:
1)
выделяется этап развития явления и
устанавливается характер динамики на
этом этапе. Этап развития явления– это
период, в течение которого формирование
уровней динамического уровня осуществляется
под воздействием определённого набора
постоянных, периодических и разовых
факторов. Решение этой задачи осуществляется
не только с помощью статистических
методов, а в основном – на базе анализа
сущности, природы явлений и общих
законов его развития.
2)
на основе предположений о той или иной
закономерности развития выбирается
форма аналитического выражения тренда,
то есть вид аппроксимирующей математической
функции.
Основанием для
выбора уравнения тренда
могут служить:
-
качественный
анализ сущности развития данного
явления; -
результаты
предыдущих исследований в данной
области; -
графическое
изображение эмпирических или скользящих
уровней ряда динамики; -
статистико-математических
критериев адекватности.
При анализе рядов
динамики используются следующие
математические модели:
-
линейная yt
= a0
+ a1t,
где
и
–
параметры уравнения;
–
начальный уровень
тренда в момент или период, принятый за
начало отсчёта времени;
–
среднее абсолютное
изменение за единицу времени;
–
обозначение
времени.
Параметр
определяет направление развития: если
,
то уровни ряда равномерно возрастают
в среднем за единицу времени на величину
,
если
,
то происходит их равномерное снижение.
-
полиноминальная(параболическая)
,
где–степень
полинома. Наиболее применяемой в
практике статистических расчётов
является уравнение параболы
второго порядка yt
= a0
+ a1t
+ a2t2.
Значение параметров
и
идентично предыдущему уравнению.
Параметр
характеризует
изменение интенсивности развития в
единицу времени. При
происходит ускорение развития, при
–
замедление развития.
Соответственно
при параболической форме тренда возможны
следующие варианты развития:
-
если
;
–
ускорение роста; -
если
;
–
замедление роста; -
если
;
–
замедление снижения; -
если
;
–
ускорение снижения.
-
экспоненциальная
,
где
–
константа ряда,
–темп
изменения в разах. При
>1
экспоненциальный тренд выражает
тенденцию ускоренного и всё более
ускоряющегося возрастания уровней, при
<1
экспоненциальный тренд означает всё
более замедляющегося снижения уровней
динамического ряда.
-
логарифмическая
.
Логарифмическая
форма тренда применяется для отображения
тенденции замедляющегося роста уровней
при отсутствии предельно возможного
значения, например, роста спортивных
достижений, производительности агрегата,
продуктивности скота. -
гиперболическая
yt
= a0
+ a1
–
применяется для отображения тенденции
процессов, ограниченных предельным
значением уровня; -
степенная
–
применяется для отображения тенденции
явлений с разной мерой пропорциональности
изменений во времени; -
логистическая
и др.
Наиболее точным
способом выбора формы тренда является
применение
статистико-математических критериев,
в качестве которых могут выступать
остаточное среднее квадратическое
отклонение, средняя ошибка аппроксимации
(
),
стандартизированная ошибка аппроксимации
(
),
относительная ошибка аппроксимации
(модифицированный коэффициент вариации):
;
,
где
y
и
—
соответственно
фактические и теоретические значения
ряда динамики;
n
– число уровней
ряда;
m
– количество
параметров в уравнении тренда.
.
Предпочтение
отдаётся той функции, которая имеет
наименьшую величину критерия.
Если
,
то точность модели тренда высокая, если
=
10-20% – точность модели тренда хорошая
(то есть уравнение достаточно хорошо
описывает основную тенденцию развития
изучаемого явления), если
=20-50%
– точность модели тренда удовлетворительная.
3) Вычисляются
параметры уравнения тренда, и по ним
производится синтезирование
трендовой модели.
Расчёт параметров
уравнений тренда может быть произведён
различными способами:
-
методом средних
значений (или линейных отклонений); -
методом конечных
разностей; -
методом наименьших
квадратов.
Наиболее точным
является аналитическое выравнивание
с помощью способа
наименьших квадратов.
Суть данного способа состоит в том, что
теоретическая линия (прямая или кривая),
выравнивающая ряд, должна проходить в
максимальной близости к фактическим
уровням ряда. Математически это означает,
что сумма квадратов отклонений (разность
между фактическими и теоретическими
уровнями) должна быть минимальной:
å
(y
–
yt)2
= min.
4) На основе
синтезированной модели тренда вычисляются
теоретические уровни.
Выявление и
характеристика основной тенденции
развития дают основание для прогнозирования,
то есть для определения возможного
варианта размеров явления в будущем.
Важное значение при прогнозировании
имеют вопросы о базе и сроках
прогнозирования.
База
прогнозирования
– длина или продолжительность базисного
периода, закономерность которого будет
распространяться на будущее.
Срок
прогнозирования
(период
упреждения)
– длина будущего периода, на который
распространяется закономерность
развития явления.
Однозначного
ответа на вопрос об определении
допустимого срока прогноза нет. В
основном придерживаются следующего
правила: срок прогноза не должен превышать
третьей части длины базы прогноза.
Однако в каждом конкретном случае
необходимо учитывать особенности
изучаемого явления. При этом необходимо,
чтобы продолжительность базисного ряда
составляла определенный этап в развитии
анализируемого явления в конкретных
исторических условий.
Установление
сроков прогнозирования зависит от цели
исследования. Однако следует иметь в
виду, особенности характера изучаемого
явления. Например, ограниченные
физиологические особенности животных
(или растений), делают невозможным
увеличение продуктивности животных
(или урожайности) до бесконечности.
Кроме того, необходимо учитывать
неустойчивость экономики в условиях
переходного периода. Поэтому чем короче
сроки прогнозирования периода, тем
надежнее результат прогноза.
Разработка
прогнозного уровня динамического ряда
может осуществляться на основе
использования различных методов,
наиболее распространённым из которых
является метод экстраполяции.
Метод экстраполяции
основывается на предположении о
неизменности основных факторов,
определяющих тенденцию данного
показателя, и заключается в распространении
закономерностей развития этого
показателя, имевших место в прошлом, на
будущее.
Более точным и
распространённым методом экстраполяции
является применение
аналитического выражения тренда,
при котором в адекватную трендовую
модель подставляются значения
в будущие годы. Прогнозирование на
основе экстраполяции дает возможность
получить точечные значения прогнозируемого
уровня исследуемого показателя.
Интерполяция–
это приближённый расчёт уровней,
находящихся внутри ряда динамики, но
почему-либо неизвестных. При интерполяции
предполагается, что характер тенденции
не претерпел существенных изменений в
том промежутке времени, уровень которого
нам не известен.
Как и экстраполяция,
интерполяция может производится на
основе на
основе выравнивания динамического ряда
по какой-либо аналитической формуле.
В Excel
сглаживание динамического ряда методом
скользящей средней осуществляется
следующим образом:
1. В диапазон ячеек
вводятся уровни ряда динамики (числовые
значения изучаемого статистического
показателя).
2.В меню Сервис
выделяется
строка Анализ
данных.
3. В открывшемся
окне Анализ
данных
выделяется процедура Скользящее
среднее и
нажимается кнопка ОК. На экране появится
диалоговое окно Скользящее
среднее.
4. В поле ввода
Входной
интервал
этого окна вводится ссылка на диапазон
ячеек, содержащий уровни исследуемого
ряда динамики. Входной интервал должен
состоять из одного столбца, «высота»
которого равна числу
уровней данного ряда динамики.
5. В поле Интервал
вводится размер окна сглаживания
(по умолчанию
=3).
6. В поле Выходной
интервал
вводится ссылка на верхнюю ячейку
столбца результатов сглаживания.
Выходной интервал всегда располагается
на том же самом рабочем листе, на котором
находится входной интервал, поэтому в
диалоговом окне процедуры нет таких
позиций, как Новый
рабочий лист
и Новая
рабочая книга.
Выходной интервал состоит по крайней
мере из одного столбца, содержащего
уровни сглаженного ряда. Высота этого
столбца равна высоте входного интервала.
При установке флажка
Стандартные погрешности
в выходном интервале появляется ещё
один столбец– столбец стандартных
погрешностей. В точках, для которых
нельзя вычислить сглаженные значения
и стандартные погрешности, процедура
выводит сообщение #
Н/Д! (Нет
данных).
7. Устанавливается
флажок Вывод
графика.
Флажок Стандартные
погрешности
устанавливается при необходимости
получения стандартных погрешностей
сглаживания. Назначение флажка Метки
рассмотрено
в 1 разделе.
8. Нажимается кнопка
ОК.
Следует иметь в
виду, что процедур Скользящее
среднее
выдаёт сглаженный ряд так называемых
адаптивных скользящих средних. Этот
ряд сдвинут на
шагов вправо относительно «канонического»
ряда скользящих средних. Для сравнения
простого и адаптивного скользящих
средних в диапазоне ячеек, число которых
на
-1
меньше числа уровней исходного ряда
динамики, свободного столбца, рассчитываются
значения скользящих средних, вычисленные
по канонической формуле =
СРЗНАЧ по
диапазону из
первых уровней динамического ряда
(например, при
=3
А1:А3). Данная формула вводится в следующую
после
по
счёту ячейку столбца, предназначенного
для расчёта канонических средних
(например, при
=3–во
вторую (С2), при
=5
(С3) и т.д.). Затем данная формула копируется
в оставшийся диапазон ячеек этого
столбца. Адаптивные скользящие средние
могут быть вычислены также с помощью
статистической процедуры Добавить
линию тренда
(см. ниже).
При проведении
экспоненциального сглаживания
использование одноимённой процедуры
аналогично выше рассмотренному порядку.
Вместо поля Интервал
диалогового
окна Скользящее
среднее в
процедуре Экспоненциальное
сглаживание
заполняется поле Фактор затухания. В
это поле вводится фактор затухания
,
где
–
параметр сглаживания (вес текущего
значения при вычислении экспоненциального
среднего,
).
Параметр
характеризует
скорость реакции экспоненциального
среднего
на изменение текущего значения
динамического
ряда и одновременно определяет его
способность сглаживать случайные
колебания. Чем больше
,
тем быстрее реакция экспоненциального
среднего на изменение динамического
ряда и тем меньше его сглаживающие
возможности. В качестве приемлемого
компромисса рекомендуется брать
в пределах от 0,1 до 0,3. Следовательно,
приемлемыми значениями фактора затухания
являются значения из интервала от 0,7 до
0,9. В статистической процедуре
Экспоненциальное
сглаживание
по умолчанию
,
что противоречит рекомендациям.
При аналитическом
выравнивании в Excel
используются статистическая процедура
Регрессия
и статистические функции регрессионного
анализа ЛИНЕЙН,
ПРЕДСКАЗ,
ЛГРФПРИБЛ,
ТЕНДЕНЦИЯ и
РОСТ,
рассмотренные в предыдущем разделе. В
этом случае при использовании
статистической процедуры Регрессия
вместо значений факторного признака
вводятся натуральные числа 1,2,….
,
обозначающие порядковые номера периодов
или моментов времени. При использовании
статистических функций натуральные
числа можно не вводить, а оставить
пропущеным аргумент известные
значения х.
Тогда при вычислениях в качестве массива
известные
значения х
используется массив натуральных чисел
1,2…и
т.д. такого же размера, как и массив
известные
значения у.
Эффективным
средством аналитического выравнивания
является процедура Добавить
линию тренда,
входящая в комплекс графических средств
табличного процессора Excel.
Она вычисляет параметры выбранной
пользователем модели тренда. При
вычислениях используется МНК. Модель
тренда выбирается из набора, включающего
в себя пять наиболее распространённых
аналитических моделей: линейную,
логарифмическую, полиноминальную
(параболическую), степенную, экспоненциальную
и модель адаптивной скользящей средней
(формулы см. выше данном разделе).
Параметры аналитических моделей
вычисляются по данным наблюдения, по
которым построен график динамического
ряда. В результате реализации процедуры
в область построения графика выводятся
график функции тренда, её аналитическое
выражение и значение коэффициента
детерминации R2.
При изменении любых значений исходного
ряда динамики процедура автоматически
пересчитывает и обновляет параметры
линии тренда и её график.
Для доступа к
процедуре Добавить
линию тренда
необходимо:
1. В диапазон ячеек
определённого столбца ввести уровни
исследуемого динамического ряда.
2. С помощью Мастера
Функций построить диаграмму (график)
ряда динамики.
3. Щелчком на
диаграмме активизировать её. На панели
меню на месте пункта Данные
появится
пункт Диаграмма.
4. В пункте меню
Диаграмма
выбрать команду Добавить
линию тренда.
Откроется диалоговое окно Линия
тренда.
5. В открывшемся
окне Линия
тренда
раскрыть вкладку Тип.
6. На этой вкладке
в разделе Построение
линии тренда (аппроксимация и сглаживание)
выбрать тип (вид) функции тренда.
7. В списке Построен
на ряде
выделить ряд данных, для которых строится
линия тренда.
8. Раскрыть вкладку
Параметры
диалогового окна Линия
тренда.
Эта вкладка содержит
следующие элементы управления:
-
группу переключателей
Название аппроксимирующей (глаженной)
кривой, состоящую из двух переключателей.
При установке переключателя автоматическое
Excel
автоматически присваивает линии тренда
имя, связанное с типом этой линии и
названием данных наблюдения, по которым
строится линия тренда, например, Линейный
(Урожайность зерновых).
При установке переключателя другое
пользователь сам устанавливает имя
линии регрессии и вводит это имя в поле
Линейный
(Ряд 1),
расположенное справа от переключателя
(максимальная длина имени 256 символов); -
группу счётчиков
Прогноз,
в которую входят два счётчика: вперёд
на…единиц
и назад
на…единиц.
С помощью этих счётчиков устанавливается
срок прогноза и производится экстраполяция
и интерполяция ряда динамики. Счётчики
недоступны в режиме Скользящее
среднее; -
флажок пересечение
кривой с осью Y
в точке.
Если этот флажок не установлен, ординататочки пересечения линии тренда с осью
Y
вычисляется по данным наблюдения. Как
правило, этот флажок не устанавливается.
Используя этот флажок и расположенное
справа от него поле ввода, можно задать
нужную ординату точки пересечения (при
активном флажке и нуле в поле ввода
линия тренда пройдет через начало
координат); -
флажок показывать
уравнение на диаграмме.
При установке этого флажка в область
построения диаграммы выводится
аналитическое выражение (формула)
функции тренда; -
флажок поместить
на диаграмму величину достоверности
аппроксимации.
При установке этого флажка в область
построения диаграммы выводится значение
коэффициента детерминации R2,
который показывает, на сколько процентов
выбранная линия тренда объясняет
разброс уровней ряда. Чем больше данный
показатель, тем более точно выбрана
линия тренда. Сравнивая величину R2
по разным аналитическим моделям можно
определить аппроксимирующую функцию.
то есть наиболее точно описывающую
основную тенденцию развития изучаемого
явления.
9. Установить нужные
переключатели, счётчики и флажки.
Щёлкнуть на кнопке ОК.
Список рекомендуемой литературы
1. Вадзинский Р.
Статистические вычисления в среде
Еxcel.
–СПб.: Питер,2008.
2. Макарова Н.В.
Трофимец В.Я. Статистика в Еxcel.–
М.: Финансы и статитсика, 2006.
3. Берк К. Кэйри П.
Анализ данных с помощью MS
Еxcel.–М.:
Вильямс, 2005.
4. Васильев А.Н.
Научные вычисления в Microsoft
Excel.–М.;
Спб.; Киев: Диалектика, 2004.
5.Вуколов Э.А. Основы
статистического анализа: практикум по
статистическим методам и исследованию
операций с использованием пакетов
STATISTICA
и Еxcel.–
М.: Форум; Инфра–М, 2004.
6. Минько А.А.
Статистический анализ в среде Еxcel.–М.,
СПб., Киев: Диалектика, 2004.
7. Гайдышев И. Анализ
и обработка данных.–СПб; М.: Питер, 2001.
8.
Елисеева И.И., Юзбашев М.М. Общая теория
статистики: Учебник. М: Финансы и
статистика, 2005
9.
Ефимова М.Р., Петрова Е.В., Румянцев В.Н.
Общая теория статистики: Учебник. –
М.: ИНФРА- М, 2006.
10.
Теория статистики: Учебник / Под ред.
Р.А. Шмойловой .4-е изд., доп. и перераб. —
М.: Финансы и статистика, 2005.
11.
Теория статистики: Учебник/ Под ред.
Г.Л. Громыко.- ИНФРА- М, 2006.
75
Процедура «Описательные статистики » пакета «Анализ данных.
В процедуре автоматически вычисляются следующие числовые характеристики выборки:
Для того чтобы выполнить вычисления, вводим в поле «Водной интервал» адреса ячеек, в которых записаны выборочные значения;
помечаем «Выходной интервал» и вводим в поле адрес первой ячейки, начиная с которой в листе Excel будет отображён резгультат; помечаем «Итоговая статистика»:
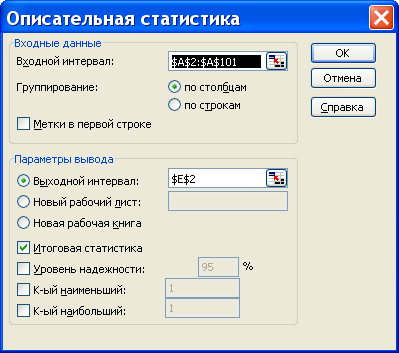
Результаты вычислений процедуры представлены в виде таблицы:
|
Столбец1 |
|
|
Среднее |
120.10 |
|
Стандартная ошибка |
0.22 |
|
Медиана |
120.12 |
|
Мода |
118.69 |
|
Стандартное отклонение |
2.15 |
|
Дисперсия выборки |
4.63 |
|
Эксцесс |
0.21 |
|
Асимметричность |
-0.16 |
|
Интервал |
11.21 |
|
Минимум |
114.46 |
|
Максимум |
125.67 |
|
Сумма |
12010.34 |
|
Счет |
100 |
Здесь: «Асимметричность» – коэффициент асимметрии, «Интервал» – размах варьирования, «Счёт» – объём выборки.
Функция «Квартиль» для вычисления квартилей и межквартильного размаха
КВАРТИЛЬ(массив;часть)
Функция вычисляет (в зависимости от значения параметра «Часть»), выборочные значения верхней квартили («Часть» = 3) или нижней квартили («Часть» = 13), медиану («Часть» = 2) , наибольшее («Часть» = 4) или наименьшее («Часть» = 03) значения для выборки, определённой как «массив»..