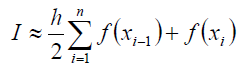В этом разделе приведены примеры решенных задач разных разделов вычислительной математики, выполненные в пакете электронных таблиц Excel.
Спасибо за ваши закладки и рекомендации
Примеры решений по численным методам в Эксель
Задача 1. Найти стационарные точки, проверить их на экстремальность, а также найти все локальные и глобальные максимумы и минимумы.
Задача 2. Решить приближенно уравнение $2x^3+3x-9=0$
Задача 3. Уплотнить часть $[a; b]$ таблицы заданной функции с шагом $H$, пользуясь интерполяционными формулами Ньютона. Составить таблицу конечных разностей. В каждом столбце, начиная с четвертого, будет на одно число меньше, чем в предыдущем. Результаты вычислений значений функции в промежуточных точках расположить в таблице.
Интерполяционные формулы Ньютона дают хороший результат в случае, когда $tin[0; 1]$. Если внутри отрезка $[a; b]$, на котором требуется уплотнить таблицу, находится узловая точка $x_i$, то на каждом из отрезков $[a; x_i]$ и $[_i; b]$ вычисления выполняются отдельно. Все задания выполнить в Excel
Задача 4. Решить систему методами Ньютона, Брауна, итераций.
Задача 5. Решить систему Ax=b методом Гаусса (схема частичного выбора). Вычислить определитель и обратную матрицу для данной матрицы на основе метода Гаусса.
Задача 6. Функция y=y(x) задана таблицей своих значений. Построить многочлены нулевой и первой степени, приближающие функцию по методу наименьших квадратов. Вычислить величину среднеквадратичного отклонения.
Построить на одном чертеже точечный график функции и графики многочленов.
Задача 7. Вычислить интеграл от заданной функции f(x) на отрезке [a,b] по формулам трапеций и Симпсона при делении отрезка на 12 равных частей. Повторить вычисления при делении отрезка на 6 равных частей. Записать ответ каждого метода, сохранив только верные цифры.
Решаем численно задачи в программе Excel на заказ
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.
Обзор методов решения в Excel
Введение
Уравнение 
называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области 
и, во всяком случае, зависит от 
. Его решением является любая функция u(x), которая этому уравнению удовлетворяет при всех x в определённом конечном или бесконечном интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид 
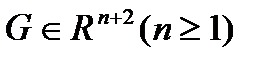
Решением этого уравнения на интервале I=[a,b] называется функция u(x).
Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что уi=F(xi)(i=1,2,…, n) и F(x0)=y0.
Таким образом, численные методы позволяют вместо нахождения функции y=F(x) (3) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений – это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически симметричных полях и многое другое)
Обзор методов решения в Excel
1.1 Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка
Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов. Наиболее употребительным методом Рунге-Кутта решения уравнения первого порядка y’ = F(x,y) (1) является метод четвертого порядка, в котором вычисления производятся по формуле:
yk+1 = yk +(k1 +2k2 +2k3 +k4 )/6, (2)
k1 = Fk h = F(xk , yk )h
Рассмотрим задачу Коши для уравнений первого порядка на отрезке [a,b]:
, 
(4)
Разобьём промежуток [a,b] на N частей 
. Обозначим , где u(x) –точное решение задачи Коши, и через 
значения приближенного решения в точках 
. Существует 2 типа численных схем :
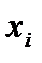
1. явные: 
) (5)
2. неявные: 
(6)
Здесь F некоторая функция, связывающая приближения. В явных схемах приближенное значение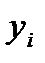 
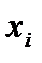
в точке определяется через некоторое число k уже определённых приближенных значений. В неявных схемах определяется не рекурентным способом, как в явных схемах, а для его определения возникает уравнение, поскольку равенство (6) представляет из себя именно уравнение на . Явные схемы проще, однако зачастую неявные схемы предпочтительнее
1.3 Метод Эйлера
Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что
Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Рассмотрим дифференциальное уравнение первого порядка (7) с начальным условием
Требуется найти решение уравнения (7) на отрезке [а,b].
Разобьем отрезок [a, b] на n равных частей и получим последовательность х0, х1, х2,…, хn, где xi=x0+ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.
В методе Эйлера приближенные значения у(хi)»yi вычисляются последовательно по формулам уi+hf(xi, yi) (i=0,1,2…).
При этом искомая интегральная кривая у=у(х), проходящая через точку М0(х0, у0), заменяется ломаной М0М1М2… с вершинами Мi(xi, yi) (i=0,1,2,…); каждое звено МiMi+1 этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (7), которая проходит через точку Мi. Если правая часть уравнения (7) в некотором прямоугольнике R<|x-x0|£a, |y-y0|£b>удовлетворяет условиям:
|df/dx|=|df/dx+f(df/dy)| £ M (M=const),
то имеет место следующая оценка погрешности:
где у(хn)-значение точного решения уравнения (7) при х=хn, а уn— приближенное значение, полученное на n-ом шаге.
Формула (13) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет: сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом h/2. Погрешность более точного значения уn * оценивается формулой
Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.
1.4 Модифицированный метод Эйлера
Рассмотрим дифференциальное уравнение (7) y / =f(x,y) с начальным условием y(x0)=y0. Разобьем наш участок интегрирования на n равных частей. На малом участ интегральную кривую заменим прямой линией.
Рисунок 1 Метод Эйлера в графическом виде
Получаем точку Мк(хк,ук). Через Мк проводим касательную:
Получаем точку Nk / . В этой точке строим следующую касательную:
Из точки Мк проводим прямую с угловым коэффициентом αк и определяем точку пересечения этой прямой с прямой Хк1. Получаем точку Мк / . В качестве ук+1 принимаем ординату точки Мк / . Тогда:
(14)-рекурентные формулы метода Эйлера.
Сначала вычисляют вспомогательные значения искомой функции ук+1/2 в точках хк+1/2, затем находят значение правой части уравнения (11) в средней точке y / k+1/2=f(xk+1/2, yk+1/2) и определяют ук+1.
Для оценки погрешности в точке хк проводят вычисления ук с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений:
где у(х)-точное решение дифференциального уравнения.
Таким образом, методом Эйлера можно решать уравнения любых порядков. Например, чтобы решить уравнение второго порядка y // =f(y / ,y,x) c начальными условиями y / (x0)=y / 0, y(x0)=y0, выполняется замена
Тем самым преобразуются начальные условия
1.5 Практическая часть
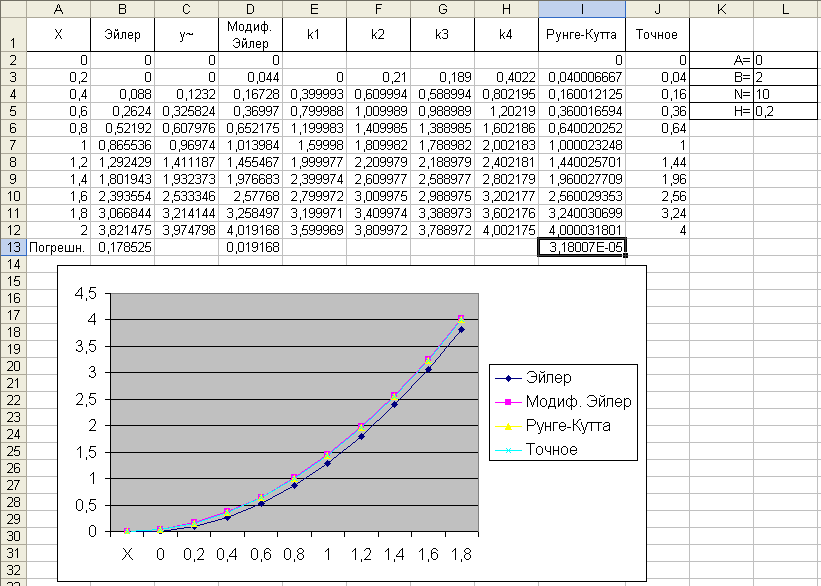
Здесь решается уравнение dy/dx = 2x-y+x 2 на интервале [0,2], начальное значение y(0)=0, для оценки точности задано также точное решение в виде функции u(x)=x 2 . Оценка погрешности делается в нормеL1, как и принято в данном случае
Численное решение дифференциальных уравнений в excel
Pers.narod.ru. Обучение. Excel: Решение обыкновенных дифференциальных уравнений (задача Коши)
Решение обыкновенных дифференциальных уравнений (ОДУ) — популярный раздел численных методов, немного теории можно почитать здесь.
В приведённом примере решается задача Коши, то есть, ищется решение дифференциального уравнения первого порядка вида dy/dx = f(x,y) на интервале x ∈ [x0,xn] при условии y(x0)=y0 и равномерном шаге сетки по x .
Решение выполняется методами Эйлера, «предиктор-корректор» (он же модифицированный метод Эйлера) и методом Рунге-Кутта 4 порядка точности. Пример может служить образцом для Ваших решений, правда, функцию придётся перепрограммировать несколько раз при различных значениях аргумента — поскольку без применения макросов на VBA Excel не позволяет создать полноценную функцию, которую было бы удобно вызывать с разными значениями аргументов.
Здесь решается уравнение dy/dx = 2x-y+x 2 на интервале [0,2] , начальное значение y(0)=0 , для оценки точности задано также точное решение в виде функции u(x)=x 2 . Оценка погрешности делается в норме L1 , как и принято в данном случае.
Скачать пример в Excel XP/2003 (28 Кб)
Рунге-Кутта VBA EXCEL
Решение дифференциальных уравнений первого порядка
методом Рунге-Кутта.
Данный проект VBA позволяет решать дифференциальные уравнения первого порядка одним из численных методов, а именно, методом Рунге-Кутта.
Исходные данные:
- границы интервала a и b;
- шаг интегрирования h;
- начальное значение для решения y(a), позволяющее правильно определить константу…
вводятся в соответствующие ячейки столбца «J».
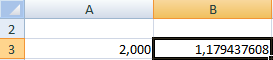
И самое главное (самая ответственная часть) необходимо без ошибок ввести формулу в ячейку «D3». Эта формула получается из заданного уравнения и представляет функцию, являющуюся производной от решения. Ее параметрами может быть как только х (т.е. ячейка «D4»), так и х совместно с у (т.е. ячейкой «D5»). На рисунке показан пример ввода формулы для заданного уравнения…
В ячейки «D4» и «D5» вводить ничего не нужно… Туда значения будет подставлять макрос…
Если не удалось запустить видео, воспользуйтесь этой ссылкой . видео на YouTube
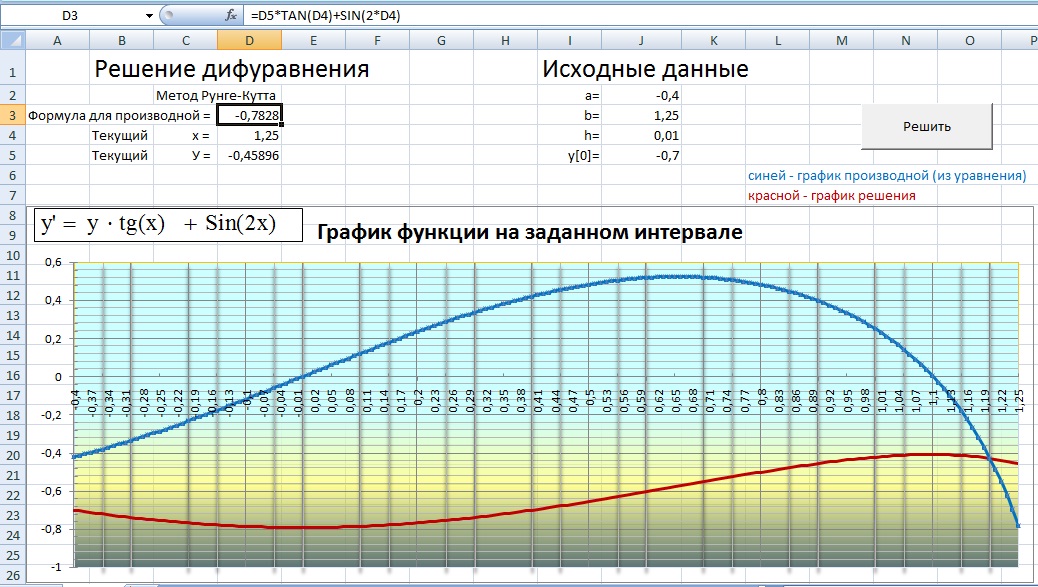
После этого остается нажать кнопку «Решить» и … если Вы не забыли включить макросы, то увидите, быстро меняющиеся текущие значения в ячейках столбца «D», а после окончания цикла расчета значений у, произойдет изменение графиков.
Графики должны быть построены на заданном Вами интервале (на рисунке от -0,4 до 1,25)…
В каждой точке, где производная (график синего цвета) пересекает ось 0У, функция решения(красная) должна иметь экстремум (максимум или минимум)…
Если терпением Вы не отличаетесь, то не задавайте очень длинный интервал и/или очень мелкий шаг…
Подсказка:
Собственно, процедура заполнения массивов х и у по методу Рунге-Кутта будет выглядеть так:
(при этом глобальная переменная D3formula предварительно инициализируется: D3formula = Range(«D3»).Formula)
Private Function func(x As Double, y As Double) As Double ‘производная
Dim f As String
‘функция вычисляется по формуле, введенной пользователем в ячейку D3 (гед D4 — это x, D5 — это y)
f = Replace(D3formula, «D4», CStr(x))
f = Replace(f, «D5», CStr(y))
Range(«D3»).FormulaLocal = f
func = Range(«D3»)
End Function
Sub MethodRungeKutta()
‘вспомогательные переменные
Dim k1 As Double, k2 As Double, k3 As Double, k4 As Double
Dim i As Integer
For i = 1 To n ‘нулевые значения уже есть
x(i) = x(0) + i * h
k1 = func(x(i — 1), y(i — 1))
k2 = func(x(i — 1) + h / 2, y(i — 1) + k1 * h / 2)
k3 = func(x(i — 1) + h / 2, y(i — 1) + k2 * h / 2)
k4 = func(x(i), y(i — 1) + k3 * h)
y(i) = y(i — 1) + h / 6 * (k1 + 2 * k2 + 2 * k3 + k4) ‘значения вычисляются
p(i — 1) = k1 ‘сохранение в массив для графика
Чтобы на диаграмме отобразились рассчитанные графики, производится заполнение соответствующих диапазонов в столбцах «AA-AB-AC»… Можете сравнить результаты с этим табличным вариантом.
источники:
http://pers.narod.ru/study/excel_odu.html
http://orenstudent.ru/RungeKuttaVBA_change_formula.htm
По теме: методические разработки, презентации и конспекты
Лабораторный практикум по численным методам
Настоящий лабораторный практикум подготовлен по дисциплине «Численные методы». Целью лабораторного практикума является усвоение и закрепление теоретического материала, приобретение практических навы…
Лекция «Численные методы решения уравнений»
Лекция по разделу «Численные методы».Рассматриваются следующие методы решения алгебраических и трансцендентных уравнений: 1) метод дихотомии (метод деления отрезка пополам),2) метод хор…
history 20 ноября 2022 г.
- Группы статей
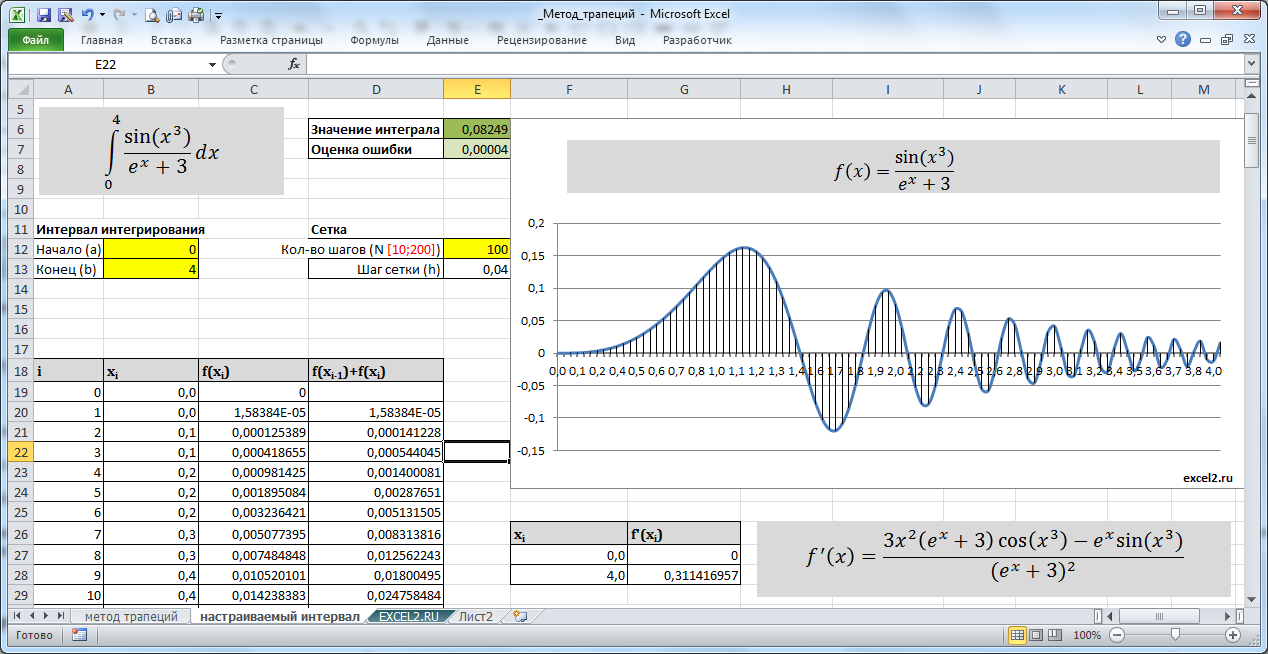
Вычислим в MS EXCEL определенный интеграл методом трапеций (англ. Trapezoidal Rule). Оценим ошибку интегрирования, построим график функции.
В интернете есть много сайтов по автоматическому вычислению интегралов аналитическими и численными методами. Но, как правило, про использованный метод численного интегрирования ничего не говорится, а корректность вычислений проверить невозможно. В данном примере все вычисления прозрачны и можно задать необходимое количество интервалов разбиения. Правда, данный метод имеет относительно невысокую точность по сравнению с другими методами (если сравнивать его с методом Симпсона и методом интерполяционного полинома Лагранжа).
Немного теории
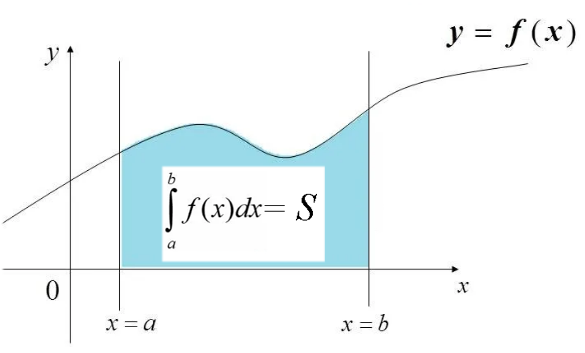
Так как функция, стоящая под знаком интеграла в общем случае может быть любая, то значение интеграла не всегда можно вычислить аналитически. Однако, можно воспользоваться тем фактом, что согласно теории, значение интеграла численно равно площади фигуры образованной графиком функции и осью Х (фигура выделена цветом).
Таким образом, задача нахождения интеграла сводится к нахождению площади этой фигуры. Площадь фигуры в общем случае можно найти численными методами, разбивая ее на простые однотипные фигуры, например трапеции. Т.к. площадь каждой трапеции найти легко, то простым суммированием площадей можно найти и интеграл. Платой за универсальность является ошибка интегрирования, которую впрочем можно оценить (будет показано далее).
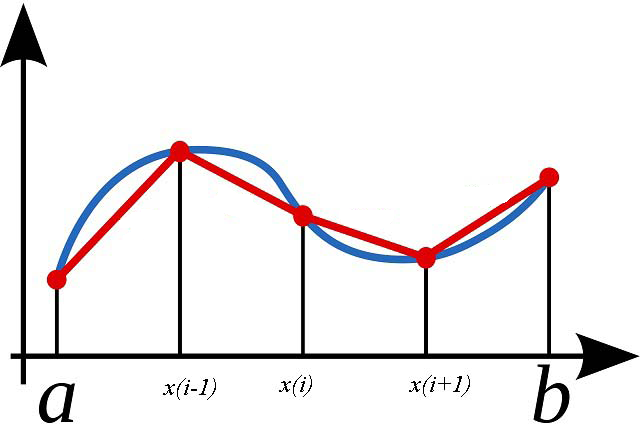
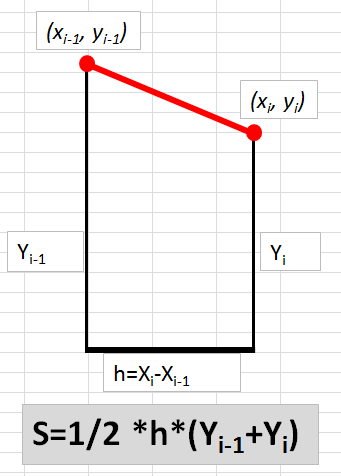
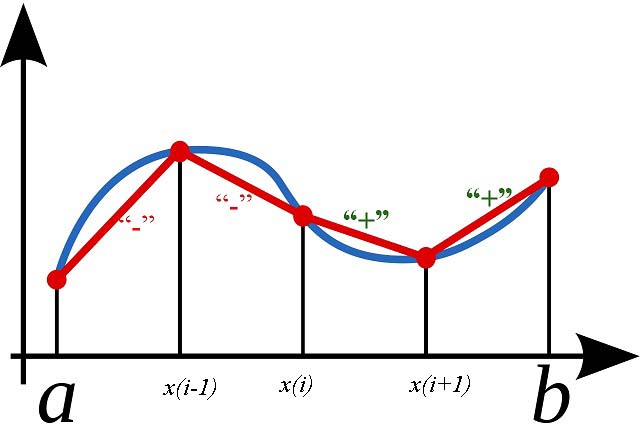
Фактически метод трапеций основан на линейной интерполяции, т.е. график функции y = f(x) представляется в виде ломаной, соединяющей точки (xi, yi) прямыми линиями.
Площадь каждой трапеции можно найти следующим образом (см. рисунок ниже).
Фактически задача по нахождению интеграла сводится в основном к построению таблицы значений функции y=f(x) для заданных Х и нахождению их суммы. Интеграл можно найти с помощью вот такой простой формулы:
Построение модели
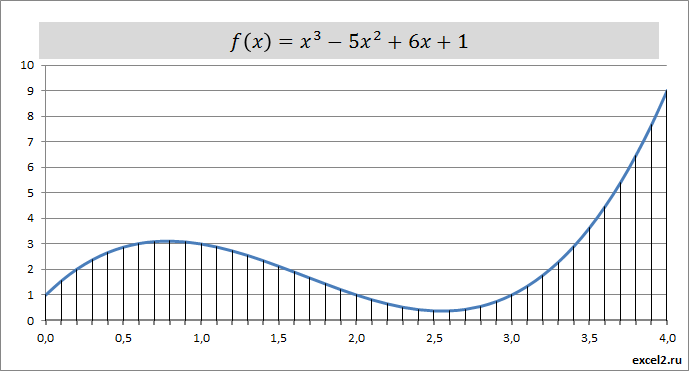
Для определенности вычислим интеграл для функции-многочлена f(𝑥)=𝑥3−5𝑥2+6𝑥+1. График этой функции в диапазоне от 0 до 4 выглядит следующим образом (см. файл примера).
Примечание: про тонкости построения графика функции можно прочитать в этой статье https://excel2.ru/articles/grafik-vs-tochechnaya-diagramma-v-ms-excel.
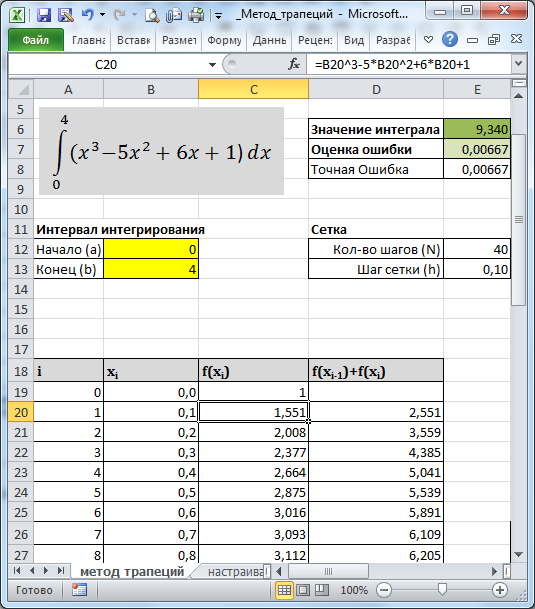
В файле примера построим таблицу значений функции для 41 точки (от 0 до 40), что составляет 40 интервалов.
Напомним, что Интеграл методом трапеций можно найти с помощью вот такой простой формулы:
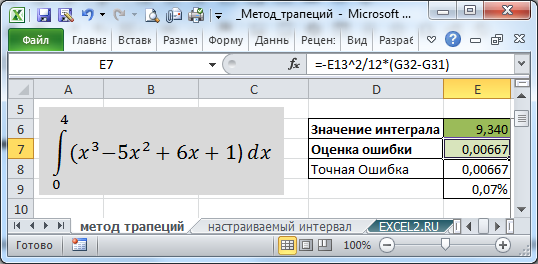
В MS EXCEL формула также будет очень простой =E13/2*СУММ(D20:D59).
Примечание: При вводе функции в столбец С нужно быть очень внимательным — ошибиться очень легко, т.к. формула будет выглядеть как месиво символов =B19^3-5*B19^2+6*B19+1.
Вычисленное приближенное значение интеграла для данной функции в интервале [0;4] равно 9,340, а точное 9,333, т.е. ошибка составляет менее 0,1%. Ниже показано как ее оценить.
В файле примера на листе «настраиваемый интервал» сделана форма для работы с разными количествами интервалов разбиения. При изменении количества интервалов график перестраивается автоматически, формулы для вычисления интеграла не нужно переписывать (как, впрочем, и расширять/ убавлять таблицу значений).
Ошибка вычисления
На рисунке ниже показано откуда появляется ошибка интегрирования. Для первых 2-х трапеций (образованы красными линиями) площадь меньше чем у истинной функции (синяя линия). Для следующих 2-х — площадь больше. Из этого следует, что метод трапеций хорошо работает для осциллирующих функций, когда ошибки компенсируют друг друга.
Простой многочлен был выбран в качестве демонстрационной функции, чтобы можно было вычислить интеграл точно и потом найти истинную ошибку, чтобы иметь возможность сравнить ее с оценкой.
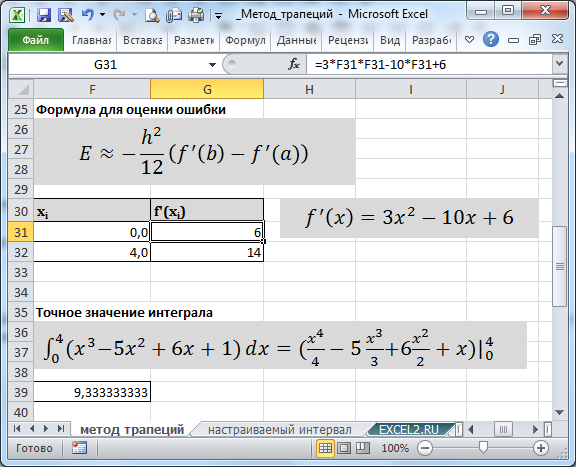
К сожалению, для нахождения оценки ошибки потребуется вычислить первую производную. Сделать это чаще всего не сложно, но автоматизировать это в EXCEL не получится. Поэтому при изменении подинтегральной функции приходится вносить изменения в несколько формул на листе, а точнее — в 2 ячейки С19 и G31 (в файле примера они выделены красным). После ввода формул их нужно скопировать вниз.
В наем случае полученная оценка ошибки совпала с истинной ошибкой, что говорит о том что мы не ошиблись при вычислении производной и вводе формул на лист.
Совет: всегда оценивайте ошибку интегрирования.
Реализация в Excel
Численные методы решения нелинейных уравнений
Постановка задачи
Дано уравнение F(x)=0. Это — общий вид нелинейного уравнения с одним неизвестным. Как правило, алгоритм нахождения корня состоит из двух этапов:
1.Отыскание приближенного значения корня или отрезка на оси абсцисс, его содержащего.
2.Уточнение приближенного значения корня до некоторой точности.
На первом этапе применяется шаговый метод отделения корней, на втором — один из методов уточнения (метод половинного деления, метод Ньютона, метод Хорд или метод простой итерации).
Шаговый метод
В качестве примера рассмотрим уравнение x2 — 11x + 30 = 0. Интервал поиска [3,5.4], шаг h = 0,3. Решим его, используя специальные возможности пакета Excel. Последовательность действий (см. рис. 1):
1.Оформить заголовок в строке 1 «Численные методы решения нелинейных уравнений».
2.Оформить заголовок в строке 3 «Шаговый метод».
3.В ячейки A6 и C6 и B6 записать данные по задаче.
4.В ячейки B9 и C9 записать заголовки рядов — соответственно x и F(x).
5.В ячейки B10 и B11 ввести первые два значения аргумента — 3 и 3.3.
6.Выделить ячейки B5-B6 и протащить ряд данных до конечного значения (3,3), убедившись в правильном выстраивании арифметической прогрессии.
7.В ячейку C10 ввести формулу «=B10*B10-11*B10+30».
8.Скопировать формулу на остальные элементы ряда, используя прием протаскивания. В интервале C10:C18 получен ряд результатов вычисления функции F(x). Видно, что функция один раз меняет знак. Корень уравнения расположен в интервале [4.8,5.1].
9.Для построения графика зависимости F(x) используем Вставка — Диаграмма (тип «Точечная», маркеры соединяются гладкими кривыми).
Метод деления отрезка пополам
В качестве примера рассмотрим уравнение x2 — 11x + 30 = 0. Интервал поиска [3,5.4], с точностью ε=0.01. Решим его, используя специальные возможности пакета Excel.
1. Ввести в ячейку B21 заголовок «Метод деления отрезков пополам».
2. Ввести в ячейку A23, C23, E23 данные по задачи.
3.В области B25:H25 оформить заголовок таблицы (ряд B — левая граница отрезка «a», ряд C — середина отрезка «x», ряд D — правая граница отрезка «b», ряд E — значение функции на левой границе отрезка «F(a)», ряд F — значение функции на середине отрезка «F(x)», ряд G — произведение «F(a)*F(x)», ряд H — проверка достижения точности «êF(x)ê<е».
4.Ввести первоначальные значения концов отрезка: в ячейку B26 «4.8», в ячейку D26 «5.1».
5.Ввести в ячейку C26 формулу «=(B26+D26)/2».
6.Ввести в ячейку E26 формулу «=B26*B26-11*B26+30».
7.Ввести в ячейку F26 формулу «=C26*C26-11*C26+30».
8.Ввести в ячейку G26 формулу «=E26*F26».
9.Ввести в ячейку H26 формулу «=ЕСЛИ(ABS(F26)<0.01;²корень²)».
1 0. Выделить область B21:H21 и протащить ее по вертикали вплоть до появления в ряду H сообщения «корень» (ячейка H29, H30).
Метод касательных (Ньютона)
В качестве примера рассмотрим уравнение x3 +2x2+3x+5= 0. Точность ε=0.01. Решим его, используя специальные возможности пакета Excel.
1. Ввести в ячейку J23 заголовок «Метод касательной (Ньютона)».
2.Ввести в ячейку L23 текст «е=», а в ячейку M23 значение точности «0.00001».
3.В области K25:N25 оформить заголовок таблицы (ряд K — значение аргумента «x», ряд L — значение функции «F(x)», ряд M — производная функции «F¢(x)», ряд N — проверка достижения точности «êF(x)ê<е».
4.В ячейку K26 ввести первоначальное значение аргумента «-2».
5.Ввести в ячейку L26 формулу «=K26*K26*K26+2*K26*K26+3*K26+5».
6.Ввести в ячейку M26 формулу «=3*K26*K26+4*K26+3».
7.Ввести в ячейку N26 формулу «=ЕСЛИ(ABS(L26)<$M$23;»корень»)».
8.Ввести в ячейку K27 формулу «=K26-L26/M26».
9.Выделить область L27:N27 и протащить ее по вертикали вплоть до появления в ряду N сообщения «корень» (ячейка N30).
Метод хорд
В качестве примера рассмотрим уравнение x3 +2x2+3x+5= 0. Точность ε=0.01. Решим его, используя специальные возможности пакета Excel.
1. Ввести в ячейку B32 заголовок «Метод хорд».
2. Ввести в ячейку C34 текст «е=», а в ячейку E34 значение точности «0.00001».
3.В области B36:D36 оформить заголовок таблицы (ряд B — значение аргумента «x», ряд C — значение функции «F(x)», ряд D — проверка достижения точности «êF(x)ê<е».
4.В ячейку B37 и B38 ввести первоначальное значение аргумента «-2» и . «-1»
5.Ввести в ячейку С37 формулу «=B37*B37*B37+2*B37*B37+3*B37+5».
6.Ввести в ячейку D37 формулу «=ЕСЛИ(ABS(B38-B37)<$D$34;»корень»)».
7.Ввести в ячейку B39 формулу «=B38-C38*(B38-B37)/(C38-C37)».
8.Выделить область C39:D39 и протащить ее по вертикали вплоть до появления в ряду D сообщения «корень» (ячейка D43).
Метод простой итерации
В качестве примера рассмотрим уравнение x2 — 11x + 30 = 0. Интервал поиска [4.8,5.1], с точностью e=0,05.
1. Ввести в ячейку K32 заголовок «Метод простой итерации»
2.Ввести в ячейку N34 текст «е=», а в ячейку O34 значение точности «0,05».
3.Выбрать функцию j(x), удовлетворяющую условию сходимости. В нашем случае такой функцией является функция S(x)=(x*x+30)/11.
4.В области K38:N38 оформить заголовок таблицы (ряд K — значение аргумента «x», ряд L — значение функции «F(x)», ряд M — значение вспомогательной функции «S(x)», ряд N — проверка достижения точности «êF(x)ê<е».
5.В ячейку K39 ввести первоначальное значение аргумента «4.8».
6.Ввести в ячейку L39 формулу «=K39*K39-11*K39+30».
7.Ввести в ячейку M39 формулу «=(K39*K39+30)/11».
8.Ввести в ячейку N39 формулу «=ЕСЛИ(ABS(L39)<$O$34;»корень»)».
9.Ввести в ячейку K40 формулу «=M39».
1 0. Скопировать ячейки L39:N39 в ячейки L40:N40.
1 1 . Выделить область L40:N40 и протащить ее по вертикали вплоть до появления в ряду N сообщения «корень» (ячейка N53).
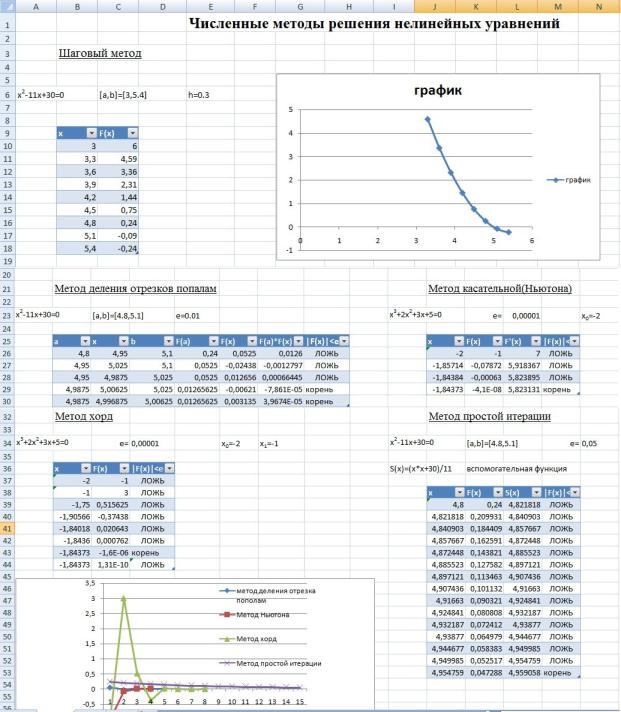
Рис.1 Решение нелинейных уравнений в среде Excel