По теме: методические разработки, презентации и конспекты
Лабораторный практикум по численным методам
Настоящий лабораторный практикум подготовлен по дисциплине «Численные методы». Целью лабораторного практикума является усвоение и закрепление теоретического материала, приобретение практических навы…
Лекция «Численные методы решения уравнений»
Лекция по разделу «Численные методы».Рассматриваются следующие методы решения алгебраических и трансцендентных уравнений: 1) метод дихотомии (метод деления отрезка пополам),2) метод хор…
Отрывок: На практике
к циклическим ссылкам прибегают, когда речь идет о реализации итерацион
ного процесса, вычислениях по рекуррентным соотношениям. В обычном
режиме Excel обнаруживает цикл и выдает сообщение о возникшей ситуации
(рисунок 2.5), требуя ее устранения. E…
| Название : | Численные методы в табличном редакторе MS Excel |
| Авторы/Редакторы : | Шляпугин А. Г. Осиновская И. В. Министерство образования и науки России Самарский государственный аэрокосмический университет им. С. П. Королева (национальный исследовательский университет) |
| Дата публикации : | 2012 |
| Библиографическое описание : | Численные методы в табличном редакторе MS Excel [Электронный ресурс] : электрон. метод. указания к лаб. работам / Минобрнауки России, Самар. гос. аэрокосм. ун-т им. С. П. Королева (нац. исслед. ун-т) ; [авт.-сост. Я. А. Ерисов, А. Г. Шляпугин, И. В. Осиновская]. — Самара, 2012. — on-line |
| Аннотация : | Ресурс закрыт даже для компьютерной сети университета Используемые программы: Adobe Acrobat. В методических указаниях к лабораторным работам приведены основные приемы работы в табличном редакторе MS Excel, численные методы вычисления определенных интегралов, заданных аналитическим выражением и таблицей значений; численные методы решения обыкновен Труды сотрудников СГАУ(электрон. версия). |
| Другие идентификаторы : | RU/НТБ СГАУ/WALL/519/Ч-671-715822 |
| Ключевые слова: | численные методы |
| Располагается в коллекциях: | Методические издания |
Все ресурсы в архиве электронных ресурсов защищены авторским правом, все права сохранены.
Информатика-2
(численные методы)
П
ермский
национальный исследовательский
политехнический университет
Строительный
факультет
Кафедра
строительной механики и вычислительных
технологий
Методические
указания и задания для лабораторных
работ
по
дисциплине
ИНФОРМАТИКА-2
для
студентов 1-го курса строительных
специальностей
бакалавр
Пермь 2012
План
УМД 20092010 уч.г.
Методические
указания и задания для лабораторных
работ
по
дисциплине
ИНФОРМАТИКА
2
Часть 2. Численные методы
Составители: Пермякова Т.Б.,
к.т.н., доцент;
Лаищева
М.Е., ст.преподаватель
Приведены
задания и рекомендации для выполнения
лабораторных работ по дисциплине
«Информатика-2», предназначенных
для студентов строительного факультета
бакалавры.
Рецензент: Г.Г.Кашеварова
д.т.н., профессор
Издание стереотипное.
Утверждено на заседании
кафедры СМиВТ
от 26.12.08.
В
ведение.
Методические
указания созданы на основе лекционного
материала и комплекса лабораторных
работ, предназначенных для студентов
первого курса строительного факультета
(бакалавры).
Темами
лабораторных работ являются численные
методы решения отдельных математических
задач, используемых в строительстве, а
Excel
служит лишь инструментом для реализации
этих методов.
Методические
указания содержат задания для лабораторных
работ, рекомендации для их выполнения,
контрольные вопросы и
отдельные
сведения об электронных таблицах Excel,.
Предполагается, что студенты владеют основными навыками работы с приложением Microsoft Excel в пределах учебного курса «Информатика-1». Литература.
-
Кашеварова
Г.Г., Пермякова Т.Б. Численные методы
решения задач строительсьва на ЭВМ.
Учебное пособие. Пермь, 2007.-351с. -
Вержбицкий
В.М. Численные методы. Линейная алгебра
и нелинейные уравнения. М. «Высшая
школа». 2000.-266с. -
Вержбицкий
В.М. Численные методы. Математический
анализ и обыкновенные дифференциальные
уравнения. М. «Высшая школа». 2001.-382с. -
Попов
А. EXCEL.
Практическое руководство. М:. 2002.
ДЕССКОМ.-301с.
Требования по оформлению пояснительной записки к отчету по лабораторным работам
Каждый
студент выполняет лабораторную
работу в
соответствии с индивидуальным заданием,
определяемым преподавателем.
Для
получения зачета по
каждой лабораторной работе
студенту необходимо подготовить отчет
в текстовом редакторе Microsoft
Word
и защитить его.
Отчет должен быть представлена на
бумажном (пояснительная записка) и
электронном (дискета) носителях.
Расчеты
должны быть выполнены с использованием
приложения Microsoft
Excel. Таблицы
и графики с расчетами из Книги
Excel можно
оформить в виде отдельных приложений
или вставить в текст записки.
Математические
формулы записываются с помощью редактора
формул Microsoft Equation.
Объем
отчета не должен превышать 3-4-х страниц
текста, включая титульный лист (Приложение
7).
Формат страницы — А4 с полями: слева –
25мм., сверху и снизу по 20мм., справа –
10мм. Шрифт: размер -12, тип – Times
New
Roman.
Верхний
колонтитул содержит: фамилию и имя
студента, код учебной группы. Страницы
должны быть пронумерованы.
Содержание отчета:
-
Тема
лабораторной работы, полный текст
задания, в соответствии с вариантом. -
Математическая
постановка задачи. -
Краткое
изложение используемых численных
методов. -
Результаты
счета на ЭВМ, включая, контрольный
пример. -
Исследовательская
часть работы. Анализ полученных
результатов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лабораторная работа
- 35 страниц
Лабораторная работа № 1 4
Лабораторная работа № 2 10
Лабораторная работа № 3 15
Лабораторная работа № 4 19
Лабораторная работа № 5 23
Лабораторная работа № 6 28
Лабораторная работа № 7 31
Лабораторная работа № 8 33
Лабораторная работа № 1
(Решение нелинейных уравнений. Метод половинного деления.)
Постановка задачи. Найти корень нелинейного уравнения методом итерации с точностью .
Решение задачи. Отделим корень уравнения на отрезке [2; 3] графическим методом. Для этого табулируем функцию на данном отрезке построим график.
Выделим отрезок [2; 3] , содержащий изолированный корень, для уточнения которого применим метод половинного деления по схеме , , , где , . Полагая , , а так же условие остановки деления отрезка пополам , составим таблицу
корень погрешность Усл.ост.
2 3 2,5 -14,18594854 6,1776 -5,71944 — 0,5 нет
2,5 3 2,75 -5,719442882 6,1776 -0,07072 — 0,25 нет
2,75 3 2,875 -0,070719841 6,1776 2,996705 — 0,125 нет
2,75 2,875 2,8125 -0,070719841 2,996705 1,446466 — 0,0625 нет
2,75 2,8125 2,78125 -0,070719841 1,446466 0,683454 — 0,03125 нет
2,75 2,78125 2,765625 -0,070719841 0,683454 0,305226 — 0,015625 нет
2,75 2,765625 2,757813 -0,070719841 0,305226 0,116964 — 0,0078125 нет
2,75 2,757813 2,753906 -0,070719841 0,116964 0,023049 — 0,00390625 нет
2,75 2,753906 2,751953 -0,070719841 0,023049 -0,02385 — 0,001953125 нет
2,751953 2,753906 2,75293 -0,023853741 0,023049 -0,00041 — 0,000976563 нет
2,75293 2,753906 2,753418 -0,000406954 0,023049 0,01132 — 0,000488281 нет
2,75293 2,753418 2,753174 -0,000406954 0,01132 0,005456 — 0,000244141 нет
2,75293 2,753174 2,753052 -0,000406954 0,005456 0,002525 — 0,00012207 нет
2,75293 2,753052 2,752991 -0,000406954 0,002525 0,001059 2,752991 0,000061035 да
Приближенное решение 2,752991, погрешность 0,000061035, число итераций .
0,000061035 Округлим 2,753 0,000009+0,000061035=0,00007.
Ответ: 2,753 0,00007
14
корень погрешность Усл.ост.
-1 2 0,5 17,82942 -14,1859 -9,33851 — 1,5 нет
-1 0,5 -0,25 17,82942 -9,33851 5,010579 — 0,75 нет
-0,25 0,5 0,125 5,010579 -9,33851 -2,47787 — 0,375 нет
-0,25 0,125 -0,0625 5,010579 -2,47787 1,253093 — 0,1875 нет
-0,0625 0,125 0,03125 1,253093 -2,47787 -0,62392 — 0,09375 нет
-0,0625 0,03125 -0,01563 1,253093 -0,62392 0,312731 — 0,046875 нет
-0,01563 0,03125 0,007813 0,312731 -0,62392 -0,15619 — 0,0234375 нет
-0,01563 0,007813 -0,00391 0,312731 -0,15619 0,07814 — 0,01171875 нет
-0,00391 0,007813 0,001953 0,07814 -0,15619 -0,03906 — 0,005859375 нет
-0,00391 0,001953 -0,00098 0,07814 -0,03906 0,019532 — 0,002929688 нет
-0,00098 0,001953 0,000488 0,019532 -0,03906 -0,00977 — 0,001464844 нет
-0,00098 0,000488 -0,00024 0,019532 -0,00977 0,004883 — 0,000732422 нет
-0,00024 0,000488 0,000122 0,004883 -0,00977 -0,00244 — 0,000366211 нет
-0,00024 0,000122 -6,1E-05 0,004883 -0,00244 0,001221 — 0,00018311 нет
-6,1E-05 0,000122 3,05E-05 0,001221 -0,00244 -0,00061 0,00003052 0,00009155 да
Приближенное решение 0,00003052, погрешность 0,000061035, число итераций 15
0,00009155 Округлим 0,00003 0,0000006.
Ответ: 0,00003 0,0000006 15
Лабораторная работа № 2
(Решение нелинейных уравнений. Метод итерации.)
Постановка задачи. Найти корень нелинейного уравнения методом итерации с точностью .
Решение задачи. Отделим корень уравнения на отрезке [2; 3] графическим методом. Для этого табулируем функцию на данном отрезке и построим график.
0,0001,
-4,
4,
Выделим отрезок [2; 3] , где находится корень, и уточним его методом итерации.
Получим равносильное уравнению уравнение .
Тогда получим следующее значение условие остановки итерационной последовательности , при выборе приближенного решения с погрешностью приближенного решения .
Результаты в таблицу получим
a= 2
b= 3
X Условие остановки
итерации
2 -1 1 нет
2,04167 -0,61448 0,04167 нет
2,067275 -0,36706 0,025605353 нет
2,082571 -0,21539 0,015295453 нет
2,091546 -0,12503 0,008975391 нет
2,096756 -0,07212 0,005210116 нет
2,099761 -0,04144 0,003005102 нет
2,101488 -0,02376 0,00172682 нет
2,102478 -0,01361 0,000990138 да
Приближенное решение 2,102478, погрешность 0,00061035, число итераций 9
0,00061035 Округлим 2,102 0,00009+0,00061035=0,0007.
Ответ: 2,102 0,0007
9
Лабораторная работа № 3
Тема: Решение нелинейных уравнений. Метод хорд.
Задание: 1) Отделить корни уравнения графически и программно.
2) Уточнить корни уравнения методом хорд с точностью .
3) Нарисовать схему применения метода к каждому корню уравнения.
7
Решение задачи. Отделим корень уравнения на отрезке [-2; 1] графическим методом. Для этого табулируем функцию f(x)= на данном отрезке построим график.
Для формализации модели используем математические формулы.
уравнение прямой, проходящей через две точки, где x1 = a, x2 = в, y1 = f(a), y2 = f(в).
После математических преобразований уравнение примет вид .
Определим корень уравнения
fb x fx abs(x1-x2) проверка условия
1,2 -1,338028 -3,001132 0,071759 —
1,2 -1,409787 -2,962267 0,000000 -1,410
1,2 -1,409787 -2,962267 0,000000 -1,410
1,2 -1,409787 -2,962267 0,000000 -1,410
1,2 -1,409787 -2,962267 0,000000 -1,410
1,2 -1,409787 -2,962267 1,409787 —
Ответ: -1,409787
Лабораторная работа № 4
Тема: Решение нелинейных уравнений. Метод касательных (Ньютона).
Задание: 1) Отделить корни уравнения графически и программно.
2) Уточнить корни уравнения методом касательных с точностью .
3) Нарисовать схему применения метода к каждому корню уравнения.
7
Найдем корни уравнения:
Используем для этого Метод Ньютона.
Пусть корень ξ уравнения f(x)=0 отделен на отрезке [a,b]. Предположим мы нашли (n-1)-ое приближение корня xn-1. Тогда n-ое приближение xn мы можем получить следующим образом. Положим:
xn = xn-1 + hn-1
Раскладывая в ряд f(x=ξ) в точке xn-1, получим:
f(xn) = f(xn-1+hn-1) = f(xn-1) + f’(xn-1)hn-1=0
Отсюда следует:
hn-1 = -f(xn-1)df/dx(xn-1)
Подставим hn-1 в формулу, получим:
xn = xn-1 -f(xn-1)df/dx(xn-1)
Геометрически метод Ньютона эквивалентен замене дуги кривой y=f(x) касательной, проведенной в некоторой точке кривой.
Находим первую производную:
dF/dx = 3×2+4x-2e2x-1
Находим вторую производную:
d2F/dx2 = 6x+4-4e2x-1
Возьмем промежуток содержащий корень [-3; -2]
Решение нелинейного уравнения методом Ньютона в Excel
a -3 -3 -3
b -2 -2 -2
F(a) dF(a) dF2(a)
-9,00091 14,99818 -14,0036
F(b) dF(b) dF2(b)
-0,00674 3,986524 -14,027
x0 -3
x1 -2
N X F(X) dF(X) h = F(X) / F'(X)
1 -3 -9,00091 14,99818 -0,600133759
2 -2,39987 -2,306 7,672552 -0,300552035
3 -2,09931 -0,44321 4,813055 -0,092085743
4 -2,00723 -0,03576 4,044702 -0,008842301
5 -1,99839 -0,00031 3,973578 -7,92218E-05
6 -1,99831 -2,5E-08 3,972943 -6,33242E-09
7 -1,99831 -1,3E-16 3,972942 -3,1656E-17
8 -1,99831 -1,3E-16 3,972942 -3,1656E-17
9 -1,99831 -1,3E-16 3,972942 -3,1656E-17
10 -1,99831 -1,3E-16 3,972942 -3,1656E-17
Возьмем промежуток содержащий корень [-1; 0]
Решение нелинейного уравнения методом Ньютона в Excel
a -1 -1 -1
b 0 0 0
F(a) dF(a) dF2(a)
0,950213 -1,09957 -2,19915
F(b) dF(b) dF2(b)
-0,36788 -0,73576 -1,47152
x0 0
x1 -1
N X F(X) dF(X) h = F(X) / F'(X)
1 0 0,950213 -1,09957 -0,86416
2 0,864164 0,067286 1,553767 0,043305
3 0,82086 0,000981 1,505382 0,000652
4 0,820208 2,82E-07 1,504516 1,87E-07
5 0,820208 2,33E-14 1,504516 1,55E-14
6 0,820208 0 1,504516 0
7 0,820208 0 1,504516 0
8 0,820208 0 1,504516 0
9 0,820208 0 1,504516 0
10 0,820208 0 1,504516 0
Возьмем промежуток содержащий корень [0; 1]
Решение нелинейного уравнения методом Ньютона в Excel
a 0 0 0
b 1 1 1
F(a) dF(a) dF2(a)
-0,36788 -0,73576 2,528482
F(b) dF(b) dF2(b)
0,281718 1,563436 -3,87313
x0 1
x1 0
N X F(X) dF(X) h = F(X) /F'(X)
1 1 -0,36788 -0,73576 0,5
2 0,5 -0,375 0,75 -0,5
3 1 0,281718 1,563436 0,180192
4 0,819808 -0,0006 1,503982 -0,0004
5 0,820208 1,07E-07 1,504516 7,09E-08
6 0,820208 3,33E-15 1,504516 2,21E-15
7 0,820208 0 1,504516 0
8 0,820208 0 1,504516 0
9 0,820208 0 1,504516 0
10 0,820208 0 1,504516 0
Возьмем промежуток содержащий корень [1; 2]
Решение нелинейного уравнения методом Ньютона в Excel
a 1 1 1
b 2 2 2
F(a) dF(a) dF2(a)
0,281718 1,563436 -0,87313
F(b) dF(b) dF2(b)
-4,08554 -20,1711 -66,3421
x0 2
x1 1
N X F(X) dF(X) h = F(X) / F'(X)
1 2 0,281718 1,563436 0,180192
2 1,819808 -1,35776 -10,8013 0,125704
3 1,694105 -0,29192 -6,40155 0,045602
4 1,648503 -0,02933 -5,14202 0,005704
5 1,642799 -0,00042 -4,99556 8,38E-05
6 1,642715 -9E-08 -4,99343 1,79E-08
7 1,642715 0 -4,99343 0
8 1,642715 0 -4,99343 0
9 1,642715 0 -4,99343 0
10 1,642715 0 -4,99343 0
Ответ:
корень ξ1=-1,99831 3,1656*10-17
корень ξ2=0,820208 1,55*10-14
корень ξ3=0,820208 2,21*10-15
корень ξ4=1,642715 1,79*10-8
Лабораторная работа № 5
Тема: Решение нелинейных уравнений.
Комбинированный метод хорд и касательных.
Задание: 1) Отделить корни уравнения графически и программно.
2) Уточнить корни уравнения данным методом с точностью .
3) Нарисовать схему применения метода к каждому корню уравнения.
7
Комбинированный метод: хорд и касательных.
f(X) = x3-5×2+x-3.2
fI(X) = 3×2-10x+1
f(4,5) < 0
f(5) >0
X* Є [4,5;5]
Хорд Косательных ε
Xo = 1,5 Xo = 2
n Xn n Xn
0 4,5 0 5
1 4,915294 1 4,930769 0,015475
2 4,928825 2 4,928837 1,19E-05
3 4,928835 3 4,928835 7,07E-12
X* = 4,928835
Ответ:
корень X1=-4,928835 7,07*10-12
Лабораторная работа № 6
Тема: Решение системы линейных уравнений методом итерации и методом Зейделя.
Задание:
1) Решить систему линейных уравнений методом итерации и методом Зейделя с точностью ;
2) Найти погрешности полученных приближенных решений;
3) Сравнить полученные приближенные решения и их погрешности.
7
Сделаем проверку. Подставим полученное решение в уравнения из системы и выполним вычисления:
2•1 — 5•1 + 2•0.5 = 2 — 5 + 1 = -2
1 + 1 — 4•0.5 = 1 + 1 — 2 = 0
-7•1 + 3•1 + 2•0.5 = -7 + 3 + 1 = -3
Проверка выполнена успешно.
x1 = 1
x2 = 1
x3 = 0.5
Решение.
Точное решение:
x1 = 1
x2 = 1
x3 = 0.5
Приведем данную систему к виду , где
Реализуем итерации.
x1 x2 x3 B
1 0 -1,4 0,3
-0,55556 1 0 0,444444
0 -0,7 1 -0,2
N x1 x2 x3 e1 e2 e3
1 0 0 0 0 0 0
2 0,3 0,444444 -0,2 0,3 0,444444 0,2
3 0,02 0,611111 0,111111 -0,28 0,166667 -0,08889
4 0,455556 0,455556 0,227778 0,435556 -0,15556 0,116667
5 0,618889 0,697531 0,118889 0,163333 0,241975 -0,10889
6 0,466444 0,788272 0,288272 -0,15244 0,090741 0,169383
7 0,70358 0,70358 0,35179 0,237136 -0,08469 0,063519
8 0,792506 0,835322 0,292506 0,088926 0,131742 -0,05928
9 0,709509 0,884726 0,384726 -0,083 0,049403 0,092219
10 0,838616 0,838616 0,419308 0,129107 -0,04611 0,034582
11 0,887031 0,910342 0,387031 0,048415 0,071726 -0,03228
12 0,841844 0,93724 0,43724 -0,04519 0,026897 0,050208
13 0,912135 0,912135 0,456068 0,070292 -0,0251 0,018828
14 0,938495 0,951186 0,438495 0,026359 0,039051 -0,01757
15 0,913893 0,96583 0,46583 -0,0246 0,014644 0,027336
16 0,952163 0,952163 0,476081 0,03827 -0,01367 0,010251
17 0,966514 0,973424 0,466514 0,014351 0,021261 -0,00957
18 0,953119 0,981397 0,481397 -0,01339 0,007973 0,014883
19 0,973955 0,973955 0,486978 0,020836 -0,00744 0,005581
20 0,981769 0,985531 0,481769 0,007813 0,011575 -0,00521
21 0,974476 0,989871 0,489871 -0,00729 0,004341 0,008103
22 0,98582 0,98582 0,49291 0,011344 -0,00405 0,003039
23 0,990074 0,992122 0,490074 0,004254 0,006302 -0,00284
24 0,986104 0,994486 0,494486 -0,00397 0,002363 0,004412
25 0,99228 0,99228 0,49614 0,006176 -0,00221 0,001654
26 0,994596 0,995711 0,494596 0,002316 0,003431 -0,00154
27 0,992434 0,996998 0,496998 -0,00216 0,001287 0,002402
28 0,995797 0,995797 0,497898 0,003363 -0,0012 0,000901
29 0,997058 0,997665 0,497058 0,001261 0,001868 -0,00084
30 0,995881 0,998365 0,498365 -0,00118 0,000701 0,001308
31 0,997712 0,997712 0,498856 0,001831 -0,00065 0,00049
32 0,998398 0,998729 0,498398 0,000687 0,001017 -0,00046
33 0,997757 0,99911 0,49911 -0,00064 0,000381 0,000712
34 0,998754 0,998754 0,499377 0,000997 -0,00036 0,000267
35 0,999128 0,999308 0,499128 0,000374 0,000554 -0,00025
36 0,998779 0,999515 0,499515 -0,00035 0,000208 0,000388
0,998779
0,999515
0,499515
Решение СЛАУ методом Зейделя
x1 x2 x3 B
-10 0 14 -3
5 -9 0 -4
0 -7 10 -2
N x1 x2 x3 e1 e2 e3
1 0 0 0 0 0 0
2 0,3 0,611111 0,227778 0,3 0,611111 0,227778
3 0,618889 0,788272 0,35179 0,318889 0,17716 0,124012
4 0,792506 0,884726 0,419308 0,173617 0,096454 0,067518
5 0,887031 0,93724 0,456068 0,094525 0,052514 0,03676
6 0,938495 0,96583 0,476081 0,051464 0,028591 0,020014
7 0,966514 0,981397 0,486978 0,028019 0,015566 0,010896
8 0,981769 0,989871 0,49291 0,015255 0,008475 0,005932
9 0,990074 0,994486 0,49614 0,008305 0,004614 0,00323
10 0,994596 0,996998 0,497898 0,004522 0,002512 0,001758
11 0,997058 0,998365 0,498856 0,002462 0,001368 0,000957
12 0,998398 0,99911 0,499377 0,00134 0,000745 0,000521
13 0,999128 0,999515 0,499661 0,00073 0,000405 0,000284
14 0,999525 0,999736 0,499815 0,000397 0,000221 0,000155
Запишем приближенное значение корня только верными значащими цифрами в узком смысле.
0,998779
0,999515
0,499515
Найдем число верных знаков
Лабораторная работа № 7
Тема: Интерполирование функции. Полином Лагранжа.
Задание:
1) Найти приближенное значение функции при заданном значении аргумента с помощью интерполяционного полинома Лагранжа, если функция задана в не равноотстоящих узлах; , ;
2) Оценить погрешность полученного значения.
x y
1.0000 0,9689
1.1000 1,0587
1.2320 1,1740
1.4796 1,3796
1.9383 1,7152
1.9577 1,7279
2.0380 1,7791
Решение.
Составляем расчетную таблицу
x 1,0000 1,1000 1,2320 1,4796 1,9383 1,9577 2,0380
y 0,9689 1,0587 1,174 1,3796 1,7152 1,7279 1,7791 ξ = 1,3000
ξ — хi 0,3000 0,2000 0,0680 -0,1796 -0,6383 -0,6577 -0,7380
xk — хi
1,0000 1,1000 1,2320 1,4796 1,9383 1,9577 2,0380
1,0000 1 0,1000 0,2320 0,4796 0,9383 0,9577 1,0380
1,1000 -0,1000 1 0,1320 0,3796 0,8383 0,8577 0,9380
1,2320 -0,2320 -0,1320 1 0,2476 0,7063 0,7257 0,8060
1,4796 -0,4796 -0,3796 -0,2476 1 0,4587 0,4781 0,5584
1,9383 -0,9383 -0,8383 -0,7063 -0,4587 1 0,0194 0,0997
1,9577 -0,9577 -0,8577 -0,7257 -0,4781 -0,0194 1 0,0803
2,0380 -1,0380 -0,9380 -0,8060 -0,5584 -0,0997 -0,0803 1
Pik=(ξ — хi)/(xk-xi) ПРik yiПРik
1,0000 1,0000 2,0000 0,2931 -0,3745 -0,6803 -0,6867 -0,7110 0,0729 0,0706
1,1000 -3,0000 1,0000 0,5152 -0,4731 -0,7614 -0,7668 -0,7868 -0,3359 -0,3556
1,2320 -1,2931 -1,5152 1,0000 -0,7254 -0,9037 -0,9063 -0,9156 1,0658 1,2512
1,4796 -0,6255 -0,5269 -0,2746 1,0000 -1,3915 -1,3757 -1,3216 0,2290 0,3159
1,9383 -0,3197 -0,2386 -0,0963 0,3915 1,0000 -33,902 -7,4022 -0,7216 -1,2377
1,9577 -0,3133 -0,2332 -0,0937 0,3757 32,9021 1,0000 -9,1905 0,7775 1,3434
2,0380 -0,2890 -0,2132 -0,0844 0,3216 6,4022 8,1905 1,0000 -0,0877 -0,1560
1,231915
1,231915
Оценим погрешность приближения с помощью выражения
Составляем расчетную таблицу.
y Δ1y Δ2y Δ3y Δ4y Δ5y Δ6y
0,9689 0,0898 0,0255 0,0648 -0,0251 -0,4675 1,7744
1,0587 0,1153 0,0903 0,0397 -0,4926 1,3069
1,174 0,2056 0,13 -0,4529 0,8143
1,3796 0,3356 -0,3229 0,3614
1,7152 0,0127 0,0385
1,7279 0,0512
1,7791
0,000227
(n+1)! 720
R = 0,0000006
Получаем решение:
1,231915
R =0,0000006
Запишем приближенное значение корня только верными значащими цифрами в узком смысле.
Округлим 1,231915 до
Получаем решение
1,231915 0,0000006
Лабораторная работа № 8
Задание:
1) Найти приближенное значение функции при заданном значении аргумента с помощью соответствующего интерполяционного полинома Ньютона, если функция задана в равноотстоящих узлах;
2) Оценить погрешность полученного значения.
x 1,0000 1,1500 1,3000 1,4500 1,6000 1,7500 1,9000
y 0,6664 0,4329 0,2406 0,0903 -0,0178 -0,0861 -0,1185
ξ = 1,5200
Решение.
Из расположения заданных точек на графике можно заключить, что искомая функция скорее всего монотонна на рассматриваемом отрезке, поэтому обратная задача имеет единственное решение.
Решим данную задачу, используя первую интерполяционную формулу Ньютона:
Таблица конечных разностей для интерполирования по формулам Ньютона
Табличные значения Конечные разности
x y Δy1 Δy2 Δy3 Δy4 Δy5 Δy6
1,00000 0,66640 -0,23350 0,04120 0,00080 -0,00060 -0,00200 0,00310
1,15000 0,43290 -0,19230 0,04200 0,00020 -0,00260 0,00110
1,30000 0,24060 -0,15030 0,04220 -0,00240 -0,00150
1,45000 0,09030 -0,10810 0,03980 -0,00390
1,60000 -0,01780 -0,06830 0,03590
1,75000 -0,08610 -0,03240
1,90000 -0,11850
Расчетная таблица.
h 1,4700 П(x-xi) n n! Δy П(h)
0,150 0,47 0,47 1 1 -0,23350 0,150000 -0,731633
0,150 0,32 0,1504 2 2 0,04120 0,022500 0,137700
0,150 0,17 0,025568 3 6 0,00080 0,003375 0,001010
0,150 0,02 0,0005114 4 24 -0,00060 0,000506 -0,000025
0,150 -0,13 -0,000066 5 120 -0,00200 0,000076 0,000015
0,150 -0,28 0,000019 6 720 0,00310 0,000011 0,000007
-0,592927 0,073473
0,073473
0,0000000017=1,7*10-9
1. Демидович Б.Н., Марон И.А. Основы вычислительной математики. -М.: Наука, 1966.- 664 с.
2. Бахвалов Н.С. Численные методы -М.: Наука, 1975. – 632 с.
3. Березин Н.С., Жидков Н.П. Методы вычислений. – Т.1. — М.: Наука, 1966. – 464 с.
4. Березин Н.С., Жидков Н.П. Методы вычислений. – Т.2. — М.: Физматгиз, 1962.- 640 с.
5. Самарский А.А. Теория разностных схем. — М.: Наука, 1983.
6. Иванов В.В. Методы вычислений на ЭВМ. Киев: Наукова думка, 1986.
7. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. -М.: Наука, 1986, — 288 с.
8. Сборник Задач по методам вычислений: Учебное пособие: Для вузов. / Под ред. П.И. Монастырского. — 2-е изд. перераб. и доп. -М.: Физматлит, 1994. -320 с.
9. Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике. -М.: Высшая школа, 1990.
10. Лапчик М.П. Рагулина М.И., Хеннер Е.К. Численные методы: Уч. Пособие для ст. вузов. –М.: Изд. Центр «Академия», 2004. – 384 с.
11. Васильев Ф.П. Численные методы решения экстремальных задач: Учебное пособие для вузов — 2-е изд., перераб. и доп. -М.: Наука, Гл. ред. физ.-мат. лит, 1988. -550 с.
12. Васильев Ф.П. Методы решения экстремальных задач -М.: Наука, 1981. -400 с.
13. Марчук Г.И. Методы вычислительной математики. – М.: Наука, 1980. -536 с.
14. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. – М.: Наука, 1976. — 544 с.
15. Самарский А.А. Введение в численные методы. – 3-е изд., перераб. – М.: Наука, 1997. — 239 с.
16. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1972.
17. Шикин Е.В., Плис А.И. Кривые и поверхности на экране компьютера. Руководство по сплайнам для пользователей. – М.: Диалог-МИФИ, 1996 – 240 с.
18. Альберг Дж., Нильсон Э., Уолш Дж. Теория сплайнов и их приложения. М.: Наука, 1972.
19. Де Бор К. Практическое руководство по сплайнам. — М.: Наука, 1983.
20. Foley J.D., van Dam A., Feiner S.K., Hugues J.F. Computer graphics. Principles and practice. Addison-Wesley Pub. Com. 991.
21. Боглаев Ю.П. Вычислительная математика и программирование. М.: Высшая школа, 1990.
22. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. -М.: Физ.-мат. лит. 1967.
23. Хайрер Э., Нерсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи: Пер. с англ. — М.: Мир, 1990. 512 c.
24. Современные численные методы решения обыкновенных дифференциальных уравнений / Под ред. Дж. Холла, Дж. Уатта. М.: Мир, 1979. 312 c.
25. Деккер К., Вервер Я. Устойчивость методов Рунге-Кутты для жестких нелинейных дифференциальных уравнений.- М.: Мир, 1988. 332 c.
26. Олемской И. В. О численном методе интегрирования систем обыкновенных дифференциальных уравнений // Оптимальное управление в механических системах. Л., 1983. C.178-185.
27. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров: Учеб. пособие. – М.: Высш. Шк., 1994. – 544 с.
28. Латыпов И.И. Численные методы. Лабораторный практикум: Учебное пособие для студентов физико-математического факультета по основам численных методов. Книга 1.– Бирск: Бирск.гос.соц.-пед.акад., 2007. – 94 с.
В работе также есть подробное решение ( все формулы отображаются)
К работе прилагается все необходимое для сдачи (Формат: Word отчет с расчетами. Расчеты прилагаются (Excel)
Работа под Лабораторный практикум Численные методы. Лабораторный практикум: Учебное пособие для студентов физико-математического факультета по основам численных методов. Книга 1.– Бирск: Бирск.гос.соц.-пед.акад., 2007. – 94 с. Латыпов И.И.
. (БирГСПА)
| Тема: | «Лабораторные работы № 1-8 по Численным методам. (БирГСПА) excel» | |
| Раздел: | Информатика | |
| Тип: | Лабораторная работа | |
| Страниц: | 35 | |
| Цена: | 2900 руб. |
Нужна похожая работа?
Закажите авторскую работу по вашему заданию.
- Цены ниже рыночных
- Удобный личный кабинет
- Необходимый уровень антиплагиата
- Прямое общение с исполнителем вашей работы
- Бесплатные доработки и консультации
- Минимальные сроки выполнения
Мы уже помогли 24535 студентам
Узнайте стоимость
написания вашей работы
Средний балл наших работ
- 4.89 из 5
Нужна уникальная работа?
Закажите новую работу, выполненную по вашим требованиям
682 автора
помогают студентам
84 задания
за последние сутки
10 минут
среднее время отклика
Лабораторная работа
Решение нелинейных
алгебраических и трансцендентных уравнений в «Excel» и «MathCAD»
Решение многих
задач приводит к исследованию сложных математических моделей. При этом в
большинстве случаев не удается получить точных аналитических решений. Тогда
используют численные методы. Решение, полученное численными методами, обычно является
приближенным, т.е. содержит некоторую погрешность. Ее источниками являются:
неполное соответствие математической модели реальной задаче: погрешность исходных
данных; погрешность самих численных методов; погрешности округления.
Цель и содержание
Целью данной
лабораторной работы является овладение практическими навыками решения
нелинейных уравнений численными методами средствами программ MS Excel и MathCAD.
Аппаратура и материалы
Лабораторная работа проводится в
компьютерном классе на IBM-совместимых персональных ЭВМ
с использованием программ MS Excel и MathCAD.
Указания по технике
безопасности
Для выполнения лабораторной работы
студент должен:
1.
Перед включением ПЭВМ подготовить рабочее место, убрать ненужные
для работы предметы; обо всех замеченных технических неисправностях сообщить
преподавателю. Запрещается включать устройства при неисправных заземлении или
кабелях питания; пользоваться поврежденными розетками, рубильниками и другими
электроустановочными приборами.
2.
После получения разрешения преподавателя включить ПЭВМ и
приступить к работе. Запрещается производить подключение или отключение
различных периферийных устройств. Запрещается работать, если при прикосновении
к корпусам оборудования ощущается действие электрического тока.
3.
После выполнения задания и получения разрешения преподавателя
необходимо закрыть активные приложения, корректно завершить работу ПЭВМ и
отключить питание.
4.
Привести в порядок рабочее место, и после получения разрешения
преподавателя покинуть помещение.
Теоретическое обоснование
Нелинейные
уравнения можно разделить на 2 класса – алгебраические и трансцендентные. Алгебраическими
уравнениями называют уравнения, содержащие только алгебраические функции
(целые, рациональные, иррациональные). В частности, многочлен является целой
алгебраической функцией. Уравнения, содержащие другие функции
(тригонометрические, показательные, логарифмические и другие) называются трансцендентными.
Часто возникающей
задачей при решении нелинейных уравнений является поиск приближенных значений
корней. Многие уравнение, например трансцендентные,
не имеют аналитических решений. Однако они могут решаться численными методами.
Пусть дано
уравнение
f(x)=0, (1)
где функция f(x) –
некоторая заданная функция.
Решить уравнение
(1) значит установить, имеет ли оно корни, сколько корней и найти значения
корней.
Методика и порядок выполнения работы
Прежде чем начать
выполнение лабораторной работы, внимательно прочтите задание на лабораторную
работу и просмотрите примеры выполнения работы. После этого запустите сначала
программу MathCAD, выполните все вычисления, необходимые для
выполнения лабораторной работы, и сохраните файл с вычислениями. Затем запустите программу MS Excel, выполните все
вычисления, необходимые для выполнения лабораторной работы, и также сохраните
файл с вычислениями. После того, как студент выполнил все вычисления, он может
приступить к формированию отчета по лабораторной работе.
Задание. Согласно данному преподавателем варианту необходимо:
1. Решить заданное
уравнение с помощью графического
метода в программе MathCAD.
2. Решить заданное
уравнение с помощью вычислительного
блока Given/Find в программе MathCAD.
3. Решить заданное уравнение с помощью метода подбора параметра в программе MS Excel.
Методика выполнения задания
Графический
метод. Рассмотрим в MathCAD графический метод, используемый для поиска приближенных значений корней нелинейных уравнений.
В качестве примера возьмем уравнение
. (2)
Чтобы определить, сколько корней оно имеет, проведем локализацию корней данного уравнения, т.е.
определим и выделим отрезки, на
каждом из которых уравнение имеет ровно один корень. Один из способов
решения данной проблемы – построение графика функции F(x), т.е.
графический метод. Для большей наглядности вводится две функции f(x)=4(1-х2) и g(x)=ех, и строятся графики этих функций (рисунок 1).
Рисунок 1 – Графики
функций f(x) и g(x)
Из графика, представленного на рисунке 1,
видно, что графики функций f(x) и g(x) пересекаются в двух точках, расположенных внутри интервалов [–2;0] и [0;2]. На каждом из этих отрезков
корень можно найти, воспользовавшись опцией root(f(x)-g(x),x,a,b), где
а и b – начальная и
конечная точки отрезка локализации.
Окончательно, результат решения нелинейного уравнения с помощью
графического метода представлен на рисунке 2.
Рисунок 2 – Графическое
определение отрезков локализации и поиск корней уравнения с помощью
графического метода
Таким образом, корнями нелинейного уравнения
(2) являются два корня: и
.
Рассмотрим также вычислительный блок Given/Find, используемый для решения нелинейного уравнения.
Вычислительный блок Given/Find. При использовании вычислительного блока Given/Find неизвестному значению
необходимо присвоить начальное значение. Неизвестной является значение
переменной х, поэтому именно она является аргументом встроенной функции Find(х), решающей нелинейное уравнение. После этого, чтобы численным
методом решить нелинейное уравнение, следует после ключевого слова Given записать нелинейное уравнение. Затем необходимо
записать функцию Find(х), поставить
знак «=», после чего на экране появится значение корня нелинейного уравнения.
Решим уравнение (2), задав начальное значение х0>0, например . Для
этого обозначим блок решения словом Given, введем уравнение с помощью булевского
оператора «=» и найдем корень уравнения с помощью опции Find (рисунок 3).
Рисунок 3 – Поиск положительного корня уравнения с помощью функции Find
Второй корень уравнения можно получить,
выбрав отрицательное начальное значение х0 , например (рисунок 4).
Рисунок 4 – Поиск отрицательного корня
уравнения с помощью функции Find
Метод
подбора параметра. Рассмотрим, как на рабочем листе при помощи подбора параметра
в MS Excel можно находить корни нелинейного уравнения с одним аргументом. В
качестве базового примера рассмотрим следующее уравнение:
.
Для нахождения
корней их первоначально надо локализовать, т.е. найти интервалы, на которых эти
корни существуют. Такими интервалами локализации корней могут служить
промежутки, на концах которых функция имеет противоположный знак. С целью
нахождения интервалов, на концах которых функция изменяет знак, необходимо
построить ее график или ее протабулировать. Например, протабулируем наш полином
на интервале [–2; 2] с шагом 0,4. С этой целью:
1.
Введите в
ячейку А2 значение -2, а в ячейку A3 – значение -1,6.
2.
Выберите
диапазон А2:АЗ, расположите указатель мыши на маркере заполнения этого
диапазона и протяните его на диапазон А4:А12. Аргумент протабулирован.
3.
В ячейку
В2 введите формулу: =4*(1–А2^2)–2,72^А2.
4.
Выберите
ячейку В2. Расположите указатель мыши на маркере заполнения этой ячейки и
протяните его на диапазон В3:В12. Функция также протабулирована.
Результаты табуляции представлены на рисунке 5.
На рисунке 6
видно, что функция меняет знак на интервалах [–1; –0,8] и [0,5; 1], и поэтому
на каждом из этих интервалов имеется свой корень. Так как квадратное уравнение
имеет не более двух корней, то они все локализованы.
Рисунок
5 – Результаты табуляции
Рисунок 6 – График функции
Прежде чем
приступить к нахождению корней при помощи подбора параметра, необходимо
выполнить некоторую подготовительную работу:
1. установите точность, с
которой находится корень. Корень при помощи подбора параметра находится методом
последовательных приближений. Для этого выберите команду Сервис→Параметры
и на вкладке Вычисления диалогового окна Параметры задайте
относительную погрешность и предельное число итераций равными 0,00001 и 1000,
соответственно.
2. Отведите на рабочем листе ячейку под
искомый корень, например, С2. Эта ячейка будет играть двойную роль. До
применения подбора параметра в ней находится начальное приближение к корню
уравнения, а после применения – найденное приближенное значение корня.
Корень при помощи
подбора параметра находим методом последовательных приближений, поэтому в
ячейку С2 надо ввести значение, являющееся приближением к искомому корню. В
нашем случае первым отрезком локализации корня является [-1; -0,8].
Следовательно, за начальное приближение к корню разумно взять среднюю точку
этого отрезка -0.9.
Отведите ячейку,
например, D2, под функцию, для которой ведется поиск корня. Причем, вместо
неизвестного, у этой функции должна указываться ссылка на ячейку, отведенную
под искомый корень. Таким образом, в ячейку D2 введите формулу
=4*(1-C2^2)-2,72^C2.
Аналогично надо
поступить с другим искомым корнем:
Отвести ячейку СЗ
под второй корень, ввести в нее начальное приближение 0,6. а в ячейку D3 ввести
следующую формулу =4*(1-C3^2)-2,72^C3.
Теперь можно
переходить к нахождению первого корня уравнения:
1. Выберите команду Сервис→Подбор
параметра. На экране отобразится диалоговое окно Подбор параметра.
2. В поле Установить в ячейке
введите ссылку на ячейку D2 (рисунок 7). В этом поле дается ссылка на ячейку, в
которой введена формула, вычисляющая значение левой части уравнения. Для
нахождения корня с помощью подбора параметра уравнение надо представить в таком
виде, чтобы его правая часть не содержала переменную.
3. В поле Значение
введите 0. Здесь указывается значение из правой части уравнения.
4. В поле Изменяя значение
ячейки введите С2. В данном поле приводится ссылка на ячейку, отведенную
под переменную.
Рисунок 7 – Локализация
корней уравнения и диалоговое окно
Подбор параметра
5. Нажмите кнопку ОК.
На экране
отображается окно Результат подбора параметра (рисунок 
работы команды Подбор параметра. Кроме того, рассматриваемое средство
помещает найденное приближенное значение корня в ячейку С2. В данном случае оно
равно -0,950483819.
Затем необходимо
провести все операции для поиска второго корня. На экране отображается окно Результат
подбора параметра (рисунок 9) с результатами работы команды Подбор
параметра. Кроме того, рассматриваемое средство помещает найденное
приближенное значение корня в ячейку С3. В данном случае оно равно 0,703322024.
Окончательно,
результат решения нелинейного уравнения с помощью метода подбора параметра
представлен на рисунке 10.
Таким образом, корнями нелинейного уравнения
(2) являются два корня: и
.
Рисунок 8 –Диалоговое окно
Результат подбора параметра
после успешного завершения
поиска первого корня
Рисунок 9 –Диалоговое окно
Результат подбора параметра
после успешного завершения
поиска второго корня
Рисунок 10 – Результат
решения нелинейного уравнения с помощью
метода подбора параметра
Варианты
заданий для самостоятельного выполнения
|
№ варианта |
Уравнение f(x)=0 |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
Вопросы для защиты работы
1. Какие бывают нелинейные
уравнения? Дать определения.
2. В чем заключается графический
метод вычисления нелинейных уравнений?
3. Как решается нелинейное
уравнение с помощью вычислительного блока Given/Find?
4.
Как можно
найти корни нелинейного уравнения при помощи подбора параметра?
Список литературы
1.
Васильев
А.Н. MathCAD 13 на примерах. – СПб.:
БХВ-Петербург, 2006. – 528 с.: ил.
2.
Гурский
Д., Турбина Е. MathCAD для студентов и школьников.
Популярный самоучитель. – СПб.: Питер, 2005. – 400 с.: ил. – (Серия «Популярный
самоучитель»)
3.
Поршнев
С.В., Беленкова
И.В. Численные методы на базе MathCAD. –
СПб.: БХВ-Петербург, 2005. – 464 с.: ил.
4.
Семененко
М.Г. Математическое моделирование в MathCAD. – М.: Альтекс-А, 2003. – 208 с.
5.
Численные
методы и инженерные расчеты в Excel.
Методические указания к выполнению лабораторных работ. – СПб.: СЗЗГТУ, 2001г.
6.
Официальный
образовательный математический сайт: http://exponenta.ru/index.php
Решение нелинейных уравнений в Excel и Mathcad (стр. 1 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Кафедра прикладной математики и вычислительной техники
Решение нелинейных уравнений в Excel и Mathcad
к выполнению лабораторных работ
по дисциплине «Вычислительная математика»
Решение нелинейных уравнений в Excel и Mathcad: Метод. указ. / Сост. , — Самара: СГАСУ, 20с.
Методические указания разработаны в соответствии с Государственным образовательным стандартом изучения дисциплины «Вычислительная математика».
Рассмотрена реализация численных методов при решении нелинейных уравнений и систем уравнений в Excel и MathCad. Приведены варианты заданий для индивидуального выполнения и вопросы для самоконтроля и тестирования.
Предназначены для студентов специальности 230201 – «Информационные системы и технологии» всех форм обучения.
Рецензент к. ф-м. н.
Ó , составление, 2012
1 Решение нелинейного уравнения
1.1 Общие сведения о решении нелинейного уравнения
1.2 Отделение корней
1.3 Уточнение корней стандартными средствами Excel и Mathcad
1.4 Метод деления отрезка пополам
1.6 Метод Ньютона (касательных)
1.7 Комбинированный метод
1.8 Метод итераций
2 Решение систем нелинейных уравнений
2.1 Общие сведения о решении систем нелинейных уравнений
2.2 Решение систем нелинейных уравнений методом Ньютона
2.3 Решение систем нелинейных уравнений методами итераций
3 Задания к лабораторным работам
Лабораторная № 1. Отделение корней и стандартные инструменты решения нелинейного уравнения
Лабораторная № 2. Сравнение методов уточнения корней нелинейного уравнения
Лабораторная № 3. Решение систем нелинейных уравнений
Лабораторная № 4. Программирование методов решения нелинейных уравнений и систем
4 Вопросы и тесты для самоконтроля
Список рекомендуемой литературы
1 Решение нелинейного уравнения
1.1 Общие сведения о решении нелинейного уравнения
Как правило, нелинейное уравнения общего вида f(х)=0 невозможно решить аналитически. Для практических задач достаточно найти приближенное значение x, в определенном смысле близкое к точному решению уравнения хточн.
В большинстве случаев поиск приближенного решения включает два этапа. На первом этапе отделяют корни, т. е. находят такие отрезки, внутри которых находится строго один корень. На втором этапе уточняют корень на одном из таких отрезков, т. е. находят его значение с требуемой точностью.
Достигнутая точность может оцениваться либо «по функции» (в найденной точке x, функция достаточно близка к 0, т. е. выполняется условие |f(x)|≤ ef, где ef требуемая точность по оси ординат), либо «по аргументу» (найден достаточно маленький отрезок [a,b], внутри которого находится корень, т. е. |b–a|≤ ex, где ex требуемая точность по оси абсцисс).
1.2 Отделение корней
Отделение корней может производиться сочетанием графического и аналитического исследования функции. Такое исследование опирается на теорему Вейерштрасса, в соответствии с которой для непрерывной на отрезке [a,b] функции f(х) и любого числа y, отвечающего условию f(a)≤y≤f(b), существует на этом отрезке точка x, в которой функция равна y. Следовательно, для непрерывной функции достаточно найти отрезок, на концах которого функция имеет разные знаки, и можно быть уверенным, что на этом отрезке есть корень уравнения f(х)=0.
Для ряда методов уточнения желательно, чтобы найденный на первом этапе отрезок содержал только один корень уравнения. Это условие выполняется, если функция на отрезке монотонна. Монотонность, можно проверить либо по графику функции, либо по знаку производной.
Пример Найти с точностью до целых все корни нелинейного уравнения y(x)=x3 ‑ 10x + 7=0 а) построив таблицу и б) построив график. Найти корень уравнения на выделенном отрезке, используя опции «Подбор параметра» и «Поиск решения».
Решение Создадим в Excel таблицу, содержащую аргументы и значения функции и по ней построим точечную диаграмму. На рисунке 1 приведен снимок решения.
На графике видно, что уравнение имеет три корня, принадлежащие отрезкам [-4, -3], [0, 1] и [2, 3]. Эти отрезки можно выявить и наблюдая за сменой знаков функции в таблице. По построенному графику можно сделать вывод, что на указанных отрезках функция f(x) монотонна и, следовательно, на каждом из них содержится только по одному корню.
Такой же анализ может быть выполнен и в пакете Mathcad. Для этого достаточно набрать определение функции f(x), используя оператор присваивания (:=) и естественные общепринятые обозначения математических операций и стандартных функций, задать цикл для изменения аргумента, например, а затем вывести на экран таблицу значений функции (расположенными в одной строке командами x= f(x)=) и график. Цикл можно задать, например, командой x:=-5,-4.5…5. Шаг цикла формируется путем задания начального и следующего за ним значений переменной, а перед конечным значением переменной ставится точка с запятой, которая будет визуально отображена на экране в виде многоточия.
Рисунок 1 – Таблица и график для отделения корней нелинейного уравнения
1.3 Уточнение корней стандартными средствами Excel и Mathcad
Во всех методах уточнения корней необходимо задать начальное приближение, которое затем и будет уточняться. Если уравнение имеет несколько корней, в зависимости от выбранного начального приближения будет найден один из них. При неудачно выбранном начальном приближении решение может и не быть найдено. Если в результате первого этапа расчетов уже выделен отрезок, содержащий единственный корень уравнения, в качестве начального приближения можно взять любую точку этого отрезка.
В Excel для уточнения значений корней можно использовать опции «Подбор параметра» и «Поиск решения». Пример оформления решения приведен на рисунках 2 и 3.
Рисунок 2 – Ввод значений для использования средств решения уравнения в Excel
Рисунок 3 – Результаты использования средств решения уравнения в Excel
В Mathcad для уточнения корней уравнения можно использовать функцию root(….) или блок решения. Пример использования функции root(…) приведен на рисунке 4, а блока решения на рисунке 5. Следует обратить внимание, что в блоке решения (после заголовка блока Given) между левой и правой частями уравнения должен стоять жирный знак равенства (тождества), который можно получить выбором из соответствующей палитры инструментов, либо нажатием одновременно клавиши Ctrl и =.

Рисунок 5 – Решение уравнения с использованием блока решения в Mathcad
Как видим, каждый стандартный инструмент находит решение уравнения с определенной точностью. Эта точность зависит от метода, используемого в пакете и, в определенной степени, настроек пакета. Управлять точностью результата здесь достаточно сложно, а часто и невозможно.
В то же время, очень просто построить собственную таблицу или написать программу, реализующие один из методов уточнения корней. Здесь можно использовать критерии точности расчета, задаваемые пользователем. При этом достигается и понимание процесса расчетов без опоры на принцип Митрофанушки: «Извозчик есть, довезет».
Далее рассмотрены несколько наиболее распространенных методов. Отметим очевидный момент: при прочих равных условиях тот метод уточнения корней будет более эффективен, в котором результат с той же погрешностью найден с меньшим числом вычислений функции f(x) (при этом достигается и максимальная точность при одинаковом числе вычислений функции).
1.4 Метод деления отрезка пополам
В этом методе на каждом шаге отрезок делится на две равные части. Затем сравнивают знаки функции на концах каждой из двух половинок (например, по знаку произведения значений функций на концах), определяют ту из них, в которой содержится решение (знаки функции на концах должны быть разные), и. сужают отрезок, перенося в найденную точку его границу (а или b). Условием окончания служит малость отрезка, где содержится корень («точность по x»), либо близость к 0 значения функции в средине отрезка («точность по y»). Решением уравнения считают середину отрезка, найденного на последнем шаге.
Пример. Построить таблицу для уточнения корня уравнения x3 –10x+7=0 на отрезке [-4, -3] методом деления отрезка пополам. Определить сколько шагов надо сделать методом деления отрезка пополам и какая при этом достигается точность по х, для достижения точности по y, равной 0,1; 0,01; 0, 001.
Решение Для решения можно использовать табличный процессор Excel, позволяющий автоматически продолжать строки. На первом шаге заносим в таблицу значения левого и правого концов выбранного начального отрезка и вычисляем значение середины отрезка с=(a+b)/2, а затем вводим формулу для вычисления функции в точке a (f(a)) и растягиваем (копируем) её для вычисления f(c) и f(b). В последнем столбца вычисляем выражение (b—a)/2, характеризующего степень точности вычислений. Все набранные формулы можно скопировать во вторую строку таблицы.
На втором шаге нужно автоматизировать процесс поиска той половины отрезка, где содержится корень. Для этого испльзуется логическая функция ЕСЛИ (Меню: Вставка

Вторую строку таблицы можно продолжить (скопировать) на необходимое число последующих строк.
Итерационный процесс завершается, когда очередное значение в последнем столбце становится меньшим, чем заданный показатель точности ex. При этом, значение середины отрезка в последнем приближении, принимается в качестве приближенного значения искомого корня нелинейного уравнения. На рисунке 6 приведен снимок решения. Для построения аналогичного процесса в Mathcad можно использовать бланк, подобный приведенному на рисунке 7. Число шагов N может варьироваться до достижения в таблице результатов требуемой точности. При этом таблица будет автоматически удлиняться или укорачиваться.
Итак, одним из трех корней нелинейного уравнения x3 – 10x + 7=0, найденным с точностью e=0,0001, является x= — 3,46686. Как мы видим, он действительно принадлежит отрезку [-4; -3].
Рисунок 6 – Уточнение корня методом деления отрезка пополам в Excel
Рисунок 7 – Уточнение корня методом деления отрезка пополам в Mathcad
1.5 Метод хорд
В этом методе нелинейная функция f(x) на отделенном интервале [а, b] заменяется линейной – уравнением хорды, т. е. прямой соединяющей граничные точки графика на отрезке. Условие применимости метода – монотонность функции на начальном отрезке, обеспечивающая единственность корня на этом отрезке. Расчет по методу хорд аналогичен расчету методом деления отрезка пополам, но теперь на каждом шаге новая точка x внутри отрезка [a,b] рассчитывается по любой из следующих формул:

1.6 Метод Ньютона (касательных)
Идея, на которой основан метод, аналогична той, которая реализована в методе хорд, только на каждом шаге кривая f(x) заменяется касательной к ней, проведенной в предыдущей найденной точке. В качестве начальной точки в зависимости от свойств функции берется или левая граница отрезка, содержащего корень – x0 = а (если f(а) f»(х) > 0), или правая его граница: x0 = b (если f(b) f»(х)>0). Расчет нового приближения на следующем шаге i+1 производится по формуле:

Алгоритм применим для монотонных функций, сохраняющих выпуклость или вогнутость в промежутке между начальным приближением и корнем уравнения (т. е. должен сохраняться знак первой и второй производных функции f(x)). работоспособен при выпуклых и монотонных функциях f(x). В расчетах нет необходимости отслеживать две границы отрезка, поэтому достаточно на каждом шаге вычислять значения x, f(x) и f′(x). При этом легко оценить «точность по y», по значению левой части уравнения на очередном шаге. Для оценки «точности по x» нужно отслеживать разницу приближений на предыдущем и последующих шагах, которая связана с разницей между найденным приближением и точным значением корня.
Следует обратить внимание на следующую особенность метода: последовательность x1, x2, x3,… приближается к корню с другой стороны, в отличие от использования метода хорд при прочих равных условиях.
Главным достоинством метода касательных является квадратичная скорость сходимости, что во многих случаях может привести к сокращению числа вычислений функции.
Уточнить корень уравнения tg (0,55x+0,1) – x2=0 на отрезке [0.6, 0.8] методом касательных до точности 0,001.
Точность вычислений можно оценить из соотношения
2 Решение систем нелинейных уравнений
2.1 Общие сведения о решении систем нелинейных уравнений
Систему n нелинейных уравнений с n неизвестными x1, x2, . xn записывают в виде:
где F1, F2,…, Fn – функции независимых переменных, среди которых есть нелинейные.
Как и в случае систем линейных уравнений, решением системы является такой вектор X*, который при подстановке обращает одновременно все уравнения системы в тождества.
Система уравнений может не иметь решений, иметь единственное решение, конечное или бесконечное количество решений. Вопрос о количестве решений должен решаться для каждой конкретной задачи отдельно.
Численные методы решения системы уравнений носят итерационный характер и требуют задания начального приближения X0.
Рассмотрим две группы таких методов: метод Ньютона с различными его модификациями и методы итераций (простых итераций и Зейделя).
2.2 Решение систем нелинейных уравнений методом Ньютона
Будем рассматривать этот метод на примере системы двух нелинейных уравнений с двумя неизвестными:
Начальные значения x0 и y0 определяются графически. Для нахождения каждого последующего приближения (xi+1, yi+1) используют вектор значений функций и матрицу значений их первых производных, рассчитанные в предыдущей точке (xi, yi).

Для расчета новых приближений на шаге i+1 используется матричная формула

Следует обратить внимание, что в последней формуле используется вычисление матрицы, обратной к матрице первых производных.
Расчет останавливают при выполнении одного (а иногда и обоих) из двух условий. Первое из них заключается в том, что на очередном шаге максимальное по модулю из изменений аргументов x и y становится меньше заданная погрешность по аргументам. В соответствии со вторым из условий, на очередном шаге максимальное по модулю значение левых частей уравнений должно отличаться от нуля меньше, чем заданная погрешность по функциям.
В упрощенном методе Ньютона матрица производных и матрица, обратная к ней вычисляются только один раз (в начальной точке) и для расчетов используется матричная формула

Приведенные формулы особенно легко записать в Mathcad, где имеются операторы для вычисления производных и действий с матрицами. Однако при правильном использовании матричных операций эти формулы достаточно просто записываются и в Excel. Правда, здесь придется заранее получить формулы для вычисления производных. Для аналитического вычисления производных также может быть использован Mathcad.
2.3 Решение систем нелинейных уравнений методами итераций
Для реализации этих методов исходную систему уравнений необходимо путем алгебраических преобразований явно выразить каждую переменную через остальные. Для случая двух уравнений с двумя неизвестными новая система будет иметь вид

Для решения такой системы задаются начальным приближением x0, y0. Уточненные решения получают по шагам, подставляя в правые части уравнений значения, найденные на предыдущем шаге. В методе простых итераций для уточнения решения используют формулы:

Если одно из решений системы и начальные значения x0 и y0 лежат в области D, задаваемой неравенствами: a ≤ x ≤ b, c ≤ y ≤ d, то расчет по методу простых итераций сходится при выполнении в области D соотношений:
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12680 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
 Решение систем линейных алгебраических уравнений в Excel
Решение систем линейных алгебраических уравнений в Excel
1. Метод обратной матрицы (решение в Excel)
Если дано уравнение:
A*X = B, где A — квадратная матрица, X,B — вектора;
причем B — известный вектор (т е столбец чисел), X — неизвестный вектор,
то решение X можно записать в виде:
X = A -1 *B, где A -1 — обратная от А матрица.
В MS Excel обратная матрица вычисляется функцией МОБР(), а перемножаются матрицы (или матрица на вектор) — функцией МУМНОЖ().
Имеются «тонкости» использования этих матричных действий в Excel. Так, чтобы вычислить обратную матрицу от матрицы А, нужно: Чтобы умножить матрицу на вектор: Есть и другой спососб, при котором используется кнопка построителя функции Excel.
Пример СЛАУ 4-го порядка
Скачать документ Excel, в котором этот пример решён различными методами.
2. Метод Гаусса
Краткое описание.
- Решаю систему уравнений: A*X=B, где A — квадратная матрица n-го порядка, X,B — вектора
- К матрице A справа приписываю вектор B. Получаю расширенную матрицу A
- В дальнейшем A обозначает расширенную матрицу (n строк, n+1 столбец)
- Aij — обозначает элемент матрицы, находящийся на i-й строке и j-м столбце
- Делю 1-ю строку на A11, т е A’1j = A1j/A11 (j = 1..n+1). В результате A’11 = 1. A’ обозначает преобразованную строку
- Преобразую остальные строки по формуле: A’ij = Aij — A’1j*Ai1 (i = 2..n; j = 1..n+1)
- В результате 1-й столбец в строках 2..n заполнится нулями
- Отметим, что все эти преобразования не нарушают правильность уравнений
- Аналогичные действия проводим для обнуления 2-го столбца в строках 3..n, то есть:
- Делю 2-ю строку на A’22, т е A»2j = A’2j/A’22 (j = 2..n+1). В результате A»22 = 1. A» обозначает резельтат 2-го преобразования строки
- Преобразую остальные строки по формуле: A»ij = A’ij — A»2j*A’i2 (i = 3..n; j = 2..n+1)
- В результате 2-й столбец в строках 3..n заполнится нулями
- Аналогичные действия проводим далее
- В результате левые n столбцов матрицы A превращаютс в верхнюю треугольную матрицу, т е ниже главной диагонали находятся только нули (а на главной диагонали — единицы) — см Рис 1. На этом рисунке вектор B — слева, S — номер шага
- Затем выполняется «обратный ход», начиная с нижней строки, из которой можно вычислить Xn = Bn/Ann, например: Х4 = 9,55741/68,6388 = 0,13924 (рис. 1)
- Затем можно вычислить X3 = (0,9065 — 2,40919*0,13924) = 0,57059
- Затем из второй строки: X2 + 2,83562*X3 + 8,17808*X4 = 2,47945 вычисляю X2, и т д
3. Метод Якоби (метод простых итераций)
Для применения метода Якоби (и метода Зейделя) необходимо, чтобы диагональные компоненты матрицы А были больше суммы остальных компонент той же строки. Заданная система не обладает таким свойством, поэтому выполняю предварительные преобразования.
Далее номер в скобках означает номер строки. Новую первую строку получаю сложением старой первой строки с другими строками, умноженными на специально подобранные коэффициенты. Записываю это в виде формулы:
Для применения метода Якоби систему уравнений нужно преобразовать к виду:
X = B2 + A2*X Преобразую:
Далее делю каждую строку на множитель левого столбца, то есть на 16, 7, 3, 70 соответственно. Тогда матрица А2 имеет вид :
А вектор В2:
Скачать
источники:
http://lumpics.ru/how-solve-system-equations-excel/
http://www.win-ni.narod.ru/exc/slau.htm
Лабораторная работа №18
«Решение задач методами численной математики в MS
Excel»
Цели:
1.
Закрепить навыки работы с
электронными таблицами и применение их для решения задач.
2.
Развивать
практические и исследовательские навыки по решению задач с помощью электронных
таблиц.
Выполнить задания:
|
Задача «Измерение температуры с помощью |
|||||||
|
1. Вычислите |
|||||||
|
2. Вычислите |
|||||||
|
Исходные данные: |
|||||||
|
R0=100 Ом |
|||||||
|
α = |
|||||||
|
RТ=R0(1+αT) |
|||||||
|
где |
|||||||
|
RТ |
— сопротивление |
||||||
|
R0 |
— сопротивление |
||||||
|
α |
— линейный |
||||||
|
Т |
— температура |
|
Результаты представить в виде таблицы |
||||||
|
1. |
Т |
R0 |
α |
RТ |
||
|
2. |
R0 |
α |
RТ |
Т |
||
2.
Сформировать на рабочем
листе ведомость «Расчет заработной платы работников научно-проектного
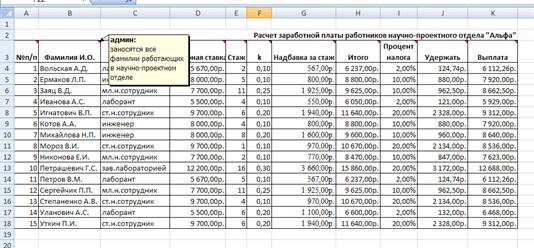
отдела «Альфа»(рис.1)
Рис. №1
Рекомендации по созданию
ведомости
·
В ячейку А2
поместить название ведомости – Расчет заработной платы работников
научно-проектного отдела «Альфа» отцентрировать по левому краю (например,
командой Формат/Ячейки/вкладка Выравнивание либо
соответствующей кнопкой По правому краю на панели
инструментов. Объединить в строке 2 столбцы от А до K.
·
В ячейки А3:К3
ввести названия полей ведомости: №п/п, Фамилия И.О., Должность, Тарифная
ставка, Стаж, k, Надбавка за стаж, Итого, Процент налога, Удержать, Выплата.
·
К шапке
ведомости – к каждому столбцу – создать скрытые примечания (рис.2). Примечания
создаются командой Вставка/Примечание (также можно использовать
панель инструментов Рецензирование, которая добавляется командой Вид/Панели
инструментов/Рецензирование
— №
п/п – номер работника отдела;
— Фамилия
И.О.— заносятся все фамилии на момент заполнения ведомости;
— Должность
– занимаемая должность на момент заполнения ведомости;
— Тарифная
ставка – денежный эквивалент занимаемой должности;
— Стаж
– вносится целое число отработанных лет на момент заполнения ведомости;
— k—
коэффициент за стаж работы
— Надбавка
за стаж – денежный эквивалент за стаж работы;
— Итого
– начисление заработной платы с учетом тарифной ставки и стажа работы;
— Процент
налога – определяет процент отчислений в бюджет;
— Удержать
– денежный эквивалент отчислений в бюджет;
— Выплата
– сумма, предназначенная к выдаче.
Рис.2
·
При расчетах к
ведомости учитывать следующее:
— k,
Надбавка за стаж, Итого, Процент налога, Удержать, Выплата – вычисляются с помощью соответствующих формул, с
использованием автозаполнения или копирования формулы.
—
Коэффициент k присваивается из следующего расчета: 0,2 – отработано
до 5 лет включительно, 0,2 – от 5 до 10 лет включительно, 0,25- от 10 до 15 лет
включительно, 0,3 – свыше 15 лет. Формула для ячейки F4:
=ЕСЛИ(Е4<=5;0,1;ЕСЛИ(И(Е4>5;E4<=10);0,2;ЕСЛИ(И(Е4>10;Е4<=15);0,25;0,3)))
— Надбавка
за стаж – денежный эквивалент за стаж работы. Формула для ячейки G4:
=D4*F4
Пользовательский
формат числа для ячейки G4:
# ##0,00р.;
(вводится
командой Формат/Ячейки/вкладка Число, из списка Числовые
форматы выбрать Все форматы и поле Тип ввести указанный
формат)
— Итого –
тарифная ставка с учетом стажа. Формула для ячейки H4:
=D4+G4
Пользовательский
формат числа для ячейки H4:
# ##0,00р.;
— Процент
налога – учитывает, что: 2%- начисление (по Итого) составляет до
7000 р. включительно, 10%- более 7000р. до 10 000 р. включительно, 20%-
более 10 000 р. до 25 000 р. включительно, 35% — превышающие
25 000 р. Формула для ячейки I4:
=ЕСЛИ(Н4<=7000;0,02;ЕСЛИ(И(H4>7000;Н4<=10000);0,1;ЕСЛИ(И(Н4>10000;H4<=25000);0,2;0,35)))
Формат числа
для ячейки I4 – Процентный
— Удержать
– денежный эквивалент налогов. Формула для ячейки J4:
=H4*14
Пользовательский
формат числа для ячейки J4:
#
##0,00р.;
— Выплата
– сумма к выдаче: Итого без Удержать
·
Требования к столбцу Стаж:
— Создать
пользовательский формат данных, учитывающий стаж работы: до 5 лет – данные
представлены желтым цветом, от 5 до 10 – синим, от 10 до 15 – зеленым, свыше 15
-красным.
—
Воспользоваться командой Формат/Ячейки и ввести пользовательский
формат для ячейки E4:
[Красный]#
##0;
— В случае
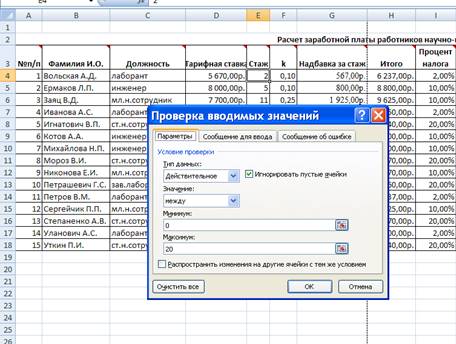
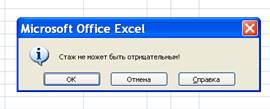
ввода отрицательного числа лет должно появляться соответствующее окно. Для
проверки ввода чисел использовать команду Данные/Проверка/вкладка Сообщение
об ошибке. (рис. 3,4)
Рис.3
Рис.4
·
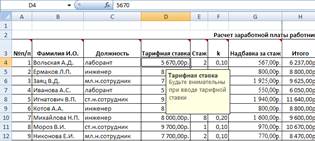
Для поля Тарифная ставка –
вывести постоянное сообщение: Тарифная ставка. Будьте внимательны при вводе
тарифной ставки (рис.5), для получения которого использовать команду Данные/Проверка/вкладка
Сообщение для ввода.
Рис.5
3.
Оформить отчет по лабораторной
работе.
4.







































































 Решение систем линейных алгебраических уравнений в Excel
Решение систем линейных алгебраических уравнений в Excel