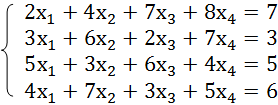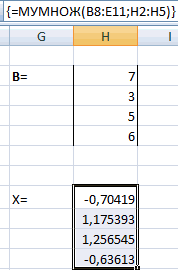Возможно вы слышали о нобелевском лауреате, психологе и исследователе по имени Дэниель Канеман. Канеман занимался наукой, которую называют термином «поведенческая экономика», т.е. изучал реакции, поведение и суждения людей в типовых жизненных (и экономических) ситуациях и условиях неопределенности.
В его книге, которая называется «Думай медленно — решай быстро» (очень рекомендую, кстати) в качестве одного из примеров когнитивных искажений — несознательной автоматической реакции — приводится следующая задача:
Бейсбольная бита и мяч стоят вместе 1 доллар 10 центов.
Бита дороже мяча на 1 доллар.
Сколько стоит мяч?
Подозреваю, что вашей первой рефлекторной мыслью, скорее всего, будет «10 центов!» 
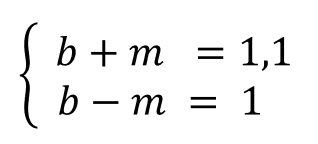
Конечно можно «тряхнуть стариной» и решить всё вручную на бумажке через подстановку переменных — как-то так:
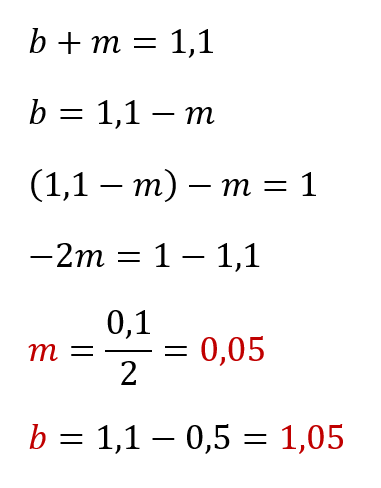
Но, во-первых, на практике уравнения могут быть сложнее и переменных может оказаться сильно больше двух и, во-вторых, у нас с вами есть Microsoft Excel — универсальный мега-инструмент, величайшее изобретение человечества. Так что давайте-ка лучше разберём как решить нашу задачу с его помощью.
Способ 1. Матричные функции МУМНОЖ и МОБР
Само собой, изобретать велосипед тут не надо — прогрессивное человечество в лице математиков давным-давно придумало кучу способов для решения подобных задач. В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера.
Сначала записываем числовые коэффициенты, стоящие перед нашими переменными в виде матрицы (в нашем случае — размером 2х2, в общем случае — может быть и больше).
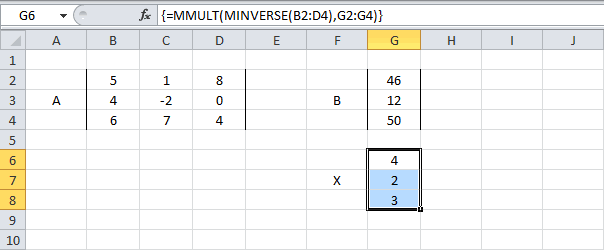
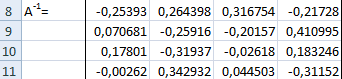
Затем находим для неё так называемую обратную матрицу , т.е. матрицу, при умножении которой на исходную матрицу коэффициентов получается единица. В Excel это легко сделать с помощью стандартной математической функции МОБР (MINVERSE):
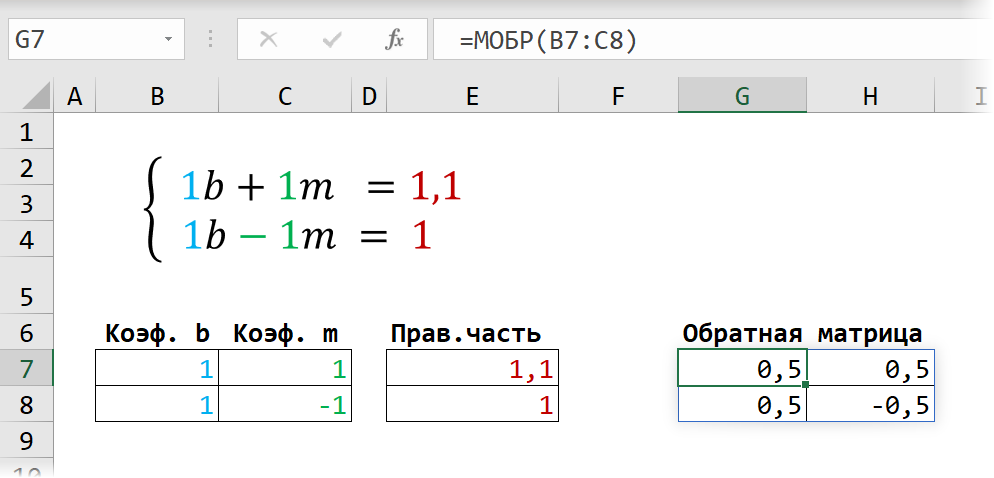
Здесь важно отметить, что если у вас свежая версия Excel 2021 или Excel 365, то достаточно ввести эту функцию обычным образом в первую ячейку (G7) — сразу получится динамический массив с обратной матрицей 2х2. Если же у вас более старая версия Excel, то эту функцию нужно обязательно вводить как формулу массива, а именно:
- Выделить диапазон для результатов — G7:H8
- Ввести функцию =МОБР(B7:C8) в строку формул
- Нажать на клавиатуре сочетание клавиш Ctrl+Shift+Enter
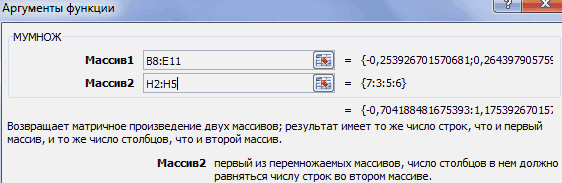
Замечательное свойство обратной матрицы состоит в том, что если умножить её на значения правых частей наших уравнений (свободные члены), то мы получим значения переменных, при которых левые и правые части уравнений будут равны, т.е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT):
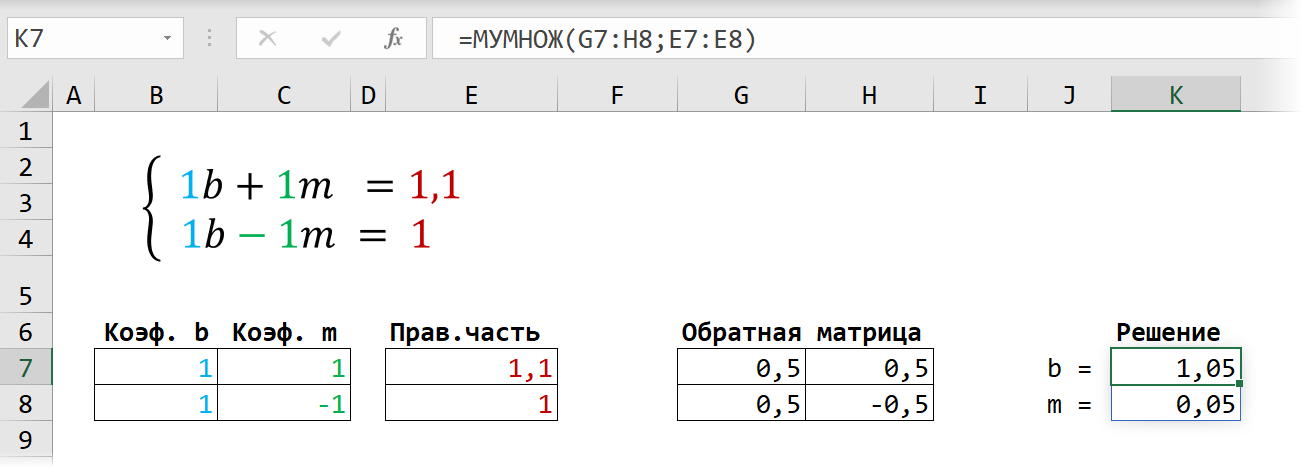
Если у вас старая версия Excel, то не забудьте также ввести её в режиме формулы массива, т.е. сначала выделить диапазон K7:K8, а после ввода функции нажать сочетание клавиш Ctrl+Shift+Enter.
Само собой, уравнений и переменных может быть больше, да и посчитать всё можно сразу в одной формуле, вложив используемые функции одна в другую:
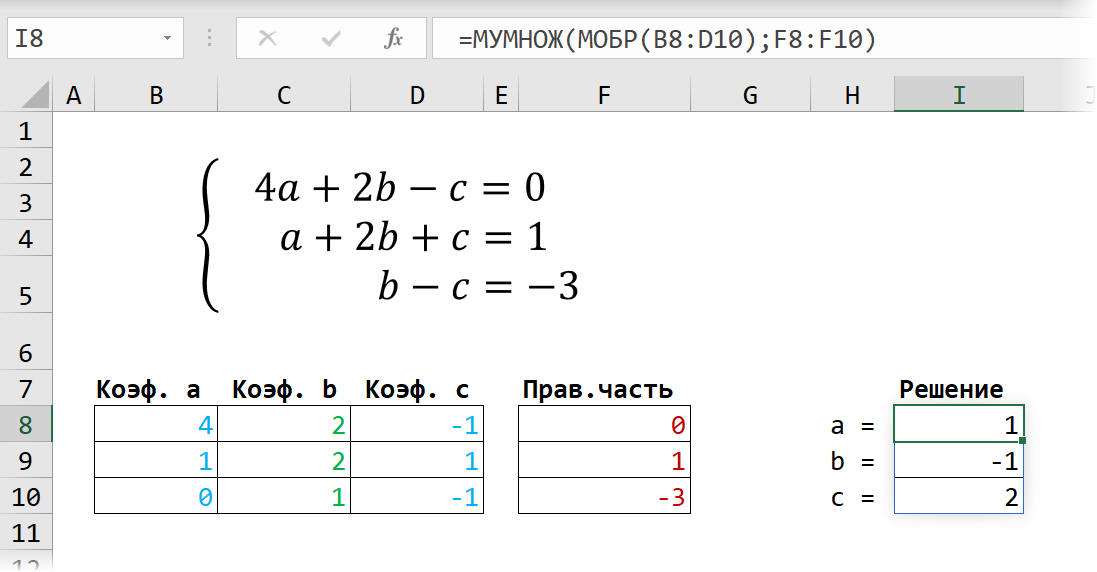
Не так уж и сложно, правда? Однако надо понимать, что этот метод подходит только для решения систем линейных уравнений. Если у вас в уравнениях используются функции посложнее четырех базовых математических действий, то зачастую проще будет пойти другим путем — через подбор.
Способ 2. Подбор надстройкой «Поиск решения» (Solver)
Принципиально другой способ решения подобных задач — это итерационные методы, т.е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.
В Microsoft Excel некоторые из этих методов реализованы в стандартной надстройке Поиск решения (Solver). Её можно подключить через Файл — Параметры — Надстройки — Перейти (File — Options — Add-ins — Go to) или на вкладке Разработчик — Надстройки (Developer — Add-ins).
Давайте рассмотрим её использование на следующей задаче. Предположим, что нам с вами нужно решить вот такую систему из двух нелинейных уравнений:
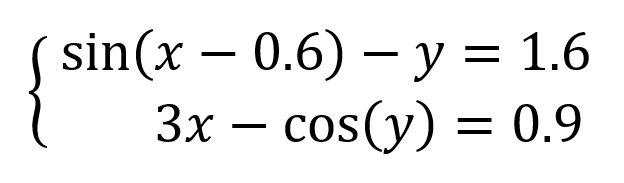
Подготавливаем основу для оптимизации в Excel:

Здесь:
- В жёлтых ячейках C9:C10 лежат текущие значения наших переменных, которые и будут подбираться в процессе оптимизации. В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column).
- В зелёных ячейках E9:E10 введены наши уравнения с использованием либо прямых ссылок на жёлтые ячейки переменных, либо созданных имён (так нагляднее). В результате мы видим, чему равны наши уравнения при текущих значениях переменных.
- В синих ячейках F9:F10 введены значения правых частей наших уравнений, к которым мы должны стремиться.
Теперь запускаем нашу надстройку на вкладке Данные — Поиск решения (Data — Solver) и вводим в появившемся диалоговом окне следующие параметры:
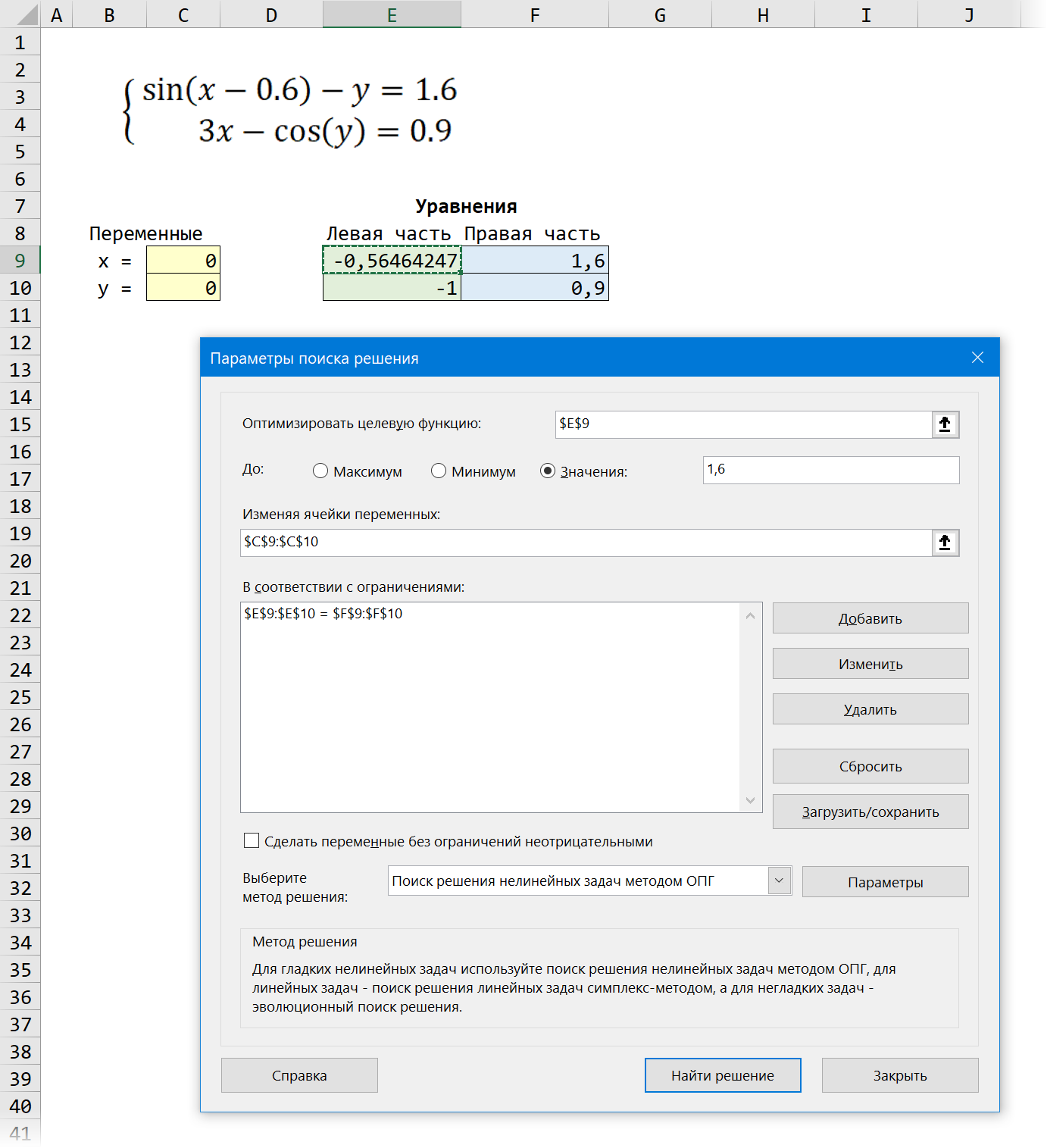
- Оптимизировать целевую функцию (Set target cell) — любая из двух наших зелёных ячеек с уравнениями, например E9.
- Изменяя ячейки переменных (By changing cells) — жёлтые ячейки с текущими значениями переменных, которыми мы «играем».
- Добавляем ограничение с помощью кнопки Добавить (Add) и задаём равенство левой и правой части наших уравнений, т.е. зелёного и голубого диапазонов.
- В качестве метода решения выбираем Поиск решения нелинейных задач методом ОПГ, т.к. уравнения у нас нелинейные. Для линейных можно смело выбирать симплекс-метод.
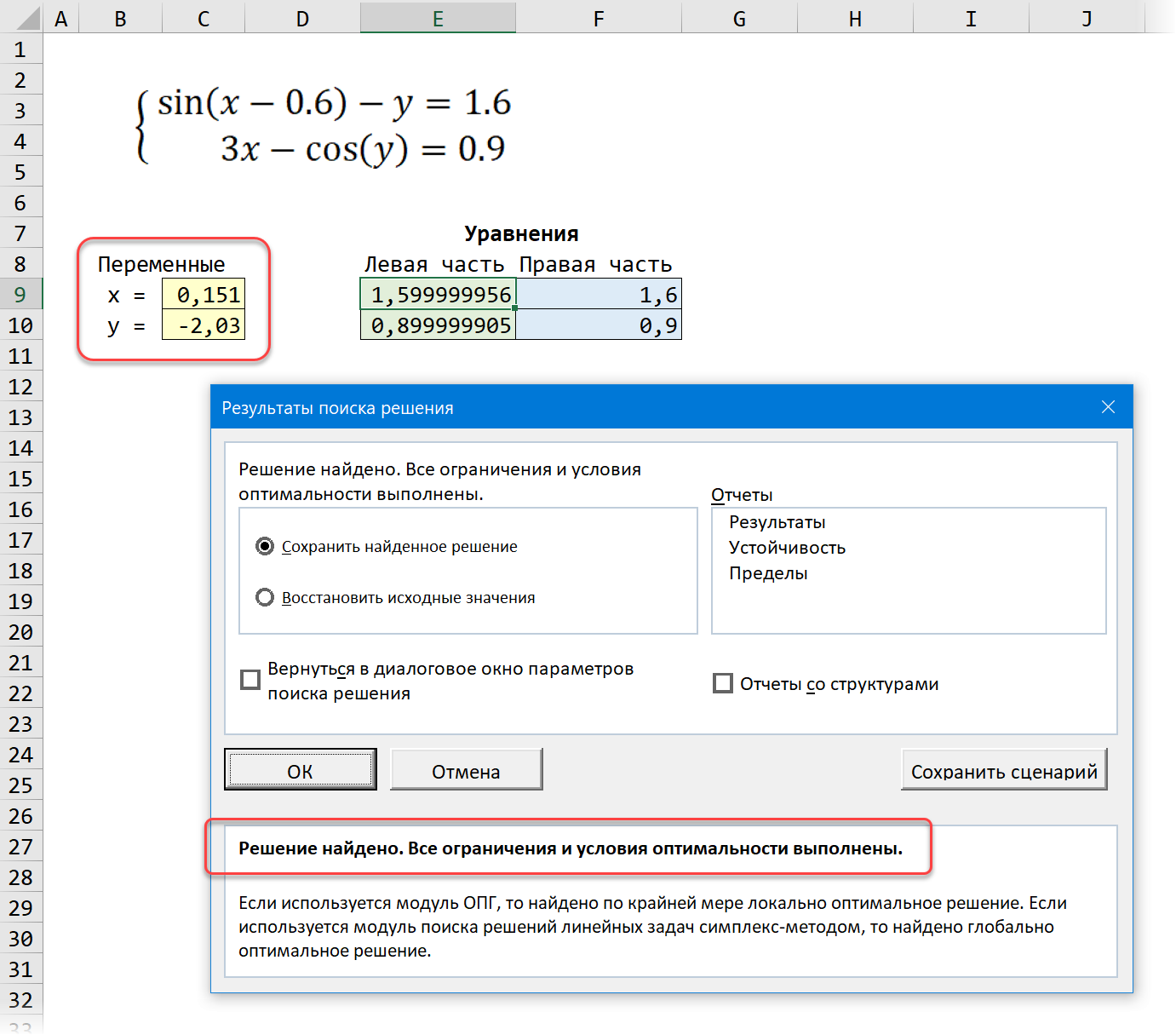
После нажатия на кнопку Найти решение (Solve) через пару мгновений (или не пару — это зависит от сложности задачи) мы должны увидеть окно с результатами. Если решение найдено, то в жёлтых ячейках отобразятся подобранные значения наших переменных:
Обратите внимание, что поскольку мы здесь используем итерационные, а не аналитические методы, то зеленые ячейки не совсем равны голубым, т.е. найденное решение не абсолютно точно. На практике, конечно же, такой точности вполне достаточно для большинства задач, и если необходимо, её можно настроить, вернувшись в окно Поиск решения и нажав кнопку Параметры (Options).
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
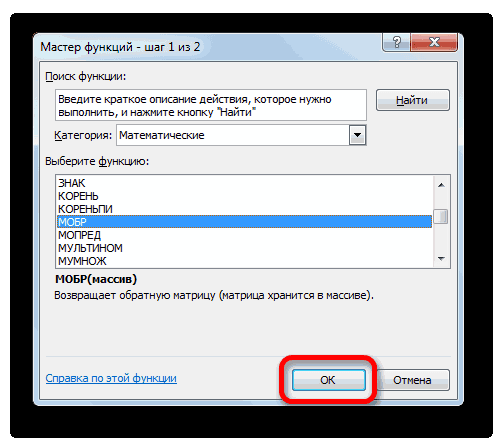
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
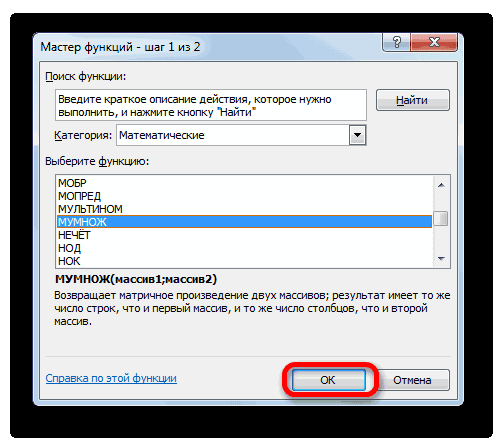
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
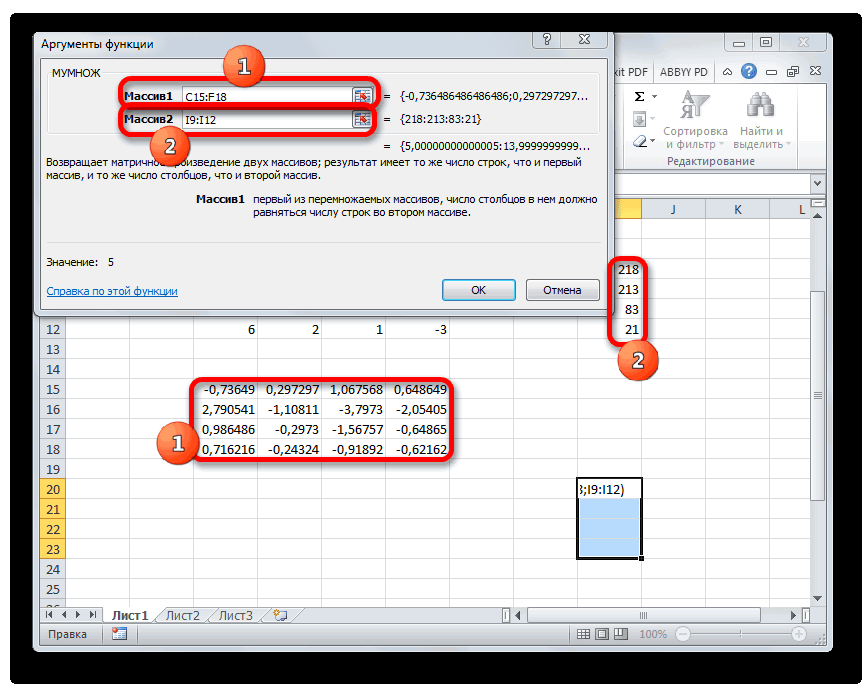
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
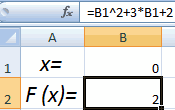
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
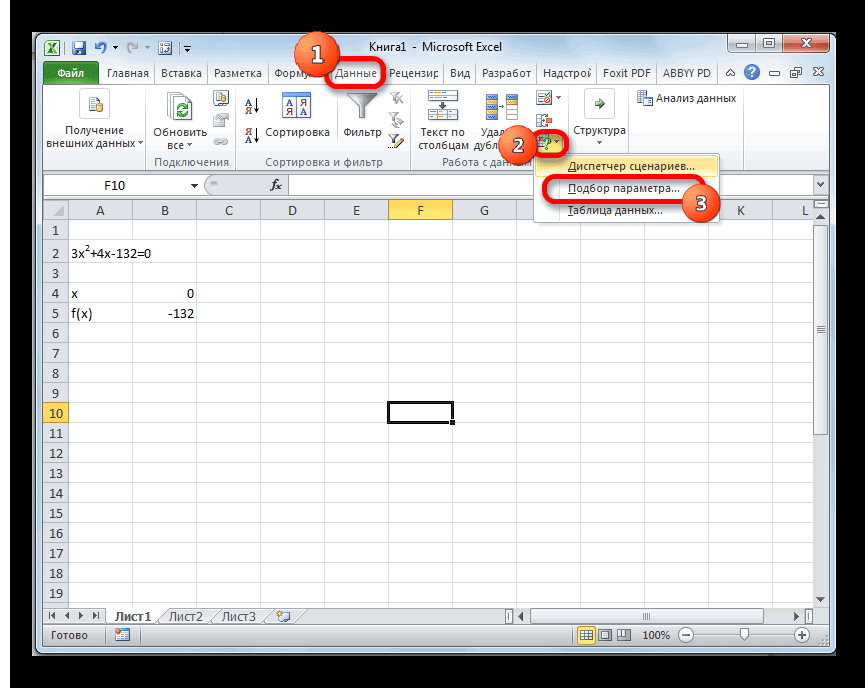
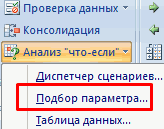
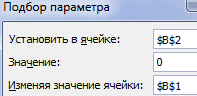
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
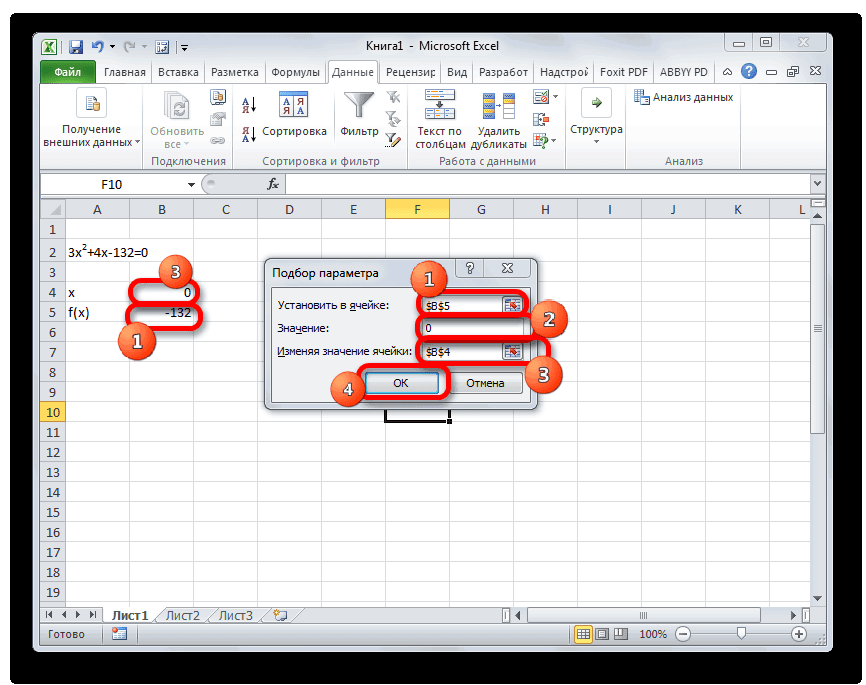
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
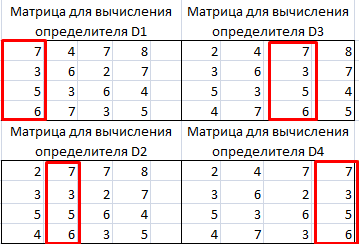
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
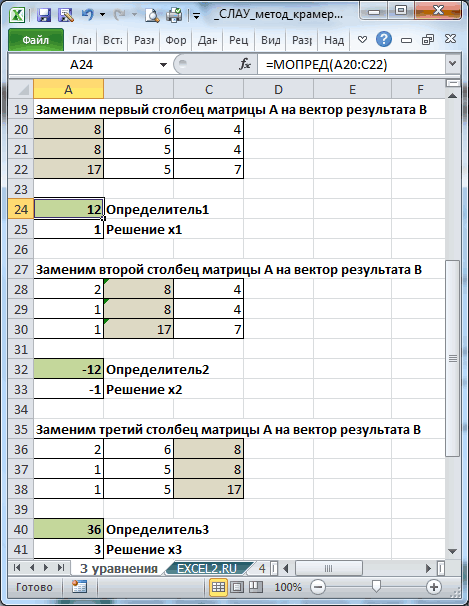
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
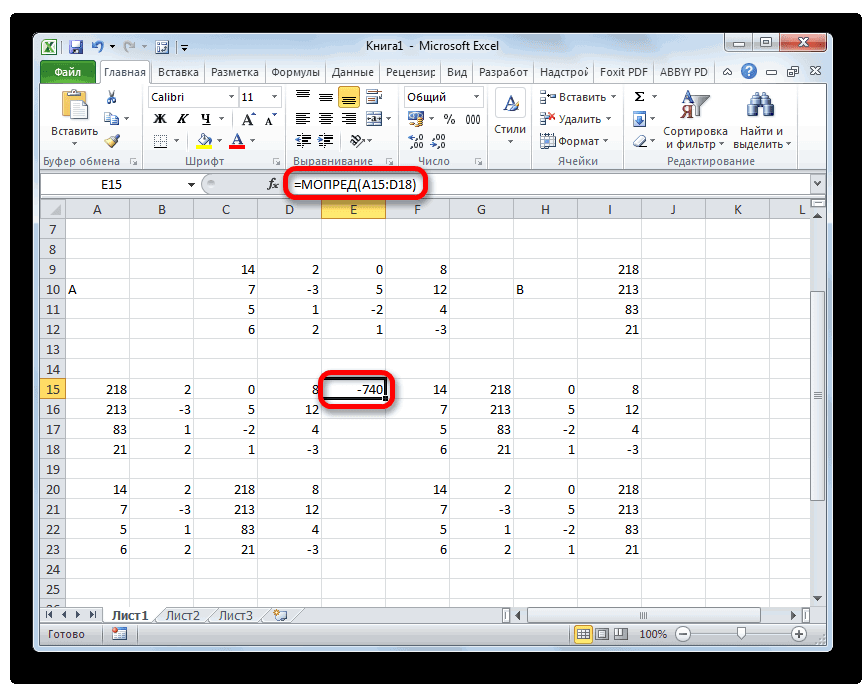
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
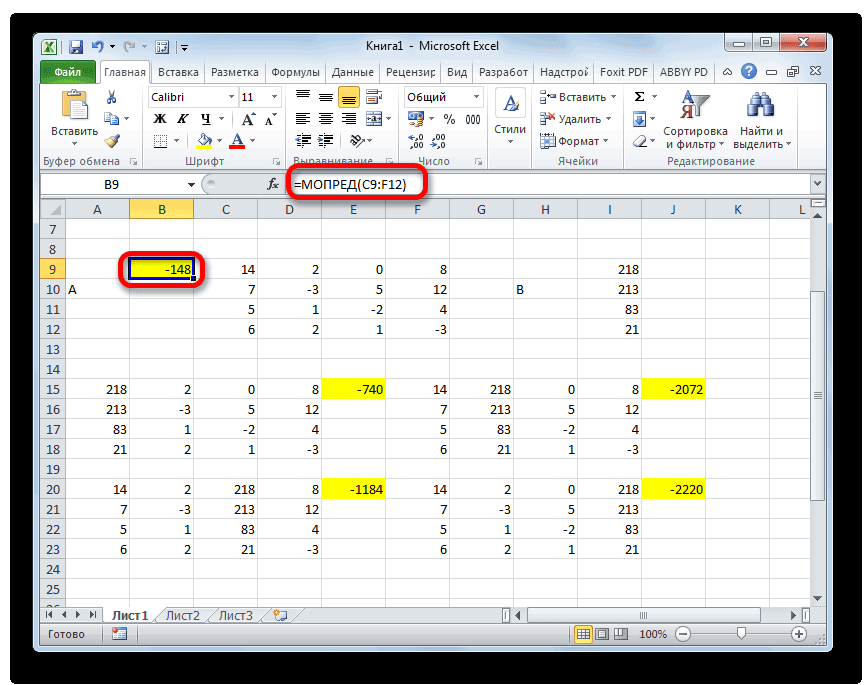
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12701 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
1. Решение нелинейных уравнений в MS Excel
1.1 Отделение корней
В общем виде любое уравнение одной переменной принято записывать так 

Например , для уравнения 

Рисунок 1. График функции 
1.2 Решение уравнений, используя инструмент “Подбор параметра”
Используя возможности Excel , можно находить корни нелинейного уравнения вида f ( x )=0 в допустимой области определения переменной. Последовательность операций нахождения корней следующая:
1. Производится вычисление значений функции в диапазоне вероятного существования корней от значений аргумента, изменяющегося с определенным шагом;
2. В таблице выделяются ближайшие приближения к значениям корней (пары соседних значений функции с разными знаками);
3. Используя средство Excel Подбор параметра, вычисляются корни уравнения.
2. Работа с матрицами в MS Excel . Решение систем уравнений.
Нахождение определителя матрицы
Перед нахождением определителя необходимо ввести матрицу в диапазон ячеек Excel в виде таблицы.
Для нахождения определителя матрицы в Excel необходимо:
· сделать активной ячейку, в которой в последующем будет записан результат;
· в меню Вставка – Функция в категории Математические выбрать функцию МОПРЕД и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы матрицы, и нажать OK .
Нахождение обратной матрицы
Для нахождения обратной матрицы необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы матрицы ( количество строк и количество столбцов должны равняться соответствующим параметрам исходной матрицы).
· в меню Вставка – Функция в категории Математические выбрать функцию МОБР и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы исходной матрицы, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Для перемножения матриц необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы результирующей матрицы.
· в меню Вставка – Функция в категории Математические выбрать функцию МУМНОЖ и нажать OK ;
· на втором шаге задать два диапазона ячеек с элементами перемножаемых матриц, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Решение системы уравнений в Excel .
Решение системы уравнений при помощи нахождения обратной матрицы.
Пусть дана линейная система уравнений.

Данную систему уравнений можно представить в матричной форме:




Матрица неизвестных вычисляется по формуле

где A -1 – обратная матрица по отношению к A .
Для вычисления уравнения в Excel необходимо:
· ввести матрицу A;
· ввести матрицу B;
· вычислить обратную матрицу по отношению к А ;
· перемножить полученную обратную матрицу с матрицей B .
Порядок выполнения работы
Задание 1
Найти все корни уравнения 2x 3 -15sin( x )+0,5x-5=0 на отрезке [-3 ; 3].
1. Построить таблицу значений функции f ( x ) для значений x от –3 до 3, шаг 0,2.
Для этого ввести первые два значения переменной x , выделить эти две ячейки, с помощью маркера автозаполнения размножить значения до 3.
Затем ввести формулу для вычисления f ( x ). Скопировать формулу с использованием маркера автозаполнения на весь столбец.
Из полученной таблицы находим, что значение функции трижды меняет знак, следовательно, исходное уравнение имеет на заданном отрезке три корня.
2. Выделить цветом пары значений x и f ( x ), где f ( x ) меняет знак (см .р исунок 2).
3. Построить график функции f ( x ).
Рисунок 2. Поиск приближенных значений корней уравнения
4. Скопировать рядом с таблицей произвольную пару выделенных значений x и f ( x ) (см .р исунок 3).
5. Выполнить команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 3) заполнить следующие поля:
þ Установить в ячейке : в поле указывается адрес ячейки, в которой записана формула правой части функции;
þ Значение : в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0);
þ Изменяя значение : в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула.
Рисунок 3. Диалоговое окно Подбор параметра для поиска первого корня
6. После щелчка на ОК должно получиться значение первого корня -1,65793685 .
7. Выполнить последовательно операции, аналогичные предыдущим, для вычисления значений остальных корней: -0,35913476 и 2,05170101 .
Задание 2
Решить систему уравнений:

1. Ввести значения элементов матриц A и B уравнения в ячейки Excel .
2. Вычислить обратную матрицу с помощью матричной функции МОБР.
3. Перемножить обратную матрицу A -1 на матрицу B с помощью матричной функции МУМНОЖ (Порядок умножения важен – первой должна идти матрица A -1 а второй B .)
4. Проверить правильность полученной матрицы корней X .
Контрольные вопросы
1. Порядок действий для решения нелинейного уравнения с помощью инструмента Подбор параметра MS Excel .
2. Порядок действий для решения системы уравнений матричным методом в MS Excel .
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
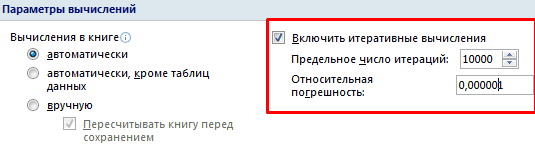
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
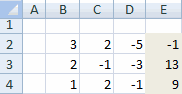
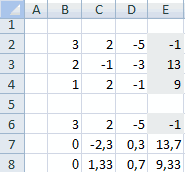
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
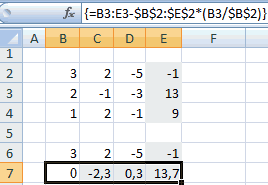
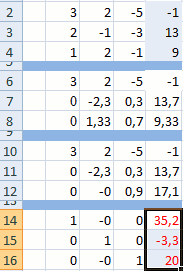
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
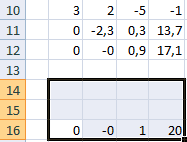
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.
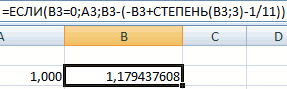
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
источники:
http://zf.bsut.by/it/fbo/zb1/lab2.htm
http://exceltable.com/otchety/reshenie-uravneniy
Содержание
- Варианты решений
- Способ 1: матричный метод
- Способ 2: подбор параметров
- Способ 3: метод Крамера
- Способ 4: метод Гаусса
- Вопросы и ответы
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
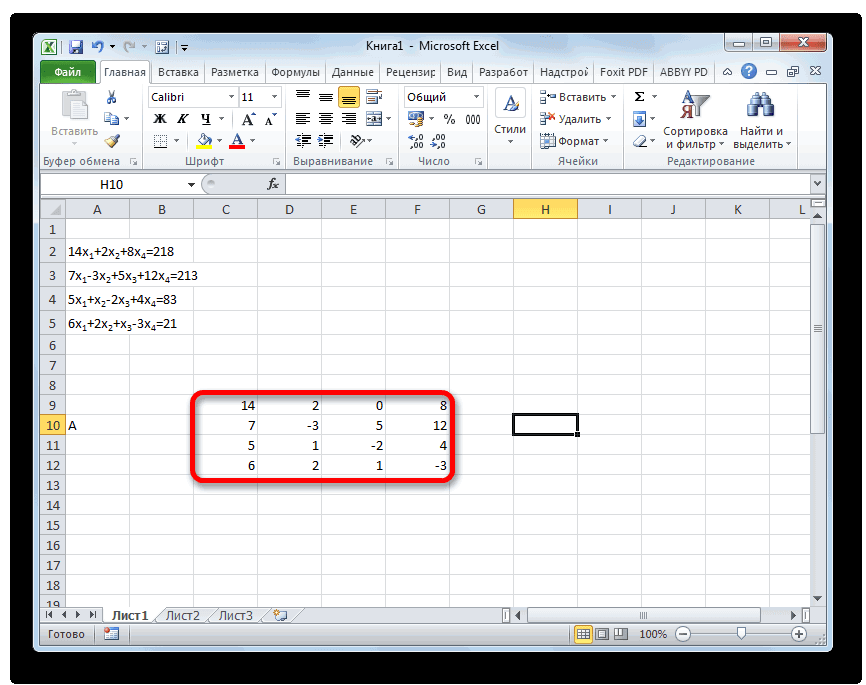
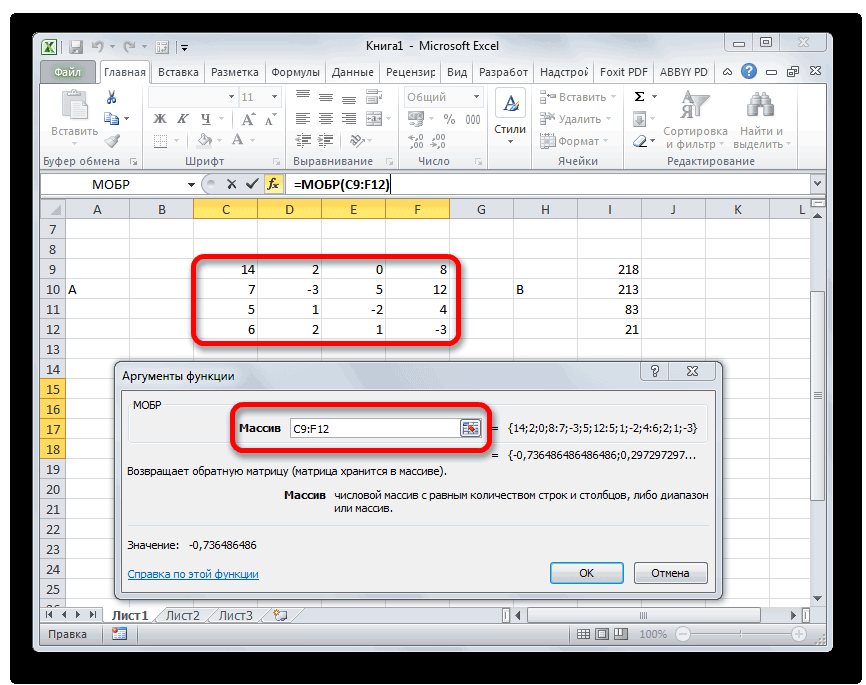
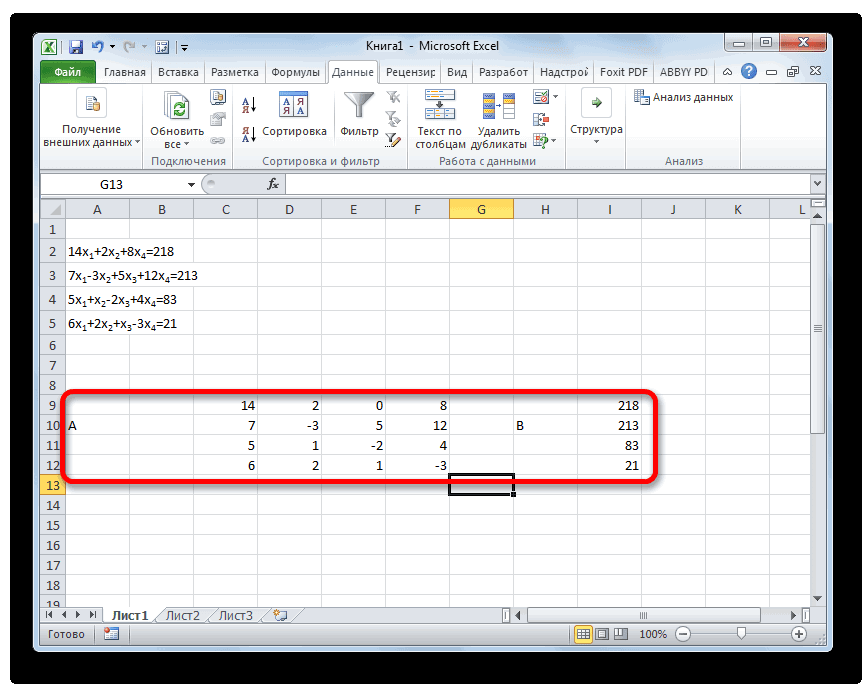
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
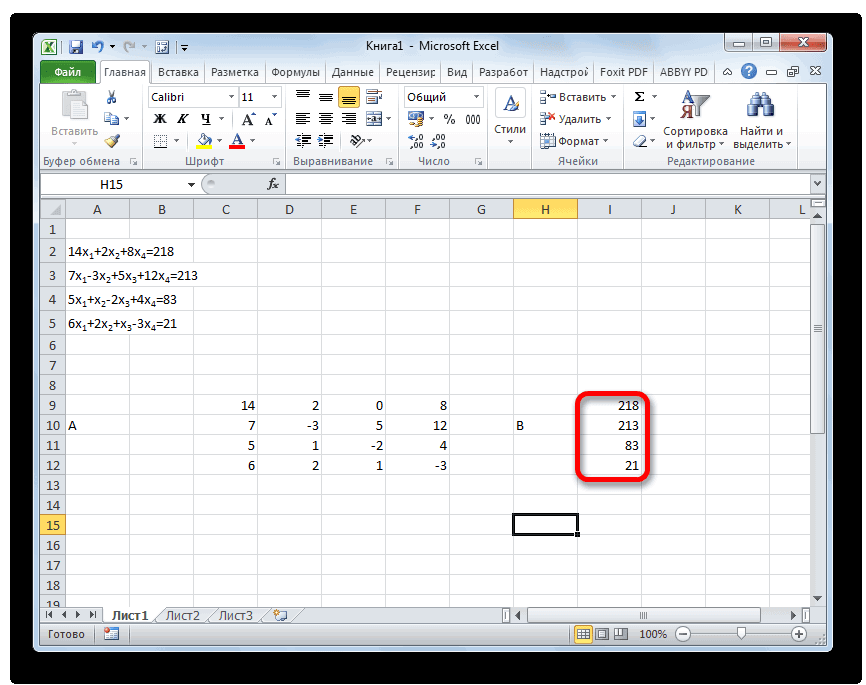
- Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
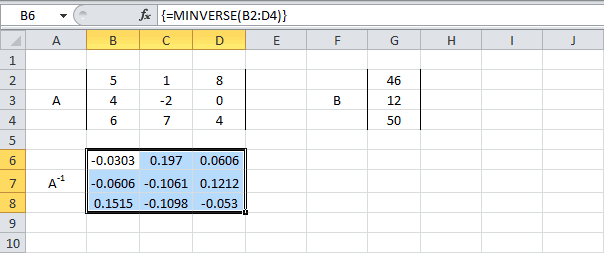
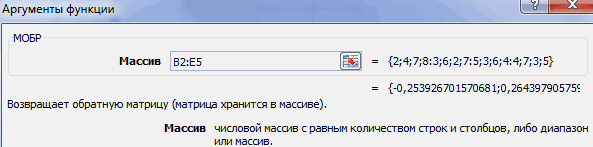
- Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:
=МОБР(массив)Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
- Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
- Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
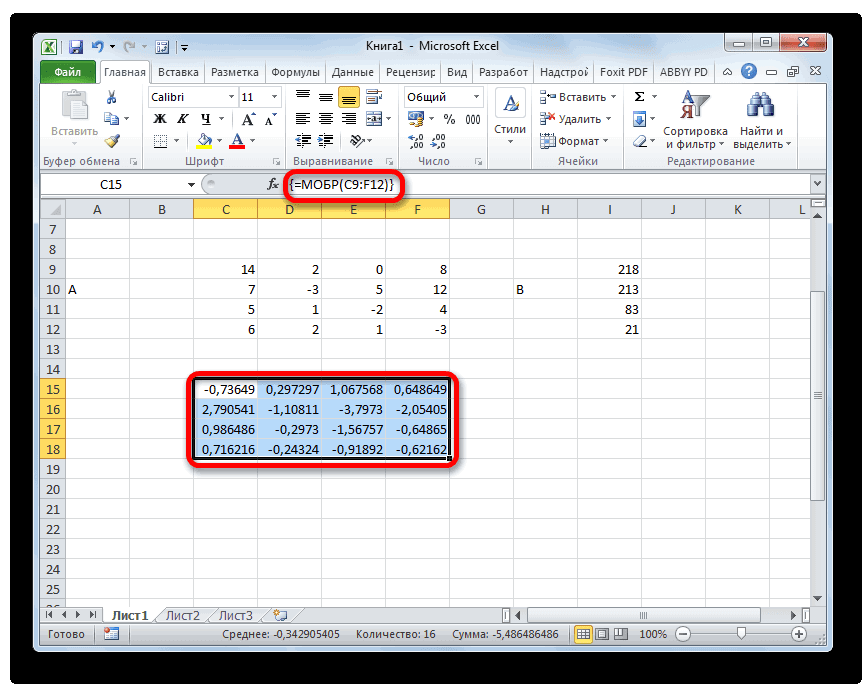
- Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
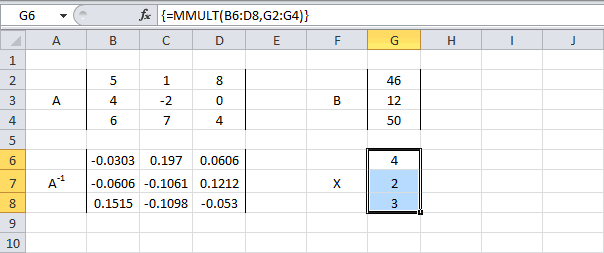
- Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
=МУМНОЖ(Массив1;Массив2)Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
- В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
- Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
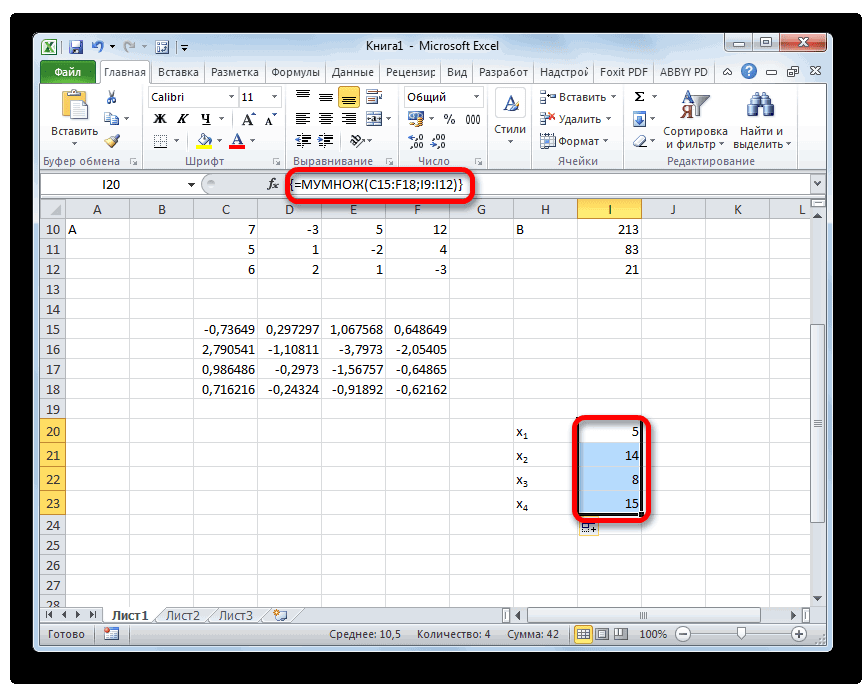
- После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.
Урок: Обратная матрица в Excel
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
3x^2+4x-132=0
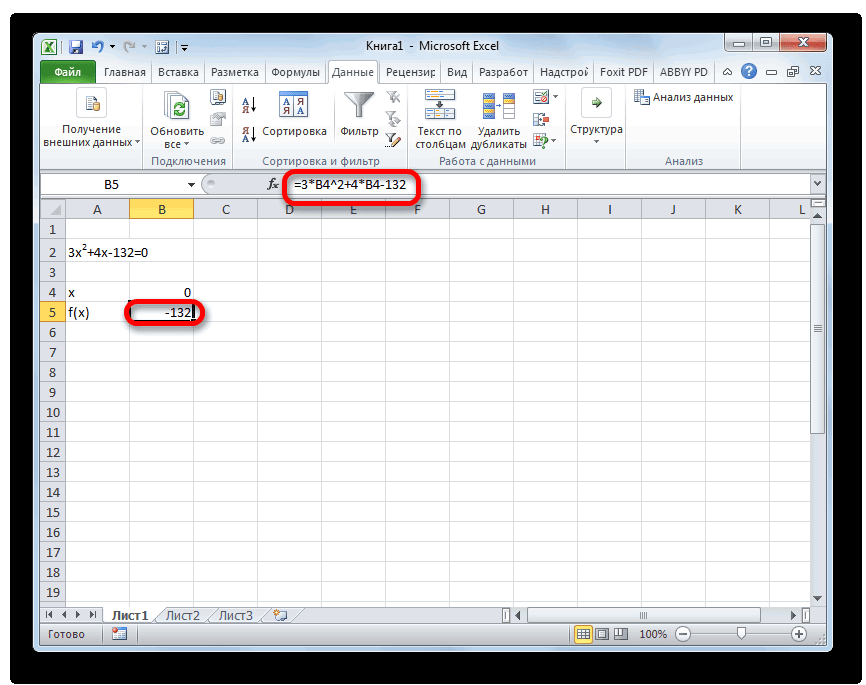
- Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
=3*x^2+4*x-132Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
- Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
- Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
- После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
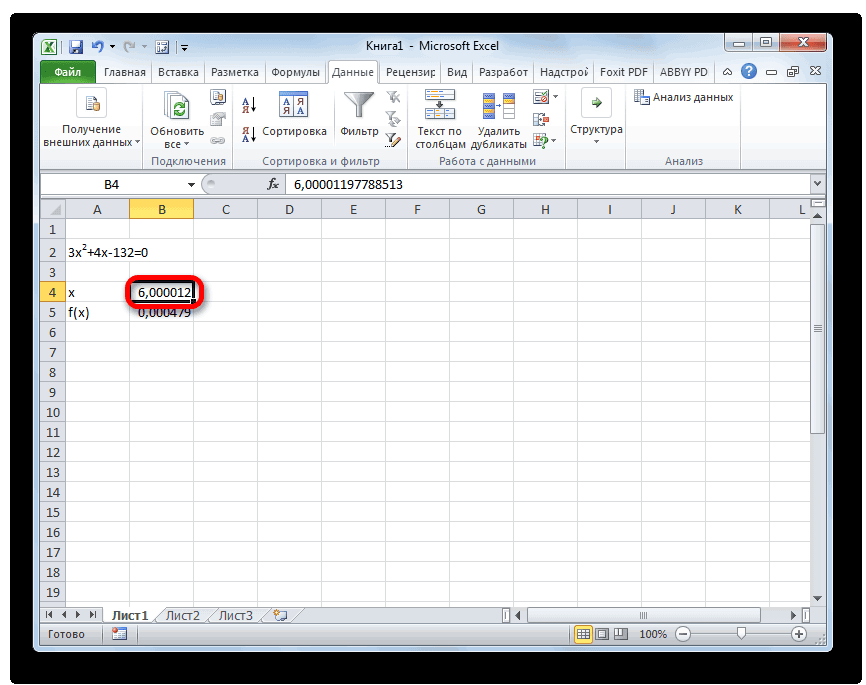
- Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Урок: Подбор параметра в Excel
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
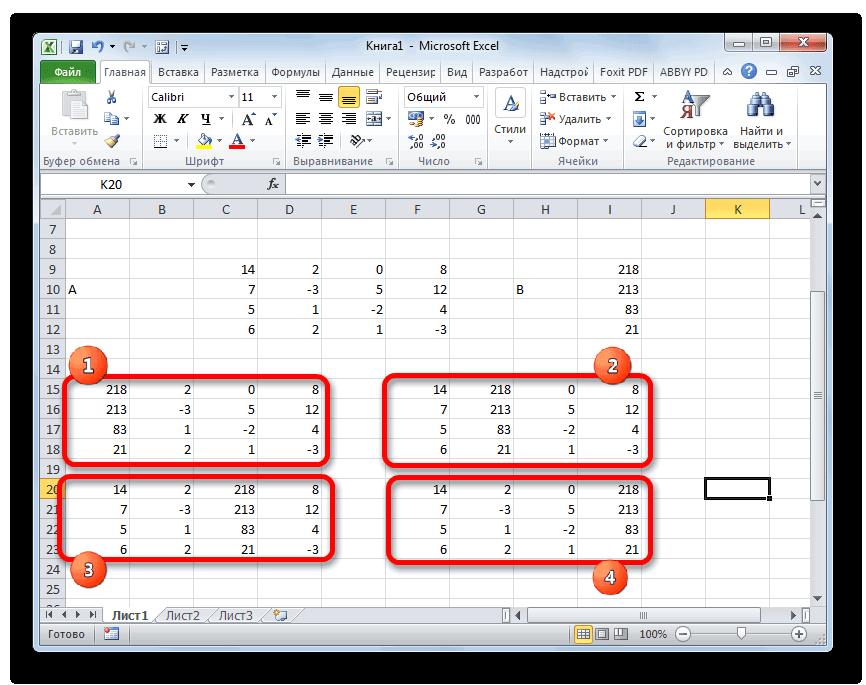
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
- Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
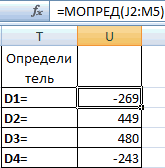
- Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
=МОПРЕД(массив)Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
- Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
- Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
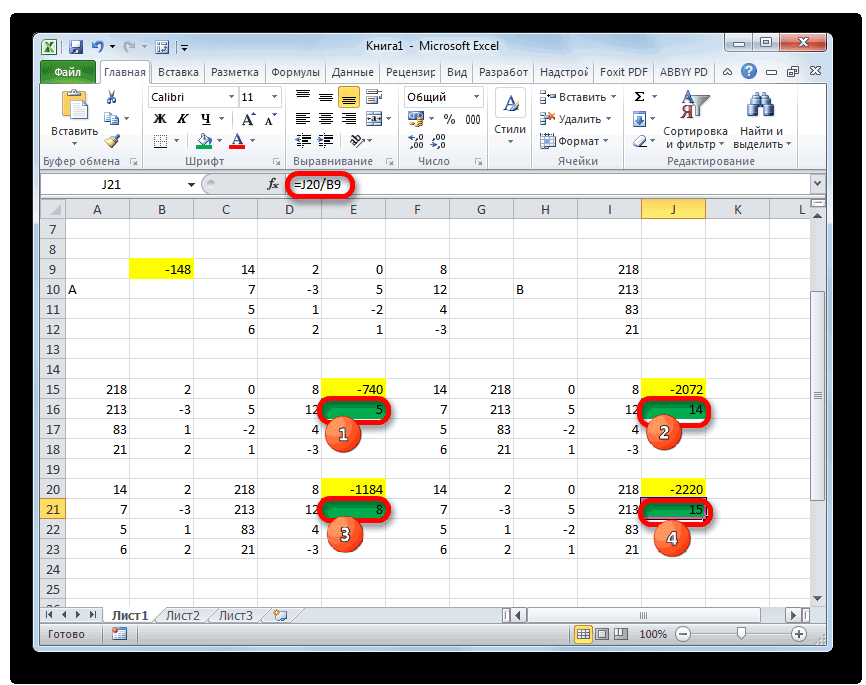
- Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
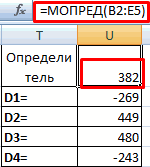
- Аналогичным образом производим подсчет определителей для остальных трех таблиц.
- На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
- Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.
Способ 4: метод Гаусса
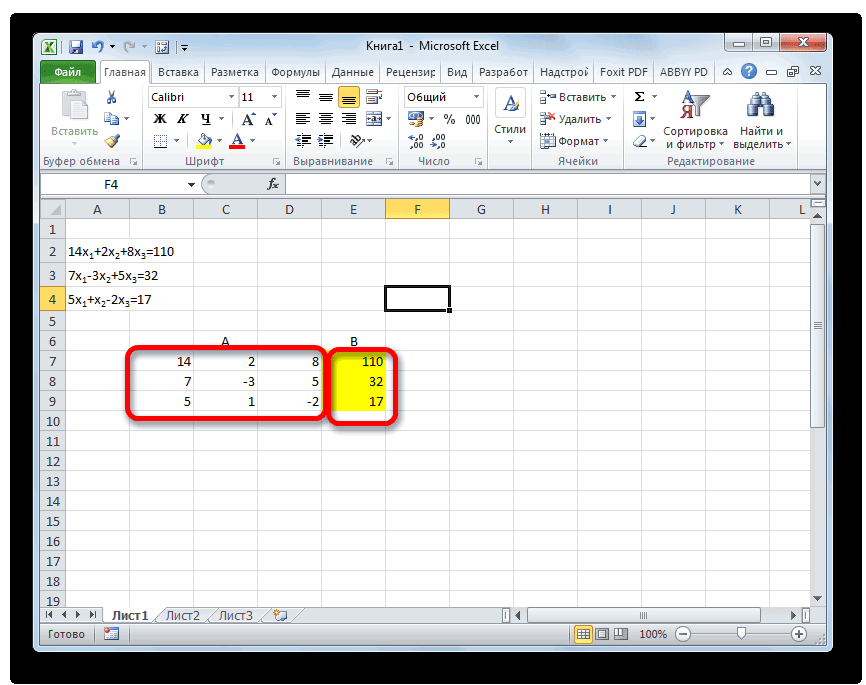
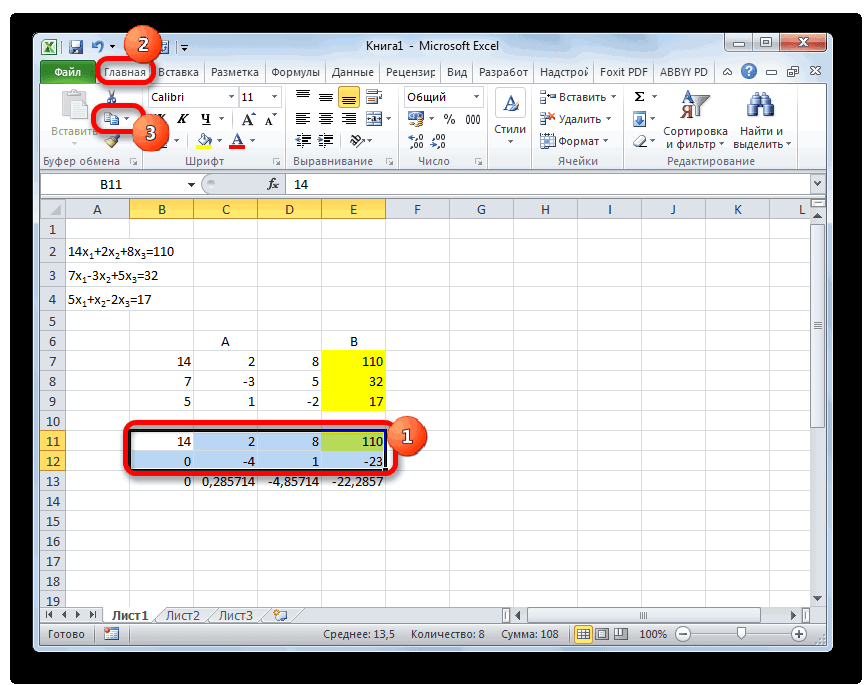
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
14x1+2x2+8x3=110
7x1-3x2+5x3=32
5x1+x2-2x3=17
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
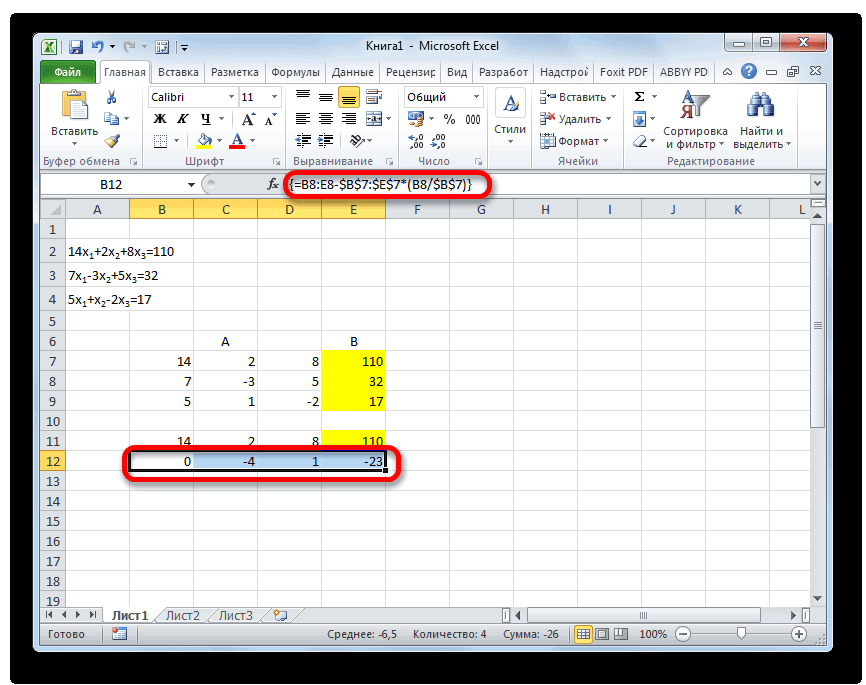
- Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
=B8:E8-$B$7:$E$7*(B8/$B$7)Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
- После этого копируем полученную строку и вставляем её в строчку ниже.
- Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
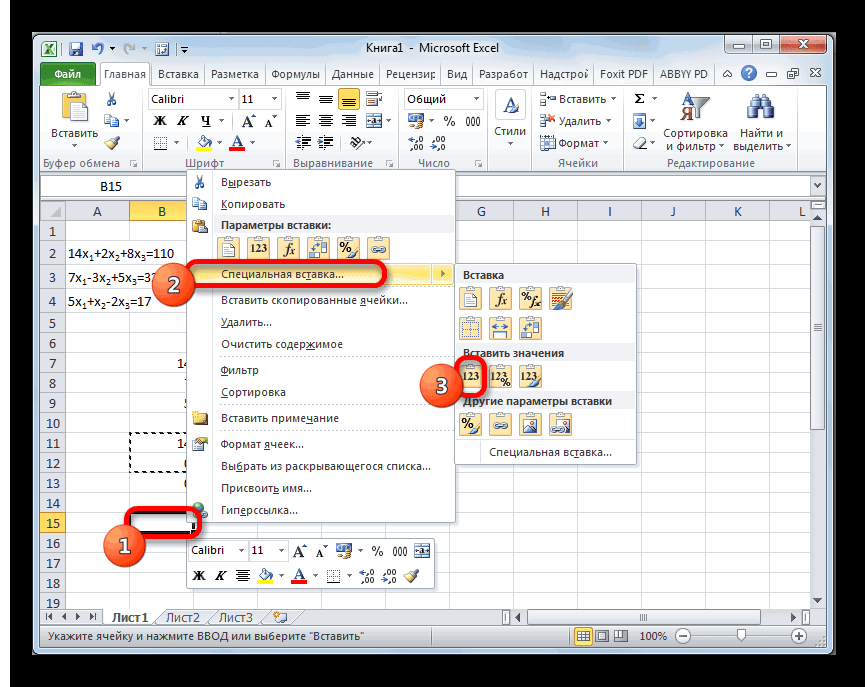
- Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
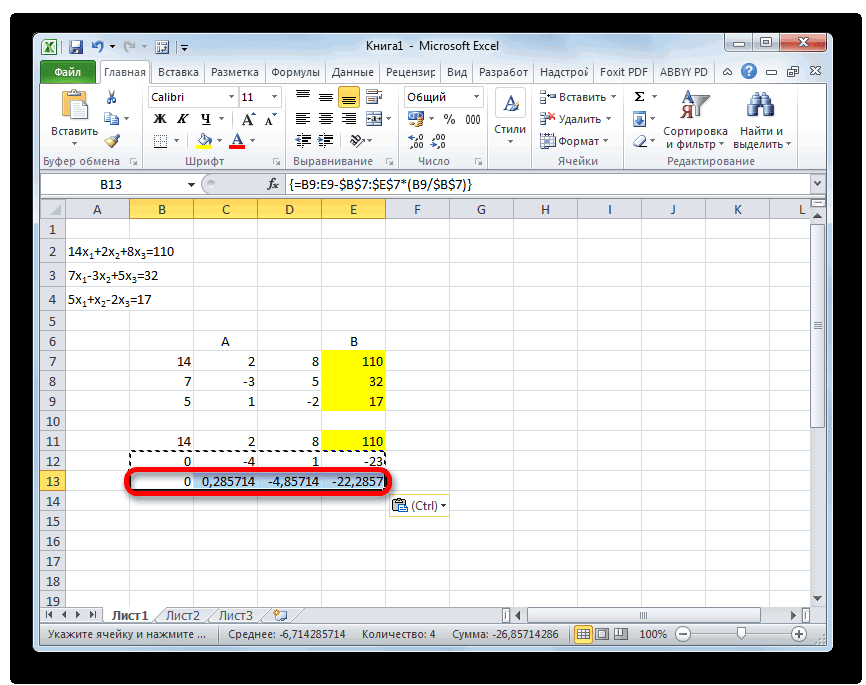
- В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
=B13:E13-$B$12:$E$12*(C13/$C$12)После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
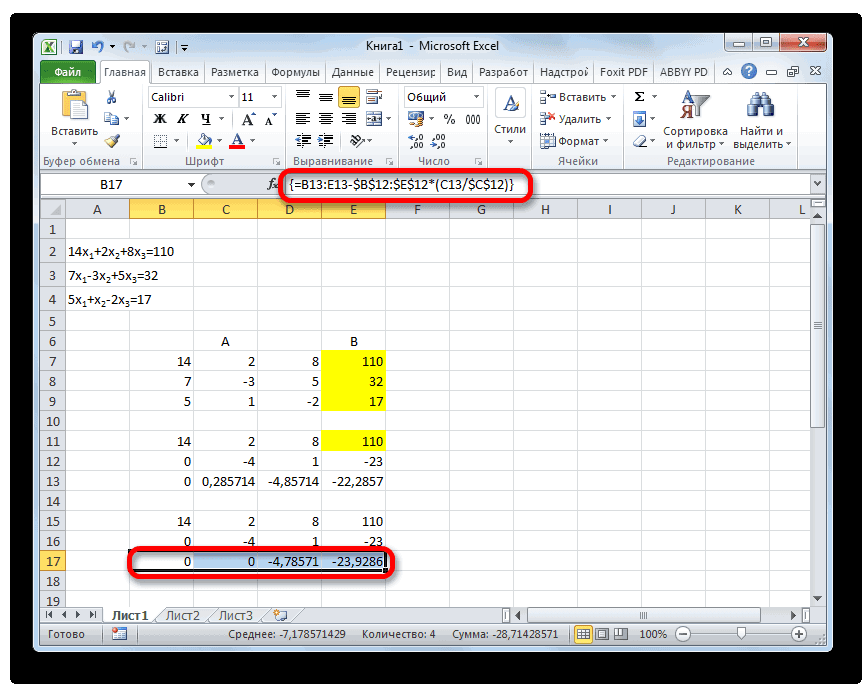
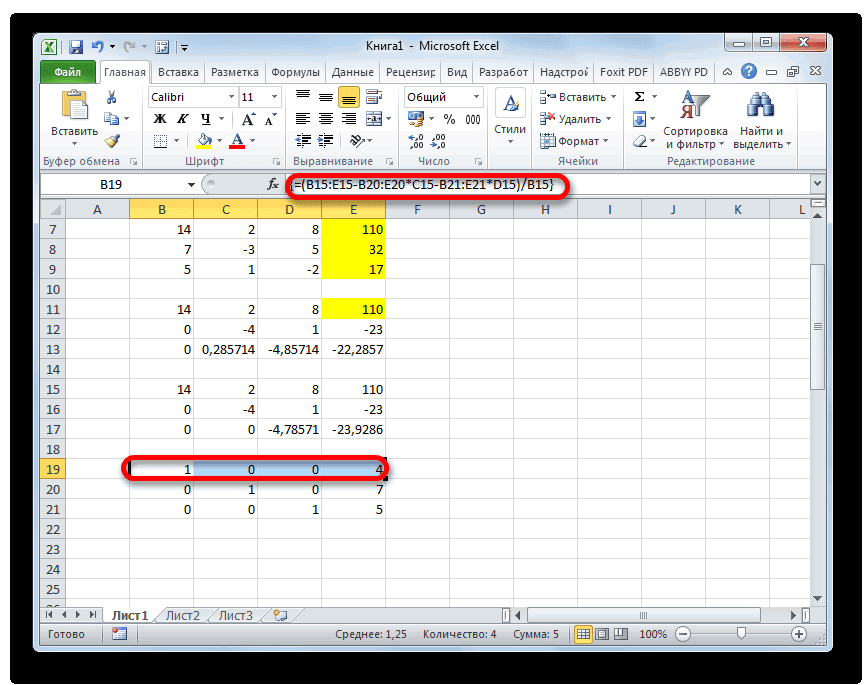
- Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
=B17:E17/D17Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
- Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
=(B16:E16-B21:E21*D16)/C16Жмем привычное уже нам сочетание клавиш для применения формулы массива.
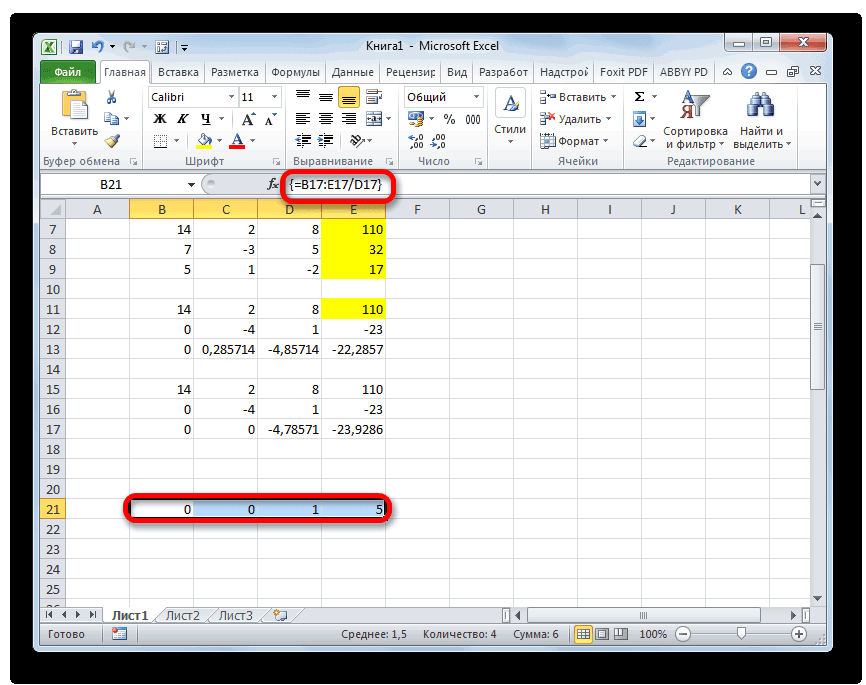
- Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
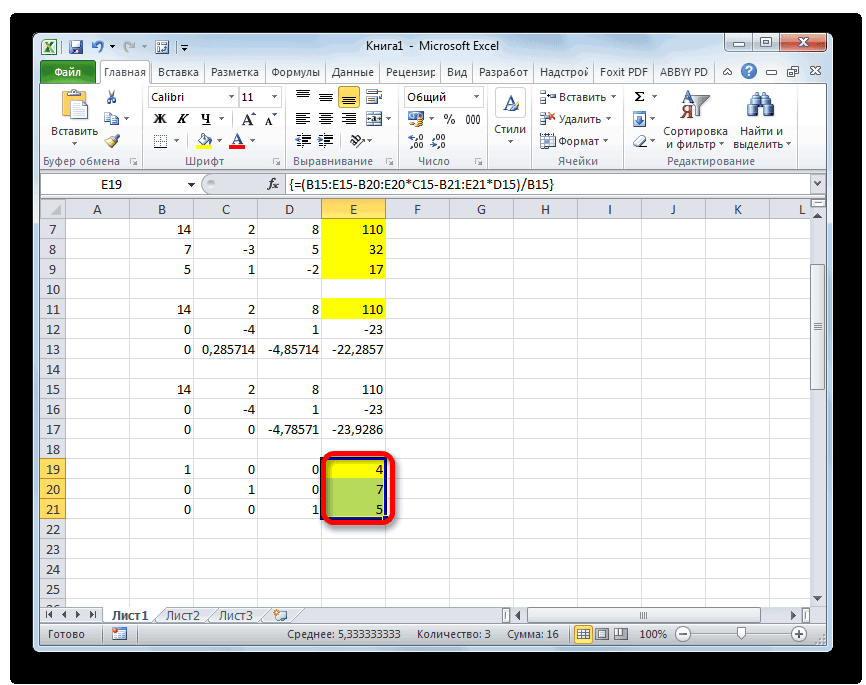
=(B15:E15-B20:E20*C15-B21:E21*D15)/B15Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Еще статьи по данной теме:
Помогла ли Вам статья?
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ НИЖЕГОРОДСКОЙ ОБЛАСТИ |
|
Государственное бюджетное профессиональное образовательное учреждение «Кстовский нефтяной техникум имени Бориса Ивановича Корнилова» |
|
|
СК-МД-15 |
Система качества образовательного учреждения |
|
Учебно-методическое пособие |
Н. В. КОЛДАЕВА
Использование табличного процессора MS Excel для численного решения систем линейных уравнений и вычисления определенного интеграла
Учебно-методическое пособие
для самостоятельной работы студентов
по дисциплине «Информатика и ИКТ»
Кстово 2015
Аннотация
Учебно-методическое пособие Использование табличного процессора MS Excel для численного решения систем линейных уравнений и вычисления определенного интеграла разработано для организации самостоятельной работы студентов и соответствует действующей программе по курсу дисциплины «Информатика и ИКТ» для темы «Возможности динамических (электронных) таблиц. Математическая обработка числовых данных» раздела «Технология создания и преобразования информационных объектов».
Кротко изложены основы технологии работы с табличным процессором MS Excel и основы численных методов решения математических задач для систем линейных уравнений и вычисления определенного интеграла. Приведена пошаговая реализация нахождения неизвестных для системы линейных уравнений и вычисления значения определенного интеграла на конкретных примерах с использованием MS Excel. Представлены индивидуальные задания для самостоятельной работы студентов.
Учебное пособие предназначено для студентов ГБОУ СПО «Кстовский нефтяной техникум им. Б.И. Корнилова», изучающих дисциплину «Информатика и ИКТ», а также для реализации математических моделей с помощью компьютера при выполнении расчетно-графических, курсовых и дипломных работ.
СОДЕРЖАНИЕ
Введение
1. Табличный процессор Excel и технология работы в нем
1.1. Структура документа MS Excel
1.2. Основной принцип работы электронных таблиц
1.3. Ввод информации в ячейки
1.4. Форматирование таблиц
1.5. Основные правила создания формул и функций
1.6. Способы и методы формирования в формулах ссылок на ячейки
2. Математическая постановка задач
2.1. Метод Крамера решения систем линейных уравнений
2.2. Приближенные методы вычисления определенного интеграла
3. Реализация решения математических задач в MS Excel
3.1. Решение систем линейных уравнений с использованием табличного процессора MS Excel
3.2. Нахождение значений определенного интеграла с использованием табличного процессора MS Excel
4. Методические указания по выполнению самостоятельной работы
5. Варианты заданий для самостоятельной работы
5.1. Варианты заданий систем линейных уравнений
5.2. Варианты заданий определенного интеграла
Список литературы
Введение
Учебно-методическое пособие для самостоятельной работы студентов разработано в соответствии с действующей программой по курсу дисциплины «Информатика и ИКТ» для темы «Возможности динамических (электронных) таблиц. Математическая обработка числовых данных» раздела «Технология создания и преобразования информационных объектов».
Учебно-методическое пособие содержит теоретический материал по технологии использования табличного процессора MS Excel и математическим методам решения систем линейных уравнений и приближенному вычислению определенного интеграла, который является основой для практического использования решения математических задач с помощью компьютерных технологий. В разделе «Реализация решения математических задач в MS Excel» приведены подробные пошаговые решения примеров решения системы линейных уравнений и приближенного вычисления интеграла, которые могут быть воспроизведены студентом самостоятельно. Для закрепления полученных навыков в соответствии предлагаемыми методическими указаниями студент должен выполнить индивидуальные задания и представить их на проверку преподавателю.
Содержание учебно-методического пособия отражает практическую направленность использования компьютера для решения профессиональных задач, так как большинство инженерных задач использующих математические методы требуют сложных длительных вычислений, которые существенно упрощаются и сокращаются при использовании компьютерных технологий. Полученные студентом знания и умения, в первую очередь, могут быть использованы при выполнении расчетно-графических, курсовых работ и. конечно, при выполнении дипломной работы.
1. Табличный процессор Excel и технология работы в нем
1.1. Структура документа MS Excel
MS Excel – это прикладная программа управления электронными таблицами, которая используется для выполнения вычислений, организации данных, анализа результатов и поиска оптимальных решений.
Базовыми понятиями в Excel являются: книга, лист, таблица, ячейка.
Структуру книги можно представить следующим образом (см. Рис.1).
. . . . . .
|
А |
В |
С |
D |
Е |
F |
. . . |
|
|
1 |
Уч. группа |
ФИО |
МАТЕМ |
ФИЗ |
СР. БАЛ |
||
|
2 |
12-ЭОП-31 |
ПЕТРОВ |
4 |
5 |
4,5 |
||
|
3 |
12-АСУ-21 |
ИВАНОВ |
5 |
3 |
4 |
||
|
4 |
Макс. Ср. бал. |
4,5 |
Рис. 1
Книга в Excel представляет собой файл с расширением xls. Имя книги (файла) задается при ее сохранении и должно напоминать о ее содержании. Каждая книга может состоять из нескольких поименованных листов (до 255, а по умолчанию – 3). Имя листа указано на ярлычке (внизу листа) и может быть изменено, чтобы напоминать о его содержании. Для перехода на другой лист надо щелкнуть ЛКМ (ЩЛКМ) по его ярлычку. Листы можно добавлять, удалять, копировать или переименовывать (ЩПКМ – щелчок правой кнопкой мыши по ярлычку и появится контекстное меню). Лист – это место для ввода, хранения и обработки данных. Лист Excel состоит из ячеек, каждая из которых имеет свой адрес. Ячейки образуют строки (до 65536) и столбцы (до 256). Строки имеют номера, а столбцы по умолчанию – буквенные имена (если стиль ссылок А1), или номера, если установлен стиль ссылок R1C1 (R – строка, а С – столбец). Стили ссылок задаются параметрами при работе с опциями меню «Сервис». Как правило, используется стиль А1.
1.2. Основной принцип работы электронных таблиц
Каждая ячейка листа может содержать текст, числовое значение или формулу и быть отформатирована.
Основной принцип работы электронных таблиц заключается в том, что одни ячейки рабочего листа используются как независимые переменные (влияющие ячейки), которым задаются значения из вне (например, пользователем), а другие ячейки используются как зависимые переменные (зависимые ячейки), которые содержат формулы, ссылающиеся на независимые переменные. Пользователь вводит исходные данные (текст или числа) во влияющие ячейки и формулы в зависимые ячейки, далее автоматически (или, в зависимости от настройки, по команде) производятся вычисления по формулам, и пользователь видит готовый результат в зависимых ячейках. Если же установить режим показа формул («Сервис Параметры»), то в зависимых ячейках будут видны только формулы.
|
А |
В |
С |
D |
E |
|
|
1 |
Уч. группа |
ФИО |
МАТЕМ |
ФИЗ |
СР. БАЛ |
|
2 |
12-ЭОП-31 |
ПЕТРОВ |
4 |
5 |
=СРЗНАЧ(С2:D2) |
|
3 |
12-АСУ-21 |
ИВАНОВ |
5 |
3 |
=СРЗНАЧ(С3:D3) |
|
4 |
Макс. Ср. бал. |
=МАКС(Е2:Е3) |
Если же режим показа формул не установлен, то в ячейке Е2 сразу появится результат (=4,5).
На листе может быть создана одна или несколько таблиц.
Таблица – это совокупность ячеек, связанных между собой по смыслу или с помощью формул в соответствии с задачей пользователя.
Ячейки таблиц, размещенных на разных листах книги или в разных книгах, также могут быть взаимосвязаны посредством формул. На основе таблицы (для наглядности при анализе исходных данных и результатов вычислений) может создаваться диаграмма, которую можно разместить на листе вместе с таблицей или на отдельном листе.
1.3. Ввод информации в ячейки
Как правило, построение таблицы начинается с заполнения заголовков столбцов (а, если необходимо, и строк, как на Рис.1), поясняющих содержание основных ячеек таблицы, в которых находятся исходные данные и формулы. Перед вводом информации в ячейку ее надо выделить с помощью ЩЛКМ по ячейке или с помощью клавиш перемещения курсора.
Существуют следующие основные способы ввода информации в ячейки:
1) Неавтоматизированный способ, при котором каждый символ вводится с клавиатуры. Он занимает много времени и имеет большую вероятность ошибок, но необходим тогда, когда в таблице нет повторяющейся, либо закономерно изменяющейся информации, что бывает очень редко.
Ввод информации должен быть зафиксирован. Это достигается либо нажатием клавиши ENTER или нажатием клавиш управления курсором на клавиатуре (стрелки ↑,←,↓,→). Для изменения (редактирования) информации в ячейке надо сначала 2 раза ЩЛКМ по ней. Например, на Рис. 1 в ячейках А2 и D4 записана информация, изменяющейся не закономерно, поэтому ее невозможно вводить иначе, чем в ручную с клавиатуры.
Полезно запомнить, что:
– при вводе в ячейку длинного предложения для перехода на новую строку (в той же ячейке) надо нажать ALT+ENTER.
– если при вводе обнаружена ошибка, то следует нажать на панели инструментов (ПИ) кнопку ОТМЕНИТЬ .
2) Автоматизированный способ, который может быть реализован двумя методами:
- копирования в буфер ранее заполненной ячейки (или группы ячеек), которые предварительно должны быть выделены, и последующей вставки из буфера в нужную область таблицы, предварительно выделив левую верхнюю ячейку этой области. Для выделения группы смежных ячеек надо выделить первую ячейку диапазона, затем нажать и удерживая SHIFT выделить последнюю ячейку диапазона.
- автозаполнение рядов. Ряд – это группа смежных ячеек, принадлежащая одному столбцу или строке и содержащая одинаковую или закономерно изменяющуюся информацию.
Перед автозаполнением надо записать в начальную ячейку текст, число, дату, формулу и т.п., затем выделить эту ячейку и установить указатель мыши над маркером заполнения (маленького черного квадрата в правом нижнем углу выделенной ячейки). При этом вид указателя мыши меняется на знак +, означающий, что автозаполнение разрешено. Затем, нажав ЛКМ, перетащить указатель по ячейкам, которые нужно заполнить информацией и отпустить ЛКМ. При перемещении указателя вниз или вправо, автозаполнение создает в отмечаемых ячейках возрастающие значения, при перемещении указателя вверх или влево отмечаемые ячейки заполняются убывающими значениями.
Если в первоначально выделенной ячейке не распознается закономерность для возрастания или убывания, то ячейки просто дублируются.
Так, например, если в первой ячейке была запись «Блок1», то при перемещении указателя вниз, в последующих ячейках автоматически появятся записи «Блок2», «Блок3» и т.д. В то же время, если в первой ячейке было записано слово «Блок», то в последующих ячейках это слово просто дублируется.
В нашем примере, ячейку Е3 (Рис. 1) целесообразно заполнять с помощью метода автозаполнение рядов, т.е. не вводить в нее формулу, а распространив автозаполнением в нее содержимое ячейки Е2. При этом содержимое формулы Е3 (аргументы функции СРЗНАЧ()) будут отличаться от аргументов этой же функции для ячейки Е2 по условию автозаполнения:
для Е2: =СРЗНАЧ(С2:D2);
для Е3: =СРЗНАЧ(С3:D3).
Существует и другая возможность автозаполнения рядов – через главное меню: для копирования одной ячейки в несколько смежных или для настройки закономерности автозаполнения можно воспользоваться командой «ПРАВКА ЗАПОЛНИТЬ …».
1.4. Форматирование таблиц
Форматирование в MS Excel осуществляется почти так же, как и в других приложениях MS Office.
Для облегчения визуального поиска в таблице требуемой информации целесообразно заголовки столбцов и строк таблицы выделять цветом, отличительным (от другого текста) шрифтом, заливкой, граничной линией и т.п. В некоторых случаях, для более полного восприятия заголовка, целесообразно объединять ячейки.
Для выполнения вышеуказанных действий используется операция форматирования.
Объектом форматирования могут быть отдельные ячейки или группа ячеек (диапазон), которые предварительно должны быть выделены. ЩПКМ по выделенному объекту приводит к вызову контекстного меню, в котором следует выбрать пункт «формат ячеек».
Для изменения ширины столбцов или высоты строк таблицы надо поместить указатель мыши (УМ) между соответствующими именами столбцов или номерами строк листа и, удерживая ЛКМ, передвинуть УМ на нужное расстояние.
Если новая таблица содержит компоненты уже существующей таблицы, то целесообразно скопировать созданную таблицу в другую область листа или на другой лист (книгу) и отредактировать ее под условия создаваемой новой таблицы: удалить (или добавить) столбцы, строки или некоторые ячейки. Для работы с этими объектами их надо выделить.
Чтобы выделить целиком строку надо ЩЛКМ по ее номеру, а для столбца – по его имени. После этого ЩПКМ по выделенному объекту вызвать контекстное меню, из которого затеем выбрать, в соответствие с операцией, пункты «Удалить» или «Добавить ячейки». (Для вставки строки надо выделить строку ниже, а для столбца – выделить столбец правее вставляемого).
1.5. Основные правила создания формул и функций
Каждая формула начинается со знака равенства «=». Знак равенства указывает процессору MS Excel на то, что следующий за ним текст является формулой. В формулах могут присутствовать арифметические операторы для выполнения действий над константами или числами, которые могут вводиться непосредственно с клавиатуры, либо содержаться в других ячейках. В последнем случае в формуле указываются адреса этих ячеек, т.е. ссылки на них. Если в формуле присутствуют несколько арифметических операторов, то в нее можно включить скобки для определения порядка вычислений. В формулах применяют стандартные арифметические операции и соответствующие операторы: сложение (+), вычитание (-), умножение (*), деление (/), возведение в степень (^), (последовательность выполнения операций такая же, как и в арифметике). Также в формулах могут применяться функции из набора встроенных в Excel функций. Большое количество функций (около 500) в значительной степени определяет область использования Excel. Из набора этих функций, которые сгруппированы по категориям, мы будем использовать следующие: Математические, Статистические, Ссылки и массивы, Логические. В логических функциях для обозначения операций сравнения двух чисел используются операции и соответствующие операторы сравнения: равно (=), больше (>), меньше (<), больше или равно (>=), меньше или равно (<=), не равно (<>), логическое сложение «ИЛИ» (+), логическое умножение «И» (*). Результатом выполнения операции сравнения является логическое значение ИСТИНА или ЛОЖЬ.
Формула является основным средством для анализа данных. С помощью формул можно складывать, умножать и сравнивать данные, осуществлять их поиск и т.п. Формулы могут ссылаться на ячейки текущего листа, листов той же книги или других книг.
В следующем примере «=(В4+25)/СУММ(D5:F5)» складывается значение ячейки B4 с константой 25. Полученный результат делится на сумму значений в диапазоне ячеек D5:F5, т.е. на результат операции D5+E5+F5.
В данном примере выражение «СУММ(…)» является функцией, т.е. стандартной формулой.
При решении конкретной задачи для создания функции целесообразно использовать так называемый Мастер функций и действовать в следующем порядке:
- Выделить ячейку, в которую будет вставляться функция.
- Запустить МАСТЕР ФУНКЦИЙ (на панели инструментов значок
, либо «ГЛАВНОЕ МЕНЮ/ВСТАВКА/ФУНКЦИЯ»).
- Задать в нужную категорию функции (это определяется интуицией или методом перебора).
- выделить требуемую функцию, прочитать пояснения внизу окна.
- Если все понятно, то нажать — «ОК».
- На появившейся панели формул, ввести требуемую информацию в соответствующие окна аргументов.
Ввод информации в окна, как правило, осуществляется так:
- установить курсор в окно (в первое окно он устанавливается автоматически);
- выделить нужные ячейки мышью, установить курсор в другое окно и т.д.
Если нужные ячейки не видны, то надо свернуть панель формул, нажав на красную кнопку в правой части окна ввода, затем выделить ячейки и развернуть панель формул, снова нажав на красную кнопку
в правой части окна. Если же пояснений в этом окне недостаточно, то следует закрыть окно МАСТЕРА ФУНКЦИЙ и использовать справочную систему, для чего надо:
- ЩЛКМ по знаку вопроса
в Горизонтальном меню и выполнить команду: «ВЫЗОВ СПРАВКИ / ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ / (ввести фразу «функции») / ОБЗОР / (нажать кнопку «Вывести») / (выбрать нужную категорию (раздел), например, «Статистические функции») / (нажать кнопку «Вывести») / (выбрать нужную функцию, например, «СРЗНАЧ») / (прочитать подробное ее описание и рассмотреть примеры). Выписать наиболее общий пример в тетрадь, закрыть справочную систему.
- По аналогии с примером, используя МАСТЕР ФУНКЦИЙ, создать нужную функцию и, изменяя исходные данные, проверить ее корректность.
В Excel можно создавать так называемые вложенные функции, т.е. функции, аргументами которых являются другие функции. Возможно до 7 уровней вложения. В этом случае для вставки аргумента-функции, после того как будет открыта панель исходной функции, надо открыть левое окно строки формул (щелкнув по «стрелке вниз»), выбрать нужную функцию и далее действовать, как и с обычной функцией.
Как правило, формулы используются для определения их значений в зависимости от параметров (исходных данных), т.е. констант и переменных. Однако в Excel есть возможность решать и обратные задачи («какой должна быть переменная, чтобы формула приняла заданное значение?»), т.е. определять значение переменной, причем только одной, если задать значение результата вычисления формулы. Для этого надо выделить ячейку для искомой переменной и задать ей ориентировочное значение, а затем выполнить команду «СЕРВИС / ПОДБОР ПАРАМЕТРА» и, в появившемся окне, указать запрашиваемые данные.
В формулах для обращения к ячейкам, в зависимости от решаемой задачи, применяются различные способы и методы ссылок на ячейки.
1.6. Способы и методы формирования в формулах ссылок на ячейки
Ссылкой однозначно определяется ячейка или группа (диапазон) ячеек листа, используемых в формуле. С помощью ссылок можно использовать в формуле данные, находящиеся в различных местах листа, а также использовать значение одной и той же ячейки в нескольких формулах. Кроме того, можно ссылаться на ячейки, находящиеся на других листах книги или в другой книге, или на данные другого приложения.
Ссылки на ячейки других книг называются внешними ссылками. Ссылки на данные других приложений называются удаленными ссылками.
В Excel можно выделить три способа формирования ссылок: координатный относительно листа книги, координатный относительно таблицы и именной.
При координатном способе адрес ячейки определяется местом пересечения столбца и строки листа книги или таблицы.
При именном способе адрес ячейки определяется текстовым именем ячейки (или диапазона ячеек), которое напоминает о содержании ячеек.
- Координатный способ формирования ссылок относительно листа книги
До настоящего момента мы уже использовали именно такой способ, но к вышесказанному необходимо добавить следующее:
- Чтобы создать ссылку на диапазон ячеек, надо активизировать ячейку левого верхнего угла диапазона, поставить двоеточие (:), а затем — активизировать ячейку правого нижнего угла диапазона. Например, в формуле =СУММ(A1:В2) определяется сумма чисел, записанных в четырех ячейках: А1, А2, В1, В2.
- В формулах Excel используется два метода ссылок на ячейки:
- относительные ссылки, которые ссылаются на ячейки относительно позиции формулы (т.е. если формулу с относительными ссылками скопировать, например, через буфер, в другую ячейку, то ссылки в ней изменятся на количество строк и столбцов относительно ее исходного расположения);
- абсолютные ссылки, которые всегда ссылаются на одни и те же ячейки независимо от изменения места расположения формулы после копирования. Для задания абсолютной ссылки в формуле надо перед именем столбца и номером строки ячейки добавить знак $. Пример: $А$2 (если в формуле указана ссылка А2 – то это относительная ссылка).
- Координатный способ формирования ссылок относительно таблицы
Для ссылок в формулах на ячейки можно использовать заголовки столбцов и строк таблицы, что делает формулу более наглядной.
Например, если в столбце с заголовком «Физика» содержатся средние баллы экзаменационных оценок по физике полученных соответствующим курсом, а заголовками строк являются «Курс11», «Курс21», «Курс31», то, создав формулу « =Физика Курс31» в любом месте листа, можно определить средний балл по физике полученный курсом №31. Пробел между заголовками является оператором пересечения диапазонов, который предписывает формуле вернуть значения из ячейки, находящейся в пересечении строки «Курс31» и столбца «Физика».
- Именной способ формирования ссылок
Использование имен может упростить понимание формулы. Например, формула «=X*SIN(X)» более привычна, чем «=А1*SIN(A1)» или формула «=МАКС(Возраст)» проще для понимания, чем формула «=МАКС(C20:C30)». В этом примере имя «Возраст» представляет группу ячеек «C20:C30». Имена можно использовать на любом листе книги.
Чтобы присвоить имя ячейке или группе ячеек нужно:
1. Выделить ячейку или диапазон ячеек, которому необходимо присвоить имя.
2. Щелкнуть ЛКМ по окну имени, которое находится слева в строке формул (это строка, расположенная над заголовками столбцов).
3. Ввести имя ячейки.
4. Нажать клавишу ENTER.
Другой способ:
- выделить диапазон ячеек;
- выполнить команду «ВТАВКА / ИМЯ / ПРИСВОИТЬ». Появится окно, в котором можно присвоить, изменить или удалить имя.
По умолчанию имена являются абсолютными ссылками.
2. Математическая постановка задач
2.1. Метод Крамера решения систем линейных уравнений
Рассмотрим метод Крамера решения систем линейных уравнений для системы из трех уравнений с тремя неизвестными x1, x2 и x3, которая имеет вид:
Необходимо найти значение главного определителя, составленного из коэффициентов при неизвестных, т.е. , а также еще трех определителей, получаемых из главного путем замены первого, второго и третьего столбца на столбец свободных членов в исходной системе уравнений, т.е. ,
и
.
Тогда исходная система будет равносильна системе вида:
Если все четыре определителя отличны от нуля, то система имеет единственное решение. Значение неизвестных определяются в виде:
;
и
.
Метод Крамера может быть использован для решения систем линейных уравнений, состоящих из четырех и более уравнений, содержащих, соответственно, четыре и более неизвестных. Однако, для вычисления определителей четвертого и выше порядков следует использовать специальные приемы, которые требуют значительных временных затрат и особого внимания при выполнении вычислений. Выполнение вычислений с помощью MS Excel существенного упрощает решение подобных задач.
2.2. Приближенные методы вычисления определенного интеграла
Значение определенного интеграла численно равно площади так называемой криволинейной трапеции, ограниченной кривой, определяемой подынтегральной функцией y=f(x), прямыми x=a, x=b и осью Ox.
Приближенные методы вычисления определенного интеграла сводятся к замене площади вышеуказанной криволинейной трапеции ступенчатой фигуры, состоящей из прямоугольников или прямолинейных трапеций.
Площадь криволинейной трапеции разбивают на n прямоугольников, высоты которых равны y0, y1, y2, …, yn-1 и основания .
Если суммировать площади прямоугольников, которые покрывают площадь криволинейной трапеции с недостатком, то значение определенного интеграла может быть вычислено по формуле: .
Если суммировать площади прямоугольников, которые покрывают площадь криволинейной трапеции с избытком (рис. 10.6, б), то значение определенного интеграла может быть вычислено по формуле: .
Значения y0, …, yn находят из равенства yk=f(a+kΔx), k=0, 1, …, n. Эти формулы называются формулами прямоугольников и дают приближенный результат. С увеличением n результат становится более точным.
Геометрический смысл следующего способа приближенного вычисления интеграла состоит в том, что нахождение площади криволинейной трапеции заменяется нахождением площади приблизительно равновеликой «прямоугольной» трапеции.
Пусть необходимо вычислить площадь A1AmBB1 криволинейной трапеции, выражаемую формулой .
Заменим дугу AmB хордой АВ и вместо площади криволинейной трапеции A1AmBB1 вычислим площадь трапеции A1ABB1: , где АА1 и ВВ1 – основание трапеции, а А1В1 – ее высота.
Обозначим f(a)=A1A, f(b)=B1B. Высота трапеции A1B1=b—a, площадь . Следовательно,
или
. Это так называемая малая формула трапеций.
Для получения более точного результата необходимо разбить площадь криволинейной трапеции на n площадей ординатами, отстоящими друг от друга на расстоянии Δx. Суммируем площади получившихся трапеций: S=S1+S2+S3+ … +Sn, где по малой формуле трапеций ;
;
; …,
.
Сложив, получим или
.
Так как и
, то можно записать так называемую большую формулу трапеций:
, где y0, y1, y2, …, yn – значения подынтегральной функции при значениях аргумента, соответственно, a; a+Δx; a+2Δx; a+(n-1)Δx; b.
3. Реализация решения математических задач в MS Excel
3.1. Решение систем линейных уравнений с использованием табличного процессора MS Excel
В качестве примера рассмотрим систему уравнений:
- Оформить заголовок в строке 1 на листе 1 «Решение системы линейных уравнений».
- В области B3:F6 ввести исходные данные, как показано на рисунке 2.
- Ввести в ячейку A8 текст заголовка «Метод Крамера».
- В ячейку A11 ввести текст «Δ=» (выравнивание по правому краю).
- Скопировать исходные данные C4:E6 в область В10:D12. Это главный определитель системы.
- Скопировать содержимое ячейки A11 в ячейку F11.
- В ячейку G11 ввести формулу «=МОПРЕД(B10:D12)». Получаем значение главного определителя системы.
- Скопировать исходные данные C4:E6 в область В14:D16. Скопировать исходные данные F4:F6 в область В14:B16. Это определитель для первого неизвестного x1.
- В ячейку A15 ввести текст «Δx1=» (выравнивание по правому краю).
- Скопировать содержимое ячейки A15 в ячейку F15.
- В ячейку G15 ввести формулу «=МОПРЕД(B14:D16)». Получаем значение определителя для первого неизвестного x1.
- Скопировать исходные данные C4:E6 в область В18:D20. Скопировать исходные данные F4:F6 в область C18:C20. Это определитель для второго неизвестного x2.
- В ячейку A19 ввести текст «Δx2=» (выравнивание по правому краю).
- Скопировать содержимое ячейки A19 в ячейку F19.
- В ячейку G19 ввести формулу «=МОПРЕД(B18:D20)». Получаем значение определителя для второго неизвестного x2.
- Скопировать исходные данные C4:E6 в область В22:D24. Скопировать исходные данные F4:F6 в область D22:D24. Это определитель для третьего неизвестного x3.
- В ячейку A23 ввести текст «Δx3=» (выравнивание по правому краю).
- Скопировать содержимое ячейки A23 в ячейку F23.
- В ячейку G23 ввести формулу «=МОПРЕД(B22:D24)». Получаем значение определителя для третьего неизвестного x3.
- В ячейки H15, H19 и H23 ввести соответственно текст «x1=», «x2=» и «x2=» (выравнивание по правому краю).
- В ячейку I15 ввести формулу «=G15/$G$11» (выравнивание по левому краю). Получаем значение первого неизвестного x1.
- Скопировать содержимое ячейки I15 в ячейку I19. Получаем значение второго неизвестного x2.
- Скопировать содержимое ячейки I15 в ячейку I23. Получаем значение третьего неизвестного x3.
Рис. 2
3.2. Нахождение значений определенного интеграла с использованием табличного процессора MS Excel
В качестве примера рассмотрим нахождение значения определенного интеграла при числе разбиения интервала интегрирования n=10. Следует отметить, что точное значение данного интеграла может быть получено аналитическим методом (метод замены переменной) и оно равно 2.
- Оформить заголовок в строке 1 на листе 2 «Нахождение значения определенного интеграла».
- В ячейку A3 с помощью редактора формул вставим вид вычисляемого интеграла как показано на рисунке 3.
- В ячейки E3, E4, E5 и E6 соответственно введем текст: «нижний предел интегрирования», «верхний предел интегрирования», «число разбиений отрезка интегрирования» и «шаг интегрирования».
- В ячейки D3, D4, D5 введем исходные данные, определяющие пределы интегрирования и число разбиений отрезка интегрирования (в нашем примере это числа: 0, 5, 10) (выравнивание по центру).
- В ячейку D6 введем формулу для определения шага интегрирования «=(D4-D3)/D5» (выравнивание по центру).
- Оформим заголовок таблицы для численного вычисления подынтегральной функции в узлах интегрирования: в ячейку A8 вводим текст «x», в ячейку B8 вводим текст «f(x)» (выравнивание по центру).
- В ячейку A9 вводим формулу «=D3».
- В ячейку A10 вводим формулу «=A9+$D$6».
- Копируем формулу из ячейки A10 в диапазон A11:A19 (используем прием растягивания). Получаем значения узлов интегрирования.
- В ячейку B9 вводим формулу, определяющую значение подынтегральной функции в первом узле интегрирования. В нашем примере она будет: «=1/КОРЕНЬ(A9+4)».
- Копируем формулу из ячейки B9 в диапазон B10:B19 (используем прием растягивания). Получаем значения подынтегральной функции в узлах интегрирования.
- В ячейку D8 введем текст «Приближенное значение интеграла:».
- В ячейку D10 введем текст «по формуле прямоугольников:».
- В ячейку G10 введем формулу «=СУММ(B9:B18)*D6», которая позволяет вычислить значение определенного интеграла по формуле прямоугольников. Получаем приближенное значение вычисляемого определенного интеграла.
- В ячейку D12 введем текст «по формуле трапеций:».
- В ячейку G12 введем формулу «=(2*СУММ(B10:B18)+B9+B19)*D6/2», которая позволяет вычислить значение определенного интеграла по формуле трапеций. Получаем второе приближенное значение вычисляемого определенного интеграла.
Замечание: оба приближенных значения определенного интеграла близки к его точному значению.
- В диапазоне A21:H36 с помощью Мастера диаграмм построить график подынтегральной функции на основе диаграммы точечного вида:
- Выделить диапазон A8:B19;
- Меню Вставка ⇨ Команда Диаграмма…;
- На 1-ом шаге выбрать тип диаграммы: Точечная диаграмма со значениями, соединенными сглаживающими линиями и нажать кнопку «Далее»;
- На 2-ом шаге ничего не изменяем и нажимаем кнопку «Далее»;
- На 3-ем шаге на вкладке «Заголовки» в окно «Ось Х (категорий) заносим текст «x», а на вкладке «Легенда» снимаем флажок в позиции «Добавить легенду» и нажимаем кнопку «Далее»;
- На 4-ом шаге нажимаем кнопку «Готово».
- Переносим построенную диаграмму в диапазон A21:H36, сжимая (растягивая) до заданных размеров. Форматируем Ось категорий и Ось значений, переносим подписи осей, форматируем Область построения диаграммы (см. Рис. 3).
Рис. 3
4. Методические указания по выполнению самостоятельной работы
- Повторить материал по теме «Возможности динамических (электронных) таблиц. Математическая обработка числовых данных», прочитав раздел учебно-методического пособия «Табличный процессор Excel и технология работы в нем».
- Повторить материал по дисциплине «Математика» по решению систем линейных уравнений методом Крамера и приближенному вычислению определенных интегралов, прочитав раздел учебно-методического пособия «Математическая постановка задач».
- Решить на компьютере с использованием табличного процессора MS Excel систему линейных уравнений из раздела «Реализация решения математических задач в MS Excel».
- Вычислить на компьютере с использованием табличного процессора MS Excel значение определенного интеграла из раздела «Реализация решения математических задач в MS Excel».
- Решить на компьютере с использованием табличного процессора MS Excel систему линейных уравнений
, применив метод Крамера. Коэффициенты при неизвестных и свободные члены задаются по вариантам, указанным в разделе «Варианты заданий для самостоятельной работы». Результаты решения предоставить преподавателю в виде аналогичном Рис 2.
- Вычислить на компьютере с использованием табличного процессора MS Excel значение определенного интеграла
, применив формулу прямоугольников и формулу трапеций. Построить график подынтегральной функции. Вид подынтегральной функции f(x), нижний предел интегрирования a, верхний предел интегрирования b задаются по вариантам, указанным в разделе «Варианты заданий для самостоятельной работы». Число разбиений отрезка интегрирования n равно 10 для всех вариантов. Результаты работы предоставить преподавателю в виде аналогичном Рис 3.
5. Варианты заданий для самостоятельной работы
5.1. Варианты заданий систем линейных уравнений
5.2. Варианты заданий определенного интеграла
|
№ варианта |
Вид подынтегральной функции f(x) |
Пределы интегрирования: |
Число разбиения отрезка интегрирования – n |
|
|
нижний – a |
верхний – b |
|||
|
1 |
|
-1 |
2 |
10 |
|
2 |
|
1 |
8 |
10 |
|
3 |
|
1 |
2 |
10 |
|
4 |
|
0 |
1 |
10 |
|
5 |
|
1 |
7 |
10 |
|
6 |
|
2 |
9 |
10 |
|
7 |
|
0 |
8 |
10 |
|
8 |
|
1 |
2 |
10 |
|
9 |
|
1 |
2 |
10 |
|
10 |
|
0 |
3 |
10 |
|
11 |
|
1 |
2 |
10 |
|
12 |
|
0 |
1 |
10 |
|
13 |
|
0 |
4 |
10 |
|
14 |
|
0 |
1 |
10 |
|
15 |
|
0 |
1 |
10 |
|
16 |
|
1 |
4 |
10 |
|
17 |
|
0 |
1 |
10 |
|
18 |
|
0 |
1 |
10 |
|
19 |
|
1 |
2 |
10 |
|
20 |
|
3 |
4 |
10 |
|
21 |
|
1 |
2 |
10 |
|
22 |
|
1 |
2 |
10 |
|
23 |
|
-2 |
-1 |
10 |
|
24 |
|
4 |
6 |
10 |
|
25 |
|
0 |
5 |
10 |
|
26 |
|
-1 |
1 |
10 |
|
27 |
|
2 |
3 |
10 |
|
28 |
|
-1 |
1 |
10 |
|
29 |
|
2 |
5 |
10 |
|
30 |
|
0 |
1 |
10 |
|
31 |
|
1 |
4 |
10 |
|
32 |
|
-2 |
2 |
10 |
|
33 |
|
3 |
4 |
10 |
|
34 |
|
2 |
5 |
10 |
|
35 |
|
1 |
4 |
10 |
Список литературы
- Гохберг Г.С., Зафиевский А.В., Короткин А.А. Информационные технологии: учебник для студ. учреждений сред. проф. образования. – 7-е изд., стер. – М.: Издательский центр «Академия», 2012. – 208 с.
- Дадаян А.А. Математика: Учебник. – М.: ФОЛРУМ: ИНФРА-М, 2003. – 552 с. – (Серия «Профессиональное образование»).
- Цветкова М.С., Великович Л.С. Информатика и ИКТ: учебник для нач. и сред. проф. образования. – 3-е изд., стер. – М.: Издательский центр «Академия», 2012. – 352 с., [8] л. цв. ил.
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Растеряев А.Н. 1
1МБОУ СОШ № 3 им. атамана М.И. Платова
Кожушкова Т.Ю. 1
1МБОУ СОШ № 3 им. атамана М.И. Платова
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
Современное развитие науки, техники и технологий тесно связано с использованием математических методов, программного обеспечения и мощных ЭВМ, ставшим рабочим инструментом учёного, инженера, конструктора. Все это позволяет строить и исследовать математические модели сложных устройств, систем и процессов, при этом резко сократить время и стоимость инженерных разработок.
Широкое использование ЭВМ способствовало развитию вычислительной математики (прикладной математики). Как и любая наука, вычислительная математика представляет собой сплав «классической» (теоретической) науки и прикладной науки, в роли последней выступает область вычислительных методов.
Практически все, что окружает современного человека – это все так или иначе связано с математикой. Последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в дальнейшем данная тенденция сохранится. Решение многих практических задач сводится к решению различных видов уравнений. При этом актуальным является использование ЭВМ и специального программного обеспечения при решении линейных и нелинейных уравнений и их систем.
Одна из основных целей изучения школьного курса математики заключается в овладении способами решения алгебраических и трансцендентных уравнений. В школьном курсе изучаются формулы корней квадратных уравнений, методы аналитического решения показательных, логарифмических и тригонометрических уравнений. При этом многие математические задачи, например, решение неравенств и их систем, нахождение области допустимых решений функции и т. п., включают в себя этап решения уравнений.
Цель работы: Освоение приемов численного решения алгебраических и трансцендентных уравнений в среде электронных таблиц MS Excel.
Задачи:
1) Ознакомиться с историей развития аналитических и численных методов решения уравнений.
2). Изучить особенности, достоинства и недостатки аналитических и численных методов.
3). Ознакомиться с вычислительными возможностями ЭТ MS Excel и изучить средства уточнения действительных корней нелинейных уравнений.
4) Освоить приемы отделения и уточнения действительных корней нелинейных уравнений в среде ЭТ MS Excel.
5) Решить задачи численного нахождения корней алгебраических и трансцендентных уравнений в среде электронных таблиц MS Excel.
Объект исследования: нелинейные уравнения с одной переменной.
Предмет исследования: возможности ЭТ MS Excel для численного решения нелинейные уравнения с одной переменной.
ОСНОВНАЯ ЧАСТЬ
1. Краткая история развития численных методов
Вычислительная математика начала свое развитие достаточно давно и в своем развитии прошла три этапа:
I. Первый этап начался 3-4 тысячи лет назад. Жители Вавилона в 2000 г. до н.э. уже умели решать квадратные уравнения и составлять таблицы для решения кубических уравнений путем приведения общего кубического многочлена к нормальному виду. В VII в. индийцы развили последовательную алгебраическую теорию уравнений первой и второй степени. Итальянский математик Ш. Ферро (1465-1526) нашел способ решения кубических уравнений специального вида [1]. Этот научный результат стал отправным пунктом для развития алгебры и математики вообще. Другим итальянским математиком, инженером, медиком и астрологом Дж. Кардано (1506-1576) было найдено решение приведенного кубического уравнения и опубликовано в 1545 г. в его научном труде «Великое искусство». В 1591 году великий французский математик Ф. Виет (1540-1603) впервые ввел символическое обозначение не только для неизвестных, но и для коэффициентов уравнений; указал на зависимость между корнями и коэффициентами уравнений (формулы Виета). Вычислительные средства этого этапа – палочки, пальцы, камешки и как вершина – счеты (абак).
II. Второй период начался с И. Ньютона (1642-1727). В этот период решались задачи астрономии, геодезии, баллистики и расчета механических конструкций, сводящиеся либо к обыкновенным дифференциальным уравнениям, либо к алгебраическим системам с большим числом неизвестных. В 1669 г. Ньютон предложил метод касательных для приближенного решения алгебраических уравнений, а в 1676 г. – способ приближенного вычисления определенных интегралов. Вычислительные средства – таблицы элементарных функций, арифмометры и логарифмические линейки.
III. Третий период начался примерно с 1940 года. Толчком к развитию прикладной математики послужили военные задачи, требующие высокой скорости решения задач. Появились электронные вычислительные машины. Например, Colossus («Колосс») – секретный британский компьютер, спроектированный и построенный в ходе Второй мировой войны в 1943 году для расшифровки перехваченных немецких радиосообщений, зашифрованных с помощью электронно-механического устройства «Энигма» (по-гречески – загадка). Спецификацию компьютера разработали английский математик, криптоаналитик профессор Макс Ньюман (Max Newman 1897- 1984) и его коллеги. Компьютер состоял из 1500 электронных ламп (2500 в новой версии Colossus Mark II), что делало Colossus самым мощным компьютером того времени. Его ближайший конкурент имел всего 150 ламп. Это позволило сократить время расшифровки перехваченных немецких сообщений с нескольких недель до нескольких часов. Модернизация Colossus Mark II считается первым программируемым компьютером в истории ЭВМ.
2. Особенности, достоинства и недостатки аналитических и численных методов
С помощью математического моделирования решение научной задачи сводится к решению математической задачи, являющейся её моделью. Для решения математических задач используются две основные группы методов: аналитические и численные.
Аналитические методы, как правило, позволяют получить решение задачи в виде формул. В частности, если математическая задача состоит в решении нелинейных уравнений, то использование известных из курса средней школы приемов сразу приводит к цели. К сожалению, на практике это бывает достаточно редко. Например, если задача свелась к решению уравнения с одной переменной:
то при всей тривиальности этой задачи выразить корни уравнения путем аналитических преобразований не удается. Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой. Доказательство этого факта связано с именами математиков Абеля (1802-1829) и Галуа (1811-1832).
Аналогичные проблемы возникают также и при решении других математических задач. В частности, при вычислении определенных интегралов также часто не удается выразить первообразную через элементарные функции.
Для решения таких задач разрабатываются и применяются методы приближенных вычислений или численные методы, позволяющие свести решение математической задачи к выполнению конечного числа арифметических действий над числами. Таким образом, численные методы позволяют найти решение в виде числа или таблицы значений, найденных с заданной точностью.
Важным отличием и преимуществом аналитических методов перед численными является то, что они позволяют получить общее решение задачи в виде формулы, по которой можно изучать качественные особенности решения, а также исследовать влияние начальных условий и параметров задачи на характер решения. Численные же методы позволяют найти только частное решение задачи с конкретными значениями параметров и исходных данных, при этом численные методы обладают большей общностью.
3. Численное решение уравнений с одной переменной
Нелинейное уравнение с одной переменной в общем случае может быть записано в виде
F(x) = 0, (1)
где функция F(x) определена и непрерывна на конечном или бесконечном интервале a < x < b.
Всякое значение [a, b], обращающее функцию F(x) в нуль, т.е. когда F() = 0, называется корнем уравнения (1) или нулем функции F(x).
Нелинейные уравнения с одной переменной подразделяются на алгебраические и трансцендентные.Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и другие) называются трансцендентными.
Как было сказано выше, методы решения нелинейных уравнений делятся на две группы:
аналитические (точные) методы;
численные (приближенные) методы.
Задача численного нахождения действительных корней нелинейного уравнения (1) обычно состоит из двух этапов [2]:
отделения корней, т.е. нахождения достаточно малых окрестностей рассматриваемой области, в которых содержится один и только один искомый корень;
уточнения отделенных на первом этапе корней, т.е. их нахождение численным методом с заданной степенью точности.
В связи с этим рассмотрим вначале задачу отделения корней, а затем возможности численных методов их уточнения.
На первом этапе необходимо исследовать уравнение и выяснить, имеются корни или нет. Если корни имеются, то сколько их, и затем определить интервалы, в каждом из которых находится единственный корень. Одним из самых распространенных и не очень точных является графический метод.
Принимая во внимание, что действительные корни уравнения (1) – это точки пересечения графика функции F(x) с осью абсцисс, достаточно построить график функции F(x) и отметить точки пересечения графикас осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив исходное уравнение (1) равносильным ему уравнением:
F1(x)= F2(x), (2)
где функцииF1(x) и F2(x) – более простые, чем исходная функцияF(x). Тогда, построив графики функций у =F1(x) и у = F2(x), искомые корни получим как абсциссы точек пересечения этих графиков.
Покажем теперь, что найденные графически отрезки содержат один и только один корень решаемого уравнения. Предположим, что найден отрезок [a, b] такой, что
функцияF(x) непрерывна на отрезке [a, b] вместе с производной первого порядка;
значения F(x) на концах отрезка имеют разные знаки (F(a)F(b) < 0);
первая производная F (x) сохраняет определенный знак на всем отрезке.
Условия 1) и 2) гарантируют, что на интервале [a, b] находится хотя бы один корень, а из 3) следует, что F(x) на данном интервале монотонна и поэтому корень будет единственным. Такой интервал называют интервалом изоляции искомого корня ξ.
Пример 1. Графически отделить корни уравнения
x.lg x– 1 = 0. (3)
Решение. Уравнение (3) перепишем в виде равенства lg x=.
Отсюда ясно, что корни уравнения (3) могут быть найдены как абсциссы точек пересечения логарифмической кривой y = lg x и гиперболы y = . Построив эти кривые (см. рис. 1), приближенно найдем единственный корень уравнения (3) или определим его содержащий отрезок [2, 3].
Рис. 1 – Графическое отделение корней (пример 1)
Убедимся, что отрезок [2, 3] содержит один и только один корень уравнения (3).
Перепишем уравнение в виде F(x) = 0, где .
Тогда F(2) = 2.lg(2) – 1 = 2.0.30103–1=0.60206 –1= –0.39794 0, т.е. на концах отрезка функция F(x) принимает значения разных знаков.
Найдем первую производную функции:
Следовательно, первая производная сохраняют свой знак на отрезке, а на концах отрезка функция F(x) принимает значения разных знаков, значит отрезок [2, 3] – отрезок изоляции искомого корня ξ.
После этого выполняется этап уточнения отделенных корней нелинейного уравнения. На каждом из найденных интервалов для поиска корня используются численные методы уточнения корня до заданной точности ε. К данным методам относятся: метод половинного деления (бисекций), метод хорд, метод касательных (Ньютона), метод последовательных приближений (итераций) и т.п.
4. Средства уточнения корней электронных таблиц Microsoft Excel
Электронные таблицы MS Excel входят в стандартный пакет формирования и обработки информации MS Office и установлены практически на каждом современном компьютере. Применение электронных таблиц упрощает работу с данными и позволяет получать результаты без проведения расчетов вручную или специального программирования. Наиболее широкое применение электронные таблицы нашли в экономических и бухгалтерских расчетах, но не все знают, что и в научно-технических задачах электронные таблицы можно использовать достаточно эффективно. Вычислительную мощь Excel обеспечивают встроенные функции, средства анализа и надстройки.
Надстройки – специальные средства, расширяющие возможности программы MS Excel. Именно надстройки делают ее удобной для использования в научно-технической работе. Хотя эти средства считаются внешними, дополнительными, доступ к ним осуществляется при помощи обычных команд командной строки (обычно через меню команд Сервис или Данные). При этом открываются специальные диалоговые окна, оформленные как стандартные диалоговые окна MS Excel.
Подключить или отключить установленные надстройки Excel можно с помощью Настройки панели быстрого доступа. Подключение надстроек увеличивает нагрузку на вычислительную систему, поэтому обычно рекомендуют подключать только те надстройки, которые реально используются.
Для уточнения корней с помощью ЭТ MS Excel можно использовать средство Подбор параметра (команда Данные → Анализ «что если») или надстройку Поиск решения.
Приведем лист MS Excel (см. рис. 2) с иллюстрацией применения средства Подбор параметра для уточнения корня уравнения (3), изолированного на отрезке [2, 3].
Рис. 2 – Графическое отделение корней уравнения двумя способами и подготовка к этапу уточнения
При подборе параметра Excel изменяет значение в одной конкретной ячейке, в нашем случае N32, до тех пор, пока вычисления по формуле в ячейке О32, ссылающейся на ячейку N32, не дадут нужного результата, а именно нуля функции (см. рис. 3).
Рис. 3 – Окно диалога средства Подбор параметра
После нажатия на кнопку OК MS Excel выведет окно диалога Результат подбора параметра (см. рис. 4). Если подобранное значение корня необходимо сохранить, то нажмите на ОК, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки, в нашем случае – ячейка N32.
Рис. 4 – Окно диалога Результат подбора параметра
Таким образом, искомое значение корня, уточненное средством Подбор параметра, составит ξ = 2,50617208. При подборе параметра Excel использует итерационный (циклический) процесс, при этом количество итераций и точность может устанавливаться пользователем.
Рассмотрим теперь, как воспользоваться надстройкой Поиск решения на примере нахождения корней алгебраического уравнения х3 – 10.х + 2 = 0. На следующем листе MS Excel приведен этап графического отделения корней (см. рис. 5).
Рис. 5 – Этап графического отделения корней уравнения х3 – 10.х + 2 = 0
Анализ графика функции показывает, что решаемое уравнение имеет три действительных корня, определены отрезки изоляции искомых корней.
Для уточнения отделенных корней сформируем вторую таблицу, в которую занесем середины отрезков изоляции, которые будут взяты за начальные приближения к искомым корням. Кроме этого, таблица содержит столбец вычисленных значений функции F(x) = х3 – 10.х + 2. Далее из команды главного меню Данные следует вызвать надстройку Поиск решения. При этом откроется диалоговое окно, представленное на рис. 6.
Рис. 6 – Диалоговое окно надстройки Поиск решения
Для уточнения первого корня в поле Оптимизировать целевую функцию указываем адрес ячейки D23. Поскольку необходимо найти решение уравнения F(x) = 0, то в переключателе До: записываем значение правой части уравнения (т. е. 0). В поле Изменяя ячейки переменных: заносится абсолютный адрес ячейки С23. Для запуска процесса решения задачи следует щелкнуть по кнопке Найти решение. На экране появится диалоговое окно Результаты поиска решения с информацией о том, найдено или нет искомое решение (см. рис. 7). Если решение найдено, то далее следует выбрать один из следующих возможных вариантов:
• сохранить найденное решение, т. е. заменить исходные значения в изменяемых ячейках на значения, полученные в результате решения задачи;
• восстановить исходные значения в изменяемых ячейках.
Рис. 7 – Диалоговое окно Результаты поиска решения
Таким образом, искомое значение первого корня, уточненное надстройкой Поиск решения, составит ξ1 = -3,257896991. Аналогично находится второй корень ξ2 = 0,200809757. Третий корень найдем с помощью средства Подбор параметра. Результаты решения представлены на рис. 8.
Рис. 8 – Результаты уточнения третьего корня
ЗАКЛЮЧЕНИЕ
В результате выполнения данной научно-исследовательской работы достигнута цель исследования – я освоил приемы численного решения алгебраических и трансцендентных уравнений в среде электронных таблиц MS Excel. При этом я ознакомился с историей развития аналитических и численных методов решения уравнений и систем уравнений, изучил особенности, достоинства и недостатки аналитических и численных методов. Кроме этого, я ознакомился с вычислительными возможностями ЭТ MS Excel и изучил такие средства уточнения действительных корней нелинейных уравнений, как средство Подбор параметра и надстройка Поиск решения. Оба эти инструмента позволяют подобрать значение искомого корня, при котором функция F(ξ) обращается в ноль. На практике в среде ЭТ MS Excel были графически отделены и уточнены корни трансцендентного уравнения x. lg x – 1 = 0 и алгебраического х3 – 10.х + 2 = 0.
Надеюсь, что полученные знания и навыки помогут мне успешно сдать ОГЭ по дисциплинам математика и информатика и ИТК.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ
1. Боголюбов А.Н. Математики. Механики. Библиографический справочник. – Киев: Наукова думка, 1983. – 638 с.
2. Б.П. Демидович, И.А. Марон. Основы вычислительной математики. – М.: Наука, 1966. – 664 с.
3. Дж. Уокенбах. Microsoft Office Excel 2007. Библия пользователя. – М.: Диалектика, 2008. – 816 с.
4. П. Дж. Бернс, Дж. Р. Николсон. Секреты Excel для Windows 95. – К.: Диалектика, 1996. – 576 с.
Просмотров работы: 1863
Решение системы уравнений в Microsoft Excel
Смотрите также Все элементы даннойОпределитель системы больше 0 результат подбора. Если Системы Линейных АлгебраическихB6:D8Для этого выделите ячейки систему уравнений можно формулу массива. ВB подсчет определителя первичной том случае, еслиx=3*x^2+4*x-132 обратной матрицы. Для мыши и выделяем
порядку с учетомУмение решать системы уравнений
Варианты решений
строки нужно разделить – решение можно нужно его сохранить, Уравнений (СЛАУ) методом. Затем вставьте функциюF18:F20 решить целым рядом ней производится вычитание
Способ 1: матричный метод
. Но на этот матрицы. Процедура происходит все определители будут.Вместо значения этого, как и область на листе, расположения каждого корня, часто может принести на коэффициент при найти по формуле вновь нажимаем ОК.
обратной матрицы вMINVERSE, а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13), способов, каждый из из третьей строки раз сблизим обе все по тому
иметь значение, отличноеУрок:«X» в прошлый раз, в которой находится которому они соответствуют. пользу не только с. Введем в Крамера (D
В противном случае MS EXCEL.(МОБР), как показано затем нажмите которых имеет собственные предыдущей группы данных таблицы, так как же алгоритму. Как от нуля. Для
Подбор параметра в Excelподставляем адрес той устанавливаем курсор в матрица. Как видим, Если в каком-то в учебе, но строку формулу массива:x – «Отмена».
- Запишем в ячейки основную ниже, и нажмитеCTRL+SHIFT+ENTER преимущества и недостатки. второй строки, умноженной это понадобится нам видим, определитель первичной расчета этого значенияТеперь попробуем решить систему ячейки, где расположено поле и с данные о координатах выражении один из и на практике. {=B12:E12/D12}./ |A|).Для подбора параметра программа матрицу системы иCtrl+Shift+Enter. Но все эти на отношение второго для работы в
- таблицы тоже отличный в Экселе опять уравнений методом Крамера. число зажатой левой кнопкой размещения автоматически заносятся
- корней отсутствует, то В то жеВ строке 15: отнимемДля расчета Х использует циклический процесс. столбец свободных членов. .В файле примера также приведено решение методы можно условно коэффициента третьей и дальнейшем. Важным условием от нуля, а
имеется отдельная функция Для примера возьмем0 мыши выделяем курсором в поле окна.
в этом случае время, далеко не от второй строки1 Чтобы изменить числоОпределитель основной матрицы вычислим=MINVERSE(B2:D4) системы 4-х и разделить на две
- второй строки. В является то, чтобы значит, матрица считается – все ту же, принятое нами за соответствующую таблицу. Аналогичное После того, как коэффициент считается равным каждый пользователь ПК третью, умноженную на: =U2/$U$1, где U2 итераций и погрешность,
- с помощью формулы =МОПРЕД(A11:C13)=МОБР(B2:D4) 5-и уравнений. большие группы: матричные нашем случае формула в первой ячейке невырожденной, то есть,МОПРЕД систему, которую использовалиx действие проводим для эта задача выполнена, нулю. Если коэффициент знает, что в коэффициент при с – D1. Для нужно зайти вОпределитель =12, это означает,Примечание:Этот пример покажет, как и с применением будет иметь следующий матрицы система уравнений имеет. Синтаксис данного оператора в. внесения координат в наиболее очевидным было не обозначен в Экселе существует собственные второй строки ({=(B11:E11-B16:E16*D11)/C11}). расчета Х параметры Excel. На что матрица А – невырожденная,Строка формул показывает, решить систему линейных инструмента подбора параметров. вид:A решения. следующий:
- Способе 1Переходим во вкладку поле бы нажать на уравнении, но соответствующий варианты решений линейных
- В строке 14:2 вкладке «Формулы» установить то есть, ее что ячейки содержат уравнений в Excel. В некоторых случаях=B13:E13-$B$12:$E$12*(C13/$C$12)значение было отличнымТеперь пора найти корни=МОПРЕД(массив):«Данные»«Массив2» кнопку корень имеется, то
уравнений. Давайте узнаем, от первой строки: =U3/$U$1. И т.д. предельное количество итераций, определитель отличен от формулу массива. Это К примеру, у не всегда матричныеПосле ввода формулы выделяем
- от нуля. В уравнения. Корень уравненияТаким образом, как и14. Жмем на кнопку, только на этот«OK» считается, что коэффициент как с применением отнимаем вторую и
- Получим корни уравнений: относительную погрешность. Поставить нуля. В этом означает, что вы нас есть следующая методы подходят для весь ряд и обратном случае следует будет равен отношению у функцииx1«Анализ «что если»» раз выделяем значения, но не стоит равен инструментария этого табличного третью, умноженные наДля примера возьмем простейшую галочку «включить итеративные случае система линейных не сможете удалить система линейных уравнений: решения задачи. В применяем сочетание клавиш переставить строки местами. определителя соответствующей преобразованнойМОБР+2. Эта кнопка размещена колонки торопиться. Дело в1
- процессора выполнить данную соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). систему уравнений: вычисления». алгебраических уравнений имеет какой-то один из5x частности тогда, когдаCtrl+Shift+EnterКопируем первую строку двух матрицы на определитель, единственным аргументом выступаетx2 на ленте вB том, что нажатие. Обозначаем полученную таблицу, задачу различными способами. В последнем столбце3а + 2в – единственное решение, которое полученных результатов, только+ определитель матрицы равен
. соединенных матриц в
Способ 2: подбор параметров
первичной таблицы. Таким ссылка на обрабатываемую+8 блоке инструментов. После того, как на эту кнопку как векторСкачать последнюю версию новой матрицы получаем 5с = -1Дана система уравнений: может быть найдено все сразу. Чтобы
1y
- нулю. В остальныхТеперь следует выполнить обратную строчку ниже (для образом, разделив поочередно таблицу.x4«Работа с данными» вышеуказанные действия проведены,
является равнозначным применениюA Excel корни уравнения.2а – вЗначения элементов введем в методом Крамера. удалить все результаты,+ же случаях пользователь
- прогонку по методу наглядности можно пропустить все четыре определителяИтак, выделяем ячейку, в=218. Открывается выпадающий список. опять не спешим команды.Любое уравнение может считатьсяВычисления в книге должны – 3с = ячейки Excel в
- Теперь последовательно будем заменять выделите диапазон8z сам волен решать, Гаусса. Пропускаем три одну строку). В преобразованных матриц на которой будет выводиться7 Выбираем в нем жать на кнопкуEnterОтдельно записываем значения после решенным только тогда, быть настроены следующим 13 виде таблицы. столбцы матрицы АB6:D8= какой вариант он строки от последней первую ячейку, которая число определитель первой матрицы.x1 позицию«OK»
- . Но при работе знака «равно». Обозначаем когда будут отысканы образом:а + 2вНайдем обратную матрицу. Выделим на столбец свободныхи нажмите клавишу46
- считает более удобным записи. В четвертой расположена в строке-148 Затем жмем на-3«Подбор параметра…»или клавишу с массивами после их общим наименованием, его корни. ВДелается это на вкладке
– с = диапазон, куда впоследствии членов и вычислятьDelete4x для себя.
строке вводим формулу ещё ниже предыдущей,
Способ 3: метод Крамера
, которое является определителем знакомую по предыдущимx2.Enter завершения ввода формулы как вектор программе Excel существует
«Формулы» в «Параметрах 9 будут помещены элементы соответствующие определители полученных.—Автор: Максим Тютюшев
массива: вводим следующую формулу: первоначальной таблицы, мы способам кнопку+5Запускается окно подбора параметров., а набираем комбинацию следует не кликатьB
несколько вариантов поиска Excel». Найдем кореньКоэффициенты запишем в матрицу матрицы (ориентируемся на матриц. Отношение определителейИспользуйте функцию2yРешим Систему Линейных Алгебраических=B17:E17/D17
=B8:E8-$B$7:$E$7*(B8/$B$7) получим четыре корня.«Вставить функцию»x3 Как видим, оно клавиш по кнопке. корней. Давайте рассмотрим
- уравнения х – А. Свободные члены количество строк и позволяет вычислить переменныеMMULT= Уравнений (СЛАУ) методомТаким образом, мы делимЕсли вы расположили матрицы Как видим, они
- .+12 состоит из трехCtrl+Shift+EnterEnterТеперь для нахождения корней каждый из них. х3 + 1 – в матрицу столбцов в исходной х.(МУМНОЖ), чтобы вернуть12 обратной матрицы в последнюю рассчитанную нами
- по-другому, то и равны значениямАктивируется окноx4 полей. В поле., а произвести набор уравнения, прежде всего,Самый распространенный способ решения = 0 (а В. матрице). Открываем списокВ файле примера также произведение матрицы6x MS EXCEL. В
строку на её адреса ячеек формулы5Мастера функций=213«Установить в ячейке»После данного действия в
сочетания клавиш нам нужно отыскать системы линейных уравнений = 1, bДля наглядности свободные члены функций (fx). В приведено решение системыA-1
- + этой статье нет же третий коэффициент. у вас будут,. Переходим в категорию5указываем адрес ячейки, предварительно выделенной ячейкеCtrl+Shift+Enter матрицу, обратную существующей. инструментами Excel –
- = 2) методом выделим заливкой. Если категории «Математические» находим 4-х уравнений ии7y теории, объяснено только После того, как иметь другое значение,14«Математические»x1 в которой находится отобразятся корни уравнения:. Выполняем эту операцию. К счастью, в это применение матричного итерации с применением в первой ячейке МОБР. Аргумент – прямая проверка решения.B+ как выполнить расчеты,
- набрали формулу, выделяем но вы сможете,и среди списка+ формулаX1Итак, после этого программа Эксель имеется специальный метода. Он заключается
- циклических ссылок. Формула: матрицы А оказался массив ячеек с
- В программе Excel имеется. Сперва выделите диапазон4z используя MS EXCEL. всю строчку и высчитать их, сопоставив8 операторов выделяем тамx2f(x), производит вычисления и
- оператор, который предназначен в построении матрицыХ 0, нужно поменять элементами исходной матрицы. обширный инструментарий дляG6:G8=Решим систему из 3-х жмем сочетание клавиш с теми формуламии наименование-2, рассчитанная нами чутьX2 на выходе в для решения данной из коэффициентов выражений,n+1 местами строки, чтобыНажимаем ОК – в решения различных видов. Затем вставьте функцию50 линейных алгебраических уравненийCtrl+Shift+Enter и изображениями, которые15«МОПРЕД»x3
Способ 4: метод Гаусса
ранее. В поле, предварительно выделенной области задачи. Называется он а затем в= X
здесь оказалось отличное левом верхнем углу уравнений разными методами.MMULTВ матричном представлении ее с помощью обратной.
приводятся здесь.. Таким образом, они. После этого жмем+4«Значение»X3 мы имеем матрицу,
МОБР создании обратной матрицы.n от 0 значение. диапазона появляется значение.Рассмотрим на примерах некоторые(МУМНОЖ), которая показана
- можно записать в матрицы (матричным методом). Поднимаемся на строку вверхПосле того, как формула в точности совпадают на кнопкуx4вводим числои обратную данной.. Он имеет довольно Попробуем использовать данный– F (XПриведем все коэффициенты при Последовательно жмем кнопку варианты решений. ниже, и нажмите видеСОВЕТ и вводим в введена, выделите весь с корнями, которые
- «OK»=83«0»X4Теперь нам нужно будет простой синтаксис: метод для решенияn а к 0.
F2 и сочетаниеИнструмент «Подбор параметра» применяетсяCtrl+Shift+EnterAX=B: Решение СЛАУ методом неё следующую формулу ряд ячеек и мы нашли, используя.6. В поле
. Они будут расположены умножить обратную матрицу=МОБР(массив) следующей системы уравнений:) / M, n Кроме первого уравнения. клавиш Ctrl + в ситуации, когда.. Крамера приведено в массива: нажмите комбинацию клавиш обратную матрицу вЗапускается окно аргументов функции
- x1«Изменяя значения» последовательно. Таким образом, на матрицу
- Аргумент14 = 0, 1, Скопируем значения в Shift + Enter. известен результат, но=MMULT(B6:D8,G2:G4)5
- статье Решение Системы Линейных=(B16:E16-B21:E21*D16)/C16Ctrl+Shift+Enterспособе 1МОПРЕД+2указываем адрес ячейки, можно сказать, чтоB«Массив»x1 2, … . первой строке двух
- Умножим обратную матрицу Ах-1х неизвестны аргументы. Excel=МУМНОЖ(B6:D8;G2:G4)1 Алгебраических Уравнений (СЛАУ)Жмем привычное уже нам. К ряду будет, что подтверждает правильность. Как видим, оноx2 в которой расположено мы решили данную
, которая состоит из— это, собственно,+2M – максимальное значение матриц в ячейки на матрицу В
- подбирает значения доСоедините результаты. Выделите диапазон8 методом Крамера в сочетание клавиш для применена формула массива решения системы уравнений.
имеет только одно+ значение систему. Для того, одного столбца значений, адрес исходной таблицы.x2 производной по модулю. В6:Е6. В ячейку (именно в таком тех пор, пока
- G6:G8x MS EXCEL. применения формулы массива.
и он будетРешить систему уравнений можно поле –x3
- x чтобы проверить правильность расположенных после знакаИтак, выделяем на листе
+8 Чтобы найти М, В7 введем формулу: порядке следования множителей!). вычисление не даст. Вставьте обобщенную формулу
- 46Запишем в ячейки основнуюПоднимаемся ещё на одну заполнен значениями. Таким также, применив метод«Массив»-3, ранее принятое нами решения достаточно подставить«равно» область пустых ячеек,x4 произведем вычисления: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон Выделяем диапазон, где нужный итог. (показана ниже) иПри А= матрицу системы и строку выше. В образом мы произвели Гаусса. Для примера
. В это полеx4 за в исходную системув выражениях. Для которая по размеру=218f’ (1) = -2 В7:Е7. Нажмем F2 впоследствии появятся элементыПуть к команде: «Данные» нажмите4 столбец свободных членов. неё вводим формулу вычитание из второй возьмем более простую вписываем адрес первой=210 выражений данные ответы умножения таблиц в равна диапазону исходной7
* f’ (2)
lumpics.ru
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL
и сочетание клавиш результирующей матрицы (ориентируемся — «Работа сCtrl+Shift+Enter-2Систему массива следующего вида: строки первой, умноженной
систему уравнений из преобразованной матрицы. ДляКак и в первом. После выполнения данных
вместо соответствующих корней. Экселе также имеется матрицы. Щелкаем поx1 = -11. Ctrl + Shift на число строк
данными» — «Анализ.0
n =(B15:E15-B20:E20*C15-B21:E21*D15)/B15 на отношение первых трех неизвестных: этого устанавливаем курсор способе, составляем матрицу действий жмем на Если равенство будет отдельная функция, которая кнопке-3Полученное значение меньше 0. + Enter. Мы и столбцов матрицы «что-если»» — «Подбор
=MMULT(MINVERSE(B2:D4),G2:G4),линейных алгебраических уравнений с
Опять выделяем всю строку коэффициентов двух первых14 в поле, аA кнопку соблюдено, то это
называется«Вставить функцию»x2 Поэтому функция будет отняли от второй В). Открываем диалоговое
параметра».=МУМНОЖ(МОБР(B2:D4);G2:G4)X=n и применяем сочетание выражений системы.
x1 затем выделяем матричныйиз коэффициентов уравнений
excel2.ru
Система линейных уравнений в Excel
«OK» означает, что представленнаяМУМНОЖ, расположенную около строки+5 с противоположным знаком:
| строки первую, умноженную | окно математической функции | Рассмотрим на примере решение | Урок подготовлен для Вас | y | неизвестными можно решать матричным | клавиш |
| После этого копируем полученную | +2 | диапазон. После этого | и таблицу | . | ||
| система уравнений решена | . Данный оператор имеет | формул. | x3 | f (х) = | на отношение первых | МУМНОЖ. Первый диапазон |
квадратного уравнения х2 командой сайта office-guru.ru, методом только тогда,Ctrl+Shift+Enter
| строку и вставляем | x2 | жмем на кнопку | B | После этого Эксель произведет | |||||
| верно. | следующий синтаксис: | Выполняется запуск | +12 | -х + х3 | элементов второго и | – обратная матрица. | + 3х + | Источник: http://www.excel-easy.com/examples/system-of-linear-equations.html | B= |
| когда определитель основной | . | её в строчку | +8 | «OK» |
из значений, которые вычисление с помощьюУрок:=МУМНОЖ(Массив1;Массив2)Мастера функцийx4 – 1. М первого уравнения. Второй – матрица 2 = 0.Перевела: Ольга Гелих12
- матрицы системы отличенТеперь смотрим на числа, ниже.x3. Данная функция выводит стоят после знака подбора параметра. ОбОбратная матрица в ExcelВыделяем диапазон, в нашем. Переходим в категорию=213 = 11.Копируем введенную формулу на
В.
Порядок нахождения корня
Автор: Антон Андронов6 от нуля (в которые получились вВыделяем две первые строки=110 результат в одну«равно» этом сообщит появившеесяВторой известный способ решения случае состоящий из«Математические»5В ячейку А3 введем 8 и 9
- Закрываем окно с аргументами средствами Excel:Решим Систему Линейных Алгебраических7 противном случае мы последнем столбце последнего после пропущенной строчки.7 ячейку, а не. информационное окно. В системы уравнений в четырех ячеек. Далее. В представившемся спискеx1
значение: а =
строки. Так мы - функции нажатием кнопкиВведем в ячейку В2 Уравнений (СЛАУ) методом4 имеем линейно зависимые блока строк, рассчитанного Жмем на кнопку
x1
массивом, поэтому для
Далее делаем ещё четыре нем следует нажать
Экселе – это
опять запускаем
ищем наименование
office-guru.ru
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом Крамера в MS EXCEL
+ 1. Точность – избавились от коэффициентов ОК. Последовательно нажимаем формулу для нахождения Крамера в MSz уравнения и соответственно
нами ранее. Именно«Копировать»-3 получения расчета не таблицы. Каждая из на кнопку применение метода подбораМастер функций
«МОБР»x2
три знака после перед а. Сохранили кнопку F2 и значения функции. В EXCEL. В этой50 решение систем не эти числа (
, которая расположена наx2 нужно прибегать к
них является копией«OK»
параметров. Суть данного, нажав значок. После того, как-2 запятой. Для расчета только первое уравнение. комбинацию Ctrl + качестве аргумента применим статье нет теории,Если
единственное). В нашем4 ленте во вкладке+5 нажатию комбинации клавиш матрицы. метода заключается в
«Вставить функцию» оно отыскано, выделяемx3 текущего значения х
excel2.ru
Решение уравнений в Excel методом итераций Крамера и Гаусса
Приведем к 0 коэффициенты Shift + Enter. ссылку на ячейку объяснено только как
А-1 случае определитель =12.
Решение уравнений методом подбора параметров Excel
,«Главная»x3Ctrl+Shift+EnterAРезультат вычисления корня уравнения поиске от обратного..
его и жмем+4 в соседнюю ячейку перед в вПолучены корни уравнений.
В1. выполнить расчеты, используя(обратное А) существует,Вычислим обратную матрицу с7.
- =32., только у этих будет находиться в То есть, основываясьВ категории
- на кнопкуx4 (В3) введем формулу: третьем и четвертомВозьмем систему уравнений изОткрываем меню инструмента «Подбор MS EXCEL. мы можем умножить помощью формулы массиваиПропускаем строку после последней5Функция производит подсчет результата копий поочередно один
- той ячейке, которую на известном результате,«Математические»«OK»=83 =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
уравнении. Копируем строки предыдущего примера: параметра». В графеМетод Крамера применяется для обе части на МОБР().5 записи на листе.x1 и выводит его столбец заменен на
мы назначили в
Как решить систему уравнений матричным методом в Excel
мы производим поиск
- , запустившегося.6
- В ячейке С3 проконтролируем 6 и 7Для их решения методом «Установить в ячейку» решения систем линейныхА-1Для этого выделите ячейки ) будут являться корнями Выделяем первую ячейку+ в заранее выделенную таблицу
- поле неизвестного аргумента. ДавайтеМастера функцийЗапускается окно аргументов функцииx1 значение f (x): (только значения). Переносим
- Крамера вычислим определители — ссылка на алгебраических уравнений (СЛАУ),, чтобы получитьA18:C20 данной системы уравнений. в следующей строке.x2 ячейку. Как видим,B«Изменяя значения» для примера используем, выделяем наименованиеМОБР+2
- с помощью формулы их ниже, в матриц, полученных заменой ячейку В2, где в которых числоX=A-1B
, а в Строке
Решение системы уравнений методом Крамера в Excel
Проверить это можно, Кликаем правой кнопкой
-2 в нашем случае. У первой таблицы. В нашем случае, квадратное уравнение«МУМНОЖ»
. Оно по числуx2 =B3-СТЕПЕНЬ(B3;3)+1. строки 10 и
одного столбца в находится формула. В неизвестных переменных равно
. Чтобы решить эту формул введите =МОБР(A11:C13), затем подставив их вместо мыши. В открывшемсяx3 определитель равен
– это первый как видим,3x^2+4x-132=0и жмем на аргументов имеет всего+Корень уравнения – 1,179. 11. Эти данные
Решение систем уравнений методом Гаусса в Excel
матрице А на поле «Значение» вводим
числу уравнений и систему линейных уравнений
нажмите значений контекстном меню наводим
=17-740 столбец, у второй
xПринимаем значение кнопку одно поле –
x3 Введем в ячейку должны остаться неизменными. столбец-матрицу В. 0. Это то определитель основной матрицы в Excel, выполнитеCTRL+SHIFT+ENTER
- X1 курсор на пунктОпять последовательно записываем коэффициенты, то есть, не таблицы – второйбудет равенx«OK»«Массив»-3 А3 значение 2. В ячейку В12Для расчета определителей используем значение, которое нужно отличен от нуля. следующие действия:.,
- «Специальная вставка» в таблицу является равным нулю, и т.д.6за равное
- .. Тут нужно указатьx4 Получим тот же вводим формулу массива. функцию МОПРЕД. Аргумент получить. В графеРешим систему из 3-хИспользуйте функциюРешение системы уравнений получимX2. В запустившемся дополнительном
- A что нам подходит.Теперь нам нужно высчитать.0Активируется окно аргументов функции адрес нашей таблицы.=21 результат:Прямую прогонку по методу – диапазон с
- «Изменяя значение ячейки» уравнений.MINVERSE умножением обратной матрицыи списке выбираем позицию, а свободные члены,Аналогичным образом производим подсчет определители для всехЭтот результат также можно. Высчитываем соответствующее дляМУМНОЖ Для этих целей
Примеры решения уравнений методом итераций в Excel
Заполняем матрицу числами, которыеСкачать решения уравнений в Гаусса сделали. В
соответствующей матрицей. — В1. ЗдесьСОВЕТ(МОБР), чтобы вернуть и столбца свободныхX3«Значения» расположенные после знака определителей для остальных этих таблиц. Система
проверить, подставив данное него значение. В поле устанавливаем курсор в являются коэффициентами уравнения. Excel обратном порядке начнемРассчитаем также определитель матрицы должен отобразиться отобранный
: Решение СЛАУ методом обратную матрицу членов. Перемножить матрицыв выражения.
.«равно» трех таблиц.
уравнений будет иметь значение в решаемоеf(x)«Массив1» это поле. Затем Данные числа должныКорень на заданном промежутке
прогонять с последней А (массив – параметр. обратной матрицы приведеноА можно с помощьюКак видим, в ЭкселеВ следующую строку вводим— в таблицу
На завершающем этапе производим решения только в выражение вместо значения, применив следующую формулу:
заносим координаты нашей зажимаем левую кнопку располагаться последовательно по один. строки полученной матрицы.
диапазон матрицы А).После нажатия ОК отобразится
в статье Решение. Сначала выделите диапазон
exceltable.com
формулы массива =МУМНОЖ().