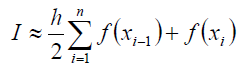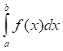Численное интегрирование метод трапеций excel - Word и Excel

history 20 ноября 2022 г.

Группы статей

Вычислим в MS EXCEL определенный интеграл методом трапеций (англ. Trapezoidal Rule). Оценим ошибку интегрирования, построим график функции.

В интернете есть много сайтов по автоматическому вычислению интегралов аналитическими и численными методами. Но, как правило, про использованный метод численного интегрирования ничего не говорится, а корректность вычислений проверить невозможно. В данном примере все вычисления прозрачны и можно задать необходимое количество интервалов разбиения. Правда, данный метод имеет относительно невысокую точность по сравнению с другими методами (если сравнивать его с методом Симпсона и методом интерполяционного полинома Лагранжа).

Немного теории

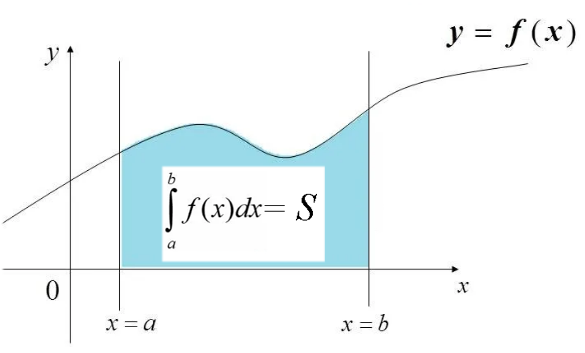
Так как функция, стоящая под знаком интеграла в общем случае может быть любая, то значение интеграла не всегда можно вычислить аналитически. Однако, можно воспользоваться тем фактом, что согласно теории, значение интеграла численно равно площади фигуры образованной графиком функции и осью Х (фигура выделена цветом).

Таким образом, задача нахождения интеграла сводится к нахождению площади этой фигуры. Площадь фигуры в общем случае можно найти численными методами, разбивая ее на простые однотипные фигуры, например трапеции. Т.к. площадь каждой трапеции найти легко, то простым суммированием площадей можно найти и интеграл. Платой за универсальность является ошибка интегрирования, которую впрочем можно оценить (будет показано далее).

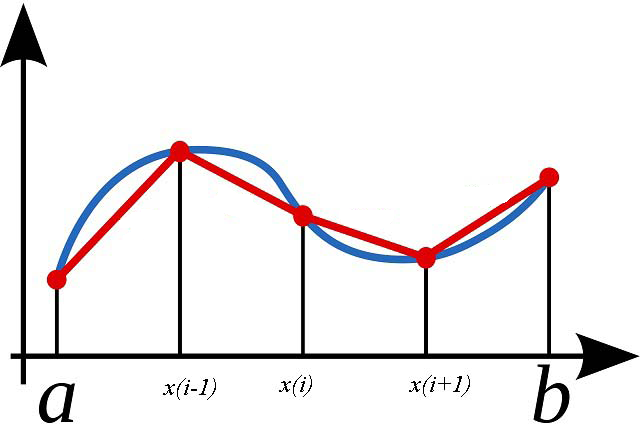
Фактически метод трапеций основан на линейной интерполяции, т.е. график функции y = f(x) представляется в виде ломаной, соединяющей точки (x_i, y_i) прямыми линиями.

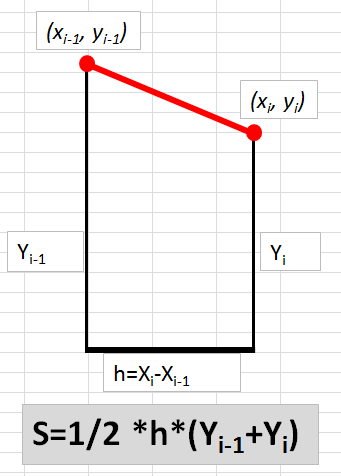
Площадь каждой трапеции можно найти следующим образом (см. рисунок ниже).

Фактически задача по нахождению интеграла сводится в основном к построению таблицы значений функции y=f(x) для заданных Х и нахождению их суммы. Интеграл можно найти с помощью вот такой простой формулы:

Построение модели

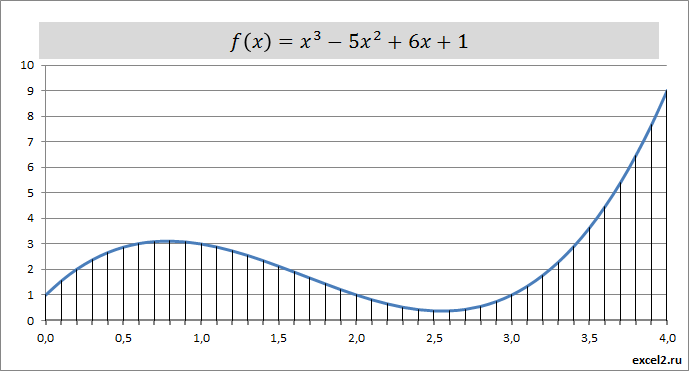
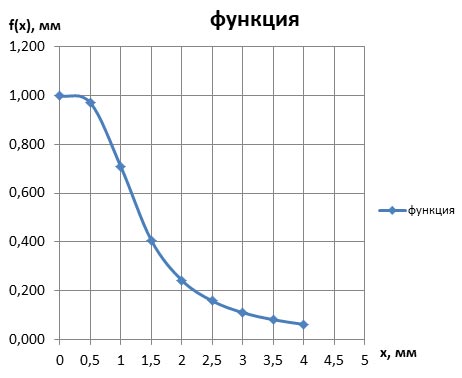
Для определенности вычислим интеграл для функции-многочлена f(𝑥)=𝑥³−5𝑥²+6𝑥+1. График этой функции в диапазоне от 0 до 4 выглядит следующим образом (см. файл примера).

Примечание: про тонкости построения графика функции можно прочитать в этой статье https://excel2.ru/articles/grafik-vs-tochechnaya-diagramma-v-ms-excel.

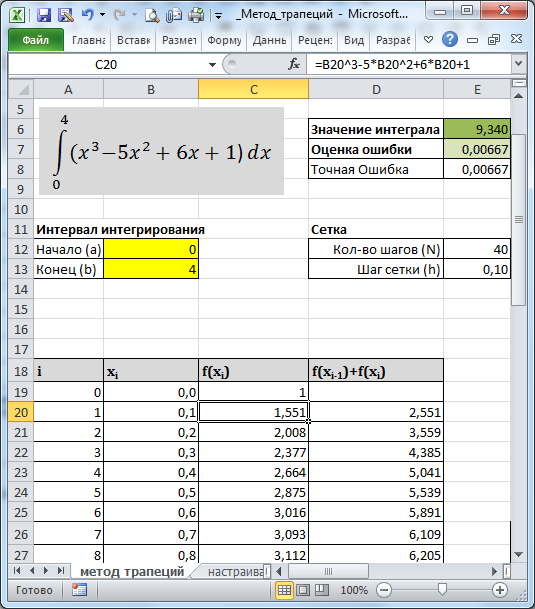
В файле примера построим таблицу значений функции для 41 точки (от 0 до 40), что составляет 40 интервалов.

Напомним, что Интеграл методом трапеций можно найти с помощью вот такой простой формулы:

В MS EXCEL формула также будет очень простой =E13/2*СУММ(D20:D59).

Примечание: При вводе функции в столбец С нужно быть очень внимательным — ошибиться очень легко, т.к. формула будет выглядеть как месиво символов =B19^3-5*B19^2+6*B19+1.

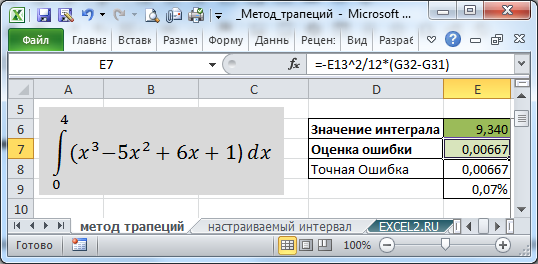
Вычисленное приближенное значение интеграла для данной функции в интервале [0;4] равно 9,340, а точное 9,333, т.е. ошибка составляет менее 0,1%. Ниже показано как ее оценить.

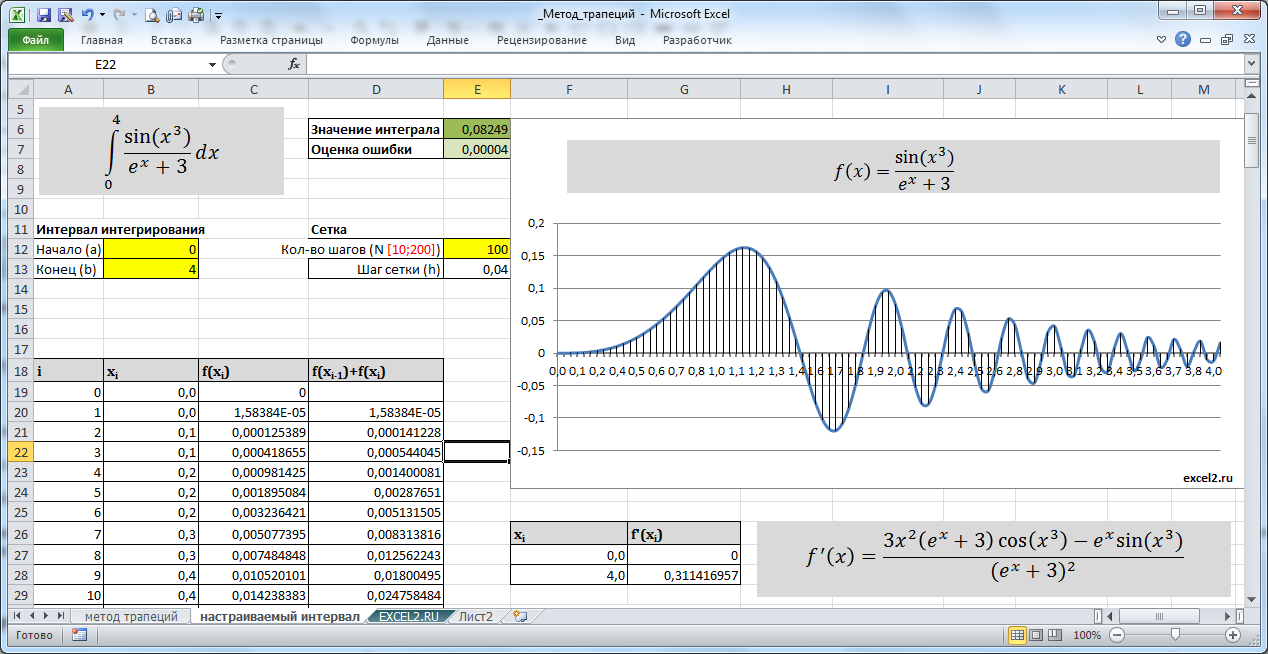
В файле примера на листе «настраиваемый интервал» сделана форма для работы с разными количествами интервалов разбиения. При изменении количества интервалов график перестраивается автоматически, формулы для вычисления интеграла не нужно переписывать (как, впрочем, и расширять/ убавлять таблицу значений).

Ошибка вычисления

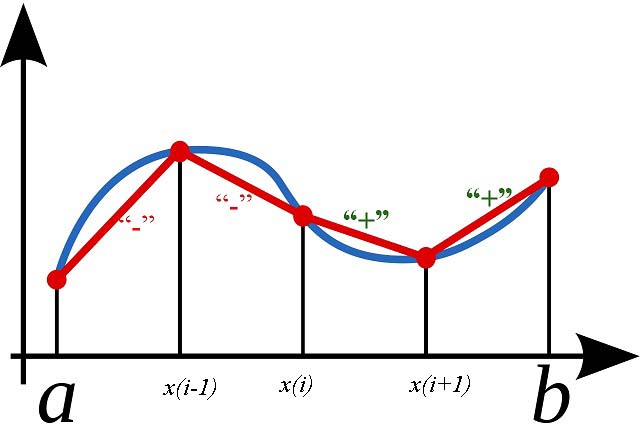
На рисунке ниже показано откуда появляется ошибка интегрирования. Для первых 2-х трапеций (образованы красными линиями) площадь меньше чем у истинной функции (синяя линия). Для следующих 2-х — площадь больше. Из этого следует, что метод трапеций хорошо работает для осциллирующих функций, когда ошибки компенсируют друг друга.

Простой многочлен был выбран в качестве демонстрационной функции, чтобы можно было вычислить интеграл точно и потом найти истинную ошибку, чтобы иметь возможность сравнить ее с оценкой.

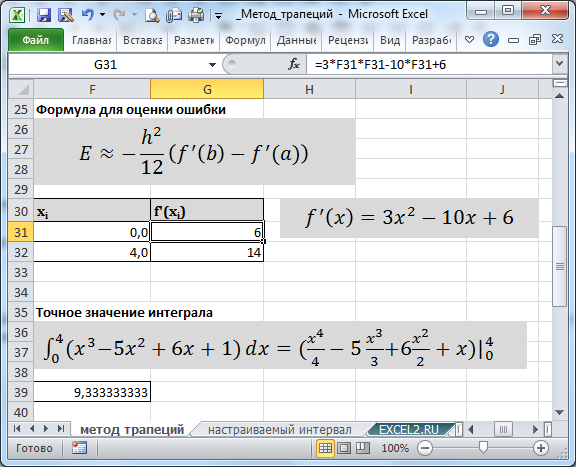
К сожалению, для нахождения оценки ошибки потребуется вычислить первую производную. Сделать это чаще всего не сложно, но автоматизировать это в EXCEL не получится. Поэтому при изменении подинтегральной функции приходится вносить изменения в несколько формул на листе, а точнее — в 2 ячейки С19 и G31 (в файле примера они выделены красным). После ввода формул их нужно скопировать вниз.

В наем случае полученная оценка ошибки совпала с истинной ошибкой, что говорит о том что мы не ошиблись при вычислении производной и вводе формул на лист.

Совет: всегда оценивайте ошибку интегрирования.

Источник

Цель урока: Совершенствование умений и навыков по теме «Численное интегрирование», применяя возможности MS Excel по вычисление определенных интегралов методом трапеции. Отработать практическое освоение соответствующих умений и навыков.

Задачи урока:

Образовательные – совершенствование умений студентов при вычисление определенных интегралов методом трапеции в среде электронных таблиц MS Excel. Выработать умение применять теоретические знания в практических расчетах;
Развивающие – познакомить студентов с применением компьютеров в качестве помощников при решении уравнений. Развивать у студентов математическую речь: создать ситуацию для применения основных понятий в речи; творческого мышления через создание условий для самореализации творческого потенциала обучающихся;
Воспитательные – выработать у студентов умение рационально использовать время и возможности компьютерных технологий при решении задач. Воспитывать интерес к предмету через ситуацию успеха и взаимодоверия.

Тип урока: комбинированный урок.

Вид урока: практическое занятие, продолжительность – 2 часа.

Оборудование урока:

Компьютеры с OS MS Windows;
Программа Microsoft Excel;
Презентация по теме, выполненная в программе PowerPoint;
Карточки с заданиями для самостоятельной работы.

Структура урока:

1.Актуализация знаний:
1.1. Мобилизующее начало, постановка целей и задач на урок;
1.2.Фронтальный опрос с целью выявления основных этапов решения задач интегрирования и методики решения;
1.3. Постановка задачи с целью повторения алгоритма вычисления определенных интегралов методом трапеции;
1.4.Подведение итогов 1 этапа урока.
2.Применение знаний, формирование умений и навыков:
2.1.Беседа с целью формулировки задания для самостоятельной работы и инструктажа по ее организации;
2.2.Самостоятельная работа в группах по выполнению задания вычисления определенных интегралов методом трапеции в среде Microsoft Excel.
2.3.Подведение итога урока.

В данном уроке особое внимание уделено визуальному представлению информации – в ходе урока с помощью проектора демонстрируются слайды, подготовленные в пакете презентационной графики Microsoft PowerPoint.

ХОД УРОКА

1. Актуализация знаний

1.1. Мобилизующее начало, постановка целей и задач на урок.

На прошлых уроках мы с Вами изучили приближенное вычисление определенных интегралов, выделили методы их решения и решали данные интегралы ручным счетом. А на сегодняшнем занятии мы будем совершенствовать умения и навыки при вычислении определенных интегралов методом трапеции в среде Microsoft Excel.

— В чем заключается вычисление интеграла?

— Важным средством вычисления определенных интегралов является формула Ньютона-Лейбница 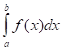. Ее применение на практике связано с существенными трудностями, возникающими при нахождении первообразной в случае подынтегральной функции. Поэтому применяют численные методы, позволяющие найти приближенное значение исходного интеграла с заданной точностью.
— Общий подход к ее решению состоит в том, чтобы аппроксимировать функцию какой-либо другой функцией , для которой интеграл вычисляется аналитически.

— Тогда для решения задачи строим с оценкой погрешности , и приближенно с очевидной оценкой погрешности .

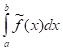
— Введем на отрезке сетку , , где , и таблицу значений , .

— Рассмотрим простой вариант построения функции , приводящий к формуле трапеций.

— При этом функция строится как кусочно-линейная интерполяция значений , на равномерной сетке с шагом .

— Тогда

— Формулы такого рода () называют механическими квадратурами, – коэффициентами (весами) квадратуры, – ее узлами.

Точность формулы трапеций зависит от гладкости функции . Если она на имеет первую производную, ограниченную числом , то , и погрешность формулы трапеций не превосходит . Если на имеет вторую производную, ограниченную числом , то погрешность формулы итераций не превосходит , поскольку .

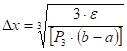
Теоретические оценки погрешностей не всегда применяются. Если требуется вычислить интеграл с погрешностью , то мало кто сначала оценит третью производную функции и вычислит шаг сетки . Эта оценка и значение константы завышены. Кроме того, само вычисление может быть трудным, особенно если задана некоторым сложным образом.

Поэтому, вычисляя интеграл с небольшим числом узлов , получают его значение ; вычисляя интеграл с удвоенным , получают . Если модуль (где ε – предельное допустимое значение погрешности расчета), то задачу считают решенной. В противном случае вычисляют и т.д. Для гладких функций часто интеграл вычисляется очень точно при малом числе узлов.

— Объясните алгоритм вычисления интеграла различными методами?

2. Применение знаний, формирование умений и навыков

Практическое задание «Вычисление определенных интегралов методом трапеции в среде Microsoft Excel.»

Состав задания:

Ознакомиться с теоретической частью задания;
Провести расчет для своего варианта индивидуального задания в Microsoft Excel
Оформить презентацию в Ms PowerPoint, включающую:
— постановку задачи;
— алгоритм расчета;
— таблицу с расчетом из Ms Excel, график исходной функции;
— результат расчета и его анализ.

Индивидуальное расчетное задание:

Найдите приближенное значение интеграла заданной функции f(x)= 1/(1+x⁴)^1/2 на отрезке [0; 4]
по формуле трапеций, разбивая отрезок [0; 4] на 8 равных частей. Оцените погрешность приближенного вычисления интеграла при таком разбиении отрезка.
Представьте графически поставленную задачу.

Постановка задачи:

Дано: f(x)= 1/(1+x⁴)^1/2 на отрезке [0; 4]

Найти: приближенное значение интеграла заданной функции по формуле трапеций, приняв предельное значение погрешности приближенного вычисления интеграла равным ε=0,02.

Таблица Исходная информация
Отрезок [a;b]	Функция f(x)
a	b	Аналитическая запись	Представление в Excel
0	4	1/(1+x⁴)^1/2	=СТЕПЕНЬ((1+СТЕПЕНЬ(B16;4));-1/2)

Анализ заданной функции и результаты вычислений в Ms Excel

Расчет площади
xi	f(xi)	Коэффициенты формулы трапеций	*Вычисление Cif(xi)**
N=2	N=4	N=8	N=2	N=4	N=8
0	1,000	0,5	0,5	0,5	0,500	0,500	0,500
0,5	0,970	0	0	1	0,000	0,000	0,970
1	0,707	0	1	1	0,000	0,707	0,707
1,5	0,406		0	1	0,000	0,000	0,406
2	0,243	1	1	1	0,243	0,243	0,243
2,5	0,158	0	0	1	0,000	0,000	0,158
3	0,110	0	1	1	0,000	0,110	0,110
3,5	0,081	0	0	1	0,000	0,000	0,081
4	0,062	0,5	0,5	0,5	0,031	0,031	0,031
Сумма	0,774	1,591	3,207
Значения интеграла
Количество узлов	N=2	N=4	N=8
S	1,55кв.мм	1,59кв.мм	1,60кв.мм
Погрешность	0,028	0,008

Ответ: приближенное значение интеграла заданной функции по формуле трапеций равна 1,60кв.мм, значение погрешности приближенного вычисления интеграла равным ε=0,008.

Задания для индивидуальной работы студентов по вариантам:

Найдите приближенное значение интеграла заданной функции f(x) на отрезке [a; b] (см. таблицу ) по формуле трапеций, разбивая отрезок [a; b] на 8 равных частей. Оцените погрешность приближенного вычисления интеграла при таком разбиении отрезка.

Представьте графически поставленную задачу.

N	отрезок [a; b]	Функция f(x)
1	[0; 4]	1/(1+x²)^1/2
2	[2; 3]	5x⁴+2x²-х
3	[2; 4]	е^х/(х+5) + x³/(х+4)
4	[0; 2]	(4+x³)^1/2
5	[0; 2]	1/(5x⁴+2x²+2)
6	[10; 18]	(х⁴/(1+x⁴)^1/2)^1/2
7	[2; 6]	6/(1+x²)^1/2
8	[2; 3]	5x⁴+2x²-х
9	[4; 8]	(х⁵/(1+x⁴)^1/2)^1/2
10	[1; 3]	12/(5x²+x+6)
11	[0; 4]	е^1/(х+5) + 1/(х+4)
12	[2; 4]	(х+x⁵)^1/2
13	[0; 4]	1/(1+x⁴)^1/2
14	[4; 8]	2+(х/(1+x⁴)^1/2)

На сегодняшнем занятии мы отработали навыки вычисления определенных интегралов методом трапеции в среде электронных таблиц MS Excel. Выработали умения применять теоретические знания в практических расчетах.

Список литературы и интернет-ресурсов

Основы компьютерной грамотности: учебное пособие / Кривенкова С.В., Радионова Л.К., Соболенко Н.А., Шванн Д.Э. М.: Издательство МЭИ, 2004.
Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989.
Федоренко Р.П. Введение в вычислительную физику. М.: Издательство МФТИ, 1994.
Физико-математические основы техники и электрофизики высоких напряжений. Учебное пособие для вузов / В.В. Базуткин, К.П. Кадомская, Е.С. Колечицкий и др. Под ред. К.П. Кадомской. М.: Энергоатомиздат, 1995.
Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad. СПб.: БХВ-Петербург, 2005.
Зенков, А.В. ЧИСЛЕННЫЕ МЕТОДЫ /А.В. Зенков. — Екатеринбург: Издательство Уральского университета, 2016. — 127с.
Вычислительные методы // Википедия. [2010—2019]. Дата обновления: 31.01.2019. URL: https://ru.wikipedia.org/?oldid=97827303 (дата обращения: 20.05.2019).
Численное решение уравнений // Википедия. [2010—2018]. Дата обновления: 01.01.2018. URL: https://ru.wikipedia.org/?oldid=89982922 (дата обращения: 20.05.2019).

Источник

Давайте разберёмся, как вычислить определённый интеграл таблично заданной функции с помощью программы Excel из состава Microsoft Office.

1Постановка физической задачина расчёт определённого интеграла

Допустим, у нас есть таблично заданная некоторая величина. Для примера пусть это будет накопленная доза радиации при авиаперелёте. Скажем, был такой эксперимент: человек с дозиметром летел на самолёте из пункта А в пункт Б и периодически измерял дозиметром мощность дозы (единицы измерений – микрозиверт в час, мкЗв/ч). Возможно, Вас это удивит, но при обычном перелёте на самолёте человек попадает под радиоактивное излучение, превышающее фоновый уровень до 10 раз и даже больше. Но воздействие это кратковременное, и поэтому не столь опасное. По результатам измерений у нас есть таблица вот такого формата: Время – Мощность дозы.

Таблично заданная величина для расчёта определённого интеграла

Необходимо посчитать суммарную накопленную за время полёта дозу.

2Геометрический смыслопределённого интеграла

Как мы помним из курса школьной алгебры, определённый интеграл – это площадь под графиком измеряемой величины. Чтобы определить накопленную дозу радиации в рассматриваемом примере, нужно определить площадь фигуры под графиком таблично заданной мощности дозы. Накопленная доза радиации равна площади фигуры под графиком мощности дозы

График изменения мощности дозы во время полёта

3Методика вычисленияопределённого интеграла

Вычислять интеграл мы будем самым простым, но довольно точным методом – методом трапеций. Напомню, площадь фигуры под графиком любой кривой можно разделить на прямоугольные трапеции. Сумма площадей этих трапеций и будет искомым значением определённого интеграла.

Площадь трапеции определяется как полусумма оснований, умноженная на высоту: S_трап = (A + B) / 2 × h Основания в нашем случае – это табличные измеренные значения мощности дозы за 2 последовательных промежутка времени, а высота – это разница времени между двумя измерениями.

Метод трапеций для вычисления значения определённого интеграла

4Согласованиеединиц измерения

В нашем примере измерения мощности дозы радиации даётся в мкЗв/час, а шкала времени – с точностью до минут. Мы не можем брать интеграл по времени, измеряемому в минутах, для величины, измеряемой в часах. Поэтому необходимо перевести мкЗв/час в мкЗв/мин.

Для перевода просто разделим мощность дозы в мкЗв/час построчно на количество минут в часе, т.е. на 60. Добавим ещё один столбец в нашу таблицу. На иллюстрации это столбец «D». В столбце «D» в строке 2 вписываем =С2/60 А потом с помощью маркера заполнения распространяем эту формулу на все остальные ячейки в столбце «D», (т.е. тянем мышью чёрный прямоугольник в правом нижнем углу ячейки). Таким образом, в столбце «D» у нас появятся значения мощности дозы радиации, измеряемые в микрозивертах в минуту для каждой минуты перелёта.

Согласуем единицы измерения по шкале времени и шкале мощности дозы

5Вычисление площадей отдельных трапеций

Теперь нужно найти площади трапеций за каждый промежуток времени. В столбце «E» будем вычислять по приведённой выше формуле площади трапеций.
Полусумма оснований – это половина суммы двух последовательных мощностей дозы из столбца «D». Так как данные идут с периодом 1 раз в минуту, а мы берём интеграл по времени, выраженному в минутах, то высота каждой трапеции будет равна единице (разница времени между каждыми двумя последовательными измерениями, например, 17ч31мин — 17ч30мин = 0ч1мин = 1мин).

Получаем формулу в ячейке «E3»: =1/2*(D3+D2)*1. Понятно, что «×1» в этой формуле можно не писать. И аналогично, с помощью маркера заполнения, распространяем формулу на весь столбец. Теперь в каждой ячейке столбца «Е» посчитана накопленная доза за 1 минуту полёта.

Вычисление площадей прямоугольных трапеций за каждый промежуток времени

Если бы данные шли не через 1 минуту, то нам нужно было бы написать формулу так:
=1/2*(D3+D2)*(МИНУТЫ(A3) – МИНУТЫ(A2)).

Правда при этом, если есть переход на следующий час, то получится отрицательное значение. Чтобы этого не произошло, впишем в формулу часы:
=1/2*(D3+D2)*(ЧАС(A3)*60+МИНУТЫ(A3)) – (ЧАС(A2)*60+МИНУТЫ(A2)).
Если переходим на следующие сутки, то нужно будет уже добавлять даты, и т.д.

5Определение площадипод графиком функции

Осталось найти сумму вычисленных площадей трапеций. Можно в ячейке «F2» написать формулу: =СУММ(E:E) Это и будет сумма всех значений в столбце «E», т.е. численное значение искомого определённого интеграла. Но давайте сделаем вот что: определим накопленную дозу в разные моменты полёта. Для этого в ячейку «F4» впишем формулу =СУММ(E$3:E4) и маркером заполнения распространим на весь столбец «F».

Обозначение E$3 говорит программе Excel, что увеличивать индекс ячейки «3» в столбце «E» при переносе формулы на следующие строки не нужно. Т.е. в строке 4 формула будет определять сумму в ячейках с «Е3» по «Е4», в строке 5 – сумму с «Е3» по «Е5», в строке 6 – с «Е3» по «Е6» и т.д.

Построим график по столбцам «F» и «A». Это график изменения накопленной дозы радиации во времени. Наглядно видно монотонное увеличение накопленной дозы радиации за время полёта. Это говорит о том, что мы правильно рассчитали интеграл. И окончательное значение накопленной за двухчасовой полёт дозы радиации, которое получается в последней ячейке этого столбца, равно примерно 4,5 микрозиверт.

Вычисление суммарной площади всех трапеций, что численно равно искомому определённому интегралу

Таким образом, мы только что нашли определённый интеграл таблично заданной функции в программе Excel на реальном физическом примере. В качестве приложения к статье – файл Excel с нашим примером.

Источник

Цель
работы:
Освоение приемов работы в Ms Excel при
вычислении сумм и интегралов.

Содержание
работы

1. Приближенное
вычисление определенных интегралов
методом прямоугольников и методом
трапеций.

2. Приближенное
вычисление длины кривой.

3. Проведение
экспериментов и решение задач.

Пояснения к выполнению работы

1.
С геометрической точки зрения определенный
интеграл
– есть площадь фигуры, ограниченной
графиком функциии прямыми,,.
Функцияназывается
подынтегральной функцией.

Чтобы
приближенно вычислить эту площадь,
разделим интервал интегрирования
наравных отрезков длинойкаждый.
Тогда координата левого концаi-го
отрезка определяется по формуле
,
где,.
Простейший приближенный расчет площади
под кривойсостоит в нахождении суммы площадей
прямоугольников, у каждого из которых
основание совпадает с отрезком,
а высота равна значению функции в точке(метод левых прямоугольников). Можно
высоту брать равной значению функции
в точке(метод правых прямоугольников) или в
точке(метод центральных прямоугольников).
При использовании метода левых
прямоугольников формула для вычисления
площади выглядит следующим образом:

Можно
повысить точность вычисления определенного
интеграла, если заменить на каждом
интервале
,дугу графикаотрезком (хордой), соединяющем точки с
координатамии.
В этом случае фигура, ограниченная
графиком функции и прямыми,,
приближенно заменяется не прямоугольником,
а трапецией, и искомый определенный
интеграл рассчитывается как сумма
площадей всех таких трапеций:

Формула
может быть существенно упрощена, но мы
оставим это для курса вычислительной
математики (сейчас можете попытаться
упростить ее самостоятельно).

2.
Замена графика функции
хордами, описанная в методе трапеций,
позволяет при помощи электронных таблиц
довольно легко определять приближенное
значение длины дуги графикана интервале.
В этой задаче рассматриваемая кривая
представляется в виде
ломанной,
длина s
которой равна сумме длин
её звеньев. Длинузвена, построенного на отрезке,
можно найти как длину гипотенузы
прямоугольного треугольника с катетами,
равнымии,
используя известную теорему Пифагора.
В результате суммирования длин всех
звеньев, получаем:

Следует
отметить, что точность приближенного
вычисления интегралов зависит от
величины
,
то есть от количества отрезков, на
которые разбивается интервал интегрирования.
При отсутствии погрешностей округления,
чем больше,
тем выше точность (с ростомN
погрешность вычислений сходится к
нулю).

3.
В качестве примера вычислим интеграл
с точностью представления результатов
вычислений до 4 знаков после запятой.

В
ячейку А6
вводим нижнюю границу интервала
интегрирования
,
равную 0,5. В следующую ячейкуА7
вводим значение 0,51, отстоящее от нижней
границы на шаг
.
Рекомендуется выбирать шаг в зависимости
от требуемой точности вычисления
интеграла. Затем выделяем обе ячейкиА6
и А7.
В правой нижней части выделенной области
есть жирная черная точка – маркер
заполнения, – тянем её мышкой вниз, пока
не получим число, соответствующее
верхней границе интеграла, т. е. значению
.
Это достигается в ячейкеА206.

Выделим
мышкой столбцы
С,
Е
и G,
указывая мышкой их заголовки. Вызовем
с помощью правой кнопки мыши контекстное
меню выделенных столбцов и выберем в
нем опцию Формат
ячеек.
Далее, на закладке Число,
выберем в качестве числового формата
– Числовой
и укажем отображаемое число десятичных
знаков 4. Нажмем клавишу OК.

3.1.
Теперь вычислим определенный интеграл
с помощью метода левых прямоугольников.
Для этого введем в ячейку С6
формулу =(А7-А6)*(Ln(А6))
(величина логарифма и есть высота
соответствующего прямоугольника).
Выделим ячейку С6
и протянем маркер заполнения вниз, до
ячейки С205.
Таким образом, в столбце C
мы получили площади всех прямоугольников.

Выделим
ячейку С206
и нажмем на кнопку Автосумма
на панели Стандартные.
Нажмем Enter,
подтверждая этим предложенную формулу.
В результате получим сумму всех выше
расположенных чисел в столбце, т. е.
значение интеграла, вычисленное методом
прямоугольников.

3.2.
Вычислим определенный интеграл с помощью
метода трапеций. Для этого введем в
ячейку Е6
следующую формулу =(А7-А6)*(Ln(А7)+Ln(А6))/2.
Выделите ячейку Е6
и протяните маркер заполнения вниз до
ячейки Е205.
Так мы вычислили площади всех трапеций.
Выделив ячейку Е206,
вычислите их сумму с помощью кнопки
Автосумма
на панели Стандартные.
Мы
получили
значение интеграла, найденное методом
трапеций.

3.3.
Вычислим длину графика функции
на интервале [0,5; 2,5].

Для
вычисления длин хорд введите в ячейку
G6
формулу
=((A7-A6)^2+(Ln(A7)-Ln(A6))^2)^(0,5).
Выделите ячейку G6
и протяните маркер заполнения вниз до
ячейки G205.
В ячейке G206,
используя Автосумму,
найдите приближенное значение искомой
длины графика.

3.4.
Повторите в соседних столбцах все
расчеты при меньшем шаге интегрирования,
например, при шаге 0,001. Сравните результаты
с полученными ранее. Проанализируйте
их и сделайте выводы.

3.5. Вычисления
провести по варианту и записать в отчет.

Соседние файлы в папке Рабочая профессия

#
#
13.03.201652.81 Кб36Графики.xlsm
#
13.03.2016656.9 Кб132Лабораторная 2.xls
#
13.03.201640.96 Кб79Лабораторная 3.xls
#
#

Источник

ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ МЕТОДОМ ТРАПЕЦИЙ В СРЕДЕ MICROSOFT EXCEL

Автор: Пилипенко Дэниил Владимирович, студент 3 курса ГБПОУ МО «Серпуховский колледж» г. Серпухов Московской области.

Научный руководитель: Соколова Марина Анатольевна, преподаватель специальных дисциплин ГБПОУ МО «Серпуховский колледж» г. Серпухов Московской области.

Аннотация.

В данной статье рассматривается численные методы решения определенных интегралов методом трапеций, с применением электронных таблиц Microsoft Excel.

Annotation.

The article shows numerical methods for solving definite integrals using the trapezoidal rule via Microsoft Excel spreadsheets.

Актуальность

Задача вычисления определенных интегралов появляется во многих областях прикладной математики, при решении практических задач. В большинстве случаев не удается найти аналитические формулы, выразить определенный интеграл в виде алгебраических и трансцендентных функций. Даже если аналитическая функция находится, то она получается более сложной, поэтому вычислять интеграл с её помощью значительно труднее, чем другими способами. Иногда подынтегральная функция задается графиком или таблицей экспериментально полученных данных. Большинство определенных интегралов не могут решиться с помощью точных методов или путем аналитических преобразований, на практике их решают только численными методами.

Задача нахождения определенного интеграла численными методами считается решенной, если они вычислены с заданной степенью точности. В своей работе я буду проводить вычисление определенного интеграла методом трапеций, с применением электронных таблиц Microsoft Excel.

Объект исследования: определенные интегралы.

Предмет исследования: методы решения определенных интегралов.

Цель работы: изучить методы решения определенных интегралов; вычислить определенный интеграл методом трапеций в среде Microsoft Excel.

Задачи работы:

1. Изучить и провести анализ литературы, интернет-ресурсов теоретической и практической основы численных методов решения определенных интегралов;

2. Исследовать различные численные методы решения определенных интегралов;

3. Вычислить определенный интеграл методом трапеций в среде Microsoft Excel.

Введение

Здесь речь пойдет об одной из самых распространенных операций – вычислении определенного интеграла . Самый общий подход к ее решению состоит в том, чтобы аппроксимировать функцию какой-либо другой функцией , для которой интеграл вычисляется аналитически. Тогда для решения задачи строим с оценкой погрешности и полагаем приближенно с очевидной оценкой погрешности .

Введем на отрезке сетку , , где , и таблицу значений , . Рассмотрим самый простой вариант построения функции , приводящий к широко распространенной формуле трапеций.

При этом функция строится как кусочно-линейная интерполяция значений , на равномерной сетке с шагом . Тогда =.

Формулы такого рода () называют механическими квадратурами, – коэффициентами (весами) квадратуры, – ее узлами.

Однако теоретические оценки погрешностей не очень популярны среди практиков. Если требуется вычислить интеграл с погрешностью , то мало кто сначала оценит третью производную функции и вычислит шаг сетки . Дело в том, что сама эта оценка завышена и завышено значение константы . Кроме того, само вычисление может быть проблематичным, особенно если задана некоторым сложным образом.

Поступают иначе. Вычисляя интеграл с небольшим числом узлов , получают его значение ; вычисляя интеграл с удвоенным , получают . Если модуль (где ε – предельное допустимое значение погрешности расчета), то задачу считают решенной. В противном случае вычисляют и т. д. Нужно иметь в виду, что для гладких функций часто интеграл вычисляется очень точно при малом числе узлов.

Постановка задачи

Дано: f(x) = 1/(1+x4)1/2 на отрезке [0; 4]

Вывод

Я изучил методы решения определенных интегралов численными методами с помощью электронных таблиц. В данной работе был рассмотрен метод расчета интеграла – метод трапеций. Результаты расчетов были сведены в таблицу. Вследствие чего было выяснено, что метод трапеций расчета интегралов является численным методом. Точное решение находится по формуле Ньютона-Лейбница.Я сделал вывод, что электронные таблицы – это очень мощный компьютерный инструмент, позволяющий проводить сложные расчеты, с заданной точностью.

Список использованных источников

Основы компьютерной грамотности: учебное пособие / Кривенкова С. В., Радионова Л. К., Соболенко Н. А., Шванн Д. Э. М.: Издательство МЭИ, 2004.
Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989.
Федоренко Р. П. Введение в вычислительную физику. М.: Издательство МФТИ, 1994.
Физико-математические основы техники и электрофизики высоких напряжений. Учебное пособие для вузов / В.В. Базуткин, К.П. Кадомская, Е.С. Колечицкий и др. Под ред. К.П. Кадомской. М.: Энергоатомиздат, 1995.
Поршнев С. В., Беленкова И. В. Численные методы на базе Mathcad. СПб.: БХВ-Петербург, 2005.

Источник

Опубликовано 10 Авг 2015
Рубрика: Справочник Excel | 13 комментариев

При стремлении постичь нечто сложное, громоздкое, непонятное следует «разбить» его на как можно большее количество простых, мелких, понятных частей, изучить их с помощью существующих инструментов, а затем «сложить» эти результаты и получить итоговый ответ.

Формулировка в предыдущем предложении определяет сущность понятия интегрирования.

Интеграл чего-либо – это сумма всех малых частей этого чего-либо. Чем больше количество этих малых частей, тем точнее значение интеграла соответствует действительности, определяя признак изучаемого объекта.

Интегрирование применимо для изучения свойств физических и философских объектов при условии, что эти свойства остаются неизменными как для «мелкой» части, так и для всего объекта в целом.

Функция – это описание зависимости некоторого признака или свойства объекта от аргумента.

Например:

Объект – плоская фигура между графиком функции и осью абсцисс.

Признак (значение функции) – высота фигуры.

Аргумент (независимая переменная) – ширина фигуры.

Функция – описание зависимости высоты от ширины.

Определенный интеграл функции – площадь фигуры. Площадь тоже является признаком фигуры, но зависит от двух переменных – высоты и ширины – и представляет собой качественно иной новый признак.

Теория.

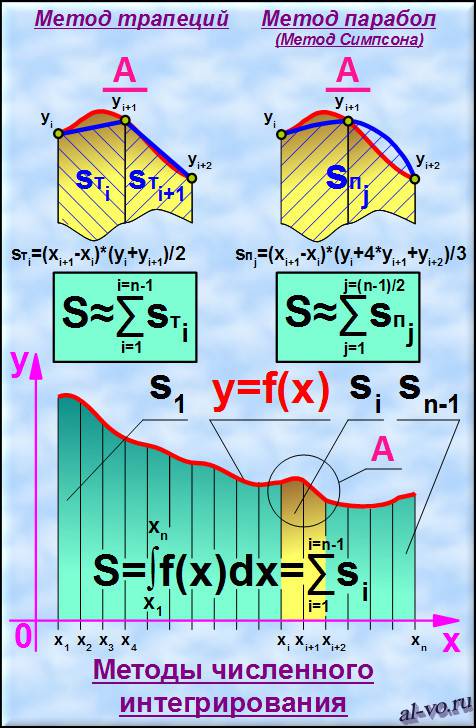
Подробно рассмотрим два наиболее точных метода численного интегрирования функции одной переменной – метод трапеций и метод парабол или метод Симпсона. Есть еще метод прямоугольников, но мы его проигнорируем из-за невысокой точности.

Все, что требуется для понимания и применения метода трапеций и метода Симпсона на практике представлено далее на рисунке.

Площадь под кривой y = f (x) разбиваем на n-1 криволинейных трапеций, у которых три стороны – это прямые линии, а одна сторона – участок кривой y=f (x). Суммарная площадь под графиком функции на участке от x₁ до x_n – это и есть искомая величина, которая является определенным интегралом функции на этом участке и находится как сумма площадей всех криволинейных трапеций.

Точно вычислить аналитически площадь криволинейной трапеции бывает сложно или даже невозможно.

Для приближенного вычисления площади криволинейной трапеции можно заменить участок кривой прямой линией и, получив простую фигуру – обычную трапецию, найти по известной формуле ее площадь. В этом суть метода трапеций.

Если участок кривой линии над двумя криволинейными трапециями заменить параболой, проведенной через три характерные точки, то получим новую криволинейную трапецию с одной из сторон в виде параболы. Количество новых фигур будет в два раза меньше, чем количество исходных трапеций. Площадь этих новых фигур вычисляется по простой формуле. В этом смысл метода Симпсона.

Идею замены участка любой кривой участком параболы высказывал Исаак Ньютон, но первым вывел формулу английский математик Томас Симпсон. Метод Симпсона для вычисления интегралов является самым точным из приближенных численных методов.

Если вычисление интегралов методом трапеций не имеет ограничений, то для того, чтобы реализовать метод Симпсона необходимо выполнить два условия.

1. Разбить площадь на четное количество частей, то есть n должно быть нечетным числом!

2. Расстояния между точками по оси x должны быть одинаковыми!

Практика вычисления интегралов в Excel.

Определенной сложностью является связать вычисление интегралов с реальными задачами из жизни. Рассмотрение примеров – лучший способ устранения подобных препятствий.

Определение тепловой энергии.

Мой знакомый из города Улан-Удэ Алексей Пыкин проводит испытания воздушных солнечных PCM-коллекторов производства КНР. Воздух из помещения подается вентилятором в коллекторы, нагревается от солнца и поступает назад в помещение. Каждую минуту измеряется и записывается температура воздуха на входе в коллекторы и на выходе при постоянном воздушном потоке. Требуется определить количество тепловой энергии полученной в течение суток.

Более подробно о преобразовании солнечной энергии в тепловую и электрическую и об экспериментах Алексея я постараюсь рассказать в отдельной статье. Многим, я думаю, это будет интересно.

Запускаем MS Excel и начинаем работу – выполняем вычисление интеграла.

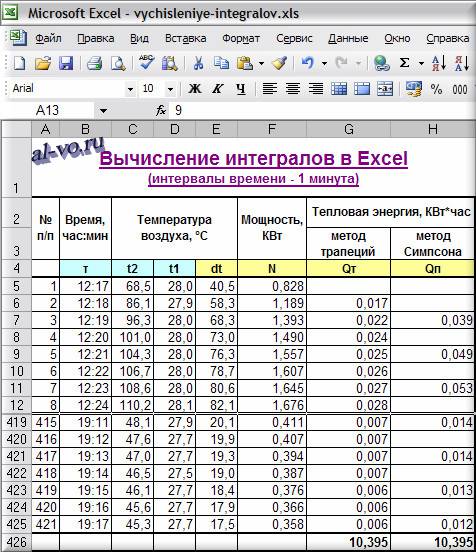
Заполним таблицу.

1. В столбец B вписываем время проведения измерения τ_i.

2. В столбец C заносим температуры нагретого воздуха t_2i, измеренные на выходе из коллекторов в градусах Цельсия.

3. В столбец D записываем температуры холодного воздуха t_1i, поступающего на вход коллекторов.

4. В столбце E вычисляем разности температур dt_i на выходе и входе

dt_i=t_2i—t_1i

5. Зная удельную теплоемкость воздуха c=1005 Дж/(кг*К) и его постоянный массовый расход (измеренная производительность вентилятора) G=0,02031 кг/с, определяем мощность установки N_i в КВт в каждый из моментов времени в столбце F

N_i=c*G*dt_i

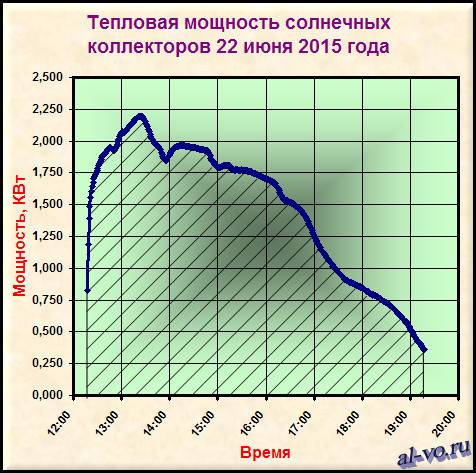
На графике ниже показана экспериментальная кривая зависимости мощности, развиваемой коллекторами, от времени.

Количество тепловой энергии, выработанной за промежуток времени – это интеграл этой функции, и значение интеграла – это заштрихованная площадь под кривой.

6. Вычисляем в ячейках столбца G площади трапеций, суммируем их и находим общее количество энергии, выработанной за день

Q_i=(N_i+1+N_i)*(τ_i+1—τ_i)/2

Q=ΣQ_i=10,395 КВт*час

7. Рассчитываем в ячейках столбца H элементарные площади по методу парабол, суммируем их и находим общее количество энергии по методу Симпсона

Q_j=(N_i+4*N_i+1+N_i+2)*(τ_i+1—τ_i)/3

Q=ΣQ_j=10,395 КВт*час

Как видим, значения не отличаются друг от друга. Оба метода демонстрируют одинаковые результаты!

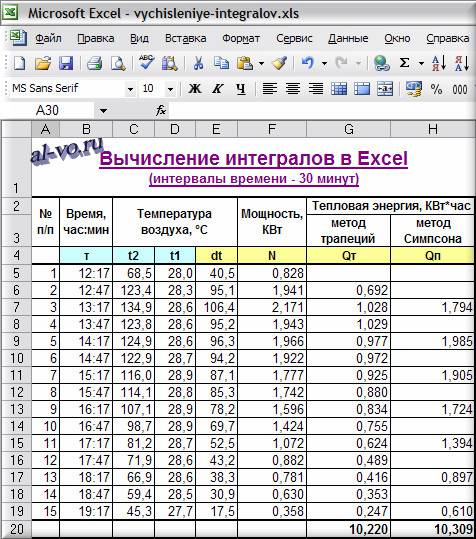
Исходная таблица содержит 421 строку. Давайте уменьшим её в 30 раз и оставим всего 15 строк, увеличив тем самым интервалы между замерами с 1 минуты до 30 минут.

По методу трапеций: Q=10,220 КВт*час (-1,684%)

По методу Симпсона: Q=10,309 КВт*час (-0,827%)

Не смотря на оставшуюся неожиданно весьма высокую точность полученных результатов, метод трапеций дает в данном случае относительную ошибку в 2 раза большую, чем метод Симпсона.

Общие выводы.

Вычисление интегралов численными методами в Excel позволяет эффективно и быстро решать сложные практические задачи, обеспечивая очень высокую точность результатов.

Так как мы существуем в пространстве и времени, то и всё окружающее нас изменяется или в пространстве или во времени. Это означает, что аргументом x функций y интересующих нас процессов или объектов чаще всего являются длина или время. Например, пройденный путь – это интеграл функции скорости (аргумент – время), площадь плотины – это интеграл функции высоты (аргумент – длина), и т.д.

Понимание сути интегрального исчисления и умение использовать его на практике вооружает вас, как специалиста, мощным оружием в осознанном изучении окружающего мира!

Ссылка на скачивание файла с примером: vychisleniye-integralov (xls 216,0KB).

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

Источник

Метод трапеций

Вы будете перенаправлены на Автор24

Метод трапеций — это метод приближённого интегрирования, полезный в тех случаях, когда нет возможности найти первообразную функции и вычислить интеграл через неё.

Помимо метода трапеций существуют другие методы приближённого интегрирования, например, метод прямоугольников и метод парабол.

Метод трапеций по сути похож на метод прямоугольников, но при этом он менее точный, чем метод средних прямоугольников.

Сущность метода трапеций

Рисунок 1. Метод трапеций для вычисления интегралов

Предположим, требуется вычислить интеграл от функции $f(x)$ на отрезке $left[a;bright]$.

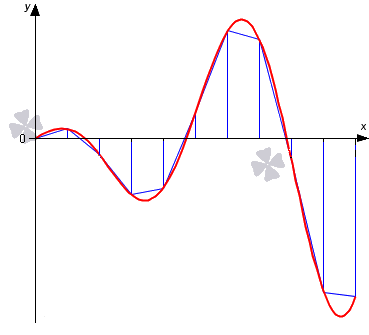
Также как и в случае с методом прямоугольников разобьём график кривой на элементарные сегменты c помощью точек с абсциссами $x_i$, и получим ломаную с вершинами в точках $(x_i;y_i)$, при этом $y_i=f(x_i)$, а $i$ принимает значения от $0$ до $n-1$.

Для этого выберем количество отрезков, на которые разбиваем исследуемый интервал и воспользуемся формулой для вычисления длины одного такого отрезка, которую мы уже использовали для метода прямоугольников:

Для вычисления по методу трапеций между собой соединяются две рядом стоящие точки разбиения, в результате образуя элементарные сегменты. Как видно дальше, значение функции $f(x)$ берётся на границах исследуемого отрезка.

Площадь первой такой трапеции составит:

а площадь $i$-ой трапеции составит:

Сложим площади всех элементарных трапеций:

Таким образом, площади всех элементарных трапеций, сложенные вместе, являются приближённой площадью фигуры, ограниченной линиями $x=a$, $x=b$, осью абсцисс и графиком кривой $f(x)$.

Готовые работы на аналогичную тему

Формула для приближённого вычисления интеграла методом трапеций:

Погрешность при использовании метода трапеций

Погрешность метода составляет:

Как видно из вышеприведённой формулы, здесь погрешность несколько больше чем погрешность метода средних прямоугольников, однако, не всегда удобно использовать именно этот метод. Метод трапеции удобен если самого графика функции нет, но есть значения, которые принимает функция $f(x)$ в точках разбиения. В случаях же когда всё же есть график, целесообразнее пользоваться методом средних прямоугольников.

Также при невозможности определения максимума функции сложно определить вычисляемую погрешность. В этом случае можно прибегнуть к следующему: сначала провести численное интегрирование методом трапеций для $n=10$, а затем на том же отрезке провести вычисление при $n=20$. Если разница двух полученных значений интегралов составляет меньше чем требуемая по условию погрешность, то в качестве ответа выбирают приближённое значение интеграла при $n=20$, а вычисления заканчивают. В противном случае если требуемая точность не достигнута, продолжают удваивать дальше количество отрезков.

Посчитайте интеграл $int_1^2 frac=ln2$ с точностью до $0, 001$, используя метод трапеций.

Разобьём нашу функцию на 10 равных сегментов.

В начале оценим погрешность вычисления:

В данном случае погрешность составляет $|δ_n|≤0.00008$, следовательно, для разбиения можно использовать 10 сегментов.

Также как и с методом прямоугольников, разобьём подынтегральную функцию на 10 отрезков, длина каждого из которых $Δx=frac<2-1><10>=0,1$ и вычислим значение подынтегральной функции $y(x)=frac<1>$ на границах каждого отрезка:

Сумма всех вычисленных значений функции $f(x)$ от первого до девятого включительно составит $6.1877$, а само значение интеграла составит:

Данное значение отвечает необходимой точности.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 21 02 2021

Метод трапеций

Сегодня мы познакомимся с еще одним методом численного интегрирования, методом трапеций. С его помощью мы будем вычислять определенные интегралы с заданной степенью точности. В статье мы опишем суть метода трапеций, разберем, как выводится формула, сравним метод трапеции с методом прямоугольника, запишем оценку абсолютной погрешности метода. Каждый из разделов мы проиллюстрируем примерами для более глубокого понимания материала.

Метод трапеций

Предположим, что нам нужно приближенно вычислить определенный интеграл ∫ a b f ( x ) d x , подынтегральная функция которого y = f ( x ) непрерывна на отрезке [ a ; b ] . Для этого разделим отрезок [ a ; b ] на несколько равных интервалов длины h точками a = x 0 x 1 x 2 . . . x n — 1 x n = b . Обозначим количество полученных интервалов как n .

Найдем шаг разбиения: h = b — a n . Определим узлы из равенства x i = a + i · h , i = 0 , 1 , . . . , n .

На элементарных отрезках рассмотрим подынтегральную функцию x i — 1 ; x i , i = 1 , 2 , . . , n .

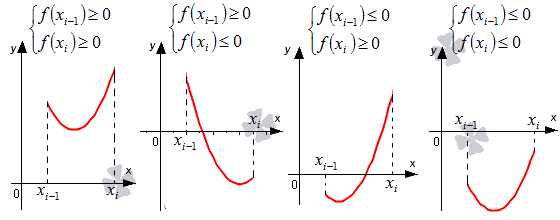
При бесконечном увеличении n сведем все случаи к четырем простейшим вариантам:

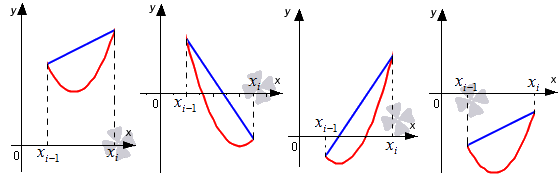
Выделим отрезки x i — 1 ; x i , i = 1 , 2 , . . . , n . Заменим на каждом из графиков функцию y = f ( x ) отрезком прямой, который проходит через точки с координатами x i — 1 ; f x i — 1 и x i ; f x i . Отметим их на рисунках синим цветом.

Возьмем выражение f ( x i — 1 ) + f ( x i ) 2 · h в качестве приближенного значения интеграла ∫ x i — 1 x i f ( x ) d x . Т.е. примем ∫ x i — 1 x i f ( x ) d x ≈ f ( x i — 1 ) + f ( x i ) 2 · h .

Давайте посмотрим, почему метод численного интегрирования, который мы изучаем, носит название метода трапеций. Для этого нам нужно выяснить, что с точки зрения геометрии означает записанное приближенное равенство.

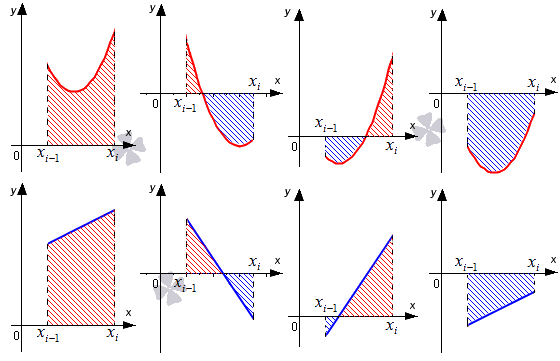
Для того, чтобы вычислить площадь трапеции, необходимо умножить полусуммы ее оснований на высоту. В первом случае площадь криволинейной трапеции примерно равна трапеции с основаниями f ( x i — 1 ) , f ( x i ) высотой h . В четвертом из рассматриваемых нами случаев заданный интеграл ∫ x i — 1 x f ( x ) d x приближенно равен площади трапеции с основаниями — f ( x i — 1 ) , — f ( x i ) и высотой h , которую необходимо взять со знаком « — ». Для того, чтобы вычислить приближенное значение определенного интеграла ∫ x i — 1 x i f ( x ) d x во втором и третьем из рассмотренных случаев, нам необходимо найти разность площадей красной и синей областей, которые мы отметили штриховкой на расположенном ниже рисунке.

Подведем итоги. Суть метода трапеций заключается в следующем: мы можем представить определенный интеграл ∫ a b f ( x ) d x в виде суммы интегралов вида ∫ x i — 1 x i f ( x ) d x на каждом элементарном отрезке и в последующей приближенной замене ∫ x i — 1 x i f ( x ) d x ≈ f ( x i — 1 ) + f ( x i ) 2 · h .

Формула метода трапеций

Вспомним пятое свойство определенного интеграла: ∫ a b f ( x ) d x = ∑ i = 1 n ∫ x i — 1 x i f ( x ) d x . Для того, чтобы получить формулу метода трапеций, необходимо вместо интегралов ∫ x i — 1 x i f ( x ) d x подставить их приближенные значения: ∫ x i — 1 x i f ( x ) d x = ∑ i = 1 n ∫ x i — 1 x i f ( x ) d x ≈ ∑ i = 1 n f ( x i — 1 ) + f ( x i ) 2 · h = = h 2 · ( f ( x 0 ) + f ( x 1 ) + f ( x 1 ) + f ( x 2 ) + f ( x 2 ) + f ( x 3 ) + . . . + f ( x n ) ) = = h 2 · f ( x 0 ) + 2 ∑ i = 1 n — 1 f ( x i ) + f ( x n ) ⇒ ∫ x i — 1 x i f ( x ) d x ≈ h 2 · f ( x 0 ) + 2 ∑ i = 1 n — 1 f ( x i ) + f ( x n )

Формула метода трапеций: ∫ x i — 1 x i f ( x ) d x ≈ h 2 · f ( x 0 ) + 2 ∑ i = 1 n — 1 f ( x i ) + f ( x n )

Оценка абсолютной погрешности метода трапеций

Оценим абсолютную погрешность метода трапеций следующим образом:

δ n ≤ m a x x ∈ [ a ; b ] f » ( x ) · n · h 3 12 = m a x x ∈ [ a ; b ] f » ( x ) · b — a 3 12 n 2

Графическая иллюстрация метода трапеций

Графическая иллюстрация метода трапеций приведена на рисунке:

Примеры вычислений

Разберем примеры использования метода трапеций для приближенного вычисления определенных интегралов. Особое внимание уделим двум разновидностям заданий:

вычисление определенного интеграла методом трапеций для данного числа разбиения отрезка n;
нахождение приближенного значения определенного интеграла с оговоренной точностью.

При заданном n все промежуточные вычисления необходимо проводить с достаточно высокой степенью точности. Точность вычислений должна быть те выше, чем больше n .

Если мы имеем заданную точность вычисления определенного интеграла, то все промежуточные вычисления необходимо проводить на два и более порядков точнее. Например, если задана точность до 0 , 01 , то промежуточные вычисления мы проводим с точностью до 0 , 0001 или 0 , 00001 . При больших n промежуточные вычисления необходимо проводить с еще более высокой точностью.

Рассмотрим приведенное выше правило на примере. Для этого сравним значения определенного интеграла, вычисленного по формуле Ньютона-Лейбница и полученного по методу трапеций.

Итак, ∫ 0 5 7 d x x 2 + 1 = 7 a r c t g ( x ) 0 5 = 7 a r c t g 5 ≈ 9 , 613805 .

Вычислим по методу трапеций определенный интеграл ∫ 0 5 7 x 2 + 1 d x для n равным 10 .

Решение

Формула метода трапеций имеет вид ∫ x i — 1 x i f ( x ) d x ≈ h 2 · f ( x 0 ) + 2 ∑ i = 1 n — 1 f ( x i ) + f ( x n )

Для того, чтобы применить формулу, нам необходимо вычислить шаг h по формуле h = b — a n , определить узлы x i = a + i · h , i = 0 , 1 , . . . , n , вычислить значения подынтегральной функции f ( x ) = 7 x 2 + 1 .

Шаг разбиения вычисляется следующим образом: h = b — a n = 5 — 0 10 = 0 . 5 . Для вычисления подынтегральной функции в узлах x i = a + i · h , i = 0 , 1 , . . . , n будем брать четыре знака после запятой:

i = 0 : x 0 = 0 + 0 · 0 . 5 = 0 ⇒ f ( x 0 ) = f ( 0 ) = 7 0 2 + 1 = 7 i = 1 : x 1 = 0 + 1 · 0 . 5 = 0 . 5 ⇒ f ( x 1 ) = f ( 0 . 5 ) = 7 0 , 5 2 + 1 = 5 , 6 . . . i = 10 : x 10 = 0 + 10 · 0 . 5 = 5 ⇒ f ( x 10 ) = f ( 5 ) = 7 5 2 + 1 ≈ 0 , 2692

Внесем результаты вычислений в таблицу:

i	0	1	2	3	4	5	6	7	8	9	10
x i	0	0 . 5	1	1 , 5	2	2 , 5	3	3 , 5	4	4 , 5	5
f ( x i )	7	5 , 6	3 , 5	2 , 1538	1 , 4	0 , 9655	0 , 7	0 , 5283	0 , 4117	0 , 3294	0 , 2692

Подставим полученные значения в формулу метода трапеций: ∫ 0 5 7 d x x 2 + 1 ≈ h 2 · f ( x 0 ) + 2 ∑ i = 1 n — 1 f ( x i ) + f ( x n ) = = 0 , 5 2 · 7 + 2 · 5 , 6 + 3 , 5 + 2 , 1538 + 1 , 4 + 0 , 9655 + 0 , 7 + 0 , 5283 + 0 , 4117 + 0 , 3294 + 0 , 2692 = 9 , 6117

Сравним наши результаты с результатами, вычисленными по формуле Ньютона-Лейбница. Полученные значения совпадают до сотых.

Ответ: ∫ 0 5 7 d x x 2 + 1 = 9 , 6117

Вычислим по методу трапеций значение определенного интеграла ∫ 1 2 1 12 x 4 + 1 3 x — 1 60 d x с точностью до 0 , 01 .

Решение

Согласно условию задачи a = 1 ; b = 2 , f ( x ) = 1 12 x 4 + 1 3 x — 1 60 ; δ n ≤ 0 , 01 .

Найдем n , которое равно количеству точек разбиения отрезка интегрирования, с помощью неравенства для оценки абсолютной погрешности δ n ≤ m a x x ∈ [ a ; b ] f » ( x ) · ( b — a ) 3 12 n 2 . Сделаем мы это следующим образом: мы найдем значения n , для которых будет выполняться неравенство m a x x ∈ [ a ; b ] f » ( x ) · ( b — a ) 3 12 n 2 ≤ 0 , 01 . При данных n формула трапеций даст нам приближенное значение определенного интеграла с заданной точностью.

Для начала найдем наибольшее значение модуля второй производной функции на отрезке [ 1 ; 2 ] .

f ‘ ( x ) = 1 12 x 4 + 1 3 x — 1 60 ‘ = 1 3 x 3 + 1 3 ⇒ f » ( x ) = 1 3 x 3 + 1 3 ‘ = x 2

Вторая производная функция является квадратичной параболой f » ( x ) = x 2 . Из ее свойств мы знаем, что она положительная и возрастает на отрезке [ 1 ; 2 ] . В связи с этим m a x x ∈ [ a ; b ] f » ( x ) = f » ( 2 ) = 2 2 = 4 .

В приведенном примере процесс нахождения m a x x ∈ [ a ; b ] f » ( x ) оказался достаточно простым. В сложных случаях для проведения вычислений можно обратиться к наибольшим и наименьшим значениям функции. После рассмотрения данного примера мы приведем альтернативный метод нахождения m a x x ∈ [ a ; b ] f » ( x ) .

Подставим полученное значение в неравенство m a x x ∈ [ a ; b ] f » ( x ) · ( b — a ) 3 12 n 2 ≤ 0 , 01

4 · ( 2 — 1 ) 3 12 n 2 ≤ 0 , 01 ⇒ n 2 ≥ 100 3 ⇒ n ≥ 5 , 7735

Количество элементарных интервалов, на которые разбивается отрезок интегрирования n является натуральным числом. Для поведения вычислений возьмем n равное шести. Такое значение n позволит нам достичь заданной точности метода трапеций при минимуме расчетов.

Вычислим шаг: h = b — a n = 2 — 1 6 = 1 6 .

Найдем узлы x i = a + i · h , i = 1 , 0 , . . . , n , определим значения подынтегральной функции в этих узлах:

i = 0 : x 0 = 1 + 0 · 1 6 = 1 ⇒ f ( x 0 ) = f ( 1 ) = 1 12 · 1 4 + 1 3 · 1 — 1 60 = 0 , 4 i = 1 : x 1 = 1 + 1 · 1 6 = 7 6 ⇒ f ( x 1 ) = f 7 6 = 1 12 · 7 6 4 + 1 3 · 7 6 — 1 60 ≈ 0 , 5266 . . . i = 6 : x 10 = 1 + 6 · 1 6 = 2 ⇒ f ( x 6 ) = f ( 2 ) = 1 12 · 2 4 + 1 3 · 2 — 1 60 ≈ 1 , 9833

Результаты вычислений запишем в виде таблицы:

i	0	1	2	3	4	5	6
x i	1	7 6	4 3	3 2	5 3	11 6	2
f x i	0 , 4	0 , 5266	0 , 6911	0 , 9052	1 , 1819	1 , 5359	1 , 9833

Подставим полученные результаты в формулу трапеций:

∫ 1 2 1 12 x 4 + 1 3 x — 1 60 d x ≈ h 2 · f ( x 0 ) + 2 ∑ i = 1 n — 1 f ( x i ) + f ( x n ) = = 1 12 · 0 , 4 + 2 · 0 , 5266 + 0 , 6911 + 0 , 9052 + 1 , 1819 + 1 , 5359 + 1 , 9833 ≈ 1 , 0054

Для проведения сравнения вычислим исходный интеграл по формуле Ньютона-Лейбница:

∫ 1 2 1 12 x 4 + 1 3 x — 1 60 d x = x 5 60 + x 2 6 — x 60 1 2 = 1

Как видим, полученной точности вычислений мы достигли.

Ответ: ∫ 1 2 1 12 x 4 + 1 3 x — 1 60 d x ≈ 1 , 0054

Для подынтегральных функций сложного вида нахождение числа n из неравенства для оценки абсолютной погрешности не всегда просто. В этом случае будет уместен следующий метод.

Обозначим приближенное значение определенного интеграла, которое было получено по методу трапеций для n узлов, как I n . Выберем произвольное число n . По формуле метода трапеций вычислим исходный интеграл при одинарном ( n = 10 ) и удвоенном ( n = 20 ) числе узлов и найдем абсолютную величину разности двух полученных приближенных значений I 20 — I 10 .

Если абсолютная величина разности двух полученных приближенных значений меньше требуемой точности I 20 — I 10 δ n , то мы прекращаем вычисления и выбираем значение I 20 , которое можно округлить до требуемого порядка точности.

Если абсолютная величина разности двух полученных приближенных значений больше требуемой точности, то необходимо повторить действия с удвоенным количеством узлов ( n = 40 ) .

Такой метод требует проведения большого объема вычислений, поэтому разумно использовать вычислительную технику для экономии времени.

Решим с помощью приведенного выше алгоритма задачу. С целью экономии времени опустим промежуточные вычисления по методу трапеций.

Необходимо вычислить определенный интеграл ∫ 0 2 x e x d x по методу трапеций с точностью до 0 , 001 .

Решение

Возьмем n равное 10 и 20 . По формуле трапеций получим I 10 = 8 , 4595380 , I 20 = 8 , 4066906 .

I 20 — I 10 = 8 , 4066906 — 8 , 4595380 = 0 , 0528474 > 0 , 001 , что требует продолжения вычислений.

Возьмем n равное 40 : I 40 = 8 , 3934656 .

I 40 — I 20 = 8 , 3934656 — 8 , 4066906 = 0 , 013225 > 0 , 001 , что также требует продолжения вычислений.

Возьмем n равное 80 : I 80 = 8 , 3901585 .

I 80 — I 40 = 8 , 3901585 — 8 , 3934656 = 0 , 0033071 > 0 , 001 , что требует проведения еще одного удвоения числа узлов.

Возьмем n равное 160 : I 160 = 8 , 3893317 .

I 160 — I 80 = 8 , 3893317 — 8 , 3901585 = 0 , 0008268 0 , 001

Получить приближенное значение исходного интеграла можно округлив I 160 = 8 , 3893317 до тысячных: ∫ 0 2 x e x d x ≈ 8 , 389 .

Для сравнения вычислим исходный определенный интеграл по формуле Ньютона-Лейбница: ∫ 0 2 x e x d x = e x · ( x — 1 ) 0 2 = e 2 + 1 ≈ 8 , 3890561 . Требуемая точность достигнута.

Ответ: ∫ 0 2 x e x d x ≈ 8 , 389

Погрешности

Промежуточные вычисления для определения значения определенного интеграла проводят в большинстве своем приближенно. Это значит, что при увеличении n начинает накапливаться вычислительная погрешность.

Сравним оценки абсолютных погрешностей метода трапеций и метода средних прямоугольников:

δ n ≤ m a x x ∈ [ a ; b ] f » ( x ) n · h 3 12 = m a x x ∈ [ a ; b ] f » ( x ) · b — a 3 12 n 2 δ n ≤ m a x x ∈ [ a ; b ] f » ( x ) n · h 3 24 = m a x x ∈ [ a ; b ] f » ( x ) · b — a 3 24 n 2 .

Метод прямоугольников для заданного n при одинаковом объеме вычислительной работы дает вдвое меньшую погрешность. Это делает метод более предпочтительным в тех случаях, когда известны значения функции в средних отрезках элементарных отрезков.

В тех случаях, когда интегрируемые функции задаются не аналитически, а в виде множества значений в узлах, мы можем использовать метод трапеций.

Если сравнивать точность метода трапеций и метода правых и левых прямоугольников, то первый метод превосходит второй в точности результата.

Вычисление определенных интегралов методом трапеции в среде Microsoft Excel

Классы: 10 , 11

Задачи урока:

Образовательные – совершенствование умений студентов при вычисление определенных интегралов методом трапеции в среде электронных таблиц MS Excel. Выработать умение применять теоретические знания в практических расчетах;
Развивающие – познакомить студентов с применением компьютеров в качестве помощников при решении уравнений. Развивать у студентов математическую речь: создать ситуацию для применения основных понятий в речи; творческого мышления через создание условий для самореализации творческого потенциала обучающихся;
Воспитательные – выработать у студентов умение рационально использовать время и возможности компьютерных технологий при решении задач. Воспитывать интерес к предмету через ситуацию успеха и взаимодоверия.

Тип урока: комбинированный урок.

Вид урока: практическое занятие, продолжительность – 2 часа.

Оборудование урока:

Компьютеры с OS MS Windows;
Программа Microsoft Excel;
Презентация по теме, выполненная в программе PowerPoint;
Карточки с заданиями для самостоятельной работы.

Структура урока:

ХОД УРОКА

1. Актуализация знаний

1.1. Мобилизующее начало, постановка целей и задач на урок.

— В чем заключается вычисление интеграла?

— Тогда для решения задачи строим с оценкой погрешности , и приближенно с очевидной оценкой погрешности .

— Введем на отрезке сетку , , где , и таблицу значений , .

— Рассмотрим простой вариант построения функции , приводящий к формуле трапеций.

— При этом функция строится как кусочно-линейная интерполяция значений , на равномерной сетке с шагом .

— Объясните алгоритм вычисления интеграла различными методами?

2. Применение знаний, формирование умений и навыков

Практическое задание «Вычисление определенных интегралов методом трапеции в среде Microsoft Excel.»

Состав задания:

Ознакомиться с теоретической частью задания;
Провести расчет для своего варианта индивидуального задания в Microsoft Excel
Оформить презентацию в Ms PowerPoint, включающую:
— постановку задачи;
— алгоритм расчета;
— таблицу с расчетом из Ms Excel, график исходной функции;
— результат расчета и его анализ.

Индивидуальное расчетное задание:

Найдите приближенное значение интеграла заданной функции f(x)= 1/(1+x 4 ) 1/2 на отрезке [0; 4]
по формуле трапеций, разбивая отрезок [0; 4] на 8 равных частей. Оцените погрешность приближенного вычисления интеграла при таком разбиении отрезка.
Представьте графически поставленную задачу.

Постановка задачи:

Таблица Исходная информация

источники:

http://zaochnik.com/spravochnik/matematika/integraly-integrirovanie/metod-trapetsij/

http://urok.1sept.ru/articles/674768

Источник