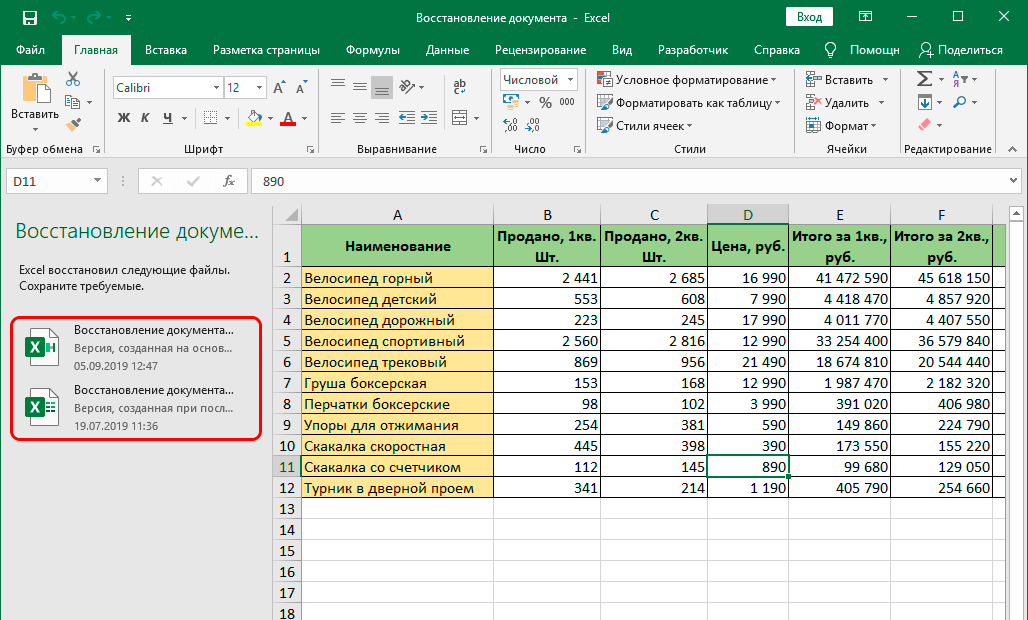
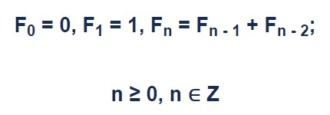Автор Антон Андронов На чтение 1 мин Опубликовано 30.05.2015
В Excel очень легко создавать практически все виды последовательностей. Например, последовательность Фибоначчи.
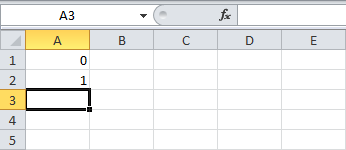
- Первые два числа в последовательности Фибоначчи – 0 и 1.
- Каждое последующее значение можно найти путем сложения двух предыдущих чисел.
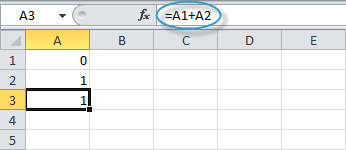
- Нажмите на правый нижний угол ячейки A3 и перетащите его вниз.
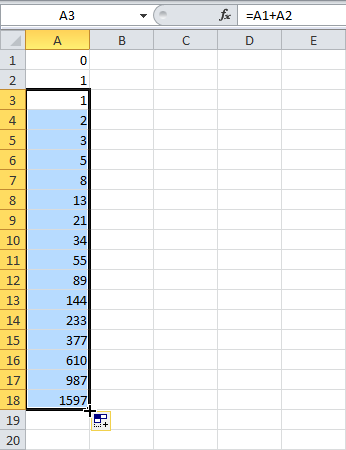
Результат: Последовательность Фибоначчи в Excel:
Оцените качество статьи. Нам важно ваше мнение:
Вам также может понравиться
Работая с таблицами Excel, иногда возникает необходимость
Тем людям, которые регулярно работают с таблицами Excel
Нередко пользователям приходится перенести часть информации
Огромное преимущество электронных таблиц Excel заключается
Пользователю Excel нередко приходится сталкиваться
Excel – одна из лучших программ для аналитика данных.
Время от времени при работе с электронными таблицами
Excel – удивительная программа, дающая возможность
Сейчас век информации. Количество данных, которые людям
Определение процента от числа – довольно частая задача
Excel – невероятно функциональная программа.
Excel – невероятно функциональная программа, позволяющая
Стандартное обозначение строк в Excel – цифровое.
Набор функций у программы Excel, конечно, поистине огромный.
При работе с Excel могут возникать различные ситуации
Важно понимать, что Excel – это не только программа
Числа Фибоначчи – это последовательность чисел, которая начинается с цифр 0 и 1, а каждое последующее значение является суммой двух предыдущих.
- Формула последовательности Фибоначчи
- Золотое сечение
- Таблица последовательности Фибоначчи
- C-код (Си-код) функции
Формула последовательности Фибоначчи
Например:
- F0 = 0
- F1 = 1
- F2 = F1+F0 = 1+0 = 1
- F3 = F2+F1 = 1+1 = 2
- F4 = F3+F2 = 2+1 = 3
- F5 = F4+F3 = 3+2 = 5
Золотое сечение
Соотношение двух последовательных чисел Фибоначчи сходится к золотому сечению:
где φ – это золотое сечение = (1 + √5) / 2 ≈ 1,61803399
Чаще всего, это значение округляют до 1,618 (или 1,62). А в округленных процентах пропорция выглядит так: 62% и 38 %.
Таблица последовательности Фибоначчи
| n | Fn |
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1597 |
| 18 | 2584 |
| 19 | 4181 |
| 20 | 6765 |
microexcel.ru
C-код (Си-код) функции
double Fibonacci(unsigned int n)
{
double f_n =n;
double f_n1=0.0;
double f_n2=1.0;
if( n > 1 ) {
for(int k=2; k<=n; k++) {
f_n = f_n1 + f_n2;
f_n2 = f_n1;
f_n1 = f_n;
}
}
return f_n;
}
|
1 / 1 / 0 Регистрация: 16.02.2010 Сообщений: 47 |
|
|
1 |
|
Число фибоначчи15.12.2010, 15:29. Показов 14627. Ответов 3
Всем доброго времени суток.
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
15.12.2010, 15:29 |
|
3 |
|
671 / 177 / 10 Регистрация: 28.07.2010 Сообщений: 253 |
|
|
15.12.2010, 16:10 |
2 |
|
А в чем проблема?
0 |
|
1 / 1 / 0 Регистрация: 16.02.2010 Сообщений: 47 |
|
|
15.12.2010, 20:13 [ТС] |
3 |
|
а это точно правильно ?
0 |
|
956 / 596 / 11 Регистрация: 11.06.2010 Сообщений: 1,345 |
|
|
15.12.2010, 20:23 |
4 |
|
а это точно правильно ? Нет, Дмитрий просто пошутил. Вот из Википедии: Чи́сла Фибона́ччи — элементы числовой последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765,… (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи)
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
15.12.2010, 20:23 |
|
4 |
ТРЕНИНГИ
Быстрый старт
Расширенный Excel
Мастер Формул
Прогнозирование
Визуализация
Макросы на VBA
КНИГИ
Готовые решения
Мастер Формул
Скульптор данных
ВИДЕОУРОКИ
Бизнес-анализ
Выпадающие списки
Даты и время
Диаграммы
Диапазоны
Дубликаты
Защита данных
Интернет, email
Книги, листы
Макросы
Сводные таблицы
Текст
Форматирование
Функции
Всякое
Коротко
Подробно
Версии
Вопрос-Ответ
Скачать
Купить
ПРОЕКТЫ
ОНЛАЙН-КУРСЫ
ФОРУМ
Excel
Работа
PLEX
© Николай Павлов, Planetaexcel, 2006-2022
info@planetaexcel.ru
Использование любых материалов сайта допускается строго с указанием прямой ссылки на источник, упоминанием названия сайта, имени автора и неизменности исходного текста и иллюстраций.
Техническая поддержка сайта
|
ООО «Планета Эксел» ИНН 7735603520 ОГРН 1147746834949 |
ИП Павлов Николай Владимирович ИНН 633015842586 ОГРНИП 310633031600071 |
In this post, I would like to explain how I have used Lambda to create a function to generate a Fibonacci series array.
This example can also be used to understand how to create an array where the value of an element in the array depends on previous elements in the same array.
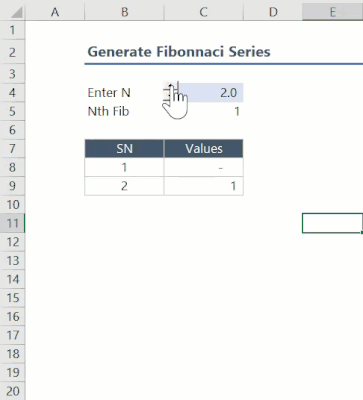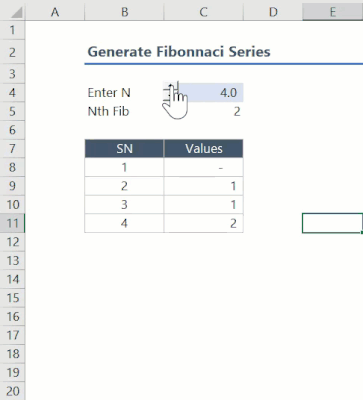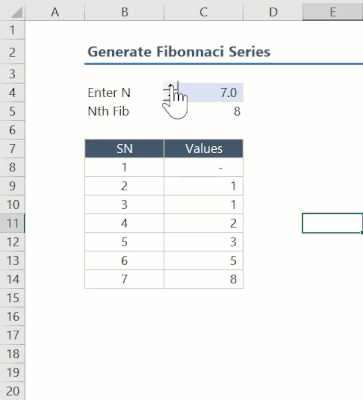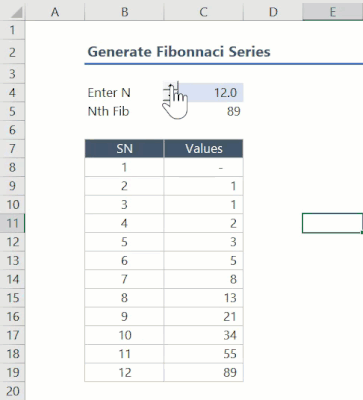
This function has been created using three function in two layers. The inner layer functions include the following:
InFib: This function generates the Nth Fibonacci number
InFibSer: This function generates the entire Fibonacci series up to the Nth number
The two functions mentioned above require arguments that are complicated and less intuitive. Therefore, we use an outer layer function (FibSeries) that generates the necessary argument and calls the two functions to generate the series.
=InFIB
‘This function returns nth Fibonacci using tail recursion
‘It takes three arguments n, a=0 , b=1 as argument and returns the nth Fibonacci value
=LAMBDA(n,a,b,IF(n=1,a,IF(n=2,b,Infib(n-1,b,a+b))))
/* The value for the arguments a and b should be passed as 0 and 1, respectively. */Example:
=InFIB(10,0,1) would generate 34 as the value
Our objective, here, is not to obtain a single value but to generate an entire array. However, here is where we have a challenge: While it is easier to manipulate an existing array, it is far more to difficult to create a new array (other than sequence array) or extend an existing array.
Therefore, in order to create a Fibonacci series, we are going to pass a dummy array of n values. This array will have 0 as the first element and 1 as the value for all the other elements.
The following image portrays the recursive addition process that converts that the initial array into a Fibonacci series.
The following code does carries out the process recursively till the maximum value of the array equals the nth Fibonacci value.
=INFIBSER
‘This inner function takes three arguments and returns a Fibonacci series
‘The three arguments are nth Fibonacci value, the initial array and a sequence array (sequential numbers from 1 to n)
‘Note, the sequence array can instead be generated inside the function but it may inefficient
=Lambda(NthFib, Initval, Sqn,
Let(
Maxval,Max(Initval),
If(Maxval = NthFib,
Initval,
Let(
NewVal,If(Maxval=1,Initval+1*(Sqn>=4),
Let(
StPos,Match(Maxval,Initval,0)+1,
adval,Large(unique(Initval),2),
Initval+adval*(Sqn>=StPos)
)
),
InFibser(NthFib,NewVal,Sqn)
)
)
)
)In the first iteration, the above function adds one to all the values from the fourth position onwards. For the subsequent iterations it adds the second largest unique value to all values that all 2 places after the position of such second largest value. The above function uses the match function to identify the position pointer.
Although the above function can generate the Fibonacci series, as mentioned earlier, it requires arguments that are less intuitive and which requires some set up.
Therefore, here we have an outer layer function that requires only one argument, n. It creates the necessary argument to be passed to the inner layer function and calls them.
=FIBSERIES
‘This outermost function generates an initial array, a sequence array, and nth fibonnaci value
‘It then calls the inner functions with these parameters
=Lambda(n,
Let(
Sqn,sequence(n),
initval,sign(Sqn-1),
Nthfib,Infib(n,0,1),
InFibser(Nthfib, Initval, Sqn)
)
)This final function can be used by the user to generate the Fibonacci series by merely passing the number of values required as argument.
Hope you found this useful. I would love to know if you think there is a way to improve the algorithm, here. I am especially looking for suggestions that could replace the match / xmatch in the InFibSer function to get the position pointer. Since the positions move sequentially, I believe a mathematical solution may exist.
Thank you
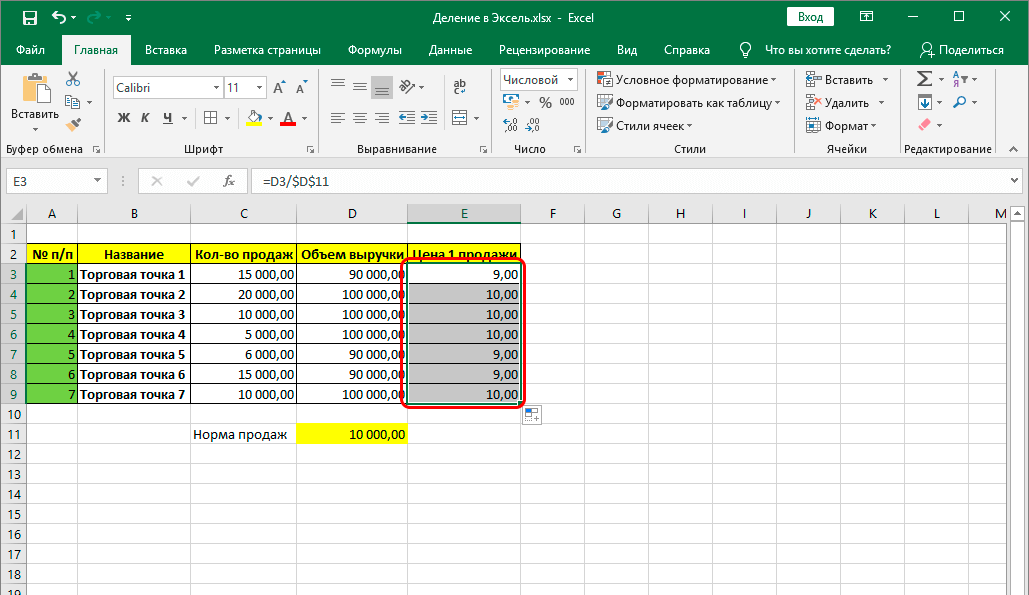
Адресация
Формулы, как известно, могут ссылаться как на отдельные ячейки, так и на блоки ячеек, которые могут находиться на данном рабочем листе либо на других листах рабочей книги.
При ссылке на ячейку можно использовать описанный ранее способ: А1, В4, С13 и т.д. Такая адресация называется относительной. При её использовании Excel запоминает адреса других ячеек формулы относительно текущей ячейки.
При перемещении формулы в новое место ссылки в формуле не изменяются.
При копировании формулы относительные адреса ссылки
автоматически настраиваются на новое местоположение в таблице.
Абсолютные адреса используются в тех случаях, когда нужно сохранить ссылку на конкретную ячейку или блок при копировании формул.

Сделать адрес абсолютным возможно и так:
§ выделить ячейку с формулой;
§ установить курсор мыши на адресе ячейки в строке формул;
§ выделить его, дважды щелкнув клавишей мыши;
§ нажать клавишу
Смешанная адресация используется, когда необходимо зафиксировать либо столбец ($A1), либо строку (A$1) в адресе ячейки. В этом случае при копировании один параметр адреса изменяется, другой — нет.

жатие её задаёт один из возможных типов адресации.

Рис.9. Иллюстрация упражнения 5.1.
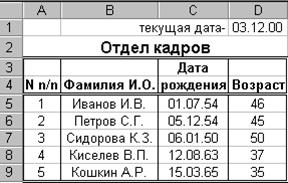
Вычислить возраст сотрудников в заданной таблице.
Порядок вычислений:
1) ввести в ячейку D1 текущую дату —
§ курсор установить на D1;
§ вызвать Мастер функций — fx;
§ выбрать группу Дата и Время;
§ функцию Сегодня, ОК;
2) ввести в ячейку D5 формулу вычисления возраста:
= D$1 – С5;
скопировать формулу из D5 на блок D6:D9.
3) задать возраст в формате года –
§ выделить столбец Возраст;
§ выполнить команду Формат ячеек /Число/(Все форматы);
§ установить формат – ГГ.
Упражнение 5.3. Вычислить значения функции двух переменных Z = X2 + Y, где X = 2, 4, 6, 8… Y = 1, 3, 5, 7, …
Решение.
1) 

2) ввести значения Y в строку 1, начиная с ячейки В1, автозаполнением;
3) ввести в ячейку В2 формулу: = А2^2+B1;
4) отредактировать её для заполнения на всю таблицу:
=$А2^2+B$1
5)
 |
заполнить формулой столбец В, затем всю таблицу.
Результат:
Задача 5.1. В таблице «Анализ спроса и продаж» (лаб. работа №1, стр.20) подсчитать выручку от продаж в долларах США, задав предварительно в качестве справки курс доллара к рублю.
Задача 5.2. Вывести на рабочем листе таблицу умножения
чисел от 1 до 10.
Задача 5.3. Имеется список персонала с соответствующим каждому окладом.
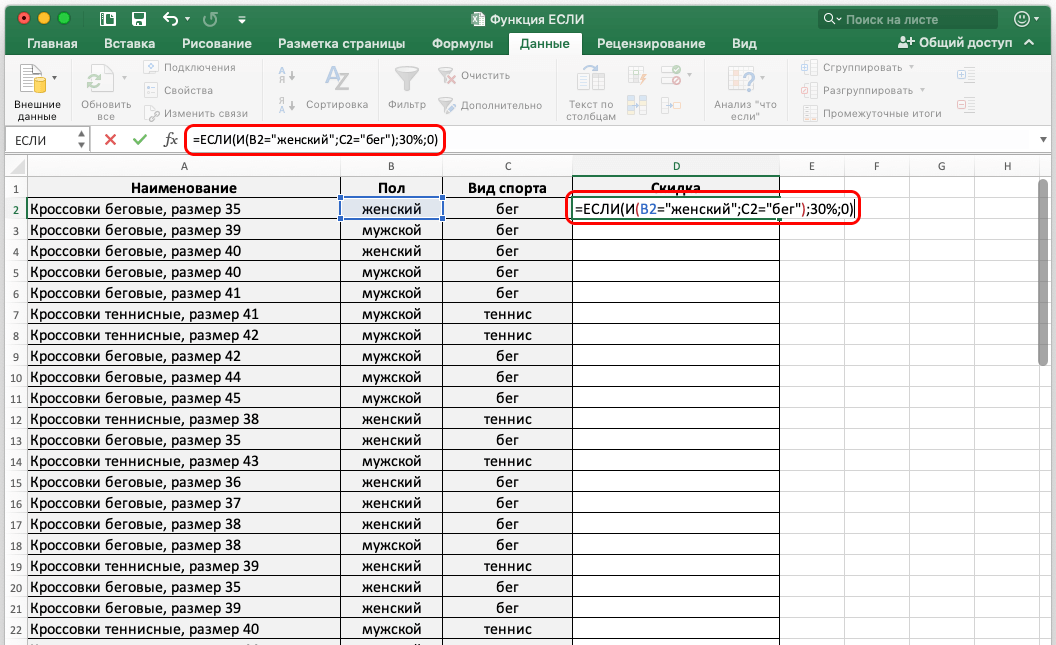
a) Всем сотрудникам нужно начислить премию в размере 20% оклада, имея в виду, что процент премии может измениться.
b) Если оклад меньше 300 руб., то премия увеличивается на 5%.
c) Премиальный фонд ограничен суммой 200 руб. Каждому сотруднику начислить премию пропорционально его окладу и так, чтобы премия была кратна 10 руб.
G Указание. Применить Сервис/Подбор параметра и
функцию округления.
d) Подсчитать зарплату каждому сотруднику.
Задача 5.4. Числа Фибоначчи определяются рекуррентной формулой: F1=0, F2=1, … Fn= Fn-1+Fn-2, где n>2.
Рассчитать первые 14 чисел Фибоначчи.

Задача 5.6. На предприятии персонал работает по графику: 12-часовая дневная смена, 12-часовая ночная смена, затем двое суток отдыха. Составить скользящий график для 8 человек на март (для 1-го — день, ночь, отдых, отдых, день,…; для 2-го — ночь, отдых, отдых, день,… и т.д.).
|
Расчетные и графические задания Равновесный объем — это объем, определяемый равенством спроса и предложения… |
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности… |
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями… |
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм… |
Обновлено: 16.04.2023
Числа Фибоначчи — это числа такой последовательности, в которой первые два элемента — 0 и 1, а каждый последующий элемент равен сумме двух предшествующих. Выглядит это так:
Примечание Иногда 0 опускается, и в этом случае ряд начинается с 1, но мы будем использовать последовательность с 0 на первой позиции.
Формула записывается следующим образом:
Вычисление ряда Фибоначчи — стандартная задача, которую задают на собеседованиях, чтобы проверить кандидата на понимание алгоритмов. Не так популярна, как сортировка, но всё же.
Давайте вычислим ряд и его отдельные элементы, использовав для этого язык Java.
Вычислить ряд Фибоначчи циклом
Предположим, что нам нужно вывести на экран первые десять чисел последовательности Фибоначчи. Мы помним, что:
- первый элемент ряда — 0, второй — 1;
- каждый последующий — сумма двух предыдущих.
Тогда наша последовательность будет иметь такой вид:
Но нам нужно вывести результат с использованием программы. Держите код с объяснениями в комментариях:
Выполнение завершится на десятом элементе. Количество элементов при этом можно менять, изменив значение в условиях цикла.
Найти число Фибоначчи через рекурсию
Рекурсивная функция — это такая функция, которая вызывает саму себя. Она также неплохо отрабатывает в алгоритмических задачах вроде чисел Фибоначчи, но ей требуется больше времени.
25–26 ноября, Москва и онлайн, От 24 000 до 52 000 ₽
Почему так происходит? Всё дело в том, что рекурсивная функция приводит к многоразовому вызову одних и тех же операций. Именно из-за этого её не рекомендуется использовать, но если уж на собеседовании прозвучит такая задача, вы будете готовы.
Рассмотрим пример, в котором нам нужно получить n-ое число в ряде Фибоначчи:
Если в качестве num задать большое значение, программа зависнет.
Тип int в Java может хранить значения до 2147483647, так что вычислить получится лишь первые 46 чисел Фибоначчи. Тип long хранит до 9223372036854775807, а это 91 число Фибоначчи. Класс BigInteger призван работать с действительно большими значениями, вот только само выполнение программы это никак не ускорит.
Использовать для вычисления Stream
Stream в Java — это компонент для самостоятельной внутренней итерации своих же элементов. Подробнее о нём вы можете почитать в нашей статье о Java Stream API.
И, разумеется, Stream подходит для вычисления элементов последовательности Фибоначчи:
В данном примере метод iterate() будет возвращать упорядоченный поток, ограниченный лимитом в num значений и созданный с применением функции к начальному массиву arr . В консоль будет выведено следующее:
А так мы получим сумму чисел последовательности по элемент num включительно:
Программистам числа Фибоначчи должны уже поднадоесть. Примеры их вычисления используются везде. Всё от того, что эти числа предоставляют простейший пример рекурсии. А ещё они являются хорошим примером динамического программирования. Но надо ли вычислять их так в реальном проекте? Не надо. Ни рекурсия, ни динамическое программирование не являются идеальными вариантами. И не замкнутая формула, использующая числа с плавающей запятой. Сейчас я расскажу, как правильно. Но сначала пройдёмся по всем известным вариантам решения.
Код предназначен для Python 3, хотя должен идти и на Python 2.
Для начала – напомню определение:
Замкнутая формула
Пропустим детали, но желающие могут ознакомиться с выводом формулы. Идея в том, чтобы предположить, что есть некий x, для которого Fn = x n , а затем найти x.
Решаем квадратное уравнение:
Откуда и растёт «золотое сечение» ϕ=(1+√5)/2. Подставив исходные значения и проделав ещё вычисления, мы получаем:
что и используем для вычисления Fn.
Хорошее:
Быстро и просто для малых n
Плохое:
Требуются операции с плавающей запятой. Для больших n потребуется большая точность.
Злое:
Использование комплексных чисел для вычисления Fn красиво с математической точки зрения, но уродливо — с компьютерной.
Рекурсия
Самое очевидное решение, которое вы уже много раз видели – скорее всего, в качестве примера того, что такое рекурсия. Повторю его ещё раз, для полноты. В Python её можно записать в одну строку:
Хорошее:
Очень простая реализация, повторяющая математическое определение
Плохое:
Экспоненциальное время выполнения. Для больших n очень медленно
Злое:
Переполнение стека
Запоминание
У решения с рекурсией есть большая проблема: пересекающиеся вычисления. Когда вызывается fib(n), то подсчитываются fib(n-1) и fib(n-2). Но когда считается fib(n-1), она снова независимо подсчитает fib(n-2) – то есть, fib(n-2) подсчитается дважды. Если продолжить рассуждения, будет видно, что fib(n-3) будет подсчитана трижды, и т.д. Слишком много пересечений.
Поэтому надо просто запоминать результаты, чтобы не подсчитывать их снова. Время и память у этого решения расходуются линейным образом. В решении я использую словарь, но можно было бы использовать и простой массив.
(В Python это можно также сделать при помощи декоратора, functools.lru_cache.)
Хорошее:
Просто превратить рекурсию в решение с запоминанием. Превращает экспоненциальное время выполнение в линейное, для чего тратит больше памяти.
Плохое:
Тратит много памяти
Злое:
Возможно переполнение стека, как и у рекурсии
Динамическое программирование
После решения с запоминанием становится понятно, что нам нужны не все предыдущие результаты, а только два последних. Кроме этого, вместо того, чтобы начинать с fib(n) и идти назад, можно начать с fib(0) и идти вперёд. У следующего кода линейное время выполнение, а использование памяти – фиксированное. На практике скорость решения будет ещё выше, поскольку тут отсутствуют рекурсивные вызовы функций и связанная с этим работа. И код выглядит проще.
Это решение часто приводится в качестве примера динамического программирования.
Хорошее:
Быстро работает для малых n, простой код
Плохое:
Всё ещё линейное время выполнения
Злое:
Да особо ничего.
Матричная алгебра
И, наконец, наименее освещаемое, но наиболее правильное решение, грамотно использующее как время, так и память. Его также можно расширить на любую гомогенную линейную последовательность. Идея в использовании матриц. Достаточно просто видеть, что
А обобщение этого говорит о том, что
Два значения для x, полученных нами ранее, из которых одно представляло собою золотое сечение, являются собственными значениями матрицы. Поэтому, ещё одним способом вывода замкнутой формулы является использование матричного уравнения и линейной алгебры.
Так чем же полезна такая формулировка? Тем, что возведение в степень можно произвести за логарифмическое время. Это делается через возведения в квадрат. Суть в том, что
где первое выражение используется для чётных A, второе для нечётных. Осталось только организовать перемножения матриц, и всё готово. Получается следующий код. Я организовал рекурсивную реализацию pow, поскольку её проще понять. Итеративную версию смотрите тут.
Хорошее:
Фиксированный объём памяти, логарифмическое время
Плохое:
Код посложнее
Злое:
Приходится работать с матрицами, хотя они не так уж и плохи
Сравнение быстродействия
Сравнивать стоит только вариант динамического программирования и матрицы. Если сравнивать их по количеству знаков в числе n, то получится, что матричное решение линейно, а решение с динамическим программированием – экспоненциально. Практический пример – вычисление fib(10 ** 6), числа, у которого будет больше двухсот тысяч знаков.
n = 10 ** 6
Вычисляем fib_matrix: у fib(n) всего 208988 цифр, расчёт занял 0.24993 секунд.
Вычисляем fib_dynamic: у fib(n) всего 208988 цифр, расчёт занял 11.83377 секунд.
Теоретические замечания
Не напрямую касаясь приведённого выше кода, данное замечание всё-таки имеет определённый интерес. Рассмотрим следующий граф:
Подсчитаем количество путей длины n от A до B. Например, для n = 1 у нас есть один путь, 1. Для n = 2 у нас опять есть один путь, 01. Для n = 3 у нас есть два пути, 001 и 101. Довольно просто можно показать, что количество путей длины n от А до В равно в точности Fn. Записав матрицу смежности для графа, мы получим такую же матрицу, которая была описана выше. Это известный результат из теории графов, что при заданной матрице смежности А, вхождения в А n — это количество путей длины n в графе (одна из задач, упоминавшихся в фильме «Умница Уилл Хантинг»).
Почему на рёбрах стоят такие обозначения? Оказывается, что при рассмотрении бесконечной последовательности символов на бесконечной в обе стороны последовательности путей на графе, вы получите нечто под названием «подсдвиги конечного типа», представляющее собой тип системы символической динамики. Конкретно этот подсдвиг конечного типа известен, как «сдвиг золотого сечения», и задаётся набором «запрещённых слов» . Иными словами, мы получим бесконечные в обе стороны двоичные последовательности и никакие пары из них не будут смежными. Топологическая энтропия этой динамической системы равна золотому сечению ϕ. Интересно, как это число периодически появляется в разных областях математики.
Читайте также:
- Как отключить сейчас в сми в яндекс браузере на телефоне андроид
- Настройка visual studio code для rust
- Скомпилированный файл справки в формате html chm конвертировать в pdf
- 1с документооборот корп это
- Билайн программа для модема 4g на компьютер