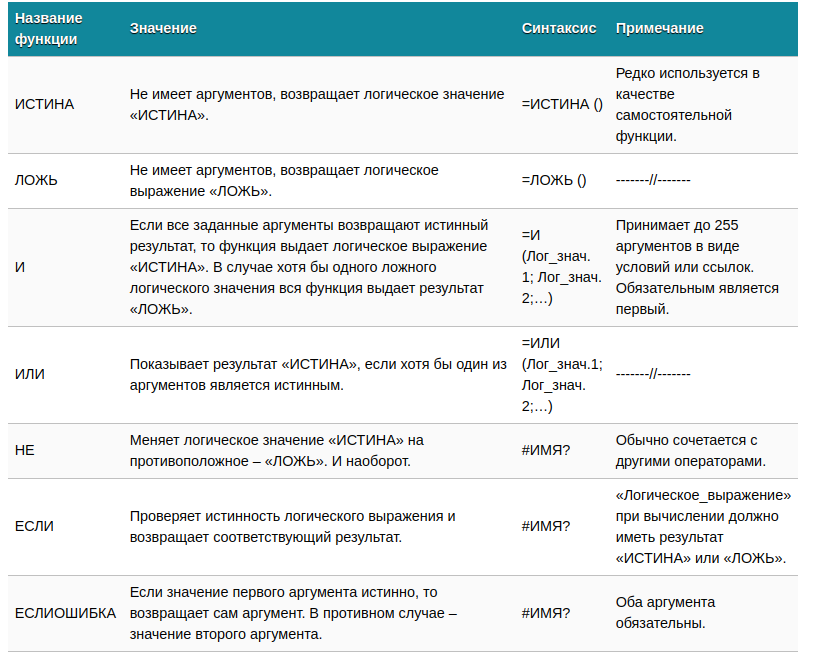
Автор Антон Андронов На чтение 1 мин Опубликовано 30.05.2015
В Excel очень легко создавать практически все виды последовательностей. Например, последовательность Фибоначчи.
- Первые два числа в последовательности Фибоначчи – 0 и 1.
- Каждое последующее значение можно найти путем сложения двух предыдущих чисел.
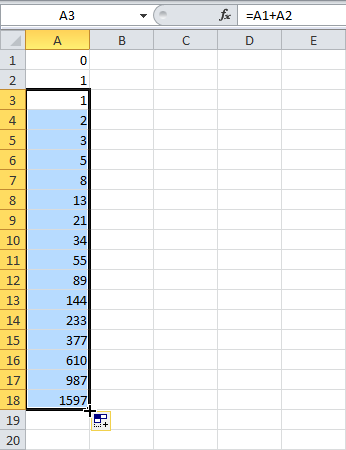
- Нажмите на правый нижний угол ячейки A3 и перетащите его вниз.
Результат: Последовательность Фибоначчи в Excel:
Оцените качество статьи. Нам важно ваше мнение:
Вам также может понравиться
Работая с таблицами Excel, иногда возникает необходимость
Тем людям, которые регулярно работают с таблицами Excel
Нередко пользователям приходится перенести часть информации
Огромное преимущество электронных таблиц Excel заключается
Пользователю Excel нередко приходится сталкиваться
Excel – одна из лучших программ для аналитика данных.
Время от времени при работе с электронными таблицами
Excel – удивительная программа, дающая возможность
Сейчас век информации. Количество данных, которые людям
Определение процента от числа – довольно частая задача
Excel – невероятно функциональная программа.
Excel – невероятно функциональная программа, позволяющая
Стандартное обозначение строк в Excel – цифровое.
Набор функций у программы Excel, конечно, поистине огромный.
При работе с Excel могут возникать различные ситуации
Важно понимать, что Excel – это не только программа
Числа Фибоначчи – это последовательность чисел, которая начинается с цифр 0 и 1, а каждое последующее значение является суммой двух предыдущих.
- Формула последовательности Фибоначчи
- Золотое сечение
- Таблица последовательности Фибоначчи
- C-код (Си-код) функции
Формула последовательности Фибоначчи
Например:
- F0 = 0
- F1 = 1
- F2 = F1+F0 = 1+0 = 1
- F3 = F2+F1 = 1+1 = 2
- F4 = F3+F2 = 2+1 = 3
- F5 = F4+F3 = 3+2 = 5
Золотое сечение
Соотношение двух последовательных чисел Фибоначчи сходится к золотому сечению:
где φ – это золотое сечение = (1 + √5) / 2 ≈ 1,61803399
Чаще всего, это значение округляют до 1,618 (или 1,62). А в округленных процентах пропорция выглядит так: 62% и 38 %.
Таблица последовательности Фибоначчи
| n | Fn |
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1597 |
| 18 | 2584 |
| 19 | 4181 |
| 20 | 6765 |
microexcel.ru
C-код (Си-код) функции
double Fibonacci(unsigned int n)
{
double f_n =n;
double f_n1=0.0;
double f_n2=1.0;
if( n > 1 ) {
for(int k=2; k<=n; k++) {
f_n = f_n1 + f_n2;
f_n2 = f_n1;
f_n1 = f_n;
}
}
return f_n;
}
As with all basic math operations in Excel, if you wish to add two or more numbers, create a formula. Formulas offer a quick way to find the sum of a few digits.
Instructions in this article apply to Excel for Microsoft 365, Excel 2019, Excel 2016, Excel 2013, Excel 2010, Excel 2007, and Excel for Mac.
Excel Formula Syntax
Some important points to remember about Excel formulas:
- Formulas in Excel begin with an equal sign.
- The equal sign is typed into the cell where the answer will appear.
- The addition sign in Excel is the plus symbol.
- Formulas are completed by pressing the Enter key.
Use Cell References in Addition Formulas
In the example data shown below, rows 2 through 4 use a formula that is located in column C to add the data in columns A and B. In row 2, the result is computed using an addition formula, =5+5.
Rows 3 and 4 show how it is better to first enter the data into worksheet cells and then use the addresses, or references, of those cells in the formula. For example, =A3+B3.
One advantage of using cell references rather than the actual data in a formula is that if you want to change the data, you’ll replace the data in the cell rather than rewrite the entire formula. The results of the formula update automatically when the data changes.
Enter Cell References With Point and Click
Although it is possible to type the above formula into cell C3 and have the correct answer appear, it’s easier to use point and click to add the cell references to formulas. This approach reduces the possibility of errors created by typing the wrong cell reference.
Point and click involves selecting the cell containing the data to add the cell reference to the formula instead of manually typing it into the cell.
Use the Addition Formula in Excel
Creating the example shown below in cell C3 is simple when you use a formula to add the values of cells A3 and B3.
Here’s how to create an addition formula:
-
Select cell C3 and type an equal sign to begin the formula.
-
Select cell A3 to add that cell reference to the formula after the equal sign.
-
Type the plus sign into the formula after A3.
-
Select cell B3 to add that cell reference to the formula after the addition sign.
-
Press Enter to complete the formula.
-
The answer 20 appears in cell C3.
Select the cell to display the formula in the formula bar above the worksheet.
Change the Formula
To change or correct a formula, select one of two options:
- Double-click the formula in the worksheet to place Excel in Edit mode and then make changes to the formula.
- Select the cell containing the formula and recreate the entire formula.
Create More Complex Formulas
To write more complex formulas that include other mathematical operators, use the steps listed above to get started and then continue to add the correct mathematical operators followed by the cell references containing the new data.
Before mixing different mathematical operations together in a formula, make sure you understand the order of operations that Excel follows when evaluating a formula.
Create a Fibonacci Sequence
A Fibonacci sequence, created by the 12th-century Italian mathematician Leonardo Pisano, forms a continuous series of increasing numbers. These series are used to explain, mathematically, different patterns found in nature such as:
- The spiral shape of seashells.
- The arrangement of leaves on a tree branch.
- The reproduction pattern of bees.
After two starting numbers, each additional number in the series is the sum of the two preceding numbers. The simplest Fibonacci sequence, shown in the image above, begins with the numbers zero and one.
Since a Fibonacci series involves addition, it can be created with an addition formula in Excel, as shown in the image above.
The steps below detail how to create a simple Fibonacci sequence using a formula. The steps involve creating the first formula in cell A3 and then copying that formula to the remaining cells using the fill handle. Each iteration, or copy, of the formula adds together the previous two numbers in the sequence.
To create the Fibonacci series shown in the example:
-
In cell A1, type 0 (a zero) and press Enter.
-
In cell A2, type 1 and press Enter.
-
In cell A3, type the formula =A1+A2 and press Enter.
-
Select cell A3 to make it the active cell.
-
Place the mouse pointer over the fill handle (it’s the dot in the bottom right corner of cell A3). The pointer changes to a black plus sign when it is over the fill handle.
-
Drag the fill handle down to cell A19.
-
Cell A19 contains the number 2584.
Thanks for letting us know!
Get the Latest Tech News Delivered Every Day
Subscribe
ТРЕНИНГИ
Быстрый старт
Расширенный Excel
Мастер Формул
Прогнозирование
Визуализация
Макросы на VBA
КНИГИ
Готовые решения
Мастер Формул
Скульптор данных
ВИДЕОУРОКИ
Бизнес-анализ
Выпадающие списки
Даты и время
Диаграммы
Диапазоны
Дубликаты
Защита данных
Интернет, email
Книги, листы
Макросы
Сводные таблицы
Текст
Форматирование
Функции
Всякое
Коротко
Подробно
Версии
Вопрос-Ответ
Скачать
Купить
ПРОЕКТЫ
ОНЛАЙН-КУРСЫ
ФОРУМ
Excel
Работа
PLEX
© Николай Павлов, Planetaexcel, 2006-2022
info@planetaexcel.ru
Использование любых материалов сайта допускается строго с указанием прямой ссылки на источник, упоминанием названия сайта, имени автора и неизменности исходного текста и иллюстраций.
Техническая поддержка сайта
|
ООО «Планета Эксел» ИНН 7735603520 ОГРН 1147746834949 |
ИП Павлов Николай Владимирович ИНН 633015842586 ОГРНИП 310633031600071 |
Использование
условных операторов и операторы цикла
при вычислении чисел Фибоначчи.
Любая
более или менее серьёзная программа
подразумевает использование управляющих
инструкций, среди которых особое место
занимают условные операторы и операторы
циклов. Рассмотрим особенности применения
таких операторов.
Общий
принцип действия условного оператора
заключается в следующем: проверяется
условие, и если оно истинно — выполняется
последовательность операций (цикл с
предусловием). Также можно определить
последовательность действий в случае
если условие ложно (цикл с постусловием,
выполняется до истинности условия).
Оператор
цикла позволяет выполнять последовательности
однотипных действий.
1)
Создадим с помощью оператора цикла FOR
макрос, который заполняет ячейки
документа числами Фибоначчи
(по
имени средневекового математика Леонардо
Пизанского, известного как Фибоначчи):
1,
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Числами
Фибоначчи называют последовательность
натуральных чисел, первые два из которых
равны 1, а каждое последующее равно сумме
двух предыдущих.
Примечание
3: Оказывается,
эта последовательность имеет множество
интересных с точки зрения математики
свойств. Вот пример: вы можете разделить
линию на два сегмента, так что соотношение
между большим и меньшим сегментом будет
пропорционально соотношению между всей
линией и большим сегментом. Этот
коэффицент пропорциональности,
приблизительно равный 1,618, известен как
золотое
сечение. В
эпоху Возрождения считалось, что именно
эта пропорция, соблюденная в архитектурных
сооружениях, больше всего радует глаз.
Если вы возьмете последовательные пары
из ряда Фибоначчи и будете делить большее
число из каждой пары на меньшее, ваш
результат будет постепенно приближаться
к золотому сечению. Другую интересную
информацию о числах Фибоначчи можно
найти в Интернете: http://elementy.ru/trefil/21136;
http://ru.wikipedia.org
и др..
Также,
в оператор For
добавим условный оператор, с помощью
которого обеспечим необходимость того,
чтобы числами ячейки заполнялись только
в том случае, если в активную ячейку
введено число большее 2. В VBA
существует условный оператор If….
Then….Else,
который реализует означенный алгоритм.
Программный код данного макроса приведен
в листинге 18:
Листинг 18: Программный код макроса Fibon ( )
Public Sub Fibon ( )
Dim N As Integer
Dim i As Integer
Dim a As Integer
Dim b As Integer
N = ActiveCell.Value
If N<2 Then
MsgBox Prompt: =
“Указано неверное значение!”, Title:
= “Ошибка!”
E
lse
a = 1
ActiveCell.Offset(1,-1).Value = 1
ActiveCell.Offset(1,0).Value = a
b = 1
For i = 2 To N
ActiveCell.Offset(i,-1).Value = i
ActiveCell.Offset(i,0).Value = b
b = b + a
a = b – a
Next i
End If
End Sub
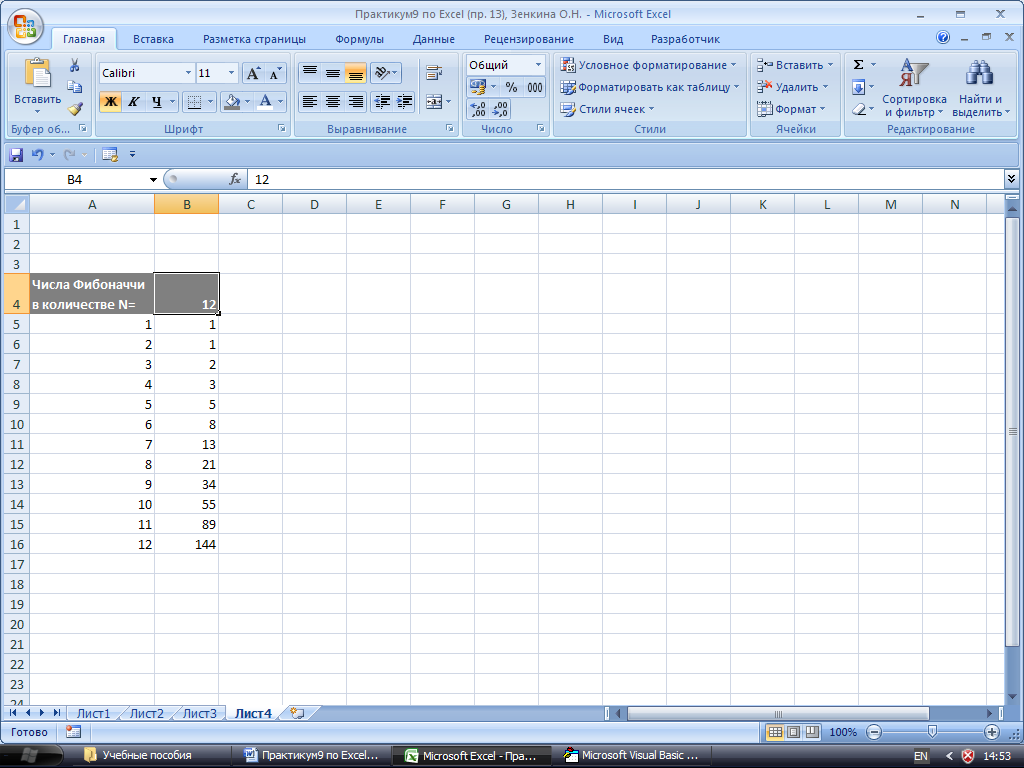
Рис.
26.
Результат выполнения задания 6, п. 1.
В
ячейку А4
введите слова: «Числа
Фибоначчи в количестве N
= »,
в ячейку В4
введите число 12 (сколько чисел Фибоначчи
будет выведено с помощью макроса), далее
выделите ячейку B4
со значением 12 (ячейка B4
станет активной) и далее запустите
макрос на выполнение. Результат выполнения
макроса будет выглядеть как на рис. 27.
Внизу, под ячейкой B4
(в ячейках B5:В16)
будут выведены 12 чисел Фибоначчи.
Поэкспериментируйте сами, с выполнением
данного макроса, задавая для вычисления
разное число чисел Фибоначчи в ячейке
B4.
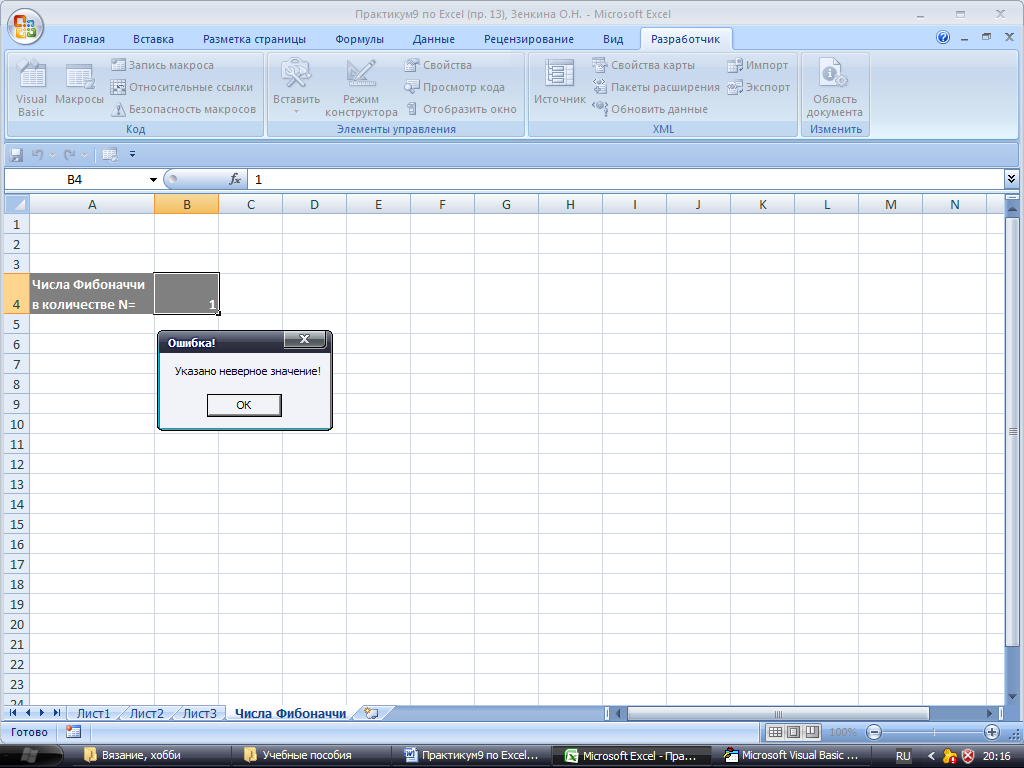
Если
в ячейку В4
будет введено число меньшее 2, то результат
будет иным, см. рис. 27:
Рис.
27. Результат
работы макроса при неверно указанном
значении ячейки.
Данный
макрос Fibon имеет
недостатки, в частности не может вывести
одно число Фибоначчи, когда значение
в
активной ячейке равно 1, а также не может
обработать случай, когда в ячейка В4
содержит нечисловое значение.
Приведённый
ниже макрос Fibon2
решает
эти проблемы (см. листинг 19):
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На чтение 4 мин. Просмотров 715 Опубликовано 03.07.2019
Содержание
- Математика не должна быть трудной, когда вы используете Excel
- Синтаксис формулы Excel
- Использовать ссылки на ячейки в формулах сложения
- Введите ссылки на ячейки с помощью точки и нажмите
- Используйте формулу сложения в Excel
- Изменить формулу
- Создать более сложные формулы
- Создать последовательность Фибоначчи
Математика не должна быть трудной, когда вы используете Excel
Как и во всех основных математических операциях в Excel, если вы хотите добавить два или более чисел, создайте формулу. Формулы быстро найти сумму из нескольких цифр.
Инструкции в этой статье относятся к Excel 2019, 2016, 2013, 2010, 2007; Excel для Office 365 и Excel для Mac.
Синтаксис формулы Excel
Вот некоторые важные моменты, которые следует помнить о формулах Excel:
- Формулы в Excel начинаются со знака равенства ( = ).
- Знак равенства вводится в ячейку, где появится ответ.
- Знак добавления в Excel – это символ плюс ( + ).
- Формулы заполняются нажатием клавиши Enter.
Использовать ссылки на ячейки в формулах сложения
В приведенных ниже примерах данных строки 2–4 используют формулу, расположенную в столбце C, для добавления данных в столбцы A и B. В строке 2 результат вычисляется с использованием формулы сложения = 5 + 5.
Строки 3 и 4 показывают, как лучше сначала ввести данные в ячейки таблицы, а затем использовать адреса или ссылки этих ячеек в формуле. Например, = A3 + B3.
Одно из преимуществ использования ссылок на ячейки, а не на фактические данные в формуле, состоит в том, что если вы хотите изменить данные, вы замените данные в ячейке, а не перепишете всю формулу. Результаты формулы обновляются автоматически при изменении данных.
Чтобы добавить несколько чисел, расположенных в одном столбце или строке на листе, используйте функцию SUM, которая предлагает ярлык для создания длинной формулы сложения.
Введите ссылки на ячейки с помощью точки и нажмите
Хотя в ячейку C3 можно ввести приведенную выше формулу и отобразить правильный ответ, проще использовать точку и щелкнуть, чтобы добавить ссылки на ячейки в формулы. Это уменьшает вероятность ошибок, созданных неправильной ссылкой на ячейку.
Укажите и щелкните, чтобы выбрать ячейку, содержащую данные, чтобы добавить ссылку на ячейку в формулу, а не вводить ее вручную в ячейку.
Используйте формулу сложения в Excel
Создать пример, показанный ниже в ячейке C3, очень просто, если вы используете формулу для добавления значений ячеек A3 и B3.
Вот как создать формулу сложения:
-
Выберите ячейку C3 и введите знак равенства ( = ), чтобы начать формулу.
-
Выберите ячейку A3 , чтобы добавить ссылку на эту ячейку в формулу после знака равенства.
-
Введите знак плюс ( + ) в формулу после A3 .
-
Выберите ячейку B3 , чтобы добавить ссылку на эту ячейку в формулу после знака добавления.
-
Нажмите Enter , чтобы завершить формулу.
-
Ответ 20 появляется в ячейке C3.
Выберите ячейку для отображения формулы на панели формул над рабочим листом.
Изменить формулу
Если вы хотите изменить или исправить формулу, у вас есть два варианта:
- Дважды щелкните формулу на листе, чтобы перевести Excel в режим редактирования , а затем внесите изменения в формулу.
- Выберите ячейку, содержащую формулу, и создайте заново всю формулу.
Создать более сложные формулы
Чтобы написать более сложные формулы, включающие другие математические операторы, используйте шаги, перечисленные выше, чтобы начать, а затем продолжайте добавлять правильные математические операторы, за которыми следуют ссылки на ячейки, содержащие новые данные.
Прежде чем смешивать различные математические операции в формуле, убедитесь, что вы понимаете порядок операций, которым следует Excel при оценке формулы.
Создать последовательность Фибоначчи
Последовательность Фибоначчи, созданная итальянским математиком XII века Леонардо Пизано, образует непрерывную серию возрастающих чисел. Эти серии используются для математического объяснения различных закономерностей, встречающихся в природе, таких как:
- Спиральная форма морских раковин.
- Расположение листьев на ветке дерева.
- Картина размножения пчел.
После двух начальных чисел каждое дополнительное число в серии является суммой двух предыдущих чисел. Простейшая последовательность Фибоначчи, показанная на рисунке выше, начинается с цифр ноль и единица.
Поскольку ряд Фибоначчи включает в себя сложение, его можно создать с помощью формулы сложения в Excel, как показано на рисунке выше.
Следующие шаги подробно описывают, как создать простую последовательность Фибоначчи, используя формулу.Шаги включают создание первой формулы в ячейке A3, а затем копирование этой формулы в оставшиеся ячейки с помощью маркера заполнения. Каждая итерация или копия формулы складывает вместе два предыдущих числа в последовательности.
Чтобы создать ряд Фибоначчи, показанный в примере:
-
В ячейке A1 введите ноль ( 0 ) и нажмите Enter .
-
В ячейке A2 введите 1 и нажмите Enter .
-
В ячейке A3 введите формулу = A1 + A2 и нажмите Enter .
-
Выберите ячейку A3 , чтобы сделать ее активной.
-
Наведите указатель мыши на маркер заливки (это точка в правом нижнем углу ячейки A3). Указатель изменится на черный знак плюс (+), когда он находится над маркером заливки.
-
Перетащите маркер заполнения вниз в ячейку A19.
-
Ячейка A19 содержит номер 2584.
Содержание
- Введение
- Квадраты и домино
- Где встречаются закономерности Фибоначчи?
- Рекурсивные алгоритмы
- Золотое сечение: тайна вселенной
- Исследования золотого сечения в 16-19 веках
- Кто такой Фибоначчи?
- Сумма чисел Фибоначчи
- Формула золотого сечения
- Витрувианский человек Леонардо
- Доказательство по индукции
- Применение пропорций в дизайне
- Золотое сечение в архитектуре
- Спираль Архимеда и золотой прямоугольник
- Простейшее определение чисел Фибоначчи
- Универсальный код природы
- Использование золотого сечения в искусстве
- Комбинаторное доказательство
- Искусство пространственных форм
- Числа Фибоначчи
- Краткая история чисел Фибоначчи
Введение
Программистам числа Фибоначчи должны уже поднадоесть. Примеры их вычисления используются везде. Всё от того, что эти числа предоставляют простейший пример рекурсии. А ещё они являются хорошим примером динамического программирования. Но надо ли вычислять их так в реальном проекте? Не надо. Ни рекурсия, ни динамическое программирование не являются идеальными вариантами. И не замкнутая формула, использующая числа с плавающей запятой. Сейчас я расскажу, как правильно. Но сначала пройдёмся по всем известным вариантам решения.
Код предназначен для Python 3, хотя должен идти и на Python 2.
Для начала – напомню определение:
Fn= Fn-1+ Fn-2
и F1= F2=1.
Квадраты и домино
Начнем с укладки квадратов и домино. Вообразим длинную горизонтальную рамку размерами 1 × 10. Мы хотим полностью заполнить ее квадратами 1 × 1 и костяшками домино 1 × 2, не оставив ни единой щели.
Для удобства обозначим число вариантов F10. Перебирать их все и потом пересчитывать — тяжелый труд, чреватый ошибками. Гораздо лучше упростить задачу. Не будем с места в карьер искать F10, начнем с F1. Это проще простого! Нам нужно заполнить рамку 1 × 1 квадратами 1 × 1 и костяшками домино 1 × 2. Домино не поместится, остается единственное решение: взять один квадрат. Другими словами, F1 = 1.
Теперь разберемся с F2. Размер рамки 1 × 2. Можно заполнить ее двумя квадратами или одной костяшкой домино. Таким образом, есть два варианта, и F2 = 2.
Дальше: сколькими способами можно заполнить рамку 1 × 3? Первый вариант: три квадрата. Два других варианта: одна костяшка домино (две не влезут) и квадрат слева или справа. Итак, F3 = 3. Еще один шаг: возьмем рамку 1 × 4. На рисунке показаны все варианты заполнения:
Мы нашли пять возможностей, но где гарантия, что мы ничего не упустили? Есть способ проверить себя. В левом конце рамки может быть или квадрат, или костяшка домино. В верхнем ряду на рисунке — варианты, когда слева квадрат, в нижнем ряду — когда слева домино.
Допустим, слева квадрат. Оставшуюся часть нужно заполнить квадратами и домино. Другими словами, нужно заполнить рамку 1 × 3. Это дает 3 варианта, так как F3 = 3. Если слева домино, размер оставшейся части 1 × 2, и заполнить ее можно двумя вариантами, так как F2 = 2.
Таким образом, у нас есть 3 + 2 = 5 вариантов, и мы удостоверились, что F4 = 5.
Теперь ваша очередь. Подумайте пару минут и найдите все варианты заполнения для рамки 1 × 5. Их немного. Решение — в конце главы. Можете отвлечься и подумать.
Вернемся к нашим квадратам. Хочется верить, что вы нашли 8 вариантов, так как есть 5 способов укладки, где слева квадрат, и еще 3 способа, где слева домино. Таким образом, F5 = 8.
Подытожим. Мы обозначили FN количество способов заполнения рамки 1 × n квадратами и костяшками домино. Нам необходимо найти F10. Вот что мы уже знаем:
Двигаемся дальше. Чему равно F6? Можно нарисовать все варианты, но это скучно. Лучше разобьем вопрос на две части. Сколькими способами можно заполнить рамку 1 × 6, если слева (a) квадрат и (b) костяшка домино? Хорошая новость: мы уже знаем ответ! В первом случае нам остается пять квадратов, а мы знаем, что F5 = 8. Во втором случае нужно заполнить четыре квадрата; нам известно, что F4 = 5. Таким образом, F5 + F4 = 13.
Чему равно F7? Исходя из тех же соображений, F7 =F6+F5=13+8=21. А как насчет F8? Очевидно, F8 = F7 + F6 = 21 + 13 = 34. И так далее. Мы обнаружили следующую взаимосвязь: Fn = Fn-1 + Fn-2.
Где встречаются закономерности Фибоначчи?
Вся мистика вокруг Фибо-чисел складывается из того, что они часто встречаются в явлениях природы:
- расположение листьев растений;
- в семенах подсолнуха;
- лепестках цветов;
- длина тела в золотом сечении у насекомых (стрекоза);
- длина фаланг пальцев у человека и во многом другом.
Нельзя сказать, что числа Фибоначчи — это панацея и ей можно посчитать абсолютно всё, но многие явления так или иначе прослеживаются в такой последовательности чисел, в том числе, это касается психологии человека и трейдинга. На этом я закончу историко-теоретическую часть и перейду непосредственно к финансовым рынкам. Для тех кому, интересна тема, небольшой и очень познавательный ролик о Фибоначчи представлен ниже.
Рекурсивные алгоритмы
Рекурсивные функции обычно решают проблему, сначала найдя решение для подмножеств проблемы (рекурсивно), а затем модифицируя это «подрешение», дабы добраться уже до верного решения. В примере выше алгоритм sumCount(value) сначала решает sumCount(value-1), а затем добавляет значение value, чтобы найти решение для sumCount(value).
Во многих рекурсивных алгоритмах некоторые данные ввода производят предсказуемые данные вывода. Например, sumCount(1) имеет предсказуемый вывод 1 (вы можете легко это вычислить и проверить самостоятельно). Случай, когда алгоритм при определённых данных ввода производит предсказуемые данные вывода, называется базовым случаем. Базовые случаи работают как условия для завершения выполнения алгоритма. Их часто можно идентифицировать, рассматривая результаты вывода для следующих значений ввода: 0, 1, «» или null.
Золотое сечение: тайна вселенной
Золотое сечение – это всеобъемлющее проявление структурной гармонии. Оно встречается во всех сферах вселенной в природе, науке, искусстве во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.
Наверняка вам не раз приходилось задумываться, почему Природа способна создавать такие удивительные гармоничные структуры, которые восхищают и радуют глаз. Почему художники, поэты, композиторы, архитекторы создают восхитительные произведения искусства из столетия в столетие. В чем же секрет и какие законы лежат в основе этих гармоничных созданий? Никто не сможет однозначно ответить на этот вопрос, но в нашей книге мы постараемся приоткрыть завесу и рассказать вам об одной из тайн мироздания – Золотом Сечении или, как его еще называют, Золотой или Божественной Пропорцией. Золотое Сечение называется числом PHI (Фи) в честь великого древнегреческого скульптора Фидия (Phidius), который использовал это число в своих скульптурах.
Не одно столетие ученые применяют уникальные математические свойства числа PHI и эти исследования продолжаются и в наши дни. Это число нашло широкое применение во всех областях современной науки, о чем мы так же попытаемся популярно рассказать на страницах нашего сайта Fib0. Также существует ряд и последовательность фибоначчи что это Вы узнаете далее…
Исследования золотого сечения в 16-19 веках
Используя золотое сечение и числа Фибоначчи, исследовательскую работу по вопросу о пропорциях продолжают уже не одно столетие. Параллельно с Леонардо да Винчи немецкий художник Альбрехт Дюрер также занимался разработкой теории правильных пропорций тела человека. Для этого им даже был создан специальный циркуль.
В 16 в. вопросу о связи числа Фибоначчи и золотого сечения были посвящены работы астронома И. Кеплера, который впервые применил эти правила для ботаники.
Новое «открытие» ожидало золотое сечение в 19 в. с опубликованием «Эстетического исследования» немецкого ученого профессора Цейзига. Он возвел эти пропорции в абсолют и объявил о том, что они универсальны для всех природных явлений. Им были проведены исследования огромного количества людей, вернее их телесных пропорций (около 2 тыс.), по итогам которых сделаны выводы о статистических подтвержденных закономерностях в соотношениях различных частей тела: длины плеч, предплечий, кистей, пальцев и т.д.
Были исследованы также предметы искусства (вазы, архитектурные сооружения), музыкальные тона, размеры при написании стихотворений — все это Цейзиг отобразил через длины отрезков и цифры, он же ввел термин «математическая эстетика». После получения результатов выяснилось, что получается ряд Фибоначчи.
Кто такой Фибоначчи?
Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.
В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.
Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.
Каждое число из ряда Фибоначчи, разделенное на последующее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.
Леонардо Пизанский — тот самый создатель числа Фибоначчи
Сумма чисел Фибоначчи
Попробуем сложить первые несколько чисел Фибоначчи. Что мы можем сказать о сумме F0 + F1 +… + Fn для любого n? Давайте проделаем кое-какие вычисления и посмотрим, что получится. Обратите внимание на результаты сложения внизу. Видите ли вы закономерность? Повремените немного, прежде чем двигаться дальше: будет лучше, если вы найдете ответ самостоятельно, а не прочтете уже готовое решение.
Хочется верить, вы увидели, что результаты суммирования, если к ним приплюсовать по единице, тоже выстраиваются в последовательность чисел Фибоначчи. Например, сложение чисел от F0 до F5 дает: F0 + F1 + F2 + F3 + F4 + F5 = 1 + 1 + 2 + 3 + 5 + 8 = 20 = F7 — 1. Сложение чисел от F0 до F6 дает 33, что на единицу меньше F8 = 34. Мы можем записать формулу для неотрицательных целых чисел n: F0 +F1 +F2 +…+Fn =Fn+2 –1. (*)
Вероятно, лично вам достаточно будет увидеть, что формула [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1.. работает в дюжине случаев, чтобы вы поверили, что она верна, но математики жаждут доказательств. Мы рады представить вам два возможных доказательства того, что она верна для всех неотрицательных целых чисел n.
Первое называется доказательством по индукции, второе — комбинаторным доказательством.
Формула золотого сечения
Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек это универсальная форма может означать: Форма предмета — взаимное расположение границ (контуров) предмета, объекта, а также взаимное расположение точек линии для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.
В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя Витрувианского человека Леонардо, создал собственную шкалу гармонических пропорций, повлиявшую на эстетику архитектуры XX века.
Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке живое разумное социальное , субъект общественно-исторической деятельности и культуры ему подчинены практически все части тела, но главный показатель золотого нечто, изготовленное из золота сечения это деление тела В математике: Тело (алгебра) — множество с двумя операциями (сложение и умножение), обладающее определёнными свойствами точкой пупа.
В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению многозначный термин, означающий: Сечение в черчении — в отличие от разреза, изображение только фигуры, образованной рассечением тела плоскостью (плоскостями) без изображения частей за этой, чем пропорции женского тела 8:5.
Витрувианский человек Леонардо
Рисунок, которым Леонардо да Винчи в 1492 г. проиллюстрировал книгу Витрувия, изображает фигуру человека в 2-х позициях с руками, разведенными в стороны. Фигура вписана в круг и квадрат. Этот рисунок принято считать каноническими пропорциями человеческого тела (мужского), описанными Леонардо на основе изучения их в трактатах римского архитектора Витрувия.
Центром тела как равноудаленной точкой от конца рук и ног считается пупок, длина рук приравнивается к росту человека, максимальная ширина плеч = 1/8 роста, расстояние от верха груди до волос = 1/7, от верха груди до верха головы =1/6 и т.д.
С тех пор рисунок используется в виде символа, показывающего внутреннюю симметрию тела человека.
Термин «Золотое сечение» Леонардо использовал для обозначения пропорциональных отношений в фигуре человека. Например, расстояние от пояса до ступней ног соотносится к аналогичному расстоянию от пупка до макушки так же, как рост к первой длине (от пояса вниз). Эти вычисление делается аналогично соотношению отрезков при вычислении золотой пропорции и стремится к 1,618.
Все эти гармоничные пропорции часто используются деятелями искусства для создания красивых и впечатляющих произведений.
Доказательство по индукции
Формула [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. представляет собой бесконечно много формул в свернутом виде. Доказать, что [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. верно для конкретного значения n, скажем для n = 6, — простая арифметическая задача. Достаточно будет записать числа от F0 до F6 и сложить их: F0 +F2 +…+F6 =1+1+2+3+5+8+13=33.
Несложно увидеть, что F8 = 34, поэтому формула действует. Перейдем к F7. Не будем тратить время и складывать все числа: мы уже знаем сумму вплоть до F6. Таким образом, (F0 +F1 +…+F6)+F7 =33+21=54. Как и раньше, все сходится: F9 = 55.
Если сейчас мы начнем проверять, работает ли формула для n = 8, наши силы окончательно иссякнут. Но все же посмотрим, что мы уже знаем и что хотим выяснить:
F0 +F1 +…+F7 =F9.
F0 +F1 +…+F7 +F7 =?
Воспользуемся предыдущим результатом: (F0 +F1 +…+F7)+F8 =(F9-1)+F8.
Мы, конечно, можем вычислить (F9-1) + F8 арифметически. Но так мы устанем еще больше. В то же время мы знаем, что F8 + F9 = F10. Таким образом, нам не нужно ничего высчитывать или заглядывать в таблицу чисел Фибоначчи:
(F0 + F1 +… + F7) + F8 = (F9-1) + F8 = (F8 + F9-1) = F10-1.
Мы удостоверились, что формула работает для n = 8, на основе того, что знали про n = 7.
В случае n = 9 мы точно так же опираемся на результат для n = 8 (убедитесь в этом самостоятельно). Разумеется, доказав верность [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. для n, мы можем быть уверены, что [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. верно и для n + 1.
Мы готовы дать полное доказательство. Как уже было сказано, [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. представляет собой бесконечное количество формул для всех значений n от нуля до бесконечности. Посмотрим, как работает доказательство.
Вначале мы доказываем [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. в простейшем случае, для n = 0. Мы просто проверяем, что F0 = F0+2 — 1. Так как F0 = 1, а F2 = 2, очевидным образом 1 = 2 — 1, а F0 = F2-1.
Дальше нам достаточно показать, что верность формулы для одного значения n (скажем, n = k) автоматически означает верность для n + 1 (в нашем примере n = k + 1). Нам лишь надо продемонстрировать, как устроено это «автоматически». Что нам нужно сделать?
Возьмем некоторое число k. Предположим, мы уже знаем, что F0+F1+…+Fk =Fk+2–1. Мы ищем величину F0 + F1 +… + Fk + Fk+1.
Мы уже знаем сумму чисел Фибоначчи вплоть до Fk, поэтому у нас получается:
(F0+F1+…+Fk)+Fk+1 =(Fk+2–1)+Fk+1.
Правая часть равна Fk+2 — 1 + Fk+1, и мы знаем, чему равна сумма следующих друг за другом чисел Фибоначчи:
Fk+2–1 + Fk+1 = (Fk+2 + Fk+1) — 1 = Fk+3– 1
Подставим в наше равенство:
(F0+F1+…+Fk)+Fk+1 =Fk+3–1
Сейчас я объясню, что мы сделали. Если мы знаем, что [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. верно, когда мы суммируем числа вплоть до Fk, тогда [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. должно быть верно, если мы приплюсуем Fk+1.
Подытожим:
— Формула [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. верна для n = 0.
— Если формула [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. верна для n, она верна и для n + 1.
Мы можем уверенно сказать, что [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. верно для любых значений n. Верно ли [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. для n = 4987? Это так, если выражение верно для n = 4986, что основано на верности выражения для n = 4985, и так далее до n = 0. Следовательно, формула [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. верна для всех возможных значений. Этот метод доказательства известен под названием математическая индукция (или доказательство по индукции). Мы проверяем базовый случай и даем шаблон, по которому каждый следующий случай может быть доказан на основе предыдущего.
Применение пропорций в дизайне
В дизайне одежды все модельеры делают новые образы и модели с учетом пропорций человеческого тела и правил золотого сечения, хотя от природы не все люди имеют идеальные пропорции.
При планировании ландшафтного дизайна и создании объемных парковых композиций с помощью растений (деревьев и кустарников), фонтанов и малых архитектурных объектов также могут применяться закономерности «божественных пропорций». Ведь композиция парка должна быть ориентирована на создание впечатления на посетителя, который свободно сможет ориентироваться в нем и находить композиционный центр.
Все элементы парка находятся в таких соотношениях, чтобы с помощью геометрического строения, взаиморасположения, освещения и света, произвести на человека впечатление гармонии и совершенства.
Золотое сечение в архитектуре
В качестве примера ученые исследовали шедевры архитектуры, созданные по правилам «золотого сечения»: египетские пирамиды, Пантеон, Парфенон, Собор Нотр-Дам де Пари, храм Василия Блаженного и др.
Парфенон — одно из красивейших зданий в Древней Греции (5 в. до н.э.) — имеет 8 колонн и 17 по разным сторонам, отношение его высоты к длине сторон равно 0,618. Выступы на его фасадах сделаны по «золотому сечению» (фото ниже).
Одним из ученых, который придумал и успешно применял усовершенствование модульной системы пропорций для архитектурных объектов (так называемый «модулор»), — был французский архитектор Ле Корбюзье. В основу модулора положена измерительная система, связанная с условным делением на части человеческого тела.
Русский архитектор М. Казаков, построивший несколько жилых домов в Москве, а также здания сената в Кремле и Голицынской больницы (сейчас 1-я Клиническая им. Н. И. Пирогова), — был одним из архитекторов, которые использовали при проектировании и строительстве законы о золотом сечении.
Спираль Архимеда и золотой прямоугольник
Спирали, очень распространенные в природе, были исследованы Архимедом, который даже вывел ее уравнение. Форма спирали основана на законах о золотом сечении. При ее раскручивании получается длина, к которой можно применить пропорции и числа Фибоначчи, увеличение шага происходит равномерно.
Параллель между числами Фибоначчи и золотым сечением можно увидеть и построив «золотой прямоугольник», у которого стороны пропорциональны, как 1,618:1. Он строится, переходя от большего прямоугольника к малым так, что длины сторон будут равны числам из ряда. Построение его можно сделать и в обратном порядке, начиная с квадратика «1». При соединении линиями углов этого прямоугольника в центре их пересечения получается спираль Фибоначчи или логарифмическая.
Простейшее определение чисел Фибоначчи
В первую очередь теоретическая часть. Числа Фибоначчи простыми словами — это последовательность чисел, где каждое следующее число равно сумме двух предыдущих. Началом последовательности, как правило, выступает единица, но в некоторых версиях и 0.
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…
Как видите, ничего особо сложного тут нет:
- 1 + 1 равняется 2;
- 1 + 2 равняется 3;
- 2 + 3 равняется 5 и т.д.
Ещё один важный факт — отношение каждого числа к предыдущему будет стремиться к числу 1,618, более известному, как «Золотое сечение». Например, если мы разделим 55 на 34, то примерно получим 1,617, чем больше числа, тем ближе будет к 1,618.
Для общего понимания этой последовательности не требуется знаний математических формул, достаточно уметь складывать числа на школьном уровне. Теперь вы примерно понимаете, о чём идёт речь. Какое именно отношение числа Фибоначчи имеют к трейдингу, я расскажу в следующих разделах, а пока немного истории.
Универсальный код природы
Даже не вдаваясь в расчеты, золотое сечение и Числа фибоначчи можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.
Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.
Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы материальный мир Вселенной, в сущности — основной объект изучения естественных наук к спиральным формам, называя спираль кривой жизни. Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.
Использование золотого сечения в искусстве
Исследователи, занимающиеся поиском в искусстве примеров использования золотого сечения, подробно исследуют различные архитектурные объекты и произведения живописи. Известны знаменитые скульптурные работы, создатели которых придерживались золотых пропорций, — статуи Зевса Олимпийского, Аполлона Бельведерского и Афины Парфенос.
Одно из творений Леонардо да Винчи — «Портрет Моны Лизы» — уже многие годы является предметом исследований ученых. Ими было обнаружено, что композиция работы целиком состоит из «золотых треугольников», объединенных вместе в правильный пятиугольник-звезду. Все работы да Винчи являются свидетельством того, насколько глубоки были его познания в строении и пропорциях тела человека, благодаря чему он и смог уловить невероятно загадочную улыбку Джоконды.
Комбинаторное доказательство
А вот совершенно другое доказательство тождества [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1.. Основной подход тут — воспользоваться тем фактом, что число Fn — это количество способов облицевать прямоугольник 1 × n квадратами и костяшками домино.
Напомню, что нам нужно доказать:
F0 + F1 + F2 +… + Fn = Fn+2- 1. (*)
Идея заключается в том, чтобы рассматривать обе части уравнения как решение задачи с облицовкой. Если мы докажем, что левая и правая часть — решение для одного и того же прямоугольника, они совпадут между собой. Эта техника носит название комбинаторного доказательства[2 ]Слово «комбинаторный» образовано от существительного «комбинаторика» — названия раздела математики, предметом которого является подсчет вариантов в задачах, схожих с облицовкой прямоугольника. Слово «комбинаторика», в свою очередь, образовано от слова «комбинации»..
На какой вопрос по комбинаторике уравнение [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. дает два верных ответа? Эта головоломка похожа на те, что встречаются в шоу Jeopardy! [3 ]Популярная в США телевикторина. Аналоги Jeopardy! выходят в разных странах; в России это — «Своя игра». — Прим. ред., где участники должны формулировать вопрос, заранее зная правильный ответ.
Правая часть выглядит проще, поэтому начнем с нее. Ответ: Fn+2– 1. Каков вопрос? Если бы ответ был равен просто Fn+2, мы с легкостью сформулировали бы вопрос: сколькими способами можно облицевать прямоугольник 1 × (n + 2) с помощью квадратов и костяшек домино? Это почти то, что нужно, но ответ меньше на единицу. Попробуем мягко поменять вопрос и уменьшить ответ. Уберем один вариант облицовки и пересчитаем оставшиеся. Сложность состоит в том, чтобы найти один вариант, который кардинально отличается от остальных. Есть ли такой?
Каждый способ облицовки подразумевает использование квадратов или домино. Только квадраты задействованы в единственном варианте, в прочих есть хотя бы одна костяшка домино. Возьмем это за основу нового вопроса.
Вопрос: Сколько существует вариантов облицовки квадратами и костяшками домино прямоугольной рамки 1 × (n + 2), включающих по меньшей мере одну костяшку домино?
Сейчас мы найдем два ответа на этот вопрос. Так как оба будут верны, между числами мы сможем уверенно поставить знак равенства.
Один из ответов мы уже обсуждали. Есть Fn+2 вариантов укладки. Только один из них подразумевает использование исключительно квадратов, без домино. Таким образом, ответ № 1 на наш вопрос таков: Fn+2– 1.
Второй ответ должен быть — я надеюсь — левой частью уравнения [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1.. Посмотрим, как это работает.
Нужно пересчитать варианты заполнения рамки, включающие хотя бы одну костяшку домино. Давайте подумаем, где будет расположена самая первая костяшка. Есть n + 2 позиций, и первая костяшка может располагаться в позициях от 1 до n + 1.
Рассмотрим случай n = 4. Мы ищем варианты заполнения рамки 1 × 6, задействующие хотя бы одну костяшку домино. Мы знаем ответ: F6 — 1 = 13 — 1 = 12, но нам необходимо получить его иным путем.
Первая костяшка домино может занимать следующие позиции:
Первая колонка демонстрирует случай, когда костяшка находится на первой позиции, вторая — когда костяшка на второй, и т. д.
Сколько вариантов в каждой колонке?
В первой колонке — пять вариантов. Если отбросить домино слева, мы получим ровно F4 = 5 вариантов для прямоугольника 1 × 4. Во второй колонке — три варианта. Отбросим домино и квадрат слева. Мы получим F3 = 3 варианта для прямоугольника 1 × 3. Аналогично для других колонок. Вот что мы обнаружили:
Таким образом, количество способов замостить квадратами и домино (хотя бы одной костяшкой) прямоугольную рамку 1 × 6 равно F4 + F3 + F2 + F1 + F0 = 12.
Вывод: F0+F1+F2+F3+F4=12=F6–1.
Рассмотрим общий случай. Нам дана рамка длиной n + 2. Сколько есть вариантов ее заполнения, при которых первая костяшка домино находится на некой позиции k? В этом случае первые k — 1 позиций заняты квадратами. Таким образом, в общей сложности занята k + 1 позиция [4 ]Число k может принимать значения от 1 до n + 1, но не больше, потому что иначе последняя костяшка домино высунется за пределы рамки.. Оставшиеся (n + 2) — (k + 1) = n — k + 1 можно заполнить любыми способами. Это дает Fn-k+1 вариантов. Построим диаграмму:
Если k меняется от 1 до n + 1, величина n — k + 1 меняется от 0 до n. Таким образом, количество вариантов заполнения нашей рамки с использованием хотя бы одной костяшки домино равно Fn + Fn-1 +… + F1 + F0.
Если поставить слагаемые в обратном порядке, мы получим левую часть выражения (*). Таким образом, мы нашли второй ответ на поставленный вопрос: F0 +F1 +…+Fn.
Итак, у нас есть два ответа на вопрос. Величины, полученные с помощью двух выведенных нами формул, совпадают, и тождество [* ]F0 +F1 +F2 +…+Fn =Fn+2 –1. доказано.
Искусство пространственных форм
Художник Василий Суриков говорил, что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика. Долгое время художники следовали этому закону интуитивно, но после Леонардо ди сер Пьеро да Винчи (итал да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек может означать: Точка — абстрактный объект в пространстве, не имеющий никаких измеримых характеристик, кроме координат золотого сечения использовал изобретенный им пропорциональный циркуль.
Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге Александр Сергеевич Пушкин в селе Михайловском, отмечает, что каждая деталь полотна, будь то камин, этажерка, кресло или сам поэт, строго вписаны в золотые пропорции.
Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.
И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.
Числа Фибоначчи
Одним из наиболее известных математических рекурсивных алгоритмов является последовательность Фибоначчи. Последовательность Фибоначчи можно увидеть даже в природе: ветвление деревьев, спираль раковин, плоды ананаса, разворачивающийся папоротник и т.д.
Спираль Фибоначчи выглядит следующим образом:
Каждое из чисел Фибоначчи — это длина горизонтальной стороны квадрата, в которой находится данное число. Математически числа Фибоначчи определяются следующим образом:
F(n) = 0, если n = 0
1, если n = 1
f(n-1) + f(n-2), если n > 1
Следовательно, довольно просто написать рекурсивную функцию для вычисления n-го числа Фибоначчи:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
#include <iostream> int fibonacci(int number) { if (number == 0) return 0 // базовый случай (условие завершения) if (number == 1) return 1 // базовый случай (условие завершения) return fibonacci(number–1) + fibonacci(number–2) } // Выводим первые 13 чисел Фибоначчи int main() { for (int count=0 count < 13 ++count) std:: cout << fibonacci(count) << ” “ return 0 } |
Результат выполнения программы выше:
0 1 1 2 3 5 8 13 21 34 55 89 144
Краткая история чисел Фибоначчи
Согласно общепринятой версии, числа придуманы Леонардо Пизанским, легендарным математиком средневековой Европы. Сама последовательность была изложена в Книге Абака в 1202-м году в виде задачи по вычислению популяции кроликов.
Интересный факт: наиболее вероятно, что сама последовательность чисел была придумана гораздо раньше, но официально зафиксирована в книге лишь у Фибоначчи. Как указывают многие источники, большую известность последовательность Фибо-чисел имела в древней Индии, и это было гораздо раньше, чем жил Леонардо Пизанский.
Источники
- https://habr.com/ru/post/261159/
- https://postnauka.ru/longreads/87836
- https://like-to-trade.ru/chisla-fibonachchi-v-trejdinge/
- https://ravesli.com/urok-107-rekursiya-chisla-fibonachchi-i-faktorial/
- https://fib0.ru/zolotoe-sechenie.html
- https://FB.ru/article/323642/chisla-fibonachchi-i-zolotoe-sechenie-vzaimosvyaz
- https://Hi-News.ru/science/chislo-fibonachchi-pochemu-ono-tak-populyarno-v-prirode.html
Увы, это доказательство не приносит полного удовлетворения, поскольку не отвечает на вопрос, откуда вообще берутся подобные удивительные формулы. Мы выясним это в разделе «Вывод формулы Бине».
Мы провели эксперимент, и выяснилось, что вычисление по формуле Бине даёт первую ошибку для числа F 71 : вместо правильного значения 308061521170129 получилось 308061521170130 .
Вывод формулы Бине
Для вывода формулы Бине мы без колебаний выбрали из миллиона различных методов самый, на наш взгляд, впечатляющий — метод производящих функций.
Пусть нас не волнует то, как именно будет вычисляться эта бесконечная сумма при тех или иных значениях z — мы отнесёмся к ней формально. Для наших целей важно лишь то, что определённые операции над последовательностями соответствуют определённым действиям над производящими функциями:
- Умножение всех элементов последовательности A на число q приводит к умножению на q её производящей функции: q A ⇄ q A z .
- Поэлементной сумме или разности двух последовательностей отвечает сумма или разность их производящих функций: A ± B ⇄ A z ± B z .
- Начальный элемент последовательности равен значению её производящей функции при нулевом z : A 0 = A 0 .
- Вставке нуля в начало последовательности соответствует умножение её производящей функции на z : ⊢ A = 0 A 0 A 1 A 2 A 3 … ⇄ z A z .
- Удаление первого элемента последовательности приводит к вычитанию этого элемента из производящей функции и последующему делению на z : ⊣ A = A 1 A 2 A 3 … ⇄ A z − A 0 z . Для удаления первых n элементов получаем ⊣ n A = A n A n + 1 A n + 2 … ⇄ A z − A 0 + A 1 z + A 2 z 2 + … + A n − 1 z n − 1 z n .
Сделаем небольшое замечание, которое читатели, не знакомые с производными, могут спокойно пропустить. Попытки вычислить A 1 как значение A z − A 0 z при нулевом z приводят к неопределённости типа 0 0 , которая раскрывается по правилу Лопиталя: A z − A 0 z 0 = A ′ 0 (штрих означает производную по z ). Впрочем, и так понятно, что A n = A n 0 n ! ( A n — n -я производная по z ).
Рекуррентное вычисление
Рекурсивная версия
Рекуррентная сводит задачу вычисления F n к задачам вычисления чисел F n − 1 и F n − 2 . Это соображение приводит нас к рекурсивному решению, в котором вычислению F n посвящена отдельная процедура F с параметром n . Она возвращает n , если n < 2 . В противном случае она дважды рекурсивно вызывает сама себя — с параметрами n − 1 и n − 2 , после чего возвращает сумму значений, возвращённых при этих вызовах. Проще некуда.
Но, несмотря на изящество и простоту алгоритма, мы получаем программу-катастрофу. Мы убедились в этом, попытавшись вычислить с её помощью всего-то F 40 — это заняло на нашем компьютере около 108 секунд. Чтобы дождаться F 50 , у нас уже не хватило терпения.
Постараемся разобраться, что же приводит к столь долгой работе программы. На рисунке 9.1. «Рекурсивные вызовы при вычислении чисел Фибоначчи» мы протянули стрелки от одного числа Фибоначчи к другому, если вычисление первого из них повлекло рекурсивный вызов для вычисления другого.
Теперь, глядя на рисунок, подсчитаем, сколько раз вызывалась рекурсивная процедура для вычисления F 5 :
| F 5 | 1 раз |
| F 4 | 1 раз (для вычисления F 5 ) |
| F 3 | 2 раза (1 раз для вычисления F 5 и 1 раз для F 4 ) |
| F 2 | 3 раза (1 раз для вычисления F 4 и 2 раза для F 3 ) |
| F 1 | 5 раз (2 раза для вычисления F 3 и 3 раза для F 2 ) |
| F 0 | 2 раза (для вычисления F 2 ) |
Всего для вычисления F 5 рекурсивная процедура вызывалась 14 раз, причём для каждого значения параметра в среднем больше двух раз. Это явный перебор, но пока это не производит столь жуткого впечатления. Что же будет при больших n ?
Рекурсивная версия с мемоизацией
Матричная версия
Матрицы
Матрица представляет собой прямоугольную таблицу, заполненную числами: a 1 , 1 a 1 , 2 ⋯ a 1 , n ⋮ ⋮ ⋮ ⋮ a k , 1 a k , 2 ⋯ a k , n . Каждое число (элемент матрицы) снабжается двумя индексами: первый — номер строки, а второй — столбца. Упомянутую матрицу можно кратко обозначить как a i , j , i = 1 ‥ k , j = 1 ‥ n .
Проиллюстрируем умножение матриц на примере: 2 3 1 − 5 4 6 − 1 7 3 0 2 4 1 5 8 − 2 0 4 = 2 ⋅ − 1 + 3 ⋅ 2 + 1 ⋅ 8 2 ⋅ 7 + 3 ⋅ 4 + 1 ⋅ − 2 2 ⋅ 3 + 3 ⋅ 1 + 1 ⋅ 0 2 ⋅ 0 + 3 ⋅ 5 + 1 ⋅ 4 − 5 ⋅ − 1 + 4 ⋅ 2 + 6 ⋅ 8 − 5 ⋅ 7 + 4 ⋅ 4 + 6 ⋅ − 2 − 5 ⋅ 3 + 4 ⋅ 1 + 6 ⋅ 0 − 5 ⋅ 0 + 4 ⋅ 5 + 6 ⋅ 4 = 12 24 9 19 61 − 31 − 11 44 .
Матричные соотношения для чисел Фибоначчи
Довольно интриговать читателей. Пора уже объяснить, какое отношение матрицы имеют к числам Фибоначчи.
Оказывается, рекуррентное соотношение для чисел Фибоначчи можно записать в матричной форме: F n + 1 F n + 2 = 0 1 1 1 F n F n + 1 = F n + 1 F n + F n + 1 . В качестве очевидного следствия этого равенства получим F n + k F n + k + 1 = 0 1 1 1 k F n F n + 1 . В частности, при n = 0 получим F k F k + 1 = 0 1 1 1 k 0 1 .
[expert_bq id=»1570″]При жизни Леонардо Пизанский очень любил математические турниры, по причине чего в своих работах Liber abaci Книга абака , 1202; Practica geometriae Практика геометрии , 1220, Flos Цветок , 1225 год исследование на тему кубических уравнений и Liber quadratorum Книга квадратов , 1225 задачи о неопределенных квадратных уравнениях очень часто разбирал всевозможные математические задачи. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq]
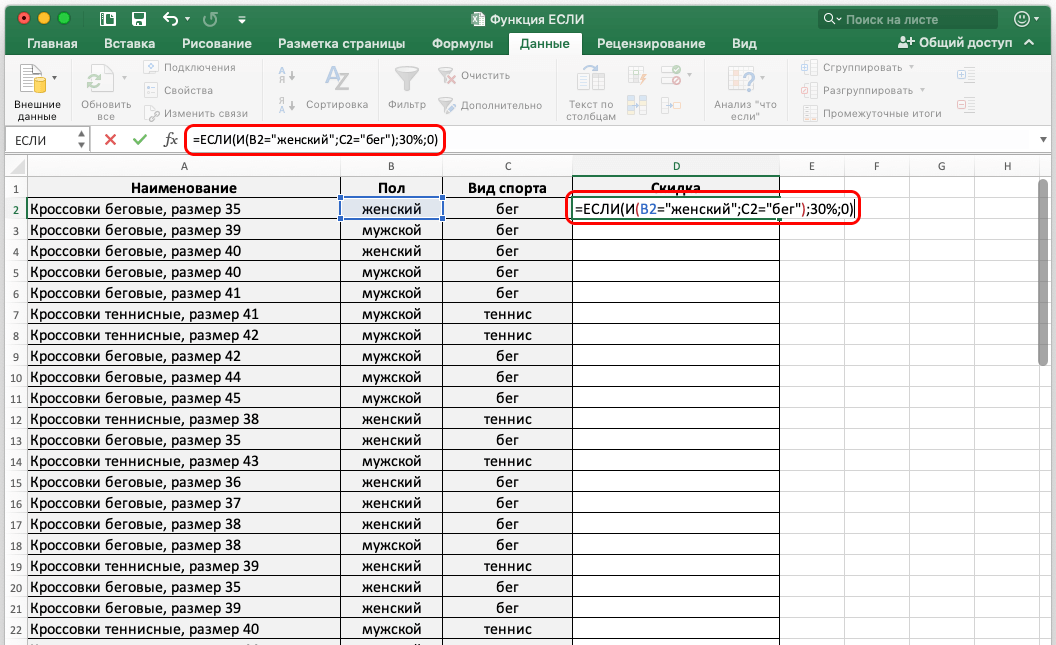
При жизни Леонардо Пизанский очень любил математические турниры, по причине чего в своих работах («Liber abaci» /«Книга абака», 1202; «Practica geometriae»/«Практика геометрии», 1220, «Flos»/«Цветок», 1225 год – исследование на тему кубических уравнений и «Liber quadratorum»/«Книга квадратов», 1225 – задачи о неопределенных квадратных уравнениях) очень часто разбирал всевозможные математические задачи.
Как вычислить миллионное число Фибоначчи на Python
- Умножение всех элементов последовательности A на число q приводит к умножению на q её производящей функции: q A ⇄ q A z .
- Поэлементной сумме или разности двух последовательностей отвечает сумма или разность их производящих функций: A ± B ⇄ A z ± B z .
- Начальный элемент последовательности равен значению её производящей функции при нулевом z : A 0 = A 0 .
- Вставке нуля в начало последовательности соответствует умножение её производящей функции на z : ⊢ A = 0 A 0 A 1 A 2 A 3 … ⇄ z A z .
- Удаление первого элемента последовательности приводит к вычитанию этого элемента из производящей функции и последующему делению на z : ⊣ A = A 1 A 2 A 3 … ⇄ A z − A 0 z . Для удаления первых n элементов получаем ⊣ n A = A n A n + 1 A n + 2 … ⇄ A z − A 0 + A 1 z + A 2 z 2 + … + A n − 1 z n − 1 z n .
Метод 5 (Оптимизированный метод 4)
Способ 4 может быть оптимизирован для работы в O (Logn) временной сложности. Мы можем сделать рекурсивное умножение, чтобы получить мощность (M, n) в преобладающем методе (аналогично оптимизации, сделанной в этом посте)
| F 5 | 1 раз |
| F 4 | 1 раз (для вычисления F 5 ) |
| F 3 | 2 раза (1 раз для вычисления F 5 и 1 раз для F 4 ) |
| F 2 | 3 раза (1 раз для вычисления F 4 и 2 раза для F 3 ) |
| F 1 | 5 раз (2 раза для вычисления F 3 и 3 раза для F 2 ) |
| F 0 | 2 раза (для вычисления F 2 ) |