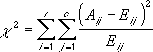Chi squared test excel

Table of Contents ( Chi-Square Test in Excel )

• Chi Square Test in Excel
• How to do Chi Square Test in Excel?

Chi Square Test in Excel

Chi Square Test in Excel is one such statistical function used to calculate the expected value from a dataset with observed values. Excel is a versatile tool to analyze data visually as well as statistically. It is one of the few spreadsheet tools around which supports advanced statistical functions. Using these functions, we can gain insights from a dataset that may not be possible by just visually analyzing them. In this article, we will learn how to calculate the Chi Square from a database using excel. Before going into detail with the Chi Square Test, let us go through a few examples.

Chi Square Test is a test of the validity of a hypothesis. The Chi Square P Value tells us if our observed results are statistically significant or not. A statistically significant result means that we reject the null hypothesis (the null hypothesis in statistics is a statement or hypothesis which is likely to be incorrect). A Chi-Square P-Value is a number between 0 and 1. A Chi-Square P-Value less than 0.05 usually lead to rejection of the null hypothesis.

How to do Chi Square Test in Excel?

Let’s understand how to do the Chi Square Test in Excel with some examples.

You can download this Chi Square Test Excel Template here – Chi Square Test Excel Template

Example #1

Chi Square test can tell us whether the proportion of a given number of items is in one place based on a random sample are statistically independent of each other or not.

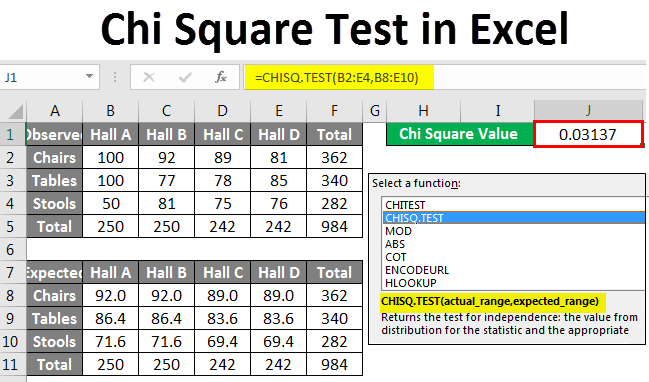
Suppose your company has 10000 pieces of furniture. About one by a tenth of them are distributed over four halls. We can find out what proportion of the total furniture is in one hall as shown below:

Observe that we have about 250 pieces of furniture in each hall. If we want to get the expected number of furniture by type, we will calculate it as follows:

Expected Value =Category Column Total X (Category Row Total/Total Sample Size)

Using this formula, we get an expected number of about 92 Chairs in Hall A as follows:

Expected Number of Chairs in Hall A = 250 X (362/984)

We will check the difference using the following formula:

((Observed Value-Expected Value)ⁿ)/expected value

In the case of the Chi Square test, n = 2

Which would give us the value 0.713928183. Similarly, we will find the values for each quantity and the sum of these values is the test statistic. This statistic has an approximate Chi-Squared distribution if each quantity is independent of the other. The following formula would determine the degree of freedom for each quantity:

(number of rows – 1)(number of columns – 1)

Which, in this case, is 6.

We find the Chi-Square P-value for the first value that is the number of chairs. The null hypothesis is that the location of the furniture is independent of the type of furniture.

The Chi Square P-value for the chairs would be calculated as:

The sum of all the Chi Square P values should be 1 if the null hypothesis is true.

If the test statistic is too large in the present dataset, then we reject the null hypothesis.

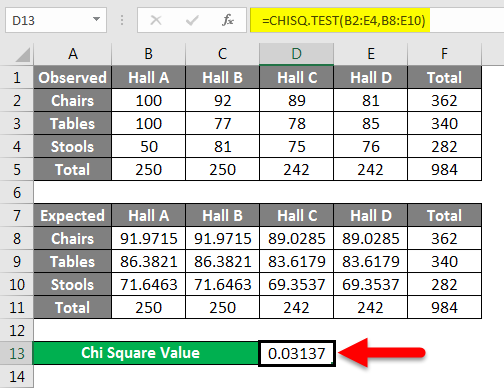
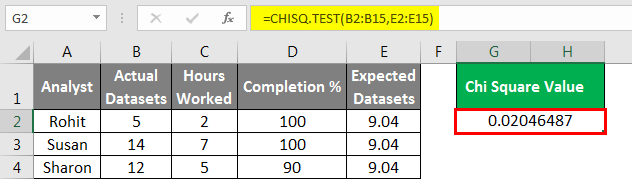
As is clear from the above example, calculating Chi Square and testing for significance of hypothesized data in statistics is a painstaking process and demands high accuracy. The above example can be analyzed using the CHISQ.TEST Function to get the Chi-Square value directly and check if our assumption that the location of the furniture is independent of the type of furniture is correct r not. In this case:

The Chi Square value is approximately 0.03. From our earlier discussion, we now know that this rejects the null hypothesis.

Example #2

To calculate the p-value in excel, we need to perform the following steps:

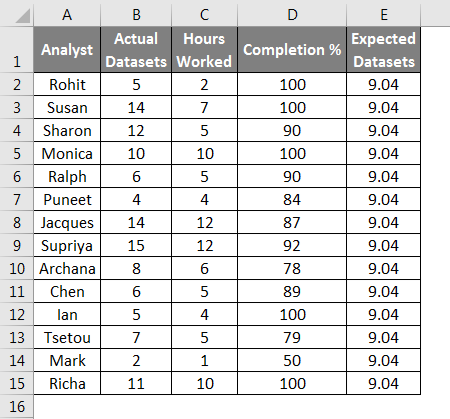
• Calculate your expected value. The expected value in chi-square is normally a simple average or mean for normally distributed datasets. For more complicated data, please check the example above.

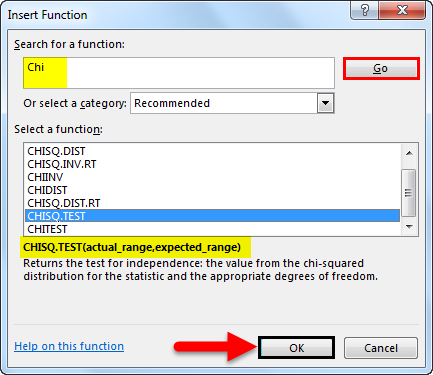
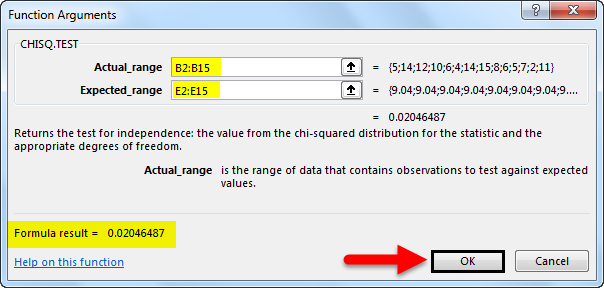
• Type your data into columns and click a blank cell where you want to show the results on the worksheet and then click the “Insert Function” button on the toolbar, a pop up would appear. Type chi in the Search for a Function box and then click “Go”.then select “CHITEST” from the list and then click “OK.”

• Select the observed and expected ranges and click “OK”.

We will get the result as follows.

Things to Remember 

1. The CHISQ.TEST is not the only Chi Square function available in excel. All the variations of Chi-Square are available and can be used depending on your proficiency in statistics.
2. The CHISQ functions can also be directly typed into a cell-like any other function. This would save time if you already know the data ranges you are working with.
3. The CHISQ function’s reliability is directly dependent on the structure and distribution of the data and the clarity of the hypotheses being tested. Particular care should be used while employing a Chi Square Test to check significance.

Recommended Articles

This has been a guide to Chi Square Testin excel. Here we discuss How to do the Chi Square Test in excel along with practical examples and a downloadable excel template. You can also go through our other suggested articles –

1. VLOOKUP Function in Excel
2. Excel STDEV Function
3. Substring in Excel
4. Excel Square Root Function

---

A Chi-Square Goodness of Fit Test is used to determine whether or not a categorical variable follows a hypothesized distribution.

This tutorial explains how to perform a Chi-Square Goodness of Fit Test in Excel.

Example: Chi-Square Goodness of Fit Test in Excel

A shop owner claims that an equal number of customers come into his shop each weekday. To test this hypothesis, an independent researcher records the number of customers that come into the shop on a given week and finds the following:

• Monday: 50 customers
• Tuesday: 60 customers
• Wednesday: 40 customers
• Thursday: 47 customers
• Friday: 53 customers

We will use the following steps to perform a Chi-Square goodness of fit test to determine if the data is consistent with the shop owner’s claim.

Step 1: Input the data.

First, we will input the data values for the expected number of customers each day in one column and the observed number of customers each day in another column:

Note: There were 250 customers total. Thus, if the shop owner expects an equal number to come into the shop each day then he would expect 50 customers per day.

Step 2: Find the difference between the observed and expected values.

The Chi-Square test statistic for the Goodness of Fit test is X² = Σ(O-E)² / E

where:

• Σ: is a fancy symbol that means “sum”
• O: observed value
• E: expected value

The following formula shows how to calculate (O-E)² / E for each row:

Step 3: Calculate the Chi-Square test statistic and the corresponding p-value.

Lastly, we will calculate the Chi-Square test statistic along with the corresponding p-value using the following formulas:

Note: The Excel function CHISQ.DIST.RT(x, deg_freedom) returns the right-tailed probability of the Chi-Square distribution associated with a test statistic x and a certain degrees of freedom. The degrees of freedom is calculated as n-1. In this case, deg_freedom = 5 – 1 = 4.

Step 4: Interpret the results.

The X² test statistic for the test is 4.36 and the corresponding p-value is 0.3595. Since this p-value is not less than 0.05, we fail to reject the null hypothesis. This means we do not have sufficient evidence to say that the true distribution of customers is different from the distribution that the shop owner claimed.

The chi-square test is a non-parametric test that compares two or more variables from randomly selected data. It helps find the relationship between two or more variables. In Excel, we calculate the chi-square p-value. Since Excel does not have an inbuilt function, mathematical formulas are used to perform the chi-square test.

There are two types of chi-square tests which are listed as follows:

1. Chi-square goodness of fit test
2. Chi-square test for independence

#1 – Chi-Square Goodness of Fit Test

The goodness of fit test helps determine whether the sample data matches the population or not. In other words, it shows how well the sample data fits a set of observations.

The symbol of the chi-square test is “x²” (i.e., “x” raised to the power 2). “x²” is the summation of the (observed count–expected count)²/expected count.

The formula of the chi-square goodness of fit test is given as follows:

Where,

• “x²” is the chi-square statistic
• “O_i” is the observed frequency
• “E_i” is the expected frequency
• “i” is the “i^th” position in the contingency table
• “k” is the category
• Degrees of freedom (df)=k-1

The Uses of the Goodness of Fit Test

The test is used in the following situations:

• To evaluate the creditworthinessCreditworthiness is a measure of judging the loan repayment history of borrowers to ascertain their worth as a debtor who should be extended a future credit or not. For instance, a defaulter’s creditworthiness is not very promising, so the lenders may avoid such a debtor out of the fear of losing their money. Creditworthiness applies to people, sovereign states, securities, and other entities whereby the creditors will analyze your creditworthiness before getting a new loan.read more of borrowers based on their age group and history of debt obligations
• To establish a relation between the performance of sales representatives and the training received by them
• To compare the returns of a single stock with the returns on stocks of the whole sector
• To evaluate the impact of a television campaign on a category of viewers

#2 – Chi-Square Test for Independence

It helps determine whether the variables are independent of one another or not. Two random variables are called independent if the probability distributionProbability distribution could be defined as the table or equations showing respective probabilities of different possible outcomes of a defined event or scenario. In simple words, its calculation shows the possible outcome of an event with the relative possibility of occurrence or non-occurrence as required.read more of one variable is not affected by the other.

The formula of the chi-square test for independence is given as follows:

Where,

• “x²” is the chi-square statistic
• “O_ij” is the observed frequency in the i^th row and j^th column
• “E_ij”is the expected frequency in the i^th row and j^th column
• “r” is the number of rows
• “c” is the number of columns
• Degrees of freedom (df)=(r-1)(c-1)

The formula for calculating the expected frequency in the i^th row and j^th column is given as follows:

The Uses of the Chi-Square Test for Independence

The test is used in the following situations:

• There are two categorical variables and the relation between them is to be determined.
• There are cross-tabulations (two-way tables) and the relationship between various categorical variables needs to be studied.
• There are non-quantifiable variables. For example, one needs to determine the reason behind variations of health plans across age groups.

The Characteristics of the Chi-Square Test

The features of the chi-square test are listed as follows:

• It evaluates whether observed frequencies vary significantly from the expected frequencies under a given set of assumptions.
• It determines how well an assumed distribution fits the data.
• It uses the contingency tables (or crosstabs) to summarize the relationship between various categorical variables.
• It supports nominal level measurements.

Note: In the simplest form, the chi-square distribution is the square of the standard normal distribution.

How to Perform the Chi-Square Test in Excel? (With Example)

You can download this Chi Square Test Excel Template here – Chi Square Test Excel Template

A restaurant manager wants to find the relationship between quality of service and the salary of customers waiting to be served.

She organizes the task in the following way:

• A random sample of 100 customers is considered.
• Every customer is asked to rate the service of the restaurant as “excellent,” “good,” and “poor.”

She constructs the following hypothesis:

• Null hypothesisNull hypothesis presumes that the sampled data and the population data have no difference or in simple words, it presumes that the claim made by the person on the data or population is the absolute truth and is always right. So, even if a sample is taken from the population, the result received from the study of the sample will come the same as the assumption.read more (H₀)–The quality of service is not dependent on the salary of customers waiting to be served.
• Alternative hypothesis (H₁)–The quality of service is dependent on the salary of customers waiting to be served.

The manager divides the customers into three categories based on their salaries–“low,” “medium,” and “high.” The level of significance (α) is 0.05.

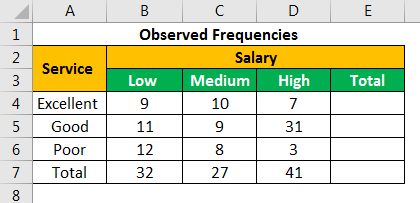
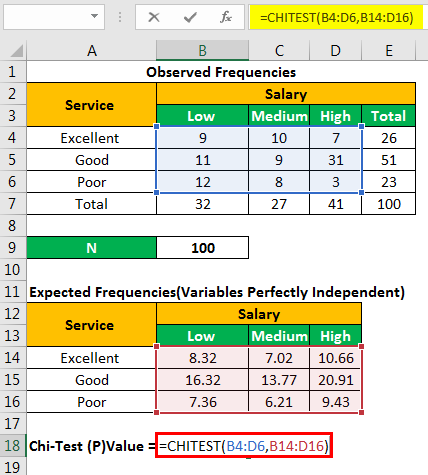
The findings are presented as nine data points shown in the following table.

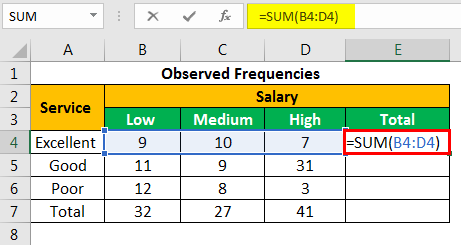
Let us calculate the sum of all the rows and columns. We apply the following SUM formula to add the numbers of the fourth row.

“=SUM(B4:D4)”

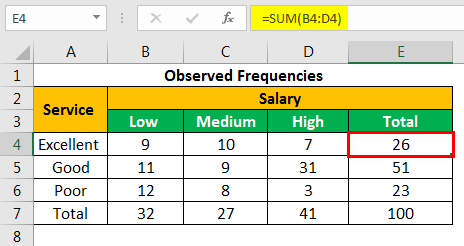
Press the “Enter” key and the sum appears in cell E4. The output is 26.

Similarly, we apply the SUM formulaThe SUM function in excel adds the numerical values in a range of cells. Being categorized under the Math and Trigonometry function, it is entered by typing “=SUM” followed by the values to be summed. The values supplied to the function can be numbers, cell references or ranges.read more to the remaining rows and columnsA cell is the intersection of rows and columns. Rows and columns make the software that is called excel. The area of excel worksheet is divided into rows and columns and at any point in time, if we want to refer a particular location of this area, we need to refer a cell.read more. There are 27 respondents with medium salary and 51 respondents who rated the service quality as “good.”

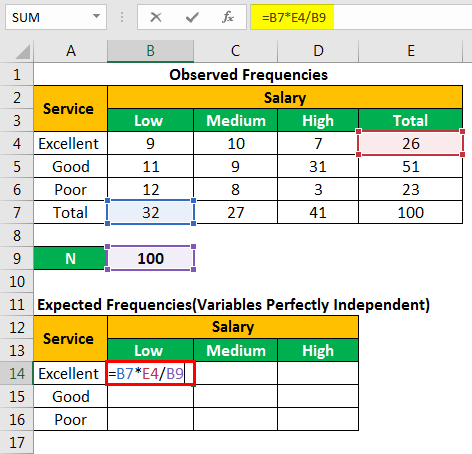
We apply the formula “(r-1)(c-1)” to calculate the degrees of freedom (df).

df=(3-1)(3-1)=2*2=4

We apply the following formula to calculate the expected frequency for column B and row 4.

“(=B7*E4/B9)”

The calculation is shown in the following image.

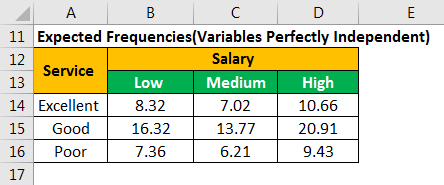
The expected number of customers who have “low” salary but rated the restaurant service as “excellent” is 8.32.

In the following calculations, E₁₁ is the expected frequency of the first row and the first column. E₁₂ is the expected frequency of the first row and the second column.

• E₁₁=(26*32)/100=8.32, E₁₂=7.02, E₁₃=10.66
• E₂₁=16.32, E₂₂=13.77, E₂₃=20.91
• E₃₁=7.36, E₃₂=6.21, E₃₃=9.43

Similarly, we calculate the expected frequencies for the entire table, as shown in the succeeding image.

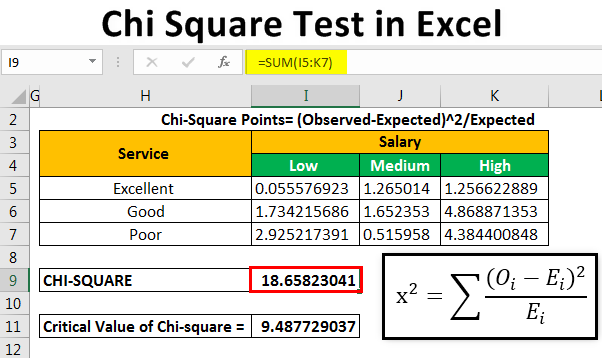
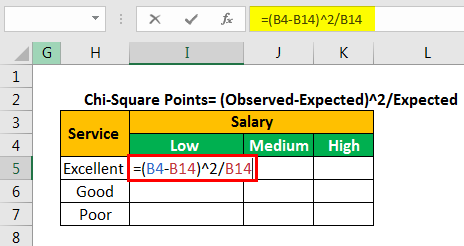
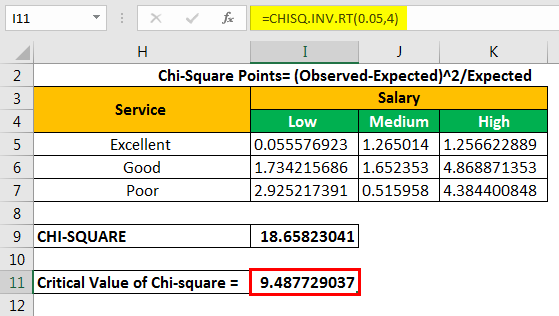
Let us calculate the chi-square data points by using the following formula.

Chi-square points=(observed-expected)^2/expected

We apply the formula “=(B4-B14)^2/B14” to calculate the first chi-square point.

We copy and paste the formula to the remaining cells. This is done to fill values in the entire table, as shown in the following image.

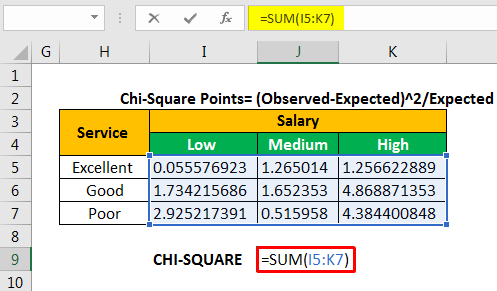
Let us calculate the chi-square calculated value by adding all the values given in the succeeding table.

The chi-square calculated value is 18.65823.

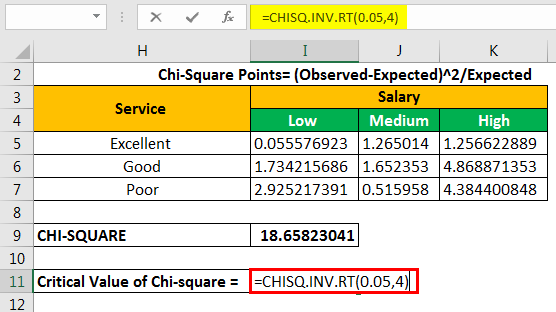
To calculate the critical value, we use either the chi-square critical value table or the CHISQ formula. The formula “CHISQ.INV.RT” contains two parameters–the probability and the degrees of freedomDegrees of freedom (df) refers to the number of independent values (variable) in a data sample used to find the missing piece of information (fixed) without violating any constraints imposed in a dynamic system. These nominal values have the freedom to vary, making it easier for users to find the unknown or missing value in a dataset.read more.

The probability is 0.05, which is a significant value. The df is equal to 4.

The chi-square critical value is 9.487729037.

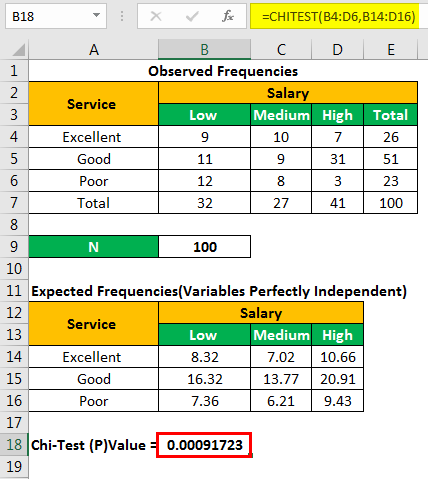
Let us find the chi-square p-value with the help of the following formula.

“=CHITEST(actual_range,expected_range)”

We apply the formula “=CHITEST(B4:D6,B14:D16).”

The chi-square p-value is= 0.00091723.

The chi-square calculated value is significant when equal to or more than the chi-square critical value (tabulated value). The null hypothesis (H₀) is rejected if the chi-square calculated value is greater than the chi-square critical value.

Here x² (calculated)>x² (tabulated) or 18.65>9.48. Hence, we reject the null hypothesis and accept the alternative hypothesis.

The p-valueP-Value, or Probability Value, is the deciding factor on the null hypothesis for the probability of an assumed result to be true, being accepted or rejected, & acceptance of an alternative result in case of the assumed results rejection. read more can also determine whether the null hypothesis must be accepted or rejected. For this, the p-value is compared with alpha (α) in the following way:

• If p-value <= α, the null hypothesis is rejected.
• If p-value > α, the null hypothesis is accepted.

In this example, p-value<α or 0.0009172<0.05. So, we reject H₀ and accept H₁.

We conclude that the quality of service is dependent on the salary of customers waiting to be served.

Frequently Asked Questions

Recommended Articles

This has been a guide to Chi-Square Test in Excel. Here we learn how to perform the chi-square test along with step by step examples. Below are some useful Excel articles-

• Z Test in Excel
• Z Test vs. T-Test
• Formula of F-Test
• T-TEST in Excel