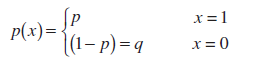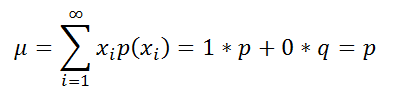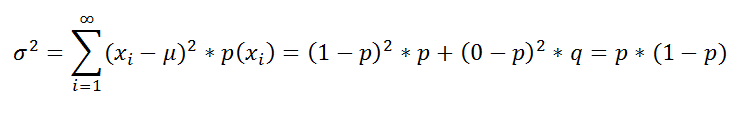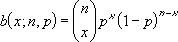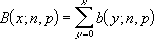Биноминальный критерий в excel

Рассмотрим Биномиальное распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL

БИНОМ.РАСП()

построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения p, математического ожидания распределения и стандартного отклонения. Также рассмотрим распределение Бернулли.

Определение

. Пусть проводятся

n

испытаний, в каждом из которых может произойти только 2 события: событие «успех» с вероятностью

p

или событие «неудача» с вероятностью

q

=1-p (так называемая

Схема Бернулли,

Bernoulli

trials

).

Вероятность получения ровно

x

успехов в этих

n

испытаниях равна:

Примечание

:

Порядок получения успехов значения не имеет. Если важен порядок, то см. статью

Отрицательное Биномиальное распределение

.

Количество успехов в выборке

x

является случайной величиной, которая имеет

Биномиальное распределение

(англ.

Binomial

distribution

)

p

и

n

–

являются параметрами этого распределения.

Примечание

: Запись

означает количество

сочетаний

из

n

элементов по

x

. Для сочетаний также используется запись

. Подробнее о сочетаниях см. статью

Сочетания без повторений: Комбинаторика в MS EXCEL

.

Напомним, что для применения

схемы Бернулли

и соответственно

Биномиального распределения,

должны быть выполнены следующие условия:

• каждое испытание должно иметь ровно два исхода, условно называемых «успехом» и «неудачей».
• результат каждого испытания не должен зависеть от результатов предыдущих испытаний (независимость испытаний).
• вероятность успеха
  
  p
  
  должна быть постоянной для всех испытаний.

Биномиальное распределение в MS EXCEL

В MS EXCEL, начиная с версии 2010, для

Биномиального распределения

имеется функция

БИНОМ.РАСП()

, английское название — BINOM.DIST(), которая позволяет вычислить вероятность того, что в выборке будет ровно

х

«успехов» (т.е.

функцию плотности вероятности

p(x), см. формулу выше), и

интегральную функцию распределения

(вероятность того, что в выборке будет

x

или меньше «успехов», включая 0).

СОВЕТ

: Подробнее о

Функции распределения

и

Плотности вероятности

см. статью

Функция распределения и плотность вероятности в MS EXCEL

.

До MS EXCEL 2010 в EXCEL была функция

БИНОМРАСП()

, которая также позволяет вычислить

функцию распределения

и

плотность вероятности

p(x).

БИНОМРАСП()

оставлена в MS EXCEL 2010 для совместимости.

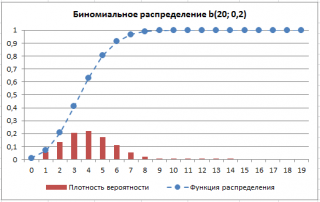
В

файле примера

приведены графики

плотности распределения вероятности

и

интегральной функции распределения

.

Биномиальное распределения

имеет обозначение

B

(

n

;

p

)

.

Примечание

: Для построения

интегральной функции распределения

идеально подходит диаграмма типа

График

, для

плотности распределения

–

Гистограмма с группировкой

. Подробнее о построении диаграмм читайте статью Основные типы диаграмм.

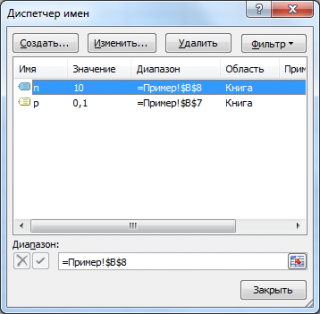
Примечание

: Для удобства написания формул в

файле примера

созданы Имена для параметров

Биномиального распределения

: n и p.

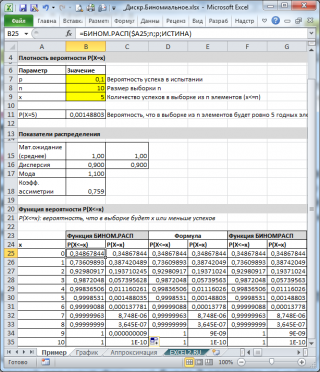
В

файле примера

приведены различные расчеты вероятности с помощью функций MS EXCEL:

Как видно на картинке выше, предполагается, что:

• В бесконечной совокупности, из которой делается выборка, содержится 10% (или 0,1) годных элементов (параметр
  
  p
  
  , третий аргумент функции =
  
  БИНОМ.РАСП()
  
  )
• Чтобы вычислить вероятность, того что в выборке из 10 элементов (параметр
  
  n
  
  , второй аргумент функции) будет ровно 5 годных элементов (первый аргумент), нужно записать формулу:
  
  =БИНОМ.РАСП(5; 10; 0,1; ЛОЖЬ)
  
• Последний, четвертый элемент, установлен =ЛОЖЬ, т.е. возвращается значение функции
  
  плотности распределения
  
  .

Если значение четвертого аргумента =ИСТИНА, то функция

БИНОМ.РАСП()

возвращает значение

интегральной функции распределения

или просто

Функцию распределения

. В этом случае можно рассчитать вероятность того, что в выборке количество годных элементов будет из определенного диапазона, например, 2 или меньше (включая 0).

Для этого нужно записать формулу: =

БИНОМ.РАСП(2; 10; 0,1; ИСТИНА)

Примечание

: При нецелом значении х,

дробная часть отбрасывается

. Например, следующие формулы вернут одно и тоже значение:

=БИНОМ.РАСП(

2

; 10; 0,1; ИСТИНА)

=БИНОМ.РАСП(

2,9

; 10; 0,1; ИСТИНА)

Примечание

: В

файле примера

плотность вероятности

и

функция распределения

также вычислены с использованием определения и функции

ЧИСЛКОМБ()

.

Показатели распределения

В

файле примера на листе Пример

имеются формулы для расчета некоторых показателей распределения:

• математического ожидания

  =n*p;

• дисперсии

  (квадрата стандартного отклонения) = n*p*(1-p);

• моды

  = (n+1)*p;

• коэффициента асимметрии

  =(1-2*p)*КОРЕНЬ(n*p*(1-p)).

Выведем формулу

математического ожидания

Биномиального распределения

, используя

Схему Бернулли

.

По определению случайная величина Х в

схеме Бернулли

(Bernoulli random variable) имеет

функцию распределения

:

Это распределение называется

распределение Бернулли

.

Примечание

:

распределение Бернулли

– частный случай

Биномиального распределения

с параметром n=1.

Найдем

математическое ожидание

(

среднее,

mean

)

распределения Бернулли

(

x

принимает только 2 значения).

Предположим, что мы провели

n

последовательных

испытаний Бернулли

и у нас сформировалась

выборка

, состоящая из n элементов: x1, x2, …, xn (каждое из которых равно 0 или 1). Сумма этих случайных величин Y=X1+X2+…+Xn, в свою очередь, также является случайной величиной и, как мы помним, будет иметь

Биномиальное распределение

с параметрами

n

и

p

.

Учитывая, что

математическое ожидание

для каждого

x

_i

равно

p

, то для соответствующего

Биномиального распределения μ=p*n.

Аналогичным образом, можно вычислить

дисперсию

Биномиального распределения.

Для этого сначала найдем

дисперсию

(

второй момент, variance

)

распределения Бернулли

:

Соответственно, дисперсия для

Биномиального распределения

равна

σ

²

=n*p*(1-p)= n*p*q.

Генерация случайных чисел. Распределение Бернулли

С помощью надстройки

Пакет анализа

можно

сгенерировать случайные числа

, извлеченные из

распределения Бернулли

.

СОВЕТ

: О надстройке

Пакет анализа

можно прочитать в статье

Надстройка Пакет анализа MS EXCEL

.

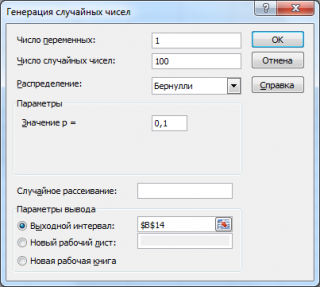
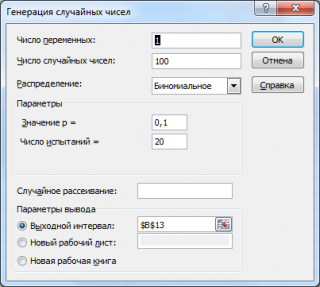
Сгенерируем 3 массива по 100 чисел с различными вероятностями успеха: 0,1; 0,5 и 0,9. Для этого в окне

Генерация случайных чисел

установим следующие параметры для каждой вероятности p:

Примечание

: Если установить опцию

Случайное рассеивание

(

Random Seed

), то можно выбрать определенный случайный набор сгенерированных чисел. Например, установив эту опцию =25 можно сгенерировать на разных компьютерах одни и те же наборы случайных чисел (если, конечно, другие параметры распределения совпадают). Значение опции может принимать целые значения от 1 до 32 767. Название опции

Случайное рассеивание

может запутать. Лучше было бы ее перевести как

Номер набора со случайными числами

.

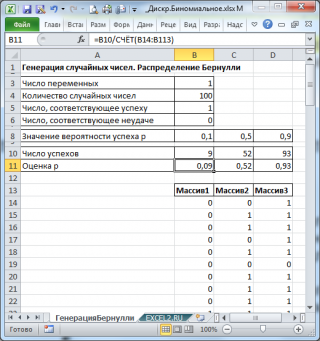
В итоге будем иметь 3 столбца по 100 чисел, на основании которых можно, например, оценить вероятность успеха

p

по формуле:

Число успехов/100

(см.

файл примера лист ГенерацияБернулли

).

Примечание

: Для

распределения Бернулли

с p=0,5 можно использовать формулу

=СЛУЧМЕЖДУ(0;1)

, которая соответствует

дискретному равномерному распределению

.

Генерация случайных чисел. Биномиальное распределение

С помощью надстройки

Пакет анализа

можно

сгенерировать случайные числа

, извлеченные из

Биномиального

распределения

.

Сгенерируем 3 массива по 100 чисел с различными вероятностями успеха: 0,1; 0,5; 0,9. Количество испытаний n установим 20. Для этого в окне

Генерация случайных чисел

установим следующие параметры для каждой вероятности p:

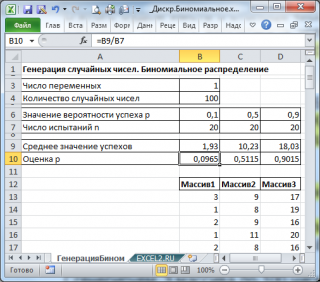
В итоге будем иметь 3 столбца чисел, на основании которых можно, например, оценить вероятность успеха

p

по формуле:

Среднее значение успехов/

n

(см.

файл примера лист ГенерацияБином

).

Примечание

: Для генерирования массива чисел, распределенных по

Биномиальному закону

, можно использовать формулу

=БИНОМ.ОБР(20; p; СЛЧИС())

, где p – вероятность успеха. Функция

СЛЧИС()

генерирует

непрерывное равномерное распределение

от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.

файл примера лист ГенерацияБином

).

Оценка параметра p

В

схеме Бернулли

оценить параметр распределения

p

можно по формуле

=СУММ(B14:B113)/СЧЁТ(B14:B113)

. В формуле предполагается, что массив случайных чисел находится в диапазоне

B14:B113

.

Оценить параметр

Биномиального распределения

p

можно по формуле

= СРЗНАЧ(B13:B112)/n

(предполагается, что случайные числа сгенерированы формулой

=БИНОМ.ОБР(n; p; СЛЧИС()

). Также в формуле предполагается, что массив случайных чисел находится в диапазоне

B13:B112

.

Обратная функция БИНОМ.ОБР()

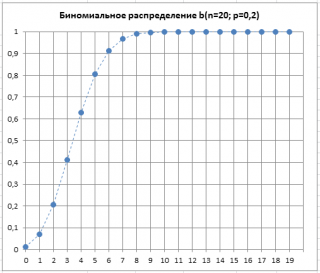
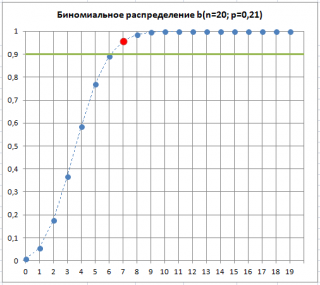
Вспомним график функции

Биномиального распределения

:

Решим задачу. Предположим, что для целей контроля качества нам требуется определить наибольшее допустимое количество дефектных изделий, которое еще позволяет обойтись без отбраковки всей партии.

Задана величина выборки из партии (

n

=20) и

р=

0,2 — доля дефектных изделий, которая обычно наблюдается в данном производственном процессе. Также пусть задана вероятность допустить

ошибку 1-го рода

(см.

статью про уровень доверия

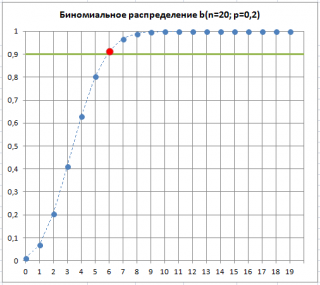
) равная 90%. Пороговый приемочный критерий можно вычислить по формуле

=БИНОМ.ОБР(20; 0,2; 90%)

. Формула вернет значение 6 — наибольшее количество дефектных изделий, допустимое в

выборке

.

Примечание

: Третий аргумент функции

БИНОМ.ОБР()

называется

Альфа

(

α error, type I error, риск производителя, альфа-риск

) и представляет собой вероятность допустить

ошибку 1-го рода

при

проверке статистической гипотезы

(см. статью

Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна)

).

Предположим, что в выборке обнаружилось 7 дефектных изделий. Это означает, что «очень вероятна» ситуация, что изменилась доля дефектных изделий

p

, которая является характеристикой нашего производственного процесса. Хотя такая ситуация «очень вероятна», но существует вероятность (альфа-риск, ошибка 1-го рода, «ложная тревога»), что все же

p

осталась без изменений, а увеличенное количество дефектных изделий обусловлено случайностью выборки.

Как видно на рисунке ниже, 7 – количество дефектных изделий, которое допустимо для процесса с p=0,21 при том же значении

Альфа

. Это служит иллюстрацией, что при превышении порогового значения дефектных изделий в выборке,

p

«скорее всего» увеличилось. Фраза «скорее всего» означает, что существует всего лишь 10% вероятность (100%-90%) того, что отклонение доли дефектных изделий выше порогового вызвано только сучайными причинами.

Таким образом, превышение порогового количества дефектных изделий в выборке, может служить сигналом, что процесс расстроился и стал выпускать б

о

льший процент бракованных изделий.

Примечание

: До MS EXCEL 2010 в EXCEL была функция

КРИТБИНОМ()

, которая эквивалентна

БИНОМ.ОБР()

.

КРИТБИНОМ()

оставлена в MS EXCEL 2010 и выше для совместимости.

Связь Биномиального распределения с другими распределениями

Если параметр

n

Биномиального распределения

стремится к бесконечности, а

p

стремится к 0, то в этом случае

Биномиальное распределение

может быть аппроксимировано

Распределением Пуассона

. Можно сформулировать условия, когда приближение

распределением Пуассона

работает хорошо:

• 
  p
  <0,1
  
  (чем меньше
  
  p
  
  и больше
  
  n
  
  , тем приближение точнее);
• 
  p
  
  >0,9
  
  (учитывая, что
  
  q
  
  =1-
  
  p
  
  , вычисления в этом случае необходимо производить через
  
  q
  
  (а
  
  х
  
  нужно заменить на
  
  n
  
  —
  
  x
  
  ). Следовательно, чем меньше
  
  q
  
  и больше
  
  n
  
  , тем приближение точнее).

При 0,1<=p<=0,9 и n*p>10

Биномиальное распределение

можно аппроксимировать

Нормальным распределением

.

В свою очередь,

Биномиальное распределение

может служить хорошим приближением

Гипергеометрического распределения

, когда размер совокупности N

Гипергеометрического распределения

гораздо больше размера выборки n (т.е., N>>n или n/N<<1).

Подробнее о связи вышеуказанных распределений, можно прочитать в статье

Взаимосвязь некоторых распределений друг с другом в MS EXCEL

. Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.

СОВЕТ

: О других распределениях MS EXCEL можно прочитать в статье

Распределения случайной величины в MS EXCEL

.

Возвращает отдельное значение биномиального распределения. Функция БИНОМРАСП используется в задачах с фиксированным числом тестов или испытаний, когда результатом любого испытания может быть только успех или неудача, испытания независимы, а вероятность успеха одинакова на протяжении всего эксперимента. Например, при помощи БИНОМРАСП можно вычислить, с какой вероятностью двое из трех следующих новорожденных будут мальчиками.

Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.

Дополнительные сведения о новом варианте этой функции см. в статье Функция БИНОМ.РАСП.

Синтаксис

БИНОМРАСП(число_успехов;число_испытаний;вероятность_успеха;интегральная)

Аргументы функции БИНОМРАСП описаны ниже.

• Число_успехов     — обязательный аргумент. Количество успешных испытаний.

• Число_испытаний     — обязательный аргумент. Количество независимых испытаний.

• Вероятность_успеха     — обязательный аргумент. Вероятность успеха каждого испытания.

• Интегральная     — обязательный аргумент. Логическое значение, определяющее форму функции. Если «накопительный» имеет number_s, функция БИНОМРАСП возвращает накопительную функцию распределения. Если имеется ложь, возвращается функция вероятностной массы, которая является вероятностью number_s успеха.

Замечания

• Число_успехов и число_испытаний усекаются до целых.

• Если number_s, испытаний или probability_s не является числом, бинОМЕТ возвращает #VALUE! значение ошибки #ЗНАЧ!.

• Если number_s < 0 или number_s >, бинОМЕТ возвращает #NUM! значение ошибки #ЗНАЧ!.

• Если probability_s < 0 или probability_s > 1, бинОМЕТ возвращает #NUM! значение ошибки #ЗНАЧ!.

• Если x = число_успехов, n = число_испытаний и p = вероятность_успеха, то весовая функция биномиального распределения выглядит следующим образом:

  

  где

  

  — ЧИСЛКОМБ(n;x).

• Если x = число_успехов, n = число_испытаний и p = вероятность_успеха, то интегральное биномиальное распределение выглядит следующим образом:

  

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
6	Количество успешных испытаний
10	Количество независимых испытаний
0,5	Вероятность успеха в каждом испытании
Формула	Описание	Результат
=БИНОМРАСП(A2;A3;A4;ЛОЖЬ)	Вероятность того, что ровно 6 испытаний из 10 будут успешными	0,2050781