This is a list of some binary codes that are (or have been) used to represent text as a sequence of binary digits «0» and «1». Fixed-width binary codes use a set number of bits to represent each character in the text, while in variable-width binary codes, the number of bits may vary from character to character.
the binary codes are used to read the computer language.
Five-bit binary codesEdit
Several different five-bit codes were used for early punched tape systems.
Five bits per character only allows for 32 different characters, so many of the five-bit codes used two sets of characters per value referred to as FIGS (figures) and LTRS (letters), and reserved two characters to switch between these sets. This effectively allowed the use of 60 characters.
Standard five-bit standard codes are:
- International Telegraph Alphabet No. 1 (ITA1) – Also commonly referred to as Baudot code[1]
- International Telegraph Alphabet No. 2 (ITA2) – Also commonly referred to as Murray code[1][2]
- American Teletypewriter code (USTTY) – A variant of ITA2 used in the USA[2]
- DIN 66006 – Developed for the presentation of ALGOL/ALCOR programs on paper tape and punch cards
The following early computer systems each used its own five-bit code:
- J. Lyons and Co. LEO (Lyon’s Electronic Office)
- English Electric DEUCE
- University of Illinois at Urbana-Champaign ILLIAC
- ZEBRA
- EMI 1100
- Ferranti Mercury, Pegasus, and Orion systems[3]
The steganographic code, commonly known as Bacon’s cipher uses groups of 5 binary-valued elements to represent letters of the alphabet.
Six-bit binary codesEdit
Six bits per character allows 64 distinct characters to be represented.
Examples of six-bit binary codes are:
- International Telegraph Alphabet No. 4 (ITA4)[4]
- Six-bit BCD (Binary Coded Decimal), used by early mainframe computers.
- Six-bit ASCII subset of the primitive seven-bit ASCII
- Braille – Braille characters are represented using six dot positions, arranged in a rectangle. Each position may contain a raised dot or not, so Braille can be considered to be a six-bit binary code.
See also: Six-bit character codes
Seven-bit binary codesEdit
Examples of seven-bit binary codes are:
- International Telegraph Alphabet No. 3 (ITA3) – derived from the Moore ARQ code, and also known as the RCA
- ASCII – The ubiquitous ASCII code was originally defined as a seven-bit character set. The ASCII article provides a detailed set of equivalent standards and variants. In addition, there are various extensions of ASCII to eight bits (see Eight-bit binary codes)
- CCIR 476 – Extends ITA2 from 5 to 7 bits, using the extra 2 bits as check digits[4]
- International Telegraph Alphabet No. 4 (ITA4)[4]
Eight-bit binary codesEdit
- Extended ASCII – A number of standards extend ASCII to eight bits by adding a further 128 characters, such as:
- HP Roman
- ISO/IEC 8859
- Mac OS Roman
- Windows-1252
- EBCDIC – Used in early IBM computers and current IBM i and System z systems.
10-bit binary codesEdit
- AUTOSPEC – Also known as Bauer code. AUTOSPEC repeats a five-bit character twice, but if the character has odd parity, the repetition is inverted.[4]
- Decabit – A datagram of electronic pulses which are transmitted commonly through power lines. Decabit is mainly used in Germany and other European countries.
16-bit binary codesEdit
- UCS-2 – An obsolete encoding capable of representing the basic multilingual plane of Unicode
32-bit binary codesEdit
- UTF-32/UCS-4 – A four-bytes-per-character representation of Unicode
Variable-length binary codesEdit
- UTF-8 – Encodes characters in a way that is mostly compatible with ASCII but can also encode the full repertoire of Unicode characters with sequences of up to four 8-bit bytes.
- UTF-16 – Extends UCS-2 to cover the whole of Unicode with sequences of one or two 16-bit elements
- GB 18030 – A full-Unicode variable-length code designed for compatibility with older Chinese multibyte encodings
- Huffman coding – A technique for expressing more common characters using shorter bit strings than are used for less common characters
Data compression systems such as Lempel–Ziv–Welch can compress arbitrary binary data. They are therefore not binary codes themselves but may be applied to binary codes to reduce storage needs
OtherEdit
- Morse code is a variable-length telegraphy code, which traditionally uses a series of long and short pulses to encode characters. It relies on gaps between the pulses to provide separation between letters and words, as the letter codes do not have the «prefix property». This means that Morse code is not necessarily a binary system, but in a sense may be a ternary system, with a 10 for a «dit» or a «dot», a 1110 for a dash, and a 00 for a single unit of separation. Morse code can be represented as a binary stream by allowing each bit to represent one unit of time. Thus a «dit» or «dot» is represented as a 1 bit, while a «dah» or «dash» is represented as three consecutive 1 bits. Spaces between symbols, letters, and words are represented as one, three, or seven consecutive 0 bits. For example, «NO U» in Morse code is «— . — — — . . —«, which could be represented in binary as «1110100011101110111000000010101110». If, however, Morse code is represented as a ternary system, «NO U» would be represented as «1110|10|00|1110|1110|1110|00|00|00|10|10|1110».
See alsoEdit
- List of computer character sets
ReferencesEdit
- ^ a b Alan G. Hobbs (1999-03-05). «Five-unit codes». NADCOMM Museum. Archived from the original on 1999-11-04.
- ^ a b Gil Smith (2001). «Teletypewriter Communication Codes» (PDF).
- ^ «Paper Tape Readers & Punches». The Ferranti Orion Web Site. Archived from the original on 2011-07-21.
- ^ a b c d «Telecipher Devices». John Savard’s Home Page.
On Convert Binary you can find the letters of the latin ASCII alphabet in their binary code representation.
Are you looking for an easy way to convert text to binary? We have an handy translator for that. You can also translate binary code to text in english or ASCII.
Alphabet in Binary (CAPITAL letters)
| Letter | Binary |
| A | 01000001 |
| B | 01000010 |
| C | 01000011 |
| D | 01000100 |
| E | 01000101 |
| F | 01000110 |
| G | 01000111 |
| H | 01001000 |
| I | 01001001 |
| J | 01001010 |
| K | 01001011 |
| L | 01001100 |
| M | 01001101 |
| N | 01001110 |
| O | 01001111 |
| P | 01010000 |
| Q | 01010001 |
| R | 01010010 |
| S | 01010011 |
| T | 01010100 |
| U | 01010101 |
| V | 01010110 |
| W | 01010111 |
| X | 01011000 |
| Y | 01011001 |
| Z | 01011010 |
Alphabet in Binary (lowercase letters)
| Letter | Binary |
| a | 01100001 |
| b | 01100010 |
| c | 01100011 |
| d | 01100100 |
| e | 01100101 |
| f | 01100110 |
| g | 01100111 |
| h | 01101000 |
| i | 01101001 |
| j | 01101010 |
| k | 01101011 |
| l | 01101100 |
| m | 01101101 |
| n | 01101110 |
| o | 01101111 |
| p | 01110000 |
| q | 01110001 |
| r | 01110010 |
| s | 01110011 |
| t | 01110100 |
| u | 01110101 |
| v | 01110110 |
| w | 01110111 |
| x | 01111000 |
| y | 01111001 |
| z | 01111010 |
Check out the binary numbers conversion table too.
Questions and Answers about the alphabet in Binary code
✏️ How do you translate binary code?
To convert binary to text, you have two options: you can either use an online translator (like the one provided for free by ConvertBinary.com, which can translate any letter or symbol), or you can do it manually.
If you want to learn how to convert binary code into text manually, you can read this guide, or watch the associated tutorial.
📛 How do I write my name in binary?
You need to convert each letter of your name to binary.
Try the Text to Binary converter over at ConvertBinary.com to instantly convert your own name into binary code!
👋 What is “hello” in Binary Code?
The word “hello” in binary code is: 0110100001100101011011000110110001101111 By dividing this into eight-digit segments it is easier to see the binary byte corresponding to each letter: 01101000 01100101 01101100 01101100 01101111 – you can verify that with the binary translator.
📄 Can I convert Text to Binary Code?
Of course! If you want to convert any plain text to binary code, you can use the instant Text to Binary Converter at ConvertBinary.com.
🔟 Can I convert Binary to Text?
Of course! If you want to convert any binary-encoded text to ASCII, you can use the Binary to Text Translator at ConvertBinary.com.
There are many types of binary codes used in digital number system which are similar to each other but each have individual significance while using them in digital electronics. These binary codes are as follows:
- Weighted Codes
- BCD (8421)
- 6311
- 2421
- Non-weighted Codes
- Excess-3
- Grey
- Alphanumeric Codes
- ASCII
- EBCDIC
- Error Detection Codes
- Parity
- Checksum
Weighted Codes
Weighted codes are those binary representation in which every bit has a certain weight depending upon their specific position. Some of those codes are discussed as below:
- BCD Code(8421)
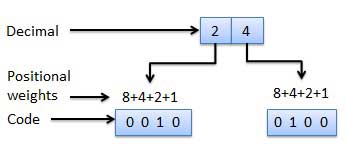
Binary coded decimal are the codes in which the value of the representation is the sum of weights defined by the position. The maximum range of BCD code is 0 to 9. Its weight of the position are 8, 4, 2 and 1 from MSB to LSB.
For example-
0101 = 0 x 8 + 1 x 4 + 0 x 2 + 1 x 1
= 0 + 4 + 0 + 1 = 5
- 6311 codes
The weight of the position are 6, 3, 1 and 1 respectively from MSB to LSB. The value of the binary representation is defined by the sum of multiplication of weight and the binary digit of that position.
For example-
1001 = 1 x 6 + 0 x 3 + 0 x 1 + 1 x 1
= 6 + 0 + 0 + 1 = 7
- 2421 codes
The weight of the position of these codes are 2, 4, 2 and 1 from MSB to LSB. Every representation is a 4-bit binary number which defines the value of a single decimal number, i.e. 0 to 9.
For example-
1010 = 1 x 2 + 0 x 4 + 1 x 2 + 0 x 1
= 2 + 0 + 2 + 0 = 4
Non-weighted Codes
Non-weighted codes are those binary representation which are independent of positional weighting. The value of any representation can be calculated by multiplying each bit from LSB with the increasing power of 2. Some of the non-weighted codes are as follows:
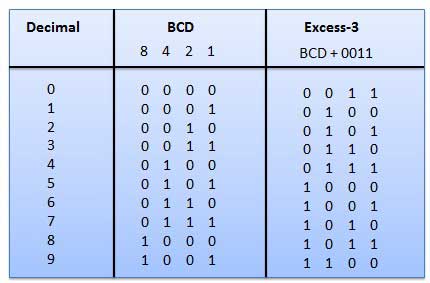
- Excess-3 Codes
Excess-3 are non-weighted codes which are also called biased representation. It is defined as the increment of 3 in its binary units when converted from any other number system.
For example-
9 is a decimal number which is written as 1001 in binary and on adding 0011, it is converted into 1100 which become an excess-3 code.
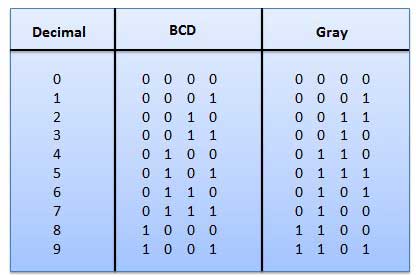
- Gray code
Gray codes are also non-weighted codes as its value is not dependent on any weights. The counting of gray codes is somewhat different from others as its digits has a difference of only 1-bit as of next number that is the reason it is also called unit-distance code. To convert a binary number into gray code, we have to take care of each bit as 1st bit from MSB is same as binary MSB and Nth bit in gray code is the XOR of N and N+1 binary bit from LSB.
For example-
7 is a decimal number which is written as 0111 in binary and when converted to grey code is represented as 0100.
| Decimal | BCD(8421) | 6311 | 2421 | Excess-3 Code | Gray Code |
| 0 | 0000 | 0000 | 0000 | 0011 | 0000 |
| 1 | 0001 | 0001 | 0001 | 0100 | 0001 |
| 2 | 0010 | 0011 | 0010 | 0101 | 0011 |
| 3 | 0011 | 0100 | 0011 | 0110 | 0010 |
| 4 | 0100 | 0101 | 0100 | 0111 | 0110 |
| 5 | 0101 | 0111 | 0101 | 1000 | 0111 |
| 6 | 0110 | 1000 | 0110 | 1001 | 0101 |
| 7 | 0111 | 1001 | 0111 | 1010 | 0100 |
| 8 | 1000 | 1011 | 1110 | 1011 | 1100 |
| 9 | 1001 | 1100 | 1111 | 1100 | 1101 |
Alphanumeric Codes
In a computer system there are different types of alphabets (upper case and lower case), numbers, symbols and other mathematical signs which are represented by a standard code. These codes are called alphanumeric codes created by some hackers to hide working machine codes which displayed as text. There are following types of alphanumeric codes exists in digital library:
- ASCII Codes
American Standard Code for Information Interchange (ASCII) is a 7-bit binary code which represents all the lower case letters (a to z), all the upper case letters (A to Z), decimal numbers (0 to 9), all special characters and symbols. There are 128 (27) different characters listed in ASCII table. In ASCII table 7-bits are divided into two parts in which 3-bits from MSB are called zone bits and 4-bits from LSB are called numeric bits.
- EBCDIC Codes
Extended Binary Coded Decimal Inter Change (EBCDIC) is an 8-bit code which was developed by IBM to operate large computer systems like mainframe. There are 256 (28) different characters and each 8-bit representation is divided into two parts in which 4-bits from MSB are zone bits and 4-bits from LSB are numeric bits.
Error Detection and Correction Codes
While transmitting a signal from transmitter to receiver, the signal is effected by some noise or other impairments. To detect the errors caused in the original signal and reconstruct those signals back to original we use error detection and correction codes. This method is also used in Hard Disk and other storage devices. There are following different methods used for detection of error:
- Parity Code
Parity method is the most widely and least expensive method which is used to check whether the data on the receiver side is error free as transmitted from the other side or corrupted. This is done by calculating the number of 1’s and then appending it as a parity bit after the signal represented in binary notation. If the number of 1’s are odd then we write 1 in the parity bit and if even, we write 0 in the parity bit. This is called even parity. The vice-versa of this i.e., if number of 1 is even then we write parity bit as 1 and 0 for odd number of 1’s is called odd parity.
If the parity bit on both the transmitter and receiver side is same then only we can assure that data is not corrupt otherwise there would be some error in the received signal.
| Data Segment | Digital Value | Parity Bit | Code Word |
| 0000 | 0 | 0 | 00000 |
| 0001 | 1 | 1 | 00011 |
| 0010 | 2 | 1 | 00101 |
| 0011 | 3 | 0 | 00110 |
| 0100 | 4 | 1 | 01001 |
| 0101 | 5 | 0 | 01010 |
| 0110 | 6 | 0 | 01100 |
| 0111 | 7 | 1 | 01111 |
| 1000 | 8 | 1 | 10001 |
| 1001 | 9 | 0 | 10010 |
| 1010 | 10 | 0 | 10100 |
| 1011 | 11 | 1 | 10111 |
| 1100
1101 1110 1111 |
12
13 14 15 |
0
1 1 0 |
11000
11011 11101 11110 |
- Checksum Code
Checksum also known as Hash-sum codes is also an error detection method in which the data is divided into different segments each of 8 bits. Each segment in the transmitter side is added using 1’s compliment arithmetic to get the sum and then the sum is complimented to get the checksum segment. The data and the checksum segment is now transmitted to the receiver. After transmission, we check each segment at the receiver end which is summed up again using 1’s compliment arithmetic. The sum is now complimented and checked that if the result is zero. If the result of the complimented sum is not zero then the data is rejected.
For example-
Let us assume four bytes of data to be transmitted which is A9H, 4FH, 20H, 81H. At transmitter end the sum of each segment is as follows:
10101001 + 01001111 = 11111000
11111000 + 00100000 = 00011000 + 1 = 00011001
00011001 + 01000001 = 01011010 = 5A <- Sum of segments
The compliment of 5A (01011010) is A5 (10100101) <- Checksum segment
Now, on the receiver end sum up the data segment received and the checksum segment.
10101001 + 01001111 = 11111000
11111000 + 00100000 = 00011000 + 1 = 00011001
00011001 + 01000001 = 01011010 + 10100101 = 11111111
Taking the compliment of the sum = 00000000
Hence, there is no error in the received signal.
In the coding, when numbers, letters or words are represented by a specific group of symbols, it is said that the number, letter or word is being encoded. The group of symbols is called as a code. The digital data is represented, stored and transmitted as group of binary bits. This group is also called as binary code. The binary code is represented by the number as well as alphanumeric letter.
Advantages of Binary Code
Following is the list of advantages that binary code offers.
-
Binary codes are suitable for the computer applications.
-
Binary codes are suitable for the digital communications.
-
Binary codes make the analysis and designing of digital circuits if we use the binary codes.
-
Since only 0 & 1 are being used, implementation becomes easy.
Classification of binary codes
The codes are broadly categorized into following four categories.
- Weighted Codes
- Non-Weighted Codes
- Binary Coded Decimal Code
- Alphanumeric Codes
- Error Detecting Codes
- Error Correcting Codes
Weighted Codes
Weighted binary codes are those binary codes which obey the positional weight principle. Each position of the number represents a specific weight. Several systems of the codes are used to express the decimal digits 0 through 9. In these codes each decimal digit is represented by a group of four bits.
Non-Weighted Codes
In this type of binary codes, the positional weights are not assigned. The examples of non-weighted codes are Excess-3 code and Gray code.
Excess-3 code
The Excess-3 code is also called as XS-3 code. It is non-weighted code used to express decimal numbers. The Excess-3 code words are derived from the 8421 BCD code words adding (0011)2 or (3)10 to each code word in 8421. The excess-3 codes are obtained as follows −
Example
Gray Code
It is the non-weighted code and it is not arithmetic codes. That means there are no specific weights assigned to the bit position. It has a very special feature that, only one bit will change each time the decimal number is incremented as shown in fig. As only one bit changes at a time, the gray code is called as a unit distance code. The gray code is a cyclic code. Gray code cannot be used for arithmetic operation.
Application of Gray code
-
Gray code is popularly used in the shaft position encoders.
-
A shaft position encoder produces a code word which represents the angular position of the shaft.
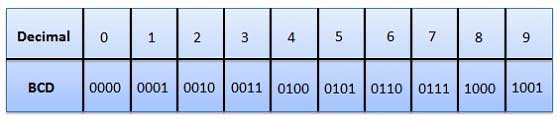
Binary Coded Decimal (BCD) code
In this code each decimal digit is represented by a 4-bit binary number. BCD is a way to express each of the decimal digits with a binary code. In the BCD, with four bits we can represent sixteen numbers (0000 to 1111). But in BCD code only first ten of these are used (0000 to 1001). The remaining six code combinations i.e. 1010 to 1111 are invalid in BCD.
Advantages of BCD Codes
- It is very similar to decimal system.
- We need to remember binary equivalent of decimal numbers 0 to 9 only.
Disadvantages of BCD Codes
-
The addition and subtraction of BCD have different rules.
-
The BCD arithmetic is little more complicated.
-
BCD needs more number of bits than binary to represent the decimal number. So BCD is less efficient than binary.
Alphanumeric codes
A binary digit or bit can represent only two symbols as it has only two states ‘0’ or ‘1’. But this is not enough for communication between two computers because there we need many more symbols for communication. These symbols are required to represent 26 alphabets with capital and small letters, numbers from 0 to 9, punctuation marks and other symbols.
The alphanumeric codes are the codes that represent numbers and alphabetic characters. Mostly such codes also represent other characters such as symbol and various instructions necessary for conveying information. An alphanumeric code should at least represent 10 digits and 26 letters of alphabet i.e. total 36 items. The following three alphanumeric codes are very commonly used for the data representation.
- American Standard Code for Information Interchange (ASCII).
- Extended Binary Coded Decimal Interchange Code (EBCDIC).
- Five bit Baudot Code.
ASCII code is a 7-bit code whereas EBCDIC is an 8-bit code. ASCII code is more commonly used worldwide while EBCDIC is used primarily in large IBM computers.
Error Codes
There are binary code techniques available to detect and correct data during data transmission.
| Error Code | Description |
|---|---|
|
Error Detection and Correction |
Error detection and correction code techniques |

Binary codes are the group of symbols which are used to encode the numbers, alphabets or special characters by using a group of bits. This group of bits is known as binary codes.
Classification of binary codes
The following figure shows the classification of binary codes.
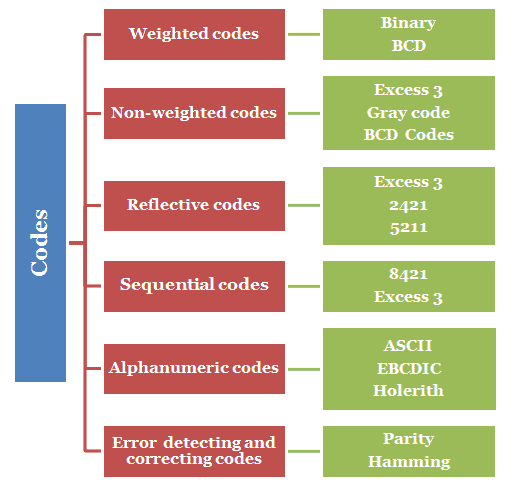
Weighted codes
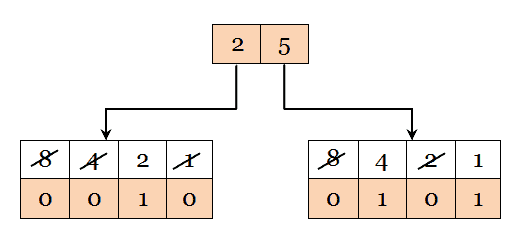
In this code, each digit position of the number represents a specific weight. In weighted code, each decimal digit is represented by a group of four bits and each bit has a weight 8, 4, 2, 1.
There are different Binary coded Decimal(BCD) like 8421 code, 2421 code, 3321 code, 4221 code, 5211 code which comes under weighted code. For example, let us consider a decimal number 25, for which the equivalent binary number in 8421 code is as follows
Non-weighted codes
In this code, no weight is assigned to any of the bit positions. Bits will not have any fixed value based on their position. Excess-3 code and gray code are the examples of non-weighted code.
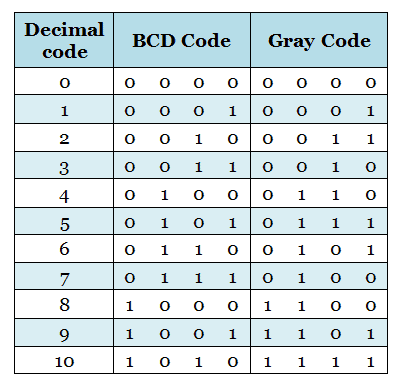
Gray code
It is a non-weighted code and known as unit-distance code. This is because, bit patterns for every consecutive number differ in only one bit position. These codes are also called cyclic codes.
The following table shows the gray code, in which you can find that, the two consecutive or two adjacent number differ only in one bit position.
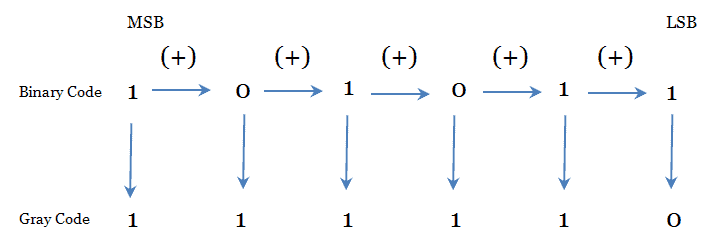
How to find a gray code from the given binary number?
- Write the MSB of the given binary code as the MSB of gray code and binary code are same.
- Perform an Ex-OR operation with the previous bit and the current bit to get the next gray digit. Ignore the carry, if any.
- Repeat 2nd step until all the binary bits have been Ex-ORed with their previous one.
Let us look at an example here. Convert a binary number (101011)2 into its equivalent gray code.
Reflective codes
A code is said to be reflective, if the code for any number is the complement of any another number.
For example, the code for 9 is 1111, whereas the code for 0 is 0000. Since 1111 and 0000 are complement of each other, the number 9 and 0 are said to be reflective codes.
BCD codes like 2421, 5211, excess-3 codes are reflective codes but 8421 is not reflective.
Sequential code
In sequential codes, each succeeding code is one binary number greater than its preceding code, which greatly helps in manipulation of mathematical data. 8421 and excess-3 codes are sequential codes but 2421 and 5211 are not sequential codes.
Alphanumeric codes
As the name suggests, the codes which consists of both numbers and alphabetic characters are called alphanumeric codes. These codes consists of symbols to represent the 26 alphabets(including capital and small letter), 0-9 numbers and other symbols. Most commonly used alphanumeric codes are.
- ASCII(American Standard code for Information Interchange) – 7 bit code
- EBCDIC (Extended Binary Coded Decimal Interchange Code) – 8 bit code
- Hollerith code
Error detecting and correcting codes
Whenever a digital information is transmitted in a binary form from one network or device to other network, there is a possibility of error to occur. This error means, the signal corresponding to 0 may change to 1 or the signal corresponding to 0 may change to 1 due to the some disturbances.
In order to main the data integrity between transmitter and receiver, an extra bit or more than one bit is added with the transmitted data. This extra bit is use to detect and correct the error that takes place in the data. the extra bit with the data, together constitute the code. There are codes which are used only to detect the error and are known as error detecting codes and there are codes which assist in detection and correction of errors are known as error detecting and correcting codes.
An Assistant Professor in the Department of Electrical and Electronics Engineering, Certified Energy Manager, Photoshop designer, a blogger and Founder of Electrically4u.
Basic Explanation
Did you know that everything a computer does is based on ones and zeroes? It’s hard to imagine, because you hear people talking about the absolutely gargantuan (huge) numbers that computers «crunch». But all those huge numbers — they’re just made up of ones and zeros.
It’s kind of like the computer is made up of a bunch of lightswitches, and each lightswitch controls just one lightbulb. On or Off. One or Zero. But if you took all of those lightbulbs together, and said «Let’s make each sequence of On-and-Off represent a different number!» Well then, you could get some pretty large numbers.
What do I mean by sequence? Let’s say you had two lightswitches. There are four different ways we could flip those switches:
Both Off
First Off, Second On
First On, Second Off
Both On
Binary Code takes each of those combinations and assigns a number to it, like this:
Both Off = 0
First Off, Second On = 1
First On, Second Off = 2
Both On = 3
Intermediate Explanation
Another way of thinking about it is this: let’s give each lightbulb a point value. We’ll say the first lightbulb is worth two points, and the second one is worth one point. Now take a look at the combinations:
Both Off = 0 + 0 = 0
First Off, Second On = 0 + 1 = 1
First On, Second Off = 2 + 0 = 2
Both On = 2 + 1 = 3
If we added in another lightbulb, we would make it worth twice as many points as the 2 pointer. Then, if all the bulbs were on, the point value would be 4 + 2 + 1 = 7. And if we added in another bulb, we would make it worth 8 points (twice as much as four). Now if they are all turned on, that’s worth 8 + 4 + 2 + 1 = 15. As you can see, it’s going to take a lot of lightbulbs to make a really big number!
Finally, even though we’re giving point values to each of those lightbulbs, when we write them down we still only write them as ones and zeros. One means On, and Zero means Off.
So let’s say we had 8 lightbulbs, and they were set up like this:
Off Off On On Off On Off Off.
The point values of those eight bulbs are:
0 + 0 + 32 + 16 + 0 + 4 + 0 + 0 (remember — we only give points if they’re turned on!)
And that adds up to 52. So we would say the sequence of bulbs is worth 52. But how do we write it? We write it like this: 00110100
So now we can say 00110100binary = 52.
And that’s Binary Code.
Go ahead and enter some text into the encoder. The computer will convert those letters into numbers, and then it will convert those numbers into binary! Did you know that to write any letter on the computer, it takes 8 «lightbulbs»? So a word with 5 letters would take 40 lightbulbs! How many lightbulbs do you think it took to make this page? I bet it was a lot!
If you want more information about binary, you might find the following pages useful:
- Connecting letters to binary with ASCII codes
- Converting base ten numbers to base two
- Encoding colors, numbers, and graphemes
English to Binary Code Converter
Those “Zeros (0)” and “Ones (1)” may not look like anything to you, but the numbers in binary code actually say «Hello!«
Text to binary converter is used to convert text into binary codes. Let’s say, what binary code of “Hey” is?
It may look 3 words word but in the «words to binary» rule, it is “01001000 01100101 01111001” long. Binary code genrator is used to convert English to binary code.
What is the binary code?
Any code using only two symbols to represent information is considered to be the binary code. Different versions of the binary code used in a variety of contexts have been around for centuries. Braille, for example, uses raised and unraised bumps to convey information to the blind, Morse code uses long and short signals to convey information, and the above example uses 0s and 1s sets to represent letters. Perhaps the most common use for binary is in computers nowadays: text to binary translator is the way, most computers and computer devices ultimately send, receive, and store information.
Look through the table below and try using UTF-8 binary code to spell something. Try the name!
For each letter of your name, translate to binary and find the 8-bit binary code sequence, write it down with a small space between each 8-bit set. For instance, if your name starts with letter A, 01000001 would be your first letter according to English to binary code genrator.
Can’t write your name using table? That’s why we have developed words to binary convertor so you can easily convert letters (alphabet) to binary code.
Examples:
hello in binary: 01001000 01100101 01101100 01101100 01101111
my name in binary (for name jhone): 01101010 01101000 01101111 01101110 01100101
Write Your Name in Binary Code in Lots of Ways
Somewhat arbitrary are the 0s and 1s of binary code. Any color, symbol, or object which can exist in two different forms or conditions like coin (heads and tails), shapes (circle and square), color (blue and green), the on and off switch can be used as a binary code.
WhyASCII to binary is a big deal?
Bits are usually transmitted electronically on computers and other computerized devices (such as calculators, printers, coffee makers, and microwaves). But this electronic information is temporary. It must be stored physically within the hardware of the device to exist for any length of time and without a power supply. That means converting every piece of binary code in a computer into a physical object or state. As it turns out, binary code is easy to convert from electronic information (e.g., 0s and 1s) to physical information, as it requires only two types of physical objects or states.
Just like when we are writing this information for you, it’s being stored in binary alphabet and letters to binary.
Does Bit Number Matter?
Arranging and reading bits in ordered groups make binary extraordinarily powerful for storing and transmitting enormous amounts of information. Comprehending why it helps to consider the alternative: what if one bit at a time was used? Well, only two types of information could be shared, one type is represented by 0 and the other type by 1. When you convert to binary the whole alphabet or signs of punctuation, you only get two types of information.
But when you group bits by two, you get four types of information:
00, 01, 10, 11
You double the amount of information by increasing from two-bit to three-bit groups:
000, 001, 010, 011, 100, 101, 110, 111
While eight types of information are still insufficient to represent a whole alphabet, you may be able to see where the pattern is heading.
Try to know how many possible bits can be combined using bits grouped by four using any binary code you want. Then try using five-grouped bits again. So now you know how to convert to binary? Let’s see how many combinations do you think you can use six or 64 bits at a time?
It’s difficult for humans to breakdown text to binary translator manually since the 8-bit code is complex and you may not convert text accurately into binary. Computers can use binary code to find, organize, send, and store more and more types of information by grouping single bits together into larger and larger groups.